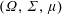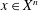We prove that Krivine’s Function Calculus is compatible with integration. Let $(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D707})$ be a finite measure space, $X$ a Banach lattice, $\mathbf{x}\in X^{n}$, and $f:\mathbb{R}^{n}\times \unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}$ a function such that 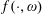$f(\cdot ,\unicode[STIX]{x1D714})$ is continuous and positively homogeneous for every 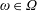$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}$, and 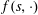$f(\mathbf{s},\cdot )$ is integrable for every 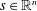$\mathbf{s}\in \mathbb{R}^{n}$. Put 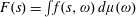$F(\mathbf{s})=\int f(\mathbf{s},\unicode[STIX]{x1D714})\,d\unicode[STIX]{x1D707}(\unicode[STIX]{x1D714})$ and define 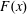$F(\mathbf{x})$ and 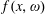$f(\mathbf{x},\unicode[STIX]{x1D714})$ via Krivine’s Function Calculus. We prove that under certain natural assumptions 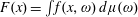$F(\mathbf{x})=\int f(\mathbf{x},\unicode[STIX]{x1D714})\,d\unicode[STIX]{x1D707}(\unicode[STIX]{x1D714})$, where the right hand side is a Bochner integral.

We study the stability of disjointness preservers on Banach lattices. In many cases, we prove that an “almost disjointness preserving” operator is well approximable by a disjointness preserving one. However, this approximation is not always possible, as our examples show.

We give a positive answer to the question of Bouras [‘Almost Dunford–Pettis sets in Banach lattices’, Rend. Circ. Mat. Palermo (2) 62 (2013), 227–236] concerning weak compactness of almost Dunford–Pettis sets in Banach lattices. That is, every almost Dunford–Pettis set in a Banach lattice $E$ is relatively weakly compact if and only if $E$ is a $\mathit{KB}$-space.

Recently, H’michane et al. [‘On the class of limited operators’, Acta Math. Sci. (submitted)] introduced the class of weak$^*$ Dunford–Pettis operators on Banach spaces, that is, operators which send weakly compact sets onto limited sets. In this paper, the domination problem for weak$^*$ Dunford–Pettis operators is considered. Let $S, T:E\to F$ be two positive operators between Banach lattices $E$ and $F$ such that $0\leq S\leq T$. We show that if $T$ is a weak$^{*}$ Dunford–Pettis operator and $F$ is $\sigma $-Dedekind complete, then $S$ itself is weak$^*$ Dunford–Pettis.

We use Krivine's form of the Grothendieck inequality to renorm the space of bounded linear maps acting between Banach lattices. We construct preduals and describe the nuclear operators associated with these preduals for this renormed space of bounded operators as well as for the spaces of $p$-convex, $p$-concave and positive $p$-summing operators acting between Banach lattices and Banach spaces. The nuclear operators obtained are described in terms of factorizations through classical Banach spaces via positive operators.

We study conditions under which every delta-convex (d.c.) mapping is the difference of two continuous convex operators, and vice versa. In particular, we prove that each d.c. mapping $F:(a,b)\to Y$ is the difference of two continuous convex operators whenever $Y$ belongs to a large class of Banach lattices which includes all $L^{p}(\mu)$ spaces ($1\leq p\leq\infty$). The proof is based on a result about Jordan decomposition of vector-valued functions. New observations on Jordan decomposition of finitely additive vector-valued measures are also presented.

It is shown that the injective tensor product of positive vector measures in certain Banach lattices is jointly continuous with respect to the weak convergence of vector measures. This result is obtained by a diagonal convergence theorem for injective tensor integrals. Our approach to this problem is based on Bartle's bilinear integration theory.

Let A and B be (not necessarily bounded) linear operators on a Banach lattice E such that |(s – B)-1x|≤ (s – A)-1|x| for all x in E and sufficiently large s ∈ R. The main purpose of this paper is to investigate the relation between the spectra σ(B) and σ(A) of B and A, respectively. We apply our results to study asymptotic properties of dominated C0-semigroups.

We investigate the relationship between the peripheral spectrum of a positive operator T on a Banach lattice E and the peripheral spectrum of the operators S dominated by T, that is, ]Sx] ≤ T]x] for all x ε E. This can be applied to obtain inheritance results for asymptotic properties of dominated operators.