Let 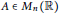 $A\,\in \,{{M}_{n}}\left( \mathbb{R} \right)$
be an invertible matrix. Consider the semi-direct product
$A\,\in \,{{M}_{n}}\left( \mathbb{R} \right)$
be an invertible matrix. Consider the semi-direct product 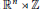 ${{\mathbb{R}}^{n}}\rtimes \,\mathbb{Z}$ where the action of
${{\mathbb{R}}^{n}}\rtimes \,\mathbb{Z}$ where the action of 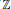 $\mathbb{Z}$ on
$\mathbb{Z}$ on 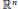 ${{\mathbb{R}}^{n}}$ is induced by the left multiplication by
${{\mathbb{R}}^{n}}$ is induced by the left multiplication by 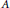 $A$. Let
$A$. Let 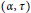 $\left( \alpha ,\,\tau \right)$ be a strongly continuous action of
$\left( \alpha ,\,\tau \right)$ be a strongly continuous action of 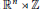 ${{\mathbb{R}}^{n}}\rtimes \,\mathbb{Z}$ on a
${{\mathbb{R}}^{n}}\rtimes \,\mathbb{Z}$ on a 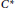 ${{C}^{*}}$-algebra
${{C}^{*}}$-algebra  $B$ where
$B$ where  $\alpha$ is a strongly continuous action of
$\alpha$ is a strongly continuous action of 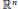 ${{\mathbb{R}}^{n}}$ and
${{\mathbb{R}}^{n}}$ and  $\tau$ is an automorphism. The map
$\tau$ is an automorphism. The map  $\tau$ induces a map
$\tau$ induces a map  $\widetilde{\tau }\,\text{on}\,\text{B}\,{{\rtimes }_{\alpha }}\,{{\mathbb{R}}^{n}}$. We show that, at the
$\widetilde{\tau }\,\text{on}\,\text{B}\,{{\rtimes }_{\alpha }}\,{{\mathbb{R}}^{n}}$. We show that, at the 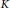 $K$-theory level,
$K$-theory level,  $\tau$ commutes with the Connes–Thom map if
$\tau$ commutes with the Connes–Thom map if  $\det \left( A \right)\,>\,0$ and anticommutes if
$\det \left( A \right)\,>\,0$ and anticommutes if  $\det \left( A \right)\,>\,0$. As an application, we recompute the
$\det \left( A \right)\,>\,0$. As an application, we recompute the 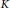 $K$-groups of the Cuntz–Li algebra associated with an integer dilation matrix.
$K$-groups of the Cuntz–Li algebra associated with an integer dilation matrix.
 $p$-Summable Operators
$p$-Summable Operators