We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
There is a problem with the proofs of [1], Lemma 4.4 and the related Theorems 4.5, 4.8 and 4.12 regarding the computation of zero-divisor cup-length of real Grassmann manifolds ${G_k({{\mathbb {R}}}^{n})}$
. The correct statements and improved estimates of the topological complexity of ${G_k({{\mathbb {R}}}^{n})}$
will appear in a separate paper by M. Radovanović [2].
Topological complexity naturally appears in the motion planning in robotics. In this paper we consider the problem of finding topological complexity of real Grassmann manifolds $G_k(\mathbb {R}^{n})$
. We use cohomology methods to give estimates on the zero-divisor cup-length of $G_k(\mathbb {R}^{n})$
for various $2\leqslant k< n$
, which in turn give us lower bounds on topological complexity. Our results correct and improve several results from Pavešić (Proc. Roy. Soc. Edinb. A 151 (2021), 2013–2029).
${{\sf {TC}}}$-generating function
For a graph 
$\Gamma$, let 
$K(H_{\Gamma },\,1)$ denote the Eilenberg–Mac Lane space associated with the right-angled Artin (RAA) group 
$H_{\Gamma }$ defined by 
$\Gamma$. We use the relationship between the combinatorics of 
$\Gamma$ and the topological complexity of 
$K(H_{\Gamma },\,1)$ to explain, and generalize to the higher TC realm, Dranishnikov's observation that the topological complexity of a covering space can be larger than that of the base space. In the process, for any positive integer 
$n$, we construct a graph 
$\mathcal {O}_n$ whose TC-generating function has polynomial numerator of degree 
$n$. Additionally, motivated by the fact that 
$K(H_{\Gamma },\,1)$ can be realized as a polyhedral product, we study the LS category and topological complexity of more general polyhedral product spaces. In particular, we use the concept of a strong axial map in order to give an estimate, sharp in a number of cases, of the topological complexity of a polyhedral product whose factors are real projective spaces. Our estimate exhibits a mixed cat-TC phenomenon not present in the case of RAA groups.
We study the existence and concentration of positive solutions for the following class of fractional p-Kirchhoff type problems:
where ɛ is a small positive parameter, a and b are positive constants, s ∈ (0, 1) and p ∈ (1, ∞) are such that 
$$ \left\{\begin{array}{@{}ll} \left(\varepsilon^{sp}a+\varepsilon^{2sp-3}b \,[u]_{s, p}^{p}\right)(-\Delta)_{p}^{s}u+V(x)u^{p-1}=f(u) & \text{in}\ \mathbb{R}^{3},\\ \noalign{ u\in W^{s, p}(\mathbb{R}^{3}), \quad u>0 & \text{in}\ \mathbb{R}^{3}, \end{array}\right.$$
$sp \in (\frac {3}{2}, 3)$, 
$(-\Delta )^{s}_{p}$ is the fractional p-Laplacian operator, f: ℝ → ℝ is a superlinear continuous function with subcritical growth and V: ℝ3 → ℝ is a continuous potential having a local minimum. We also prove a multiplicity result and relate the number of positive solutions with the topology of the set where the potential V attains its minimum values. Finally, we obtain an existence result when f(u) = uq−1 + γur−1, where γ > 0 is sufficiently small, and the powers q and r satisfy 2p < q < p*s ⩽ r. The main results are obtained by using some appropriate variational arguments.
A subset 
$W$ of a closed manifold 
$M$ is 
$K$-contractible, where $K$ is a torus or Klein bottle if the inclusion 
$W\,\to \,M$ factors homotopically through a map to $K$. The image of 
${{\pi }_{1}}\left( W \right)$ (for any base point) is a subgroup of 
${{\pi }_{1}}\left( M \right)$ that is isomorphic to a subgroup of a quotient group of 
${{\pi }_{1}}\left( K \right)$. Subsets of $M$ with this latter property are called 
${{\mathcal{G}}_{K}}$-contractible. We obtain a list of the closed 3-manifolds that can be covered by two open ${{\mathcal{G}}_{K}}$-contractible subsets. This is applied to obtain a list of the possible closed prime 3-manifolds that can be covered by two open $K$-contractible subsets.
We give conditions which determine if cat of a map go up when extending over a cofibre. We apply this to reprove a result of Roitberg giving an example of a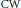 
$\text{CW}$ complex 
$Z$ such that 
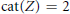$\text{cat}(Z)\,=\,2$ but every skeleton of $Z$ is of category 1. We also find conditions when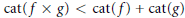 
$\text{cat}(f\,\times \,g)\,<\,\text{cat}(f)\,+\,\text{cat}(g)$. We apply our result to show that under suitable conditions for rational maps 
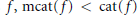$f,\,\text{mcat}(f)\,<\,\text{cat}(f)$ is equivalent to 
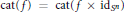$\text{cat(}f)\,=\,\text{cat(}f\,\times \,\text{i}{{\text{d}}_{{{S}^{n}}}})$. Many examples with 
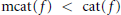$\text{mcat}(f)\,<\,\text{cat}(f)$ satisfying our conditions are constructed. We also answer a question of Iwase by constructing 
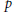$p$-local spaces 
$X$ such that 
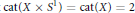$\text{cat(}X\ \times \,{{S}^{1}}\text{)}\,\text{=}\,\text{cat(}X\text{)}\,\text{=2}$. In fact for our spaces and every 
$Y\,\not{\simeq }\,*,\,\text{cat}(X\,\times \,Y)\,\le \,\text{cat}(Y)\,+\,1\,\text{cat}(Y)\,+\,\text{cat}(X)$. We show that this same $X$ has the property 
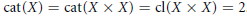$\text{cat}(X)=\,\text{cat}(X\,\times \,X)\,=\,\text{cl}(X\,\times \,X)\,=\,2$.
Nous montrons que la 
$\text{A}$-catégorie d’un espace simplement connexe de type fini est inférieure ou égale à 
$n$ si et seulement si son modèle d’Adams-Hilton est un rétracte homotopique d’une algèbre différentielle à $n$ étages. Nous en déduisons que l’invariant Acat augmente au plus de 1 lors de l’attachement d’une cellule à un espace.
