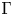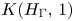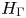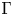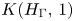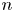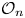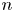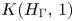1. Main results
The ![]() ${{\sf {TC}}}$ generating function of a space
${{\sf {TC}}}$ generating function of a space ![]() $X$, introduced in [Reference Farber and Oprea16], is defined in terms of all the higher topological complexities
$X$, introduced in [Reference Farber and Oprea16], is defined in terms of all the higher topological complexities ![]() ${{\sf {TC}}}_r(X)$:
${{\sf {TC}}}_r(X)$:
 \[ \mathcal{F}_X (x) = \, \sum_{r=1}^{\infty} {{\sf{TC}}}_{r+1}(X)\cdot x^{r}. \]
\[ \mathcal{F}_X (x) = \, \sum_{r=1}^{\infty} {{\sf{TC}}}_{r+1}(X)\cdot x^{r}. \]
We focus on the integral power series ![]() $P_X(x)=(1-x)^{2}\cdot \mathcal {F}_X (x)$. Note that
$P_X(x)=(1-x)^{2}\cdot \mathcal {F}_X (x)$. Note that ![]() $P_X(0)=0$, whereas
$P_X(0)=0$, whereas ![]() $P_X(x)$ vanishes if and only if
$P_X(x)$ vanishes if and only if ![]() $X$ is contractible. Furthermore, as it was first observed in [Reference Farber and Oprea16, § 8.2],
$X$ is contractible. Furthermore, as it was first observed in [Reference Farber and Oprea16, § 8.2], ![]() $P_X(x)$ is a polynomial if and only if, for all
$P_X(x)$ is a polynomial if and only if, for all ![]() $r$ large enough, the differences
$r$ large enough, the differences ![]() ${{\sf {TC}}}_{r+1}(X) - {{\sf {TC}}}_r(X)$ are constant, say with value
${{\sf {TC}}}_{r+1}(X) - {{\sf {TC}}}_r(X)$ are constant, say with value ![]() $K_X$. In such a case, for non-contractible
$K_X$. In such a case, for non-contractible ![]() $X$, the degree of
$X$, the degree of ![]() $P_X(x)$ is the smallest integer
$P_X(x)$ is the smallest integer ![]() $e\geq 1$ such that
$e\geq 1$ such that ![]() ${{\sf {TC}}}_{r+1}(X) - {{\sf {TC}}}_r(X)=K_X$ for all
${{\sf {TC}}}_{r+1}(X) - {{\sf {TC}}}_r(X)=K_X$ for all ![]() $r\geq e$ (see lemma 2.2).
$r\geq e$ (see lemma 2.2).
All generating functions arising in [Reference Farber and Oprea16] turn out to have a polynomial numerator ![]() $P_X(x)$ of degree one or two. To get a much richer source of examples, we consider the Eilenberg–Mac Lane space
$P_X(x)$ of degree one or two. To get a much richer source of examples, we consider the Eilenberg–Mac Lane space ![]() $K(H_{\Gamma },\,1)$ associated with a right-angled Artin (RAA) group
$K(H_{\Gamma },\,1)$ associated with a right-angled Artin (RAA) group ![]() $H_\Gamma$. Here,
$H_\Gamma$. Here, ![]() $\Gamma$ is a simplicial graph (i.e. containing neither loops nor repeated edges), and
$\Gamma$ is a simplicial graph (i.e. containing neither loops nor repeated edges), and ![]() $H_\Gamma$ is generated by
$H_\Gamma$ is generated by ![]() $V_\Gamma$, the vertex set of
$V_\Gamma$, the vertex set of ![]() $\Gamma$, with relations
$\Gamma$, with relations ![]() $uv=vu$ whenever
$uv=vu$ whenever ![]() $u$ and
$u$ and ![]() $v$ are adjacent vertices in
$v$ are adjacent vertices in ![]() $\Gamma$. We write
$\Gamma$. We write ![]() $\mathcal {F}_{H_\Gamma }(x)$,
$\mathcal {F}_{H_\Gamma }(x)$, ![]() $P_{H_\Gamma }(x)$,
$P_{H_\Gamma }(x)$, ![]() $K_{H_\Gamma }$,
$K_{H_\Gamma }$, ![]() ${{\sf {TC}}}_r(H_\Gamma )$ and
${{\sf {TC}}}_r(H_\Gamma )$ and ![]() ${{\sf {cat}}}(H_\Gamma )$ when referring to the corresponding objects for
${{\sf {cat}}}(H_\Gamma )$ when referring to the corresponding objects for ![]() $X=K(H_{\Gamma },\,1)$. This is a standard shorthand based on the fact that
$X=K(H_{\Gamma },\,1)$. This is a standard shorthand based on the fact that ![]() ${{\sf {cat}}}(X)$ and
${{\sf {cat}}}(X)$ and ![]() ${{\sf {TC}}}_r(X)$ are homotopy invariants of
${{\sf {TC}}}_r(X)$ are homotopy invariants of ![]() $X$.
$X$.
Theorem 1.1 There is a family ![]() $\{\mathcal {O}_n\}_{n\geq 1}$ of graphs with
$\{\mathcal {O}_n\}_{n\geq 1}$ of graphs with ![]() $\deg (P_{H_{\mathcal {O}_n}}(x))=n$.
$\deg (P_{H_{\mathcal {O}_n}}(x))=n$.
We also use the graph theoretic viewpoint to explain a topological complexity phenomenon that was thought to be anomalous. Namely, Dranishnikov has shown in [Reference Dranishnikov7] that the topological complexity of a covering space can be greater than that of the base space. Our explanation of such a fact is done through the double ![]() $D_v(\Gamma )$ of a graph
$D_v(\Gamma )$ of a graph ![]() $\Gamma$ around a vertex
$\Gamma$ around a vertex ![]() $v$ (the construction is reviewed in § 4). A key fact we need comes from [Reference Kim and Koberda23]: There is an inclusion of RAA groups
$v$ (the construction is reviewed in § 4). A key fact we need comes from [Reference Kim and Koberda23]: There is an inclusion of RAA groups ![]() $H_{D_v(\Gamma )} \leq H_\Gamma$. Using the topological consequence that
$H_{D_v(\Gamma )} \leq H_\Gamma$. Using the topological consequence that ![]() $K(H_{D_v(\Gamma )},\,1)$ covers
$K(H_{D_v(\Gamma )},\,1)$ covers ![]() $K(H_\Gamma ,\,1)$ together with the combinatorial description of
$K(H_\Gamma ,\,1)$ together with the combinatorial description of ![]() ${{\sf {TC}}}_r$ for RAA groups given in [Reference Farber and Oprea16, Reference González, Gutiérrez and Yuzvinsky20], we give a set of combinatorial conditions that generalize Dranishnikov's observation at the
${{\sf {TC}}}_r$ for RAA groups given in [Reference Farber and Oprea16, Reference González, Gutiérrez and Yuzvinsky20], we give a set of combinatorial conditions that generalize Dranishnikov's observation at the ![]() $r$-th topological complexity level:
$r$-th topological complexity level:
Theorem 1.2 Fix ![]() $r\geq 2$ and let
$r\geq 2$ and let ![]() $v$ be a vertex and
$v$ be a vertex and ![]() $C_1$,
$C_1$, ![]() $C_2$ be cliques of
$C_2$ be cliques of ![]() $\;\Gamma$ satisfying:
$\;\Gamma$ satisfying:
•
 $|C_1|\geq |C_2|$;
$|C_1|\geq |C_2|$;• no vertex in
 $C_1\cap C_2$ is either
$C_1\cap C_2$ is either  $v$ or adjacent to
$v$ or adjacent to  $v$;
$v$;•
 $(r-1)|C_1|+|C_2|$ is strictly larger than any sum
$(r-1)|C_1|+|C_2|$ is strictly larger than any sum  $\sum _{i=1}^{r}\vert D_i\vert$ of
$\sum _{i=1}^{r}\vert D_i\vert$ of  $\,r$ cliques
$\,r$ cliques  $D_1,\,\ldots ,\,D_r$ of
$D_1,\,\ldots ,\,D_r$ of  $\;\Gamma$ with empty intersection (in particular
$\;\Gamma$ with empty intersection (in particular  $C_1\cap C_2\neq \varnothing$).
$C_1\cap C_2\neq \varnothing$).
Then ![]() ${{\sf {TC}}}_{{}{r}}(H_{D_v(\Gamma )}) > {{\sf {TC}}}_{{}{r}}(H_\Gamma ).$
${{\sf {TC}}}_{{}{r}}(H_{D_v(\Gamma )}) > {{\sf {TC}}}_{{}{r}}(H_\Gamma ).$
Explicit examples satisfying the conditions in theorem 1.2 (including Dranishnikov's double cover) are given in § 4.
Motivated by the fact that the Eilenberg–Mac Lane spaces associated with RAA groups may be realized as polyhedral products, we shall consider the LS category and higher topological complexities of general polyhedral product spaces ![]() $\underline {X}^{K}$ defined in terms of a family
$\underline {X}^{K}$ defined in terms of a family ![]() $\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$ of based spaces and a simplicial complex
$\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$ of based spaces and a simplicial complex ![]() $K$ on vertices
$K$ on vertices ![]() $[m]:=\{1,\,2,\,\ldots ,\,m\}$ (explicit definitions are given in § 6.3). We need:
$[m]:=\{1,\,2,\,\ldots ,\,m\}$ (explicit definitions are given in § 6.3). We need:
Definition 1.3 A family ![]() $\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$ of based spaces is said to be LS-logarithmic provided
$\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$ of based spaces is said to be LS-logarithmic provided
whenever ![]() $i_1<\cdots < i_k$. Likewise, for an integer
$i_1<\cdots < i_k$. Likewise, for an integer ![]() $r\geq 2$,
$r\geq 2$, ![]() $\underline {X}$ is said to be
$\underline {X}$ is said to be ![]() ${{\sf {TC}}}_r$-logarithmic provided
${{\sf {TC}}}_r$-logarithmic provided
whenever ![]() $i_1<\cdots < i_k$.
$i_1<\cdots < i_k$.
We shall see that the assumption of LS-logarithmicity powerfully constrains TC-generating functions (proposition 3.1). The following result generalizes [Reference Félix and Tanré18, proposition 4] (note that we do not need any simple-connectivity assumption):
Theorem 1.4 For an LS-logarithmic family ![]() $\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$,
$\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$,
where the maximum is taken over all simplices ![]() $[i_1,\,\ldots ,\,i_n]$ of
$[i_1,\,\ldots ,\,i_n]$ of ![]() $K$.
$K$.
The notation ![]() $[i_1,\,\ldots ,\,i_m]$ for simplices is used to stress the fact that no repetition of indices is allowed. Regarding higher topological complexity, we prove:
$[i_1,\,\ldots ,\,i_m]$ for simplices is used to stress the fact that no repetition of indices is allowed. Regarding higher topological complexity, we prove:
Theorem 1.5 Fix ![]() $r\geq 2$ and assume a family
$r\geq 2$ and assume a family ![]() $\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$ is both LS-logarithmic and
$\underline {X}=\{(X_i,\,*)\}_{i=1}^{m}$ is both LS-logarithmic and ![]() ${{\sf {TC}}}_r$-logarithmic with
${{\sf {TC}}}_r$-logarithmic with
Then
where the maximum is taken over all simplices ![]() $[i_1,\,\ldots ,\,i_n]$ of
$[i_1,\,\ldots ,\,i_n]$ of ![]() $K$.
$K$.
We shall see in § 6 that the logarithmicity assumptions in theorem 1.5 are satisfied when each ![]() $X_i$ is a
$X_i$ is a ![]() $K(H_{\Gamma _i},\,1)$, while condition (1.1) depends on the structure of the graphs
$K(H_{\Gamma _i},\,1)$, while condition (1.1) depends on the structure of the graphs ![]() $\Gamma _i$. Examples outside the RAA-group realm where theorem 1.5 applies are given by:
$\Gamma _i$. Examples outside the RAA-group realm where theorem 1.5 applies are given by:
Corollary 1.6 For large enough ![]() $r$ and a family
$r$ and a family ![]() $\underline {P}=\{(P^{n_i},\,\ast )\}_{i=1}^{m}$ of real projective spaces with all
$\underline {P}=\{(P^{n_i},\,\ast )\}_{i=1}^{m}$ of real projective spaces with all ![]() $n_i$ even,
$n_i$ even,
where the maximum is taken over all simplices ![]() $[i_1,\,\ldots ,\,i_\ell ]$ of
$[i_1,\,\ldots ,\,i_\ell ]$ of ![]() $K$.
$K$.
The proof of corollary 1.6 may be found directly after proposition 7.3. Families ![]() $\underline {P}=\{(P^{n_i},\,\ast )\}_{i=1}^{m}$ of real projective spaces exhibit
$\underline {P}=\{(P^{n_i},\,\ast )\}_{i=1}^{m}$ of real projective spaces exhibit ![]() ${{\sf {TC}}}_2$-phenomena that do not seem to have a counterpart in the RAA group realm, namely, a combined maximum taken over sums of both cat and TC terms (a situation best illustrated by example 7.2):
${{\sf {TC}}}_2$-phenomena that do not seem to have a counterpart in the RAA group realm, namely, a combined maximum taken over sums of both cat and TC terms (a situation best illustrated by example 7.2):
Theorem 1.7 ![]() ${{\sf {TC}}}_2(\underline {P}^{K})$ is estimated from above by
${{\sf {TC}}}_2(\underline {P}^{K})$ is estimated from above by
 \[ {{\sf{TC}}}_2(\underline{P}^{K})\leq\max\left\{\sum_{i\in \sigma_{1}{\bigtriangleup}\sigma_{2}}n_i+\sum_{i\in \sigma_1\cap\sigma_{2}}{{\sf{TC}}}_2({P}^{n_i}):\sigma_{1},\sigma_{2}\in K\right\}, \]
\[ {{\sf{TC}}}_2(\underline{P}^{K})\leq\max\left\{\sum_{i\in \sigma_{1}{\bigtriangleup}\sigma_{2}}n_i+\sum_{i\in \sigma_1\cap\sigma_{2}}{{\sf{TC}}}_2({P}^{n_i}):\sigma_{1},\sigma_{2}\in K\right\}, \]
where ![]() $\sigma _{1}{\bigtriangleup} \sigma _{2}=(\sigma _{1}\setminus \sigma _{2})\cup (\sigma _{2}\setminus \sigma _{1})$, the symmetric difference of
$\sigma _{1}{\bigtriangleup} \sigma _{2}=(\sigma _{1}\setminus \sigma _{2})\cup (\sigma _{2}\setminus \sigma _{1})$, the symmetric difference of ![]() $\sigma _1$ and
$\sigma _1$ and ![]() $\sigma _2$.
$\sigma _2$.
The lower estimate for ![]() ${{\sf {TC}}}_2(\underline {P}^{K})$ in proposition 1.8 below, with the flavour of theorem 1.7, is closely related to the fact that the inequality in theorem 1.7 is in fact sharp in a number of cases (for instance when
${{\sf {TC}}}_2(\underline {P}^{K})$ in proposition 1.8 below, with the flavour of theorem 1.7, is closely related to the fact that the inequality in theorem 1.7 is in fact sharp in a number of cases (for instance when ![]() $\mathrm {dim}(K)=0$, or when every
$\mathrm {dim}(K)=0$, or when every ![]() $P^{n_i}$ is parallelizable; see the more detailed discussion in § 7).
$P^{n_i}$ is parallelizable; see the more detailed discussion in § 7).
Proposition 1.8 ![]() ${{\sf {TC}}}_2(\underline {P}^{K})$ is estimated from below by
${{\sf {TC}}}_2(\underline {P}^{K})$ is estimated from below by
 \[ {{\sf{TC}}}_2(\underline{P}^{K})\geq\max\left\{\sum_{i\in \sigma_{1}{\bigtriangleup}\sigma_{2}}n_i+\sum_{i\in \sigma_{1}\cap\sigma_{2}}{{\sf{zcl}}}(P^{n_i}): \sigma_{1}, \sigma_{2}\in K\right\}, \]
\[ {{\sf{TC}}}_2(\underline{P}^{K})\geq\max\left\{\sum_{i\in \sigma_{1}{\bigtriangleup}\sigma_{2}}n_i+\sum_{i\in \sigma_{1}\cap\sigma_{2}}{{\sf{zcl}}}(P^{n_i}): \sigma_{1}, \sigma_{2}\in K\right\}, \]
where ![]() ${{\sf {zcl}}}$ stands for zero-divisors cup-length with mod 2 coefficients.
${{\sf {zcl}}}$ stands for zero-divisors cup-length with mod 2 coefficients.
2. Background
Topological complexity ![]() ${{\sf {TC}}}(X)$, a homotopy invariant of a path-connected space
${{\sf {TC}}}(X)$, a homotopy invariant of a path-connected space ![]() $X$, was introduced in [Reference Farber10] motivated by topological aspects of the motion planning problem in robotics. Topological complexity is a close relative of the Lusternik–Schnirelmann (LS) category
$X$, was introduced in [Reference Farber10] motivated by topological aspects of the motion planning problem in robotics. Topological complexity is a close relative of the Lusternik–Schnirelmann (LS) category ![]() ${{\sf {cat}}}(X)$, and both are special cases of Schwarz’ sectional category of a fibration. We review basic definitions, referring the reader to the monographs [Reference Cornea, Lupton, Oprea and Tanré6, Reference Farber11, Reference Rudyak26, Reference Schwarz29] for further details.
${{\sf {cat}}}(X)$, and both are special cases of Schwarz’ sectional category of a fibration. We review basic definitions, referring the reader to the monographs [Reference Cornea, Lupton, Oprea and Tanré6, Reference Farber11, Reference Rudyak26, Reference Schwarz29] for further details.
The sectional category of a fibration ![]() $p \colon E \to B$, denoted by
$p \colon E \to B$, denoted by ![]() ${{\sf {secat}}}(p)$, is the smallest
${{\sf {secat}}}(p)$, is the smallest ![]() $n$ for which there is an open covering
$n$ for which there is an open covering ![]() $\{ U_0,\, \ldots ,\, U_n \}$ of
$\{ U_0,\, \ldots ,\, U_n \}$ of ![]() $B$ by
$B$ by ![]() $n+1$ open sets, on each of which there is a continuous local section
$n+1$ open sets, on each of which there is a continuous local section ![]() $s_i \colon U_i \to E$ of
$s_i \colon U_i \to E$ of ![]() $p$, i.e.
$p$, i.e. ![]() $p\circ s_i = j_i \colon U_i \hookrightarrow B$. We agree to set
$p\circ s_i = j_i \colon U_i \hookrightarrow B$. We agree to set ![]() ${{\sf {secat}}}(p)=\infty$ if the corresponding finite coverings fail to exist. The Lusternik–Schnirelmann category is then defined to be
${{\sf {secat}}}(p)=\infty$ if the corresponding finite coverings fail to exist. The Lusternik–Schnirelmann category is then defined to be ![]() ${{\sf {cat}}}(X)={{\sf {secat}}}(PX \to X)$, where
${{\sf {cat}}}(X)={{\sf {secat}}}(PX \to X)$, where ![]() $PX$ is the space of based paths in
$PX$ is the space of based paths in ![]() $X$ and the map
$X$ and the map ![]() $PX \to X$ takes a path to its endpoint.
$PX \to X$ takes a path to its endpoint.
For an integer ![]() $r\geq 2$, the
$r\geq 2$, the ![]() $r$th topological complexity of a space
$r$th topological complexity of a space ![]() $X$,
$X$, ![]() ${{\sf {TC}}}_r(X)$, is defined by
${{\sf {TC}}}_r(X)$, is defined by ![]() ${{\sf {TC}}}_r(X)={{\sf {secat}}}(p_r)$, where
${{\sf {TC}}}_r(X)={{\sf {secat}}}(p_r)$, where ![]() $p_r \colon X^{I}\to X^{r}$ is the fibration given by
$p_r \colon X^{I}\to X^{r}$ is the fibration given by
for ![]() $\alpha \in X^{I}.$ Here,
$\alpha \in X^{I}.$ Here, ![]() $X^{I}$ denotes the space of free paths
$X^{I}$ denotes the space of free paths ![]() $\alpha : I=[0,\, 1]\to X$ and
$\alpha : I=[0,\, 1]\to X$ and ![]() $X^{r}=X\times \dots \times X$, the Cartesian product of
$X^{r}=X\times \dots \times X$, the Cartesian product of ![]() $r$ copies of
$r$ copies of ![]() $X$. When
$X$. When ![]() $r>2$, we say that the
$r>2$, we say that the ![]() ${{\sf {TC}}}_r(X)$ are higher or sequential topological complexities of
${{\sf {TC}}}_r(X)$ are higher or sequential topological complexities of ![]() $X$ and when
$X$ and when ![]() $r=2$, we say that
$r=2$, we say that ![]() ${{\sf {TC}}}(X):={{\sf {TC}}}_2(X)$ is simply the topological complexity of
${{\sf {TC}}}(X):={{\sf {TC}}}_2(X)$ is simply the topological complexity of ![]() $X$.
$X$.
Just as LS category is very difficult to compute, so also is topological complexity. Indeed, it is usually the case for both invariants that lower and upper bounds are derived. The fundamental such bounds are:
Theorem 2.1 For any space ![]() $X$,
$X$, ![]() ${{\sf {cat}}}(X^{r-1}) \leq {{\sf {TC}}}_r(X) \leq {{\sf {cat}}}(X^{r})$.
${{\sf {cat}}}(X^{r-1}) \leq {{\sf {TC}}}_r(X) \leq {{\sf {cat}}}(X^{r})$.
When ![]() $X=K(\pi ,\,1)$ is aspherical, the category
$X=K(\pi ,\,1)$ is aspherical, the category ![]() ${{\sf {cat}}}(X)$ and topological complexities
${{\sf {cat}}}(X)$ and topological complexities ![]() ${{\sf {TC}}}_r(X)$ depend only on
${{\sf {TC}}}_r(X)$ depend only on ![]() $\pi$ and we may write
$\pi$ and we may write ![]() ${{\sf {cat}}}(X)={{\sf {cat}}}(\pi )$ and
${{\sf {cat}}}(X)={{\sf {cat}}}(\pi )$ and ![]() ${{\sf {TC}}}_r(X)={{\sf {TC}}}_r(\pi )$. It is easy to see (using the Eilenberg–Ganea theorem [Reference Eilenberg and Ganea9]) that
${{\sf {TC}}}_r(X)={{\sf {TC}}}_r(\pi )$. It is easy to see (using the Eilenberg–Ganea theorem [Reference Eilenberg and Ganea9]) that ![]() ${{\sf {TC}}}_r(\pi )$ is finite if and only if there exists a finite dimensional
${{\sf {TC}}}_r(\pi )$ is finite if and only if there exists a finite dimensional ![]() $K(\pi ,\,1)$. Various results about
$K(\pi ,\,1)$. Various results about ![]() ${{\sf {TC}}}_r(\pi )$ have been obtained (e.g. [Reference Farber, Grant, Lupton and Oprea12, Reference Farber and Mescher15, Reference Grant, Lupton and Oprea22]), but there is no definitive result at this time.
${{\sf {TC}}}_r(\pi )$ have been obtained (e.g. [Reference Farber, Grant, Lupton and Oprea12, Reference Farber and Mescher15, Reference Grant, Lupton and Oprea22]), but there is no definitive result at this time.
We shall need the following extract of [Reference Farber, Kishimoto and Stanley14, lemma 1] and its proof:
Lemma 2.2 Let ![]() $X$ be a finite CW complex.
$X$ be a finite CW complex. ![]() $P_X(x)$ is a polynomial if and only if there is an integer
$P_X(x)$ is a polynomial if and only if there is an integer ![]() $K_X$ satisfying
$K_X$ satisfying ![]() ${{\sf {TC}}}_{r+1}(X) = {{\sf {TC}}}_r(X) + K_X$ for all
${{\sf {TC}}}_{r+1}(X) = {{\sf {TC}}}_r(X) + K_X$ for all ![]() $r$ large enough. If these conditions hold, then:
$r$ large enough. If these conditions hold, then:
(a)
 $K_X$ is determined by
$K_X$ is determined by  $P_X$,
$P_X$,  $K_X=P_X(1)$. Conversely, setting
$K_X=P_X(1)$. Conversely, setting  ${{\sf {TC}}}_1(X):=0$ and
${{\sf {TC}}}_1(X):=0$ and  $e:=\text {min}\{s\geq 1\colon {{\sf {TC}}}_{r+1}(X) = {{\sf {TC}}}_r(X) + K_X,\, \text { for all } r\geq s\}$, we have
$e:=\text {min}\{s\geq 1\colon {{\sf {TC}}}_{r+1}(X) = {{\sf {TC}}}_r(X) + K_X,\, \text { for all } r\geq s\}$, we have
 \[ P_X(x)=(1-x)^{2}\left(\sum_{i=2}^{e-1}{{\sf{TC}}}_i(X)\cdot x^{i-1}\right)+{{\sf{TC}}}_e(X)\cdot x^{e-1}(1-x)+K_X\cdot x^{e}. \]
\[ P_X(x)=(1-x)^{2}\left(\sum_{i=2}^{e-1}{{\sf{TC}}}_i(X)\cdot x^{i-1}\right)+{{\sf{TC}}}_e(X)\cdot x^{e-1}(1-x)+K_X\cdot x^{e}. \](b)
 $P_X'(1)=eK_X-{{\sf {TC}}}_e(X)$.
$P_X'(1)=eK_X-{{\sf {TC}}}_e(X)$.(c)
 $\deg (P_X)=e$ provided
$\deg (P_X)=e$ provided  $X\not \simeq \star .$
$X\not \simeq \star .$
2.1 Higher topological complexity of RAA groups
We use the notation set forth in § 1 regarding RAA groups. The higher topological complexity ![]() ${{\sf {TC}}}_r(H_\Gamma )$ was computed in [Reference González, Gutiérrez and Yuzvinsky20] in terms of the structure of cliques in
${{\sf {TC}}}_r(H_\Gamma )$ was computed in [Reference González, Gutiérrez and Yuzvinsky20] in terms of the structure of cliques in ![]() $\Gamma$. The answer is spelled out in theorem 2.4 below in terms of the simplified expression in [Reference Farber and Oprea16].
$\Gamma$. The answer is spelled out in theorem 2.4 below in terms of the simplified expression in [Reference Farber and Oprea16].
Definition 2.3 For an integer ![]() $r\ge 2$ and a graph
$r\ge 2$ and a graph ![]() $\Gamma$, we define the number
$\Gamma$, we define the number ![]() $z_r(\Gamma )$ as the maximal total cardinality
$z_r(\Gamma )$ as the maximal total cardinality ![]() $\sum _{i=1}^{r} |C_i|$ of
$\sum _{i=1}^{r} |C_i|$ of ![]() $r$ cliques
$r$ cliques ![]() $C_1,\, \dots ,\, C_r$ of
$C_1,\, \dots ,\, C_r$ of ![]() $\,\Gamma$ with empty intersection,
$\,\Gamma$ with empty intersection, ![]() $\cap _{i=1}^{r} C_i=\varnothing$.
$\cap _{i=1}^{r} C_i=\varnothing$.
The maximum sum in definition 2.3 giving the value of ![]() $z_r(\Gamma )$ might not be realized by cliques whose cardinality is maximal.
$z_r(\Gamma )$ might not be realized by cliques whose cardinality is maximal.
Theorem 2.4 [Reference Farber and Oprea16, Reference González, Gutiérrez and Yuzvinsky20]
For any graph ![]() $\Gamma$ and
$\Gamma$ and ![]() $r\geq 2$,
$r\geq 2$, ![]() ${{\sf {TC}}}_r(H_\Gamma ) = z_r(\Gamma )$.
${{\sf {TC}}}_r(H_\Gamma ) = z_r(\Gamma )$.
3.  ${{\sf {TC}}}$-generating function and LS-logarithmicity
${{\sf {TC}}}$-generating function and LS-logarithmicity
A number of examples of finite CW complexes ![]() $X$ were given in [Reference Farber and Oprea16] for which
$X$ were given in [Reference Farber and Oprea16] for which ![]() $P_X(x)$ is a polynomial satisfying
$P_X(x)$ is a polynomial satisfying ![]() $P_X(1)={{\sf {cat}}}(X)$ (cf. lemma 2.2(a)). Real projective spaces
$P_X(1)={{\sf {cat}}}(X)$ (cf. lemma 2.2(a)). Real projective spaces ![]() $P^{n}$ give additional such examples provided
$P^{n}$ give additional such examples provided ![]() $n$ is a 2-power. Indeed, [Reference Cadavid-Aguilar, González, Gutiérrez, Guzmán-Sáenz and Lara4, proposition 6.2] implies
$n$ is a 2-power. Indeed, [Reference Cadavid-Aguilar, González, Gutiérrez, Guzmán-Sáenz and Lara4, proposition 6.2] implies ![]() $P_{P^{2^{e}}}(x)=(2^{e+1}-1)x -2(2^{e-1}-1)x^{2}-x^{3}$, so
$P_{P^{2^{e}}}(x)=(2^{e+1}-1)x -2(2^{e-1}-1)x^{2}-x^{3}$, so ![]() $P_{P^{2^{e}}}(1)=2^{e}={{\sf {cat}}}(P^{2^{e}})$. Note that all these examples deal with LS-logarithmic spaces, i.e. spaces
$P_{P^{2^{e}}}(1)=2^{e}={{\sf {cat}}}(P^{2^{e}})$. Note that all these examples deal with LS-logarithmic spaces, i.e. spaces ![]() $X$ satisfyingFootnote 1
$X$ satisfyingFootnote 1 ![]() ${{\sf {cat}}}(X^{r})=r\cdot {{\sf {cat}}}(X)$ for any
${{\sf {cat}}}(X^{r})=r\cdot {{\sf {cat}}}(X)$ for any ![]() $r$. In this short section we prove that whether a space is LS-logarithmic has a great influence on the structure of its
$r$. In this short section we prove that whether a space is LS-logarithmic has a great influence on the structure of its ![]() ${{\sf {TC}}}$-generating function.
${{\sf {TC}}}$-generating function.
Proposition 3.1 If an LS-logarithmic space ![]() $X$ satisfies
$X$ satisfies ![]() ${{\sf {TC}}}_{r+1}(X)-{{\sf {TC}}}_r(X)=K$ for all
${{\sf {TC}}}_{r+1}(X)-{{\sf {TC}}}_r(X)=K$ for all ![]() $r$ large enough, then
$r$ large enough, then ![]() $K = {{\sf {cat}}}(X)$. Consequently
$K = {{\sf {cat}}}(X)$. Consequently ![]() $P_X(1)={{\sf {cat}}}(X)$.
$P_X(1)={{\sf {cat}}}(X)$.
Proof. Fix a positive integer ![]() $n$ with
$n$ with ![]() ${{\sf {TC}}}_r(X)={{\sf {TC}}}_n(X)+(r-n)K$ for
${{\sf {TC}}}_r(X)={{\sf {TC}}}_n(X)+(r-n)K$ for ![]() $r\geq n$. The numbers
$r\geq n$. The numbers ![]() $s_r:={{\sf {TC}}}_{r+1}(X)-r{{\sf {cat}}}(X)$ (
$s_r:={{\sf {TC}}}_{r+1}(X)-r{{\sf {cat}}}(X)$ (![]() $r\geq n$) satisfy
$r\geq n$) satisfy ![]() $s_r - s_{r+1}={{\sf {cat}}}(X)-K$. The relation
$s_r - s_{r+1}={{\sf {cat}}}(X)-K$. The relation ![]() $K\neq {{\sf {cat}}}(X)$ would then imply that the sequence of integers
$K\neq {{\sf {cat}}}(X)$ would then imply that the sequence of integers ![]() $s_n,\,s_{n+1},\,\ldots$ is either strictly increasing or strictly decreasing, which is impossible as
$s_n,\,s_{n+1},\,\ldots$ is either strictly increasing or strictly decreasing, which is impossible as ![]() $0\leq s_r\leq {{\sf {cat}}}(X)$ in view of theorem 2.1 and the LS-logarithmicity hypothesis.
$0\leq s_r\leq {{\sf {cat}}}(X)$ in view of theorem 2.1 and the LS-logarithmicity hypothesis.
Example 3.2 Theorem 5.7 in [Reference Cadavid-Aguilar, González, Gutiérrez, Guzmán-Sáenz and Lara4] shows ![]() ${{\sf {TC}}}_r(P^{m})=rm$ for
${{\sf {TC}}}_r(P^{m})=rm$ for ![]() $m$ even and
$m$ even and ![]() $r$ (moderately) large. Since
$r$ (moderately) large. Since ![]() $P^{m}$ is LS-logarithmic, proposition 3.1 implies
$P^{m}$ is LS-logarithmic, proposition 3.1 implies ![]() $P_{P^{m}}(1)=m$, even though the polynomial
$P_{P^{m}}(1)=m$, even though the polynomial ![]() $P_{P^{m}}(x)$ is unknown. (Recall from [Reference Farber, Tabachnikov and Yuzvinsky17] that
$P_{P^{m}}(x)$ is unknown. (Recall from [Reference Farber, Tabachnikov and Yuzvinsky17] that ![]() ${{\sf {TC}}}(P^{m})$ is the Euclidean immersion dimension of
${{\sf {TC}}}(P^{m})$ is the Euclidean immersion dimension of ![]() $P^{m}$.)
$P^{m}$.)
If the LS-logarithmicity hypothesis in proposition 3.1 is removed, the conclusion ![]() $P_X(1)={{\sf {cat}}}(X)$ may be lost. Indeed, a remarkable 3-cell complex
$P_X(1)={{\sf {cat}}}(X)$ may be lost. Indeed, a remarkable 3-cell complex ![]() $X$ is constructed in [Reference Stanley30] with the property that
$X$ is constructed in [Reference Stanley30] with the property that ![]() ${{\sf {cat}}}(X \times X)={{\sf {cat}}}(X)=2$. In [Reference Farber, Kishimoto and Stanley14], the higher topological complexities of
${{\sf {cat}}}(X \times X)={{\sf {cat}}}(X)=2$. In [Reference Farber, Kishimoto and Stanley14], the higher topological complexities of ![]() $X$ were shown to be
$X$ were shown to be ![]() ${{\sf {TC}}}_r(X)=r={{\sf {cat}}}({}{X^{r}})$ (
${{\sf {TC}}}_r(X)=r={{\sf {cat}}}({}{X^{r}})$ (![]() $r\geq 2$). In view of lemma 2.2, this yields
$r\geq 2$). In view of lemma 2.2, this yields ![]() $P_X(1)=1<{{\sf {cat}}}(X)$. The point to remark here is that, as observed in [Reference Farber, Kishimoto and Stanley14], in this example
$P_X(1)=1<{{\sf {cat}}}(X)$. The point to remark here is that, as observed in [Reference Farber, Kishimoto and Stanley14], in this example ![]() $P_X(1)$ agrees with
$P_X(1)$ agrees with ![]() ${{\sf {cup}}}(X)$, the cup-length of
${{\sf {cup}}}(X)$, the cup-length of ![]() $X$. To the best of our knowledge, the equality
$X$. To the best of our knowledge, the equality ![]() $P_X(1)={{\sf {cup}}}(X)$ holds true in all cases where all
$P_X(1)={{\sf {cup}}}(X)$ holds true in all cases where all ![]() ${{\sf {TC}}}_r(X)$ are known. It is thus tempting to insert such a clause in the modified form of the rationality conjecture at the end of [Reference Farber, Kishimoto and Stanley14].
${{\sf {TC}}}_r(X)$ are known. It is thus tempting to insert such a clause in the modified form of the rationality conjecture at the end of [Reference Farber, Kishimoto and Stanley14].
4.  ${{\sf {TC}}}_r$ and coverings of RAA groups
${{\sf {TC}}}_r$ and coverings of RAA groups
We use RAA groups to explain on combinatorial grounds, and generalize to the higher TC realm, Dranishnikov's example of a covering space ![]() $E\to B$ having
$E\to B$ having ![]() ${{\sf {TC}}}(E)>{{\sf {TC}}}(B)$. In fact, from this perspective it is clear that such a phenomenon is more common than it was originally thought.
${{\sf {TC}}}(E)>{{\sf {TC}}}(B)$. In fact, from this perspective it is clear that such a phenomenon is more common than it was originally thought.
We follow the notation set forth in § 1 regarding RAA groups. Additionally, the double of a graph ![]() $\Gamma$ around one of its vertices
$\Gamma$ around one of its vertices ![]() $v$, denoted by
$v$, denoted by ![]() $D_v(\Gamma )$, is defined to be the graph formed by taking two copies of
$D_v(\Gamma )$, is defined to be the graph formed by taking two copies of ![]() $\Gamma$ and identifying the copies of
$\Gamma$ and identifying the copies of ![]() $\mathrm {St}(v)$ in each. Here, the star of
$\mathrm {St}(v)$ in each. Here, the star of ![]() $v$ in
$v$ in ![]() $\Gamma$,
$\Gamma$, ![]() $\mathrm {St}(v)$, is the induced subgraph of
$\mathrm {St}(v)$, is the induced subgraph of ![]() $\Gamma$ containing
$\Gamma$ containing ![]() $v$ and all vertices connected to
$v$ and all vertices connected to ![]() $v$ by an edge. Figures 1 and 2 illustrate the construction.
$v$ by an edge. Figures 1 and 2 illustrate the construction.

FIGURE 1. ![]() ${{\sf {TC}}}_r(H_\Gamma )={}{2r-1}\hspace {.6mm}$ and
${{\sf {TC}}}_r(H_\Gamma )={}{2r-1}\hspace {.6mm}$ and ![]() $\,{{\sf {TC}}}_r(H_{D_v(\Gamma )})={}{2r}$.
$\,{{\sf {TC}}}_r(H_{D_v(\Gamma )})={}{2r}$.

FIGURE 2. ![]() ${{\sf {TC}}}_r(H_\Gamma )={}{3r-2}$ and
${{\sf {TC}}}_r(H_\Gamma )={}{3r-2}$ and ![]() ${{\sf {TC}}}_r(H_{D_v(\Gamma )})={}{3r-1}$.
${{\sf {TC}}}_r(H_{D_v(\Gamma )})={}{3r-1}$.
In view of theorem 2.4, theorem 1.2 is the second assertion of:
Theorem 4.1 If no vertex of ![]() $\mathrm {St}(v)$ belongs to a clique
$\mathrm {St}(v)$ belongs to a clique ![]() $C$ of
$C$ of ![]() $\,\Gamma$ of maximal cardinality, then
$\,\Gamma$ of maximal cardinality, then ![]() ${{\sf {TC}}}_r(H_{D_v(\Gamma )})=r\cdot {\textrm {cd}}(H_{D_v(\Gamma )}) = r \cdot {\textrm {{cd}}}(H_\Gamma )$, for all
${{\sf {TC}}}_r(H_{D_v(\Gamma )})=r\cdot {\textrm {cd}}(H_{D_v(\Gamma )}) = r \cdot {\textrm {{cd}}}(H_\Gamma )$, for all ![]() $r\geq 2$. In particular,
$r\geq 2$. In particular, ![]() $P_{H_{D_v(\Gamma )}}(x)=|C|\cdot x(2-x)$. On the other hand, if no vertex of
$P_{H_{D_v(\Gamma )}}(x)=|C|\cdot x(2-x)$. On the other hand, if no vertex of ![]() $\mathrm {St}(v)$ is common to a pair of cliques
$\mathrm {St}(v)$ is common to a pair of cliques ![]() $C_1$ and
$C_1$ and ![]() $C_2$ of
$C_2$ of ![]() $\,\Gamma$ with
$\,\Gamma$ with ![]() $|C_1|\geq |C_2|$ and
$|C_1|\geq |C_2|$ and ![]() $(r-1)|C_1|+|C_2|> {{\sf {TC}}}_r(H_\Gamma )$, then
$(r-1)|C_1|+|C_2|> {{\sf {TC}}}_r(H_\Gamma )$, then ![]() ${{\sf {TC}}}_{{}{r}}(H_{D_v(\Gamma )}) > {{\sf {TC}}}_{{}{r}}(H_\Gamma ).$
${{\sf {TC}}}_{{}{r}}(H_{D_v(\Gamma )}) > {{\sf {TC}}}_{{}{r}}(H_\Gamma ).$
Here ![]() ${\textrm {cd}}(G)$ stands for the cohomological dimension of the group
${\textrm {cd}}(G)$ stands for the cohomological dimension of the group ![]() $G$. It is well-known that
$G$. It is well-known that
where ![]() $c(\Gamma )$ stands for the size of the largest clique in
$c(\Gamma )$ stands for the size of the largest clique in ![]() $\Gamma$.
$\Gamma$.
Proof of theorem 4.1. By the hypothesis and the construction of ![]() $D_v(\Gamma )$, we see that
$D_v(\Gamma )$, we see that ![]() $D_v(\Gamma )$ contains two disjoint cliques of maximal cardinality,
$D_v(\Gamma )$ contains two disjoint cliques of maximal cardinality, ![]() $C$ and
$C$ and ![]() $C'$ (where the prime denotes inclusion in
$C'$ (where the prime denotes inclusion in ![]() $\Gamma '$, the second copy of
$\Gamma '$, the second copy of ![]() $\Gamma$). Since no other clique has larger size, we get the first assertion of the theorem, i.e.
$\Gamma$). Since no other clique has larger size, we get the first assertion of the theorem, i.e.
while the expression for ![]() $P_{H_{D_v(\Gamma )}}(x)$ follows directly from lemma 2.2. On the other hand, for cliques
$P_{H_{D_v(\Gamma )}}(x)$ follows directly from lemma 2.2. On the other hand, for cliques ![]() $C_i$ as in the last assertion of the theorem, the condition that no vertex of
$C_i$ as in the last assertion of the theorem, the condition that no vertex of ![]() $\mathrm {St}(v)$ is common to
$\mathrm {St}(v)$ is common to ![]() $C_1$ and
$C_1$ and ![]() $C_2$ implies
$C_2$ implies ![]() $C_1 \cap C_2' = \varnothing$ (where, again, primes denote copies in the copy of
$C_1 \cap C_2' = \varnothing$ (where, again, primes denote copies in the copy of ![]() $\Gamma$,
$\Gamma$, ![]() $\Gamma ' \subset D_v(\Gamma )$). So
$\Gamma ' \subset D_v(\Gamma )$). So
which completes the proof.
Dranishnikov's example in [Reference Dranishnikov7, theorem 3.8(a)] of a double covering space ![]() $p\colon E\simeq T^{2}\vee S^{1}\vee T^{2}\to B=S^{1} \vee T^{2}$ with
$p\colon E\simeq T^{2}\vee S^{1}\vee T^{2}\to B=S^{1} \vee T^{2}$ with ![]() ${{\sf {TC}}}(E)>{{\sf {TC}}}(B)$ arises from the graph
${{\sf {TC}}}(E)>{{\sf {TC}}}(B)$ arises from the graph ![]() $\Gamma$ in figure 1 given by a
$\Gamma$ in figure 1 given by a ![]() $2$-clique
$2$-clique ![]() $C$ and a disjoint vertex
$C$ and a disjoint vertex ![]() $v$. In this case theorem 4.1 is applied with
$v$. In this case theorem 4.1 is applied with ![]() $C_1=C_2=C$. Note that
$C_1=C_2=C$. Note that ![]() $P_B(x)=3x-x^{2}$ and
$P_B(x)=3x-x^{2}$ and ![]() $P_{E}(x)=4x-2x^{2}$, both of degree 2.
$P_{E}(x)=4x-2x^{2}$, both of degree 2.
Wedges in Dranishnikov's example correspond to disconnected graphs (so that the associated RAA groups decompose as free products). But this is an unnecessary restriction. Consider for instance the situation in figure 2, where
for all ![]() $r\geq 2$ in view of theorem 2.4. Note that theorem 4.1 is used with
$r\geq 2$ in view of theorem 2.4. Note that theorem 4.1 is used with ![]() $C_2=C_1\setminus \mbox {St}(v)$. This time
$C_2=C_1\setminus \mbox {St}(v)$. This time ![]() $P_{H_\Gamma }(x)=4x-x^{2}$ and
$P_{H_\Gamma }(x)=4x-x^{2}$ and ![]() $P_{H_{D_v(\Gamma )}}(x)=5x-2x^{2}$.
$P_{H_{D_v(\Gamma )}}(x)=5x-2x^{2}$.
More interesting is the situation for the graph ![]() $\Gamma$ shown in figure 3, for only
$\Gamma$ shown in figure 3, for only ![]() ${{\sf {TC}}}_2$ of the corresponding covering space is strictly larger than that of the base space. We leave it to the reader to show that, while
${{\sf {TC}}}_2$ of the corresponding covering space is strictly larger than that of the base space. We leave it to the reader to show that, while ![]() ${{\sf {TC}}}_2(H_{D_v(\Gamma )}) = 8$ and
${{\sf {TC}}}_2(H_{D_v(\Gamma )}) = 8$ and ![]() ${{\sf {TC}}}_2(H_\Gamma )=7$, we have
${{\sf {TC}}}_2(H_\Gamma )=7$, we have ![]() ${{\sf {TC}}}_r(H_{D_v(\Gamma )})={{\sf {TC}}}_r(H_\Gamma )$ for
${{\sf {TC}}}_r(H_{D_v(\Gamma )})={{\sf {TC}}}_r(H_\Gamma )$ for ![]() $r>2$. This phenomenon reflects the fact that the hypotheses in the second half of theorem 4.1 fail for
$r>2$. This phenomenon reflects the fact that the hypotheses in the second half of theorem 4.1 fail for ![]() $C_1$ and
$C_1$ and ![]() $C_2$ if
$C_2$ if ![]() $r\geq 3$. Note that in this case
$r\geq 3$. Note that in this case ![]() $P_{H_\Gamma }(x)=7x-x^{2}-x^{3}$ while
$P_{H_\Gamma }(x)=7x-x^{2}-x^{3}$ while ![]() $P_{H_{D_v(\Gamma )}}(x)=8x-3x^{2}$, a smaller degree polynomial.
$P_{H_{D_v(\Gamma )}}(x)=8x-3x^{2}$, a smaller degree polynomial.

FIGURE 3. ![]() ${{\sf {TC}}}(H_\Gamma )=7$ and
${{\sf {TC}}}(H_\Gamma )=7$ and ![]() ${{\sf {TC}}}(H_{D_v(\Gamma )})=8$.
${{\sf {TC}}}(H_{D_v(\Gamma )})=8$.
The examples above would suggest a positive answer to:
Problem 4.2 Is it true that ![]() $\deg (P_E(x))\leq \deg (P_B(x))$ holds for any covering
$\deg (P_E(x))\leq \deg (P_B(x))$ holds for any covering ![]() $E\to B$?
$E\to B$?
5.  $P_X$ of degree greater than
$P_X$ of degree greater than  $3$
$3$
All examples of ![]() ${{\sf {TC}}}$-generating functions dealt with so far have
${{\sf {TC}}}$-generating functions dealt with so far have ![]() $\deg (P_X(x))\leq 3$. We now construct examples with arbitrary
$\deg (P_X(x))\leq 3$. We now construct examples with arbitrary ![]() $\deg (P_X(x))$. We need the following equivalent statement of [Reference Farber and Oprea16, lemma 8.3]:
$\deg (P_X(x))$. We need the following equivalent statement of [Reference Farber and Oprea16, lemma 8.3]:
Lemma 5.1 If ![]() $z_r(\Gamma )$ can be realized by a sequence of cliques
$z_r(\Gamma )$ can be realized by a sequence of cliques ![]() $C_1,\,\ldots ,\,C_r$ of
$C_1,\,\ldots ,\,C_r$ of ![]() $\Gamma$, where
$\Gamma$, where ![]() $\cap _{s=1}^{k} C_{i_s} = \varnothing$ for some subsequence of length
$\cap _{s=1}^{k} C_{i_s} = \varnothing$ for some subsequence of length ![]() $k$, then
$k$, then ![]() $z_r(\Gamma ) = z_k(\Gamma ) + (r-k)c(\Gamma )$.
$z_r(\Gamma ) = z_k(\Gamma ) + (r-k)c(\Gamma )$.
The following example paves the way for the main result in this section.
Example 5.2 The graph ![]() $\mathcal {O}_3$ in figure 4, with 6 vertices and 9 edges, has a central triangle with each side being the base of another triangle. Then, because we require cliques that are disjoint, we have
$\mathcal {O}_3$ in figure 4, with 6 vertices and 9 edges, has a central triangle with each side being the base of another triangle. Then, because we require cliques that are disjoint, we have ![]() $z_2(\mathcal {O}_3)=5$. However, for
$z_2(\mathcal {O}_3)=5$. However, for ![]() $z_3(\mathcal {O}_3)$, we only require empty intersection, so we can take
$z_3(\mathcal {O}_3)$, we only require empty intersection, so we can take ![]() $C_1,\,C_2,\,C_3$ with each
$C_1,\,C_2,\,C_3$ with each ![]() $C_j$ being one of the side triangles. This yields the maximum possible
$C_j$ being one of the side triangles. This yields the maximum possible ![]() $z_3(\mathcal {O}_3)=9$. Note that we do not have
$z_3(\mathcal {O}_3)=9$. Note that we do not have ![]() $z_3(\mathcal {O}_3)=z_2(\mathcal {O}_3)+c(\Gamma )$ in this case. This is because the cliques
$z_3(\mathcal {O}_3)=z_2(\mathcal {O}_3)+c(\Gamma )$ in this case. This is because the cliques ![]() $C_j$ have
$C_j$ have ![]() $C_i \cap C_j \not = \varnothing$ for all choices of
$C_i \cap C_j \not = \varnothing$ for all choices of ![]() $i,\,j=1,\,2,\,3$, so the hypothesis of lemma 5.1 never holds. However, because the triangles
$i,\,j=1,\,2,\,3$, so the hypothesis of lemma 5.1 never holds. However, because the triangles ![]() $C_j$ use up all the vertices of the graph, any longer sequence
$C_j$ use up all the vertices of the graph, any longer sequence ![]() $C_1,\,\ldots ,\,C_r$ can do no better than starting with the triangles. Therefore, we must have, for any
$C_1,\,\ldots ,\,C_r$ can do no better than starting with the triangles. Therefore, we must have, for any ![]() $r\geq 3$,
$r\geq 3$,
which is the largest possible. As a consequence ![]() $P_{H_{\mathcal {O}_3}}(x)=-x^{3}-x^{2}+5x$, a polynomial of degree 3.
$P_{H_{\mathcal {O}_3}}(x)=-x^{3}-x^{2}+5x$, a polynomial of degree 3.

FIGURE 4. ![]() $\mathcal {O}_3$.
$\mathcal {O}_3$.
More generally, let ![]() $K_n$ be the complete graph on
$K_n$ be the complete graph on ![]() $n$ vertices. This forms the central clique akin to the central triangle of
$n$ vertices. This forms the central clique akin to the central triangle of ![]() $\mathcal {O}_3$. Now, there are
$\mathcal {O}_3$. Now, there are ![]() $n$ subsets of
$n$ subsets of ![]() $(n-1)$ vertices in
$(n-1)$ vertices in ![]() $K_n$ and for each of these take the join with a single new vertex. The graph
$K_n$ and for each of these take the join with a single new vertex. The graph ![]() $\mathcal {O}_n$ consists of
$\mathcal {O}_n$ consists of ![]() $K_n$ and the
$K_n$ and the ![]() $n$ cliques
$n$ cliques ![]() $C_1,\,\ldots ,\,C_n$ (also of size
$C_1,\,\ldots ,\,C_n$ (also of size ![]() $n$) corresponding to each of these joins.
$n$) corresponding to each of these joins.
Proof of theorem 1.1. We compute the numbers ![]() $z_r:=z_r(\mathcal {O}_n)$. For
$z_r:=z_r(\mathcal {O}_n)$. For ![]() $z_2$, we see that any two cliques
$z_2$, we see that any two cliques ![]() $C_i$ and
$C_i$ and ![]() $C_j$ intersect in
$C_j$ intersect in ![]() $n-2$ vertices, so we are forced to take any
$n-2$ vertices, so we are forced to take any ![]() $C_j$ and then use the central vertex not in
$C_j$ and then use the central vertex not in ![]() $C_j$ with one of the new vertices attached to it to get
$C_j$ with one of the new vertices attached to it to get ![]() $z_2=n+2$. For
$z_2=n+2$. For ![]() $z_3$, as noted above,
$z_3$, as noted above, ![]() $C_i \cap C_j$ overlap in
$C_i \cap C_j$ overlap in ![]() $n-2$ central vertices, so the two vertices not in the intersection can be used with a new vertex to form a
$n-2$ central vertices, so the two vertices not in the intersection can be used with a new vertex to form a ![]() $K_3$ clique. Hence,
$K_3$ clique. Hence, ![]() $z_3=2n+3$. For
$z_3=2n+3$. For ![]() $z_4$, we see that any
$z_4$, we see that any ![]() $C_i \cap C_j \cap C_k$ consists of
$C_i \cap C_j \cap C_k$ consists of ![]() $n-3$ central vertices, so the three central vertices not in the intersection can be used with a new vertex (not in
$n-3$ central vertices, so the three central vertices not in the intersection can be used with a new vertex (not in ![]() $C_i$,
$C_i$, ![]() $C_j$ or
$C_j$ or ![]() $C_k$ of course) to obtain a
$C_k$ of course) to obtain a ![]() $K_4$ clique. Hence,
$K_4$ clique. Hence, ![]() $z_4=3n+4$. This same argument works up to
$z_4=3n+4$. This same argument works up to ![]() $z_{n-1}=(n-2)n+n-1$ since any
$z_{n-1}=(n-2)n+n-1$ since any ![]() $n-2$ of the
$n-2$ of the ![]() $C_i$ cliques intersect in
$C_i$ cliques intersect in ![]() $n-(n-2)=2$ central vertices, thus allowing a
$n-(n-2)=2$ central vertices, thus allowing a ![]() $K_{n-1}$ clique to be formed. However, for
$K_{n-1}$ clique to be formed. However, for ![]() $z_n$, we may use all the
$z_n$, we may use all the ![]() $C_i$ since
$C_i$ since ![]() $\cap _{i=1}^{n} C_i = \varnothing$, so
$\cap _{i=1}^{n} C_i = \varnothing$, so ![]() $z_n=n^{2}$. Then, by lemma 5.1, we have
$z_n=n^{2}$. Then, by lemma 5.1, we have ![]() $z_r = z_n + (r-n)n=rn$ for
$z_r = z_n + (r-n)n=rn$ for ![]() $r>n$. The result now follows from part (c) in lemma 2.2.
$r>n$. The result now follows from part (c) in lemma 2.2.
Remark 5.3 For a simplicial graph ![]() $\Gamma$ with
$\Gamma$ with ![]() $m$ vertices, part (c) in lemma 2.2 and theorems 8.2 and 8.5 in [Reference Farber and Oprea16] yield
$m$ vertices, part (c) in lemma 2.2 and theorems 8.2 and 8.5 in [Reference Farber and Oprea16] yield
This is a rather coarse bound in general. For instance ![]() $P_{H_\Gamma }(x)=kx+\ell x(1-x)$ if
$P_{H_\Gamma }(x)=kx+\ell x(1-x)$ if ![]() $\Gamma$ is the disjoint union of two cliques of cardinalities
$\Gamma$ is the disjoint union of two cliques of cardinalities ![]() $k$ and
$k$ and ![]() $\ell$, with
$\ell$, with ![]() $k\geq \ell$ (as follows from lemma 2.2 and [Reference Rudyak27]). The estimate in (5.1) is somehow closer to optimal in the case of the graphs
$k\geq \ell$ (as follows from lemma 2.2 and [Reference Rudyak27]). The estimate in (5.1) is somehow closer to optimal in the case of the graphs ![]() $\mathcal {O}_n$, for
$\mathcal {O}_n$, for ![]() $\deg (P_{H_{\mathcal {O}_n}})$ is half the number of vertices of
$\deg (P_{H_{\mathcal {O}_n}})$ is half the number of vertices of ![]() $\mathcal {O}_n$. It would be interesting to know whether (5.1) is sharp in particular cases.
$\mathcal {O}_n$. It would be interesting to know whether (5.1) is sharp in particular cases.
6. Consequences of the LS-logarithmic condition
We have seen in § 3 that the LS-logarithmicity hypothesis entails interesting consequences. Here we give further instances of the influence of the LS-logarithmicity hypothesis. In what follows all spaces are assumed to be normal and path-connected.
6.1 Open covers
We recall certain techniques involving open covers of spaces. These techniques go back at least to [Reference Ostrand25, Reference Schwarz29] and more recently have been used in [Reference Dranishnikov7, Reference Farber, Grant, Lupton and Oprea13, Reference Oprea and Strom24]. We shall use them in our study of the category and higher topological complexity of polyhedral products.
Lemma 6.1 Suppose ![]() $U_0,\, \ldots ,\,U_k$ is an open covering of the space
$U_0,\, \ldots ,\,U_k$ is an open covering of the space ![]() $X$. Then, for any integer
$X$. Then, for any integer ![]() $m \geq 0$, the open cover may be extended (recursively) to an open cover
$m \geq 0$, the open cover may be extended (recursively) to an open cover ![]() $U_0,\, \ldots ,\, U_{k+m}$ with the property that any
$U_0,\, \ldots ,\, U_{k+m}$ with the property that any ![]() $(k+1)$ subsets still cover
$(k+1)$ subsets still cover ![]() $X$. Moreover, the added subsets
$X$. Moreover, the added subsets ![]() $U_{k+1},\,\ldots ,\,U_{k+m}$ are formed by taking disjoint unions of subsets of the original
$U_{k+1},\,\ldots ,\,U_{k+m}$ are formed by taking disjoint unions of subsets of the original ![]() $U_0,\, \ldots ,\,U_k$.
$U_0,\, \ldots ,\,U_k$.
Remark 6.2 If the cover ![]() $U_0,\, \ldots ,\,U_k$ is categorical (i.e. each
$U_0,\, \ldots ,\,U_k$ is categorical (i.e. each ![]() $U_j$ is contractible to a point in
$U_j$ is contractible to a point in ![]() $X$), then the extended cover
$X$), then the extended cover ![]() $U_0,\, \ldots ,\, U_{k+m}$ is also categorical by simply restricting the original contracting homotopies to open subsets. Notice that no problem is incurred with intersections since the extended cover consists of disjoint unions of subsets of the cover
$U_0,\, \ldots ,\, U_{k+m}$ is also categorical by simply restricting the original contracting homotopies to open subsets. Notice that no problem is incurred with intersections since the extended cover consists of disjoint unions of subsets of the cover ![]() $U_0,\, \ldots ,\, U_{k}$.
$U_0,\, \ldots ,\, U_{k}$.
An open covering ![]() $U_0,\,\ldots ,\,U_{k+m}$ having the property of lemma 6.1, i.e. that any
$U_0,\,\ldots ,\,U_{k+m}$ having the property of lemma 6.1, i.e. that any ![]() $(k+1)$ subsets cover
$(k+1)$ subsets cover ![]() $X$, is called a
$X$, is called a ![]() $(k+1)$-cover. We then have:
$(k+1)$-cover. We then have:
Lemma 6.3 If ![]() $U_0,\,\ldots ,\,U_{k+m}$ is a
$U_0,\,\ldots ,\,U_{k+m}$ is a ![]() $(k+1)$-cover of
$(k+1)$-cover of ![]() $X$, then each point
$X$, then each point ![]() $x \in X$ is in at least
$x \in X$ is in at least ![]() $m+1$ of the subsets.
$m+1$ of the subsets.
Proof. Suppose not. Then some ![]() $x \in X$ lies in only (at most)
$x \in X$ lies in only (at most) ![]() $m$ of the subsets, say
$m$ of the subsets, say ![]() $U_0,\,\ldots ,\,U_{m-1}$. But then
$U_0,\,\ldots ,\,U_{m-1}$. But then ![]() $x$ does not lie in any of the
$x$ does not lie in any of the ![]() $k+1$ subsets
$k+1$ subsets ![]() $U_m,\,\ldots ,\,U_{k+m}$, and this contradicts the cover being a
$U_m,\,\ldots ,\,U_{k+m}$, and this contradicts the cover being a ![]() $(k+1)$-cover.
$(k+1)$-cover.
Proposition 6.4 Let ![]() $X=\prod _{i=1}^{n} X_i$ be a product where each
$X=\prod _{i=1}^{n} X_i$ be a product where each ![]() $X_i$ has an open covering
$X_i$ has an open covering ![]() ${}{\mathcal {U}_i}=\{{}_iU_j\}_{j=0}^{k_i}$. For each
${}{\mathcal {U}_i}=\{{}_iU_j\}_{j=0}^{k_i}$. For each ![]() $i$, extend
$i$, extend ![]() $\mathcal {U}_i$ to a
$\mathcal {U}_i$ to a ![]() $(k_i+1)$-cover
$(k_i+1)$-cover ![]() $\{{}_iU_j\}_{j=0}^{S}$ where
$\{{}_iU_j\}_{j=0}^{S}$ where ![]() $S=\sum _{i=1}^{n} k_i$ (this can be done in view of lemma 6.1). Then the sets
$S=\sum _{i=1}^{n} k_i$ (this can be done in view of lemma 6.1). Then the sets ![]() $W_j=\prod _{i=1}^{n} {}_iU_j$, with
$W_j=\prod _{i=1}^{n} {}_iU_j$, with ![]() $j=0,\,1,\,\ldots ,\, S$, form an open covering of
$j=0,\,1,\,\ldots ,\, S$, form an open covering of ![]() $X$.
$X$.
Proof. Let ![]() $(x_1,\,x_2,\,\ldots ,\,x_n)\in X$. By lemma 6.3, the first coordinate
$(x_1,\,x_2,\,\ldots ,\,x_n)\in X$. By lemma 6.3, the first coordinate ![]() $x_1$ lies in at least
$x_1$ lies in at least ![]() $S-k_1+1$ subsets, so without loss of generality take these to be
$S-k_1+1$ subsets, so without loss of generality take these to be ![]() ${}_1U_0,\,\ldots ,\,{}_1U_{S-k_1}$. The point
${}_1U_0,\,\ldots ,\,{}_1U_{S-k_1}$. The point ![]() $x_2$ lies in at least
$x_2$ lies in at least ![]() $S-k_2+1$ of the subsets, so it must be in at least
$S-k_2+1$ of the subsets, so it must be in at least ![]() $S-k_1 - k_2 +1$ of the sets
$S-k_1 - k_2 +1$ of the sets ![]() ${}_2U_0,\,\ldots ,\,{}_2U_{S-k_1}$. Again, we may take these to be
${}_2U_0,\,\ldots ,\,{}_2U_{S-k_1}$. Again, we may take these to be ![]() ${}_2U_0,\,\ldots ,\,{}_2U_{S-k_1-k_2}$. Similar arguments say that
${}_2U_0,\,\ldots ,\,{}_2U_{S-k_1-k_2}$. Similar arguments say that ![]() $x_p$ lies in
$x_p$ lies in ![]() $S-\sum _{j=1}^{p} k_j +1$ of the sets
$S-\sum _{j=1}^{p} k_j +1$ of the sets ![]() ${}_pU_0,\,\ldots ,\,{}_pU_{S-T}$, where
${}_pU_0,\,\ldots ,\,{}_pU_{S-T}$, where ![]() $T=\sum _{j=1}^{p-1} k_j$, and we may take these to be
$T=\sum _{j=1}^{p-1} k_j$, and we may take these to be ![]() ${}_pU_0,\,\ldots ,\,{}_2U_{S-T-k_p}$. Finally,
${}_pU_0,\,\ldots ,\,{}_2U_{S-T-k_p}$. Finally, ![]() $x_n$ lies in at least
$x_n$ lies in at least ![]() $S-S+1=1$ set which may be taken to be
$S-S+1=1$ set which may be taken to be ![]() $_nU_0$. But then
$_nU_0$. But then ![]() $(x_1,\,\ldots ,\,x_n)\in W_0$. Hence
$(x_1,\,\ldots ,\,x_n)\in W_0$. Hence ![]() $\{W_j\}$ covers.
$\{W_j\}$ covers.
6.2 LS category of products
As a reference for our later use of open cover properties (proof of lemma 6.7), we give an easy proof of the standard product inequality for LS category:
Proposition 6.5 For ![]() $X$ and
$X$ and ![]() $Y$ normal,
$Y$ normal, ![]() ${{\sf {cat}}}(X \times Y) \leq {{\sf {cat}}}(X)+ {{\sf {cat}}}(Y)$.
${{\sf {cat}}}(X \times Y) \leq {{\sf {cat}}}(X)+ {{\sf {cat}}}(Y)$.
Proof. Let ![]() ${{\sf {cat}}}(X)=k$ and
${{\sf {cat}}}(X)=k$ and ![]() ${{\sf {cat}}}(Y)=m$ be represented by respective open covers
${{\sf {cat}}}(Y)=m$ be represented by respective open covers ![]() $U_0,\,\ldots ,\,U_k$ and
$U_0,\,\ldots ,\,U_k$ and ![]() $V_0,\,\ldots ,\,V_m$. Then by lemma 6.1, we may extend these covers to categorical covers
$V_0,\,\ldots ,\,V_m$. Then by lemma 6.1, we may extend these covers to categorical covers ![]() $U_0,\,\ldots ,\,U_{k+m}$ and
$U_0,\,\ldots ,\,U_{k+m}$ and ![]() $V_0,\,\ldots ,\,V_{k+m}$ where the former is a
$V_0,\,\ldots ,\,V_{k+m}$ where the former is a ![]() $(k+1)$-cover and the latter is an
$(k+1)$-cover and the latter is an ![]() $(m+1)$-cover. Let
$(m+1)$-cover. Let ![]() $W_j=U_j \times V_j$ for
$W_j=U_j \times V_j$ for ![]() $j=0,\,\ldots ,\,k+m$. Clearly, each
$j=0,\,\ldots ,\,k+m$. Clearly, each ![]() $W_j$ is contractible in
$W_j$ is contractible in ![]() $X \times Y$ since we may use the product of the individual contracting homotopies in
$X \times Y$ since we may use the product of the individual contracting homotopies in ![]() $X$ and
$X$ and ![]() $Y$. By proposition 6.4, we know that
$Y$. By proposition 6.4, we know that ![]() $\{W_j\}$ covers
$\{W_j\}$ covers ![]() $X \times Y$ and therefore,
$X \times Y$ and therefore, ![]() ${{\sf {cat}}}(X \times Y) \leq k+m$.
${{\sf {cat}}}(X \times Y) \leq k+m$.
Remark 6.6 The exact same proof as above applies to show
 \[ {{\sf{cat}}}\left(\prod_{i=1}^{m} X_i\right) \leq \sum_{i=1}^{m} {{\sf{cat}}}(X_i). \]
\[ {{\sf{cat}}}\left(\prod_{i=1}^{m} X_i\right) \leq \sum_{i=1}^{m} {{\sf{cat}}}(X_i). \]
Here, each open categorical cover is extended to one of the form ![]() $U_0,\, \ldots ,\, U_s$, where
$U_0,\, \ldots ,\, U_s$, where ![]() $s=\sum _{i=1}^{m} {{\sf {cat}}}(X_i)$.
$s=\sum _{i=1}^{m} {{\sf {cat}}}(X_i)$.
6.3 LS category of polyhedral products
Let ![]() $\{(X_i,\,A_i)\}_{i=1}^{m}$ be a family of pairs of spaces, and
$\{(X_i,\,A_i)\}_{i=1}^{m}$ be a family of pairs of spaces, and ![]() $K$ be a simplicial complex on vertices
$K$ be a simplicial complex on vertices ![]() $[m]:=\{1,\,2,\,\ldots ,\,m\}$. For a subset
$[m]:=\{1,\,2,\,\ldots ,\,m\}$. For a subset ![]() $\sigma \subseteq [m]$, let
$\sigma \subseteq [m]$, let
 \[ X^{\sigma} = \prod_{i=1}^{m} Y_i, \quad \textrm{where} \quad Y_i =\begin{cases} X_i & \textrm{if}\ i \in \sigma; \\ A_i & \textrm{if}\ i \not\in\sigma. \end{cases} \]
\[ X^{\sigma} = \prod_{i=1}^{m} Y_i, \quad \textrm{where} \quad Y_i =\begin{cases} X_i & \textrm{if}\ i \in \sigma; \\ A_i & \textrm{if}\ i \not\in\sigma. \end{cases} \]
The polyhedral product ![]() $\mathcal {Z}(\{X_i,\,A_i\},\,K)$ is the union of all
$\mathcal {Z}(\{X_i,\,A_i\},\,K)$ is the union of all ![]() $X^{\sigma }$ with
$X^{\sigma }$ with ![]() $\sigma$ running over the simplicesFootnote 2 of
$\sigma$ running over the simplicesFootnote 2 of ![]() $K$,
$K$,
We are only interested in the case where all ![]() $A_i = *$, and use the notation
$A_i = *$, and use the notation ![]() $\underline {X}^{K}=\mathcal {Z}(\{X_i,\,A_i\},\,K)$. If in addition all
$\underline {X}^{K}=\mathcal {Z}(\{X_i,\,A_i\},\,K)$. If in addition all ![]() $X_i = X$, we simply write
$X_i = X$, we simply write ![]() $X^{K}$. The connection to our earlier work, and motivation for the results given below is apparent once it is realized that any
$X^{K}$. The connection to our earlier work, and motivation for the results given below is apparent once it is realized that any ![]() $K(H_\Gamma ,\,1)$ is the polyhedral product
$K(H_\Gamma ,\,1)$ is the polyhedral product ![]() $(S^{1})^{K}$, where
$(S^{1})^{K}$, where ![]() $K$ is the flag complex with
$K$ is the flag complex with ![]() $1$-skeleton given by
$1$-skeleton given by ![]() $\Gamma$.
$\Gamma$.
In [Reference Félix and Tanré18], the category of ![]() $X^{K}$ was computed to be
$X^{K}$ was computed to be ![]() ${{\sf {cat}}}(X)\cdot (1+ \mathrm {dim}(K))$ provided that
${{\sf {cat}}}(X)\cdot (1+ \mathrm {dim}(K))$ provided that ![]() $X$ is LS-logarithmic. Here, we shall generalize this result to polyhedral products
$X$ is LS-logarithmic. Here, we shall generalize this result to polyhedral products ![]() $\underline {X}^{K}$. We start with the following result that is reminiscent of [Reference González, Gutiérrez and Yuzvinsky20, theorem 5.3].
$\underline {X}^{K}$. We start with the following result that is reminiscent of [Reference González, Gutiérrez and Yuzvinsky20, theorem 5.3].
Lemma 6.7 Let ![]() $\{(X_i,\,*)\}_{i=1}^{m}$ be a family of based spaces and
$\{(X_i,\,*)\}_{i=1}^{m}$ be a family of based spaces and ![]() $K$ be a simplicial complex on vertices
$K$ be a simplicial complex on vertices ![]() $[m]$. Then
$[m]$. Then
where the maximum is taken over all Footnote 3 simplices ![]() $[i_1,\,\ldots ,\,i_n]$ of
$[i_1,\,\ldots ,\,i_n]$ of ![]() $K$.
$K$.
Proof. Let ![]() ${}_iU_0,\,\ldots ,\,{}_iU_{k_i}$ denote an open cover of the space
${}_iU_0,\,\ldots ,\,{}_iU_{k_i}$ denote an open cover of the space ![]() $X_i$ realizing
$X_i$ realizing ![]() ${{{\sf {cat}}}(X_i)=k_i}$. Fix homotopies
${{{\sf {cat}}}(X_i)=k_i}$. Fix homotopies ![]() ${}_iH_j$ contracting
${}_iH_j$ contracting ![]() ${}_iU_j$ to a point in
${}_iU_j$ to a point in ![]() $X_i$. (These may be taken to be base pointed by [Reference Cornea, Lupton, Oprea and Tanré6, lemma 1.25].) Let
$X_i$. (These may be taken to be base pointed by [Reference Cornea, Lupton, Oprea and Tanré6, lemma 1.25].) Let ![]() $\sigma =[i_1,\,\ldots ,\,i_n]$ be a maximal simplex giving a ‘subproduct’
$\sigma =[i_1,\,\ldots ,\,i_n]$ be a maximal simplex giving a ‘subproduct’
 \[ X^{\sigma} = \prod_{j=1}^{n} X_{i_j} \subseteq \underline{X}^{K}. \]
\[ X^{\sigma} = \prod_{j=1}^{n} X_{i_j} \subseteq \underline{X}^{K}. \]
Here, an element of ![]() $X^{\sigma }$ is thought of as element of
$X^{\sigma }$ is thought of as element of ![]() $\underline {X}^{K}$ by completing with base points in the coordinates corresponding to vertices not in
$\underline {X}^{K}$ by completing with base points in the coordinates corresponding to vertices not in ![]() $\sigma$. By the proof of proposition 6.5 and remark 6.6, we see that
$\sigma$. By the proof of proposition 6.5 and remark 6.6, we see that ![]() $X^{\sigma }$ is covered by
$X^{\sigma }$ is covered by ![]() $W_0^{\sigma },\,\ldots ,\,W_s^{\sigma }$, where
$W_0^{\sigma },\,\ldots ,\,W_s^{\sigma }$, where ![]() $s=\sum _{j=1}^{n} k_{i_j}$ and
$s=\sum _{j=1}^{n} k_{i_j}$ and ![]() $W_j^{\sigma } = {}_{i_1}U_j \times \cdots \times {}_{i_n}U_j$ for extended covers
$W_j^{\sigma } = {}_{i_1}U_j \times \cdots \times {}_{i_n}U_j$ for extended covers ![]() ${}_{i_j}U_0,\, \ldots ,\, {}_{i_j}U_s$ for each space appearing in the product
${}_{i_j}U_0,\, \ldots ,\, {}_{i_j}U_s$ for each space appearing in the product ![]() $X^{\sigma }$. Note that, by remark 6.2, the contracting homotopies for the extended covers are simply restrictions of the
$X^{\sigma }$. Note that, by remark 6.2, the contracting homotopies for the extended covers are simply restrictions of the ![]() ${}_{i_j}H_r$. This is, in fact, the key point. If
${}_{i_j}H_r$. This is, in fact, the key point. If ![]() $\tau =[r_1,\,\ldots ,\,r_p]$ is another maximal simplex of
$\tau =[r_1,\,\ldots ,\,r_p]$ is another maximal simplex of ![]() $K$, then we obtain
$K$, then we obtain
for ![]() $j =0,\,\ldots ,\, z=\sum _{i=1}^{p} k_{r_i}$. Here, we use the fact that if
$j =0,\,\ldots ,\, z=\sum _{i=1}^{p} k_{r_i}$. Here, we use the fact that if ![]() $m >p$, then the extended open cover
$m >p$, then the extended open cover ![]() $U_0,\,\ldots ,\,U_m$ of lemma 6.1 is an extension of
$U_0,\,\ldots ,\,U_m$ of lemma 6.1 is an extension of ![]() $U_0,\,\ldots ,\,U_p$. Now, if
$U_0,\,\ldots ,\,U_p$. Now, if ![]() $s > z$, then for
$s > z$, then for ![]() $s \geq j > z$, let
$s \geq j > z$, let ![]() $W_j^{\tau } = \varnothing$. Then, because the open covers and homotopies are fixed for each
$W_j^{\tau } = \varnothing$. Then, because the open covers and homotopies are fixed for each ![]() $X_i$, if
$X_i$, if ![]() $W_j^{\sigma } \cap W_j^{\tau } \not = \varnothing$, the homotopies and open subsets agree on the intersection. Hence, they can be pieced together to contract
$W_j^{\sigma } \cap W_j^{\tau } \not = \varnothing$, the homotopies and open subsets agree on the intersection. Hence, they can be pieced together to contract ![]() $W_j^{\sigma } \cup W_j^{\tau }$ to a point in
$W_j^{\sigma } \cup W_j^{\tau }$ to a point in ![]() $\underline {X}^{K}$. This can then be done for all maximal simplices, so we define
$\underline {X}^{K}$. This can then be done for all maximal simplices, so we define ![]() $W_j^{K} = \cup _\sigma W_j^{\sigma }$, where
$W_j^{K} = \cup _\sigma W_j^{\sigma }$, where ![]() $\sigma$ is maximal. Here, we have
$\sigma$ is maximal. Here, we have ![]() $j=0,\,\ldots ,\, \max _{\sigma =[i_1,\ldots ,i_n]}\{k_{i_1}+\cdots + k_{i_n}\}$, where the maximum is taken over maximal simplices. Notice that by taking unions, we only require the maximal simplex with the greatest number of open sets.
$j=0,\,\ldots ,\, \max _{\sigma =[i_1,\ldots ,i_n]}\{k_{i_1}+\cdots + k_{i_n}\}$, where the maximum is taken over maximal simplices. Notice that by taking unions, we only require the maximal simplex with the greatest number of open sets.
Proof of theorem 1.4. By lemma 6.7, we need only show
Let ![]() ${}{\sigma _0}$ be a simplex realizing the maximum. But
${}{\sigma _0}$ be a simplex realizing the maximum. But ![]() $X^{{}{\sigma _0}} \subseteq \underline {X}^{K}$ is a subproduct with a retraction
$X^{{}{\sigma _0}} \subseteq \underline {X}^{K}$ is a subproduct with a retraction ![]() $\underline {X}^{K} \to X^{{}{\sigma _0}}$ obtained by taking all other coordinates to base points. Since retracts have smaller category, we are done by the logarithmicity hypothesis.
$\underline {X}^{K} \to X^{{}{\sigma _0}}$ obtained by taking all other coordinates to base points. Since retracts have smaller category, we are done by the logarithmicity hypothesis.
Example 6.8 We illustrate how theorem 1.4 can be used to make (4.1) explicit in particular cases. Let ![]() $\{\Gamma _i\}_{i=1}^{m}$ be a family of graphs whose sets of vertices are pairwise disjoint. The set of vertices of the graph join
$\{\Gamma _i\}_{i=1}^{m}$ be a family of graphs whose sets of vertices are pairwise disjoint. The set of vertices of the graph join ![]() $\Gamma :=\Gamma _1\ast \cdots \ast \Gamma _m$ is the union of the vertices of all the graphs
$\Gamma :=\Gamma _1\ast \cdots \ast \Gamma _m$ is the union of the vertices of all the graphs ![]() $\Gamma _i$ where, besides the adjacencies in the individual graphs, each vertex of
$\Gamma _i$ where, besides the adjacencies in the individual graphs, each vertex of ![]() $\Gamma _i$ is taken to be adjacent in
$\Gamma _i$ is taken to be adjacent in ![]() $\Gamma$ to each vertex of
$\Gamma$ to each vertex of ![]() $\Gamma _j$ whenever
$\Gamma _j$ whenever ![]() $i\neq j$. Therefore, cliques
$i\neq j$. Therefore, cliques ![]() $C_i$ of
$C_i$ of ![]() $\Gamma _i$ (
$\Gamma _i$ (![]() $1\leq i\leq m$) form a new clique
$1\leq i\leq m$) form a new clique ![]() $C_1\ast \cdots \ast C_m$ (of size
$C_1\ast \cdots \ast C_m$ (of size ![]() $\sum _i |C_i|$) of
$\sum _i |C_i|$) of ![]() $\Gamma$. Hence, the size of the largest clique in
$\Gamma$. Hence, the size of the largest clique in ![]() $\Gamma$ is the sum of the sizes of the largest cliques in the individual graphs,
$\Gamma$ is the sum of the sizes of the largest cliques in the individual graphs,
 \begin{equation} c(\Gamma)=\sum_{i=1}^{m}c(\Gamma_i). \end{equation}
\begin{equation} c(\Gamma)=\sum_{i=1}^{m}c(\Gamma_i). \end{equation}
In terms of the RAA groups, we have disjoint subgroups so that elements in different subgroups commute; hence, ![]() $H_\Gamma =H_{\Gamma _1} \times \cdots \times H_{\Gamma _m}$, and (6.2) gives
$H_\Gamma =H_{\Gamma _1} \times \cdots \times H_{\Gamma _m}$, and (6.2) gives
 \[ \textrm{{cd}}(H_{\Gamma})={\textrm{cd}}(H_{\Gamma_1} \times \cdots \times H_{\Gamma_m}) = \sum_{i=1}^{m} \textrm{{cd}}(H_{\Gamma_i}). \]
\[ \textrm{{cd}}(H_{\Gamma})={\textrm{cd}}(H_{\Gamma_1} \times \cdots \times H_{\Gamma_m}) = \sum_{i=1}^{m} \textrm{{cd}}(H_{\Gamma_i}). \]
The point to stress is that, in terms of classifying spaces, the above discussion shows that any collection ![]() $\underline {H_\Gamma }:=\{(K(H_{\Gamma _i},\,1),\,\ast )\}_{i=1}^{m}$ is LS-logarithmic. Note that the associated polyhedral product
$\underline {H_\Gamma }:=\{(K(H_{\Gamma _i},\,1),\,\ast )\}_{i=1}^{m}$ is LS-logarithmic. Note that the associated polyhedral product ![]() $\underline {H_\Gamma }^{K}:=\mathcal {Z}(\{K(H_{\Gamma _i},\,1),\,\ast \},\,K)$ classifies an RAA group, so its category is given by (4.1). Theorem 1.4 then yields an explicit formula for
$\underline {H_\Gamma }^{K}:=\mathcal {Z}(\{K(H_{\Gamma _i},\,1),\,\ast \},\,K)$ classifies an RAA group, so its category is given by (4.1). Theorem 1.4 then yields an explicit formula for ![]() ${{\sf {cat}}}(\hspace {.4mm}\underline {H_\Gamma }^{K})$ in terms of the simplicial complex
${{\sf {cat}}}(\hspace {.4mm}\underline {H_\Gamma }^{K})$ in terms of the simplicial complex ![]() $K$ and the cliques of the graphs
$K$ and the cliques of the graphs ![]() $\Gamma _i$.
$\Gamma _i$.
6.4 TC of polyhedral products
For reference purposes, we record the following easy consequence of theorem 2.1 and lemma 6.7:
Corollary 6.9 For an integer ![]() $r\geq 2$, a family
$r\geq 2$, a family ![]() $\{(X_i,\,*)\}_{i=1}^{m}$ of based spaces and a simplicial complex
$\{(X_i,\,*)\}_{i=1}^{m}$ of based spaces and a simplicial complex ![]() $K$ on
$K$ on ![]() $[m]$ vertices, we have
$[m]$ vertices, we have
where the maximum is taken over all simplices ![]() $[i_1,\,\ldots ,\,i_n]$ of
$[i_1,\,\ldots ,\,i_n]$ of ![]() $K$.
$K$.
Proof of theorem 1.5. In view of corollary 6.9, it suffices to show
Let ![]() $\sigma _{{}{0}}$ be a simplex realizing the maximum. As in the proof of theorem 1.4,
$\sigma _{{}{0}}$ be a simplex realizing the maximum. As in the proof of theorem 1.4, ![]() $X^{\sigma _{{}{0}}}$ is a retract of
$X^{\sigma _{{}{0}}}$ is a retract of ![]() $\underline {X}^{K}$, so
$\underline {X}^{K}$, so ![]() ${{\sf {TC}}}_{{}{r}}(X^{\sigma _{{}{0}}}) \leq {{\sf {TC}}}_{{}{r}}(\underline {X}^{K})$, and we are done by the logarithmicity hypothesis.
${{\sf {TC}}}_{{}{r}}(X^{\sigma _{{}{0}}}) \leq {{\sf {TC}}}_{{}{r}}(\underline {X}^{K})$, and we are done by the logarithmicity hypothesis.
For ![]() $r\geq 2$, we say that
$r\geq 2$, we say that ![]() $X$ is
$X$ is ![]() ${{\sf {TC}}}_{{}{r}}$-logarithmic if
${{\sf {TC}}}_{{}{r}}$-logarithmic if ![]() ${{\sf {TC}}}_{{}{r}}(X^{s})=s\cdot {{\sf {TC}}}_{{}{r}}(X)$ for all
${{\sf {TC}}}_{{}{r}}(X^{s})=s\cdot {{\sf {TC}}}_{{}{r}}(X)$ for all ![]() $s \geq 2$.
$s \geq 2$.
Corollary 6.10 For a family ![]() $\{(X,\,*)\}_{i=1}^{m}$ of
$\{(X,\,*)\}_{i=1}^{m}$ of ![]() $m$-copies of the same based space
$m$-copies of the same based space ![]() $X$ and a simplicial complex
$X$ and a simplicial complex ![]() $K$ on
$K$ on ![]() $[m]$ vertices, if
$[m]$ vertices, if ![]() ${{\sf {TC}}}_{{}{r}}(X)={}{r}\,{{\sf {cat}}}(X)$ and
${{\sf {TC}}}_{{}{r}}(X)={}{r}\,{{\sf {cat}}}(X)$ and ![]() $X$ is both LS- and
$X$ is both LS- and ![]() ${{\sf {TC}}}_{{}{r}}$-logarithmic for some
${{\sf {TC}}}_{{}{r}}$-logarithmic for some ![]() $r\geq 2$, then
$r\geq 2$, then
Remark 6.11 In [Reference González, Gutiérrez and Yuzvinsky20, theorem 5.3], a result similar to theorem 1.5 was proven using the hypotheses that, for each ![]() $i$,
$i$, ![]() ${{\sf {TC}}}_{{}{r}}(X_i)$ is given by rational
${{\sf {TC}}}_{{}{r}}(X_i)$ is given by rational ![]() $r$-th zero-divisor cup-length and it equals twice the cone-length. Such hypotheses imply that the family
$r$-th zero-divisor cup-length and it equals twice the cone-length. Such hypotheses imply that the family ![]() $\{(X_i,\,*)\}_{i=1}^{m}$ is both LS- and
$\{(X_i,\,*)\}_{i=1}^{m}$ is both LS- and ![]() ${{\sf {TC}}}_r$-logarithmic. In this sense, theorem 1.5 is a generalization of that of [Reference González, Gutiérrez and Yuzvinsky20].
${{\sf {TC}}}_r$-logarithmic. In this sense, theorem 1.5 is a generalization of that of [Reference González, Gutiérrez and Yuzvinsky20].
Example 6.8 gives the LS-logarithmicity hypothesis in theorem 1.5 for families of RAA groups; the ![]() ${{\sf {TC}}}$-logarithmicity hypothesis also holds:
${{\sf {TC}}}$-logarithmicity hypothesis also holds:
Proposition 6.12 For any ![]() $r\geq 2$ and any family
$r\geq 2$ and any family ![]() $\{\Gamma _i\}_{i=1}^{m}$ of simplicial graphs,
$\{\Gamma _i\}_{i=1}^{m}$ of simplicial graphs,
Proof. It suffices to consider the case ![]() $m=2$. Let
$m=2$. Let ![]() $\Gamma$ and
$\Gamma$ and ![]() ${\Gamma '}$ be simplicial graphs and choose
${\Gamma '}$ be simplicial graphs and choose ![]() $C_1,\, \ldots ,\, C_r$ and
$C_1,\, \ldots ,\, C_r$ and ![]() $D_1,\,\ldots ,\,D_r$ cliques in
$D_1,\,\ldots ,\,D_r$ cliques in ![]() $\Gamma$ and
$\Gamma$ and ![]() $\Gamma '$ respectively with
$\Gamma '$ respectively with ![]() $\cap _{i=1}^{r} C_i = \varnothing$ and
$\cap _{i=1}^{r} C_i = \varnothing$ and ![]() $\cap _{i=1}^{r} D_i = \varnothing$ that realize
$\cap _{i=1}^{r} D_i = \varnothing$ that realize ![]() ${{\sf {TC}}}_r(H_\Gamma )$ and
${{\sf {TC}}}_r(H_\Gamma )$ and ![]() ${{\sf {TC}}}_r({H_\Gamma '})$. Let
${{\sf {TC}}}_r({H_\Gamma '})$. Let ![]() $E_i = C_i * D_i$ (where
$E_i = C_i * D_i$ (where ![]() $*$ again denotes the graph join). Clearly,
$*$ again denotes the graph join). Clearly, ![]() $\cap _{i=1}^{r} E_i = \varnothing$, for all
$\cap _{i=1}^{r} E_i = \varnothing$, for all ![]() $C_i$ are pairwise disjoint from all
$C_i$ are pairwise disjoint from all ![]() $D_j$ and the total intersections of the
$D_j$ and the total intersections of the ![]() $C_i$ and
$C_i$ and ![]() $D_i$ are individually empty. Then, using theorem 2.4, we obtain
$D_i$ are individually empty. Then, using theorem 2.4, we obtain
 \begin{align*} \sum_{i=1}^{r} |C_i| + \sum_{i=1}^{r} |D_i| & = \sum_{i=1}^{r} |E_i| \leq {{\sf{TC}}}_r(H_{\Gamma \ast {\Gamma'}}) \\ & \leq {{\sf{TC}}}_r(H_\Gamma) + {{\sf{TC}}}(H_{\Gamma'}) = \sum_{i=1}^{r} |C_i| + \sum_{i=1}^{r} |D_i|. \end{align*}
\begin{align*} \sum_{i=1}^{r} |C_i| + \sum_{i=1}^{r} |D_i| & = \sum_{i=1}^{r} |E_i| \leq {{\sf{TC}}}_r(H_{\Gamma \ast {\Gamma'}}) \\ & \leq {{\sf{TC}}}_r(H_\Gamma) + {{\sf{TC}}}(H_{\Gamma'}) = \sum_{i=1}^{r} |C_i| + \sum_{i=1}^{r} |D_i|. \end{align*}Hence, all inequalities are equalities and we are done.
The validity of the first hypothesis in theorem 1.5 for families of RAA groups depends on the actual structure of the graphs ![]() $\Gamma _i$. For instance, if a graph
$\Gamma _i$. For instance, if a graph ![]() $\Gamma$ has two disjoint cliques of the maximal cardinality (as is the case for
$\Gamma$ has two disjoint cliques of the maximal cardinality (as is the case for ![]() $D_v(\Gamma )$ in the first part of theorem 4.1), then
$D_v(\Gamma )$ in the first part of theorem 4.1), then ![]() ${{\sf {TC}}}_{{}{r}}(H_\Gamma )={}{r}\cdot {\textrm {cd}}(H_\Gamma )$, in view of theorem 2.4. Thus:
${{\sf {TC}}}_{{}{r}}(H_\Gamma )={}{r}\cdot {\textrm {cd}}(H_\Gamma )$, in view of theorem 2.4. Thus:
Corollary 6.13 If ![]() $\{\Gamma _i\}_{i=1}^{n}$ is a family of simplicial graphs such that each
$\{\Gamma _i\}_{i=1}^{n}$ is a family of simplicial graphs such that each ![]() $\Gamma _i$ has two disjoint cliques of the maximal cardinality, then for any simplicial complex
$\Gamma _i$ has two disjoint cliques of the maximal cardinality, then for any simplicial complex ![]() $K$ and any
$K$ and any ![]() $r\geq 2$,
$r\geq 2$,
where the maximum is taken over all maximal simplices ![]() $[i_1,\,\ldots ,\,i_n]$ of
$[i_1,\,\ldots ,\,i_n]$ of ![]() $K$. Here, we follow the notation in example 6.8, in particular
$K$. Here, we follow the notation in example 6.8, in particular ![]() $\Gamma =\Gamma _1\ast \cdots \ast \Gamma _m$.
$\Gamma =\Gamma _1\ast \cdots \ast \Gamma _m$.
It would be interesting to know whether one or both of the logarithmicity hypotheses could be waived in theorem 1.5. The hypothesis ![]() ${{\sf {TC}}}_r=r\cdot {{\sf {cat}}}$ for the polyhedral product factors however, plays a crucial role even for
${{\sf {TC}}}_r=r\cdot {{\sf {cat}}}$ for the polyhedral product factors however, plays a crucial role even for ![]() ${{\sf {TC}}}_2$, as will be clear in the next and final section.
${{\sf {TC}}}_2$, as will be clear in the next and final section.
We close the section with a general lower estimate (used later in the paper) for the topological complexity of polyhedral products. We need:
Theorem 6.14 [Reference Grant, Lupton and Oprea21, corollary 2.4]
If ![]() $F \to E \to B$ is a fibration of connected CW complexes admitting a (homotopy) section, then
$F \to E \to B$ is a fibration of connected CW complexes admitting a (homotopy) section, then ![]() ${{\sf {cat}}}(B \times F \times E^{r-2}) \leq {{\sf {TC}}}_r(E)$.
${{\sf {cat}}}(B \times F \times E^{r-2}) \leq {{\sf {TC}}}_r(E)$.
Corollary 6.15 Let ![]() $\sigma _1,\,\ldots ,\,\sigma _r$ be an
$\sigma _1,\,\ldots ,\,\sigma _r$ be an ![]() $r$-tuple of simplices in
$r$-tuple of simplices in ![]() $K$ such that at least two simplices are disjoint. Then, for any family
$K$ such that at least two simplices are disjoint. Then, for any family ![]() $\{(X_i,\,\ast )\}_{i=1}^{m}$,
$\{(X_i,\,\ast )\}_{i=1}^{m}$,
Here ![]() ${X}^{\sigma _i}$ stands for the product
${X}^{\sigma _i}$ stands for the product ![]() $\prod _{j\in \sigma _i}X_j$ (see the proof of corollary 6.7).
$\prod _{j\in \sigma _i}X_j$ (see the proof of corollary 6.7).
Proof. Without loss of generality we can take ![]() $\sigma _1 \cap \sigma _2 = \varnothing$. Consider the projection
$\sigma _1 \cap \sigma _2 = \varnothing$. Consider the projection ![]() $p_1\colon {}{\underline {X}}^{K} \to {}{{X}}^{\sigma _1}$ with homotopy fibre
$p_1\colon {}{\underline {X}}^{K} \to {}{{X}}^{\sigma _1}$ with homotopy fibre ![]() $F$. The inclusion
$F$. The inclusion ![]() $i_1\colon {}{{X}}^{\sigma _1} \to {}{\underline {X}}^{K}$ satisfies
$i_1\colon {}{{X}}^{\sigma _1} \to {}{\underline {X}}^{K}$ satisfies ![]() $p_1 \circ i_1 = \mathrm {id}$, so
$p_1 \circ i_1 = \mathrm {id}$, so ![]() ${}{{X}}^{\sigma _1}$ is a retract of
${}{{X}}^{\sigma _1}$ is a retract of ![]() ${}{\underline {X}}^{K}$. Hence, we may consider
${}{\underline {X}}^{K}$. Hence, we may consider ![]() $i_1$ to be a homotopy section of the homotopy fibration
$i_1$ to be a homotopy section of the homotopy fibration ![]() $p_1$. By theorem 6.14,
$p_1$. By theorem 6.14,
The inclusion ![]() $i_2\colon {}{{X}}^{\sigma _2} \to {}{\underline {X}}^{K}$ (with associated retraction
$i_2\colon {}{{X}}^{\sigma _2} \to {}{\underline {X}}^{K}$ (with associated retraction ![]() $p_2\colon {}{\underline {X}}^{K} \to {}{{X}}^{\sigma _2}$) has
$p_2\colon {}{\underline {X}}^{K} \to {}{{X}}^{\sigma _2}$) has ![]() $p_1 \circ i_2 = *$, since
$p_1 \circ i_2 = *$, since ![]() $\sigma _1 \cap \sigma _2 = \varnothing$, so
$\sigma _1 \cap \sigma _2 = \varnothing$, so ![]() $i_2$ factors up to homotopy through the fibre
$i_2$ factors up to homotopy through the fibre ![]() $F$. Moreover, composing the resulting homotopy class
$F$. Moreover, composing the resulting homotopy class ![]() ${X}^{\sigma _2}\to F$ with the fibre inclusion and
${X}^{\sigma _2}\to F$ with the fibre inclusion and ![]() $p_2$ gives the identity on
$p_2$ gives the identity on ![]() ${}{{X}}^{\sigma _2}$ (for
${}{{X}}^{\sigma _2}$ (for ![]() $p_2\circ i_2=\text {id}$), so
$p_2\circ i_2=\text {id}$), so ![]() ${}{{X}}^{\sigma _2}$ is a homotopy retract of
${}{{X}}^{\sigma _2}$ is a homotopy retract of ![]() $F$. Of course, it is also the case that
$F$. Of course, it is also the case that ![]() ${}{{X}}^{\sigma _3} \times \cdots \times {}{{X}}^{\sigma _r}$ is a retract of
${}{{X}}^{\sigma _3} \times \cdots \times {}{{X}}^{\sigma _r}$ is a retract of ![]() $({}{\underline {X}}^{K})^{r-2}$ as well, so
$({}{\underline {X}}^{K})^{r-2}$ as well, so ![]() ${}{{X}}^{\sigma _1} \times \cdots \times {}{{X}}^{\sigma _r}$ is a homotopy retract of
${}{{X}}^{\sigma _1} \times \cdots \times {}{{X}}^{\sigma _r}$ is a homotopy retract of ![]() ${}{{X}}^{\sigma _1} \times F \times ({}{\underline {X}}^{K})^{r-2}$. Thus
${}{{X}}^{\sigma _1} \times F \times ({}{\underline {X}}^{K})^{r-2}$. Thus
which yields the result.
7. Real projective spaces
For a family ![]() $\underline {P}=\{(P^{n_i},\,\ast )\}_{i=1}^{m}$ of real projective spaces, and a simplicial complex
$\underline {P}=\{(P^{n_i},\,\ast )\}_{i=1}^{m}$ of real projective spaces, and a simplicial complex ![]() $K$ with vertices
$K$ with vertices ![]() $[m]$, set
$[m]$, set
 \begin{equation} \mathcal{N}^{(n_1,\ldots,n_m)}(K):=\max\left\{\sum_{i\in \sigma_{1}{\bigtriangleup}\sigma_{2}}n_i+\sum_{i\in \sigma_1\cap\sigma_{2}}{{\sf{TC}}}({P}^{n_i}):\sigma_{1},\sigma_{2}\in K\right\} \end{equation}
\begin{equation} \mathcal{N}^{(n_1,\ldots,n_m)}(K):=\max\left\{\sum_{i\in \sigma_{1}{\bigtriangleup}\sigma_{2}}n_i+\sum_{i\in \sigma_1\cap\sigma_{2}}{{\sf{TC}}}({P}^{n_i}):\sigma_{1},\sigma_{2}\in K\right\} \end{equation}
(recall that ![]() ${{\sf {TC}}}={{\sf {TC}}}_2$), where
${{\sf {TC}}}={{\sf {TC}}}_2$), where ![]() $\sigma _{1}{\bigtriangleup} \sigma _{2}=(\sigma _{1}\setminus \sigma _{2})\cup (\sigma _{2}\setminus \sigma _{1})$, the symmetric difference of
$\sigma _{1}{\bigtriangleup} \sigma _{2}=(\sigma _{1}\setminus \sigma _{2})\cup (\sigma _{2}\setminus \sigma _{1})$, the symmetric difference of ![]() $\sigma _1$ and
$\sigma _1$ and ![]() $\sigma _2$. In these terms, theorem 1.7 reads:
$\sigma _2$. In these terms, theorem 1.7 reads:
Since ![]() ${{\sf {TC}}}(P^{n})<2n=2\,{{\sf {cat}}}(P^{n})$, theorem 1.7 is an improvement (for families of real projective spaces) of the upper estimate in corollary 6.9 (for
${{\sf {TC}}}(P^{n})<2n=2\,{{\sf {cat}}}(P^{n})$, theorem 1.7 is an improvement (for families of real projective spaces) of the upper estimate in corollary 6.9 (for ![]() $r=2$). On the other hand, by taking
$r=2$). On the other hand, by taking ![]() $\sigma _1=\sigma _2$ in (7.1), we see that the value that theorem 1.5 would predict for
$\sigma _1=\sigma _2$ in (7.1), we see that the value that theorem 1.5 would predict for ![]() ${{\sf {TC}}}(\underline {P}^{K})$ could turn out to be smaller than the actual value of this invariant (of course, hypothesis (1) in theorem 1.5 does not hold for the family
${{\sf {TC}}}(\underline {P}^{K})$ could turn out to be smaller than the actual value of this invariant (of course, hypothesis (1) in theorem 1.5 does not hold for the family ![]() $\underline {P}$). Example 7.2 below illustrates a concrete such situation.
$\underline {P}$). Example 7.2 below illustrates a concrete such situation.
The inequality in (7.2) is sharp in a number of situations. The simplest one is when each ![]() $P^{n_i}$ is parallelizable, for then
$P^{n_i}$ is parallelizable, for then ![]() ${{\sf {TC}}}(P^{n_i})=n_i$, so equality in theorem 1.7 follows from corollary 6.15 and the obvious fact that families of real projective spaces are LS-logarithmic. More generally, proposition 1.8 implies that (7.2) is optimal as long as, for each
${{\sf {TC}}}(P^{n_i})=n_i$, so equality in theorem 1.7 follows from corollary 6.15 and the obvious fact that families of real projective spaces are LS-logarithmic. More generally, proposition 1.8 implies that (7.2) is optimal as long as, for each ![]() $i$,
$i$, ![]() ${{\sf {TC}}}(P^{n_i})$ agrees with
${{\sf {TC}}}(P^{n_i})$ agrees with ![]() ${{\sf {zcl}}}(P^{n_i})$, the zero-divisors cup-length of
${{\sf {zcl}}}(P^{n_i})$, the zero-divisors cup-length of ![]() $P^{n_i}$ with mod-2 coefficients, i.e. the maximal number of elements
$P^{n_i}$ with mod-2 coefficients, i.e. the maximal number of elements ![]() $z_j$ in the kernel of the cup-multiplication
$z_j$ in the kernel of the cup-multiplication ![]() $H^{*}(P^{n_i})\otimes H^{*}(P^{n_i})\to H^{*}(P^{n_i})$ with
$H^{*}(P^{n_i})\otimes H^{*}(P^{n_i})\to H^{*}(P^{n_i})$ with ![]() $\prod z_j\neq 0$.
$\prod z_j\neq 0$.
Remark 7.1 It is known that the equality ![]() ${{\sf {TC}}}(P^{n})={{\sf {zcl}}}(P^{n})$ holds precisely in the following (non-mutually exclusive) cases: (1)
${{\sf {TC}}}(P^{n})={{\sf {zcl}}}(P^{n})$ holds precisely in the following (non-mutually exclusive) cases: (1) ![]() $n\in \{1,\,3,\,7\}$, i.e.
$n\in \{1,\,3,\,7\}$, i.e. ![]() $P^{n}$ is parallelizable; (2)
$P^{n}$ is parallelizable; (2) ![]() $n=2^{e}+\delta$ with
$n=2^{e}+\delta$ with ![]() $e\geq 1$ and
$e\geq 1$ and ![]() $\delta =0,\,1$; (3)
$\delta =0,\,1$; (3) ![]() $n=6$.
$n=6$.
Since ![]() $n\leq {{\sf {zcl}}}(P^{n})\leq {{\sf {TC}}}(P^{n})$ for any
$n\leq {{\sf {zcl}}}(P^{n})\leq {{\sf {TC}}}(P^{n})$ for any ![]() $n$, both maximums in theorem 1.7 and proposition 1.8 are always realized by maximal simplices
$n$, both maximums in theorem 1.7 and proposition 1.8 are always realized by maximal simplices ![]() $\sigma _1$ and
$\sigma _1$ and ![]() $\sigma _2$ of
$\sigma _2$ of ![]() $K$, i.e. simplices that are not contained in any other simplex of
$K$, i.e. simplices that are not contained in any other simplex of ![]() $K$. Nonetheless, it can be the case that these maximums are realized by sums that necessarily involve both
$K$. Nonetheless, it can be the case that these maximums are realized by sums that necessarily involve both ![]() ${{\sf {cat}}}$ and
${{\sf {cat}}}$ and ![]() ${{\sf {TC}}}$ terms. In other words, our estimates exhibit a mixed
${{\sf {TC}}}$ terms. In other words, our estimates exhibit a mixed ![]() ${{\sf {cat}}}$/
${{\sf {cat}}}$/![]() ${{\sf {TC}}}$ behaviour not present for RAA groups. For instance:
${{\sf {TC}}}$ behaviour not present for RAA groups. For instance:
Example 7.2 Let ![]() $K=\partial \Delta ^{2}$, the simplicial complex with vertices
$K=\partial \Delta ^{2}$, the simplicial complex with vertices ![]() $1,\,2,\,3$ and facets
$1,\,2,\,3$ and facets ![]() $[1,\,2]$,
$[1,\,2]$, ![]() $[1,\,3]$ and
$[1,\,3]$ and ![]() $[2,\,3]$, and take
$[2,\,3]$, and take ![]() $n_1=n_2=n_3=2^{e}$ with
$n_1=n_2=n_3=2^{e}$ with ![]() $e\geq 0$. Since
$e\geq 0$. Since ![]() ${{\sf {TC}}}(P^{2^{e}})=2^{e+1}-1$, theorem 1.7 and proposition 1.8 yield
${{\sf {TC}}}(P^{2^{e}})=2^{e+1}-1$, theorem 1.7 and proposition 1.8 yield ![]() ${{\sf {TC}}}(\underline {P}^{K})=2^{e+2}-1$, a maximum that is realized only with different maximal simplices
${{\sf {TC}}}(\underline {P}^{K})=2^{e+2}-1$, a maximum that is realized only with different maximal simplices ![]() $\sigma _1$ and
$\sigma _1$ and ![]() $\sigma _2$, so that
$\sigma _2$, so that ![]() $|\sigma _1\cap \sigma _2|=1$ and
$|\sigma _1\cap \sigma _2|=1$ and ![]() $|\sigma _{1}{\bigtriangleup} \sigma _{2}|=2$.
$|\sigma _{1}{\bigtriangleup} \sigma _{2}|=2$.
Proposition 7.3 below shows that (7.2) is also sharp if ![]() $\mathrm {dim}(K)=0$ (for unrestricted
$\mathrm {dim}(K)=0$ (for unrestricted ![]() $n_i$'s, and with no mixed
$n_i$'s, and with no mixed ![]() ${{\sf {cat}}}$/
${{\sf {cat}}}$/![]() ${{\sf {TC}}}$ behaviour). This is proved using [Reference Dranishnikov and Sadykov8, theorem 6] by induction on the number of vertices of
${{\sf {TC}}}$ behaviour). This is proved using [Reference Dranishnikov and Sadykov8, theorem 6] by induction on the number of vertices of ![]() $K$. The easy proof details are left as an exercise for the interested reader.
$K$. The easy proof details are left as an exercise for the interested reader.
Proposition 7.3 If ![]() $n_1\geq n_2\geq \cdots \geq n_m$, then
$n_1\geq n_2\geq \cdots \geq n_m$, then
 \[ {{\sf{TC}}}\left({\bigvee_iP}^{n_i}\right)=\max\left\{n_1+n_2,{{\sf{TC}}}(P^{n_1})\right\}. \]
\[ {{\sf{TC}}}\left({\bigvee_iP}^{n_i}\right)=\max\left\{n_1+n_2,{{\sf{TC}}}(P^{n_1})\right\}. \]Proof of corollary 1.6. This is a consequence of theorem 1.5; we need only check the three relevant hypotheses. The LS-logarithmicity hypothesis is obvious, while the ![]() ${{\sf {TC}}}_r=r\,{{\sf {cat}}}$ condition is given by [Reference Cadavid-Aguilar, González, Gutiérrez, Guzmán-Sáenz and Lara4, equation (5.2) and theorem 5.7]. Namely, under the present hypotheses (large
${{\sf {TC}}}_r=r\,{{\sf {cat}}}$ condition is given by [Reference Cadavid-Aguilar, González, Gutiérrez, Guzmán-Sáenz and Lara4, equation (5.2) and theorem 5.7]. Namely, under the present hypotheses (large ![]() $r$ and even
$r$ and even ![]() $n_i$),
$n_i$),
for all ![]() $i$, where
$i$, where ![]() ${{\sf {zcl}}}_r$ stands for
${{\sf {zcl}}}_r$ stands for ![]() $r$-th zero-divisors cup-length, see [Reference Basabe, González, Rudyak and Tamaki3, definition 3.8]. Lastly, the
$r$-th zero-divisors cup-length, see [Reference Basabe, González, Rudyak and Tamaki3, definition 3.8]. Lastly, the ![]() ${{\sf {TC}}}_r$-hypothesis follows from
${{\sf {TC}}}_r$-hypothesis follows from
 \[ r\left(\sum_{j=1}^{\ell} n_{i_j}\right)\hspace{-.2mm}\geq \hspace{-.2mm}{{\sf{TC}}}_r\left(\prod_{j=1}^{\ell} P^{n_{i_j}}\right)\hspace{-.2mm}\geq\hspace{-.2mm}{{\sf{zcl}}}_r\left(\prod_{j=1}^{\ell} P^{n_{i_j}}\right)\hspace{-.2mm}\geq\hspace{-.2mm}\sum_{j=1}^{\ell}{{\sf{zcl}}}_r(P^{n_{i_j}})\hspace{-.2mm}=\hspace{-.2mm}r\left(\sum_{j=1}^{\ell} n_{i_j}\right)\hspace{-.8mm}, \]
\[ r\left(\sum_{j=1}^{\ell} n_{i_j}\right)\hspace{-.2mm}\geq \hspace{-.2mm}{{\sf{TC}}}_r\left(\prod_{j=1}^{\ell} P^{n_{i_j}}\right)\hspace{-.2mm}\geq\hspace{-.2mm}{{\sf{zcl}}}_r\left(\prod_{j=1}^{\ell} P^{n_{i_j}}\right)\hspace{-.2mm}\geq\hspace{-.2mm}\sum_{j=1}^{\ell}{{\sf{zcl}}}_r(P^{n_{i_j}})\hspace{-.2mm}=\hspace{-.2mm}r\left(\sum_{j=1}^{\ell} n_{i_j}\right)\hspace{-.8mm}, \]where the first inequality comes from theorem 2.1, the second one comes from [Reference Basabe, González, Rudyak and Tamaki3, theorem 3.9], and the third one comes from [Reference Cohen and Farber5, lemma 2.1].
7.1 Proof of proposition 1.8
Recall from [Reference Bahri, Bendersky, Cohen and Gitler2, theorem 2.35] that the mod-2 cohomology ring of ![]() $\underline {P}^{K}$ is
$\underline {P}^{K}$ is
 \[ H^{*}(\underline{P}^{K})\cong \bigotimes_{i=1}^{m}H^{*}({P}^{n_i})/I_K. \]
\[ H^{*}(\underline{P}^{K})\cong \bigotimes_{i=1}^{m}H^{*}({P}^{n_i})/I_K. \]
Here, ![]() $I_K$ is the generalized Stanley–Reisner ideal generated by all elements
$I_K$ is the generalized Stanley–Reisner ideal generated by all elements ![]() $x_{r_1}\otimes x_{r_2}\otimes \cdots \otimes x_{r_t},$ satisfying
$x_{r_1}\otimes x_{r_2}\otimes \cdots \otimes x_{r_t},$ satisfying ![]() $x_{r_{i}}\in \overline {H}^{ * }({P}^{n_{r_i}})$ and
$x_{r_{i}}\in \overline {H}^{ * }({P}^{n_{r_i}})$ and ![]() $[r_{1},\,\ldots ,\,r_{t}]\notin {K}$. For each
$[r_{1},\,\ldots ,\,r_{t}]\notin {K}$. For each ![]() $i\in [m]$, let
$i\in [m]$, let ![]() $u_{i}\in H^{*}(\underline {P}^{K})$ be the pullback of the generator of
$u_{i}\in H^{*}(\underline {P}^{K})$ be the pullback of the generator of ![]() $H^{1}({P}^{n_i})$ under the canonical projection
$H^{1}({P}^{n_i})$ under the canonical projection ![]() $\underline {P}^{K}\to {P}^{n_i}$ onto the
$\underline {P}^{K}\to {P}^{n_i}$ onto the ![]() $i$-th coordinate. In these terms,
$i$-th coordinate. In these terms, ![]() $I_K$ is generated by the powers
$I_K$ is generated by the powers ![]() $u_{i}^{n_{i}+1}$ and the products
$u_{i}^{n_{i}+1}$ and the products ![]() $u_{r_1}\cdots u_{r_t}$ with
$u_{r_1}\cdots u_{r_t}$ with ![]() $[r_1,\,\ldots ,\,r_t]\notin {K}$. In particular, a graded basis for
$[r_1,\,\ldots ,\,r_t]\notin {K}$. In particular, a graded basis for ![]() $H^{*}(\underline {P}^{K})$ is given by the monomials
$H^{*}(\underline {P}^{K})$ is given by the monomials ![]() $u_{1}^{e_1}\cdots u_{m}^{e_m}$ having
$u_{1}^{e_1}\cdots u_{m}^{e_m}$ having ![]() $0\leq e_{i}\leq n_i$ and
$0\leq e_{i}\leq n_i$ and ![]() $[i: e_{i}>0]\in {K}$. Note that
$[i: e_{i}>0]\in {K}$. Note that ![]() $u_{i}\otimes 1+1\otimes u_{i}\in [H^{*}(\underline {P}^{K})]^{\otimes 2}$ is a zero divisor for each
$u_{i}\otimes 1+1\otimes u_{i}\in [H^{*}(\underline {P}^{K})]^{\otimes 2}$ is a zero divisor for each ![]() $i\in \{1,\,\ldots ,\,m\}$.
$i\in \{1,\,\ldots ,\,m\}$.
Let ![]() $\sigma _{1},\,\sigma _{2}\in {K}$, say with
$\sigma _{1},\,\sigma _{2}\in {K}$, say with ![]() $\sigma _{1}\setminus \sigma _{2}=[i_1,\,\ldots ,\,i_{r}]$,
$\sigma _{1}\setminus \sigma _{2}=[i_1,\,\ldots ,\,i_{r}]$, ![]() $\sigma _{2}\setminus \sigma _{1}=[j_1,\,\ldots ,\,j_{s}]$, and
$\sigma _{2}\setminus \sigma _{1}=[j_1,\,\ldots ,\,j_{s}]$, and ![]() $\sigma _{1}\cap \sigma _{2}=[k_{1},\,\ldots ,\,k_{w}]$. It suffices to show that, in
$\sigma _{1}\cap \sigma _{2}=[k_{1},\,\ldots ,\,k_{w}]$. It suffices to show that, in ![]() $[H^{*}(\underline {P}^{K})]^{\otimes 2}$,
$[H^{*}(\underline {P}^{K})]^{\otimes 2}$,
 \begin{equation} \left(\prod_{i\in\sigma_{1}{\bigtriangleup}\sigma_2}(u_{i}\otimes 1+1\otimes u_{i})^{n_i}\right)\left(\,\prod_{i\in\sigma_{1}\cap\sigma_2}(u_{i}\otimes 1+1\otimes u_{i})^{{{\sf{zcl}}}(P^{n_i})}\right)\neq 0. \end{equation}
\begin{equation} \left(\prod_{i\in\sigma_{1}{\bigtriangleup}\sigma_2}(u_{i}\otimes 1+1\otimes u_{i})^{n_i}\right)\left(\,\prod_{i\in\sigma_{1}\cap\sigma_2}(u_{i}\otimes 1+1\otimes u_{i})^{{{\sf{zcl}}}(P^{n_i})}\right)\neq 0. \end{equation}Expanding the first factor on the left-hand side of (7.3), we get
 \begin{align} &\left(\sum_{\ell_{1}=0}^{n_{i_1}}\binom{n_{i_1}}{\ell_1}\right.\left.u_{i_1}^{n_{i_1}-\ell_1}\otimes u_{i_1}^{\ell_1}\rule{0mm}{7.5mm}\right) \cdots\left(\sum_{\ell_{r}=0}^{n_{i_r}}\binom{n_{i_r}}{\ell_r}u_{i_{r}}^{n_{i_r}-\ell_{r}}\otimes u_{i_{r}}^{\ell_{r}}\right)\nonumber\\ &\qquad\cdot\left(\sum_{q_{1}=0}^{n_{j_1}}\right.\left.\binom{n_{j_1}}{q_1}u_{j_1}^{n_{j_1}-q_1}\otimes u_{j_1}^{q_1}\rule{0mm}{7.5mm}\right) \cdots\left(\sum_{q_{s}=0}^{n_{j_s}}\binom{n_{j_s}}{q_s}u_{j_s}^{n_{j_s}-q_{s}}\otimes u_{j_{s}}^{q_{s}}\right) \nonumber\\ &\qquad\qquad=\left(\sum_{\substack{0\leq \ell_{t}\leq n_{i_t}\\ 1\leq t\leq r}}\binom{n_{i_1}}{\ell_1}\cdots\binom{n_{i_r}}{\ell_r}u_{i_1}^{n_{i_1}-\ell_1}\cdots u_{i_r}^{n_{i_r}-\ell_r}\otimes u_{i_1}^{\ell_1}\cdots u_{i_r}^{\ell_r}\right) \end{align}
\begin{align} &\left(\sum_{\ell_{1}=0}^{n_{i_1}}\binom{n_{i_1}}{\ell_1}\right.\left.u_{i_1}^{n_{i_1}-\ell_1}\otimes u_{i_1}^{\ell_1}\rule{0mm}{7.5mm}\right) \cdots\left(\sum_{\ell_{r}=0}^{n_{i_r}}\binom{n_{i_r}}{\ell_r}u_{i_{r}}^{n_{i_r}-\ell_{r}}\otimes u_{i_{r}}^{\ell_{r}}\right)\nonumber\\ &\qquad\cdot\left(\sum_{q_{1}=0}^{n_{j_1}}\right.\left.\binom{n_{j_1}}{q_1}u_{j_1}^{n_{j_1}-q_1}\otimes u_{j_1}^{q_1}\rule{0mm}{7.5mm}\right) \cdots\left(\sum_{q_{s}=0}^{n_{j_s}}\binom{n_{j_s}}{q_s}u_{j_s}^{n_{j_s}-q_{s}}\otimes u_{j_{s}}^{q_{s}}\right) \nonumber\\ &\qquad\qquad=\left(\sum_{\substack{0\leq \ell_{t}\leq n_{i_t}\\ 1\leq t\leq r}}\binom{n_{i_1}}{\ell_1}\cdots\binom{n_{i_r}}{\ell_r}u_{i_1}^{n_{i_1}-\ell_1}\cdots u_{i_r}^{n_{i_r}-\ell_r}\otimes u_{i_1}^{\ell_1}\cdots u_{i_r}^{\ell_r}\right) \end{align} \begin{align} &\cdot\left(\sum_{\substack{0\leq q_{t}\leq n_{j_t}\\ 1\leq t\leq s}}\binom{n_{j_1}}{q_1}\cdots\binom{n_{j_s}}{q_s}u_{j_1}^{n_{j_1}-q_1}\cdots u_{j_s}^{n_{j_s}-q_s}\otimes u_{j_1}^{q_1}\cdots u_{j_s}^{q_s}\right). \end{align}
\begin{align} &\cdot\left(\sum_{\substack{0\leq q_{t}\leq n_{j_t}\\ 1\leq t\leq s}}\binom{n_{j_1}}{q_1}\cdots\binom{n_{j_s}}{q_s}u_{j_1}^{n_{j_1}-q_1}\cdots u_{j_s}^{n_{j_s}-q_s}\otimes u_{j_1}^{q_1}\cdots u_{j_s}^{q_s}\right). \end{align}
On the other hand, it is elementary to see that ![]() ${{\sf {zcl}}}(P^{n_i})=2^{\theta _i}-1$ where
${{\sf {zcl}}}(P^{n_i})=2^{\theta _i}-1$ where ![]() $2^{\theta _{i}-1}\leq n_i<2^{\theta _{i}}$. In particular
$2^{\theta _{i}-1}\leq n_i<2^{\theta _{i}}$. In particular ![]() $n_i\leq 2^{\theta _i}-1<2n_{i}$. With this in mind, the second factor on the right-hand side of (7.3) becomes
$n_i\leq 2^{\theta _i}-1<2n_{i}$. With this in mind, the second factor on the right-hand side of (7.3) becomes
 \begin{align} &\left(\sum_{h_{1}=2^{\theta_{k_1}}-1-n_{k_1}}^{n_{k_1}}u_{k_1}^{2^{\theta_{k_1}}-1-h_1}\otimes u_{k_1}^{h_1}\rule{0mm}{9mm}\right)\cdots\left(\sum_{h_{w}=2^{\theta_{k_w}}-1-n_{k_w}}^{n_{k_w}}u_{k_w}^{2^{\theta_{k_w}}-1-h_w}\otimes u_{k_w}^{h_w}\right) \nonumber\\ &\quad = \left(\sum_{\substack{2^{\theta_{k_t}}-1-n_{k_t}\leq h_{t}\leq n_{k_t}\\ 1\leq t\leq w}}u_{k_1}^{2^{\theta_{k_1}}-1-h_1}\cdots u_{k_w}^{2^{\theta_{k_w}}-1-h_w}\otimes u_{k_1}^{h_1}\cdots u_{k_w}^{h_w}\right). \end{align}
\begin{align} &\left(\sum_{h_{1}=2^{\theta_{k_1}}-1-n_{k_1}}^{n_{k_1}}u_{k_1}^{2^{\theta_{k_1}}-1-h_1}\otimes u_{k_1}^{h_1}\rule{0mm}{9mm}\right)\cdots\left(\sum_{h_{w}=2^{\theta_{k_w}}-1-n_{k_w}}^{n_{k_w}}u_{k_w}^{2^{\theta_{k_w}}-1-h_w}\otimes u_{k_w}^{h_w}\right) \nonumber\\ &\quad = \left(\sum_{\substack{2^{\theta_{k_t}}-1-n_{k_t}\leq h_{t}\leq n_{k_t}\\ 1\leq t\leq w}}u_{k_1}^{2^{\theta_{k_1}}-1-h_1}\cdots u_{k_w}^{2^{\theta_{k_w}}-1-h_w}\otimes u_{k_1}^{h_1}\cdots u_{k_w}^{h_w}\right). \end{align}The conclusion then follows by observing that, in the product of the expressions above, the basis element
arises only from the product of:
•
 $u_{i_1}^{n_{i_1}}\cdots u_{i_r}^{n_{i_r}}\otimes 1\,$ in (7.4), with
$u_{i_1}^{n_{i_1}}\cdots u_{i_r}^{n_{i_r}}\otimes 1\,$ in (7.4), with  $\ell _{t}=0$ for all
$\ell _{t}=0$ for all  $t\in \{1,\,\ldots ,\,r\}$;
$t\in \{1,\,\ldots ,\,r\}$;•
 $1\otimes u_{j_1}^{n_{j_1}}\cdots u_{j_s}^{n_{j_s}}\,$ in (7.5), with
$1\otimes u_{j_1}^{n_{j_1}}\cdots u_{j_s}^{n_{j_s}}\,$ in (7.5), with  $q_{t}=n_{j_t}$ for all
$q_{t}=n_{j_t}$ for all  $t\in \{1,\,\ldots ,\,s\}$;
$t\in \{1,\,\ldots ,\,s\}$;•
 $u_{k_1}^{n_{k_1}}\cdots u_{k_w}^{n_{k_w}}\otimes u_{k_1}^{2^{\theta _{k_1}}-1-n_{k_1}}\cdots u_{k_w}^{2^{\theta _{k_w}}-1-n_{k_w}}\,$ in (7.6), with
$u_{k_1}^{n_{k_1}}\cdots u_{k_w}^{n_{k_w}}\otimes u_{k_1}^{2^{\theta _{k_1}}-1-n_{k_1}}\cdots u_{k_w}^{2^{\theta _{k_w}}-1-n_{k_w}}\,$ in (7.6), with  $h_{t}=2^{\theta _{k_t}}-1-n_{k_t}$ for all
$h_{t}=2^{\theta _{k_t}}-1-n_{k_t}$ for all  $t\in \{1,\,\ldots ,\,w\}$.
$t\in \{1,\,\ldots ,\,w\}$.
7.2 Axial and nonsingular maps
The rest of the paper is devoted to the proof of theorem 1.7. For this, we need the full force of the concept of axial map and its relationship to the topological complexity of real projective spaces. We review the needed details.
Definition 7.4 Let ![]() $n$ and
$n$ and ![]() $k$ be nonnegative integers. A continuous map
$k$ be nonnegative integers. A continuous map ![]() $f\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{k+1}$ is called nonsingular provided (a)
$f\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{k+1}$ is called nonsingular provided (a) ![]() $f(\lambda x,\,\mu y)=\lambda \mu f(x,\,y)$ for all
$f(\lambda x,\,\mu y)=\lambda \mu f(x,\,y)$ for all ![]() $x,\,y\in \mathbb {R}^{n+1}$,
$x,\,y\in \mathbb {R}^{n+1}$, ![]() $\lambda ,\,\mu \in \mathbb {R}^{}$, and (b)
$\lambda ,\,\mu \in \mathbb {R}^{}$, and (b) ![]() $f(x,\,y)=0$ implies either
$f(x,\,y)=0$ implies either ![]() $x=0$ or
$x=0$ or ![]() $y=0$. If in addition
$y=0$. If in addition ![]() $f(x,\,\ast )=x$ and
$f(x,\,\ast )=x$ and ![]() $f(\ast ,\,x)=x$ for all
$f(\ast ,\,x)=x$ for all ![]() $x\in \mathbb {R}^{n+1}$,
$x\in \mathbb {R}^{n+1}$, ![]() $f$ is called a strong nonsingular map. Here,
$f$ is called a strong nonsingular map. Here, ![]() $\ast$ stands for the base point
$\ast$ stands for the base point ![]() $(1,\,0,\,\ldots ,\,0)$ of
$(1,\,0,\,\ldots ,\,0)$ of ![]() $\mathbb {R}^{n+1}$. Furthermore, we use the canonical embedding
$\mathbb {R}^{n+1}$. Furthermore, we use the canonical embedding ![]() $\mathbb {R}^{n+1}\hookrightarrow \mathbb {R}^{k+1}$ to identify
$\mathbb {R}^{n+1}\hookrightarrow \mathbb {R}^{k+1}$ to identify ![]() $(x_1,\,\ldots ,\,x_{n+1})\in \mathbb {R}^{n+1}$ with
$(x_1,\,\ldots ,\,x_{n+1})\in \mathbb {R}^{n+1}$ with ![]() $(x_1,\,\ldots ,\,x_{n+1},\,0,\,\ldots ,\,0)\in \mathbb {R}^{k+1}$.
$(x_1,\,\ldots ,\,x_{n+1},\,0,\,\ldots ,\,0)\in \mathbb {R}^{k+1}$.
It is classical that a nonsingular map as above exists only for ![]() $k\geq n$, and that
$k\geq n$, and that ![]() $k=n$ is possible only for
$k=n$ is possible only for ![]() $n\in \{1,\,3,\,7\}$, in which case the complex, quaternion, and octonion multiplications can be used. In the latter cases, the multiplication
$n\in \{1,\,3,\,7\}$, in which case the complex, quaternion, and octonion multiplications can be used. In the latter cases, the multiplication ![]() $\omega \cdot z$ yields a strong nonsingular map, while the multiplication
$\omega \cdot z$ yields a strong nonsingular map, while the multiplication ![]() $\omega \cdot \overline {z}$ yields a nonsingular map
$\omega \cdot \overline {z}$ yields a nonsingular map ![]() $f\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{n+1}$ satisfying
$f\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{n+1}$ satisfying
with ![]() $\lambda _x>0$ for
$\lambda _x>0$ for ![]() $x\neq 0$. From the polyhedral product viewpoint, the latter condition allows us to detect the
$x\neq 0$. From the polyhedral product viewpoint, the latter condition allows us to detect the ![]() ${{\sf {cat}}}$/
${{\sf {cat}}}$/![]() ${{\sf {TC}}}$ mixed behaviour illustrated in example 7.2 – see the discussion following the next definition.
${{\sf {TC}}}$ mixed behaviour illustrated in example 7.2 – see the discussion following the next definition.
Definition 7.5 Let ![]() $n$ and
$n$ and ![]() $k$ be nonnegative integers. A continuous map
$k$ be nonnegative integers. A continuous map ![]() $\alpha :{P}^{n}\times {P}^{n}\to {P}^{k}$ is called axial if its restrictions
$\alpha :{P}^{n}\times {P}^{n}\to {P}^{k}$ is called axial if its restrictions ![]() $\alpha |_{{P}^{n}\times \ast }$ and
$\alpha |_{{P}^{n}\times \ast }$ and ![]() $\alpha |_{\ast \times {P}^{n}}$ are detected in mod 2 cohomology (so
$\alpha |_{\ast \times {P}^{n}}$ are detected in mod 2 cohomology (so ![]() $k\geq n$ is forced). If in fact
$k\geq n$ is forced). If in fact ![]() $\alpha |_{{P}^{n}\times \ast }$ and
$\alpha |_{{P}^{n}\times \ast }$ and ![]() $\alpha |_{\ast \times {P}^{n}}$ are the equatorial inclusions, i.e. if
$\alpha |_{\ast \times {P}^{n}}$ are the equatorial inclusions, i.e. if ![]() $\alpha (A,\,\ast )=A$ and
$\alpha (A,\,\ast )=A$ and ![]() $\alpha (\ast ,\,A)=A$ hold for any
$\alpha (\ast ,\,A)=A$ hold for any ![]() $A\in {P}^{n}\subset {P}^{k}$, then
$A\in {P}^{n}\subset {P}^{k}$, then ![]() $\alpha$ is called a strong axial map. Here,
$\alpha$ is called a strong axial map. Here, ![]() $\ast$ is the base point of
$\ast$ is the base point of ![]() ${P}^{\ell }$ given by the equivalence class of
${P}^{\ell }$ given by the equivalence class of ![]() $(1,\,0,\,\ldots ,\,0)\in \mathbb {R}^{\ell +1}$.
$(1,\,0,\,\ldots ,\,0)\in \mathbb {R}^{\ell +1}$.
It is elementary to see that a nonsingular map ![]() $f\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{k+1}$ induces and is induced by an axial map
$f\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{k+1}$ induces and is induced by an axial map ![]() $\alpha \colon {P}^{n}\times {P}^{n}\longrightarrow {P}^{k}$, and that, in these conditions,
$\alpha \colon {P}^{n}\times {P}^{n}\longrightarrow {P}^{k}$, and that, in these conditions, ![]() $f$ is strong if and only if
$f$ is strong if and only if ![]() $\alpha$ is strong. In turn, a strong axial map
$\alpha$ is strong. In turn, a strong axial map ![]() ${P}^{n}\times {P}^{n}\to {P}^{k}$ can be constructed out of a smooth immersion
${P}^{n}\times {P}^{n}\to {P}^{k}$ can be constructed out of a smooth immersion ![]() ${P}^{n}\looparrowright \mathbb {R}^{k}$ ([Reference Sanderson28, theorem 2.1]; note that
${P}^{n}\looparrowright \mathbb {R}^{k}$ ([Reference Sanderson28, theorem 2.1]; note that ![]() $k>n$ is forced). Conversely, for
$k>n$ is forced). Conversely, for ![]() $k>n$, the existence of a (not necessarily strong) axial map
$k>n$, the existence of a (not necessarily strong) axial map ![]() ${P}^{n}\times {P}^{n}\to {P}^{k}$ implies the existence of a smooth immersion
${P}^{n}\times {P}^{n}\to {P}^{k}$ implies the existence of a smooth immersion ![]() ${P}^{n}\looparrowright \mathbb {R}^{k}$ ([Reference Adem, Gitler and James1]). The ‘strong’ requirement, which is then free when
${P}^{n}\looparrowright \mathbb {R}^{k}$ ([Reference Adem, Gitler and James1]). The ‘strong’ requirement, which is then free when ![]() $k>n$, is central in what follows. (The situation
$k>n$, is central in what follows. (The situation ![]() $n=k$ is special in that there cannot be a smooth immersion
$n=k$ is special in that there cannot be a smooth immersion ![]() ${P}^{n}\looparrowright \mathbb {R}^{n}$, and yet an axial map
${P}^{n}\looparrowright \mathbb {R}^{n}$, and yet an axial map ![]() ${P}^{n}\times {P}^{n}\to {P}^{n}$ exists if and only if
${P}^{n}\times {P}^{n}\to {P}^{n}$ exists if and only if ![]() $n\in \{1,\,3,\,7\}$.)
$n\in \{1,\,3,\,7\}$.)
These facts imply that, for ![]() $n\neq 1,\,3,\,7$,
$n\neq 1,\,3,\,7$, ![]() ${{\sf {TC}}}({P}^{n})= \operatorname {Imm}({P}^{n})$, the Euclidean immersion dimension of
${{\sf {TC}}}({P}^{n})= \operatorname {Imm}({P}^{n})$, the Euclidean immersion dimension of ![]() $P^{n}$ ([Reference Farber, Tabachnikov and Yuzvinsky17, theorem 7.1]), which also agrees with the smallest integer
$P^{n}$ ([Reference Farber, Tabachnikov and Yuzvinsky17, theorem 7.1]), which also agrees with the smallest integer ![]() $k$ greater than
$k$ greater than ![]() $n$ for which there is a strong axial map
$n$ for which there is a strong axial map ![]() $P^{n}\times P^{n}\to P^{k}$. Furthermore, if
$P^{n}\times P^{n}\to P^{k}$. Furthermore, if ![]() $k>n$, an axial map
$k>n$, an axial map ![]() $P^{n}\times P^{n}\to P^{k}$ is known to be null-homotopic on the diagonal. The combination of such a behaviour with the strong condition for axial maps yields the main ingredient in the proof of theorem 1.7. Actually, the strong property for axial maps is directly responsible for the mixed
$P^{n}\times P^{n}\to P^{k}$ is known to be null-homotopic on the diagonal. The combination of such a behaviour with the strong condition for axial maps yields the main ingredient in the proof of theorem 1.7. Actually, the strong property for axial maps is directly responsible for the mixed ![]() ${{\sf {cat}}}$/
${{\sf {cat}}}$/![]() ${{\sf {TC}}}$ behaviour – and resulting apparent sharpness – of theorem 1.7 (see (7.9) below).
${{\sf {TC}}}$ behaviour – and resulting apparent sharpness – of theorem 1.7 (see (7.9) below).
The following fact is adapted from [Reference Farber, Tabachnikov and Yuzvinsky17, lemma 5.7]. We leave the proof as a standard algebraic topology exercise for the reader.
Lemma 7.6 For ![]() $n\neq 1,\,3,\,7$, there is an axial map
$n\neq 1,\,3,\,7$, there is an axial map ![]() $\alpha :{P}^{n}\times {P}^{n}\to {P}^{{{\sf {TC}}}({P}^{n})}$ that is strong and satisfies
$\alpha :{P}^{n}\times {P}^{n}\to {P}^{{{\sf {TC}}}({P}^{n})}$ that is strong and satisfies ![]() $\alpha (A,\,A)=\ast$ for all
$\alpha (A,\,A)=\ast$ for all ![]() $A\in P^{n}$. Consequently, there is a strong nonsingular map
$A\in P^{n}$. Consequently, there is a strong nonsingular map ![]() $f:\mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{{{\sf {TC}}}({P}^{n})+1}$ such that
$f:\mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}^{{{\sf {TC}}}({P}^{n})+1}$ such that ![]() $f(x,\,x)=(\lambda _{x},\,0,\,\ldots ,\,0)$,
$f(x,\,x)=(\lambda _{x},\,0,\,\ldots ,\,0)$, ![]() $\lambda _{x}\geq 0$, for all
$\lambda _{x}\geq 0$, for all ![]() $x\in \mathbb {R}^{n+1}$, and
$x\in \mathbb {R}^{n+1}$, and ![]() $\lambda _{x}= 0$ only for
$\lambda _{x}= 0$ only for ![]() $x=0$.
$x=0$.
7.3 Proof of theorem 1.7
For each ![]() $i\in \{1,\,\ldots ,\,m\}$, fix once and for all a nonsingular map
$i\in \{1,\,\ldots ,\,m\}$, fix once and for all a nonsingular map ![]() $f_{i}:\mathbb {R}^{n_{i}+1}\times \mathbb {R}^{n_{i}+1}\to \mathbb {R}^{{{\sf {TC}}}({P}^{n_i})+1}$ such that
$f_{i}:\mathbb {R}^{n_{i}+1}\times \mathbb {R}^{n_{i}+1}\to \mathbb {R}^{{{\sf {TC}}}({P}^{n_i})+1}$ such that
for all ![]() $x\in \mathbb {R}^{n_i+1}$, with
$x\in \mathbb {R}^{n_i+1}$, with ![]() $\lambda _x>0$ for
$\lambda _x>0$ for ![]() $x\neq 0$. Furthermore, if
$x\neq 0$. Furthermore, if ![]() $n_i\neq 1,\,3,\,7$, we also require
$n_i\neq 1,\,3,\,7$, we also require ![]() $f_i$ to be strong:
$f_i$ to be strong:
For ![]() $k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$, let
$k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$, let ![]() $f_{ik}$ denote the
$f_{ik}$ denote the ![]() $(k+1)$-st coordinate map of
$(k+1)$-st coordinate map of ![]() $f_{i}$, and consider the subsets
$f_{i}$, and consider the subsets ![]() $V_{ik}\subset P^{n_i}\times P^{n_i}$ defined by
$V_{ik}\subset P^{n_i}\times P^{n_i}$ defined by
Observe that ![]() $\{V_{i0},\,V_{i1},\,\ldots ,\,V_{i{{\sf {TC}}}({P}^{n_i})}\}$ is an open cover of
$\{V_{i0},\,V_{i1},\,\ldots ,\,V_{i{{\sf {TC}}}({P}^{n_i})}\}$ is an open cover of ![]() ${P}^{n_i}\times {P}^{n_i}$, with the diagonal of
${P}^{n_i}\times {P}^{n_i}$, with the diagonal of ![]() ${P}^{n_i}$ contained in
${P}^{n_i}$ contained in ![]() $V_{i0}$, in view of (7.7).
$V_{i0}$, in view of (7.7).
Remark 7.7 As observed in [Reference Farber, Tabachnikov and Yuzvinsky17], on each set ![]() $V_{ik}$, the end-points evaluation map
$V_{ik}$, the end-points evaluation map ![]() $({P}^{n_i})^{[0,1]}\to {P}^{n_i}\times {P}^{n_i}$ has a continuous local section
$({P}^{n_i})^{[0,1]}\to {P}^{n_i}\times {P}^{n_i}$ has a continuous local section ![]() $\lambda _{ik}:V_{ik}\to ({P}^{n_i})^{[0,1]}$ defined as follows: in the diagonal,
$\lambda _{ik}:V_{ik}\to ({P}^{n_i})^{[0,1]}$ defined as follows: in the diagonal, ![]() $\lambda _{i0}(A,\,A)$ is the constant path at
$\lambda _{i0}(A,\,A)$ is the constant path at ![]() $A$. Otherwise, for
$A$. Otherwise, for ![]() $A\neq B$, choose unit vectors
$A\neq B$, choose unit vectors ![]() $a\in A$ and
$a\in A$ and ![]() $b\in B$ with
$b\in B$ with ![]() $f_{ik}(a,\,b)>0$. The only other pair of unit vectors satisfying the latter condition is
$f_{ik}(a,\,b)>0$. The only other pair of unit vectors satisfying the latter condition is ![]() $(-a,\,-b)$. Both pairs
$(-a,\,-b)$. Both pairs ![]() $(a,\,b)$ and
$(a,\,b)$ and ![]() $(-a,\,-b)$ determine the same orientation of the plane spanned by
$(-a,\,-b)$ determine the same orientation of the plane spanned by ![]() $A$ and
$A$ and ![]() $B$. We then set
$B$. We then set ![]() $\lambda _{ik}(A,\,B)$ to be the rotation with constant velocity from
$\lambda _{ik}(A,\,B)$ to be the rotation with constant velocity from ![]() $A$ towards
$A$ towards ![]() $B$ in the plane spanned by
$B$ in the plane spanned by ![]() $A$ and
$A$ and ![]() $B$, following the direction determined by the above orientation. Notice that the continuity of
$B$, following the direction determined by the above orientation. Notice that the continuity of ![]() $\lambda _{i0}$ on
$\lambda _{i0}$ on ![]() $V_{i0}$ follows from (7.7), as
$V_{i0}$ follows from (7.7), as ![]() $\lambda _{i0}(A,\,A)$ is constant.
$\lambda _{i0}(A,\,A)$ is constant.
We replace the covering ![]() $\{V_{ik}\}_k$ of each
$\{V_{ik}\}_k$ of each ![]() $P^{n_i}$ by one which consists of pairwise disjoint sets. Put
$P^{n_i}$ by one which consists of pairwise disjoint sets. Put ![]() $U_{ik}:=V_{ik}\setminus (V_{i0}\cup \cdots \cup V_{i(k-1)})$ (so
$U_{ik}:=V_{ik}\setminus (V_{i0}\cup \cdots \cup V_{i(k-1)})$ (so ![]() $U_{i0}=V_{i0}$). We say that an ordered pair of lines
$U_{i0}=V_{i0}$). We say that an ordered pair of lines ![]() $(A,\,B)$ in
$(A,\,B)$ in ![]() $\mathbb {R}^{n_{i}+1}$ produces
$\mathbb {R}^{n_{i}+1}$ produces ![]() $k$ zeroes (
$k$ zeroes (![]() $k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$) when
$k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$) when ![]() $(A,\,B)\in U_{ik}$. The justification of the latter convention comes by observing that
$(A,\,B)\in U_{ik}$. The justification of the latter convention comes by observing that ![]() $(A,\,B)\in U_{ik}$ if and only if
$(A,\,B)\in U_{ik}$ if and only if
for some (and therefore any) vectors ![]() $a\in A$ and
$a\in A$ and ![]() $b\in B$. The number of zeroes produced by
$b\in B$. The number of zeroes produced by ![]() $(A,\,B)$ is denoted
$(A,\,B)$ is denoted ![]() $Z(A,\,B)$.
$Z(A,\,B)$.
For simplicity we write ![]() $X=\underline {P}^{K}$, the polyhedral product in theorem 1.7, but keep the notation
$X=\underline {P}^{K}$, the polyhedral product in theorem 1.7, but keep the notation ![]() ${P}^{\sigma }$ for the ‘subproducts’ in corollary 6.15. An element
${P}^{\sigma }$ for the ‘subproducts’ in corollary 6.15. An element ![]() $(A_1,\,A_2)$ of
$(A_1,\,A_2)$ of ![]() $X^{2}$ will be thought of as a matrix of size
$X^{2}$ will be thought of as a matrix of size ![]() $m\times 2$, i.e.
$m\times 2$, i.e.
 \begin{equation} \nonumber (A_1,A_2)= \begin{pmatrix} A_{11} & A_{12}\\ \vdots & \vdots\\ A_{m1} & A_{m2}\end{pmatrix}, \end{equation}
\begin{equation} \nonumber (A_1,A_2)= \begin{pmatrix} A_{11} & A_{12}\\ \vdots & \vdots\\ A_{m1} & A_{m2}\end{pmatrix}, \end{equation}
where each column belongs to ![]() $X$, say
$X$, say ![]() $(A_{1j},\,\ldots ,\,A_{mj})\in {P}^{\sigma _{j}}$ with
$(A_{1j},\,\ldots ,\,A_{mj})\in {P}^{\sigma _{j}}$ with ![]() $\sigma _{1},\,\sigma _{2}\in {K}$. Each row
$\sigma _{1},\,\sigma _{2}\in {K}$. Each row ![]() $(A_{i1},\,A_{i2})$ of the matrix
$(A_{i1},\,A_{i2})$ of the matrix ![]() $(A_1,\,A_2)$ lies in a unique set
$(A_1,\,A_2)$ lies in a unique set ![]() $U_{ik}$ with
$U_{ik}$ with ![]() $k=Z(A_{i1},\,A_{i2})$. The number of zeroes determined by
$k=Z(A_{i1},\,A_{i2})$. The number of zeroes determined by ![]() $(A_1,\,A_2)$, denoted by
$(A_1,\,A_2)$, denoted by ![]() $Z(A_1,\,A_2)$, is the sum of zeroes produced by the rows of
$Z(A_1,\,A_2)$, is the sum of zeroes produced by the rows of ![]() $(A_1,\,A_2)$,
$(A_1,\,A_2)$,
 \[ Z(A_1,A_2)=\sum_{i=1}^{m}Z(A_{i1},A_{i2}). \]
\[ Z(A_1,A_2)=\sum_{i=1}^{m}Z(A_{i1},A_{i2}). \]
It is apparent that ![]() $Z(A_1,\,A_2)\leq \sum _{i\in \sigma _{1}\cup \sigma _{2}}{{\sf {TC}}}({P}^{n_i})$. However, in view of (7.8), the number of zeroes produced by rows of type either
$Z(A_1,\,A_2)\leq \sum _{i\in \sigma _{1}\cup \sigma _{2}}{{\sf {TC}}}({P}^{n_i})$. However, in view of (7.8), the number of zeroes produced by rows of type either ![]() $(A_{i1},\,\ast )$ or
$(A_{i1},\,\ast )$ or ![]() $(\ast ,\, A_{i2})$ of
$(\ast ,\, A_{i2})$ of ![]() $(A_1,\,A_2)$ calls for a more careful consideration. Namely, note that
$(A_1,\,A_2)$ calls for a more careful consideration. Namely, note that ![]() $Z(A_{i1},\,A_{i2})=Z(A_{i1},\,\ast )\leq n_i$ for
$Z(A_{i1},\,A_{i2})=Z(A_{i1},\,\ast )\leq n_i$ for ![]() $i\in \sigma _{1}\setminus \sigma _{2}$, because
$i\in \sigma _{1}\setminus \sigma _{2}$, because ![]() $f_{i}$ fulfils (7.8) when
$f_{i}$ fulfils (7.8) when ![]() $n_i\neq 1,\,3,\,7$ (recall that
$n_i\neq 1,\,3,\,7$ (recall that ![]() $n_i={{\sf {TC}}}({P}^{n_i})$ if
$n_i={{\sf {TC}}}({P}^{n_i})$ if ![]() $n_i=1,\,3,\,7$). Likewise, if
$n_i=1,\,3,\,7$). Likewise, if ![]() $i\in \sigma _{2}\setminus \sigma _{1}$, then
$i\in \sigma _{2}\setminus \sigma _{1}$, then ![]() $Z(A_{i1},\,A_{i2})=Z(\ast ,\,A_{i2})\leq n_i$. Therefore
$Z(A_{i1},\,A_{i2})=Z(\ast ,\,A_{i2})\leq n_i$. Therefore
and we have proved:
Proposition 7.8 A pairwise disjoint covering of ![]() $X^{2}$ is given by the sets
$X^{2}$ is given by the sets ![]() $W_{j}=\{(A_1,\,A_2)\in X^{2}: Z(A_1,\,A_2)=j\}$, with
$W_{j}=\{(A_1,\,A_2)\in X^{2}: Z(A_1,\,A_2)=j\}$, with ![]() $j\in \{0,\,1,\,\ldots ,\,\mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$.
$j\in \{0,\,1,\,\ldots ,\,\mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$.
Remark 7.9 The sets ![]() $W_j$ fail to give an open covering. However, they can be used to calculate the generalized topological complexity of
$W_j$ fail to give an open covering. However, they can be used to calculate the generalized topological complexity of ![]() $X$,
$X$, ![]() ${{\sf {TC}}}_{g}(X)$ (not to be confused with a higher
${{\sf {TC}}}_{g}(X)$ (not to be confused with a higher ![]() ${{\sf {TC}}}_g$). This generalized topological complexity is defined in the same way as
${{\sf {TC}}}_g$). This generalized topological complexity is defined in the same way as ![]() ${{\sf {TC}}}(X)$, except that the openness condition imposed on the cover of
${{\sf {TC}}}(X)$, except that the openness condition imposed on the cover of ![]() $X^{2}$ is not required. In our case,
$X^{2}$ is not required. In our case, ![]() ${{\sf {TC}}}(X)$ and
${{\sf {TC}}}(X)$ and ![]() ${{\sf {TC}}}_{g}(X)$ agree since
${{\sf {TC}}}_{g}(X)$ agree since ![]() $X$ is a
$X$ is a ![]() $ \operatorname {CW}$ complex (see [Reference García-Calcines19, corollary 2.8]).
$ \operatorname {CW}$ complex (see [Reference García-Calcines19, corollary 2.8]).
The proof of theorem 1.7 will be complete once a local rule (i.e. a local section for the end-points evaluation map ![]() $X^{[0,1]}\to X\times X$) is constructed on each
$X^{[0,1]}\to X\times X$) is constructed on each ![]() $W_{j}$. This will be achieved by splitting
$W_{j}$. This will be achieved by splitting ![]() $W_{j}$ into topologically disjoint subsets (proposition 7.10 below), and then showing that each such subset admits a local rule.
$W_{j}$ into topologically disjoint subsets (proposition 7.10 below), and then showing that each such subset admits a local rule.
A partition of an integer ![]() $j\in \{0,\,1,\,\ldots ,\, \mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$ is an ordered tuple
$j\in \{0,\,1,\,\ldots ,\, \mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$ is an ordered tuple ![]() $(j_1,\,\ldots ,\, j_{m})$ of integers satisfying
$(j_1,\,\ldots ,\, j_{m})$ of integers satisfying ![]() $j=j_{1}+\cdots +j_{m}$ and
$j=j_{1}+\cdots +j_{m}$ and ![]() $0\leq j_{i}\leq {{\sf {TC}}}({P}^{n_i})$ for each
$0\leq j_{i}\leq {{\sf {TC}}}({P}^{n_i})$ for each ![]() $i=1,\,\ldots ,\,m$. For such a partition we set
$i=1,\,\ldots ,\,m$. For such a partition we set
We show that the resulting set-theoretic partition ![]() $W_{j}=\displaystyle {\bigsqcup} W_{(j_1,\ldots , j_{m})}$, where the union runs over the partitions
$W_{j}=\displaystyle {\bigsqcup} W_{(j_1,\ldots , j_{m})}$, where the union runs over the partitions ![]() $(j_1,\,\ldots ,\,j_m)$ of
$(j_1,\,\ldots ,\,j_m)$ of ![]() $j$, is topological, i.e.
$j$, is topological, i.e. ![]() $W_{j}$ has the weak topology determined by the several
$W_{j}$ has the weak topology determined by the several ![]() $W_{(j_1,\ldots , j_{m})}$. In fact:
$W_{(j_1,\ldots , j_{m})}$. In fact:
Proposition 7.10 Two different partitions ![]() $(j_1,\,\ldots ,\, j_{m})$ and
$(j_1,\,\ldots ,\, j_{m})$ and ![]() $(r_1,\,\ldots ,\, r_{m})$ of the same
$(r_1,\,\ldots ,\, r_{m})$ of the same ![]() $j\in \{0,\,1,\,\ldots ,\,\mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$ have
$j\in \{0,\,1,\,\ldots ,\,\mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$ have
Proof. It suffices to show the first equality assuming ![]() $j_{\ell }< r_{\ell }$ for some
$j_{\ell }< r_{\ell }$ for some ![]() $\ell \in [m]$. For elements
$\ell \in [m]$. For elements ![]() $(A_{1},\,A_{2})\in W_{(j_1,\ldots ,j_{m})}$ and
$(A_{1},\,A_{2})\in W_{(j_1,\ldots ,j_{m})}$ and ![]() $(B_{1},\,B_{2})\in W_{(r_1,\ldots ,r_{m})}$ we have
$(B_{1},\,B_{2})\in W_{(r_1,\ldots ,r_{m})}$ we have
The assertion then follows since the latter condition is inherited by elements of ![]() $\overline {W_{(r_1,\ldots ,r_{m})}}$.
$\overline {W_{(r_1,\ldots ,r_{m})}}$.
In the rest of the paper we construct a local rule on each ![]() $W_{(j_1,\ldots ,j_m)}$. For
$W_{(j_1,\ldots ,j_m)}$. For ![]() $i\in \{1,\,\ldots ,\,m\}$, consider the canonical Riemannian structure on the unit
$i\in \{1,\,\ldots ,\,m\}$, consider the canonical Riemannian structure on the unit ![]() $n_i$-sphere
$n_i$-sphere ![]() $S^{n_i}$. Since the antipodal involution
$S^{n_i}$. Since the antipodal involution ![]() ${S}^{n_i}\to {S}^{n_i}$ is a fixed-point free properly discontinuous isometry,
${S}^{n_i}\to {S}^{n_i}$ is a fixed-point free properly discontinuous isometry, ![]() ${P}^{n_i}$ inherits a canonical quotient Riemannian structure
${P}^{n_i}$ inherits a canonical quotient Riemannian structure ![]() $g_i$. Let
$g_i$. Let ![]() $L_{i}(\gamma )$ denote the resulting length of a smooth curve
$L_{i}(\gamma )$ denote the resulting length of a smooth curve ![]() $\gamma$ in
$\gamma$ in ![]() ${P}^{n_i}$, and let
${P}^{n_i}$, and let
be the associated metric. Note that the curves ![]() $\lambda _{ik}(A,\,B)$ described in remark 7.7 are geodesic on
$\lambda _{ik}(A,\,B)$ described in remark 7.7 are geodesic on ![]() ${P}^{n_i}$. Without loss of generality we can assume that each
${P}^{n_i}$. Without loss of generality we can assume that each ![]() $g_i$ is normalized so that any geodesic
$g_i$ is normalized so that any geodesic ![]() $\gamma$ on
$\gamma$ on ![]() ${P}^{n_i}$ satisfies
${P}^{n_i}$ satisfies ![]() $L_{i}(\gamma )\leq 1/2$.
$L_{i}(\gamma )\leq 1/2$.
As a first step, we reparametrize the families of paths ![]() $\lambda _{ik}$. Explicitly, for
$\lambda _{ik}$. Explicitly, for ![]() $k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$, consider the section
$k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$, consider the section ![]() $\tau _{ik}:U_{ik}\to ({P}^{n_i})^{[0,1]}$ of the end-points evaluation map
$\tau _{ik}:U_{ik}\to ({P}^{n_i})^{[0,1]}$ of the end-points evaluation map ![]() $({P}^{n_i})^{[0,1]}\to {P}^{n_i}\times {P}^{n_i}$ given by
$({P}^{n_i})^{[0,1]}\to {P}^{n_i}\times {P}^{n_i}$ given by
 \[ \tau_{ik}(A_{1},A_{2})(t)=\begin{cases} A_1, & \hspace{1mm}\text{if }\hspace{1mm} d_{i1}+d_{i2}=0;\\ \lambda_{ik}(A_1,A_2)\left(\displaystyle\frac{t}{d_{i1}+d_{i2}}\right), & \hspace{1mm}\text{if }\hspace{1mm} 0\leq t\leq (d_{i1}+d_{i2})\neq 0;\\ A_{2}, & \hspace{1mm}\text{if }\hspace{1mm} 0\neq (d_{i1}+d_{i2})\leq t\leq 1, \end{cases} \]
\[ \tau_{ik}(A_{1},A_{2})(t)=\begin{cases} A_1, & \hspace{1mm}\text{if }\hspace{1mm} d_{i1}+d_{i2}=0;\\ \lambda_{ik}(A_1,A_2)\left(\displaystyle\frac{t}{d_{i1}+d_{i2}}\right), & \hspace{1mm}\text{if }\hspace{1mm} 0\leq t\leq (d_{i1}+d_{i2})\neq 0;\\ A_{2}, & \hspace{1mm}\text{if }\hspace{1mm} 0\neq (d_{i1}+d_{i2})\leq t\leq 1, \end{cases} \]
for ![]() $(A_1,\,A_2)\in U_{ik}$, where
$(A_1,\,A_2)\in U_{ik}$, where ![]() $d_{ij}=d_{i}(A_j,\,\ast )$,
$d_{ij}=d_{i}(A_j,\,\ast )$, ![]() $j=1,\,2$. Note that
$j=1,\,2$. Note that ![]() $\tau _{ik}$ is continuous on the open subset of
$\tau _{ik}$ is continuous on the open subset of ![]() $U_{ik}$ determined by the condition
$U_{ik}$ determined by the condition ![]() $d_{i1}+d_{i2}\neq 0$. The latter open subset of
$d_{i1}+d_{i2}\neq 0$. The latter open subset of ![]() $U_{ik}$ equals in fact
$U_{ik}$ equals in fact ![]() $U_{ik}$ unless
$U_{ik}$ unless ![]() $k=0$, so that
$k=0$, so that ![]() $\tau _{ik}$ is continuous on the whole
$\tau _{ik}$ is continuous on the whole ![]() $U_{ik}$ for
$U_{ik}$ for ![]() $k\in \{1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$. The continuity of
$k\in \{1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$. The continuity of ![]() $\tau _{i0}$ on
$\tau _{i0}$ on ![]() $U_{i0}$ follows from the continuity of
$U_{i0}$ follows from the continuity of ![]() $\lambda _{i0}$ and the fact that
$\lambda _{i0}$ and the fact that ![]() $\lambda _{i0}(A,\,A)$ is the constant path for all
$\lambda _{i0}(A,\,A)$ is the constant path for all ![]() $A\in {P}^{n_i}$. Note in addition that
$A\in {P}^{n_i}$. Note in addition that ![]() $\tau _{ik}$ reaches its end point at time
$\tau _{ik}$ reaches its end point at time ![]() $d_{i1}+d_{i2}$ (this is function-wise speaking). In particular
$d_{i1}+d_{i2}$ (this is function-wise speaking). In particular ![]() $\tau _{ik}(A_1,\,\ast )$ reaches
$\tau _{ik}(A_1,\,\ast )$ reaches ![]() $\ast$ at time
$\ast$ at time ![]() $d_{i1}$.
$d_{i1}$.
The map ![]() $\varphi :X^{2}\to (\prod _{i=1}^{m}{P}^{n_i})^{[0,1]}$ we are after is defined by
$\varphi :X^{2}\to (\prod _{i=1}^{m}{P}^{n_i})^{[0,1]}$ we are after is defined by
with ![]() $i$-th coordinate
$i$-th coordinate ![]() $\varphi _{i}(A_{i1},\,A_{i2})$, the path in
$\varphi _{i}(A_{i1},\,A_{i2})$, the path in ![]() ${P}^{n_i}$ from
${P}^{n_i}$ from ![]() $A_{i1}$ to
$A_{i1}$ to ![]() $A_{i2}$ given by
$A_{i2}$ given by
 \begin{equation} \varphi_{i}(A_{i1},A_{i2})(t)=\begin{cases} A_{i1}, & \hspace{1mm}\text{if }\hspace{1mm} 0\leq t\leq t_{A_{i1}};\\ \mu(A_{i1},A_{i2})(t-t_{A_{i1}}), & \hspace{1mm}\text{if }\hspace{1mm} t_{A_{i1}}\leq t\leq 1. \end{cases} \end{equation}
\begin{equation} \varphi_{i}(A_{i1},A_{i2})(t)=\begin{cases} A_{i1}, & \hspace{1mm}\text{if }\hspace{1mm} 0\leq t\leq t_{A_{i1}};\\ \mu(A_{i1},A_{i2})(t-t_{A_{i1}}), & \hspace{1mm}\text{if }\hspace{1mm} t_{A_{i1}}\leq t\leq 1. \end{cases} \end{equation}
Here, ![]() $t_{A_{i1}}=1/2-d_{i}(A_{i1},\,\ast )$ and
$t_{A_{i1}}=1/2-d_{i}(A_{i1},\,\ast )$ and
 \begin{equation} \mu(A_{i1},A_{i2})=\begin{cases} \tau_{i0}(A_{i1},A_{i2}), & \hspace{1mm}\text{if }\hspace{1mm} (A_{i1},A_{i2})\in U_{i0};\\ \hspace{1mm}\vdots & \hspace{2mm}\vdots\\ \tau_{i{{\sf{TC}}}({P}^{n_i})}(A_{i1},A_{i2}), & \hspace{1mm}\text{if }\hspace{1mm} (A_{i1},A_{i2})\in U_{i{{\sf{TC}}}({P}^{n_i})}.\end{cases} \end{equation}
\begin{equation} \mu(A_{i1},A_{i2})=\begin{cases} \tau_{i0}(A_{i1},A_{i2}), & \hspace{1mm}\text{if }\hspace{1mm} (A_{i1},A_{i2})\in U_{i0};\\ \hspace{1mm}\vdots & \hspace{2mm}\vdots\\ \tau_{i{{\sf{TC}}}({P}^{n_i})}(A_{i1},A_{i2}), & \hspace{1mm}\text{if }\hspace{1mm} (A_{i1},A_{i2})\in U_{i{{\sf{TC}}}({P}^{n_i})}.\end{cases} \end{equation} By construction, ![]() $\varphi$ is a global section of the end-points evaluation map
$\varphi$ is a global section of the end-points evaluation map
 \[ \left(\prod_{i=1}^{m}{P}^{n_i}\right)^{[0,1]}\longrightarrow \,\left(\prod_{i=1}^{m}{P}^{n_i}\right)^{2}. \]
\[ \left(\prod_{i=1}^{m}{P}^{n_i}\right)^{[0,1]}\longrightarrow \,\left(\prod_{i=1}^{m}{P}^{n_i}\right)^{2}. \]
Although ![]() $\varphi$ is not globally continuous, the restriction of
$\varphi$ is not globally continuous, the restriction of ![]() $\varphi$ to each
$\varphi$ to each ![]() $W_{(j_1,\ldots , j_{m})}$, where
$W_{(j_1,\ldots , j_{m})}$, where ![]() $(j_1,\,\ldots ,\,j_{m})$ is a partition of
$(j_1,\,\ldots ,\,j_{m})$ is a partition of ![]() $j\in \{0,\,1,\,\ldots ,\, \mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$, is continuous because formulas (7.11) can be rewritten as
$j\in \{0,\,1,\,\ldots ,\, \mathcal {N}^{(n_1,\,\ldots ,\,n_m)}(K)\}$, is continuous because formulas (7.11) can be rewritten as
 \[ \mu=\begin{cases} \tau_{i0}, & \hspace{1mm}\text{if }\hspace{1mm} j_{i}=0;\\ \hspace{1mm}\vdots & \hspace{2mm}\vdots\\ \tau_{i{{\sf{TC}}}({P}^{n_i})}, & \hspace{1mm}\text{if }\hspace{1mm} j_{i}={{\sf{TC}}}({P}^{n_i}). \end{cases} \]
\[ \mu=\begin{cases} \tau_{i0}, & \hspace{1mm}\text{if }\hspace{1mm} j_{i}=0;\\ \hspace{1mm}\vdots & \hspace{2mm}\vdots\\ \tau_{i{{\sf{TC}}}({P}^{n_i})}, & \hspace{1mm}\text{if }\hspace{1mm} j_{i}={{\sf{TC}}}({P}^{n_i}). \end{cases} \]
So, the crux of the matter is to show (in proposition 7.14 below) that the restriction of ![]() $\varphi$ to each
$\varphi$ to each ![]() $W_{(j_1,\ldots ,j_m)}$ lands in
$W_{(j_1,\ldots ,j_m)}$ lands in ![]() $X^{[0,1]}$.
$X^{[0,1]}$.
Remark 7.11 We spell out the motion planning instructions at the level of each factor in the polyhedral product. For ![]() $(A_{i1},\,A_{i2})\in U_{ik}$ with
$(A_{i1},\,A_{i2})\in U_{ik}$ with ![]() $k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$, the navigational instruction is:
$k\in \{0,\,1,\,\ldots ,\,{{\sf {TC}}}({P}^{n_i})\}$, the navigational instruction is:
• stay at
 $A_{i1}$, for times
$A_{i1}$, for times  $t\in [0,\,1/2-d_{i}(A_{i1},\,\ast )]$;
$t\in [0,\,1/2-d_{i}(A_{i1},\,\ast )]$;• move from
 $A_{i1}$ to
$A_{i1}$ to  $A_{i2}$ at constant speed (recall the normalization) via
$A_{i2}$ at constant speed (recall the normalization) via  $\tau _{ik}$, for times
$\tau _{ik}$, for times  $t\in [1/2-d_{i}(A_{i1},\,\ast ),\,1/2+d_{i}(A_{i2},\,\ast )]$;
$t\in [1/2-d_{i}(A_{i1},\,\ast ),\,1/2+d_{i}(A_{i2},\,\ast )]$;• stay at
 $A_{i2}$, for times
$A_{i2}$, for times  $t\in [1/2+d_{i}(A_{i2},\,\ast ),\,1]$.
$t\in [1/2+d_{i}(A_{i2},\,\ast ),\,1]$.
Example 7.12 Suppose ![]() $A_{i1}=\ast$ and let
$A_{i1}=\ast$ and let ![]() $A_{i2}$ be any line through the origin in
$A_{i2}$ be any line through the origin in ![]() $\mathbb {R}^{{n_i}+1}$. In this case,
$\mathbb {R}^{{n_i}+1}$. In this case, ![]() $t_{A_{i1}}=1/2-d_{i}(A_{i1},\,\ast )=1/2-0=1/2$. By remark 7.11, the path
$t_{A_{i1}}=1/2-d_{i}(A_{i1},\,\ast )=1/2-0=1/2$. By remark 7.11, the path ![]() $\varphi _{i}(A_{i1},\,A_{i2})$ obeys the instructions:
$\varphi _{i}(A_{i1},\,A_{i2})$ obeys the instructions:
• for
 $t\in [0,\,1/2]$, stay at
$t\in [0,\,1/2]$, stay at  $\ast$;
$\ast$;• for
 $t\in [1/2,\,1/2+d_{i}(A_{i2},\,\ast )]$, move from
$t\in [1/2,\,1/2+d_{i}(A_{i2},\,\ast )]$, move from  $\ast$ to
$\ast$ to  $A_{i2}$ at constant speed;
$A_{i2}$ at constant speed;• for
 $t\in [1/2+d_{i}(A_{i2},\,\ast ),\,1]$, stay at
$t\in [1/2+d_{i}(A_{i2},\,\ast ),\,1]$, stay at  $A_{i2}$.
$A_{i2}$.
Example 7.13 Suppose ![]() $A_{i2}=\ast$ (so that
$A_{i2}=\ast$ (so that ![]() $d_i(A_{i2},\,\ast )=0$) and let
$d_i(A_{i2},\,\ast )=0$) and let ![]() $A_{i1}$ be any line through the origin in
$A_{i1}$ be any line through the origin in ![]() $\mathbb {R}^{n_{i}+1}$. Then the path
$\mathbb {R}^{n_{i}+1}$. Then the path ![]() $\varphi _{i}(A_{i1},\,A_{i2})$ obeys the instructions:
$\varphi _{i}(A_{i1},\,A_{i2})$ obeys the instructions:
• for
 $t\in [0,\,1/2-d_{i}(A_{i1},\,\ast )]$, stay at
$t\in [0,\,1/2-d_{i}(A_{i1},\,\ast )]$, stay at  $A_{i1}$;
$A_{i1}$;• for
 $t\in [1/2-d_{i}(A_{i1},\,\ast ),\,1/2]$, move from
$t\in [1/2-d_{i}(A_{i1},\,\ast ),\,1/2]$, move from  $A_{i1}$ to
$A_{i1}$ to  $\ast$ at constant speed;
$\ast$ at constant speed;• for
 $t\in [1/2,\,1]$, stay at
$t\in [1/2,\,1]$, stay at  $\ast$.
$\ast$.
Proposition 7.14 The image of ![]() $\varphi$ is contained in
$\varphi$ is contained in ![]() $X^{[0,1]}$.
$X^{[0,1]}$.
Proof. Let ![]() $(A_{1},\,A_{2})\in X^{2}$, say
$(A_{1},\,A_{2})\in X^{2}$, say ![]() $(A_{1j},\,\ldots ,\,A_{mj})\in {P}^{\sigma _{j}}$ with
$(A_{1j},\,\ldots ,\,A_{mj})\in {P}^{\sigma _{j}}$ with ![]() $\sigma _1,\,\sigma _{2}\in {K}$. Then, for
$\sigma _1,\,\sigma _{2}\in {K}$. Then, for ![]() $i\notin \sigma _{1}$, example 7.12 shows that
$i\notin \sigma _{1}$, example 7.12 shows that ![]() $A_{i1}=\ast$ keeps its position through time
$A_{i1}=\ast$ keeps its position through time ![]() $t\leq 1/2$. Consequently
$t\leq 1/2$. Consequently ![]() $\varphi (A_1,\,A_{2})([0,\,1/2])\subseteq {P}^{\sigma _1}\subseteq X$. Likewise, for
$\varphi (A_1,\,A_{2})([0,\,1/2])\subseteq {P}^{\sigma _1}\subseteq X$. Likewise, for ![]() $i\notin \sigma _{2}$, example 7.13 shows that the path
$i\notin \sigma _{2}$, example 7.13 shows that the path ![]() $\varphi _{i}(A_{i1},\,A_{i2})$ has reached its final position
$\varphi _{i}(A_{i1},\,A_{i2})$ has reached its final position ![]() $A_{i2}=\ast$ at time
$A_{i2}=\ast$ at time ![]() $1/2$, so that
$1/2$, so that ![]() $\varphi (A_1,\,A_{2})([1/2,\,1])\subseteq {P}^{\sigma _{2}}\subseteq X$.
$\varphi (A_1,\,A_{2})([1/2,\,1])\subseteq {P}^{\sigma _{2}}\subseteq X$.