For the Bergman projection operator $P$ we prove that

$$\left\| P:\,{{L}^{1}}\left( B,\,d\lambda \right)\,\to \,{{B}_{1}} \right\|\,=\,\frac{\left( 2n\,+\,1 \right)!}{n!}.$$

Here $\lambda$ stands for the hyperbolic metric in the unit ball $B$ of 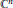${{\mathbb{C}}^{n}}$, and 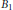${{B}_{1}}$ denotes the Besov space with an adequate semi-norm. We also consider a generalization of this result. This generalizes some recent results due to Perälä.

We give some new characterizations for compactness of weighted composition operators $u{{C}_{\varphi }}$ acting on Bloch-type spaces in terms of the power of the components of $\varphi$, where $\varphi$ is a holomorphic self-map of the polydisk ${{\mathbb{D}}^{n}}$, thus generalizing the results obtained by Hyvärinen and Lindström in 2012.

In general, multiplication of operators is not essentially commutative in an algebra generated by integral-type operators and composition operators. In this paper, we characterize the essential commutativity of the integral operators and composition operators from a mixed-norm space to a Bloch-type space, and give a complete description of the universal set of integral operators. Corresponding results for boundedness and compactness are also obtained.

The aim of this paper is to prove a theorem concerning asymptotic estimates of eigenvalues of certain positive integral operators with Laplace transform-type kernels.

In this paper, we prove a theorem concerning asymptotic estimates of the eigenvalues of certain positive integral operators with Laplace transform type kernels.

Using a canonical linear embedding of the algebra ${{G}^{\infty }}\left( \Omega \right)$ of Colombeau generalized functions in the space of $\overline{\mathbb{C}}$ -valued $\mathbb{C}$-linear maps on the space $D\left( \Omega \right)$ of smooth functions with compact support, we give vanishing conditions for functions and linear integral operators of class ${{G}^{\infty }}$ . These results are then applied to the zeros of holomorphic generalized functions in dimension greater than one.

Let m be a vector measure with values in a Banach space X. If L1(m) denotes the space of all m integrable functions then, with respect to the mean convergence topology, L1(m) is a Banach space. A natural operator associated with m is its integration map Im which sends each f of L1(m) to the element ∫fdm (of X). Many properties of the (continuous) operator Im are closely related to the nature of the space L1(m). In general, it is difficult to identify L1(m). We aim to exhibit non-trivial examples of measures m in (non-reflexive) spaces X for which L1(m) can be explicitly computed and such that Im is not weakly compact. The examples include some well known operators from analysis (the Fourier transform on L1 ([−π, π]), the Volterra operator on L1 ([0, 1]), compact self-adjoint operators in a Hilbert space); such operators can be identified with integration maps Im (or their restrictions) for suitable measures m.