We develop multisummability, in the positive real direction, for generalized power series with natural support, and we prove o-minimality of the expansion of the real field by all multisums of these series. This resulting structure expands both $\mathbb {R}_{\mathcal {G}}$ and the reduct of $\mathbb {R}_{\text {an}^*}$ generated by all convergent generalized power series with natural support; in particular, its expansion by the exponential function defines both the gamma function on $(0,\infty )$ and the zeta function on $(1,\infty )$.

In this paper, we establish an infinite series expansion of Leray–Trudinger inequality, which is closely related with Hardy inequality and Moser Trudinger inequality. Our result extends early results obtained by Mallick and Tintarev [A. Mallick and C. Tintarev. An improved Leray-Trudinger inequality. Commun. Contemp. Math. 20 (2018), 17501034. OP 21] to the case with many logs. It should be pointed out that our result is about series expansion of Hardy inequality under the case $p=n$, which case is not considered by Gkikas and Psaradakis in [K. T. Gkikas and G. Psaradakis. Optimal non-homogeneous improvements for the series expansion of Hardy's inequality. Commun. Contemp. Math. doi:10.1142/S0219199721500310]. However, we can't obtain the optimal form by our method.

We show that if $X$ is an $m$-dimensional definable set in $\mathbb {R}_\text {an}^\text{pow}$, the structure of real subanalytic sets with real power maps added, then for any positive integer $r$ there exists a $C^{r}$-parameterization of $X$ consisting of $cr^{m^{3}}$ maps for some constant $c$. Moreover, these maps are real analytic and this bound is uniform for a definable family.

By an influential theorem of Boman, a function $f$ on an open set $U$ in $\mathbb{R}^{d}$ is smooth (${\mathcal{C}}^{\infty }$) if and only if it is arc-smooth, that is, $f\,\circ \,c$ is smooth for every smooth curve $c:\mathbb{R}\rightarrow U$. In this paper we investigate the validity of this result on closed sets. Our main focus is on sets which are the closure of their interior, so-called fat sets. We obtain an analogue of Boman’s theorem on fat closed sets with Hölder boundary and on fat closed subanalytic sets with the property that every boundary point has a basis of neighborhoods each of which intersects the interior in a connected set. If $X\subseteq \mathbb{R}^{d}$ is any such set and $f:X\rightarrow \mathbb{R}$ is arc-smooth, then $f$ extends to a smooth function defined on $\mathbb{R}^{d}$. We also get a version of the Bochnak–Siciak theorem on all closed fat subanalytic sets and all closed sets with Hölder boundary: if $f:X\rightarrow \mathbb{R}$ is the restriction of a smooth function on $\mathbb{R}^{d}$ which is real analytic along all real analytic curves in $X$, then $f$ extends to a holomorphic function on a neighborhood of $X$ in $\mathbb{C}^{d}$. Similar results hold for non-quasianalytic Denjoy–Carleman classes (of Roumieu type). We will also discuss sharpness and applications of these results.

We prove two main results on Denjoy–Carleman classes: (1) a composite function theorem which asserts that a function $f(x)$ in a quasianalytic Denjoy–Carleman class ${\mathcal{Q}}_{M}$, which is formally composite with a generically submersive mapping $y=\unicode[STIX]{x1D711}(x)$ of class ${\mathcal{Q}}_{M}$, at a single given point in the source (or in the target) of $\unicode[STIX]{x1D711}$ can be written locally as $f=g\circ \unicode[STIX]{x1D711}$, where $g(y)$ belongs to a shifted Denjoy–Carleman class ${\mathcal{Q}}_{M^{(p)}}$; (2) a statement on a similar loss of regularity for functions definable in the $o$-minimal structure given by expansion of the real field by restricted functions of quasianalytic class ${\mathcal{Q}}_{M}$. Both results depend on an estimate for the regularity of a ${\mathcal{C}}^{\infty }$ solution $g$ of the equation $f=g\circ \unicode[STIX]{x1D711}$, with $f$ and $\unicode[STIX]{x1D711}$ as above. The composite function result depends also on a quasianalytic continuation theorem, which shows that the formal assumption at a given point in (1) propagates to a formal composition condition at every point in a neighbourhood.

Let ${{C}^{M}}$ denote a Denjoy–Carleman class of ${{C}^{\infty }}$ functions (for a given logarithmically-convex sequence $M\,=\,\left( {{M}_{n}} \right))$. We construct: (1) a function in ${{C}^{M}}\left( \left( -1,\,1 \right) \right)$ that is nowhere in any smaller class; (2) a function on $\mathbb{R}$ that is formally ${{C}^{M}}$ at every point, but not in ${{C}^{M}}\left( \mathbb{R} \right)$; (3) (under the assumption of quasianalyticity) a smooth function on ${{\mathbb{R}}^{p}}\,\left( p\,\ge \,2 \right)$ that is ${{C}^{M}}$ on every ${{C}^{M}}$ curve, but not in ${{C}^{M}}\left( {{\mathbb{R}}^{p}} \right)$.

Consider quasianalytic local rings of germs of smooth functions closed under composition, implicit equation, and monomial division. We show that if the Weierstrass Preparation Theoremholds in such a ring, then all elements of it are germs of analytic functions.

On se donne un intervalle ouvert non vide 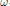$\omega $ de $\mathbb{R}$, un ouvert connexe non vide $\Omega $ de 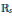${{\mathbb{R}}_{5}}$ et unpolynôme unitaire

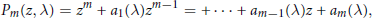$${{P}_{m}}\left( z,\text{ }\!\!\lambda\!\!\text{ } \right)={{z}^{m}}+{{a}_{1}}\left( \text{ }\!\!\lambda\!\!\text{ } \right){{z}^{m-1}}=+\cdot \cdot \cdot +{{a}_{m-1}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)z+{{a}_{m}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)$$

de degré $m>0$, dépendant du paramètre 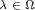$\lambda \in \Omega $. Un tel polynôme est dit 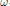$\omega $-hyperbolique si, pour tout 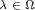$\lambda \in \Omega $, ses racines sont réelles et appartiennent à 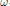$\omega $.

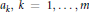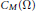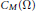On suppose que les fonctions ${{a}_{k}},k=1,\cdot \cdot \cdot ,m$, appartiennent à une classe ultradifférentiable ${{C}_{M}}\left( \Omega \right)$. On s‘intéresse au problème suivant. Soit $f$ appartient à ${{C}_{M}}\left( \Omega \right)$, existe-t-il des fonctions 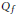${{Q}_{f}}$ et 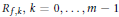${{R}_{f,k}},k=0,\cdot \cdot \cdot ,m-1$, appartenant respectivement à 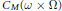${{C}_{M}}\left( \omega \,\times \,\Omega \right)$ et à 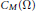${{C}_{M}}\left( \Omega \right)$, telles que l’on ait, pour 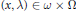$\left( x,\,\lambda \right)\,\in \,\omega \,\times \,\Omega$,

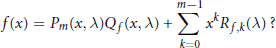$$f\left( x \right)={{P}_{m}}\left( x,\text{ }\!\!\lambda\!\!\text{ } \right){{Q}_{f}}\left( x,\text{ }\!\!\lambda\!\!\text{ } \right)+\sum\limits_{k=0}^{m-1}{{{x}^{k}}{{R}_{f,k}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)?}$$

On donne ici une réponse positive dès que le polynôme est 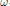$\omega$-hyperbolique, que la class untradifférentiable soit quasi-analytique ou non ; on obtient alors, des exemples d’idéaux fermés dan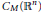s ${{C}_{M}}\left( {{\mathbb{R}}^{n}} \right)$ . On complète ce travail par une généralisation d’un résultat de C. L. Childress dans le cadre quasi-analytique et quelques remarques.