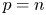1. Introduction
Let $\Omega$![]() be a bounded domain of $\mathbb {R}^{n}$
be a bounded domain of $\mathbb {R}^{n}$![]() containing the origin, $n\geq 2$
containing the origin, $n\geq 2$![]() and $p>1$
and $p>1$![]() , the classical p-Hardy inequality asserts that
, the classical p-Hardy inequality asserts that
with $\left |\frac {n-p}{p}\right |^{p}$![]() being the best constant and never achieved [Reference Brezis and Marcus6, Reference Brezis, Marcus and Shafrir7, Reference Davies10, Reference Hardy, Littlewood and Pólya15, Reference Opic and Kufner20, Reference Vazquez and Zuazua24]. Many improvements of Hardy inequality can be obtained by adding the error term in the right side of (1.1) [Reference Brezis and Vazquez8, Reference Gazzola, Grunau and Mitidieri12]. The first improvement was obtained by Brezis and Vazquez [Reference Brezis and Vazquez8]. When $p=2$
being the best constant and never achieved [Reference Brezis and Marcus6, Reference Brezis, Marcus and Shafrir7, Reference Davies10, Reference Hardy, Littlewood and Pólya15, Reference Opic and Kufner20, Reference Vazquez and Zuazua24]. Many improvements of Hardy inequality can be obtained by adding the error term in the right side of (1.1) [Reference Brezis and Vazquez8, Reference Gazzola, Grunau and Mitidieri12]. The first improvement was obtained by Brezis and Vazquez [Reference Brezis and Vazquez8]. When $p=2$![]() , they have shown that (1.1) can be improved by adding subcritical Sobolev term $\int _{\Omega }|u|^{q}\,\textrm {d}x (1\leq q<2^{*}=\frac {2n}{n-2})$
, they have shown that (1.1) can be improved by adding subcritical Sobolev term $\int _{\Omega }|u|^{q}\,\textrm {d}x (1\leq q<2^{*}=\frac {2n}{n-2})$![]() . After that, Chaudhuri and Ramaswamy [Reference Chaudhuri and Ramaswamy9] improved inequality (1.1) by introducing a subcritical Hardy–Sobolev term $\int _{\Omega }\frac {|u|^{q}}{|x|^{\beta }}\,\textrm {d}x \ \ (0\leq \beta <2$
. After that, Chaudhuri and Ramaswamy [Reference Chaudhuri and Ramaswamy9] improved inequality (1.1) by introducing a subcritical Hardy–Sobolev term $\int _{\Omega }\frac {|u|^{q}}{|x|^{\beta }}\,\textrm {d}x \ \ (0\leq \beta <2$![]() , $1\leq q<2^{*}_{\beta }:=\frac {2(n-\beta )}{n-2})$
, $1\leq q<2^{*}_{\beta }:=\frac {2(n-\beta )}{n-2})$![]() [Reference Adimurthi and Tertikas1]. Later, Adimurthi, Chaudhuri and Ramaswamy [Reference Adimurthi and Ramaswamy2] extended their results to general $L_p$
[Reference Adimurthi and Tertikas1]. Later, Adimurthi, Chaudhuri and Ramaswamy [Reference Adimurthi and Ramaswamy2] extended their results to general $L_p$![]() Hardy inequality for $2\leq p< n$
Hardy inequality for $2\leq p< n$![]() . In [Reference Filippas and Tertikas11], Filippas and Tertikas pointed out that the critical Sobolev type improvement for $p=2$
. In [Reference Filippas and Tertikas11], Filippas and Tertikas pointed out that the critical Sobolev type improvement for $p=2$![]() could be established by adding a logarithmic term. Their result is as follows.
could be established by adding a logarithmic term. Their result is as follows.
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n}(n\geq 3)$
be a bounded domain in $\mathbb {R}^{n}(n\geq 3)$![]() containing the origin, $R_{\Omega }:=\sup _{x\in \Omega }|x|$
containing the origin, $R_{\Omega }:=\sup _{x\in \Omega }|x|$![]() , then for any $u\in H^{1}_0(\Omega )$
, then for any $u\in H^{1}_0(\Omega )$![]() and $R\geq R_{\Omega }$
and $R\geq R_{\Omega }$![]() , there exists a constant $C_n>0$
, there exists a constant $C_n>0$![]() depending only on $n$
depending only on $n$![]() , such that
, such that

Here
Inequality (1.2) was sharp in the sense that $X_1^{1+\frac {2^{*}}{2}}$![]() cannot be replaced by a smaller power of $X_1$
cannot be replaced by a smaller power of $X_1$![]() .
.
In [Reference Filippas and Tertikas11], the authors also established the series expansion of Hardy inequality. Their results were extended to the following general $L_p$![]() ($p\neq n$
($p\neq n$![]() ) Hardy inequality [Reference Barbatis, Filippas and Tertikas5].
) Hardy inequality [Reference Barbatis, Filippas and Tertikas5].
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n}(n\geq 3)$
be a bounded domain in $\mathbb {R}^{n}(n\geq 3)$![]() containing the origin, $R_{\Omega }:=\sup _{x\in \Omega }|x|$
containing the origin, $R_{\Omega }:=\sup _{x\in \Omega }|x|$![]() , then for any $u\in W^{1,p}_0(\Omega \setminus \{0\})$
, then for any $u\in W^{1,p}_0(\Omega \setminus \{0\})$![]() and $R\geq R_{\Omega }$
and $R\geq R_{\Omega }$![]() , there holds
, there holds

Here
In [Reference Filippas and Tertikas11], the authors also proved the following series expansion of Hardy inequality for $p=2$![]() with critical sobolev term.
with critical sobolev term.

The exponent $1+\frac {2^{*}}{2}$![]() on $X_{k+1}$
on $X_{k+1}$![]() cannot be decreased.
cannot be decreased.
Recently, Gkikas and Psaradakis [Reference Gkikas and Psaradakis13] generalized inequality (1.6) to the general case $1< p< n$![]() and $p>n$
and $p>n$![]() . When $1< p< n$
. When $1< p< n$![]() , by adding an optimally weighted critical Sobolev norm, they obtained the following results.
, by adding an optimally weighted critical Sobolev norm, they obtained the following results.
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n}$
be a bounded domain in $\mathbb {R}^{n}$![]() containing the origin, $n\geq 2$
containing the origin, $n\geq 2$![]() and $1< p< n$
and $1< p< n$![]() , $R_{\Omega }:=\sup _{x\in \Omega }|x|$
, $R_{\Omega }:=\sup _{x\in \Omega }|x|$![]() , there exist constants $C_n>0$
, there exist constants $C_n>0$![]() depending only on $n$
depending only on $n$![]() and $B:=B(n,\,p)\geq 1$
and $B:=B(n,\,p)\geq 1$![]() , such that for any $u\in W^{1,p}_0(\Omega )$
, such that for any $u\in W^{1,p}_0(\Omega )$![]() , $R\geq B R_{\Omega }$
, $R\geq B R_{\Omega }$![]() and $k\in \mathbb {N}$
and $k\in \mathbb {N}$![]() , there holds
, there holds

The exponent $1+\frac {p^{*}}{p}$![]() on $X_{k+1}$
on $X_{k+1}$![]() cannot be decreased. When $p>n$
cannot be decreased. When $p>n$![]() , they established the series expansion of $L_p$
, they established the series expansion of $L_p$![]() Hardy inequality by adding the optimally weighted Hölder seminorm.
Hardy inequality by adding the optimally weighted Hölder seminorm.
All the previous results we mentioned are concerning about the case $p\neq n$![]() . When $p=n$
. When $p=n$![]() , Hardy inequality can be stated as follows [Reference Adimurthi and Ramaswamy2–Reference Barbatis, Filippas and Tertikas4, Reference Leray16].
, Hardy inequality can be stated as follows [Reference Adimurthi and Ramaswamy2–Reference Barbatis, Filippas and Tertikas4, Reference Leray16].
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$
be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$![]() , containing the origin, then for any $R\geq R_{\Omega }$
, containing the origin, then for any $R\geq R_{\Omega }$![]() and $u\in W_0^{1,n}(\Omega )$
and $u\in W_0^{1,n}(\Omega )$![]() , one has
, one has
Barbatis, Filippas and Tertikas [Reference Barbatis, Filippas and Tertikas5] established the following series expansion of Hardy inequality for the case $p=n$![]() .
.
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$
be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$![]() containing the origin, then for any $R>R_{\Omega }$
containing the origin, then for any $R>R_{\Omega }$![]() and for all $u\in W^{1,n}_0(\Omega \setminus \{0\})$
and for all $u\in W^{1,n}_0(\Omega \setminus \{0\})$![]() , one has
, one has

In analogy with inequality (1.1), it is natural to ask whether similar critical Sobolev term can be added into inequality (1.8). Since the limit case of critical Sobolev inequality is Moser–Trudinger inequality [Reference Li and Ruf17, Reference Moser18, Reference Ruf22, Reference Tintarev23], the natural substitute of critical Sobolev term is some exponential function. Recently, Psaradakis and Spector [Reference Psaradakis and Spector21] established the following Leray–Trudinger inequality.
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$
be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$![]() containing the origin, then for any $\epsilon >0$
containing the origin, then for any $\epsilon >0$![]() and $R\geq R_{\Omega }$
and $R\geq R_{\Omega }$![]() , there exist positive constants $A_{n,\epsilon }$
, there exist positive constants $A_{n,\epsilon }$![]() and $B_{n}$
and $B_{n}$![]() , such that for all $u\in W_0^{1,n}(\Omega )$
, such that for all $u\in W_0^{1,n}(\Omega )$![]() satisfying $I_1(u)\leq 1$
satisfying $I_1(u)\leq 1$![]() , one has
, one has
where $I_1(u)$![]() is defined by
is defined by
Moreover, inequality (1.10) failed for $\epsilon =0$![]() .
.
Inequality (1.10) is closely related with Hardy inequality and Moser–Trudinger inequality. Subsequently, Mallick and Tintarev [Reference Mallick and Tintarev19] extended inequality (1.10) to the following form:
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$
be a bounded domain in $\mathbb {R}^{n} (n\geq 2)$![]() containing the origin, then for any $\beta \geq \frac {2}{n}$
containing the origin, then for any $\beta \geq \frac {2}{n}$![]() and $R\geq R_{\Omega }$
and $R\geq R_{\Omega }$![]() , there exist positive constants $A_n$
, there exist positive constants $A_n$![]() and $B_n$
and $B_n$![]() , such that for any $0< c< A_n$
, such that for any $0< c< A_n$![]() and for all $u\in W_0^{1,n}(\Omega )$
and for all $u\in W_0^{1,n}(\Omega )$![]() satisfying $I_1(u)\leq 1$
satisfying $I_1(u)\leq 1$![]() , one has
, one has
where $X_2(t):=X_1(X_1(t))$![]() . Moreover, inequality (1.12) failed if $\beta <\frac {1}{n}$
. Moreover, inequality (1.12) failed if $\beta <\frac {1}{n}$![]() for any $c>0$
for any $c>0$![]() .
.
The relationship of inequality (1.10) and inequality (1.12) motivates us to investigate whether inequality (1.12) can be improved to be series expansion. In this paper, we establish the following series expansion of Leray–Trudinger inequality. Our main result is as follows.
Theorem 1.1 Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{n}$
be a bounded domain in $\mathbb {R}^{n}$![]() containing the origin, $n\geq 2$
containing the origin, $n\geq 2$![]() and $R_{\Omega }:=\sup _{x\in \Omega }|x|$
and $R_{\Omega }:=\sup _{x\in \Omega }|x|$![]() . Then for any $k\in \mathbb {N},$
. Then for any $k\in \mathbb {N},$![]() $k\geq 1$
$k\geq 1$![]() and $R\geq R_{\Omega },$
and $R\geq R_{\Omega },$![]() there exist constants $A(k,\,n)$
there exist constants $A(k,\,n)$![]() and $B(k,\,n),$
and $B(k,\,n),$![]() such that for any $0< C< A(k,\,n)$
such that for any $0< C< A(k,\,n)$![]() and $u\in W_0^{1,n}(\Omega )$
and $u\in W_0^{1,n}(\Omega )$![]() satisfying $I_k(u)\leq 1,$
satisfying $I_k(u)\leq 1,$![]() one has
one has

where $I_1(u)$![]() is defined by (1.11) and for $k\geq 2,$
is defined by (1.11) and for $k\geq 2,$![]() $I_k(u)$
$I_k(u)$![]() is defined by
is defined by
Moreover, if replacing $X_{k+1}^{2}$![]() by $X_{k+1}^{\beta },$
by $X_{k+1}^{\beta },$![]() one has that inequality (1.13) holds for any $\beta \geq \frac {2}{n}$
one has that inequality (1.13) holds for any $\beta \geq \frac {2}{n}$![]() .
.
Remark 1.2 When $k=1$![]() , inequality (1.13) becomes inequality (1.12). Hence our result extends early results obtained by Mallick and Tintarev [Reference Mallick and Tintarev19] to series expansion form. However, in [Reference Mallick and Tintarev19], they obtained that inequality (1.12) holds when $\beta \geq \frac {2}{n}$
, inequality (1.13) becomes inequality (1.12). Hence our result extends early results obtained by Mallick and Tintarev [Reference Mallick and Tintarev19] to series expansion form. However, in [Reference Mallick and Tintarev19], they obtained that inequality (1.12) holds when $\beta \geq \frac {2}{n}$![]() and fails when $\beta <\frac {1}{n}$
and fails when $\beta <\frac {1}{n}$![]() . Here we can't show that inequality (1.13) fails when $\beta <\frac {1}{n}$
. Here we can't show that inequality (1.13) fails when $\beta <\frac {1}{n}$![]() . Moreover, as we mentioned before, Gkikas and Psaradakis [Reference Gkikas and Psaradakis13] obtained series optimal forms of Hardy inequality for $1< p< n$
. Moreover, as we mentioned before, Gkikas and Psaradakis [Reference Gkikas and Psaradakis13] obtained series optimal forms of Hardy inequality for $1< p< n$![]() and $p>n$
and $p>n$![]() but didn't consider $p=n$
but didn't consider $p=n$![]() , our result is about this case. However, we can't obtain optimal forms by our method.
, our result is about this case. However, we can't obtain optimal forms by our method.
To prove the main result, we follow closely Trudinger's original proof (see [Reference Gilbarg and Trudinger14]), which has been used in [Reference Psaradakis and Spector21] and [Reference Mallick and Tintarev19]. Our main steps are as follows. Firstly, we find a suitable function (2.6), which is a supersolution of some Laplace equation (lemma 2.5). By this function, we define corresponding transform to obtain $L^{q}$![]() estimate (proposition 3.1). After that, we obtain the exponential integrability.
estimate (proposition 3.1). After that, we obtain the exponential integrability.
This paper is organized as follows. In § 2, we establish some important preliminaries. In § 3, we give the proof of theorem 1.1.
2. Preliminaries
In this section, we list some important preliminaries.
By the definition of $X_k(t)$![]() (see (1.5)), we define
(see (1.5)), we define

The following proposition is due to the derivative of $X_k$![]() ,$Y_k$
,$Y_k$![]() and $Z_k$
and $Z_k$![]() .
.
Proposition 2.1 For any $k\in \mathbb {N}$![]() and $k\geq 2,$
and $k\geq 2,$![]() one has
one has

Proof. The first one is proved in [Reference Gkikas and Psaradakis13], lemma 2.2. Since $Y_k$![]() and $Z_k$
and $Z_k$![]() are different from definition 2.1 appeared in [Reference Gkikas and Psaradakis13]. We list the proof of (2.3) and (2.4) as follows.
are different from definition 2.1 appeared in [Reference Gkikas and Psaradakis13]. We list the proof of (2.3) and (2.4) as follows.

From the elementary identity

one has

Defining $Z_{\infty }(t):=\sum \limits _{i=2}^{\infty }Y_k(t)$![]() , it converges if and only if $t\in (0,\,1)$
, it converges if and only if $t\in (0,\,1)$![]() , see [Reference Gkikas and Psaradakis13].
, see [Reference Gkikas and Psaradakis13].
Concerning $I_k(u)$![]() , the following results hold, see [Reference Barbatis, Filippas and Tertikas5].
, the following results hold, see [Reference Barbatis, Filippas and Tertikas5].
Proposition 2.2 Theorem B [Reference Barbatis, Filippas and Tertikas5]
For any $k\in \mathbb {N},$![]() $R\geq R_{\Omega }$
$R\geq R_{\Omega }$![]() and $u\in C_c^{\infty }(\Omega \setminus \{0\}),$
and $u\in C_c^{\infty }(\Omega \setminus \{0\}),$![]() one has
one has
The following lemma is a standard representation formula for smooth functions.
Lemma 2.3 [Reference Gilbarg and Trudinger14], Lemma 7.14
Let $\Omega$![]() be any open set in $\mathbb {R}^{n},$
be any open set in $\mathbb {R}^{n},$![]() $n\geq 2,$
$n\geq 2,$![]() $u\in C_c^{1}(\Omega ),$
$u\in C_c^{1}(\Omega ),$![]() then
then
where $w_n$![]() is the volume of unit ball in $\mathbb {R}^{n}$
is the volume of unit ball in $\mathbb {R}^{n}$![]() .
.
In [Reference Psaradakis and Spector21], let $u(x)=X_1^{\frac {1-n}{n}}(\frac {|x|}{R})v(x),$![]() the authors obtained the following lower bound of $I_1(u)$
the authors obtained the following lower bound of $I_1(u)$![]() . That is,
. That is,
where $C_1(n)=\frac {1}{2^{n-1}-1}$![]() . In the following, we are going to extend their result to arbitrary $k\in \mathbb {N}$
. In the following, we are going to extend their result to arbitrary $k\in \mathbb {N}$![]() . Precisely, we have
. Precisely, we have
Theorem 2.4 For any $R\geq R_{\Omega },$![]() $k\in \mathbb {N}$
$k\in \mathbb {N}$![]() and $k\geq 2,$
and $k\geq 2,$![]() set
set
then for all $u\in C_c^{\infty }(\Omega \setminus \{0\}),$![]() one has
one has
where $v$![]() is defined by $u(x):=w_k(x)v(x)$
is defined by $u(x):=w_k(x)v(x)$![]() .
.
In order to prove theorem 2.4, the following key lemma is needed.
Lemma 2.5 For any $k\in \mathbb {N},$![]() the function $w_k$
the function $w_k$![]() defined by (2.6), is a supersolution of the following Laplace equation:
defined by (2.6), is a supersolution of the following Laplace equation:

Proof. Let $A_k(x)=X_1(\frac {|x|}{R})(\frac {1-n}{n}-\frac {1}{n}Z_k(\frac {|x|}{R}))$![]() , then by direct calculation, one has
, then by direct calculation, one has
Hence,

While
and
thus

In order to prove the result, we should prove that

When $n=2$![]() , inequality (2.8) naturally holds true. In the following, we just consider the case of $n>2$
, inequality (2.8) naturally holds true. In the following, we just consider the case of $n>2$![]() . Let $t=\frac {Z_k}{n}$
. Let $t=\frac {Z_k}{n}$![]() , $h=\frac {1-n}{n}$
, $h=\frac {1-n}{n}$![]() and $\lambda =\frac {n-1}{2n}\sum \limits _{i=2}^{k}Y_i^{2}$
and $\lambda =\frac {n-1}{2n}\sum \limits _{i=2}^{k}Y_i^{2}$![]() , then inequality (2.8) can be written by
, then inequality (2.8) can be written by

Consider function $g(x)=\left |1-x\right |^{2-n}$![]() , by Taylor expansion at $x=0$
, by Taylor expansion at $x=0$![]() (see [Reference Gkikas and Psaradakis13]), one has
(see [Reference Gkikas and Psaradakis13]), one has
Therefore, inequality (2.9) is equivalent to
While inequality (2.10) holds since $n>2$![]() and $h<0$
and $h<0$![]() . Therefore, we complete our proof.
. Therefore, we complete our proof.
The proof of theorem 2.4. Setting $u(x)=w_k(x)v(x)$![]() , from the following inequality (see [Reference Gkikas and Psaradakis13, Reference Psaradakis and Spector21])
, from the following inequality (see [Reference Gkikas and Psaradakis13, Reference Psaradakis and Spector21])
and integrating by parts, we deduce that

3. Proof of theorem 1.1
In this section, we give the proof of theorem 1.1. Firstly, we prove the following $L^{q}$![]() estimate.
estimate.
Proposition 3.1 Let $u\in W_0^{1,n}(\Omega ),$![]() for any $q>n$
for any $q>n$![]() and $R\geq R_{\Omega },$
and $R\geq R_{\Omega },$![]() we have
we have

where $C(k,\,n)= (\frac {1}{C_1(n)^{\frac {1}{n}}}+2^{\frac {1}{n}}C^{'}(k,\,n)(\frac {n}{n-1})^{\frac {n-1}{n}})\frac {1}{n w_n^{\frac {1}{n}}}$![]() .
.
Proof. Let $u\in C_c^{\infty }(\Omega \setminus \{0\})$![]() , we define $u(x)=w_k(x)v(x)$
, we define $u(x)=w_k(x)v(x)$![]() , then inequality (2.5) implies that
, then inequality (2.5) implies that

By proposition 2.1, we get

Hence we deduce

where

and
Then for $q>n$![]() , one has
, one has
Define $r$![]() by $\frac {1}{n}+\frac {1}{r}=1+\frac {1}{q}$
by $\frac {1}{n}+\frac {1}{r}=1+\frac {1}{q}$![]() . In order to estimate $\|S\|_{L^{q}(\Omega )}$
. In order to estimate $\|S\|_{L^{q}(\Omega )}$![]() , we write
, we write

and define
Then by Hölder's inequality, we get

Integrating $S(x)$![]() and using Tonelli’ Theorem, one has
and using Tonelli’ Theorem, one has

From theorem 2.4, we get
To estimate $\|T\|_{L^{q}(\Omega )}$![]() , we use similar steps. Firstly, we write that
, we use similar steps. Firstly, we write that

Applying H$\ddot {\mbox {o}}$![]() lder's inequality and taking the $L^{q}$
lder's inequality and taking the $L^{q}$![]() -norm of the both sides, we obtain
-norm of the both sides, we obtain

Using the conclusion of proposition 2.2, one has

Thus using the following estimate ([Reference Mallick and Tintarev19],(3.4))

we get

where $C(k,\,n)$![]() is defined by $C(k,\,n)= (\frac {1}{C_1(n)^{\frac {1}{n}}}+2^{\frac{1}{n}}C^{'}(k,\,n)(\frac {n}{n-1})^{\frac {n-1}{n}})\frac {1}{n w_n^{\frac {1}{n}}}$
is defined by $C(k,\,n)= (\frac {1}{C_1(n)^{\frac {1}{n}}}+2^{\frac{1}{n}}C^{'}(k,\,n)(\frac {n}{n-1})^{\frac {n-1}{n}})\frac {1}{n w_n^{\frac {1}{n}}}$![]() . Thus, we complete the proof of proposition 3.1.
. Thus, we complete the proof of proposition 3.1.
In the following, we prove theorem 1.1.
Proof. Let $u\in W_0^{1,n}(\Omega )$![]() such that $I_k(u)\leq 1$
such that $I_k(u)\leq 1$![]() . Applying proposition 3.1 with $q=\frac {ns}{n-1},\, s\in \{n,\,n+1,\,\cdots \}$
. Applying proposition 3.1 with $q=\frac {ns}{n-1},\, s\in \{n,\,n+1,\,\cdots \}$![]() , we have
, we have

Given $C>0$![]() , multiplying both sides by $\frac {C^{s}}{s!}$
, multiplying both sides by $\frac {C^{s}}{s!}$![]() and adding from $n$
and adding from $n$![]() to $m$
to $m$![]() $(m\geq n)$
$(m\geq n)$![]() , it yields
, it yields

Clearly, the right side above inequality converges as $m\to \infty$![]() if and only if
if and only if
While each term of the finite sum

is bounded by a constant depending only on $k,\,n$![]() due to Hölder inequality. And so, there exist constants $A(k,\,n)$
due to Hölder inequality. And so, there exist constants $A(k,\,n)$![]() and $B(k,\,n)$
and $B(k,\,n)$![]() such that for any $0< C< A(k,\,n)$
such that for any $0< C< A(k,\,n)$![]() , there has
, there has

The left side inequality (3.10) is the power series expansion of $e^{C\left |u(x)Y_{k+1}^{\frac{2}{n}}(\frac {|x|}{R})\right |^{\frac {n}{n-1}}}$![]() . Thus, theorem 1.1 is valid, and for $\beta >\frac {2}{n}$
. Thus, theorem 1.1 is valid, and for $\beta >\frac {2}{n}$![]() , the result is also valid because of $X_{k+1}(\frac {|x|}{R})<1$
, the result is also valid because of $X_{k+1}(\frac {|x|}{R})<1$![]() .
.
Acknowledgments
The first author was supported by National Natural Science Foundation of China (No. 11601173 and No. 61772223).