Let 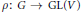 $\rho :\,G\,\to \,\text{GL}\left( V \right)$ be a rational finite dimensional complex representation of a reductive linear algebraic group
$\rho :\,G\,\to \,\text{GL}\left( V \right)$ be a rational finite dimensional complex representation of a reductive linear algebraic group 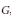 $G$, and let
$G$, and let 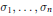 ${{\sigma }_{1}},\ldots ,{{\sigma }_{n}}$ be a system of generators of the algebra of invariant polynomials
${{\sigma }_{1}},\ldots ,{{\sigma }_{n}}$ be a system of generators of the algebra of invariant polynomials 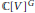 $\mathbb{C}{{\left[ V \right]}^{G}}$. We study the problem of lifting mappings
$\mathbb{C}{{\left[ V \right]}^{G}}$. We study the problem of lifting mappings 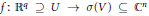 $f:\,{{\mathbb{R}}^{q}}\,\supseteq \,U\,\to \,\sigma \left( V \right)\,\subseteq \,{{\mathbb{C}}^{n}}$ over the mapping of invariants
$f:\,{{\mathbb{R}}^{q}}\,\supseteq \,U\,\to \,\sigma \left( V \right)\,\subseteq \,{{\mathbb{C}}^{n}}$ over the mapping of invariants 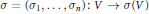 $\sigma \,=\,\left( {{\sigma }_{1}},\ldots ,{{\sigma }_{n}} \right):\,V\,\to \,\sigma \left( V \right)$. Note that
$\sigma \,=\,\left( {{\sigma }_{1}},\ldots ,{{\sigma }_{n}} \right):\,V\,\to \,\sigma \left( V \right)$. Note that 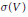 $\sigma \left( V \right)$ can be identified with the categorical quotient
$\sigma \left( V \right)$ can be identified with the categorical quotient 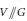 $V//G$ and its points correspond bijectively to the closed orbits in
$V//G$ and its points correspond bijectively to the closed orbits in 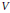 $V$. We prove that if
$V$. We prove that if 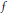 $f$ belongs to a quasianalytic subclass
$f$ belongs to a quasianalytic subclass 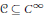 $C\subseteq {{C}^{\infty }}$ satisfying some mild closedness properties that guarantee resolution of singularities in
$C\subseteq {{C}^{\infty }}$ satisfying some mild closedness properties that guarantee resolution of singularities in 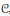 $C$, e.g., the real analytic class, then
$C$, e.g., the real analytic class, then 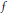 $f$ admits a lift of the same class
$f$ admits a lift of the same class 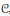 $C$ after desingularization by local blow-ups and local power substitutions. As a consequence we show that
$C$ after desingularization by local blow-ups and local power substitutions. As a consequence we show that 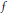 $f$ itself allows for a lift that belongs to
$f$ itself allows for a lift that belongs to  $\text{SB}{{\text{V}}_{\text{loc}}}$, i.e., special functions of bounded variation. If
$\text{SB}{{\text{V}}_{\text{loc}}}$, i.e., special functions of bounded variation. If 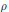 $\rho $ is a real representation of a compact Lie group, we obtain stronger versions.
$\rho $ is a real representation of a compact Lie group, we obtain stronger versions.