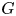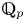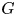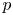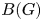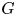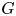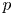Introduction
Dans notre travail en commun avec J.-M. Fontaine [Reference Fargues and FontaineFF18] on a défini une ‘courbe’ sur ![]() $\mathbb {Q}_p$. Il s'agit d'un schéma noethérien régulier de dimension
$\mathbb {Q}_p$. Il s'agit d'un schéma noethérien régulier de dimension ![]() $1$,
$1$, ![]() $X$ sur
$X$ sur ![]() ${\rm Spec} (\mathbb {Q}_p)$ associé au choix d'un corps perfectoïde
${\rm Spec} (\mathbb {Q}_p)$ associé au choix d'un corps perfectoïde ![]() $F$ de caractéristique
$F$ de caractéristique ![]() $p$. On a également classifié les fibrés vectoriels sur
$p$. On a également classifié les fibrés vectoriels sur ![]() $X$. Plus précisément, à chaque choix d'un nombre rationnel
$X$. Plus précisément, à chaque choix d'un nombre rationnel ![]() $\lambda$ est associé un fibré vectoriel
$\lambda$ est associé un fibré vectoriel ![]() $\mathcal {O}_X(\lambda )$ semi-stable de pente
$\mathcal {O}_X(\lambda )$ semi-stable de pente ![]() $\lambda$ sur
$\lambda$ sur ![]() $X$. On a alors démontré que si
$X$. On a alors démontré que si ![]() $F$ est algébriquement clos tout fibré vectoriel est somme directe de fibrés
$F$ est algébriquement clos tout fibré vectoriel est somme directe de fibrés ![]() $\mathcal {O}_X (\lambda )$.
$\mathcal {O}_X (\lambda )$.
Cette classification se traduit en termes d'algèbres semi-linéaires : à tout isocristal ![]() $(D,\varphi )$ on peut associer naturellement un fibré vectoriel
$(D,\varphi )$ on peut associer naturellement un fibré vectoriel ![]() $\mathscr {E}(D,\varphi )$ sur
$\mathscr {E}(D,\varphi )$ sur ![]() $X$ et alors la correspondance précédent induit une bijection entre classes d'isomorphismes d'isocristaux et de fibrés.
$X$ et alors la correspondance précédent induit une bijection entre classes d'isomorphismes d'isocristaux et de fibrés.
Soit maintenant ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $\mathbb {Q}_p$ (ou plus généralement une extension de degré fini mais on se restreint dans cette introduction au cas de
$\mathbb {Q}_p$ (ou plus généralement une extension de degré fini mais on se restreint dans cette introduction au cas de ![]() $\mathbb {Q}_p$). Dans ce texte on étudie les
$\mathbb {Q}_p$). Dans ce texte on étudie les ![]() $G$-fibrés sur
$G$-fibrés sur ![]() $X$ du point de vue des travaux fondateurs de Kottwitz sur les
$X$ du point de vue des travaux fondateurs de Kottwitz sur les ![]() $G$-isocristaux [Reference KottwitzKot85, Reference Rapoport and RichartzRR96, Reference KottwitzKot97]. Notons
$G$-isocristaux [Reference KottwitzKot85, Reference Rapoport and RichartzRR96, Reference KottwitzKot97]. Notons ![]() $L=\widehat {\mathbb {Q}_p^{nr}}$ muni de son Frobenius
$L=\widehat {\mathbb {Q}_p^{nr}}$ muni de son Frobenius ![]() $\sigma$ et
$\sigma$ et ![]() $B(G)$ les classes de
$B(G)$ les classes de ![]() $\sigma$-conjugaison dans
$\sigma$-conjugaison dans ![]() $G(L)$. Étant donné
$G(L)$. Étant donné ![]() $b\in G(L)$ on construit un
$b\in G(L)$ on construit un ![]() $G$-fibré
$G$-fibré ![]() $\mathscr {E}_b$ sur
$\mathscr {E}_b$ sur ![]() $X$. Le résultat principal de cet article est alors le suivant qui généralise le précédent pour le groupe linéaire.
$X$. Le résultat principal de cet article est alors le suivant qui généralise le précédent pour le groupe linéaire.
Théorème 5.1 Il y a une bijection
 \begin{align*} B(G) &\xrightarrow{\;\sim\;} H^1_{\rm{\acute{e}t}} (X,G)\\ {[} b] &\longmapsto [\mathscr{E}_b] \end{align*}
\begin{align*} B(G) &\xrightarrow{\;\sim\;} H^1_{\rm{\acute{e}t}} (X,G)\\ {[} b] &\longmapsto [\mathscr{E}_b] \end{align*}
entre classes de ![]() $\sigma$-conjugaison dans
$\sigma$-conjugaison dans ![]() $G$ et classes d'isomorphisme de
$G$ et classes d'isomorphisme de ![]() $G$-fibrés sur
$G$-fibrés sur ![]() $X$.
$X$.
Les résultats de Kottwitz sur la structure de l'ensemble ![]() $B(G)$ s'interprètent alors agréablement du point de vue géométrique. Donnons quelques exemples (cf. sec. 6 et 8) :
$B(G)$ s'interprètent alors agréablement du point de vue géométrique. Donnons quelques exemples (cf. sec. 6 et 8) :
— L'inclusion de la cohomologie galoisienne
 $H^1(\mathbb {Q}_p,G) \subset B(G)$ comme sous-ensemble des
$H^1(\mathbb {Q}_p,G) \subset B(G)$ comme sous-ensemble des  $G$-isocristaux ‘racines de l'unité’ s'interprète comme l'application
$G$-isocristaux ‘racines de l'unité’ s'interprète comme l'application
 \[ H^1_{\rm{\acute{e}t}} ({\rm Spec} ( \mathbb{Q}_p),G)\longrightarrow H^1_{\rm{\acute{e}t}} (X,G). \]
\[ H^1_{\rm{\acute{e}t}} ({\rm Spec} ( \mathbb{Q}_p),G)\longrightarrow H^1_{\rm{\acute{e}t}} (X,G). \]— Le
 $G$-torseur
$G$-torseur  $\mathscr {E}_b$ est semi-stable si et seulement si
$\mathscr {E}_b$ est semi-stable si et seulement si  $b$ est basique.
$b$ est basique.— Le morphisme des pentes
 $\nu _b$ associé à
$\nu _b$ associé à  $b$ par la théorie de Dieudonné-Manin s'interprète comme un polygone de Harder-Narasimhan généralisé.
$b$ par la théorie de Dieudonné-Manin s'interprète comme un polygone de Harder-Narasimhan généralisé.— L'application
 $\kappa :B(G)\rightarrow \pi _1(G)_{\Gamma }$ de Kottwitz s'interprète comme une classe de Chern
$\kappa :B(G)\rightarrow \pi _1(G)_{\Gamma }$ de Kottwitz s'interprète comme une classe de Chern  $G$-équivariante.
$G$-équivariante.
La théorie de la réduction des ![]() $G$-torseurs au sens d'Atiyah-Bott permet d’éclairer sous un nouveau jour les résultats de Kottwitz. Réciproquement, celle-ci est essentielle dans la démonstration du théorème 5.1.
$G$-torseurs au sens d'Atiyah-Bott permet d’éclairer sous un nouveau jour les résultats de Kottwitz. Réciproquement, celle-ci est essentielle dans la démonstration du théorème 5.1.
Il se trouve qu'au cours de la démonstration du théorème 5.1 l'auteur est tombé sur un certains nombre de faits frappants concernant la cohomologie étale de la courbe ![]() $X$ en relation avec la théorie du corps de classe local. Voici quelques exemples :
$X$ en relation avec la théorie du corps de classe local. Voici quelques exemples :
— La cohomologie étale de la courbe à coefficients dans un système local s'identifie à la cohomologie galoisienne de
 $\mathbb {Q}_p$ (théo. 3.7).
$\mathbb {Q}_p$ (théo. 3.7).— La dualité de Tate-Nakayama s'interprète comme une dualité de Poincaré sur
 $X$ (coro. 3.8).
$X$ (coro. 3.8).— La classe fondamentale de la courbe coïncide avec la classe fondamentale de la théorie du corps de classe (sec. 3.1).
Notons également que le théorème 5.1 fournit une nouvelle démonstration de la théorie du corps de classe local (sec. 2.2) qui, bien que fort compliquée si l'on tient compte de tous les arguments mis bout à bout, est assez naturelle et différente des autres preuves.
Il se trouve finalement que c'est durant l’élaboration de cet article que l'auteur est tombé sur certaines conjectures reliant les correspondances de Langlands locales et l'espace de module des ![]() $G$-torseurs sur cette courbe. On renvoie à [Reference FarguesFar16] et [Reference Fargues and ScholzeFS] pour cela.
$G$-torseurs sur cette courbe. On renvoie à [Reference FarguesFar16] et [Reference Fargues and ScholzeFS] pour cela.
1. Généralités
Soient ![]() $F$ un corps perfectoïde algébriquement clos de caractéristique
$F$ un corps perfectoïde algébriquement clos de caractéristique ![]() $p$ et
$p$ et ![]() $E$ une extension de degré fini de
$E$ une extension de degré fini de ![]() $\mathbb {Q}_p$ de corps résiduel
$\mathbb {Q}_p$ de corps résiduel ![]() $\mathbb {F}_q$ que l'on suppose plongé dans
$\mathbb {F}_q$ que l'on suppose plongé dans ![]() $F$. À ces données est associé un schéma
$F$. À ces données est associé un schéma
que l'on abrégera la plupart du temps en ![]() $X$ lorsqu'il n'y a pas d'ambigüité sur
$X$ lorsqu'il n'y a pas d'ambigüité sur ![]() $E$ et
$E$ et ![]() $F$ [Reference Fargues and FontaineFF11, Reference Fargues and FontaineFF12, Reference Fargues and FontaineFF14, Reference Fargues and FontaineFF18]. Dans la notation précédente
$F$ [Reference Fargues and FontaineFF11, Reference Fargues and FontaineFF12, Reference Fargues and FontaineFF14, Reference Fargues and FontaineFF18]. Dans la notation précédente ![]() $\pi _E$ est une uniformisante de
$\pi _E$ est une uniformisante de ![]() $E$, cependant
$E$, cependant ![]() $X_{F,E}$ ne dépend pas canoniquement du choix de cette uniformisante. On note
$X_{F,E}$ ne dépend pas canoniquement du choix de cette uniformisante. On note ![]() $\bar {\mathbb {F}}_q$ la clôture algébrique de
$\bar {\mathbb {F}}_q$ la clôture algébrique de ![]() $\mathbb {F}_q$ dans
$\mathbb {F}_q$ dans ![]() $F$ et
$F$ et ![]() $L$ le complété de l'extension maximale non-ramifiée de
$L$ le complété de l'extension maximale non-ramifiée de ![]() $E$ de corps résiduel
$E$ de corps résiduel ![]() $\bar {\mathbb {F}}_q$. Dans la suite, lorsqu'on considérera une extension algébrique
$\bar {\mathbb {F}}_q$. Dans la suite, lorsqu'on considérera une extension algébrique ![]() $E^{\prime}$ de
$E^{\prime}$ de ![]() $E$ on supposera toujours son corps résiduel plongé dans
$E$ on supposera toujours son corps résiduel plongé dans ![]() $\bar {\mathbb {F}}_q$ et donc
$\bar {\mathbb {F}}_q$ et donc
On notera également ![]() $E_h$ l'extension non-ramifiée de degré
$E_h$ l'extension non-ramifiée de degré ![]() $h$ de
$h$ de ![]() $E$. Enfin on note parfois
$E$. Enfin on note parfois ![]() $\Gamma ={\rm Gal} (\bar {E}|E)$ pour une clôture algébrique
$\Gamma ={\rm Gal} (\bar {E}|E)$ pour une clôture algébrique ![]() $\bar {E}$ de
$\bar {E}$ de ![]() $E$.
$E$.
Notons ![]() ${\rm Fib}_X$ la catégorie des fibrés vectoriels sur
${\rm Fib}_X$ la catégorie des fibrés vectoriels sur ![]() $X$. Soit
$X$. Soit ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $E$. On dispose de deux points de vue sur les
$E$. On dispose de deux points de vue sur les ![]() $G$-fibrés sur
$G$-fibrés sur ![]() $X$ :
$X$ :
(1) Le point de vue des
 $G$-torseurs sur
$G$-torseurs sur  $X$ localement triviaux pour la topologie étale ou, ce qui est équivalent puisque
$X$ localement triviaux pour la topologie étale ou, ce qui est équivalent puisque  $G$ est lisse, pour la topologie fppf.
$G$ est lisse, pour la topologie fppf.(2) Le point de vue Tannakien des fibrés munis d'une
 $G$-structure, c'est à dire les foncteurs exactes compatibles au produit tensoriel
$G$-structure, c'est à dire les foncteurs exactes compatibles au produit tensoriel
 \[ {\rm Rep}_E\, G\longrightarrow {\rm Fib}_X. \]
\[ {\rm Rep}_E\, G\longrightarrow {\rm Fib}_X. \]
Ces deux points de vue sont équivalents. Plus précisément, si ![]() $\mathscr {T}\rightarrow X$ est un
$\mathscr {T}\rightarrow X$ est un ![]() $G$-torseur il définit le fibré muni d'une
$G$-torseur il définit le fibré muni d'une ![]() $G$-structure
$G$-structure
 \begin{align*} \omega_{\mathscr{T}}:{\rm Rep}_E\, G&\longrightarrow{\rm Fib}_X \\ (V,\rho) & \longmapsto \mathscr{T}\underset{G,\rho}{\times} V. \end{align*}
\begin{align*} \omega_{\mathscr{T}}:{\rm Rep}_E\, G&\longrightarrow{\rm Fib}_X \\ (V,\rho) & \longmapsto \mathscr{T}\underset{G,\rho}{\times} V. \end{align*}
Dans l'autre sens, si ![]() $\omega :{\rm Rep}_E\, G\rightarrow {\rm Fib}_X$, d'après [Reference DeligneDel90] theo. 1.12,
$\omega :{\rm Rep}_E\, G\rightarrow {\rm Fib}_X$, d'après [Reference DeligneDel90] theo. 1.12,
est un ![]() $G$-torseur où
$G$-torseur où ![]() $\omega _{{\rm can}}(V,\rho )=V\otimes _E \mathcal {O}_X$ et toujours d'après [Reference DeligneDel90] cela définit une équivalence entre nos deux catégories.
$\omega _{{\rm can}}(V,\rho )=V\otimes _E \mathcal {O}_X$ et toujours d'après [Reference DeligneDel90] cela définit une équivalence entre nos deux catégories.
Notons ![]() $\varphi \text {-Mod}_L$ la catégorie des isocristaux associée à
$\varphi \text {-Mod}_L$ la catégorie des isocristaux associée à ![]() $L|E$ et
$L|E$ et ![]() $\sigma$ le relèvement de
$\sigma$ le relèvement de ![]() ${\rm Frob}_q$. Rappelons qu'il y a un foncteur ([Reference Fargues and FontaineFF18] sec. 8.2.3])
${\rm Frob}_q$. Rappelons qu'il y a un foncteur ([Reference Fargues and FontaineFF18] sec. 8.2.3])
Ce foncteur est exact fidèle mais non plein ce qui explique pourquoi le théorème principal 5.1 est absolument non-évident.
Définition 1.1 Pour ![]() $b\in G(L)$ on note
$b\in G(L)$ on note ![]() $\mathscr {E}_b$ le
$\mathscr {E}_b$ le ![]() $G$-fibré défini par le foncteur composé
$G$-fibré défini par le foncteur composé
 \begin{align*} {\rm Rep}_E\, G & \longrightarrow \varphi\text{-Mod}_L \xrightarrow{\ \mathscr{E}(-)\ } {\rm Fib}_X \\ (V,\rho) & \longmapsto (V_L,\rho(b)\sigma). \end{align*}
\begin{align*} {\rm Rep}_E\, G & \longrightarrow \varphi\text{-Mod}_L \xrightarrow{\ \mathscr{E}(-)\ } {\rm Fib}_X \\ (V,\rho) & \longmapsto (V_L,\rho(b)\sigma). \end{align*} Rappelons [Reference KottwitzKot85] que ![]() $B(G)$ désigne les classes de
$B(G)$ désigne les classes de ![]() $\sigma$-conjugaison dans
$\sigma$-conjugaison dans ![]() $G(L)$. La construction précédente définit une application
$G(L)$. La construction précédente définit une application
 \begin{align*} B(G) & \longrightarrow H^1_{\rm{\acute{e}t}} (X,G) \\ \, [b] & \longmapsto [\mathscr{E}_{b}]. \end{align*}
\begin{align*} B(G) & \longrightarrow H^1_{\rm{\acute{e}t}} (X,G) \\ \, [b] & \longmapsto [\mathscr{E}_{b}]. \end{align*}
Lorsque ![]() $G$ est un tore il y a une identification
$G$ est un tore il y a une identification
et cette application est un morphisme de groupe.
Remarque 1.2 Dans ce texte on ne considère que des torseurs sous un groupe constants sur ![]() $X$ c'est à dire de la forme
$X$ c'est à dire de la forme ![]() $G\times X$ avec
$G\times X$ avec ![]() $G$ défini sur
$G$ défini sur ![]() $E$. Néanmoins il semblerait intéressant, et même plus naturel en un certain sens, d’étudier les torseurs sous des schémas en groupes réductifs plus généraux sur
$E$. Néanmoins il semblerait intéressant, et même plus naturel en un certain sens, d’étudier les torseurs sous des schémas en groupes réductifs plus généraux sur ![]() $X$. C'est en fait déjà le point de vue adopté partiellement dans le chapitre IX de [Reference Dat, Orlik and RapoportDOR10]. En effet, tout schéma en groupes dans la catégorie
$X$. C'est en fait déjà le point de vue adopté partiellement dans le chapitre IX de [Reference Dat, Orlik and RapoportDOR10]. En effet, tout schéma en groupes dans la catégorie ![]() $\varphi \text {-Mod}_L$ au sens de [Reference Dat, Orlik and RapoportDOR10], déf. 9.1.8, définit un schéma en groupes sur
$\varphi \text {-Mod}_L$ au sens de [Reference Dat, Orlik and RapoportDOR10], déf. 9.1.8, définit un schéma en groupes sur ![]() $X$. Par exemple, si
$X$. Par exemple, si ![]() $(D,\varphi )$ est un isocristal le schéma en groupe réductif associé à
$(D,\varphi )$ est un isocristal le schéma en groupe réductif associé à ![]() $(D,\varphi )$ via l'exemple 9.1.10 de [Reference Dat, Orlik and RapoportDOR10] est
$(D,\varphi )$ via l'exemple 9.1.10 de [Reference Dat, Orlik and RapoportDOR10] est ![]() ${\textit{GL}} (\mathscr {E}(D,\varphi ))$. Il semblerait donc intéressant de reprendre les résultats de [Reference Dat, Orlik and RapoportDOR10] dans le cadre de cet article.
${\textit{GL}} (\mathscr {E}(D,\varphi ))$. Il semblerait donc intéressant de reprendre les résultats de [Reference Dat, Orlik and RapoportDOR10] dans le cadre de cet article.
2. Le cas des tores
Dans cette section on commence par étudier la cohomologie étale de la courbe ![]() $X$ à coefficients dans un tore. Cela donne une démonstration (théo. 2.9) du théorème principal 5.1 de cet article pour les tores indépendante de celle donnée en toute généralité dans la section 5 pour tout groupe réductif. Cela nous amène à étudier la cohomologie étale de la courbe à coefficients de torsion qui se révèle avoir des liens très intéressants avec la théorie du corps de classe.
$X$ à coefficients dans un tore. Cela donne une démonstration (théo. 2.9) du théorème principal 5.1 de cet article pour les tores indépendante de celle donnée en toute généralité dans la section 5 pour tout groupe réductif. Cela nous amène à étudier la cohomologie étale de la courbe à coefficients de torsion qui se révèle avoir des liens très intéressants avec la théorie du corps de classe.
2.1 Annulation du groupe de Brauer de la courbe
On sait que ![]() ${\rm Pic} (X)=\mathbb {Z}$ engendré par la classe du fibré
${\rm Pic} (X)=\mathbb {Z}$ engendré par la classe du fibré ![]() $\mathcal {O}_X(1)$. On va avoir besoin dans la suite de connaître
$\mathcal {O}_X(1)$. On va avoir besoin dans la suite de connaître
D'après Grothendieck ([Reference GrothendieckGro68] coro. 2.2), puisque ![]() $X$ est noethérien de dimension
$X$ est noethérien de dimension ![]() $1$,
$1$,
où le groupe de Brauer est celui classifiant les classes d’équivalence d'algèbres d'Azumaya sur ![]() $X$. Commençons par remarquer le résultat suivant.
$X$. Commençons par remarquer le résultat suivant.
Proposition 2.1 Le morphisme ![]() ${\rm Br}(E)\longrightarrow {\rm Br}(X)$ est nul.
${\rm Br}(E)\longrightarrow {\rm Br}(X)$ est nul.
Proof Démonstration D'après la théorie du corps de classe local on sait que si ![]() $[B]\in {\rm Br}(E)$, où
$[B]\in {\rm Br}(E)$, où ![]() $B$ est une algèbre simple sur
$B$ est une algèbre simple sur ![]() $E$, il existe un isocristal
$E$, il existe un isocristal ![]() $(D,\varphi )\in \varphi \text {-Mod}_L$ isocline tel que
$(D,\varphi )\in \varphi \text {-Mod}_L$ isocline tel que
Mais pour un tel isocristal
Théorème 2.2 On a ![]() ${\rm Br}(X)=0$.
${\rm Br}(X)=0$.
Proof Démonstration Soit ![]() $\mathscr {A}$ une algèbre d'Azumaya sur
$\mathscr {A}$ une algèbre d'Azumaya sur ![]() $X$. Pour
$X$. Pour ![]() $\lambda \in \mathbb {Q}$ on note
$\lambda \in \mathbb {Q}$ on note ![]() $\mathscr {A}^{\geq \lambda }$ , resp.
$\mathscr {A}^{\geq \lambda }$ , resp. ![]() $\mathscr {A}^{>\lambda }$, la partie de pente
$\mathscr {A}^{>\lambda }$, la partie de pente ![]() $\geq \lambda$, resp.
$\geq \lambda$, resp. ![]() $ > \lambda$, dans la filtration de Harder-Narasimhan de
$ > \lambda$, dans la filtration de Harder-Narasimhan de ![]() $\mathscr {A}$. Il résulte du théorème de classification 8.2.10 de [Reference Fargues and FontaineFF18] que le produit tensoriel de deux fibrés semi-stables est semi-stable. On en déduit en regardant le morphisme
$\mathscr {A}$. Il résulte du théorème de classification 8.2.10 de [Reference Fargues and FontaineFF18] que le produit tensoriel de deux fibrés semi-stables est semi-stable. On en déduit en regardant le morphisme
défini par la loi d'algèbre que
De plus la section unité de ![]() $\mathscr {A}$, définie par un morphisme
$\mathscr {A}$, définie par un morphisme ![]() $\mathcal {O}_X\xrightarrow {e} \mathscr {A}$, est à valeurs dans
$\mathcal {O}_X\xrightarrow {e} \mathscr {A}$, est à valeurs dans ![]() $\mathscr {A}^{\geq 0}$. Il s'en suit que
$\mathscr {A}^{\geq 0}$. Il s'en suit que ![]() $\mathscr {A}^{\geq 0}$ est une sous-algèbre de
$\mathscr {A}^{\geq 0}$ est une sous-algèbre de ![]() $\mathscr {A}$ et
$\mathscr {A}$ et ![]() $\mathscr {A}^{>0}$ un idéal bilatère nilpotent dans
$\mathscr {A}^{>0}$ un idéal bilatère nilpotent dans ![]() $\mathscr {A}^{\geq 0}$. Posons
$\mathscr {A}^{\geq 0}$. Posons
comme ![]() $X$-schéma en groupes lisse. Montrons que
$X$-schéma en groupes lisse. Montrons que ![]() $H$ est un sous-groupe parabolique du groupe semi-simple
$H$ est un sous-groupe parabolique du groupe semi-simple ![]() $\mathscr {A}^{\times }/e(\mathcal {O}_X^{\times })$ de radical unipotent
$\mathscr {A}^{\times }/e(\mathcal {O}_X^{\times })$ de radical unipotent ![]() $1+\mathscr {A}^{>0}$. Remarquons d'abord que
$1+\mathscr {A}^{>0}$. Remarquons d'abord que ![]() $e(\mathcal {O}_X)\cap \mathscr {A}^{>0}=0$ puisque
$e(\mathcal {O}_X)\cap \mathscr {A}^{>0}=0$ puisque ![]() $\mathscr {A}^{>0}$ est nilpotent. La filtration de Harder-Narasimhan de
$\mathscr {A}^{>0}$ est nilpotent. La filtration de Harder-Narasimhan de
 \begin{align*} \mathscr{E} &:= \mathscr{A}/e(\mathcal{O}_X)\\ &\phantom{:}= {\rm Lie} ( \mathscr{A}^\times/e(\mathcal{O}_X^\times) ) \end{align*}
\begin{align*} \mathscr{E} &:= \mathscr{A}/e(\mathcal{O}_X)\\ &\phantom{:}= {\rm Lie} ( \mathscr{A}^\times/e(\mathcal{O}_X^\times) ) \end{align*}est donnée par :
—
 $\mathscr {E}^{\geq \lambda }=\mathscr {A}^{\geq \lambda }/e(\mathcal {O}_X)$ si
$\mathscr {E}^{\geq \lambda }=\mathscr {A}^{\geq \lambda }/e(\mathcal {O}_X)$ si  $\lambda \leq 0$;
$\lambda \leq 0$;—
 $\mathscr {E}^{\geq \lambda }=\mathscr {A}^{\geq \lambda }$ si
$\mathscr {E}^{\geq \lambda }=\mathscr {A}^{\geq \lambda }$ si  $\lambda >0$.
$\lambda >0$.
Considérons la forme de Killing
Puisque l'algèbre de Lie ![]() $\mathscr {E}$ est localement isomorphe pour la topologie étale à
$\mathscr {E}$ est localement isomorphe pour la topologie étale à ![]() $pgl_n$, où
$pgl_n$, où ![]() ${\rm rg} \mathscr {A}=n^2$, c'est une forme parfaite et elle induit des isomorphismes
${\rm rg} \mathscr {A}=n^2$, c'est une forme parfaite et elle induit des isomorphismes
où l’égalité de droite est valable pour la filtration de Harder-Narasimhan de n'importe quel fibré. Par définition ([Reference Gille and PoloSGA3] exp. XXVI déf. 1.1) ![]() $H$ est un sous-groupe parabolique si et seulement si c'est le cas après spécialisation en chaque fibre géométrique de
$H$ est un sous-groupe parabolique si et seulement si c'est le cas après spécialisation en chaque fibre géométrique de ![]() $X$. Soit donc
$X$. Soit donc ![]() $\bar {x}\rightarrow X$ un point géométrique de
$\bar {x}\rightarrow X$ un point géométrique de ![]() $X$. Par spécialisation de (1) on obtient que sous la forme de Killing de
$X$. Par spécialisation de (1) on obtient que sous la forme de Killing de ![]() $\mathscr {E}\otimes k(\bar {x})$
$\mathscr {E}\otimes k(\bar {x})$
D'après la proposition 3.1 de [Reference GraysonGra86] on en déduit que l'algèbre ![]() $\mathscr {E}^{\geq 0}\otimes k(\bar {x})$ est parabolique de radical nilpotent
$\mathscr {E}^{\geq 0}\otimes k(\bar {x})$ est parabolique de radical nilpotent ![]() $\mathscr {E}^{>0}\otimes k(\bar {x})$. Puisque
$\mathscr {E}^{>0}\otimes k(\bar {x})$. Puisque ![]() $k(\bar {x})$ est de caractéristique
$k(\bar {x})$ est de caractéristique ![]() $0$, on en déduit que
$0$, on en déduit que ![]() $H$ est un sous-groupe parabolique de radical unipotent
$H$ est un sous-groupe parabolique de radical unipotent ![]() $1+\mathscr {A}^{> 0}$.
$1+\mathscr {A}^{> 0}$.
Soit ![]() $P\subset {\rm PGL}_n$ le sous-groupe parabolique standard de type celui défini par
$P\subset {\rm PGL}_n$ le sous-groupe parabolique standard de type celui défini par ![]() $H\subset \mathscr {A}^\times /e(\mathcal {O}_X^\times )$. Puisque
$H\subset \mathscr {A}^\times /e(\mathcal {O}_X^\times )$. Puisque ![]() $H$ et
$H$ et ![]() $P$ sont localement conjugués pour la topologie étale ([Reference Gille and PoloSGA3] exp. XXVI prop. 1.3), la classe de cohomologie
$P$ sont localement conjugués pour la topologie étale ([Reference Gille and PoloSGA3] exp. XXVI prop. 1.3), la classe de cohomologie
provient d'une classe de cohomologie dans
i.e. le ![]() ${\rm PGL}_n$-torseur défini par
${\rm PGL}_n$-torseur défini par ![]() $\mathscr {A}$ possède une réduction canonique à
$\mathscr {A}$ possède une réduction canonique à ![]() $P$ (cf. rem. 2.4 qui suit). Cette classe de cohomologie est donnée par le
$P$ (cf. rem. 2.4 qui suit). Cette classe de cohomologie est donnée par le ![]() $P$-torseur
$P$-torseur
où ![]() $\tilde {P}$ est le sous-groupe parabolique de
$\tilde {P}$ est le sous-groupe parabolique de ![]() $\hbox {GL}_n$ image réciproque de
$\hbox {GL}_n$ image réciproque de ![]() $P$.
$P$.
Notons ![]() $\alpha \in H^1_{\rm{\acute {e}t}}(X,P)$ cette classe. Soit
$\alpha \in H^1_{\rm{\acute {e}t}}(X,P)$ cette classe. Soit ![]() $\mathscr {U}_\alpha$ la forme tordue du radical unipotent
$\mathscr {U}_\alpha$ la forme tordue du radical unipotent ![]() $U$ de
$U$ de ![]() $P$ par
$P$ par ![]() $\alpha$ via l'action de
$\alpha$ via l'action de ![]() $P$ sur
$P$ sur ![]() $U$ par automorphismes intérieurs. Le groupe
$U$ par automorphismes intérieurs. Le groupe ![]() $\mathscr {U}_\alpha$ est filtré par
$\mathscr {U}_\alpha$ est filtré par
de gradués
On note ![]() $M$ le quotient de Levi de
$M$ le quotient de Levi de ![]() $P$. La fibre de l'application
$P$. La fibre de l'application
au dessus de l'image de ![]() $\alpha$ s'identifie à l'ensemble pointé
$\alpha$ s'identifie à l'ensemble pointé
dont la classe triviale correspond à ![]() $\alpha$. Cet ensemble de cohomologie se dévisse alors par récurrence en les
$\alpha$. Cet ensemble de cohomologie se dévisse alors par récurrence en les
qui sont nuls puisque ![]() $\mathscr {A}^{\geq \lambda }/\mathscr {A}^{>\lambda }$ est semi-stable de pente positive. On en déduit que
$\mathscr {A}^{\geq \lambda }/\mathscr {A}^{>\lambda }$ est semi-stable de pente positive. On en déduit que ![]() $\alpha$ est complètement déterminée par son image dans
$\alpha$ est complètement déterminée par son image dans ![]() $H^1_{\rm{\acute {e}t}}(X,M)$.
$H^1_{\rm{\acute {e}t}}(X,M)$.
Notons ![]() $\beta \in H^1_{\rm{\acute {e}t}}(X,M)$ l'image de
$\beta \in H^1_{\rm{\acute {e}t}}(X,M)$ l'image de ![]() $\alpha$. La
$\alpha$. La ![]() $\mathcal {O}_X$-algèbre
$\mathcal {O}_X$-algèbre ![]() $\mathscr {A}^{\geq 0}/\mathscr {A}^{>0}$ est de la forme
$\mathscr {A}^{\geq 0}/\mathscr {A}^{>0}$ est de la forme
où les ![]() $\mathscr {B}_i$ sont des algèbres d'Azumaya. Le fibré
$\mathscr {B}_i$ sont des algèbres d'Azumaya. Le fibré ![]() $\mathscr {A}^{\geq 0}/\mathscr {A}^{>0}$ est semi-stable de pente
$\mathscr {A}^{\geq 0}/\mathscr {A}^{>0}$ est semi-stable de pente ![]() $0$ or il y a une équivalence tensorielle
$0$ or il y a une équivalence tensorielle
Il existe donc des algèbres semi-simples ![]() $B_1,\dots ,B_r$ centrales sur
$B_1,\dots ,B_r$ centrales sur ![]() $E$ telles que
$E$ telles que
On a ![]() $M=(\prod _{i=1}^{r} \hbox {GL}_{m_i})/\mathbb {G}_m$ avec
$M=(\prod _{i=1}^{r} \hbox {GL}_{m_i})/\mathbb {G}_m$ avec ![]() $\dim _E B_i=m_i^2$. De la proposition 2.1 on en déduit que l'image par le morphisme
$\dim _E B_i=m_i^2$. De la proposition 2.1 on en déduit que l'image par le morphisme
 \[ M\longrightarrow \prod_{i=1}^{r} {\rm PGL}_{m_i} \]
\[ M\longrightarrow \prod_{i=1}^{r} {\rm PGL}_{m_i} \]
de notre classe de ![]() $\beta$ est celle de l'algèbre d'Azumaya
$\beta$ est celle de l'algèbre d'Azumaya
 \[ \prod_{i=1}^r \mathscr{E}nd (\mathscr{E}_i) \]
\[ \prod_{i=1}^r \mathscr{E}nd (\mathscr{E}_i) \]
pour des fibré vectoriels ![]() $\mathscr {E}_i$ de rang
$\mathscr {E}_i$ de rang ![]() $m_i$. La suite exacte
$m_i$. La suite exacte
 \[ 1\longrightarrow \mathbb{G}_m^r/\mathbb{G}_m\longrightarrow M\longrightarrow \prod_{i=1}^r {\rm PGL}_{m_i}\longrightarrow 1 \]
\[ 1\longrightarrow \mathbb{G}_m^r/\mathbb{G}_m\longrightarrow M\longrightarrow \prod_{i=1}^r {\rm PGL}_{m_i}\longrightarrow 1 \]
montre alors qu'il existe des fibrés en droites ![]() $\mathscr {L}_1,\dots ,\mathscr {L}_r$ tels que
$\mathscr {L}_1,\dots ,\mathscr {L}_r$ tels que
 \[ \mathscr{A}\simeq {\rm End} \Big ( \bigoplus_{i=1}^r \mathscr{E}_i\otimes \mathscr{L}_i\Big ) \]
\[ \mathscr{A}\simeq {\rm End} \Big ( \bigoplus_{i=1}^r \mathscr{E}_i\otimes \mathscr{L}_i\Big ) \]ce qui conclut la preuve.
Remarque 2.3 La preuve précédente s'applique pour montrer que si ![]() $k$ est un corps
$k$ est un corps ![]() ${\rm Br}(k)\xrightarrow {\sim }{\rm Br}(\mathbb {P}^1_k)$ sans utiliser le théorème de Tsen.
${\rm Br}(k)\xrightarrow {\sim }{\rm Br}(\mathbb {P}^1_k)$ sans utiliser le théorème de Tsen.
Remarque 2.4 La première partie de la preuve précédente consiste à montrer l'existence d'une réduction canonique du type Atiyah-Bott d'un ![]() ${\rm PGL}_n$-torseur en termes d'algèbres de Lie. Comme dans les travaux de Behrend [Reference BehrendBeh95] cela se formule en la construction d'un sous-schéma en groupes parabolique de la forme intérieure de
${\rm PGL}_n$-torseur en termes d'algèbres de Lie. Comme dans les travaux de Behrend [Reference BehrendBeh95] cela se formule en la construction d'un sous-schéma en groupes parabolique de la forme intérieure de ![]() ${\rm PGL}_n$ associée à notre torseur. Dans notre situation cette forme intérieure est
${\rm PGL}_n$ associée à notre torseur. Dans notre situation cette forme intérieure est ![]() $\mathscr {A}^\times$. On renvoie également à la section 5.1.
$\mathscr {A}^\times$. On renvoie également à la section 5.1.
On note ![]() $E(X)$ le corps des fonctions de la courbe. Notons le corollaire suivant que nous n'utiliserons pas.
$E(X)$ le corps des fonctions de la courbe. Notons le corollaire suivant que nous n'utiliserons pas.
Corollaire 2.5 Le groupe de Brauer de ![]() $E(X)$ est trivial.
$E(X)$ est trivial.
Proof Démonstration Pour tout entier ![]() $n\geq 1$ on a
$n\geq 1$ on a
où ![]() $U$ parcourt les ouverts non vides de
$U$ parcourt les ouverts non vides de ![]() $X$. D'après le théorème de pureté absolu de Gabber [Reference FujiwaraFuj02] pour un tel
$X$. D'après le théorème de pureté absolu de Gabber [Reference FujiwaraFuj02] pour un tel ![]() $U$ l'application
$U$ l'application
est surjective. D'après le théorème 2.2 toute classe dans ![]() $H^2 (X,\mu _n)$ est la classe de Chern d'un fibré en droites sur
$H^2 (X,\mu _n)$ est la classe de Chern d'un fibré en droites sur ![]() $X$. La restriction d'un tel fibré en droites à
$X$. La restriction d'un tel fibré en droites à ![]() $U\subsetneq X$ est triviale (
$U\subsetneq X$ est triviale (![]() $U$ est le spectre d'un anneau principal). On en déduit que l'image d'une telle classe dans
$U$ est le spectre d'un anneau principal). On en déduit que l'image d'une telle classe dans ![]() $H^2(U,\mu _n)$ est nulle.
$H^2(U,\mu _n)$ est nulle.
2.2 Une nouvelle preuve de la théorie du corps de classe locale
En fait le théorème 2.2 précédent résulte du théorème principal 5.1 qui sera démontré indépendamment. En effet, si l'application ![]() $B({\rm PGL}_n)\rightarrow H^1_{\rm{\acute {e}t}} (X,{\rm PGL}_n)$ est surjective, puisque
$B({\rm PGL}_n)\rightarrow H^1_{\rm{\acute {e}t}} (X,{\rm PGL}_n)$ est surjective, puisque ![]() $B(\hbox {GL}_n)\rightarrow B({\rm PGL}_n)$ est surjective l'application
$B(\hbox {GL}_n)\rightarrow B({\rm PGL}_n)$ est surjective l'application ![]() $H^1_{\rm{\acute {e}t}} (X,GL_n)\rightarrow H^1_{\rm{\acute {e}t}} ( X,{\rm PGL}_n)$ l'est également. On a tout de même préféré donné une preuve indépendante du théorème 2.2. car le lien avec la théorie du corps de classe de
$H^1_{\rm{\acute {e}t}} (X,GL_n)\rightarrow H^1_{\rm{\acute {e}t}} ( X,{\rm PGL}_n)$ l'est également. On a tout de même préféré donné une preuve indépendante du théorème 2.2. car le lien avec la théorie du corps de classe de ![]() $E$ y fait déjà son apparition (cf. prop. 2.1) ce dont l'auteur ne se serait pas rendu compte s'il ne s’était intéressé qu'au théorème 5.1. En renversant les arguments on trouve alors l’énoncé suivant.
$E$ y fait déjà son apparition (cf. prop. 2.1) ce dont l'auteur ne se serait pas rendu compte s'il ne s’était intéressé qu'au théorème 5.1. En renversant les arguments on trouve alors l’énoncé suivant.
Théorème 2.6 Le théorème 5.1 implique la théorie du corps de classe local associée à ![]() $E$ au sens où l'application qui à un isocristal
$E$ au sens où l'application qui à un isocristal ![]() $(D,\varphi )$ simple de pente
$(D,\varphi )$ simple de pente ![]() $\lambda$ associe la classe
$\lambda$ associe la classe ![]() $[{\rm End} (D,\varphi )]\in {\rm Br}(E)$ induit un isomorphisme
$[{\rm End} (D,\varphi )]\in {\rm Br}(E)$ induit un isomorphisme
Proof Démonstration Comme expliqué précédemment, si le théorème 5.1 est vérifié et ![]() $B$ est une algèbre centrale simple sur
$B$ est une algèbre centrale simple sur ![]() $E$ alors
$E$ alors ![]() $B\otimes _E \mathcal {O}_X\simeq \mathscr {E}nd (\mathscr {E})$ pour un fibré vectoriel
$B\otimes _E \mathcal {O}_X\simeq \mathscr {E}nd (\mathscr {E})$ pour un fibré vectoriel ![]() $\mathscr {E}$ sur
$\mathscr {E}$ sur ![]() $X$. Puisque
$X$. Puisque ![]() $B\otimes _E \mathcal {O}_X$ est un fibré semi-stable de pente
$B\otimes _E \mathcal {O}_X$ est un fibré semi-stable de pente ![]() $0$,
$0$, ![]() $\mathscr {E}$ est semi-stable et donc d'après le théorème de classification des fibrés sur
$\mathscr {E}$ est semi-stable et donc d'après le théorème de classification des fibrés sur ![]() $X$ il existe un isocristal simple
$X$ il existe un isocristal simple ![]() $(D,\varphi )$ tel que
$(D,\varphi )$ tel que ![]() $\mathscr {E}\simeq \mathscr {E}(D,\varphi )$. On conclut puisque
$\mathscr {E}\simeq \mathscr {E}(D,\varphi )$. On conclut puisque ![]() $B=H^0 (X,B\otimes _E \mathcal {O}_X)={\rm End} (D,\varphi )$.
$B=H^0 (X,B\otimes _E \mathcal {O}_X)={\rm End} (D,\varphi )$.
Cette preuve repose sur le théorème de classification des fibrés de [Reference Fargues and FontaineFF18] qui n'utilise a aucun moment la théorie du corps de classe locale. Elle est différente des preuves usuelles au sens où elle n'utilise pas d'argument de comptage d'ordre de certains groupes de cohomologie galoisienne.
2.3 Annulation du second groupe de cohomologie des tores
Soit ![]() $T$ un tore algébrique sur
$T$ un tore algébrique sur ![]() $E$. On va maintenant généraliser le théorème 2.2 au cas de
$E$. On va maintenant généraliser le théorème 2.2 au cas de ![]() $T$. Notons
$T$. Notons
On note encore ![]() $T$ pour
$T$ pour ![]() $T\times _E X$ par abus de notation. Puisque
$T\times _E X$ par abus de notation. Puisque ![]() $\Gamma (X_{\bar {E}},\mathcal {O}_{X_{\bar {E}}})=\bar {E}$ on a
$\Gamma (X_{\bar {E}},\mathcal {O}_{X_{\bar {E}}})=\bar {E}$ on a
Puisque ![]() ${\rm Pic} (X_{\bar {E}})=\mathbb {Q}$ on a
${\rm Pic} (X_{\bar {E}})=\mathbb {Q}$ on a
comme module galoisien. Enfin, le théorème 2.2 fournit
Théorème 2.7 On a ![]() $H^2_{\rm{\acute {e}t}}(X,T)=0$.
$H^2_{\rm{\acute {e}t}}(X,T)=0$.
Proof Démonstration Considérons la suite spectrale de Hochschild-Serre
On a :
—
 $E^{02}_2=0$ d'après (4);
$E^{02}_2=0$ d'après (4);—
 $E^{11}_2= H^1 ({\rm Gal} (\bar {E}|E),X_*(T)_\mathbb {Q})=0$ d'après (3);
$E^{11}_2= H^1 ({\rm Gal} (\bar {E}|E),X_*(T)_\mathbb {Q})=0$ d'après (3);—
 $E^{20}_2= H^2({\rm Gal} (\bar {E}|E),T(\bar {E}))$ d'après (2), qui est le dual de Pontryagin de
$E^{20}_2= H^2({\rm Gal} (\bar {E}|E),T(\bar {E}))$ d'après (2), qui est le dual de Pontryagin de  $H^0 ({\rm Gal} (\bar {E}|E),X^*(T))$ d'après Tate-Nakayama.
$H^0 ({\rm Gal} (\bar {E}|E),X^*(T))$ d'après Tate-Nakayama.
On en déduit que ![]() $H^2_{\rm{\acute {e}t}}(X,T)$ est un groupe divisible.
$H^2_{\rm{\acute {e}t}}(X,T)$ est un groupe divisible.
Soit maintenant ![]() $E^{\prime}|E$ une extension galoisienne scindant
$E^{\prime}|E$ une extension galoisienne scindant ![]() $T$. Regardons la suite spectrale
$T$. Regardons la suite spectrale
Dans la catégorie quotient des groupes abéliens par la sous catégorie épaisse formée des groupes de torsion bornée (annulés par un entier) on a :
—
 $E^{11}_2=E^{20}_2=0$ puisqu'ils sont annulés par
$E^{11}_2=E^{20}_2=0$ puisqu'ils sont annulés par  $[E^{\prime}:E]$;
$[E^{\prime}:E]$;—
 $E^{02}_2= 0$ d'après le théorème 2.2.
$E^{02}_2= 0$ d'après le théorème 2.2.
On en déduit que ![]() $H^2_{\rm{\acute {e}t}}(X,T)$ est de torsion bornée ce qui permet de conclure.
$H^2_{\rm{\acute {e}t}}(X,T)$ est de torsion bornée ce qui permet de conclure.
Remarque 2.8 On a vu que le théorème 5.1 implique directement l'annulation de ![]() $\mathrm {Br} (X)$ (cf. intro. sec. 2.2). Il implique en fait plus généralement 2.7 indépendamment de tout l'arsenal de la théorie du corps de classe (en particulier la dualité de Tate-Nakayama). Considérons en effet une suite exacte de tores
$\mathrm {Br} (X)$ (cf. intro. sec. 2.2). Il implique en fait plus généralement 2.7 indépendamment de tout l'arsenal de la théorie du corps de classe (en particulier la dualité de Tate-Nakayama). Considérons en effet une suite exacte de tores ![]() $0\rightarrow T\rightarrow T'\rightarrow T''\rightarrow 0$ avec
$0\rightarrow T\rightarrow T'\rightarrow T''\rightarrow 0$ avec ![]() $T'$ un tore induit. L'application
$T'$ un tore induit. L'application ![]() $B(T')\rightarrow B(T'')$ est surjective (Steinberg). L'annulation de
$B(T')\rightarrow B(T'')$ est surjective (Steinberg). L'annulation de ![]() $H^2 (X,T')$ implique alors celle de
$H^2 (X,T')$ implique alors celle de ![]() $H^2(X,T)$.
$H^2(X,T)$.
2.4 L'isomorphisme entre  $B(T)$ et
$B(T)$ et  $H^1_{\rm{\acute {e}t}}(X,T)$
$H^1_{\rm{\acute {e}t}}(X,T)$
On peut maintenant montrer le résultat principal, le théorème 5.1, dans le cas des tores.
Théorème 2.9 Il y a un isomorphisme
 \begin{align*} B(T) & \xrightarrow{\;\sim\;} H^1_{\rm{\acute{e}t}}(X,T)\\ \, [b] & \longmapsto [\mathscr{E}_b]. \end{align*}
\begin{align*} B(T) & \xrightarrow{\;\sim\;} H^1_{\rm{\acute{e}t}}(X,T)\\ \, [b] & \longmapsto [\mathscr{E}_b]. \end{align*}Proof Démonstration Le foncteur qui à ![]() $E$ et un tore
$E$ et un tore ![]() $T$ sur
$T$ sur ![]() $E$ associe
$E$ associe ![]() $H^1_{\rm{\acute {e}t}}(X_{E},T)$ vérifie :
$H^1_{\rm{\acute {e}t}}(X_{E},T)$ vérifie :
— il est exacte à droite d'après le théorème 2.7;
— il est compatible à la restriction des scalaires c'est à dire pour
 $E^{\prime}|E$ finie et
$E^{\prime}|E$ finie et  $T$ sur
$T$ sur  $E^{\prime}$
$E^{\prime}$
 \[ H^1_{\rm{\acute{e}t}}(X_E,{\rm Res}_{E^{\prime}/E} T)= H^1_{\rm{\acute{e}t}}(X_{E^{\prime}},T). \]
\[ H^1_{\rm{\acute{e}t}}(X_E,{\rm Res}_{E^{\prime}/E} T)= H^1_{\rm{\acute{e}t}}(X_{E^{\prime}},T). \]
Il en est de même pour ![]() $T\mapsto B(T)$. De plus la transformation naturelle de foncteurs
$T\mapsto B(T)$. De plus la transformation naturelle de foncteurs
vérifie :
— elle est compatible aux identifications
 $B({\rm Res}_{E^{\prime}/E} T)=B(T)$ et
$B({\rm Res}_{E^{\prime}/E} T)=B(T)$ et  $H^1_{\rm{\acute {e}t}}(X_E,{\rm Res}_{E^{\prime}/E} T)= H^1_{\rm{\acute {e}t}}(X_{E^{\prime}},T)$;
$H^1_{\rm{\acute {e}t}}(X_E,{\rm Res}_{E^{\prime}/E} T)= H^1_{\rm{\acute {e}t}}(X_{E^{\prime}},T)$;— si
 $T=\mathbb {G}_m$ c'est un isomorphisme d'après le calcul de
$T=\mathbb {G}_m$ c'est un isomorphisme d'après le calcul de  ${\rm Pic} (X_E)$.
${\rm Pic} (X_E)$.
Le lemme 2.2 de [Reference KottwitzKot85] permet alors de conclure que c'est un isomorphisme.
Avec les notations de la section 2.3, il y a un triangle exacte

qui est le dévissage de ![]() $\tau _{\leq 2} Rf_*T$ en
$\tau _{\leq 2} Rf_*T$ en ![]() $f_*T$ et
$f_*T$ et ![]() $R^1 f_*T$. Il induit une suite exacte
$R^1 f_*T$. Il induit une suite exacte
Via l'isomorphisme de Kottwitz ([Reference KottwitzKot85] sec. 2.4)
cette suite exacte coïncide avec la suite exacte
où la flèche de droite s'interprète comme étant l'application ![]() $[b]\mapsto [\nu _b]$. Il suffit pour cela de vérifier que les différentes flêches sont compatibles à la restriction des scalaires des tores et que ces deux suites exactes s'identifient pour
$[b]\mapsto [\nu _b]$. Il suffit pour cela de vérifier que les différentes flêches sont compatibles à la restriction des scalaires des tores et que ces deux suites exactes s'identifient pour ![]() $T=\mathbb {G}_m$, ce qui ne pose pas de problème.
$T=\mathbb {G}_m$, ce qui ne pose pas de problème.
3. Cohomologie de la courbe à coefficients de torsion
Dans la section précédente on a étudié la cohomologie étale de ![]() $X$ à coefficients dans un tore. On va maintenant étudier la cohomologie étale du schémas
$X$ à coefficients dans un tore. On va maintenant étudier la cohomologie étale du schémas ![]() $X$ à coefficients dans des systèmes locaux de torsion.
$X$ à coefficients dans des systèmes locaux de torsion.
3.1 La classe fondamentale de la courbe
Commençons par le calcul suivant.
Proposition 3.1 Il y a un isomorphisme canonique
via lequel ![]() ${\rm tr}(c_1(\mathcal {O}_X(1)))=\bar {1}$.
${\rm tr}(c_1(\mathcal {O}_X(1)))=\bar {1}$.
Proof Démonstration Il suffit d'utiliser la théorie de Kummer couplée au théorème d'annulation, le théorème 2.2, et le calcul de ![]() ${\rm Pic}(X)=\mathbb {Z}=\langle [\mathcal {O}_X (1)]\rangle$.
${\rm Pic}(X)=\mathbb {Z}=\langle [\mathcal {O}_X (1)]\rangle$.
Remarquons que d'après le théorème de pureté de Gabber [Reference FujiwaraFuj02], puisque ![]() $X$ est régulier de dimension
$X$ est régulier de dimension ![]() $1$, si
$1$, si ![]() $i:Z\hookrightarrow X$ est un sous-schéma fermé propre, il y a un isomorphisme canonique
$i:Z\hookrightarrow X$ est un sous-schéma fermé propre, il y a un isomorphisme canonique
On dispose donc d'une application classe de cycle
et on vérifie qu'elle est compatible à la première classe de Chern utilisée précédemment via l'isomorphisme
Définition 3.2 On note
pour n'importe quel ![]() $x\in |X_E|$ la classe fondamentale de la courbe.
$x\in |X_E|$ la classe fondamentale de la courbe.
Remarquons la propriété suivante de compatibilité lorsque le corps ![]() $E$ varie.
$E$ varie.
Proposition 3.3 Soit ![]() $E^{\prime}|E$ de degré fini. Notons
$E^{\prime}|E$ de degré fini. Notons ![]() $\pi _{E^{\prime}/E}:X_{E^{\prime}}\rightarrow X_E$.
$\pi _{E^{\prime}/E}:X_{E^{\prime}}\rightarrow X_E$.
(1) Le diagramme suivant commute
et donc
 \[ \pi_{E^{\prime}/E}^*\, \eta_{X_E} = [E^{\prime}:E] \eta_{X_{E^{\prime}}}. \]
\[ \pi_{E^{\prime}/E}^*\, \eta_{X_E} = [E^{\prime}:E] \eta_{X_{E^{\prime}}}. \](2) Le diagramme suivante
et donc
 \[ \pi_{E^{\prime}/E!}\,\eta_{X_{E^{\prime}}} = \eta_{X_E}. \]
\[ \pi_{E^{\prime}/E!}\,\eta_{X_{E^{\prime}}} = \eta_{X_E}. \]
Proof Démonstration On utilise les notations de la section 8.2 de [Reference Fargues and FontaineFF18]. Le point (1) est une conséquence de ce que l'image réciproque de ![]() $\mathcal {O}_{X_E}(1)$ à
$\mathcal {O}_{X_E}(1)$ à ![]() $X_{E^{\prime}}$ est isomorphe à
$X_{E^{\prime}}$ est isomorphe à ![]() $\mathcal {O}_{X_{E^{\prime}}}([E^{\prime}:E])$. Le point (2) quant à lui résulte de ce que
$\mathcal {O}_{X_{E^{\prime}}}([E^{\prime}:E])$. Le point (2) quant à lui résulte de ce que
 \begin{align*} \det (\pi_{E^{\prime}/E*} \mathcal{O}_{X_{E^{\prime}}}(1)) &= \det \biggl(\mathcal{O}_{X_{E}} \biggl(\frac{1}{[E^{\prime}:E]}\biggr)\biggr) \\ &\simeq \mathcal{O}_{X_{E}} (1) \end{align*}
\begin{align*} \det (\pi_{E^{\prime}/E*} \mathcal{O}_{X_{E^{\prime}}}(1)) &= \det \biggl(\mathcal{O}_{X_{E}} \biggl(\frac{1}{[E^{\prime}:E]}\biggr)\biggr) \\ &\simeq \mathcal{O}_{X_{E}} (1) \end{align*}et de ce que
Normalisons la théorie du corps de classe de telle manière que le Frobenius arithmétique corresponde à une uniformisante.
Proposition 3.4 Via l'application ![]() ${\rm Br}(E)[n]=H^2 (E,\mu _n)\longrightarrow H^2_{\rm{\acute {e}t}}(X_E,\mu _n)$ la classe fondamentale de la théorie du corps de classe s'envoie sur la classe fondamentale de la courbe
${\rm Br}(E)[n]=H^2 (E,\mu _n)\longrightarrow H^2_{\rm{\acute {e}t}}(X_E,\mu _n)$ la classe fondamentale de la théorie du corps de classe s'envoie sur la classe fondamentale de la courbe ![]() $\eta _{X_E}$.
$\eta _{X_E}$.
Proof Démonstration Soit ![]() $D_{1/n}$ l'algèbre à division sur
$D_{1/n}$ l'algèbre à division sur ![]() $E$ des automorphismes de l'isocristal isocline de pente
$E$ des automorphismes de l'isocristal isocline de pente ![]() $-1/n$. Sa classe dans le groupe de Brauer de
$-1/n$. Sa classe dans le groupe de Brauer de ![]() $E$ est la classe fondamentale de la théorie du corps de classe associée à l'extension non-ramifiée de degré
$E$ est la classe fondamentale de la théorie du corps de classe associée à l'extension non-ramifiée de degré ![]() $n$ de
$n$ de ![]() $E$. De plus
$E$. De plus
On a un diagramme commutatif
duquel on déduit en chassant les cocycles de Cech non abéliens que l'application composée
coïncide avec
La proposition découle alors de ce que
Remarque 3.5 Traditionnellement ([Reference SerreSer68] chap. XI § 3) la classe fondamentale en théorie du corps de classe local est associée à une extension de degré fini ![]() $E^{\prime}|E$. Du point de vue de la courbe on définit
$E^{\prime}|E$. Du point de vue de la courbe on définit ![]() $u_{E^{\prime}/E}\in H^2 (E^{\prime}|E,\mathbb {G}_m)$ de la façon suivante. On remarque que
$u_{E^{\prime}/E}\in H^2 (E^{\prime}|E,\mathbb {G}_m)$ de la façon suivante. On remarque que ![]() $\pi _{E^{\prime}/E}^*\mathcal {O}_{X_E}(1)\simeq \mathcal {O}_{X_{E^{\prime}}}([E^{\prime}:E])$. Posons
$\pi _{E^{\prime}/E}^*\mathcal {O}_{X_E}(1)\simeq \mathcal {O}_{X_{E^{\prime}}}([E^{\prime}:E])$. Posons ![]() $n=[E^{\prime}:E]$. La
$n=[E^{\prime}:E]$. La ![]() $\mu _n$-gerbe des racines
$\mu _n$-gerbe des racines ![]() $n$-ièmes de
$n$-ièmes de ![]() $\mathcal {O}_{X_E}(1)$ est donc neutralisée par le revêtement
$\mathcal {O}_{X_E}(1)$ est donc neutralisée par le revêtement ![]() $X_{E^{\prime}}\rightarrow X_E$. Il s'en suit que
$X_{E^{\prime}}\rightarrow X_E$. Il s'en suit que ![]() $c_1(\mathcal {O}_{X_E}(1))\in \check {H}^2 (X_{E^{\prime}}/X_{E},\mu _n)$ qui est la classe de cohomologie de cette gerbe.
$c_1(\mathcal {O}_{X_E}(1))\in \check {H}^2 (X_{E^{\prime}}/X_{E},\mu _n)$ qui est la classe de cohomologie de cette gerbe.
Remarque 3.6 Le problème existentiel usuel des théoriciens des nombres qui consiste à savoir si l'on doit normaliser la théorie du corps de classe en se faisant se correspondre un Frobenius ou bien un Frobenius géométrique et une uniformisante se reflète ici en le choix d'un générateur de ![]() ${\rm Pic} (X)$ :
${\rm Pic} (X)$ : ![]() $[\mathcal {O}_X(1)]$ (choix du générateur ample) ou bien
$[\mathcal {O}_X(1)]$ (choix du générateur ample) ou bien ![]() $[\mathcal {O}_X(-1)]$ (générateur anti-ample).
$[\mathcal {O}_X(-1)]$ (générateur anti-ample).
3.2 Cohomologie de la courbe à coefficients dans un système local
On peut maintenant en venir au point principal qui dit que l'on peut calculer la cohomologie galoisienne de ![]() $E$ à coefficients de torsion en termes de la cohomologie étale de la courbe.
$E$ à coefficients de torsion en termes de la cohomologie étale de la courbe.
Théorème 3.7 Notons ![]() $f:X\rightarrow {\rm Spec} (E)$ et soit
$f:X\rightarrow {\rm Spec} (E)$ et soit ![]() $\mathscr {F}$ un système locale étale de torsion sur
$\mathscr {F}$ un système locale étale de torsion sur ![]() ${\rm Spec} (E)$. Pour
${\rm Spec} (E)$. Pour ![]() $0\leq i\leq 2$ il y a un isomorphisme
$0\leq i\leq 2$ il y a un isomorphisme
Proof Démonstration Commençons par vérifier que pour ![]() $i\in \{1,2\}$ on a
$i\in \{1,2\}$ on a
Pour cela il suffit de vérifier que pour tout entier ![]() $n\geq 1$,
$n\geq 1$,
Cela résulte alors de la suite exacte longue de Kummer couplée au fait que
 \begin{align*} {\rm Pic} (X_{\bar{E}})&= \mathbb{Q}, \\ H^2_{\rm{\acute{e}t}} (X_{\bar{E}},\mathbb{G}_m) &= \underset{E^{\prime}|E{\rm finie}}{\underset{\longrightarrow}{{\rm lim }}\;} H^2_{\rm{\acute{e}t}} (X_{E^{\prime}},\mathbb{G}_m) \\ &= 0 \end{align*}
\begin{align*} {\rm Pic} (X_{\bar{E}})&= \mathbb{Q}, \\ H^2_{\rm{\acute{e}t}} (X_{\bar{E}},\mathbb{G}_m) &= \underset{E^{\prime}|E{\rm finie}}{\underset{\longrightarrow}{{\rm lim }}\;} H^2_{\rm{\acute{e}t}} (X_{E^{\prime}},\mathbb{G}_m) \\ &= 0 \end{align*}d'après le théorème 2.2.
On peut maintenant appliquer la suite spectrale de Hochschild-Serre
pour conclure.
Rappelons que ![]() $X_{\bar {E}}$ est simplement connexe ([Reference Fargues and FontaineFF18] théo. 8.6.1). On en déduit le résultat suivant en utilisant la dualité de Tate-Nakayama et la formule de Tate pour la caractéristique d'Euler-Poincaré de la cohomologie galoisienne ([Reference SerreSer94] chap. II § 5 5.7).
$X_{\bar {E}}$ est simplement connexe ([Reference Fargues and FontaineFF18] théo. 8.6.1). On en déduit le résultat suivant en utilisant la dualité de Tate-Nakayama et la formule de Tate pour la caractéristique d'Euler-Poincaré de la cohomologie galoisienne ([Reference SerreSer94] chap. II § 5 5.7).
Corollaire 3.8 Soit ![]() $\mathscr {G}$ un système local étale de torsion sur
$\mathscr {G}$ un système local étale de torsion sur ![]() $X$. Si
$X$. Si ![]() $f:X\rightarrow {\rm Spec} (E)$ on a alors
$f:X\rightarrow {\rm Spec} (E)$ on a alors
De plus si ![]() $\mathscr {G}^{\vee }$ désigne son dual de Pontryagin :
$\mathscr {G}^{\vee }$ désigne son dual de Pontryagin :
(1) Il y a un accouplement parfait de dualité de Poincaré pour
 $0\leq i\leq 2$
qui s'interprète comme la dualité de Tate-Nakayama.
$0\leq i\leq 2$
qui s'interprète comme la dualité de Tate-Nakayama. \[ H^i_{\rm{\acute{e}t}} (X,\mathscr{G})\times H^{2-i}_{\rm{\acute{e}t}} (X,\mathscr{G}^{\vee}(1))\longrightarrow H^2 (X,\mathbb{Q}/\mathbb{Z} (1))\underset{\sim}{\xrightarrow{\ {\rm tr}\ }} \mathbb{Q}/\mathbb{Z} \]
\[ H^i_{\rm{\acute{e}t}} (X,\mathscr{G})\times H^{2-i}_{\rm{\acute{e}t}} (X,\mathscr{G}^{\vee}(1))\longrightarrow H^2 (X,\mathbb{Q}/\mathbb{Z} (1))\underset{\sim}{\xrightarrow{\ {\rm tr}\ }} \mathbb{Q}/\mathbb{Z} \](2) On dispose d'une formule pour la caractéristique d'Euler-Poincaré
qui s'interprète comme la formule de Tate. \[ \prod_{i=0}^2 \big | H^i_{\rm{\acute{e}t}} (X,\mathscr{G})\big |^{(-1)^i} = |\mathscr{G}|_E. \]
\[ \prod_{i=0}^2 \big | H^i_{\rm{\acute{e}t}} (X,\mathscr{G})\big |^{(-1)^i} = |\mathscr{G}|_E. \]
3.3 Quelques conjectures
À la vue des résultats précédents la conjecture suivante s'impose.
Conjecture 3.9 Pour ![]() $\mathscr {F}$ un faisceau étale de torsion sur
$\mathscr {F}$ un faisceau étale de torsion sur ![]() $X$ on a
$X$ on a ![]() $H^i(X,\mathscr {F})=0$ lorsque
$H^i(X,\mathscr {F})=0$ lorsque ![]() $i\geq 3$.
$i\geq 3$.
La conjecture se ramène bien sûr au cas des faisceaux constructibles et donc au cas de ![]() $j_!\mathscr {G}$ où
$j_!\mathscr {G}$ où ![]() $j:U\hookrightarrow X$ est l'inclusion d'un ouvert non vide de
$j:U\hookrightarrow X$ est l'inclusion d'un ouvert non vide de ![]() $X$ et
$X$ et ![]() $\mathscr {G}$ un système local sur
$\mathscr {G}$ un système local sur ![]() $U$. Dans la suite on notera
$U$. Dans la suite on notera
Voici deux méthodes pour attaquer cette conjecture. La première est de constater qu'elle résulte de la suivante (théorème de Tsen pour les courbes ‘usuelles’ sur un corps algébriquement clos).
Conjecture 3.10 Le corps des fonctions rationnelles sur ![]() $X$,
$X$, ![]() $E(X)$, est (C1).
$E(X)$, est (C1).
Une des motivations est qu'il semble qu'un analogue de la courbe ![]() $X_E$ dans le cas
$X_E$ dans le cas ![]() $E=\mathbb {R}$ soit lié à la conique sans point réel
$E=\mathbb {R}$ soit lié à la conique sans point réel ![]() $x^2+y^2+z^2=0$,
$x^2+y^2+z^2=0$, ![]() $[x:y:z]\in \mathbb {P}^2_\mathbb {R}$, c'est à dire la forme tordue de
$[x:y:z]\in \mathbb {P}^2_\mathbb {R}$, c'est à dire la forme tordue de ![]() $\mathbb {P}^1_{\mathbb {R}}$ sans points réels. Or, il est conjecturé que le corps des fonctions de cette courbe est (C1) ([Reference LangLan53] p. 379) contrairement au corps des fonctions de
$\mathbb {P}^1_{\mathbb {R}}$ sans points réels. Or, il est conjecturé que le corps des fonctions de cette courbe est (C1) ([Reference LangLan53] p. 379) contrairement au corps des fonctions de ![]() $\mathbb {P}^1_{\mathbb {R}}$ qui n'est pas (C1) pour des raisons évidentes. Bien sûr lorsque
$\mathbb {P}^1_{\mathbb {R}}$ qui n'est pas (C1) pour des raisons évidentes. Bien sûr lorsque ![]() $E=\mathbb {C}$ ce corps est (C1) d'après Tsen.
$E=\mathbb {C}$ ce corps est (C1) d'après Tsen.
Une autre façon d'attaquer la conjecture 3.9 est la suivante. Rappelons que l'on peut définir un pendant adique ![]() $X^{ad}$ de la courbe schématique
$X^{ad}$ de la courbe schématique ![]() $X$ ([Reference FarguesFar15] sec. 2 et [Reference FarguesFar16]). Il y un morphisme continu de sites étales
$X$ ([Reference FarguesFar15] sec. 2 et [Reference FarguesFar16]). Il y un morphisme continu de sites étales
Avec les notations de [Reference Fargues and FontaineFF18] cela résulte de l'existence d'un morphisme de ind-schémas ![]() $\varphi$-invariant
$\varphi$-invariant
et de ce que les algèbres de Banach ![]() $B_I$ sont fortement noethériennes [Reference KedlayaKed14]. En effet, puisque
$B_I$ sont fortement noethériennes [Reference KedlayaKed14]. En effet, puisque ![]() $B_I$ est fortement noethérienne, pour
$B_I$ est fortement noethérienne, pour ![]() $U\rightarrow {\rm Spec} (B_I)$ étale on peut définir naturellement son adifié qui est un morphisme étale
$U\rightarrow {\rm Spec} (B_I)$ étale on peut définir naturellement son adifié qui est un morphisme étale ![]() $U^{ad}\rightarrow \hbox {Spa} (B_I,B_I^{\circ })$ et cela définit un morphisme continu de sites
$U^{ad}\rightarrow \hbox {Spa} (B_I,B_I^{\circ })$ et cela définit un morphisme continu de sites
On peut alors formuler la conjecture suivante.
Conjecture 3.11 Pour tout faisceau étale de torsion ![]() $\mathscr {F}$ sur
$\mathscr {F}$ sur ![]() $X$ le morphisme continu
$X$ le morphisme continu ![]() $X^{ad}_{\rm{\acute {e}t}}\rightarrow X_{\rm{\acute {e}t}}$ induit un isomorphisme
$X^{ad}_{\rm{\acute {e}t}}\rightarrow X_{\rm{\acute {e}t}}$ induit un isomorphisme
Passons maintenant à la question de l'extension de la dualité de Poincaré aux faisceaux constructibles qui se dévisse à la conjecture suivante.
Conjecture 3.12 Soit ![]() $U\subset X$ un ouvert non vide de
$U\subset X$ un ouvert non vide de ![]() $X$ et
$X$ et ![]() $\mathscr {F}$ un système local étale de torsion sur
$\mathscr {F}$ un système local étale de torsion sur ![]() $U$. Pour
$U$. Pour ![]() $0\leq i\leq 2$ l'accouplement
$0\leq i\leq 2$ l'accouplement
est parfait.
Cette conjecture étant supposée vérifiée, se pose la question de son interprétation comme généralisation de la dualité de Tate-Nakayama. On peut également se demander si la bonne notion qui s'interprète agréablement comme généralisation de la dualité de Tate-Nakayama n'est pas plutôt la cohomologie d'intersection ![]() $\mathbb {H}^i (X,\mathscr {F}):=H^i(X,j_*\mathscr {F})$ qui devrait être autoduale.
$\mathbb {H}^i (X,\mathscr {F}):=H^i(X,j_*\mathscr {F})$ qui devrait être autoduale.
4. Interprétation de l'application  $\kappa$ de Kottwitz pour les tores en termes de classe de Chern équivariante
$\kappa$ de Kottwitz pour les tores en termes de classe de Chern équivariante
Si ![]() $T$ est un tore sur un corps algébriquement clos de caractéristique
$T$ est un tore sur un corps algébriquement clos de caractéristique ![]() $0$ il y a un unique isomorphisme
$0$ il y a un unique isomorphisme
fonctoriel en ![]() $T$ et tel que pour
$T$ et tel que pour ![]() $T=\mathbb {G}_m$ celui-si soit donné par la classe de Chern d'un fibré en droites. Soit maintenant
$T=\mathbb {G}_m$ celui-si soit donné par la classe de Chern d'un fibré en droites. Soit maintenant ![]() $T$ un tore sur
$T$ un tore sur ![]() $E$. On note
$E$. On note ![]() $\Gamma ={\rm Gal} (\bar {E}|E)$. La suite spectrale de Hochschild-Serre fournit une suite exacte
$\Gamma ={\rm Gal} (\bar {E}|E)$. La suite spectrale de Hochschild-Serre fournit une suite exacte
 \[ 0\longrightarrow \mathrm{Br} (E)\longrightarrow H^2_{\rm{\acute{e}t}} (BT,\mathbb{Q}/\mathbb{Z} (1)) \longrightarrow \underbrace{\big ( X^*(T)\otimes_\mathbb{Z} \mathbb{Q}/\mathbb{Z}\big )^\Gamma }_{(X_*(T)_\Gamma)^D}\longrightarrow 0 \]
\[ 0\longrightarrow \mathrm{Br} (E)\longrightarrow H^2_{\rm{\acute{e}t}} (BT,\mathbb{Q}/\mathbb{Z} (1)) \longrightarrow \underbrace{\big ( X^*(T)\otimes_\mathbb{Z} \mathbb{Q}/\mathbb{Z}\big )^\Gamma }_{(X_*(T)_\Gamma)^D}\longrightarrow 0 \]
où ![]() $(-)^D$ désigne la dualité de Pontryagin. En écrivant
$(-)^D$ désigne la dualité de Pontryagin. En écrivant
on obtient un accouplement
via l'isomorphisme trace (prop. 3.1). Puisque l'application ![]() $\mathrm {Br}(E)\rightarrow \mathrm {Br}(X)$ est nulle (prop. 2.1), cet accouplement est nul sur
$\mathrm {Br}(E)\rightarrow \mathrm {Br}(X)$ est nulle (prop. 2.1), cet accouplement est nul sur ![]() $\mathrm {Br}(E)\subset H^2_{\rm{\acute {e}t}} (BT,\mathbb {Q}/\mathbb {Z} (1))$. Il induit donc un morphisme
$\mathrm {Br}(E)\subset H^2_{\rm{\acute {e}t}} (BT,\mathbb {Q}/\mathbb {Z} (1))$. Il induit donc un morphisme
le complété profini de ![]() $X_*(T)_{\Gamma }$. Rappelons maintenant que Kottwitz a construit dans [Reference KottwitzKot85] un isomorphisme canonique
$X_*(T)_{\Gamma }$. Rappelons maintenant que Kottwitz a construit dans [Reference KottwitzKot85] un isomorphisme canonique
dont l'inverse est noté ![]() $\kappa$.
$\kappa$.
Proposition 4.1 Via l'isomorphisme ![]() $B(T)\xrightarrow {\sim } H^1_{\rm{\acute {e}t}}(X,T)$ l'application classe Chern
$B(T)\xrightarrow {\sim } H^1_{\rm{\acute {e}t}}(X,T)$ l'application classe Chern ![]() $T$-équivariante
$T$-équivariante ![]() $c_1^T$ coïncide avec l'opposé de l'application
$c_1^T$ coïncide avec l'opposé de l'application ![]() $\kappa$ de Kottwitz composée avec l'inclusion de
$\kappa$ de Kottwitz composée avec l'inclusion de ![]() $X_* (T)_\Gamma$ dans son complété profini.
$X_* (T)_\Gamma$ dans son complété profini.
Proof Démonstration Le morphisme ![]() $c_1^T$ est fonctoriel en
$c_1^T$ est fonctoriel en ![]() $T$. De plus, si
$T$. De plus, si ![]() $E^{\prime}|E$ le diagramme
$E^{\prime}|E$ le diagramme
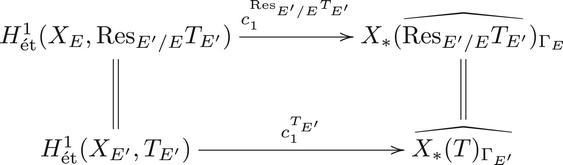
commute. Lorsque ![]() $T=\mathbb {G}_m$ les deux applications
$T=\mathbb {G}_m$ les deux applications ![]() $c_1^{\mathbb {G}_m}$ et
$c_1^{\mathbb {G}_m}$ et ![]() $-\kappa$ coïncident car à une uniformisante
$-\kappa$ coïncident car à une uniformisante ![]() $\pi _E\in T(E)$ est associé le fibré
$\pi _E\in T(E)$ est associé le fibré ![]() $\mathcal {O}_{X_E}(-1)$ de classe de Chern
$\mathcal {O}_{X_E}(-1)$ de classe de Chern ![]() $-1$. Les deux foncteurs
$-1$. Les deux foncteurs ![]() $T\mapsto H^1_{\rm{\acute {e}t}}(X,T)$ et
$T\mapsto H^1_{\rm{\acute {e}t}}(X,T)$ et ![]() $T\mapsto \widehat {X_*(T)_\Gamma }$ étant exactes à droite on en déduit le résultat (cf. [Reference KottwitzKot85] sec. 2.1).
$T\mapsto \widehat {X_*(T)_\Gamma }$ étant exactes à droite on en déduit le résultat (cf. [Reference KottwitzKot85] sec. 2.1).
5. Classification des  $G$-torseurs
$G$-torseurs
Dans cette section on montre le résultat principal suivant.
Théorème 5.1 Pour ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $E$ il y a une bijection d'ensembles pointés
$E$ il y a une bijection d'ensembles pointés
 \begin{align*} B(G) & \xrightarrow{\;\sim\;} H^1_{\rm{\acute{e}t}}(X,G) \\ {[} b] & \longmapsto [\mathscr{E}_b]. \end{align*}
\begin{align*} B(G) & \xrightarrow{\;\sim\;} H^1_{\rm{\acute{e}t}}(X,G) \\ {[} b] & \longmapsto [\mathscr{E}_b]. \end{align*}Le plan de la preuve est le suivant :
— On commence par montrer dans la section 5.2 que les classes d'isomorphisme de
 $G$-torseurs sur
$G$-torseurs sur  $X$ s'identifient aux classes de
$X$ s'identifient aux classes de  $\varphi$-conjugaison dans
$\varphi$-conjugaison dans  $G(\bar {B})$ où
$G(\bar {B})$ où  $\bar {B}$ est un anneau de théorie de Hodge
$\bar {B}$ est un anneau de théorie de Hodge  $p$-adique introduit dans [Reference Fargues and FontaineFF18].
$p$-adique introduit dans [Reference Fargues and FontaineFF18].— On traite ensuite le cas où le groupe
 $G$ est quasi-déployé dans la section 5.3. Ce cas là se divise en deux :
$G$ est quasi-déployé dans la section 5.3. Ce cas là se divise en deux :
• Le cas semi-stable (sec. 5.3.1) que l'on traite via les classes de
 $\varphi$-conjugaison dans
$\varphi$-conjugaison dans  $G(\bar {B})$.
$G(\bar {B})$.• La réduction au cas semi-stable qui se ramène au cas précédent en montrant que tout torseur possède une réduction semi-stable à un sous-groupe de Levi (sec. 5.3.2), un énoncé analogue au fait que pour
 $G=\hbox {GL}_n$ la filtration de Harder-Narasimhan est scindée.
$G=\hbox {GL}_n$ la filtration de Harder-Narasimhan est scindée.
— On conclut le cas
 $G$ général par un argument de descente galoisienne non-ramifiée dans la section 5.4.
$G$ général par un argument de descente galoisienne non-ramifiée dans la section 5.4.
5.1 Réduction canonique d'un  $G$-torseur
$G$-torseur
La théorie de Harder-Narasimhan de la réduction des ![]() $\hbox {GL}_n$-torseurs sur les courbes propres et lisses sur un corps [Reference Harder and NarasimhanHN74] a été étendue au cadre des groupes réductifs par Atiyah et Bott dans [Reference Atiyah and BottAB83]. Atiyah et Bott se placent dans le contexte des torseurs sur une surface de Riemann compacte. Cependant Biswas et Holla montrent dans [Reference Biswas and HollaBH04] qu'une telle théorie existe dans le contexte des
$\hbox {GL}_n$-torseurs sur les courbes propres et lisses sur un corps [Reference Harder and NarasimhanHN74] a été étendue au cadre des groupes réductifs par Atiyah et Bott dans [Reference Atiyah and BottAB83]. Atiyah et Bott se placent dans le contexte des torseurs sur une surface de Riemann compacte. Cependant Biswas et Holla montrent dans [Reference Biswas and HollaBH04] qu'une telle théorie existe dans le contexte des ![]() $G$-torseurs sur une courbe propre et lisse sur un corps algébriquement clos de caractéristique
$G$-torseurs sur une courbe propre et lisse sur un corps algébriquement clos de caractéristique ![]() $0$. Ici
$0$. Ici ![]() $G$ est un groupe réductif constant c'est à dire défini sur le corps de base. Lorsque
$G$ est un groupe réductif constant c'est à dire défini sur le corps de base. Lorsque ![]() $G$ n'est plus constant, c'est à dire est un schéma en groupes réductifs sur la courbe, Behrend a développé dans [Reference BehrendBeh95] une théorie de la réduction d'un
$G$ n'est plus constant, c'est à dire est un schéma en groupes réductifs sur la courbe, Behrend a développé dans [Reference BehrendBeh95] une théorie de la réduction d'un ![]() $G$-torseur
$G$-torseur ![]() $\mathscr {T}$ en termes de sous-groupe parabolique canonique du schéma en groupes réductif
$\mathscr {T}$ en termes de sous-groupe parabolique canonique du schéma en groupes réductif ![]() $\underline {{\rm Aut}}(\mathscr {T})$ forme intérieure de
$\underline {{\rm Aut}}(\mathscr {T})$ forme intérieure de ![]() $G$. Enfin, remarquons qu'un point de vue Tannakien sur les filtrations dans les catégories Tannakiennes est étudié en détails dans [Reference ZieglerZie15] en complément des résultats de [Reference Saavedra RivanoSR72] dont nous utiliserons parfois les résultats. On pourra également se référer à [Reference CornutCor] pour des résultats généralisant ceux de [Reference ZieglerZie15] pour les groupes non constants.
$G$. Enfin, remarquons qu'un point de vue Tannakien sur les filtrations dans les catégories Tannakiennes est étudié en détails dans [Reference ZieglerZie15] en complément des résultats de [Reference Saavedra RivanoSR72] dont nous utiliserons parfois les résultats. On pourra également se référer à [Reference CornutCor] pour des résultats généralisant ceux de [Reference ZieglerZie15] pour les groupes non constants.
Revenons à notre courbe ![]() $X$ sur
$X$ sur ![]() $E$. Soit
$E$. Soit ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $E$. Si
$E$. Si ![]() $\mathscr {T}$ est un
$\mathscr {T}$ est un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$ et
$X$ et ![]() $H$ un sous-groupe algébrique de
$H$ un sous-groupe algébrique de ![]() $G$ par définition une réduction de
$G$ par définition une réduction de ![]() $\mathscr {T}$ à
$\mathscr {T}$ à ![]() $H$ est la donnée d'un
$H$ est la donnée d'un ![]() $H$-torseur
$H$-torseur ![]() $\mathscr {T}_H$ ainsi que d'un isomorphisme
$\mathscr {T}_H$ ainsi que d'un isomorphisme
Par abus de notations on notera ![]() $\mathscr {T}_H$ une telle réduction, l'isomorphisme précédent étant supposé fixé. Rappelons également qu'une réduction de
$\mathscr {T}_H$ une telle réduction, l'isomorphisme précédent étant supposé fixé. Rappelons également qu'une réduction de ![]() $\mathscr {T}$ coïncide avec la donné d'une section de la fibration
$\mathscr {T}$ coïncide avec la donné d'une section de la fibration
étale localement triviale de fibre ![]() $G/H$. On vérifie que les résultats de [Reference Biswas and HollaBH04] s'appliquent aux
$G/H$. On vérifie que les résultats de [Reference Biswas and HollaBH04] s'appliquent aux ![]() $G$-torseurs sur
$G$-torseurs sur ![]() $X_{\bar {E}}$. Supposons maintenant de plus que
$X_{\bar {E}}$. Supposons maintenant de plus que ![]() $G$ est quasi-déployé et fixons un sous-groupe de Borel
$G$ est quasi-déployé et fixons un sous-groupe de Borel ![]() $B$ de
$B$ de ![]() $G$. Soit
$G$. Soit ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X_E$ et
$X_E$ et ![]() $\mathscr {T}_{\bar {E}}$ son image réciproque sur
$\mathscr {T}_{\bar {E}}$ son image réciproque sur ![]() $X_{\bar {E}}$. Il existe alors un sous-groupe parabolique standard
$X_{\bar {E}}$. Il existe alors un sous-groupe parabolique standard ![]() $P$ dans
$P$ dans ![]() $G_{\bar {E}}$ et une réduction canonique
$G_{\bar {E}}$ et une réduction canonique ![]() $\mathscr {T}_{\bar {E},P}$ de
$\mathscr {T}_{\bar {E},P}$ de ![]() $\mathscr {T}_{\bar {E}}$ à
$\mathscr {T}_{\bar {E}}$ à ![]() $P$ telle que si
$P$ telle que si ![]() $M$ désigne le quotient de Levi de
$M$ désigne le quotient de Levi de ![]() $P$
$P$
soit semi-stable. Appliquant la propriété de canonicité à ![]() $(P^\sigma ,\mathscr {T}_{\bar {E},P}^{\sigma })$ pour
$(P^\sigma ,\mathscr {T}_{\bar {E},P}^{\sigma })$ pour ![]() $\sigma \in {\rm Gal} (\bar {E}|E)$ on constate alors que
$\sigma \in {\rm Gal} (\bar {E}|E)$ on constate alors que ![]() $(P,\mathscr {T}_{\bar {E},P})$ descendent sur
$(P,\mathscr {T}_{\bar {E},P})$ descendent sur ![]() $E$ en un couple
$E$ en un couple ![]() $(Q,\mathscr {T}_Q)$ que l'on appelle la réduction canonique de
$(Q,\mathscr {T}_Q)$ que l'on appelle la réduction canonique de ![]() $\mathscr {T}$.
$\mathscr {T}$.
Étant donné un ![]() $G$-torseur
$G$-torseur ![]() $\mathscr {T}$ sur
$\mathscr {T}$ sur ![]() $X$ on note
$X$ on note
 \begin{align*} {\rm Ad} (\mathscr{T}) &= \mathscr{T}\underset{G,{\rm Ad}}{\times} {\rm Lie}\, G \\ &= {\rm Lie} ( \underline{{\rm Aut}} (\mathscr{T})) \end{align*}
\begin{align*} {\rm Ad} (\mathscr{T}) &= \mathscr{T}\underset{G,{\rm Ad}}{\times} {\rm Lie}\, G \\ &= {\rm Lie} ( \underline{{\rm Aut}} (\mathscr{T})) \end{align*}
le fibré vectoriel en algèbres de Lie associé via la représentation adjointe. Dans la formule précédente ![]() $\underline {{\rm Aut}}(\mathscr {T})$ s'interprète également comme étant la forme intérieure de
$\underline {{\rm Aut}}(\mathscr {T})$ s'interprète également comme étant la forme intérieure de ![]() $G\times X$ obtenue par torsion par
$G\times X$ obtenue par torsion par ![]() $\mathscr {T}$ via l'action par automorphismes intérieures de
$\mathscr {T}$ via l'action par automorphismes intérieures de ![]() $G$ sur lui-même.
$G$ sur lui-même.
Notons ![]() $A\subset T\subset B$ où
$A\subset T\subset B$ où ![]() $A$ est un tore déployé maximal,
$A$ est un tore déployé maximal, ![]() $T$ un tore maximal et
$T$ un tore maximal et ![]() $B$ un sous-groupe de Borel. On utilisera dans la suite les propriétés suivantes pour
$B$ un sous-groupe de Borel. On utilisera dans la suite les propriétés suivantes pour ![]() $\mathscr {T}$ de réduction canonique
$\mathscr {T}$ de réduction canonique ![]() $\mathscr {T}_P$ :
$\mathscr {T}_P$ :
(1)
 $\mathscr {T}$ est semi-stable si et seulement si le fibré de pente
$\mathscr {T}$ est semi-stable si et seulement si le fibré de pente  $0$
$0$  ${\rm Ad}(\mathscr {T})$ est semi-stable.
${\rm Ad}(\mathscr {T})$ est semi-stable.(2) L'application
est Galois invariante et définit donc un élément \begin{align*} X^* (P) & \longrightarrow \mathbb{Z} \\ \chi & \longmapsto \deg \big ( \chi_* \mathscr{T}_P\big ) \end{align*}que l'on voit comme étant un morphisme
\begin{align*} X^* (P) & \longrightarrow \mathbb{Z} \\ \chi & \longmapsto \deg \big ( \chi_* \mathscr{T}_P\big ) \end{align*}que l'on voit comme étant un morphisme \[ \nu_{\mathscr{T}}\in X_*(A)_\mathbb{Q} = X_*(T)_\mathbb{Q}^{{\rm Gal} (\bar{E}|E)} = {\rm Hom} (X^*(P),\mathbb{Q})^{{\rm Gal} (\bar{E}|E)} \]où
\[ \nu_{\mathscr{T}}\in X_*(A)_\mathbb{Q} = X_*(T)_\mathbb{Q}^{{\rm Gal} (\bar{E}|E)} = {\rm Hom} (X^*(P),\mathbb{Q})^{{\rm Gal} (\bar{E}|E)} \]où \[ \nu_{\mathscr{T}} :\mathbb{D}\longrightarrow A \]
\[ \nu_{\mathscr{T}} :\mathbb{D}\longrightarrow A \] $\mathbb {D}$ est le pro-tore des pentes,
$\mathbb {D}$ est le pro-tore des pentes,  $X^*(D)=\mathbb {Q}$.
$X^*(D)=\mathbb {Q}$.(3) On a
la chambre de Weyl positive relativement au sous-groupe de Borel \[ \nu_{\mathscr{T}} \in X^*(A)_{\mathbb{Q}}^+ \]
\[ \nu_{\mathscr{T}} \in X^*(A)_{\mathbb{Q}}^+ \] $B$.
$B$.(4) Le sous-groupe parabolique
 $P$ est celui associé à
$P$ est celui associé à  $\nu _{\mathscr {T}}$.
$\nu _{\mathscr {T}}$.(5) Pour
 $\lambda \in \mathbb {Q}$ soit
$\lambda \in \mathbb {Q}$ soit  ${\rm Ad} (\mathscr {T})^{\geq \lambda }$ la partie de pente
${\rm Ad} (\mathscr {T})^{\geq \lambda }$ la partie de pente  $\geq \lambda$ dans la filtration de Harder-Narasimhan de
$\geq \lambda$ dans la filtration de Harder-Narasimhan de  ${\rm Ad} (\mathscr {T})$. On a alors
${\rm Ad} (\mathscr {T})$. On a alors
 \begin{align*} [ {\rm Ad} (\mathscr{T})^{\geq \lambda}, {\rm Ad} (\mathscr{T})^{\geq \mu}] & \subset {\rm Ad} (\mathscr{T})^{\geq \lambda+\mu},\\ {\rm Lie} (\underline{{\rm Aut}} (\mathscr{T}_P)) & = {\rm Ad} (\mathscr{T})^{\geq 0}, \\ {\rm Lie} (R_u \underline{{\rm Aut}} (\mathscr{T}_P)) & = {\rm Ad} (\mathscr{T})^{>0}. \end{align*}
\begin{align*} [ {\rm Ad} (\mathscr{T})^{\geq \lambda}, {\rm Ad} (\mathscr{T})^{\geq \mu}] & \subset {\rm Ad} (\mathscr{T})^{\geq \lambda+\mu},\\ {\rm Lie} (\underline{{\rm Aut}} (\mathscr{T}_P)) & = {\rm Ad} (\mathscr{T})^{\geq 0}, \\ {\rm Lie} (R_u \underline{{\rm Aut}} (\mathscr{T}_P)) & = {\rm Ad} (\mathscr{T})^{>0}. \end{align*}(6) Le sous-groupe parabolique
 $\mathscr {P}=\underline {{\rm Aut}} (\mathscr {T}_P)\subset \underline {{\rm Aut}} (\mathscr {T})$ est le groupe des automorphismes du foncteur fibre filtré
au sens de [Reference ZieglerZie15] (théo. 4.40) donné par la filtration de Harder-Narasimhan d'un fibré vectoriel. Il admet une filtration
$\mathscr {P}=\underline {{\rm Aut}} (\mathscr {T}_P)\subset \underline {{\rm Aut}} (\mathscr {T})$ est le groupe des automorphismes du foncteur fibre filtré
au sens de [Reference ZieglerZie15] (théo. 4.40) donné par la filtration de Harder-Narasimhan d'un fibré vectoriel. Il admet une filtration
 $\mathscr {P}^{\geq \lambda }$,
$\mathscr {P}^{\geq \lambda }$,  $\lambda \in \mathbb {Q}_{\geq 0}$, telle que
et pour
$\lambda \in \mathbb {Q}_{\geq 0}$, telle que
et pour \[ \mathscr{P}^{>0}=R_u \mathscr{P} \]
\[ \mathscr{P}^{>0}=R_u \mathscr{P} \] $\lambda >0$,
On a de plus pour
$\lambda >0$,
On a de plus pour \[ \mathscr{P}^{\geq\lambda}/\mathscr{P}^{>\lambda} \xrightarrow{\;\sim\;} {\rm Ad} (\mathscr{T})^{\geq \lambda}/{\rm Ad} (\mathscr{T})^{>\lambda}\otimes \mathbb{G}_a. \]
\[ \mathscr{P}^{\geq\lambda}/\mathscr{P}^{>\lambda} \xrightarrow{\;\sim\;} {\rm Ad} (\mathscr{T})^{\geq \lambda}/{\rm Ad} (\mathscr{T})^{>\lambda}\otimes \mathbb{G}_a. \] $\lambda >0$
$\lambda >0$
 \[ \mathscr{P}^{\geq \lambda} = \{g\in \underline{{\rm Aut}}(\mathscr{T})\ |\ ({\rm Ad} (g)-{\rm Id}) ({\rm Ad} (\mathscr{T})^{\geq \bullet}) \subset {\rm Ad} (\mathscr{T})^{\geq \bullet +\lambda} \}. \]
\[ \mathscr{P}^{\geq \lambda} = \{g\in \underline{{\rm Aut}}(\mathscr{T})\ |\ ({\rm Ad} (g)-{\rm Id}) ({\rm Ad} (\mathscr{T})^{\geq \bullet}) \subset {\rm Ad} (\mathscr{T})^{\geq \bullet +\lambda} \}. \]
Enfin, on remarquera que même si ![]() $G$ n'est pas quasidéployé le théorème 4.40 de [Reference ZieglerZie15] s'applique et tout
$G$ n'est pas quasidéployé le théorème 4.40 de [Reference ZieglerZie15] s'applique et tout ![]() $G$-torseur définit un tel sous-groupe parabolique, la différence étant qu'en général ce n'est pas une forme tordue d'un groupe constant sur
$G$-torseur définit un tel sous-groupe parabolique, la différence étant qu'en général ce n'est pas une forme tordue d'un groupe constant sur ![]() $E$.
$E$.
5.2 Classification des  $G$-fibrés en termes de classes de
$G$-fibrés en termes de classes de  $\varphi$-conjugaison
$\varphi$-conjugaison
5.2.1 Rappels sur l'anneau  $\bar {B}$
$\bar {B}$
Rappelons ([Reference Fargues and FontaineFF18] sec. 1.10) que l'on dispose d'une ![]() $L$-algèbre
$L$-algèbre
où lorsque ![]() $E=\mathbb {Q}_p$
$E=\mathbb {Q}_p$
pour ![]() $\varpi _F\in F$ vérifiant
$\varpi _F\in F$ vérifiant ![]() $0<|\varpi _F|<1$. De plus, si
$0<|\varpi _F|<1$. De plus, si ![]() $B^{b,+}=W_{\mathcal {O}_E}(\mathcal {O}_F)[\tfrac {1}{\pi _E}]$
$B^{b,+}=W_{\mathcal {O}_E}(\mathcal {O}_F)[\tfrac {1}{\pi _E}]$
On a alors
sur lequel ![]() $\varphi$ est bijectif ([Reference Fargues and FontaineFF18] sec. 1.10.4). Les anneaux
$\varphi$ est bijectif ([Reference Fargues and FontaineFF18] sec. 1.10.4). Les anneaux ![]() $B^{b,+}/[\varpi _F]$ et
$B^{b,+}/[\varpi _F]$ et ![]() $\bar {B}$ sont locaux de corps résiduel
$\bar {B}$ sont locaux de corps résiduel ![]() $W_{\mathcal {O}_E}(k_F)_\mathbb {Q}$. De plus ([Reference Fargues and FontaineFF18] théo. 11.1.7), la réduction des scalaires induit une équivalence
$W_{\mathcal {O}_E}(k_F)_\mathbb {Q}$. De plus ([Reference Fargues and FontaineFF18] théo. 11.1.7), la réduction des scalaires induit une équivalence
où par ![]() $\varphi$-module on entend ici des modules libres de rang fini munis d'un isomorphisme semi-linéaire. Lorsque
$\varphi$-module on entend ici des modules libres de rang fini munis d'un isomorphisme semi-linéaire. Lorsque ![]() $E=\mathbb {Q}_p$ la catégorie
$E=\mathbb {Q}_p$ la catégorie ![]() $\varphi \text {-Mod}_{B^+}$ s'identifie à celle des
$\varphi \text {-Mod}_{B^+}$ s'identifie à celle des ![]() $F$-isocristaux sur
$F$-isocristaux sur ![]() ${\rm Spec} (\mathcal {O}_F/[\varpi _F])$. Il y a une équivalence de catégories (théo. 11.1.9 de [Reference Fargues and FontaineFF18])
${\rm Spec} (\mathcal {O}_F/[\varpi _F])$. Il y a une équivalence de catégories (théo. 11.1.9 de [Reference Fargues and FontaineFF18])
Mais il faut prendre garde que ce n'est pas une équivalence de catégories exactes (cf. exemple 5.2 qui suit), les ![]() $\varphi$-modules sur
$\varphi$-modules sur ![]() $B^+$ constituant une sorte de ‘modèle entier des fibrés où
$B^+$ constituant une sorte de ‘modèle entier des fibrés où ![]() $[\varpi _F]$ n'est pas inversé’ et l'application qui à un fibré associe un tel ‘model entier’ tue l'exactitude. Au final on a alors :
$[\varpi _F]$ n'est pas inversé’ et l'application qui à un fibré associe un tel ‘model entier’ tue l'exactitude. Au final on a alors :
— une équivalence de catégories tensorielle additives
 \[ {\rm Fib}_{X}\xrightarrow{\;\sim\;} \varphi\text{-Mod}_{\bar{B}}, \]
\[ {\rm Fib}_{X}\xrightarrow{\;\sim\;} \varphi\text{-Mod}_{\bar{B}}, \]— un foncteur de réduction sur le corps résiduel de
 $\bar {B}$
$\bar {B}$
 \[ \varphi\text{-Mod}_{\bar{B}} \longrightarrow \varphi\text{-Mod}_{W_{\mathcal{O}_E}(k_F)_\mathbb{Q}}, \]
\[ \varphi\text{-Mod}_{\bar{B}} \longrightarrow \varphi\text{-Mod}_{W_{\mathcal{O}_E}(k_F)_\mathbb{Q}}, \]— d'après le théorème de Dieudonné-Manin, puisque
 $k_F$ est algébriquement clos, une équivalence entre catégories d'isocristaux
de la quelle on déduit un foncteur
$k_F$ est algébriquement clos, une équivalence entre catégories d'isocristaux
de la quelle on déduit un foncteur \[ \varphi\text{-Mod}_{L} \xrightarrow{\;\sim\;} \varphi\text{-Mod}_{W_{\mathcal{O}_E}(k_F)_\mathbb{Q}} \]
\[ \varphi\text{-Mod}_{L} \xrightarrow{\;\sim\;} \varphi\text{-Mod}_{W_{\mathcal{O}_E}(k_F)_\mathbb{Q}} \] \[ red_{\bar{B},L}:\varphi\text{-Mod}_{\bar{B}}\longrightarrow \varphi\text{-Mod}_L. \]
\[ red_{\bar{B},L}:\varphi\text{-Mod}_{\bar{B}}\longrightarrow \varphi\text{-Mod}_L. \]— D'après le théorème 11.1.7 de [Reference Fargues and FontaineFF18] pour
 $(M,\varphi )\in \varphi \text {-Mod}_{\bar {B}}$ il y a alors un isomorphisme (non canonique)
$(M,\varphi )\in \varphi \text {-Mod}_{\bar {B}}$ il y a alors un isomorphisme (non canonique)
 \[ (M,\varphi)\simeq red_{\bar{B},L} (M,\varphi)\otimes_L \bar{B}. \]
\[ (M,\varphi)\simeq red_{\bar{B},L} (M,\varphi)\otimes_L \bar{B}. \]
Exemple 5.2 Soient ![]() $t_1,t_2\in B^{\varphi =\pi _E}$ non colinéaires. Ils induisent une suite exacte de fibrés
$t_1,t_2\in B^{\varphi =\pi _E}$ non colinéaires. Ils induisent une suite exacte de fibrés
où ![]() $u(a)=(-at_2,at_1)$ et
$u(a)=(-at_2,at_1)$ et ![]() $v(b,c)=bt_1+ct_2$. La suite associée de
$v(b,c)=bt_1+ct_2$. La suite associée de ![]() $\varphi$-modules sur
$\varphi$-modules sur ![]() $B^+$ n'est pas exacte puisque le morphisme
$B^+$ n'est pas exacte puisque le morphisme
n'est pas surjectif comme on le voit en réduisant modulo ![]() $[\varpi _F]$ puis sur le corps résiduel de
$[\varpi _F]$ puis sur le corps résiduel de ![]() $B^+/[\varpi _F]$ où c'est le morphisme nul.
$B^+/[\varpi _F]$ où c'est le morphisme nul.
Remarque 5.3 Bien que ce ne soit pas une équivalence de catégories exactes, l’équivalence ![]() $\varphi \text {-Mod}_{B^+}\xrightarrow {\sim } {\rm Fib}_X$ est compatible à la filtration de Harder-Narasimhan d'un fibré et tout
$\varphi \text {-Mod}_{B^+}\xrightarrow {\sim } {\rm Fib}_X$ est compatible à la filtration de Harder-Narasimhan d'un fibré et tout ![]() $\varphi$-module sur
$\varphi$-module sur ![]() $B^+$ est canoniquement muni d'une telle filtration.
$B^+$ est canoniquement muni d'une telle filtration.
5.2.2 La classe de  $\sigma$-conjugaison associée à un torseur
$\sigma$-conjugaison associée à un torseur
Le lemme suivant va nous permettre de nous débarrasser du problème de non-exactitude de l’équivalence entre ![]() ${\rm Fib}_X$ et
${\rm Fib}_X$ et ![]() $\varphi \text {-Mod}_{\bar {B}}$.
$\varphi \text {-Mod}_{\bar {B}}$.
Lemme 5.4 Soient ![]() $k$ un corps de caractéristique
$k$ un corps de caractéristique ![]() $0$,
$0$, ![]() $H$ un groupe réductif sur
$H$ un groupe réductif sur ![]() $k$ et
$k$ et ![]() $R$ une
$R$ une ![]() $k$-algèbre non nulle. Un foncteur
$k$-algèbre non nulle. Un foncteur
à valeurs dans les ![]() $R$-modules projectifs de type fini est un foncteur fibre si et seulement si c'est un foncteur additif compatible au produit tensoriel.
$R$-modules projectifs de type fini est un foncteur fibre si et seulement si c'est un foncteur additif compatible au produit tensoriel.
Proof Démonstration Puisque ![]() $k$ est de caractéristique zéro
$k$ est de caractéristique zéro ![]() $H$ est linéairement réductif et toute suite exacte dans
$H$ est linéairement réductif et toute suite exacte dans ![]() ${\rm Rep}\, H$ est scindée. Un tel foncteur est donc automatiquement exact. D'après le corollaire 2.10 de [Reference DeligneDel90] un tel foncteur est automatiquement fidèle.
${\rm Rep}\, H$ est scindée. Un tel foncteur est donc automatiquement exact. D'après le corollaire 2.10 de [Reference DeligneDel90] un tel foncteur est automatiquement fidèle.
Soit maintenant ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$. D'après le lemme 5.4 le foncteur composé
$X$. D'après le lemme 5.4 le foncteur composé
est un foncteur fibre.
Définition 5.5 On note ![]() $[b_{\mathscr {T}}]\in B(G)$ la classe de
$[b_{\mathscr {T}}]\in B(G)$ la classe de ![]() $\sigma$-conjugaison définissant le
$\sigma$-conjugaison définissant le ![]() $G$-isocristal associé au foncteur composé (5).
$G$-isocristal associé au foncteur composé (5).
Le but est maintenant de démontrer le théorème suivant.
Théorème 5.6 Pour tout ![]() $G$-torseur
$G$-torseur ![]() $\mathscr {T}$ sur
$\mathscr {T}$ sur ![]() $X$ il y a un isomorphisme
$X$ il y a un isomorphisme
Ce théorème implique aussitôt le théorème principal 5.1.
5.2.3 La classe de  $\varphi$-conjugaison dans
$\varphi$-conjugaison dans  $\bar {B}$ associée à un torseur
$\bar {B}$ associée à un torseur
On va maintenant voir que l'on peut raffiner la classe de ![]() $\sigma$-conjugaison
$\sigma$-conjugaison ![]() $b_\mathscr {T}$ dans
$b_\mathscr {T}$ dans ![]() $G(L)$ en une classe de
$G(L)$ en une classe de ![]() $\varphi$-conjugaison dans
$\varphi$-conjugaison dans ![]() $G(\bar {B})$. Pour cela nous aurons besoin du résultat suivant.
$G(\bar {B})$. Pour cela nous aurons besoin du résultat suivant.
Proposition 5.7 L'anneau local ![]() $\bar {B}$ est hensélien.
$\bar {B}$ est hensélien.
Pour tout ![]() $\rho \in\ ]0,1[$ on a
$\rho \in\ ]0,1[$ on a ![]() $B^+_\rho =B^+_{[\rho ,1]}$ et une égalité
$B^+_\rho =B^+_{[\rho ,1]}$ et une égalité ![]() $B^+_\rho /[\varpi _F]= B^{b,+}/[\varpi _F]$. On montre en fait le résultat plus général suivant.
$B^+_\rho /[\varpi _F]= B^{b,+}/[\varpi _F]$. On montre en fait le résultat plus général suivant.
Proposition 5.8 Le couple ![]() $(\underset{\longrightarrow }{{\rm lim }}_{\rho \underset {<}{\rightarrow }1} B^+_\rho , \mathfrak {m} )$ est hensélien où
$(\underset{\longrightarrow }{{\rm lim }}_{\rho \underset {<}{\rightarrow }1} B^+_\rho , \mathfrak {m} )$ est hensélien où ![]() $\mathfrak {m}$ est le noyau de la surjection vers
$\mathfrak {m}$ est le noyau de la surjection vers ![]() $W_{\mathcal {O}_E}(k_F)_\mathbb {Q}$.
$W_{\mathcal {O}_E}(k_F)_\mathbb {Q}$.
Proof Démonstration Soient ![]() $\rho \in\ ]0,1[$,
$\rho \in\ ]0,1[$, ![]() $P\in B^+_{\rho } [X]$ unitaire et
$P\in B^+_{\rho } [X]$ unitaire et ![]() $x\in B^+_{\rho }$ satisfaisant
$x\in B^+_{\rho }$ satisfaisant
Dire que ![]() $P'(x)\notin \mathfrak {m}$ est équivalent à ce que le polygone de Newton de
$P'(x)\notin \mathfrak {m}$ est équivalent à ce que le polygone de Newton de ![]() $P'(x)$ satisfasse
$P'(x)$ satisfasse
Cela implique que quitte à agrandir ![]() $\rho$ dans
$\rho$ dans ![]() $]0,1[$ on peut supposer que
$]0,1[$ on peut supposer que
En regardant ce même polygone de Newton on constate également qu'il existe ![]() $\rho _0 \in\ ]0,1[$ ainsi que
$\rho _0 \in\ ]0,1[$ ainsi que ![]() $n\in \mathbb {Z}$ (la plus petite abscisse où le polygone de Newton touche l'axe des abscisses) tels que
$n\in \mathbb {Z}$ (la plus petite abscisse où le polygone de Newton touche l'axe des abscisses) tels que
Quitte à remplacer ![]() $x$ par
$x$ par ![]() $\pi _E^kx$ et
$\pi _E^kx$ et ![]() $P(X)$ par
$P(X)$ par ![]() $\pi _E^{k\deg P} P ({X}/{\pi _E^k} )$ pour
$\pi _E^{k\deg P} P ({X}/{\pi _E^k} )$ pour ![]() $k\gg 0$ on peut de plus supposer que
$k\gg 0$ on peut de plus supposer que ![]() $n\geq 1$.
$n\geq 1$.
Puisque ![]() $P(x)\in \mathfrak {m}$ son polygone de Newton ne touche pas l'axe des abscisses. On en déduit que quitte à agrandir
$P(x)\in \mathfrak {m}$ son polygone de Newton ne touche pas l'axe des abscisses. On en déduit que quitte à agrandir ![]() $\rho _0$ on peut supposer que
$\rho _0$ on peut supposer que
où ![]() $m(\rho )\geq n$ et
$m(\rho )\geq n$ et ![]() $m(\rho )\underset {\rho \rightarrow 1}{\longrightarrow } +\infty$.
$m(\rho )\underset {\rho \rightarrow 1}{\longrightarrow } +\infty$.
On a donc pour ![]() $\rho \in [\rho _0,1]$
$\rho \in [\rho _0,1]$
L'algorithme de Newton nous dit alors qu'il existe une racine ![]() $z\in B^+_{\rho _0}$ de
$z\in B^+_{\rho _0}$ de ![]() $P$ satisfaisant
$P$ satisfaisant
Ces inégalité implique que le polygone de Newton de ![]() $z-x$ ne touche pas l'axe des abscisses et que donc
$z-x$ ne touche pas l'axe des abscisses et que donc ![]() $z-x\in \mathfrak {m}$.
$z-x\in \mathfrak {m}$.
Remarque 5.9 Avec les notations de ce résultat est le pendant au voisinage de ![]() $\{\delta =1\}=V([\varpi _F])$ dans l'espace
$\{\delta =1\}=V([\varpi _F])$ dans l'espace ![]() $\mathscr {Y}$ de l’énoncé usuel au voisinage de
$\mathscr {Y}$ de l’énoncé usuel au voisinage de ![]() $\{\delta =0\} =V(\pi _E)$ qui dit que l'anneau des entiers de l'anneau de Robba borné,
$\{\delta =0\} =V(\pi _E)$ qui dit que l'anneau des entiers de l'anneau de Robba borné, ![]() $\mathcal {O}_{\mathscr {E}^\dagger }$, est hensélien ([Reference Fargues and FontaineFF18] prop. 1.8.2). En effet, on a
$\mathcal {O}_{\mathscr {E}^\dagger }$, est hensélien ([Reference Fargues and FontaineFF18] prop. 1.8.2). En effet, on a
 \begin{align*} \underset{\rho \underset{<}{\rightarrow}1}{\underset{\longrightarrow}{\text{ lim }}\;} B^+_\rho &= \underset{\rho \underset{<}{\rightarrow}1}{\underset{\longrightarrow}{\text{ lim }}\;} \Gamma (\mathscr{Y}_{[\rho,1]},\mathcal{O}_{\mathscr{Y}}) ,\\ \mathcal{O}_{\mathscr{E}^\dagger} &= \underset{\rho\underset{>}{\rightarrow} 0}{\underset{\longrightarrow}{\text{ lim }}\;} \Gamma (\mathscr{Y}_{[0,\rho]},\mathcal{O}_{\mathscr{Y}}) \end{align*}
\begin{align*} \underset{\rho \underset{<}{\rightarrow}1}{\underset{\longrightarrow}{\text{ lim }}\;} B^+_\rho &= \underset{\rho \underset{<}{\rightarrow}1}{\underset{\longrightarrow}{\text{ lim }}\;} \Gamma (\mathscr{Y}_{[\rho,1]},\mathcal{O}_{\mathscr{Y}}) ,\\ \mathcal{O}_{\mathscr{E}^\dagger} &= \underset{\rho\underset{>}{\rightarrow} 0}{\underset{\longrightarrow}{\text{ lim }}\;} \Gamma (\mathscr{Y}_{[0,\rho]},\mathcal{O}_{\mathscr{Y}}) \end{align*}
i.e. l'anneau des germes de fonctions holomorphes au voisinage du diviseur ![]() $V([\varpi _F])$, resp.
$V([\varpi _F])$, resp. ![]() $V(\pi _E)$, est hensélien.
$V(\pi _E)$, est hensélien.
Soient maintenant ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur et
$G$-torseur et ![]() $\omega _{\mathscr {T}}$ le foncteur fibre associé.
$\omega _{\mathscr {T}}$ le foncteur fibre associé.
Proposition 5.10 Le foncteur composé
est un foncteur fibre isomorphe à ![]() $\omega _{{\rm can}}$ où
$\omega _{{\rm can}}$ où ![]() $\omega _{{\rm can}}(V,\rho )=V\otimes _E \bar {B}$.
$\omega _{{\rm can}}(V,\rho )=V\otimes _E \bar {B}$.
Proof Démonstration Le fait que ce soit un foncteur fibre résulte du lemme 5.4. D'après [Reference DeligneDel90] théo. 1.12,
est un ![]() $G$-torseur sur
$G$-torseur sur ![]() ${\rm Spec} (\bar {B})$. Puisque
${\rm Spec} (\bar {B})$. Puisque
d'après Steinberg, ce ![]() $G$-torseur devient trivial sur le corps résiduel de
$G$-torseur devient trivial sur le corps résiduel de ![]() $\bar {B}$. Puisque
$\bar {B}$. Puisque ![]() $\bar {B}$ est hensélien (prop. 5.7) on conclut que ce torseur est en fait trivial sur
$\bar {B}$ est hensélien (prop. 5.7) on conclut que ce torseur est en fait trivial sur ![]() ${\rm Spec} (\bar {B})$ (puisque
${\rm Spec} (\bar {B})$ (puisque ![]() $G$ est lisse ce torseur est lisse et il suffit d'appliquer l'existence de quasi-sections localement pour la topologie étale, cf. [Reference GrothendieckGro67] sec. 17.16).
$G$ est lisse ce torseur est lisse et il suffit d'appliquer l'existence de quasi-sections localement pour la topologie étale, cf. [Reference GrothendieckGro67] sec. 17.16).
On en déduit aussitôt le résultat suivant qui donne une correspondance entre ![]() $G$-torseurs et algèbre semi-linéaire.
$G$-torseurs et algèbre semi-linéaire.
Proposition 5.11 Les classes d'isomorphisme de ![]() $G$-fibrés sur
$G$-fibrés sur ![]() $X$ sont en bijection avec les classes de
$X$ sont en bijection avec les classes de ![]() $\varphi$-conjugaison dans
$\varphi$-conjugaison dans ![]() $G(\bar {B})$.
$G(\bar {B})$.
5.3 Le cas quasi-déployé
Le but de cette section est de démontrer le théorème 5.6 lorsque ![]() $G$ est quasi-déployé. Dans cette section on suppose donc
$G$ est quasi-déployé. Dans cette section on suppose donc ![]() $G$ quasi-déployé.
$G$ quasi-déployé.
5.3.1 Le cas semi-stable
Commençons par remarquer le point clef suivant.
Proposition 5.12 Pour ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$ sont équivalents :
$X$ sont équivalents :
(1)
 $\mathscr {T}$ est semi-stable;
$\mathscr {T}$ est semi-stable;(2) la classe de
 $\sigma$-conjugaison
$\sigma$-conjugaison  $[b_\mathscr {T}]$ est basique.
$[b_\mathscr {T}]$ est basique.
Proof Démonstration En effet, le torseur ![]() $\mathscr {T}$ est semi-stable si et seulement si le fibré
$\mathscr {T}$ est semi-stable si et seulement si le fibré ![]() ${\rm Ad} (\mathscr {T})$ l'est. De plus
${\rm Ad} (\mathscr {T})$ l'est. De plus ![]() $[b]\in B(G)$ est basique si et seulement si
$[b]\in B(G)$ est basique si et seulement si ![]() $[{\rm Ad}(b)]\in B (\hbox {GL} ({\rm Lie}\, G) )$ est isocline (de pente
$[{\rm Ad}(b)]\in B (\hbox {GL} ({\rm Lie}\, G) )$ est isocline (de pente ![]() $0$ automatiquement). Cela résulte de ce que
$0$ automatiquement). Cela résulte de ce que ![]() $\nu _{{\rm Ad} (b)}={\rm Ad}\circ \nu _b$. On a de plus
$\nu _{{\rm Ad} (b)}={\rm Ad}\circ \nu _b$. On a de plus
On conclut en utilisant que si via le foncteur ![]() ${\rm Fib}_X\longrightarrow \varphi \text {-Mod}_L$ le fibré
${\rm Fib}_X\longrightarrow \varphi \text {-Mod}_L$ le fibré ![]() $\mathscr {E}$ s'envoie sur l'isocristal
$\mathscr {E}$ s'envoie sur l'isocristal ![]() $(D,\varphi )$ alors
$(D,\varphi )$ alors ![]() $\mathscr {E}$ est semi-stable si et seulement si
$\mathscr {E}$ est semi-stable si et seulement si ![]() $(D,\varphi )$ est isocline.
$(D,\varphi )$ est isocline.
Proposition 5.13 Si ![]() $\mathscr {T}$ est un
$\mathscr {T}$ est un ![]() $G$-torseur semi-stable sur
$G$-torseur semi-stable sur ![]() $X$ on a
$X$ on a
Dans la preuve de cette proposition nous aurons besoin du lemme intermédiaire suivant.
Lemme 5.14 Soit ![]() $\mathcal {G}$ un
$\mathcal {G}$ un ![]() $\mathcal {O}_E$-schéma en groupe lisse de fibre spéciale
$\mathcal {O}_E$-schéma en groupe lisse de fibre spéciale ![]() $\mathcal {G}_{\mathbb {F}_q}$ connexe. Notons
$\mathcal {G}_{\mathbb {F}_q}$ connexe. Notons ![]() ${\mathbf {A}}=W_{\mathcal {O}_E}(\mathcal {O}_F)$ et
${\mathbf {A}}=W_{\mathcal {O}_E}(\mathcal {O}_F)$ et
Pour tout entier ![]() $s\geq 1$ tout élément de
$s\geq 1$ tout élément de ![]() $\mathcal {G} (\bar {{\mathbf {A}}})$ est
$\mathcal {G} (\bar {{\mathbf {A}}})$ est ![]() $\varphi ^s$-conjugué à
$\varphi ^s$-conjugué à ![]() $1$.
$1$.
Proof Démonstration Puisque ![]() $\mathcal {G}$ est de présentation finie un élément de
$\mathcal {G}$ est de présentation finie un élément de ![]() $\mathcal {G}({\bf \bar{A}})$ est la réduction d'un élément de
$\mathcal {G}({\bf \bar{A}})$ est la réduction d'un élément de ![]() $\mathcal {G} ( {\boldsymbol {\text A}}/[a])$ pour un
$\mathcal {G} ( {\boldsymbol {\text A}}/[a])$ pour un ![]() $a\in F$ satisfaisant
$a\in F$ satisfaisant ![]() $0 < |a| < 1$. L'anneau
$0 < |a| < 1$. L'anneau ![]() $R= {\boldsymbol {\text A}}/[a]$ est
$R= {\boldsymbol {\text A}}/[a]$ est ![]() $\pi _E$-adique et vérifie
$\pi _E$-adique et vérifie
Puisque ![]() $\mathcal {G}$ est lisse l'application
$\mathcal {G}$ est lisse l'application
est surjective. Posons pour tout entier ![]() $n\geq 1$
$n\geq 1$
qui définit une filtration relativement à laquelle ![]() $\mathcal {G}(R)$ est séparé complet. On a
$\mathcal {G}(R)$ est séparé complet. On a
 \begin{align*} \mathcal{G}(R)/\mathrm{Fil}^1\mathcal{G}(R) & = \mathcal{G} (\mathcal{O}_F/a) ,\\ \mathrm{Fil}^n\mathcal{G} (R)/\mathrm{Fil}^{n+1}\mathcal{G}(R) & = {\rm Lie}\, \mathcal{G}_{\mathbb{F}_q}\otimes_{\mathbb{F}_q} \mathcal{O}_F/a. \end{align*}
\begin{align*} \mathcal{G}(R)/\mathrm{Fil}^1\mathcal{G}(R) & = \mathcal{G} (\mathcal{O}_F/a) ,\\ \mathrm{Fil}^n\mathcal{G} (R)/\mathrm{Fil}^{n+1}\mathcal{G}(R) & = {\rm Lie}\, \mathcal{G}_{\mathbb{F}_q}\otimes_{\mathbb{F}_q} \mathcal{O}_F/a. \end{align*}
D'après Lang, puisque ![]() $\mathcal {G}_{\mathbb {F}_q}$ est connexe et
$\mathcal {G}_{\mathbb {F}_q}$ est connexe et ![]() $F$ algébriquement clos, tout élément de
$F$ algébriquement clos, tout élément de ![]() $\mathcal {G} (\mathcal {O}_F/a)$ est
$\mathcal {G} (\mathcal {O}_F/a)$ est ![]() ${\rm Frob}_q^s$-conjugué à
${\rm Frob}_q^s$-conjugué à ![]() $1$. Puisque
$1$. Puisque ![]() $F$ est algébriquement clos,
$F$ est algébriquement clos,
est surjectif. On conclut facilement.
Nous allons également utiliser le lemme suivant dont la preuve élémentaire est laissée au lecteur. Du point de vue des torseur ce lemme revient à étudier les torseurs sur ![]() $X_E$ qui deviennent isomorphes après tiré en arrière sur le revêtement
$X_E$ qui deviennent isomorphes après tiré en arrière sur le revêtement ![]() $X_{E^{\prime}}\rightarrow X_E$ où
$X_{E^{\prime}}\rightarrow X_E$ où ![]() $E^{\prime}|E$ est non-ramifiée.
$E^{\prime}|E$ est non-ramifiée.
Lemme 5.15 Soit ![]() $s\in \mathbb {N}_{\geq 1}$. Pour
$s\in \mathbb {N}_{\geq 1}$. Pour ![]() $g\in G(\bar {B})$ notons
$g\in G(\bar {B})$ notons
qui définit une application
Pour ![]() $h\in G(\bar {B})$ on note également
$h\in G(\bar {B})$ on note également
le ![]() $\varphi ^s$-centralisateur de
$\varphi ^s$-centralisateur de ![]() $h$.
$h$.
Pour ![]() $g\in G(\bar {B})$ on a alors :
$g\in G(\bar {B})$ on a alors :
(1) Il y a une action de
 $\mathbb {Z}/s\mathbb {Z}$ sur
$\mathbb {Z}/s\mathbb {Z}$ sur  $I_{N_s(g),s}$ telle que
$I_{N_s(g),s}$ telle que  $\bar {1}\in \mathbb {Z}/s\mathbb {Z}$ agisse via
$\bar {1}\in \mathbb {Z}/s\mathbb {Z}$ agisse via  $x\mapsto g \varphi (x) g^{-1}$.
$x\mapsto g \varphi (x) g^{-1}$.(2) Il y a une bijection d'ensembles pointés

Preuve de la proposition 5.13. On note dans cette preuve
Fixons une section ![]() $k_F\hookrightarrow \mathcal {O}_F$ de la projection de
$k_F\hookrightarrow \mathcal {O}_F$ de la projection de ![]() $\mathcal {O}_F$ vers son corps résiduel. Cela définit un plongement
$\mathcal {O}_F$ vers son corps résiduel. Cela définit un plongement ![]() $L'\hookrightarrow \bar {B}$ et donc une section de la projection
$L'\hookrightarrow \bar {B}$ et donc une section de la projection
Soit
associé à ![]() $\mathscr {T}$ par la proposition 5.11. Notons
$\mathscr {T}$ par la proposition 5.11. Notons
la réduction de ![]() $g$.
$g$.
On note ![]() $\nu _b:\mathbb {D}\rightarrow G$ le morphisme des pentes [Reference KottwitzKot85]. D'après la proposition 5.12
$\nu _b:\mathbb {D}\rightarrow G$ le morphisme des pentes [Reference KottwitzKot85]. D'après la proposition 5.12 ![]() $b$ est basique et donc
$b$ est basique et donc ![]() $\nu _b$ est central. Quitte à
$\nu _b$ est central. Quitte à ![]() $\sigma$-conjuguer, resp.
$\sigma$-conjuguer, resp. ![]() $\varphi$-conjuguer,
$\varphi$-conjuguer, ![]() $b$ et
$b$ et ![]() $g$ par un même élément de
$g$ par un même élément de ![]() $G(L')$ on peut supposer
$G(L')$ on peut supposer ![]() $b$ décent c'est à dire pour un
$b$ décent c'est à dire pour un ![]() $s\in \mathbb {N}_{\geq 1}$
$s\in \mathbb {N}_{\geq 1}$
Notons
Soit ![]() $\mathcal {G}$ un modèle entier lisse de
$\mathcal {G}$ un modèle entier lisse de ![]() $G$ sur
$G$ sur ![]() $\mathcal {O}_E$ à fibre spéciale connexe. Il y a un diagramme cartésien
$\mathcal {O}_E$ à fibre spéciale connexe. Il y a un diagramme cartésien

duquel on déduit que
D'après le lemme 5.14 ![]() $h$ est
$h$ est ![]() $\varphi ^s$-conjugué à
$\varphi ^s$-conjugué à ![]() $1$ et donc, puisque
$1$ et donc, puisque ![]() $\nu _b$ est central,
$\nu _b$ est central, ![]() $N_s(g)$ est
$N_s(g)$ est ![]() $\varphi ^s$-conjugué à
$\varphi ^s$-conjugué à ![]() $N_s(b)$ i.e. on a montré le résultat après ‘extension des scalaires’ à
$N_s(b)$ i.e. on a montré le résultat après ‘extension des scalaires’ à ![]() $E_s$ l'extension non-ramifiée de degré
$E_s$ l'extension non-ramifiée de degré ![]() $s$. Soit
$s$. Soit ![]() $J_b$ le
$J_b$ le ![]() $\sigma$-centralisateur de
$\sigma$-centralisateur de ![]() $b$ comme groupe algébrique sur
$b$ comme groupe algébrique sur ![]() $E$ [Reference KottwitzKot85].
$E$ [Reference KottwitzKot85].
On utilise maintenant le lemme 5.15 ainsi que ses notations.
Puisque ![]() $\bar {B}^{\varphi ^s={\rm Id}}=E_s$ on a
$\bar {B}^{\varphi ^s={\rm Id}}=E_s$ on a
où l'action de ![]() $\mathbb {Z}/s\mathbb {Z}$ sur le groupe de gauche coïncide avec celle de
$\mathbb {Z}/s\mathbb {Z}$ sur le groupe de gauche coïncide avec celle de ![]() ${\rm Gal} (E_s|E)$. En effet, puisque
${\rm Gal} (E_s|E)$. En effet, puisque ![]() $(b\sigma )^s=(s.\nu _b) (\pi _E)\sigma ^s$ avec
$(b\sigma )^s=(s.\nu _b) (\pi _E)\sigma ^s$ avec ![]() $\nu _b$ central,
$\nu _b$ central, ![]() $I_{N_s (g),s}$ s'identifie à
$I_{N_s (g),s}$ s'identifie à ![]() $G(\bar {B})^{\varphi ^s={\rm Id}}$. L'obstruction à ce que
$G(\bar {B})^{\varphi ^s={\rm Id}}$. L'obstruction à ce que ![]() $g$ et
$g$ et ![]() $b$ soient
$b$ soient ![]() $\varphi$-conjugués dans
$\varphi$-conjugués dans ![]() $G(\bar {B})$ est un élément de
$G(\bar {B})$ est un élément de
mais l'image par l'application de réduction ![]() $I_{N_s(g),s}\rightarrow J_b (E_s)$ de cette obstruction dans l'ensemble pointé
$I_{N_s(g),s}\rightarrow J_b (E_s)$ de cette obstruction dans l'ensemble pointé ![]() $H^1({\rm Gal} (E_s|E),J_b (E_s))$ est triviale puisque
$H^1({\rm Gal} (E_s|E),J_b (E_s))$ est triviale puisque ![]() $g$ et
$g$ et ![]() $b$ deviennent
$b$ deviennent ![]() $\sigma$-conjugué par réduction vers
$\sigma$-conjugué par réduction vers ![]() $L'$. On conclut.□
$L'$. On conclut.□
5.3.2 Réduction au cas semi-stable
On suppose toujours ![]() $G$ quasi-déployé. Le cas quelconque du théorème 5.6 résulte alors du cas semi-stable (5.13) et de la proposition suivante. Pour
$G$ quasi-déployé. Le cas quelconque du théorème 5.6 résulte alors du cas semi-stable (5.13) et de la proposition suivante. Pour ![]() $\hbox {GL}_n$ cette proposition est une reformulation du fait que la filtration de Harder-Narasimhan d'un fibré est scindée.
$\hbox {GL}_n$ cette proposition est une reformulation du fait que la filtration de Harder-Narasimhan d'un fibré est scindée.
Proposition 5.16 Soit ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur de réduction canonique
$G$-torseur de réduction canonique ![]() $\mathscr {T}_P$ où l'on suppose
$\mathscr {T}_P$ où l'on suppose ![]() $P$ en position standard relativement à un sous-groupe de Borel. Notons
$P$ en position standard relativement à un sous-groupe de Borel. Notons ![]() $M$ le quotient de Levi de
$M$ le quotient de Levi de ![]() $P$ et soit
$P$ et soit ![]() $i:M\hookrightarrow P$ le facteur de Levi standard. Il y a alors un isomorphisme
$i:M\hookrightarrow P$ le facteur de Levi standard. Il y a alors un isomorphisme
et donc ![]() $\mathscr {T}$ possède une réduction semi-stable à un sous-groupe de Levi.
$\mathscr {T}$ possède une réduction semi-stable à un sous-groupe de Levi.
Proof Démonstration Soit ![]() $U$ le radical unipotent de
$U$ le radical unipotent de ![]() $P$ et
$P$ et ![]() $\mathscr {U}$ la forme de
$\mathscr {U}$ la forme de ![]() $U\times X$ définie par torsion par
$U\times X$ définie par torsion par ![]() $\mathscr {T}_P$ via l'action par conjugaison de
$\mathscr {T}_P$ via l'action par conjugaison de ![]() $P$ sur
$P$ sur ![]() $U$. Le schéma en groupes unipotent
$U$. Le schéma en groupes unipotent ![]() $\mathscr {U}$ possède une filtration
$\mathscr {U}$ possède une filtration
vérifiant
La fibre de l'application
au dessus de l'image de ![]() $[\mathscr {T}_P]$ s'identifie à
$[\mathscr {T}_P]$ s'identifie à
Ce groupe de cohomologie est trivial puisque pour tout ![]() $\lambda >0$,
$\lambda >0$, ![]() ${\rm Ad}(\mathscr {T}) ^{\geq \lambda }/{\rm Ad} (\mathscr {T})^{>\lambda }$ est semi-stable de pente positive et donc
${\rm Ad}(\mathscr {T}) ^{\geq \lambda }/{\rm Ad} (\mathscr {T})^{>\lambda }$ est semi-stable de pente positive et donc
5.4 Le cas général
5.4.1 Le sous-groupe parabolique associé à un torseur
Soit ![]() $(M,\varphi )\in \varphi \text {-Mod}_{\bar {B}}$. D'après le théorème 11.1.7 de [Reference Fargues and FontaineFF18]
$(M,\varphi )\in \varphi \text {-Mod}_{\bar {B}}$. D'après le théorème 11.1.7 de [Reference Fargues and FontaineFF18] ![]() $(M,\varphi )$ admet une décomposition de Dieudonné-Manin. Bien que non-unique, la filtration associée
$(M,\varphi )$ admet une décomposition de Dieudonné-Manin. Bien que non-unique, la filtration associée
avec ![]() ${\rm gr}^\lambda M$ isocline de pente
${\rm gr}^\lambda M$ isocline de pente ![]() $-\lambda$ est unique. Elle correspond à la filtration de Harder-Narasimhan du fibré associé à
$-\lambda$ est unique. Elle correspond à la filtration de Harder-Narasimhan du fibré associé à ![]() $(M,\varphi )$ (cf. rem. 5.3).
$(M,\varphi )$ (cf. rem. 5.3).
Soient ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $E$ et
$E$ et ![]() $\beta \in G(\bar {B})$ que l'on pense comme étant associé à un
$\beta \in G(\bar {B})$ que l'on pense comme étant associé à un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$, cf. prop. 5.11. On ne suppose pas
$X$, cf. prop. 5.11. On ne suppose pas ![]() $G$ quasi-déployé. Le foncteur
$G$ quasi-déployé. Le foncteur
défini par la filtration précédente de Harder-Narasimhan est un foncteur fibre filtré au sens de [Reference ZieglerZie15] (utiliser que ![]() $E$ est de caractéristique
$E$ est de caractéristique ![]() $0$ ce qui implique que
$0$ ce qui implique que ![]() $G$ est linéairement réductif et donc le gradué de la filtration de Harder-Narasimhan définit un foncteur exact). D'après le théorème 4.40 de [Reference ZieglerZie15] on peut lui associer un sous-groupe parabolique
$G$ est linéairement réductif et donc le gradué de la filtration de Harder-Narasimhan définit un foncteur exact). D'après le théorème 4.40 de [Reference ZieglerZie15] on peut lui associer un sous-groupe parabolique
Notons
la représentation adjointe. La filtration de Harder-Narasimhan de ![]() $(\mathfrak {g}\otimes _E \bar {B},{\rm Ad} (\beta )\varphi )$ définit une filtration
$(\mathfrak {g}\otimes _E \bar {B},{\rm Ad} (\beta )\varphi )$ définit une filtration
telle que
Le sous-groupe parabolique ![]() $\mathscr {P}$ est filtré par
$\mathscr {P}$ est filtré par ![]() $(\mathscr {P}^{\geq \lambda })_{\lambda \geq 0}$ avec
$(\mathscr {P}^{\geq \lambda })_{\lambda \geq 0}$ avec
 \begin{align*} \mathscr{P}^{>0} &= R_u \mathscr{P} \\ \forall \lambda>0,\ \mathscr{P}^{\geq \lambda}/\mathscr{P}^{>\lambda} &\xrightarrow{\;\sim\;} {\rm gr}^\lambda \mathfrak{g}_{\bar{B}}\otimes \mathbb{G}_a. \end{align*}
\begin{align*} \mathscr{P}^{>0} &= R_u \mathscr{P} \\ \forall \lambda>0,\ \mathscr{P}^{\geq \lambda}/\mathscr{P}^{>\lambda} &\xrightarrow{\;\sim\;} {\rm gr}^\lambda \mathfrak{g}_{\bar{B}}\otimes \mathbb{G}_a. \end{align*}5.4.2 Structure du groupe des automorphismes d'un  $G$-torseur
$G$-torseur
On continue avec les hypothèses et notations précédentes. Notons maintenant
le ![]() $\varphi$-centralisateur de
$\varphi$-centralisateur de ![]() $\beta$. Il s'identifie au groupe des automorphismes d'un
$\beta$. Il s'identifie au groupe des automorphismes d'un ![]() $G$-torseur associé. Puisque
$G$-torseur associé. Puisque
 \begin{align*} \mathscr{P} & = \{ g\in G_{\bar{B}}\ |\ {\rm Ad} (g) ( \mathfrak{g}_{\bar{B}}^{\geq \bullet} ) = ( \mathfrak{g}_{\bar{B}}^{\geq \bullet} ) \},\\ I_\beta & \subset \mathscr{P} (\bar{B}). \end{align*}
\begin{align*} \mathscr{P} & = \{ g\in G_{\bar{B}}\ |\ {\rm Ad} (g) ( \mathfrak{g}_{\bar{B}}^{\geq \bullet} ) = ( \mathfrak{g}_{\bar{B}}^{\geq \bullet} ) \},\\ I_\beta & \subset \mathscr{P} (\bar{B}). \end{align*}Il y a une action
 \begin{align*} \psi: \mathscr{P} (\bar{B}) &\xrightarrow{\;\sim\;} \mathscr{P} (\bar{B}) \\ g & \longmapsto (\beta \varphi) g (\beta \varphi)^{-1} \end{align*}
\begin{align*} \psi: \mathscr{P} (\bar{B}) &\xrightarrow{\;\sim\;} \mathscr{P} (\bar{B}) \\ g & \longmapsto (\beta \varphi) g (\beta \varphi)^{-1} \end{align*}pour laquelle
Pour ![]() $\lambda \geq 0$ l'action de
$\lambda \geq 0$ l'action de ![]() $\psi$ sur
$\psi$ sur
est donnée par ![]() ${\rm Ad} (\beta )\varphi$. Pour
${\rm Ad} (\beta )\varphi$. Pour ![]() $(M,\varphi )\in \varphi \text {-Mod}_{\bar {B}}$ on a
$(M,\varphi )\in \varphi \text {-Mod}_{\bar {B}}$ on a
([Reference Fargues and FontaineFF18] lemme 11.1.6). On en déduit que si ![]() $(I_\beta ^{\geq \lambda })_{\lambda \geq 0}$ désigne la filtration associée,
$(I_\beta ^{\geq \lambda })_{\lambda \geq 0}$ désigne la filtration associée, ![]() $I_\beta ^{\geq \lambda } = I_\beta \cap \mathscr {P}^{\geq \lambda }(\bar {B})$ alors si
$I_\beta ^{\geq \lambda } = I_\beta \cap \mathscr {P}^{\geq \lambda }(\bar {B})$ alors si ![]() $\lambda >0$
$\lambda >0$
qui est isomorphe à une somme finie de copies de ![]() $\bar {B}^{\varphi ^h=\pi _E^d}=H^0(X,\mathcal {O}_X(\lambda ))$ si
$\bar {B}^{\varphi ^h=\pi _E^d}=H^0(X,\mathcal {O}_X(\lambda ))$ si ![]() $\lambda =d/h$ avec
$\lambda =d/h$ avec ![]() $(d,h)=1$. De plus,
$(d,h)=1$. De plus,
 \begin{align*} I_\beta/I_\beta^{>0}&= {\rm Aut} ( {\rm gr}^0 \mathfrak{g}_{\bar{B}}, {\rm Ad} (\beta)\varphi) \\ &\simeq J_b (E) \end{align*}
\begin{align*} I_\beta/I_\beta^{>0}&= {\rm Aut} ( {\rm gr}^0 \mathfrak{g}_{\bar{B}}, {\rm Ad} (\beta)\varphi) \\ &\simeq J_b (E) \end{align*}
après le choix d'une ![]() $\varphi$-conjugaison entre
$\varphi$-conjugaison entre ![]() ${\rm Ad} (\beta )$ et
${\rm Ad} (\beta )$ et ![]() ${\rm Ad} (b)$.
${\rm Ad} (b)$.
5.4.3 Fin de la preuve du théorème 5.1 par descente galoisienne non-ramifiée
Voyons maintenant comment conclure la preuve du théorème 5.6 lorsque ![]() $G$ n'est pas forcément quasi-déployé. Soit donc
$G$ n'est pas forcément quasi-déployé. Soit donc ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $E$. Puisque
$E$. Puisque ![]() $H^1 (E^{nr},G_{ad})$ est trivial (Steinberg)
$H^1 (E^{nr},G_{ad})$ est trivial (Steinberg) ![]() $G$ est quasi-déployé sur une extension non-ramifiée de
$G$ est quasi-déployé sur une extension non-ramifiée de ![]() $E$. Soit donc
$E$. Soit donc ![]() $h\geq 1$ tel que
$h\geq 1$ tel que ![]() $G_{E_h}$ soit quasi-déployé. Soit
$G_{E_h}$ soit quasi-déployé. Soit ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X_E$,
$X_E$, ![]() $\beta \in G(\bar {B})$ et
$\beta \in G(\bar {B})$ et ![]() $b\in G(L)$ associés. On veut montrer que
$b\in G(L)$ associés. On veut montrer que ![]() $\beta$ et
$\beta$ et ![]() $b$ sont
$b$ sont ![]() $\varphi$-conjugués.
$\varphi$-conjugués.
On utilise les notations du lemme 5.15. On sait d'après la section 5.3 précédente que ![]() $N_h(\beta )$ et
$N_h(\beta )$ et ![]() $N_h (b)$ sont
$N_h (b)$ sont ![]() $\varphi ^h$-conjugués. L'action de
$\varphi ^h$-conjugués. L'action de ![]() ${\rm Gal} (E_h|E)$ sur
${\rm Gal} (E_h|E)$ sur ![]() $I_{N_h(\beta )}$ du lemme 5.15 est compatible à la filtration définie précédemment. De plus, pour
$I_{N_h(\beta )}$ du lemme 5.15 est compatible à la filtration définie précédemment. De plus, pour ![]() $\lambda >0$
$\lambda >0$
 \begin{align*} H^1 \big ({\rm Gal} (E_h|E), I_{N_h(\beta),h}^{\geq \lambda}/I_{N_h(\beta),h}^{>\lambda}\big ) &= H^1 \big ({\rm Gal} (E_h|E), ({\rm gr}^\lambda \mathfrak{g}_{\bar{B}})^{({\rm Ad} (\beta)\varphi)^h={\rm Id}} \big ) \\ &= 0 \end{align*}
\begin{align*} H^1 \big ({\rm Gal} (E_h|E), I_{N_h(\beta),h}^{\geq \lambda}/I_{N_h(\beta),h}^{>\lambda}\big ) &= H^1 \big ({\rm Gal} (E_h|E), ({\rm gr}^\lambda \mathfrak{g}_{\bar{B}})^{({\rm Ad} (\beta)\varphi)^h={\rm Id}} \big ) \\ &= 0 \end{align*}
puisqu'on regarde la cohomologie d'un groupe fini à valeurs dans un ![]() $\mathbb {Q}$-espace vectoriel. On en déduit que l'application
$\mathbb {Q}$-espace vectoriel. On en déduit que l'application
est un isomorphisme. Le résultat s'en déduit par application du lemme 5.15 puisque
6. Le dictionnaire entre Kottwitz et Atiyah-Bott
On dispose maintenant du théorème 5.1. Dans cette section on interprète certains résultats de [Reference KottwitzKot85] et [Reference KottwitzKot97] en termes de torseurs.
6.1 Classification sur  $\bar {E}$
$\bar {E}$
Soit ![]() $G$ un groupe réductif sur
$G$ un groupe réductif sur ![]() $E$. Il y a une application
$E$. Il y a une application
 \begin{align*} B(G) & \longrightarrow \big [ {\rm Hom}(\mathbb{D}_{E^{nr}}, G_{E^{nr}})/G(E^{nr})\text{-conj.}\big ]^{\sigma={\rm Id}} \\ {[} b] & \longmapsto {[}\nu_b] \end{align*}
\begin{align*} B(G) & \longrightarrow \big [ {\rm Hom}(\mathbb{D}_{E^{nr}}, G_{E^{nr}})/G(E^{nr})\text{-conj.}\big ]^{\sigma={\rm Id}} \\ {[} b] & \longmapsto {[}\nu_b] \end{align*}
si ![]() $b$ est décent, auquel cas
$b$ est décent, auquel cas ![]() $\nu _b$ est défini sur
$\nu _b$ est défini sur ![]() $E^{nr}$. Rappelons maintenant que la catégorie Tannakienne des isocristaux
$E^{nr}$. Rappelons maintenant que la catégorie Tannakienne des isocristaux ![]() $\varphi \text {-Mod}_L$ est
$\varphi \text {-Mod}_L$ est ![]() $E$-linéaire neutre sur
$E$-linéaire neutre sur ![]() $E^{nr}$. Il y a en effet un foncteur fibre
$E^{nr}$. Il y a en effet un foncteur fibre
 \begin{align*} \varphi\text{-Mod}_L & \longrightarrow {\rm Vect}_{E^{nr}} \\ (D,\varphi) & \longmapsto \bigoplus_{\lambda\in \mathbb{Q}} \bigcup_{h\geq 1\atop h\lambda\in \mathbb{Z}} D^{\varphi^h =\pi_E^{h\lambda}}. \end{align*}
\begin{align*} \varphi\text{-Mod}_L & \longrightarrow {\rm Vect}_{E^{nr}} \\ (D,\varphi) & \longmapsto \bigoplus_{\lambda\in \mathbb{Q}} \bigcup_{h\geq 1\atop h\lambda\in \mathbb{Z}} D^{\varphi^h =\pi_E^{h\lambda}}. \end{align*}
Ce foncteur fibre est ![]() $\mathbb {Q}$-gradué et le lien associé est le pro-tore des pentes
$\mathbb {Q}$-gradué et le lien associé est le pro-tore des pentes ![]() $\mathbb {D}$. Il s'en suit que si
$\mathbb {D}$. Il s'en suit que si ![]() $b\in G(L)$ est décent le
$b\in G(L)$ est décent le ![]() $G$-isocristal associé est complètement déterminé après extension des scalaires à
$G$-isocristal associé est complètement déterminé après extension des scalaires à ![]() $E^{nr}$ par
$E^{nr}$ par ![]() $\nu _b$.
$\nu _b$.
Traduisons maintenant cela du coté de la courbe ![]() $X$. Pour
$X$. Pour ![]() $h\in \mathbb {N}_{\geq 1}$ on note
$h\in \mathbb {N}_{\geq 1}$ on note ![]() $X_h=X_{E_h}$,
$X_h=X_{E_h}$, ![]() $X=X_1$. Notons
$X=X_1$. Notons
le ![]() $\mathbb {G}_m$-torseur sur
$\mathbb {G}_m$-torseur sur ![]() $X_h$ associé au fibré en droites
$X_h$ associé au fibré en droites ![]() $\mathcal {O}_{X_h}(1)$. Si
$\mathcal {O}_{X_h}(1)$. Si ![]() $h|h'$ et
$h|h'$ et ![]() $\pi _{h',h}:X_{h'}\rightarrow X_h$ il y a un isomorphisme canonique
$\pi _{h',h}:X_{h'}\rightarrow X_h$ il y a un isomorphisme canonique
Cela définit un morphisme
Définition 6.1 On pose
où la limite projective est prise suivant les applications de transition (6). C'est un ![]() $\mathbb {D}$-torseur sur
$\mathbb {D}$-torseur sur ![]() $X_{E^{nr}}$.
$X_{E^{nr}}$.
On obtient alors le résultat suivant.
Proposition 6.2 Si ![]() $b$ est décent il y a un isomorphisme de
$b$ est décent il y a un isomorphisme de ![]() $G$-torseurs sur
$G$-torseurs sur ![]() $X_{E^{nr}}$
$X_{E^{nr}}$
Remarque 6.3 Dans la proposition précédente c'est ![]() $-\nu _b$ qui intervient et non
$-\nu _b$ qui intervient et non ![]() $\nu _b$ car les pentes de Newton et de Harder-Narasimhan sont opposées, le fibré associé à
$\nu _b$ car les pentes de Newton et de Harder-Narasimhan sont opposées, le fibré associé à ![]() $[\pi _E]\in B(\mathbb {G}_m)$ est
$[\pi _E]\in B(\mathbb {G}_m)$ est ![]() $\mathcal {O}_{X}(-1)$.
$\mathcal {O}_{X}(-1)$.
Remarque 6.4 Il faut faire attention que si ![]() $E^{\prime}|E$ est ramifiée bien que
$E^{\prime}|E$ est ramifiée bien que ![]() $\pi _{E^{\prime}/E}^*\mathcal {O}_{X_E}(1)\simeq \mathcal {O}_{X_{E^{\prime}}} ([E^{\prime}:E])$, il n'y a pas de tel isomorphisme canonique. Cela provient du fait que le fibré en droites
$\pi _{E^{\prime}/E}^*\mathcal {O}_{X_E}(1)\simeq \mathcal {O}_{X_{E^{\prime}}} ([E^{\prime}:E])$, il n'y a pas de tel isomorphisme canonique. Cela provient du fait que le fibré en droites ![]() $\mathcal {O}_{X_E}(1)$ dépend du choix d'une uniformisante que l'on a fixée depuis le début
$\mathcal {O}_{X_E}(1)$ dépend du choix d'une uniformisante que l'on a fixée depuis le début ![]() $\pi _E$ et qu'afin de fixer un isomorphisme entre
$\pi _E$ et qu'afin de fixer un isomorphisme entre ![]() $\pi _{E^{\prime}/E}^*\mathcal {O}_{X_E}(1)$ et
$\pi _{E^{\prime}/E}^*\mathcal {O}_{X_E}(1)$ et ![]() $\mathcal {O}_{X_{E^{\prime}}} ([E^{\prime}:E])$ il faut choisir un élément
$\mathcal {O}_{X_{E^{\prime}}} ([E^{\prime}:E])$ il faut choisir un élément ![]() $u\in L^\times$ tel que
$u\in L^\times$ tel que ![]() $\pi _{E^{\prime}}^{e_{E^{\prime}/E}}/\pi _E=u^{\sigma -1}$, cf. [Reference Fargues and FontaineFF18].
$\pi _{E^{\prime}}^{e_{E^{\prime}/E}}/\pi _E=u^{\sigma -1}$, cf. [Reference Fargues and FontaineFF18].
En appliquant maintenant le théorème 5.1 on obtient le résultat suivant.
Théorème 6.5 Soit ![]() $E^{\prime}|E^{nr}$ une extension algébrique. Il y a une bijection
$E^{\prime}|E^{nr}$ une extension algébrique. Il y a une bijection
 \begin{align*} {\rm Hom} ( \mathbb{D}_{E^{\prime}}, G_{E^{\prime}} )/G(E^{\prime})\text{-conj.} &\xrightarrow{\;\sim\;} \big \{G\text{-torseurs sur }X_{E^{\prime}}\big \}/\sim \\ {[} \nu] & \longmapsto \big [ \nu_*\mathscr{T}_\infty\big ]. \end{align*}
\begin{align*} {\rm Hom} ( \mathbb{D}_{E^{\prime}}, G_{E^{\prime}} )/G(E^{\prime})\text{-conj.} &\xrightarrow{\;\sim\;} \big \{G\text{-torseurs sur }X_{E^{\prime}}\big \}/\sim \\ {[} \nu] & \longmapsto \big [ \nu_*\mathscr{T}_\infty\big ]. \end{align*}6.2 Plongement de la cohomologie galoisienne dans  $B(G)$
$B(G)$
Soit ![]() $[b]\in B(G)$ et
$[b]\in B(G)$ et ![]() $J_b$ le groupe algébrique associé tel que
$J_b$ le groupe algébrique associé tel que ![]() $J_b (E)$ soit
$J_b (E)$ soit ![]() $\sigma$-centralisateur de
$\sigma$-centralisateur de ![]() $b$. Pour
$b$. Pour ![]() $R$ une
$R$ une ![]() $E$-algèbre
$E$-algèbre ![]() $J_b (R)$ est le groupe des automorphismes compatibles au produit tensoriel du foncteur
$J_b (R)$ est le groupe des automorphismes compatibles au produit tensoriel du foncteur
D'après [Reference Rapoport and RichartzRR96] prop. 1.17 ou bien [Reference KottwitzKot97] 3.5 il y a une identification
et en particulier
qui identifie la cohomologie galoisienne de ![]() $G$ avec les ‘
$G$ avec les ‘![]() $G$-isocristaux unités’.
$G$-isocristaux unités’.
Ces plongements s'interprètent de la façon suivante en termes de ![]() $G$-torseurs sur
$G$-torseurs sur ![]() $X$. Il y a un plongement de
$X$. Il y a un plongement de ![]() $X$-schémas en groupes réductifs
$X$-schémas en groupes réductifs
Dès lors l'application (7) est donnée par
 \begin{align*} \{J_b\text{-torseurs}\} & \longrightarrow \{ G\text{-torseurs sur }X\} \\ \mathscr{T} & \longmapsto \mathscr{E}_b\underset{J_b\times X}{\times} (\mathscr{T}\times X ). \end{align*}
\begin{align*} \{J_b\text{-torseurs}\} & \longrightarrow \{ G\text{-torseurs sur }X\} \\ \mathscr{T} & \longmapsto \mathscr{E}_b\underset{J_b\times X}{\times} (\mathscr{T}\times X ). \end{align*}En particulier l'inclusion (8) est donnée par l'image réciproque
où ![]() $f:X\rightarrow {\rm Spec} (E)$.
$f:X\rightarrow {\rm Spec} (E)$.
6.3 Morphisme des pentes et polygone de Harder-Narasimhan
On suppose maintenant ![]() $G$ quasi-déployé. On a déjà vu (prop. 5.12) que
$G$ quasi-déployé. On a déjà vu (prop. 5.12) que ![]() $b\in B(G)$ est basique si et seulement si
$b\in B(G)$ est basique si et seulement si ![]() $\mathscr {E}_b$ est semi-stable et donc
$\mathscr {E}_b$ est semi-stable et donc
Fixons ![]() $A\subset T\subset B$ où
$A\subset T\subset B$ où ![]() $A$ est un tore déployé maximal,
$A$ est un tore déployé maximal, ![]() $T$ un tore maximal et
$T$ un tore maximal et ![]() $B$ un sous-groupe de Borel. Puisque
$B$ un sous-groupe de Borel. Puisque ![]() $G$ est quasi-déployé
$G$ est quasi-déployé
et on voit donc ![]() $[\nu _b]$ pour
$[\nu _b]$ pour ![]() $[b]\in B(G)$ comme un élément de la chambre de Weyl positive. Rappelons également (sec. 5.1) qu’étant donné un
$[b]\in B(G)$ comme un élément de la chambre de Weyl positive. Rappelons également (sec. 5.1) qu’étant donné un ![]() $G$-torseur
$G$-torseur ![]() $\mathscr {T}$ sur
$\mathscr {T}$ sur ![]() $X$ on peut définir son polygone de Harder-Narasimhan généralisé
$X$ on peut définir son polygone de Harder-Narasimhan généralisé ![]() $\nu _\mathscr {T}\in X_*(A)_\mathbb {Q}^+$. On vérifie alors aussitôt la proposition suivante (cf. remarque 6.3 pour le signe
$\nu _\mathscr {T}\in X_*(A)_\mathbb {Q}^+$. On vérifie alors aussitôt la proposition suivante (cf. remarque 6.3 pour le signe ![]() $-$).
$-$).
Proposition 6.6 On a l’égalité suivante dans la chambre de Weyl positive
où ![]() $w_0$ est l’élément de plus grande longueur dans le groupe de Weyl. En particulier le sous-groupe parabolique associé à la réduction canonique de
$w_0$ est l’élément de plus grande longueur dans le groupe de Weyl. En particulier le sous-groupe parabolique associé à la réduction canonique de ![]() $\mathscr {E}_b$ est le sous-groupe parabolique opposé associé à
$\mathscr {E}_b$ est le sous-groupe parabolique opposé associé à ![]() $\nu _b$.
$\nu _b$.
Quitte à ![]() $\sigma$-conjuguer
$\sigma$-conjuguer ![]() $b$ on peut supposer que
$b$ on peut supposer que ![]() $\nu _b:\mathbb {D}\rightarrow A$. Soit alors
$\nu _b:\mathbb {D}\rightarrow A$. Soit alors ![]() $M_b$ le centralisateur de
$M_b$ le centralisateur de ![]() $\nu _b$, un sous-groupe de Levi standard. Alors,
$\nu _b$, un sous-groupe de Levi standard. Alors, ![]() $b\in M_b (L)$ et si on note
$b\in M_b (L)$ et si on note ![]() $b'=b$ vu comme élément de
$b'=b$ vu comme élément de ![]() $M_b (L)$
$M_b (L)$
qui est la réduction canonique de ![]() $\mathscr {E}$ (on a déjà vu que
$\mathscr {E}$ (on a déjà vu que ![]() $\mathscr {E}$ possède une réduction au Levi, cf. prop. 5.16).
$\mathscr {E}$ possède une réduction au Levi, cf. prop. 5.16).
7. Un analogue d'un résultat de Drinfeld-Simpson
Voici un analogue du théorème principal de [Reference Drinfeld and SimpsonDS95]. On remarquera que contrairement à [Reference Drinfeld and SimpsonDS95] on n'a pas besoin de supposer que ![]() $G$ est semi-simple. Cela résulte du fait que dans notre cas
$G$ est semi-simple. Cela résulte du fait que dans notre cas ![]() ${\rm Pic}^0(X)=0$.
${\rm Pic}^0(X)=0$.
Théorème 7.1 Supposons ![]() $G$ quasi-déployé. Soit
$G$ quasi-déployé. Soit ![]() $\infty \in |X|$ un point fermé de
$\infty \in |X|$ un point fermé de ![]() $X$. Pour
$X$. Pour ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$,
$X$, ![]() $\mathscr {T}_{|X\setminus \{\infty \}}$ est trivial c'est à dire possède une section.
$\mathscr {T}_{|X\setminus \{\infty \}}$ est trivial c'est à dire possède une section.
Concrètement, à la vue du théorème 5.1, le théorème précédent se traduit de la façon suivante. Soit ![]() $t\in B^{\varphi =\pi _E}$ non nul tel que
$t\in B^{\varphi =\pi _E}$ non nul tel que ![]() $V^+(t)=\{\infty \}$. Notons
$V^+(t)=\{\infty \}$. Notons ![]() $B_e=B[{1}/{t}]^{\varphi ={\rm Id}}$,
$B_e=B[{1}/{t}]^{\varphi ={\rm Id}}$, ![]() $X\setminus \{\infty \}= {\rm Spec} (B_e)$. Soit
$X\setminus \{\infty \}= {\rm Spec} (B_e)$. Soit ![]() $b\in G(L)$. Le théorème dit alors que les deux foncteurs fibres sur
$b\in G(L)$. Le théorème dit alors que les deux foncteurs fibres sur ![]() ${\rm Rep}\, G$ à valeurs dans les
${\rm Rep}\, G$ à valeurs dans les ![]() $B_e$-modules libres
$B_e$-modules libres
sont isomorphes.
Avant d'entamer la preuve remarquons le résultat suivant.
Proposition 7.2 Si ![]() $G$ est quasi-déployé tout
$G$ est quasi-déployé tout ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$ possède une réduction à un sous-tore de
$X$ possède une réduction à un sous-tore de ![]() $G$.
$G$.
Proof Démonstration C'est une conséquence du théorème 5.1, du fait que toute classe de ![]() $\sigma$-conjugaison dans
$\sigma$-conjugaison dans ![]() $G$ possède une réduction basique à un sous-groupe de Levi et de ce que si
$G$ possède une réduction basique à un sous-groupe de Levi et de ce que si ![]() $M$ est un sous-groupe de Levi d'un sous-groupe parabolique de
$M$ est un sous-groupe de Levi d'un sous-groupe parabolique de ![]() $G$ et
$G$ et ![]() $T$ un tore elliptique dans
$T$ un tore elliptique dans ![]() $M$ alors l'application
$M$ alors l'application
est surjective ([Reference KottwitzKot85] prop. 5.3).
Preuve du théorème 7.1. D'après la proposition 7.2 on peut supposer que ![]() $G$ est un tore que l'on note maintenant
$G$ est un tore que l'on note maintenant ![]() $T$. Il s'agit de montrer que le morphisme de groupes
$T$. Il s'agit de montrer que le morphisme de groupes
est nul. Soit ![]() $E^{\prime}|E$ une extension galoisienne scindant
$E^{\prime}|E$ une extension galoisienne scindant ![]() $T$. Il y a une suite exacte de tores
$T$. Il y a une suite exacte de tores
D'après le théorème 2.7 (cf. également rem. 2.8 qui montre que la preuve que nous sommes en train d'effectuer est indépendante de l'arsenal de la théorie du corps de classe) on a ![]() $H^2(X, T')=0$. Il y a donc un diagramme.
$H^2(X, T')=0$. Il y a donc un diagramme.

Il suffit maintenant de constater que puisque ![]() ${\rm Pic}^0 (X_{E^{\prime}})=0$,
${\rm Pic}^0 (X_{E^{\prime}})=0$,
Remarque 7.3 Du point de vue de [Reference Drinfeld and SimpsonDS95] le théorème 7.1 peut s'interpréter de la façon suivant. Soit ![]() $F|\mathbb {F}_q$ un corps perfectoïde non nécessairement algébriquement clos (contrairement à l'hypothèse faite dans tout cet article) et
$F|\mathbb {F}_q$ un corps perfectoïde non nécessairement algébriquement clos (contrairement à l'hypothèse faite dans tout cet article) et ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X_F$. Soit
$X_F$. Soit ![]() $\infty \in |X_F|$ un point fermé. Alors, après le revêtement pro-étale
$\infty \in |X_F|$ un point fermé. Alors, après le revêtement pro-étale ![]() $\hbox {Spa} (\hat {\bar {F}}\big )\rightarrow \hbox {Spa} (F)$, via le morphisme
$\hbox {Spa} (\hat {\bar {F}}\big )\rightarrow \hbox {Spa} (F)$, via le morphisme ![]() $X_{\hat {\bar {F}}}\rightarrow X_F$, le tiré en arrière de
$X_{\hat {\bar {F}}}\rightarrow X_F$, le tiré en arrière de ![]() $\mathscr {T}_{|X\setminus \{\infty \}}$ devient trivial.
$\mathscr {T}_{|X\setminus \{\infty \}}$ devient trivial.
Corollaire 7.4 Sous les hypothèses du théorème 7.1 y a une bijection
Notons également le corollaire suivant qui pourrait s'avérer utile.
Corollaire 7.5 Si ![]() $G$ est quasi-déployé et
$G$ est quasi-déployé et ![]() $B$ est un sous-groupe de Borel de
$B$ est un sous-groupe de Borel de ![]() $G$ alors tout
$G$ alors tout ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$ possède une réduction à
$X$ possède une réduction à ![]() $B$.
$B$.
Proof Démonstration Choisissons un point fermé ![]() $\infty \in |X|$ et soit
$\infty \in |X|$ et soit ![]() $\mathscr {T}$ un
$\mathscr {T}$ un ![]() $G$-torseur sur
$G$-torseur sur ![]() $X$. D'après le théorème 7.1
$X$. D'après le théorème 7.1 ![]() $\mathscr {T}_{|X\setminus \{\infty \}}$ possède une réduction à
$\mathscr {T}_{|X\setminus \{\infty \}}$ possède une réduction à ![]() $B$ c'est à dire une section au dessus de
$B$ c'est à dire une section au dessus de ![]() $X\setminus \{\infty \}$ de la fibration localement triviale pour la topologie étale
$X\setminus \{\infty \}$ de la fibration localement triviale pour la topologie étale
de fibre ![]() $G/B$. Puisque ce morphisme est propre, par le critère valuatif de propreté une telle section s’étend automatiquement à
$G/B$. Puisque ce morphisme est propre, par le critère valuatif de propreté une telle section s’étend automatiquement à ![]() $X$.
$X$.
Remarque 7.6 Le corollaire précédent illustre bien la ‘souplesse géométrique’ qu'apportent les fibrés par rapport aux isocristaux. Par exemple, bien qu'un isocristal simple de hauteur ![]() $>1$ n'ait pas de réduction à un sous-groupe de Borel, le fibré associé est (non canoniquement) une extension successive de fibrés en droites.
$>1$ n'ait pas de réduction à un sous-groupe de Borel, le fibré associé est (non canoniquement) une extension successive de fibrés en droites.
8. Interprétation de l'application de  $\kappa$ de Kottwitz en termes de classe de Chern
$\kappa$ de Kottwitz en termes de classe de Chern
Notons ![]() $\pi _1 (G)$ le groupe fondamental au sens de Borovoi de
$\pi _1 (G)$ le groupe fondamental au sens de Borovoi de ![]() $G$. Kottwitz a défini dans [Reference KottwitzKot85] une application
$G$. Kottwitz a défini dans [Reference KottwitzKot85] une application
qui généralise celle de la section 4 dans le cas des tores. Voici une description en termes de cohomologie abélianisée de Borovoi [Reference BorovoiBor98] et de cohomologie de modules croisés à la Breen [Reference LabesseLab99]. Considérons le module croisé ![]() $[G_{sc}\rightarrow G]$ où
$[G_{sc}\rightarrow G]$ où ![]() $G_{sc}$ désigne le revêtement universel de
$G_{sc}$ désigne le revêtement universel de ![]() $G_{der}$ et
$G_{der}$ et ![]() $G$ agit sur
$G$ agit sur ![]() $G_{sc}$ par automorphismes intérieurs. Breen a défini dans l'appendice B de [Reference LabesseLab99] la cohomologie à valeurs dans module croisé dans n'importe quel topos. On considère ici le cas du topos étale de
$G_{sc}$ par automorphismes intérieurs. Breen a défini dans l'appendice B de [Reference LabesseLab99] la cohomologie à valeurs dans module croisé dans n'importe quel topos. On considère ici le cas du topos étale de ![]() $X$.
$X$.
Le morphisme de modules croisés
induit un morphisme
Maintenant, si ![]() $T$ est un tore maximal dans
$T$ est un tore maximal dans ![]() $G$ et
$G$ et ![]() $T_{sc}$ désigne son image réciproque à
$T_{sc}$ désigne son image réciproque à ![]() $G_{sc}$, l'inclusion
$G_{sc}$, l'inclusion
est un quasi-isomorphisme i.e. induit un isomorphisme sur les ![]() $\pi _1$ et
$\pi _1$ et ![]() $\pi _0$. On en déduit un isomorphisme
$\pi _0$. On en déduit un isomorphisme
Mais puisque ![]() $H^2 (X,T_{sc})=0$ (théo. 2.7)
$H^2 (X,T_{sc})=0$ (théo. 2.7)
Qui s'identifie via l'isomorphisme ![]() $\kappa$ pour les tores à
$\kappa$ pour les tores à
puisque ![]() $X_* (T_{sc})\subset X_*(T)$ s'identifie au sous-groupe engendré par les coracines associée à un sous-groupe de Borel de
$X_* (T_{sc})\subset X_*(T)$ s'identifie au sous-groupe engendré par les coracines associée à un sous-groupe de Borel de ![]() $G_{\bar {E}}$ de Levi
$G_{\bar {E}}$ de Levi ![]() $T_{\bar {E}}$. On en déduit une application
$T_{\bar {E}}$. On en déduit une application
dont on vérifie que c'est celle définie par Kottwitz via la bijection ![]() $B(G)\xrightarrow {\sim } H^1(X,G)$.
$B(G)\xrightarrow {\sim } H^1(X,G)$.
Si ![]() $H$ est un groupe réductif sur un corps algébriquement clos et
$H$ est un groupe réductif sur un corps algébriquement clos et ![]() $\ell$ un nombre premier différent de la caractéristique de ce corps l'inclusion d'un tore maximal
$\ell$ un nombre premier différent de la caractéristique de ce corps l'inclusion d'un tore maximal ![]() $T\subset H$ induit un morphisme de champs algébriques
$T\subset H$ induit un morphisme de champs algébriques
qui induit un isomorphisme
où ![]() $W$ désigne le groupe de Weyl de
$W$ désigne le groupe de Weyl de ![]() $T$ [Reference GrothendieckGro58]. Ainsi, la cohomologie de
$T$ [Reference GrothendieckGro58]. Ainsi, la cohomologie de ![]() $BH$ est concentrée en degrés pairs et
$BH$ est concentrée en degrés pairs et
On en déduit en particulier un isomorphisme
En général, pour des groupes autre que le groupe linéaire, la cohomologie entière ![]() $H^\bullet (BH,\mathbb {Z}_\ell )$ possède de la torsion ‘exotique’ (cf. [Reference GrothendieckGro58] et [Reference TotaroTot05]). Néanmoins il y a toujours un morphisme
$H^\bullet (BH,\mathbb {Z}_\ell )$ possède de la torsion ‘exotique’ (cf. [Reference GrothendieckGro58] et [Reference TotaroTot05]). Néanmoins il y a toujours un morphisme
Il se décrit de la façon suivante en utilisant la cohomologie des topos à valeurs dans un module croisé de Breen et le topos lisse du champ algébrique ![]() $BH$ (sec. 2 de [Reference Illusie and ZhengIZ16]). Soit
$BH$ (sec. 2 de [Reference Illusie and ZhengIZ16]). Soit ![]() $EH\rightarrow BH$ le
$EH\rightarrow BH$ le ![]() $H$-torseur universel. Le poussé en avant du
$H$-torseur universel. Le poussé en avant du ![]() $H$-torseur universel
$H$-torseur universel ![]() $E H$ par
$E H$ par ![]() $[1\rightarrow H]\rightarrow [H_{sc}\rightarrow H]$ définit un élément de
$[1\rightarrow H]\rightarrow [H_{sc}\rightarrow H]$ définit un élément de ![]() $H^1 ( BH, [H_{sc}\rightarrow H])$. Si maintenant
$H^1 ( BH, [H_{sc}\rightarrow H])$. Si maintenant ![]() $T$ est un tore maximal dans
$T$ est un tore maximal dans ![]() $H$ il y a un isomorphisme
$H$ il y a un isomorphisme ![]() $H^1 ( BH, [T_{sc}\rightarrow T])\xrightarrow {\sim } H^1(BH, [H_{sc}\rightarrow H])$. Pour un entier
$H^1 ( BH, [T_{sc}\rightarrow T])\xrightarrow {\sim } H^1(BH, [H_{sc}\rightarrow H])$. Pour un entier ![]() $n\geq 1$ la suite exacte
$n\geq 1$ la suite exacte
 \[ 0\longrightarrow \underbrace{[T_{sc}[n]\rightarrow T[n] ]}_{\pi_1(H)\overset{\mathbb{L}}{\otimes} {\mathbb{Z}/n\mathbb{Z}(1)}} \longrightarrow [T_{sc}\rightarrow T]\xrightarrow{\ \times n\ } [T_{sc}\rightarrow T]\longrightarrow 0 \]
\[ 0\longrightarrow \underbrace{[T_{sc}[n]\rightarrow T[n] ]}_{\pi_1(H)\overset{\mathbb{L}}{\otimes} {\mathbb{Z}/n\mathbb{Z}(1)}} \longrightarrow [T_{sc}\rightarrow T]\xrightarrow{\ \times n\ } [T_{sc}\rightarrow T]\longrightarrow 0 \]nous permet de définir la classe de Chern de notre classe comme un élément de
Lorsque ![]() $n$ varie cela fournit une classe dans
$n$ varie cela fournit une classe dans ![]() $H^2 (BH, \widehat {\pi _1(H)} (1) )$ (complétion profinie) qui nous donne le morphisme (9) cherché.
$H^2 (BH, \widehat {\pi _1(H)} (1) )$ (complétion profinie) qui nous donne le morphisme (9) cherché.
Revenons maintenant à ![]() $G$ sur
$G$ sur ![]() $E$. Comme dans la section 4 on a une application
$E$. Comme dans la section 4 on a une application
On a ![]() $H^1 (BG_{\bar {E}}, \mathbb {Q}/\mathbb {Z} (1))=0$ par connexité de
$H^1 (BG_{\bar {E}}, \mathbb {Q}/\mathbb {Z} (1))=0$ par connexité de ![]() $G$ et donc une suite exacte
$G$ et donc une suite exacte
D'après la proposition 2.1 l'accouplement précédent est nul sur ![]() $\mathrm {Br} (E)$ et on obtient donc un accouplement
$\mathrm {Br} (E)$ et on obtient donc un accouplement
c'est à dire encore une application classe de Chern
Du cas des tores (prop. 4.1) on déduit que via le théorème 5.1
Acknowledgements
J'aimerais remercier Michael Rapoport et Peter Scholze pour de nombreuses discussions sur le sujet. J'aimerais également remercier Arthur-César Le Bras qui m'a fait remarquer que la conjecture 3.10 admet un analogue archimédien et Urs Hartl pour des corrections.