There are several ways to convert a closure or interior operation to a different operation that has particular desirable properties. In this paper, we axiomatize three ways to do so, drawing on disparate examples from the literature, including tight closure, basically full closure, and various versions of integral closure. In doing so, we explore several such desirable properties, including hereditary, residual, and cofunctorial, and see how they interact with other properties such as the finitistic property.

In this article, we prove that a complete Noetherian local domain of mixed characteristic $p>0$ with perfect residue field has an integral extension that is an integrally closed, almost Cohen–Macaulay domain such that the Frobenius map is surjective modulo p. This result is seen as a mixed characteristic analog of the fact that the perfect closure of a complete local domain in positive characteristic is almost Cohen–Macaulay. To this aim, we carry out a detailed study of decompletion of perfectoid rings and establish the Witt-perfect (decompleted) version of André’s perfectoid Abhyankar’s lemma and Riemann’s extension theorem.

Let $f\colon Y \to X$ be a proper flat morphism of locally noetherian schemes. Then the locus in $X$ over which $f$ is smooth is stable under generization. We prove that, under suitable assumptions on the formal fibers of $X$, the same property holds for other local properties of morphisms, even if $f$ is only closed and flat. Our proof of this statement reduces to a purely local question known as Grothendieck's localization problem. To answer Grothendieck's problem, we provide a general framework that gives a uniform treatment of previously known cases of this problem, and also solves this problem in new cases, namely for weak normality, seminormality, $F$-rationality, and the ‘Cohen–Macaulay and $F$-injective’ property. For the weak normality statement, we prove that weak normality always lifts from Cartier divisors. We also solve Grothendieck's localization problem for terminal, canonical, and rational singularities in equal characteristic zero.

We prove a Noether–Deuring theorem for the derived category of bounded complexes of modules over a Noetherian algebra.

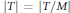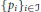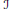Let $\left( T,\,M \right)$ be a complete local (Noetherian) ring such that $\dim\,T\,\ge \,2$ and $\left| T \right|\,=\,\left| T/M \right|$ and let ${{\left\{ {{p}_{i}} \right\}}_{i\in \Im }}$ be a collection of elements of $T$ indexed by a set $\mathcal{J}$ so that $\left| \mathcal{J} \right|\,<\,\left| T \right|$. For each 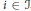$i\,\in \,\mathcal{J}$, let ${{C}_{i}}:=\left\{ {{Q}_{i1}},...,{{Q}_{i{{n}_{i}}}} \right\}$ be a set of nonmaximal prime ideals containing ${{p}_{i}}$ such that the ${{Q}_{ij}}$ are incomparable and ${{p}_{i}}\in {{Q}_{jk}}$ if and only if 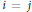$i\,=\,j$. We provide necessary and sufficient conditions so that $T$ is the 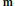$\mathbf{m}$-adic completion of a local unique factorization domain $\left( A,\,\mathbf{m} \right)$, and for each 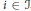$i\,\in \,\mathcal{J}$, there exists a unit ${{t}_{i}}$ of $T$ so that 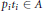${{p}_{i}}{{t}_{i}}\in A$ and 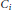${{C}_{i}}$ is the set of prime ideals 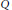$Q$ of $T$ that are maximal with respect to the condition that $Q\cap A={{p}_{i}}{{t}_{i}}A$.

We then use this result to construct a (nonexcellent) unique factorization domain containing many ideals for which tight closure and completion do not commute. As another application, we construct a unique factorization domain 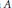$A$ most of whose formal fibers are geometrically regular.

We obtain a uniform linear bound for the Chevalley function at a point in the source of an analytic mapping that is regular in the sense of Gabrielov. There is a version of Chevalley’s lemma also along a fibre, or at a point of the image of a proper analytic mapping. We get a uniform linear bound for the Chevalley function of a closed Nash (or formally Nash) subanalytic set.

A topology on $\mathbb{Z}$, which gives a nice proof that the set of prime integers is infinite, is characterised and examined. It is found to be homeomorphic to $\mathbb{Q}$, with a compact completion homeomorphic to the Cantor set. It has a natural place in a family of topologies on $\mathbb{Z}$, which includes the $p$-adics, and one in which the set of rational primes $\mathbb{P}$ is dense. Examples from number theory are given, including the primes and squares, Fermat numbers, Fibonacci numbers and $k$-free numbers.

This paper is concerned with a finitely generated module M over a (commutative Noetherian) local ring R. In the case when R is a homomorphic image of a Gorenstein local ring, one can use the well-known associativity formula for multiplicities, together with local duality and Matlis duality, to produce analogous associativity formulae for the local cohomology modules of M with respect to the maximal ideal. The main purpose of this paper is to show that these formulae also hold in the case when R is universally catenary and such that all its formal fibres are Cohen–Macaulay.

These formulae involve certain subsets of the spectrum of R called the pseudosupports of M; these pseudo-supports are closed in the Zariski topology when R is universally catenary and has the property that all its formal fibres are Cohen–Macaulay. However, examples are provided to show that, in general, these pseudo-supports need not be closed. We are able to conclude that the above-mentioned associativity formulae for local cohomology modules do not hold over all local rings.