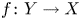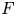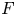1. Introduction
Let ![]() $f\colon Y \to X$ be a proper flat morphism of locally noetherian schemes. By [Reference Grothendieck and DieudonnéEGAIV3, Théorème 12.2.4(iii)], the locus of points
$f\colon Y \to X$ be a proper flat morphism of locally noetherian schemes. By [Reference Grothendieck and DieudonnéEGAIV3, Théorème 12.2.4(iii)], the locus of points ![]() $x \in X$ such that
$x \in X$ such that ![]() $f^{-1}(x)$ is smooth over
$f^{-1}(x)$ is smooth over ![]() $\kappa (x)$ is open, and, in particular, is stable under generization. In [Reference Grothendieck and DieudonnéEGAIV3, (12.0.2)], Grothendieck and Dieudonné asked whether similar statements hold for other local properties of morphisms, in the following sense.
$\kappa (x)$ is open, and, in particular, is stable under generization. In [Reference Grothendieck and DieudonnéEGAIV3, (12.0.2)], Grothendieck and Dieudonné asked whether similar statements hold for other local properties of morphisms, in the following sense.
Question 1.1 Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a proper flat morphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a proper flat morphism ![]() $f\colon Y \to X$ of locally noetherian schemes. Is the locus
$f\colon Y \to X$ of locally noetherian schemes. Is the locus
stable under generization?
Question 1.1 was answered for many properties ![]() $\mathbf {R}$ in [Reference Grothendieck and DieudonnéEGAIV3, § 12], and is a global version of Problem 1.2 below, which is known as Grothendieck's localization problem (see, for example, [Reference Avramov and FoxbyAF94]). Our goal is to provide a general framework with which to answer Question 1.1, assuming that
$\mathbf {R}$ in [Reference Grothendieck and DieudonnéEGAIV3, § 12], and is a global version of Problem 1.2 below, which is known as Grothendieck's localization problem (see, for example, [Reference Avramov and FoxbyAF94]). Our goal is to provide a general framework with which to answer Question 1.1, assuming that ![]() $\mathbf {R}$ is well behaved in the sense that it satisfies the following four permanence conditions.
$\mathbf {R}$ is well behaved in the sense that it satisfies the following four permanence conditions.
 $({\text {R}'_{\text {I}}})$ (Ascent via geometrically
$({\text {R}'_{\text {I}}})$ (Ascent via geometrically  $\mathbf {R}$ homomorphisms) For every flat local homomorphism
$\mathbf {R}$ homomorphisms) For every flat local homomorphism  $A \to B$ of noetherian local rings with geometrically
$A \to B$ of noetherian local rings with geometrically  $\mathbf {R}$ fibers, if
$\mathbf {R}$ fibers, if  $A$ satisfies
$A$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $B$ satisfies
$B$ satisfies  $\mathbf {R}$.
$\mathbf {R}$. $({\text {R}_{\text {II}}})$ (Descent) For every flat local homomorphism
$({\text {R}_{\text {II}}})$ (Descent) For every flat local homomorphism  $A \to B$ of noetherian local rings, if
$A \to B$ of noetherian local rings, if  $B$ satisfies
$B$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $A$ satisfies
$A$ satisfies  $\mathbf {R}$.
$\mathbf {R}$. $({\text {R}_{\text {IV}}})$ (Lifting from Cartier divisors) For every noetherian local ring
$({\text {R}_{\text {IV}}})$ (Lifting from Cartier divisors) For every noetherian local ring  $A$ and for every nonzerodivisor
$A$ and for every nonzerodivisor  $t$ in its maximal ideal, if
$t$ in its maximal ideal, if  $A/tA$ satisfies
$A/tA$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $A$ satisfies
$A$ satisfies  $\mathbf {R}$.
$\mathbf {R}$. $({\text {R}_{\text {V}}})$ (Localization) If a noetherian local ring
$({\text {R}_{\text {V}}})$ (Localization) If a noetherian local ring  $A$ satisfies
$A$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $A_\mathfrak {p}$ satisfies
$A_\mathfrak {p}$ satisfies  $\mathbf {R}$ for every prime ideal
$\mathbf {R}$ for every prime ideal  $\mathfrak {p} \subseteq A$.
$\mathfrak {p} \subseteq A$.
These conditions on ![]() $\mathbf {R}$ are studied in [Reference Grothendieck and DieudonnéEGAIV2, § 7] (see also Conditions 3.1), and are satisfied by many common properties
$\mathbf {R}$ are studied in [Reference Grothendieck and DieudonnéEGAIV2, § 7] (see also Conditions 3.1), and are satisfied by many common properties ![]() $\mathbf {R}$ (see Table 2). The notation
$\mathbf {R}$ (see Table 2). The notation ![]() $({\text {R}'_{\text {I}}})$ is used instead of
$({\text {R}'_{\text {I}}})$ is used instead of ![]() $({\text {R}_{\text {I}}})$ because the latter condition in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.10)] asserts that
$({\text {R}_{\text {I}}})$ because the latter condition in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.10)] asserts that ![]() $\mathbf {R}$ ascends via geometrically regular homomorphisms. The condition
$\mathbf {R}$ ascends via geometrically regular homomorphisms. The condition ![]() $({\text {R}_{\text {IV}}})$ is called ‘deformation’ in commutative algebra, is related to inversion of adjunction-type results in birational geometry, and can also be thought of as an inverse to local Bertini-type theorems. The terminology ‘lifts from Cartier divisors’ was suggested to us by János Kollár.
$({\text {R}_{\text {IV}}})$ is called ‘deformation’ in commutative algebra, is related to inversion of adjunction-type results in birational geometry, and can also be thought of as an inverse to local Bertini-type theorems. The terminology ‘lifts from Cartier divisors’ was suggested to us by János Kollár.
Our main result says that under an additional assumption on the formal fibers of the local rings of ![]() $X$, a more general version of Question 1.1 holds.
$X$, a more general version of Question 1.1 holds.
Theorem A Let ![]() $\mathbf {R}$ be a property of noetherian local rings satisfying
$\mathbf {R}$ be a property of noetherian local rings satisfying ![]() $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$, ![]() $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$, ![]() $({\text {R}_{\text {IV}}})$, and
$({\text {R}_{\text {IV}}})$, and ![]() $({\text {R}_{\text {V}}})$, such that regular local rings satisfy
$({\text {R}_{\text {V}}})$, such that regular local rings satisfy ![]() $\mathbf {R}$. Consider a flat morphism
$\mathbf {R}$. Consider a flat morphism ![]() $f\colon Y \to X$ of locally noetherian schemes.
$f\colon Y \to X$ of locally noetherian schemes.
(i) Suppose that
 $f$ maps closed to closed points, and that the local rings of
$f$ maps closed to closed points, and that the local rings of  $X$ at closed points have geometrically
$X$ at closed points have geometrically  $\mathbf {R}$ formal fibers. If every closed fiber of
$\mathbf {R}$ formal fibers. If every closed fiber of  $f$ is geometrically
$f$ is geometrically  $\mathbf {R}$, then all fibers of
$\mathbf {R}$, then all fibers of  $f$ are geometrically
$f$ are geometrically  $\mathbf {R}$.
$\mathbf {R}$.(ii) Suppose that
 $f$ is closed, and that the local rings of
$f$ is closed, and that the local rings of  $X$ have geometrically
$X$ have geometrically  $\mathbf {R}$ formal fibers. Then the locus
is stable under generization.
$\mathbf {R}$ formal fibers. Then the locus
is stable under generization. \[ U_\mathbf{R}(f) := \{x \in X \,|\, f^{{-}1}(x)\ \text{is geometrically}\ \mathbf{R}\ \text{over}\ \kappa(x)\} \subseteq X \]
\[ U_\mathbf{R}(f) := \{x \in X \,|\, f^{{-}1}(x)\ \text{is geometrically}\ \mathbf{R}\ \text{over}\ \kappa(x)\} \subseteq X \]
In the statement above, a locally noetherian scheme ![]() $X$ over a field
$X$ over a field ![]() $k$ is geometrically
$k$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $k$ if, for all finite field extensions
$k$ if, for all finite field extensions ![]() $k \subseteq k'$, every local ring of
$k \subseteq k'$, every local ring of ![]() $X \otimes _k k'$ satisfies
$X \otimes _k k'$ satisfies ![]() $\mathbf {R}$. We consider the fiber
$\mathbf {R}$. We consider the fiber ![]() $f^{-1}(x)$ of a morphism
$f^{-1}(x)$ of a morphism ![]() $f$ as a scheme over the residue field
$f$ as a scheme over the residue field ![]() $\kappa (x)$ at
$\kappa (x)$ at ![]() $x \in X$. We will use similar terminology for noetherian algebras over a field
$x \in X$. We will use similar terminology for noetherian algebras over a field ![]() $k$ and homomorphisms of noetherian rings. A semi-local noetherian ring
$k$ and homomorphisms of noetherian rings. A semi-local noetherian ring ![]() $A$ has geometrically
$A$ has geometrically ![]() $\mathbf {R}$ formal fibers if the
$\mathbf {R}$ formal fibers if the ![]() $\mathfrak {m}$-adic completion homomorphism
$\mathfrak {m}$-adic completion homomorphism ![]() $A \to \hat {A}$ has geometrically
$A \to \hat {A}$ has geometrically ![]() $\mathbf {R}$ fibers, where
$\mathbf {R}$ fibers, where ![]() $\mathfrak {m}$ is the product of the maximal ideals in
$\mathfrak {m}$ is the product of the maximal ideals in ![]() $A$.
$A$.
Theorem A(ii) answers Question 1.1 since proper morphisms are closed. Combined with the constructibility results proved in [Reference Grothendieck and DieudonnéEGAIV3, § 9] and [Reference Bingener and FlennerBF93, § 7], Theorem A(ii) implies that many properties of fibers are open on the target for closed flat morphisms of finite type between locally noetherian schemes with nice formal fibers. In Theorem A(i), the condition that a morphism maps closed points to closed points is much weaker than properness or even closedness, since it is satisfied by all morphisms locally of finite type between algebraic varieties, or more generally between Jacobson schemes [Reference Grothendieck and DieudonnéEGAInew, Corollaire 6.4.7 and Proposition 6.5.2].
Theorem A does not need to assume that ![]() $f$ is proper or even of finite type, and therefore answers a question of Shimomoto [Reference ShimomotoShi17, p. 1058]. Shimomoto proved versions of (i) and (ii) for morphisms of finite type between excellent noetherian schemes [Reference ShimomotoShi17, Main Theorem 1 and Corollary 3.8], and asked whether similar results hold without finite type hypotheses.
$f$ is proper or even of finite type, and therefore answers a question of Shimomoto [Reference ShimomotoShi17, p. 1058]. Shimomoto proved versions of (i) and (ii) for morphisms of finite type between excellent noetherian schemes [Reference ShimomotoShi17, Main Theorem 1 and Corollary 3.8], and asked whether similar results hold without finite type hypotheses.
The main ingredient in the proof of Theorem A is a purely commutative-algebraic statement, which is of independent interest. In [Reference Grothendieck and DieudonnéEGAIV2], Grothendieck and Dieudonné asked whether the following local version of Question 1.1 holds.
Problem 1.2 (Grothendieck's localization problem; see [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.5.4(i)])
Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism ![]() $\varphi \colon A \to B$ of noetherian local rings. If
$\varphi \colon A \to B$ of noetherian local rings. If ![]() $A$ has geometrically
$A$ has geometrically ![]() $\mathbf {R}$ formal fibers and the closed fiber of
$\mathbf {R}$ formal fibers and the closed fiber of ![]() $\varphi$ is geometrically
$\varphi$ is geometrically ![]() $\mathbf {R}$, then are all fibers of
$\mathbf {R}$, then are all fibers of ![]() $\varphi$ geometrically
$\varphi$ geometrically ![]() $\mathbf {R}$?
$\mathbf {R}$?
In other words, Problem 1.2 asks whether the property of having geometrically ![]() $\mathbf {R}$ fibers localizes for flat local homomorphisms of noetherian local rings. We call Problem 1.2 ‘Grothendieck's localization problem’ following Avramov and Foxby [Reference Avramov and FoxbyAF94], who proved many cases of this problem; see Table 1. We resolve Problem 1.2 for well-behaved properties
$\mathbf {R}$ fibers localizes for flat local homomorphisms of noetherian local rings. We call Problem 1.2 ‘Grothendieck's localization problem’ following Avramov and Foxby [Reference Avramov and FoxbyAF94], who proved many cases of this problem; see Table 1. We resolve Problem 1.2 for well-behaved properties ![]() $\mathbf {R}$, extending [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8] and [Reference MarotMar84, Theorem 2.1] to non-zero residue characteristic.
$\mathbf {R}$, extending [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8] and [Reference MarotMar84, Theorem 2.1] to non-zero residue characteristic.
Theorem B Problem 1.2 holds for properties ![]() $\mathbf {R}$ of noetherian local rings satisfying
$\mathbf {R}$ of noetherian local rings satisfying ![]() $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$, ![]() $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$, ![]() $({\text {R}_{\text {IV}}})$, and
$({\text {R}_{\text {IV}}})$, and ![]() $({\text {R}_{\text {V}}})$, such that regular local rings satisfy
$({\text {R}_{\text {V}}})$, such that regular local rings satisfy ![]() $\mathbf {R}$.
$\mathbf {R}$.
Table 1. Special cases of Problems 1.2 and 1.3. All results except those in the bottom section can be obtained from our methods.

Note: ‘C–M’ stands for ‘Cohen–Macaulay’.
See [Reference Avramov and FoxbyAF94, Remark 4.2 and pp. 1–2] for definitions of ![]() $(CI_n)$,
$(CI_n)$, ![]() $(G_n)$,
$(G_n)$, ![]() $(S_n)$,
$(S_n)$, ![]() ${\rm cid}$, and
${\rm cid}$, and ![]() ${\rm cmd}$.
${\rm cmd}$.
We list necessary assumptions for the results in the bottom two sections of the table.
![]() $^{1}$ Either
$^{1}$ Either ![]() $B$ is universally catenary, or
$B$ is universally catenary, or ![]() $B \otimes _A k$ has geometrically (normal
$B \otimes _A k$ has geometrically (normal ![]() $+$
$+$ ![]() $(R_n)$) formal fibers.
$(R_n)$) formal fibers.
![]() $^{2}$
$^{2}$ ![]() $A$ is quasi-excellent.
$A$ is quasi-excellent.
![]() $^{3}$
$^{3}$ ![]() $A$ is quasi-excellent and
$A$ is quasi-excellent and ![]() $B$ is excellent.
$B$ is excellent.
![]() $^{4}$
$^{4}$ ![]() $\hat {B}$ is equidimensional.
$\hat {B}$ is equidimensional.
![]() $^{5}$
$^{5}$ ![]() $A$ has complete intersection formal fibers.
$A$ has complete intersection formal fibers.
![]() $^{6}$
$^{6}$ ![]() $A$ has Cohen–Macaulay formal fibers.
$A$ has Cohen–Macaulay formal fibers.
![]() $^{7}$
$^{7}$ ![]() $A$ is universally catenary.
$A$ is universally catenary.
![]() $^{\rm {N}}$
$^{\rm {N}}$ ![]() $A/I$ is Nagata.
$A/I$ is Nagata.
![]() $^{\mathbf {Q}}$
$^{\mathbf {Q}}$ ![]() $A$ and
$A$ and ![]() $B$ are quasi-excellent
$B$ are quasi-excellent ![]() $\mathbf {Q}$-algebras.
$\mathbf {Q}$-algebras.
![]() $^{\rm {char0}}$
$^{\rm {char0}}$ ![]() $A$ is a quasi-excellent
$A$ is a quasi-excellent ![]() $\mathbf {Q}$-algebra and
$\mathbf {Q}$-algebra and ![]() $B$ is essentially of finite type over a field of characteristic zero.
$B$ is essentially of finite type over a field of characteristic zero.
The proof of Theorems A and B now proceeds as follows.
(I) We reduce Theorem A to Theorem B by replacing
 $X$ and
$X$ and  $Y$ with
$Y$ with  ${\rm Spec}(\mathcal {O}_{X,x})$ and
${\rm Spec}(\mathcal {O}_{X,x})$ and  ${\rm Spec}(\mathcal {O}_{Y,y})$ for suitable points
${\rm Spec}(\mathcal {O}_{Y,y})$ for suitable points  $x \in X$ and
$x \in X$ and  $y \in Y$. This step uses the assumption either that
$y \in Y$. This step uses the assumption either that  $f$ maps closed points to closed points, or that
$f$ maps closed points to closed points, or that  $f$ is closed.
$f$ is closed.(II) We reduce to the case when
 $A$ is quasi-excellent by replacing
$A$ is quasi-excellent by replacing  $A$ with its completion
$A$ with its completion  $\hat {A}$. This step uses
$\hat {A}$. This step uses  $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$,  $({\text {R}_{\text {II}}})$, and the condition on the formal fibers of
$({\text {R}_{\text {II}}})$, and the condition on the formal fibers of  $A$.
$A$.(III) We reduce to the case when
 $A$ is a regular local ring by applying Gabber's weak local uniformization theorem [Reference Illusie, Laszlo and OrgogozoILO14, Exposé VII, Théorème 1.1]. This step uses
$A$ is a regular local ring by applying Gabber's weak local uniformization theorem [Reference Illusie, Laszlo and OrgogozoILO14, Exposé VII, Théorème 1.1]. This step uses  $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$,  $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$,  $({\text {R}_{\text {IV}}})$,
$({\text {R}_{\text {IV}}})$,  $({\text {R}_{\text {V}}})$, and the quasi-excellence of
$({\text {R}_{\text {V}}})$, and the quasi-excellence of  $A$ obtained in (II).
$A$ obtained in (II).(IV) Finally, we are in a situation where we can apply [Reference Grothendieck and DieudonnéEGAIV2, Lemme 7.5.1.1], which is a statement similar to Problem 1.2 when
 $A$ is regular. This step uses
$A$ is regular. This step uses  $({\text {R}_{\text {IV}}})$.
$({\text {R}_{\text {IV}}})$.
The main innovation in our approach to Theorems A and B is the use of Gabber's theorem in (III). Grothendieck and Dieudonné [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8] and Marot [Reference MarotMar84, Theorem 2.1] separately proved versions of Theorem B under the assumption that every reduced module-finite ![]() $A$-algebra has a resolution of singularities. This assumption on resolutions of singularities holds when
$A$-algebra has a resolution of singularities. This assumption on resolutions of singularities holds when ![]() $A$ is a quasi-excellent
$A$ is a quasi-excellent ![]() $\mathbf {Q}$-algebra [Reference HironakaHir64, Chapter I, § 3, Main Theorem I
$\mathbf {Q}$-algebra [Reference HironakaHir64, Chapter I, § 3, Main Theorem I![]() $(n)$], or when
$(n)$], or when ![]() $A$ is quasi-excellent of dimension at most three [Reference LipmanLip78, Theorem; Reference Cossart and PiltantCP19, Theorem 1.1], but is not known to hold in general.
$A$ is quasi-excellent of dimension at most three [Reference LipmanLip78, Theorem; Reference Cossart and PiltantCP19, Theorem 1.1], but is not known to hold in general.
On the other hand, Gabber's weak local uniformization theorem says that a variant of resolutions of singularities exists for arbitrary quasi-excellent noetherian schemes [Reference Illusie, Laszlo and OrgogozoILO14, Exposé VII, Théorème 1.1]. Gabber's theorem is a version of de Jong's alteration theorem [Reference de JongdJ96, Theorem 4.1] for quasi-excellent noetherian schemes that are not necessarily of finite type over a field or a discrete rank one valuation ring (DVR). Both of their theorems say that variants of resolutions of singularities exist after possibly passing to a finite extension of the function field. As presented by Kurano and Shimomoto [Reference Kurano and ShimomotoKS21, Main Theorem 2], Gabber previously used this theorem to prove that quasi-excellence is preserved under ideal-adic completion.
We note that one can also ask about generization on the source space ![]() $Y$ in the context of Theorem A. Such a statement follows from Theorem B for arbitrary flat morphisms
$Y$ in the context of Theorem A. Such a statement follows from Theorem B for arbitrary flat morphisms ![]() $f\colon Y \to X$ of locally noetherian schemes, with appropriate assumptions on the formal fibers of the local rings of
$f\colon Y \to X$ of locally noetherian schemes, with appropriate assumptions on the formal fibers of the local rings of ![]() $X$; cf. [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.9.10(ii)].
$X$; cf. [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.9.10(ii)].
In the second half of this paper, we answer Question 1.1 and Problem 1.2 in specific cases. Starting with André's theorem on the localization of formal smoothness [Reference AndréAnd74, Théorème on p. 297], previous cases of Problem 1.2 were proved using a variety of methods, including André–Quillen homology [Reference AndréAnd67, Reference QuillenQui70], Grothendieck duality [Reference HartshorneHar66], and the Cohen factorizations of Avramov, Foxby, and Herzog [Reference Avramov, Foxby and HerzogAFH94]. See Table 1 for known cases of Problem 1.2. By checking the conditions ![]() $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$, ![]() $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$, ![]() $({\text {R}_{\text {IV}}})$, and
$({\text {R}_{\text {IV}}})$, and ![]() $({\text {R}_{\text {V}}})$ (see Table 2), we give a uniform treatment of most of the results in Table 1 using Theorem B. Additionally, Theorem B resolves Problem 1.2 for weak normality, seminormality,
$({\text {R}_{\text {V}}})$ (see Table 2), we give a uniform treatment of most of the results in Table 1 using Theorem B. Additionally, Theorem B resolves Problem 1.2 for weak normality, seminormality, ![]() $F$-rationality, and the ‘Cohen–Macaulay and
$F$-rationality, and the ‘Cohen–Macaulay and ![]() $F$-injective’ property, the latter three of which were previously known only under additional finiteness assumptions [Reference HashimotoHas01, Theorem 5.8 and Remark 6.7; Reference ShimomotoShi17, Corollaries 3.4 and 3.10; Reference Patakfalvi, Schwede and ZhangPSZ18, Theorem 5.13]. The result for
$F$-injective’ property, the latter three of which were previously known only under additional finiteness assumptions [Reference HashimotoHas01, Theorem 5.8 and Remark 6.7; Reference ShimomotoShi17, Corollaries 3.4 and 3.10; Reference Patakfalvi, Schwede and ZhangPSZ18, Theorem 5.13]. The result for ![]() $F$-rationality completely answers a question of Hashimoto [Reference HashimotoHas01, Remark 6.7].
$F$-rationality completely answers a question of Hashimoto [Reference HashimotoHas01, Remark 6.7].
Table 2. Properties satisfying Conditions 3.1. The conditions hold under additional assumptions for the properties in the second and third sections of the table.

Note: ‘C–M’ stands for ‘Cohen–Macaulay’. See [Reference Avramov and FoxbyAF94, Remark 4.2 and pp. 1–2] for definitions of ![]() $(CI_n)$,
$(CI_n)$, ![]() $(G_n)$,
$(G_n)$, ![]() $(S_n)$,
$(S_n)$, ![]() ${\rm cid}$, and
${\rm cid}$, and ![]() ${\rm cmd}$.
${\rm cmd}$.
![]() $^{1}$
$^{1}$ ![]() $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$ is false when
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$ is false when ![]() $\mathbf {R} =$ ‘
$\mathbf {R} =$ ‘![]() $(R_n)$’ [Reference Grothendieck and DieudonnéEGAIV2, Remarque 5.12.6], but holds if one restricts
$(R_n)$’ [Reference Grothendieck and DieudonnéEGAIV2, Remarque 5.12.6], but holds if one restricts ![]() ${\mathscr {C}}$ to be the category of equidimensional catenary noetherian rings. For ‘normal
${\mathscr {C}}$ to be the category of equidimensional catenary noetherian rings. For ‘normal ![]() $+$
$+$ ![]() $(R_n)$’, we note that normal local rings are equidimensional.
$(R_n)$’, we note that normal local rings are equidimensional.
![]() $^{2}$
$^{2}$ ![]() $({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$ is false when
$({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$ is false when ![]() $\mathbf {R} =$ ‘domain’ [Reference Grothendieck and DieudonnéEGAIV2, Remarques 6.5.5(ii) and 6.15.11(ii)].
$\mathbf {R} =$ ‘domain’ [Reference Grothendieck and DieudonnéEGAIV2, Remarques 6.5.5(ii) and 6.15.11(ii)].
![]() $^{3}$
$^{3}$ ![]() $({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$ holds when
$({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$ holds when ![]() $\mathbf {R} =$ ‘
$\mathbf {R} =$ ‘![]() $F$-rational’ if
$F$-rational’ if ![]() ${\mathscr {C}}$ is the category of excellent rings; cf. [Reference HashimotoHas01, Theorem 6.4]. Enescu assumes that
${\mathscr {C}}$ is the category of excellent rings; cf. [Reference HashimotoHas01, Theorem 6.4]. Enescu assumes that ![]() $B/\mathfrak {m} B \otimes _{A/\mathfrak {m}} F^e_*(A/\mathfrak {m})$ is noetherian for every
$B/\mathfrak {m} B \otimes _{A/\mathfrak {m}} F^e_*(A/\mathfrak {m})$ is noetherian for every ![]() $e > 0$, which is used in the proof of [Reference EnescuEne00, Theorem 2.19]. Enescu states that this latter result holds without this assumption as long as ideals generated by systems of parameters in the rings
$e > 0$, which is used in the proof of [Reference EnescuEne00, Theorem 2.19]. Enescu states that this latter result holds without this assumption as long as ideals generated by systems of parameters in the rings ![]() $B/\mathfrak {m} B \otimes _{A/\mathfrak {m}} F^e_*(A/\mathfrak {m})$ are Frobenius closed in [Reference EnescuEne00, Remark 2.20]. This condition holds by the proof of [Reference Datta and MurayamaDM20, Proposition 3.11].
$B/\mathfrak {m} B \otimes _{A/\mathfrak {m}} F^e_*(A/\mathfrak {m})$ are Frobenius closed in [Reference EnescuEne00, Remark 2.20]. This condition holds by the proof of [Reference Datta and MurayamaDM20, Proposition 3.11].
![]() $^{4}$
$^{4}$ ![]() $({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$ holds for complete intersection (respectively, Cohen–Macaulay) homomorphisms when
$({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$ holds for complete intersection (respectively, Cohen–Macaulay) homomorphisms when ![]() $\mathbf {R} =$ ‘
$\mathbf {R} =$ ‘![]() ${\rm cid} \leqslant n$’ (respectively, ‘
${\rm cid} \leqslant n$’ (respectively, ‘![]() ${\rm cmd} \leqslant n$’). The cited references relate the complete intersection (respectively, Cohen–Macaulay) defects of the domain and fiber to that of the codomain.
${\rm cmd} \leqslant n$’). The cited references relate the complete intersection (respectively, Cohen–Macaulay) defects of the domain and fiber to that of the codomain.
![]() $^{e}$ This property holds if
$^{e}$ This property holds if ![]() ${\mathscr {C}}$ is the category of excellent rings.
${\mathscr {C}}$ is the category of excellent rings.
![]() $^{\mathbf {Q}}$
$^{\mathbf {Q}}$ ![]() $({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$,
$({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$, ![]() $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$, and
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$, and ![]() $({\rm R}_{\rm V}^{{\mathscr {C}}})$ hold when
$({\rm R}_{\rm V}^{{\mathscr {C}}})$ hold when ![]() ${\mathscr {C}}$ is the category of
${\mathscr {C}}$ is the category of ![]() $\mathbf {Q}$-algebras whose local rings are quasi-excellent, and
$\mathbf {Q}$-algebras whose local rings are quasi-excellent, and ![]() $({\rm R}_{{\rm III}})$ holds for complete local
$({\rm R}_{{\rm III}})$ holds for complete local ![]() $\mathbf {Q}$-algebras. For
$\mathbf {Q}$-algebras. For ![]() $({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$, Elkik works with rings essentially of finite type over a field of characteristic zero, but the same proof works after replacing [Reference ElkikElk78, Théorème 2] with Proposition 4.17.
$({\rm R}_{{\rm I}}^{{\mathscr {C}}\prime })$, Elkik works with rings essentially of finite type over a field of characteristic zero, but the same proof works after replacing [Reference ElkikElk78, Théorème 2] with Proposition 4.17.
![]() $^{\rm {rc}}$ This property holds for pseudo-rationality if
$^{\rm {rc}}$ This property holds for pseudo-rationality if ![]() ${\mathscr {C}}$ is the category of noetherian rings that have a residual complex in the sense of [Reference HartshorneHar66, Definition on p. 304].
${\mathscr {C}}$ is the category of noetherian rings that have a residual complex in the sense of [Reference HartshorneHar66, Definition on p. 304].
![]() $^{\rm {CM}}$ This property holds if
$^{\rm {CM}}$ This property holds if ![]() ${\mathscr {C}}$ is the category of homomorphic images of Cohen–Macaulay rings.
${\mathscr {C}}$ is the category of homomorphic images of Cohen–Macaulay rings.
![]() $^{\rm {char0}}$
$^{\rm {char0}}$ ![]() $({\rm R}_{{\rm III}})$ holds for complete local
$({\rm R}_{{\rm III}})$ holds for complete local ![]() $\mathbf {Q}$-algebras since resolutions of singularities exist [Reference HironakaHir64, Chapter I, § 3, Main Theorem I
$\mathbf {Q}$-algebras since resolutions of singularities exist [Reference HironakaHir64, Chapter I, § 3, Main Theorem I![]() $(n)$], and the other properties hold if
$(n)$], and the other properties hold if ![]() ${\mathscr {C}}$ is the category of rings essentially of finite type over possibly different fields of characteristic zero. The results for
${\mathscr {C}}$ is the category of rings essentially of finite type over possibly different fields of characteristic zero. The results for ![]() $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$ require some extra work; see Proposition 4.15.
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$ require some extra work; see Proposition 4.15.
For weak normality, we prove that weak normality lifts from Cartier divisors for all noetherian local rings (Proposition 4.10), extending a result of Bingener and Flenner [Reference Bingener and FlennerBF93, Corollary 4.1] to non-excellent rings. We also solve Grothendieck's localization problem for terminal, canonical, and rational singularities in equal characteristic zero (Corollary 4.18) using [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8].
As an application of Theorem B, we consider the following version of Grothendieck's lifting problem for semi-local rings.
Problem 1.3 (Local lifting problem; cf. [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.4.8A])
Let ![]() $A$ be a noetherian semi-local ring that is
$A$ be a noetherian semi-local ring that is ![]() $I$-adically complete with respect to an ideal
$I$-adically complete with respect to an ideal ![]() $I \subseteq A$. If
$I \subseteq A$. If ![]() $A/I$ has geometrically
$A/I$ has geometrically ![]() $\mathbf {R}$ formal fibers, then does
$\mathbf {R}$ formal fibers, then does ![]() $A$ have geometrically
$A$ have geometrically ![]() $\mathbf {R}$ formal fibers?
$\mathbf {R}$ formal fibers?
We call Problem 1.3 the ‘local lifting problem’ following Nishimura and Nishimura [Reference Nishimura and NishimuraNN88], in order to distinguish Problem 1.3 from Grothendieck's original lifting problem asked in [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.4.8A], which does not restrict to semi-local rings. Using Theorem B and the axiomatic approach to Problem 1.3 due to Brezuleanu and Ionescu [Reference Brezuleanu and IonescuBI84, Theorem 2.3], we give a solution to Problem 1.3 under the additional assumption that ![]() $A/I$ is Nagata. This result extends [Reference MarotMar84, Theorem 5.2] to non-zero residue characteristic.
$A/I$ is Nagata. This result extends [Reference MarotMar84, Theorem 5.2] to non-zero residue characteristic.
Theorem C Let ![]() $\mathbf {R}$ be a property of noetherian local rings that satisfies the hypotheses in Theorem B. Suppose, moreover, that the locus
$\mathbf {R}$ be a property of noetherian local rings that satisfies the hypotheses in Theorem B. Suppose, moreover, that the locus
is open for every noetherian complete local ring ![]() $C$. If
$C$. If ![]() $A$ is a noetherian semi-local ring that is
$A$ is a noetherian semi-local ring that is ![]() $I$-adically complete with respect to an ideal
$I$-adically complete with respect to an ideal ![]() $I \subseteq A$, and if
$I \subseteq A$, and if ![]() $A/I$ is Nagata and has geometrically
$A/I$ is Nagata and has geometrically ![]() $\mathbf {R}$ formal fibers, then
$\mathbf {R}$ formal fibers, then ![]() $A$ is Nagata and has geometrically
$A$ is Nagata and has geometrically ![]() $\mathbf {R}$ formal fibers.
$\mathbf {R}$ formal fibers.
The condition on ![]() $U_\mathbf {R}({\rm Spec}(C))$ is condition
$U_\mathbf {R}({\rm Spec}(C))$ is condition ![]() $({\rm R}_{{\rm III}})$ in Conditions 3.1. Recall that a noetherian semi-local ring is Nagata if and only if it has geometrically reduced formal fibers; see Remark 2.5. Theorem C therefore answers Problem 1.3 for properties
$({\rm R}_{{\rm III}})$ in Conditions 3.1. Recall that a noetherian semi-local ring is Nagata if and only if it has geometrically reduced formal fibers; see Remark 2.5. Theorem C therefore answers Problem 1.3 for properties ![]() $\mathbf {R}$ such that regular
$\mathbf {R}$ such that regular ![]() $\Rightarrow$
$\Rightarrow$ ![]() $\mathbf {R}$
$\mathbf {R}$ ![]() $\Rightarrow$ reduced, and gives a uniform treatment of most known cases of Problem 1.3; see Table 1. Theorem C also implies that for semi-local Nagata rings, the property of having geometrically
$\Rightarrow$ reduced, and gives a uniform treatment of most known cases of Problem 1.3; see Table 1. Theorem C also implies that for semi-local Nagata rings, the property of having geometrically ![]() $\mathbf {R}$ formal fibers is preserved under ideal-adic completion; see Corollary 3.11.
$\mathbf {R}$ formal fibers is preserved under ideal-adic completion; see Corollary 3.11.
We end this introduction with one question that is still open. Nishimura showed that the non-local version of Problem 1.3 is false for all properties ![]() $\mathbf {R}$ such that regular
$\mathbf {R}$ such that regular ![]() $\Rightarrow$
$\Rightarrow$ ![]() $\mathbf {R}$
$\mathbf {R}$ ![]() $\Rightarrow$ reduced [Reference NishimuraNis81, Example 5.3], and Greco showed that similar questions for the properties ‘universally catenary’ and ‘excellent’ are also false [Reference GrecoGre82, Proposition 1.1]. Instead, inspired by the axiomatic approach of Valabrega [Reference ValabregaVal78, Theorem 3], Imbesi conjectured that the following formulation of Problem 1.3 for non-semi-local rings may hold.
$\Rightarrow$ reduced [Reference NishimuraNis81, Example 5.3], and Greco showed that similar questions for the properties ‘universally catenary’ and ‘excellent’ are also false [Reference GrecoGre82, Proposition 1.1]. Instead, inspired by the axiomatic approach of Valabrega [Reference ValabregaVal78, Theorem 3], Imbesi conjectured that the following formulation of Problem 1.3 for non-semi-local rings may hold.
Problem 1.4 [Reference ImbesiImb95, p. 54]
Let ![]() $A$ be a noetherian ring that is
$A$ be a noetherian ring that is ![]() $I$-adically complete with respect to an ideal
$I$-adically complete with respect to an ideal ![]() $I \subseteq A$. If
$I \subseteq A$. If ![]() $A/I$ satisfies
$A/I$ satisfies ![]() $\mathbf {R} - 2$ and every local ring of
$\mathbf {R} - 2$ and every local ring of ![]() $A/I$ has geometrically
$A/I$ has geometrically ![]() $\mathbf {R}$ formal fibers, then is it true that
$\mathbf {R}$ formal fibers, then is it true that ![]() $A$ satisfies
$A$ satisfies ![]() $\mathbf {R} - 2$ and that every local ring of
$\mathbf {R} - 2$ and that every local ring of ![]() $A$ has geometrically
$A$ has geometrically ![]() $\mathbf {R}$ formal fibers?
$\mathbf {R}$ formal fibers?
Here, a ring ![]() $A$ satisfies
$A$ satisfies ![]() $\mathbf {R} - 2$ if for every
$\mathbf {R} - 2$ if for every ![]() $A$-algebra
$A$-algebra ![]() $B$ of finite type, the locus
$B$ of finite type, the locus ![]() $U_\mathbf {R}({\rm Spec}(B))$ is open in
$U_\mathbf {R}({\rm Spec}(B))$ is open in ![]() ${\rm Spec}(B)$ [Reference ValabregaVal78, Definition 1]. Nishimura's aforementioned example [Reference NishimuraNis81, Example 5.3] shows that Problem 1.4 does not hold when
${\rm Spec}(B)$ [Reference ValabregaVal78, Definition 1]. Nishimura's aforementioned example [Reference NishimuraNis81, Example 5.3] shows that Problem 1.4 does not hold when ![]() $\mathbf {R} =$ ‘reduced’. On the other hand, Problem 1.4 for
$\mathbf {R} =$ ‘reduced’. On the other hand, Problem 1.4 for ![]() $\mathbf {R} =$ ‘normal’ follows from a result proved by Brezuleanu and Rotthaus [Reference Brezuleanu and RotthausBR82, Satz 1] and by Chiriacescu [Reference ChiriacescuChi82, Theorem 1.5] around the same time, and a result due to Nishimura and Nishimura [Reference Nishimura and NishimuraNN88, Theorem A]. Moreover, Gabber proved Problem 1.4 for
$\mathbf {R} =$ ‘normal’ follows from a result proved by Brezuleanu and Rotthaus [Reference Brezuleanu and RotthausBR82, Satz 1] and by Chiriacescu [Reference ChiriacescuChi82, Theorem 1.5] around the same time, and a result due to Nishimura and Nishimura [Reference Nishimura and NishimuraNN88, Theorem A]. Moreover, Gabber proved Problem 1.4 for ![]() $\mathbf {R} =$ ‘regular’ [Reference Kurano and ShimomotoKS21, Main Theorem 1].
$\mathbf {R} =$ ‘regular’ [Reference Kurano and ShimomotoKS21, Main Theorem 1].
Outline
This paper is structured as follows.
In the first half of the paper, we set up the general framework with which we prove Theorems A, B, and C. To so do, we define geometrically ![]() $\mathbf {R}$ morphisms and formal fibers, and review the necessary background on (quasi-)excellent rings and on Gabber's weak local uniformization theorem in § 2. In § 3 we state the various conditions we put on local properties
$\mathbf {R}$ morphisms and formal fibers, and review the necessary background on (quasi-)excellent rings and on Gabber's weak local uniformization theorem in § 2. In § 3 we state the various conditions we put on local properties ![]() $\mathbf {R}$ of noetherian rings, and then prove Theorem B, first in the quasi-excellent case (Theorem 3.4), and then for rings with geometrically
$\mathbf {R}$ of noetherian rings, and then prove Theorem B, first in the quasi-excellent case (Theorem 3.4), and then for rings with geometrically ![]() $\mathbf {R}$ formal fibers (Corollary 3.6). We obtain Theorems A and C as consequences.
$\mathbf {R}$ formal fibers (Corollary 3.6). We obtain Theorems A and C as consequences.
The second half of the paper consists of § 4, where we verify the necessary conditions to apply Theorems A, B, and C to specific properties ![]() $\mathbf {R}$, in particular proving that weak normality lifts from Cartier divisors (Proposition 4.10). We then solve Problem 1.2 for terminal, canonical, and rational singularities in equal characteristic zero (Corollary 4.18) using [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8]. Finally, we conclude this paper with two tables: Table 1 contains references for special cases of Problems 1.2 and 1.3, and Table 2 contains references for the conditions used in our theorems.
$\mathbf {R}$, in particular proving that weak normality lifts from Cartier divisors (Proposition 4.10). We then solve Problem 1.2 for terminal, canonical, and rational singularities in equal characteristic zero (Corollary 4.18) using [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8]. Finally, we conclude this paper with two tables: Table 1 contains references for special cases of Problems 1.2 and 1.3, and Table 2 contains references for the conditions used in our theorems.
Notation
All rings are commutative with identity, and all ring homomorphisms are unital. We follow the notation in Definition 2.1 for properties ![]() $\mathbf {R}$ of noetherian local rings and their associated properties of morphisms and of formal fibers. We also follow the notation in Conditions 3.1 for the conditions on
$\mathbf {R}$ of noetherian local rings and their associated properties of morphisms and of formal fibers. We also follow the notation in Conditions 3.1 for the conditions on ![]() $\mathbf {R}$ appearing in our results. In addition, if
$\mathbf {R}$ appearing in our results. In addition, if ![]() $\mathbf {R}$ is a property of noetherian local rings, then, following [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.12], the
$\mathbf {R}$ is a property of noetherian local rings, then, following [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.12], the ![]() $\mathbf {R}$ locus in a locally noetherian scheme
$\mathbf {R}$ locus in a locally noetherian scheme ![]() $X$ is the locus
$X$ is the locus
at which ![]() $X$ satisfies
$X$ satisfies ![]() $\mathbf {R}$.
$\mathbf {R}$.
2. Preliminaries
2.1 Geometrically  $\mathbf {R}$ morphisms and formal fibers
$\mathbf {R}$ morphisms and formal fibers
We begin by defining geometrically ![]() $\mathbf {R}$ morphisms and rings with geometrically
$\mathbf {R}$ morphisms and rings with geometrically ![]() $\mathbf {R}$ formal fibers.
$\mathbf {R}$ formal fibers.
Definition 2.1 [Reference Grothendieck and DieudonnéEGAIV2, (7.3.1), (7.5.0), and (7.3.13)]
Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and let
$\mathbf {R}$ be a property of noetherian local rings, and let ![]() $k$ be a field. A locally noetherian
$k$ be a field. A locally noetherian ![]() $k$-scheme
$k$-scheme ![]() $X$ is geometrically
$X$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $k$ if
$k$ if ![]() $X$ satisfies the following property.
$X$ satisfies the following property.
A noetherian ![]() $k$-algebra
$k$-algebra ![]() $A$ is geometrically
$A$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $k$ if
$k$ if ![]() ${\rm Spec}(A)$ is geometrically
${\rm Spec}(A)$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $k$.
$k$.
A morphism ![]() $f \colon Y \to X$ of locally noetherian schemes is geometrically
$f \colon Y \to X$ of locally noetherian schemes is geometrically ![]() $\mathbf {R}$ if it is flat and if the scheme
$\mathbf {R}$ if it is flat and if the scheme ![]() $f^{-1}(x)$ is geometrically
$f^{-1}(x)$ is geometrically ![]() $\mathbf {R}$ for every
$\mathbf {R}$ for every ![]() $x \in X$. We consider the fiber
$x \in X$. We consider the fiber ![]() $f^{-1}(x)$ of a morphism
$f^{-1}(x)$ of a morphism ![]() $f$ as a scheme over the residue field
$f$ as a scheme over the residue field ![]() $\kappa (x)$ at
$\kappa (x)$ at ![]() $x \in X$. A ring homomorphism
$x \in X$. A ring homomorphism ![]() $\varphi \colon A \to B$ is geometrically
$\varphi \colon A \to B$ is geometrically ![]() $\mathbf {R}$ if
$\mathbf {R}$ if ![]() ${\rm Spec}(\varphi )$ is geometrically
${\rm Spec}(\varphi )$ is geometrically ![]() $\mathbf {R}$. The geometrically
$\mathbf {R}$. The geometrically ![]() $\mathbf {R}$ locus of a flat morphism
$\mathbf {R}$ locus of a flat morphism ![]() $f\colon Y \to X$ of locally noetherian schemes is the locus
$f\colon Y \to X$ of locally noetherian schemes is the locus
of points in ![]() $X$ over which
$X$ over which ![]() $f$ is geometrically
$f$ is geometrically ![]() $\mathbf {R}$.
$\mathbf {R}$.
A noetherian semi-local ring ![]() $A$ has geometrically
$A$ has geometrically ![]() $\mathbf {R}$ formal fibers if the
$\mathbf {R}$ formal fibers if the ![]() $\mathfrak {m}$-adic completion homomorphism
$\mathfrak {m}$-adic completion homomorphism ![]() $A \to \hat {A}$ is geometrically
$A \to \hat {A}$ is geometrically ![]() $\mathbf {R}$, where
$\mathbf {R}$, where ![]() $\mathfrak {m}$ is the product of the maximal ideals in
$\mathfrak {m}$ is the product of the maximal ideals in ![]() $A$.
$A$.
Remark 2.2 We note that the property in (1) is called ![]() $\mathbf {P}$ in [Reference Grothendieck and DieudonnéEGAIV2, (7.5.0)]. Following this terminology, geometrically
$\mathbf {P}$ in [Reference Grothendieck and DieudonnéEGAIV2, (7.5.0)]. Following this terminology, geometrically ![]() $\mathbf {R}$ morphisms are called
$\mathbf {R}$ morphisms are called ![]() $\mathbf {P}$-morphisms in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.1)], and semi-local rings with geometrically
$\mathbf {P}$-morphisms in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.1)], and semi-local rings with geometrically ![]() $\mathbf {R}$ formal fibers are called
$\mathbf {R}$ formal fibers are called ![]() $\mathbf {P}$-rings in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.13)].
$\mathbf {P}$-rings in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.13)].
2.2 (Quasi-)excellent rings and schemes
We next define (quasi-)excellent rings and schemes. In the definition below, we recall that a noetherian ring ![]() $A$ is a
$A$ is a ![]() $G$-ring if
$G$-ring if ![]() $A_\mathfrak {p}$ has geometrically regular formal fibers for every prime ideal
$A_\mathfrak {p}$ has geometrically regular formal fibers for every prime ideal ![]() $\mathfrak {p} \subseteq A$ [Reference MatsumuraMat89, p. 256].
$\mathfrak {p} \subseteq A$ [Reference MatsumuraMat89, p. 256].
Definition 2.3 [Reference Grothendieck and DieudonnéEGAIV2, Définition 7.8.2 and (7.8.5)] (cf. [Reference MatsumuraMat89, Definition on p. 260])
A noet-herian ring ![]() $A$ is quasi-excellent if
$A$ is quasi-excellent if ![]() $A$ is a
$A$ is a ![]() $G$-ring and if
$G$-ring and if ![]() $A$ is
$A$ is ![]() $J - 2$, that is, if for every
$J - 2$, that is, if for every ![]() $A$-algebra
$A$-algebra ![]() $B$ of finite type the regular locus in
$B$ of finite type the regular locus in ![]() ${\rm Spec}(B)$ is open. A quasi-excellent ring
${\rm Spec}(B)$ is open. A quasi-excellent ring ![]() $A$ is excellent if
$A$ is excellent if ![]() $A$ is universally catenary.
$A$ is universally catenary.
A locally noetherian scheme ![]() $X$ is quasi-excellent (respectively, excellent) if it admits an open affine covering
$X$ is quasi-excellent (respectively, excellent) if it admits an open affine covering ![]() $X = \bigcup _i{\rm Spec}(A_i)$, such that every
$X = \bigcup _i{\rm Spec}(A_i)$, such that every ![]() $A_i$ is quasi-excellent (respectively, excellent).
$A_i$ is quasi-excellent (respectively, excellent).
The condition ![]() $J - 2$ is the condition
$J - 2$ is the condition ![]() $\mathbf {R} - 2$ for
$\mathbf {R} - 2$ for ![]() $\mathbf {R} =$ ‘regular’ in the sense mentioned in § 1. We also define the following closely related notion.
$\mathbf {R} =$ ‘regular’ in the sense mentioned in § 1. We also define the following closely related notion.
Definition 2.4 [Reference Grothendieck and DieudonnéEGAIV1, Chapitre 0, Définition 23.1.1]
A noetherian domain ![]() $A$ is Japanese if, for every finite extension
$A$ is Japanese if, for every finite extension ![]() $L$ of the fraction field of
$L$ of the fraction field of ![]() $A$, the integral closure of
$A$, the integral closure of ![]() $A$ inside
$A$ inside ![]() $L$ is module-finite over
$L$ is module-finite over ![]() $A$. A noetherian ring
$A$. A noetherian ring ![]() $A$ is Nagata or universally Japanese if every domain
$A$ is Nagata or universally Japanese if every domain ![]() $B$ of finite type over
$B$ of finite type over ![]() $A$ is Japanese.
$A$ is Japanese.
Every quasi-excellent noetherian ring is Nagata [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 7.7.3].
Remark 2.5 By theorems of Zariski and Nagata [Reference Grothendieck and DieudonnéEGAIV2, Théorèmes 7.6.4 and 7.7.2] (see also [Reference MatsumuraMat89, p. 264]), a noetherian ring ![]() $A$ is Nagata if and only if:
$A$ is Nagata if and only if:
(a)
 $A_\mathfrak {p}$ has geometrically reduced formal fibers for every prime ideal
$A_\mathfrak {p}$ has geometrically reduced formal fibers for every prime ideal  $\mathfrak {p} \subseteq A$; and
$\mathfrak {p} \subseteq A$; and(b) for every domain
 $B$ that is module-finite over
$B$ that is module-finite over  $A$, the normal locus is open in
$A$, the normal locus is open in  ${\rm Spec}(B)$.
${\rm Spec}(B)$.
For semi-local rings ![]() $A$, (a) implies (b) by [Reference Grothendieck and DieudonnéEGAIV2, Théorème 7.6.4 and Corollaire 7.6.5], and (a) holds if and only if
$A$, (a) implies (b) by [Reference Grothendieck and DieudonnéEGAIV2, Théorème 7.6.4 and Corollaire 7.6.5], and (a) holds if and only if ![]() $A$ has geometrically reduced formal fibers [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.14 and Corollaire 7.4.5]. Thus, a semi-local ring is Nagata if and only if it has geometrically reduced formal fibers.
$A$ has geometrically reduced formal fibers [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.14 and Corollaire 7.4.5]. Thus, a semi-local ring is Nagata if and only if it has geometrically reduced formal fibers.
2.3 Gabber's weak local uniformization theorem
We now recall Gabber's weak local uniformization theorem, which is a variant of resolutions of singularities for arbitrary quasi-excellent noetherian schemes. Gabber's result is a version of de Jong's alteration theorem [Reference de JongdJ96, Theorem 4.1] for quasi-excellent noetherian schemes that are not necessarily of finite type over a field or a DVR.
To state Gabber's result, we first need to define maximally dominating morphisms. We recall that a point ![]() $x$ on a scheme
$x$ on a scheme ![]() $X$ is maximal if it is the generic point of an irreducible component of
$X$ is maximal if it is the generic point of an irreducible component of ![]() $X$ [Reference Grothendieck and DieudonnéEGAInew, Chapitre 0, (2.1.1)]. We then have the following definition.
$X$ [Reference Grothendieck and DieudonnéEGAInew, Chapitre 0, (2.1.1)]. We then have the following definition.
Definition 2.6 [Reference Illusie, Laszlo and OrgogozoILO14, Exposé II, Définition 1.1.2]
A morphism ![]() $f\colon Y \to X$ of schemes is maximally dominating if every maximal point of
$f\colon Y \to X$ of schemes is maximally dominating if every maximal point of ![]() $Y$ maps to a maximal point of
$Y$ maps to a maximal point of ![]() $X$.
$X$.
We now define the alteration topology on a noetherian scheme.
Definition 2.7 [Reference Illusie, Laszlo and OrgogozoILO14, Exposé II, Définition 1.2.2 and (2.3.1)]
Let ![]() $X$ be a noetherian scheme. The category
$X$ be a noetherian scheme. The category ![]() $\mathrm {alt}/X$ is the category whose objects are reduced schemes that are maximally dominating, generically finite, and of finite type over
$\mathrm {alt}/X$ is the category whose objects are reduced schemes that are maximally dominating, generically finite, and of finite type over ![]() $X$, and whose morphisms are morphisms as schemes over
$X$, and whose morphisms are morphisms as schemes over ![]() $X$. All morphisms in
$X$. All morphisms in ![]() $\mathrm {alt}/X$ are maximally dominating, generically finite, and of finite type [Reference Illusie, Laszlo and OrgogozoILO14, Exposé II, Définition 1.2.2 and (2.3.1)].
$\mathrm {alt}/X$ are maximally dominating, generically finite, and of finite type [Reference Illusie, Laszlo and OrgogozoILO14, Exposé II, Définition 1.2.2 and (2.3.1)].
The alteration topology on ![]() $X$ is the Grothendieck topology on
$X$ is the Grothendieck topology on ![]() $\mathrm {alt}/X$ associated to the pretopology generated by:
$\mathrm {alt}/X$ associated to the pretopology generated by:
(i) étale coverings; and
(ii) proper surjective morphisms that are maximally dominating and generically finite.
We will use the following alternative characterization for coverings in the alteration topology when ![]() $X$ is irreducible. This result implies that coverings in the alteration topology on
$X$ is irreducible. This result implies that coverings in the alteration topology on ![]() $\mathrm {alt}/X$ are coverings in Voevodsky's
$\mathrm {alt}/X$ are coverings in Voevodsky's ![]() $h$-topology [Reference VoevodskyVoe96, Definition 3.1.2]; see [Reference Illusie, Laszlo and OrgogozoILO14, p. 263].
$h$-topology [Reference VoevodskyVoe96, Definition 3.1.2]; see [Reference Illusie, Laszlo and OrgogozoILO14, p. 263].
Theorem 2.8 [Reference Illusie, Laszlo and OrgogozoILO14, Exposé II, Théorème 3.2.1]
Let ![]() $X$ be an irreducible noetherian scheme. Then, for every finite covering
$X$ be an irreducible noetherian scheme. Then, for every finite covering ![]() $\{Y_i \to X\}_{i=1}^m$ in the alteration topology on
$\{Y_i \to X\}_{i=1}^m$ in the alteration topology on ![]() $X$, there exist a proper surjective morphism
$X$, there exist a proper surjective morphism ![]() $\pi \colon V \to X$ in
$\pi \colon V \to X$ in ![]() $\mathrm {alt}/X$ such that
$\mathrm {alt}/X$ such that ![]() $V$ is integral, and a Zariski open covering
$V$ is integral, and a Zariski open covering ![]() $V = \bigcup _{i=1}^m V_i$, together with a collection
$V = \bigcup _{i=1}^m V_i$, together with a collection ![]() $\{h_i\colon V_i \to Y_i\}_{i=1}^m$ of morphisms, such that the diagram
$\{h_i\colon V_i \to Y_i\}_{i=1}^m$ of morphisms, such that the diagram

commutes for every ![]() $i \in \{1,2,\ldots,m\}$, where the morphisms
$i \in \{1,2,\ldots,m\}$, where the morphisms ![]() $V_i \hookrightarrow V$ are the natural open immersions.
$V_i \hookrightarrow V$ are the natural open immersions.
We now state a special case of Gabber's weak local uniformization result, which is the main technical ingredient in the proof of Theorem B.
Theorem 2.9 (Gabber [Reference Illusie, Laszlo and OrgogozoILO14, Exposé VII, Théorème 1.1])
Let ![]() $X$ be a quasi-excellent noetherian scheme. Then there exists a finite covering
$X$ be a quasi-excellent noetherian scheme. Then there exists a finite covering ![]() $\{Y_i \to X\}_{i=1}^m$ in the alteration topology on
$\{Y_i \to X\}_{i=1}^m$ in the alteration topology on ![]() $X$, such that
$X$, such that ![]() $Y_i$ is regular and integral for every
$Y_i$ is regular and integral for every ![]() $i \in \{1,2,\ldots,m\}$.
$i \in \{1,2,\ldots,m\}$.
3. Grothendieck's localization problem and the local lifting problem
In this section we solve Grothendieck's localization problem (Problem 1.2) by proving Theorem B in a sequence of steps. We first fix notation for our conditions on local properties ![]() $\mathbf {R}$ in § 3.1. In § 3.2 we prove Theorem B under the additional assumption that
$\mathbf {R}$ in § 3.1. In § 3.2 we prove Theorem B under the additional assumption that ![]() $A$ is quasi-excellent (Theorem 3.4), in which case Gabber's weak local uniformization theorem (Theorem 2.9) applies. We then prove Theorem B in § 3.3 by taking a completion to reduce to the quasi-excellent case, using
$A$ is quasi-excellent (Theorem 3.4), in which case Gabber's weak local uniformization theorem (Theorem 2.9) applies. We then prove Theorem B in § 3.3 by taking a completion to reduce to the quasi-excellent case, using ![]() $({\text {R}'_{\text {I}}})$ and the fact that
$({\text {R}'_{\text {I}}})$ and the fact that ![]() $A$ has geometrically
$A$ has geometrically ![]() $\mathbf {R}$ formal fibers. Finally, we obtain Theorems A and C as consequences in §§ 3.4 and 3.5, respectively.
$\mathbf {R}$ formal fibers. Finally, we obtain Theorems A and C as consequences in §§ 3.4 and 3.5, respectively.
3.1 Conditions on  $\mathbf {R}$
$\mathbf {R}$
We fix the following notational conventions for permanence conditions on the local properties ![]() $\mathbf {R}$.
$\mathbf {R}$.
Conditions 3.1 Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian rings, and let
${\mathscr {C}}$ of the category of noetherian rings, and let ![]() $\mathbf {R}$ be a property of noetherian local rings. We consider the following conditions on the property
$\mathbf {R}$ be a property of noetherian local rings. We consider the following conditions on the property ![]() $\mathbf {R}$.
$\mathbf {R}$.
 $({\rm R}_0)$ The property
$({\rm R}_0)$ The property  $\mathbf {R}$ holds for every field
$\mathbf {R}$ holds for every field  $k$.
$k$. $(\text {R}_{\text {I}}^{\mathscr {C}})$ (Ascent via geometrically regular homomorphisms) For every geometrically regular local homomorphism
$(\text {R}_{\text {I}}^{\mathscr {C}})$ (Ascent via geometrically regular homomorphisms) For every geometrically regular local homomorphism  $\varphi \colon A \to B$ of noetherian local rings in
$\varphi \colon A \to B$ of noetherian local rings in  ${\mathscr {C}}$, if
${\mathscr {C}}$, if  $A$ satisfies
$A$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $B$ satisfies
$B$ satisfies  $\mathbf {R}$.
$\mathbf {R}$. $(\text {R}_{\text {II}}^{\mathscr {C}})$ (Descent) For every flat local homomorphism
$(\text {R}_{\text {II}}^{\mathscr {C}})$ (Descent) For every flat local homomorphism  $\varphi \colon A \to B$ of noetherian local rings such that
$\varphi \colon A \to B$ of noetherian local rings such that  $B$ is in
$B$ is in  ${\mathscr {C}}$, if
${\mathscr {C}}$, if  $B$ satisfies
$B$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $A$ satisfies
$A$ satisfies  $\mathbf {R}$.
$\mathbf {R}$. $({\rm R}_{{\rm III}})$ (Openness) For every noetherian complete local ring
$({\rm R}_{{\rm III}})$ (Openness) For every noetherian complete local ring  $C$, the locus
$C$, the locus  $U_\mathbf {R}({\rm Spec}(C))$ is open.
$U_\mathbf {R}({\rm Spec}(C))$ is open. $(\text {R}_{\text {IV}}^{\mathscr {C}})$ (Lifting from Cartier divisors) For every noetherian local ring
$(\text {R}_{\text {IV}}^{\mathscr {C}})$ (Lifting from Cartier divisors) For every noetherian local ring  $A$ in
$A$ in  ${\mathscr {C}}$ and for every nonzerodivisor
${\mathscr {C}}$ and for every nonzerodivisor  $t$ in its maximal ideal, if
$t$ in its maximal ideal, if  $A/tA$ satisfies
$A/tA$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $A$ satisfies
$A$ satisfies  $\mathbf {R}$.
$\mathbf {R}$. $(\text {R}_{\text {V}}^{\mathscr {C}})$ (Localization) If a noetherian local ring
$(\text {R}_{\text {V}}^{\mathscr {C}})$ (Localization) If a noetherian local ring  $A$ in
$A$ in  ${\mathscr {C}}$ satisfies
${\mathscr {C}}$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $A_\mathfrak {p}$ satisfies
$A_\mathfrak {p}$ satisfies  $\mathbf {R}$ for every prime ideal
$\mathbf {R}$ for every prime ideal  $\mathfrak {p} \subseteq A$.
$\mathfrak {p} \subseteq A$.
In addition, we consider the following variant of ![]() $({\rm R}_{\rm {I}}^{{\mathscr {C}}})$.
$({\rm R}_{\rm {I}}^{{\mathscr {C}}})$.
 $(\text {R}^{{\mathscr {C}}\prime }_{\text {I}})$ (Ascent via geometrically
$(\text {R}^{{\mathscr {C}}\prime }_{\text {I}})$ (Ascent via geometrically  $\mathbf {R}$ homomorphisms) For every local geometrically
$\mathbf {R}$ homomorphisms) For every local geometrically  $\mathbf {R}$ homomorphism
$\mathbf {R}$ homomorphism  $\varphi \colon A \to B$ of noetherian local rings in
$\varphi \colon A \to B$ of noetherian local rings in  ${\mathscr {C}}$, if
${\mathscr {C}}$, if  $A$ satisfies
$A$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $B$ satisfies
$B$ satisfies  $\mathbf {R}$.
$\mathbf {R}$.
We also consider the following conditions for ![]() $\mathbf {R}$ that affect geometrically
$\mathbf {R}$ that affect geometrically ![]() $\mathbf {R}$ homomorphisms.
$\mathbf {R}$ homomorphisms.
 $(\text {P}_{\text {I}}^{\mathscr {C}})$ If
$(\text {P}_{\text {I}}^{\mathscr {C}})$ If  $\varphi \colon A \to B$ and
$\varphi \colon A \to B$ and  $\psi \colon B \to C$ are a geometrically
$\psi \colon B \to C$ are a geometrically  $\mathbf {R}$ homomorphism and a geometrically regular homomorphism of noetherian rings, respectively, and
$\mathbf {R}$ homomorphism and a geometrically regular homomorphism of noetherian rings, respectively, and  $B$ and
$B$ and  $C$ are in
$C$ are in  ${\mathscr {C}}$, then
${\mathscr {C}}$, then  $\psi \circ \varphi$ is a geometrically
$\psi \circ \varphi$ is a geometrically  $\mathbf {R}$ homomorphism.
$\mathbf {R}$ homomorphism. $(\text {P}_{\text {II}}^{\mathscr {C}})$ (Descent) If
$(\text {P}_{\text {II}}^{\mathscr {C}})$ (Descent) If  $\varphi \colon A \to B$ and
$\varphi \colon A \to B$ and  $\psi \colon B \to C$ are two homomorphisms of noetherian rings such that
$\psi \colon B \to C$ are two homomorphisms of noetherian rings such that  $\psi \circ \varphi$ is geometrically
$\psi \circ \varphi$ is geometrically  $\mathbf {R}$,
$\mathbf {R}$,  $\psi$ is faithfully flat, and
$\psi$ is faithfully flat, and  $C$ is in
$C$ is in  ${\mathscr {C}}$, then
${\mathscr {C}}$, then  $\varphi$ is geometrically
$\varphi$ is geometrically  $\mathbf {R}$.
$\mathbf {R}$. $({\rm P}_{{\rm III}})$ Every field
$({\rm P}_{{\rm III}})$ Every field  $k$ is geometrically
$k$ is geometrically  $\mathbf {R}$ over itself.
$\mathbf {R}$ over itself. $(\text {P}_{\text {IV}}^{\mathscr {C}})$ (Stability under finitely generated ground field extensions) If a noetherian ring
$(\text {P}_{\text {IV}}^{\mathscr {C}})$ (Stability under finitely generated ground field extensions) If a noetherian ring  $A$ in
$A$ in  ${\mathscr {C}}$ is geometrically
${\mathscr {C}}$ is geometrically  $\mathbf {R}$ over a field
$\mathbf {R}$ over a field  $k$, then, for all finitely generated field extensions
$k$, then, for all finitely generated field extensions  $k \subseteq k'$, the ring
$k \subseteq k'$, the ring  $A \otimes _k k'$ is geometrically
$A \otimes _k k'$ is geometrically  $\mathbf {R}$ over
$\mathbf {R}$ over  $k'$.
$k'$.
In addition, we consider the following variant of ![]() $({\rm {P}}_{{\rm I}}^{{\mathscr {C}}})$.
$({\rm {P}}_{{\rm I}}^{{\mathscr {C}}})$.
 $({\rm P}_{\rm {I}}^{{\mathscr {C}}})$ If
$({\rm P}_{\rm {I}}^{{\mathscr {C}}})$ If  $\varphi \colon A \to B$ and
$\varphi \colon A \to B$ and  $\psi \colon B \to C$ are geometrically
$\psi \colon B \to C$ are geometrically  $\mathbf {R}$ homomorphisms of noetherian rings such that
$\mathbf {R}$ homomorphisms of noetherian rings such that  $B$ and
$B$ and  $C$ are in
$C$ are in  ${\mathscr {C}}$, then
${\mathscr {C}}$, then  $\psi \circ \varphi$ is also geometrically
$\psi \circ \varphi$ is also geometrically  $\mathbf {R}$.
$\mathbf {R}$.
We drop ![]() ${\mathscr {C}}$ from our notation if
${\mathscr {C}}$ from our notation if ![]() ${\mathscr {C}}$ is the entire category of noetherian rings.
${\mathscr {C}}$ is the entire category of noetherian rings.
Remark 3.2 The list in Conditions 3.1 is a subset of that in [Reference MarotMar84, Conditions 1.1 and 1.2], although our naming convention mostly follows [Reference Grothendieck and DieudonnéEGAIV2]. Specifically,
–
 $(\rm {R}_0)$,
$(\rm {R}_0)$,  $({\text {R}_{\text {I}}})$, and
$({\text {R}_{\text {I}}})$, and  $({\text {R}_{\text {II}}})$ appear in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.10)], although
$({\text {R}_{\text {II}}})$ appear in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.10)], although  $(\rm {R}_0)$ is not named;
$(\rm {R}_0)$ is not named;–
 $({\rm {R}}_{{\rm III}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.18];
$({\rm {R}}_{{\rm III}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.18];–
 $({\rm {R}}_{{\rm IV}}^{{\mathscr {C}}})$ specializes to the condition
$({\rm {R}}_{{\rm IV}}^{{\mathscr {C}}})$ specializes to the condition  $(\text {R}_{\text {IV}})$ in [Reference Grothendieck and DieudonnéEGAIV2, Théorème 7.5.1] when
$(\text {R}_{\text {IV}})$ in [Reference Grothendieck and DieudonnéEGAIV2, Théorème 7.5.1] when  ${\mathscr {C}}$ is the category of noetherian complete local rings;
${\mathscr {C}}$ is the category of noetherian complete local rings;–
 $({\rm {R}}_{\rm {V}}^{{\mathscr {C}}})$ is unrelated to the condition
$({\rm {R}}_{\rm {V}}^{{\mathscr {C}}})$ is unrelated to the condition  $(\text {R}_{\text {V}})$ in [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 7.5.2];
$(\text {R}_{\text {V}})$ in [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 7.5.2];–
 $({\text {R}'_{\text {I}}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.3.11];
$({\text {R}'_{\text {I}}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.3.11];–
 $({\text {P}_{\text {I}}})$,
$({\text {P}_{\text {I}}})$,  $({\text {P}_{\text {II}}})$, and
$({\text {P}_{\text {II}}})$, and  $({\rm P}_{{\rm III}})$ appear in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.4)];
$({\rm P}_{{\rm III}})$ appear in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.4)];–
 $({\text {P}_{\text {IV}}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.6)]; and
$({\text {P}_{\text {IV}}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, (7.3.6)]; and–
 $({\text {P}'_{\text {I}}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.3.5(iii)].
$({\text {P}'_{\text {I}}})$ appears in [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.3.5(iii)].
See also [Reference Grothendieck and DieudonnéEGAIV2, (7.9.7)], [Reference ValabregaVal78, p. 201], and [Reference Brezuleanu and IonescuBI84, (2.1) and (2.4)].
We will use the following relationships between different conditions on ![]() $\mathbf {R}$.
$\mathbf {R}$.
Lemma 3.3 (cf. [Reference Grothendieck and DieudonnéEGAIV2, (7.3.10), Remarque 7.3.11, and Lemme 7.3.7; Reference Datta and MurayamaDM20, Proposition 4.10])
Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type, and let
${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type, and let ![]() $\mathbf {R}$ be a property of noetherian local rings.
$\mathbf {R}$ be a property of noetherian local rings.
(i) If
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm R}_0)$, then
$({\rm R}_0)$, then  $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm {P}}_{{\rm III}})$.
$({\rm {P}}_{{\rm III}})$.(ii) Let
 $\mathbf {R}'$ be another property of noetherian local rings. Suppose that, for every local geometrically
$\mathbf {R}'$ be another property of noetherian local rings. Suppose that, for every local geometrically  $\mathbf {R}'$ homomorphism
$\mathbf {R}'$ homomorphism  $B \to C$ of noetherian local rings in
$B \to C$ of noetherian local rings in  ${\mathscr {C}}$, if
${\mathscr {C}}$, if  $B$ satisfies
$B$ satisfies  $\mathbf {R}$, then
$\mathbf {R}$, then  $C$ satisfies
$C$ satisfies  $\mathbf {R}$. If
$\mathbf {R}$. If  $\varphi \colon A \to B$ and
$\varphi \colon A \to B$ and  $\psi \colon B \to C$ are geometrically
$\psi \colon B \to C$ are geometrically  $\mathbf {R}$ and geometrically
$\mathbf {R}$ and geometrically  $\mathbf {R}'$ homomorphisms of noetherian rings, respectively, and
$\mathbf {R}'$ homomorphisms of noetherian rings, respectively, and  $B$ and
$B$ and  $C$ are in
$C$ are in  ${\mathscr {C}}$, then
${\mathscr {C}}$, then  $\psi \circ \varphi$ is geometrically
$\psi \circ \varphi$ is geometrically  $\mathbf {R}$.
$\mathbf {R}$.In particular, if
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm R}_{\rm I}^{{\mathscr {C}}})$, then
$({\rm R}_{\rm I}^{{\mathscr {C}}})$, then  $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm P}_{{\rm I}}^{{\mathscr {C}}})$, and if
$({\rm P}_{{\rm I}}^{{\mathscr {C}}})$, and if  $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm R}_{\rm I}^{{\mathscr {C}}'})$, then
$({\rm R}_{\rm I}^{{\mathscr {C}}'})$, then  $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm P}_{{\rm I}}^{{\mathscr {C}}'})$.
$({\rm P}_{{\rm I}}^{{\mathscr {C}}'})$.(iii) If
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$, then
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$, then  $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm P}_{{\rm II}}^{{\mathscr {C}}})$.
$({\rm P}_{{\rm II}}^{{\mathscr {C}}})$.(iv) If
 $\mathbf {R}$ satisfies the special cases of
$\mathbf {R}$ satisfies the special cases of  $({\rm R}_{\rm I}^{{\mathscr {C}}})$ and
$({\rm R}_{\rm I}^{{\mathscr {C}}})$ and  $({\rm R}_{\rm II}^{{\mathscr {C}}})$ when the homomorphisms
$({\rm R}_{\rm II}^{{\mathscr {C}}})$ when the homomorphisms  $\varphi$ are essentially of finite type, then
$\varphi$ are essentially of finite type, then  $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm P}_{\rm IV}^{{\mathscr {C}}})$.
$({\rm P}_{\rm IV}^{{\mathscr {C}}})$.(v) If
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm P}_{\rm IV}^{{\mathscr {C}}})$, and if
$({\rm P}_{\rm IV}^{{\mathscr {C}}})$, and if  $\varphi \colon A \to B$ is a geometrically
$\varphi \colon A \to B$ is a geometrically  $\mathbf {R}$ homomorphism of noetherian rings such that
$\mathbf {R}$ homomorphism of noetherian rings such that  $B$ is in
$B$ is in  ${\mathscr {C}}$, then for every
${\mathscr {C}}$, then for every  $A$-algebra
$A$-algebra  $C$ essentially of finite type, the base change
$C$ essentially of finite type, the base change  $\varphi \otimes _A \mathrm {id}_C \colon C \to B \otimes _A C$ is geometrically
$\varphi \otimes _A \mathrm {id}_C \colon C \to B \otimes _A C$ is geometrically  $\mathbf {R}$.
$\mathbf {R}$.
Proof. (i) is clear from definition of being geometrically ![]() $\mathbf {R}$.
$\mathbf {R}$.
To show (ii) and (iii), it suffices to consider the case when ![]() $A$ is a field
$A$ is a field ![]() $k$ by transitivity of fibers; see [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.3.5(ii)]. Note that for (ii) (respectively, (iii)), we use the hypothesis on
$k$ by transitivity of fibers; see [Reference Grothendieck and DieudonnéEGAIV2, Remarque 7.3.5(ii)]. Note that for (ii) (respectively, (iii)), we use the hypothesis on ![]() ${\mathscr {C}}$ to guarantee that after this reduction,
${\mathscr {C}}$ to guarantee that after this reduction, ![]() $B$ and
$B$ and ![]() $C$ (respectively,
$C$ (respectively, ![]() $C$) are still in
$C$) are still in ![]() ${\mathscr {C}}$. Consider the composition
${\mathscr {C}}$. Consider the composition
of homomorphisms of noetherian rings, and consider the base change
for a finite field extension ![]() $k \subseteq k'$. For (ii), we first note that since
$k \subseteq k'$. For (ii), we first note that since ![]() $B \to B \otimes _k k'$ is a module-finite homomorphism, it induces finite field extensions on residue fields. Thus, the base change
$B \to B \otimes _k k'$ is a module-finite homomorphism, it induces finite field extensions on residue fields. Thus, the base change ![]() $\psi \otimes _k \mathrm {id}_{k'}$ of
$\psi \otimes _k \mathrm {id}_{k'}$ of ![]() $\psi$ is geometrically
$\psi$ is geometrically ![]() $\mathbf {R}'$. Since the local rings of
$\mathbf {R}'$. Since the local rings of ![]() $B \otimes _k k'$ satisfy
$B \otimes _k k'$ satisfy ![]() $\mathbf {R}$ by assumption, we see that the local rings of
$\mathbf {R}$ by assumption, we see that the local rings of ![]() $C \otimes _k k'$ also satisfy
$C \otimes _k k'$ also satisfy ![]() $\mathbf {R}$. For (iii), we note that in (2), the local rings of
$\mathbf {R}$. For (iii), we note that in (2), the local rings of ![]() $C \otimes _k k'$ satisfy
$C \otimes _k k'$ satisfy ![]() $\mathbf {R}$ by assumption. Thus, the local rings of
$\mathbf {R}$ by assumption. Thus, the local rings of ![]() $B \otimes _k k'$ also satisfy
$B \otimes _k k'$ also satisfy ![]() $\mathbf {R}$ by
$\mathbf {R}$ by ![]() $({\rm R}_{{\rm II}}^{\mathscr {C}})$, since
$({\rm R}_{{\rm II}}^{\mathscr {C}})$, since ![]() $\psi \otimes _k \mathrm {id}_{k'}$ is faithfully flat by base change.
$\psi \otimes _k \mathrm {id}_{k'}$ is faithfully flat by base change.
For (iv), let ![]() $k \subseteq k'$ be a finitely generated field extension. By [Reference Datta and MurayamaDM20, Lemma 4.9], there exist a finite extension
$k \subseteq k'$ be a finitely generated field extension. By [Reference Datta and MurayamaDM20, Lemma 4.9], there exist a finite extension ![]() $k \subseteq k_1$ and a diagram
$k \subseteq k_1$ and a diagram

of finitely generated field extensions, where ![]() $k_1 \subseteq k_2 := (k' \otimes _k k_1)_\mathrm {red}$ is a separable field extension. Since
$k_1 \subseteq k_2 := (k' \otimes _k k_1)_\mathrm {red}$ is a separable field extension. Since ![]() $A$ is geometrically
$A$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $k$, the local rings of
$k$, the local rings of ![]() $A \otimes _k k_1$ satisfy
$A \otimes _k k_1$ satisfy ![]() $\mathbf {R}$. We therefore see that the local rings of
$\mathbf {R}$. We therefore see that the local rings of ![]() $A \otimes _k k_2$ also satisfy
$A \otimes _k k_2$ also satisfy ![]() $\mathbf {R}$, since
$\mathbf {R}$, since ![]() $k_1 \to k_2$ is regular and both
$k_1 \to k_2$ is regular and both ![]() $A \otimes _k k_1$ and
$A \otimes _k k_1$ and ![]() $A \otimes _k k_2$ are in
$A \otimes _k k_2$ are in ![]() ${\mathscr {C}}$. Finally, the local rings of
${\mathscr {C}}$. Finally, the local rings of ![]() $A \otimes _k k'$ satisfy
$A \otimes _k k'$ satisfy ![]() $\mathbf {R}$ by
$\mathbf {R}$ by ![]() $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$.
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$.
For (v), we note that ![]() $\varphi \otimes _A \mathrm {id}_C$ is flat by base change, and hence it suffices to show that, for every prime ideal
$\varphi \otimes _A \mathrm {id}_C$ is flat by base change, and hence it suffices to show that, for every prime ideal ![]() $\mathfrak {q} \subseteq C$, the fiber
$\mathfrak {q} \subseteq C$, the fiber ![]() $B \otimes _A C \otimes _C \kappa (\mathfrak {q})$ is geometrically
$B \otimes _A C \otimes _C \kappa (\mathfrak {q})$ is geometrically ![]() $\mathbf {R}$. Letting
$\mathbf {R}$. Letting ![]() $\mathfrak {p} = \mathfrak {q} \cap A$, the field extension
$\mathfrak {p} = \mathfrak {q} \cap A$, the field extension ![]() $\kappa (\mathfrak {p}) \subseteq \kappa (\mathfrak {q})$ is finitely generated since
$\kappa (\mathfrak {p}) \subseteq \kappa (\mathfrak {q})$ is finitely generated since ![]() $A \to C$ is essentially of finite type [Reference Grothendieck and DieudonnéEGAInew, Proposition 6.5.10]. Since
$A \to C$ is essentially of finite type [Reference Grothendieck and DieudonnéEGAInew, Proposition 6.5.10]. Since
we see that ![]() $B \otimes _A C \otimes _C \kappa (\mathfrak {q})$ is geometrically
$B \otimes _A C \otimes _C \kappa (\mathfrak {q})$ is geometrically ![]() $\mathbf {R}$ by
$\mathbf {R}$ by ![]() $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
3.2 Problem 1.2 for quasi-excellent bases
The following result solves Grothendieck's localization problem when the ring ![]() $A$ is quasi-excellent. This step corresponds to
$A$ is quasi-excellent. This step corresponds to ![]() $({\rm {III}})$ in § 1, and forms the technical core of the proof of Theorem B.
$({\rm {III}})$ in § 1, and forms the technical core of the proof of Theorem B.
Theorem 3.4 (cf. [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8; Reference MarotMar84, Theorem 2.1])
Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let
${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism ![]() $\varphi \colon (A,\mathfrak {m},k) \to (B,\mathfrak {n},l)$ of noetherian local rings. Assume the following:
$\varphi \colon (A,\mathfrak {m},k) \to (B,\mathfrak {n},l)$ of noetherian local rings. Assume the following:
(i) the ring
 $A$ is quasi-excellent;
$A$ is quasi-excellent;(ii) the ring
 $B$ appears in
$B$ appears in  ${\mathscr {C}}$; and
${\mathscr {C}}$; and(iii) the property
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$,  $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,  $({\rm R}_{{\rm V}}^{{\mathscr {C}}})$, and
$({\rm R}_{{\rm V}}^{{\mathscr {C}}})$, and  $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
If the closed fiber of ![]() $\varphi$ is geometrically
$\varphi$ is geometrically ![]() $\mathbf {R}$, then all fibers of
$\mathbf {R}$, then all fibers of ![]() $\varphi$ are geometrically
$\varphi$ are geometrically ![]() $\mathbf {R}$.
$\mathbf {R}$.
The proof in [Reference MarotMar84] relies on the existence of resolutions of singularities, which we avoid by using Gabber's weak local uniformization theorem. As far as we are aware, the idea of using alterations instead of resolutions of singularities first appeared in [Reference HashimotoHas01, Remark 6.7], where Hashimoto proves Grothendieck's localization problem for ![]() $F$-rationality when the base ring
$F$-rationality when the base ring ![]() $A$ is essentially of finite type over a field of positive characteristic using de Jong's alteration theorem [Reference de JongdJ96, Theorem 4.1]. When
$A$ is essentially of finite type over a field of positive characteristic using de Jong's alteration theorem [Reference de JongdJ96, Theorem 4.1]. When ![]() $\mathbf {R} =$ Cohen–Macaulay or
$\mathbf {R} =$ Cohen–Macaulay or ![]() $(S_n)$, one can use Kawasaki's Macaulayfication theorem [Reference KawasakiKaw02, Theorem 1.1] to prove Theorem 3.4; see [Reference Brezuleanu and IonescuBI84, Proposition 3.1; Reference IonescuIon08, Theorem 4.1 and Remark 4.2].
$(S_n)$, one can use Kawasaki's Macaulayfication theorem [Reference KawasakiKaw02, Theorem 1.1] to prove Theorem 3.4; see [Reference Brezuleanu and IonescuBI84, Proposition 3.1; Reference IonescuIon08, Theorem 4.1 and Remark 4.2].
Our strategy will be to ultimately reduce to the following version of Problem 1.2 for regular bases. This statement corresponds to (IV) in § 1.
Lemma 3.5 [Reference Grothendieck and DieudonnéEGAIV2, Lemme 7.5.1.1]
Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian local rings that is stable under quotients. Let
${\mathscr {C}}$ of the category of noetherian local rings that is stable under quotients. Let ![]() $\mathbf {R}$ be a property of noetherian local rings satisfying
$\mathbf {R}$ be a property of noetherian local rings satisfying ![]() $({\rm {R}}_{{\rm IV}}^{{\mathscr {C}}})$, and consider a flat local homomorphism
$({\rm {R}}_{{\rm IV}}^{{\mathscr {C}}})$, and consider a flat local homomorphism ![]() $\varphi \colon (C,\mathfrak {m},k) \to (D,\mathfrak {n},l)$ of noetherian local rings in
$\varphi \colon (C,\mathfrak {m},k) \to (D,\mathfrak {n},l)$ of noetherian local rings in ![]() ${\mathscr {C}}$, where
${\mathscr {C}}$, where ![]() $C$ is regular. If
$C$ is regular. If ![]() $D \otimes _C k$ satisfies
$D \otimes _C k$ satisfies ![]() $\mathbf {R}$, then
$\mathbf {R}$, then ![]() $D$ satisfies
$D$ satisfies ![]() $\mathbf {R}$.
$\mathbf {R}$.
We now prove Theorem 3.4.
Proof Proof of Theorem 3.4
We want to show that, for every prime ideal ![]() $\mathfrak {p} \subseteq A$, the
$\mathfrak {p} \subseteq A$, the ![]() $\kappa (\mathfrak {p})$-algebra
$\kappa (\mathfrak {p})$-algebra ![]() $B \otimes _A \kappa (\mathfrak {p})$ is geometrically
$B \otimes _A \kappa (\mathfrak {p})$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\mathfrak {p})$. By noetherian induction, it suffices to show that if
$\kappa (\mathfrak {p})$. By noetherian induction, it suffices to show that if ![]() $\mathfrak {p}_0 \subseteq A$ is a prime ideal and
$\mathfrak {p}_0 \subseteq A$ is a prime ideal and ![]() $B \otimes _A \kappa (\mathfrak {p})$ is geometrically
$B \otimes _A \kappa (\mathfrak {p})$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\mathfrak {p})$ for every prime ideal
$\kappa (\mathfrak {p})$ for every prime ideal ![]() $\mathfrak {p} \supsetneq \mathfrak {p}_0$, then
$\mathfrak {p} \supsetneq \mathfrak {p}_0$, then ![]() $B \otimes _A \kappa (\mathfrak {p}_0)$ is geometrically
$B \otimes _A \kappa (\mathfrak {p}_0)$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\mathfrak {p}_0)$. Replacing
$\kappa (\mathfrak {p}_0)$. Replacing ![]() $A$ by
$A$ by ![]() $A/\mathfrak {p}_0$ and
$A/\mathfrak {p}_0$ and ![]() $B$ by
$B$ by ![]() $B/\mathfrak {p}_0 B$, we may therefore assume that
$B/\mathfrak {p}_0 B$, we may therefore assume that ![]() $A$ is a domain and that
$A$ is a domain and that ![]() $B \otimes _A \kappa (\mathfrak {p})$ is geometrically
$B \otimes _A \kappa (\mathfrak {p})$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\mathfrak {p})$ for every non-zero prime ideal
$\kappa (\mathfrak {p})$ for every non-zero prime ideal ![]() $\mathfrak {p} \subseteq A$. We note that
$\mathfrak {p} \subseteq A$. We note that ![]() $A/\mathfrak {p}_0$ is quasi-excellent by [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.15(i)], and that
$A/\mathfrak {p}_0$ is quasi-excellent by [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.15(i)], and that ![]() $B/\mathfrak {p}_0 B$ appears in
$B/\mathfrak {p}_0 B$ appears in ![]() ${\mathscr {C}}$ by (ii).
${\mathscr {C}}$ by (ii).
We now reduce to showing that the local rings of ![]() $B \otimes _A K$ satisfy
$B \otimes _A K$ satisfy ![]() $\mathbf {R}$, where
$\mathbf {R}$, where ![]() $K := {\rm Frac}(A)$. We want to show that, for every finite field extension
$K := {\rm Frac}(A)$. We want to show that, for every finite field extension ![]() $K \subseteq K'$, the local rings of
$K \subseteq K'$, the local rings of ![]() $B \otimes _A K'$ satisfy
$B \otimes _A K'$ satisfy ![]() $\mathbf {R}$. Let
$\mathbf {R}$. Let ![]() $A \subseteq A'$ be a module-finite extension such that
$A \subseteq A'$ be a module-finite extension such that ![]() $A'$ is a domain and such that
$A'$ is a domain and such that ![]() $K' = {\rm Frac}(A')$. Then
$K' = {\rm Frac}(A')$. Then ![]() $A'$ is a semi-local ring, and setting
$A'$ is a semi-local ring, and setting ![]() $B' := B \otimes _A A'$, we have
$B' := B \otimes _A A'$, we have ![]() $B \otimes _A K' \simeq B' \otimes _{A'} K'$. Note that every local ring of
$B \otimes _A K' \simeq B' \otimes _{A'} K'$. Note that every local ring of ![]() $B \otimes _A K'$ is a local ring of
$B \otimes _A K'$ is a local ring of ![]() $B'_\mathfrak {q} \otimes _{A'_\mathfrak {p}} K'$ for some prime ideals
$B'_\mathfrak {q} \otimes _{A'_\mathfrak {p}} K'$ for some prime ideals ![]() $\mathfrak {p} \subseteq A'$ and
$\mathfrak {p} \subseteq A'$ and ![]() $\mathfrak {q} \subseteq B'$. Moreover, denoting by
$\mathfrak {q} \subseteq B'$. Moreover, denoting by ![]() $k'$ the residue field of
$k'$ the residue field of ![]() $A'_\mathfrak {p}$, we have
$A'_\mathfrak {p}$, we have
Thus, ![]() $B'_\mathfrak {q} \otimes _{A'_\mathfrak {p}} k'$ is a localization of
$B'_\mathfrak {q} \otimes _{A'_\mathfrak {p}} k'$ is a localization of ![]() $B \otimes _A k'$, and hence
$B \otimes _A k'$, and hence ![]() $B'_\mathfrak {q} \otimes _{A'_\mathfrak {p}} k'$ is geometrically
$B'_\mathfrak {q} \otimes _{A'_\mathfrak {p}} k'$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $k'$. We may therefore replace
$k'$. We may therefore replace ![]() $A$ by
$A$ by ![]() $A'_\mathfrak {p}$,
$A'_\mathfrak {p}$, ![]() $B$ by
$B$ by ![]() $B'_\mathfrak {q}$, and
$B'_\mathfrak {q}$, and ![]() $K$ by
$K$ by ![]() $K'$, in which case it suffices to show that the local rings of
$K'$, in which case it suffices to show that the local rings of ![]() $B \otimes _A K$ satisfy
$B \otimes _A K$ satisfy ![]() $\mathbf {R}$. We note that
$\mathbf {R}$. We note that ![]() $A'_\mathfrak {p}$ is quasi-excellent by [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.15(i) and Théorème 7.7.2], and that
$A'_\mathfrak {p}$ is quasi-excellent by [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.15(i) and Théorème 7.7.2], and that ![]() $B'_\mathfrak {q}$ appears in
$B'_\mathfrak {q}$ appears in ![]() ${\mathscr {C}}$ by (ii).
${\mathscr {C}}$ by (ii).
We now apply Gabber's weak local uniformization theorem. Since ![]() $X:= {\rm Spec}(A)$ is quasi-excellent by (i), Theorem 2.9 implies there exists a finite covering
$X:= {\rm Spec}(A)$ is quasi-excellent by (i), Theorem 2.9 implies there exists a finite covering ![]() $\{f_i\colon Y_i \to X\}_{i=1}^m$ of
$\{f_i\colon Y_i \to X\}_{i=1}^m$ of ![]() $X$ in the alteration topology, where
$X$ in the alteration topology, where ![]() $Y_i$ is regular and integral for every
$Y_i$ is regular and integral for every ![]() $i$. Note that
$i$. Note that ![]() $X$ is irreducible by our reduction in the first paragraph and by construction of
$X$ is irreducible by our reduction in the first paragraph and by construction of ![]() $A'$ in the previous paragraph. Thus, Theorem 2.8 implies there exist a proper surjective morphism
$A'$ in the previous paragraph. Thus, Theorem 2.8 implies there exist a proper surjective morphism ![]() $\pi \colon V \to X$ and a Zariski open covering
$\pi \colon V \to X$ and a Zariski open covering ![]() $V = \bigcup _{i=1}^m V_i$ fitting into a commutative diagram
$V = \bigcup _{i=1}^m V_i$ fitting into a commutative diagram

for every ![]() $i$. By base change along the morphism
$i$. By base change along the morphism ![]() ${\rm Spec}(\varphi )\colon X' \to X$, where
${\rm Spec}(\varphi )\colon X' \to X$, where ![]() $X' := {\rm Spec}(B)$, we obtain the commutative diagram
$X' := {\rm Spec}(B)$, we obtain the commutative diagram

with cartesian squares for every ![]() $i$. We now consider a point
$i$. We now consider a point ![]() $\eta ' \in X'$ lying over the generic point of
$\eta ' \in X'$ lying over the generic point of ![]() $X$. We want to show that
$X$. We want to show that ![]() $\mathcal {O}_{X',\eta '}$ satisfies
$\mathcal {O}_{X',\eta '}$ satisfies ![]() $\mathbf {R}$. Since
$\mathbf {R}$. Since ![]() $\pi '$ is surjective, there exists a point
$\pi '$ is surjective, there exists a point ![]() $\xi ' \in V'$ such that
$\xi ' \in V'$ such that ![]() $\pi '(\xi ') = \eta '$. Since
$\pi '(\xi ') = \eta '$. Since ![]() $\pi '$ is closed, the specialization
$\pi '$ is closed, the specialization ![]() $\eta ' \rightsquigarrow \mathfrak {n}$ in
$\eta ' \rightsquigarrow \mathfrak {n}$ in ![]() $X' = {\rm Spec}(B)$ then lifts to a specialization
$X' = {\rm Spec}(B)$ then lifts to a specialization ![]() $\xi ' \rightsquigarrow v'$ in
$\xi ' \rightsquigarrow v'$ in ![]() $V'$ [Sta20, Tag 0066]. Since
$V'$ [Sta20, Tag 0066]. Since ![]() $V' = \bigcup _{i=1}^m V'_i$ is a Zariski open covering, there exists an index
$V' = \bigcup _{i=1}^m V'_i$ is a Zariski open covering, there exists an index ![]() $i_0 \in \{1,2,\ldots,m\}$ such that
$i_0 \in \{1,2,\ldots,m\}$ such that ![]() $v' \in V_{i_0}'$, and since open sets are stable under generization, we have
$v' \in V_{i_0}'$, and since open sets are stable under generization, we have ![]() $\xi ' \in V_{i_0}'$ as well. We claim that it suffices to show that
$\xi ' \in V_{i_0}'$ as well. We claim that it suffices to show that ![]() $\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies
$\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies ![]() $\mathbf {R}$. Since the morphism
$\mathbf {R}$. Since the morphism ![]() $f_{i_0}$ is maximally dominating, base-changing the bottom square in (
$f_{i_0}$ is maximally dominating, base-changing the bottom square in (
) for ![]() $i = i_0$ along the morphism
$i = i_0$ along the morphism ![]() ${\rm Spec}(K) \to X = {\rm Spec}(A)$, localizing at the generic point of
${\rm Spec}(K) \to X = {\rm Spec}(A)$, localizing at the generic point of ![]() $Y_{i_0}$, and taking global sections yields the cocartesian square
$Y_{i_0}$, and taking global sections yields the cocartesian square

of rings, where ![]() $L_{i_0}$ is the function field of
$L_{i_0}$ is the function field of ![]() $Y_{i_0}$. The bottom horizontal arrow is faithfully flat; thus, the top horizontal arrow is also faithfully flat by base change. After localizing, we therefore obtain a faithfully flat homomorphism
$Y_{i_0}$. The bottom horizontal arrow is faithfully flat; thus, the top horizontal arrow is also faithfully flat by base change. After localizing, we therefore obtain a faithfully flat homomorphism
and ![]() $({\rm R}_{\rm II}^{{\mathscr {C}}})$ implies that if
$({\rm R}_{\rm II}^{{\mathscr {C}}})$ implies that if ![]() $\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies
$\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies ![]() $\mathbf {R}$, then
$\mathbf {R}$, then ![]() $\mathcal {O}_{X',\eta '}$ satisfies
$\mathcal {O}_{X',\eta '}$ satisfies ![]() $\mathbf {R}$. Here we use the fact that
$\mathbf {R}$. Here we use the fact that ![]() $(B \otimes _A L_{i_0})_{h_{i_0}'(\xi ')}$ is in
$(B \otimes _A L_{i_0})_{h_{i_0}'(\xi ')}$ is in ![]() ${\mathscr {C}}$ by (ii).
${\mathscr {C}}$ by (ii).
It remains to show that ![]() $\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies
$\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies ![]() $\mathbf {R}$. Setting
$\mathbf {R}$. Setting ![]() $y' := h_{i_0}'(v')$ and
$y' := h_{i_0}'(v')$ and ![]() $y := g_{i_0}(y')$, the residue field extension
$y := g_{i_0}(y')$, the residue field extension ![]() $k \subseteq \kappa (y)$ is finitely generated since
$k \subseteq \kappa (y)$ is finitely generated since ![]() $f_{i_0}$ is of finite type. Thus, the closed fiber of the flat homomorphism
$f_{i_0}$ is of finite type. Thus, the closed fiber of the flat homomorphism ![]() $\psi$ in the commutative diagram
$\psi$ in the commutative diagram

is geometrically ![]() $\mathbf {R}$ by
$\mathbf {R}$ by ![]() $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$, since
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$, since ![]() $B \otimes _A k$ is in
$B \otimes _A k$ is in ![]() ${\mathscr {C}}$ by (ii). Since
${\mathscr {C}}$ by (ii). Since ![]() $\mathcal {O}_{Y_{i_0},y}$ is regular by construction and
$\mathcal {O}_{Y_{i_0},y}$ is regular by construction and ![]() $\mathcal {O}_{Y'_{i_0},y'}$ appears in
$\mathcal {O}_{Y'_{i_0},y'}$ appears in ![]() ${\mathscr {C}}$ by (ii), we can apply Lemma 3.5 (which uses
${\mathscr {C}}$ by (ii), we can apply Lemma 3.5 (which uses ![]() $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$) to deduce that
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$) to deduce that ![]() $\mathcal {O}_{Y'_{i_0},y'}$ satisfies
$\mathcal {O}_{Y'_{i_0},y'}$ satisfies ![]() $\mathbf {R}$. Finally,
$\mathbf {R}$. Finally, ![]() $({\rm R}_{{\rm V}}^{{\mathscr {C}}})$ implies that
$({\rm R}_{{\rm V}}^{{\mathscr {C}}})$ implies that ![]() $\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies
$\mathcal {O}_{Y_{i_0}',h_{i_0}'(\xi ')}$ satisfies ![]() $\mathbf {R}$, since the specialization
$\mathbf {R}$, since the specialization ![]() $\xi ' \rightsquigarrow v'$ in
$\xi ' \rightsquigarrow v'$ in ![]() $V'$ maps to the specialization
$V'$ maps to the specialization ![]() $h_{i_0}'(\xi ') \rightsquigarrow h_{i_0}'(v') = y'$ by continuity.
$h_{i_0}'(\xi ') \rightsquigarrow h_{i_0}'(v') = y'$ by continuity.
3.3 Problem 1.2 in general and the proof of Theorem B
We now prove Theorem B by reducing to the complete (hence quasi-excellent) case proved in Theorem 3.4. This step corresponds to (II) in § 1.
We first show the following stronger statement that is more specific about what conditions from Conditions 3.1 are needed.
Corollary 3.6 (cf. [Reference MarotMar84, Theorem 2.2; Reference Brezuleanu and IonescuBI84, Proposition 1.2])
Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let
${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism ![]() $\varphi \colon (A,\mathfrak {m},k) \to (B,\mathfrak {n},l)$ of noetherian local rings. Assume the following:
$\varphi \colon (A,\mathfrak {m},k) \to (B,\mathfrak {n},l)$ of noetherian local rings. Assume the following:
(i) the ring
 $A$ has geometrically
$A$ has geometrically  $\mathbf {R}$ formal fibers;
$\mathbf {R}$ formal fibers;(ii) the rings
 $\hat {A}$ and
$\hat {A}$ and  $B^*$ appear in
$B^*$ appear in  ${\mathscr {C}}$, where
${\mathscr {C}}$, where  $\hat {A}$ and
$\hat {A}$ and  $B^*$ denote the
$B^*$ denote the  $\mathfrak {m}$-adic completions of
$\mathfrak {m}$-adic completions of  $A$ and
$A$ and  $B$, respectively; and
$B$, respectively; and(iii) the property
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$,  $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,  $({\rm R}_{{\rm V}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm V}}^{{\mathscr {C}}})$,  $({\rm P}_{{\rm I}}^{{\mathscr {C}}'})$, and
$({\rm P}_{{\rm I}}^{{\mathscr {C}}'})$, and  $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
If the closed fiber of ![]() $\varphi$ is geometrically
$\varphi$ is geometrically ![]() $\mathbf {R}$, then all fibers of
$\mathbf {R}$, then all fibers of ![]() $\varphi$ are geometrically
$\varphi$ are geometrically ![]() $\mathbf {R}$.
$\mathbf {R}$.
Proof. We have the commutative square

where ![]() $\sigma$ and
$\sigma$ and ![]() $\tau$ are the canonical
$\tau$ are the canonical ![]() $\mathfrak {m}$-adic completion homomorphisms. By (i), the homomorphism
$\mathfrak {m}$-adic completion homomorphisms. By (i), the homomorphism ![]() $\sigma$ is geometrically
$\sigma$ is geometrically ![]() $\mathbf {R}$. We claim that
$\mathbf {R}$. We claim that ![]() $\varphi ^*$ is geometrically
$\varphi ^*$ is geometrically ![]() $\mathbf {R}$. By [Reference Grothendieck and DieudonnéEGAInew, Chapitre 0, Lemme 6.8.3.1], the ring
$\mathbf {R}$. By [Reference Grothendieck and DieudonnéEGAInew, Chapitre 0, Lemme 6.8.3.1], the ring ![]() $B^*$ is a noetherian local ring, and we have
$B^*$ is a noetherian local ring, and we have
Theorem 3.4 therefore implies that ![]() $\varphi ^*$ is geometrically
$\varphi ^*$ is geometrically ![]() $\mathbf {R}$, where we use the fact that the complete local ring
$\mathbf {R}$, where we use the fact that the complete local ring ![]() $\hat {A}$ is excellent by [Reference Grothendieck and DieudonnéEGAIV2, Scholie 7.8.3(iii)]. The composition
$\hat {A}$ is excellent by [Reference Grothendieck and DieudonnéEGAIV2, Scholie 7.8.3(iii)]. The composition ![]() $\tau \circ \varphi = \varphi ^* \circ \sigma$ is geometrically
$\tau \circ \varphi = \varphi ^* \circ \sigma$ is geometrically ![]() $\mathbf {R}$ by
$\mathbf {R}$ by ![]() $({\rm P}_{{\rm I}}^{{\mathscr {C}}'})$, and therefore
$({\rm P}_{{\rm I}}^{{\mathscr {C}}'})$, and therefore ![]() $\varphi$ is also by
$\varphi$ is also by ![]() $({\rm P}_{{\rm II}}^{{\mathscr {C}}})$ (which holds by
$({\rm P}_{{\rm II}}^{{\mathscr {C}}})$ (which holds by ![]() $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$ and Lemma 3.3(iii)) since
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$ and Lemma 3.3(iii)) since ![]() $\tau$ is faithfully flat [Reference MatsumuraMat89, Theorem 8.14].
$\tau$ is faithfully flat [Reference MatsumuraMat89, Theorem 8.14].
We now deduce Theorem B as a consequence.
Theorem B Problem 1.2 holds for properties ![]() $\mathbf {R}$ of noetherian local rings satisfying
$\mathbf {R}$ of noetherian local rings satisfying ![]() $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$, ![]() $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$, ![]() $({\text {R}_{\text {IV}}})$, and
$({\text {R}_{\text {IV}}})$, and ![]() $({\text {R}_{\text {V}}})$, such that regular local rings satisfy
$({\text {R}_{\text {V}}})$, such that regular local rings satisfy ![]() $\mathbf {R}$.
$\mathbf {R}$.
Proof. It suffices to show that the hypotheses in Theorem B imply those in Corollary 3.6 when ![]() ${\mathscr {C}}$ is the entire category of noetherian rings. Note that (i) is already a hypothesis in Theorem B and that (ii) is vacuously true. It therefore suffices to note that
${\mathscr {C}}$ is the entire category of noetherian rings. Note that (i) is already a hypothesis in Theorem B and that (ii) is vacuously true. It therefore suffices to note that ![]() $({\text {R}'_{\text {I}}})$ implies
$({\text {R}'_{\text {I}}})$ implies ![]() $({\text {P}'_{\text {I}}})$ by Lemma 3.3(ii), and that
$({\text {P}'_{\text {I}}})$ by Lemma 3.3(ii), and that ![]() $({\text {R}_{\text {I}}})$ and
$({\text {R}_{\text {I}}})$ and ![]() $({\text {R}_{\text {II}}})$ imply
$({\text {R}_{\text {II}}})$ imply ![]() $({\text {P}_{\text {IV}}})$ by Lemma 3.3(iv). Here,
$({\text {P}_{\text {IV}}})$ by Lemma 3.3(iv). Here, ![]() $({\text {R}_{\text {I}}})$ holds by
$({\text {R}_{\text {I}}})$ holds by ![]() $({\text {R}'_{\text {I}}})$ and the assumption that regular local rings satisfy
$({\text {R}'_{\text {I}}})$ and the assumption that regular local rings satisfy ![]() $\mathbf {R}$.
$\mathbf {R}$.
We can also prove a version of Corollary 3.6 for a specific choice of the category ![]() ${\mathscr {C}}$, as long as we put an extra condition on
${\mathscr {C}}$, as long as we put an extra condition on ![]() $B \otimes _A k$.
$B \otimes _A k$.
Corollary 3.7 (cf. [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 7.5.2; Reference Brezuleanu and IonescuBI84, Proposition 1.2])
Denote by ![]() ${\mathscr {C}}$ the smallest full subcategory of the category of noetherian rings containing noetherian complete local rings that is stable under homomorphisms essentially of finite type. Let
${\mathscr {C}}$ the smallest full subcategory of the category of noetherian rings containing noetherian complete local rings that is stable under homomorphisms essentially of finite type. Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a flat local homomorphism ![]() $\varphi \colon (A,\mathfrak {m},k) \to (B,\mathfrak {n},l)$ of noetherian local rings. Assume the following:
$\varphi \colon (A,\mathfrak {m},k) \to (B,\mathfrak {n},l)$ of noetherian local rings. Assume the following:
(i) the rings
 $A$ and
$A$ and  $B \otimes _A k$ have geometrically
$B \otimes _A k$ have geometrically  $\mathbf {R}$ formal fibers; and
$\mathbf {R}$ formal fibers; and(ii) the property
 $\mathbf {R}$ satisfies
$\mathbf {R}$ satisfies  $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$,  $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$,  $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,  $({\rm R}_{{\rm V}}^{{\mathscr {C}}})$, and
$({\rm R}_{{\rm V}}^{{\mathscr {C}}})$, and  $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$.
If the closed fiber of ![]() $\varphi$ is geometrically
$\varphi$ is geometrically ![]() $\mathbf {R}$, then all fibers of
$\mathbf {R}$, then all fibers of ![]() $\varphi$ are geometrically
$\varphi$ are geometrically ![]() $\mathbf {R}$.
$\mathbf {R}$.
Proof. We have the commutative square

where ![]() $\sigma$ and
$\sigma$ and ![]() $\tau$ are the canonical
$\tau$ are the canonical ![]() $\mathfrak {m}$-adic and
$\mathfrak {m}$-adic and ![]() $\mathfrak {n}$-adic completion homomorphisms, respectively. By (i), the homomorphism
$\mathfrak {n}$-adic completion homomorphisms, respectively. By (i), the homomorphism ![]() $\sigma$ is geometrically
$\sigma$ is geometrically ![]() $\mathbf {R}$. We claim that
$\mathbf {R}$. We claim that ![]() $\hat {\varphi }$ is geometrically
$\hat {\varphi }$ is geometrically ![]() $\mathbf {R}$. Note that
$\mathbf {R}$. Note that ![]() $\hat {\varphi }$ is flat by [Reference MatsumuraMat89, Theorem 22.4(i)], and that
$\hat {\varphi }$ is flat by [Reference MatsumuraMat89, Theorem 22.4(i)], and that ![]() $B \otimes _A k$ has geometrically
$B \otimes _A k$ has geometrically ![]() $\mathbf {R}$ formal fibers by (i). Thus, the composition
$\mathbf {R}$ formal fibers by (i). Thus, the composition
is geometrically ![]() $\mathbf {R}$ by applying
$\mathbf {R}$ by applying ![]() $({\text {P}'_{\text {I}}})$ (which holds by
$({\text {P}'_{\text {I}}})$ (which holds by ![]() $({\text {R}'_{\text {I}}})$ and Lemma 3.3(ii)). Since this composition is equal to
$({\text {R}'_{\text {I}}})$ and Lemma 3.3(ii)). Since this composition is equal to ![]() $\hat {\varphi } \otimes _{\hat {A}} \mathrm {id}_k$, Theorem 3.4 implies that
$\hat {\varphi } \otimes _{\hat {A}} \mathrm {id}_k$, Theorem 3.4 implies that ![]() $\hat {\varphi }$ is geometrically
$\hat {\varphi }$ is geometrically ![]() $\mathbf {R}$, where we use the fact that the complete local ring
$\mathbf {R}$, where we use the fact that the complete local ring ![]() $\hat {A}$ is excellent by [Reference Grothendieck and DieudonnéEGAIV2, Scholie 7.8.3(iii)].
$\hat {A}$ is excellent by [Reference Grothendieck and DieudonnéEGAIV2, Scholie 7.8.3(iii)].
The composition ![]() $\tau \circ \varphi = \varphi ^* \circ \sigma$ is geometrically
$\tau \circ \varphi = \varphi ^* \circ \sigma$ is geometrically ![]() $\mathbf {R}$ by
$\mathbf {R}$ by ![]() $({\text {P}'_{\text {I}}})$, and therefore
$({\text {P}'_{\text {I}}})$, and therefore ![]() $\varphi$ is also by
$\varphi$ is also by ![]() $({\rm P}_{{\rm I}}')$ (which holds by
$({\rm P}_{{\rm I}}')$ (which holds by ![]() $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$ and Lemma 3.3(iii)) since
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$ and Lemma 3.3(iii)) since ![]() $\tau$ is faithfully flat [Reference MatsumuraMat89, Theorem 8.14].
$\tau$ is faithfully flat [Reference MatsumuraMat89, Theorem 8.14].
3.4 Global applications and the proof of Theorem A
We now prove Theorem A by reducing to the local statements proved above. This step corresponds to (I) in § 1.
We first give global versions of Theorem 3.4 and Corollaries 3.6 and 3.7. Theorem A(i) will be deduced from (ii) below. These results are related to a theorem of Shimomoto [Reference ShimomotoShi17, Main Theorem 1], which applies to morphisms of finite type between excellent noetherian schemes.
Proposition 3.8 (cf. [Reference ShimomotoShi17, Main Theorem 1])
Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let
${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a flat morphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a flat morphism ![]() $f\colon Y \to X$ of locally noetherian schemes mapping closed points to closed points. Assume one of the following:
$f\colon Y \to X$ of locally noetherian schemes mapping closed points to closed points. Assume one of the following:
(i)
 $\mathbf {R}$ satisfies the hypotheses of Theorem 3.4 for the category
$\mathbf {R}$ satisfies the hypotheses of Theorem 3.4 for the category  ${\mathscr {C}}$, the local rings of
${\mathscr {C}}$, the local rings of  $X$ at closed points are quasi-excellent, and the local rings of
$X$ at closed points are quasi-excellent, and the local rings of  $Y$ at closed points appear in
$Y$ at closed points appear in  ${\mathscr {C}}$;
${\mathscr {C}}$;(ii)
 $\mathbf {R}$ satisfies the hypotheses of Corollary 3.6 for the category
$\mathbf {R}$ satisfies the hypotheses of Corollary 3.6 for the category  ${\mathscr {C}}$, the local rings of
${\mathscr {C}}$, the local rings of  $X$ at closed points have geometrically
$X$ at closed points have geometrically  $\mathbf {R}$ formal fibers, and the rings
$\mathbf {R}$ formal fibers, and the rings  $\hat {\mathcal {O}}_{X,f(y)}$ and
$\hat {\mathcal {O}}_{X,f(y)}$ and  $\mathcal {O}_{Y,y}^*$ appear in
$\mathcal {O}_{Y,y}^*$ appear in  ${\mathscr {C}}$ for every closed point
${\mathscr {C}}$ for every closed point  $y \in Y$, where
$y \in Y$, where  $\mathcal {O}_{Y,y}^*$ denotes the
$\mathcal {O}_{Y,y}^*$ denotes the  $\mathfrak {m}_{f(y)}$-adic completion of
$\mathfrak {m}_{f(y)}$-adic completion of  $\mathcal {O}_{Y,y}$; or
$\mathcal {O}_{Y,y}$; or(iii)
 $\mathbf {R}$ satisfies the hypotheses of Corollary 3.7 for the specific choice of
$\mathbf {R}$ satisfies the hypotheses of Corollary 3.7 for the specific choice of  ${\mathscr {C}}$ therein, the local rings of
${\mathscr {C}}$ therein, the local rings of  $X$ at closed points have geometrically
$X$ at closed points have geometrically  $\mathbf {R}$ formal fibers, and the local rings
$\mathbf {R}$ formal fibers, and the local rings  $\mathcal {O}_{f^{-1}(x),y}$ have geometrically
$\mathcal {O}_{f^{-1}(x),y}$ have geometrically  $\mathbf {R}$ formal fibers for every closed point
$\mathbf {R}$ formal fibers for every closed point  $x \in X$ and every closed point
$x \in X$ and every closed point  $y \in f^{-1}(x)$.
$y \in f^{-1}(x)$.
If every closed fiber of ![]() $f$ is geometrically
$f$ is geometrically ![]() $\mathbf {R}$, then all fibers of
$\mathbf {R}$, then all fibers of ![]() $f$ are geometrically
$f$ are geometrically ![]() $\mathbf {R}$.
$\mathbf {R}$.
Proof. Let ![]() $\xi \in Y$ be an arbitrary point, and let
$\xi \in Y$ be an arbitrary point, and let ![]() $\eta = f(\xi )$. We want to show that
$\eta = f(\xi )$. We want to show that ![]() $\mathcal {O}_{Y,\xi }$ is geometrically
$\mathcal {O}_{Y,\xi }$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\eta )$. By [Sta20, Tag 02IL], the point
$\kappa (\eta )$. By [Sta20, Tag 02IL], the point ![]() $\xi$ specializes to a closed point
$\xi$ specializes to a closed point ![]() $y \in Y$. Since
$y \in Y$. Since ![]() $f$ maps closed points to closed points, the point
$f$ maps closed points to closed points, the point ![]() $x = f(y)$ is closed in
$x = f(y)$ is closed in ![]() $X$. After localization, we then obtain a flat local homomorphism
$X$. After localization, we then obtain a flat local homomorphism
whose closed fiber is geometrically ![]() $\mathbf {R}$ by assumption. Finally, we can apply Theorem 3.4, Corollary 3.6, and Corollary 3.7 to the homomorphism
$\mathbf {R}$ by assumption. Finally, we can apply Theorem 3.4, Corollary 3.6, and Corollary 3.7 to the homomorphism ![]() $\varphi$ under the assumptions in (i), (ii), and (iii), respectively, to conclude that
$\varphi$ under the assumptions in (i), (ii), and (iii), respectively, to conclude that ![]() $\mathcal {O}_{Y,\xi }$ is geometrically
$\mathcal {O}_{Y,\xi }$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\eta )$.
$\kappa (\eta )$.
We also prove that the locus over which ![]() $f$ has geometrically
$f$ has geometrically ![]() $\mathbf {R}$ fibers is stable under generization for closed flat morphisms. Theorem A(i) will be deduced from (ii) below.
$\mathbf {R}$ fibers is stable under generization for closed flat morphisms. Theorem A(i) will be deduced from (ii) below.
Proposition 3.9 Fix a full subcategory ![]() ${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let
${\mathscr {C}}$ of the category of noetherian rings that is stable under homomorphisms essentially of finite type. Let ![]() $\mathbf {R}$ be a property of noetherian local rings, and consider a closed flat morphism
$\mathbf {R}$ be a property of noetherian local rings, and consider a closed flat morphism ![]() $f\colon Y \to X$ of locally noetherian schemes. Assume one
$f\colon Y \to X$ of locally noetherian schemes. Assume one
of the following:
(i)
 $\mathbf {R}$ satisfies the hypotheses of Theorem 3.4 for the category
$\mathbf {R}$ satisfies the hypotheses of Theorem 3.4 for the category  ${\mathscr {C}}$, the local rings of
${\mathscr {C}}$, the local rings of  $X$ are quasi-excellent, and the local rings of
$X$ are quasi-excellent, and the local rings of  $Y$ appear in
$Y$ appear in  ${\mathscr {C}}$;
${\mathscr {C}}$;(ii)
 $\mathbf {R}$ satisfies the hypotheses of Corollary 3.6 for the category
$\mathbf {R}$ satisfies the hypotheses of Corollary 3.6 for the category  ${\mathscr {C}}$, the local rings of
${\mathscr {C}}$, the local rings of  $X$ have geometrically
$X$ have geometrically  $\mathbf {R}$ formal fibers, and the rings
$\mathbf {R}$ formal fibers, and the rings  $\hat {\mathcal {O}}_{X,f(y)}$ and
$\hat {\mathcal {O}}_{X,f(y)}$ and  $\mathcal {O}_{Y,y}^*$ appear in
$\mathcal {O}_{Y,y}^*$ appear in  ${\mathscr {C}}$ for every
${\mathscr {C}}$ for every  $y \in Y$, where
$y \in Y$, where  $\mathcal {O}_{Y,y}^*$ denotes the
$\mathcal {O}_{Y,y}^*$ denotes the  $\mathfrak {m}_{f(y)}$-adic completion of
$\mathfrak {m}_{f(y)}$-adic completion of  $\mathcal {O}_{Y,y}$; or
$\mathcal {O}_{Y,y}$; or(iii)
 $\mathbf {R}$ satisfies the hypotheses of Corollary 3.7 for the specific choice of
$\mathbf {R}$ satisfies the hypotheses of Corollary 3.7 for the specific choice of  ${\mathscr {C}}$ therein, the local rings of
${\mathscr {C}}$ therein, the local rings of  $X$ have geometrically
$X$ have geometrically  $\mathbf {R}$ formal fibers, and the local rings
$\mathbf {R}$ formal fibers, and the local rings  $\mathcal {O}_{f^{-1}(x),y}$ have geometrically
$\mathcal {O}_{f^{-1}(x),y}$ have geometrically  $\mathbf {R}$ formal fibers for every
$\mathbf {R}$ formal fibers for every  $x \in X$ and every
$x \in X$ and every  $y \in f^{-1}(x)$.
$y \in f^{-1}(x)$.
Then the locus
is stable under generization.
Proof. Consider a specialization ![]() $\eta \rightsquigarrow x$ in
$\eta \rightsquigarrow x$ in ![]() $X$, and suppose that
$X$, and suppose that ![]() $f^{-1}(x)$ is geometrically
$f^{-1}(x)$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (x)$. We want to show that
$\kappa (x)$. We want to show that ![]() $f^{-1}(\eta )$ is geometrically
$f^{-1}(\eta )$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\eta )$. It suffices to show that, for every
$\kappa (\eta )$. It suffices to show that, for every ![]() $\xi \in f^{-1}(\eta )$, the local ring
$\xi \in f^{-1}(\eta )$, the local ring ![]() $\mathcal {O}_{Y,\xi }$ is geometrically
$\mathcal {O}_{Y,\xi }$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\kappa (\eta )$. Since
$\kappa (\eta )$. Since ![]() $f$ is closed, the specialization
$f$ is closed, the specialization ![]() $\eta \rightsquigarrow x$ lifts to a specialization
$\eta \rightsquigarrow x$ lifts to a specialization ![]() $\xi \rightsquigarrow y$ [Sta20, Tag 0066]. After localization, we then obtain a flat local homomorphism
$\xi \rightsquigarrow y$ [Sta20, Tag 0066]. After localization, we then obtain a flat local homomorphism
whose closed fiber is geometrically ![]() $\mathbf {R}$ by assumption. Finally, we can apply Theorem 3.4, Corollary 3.6, and Corollary 3.7 to the homomorphism
$\mathbf {R}$ by assumption. Finally, we can apply Theorem 3.4, Corollary 3.6, and Corollary 3.7 to the homomorphism ![]() $\varphi$ under the assumptions in (i), (ii), and (iii), respectively, to conclude that
$\varphi$ under the assumptions in (i), (ii), and (iii), respectively, to conclude that ![]() $\mathcal {O}_{Y,\xi }$ is geometrically
$\mathcal {O}_{Y,\xi }$ is geometrically ![]() $\mathbf {R}$ over
$\mathbf {R}$ over ![]() $\eta$.
$\eta$.
We now deduce Theorem A as a consequence of Propositions 3.8 and 3.9.
Theorem A Let ![]() $\mathbf {R}$ be a property of noetherian local rings satisfying
$\mathbf {R}$ be a property of noetherian local rings satisfying ![]() $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$, ![]() $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$, ![]() $({\text {R}_{\text {IV}}})$, and
$({\text {R}_{\text {IV}}})$, and ![]() $({\text {R}_{\text {V}}})$, such that regular local rings satisfy
$({\text {R}_{\text {V}}})$, such that regular local rings satisfy ![]() $\mathbf {R}$. Consider a flat morphism
$\mathbf {R}$. Consider a flat morphism ![]() $f\colon Y \to X$ of locally noetherian schemes.
$f\colon Y \to X$ of locally noetherian schemes.
(i) Suppose that
 $f$ maps closed to closed points, and that the local rings of
$f$ maps closed to closed points, and that the local rings of  $X$ at closed points have geometrically
$X$ at closed points have geometrically  $\mathbf {R}$ formal fibers. If every closed fiber of
$\mathbf {R}$ formal fibers. If every closed fiber of  $f$ is geometrically
$f$ is geometrically  $\mathbf {R}$, then all fibers of
$\mathbf {R}$, then all fibers of  $f$ are geometrically
$f$ are geometrically  $\mathbf {R}$.
$\mathbf {R}$.(ii) Suppose that
 $f$ is closed, and that the local rings of
$f$ is closed, and that the local rings of  $X$ have geometrically
$X$ have geometrically  $\mathbf {R}$ formal fibers. Then the locus
is stable under generization.
$\mathbf {R}$ formal fibers. Then the locus
is stable under generization. \[ U_\mathbf{R}(f) := \{x \in X \,|\, f^{{-}1}(x)\ \text{is geometrically}\ \mathbf{R}\ \text{over}\ \kappa(x)\} \subseteq X \]
\[ U_\mathbf{R}(f) := \{x \in X \,|\, f^{{-}1}(x)\ \text{is geometrically}\ \mathbf{R}\ \text{over}\ \kappa(x)\} \subseteq X \]
3.5 The local lifting problem
To solve the local lifting problem, we use the following theorem of Brezuleanu and Ionescu. We state their theorem using the notation in Conditions 3.1 instead of that in [Reference Brezuleanu and IonescuBI84, (2.1)].
Theorem 3.10 [Reference Brezuleanu and IonescuBI84, Theorem 2.3]
Let ![]() $\mathbf {R}'$ be a property of noetherian local rings. Assume the following:
$\mathbf {R}'$ be a property of noetherian local rings. Assume the following:
(i) we have the sequence of implications regular
 $\Rightarrow$
$\Rightarrow$  $\mathbf {R}'$
$\mathbf {R}'$  $\Rightarrow$ reduced;
$\Rightarrow$ reduced;(ii) the property
 $\mathbf {R}'$ satisfies
$\mathbf {R}'$ satisfies  $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$,  $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$,  $({\text {R}_{\text {III}}})$, and
$({\text {R}_{\text {III}}})$, and  $({\text {R}_{\text {V}}})$;
$({\text {R}_{\text {V}}})$;(iii) for every flat local homomorphism
 $\varphi \colon A \to B$ of noetherian complete local rings, if the closed fiber of
$\varphi \colon A \to B$ of noetherian complete local rings, if the closed fiber of  $\varphi$ is geometrically
$\varphi$ is geometrically  $\mathbf {R}'$, then all fibers of
$\mathbf {R}'$, then all fibers of  $\varphi$ are geometrically
$\varphi$ are geometrically  $\mathbf {R}'$.
$\mathbf {R}'$.
Let ![]() $A$ be a noetherian semi-local ring that is
$A$ be a noetherian semi-local ring that is ![]() $I$-adically complete with respect to an ideal
$I$-adically complete with respect to an ideal ![]() $I \subseteq A$. If
$I \subseteq A$. If ![]() $A/I$ is has geometrically
$A/I$ is has geometrically ![]() $\mathbf {R}'$ formal fibers, then
$\mathbf {R}'$ formal fibers, then ![]() $A$ has geometrically
$A$ has geometrically ![]() $\mathbf {R}'$ formal fibers.
$\mathbf {R}'$ formal fibers.
We obtain Theorem C and an important corollary as immediate consequences.
Theorem C Let ![]() $\mathbf {R}$ be a property of noetherian local rings that satisfies the hypotheses in Theorem B. Suppose, moreover, that the locus
$\mathbf {R}$ be a property of noetherian local rings that satisfies the hypotheses in Theorem B. Suppose, moreover, that the locus
is open for every noetherian complete local ring ![]() $C$. If
$C$. If ![]() $A$ is a noetherian semi-local ring that is
$A$ is a noetherian semi-local ring that is ![]() $I$-adically complete with respect to an ideal
$I$-adically complete with respect to an ideal ![]() $I \subseteq A$, and if
$I \subseteq A$, and if ![]() $A/I$ is Nagata and has geometrically
$A/I$ is Nagata and has geometrically ![]() $\mathbf {R}$ formal fibers, then
$\mathbf {R}$ formal fibers, then ![]() $A$ is Nagata and has geometrically
$A$ is Nagata and has geometrically ![]() $\mathbf {R}$ formal fibers.
$\mathbf {R}$ formal fibers.
Proof. Since a noetherian semi-local ring is Nagata if and only if it has geometrically reduced formal fibers (Remark 2.5), it suffices to verify the hypotheses in Theorem 3.10 for ![]() $\mathbf {R}' = \mathbf {R} +$ ‘reduced’. Both (i) and (ii) hold by assumption. Theorem B implies (iii) holds, since complete local rings have geometrically
$\mathbf {R}' = \mathbf {R} +$ ‘reduced’. Both (i) and (ii) hold by assumption. Theorem B implies (iii) holds, since complete local rings have geometrically ![]() $\mathbf {R}$ formal fibers by the assumption that regular local rings satisfy
$\mathbf {R}$ formal fibers by the assumption that regular local rings satisfy ![]() $\mathbf {R}$.
$\mathbf {R}$.
Corollary 3.11 With assumptions as in Theorem C, if ![]() $B$ is a noetherian semi-local Nagata ring that has geometrically
$B$ is a noetherian semi-local Nagata ring that has geometrically ![]() $\mathbf {R}$ formal fibers, then for every ideal
$\mathbf {R}$ formal fibers, then for every ideal ![]() $I \subseteq B$ the
$I \subseteq B$ the ![]() $I$-adic completion of
$I$-adic completion of ![]() $B$ is Nagata and has geometrically
$B$ is Nagata and has geometrically ![]() $\mathbf {R}$ formal fibers.
$\mathbf {R}$ formal fibers.
Proof. The ![]() $I$-adic completion
$I$-adic completion ![]() $\hat {B}$ of
$\hat {B}$ of ![]() $B$ is a noetherian semi-local ring that is
$B$ is a noetherian semi-local ring that is ![]() $I\hat {B}$-adically complete by [Reference BourbakiBou98, Chapter III, § 3,
$I\hat {B}$-adically complete by [Reference BourbakiBou98, Chapter III, § 3, ![]() ${\rm n}^{{\rm o}}$ 4, Proposition 8]. Thus, by Theorem C, it suffices to show that
${\rm n}^{{\rm o}}$ 4, Proposition 8]. Thus, by Theorem C, it suffices to show that ![]() $\hat {B}/I\hat {B} \simeq B/I$ is a Nagata ring with geometrically
$\hat {B}/I\hat {B} \simeq B/I$ is a Nagata ring with geometrically ![]() $\mathbf {R}$ formal fibers. But
$\mathbf {R}$ formal fibers. But ![]() $B/I$ has geometrically
$B/I$ has geometrically ![]() $\mathbf {R}$ formal fibers by [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.15(i)], and is also Nagata by Definition 2.4.
$\mathbf {R}$ formal fibers by [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.3.15(i)], and is also Nagata by Definition 2.4.
4. Specific properties  $\mathbf {R}$
$\mathbf {R}$
We now explicitly consider our new cases of Grothendieck's localization problem and the local lifting problem. We have listed known cases of conditions ![]() $({\text {R}'_{\text {I}}})$,
$({\text {R}'_{\text {I}}})$, ![]() $({\text {R}_{\text {II}}})$,
$({\text {R}_{\text {II}}})$, ![]() $({\rm R}_{{\rm III}})$,
$({\rm R}_{{\rm III}})$, ![]() $({\text {R}_{\text {IV}}})$, and
$({\text {R}_{\text {IV}}})$, and ![]() $({\text {R}_{\text {V}}})$ in Table 2. While Problem 1.2 follows readily from these results when
$({\text {R}_{\text {V}}})$ in Table 2. While Problem 1.2 follows readily from these results when ![]() $\mathbf {R} =$ ‘domain’, ‘Cohen–Macaulay and
$\mathbf {R} =$ ‘domain’, ‘Cohen–Macaulay and ![]() $F$-injective’, and ‘
$F$-injective’, and ‘![]() $F$-rational’, we will have to verify
$F$-rational’, we will have to verify ![]() $({\text {R}_{\text {IV}}})$ for weak normality (Proposition 4.10). We will deduce our results for terminal, canonical, and rational singularities from [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8] instead of Theorems A and B.
$({\text {R}_{\text {IV}}})$ for weak normality (Proposition 4.10). We will deduce our results for terminal, canonical, and rational singularities from [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8] instead of Theorems A and B.
We will not explicitly formulate versions of Theorem A below, except for terminal, canonical, and rational singularities (Corollary 4.19).
4.1 Domain
We first note that a version of Problem 1.2 holds for ![]() $\mathbf {R} =$ ‘domain’. This property satisfies the hypotheses in Theorem 3.4 (see Table 2). This extends a result of Marot [Reference MarotMar84], which holds in residue characteristic zero. We use the terminology ‘geometrically punctually integral’ following [Reference Grothendieck and DieudonnéEGAIV2, Définition 4.6.9] for the property obtained by applying Definition 2.1 to
$\mathbf {R} =$ ‘domain’. This property satisfies the hypotheses in Theorem 3.4 (see Table 2). This extends a result of Marot [Reference MarotMar84], which holds in residue characteristic zero. We use the terminology ‘geometrically punctually integral’ following [Reference Grothendieck and DieudonnéEGAIV2, Définition 4.6.9] for the property obtained by applying Definition 2.1 to ![]() $\mathbf {R} =$ ‘domain’.
$\mathbf {R} =$ ‘domain’.
Corollary 4.1 (cf. [Reference MarotMar84, Theorem 2.1])
Let ![]() $\varphi \colon A \to B$ be a flat local homomorphism of noetherian local rings, and assume that
$\varphi \colon A \to B$ be a flat local homomorphism of noetherian local rings, and assume that ![]() $A$ is quasi-excellent. If the closed fiber of
$A$ is quasi-excellent. If the closed fiber of ![]() $\varphi$ is geometrically punctually integral, then all fibers of
$\varphi$ is geometrically punctually integral, then all fibers of ![]() $\varphi$ are geometrically punctually integral.
$\varphi$ are geometrically punctually integral.
Remark 4.2 Since ![]() $({\rm R}_{{\rm I}}^{{\mathscr {C}}'})$ is false for the property
$({\rm R}_{{\rm I}}^{{\mathscr {C}}'})$ is false for the property ![]() $\mathbf {R} =$ ‘domain’ [Reference Grothendieck and DieudonnéEGAIV2, Remarques 6.5.5(ii) and 6.15.11(ii)], we only know that global versions of Corollary 4.1 hold under quasi-excellence assumptions by applying Propositions 3.8(i) and 3.9(i). See also [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 7.9.9 and Remarque 7.9.10
$\mathbf {R} =$ ‘domain’ [Reference Grothendieck and DieudonnéEGAIV2, Remarques 6.5.5(ii) and 6.15.11(ii)], we only know that global versions of Corollary 4.1 hold under quasi-excellence assumptions by applying Propositions 3.8(i) and 3.9(i). See also [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 7.9.9 and Remarque 7.9.10![]() $({\rm i})$].
$({\rm i})$].
4.2 F-singularities
We now solve Problems 1.2 and 1.3 for ‘Cohen–Macaulay and ![]() $F$-injective’ and for
$F$-injective’ and for ![]() $F$-rationality. See [Reference FedderFed83, Definition on p. 473] and [Reference Hochster and HunekeHH94, Definition 4.1] for the definitions of
$F$-rationality. See [Reference FedderFed83, Definition on p. 473] and [Reference Hochster and HunekeHH94, Definition 4.1] for the definitions of ![]() $F$-injectivity and
$F$-injectivity and ![]() $F$-rationality, respectively. We recall (see [Reference Datta and MurayamaDM20, Remark A.4]) that we have the following sequence of implications:
$F$-rationality, respectively. We recall (see [Reference Datta and MurayamaDM20, Remark A.4]) that we have the following sequence of implications:
Since the ‘Cohen–Macaulay and ![]() $F$-injective’ property satisfies the hypotheses in Theorems B and C (see Table 2 and (4)), we can solve Problems 1.2 and 1.3 for this property. The result for Problem 1.2 extends a result of Hashimoto [Reference HashimotoHas01] to the non-
$F$-injective’ property satisfies the hypotheses in Theorems B and C (see Table 2 and (4)), we can solve Problems 1.2 and 1.3 for this property. The result for Problem 1.2 extends a result of Hashimoto [Reference HashimotoHas01] to the non-![]() $F$-finite case.
$F$-finite case.
Corollary 4.3 (cf. [Reference HashimotoHas01, Theorem 5.8])
Grothendieck's localization problem and the local lifting problem hold for ‘Cohen–Macaulay and ![]() $F$-injective’, where
$F$-injective’, where ![]() $A$ is assumed to be of prime characteristic
$A$ is assumed to be of prime characteristic ![]() $p > 0$.
$p > 0$.
Remark 4.4 Shimomoto and Zhang proved Grothendieck's localization problem for the ‘Gorenstein and ![]() $F$-pure’ property when
$F$-pure’ property when ![]() $A$ and
$A$ and ![]() $B$ are
$B$ are ![]() $F$-finite [Reference Shimomoto and ZhangSZ09, Theorem 3.10]. Their result is a special case of Hashimoto's result, since
$F$-finite [Reference Shimomoto and ZhangSZ09, Theorem 3.10]. Their result is a special case of Hashimoto's result, since ![]() $F$-purity and
$F$-purity and ![]() $F$-injectivity coincide for Gorenstein rings [Reference FedderFed83, Lemma 3.3], and since Problem 1.2 holds for Gorensteinness [Reference MarotMar84, Theorem 3.2]. Corollary 4.3 also extends Shimomoto and Zhang's result to the non-
$F$-injectivity coincide for Gorenstein rings [Reference FedderFed83, Lemma 3.3], and since Problem 1.2 holds for Gorensteinness [Reference MarotMar84, Theorem 3.2]. Corollary 4.3 also extends Shimomoto and Zhang's result to the non-![]() $F$-finite case. See also Remark 4.6.
$F$-finite case. See also Remark 4.6.
Next, we consider Grothendieck's localization problem for ![]() $F$-rationality. The following extends a result of Hashimoto [Reference HashimotoHas01] to rings
$F$-rationality. The following extends a result of Hashimoto [Reference HashimotoHas01] to rings ![]() $A$ not necessarily essentially of finite type over a field, and a result of Shimomoto [Reference ShimomotoShi17] to homomorphisms not necessarily of finite type, giving a complete answer to a question of Hashimoto [Reference HashimotoHas01, Remark 6.7].
$A$ not necessarily essentially of finite type over a field, and a result of Shimomoto [Reference ShimomotoShi17] to homomorphisms not necessarily of finite type, giving a complete answer to a question of Hashimoto [Reference HashimotoHas01, Remark 6.7].
Corollary 4.5 (cf. [Reference HashimotoHas01, Remark 6.7; Reference ShimomotoShi17, Corollary 3.10])
Let ![]() $\varphi \colon A \to B$ be a flat local homomorphism of noetherian local rings of prime characteristic
$\varphi \colon A \to B$ be a flat local homomorphism of noetherian local rings of prime characteristic ![]() $p > 0$. Assume that
$p > 0$. Assume that ![]() $A$ is quasi-excellent and that
$A$ is quasi-excellent and that ![]() $B$ is excellent. If the closed fiber of
$B$ is excellent. If the closed fiber of ![]() $\varphi$ is geometrically
$\varphi$ is geometrically ![]() $F$-rational, then all fibers of
$F$-rational, then all fibers of ![]() $\varphi$ are geometrically
$\varphi$ are geometrically ![]() $F$-rational.
$F$-rational.
Proof. We apply Theorem 3.4 when ![]() ${\mathscr {C}}$ is the category of excellent rings, which is stable under homomorphisms essentially of finite type by [Reference Grothendieck and DieudonnéEGAIV2, Scholie 7.8.3(ii)]. To verify the hypotheses of Theorem 3.4, it suffices to note that excellent local rings are homomorphic images of Cohen–Macaulay rings [Reference KawasakiKaw02, Corollary 1.2], and hence
${\mathscr {C}}$ is the category of excellent rings, which is stable under homomorphisms essentially of finite type by [Reference Grothendieck and DieudonnéEGAIV2, Scholie 7.8.3(ii)]. To verify the hypotheses of Theorem 3.4, it suffices to note that excellent local rings are homomorphic images of Cohen–Macaulay rings [Reference KawasakiKaw02, Corollary 1.2], and hence ![]() $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$,
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$, ![]() $({\rm R}_{{\rm V}}^{{\mathscr {C}}})$, and
$({\rm R}_{{\rm V}}^{{\mathscr {C}}})$, and ![]() $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$ hold by Table 2.
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$ hold by Table 2.
Remark 4.6 Patakfalvi, Schwede, and Zhang also obtained a version of Problem 1.2 for proper flat morphisms ![]() $f \colon Y \to X$, showing that the locus
$f \colon Y \to X$, showing that the locus ![]() $U_\mathbf {R}(f)$ defined in Definition 2.1 is open when
$U_\mathbf {R}(f)$ defined in Definition 2.1 is open when ![]() $\mathbf {R} =$ ‘Cohen–Macaulay and
$\mathbf {R} =$ ‘Cohen–Macaulay and ![]() $F$-injective’ (respectively, ‘
$F$-injective’ (respectively, ‘![]() $F$-rational’) under the assumption that
$F$-rational’) under the assumption that ![]() $X$ is an excellent integral scheme with a dualizing complex [Reference Patakfalvi, Schwede and ZhangPSZ18, Theorem 5.13]. Theorem A(ii) (respectively, Proposition 3.9(i)) implies that the locus
$X$ is an excellent integral scheme with a dualizing complex [Reference Patakfalvi, Schwede and ZhangPSZ18, Theorem 5.13]. Theorem A(ii) (respectively, Proposition 3.9(i)) implies that the locus ![]() $U_\mathbf {R}(f)$ is stable under generization, even if
$U_\mathbf {R}(f)$ is stable under generization, even if ![]() $f$ is only closed and flat (respectively,
$f$ is only closed and flat (respectively, ![]() $f$ is closed and flat,
$f$ is closed and flat, ![]() $X$ is quasi-excellent, and
$X$ is quasi-excellent, and ![]() $Y$ is excellent).
$Y$ is excellent).
For ![]() $F$-rationality, we note that Theorem A(i) does not apply, but one can apply Proposition 3.8(i) instead.
$F$-rationality, we note that Theorem A(i) does not apply, but one can apply Proposition 3.8(i) instead.
4.3 Weak normality and seminormality
In this subsection we prove that weak normality lifts from Cartier divisors. We then solve Problems 1.2 and 1.3 for both weak normality and seminormality.
To fix notation, we first define weak normality and seminormality.
Definition 4.7 (see [Reference KollárKol16, Definition 50])
Let ![]() $X$ be a noetherian scheme. A morphism
$X$ be a noetherian scheme. A morphism ![]() $g\colon X' \to X$ is a partial normalization if
$g\colon X' \to X$ is a partial normalization if ![]() $X'$ is reduced,
$X'$ is reduced, ![]() $g$ is integral, and
$g$ is integral, and ![]() $X' \to X_\mathrm {red}$ is birational. A partial normalization is a partial weak normalization if
$X' \to X_\mathrm {red}$ is birational. A partial normalization is a partial weak normalization if ![]() $g$ is a universal homeomorphism. A partial weak normalization is a partial seminormalization if the induced extensions of residue fields
$g$ is a universal homeomorphism. A partial weak normalization is a partial seminormalization if the induced extensions of residue fields
are bijective for all ![]() $x \in X$.
$x \in X$.
We say that ![]() $X$ is weakly normal (respectively, seminormal) if every finite partial weak normalization (respectively, finite partial seminormalization)
$X$ is weakly normal (respectively, seminormal) if every finite partial weak normalization (respectively, finite partial seminormalization) ![]() $g\colon X' \to X$ is an isomorphism. A noetherian ring
$g\colon X' \to X$ is an isomorphism. A noetherian ring ![]() $A$ is weakly normal (respectively, seminormal) if
$A$ is weakly normal (respectively, seminormal) if ![]() ${\rm Spec}(A)$ is weakly normal (respectively, seminormal).
${\rm Spec}(A)$ is weakly normal (respectively, seminormal).
We have the sequence of implications
where for the last implication, we use that ![]() $X_\mathrm {red} \to X$ is a finite partial seminormalization; see [Reference KollárKol16, (4.4)]. We also note that a partial normalization is a partial weak normalization if and only if the extensions (5) are purely inseparable for all
$X_\mathrm {red} \to X$ is a finite partial seminormalization; see [Reference KollárKol16, (4.4)]. We also note that a partial normalization is a partial weak normalization if and only if the extensions (5) are purely inseparable for all ![]() $x \in X$ by [Reference Grothendieck and DieudonnéEGAIV4, Corollaire 18.12.11].
$x \in X$ by [Reference Grothendieck and DieudonnéEGAIV4, Corollaire 18.12.11].
To show that weak normality lifts from Cartier divisors, we follow the proof in [Reference Bingener and FlennerBF93], with suitable modifications to avoid excellence hypotheses.
Lemma 4.8 (cf. [Reference Bingener and FlennerBF93, Proposition 4.7])
Let ![]() $(A,\mathfrak {m}_A)$ be a noetherian local ring with
$(A,\mathfrak {m}_A)$ be a noetherian local ring with ![]() ${\rm depth}(A_\mathrm {red}) \geqslant 2$, and let
${\rm depth}(A_\mathrm {red}) \geqslant 2$, and let ![]() $B$ be a module-finite
$B$ be a module-finite ![]() $A$-algebra such that
$A$-algebra such that ![]() ${\rm Spec}(B) \to {\rm Spec}(A)$ is a partial weak normalization. Set
${\rm Spec}(B) \to {\rm Spec}(A)$ is a partial weak normalization. Set ![]() $U := {\rm Spec}(A) - \{\mathfrak {m}_A\}$. Then the local hull
$U := {\rm Spec}(A) - \{\mathfrak {m}_A\}$. Then the local hull
is a module-finite local ![]() $B$-algebra with
$B$-algebra with ![]() ${\rm depth}(C) \geqslant 2$, such that
${\rm depth}(C) \geqslant 2$, such that ![]() ${\rm Spec}(C) \to {\rm Spec}(B)$ is a partial weak normalization.
${\rm Spec}(C) \to {\rm Spec}(B)$ is a partial weak normalization.
Here, ![]() $\tilde {\cdot }$ denotes the sheaf associated to a module on an affine scheme.
$\tilde {\cdot }$ denotes the sheaf associated to a module on an affine scheme.
Proof. Throughout this proof, if ![]() $R$ is a local ring, then we denote by
$R$ is a local ring, then we denote by ![]() $\mathfrak {m}_R$ and
$\mathfrak {m}_R$ and ![]() $k_R$ the maximal ideal and residue field of
$k_R$ the maximal ideal and residue field of ![]() $R$, respectively. By replacing
$R$, respectively. By replacing ![]() $A$ with its reduction
$A$ with its reduction ![]() $A_\mathrm {red}$, it suffices to consider the case when
$A_\mathrm {red}$, it suffices to consider the case when ![]() $A$ is reduced.
$A$ is reduced.
We first show that ![]() $B \to C$ is module-finite, for which it suffices to show that
$B \to C$ is module-finite, for which it suffices to show that ![]() $A \to C$ is module-finite. By Kollár's finiteness theorem [Reference KollárKol17, Theorem 2],
$A \to C$ is module-finite. By Kollár's finiteness theorem [Reference KollárKol17, Theorem 2], ![]() $(5) \Rightarrow (1)$, it suffices to show that for every
$(5) \Rightarrow (1)$, it suffices to show that for every ![]() $\mathfrak {p} \in {\rm Ass}_A(B)$, the local hull
$\mathfrak {p} \in {\rm Ass}_A(B)$, the local hull
is a finitely generated ![]() $A$-module. Since
$A$-module. Since ![]() $A$ and
$A$ and ![]() $B$ are reduced and
$B$ are reduced and ![]() ${\rm Spec}(B) \to {\rm Spec}(A)$ is a homeomorphism, we see that
${\rm Spec}(B) \to {\rm Spec}(A)$ is a homeomorphism, we see that ![]() ${\rm Ass}_A(A) = {\rm Ass}_A(B)$. Thus, applying Kollár's finiteness theorem [Reference KollárKol17, Theorem 2],
${\rm Ass}_A(A) = {\rm Ass}_A(B)$. Thus, applying Kollár's finiteness theorem [Reference KollárKol17, Theorem 2], ![]() $(1) \Rightarrow (5)$ to
$(1) \Rightarrow (5)$ to ![]() $F = \mathcal {O}_{{\rm Spec}(A)}$, it suffices to show that the local hull
$F = \mathcal {O}_{{\rm Spec}(A)}$, it suffices to show that the local hull ![]() $\Gamma (U,\tilde {A}\rvert _U)$ is a finitely generated
$\Gamma (U,\tilde {A}\rvert _U)$ is a finitely generated ![]() $A$-module. But this is automatic since the natural homomorphism
$A$-module. But this is automatic since the natural homomorphism ![]() $A \to \Gamma (U,\tilde {A}\rvert _U)$ is an isomorphism by [Reference KollárKol17, Lemma 14], using the condition
$A \to \Gamma (U,\tilde {A}\rvert _U)$ is an isomorphism by [Reference KollárKol17, Lemma 14], using the condition ![]() ${\rm depth}(A) \geqslant 2$.
${\rm depth}(A) \geqslant 2$.
We now show that ![]() ${\rm Spec}(C) \to {\rm Spec}(B)$ is a universal homeomorphism. Let
${\rm Spec}(C) \to {\rm Spec}(B)$ is a universal homeomorphism. Let ![]() $A' := A^\mathrm {sh}$ be a strict Henselization of
$A' := A^\mathrm {sh}$ be a strict Henselization of ![]() $A$, and set
$A$, and set ![]() $U' := {\rm Spec}(A') - \{\mathfrak {m}_{A'}\}$. Denoting
$U' := {\rm Spec}(A') - \{\mathfrak {m}_{A'}\}$. Denoting ![]() $B' := B \otimes _A A^\mathrm {sh}$ and
$B' := B \otimes _A A^\mathrm {sh}$ and ![]() $C' := C \otimes _A A^\mathrm {sh}$, it suffices to show that the morphism
$C' := C \otimes _A A^\mathrm {sh}$, it suffices to show that the morphism
is a universal homeomorphism by [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 2.6.4(iv)] since ![]() $A \to A'$ is faithfully flat. Setting
$A \to A'$ is faithfully flat. Setting
we see that (7) is an isomorphism over ![]() $V'$, and hence it suffices to show that there is only one prime ideal in
$V'$, and hence it suffices to show that there is only one prime ideal in ![]() $C'$ lying over
$C'$ lying over ![]() $\mathfrak {m}_{B'}$, and that the residue field extension
$\mathfrak {m}_{B'}$, and that the residue field extension ![]() $k_{B'} \to k_{C'}$ is purely inseparable [Reference Grothendieck and DieudonnéEGAIV4, Corollaire 18.12.11]. First, since
$k_{B'} \to k_{C'}$ is purely inseparable [Reference Grothendieck and DieudonnéEGAIV4, Corollaire 18.12.11]. First, since ![]() ${\rm depth}(A') \geqslant 2$ by [Reference Bruns and HerzogBH98, Proposition 1.2.16(a)], Hartshorne's connectedness theorem [Reference Grothendieck and DieudonnéEGAIV2, Théorème 5.10.7] implies that the punctured spectrum
${\rm depth}(A') \geqslant 2$ by [Reference Bruns and HerzogBH98, Proposition 1.2.16(a)], Hartshorne's connectedness theorem [Reference Grothendieck and DieudonnéEGAIV2, Théorème 5.10.7] implies that the punctured spectrum ![]() $U'$ is connected, and thus,
$U'$ is connected, and thus, ![]() $V'$ is also connected by the fact that
$V'$ is also connected by the fact that ![]() ${\rm Spec}(B') \to {\rm Spec}(A')$ is a homeomorphism. By the Henselian property of
${\rm Spec}(B') \to {\rm Spec}(A')$ is a homeomorphism. By the Henselian property of ![]() $A' = A^\mathrm {sh}$, the semi-local ring
$A' = A^\mathrm {sh}$, the semi-local ring ![]() $C'$ is a direct product of local rings [Reference Grothendieck and DieudonnéEGAIV4, Proposition 18.5.9
$C'$ is a direct product of local rings [Reference Grothendieck and DieudonnéEGAIV4, Proposition 18.5.9![]() ${\rm (ii)}$]. But the fact that
${\rm (ii)}$]. But the fact that ![]() $V'$ is connected forces there to be only one factor in this decomposition, since the morphism (7) is an isomorphism over
$V'$ is connected forces there to be only one factor in this decomposition, since the morphism (7) is an isomorphism over ![]() $V'$, and the support of
$V'$, and the support of
is the closure of the inverse image of ![]() $V'$ under (7) by [Reference KollárKol17, Definition 1,
$V'$ under (7) by [Reference KollárKol17, Definition 1, ![]() $(3')$]. Thus,
$(3')$]. Thus, ![]() $C'$ is a local ring, and there is therefore only one prime ideal in
$C'$ is a local ring, and there is therefore only one prime ideal in ![]() $C'$ lying over
$C'$ lying over ![]() $\mathfrak {m}_{B'}$. Note that the isomorphism (8) follows from flat base change for local hulls [Reference KollárKol17, (13)] since the preimage of
$\mathfrak {m}_{B'}$. Note that the isomorphism (8) follows from flat base change for local hulls [Reference KollárKol17, (13)] since the preimage of ![]() $\{\mathfrak {m}_B\}$ in
$\{\mathfrak {m}_B\}$ in ![]() ${\rm Spec}(B')$ is
${\rm Spec}(B')$ is ![]() $\{\mathfrak {m}_{B'}\}$. Finally, since
$\{\mathfrak {m}_{B'}\}$. Finally, since ![]() $k_{A'}$ is separably closed, the residue field extension
$k_{A'}$ is separably closed, the residue field extension ![]() $k_{B'} \to k_{C'}$ is purely inseparable, and hence (7) is a universal homeomorphism.
$k_{B'} \to k_{C'}$ is purely inseparable, and hence (7) is a universal homeomorphism.
We now note that
where the first equality is [Reference Grothendieck and DieudonnéEGAIV1, Chapitre 0, Proposition 16.4.8], and the second inequality follows from [Reference KollárKol17, Lemma 14] since ![]() $C$ is module-finite over
$C$ is module-finite over ![]() $A$. Moreover, the morphism
$A$. Moreover, the morphism ![]() ${\rm Spec}(C) \to {\rm Spec}(B)$ is birational since it induces an isomorphism between
${\rm Spec}(C) \to {\rm Spec}(B)$ is birational since it induces an isomorphism between ![]() ${\rm Spec}(B) - \{\mathfrak {m}_B\}$ and
${\rm Spec}(B) - \{\mathfrak {m}_B\}$ and ![]() ${\rm Spec}(C) - \{\mathfrak {m}_C\}$, which are dense in
${\rm Spec}(C) - \{\mathfrak {m}_C\}$, which are dense in ![]() ${\rm Spec}(B)$ and
${\rm Spec}(B)$ and ![]() ${\rm Spec}(C)$, respectively. It remains to show that
${\rm Spec}(C)$, respectively. It remains to show that ![]() $C$ is reduced. Since
$C$ is reduced. Since ![]() ${\rm Spec}(C) \to {\rm Spec}(B)$ is birational, we see that
${\rm Spec}(C) \to {\rm Spec}(B)$ is birational, we see that ![]() $C$ satisfies
$C$ satisfies ![]() $(R_0)$, and satisfies
$(R_0)$, and satisfies ![]() $(S_1)$ everywhere except possibly at
$(S_1)$ everywhere except possibly at ![]() $\mathfrak {m}_C$. But (9) implies
$\mathfrak {m}_C$. But (9) implies
Thus, ![]() $C$ satisfies
$C$ satisfies ![]() $(S_1)$ at
$(S_1)$ at ![]() $\mathfrak {m}_C$, and
$\mathfrak {m}_C$, and ![]() $C$ is therefore reduced.
$C$ is therefore reduced.
The following result allows us to restrict a partial weak normalization to a reduced Cartier divisor.
Lemma 4.9 (cf. [Reference Bingener and FlennerBF93, Proposition 4.8])
Let ![]() $(A,\mathfrak {m}_A)$ be a noetherian local ring, and let
$(A,\mathfrak {m}_A)$ be a noetherian local ring, and let ![]() $t \in \mathfrak {m}$ be a nonzerodivisor such that
$t \in \mathfrak {m}$ be a nonzerodivisor such that ![]() $A/tA$ is reduced of dimension
$A/tA$ is reduced of dimension ![]() $\geqslant 1$. Let
$\geqslant 1$. Let ![]() $B$ be a module-finite
$B$ be a module-finite ![]() $A$-algebra such that
$A$-algebra such that ![]() ${\rm Spec}(B) \to {\rm Spec}(A)$ is a partial weak normalization that is an isomorphism along
${\rm Spec}(B) \to {\rm Spec}(A)$ is a partial weak normalization that is an isomorphism along ![]() $V(t) - \{\mathfrak {m}_A\}$. Then the local hull
$V(t) - \{\mathfrak {m}_A\}$. Then the local hull
is a module-finite local ![]() $B$-algebra such that the composition
$B$-algebra such that the composition
is a partial weak normalization.
Proof. Throughout this proof, if ![]() $R$ is a local ring, then we denote by
$R$ is a local ring, then we denote by ![]() $\mathfrak {m}_R$ the maximal ideal of
$\mathfrak {m}_R$ the maximal ideal of ![]() $R$. We note that
$R$. We note that ![]() $A$ is reduced since reducedness lifts from Cartier divisors [Reference Grothendieck and DieudonnéEGAIV2, Proposition 3.4.6].
$A$ is reduced since reducedness lifts from Cartier divisors [Reference Grothendieck and DieudonnéEGAIV2, Proposition 3.4.6].
Set ![]() $\bar {A} := A/tA$ and
$\bar {A} := A/tA$ and ![]() $\bar {C} := C/tC$. We have
$\bar {C} := C/tC$. We have
since ![]() $A/tA$ satisfies
$A/tA$ satisfies ![]() $(S_1)$ [Reference Grothendieck and DieudonnéEGAIV2, Proposition 5.8.5]. Thus, we have
$(S_1)$ [Reference Grothendieck and DieudonnéEGAIV2, Proposition 5.8.5]. Thus, we have ![]() ${\rm depth}(A) \geqslant 2$ by [Reference Bruns and HerzogBH98, Proposition 1.2.10(d)], and hence
${\rm depth}(A) \geqslant 2$ by [Reference Bruns and HerzogBH98, Proposition 1.2.10(d)], and hence ![]() ${\rm Spec}(C) \to {\rm Spec}(B)$ is a partial weak normalization by Lemma 4.8. Since
${\rm Spec}(C) \to {\rm Spec}(B)$ is a partial weak normalization by Lemma 4.8. Since ![]() $g \circ h$ is an integral universal homeomorphism by base change, to show that
$g \circ h$ is an integral universal homeomorphism by base change, to show that ![]() $g \circ h$ is a partial weak normalization, it suffices to show that
$g \circ h$ is a partial weak normalization, it suffices to show that ![]() $g \circ h$ is birational and that
$g \circ h$ is birational and that ![]() $\bar {C}$ is reduced.
$\bar {C}$ is reduced.
We start by showing that ![]() $g \circ h$ is birational. Since
$g \circ h$ is birational. Since ![]() $g \circ h$ is a universal homeomorphism and
$g \circ h$ is a universal homeomorphism and ![]() $\bar {A}$ is reduced, to show that
$\bar {A}$ is reduced, to show that ![]() $g \circ h$ is birational, it suffices to show that
$g \circ h$ is birational, it suffices to show that ![]() $\bar {A} \to \bar {C}$ localizes to an isomorphism
$\bar {A} \to \bar {C}$ localizes to an isomorphism ![]() $\bar {A}_{\bar {\mathfrak {p}}} \overset {\sim }{\to } \bar {C}_{\bar {\mathfrak {p}}}$ at every minimal prime
$\bar {A}_{\bar {\mathfrak {p}}} \overset {\sim }{\to } \bar {C}_{\bar {\mathfrak {p}}}$ at every minimal prime ![]() $\bar {\mathfrak {p}} \subseteq \bar {A}$. Let
$\bar {\mathfrak {p}} \subseteq \bar {A}$. Let ![]() $\mathfrak {p} \subseteq A$ be the prime in
$\mathfrak {p} \subseteq A$ be the prime in ![]() $A$ corresponding to such a minimal prime
$A$ corresponding to such a minimal prime ![]() $\bar {\mathfrak {p}}$. Since regularity lifts from Cartier divisors [Reference Grothendieck and DieudonnéEGAIV1, Chapitre 0, Corollaire 17.1.8] and
$\bar {\mathfrak {p}}$. Since regularity lifts from Cartier divisors [Reference Grothendieck and DieudonnéEGAIV1, Chapitre 0, Corollaire 17.1.8] and ![]() $\bar {A}$ is reduced, we see that
$\bar {A}$ is reduced, we see that ![]() $A_\mathfrak {p}$ is regular, in which case the homomorphism
$A_\mathfrak {p}$ is regular, in which case the homomorphism ![]() $A \to C$ induces an isomorphism
$A \to C$ induces an isomorphism ![]() $A_\mathfrak {p} \overset {\sim }{\to } C_\mathfrak {p}$ by the fact that regular rings are weakly normal; see (6). Thus,
$A_\mathfrak {p} \overset {\sim }{\to } C_\mathfrak {p}$ by the fact that regular rings are weakly normal; see (6). Thus, ![]() $g \circ h$ is birational.
$g \circ h$ is birational.
We now show that ![]() $\bar {C}$ is reduced. By our assumption that
$\bar {C}$ is reduced. By our assumption that ![]() ${\rm Spec}(B) \to {\rm Spec}(A)$ is an isomorphism along
${\rm Spec}(B) \to {\rm Spec}(A)$ is an isomorphism along ![]() $V(t) - \{\mathfrak {m}_A\}$, we know that
$V(t) - \{\mathfrak {m}_A\}$, we know that ![]() ${\rm Spec}(C) \to {\rm Spec}(B) \to {\rm Spec}(A)$ is an isomorphism along
${\rm Spec}(C) \to {\rm Spec}(B) \to {\rm Spec}(A)$ is an isomorphism along ![]() $V(t) - \{\mathfrak {m}_A\}$ by [Reference KollárKol17, Definition 1,
$V(t) - \{\mathfrak {m}_A\}$ by [Reference KollárKol17, Definition 1, ![]() $(4')$]. Since
$(4')$]. Since ![]() $\bar {A}$ is reduced and
$\bar {A}$ is reduced and ![]() $g \circ h$ is birational, we see that
$g \circ h$ is birational, we see that ![]() $\bar {A} \to \bar {C}$ is injective by [Reference Grothendieck and DieudonnéEGAInew, Corollaire 1.2.6]. Thus, the homomorphism
$\bar {A} \to \bar {C}$ is injective by [Reference Grothendieck and DieudonnéEGAInew, Corollaire 1.2.6]. Thus, the homomorphism ![]() $\bar {A} \to \bar {C}$ restricts to an isomorphism
$\bar {A} \to \bar {C}$ restricts to an isomorphism
over ![]() $\bar {U} := {\rm Spec}(\bar {A}) - \{\mathfrak {m}_{\bar {A}}\}$. Since
$\bar {U} := {\rm Spec}(\bar {A}) - \{\mathfrak {m}_{\bar {A}}\}$. Since ![]() $\bar {A}$ is reduced, this shows that
$\bar {A}$ is reduced, this shows that ![]() $\bar {C}$ satisfies
$\bar {C}$ satisfies ![]() $(R_0)$, and satisfies
$(R_0)$, and satisfies ![]() $(S_1)$ everywhere except possibly at
$(S_1)$ everywhere except possibly at ![]() $\mathfrak {m}_{\bar {C}}$. It suffices to show
$\mathfrak {m}_{\bar {C}}$. It suffices to show ![]() ${\rm depth}(\bar {C}) \geqslant 1$, since this would imply
${\rm depth}(\bar {C}) \geqslant 1$, since this would imply
by the assumption that ![]() $\dim (\bar {A}) = \dim (\bar {C}) \geqslant 1$. Note that
$\dim (\bar {A}) = \dim (\bar {C}) \geqslant 1$. Note that ![]() ${\rm depth}(C) \geqslant 2$ by Lemma 4.8, and hence it suffices to show that
${\rm depth}(C) \geqslant 2$ by Lemma 4.8, and hence it suffices to show that ![]() $t$ is a nonzerodivisor on
$t$ is a nonzerodivisor on ![]() $C$ by [Reference Bruns and HerzogBH98, Proposition 1.2.10(d)]. Consider the commutative diagram
$C$ by [Reference Bruns and HerzogBH98, Proposition 1.2.10(d)]. Consider the commutative diagram

where the isomorphism of total rings of fractions on the bottom holds by the birationality of ![]() $g \circ h$ and the two vertical homomorphisms are injective since
$g \circ h$ and the two vertical homomorphisms are injective since ![]() $A$ and
$A$ and ![]() $C$ are reduced. Since
$C$ are reduced. Since ![]() $A \to {\rm Frac}(A)$ is flat, it maps
$A \to {\rm Frac}(A)$ is flat, it maps ![]() $t$ to a nonzerodivisor on
$t$ to a nonzerodivisor on ![]() ${\rm Frac}(A)$. By the commutativity of the diagram,
${\rm Frac}(A)$. By the commutativity of the diagram, ![]() $t$ is therefore a nonzerodivisor on
$t$ is therefore a nonzerodivisor on ![]() $C$.
$C$.
We can now show that weak normality satisfies ![]() $({\text {R}_{\text {IV}}})$. This statement is due to Bingener and Flenner in the excellent case [Reference Bingener and FlennerBF93].
$({\text {R}_{\text {IV}}})$. This statement is due to Bingener and Flenner in the excellent case [Reference Bingener and FlennerBF93].
Proposition 4.10 (cf. [Reference Bingener and FlennerBF93, Corollary 4.1])
Let ![]() $(A,\mathfrak {m})$ be a noetherian local ring, and let
$(A,\mathfrak {m})$ be a noetherian local ring, and let ![]() $t \in \mathfrak {m}$ be a nonzerodivisor. If
$t \in \mathfrak {m}$ be a nonzerodivisor. If ![]() $A/tA$ is weakly normal, then
$A/tA$ is weakly normal, then ![]() $A$ is weakly normal.
$A$ is weakly normal.
Proof. We want to show that, for every module-finite ![]() $A$-algebra
$A$-algebra ![]() $B$ such that
$B$ such that ![]() ${\rm Spec}(B) \to {\rm Spec}(A)$ is a partial weak normalization, the homomorphism
${\rm Spec}(B) \to {\rm Spec}(A)$ is a partial weak normalization, the homomorphism ![]() $A \to B$ is an isomorphism. We will show that
$A \to B$ is an isomorphism. We will show that ![]() $A_\mathfrak {p} \to B_\mathfrak {p}$ is an isomorphism for every prime ideal
$A_\mathfrak {p} \to B_\mathfrak {p}$ is an isomorphism for every prime ideal ![]() $\mathfrak {p} \subseteq A$ containing
$\mathfrak {p} \subseteq A$ containing ![]() $t$, which would suffice since
$t$, which would suffice since ![]() $\mathfrak {m}$ is a prime ideal containing
$\mathfrak {m}$ is a prime ideal containing ![]() $t$.
$t$.
Set ![]() $\bar {A} := A/tA$ and
$\bar {A} := A/tA$ and ![]() $\bar {B} := B/tB$. We induce on the height of
$\bar {B} := B/tB$. We induce on the height of ![]() $\bar {\mathfrak {p}} := \mathfrak {p}\bar {A}$. If
$\bar {\mathfrak {p}} := \mathfrak {p}\bar {A}$. If ![]() ${\rm ht}(\bar {\mathfrak {p}}) = 0$, then
${\rm ht}(\bar {\mathfrak {p}}) = 0$, then ![]() $\bar {A}_{\bar {\mathfrak {p}}} \simeq A_\mathfrak {p}/tA_\mathfrak {p}$ is regular since
$\bar {A}_{\bar {\mathfrak {p}}} \simeq A_\mathfrak {p}/tA_\mathfrak {p}$ is regular since ![]() $\bar {A}$ is reduced by (6), and hence
$\bar {A}$ is reduced by (6), and hence ![]() $A_\mathfrak {p}$ is regular since regularity lifts from Cartier divisors [Reference Grothendieck and DieudonnéEGAIV1, Chapitre 0, Corollaire 17.1.8]. Thus,
$A_\mathfrak {p}$ is regular since regularity lifts from Cartier divisors [Reference Grothendieck and DieudonnéEGAIV1, Chapitre 0, Corollaire 17.1.8]. Thus, ![]() $A_\mathfrak {p}$ is weakly normal by (6), and
$A_\mathfrak {p}$ is weakly normal by (6), and ![]() $A_\mathfrak {p} \to B_\mathfrak {p}$ is an isomorphism.
$A_\mathfrak {p} \to B_\mathfrak {p}$ is an isomorphism.
Now suppose that ![]() ${\rm ht}(\bar {\mathfrak {p}}) > 0$. By the inductive hypothesis, we know that
${\rm ht}(\bar {\mathfrak {p}}) > 0$. By the inductive hypothesis, we know that ![]() $A_\mathfrak {p} \to B_\mathfrak {p}$ is an isomorphism along
$A_\mathfrak {p} \to B_\mathfrak {p}$ is an isomorphism along ![]() $V(t) - \{\mathfrak {p} A_\mathfrak {p}\} \subseteq {\rm Spec}(A_\mathfrak {p})$. Applying Lemmas 4.8 and 4.9 on
$V(t) - \{\mathfrak {p} A_\mathfrak {p}\} \subseteq {\rm Spec}(A_\mathfrak {p})$. Applying Lemmas 4.8 and 4.9 on ![]() $A_\mathfrak {p}$, the local hull
$A_\mathfrak {p}$, the local hull
is module-finite over ![]() $A$ and yields a partial weak normalization
$A$ and yields a partial weak normalization ![]() ${\rm Spec}(C) \to {\rm Spec}(B)$ such that the composition
${\rm Spec}(C) \to {\rm Spec}(B)$ such that the composition
is a partial weak normalization. Since ![]() $\bar {A}_{\bar {\mathfrak {p}}} \simeq A_\mathfrak {p}/tA_\mathfrak {p}$ is weakly normal by [Reference ManaresiMan80, Corollary IV.2], we see that this composition is an isomorphism. The Nakayama–Azumaya–Krull lemma [Reference MatsumuraMat89, Theorem 2.2] then implies that
$\bar {A}_{\bar {\mathfrak {p}}} \simeq A_\mathfrak {p}/tA_\mathfrak {p}$ is weakly normal by [Reference ManaresiMan80, Corollary IV.2], we see that this composition is an isomorphism. The Nakayama–Azumaya–Krull lemma [Reference MatsumuraMat89, Theorem 2.2] then implies that ![]() $A_\mathfrak {p} \to C$ is an isomorphism. Since
$A_\mathfrak {p} \to C$ is an isomorphism. Since ![]() $B_\mathfrak {p} \to C$ is injective by [Reference Grothendieck and DieudonnéEGAInew, Corollaire 1.2.6], we see that
$B_\mathfrak {p} \to C$ is injective by [Reference Grothendieck and DieudonnéEGAInew, Corollaire 1.2.6], we see that ![]() $B_\mathfrak {p} \to C$ is an isomorphism as well, and hence
$B_\mathfrak {p} \to C$ is an isomorphism as well, and hence ![]() $A_\mathfrak {p} \to B_\mathfrak {p}$ is also an isomorphism.
$A_\mathfrak {p} \to B_\mathfrak {p}$ is also an isomorphism.
Since we have seen that both weak normality and seminormality satisfy the hypotheses in Theorems B and C (see Table 2 and (6)), we can solve Problems 1.2 and 1.3 for both weak normality and seminormality. The proof of Problem 1.2 for seminormality extends a result of Shimomoto [Reference ShimomotoShi17] in the finite type case.
Corollary 4.11 (cf. [Reference ShimomotoShi17, Corollary 3.4])
Grothendieck's localization problem and the local lifting problem hold for weak normality and seminormality.
4.4 Terminal, canonical, and rational singularities
We now consider Problem 1.2 for terminal, canonical, and rational singularities in equal characteristic zero, using the version of Theorem B in [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8].
See [Reference KollárKol13, Definition 2.8] for the definition of terminal and canonical singularities, which apply to excellent noetherian schemes with dualizing complexes. For rational singularities, we will work with the following definition.
Definition 4.12 [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, p. 51; Reference MurayamaMur21, Definition 7.2]
Let ![]() $A$ be a quasi-excellent local
$A$ be a quasi-excellent local ![]() $\mathbf {Q}$-algebra. We say that
$\mathbf {Q}$-algebra. We say that ![]() $A$ has rational singularities if
$A$ has rational singularities if ![]() $A$ is normal and if, for every resolution of singularities
$A$ is normal and if, for every resolution of singularities ![]() $f\colon W \to {\rm Spec}(A)$, we have
$f\colon W \to {\rm Spec}(A)$, we have ![]() $R^if_*\mathcal {O}_W = 0$ for all
$R^if_*\mathcal {O}_W = 0$ for all ![]() $i > 0$. If
$i > 0$. If ![]() $X$ is a locally noetherian
$X$ is a locally noetherian ![]() $\mathbf {Q}$-scheme whose local rings
$\mathbf {Q}$-scheme whose local rings ![]() $\mathcal {O}_{X,x}$ are quasi-excellent, we say that
$\mathcal {O}_{X,x}$ are quasi-excellent, we say that ![]() $X$ has rational singularities if
$X$ has rational singularities if ![]() $\mathcal {O}_{X,x}$ has rational singularities for every
$\mathcal {O}_{X,x}$ has rational singularities for every ![]() $x \in X$. By [Reference MurayamaMur21, Lemma 7.3], a quasi-excellent local
$x \in X$. By [Reference MurayamaMur21, Lemma 7.3], a quasi-excellent local ![]() $\mathbf {Q}$-algebra R has rational singularities if and only if
$\mathbf {Q}$-algebra R has rational singularities if and only if ![]() ${\rm Spec}(R)$ has rational singularities.
${\rm Spec}(R)$ has rational singularities.
Remark 4.13 (cf. [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, p. 51; Reference KollárKol13, Corollary 2.86)]
The object ![]() $\mathbf {R} f_*\mathcal {O}_W$ does not depend on the choice of resolution
$\mathbf {R} f_*\mathcal {O}_W$ does not depend on the choice of resolution ![]() $f\colon W \to {\rm Spec}(A)$, since higher direct images of structure sheaves vanish for morphisms of noetherian schemes of finite type over a quasi-excellent local
$f\colon W \to {\rm Spec}(A)$, since higher direct images of structure sheaves vanish for morphisms of noetherian schemes of finite type over a quasi-excellent local ![]() $\mathbf {Q}$-algebra (one combines the strategy of [Reference HironakaHir64, (2) on pp. 144–145] with the version of elimination of indeterminacies in [Reference HironakaHir64, Chapter I, § 3, Main Theorem II(N)]). Thus, to show that a quasi-excellent local
$\mathbf {Q}$-algebra (one combines the strategy of [Reference HironakaHir64, (2) on pp. 144–145] with the version of elimination of indeterminacies in [Reference HironakaHir64, Chapter I, § 3, Main Theorem II(N)]). Thus, to show that a quasi-excellent local ![]() $\mathbf {Q}$-algebra has rational singularities, it suffices to show that
$\mathbf {Q}$-algebra has rational singularities, it suffices to show that ![]() $A$ is normal and that there exists a resolution of singularities
$A$ is normal and that there exists a resolution of singularities ![]() $f\colon W \to {\rm Spec}(A)$ such that
$f\colon W \to {\rm Spec}(A)$ such that ![]() $R^if_*\mathcal {O}_W = 0$ for all
$R^if_*\mathcal {O}_W = 0$ for all ![]() $i > 0$.
$i > 0$.
In particular, this shows that if ![]() $X$ is a quasi-excellent
$X$ is a quasi-excellent ![]() $\mathbf {Q}$-scheme of finite Krull dimension, then the rational locus is open in
$\mathbf {Q}$-scheme of finite Krull dimension, then the rational locus is open in ![]() $X$: since resolutions of singularities exist in this context [Reference TemkinTem08, Theorem 1.1], the rational locus is the normal locus intersected with the complement of
$X$: since resolutions of singularities exist in this context [Reference TemkinTem08, Theorem 1.1], the rational locus is the normal locus intersected with the complement of ![]() $\bigcup _{i>0} {\rm Supp}(R^if_*\mathcal {O}_W)$, where
$\bigcup _{i>0} {\rm Supp}(R^if_*\mathcal {O}_W)$, where ![]() $f\colon W \to X$ is a resolution of singularities.
$f\colon W \to X$ is a resolution of singularities.
We now show the following strong version of ![]() $({\text {P}_{\text {IV}}})$.
$({\text {P}_{\text {IV}}})$.
Lemma 4.14 Let ![]() $R$ be a quasi-excellent local
$R$ be a quasi-excellent local ![]() $\mathbf {Q}$-algebra, and let
$\mathbf {Q}$-algebra, and let ![]() $k \to R$ be a homomorphism from a field of characteristic zero.
$k \to R$ be a homomorphism from a field of characteristic zero.
(i) If
 $R$ has a dualizing complex, then
$R$ has a dualizing complex, then  ${\rm Spec}(R)$ has terminal (respectively, canonical) singularities if and only if
${\rm Spec}(R)$ has terminal (respectively, canonical) singularities if and only if  ${\rm Spec}(R \otimes _k k')$ has terminal (respectively, canonical) singularities for every finitely generated field extension
${\rm Spec}(R \otimes _k k')$ has terminal (respectively, canonical) singularities for every finitely generated field extension  $k \subseteq k'$.
$k \subseteq k'$.(ii)
 ${\rm Spec}(R)$ has rational singularities if and only if
${\rm Spec}(R)$ has rational singularities if and only if  ${\rm Spec}(R \otimes _k k')$ has rational singularities for every finitely generated field extension
${\rm Spec}(R \otimes _k k')$ has rational singularities for every finitely generated field extension  $k \subseteq k'$.
$k \subseteq k'$.
Proof. ![]() $\Leftarrow$ holds by setting
$\Leftarrow$ holds by setting ![]() $k = k'$. It therefore suffices to show the converse. The terminal and canonical cases follow from [Reference KollárKol13, Proposition 2.15], since
$k = k'$. It therefore suffices to show the converse. The terminal and canonical cases follow from [Reference KollárKol13, Proposition 2.15], since ![]() $R \to R \otimes _k k'$ is surjective and essentially smooth by base change [Reference Grothendieck and DieudonnéEGAIV2, Proposition 6.8.3(iii); Reference Grothendieck and DieudonnéEGAIV4, Théorème 17.5.1]. Here, we note that
$R \to R \otimes _k k'$ is surjective and essentially smooth by base change [Reference Grothendieck and DieudonnéEGAIV2, Proposition 6.8.3(iii); Reference Grothendieck and DieudonnéEGAIV4, Théorème 17.5.1]. Here, we note that ![]() $R \otimes _k k'$ has a dualizing complex by [Reference HartshorneHar66, (2) on p. 299]. For the rational case, we use the criterion for rational singularities stated in Remark 4.13. Let
$R \otimes _k k'$ has a dualizing complex by [Reference HartshorneHar66, (2) on p. 299]. For the rational case, we use the criterion for rational singularities stated in Remark 4.13. Let ![]() $f\colon W \to {\rm Spec}(R)$ be a resolution of singularities. Since
$f\colon W \to {\rm Spec}(R)$ be a resolution of singularities. Since ![]() $R \to R \otimes _k k'$ is flat with geometrically regular fibers, the morphism
$R \to R \otimes _k k'$ is flat with geometrically regular fibers, the morphism ![]() $f'\colon W \otimes _k k' \to {\rm Spec}(R \otimes k')$ is a resolution of singularities [Reference MatsumuraMat89, Theorem 23.7] and satisfies
$f'\colon W \otimes _k k' \to {\rm Spec}(R \otimes k')$ is a resolution of singularities [Reference MatsumuraMat89, Theorem 23.7] and satisfies ![]() $R^if'_*\mathcal {O}_{W \otimes _k k'} = 0$ for all
$R^if'_*\mathcal {O}_{W \otimes _k k'} = 0$ for all ![]() $i > 0$ by flat base change. Finally,
$i > 0$ by flat base change. Finally, ![]() $R \otimes _k k'$ is normal by [Reference MatsumuraMat89, Corollary to Theorem 23.9].
$R \otimes _k k'$ is normal by [Reference MatsumuraMat89, Corollary to Theorem 23.9].
The main ingredient for terminal and canonical singularities is the following version of ![]() $({\text {R}_{\text {IV}}})$, which follows from the deformation results for complex varieties due to Kawamata [Reference KawamataKaw99] for canonical singularities and Nakayama [Reference NakayamaNak04] for terminal singularities. Note that similar results do not hold for Kawamata log terminal or log canonical singularities without assuming that the canonical divisor on
$({\text {R}_{\text {IV}}})$, which follows from the deformation results for complex varieties due to Kawamata [Reference KawamataKaw99] for canonical singularities and Nakayama [Reference NakayamaNak04] for terminal singularities. Note that similar results do not hold for Kawamata log terminal or log canonical singularities without assuming that the canonical divisor on ![]() $A$ is
$A$ is ![]() $\mathbf {Q}$-Cartier; see [Reference IshiiIsh18, Example 9.1.7 and Remark 9.1.15].
$\mathbf {Q}$-Cartier; see [Reference IshiiIsh18, Example 9.1.7 and Remark 9.1.15].
Proposition 4.15 (cf. [Reference KawamataKaw99, Main Theorem; Reference NakayamaNak04, Chapter VI, Theorem 5.2(2)])
Let ![]() ${(A, \mathfrak {m})}$ be a local ring essentially of finite type over a field
${(A, \mathfrak {m})}$ be a local ring essentially of finite type over a field ![]() $k$ of characteristic zero, and let
$k$ of characteristic zero, and let ![]() $t \in \mathfrak {m}$ be a nonzerodivisor. If
$t \in \mathfrak {m}$ be a nonzerodivisor. If ![]() $A/tA$ has terminal (respectively, canonical) singularities, then
$A/tA$ has terminal (respectively, canonical) singularities, then ![]() $A$ has terminal (respectively, canonical) singularities.
$A$ has terminal (respectively, canonical) singularities.
Proof. Note that ![]() $A$ is a normal domain by [Reference SeydiSey72, Proposition I.7.4] and [Reference Grothendieck and DieudonnéEGAIV2, Proposition 3.4.5].
$A$ is a normal domain by [Reference SeydiSey72, Proposition I.7.4] and [Reference Grothendieck and DieudonnéEGAIV2, Proposition 3.4.5].
Step 1 It suffices to show that if ![]() $A'$ is a normal domain of finite type over
$A'$ is a normal domain of finite type over ![]() $k$, and
$k$, and ![]() $t' \in A'$ is a non-zero element such that
$t' \in A'$ is a non-zero element such that ![]() $A'/t'$ has terminal (respectively, canonical) singularities, then
$A'/t'$ has terminal (respectively, canonical) singularities, then ![]() $A'$ has terminal (respectively, canonical) singularities along
$A'$ has terminal (respectively, canonical) singularities along ![]() $V(t')$.
$V(t')$.
Since ![]() $A$ is essentially of finite type over
$A$ is essentially of finite type over ![]() $k$, there exist a ring
$k$, there exist a ring ![]() $A'$ of finite type over
$A'$ of finite type over ![]() $k$, a prime ideal
$k$, a prime ideal ![]() $\mathfrak {p} \subseteq A'$ such that
$\mathfrak {p} \subseteq A'$ such that ![]() $A = A'_\mathfrak {p}$, and an element
$A = A'_\mathfrak {p}$, and an element ![]() $t' \in A'$ such that
$t' \in A'$ such that ![]() $t'$ maps to
$t'$ maps to ![]() $t \in A$. Since the normal locus in
$t \in A$. Since the normal locus in ![]() ${\rm Spec}(A')$ is open [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 6.13.5], we can replace
${\rm Spec}(A')$ is open [Reference Grothendieck and DieudonnéEGAIV2, Corollaire 6.13.5], we can replace ![]() ${\rm Spec}(A')$ by an affine open subset containing
${\rm Spec}(A')$ by an affine open subset containing ![]() $\mathfrak {p}$ to assume that
$\mathfrak {p}$ to assume that ![]() $A'$ is normal domain and that
$A'$ is normal domain and that ![]() $t'$ is non-zero. Since the locus over which
$t'$ is non-zero. Since the locus over which ![]() ${\rm Spec}(A'/t')$ has terminal (respectively, canonical) singularities is open by [Reference KollárKol13, Corollary 2.12], we can replace
${\rm Spec}(A'/t')$ has terminal (respectively, canonical) singularities is open by [Reference KollárKol13, Corollary 2.12], we can replace ![]() $A'$ by an affine open subset again to assume that
$A'$ by an affine open subset again to assume that ![]() $A'/t'$ has terminal (respectively, canonical) singularities. Then
$A'/t'$ has terminal (respectively, canonical) singularities. Then ![]() $A'$ has terminal (respectively, canonical) singularities by assumption, and hence
$A'$ has terminal (respectively, canonical) singularities by assumption, and hence ![]() $A'_\mathfrak {p}$ has terminal (respectively, canonical) singularities by [Reference KollárKol13, Corollary 2.12].
$A'_\mathfrak {p}$ has terminal (respectively, canonical) singularities by [Reference KollárKol13, Corollary 2.12].
Step 2 It suffices to show that the statement in Step 1 holds when ![]() $k = \mathbf {C}$.
$k = \mathbf {C}$.
Since ![]() $A$ is of finite type over
$A$ is of finite type over ![]() $k$, there exists a subfield
$k$, there exists a subfield ![]() $k_0 \subseteq k$ that is a finitely generated field extension of
$k_0 \subseteq k$ that is a finitely generated field extension of ![]() $\mathbf {Q}$ together with a ring
$\mathbf {Q}$ together with a ring ![]() $A_0$ of finite type over
$A_0$ of finite type over ![]() $k_0$ such that
$k_0$ such that ![]() $A \simeq A_0 \otimes _{k_0} k$, and such that there exists an element
$A \simeq A_0 \otimes _{k_0} k$, and such that there exists an element ![]() $t_0 \in A_0$ mapping to
$t_0 \in A_0$ mapping to ![]() $t \in A$ under the homomorphism
$t \in A$ under the homomorphism ![]() $A_0 \to A$. Note that
$A_0 \to A$. Note that ![]() $A_0$ is a normal domain by [Reference MatsumuraMat89, Corollary to Theorem 23.9] and [Reference Grothendieck and DieudonnéEGAIV2, Proposition 2.1.14]. Since
$A_0$ is a normal domain by [Reference MatsumuraMat89, Corollary to Theorem 23.9] and [Reference Grothendieck and DieudonnéEGAIV2, Proposition 2.1.14]. Since ![]() $A_0/t_0A_0 \otimes _{k_0} k \simeq A/tA$, applying Lemma 4.14, we know that
$A_0/t_0A_0 \otimes _{k_0} k \simeq A/tA$, applying Lemma 4.14, we know that ![]() $A_0/t_0A_0 \otimes _{k_0} \mathbf {C}$ has terminal (respectively, canonical) singularities, and, moreover, that
$A_0/t_0A_0 \otimes _{k_0} \mathbf {C}$ has terminal (respectively, canonical) singularities, and, moreover, that ![]() $A$ has terminal (respectively, canonical) singularities if
$A$ has terminal (respectively, canonical) singularities if ![]() $A_0 \otimes _{k_0} \mathbf {C}$ does. Note that the image of
$A_0 \otimes _{k_0} \mathbf {C}$ does. Note that the image of ![]() $t_0$ in
$t_0$ in ![]() $A_0 \otimes _{k_0} \mathbf {C}$ is a nonzerodivisor by flat base change, and that
$A_0 \otimes _{k_0} \mathbf {C}$ is a nonzerodivisor by flat base change, and that ![]() $A_0 \otimes _{k_0} \mathbf {C}$ is normal by [Reference MatsumuraMat89, Corollary to Theorem 23.9]. Working one direct factor of
$A_0 \otimes _{k_0} \mathbf {C}$ is normal by [Reference MatsumuraMat89, Corollary to Theorem 23.9]. Working one direct factor of ![]() $A_0 \otimes _{k_0} \mathbf {C}$ at a time, the statement in Step 1 for
$A_0 \otimes _{k_0} \mathbf {C}$ at a time, the statement in Step 1 for ![]() $k = \mathbf {C}$ implies that
$k = \mathbf {C}$ implies that ![]() $A_0 \otimes _{k_0} \mathbf {C}$ has terminal (respectively, canonical) singularities.
$A_0 \otimes _{k_0} \mathbf {C}$ has terminal (respectively, canonical) singularities.
Step 3 The statement in Step 1 holds for ![]() $k = \mathbf {C}$.
$k = \mathbf {C}$.
The terminal case is [Reference NakayamaNak04, Chapter VI, Theorem 5.2(2)] and the canonical case is [Reference KawamataKaw99, Main Theorem] (see also [Reference NakayamaNak04, Chapter VI, Theorem 5.2(1)]).
For rational singularities, we prove ![]() $({\text {R}_{\text {IV}}})$ in greater generality. For the proof, we will work with the notion of pseudo-rational rings defined below, which gives a characteristic-free version of rational singularities.
$({\text {R}_{\text {IV}}})$ in greater generality. For the proof, we will work with the notion of pseudo-rational rings defined below, which gives a characteristic-free version of rational singularities.
Definition 4.16 [Reference Lipman and TeissierLT81, § 2]
Let ![]() $(A,\mathfrak {m})$ be a noetherian local ring of dimension
$(A,\mathfrak {m})$ be a noetherian local ring of dimension ![]() $d$. We say that
$d$. We say that ![]() $A$ is pseudo-rational if:
$A$ is pseudo-rational if:
(i)
 $A$ is normal;
$A$ is normal;(ii)
 $A$ is Cohen–Macaulay;
$A$ is Cohen–Macaulay;(iii) the
 $\mathfrak {m}$-adic completion
$\mathfrak {m}$-adic completion  $\hat {A}$ of
$\hat {A}$ of  $A$ is reduced; and
$A$ is reduced; and(iv) for every proper birational morphism
 $f\colon W \to {\rm Spec}(A)$ with
$f\colon W \to {\rm Spec}(A)$ with  $W$ normal, if
$W$ normal, if  $E = f^{-1}(\{\mathfrak {m}\})$ is the closed fiber, then the canonical homomorphism
appearing as the edge map in the Leray–Serre spectral sequence for the composition of functors
$E = f^{-1}(\{\mathfrak {m}\})$ is the closed fiber, then the canonical homomorphism
appearing as the edge map in the Leray–Serre spectral sequence for the composition of functors \[ H^d_\mathfrak{m}(A) = H^d_{\{\mathfrak{m}\}}(f_*\mathcal{O}_W) \xrightarrow{\delta^d_f(\mathcal{O}_W)} H^d_E(\mathcal{O}_W) \]
\[ H^d_\mathfrak{m}(A) = H^d_{\{\mathfrak{m}\}}(f_*\mathcal{O}_W) \xrightarrow{\delta^d_f(\mathcal{O}_W)} H^d_E(\mathcal{O}_W) \] $\Gamma _{\{\mathfrak {m}\}} \circ f_* = \Gamma _E$ is injective.
$\Gamma _{\{\mathfrak {m}\}} \circ f_* = \Gamma _E$ is injective.
We now prove ![]() $({\text {R}_{\text {IV}}})$ for rational singularities using the strategy in [Reference Ma and SchwedeMS21, Proposition 3.4]. The case when
$({\text {R}_{\text {IV}}})$ for rational singularities using the strategy in [Reference Ma and SchwedeMS21, Proposition 3.4]. The case when ![]() $A$ is essentially of finite type over a field of characteristic zero is due to Elkik [Reference ElkikElk78].
$A$ is essentially of finite type over a field of characteristic zero is due to Elkik [Reference ElkikElk78].
Proposition 4.17 (cf. [Reference ElkikElk78, Théorème 5])
Let ![]() $(A,\mathfrak {m})$ be a quasi-excellent local
$(A,\mathfrak {m})$ be a quasi-excellent local ![]() $\mathbf {Q}$-algebra, and let
$\mathbf {Q}$-algebra, and let ![]() $t \in \mathfrak {m}$ be a nonzerodivisor. If
$t \in \mathfrak {m}$ be a nonzerodivisor. If ![]() $A/tA$ has rational singularities, then
$A/tA$ has rational singularities, then ![]() $A$ has rational singularities.
$A$ has rational singularities.
Proof. By [Reference MurayamaMur21, Remark 7.4], a quasi-excellent local ![]() $\mathbf {Q}$-algebra has rational singularities if and only if it is pseudo-rational. Since
$\mathbf {Q}$-algebra has rational singularities if and only if it is pseudo-rational. Since ![]() $A$ is normal and Cohen–Macaulay by [Reference SeydiSey72, Proposition I.7.4] and [Reference Bruns and HerzogBH98, Theorem 2.1.3(a)], and
$A$ is normal and Cohen–Macaulay by [Reference SeydiSey72, Proposition I.7.4] and [Reference Bruns and HerzogBH98, Theorem 2.1.3(a)], and ![]() $\hat {A}$ is reduced by [Reference MatsumuraMat89, Corollary to Theorem 23.9], it suffices to show that for every resolution of singularities
$\hat {A}$ is reduced by [Reference MatsumuraMat89, Corollary to Theorem 23.9], it suffices to show that for every resolution of singularities ![]() $f\colon W \to {\rm Spec}(A)$, the homomorphism
$f\colon W \to {\rm Spec}(A)$, the homomorphism ![]() $\delta ^d_f(\mathcal {O}_W)$ is injective, where
$\delta ^d_f(\mathcal {O}_W)$ is injective, where ![]() $d = \dim (A)$.
$d = \dim (A)$.
Let ![]() $E = f^{-1}(\{\mathfrak {m}\})$. Set
$E = f^{-1}(\{\mathfrak {m}\})$. Set ![]() $W_t = f^{-1}(V(t))$, and let
$W_t = f^{-1}(V(t))$, and let ![]() $g\colon W'_t \to W_t$ be a resolution of singularities, which exists by [Reference HironakaHir64, Chapter I, § 3, Main Theorem I
$g\colon W'_t \to W_t$ be a resolution of singularities, which exists by [Reference HironakaHir64, Chapter I, § 3, Main Theorem I![]() $(n)$]. Consider the commutative diagram
$(n)$]. Consider the commutative diagram

where the top half is obtained from [Reference MurayamaMur21, Lemma 3.12]. The top left arrow is injective since the composition in the left column is injective by the hypothesis that ![]() $A/tA$ has rational singularities, where we use the fact that the edge maps in Definition 4.16(iv) behave well under composition of morphisms [Reference SmithSmi97, Proposition 1.12]. The rows are exact on the left by the fact that
$A/tA$ has rational singularities, where we use the fact that the edge maps in Definition 4.16(iv) behave well under composition of morphisms [Reference SmithSmi97, Proposition 1.12]. The rows are exact on the left by the fact that ![]() $A$ is Cohen–Macaulay and by the version of Grauert–Riemenschneider vanishing in [Reference MurayamaMur21, Theorem B*(i)], respectively.
$A$ is Cohen–Macaulay and by the version of Grauert–Riemenschneider vanishing in [Reference MurayamaMur21, Theorem B*(i)], respectively.
Now suppose there exists an element ![]() $0 \ne \eta \in \ker (\delta ^d_f(\mathcal {O}_W))$. Since every element in
$0 \ne \eta \in \ker (\delta ^d_f(\mathcal {O}_W))$. Since every element in ![]() $H^d_\mathfrak {m}(A)$ is annihilated by a power of
$H^d_\mathfrak {m}(A)$ is annihilated by a power of ![]() $t$, after multiplying
$t$, after multiplying ![]() $\eta$ by a power of
$\eta$ by a power of ![]() $t$ we may assume that
$t$ we may assume that ![]() $t\eta = 0$, in which case
$t\eta = 0$, in which case ![]() $\eta$ lies in the image of
$\eta$ lies in the image of ![]() $H^{d-1}_\mathfrak {m}(A/tA)$ in the top row. The commutativity of the diagram implies that the composition
$H^{d-1}_\mathfrak {m}(A/tA)$ in the top row. The commutativity of the diagram implies that the composition ![]() $H^{d-1}_\mathfrak {m}(A/tA) \to H^d_\mathfrak {m}(\mathcal {O}_W)$ is injective. Since
$H^{d-1}_\mathfrak {m}(A/tA) \to H^d_\mathfrak {m}(\mathcal {O}_W)$ is injective. Since ![]() $\eta \in \ker (\delta ^d_f(\mathcal {O}_W))$ by assumption, this shows that
$\eta \in \ker (\delta ^d_f(\mathcal {O}_W))$ by assumption, this shows that ![]() $\eta = 0$, which is a contradiction.
$\eta = 0$, which is a contradiction.
We can now solve Grothendieck's localization problem for terminal, canonical, and rational singularities using [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8]. While our Theorems B and 3.4 apply to positive or mixed characteristic, we are not able to prove this result in these contexts in part because we do not know whether Propositions 4.15 and 4.17 hold in positive or mixed characteristic.
Corollary 4.18 Let ![]() $\varphi \colon A \to B$ be a flat local homomorphism of quasi-excellent local
$\varphi \colon A \to B$ be a flat local homomorphism of quasi-excellent local ![]() $\mathbf {Q}$-algebras.
$\mathbf {Q}$-algebras.
(i) Suppose that
 $B$ is essentially of finite type over a field of characteristic zero. If the closed fiber of
$B$ is essentially of finite type over a field of characteristic zero. If the closed fiber of  $\varphi$ has terminal (respectively, canonical) singularities, then all fibers of
$\varphi$ has terminal (respectively, canonical) singularities, then all fibers of  $\varphi$ have terminal (respectively, canonical) singularities.
$\varphi$ have terminal (respectively, canonical) singularities.(ii) If the closed fiber of
 $\varphi$ has rational singularities, then all fibers of
$\varphi$ has rational singularities, then all fibers of  $\varphi$ have rational singularities.
$\varphi$ have rational singularities.
Proof. By Lemma 4.14, we do not need to distinguish between ‘has terminal (respectively, canonical, rational) singularities’ and ‘geometrically has terminal (respectively, canonical, rational) singularities’. We want to apply [Reference Grothendieck and DieudonnéEGAIV2, Proposition 7.9.8] where the category C in their notation is the category of schemes essentially of finite type over a field of characteristic zero in situation (i), and the category of schemes locally essentially of finite type over a quasi-excellent local ![]() $\mathbf {Q}$-algebra in situation (ii).
$\mathbf {Q}$-algebra in situation (ii).
– For [Reference Grothendieck and DieudonnéEGAIV2, (7.9.7.1)], the category C is stable under morphisms locally essentially of finite type by definition.
– For [Reference Grothendieck and DieudonnéEGAIV2, (7.9.7.2)], the terminal and canonical locus of a scheme
 $X$ in C is open by [Reference KollárKol13, Corollary 2.12], and the rational locus of a scheme
$X$ in C is open by [Reference KollárKol13, Corollary 2.12], and the rational locus of a scheme  $X$ in C is open by Remark 4.13.
$X$ in C is open by Remark 4.13.– The condition [Reference Grothendieck and DieudonnéEGAIV2, (7.9.7.3)] is our condition
 $({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$ when
$({\rm R}_{{\rm IV}}^{{\mathscr {C}}})$ when  ${\mathscr {C}}$ is the category of rings whose spectra are in C, which holds by Propositions 4.15 and 4.17.
${\mathscr {C}}$ is the category of rings whose spectra are in C, which holds by Propositions 4.15 and 4.17.– The condition [Reference Grothendieck and DieudonnéEGAIV2, (7.9.7.4)] is a version of our condition
 $({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$ when
$({\rm P}_{{\rm IV}}^{{\mathscr {C}}})$ when  ${\mathscr {C}}$ is the category of rings whose spectra are in C, which holds by Lemma 4.14.
${\mathscr {C}}$ is the category of rings whose spectra are in C, which holds by Lemma 4.14.– For [Reference Grothendieck and DieudonnéEGAIV2, (7.9.8.2)], every module-finite
 $A$-algebra has a resolution of singularities by [Reference HironakaHir64, Chapter I, § 3, Main Theorem I
$A$-algebra has a resolution of singularities by [Reference HironakaHir64, Chapter I, § 3, Main Theorem I $(n)$].
$(n)$].
We state a global version of this result as well. A similar statement for the behavior of rational singularities in proper flat families was shown to us by János Kollár; see also [Reference ElkikElk78, Théorème 4].
Corollary 4.19 Let ![]() $f\colon Y \to X$ be a flat morphism of locally noetherian
$f\colon Y \to X$ be a flat morphism of locally noetherian ![]() $\mathbf {Q}$-schemes, such that the local rings of
$\mathbf {Q}$-schemes, such that the local rings of ![]() $X$ and
$X$ and ![]() $Y$ are quasi-excellent.
$Y$ are quasi-excellent.
(i) Suppose
 $f$ maps closed points to closed points. If every closed fiber of
$f$ maps closed points to closed points. If every closed fiber of  $f$ has rational singularities, then all fibers of
$f$ has rational singularities, then all fibers of  $f$ have rational singularities. If the local rings of
$f$ have rational singularities. If the local rings of  $Y$ are essentially of finite type over fields of characteristic zero, and every closed fiber of
$Y$ are essentially of finite type over fields of characteristic zero, and every closed fiber of  $f$ has terminal (respectively, canonical) singularities, then all fibers of
$f$ has terminal (respectively, canonical) singularities, then all fibers of  $f$ have terminal (respectively, canonical) singularities.
$f$ have terminal (respectively, canonical) singularities.(ii) Suppose
 $f$ is closed. Then the locus of points
$f$ is closed. Then the locus of points  $x \in X$ over which
$x \in X$ over which  $f^{-1}(x)$ has rational singularities is stable under generization. If the local rings of
$f^{-1}(x)$ has rational singularities is stable under generization. If the local rings of  $Y$ are essentially of finite type over fields of characteristic zero, then the locus of points
$Y$ are essentially of finite type over fields of characteristic zero, then the locus of points  $x \in X$ over which
$x \in X$ over which  $f^{-1}(x)$ has terminal (respectively, canonical) singularities is stable under generization.
$f^{-1}(x)$ has terminal (respectively, canonical) singularities is stable under generization.
For completeness, we end by showing that pseudo-rationality satisfies ![]() $({\rm R}_{{\rm II}}^{{\mathscr {C}}})$ when
$({\rm R}_{{\rm II}}^{{\mathscr {C}}})$ when ![]() ${\mathscr {C}}$ is the category of noetherian rings with residual complexes in the sense of [Reference HartshorneHar66, Definition on p. 304]. A special case of this statement was shown to us by Karl Schwede. Similar results hold for cyclically pure homomorphisms of
${\mathscr {C}}$ is the category of noetherian rings with residual complexes in the sense of [Reference HartshorneHar66, Definition on p. 304]. A special case of this statement was shown to us by Karl Schwede. Similar results hold for cyclically pure homomorphisms of ![]() $\mathbf {Q}$-algebras whose local rings are quasi-excellent; see [Reference BoutotBou87, Théorème on p. 65; Reference MurayamaMur21, Theorem C].
$\mathbf {Q}$-algebras whose local rings are quasi-excellent; see [Reference BoutotBou87, Théorème on p. 65; Reference MurayamaMur21, Theorem C].
Proposition 4.20 Let ![]() $\varphi \colon (A,\mathfrak {m}) \to (B,\mathfrak {n})$ be a flat local homomorphism of noetherian local rings, such that
$\varphi \colon (A,\mathfrak {m}) \to (B,\mathfrak {n})$ be a flat local homomorphism of noetherian local rings, such that ![]() $B$ has a residual complex. If
$B$ has a residual complex. If ![]() $B$ is pseudo-rational, then
$B$ is pseudo-rational, then ![]() $A$ is pseudo-rational.
$A$ is pseudo-rational.
Proof. First, we know that ![]() $A$ is normal [Reference MatsumuraMat89, Corollary to Theorem 23.9] and Cohen–Macaulay [Reference Bruns and HerzogBH98, Theorem 2.1.7]. To prove that
$A$ is normal [Reference MatsumuraMat89, Corollary to Theorem 23.9] and Cohen–Macaulay [Reference Bruns and HerzogBH98, Theorem 2.1.7]. To prove that ![]() $\hat {A}$ is reduced, we note that
$\hat {A}$ is reduced, we note that
is flat, where ![]() $\hat {B}$ is the
$\hat {B}$ is the ![]() $\mathfrak {n}$-adic completion of
$\mathfrak {n}$-adic completion of ![]() $B$ [Reference MatsumuraMat89, Theorem 22.4(i)]. But
$B$ [Reference MatsumuraMat89, Theorem 22.4(i)]. But ![]() $\hat {B}$ is reduced by assumption, and hence
$\hat {B}$ is reduced by assumption, and hence ![]() $\hat {A}$ is reduced by [Reference MatsumuraMat89, Corollary to Theorem 23.9].
$\hat {A}$ is reduced by [Reference MatsumuraMat89, Corollary to Theorem 23.9].
It remains to show that condition (iv) holds. Let ![]() $\mathfrak {q} \subseteq B$ be a minimal prime lying over
$\mathfrak {q} \subseteq B$ be a minimal prime lying over ![]() $\mathfrak {m}$. The localization
$\mathfrak {m}$. The localization ![]() $B_\mathfrak {q}$ is pseudo-rational since
$B_\mathfrak {q}$ is pseudo-rational since ![]() $B$ has a residual complex [Reference Lipman and TeissierLT81, § 4, Corollary of (iii)]. By replacing
$B$ has a residual complex [Reference Lipman and TeissierLT81, § 4, Corollary of (iii)]. By replacing ![]() $B$ with
$B$ with ![]() $B_\mathfrak {q}$, we reduce to the case where
$B_\mathfrak {q}$, we reduce to the case where ![]() $B/\mathfrak {m} B$ is zero-dimensional, in which case
$B/\mathfrak {m} B$ is zero-dimensional, in which case ![]() $\sqrt {\mathfrak {m} B} = \mathfrak {n}$. Let
$\sqrt {\mathfrak {m} B} = \mathfrak {n}$. Let ![]() $f\colon W \to X := {\rm Spec}(A)$ be a proper birational morphism, where
$f\colon W \to X := {\rm Spec}(A)$ be a proper birational morphism, where ![]() $W$ is normal. Set
$W$ is normal. Set ![]() $Y := {\rm Spec}(B)$, and consider the commutative diagram
$Y := {\rm Spec}(B)$, and consider the commutative diagram

where the square is cartesian, where ![]() $g := {\rm Spec}(\varphi )$, and where
$g := {\rm Spec}(\varphi )$, and where ![]() $\nu$ is the normalization of
$\nu$ is the normalization of ![]() $W' := W \times _X Y$. Note that
$W' := W \times _X Y$. Note that ![]() $f'$ is proper by base change and birational by flat base change [Reference Grothendieck and DieudonnéEGAInew, Proposition 3.9.9], and hence
$f'$ is proper by base change and birational by flat base change [Reference Grothendieck and DieudonnéEGAInew, Proposition 3.9.9], and hence ![]() $\nu$ is finite by [Reference Lipman and TeissierLT81,
$\nu$ is finite by [Reference Lipman and TeissierLT81, ![]() $({\rm iv})''$ in Remark (a) on pp. 102–103]. We then have the commutative diagram
$({\rm iv})''$ in Remark (a) on pp. 102–103]. We then have the commutative diagram

where the top half of the diagram is from [Reference SmithSmi97, Proposition 1.12], and the bottom half is from the naturality of ![]() $\delta ^d_f(-)$ applied to the pullback map
$\delta ^d_f(-)$ applied to the pullback map ![]() $\mathcal {O}_W \to (g' \circ \nu )_*\mathcal {O}_Z$ [Reference SmithSmi97, Lemma 1.11]. The horizontal arrow on the top left is injective by the assumption that
$\mathcal {O}_W \to (g' \circ \nu )_*\mathcal {O}_Z$ [Reference SmithSmi97, Lemma 1.11]. The horizontal arrow on the top left is injective by the assumption that ![]() $B$ is pseudo-rational, the vertical arrow on the top right is an equality since
$B$ is pseudo-rational, the vertical arrow on the top right is an equality since ![]() $\sqrt {\mathfrak {m} B} = \mathfrak {n}$, and the vertical arrow on the bottom right is injective by the flatness of
$\sqrt {\mathfrak {m} B} = \mathfrak {n}$, and the vertical arrow on the bottom right is injective by the flatness of ![]() $\varphi$. The commutativity of the diagram shows that
$\varphi$. The commutativity of the diagram shows that ![]() $\delta ^d_f(\mathcal {O}_W)$ is injective as required.
$\delta ^d_f(\mathcal {O}_W)$ is injective as required.
Acknowledgements
I am grateful to Sándor Kovács, Linquan Ma, Yohsuke Matsuzawa, Zsolt Patakfalvi, Karl Schwede, Kazuma Shimomoto, Austyn Simpson, and Farrah Yhee for helpful conversations. I would especially like to thank Rankeya Datta, Charles Godfrey, János Kollár, and Mircea Mustaţă for insightful comments on previous drafts of this paper. This paper arose out of discussions with Rankeya about Grothendieck's localization problem for the ‘Cohen–Macaulay and ![]() $F$-injective’ property that occurred while writing [Reference Datta and MurayamaDM20], and I am grateful to Rankeya for allowing me to write this standalone paper. Finally, I am indebted to the anonymous referees for helpful suggestions and corrections which improved the quality of this paper.
$F$-injective’ property that occurred while writing [Reference Datta and MurayamaDM20], and I am grateful to Rankeya for allowing me to write this standalone paper. Finally, I am indebted to the anonymous referees for helpful suggestions and corrections which improved the quality of this paper.