We generalize our previous method on the subconvexity problem for $\text{GL}_{2}\times \text{GL}_{1}$ with cuspidal representations to Eisenstein series, and deduce a Burgess-like subconvex bound for Hecke characters, that is, the bound $|L(1/2,\unicode[STIX]{x1D712})|\ll _{\mathbf{F},\unicode[STIX]{x1D716}}\mathbf{C}(\unicode[STIX]{x1D712})^{1/4-(1-2\unicode[STIX]{x1D703})/16+\unicode[STIX]{x1D716}}$ for varying Hecke characters $\unicode[STIX]{x1D712}$ over a number field $\mathbf{F}$ with analytic conductor $\mathbf{C}(\unicode[STIX]{x1D712})$. As a main tool, we apply the extended theory of regularized integrals due to Zagier developed in a previous paper to obtain the relevant triple product formulas of Eisenstein series.

We study the number of non-trivial simple zeros of the Dedekind zeta-function of a quadratic number field in the rectangle $\{\unicode[STIX]{x1D70E}+\text{i}t:0<\unicode[STIX]{x1D70E}<1,0<t<T\}$. We prove that such a number exceeds $T^{6/7-\unicode[STIX]{x1D700}}$ if $T$ is sufficiently large. This improves upon the classical lower bound $T^{6/11}$ established by Conrey et al [Simple zeros of the zeta function of a quadratic number field. I. Invent. Math.86 (1986), 563–576].

We formulate a conjecture which generalizes Darmon’s ‘refined class number formula’. We discuss relations between our conjecture and the equivariant leading term conjecture of Burns. As an application, we give another proof of the ‘except $2$-part’ of Darmon’s conjecture, which was first proved by Mazur and Rubin.

Let 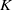$K$ be a number field of degree $n$, and let 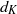$d_K$ be its discriminant. Then, under the Artin conjecture, the generalized Riemann hypothesis and a certain zero-density hypothesis, we show that the upper and lower bounds of the logarithmic derivatives of Artin 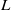$L$-functions attached to $K$ at 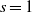$s=1$ are 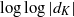$\log \log |d_K|$ and 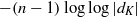$-(n-1) \log \log |d_K|$, respectively. Unconditionally, we show that there are infinitely many number fields with the extreme logarithmic derivatives; they are families of number fields whose Galois closures have the Galois group $C_n$ for $n=2,3,4,6$, 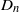$D_n$ for 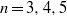$n=3,4,5$, 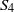$S_4$ or 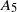$A_5$.

We use the theory of Kolyvagin systems to prove (most of) a refined class number formula conjectured by Darmon. We show that, for every odd prime p, each side of Darmon’s conjectured formula (indexed by positive integers n) is ‘almost’ a p-adic Kolyvagin system as n varies. Using the fact that the space of Kolyvagin systems is free of rank one over ℤp, we show that Darmon’s formula for arbitrary n follows from the case n=1, which in turn follows from classical formulas.

Let L/k be a finite Galois extension of number fields with Galois group G. For every odd prime p satisfying certain mild technical hypotheses, we use values of Artin L-functions to construct an element in the centre of the group ring ℤ(p)[G] that annihilates the p-part of the class group of L.

We formulate an explicit conjecture for the leading term at s=1 of the equivariant Dedekind zeta-function that is associated to a Galois extension of number fields. We show that this conjecture refines well-known conjectures of Stark and Chinburg, and we use the functional equation of the zeta-function to compare it to a natural conjecture for the leading term at s=0.

Explicit bounds are given for the residues at $s\,{=}\,1$ of the Dedekind zeta functions of number fields. As a consequence, a simple proof of the Brauer-Siegel theorem and explicit lower bounds for class numbers of number fields are obtained. Compared with Stark's original approach, the paper is explicit and more satisfactory for number fields containing quadratic subfields. Examples are given of fully explicit lower bounds for class numbers of various types of number fields, for example normal and non-normal number fields of odd degree, with an emphasis on cubic fields, real cyclic quartic number fields, and non-normal quartic number fields containing an imaginary quadratic subfield.

Gross and Rubin have made conjectures about special values of equivariant L-functions associated to abelian extensions of global fields. We describe a common refinement, due to Burns, and give evidence in favour of this conjecture for quadratic extensions and cyclotomic fields. We also note that the statement provides a new interpretation of further conjectures of Darmon and Gross.