In this paper, we study transcendence theory for Thakur multizeta values in positive characteristic. We prove an analogue of the strong form of Goncharov’s conjecture. The same result is also established for Carlitz multiple polylogarithms at algebraic points.

We formulate a conjecture which generalizes Darmon’s ‘refined class number formula’. We discuss relations between our conjecture and the equivariant leading term conjecture of Burns. As an application, we give another proof of the ‘except $2$-part’ of Darmon’s conjecture, which was first proved by Mazur and Rubin.

A trisymplectic structure on a complex $2n$-manifold is a three-dimensional space ${\rm\Omega}$ of closed holomorphic forms such that any element of ${\rm\Omega}$ has constant rank $2n$, $n$ or zero, and degenerate forms in 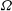${\rm\Omega}$ belong to a non-degenerate quadric hypersurface. We show that a trisymplectic manifold is equipped with a holomorphic 3-web and the Chern connection of this 3-web is holomorphic, torsion-free, and preserves the three symplectic forms. We construct a trisymplectic structure on the moduli of regular rational curves in the twistor space of a hyperkähler manifold, and define a trisymplectic reduction of a trisymplectic manifold, which is a complexified form of a hyperkähler reduction. We prove that the trisymplectic reduction in the space of regular rational curves on the twistor space of a hyperkähler manifold $M$ is compatible with the hyperkähler reduction on $M$. As an application of these geometric ideas, we consider the ADHM construction of instantons and show that the moduli space of rank $r$, charge $c$ framed instanton bundles on 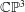$\mathbb{C}\mathbb{P}^{3}$ is a smooth trisymplectic manifold of complex dimension 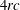$4rc$. In particular, it follows that the moduli space of rank two, charge $c$ instanton bundles on 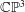$\mathbb{C}\mathbb{P}^{3}$ is a smooth complex manifold dimension $8c-3$, thus settling part of a 30-year-old conjecture.

Let $X$ be a compact Kähler manifold and let $(L,{\it\varphi})$ be a pseudo-effective line bundle on $X$. We first define a notion of numerical dimension for pseudo-effective line bundles with singular metrics, and then discuss the properties of this numerical dimension. Finally, we prove a very general Kawamata–Viehweg–Nadel-type vanishing theorem on an arbitrary compact Kähler manifold.

Let $W$ be an extended affine Weyl group. We prove that the minimal length elements $w_{{\mathcal{O}}}$ of any conjugacy class ${\mathcal{O}}$ of $W$ satisfy some nice properties, generalizing results of Geck and Pfeiffer [On the irreducible characters of Hecke algebras, Adv. Math. 102 (1993), 79–94] on finite Weyl groups. We also study a special class of conjugacy classes, the straight conjugacy classes. These conjugacy classes are in a natural bijection with the Frobenius-twisted conjugacy classes of some $p$-adic group and satisfy additional interesting properties. Furthermore, we discuss some applications to the affine Hecke algebra $H$. We prove that $T_{w_{{\mathcal{O}}}}$, where ${\mathcal{O}}$ ranges over all the conjugacy classes of $W$, forms a basis of the cocenter $H/[H,H]$. We also introduce the class polynomials, which play a crucial role in the study of affine Deligne–Lusztig varieties He [Geometric and cohomological properties of affine Deligne–Lusztig varieties, Ann. of Math. (2) 179 (2014), 367–404].

Let $G$ and $\tilde{G}$ be Kleinian groups whose limit sets $S$ and $\tilde{S}$, respectively, are homeomorphic to the standard Sierpiński carpet, and such that every complementary component of each of $S$ and $\tilde{S}$ is a round disc. We assume that the groups $G$ and $\tilde{G}$ act cocompactly on triples on their respective limit sets. The main theorem of the paper states that any quasiregular map (in a suitably defined sense) from an open connected subset of $S$ to $\tilde{S}$ is the restriction of a Möbius transformation that takes $S$ onto $\tilde{S}$, in particular it has no branching. This theorem applies to the fundamental groups of compact hyperbolic 3-manifolds with non-empty totally geodesic boundaries. One consequence of the main theorem is the following result. Assume that $G$ is a torsion-free hyperbolic group whose boundary at infinity $\partial _{\infty }G$ is a Sierpiński carpet that embeds quasisymmetrically into the standard 2-sphere. Then there exists a group $H$ that contains $G$ as a finite index subgroup and such that any quasisymmetric map $f$ between open connected subsets of $\partial _{\infty }G$ is the restriction of the induced boundary map of an element $h\in H$.

We investigate subgroups of $\text{SL}(n,\mathbb{Z})$ which preserve an open nondegenerate convex cone in $\mathbb{R}^{n}$ and admit in that cone as fundamental domain a polyhedral cone of which some faces are allowed to lie on the boundary. Examples are arithmetic groups acting on self-dual cones, Weyl groups of certain Kac–Moody algebras, and they do occur in algebraic geometry as the automorphism groups of projective manifolds acting on their ample cones.