1 Introduction
Let
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
be the quantized enveloping algebra of
${{\mathbf {U}}(\mathfrak {gl}_n)}$
be the quantized enveloping algebra of
![]() $\mathfrak {gl}_n$
over
$\mathfrak {gl}_n$
over
![]() $\mathbb Q(v)$
(v an indeterminate) with Chevalley type generators
$\mathbb Q(v)$
(v an indeterminate) with Chevalley type generators
![]() $E_i$
,
$E_i$
,
![]() $F_i$
, and
$F_i$
, and
![]() $K_j^{\pm 1}$
for
$K_j^{\pm 1}$
for
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() $1\leqslant j\leqslant n$
. Beilinson, Lusztig, and MacPherson (BLM) [Reference Beilinson, Lusztig and MacPherson3] constructed a realization for the quantum group
$1\leqslant j\leqslant n$
. Beilinson, Lusztig, and MacPherson (BLM) [Reference Beilinson, Lusztig and MacPherson3] constructed a realization for the quantum group
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
via a geometric setting of q-Schur algebras. A presentation of the q-Schur algebra
${{\mathbf {U}}(\mathfrak {gl}_n)}$
via a geometric setting of q-Schur algebras. A presentation of the q-Schur algebra
![]() ${\boldsymbol {\mathcal S}}(n,d)$
was given by Doty–Giaquinto [Reference Doty and Giaquinto8]. Du–Parshall [Reference Du and Parshall15] provided an approach to the
${\boldsymbol {\mathcal S}}(n,d)$
was given by Doty–Giaquinto [Reference Doty and Giaquinto8]. Du–Parshall [Reference Du and Parshall15] provided an approach to the
![]() $\mathfrak {sl}_n$
type presentation of the q-Schur algebra
$\mathfrak {sl}_n$
type presentation of the q-Schur algebra
![]() ${\boldsymbol {\mathcal S}}(n,d)$
using the Beilinson–Lusztig–MacPherson’s construction of
${\boldsymbol {\mathcal S}}(n,d)$
using the Beilinson–Lusztig–MacPherson’s construction of
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
. The problem of describing the defining relations of a generalized q-Schur algebra as a quotient of a quantized enveloping algebra was investigated by Doty [Reference Doty7], Doty–Giaquinto–Sullivan [Reference Doty, Giaquinto and Sullivan9], [Reference Doty, Giaquinto and Sullivan10].
${{\mathbf {U}}(\mathfrak {gl}_n)}$
. The problem of describing the defining relations of a generalized q-Schur algebra as a quotient of a quantized enveloping algebra was investigated by Doty [Reference Doty7], Doty–Giaquinto–Sullivan [Reference Doty, Giaquinto and Sullivan9], [Reference Doty, Giaquinto and Sullivan10].
Infinitesimal Schur algebras are certain important subalgebras of Schur algebras (cf. [Reference Doty, Nakano and Peters11]). The polynomial representations of the group scheme
![]() $G_r T$
of degree d are equivalent to the representation theory of the infinitesimal Schur algebras
$G_r T$
of degree d are equivalent to the representation theory of the infinitesimal Schur algebras ![]() . Here,
. Here,
![]() $G_r$
is the r-th Frobenius kernel of the general linear group G over
$G_r$
is the r-th Frobenius kernel of the general linear group G over ![]() , and T is the subscheme of G arising from diagonal elements. A theory of the infinitesimal q-Schur algebra was studied by Cox [Reference Cox4], [Reference Cox5].
, and T is the subscheme of G arising from diagonal elements. A theory of the infinitesimal q-Schur algebra was studied by Cox [Reference Cox4], [Reference Cox5].
Let
![]() ${\mathcal Z}=\mathbb Z[v,v^{-1}]$
and
${\mathcal Z}=\mathbb Z[v,v^{-1}]$
and ![]() be a commutative ring of characteristic p. Let
be a commutative ring of characteristic p. Let ![]() be a primitive
be a primitive
![]() $l'$
th root of
$l'$
th root of
![]() $1$
. We will regard
$1$
. We will regard ![]() as a
as a
![]() ${\mathcal Z}$
-module by specializing v to
${\mathcal Z}$
-module by specializing v to
![]() $\varepsilon $
. Let
$\varepsilon $
. Let ![]() , where
, where
![]() ${U_{\mathcal Z}(\mathfrak {gl}_n)}$
is the
${U_{\mathcal Z}(\mathfrak {gl}_n)}$
is the
![]() ${\mathcal Z}$
-subalgebra of
${\mathcal Z}$
-subalgebra of
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
generated by the elements
${{\mathbf {U}}(\mathfrak {gl}_n)}$
generated by the elements
![]() $E_i^{(m)}$
,
$E_i^{(m)}$
,
![]() $F_i^{(m)}$
,
$F_i^{(m)}$
,
![]() $K_j^{\pm 1}$
, and
$K_j^{\pm 1}$
, and
![]() $\big [ {K_j;0 \atop t} \big ]$
for
$\big [ {K_j;0 \atop t} \big ]$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $1\leqslant j\leqslant n$
and
$1\leqslant j\leqslant n$
and
![]() $m,t\in \mathbb N$
. For
$m,t\in \mathbb N$
. For
![]() $r\geqslant 1$
, let
$r\geqslant 1$
, let ![]() be the
be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}$
,
$E_{i}^{(m)}$
,
![]() $F_{i}^{(m)}$
,
$F_{i}^{(m)}$
,
![]() $K_{j}^{\pm 1}$
, and
$K_{j}^{\pm 1}$
, and
![]() $\big [{K_j;0 \atop t} \big ]$
for
$\big [{K_j;0 \atop t} \big ]$
for
![]() $1 \leqslant i \leqslant n-1$
,
$1 \leqslant i \leqslant n-1$
,
![]() $1 \leqslant j \leqslant n$
,
$1 \leqslant j \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $0 \leqslant m,t<l p^{r-1}$
, where
$0 \leqslant m,t<l p^{r-1}$
, where
![]() $l=l'$
if
$l=l'$
if
![]() $l'$
is odd, and
$l'$
is odd, and
![]() $l=l'/2$
otherwise. Furthermore, let
$l=l'/2$
otherwise. Furthermore, let ![]() , where
, where ![]() is the zero part of
is the zero part of ![]() . Then, we have
. Then, we have
and ![]() . In the case where
. In the case where
![]() $l'=l$
is an odd number, let
$l'=l$
is an odd number, let
The algebra ![]() is the Lusztig’s small quantum group, and
is the Lusztig’s small quantum group, and ![]() is called Frobenius–Lusztig kernels of
is called Frobenius–Lusztig kernels of ![]() (cf. [Reference Drupieski12], [Reference Lusztig22]). The representation theory of
(cf. [Reference Drupieski12], [Reference Lusztig22]). The representation theory of ![]() and
and ![]() was studied in [Reference Drupieski12].
was studied in [Reference Drupieski12].
Jimbo [Reference Jimbo20] proved that there is a natural surjective algebra homomorphism
![]() $\zeta _d$
from
$\zeta _d$
from
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
to the q-Schur algebra
${{\mathbf {U}}(\mathfrak {gl}_n)}$
to the q-Schur algebra
![]() ${\boldsymbol {\mathcal S}}(n,d)$
. The map
${\boldsymbol {\mathcal S}}(n,d)$
. The map
![]() $\zeta _d:{{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
induces a surjective algebra homomorphism
$\zeta _d:{{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
induces a surjective algebra homomorphism
where ![]() is the infinitesimal q-Schur algebra over
is the infinitesimal q-Schur algebra over ![]() (cf. [Reference Fu18, Prop. 6.1]). Note that
(cf. [Reference Fu18, Prop. 6.1]). Note that ![]() is a quotient algebra of
is a quotient algebra of ![]() in the case where
in the case where
![]() $l'=l$
is odd. We prove in Theorem 4.10 that
$l'=l$
is odd. We prove in Theorem 4.10 that
![]() $\ker \zeta _{d,r}$
is generated by the elements
$\ker \zeta _{d,r}$
is generated by the elements
![]() $1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }$
,
$1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }$
,
![]() $K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
,
$K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
,
![]() $\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
$\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
![]() $1 \leqslant i \leqslant n$
,
$1 \leqslant i \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $\lambda \in \Lambda (n,d)$
, where
$\lambda \in \Lambda (n,d)$
, where
![]() $\Lambda (n,d)$
is the set of all compositions of d into n parts.
$\Lambda (n,d)$
is the set of all compositions of d into n parts.
Let
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
be the modified quantum group with generators
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
be the modified quantum group with generators
![]() $E_i1_{\lambda }$
,
$E_i1_{\lambda }$
,
![]() $1_{\lambda } F_i$
, and
$1_{\lambda } F_i$
, and
![]() $1_{\lambda }$
for
$1_{\lambda }$
for
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() ${\lambda }\in \mathbb Z^{n}$
. The map
${\lambda }\in \mathbb Z^{n}$
. The map
![]() $\zeta _d:{{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
induces a surjective algebra homomorphism
$\zeta _d:{{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
induces a surjective algebra homomorphism
Let ![]() , where
, where
![]() $\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)$
is the
$\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)$
is the
![]() ${\mathcal Z}$
-subalgebra of
${\mathcal Z}$
-subalgebra of
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
generated by the elements
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
generated by the elements
![]() $E_i^{(m)}1_{\lambda }$
,
$E_i^{(m)}1_{\lambda }$
,
![]() $1_{\lambda } F_i^{(m)}$
for
$1_{\lambda } F_i^{(m)}$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $m\in \mathbb N$
and
$m\in \mathbb N$
and
![]() ${\lambda }\in \mathbb Z^{n}$
. Let
${\lambda }\in \mathbb Z^{n}$
. Let ![]() be the
be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}1_{\lambda }$
and
$E_{i}^{(m)}1_{\lambda }$
and
![]() $1_{\lambda } F_{i}^{(m)}$
for
$1_{\lambda } F_{i}^{(m)}$
for
![]() $1 \leqslant i \leqslant n-1$
,
$1 \leqslant i \leqslant n-1$
,
![]() $\lambda \in \mathbb Z^{n}$
and
$\lambda \in \mathbb Z^{n}$
and
![]() $0 \leqslant m<l p^{r-1}$
. The map
$0 \leqslant m<l p^{r-1}$
. The map
![]() $\dot {\zeta }_d:\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
induces a surjective algebra homomorphism
$\dot {\zeta }_d:\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
induces a surjective algebra homomorphism
We prove in Theorem 5.5 that
![]() $\ker \dot {\zeta }_{d,r}$
is generated by the elements
$\ker \dot {\zeta }_{d,r}$
is generated by the elements
![]() $1_{\lambda }$
for
$1_{\lambda }$
for
![]() ${\lambda }\not \in \Lambda (n,d)$
.
${\lambda }\not \in \Lambda (n,d)$
.
The organization of the paper is as follows. We recall the BLM construction of the quantum group
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
in Section 2. In Section 3, we introduce the infinitesimal q-Schur algebra
${{\mathbf {U}}(\mathfrak {gl}_n)}$
in Section 2. In Section 3, we introduce the infinitesimal q-Schur algebra ![]() . A generating set for the kernel of the epimorphism
. A generating set for the kernel of the epimorphism ![]() is obtained in Section 4. In Section 5, we investigate the kernel of the epimorphism
is obtained in Section 4. In Section 5, we investigate the kernel of the epimorphism ![]() . In Section 6, we discuss the classical case. In Section 7, we investigate Borel subalgebras of the infinitesimal q-Schur algebra
. In Section 6, we discuss the classical case. In Section 7, we investigate Borel subalgebras of the infinitesimal q-Schur algebra ![]() . As an application, we give a classification of irreducible
. As an application, we give a classification of irreducible ![]() -modules over a field of characteristic p in Section 8.
-modules over a field of characteristic p in Section 8.
Throughout this paper, let
![]() ${\mathcal Z}=\mathbb Z[v,v^{-1}]$
where v is an indeterminate. For
${\mathcal Z}=\mathbb Z[v,v^{-1}]$
where v is an indeterminate. For
![]() $i\in \mathbb Z$
let
$i\in \mathbb Z$
let
![]() $[i]=\frac {v^i-v^{-i}}{v-v^{-1}}$
. For integers
$[i]=\frac {v^i-v^{-i}}{v-v^{-1}}$
. For integers
![]() $N,t$
with
$N,t$
with
![]() $t\geqslant 0$
, let
$t\geqslant 0$
, let
 $$ \begin{align*} \left[{N\atop t}\right]=\frac{[N][N-1]\cdots[N-t+1]}{[t]^!}\in{\mathcal Z,} \end{align*} $$
$$ \begin{align*} \left[{N\atop t}\right]=\frac{[N][N-1]\cdots[N-t+1]}{[t]^!}\in{\mathcal Z,} \end{align*} $$
where
![]() $[t]^{!}=[1][2]\cdots [t]$
.
$[t]^{!}=[1][2]\cdots [t]$
.
Let ![]() be a commutative ring containing a primitive
be a commutative ring containing a primitive
![]() $l'$
th root
$l'$
th root
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $1$
with
$1$
with
![]() $l'\geqslant 1$
. Let
$l'\geqslant 1$
. Let
![]() $l\geqslant 1$
be defined by
$l\geqslant 1$
be defined by
 $$ \begin{align*}l= \begin{cases} l'&\text{if } l' \text{ is odd},\\ l'/2&\text{if } l' \text{ is even}. \end{cases}\end{align*} $$
$$ \begin{align*}l= \begin{cases} l'&\text{if } l' \text{ is odd},\\ l'/2&\text{if } l' \text{ is even}. \end{cases}\end{align*} $$
Let p be the characteristic of ![]() . The commutative ring
. The commutative ring ![]() will be viewed as a
will be viewed as a
![]() ${\mathcal Z}$
-module by specializing v to
${\mathcal Z}$
-module by specializing v to
![]() $\varepsilon $
. For
$\varepsilon $
. For
![]() $c\in \mathbb Z$
and
$c\in \mathbb Z$
and
![]() $t\in \mathbb N$
, we will denote the image of
$t\in \mathbb N$
, we will denote the image of
![]() $\big [{c\atop t}\big ]\in {\mathcal Z}$
in
$\big [{c\atop t}\big ]\in {\mathcal Z}$
in ![]() by
by
![]() $\big [{c\atop t}\big ]_{\varepsilon }$
. For
$\big [{c\atop t}\big ]_{\varepsilon }$
. For
![]() $\mu \in \mathbb Z^{n}$
and
$\mu \in \mathbb Z^{n}$
and
![]() ${\lambda }\in \mathbb N^{n}$
let
${\lambda }\in \mathbb N^{n}$
let
![]() $\big [{\mu \atop {\lambda }}\big ]_{\varepsilon }=\big [{\mu _1\atop {\lambda }_1}\big ]_{\varepsilon }\cdots \big [{\mu _n\atop {\lambda }_n}\big ]_{\varepsilon }.$
$\big [{\mu \atop {\lambda }}\big ]_{\varepsilon }=\big [{\mu _1\atop {\lambda }_1}\big ]_{\varepsilon }\cdots \big [{\mu _n\atop {\lambda }_n}\big ]_{\varepsilon }.$
2 The BLM construction of
 $ {{\mathbf {U}}(\mathfrak {gl}_n)} $
$ {{\mathbf {U}}(\mathfrak {gl}_n)} $
Following [Reference Jimbo20], we define the quantized enveloping algebra
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
of
${{\mathbf {U}}(\mathfrak {gl}_n)}$
of
![]() $\mathfrak {gl}_n$
to be the
$\mathfrak {gl}_n$
to be the
![]() $\mathbb Q(v)$
algebra with generators
$\mathbb Q(v)$
algebra with generators
and relations
![]() $\mathrm{(a)}\ K_{i}K_{j}=K_{j}K_{i},\ K_{i}K_{i}^{-1}=1;$
$\mathrm{(a)}\ K_{i}K_{j}=K_{j}K_{i},\ K_{i}K_{i}^{-1}=1;$
![]() $\mathrm{(b)}\ K_{i}E_j=v^{\delta _{i,j}-\delta _{i,j+1}} E_jK_{i};$
$\mathrm{(b)}\ K_{i}E_j=v^{\delta _{i,j}-\delta _{i,j+1}} E_jK_{i};$
![]() $\mathrm{(c)}\ K_{i}F_j=v^{\delta _{i,j+1}-\delta _{i,j}} F_jK_{i};$
$\mathrm{(c)}\ K_{i}F_j=v^{\delta _{i,j+1}-\delta _{i,j}} F_jK_{i};$
![]() $\mathrm{(d)}\ E_iE_j=E_jE_i,\ F_iF_j=F_jF_i\ when\ |i-j|>1;$
$\mathrm{(d)}\ E_iE_j=E_jE_i,\ F_iF_j=F_jF_i\ when\ |i-j|>1;$
![]() $\mathrm{(e)}\ E_iF_j-F_jE_i=\delta _{i,j}\frac {\widetilde K_{i} -\widetilde K_{i}^{-1}}{v-v^{-1}},\ where \ \widetilde K_i =K_{i}K_{i+1}^{-1};$
$\mathrm{(e)}\ E_iF_j-F_jE_i=\delta _{i,j}\frac {\widetilde K_{i} -\widetilde K_{i}^{-1}}{v-v^{-1}},\ where \ \widetilde K_i =K_{i}K_{i+1}^{-1};$
![]() $\mathrm{(f)}\ E_i^2E_j-(v+v^{-1})E_iE_jE_i+E_jE_i^2=0\ when\ |i-j|=1;$
$\mathrm{(f)}\ E_i^2E_j-(v+v^{-1})E_iE_jE_i+E_jE_i^2=0\ when\ |i-j|=1;$
![]() $\mathrm{(g)}\ F_i^2F_j-(v+v^{-1})F_iF_jF_i+F_jF_i^2=0\ when\ |i-j|=1.$
$\mathrm{(g)}\ F_i^2F_j-(v+v^{-1})F_iF_jF_i+F_jF_i^2=0\ when\ |i-j|=1.$
Following [Reference Lusztig22], let
![]() ${U_{\mathcal Z}(\mathfrak {gl}_n)}$
be the Lusztig integral form of
${U_{\mathcal Z}(\mathfrak {gl}_n)}$
be the Lusztig integral form of
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
generated by
${{\mathbf {U}}(\mathfrak {gl}_n)}$
generated by
![]() $E_{i}^{(m)}, F_{i}^{(m)}$
,
$E_{i}^{(m)}, F_{i}^{(m)}$
,
![]() $K_{j}^{\pm 1}$
, and
$K_{j}^{\pm 1}$
, and
![]() $\big [{K_j;c \atop t}\big ](1 \leqslant i \leqslant n-1,1 \leqslant j \leqslant n, m, t \in \mathbb {N}, c \in \mathbb {Z})$
, where
$\big [{K_j;c \atop t}\big ](1 \leqslant i \leqslant n-1,1 \leqslant j \leqslant n, m, t \in \mathbb {N}, c \in \mathbb {Z})$
, where
 $$ \begin{align*}E_{i}^{(m)}=\frac{E_{i}^{m}}{[m]^!}, \quad F_{i}^{(m)}=\frac{F_{i}^{m}}{[m]^!} \quad \text{and} \quad \left[{K_{j}; c \atop t}\right]=\prod_{s=1}^{t} \frac{K_{j} v^{c-s+1}-K_{j}^{-1} v^{-c+s-1}}{v^{s}-v^{-s}}, \end{align*} $$
$$ \begin{align*}E_{i}^{(m)}=\frac{E_{i}^{m}}{[m]^!}, \quad F_{i}^{(m)}=\frac{F_{i}^{m}}{[m]^!} \quad \text{and} \quad \left[{K_{j}; c \atop t}\right]=\prod_{s=1}^{t} \frac{K_{j} v^{c-s+1}-K_{j}^{-1} v^{-c+s-1}}{v^{s}-v^{-s}}, \end{align*} $$
with
![]() $[m]^{!}=[1][2] \cdots [m]$
and
$[m]^{!}=[1][2] \cdots [m]$
and
![]() $[i]=\frac {v^{i}-v^{-i}}{v-v^{-1}}$
. The following result is given by Lusztig [Reference Lusztig21].
$[i]=\frac {v^{i}-v^{-i}}{v-v^{-1}}$
. The following result is given by Lusztig [Reference Lusztig21].
Lemma 2.1. The following formulas hold in
![]() ${U_{\mathcal Z}(\mathfrak {gl}_n)}:$
${U_{\mathcal Z}(\mathfrak {gl}_n)}:$
-
(1)
 $E_i^{(m)}\big [{K_j;c\atop t}\big ]=\big [{K_j;c+m(-\delta _{i,j}+\delta _{i+1,j})\atop t}\big ] E_i^{(m)};$
$E_i^{(m)}\big [{K_j;c\atop t}\big ]=\big [{K_j;c+m(-\delta _{i,j}+\delta _{i+1,j})\atop t}\big ] E_i^{(m)};$
-
(2)
 $F_i^{(m)}\big [{K_j;c\atop t}\big ]=\big [{K_j;c-m(-\delta _{i,j}+\delta _{i+1,j})\atop t}\big ] F_i^{(m)};$
$F_i^{(m)}\big [{K_j;c\atop t}\big ]=\big [{K_j;c-m(-\delta _{i,j}+\delta _{i+1,j})\atop t}\big ] F_i^{(m)};$
-
(3) For
 $k,l\in \mathbb N$
, we have
$k,l\in \mathbb N$
, we have  $$ \begin{align*}E_i^{(k)}F_i^{(l)}=\sum_{0\leqslant t\leqslant k\atop t\leqslant l}F_i^{(l-t)} \bigg[{\widetilde K_i;2t-k-l\atop t}\bigg]E_i^{(k-t)},\end{align*} $$
$$ \begin{align*}E_i^{(k)}F_i^{(l)}=\sum_{0\leqslant t\leqslant k\atop t\leqslant l}F_i^{(l-t)} \bigg[{\widetilde K_i;2t-k-l\atop t}\bigg]E_i^{(k-t)},\end{align*} $$
where
 $\big [ {\widetilde K_i;c \atop t} \big ] = \prod _{s=1}^t \frac {\widetilde K_iv^{c-s+1}-\widetilde K_i^{-1}v^{-c+s-1}}{v^s-v^{-s}}$
.
$\big [ {\widetilde K_i;c \atop t} \big ] = \prod _{s=1}^t \frac {\widetilde K_iv^{c-s+1}-\widetilde K_i^{-1}v^{-c+s-1}}{v^s-v^{-s}}$
.
Let
![]() $\Pi (n)=\{\alpha _i\mid 1\leqslant i\leqslant n-1\}$
, where
$\Pi (n)=\{\alpha _i\mid 1\leqslant i\leqslant n-1\}$
, where
![]() $\alpha _i=\boldsymbol {e}_i-\boldsymbol {e}_{i+1}$
with
$\alpha _i=\boldsymbol {e}_i-\boldsymbol {e}_{i+1}$
with
![]() $\boldsymbol e_i=(0,\ldots ,0,\underset i1,0\cdots ,0)\in \mathbb Z^n.$
We have the following direct sum decomposition:
$\boldsymbol e_i=(0,\ldots ,0,\underset i1,0\cdots ,0)\in \mathbb Z^n.$
We have the following direct sum decomposition:
 $$ \begin{align*} {{\mathbf{U}}(\mathfrak{gl}_n)}=\bigoplus\limits_{\nu\in\mathbb Z\Pi(n)}{{\mathbf{U}}(\mathfrak{gl}_n)}_\nu, \end{align*} $$
$$ \begin{align*} {{\mathbf{U}}(\mathfrak{gl}_n)}=\bigoplus\limits_{\nu\in\mathbb Z\Pi(n)}{{\mathbf{U}}(\mathfrak{gl}_n)}_\nu, \end{align*} $$
where
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}_\nu $
is defined by the conditions
${{\mathbf {U}}(\mathfrak {gl}_n)}_\nu $
is defined by the conditions
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu '}{{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu "}\subseteq {{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu '+\nu "}$
,
${{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu '}{{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu "}\subseteq {{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu '+\nu "}$
,
![]() $K_j^{\pm 1}\in {{\mathbf {U}}(\mathfrak {gl}_n)}_0$
,
$K_j^{\pm 1}\in {{\mathbf {U}}(\mathfrak {gl}_n)}_0$
,
![]() $E_i\in {{\mathbf {U}}(\mathfrak {gl}_n)}_{\alpha _i}$
,
$E_i\in {{\mathbf {U}}(\mathfrak {gl}_n)}_{\alpha _i}$
,
![]() $F_i\in {{\mathbf {U}}(\mathfrak {gl}_n)}_{-\alpha _i}$
for all
$F_i\in {{\mathbf {U}}(\mathfrak {gl}_n)}_{-\alpha _i}$
for all
![]() $\nu ',\nu "\in \mathbb Z\Pi (n)$
,
$\nu ',\nu "\in \mathbb Z\Pi (n)$
,
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() $1\leqslant j\leqslant n$
.
$1\leqslant j\leqslant n$
.
Following [Reference Lusztig23, 23.1], we introduce the modified quantum group
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
associated with
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
associated with
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
as follows. Let
${{\mathbf {U}}(\mathfrak {gl}_n)}$
as follows. Let
 $$ \begin{align*}\dot{{{\mathbf{U}}}}(\mathfrak{gl}_n)=\bigoplus\limits_{{\lambda},\mu\in\mathbb Z^{n}}{}_{\lambda}{{\mathbf{U}}(\mathfrak{gl}_n)}_\mu,\end{align*} $$
$$ \begin{align*}\dot{{{\mathbf{U}}}}(\mathfrak{gl}_n)=\bigoplus\limits_{{\lambda},\mu\in\mathbb Z^{n}}{}_{\lambda}{{\mathbf{U}}(\mathfrak{gl}_n)}_\mu,\end{align*} $$
where
 $$ \begin{align*}{}_{\lambda}{{\mathbf{U}}(\mathfrak{gl}_n)}_\mu={{\mathbf{U}}(\mathfrak{gl}_n)}/\left(\sum_{{\mathbf{j}}\in\mathbb Z^{n}}(K^{\mathbf{j}}- v^{{\lambda}\cdot{\mathbf{j}}}){{\mathbf{U}}(\mathfrak{gl}_n)}+\sum_{{\mathbf{j}}\in\mathbb Z^{n}}{{\mathbf{U}}(\mathfrak{gl}_n)}(K^{\mathbf{j}} -v^{\mu\cdot{\mathbf{j}}})\right),\end{align*} $$
$$ \begin{align*}{}_{\lambda}{{\mathbf{U}}(\mathfrak{gl}_n)}_\mu={{\mathbf{U}}(\mathfrak{gl}_n)}/\left(\sum_{{\mathbf{j}}\in\mathbb Z^{n}}(K^{\mathbf{j}}- v^{{\lambda}\cdot{\mathbf{j}}}){{\mathbf{U}}(\mathfrak{gl}_n)}+\sum_{{\mathbf{j}}\in\mathbb Z^{n}}{{\mathbf{U}}(\mathfrak{gl}_n)}(K^{\mathbf{j}} -v^{\mu\cdot{\mathbf{j}}})\right),\end{align*} $$
and
![]() ${\lambda }\cdot {\mathbf {j}}=\sum _{1\leqslant i\leqslant n}{\lambda }_ij_i$
. Let
${\lambda }\cdot {\mathbf {j}}=\sum _{1\leqslant i\leqslant n}{\lambda }_ij_i$
. Let
![]() $\pi _{{\lambda },\mu }: {{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {}_{{\lambda }}{{\mathbf {U}}(\mathfrak {gl}_n)}_{\mu }$
be the canonical projection.
$\pi _{{\lambda },\mu }: {{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {}_{{\lambda }}{{\mathbf {U}}(\mathfrak {gl}_n)}_{\mu }$
be the canonical projection.
We define the product in
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
as follows. For
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
as follows. For
![]() ${\lambda }', \mu ', {\lambda }", \mu " \in \mathbb Z^{n}$
with
${\lambda }', \mu ', {\lambda }", \mu " \in \mathbb Z^{n}$
with
![]() ${\lambda }'-\mu '$
,
${\lambda }'-\mu '$
,
![]() ${\lambda }"-\mu " \in \mathbb Z \Pi (n)$
and any
${\lambda }"-\mu " \in \mathbb Z \Pi (n)$
and any
![]() $t \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{{\lambda }'-\mu '}$
,
$t \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{{\lambda }'-\mu '}$
,
![]() $s \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{{\lambda }"-\mu "}$
, define
$s \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{{\lambda }"-\mu "}$
, define
 $$ \begin{align*}\pi_{{\lambda}',\mu'}(t) \pi_{{\lambda}", \mu"}(s)= \begin{cases}\pi_{{\lambda}',\mu"}(t s), & \text { if } \mu'={\lambda}" ,\\ 0 & \text { otherwise. }\end{cases} \end{align*} $$
$$ \begin{align*}\pi_{{\lambda}',\mu'}(t) \pi_{{\lambda}", \mu"}(s)= \begin{cases}\pi_{{\lambda}',\mu"}(t s), & \text { if } \mu'={\lambda}" ,\\ 0 & \text { otherwise. }\end{cases} \end{align*} $$
Then
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
becomes an associative
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
becomes an associative
![]() $\mathbb Q(v)$
-algebra with the above product. Moreover, the algebra
$\mathbb Q(v)$
-algebra with the above product. Moreover, the algebra
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
is naturally a
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
is naturally a
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
-bimodule defined by
${{\mathbf {U}}(\mathfrak {gl}_n)}$
-bimodule defined by
![]() $t' \pi _{{\lambda }', {\lambda }"}(s) t"=\pi _{{\lambda }'+\nu ', {\lambda }"-\nu "}(t' s t")$
for
$t' \pi _{{\lambda }', {\lambda }"}(s) t"=\pi _{{\lambda }'+\nu ', {\lambda }"-\nu "}(t' s t")$
for
![]() $t' \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu '}, s \in {{\mathbf {U}}(\mathfrak {gl}_n)}, t" \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu "}$
, and
$t' \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu '}, s \in {{\mathbf {U}}(\mathfrak {gl}_n)}, t" \in {{\mathbf {U}}(\mathfrak {gl}_n)}_{\nu "}$
, and
![]() ${\lambda }', {\lambda }" \in \mathbb Z^{n} .$
Let
${\lambda }', {\lambda }" \in \mathbb Z^{n} .$
Let
![]() $\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)$
be the
$\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)$
be the
![]() ${\mathcal Z}$
-subalgebra of
${\mathcal Z}$
-subalgebra of
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
generated by the elements
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
generated by the elements
![]() $E_{i}^{(m)} 1_{\lambda }$
and
$E_{i}^{(m)} 1_{\lambda }$
and
![]() $1_{\lambda } F_{i}^{(m)}$
for
$1_{\lambda } F_{i}^{(m)}$
for
![]() $1 \leqslant i \leqslant n-1$
and
$1 \leqslant i \leqslant n-1$
and
![]() $m \in \mathbb {N}$
, where
$m \in \mathbb {N}$
, where
![]() $1_{\lambda }=\pi _{\lambda , \lambda }(1)$
.
$1_{\lambda }=\pi _{\lambda , \lambda }(1)$
.
We now follow [Reference Dipper and James6] to recall the definition of q-Schur algebras as follows. The Hecke algebra
![]() ${{\mathcal H}_{\mathcal Z}(d)}$
associated with
${{\mathcal H}_{\mathcal Z}(d)}$
associated with
![]() ${\mathfrak S}_d$
is the
${\mathfrak S}_d$
is the
![]() ${\mathcal Z}$
-algebra generated by
${\mathcal Z}$
-algebra generated by
![]() $T_i$
(
$T_i$
(
![]() $1\leqslant i\leqslant d-1$
), with the following relations:
$1\leqslant i\leqslant d-1$
), with the following relations:
where
![]() $q=v^2$
. Let
$q=v^2$
. Let
![]() ${\boldsymbol {\mathcal H}}(d)={{\mathcal H}_{\mathcal Z}(d)}\otimes _{\mathcal Z}\mathbb Q(v)$
. If
${\boldsymbol {\mathcal H}}(d)={{\mathcal H}_{\mathcal Z}(d)}\otimes _{\mathcal Z}\mathbb Q(v)$
. If
![]() $w=s_{i_1}s_{i_2}\cdots s_{i_m}$
is reduced let
$w=s_{i_1}s_{i_2}\cdots s_{i_m}$
is reduced let
![]() $T_w=T_{i_1}T_{i_2}\cdots T_{i_m}$
. Then the set
$T_w=T_{i_1}T_{i_2}\cdots T_{i_m}$
. Then the set
![]() $\{T_w\mid w\in {\mathfrak S}_d\}$
forms a
$\{T_w\mid w\in {\mathfrak S}_d\}$
forms a
![]() ${\mathcal Z}$
-basis for
${\mathcal Z}$
-basis for
![]() ${{\mathcal H}_{\mathcal Z}(d)}$
. Let
${{\mathcal H}_{\mathcal Z}(d)}$
. Let
![]() $\Lambda (n,d)=\{{\lambda }\in \mathbb N^{n}\mid \sigma ({\lambda })=d\}$
, where
$\Lambda (n,d)=\{{\lambda }\in \mathbb N^{n}\mid \sigma ({\lambda })=d\}$
, where
![]() $\sigma ({\lambda })=\sum _{1\leqslant i\leqslant n}{\lambda }_i$
. For
$\sigma ({\lambda })=\sum _{1\leqslant i\leqslant n}{\lambda }_i$
. For
![]() ${\lambda }\in \Lambda (n,d)$
, let
${\lambda }\in \Lambda (n,d)$
, let
![]() $x_{{\lambda }}=\sum _{w\in {\mathfrak S}_{{\lambda }}}T_w$
, where
$x_{{\lambda }}=\sum _{w\in {\mathfrak S}_{{\lambda }}}T_w$
, where
![]() ${\mathfrak S}_{{\lambda }}$
is the Young subgroup of
${\mathfrak S}_{{\lambda }}$
is the Young subgroup of
![]() ${\mathfrak S}_d$
. The endomorphism algebras
${\mathfrak S}_d$
. The endomorphism algebras
 $$ \begin{align*}{\mathcal S}_{\mathcal Z}(n,d):=\operatorname{End}_{{{\mathcal H}_{\mathcal Z}(d)}}\bigg( \bigoplus_{{\lambda}\in\Lambda(n,d)}x_{{\lambda}}{{\mathcal H}_{\mathcal Z}(d)}\bigg),\quad {\boldsymbol{\mathcal S}}(n,d):=\operatorname{End}_{{\boldsymbol{\mathcal H}}(d)}\bigg( \bigoplus_{{\lambda}\in\Lambda(n,d)}x_{{\lambda}}{\boldsymbol{\mathcal H}}(d)\bigg),\end{align*} $$
$$ \begin{align*}{\mathcal S}_{\mathcal Z}(n,d):=\operatorname{End}_{{{\mathcal H}_{\mathcal Z}(d)}}\bigg( \bigoplus_{{\lambda}\in\Lambda(n,d)}x_{{\lambda}}{{\mathcal H}_{\mathcal Z}(d)}\bigg),\quad {\boldsymbol{\mathcal S}}(n,d):=\operatorname{End}_{{\boldsymbol{\mathcal H}}(d)}\bigg( \bigoplus_{{\lambda}\in\Lambda(n,d)}x_{{\lambda}}{\boldsymbol{\mathcal H}}(d)\bigg),\end{align*} $$
are called q-Schur algebras over
![]() ${\mathcal Z}$
and over
${\mathcal Z}$
and over
![]() $\mathbb Q(v)$
, respectively.
$\mathbb Q(v)$
, respectively.
We now recall the BLM construction of
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
. Let
${{\mathbf {U}}(\mathfrak {gl}_n)}$
. Let
![]() $\widetilde {\Theta }(n)$
be the set of all
$\widetilde {\Theta }(n)$
be the set of all
![]() $n \times n$
matrices over
$n \times n$
matrices over
![]() $\mathbb {Z}$
with all off diagonal entries in
$\mathbb {Z}$
with all off diagonal entries in
![]() $\mathbb {N}$
. Let
$\mathbb {N}$
. Let
![]() $\Theta (n)$
be the set of all
$\Theta (n)$
be the set of all
![]() $n\times n$
matrices over
$n\times n$
matrices over
![]() $\mathbb N$
. Let
$\mathbb N$
. Let
![]() ${\Theta (n,d)}$
be the set of all
${\Theta (n,d)}$
be the set of all
![]() $n \times n$
matrices A over
$n \times n$
matrices A over
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $\sigma (A)=d$
, where
$\sigma (A)=d$
, where
![]() $\sigma (A)=\sum _{1 \leqslant i, j \leqslant n} a_{i, j}$
. For
$\sigma (A)=\sum _{1 \leqslant i, j \leqslant n} a_{i, j}$
. For
![]() $A \in \widetilde {\Theta }(n)$
, let
$A \in \widetilde {\Theta }(n)$
, let
![]() $\operatorname {ro}(A)=(\sum _{j} a_{1, j}, \ldots , \sum _{j} a_{n, j})$
and
$\operatorname {ro}(A)=(\sum _{j} a_{1, j}, \ldots , \sum _{j} a_{n, j})$
and
![]() $\operatorname {co}(A)=$
$\operatorname {co}(A)=$
![]() $(\sum _{i} a_{i, 1}, \ldots , \sum _{i} a_{i, n})$
.
$(\sum _{i} a_{i, 1}, \ldots , \sum _{i} a_{i, n})$
.
The q-Schur algebra
![]() ${\mathcal S}_{\mathcal Z}(n,d)$
was reconstructed using the geometry of pairs of n-step filtrations on a d-dimensional vector space in [Reference Beilinson, Lusztig and MacPherson3]. In particular, a normalized
${\mathcal S}_{\mathcal Z}(n,d)$
was reconstructed using the geometry of pairs of n-step filtrations on a d-dimensional vector space in [Reference Beilinson, Lusztig and MacPherson3]. In particular, a normalized
![]() ${\mathcal Z}$
-basis
${\mathcal Z}$
-basis
![]() $\{[A]\}_{A \in {\Theta (n,d)}}$
for
$\{[A]\}_{A \in {\Theta (n,d)}}$
for
![]() ${\mathcal S}_{\mathcal Z}(n,d)$
was constructed. Using the stabilization property of multiplication for q-Schur algebra, an important
${\mathcal S}_{\mathcal Z}(n,d)$
was constructed. Using the stabilization property of multiplication for q-Schur algebra, an important
![]() ${\mathcal Z}$
-algebra
${\mathcal Z}$
-algebra
![]() $K_{\mathcal Z}(n)$
(without
$K_{\mathcal Z}(n)$
(without
![]() $ 1 $
), with basis
$ 1 $
), with basis
![]() $\{[A]\}_{A \in \widetilde {\Theta }(n)} $
, was constructed in [1, §4]. Let
$\{[A]\}_{A \in \widetilde {\Theta }(n)} $
, was constructed in [1, §4]. Let
![]() ${\mathbf K}(n)=K_{\mathcal Z}(n)\otimes _{\mathcal Z}\mathbb Q(v)$
. Following [Reference Beilinson, Lusztig and MacPherson3, 5.1], we define
${\mathbf K}(n)=K_{\mathcal Z}(n)\otimes _{\mathcal Z}\mathbb Q(v)$
. Following [Reference Beilinson, Lusztig and MacPherson3, 5.1], we define
![]() $\widehat {{\mathbf K}}(n)$
to be the vector space of all formal (possibly infinite)
$\widehat {{\mathbf K}}(n)$
to be the vector space of all formal (possibly infinite)
![]() $\mathbb {Q}(v)$
-linear combinations
$\mathbb {Q}(v)$
-linear combinations
![]() $\sum _{A \in \widetilde {\Theta }(n)} \beta _{A}[A]$
satisfying the following property: for any
$\sum _{A \in \widetilde {\Theta }(n)} \beta _{A}[A]$
satisfying the following property: for any
![]() ${\mathbf {x}} \in \mathbb Z^{n}$
, the sets
${\mathbf {x}} \in \mathbb Z^{n}$
, the sets
![]() $\{A \in \widetilde {\Theta }(n) \mid \beta _{A} \neq 0, \operatorname {ro}(A)={\mathbf {x}}\}$
and
$\{A \in \widetilde {\Theta }(n) \mid \beta _{A} \neq 0, \operatorname {ro}(A)={\mathbf {x}}\}$
and
![]() $\{A \in \widetilde {\Theta }(n) \mid \beta _{A} \neq 0, \operatorname {co}(A)={\mathbf {x}}\}$
are finite. The product of two elements
$\{A \in \widetilde {\Theta }(n) \mid \beta _{A} \neq 0, \operatorname {co}(A)={\mathbf {x}}\}$
are finite. The product of two elements
![]() $\sum _{A \in \widetilde {\Theta }(n)} \beta _{A}[A]$
,
$\sum _{A \in \widetilde {\Theta }(n)} \beta _{A}[A]$
,
![]() $\sum _{B \in \widetilde {\Theta }(n)} \gamma _{B}[B]$
in
$\sum _{B \in \widetilde {\Theta }(n)} \gamma _{B}[B]$
in
![]() $\widehat {{\mathbf K}}(n)$
is defined to be
$\widehat {{\mathbf K}}(n)$
is defined to be
![]() $\sum _{A, B} \beta _{A} \gamma _{B}[A] \cdot [B]$
, where
$\sum _{A, B} \beta _{A} \gamma _{B}[A] \cdot [B]$
, where
![]() $[A] \cdot [B]$
is the product in
$[A] \cdot [B]$
is the product in
![]() $K_{\mathcal Z}(n).$
Then
$K_{\mathcal Z}(n).$
Then
![]() $\widehat {{\mathbf K}}(n)$
is an associative algebra.
$\widehat {{\mathbf K}}(n)$
is an associative algebra.
Let
![]() $\Theta ^\pm (n)$
be the set of all
$\Theta ^\pm (n)$
be the set of all
![]() $A \in \Theta (n)$
such that all diagonal entries are zero. For
$A \in \Theta (n)$
such that all diagonal entries are zero. For
![]() $A \in \Theta ^\pm (n)$
and
$A \in \Theta ^\pm (n)$
and
![]() ${\mathbf {j}} \in \mathbb {Z}^{n}$
, let
${\mathbf {j}} \in \mathbb {Z}^{n}$
, let
 $$ \begin{align*}\begin{aligned} A({\mathbf{j}},d) &=\sum_{\lambda \in \Lambda(n,d-\sigma(A))} v^{\lambda \cdot {\mathbf{j}}}[A+\operatorname{diag}(\lambda)] \in {\boldsymbol{\mathcal S}}(n,d), \\ A({\mathbf{j}}) &=\sum_{\lambda \in \mathbb{Z}^{n}} v^{\lambda \cdot {\mathbf{j}}}[A+\operatorname{diag}(\lambda)] \in \widehat{{\mathbf K}}(n), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} A({\mathbf{j}},d) &=\sum_{\lambda \in \Lambda(n,d-\sigma(A))} v^{\lambda \cdot {\mathbf{j}}}[A+\operatorname{diag}(\lambda)] \in {\boldsymbol{\mathcal S}}(n,d), \\ A({\mathbf{j}}) &=\sum_{\lambda \in \mathbb{Z}^{n}} v^{\lambda \cdot {\mathbf{j}}}[A+\operatorname{diag}(\lambda)] \in \widehat{{\mathbf K}}(n), \end{aligned} \end{align*} $$
where
![]() ${\lambda }\cdot{{\mathbf {j}}}=\sum _{1\leqslant i\leqslant n}{\lambda }_i{j_i}$
.
${\lambda }\cdot{{\mathbf {j}}}=\sum _{1\leqslant i\leqslant n}{\lambda }_i{j_i}$
.
We shall denote by
![]() $\mathbf {V}(n)$
the subspace of
$\mathbf {V}(n)$
the subspace of
![]() $\widehat {{\mathbf K}}(n)$
spanned by the elements
$\widehat {{\mathbf K}}(n)$
spanned by the elements
![]() $A({\mathbf {j}})$
for
$A({\mathbf {j}})$
for
![]() $A \in \Theta ^{\pm }(n)$
and
$A \in \Theta ^{\pm }(n)$
and
![]() ${\mathbf {j}} \in \mathbb {Z}^{n}$
. For
${\mathbf {j}} \in \mathbb {Z}^{n}$
. For
![]() $1 \leqslant i, j \leqslant n$
, let
$1 \leqslant i, j \leqslant n$
, let
![]() $E_{i, j} \in \Theta (n)$
be the matrix whose
$E_{i, j} \in \Theta (n)$
be the matrix whose
![]() $(i,j)$
-entry is
$(i,j)$
-entry is
![]() $1$
and the other entries are
$1$
and the other entries are
![]() $0$
. The following result was given by Beilinson–Lusztig–MacPherson [Reference Beilinson, Lusztig and MacPherson3].
$0$
. The following result was given by Beilinson–Lusztig–MacPherson [Reference Beilinson, Lusztig and MacPherson3].
Theorem 2.2.
![]() $(1)$
$(1)$
![]() $\mathbf {V}(n)$
is a subalgebra of
$\mathbf {V}(n)$
is a subalgebra of
![]() $\widehat {{\mathbf K}}(n)$
and there is an algebra isomorphism
$\widehat {{\mathbf K}}(n)$
and there is an algebra isomorphism
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}\stackrel {\thicksim }{\,\rightarrow }\mathbf {V}(n)$
satisfying
${{\mathbf {U}}(\mathfrak {gl}_n)}\stackrel {\thicksim }{\,\rightarrow }\mathbf {V}(n)$
satisfying
![]() $(2)$
There is an algebra epimorphism
$(2)$
There is an algebra epimorphism
![]() $\zeta _d:{{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
satisfying
$\zeta _d:{{\mathbf {U}}(\mathfrak {gl}_n)}\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
satisfying
We shall identify
![]() ${{\mathbf {U}}(\mathfrak {gl}_n)}$
with
${{\mathbf {U}}(\mathfrak {gl}_n)}$
with
![]() $\mathbf {V}(n)$
. By [Reference Du and Fu14] we have the following result (cf. [Reference Fu17]).
$\mathbf {V}(n)$
. By [Reference Du and Fu14] we have the following result (cf. [Reference Fu17]).
Lemma 2.3.
![]() $(1)$
There is an algebra isomorphism
$(1)$
There is an algebra isomorphism
![]() $\varphi :\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)\rightarrow {\mathbf K}(n)$
satisfying
$\varphi :\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)\rightarrow {\mathbf K}(n)$
satisfying
for all
![]() $u\in {{\mathbf {U}}(\mathfrak {gl}_n)}$
and
$u\in {{\mathbf {U}}(\mathfrak {gl}_n)}$
and
![]() ${\lambda },\mu \in \mathbb Z^{n}$
. Furthermore, we have
${\lambda },\mu \in \mathbb Z^{n}$
. Furthermore, we have
![]() $\varphi (\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n))=K_{\mathcal Z}(n)$
.
$\varphi (\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n))=K_{\mathcal Z}(n)$
.
![]() $(2)$
There is a surjective algebra homomorphism
$(2)$
There is a surjective algebra homomorphism
![]() $\dot {\zeta }_d:{\mathbf K}(n)\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
such that
$\dot {\zeta }_d:{\mathbf K}(n)\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
such that
 $$ \begin{align*} { \dot{\zeta}_d([A])=\begin{cases}[A], &\text{ if } A\in{\Theta(n,d)};\\ 0, &\text{ otherwise.} \end{cases}} \end{align*} $$
$$ \begin{align*} { \dot{\zeta}_d([A])=\begin{cases}[A], &\text{ if } A\in{\Theta(n,d)};\\ 0, &\text{ otherwise.} \end{cases}} \end{align*} $$
We shall identify
![]() $\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)$
with
$\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)$
with
![]() $K_{\mathcal Z}(n)$
.
$K_{\mathcal Z}(n)$
.
3 The infinitesimal q-Schur algebra 
Let ![]() . We shall denote the images of
. We shall denote the images of
![]() $E_{i}^{(m)}, F_{i}^{(m)}$
, etc. in
$E_{i}^{(m)}, F_{i}^{(m)}$
, etc. in ![]() by the same letters. Let
by the same letters. Let ![]() (resp.
(resp. ![]() ) be the subalgebra of
) be the subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}$
(resp.
$E_{i}^{(m)}$
(resp.
![]() $F_{i}^{(m)}$
) for
$F_{i}^{(m)}$
) for
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() $m\in \mathbb N$
. Let
$m\in \mathbb N$
. Let ![]() be the subalgebra of
be the subalgebra of ![]() generated by the elements
generated by the elements
![]() $K_{j}^{\pm 1}$
and
$K_{j}^{\pm 1}$
and
![]() $\big [{K_j;0 \atop t} \big ]$
for
$\big [{K_j;0 \atop t} \big ]$
for
![]() $1 \leqslant j \leqslant n$
and
$1 \leqslant j \leqslant n$
and
![]() $t \in \mathbb {N}$
. Then we have
$t \in \mathbb {N}$
. Then we have ![]() . The algebras
. The algebras ![]() and
and ![]() are both
are both
![]() $\mathbb {N}$
-graded in terms of the degrees of monomials in the
$\mathbb {N}$
-graded in terms of the degrees of monomials in the
![]() $E_{i}^{(m)}$
and
$E_{i}^{(m)}$
and
![]() $F_{i}^{(m)}$
.
$F_{i}^{(m)}$
.
For
![]() $r\geqslant 1$
, let
$r\geqslant 1$
, let ![]() be the
be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}$
,
$E_{i}^{(m)}$
,
![]() $F_{i}^{(m)}$
,
$F_{i}^{(m)}$
,
![]() $K_{j}^{\pm 1}$
, and
$K_{j}^{\pm 1}$
, and
![]() $\big [{K_j;0 \atop t} \big ]$
for
$\big [{K_j;0 \atop t} \big ]$
for
![]() $1 \leqslant i \leqslant n-1$
,
$1 \leqslant i \leqslant n-1$
,
![]() $1 \leqslant j \leqslant n$
,
$1 \leqslant j \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $0 \leqslant m,t<l p^{r-1}$
. Furthermore, let
$0 \leqslant m,t<l p^{r-1}$
. Furthermore, let
Clearly, the algebra ![]() is a Hopf subalgebra of
is a Hopf subalgebra of ![]() . Let
. Let ![]() (resp.
(resp. ![]() ) be the subalgebra of
) be the subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}$
(resp.
$E_{i}^{(m)}$
(resp.
![]() $F_{i}^{(m)}$
) for
$F_{i}^{(m)}$
) for
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() $0 \leqslant m<l p^{r-1}$
. Then we have
$0 \leqslant m<l p^{r-1}$
. Then we have ![]() .
.
Let
![]() $\Theta ^+(n)=\left \{A \in \Theta (n) \mid a_{i, j}=0, \forall i \geqslant j\right \}$
and
$\Theta ^+(n)=\left \{A \in \Theta (n) \mid a_{i, j}=0, \forall i \geqslant j\right \}$
and
![]() $\Theta ^-(n)=\left \{A \in \Theta (n) \mid a_{i, j}=0, \forall i \leqslant j\right \}$
. For
$\Theta ^-(n)=\left \{A \in \Theta (n) \mid a_{i, j}=0, \forall i \leqslant j\right \}$
. For
![]() $A \in \widetilde \Theta (n)$
, write
$A \in \widetilde \Theta (n)$
, write
![]() $A=A^{+}+\operatorname {diag}({\lambda })+A^{-}$
with
$A=A^{+}+\operatorname {diag}({\lambda })+A^{-}$
with
![]() $A^{+} \in \Theta ^+(n)$
,
$A^{+} \in \Theta ^+(n)$
,
![]() $A^{-} \in \Theta ^-(n)$
and
$A^{-} \in \Theta ^-(n)$
and
![]() ${\lambda }\in \mathbb Z^{n}$
. Let
${\lambda }\in \mathbb Z^{n}$
. Let
Let
For
![]() $A \in \Theta ^\pm (n)_r$
, let
$A \in \Theta ^\pm (n)_r$
, let
where
and
For
![]() $A \in \Theta ^\pm (n)$
let
$A \in \Theta ^\pm (n)$
let
 $$ \begin{align*}\operatorname{deg}(A)= \sum_{1 \leqslant i, j \leqslant n}|j-i| a_{i, j}.\end{align*} $$
$$ \begin{align*}\operatorname{deg}(A)= \sum_{1 \leqslant i, j \leqslant n}|j-i| a_{i, j}.\end{align*} $$
Then we have
![]() $\textrm {deg}(E^{(A^+)})=\textrm {deg}(A^+)$
and
$\textrm {deg}(E^{(A^+)})=\textrm {deg}(A^+)$
and
![]() $\textrm {deg}(F^{(A^-)})=\textrm { deg}(A^-)$
for
$\textrm {deg}(F^{(A^-)})=\textrm { deg}(A^-)$
for
![]() $A\in \Theta ^\pm (n)$
. For
$A\in \Theta ^\pm (n)$
. For
![]() ${\lambda }\in \mathbb N^{n}$
and
${\lambda }\in \mathbb N^{n}$
and
![]() ${\mathbf {j}}\in \mathbb Z^{n}$
let
${\mathbf {j}}\in \mathbb Z^{n}$
let
 $$ \begin{align*}K_{\lambda}=\prod_{1 \leqslant i \leqslant n}\bigg[ {K_i;0 \atop {\lambda}_i} \bigg],\,K^{{\mathbf{j}}}=\prod_{1 \leqslant i \leqslant n}K_i^{j_i}.\end{align*} $$
$$ \begin{align*}K_{\lambda}=\prod_{1 \leqslant i \leqslant n}\bigg[ {K_i;0 \atop {\lambda}_i} \bigg],\,K^{{\mathbf{j}}}=\prod_{1 \leqslant i \leqslant n}K_i^{j_i}.\end{align*} $$
The following result is given in [Reference Fu18, Lem. 6.3].
Proposition 3.1.
![]() $(1)$
The set
$(1)$
The set
![]() $\big \{E^{(A^+)} K^\delta K_{\lambda } F^{(A^-)} \mid A \in \Theta ^\pm (n)_r,\, \delta ,{\lambda } \in \mathbb N^{n},\, \delta _{i} \in \{0,1\},\,\forall i\big \}$
forms a
$\big \{E^{(A^+)} K^\delta K_{\lambda } F^{(A^-)} \mid A \in \Theta ^\pm (n)_r,\, \delta ,{\lambda } \in \mathbb N^{n},\, \delta _{i} \in \{0,1\},\,\forall i\big \}$
forms a ![]() -basis for
-basis for ![]() .
.
![]() $(2)$
The set
$(2)$
The set
![]() $\big \{E^{(A^+)} \mid A \in \Theta ^+(n)_r\}$
(resp.
$\big \{E^{(A^+)} \mid A \in \Theta ^+(n)_r\}$
(resp.
![]() $\big \{F^{(A^-)} \mid A \in \Theta ^-(n)_r\}$
) forms a
$\big \{F^{(A^-)} \mid A \in \Theta ^-(n)_r\}$
) forms a ![]() -basis for
-basis for ![]() (resp.
(resp. ![]() ).
).
For
![]() $A\in \widetilde \Theta (n)$
let
$A\in \widetilde \Theta (n)$
let
 $$ \begin{align*}\sigma_{i,j}(A) =\begin{cases} \sum_{s\leqslant i;t\geqslant j}a_{s,t}&\text{if } i<j\\ \sum_{s\geqslant i;t\leqslant j}a_{s,t}&\text{if } i>j. \end{cases}\end{align*} $$
$$ \begin{align*}\sigma_{i,j}(A) =\begin{cases} \sum_{s\leqslant i;t\geqslant j}a_{s,t}&\text{if } i<j\\ \sum_{s\geqslant i;t\leqslant j}a_{s,t}&\text{if } i>j. \end{cases}\end{align*} $$
Following [Reference Beilinson, Lusztig and MacPherson3], for
![]() $A,B\in \widetilde \Theta (n)$
, define
$A,B\in \widetilde \Theta (n)$
, define
![]() $B \preccurlyeq A$
if and only if
$B \preccurlyeq A$
if and only if
![]() $\sigma _{i,j}( B )\leqslant \sigma _{i,j}(A)$
for all
$\sigma _{i,j}( B )\leqslant \sigma _{i,j}(A)$
for all
![]() $i\not =j$
. Put
$i\not =j$
. Put
![]() $ B \prec A$
if
$ B \prec A$
if
![]() $ B \preccurlyeq A$
and
$ B \preccurlyeq A$
and
![]() $\sigma _{i,j}( B )<\sigma _{i,j}(A)$
for some
$\sigma _{i,j}( B )<\sigma _{i,j}(A)$
for some
![]() $i\not =j$
.
$i\not =j$
.
Proposition 3.2.
![]() $(1)$
The set
$(1)$
The set
![]() $\big \{A^+(\mathbf {0}) K^\delta K_{\lambda } A^-(\mathbf {0}) \mid A \in \Theta ^\pm (n)_r,\,\delta ,\lambda \in \mathbb {N}^{n},\, \delta _{i} \in \{0,1\}, \forall i \big \}$
forms a -basis for
$\big \{A^+(\mathbf {0}) K^\delta K_{\lambda } A^-(\mathbf {0}) \mid A \in \Theta ^\pm (n)_r,\,\delta ,\lambda \in \mathbb {N}^{n},\, \delta _{i} \in \{0,1\}, \forall i \big \}$
forms a -basis for ![]() .
.
![]() $(2)$
The set
$(2)$
The set
![]() $\big \{A(\mathbf {0}) \mid A \in \Theta ^+(n)_r\}$
(resp.
$\big \{A(\mathbf {0}) \mid A \in \Theta ^+(n)_r\}$
(resp.
![]() $\big \{A(\mathbf {0}) \mid A \in \Theta ^-(n)_r\}$
) forms a
$\big \{A(\mathbf {0}) \mid A \in \Theta ^-(n)_r\}$
) forms a ![]() -basis for
-basis for ![]() (resp.
(resp. ![]() ).
).
Proof. By [Reference Beilinson, Lusztig and MacPherson3, 4.6(c)] for
![]() $A \in \Theta ^\pm (n)_r$
, we have
$A \in \Theta ^\pm (n)_r$
, we have
where f is a ![]() -linear combination of
-linear combination of
![]() $B(\mathbf {0})$
for
$B(\mathbf {0})$
for
![]() $B\in \Theta ^+(n)$
with
$B\in \Theta ^+(n)$
with
![]() $B\prec A^+$
and g is a
$B\prec A^+$
and g is a ![]() -linear combination of
-linear combination of
![]() $C(\mathbf {0})$
for
$C(\mathbf {0})$
for
![]() $C\in \Theta ^-(n)$
with
$C\in \Theta ^-(n)$
with
![]() $C\prec A^-$
. By [Reference Fu18, Lem. 6.3] we know that f must a
$C\prec A^-$
. By [Reference Fu18, Lem. 6.3] we know that f must a ![]() -linear combination of
-linear combination of
![]() $B(\mathbf {0})$
for
$B(\mathbf {0})$
for
![]() $B\in \Theta ^+(n)_r$
with
$B\in \Theta ^+(n)_r$
with
![]() $B\prec A^+$
and g is a
$B\prec A^+$
and g is a ![]() -linear combination of
-linear combination of
![]() $C(\mathbf {0})$
for
$C(\mathbf {0})$
for
![]() $C\in \Theta ^-(n)_r$
with
$C\in \Theta ^-(n)_r$
with
![]() $C\prec A^-$
. Now the assertion follows from Proposition 3.1.
$C\prec A^-$
. Now the assertion follows from Proposition 3.1.
Let ![]() . We shall denote the images of
. We shall denote the images of
![]() $E_{i}^{(m)}1_{\lambda }$
,
$E_{i}^{(m)}1_{\lambda }$
,
![]() $1_{\lambda } F_{i}^{(m)}$
,
$1_{\lambda } F_{i}^{(m)}$
,
![]() $E^{(A^+)} 1_{\lambda }$
,
$E^{(A^+)} 1_{\lambda }$
,
![]() $1_{\lambda }F^{(A^-)}$
in
$1_{\lambda }F^{(A^-)}$
in ![]() by the same letters. For
by the same letters. For
![]() $A\in \widetilde \Theta (n)$
let
$A\in \widetilde \Theta (n)$
let
Let ![]() be the
be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}1_{\lambda }$
and
$E_{i}^{(m)}1_{\lambda }$
and
![]() $1_{\lambda } F_{i}^{(m)}$
for
$1_{\lambda } F_{i}^{(m)}$
for
![]() $1 \leqslant i \leqslant n-1$
,
$1 \leqslant i \leqslant n-1$
,
![]() $\lambda \in \mathbb Z^{n}$
and
$\lambda \in \mathbb Z^{n}$
and
![]() $0 \leqslant m<l p^{r-1}$
.
$0 \leqslant m<l p^{r-1}$
.
For
![]() $ A \in \widetilde \Theta (n)$
and
$ A \in \widetilde \Theta (n)$
and
![]() $1 \leqslant i \leqslant n$
, let
$1 \leqslant i \leqslant n$
, let
where
![]() $ \sigma _{i}(A)=a_{i,i}+\sum _{1 \leqslant j<i}(a_{i j}+a_{j i})$
. Let
$ \sigma _{i}(A)=a_{i,i}+\sum _{1 \leqslant j<i}(a_{i j}+a_{j i})$
. Let
We have the following monomial, BLM and PBW bases of ![]() .
.
Proposition 3.3. Each of the following sets forms a ![]() -basis of
-basis of ![]() :
:
-
(1)
 ${\mathscr M}_r:=\{E^{(A^+)} 1_{{\boldsymbol \sigma }(A)} F^{(A^-)} \mid A\in \widetilde \Theta (n)_r\};$
${\mathscr M}_r:=\{E^{(A^+)} 1_{{\boldsymbol \sigma }(A)} F^{(A^-)} \mid A\in \widetilde \Theta (n)_r\};$
-
(2)
 ${\mathscr L}_r:=\{[A]_{\varepsilon }\mid A\in \widetilde \Theta (n)_r\};$
${\mathscr L}_r:=\{[A]_{\varepsilon }\mid A\in \widetilde \Theta (n)_r\};$
-
(3)
 ${\mathscr P}_r:=\{A^+(\mathbf {0}) 1_{{\boldsymbol \sigma }(A)} A^-(\mathbf {0}) \mid A\in \widetilde \Theta (n)_r\}$
.
${\mathscr P}_r:=\{A^+(\mathbf {0}) 1_{{\boldsymbol \sigma }(A)} A^-(\mathbf {0}) \mid A\in \widetilde \Theta (n)_r\}$
.
Proof. Let ![]() be the
be the ![]() -submodule of
-submodule of ![]() spanned by the elements
spanned by the elements
![]() $[A]_{\varepsilon }$
for
$[A]_{\varepsilon }$
for
![]() $A\in \widetilde \Theta (n)_r$
. By [Reference Beilinson, Lusztig and MacPherson3, 4.6(a)] for
$A\in \widetilde \Theta (n)_r$
. By [Reference Beilinson, Lusztig and MacPherson3, 4.6(a)] for
![]() $1\leqslant h\leqslant n-1$
,
$1\leqslant h\leqslant n-1$
,
![]() $0\leqslant m<lp^{r-1}$
,
$0\leqslant m<lp^{r-1}$
,
![]() $A\in \widetilde \Theta (n)_r$
, we have
$A\in \widetilde \Theta (n)_r$
, we have
 $$ \begin{align*}E_h^{(m)} [A]_{\varepsilon}=\sum_{{\mathbf{t}}\in\Lambda(n,m)\atop a_{h+1,u}\geqslant t_u,\,\forall u\not=h+1}\varepsilon^{\beta({\mathbf{t}})} \prod_{1\leq u\leq n}{\bigg[{a_{h,u}+t_u\atop t_u}\bigg]_{\varepsilon}}\big[A+\sum_{1\leq u\leq n}t_u(E_{h,u}-E_{h+1,u})\big]_{\varepsilon},\end{align*} $$
$$ \begin{align*}E_h^{(m)} [A]_{\varepsilon}=\sum_{{\mathbf{t}}\in\Lambda(n,m)\atop a_{h+1,u}\geqslant t_u,\,\forall u\not=h+1}\varepsilon^{\beta({\mathbf{t}})} \prod_{1\leq u\leq n}{\bigg[{a_{h,u}+t_u\atop t_u}\bigg]_{\varepsilon}}\big[A+\sum_{1\leq u\leq n}t_u(E_{h,u}-E_{h+1,u})\big]_{\varepsilon},\end{align*} $$
where
![]() $\beta ({\mathbf {t}})=\sum _{j> u}(a_{h,j}-a_{h+1,j})t_u+\sum _{u<u'}t_ut_{u'}$
. If
$\beta ({\mathbf {t}})=\sum _{j> u}(a_{h,j}-a_{h+1,j})t_u+\sum _{u<u'}t_ut_{u'}$
. If
![]() $A+\sum _{u}t_u(E_{h,u}-E_{h+1,u})\not \in \widetilde \Theta (n)_r$
for some
$A+\sum _{u}t_u(E_{h,u}-E_{h+1,u})\not \in \widetilde \Theta (n)_r$
for some
![]() ${\mathbf {t}}\in \Lambda (n,m)$
, then we have
${\mathbf {t}}\in \Lambda (n,m)$
, then we have
![]() $a_{h,u}+t_u\geqslant lp^{r-1}$
for some
$a_{h,u}+t_u\geqslant lp^{r-1}$
for some
![]() $u\not =h$
. Since
$u\not =h$
. Since
![]() $A\in \widetilde \Theta (n)_r$
,
$A\in \widetilde \Theta (n)_r$
,
![]() ${\mathbf {t}}\in \Lambda (n,m)$
and
${\mathbf {t}}\in \Lambda (n,m)$
and
![]() $m<lp^{r-1}$
, we have
$m<lp^{r-1}$
, we have
![]() $a_{h,u}<lp^{r-1}$
and
$a_{h,u}<lp^{r-1}$
and
![]() $t_u<lp^{r-1}$
. Hence, by [Reference Fu18, Cor. 3.4] we have
$t_u<lp^{r-1}$
. Hence, by [Reference Fu18, Cor. 3.4] we have
![]() $\big [{a_{h,u}+t_u\atop t_u}\big ]_{\varepsilon }=0$
. Therefore, we have
$\big [{a_{h,u}+t_u\atop t_u}\big ]_{\varepsilon }=0$
. Therefore, we have
Similarly, we have
for
![]() $1\leqslant h\leqslant n-1$
and
$1\leqslant h\leqslant n-1$
and
![]() $0\leqslant m<lp^{r-1}$
. Consequently, we have
$0\leqslant m<lp^{r-1}$
. Consequently, we have
Furthermore, by [Reference Beilinson, Lusztig and MacPherson3, 4.6(c)] for
![]() $A \in \widetilde \Theta (n)_r$
,
$A \in \widetilde \Theta (n)_r$
,
where f is a ![]() -linear combination of
-linear combination of
![]() $[B]_{\varepsilon }$
for
$[B]_{\varepsilon }$
for
![]() $B\in \widetilde \Theta (n)$
with
$B\in \widetilde \Theta (n)$
with
![]() $B\prec A$
. By (3.3), we see that f must be a
$B\prec A$
. By (3.3), we see that f must be a ![]() -linear combination of
-linear combination of
![]() $[B]_{\varepsilon }$
for
$[B]_{\varepsilon }$
for
![]() $B\in \widetilde \Theta (n)_r$
with
$B\in \widetilde \Theta (n)_r$
with
![]() $B\prec A$
. It follows from (3.2) that
$B\prec A$
. It follows from (3.2) that
where g is a ![]() -linear combination of
-linear combination of
![]() $[B]_{\varepsilon }$
for
$[B]_{\varepsilon }$
for
![]() $B\in \widetilde \Theta (n)_r$
with
$B\in \widetilde \Theta (n)_r$
with
![]() $B\prec A$
. Therefore, each of the sets
$B\prec A$
. Therefore, each of the sets
![]() ${\mathscr M}_r$
,
${\mathscr M}_r$
,
![]() ${\mathscr L}_r$
,
${\mathscr L}_r$
,
![]() ${\mathscr P}_r$
forms a
${\mathscr P}_r$
forms a ![]() -basis of
-basis of ![]() and
and
Hence, by (3.3) we have ![]() . The proof is completed.
. The proof is completed.
Let ![]() . By [Reference Du13] we have
. By [Reference Du13] we have
![]() $\zeta _d({U_{\mathcal Z}(\mathfrak {gl}_n)})={\mathcal S}_{\mathcal Z}(n,d)$
. Therefore, the map
$\zeta _d({U_{\mathcal Z}(\mathfrak {gl}_n)})={\mathcal S}_{\mathcal Z}(n,d)$
. Therefore, the map
![]() $\zeta _d: {{\mathbf {U}}(\mathfrak {gl}_n)} \rightarrow {\boldsymbol {\mathcal S}}(n,d)$
given in Theorem 2.2 restricts to a surjective algebra homomorphism
$\zeta _d: {{\mathbf {U}}(\mathfrak {gl}_n)} \rightarrow {\boldsymbol {\mathcal S}}(n,d)$
given in Theorem 2.2 restricts to a surjective algebra homomorphism
A generating set for the kernel of
![]() $\zeta _{d}:{U_{\mathcal Z}(\mathfrak {gl}_n)} \rightarrow {\mathcal S}_{\mathcal Z}(n,d)$
was given in [Reference Fu and Gao19]. The map
$\zeta _{d}:{U_{\mathcal Z}(\mathfrak {gl}_n)} \rightarrow {\mathcal S}_{\mathcal Z}(n,d)$
was given in [Reference Fu and Gao19]. The map
![]() $\zeta _{d}$
induces, upon tensoring with
$\zeta _{d}$
induces, upon tensoring with ![]() , a surjective algebra homomorphism
, a surjective algebra homomorphism
Let
for
![]() $1 \leqslant i \leqslant n-1$
and
$1 \leqslant i \leqslant n-1$
and
![]() $1\leqslant j \leqslant n$
. For
$1\leqslant j \leqslant n$
. For
![]() $A \in \Theta (n)$
and
$A \in \Theta (n)$
and
![]() ${\lambda }\in \mathbb N^{n} $
, let
${\lambda }\in \mathbb N^{n} $
, let
For
![]() $ A \in {\Theta (n,d)}$
, let
$ A \in {\Theta (n,d)}$
, let
By [Reference Du and Parshall15, Cor. 5.3], we have
for
![]() ${\lambda }\in \Lambda (n,d)$
.
${\lambda }\in \Lambda (n,d)$
.
Let ![]() be the infinitesimal q-Schur algebra introduced in [Reference Cox4]. The algebra
be the infinitesimal q-Schur algebra introduced in [Reference Cox4]. The algebra ![]() is a
is a ![]() -subalgebra of the q-Schur algebra
-subalgebra of the q-Schur algebra ![]() . Let
. Let
According to [Reference Cox4, 5.3.1] and the proof of [Reference Fu16, Th. 5.5], we have the following result.
Lemma 3.4. The set
![]() ${\mathscr L}_{d,r}:=\{[A]_{\varepsilon } \mid A \in \Theta (n,d)_r\}$
forms a
${\mathscr L}_{d,r}:=\{[A]_{\varepsilon } \mid A \in \Theta (n,d)_r\}$
forms a ![]() -basis of
-basis of ![]() .
.
By [Reference Fu18, Prop. 6.4], we have the following result.
Lemma 3.5. For
![]() $d\in \mathbb N$
we have
$d\in \mathbb N$
we have ![]()
The map
![]() $\dot {\zeta }_d: \dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)={\mathbf K}(n)\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
given in Lemma 2.3 restricts to a surjective algebra homomorphism
$\dot {\zeta }_d: \dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)={\mathbf K}(n)\rightarrow {\boldsymbol {\mathcal S}}(n,d)$
given in Lemma 2.3 restricts to a surjective algebra homomorphism
tensoring with ![]() , we obtain a surjective algebra homomorphism
, we obtain a surjective algebra homomorphism
Combining Lemma 2.3 with Proposition 3.3, we obtain the following result.
Lemma 3.6. For
![]() $d\in \mathbb N$
we have
$d\in \mathbb N$
we have ![]() .
.
For
![]() ${\lambda },\mu \in \mathbb Z^{n}$
, write
${\lambda },\mu \in \mathbb Z^{n}$
, write
![]() ${\lambda }\leqslant \mu \Leftrightarrow {\lambda }_i\leqslant \mu _i$
for
${\lambda }\leqslant \mu \Leftrightarrow {\lambda }_i\leqslant \mu _i$
for
![]() $1\leqslant i\leqslant n$
. We have the following monomial and PBW bases of
$1\leqslant i\leqslant n$
. We have the following monomial and PBW bases of ![]() .
.
Proposition 3.7. Each of the following set forms a ![]() -basis of
-basis of ![]() :
:
-
(1)
 ${\mathscr M}_{d,r}=\{{\mathtt e}^{(A^+)}\mathtt {k}_{{\lambda }} {\mathtt f}^{(A^-)} \mid A \in \Theta ^\pm (n)_r,\,{\lambda }\in \Lambda (n,d),\,{\lambda }\geqslant {\boldsymbol \sigma }(A)\};$
${\mathscr M}_{d,r}=\{{\mathtt e}^{(A^+)}\mathtt {k}_{{\lambda }} {\mathtt f}^{(A^-)} \mid A \in \Theta ^\pm (n)_r,\,{\lambda }\in \Lambda (n,d),\,{\lambda }\geqslant {\boldsymbol \sigma }(A)\};$
-
(2)
 ${\mathscr P}_{d,r}=\{A^+(\mathbf {0},d) \mathtt {k}_{{\lambda }} A^-(\mathbf {0},d) \mid A \in \Theta ^\pm (n)_r,\,{\lambda }\in \Lambda (n,d),\,{\lambda }\geqslant {\boldsymbol \sigma }(A)\}.$
${\mathscr P}_{d,r}=\{A^+(\mathbf {0},d) \mathtt {k}_{{\lambda }} A^-(\mathbf {0},d) \mid A \in \Theta ^\pm (n)_r,\,{\lambda }\in \Lambda (n,d),\,{\lambda }\geqslant {\boldsymbol \sigma }(A)\}.$
Proof. By Lemma 2.3, (3.4), (3.5), and (3.8), for
![]() $A \in \Theta ^\pm (n)_r$
,
$A \in \Theta ^\pm (n)_r$
,
![]() ${\lambda }\in \Lambda (n,d)$
with
${\lambda }\in \Lambda (n,d)$
with
![]() ${\lambda }\geqslant {\boldsymbol \sigma }(A)$
, we have
${\lambda }\geqslant {\boldsymbol \sigma }(A)$
, we have
 $$ \begin{align*} \begin{aligned} {\mathtt e}^{(A^+)} \mathtt{k}_{{\lambda}} {\mathtt f}^{(A^-)} &=\dot{\zeta}_{d}(E^{(A^+)} 1_{{\lambda}}F^{(A^-)})=[A+{\lambda}-{\boldsymbol\sigma}(A)]_{\varepsilon} +f,\\ A^+(\mathbf{0},d) \mathtt{k}_{{\lambda}} A^-(\mathbf{0},d) &=[A+{\lambda}-{\boldsymbol\sigma}(A)]_{\varepsilon} +g,\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\mathtt e}^{(A^+)} \mathtt{k}_{{\lambda}} {\mathtt f}^{(A^-)} &=\dot{\zeta}_{d}(E^{(A^+)} 1_{{\lambda}}F^{(A^-)})=[A+{\lambda}-{\boldsymbol\sigma}(A)]_{\varepsilon} +f,\\ A^+(\mathbf{0},d) \mathtt{k}_{{\lambda}} A^-(\mathbf{0},d) &=[A+{\lambda}-{\boldsymbol\sigma}(A)]_{\varepsilon} +g,\\ \end{aligned} \end{align*} $$
where ![]() . Now the assertion follows from Lemma 3.4.
. Now the assertion follows from Lemma 3.4.
4 The algebra 
For
![]() $d\in \mathbb N$
let
$d\in \mathbb N$
let
where
![]() $I_{d,r}$
is the two-sided ideal of
$I_{d,r}$
is the two-sided ideal of ![]() generated by the elements
generated by the elements
![]() $1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }$
,
$1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }$
,
![]() $K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
and
$K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
and
![]() $\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
$\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
![]() $1 \leqslant i \leqslant n$
,
$1 \leqslant i \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $\lambda \in \Lambda (n,d)$
. For
$\lambda \in \Lambda (n,d)$
. For
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $t\in \mathbb N$
and
$t\in \mathbb N$
and
![]() $0\leqslant m<lp^{r-1}$
let
$0\leqslant m<lp^{r-1}$
let
Furthermore, for
![]() $1\leqslant j\leqslant n$
,
$1\leqslant j\leqslant n$
,
![]() $c\in \mathbb Z$
,
$c\in \mathbb Z$
,
![]() $t\in \mathbb N$
and
$t\in \mathbb N$
and
![]() ${\lambda }\in \mathbb N^{n}$
let
${\lambda }\in \mathbb N^{n}$
let
 $$ \begin{align*}\mathbf{k}_j=K_j+I_{d,r},\, \bigg[{\mathbf{k}_j;c \atop t}\bigg]=\bigg[{K_j;c \atop t}\bigg]+I_{d,r},\,\mathbf{k}_{\lambda}=K_{\lambda}+I_{d,r}.\end{align*} $$
$$ \begin{align*}\mathbf{k}_j=K_j+I_{d,r},\, \bigg[{\mathbf{k}_j;c \atop t}\bigg]=\bigg[{K_j;c \atop t}\bigg]+I_{d,r},\,\mathbf{k}_{\lambda}=K_{\lambda}+I_{d,r}.\end{align*} $$
We will prove in Theorem 4.10 that the algebra ![]() is isomorphic to the infinitesimal q-Schur algebra
is isomorphic to the infinitesimal q-Schur algebra ![]() .
.
Lemma 4.1.
![]() $(1)$
For
$(1)$
For
![]() ${\lambda },\mu \in \Lambda (n,d)$
we have
${\lambda },\mu \in \Lambda (n,d)$
we have
![]() $\mathbf {k}_{\lambda }\mathbf {k}_\mu =\delta _{{\lambda },\mu }\mathbf {k}_{\lambda }$
.
$\mathbf {k}_{\lambda }\mathbf {k}_\mu =\delta _{{\lambda },\mu }\mathbf {k}_{\lambda }$
.
![]() $(2)$
Assume
$(2)$
Assume
![]() $\nu \in \mathbb N^{n}$
is such that
$\nu \in \mathbb N^{n}$
is such that
![]() $\sigma (\nu )>d$
. Then we have
$\sigma (\nu )>d$
. Then we have
![]() $\mathbf {k}_\nu =0$
.
$\mathbf {k}_\nu =0$
.
Proof. For
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $t\in \mathbb N$
, we have
$t\in \mathbb N$
, we have
![]() $\big [{\mathbf {k}_i;0 \atop t}\big ]\mathbf {k}_\mu = \big [{ \mu _i\atop t}\big ]_{\varepsilon } \mathbf {k}_\mu $
. It follows that
$\big [{\mathbf {k}_i;0 \atop t}\big ]\mathbf {k}_\mu = \big [{ \mu _i\atop t}\big ]_{\varepsilon } \mathbf {k}_\mu $
. It follows that
 $$ \begin{align*}\mathbf{k}_{\lambda} \mathbf{k}_\mu = \bigg[{ \mu\atop{\lambda}}\bigg]_{\varepsilon} \mathbf{k}_\mu.\end{align*} $$
$$ \begin{align*}\mathbf{k}_{\lambda} \mathbf{k}_\mu = \bigg[{ \mu\atop{\lambda}}\bigg]_{\varepsilon} \mathbf{k}_\mu.\end{align*} $$
If
![]() $\big [{ \mu \atop {\lambda }}\big ]_{\varepsilon }\not =0$
, then we have
$\big [{ \mu \atop {\lambda }}\big ]_{\varepsilon }\not =0$
, then we have
![]() $\mu \geqslant {\lambda }$
. This implies that
$\mu \geqslant {\lambda }$
. This implies that
![]() $\mu ={\lambda }$
since
$\mu ={\lambda }$
since
![]() ${\lambda },\mu \in \Lambda (n,d)$
. Therefore, we have
${\lambda },\mu \in \Lambda (n,d)$
. Therefore, we have
![]() $\mathbf {k}_{\lambda }\mathbf {k}_\mu =\delta _{{\lambda },\mu }\mathbf {k}_{\lambda }$
. Furthermore, since
$\mathbf {k}_{\lambda }\mathbf {k}_\mu =\delta _{{\lambda },\mu }\mathbf {k}_{\lambda }$
. Furthermore, since
![]() $1=\sum _{{\gamma } \in \Lambda (n,d)}\mathbf {k}_{\gamma }$
and
$1=\sum _{{\gamma } \in \Lambda (n,d)}\mathbf {k}_{\gamma }$
and
![]() $\sigma (\nu )>d$
, we have
$\sigma (\nu )>d$
, we have
 $$ \begin{align*}\mathbf{k}_\nu= \sum_{{\gamma} \in \Lambda(n,d)}\mathbf{k}_\nu\mathbf{k}_{\gamma} =\sum_{{\gamma} \in \Lambda(n,d)}\bigg[{ {\gamma}\atop\nu}\bigg]_{\varepsilon} \mathbf{k}_{\gamma}=\sum_{{\gamma} \in \Lambda(n,d)\atop\sigma({\gamma})\geqslant\sigma(\nu)>d}\bigg[{ {\gamma}\atop\nu}\bigg]_{\varepsilon} \mathbf{k}_{\gamma}=0.\end{align*} $$
$$ \begin{align*}\mathbf{k}_\nu= \sum_{{\gamma} \in \Lambda(n,d)}\mathbf{k}_\nu\mathbf{k}_{\gamma} =\sum_{{\gamma} \in \Lambda(n,d)}\bigg[{ {\gamma}\atop\nu}\bigg]_{\varepsilon} \mathbf{k}_{\gamma}=\sum_{{\gamma} \in \Lambda(n,d)\atop\sigma({\gamma})\geqslant\sigma(\nu)>d}\bigg[{ {\gamma}\atop\nu}\bigg]_{\varepsilon} \mathbf{k}_{\gamma}=0.\end{align*} $$
The proof is completed.
For
![]() $a,b\in \mathbb Z$
, we have
$a,b\in \mathbb Z$
, we have
 $$ \begin{align} \begin{aligned} \bigg[{b+a\atop t}\bigg]_{\varepsilon}&=\sum_{0\leqslant j\leqslant t}\varepsilon^{a(t-j)-bj}\bigg[{a\atop j}\bigg]_{\varepsilon}\bigg[{b\atop t-j}\bigg]_{\varepsilon}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \bigg[{b+a\atop t}\bigg]_{\varepsilon}&=\sum_{0\leqslant j\leqslant t}\varepsilon^{a(t-j)-bj}\bigg[{a\atop j}\bigg]_{\varepsilon}\bigg[{b\atop t-j}\bigg]_{\varepsilon}. \end{aligned} \end{align} $$
Lemma 4.2. Let
![]() ${\lambda }\in \Lambda (n,d)$
. Then we have
${\lambda }\in \Lambda (n,d)$
. Then we have
![]() $\big [{\mathbf {k}_i;c\atop t}\big ] \mathbf {k}_{\lambda }=\big [{{\lambda }_i+c\atop t}\big ]_{\varepsilon } \mathbf {k}_{\lambda }$
for
$\big [{\mathbf {k}_i;c\atop t}\big ] \mathbf {k}_{\lambda }=\big [{{\lambda }_i+c\atop t}\big ]_{\varepsilon } \mathbf {k}_{\lambda }$
for
![]() $1\leqslant i\leqslant n$
,
$1\leqslant i\leqslant n$
,
![]() $c\in \mathbb Z$
,
$c\in \mathbb Z$
,
![]() $t\in \mathbb N$
.
$t\in \mathbb N$
.
Proof. Assume
![]() $c\geqslant 0$
. By [Reference Lusztig22, 2.3 (g9), (g10)], we have
$c\geqslant 0$
. By [Reference Lusztig22, 2.3 (g9), (g10)], we have
 $$ \begin{align*}\left[{\mathbf{k}_i;\pm c\atop t}\right]=\sum_{0\leqslant j\leqslant t}\varepsilon^{c(t-j)}\left[{\pm c\atop j}\right]_{\varepsilon}\mathbf{k}_i^{\mp j}\left[{\mathbf{k}_i;0\atop t-j}\right]. \end{align*} $$
$$ \begin{align*}\left[{\mathbf{k}_i;\pm c\atop t}\right]=\sum_{0\leqslant j\leqslant t}\varepsilon^{c(t-j)}\left[{\pm c\atop j}\right]_{\varepsilon}\mathbf{k}_i^{\mp j}\left[{\mathbf{k}_i;0\atop t-j}\right]. \end{align*} $$
Hence, by (4.1), we have
 $$ \begin{align*} \left[{\mathbf{k}_i;\pm c\atop t}\right]\mathbf{k}_{\lambda} =\sum_{0\leqslant j\leqslant t}\varepsilon^{c(t-j)\mp j{\lambda}_i}\left[{\pm c\atop j}\right]_{\varepsilon}\left[{{\lambda}_i\atop t-j}\right]_{\varepsilon}\mathbf{k}_{\lambda}=\bigg[{{\lambda}_i\pm c\atop t}\bigg]_{\varepsilon}\mathbf{k}_{\lambda}. \end{align*} $$
$$ \begin{align*} \left[{\mathbf{k}_i;\pm c\atop t}\right]\mathbf{k}_{\lambda} =\sum_{0\leqslant j\leqslant t}\varepsilon^{c(t-j)\mp j{\lambda}_i}\left[{\pm c\atop j}\right]_{\varepsilon}\left[{{\lambda}_i\atop t-j}\right]_{\varepsilon}\mathbf{k}_{\lambda}=\bigg[{{\lambda}_i\pm c\atop t}\bigg]_{\varepsilon}\mathbf{k}_{\lambda}. \end{align*} $$
The proof is completed.
By the definition of ![]() , we have the following result.
, we have the following result.
Lemma 4.3. There is an algebra anti-automorphism
![]() $\tau _d$
on
$\tau _d$
on ![]() such that
such that
 $$ \begin{align*}\tau_d(\mathbf{e}_i^{(m)})=\mathbf{f}_i^{(m)},\quad \tau_d(\mathbf{f}_i^{(m)})=\mathbf{e}_i^{(m)}, \quad \tau_d(\mathbf{k}_j)=\mathbf{k}_j,\quad\tau_d\bigg(\bigg[{\mathbf{k}_j;0\atop t}\bigg]\bigg)=\bigg[{\mathbf{k}_j;0\atop t}\bigg], \end{align*} $$
$$ \begin{align*}\tau_d(\mathbf{e}_i^{(m)})=\mathbf{f}_i^{(m)},\quad \tau_d(\mathbf{f}_i^{(m)})=\mathbf{e}_i^{(m)}, \quad \tau_d(\mathbf{k}_j)=\mathbf{k}_j,\quad\tau_d\bigg(\bigg[{\mathbf{k}_j;0\atop t}\bigg]\bigg)=\bigg[{\mathbf{k}_j;0\atop t}\bigg], \end{align*} $$
for
![]() $1\leqslant i \leqslant n-1$
,
$1\leqslant i \leqslant n-1$
,
![]() $1\leqslant j \leqslant n$
,
$1\leqslant j \leqslant n$
,
![]() $t\in \mathbb N$
and
$t\in \mathbb N$
and
![]() $0\leqslant m<lp^{r-1}$
.
$0\leqslant m<lp^{r-1}$
.
Lemma 4.4. Let
![]() ${\lambda },\mu \in \Lambda (n,d)$
and
${\lambda },\mu \in \Lambda (n,d)$
and
![]() $a\in \mathbb N$
.
$a\in \mathbb N$
.
![]() $(1)$
If
$(1)$
If
![]() ${\lambda }_{i+1}<a$
for some
${\lambda }_{i+1}<a$
for some
![]() $1\leqslant i \leqslant n-1$
, then we have
$1\leqslant i \leqslant n-1$
, then we have
![]() $\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=0$
.
$\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=0$
.
![]() $(2)$
If
$(2)$
If
![]() $\mu _{j}<a$
for some
$\mu _{j}<a$
for some
![]() $1\leqslant j \leqslant n-1$
, then we have
$1\leqslant j \leqslant n-1$
, then we have
![]() $\mathbf {k}_\mu \mathbf {e}_j^{(a)}=\mathbf {f}_j^{(a)}\mathbf {k}_\mu =0$
.
$\mathbf {k}_\mu \mathbf {e}_j^{(a)}=\mathbf {f}_j^{(a)}\mathbf {k}_\mu =0$
.
Proof. By Lemma 2.1 and 4.2, we have
 $$ \begin{align*} \begin{aligned} \mathbf{e}_i^{(a)}\mathbf{k}_{\lambda}&=\mathbf{e}_i^{(a)}\prod_{s\not=i,i+1} \left[{\mathbf{k}_s;0\atop{\lambda}_s}\right]\left[{\mathbf{k}_i;a\atop{\lambda}_i+a}\right]\mathbf{k}_{\lambda} =\mathbf{k}_{{\lambda}+a\boldsymbol{e}_i-{\lambda}_{i+1}\boldsymbol{e}_{i+1}}\mathbf{e}_i^{(a)}\mathbf{k}_{\lambda},\\ \mathbf{k}_\mu\mathbf{e}_j^{(a)}&=\mathbf{k}_\mu\prod_{s\not=j,j+1} \left[{\mathbf{k}_s;0\atop\mu_s}\right]\left[{\mathbf{k}_{j+1};a\atop\mu_{j+1}+a}\right]\mathbf{e}_j^{(a)} =\mathbf{k}_\mu\mathbf{e}_j^{(a)}\mathbf{k}_{{\lambda}+a\boldsymbol{e}_{j+1}-\mu_j\boldsymbol{e}_j}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathbf{e}_i^{(a)}\mathbf{k}_{\lambda}&=\mathbf{e}_i^{(a)}\prod_{s\not=i,i+1} \left[{\mathbf{k}_s;0\atop{\lambda}_s}\right]\left[{\mathbf{k}_i;a\atop{\lambda}_i+a}\right]\mathbf{k}_{\lambda} =\mathbf{k}_{{\lambda}+a\boldsymbol{e}_i-{\lambda}_{i+1}\boldsymbol{e}_{i+1}}\mathbf{e}_i^{(a)}\mathbf{k}_{\lambda},\\ \mathbf{k}_\mu\mathbf{e}_j^{(a)}&=\mathbf{k}_\mu\prod_{s\not=j,j+1} \left[{\mathbf{k}_s;0\atop\mu_s}\right]\left[{\mathbf{k}_{j+1};a\atop\mu_{j+1}+a}\right]\mathbf{e}_j^{(a)} =\mathbf{k}_\mu\mathbf{e}_j^{(a)}\mathbf{k}_{{\lambda}+a\boldsymbol{e}_{j+1}-\mu_j\boldsymbol{e}_j}. \end{aligned} \end{align*} $$
Hence, by Lemma 4.1 we have
![]() $\mathbf {k}_{{\lambda }+a\boldsymbol {e}_i-{\lambda }_{i+1}\boldsymbol {e}_{i+1}}=0$
and
$\mathbf {k}_{{\lambda }+a\boldsymbol {e}_i-{\lambda }_{i+1}\boldsymbol {e}_{i+1}}=0$
and
![]() $\mathbf {k}_{{\lambda }+a\boldsymbol {e}_{j+1}-\mu _j\boldsymbol {e}_j}=0$
, since
$\mathbf {k}_{{\lambda }+a\boldsymbol {e}_{j+1}-\mu _j\boldsymbol {e}_j}=0$
, since
![]() ${\lambda }_{i+1}<a$
,
${\lambda }_{i+1}<a$
,
![]() $\mu _j<a$
and
$\mu _j<a$
and
![]() ${\lambda },\mu \in \Lambda (n,d)$
. Therefore we have
${\lambda },\mu \in \Lambda (n,d)$
. Therefore we have
![]() $\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_\mu \mathbf {e}_j^{(a)}=0$
. Consequently, we have
$\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_\mu \mathbf {e}_j^{(a)}=0$
. Consequently, we have
![]() $\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\tau _d(\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda })=0$
and
$\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\tau _d(\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda })=0$
and
![]() $\mathbf {f}_j^{(a)}\mathbf {k}_\mu =\tau _d(\mathbf {k}_\mu \mathbf {e}_j^{(a)})=0$
.
$\mathbf {f}_j^{(a)}\mathbf {k}_\mu =\tau _d(\mathbf {k}_\mu \mathbf {e}_j^{(a)})=0$
.
Lemma 4.5. Let
![]() ${\lambda } \in \Lambda (n,d)$
and
${\lambda } \in \Lambda (n,d)$
and
![]() $a\in \mathbb N$
. If
$a\in \mathbb N$
. If
![]() ${\lambda }_{i+1}\geqslant a$
for some
${\lambda }_{i+1}\geqslant a$
for some
![]() $1\leqslant i \leqslant n-1$
, then we have
$1\leqslant i \leqslant n-1$
, then we have
![]() $\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_{{\lambda }+a\alpha _i}\mathbf {e}_i^{(a)}$
and
$\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_{{\lambda }+a\alpha _i}\mathbf {e}_i^{(a)}$
and
![]() $\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\mathbf {f}_i^{(a)}\mathbf {k}_{{\lambda }+a\alpha _i}$
, where
$\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\mathbf {f}_i^{(a)}\mathbf {k}_{{\lambda }+a\alpha _i}$
, where
![]() $\alpha _i=\boldsymbol {e}_i-\boldsymbol {e}_{i+1}$
.
$\alpha _i=\boldsymbol {e}_i-\boldsymbol {e}_{i+1}$
.
Proof. By Lemma 2.1 and 4.2, we have
 $$ \begin{align*} \begin{aligned} \mathbf{e}_i^{(a)}\mathbf{k}_{\lambda} &=\prod_{j\not=i,i+1}\left[{\mathbf{k}_j;0\atop{\lambda}_j}\right] \left[{\mathbf{k}_i;-a\atop{\lambda}_i}\right]\left[{\mathbf{k}_{i+1};a\atop{\lambda}_{i+1}}\right] \mathbf{e}_i^{(a)}\\ &= \sum_{\mu\in\Lambda(n,d)} \prod_{j\not=i,i+1}\left[{\mathbf{k}_j;0\atop{\lambda}_j}\right] \left[{\mathbf{k}_i;-a\atop{\lambda}_i}\right]\left[{\mathbf{k}_{i+1};a\atop{\lambda}_{i+1}}\right] \mathbf{k}_\mu \mathbf{e}_i^{(a)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathbf{e}_i^{(a)}\mathbf{k}_{\lambda} &=\prod_{j\not=i,i+1}\left[{\mathbf{k}_j;0\atop{\lambda}_j}\right] \left[{\mathbf{k}_i;-a\atop{\lambda}_i}\right]\left[{\mathbf{k}_{i+1};a\atop{\lambda}_{i+1}}\right] \mathbf{e}_i^{(a)}\\ &= \sum_{\mu\in\Lambda(n,d)} \prod_{j\not=i,i+1}\left[{\mathbf{k}_j;0\atop{\lambda}_j}\right] \left[{\mathbf{k}_i;-a\atop{\lambda}_i}\right]\left[{\mathbf{k}_{i+1};a\atop{\lambda}_{i+1}}\right] \mathbf{k}_\mu \mathbf{e}_i^{(a)}. \end{aligned} \end{align*} $$
Hence, by Lemma 4.4, we have
 $$ \begin{align*} \mathbf{e}_i^{(a)}\mathbf{k}_{\lambda} =\sum_{\mu\in\Lambda(n,d)\atop\mu_i\geqslant a}\left[{\mu-a\alpha_i\atop{\lambda}}\right]_{\varepsilon} \mathbf{k}_\mu \mathbf{e}_i^{(a)} =\sum_{\mu\in\Lambda(n,d),\,\mu-a\alpha_i\geqslant{\lambda}}\left[{\mu-a\alpha_i\atop{\lambda}}\right]_{\varepsilon} \mathbf{k}_\mu \mathbf{e}_i^{(a)}=\mathbf{k}_{{\lambda}+a\alpha_i} \mathbf{e}_i^{(a)}. \end{align*} $$
$$ \begin{align*} \mathbf{e}_i^{(a)}\mathbf{k}_{\lambda} =\sum_{\mu\in\Lambda(n,d)\atop\mu_i\geqslant a}\left[{\mu-a\alpha_i\atop{\lambda}}\right]_{\varepsilon} \mathbf{k}_\mu \mathbf{e}_i^{(a)} =\sum_{\mu\in\Lambda(n,d),\,\mu-a\alpha_i\geqslant{\lambda}}\left[{\mu-a\alpha_i\atop{\lambda}}\right]_{\varepsilon} \mathbf{k}_\mu \mathbf{e}_i^{(a)}=\mathbf{k}_{{\lambda}+a\alpha_i} \mathbf{e}_i^{(a)}. \end{align*} $$
Therefore, we have
![]() $\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\tau _d(\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda })= \tau _d(\mathbf {k}_{{\lambda }+a\alpha _i} \mathbf {e}_i^{(a)} )=\mathbf {f}_i^{(a)}\mathbf {k}_{{\lambda }+a\alpha _i}$
.
$\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\tau _d(\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda })= \tau _d(\mathbf {k}_{{\lambda }+a\alpha _i} \mathbf {e}_i^{(a)} )=\mathbf {f}_i^{(a)}\mathbf {k}_{{\lambda }+a\alpha _i}$
.
For simplicity, we set
![]() $\mathbf {k}_{\lambda }=0$
if
$\mathbf {k}_{\lambda }=0$
if
![]() ${\lambda }\not \in \mathbb N^{n}$
with
${\lambda }\not \in \mathbb N^{n}$
with
![]() $\sigma ({\lambda })=d$
, where
$\sigma ({\lambda })=d$
, where
![]() $\sigma ({\lambda })=\sum _{1\leqslant i\leqslant n}{\lambda }_i$
. Then, by Lemma 4.4 and 4.5, we have the following result.
$\sigma ({\lambda })=\sum _{1\leqslant i\leqslant n}{\lambda }_i$
. Then, by Lemma 4.4 and 4.5, we have the following result.
Lemma 4.6. For
![]() ${\lambda } \in \mathbb Z^{n}$
with
${\lambda } \in \mathbb Z^{n}$
with
![]() $\sigma ({\lambda })=d$
and
$\sigma ({\lambda })=d$
and
![]() $a\in \mathbb N$
we have
$a\in \mathbb N$
we have
![]() $\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_{{\lambda }+a\alpha _i}\mathbf {e}_i^{(a)}$
and
$\mathbf {e}_i^{(a)}\mathbf {k}_{\lambda }=\mathbf {k}_{{\lambda }+a\alpha _i}\mathbf {e}_i^{(a)}$
and
![]() $\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\mathbf {f}_i^{(a)}\mathbf {k}_{{\lambda }+a\alpha _i}$
.
$\mathbf {k}_{\lambda }\mathbf {f}_i^{(a)}=\mathbf {f}_i^{(a)}\mathbf {k}_{{\lambda }+a\alpha _i}$
.
For
![]() $A\in \Theta ^\pm (n)$
let
$A\in \Theta ^\pm (n)$
let
![]() $\mathbf {e}^{(A^+)}=E^{(A^+)}+I_{d,r}$
and
$\mathbf {e}^{(A^+)}=E^{(A^+)}+I_{d,r}$
and
![]() $\mathbf {f}^{(A^-)}=F^{(A^-)}+I_{d,r}$
.
$\mathbf {f}^{(A^-)}=F^{(A^-)}+I_{d,r}$
.
Lemma 4.7. Let
![]() $A\in \Theta ^\pm (n)_r$
and
$A\in \Theta ^\pm (n)_r$
and
![]() ${\lambda } \in \mathbb Z^{n}$
with
${\lambda } \in \mathbb Z^{n}$
with
![]() $\sigma ({\lambda })=d$
. Then, we have
$\sigma ({\lambda })=d$
. Then, we have
![]() $\mathbf {e}^{(A^+)}\mathbf {k}_{\lambda }=\mathbf { k}_{{\lambda }-\textrm {co}(A^+)+\textrm {ro}(A^+)}\mathbf {e}^{(A^+)}$
and
$\mathbf {e}^{(A^+)}\mathbf {k}_{\lambda }=\mathbf { k}_{{\lambda }-\textrm {co}(A^+)+\textrm {ro}(A^+)}\mathbf {e}^{(A^+)}$
and
![]() $\mathbf {k}_{\lambda }\mathbf {f}^{(A^-)}= \mathbf {f}^{(A^-)}\mathbf {k}_{{\lambda }+\textrm {co}(A^-)-\textrm {ro}(A^-)}$
.
$\mathbf {k}_{\lambda }\mathbf {f}^{(A^-)}= \mathbf {f}^{(A^-)}\mathbf {k}_{{\lambda }+\textrm {co}(A^-)-\textrm {ro}(A^-)}$
.
Proof. By Lemma 4.6, we have
![]() $ \mathbf {e}^{(A^+)}\mathbf {k}_{\lambda }=\mathbf {k}_\mu \mathbf {e}^{(A^+)}$
and
$ \mathbf {e}^{(A^+)}\mathbf {k}_{\lambda }=\mathbf {k}_\mu \mathbf {e}^{(A^+)}$
and
![]() $\mathbf {k}_{\lambda }\mathbf {f}^{(A^-)}=\mathbf {f}^{(A^-)}\mathbf {k}_\nu $
where
$\mathbf {k}_{\lambda }\mathbf {f}^{(A^-)}=\mathbf {f}^{(A^-)}\mathbf {k}_\nu $
where
 $$ \begin{align*}\mu={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{k,j}\sum_{k\leqslant s<j}\alpha_s={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{k,j}(\boldsymbol{e}_k-\boldsymbol{e}_j)={\lambda}-\textrm{co}(A^+)+\textrm{ro}(A^+), \end{align*} $$
$$ \begin{align*}\mu={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{k,j}\sum_{k\leqslant s<j}\alpha_s={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{k,j}(\boldsymbol{e}_k-\boldsymbol{e}_j)={\lambda}-\textrm{co}(A^+)+\textrm{ro}(A^+), \end{align*} $$
and
 $$ \begin{align*}\nu={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{j,k}\sum_{k\leqslant s<j}\alpha_s ={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{j,k}(\boldsymbol{e}_k-\boldsymbol{e}_j)={\lambda}+\textrm{co}(A^-)-\textrm{ro}(A^-).\end{align*} $$
$$ \begin{align*}\nu={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{j,k}\sum_{k\leqslant s<j}\alpha_s ={\lambda}+\sum_{2\leqslant j\leqslant n}\sum_{1\leqslant k<j}a_{j,k}(\boldsymbol{e}_k-\boldsymbol{e}_j)={\lambda}+\textrm{co}(A^-)-\textrm{ro}(A^-).\end{align*} $$
The proof is completed.
Recall the sets
![]() $\Theta ^+(n)_r$
and
$\Theta ^+(n)_r$
and
![]() $\Theta ^-(n)_r$
defined in (3.1).
$\Theta ^-(n)_r$
defined in (3.1).
Lemma 4.8. Let
![]() ${\lambda } \in \Lambda (n,d)$
.
${\lambda } \in \Lambda (n,d)$
.
-
(1) If
 $A \in \Theta ^+(n)_r$
and
$A \in \Theta ^+(n)_r$
and
 ${\lambda }_i<\sigma _i(A)$
for some i, then we have
${\lambda }_i<\sigma _i(A)$
for some i, then we have
 $\mathbf {e}^{(A)}\mathbf {k}_{\lambda }=0$
.
$\mathbf {e}^{(A)}\mathbf {k}_{\lambda }=0$
. -
(2) If
 $A \in \Theta ^-(n)_r$
and
$A \in \Theta ^-(n)_r$
and
 ${\lambda }_i<\sigma _i(A)$
for some i, then we have
${\lambda }_i<\sigma _i(A)$
for some i, then we have
 $\mathbf {k}_{\lambda }\mathbf {f}^{(A)}=0$
.
$\mathbf {k}_{\lambda }\mathbf {f}^{(A)}=0$
.
Proof. If
![]() $A \in \Theta ^+(n)_r$
and
$A \in \Theta ^+(n)_r$
and
![]() ${\lambda }_i<\sigma _i(A)$
for some i, then by Lemma 4.6 we have
${\lambda }_i<\sigma _i(A)$
for some i, then by Lemma 4.6 we have
where
![]() $\mathbf {m}_j=\mathbf {e}^{(a_{j-1,j})}_{j-1}(\mathbf {e}_{j-2}^{(a_{j-2, j})} \mathbf {e}_{j-1}^{(a_{j-2, j})}) \cdots (\mathbf {e}_{1}^{(a_{1, j})} \mathbf { e}_{2}^{(a_{1, j})} \cdots \mathbf {e}_{j-1}^{(a_{1, j})})$
and
$\mathbf {m}_j=\mathbf {e}^{(a_{j-1,j})}_{j-1}(\mathbf {e}_{j-2}^{(a_{j-2, j})} \mathbf {e}_{j-1}^{(a_{j-2, j})}) \cdots (\mathbf {e}_{1}^{(a_{1, j})} \mathbf { e}_{2}^{(a_{1, j})} \cdots \mathbf {e}_{j-1}^{(a_{1, j})})$
and
 $$ \begin{align*}\mu={\lambda}+\sum_{2\leqslant j\leqslant i}\sum_{1\leqslant k<j}a_{k,j}\sum_{k\leqslant s<j}\alpha_s={\lambda}+\sum_{2\leqslant j\leqslant i}\sum_{1\leqslant k<j}a_{k,j}(\boldsymbol{e}_k-\boldsymbol{e}_j). \end{align*} $$
$$ \begin{align*}\mu={\lambda}+\sum_{2\leqslant j\leqslant i}\sum_{1\leqslant k<j}a_{k,j}\sum_{k\leqslant s<j}\alpha_s={\lambda}+\sum_{2\leqslant j\leqslant i}\sum_{1\leqslant k<j}a_{k,j}(\boldsymbol{e}_k-\boldsymbol{e}_j). \end{align*} $$
Since
![]() $\mu _i={\lambda }_i-\sigma _i(A)<0$
we have
$\mu _i={\lambda }_i-\sigma _i(A)<0$
we have
![]() $\mathbf {k}_\mu =0$
. Hence, we have
$\mathbf {k}_\mu =0$
. Hence, we have
![]() $\mathbf {e}^{(A)}\mathbf {k}_{\lambda }=0$
. Assume now that
$\mathbf {e}^{(A)}\mathbf {k}_{\lambda }=0$
. Assume now that
![]() $A \in \Theta ^-(n)_r$
and
$A \in \Theta ^-(n)_r$
and
![]() ${\lambda }_i<\sigma _i(A)$
for some i. Then, we have
${\lambda }_i<\sigma _i(A)$
for some i. Then, we have
![]() $\mathbf {k}_{\lambda }\mathbf {f}^{(A)}=\tau _d(\mathbf {e}^{({}^tA)}\mathbf {k}_{\lambda })=0$
. The proof is completed.
$\mathbf {k}_{\lambda }\mathbf {f}^{(A)}=\tau _d(\mathbf {e}^{({}^tA)}\mathbf {k}_{\lambda })=0$
. The proof is completed.
For
![]() $A \in \Theta ^\pm (n)_r$
and
$A \in \Theta ^\pm (n)_r$
and
![]() ${\lambda } \in \Lambda (n,d)$
, let
${\lambda } \in \Lambda (n,d)$
, let
Proposition 4.9. The set
![]() $\mathbf {M}_{d,r}=\{\mathbf {m}^{(A,{\lambda })}| A \in \Theta ^\pm (n)_r,\, {\lambda } \in \Lambda (n,d),\, {\lambda }\geqslant {\boldsymbol \sigma }(A)\}$
is a spanning set for
$\mathbf {M}_{d,r}=\{\mathbf {m}^{(A,{\lambda })}| A \in \Theta ^\pm (n)_r,\, {\lambda } \in \Lambda (n,d),\, {\lambda }\geqslant {\boldsymbol \sigma }(A)\}$
is a spanning set for ![]() .
.
Proof. By the definition of
![]() $I_{d,r}$
we have
$I_{d,r}$
we have
![]() $\mathbf {k}_i=\sum _{{\lambda }\in \Lambda (n,d)}\varepsilon ^{{\lambda }_i}\mathbf {k}_{\lambda }$
and
$\mathbf {k}_i=\sum _{{\lambda }\in \Lambda (n,d)}\varepsilon ^{{\lambda }_i}\mathbf {k}_{\lambda }$
and
![]() $\mathbf {k}_{\lambda }=\sum _{\mu \in \Lambda (n,d)} \big [{\mu \atop {\lambda }}\big ]_{\varepsilon }\mathbf {k}_\mu $
for
$\mathbf {k}_{\lambda }=\sum _{\mu \in \Lambda (n,d)} \big [{\mu \atop {\lambda }}\big ]_{\varepsilon }\mathbf {k}_\mu $
for
![]() ${\lambda }\in \Lambda (n,d)$
and
${\lambda }\in \Lambda (n,d)$
and
![]() $1\leqslant i\leqslant n$
. Hence, by Proposition 3.1, we see that the algebra
$1\leqslant i\leqslant n$
. Hence, by Proposition 3.1, we see that the algebra ![]() is spanned by the elements
is spanned by the elements
![]() $\mathbf {e}^{(A^+)} \mathbf {k}_{\lambda } \mathbf {f}^{(A^-)}$
for
$\mathbf {e}^{(A^+)} \mathbf {k}_{\lambda } \mathbf {f}^{(A^-)}$
for
![]() $A\in \Theta ^\pm (n)_r$
and
$A\in \Theta ^\pm (n)_r$
and
![]() $\lambda \in \Lambda (n,d)$
. Therefore, to prove the proposition, we have to show that if
$\lambda \in \Lambda (n,d)$
. Therefore, to prove the proposition, we have to show that if
![]() ${\lambda }_i< \sigma _i(A)$
for some i, then
${\lambda }_i< \sigma _i(A)$
for some i, then
![]() $\mathbf {m}^{(A,{\lambda })}$
lies in the span of
$\mathbf {m}^{(A,{\lambda })}$
lies in the span of
![]() $\mathbf {M}_{d,r}$
.
$\mathbf {M}_{d,r}$
.
We argue by induction on
![]() $\textrm {deg}(A)$
. The result follows from Lemma 4.4 in the cases where
$\textrm {deg}(A)$
. The result follows from Lemma 4.4 in the cases where
![]() $\textrm {deg}(A)=1$
. Assume now that
$\textrm {deg}(A)=1$
. Assume now that
![]() $\textrm {deg}(A)>1$
, and suppose
$\textrm {deg}(A)>1$
, and suppose
![]() ${\lambda }_i<\sigma _i(A)$
for some
${\lambda }_i<\sigma _i(A)$
for some
![]() $1\leqslant i\leqslant n$
. For
$1\leqslant i\leqslant n$
. For
![]() $2\leqslant j\leqslant n$
let
$2\leqslant j\leqslant n$
let
 $$ \begin{align*} \begin{aligned} \mathbf{m}_j&=\mathbf{e}^{(a_{j-1,j})}_{j-1}(\mathbf{e}_{j-2}^{(a_{j-2, j})} \mathbf{e}_{j-1}^{(a_{j-2, j})}) \cdots(\mathbf{e}_{1}^{(a_{1, j})} \mathbf{ e}_{2}^{(a_{1, j})} \cdots \mathbf{e}_{j-1}^{(a_{1, j})}),\\ \mathbf{m}_j'&=(\mathbf{f}_{j-1}^{(a_{j, 1})} \cdots \mathbf{f}_{2}^{(a_{j, 1})} \mathbf{ f}_{1}^{(a_{j, 1})}) \cdots(\mathbf{f}_{j-1}^{(a_{j, j-2})} \mathbf{f}_{j-2}^{(a_{j, j-2})}) \mathbf{f}_{j-1}^{(a_{j, j-1})}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathbf{m}_j&=\mathbf{e}^{(a_{j-1,j})}_{j-1}(\mathbf{e}_{j-2}^{(a_{j-2, j})} \mathbf{e}_{j-1}^{(a_{j-2, j})}) \cdots(\mathbf{e}_{1}^{(a_{1, j})} \mathbf{ e}_{2}^{(a_{1, j})} \cdots \mathbf{e}_{j-1}^{(a_{1, j})}),\\ \mathbf{m}_j'&=(\mathbf{f}_{j-1}^{(a_{j, 1})} \cdots \mathbf{f}_{2}^{(a_{j, 1})} \mathbf{ f}_{1}^{(a_{j, 1})}) \cdots(\mathbf{f}_{j-1}^{(a_{j, j-2})} \mathbf{f}_{j-2}^{(a_{j, j-2})}) \mathbf{f}_{j-1}^{(a_{j, j-1})}. \end{aligned} \end{align*} $$
Then, we have
![]() $\mathbf {e}^{(A^+)} =\mathbf {m}_n\mathbf {m}_{n-1}\cdots \mathbf {m}_2$
and
$\mathbf {e}^{(A^+)} =\mathbf {m}_n\mathbf {m}_{n-1}\cdots \mathbf {m}_2$
and
![]() $\mathbf {f}^{(A^-)} =\mathbf {m}_2^{\prime }\mathbf {m}_{3}^{\prime }\cdots \mathbf {m}_n'$
. Let
$\mathbf {f}^{(A^-)} =\mathbf {m}_2^{\prime }\mathbf {m}_{3}^{\prime }\cdots \mathbf {m}_n'$
. Let
![]() $A_i$
be the submatrix of A consisting of the first i rows and columns, and write
$A_i$
be the submatrix of A consisting of the first i rows and columns, and write
![]() $\mathbf {e}^{(A^+)}=\mathbf {x}_1 \mathbf {e}^{(A_i^{+})}, \mathbf { f}^{(A^-)}=\mathbf {f}^{(A_i^-)}\mathbf {x}_1^\prime $
. Then,
$\mathbf {e}^{(A^+)}=\mathbf {x}_1 \mathbf {e}^{(A_i^{+})}, \mathbf { f}^{(A^-)}=\mathbf {f}^{(A_i^-)}\mathbf {x}_1^\prime $
. Then,
where
![]() $\mathbf {x}_1=\mathbf {m}_n\mathbf {m}_{n-1}\cdots \mathbf {m}_{i+1}$
and
$\mathbf {x}_1=\mathbf {m}_n\mathbf {m}_{n-1}\cdots \mathbf {m}_{i+1}$
and
![]() $\mathbf {x}_1^{\prime }=\mathbf {m}_{i+1}^{\prime }\mathbf {m}_{i+2}^{\prime }\cdots \mathbf {m}_{n}^{\prime }$
. By Lemma 4.8, we may assume that
$\mathbf {x}_1^{\prime }=\mathbf {m}_{i+1}^{\prime }\mathbf {m}_{i+2}^{\prime }\cdots \mathbf {m}_{n}^{\prime }$
. By Lemma 4.8, we may assume that
![]() ${\lambda }_i\geqslant \sigma _i(A_i^{+})=\sigma _i(A^{+})$
. Furthermore, by Lemma 4.7, we have
${\lambda }_i\geqslant \sigma _i(A_i^{+})=\sigma _i(A^{+})$
. Furthermore, by Lemma 4.7, we have
where
![]() ${\lambda }^\prime ={\lambda }-\textrm {co}(A_i^{+})+\textrm {ro}(A_i^+)$
. By Lemma 2.1,
${\lambda }^\prime ={\lambda }-\textrm {co}(A_i^{+})+\textrm {ro}(A_i^+)$
. By Lemma 2.1,
where f is a ![]() -linear combination of
-linear combination of
![]() $\mathbf {x}_j^{\mathbf {e}}\mathbf {h}_j \mathbf {x}^{\mathbf {f}}_j$
with
$\mathbf {x}_j^{\mathbf {e}}\mathbf {h}_j \mathbf {x}^{\mathbf {f}}_j$
with ![]() and
and
![]() $\textrm {deg}(\mathbf {x}_j^{\mathbf {e}})+\textrm {deg} (\mathbf {x}_j^{\mathbf { f}}) < \textrm {deg}(A_i)$
. Here,
$\textrm {deg}(\mathbf {x}_j^{\mathbf {e}})+\textrm {deg} (\mathbf {x}_j^{\mathbf { f}}) < \textrm {deg}(A_i)$
. Here,
![]() $\mathbf {x}_j^{\mathbf {e}}$
(resp.
$\mathbf {x}_j^{\mathbf {e}}$
(resp.
![]() $\mathbf {x}_j^{\mathbf {f}}$
) denotes a monomial in the
$\mathbf {x}_j^{\mathbf {f}}$
) denotes a monomial in the
![]() $\mathbf {e}_i^{(a)}$
(resp.
$\mathbf {e}_i^{(a)}$
(resp.
![]() $\mathbf {f}_i^{(a)}$
). Thus,
$\mathbf {f}_i^{(a)}$
). Thus,
![]() $\textrm {deg}(\mathbf {x}_1)+\textrm {deg}(\mathbf {x}_j^{\mathbf {e}})+\textrm {deg}(\mathbf {x}^{\mathbf {f}}_j)+\textrm {deg}(\mathbf {x}_1')<\textrm {deg}(A)$
. Since
$\textrm {deg}(\mathbf {x}_1)+\textrm {deg}(\mathbf {x}_j^{\mathbf {e}})+\textrm {deg}(\mathbf {x}^{\mathbf {f}}_j)+\textrm {deg}(\mathbf {x}_1')<\textrm {deg}(A)$
. Since
![]() ${\lambda }_i<\sigma _i(A)$
, we have
${\lambda }_i<\sigma _i(A)$
, we have
![]() ${\lambda }_i^{\prime }={\lambda }_i-\sigma _i(A_i^+)<\sigma _i(A)-\sigma _i(A_i^+)=\sigma _i(A_i^-)$
. It follows from Lemma 4.7 that
${\lambda }_i^{\prime }={\lambda }_i-\sigma _i(A_i^+)<\sigma _i(A)-\sigma _i(A_i^+)=\sigma _i(A_i^-)$
. It follows from Lemma 4.7 that
![]() $ \mathbf {k}_{{\lambda }'}\mathbf {f}^{(A_i^-)}=0$
. Hence, we have
$ \mathbf {k}_{{\lambda }'}\mathbf {f}^{(A_i^-)}=0$
. Hence, we have
Furthermore, by Proposition 3.1, we see that each
![]() $\mathbf {x}_1\mathbf {x}_j^{\mathbf {e}}$
is a
$\mathbf {x}_1\mathbf {x}_j^{\mathbf {e}}$
is a ![]() -linear combination of
-linear combination of
![]() $\mathbf { e}^{(B)}$
with
$\mathbf { e}^{(B)}$
with
![]() $B\in \Theta ^+(n)_r$
,
$B\in \Theta ^+(n)_r$
,
![]() $\textrm {deg}(B)=\textrm {deg}(\mathbf {x}_1\mathbf {x}_j^{\mathbf {e}})$
and each
$\textrm {deg}(B)=\textrm {deg}(\mathbf {x}_1\mathbf {x}_j^{\mathbf {e}})$
and each
![]() $\mathbf {x}_j^{\mathbf {f}} \mathbf {x}_1^\prime $
is a
$\mathbf {x}_j^{\mathbf {f}} \mathbf {x}_1^\prime $
is a ![]() -linear combination of
-linear combination of
![]() $\mathbf {f}^{(C)}$
with
$\mathbf {f}^{(C)}$
with
![]() $C\in \Theta ^-(n)_r$
,
$C\in \Theta ^-(n)_r$
,
![]() $\textrm {deg}(C)=\textrm { deg}(\mathbf {x}_j^{\mathbf {f}} \mathbf {x}_1^\prime )$
. Therefore, by Lemma 4.7 each
$\textrm {deg}(C)=\textrm { deg}(\mathbf {x}_j^{\mathbf {f}} \mathbf {x}_1^\prime )$
. Therefore, by Lemma 4.7 each
![]() $\mathbf {x}_1 \mathbf {k}_{{\lambda }'} \mathbf {x}_j^{\mathbf {e}}\mathbf {h}_j \mathbf {x}^{\mathbf {f}}_j\mathbf {x}_1^\prime $
is a
$\mathbf {x}_1 \mathbf {k}_{{\lambda }'} \mathbf {x}_j^{\mathbf {e}}\mathbf {h}_j \mathbf {x}^{\mathbf {f}}_j\mathbf {x}_1^\prime $
is a ![]() -linear combination of
-linear combination of
![]() $\mathbf {m}^{(A',\mu )}$
with
$\mathbf {m}^{(A',\mu )}$
with
![]() $\textrm {deg}(A')<\textrm {deg}(A)$
, since
$\textrm {deg}(A')<\textrm {deg}(A)$
, since
![]() $\textrm {deg}(\mathbf {x}_1)+\textrm {deg}(\mathbf {x}_j^{\mathbf {e}})+\textrm {deg}(\mathbf {x}^{\mathbf {f}}_j)+\textrm {deg}(\mathbf {x}_1')<\textrm {deg}(A)$
. Consequently, by induction, we have
$\textrm {deg}(\mathbf {x}_1)+\textrm {deg}(\mathbf {x}_j^{\mathbf {e}})+\textrm {deg}(\mathbf {x}^{\mathbf {f}}_j)+\textrm {deg}(\mathbf {x}_1')<\textrm {deg}(A)$
. Consequently, by induction, we have ![]() . The proof is completed.
. The proof is completed.
By Lemma 3.5, we have ![]() Therefore, the map
Therefore, the map ![]() given in (3.7) restricts to a surjective algebra homomorphism
given in (3.7) restricts to a surjective algebra homomorphism
By (3.8), we have
for
![]() ${\lambda }\in \Lambda (n,d)$
. So, we have
${\lambda }\in \Lambda (n,d)$
. So, we have
![]() $\zeta _{d,r} (I_{d,r})=0$
. Hence, the map
$\zeta _{d,r} (I_{d,r})=0$
. Hence, the map ![]() induces a surjective algebra homomorphism
induces a surjective algebra homomorphism
Theorem 4.10. The map
![]() $\zeta _{d,r}^{\prime }$
is an algebra isomorphism. In particular, the kernel of the map
$\zeta _{d,r}^{\prime }$
is an algebra isomorphism. In particular, the kernel of the map ![]() is generated by the elements
is generated by the elements
![]() $1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }$
,
$1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }$
,
![]() $K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
and
$K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
and
![]() $\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
$\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
![]() $1 \leqslant i \leqslant n$
,
$1 \leqslant i \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $\lambda \in \Lambda (n,d)$
.
$\lambda \in \Lambda (n,d)$
.
5 The algebra 
For
![]() $d\in \mathbb N$
, let
$d\in \mathbb N$
, let
where
![]() $J_{d,r}$
is the two-sided ideal of
$J_{d,r}$
is the two-sided ideal of ![]() generated by the elements
generated by the elements
![]() $1_{\lambda }$
for
$1_{\lambda }$
for
![]() $\lambda \notin \Lambda (n,d)$
. For
$\lambda \notin \Lambda (n,d)$
. For
![]() ${\lambda }\in \mathbb Z^{n}$
, let
${\lambda }\in \mathbb Z^{n}$
, let
Then, we have
![]() $1=\sum _{{\lambda }\in \Lambda (n,d)}\mathfrak {k}_{\lambda }$
. For
$1=\sum _{{\lambda }\in \Lambda (n,d)}\mathfrak {k}_{\lambda }$
. For
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() $0\leqslant m<lp^{r-1}$
, let
$0\leqslant m<lp^{r-1}$
, let
 $$ \begin{align*}\mathfrak{e}_i^{(m)}=\sum_{{\lambda}\in\Lambda(n,d)}E_i^{(m)}1_{\lambda}+J_{d,r},\ \mathfrak{f}_i^{(m)}=\sum_{{\lambda}\in\Lambda(n,d)}1_{\lambda} F_i^{(m)}+J_{d,r}.\end{align*} $$
$$ \begin{align*}\mathfrak{e}_i^{(m)}=\sum_{{\lambda}\in\Lambda(n,d)}E_i^{(m)}1_{\lambda}+J_{d,r},\ \mathfrak{f}_i^{(m)}=\sum_{{\lambda}\in\Lambda(n,d)}1_{\lambda} F_i^{(m)}+J_{d,r}.\end{align*} $$
For
![]() $A\in \Theta ^\pm (n)_r$
, let. Furthermore for
$A\in \Theta ^\pm (n)_r$
, let. Furthermore for
![]() $1\leqslant i\leqslant n$
,
$1\leqslant i\leqslant n$
,
![]() $1\leqslant j\leqslant n-1$
,
$1\leqslant j\leqslant n-1$
,
![]() $c\in\mathbb{Z}$
and
$c\in\mathbb{Z}$
and
![]() $t\in\mathbb{N}$
let
$t\in\mathbb{N}$
let
 $$ \begin{align*}\mathfrak{k}_i=\sum_{\lambda\in\Lambda(n,d)}K_i1_\lambda+J_{d,r},\ \bigg[{\mathfrak{k}_i;c\atop t}\bigg]=\sum_{\lambda\in\Lambda(n,d)}\bigg[{K_i;c\atop t}\bigg]1_\lambda+J_{d,r},\ \bigg[{\widetilde{\mathfrak{k}}_j;c\atop t}\bigg]=\sum_{\lambda\in\Lambda(n,d)}\bigg[{\widetilde K_j;c\atop t}\bigg]1_\lambda+J_{d,r}.\end{align*} $$
$$ \begin{align*}\mathfrak{k}_i=\sum_{\lambda\in\Lambda(n,d)}K_i1_\lambda+J_{d,r},\ \bigg[{\mathfrak{k}_i;c\atop t}\bigg]=\sum_{\lambda\in\Lambda(n,d)}\bigg[{K_i;c\atop t}\bigg]1_\lambda+J_{d,r},\ \bigg[{\widetilde{\mathfrak{k}}_j;c\atop t}\bigg]=\sum_{\lambda\in\Lambda(n,d)}\bigg[{\widetilde K_j;c\atop t}\bigg]1_\lambda+J_{d,r}.\end{align*} $$
 $$ \begin{align*}\mathfrak{e}^{(A^+)}=\sum_{{\lambda}\in\Lambda(n,d)}E^{(A^+)} 1_{\lambda}+J_{d,r},\ \mathfrak{f}^{(A^-)}=\sum_{{\lambda}\in\Lambda(n,d)}1_{\lambda}F^{(A^-)} +J_{d,r}.\end{align*} $$
$$ \begin{align*}\mathfrak{e}^{(A^+)}=\sum_{{\lambda}\in\Lambda(n,d)}E^{(A^+)} 1_{\lambda}+J_{d,r},\ \mathfrak{f}^{(A^-)}=\sum_{{\lambda}\in\Lambda(n,d)}1_{\lambda}F^{(A^-)} +J_{d,r}.\end{align*} $$
We will prove in Theorem 5.5 that the algebra ![]() is isomorphic to the infinitesimal q-Schur algebra
is isomorphic to the infinitesimal q-Schur algebra ![]() .
.
By [Reference Beilinson, Lusztig and MacPherson3, Lem. 3.10 and Prop. 4.2], we have the following result.
Lemma 5.1. There is an unique algebra antiautomorphism
![]() $\dot \tau _d$
on
$\dot \tau _d$
on ![]() such that
such that
![]() $\dot \tau _d(\mathfrak {e}_i^{(m)})=\mathfrak {f}_i^{(m)}$
,
$\dot \tau _d(\mathfrak {e}_i^{(m)})=\mathfrak {f}_i^{(m)}$
,
![]() $\dot \tau _d(\mathfrak {f}_i^{(m)})=\mathfrak {e}_i^{(m)}$
and
$\dot \tau _d(\mathfrak {f}_i^{(m)})=\mathfrak {e}_i^{(m)}$
and
![]() $\dot \tau _d(\mathfrak {k}_{\lambda })=\mathfrak {k}_{\lambda }$
for
$\dot \tau _d(\mathfrak {k}_{\lambda })=\mathfrak {k}_{\lambda }$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $0\leqslant m<lp^{r-1}$
and
$0\leqslant m<lp^{r-1}$
and
![]() ${\lambda }\in \Lambda (n,d)$
.
${\lambda }\in \Lambda (n,d)$
.
Clearly we have the following result.
Lemma 5.2. Let
![]() $1 \leqslant i \leqslant n, 1\leqslant j\leqslant n-1$
,
$1 \leqslant i \leqslant n, 1\leqslant j\leqslant n-1$
,
![]() $c\in \mathbb Z$
,
$c\in \mathbb Z$
,
![]() $t\in \mathbb N$
and
$t\in \mathbb N$
and
![]() $\lambda \in \mathbb {Z}^{n}$
. The following formulas hold in
$\lambda \in \mathbb {Z}^{n}$
. The following formulas hold in ![]()
 $$ \begin{align*}\mathfrak{k}_{i}\mathfrak{k}_{\lambda}=\varepsilon^{\lambda_{i}}\mathfrak{k}_{\lambda},\ \bigg[{\mathfrak{k}_i;c\atop t}\bigg]\mathfrak{k}_{\lambda}=\bigg[{{\lambda}_i+c \atop t}\bigg]_{\varepsilon}\mathfrak{k}_{\lambda},\ \bigg[{\widetilde{\mathfrak{k}}_j;c \atop t}\bigg]\mathfrak{k}_{\lambda}=\bigg[{{\lambda}_j-{\lambda}_{j+1}+c \atop t}\bigg]_{\varepsilon} \mathfrak{k}_{\lambda}.\end{align*} $$
$$ \begin{align*}\mathfrak{k}_{i}\mathfrak{k}_{\lambda}=\varepsilon^{\lambda_{i}}\mathfrak{k}_{\lambda},\ \bigg[{\mathfrak{k}_i;c\atop t}\bigg]\mathfrak{k}_{\lambda}=\bigg[{{\lambda}_i+c \atop t}\bigg]_{\varepsilon}\mathfrak{k}_{\lambda},\ \bigg[{\widetilde{\mathfrak{k}}_j;c \atop t}\bigg]\mathfrak{k}_{\lambda}=\bigg[{{\lambda}_j-{\lambda}_{j+1}+c \atop t}\bigg]_{\varepsilon} \mathfrak{k}_{\lambda}.\end{align*} $$
Recall from (3.1) that
![]() $\Theta ^\pm (n)_r=\{A\in \Theta ^\pm (n) \mid 0 \leqslant a_{ij} < lp^{r-1}, \forall i \neq j\} $
,
$\Theta ^\pm (n)_r=\{A\in \Theta ^\pm (n) \mid 0 \leqslant a_{ij} < lp^{r-1}, \forall i \neq j\} $
,
![]() $\Theta ^+(n)_r=\{A\in \Theta ^+(n) \mid 0 \leqslant a_{ij} < lp^{r-1}, \forall i < j \}$
and
$\Theta ^+(n)_r=\{A\in \Theta ^+(n) \mid 0 \leqslant a_{ij} < lp^{r-1}, \forall i < j \}$
and
![]() $\Theta ^-(n)_r=\{A\in \Theta ^-(n) \mid 0 \leqslant a_{ij} < lp^{r-1}, \forall i> j \}$
.
$\Theta ^-(n)_r=\{A\in \Theta ^-(n) \mid 0 \leqslant a_{ij} < lp^{r-1}, \forall i> j \}$
.
Lemma 5.3. Let
![]() $\lambda \in \Lambda (n,d)$
. The following results hold in
$\lambda \in \Lambda (n,d)$
. The following results hold in ![]() . (1) If
. (1) If
![]() $A \in \Theta ^+(n)_r$
and
$A \in \Theta ^+(n)_r$
and
![]() $\lambda _{i}<\sigma _{i}(A)$
for some i, then
$\lambda _{i}<\sigma _{i}(A)$
for some i, then
![]() $\mathfrak {e}^{(A)}\mathfrak {k}_{\lambda } =0$
. (2) If
$\mathfrak {e}^{(A)}\mathfrak {k}_{\lambda } =0$
. (2) If
![]() $A \in \Theta ^-(n)_r$
and
$A \in \Theta ^-(n)_r$
and
![]() $\lambda _{i}<\sigma _{i}(A)$
for some i, then
$\lambda _{i}<\sigma _{i}(A)$
for some i, then
![]() $\mathfrak {k}_{\lambda }\mathfrak {f}^{(A)}=0$
.
$\mathfrak {k}_{\lambda }\mathfrak {f}^{(A)}=0$
.
Proof. Assume
![]() $A\in \Theta ^+(n)_r$
and
$A\in \Theta ^+(n)_r$
and
![]() ${\lambda }_i<\sigma _i(A)$
for some i. For
${\lambda }_i<\sigma _i(A)$
for some i. For
![]() $\mu \in \mathbb Z^{n}, 1 \leqslant j \leqslant n-1$
, we have
$\mu \in \mathbb Z^{n}, 1 \leqslant j \leqslant n-1$
, we have
![]() $\mathfrak {e}_j\mathfrak {k}_\mu =\mathfrak {k}_{\mu +\alpha _j} \mathfrak {e}_j$
. This implies that
$\mathfrak {e}_j\mathfrak {k}_\mu =\mathfrak {k}_{\mu +\alpha _j} \mathfrak {e}_j$
. This implies that
where
![]() $\mathfrak {m}_{j} =\mathfrak {e}_{j-1}^{(a_{j-1, j})}(\mathfrak {e}_{j-2}^{(a_{j-2, j})} \mathfrak {e}_{j-1}^{(a_{j-2, j})}) \cdots (\mathfrak {e}_{1}^{(a_{1, j})} \mathfrak {e}_{2}^{(a_{1, j})} \cdots \mathfrak {e}_{j-1}^{(a_{1, j})})$
and
$\mathfrak {m}_{j} =\mathfrak {e}_{j-1}^{(a_{j-1, j})}(\mathfrak {e}_{j-2}^{(a_{j-2, j})} \mathfrak {e}_{j-1}^{(a_{j-2, j})}) \cdots (\mathfrak {e}_{1}^{(a_{1, j})} \mathfrak {e}_{2}^{(a_{1, j})} \cdots \mathfrak {e}_{j-1}^{(a_{1, j})})$
and
 $$ \begin{align*}\nu=\sum_{2\leqslant j\leqslant i}\bigg(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\boldsymbol{e}_s-(\sum_{1\leqslant s\leqslant j-1}a_{s,j})\boldsymbol{e}_j\bigg).\end{align*} $$
$$ \begin{align*}\nu=\sum_{2\leqslant j\leqslant i}\bigg(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\boldsymbol{e}_s-(\sum_{1\leqslant s\leqslant j-1}a_{s,j})\boldsymbol{e}_j\bigg).\end{align*} $$
Thus, we have
![]() $ {\mathfrak {e}^{(A)}\mathfrak {k}_{\lambda }}= {\mathfrak {m}_n \mathfrak {m}_{n-1} \cdots \mathfrak {m}_{i+1} \mathfrak {k}_{{\lambda }+\nu } \mathfrak {m}_i \mathfrak {m}_{i-1} \cdots \mathfrak {m}_2 }.$
Since
$ {\mathfrak {e}^{(A)}\mathfrak {k}_{\lambda }}= {\mathfrak {m}_n \mathfrak {m}_{n-1} \cdots \mathfrak {m}_{i+1} \mathfrak {k}_{{\lambda }+\nu } \mathfrak {m}_i \mathfrak {m}_{i-1} \cdots \mathfrak {m}_2 }.$
Since
![]() ${\lambda }_i<\sigma _i(A)$
, we have
${\lambda }_i<\sigma _i(A)$
, we have
![]() ${\lambda }+\nu \not \in \Lambda (n,d)$
. It follows that
${\lambda }+\nu \not \in \Lambda (n,d)$
. It follows that
![]() $\mathfrak {k}_{{\lambda }+\nu }=0$
. Therefore, we have
$\mathfrak {k}_{{\lambda }+\nu }=0$
. Therefore, we have
![]() $\mathfrak {e}^{(A)}\mathfrak {k}_{\lambda }=0$
. Applying
$\mathfrak {e}^{(A)}\mathfrak {k}_{\lambda }=0$
. Applying
![]() $\dot \tau _d$
to the identity in (1) gives that in (2).
$\dot \tau _d$
to the identity in (1) gives that in (2).
Proposition 5.4. Let
![]() ${\mathfrak M}_{d,r}=\{\mathfrak {e}^{(A^+)}\mathfrak {k}_{\lambda }\mathfrak {f}^{(A^-)} \mid A \in \Theta ^\pm (n)_r,\, \lambda \in \Lambda (n,d),\, \lambda \geqslant {\boldsymbol \sigma }(A) \}$
. Then, the algebra
${\mathfrak M}_{d,r}=\{\mathfrak {e}^{(A^+)}\mathfrak {k}_{\lambda }\mathfrak {f}^{(A^-)} \mid A \in \Theta ^\pm (n)_r,\, \lambda \in \Lambda (n,d),\, \lambda \geqslant {\boldsymbol \sigma }(A) \}$
. Then, the algebra ![]() is spanned as a
is spanned as a ![]() -module by the elements in
-module by the elements in
![]() ${\mathfrak M}_{d,r}$
.
${\mathfrak M}_{d,r}$
.
Proof. By Proposition 3.3, we have
Thus, it is enough to prove that if
![]() ${\lambda } \in \Lambda (n,d)$
and
${\lambda } \in \Lambda (n,d)$
and
![]() $ {\lambda }_i <\sigma _i(A) $
for some i,
$ {\lambda }_i <\sigma _i(A) $
for some i, ![]() . We apply induction on
. We apply induction on
![]() $\textrm {deg}(A)$
. If
$\textrm {deg}(A)$
. If
![]() $\textrm {deg}(A)=1$
, then by Lemma 5.3 we have
$\textrm {deg}(A)=1$
, then by Lemma 5.3 we have
![]() $\mathfrak {e}^{(A^+)}\mathfrak {k}_{\lambda }\mathfrak {f}^{(A^-)}=0$
. Now suppose
$\mathfrak {e}^{(A^+)}\mathfrak {k}_{\lambda }\mathfrak {f}^{(A^-)}=0$
. Now suppose
![]() $\textrm {deg}(A)>1$
. For
$\textrm {deg}(A)>1$
. For
![]() $2\leqslant j\leqslant n$
let
$2\leqslant j\leqslant n$
let
 $$ \begin{align*} \begin{aligned} \mathfrak{m}_{j}&=\mathfrak{e}_{j-1}^{(a_{j-1, j})}(\mathfrak{e}_{j-2}^{(a_{j-2, j})} \mathfrak{e}_{j-1}^{(a_{j-2, j})}) \cdots(\mathfrak{e}_{1}^{(a_{1, j})} \mathfrak{e}_{2}^{(a_{1, j})} \cdots \mathfrak{e}_{j-1}^{(a_{1, j})}) \\ \mathfrak{m}_j'&=(\mathfrak{f}_{j-1}^{(a_{j, 1})} \cdots \mathfrak{f}_{2}^{(a_{j, 1})} \mathfrak{f}_{1}^{(a_{j, 1})}) \cdots(\mathfrak{f}_{j-1}^{(a_{j, j-2})} \mathfrak{f}_{j-2}^{(a_{j, j-2})}) \mathfrak{f}_{j-1}^{(a_{j, j-1})}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathfrak{m}_{j}&=\mathfrak{e}_{j-1}^{(a_{j-1, j})}(\mathfrak{e}_{j-2}^{(a_{j-2, j})} \mathfrak{e}_{j-1}^{(a_{j-2, j})}) \cdots(\mathfrak{e}_{1}^{(a_{1, j})} \mathfrak{e}_{2}^{(a_{1, j})} \cdots \mathfrak{e}_{j-1}^{(a_{1, j})}) \\ \mathfrak{m}_j'&=(\mathfrak{f}_{j-1}^{(a_{j, 1})} \cdots \mathfrak{f}_{2}^{(a_{j, 1})} \mathfrak{f}_{1}^{(a_{j, 1})}) \cdots(\mathfrak{f}_{j-1}^{(a_{j, j-2})} \mathfrak{f}_{j-2}^{(a_{j, j-2})}) \mathfrak{f}_{j-1}^{(a_{j, j-1})}. \end{aligned} \end{align*} $$
Then, we have
where
![]() $X_1=\mathfrak {m}_n\mathfrak {m}_{n-1}\cdots \mathfrak {m}_{i+1}$
,
$X_1=\mathfrak {m}_n\mathfrak {m}_{n-1}\cdots \mathfrak {m}_{i+1}$
,
![]() $X_2=\mathfrak {m}_i\mathfrak {m}_{i-1}\cdots \mathfrak {m}_2$
,
$X_2=\mathfrak {m}_i\mathfrak {m}_{i-1}\cdots \mathfrak {m}_2$
,
![]() $Y_1=\mathfrak {m}_2^{\prime }\mathfrak {m}_3^{\prime }\cdots \mathfrak {m}_i^{\prime }$
,
$Y_1=\mathfrak {m}_2^{\prime }\mathfrak {m}_3^{\prime }\cdots \mathfrak {m}_i^{\prime }$
,
![]() $Y_2=\mathfrak {m}_{i+1}^{\prime }\mathfrak {m}_{i+2}^{\prime }\cdots \mathfrak {m}_{n}^{\prime }$
and
$Y_2=\mathfrak {m}_{i+1}^{\prime }\mathfrak {m}_{i+2}^{\prime }\cdots \mathfrak {m}_{n}^{\prime }$
and
 $$ \begin{align*}{\lambda}'={\lambda}+\sum_{2\leqslant j\leqslant i}\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\boldsymbol{e}_s-\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\right)\boldsymbol{e}_j\right).\end{align*} $$
$$ \begin{align*}{\lambda}'={\lambda}+\sum_{2\leqslant j\leqslant i}\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\boldsymbol{e}_s-\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\right)\boldsymbol{e}_j\right).\end{align*} $$
By Lemma 2.1 and 5.2, we have
![]() $\mathfrak {k}_{{\lambda }'}X_2Y_1=\mathfrak {k}_{{\lambda }'}Y_1X_2+\mathfrak {k}_{{\lambda }'}f_1f_2$
where
$\mathfrak {k}_{{\lambda }'}X_2Y_1=\mathfrak {k}_{{\lambda }'}Y_1X_2+\mathfrak {k}_{{\lambda }'}f_1f_2$
where
![]() $f_1$
is a
$f_1$
is a ![]() -linear combination of monomials
-linear combination of monomials
![]() $f_{1,k}$
in the
$f_{1,k}$
in the
![]() $\mathfrak {e}_s^{(a)}$
,
$\mathfrak {e}_s^{(a)}$
,
![]() $f_{2}$
is a
$f_{2}$
is a ![]() -linear combination of monomials
-linear combination of monomials
![]() $f_{2,k}$
in the
$f_{2,k}$
in the
![]() $\mathfrak {f}_s^{(a)}$
, and
$\mathfrak {f}_s^{(a)}$
, and
![]() $\textrm {deg}(f_{1,k})+\textrm {deg}(f_{2,k})<\textrm {deg}(X_2)+\textrm {deg}(Y_1)$
. Since
$\textrm {deg}(f_{1,k})+\textrm {deg}(f_{2,k})<\textrm {deg}(X_2)+\textrm {deg}(Y_1)$
. Since
![]() ${\lambda }_i<\sigma _i(A)$
, we have
${\lambda }_i<\sigma _i(A)$
, we have
![]() ${\lambda }_i^{\prime }<\sigma _i(A^-)$
. Hence by Lemma 5.3, we have
${\lambda }_i^{\prime }<\sigma _i(A^-)$
. Hence by Lemma 5.3, we have
![]() $\mathfrak {k}_{{\lambda }'}Y_1=0$
. This implies that
$\mathfrak {k}_{{\lambda }'}Y_1=0$
. This implies that
where
 $$ \begin{align*}{\lambda}"={\lambda}+\sum_{2\leqslant j\leqslant n}\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\boldsymbol{e}_s-\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\right)\boldsymbol{e}_j\right).\end{align*} $$
$$ \begin{align*}{\lambda}"={\lambda}+\sum_{2\leqslant j\leqslant n}\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\boldsymbol{e}_s-\left(\sum_{1\leqslant s\leqslant j-1}a_{s,j}\right)\boldsymbol{e}_j\right).\end{align*} $$
By Proposition 3.1, we have ![]() and
and ![]() . Thus,
. Thus,
By induction, we have ![]() for
for
![]() $B\in \Theta ^\pm (n)_r$
with
$B\in \Theta ^\pm (n)_r$
with
![]() $\textrm {deg}(B)<\textrm {deg}(A)$
. Therefore,
$\textrm {deg}(B)<\textrm {deg}(A)$
. Therefore, ![]() .
.
By Lemma 3.6, we have ![]() Therefore, the map
Therefore, the map ![]() given in (3.10) restricts to a surjective algebra homomorphism
given in (3.10) restricts to a surjective algebra homomorphism
Since
![]() $\dot {\zeta }_{d,r} (J_{d,r})=0$
, the map
$\dot {\zeta }_{d,r} (J_{d,r})=0$
, the map ![]() induces a surjective algebra homomorphism
induces a surjective algebra homomorphism
A presentation of ![]() was given in [Reference Fu16, Th. 3.9] in the case where
was given in [Reference Fu16, Th. 3.9] in the case where
![]() $r=1$
,
$r=1$
, ![]() is a field and
is a field and
![]() $l'$
is odd. We now generalize this result to the general case.
$l'$
is odd. We now generalize this result to the general case.
Theorem 5.5. The map ![]() is an algebra isomorphism. In particular, the kernel of the map
is an algebra isomorphism. In particular, the kernel of the map ![]() is generated by the elements
is generated by the elements
![]() $1_{\lambda }$
for
$1_{\lambda }$
for
![]() $\lambda \notin \Lambda (n,d)$
.
$\lambda \notin \Lambda (n,d)$
.
6 The classical case
Let
![]() ${\mathcal U}(\mathfrak {gl}_n)$
be the
${\mathcal U}(\mathfrak {gl}_n)$
be the
![]() $\mathbb Q$
-algebra defined by the generators
$\mathbb Q$
-algebra defined by the generators
and the relations
-
(a)
 $H_iH_j=H_jH_i;$
$H_iH_j=H_jH_i;$
-
(b)
 $H_{i}\bar E_j-\bar E_jH_i=(\delta _{i,j}-\delta _{i,j+1}) \bar E_j;$
$H_{i}\bar E_j-\bar E_jH_i=(\delta _{i,j}-\delta _{i,j+1}) \bar E_j;$
-
(c)
 $H_{i}\bar F_j-\bar F_jH_i=(-\delta _{i,j}+\delta _{i,j+1}) \bar F_j;$
$H_{i}\bar F_j-\bar F_jH_i=(-\delta _{i,j}+\delta _{i,j+1}) \bar F_j;$
-
(d)
 $ \bar E_i\bar E_j=\bar E_j\bar E_i,\ \bar F_i\bar F_j=\bar F_j\bar F_i\ when\ |i-j|>1;$
$ \bar E_i\bar E_j=\bar E_j\bar E_i,\ \bar F_i\bar F_j=\bar F_j\bar F_i\ when\ |i-j|>1;$
-
(e)
 $\bar E_i\bar F_j-\bar F_j\bar E_i=\delta _{i,j}H_i;$
$\bar E_i\bar F_j-\bar F_j\bar E_i=\delta _{i,j}H_i;$
-
(f)
 $ \bar E_i^2\bar E_j-2\bar E_i\bar E_j\bar E_i+\bar E_j\bar E_i^2=0\ when\ |i-j|=1;$
$ \bar E_i^2\bar E_j-2\bar E_i\bar E_j\bar E_i+\bar E_j\bar E_i^2=0\ when\ |i-j|=1;$
-
(g)
 $ \bar F_i^2\bar F_j-2\bar F_i\bar F_j\bar F_i+\bar F_j\bar F_i^2=0\ when\ |i-j|=1.$
$ \bar F_i^2\bar F_j-2\bar F_i\bar F_j\bar F_i+\bar F_j\bar F_i^2=0\ when\ |i-j|=1.$
Then,
![]() ${\mathcal U}(\mathfrak {gl}_n)$
is the universal enveloping algebra of
${\mathcal U}(\mathfrak {gl}_n)$
is the universal enveloping algebra of
![]() $\mathfrak {gl}_n$
. Let
$\mathfrak {gl}_n$
. Let
![]() ${\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
be the
${\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
be the
![]() $\mathbb Z$
-subalgebra of
$\mathbb Z$
-subalgebra of
![]() ${\mathcal U}(\mathfrak {gl}_n)$
generated by
${\mathcal U}(\mathfrak {gl}_n)$
generated by
![]() $\bar E_i^{(m)}$
,
$\bar E_i^{(m)}$
,
![]() $\bar F_i^{(m)}$
, and
$\bar F_i^{(m)}$
, and
![]() $\big ({H_j\atop t}\big )$
for
$\big ({H_j\atop t}\big )$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $1\leqslant j\leqslant n$
and
$1\leqslant j\leqslant n$
and
![]() $m,t\in \mathbb N$
, where
$m,t\in \mathbb N$
, where
 $$ \begin{align*}\bar E_i^{(m)}=\frac{\bar E_i^m}{m!},\, \bar F_i^{(m)}=\frac{\bar F_i^m}{m!},\, \left({H_j\atop t}\right)=\frac{H_j(H_{j}-1)\cdots (H_{j}-t+1)}{t!}.\end{align*} $$
$$ \begin{align*}\bar E_i^{(m)}=\frac{\bar E_i^m}{m!},\, \bar F_i^{(m)}=\frac{\bar F_i^m}{m!},\, \left({H_j\atop t}\right)=\frac{H_j(H_{j}-1)\cdots (H_{j}-t+1)}{t!}.\end{align*} $$
Let
![]() ${U_{\mathbb Z}(\mathfrak {gl}_n)}={U_{\mathcal Z}(\mathfrak {gl}_n)}\otimes _{\mathcal Z}\mathbb Z$
, where
${U_{\mathbb Z}(\mathfrak {gl}_n)}={U_{\mathcal Z}(\mathfrak {gl}_n)}\otimes _{\mathcal Z}\mathbb Z$
, where
![]() $\mathbb Z$
is viewed as
$\mathbb Z$
is viewed as
![]() ${\mathcal Z}$
-modules by specializing v to
${\mathcal Z}$
-modules by specializing v to
![]() $1$
. Let
$1$
. Let
![]() ${\bar U_{\mathbb Z}(\mathfrak {gl}_n)}={U_{\mathbb Z}(\mathfrak {gl}_n)}/\langle K_i-1\mid 1\leqslant i\leqslant n\rangle $
. We shall denote the images of
${\bar U_{\mathbb Z}(\mathfrak {gl}_n)}={U_{\mathbb Z}(\mathfrak {gl}_n)}/\langle K_i-1\mid 1\leqslant i\leqslant n\rangle $
. We shall denote the images of
![]() $E_i^{(m)}$
,
$E_i^{(m)}$
,
![]() $F_i^{(m)}$
, etc. in
$F_i^{(m)}$
, etc. in
![]() ${\bar U_{\mathbb Z}(\mathfrak {gl}_n)}$
by the same letters. By [Reference Lusztig22, 6.7(c)], there is an algebra isomorphism
${\bar U_{\mathbb Z}(\mathfrak {gl}_n)}$
by the same letters. By [Reference Lusztig22, 6.7(c)], there is an algebra isomorphism
such that
![]() $\theta (E_i^{(m)})=\bar E_i^{(m)}$
,
$\theta (E_i^{(m)})=\bar E_i^{(m)}$
,
![]() $\theta (F_i^{(m)})=\bar F_i^{(m)}$
,
$\theta (F_i^{(m)})=\bar F_i^{(m)}$
,
![]() $\theta (\big [{K_j;0\atop t}\big ])=\big ({H_j\atop t}\big )$
for
$\theta (\big [{K_j;0\atop t}\big ])=\big ({H_j\atop t}\big )$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $1\leqslant j\leqslant n$
,
$1\leqslant j\leqslant n$
,
![]() $m,t\in \mathbb N$
. We will identify
$m,t\in \mathbb N$
. We will identify
![]() ${\bar U_{\mathbb Z}(\mathfrak {gl}_n)}$
with
${\bar U_{\mathbb Z}(\mathfrak {gl}_n)}$
with
![]() ${\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
.
${\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
.
Let
![]() ${\mathcal S}_{\mathbb Z}(n,d)={\mathcal S}_{\mathcal Z}(n,d)\otimes _{\mathcal Z}\mathbb Z$
where
${\mathcal S}_{\mathbb Z}(n,d)={\mathcal S}_{\mathcal Z}(n,d)\otimes _{\mathcal Z}\mathbb Z$
where
![]() $\mathbb Z$
is viewed as
$\mathbb Z$
is viewed as
![]() ${\mathcal Z}$
-modules by specializing v to
${\mathcal Z}$
-modules by specializing v to
![]() $1$
. The map
$1$
. The map
![]() $\zeta _{d}$
given in (3.6) induces, upon tensoring with
$\zeta _{d}$
given in (3.6) induces, upon tensoring with
![]() $\mathbb Z$
, a surjective algebra homomorphism
$\mathbb Z$
, a surjective algebra homomorphism
Since
![]() $\xi _{d}(K_i)=1$
, the map
$\xi _{d}(K_i)=1$
, the map
![]() $\xi _{d}$
induces a surjective algebra homomorphism
$\xi _{d}$
induces a surjective algebra homomorphism
In the remainder of this section, we assume that
![]() $l'=l=1$
. Let
$l'=l=1$
. Let
We shall denote the images of
![]() $\bar E_{i}^{(m)}$
,
$\bar E_{i}^{(m)}$
,
![]() $\bar F_{i}^{(m)}$
, etc. in
$\bar F_{i}^{(m)}$
, etc. in ![]() by the same letters. For
by the same letters. For
![]() $A\in {\Theta (n,d)}$
, let
$A\in {\Theta (n,d)}$
, let
![]() $[A]_1$
be the image of
$[A]_1$
be the image of
![]() $[A]$
in
$[A]$
in ![]() . The map
. The map
![]() $\xi _{d}$
induces, upon tensoring with
$\xi _{d}$
induces, upon tensoring with ![]() , a surjective algebra homomorphism
, a surjective algebra homomorphism
Let ![]() be the infinitesimal Schur algebra introduced in [Reference Doty, Nakano and Peters11]. By [Reference Doty, Nakano and Peters11, (5.3.4)], the set
be the infinitesimal Schur algebra introduced in [Reference Doty, Nakano and Peters11]. By [Reference Doty, Nakano and Peters11, (5.3.4)], the set
![]() $\{[A]_1\mid A\in {\Theta (n,d)},\,a_{i,j}<p^r,\,\forall i,j\}$
forms a
$\{[A]_1\mid A\in {\Theta (n,d)},\,a_{i,j}<p^r,\,\forall i,j\}$
forms a ![]() -basis for
-basis for ![]() . Hence, we have
. Hence, we have
Let ![]() be the
be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $\bar E_i^{(m)}$
,
$\bar E_i^{(m)}$
,
![]() $\bar F_i^{(m)}$
,
$\bar F_i^{(m)}$
,
![]() $\big ({H_j\atop t}\big )$
for
$\big ({H_j\atop t}\big )$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() $1\leqslant j\leqslant n$
,
$1\leqslant j\leqslant n$
,
![]() $t\in \mathbb N$
and
$t\in \mathbb N$
and
![]() $0\leqslant m<p^{r}$
. Then, by (6.1), we have
$0\leqslant m<p^{r}$
. Then, by (6.1), we have
Therefore, by Lemma 3.5, we have ![]() . Hence, by restricting the map
. Hence, by restricting the map
![]() $\xi _{d}$
to
$\xi _{d}$
to ![]() , we obtain a surjective algebra homomorphism
, we obtain a surjective algebra homomorphism
By Theorem 4.10, we obtain the following result.
Theorem 6.1. The kernel of the map ![]() is generated by the elements
is generated by the elements
![]() $1-\sum _{\mu \in \Lambda (n,d)} H_{\mu }$
and
$1-\sum _{\mu \in \Lambda (n,d)} H_{\mu }$
and
![]() $\big ({H_i \atop t}\big ) H_{\lambda }-\big ({{\lambda }_i \atop t}\big ) H_{\lambda }$
for
$\big ({H_i \atop t}\big ) H_{\lambda }-\big ({{\lambda }_i \atop t}\big ) H_{\lambda }$
for
![]() $1 \leqslant i \leqslant n$
,
$1 \leqslant i \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $\lambda \in \Lambda (n,d)$
, where
$\lambda \in \Lambda (n,d)$
, where
![]() $H_{\lambda }=\prod _{1\leqslant i\leqslant n}\big ({H_i\atop {\lambda }_i}\big ).$
$H_{\lambda }=\prod _{1\leqslant i\leqslant n}\big ({H_i\atop {\lambda }_i}\big ).$
Let
 $$ \begin{align*}\dot{\mathcal U}(\mathfrak{gl}_n):=\bigoplus_{{\lambda},\mu\in\mathbb Z^{n}}{}_{\lambda}{\mathcal U}(\mathfrak{gl}_n)_\mu,\end{align*} $$
$$ \begin{align*}\dot{\mathcal U}(\mathfrak{gl}_n):=\bigoplus_{{\lambda},\mu\in\mathbb Z^{n}}{}_{\lambda}{\mathcal U}(\mathfrak{gl}_n)_\mu,\end{align*} $$
where
 $$ \begin{align*} {}_{\lambda}{\mathcal U}(\mathfrak{gl}_n)_\mu={\mathcal U}(\mathfrak{gl}_n)/\left(\sum_{{\mathbf{j}}\in\mathbb Z^{n}}\big(H^{\mathbf{j}}-{\lambda}^{{\mathbf{j}}}\big) {\mathcal U}(\mathfrak{gl}_n)+\sum_{{\mathbf{j}}\in\mathbb Z^{n}}{\mathcal U}(\mathfrak{gl}_n)\big(H^{\mathbf{j}}-\mu^{{\mathbf{j}}})\right), \end{align*} $$
$$ \begin{align*} {}_{\lambda}{\mathcal U}(\mathfrak{gl}_n)_\mu={\mathcal U}(\mathfrak{gl}_n)/\left(\sum_{{\mathbf{j}}\in\mathbb Z^{n}}\big(H^{\mathbf{j}}-{\lambda}^{{\mathbf{j}}}\big) {\mathcal U}(\mathfrak{gl}_n)+\sum_{{\mathbf{j}}\in\mathbb Z^{n}}{\mathcal U}(\mathfrak{gl}_n)\big(H^{\mathbf{j}}-\mu^{{\mathbf{j}}})\right), \end{align*} $$
![]() $H^{\mathbf {j}}=\prod _{1\leqslant i\leqslant n} H_i^{j_i}$
and
$H^{\mathbf {j}}=\prod _{1\leqslant i\leqslant n} H_i^{j_i}$
and
![]() ${\lambda }^{{\mathbf {j}}}=\prod _{1\leqslant i\leqslant n}{\lambda }_i^{j_i}$
. Let
${\lambda }^{{\mathbf {j}}}=\prod _{1\leqslant i\leqslant n}{\lambda }_i^{j_i}$
. Let
![]() $\bar \pi _{{\lambda },\mu }:{\mathcal U}(\mathfrak {gl}_n)\rightarrow {}_{\lambda }{\mathcal U}(\mathfrak {gl}_n)_\mu $
be the canonical projection. Let
$\bar \pi _{{\lambda },\mu }:{\mathcal U}(\mathfrak {gl}_n)\rightarrow {}_{\lambda }{\mathcal U}(\mathfrak {gl}_n)_\mu $
be the canonical projection. Let
![]() $\bar 1_{\lambda }=\bar \pi _{{\lambda },{\lambda }}(1)$
. As in the case of
$\bar 1_{\lambda }=\bar \pi _{{\lambda },{\lambda }}(1)$
. As in the case of
![]() $\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
, there is a natural associative
$\dot {{{\mathbf {U}}}}(\mathfrak {gl}_n)$
, there is a natural associative
![]() $\mathbb Q$
-algebra structure on
$\mathbb Q$
-algebra structure on
![]() $\dot {\mathcal U}(\mathfrak {gl}_n)$
inherited from that of
$\dot {\mathcal U}(\mathfrak {gl}_n)$
inherited from that of
![]() ${\mathcal U}(\mathfrak {gl}_n)$
, and
${\mathcal U}(\mathfrak {gl}_n)$
, and
![]() $\dot {\mathcal U}(\mathfrak {gl}_n)$
is naturally a
$\dot {\mathcal U}(\mathfrak {gl}_n)$
is naturally a
![]() ${\mathcal U}(\mathfrak {gl}_n)$
-bimodule. Let
${\mathcal U}(\mathfrak {gl}_n)$
-bimodule. Let
![]() $\dot {\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
be the
$\dot {\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
be the
![]() $\mathbb Z$
-subalgebra of
$\mathbb Z$
-subalgebra of
![]() $\dot {\mathcal U}(\mathfrak {gl}_n)$
generated by the elements
$\dot {\mathcal U}(\mathfrak {gl}_n)$
generated by the elements
![]() $\bar E_i^{(m)}\bar 1_{\lambda }$
and
$\bar E_i^{(m)}\bar 1_{\lambda }$
and
![]() $\bar 1_{\lambda }\bar F_i^{(m)}$
for
$\bar 1_{\lambda }\bar F_i^{(m)}$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() ${\lambda }\in \mathbb Z^{n}$
and
${\lambda }\in \mathbb Z^{n}$
and
![]() $m\in \mathbb N$
.
$m\in \mathbb N$
.
Let
![]() ${\dot U_{\mathbb Z}(\mathfrak {gl}_n)}=\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)\otimes _{\mathcal Z}\mathbb Z$
, where
${\dot U_{\mathbb Z}(\mathfrak {gl}_n)}=\dot {{U}}_{\mathcal Z}(\mathfrak {gl}_n)\otimes _{\mathcal Z}\mathbb Z$
, where
![]() $\mathbb Z$
is viewed as a
$\mathbb Z$
is viewed as a
![]() ${\mathcal Z}$
-module by specializing v to
${\mathcal Z}$
-module by specializing v to
![]() $1$
. By (6.1), we have
$1$
. By (6.1), we have
We will identify
![]() ${\dot U_{\mathbb Z}(\mathfrak {gl}_n)}$
with
${\dot U_{\mathbb Z}(\mathfrak {gl}_n)}$
with
![]() $\dot {\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
. The map
$\dot {\mathcal U}_{\mathbb Z}(\mathfrak {gl}_n)$
. The map
![]() $\dot {\zeta }_{d}$
given in (3.9) induces, upon tensoring with
$\dot {\zeta }_{d}$
given in (3.9) induces, upon tensoring with
![]() $\mathbb Z$
, a surjective algebra homomorphism
$\mathbb Z$
, a surjective algebra homomorphism
Let ![]() . We shall denote the images of
. We shall denote the images of
![]() $\bar E_{i}^{(m)}\bar 1_{\lambda }$
,
$\bar E_{i}^{(m)}\bar 1_{\lambda }$
,
![]() $\bar 1_{\lambda }\bar F_{i}^{(m)}$
in
$\bar 1_{\lambda }\bar F_{i}^{(m)}$
in ![]() by the same letters. The map
by the same letters. The map
![]() $\dot \xi _{d}$
induces, upon tensoring with
$\dot \xi _{d}$
induces, upon tensoring with ![]() , a surjective algebra homomorphism
, a surjective algebra homomorphism
Let ![]() be the
be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $\bar E_i^{(m)}\bar 1_{\lambda }$
,
$\bar E_i^{(m)}\bar 1_{\lambda }$
,
![]() $\bar 1_{\lambda }\bar F_i^{(m)}$
for
$\bar 1_{\lambda }\bar F_i^{(m)}$
for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() ${\lambda }\in \mathbb Z^{n}$
and
${\lambda }\in \mathbb Z^{n}$
and
![]() $0\leqslant m<p^{r}$
. Then, by (6.2), we have
$0\leqslant m<p^{r}$
. Then, by (6.2), we have
By Lemma 3.6, we have ![]() . Hence, by restricting the map
. Hence, by restricting the map
![]() $\dot {\xi }_{d}$
to
$\dot {\xi }_{d}$
to ![]() , we obtain a surjective algebra homomorphism
, we obtain a surjective algebra homomorphism
By Theorem 5.5, we obtain the following result.
Theorem 6.2. The kernel of the map ![]() is generated by the elements
is generated by the elements
![]() $\bar 1_{\lambda }$
for
$\bar 1_{\lambda }$
for
![]() ${\lambda }\not \in \Lambda (n,d)$
.
${\lambda }\not \in \Lambda (n,d)$
.
7 Borel subalgebras of the infinitesimal q-Schur algebra 
In this section, we investigate Borel subalgebras of the infinitesimal q-Schur algebra ![]() . In what follows, we focus entirely on the quantum case as the corresponding results for the classical cases are essentially the same.
. In what follows, we focus entirely on the quantum case as the corresponding results for the classical cases are essentially the same.
Let ![]() and
and ![]() . These algebras are called Borel subalgebras of
. These algebras are called Borel subalgebras of ![]() . Furthermore, let
. Furthermore, let ![]() (resp.
(resp. ![]() ) be the
) be the ![]() -subalgebra of
-subalgebra of ![]() generated by the elements
generated by the elements
![]() $E_{i}^{(m)}1_{\lambda }$
(resp.
$E_{i}^{(m)}1_{\lambda }$
(resp.
![]() $1_{\lambda } F_{i}^{(m)}$
) for
$1_{\lambda } F_{i}^{(m)}$
) for
![]() $1\leqslant i\leqslant n-1$
,
$1\leqslant i\leqslant n-1$
,
![]() ${\lambda }\in \mathbb Z^{n}$
and
${\lambda }\in \mathbb Z^{n}$
and
![]() $0\leqslant m<lp^{r-1}$
.
$0\leqslant m<lp^{r-1}$
.
Let ![]() (resp.
(resp. ![]() ) be the
) be the ![]() -subalgebra of
-subalgebra of ![]() generated by
generated by
![]() $\mathtt {e}_i^{(m)}$
(resp.
$\mathtt {e}_i^{(m)}$
(resp.
![]() $\mathtt {f}_i^{(m)}$
) and
$\mathtt {f}_i^{(m)}$
) and
![]() $\mathtt {k}_\lambda $
for
$\mathtt {k}_\lambda $
for
![]() $1 \leqslant i \leqslant n-1$
,
$1 \leqslant i \leqslant n-1$
,
![]() $0\leqslant m<lp^{r-1}$
and
$0\leqslant m<lp^{r-1}$
and
![]() $\lambda \in \Lambda (n,d)$
. These algebras are called Borel subalgebras of
$\lambda \in \Lambda (n,d)$
. These algebras are called Borel subalgebras of ![]() .
.
Let ![]() (resp.
(resp. ![]() ) be the
) be the ![]() -subalgebra of
-subalgebra of ![]() generated by
generated by
![]() $\mathtt {e}_i^{(m)}$
(resp.
$\mathtt {e}_i^{(m)}$
(resp.
![]() $\mathtt {f}_i^{(m)}$
) for
$\mathtt {f}_i^{(m)}$
) for
![]() $1\leqslant i\leqslant n-1$
and
$1\leqslant i\leqslant n-1$
and
![]() $0\leqslant m<lp^{r-1}$
.
$0\leqslant m<lp^{r-1}$
.
Lemma 7.1. Each of the following set forms a ![]() -basis of
-basis of ![]() :
:
-
(1)
 ${\mathscr M}_{d,r}^+:=\{\mathtt {e}^{(A)} \mid A \in \Theta ^+(n)_r,\,\sigma (A)\leqslant d\}$
;
${\mathscr M}_{d,r}^+:=\{\mathtt {e}^{(A)} \mid A \in \Theta ^+(n)_r,\,\sigma (A)\leqslant d\}$
; -
(2)
 ${\mathscr P}_{d,r}^+:=\{A(\mathbf {0},d)\mid A\in \Theta ^+(n)_r,\,\sigma (A)\leqslant d\}$
.
${\mathscr P}_{d,r}^+:=\{A(\mathbf {0},d)\mid A\in \Theta ^+(n)_r,\,\sigma (A)\leqslant d\}$
.
A similar result holds for ![]() .
.
Proof. By [Reference Doty and Giaquinto8, Prop. 8.2], we have
![]() $1=\sum _{{\lambda }\in \Lambda (n,d)}\mathtt {k}_{\lambda }$
. Hence, by [Reference Du and Parshall15, Lem. 4.10], we have
$1=\sum _{{\lambda }\in \Lambda (n,d)}\mathtt {k}_{\lambda }$
. Hence, by [Reference Du and Parshall15, Lem. 4.10], we have
 $$ \begin{align} {\mathtt e}^{(A)}=\sum_{{\lambda}\in\Lambda(n,d) }{\mathtt e}^{(A)}\mathtt{k}_{\lambda}=\sum_{{\lambda}\in\Lambda(n,d)\atop{\lambda}\geqslant{\boldsymbol\sigma}(A)}{\mathtt e}^{(A)}\mathtt{k}_{\lambda}, \end{align} $$
$$ \begin{align} {\mathtt e}^{(A)}=\sum_{{\lambda}\in\Lambda(n,d) }{\mathtt e}^{(A)}\mathtt{k}_{\lambda}=\sum_{{\lambda}\in\Lambda(n,d)\atop{\lambda}\geqslant{\boldsymbol\sigma}(A)}{\mathtt e}^{(A)}\mathtt{k}_{\lambda}, \end{align} $$
for
![]() $A\in \Theta ^+(n)_r$
. Furthermore, we have
$A\in \Theta ^+(n)_r$
. Furthermore, we have
 $$ \begin{align} A(\mathbf{0},d)=\sum_{{\lambda}\in\Lambda(n,d)}A(\mathbf{0},d)[\operatorname{diag}({\lambda})]_{\varepsilon}=\sum_{{\lambda}\in\Lambda(n,d)\atop{\lambda}\geqslant{\boldsymbol\sigma}(A)} A(\mathbf{0},d)[\operatorname{diag}({\lambda})]_{\varepsilon}, \end{align} $$
$$ \begin{align} A(\mathbf{0},d)=\sum_{{\lambda}\in\Lambda(n,d)}A(\mathbf{0},d)[\operatorname{diag}({\lambda})]_{\varepsilon}=\sum_{{\lambda}\in\Lambda(n,d)\atop{\lambda}\geqslant{\boldsymbol\sigma}(A)} A(\mathbf{0},d)[\operatorname{diag}({\lambda})]_{\varepsilon}, \end{align} $$
for
![]() $A\in \Theta ^+(n)_r$
, since
$A\in \Theta ^+(n)_r$
, since
![]() $1=\sum _{{\lambda }\in \Lambda (n,d)}[\operatorname {diag}({\lambda })]_{\varepsilon }$
. Therefore, we have
$1=\sum _{{\lambda }\in \Lambda (n,d)}[\operatorname {diag}({\lambda })]_{\varepsilon }$
. Therefore, we have
for
![]() $A\in \Theta ^+(n)_r$
with
$A\in \Theta ^+(n)_r$
with
![]() $\sigma (A)>d$
. Hence, by Proposition 3.1 and 3.2, we conclude that
$\sigma (A)>d$
. Hence, by Proposition 3.1 and 3.2, we conclude that ![]() . Furthermore, by Proposition 3.7, the sets
. Furthermore, by Proposition 3.7, the sets
![]() ${\mathscr M}_{d,r}^+$
and
${\mathscr M}_{d,r}^+$
and
![]() ${\mathscr P}_{d,r}^+$
are both linearly independent. Our assertion follows.
${\mathscr P}_{d,r}^+$
are both linearly independent. Our assertion follows.
Lemma 7.2. Each of the following set forms a ![]() -basis of
-basis of ![]() :
:
-
(1)
 ${\mathscr M}_{d,r}^{\geqslant 0}:=\{{\mathtt e}^{(A)}\mathtt {k}_\lambda \mid A \in \Theta ^+(n)_r,\,{\lambda }\in \Lambda (n,d),\, \lambda \geqslant {\boldsymbol \sigma }(A)\}$
;
${\mathscr M}_{d,r}^{\geqslant 0}:=\{{\mathtt e}^{(A)}\mathtt {k}_\lambda \mid A \in \Theta ^+(n)_r,\,{\lambda }\in \Lambda (n,d),\, \lambda \geqslant {\boldsymbol \sigma }(A)\}$
; -
(2)
 ${\mathscr L}_{d,r}^{\geqslant 0}:= \{[A+\operatorname {diag}({\lambda })]_{\varepsilon } \mid A \in \Theta ^+(n)_r,\, {\lambda }\in \Lambda (n,d-\sigma (A)) \}$
.
${\mathscr L}_{d,r}^{\geqslant 0}:= \{[A+\operatorname {diag}({\lambda })]_{\varepsilon } \mid A \in \Theta ^+(n)_r,\, {\lambda }\in \Lambda (n,d-\sigma (A)) \}$
.
A similar result holds for ![]() .
.
Proof. From Lemma 7.1, (7.1) and (7.2), it follows that ![]() . Therefore, the result follows from Proposition 3.7.
. Therefore, the result follows from Proposition 3.7.
Let ![]() be the quotient of
be the quotient of ![]() by
by
![]() $I_{d,r}^{\geqslant 0}$
, where
$I_{d,r}^{\geqslant 0}$
, where
![]() $I_{d,r}^{\geqslant 0}$
is the two-sided ideal of
$I_{d,r}^{\geqslant 0}$
is the two-sided ideal of ![]() generated by the elements
generated by the elements
![]() $1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }, K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
and
$1-\sum _{\mu \in \Lambda (n,d)} K_{\mu }, K_{i} K_{\lambda }-\varepsilon ^{\lambda _{i}} K_{\lambda }$
and
![]() $\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
$\big [{K_i;0 \atop t}\big ] K_{\lambda }-\big [{{\lambda }_i \atop t}\big ]_{\varepsilon } K_{\lambda }$
for
![]() $1 \leqslant i \leqslant n$
,
$1 \leqslant i \leqslant n$
,
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() $\lambda \in \Lambda (n,d)$
.
$\lambda \in \Lambda (n,d)$
.
By restricting the map
![]() $\zeta _{d,r}$
given in (4.2) to
$\zeta _{d,r}$
given in (4.2) to ![]() , we obtain a surjective algebra homomorphism
, we obtain a surjective algebra homomorphism ![]() . Since
. Since
![]() $\zeta _{d,r}(I_{d,r}^{\geqslant 0})=0$
, the map
$\zeta _{d,r}(I_{d,r}^{\geqslant 0})=0$
, the map
![]() $\zeta _{d,r}$
induces an epimorphism
$\zeta _{d,r}$
induces an epimorphism
Theorem 7.3. The map ![]() is an algebra isomorphism. In particular, the kernel of the map
is an algebra isomorphism. In particular, the kernel of the map ![]() is
is
![]() $I_{d,r}^{\geqslant 0}$
. A similar result holds for
$I_{d,r}^{\geqslant 0}$
. A similar result holds for ![]() .
.
Proof. Using an argument similar to the proof of Proposition 4.9, we can show that the algebra ![]() is spanned as a
is spanned as a ![]() -module by the elements
-module by the elements
![]() $E^{(A)} K_{\lambda }+I_{d,r}^{\geqslant 0}$
for
$E^{(A)} K_{\lambda }+I_{d,r}^{\geqslant 0}$
for
![]() $A \in \Theta ^+(n)_r$
,
$A \in \Theta ^+(n)_r$
,
![]() $\lambda \in \Lambda (n,d)$
and
$\lambda \in \Lambda (n,d)$
and
![]() $\lambda \geqslant {\boldsymbol \sigma }(A)$
. Furthermore, by Lemma 7.2, the set
$\lambda \geqslant {\boldsymbol \sigma }(A)$
. Furthermore, by Lemma 7.2, the set
forms a ![]() -basis for
-basis for ![]() . Hence,
. Hence,
![]() $\zeta _{d,r}' $
is an algebra isomorphism.
$\zeta _{d,r}' $
is an algebra isomorphism.
Let ![]() be the quotient of
be the quotient of ![]() by
by
![]() $J_{d,r}^{\geqslant 0}$
, where
$J_{d,r}^{\geqslant 0}$
, where
![]() $J_{d,r}^{\geqslant 0}$
is the two-sided ideal of
$J_{d,r}^{\geqslant 0}$
is the two-sided ideal of ![]() generated by the elements
generated by the elements
![]() $1_{\lambda }$
for
$1_{\lambda }$
for
![]() $\lambda \not \in \Lambda (n,d)$
.
$\lambda \not \in \Lambda (n,d)$
.
By restricting the map
![]() $\dot {\zeta }_{d,r}$
given in (5.1) to
$\dot {\zeta }_{d,r}$
given in (5.1) to ![]() , we obtain a surjective algebra homomorphism
, we obtain a surjective algebra homomorphism ![]() . Since
. Since
![]() $\dot {\zeta }_{d,r}(J_{d,r}^{\geqslant 0})=0$
, the map
$\dot {\zeta }_{d,r}(J_{d,r}^{\geqslant 0})=0$
, the map
![]() $\dot {\zeta }_{d,r}$
induces an epimorphism
$\dot {\zeta }_{d,r}$
induces an epimorphism
Theorem 7.4. The map ![]() is an algebra isomorphism. In particular, the kernel of the map
is an algebra isomorphism. In particular, the kernel of the map ![]() is
is
![]() $J_{d,r}^{\geqslant 0}$
. A similar result holds for
$J_{d,r}^{\geqslant 0}$
. A similar result holds for ![]() .
.
Proof. Using an argument similar to the proof of Proposition 5.4, we can show that the algebra ![]() is spanned as a
is spanned as a ![]() -module by the elements
-module by the elements
![]() $E^{(A)}1_{\lambda }+J_{d,r}^{\geqslant 0}$
for
$E^{(A)}1_{\lambda }+J_{d,r}^{\geqslant 0}$
for
![]() $A\in \Theta ^+(n)_r$
,
$A\in \Theta ^+(n)_r$
,
![]() ${\lambda } \in \Lambda (n,d)$
and
${\lambda } \in \Lambda (n,d)$
and
![]() ${\lambda } \geqslant {\boldsymbol \sigma }(A)$
. Furthermore, by Lemma 7.2, the set
${\lambda } \geqslant {\boldsymbol \sigma }(A)$
. Furthermore, by Lemma 7.2, the set
forms a ![]() -basis of
-basis of ![]() . Therefore,
. Therefore,
![]() $\dot {\zeta }_{d,r}'$
is an algebra isomorphism.
$\dot {\zeta }_{d,r}'$
is an algebra isomorphism.
8 Irreducible  -modules
-modules
In this section, we assume that ![]() is a field,
is a field,
![]() $p>0$
and
$p>0$
and
![]() $l'=l$
is odd. Let
$l'=l$
is odd. Let
![]() $X=\mathbb Z^{n}$
and
$X=\mathbb Z^{n}$
and
![]() $X^+=\{{\lambda }\in X\mid {\lambda }_1\geqslant {\lambda }_{2}\geqslant \cdots \geqslant {\lambda }_n\}$
. For
$X^+=\{{\lambda }\in X\mid {\lambda }_1\geqslant {\lambda }_{2}\geqslant \cdots \geqslant {\lambda }_n\}$
. For
![]() ${\lambda }\in X^+$
, let
${\lambda }\in X^+$
, let
![]() $L({\lambda })$
be the simple integrable
$L({\lambda })$
be the simple integrable ![]() -module of highest weight
-module of highest weight
![]() ${\lambda }$
. Let
${\lambda }$
. Let
![]() $\text {Ind}^{U_2}_{U_1}(-)= H^0(U_2/U_1,-)$
be the induction functor for quantized enveloping algebras defined in [Reference Andersen, Polo and Wen1], [Reference Andersen, Polo and Wen2].
$\text {Ind}^{U_2}_{U_1}(-)= H^0(U_2/U_1,-)$
be the induction functor for quantized enveloping algebras defined in [Reference Andersen, Polo and Wen1], [Reference Andersen, Polo and Wen2].
For
![]() ${\lambda }\in X$
, let
${\lambda }\in X$
, let
Let
![]() $P_r=\{{\lambda }\in \mathbb N^{n}\mid 0\leqslant {\lambda }_i-{\lambda }_{i+1}<lp^{r-1}\text { for }1\leqslant i\leqslant n \}$
, where
$P_r=\{{\lambda }\in \mathbb N^{n}\mid 0\leqslant {\lambda }_i-{\lambda }_{i+1}<lp^{r-1}\text { for }1\leqslant i\leqslant n \}$
, where
![]() ${\lambda }_{n+1}=0$
. The following result was given in [Reference Drupieski12, Ths. 3.4.1 & 3.4.3].
${\lambda }_{n+1}=0$
. The following result was given in [Reference Drupieski12, Ths. 3.4.1 & 3.4.3].
Theorem 8.1.
![]() $(1)$
The set
$(1)$
The set
![]() $\{\widehat L_r({\lambda })\mid {\lambda }\in X\}$
form a complete set of pairwise nonisomorphic irreducible integrable
$\{\widehat L_r({\lambda })\mid {\lambda }\in X\}$
form a complete set of pairwise nonisomorphic irreducible integrable ![]() -modules.
-modules.
![]() $(2)$
For
$(2)$
For
![]() ${\lambda },\mu \in X$
, we have
${\lambda },\mu \in X$
, we have
![]() $\widehat L_r({\lambda }+lp^{r-1}\mu )\cong \widehat L_r({\lambda })\otimes lp^{r-1}\mu $
.
$\widehat L_r({\lambda }+lp^{r-1}\mu )\cong \widehat L_r({\lambda })\otimes lp^{r-1}\mu $
.
![]() $(3)$
For
$(3)$
For
![]() ${\lambda }\in P_r$
, we have
${\lambda }\in P_r$
, we have ![]() .
.
If M is a ![]() -module and
-module and
![]() ${\lambda }\in X$
let
${\lambda }\in X$
let
 $$ \begin{align*}M_{\lambda}=\{w\in M\mid K_iw=\varepsilon^{{\lambda}_i}w,\,\left[{K_i;0\atop t}\right]w=\left[{{\lambda}_i\atop t}\right]_{\varepsilon} w \text{ for }1\leqslant i\leqslant n,\,t\in\mathbb N\}.\end{align*} $$
$$ \begin{align*}M_{\lambda}=\{w\in M\mid K_iw=\varepsilon^{{\lambda}_i}w,\,\left[{K_i;0\atop t}\right]w=\left[{{\lambda}_i\atop t}\right]_{\varepsilon} w \text{ for }1\leqslant i\leqslant n,\,t\in\mathbb N\}.\end{align*} $$
Let
![]() ${\Gamma }_r=P_r+lp^{r-1}\mathbb N^{n}$
and
${\Gamma }_r=P_r+lp^{r-1}\mathbb N^{n}$
and
![]() ${\Gamma }_r^d=\big \{{\lambda }\in {\Gamma }_r\big |\sum _{i=1}^n{\lambda }_i=d\big \}.$
For
${\Gamma }_r^d=\big \{{\lambda }\in {\Gamma }_r\big |\sum _{i=1}^n{\lambda }_i=d\big \}.$
For
![]() ${\lambda },\mu \in \mathbb Z^{n}$
with
${\lambda },\mu \in \mathbb Z^{n}$
with
![]() $\sum _{1\leqslant i\leqslant n}{\lambda }_i=\sum _{1\leqslant i\leqslant n}\mu _i$
we write
$\sum _{1\leqslant i\leqslant n}{\lambda }_i=\sum _{1\leqslant i\leqslant n}\mu _i$
we write
![]() ${\lambda }\trianglelefteq \mu $
if
${\lambda }\trianglelefteq \mu $
if
![]() $\sum _{1\leqslant s\leqslant i}{\lambda }_s\leqslant \sum _{1\leqslant s\leqslant i}\mu _s$
for
$\sum _{1\leqslant s\leqslant i}{\lambda }_s\leqslant \sum _{1\leqslant s\leqslant i}\mu _s$
for
![]() $1\leqslant i\leqslant n$
.
$1\leqslant i\leqslant n$
.
Lemma 8.2. For
![]() ${\lambda }\in {\Gamma }_r^d$
we have
${\lambda }\in {\Gamma }_r^d$
we have
![]() $\widehat L_r({\lambda })=\oplus _{\mu \in \Lambda (n,d)}\widehat L_r({\lambda })_\mu $
.
$\widehat L_r({\lambda })=\oplus _{\mu \in \Lambda (n,d)}\widehat L_r({\lambda })_\mu $
.
Proof. We write
![]() ${\lambda }=\alpha +lp^{r-1}\beta $
with
${\lambda }=\alpha +lp^{r-1}\beta $
with
![]() $\alpha \in P_r$
and
$\alpha \in P_r$
and
![]() $\beta \in \mathbb N^{n}$
. By Theorem 8.1, we have
$\beta \in \mathbb N^{n}$
. By Theorem 8.1, we have
![]() $\widehat L_r({\lambda })\cong L(\alpha )\otimes lp^{r-1}\beta .$
Hence, it suffices to show that
$\widehat L_r({\lambda })\cong L(\alpha )\otimes lp^{r-1}\beta .$
Hence, it suffices to show that
![]() $L(\alpha )=\oplus _{\mu \in \Lambda (n,d')}L(\alpha )_\mu $
, where
$L(\alpha )=\oplus _{\mu \in \Lambda (n,d')}L(\alpha )_\mu $
, where
![]() $d'=\sum _{1\leqslant i\leqslant n}\alpha _i$
. If
$d'=\sum _{1\leqslant i\leqslant n}\alpha _i$
. If
![]() $L(\alpha )_\mu \not =0$
for some
$L(\alpha )_\mu \not =0$
for some
![]() $\mu \in \mathbb Z^{n}$
with
$\mu \in \mathbb Z^{n}$
with
![]() $\sum _{1\leqslant i\leqslant n}\mu _i=d'$
. We claim that
$\sum _{1\leqslant i\leqslant n}\mu _i=d'$
. We claim that
![]() $\mu \in \mathbb N^{n}$
. Otherwise, there exists some element w in the symmetric group
$\mu \in \mathbb N^{n}$
. Otherwise, there exists some element w in the symmetric group
![]() $\mathfrak {S}_n$
such that
$\mathfrak {S}_n$
such that
![]() $\gamma =(\mu _{w(1)},\ldots ,\mu _{w(n)})$
and
$\gamma =(\mu _{w(1)},\ldots ,\mu _{w(n)})$
and
![]() $\gamma _n<0$
. Since
$\gamma _n<0$
. Since
![]() $L(\alpha )_\mu \not =0$
, we have
$L(\alpha )_\mu \not =0$
, we have
![]() $L(\alpha )_{\gamma }\not =0$
and hence
$L(\alpha )_{\gamma }\not =0$
and hence
![]() ${\gamma }\unlhd \alpha $
. This implies that
${\gamma }\unlhd \alpha $
. This implies that
![]() $\sum _{1\leqslant i\leqslant n-1}\gamma _i\leqslant \sum _{1\leqslant i\leqslant n-1}\alpha _i\leqslant d'$
. Hence, since
$\sum _{1\leqslant i\leqslant n-1}\gamma _i\leqslant \sum _{1\leqslant i\leqslant n-1}\alpha _i\leqslant d'$
. Hence, since
![]() ${\gamma }_n<0$
, we have
${\gamma }_n<0$
, we have
![]() $\sum _{1\leqslant i\leqslant n}\gamma _i<d'$
. This is a contradiction. The assertion follows.
$\sum _{1\leqslant i\leqslant n}\gamma _i<d'$
. This is a contradiction. The assertion follows.
The irreducible modules for infinitesimal q-Schur algebras were classified in [Reference Cox4, Sec. 5.1]. We now use Theorem 4.10 to give a classification of irreducible ![]() -modules.
-modules.
Theorem 8.3. The set
![]() $\{\widehat L_r({\lambda })\mid {\lambda }\in {\Gamma }_r^d\}$
forms a completed set of pairwise nonisomorphic irreducible
$\{\widehat L_r({\lambda })\mid {\lambda }\in {\Gamma }_r^d\}$
forms a completed set of pairwise nonisomorphic irreducible ![]() -modules.
-modules.
Proof. Let
![]() ${\lambda }\in {\Gamma }_r^d$
. By Lemma 8.2, we have
${\lambda }\in {\Gamma }_r^d$
. By Lemma 8.2, we have
![]() $\widehat L_r({\lambda })=\oplus _{\mu \in \Lambda (n,d)}\widehat L_r({\lambda })_\mu $
. Let
$\widehat L_r({\lambda })=\oplus _{\mu \in \Lambda (n,d)}\widehat L_r({\lambda })_\mu $
. Let
![]() $w_\mu $
be a nonzero vector in
$w_\mu $
be a nonzero vector in
![]() $\widehat L_r({\lambda })_\mu $
for some
$\widehat L_r({\lambda })_\mu $
for some
![]() $\mu \in \Lambda (n,d)$
. Since
$\mu \in \Lambda (n,d)$
. Since
![]() $\mu \in \Lambda (n,d)$
, we have
$\mu \in \Lambda (n,d)$
, we have
![]() $K_\alpha w_\mu =\big [{\mu \atop \alpha }\big ]_{\varepsilon } w_\mu =\delta _{\alpha ,\mu }w_\mu $
for
$K_\alpha w_\mu =\big [{\mu \atop \alpha }\big ]_{\varepsilon } w_\mu =\delta _{\alpha ,\mu }w_\mu $
for
![]() $\alpha \in \Lambda (n,d)$
. It follows that
$\alpha \in \Lambda (n,d)$
. It follows that
 $$ \begin{align*} \begin{aligned} \sum_{\beta\in\Lambda(n,d)}K_\beta w_\mu&=\sum_{\beta\in\Lambda(n,d)}\delta_{\beta,\mu} w_\mu=w_\mu, \\ (K_i-\varepsilon^{\alpha_i})K_\alpha w_\mu&=\delta_{\alpha,\mu}K_iw_\mu-\varepsilon^{\alpha_i}\delta_{\alpha,\mu}w_\mu=0,\\ \bigg(\bigg[{K_i;0\atop t}\bigg] -\bigg[{\alpha_i\atop t}\bigg]\bigg)K_\alpha w_\mu&= \delta_{\alpha,\mu}\bigg[{K_i;0\atop t}\bigg] w_\mu-\bigg[{\alpha_i\atop t}\bigg]\delta_{\alpha,\mu} w_\mu=0, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{\beta\in\Lambda(n,d)}K_\beta w_\mu&=\sum_{\beta\in\Lambda(n,d)}\delta_{\beta,\mu} w_\mu=w_\mu, \\ (K_i-\varepsilon^{\alpha_i})K_\alpha w_\mu&=\delta_{\alpha,\mu}K_iw_\mu-\varepsilon^{\alpha_i}\delta_{\alpha,\mu}w_\mu=0,\\ \bigg(\bigg[{K_i;0\atop t}\bigg] -\bigg[{\alpha_i\atop t}\bigg]\bigg)K_\alpha w_\mu&= \delta_{\alpha,\mu}\bigg[{K_i;0\atop t}\bigg] w_\mu-\bigg[{\alpha_i\atop t}\bigg]\delta_{\alpha,\mu} w_\mu=0, \end{aligned} \end{align*} $$
for
![]() $\alpha \in \Lambda (n,d)$
,
$\alpha \in \Lambda (n,d)$
,
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $t\in \mathbb N$
. Thus, by Theorem 4.10, we conclude that
$t\in \mathbb N$
. Thus, by Theorem 4.10, we conclude that
![]() $\widehat L_r({\lambda })$
can be regarded as a
$\widehat L_r({\lambda })$
can be regarded as a ![]() -module.
-module.
On the other hand, let L be an irreducible ![]() -module. By Theorem 8.1, we conclude that
-module. By Theorem 8.1, we conclude that
![]() $L\cong \widehat L_r(\nu +lp^{r-1}\delta )\cong L(\nu )\otimes lp^{r-1}\delta $
for some
$L\cong \widehat L_r(\nu +lp^{r-1}\delta )\cong L(\nu )\otimes lp^{r-1}\delta $
for some
![]() $\nu \in P_r$
and
$\nu \in P_r$
and
![]() $\delta \in \mathbb Z^{n}$
. Hence, since L is a
$\delta \in \mathbb Z^{n}$
. Hence, since L is a ![]() -module, we have
-module, we have
![]() $(\nu _{w(1)},\nu _{w(2)},\ldots ,\nu _{w(n)})+ lp^{r-1}\delta \in \Lambda (n,d)$
for any w in the symmetric group
$(\nu _{w(1)},\nu _{w(2)},\ldots ,\nu _{w(n)})+ lp^{r-1}\delta \in \Lambda (n,d)$
for any w in the symmetric group
![]() ${\mathfrak S}_n$
. It follows that
${\mathfrak S}_n$
. It follows that
![]() $\nu _n+lp^{r-1}\delta _j\geqslant 0$
for
$\nu _n+lp^{r-1}\delta _j\geqslant 0$
for
![]() $1\leqslant j\leqslant n$
. Furthermore, since
$1\leqslant j\leqslant n$
. Furthermore, since
![]() $\nu \in P_r$
, we have
$\nu \in P_r$
, we have
![]() $0\leqslant \nu _n<lp^{r-1}$
. Therefore, we have
$0\leqslant \nu _n<lp^{r-1}$
. Therefore, we have
![]() $\delta _j\geqslant 0$
for
$\delta _j\geqslant 0$
for
![]() $1\leqslant j\leqslant n$
. Consequently, we have
$1\leqslant j\leqslant n$
. Consequently, we have
![]() $\nu +lp^{r-1}\delta \in {\Gamma }_r^d$
. The proof is completed.
$\nu +lp^{r-1}\delta \in {\Gamma }_r^d$
. The proof is completed.
Acknowledgement
Supported by the National Natural Science Foundation of China (12371032, 12431002).



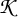 be a commutative ring containing a primitive
be a commutative ring containing a primitive 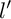
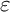
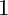
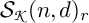 over
over  form an ascending chain of subalgebras of the
form an ascending chain of subalgebras of the 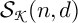 , which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let
, which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let  be the quantized enveloping algebra of
be the quantized enveloping algebra of 
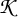 . There is a natural surjective algebra homomorphism
. There is a natural surjective algebra homomorphism 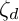
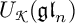 to
to 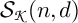 . The map
. The map 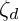
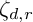
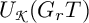 to
to 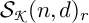 , where
, where 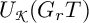 is a certain Hopf subalgebra of
is a certain Hopf subalgebra of 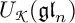 , which is closely related to Frobenius–Lusztig kernels of
, which is closely related to Frobenius–Lusztig kernels of 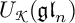 . We give the extra defining relations needed to define the infinitesimal
. We give the extra defining relations needed to define the infinitesimal 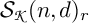 as a quotient of
as a quotient of  . The map
. The map 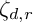
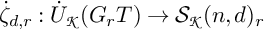 , where
, where 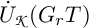 is the modified quantum algebra associated with
is the modified quantum algebra associated with 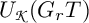 . We also give a generating set for the kernel of
. We also give a generating set for the kernel of 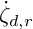
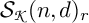 -modules over a field of characteristic
-modules over a field of characteristic 

