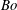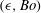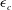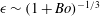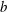1. Introduction
Understanding small-scale wave structures in the ocean is of fundamental importance in order to quantify wave dissipation and air–sea interactions, including gas and momentum exchange, and to improve parametrization for ocean–atmosphere exchange in weather and climate models. The understanding of dissipation induced by breaking waves at various scales has been the topic of intensive research in recent decades, combining field work in the open ocean (Melville Reference Melville1996; Melville & Matusov Reference Melville and Matusov2002; Veron, Melville & Lenain Reference Veron, Melville and Lenain2008; Sutherland & Melville Reference Sutherland and Melville2013), laboratory experiments on wave breaking (Melville & Rapp Reference Melville and Rapp1985; Rapp & Melville Reference Rapp and Melville1990; Tulin & Waseda Reference Tulin and Waseda1999; Melville, Veron & White Reference Melville, Veron and White2002; Banner & Peirson Reference Banner and Peirson2007; Drazen, Melville & Lenain Reference Drazen, Melville and Lenain2008) and the dissipation induced by smaller scales involving surface tension, such as micro-breaking, spilling breaking (Duncan, Qiao & Philomin Reference Duncan, Qiao and Philomin1999; Duncan Reference Duncan2001; Liu & Duncan Reference Liu and Duncan2003, Reference Liu and Duncan2006) and parasitic capillary waves (Su Reference Su1982; Perlin, Lin & Ting Reference Perlin, Lin and Ting1993; Caulliez, Ricci & Dupont Reference Caulliez, Ricci and Dupont1998; Fedorov, Melville & Rozenberg Reference Fedorov, Melville and Rozenberg1998; Jiang et al.
Reference Jiang, Lin, Schultz and Perlin1999; Caulliez Reference Caulliez2013). The importance of small scales,
![]() $O(1{-}10)~\text{cm}$
in the global ocean wave energy fluxes is still an open question and needs further investigation.
$O(1{-}10)~\text{cm}$
in the global ocean wave energy fluxes is still an open question and needs further investigation.
Theoretical approaches to describe these wave phenomena have been based mainly on potential theory, and provide insights into wave stability and the onset of wave breaking (McLean Reference McLean1982; Peregrine, Cokelet & McIver Reference Peregrine, Cokelet and McIver1993; Longuet-Higgins & Tanaka Reference Longuet-Higgins and Tanaka1997; Dias & Kharif Reference Dias and Kharif1999). Geometrical, kinematic and dynamical criteria for the onset of wave breaking have been the subject of constant debate (e.g. the review of Peregrine et al. Reference Peregrine, Cokelet and McIver1993; Perlin, Choi & Tian Reference Perlin, Choi and Tian2013). Regarding surface tension effects, boundary layer theory has provided a general description of the appearance of capillary ripples on the front of carrier gravity waves (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998; Melville & Fedorov Reference Melville and Fedorov2015) and were first observed numerically by Mui & Dommermuth (Reference Mui and Dommermuth1995). Numerical simulations of gravity–capillary waves are based on potential theory with a boundary layer near the interface (Yang & Tryggvason Reference Yang and Tryggvason1998; Furhman, Madsen & Bingham Reference Furhman, Madsen and Bingham2004; Fructus et al. Reference Fructus, Clamond, Grue and Kristiansen2005), or on the Navier–Stokes equations (Mui & Dommermuth Reference Mui and Dommermuth1995; Tsai & Hung Reference Tsai and Hung2007, Reference Tsai and Hung2010), not taking into account the air flow, or the air being modelled by a pressure forcing (Fedorov & Melville Reference Fedorov and Melville1998; Melville & Fedorov Reference Melville and Fedorov2015). They provide qualitative and quantitative comparisons with the various wave patterns and phenomenology observed experimentally. The enhancement of dissipation by parasitic capillaries has also been described, both experimentally (Zhang Reference Zhang1995; Fedorov et al. Reference Fedorov, Melville and Rozenberg1998; Caulliez Reference Caulliez2013) and numerically (Fedorov & Melville Reference Fedorov and Melville1998; Tsai & Hung Reference Tsai and Hung2007, Reference Tsai and Hung2010; Melville & Fedorov Reference Melville and Fedorov2015). Numerical simulations of the complete two-phase flow remain relatively rare and have focused on the resolution of the wave breaking and post-impact dynamics, which are numerically challenging (Chen et al. Reference Chen, Kharif, Zaleski and Li1999; Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2009, Reference Iafrati2011; Iafrati, Babanin & Onorato Reference Iafrati, Babanin and Onorato2013). Most of these numerical studies (Chen et al. Reference Chen, Kharif, Zaleski and Li1999; Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2009, Reference Iafrati2011) use arbitrarily steep Stokes waves to study breaking, without considering the processes that lead to breaking, such as modulation instability, wave focusing or three-dimensional instabilities. The use of steep Stokes waves as initial data permits detailed studies of wave breaking processes such as dissipation, vorticity generation, air entrainment and aspects of the post-breaking flow. The numerical investigation of capillary effects has been limited to wave breaking at high steepness (Song & Sirviente Reference Song and Sirviente2004). The influence of capillary effects on the wave breaking dynamics is discussed extensively experimentally (e.g. the review of Duncan Reference Duncan2001) while the significance of surface tension effects can be experimentally studied by adding surfactants that are able to modify the breaking kinematic and dissipation effects (Liu & Duncan Reference Liu and Duncan2003, Reference Liu and Duncan2006).
Most recently Melville & Fedorov (Reference Melville and Fedorov2015) using the theory of Fedorov & Melville (Reference Fedorov and Melville1998) have shown that the dissipative effects of parasitic capillaries on short,
![]() $O(1{-}10)~\text{cm}$
, gravity–capillary waves may be enough to balance the wind input and also be consistent with the inertial scaling of the breaking parameter,
$O(1{-}10)~\text{cm}$
, gravity–capillary waves may be enough to balance the wind input and also be consistent with the inertial scaling of the breaking parameter,
![]() $b$
, presented first for plunging waves by Drazen et al. (Reference Drazen, Melville and Lenain2008), and extended by Romero, Melville & Kleiss (Reference Romero, Melville and Kleiss2012) to encompass the full range of breaking strengths, including spilling breakers (Pizzo & Melville Reference Pizzo and Melville2013).
$b$
, presented first for plunging waves by Drazen et al. (Reference Drazen, Melville and Lenain2008), and extended by Romero, Melville & Kleiss (Reference Romero, Melville and Kleiss2012) to encompass the full range of breaking strengths, including spilling breakers (Pizzo & Melville Reference Pizzo and Melville2013).
In this paper, we present two-dimensional direct numerical simulations (DNS) of the Navier–Stokes equations in the two phases, air and water. The wave dynamics is described as a function of the initial wave steepness and the Bond number (the ratio between gravity and surface tension forces). Various small-scale wave patterns are observed: non-breaking gravity waves, parasitic capillary ripples on gravity waves, spilling breakers and plunging breakers. We investigate the influence of surface tension and the initial steepness on the various wave regimes. All of these regimes are obtained by changing the initial steepness of the wave and the Bond number while the Reynolds number, the density ratio and the viscosity ratio are kept constant. A wave-state diagram is presented and the asymptotic critical steepness at high Bond number is compared with theoretical and experimental results. At low Bond number, the influence of surface tension is quantified through two boundaries separating first gravity–capillary waves and breakers, and second spilling and plunging breakers. Both boundaries are found to scale as
![]() ${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$
, which can be explained by balancing the vorticity generated by gravity–capillary waves (Longuet-Higgins Reference Longuet-Higgins1992) and the pressure due to surface tension effects. Finally, a description of the wave dissipation for the various wave states is presented and capillary effects on wave dissipation are discussed. The dissipation rate during the breaking stages is estimated and the breaking parameter
${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$
, which can be explained by balancing the vorticity generated by gravity–capillary waves (Longuet-Higgins Reference Longuet-Higgins1992) and the pressure due to surface tension effects. Finally, a description of the wave dissipation for the various wave states is presented and capillary effects on wave dissipation are discussed. The dissipation rate during the breaking stages is estimated and the breaking parameter
![]() $b$
defined by Duncan (Reference Duncan1981) and Phillips (Reference Phillips1985) is compared with experimental results (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). Very good agreement between the numerical results presented here and the available experimental data is found for plunging and spilling breakers and the dissipation due to parasitic capillaries is found to be comparable with the dissipation by breaking waves.
$b$
defined by Duncan (Reference Duncan1981) and Phillips (Reference Phillips1985) is compared with experimental results (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). Very good agreement between the numerical results presented here and the available experimental data is found for plunging and spilling breakers and the dissipation due to parasitic capillaries is found to be comparable with the dissipation by breaking waves.
This paper is organized as follows. First we present the configuration of the numerical experiment in § 2: the flow solver Gerris is briefly introduced, the physical parameters of gravity–capillary waves are described and the classical potential theory of water waves which is used to define the initial conditions is reviewed. In § 3 we first describe the various wave regimes obtained for different values of the Bond number and the initial wave steepness. Then the parametric study is presented and the wave state is systematically investigated as a function of the initial steepness and Bond number. The wave state diagram is then presented and discussed. Finally in § 4 the energy dissipation for the various wave states is discussed. Comparisons between the wave regime diagram and existing experiments are discussed in § 5 and conclusions are presented in § 6.
2. Configuration of the numerical experiment
2.1. Gerris flow solver
The open-source flow solver Gerris described in Popinet (Reference Popinet2003, Reference Popinet2009) is used is this study. Gerris is based on a quad/octree adaptive spatial discretization, multilevel Poisson solver. The full Navier–Stokes equations in a two-phase flow are solved in two dimensions, including surface tension. The interface between the high-density liquid (water) and the low-density gas (air) is reconstructed by a volume of fluid (VOF) method. The multifluid interface is traced by a function
![]() $\mathscr{T}(\boldsymbol{x},t)$
, defined as the volume fraction of a given fluid in each cell of the computational mesh. The density and viscosity can thus be written as
$\mathscr{T}(\boldsymbol{x},t)$
, defined as the volume fraction of a given fluid in each cell of the computational mesh. The density and viscosity can thus be written as
![]() ${\it\rho}(\mathscr{T})=\mathscr{T}{\it\rho}_{w}+(1-\mathscr{T}){\it\rho}_{a}$
,
${\it\rho}(\mathscr{T})=\mathscr{T}{\it\rho}_{w}+(1-\mathscr{T}){\it\rho}_{a}$
,
![]() ${\it\mu}(\mathscr{T})=\mathscr{T}{\it\mu}_{w}+(1-\mathscr{T}){\it\mu}_{a}$
, with
${\it\mu}(\mathscr{T})=\mathscr{T}{\it\mu}_{w}+(1-\mathscr{T}){\it\mu}_{a}$
, with
![]() ${\it\rho}_{w}$
,
${\it\rho}_{w}$
,
![]() ${\it\rho}_{a}$
and
${\it\rho}_{a}$
and
![]() ${\it\mu}_{w}$
,
${\it\mu}_{w}$
,
![]() ${\it\mu}_{a}$
the density and viscosity of the two fluids (water and air), respectively. A detailed description of the numerical methods can be found in Popinet (Reference Popinet2003, Reference Popinet2009). This solver has been used recently to study complex phenomena involving multiphase flow, such as atomization processes (Fuster et al.
Reference Fuster, Agbaglah, Josserand, Popinet and Zaleski2009; Agbaglah et al.
Reference Agbaglah, Delaux, Fuster, Hoepffner, Josserand, Popinet, Ray, Scardovelli and Zaleski2011). It has been validated extensively, in particular through comparisons with wave-like solutions for capillary waves (Popinet Reference Popinet2009) as well as shear-layer instabilities (Bague et al.
Reference Bague, Fuster, Popinet, Scardovelli and Zaleski2010; Fuster et al.
Reference Fuster, Matas, Marty, Popinet, Hoepffner, Cartellier and Zaleski2013). The incompressible, variable density, Navier–Stokes equations with surface tension can be written
${\it\mu}_{a}$
the density and viscosity of the two fluids (water and air), respectively. A detailed description of the numerical methods can be found in Popinet (Reference Popinet2003, Reference Popinet2009). This solver has been used recently to study complex phenomena involving multiphase flow, such as atomization processes (Fuster et al.
Reference Fuster, Agbaglah, Josserand, Popinet and Zaleski2009; Agbaglah et al.
Reference Agbaglah, Delaux, Fuster, Hoepffner, Josserand, Popinet, Ray, Scardovelli and Zaleski2011). It has been validated extensively, in particular through comparisons with wave-like solutions for capillary waves (Popinet Reference Popinet2009) as well as shear-layer instabilities (Bague et al.
Reference Bague, Fuster, Popinet, Scardovelli and Zaleski2010; Fuster et al.
Reference Fuster, Matas, Marty, Popinet, Hoepffner, Cartellier and Zaleski2013). The incompressible, variable density, Navier–Stokes equations with surface tension can be written
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}{\it\rho}(\partial _{t}\boldsymbol{u}+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u})=-\boldsymbol{{\rm\nabla}}p+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(2{\it\mu}\unicode[STIX]{x1D63F})+{\it\gamma}{\it\kappa}{\it\delta}_{S}\boldsymbol{n}\\ \partial _{t}{\it\rho}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{u})=0\\ \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}{\it\rho}(\partial _{t}\boldsymbol{u}+(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{u})=-\boldsymbol{{\rm\nabla}}p+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(2{\it\mu}\unicode[STIX]{x1D63F})+{\it\gamma}{\it\kappa}{\it\delta}_{S}\boldsymbol{n}\\ \partial _{t}{\it\rho}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\rho}\boldsymbol{u})=0\\ \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with
![]() $\boldsymbol{u}=(u,v,w)$
the fluid velocity,
$\boldsymbol{u}=(u,v,w)$
the fluid velocity,
![]() ${\it\rho}\equiv {\it\rho}(\boldsymbol{x},t)$
the fluid density,
${\it\rho}\equiv {\it\rho}(\boldsymbol{x},t)$
the fluid density,
![]() ${\it\mu}\equiv {\it\mu}(\boldsymbol{x},t)$
the dynamic viscosity and
${\it\mu}\equiv {\it\mu}(\boldsymbol{x},t)$
the dynamic viscosity and
![]() $\unicode[STIX]{x1D63F}$
the deformation tensor defined as
$\unicode[STIX]{x1D63F}$
the deformation tensor defined as
![]() $\unicode[STIX]{x1D60B}_{ij}\equiv (\partial _{i}u_{j}+\partial _{j}u_{i})/2$
. The Dirac delta,
$\unicode[STIX]{x1D60B}_{ij}\equiv (\partial _{i}u_{j}+\partial _{j}u_{i})/2$
. The Dirac delta,
![]() ${\it\delta}_{S}$
, expresses the fact that the surface tension term is concentrated on the interface, where
${\it\delta}_{S}$
, expresses the fact that the surface tension term is concentrated on the interface, where
![]() ${\it\gamma}$
is the surface tension coefficient,
${\it\gamma}$
is the surface tension coefficient,
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() $\boldsymbol{n}$
the curvature and normal to the interface. Surface tension effects in (2.1) are represented explicitly using the method described in Popinet (Reference Popinet2009). The computations are performed with a uniform surface tension.
$\boldsymbol{n}$
the curvature and normal to the interface. Surface tension effects in (2.1) are represented explicitly using the method described in Popinet (Reference Popinet2009). The computations are performed with a uniform surface tension.
Current problems about computational time in fluid flow modelling are linked to the wide range of spatial scales often encountered. Consequently, adaptive mesh refinement, where the spatial discretization is adjusted to follow the scale and temporal evolution of flow structures presents evident benefits. The spatial discretization uses a quad (2D) or octree (3D) scheme. Each cell may be the parent of either four (2D) or eight (3D) children. The root cell is the base of the tree and a leaf cell is a cell without child. The level of a cell is defined by starting from zero for the root cell and by adding one every time a group of four descendant children is added. We will call the maximum grid level
![]() $L_{\mathit{MAX}}$
. It gives the finest refinement used in the simulation. In surface wave simulations we need to have a high resolution of the interface and the boundary layer where energy will be dissipated. Thus, the chosen refinement criteria focus on the flow vorticity and the interface between the liquid and the gas phases. Further away from the interface, the resolution decreases since the quasi-irrotational motion can be appropriately described with a coarser mesh. The parameter
$L_{\mathit{MAX}}$
. It gives the finest refinement used in the simulation. In surface wave simulations we need to have a high resolution of the interface and the boundary layer where energy will be dissipated. Thus, the chosen refinement criteria focus on the flow vorticity and the interface between the liquid and the gas phases. Further away from the interface, the resolution decreases since the quasi-irrotational motion can be appropriately described with a coarser mesh. The parameter
![]() $L_{\mathit{MAX}}$
allows comparison of our results to simulations with a fixed grid. For example, our
$L_{\mathit{MAX}}$
allows comparison of our results to simulations with a fixed grid. For example, our
![]() $L_{\mathit{MAX}}=9$
(
$L_{\mathit{MAX}}=9$
(
![]() $2^{9}=512$
) is equivalent to the
$2^{9}=512$
) is equivalent to the
![]() $512\times 512$
grid used in previous studies for DNS of breaking waves (Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2011). We have checked that no significant changes are observed when the maximum grid level is increased to
$512\times 512$
grid used in previous studies for DNS of breaking waves (Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2011). We have checked that no significant changes are observed when the maximum grid level is increased to
![]() $L_{\mathit{MAX}}=10$
, thus all results presented here on the wave energy evolution and the interface dynamics have converged regarding the grid resolution.
$L_{\mathit{MAX}}=10$
, thus all results presented here on the wave energy evolution and the interface dynamics have converged regarding the grid resolution.
2.2. Physical parameters of gravity–capillary waves
Two-dimensional simulations of surface waves are computed, in a two-phase flow: the liquid on the bottom and the gas on the top. Therefore, within the 2D constraint, we capture naturally all of the physical phenomena taking place at the interface without resorting to any simplification of the model. We are solving the complete Navier–Stokes equations, including surface tension and viscosity (see (2.1)) to investigate the capillary effects on breaking waves.
A wave is initialized and propagates in the
![]() $x$
direction with periodic boundary conditions. The top and bottom walls are free-slip. The wavelength of the initial wave is the length of the box. The study is conducted in terms of dimensionless parameters, with the wavelength and gravity set to unity,
$x$
direction with periodic boundary conditions. The top and bottom walls are free-slip. The wavelength of the initial wave is the length of the box. The study is conducted in terms of dimensionless parameters, with the wavelength and gravity set to unity,
![]() ${\it\lambda}=1$
,
${\it\lambda}=1$
,
![]() $g=1$
. The parameters of the problem with a finite depth are then defined as follows. (i) The air–water density ratio
$g=1$
. The parameters of the problem with a finite depth are then defined as follows. (i) The air–water density ratio
![]() ${\it\alpha}={\it\rho}_{a}/{\it\rho}_{w}=1/850$
. (ii) The air–water dynamic viscosity ratio
${\it\alpha}={\it\rho}_{a}/{\it\rho}_{w}=1/850$
. (ii) The air–water dynamic viscosity ratio
![]() ${\it\beta}={\it\mu}_{a}/{\it\mu}_{w}=17.4\times 10^{-6}/8.9\times 10^{-4}=1.96\times 10^{-2}$
. (iii) The Reynolds number in the water
${\it\beta}={\it\mu}_{a}/{\it\mu}_{w}=17.4\times 10^{-6}/8.9\times 10^{-4}=1.96\times 10^{-2}$
. (iii) The Reynolds number in the water
![]() $\mathit{Re}=cL/{\it\nu}_{w}$
, with
$\mathit{Re}=cL/{\it\nu}_{w}$
, with
![]() $L={\it\lambda}$
the length scale,
$L={\it\lambda}$
the length scale,
![]() $c$
the linear gravity wave phase speed
$c$
the linear gravity wave phase speed
![]() $c=\sqrt{g/k}$
, with
$c=\sqrt{g/k}$
, with
![]() $k=2{\rm\pi}/{\it\lambda}$
the wavenumber. Consequently
$k=2{\rm\pi}/{\it\lambda}$
the wavenumber. Consequently
![]() $\mathit{Re}=\sqrt{g{\it\lambda}^{3}}/{\it\nu}$
and we keep the Reynolds number constant in all of the simulations presented here, with
$\mathit{Re}=\sqrt{g{\it\lambda}^{3}}/{\it\nu}$
and we keep the Reynolds number constant in all of the simulations presented here, with
![]() $\mathit{Re}=40\,000$
. This choice is a compromise between our desire to work at high Reynolds number in order to focus on the effects of the wave amplitude and surface tension rather than that of viscosity, and the grid resolution necessary to capture the viscous processes. (iv) The depth ratio
$\mathit{Re}=40\,000$
. This choice is a compromise between our desire to work at high Reynolds number in order to focus on the effects of the wave amplitude and surface tension rather than that of viscosity, and the grid resolution necessary to capture the viscous processes. (iv) The depth ratio
![]() $h/{\it\lambda}=1/2$
with
$h/{\it\lambda}=1/2$
with
![]() $h$
the depth of the water and
$h$
the depth of the water and
![]() $L$
the horizontal box size. The depth effects on the wave evolution are negligible, which was checked with simulations for larger
$L$
the horizontal box size. The depth effects on the wave evolution are negligible, which was checked with simulations for larger
![]() $h$
. (v) The initial steepness
$h$
. (v) The initial steepness
![]() ${\it\epsilon}=ak$
, with
${\it\epsilon}=ak$
, with
![]() $a$
the initial amplitude of the wave and
$a$
the initial amplitude of the wave and
![]() $k$
the wavenumber. (vi) The Bond number
$k$
the wavenumber. (vi) The Bond number
![]() $\mathit{Bo}={\rm\Delta}{\it\rho}g/({\it\gamma}k^{2})$
, with
$\mathit{Bo}={\rm\Delta}{\it\rho}g/({\it\gamma}k^{2})$
, with
![]() ${\rm\Delta}{\it\rho}$
the density difference between the two fluids and
${\rm\Delta}{\it\rho}$
the density difference between the two fluids and
![]() ${\it\gamma}$
the surface tension.
${\it\gamma}$
the surface tension.
As discussed by Chen et al. (Reference Chen, Kharif, Zaleski and Li1999), there are two dimensionless numbers which are related to the length scale (i.e. the wavelength): the Reynolds number
![]() $\mathit{Re}$
and the Bond number
$\mathit{Re}$
and the Bond number
![]() $\mathit{Bo}$
. Based on these two numbers and for a given liquid, one then obtains two different length scales, say
$\mathit{Bo}$
. Based on these two numbers and for a given liquid, one then obtains two different length scales, say
![]() $l_{\mathit{Re}}$
and
$l_{\mathit{Re}}$
and
![]() $l_{\mathit{Bo}}$
, respectively. Thus, our working hypothesis is that the wavelength is given by
$l_{\mathit{Bo}}$
, respectively. Thus, our working hypothesis is that the wavelength is given by
![]() $l_{\mathit{Bo}}$
and the processes we are studying are asymptotically independent of the Reynolds number, a commonly proven assumption in wave and turbulence dynamics. The Reynolds number is set to 40 000 which allows us to solve the viscous scales properly with the mesh size we use. We have to keep in mind that when the Reynolds number becomes too large, one expects the boundary layers to be smaller than the mesh size and a loss of accuracy in the simulations.
$l_{\mathit{Bo}}$
and the processes we are studying are asymptotically independent of the Reynolds number, a commonly proven assumption in wave and turbulence dynamics. The Reynolds number is set to 40 000 which allows us to solve the viscous scales properly with the mesh size we use. We have to keep in mind that when the Reynolds number becomes too large, one expects the boundary layers to be smaller than the mesh size and a loss of accuracy in the simulations.
The results are presented in non-dimensional units. The evolution in time is normalized by the period of the principal wave
![]() $T=1/f=2{\rm\pi}/\sqrt{gk}$
, given by the linear dispersion relation of the main gravity wave. The two-dimensional vorticity field
$T=1/f=2{\rm\pi}/\sqrt{gk}$
, given by the linear dispersion relation of the main gravity wave. The two-dimensional vorticity field
![]() ${\it\Gamma}=\partial v/\partial x-\partial u/\partial y$
is normalized by
${\it\Gamma}=\partial v/\partial x-\partial u/\partial y$
is normalized by
![]() ${\it\Gamma}_{0}=\sqrt{g{\it\lambda}}/{\it\lambda}$
(
${\it\Gamma}_{0}=\sqrt{g{\it\lambda}}/{\it\lambda}$
(
![]() $\boldsymbol{u}=(u,v)$
denotes the velocity field).
$\boldsymbol{u}=(u,v)$
denotes the velocity field).
We will now describe the initial conditions of the wave simulations.
2.3. Initialization with a third-order Stokes solution
The simulation is initialized with a modified potential solution for gravity waves, a third-order Stokes wave. Note that this solution does not include surface tension effects. Considering a free surface over a liquid of depth
![]() $h$
,
$h$
,
![]() $x$
the horizontal direction and
$x$
the horizontal direction and
![]() $y$
the vertical direction, the initial fluid flow is assumed to be irrotational. Hence, we have (Lamb Reference Lamb1932)
$y$
the vertical direction, the initial fluid flow is assumed to be irrotational. Hence, we have (Lamb Reference Lamb1932)
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial ^{2}{\it\phi}}{\partial x^{2}}+\frac{\partial ^{2}{\it\phi}}{\partial y^{2}}=0,\quad -h<y<{\it\eta}\\ \displaystyle \frac{\partial {\it\phi}}{\partial y}=0\quad \text{as }y=-h\\ \displaystyle \frac{\partial {\it\phi}}{\partial t}+g{\it\eta}+\frac{1}{2}\left(\left(\frac{\partial {\it\phi}}{\partial x}\right)^{2}+\left(\frac{\partial {\it\phi}}{\partial y}\right)^{2}\right)=\frac{1}{2}c^{2}\\ \displaystyle \frac{\partial {\it\eta}}{\partial t}+\frac{\partial {\it\phi}}{\partial x}\frac{\partial {\it\eta}}{\partial x}+\frac{\partial {\it\phi}}{\partial y}=0\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial ^{2}{\it\phi}}{\partial x^{2}}+\frac{\partial ^{2}{\it\phi}}{\partial y^{2}}=0,\quad -h<y<{\it\eta}\\ \displaystyle \frac{\partial {\it\phi}}{\partial y}=0\quad \text{as }y=-h\\ \displaystyle \frac{\partial {\it\phi}}{\partial t}+g{\it\eta}+\frac{1}{2}\left(\left(\frac{\partial {\it\phi}}{\partial x}\right)^{2}+\left(\frac{\partial {\it\phi}}{\partial y}\right)^{2}\right)=\frac{1}{2}c^{2}\\ \displaystyle \frac{\partial {\it\eta}}{\partial t}+\frac{\partial {\it\phi}}{\partial x}\frac{\partial {\it\eta}}{\partial x}+\frac{\partial {\it\phi}}{\partial y}=0\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() ${\it\phi}(x,y,t)$
is the velocity potential,
${\it\phi}(x,y,t)$
is the velocity potential,
![]() $y={\it\eta}(x,y,t)$
is the free surface,
$y={\it\eta}(x,y,t)$
is the free surface,
![]() $c$
the phase speed of the unperturbed wave of wavelength
$c$
the phase speed of the unperturbed wave of wavelength
![]() ${\it\lambda}$
and
${\it\lambda}$
and
![]() $g$
the acceleration of gravity. These equations admit, in the frame of reference moving with the wave, a steady solution of the form of a sum over all Fourier components (McLean Reference McLean1982). Equation (2.2) can be solved numerically (Fenton Reference Fenton1988), and the complete Stokes wave can be used in potential simulations (Furhman et al.
Reference Furhman, Madsen and Bingham2004; Fructus et al.
Reference Fructus, Clamond, Grue and Kristiansen2005; Tsai & Hung Reference Tsai and Hung2007). Following previous work on breaking waves (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999; Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2011), we use the third-order solution of (2.2) that can be solved explicitly through a perturbation approach (Lamb Reference Lamb1932). At the third order in
$g$
the acceleration of gravity. These equations admit, in the frame of reference moving with the wave, a steady solution of the form of a sum over all Fourier components (McLean Reference McLean1982). Equation (2.2) can be solved numerically (Fenton Reference Fenton1988), and the complete Stokes wave can be used in potential simulations (Furhman et al.
Reference Furhman, Madsen and Bingham2004; Fructus et al.
Reference Fructus, Clamond, Grue and Kristiansen2005; Tsai & Hung Reference Tsai and Hung2007). Following previous work on breaking waves (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999; Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2011), we use the third-order solution of (2.2) that can be solved explicitly through a perturbation approach (Lamb Reference Lamb1932). At the third order in
![]() ${\it\varepsilon}$
, with a fixed bottom
${\it\varepsilon}$
, with a fixed bottom
![]() $-h$
, the interface elevation is given by Lamb (Reference Lamb1932):
$-h$
, the interface elevation is given by Lamb (Reference Lamb1932):
 $$\begin{eqnarray}\displaystyle {\it\eta} & = & \displaystyle a_{0}\cos (kx)+{\it\varepsilon}\frac{a_{0}}{4}{\it\chi}(3{\it\chi}^{2}-1)\cos (2kx)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\varepsilon}^{2}a_{0}\left(-\frac{3}{8}({\it\chi}^{4}-3{\it\chi}^{2}+3)\cos (kx)+\frac{3}{64}(8{\it\chi}^{6}+({\it\chi}^{2}-1)^{2})\cos (3kx)\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\eta} & = & \displaystyle a_{0}\cos (kx)+{\it\varepsilon}\frac{a_{0}}{4}{\it\chi}(3{\it\chi}^{2}-1)\cos (2kx)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\varepsilon}^{2}a_{0}\left(-\frac{3}{8}({\it\chi}^{4}-3{\it\chi}^{2}+3)\cos (kx)+\frac{3}{64}(8{\it\chi}^{6}+({\it\chi}^{2}-1)^{2})\cos (3kx)\right)\end{eqnarray}$$
where
![]() ${\it\chi}=1/\tanh (kh)$
. The velocity potential is given by
${\it\chi}=1/\tanh (kh)$
. The velocity potential is given by
 $$\begin{eqnarray}\displaystyle {\it\phi} & = & \displaystyle \frac{a_{0}g}{{\it\omega}}\frac{\cosh (k(y+h))}{\cosh (kh)}\sin (kx)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\varepsilon}\frac{3a_{0}g}{{\it\omega}}\frac{({\it\chi}^{2}-1)^{2}}{8{\it\chi}}\frac{\cosh (2k(y+h))}{\cosh (2kh)}\sin (2kx)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\varepsilon}^{2}\frac{a_{0}g}{64{\it\omega}}({\it\chi}^{2}-1)({\it\chi}^{2}+3)(9{\it\chi}^{2}-13)\frac{\cosh (3k(y+h))}{\cosh (3kh)}\sin (3kx)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\phi} & = & \displaystyle \frac{a_{0}g}{{\it\omega}}\frac{\cosh (k(y+h))}{\cosh (kh)}\sin (kx)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\varepsilon}\frac{3a_{0}g}{{\it\omega}}\frac{({\it\chi}^{2}-1)^{2}}{8{\it\chi}}\frac{\cosh (2k(y+h))}{\cosh (2kh)}\sin (2kx)\nonumber\\ \displaystyle & & \displaystyle +\,{\it\varepsilon}^{2}\frac{a_{0}g}{64{\it\omega}}({\it\chi}^{2}-1)({\it\chi}^{2}+3)(9{\it\chi}^{2}-13)\frac{\cosh (3k(y+h))}{\cosh (3kh)}\sin (3kx)\end{eqnarray}$$
where
![]() ${\it\omega}=\sqrt{gk\tanh (kh)(1+{\it\varepsilon}^{2}((9/8)({\it\chi}^{2}-1)^{2}+{\it\chi}^{2}))}$
is the dispersion relation at the third order, and
${\it\omega}=\sqrt{gk\tanh (kh)(1+{\it\varepsilon}^{2}((9/8)({\it\chi}^{2}-1)^{2}+{\it\chi}^{2}))}$
is the dispersion relation at the third order, and
![]() ${\it\varepsilon}=a_{0}k$
the steepness of the linear wave and the small parameter of the nonlinear expansion. Previous studies have discussed the use of third-order solutions as initial conditions being relevant for the simulation of breaking waves (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999; Iafrati Reference Iafrati2011).
${\it\varepsilon}=a_{0}k$
the steepness of the linear wave and the small parameter of the nonlinear expansion. Previous studies have discussed the use of third-order solutions as initial conditions being relevant for the simulation of breaking waves (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999; Iafrati Reference Iafrati2011).
The velocity potential in the liquid is obtained assuming a free surface, i.e. the variation in the gas pressure is negligible. In our two-phase simulations the gas phase also has to be initialized. Fixing the initial velocity in the air to zero creates too much shear and the interface becomes unstable due to Kelvin–Helmoltz instabilities. To obtain a smoother, more physical initial condition, we follow Yang & Tryggvason (Reference Yang and Tryggvason1998) and add a vortex sheet compatible with the potential solution described above.
A thin vorticity field
![]() ${\it\Omega}$
at the interface is initialized and the Poisson equation
${\it\Omega}$
at the interface is initialized and the Poisson equation
![]() ${\rm\nabla}^{2}{\it\Psi}={\it\Omega}$
, with
${\rm\nabla}^{2}{\it\Psi}={\it\Omega}$
, with
![]() ${\it\Psi}$
the stream function, is solved to obtain the initial velocity field in both phases. The initial vortex sheet is of the form
${\it\Psi}$
the stream function, is solved to obtain the initial velocity field in both phases. The initial vortex sheet is of the form
![]() ${\it\Omega}={\it\Gamma}_{I}{\it\delta}_{S}$
, with
${\it\Omega}={\it\Gamma}_{I}{\it\delta}_{S}$
, with
![]() ${\it\delta}_{S}$
a Dirac distribution on the interface and
${\it\delta}_{S}$
a Dirac distribution on the interface and
![]() ${\it\Gamma}_{I}$
the initial vorticity. Following Schwartz (Reference Schwartz1966), the initial vorticity field, compatible with the velocity potential in the liquid given by (2.4) and a steady state in the gas with no velocity can be expressed as
${\it\Gamma}_{I}$
the initial vorticity. Following Schwartz (Reference Schwartz1966), the initial vorticity field, compatible with the velocity potential in the liquid given by (2.4) and a steady state in the gas with no velocity can be expressed as
The Dirac distribution of the previous equation has to be modelled with a finite boundary layer. Considering the steady Navier–Stokes equations with viscosity and the condition of incompressibility, and assuming the boundary layer thickness
![]() ${\it\delta}$
to be much smaller than the wavelength
${\it\delta}$
to be much smaller than the wavelength
![]() ${\it\lambda}$
, we get (Batchelor Reference Batchelor1967)
${\it\lambda}$
, we get (Batchelor Reference Batchelor1967)
![]() ${\it\delta}\approx {\it\lambda}/\sqrt{\mathit{Re}}$
. So an asymmetric Gaussian distribution is used to describe the Dirac distribution with a thickness given by the boundary layer
${\it\delta}\approx {\it\lambda}/\sqrt{\mathit{Re}}$
. So an asymmetric Gaussian distribution is used to describe the Dirac distribution with a thickness given by the boundary layer
![]() ${\it\delta}$
: in the water
${\it\delta}$
: in the water
![]() ${\it\delta}_{w}=\sqrt{2{\it\nu}_{l}/ck}$
and in the air
${\it\delta}_{w}=\sqrt{2{\it\nu}_{l}/ck}$
and in the air
![]() ${\it\delta}_{a}=\sqrt{2{\it\nu}g/ck}$
. Thus, the boundary-layer thickness in the air is
${\it\delta}_{a}=\sqrt{2{\it\nu}g/ck}$
. Thus, the boundary-layer thickness in the air is
![]() $\sqrt{{\it\nu}_{w}/{\it\nu}a}\approx 4$
times larger than that in the water. Note that this hypothesis is in agreement with Lamb (Reference Lamb1932) which shows that for wave oscillations under the influence of viscosity, vorticity remains in a thin layer
$\sqrt{{\it\nu}_{w}/{\it\nu}a}\approx 4$
times larger than that in the water. Note that this hypothesis is in agreement with Lamb (Reference Lamb1932) which shows that for wave oscillations under the influence of viscosity, vorticity remains in a thin layer
![]() ${\it\delta}=\sqrt{2{\it\nu}/ck}$
and this thickness was previously used to study gravity–capillary waves and develop a boundary-layer theory where boundary conditions outside the layer are given by the potential theory (Longuet-Higgins Reference Longuet-Higgins1992; Fedorov & Melville Reference Fedorov and Melville1998). Finally the Dirac distribution is approximated by
${\it\delta}=\sqrt{2{\it\nu}/ck}$
and this thickness was previously used to study gravity–capillary waves and develop a boundary-layer theory where boundary conditions outside the layer are given by the potential theory (Longuet-Higgins Reference Longuet-Higgins1992; Fedorov & Melville Reference Fedorov and Melville1998). Finally the Dirac distribution is approximated by
 $$\begin{eqnarray}\displaystyle {\it\delta}_{S}(y-{\it\eta}) & {\approx} & \displaystyle D(y-{\it\eta})\nonumber\\ \displaystyle & = & \displaystyle \frac{2}{\sqrt{2{\rm\pi}{\it\delta}_{a}^{2}}+\sqrt{2{\rm\pi}{\it\delta}_{w}^{2}}}\!\left(\!\mathscr{T}\!\exp -\frac{(y-{\it\eta}(x))^{2}}{2{\it\delta}_{w}}+(1-\mathscr{T})\exp -\frac{(y-{\it\eta}(x))^{2}}{2{\it\delta}_{a}}\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\delta}_{S}(y-{\it\eta}) & {\approx} & \displaystyle D(y-{\it\eta})\nonumber\\ \displaystyle & = & \displaystyle \frac{2}{\sqrt{2{\rm\pi}{\it\delta}_{a}^{2}}+\sqrt{2{\rm\pi}{\it\delta}_{w}^{2}}}\!\left(\!\mathscr{T}\!\exp -\frac{(y-{\it\eta}(x))^{2}}{2{\it\delta}_{w}}+(1-\mathscr{T})\exp -\frac{(y-{\it\eta}(x))^{2}}{2{\it\delta}_{a}}\right)\end{eqnarray}$$
where
![]() $\mathscr{T}$
is equal to 1 in the liquid and 0 in the gas. Here
$\mathscr{T}$
is equal to 1 in the liquid and 0 in the gas. Here
![]() $D(y-{\it\eta})$
is numerically evaluated with the finest grid resolution, both in
$D(y-{\it\eta})$
is numerically evaluated with the finest grid resolution, both in
![]() $x$
and
$x$
and
![]() $y$
directions, i.e.
$y$
directions, i.e.
![]() $\text{d}x=\text{d}y={\it\lambda}/2^{9}$
.
$\text{d}x=\text{d}y={\it\lambda}/2^{9}$
.
This initialization allows the simulation of surface waves with various Bond numbers, Reynolds numbers and slopes. Note again that surface tension is not taken into account in the initial conditions and will act once the wave starts to propagate.
3. Gravity–capillary waves: parametric study as a function of the Bond number and initial steepness
3.1. Wave patterns
We will now describe the waves obtained for different Bond numbers
![]() $\mathit{Bo}$
and initial steepnesses
$\mathit{Bo}$
and initial steepnesses
![]() ${\it\epsilon}$
, at
${\it\epsilon}$
, at
![]() $\mathit{Re}=40\,000$
. This permits us to investigate the effects of surface tension while the viscosity remains constant.
$\mathit{Re}=40\,000$
. This permits us to investigate the effects of surface tension while the viscosity remains constant.
3.1.1. Non-breaking gravity wave
Figure 1 shows two examples of gravity waves with negligible surface tension (
![]() $\mathit{Bo}=1000$
) and initial steepness,
$\mathit{Bo}=1000$
) and initial steepness,
![]() ${\it\epsilon}=0.2$
and
${\it\epsilon}=0.2$
and
![]() ${\it\epsilon}=0.25$
. The black line corresponds to the interface between the liquid (bottom) and the gas (top). The color scale represents the two-dimensional normalized vorticity field
${\it\epsilon}=0.25$
. The black line corresponds to the interface between the liquid (bottom) and the gas (top). The color scale represents the two-dimensional normalized vorticity field
![]() ${\it\Gamma}^{\ast }={\it\Gamma}/{\it\Gamma}_{0}$
. In both cases, the wave propagates with a decreasing amplitude due to viscous damping, with the wave profile becoming steeper during the propagation. The wave becomes more asymmetric when the initial steepness is higher and a stronger vorticity field is also observed both in the air and water. Both effects are the signatures of nonlinearity and can be seen as the beginning of the process that will eventually lead to wave breaking for higher steepnesses. The vorticity field in the water remains located in the thin boundary layer. Moreover, a steeper wave propagates faster due to nonlinear effects (Lamb Reference Lamb1932). However, for these relatively low initial steepnesses, the wave remains stable (non-breaking) and propagates smoothly without dramatic changes of the wave shape. The vorticity remains localized at the interface, within a thin boundary layer and deeper into the liquid the fluid motion remains irrotational. Dissipation processes are consequently localized near the interface as expected for waves of small amplitude (Lamb Reference Lamb1932). These waves are obtained for small slopes and high Bond numbers.
${\it\Gamma}^{\ast }={\it\Gamma}/{\it\Gamma}_{0}$
. In both cases, the wave propagates with a decreasing amplitude due to viscous damping, with the wave profile becoming steeper during the propagation. The wave becomes more asymmetric when the initial steepness is higher and a stronger vorticity field is also observed both in the air and water. Both effects are the signatures of nonlinearity and can be seen as the beginning of the process that will eventually lead to wave breaking for higher steepnesses. The vorticity field in the water remains located in the thin boundary layer. Moreover, a steeper wave propagates faster due to nonlinear effects (Lamb Reference Lamb1932). However, for these relatively low initial steepnesses, the wave remains stable (non-breaking) and propagates smoothly without dramatic changes of the wave shape. The vorticity remains localized at the interface, within a thin boundary layer and deeper into the liquid the fluid motion remains irrotational. Dissipation processes are consequently localized near the interface as expected for waves of small amplitude (Lamb Reference Lamb1932). These waves are obtained for small slopes and high Bond numbers.

Figure 1. Non-breaking gravity waves propagating to the right and the vorticity field
![]() ${\it\Gamma}^{\ast }={\it\Gamma}/{\it\Gamma}_{0}$
at
${\it\Gamma}^{\ast }={\it\Gamma}/{\it\Gamma}_{0}$
at
![]() $t/T=1$
, for two different steepness: 0.2 (a,b) and 0.25 (c,d). The vorticity field is displayed both in the air and water (a,c) and only in the water (b,d) with a different colour scale. Here
$t/T=1$
, for two different steepness: 0.2 (a,b) and 0.25 (c,d). The vorticity field is displayed both in the air and water (a,c) and only in the water (b,d) with a different colour scale. Here
![]() $\mathit{Re}=4\times 10^{4}$
,
$\mathit{Re}=4\times 10^{4}$
,
![]() $\mathit{Bo}=1000$
. We can see that the wave is more asymmetric for
$\mathit{Bo}=1000$
. We can see that the wave is more asymmetric for
![]() ${\it\epsilon}=0.25$
, due to stronger nonlinear effects.
${\it\epsilon}=0.25$
, due to stronger nonlinear effects.
3.1.2. Plunging breaker
Figure 2 shows a typical plunging wave, obtained for
![]() ${\it\epsilon}=0.55$
and with almost no surface tension,
${\it\epsilon}=0.55$
and with almost no surface tension,
![]() $\mathit{Bo}=1000$
. The formation and the evolution of the plunging breaker is similar to the description of plunging breakers observed in laboratory experiments, e.g. Rapp & Melville (Reference Rapp and Melville1990): the wave becomes steeper, the interface becomes vertical and a jet forms at the crest. Then under the influence of gravity the jet splashes down into the surface causing air entrainment and vortical motion beneath the surface. Liquid droplets and gas bubbles are formed when the overturning wave hits the liquid. Plunging breakers generate significant air entrainment when the jet reconnects to the liquid surface. During the breaking process the positive (anticlockwise) vorticity remains located at the crest (the tip of the jet), and is stronger than the negative vorticity in the trough. We can also observe separation of the vorticity layer in the air behind the crest. There is a dramatic change in vorticity after the jet reentry to the water since vorticity is created during the overturning. The vorticity of largest magnitude is observed during the splash-up phenomenon. Vorticity is created by viscous shear torque (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999) and by the generation of vorticity close to high-curvature regions of the interface (Batchelor Reference Batchelor1967; Longuet-Higgins Reference Longuet-Higgins1992). The topological changes of the flow, such as the jet plunging and reconnection are also responsible for vorticity generation (Hornung, Willert & Turner Reference Hornung, Willert and Turner1995). The splashing process and air entrainment generated bubbles and droplets with associated vortical structure, also related to topological changes (Zhang, Duncan & Chahine Reference Zhang, Duncan and Chahine1993; Iafrati Reference Iafrati2009).
$\mathit{Bo}=1000$
. The formation and the evolution of the plunging breaker is similar to the description of plunging breakers observed in laboratory experiments, e.g. Rapp & Melville (Reference Rapp and Melville1990): the wave becomes steeper, the interface becomes vertical and a jet forms at the crest. Then under the influence of gravity the jet splashes down into the surface causing air entrainment and vortical motion beneath the surface. Liquid droplets and gas bubbles are formed when the overturning wave hits the liquid. Plunging breakers generate significant air entrainment when the jet reconnects to the liquid surface. During the breaking process the positive (anticlockwise) vorticity remains located at the crest (the tip of the jet), and is stronger than the negative vorticity in the trough. We can also observe separation of the vorticity layer in the air behind the crest. There is a dramatic change in vorticity after the jet reentry to the water since vorticity is created during the overturning. The vorticity of largest magnitude is observed during the splash-up phenomenon. Vorticity is created by viscous shear torque (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999) and by the generation of vorticity close to high-curvature regions of the interface (Batchelor Reference Batchelor1967; Longuet-Higgins Reference Longuet-Higgins1992). The topological changes of the flow, such as the jet plunging and reconnection are also responsible for vorticity generation (Hornung, Willert & Turner Reference Hornung, Willert and Turner1995). The splashing process and air entrainment generated bubbles and droplets with associated vortical structure, also related to topological changes (Zhang, Duncan & Chahine Reference Zhang, Duncan and Chahine1993; Iafrati Reference Iafrati2009).

Figure 2. Evolution of a breaking wave and the vorticity field
![]() ${\it\Gamma}^{\ast }$
, displayed both in the air and water (a,c,e,g,i,k,m) and only in the water (b,d,f,h,j,l,n) with a different colour scale. Initial parameters:
${\it\Gamma}^{\ast }$
, displayed both in the air and water (a,c,e,g,i,k,m) and only in the water (b,d,f,h,j,l,n) with a different colour scale. Initial parameters:
![]() $\mathit{Re}=4\times 10^{4}$
,
$\mathit{Re}=4\times 10^{4}$
,
![]() $\mathit{Bo}=1000$
,
$\mathit{Bo}=1000$
,
![]() ${\it\epsilon}=0.55$
. The wave is moving from left to right. The wave becomes asymmetric (a,b), leading to a jet (c–f), which overturns (e–h) and reconnects (g,h) to finally splash up (i,n), where bubbles and spray are generated as well as large vortical structures both in the air and water.
${\it\epsilon}=0.55$
. The wave is moving from left to right. The wave becomes asymmetric (a,b), leading to a jet (c–f), which overturns (e–h) and reconnects (g,h) to finally splash up (i,n), where bubbles and spray are generated as well as large vortical structures both in the air and water.
DNS of plunging breakers have been previously performed for high initial steepness (Chen et al.
Reference Chen, Kharif, Zaleski and Li1999; Song & Sirviente Reference Song and Sirviente2004; Iafrati Reference Iafrati2009, Reference Iafrati2011) and show similar dynamics to that described here. When surface tension is increased (i.e.
![]() $\mathit{Bo}$
decreases), plunging waves are still observed for moderate Bond numbers (not shown) but the jet becomes smoother, leading to a significant reduction of the jet velocity and air entrapment. For these Bond numbers, the surface tension tends to inhibit the wave overturning but this effect is not sufficient to prevent wave breaking. Surface tension effects on plunging waves have been investigated numerically by Song & Sirviente (Reference Song and Sirviente2004) for high steepness (
$\mathit{Bo}$
decreases), plunging waves are still observed for moderate Bond numbers (not shown) but the jet becomes smoother, leading to a significant reduction of the jet velocity and air entrapment. For these Bond numbers, the surface tension tends to inhibit the wave overturning but this effect is not sufficient to prevent wave breaking. Surface tension effects on plunging waves have been investigated numerically by Song & Sirviente (Reference Song and Sirviente2004) for high steepness (
![]() ${\it\epsilon}>0.5$
) and show similar behaviour. Thus, plunging breakers are observed for high initial steepnesses and moderate to high Bond numbers.
${\it\epsilon}>0.5$
) and show similar behaviour. Thus, plunging breakers are observed for high initial steepnesses and moderate to high Bond numbers.
3.1.3. Parasitic capillary waves
Figure 3 shows the evolution of a wave with strong surface tension effects,
![]() $\mathit{Bo}=25$
, and an initial steepness,
$\mathit{Bo}=25$
, and an initial steepness,
![]() ${\it\epsilon}=0.3$
. The wave behaviour is quite different from the pure gravity wave case described above. Starting with a profile corresponding to a pure gravity wave, parasitic capillaries develop on the forward face of the wave, positive vorticity is located on the main wave crest as well as on the capillary crests while negative vorticity is at the corresponding troughs (both in the air and in the water). Negative vorticity in the trough is higher than positive vorticity on the crest. This mirrors the characteristic asymmetry in curvature of capillary waves (troughs are more curved than crests). We can see the progressive formation of the capillary ripples. The first one appears between
${\it\epsilon}=0.3$
. The wave behaviour is quite different from the pure gravity wave case described above. Starting with a profile corresponding to a pure gravity wave, parasitic capillaries develop on the forward face of the wave, positive vorticity is located on the main wave crest as well as on the capillary crests while negative vorticity is at the corresponding troughs (both in the air and in the water). Negative vorticity in the trough is higher than positive vorticity on the crest. This mirrors the characteristic asymmetry in curvature of capillary waves (troughs are more curved than crests). We can see the progressive formation of the capillary ripples. The first one appears between
![]() $t/T=0.64$
and
$t/T=0.64$
and
![]() $t/T=0.76$
, vorticity both in the water and in the air being focused on the front of the wave. Then we observe the formation of a train of ripples, with high positive vorticity on the crest and negative vorticity in the through. The capillary train remains stationary in the frame of the main wave and is then simply damped by viscosity. We observe that vorticity remains localized in thin boundary layers in both the air and the water.
$t/T=0.76$
, vorticity both in the water and in the air being focused on the front of the wave. Then we observe the formation of a train of ripples, with high positive vorticity on the crest and negative vorticity in the through. The capillary train remains stationary in the frame of the main wave and is then simply damped by viscosity. We observe that vorticity remains localized in thin boundary layers in both the air and the water.

Figure 3. Parasitic capillary waves on a gravity wave and the vorticity field
![]() ${\it\Gamma}^{\ast }$
, displayed both in the air and water (a,c,e,g,i,k) and only in the water (b,d,f,h,j,l) with a different colour scale. Initial parameters:
${\it\Gamma}^{\ast }$
, displayed both in the air and water (a,c,e,g,i,k) and only in the water (b,d,f,h,j,l) with a different colour scale. Initial parameters:
![]() $\mathit{Re}=4\times 10^{4}$
,
$\mathit{Re}=4\times 10^{4}$
,
![]() $\mathit{Bo}=25$
,
$\mathit{Bo}=25$
,
![]() ${\it\epsilon}=0.3$
. Parasitic capillaries are generated on the front of the carrier gravity wave when the wave becomes steep enough (a–d). A train of parasitic capillaries is then formed (c–h) and propagates with the main wave. The amplitude of the carrier decays through viscous effects (i–l). Positive vorticity is located in the crest of the capillaries and negative vorticity in the trough.
${\it\epsilon}=0.3$
. Parasitic capillaries are generated on the front of the carrier gravity wave when the wave becomes steep enough (a–d). A train of parasitic capillaries is then formed (c–h) and propagates with the main wave. The amplitude of the carrier decays through viscous effects (i–l). Positive vorticity is located in the crest of the capillaries and negative vorticity in the trough.
These gravity–capillary waves are nonlinear surface waves for which both gravity and surface tension are important, where two typical length scales can be defined, the longer scale corresponds to the main wavelength (
![]() ${\it\lambda}$
) and the shorter scale to the capillary ripples we observe in the front of the wave (
${\it\lambda}$
) and the shorter scale to the capillary ripples we observe in the front of the wave (
![]() ${\it\lambda}_{c}=2{\rm\pi}\sqrt{{\it\gamma}/(g{\rm\Delta}{\it\rho})}$
). Parasitic capillary waves on steep gravity waves have been described theoretically (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998): assuming an underlying pure Stokes wave, high curvature and surface tension effects are localized at the crest of the gravity wave and act as a forcing term. Parasitic capillaries appear initially as a linear response to the local forcing on the Stokes wave and finally are damped by viscosity. In this description, vorticity remains located in a thin boundary layer and parasitic capillaries are responsible for significant dissipation enhancement (Mui & Dommermuth Reference Mui and Dommermuth1995; Fedorov & Melville Reference Fedorov and Melville1998; Melville & Fedorov Reference Melville and Fedorov2015).
${\it\lambda}_{c}=2{\rm\pi}\sqrt{{\it\gamma}/(g{\rm\Delta}{\it\rho})}$
). Parasitic capillary waves on steep gravity waves have been described theoretically (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998): assuming an underlying pure Stokes wave, high curvature and surface tension effects are localized at the crest of the gravity wave and act as a forcing term. Parasitic capillaries appear initially as a linear response to the local forcing on the Stokes wave and finally are damped by viscosity. In this description, vorticity remains located in a thin boundary layer and parasitic capillaries are responsible for significant dissipation enhancement (Mui & Dommermuth Reference Mui and Dommermuth1995; Fedorov & Melville Reference Fedorov and Melville1998; Melville & Fedorov Reference Melville and Fedorov2015).
These waves are observed for initial steepnesses below a breaking threshold and for small Bond number (
![]() $\mathit{Bo}\lesssim 70$
). Note also that the steepness must be high enough to observe the formation of parasitic capillaries and that the intensity of the vorticity field under the capillaries is related to the wave steepness (Longuet-Higgins Reference Longuet-Higgins1992). The present behaviour is in agreement with the theoretical description given by Longuet-Higgins (Reference Longuet-Higgins1963) and Fedorov & Melville (Reference Fedorov and Melville1998).
$\mathit{Bo}\lesssim 70$
). Note also that the steepness must be high enough to observe the formation of parasitic capillaries and that the intensity of the vorticity field under the capillaries is related to the wave steepness (Longuet-Higgins Reference Longuet-Higgins1992). The present behaviour is in agreement with the theoretical description given by Longuet-Higgins (Reference Longuet-Higgins1963) and Fedorov & Melville (Reference Fedorov and Melville1998).
3.1.4. Spilling breakers
Spilling breakers are usually defined as breaking waves without an overturning entrainment of air. The overturning entrainment is avoided either because the slope of the wave is too low, resulting in a gentle spilling wave (Rapp & Melville Reference Rapp and Melville1990), or due to stabilization by surface tension effects (Duncan et al.
Reference Duncan, Qiao and Philomin1999; Duncan Reference Duncan2001). These waves have been observed and described in laboratory experiments (Rapp & Melville Reference Rapp and Melville1990; Lin & Rockwell Reference Lin and Rockwell1995; Duncan et al.
Reference Duncan, Qiao and Philomin1999; Qiao & Duncan Reference Qiao and Duncan2001; Liu & Duncan Reference Liu and Duncan2003, Reference Liu and Duncan2006) and numerically by Iafrati & Campana (Reference Iafrati and Campana2005). This regime is also obtained in our simulations as illustrated in figure 4, for a relative high initial steepness and low Bond number (
![]() $\mathit{Bo}=25$
,
$\mathit{Bo}=25$
,
![]() ${\it\epsilon}=0.45$
). The spilling breaker dynamics can be described as follows: due to surface tension effects, the free surface does not overturn and the beginning of the breaking process is marked by the formation of a bulge in the profile at the crest on the forward face of the wave (figure 4
a–d). The leading edge is sometimes called the ‘toe of the wave’, and as the breaking process continues, the bulge becomes more pronounced while the toe remains in nearly a fixed position relative to the crest (figure 4
c–f). Concurrent with the growth of the bulge, capillary waves appear and grow in amplitude upstream of the toe (figure 4
e–j). After a short time, the toe begins a rapid motion down the wave face and during this motion a train of large amplitude well organized ripples is formed between the toe and the crest. These ripples grow rapidly and then break down into a random pattern indicating that the underlying flow has become turbulent (figure 4
k–n). The wave evolution from (a) to (b) and (c) may support the theoretical considerations from Longuet-Higgins (Reference Longuet-Higgins1994) and Longuet-Higgins & Cleaver (Reference Longuet-Higgins and Cleaver1994) that the bulge formation is due to both the negative curvature at the crest and the positive curvature at the toe. Both in the air and water, the vorticity field is positive on the crest and negative in the trough. The negative vorticity field in the water appears much stronger, and the initial boundary layer becomes thicker together with an increase of the magnitude of the vorticity, which induces a flow separation from the main wave. The turbulent structures then break up and give birth to counter-rotating vortices. Banner & Melville (Reference Banner and Melville1976) considered separation of the airflow over a quasi-steady spilling breaker but in that case the flow in the water must separate also. In the quasi-steady case, in the frame of reference of the wave, breaking requires a stagnation point at the surface. If the wave is moving to the right, then in the reference frame of the wave the flow at the surface in the water is to the left coming to zero at the stagnation point. From the no-slip condition at the interface the flow in the air at the surface is the same. Therefore, both the air and the water flows separate at the stagnation point. Note that to leading order the vorticity follows the flow, so separation should also show vorticity being advected, rather than diffused, away from the surface in both fluids. In fact, another definition of separation is the advection of vorticity away from the boundary.
${\it\epsilon}=0.45$
). The spilling breaker dynamics can be described as follows: due to surface tension effects, the free surface does not overturn and the beginning of the breaking process is marked by the formation of a bulge in the profile at the crest on the forward face of the wave (figure 4
a–d). The leading edge is sometimes called the ‘toe of the wave’, and as the breaking process continues, the bulge becomes more pronounced while the toe remains in nearly a fixed position relative to the crest (figure 4
c–f). Concurrent with the growth of the bulge, capillary waves appear and grow in amplitude upstream of the toe (figure 4
e–j). After a short time, the toe begins a rapid motion down the wave face and during this motion a train of large amplitude well organized ripples is formed between the toe and the crest. These ripples grow rapidly and then break down into a random pattern indicating that the underlying flow has become turbulent (figure 4
k–n). The wave evolution from (a) to (b) and (c) may support the theoretical considerations from Longuet-Higgins (Reference Longuet-Higgins1994) and Longuet-Higgins & Cleaver (Reference Longuet-Higgins and Cleaver1994) that the bulge formation is due to both the negative curvature at the crest and the positive curvature at the toe. Both in the air and water, the vorticity field is positive on the crest and negative in the trough. The negative vorticity field in the water appears much stronger, and the initial boundary layer becomes thicker together with an increase of the magnitude of the vorticity, which induces a flow separation from the main wave. The turbulent structures then break up and give birth to counter-rotating vortices. Banner & Melville (Reference Banner and Melville1976) considered separation of the airflow over a quasi-steady spilling breaker but in that case the flow in the water must separate also. In the quasi-steady case, in the frame of reference of the wave, breaking requires a stagnation point at the surface. If the wave is moving to the right, then in the reference frame of the wave the flow at the surface in the water is to the left coming to zero at the stagnation point. From the no-slip condition at the interface the flow in the air at the surface is the same. Therefore, both the air and the water flows separate at the stagnation point. Note that to leading order the vorticity follows the flow, so separation should also show vorticity being advected, rather than diffused, away from the surface in both fluids. In fact, another definition of separation is the advection of vorticity away from the boundary.

Figure 4. Evolution of a spilling breaker and its vorticity field
![]() ${\it\Gamma}^{\ast }$
at different times, displayed both in the air and water (a,c,e,g,i,k,m,o) and only in the water (b,d,f,h,j,l,n,p) with a different colour scale. Initial conditions
${\it\Gamma}^{\ast }$
at different times, displayed both in the air and water (a,c,e,g,i,k,m,o) and only in the water (b,d,f,h,j,l,n,p) with a different colour scale. Initial conditions
![]() $\mathit{Re}=4\times 10^{4}$
,
$\mathit{Re}=4\times 10^{4}$
,
![]() $\mathit{Bo}=25$
,
$\mathit{Bo}=25$
,
![]() ${\it\epsilon}=0.45$
. The wave becomes steeper and begins to break (a–d) but the overturning motion is avoided due to capillary effects and capillaries propagate on the front of the toe (c–i). A separation of the boundary layers in water is observed, without air entrainment but with the formation of vortex dipoles in the water after breaking (m–p).
${\it\epsilon}=0.45$
. The wave becomes steeper and begins to break (a–d) but the overturning motion is avoided due to capillary effects and capillaries propagate on the front of the toe (c–i). A separation of the boundary layers in water is observed, without air entrainment but with the formation of vortex dipoles in the water after breaking (m–p).
Another example of a spilling breaker, for higher Bond number, is shown in figure 5 (
![]() $\mathit{Bo}=70$
,
$\mathit{Bo}=70$
,
![]() ${\it\epsilon}=0.45$
). The previous description of a spilling breaker is still valid but the wave is closer to overturning and thus more mixing and aeration is observed. In this case more bubbles are created and the vorticity field in the fluid underneath is more turbulent, and interface reconnection is also observed, these topological changes increasing the vorticity generation. Several vortex dipoles are also generated in the water and start to move deeper. Thus, it appears that for this intermediate steepness, a small change in the surface tension can cause qualitative changes in the wave dynamics. These types of wave structure changes have been explored experimentally by adding surfactants to water (Liu & Duncan Reference Liu and Duncan2003, Reference Liu and Duncan2006). Air entrainment by breaking waves has been investigated experimentally (Lamarre & Melville Reference Lamarre and Melville1991, Reference Lamarre and Melville1994; Loewen, O’Dor & Skafel Reference Loewen, O’Dor and Skafel1996; Blenkinsopp & Chaplin Reference Blenkinsopp and Chaplin2007; Rojas & Loewen Reference Rojas and Loewen2010) but detailed comparisons require the extension of the present simulation to three dimensions.
${\it\epsilon}=0.45$
). The previous description of a spilling breaker is still valid but the wave is closer to overturning and thus more mixing and aeration is observed. In this case more bubbles are created and the vorticity field in the fluid underneath is more turbulent, and interface reconnection is also observed, these topological changes increasing the vorticity generation. Several vortex dipoles are also generated in the water and start to move deeper. Thus, it appears that for this intermediate steepness, a small change in the surface tension can cause qualitative changes in the wave dynamics. These types of wave structure changes have been explored experimentally by adding surfactants to water (Liu & Duncan Reference Liu and Duncan2003, Reference Liu and Duncan2006). Air entrainment by breaking waves has been investigated experimentally (Lamarre & Melville Reference Lamarre and Melville1991, Reference Lamarre and Melville1994; Loewen, O’Dor & Skafel Reference Loewen, O’Dor and Skafel1996; Blenkinsopp & Chaplin Reference Blenkinsopp and Chaplin2007; Rojas & Loewen Reference Rojas and Loewen2010) but detailed comparisons require the extension of the present simulation to three dimensions.

Figure 5. Evolution of a spilling–overturning breaker and its vorticity field
![]() ${\it\Gamma}^{\ast }$
at different times, displayed both in the air and water (a,c,e,g,i,k,m,o) and only in the water (b,d,f,h,j,l,n,p) with a different colour scale. Initial conditions:
${\it\Gamma}^{\ast }$
at different times, displayed both in the air and water (a,c,e,g,i,k,m,o) and only in the water (b,d,f,h,j,l,n,p) with a different colour scale. Initial conditions:
![]() $\mathit{Re}=4\times 10^{4}$
,
$\mathit{Re}=4\times 10^{4}$
,
![]() $\mathit{Bo}=70$
,
$\mathit{Bo}=70$
,
![]() ${\it\epsilon}=0.45$
. The wave begins to break (a–d) similar to figure 4 but with the interface almost overturning (c,d) and formation of bubbles after the breaking stage (i,j). The turbulent breakdown appears stronger and several vortices are generated in the water (k,l).
${\it\epsilon}=0.45$
. The wave begins to break (a–d) similar to figure 4 but with the interface almost overturning (c,d) and formation of bubbles after the breaking stage (i,j). The turbulent breakdown appears stronger and several vortices are generated in the water (k,l).
3.2. Wave regime diagram
The different wave regimes observed and described previously are summarized in the state diagram in figure 7. We first present the criteria chosen to distinguish each of them and then discuss the diagram. The different wave regimes are (i) non-breaking gravity waves (phase NB), (ii) parasitic capillary waves on gravity wave (phase PCW), (iii) plunging breakers (phase PB), (iv) spilling breakers (phase SB).
Using the criteria defined below, numerical simulations can be used to automatically estimate the critical values of the steepness and Bond numbers for which transitions occur. To do this efficiently, we used an automatic iteration in the
![]() $({\it\epsilon},\mathit{Bo})$
phase space. Simulations are repeated on either side of the transition boundary until convergence. The symbols in figure 7 are the results of this iterative process. Each symbol on the diagram thus represents the result of typically 5–10 simulations. This systematic phase-space exploration was greatly facilitated by the overall speed of the adaptive grid method.
$({\it\epsilon},\mathit{Bo})$
phase space. Simulations are repeated on either side of the transition boundary until convergence. The symbols in figure 7 are the results of this iterative process. Each symbol on the diagram thus represents the result of typically 5–10 simulations. This systematic phase-space exploration was greatly facilitated by the overall speed of the adaptive grid method.
3.2.1. Wave regime criteria
Breaking criteria. Vertical interface. Wave breaking criteria have been the subject of strong debates over the years and we choose to characterize the onset of wave breaking by the appearance of a local vertical interface (Peregrine et al.
Reference Peregrine, Cokelet and McIver1993; Perlin et al.
Reference Perlin, Choi and Tian2013). A wave is classified as breaking when it exhibits a vertical interface, as shown on the sketch figure 6(a). The boundary between non-breaking and breaking waves using this criterion is indicated by (▪) on figure 7 and will be called the breaking boundary in the following. The breaking boundary exhibits two transitions: at high Bond number (
![]() $\mathit{Bo}\gg 100$
), a critical steepness
$\mathit{Bo}\gg 100$
), a critical steepness
![]() ${\it\epsilon}_{c}=0.32$
determines whether the two-dimensional wave will break, while at low Bond number, the breaking boundary depends on the Bond number. The wave breaking boundary can be described at high steepness and low Bond number by the following relation:
${\it\epsilon}_{c}=0.32$
determines whether the two-dimensional wave will break, while at low Bond number, the breaking boundary depends on the Bond number. The wave breaking boundary can be described at high steepness and low Bond number by the following relation:
![]() ${\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
, for which we present a physical interpretation in § 3.3. Here
${\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
, for which we present a physical interpretation in § 3.3. Here
![]() $K_{B}=1.12$
is a dimensionless constant fitted to the data. The constant
$K_{B}=1.12$
is a dimensionless constant fitted to the data. The constant
![]() $K_{B}$
can be interpreted as a critical Bond number
$K_{B}$
can be interpreted as a critical Bond number
![]() $\mathit{Bo}_{B}=K_{B}^{3}=1.4$
, below which no breaking wave can exist.
$\mathit{Bo}_{B}=K_{B}^{3}=1.4$
, below which no breaking wave can exist.

Figure 6. Topological wave state criteria: (a) breaking criterion with the interface presenting a vertical segment (
![]() $-90^{\circ }$
angle); (b) overturning wave with the interface presenting both vertical and horizontal segments (
$-90^{\circ }$
angle); (b) overturning wave with the interface presenting both vertical and horizontal segments (
![]() $-180^{\circ }$
angle).
$-180^{\circ }$
angle).

Figure 7. Wave regime diagram
![]() $(\mathit{Bo},{\it\epsilon})$
. Symbols indicate the boundaries between the wave regimes obtained numerically (see the text). ▪: wave breaking boundary, presence of a vertical interface. ▾: spilling-plunging boundary, presence of an horizontal interface. Zone (PB): plunging breakers (as in figure 2); (SB): spilling breakers (as in figure 4); (PCW): parasitic capillary waves (as in figure 3); (NB): non-breaking gravity waves (as in figure 1). Horizontal solid line (black) indicates the critical steepness
$(\mathit{Bo},{\it\epsilon})$
. Symbols indicate the boundaries between the wave regimes obtained numerically (see the text). ▪: wave breaking boundary, presence of a vertical interface. ▾: spilling-plunging boundary, presence of an horizontal interface. Zone (PB): plunging breakers (as in figure 2); (SB): spilling breakers (as in figure 4); (PCW): parasitic capillary waves (as in figure 3); (NB): non-breaking gravity waves (as in figure 1). Horizontal solid line (black) indicates the critical steepness
![]() ${\it\epsilon}_{c}=0.32$
. Black dashed line indicates the boundary between breaking and non-breaking waves:
${\it\epsilon}_{c}=0.32$
. Black dashed line indicates the boundary between breaking and non-breaking waves:
![]() ${\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
, with
${\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
, with
![]() $K_{B}=1.12$
a fitted parameter. Solid grey line (red online) indicates the overturning boundary (between spilling and plunging breakers):
$K_{B}=1.12$
a fitted parameter. Solid grey line (red online) indicates the overturning boundary (between spilling and plunging breakers):
![]() ${\it\epsilon}_{SP}=K_{SP}(1+\mathit{Bo})^{-1/3}$
, with
${\it\epsilon}_{SP}=K_{SP}(1+\mathit{Bo})^{-1/3}$
, with
![]() $K_{SP}=1.75$
a fitted parameter. Dot-dashed line:
$K_{SP}=1.75$
a fitted parameter. Dot-dashed line:
![]() $\mathit{Bo}_{c}=67$
, the observed critical Bond number for the appearance of parasitic capillaries.
$\mathit{Bo}_{c}=67$
, the observed critical Bond number for the appearance of parasitic capillaries.
Overturning wave. Horizontal interface. Plunging and spilling waves (figures 2 and 4) display different interface profiles at and after breaking. Spilling and plunging breakers both exhibit a vertical interface but a plunging wave also exhibits a horizontal interface, as shown in figure 6, and described by Duncan (Reference Duncan2001). We choose the presence of an horizontal interface to distinguish plunging and spilling breakers. The plunging breaker in figure 2 satisfies both the breaking (vertical interface) and the overturning wave (horizontal interface) criteria, since a horizontal interface is seen once the jet is formed. On the other hand, the spilling breaker in figure 4 only satisfies the breaking (vertical interface) criterion, since the jet formation is prevented by surface tension effects.
The boundary between spilling and plunging breakers is shown in figure 7 by ▾. At high Bond numbers, the same critical steepness
![]() ${\it\epsilon}_{c}$
as before is obtained and there is no difference between the breaking boundary and the overturning boundary. At low Bond number and high steepness, the overturning boundary can be described by a similar function as the breaking boundary,
${\it\epsilon}_{c}$
as before is obtained and there is no difference between the breaking boundary and the overturning boundary. At low Bond number and high steepness, the overturning boundary can be described by a similar function as the breaking boundary,
![]() ${\it\epsilon}_{SP}=K_{SP}(1+\mathit{Bo})^{-1/3}$
, having the same power law but with a different constant,
${\it\epsilon}_{SP}=K_{SP}(1+\mathit{Bo})^{-1/3}$
, having the same power law but with a different constant,
![]() $K_{SP}=1.75$
. Again, the constant
$K_{SP}=1.75$
. Again, the constant
![]() $K_{SP}$
can be interpreted as a critical Bond number
$K_{SP}$
can be interpreted as a critical Bond number
![]() $\mathit{Bo}_{SP}=K_{SP}^{3}=4.8$
below which no plunging breaker can exist.
$\mathit{Bo}_{SP}=K_{SP}^{3}=4.8$
below which no plunging breaker can exist.
3.2.2. Existence of a critical steepness at high Bond number
 ${\it\epsilon}_{c}$
${\it\epsilon}_{c}$
At high Bond numbers (
![]() $\mathit{Bo}\gg 100$
) the breaking boundary corresponds to the existence of a critical steepness, here
$\mathit{Bo}\gg 100$
) the breaking boundary corresponds to the existence of a critical steepness, here
![]() ${\it\epsilon}_{c}=0.32$
. For
${\it\epsilon}_{c}=0.32$
. For
![]() ${\it\epsilon}<{\it\epsilon}_{c}$
the wave does not break (phase S in figure 7), while for
${\it\epsilon}<{\it\epsilon}_{c}$
the wave does not break (phase S in figure 7), while for
![]() ${\it\epsilon}>{\it\epsilon}_{c}$
the wave breaks. This critical steepness defines the breaking of a gravity wave and we remark that the breaking and the overturning boundary exhibit the same critical steepness at high Bond number. Thus, the spilling breaker regime at high Bond number (low surface tension) can be seen as a transition regime between non-breaking and breaking waves. Note that the existence of a critical steepness for wave breaking is a meaningful physical result, but the particular value of the critical steepness in idealized numerical simulations strongly depends on the initial conditions.
${\it\epsilon}>{\it\epsilon}_{c}$
the wave breaks. This critical steepness defines the breaking of a gravity wave and we remark that the breaking and the overturning boundary exhibit the same critical steepness at high Bond number. Thus, the spilling breaker regime at high Bond number (low surface tension) can be seen as a transition regime between non-breaking and breaking waves. Note that the existence of a critical steepness for wave breaking is a meaningful physical result, but the particular value of the critical steepness in idealized numerical simulations strongly depends on the initial conditions.
The finding of an accurate critical steepness for wave breaking remains an open challenge theoretically and has been the scope of many experimental studies (e.g. Perlin et al.
Reference Perlin, Choi and Tian2013). When breaking is triggered by modulational instabilities, plunging waves can be observed for initial slopes
![]() ${\it\epsilon}\approx 0.11$
(Melville Reference Melville1982; Tulin & Waseda Reference Tulin and Waseda1999; Song & Banner Reference Song and Banner2002; Banner & Peirson Reference Banner and Peirson2007; Iafrati et al.
Reference Iafrati, Babanin and Onorato2013). In focusing experiments a critical slope of the same order is described when considering the dissipation by breaking, and
${\it\epsilon}\approx 0.11$
(Melville Reference Melville1982; Tulin & Waseda Reference Tulin and Waseda1999; Song & Banner Reference Song and Banner2002; Banner & Peirson Reference Banner and Peirson2007; Iafrati et al.
Reference Iafrati, Babanin and Onorato2013). In focusing experiments a critical slope of the same order is described when considering the dissipation by breaking, and
![]() ${\it\epsilon}\approx 0.08$
(Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012). Note also, that when only considering the shape of the interface as a breaking criterion, higher values of the slope can be considered and
${\it\epsilon}\approx 0.08$
(Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012). Note also, that when only considering the shape of the interface as a breaking criterion, higher values of the slope can be considered and
![]() ${\it\epsilon}\approx 0.25$
(Rapp & Melville Reference Rapp and Melville1990). In these focusing cases, the slope is often evaluated by the sum of all linear components of the initial wavepacket. Thus, the particular value of
${\it\epsilon}\approx 0.25$
(Rapp & Melville Reference Rapp and Melville1990). In these focusing cases, the slope is often evaluated by the sum of all linear components of the initial wavepacket. Thus, the particular value of
![]() ${\it\epsilon}_{c}$
depends on the initial conditions, on the physical processes that lead to breaking and on the breaking criterion. Note also that in focusing experiments, a dependency on the bandwidth of the wave packet is evident (Rapp & Melville Reference Rapp and Melville1990; Banner & Peirson Reference Banner and Peirson2007; Drazen et al.
Reference Drazen, Melville and Lenain2008).
${\it\epsilon}_{c}$
depends on the initial conditions, on the physical processes that lead to breaking and on the breaking criterion. Note also that in focusing experiments, a dependency on the bandwidth of the wave packet is evident (Rapp & Melville Reference Rapp and Melville1990; Banner & Peirson Reference Banner and Peirson2007; Drazen et al.
Reference Drazen, Melville and Lenain2008).
3.2.3. Parasitic capillaries and spilling breakers at low Bond number, critical steepness breaking curve
 ${\it\epsilon}_{B}(\mathit{Bo})$
${\it\epsilon}_{B}(\mathit{Bo})$
Let us now discuss the breaking wave regimes. At high Bond number and high steepness plunging waves are observed above the critical steepness. Plunging waves are also observed at higher surface tension with a smoother jet. Increasing the surface tension eventually leads to the inhibition of the jet formation and while spilling breakers are observed at high steepness (as in figure 4), parasitic capillaries are observed at relatively low steepness as in figure 3. While spilling breakers satisfy the breaking criterion, parasitic capillaries are not considered breaking waves.
At high steepness and low Bond number, the breaking boundary is described by a steepness depending on the Bond number,
![]() ${\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
, the corresponding function being shown on the state diagram of figure 7.
${\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
, the corresponding function being shown on the state diagram of figure 7.
Thus, the breaking wave boundary permits us to define the parameter space where parasitic capillaries are present. For
![]() $\mathit{Bo}>\mathit{Bo}_{c}=67$
, a critical steepness alone defines the transition from non-breaking to breaking waves. For
$\mathit{Bo}>\mathit{Bo}_{c}=67$
, a critical steepness alone defines the transition from non-breaking to breaking waves. For
![]() $\mathit{Bo}<\mathit{Bo}_{c}$
, surface tension stabilizes the wave and a higher initial steepness is needed to observe wave breaking, the breaking to non-breaking wave boundary is described by the
$\mathit{Bo}<\mathit{Bo}_{c}$
, surface tension stabilizes the wave and a higher initial steepness is needed to observe wave breaking, the breaking to non-breaking wave boundary is described by the
![]() ${\it\epsilon}_{B}(\mathit{Bo})$
curve. This critical Bond number
${\it\epsilon}_{B}(\mathit{Bo})$
curve. This critical Bond number
![]() $\mathit{Bo}_{c}$
describes the appearance of parasitic capillary waves: for
$\mathit{Bo}_{c}$
describes the appearance of parasitic capillary waves: for
![]() $\mathit{Bo}<\mathit{Bo}_{c}$
and
$\mathit{Bo}<\mathit{Bo}_{c}$
and
![]() ${\it\epsilon}<{\it\epsilon}_{B}$
, we observe the appearance of parasitic capillary waves (as in figure 3), where capillaries can be treated as a perturbation of the main gravity wave (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998). Note that according to the Bond number, the corresponding wavelength in the air–water case is
${\it\epsilon}<{\it\epsilon}_{B}$
, we observe the appearance of parasitic capillary waves (as in figure 3), where capillaries can be treated as a perturbation of the main gravity wave (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998). Note that according to the Bond number, the corresponding wavelength in the air–water case is
![]() ${\it\lambda}_{c}=2{\rm\pi}\sqrt{{\it\gamma}\mathit{Bo }_{c}/({\it\rho}g)}\approx 14~\text{cm}$
, which is consistent with the experimental scale where parasitic capillaries are observed for
${\it\lambda}_{c}=2{\rm\pi}\sqrt{{\it\gamma}\mathit{Bo }_{c}/({\it\rho}g)}\approx 14~\text{cm}$
, which is consistent with the experimental scale where parasitic capillaries are observed for
![]() ${\it\lambda}\sim O(10~\text{cm})$
or less (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998).
${\it\lambda}\sim O(10~\text{cm})$
or less (Longuet-Higgins Reference Longuet-Higgins1963; Fedorov & Melville Reference Fedorov and Melville1998).
3.2.4. Spilling and plunging breakers, critical steepness curve at low Bond number
 ${\it\epsilon}_{SP}(\mathit{Bo})$
${\it\epsilon}_{SP}(\mathit{Bo})$
As already noted, at high Bond number the spilling–plunging boundary is described by
![]() ${\it\epsilon}_{c}$
. At low Bond numbers the spilling–plunging boundary is described by the curve
${\it\epsilon}_{c}$
. At low Bond numbers the spilling–plunging boundary is described by the curve
![]() ${\it\epsilon}_{B}=K_{SP}(1+\mathit{Bo})^{-1/3}$
. Above the stability boundary and below the plunging boundary, i.e.
${\it\epsilon}_{B}=K_{SP}(1+\mathit{Bo})^{-1/3}$
. Above the stability boundary and below the plunging boundary, i.e.
![]() ${\it\epsilon}_{B}<{\it\epsilon}<{\it\epsilon}_{SP}$
, spilling breakers (as in figure 4) are observed (zone BS). The wave still breaks but no overturning is observed. This dynamics is similar to gentle (weak) spilling breakers, observed experimentally (Rapp & Melville Reference Rapp and Melville1990; Duncan Reference Duncan2001).
${\it\epsilon}_{B}<{\it\epsilon}<{\it\epsilon}_{SP}$
, spilling breakers (as in figure 4) are observed (zone BS). The wave still breaks but no overturning is observed. This dynamics is similar to gentle (weak) spilling breakers, observed experimentally (Rapp & Melville Reference Rapp and Melville1990; Duncan Reference Duncan2001).
The fact that for Bond number around 100, the boundary between plunging breakers and spilling breakers is a smooth transition corresponds to the existence of spilling breakers as shown in figure 5, where significant bubble formation and air entrainment appear and, thus, horizontal interfaces may exist. These highly aerated spilling breakers satisfy both the breaking and the overturning criteria, but without jet formation. Note finally that at high steepness (
![]() ${\it\epsilon}>0.6$
) and high surface tension, we observe highly nonlinear waves similar to pure nonlinear capillary waves, with interface reconnection and air entrapment (not shown). These features appear comparable with limiting Crapper waves (Crapper Reference Crapper1957).
${\it\epsilon}>0.6$
) and high surface tension, we observe highly nonlinear waves similar to pure nonlinear capillary waves, with interface reconnection and air entrapment (not shown). These features appear comparable with limiting Crapper waves (Crapper Reference Crapper1957).
3.3. A scaling for capillary effects on wave breaking
We have shown that the separation between breaking and non-breaking waves when surface tension effects are important scales as
![]() ${\it\epsilon}_{B}\sim (1+\mathit{Bo})^{-1/3}$
. It is very interesting to note that this scaling is also valid for separating the spilling and plunging breakers in the
${\it\epsilon}_{B}\sim (1+\mathit{Bo})^{-1/3}$
. It is very interesting to note that this scaling is also valid for separating the spilling and plunging breakers in the
![]() $({\it\epsilon},\mathit{Bo})$
space. We discuss here a possible explanation for this boundary, using the balance between the generation of vorticity by gravity–capillary waves, given by Longuet-Higgins (Reference Longuet-Higgins1992) and the Laplace pressure due to the capillary effects
$({\it\epsilon},\mathit{Bo})$
space. We discuss here a possible explanation for this boundary, using the balance between the generation of vorticity by gravity–capillary waves, given by Longuet-Higgins (Reference Longuet-Higgins1992) and the Laplace pressure due to the capillary effects
![]() $p={\it\gamma}{\it\kappa}$
, with
$p={\it\gamma}{\it\kappa}$
, with
![]() ${\it\kappa}$
the wave curvature.
${\it\kappa}$
the wave curvature.
We want to connect the vorticity generated by the wave to the pressure. Following Douady, Couder & Brachet (Reference Douady, Couder and Brachet1991) and taking the divergence of the Navier–Stokes equations in the water (2.1):
with
![]() ${\it\Gamma}$
the vorticity and
${\it\Gamma}$
the vorticity and
![]() $\unicode[STIX]{x1D60B}_{ij}$
the deformation tensor, linked to the dissipation. Thus, the vorticity concentrations will act as source of pressure. At high Reynolds number we have
$\unicode[STIX]{x1D60B}_{ij}$
the deformation tensor, linked to the dissipation. Thus, the vorticity concentrations will act as source of pressure. At high Reynolds number we have
![]() $\unicode[STIX]{x1D60B}_{ij}^{2}\ll {\it\Gamma}^{2}$
, which was checked by the DNS results to be valid in our simulations. Thus, one obtains the following relation between vorticity and pressure:
$\unicode[STIX]{x1D60B}_{ij}^{2}\ll {\it\Gamma}^{2}$
, which was checked by the DNS results to be valid in our simulations. Thus, one obtains the following relation between vorticity and pressure:
We consider the pressure due to capillary effects,
with
![]() $a$
the wave amplitude. The vorticity is given by Longuet-Higgins (Reference Longuet-Higgins1992) for a nonlinear gravity–capillary wave:
$a$
the wave amplitude. The vorticity is given by Longuet-Higgins (Reference Longuet-Higgins1992) for a nonlinear gravity–capillary wave:
with
![]() ${\it\omega}=\sqrt{gk+{\it\gamma}/{\it\rho}k^{3}}$
the dispersion relation. Thus, we obtain
${\it\omega}=\sqrt{gk+{\it\gamma}/{\it\rho}k^{3}}$
the dispersion relation. Thus, we obtain
and since the Bond number is given by
![]() $\mathit{Bo}={\it\rho}_{w}g/({\it\gamma}k^{2})$
, we finally obtain the following scaling:
$\mathit{Bo}={\it\rho}_{w}g/({\it\gamma}k^{2})$
, we finally obtain the following scaling:
which corresponds to the boundary between breaking and non-breaking waves when surface tension effects are strong. Thus, this simple scaling argument appears to describe the transition from a non-breaking gravity–capillary wave to breakers with strong surface tension and the same scaling holds for describing the transition from spilling breakers to plunging breakers.
4. Energy dissipation
4.1. Evolution of the various energy components
We will now discuss the capillary effects on wave dissipation for the various wave patterns described previously. We calculate the various energy components of the propagating wave, the kinetic energy
the gravitational potential energy
the surface tension potential energy
where
![]() $\mathscr{L}$
is the arclength of the interface, and the total energy
$\mathscr{L}$
is the arclength of the interface, and the total energy
The constant
![]() $1/8$
in the gravitational potential energy equation is introduced to define a zero potential energy for an unperturbed surface.
$1/8$
in the gravitational potential energy equation is introduced to define a zero potential energy for an unperturbed surface.
Figure 8 shows the different wave energy components for various parameters
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() $\mathit{Bo}$
. In all cases, the total wave energy decreases in time due to dissipative processes.
$\mathit{Bo}$
. In all cases, the total wave energy decreases in time due to dissipative processes.

Figure 8. Normalized wave energy components as functions of time
![]() $t/T$
, the total energy
$t/T$
, the total energy
![]() $E/E_{0}$
(▫), kinetic energy
$E/E_{0}$
(▫), kinetic energy
![]() $E_{k}/E_{0}$
(*), gravitational potential energy
$E_{k}/E_{0}$
(*), gravitational potential energy
![]() $E_{g}/E_{0}$
(○) and surface tension potential energy
$E_{g}/E_{0}$
(○) and surface tension potential energy
![]() $E_{s}/E_{0}$
(▿), for various
$E_{s}/E_{0}$
(▿), for various
![]() $\mathit{Bo}$
and initial
$\mathit{Bo}$
and initial
![]() $ak$
: (a)
$ak$
: (a)
![]() $\mathit{Bo}=1000$
and
$\mathit{Bo}=1000$
and
![]() ${\it\epsilon}=0.3$
; (b)
${\it\epsilon}=0.3$
; (b)
![]() $\mathit{Bo}=1000$
and
$\mathit{Bo}=1000$
and
![]() ${\it\epsilon}=0.45$
; (c)
${\it\epsilon}=0.45$
; (c)
![]() $\mathit{Bo}=50$
and
$\mathit{Bo}=50$
and
![]() ${\it\epsilon}=0.3$
; (d)
${\it\epsilon}=0.3$
; (d)
![]() $\mathit{Bo}=50$
and
$\mathit{Bo}=50$
and
![]() ${\it\epsilon}=0.45$
; (e)
${\it\epsilon}=0.45$
; (e)
![]() $\mathit{Bo}=10$
and
$\mathit{Bo}=10$
and
![]() ${\it\epsilon}=0.3$
; (f)
${\it\epsilon}=0.3$
; (f)
![]() $\mathit{Bo}=10$
and
$\mathit{Bo}=10$
and
![]() ${\it\epsilon}=0.45$
. Here
${\it\epsilon}=0.45$
. Here
![]() $E_{0}$
is the initial total energy. The (red online) dot-dashed line is the theoretical linear viscous dissipation
$E_{0}$
is the initial total energy. The (red online) dot-dashed line is the theoretical linear viscous dissipation
![]() $E/E_{0}=\exp (-4{\it\nu}k^{2}t)$
. The black dashed line is an exponential fit
$E/E_{0}=\exp (-4{\it\nu}k^{2}t)$
. The black dashed line is an exponential fit
![]() $E=E(t/T=1)\exp (-{\it\zeta}t)$
to the energy decay in the time interval
$E=E(t/T=1)\exp (-{\it\zeta}t)$
to the energy decay in the time interval
![]() $t/T\in [1:2]$
.
$t/T\in [1:2]$
.
First, we focus on the low surface tension case
![]() $(\mathit{Bo}=1000)$
. When the steepness is below the breaking threshold (
$(\mathit{Bo}=1000)$
. When the steepness is below the breaking threshold (
![]() ${\it\epsilon}<0.32$
),
${\it\epsilon}<0.32$
),
![]() $E$
decreases exponentially at a constant decay rate, as shown by figure 8(a), and is close to the theoretical linear viscous decay rate
$E$
decreases exponentially at a constant decay rate, as shown by figure 8(a), and is close to the theoretical linear viscous decay rate
![]() $E/E_{0}=\exp (-4{\it\nu}k^{2}t)$
. The kinetic and potential energies oscillate at half the wave frequency but with opposite phase, showing exchanges between the kinetic and potential energy components, and decay at similar rates. The surface tension potential energy remains negligible throughout the propagation. This case corresponds to a non-breaking gravity wave. For a higher steepness, when wave breaking occurs (
$E/E_{0}=\exp (-4{\it\nu}k^{2}t)$
. The kinetic and potential energies oscillate at half the wave frequency but with opposite phase, showing exchanges between the kinetic and potential energy components, and decay at similar rates. The surface tension potential energy remains negligible throughout the propagation. This case corresponds to a non-breaking gravity wave. For a higher steepness, when wave breaking occurs (
![]() ${\it\epsilon}=0.45$
, figure 8
b), an abrupt decrease of the total energy is observed during the breaking event (starting at
${\it\epsilon}=0.45$
, figure 8
b), an abrupt decrease of the total energy is observed during the breaking event (starting at
![]() $t/T\approx 1$
), and around 70 % of the wave energy is dissipated in a few wave periods. During the breaking, the gravitational potential energy is almost completely dissipated, and only kinetic energy remains after a few wave periods. Surface tension potential energy remains small during the whole process, even if an increase is observed during the breaking stage, due to high surface curvature, and the generation of droplets and bubbles. The peak value of surface tension energy represents
$t/T\approx 1$
), and around 70 % of the wave energy is dissipated in a few wave periods. During the breaking, the gravitational potential energy is almost completely dissipated, and only kinetic energy remains after a few wave periods. Surface tension potential energy remains small during the whole process, even if an increase is observed during the breaking stage, due to high surface curvature, and the generation of droplets and bubbles. The peak value of surface tension energy represents
![]() ${\approx}8\,\%$
of the total energy dissipated, which is similar to the finding of Iafrati (Reference Iafrati2011). The abrupt decrease of energy during the breaking process can be fitted by an exponential curve between
${\approx}8\,\%$
of the total energy dissipated, which is similar to the finding of Iafrati (Reference Iafrati2011). The abrupt decrease of energy during the breaking process can be fitted by an exponential curve between
![]() $t/T=1$
and
$t/T=1$
and
![]() $t/T=2$
:
$t/T=2$
:
![]() $E=E(t/T=1)\exp (-{\it\zeta}t)$
, where
$E=E(t/T=1)\exp (-{\it\zeta}t)$
, where
![]() ${\it\zeta}$
is the decay rate during the breaking process and
${\it\zeta}$
is the decay rate during the breaking process and
![]() $E(t/T=1)$
is the energy at
$E(t/T=1)$
is the energy at
![]() $t/T=1$
. This case corresponds to a plunging breaker.
$t/T=1$
. This case corresponds to a plunging breaker.
Chen et al. (Reference Chen, Kharif, Zaleski and Li1999) studied a plunging breaker at high Bond number and found a decay rate
![]() $E\sim \text{e}^{-2{\it\gamma}_{2}(t-t_{1})}$
, where
$E\sim \text{e}^{-2{\it\gamma}_{2}(t-t_{1})}$
, where
![]() $t_{1}$
is a breaking time and
$t_{1}$
is a breaking time and
![]() ${\it\gamma}_{2}=0.16$
, which using our notation gives
${\it\gamma}_{2}=0.16$
, which using our notation gives
![]() ${\it\zeta}_{Chen}=2{\it\gamma}_{2}=0.32$
. The value of
${\it\zeta}_{Chen}=2{\it\gamma}_{2}=0.32$
. The value of
![]() ${\it\zeta}$
in our simulation for
${\it\zeta}$
in our simulation for
![]() $\mathit{Bo}=1000$
and
$\mathit{Bo}=1000$
and
![]() ${\it\epsilon}=0.45$
is
${\it\epsilon}=0.45$
is
![]() ${\it\zeta}=0.18$
, and for
${\it\zeta}=0.18$
, and for
![]() ${\it\epsilon}=0.55$
,
${\it\epsilon}=0.55$
,
![]() ${\it\zeta}=0.22$
, so our values of decay rate are slightly smaller than that from Chen et al. (Reference Chen, Kharif, Zaleski and Li1999) for a plunging breaker. This is coherent with the fact that Chen et al. (Reference Chen, Kharif, Zaleski and Li1999) reports a loss of 80 % of the initial wave energy for a plunging breaker after four wave periods while we observe a loss of
${\it\zeta}=0.22$
, so our values of decay rate are slightly smaller than that from Chen et al. (Reference Chen, Kharif, Zaleski and Li1999) for a plunging breaker. This is coherent with the fact that Chen et al. (Reference Chen, Kharif, Zaleski and Li1999) reports a loss of 80 % of the initial wave energy for a plunging breaker after four wave periods while we observe a loss of
![]() ${\approx}65\,\%$
. For a similar plunging wave, Iafrati (Reference Iafrati2011) reports a loss of around 60 % of the energy after four wave periods. Note also that for
${\approx}65\,\%$
. For a similar plunging wave, Iafrati (Reference Iafrati2011) reports a loss of around 60 % of the energy after four wave periods. Note also that for
![]() $\mathit{Bo}=1000$
, the energy after breaking for
$\mathit{Bo}=1000$
, the energy after breaking for
![]() ${\it\epsilon}=0.35$
and
${\it\epsilon}=0.35$
and
![]() ${\it\epsilon}=0.45$
is close to the initial energy of the steepest non-breaking wave (
${\it\epsilon}=0.45$
is close to the initial energy of the steepest non-breaking wave (
![]() ${\it\epsilon}=0.31$
), in qualitative agreement with the result discussed by Iafrati (Reference Iafrati2011) that the energy of the residual wave after a spilling breaking process at high Bond number is close to that of the steepest non-breaking wave.
${\it\epsilon}=0.31$
), in qualitative agreement with the result discussed by Iafrati (Reference Iafrati2011) that the energy of the residual wave after a spilling breaking process at high Bond number is close to that of the steepest non-breaking wave.
We now consider the case where surface tension effects become important (
![]() $\mathit{Bo}<100$
). Figure 8(c) shows the evolution of the energy components during wave propagation at relatively low steepness (
$\mathit{Bo}<100$
). Figure 8(c) shows the evolution of the energy components during wave propagation at relatively low steepness (
![]() ${\it\epsilon}=0.3$
) for
${\it\epsilon}=0.3$
) for
![]() $\mathit{Bo}=50$
. During the first wave period, the total energy decays exponentially with the classical decay rate, while at
$\mathit{Bo}=50$
. During the first wave period, the total energy decays exponentially with the classical decay rate, while at
![]() $t/T\approx 1$
, the decay of energy is enhanced, due to the appearance of parasitic capillaries. An increase of the surface tension energy is observed at this moment. The kinetic and potential energies oscillate with opposite phase at half the wave frequency, as observed previously. For the same value of
$t/T\approx 1$
, the decay of energy is enhanced, due to the appearance of parasitic capillaries. An increase of the surface tension energy is observed at this moment. The kinetic and potential energies oscillate with opposite phase at half the wave frequency, as observed previously. For the same value of
![]() ${\it\epsilon}=0.3$
, when the surface tension is further increased (
${\it\epsilon}=0.3$
, when the surface tension is further increased (
![]() $\mathit{Bo}=10$
, see figure 8
e), the previous observations hold but with increased capillary effects. The surface tension energy during the appearance of the capillaries is higher and the dissipation rate is increased. The peak value of surface tension energy represents between 5 % and 10 % of the total dissipated energy of the wave. These two cases correspond to gravity–capillary waves. For higher initial steepness (
$\mathit{Bo}=10$
, see figure 8
e), the previous observations hold but with increased capillary effects. The surface tension energy during the appearance of the capillaries is higher and the dissipation rate is increased. The peak value of surface tension energy represents between 5 % and 10 % of the total dissipated energy of the wave. These two cases correspond to gravity–capillary waves. For higher initial steepness (
![]() ${\it\epsilon}=0.45$
), a dramatic decrease of the energy is observed, corresponding to a spilling breaker (see figure 8
d,f) and surface tension energy is up to 10 % of the dissipated energy. Again, after the breaking, mostly kinetic energy remains in the system, while potential energy has been dissipated. For non-breaking waves, more energy is dissipated when the Bond number is lower, while for breaking waves, the total energy dissipated depends less on the Bond number.
${\it\epsilon}=0.45$
), a dramatic decrease of the energy is observed, corresponding to a spilling breaker (see figure 8
d,f) and surface tension energy is up to 10 % of the dissipated energy. Again, after the breaking, mostly kinetic energy remains in the system, while potential energy has been dissipated. For non-breaking waves, more energy is dissipated when the Bond number is lower, while for breaking waves, the total energy dissipated depends less on the Bond number.
4.2. Influence of
 $\mathit{Bo}$
and
$\mathit{Bo}$
and
 ${\it\epsilon}$
${\it\epsilon}$
Figure 9 shows the decay of the total energy,
![]() $E/E_{0}$
. Figure 9(a,b) show the influence of the initial steepness at a given Bond number (
$E/E_{0}$
. Figure 9(a,b) show the influence of the initial steepness at a given Bond number (
![]() $\mathit{Bo}=10$
and
$\mathit{Bo}=10$
and
![]() $\mathit{Bo}=1000$
, respectively), with
$\mathit{Bo}=1000$
, respectively), with
![]() ${\it\epsilon}$
increasing from top to bottom. In the high-Bond-number case (almost no surface tension,
${\it\epsilon}$
increasing from top to bottom. In the high-Bond-number case (almost no surface tension,
![]() $\mathit{Bo}=1000$
), energy dissipation is increased for steepness higher than the breaking threshold (
$\mathit{Bo}=1000$
), energy dissipation is increased for steepness higher than the breaking threshold (
![]() ${\it\epsilon}_{c}=0.32$
). For
${\it\epsilon}_{c}=0.32$
). For
![]() ${\it\epsilon}<{\it\epsilon}_{c}$
, at high Bond number, the wave dissipation is close to the classical viscous dissipation. For
${\it\epsilon}<{\it\epsilon}_{c}$
, at high Bond number, the wave dissipation is close to the classical viscous dissipation. For
![]() ${\it\epsilon}>{\it\epsilon}_{c}$
, a dramatic loss of energy is observed between
${\it\epsilon}>{\it\epsilon}_{c}$
, a dramatic loss of energy is observed between
![]() $t/T=1$
and
$t/T=1$
and
![]() $t/T=2$
corresponding to the breaking event. The total energy dissipated after four wave periods increases with the initial steepness, for
$t/T=2$
corresponding to the breaking event. The total energy dissipated after four wave periods increases with the initial steepness, for
![]() ${\it\epsilon}=0.35$
around 40 % of the wave energy is lost while up to 70 % is lost for
${\it\epsilon}=0.35$
around 40 % of the wave energy is lost while up to 70 % is lost for
![]() ${\it\epsilon}=0.55$
. In the case of strong surface tension effects (
${\it\epsilon}=0.55$
. In the case of strong surface tension effects (
![]() $\mathit{Bo}=10$
), only the lowest steepness (
$\mathit{Bo}=10$
), only the lowest steepness (
![]() ${\it\epsilon}=0.15$
) presents a decay close to the classical viscous decay. When the steepness is increased to
${\it\epsilon}=0.15$
) presents a decay close to the classical viscous decay. When the steepness is increased to
![]() ${\it\epsilon}=0.25$
, energy dissipation is enhanced by the appearance of parasitic capillaries. The total dissipation is then further increased when the initial steepness is increased.
${\it\epsilon}=0.25$
, energy dissipation is enhanced by the appearance of parasitic capillaries. The total dissipation is then further increased when the initial steepness is increased.

Figure 9. Normalized wave energy
![]() $E/E_{0}$
as a function of time
$E/E_{0}$
as a function of time
![]() $t/T$
. (a,b) Effect of increasing steepness for (a)
$t/T$
. (a,b) Effect of increasing steepness for (a)
![]() $\mathit{Bo}=10$
and (b)
$\mathit{Bo}=10$
and (b)
![]() $\mathit{Bo}=1000$
. From top to bottom
$\mathit{Bo}=1000$
. From top to bottom
![]() ${\it\epsilon}=0.15,0.25,0.35,0.45$
and 0.55. (c,d) Effect of increasing surface tension at a given steepness, (c)
${\it\epsilon}=0.15,0.25,0.35,0.45$
and 0.55. (c,d) Effect of increasing surface tension at a given steepness, (c)
![]() ${\it\epsilon}=0.3$
and (d)
${\it\epsilon}=0.3$
and (d)
![]() ${\it\epsilon}=0.45$
. From bottom to top
${\it\epsilon}=0.45$
. From bottom to top
![]() $\mathit{Bo}=2,5,10,20$
and 100. Black dashed line is the theoretical linear viscous dissipation
$\mathit{Bo}=2,5,10,20$
and 100. Black dashed line is the theoretical linear viscous dissipation
![]() $E/E_{0}=\exp (-4{\it\nu}k^{2}t)$
.
$E/E_{0}=\exp (-4{\it\nu}k^{2}t)$
.
Breaking waves are thus characterized by a strong loss of energy during the breaking stage and the influence of the steepness is similar for low and high values of surface tension, the main difference being that in the presence of surface tension the critical steepness for which dissipation is enhanced is smaller, due to the appearance of parasitic capillaries.
Figure 9(c,d) show the decay of the total energy
![]() $E/E_{0}$
and the influence of the surface tension at a given initial steepness (
$E/E_{0}$
and the influence of the surface tension at a given initial steepness (
![]() ${\it\epsilon}=0.3$
and
${\it\epsilon}=0.3$
and
![]() ${\it\epsilon}=0.45$
, respectively).
${\it\epsilon}=0.45$
, respectively).
At low steepness (
![]() ${\it\epsilon}<0.3$
) and without surface tension effects (
${\it\epsilon}<0.3$
) and without surface tension effects (
![]() $\mathit{Bo}=1000$
), the wave dissipation is close to the classical theoretical dissipation (see figure 9) of a linear sinusoidal wave at small amplitude. When the Bond number decreases (surface tension increases), an abrupt decrease of the energy is observed around
$\mathit{Bo}=1000$
), the wave dissipation is close to the classical theoretical dissipation (see figure 9) of a linear sinusoidal wave at small amplitude. When the Bond number decreases (surface tension increases), an abrupt decrease of the energy is observed around
![]() $t/T\approx 1$
(figure 9
c,
$t/T\approx 1$
(figure 9
c,
![]() $\mathit{Bo}=10,25,50,100$
), which corresponds to the time when capillaries appear on the main gravity wave (see figure 3), while when surface tension is too low to induce the appearance of capillaries, the energy decay remains smooth (two top curves in figure 9
c,
$\mathit{Bo}=10,25,50,100$
), which corresponds to the time when capillaries appear on the main gravity wave (see figure 3), while when surface tension is too low to induce the appearance of capillaries, the energy decay remains smooth (two top curves in figure 9
c,
![]() $\mathit{Bo}=500,1000$
).
$\mathit{Bo}=500,1000$
).
The appearance of parasitic capillaries induces a global enhancement of the wave energy dissipation. Moreover, the final state of gravity–capillary waves depends on the intensity of the capillary effects: at
![]() $t/T=4$
, 60 % of the energy has been dissipated for
$t/T=4$
, 60 % of the energy has been dissipated for
![]() $\mathit{Bo}=10$
, while 30 % has been dissipated for
$\mathit{Bo}=10$
, while 30 % has been dissipated for
![]() $\mathit{Bo}=25$
,
$\mathit{Bo}=25$
,
![]() ${\approx}20\,\%$
for
${\approx}20\,\%$
for
![]() $\mathit{Bo}=50$
, 10 % for
$\mathit{Bo}=50$
, 10 % for
![]() $\mathit{Bo}=100$
and only less than 5 % can be attributed to the classical viscous dissipation. Thus, at steepness below the breaking threshold, capillary effects strongly increase the wave energy dissipation.
$\mathit{Bo}=100$
and only less than 5 % can be attributed to the classical viscous dissipation. Thus, at steepness below the breaking threshold, capillary effects strongly increase the wave energy dissipation.
At higher steepnesses,
![]() ${\it\epsilon}=0.45$
(see figure 4
d), wave breaking occurs and the total amounts of dissipated energy are similar for the various Bond numbers. Thus, even if the breaking process is qualitatively different (plunging or spilling wave), the total amount of energy dissipated is similar at high wave steepness.
${\it\epsilon}=0.45$
(see figure 4
d), wave breaking occurs and the total amounts of dissipated energy are similar for the various Bond numbers. Thus, even if the breaking process is qualitatively different (plunging or spilling wave), the total amount of energy dissipated is similar at high wave steepness.
Surface wave dissipation is thus first determined by the stability of the wave, given by the initial steepness. Breaking waves exhibit strong dissipation in agreement with previous results, both experimental and numerical. However, at smaller steepnesses, dissipation processes are strongly affected by the appearance of capillaries on the main propagating wave. Spilling breakers with high surface tension exhibit global dissipation of the same order as plunging breakers, while gravity–capillary waves show a global dissipation much higher than that due to linear viscous dissipation, in agreement with Mui & Dommermuth (Reference Mui and Dommermuth1995) and Fedorov & Melville (Reference Fedorov and Melville1998).
4.3. Estimation of the breaking parameter
 $b$
$b$
We observe a dramatic decay of the wave energy during breaking events and the formation of parasitic capillaries, and showed that during these events, the decay has an exponential form
![]() $E\sim \exp [-{\it\zeta}({\it\epsilon},\mathit{Bo})t]$
. We will now compare the decay rate obtained in the present simulations to experimental and theoretical results. The variation of the Bond number corresponds for air–water surface waves to various wavelengths, however, we have to keep in mind that the Reynolds number is constant in our study.
$E\sim \exp [-{\it\zeta}({\it\epsilon},\mathit{Bo})t]$
. We will now compare the decay rate obtained in the present simulations to experimental and theoretical results. The variation of the Bond number corresponds for air–water surface waves to various wavelengths, however, we have to keep in mind that the Reynolds number is constant in our study.
The dissipation induced by a breaking wave is usually described by the dissipation rate per unit length of breaking crest
![]() ${\it\varepsilon}_{l}$
. Following Duncan (Reference Duncan1981) and Phillips (Reference Phillips1985),
${\it\varepsilon}_{l}$
. Following Duncan (Reference Duncan1981) and Phillips (Reference Phillips1985),
where
![]() $c$
is the phase velocity at breaking and
$c$
is the phase velocity at breaking and
![]() $b$
is a non-dimensional parameter, called the breaking parameter. This formulation is the starting point for statistical modelling of wave breaking in the ocean (Phillips Reference Phillips1985; Romero et al.
Reference Romero, Melville and Kleiss2012). While the breaking parameter was first assumed to be constant (Phillips Reference Phillips1985), a large variation of the measured values of
$b$
is a non-dimensional parameter, called the breaking parameter. This formulation is the starting point for statistical modelling of wave breaking in the ocean (Phillips Reference Phillips1985; Romero et al.
Reference Romero, Melville and Kleiss2012). While the breaking parameter was first assumed to be constant (Phillips Reference Phillips1985), a large variation of the measured values of
![]() $b$
has been observed in various experiments. A scaling law, based on inertial arguments was derived for plunging waves (Drazen et al.
Reference Drazen, Melville and Lenain2008) and leads to the following result
$b$
has been observed in various experiments. A scaling law, based on inertial arguments was derived for plunging waves (Drazen et al.
Reference Drazen, Melville and Lenain2008) and leads to the following result
![]() $b\sim S^{-5/2}$
, where
$b\sim S^{-5/2}$
, where
![]() $S$
is the slope of the breaking wave. This result was then extended to spilling breakers by Pizzo & Melville (Reference Pizzo and Melville2013). By assuming a threshold for breaking, the following general parametrization was supported by laboratory measurements and used for ocean wave modelling (Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013):
$S$
is the slope of the breaking wave. This result was then extended to spilling breakers by Pizzo & Melville (Reference Pizzo and Melville2013). By assuming a threshold for breaking, the following general parametrization was supported by laboratory measurements and used for ocean wave modelling (Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013):
The dissipation rate per unit length
![]() ${\it\varepsilon}_{l}$
is simply given by
${\it\varepsilon}_{l}$
is simply given by
![]() $E_{0}{\it\zeta}$
, where
$E_{0}{\it\zeta}$
, where
![]() $E_{0}$
is the initial wave energy (with the dimension of an energy per unit length) and
$E_{0}$
is the initial wave energy (with the dimension of an energy per unit length) and
![]() ${\it\zeta}$
the observed decay rate during breaking. The velocity
${\it\zeta}$
the observed decay rate during breaking. The velocity
![]() $c$
is estimated by the linear phase velocity of the gravity–capillary wave
$c$
is estimated by the linear phase velocity of the gravity–capillary wave
![]() $c=\sqrt{g/k+({\it\gamma}/{\it\rho}_{w})k}$
. Thus,
$c=\sqrt{g/k+({\it\gamma}/{\it\rho}_{w})k}$
. Thus,
![]() $b={\it\varepsilon}_{l}g/({\it\rho}_{w}c^{5})=E_{0}{\it\zeta}g/({\it\rho}_{w}c^{5})$
, is shown in figure 10 as a function of the wave slope
$b={\it\varepsilon}_{l}g/({\it\rho}_{w}c^{5})=E_{0}{\it\zeta}g/({\it\rho}_{w}c^{5})$
, is shown in figure 10 as a function of the wave slope
![]() ${\it\epsilon}$
for all the breaking waves, the gravity–capillary waves and non-breaking waves. At steepness higher than the breaking threshold observed in these simulations
${\it\epsilon}$
for all the breaking waves, the gravity–capillary waves and non-breaking waves. At steepness higher than the breaking threshold observed in these simulations
![]() ${\it\epsilon}>0.32$
, a very good agreement is observed between the numerical results and the semi-empirical
${\it\epsilon}>0.32$
, a very good agreement is observed between the numerical results and the semi-empirical
![]() ${\sim}{\it\epsilon}^{5/2}$
scaling. Moreover, the value of
${\sim}{\it\epsilon}^{5/2}$
scaling. Moreover, the value of
![]() $b$
at high steepness appears independent of the Bond number, which is consistent with experimental results where
$b$
at high steepness appears independent of the Bond number, which is consistent with experimental results where
![]() $b$
is independent of the wavelength (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). For non-breaking waves (
$b$
is independent of the wavelength (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). For non-breaking waves (
![]() ${\it\epsilon}<0.32$
) the definition and estimation of
${\it\epsilon}<0.32$
) the definition and estimation of
![]() $b$
is not meaningful which explains the observed discrepancy in figure 10. However, it is remarkable to note that for the strong capillary effects cases,
$b$
is not meaningful which explains the observed discrepancy in figure 10. However, it is remarkable to note that for the strong capillary effects cases,
![]() $\mathit{Bo}=10$
, and
$\mathit{Bo}=10$
, and
![]() $\mathit{Bo}=25$
, the values of
$\mathit{Bo}=25$
, the values of
![]() $b$
at low steepness are in good agreement with the semi-empirical curve for breaking. Thus, for these numerical solutions, the increase of dissipation induced by capillarity at low Bond number is consistent with the experimental scaling for breaking.
$b$
at low steepness are in good agreement with the semi-empirical curve for breaking. Thus, for these numerical solutions, the increase of dissipation induced by capillarity at low Bond number is consistent with the experimental scaling for breaking.

Figure 10. Breaking parameter
![]() $b$
as a function of steepness for various Bond numbers. The (red online) dashed line is the semi-empirical dissipation function:
$b$
as a function of steepness for various Bond numbers. The (red online) dashed line is the semi-empirical dissipation function:
![]() $b=0.4({\it\epsilon}-0.08)^{5/2}$
(4.6) from Romero et al. (Reference Romero, Melville and Kleiss2012). The vertical dot-dashed line indicates the breaking threshold in the present work,
$b=0.4({\it\epsilon}-0.08)^{5/2}$
(4.6) from Romero et al. (Reference Romero, Melville and Kleiss2012). The vertical dot-dashed line indicates the breaking threshold in the present work,
![]() ${\it\epsilon}_{c}=0.32$
.
${\it\epsilon}_{c}=0.32$
.
5. Discussion on the wave regime diagram
We will now discuss in more detail the application of the state diagram shown in figure 7 to waves observed in published experiments. Table 1 summarizes experimental observations of breaking and parasitic capillary waves, for which both the slope and the Bond number could easily be extracted. The Bond number is estimated from the wavelength and the liquid properties (
![]() $\mathit{Bo}={\it\rho}g/({\it\gamma}k^{2})$
), and we also indicate the Reynolds numbers of the experiments (
$\mathit{Bo}={\it\rho}g/({\it\gamma}k^{2})$
), and we also indicate the Reynolds numbers of the experiments (
![]() $\mathit{Re}=\sqrt{g{\it\lambda}^{3}}/{\it\nu}$
), which are often larger (especially for wave breaking) than that used in the present simulations.
$\mathit{Re}=\sqrt{g{\it\lambda}^{3}}/{\it\nu}$
), which are often larger (especially for wave breaking) than that used in the present simulations.
Table 1. Experimental parameters of observed parasitic capillary waves, spilling and plunging breakers observed in the literature. The generation and measurement techniques are briefly summarized. Breaking waves due to the modulation instability are indicated (MI) and the distinction between spilling or plunging breakers is not made in these papers.

In these experiments, the waves are either generated by wind or by a wave maker. Breaking waves are either obtained through a focusing wavepacket or are triggered by a modulational instability. In the first case, a wavepacket is generated by the wave maker, defining the central wavelength and the linear slope (through the sum of all frequency components of the initial packet). This slope is close (slightly smaller in general) to the slope at breaking that can be directly measured. This protocol has been used to study both spilling and plunging breakers. On the other hand, breaking triggered by the modulational instability corresponds to the instability of an initial wave (of a given wavelength) and the slope indicated in table 1 corresponds to the initial linear slope. In this case, the distinction between spilling and breaking wave is not necessarily done in the original papers and we will simply call these waves breakers. In the case of mechanically generated parasitic capillary waves, both the wavelength and amplitude of the carrier wave are initial parameters of the experiment. Finally, for the wind-generated waves, both the wavelength and the amplitude can be extracted from the figures of Zhang (Reference Zhang1995) and Caulliez (Reference Caulliez2013).
Figure 11 shows the boundaries of the wave regime diagram of figure 7, together with the experimental data summarized in table 1. For simplicity, we do not distinguish the various studies in the diagram but only the observed wave state, breaking triggered by modulation instability, plunging breakers, spilling breakers and parasitic capillary waves.

Figure 11. Wave state diagram, compares the regimes obtained through the simulation and described in figure 7 with the experimental studies summarized in table 1. Experimental studies: (*) breakers triggered by modulation instability, (▾) plunging breakers, (●) spilling breakers, (♦) parasitic capillary waves.
The first obvious observation is that, at high Bond number (i.e. large wavelength) breaking is observed in numerous experiments for much smaller initial values of the wave slope than what is described in the present numerical work. Breaking through modulational instabilities is observed from
![]() ${\it\epsilon}\sim 0.11$
and spilling breakers are observed in focusing experiments for
${\it\epsilon}\sim 0.11$
and spilling breakers are observed in focusing experiments for
![]() ${\it\epsilon}\sim 0.25$
. Our breaking threshold at
${\it\epsilon}\sim 0.25$
. Our breaking threshold at
![]() ${\it\epsilon}_{c}=0.32$
is thus related to our initial conditions. However, this allows observation of a critical value of the Bond number necessary for the influence of surface tension in the wave dynamics. The plunging breakers generated in focusing experiments have very high steepness (
${\it\epsilon}_{c}=0.32$
is thus related to our initial conditions. However, this allows observation of a critical value of the Bond number necessary for the influence of surface tension in the wave dynamics. The plunging breakers generated in focusing experiments have very high steepness (
![]() ${\it\epsilon}>0.35$
) and high Bond numbers (
${\it\epsilon}>0.35$
) and high Bond numbers (
![]() $\mathit{Bo}>1000$
) and are indeed located in the plunging regime of our diagram (PB).
$\mathit{Bo}>1000$
) and are indeed located in the plunging regime of our diagram (PB).
Note that most of the spilling breakers described experimentally (Rapp & Melville Reference Rapp and Melville1990; Duncan Reference Duncan2001; Liu & Duncan Reference Liu and Duncan2003, Reference Liu and Duncan2006) correspond to relatively high Bond number (
![]() $\mathit{Bo}>1000$
) and have typical slopes
$\mathit{Bo}>1000$
) and have typical slopes
![]() ${\it\epsilon}\in [0.25:0.35]$
close to our critical steepness. This tends to confirm the idea that spilling breakers at large Bond number (large scale) is a transition regime between non-breaking and plunging wave. On the other hand, the wind-generated small-scale spilling breakers described by Caulliez (Reference Caulliez2013) correspond to smaller Bond number (
${\it\epsilon}\in [0.25:0.35]$
close to our critical steepness. This tends to confirm the idea that spilling breakers at large Bond number (large scale) is a transition regime between non-breaking and plunging wave. On the other hand, the wind-generated small-scale spilling breakers described by Caulliez (Reference Caulliez2013) correspond to smaller Bond number (
![]() $\mathit{Bo}<100$
) and larger slope and are located inside the spilling zone (SB).
$\mathit{Bo}<100$
) and larger slope and are located inside the spilling zone (SB).
Finally, at low Bond number, the experimentally observed parasitic capillary waves have Bond numbers smaller than
![]() $\mathit{Bo}_{c}$
and a slope smaller than the breaking steepness,
$\mathit{Bo}_{c}$
and a slope smaller than the breaking steepness,
![]() ${\it\epsilon}<{\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
. However, only a few data points exist at high steepness close to the boundary
${\it\epsilon}<{\it\epsilon}_{B}=K_{B}(1+\mathit{Bo})^{-1/3}$
. However, only a few data points exist at high steepness close to the boundary
![]() ${\it\epsilon}_{B}$
.
${\it\epsilon}_{B}$
.
To conclude this comparison, when surface tension effects are important (
![]() $\mathit{Bo}<100$
), the phase diagram described by the numerical simulation appears compatible with numerous experimental observations of parasitic capillary waves and small-scale spilling breakers. However, further studies are needed to validate experimentally the scaling of the breaking and the spilling–plunging boundaries at high steepness,
$\mathit{Bo}<100$
), the phase diagram described by the numerical simulation appears compatible with numerous experimental observations of parasitic capillary waves and small-scale spilling breakers. However, further studies are needed to validate experimentally the scaling of the breaking and the spilling–plunging boundaries at high steepness,
![]() ${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$
.
${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$
.
The present DNS have been performed assuming a uniform surface tension. The presence of surfactants on the air–water interface can modify the wave dynamics. Liu & Duncan (Reference Liu and Duncan2003, Reference Liu and Duncan2006) have found that adding surfactants significantly changes the breaking process. For high surfactant concentrations, they observe a small plunging jet issued from the front face of the wave at a point below the wave crest. Note that their data are included in figure 11 and their spilling breakers for various surfactant concentrations are inside the spilling phase. They also observed that the capillary ripples found upstream of the spilling breaker toe in the clean-water case are dramatically reduced for all concentrations of surfactants. Similar results were found by Ceniceros (Reference Ceniceros2003) who investigated numerically the effect of surfactant on parasitic capillaries.
6. Conclusion
A parametric study of the influence of the wave steepness and Bond number on surface wave evolution is presented, using DNS of the two-phase flow, in air and water, including surface tension and viscosity. The study is conducted at a given high Reynolds number in order to study the effects of surface tension on wave breaking. A regime diagram is presented in which we report the observation of pure gravity waves, gravity–capillary waves, plunging breakers and spilling breakers. We are able to go continuously from one wave pattern to another by changing the Bond number and the initial steepness of the wave. For our initial conditions, we observe that when surface tension effects are small, a critical steepness
![]() ${\it\epsilon}_{c}$
can be defined to distinguish breaking from non-breaking waves, as already discussed theoretically as well as through experiments and numerical studies (Rapp & Melville Reference Rapp and Melville1990; Peregrine et al.
Reference Peregrine, Cokelet and McIver1993; Song & Banner Reference Song and Banner2002; Banner & Peirson Reference Banner and Peirson2007; Perlin et al.
Reference Perlin, Choi and Tian2013). When surface tension becomes important, its influence is quantified through two boundaries separating first gravity–capillary waves and breakers, and second spilling and plunging breakers. Both boundaries scale as
${\it\epsilon}_{c}$
can be defined to distinguish breaking from non-breaking waves, as already discussed theoretically as well as through experiments and numerical studies (Rapp & Melville Reference Rapp and Melville1990; Peregrine et al.
Reference Peregrine, Cokelet and McIver1993; Song & Banner Reference Song and Banner2002; Banner & Peirson Reference Banner and Peirson2007; Perlin et al.
Reference Perlin, Choi and Tian2013). When surface tension becomes important, its influence is quantified through two boundaries separating first gravity–capillary waves and breakers, and second spilling and plunging breakers. Both boundaries scale as
![]() ${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$
. This scaling is consistent with a balance between the generation of vorticity by gravity–capillary waves (Longuet-Higgins Reference Longuet-Higgins1992) and the pressure due to capillary effects. When surface tension effects are important, our regime diagram appears compatible with the available experimental data.
${\it\epsilon}\sim (1+\mathit{Bo})^{-1/3}$
. This scaling is consistent with a balance between the generation of vorticity by gravity–capillary waves (Longuet-Higgins Reference Longuet-Higgins1992) and the pressure due to capillary effects. When surface tension effects are important, our regime diagram appears compatible with the available experimental data.
The wave energy is computed for each wave state and confirms the importance of breaking processes in surface wave dissipation. Plunging and spilling breakers both exhibit dramatic loss of energy during the breaking stage, with little potential energy remaining in the system. This is a result of the periodic boundary conditions, in an open system we would expect equipartition in the surviving wavefield. At low steepness, the wave dissipation is strongly enhanced when surface tension effects are important, while decay rates are comparable in the case of breaking waves for various Bond numbers. Moreover, from the wave energy decay rate during breaking, we are able to estimate the breaking parameter
![]() $b$
and our simulations appear fully consistent with the inertial scaling for breaking waves
$b$
and our simulations appear fully consistent with the inertial scaling for breaking waves
![]() $b\sim {\it\epsilon}^{5/2}$
obtained using scaling arguments and observed experimentally (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). The fact that non-breaking parasitic capillaries exhibit dissipation rates compatible with the breaking dissipation scaling is a very promising result that deserves further investigations. Note that these results are in qualitative agreement with the recent study of dissipation due to parasitic capillaries by Melville & Fedorov (Reference Melville and Fedorov2015) based on the theory of Fedorov & Melville (Reference Fedorov and Melville1998).
$b\sim {\it\epsilon}^{5/2}$
obtained using scaling arguments and observed experimentally (Drazen et al.
Reference Drazen, Melville and Lenain2008; Romero et al.
Reference Romero, Melville and Kleiss2012; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). The fact that non-breaking parasitic capillaries exhibit dissipation rates compatible with the breaking dissipation scaling is a very promising result that deserves further investigations. Note that these results are in qualitative agreement with the recent study of dissipation due to parasitic capillaries by Melville & Fedorov (Reference Melville and Fedorov2015) based on the theory of Fedorov & Melville (Reference Fedorov and Melville1998).
In this study, we have focused on the influence of surface tension, by changing the Bond number and keeping the Reynolds number constant. A natural development would be to now to study waves of various wavelengths, which would allow a closer comparison with experimental results. Furthermore, this has been a 2D study and 3D simulations are required to confirm the evolution of the resulting turbulent flows.
Acknowledgements
We thank M. Smith and N. Pizzo for helpful discussions. This work was started by L.D. when a visiting student at NIWA and completed as a postdoctoral researcher at SIO. At SIO, L.D. and W.K.M. were supported by grants to W.K.M. from NSF (OCE) and ONR (Physical Oceanography).