Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T15:17:36.768Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametric up-conversion of a trivelpiece–gould mode in a beam–plasma system

Published online by Cambridge University Press:  01 March 2004

D.N. GUPTA  and
A.K. SHARMA
D.N. GUPTA
Affiliation:
Department of Physics, University of Rajasthan, Jaipur, India
A.K. SHARMA
Affiliation:
Center for Energy Studies, Indian Institute of Technology, New Delhi, India
Rights & Permissions [Opens in a new window]

Abstract

A large amplitude Trivelpiece–Gould (TG) mode, in a strongly magnetized beam–plasma system, parametrically couples to a beam space charge mode and a TG mode sideband. The density perturbation associated with the beam mode couples with the electron oscillatory velocity, due to the pump wave, to produce a nonlinear current, driving the sideband. The pump and the sideband waves exert a ponderomotive force on the electrons with a component parallel to the ambient magnetic field, driving the beam mode. For a pump wave having k0·v0b0/ω0 < 0, where ω0, k0 are the frequency and the wave number of the pump, and v0b0 is the beam velocity, the sideband is frequency upshifted. At low beam density (Compton regime) the growth rate of the parametric instability scales as two-thirds power of the pump amplitude, and one-third power of beam density. In the Raman regime, the growth rate scales as half power of beam density and linearly with pump amplitude. The background plasma has a destabilizing role on the instability.

Keywords

Beam–plasma systemParametric up-conversionTG mode
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 1 , March 2004 , pp. 89 - 94
Copyright
2004 Cambridge University Press

1. INTRODUCTION

A magnetized beam–plasma system supports a variety of electrostatic and electromagnetic modes. These modes can either be launched externally or excited in situ via linear and nonlinear mechanisms. At higher amplitudes they are coupled and can exchange energy and momentum with each other. Such nonlinear interactions are important in many laboratory experiments and space plasmas. The parametric instability in magnetized plasma is a particular type of nonlinear coherent wave phenomena (Chang et al., 1971).

Large amplitude Trivelpiece–Gould (TG) modes or lower hybrid waves have been observed in several experiments by using axial and spiraling electron and ion beams (Sharma et al., 1998; Krafft, Volokitin & Fle, 2000; Maslennikov, Mikhailenko & Stepanov, 2000; Volokitin & Krafft, 2001). Prabhuram and Sharma (1992) have observed the excitation of higher harmonics of a TG mode in a low-energy beam–plasma system. Large amplitude TG modes, also known as lower hybrid waves, have been employed for heating and for current drive in tokamak (Taylor et al., 1989) and suppression of microinstabilities in Q-machine (Berger et al., 1976; Amatucci et al., 1996; Koepkr, 2002, and reference therein). These waves have also been observed as a dominant instability in magnetized beam–plasma systems where they are called the TG mode (Sakawa et al., 1993). They give rise to a variety of nonlinear phenomena, for example, harmonic generation, modulational instability, and parametric instabilities. Liu et al. (1984) and Porkolab (1974) have given a detailed survey of parametric instabilities of lower hybrid waves in tokamaks. Seiler et al. (1976) have reported experimental results on the excitation of a lower hybrid instability by a spiraling ion beam in the linear Princeton Q-1 device.

Plasma heating by high-energy particle-beam injection is considered to be one of the most promising methods of obtaining the ion temperatures necessary for a thermonuclear plasma. The mechanism by which the beam transfers its energy to the target plasma has been a subject of intense research (Yatsui & Imai, 1975; Porkolab et al., 1977). An electron beam injected parallel to the confining magnetic field of a low-β, isothermal (Te ≈ Ti) plasma is density modulated at or above the lower hybrid frequency (ωLH) of the target plasma. Allen et al. (1978) have observed that such a modulation can parametrically excite a lower hybrid wave and either an ion quasimode or an ion-cyclotron mode.

In this article, we study the nonlinear coupling of a large amplitude TG mode with the beam mode in a magnetized beam–plasma system. The TG mode (ω0, k0), imparts oscillatory velocity to electrons that couples with the density perturbation associated with the beam mode (ω ≈ kzv0b0,b) to produce a nonlinear current, deriving a TG mode sideband (ω1 = ω0 + ω, k1 = k0 + k). The sideband beats with the pump to exert a parallel ponderomotive force on electrons, driving the beam mode.

In Section 2 we carry out the instability analysis following the fluid approach and obtain an expression for the growth rate of the parametric instability under beam-dominated decay (Wang et al., 1996) in Compton and Raman regimes. A brief discussion of results is presented in Section 3.

2. INSTABILITY ANALYSIS

Consider a magnetized beam–plasma system with electron density n00 and static magnetic field

. An electron beam of density n0b0 propagates through it with velocity

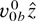
. A large amplitude TG mode exists in the plasma. If we ignore finite boundary effects, the potential of the TG mode can be written as

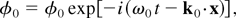
where

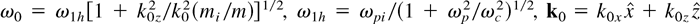
, ωp and ωc are the electron plasma and cyclotron frequencies, ωpi is the ion plasma frequency, and mi and m are the ion and electron masses, respectively.

The TG mode imparts oscillatory velocity to plasma and beam electrons. Solving the equations of motion and continuity, the velocity and density perturbations of the beam electrons can be written as

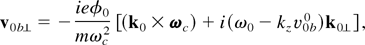
where subscripts ⊥ and ∥ refer to the perpendicular and parallel components with respect to magnetic field Bs. Corresponding quantities for plasma electrons, v0 and n0, can be deduced from Eqs. (2)–(4) by dropping the subscript b and taking v0b0 = 0. Eqs. (2) and (4) are valid for ω0 << ωc.

The pump wave decays into a low frequency electrostatic wave (beam mode) with potential φ(ω,k) and a TG mode sideband wave of potential φ1(ω1,k1), where ω1 ≡ ω0 + ω, k1 ≡ k0 + k. The linear response at (ω1,k1) is the same as given by Eqs. (2)–(4), with ω0, k0 replaced by ω1, k1. The sideband of potential φ1(ω1,k1) couples with the pump to produce a low-frequency ponderomotive force Fp = mv·∇v on the electrons. Fp has two components, one perpendicular to the static magnetic field Bs and the other parallel to it. The response of electrons to Fp⊥ is strongly suppressed by the magnetic field and is usually weak (for ωp << ωc). In the parallel direction, the electrons can effectively respond to Fp∥; hence, the low-frequency nonlinearity arises mainly through Fp∥ = −mv·∇v∥. For ω < k∥vth (vth being the electron thermal speed), the electron can spontaneously follow the ponderomotive force and the nonlinearity is strong. At longer wavelengths ω > k∥vth, the electrons' response in the parallel direction is slow and the nonlinearity is weak. The parallel ponderomotive force on the beam electrons can be explicitly written as

where we have dropped the v0∥∇∥ and v1∥∇∥ terms as these are kzk0zω0 /kk0ωc = (m/mi)1/2 times the terms retained. Substituting for v0b⊥* and v1b⊥*, and considering only dominant E × Bs terms, one may simplify Eq. (5) to write Fpb∥ = eikzφpb, where

The ponderomotive potential φp for plasma electrons can be deduced from Eq. (6) taking v0b0 = 0. φpb and φp at (ω,k) produce a low-frequency beam electron density perturbation

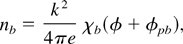
where χb = −ωpb2(kz2/k2)/(ω − kzv0b0)2. We neglected the role of E⊥ on beam electrons assuming (ω − kzv0b0)2 << ωc2kz2/k⊥2.

The low-frequency plasma electron density perturbation is

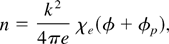
where χe = −ωp2(kz2/k2)/ω2 − ωp2(k⊥2/k2)/ωc2 for ωc >> ω. Using the density perturbations in Poisson's equation, we obtain

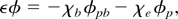
where ε = 1 + χe + χb. The nonlinear density perturbations n1bNL and n1NL at (ω,k) can be obtained from equation of continuity

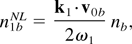
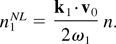
Using Eqs. (10) and (11) in the Poisson's equation for the sideband wave, we obtain

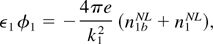
where ε1 = 1 + ωp2(k1⊥2/k12)/ωc2 − ωp2(k1z2/k12)/ω12.

Eqs. (9) and (12) are the nonlinear-coupled equations for φ and φ1 from which the nonlinear dispersion relation can be obtained:

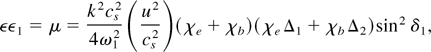
where Δ1 = [1 − ω(k0z /kz)/ω0], Δ2 = [1 − ω(k0z /kz)/(ω0 − kzv0b0)], u = ek0|φ0*|/mωc is the magnitude of E × Bs electron velocity, δ1 is the angle between k1⊥ and k0⊥, and cs is the sound speed.

Using χe + χb + 1 ≈ 0 in Eq. (13), we get

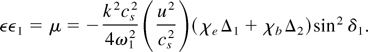
In the case when ω, k wave is the beam mode (ω ≈ kzv0b0), χb >> χe (beam-dominated decay), μ simplifies to

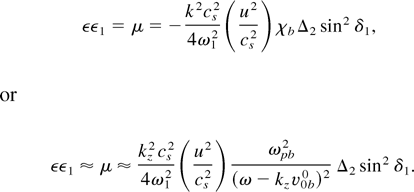
We solve Eq. (14) in two distinct cases of interest.

2.1. Compton regime

In the case when beam density (or the beam current) is small, χb << 1, self-consistent potential of the beam can be neglected as compared to ponderomotive potential (φ << φpb), and Eq. (14) can be written as

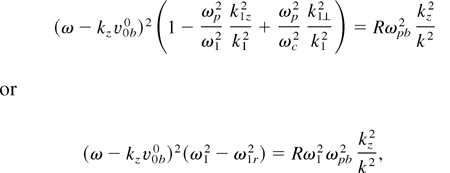
where R = (kz2cs2/4ω12)(u2/cs2)Δ2 sin2 δ1, and ω1r2 = [ωp2k1z2/k12 − ωp2(k1⊥2/k12)ω12/ωc2].

The maximum growth rate of the instability occurs near the simultaneous zeroes of the left-hand side. Choosing ω = kz v0b0 + δ, and ω1 = ω1r + δ, where δ is the frequency mismatch, Eq. (15) gives

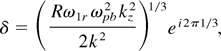
where 1 = 0, 1, 2. The growth rate turns out to be

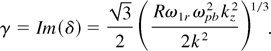
Because k1 = k0 + k and ω1 = ω0 + ω, we get

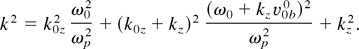
The growth rate of the parametric instability scales as two-thirds power of the pump amplitude and one-third power of beam density. This treatment, however, is valid when γ2 > ωpb2 (weak beam limit).

To calculate the normalized growth rate γ/ωpb in a Compton regime, we estimate k/k0z for different values of kz /k0z = 0, 0.2, 0.4, 0.6, 0.8, 1.0 from Eq. (17) first. Using ω1 = ωpk1z /k1 (for TG mode sideband), ω1 = ω0 − ω, k1z = k0z − kz, and ω = kzv0b0 (for beam mode), we calculate the normalized growth rate from Eq. (16).

In Figure 1, we have plotted the normalized growth rate γ/ωpb of the parametric instability in the Compton regime as a function of the normalized parallel wave number of the beam mode kz /k0z for upper sideband generation in a beam–plasma system. The parameters are −v0b0/c = 0.1, k0zc/ω0 = 3, cs /c = 10−5, δ1 = π/2, u2/cs2 = 1, ωpb /ωp = 0.2, and ω0 /ωp = 0.1, 0.2. The normalized growth rate of the parametric instability in the Compton regime increases with the normalized wave number of the beam mode. One may also see that for a pump wave counterpropagating with the beam, the sideband is frequency upshifted, whereas, for copropagating with a beam, the sideband is frequency downshifted. Figure 1 also shows the effect of background plasma on the growth rate of instability. The rate of growth increases with background plasma density.

Variation of the normalized growth rate of the parametric instability in the Compton regime as a function of the normalized parallel wave number of the beam mode. The parameters are −v0b0/c = 0.1, k0zc/ω0 = 3, cs /c = 10−5, δ1 = π/2, u2/cs2 = 1, ωpb /ωp = 0.2, and ω0 /ωp = 0.1, 0.2.

2.2. Raman regime

At high beam density, one may have ε ≈ 0. In this case, self-consistent potential far exceeds the ponderomotive one (φ >> φpb). Then one looks for a solution of Eq. (14) around the simultaneous zeroes of the left-hand side. Eq. (14) takes the form

where

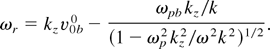
We choose ω = ωr + δ and ω1 = ω1r + δ for maximum growth and solve Eq. (18) for δ. The growth rate turns out to be

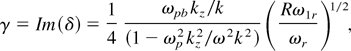
where

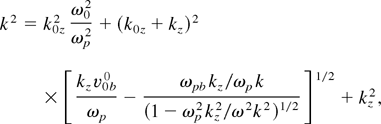
from phase matching conditions.

The growth rate of the parametric instability scales as half power of beam density and linearly with pump amplitude. This theory is also applicable for lower sideband generation when the beam travels along the direction of the pump wave.

We calculate the normalized growth rate γ/ωpb in the Raman regime from Eqs. (19) and (20) by using the mathematical method used in the Compton regime.

In Figure 2 we have plotted the growth rate in the Raman regime as a function of kz /k0z for the corresponding value of ωpb /ωp = 0.5. The normalized growth rate increases with the normalized parallel wave number of the beam mode kz /k0z. The background plasma plays a significant role and enhances the growth rate of the instability.

Variation of the normalized growth rate of the parametric instability in the Raman regime as a function of the normalized parallel wave number of the beam mode for the same parameters as those in Figure 1 and ωpb /ωp = 0.5.

3. DISCUSSION

A nonlinear dispersion relation describing three-wave interaction and instability growth rates are found. The theoretical results obtained above are applicable to the explanation of phenomena observed in laboratory plasmas as well as in space plasmas. We present the theory on parametric instabilities in space-charge-dominated beams, which are important to the design and development of induction accelerators as heavy ion fusion drivers (Wang et al., 1996).

A large amplitude TG mode propagating through a magnetized plasma, in the presence of an electron beam, undergoes parametric coupling with a negative energy beam space charge mode and a TG mode sideband. For ω ≈ kzv0b0, the coupling is caused by a ponderomotive-force-driven beam mode and one obtains upper sideband generation. However, in the Raman regime, one obtains an upper sideband for ω < kzv0b0. The sideband frequency is upshifted for the negative energy beam space charge mode. The presence of plasma enhances the growth rate of the up-conversion process.

For a low-density beam the growth rate of the parametric instability scales as two-thirds power of the pump amplitude and one-third power of the beam density, whereas, in the case of a high-density beam the rate of growth of the parametric instability scales as half power of beam density and linearly with pump amplitude. Hence, the beam density enhances the rate of growth of the parametric instability in a beam–plasma system.

The two-stream instability competes with this instability. The former has a growth rate

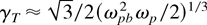
that may be higher than the growth rate of the parametric instability. The parametric instability would then arise after the two-stream instability has been saturated. However, the beam would acquire a finite velocity spread due to the two-stream instability, and one must employ a kinetic theory for the parametric coupling. Stimulated Compton scattering may be suppressed totally by kinetic effects but the stimulated Raman scattering would exist with roughly the same growth rate as above. Obiki et al. (1968) have reported an experimental study of suppression of a two-stream instability in a beam–plasma system by external ac electric fields. Davydova et al. (1986) have shown theoretically that a nonuniform external rf field can suppress a resonant instability of TG waves excited by a monoenergetic electron beam. In these situations, the parametric instability discussed above could be prominent.

ACKNOWLEDGMENT

D.N. Gupta is grateful to Professor V.K. Tripathi for stimulating and valuable discussion.

References

REFERENCES

Allen, G.R., Owens, D.K., Seiler, S.W., Yamada, M., Ikezi, H. & Porkolab, M. (1978). Parametric lower-hybrid instability driven by modulated electron-beam injection. Phys. Rev. Lett. 41, 1045–1048.CrossRefGoogle Scholar
Amatucci, W.E., Walker, D.N., Ganguli, G., Antoniades, J.A., Duncan, D., Bowles, J.H., Gavrishchaka, V. & Koepke, M.E. (1996). Plasma response to strongly sheared flow. Phys. Rev. Lett. 77, 1978–1981.CrossRefGoogle Scholar
Berger, R.L., Chen, L., Kaw, P.K. & Perkins, F.W. (1976). Lower hybrid parametric instabilities-nonuniform pump waves and tokamak applications. Phys, Fluids 20, 1864–1875.Google Scholar
Chang, J., Raether, M. & Tanaka, S. (1971). Experimental observation of wave-wave coupling in a beam-plasma system. Phys. Rev. Lett. 27, 1263–1266.CrossRefGoogle Scholar
Davydova, T.A., Lashkin, V.M, Shamrai, K.P. (1986). Effect of external rf field on instability of Trivelpiece-Gould waves in a plasma with an electron beam. Sov. J. Plasma Phys 12, 235–237.Google Scholar
Koepkr, M.E. (2002). Contributions of Q-machine experiments to understanding auroral particle acceleration processes. Phys. Plasmas 9, 2420–2427, and reference therein.Google Scholar
Krafft, C., Volokitin, A.S. & Fle, M. (2000). Nonlinear electron beam interaction with a whistler wave packet. Phys. Plasmas 7, 4423–4432.CrossRefGoogle Scholar
Liu, C.S., Tripathi, V.K., Chan, V.S. & Stefan, V. (1984). Density threshold for parametric instability of lower-hybrid waves in tokamaks. Phys. Fluids 27, 1709–1717.CrossRefGoogle Scholar
Maslennikov, D.I., Mikhailenko, V.S. & Stepanov, K.N. (2000). Decay instability of a lower hybrid wave. Plasma Physics Report 26, 139–146.CrossRefGoogle Scholar
Obiki, T., Itatani, R. & Otani, Y. (1968). Suppression of a two-stream interaction in a beam-plasma system by external ac electric fields. Phys. Rev. Lett. 20, 184–187.CrossRefGoogle Scholar
Porkolab, M. (1974). Theory of parametric instability near the lower-hybrid frequency. Phys. Fluids 17, 1432–1442.CrossRefGoogle Scholar
Porkolab, M., Bernabei, S., Hooke, W.M., Motley, R.W. & Nagashima, T. (1977). Observation of parametric instabilities in lower-hybrid radio frequency heating of tokamaks. Phys. Rev. Lett. 38, 230–233.CrossRefGoogle Scholar
Prabhuram, G. & Sharma, A.K. (1992). Second harmonic excitation of TG mode in a beam plasma system. J. Plasma Phys. 48, 3–12.CrossRefGoogle Scholar
Sakawa, Y., Joshi, C., Kaw, P.K., Chen, F.F., Jain, V.K. (1993). Excitation of the modified Simon–Hoh instability in an electron beam produced plasma. Phys. FluidsB5(6), 1681–1694.CrossRef
Seiler, S., Yamada, M. & Ikezi, H. (1976). Lower hybrid instability driven by a spiraling ion beam. Phys. Rev. Lett. 37, 700–703.CrossRefGoogle Scholar
Sharma, S.C., Srivastava, M.P., Sugawa, M. & Tripathi, V.K. (1998). Excitation of lower hybrid waves by a density-modulated electron beam in a plasma cylinder. Phys. Plasmas 5, 3161–3164.CrossRefGoogle Scholar
Taylor, R.J., Brown, M.L., Fried, B.D., Grote, H., Liberati, J.R., Morales, G.J., Pribyl, P., Darrow, D. & Ono, M. (1989). H-mode behavior induced by cross-field currents in a tokamak. Phys. Rev. Lett. 63, 2365–2368.CrossRefGoogle Scholar
Volokitin, A.S. & Krafft, C. (2001). Electron beam interaction with lower hybrid waves at Cherenkov and cyclotron resonances. Phys. Plasmas 8, 3748–3758.CrossRefGoogle Scholar
Wang, J.G., Suk, H. & Reiser, M. (1996). Experimental studies of space-charge waves and resistive-wall instability in space-charge-dominated electron beams. Fusion Engineering and Design 32–33, 141–148.CrossRefGoogle Scholar
Yatsui, K. & Imai, T. (1975). Plasma heating by lower-hybrid parametric instability pumped by an electron beam. Phys. Rev. Lett. 35, 1279–1282.CrossRefGoogle Scholar
Figure 0

Variation of the normalized growth rate of the parametric instability in the Compton regime as a function of the normalized parallel wave number of the beam mode. The parameters are −v0b0/c = 0.1, k0zc/ω0 = 3, cs /c = 10−5, δ1 = π/2, u2/cs2 = 1, ωpb /ωp = 0.2, and ω0 /ωp = 0.1, 0.2.

Figure 1

Variation of the normalized growth rate of the parametric instability in the Raman regime as a function of the normalized parallel wave number of the beam mode for the same parameters as those in Figure 1 and ωpb /ωp = 0.5.