3.1 The larger-scale vortices

As previously seen in figure 1, the large-scale swirling flow around the diagonal of a fundamental box is sustained by fixing the amplitude of a number of Fourier coefficients in time (see (2.4)). Taking into account the flow characteristics, we decompose the velocity vector $\boldsymbol{u}$ and the vorticity vector $\unicode[STIX]{x1D74E}$ into three mutually perpendicular components in a cylindrical coordinate system $(r,\unicode[STIX]{x1D703},z)$ whose longitudinal axis is defined by the diagonal line of a fundamental box (see figure 5). In the cylindrical coordinate system, velocity vector $\boldsymbol{u}$ is expressed as $\boldsymbol{u}=(u_{r},u_{\unicode[STIX]{x1D703}},u_{z})$ , where $u_{r}$ is the radial velocity, $u_{\unicode[STIX]{x1D703}}$ the circumferential velocity, $u_{z}$ the axial velocity. They are obtained by solving the following system of linear equations,

(3.1) $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}c@{}}u_{r}\\ u_{\unicode[STIX]{x1D703}}\\ u_{z}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}\boldsymbol{e}_{r} & \boldsymbol{e}_{\unicode[STIX]{x1D703}} & \boldsymbol{e}_{z}\end{array}\right)^{-1}\left(\begin{array}{@{}c@{}}u_{1}\\ u_{2}\\ u_{3}\end{array}\right), & & \displaystyle\end{eqnarray}$$

where the $3\times 3$ matrix, which is dependent upon $\boldsymbol{x}$ , is composed of the three unit vectors: $\boldsymbol{e}_{r}=\boldsymbol{r}/|\boldsymbol{r}|=(\boldsymbol{x}-\boldsymbol{z})/|\boldsymbol{x}-\boldsymbol{z}|$ , $\boldsymbol{e}_{\unicode[STIX]{x1D703}}=(\boldsymbol{z}\times \boldsymbol{r})/|\boldsymbol{z}\times \boldsymbol{r}|$ and $\boldsymbol{e}_{z}=\boldsymbol{z}/|\boldsymbol{z}|=1/\sqrt{3}(1,1,1)$ . Vorticity vector $\unicode[STIX]{x1D74E}$ is similarly expressed as $\unicode[STIX]{x1D74E}=(\unicode[STIX]{x1D714}_{r},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D714}_{z})$ , where $\unicode[STIX]{x1D714}_{r}$ is the radial vorticity, $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$ the circumferential vorticity and $\unicode[STIX]{x1D714}_{z}$ the axial vorticity. Figure 6 shows the time evolutions of $\langle u_{r}^{2}\rangle _{f}$ , $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ and $\langle u_{z}^{2}\rangle _{f}$ as well as $\langle \unicode[STIX]{x1D714}_{r}^{2}\rangle _{f}$ , $\langle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ and $\langle \unicode[STIX]{x1D714}_{z}^{2}\rangle _{f}$ for the period-5 motion, where $\langle \cdot \rangle _{f}$ indicates the spatially averaged value over the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ). Over the whole time period, the temporal mean of $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ is much larger than those of $\langle u_{r}^{2}\rangle _{f}$ and $\langle u_{z}^{2}\rangle _{f}$ , and that of $\langle \unicode[STIX]{x1D714}_{z}^{2}\rangle _{f}$ is much larger than those of $\langle \unicode[STIX]{x1D714}_{r}^{2}\rangle _{f}$ and $\langle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ . It is therefore considered that, in a fundamental box, the swirling flow around the diagonal is dominant and the corresponding columnar vortex is the dominant flow structure. Hereinafter, we shall refer to the columnar vortex as the larger-scale vortex. It is statistically sustained by the external forcing preserving a high-symmetric flow field (Kida Reference Kida1985). Figure 6(a) also shows that $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ fluctuates around its temporal mean with large amplitude and shows five peaks. The global intensity of the large-scale swirling flow over the fundamental box becomes active and quiescent alternately corresponding to the time variation of $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ . Incidentally, the last two large-amplitude oscillations of $\langle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}^{2}\rangle$ correspond to generation and circumferential vortex stretching of strong smaller-scale vortices, which will be presented in the next subsection (§ 3.2).

Figure 6. Time evolutions of the spatially averaged quantities over the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ). (a) Blue dash-dotted, $\langle u_{r}^{2}\rangle _{f}/[2\langle K\rangle ]$ ; green solid, $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}/[2\langle K\rangle ]$ ; red dashed, $\langle u_{z}^{2}\rangle _{f}/[2\langle K\rangle ]$ . (b) Blue dash-dotted, $\langle \unicode[STIX]{x1D714}_{r}^{2}\rangle _{f}/[2\langle {\mathcal{Q}}\rangle ]$ ; green solid, $\langle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}/[2\langle {\mathcal{Q}}\rangle ]$ ; red dashed, $\langle \unicode[STIX]{x1D714}_{z}^{2}\rangle _{f}/[2\langle {\mathcal{Q}}\rangle ]$ .

The period-5 motion includes active and quiescent periods of time. Since we will later discuss the closed regenerative cycle of the large-amplitude axial waves, which is reminiscent of the regeneration cycle of near-wall turbulence structures (Hamilton et al. Reference Hamilton, Kim and Waleffe1995), it is convenient to have a well-defined period of time. In this paper, by focusing on the time evolution of the global intensity of the large-scale swirling flow over the fundamental box, we define a single cycle as the time period from one time when $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ attains a local maximum to the time when it attains the next local one. Figure 7 shows the time period ( $6.27\leqslant t/T\leqslant 9.18$ ) including one of the five cycles during which the most intense energy dissipation event takes place. During this time period, $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ attains its local maxima at $t=t_{1}$ and $t_{7}$ , and its local minimum at $t=t_{4}$ ; $\unicode[STIX]{x1D716}$ attains its local maximum at $t=t_{2}$ and its local minimum at $t=t_{5}$ . This time period will be used when investigating the oscillatory evolution in detail in § 5. Here, it is important to emphasise that, although we select it for investigation, our proposed mechanism, a vortex interaction mechanism, plays an important role in generating global oscillations whether or not the period includes the most intense energy dissipation event. Indeed, in § 6 we will find its significance even in decaying high-symmetric turbulence whose turbulence intensity is significantly decreasing with time.

Figure 7. Time evolutions of $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ (green solid line) and the total energy dissipation rate $\unicode[STIX]{x1D716}$ (blue dashed line) ( $6.27\leqslant t/T\leqslant 9.18$ ). The seven dashed straight lines from left to right indicate times $t_{1}-t_{7}$ : $t_{1}=6.74T$ , $t_{2}=7.04T$ , $t_{3}=7.40T$ , $t_{4}=7.66T$ , $t_{5}=8.09T$ , $t_{6}=8.38T$ and $t_{7}=8.70T$ . $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ attains its local maxima at $t=t_{1}$ and $t_{7}$ and its local minimum at $t=t_{4}$ . $\unicode[STIX]{x1D716}$ attains its local maximum at $t=t_{2}$ and its local minimum at $t=t_{5}$ .

3.2 The smaller-scale vortices

3.2.1 Classification of smaller-scale vortices

Here, we shall introduce the smaller-scale vortices, the dynamics of which is spatio-temporally simplified because of the symmetry constraint. We shall consider smaller-scale vortices in the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ). At this moderate Reynolds number ( $\langle R_{\unicode[STIX]{x1D706}}\rangle =69.6$ ), we can classify all the smaller-scale vortices into two types, both of which are generated and stretched in the strong straining fields appearing between the larger-scale vortices. Vortices of one type are created in the strong straining fields near the origin O while vortices of the other type are created in those near the point $\text{A}(\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}/2)$ . Recall that the generation mechanism of smaller-scale vortices in strong straining regions between the larger-scale vortices was previously reported by means of DNS of homogeneous isotropic turbulence at higher Reynolds numbers (Goto Reference Goto2008, Reference Goto2012; Leung, Swaminathan & Davidson Reference Leung, Swaminathan and Davidson2012; Goto, Saito & Kawahara Reference Goto, Saito and Kawahara2017) and is not specific to high-symmetric turbulence. Once they are created in such a way, the former vortices start to move towards the origin O and the latter towards the point A. Therefore, we hereinafter refer to the former group of vortices as SV-O and the latter as SV-A. Note that both the origin O and the point A are stagnation points of the velocity vector field. In order to grasp the spatial arrangement of smaller-scale vortices, we plot in figure 8 an instantaneous flow field of the period-5 motion in the 64 fundamental boxes ( $-\unicode[STIX]{x03C0}\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}$ ). The cubic domain drawn by thick black lines is $-\unicode[STIX]{x03C0}/4\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/4$ , whose centre is the origin O, towards which the SV-O vortices converge. The cuboid domain drawn by thick red lines is the two fundamental boxes ( $0\leqslant x_{1}\leqslant \unicode[STIX]{x03C0}$ and $0\leqslant x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ). In this domain, we observe not only the SV-O but also SV-A vortices which converge towards the point A.

Figure 8. Snapshot of the flow field of the period-5 motion taken at $t/T=4.47$ . The largest cubic domain drawn by thin black lines (64 fundamental boxes) is $-\unicode[STIX]{x03C0}\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}$ . The cubic subdomain drawn by thick black lines is $-\unicode[STIX]{x03C0}/4\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/4$ , whose centre is the origin O, which will appear in figure 9. The cuboid subdomain drawn by thick red lines is $0\leqslant x_{1}\leqslant \unicode[STIX]{x03C0}$ and $0\leqslant x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ , which will be shown in figure 10. The smaller-scale vortices are visualised by grey-coloured isosurfaces of $|\unicode[STIX]{x1D74E}|^{2}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle ^{2}=12$ , but they are coloured in green inside the subdomains. The blue-coloured plane including three points O, A $(\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}/2)$ and $(0,\unicode[STIX]{x03C0}/2,0)$ will be used in figures 17 and 18.

Figure 9. Snapshots of the flow fields in the cubic domain $-\unicode[STIX]{x03C0}/4\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/4$ whose centroid is the origin O. They are taken at (a)  $t=8.29T$ , (b)  $8.78T$ , (c)  $9.14T$ , (d)  $9.32T$ , (e)  $9.45T$ , (f)  $9.68T$ . The grey and green isosurfaces indicate pressure $p/[\unicode[STIX]{x1D70C}\langle u^{\prime }\rangle ^{2}]=-2$ and $|\unicode[STIX]{x1D74E}|^{2}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle ^{2}=18$ , respectively. The streamlines of the instantaneous velocity fields are shown, where the red ones are in the domain $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/4$ and the blue ones are in the domain $0\leqslant x_{1},x_{3}\leqslant \unicode[STIX]{x03C0}/4$ and $-\unicode[STIX]{x03C0}/4\leqslant x_{2}\leqslant 0$ . The mirror symmetries with respect to the three planes $x_{1}=0$ , $x_{2}=0$ and $x_{3}=0$ are observed. (a) The arrows show the rotation directions of the large-scale swirling flows. (b) The arrows indicate a counter-rotating vortex pair (a dipole).

Figure 10. Snapshots of the flow fields in the two neighbouring fundamental boxes ( $0\leqslant x_{1}\leqslant \unicode[STIX]{x03C0}$ and $0\leqslant x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ). They are taken at (a)  $t=8.06T$ , (b)  $8.19T$ , (c)  $8.37T$ , (d)  $8.51T$ , (e)  $8.82T$ and (f)  $9.40T$ . The light-grey, dark-grey and green isosurfaces indicate $p/[\unicode[STIX]{x1D70C}\langle u^{\prime }\rangle ^{2}]=-2$ , $\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle ^{2}=12$ and $|\unicode[STIX]{x1D74E}|^{2}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle ^{2}=18$ , respectively. The red streamlines of the instantaneous velocity fields are shown. (a) The arrows show the rotation direction of the large-scale swirling flows. (c) The elliptic area denoted by B indicates the region where strong straining fields are generated. (d) The arrows indicate a counter-rotating vortex pair (a dipole). (e) The double arrow shows the directions of stretching by the larger-scale vortices. The SV-A vortices are observed in the shape of the letter S being wrapped around the larger-scale vortices.

These vortices are similar to those in decaying high-symmetric turbulence which were previously found and investigated by Boratav & Pelz (Reference Boratav and Pelz1994, Reference Boratav and Pelz1995). They performed DNS of decaying turbulence which starts with the initial velocity field (2.5), and observed the smaller-scale vortices moving towards the stagnation points. In the following, we will consider time evolutions of the SV-O and SV-A vortices in high-symmetric flow with the external forcing (2.4).

3.2.2 Time evolutions and creation mechanisms of the SV-O and SV-A vortices

Firstly, we shall consider the time evolution and creation mechanism of the SV-O vortices. Figure 9 shows the time evolution of the SV-O vortices visualised by isosurfaces of enstrophy and the larger-scale vortices visualised by isosurfaces of low pressure. To provide the information of the three-dimensional velocity field, we also plot streamlines of the instantaneous velocity field. Since the velocity field has three mirror symmetries with respect to three planes $x_{1}=0$ , $x_{2}=0$ and $x_{3}=0$ , the origin O is a stagnation point of the velocity vector field. This point is surrounded by the eight large-scale swirling flows with different orientations. Because of the arrangement of the larger-scale swirling flows, strong straining fields tend to be generated near three planes $x_{1}=0$ , $x_{2}=0$ and $x_{3}=0$ . The SV-O vortices are stretched and created in the straining fields generated by local high-speed rotational motions around the central axis of the larger-scale vortices (see figure 9 a); they appear in the form of counter-rotating vortex pairs (dipoles) (figure 9 b). It is confirmed that, once they are created, the SV-O vortices start to converge towards the origin O (figure 9 b–e). This convergence of the SV-O vortices has been explained in terms of the mutual induction between the 12 vortices (six dipoles) (Boratav & Pelz Reference Boratav and Pelz1995; Pelz Reference Pelz2001; Kimura Reference Kimura2010). In the late stage of their convergence, they dissipate and diminish strongly affected by viscosity; in the meantime, the new SV-O vortices are generated far from the origin O as seen in figure 9(f). This is the beginning of the next cycle.

Secondly, we discuss the SV-A vortices. In a fundamental box, we can only observe parts of the SV-A vortices. In order to observe the whole picture of the individual SV-A vortices, it is necessary to consider neighbouring fundamental boxes. This is because these vortices cross a boundary plane between two fundamental boxes. As for the fundamental box whose spatial domain is $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ , the SV-A vortices cross three planes: $x_{1}=\unicode[STIX]{x03C0}/2$ , $x_{2}=\unicode[STIX]{x03C0}/2$ and $x_{3}=\unicode[STIX]{x03C0}/2$ . In the following, therefore, we shall consider the flow field in the two neighbouring fundamental boxes whose domain is $0\leqslant x_{1}\leqslant \unicode[STIX]{x03C0}$ and $0\leqslant x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ , where the whole picture of the SV-A vortices crossing the plane $x_{1}=\unicode[STIX]{x03C0}/2$ is observed.

Figure 10 shows the time evolution of the SV-A vortices. The two larger-scale vortices in the left and right fundamental boxes are visualised by the light-grey isosurfaces of low pressure surrounded by streamlines of the instantaneous velocity field, and the SV-A vortices are visualised by the green isosurfaces of enstrophy; the strong straining flow fields are visualised by the dark-grey isosurfaces of $\unicode[STIX]{x1D61A}_{ij}\unicode[STIX]{x1D61A}_{ij}$ , where $\unicode[STIX]{x1D61A}_{ij}=1/2(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})$ is the strain-rate tensor. The boundary plane $x_{1}=\unicode[STIX]{x03C0}/2$ between the two adjacent fundamental boxes is located between the two identical large-scale swirling flows with different orientations. When local rotational motions near the point A start to get faster, strong straining fields are generated near the plane $x_{1}=\unicode[STIX]{x03C0}/2$ (see the region B in figure 10 c). In the vicinity of the strong strain fields, the two SV-A vortices are created in the form of a counter-rotating vortex pair (a dipole) and converge towards the stagnation point A being rolled up by the larger-scale vortices (a counter-rotating vortex pair is denoted by the yellow arrows in figure 10 d). This convergence may be caused by the mutual induction of the SV-A vortices as in the case of the SV-O vortices. As a result of being wrapped around the larger-scale vortex, the isosurfaces of enstrophy are formed in the shape of the letter S (see figure 10 e). Eventually, the SV-A vortices dissipate because of viscosity. Although not shown in figure 10, a total of 24 SV-A vortices (12 dipoles) in the eight neighbouring fundamental boxes approach the stagnation point A.

Note that, although we have selected to demonstrate the six snapshots which are taken from one of the five cyclic events, qualitatively similar spatio-temporal evolutions of SV-O and SV-A vortices are also observed in the other events.

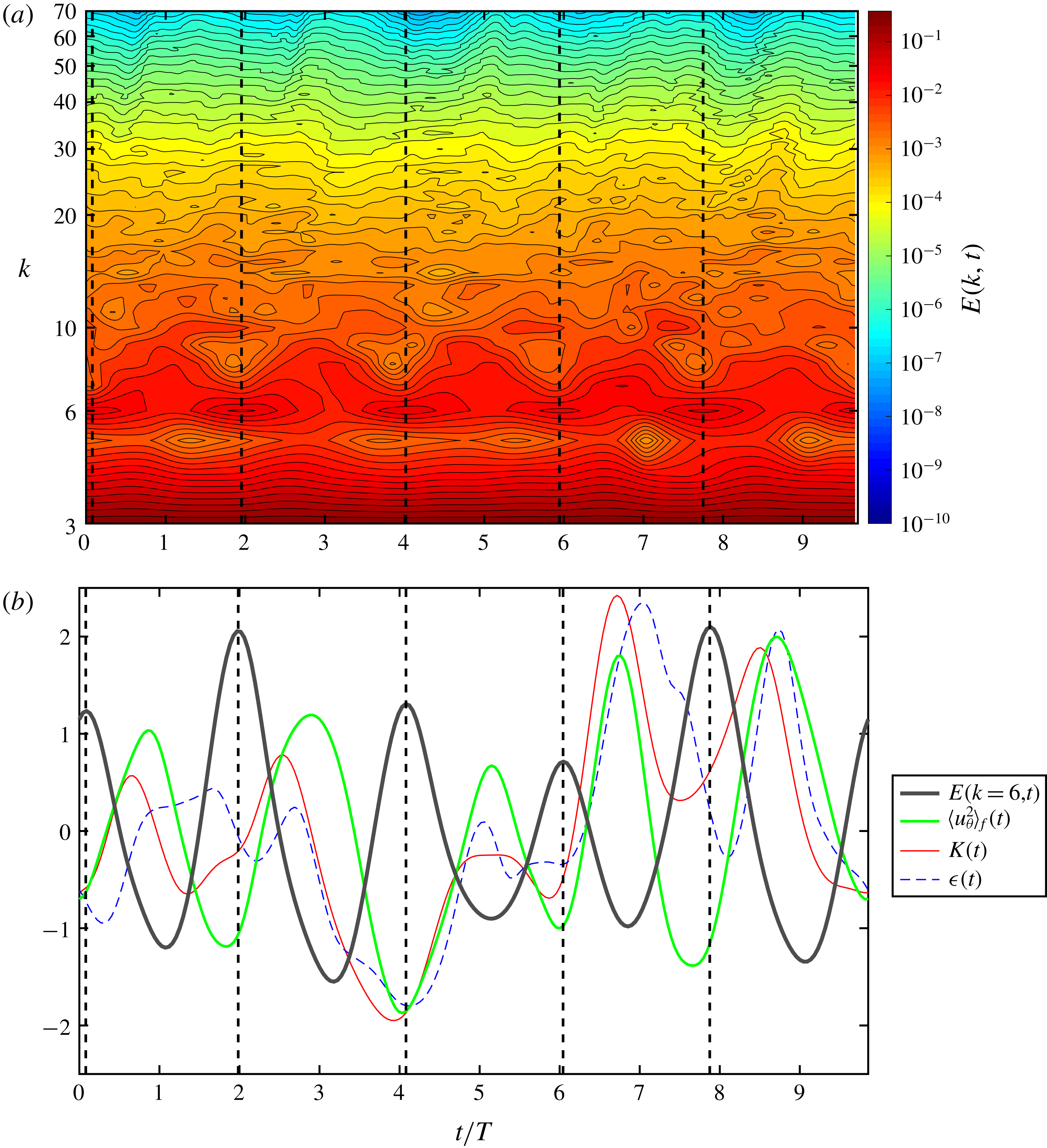
Figure 11. (a) Time evolution of energy spectrum of the period-5 motion. The horizontal and longitudinal axes represent the time and wavenumber, respectively. The contours are not shown in the wavenumber range beyond $k=70$ for clarity. (b) Temporal fluctuations of global quantities around their temporal mean normalised by their temporal standard deviation. The grey, green, red and blue lines correspond to $E(k=6,t)$ , $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}(t)$ , $K(t)$ and $\unicode[STIX]{x1D716}(t)$ , respectively. (a,b) The five dashed straight lines indicate the times when $E(k=6,t)$ attains its local maximum. The times are $t=0.0793T$ , $1.95T$ , $4.02T$ , $5.95T$ and $7.75T$ from left to right.

4.1 Cyclic energy transfer dynamics

In figure 11(a), we show the time evolution of three-dimensional energy spectrum $E(k,t)$ of the period-5 motion, as was shown by van Veen et al. (Reference van Veen, Kida and Kawahara2006). This contour plot demonstrates that fluctuating energy is transferred from smaller to larger wavenumbers in the high-wavenumber dissipation range (i.e. forward energy transfer). Our new finding in this plot is the presence of large-amplitude temporal fluctuation in $E(k=6,t)$ , which has five peaks at times $t=0.0793T$ , $1.95T$ , $4.02T$ , $5.95T$ and $7.75T$ . Here, the wavenumber $k=6$ is smaller than $k_{L}$ and $k_{\unicode[STIX]{x1D706}}$ by a factor of 1.65 and 2.43, respectively, and about double the forcing wavenumber ( $k_{F}=\sqrt{11}$ ). It is important to mention that intense forward energy transfer events are confirmed after the maximum peaks of $E(k=6,t)$ by ridges of contour lines of energy spectrum (figure 11 a).

The temporal fluctuation of $E(k=6,t)$ is plotted in figure 11(b) alongside with those of $K(t)$ , $\unicode[STIX]{x1D716}(t)$ and $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}(t)$ . The local maxima of $E(k=6,t)$ are located between two adjacent times which take a local maximum value of $K(t)$ , $\unicode[STIX]{x1D716}(t)$ and $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}(t)$ . The time period of oscillation in $E(k=6,t)$ and the time lag of oscillations of $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}(t)$ relative to $E(k=6,t)$ are, respectively, estimated by the first peak of auto-correlation function of time series of $E(k=6,t)$ and that of cross-correlation function between those of $E(k=6,t)$ and $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}(t)$ , where the former is $2.02T$ and the latter is $0.896T$ . This time lag and our qualitative observation of the cyclic intense forward energy transfer events in figure 11(a) suggest to us that the increase of $E(k=6,t)$ subsequently leads to those of $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}(t)$ , $K(t)$ and $\unicode[STIX]{x1D716}(t)$ through an intense forward energy transfer and that the excitation of $E(k=6,t)$ is a key ingredient in the cyclic energy transfer dynamics.

4.2 Scale-by-scale anisotropic fluctuations

The three-dimensional energy spectrum $E(k,t)$ , which has been discussed above, is an orientation-averaged quantity in wave space, for a given wavenumber $k$ . Note that it does not include any information on anisotropic fluctuations because of the orientation average. So far we have found that the flow is globally anisotropic and directional in the fundamental box; the axis of the larger-scale vortex is oriented in the $z$ -direction and the smaller-scale vortices which are generated in the straining regions appearing between larger-scale vortices also seem to have some preferential orientations (see figures 9 and 10). Taking into account such a directional dependency in scales, we investigate the preferential directions of fluctuations of each mode so as to find a clearer connection between the observed coherent structures and anisotropic fluctuations. To attempt this, we introduce a multi-scale and multi-orientation decomposition: velocity and vorticity fields are decomposed into Fourier modes and three mutually orthogonal directions defined in the cylindrical coordinate system (figure 5).

For the decomposition, we first compute $k$ th-mode velocity $\boldsymbol{u}^{(k)}(\boldsymbol{x},t)$ and $k$ th-mode vorticity $\unicode[STIX]{x1D74E}^{(k)}(\boldsymbol{x},t)$ in the Cartesian coordinate system which are, respectively, written as

(4.1a,b ) $$\begin{eqnarray}\displaystyle \boldsymbol{u}^{(k)}(\boldsymbol{x},t)=\mathop{\sum }_{k-1/2\leqslant |\boldsymbol{k}^{\prime }|<k+1/2}\widetilde{\boldsymbol{u}}(\boldsymbol{k}^{\prime },t)\text{e}^{\text{i}\boldsymbol{k}^{\prime }\boldsymbol{\cdot }\boldsymbol{x}},\quad \unicode[STIX]{x1D74E}^{(k)}(\boldsymbol{x},t)=\mathop{\sum }_{k-1/2\leqslant |\boldsymbol{k}^{\prime }|<k+1/2}\widetilde{\unicode[STIX]{x1D74E}}(\boldsymbol{k}^{\prime },t)\text{e}^{\text{i}\boldsymbol{k}^{\prime }\boldsymbol{\cdot }\boldsymbol{x}}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Using (3.1), we subsequently compute $k$ th-mode radial velocity $u_{r}^{(k)}$ , $k$ th-mode circumferential velocity $u_{\unicode[STIX]{x1D703}}^{(k)}$ , $k$ th-mode axial velocity $u_{z}^{(k)}$ from $\boldsymbol{u}^{(k)}$ and $k$ th-mode radial vorticity $\unicode[STIX]{x1D714}_{r}^{(k)}$ , $k$ th-mode circumferential vorticity $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}^{(k)}$ , $k$ th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(k)}$ from $\unicode[STIX]{x1D74E}^{(k)}$ . By spatially averaging squared values of these quantities over the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ) and halving them, we finally obtain the radial energy spectrum $E_{r}(k,t)\equiv 1/2\langle (u_{r}^{(k)})^{2}\rangle _{f}(t)$ , circumferential energy spectrum $E_{\unicode[STIX]{x1D703}}(k,t)\equiv 1/2\langle (u_{\unicode[STIX]{x1D703}}^{(k)})^{2}\rangle _{f}(t)$ , axial energy spectrum $E_{z}(k,t)\equiv 1/2\langle (u_{z}^{(k)})^{2}\rangle _{f}(t)$ for velocity, and the radial enstrophy spectrum $D_{r}(k,t)\equiv 1/2\langle (\unicode[STIX]{x1D714}_{r}^{(k)})^{2}\rangle _{f}(t)$ , circumferential enstrophy spectrum $D_{\unicode[STIX]{x1D703}}(k,t)\equiv 1/2\langle (\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}^{(k)})^{2}\rangle _{f}(t)$ , axial enstrophy spectrum $D_{z}(k,t)\equiv 1/2\langle (\unicode[STIX]{x1D714}_{z}^{(k)})^{2}\rangle _{f}(t)$ for vorticity. The non-decomposed energy spectrum and enstrophy spectrum are respectively written as $E_{tot}(k,t)\equiv 1/2\langle (\boldsymbol{u}^{(k)})^{2}\rangle _{f}(t)$ and $D_{tot}(k,t)\equiv 1/2\langle (\unicode[STIX]{x1D74E}^{(k)})^{2}\rangle _{f}(t)$ , where $E_{tot}(k,t)=[E_{r}+E_{\unicode[STIX]{x1D703}}+E_{z}](k,t)$ and $D_{tot}(k,t)=[D_{r}+D_{\unicode[STIX]{x1D703}}+D_{z}](k,t)$ .

Figure 12. Time evolutions of the directionally decomposed energy spectra and the non-decomposed energy spectrum. The blue, green, red and black lines correspond to $E_{r}(k=6,t)$ , $E_{\unicode[STIX]{x1D703}}(k=6,t)$ , $E_{z}(k=6,t)$ and $E_{tot}(k=6,t)$ , respectively.

Figure 13. Linear-log plots of temporal standard deviations of directionally decomposed and non-decomposed spectra. Circles, triangles, squares and diamonds correspond respectively to (a) $E_{r}$ , $E_{\unicode[STIX]{x1D703}}$ , $E_{z}$ , $E_{tot}$ and (b) $D_{r}$ , $D_{\unicode[STIX]{x1D703}}$ , $D_{z}$ , $D_{tot}$ which are defined in § 4. The 4th and 6th modes are highlighted by the black dashed vertical lines. The red and blue dash-dotted vertical lines indicate the wavenumbers $k_{L}$ and $k_{\unicode[STIX]{x1D706}}$ , respectively.

To demonstrate an example of the decomposition we plot, in figure 12, the time evolutions of three directionally decomposed energy spectra and non-decomposed energy spectrum at $k=6$ . The time-averaged circumferential energy spectrum $\langle E_{\unicode[STIX]{x1D703}}\rangle (k=6)$ is more than four times as large as $\langle E_{r}\rangle (k=6)$ and $\langle E_{z}\rangle (k=6)$ : $\langle E_{\unicode[STIX]{x1D703}}\rangle (k=6)/\langle E_{r}\rangle (k=6)=5.20$ and $\langle E_{\unicode[STIX]{x1D703}}\rangle (k=6)/\langle E_{z}\rangle (k=6)=4.23$ . The amplitude of temporal fluctuation of $E_{\unicode[STIX]{x1D703}}(k=6,t)$ around its temporal mean is much larger than those of $E_{r}(k=6,t)$ and $E_{z}(k=6,t)$ ; the temporal standard deviation of $E_{\unicode[STIX]{x1D703}}(k=6,t)$ is larger than those of $E_{r}(k=6,t)$ and $E_{z}(k=6,t)$ by a factor of 6.26 and 4.93, respectively (i.e.  $\unicode[STIX]{x1D70E}_{E_{\unicode[STIX]{x1D703}}(k=6)}/\unicode[STIX]{x1D70E}_{E_{r}(k=6)}=6.26$ and $\unicode[STIX]{x1D70E}_{E_{\unicode[STIX]{x1D703}}(k=6)}/\unicode[STIX]{x1D70E}_{E_{z}(k=6)}=4.93$ ). This means that the temporal variation of $E_{tot}(k=6,t)$ is mainly reflected by that of large-scale swirling flow around the central axis of the larger-scale vortex.

Besides the 6th mode, let us examine anisotropic fluctuations of other modes. Figure 13(a) shows the temporal standard deviations of the directionally decomposed energy spectra $E_{r}(k,t)$ , $E_{\unicode[STIX]{x1D703}}(k,t)$ and $E_{z}(k,t)$ , and the non-decomposed energy spectrum $E_{tot}(k,t)$ , as a function of wavenumber. All the lower modes than the 3rd mode are not shown because Kida’s high symmetry (Kida Reference Kida1985) sets their values to zero. It is clear that temporal fluctuations of spectra are strongly directional at low Fourier modes, including the 6th mode, such that the circumferential component is dominant (see figure 13 a). For the 4th mode, for instance, we verify that $\unicode[STIX]{x1D70E}_{E_{\unicode[STIX]{x1D703}}(k=4)}/\unicode[STIX]{x1D70E}_{E_{r}(k=4)}=4.46$ and $\unicode[STIX]{x1D70E}_{E_{\unicode[STIX]{x1D703}}(k=4)}/\unicode[STIX]{x1D70E}_{E_{z}(k=4)}=4.29$ .

Figure 13(b) shows the temporal standard deviations of $D_{r}(k,t)$ , $D_{\unicode[STIX]{x1D703}}(k,t)$ , $D_{z}(k,t)$ , and $D_{tot}(k,t)$ . The temporal standard deviation of $D_{z}(k,t)$ is larger than those of $D_{r}(k,t)$ and $D_{\unicode[STIX]{x1D703}}(k,t)$ at low modes ( $4\leqslant k\leqslant k_{L}$ ) with the exception of the 7th mode. However, as the mode is increased from the 3rd mode, the temporal standard deviation of $D_{\unicode[STIX]{x1D703}}(k,t)$ is increasing significantly; for several moderate modes comparable to $k_{\unicode[STIX]{x1D706}}$ , it is much larger than that of $D_{z}(k,t)$ . This demonstrates that, at moderate wavenumbers, the temporal fluctuation of $D_{tot}(k,t)$ is strongly affected by the events of generation, circumferential vortex stretching and dissipation of the smaller-scale vortices.

4.3 Spatial distribution of intense anisotropic fluctuations

As the global fluctuations have been analysed into different directions and scales, we next seek for the spatial origin of intense fluctuations of quantities based on multi-scale and multi-orientation decomposition. In order to do this, we extract turbulent spatial fluctuations of different scales from multi-scale turbulent flow fields by using a bandpass-filtering approach which has been exploited in the literature (Leung et al. Reference Leung, Swaminathan and Davidson2012; Cardesa, Vela-Martín & Jiménez Reference Cardesa, Vela-Martín and Jiménez2017; Goto et al. Reference Goto, Saito and Kawahara2017). For the filter, we employ a sharp-cutoff bandpass filter since the Fourier mode decomposition has been used in our preceding discussion. We compute the bandpass-filtered vorticity field $\widehat{\unicode[STIX]{x1D74E}}(\boldsymbol{x},t)$ in physical space by applying the sharp-cutoff bandpass filter $G(\boldsymbol{k})$ to the vorticity field in Fourier space as

(4.2) $$\begin{eqnarray}\displaystyle \widehat{\unicode[STIX]{x1D74E}}(\boldsymbol{x},t)=\mathop{\sum }_{\boldsymbol{k}}G(\boldsymbol{k})\widetilde{\unicode[STIX]{x1D74E}}(\boldsymbol{k},t)\text{e}^{\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}}, & & \displaystyle\end{eqnarray}$$

where

(4.3) $$\begin{eqnarray}\displaystyle G(\boldsymbol{k}) & = & \displaystyle 1,\quad \text{for}~k_{low}-{\textstyle \frac{1}{2}}\leqslant |\boldsymbol{k}|<k_{high}+{\textstyle \frac{1}{2}},\nonumber\\ \displaystyle & = & \displaystyle 0,\quad \text{otherwise},\end{eqnarray}$$

and $k_{low}$ and $k_{high}$ are the lower and higher cutoff wavenumbers, respectively. Considering the dependency of anisotropic enstrophy fluctuation on different modes (figure 13 b), we use three wavenumber ranges: [R1] $(k_{low},k_{high})=(3,6)$ ; [R2] $(k_{low},k_{high})=(9,16)$ ; [R3] $(k_{low},k_{high})=(16,32)$ . Here, we set the range [R1] to include the fixed modes and intensely fluctuating modes of circumferential velocity and axial vorticity, which are 4th and 6th modes, the range [R2] to include the modes showing relatively strong fluctuation in circumferential enstrophy spectrum seen in figure 13(b), and the range [R3] to have dissipative small scales. Using (3.1), the filtered vorticity obtained is finally decomposed into the filtered radial vorticity $\widehat{\unicode[STIX]{x1D714}}_{r}(\boldsymbol{x},t)$ , the filtered circumferential vorticity $\widehat{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D703}}(\boldsymbol{x},t)$ and the filtered axial vorticity $\widehat{\unicode[STIX]{x1D714}}_{z}(\boldsymbol{x},t)$ .

Because of Kida’s high symmetry (Kida Reference Kida1985), which fixes in space the central axes of larger-scale vortices, strongly fluctuating regions are spatially localised inside a fundamental box. In order to detect such regions, we compute the temporal standard deviation field $\unicode[STIX]{x1D6F4}(\boldsymbol{x};A)$ of scalar quantity $A$ , which is defined as

(4.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(\boldsymbol{x};A)=\sqrt{\frac{1}{T_{p}}\int _{0}^{T_{p}}(A(\boldsymbol{x},t)-\langle A\rangle (\boldsymbol{x}))^{2}\,\text{d}t}, & & \displaystyle\end{eqnarray}$$

where $T_{p}$ is set to the time period of the period-5 motion.

Figure 14. Visualisations of temporal standard deviation fields of (a) filtered axial vorticity $\widehat{\unicode[STIX]{x1D714}}_{z}$ , (b) filtered radial vorticity $\widehat{\unicode[STIX]{x1D714}}_{r}$ and (c) filtered circumferential vorticity $\widehat{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D703}}$ . Red, blue and green isosurfaces correspond respectively to the filtered vorticity obtained with the ranges [R1] $(k_{low},k_{high})=(3,6)$ , [R2] $(9,16)$ and [R3] $(16,32)$ , which are explained in § 4.3. (a) Red, $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\widehat{\unicode[STIX]{x1D714}}_{z})=0.16\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ ; blue, green, $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\widehat{\unicode[STIX]{x1D714}}_{z})=0.8\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ . (b) Red, $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\widehat{\unicode[STIX]{x1D714}}_{r})=0.16\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ ; blue, green, $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\widehat{\unicode[STIX]{x1D714}}_{r})=0.8\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ . (c) Red, $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\widehat{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D703}})=0.2\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ ; blue, green, $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\widehat{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D703}})=\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ .

Figure 14(a) shows the isosurfaces of large values of $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\hat{\unicode[STIX]{x1D714}}_{z})$ . As for the wavenumber range [R1], the isosurfaces which demonstrate the intensely fluctuating regions of filtered axial vorticity are found on the diagonal, i.e. the central axis of larger-scale vortex. Taking into account the fact that temporal fluctuation of $D_{z}(k=6,t)$ is much larger than those of $D_{r}(k=6,t)$ and $D_{\unicode[STIX]{x1D703}}(k=6,t)$ , the spatial origin of excitation of lower modes is considered to be the locations where the isosurfaces are detected. Crucially, even for the filtered axial vorticity obtained with higher wavenumber ranges [R2] and [R3] some isosurfaces of the high values which exhibit strongly fluctuating regions are observed on the diagonal, even in the central region of the fundamental box. The observed regions are associated with axial stretching and compression dynamics by the nonlinear axial waves, which will appear in the next section.

Figures 14(b) and 14(c) demonstrate the temporal standard deviation fields $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\hat{\unicode[STIX]{x1D714}}_{r})$ and $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\hat{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D703}})$ , respectively. It is found in the field of $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\hat{\unicode[STIX]{x1D714}}_{r})$ (figure 14 b) that, unlike $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\hat{\unicode[STIX]{x1D714}}_{z})$ , none of the isosurfaces appears on the diagonal. For $\unicode[STIX]{x1D6F4}(\boldsymbol{x};\hat{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D703}})$ , on the other hand, some isosurfaces appear on the diagonal with the ranges [R2] and [R3] (figure 14 c). This result suggests that, since the smaller-scale vortices own strong circumferential vorticity, there would be significant dynamical interactions between the axial waves and smaller-scale vortices which induce axial flows on the diagonal. This dynamical interaction will be discussed in § 5.2.

5.1 Large-amplitude axial waves on larger-scale vortices

In § 4.1, we have detected the intense cyclic forward energy transfer events in the period-5 motion, which are caused after excitations of the 6th mode. We have also found that intensely fluctuating regions of bandpass-filtered axial vorticity obtained with the low wavenumber range [R1] including the wavenumber $k=6$ are located on the central axis of the larger-scale vortex (§ 4.3). Based on these results, a question arises: What physical mechanism causes excitations of the key mode, i.e. the 6th mode? This question will be tackled by investigating nonlinear axial waves on the larger-scale vortices. We will demonstrate that the large-amplitude oscillations of the larger-scale vortices are caused with the aid of the nonlinear axial waves, which are excited by the dynamical effect of smaller-scale vortices. Such a sustenance mechanism can be described in terms of supportive dynamical interactions between the larger-scale and smaller-scale vortices, which will be schematically summarised in a cycle diagram (see figure 20). It is reminiscent of the regeneration cycle of turbulent structures in wall-bounded shear flows (Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Waleffe Reference Waleffe1997) and transitional flows (Shimizu & Kida Reference Shimizu and Kida2009).

We emphasise that nonlinear axial waves on larger-scale vortices are essential in the cyclic process. The larger-scale vortices are the largest structures in high-symmetric turbulence. Since there is no larger-scale strain field which gives rise to global stretching or compression of the larger-scale vortices, they should be locally stretched or compressed through nonlinear axial waves to oscillate. We will therefore pay attention to axial motions along the central axes of the larger-scale vortices. In order to clarify this oscillation mechanism, we shall proceed with our discussion based on the following perspectives: (i) local vortex stretching and compression along the central axes of the larger-scale vortices and (ii) dynamical feedbacks from smaller-scale vortices. To begin with, we shall confirm the axial waves.

Figure 15. Time evolutions of physical quantities on the diagonal line of the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ) for the period-5 motion. Contour values denote (a) axial velocity $u_{z}$ , (b) axial vorticity $\unicode[STIX]{x1D714}_{z}$ , (c) axial vorticity stretching rate $\unicode[STIX]{x1D714}_{z}(\unicode[STIX]{x2202}u_{z}/\unicode[STIX]{x2202}z)$ and (d) pressure $p$ . Horizontal and vertical axes represent the time and coordinates on the diagonal line ( $0\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 1$ ).  $z=0$ and $z=\sqrt{3}\unicode[STIX]{x03C0}/2$ correspond to the origin O and point A, respectively. The thick and thin dashed lines represent times when $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ attains a local maximum and when $E(k=6,t)$ attains a local maximum, respectively. (b) The filled (open) inverted triangles indicate the local maximum (local minimum) of axial vorticity along the diagonal in the range $0\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 0.3$ . The filled (open) triangles indicate the local maximum (local minimum) of axial vorticity along the diagonal in the range $0.6\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 1$ .

We turn to figure 15 which shows the time evolution of axial motions along the central axis of the larger-scale vortex in the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ) for the period-5 motion. Within this time period ( $0\leqslant t/T\leqslant 9.85$ ), all the quantities shown in the figure (axial velocity $u_{z}$ , axial vorticity $\unicode[STIX]{x1D714}_{z}$ , axial vorticity stretching rate $\unicode[STIX]{x1D714}_{z}(\unicode[STIX]{x2202}u_{z}/\unicode[STIX]{x2202}z)$ and pressure $p$ ) fluctuate cyclically, with large amplitude, five times. Along the central axis, the axial vorticity $\unicode[STIX]{x1D714}_{z}$ is not homogeneous; the area of lower vorticity (local lower-speed rotational motion) and that of higher vorticity (local higher-speed rotational motion) are alternately aligned. An important observation in figure 15 is that the axial waves on the larger-scale vortex include a standing wave pattern and two travelling wave patterns, depending on the axial position $z$ ( $0\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 1$ ; $z=0$ (or $z=\sqrt{3}\unicode[STIX]{x03C0}/2$ ) represents the origin O (or the point A)). For convenience, we hereinafter refer to the range $0.3\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 0.6$ as the inner region, where a standing wave pattern is observed, and the ranges $0\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 0.3$ and $0.6\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 1$ , where travelling wave patterns are observed, as the outer-O region and the outer-A region, respectively.

The standing wave pattern is observed in figure 15(b) such that the time evolution of $\unicode[STIX]{x1D714}_{z}$ in the range $0.3\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 0.6$ shows temporal alternations of low and high axial vorticity. The areas of low vorticity have often been called ‘bubbles’ in the literature (e.g. Leibovich & Kribus Reference Leibovich and Kribus1990; Melander & Hussain Reference Melander and Hussain1994; Verzicco et al. Reference Verzicco, Jiménez and Orlandi1995); they are considered as a consequence of local axial vorticity compression in a longitudinal wave along the central axis of a columnar vortex. They are not permanent flow structures (except in stationary flows or equilibrium solutions), but decay because of local axial vorticity stretching which subsequently happens. Such axial vorticity compression and stretching are caused by the axial flows accelerated by the axial pressure gradient from the areas of lower axial vorticity, which nearly corresponds to the higher-pressure areas, to those of higher axial vorticity, which nearly corresponds to the lower-pressure areas. The reason why the areas of lower (or higher) axial vorticity nearly correspond to those of higher (or lower) pressure is due to the centrifugal force: If rotational motion around the central axis of a larger-scale vortex gets faster (i.e. the axial vorticity $\unicode[STIX]{x1D714}_{z}$ becomes larger), then shortly pressure on the axis gets lower to counter-balance the centrifugal force because of strong swirling motion induced by the rotational motion. Because of the axial pressure gradient and the centrifugal force, axial inhomogeneity in axial vorticity and pressure is a driving source of axial waves. Alternative explanations of axisymmetric standing waves can be found in the literature (Melander & Hussain Reference Melander and Hussain1994; Fabre et al. Reference Fabre, Sipp and Jacquin2006).

Figure 16. Similar to figure 15, but focusing on the time period ( $6.27\leqslant t/T\leqslant 9.18$ ) shown in figure 7. The thick dashed lines correspond to times 1–7 shown in figure 7. The thin dashed line denotes the time when $E(k=6,t)$ is maximal ( $t=7.75T$ ). The double triangle and double inverted triangle indicate the locations of local minimum pressure at $t=t_{4}$ in the outer-A region and inner region, respectively. The double circle indicates the zero-crossing point of axial velocity at $t=t_{5}$ .

Figure 17. Snapshots of the flow fields in the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ), taken at the corresponding times in figure 7: (a)  $t=t_{1}$ ( $6.74T$ ), (b)  $t_{2}$ ( $7.04T$ ), (c)  $t_{3}$ ( $7.40T$ ), (d)  $t_{4}$ ( $7.66T$ ), (e)  $t_{5}$ ( $8.09T$ ), (f)  $t_{6}$ ( $8.38T$ ), (g)  $t_{7}$ ( $8.70T$ ). The grey, yellow and blue-coloured isosurfaces represent $p/[\unicode[STIX]{x1D70C}\langle u^{\prime }\rangle ^{2}]=-2$ , $\unicode[STIX]{x1D714}_{z}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle =4.54$ and $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle =-4.54$ , respectively. The two-dimensional velocity vectors are shown on the plane including the points O, A and $(0,\unicode[STIX]{x03C0}/2,0)$ . The double triangle and double inverted triangle indicate the locations of local minimum pressure at $t=t_{4}$ in the outer-A region and inner region, respectively. The double circle indicates the zero-crossing point of axial velocity at $t=t_{5}$ . See the supplementary movie of the corresponding time evolution available at https://doi.org/10.1017/jfm.2019.370.

Figure 18. Snapshots of the flow fields in the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ). They are taken at (a)  $t=t_{1}$ ( $6.74T$ ), (b)  $t_{2}$ ( $7.04T$ ), (c)  $t_{3}$ ( $7.40T$ ), (d)  $t_{4}$ ( $7.66T$ ). The grey, yellow, red and blue-coloured isosurfaces represent $p/[\unicode[STIX]{x1D70C}\langle u^{\prime }\rangle ^{2}]=-2$ , $\unicode[STIX]{x1D714}_{z}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle =4.54$ , $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle =4.54$ and $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}/\langle \unicode[STIX]{x1D714}^{\prime }\rangle =-4.54$ , respectively. The two-dimensional velocity vectors are shown on the plane including the points O, A and $(0,\unicode[STIX]{x03C0}/2,0)$ . The SV-A vortex denoted by the arrow is approaching towards the central axis of larger-scale vortex and induces the strong axial flow ( $u_{z}<0$ ).

Figure 19. Similar to figure 16, but the time evolutions of (a) 4th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(4)}$ and (b) 6th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(6)}$ on the diagonal line of the fundamental box ( $0\leqslant x_{1},x_{2},x_{3}\leqslant \unicode[STIX]{x03C0}/2$ ) for the period-5 motion.

The travelling wave pattern is, on the other hand, observed such that the areas of lower and higher vorticity in the range $0\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 0.3$ (the outer-O region) move towards the origin O; those in $0.6\leqslant z/(\sqrt{3}\unicode[STIX]{x03C0}/2)\leqslant 1$ (the outer-A region) move towards the point A. In order to make this point more evident, we plot in figure 15(b) the triangles along the central axis where the local maxima and minima of axial vorticity $\unicode[STIX]{x1D714}_{z}$ are detected. The plot of the filled (open) inverted triangles indicates that the local maximum (local minimum) of axial vorticity propagates towards the origin O, whereas that of the filled (open) triangles indicates that the local maximum (local minimum) of axial vorticity propagates towards the point A.

Here, we shall explain in more detail the travelling wave pattern in the outer-A region within the time period $6.27\leqslant t/T\leqslant 9.18$ (see figure 16). In the contour plot of $\unicode[STIX]{x1D714}_{z}$ (figure 16 b), we observe that the strong axial vorticity region is moving from its onset point towards the endpoint A of the diagonal. Within the shown time period ( $6.27\leqslant t/T\leqslant 9.18$ ), the event of local maximum of axial vorticity propagating towards the point A is observed twice. For the first propagation event, local maximum of axial vorticity attains at $(t,z/(\sqrt{3}\unicode[STIX]{x03C0}/2))=(t_{1},0.656)$ , $(t_{2},0.758)$ , $(t_{3},0.805)$ , $(t_{4},0.867)$ , $(t_{5},0.914)$ , $(t_{6},0.938)$ and $(t_{7},0.945)$ , while $(t,z/(\sqrt{3}\unicode[STIX]{x03C0}/2))=(t_{5},0.648)$ , $(t_{6},0.712)$ and $(t_{7},0.766)$ for the second propagation event. We verify in our flow visualisation (figure 17) that the yellow isosurface of the large value of $\unicode[STIX]{x1D714}_{z}$ ( $=4.54\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ ) is moving towards the point A from $t=t_{1}$ to $t_{5}$ (the first propagation event). We also find a strong spatio-temporal correlation between large axial vorticity and low pressure regions (compare figures 16 b and 16 d). This occurs because of the centrifugal force as discussed earlier. This high-speed rotation is moving together with the SV-A vortices visualised by the blue isosurfaces of $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$ (figure 17).

In § 4, we have confirmed that the 4th and 6th modes are relevant for large-amplitude fluctuations of larger-scale swirling flows (figure 13) and that an excitation of the 6th mode is followed by an intense forward energy transfer event (figure 11). We have also observed that intensely fluctuating regions of bandpass-filtered axial vorticity obtained with the range [R1] that includes both 4th and 6th modes appear on the diagonal (figure 14 a). For later discussion regarding the association of these modes with the vortex interaction mechanism, we shall confirm time evolutions of the 4th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(4)}$ and the 6th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(6)}$ on the diagonal in figure 19. In the figure, we find that both $\unicode[STIX]{x1D714}_{z}^{(4)}$ and $\unicode[STIX]{x1D714}_{z}^{(6)}$ oscillate significantly on the axis and that the significant oscillation of $\unicode[STIX]{x1D714}_{z}^{(4)}$ is happening in the inner region while that of $\unicode[STIX]{x1D714}_{z}^{(6)}$ in the outer-O region and outer-A region. Such oscillations of the 4th and 6th modes can be related respectively to the second and third harmonic standing waves along the diagonal of the fundamental box whose endpoints are the origin O and the point A. Here, the wavelength $\unicode[STIX]{x1D706}_{m}$ of the $m$ th harmonic standing wave is $\sqrt{3}\unicode[STIX]{x03C0}/m$ and the length $L_{D}$ of the diagonal of the $(2\unicode[STIX]{x03C0})^{3}$ periodic box is $2\sqrt{3}\unicode[STIX]{x03C0}$ so that the corresponding mode $k$ is calculated by the equation $k=L_{D}/\unicode[STIX]{x1D706}_{m}=2m$ . This gives $k=4$ and 6 for the second harmonic ( $m=2$ ) and the third harmonic ( $m=3$ ), respectively. Note also that $\unicode[STIX]{x1D714}_{z}^{(6)}$ becomes large in the outer-O region and outer-A region when $E(k=6,t)$ attains a local maximum, which demonstrates that the temporal fluctuation of $\unicode[STIX]{x1D714}_{z}^{(6)}$ in the local regions and that of $E(k=6,t)$ are temporally correlated, and that there exists a time lag between excitations of $\unicode[STIX]{x1D714}_{z}^{(4)}$ and $\unicode[STIX]{x1D714}_{z}^{(6)}$ so that they are not excited at the same time.

Figure 20. A vortex interaction mechanism for generating large-amplitude axial waves.

5.2 A vortex interaction mechanism

We are now ready to describe the vortex interaction mechanism (figure 20). This mechanism forms a cyclic process characterised by three distinct phases. In order to describe each phase, we shall follow the dynamical events by referring to the time evolutions of the physical quantities on the central axis of the larger-scale vortex seen in figure 16 ( $6.27\leqslant t/T\leqslant 9.18$ ).

In figure 16, the time evolution starts off at around when the rate of rotation in the outer-A region is high (see figure 16 b). Around $t=t_{1}$ , when $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ attains its first local maximum, strong SV-A vortices are generated in the strong strain regions appearing between high-speed rotational motions of larger-scale vortices visualised by the isosurface of $\unicode[STIX]{x1D714}_{z}$ in figure 17(a). This event corresponds to the event (a) in the vortex interaction mechanism (see figure 20).

Once they have been generated, the SV-A vortices start to move towards the stagnation point A. Together with them, the large axial vorticity region (corresponding approximately to the low pressure region due to the centrifugal force) is moving towards the point A, from $t_{1}$ to $t_{5}$ (see figure 17 a–e). An important temporal behaviour to note here is that the axial vorticity can get stronger despite being damped due to the effect of viscosity while propagating. For the first propagation event, the axial vorticity is getting stronger from $t_{3}$ to $t_{5}$ while it is getting weaker from $t_{1}$ to $t_{3}$ (see figure 16 b). This axial vorticity growth is caused with the aid of the dynamical effect of smaller-scale vortices, which is explained as follows.

While travelling, the SV-A vortices are moving towards the central axis of larger-scale vortices and some of them induce strong axial flow ( $u_{z}<0$ ) in the negative direction. These axial flows cause strong axial vorticity stretching leading to the axial vorticity growth mentioned above. The four snapshots shown in figure 18 demonstrate how the SV-A vortices are moving towards the central axis and induce the strong axial flow ( $u_{z}<0$ ) during the first propagation event. In the figure, the SV-A vortices are visualised by using isosurfaces of positive circumferential vorticity ( $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}=4.54\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ ) and negative circumferential vorticity ( $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}=-4.54\langle \unicode[STIX]{x1D714}^{\prime }\rangle$ ); the latter ones appear closer to the central axis. Here, let us focus on the evolution of one of the latter ones denoted by the green arrow. It crosses the plane including the points O, A and $(0,\unicode[STIX]{x03C0}/2,0)$ . From the two-dimensional velocity vector field on the plane, we find that, approaching the central axis, it assists in generating the strong axial flow ( $u_{z}<0$ ) in the negative direction (figure 18 d). Note that, because of the $2\unicode[STIX]{x03C0}/3$ rotational symmetry around the axis, generating the strong axial flow ( $u_{z}<0$ ) is assisted by the three vortices visualised by the blue isosurfaces which appear closer to the axis than the other three. The other three SV-A vortices (visualised by the red isosurfaces) assist in generating the axial flow ( $u_{z}<0$ ) along the other axes. The effect of this axial vorticity stretching is, because of the centrifugal force, that of lowering pressure locally and significantly which sets a strong inhomogeneity along the central axis in pressure and, therefore, strong axial pressure gradients. This is the process (b) in the mechanism (see figure 20).

Figure 21. Cartoons of two different phases from the temporally cyclic process. Larger-scale vortices (white) and SV-A vortices (green) are shown. Dashed straight lines denote the central axis of larger-scale vortices. Black and yellow arrows denote the direction of axial flows and rotational motions, respectively. (a) Local rotational motions of larger-scale vortices strengthened by axial flows generate strong strain fields (see the phase (a) in figure 20). (b) SV-A vortices induce strong axial flows being wrapped around larger-scale vortices (see the phase (b) in figure 20).

It is observed that the strong axial inhomogeneity in pressure is set around $t=t_{4}$ when $\langle u_{\unicode[STIX]{x1D703}}^{2}\rangle _{f}$ attains its local minimum (figure 16 d). In figure 16(d), we denote two low-pressure regions by the double triangle and inverted double triangle for the outer-A region and inner region, respectively. Because of the low-pressure regions, strong axial pressure gradients are formed. The axial pressure gradients generated in such a way cause the strong axial flows with positive direction ( $u_{z}>0$ ) and negative direction ( $u_{z}<0$ ). At $t=t_{5}$ , we observe that axial vorticity stretching is caused by the strong axial flows in two opposite directions generated because of the axial pressure gradients; one accelerated axial flow is the strong axial flow ( $u_{z}>0$ ) towards the region where the pressure decreases (denoted by the red arrow in figure 16 a) and the other one is the one towards the inner region (denoted by the blue arrow). These accelerated axial flows by the axial pressure gradients cause the strong axial vorticity stretching in the outer-A region (figure 16 c, $t=t_{5}$ – $t_{7}$ ) so that the rate of rotation in the region becomes higher. It leads to the second propagation event. This process corresponds to (c) in the vortex interaction mechanism.

As seen in figure 19(b), this axial vortex stretching excites the 6th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(6)}$ which corresponds to the local rotational motion of the larger-scale vortex in the outer-A region. In other words, the 6th-mode axial vorticity $\unicode[STIX]{x1D714}_{z}^{(6)}$ in the outer-A region fluctuates significantly with the aid of the dynamical effects of SV-A vortices. After the excitation of the 6th mode, an intense forward energy transfer event occurs, which subsequently leads to the increase of the total kinetic energy and total energy dissipation rate (figure 11). It may be considered that significant temporal modulation of the 4th-mode axial vorticity (figure 19 a) is caused through the excited axial waves and therefore there exists a time delay between the excitations of 4th and 6th modes.

In summary, the coherent structures of the larger-scale and SV-A vortices undergo the following temporally cyclic process through nonlinear axial waves ((i) $\rightarrow$ (ii) $\rightarrow$ (iii) $\rightarrow$ (i)):

1. (i) The local high-speed rotational motions of larger-scale vortices generate the straining fields; because of these fields, the SV-A vortices are stretched and generated (see the cartoon in figure 21 a).

2. (ii) The SV-A vortices are approaching the axis of the larger-scale vortices being mutually induced by the other SV-A vortices and wrapped around the larger-scale vortices; they induce the axial flows which cause strong axial vorticity stretching leading to significant pressure reduction because of the centrifugal force, which sets strong axial pressure gradients (see the cartoon in figure 21 b).

3. (iii) The axial flows are accelerated by the axial pressure gradients; they cause the axial vorticity stretching in the outer-A region. As a result, the local rotational motions of the larger-scale vortices are intensified.

Although not shown here for economy of space, such a temporally cyclic process is also present between the larger-scale and SV-O vortices. Based on the discussion above, we propose a vortex interaction mechanism for generating large-amplitude axial waves leading to fluctuations of globally averaged quantities, which is schematically illustrated in the form of a cyclic process (figure 20).