Model equations for laser and plasma oscillations

The propagation dynamics of the laser beam and plasma oscillations in a collisionless plasma coupled through ponderomotive and relativistic non-linearity have been obtained as follows.

Equation for the laser

The propagation of a linearly polarized intense laser pump of frequency ω₀ along z-direction in an under-dense plasma, of equilibrium electron density, n ₀ has been considered.

The laser is considered to be propagating in a medium with plasma density oscillations in the background. The laser beam dynamical equation can be obtained (Ginzburg, Reference Ginzburg1970) from the equations of continuity and momentum balance and also with the Maxwell's equations:

(1)$$\displaystyle{{\partial n_j} \over {\partial t}} + \nabla. (n_j\vec{v}_j) = 0$$

(2)$$\displaystyle{{\partial \lpar {m_j{\vec{v}}_j} \rpar } \over {\partial t}} + \vec{v}_j.\nabla \lpar {m_j{\vec{v}}_j} \rpar = \,\;q_j\left\{ {\vec{E} + \displaystyle{{({\vec{v}}_j \times \vec{B})} \over c}} \right\}$$

(3)$$\nabla \times \vec{E} = -\displaystyle{1 \over c}\displaystyle{{\partial \vec{B}} \over {\partial t}}$$

(4)$$\nabla \times \vec{B} = \displaystyle{{4{\rm \pi}} \over c}\,\vec{J} + \displaystyle{1 \over c}\displaystyle{{\partial \vec{E}} \over {\partial t}}$$

where, j symbolizes plasma species (e for electron and i for ion) and q _j, m _j, v _j, n _j and T _j symbolize the charge, mass, velocity, number density, and energy of the plasma species, respectively. The wave equation in the x-component of the electric field can be obtained by combining Eqs. (3) and (4)

(5)$$\nabla ^2E_x-\lpar {\nabla \lpar {\nabla. \vec{E}} \rpar } \rpar _x = \displaystyle{{4{\rm \pi}} \over {c^2}}\displaystyle{{\partial J_x} \over {\partial t}} + \displaystyle{1 \over {c^2}}\displaystyle{{\partial ^2E_x} \over {\partial t^2}}$$

For $\nabla {\rm \varepsilon} /{\rm \varepsilon} \;\ll 1$, one may ignore $\lpar {\nabla \lpar {\nabla. \vec{E}} \rpar } \rpar _x$ term in the wave equation (Sodha et al., Reference Sodha, Ghatak and Tripathi1976), where ε is the non-linear plasma dielectric constant.

The solution of Eq. (5) can be written as follows (Sodha et al., Reference Sodha, Ghatak and Tripathi1976):

(6)$$E_x = A\lpar {x,z,t} \rpar \exp \lcub {-i\lpar {{\rm \omega}_0t-k_0z} \rpar } \rcub $$

where A(x, z, t) is the wave amplitude of slow space and time dependence,

$$k_0 = \displaystyle{{{\rm \omega} _0} \over c}\left[ {1-\displaystyle{{{\rm \omega}_{{\rm p}0}^2} \over {{\rm \gamma} {\rm \omega}_0^2}}} \right]^{1/2}$$

and ${\rm \omega} _{{\rm p}0}^2 = 4{\rm \pi} n_0e^2/m_{{\rm e}0}$, m _e0 is the electron rest mass and γ{ = (1 + a ²/2)^1/2} is the relativistic factor and

$$a = \displaystyle{{e\vert A \vert } \over {m_{{\rm e}0}{\rm \omega} _0c}}$$

By using the relation, J _x = −en _ev _e, where n _e = n _o + n ₁; $\vec{v}_{\rm e}\lpar { = e\vec{E}/m_{\rm e}i{\rm \omega}_0} \rpar $ is the drift velocity of electrons and we obtain

(7)$$J_x = -\displaystyle{{n_{\rm e}e^2} \over {m_{\rm e}i{\rm \omega} _0}}\left[ {E_x-\displaystyle{i \over {{\rm \omega}_0}}\displaystyle{{\partial A} \over {\partial t}}e^{-i({\rm \omega}_0t-k_0z)}} \right]$$

Using Eqs. (6) and (7) in Eq. (5), we derive in the WKB approximation (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968).

(8)$$2ik_0\displaystyle{{\partial A} \over {\partial z}} + \displaystyle{{\partial ^2A} \over {\partial x^2}} + \displaystyle{{2i{\rm \omega} _0} \over {c^2}}\displaystyle{{\partial A} \over {\partial t}} = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {c^2{\rm \gamma}}} \displaystyle{{n_1} \over {n_0}}A$$

Dynamics of plasma oscillation

A laser with non-uniform amplitude (e.g., Periodic) along its wavefront exerts a relativistic ponderomotive force ($\overrightarrow F _{\rm p}\lcub { = -m_{{\rm e}0}c^2\nabla \lpar {{\rm \gamma} -1} \rpar } \rcub $) on electrons and electrons move away under the influence of this force, from the maximum field amplitude region (Brandi et al., Reference Brandi, Manus and Mainfray1993). For the case, when the pulse duration is shorter than ion plasma period, the ions do not have enough time to move, which creates charge imbalance between ions and electrons which results in a space charge field ($\vec{E}_{\rm p}$). Taking the time derivative of the continuity equation [Eq. (1)] and using the equation of motion of the electron [Eq. (2)], we get the following equation of electron density

(9)$$\eqalign{\displaystyle{{\partial ^2n_{\rm e}} \over {\partial t^2}}-\displaystyle{{e\nabla. \lpar {n_{\rm e}\vec{E}} \rpar } \over {m_{{\rm e}0}{\rm \gamma}}} & = \nabla. \left\{ {\displaystyle{{{\vec{v}}_{\rm e}.\nabla \lpar {{\rm \gamma} {\vec{v}}_{\rm e}} \rpar } \over {\rm \gamma}} + \displaystyle{{e{\vec{v}}_{\rm e} \times \vec{B}} \over {m_{{\rm e}0}{\rm \gamma} c}}} \right\}n_{\rm e} \cr & -\nabla. \left\{ {-\displaystyle{{n_{\rm e}} \over {\rm \gamma}} \displaystyle{{\partial {\rm \gamma}} \over {\partial t}} + \displaystyle{{\partial n_{\rm e}} \over {\partial t}}} \right\}\overrightarrow v _{\rm e}} $$

To get the equation for plasma oscillation, we linearize (n _e = n _o + n ₁, wheren _o ≫ n ₁) Eq. (9) and using the Poisson equation $\lpar {\nabla. {\vec{E}}_{\rm p} = -4{\rm \pi} n_1e} \rpar $, we get

(10)$$\eqalign{\left( {\displaystyle{{\partial^2} \over {\partial t^2}} + \displaystyle{{{\rm \omega}_{{\rm p}0}^2} \over {\rm \gamma}}} \right)n_1 &= -\displaystyle{{c^2n_0} \over {4{\rm \gamma} ^2}}\left[ {{\left( {\displaystyle{e \over {m_{{\rm e}0}{\rm \omega}_0c}}} \right)}^2\left( {\displaystyle{{\partial^2{\vert A \vert }^2} \over {\partial x^2}} + \displaystyle{{\partial^2{\vert A \vert }^2} \over {\partial z^2}}} \right)\right}\right} \cr &\quad\quad\quad+ { \left\left( {\displaystyle{e \over {m_{{\rm e}0}{\rm \omega}_0c}}} \right)}^4\left( {{\left( {\displaystyle{{\partial {\vert A \vert }^2} \over {\partial x}}} \right)}^2 + {\left( {\displaystyle{{\partial {\vert A \vert }^2} \over {\partial z}}} \right)}^2} \right)} \right]$$

Equation (10) represents the non-linear dynamical equation of plasma oscillation under the non-linear force due to the laser pump. We can write the dimensionless form of Eqs. (8) and (10) as follows:

(11)$$i\displaystyle{{\partial {A}^{\prime}} \over {\partial {t}^{\prime}}} + i\displaystyle{{\partial {A}^{\prime}} \over {\partial z^{\prime}}} + \displaystyle{{\partial ^2{A}^{\prime}} \over {\partial {{x}^{\prime}}^2}} = c_4{n}^{\prime}{A}^{\prime}$$

(12)$$\displaystyle{{\partial ^2{n}^{\prime}} \over {\partial {{t}^{\prime}}^2}} + c_1{n}^{\prime} = -c_2\left[ {\displaystyle{{\partial^2{\vert {{A}^{\prime}} \vert }^2} \over {\partial x^{\prime 2}}} + {\left( {\displaystyle{{\partial {\vert {{A}^{\prime}} \vert }^2} \over {\partial x^{\prime}}}} \right)}^2} \right]-c_3\left[ {\displaystyle{{\partial^2{\vert {{A}^{\prime}} \vert }^2} \over {\partial z^{\prime 2}}} + {\left( {\displaystyle{{\partial {\vert {{A}^{\prime}} \vert }^2} \over {\partial z^{\prime}}}} \right)}^2} \right]$$

here,

$$c_1 = \displaystyle{{{\rm \omega} _{{\rm p}0}^2 \,t_{\rm n}^2} \over {\rm \gamma}}, \quad c_2 = \displaystyle{{c^2t_{\rm n}^2 n_0} \over {4{\rm \gamma} ^2x_{\rm n}^2 n_{\rm n}}},\quad c_3 = \displaystyle{{c^2t_{\rm n}^2 n_0} \over {4{\rm \gamma} ^2z_{\rm n}^2 n_{\rm n}}}\;{\rm and}\;c_4 = \displaystyle{1 \over {\rm \gamma}}. $$

In the above equations, primed values represent the normalized quantities:

$$t_{\rm n} = \displaystyle{{2\,{\rm \eta} \,{\rm \omega} _0} \over {c^2k_0^2}}, \quad x_{\rm n} = \displaystyle{{{\lpar {\rm \eta} \rpar }^{0.5}} \over {k_0}},\quad z_{\rm n} = \displaystyle{{\rm \eta} \over {k_0}},\quad n_{\rm n} = \displaystyle{{c^2k_0^2} \over {{\rm \eta} \,{\rm \omega} _{{\rm p}0}^2}} \,n_0\;{\rm and}\;A_{\rm n} = \displaystyle{{{\rm \varsigma} m_{{\rm e}0}{\rm \omega} _0c} \over e}$$

where, η = 1200 and ${\rm \varsigma} = 10$.

The normalizing parameters, $z_{\rm n}^{-1} $ and n _n are a fraction of the wave number k ₀ of the pump laser beam and background number density n ₀, respectively. Now to investigate the impact of plasma oscillations on the localization process of laser and harmonics generation of plasma oscillations, we solve Eqs. (11) and (12) numerically.

Numerical simulation and results

The initial condition of the simulation is considered as

(13a)$${A}^{\prime}{\kern 1pt} {\kern 1pt} \lpar {x,z,0} \rpar \; = \;A_0\lpar {1 + {\rm \beta} \,cos\lpar {{\rm \alpha}_x{x}^{\prime}} \rpar } \rpar \lpar {1 + {\rm \beta} \;\cos \lpar {{\rm \alpha}_z{z}^{\prime}} \rpar } \rpar $$

(13b)$${n}^{\prime}\lpar {x,z,0} \rpar = -n_{10}\vert {{A}^{\prime}(x,z,0)} \vert ^2$$

The initial amplitude of the laser beam and electron plasma density fluctuations are taken as A ₀ = 1 and n ₁₀ = 1, respectively. The perturbation magnitude, β is considered 0.1 for this study. Here, α_x and α_z represent the perturbation wave number and their value is considered 0.1. The equations are numerically solved in a spatial periodic domain of step size (2π/α_x) × (2π/α_z) having 256 × 256 grid points. For space integration, the pseudo-spectral method is used and the finite difference method is used for time evolution with a predictor corrector scheme (Canuto et al., Reference Canuto, Hussaini, Quarteroni and Zang1988). The time step width is “dt” taken as 5 × 10⁻⁶. The veracity of the present algorithm has been established by first using it for a non-linear Schrödinger equation to give a constant Plasmon number. Thereafter, this algorithm is altered to solve our present equations.

The parameters used in the simulation are: ω₀ = 2.35 × 10¹⁵ rad/s, ω_p0 = 0.001ω₀, n ₀ = 1.74 × 10¹⁵/cm³ (under-dense region), a = 1.0, and k _0z = 7.84 × 10⁴ /cm. The normalizing parameters are x _n = 4.4 × 10⁻⁴ cm, z _n = 3.05 × 10⁻² cm, t _n = 1.02 ps, and E _n = 1.34 × 10⁷ stat V/cm. Figure 1a–1c shows the localized structures of field intensity, |A ^′|²of the laser beam in the x-z plane at a distinct time.

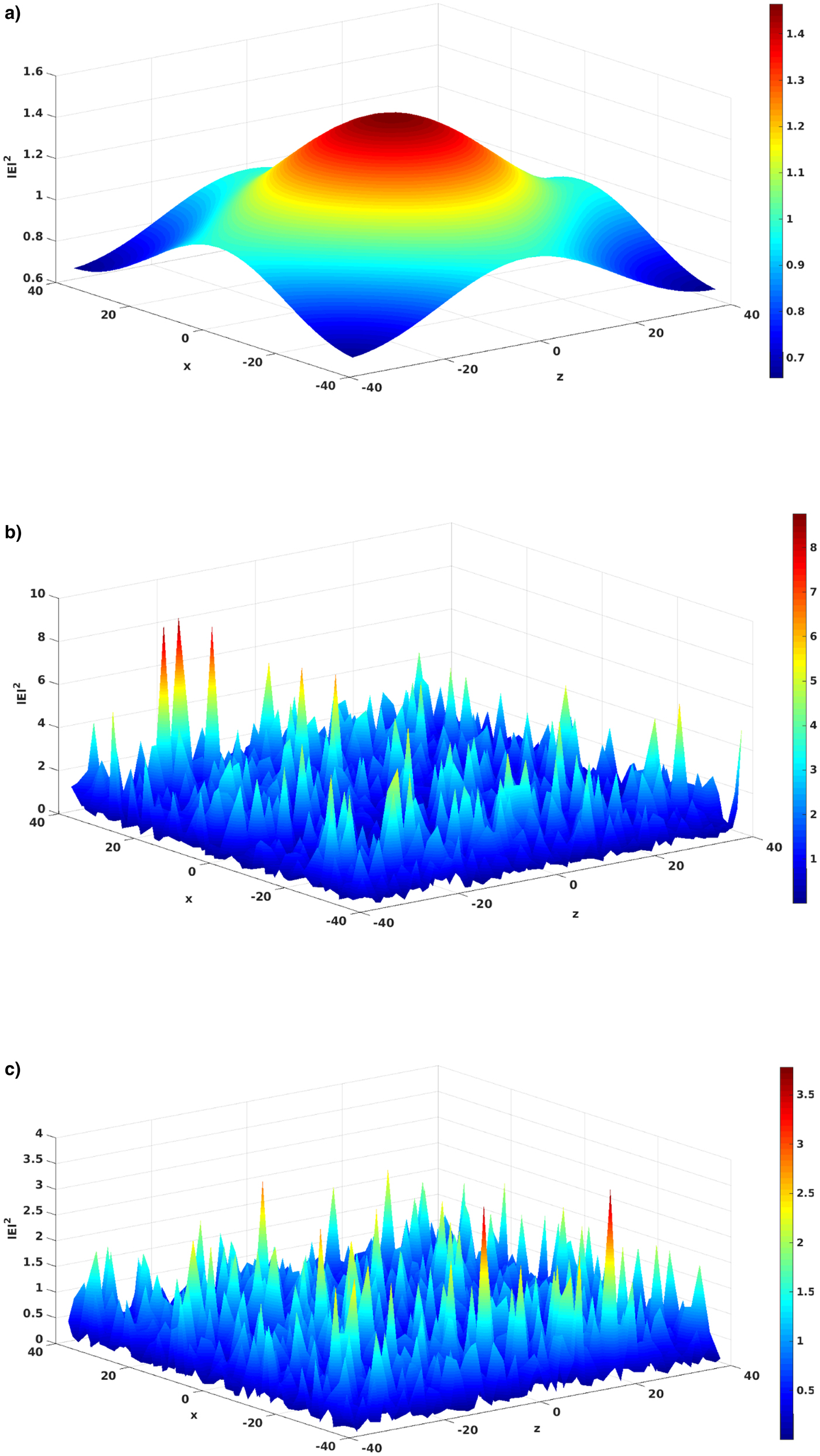
Fig. 1. Normalized intensity profile of the laser beam in the x-z plane at a distinct time (a) t ^′ = 0, (b) t ^′ = 8, and (c) t ^′ = 16.

Electron plasma oscillations perturb the background electron density because the non-linear force arises from the laser pump. This causes the variation of density in the form of modes/harmonic and non-linear coupling between plasma oscillation and laser pump. The density variation or non-linear coupling causes filamentation of laser pump that results in localized structures. Figure 1a shows the commencement of the localized structure formation that progressively grows into a complex localized structure as shown in Figure 1b, 1c. Figure 2 depicts the variation of electron density in the x-z plane at a normalized time, t ^′ = 5. It shows the density depletion in some regions of the x-z plane. The density cavity formations are observed at a distinct time related to the electric field coherent structures. Figure 3 represents the frequency spectrum of the electron plasma oscillations. In this figure, one can observe the excitation of plasma oscillation of THz frequency, appearing due to the density oscillations generated at k _x = α_x,  2α_x, 3α_x  upto 64α_x and the oscillations' peak lies in the THz frequency region. In laser–plasma interaction, the generation of an acoustic wave in the THz region has been experimentally reported by Adak et al. (Reference Adak, Robinson, Singh, Chatterjee, Lad, Pasley and Kumar2015). Figure 4a, 4b shows the normalized density mode | n| variation with k _x (when k _z = 0) at a distinct time. With time, the higher order density modes are generated. The non-linear force due to the laser beam, which is given in R.H.S. of eqn. (12), is responsible for the generation of harmonic in the density (Hussain et al., Reference Hussain, Sharma, Singh, Uma and Sharma2017). When k _z = α_z = 0, at any time we may write Eqs. (13a) and (13b) as follows

(14)$${A}^{\prime}\lpar {x^{\prime},0} \rpar = 1 + {\rm \beta} \cos \lpar {{\rm \alpha}_xx^{\prime}} \rpar $$

(15)$$n^{\prime}\lpar {x^{\prime},0} \rpar = -\lpar {1 + {\rm \beta} \cos \lpar {{\rm \alpha}_xx^{\prime}} \rpar } \rpar ^2 = -\lpar {1 + {\rm \beta}^2{\cos}^2\lpar {{\rm \alpha}_xx^{\prime}} \rpar + 2{\rm \beta} \cos \lpar {{\rm \alpha}_xx^{\prime}} \rpar } \rpar $$

Fig. 2. Plot of the normalized electron density in the x-z plane at a normalized time, t ^′ = 5.

Fig. 3. Plot of the normalized frequency spectrum of the plasma density oscillations.

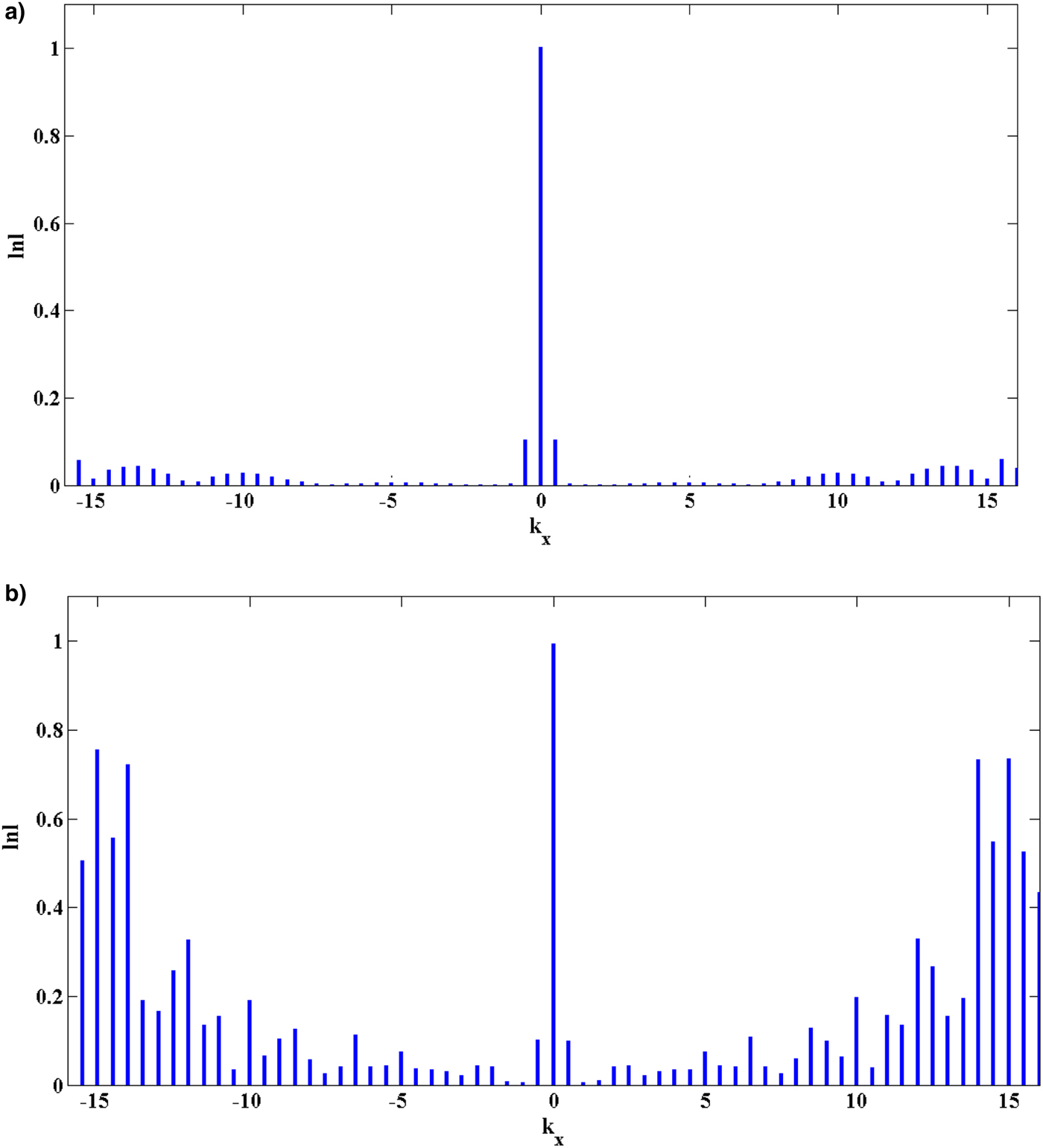
Fig. 4. Variation of the normalized electron density | n|versus k _x (at fixed k _z) for a normalized time (a) t ^′ = 3 and (b) t ^′ = 23.

Equation (15) signifies the generation of density harmonics at α_x and 2α_x. Using Eqs. (14) and (15), the R.H.S. term n ^′A ^′ of Eq. (11) can be expressed as

(16)$${n}^{\prime}{A}^{\prime} = -\lpar {1 + {\rm \beta} {\kern 1pt} \cos \lpar {{\rm \alpha}_x{\kern 1pt} x^{\prime}} \rpar } \rpar \lpar {1 + {\rm \beta}^2{\cos}^2\lpar {{\rm \alpha}_x{\kern 1pt} x^{\prime}} \rpar + 2{\rm \beta} \cos \lpar {{\rm \alpha}_x{\kern 1pt} x^{\prime}} \rpar } \rpar $$

Equation (15) shows the generation of density harmonics corresponding to α_x and 2α_x. Combining Eqs. (14), (15), and (11) one can observe the generation of density harmonics corresponding to α_x, 2α_x, and 3α_x as given in Eq. (16).

Transient self-focusing: a semi-analytical approach

In this section, a semi-analytical approach is discussed using the results acquired from the simulation to describe the role of the non-linear progression of the laser beam as the localized structure and varying number density (Sharma et al., Reference Sharma, Hussain and Gaur2015; Hussain et al., Reference Hussain, Sharma, Singh, Uma and Sharma2017). For a wave having rapid phase variation, the wave equation in the WKB approximation by neglecting the time variation can be written as

(17)$$2ik_0\displaystyle{{\partial A} \over {\partial z}} + \displaystyle{{\partial ^2A} \over {\partial x^2}}-\displaystyle{{k_0^2} \over {{\rm \eta} \,{\rm \gamma}}} \left( {\displaystyle{{n_{\rm e}} \over {n_{\rm n}}}} \right)A = 0$$

where n _n is the normalizing electron density and the time-dependent term (n _e/n _n) can be obtained from simulation results. The time-dependent term is further expanded to incorporate its dependency in Eq. (17).

(18)$$\displaystyle{{n_{\rm e}} \over {n_{\rm n}}} = N + \sum\limits_{\,j = 1}^{64} {n_j\lpar {\cos \lpar {\,j{\rm \alpha}_x{x}^{\prime}} \rpar } \rpar } \,\, = N + \sum\limits_{\,j = 1}^{64} {n_j\left( {1-\displaystyle{{\,j^2{{x}^{\prime}}^2{\rm \alpha}_x^2} \over 2} + \ldots} \right)} $$

Here, N and n _j are the Plasmon number and the number density of harmonics obtained through simulation for j = 1 to 64. One may write the solution of Eq. (17) as follows (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968).

(19)$$A = A_0\lpar {x,z} \rpar e^{ik_0s\lpar {x,z} \rpar }$$

Using the Eqs. (18) and (19) in Eq. (17), and thereafter equating the real and imaginary parts we get Eqs. (20) and (21)

(20)$$-2k_0^2 A_0\displaystyle{{\partial S} \over {\partial z}} + \displaystyle{{\partial ^2A_0} \over {\partial x^2}}-k_0^2 A_0\left( {\displaystyle{{\partial S} \over {\partial x}}} \right)^2-\displaystyle{{k_0^2} \over {{\rm \xi} \,{\rm \gamma}}} A_0\left( {N + \sum\limits_{\,j = 1}^{64} {n_j\left( {1-\displaystyle{{\,j^2{{x}^{\prime}}^2{\rm \alpha}_x^2} \over 2} + \ldots} \right)}} \right) = 0$$

and

(21)$$2\displaystyle{{\partial A_0} \over {\partial z}} + 2\displaystyle{{\partial A_0} \over {\partial x}}\displaystyle{{\partial S} \over {\partial x}} + A_0\displaystyle{{\partial ^2S} \over {\partial x^2}} = 0$$

Introducing an eikonal and initially Gaussian beam of initial beam width r ₀,

(22)$$A_0 = \displaystyle{{E_{00}} \over {\,f^{1/2}}}\exp \left( {-\displaystyle{{x^2} \over {2r_0^2 f^2}}} \right)$$

and

(23)$$S = \displaystyle{{x^2} \over {2f}}\displaystyle{{\partial f} \over {\partial z}}$$

here, E ₀₀ is the initial amplitude of the laser beam. On substituting Eqs. (22) and (23) in Eq. (20) and equating the x ² coefficients; in the paraxial ray approximation, the beam width parameter f is given by

(24)$$\displaystyle{{d^2f} \over {d{\rm \xi} ^2}} = \displaystyle{1 \over {\,f^3}}-\displaystyle{1 \over {{\rm \xi} {\rm \gamma}}} \left( {\displaystyle{{r_0^2 {\rm \omega}_0^2} \over {c^2}}} \right)\displaystyle{1 \over {\,f^2}}\left( {\displaystyle{{E_{00}} \over {E_{\rm n}}}} \right)^2-\displaystyle{1 \over {{\rm \xi} {\rm \gamma}}} \left( {\displaystyle{{r_0^4 {\rm \omega}_0^2} \over {c^2}}} \right)\displaystyle{{\,f\,{\rm \alpha} _x^2} \over 2}\sum\limits_{\,j = 1}^{64} {n_jj^2} $$

where ${\rm \xi} \lpar { = \lpar {c\,z/r_0^2 {\rm \omega}_0} \rpar } \rpar $ is the dimensionless distance of propagation and r ₀( = 10 μm) is the transverse scale size of the wave. Runge Kutta method (fourth order) has been adopted to solve Eq. (24) with the initial boundary conditions$f = 1,\;d{\kern 1pt} f/d {\rm \xi} = 0$ at ξ = 0. The wave can propagate without divergence and convergence when the diffraction term [due to the first part of the R.H.S. of Eq. (24)] balances the non-linear part term [due to the second and third part of the R.H.S. of Eq. (24)]. It is the third term of Eq. (24) that accommodates the transient progression as the magnitude of spectral modes varies with time, thus the transient progression effect of laser pulse occurs. When the laser travels in the plasma, the non-linearity arises in the beam and it suffers self-focusing. With time, the decrease of non-linearity becomes more prominent due to the dominance of natural diffraction and causes the beam defocusing. This phenomenon leads to the competition among the diverging and the converging term (due to the relativistic ponderomotive non-linearity and density oscillations contribution) and leads to the oscillatory self-focusing of the beam. Figure 5a, 5b shows the laser beam localization for two different times, one can notice from the figure that in early time when the impact of the density oscillations via non-linearity is trivial initially then there is no beam focusing. However, the contribution from the density oscillations turns out to be important and leads into a laser beam focusing in a later time.

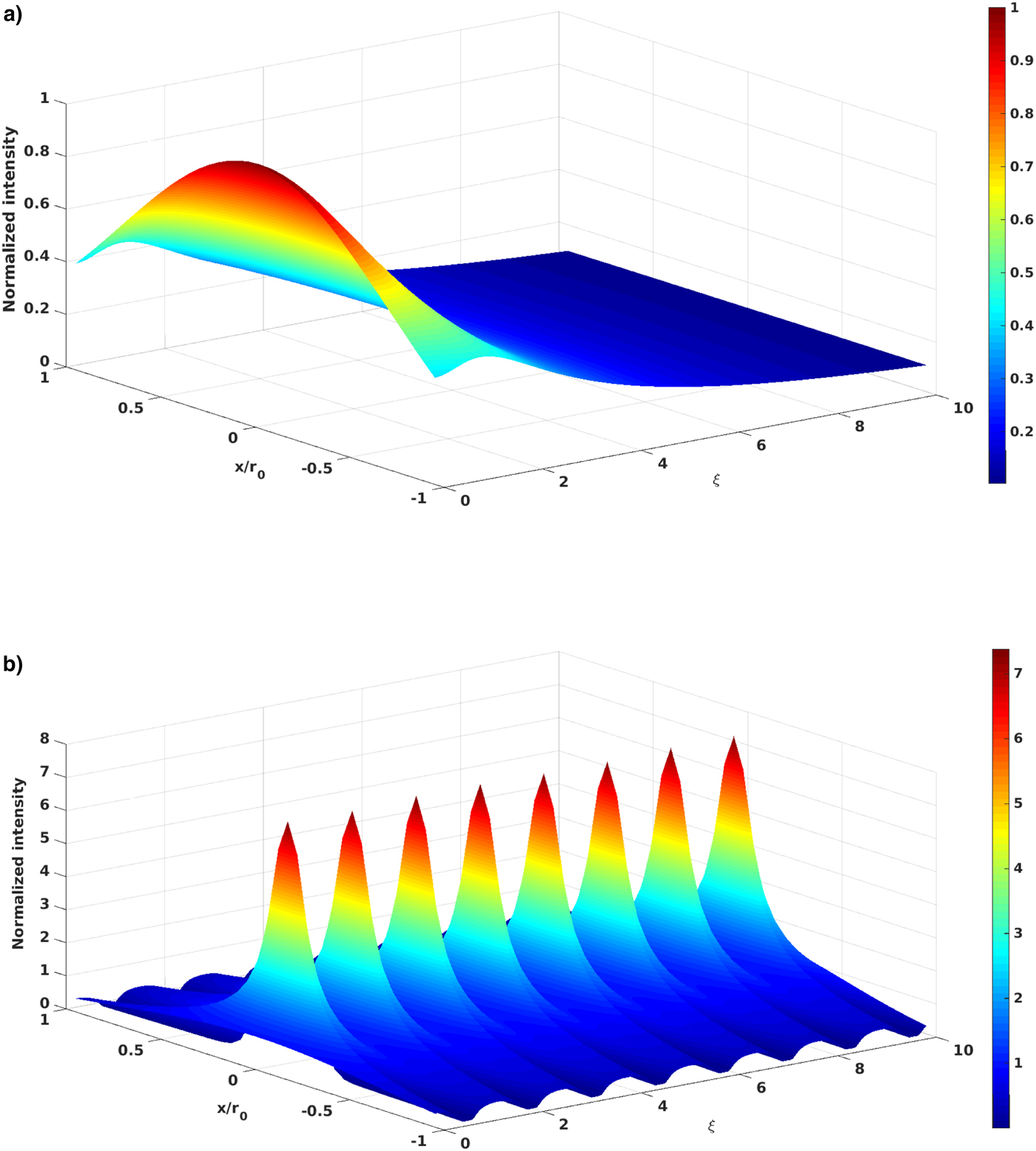
Fig. 5. Normalized intensity profile of the laser beam in the paraxial regime obtained by a semi-analytical model in the x-z plane at a distinct time (a) t ^′ = 2 and (b) t ^′ = 23.