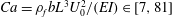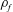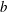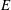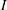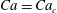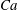1 Introduction
Flow-induced, unsteady dynamics of flexible objects is a ubiquitous phenomenon. Characterization and quantification of the dominant modes of oscillation and the distinctive coupling between flow and structures remain as longstanding open problems. Substantial investigations have focused on understanding the mechanisms modulating the mean bending and drag reduction of wall-mounted elastic structures. Body deformation modifies the drag scaling
![]() $F\propto U^{2}$
common in rigid counterparts to
$F\propto U^{2}$
common in rigid counterparts to
![]() $\propto U^{2+V}$
, where
$\propto U^{2+V}$
, where
![]() $U$
is the flow velocity and
$U$
is the flow velocity and
![]() $V$
is the so-called Vogel exponent. For large flow velocity,
$V$
is the so-called Vogel exponent. For large flow velocity,
![]() $V=-2/3$
, and slender structures typically exhibit quasi-parabolic deformation (Alben, Shelley & Zhang Reference Alben, Shelley and Zhang2002, Reference Alben, Shelley and Zhang2004). The effects of other factors, including buoyancy (Luhar & Nepf Reference Luhar and Nepf2011), skin friction (Bhati et al.
Reference Bhati, Sawanni, Kulkarni and Bhardwaj2018) and mean shear of incoming velocity (Leclercq & De Langre Reference Leclercq and De Langre2016), have also been explored recently to estimate structure reconfiguration. Schouveiler & Boudaoud (Reference Schouveiler and Boudaoud2006) investigated the deformation of a radially cut disk and formulated a model that matched very well the disk drag; it predicts
$V=-2/3$
, and slender structures typically exhibit quasi-parabolic deformation (Alben, Shelley & Zhang Reference Alben, Shelley and Zhang2002, Reference Alben, Shelley and Zhang2004). The effects of other factors, including buoyancy (Luhar & Nepf Reference Luhar and Nepf2011), skin friction (Bhati et al.
Reference Bhati, Sawanni, Kulkarni and Bhardwaj2018) and mean shear of incoming velocity (Leclercq & De Langre Reference Leclercq and De Langre2016), have also been explored recently to estimate structure reconfiguration. Schouveiler & Boudaoud (Reference Schouveiler and Boudaoud2006) investigated the deformation of a radially cut disk and formulated a model that matched very well the disk drag; it predicts
![]() $V=-4/3$
under sufficient deformation.
$V=-4/3$
under sufficient deformation.
Flow instability may modulate body oscillations around the equilibrium bending. Such phenomenon has been extensively explored for the cases of flexible filaments parallel to uniform flows; distinctive, high-amplitude flapping motions may be triggered in individual and tandem configurations (Alben & Shelley Reference Alben and Shelley2008; Jia & Yin Reference Jia and Yin2008; Ristroph & Zhang Reference Ristroph and Zhang2008; Kim, Huang & Sung Reference Kim, Huang and Sung2010; Uddin, Huang & Sung Reference Uddin, Huang and Sung2013). Comparatively, flow-induced oscillations of wall-mounted elastic plates facing a flow are usually less distinctive. Despite the fact that wake fluctuations may induce unsteady force on bent structures, the unsteady force is usually a relatively small fraction of the mean drag (Luhar & Nepf Reference Luhar and Nepf2011) and a secondary factor in determining the structure posture. In those configurations, the plate oscillations may be strongly dominated by the natural frequency, whereas distinctive Kármán vortex shedding may modulate the wake fluctuations (Jin, Kim & Chamorro Reference Jin, Kim and Chamorro2018a ; Jin et al. Reference Jin, Kim, Mao and Chamorro2018b ).
In nature and engineering applications, structures can often be inclined with respect to the incoming flow. Aero/hydrodynamic loads and wake characteristics are significantly influenced by the angle of attack (Fage & Johansen Reference Fage and Johansen1927; Modi et al. Reference Modi, Wiland, Dikshit and Yokomizo1992; Amandolese, Michelin & Choquel Reference Amandolese, Michelin and Choquel2013). Experimental investigations by Lam (Reference Lam1996) and Lam & Leung (Reference Lam and Leung2005) showed the distinctive vortex shedding from inclined rigid plates. Trailing-edge vortices were found to induce more fluid circulation and production of Reynolds stress compared to the leading-edge vortices. Inclined structures produce asymmetric wakes and net aero/hydrodynamic torque on the plate, which may trigger complex rotation or pitching motions dependent on the incoming velocity, plate geometry and structure stiffness (Iversen Reference Iversen1979; Mirzaeisefat & Fernandes Reference Mirzaeisefat and Fernandes2013; Onoue et al. Reference Onoue, Song, Strom and Breuer2015; Jin et al. Reference Jin, Ji, Liu and Chamorro2016). A recent study by Onoue et al. (Reference Onoue, Song, Strom and Breuer2015) reported that the pitching amplitude of a rigid flat plate may exhibit hysteresis and abrupt changes as a function of structure torsional stiffness. Despite this common scenario, the physics modulating the dynamics of wall-mounted inclined flexible plates has not been uncovered.
In this study, we explore such phenomena using theoretical arguments and carefully designed laboratory experiments. We describe three dominant, distinctive modes of plate oscillations, namely, fluttering, twisting and orbital motions. We also show that the intensity of force fluctuations increases significantly past a critical condition, which coincides with the transition from small-amplitude fluttering to twisting. The experimental results and theoretical formulation offer a framework to characterize complex structure motions under flows with arbitrary direction, and insight on the aerodynamic load of elastic structures under a variety of flow fields. The paper is organized as follows: the experimental set-up is elaborated in § 2, the results and analysis are discussed in § 3, and conclusions are provided in § 4.
2 Experimental set-up
Selected laboratory experiments were conducted in the free-stream region of the Talbot wind tunnel at the University of Illinois. The wind tunnel has a test section 6 m long, 0.46 m high and 0.914 m wide; see details of the facility in Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000). A flexible flat plate made of acrylic was mounted over a Velmex rotary table and vertically hung from the top wall of the wind tunnel as a cantilever beam (figure 1
a). The elastic plate was fixed near the entrance of the wind tunnel, at 0.7 m from the inlet, where the boundary layer effects are negligible. The plate has a height
![]() $L=240~\text{mm}$
, width
$L=240~\text{mm}$
, width
![]() $b=60~\text{mm}$
, thickness
$b=60~\text{mm}$
, thickness
![]() $c=0.5~\text{mm}$
, Young’s modulus
$c=0.5~\text{mm}$
, Young’s modulus
![]() $E=2.4~\text{GPa}$
and density
$E=2.4~\text{GPa}$
and density
![]() $\unicode[STIX]{x1D70C}_{m}=1180~\text{kg}~\text{m}^{-3}$
. The high mass ratio
$\unicode[STIX]{x1D70C}_{m}=1180~\text{kg}~\text{m}^{-3}$
. The high mass ratio
![]() $\unicode[STIX]{x1D70C}_{m}/\unicode[STIX]{x1D70C}_{f}\approx 10^{3}$
ensured minor influence of the added mass in the structure dynamics. The unsteady dynamics of the plate was characterized at 35 incoming velocities
$\unicode[STIX]{x1D70C}_{m}/\unicode[STIX]{x1D70C}_{f}\approx 10^{3}$
ensured minor influence of the added mass in the structure dynamics. The unsteady dynamics of the plate was characterized at 35 incoming velocities
![]() $U_{0}\in [3.2,11.1]~\text{m}~\text{s}^{-1}$
every
$U_{0}\in [3.2,11.1]~\text{m}~\text{s}^{-1}$
every
![]() $\unicode[STIX]{x0394}U_{0}\approx 0.23~\text{m}~\text{s}^{-1}$
, resulting in Reynolds numbers
$\unicode[STIX]{x0394}U_{0}\approx 0.23~\text{m}~\text{s}^{-1}$
, resulting in Reynolds numbers
![]() $Re=U_{0}b/\unicode[STIX]{x1D708}\in [1.3,4.4]\times 10^{4}$
, or Cauchy numbers
$Re=U_{0}b/\unicode[STIX]{x1D708}\in [1.3,4.4]\times 10^{4}$
, or Cauchy numbers
![]() $Ca=\unicode[STIX]{x1D70C}_{f}bL^{3}U_{0}^{2}/(EI)\in [7,81]$
(Lu et al.
Reference Lu, Guo, Tang, Liu, Chen and Xie2016); here
$Ca=\unicode[STIX]{x1D70C}_{f}bL^{3}U_{0}^{2}/(EI)\in [7,81]$
(Lu et al.
Reference Lu, Guo, Tang, Liu, Chen and Xie2016); here
![]() $I=bc^{3}/12$
. For each velocity, the plate was placed at an inclination angle
$I=bc^{3}/12$
. For each velocity, the plate was placed at an inclination angle
![]() $\unicode[STIX]{x1D6FC}=0^{\circ },30^{\circ }$
and
$\unicode[STIX]{x1D6FC}=0^{\circ },30^{\circ }$
and
![]() $45^{\circ }$
controlled by the rotary table with an accuracy of 100 arcsec. The angle
$45^{\circ }$
controlled by the rotary table with an accuracy of 100 arcsec. The angle
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
refers to the plate facing the incoming flow (see figure 1
b).
$\unicode[STIX]{x1D6FC}=0^{\circ }$
refers to the plate facing the incoming flow (see figure 1
b).

Figure 1. (a) Schematic of the experimental set-up illustrating the force sensor, rotary table and PTV system. (b) Basic definitions; the origin of the coordinate system is fixed at the centre of the plate base, the black and red fiducial points denote the tips used in other figures, and
![]() $\unicode[STIX]{x1D6FC}$
is the inclination angle at the plate base with respect to the mean flow
$\unicode[STIX]{x1D6FC}$
is the inclination angle at the plate base with respect to the mean flow
![]() $U_{0}$
.
$U_{0}$
.
The instantaneous flow-induced force acting on the elastic plate was measured at a frequency of 1 kHz for periods of 30 s using a high-resolution ATI Gamma load cell connected at the plate base, which was mounted outside of the test section (Jin & Chamorro Reference Jin and Chamorro2017; Jin, Hayat & Chamorro Reference Jin, Hayat and Chamorro2017). The dynamics of the plate tips was tracked using a three-dimensional (3D) particle tracking velocimetry (PTV) system at a frequency of 300 Hz for periods of 30 s with camera views at the bottom and one side of the plate to track instantaneous 3D motions (figure 1
a). The plate was illuminated with two Stanley lithium ion halogen spotlights and captured within an investigation volume of
![]() $240~\text{mm}\times 160~\text{mm}\times 160~\text{mm}$
using two 4 MP Mikrotron EoSens 4CXP MC4082 high-speed cameras. Nikon AF Micro-Nikkor 50 mm lens with a focal ratio
$240~\text{mm}\times 160~\text{mm}\times 160~\text{mm}$
using two 4 MP Mikrotron EoSens 4CXP MC4082 high-speed cameras. Nikon AF Micro-Nikkor 50 mm lens with a focal ratio
![]() $f/2.8$
were used to maximize the focus on the selected investigation volume. The centroid of illuminated fiducial points was detected at subpixel level and tracked using the Hungarian algorithm and linked by performing a three-frame gap closing to obtain linked trajectories. A robust calibration is required to minimize the position error of detected points. The investigation volume was calibrated using a
$f/2.8$
were used to maximize the focus on the selected investigation volume. The centroid of illuminated fiducial points was detected at subpixel level and tracked using the Hungarian algorithm and linked by performing a three-frame gap closing to obtain linked trajectories. A robust calibration is required to minimize the position error of detected points. The investigation volume was calibrated using a
![]() $200~\text{mm}\times 200~\text{mm}$
planar target containing 342 fiducial points placed 10 mm apart. The root mean square (r.m.s.) of the recognized calibration points was
$200~\text{mm}\times 200~\text{mm}$
planar target containing 342 fiducial points placed 10 mm apart. The root mean square (r.m.s.) of the recognized calibration points was
![]() ${\approx}2\times 10^{-4}\,L$
. The calibration process was performed for each case by carefully placing the calibration target in the vicinity of the plate oscillation centre to account for the change in pixel/millimetre ratio along the camera view. To further reduce the error of velocity estimation, the PTV data were smoothed by using the least-squares spline method. More details about the PTV set-up can be found in Kim et al. (Reference Kim, Kim, Liberzon and Chamorro2016). To minimize any initial transient effect, the force fluctuations and tip motions were sampled after the steady state was reached (waiting time of at least 60 s).
${\approx}2\times 10^{-4}\,L$
. The calibration process was performed for each case by carefully placing the calibration target in the vicinity of the plate oscillation centre to account for the change in pixel/millimetre ratio along the camera view. To further reduce the error of velocity estimation, the PTV data were smoothed by using the least-squares spline method. More details about the PTV set-up can be found in Kim et al. (Reference Kim, Kim, Liberzon and Chamorro2016). To minimize any initial transient effect, the force fluctuations and tip motions were sampled after the steady state was reached (waiting time of at least 60 s).

Figure 2. (a) The normal-force coefficient (
![]() $C_{N}$
) for various
$C_{N}$
) for various
![]() $Ca$
and
$Ca$
and
![]() $\unicode[STIX]{x1D6FC}$
. (b) Intensity of the normal-force fluctuations (
$\unicode[STIX]{x1D6FC}$
. (b) Intensity of the normal-force fluctuations (
![]() $I_{N}$
) across various
$I_{N}$
) across various
![]() $Ca$
and
$Ca$
and
![]() $\unicode[STIX]{x1D6FC}$
. (c,d) Sample time series of the normal force
$\unicode[STIX]{x1D6FC}$
. (c,d) Sample time series of the normal force
![]() $F_{N}$
at the plate base right below (
$F_{N}$
at the plate base right below (
![]() $Ca=20.5$
for panel c) and above (
$Ca=20.5$
for panel c) and above (
![]() $Ca=24$
for panel d)
$Ca=24$
for panel d)
![]() $Ca_{c}$
at
$Ca_{c}$
at
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. (e–g) Snapshots of plate dynamics at
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. (e–g) Snapshots of plate dynamics at
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
and various
$\unicode[STIX]{x1D6FC}=45^{\circ }$
and various
![]() $Ca$
: (e)
$Ca$
: (e)
![]() $Ca=9$
, (f)
$Ca=9$
, (f)
![]() $Ca=32$
and (g)
$Ca=32$
and (g)
![]() $Ca=68$
. Here (i), (ii) and (iii) are instants highlighting dominant modes of tip motion.
$Ca=68$
. Here (i), (ii) and (iii) are instants highlighting dominant modes of tip motion.
3 Results
3.1 Aerodynamic force fluctuations and plate dynamics
Characterization of the plate motions and fluctuations of the aerodynamic force across
![]() $Ca$
and
$Ca$
and
![]() $\unicode[STIX]{x1D6FC}$
revealed distinctive patterns. First, quantification of the normal-force coefficient
$\unicode[STIX]{x1D6FC}$
revealed distinctive patterns. First, quantification of the normal-force coefficient
![]() $C_{N}=2F_{N}/(\unicode[STIX]{x1D70C}_{f}U_{0}^{2}bL)$
is illustrated in figure 2(a); here,
$C_{N}=2F_{N}/(\unicode[STIX]{x1D70C}_{f}U_{0}^{2}bL)$
is illustrated in figure 2(a); here,
![]() $F_{N}$
is the force component normal to the plate base. Despite the large variation of the inclination angle
$F_{N}$
is the force component normal to the plate base. Despite the large variation of the inclination angle
![]() $\unicode[STIX]{x1D6FC}$
, the trends of
$\unicode[STIX]{x1D6FC}$
, the trends of
![]() $C_{N}$
as a function of
$C_{N}$
as a function of
![]() $Ca$
are comparable. For
$Ca$
are comparable. For
![]() $Ca\lesssim 20$
one has
$Ca\lesssim 20$
one has
![]() $C_{N}\propto Ca^{-1/3}$
and for
$C_{N}\propto Ca^{-1/3}$
and for
![]() $Ca\gtrsim 20$
one has
$Ca\gtrsim 20$
one has
![]() $C_{N}\propto Ca^{-2/3}$
, corresponding to Vogel exponents of
$C_{N}\propto Ca^{-2/3}$
, corresponding to Vogel exponents of
![]() $V=-2/3$
and
$V=-2/3$
and
![]() $-4/3$
. Similar results were noted by Gosselin, De Langre & Machado-Almeida (Reference Gosselin, De Langre and Machado-Almeida2010) on flexible rectangular plates (their figure 5), indicating that strong plate deformation may alter the interaction mechanism between the plate and flow. Bulk quantification of the plate dynamics can be obtained with the intensity of the force fluctuations. In particular, distributions of the component normal to the base of the plate
$-4/3$
. Similar results were noted by Gosselin, De Langre & Machado-Almeida (Reference Gosselin, De Langre and Machado-Almeida2010) on flexible rectangular plates (their figure 5), indicating that strong plate deformation may alter the interaction mechanism between the plate and flow. Bulk quantification of the plate dynamics can be obtained with the intensity of the force fluctuations. In particular, distributions of the component normal to the base of the plate
![]() $I_{N}$
(
$I_{N}$
(
![]() $=2\unicode[STIX]{x1D70E}_{N}/(\unicode[STIX]{x1D70C}_{f}U_{0}^{2}bL)$
, where
$=2\unicode[STIX]{x1D70E}_{N}/(\unicode[STIX]{x1D70C}_{f}U_{0}^{2}bL)$
, where
![]() $\unicode[STIX]{x1D70E}_{N}$
is the standard deviation of
$\unicode[STIX]{x1D70E}_{N}$
is the standard deviation of
![]() $F_{N}$
) as a function of
$F_{N}$
) as a function of
![]() $Ca$
are illustrated in figure 2(b). It shows negligible differences between plate inclinations for sufficiently low
$Ca$
are illustrated in figure 2(b). It shows negligible differences between plate inclinations for sufficiently low
![]() $Ca$
, and abrupt increase of the force fluctuations past a critical
$Ca$
, and abrupt increase of the force fluctuations past a critical
![]() $Ca=Ca_{c}$
threshold that depended on the inclination angle. Such a critical condition occurred at
$Ca=Ca_{c}$
threshold that depended on the inclination angle. Such a critical condition occurred at
![]() $Ca_{c}=34$
and 22 for
$Ca_{c}=34$
and 22 for
![]() $\unicode[STIX]{x1D6FC}=30^{\circ }$
and
$\unicode[STIX]{x1D6FC}=30^{\circ }$
and
![]() $45^{\circ }$
cases, but it was absent at
$45^{\circ }$
cases, but it was absent at
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
. To highlight the sharp change on the force fluctuations, figure 2(c,d) illustrates a sample time series of the normal force at the plate base
$\unicode[STIX]{x1D6FC}=0^{\circ }$
. To highlight the sharp change on the force fluctuations, figure 2(c,d) illustrates a sample time series of the normal force at the plate base
![]() $F_{N}$
for the case
$F_{N}$
for the case
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
right before (
$\unicode[STIX]{x1D6FC}=45^{\circ }$
right before (
![]() $Ca=20.5$
) and after (
$Ca=20.5$
) and after (
![]() $Ca=24$
)
$Ca=24$
)
![]() $Ca_{c}$
. Despite the similar averaged values, distinctive high-amplitude periodic oscillations occurred right within
$Ca_{c}$
. Despite the similar averaged values, distinctive high-amplitude periodic oscillations occurred right within
![]() $Ca>Ca_{c}$
implying the onset of a different oscillation mode. This is also consistent with recent work by Leclercq, Peake & de Langre (Reference Leclercq, Peake and de Langre2018), where plate motions had a minor influence on the time-averaged flow-induced loads.
$Ca>Ca_{c}$
implying the onset of a different oscillation mode. This is also consistent with recent work by Leclercq, Peake & de Langre (Reference Leclercq, Peake and de Langre2018), where plate motions had a minor influence on the time-averaged flow-induced loads.
The instantaneous snapshots shown in figure 2(e–g) provide a basic linkage of the force fluctuation and distinctive dynamics of the plate motions for the particular case with
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. At
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. At
![]() $Ca<Ca_{c}$
(figure 2
e), the plate exhibited small-amplitude fluttering around the bending equilibrium. The increase of
$Ca<Ca_{c}$
(figure 2
e), the plate exhibited small-amplitude fluttering around the bending equilibrium. The increase of
![]() $Ca$
over
$Ca$
over
![]() $Ca_{c}$
(figure 2
f) resulted in twisting oscillations around a relatively larger bending. At sufficiently high
$Ca_{c}$
(figure 2
f) resulted in twisting oscillations around a relatively larger bending. At sufficiently high
![]() $Ca$
, the plate tips exhibited comparatively large-scale orbital motions; this condition happened at
$Ca$
, the plate tips exhibited comparatively large-scale orbital motions; this condition happened at
![]() $Ca\gtrsim 43$
(
$Ca\gtrsim 43$
(
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
). There, the tip was dominated by anticlockwise orbits coupled with twisting oscillations, as illustrated in figure 2(g). See additional details in the supplementary movies available at https://doi.org/10.1017/jfm.2019.40.
$\unicode[STIX]{x1D6FC}=45^{\circ }$
). There, the tip was dominated by anticlockwise orbits coupled with twisting oscillations, as illustrated in figure 2(g). See additional details in the supplementary movies available at https://doi.org/10.1017/jfm.2019.40.
The trajectories of the tip motions for various
![]() $Ca$
and
$Ca$
and
![]() $\unicode[STIX]{x1D6FC}$
illustrate the dominant modes of oscillation. Indeed, figure 3(a–c) shows minor fluttering corresponding to low
$\unicode[STIX]{x1D6FC}$
illustrate the dominant modes of oscillation. Indeed, figure 3(a–c) shows minor fluttering corresponding to low
![]() $I_{N}$
around the bending equilibrium for
$I_{N}$
around the bending equilibrium for
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
. Such a mode is also observed under
$\unicode[STIX]{x1D6FC}=0^{\circ }$
. Such a mode is also observed under
![]() $\unicode[STIX]{x1D6FC}=30^{\circ }$
and
$\unicode[STIX]{x1D6FC}=30^{\circ }$
and
![]() $45^{\circ }$
within
$45^{\circ }$
within
![]() $Ca<Ca_{c}$
(figure 3
d,g). At
$Ca<Ca_{c}$
(figure 3
d,g). At
![]() $Ca_{c}$
, the plate experienced the onset of twisting oscillations. This resulted in stronger tip motions and, consequently, increased
$Ca_{c}$
, the plate experienced the onset of twisting oscillations. This resulted in stronger tip motions and, consequently, increased
![]() $I_{N}$
(figure 3
e,f,h,i). As expected, the intensity of tip oscillations increased with
$I_{N}$
(figure 3
e,f,h,i). As expected, the intensity of tip oscillations increased with
![]() $Ca$
and
$Ca$
and
![]() $\unicode[STIX]{x1D6FC}$
. Dominant 3D orbital motions occurred at a specific threshold, which is the case in figure 3(i) at
$\unicode[STIX]{x1D6FC}$
. Dominant 3D orbital motions occurred at a specific threshold, which is the case in figure 3(i) at
![]() $Ca=68$
and
$Ca=68$
and
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. It is worth noting that such 3D dynamics led to significant deviations of the plate tips from the bending equilibrium; in this case the orbits from each tip overlapped.
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. It is worth noting that such 3D dynamics led to significant deviations of the plate tips from the bending equilibrium; in this case the orbits from each tip overlapped.

Figure 3. Trajectories of the tips for various
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $Ca$
: (a–c)
$Ca$
: (a–c)
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
with
$\unicode[STIX]{x1D6FC}=0^{\circ }$
with
![]() $Ca=7$
, 41 and 68; (d–f) same as (a–c) with
$Ca=7$
, 41 and 68; (d–f) same as (a–c) with
![]() $\unicode[STIX]{x1D6FC}=30^{\circ }$
; (g–i) same as (a–c) with
$\unicode[STIX]{x1D6FC}=30^{\circ }$
; (g–i) same as (a–c) with
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. Here
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. Here
![]() $x^{\ast }=x/L$
,
$x^{\ast }=x/L$
,
![]() $y^{\ast }=y/L$
and
$y^{\ast }=y/L$
and
![]() $z^{\ast }=z/L$
denote the normalized tip locations. The blue lines represent the location of the plate base.
$z^{\ast }=z/L$
denote the normalized tip locations. The blue lines represent the location of the plate base.
Specific insight on the distinctive modes of oscillation is obtained by examining the representative trajectories and spectra of the tip velocity. In the fluttering-like mode, the bending deformation dominates the reconfiguration of the elastic plate where the tip is nearly parallel to the base. As noted in figure 4(a), the streamwise velocity spectrum
![]() $\unicode[STIX]{x1D6F7}^{\ast }$
of one of the tip edges evidences the modulation of the first- and second-order natural frequencies of the bending; these are given by
$\unicode[STIX]{x1D6F7}^{\ast }$
of one of the tip edges evidences the modulation of the first- and second-order natural frequencies of the bending; these are given by
![]() $f_{b,r}=(j_{r}/L^{2})\sqrt{EI/(\unicode[STIX]{x1D70C}_{m}bc)}$
, where
$f_{b,r}=(j_{r}/L^{2})\sqrt{EI/(\unicode[STIX]{x1D70C}_{m}bc)}$
, where
![]() $j_{1}=0.56$
and
$j_{1}=0.56$
and
![]() $j_{2}=3.51$
. As reported in previous works (Fage & Johansen Reference Fage and Johansen1927; Modi et al.
Reference Modi, Wiland, Dikshit and Yokomizo1992; Onoue et al.
Reference Onoue, Song, Strom and Breuer2015; Liu et al.
Reference Liu, Hamed, Jin and Chamorro2017), for a thin flat plate inclined with respect to the mean flow, the aerodynamic load produces a torque
$j_{2}=3.51$
. As reported in previous works (Fage & Johansen Reference Fage and Johansen1927; Modi et al.
Reference Modi, Wiland, Dikshit and Yokomizo1992; Onoue et al.
Reference Onoue, Song, Strom and Breuer2015; Liu et al.
Reference Liu, Hamed, Jin and Chamorro2017), for a thin flat plate inclined with respect to the mean flow, the aerodynamic load produces a torque
![]() $M$
that tends to twist the frontal surface perpendicular to the free-stream flow. Its magnitude is given by
$M$
that tends to twist the frontal surface perpendicular to the free-stream flow. Its magnitude is given by
where
![]() $C_{M}(\unicode[STIX]{x1D6FC})$
is the moment coefficient,
$C_{M}(\unicode[STIX]{x1D6FC})$
is the moment coefficient,
![]() $U_{e}$
is the effective wind speed and
$U_{e}$
is the effective wind speed and
![]() $A$
represents a characteristic area of the structure. An increase of the velocity results in an increment of the torque and the likelihood of tip twisting, which is controlled by the body stiffness. Such modulation, however, is continuously disturbed by the wake fluctuations resulting in twisting oscillations (figure 4
b). The height difference between the tips (
$A$
represents a characteristic area of the structure. An increase of the velocity results in an increment of the torque and the likelihood of tip twisting, which is controlled by the body stiffness. Such modulation, however, is continuously disturbed by the wake fluctuations resulting in twisting oscillations (figure 4
b). The height difference between the tips (
![]() $\unicode[STIX]{x0394}z_{t}^{\ast }$
) leads to the tip not being parallel to the base. In such cases, the tip velocity was substantially higher than the fluttering-like mode and exhibited semi-periodic variations. This is reflected by the dominating frequency component
$\unicode[STIX]{x0394}z_{t}^{\ast }$
) leads to the tip not being parallel to the base. In such cases, the tip velocity was substantially higher than the fluttering-like mode and exhibited semi-periodic variations. This is reflected by the dominating frequency component
![]() $f_{t}$
in the spectral domain. It is worth noting that
$f_{t}$
in the spectral domain. It is worth noting that
![]() $f_{t}$
remains nearly constant within all the twisting configurations, indicating that it is determined only by the characteristics of the structure.
$f_{t}$
remains nearly constant within all the twisting configurations, indicating that it is determined only by the characteristics of the structure.

Figure 4. Sampled tip trajectories and normalized streamwise velocity spectra
![]() $\unicode[STIX]{x1D6F7}^{\ast }=\unicode[STIX]{x1D6F7}/\text{max}\{\unicode[STIX]{x1D6F7}\}$
of a tip under (a)
$\unicode[STIX]{x1D6F7}^{\ast }=\unicode[STIX]{x1D6F7}/\text{max}\{\unicode[STIX]{x1D6F7}\}$
of a tip under (a)
![]() $Ca=7$
and
$Ca=7$
and
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
, (b)
$\unicode[STIX]{x1D6FC}=0^{\circ }$
, (b)
![]() $Ca=41$
and
$Ca=41$
and
![]() $\unicode[STIX]{x1D6FC}=30^{\circ }$
, (c)
$\unicode[STIX]{x1D6FC}=30^{\circ }$
, (c)
![]() $Ca=41$
and
$Ca=41$
and
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
, and (d)
$\unicode[STIX]{x1D6FC}=45^{\circ }$
, and (d)
![]() $Ca=68$
and
$Ca=68$
and
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. The colour bar indicates the normalized height difference between the tips (
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. The colour bar indicates the normalized height difference between the tips (
![]() $\unicode[STIX]{x0394}z_{t}^{\ast }$
). The two-headed blue arrow in (b) denotes the twisting oscillations, whereas the anticlockwise arrow in (d) indicates the 3D orbital motion of the tips composed of three stages. The insets show the (red) tip streamwise velocity
$\unicode[STIX]{x0394}z_{t}^{\ast }$
). The two-headed blue arrow in (b) denotes the twisting oscillations, whereas the anticlockwise arrow in (d) indicates the 3D orbital motion of the tips composed of three stages. The insets show the (red) tip streamwise velocity
![]() $u_{t}$
.
$u_{t}$
.

Figure 5. Normalized base normal-force spectra
![]() $\unicode[STIX]{x1D6F7}_{N}^{\ast }=\unicode[STIX]{x1D6F7}/\text{max}\{\unicode[STIX]{x1D6F7}\}$
at
$\unicode[STIX]{x1D6F7}_{N}^{\ast }=\unicode[STIX]{x1D6F7}/\text{max}\{\unicode[STIX]{x1D6F7}\}$
at
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
and (a)
$\unicode[STIX]{x1D6FC}=45^{\circ }$
and (a)
![]() $Ca=36.3$
, (b)
$Ca=36.3$
, (b)
![]() $Ca=38.6$
and (c)
$Ca=38.6$
and (c)
![]() $Ca=41$
. The dashed arrows indicate the gradual increase of the frequency component corresponding to the orbital motions.
$Ca=41$
. The dashed arrows indicate the gradual increase of the frequency component corresponding to the orbital motions.

Figure 6. Instantaneous tip heights
![]() $z^{\ast }=z/L$
during one representative orbital cycle under
$z^{\ast }=z/L$
during one representative orbital cycle under
![]() $Ca=68$
and
$Ca=68$
and
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
; here
$\unicode[STIX]{x1D6FC}=45^{\circ }$
; here
![]() $T_{r}=1/f_{r}$
is the period of orbital motion. The black and red points denote each tip.
$T_{r}=1/f_{r}$
is the period of orbital motion. The black and red points denote each tip.
Unlike the abrupt occurrence of the twisting mode from fluttering with
![]() $Ca$
, the transition from twisting to 3D orbits is comparatively a gradual process, where
$Ca$
, the transition from twisting to 3D orbits is comparatively a gradual process, where
![]() $I_{N}$
remains approximately constant. Indeed, the gradual development of the orbital motions may be noted from the changes on the normalized spectra
$I_{N}$
remains approximately constant. Indeed, the gradual development of the orbital motions may be noted from the changes on the normalized spectra
![]() $\unicode[STIX]{x1D6F7}_{N}^{\ast }$
of the base normal force
$\unicode[STIX]{x1D6F7}_{N}^{\ast }$
of the base normal force
![]() $F_{N}$
with
$F_{N}$
with
![]() $Ca$
(figure 5). Within the transition between twisting and orbital modes, the twisting mode
$Ca$
(figure 5). Within the transition between twisting and orbital modes, the twisting mode
![]() $f_{t}$
dominates the force fluctuations, whereas the signature of the orbital motions,
$f_{t}$
dominates the force fluctuations, whereas the signature of the orbital motions,
![]() $f_{r}$
, exhibits a monotonic increase with
$f_{r}$
, exhibits a monotonic increase with
![]() $Ca$
. In such a process, the force fluctuation intensity
$Ca$
. In such a process, the force fluctuation intensity
![]() $\unicode[STIX]{x1D70E}_{N}^{2}=\int \unicode[STIX]{x1D6F7}\,\text{d}f$
does not show abrupt changes due to the very similar
$\unicode[STIX]{x1D70E}_{N}^{2}=\int \unicode[STIX]{x1D6F7}\,\text{d}f$
does not show abrupt changes due to the very similar
![]() $\unicode[STIX]{x1D6F7}$
distributions across
$\unicode[STIX]{x1D6F7}$
distributions across
![]() $Ca$
. The corresponding tip dynamics in the transition to orbital motions is illustrated with tip trajectories in figure 4(c) at
$Ca$
. The corresponding tip dynamics in the transition to orbital motions is illustrated with tip trajectories in figure 4(c) at
![]() $Ca=41$
and
$Ca=41$
and
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. It is characterized by twisting and 3D orbital motions. The associated tip velocity spectrum also reveals a dominant effect of the twisting mode (
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. It is characterized by twisting and 3D orbital motions. The associated tip velocity spectrum also reveals a dominant effect of the twisting mode (
![]() $f_{t}$
) and the orbital motion
$f_{t}$
) and the orbital motion
![]() $f_{r}$
. The distinctive mode of orbital motions is observed only under
$f_{r}$
. The distinctive mode of orbital motions is observed only under
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
and
$\unicode[STIX]{x1D6FC}=45^{\circ }$
and
![]() $Ca\gtrsim 43$
, which is a result of the coupling between plate twisting and bending as a three-stage process illustrated in figure 4(d) and figure 6 with instantaneous tip heights. The flow-induced torque at sufficiently high
$Ca\gtrsim 43$
, which is a result of the coupling between plate twisting and bending as a three-stage process illustrated in figure 4(d) and figure 6 with instantaneous tip heights. The flow-induced torque at sufficiently high
![]() $Ca$
and
$Ca$
and
![]() $\unicode[STIX]{x1D6FC}$
leads to distinctive twisting of the plate near the tip such that the local projected area to the incoming flow increases (stage 1); this induces an abrupt increase of the aerodynamic load in the vicinity of the tip and substantial structure bending as highlighted by the decrease of
$\unicode[STIX]{x1D6FC}$
leads to distinctive twisting of the plate near the tip such that the local projected area to the incoming flow increases (stage 1); this induces an abrupt increase of the aerodynamic load in the vicinity of the tip and substantial structure bending as highlighted by the decrease of
![]() $z^{\ast }$
of both tips (stage 2). As depicted in figure 2(f,ii), relatively high load can substantially deform the elastic plate; local bending angle of the plate near the tip relative to the vertical axis can reach or even be larger than
$z^{\ast }$
of both tips (stage 2). As depicted in figure 2(f,ii), relatively high load can substantially deform the elastic plate; local bending angle of the plate near the tip relative to the vertical axis can reach or even be larger than
![]() $90^{\circ }$
. In this scenario (stage 3), the tip aerodynamic load drops significantly due to the reduced projected area. The structure restoring force governs the motion of the plate, pushing the tip back to the posture at stage 1, which completes an orbital cycle. Similar to the twisting mode,
$90^{\circ }$
. In this scenario (stage 3), the tip aerodynamic load drops significantly due to the reduced projected area. The structure restoring force governs the motion of the plate, pushing the tip back to the posture at stage 1, which completes an orbital cycle. Similar to the twisting mode,
![]() $f_{r}$
is independent of
$f_{r}$
is independent of
![]() $Ca$
within the inspected configurations, despite the significant variation of the intensity of the orbital motions.
$Ca$
within the inspected configurations, despite the significant variation of the intensity of the orbital motions.
3.2 Theoretical estimation of the critical
 $Ca$
or
$Ca$
or
 $Ca_{c}$
$Ca_{c}$
An uncovered key quantity is the threshold
![]() $Ca_{c}$
that defines the condition of abrupt increase of force fluctuations leading to substantial unsteady loading. The aerodynamic load of an elastic structure undergoing simultaneous bending and twisting involves a number of physical processes. To tackle this problem quantitatively, we consider that the plate experiences minor deformation in a portion close to the tip. This assumption is well supported by the tracking of plate postures under
$Ca_{c}$
that defines the condition of abrupt increase of force fluctuations leading to substantial unsteady loading. The aerodynamic load of an elastic structure undergoing simultaneous bending and twisting involves a number of physical processes. To tackle this problem quantitatively, we consider that the plate experiences minor deformation in a portion close to the tip. This assumption is well supported by the tracking of plate postures under
![]() $Ca<Ca_{c}$
(figure 2
d) and previous studies (Schouveiler, Eloy & Le Gal Reference Schouveiler, Eloy and Le Gal2005). Also, the plate dynamics shows that the plate remains nearly parallel to its base before the occurrence of the twisting mode. Hence, as a first-order approximation, we focus our analysis on the plate tip region with a constant local bending angle (
$Ca<Ca_{c}$
(figure 2
d) and previous studies (Schouveiler, Eloy & Le Gal Reference Schouveiler, Eloy and Le Gal2005). Also, the plate dynamics shows that the plate remains nearly parallel to its base before the occurrence of the twisting mode. Hence, as a first-order approximation, we focus our analysis on the plate tip region with a constant local bending angle (
![]() $\unicode[STIX]{x1D703}$
) and inclination angle
$\unicode[STIX]{x1D703}$
) and inclination angle
![]() $\unicode[STIX]{x1D6FC}$
relative to the free-stream flow at equilibrium, as illustrated in figure 7(a). There, the governing equation of the twisting dynamics of the plate can be characterized by
$\unicode[STIX]{x1D6FC}$
relative to the free-stream flow at equilibrium, as illustrated in figure 7(a). There, the governing equation of the twisting dynamics of the plate can be characterized by
where
![]() $\hat{\unicode[STIX]{x1D6FC}}$
is the modified inclination angle due to plate bending,
$\hat{\unicode[STIX]{x1D6FC}}$
is the modified inclination angle due to plate bending,
![]() $I_{w},~c_{w}$
and
$I_{w},~c_{w}$
and
![]() $k_{w}$
represent the polar moment of inertia, damping coefficient and torsional stiffness corresponding to the section under inspection, and
$k_{w}$
represent the polar moment of inertia, damping coefficient and torsional stiffness corresponding to the section under inspection, and
![]() $\hat{\unicode[STIX]{x1D6FC}}_{e}$
is the effective inclination angle modulated by the plate angular velocity. Here, the positive
$\hat{\unicode[STIX]{x1D6FC}}_{e}$
is the effective inclination angle modulated by the plate angular velocity. Here, the positive
![]() $M$
is defined to induce a decrease of
$M$
is defined to induce a decrease of
![]() $\hat{\unicode[STIX]{x1D6FC}}$
. For an inclined bent plate, the effective wind speed
$\hat{\unicode[STIX]{x1D6FC}}$
. For an inclined bent plate, the effective wind speed
![]() $U_{e}$
is taken as the velocity component normal to the plate span (figure 7
a), whereas the modified inclination angle at the equilibrium (
$U_{e}$
is taken as the velocity component normal to the plate span (figure 7
a), whereas the modified inclination angle at the equilibrium (
![]() $\hat{\unicode[STIX]{x1D6FC}}_{s}$
) is defined between
$\hat{\unicode[STIX]{x1D6FC}}_{s}$
) is defined between
![]() $U_{e}$
and the normal vector
$U_{e}$
and the normal vector
![]() $\boldsymbol{n}$
of the plate surface at the equilibrium bending position, as follows:
$\boldsymbol{n}$
of the plate surface at the equilibrium bending position, as follows:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle U_{e}=U_{0}\sqrt{1-\cos ^{2}\unicode[STIX]{x1D6FC}\sin ^{2}\unicode[STIX]{x1D703}},\\[4.0pt] \displaystyle \sin \hat{\unicode[STIX]{x1D6FC}}_{s}=\frac{\sin \unicode[STIX]{x1D6FC}}{\sqrt{1-\cos ^{2}\unicode[STIX]{x1D6FC}\sin ^{2}\unicode[STIX]{x1D703}}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle U_{e}=U_{0}\sqrt{1-\cos ^{2}\unicode[STIX]{x1D6FC}\sin ^{2}\unicode[STIX]{x1D703}},\\[4.0pt] \displaystyle \sin \hat{\unicode[STIX]{x1D6FC}}_{s}=\frac{\sin \unicode[STIX]{x1D6FC}}{\sqrt{1-\cos ^{2}\unicode[STIX]{x1D6FC}\sin ^{2}\unicode[STIX]{x1D703}}}.\end{array}\right\}\end{eqnarray}$$

Figure 7. (a) Schematic illustrating parameters near plate tip region with bending angle
![]() $\unicode[STIX]{x1D703}$
. (b) Schematic of the cross-section of the plate undergoing twisting motion under the influence of instantaneous angular velocity. The ‘
$\unicode[STIX]{x1D703}$
. (b) Schematic of the cross-section of the plate undergoing twisting motion under the influence of instantaneous angular velocity. The ‘
![]() $+$
’ symbol denotes the plate centre. (c) Distribution of the plate tips projected in the
$+$
’ symbol denotes the plate centre. (c) Distribution of the plate tips projected in the
![]() $x{-}z$
plane under
$x{-}z$
plane under
![]() $Ca=7$
and (i)
$Ca=7$
and (i)
![]() $\unicode[STIX]{x1D6FC}=0^{\circ }$
, (ii)
$\unicode[STIX]{x1D6FC}=0^{\circ }$
, (ii)
![]() $\unicode[STIX]{x1D6FC}=30^{\circ }$
and (iii)
$\unicode[STIX]{x1D6FC}=30^{\circ }$
and (iii)
![]() $\unicode[STIX]{x1D6FC}=45^{\circ }$
. (d) Distribution of
$\unicode[STIX]{x1D6FC}=45^{\circ }$
. (d) Distribution of
![]() $C_{M}=2M/(\unicode[STIX]{x1D70C}_{f}U_{0}^{2}b^{2}L)$
with
$C_{M}=2M/(\unicode[STIX]{x1D70C}_{f}U_{0}^{2}b^{2}L)$
with
![]() $\unicode[STIX]{x1D6FC}$
of a rigid plate with the same geometry.
$\unicode[STIX]{x1D6FC}$
of a rigid plate with the same geometry.
The effective inclination angle
![]() $\hat{\unicode[STIX]{x1D6FC}}_{e}$
is influenced by the instantaneous angular velocity of the plate. Following the linear quasi-steady analysis characterizing the torsional instability (Païdoussis, Price & De Langre Reference Païdoussis, Price and De Langre2010), we consider an instant where the plate is in a given
$\hat{\unicode[STIX]{x1D6FC}}_{e}$
is influenced by the instantaneous angular velocity of the plate. Following the linear quasi-steady analysis characterizing the torsional instability (Païdoussis, Price & De Langre Reference Païdoussis, Price and De Langre2010), we consider an instant where the plate is in a given
![]() $\hat{\unicode[STIX]{x1D6FC}}$
with an instantaneous angular velocity
$\hat{\unicode[STIX]{x1D6FC}}$
with an instantaneous angular velocity
![]() $\text{d}\hat{\unicode[STIX]{x1D6FC}}/\text{d}t$
(figure 7
b). To represent the varying relative flow velocity along the width, we define a reference radius
$\text{d}\hat{\unicode[STIX]{x1D6FC}}/\text{d}t$
(figure 7
b). To represent the varying relative flow velocity along the width, we define a reference radius
![]() $b\unicode[STIX]{x1D709}$
such that the plate velocity is considered as
$b\unicode[STIX]{x1D709}$
such that the plate velocity is considered as
![]() $v=(\text{d}\hat{\unicode[STIX]{x1D6FC}}/\text{d}t)b\unicode[STIX]{x1D709}$
of the cross-section (Slater Reference Slater1969; Blevins Reference Blevins1990) and assumed to undergo minor variations within the investigated inclination angles (Tadrist et al.
Reference Tadrist, Julio, Saudreau and De Langre2015). This leads to the relative wind velocity (
$v=(\text{d}\hat{\unicode[STIX]{x1D6FC}}/\text{d}t)b\unicode[STIX]{x1D709}$
of the cross-section (Slater Reference Slater1969; Blevins Reference Blevins1990) and assumed to undergo minor variations within the investigated inclination angles (Tadrist et al.
Reference Tadrist, Julio, Saudreau and De Langre2015). This leads to the relative wind velocity (
![]() $\boldsymbol{U}_{rel}$
) and effective inclination angle as
$\boldsymbol{U}_{rel}$
) and effective inclination angle as
For relatively small
![]() $\unicode[STIX]{x1D6FE}$
(small plate velocity compared to
$\unicode[STIX]{x1D6FE}$
(small plate velocity compared to
![]() $U_{e}$
) and low-amplitude twisting around the equilibrium,
$U_{e}$
) and low-amplitude twisting around the equilibrium,
and, therefore,
Then, using Taylor’s expansion, the moment coefficient can be approximated as
The condition leading to the sudden increase of twisting motion denotes the loss of the system stability, which occurs when damping vanishes, i.e. the terms in
![]() $\text{d}\hat{\unicode[STIX]{x1D6FC}}/\text{d}t$
(combining (3.2), (3.6) and (3.7)) are zero:
$\text{d}\hat{\unicode[STIX]{x1D6FC}}/\text{d}t$
(combining (3.2), (3.6) and (3.7)) are zero:
where
![]() $C$
is a constant. Key for evaluating the model is the estimation of the plate tip bending angle
$C$
is a constant. Key for evaluating the model is the estimation of the plate tip bending angle
![]() $\unicode[STIX]{x1D703}$
and, thus,
$\unicode[STIX]{x1D703}$
and, thus,
![]() $\hat{\unicode[STIX]{x1D6FC}}_{s}$
at each
$\hat{\unicode[STIX]{x1D6FC}}_{s}$
at each
![]() $Ca_{c}$
. Despite the variation of
$Ca_{c}$
. Despite the variation of
![]() $\unicode[STIX]{x1D6FC}$
, the equilibrium tip height resulted very close at a given
$\unicode[STIX]{x1D6FC}$
, the equilibrium tip height resulted very close at a given
![]() $Ca$
within
$Ca$
within
![]() $Ca<Ca_{c}$
(see example in figure 7
c), indicating similar plate bending; therefore,
$Ca<Ca_{c}$
(see example in figure 7
c), indicating similar plate bending; therefore,
![]() $\unicode[STIX]{x1D703}$
can be inferred from the case with
$\unicode[STIX]{x1D703}$
can be inferred from the case with
![]() $\unicode[STIX]{x1D6FC}=0$
at each
$\unicode[STIX]{x1D6FC}=0$
at each
![]() $Ca_{c}$
directly from the PTV measurements. To determine
$Ca_{c}$
directly from the PTV measurements. To determine
![]() $\unicode[STIX]{x2202}C_{M}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\hat{\unicode[STIX]{x1D6FC}}_{s}}$
, the aerodynamic torque of a rigid metallic plate with the same geometry of the elastic counterpart was measured across various
$\unicode[STIX]{x2202}C_{M}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}|_{\hat{\unicode[STIX]{x1D6FC}}_{s}}$
, the aerodynamic torque of a rigid metallic plate with the same geometry of the elastic counterpart was measured across various
![]() $\unicode[STIX]{x1D6FC}$
as shown in figure 7(d), where the distribution of
$\unicode[STIX]{x1D6FC}$
as shown in figure 7(d), where the distribution of
![]() $C_{M}$
follows a power-law function with
$C_{M}$
follows a power-law function with
![]() $\unicode[STIX]{x1D6FC}$
(see dashed line with power 1/2). Noting that
$\unicode[STIX]{x1D6FC}$
(see dashed line with power 1/2). Noting that
![]() $Ca\propto U_{0}^{2}$
for a given structure and combing (3.3) and (3.8), we can then define a dimensionless quantity
$Ca\propto U_{0}^{2}$
for a given structure and combing (3.3) and (3.8), we can then define a dimensionless quantity
![]() $C_{t}$
characterizing the threshold of
$C_{t}$
characterizing the threshold of
![]() $Ca_{c}$
:
$Ca_{c}$
:
Additional experiments were conducted to test equation (3.9), with the plate under various
![]() $\unicode[STIX]{x1D6FC}$
. As shown in figure 8,
$\unicode[STIX]{x1D6FC}$
. As shown in figure 8,
![]() $Ca_{c}$
decreased monotonically with
$Ca_{c}$
decreased monotonically with
![]() $\unicode[STIX]{x1D6FC}$
; remarkably,
$\unicode[STIX]{x1D6FC}$
; remarkably,
![]() $C_{t}\approx 0.2\pm 0.005$
across all investigated
$C_{t}\approx 0.2\pm 0.005$
across all investigated
![]() $\unicode[STIX]{x1D6FC}$
. It is worth pointing out that, compared to previous studies with rigid structures (Larsen Reference Larsen2002; Païdoussis et al.
Reference Païdoussis, Price and De Langre2010; Fernandes & Armandei Reference Fernandes and Armandei2014),
$\unicode[STIX]{x1D6FC}$
. It is worth pointing out that, compared to previous studies with rigid structures (Larsen Reference Larsen2002; Païdoussis et al.
Reference Païdoussis, Price and De Langre2010; Fernandes & Armandei Reference Fernandes and Armandei2014),
![]() $\hat{\unicode[STIX]{x1D6FC}}_{s}$
accounts for the influence of plate flexibility on the onset of twisting motions. As indicated in (3.3), strong plate deformation (i.e. large bending angle
$\hat{\unicode[STIX]{x1D6FC}}_{s}$
accounts for the influence of plate flexibility on the onset of twisting motions. As indicated in (3.3), strong plate deformation (i.e. large bending angle
![]() $\unicode[STIX]{x1D703}$
) leads to significant deviation of
$\unicode[STIX]{x1D703}$
) leads to significant deviation of
![]() $\hat{\unicode[STIX]{x1D6FC}}_{s}$
from the base inclination angle
$\hat{\unicode[STIX]{x1D6FC}}_{s}$
from the base inclination angle
![]() $\unicode[STIX]{x1D6FC}$
, and therefore different local
$\unicode[STIX]{x1D6FC}$
, and therefore different local
![]() $\unicode[STIX]{x2202}C_{M}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
due to the nonlinear dependence of
$\unicode[STIX]{x2202}C_{M}/\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}$
due to the nonlinear dependence of
![]() $C_{M}$
with
$C_{M}$
with
![]() $\unicode[STIX]{x1D6FC}$
(figure 7
d). Also, it should be noted that, for flexible plates with different geometry and material, the parameters on the right-hand side of (3.8) may vary and lead to different
$\unicode[STIX]{x1D6FC}$
(figure 7
d). Also, it should be noted that, for flexible plates with different geometry and material, the parameters on the right-hand side of (3.8) may vary and lead to different
![]() $C_{t}$
; however, the critical
$C_{t}$
; however, the critical
![]() $Ca_{c}$
should still follow (3.9) for a given structure. That is, the abrupt force fluctuations are triggered by instability mechanisms in an inclined bent plate relative to the mean flow.
$Ca_{c}$
should still follow (3.9) for a given structure. That is, the abrupt force fluctuations are triggered by instability mechanisms in an inclined bent plate relative to the mean flow.

Figure 8.
![]() $Ca_{c}$
and dimensionless quantity
$Ca_{c}$
and dimensionless quantity
![]() $C_{t}$
(3.9) characterizing the threshold of twisting motions; the dashed line marks the averaged value of
$C_{t}$
(3.9) characterizing the threshold of twisting motions; the dashed line marks the averaged value of
![]() $C_{t}$
across
$C_{t}$
across
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
4 Conclusions
Overall, we have shown the distinctive force fluctuations and dynamics of inclined flexible plates under various flows. Our experiments revealed a sharp increase of the unsteady force, where the plate tip motions shifted from small-amplitude fluttering to twisting oscillations past a critical
![]() $Ca$
. Further increase of the incoming velocity or
$Ca$
. Further increase of the incoming velocity or
![]() $Ca$
under sufficiently large
$Ca$
under sufficiently large
![]() $\unicode[STIX]{x1D6FC}$
led to distinctive 3D orbital dynamics induced by the coupled twisting and bending deformations. The agreement between our theoretical arguments and experiments demonstrates the dominating role of the dynamic instability in triggering twisting oscillations. These findings provide novel insights for examining the reconfiguration and, particularly, the large-amplitude 3D orbital motions of elastic structures under complex flow fields. Theoretical inspection of the onset of abrupt force fluctuations may be used to determine conditions for structure fatigue and design various engineering structures and processes exposed to flows. Future work will focus on the effects of mass ratio, plate geometry and other parameters in the structure dynamics and induced flow.
$\unicode[STIX]{x1D6FC}$
led to distinctive 3D orbital dynamics induced by the coupled twisting and bending deformations. The agreement between our theoretical arguments and experiments demonstrates the dominating role of the dynamic instability in triggering twisting oscillations. These findings provide novel insights for examining the reconfiguration and, particularly, the large-amplitude 3D orbital motions of elastic structures under complex flow fields. Theoretical inspection of the onset of abrupt force fluctuations may be used to determine conditions for structure fatigue and design various engineering structures and processes exposed to flows. Future work will focus on the effects of mass ratio, plate geometry and other parameters in the structure dynamics and induced flow.
Acknowledgements
This work was supported by the Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, as part of the start-up package of L.P.C.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.40.