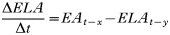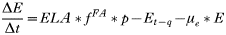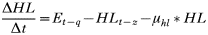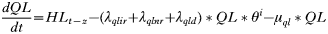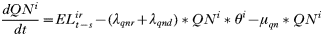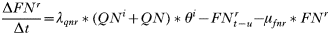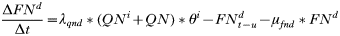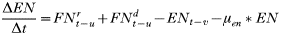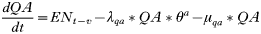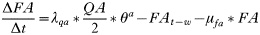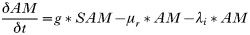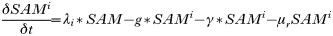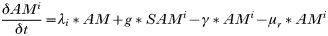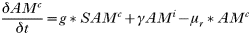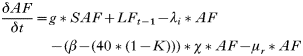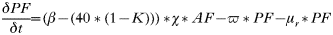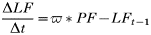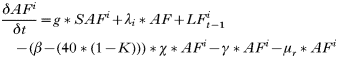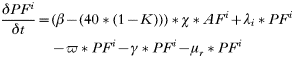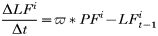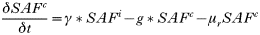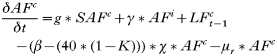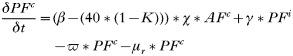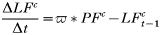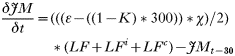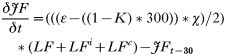Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T10:23:30.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Vector seasonality, host infection dynamics and fitness of pathogens transmitted by the tick Ixodes scapularis

Published online by Cambridge University Press:  11 October 2006

N. H. OGDEN ,
M. BIGRAS-POULIN ,
C. J. O'CALLAGHAN ,
I. K. BARKER ,
K. KURTENBACH ,
L. R. LINDSAY  and
D. F. CHARRON
N. H. OGDEN
Affiliation:
Faculté de médecine vétérinaire, Université de Montréal, C.P. 5000, Saint-Hyacinthe, QC, J2S 7C6 Public Health Agency of Canada, Foodborne, Waterborne and Zoonotic Infections Division, Canada
M. BIGRAS-POULIN
Affiliation:
Faculté de médecine vétérinaire, Université de Montréal, C.P. 5000, Saint-Hyacinthe, QC, J2S 7C6
C. J. O'CALLAGHAN
Affiliation:
Department of Community Health and Epidemiology, Queen's University, Kingston, ON, Canada
I. K. BARKER
Affiliation:
Canadian Cooperative Wildlife Health Centre, Department of Pathobiology, University of Guelph, ON, Canada
K. KURTENBACH
Affiliation:
Department of Biology and Biochemistry, University of Bath, UK
L. R. LINDSAY
Affiliation:
Public Health Agency of Canada, Zoonotic Diseases and Special Pathogens Section, National Microbiology Laboratory, Canada
D. F. CHARRON
Affiliation:
Public Health Agency of Canada, Foodborne, Waterborne and Zoonotic Infections Division, Canada
Rights & Permissions [Opens in a new window]

Abstract

Fitness of tick-borne pathogens may be determined by the degree to which their infection dynamics in vertebrate hosts permits transmission cycles if infective and uninfected tick stages are active at different times of the year. To investigate this hypothesis we developed a simulation model that integrates the transmission pattern imposed by seasonally asynchronous nymphal and larval Ixodes scapularis ticks in northeastern North America, with a model of infection in white-footed mice (Peromyscus leucopus) reservoir hosts, using the bacteria Borrelia burgdorferi and Anaplasma phagocytophilum as examples. In simulations, survival of microparasites, their sensitivity to reduced rodent and tick abundance, and to ‘dilution’ by a reservoir-incompetent host depended on traits that allowed (i) highly efficient transmission from acutely-infected hosts, (ii) long-lived acute or ‘carrier’ host infections, and/or (iii) transmission amongst co-feeding ticks. Minimum values for transmission efficiency to ticks, and duration of host infectivity, necessary for microparasite persistence, were always higher when nymphal and larval ticks were seasonally asynchronous than when these instars were synchronous. Thus, traits influencing duration of host infectivity, transmission efficiency to ticks and co-feeding transmission are likely to be dominant determinants of fitness in I. scapularis-borne microparasites in northeastern North America due to abiotic forcings influencing I. scapularis seasonality.

Keywords

Ixodes scapularisPeromyscus leucopuswhite-footed mousemodelfitnessBorrelia burgdorferiAnaplasma phagocytophilum
Type
Research Article
Information
Parasitology , Volume 134 , Issue 2 , February 2007 , pp. 209 - 227
Copyright
2006 Cambridge University Press

INTRODUCTION

Ixodes scapularis is the tick vector of a number of tick borne zoonoses, including Lyme borreliosis, one of the most frequent vector-borne zoonoses in temperate zones (Thompson et al. 2001), which is caused by the bacterium Borrelia burgdorferi in northeastern North America. It is believed that transmission cycles of B. burgdorferi are very efficient in northeastern North America because the seasonal activity of nymphal and larval Ixodes scapularis ticks is asynchronous (Wilson and Spielman, 1985). Typically, infected nymphs become active in spring and early summer transmitting the bacteria to rodents (particularly white footed mice: Peromyscus leucopus). Non-infected larvae that are active in mid to late summer then acquire the infection from persistently infected rodents. Larvae maintain infection through the molt, giving rise to a new population of infected host-seeking nymphs in the following spring (Yuval and Spielman, 1990). The efficiency of this cycle leads to a high prevalence of B. burgdorferi infection in questing nymphal ticks, and a high public health risk in the region (Thompson et al. 2001).

In addition to B. burgdorferi, I. scapularis ticks and P. leucopus rodents maintain the bacterium Anaplasma phagocytophilum and the protozoan Babesia microti, which cause human granulocytic anaplasmosis and human babesiosis respectively (Thompson et al. 2001). The transmission efficiency of most strains of B. burgdorferi from acutely infected rodent hosts to ticks is usually very high (>50%: Donahue et al. 1987; Derdáková et al. 2004), compared with A. phagocytophilum and B. microti (Mather et al. 1990; Massung et al. 2004). Typically, B. burgdorferi is transmitted with high efficiency from P. leucopus rodents almost life-long (Donahue et al. 1987), but some strains and A. phagocytophilum have short infective periods in rodent hosts (Lindsay et al. 1997; Derdáková et al. 2004; Massung et al. 2004). Variation in longevity and transmissibility of host infections with these pathogens is likely to affect the public health risk via effects on infection prevalence in questing nymphs (Porco, 1999).

For the pathogens to survive in an I. scapularis-rodent cycle, the duration of rodent infectivity for ticks must span any gap between the seasons of nymphal and larval activity (Randolph, 2001). The duration of infectivity is a crucial measure of fitness in different host species for vector-borne pathogens and particularly for B. burgdorferi in northeastern USA (Brisson and Dykhuizen, 2004; Tsao et al. 2004; Hanincová et al. 2006) and it has been suggested that B. burgdorferi strains that are short-lived in rodents are better adapted to alternative reservoir hosts (Derdáková et al. 2004). However, for I. scapularis-borne zoonoses investigated to date, recovery of rodents from acute, highly transmissible infections (if they actually do recover) is not complete, and the rodents remain persistently infective ‘carriers’ that transmit infection to ticks with low efficiency (Derdáková et al. 2004; Levin and Ross, 2004). The potential capacity for B. burgdorferi and A. phagocytophilum to be transmitted between ticks co-feeding on the same host irrespective of systemic host infection (co-feeding transmission: Randolph et al. 1996; Levin and Fish, 2000) adds further complexity to the transmission dynamics. Furthermore, relative rates of rodent birth and death rates between nymphal and larval appearance each year very likely affect transmission cycles (Schauber and Ostfeld, 2002).

Together, these observations suggest that (i) the efficiency with which ticks acquire infection from infected hosts, (ii) the duration of host infectivity relative to the timing of tick activity and (iii) the capacity for co-feeding transmission may be particularly crucial as fitness determinants for pathogens transmitted by I. scapularis and other ticks where different instars are seasonally asynchronous in comparison to other vector-borne pathogens. If so, then the evolutionary ‘strain space’ (Gog and Grenfell, 2002) of I. scapularis-borne microparasite populations may be shaped by abiotic forcings via their influence on tick phenology. Because I. scapularis phenology is mostly temperature-related (Ogden et al. 2004) both the quantity (numbers of infected ticks per unit area, per unit time) and quality (pathogen species and genotypes) of the public health risk posed by I. scapularis ticks could be predictable. Here we investigate these hypotheses using a simulation model that combines seasonal life-history events of I. scapularis ticks, P. leucopus rodent hosts, and cycles of pathogen transmission between these two populations.

MATERIALS AND METHODS

Model construction

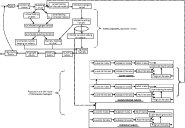
The model was constructed in STELLA 7.0.3 for Windows software (High Performance Systems Inc. NH). A diagram of the conceptual model is presented as Fig. 1. The model comprised 2 components: (i) a simulation model of I. scapularis populations that provided values for the daily number of infected and uninfected ticks attaching to, and detaching from, hosts in a seasonal cycle representative of conditions in northeastern North America, and (ii) an SIR model of a host for larval and nymphal I. scapularis, and tick-borne microparasites, based on published values for seasonal population processes of P. leucopus in northeastern North America. The model was calibrated with data from the field and laboratory so that the phenologies of tick attachment rates to rodents, and annual cycles of rodent abundance, approximated to those seen in the field each year. By using laboratory data on P. leucopus infectivity for ticks with different microparasites, we could then investigate how seasonal asynchrony of immature I. scapularis may affect microparasite survival, and thus fitness, in nature.

Fig. 1. A diagram of the combined Ixodes scapularis and SIR Peromyscus leucopus rodent models. The bold dotted lines indicate infection transmission between tick and rodent populations. For simplicity, not all flows to indicate mortality, nor linkage of P. leucopus abundance to host-finding success of immature ticks, are shown.

  • Ixodes scapularis population model

Rates of inter-stadial development of I. scapularis are mostly controlled by ambient temperature in northeastern North America, although nymph-to-adult development is likely also controlled by temperature-independent diapause (Ogden et al. 2004). The model uses site-specific temperature data (while accounting for diapause) to drive simulations of abundance and seasonality of I. scapularis populations at specific geographical locations (for details see Ogden et al. 2005). For this study, the model was modified from that in Ogden et al. (2005) in 2 ways: (i) immature ticks could feed on reservoir-incompetent deer as well as reservoir-competent rodents, and (ii) larvae and nymphs could feed on infective or uninfected rodents. The proportion of feeding larvae acquiring infection from the rodent population at any one time was calculated from the proportions of larvae attaching to acutely-infected and carrier mice, and the transmission coefficients from these rodents.

Nearly all simulations were run using tick development times calculated from 1971–2000 temperature normals (Ogden et al. 2005) from the Chatham, Ontario meteorological station (42 °23′N, 82 °12′W), which is close to an established population of I. scapularis (Ogden et al. 2005). These data simulate the asynchronous pattern of seasonal activity of immature I. scapularis (Ogden et al. 2006) typical for northeastern North America (Wilson and Spielman, 1985). For some comparisons, the model was calibrated to simulate hypothetical, more synchronous larval and nymphal activity periods. In this case, tick mortality rates were adjusted so that peak and total numbers of larvae and nymphs feeding on rodents were lower than when the ticks were asynchronous. This was necessary to be sure that any survival advantage due to synchronous tick activity was not attributable simply to increases in tick abundance overall, which occur due to faster development of ticks in the model (Ogden et al. 2006), and would increase tick infestation levels of rodents and affect transmission cycles (see results of sensitivity analyses).

Model parameters and their estimates are presented in Table 1 and model equations are presented in Appendix 1. In all simulations the model was seeded with 1000 questing adults and 100 infected questing nymphs to establish ticks and infection in the model in the first year. The model then took a number of years of tick and pathogen reproduction (with ticks regulated by density-dependent effects) to come to a stable cyclical equilibrium.

Table 1. Parameter definitions in the Ixodes scapularis model and their initial values (The right hand column indicates the source of the value: M, model derived; L, laboratory study; F, field study; A, assumed in the model; A/F, assumed based on field observations. The parameter values and their sources are explained in detail in Ogden et al. (2005).)

Peromyscus leucopus population model

Rodent numbers simulated by the rodent population model replaced the constant rodent density in the original I. scapularis model (Ogden et al. 2005). Male and female rodents in the model each comprised 3 states: (i) juveniles, considered here to equate with ‘non-trappable’ juveniles still in the nest in field studies, (ii) trappable juveniles/subadults (TJSAs), and (iii) adults. Peromyscus leucopus can remain non-trappable juveniles up to 30 days of age, they can become subadults at 42 days, and adults at 56 days (Rintamaa et al. 1976; Schug et al. 1991). Residence time as a non-trappable juvenile was fixed at 30 days, while TJSAs became adults at a per capita daily rate of 1/25 (i.e. a TJSA became an adult after a mean of 25 days). The basic daily per capita mortality rate of all TJSAs and adult rodents was 0·012 (Schug et al. 1991). Mortality of ‘non-trappable’ juveniles in the model was accounted for in the litter size of ‘litter-bearing females’ (see below).

The daily per capita rate at which ‘adult females’ became ‘pregnant females’ was termed the ‘breeding proportion’. This rate reflected the winter decline in breeding in P. leucopus (Wolff, 1985), being zero on 31 December, rising to unity from 1 April to 30 September, after which the proportion declined again. Rises and falls in the ‘breeding proportion’ were sigmoid. The ‘pregnant females’ remained in this state for a mean 28 days (Lewellen and Vessey, 1998) at which point they gave birth (as ‘litter-bearing females’). ‘Litter-bearing females’ remained in this state for 1 day ensuring that they did not give rise to more than 1 litter before returning to the ‘adult female’ state. Females returned to the adult female state immediately after giving birth: there is little evidence of lactational anoestrus in P. leucopus (Lewellen and Vessey, 1998).

For simplicity, in most simulations it was assumed that there was no midsummer hiatus in breeding (Rintamaa et al. 1976), i.e. the model represented more northern populations of P. leucopus (Millar and Gyug, 1981). An index of habitat carrying capacity (K) simulated reduced ‘food supply’ through autumn to early spring (1 September through to 1 April), i.e. the simulations assumed no ‘mast years’ occurred, which could increase rather than decrease winter/spring survival (Jones et al. 1998). K could alter a number of the model variables simultaneously. The ‘breeding proportion’ and the numbers of rodents per litter declined with reduced K (Rintamaa et al. 1976; Nadeau et al. 1981; Wolff, 1985; Schug et al. 1991), while the daily per capita mortality rate of all rodents increased inversely with K (Linzey and Kesner, 1991; Schug et al. 1991) (Table 2).

Table 2. Parameter definitions in the Peromuscus leucopus model and their initial values (The right hand column indicates the source of the value: M, model derived; L, laboratory study; F, field study; A, assumed in the model; A/F, assumed based on field observations; A/L, assumed based on laboratory observations.)

The P. leucopus population in the model was regulated by density-dependent effects on reproduction (as suggested by analysis of field data: Lewellen and Vessey, 1998), by reducing the ‘breeding proportion’, and the numbers of rodents born and surviving to be trappable (see Table 2).

Empirical validation and sensitivity analyses were re-run using 2 variants of the model. In the first variant, we included a midsummer hiatus in P. leucopus breeding: a physiological cessation of male and female reproductive activity due to unknown cues (Terman and Terman, 1999). Where this occurs in northeastern USA, it typically does so in July and early August (Rintamaa et al. 1976), and to model its potential effects, the ‘breeding proportion’ in the model was reduced to zero from mid-July to mid-August. To compensate for an overall reduced abundance of rodents (which could affect both tick and microparasite abundance and invalidate comparisons amongst model variants), the basic mortality rate was reduced from 0·012 to 0·0115. In the second variant, a more complex seasonal pattern of rodent mortality as suggested by Schug et al. (1991) was introduced. In this version, adult rodent mortality in winter was unaffected by K but adult female mortality increased in spring and summer associated with intraspecific competition associated with breeding. To achieve this, adult female mortality was increased by one four hundredth of the breeding proportion, and this also necessitated a slight decrease in the basic rate of mortality to obtain rodent numbers that were comparable amongst model variants.

Model parameters and their estimates are presented in Table 2 and model equations are presented in Appendix 2. All versions of the model were initially seeded with 60 non-pregnant adult females and 60 adult males. Ten of each of these were in the acute-infected class to seed infection in the model (see below). Although the model does not explicitly have a spatial dimension, the rodent numbers were scaled to those typically captured in 10–20 ha grids in the northern part of the rodent's range (Harland et al. 1979; Nadeau et al. 1981), and deer densities were scaled high (equivalent to 1–2 per ha in comparison to rodent numbers, where 1–2 per hectare is considered a high natural density for white-tailed deer: Kilpatrick et al. 2001) to account for the absence of other hosts for adult and immature ticks.

Modelling infection in rodent and tick populations

All states in the rodent population could acquire infection except juveniles and ‘litter-bearing’ females. Non-trappable juveniles confined to the nest are unlikely to acquire ticks (Hofmeister et al. 1999), and litter-bearing females were in that state for 1 day only. Tick-to-rodent transmission efficiency was set at 100%. The per capita daily rate at which naïve mice became ‘acutely-infected’ mice was then the number of infected questing nymphs that attached to a rodent on that day. The daily per capita rate at which ‘acutely-infected’ mice recovered was 1·3/Infection Duration, where duration of acute infections in rodents was approximated from laboratory studies (Table 3). This relationship was designed to capture some of the variation in transmission efficiency during the acute infection period (Derdáková et al. 2004; Levin and Ross, 2004). Our examples are simplifications, and do not cover the full gamut of possible values for duration of host infection and transmission efficiency, and variations in transmission efficiency over time post-infection that may occur in nature (Burgdorfer and Schwan, 1991; Derdáková et al. 2004). All recovered mice became ‘carrier’ mice although ‘carrier’ mice could also be completely ‘recovered/immune’ mice by setting the transmission efficiency from these mice (see below) to zero. To simulate life-long ‘acute’ infections in some Borrelia burgdorferi strains, infection duration was raised higher than the maximum rodent life-expectancy (>1000 days). There was no additional rodent mortality associated with infection in the model (Hofmeister et al. 1999; Bunikis et al. 2004) except in some sensitivity analyses. Four different ‘pathogens’ were simulated: A. phagocytophilum and B. burgdorferi strains BL206 and B348 from northeastern USA, and LI-231 from Ontario, Canada. Simulations of the latter were used in empirical validation only. BL206 is transmitted from P. leucopus to ticks life-long with high efficiency (Donahue et al. 1987; Derdáková et al. 2004), while strains B348 and LI-231 are efficiently transmitted for a short period, although recovered rodents may remain ‘carriers’ (Lindsay et al. 1997; Derdáková et al. 2004) (Table 3). For A. phagocytophilum and B. burgdorferi B348 and LI-231, the decline in transmission efficiency from acute to carrier was exponential (Table 2). Recovered rodents or ‘carriers’ of A. phagocytophilum and B. burgdorferi B348 and LI-231 could not revert to the acute-infected status by re-infection (Stafford et al. 1999; Derdáková et al. 2004). The proportion of larvae acquiring infection from the rodent population at any one time was calculated as:

where TE is the efficiency of transmission from host-to-larva, Rai and Rci are the numbers of acutely infected and carrier rodents and R is the total number of trappable and infectable rodents.

Table 3. Infection and transmission characteristics of the tick-borne pathogens used in model simulations, and the studies from which these values were approximated (* Transmission cycles died out in simulations using these values and only values obtained by Levin and Ross (2004) are considered in the results.)

To investigate how co-feeding transmission may contribute to transmission cycles, in some simulations we included a ‘co-feeding proportion’ in the calculation of the proportion of larvae acquiring infection from the rodent population at any one time. The co-feeding proportion’ (κ in Table 1) was calculated as 0·67∗Ln(T+1·001) (where T is the instantaneous number of infective nymphs attached per rodent) thus an additional rodent-to-larva transmission coefficient was accorded to all acutely infected and ‘carrier’ rodents that was ‘tick infestation intensity dependent’ rising from 6% when rodents carried 1 nymph, to a potential maximum of 84% were rodents to carry 5 nymphs, of which 2 may be infected in the most efficient of simulated transmission cycles. This relationship was used in order to give values of transmission efficiency observed in field and laboratory studies and attributed to co-feeding transmission (Gern and Rais, 1996; Ogden et al. 1997, 2003; Richter et al. 2002; Derdáková et al. 2004). In 3 of these studies there was evidence for density dependence in transmission: uninfected larvae were more likely to co-feed with an infective nymph (or uninfected nymph with infected adult) the higher was the number of infected ticks feeding on the host (Ogden et al. 1997; Richter et al. 2002; Ogden et al. 2003). The total combined proportion of feeding larvae acquiring infection from rodents via systemic infections and co-feeding transmission was constrained to a maximum 0·99 by the IF, AND, ELSE logic of STELLA.

In all simulations, the model was seeded with infected nymphs (see description of I. scapularis population model), and with 10 infected adult female and 10 infected adult male mice (see description of P. leucopus model), and the simulation length was 40 years.

Empirical validation

A number of values at model equilibrium were compared against field observations: (i) seasonal variations in numbers of ‘trappable’ rodents, (ii) seasonal variations in immature tick infestations of rodents, (iii) questing nymph infection prevalence, and (iv) seasonal variation in rodent infection prevalence. For the latter, simulations of B. burgdorferi strain BL206 were compared with observations from 2 field studies in Connecticut, USA (Anderson et al. 1987; Bunikis et al. 2004). In the study of Bunikis et al. (2004) the dominant genotypes were those related to B. burgdorferi BL206 (Tsao et al. 2004). A period between infection and seroconversion of 2·5 weeks was accounted for where infections were detected serologically (Schwan et al. 1989). Simulations of B. burgdorferi strain LI-231 were compared with observations at the site (Long Point, Ontario) where the isolate in transmission studies was obtained (Lindsay et al. 1997). All of the simulations were run with and without the ‘co-feeding proportion’.

Local sensitivity analyses

A comparative index (Keeling and Gilligan, 2000) was used to test the sensitivity of the 3 model domains (rodent population, tick population and pathogen transmission) to individual model variables:

where To is the outcome parameter at equilibrium using starting values for all variables (see Table 1), and Ti is the outcome parameter, at equilibrium, when the variable under investigation V is increased by a small amount (5%), from its starting value Vo, to Vi.

Five outcome parameters were measured: (i) annual peak rodent numbers, (ii) annual peak questing nymph numbers, (iii) annual mean infection prevalence in questing nymphs, (iv) annual mean infection prevalence in rodents, and (v) ‘risk’ of human infection (being the product of peak questing nymph numbers and infection prevalence). We tested the sensitivity of these outcomes to 5% changes in rodent population parameters (density-dependent effects, mortality and reproduction rates and fecundity), tick population parameters (mortality and host finding rates) and deer numbers. For brevity, sensitivity analyses were not performed for B. burgdorferi strain LI-231, and the ‘co-feeding proportion’ was not included.

Global sensitivity analyses

We assessed the global sensitivity of simulated microparasite transmission cycles to the degree of seasonal synchrony of immature ticks and to the inclusion of co-feeding transmission. Simulations were run with and without the co-feeding proportion, and when the simulated seasonal activities of larval and nymphal I. scapularis were synchronous or asynchronous (see Fig. 3). Four analyses were performed. First, we estimated the minimum values for the duration of acute infection, below which deterministic die-out of microparasites occurred, for microparasites transmitted with 40%, 60% or 75% efficiency from acute-infected hosts to ticks. These values were obtained when transmission efficiency from ‘carrier’ animals was 2·5% or 0% (i.e. infected animals recovered completely after the acute phase of infection). Second, we estimated the minimum transmission efficiency from acutely infected animals, below which deterministic die-out of the microparasites occurred, when the duration of the acute phase was set at 14 days, and the transmission efficiency from ‘carrier’ animals was either 2·5% or 0%. Third, we estimated the increase in mortality of acutely infected rodents needed to cause deterministic die-out of B. burgdorferi B348. Fourth, the degree of (i) increase in mortality rates of non-feeding ticks of all stages, (ii) increase in the basic rodent mortality rate, and (iii) decrease in transmission efficiency from ‘carrier’ animals to larvae (for A. phagocytophilum and B. burgdorferi B348) required for deterministic die out of infection were recorded for each pathogen.

Interplay of rodent and deer host densities

We investigated the susceptibility of each pathogen to the ‘dilution effect’ of increasing densities of reservoir-incompetent deer relative to reservoir-competent rodents by plotting how threshold densities of rodents for pathogen survival varied with different deer densities (‘joint threshold curves’; Norman et al. 1999). Equilibrium rodent numbers were reduced stepwise by increasing the basic rodent mortality rate, and at each step multiple simulations were run with deer numbers varying from zero to 1000. At each step, the annual maximum number of rodents was recorded as were the deer numbers at which deterministic die-out of the ticks and/or the pathogen occurred. Threshold deer numbers were then plotted against the corresponding number of rodents. The process was repeated to produce a joint threshold curve for each B. burgdorferi strains BL206 and B348, and A. phagocytophilum. A joint threshold curve was also created for a hypothetical pathogen, which had the transmission characteristics of B. burgdorferi B348 but a longer 28-day duration of acute infection. The curve for A. phagocytophilum was repeated using more synchronous seasonal larval and nymphal I. scapularis activity.

RESULTS

Simulated tick and rodent populations reached a stable cyclical equilibrium within 10 years. Transmission cycles of tick-borne pathogens reached stable cyclical equilibria within 15 years. In the absence of simulated co-feeding transmission, A. phagocytophilum infection died out when the transmission coefficient from acutely infected rodents to larvae was set at 25%, so results of simulations using the higher transmission efficiency value of 40% are presented. The model reached the same equilibria irrespective of the way in which it was initially seeded with ticks, rodents and infection, providing the seeding methods permitted survival for the first years.

Empirical validation

The P. leucopus population model obtained a stable, cyclical equilibrium with the seasonal variations in juvenile/subadult, adult and total rodent numbers observed in the field in northeastern North America (Harland et al. 1979; Nadeau et al. 1981; Yunger, 2002; Fig. 2). A similar pattern was observed under 2 different scenarios of seasonal rodent mortality and reproduction (Fig. 2).

Fig. 2. Monthly variations in the numbers of ‘trappable’ Peromyscus leucopus at model equilibrium (A), compared against field observations in northeastern USA (Nadeau et al. 1981) (B). Field observations are mean monthly values (+/− maximum and minimum over 5 years) of the minimum numbers of P. leucopus known alive (MNKA). Also shown are simulated monthly variations in P. leucopus numbers when the model included a mid-summer hiatus in rodent breeding (C) and when adult rodent mortality was set higher in spring and summer than in winter (D).

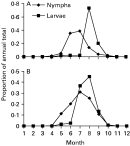
The peak mean monthly nymph infestation of rodents in simulations was 5 nymphs per rodent (in June, Fig. 3A), comparable with the 2–8 nymphs per P. leucopus observed in the field (Wilson and Spielman 1985; Lindsay et al. 1999; Schmidt et al. 1999; LoGiudice et al. 2003). Peak mean monthly larval infestations were 61 per rodent in August (Fig. 3A). Peak infestations of 30–40 per rodent are normal in the field (Wilson and Spielman 1985; Lindsay et al. 1999; Schmidt et al. 1999), but can reach >100 (Levin et al. 1999; LoGiudice et al. 2003).

Fig. 3. The seasonal variation in monthly nymphal and larval Ixodes scapularis infestations of mice at model equilibrium expressed as a proportion of the total annual numbers infesting the mice. In (A) the model simulated the classical immature tick seasonality in northeastern North America. The model in (B), calibrated to produce a hypothetical synchronous pattern of immature tick activity, was used in comparisons.

When transmission cycles of 4 tick-borne pathogen species or strains with different characteristics of transmission from the host (Table 3) were simulated, infection prevalence in questing nymphs was stable through the year (Fig. 4) and comparable with field studies (Table 4).

Fig. 4. Mean monthly prevalence of infection in questing nymphs for each pathogen at model equilibrium, obtained with and without co-feeding transmission.

Table 4. The mean annual prevalence of infection in questing nymphal ticks at model equilibrium alongside comparable estimates obtained in field studies (NIP, nymphal infection prevalence; TE, host-to-tick transmission efficiency from acutely-infected hosts (%).)

In simulations of B. burgdorferi strain BL206, seasonal prevalence of infection in rodents was similar to that observed in longitudinal studies in Connecticut (Anderson et al. 1987; Bunikis et al. 2004; Fig. 5), and cross-sectional studies elsewhere in northeastern USA (Levine et al. 1985; Mather et al. 1989). In simulations of B. burgdorferi strain LI-231 and A. phagocytophilum, the prevalence of infective rodents was much lower, and the seasonal prevalence of B. burgdorferi LI-231 infection in rodents was similar to that observed in the field (Lindsay et al. 1997) (Fig. 5). These seasonal patterns were consistent under 2 different scenarios of seasonal rodent mortality and reproduction (Fig. 5). Incorporating co-feeding transmission did not alter the seasonal patterns but increased the prevalence of rodents infective for B. burgdorferi BL206 by 5% throughout the year, and almost doubled peak prevalence of infection with A. phagocytophilum and B. burgdorferi LI-231.

Fig. 5. The monthly variations in rodent infection prevalence with Borrelia burgdorferi BL206 (solid line with filled triangles), B. burgdorferi LI-231 (broken line with filled squares), and A. phagocytophilum (broken line with filled circles), predicted by the model at equilibrium without effects of co-feeding transmission. Also shown are field observations of B. burgdorferi infection prevalence in Peromyscus leucopus in studies in Connecticut, USA (open circles [mean values across 2 years and sites: Anderson et al. 1987] and crosses [mean values across 2 years: Bunikis et al. 2004]) and Ontario, Canada (open squares [Lindsay et al. 1997]). Vertical bars indicate the range of values obtained at different observations (for the field studies in Connecticut), or 95% confidence intervals (for the field study in Ontario). P. leucopus mortality and reproduction parameters were at their most simple in (A). In (B) the model included a mid-summer hiatus in rodent breeding, and in (C) adult rodent mortality was higher in spring and summer than in winter.

Local sensitivity analyses

Rodent numbers were sensitive to rodent mortality and reproduction rates. Questing nymph abundance was sensitive to off-host tick mortality, host finding rates, deer abundance, and variables that altered rodent abundance (Fig. 6).

Fig. 6. The sensitivity of model equilibrium parameter values for (left to right) (i) annual maximum rodent and tick numbers, (ii) mean annual infection prevalence in questing nymphal ticks, (iii) mean annual infection prevalence in rodents, and (iv) infection ‘risk’ (the product of mean annual prevalence in questing nymphal ticks, and maximum numbers of questing nymphs), to 5% increases in the variables on the left hand side of the figure. DD rodents: density dependent regulation of rodent breeding. Peromyscus leucopus mortality and reproduction parameters were at their most simple in (A). In (B) the model included a mid-summer hiatus in rodent breeding, and in (C) adult rodent mortality was higher in spring and summer than in winter.

Infection prevalence in questing nymph and rodents, and ‘risk’ (the product of peak questing nymph numbers and mean infection prevalence and an index of the risk of human infection) were each sensitive to rates of tick and rodent mortality, and of rodent reproduction. The direction of changes in questing nymph and rodent infection prevalence, and ‘risk’ were consistent amongst the tick-borne pathogens, except that small increases in deer numbers increased A. phagocytophilum prevalence in ticks and rodents (i.e. ‘rescued’ the transmission cycles), but reduced B. burgdorferi prevalence in questing nymphal ticks (Fig. 6). Except for infected rodent mortality rates, to which B. burgdorferi BL206 was the most sensitive, prevalence and ‘risk’ values for A. phagocytophilum were an order of magnitude more sensitive to all variables than those for the B. burgdorferi strains, and B348 was the more sensitive of the 2 B. burgdorferi strains. The pattern of model sensitivity was similar under 2 different scenarios of seasonal rodent mortality and reproduction, although increased summer mortality of adult rodents reduced the overall sensitivity of infection parameters to changes in rodent and tick abundance (Fig. 6).

Global sensitivity analyses

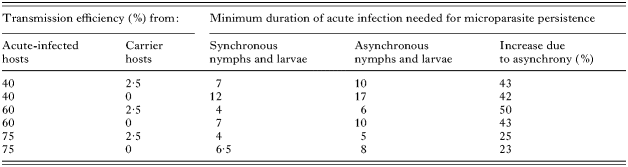
The duration of acute infection in the host required to prevent deterministic die out was always higher (by between 23 and 50%) when seasonal activity of immature I. scapularis was asynchronous rather than synchronous (Fig. 3B, Table 5). When the duration of acute infection was set at 14 days and transmission efficiency from carrier rodents to ticks was 2·5%, the minimum transmission efficiency to ticks from acute-infected hosts was 22% when immature ticks were synchronous and 29% when they were asynchronous. When the transmission efficiency from carrier rodents to ticks was set at 0%, the minimum transmission efficiency to ticks from acute-infected hosts was 32% when immature ticks were synchronous and 45% when they were asynchronous.

Table 5. The minimum duration of acute infection in hosts (in days), below which deterministic die out occurred, for a range of values for transmission efficiency to ticks from acute-infected and carrier hosts (These values are compared for simulations run using synchronous and asynchronous patterns of seasonal activity of larval and nymphal Ixodes scapularis.)

When immature tick activity was synchronous, B. burgdorferi B348 died out if the mortality rate of acute-infected rodents was increased 15-fold, but when the ticks were asynchronous this microparasite died out if acute-infected rodent mortality was increased 9-fold.

When co-feeding transmission was included in the models, transmission cycles could be maintained in the absence of systemic host infections (i.e. when host-to-tick transmission efficiency from acute-infected and carrier animals was set to zero) provided that tick abundance did not fall below the levels obtained by increasing tick mortality as described in Table 6.

Table 6. A comparison of the percentage increase in mortality rates of non-feeding ticks, and the basic mortality rate of rodents, required to cause deterministic die out of the different pathogens, and Ixodes scapularis and Peromyscus leucopus populations (Figures in parentheses are values obtained using a model with coincident seasonal activity of nymphal and larval I. scapularis.)

B. burgdorferi BL206 was the most resistant, and A. phagocytophilum the least resistant to deterministic die out due to increases in tick and rodent mortality rates (Table 6). These differences were less marked when the seasonal activity periods for larval and nymphal I. scapularis were more synchronous (Table 6). Co-feeding transmission increased resistance to die-out, particularly for A. phagocytophilum and B. burgdorferi B348. In all cases microparasite die-out preceded die-out of ticks and rodents. A. phagocytophilum died out unless recovered rodents became ‘carriers’ and at least 1·15% of larvae acquired infection when feeding on these rodents, but ‘carriers’ were unnecessary if co-feeding transmission was included. Carriers were also unnecessary to maintain B. burgdorferi B348, but their absence reduced mean annual questing nymph and rodent infection prevalence by 20% and 14%, respectively. When immature tick seasonal activity was set to be synchronous, transmission from carriers was not necessary to maintain A. phagocytophilum or B. burgdorferi strain B348, and had little effect on infection prevalence in ticks and rodents.

Interplay of rodent and deer host densities

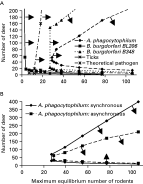
When rodent numbers were low, increasing numbers of reservoir-incompetent deer could permit maintenance of transmission cycles by increasing tick abundance (transmission cycle ‘rescue’: Norman et al. 1999, Fig. 7). As rodent numbers declined below a certain threshold the numbers of deer required to ‘rescue’ the transmission cycles increased exponentially. This threshold was inversely related to the transmission efficiency from acutely-infected hosts to larvae, i.e. the ‘elbow’ of the joint threshold curves in Fig. 7 moved to the left as transmission efficiency increased. For A. phagocytophilum and B. burgdorferi B348, high as well as low deer numbers could cause pathogens to die out, i.e. at high deer densities a ‘dilution effect’ occurred for these pathogens (as in Norman et al. 1999, Fig. 7). The numbers of deer needed to obtain a ‘dilution effect’ was lower for A. phagocytophilum than for B. burgdorferi B348, but numbers of deer sufficient to dilute transmission cycles of B. burgdorferi BL206 (>2000) were not reached in the simulations. A hypothetical pathogen, with transmission characteristics of B. burgdorferi B348 but a longer duration of acute infection, also did not suffer a ‘dilution effect’ with the range of deer numbers tested. Therefore, susceptibility to the ‘dilution effect’ varied with both the duration of acute infection, and acute phase host-to-tick transmission efficiency (Fig. 7). When seasonal nymphal and larval activity was more synchronous, higher deer numbers were needed to obtain a dilution effect for A. phagocytophilum (Fig. 7).

Fig. 7. Joint threshold curves for persistence of ticks and tick-borne pathogens obtained in model simulations under conditions of different deer and rodent host densities. In (A) separate curves are shown for the ticks and each of 4 pathogens: Borrelia burgdorferi strains BL206 and B348, Anaplasma phagocytophilum and a theoretical pathogen as described in the text. Arrows indicate the sides of the curves on which rodent and deer densities permit persistence of the pathogens. In (B) the curve obtained for A. phagocytophilum when larval and nymphal Ixodes scapularis were seasonally asynchronous was compared against that obtained when these instars were more synchronous.

DISCUSSION

We have developed a model that simulates a seasonal pattern of rodent demography, tick vector abundance and attachment rates, and infection prevalence in rodents and questing ticks, which approximate the situation in northeastern North America. We used this system to compare the consequences of reductions in host and tick abundance on, and limits of host-to-tick transmission characteristics for, the survival of different strains and species of I. scapularis-borne bacteria. We have then compared results obtained when larval and nymphal ticks were asynchronous and synchronous.

Sensitivity analyses demonstrated the interrelatedness of rodent, tick and microparasite abundance in terms of both the ecology of the system, and the public health risk that may arise. This underlines the need to model how variations in the host community simultaneously affect microparasite survival directly by varying densities of competent reservoir species, and indirectly by affecting tick vector abundance (Begon, 2006). These also suggest that parameterization of rodent model parameters are important to model outcomes and require further study.

Quantitative limits for characteristics of host infection and host-to-tick infectivity and transmission were obtained from the model under conditions of seasonally asynchronous activity of immature I. scapularis. In the absence of co-feeding transmission, a number of combinations of levels of transmission efficiency from acute-infected and carrier animals, and persistence of acute infection, could permit maintenance of microparasites in the model system. Higher transmission efficiency from acutely infected rodents to ticks and longer duration of acute host infections increased resistance to deterministic die-out due to reduced tick and rodent abundance and, possibly, to the ‘dilution effect’. Here, the dilution effect was explored using a theoretical two-host system to compare our model with that of Norman et al. (1999), and produced qualitatively similar results. However, a ‘dilution effect’ occurred only when numbers of deer were unrealistically high, even though deer are completely reservoir incompetent (in the model and in nature for B. burgdorferi). Further studies are required, therefore, to more fully and practically investigate under what circumstances, and for what pathogens, the ‘dilution effect’ may occur using more complex models containing hosts that are considered important dilution hosts in nature (LoGiudice et al. 2003). When immature I. scapularis were seasonally asynchronous rather than synchronous, infections had to persist longer and/or be transmitted with higher efficiency to survive, transmission cycles were much more sensitive to microparasite-induced mortality of rodents, and to the ‘dilution effect’ caused by a non-reservoir tick host (as defined in Norman et al. 1999), and differences in susceptibility to die-out amongst the pathogens were much more marked. As long as co-feeding transmission is efficient, it may buffer any limitations duration and transmission of systemic host infections may have on microparasite survival, even where ticks are not completely synchronous. However, co-feeding transmission is itself likely to be most efficient when nymphal and larval ticks are synchronous (Randolph et al. 2000).

Seasonal asynchrony of immature I. scapularis tick vectors and strong inter-annual fluctuations in P. leucopus rodent and I. scapularis vector abundance are the norm in nature in northeastern USA (Jones et al. 1998). Our model suggests, therefore, that traits permitting one of (i) highly efficient transmission from acutely infected hosts, (ii) longer lived acute or ‘carrier’ infections in the host, and (iii) efficient transmission amongst co-feeding ticks are essential for emergence and persistence of I. scapularis-borne pathogens in northeastern North America.

Persistent, highly transmissible microparasite infections require efficient but costly mechanisms to evade host immunity such as binding of host proteins and down-regulation of immunogenic surface proteins (for B. burgdorferi s.l.: Kurtenbach et al. 2002; Liang et al. 2004; Lederer et al. 2005) or antigenic variation (for A. phagocytophilum: Barbet et al. 2003), which may entail specialization for a host species (Nelson et al. 2005). The high mortality often associated with highly efficient host-to-tick transmission in livestock (O'Callaghan et al. 1998; Ogden et al. 2003) is not seen in P. leucopus infected with B. burgdorferi (Hofmeister et al. 1999; Bunikis et al. 2004). By implication, B. burgdorferi strain BL206 is more specialized for P. leucopus than strain B348 by having an immune-evasion mechanism that is more effective in this host, enhances pathogen survival, yet the greater abundance of the microparasite doesn't increase host mortality (Gilchrist and Sasaki 2002; Alizon and van Baalen, 2005). This raises the hypothesis that seasonal asynchrony of immature I. scapularis drives specialization for different host species (multiple niche polymorphism: Levene, 1953).

The dynamics of infection in, and transmission from experimental mice, and the capacity for local dissemination (and thus possibly co-feeding transmission: Ogden et al.1997; Richter et al. 2002) vary amongst B. burgdorferi strains and in part correlate with clinical disease in humans (Liveris et al. 2002; Wang et al. 2002; Steere et al. 2004). Thus, traits that evolve to enhance transmission from natural hosts could affect the severity or type of clinical disease seen in humans.

Our study suggests that the degree of seasonal asynchrony between nymphal I. scapularis infecting hosts, and larvae acquiring infection from hosts sets minimum values for the duration and efficiency of transmission of host infections (or co-feeding transmission) that are consistent with survival of the I. scapularis-borne microparasites. This may in turn drive host specialization amongst populations of I. scapularis-borne microparasites. Thus, abiotic forcings that determine the degree of asynchrony in seasonal tick abundance (day length and climate: Yuval and Spielman, 1990; Ogden et al. 2006) may have important implications for the public health risk from tick-borne zoonoses because: (i) adaptation to different host species may be associated with differences in pathogenicity and clinical disease in humans; and (ii) variations in tick seasonality at different latitudes, and with climate change (Ogden et al. 2006), may result in variation in the geographical range of different species and strains of tick-borne zoonoses. Further modelling and empirical studies are required to specifically investigate effects of host infection dynamics and transmission (related to different species and genotypes), rodent population biology and the dilution effect on transmission cycles and public health risk from tick-borne zoonoses. Our study highlights the importance in general of field and laboratory studies to more fully parameterize and validate models of tick-borne zoonoses transmission, and to investigate the predictions for pathogen evolution and geographical distribution of our modelling studies.

We thank Rick Ostfeld for very helpful comments in the preparation of this manuscript.

APPENDIX 1

Equations of the Ixodes scapularis population model

STELLA calculates changes at four steps per time unit using difference equations, but approximates a differential equation by integration of the difference equation (Peterson and Richmond, 1997). Equations have left-hand-side notation as for a differential equation, except those containing predictions for tick development events, which have a resolution of one day.

  1. Rate of change of egg-laying adult females:
  2. Rate of change of number of eggs:
  3. Rate of change in the number of hardening larvae:
  4. Rate of change in the number of questing larvae:
  5. Rate of change in the number of feeding larvae acquiring infection from rodents:
  6. Rate of change in the number of feeding larvae not acquiring infection from rodents:
  7. Rate of change in the number of larvae feeding on deer:
  8. Rate of change in the number of infected engorged larvae that fed on rodents:
  9. Rate of change in the number of uninfected engorged larvae that fed on rodents:
  10. Rate of change in the number of engorged larvae that fed on deer:
  11. Rate of change in the number of uninfected questing nymphs:
  12. Rate of change in the number of infected questing nymphs:
  13. Rate of change in the number of nymphs feeding on rodents:
  14. Rate of change in the number of nymphs feeding on deer:
  15. Rate of change in the number of engorged nymphs:
  16. Rate of change in the number of questing adults:
  17. Rate of change in the number of feeding adults:
  18. Rate of change in the number of engorged adult females:

APPENDIX 2

Equations of the Peromyscus leucopus population model

  1. Rate of change in the number of uninfected trappable juvenile/sub-adult males:
  2. Rate of change in the number of uninfected adult males:
  3. Rate of change in the number of trappable juvenile/sub-adult males with acute infections:
  4. Rate of change in the number of adult males with acute infections:
  5. Rate of change in the number of trappable juvenile/sub-adult males with carrier infections:
  6. Rate of change in the number of adult males with carrier infections:
  7. Rate of change in the number of uninfected trappable juvenile/sub-adult females:
  8. Rate of change in the number of uninfected adult females:
  9. Rate of change in the number of uninfected pregnant females:
  10. Rate of change in the number of uninfected litter-bearing females:
  11. Rate of change in the number of trappable juvenile/sub-adult females with acute infections:
  12. Rate of change in the number of adult females with acute infections:
  13. Rate of change in the number of pregnant females with acute infections:
  14. Rate of change in the number of litter-bearing females with acute infections:
  15. Rate of change in the number of trappable juvenile/sub-adult females with carrier infections:
  16. Rate of change in the number of adult females with carrier infections:
  17. Rate of change in the number of pregnant females with carrier infections:
  18. Rate of change in the number of litter-bearing females with carrier infections:
  19. Rate of change in the numbers of non-trappable juvenile males:
  20. Rate of change in the numbers of non-trappable juvenile females:

References

REFERENCES

Adelson, M. E., Rao, R. V., Tilton, R. C., Cabets, K., Eskow, E., Fein, L., Occi, J. L. and Mordechai, E. ( 2004). Prevalence of Borrelia burgdorferi, Bartonella spp., Babesia microti, and Anaplasma phagocytophila in Ixodes scapularis ticks collected in Northern New Jersey. Journal of Clinical Microbiology 42, 2799–2801.Google Scholar
Alizon, S. and van Baalen, M. ( 2005). Emergence of a convex trade-off between transmission and virulence. American Naturalist 165, 155–167.CrossRefGoogle Scholar
Anderson, J. F., Johnson, R. C. and Magnarelli, L. A. ( 1987). Seasonal prevalence of Borrelia burgdorferi in natural populations of white-footed mice, Peromyscus leucopus. Journal of Clinical Microbiology 25, 1564–1566.Google Scholar
Barbet, A. F., Meeus, P. F., Belanger, M., Bowie, M. V., Yi, J., Lundgren, A. M., Alleman, A. R., Wong, S. J., Chu, F. K., Munderloh, U. G. and Jauron, S. D. ( 2003). Expression of multiple outer membrane protein sequence variants from a single genomic locus of Anaplasma phagocytophilum. Infection and Immunity 71, 1706–1718.CrossRefGoogle Scholar
Begon, M. ( 2006). Effects of host diversity on disease dynamics. In Ecology of Infectious Diseases: Effects of Ecosystems on Disease and of Disease on Ecosystems ( ed. Ostfeld, R. S., Keesing, F. and Eviner, V.). Princeton University Press (in the Press).
Brisson, D. and Dykhuizen, D. E. ( 2004). OspC diversity in Borrelia burgdorferi: different hosts are different niches. Genetics 168, 713–722.CrossRefGoogle Scholar
Bunikis, J., Tsao, J., Luke, C. L., Luna, M. G., Fish, D. and Barbour, A. G. ( 2004). Borrelia burgdorferi infection in a natural population of Peromyscus leucopus mice: a longitudinal study in an area where Lyme Borreliosis is highly endemic. Journal of Infectious Diseases 189, 1515–1524.CrossRefGoogle Scholar
Burgdorfer, W. and Schwan, T. G. ( 1991). Lyme borreliosis: a relapsing fever-like disease? Scandinavian Journal of Infectious Diseases Supplements 77, 17–22.Google Scholar
Daniels, T. J., Boccia, T. M., Varde, S., Marcus, J., Le, J., Bucher, D. J., Falco, R. C. and Schwartz, I. ( 1998). Geographic risk for Lyme disease and human granulocytic ehrlichiosis in southern New York State. Applied and Environmental Microbiology 64, 4663–4669.Google Scholar
Derdáková, M., Dudiòák, V., Brei, B., Brownstein, J. S., Schwartz, I. and Fish, D. ( 2004). Interaction and transmission of two Borrelia burgdorferi sensu stricto strains in a tick-rodent maintenance system. Applied and Environmental Microbiology 70, 6783–6788.CrossRefGoogle Scholar
Donahue, J. G., Piesman, J. and Spielman, A. ( 1987). Reservoir competence of white-footed mice for Lyme disease spirochetes. American Journal of Tropical Medicine and Hygiene 36, 92–96.CrossRefGoogle Scholar
Gern, L. and Rais, O. ( 1996). Efficient transmission of Borrelia burgdorferi between cofeeding Ixodes ricinus ticks (Acari: Ixodidae). Journal of Medical Entomology 33, 189–192.CrossRefGoogle Scholar
Gilchrist, M. A. and Sasaki, A. ( 2002). Modeling host-parasite coevolution: a nested approach based on mechanistic models. Journal of Theoretical Biology 218, 219–308.CrossRefGoogle Scholar
Gog, J. R. and Grenfell, B. T. ( 2002). Dynamics and selection of many-strain pathogens. Proceedings of the National Academy of Sciences, USA 99, 17209–17214.CrossRefGoogle Scholar
Hanincová, K., Kurtenbach, K., Diuk-Wasser, M., Brei, B. and Fish, D. ( 2006). Epidemic spread of Lyme borreliosis, northeastern United States. Emerging Infectious Diseases 12, 604–611.CrossRefGoogle Scholar
Harland, R. M., Blancher, P. J. and Millar, J. S. ( 1979). Demography of a population of Peromyscus leucopus. Canadian Journal of Zoology-Revue Canadienne de Zoologie 57, 323–328.CrossRefGoogle Scholar
Hofmeister, E. K., Ellis, B. A., Glass, G. E. and Childs, J. E. ( 1999). Longitudinal study of infection with Borrelia burgdorferi in a population of Peromyscus leucopus at a Lyme disease-enzootic site in Maryland. American Journal of Tropical Medicine and Hygiene 60, 598–609.CrossRefGoogle Scholar
Jones, C. G., Ostfeld, R. S., Richard, M. P., Schauber, E. M. and Wolff, J. O. ( 1998). Chain reactions linking acorns to gypsy moth outbreaks and Lyme disease risk. Science 279, 1023–1026.CrossRefGoogle Scholar
Keeling, M. J. and Gilligan, C. A. ( 2000). Bubonic plague: a metapopulation model of a zoonosis. Proceedings of the Royal Society of London, B 267, 2219–2230.CrossRefGoogle Scholar
Kilpatrick, H. J., Spohr, S. M. and Lima, K. K. ( 2001). Effects of population reduction on home ranges of female white-tailed deer at high densities. Canadian Journal of Zoology-Revue Canadienne De Zoologie 79, 949–954.CrossRefGoogle Scholar
Kurtenbach, K., De Michelis, S., Etti, S., Schäfer, S. M., Sewell, H.-S., Brade, V. and Kraiczy, P. ( 2002). Host association of Borrelia burgdorferi sensu lato – the key role of host complement. Trends in Microbiology 10, 74–79.CrossRefGoogle Scholar
Lederer, S., Brenner, C., Stehle, T., Gern, L., Wallich, R. and Simon, M. M. ( 2005). Quantitative analysis of Borrelia burgdorferi gene expression in naturally (tick) infected mouse strains. Medical Microbiology and Immunology 194, 81–90.CrossRefGoogle Scholar
Levene, H. ( 1953). Genetic equilibrium when more than one ecological niche is available. American Naturalist 87, 331–333.CrossRefGoogle Scholar
Levin, M. L. and Fish, D. ( 2000). Immunity reduces reservoir host competence of Peromyscus leucopus for Ehrlichia phagocytophila. Infection and Immunity 68, 1514–1518.CrossRefGoogle Scholar
Levin, M. L. and Ross D. E. ( 2004). Acquisition of different isolates of Anaplasma phagocytophilum by Ixodes scapularis from a model animal. Vector Borne Zoonotic Diseases 4, 53–59.CrossRefGoogle Scholar
Levin, M. L., des Vignes, F. and Fish, D. ( 1999). Disparity in the natural cycles of Borrelia burgdorferi and the agent of human granulocytic ehrlichiosis. Emerging Infectious Diseases 5, 204–208.CrossRefGoogle Scholar
Levine, J. F., Wilson, M. L. and Spielman, A. ( 1985). Mice as reservoirs of the Lyme disease spirochete. American Journal of Tropical Medicine and Hygiene 34, 355–360.CrossRefGoogle Scholar
Lewellen, R. H. and Vessey, S. H. ( 1998). The effect of density dependence and weather on population size of a polyvoltine species. Ecological Monographs 68, 571–594.CrossRefGoogle Scholar
Liang, F. T., Yan, J., Mbow, M. L., Sviat, S. L., Gilmore, R. D., Mamula, M. and Fikrig, E. ( 2004). Borrelia burgdorferi changes its surface antigenic expression in response to host immune responses. Infection and Immunity 72, 5759–5767.CrossRefGoogle Scholar
Lindsay, L. R., Barker, I. K., Surgeoner, G. A., McEwen, S. A. and Campbell, G. D. ( 1997). Duration of Borrelia burgdorferi infectivity in white-footed mice for the tick vector Ixodes scapularis under laboratory and field conditions in Ontario. Journal of Wildlife Diseases 33, 766–775.CrossRefGoogle Scholar
Lindsay, L. R., Mathison, S. W., Barker, I. K., McEwen, S. A., Gillespie, T. J. and Surgeoner, G. A. ( 1999). Microclimate and habitat in relation to Ixodes scapularis (Acari: Ixodidae) populations on Long Point, Ontario, Canada. Journal of Medical Entomology 36, 255–262.CrossRefGoogle Scholar
Linzey, A. V. and Kesner, M. H. ( 1991). Population regulation in white-footed mice (Peromyscus leucopus) in a suboptimal habitat. Canadian Journal of Zoology-Revue Canadienne de Zoologie 69, 76–81.CrossRefGoogle Scholar
Liveris, D., Wang, G., Girao, G., Byrne, D. W., Nowakowski, J., McKenna, D., Nadelman, R., Wormser, G. P. and Schwartz, I. ( 2002). Quantitative detection of Borrelia burgdorferi in 2-millimeter skin samples of erythema migrans lesions: correlation of results with clinical and laboratory findings. Journal of Clinical Microbiology 40, 1249–1253.CrossRefGoogle Scholar
LoGiudice, K., Ostfeld, R. S., Schmidt, K. A. and Keesing, F. ( 2003). The ecology of infectious disease: effects of host diversity and community composition on Lyme disease risk. Proceedings of the National Academy of Sciences, USA 100, 567–571.CrossRefGoogle Scholar
Massung, R. F., Priestly, R. A. and Levin, M. L. ( 2004). Transmission route and kinetics of Anaplasma phagocytophilum infection in the white-footed mouse Peromyscus leucopus. Vector-Borne Zoonotic Diseases 4, 310–318.CrossRefGoogle Scholar
Mather, T. N., Wilson, M. L., Moore, S. I., Ribeiro, J. M. and Spielman, A. ( 1989). Comparing the relative potential of rodents as reservoirs of the Lyme disease spirochete (Borrelia burgdorferi). American Journal of Epidemiology 130, 143–150.CrossRefGoogle Scholar
Mather, T. N., Telford, S. R. 3rd, Moore, S. I. and Spielman, A. ( 1990). Borrelia burgdorferi and Babesia microti: efficiency of transmission from reservoirs to vector ticks (Ixodes dammini). Experimental Parasitology 70, 55–61.CrossRefGoogle Scholar
Millar, J. S. and Gyug, L. W. ( 1981). Initiation of breeding by northern Peromyscus in relation to temperature. Canadian Journal of Zoology-Revue Canadienne de Zoologie 59, 1094–1098.CrossRefGoogle Scholar
Nadeau, J. H., Lombardi, R. T. and Tamarin, R. H. ( 1981). Population-structure and dispersal of Peromyscus leucopus on Muskeget island. Canadian Journal of Zoology-Revue Canadienne de Zoologie 59, 793–799.CrossRefGoogle Scholar
Nelson, D. E., Virok, D. P., Wood, H., Roshick, C., Johnson, R. M., Whitmire, W. M., Crane, D. D., Steele-Mortimer, O., Kari, L., McClarty, G. and Caldwell, H. D. ( 2005). Chlamydial IFN-gamma immune evasion is linked to host infection tropism. Proceedings of the National Academy of Sciences, USA 102, 10658–10663.CrossRefGoogle Scholar
Norman, R., Bowers, R. G., Begon, M. and Hudson, P. J. ( 1999). Persistence of tick-borne virus in the presence of multiple host species: tick reservoirs and parasite-mediated competition. Journal of Theoretical Biology 200, 111–118.CrossRefGoogle Scholar
O'Callaghan, C. J., Medley, G. F., Peter, T. F. and Perry, B. D. ( 1998). Investigating the epidemiology of heartwater (Cowdria ruminantium infection) by means of a transmission dynamics model. Parasitology 117, 49–61.CrossRefGoogle Scholar
Ogden, N. H., Nuttall, P. A. and Randolph, S. E. ( 1997). Natural Lyme disease cycles maintained via sheep by cofeeding ticks. Parasitology 115, 591–599.CrossRefGoogle Scholar
Ogden, N. H., Casey, A. N. J., Woldehiwet, Z. and French, N. P. ( 2003). Transmission of Anaplasma phagocytophilum to Ixodes ricinus ticks from sheep in the acute and post-acute phase of infection. Infection and Immunity 71, 2071–2078.CrossRefGoogle Scholar
Ogden, N. H., Lindsay, L. R., Beauchamp, G., Charron, D., Maarouf, A., O'Callaghan, C. J., Waltner-Toews D. and Barker, I. K. ( 2004). Investigation of the relationships between temperature and development rates of the tick Ixodes scapularis (Acari: Ixodidae) in the laboratory and field. Journal of Medical Entomology 41, 622–633.CrossRefGoogle Scholar
Ogden, N. H., Bigras-Poulin, M., O'Callaghan, C. J., Barker, I. K., Lindsay, L. R., Maarouf, A., Smoyer-Tomic, K. E., Waltner-Toews, D. and Charron, D. ( 2005). A dynamic population model to investigate effects of climate on geographic range and seasonality of the tick Ixodes scapularis. International Journal for Parasitology 35, 375–389.CrossRefGoogle Scholar
Ogden, N. H., Maarouf, A., Barker, I. K., Bigras-Poulin, M., Lindsay, L. R., Morshed M. G., O'Callaghan, C. J., Ramay, F., Waltner-Toews, D. and Charron, D. F. ( 2006). Projections for range expansion of the Lyme disease vector Ixodes scapularis, in response to climate change. International Journal for Parasitology 36, 63–70.CrossRefGoogle Scholar
Pancholi, P., Kolbert, C. P., Mitchell, P. D., Reed, K. D. Jr, Dumler, J. S., Bakken, J. S., Telford, S. R. 3rd and Persing, D. H. ( 1995). Ixodes dammini as a potential vector of human granulocytic ehrlichiosis. Journal of Infectious Diseases 172, 1007–1012.CrossRefGoogle Scholar
Peterson, S. and Richmond, B. ( 1997). Stella Technical Documentation, High Performance Systems, Inc., 13.2–13.5.
Porco, T. C. ( 1999). A mathematical model of the ecology of Lyme disease. IMA Journal of Mathematics Applied in Medicine and Biology 16, 261–296.CrossRefGoogle Scholar
Randolph, S. E. ( 2001). The shifting landscape of tick-borne zoonoses: tick-borne encephalitis and Lyme borreliosis in Europe. Philosophical Transactions of the Royal Society, B. 356, 1045–1056.CrossRefGoogle Scholar
Randolph, S. E., Gern, L. and Nuttall, P. A. ( 1996). Co-feeding ticks: epidemiological significance for tick-borne pathogen transmission. Parasitology Today 12, 472–479.CrossRefGoogle Scholar
Randolph, S. E., Mikslová, D., Rogers, D. J. and Labuda, M. ( 1999). Incidence from coincidence: patterns of tick infestations on rodents facilitate transmission of tick-borne encephalitis virus. Parasitology 118, 177–186.CrossRefGoogle Scholar
Randolph, S. E., Green, R. M., Peacey, M. F. and Rogers, D. J. ( 2000). Seasonal synchrony: the key to tick-borne encephalitis foci identified by satellite data. Parasitology 121, 15–23.CrossRefGoogle Scholar
Richter, D., Allgower, R. and Matuschka, F. R. ( 2002). Cofeeding transmission and its contribution to the perpetuation of the lyme disease spirochete Borrelia afzelii. Emerging Infectious Diseases 8, 1421–1425.CrossRefGoogle Scholar
Rintamaa, D. L., Mazur, P. A. and Vessey, S. H. ( 1976). Reproduction during two annual cycles in a population of Peromyscus leucopus noveboracensis. Journal of Mammalogy 57, 593–595.CrossRefGoogle Scholar
Schauber, E. M. and Ostfeld, R. S. ( 2002). Modeling the effects of reservoir competence decay and demographic turnover in Lyme disease ecology. Ecological Applications 12, 1142–1162.CrossRefGoogle Scholar
Schmidt, K. A., Ostfeld, R. S. and Schauber, E. M. ( 1999). Infestation of Peromyscus leucopus and Tamias striatus by Ixodes scapularis (Acari: Ixodidae) in relation to the abundance of hosts and parasites. Journal of Medical Entomology 36, 749–757.CrossRefGoogle Scholar
Schug, M. D., Vessey, S. H. and Korytko, A. I. ( 1991). Longevity and survival in a population of white-footed mice (Peromyscus leucopus). Journal of Mammalogy 72, 360–366.CrossRefGoogle Scholar
Schwan, T. G., Kime, K. K., Schrumpf, M. E., Coe, J. E. and Simpson, W. J. ( 1989). Antibody response in white footed mice (Peromyscus leucopus) experimentally infected with the Lyme disease spirochaete (Borrelia burgdorferi). Infection and Immunity 57, 3445–3451.Google Scholar
Stafford, K. C. 3rd, Massung, R. F., Magnarelli, L. A., Ijdo, J. W. and Anderson, J. F. ( 1999). Infection with agents of human granulocytic ehrlichiosis, Lyme disease, and babesiosis in wild white-footed mice (Peromyscus leucopus) in Connecticut. Journal of Clinical Microbiology 37, 2887–2892.Google Scholar
Steere, A. C., Coburn, J. and Glickstein, L. ( 2004). The emergence of Lyme disease. Journal of Clinical Investigation 113, 1093–1101.CrossRefGoogle Scholar
Terman, C. R. and Terman, J. R. ( 1999). Early summer reproductive hiatus in wild adult white-footed mice. Journal of Mammalogy 80, 1251–1256.CrossRefGoogle Scholar
Thompson, C., Spielman, A. and Krause, P. J. ( 2001). Coinfecting deer-associated zoonoses: Lyme disease, babesiosis, and ehrlichiosis. Clinical Infectious Diseases 33, 676–685.CrossRefGoogle Scholar
Tsao, J. I., Wootton, J. T., Bunikis, J., Luna, M. G., Fish, D. and Barbour, A. G. ( 2004). An ecological approach to preventing human infection: vaccinating wild mouse reservoirs intervenes in the Lyme disease cycle. Proceedings of the National Academy of Sciences, USA 101, 18159–18164.CrossRefGoogle Scholar
Wang, G., Ojaimi, C., Wu, H., Saksenberg, V., Iyer, R., Liveris, D., McClain, S. A., Wormser, G. P. and Schwartz, I. ( 2002). Disease severity in a murine model of Lyme borreliosis is associated with the genotype of the infecting Borrelia burgdorferi sensu stricto strain. Journal of Infectious Diseases 186, 782–791.CrossRefGoogle Scholar
Wilson, M. L. and Spielman, A. ( 1985). Seasonal activity of immature Ixodes dammini (Acari: Ixodidae). Journal of Medical Entomology 26, 408–414.CrossRefGoogle Scholar
Wolff, J. O. ( 1985). Comparative population ecology of Peromyscus leucopus and Peromyscus maniculatus. Canadian Journal of Zoology-Revue Canadienne de Zoologie 63, 1548–1555.CrossRefGoogle Scholar
Yunger, J. A. ( 2002). Response of two low-density populations of Peromyscus leucopus to increased food availability. Journal of Mammalogy 83, 267–279.2.0.CO;2>CrossRefGoogle Scholar
Yuval, B. and Spielman, A. ( 1990). Duration and regulation of the developmental cycle of Ixodes dammini (Acari: Ixodidae). Journal of Medical Entomology 27, 196–201.CrossRefGoogle Scholar
Figure 0

Fig. 1. A diagram of the combined Ixodes scapularis and SIR Peromyscus leucopus rodent models. The bold dotted lines indicate infection transmission between tick and rodent populations. For simplicity, not all flows to indicate mortality, nor linkage of P. leucopus abundance to host-finding success of immature ticks, are shown.

Figure 1

Table 1. Parameter definitions in the Ixodes scapularis model and their initial values

Figure 2

Table 2. Parameter definitions in the Peromuscus leucopus model and their initial values

Figure 3

Table 3. Infection and transmission characteristics of the tick-borne pathogens used in model simulations, and the studies from which these values were approximated

Figure 4

Fig. 2. Monthly variations in the numbers of ‘trappable’ Peromyscus leucopus at model equilibrium (A), compared against field observations in northeastern USA (Nadeau et al. 1981) (B). Field observations are mean monthly values (+/− maximum and minimum over 5 years) of the minimum numbers of P. leucopus known alive (MNKA). Also shown are simulated monthly variations in P. leucopus numbers when the model included a mid-summer hiatus in rodent breeding (C) and when adult rodent mortality was set higher in spring and summer than in winter (D).

Figure 5

Fig. 3. The seasonal variation in monthly nymphal and larval Ixodes scapularis infestations of mice at model equilibrium expressed as a proportion of the total annual numbers infesting the mice. In (A) the model simulated the classical immature tick seasonality in northeastern North America. The model in (B), calibrated to produce a hypothetical synchronous pattern of immature tick activity, was used in comparisons.

Figure 6

Fig. 4. Mean monthly prevalence of infection in questing nymphs for each pathogen at model equilibrium, obtained with and without co-feeding transmission.

Figure 7

Table 4. The mean annual prevalence of infection in questing nymphal ticks at model equilibrium alongside comparable estimates obtained in field studies

Figure 8

Fig. 5. The monthly variations in rodent infection prevalence with Borrelia burgdorferi BL206 (solid line with filled triangles), B. burgdorferi LI-231 (broken line with filled squares), and A. phagocytophilum (broken line with filled circles), predicted by the model at equilibrium without effects of co-feeding transmission. Also shown are field observations of B. burgdorferi infection prevalence in Peromyscus leucopus in studies in Connecticut, USA (open circles [mean values across 2 years and sites: Anderson et al. 1987] and crosses [mean values across 2 years: Bunikis et al. 2004]) and Ontario, Canada (open squares [Lindsay et al. 1997]). Vertical bars indicate the range of values obtained at different observations (for the field studies in Connecticut), or 95% confidence intervals (for the field study in Ontario). P. leucopus mortality and reproduction parameters were at their most simple in (A). In (B) the model included a mid-summer hiatus in rodent breeding, and in (C) adult rodent mortality was higher in spring and summer than in winter.

Figure 9

Fig. 6. The sensitivity of model equilibrium parameter values for (left to right) (i) annual maximum rodent and tick numbers, (ii) mean annual infection prevalence in questing nymphal ticks, (iii) mean annual infection prevalence in rodents, and (iv) infection ‘risk’ (the product of mean annual prevalence in questing nymphal ticks, and maximum numbers of questing nymphs), to 5% increases in the variables on the left hand side of the figure. DD rodents: density dependent regulation of rodent breeding. Peromyscus leucopus mortality and reproduction parameters were at their most simple in (A). In (B) the model included a mid-summer hiatus in rodent breeding, and in (C) adult rodent mortality was higher in spring and summer than in winter.

Figure 10

Table 5. The minimum duration of acute infection in hosts (in days), below which deterministic die out occurred, for a range of values for transmission efficiency to ticks from acute-infected and carrier hosts

Figure 11

Table 6. A comparison of the percentage increase in mortality rates of non-feeding ticks, and the basic mortality rate of rodents, required to cause deterministic die out of the different pathogens, and Ixodes scapularis and Peromyscus leucopus populations

Figure 12

Fig. 7. Joint threshold curves for persistence of ticks and tick-borne pathogens obtained in model simulations under conditions of different deer and rodent host densities. In (A) separate curves are shown for the ticks and each of 4 pathogens: Borrelia burgdorferi strains BL206 and B348, Anaplasma phagocytophilum and a theoretical pathogen as described in the text. Arrows indicate the sides of the curves on which rodent and deer densities permit persistence of the pathogens. In (B) the curve obtained for A. phagocytophilum when larval and nymphal Ixodes scapularis were seasonally asynchronous was compared against that obtained when these instars were more synchronous.