1. INTRODUCTION
Valid asymptotic corrections to limiting distributions, in the form
of Edgeworth expansions, are available for a variety of econometric
estimators and tests. However, the use of such expansions specifically
as inferential tools has proved somewhat limited. Instead, Bartlett
correction, the bootstrap, and Laplace or saddlepoint approximations
have proved more popular. In fact, all of these techniques rely on the
theory of Edgeworth expansions to justify their higher order validity.
For example, see the derivation of Bartlett corrections in McCullagh
(1987), the synthesis of the bootstrap and
Edgeworth expansion in Hall (1992), and the
derivations of saddlepoint approximations in Daniels (1954) and Durbin (1980),
all of which illustrate this point.
This paper attempts to make use of the Edgeworth expansion as a
practical tool. First we detail precisely the conditions under which
the expansion is justified, ensuring that the required conditions are
verifiable in a straightforward way. Second we consider the statistic
for which we want the expansion as a choice in itself, specifically by
choosing a nonlinear transformation so as to fix the properties of the
resultant expansion. For example, it will be shown that it is possible
to improve the rate of convergence of the leading term, from
O(N−1/2) to
O(N−1), where N is the
asymptotic argument of the series, in most applications the sample
size.
The effect of nonlinear transformations upon the efficacy of
asymptotic expansions has been considered in the literature. Phillips
and Park (1988) examine the effect that
different algebraic formulations of nonlinear hypotheses have on the
Wald test. Phillips (1979a) and Niki and
Konishi (1986) derive Edgeworth expansions
for transformations of a univariate statistic, whereas Phillips (1979b), Taniguchi (1991),
and Marsh (2001) consider the Edgeworth
expansion of Fisher's z-transformation of the serial
correlation coefficient.
Here these results are generalized in the following way. It will be
assumed that the statistic, or indeed an approximation to it suitable
in distribution, permits a valid, that is, with known order of error,
Edgeworth expansion. The statistic may be multivariate and the data
from which it is derived may be dependent and heterogeneously
distributed. Then we identify what is perceived to be a fundamental
difficulty in the usage of such expansions. This is that the
oscillatory nature of the polynomial corrections to the leading term
asymptotic distribution causes nonmonotonicity, particularly in the
tails of the distribution, so-called tail difficulty (see Niki and Konishi, 1986; Hall, 1992, App. V). The suggested transformation will,
as in Niki and Konishi (1986), thus be that
which eliminates the asymptotic skewness coefficient and thereby limits
this tail difficulty to the greatest extent.
The main results of this paper are contained in two theorems and two
corollaries. The first theorem derives the set of equations (a cube of
coupled second-order partial differential equations) that the
transformation that removes asymptotic skewness must satisfy. There
will be, in general, a multiplicity of solutions to these equations.
Specializing the problem slightly (essentially requiring that the
moments depend upon some set of parameters of fixed dimension) the
second theorem yields a particular solution. The first corollary shows
that we may find a transformation such that the leading term has an
order of error of O(N−1), rather
than the usual O(N−1/2).
Similarly, the second corollary shows that if the bootstrap is used to
approximate the distribution of the transformed statistic the order of
error committed is O(N−3/2).
Although these results are simply the usual orders of errors for both
the limiting and bootstrap approximations applied to symmetrically
distributed statistics, and are therefore somewhat obvious, they
highlight a key point of the paper, which is that the Edgeworth
expansion may be employed in such a way as to turn a first-order
problem into a second-order one.
To be of practical use these results need to offer at least some
advantage over the techniques mentioned at the beginning of this
introduction. It is certainly true that derivation of Edgeworth
expansions can be a formidable exercise, as exemplified by the
derivations contained in Sargan (1976),
Phillips (1977a, 1977b), Satchell (1984),
Sargan and Satchell (1986), and more recently
Linton (1997). However, the same is true for
both Bartlett corrections and saddlepoint approximations, and indeed
the latter are only available under more restrictive conditions.
The bootstrap has become by far the most widely used higher order
inferential tool in econometrics. See, for example, Hall (1992), Horowitz and Savin (2000), and Horowitz (2001), among many others. Although it depends upon
Edgeworth-type expansions for its validity, appropriate resampling
schemes negate the necessity of calculating the expansion itself. Thus
the theoretical complexity of the expansion is replaced by the
computational complexity of Monte Carlo and resampling. However, unlike
approximations derived from an expansion those from the bootstrap are
conditional upon the sample, that is, they apply to the data, rather
than the model. For any given sample, calculation of bootstrap critical
values for a test is trivial given modern equipment and software;
however this needs to be repeated for every sample. To overcome the
computational burden in nonlinear models Davidson and MacKinnon (1999) and Andrews (2002)
propose a more convenient procedure requiring only a finite number of
steps in an iterative optimization routine. Combined with double
bootstrap, or prepivoting in the language of Beran (1988), and requiring only two steps in the
optimization we have potentially a very powerful tool, delivering an
order of error of O(N−3/2).
However, even with a relatively modest sample size, number of bootstrap
iterations (at both levels), and Monte Carlo replications in the
thousands, a single experiment would require the generation of billions
of pseudorandom numbers, even for a univariate statistic. Although
perfectly feasible, this does require both time and the availability of
sophisticated pseudorandom number generators having very long
periods.
Recalling that a one-level bootstrap will, in general, have an order
of error of O(N−1), in coverage
probability, and for the two-level bootstrap it will be
O(N−3/2) (see Beran, 1988), this puts the results of the two
corollaries of this paper in context. That is we may deliver the same
order of error but at a significantly lower computational cost,
although this must be offset by the cost in deriving the relevant
transformation. The computational saving may be quantified. If the last
bootstrap level consists of 100 × B iterations, the
computation length for the methods of this paper are
(1/B)% of those for the bootstrap yielding the same order
of error. In some circumstances, such as calculation of a symmetric
confidence interval or application of a symmetric test, the error in
coverage and rejection probabilities for the one-level bootstrap are
O(N−2). In such cases the practical
relevance of transformation methods appears limited in comparison,
because this order of error cannot always be attained by a leading term
approximation.
The methods of this paper are illustrated in two separate sections.
The first applies the theorems to the distribution of the sufficient
statistic in the exponential family. Doing so reveals that the
transformation required depends only upon the log-likelihood and its
derivatives. This result adds to those, including, for example, Durbin
(1980) and Armstrong and Hillier (1999), in which properties of, for instance,
maximum likelihood estimators (MLE), are derived directly from the
likelihood, not from the form of the statistic itself. The second
illustration concerns the numerical properties of the two corollaries.
Over four nonlinear regression models (probit, logit, Poisson, and
exponential regressions), the transformation that removes asymptotic
skewness and delivers asymptotic normal inference of order
O(N−1) is found. Then standard
normal quantiles are used as approximations to those of the MLEs (as
obtained by Monte Carlo simulation) and those of the transformed
statistic. Similarly, bootstrap critical values are obtained for both
statistics, in the logit and exponential regression cases, and the
nominal and true rejection probabilities analyzed.
The plan of the paper is as follows. Section 2 describes the notation
used and the assumption required to justify the Edgeworth expansion for
the density and distribution of a multivariate statistic, and it
motivates consideration of transformations of that statistic. The main
results are then contained in Section 3. Section 4 applies the theorems
to the cases where the statistic of interest is the sufficient
statistic and a linear combination of its elements. Section 5 provides
a numerical comparison first with respect to the limiting standard
normal and second with respect to the bootstrap within the nonlinear
models mentioned previously, Section 6 then concludes. The proofs of
the two theorems are contained in the Appendix.
2. PRELIMINARIES AND MOTIVATION
Before fixing the conditions under which the results of this paper
apply, some notation is required for expansions for multivariate
statistics. Let XN be a k ×
1 random vector with density
fN(x), distribution
FN(x), characteristic function
MX(λ), cumulant generating function
KX(λ) =
ln[MX(λ)], and vth
cumulant defined by
For a full account of the notation involved see McCullagh (1987, Ch. 2), in particular for the generalities of
index notation and the summation convention. The statistic
XN may be, for example, an estimator or a
test derived from some sample of size N, or indeed an
in-distribution approximation to it, of suitable order. In general we
will assume that as N → ∞,
XN →d
N(0,κXi1,i2 )
and that the density fN(x) may be
expanded as
for some b ≥ 3 and where
φk(x;κXi1,i2 )
is the k-dimension normal density with covariance
κXi1,i2 ,
the coefficients cj,N(κ) are
an asymptotic sequence in N and depend upon the cumulants of
XN, and the
qj(x) are (Hermite tensoral)
polynomials of degree 3j in the elements of x.
For details of relevant conditions and assumptions under which (1)
holds, the reader is referred to Sargan (1976), Phillips (1977a),
Bhattacharya and Ghosh (1978), Durbin (1980), Sargan and Satchell (1986), and Hall (1992),
among many others. A sufficient—and, more important,
verifiable—condition is given when the cumulants of
XN satisfy the following condition.
Assumption 1. Let
κXIj be
the jth cumulant of XN. Then
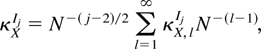
where the O(1) cumulant coefficients
κX,lIj
are free of N and we also assume
κX,1I1 = 0.
Assumption 1 guarantees that in (1) the coefficients
cj,N(κ) are of order
O(N−(j−2)/2),
which in turn determine the rate of convergence of the approximation.
However, this paper is concerned with the application of (1) as an
approximation to the finite sample density of
XN. Two aspects influence the accuracy of
such approximations. Apart from the number of correction terms
included, (i.e., b − 2), the accuracy will depend upon
where, in the sample space for XN, we
evaluate the approximation. As noted by Niki and Konishi (1986) the polynomials
qj(x) tend to be highly
oscillatory in particular for large x (i.e., in the tail
areas). Moreover, they find that the highest order polynomial occurs,
for every b, with the asymptotic skewness term
κX,1I3.
Therefore, for the univariate case they suggest transforming
XN via a nonlinear function to remove this
term. Other investigations of the impact of nonlinear transformations
on the accuracy of asymptotic approximations are contained in Hougaard
(1982) (for univariate likelihood), Phillips
(1979b) (in autoregression), and Phillips and
Park (1988) (for Wald tests of nonlinear
restrictions).
An interesting slant on the problem is provided by Hall (1992, App. V), who shows that, the product
φk(x;κXi1,i2 )cj,N(κ)qj(x)
involves the dominant term
so that the integral, and hence the approximating distribution, will
not converge at all if x =
O(N1/6). This is relevant because, for
example, if we follow some procedure that decreases the size of a
hypothesis test for larger sample sizes, then the critical value of the
test will grow with N. If we eliminate asymptotic skewness
then the polynomials qj(x) become
of degree 2j (if j is even) or 2j − 1
(if j is odd), and so the distribution will not converge if
now x = O(N1/4).
Evidence that the oscillations of the polynomials
qj(x) do cause tail difficulty
that is of concern may be found in the numerical analysis of the
Edgeworth series for the ordinary least squares (OLS) estimator for the
autoregressive parameter in an AR(1), contained in Phillips (1977b). Nonmonotone behavior of the approximating
distribution function manifests itself even for moderate values of the
parameter and in reasonable sample sizes. Similar results are contained
in the analysis of Edgeworth approximations for the information matrix
test in Chesher and Spady (1991).
Later in this paper we consider a family of nonlinear regression
models involving a single covariate,
{wi}i=1N.
For each, it will be shown that the asymptotic skewness coefficient of
the bias-corrected MLE (for the coefficient on that covariate) takes
the form,
where
is the bias-corrected version of the MLE
,
kα is a constant depending upon the particular
model characteristics, and rw is the
skewness coefficient of the covariates wi
(precise details are given in Section 5). To order
O(N−1) the Edgeworth expansion for
the distribution of
is
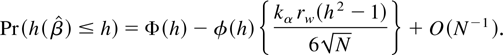
The approximation for the exponential regression case for which
kα = −1 for a sample size of N =
25 and for two different covariate configurations having skewness of
approximately rw ≈ 12.5 and
rw ≈ 5.7, respectively, is plotted in
Figure 1.
Edgeworth approximation (3) for the distribution of
,
with N = 25, for rw ≈ 12.5
(solid) and rw ≈ 5.7 (dashed) in the
exponential case.
Clearly the approximation is nonmonotonic; in fact for (3) to be
monotonic when rw ≈ 12.5, we would
require over 50,000 observations. If higher order inference based upon
Edgeworth expansions is to be made more practical, then the issue of
nonmonotonicity, and hence tail difficulty, needs to be overcome.
3. OPTIMAL TRANSFORMATIONS
In this section we first generalize the results of Phillips (1979a) and Niki and Konishi (1986) to the multivariate case. Following the
heuristic argument of the previous section, we call a transformation
optimal if it removes asymptotic skewness, thereby reducing the degree
of the highest order polynomial in (1). Suppose that we have the
k-dimension statistic X =
XN, with density
fN(x), satisfying Assumption 1,
with Edgeworth expansion given by (1) and cumulants
κXIj
and consider an arbitrary nonlinear transformation of the form
g = g(X). We will consider transformations
satisfying the following assumption.
Assumption 2.
(i) Let the dimension of g(X) be d,
where d ≤ k.
(ii) g(X) is v times differentiable,
where v > b, with derivatives
with the gIv
continuous in a neighbourhood of τ =
κXI1 =
E [X] and all minors of
gI1 bounded away from zero.
Assumption 2 requires the following. First, because we are
transforming a multivariate statistic, we require the dimension of the
transformation to be no larger than the original statistic. Second, we
will require that the function g = g(X) may
be expanded, around τ, as a power series of the form
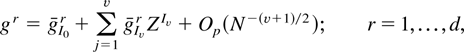
where
Under Assumption 2, the density and distribution of
g(X) permit a valid Edgeworth approximation (see
Skovgaard, 1981; Sargan
and Satchell, 1986). This assumption is stronger than those used
in the latter two papers only in that we desire a transformation that
will affect each of the terms in the expansion up to, and including,
order b. The density of g may be approximated, for
example, to O(N−3/2), by
In (5)
κg,jIv
is the jth term in the expansion of the vth cumulant
array of the statistic g. Because g is expressible as
a power series in X, then the cumulants of g are thus
the generalized cumulants of X, as detailed in the Appendix.
The transformation we want is such that the asymptotic skewness term
vanishes, that is,
κg,1I3 = 0. This
is achieved in the following theorem.
THEOREM 1. Suppose X satisfies Assumption 1 and g =
g(X) satisfies Assumption 2. Then
if and only if g(.) solves the d-cube of coupled
partial differential equations
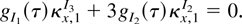
Remarks.
(i) The set of differential equations (6) are invariant with respect
to affine transformation; hence issues of standardization (with respect
to the mean and variance) do not impact upon solutions to them.
(ii) To eliminate asymptotic skewness g(.) must satisfy (6).
However, sometimes the exact cumulants of X will be known,
rather than their expansion. Because by definition the exact cumulants
and their leading term coincide asymptotically, it may be simpler to
solve
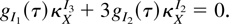
(iii) In general, (6) and (7) describe a set of
d3 coupled second-order partial differential
equations. Hence, solutions, even when they exist, may be difficult to
find (see Hougaard, 1982), whereas if
d < k then there will not exist an orthogonal
basis for a solution (see McCullagh, 1987,
Ch. 5). Overcoming this problem will be the purpose of the next
theorem.
(iv) The requirement here is only that asymptotic skewness be
eliminated, a much weaker condition than requiring that all excess
skewness be removed. Thus, to simplify the problem, we need only look
for local (up to an asymptotic order of
O(N−1/2)) solutions. This is
still true even if the form (7) is used.
To implement the transformation, that is, to find a feasible solution
to (6), we need to specialize the problem. Specifically we impose a
parameterization that the density of X is
fN(x;θ) depending on a
d-vector of parameters θ and so X has cumulants
given by
κXIv =
κXIv(θ).
In this setup, to solve (6) we make a preliminary transformation of the
form
depending both upon the statistic and the parameter. Again we assume
that h satisfies Assumption 1 and so permits a valid Edgeworth
approximation. The transformation is now g =
g(h). Hence a solution to (6) is given by the
following theorem.
THEOREM 2. Let
gii and
giii denote the
first and second derivatives of the ith element of g with respect to the
ith element of h, evaluated at
κh,1i1. Then a
solution to the set of d ordinary differential equations
where
kh,1i,i,i
is the leading term of the expansion of
cum(hi,hi,hi),
is also a solution to (6). Moreover a solution to (8) exists, unique up
to constants of integration.
Although Theorems 1 and 2 deliver transformations that remove the
highest order Hermite polynomial from any bth order
approximation, often we are able to obtain a stronger result.
COROLLARY 1. Suppose that there exists an affine transformation
of h, h → h = d + Dh,
so that τh = E
[h] = 0 + O(N−1)
and hence κh,21 = 0.
Defining the transformation, g = g(h),
satisfying (8) and letting
where
κg,1i1,i2
is the asymptotic covariance of g, then
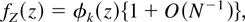
where φk(z) is the
standard normal density.
Proof. Because now also κh,21 = 0
then the only other term of order N−1/2 is
c, as defined previously, which may be removed because (8) is
invariant to affine transformation. █
We may also consider the transformation in conjunction with an
appropriate one-step bootstrap. Suppose that we have a sample
YN =
(y1,…,yN)
having distribution PN,θ. The
statistic of interest is X = XN =
X(y1,…,yN),
which may be, for example, an estimator for, or test upon, the unknown
parameter of interest θ. Let
be an
-consistent
estimator of θ. Let YN* be resampled
observations having distribution
,
that is, the empirical distribution of YN,
and similarly let X*, h*, and g* denote the
bootstrapped versions of the statistics considered in Theorems 1 and 2
and Corollary 1. The cumulative distribution functions of X,
h, and g will be denoted by
FN(.,θ), which are to be approximated by
,
the empirical distribution of the bootstrapped statistics.
COROLLARY 2. Suppose that X has an Edgeworth expansion given
by (1), h satisfies the conditions of Corollary 1, and
g = g(h) solves (8). Then
Proof. Following Beran (1988) the empirical
distributions
permit expansions, uniform in the first argument and local in θ,
of the form
where f1(X,θ) and
f2(g,θ) are polynomials derived
from the respective Edgeworth expansions for X and g
and the rate of convergence is determined by the leading term in that
expansion, that is, respectively, from (1) and (9). Consequently,
expanding f1(X,θ) and
f2(g,θ) around
and noting
proves the result. █
Provided that there is an affine transformation that removes the
O(N−1/2) term in the expansion
of the mean, Corollary 1 contains the stronger result that asymptotic
inference is optimized via use of a transformed statistic given by
Theorem 2. That is, if we use the limiting normal to obtain
probabilities or quantiles, then the transformation minimizes the order
of error for these values. Similarly, Corollary 2 optimizes the use of
a one-step bootstrap, in the sense that, as is well known, the
bootstrap has a faster convergence rate for symmetric rather than
asymmetric distributions. In fact, the one-step bootstrap applied to
the transformed statistic can have a convergence rate equal to that of
the two-step bootstrap applied to the original statistic.
With the general results in the preceding theorems and corollaries,
in the next two sections we will analyze the resulting properties of
such transformations, first their analytic and then their numerical
properties.
4. ANALYTIC PROPERTIES IN THE EXPONENTIAL
FAMILY
4.1. General Functions of the Sufficient Statistic
As a general application, consider a sample Y =
{y1,…,yN}′,
generated from a member of the exponential family, with density
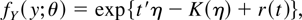
where η = η(θ), properties of which are detailed in
Barndorff-Nielsen and Cox (1989). Many
interesting Gaussian econometric models are exponential models,
examples of which are contained in van Garderen (1997).
Inference about θ will be conducted through functions of the
minimal sufficient statistic, t. In this section we will
derive the transformation of t, as described in the previous
section. In particular, it will be seen that this transformation is
defined only by the properties of the sample density itself. First we
need to check when Assumption 1 holds. The cumulant generating function
of t is
and hence the cumulants are
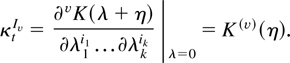
To proceed, note that if s = At + a, where
A and a may depend upon N but not η,
then (i) s is a canonical statistic and (ii) the sample
density may be written
Thus the exponential form of the density is preserved by affine
transformations, and moreover we may assume without loss of generality
that E [t] = 0 by choosing the constant
a appropriately. In particular we can define a canonical
statistic S = N1/2t, and if
in addition the cumulants of S satisfy
then Assumption 1 holds because for S, γ =
N−1/2η, then (12) implies
noting that higher order terms in the cumulant expansion vanish. As a
consequence, the density of t admits a formal Edgeworth
expansion.
An analogous result for a nonlinear transformation, g =
g(t), may be established, given only that (12) holds,
as in the following theorem, proved in Marsh (2001).
THEOREM 3. Given a transformation t →
g(t), satisfying Assumption 2, the density of
g permits a valid Edgeworth expansion provided only that there
exists an S satisfying (12).
Because both t and g permit Edgeworth
approximations for their densities, we may apply the criterion of an
“optimal” transformation. If we consider the case where
η = θ, implying that
fY(y;θ) is full exponential
(i.e., k = d), then applying Theorem 2, g(.)
must satisfy, using (11),
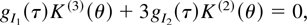
where τ = E(t) = K′(θ).
Notice that (14) is specified purely in terms of the properties of the
sample density. That is, if we define the log-likelihood for the sample
by l(θ) = θ′t −
K(θ) + h(y), then
K(v)(θ) =
−l(v)(θ) for v ≥ 2,
and τ = t − l′(θ). A solution to
(14) is found by applying Theorem 2. Define a symmetric P =
pji such that
and let z = Pt, so the cumulants of z are
then the optimal transformation must satisfy
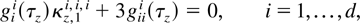
where τz = Pτ.
This explicit dependence on the likelihood is a further result in the
spirit of Durbin (1980), Hougaard (1982), and Armstrong and Hillier (1999). In those papers the object is to derive
exact or higher order asymptotic densities of estimators and tests,
purely in terms of functionals of the likelihood and its derivatives.
Here, the optimal transformation is defined entirely in terms of a
differential equation in the derivatives of the log-likelihood.
4.2. Tests of a Particular Form
Often, even for multivariable hypotheses, we require a univariate
statistic. In this section we analyze the properties of the
transformation acting upon a weighted average of the components of the
sufficient statistic. In a slightly altered setup, consider the full
exponential model
where s =
{s1,…,sk}′
and γ = {γ1,…,γk},
and the set of statistics defined by
the set of weighted averages of the canonical statistic. Statistics
such as (16) encompass point optimal and locally most powerful tests of
H0 : γ = γ0 against
H1 : γ = γ1 (see van Garderen, 1998) and also statistics with
asymptotically optimal properties (see Elliott,
Rothenberg, and Stock, 1996). As a consequence, we look for a
transformation of h, g = g(h),
satisfying the conditions of Theorem 2. Defining
then the density may be written
and h then becomes
.
Now from (11), the cumulants of t are
and hence the cumulants of h are
and in particular
so that
On applying Theorem 1, the optimal transformation of h is
given by
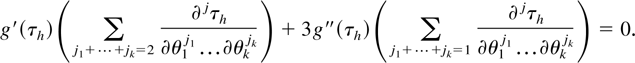
Solutions to (18) will obviously depend upon the particular form of
the likelihood; however, rearranging gives
so that, noting (17), the shape of the transformation, once again, is
explicitly determined by the shape of the likelihood. The general
solution to (18) is
for constants C1 and C2.
5. NUMERICAL ANALYSIS
In this section we apply the results of Section 3 to some simple
likelihood based analysis of nonlinear regression problems. In
particular, we consider (a) exponential and (b) Poisson regression
models and also two binary choice regression models (c) logit and (d)
probit. In general, small sample results for these models are
relatively scarce. Some exceptions are the work of McCullagh (1987, Ch. 7), who calculates Bartlett corrections
for the first two models, Armstrong and Hillier (1999), who derive an expression for the exact
distribution of the MLE for exponential regression, and Horowitz (1994) and Horowitz and Savin (2000) who apply higher order bootstrap methods in
binary probit.
Before proceeding, we note some crucial properties of likelihood
based on independent observations, which will vastly simplify
application of the transformation for all these models. Let
yi, i = 1,…,N, be
independent observations with density
fi(β) depending upon some d
× 1 parameter, β, and with sample log-likelihood
and denote the MLE for β by
.
Define the generalized mean information measures (see McCullagh, 1987, Ch. 7) by
where [sum ]l jl =
v and, for example,
is Fisher information. As a consequence, the first three cumulants of
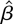
are asymptotically
For all the models listed previously we will consider approximating
the distribution of the standardized, bias-corrected MLE, given by
with asymptotic cumulants
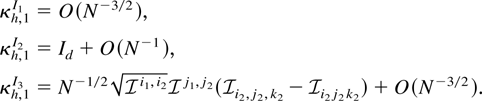
Crucially, by standardizing the MLE as in (20), the following points
should be noted. From (21) Assumption 1 holds for
(with b = 3) and moreover for any function satisfying Assumption 2.
The elements of
,
are asymptotically independent, and therefore the conditions for Theorem 2
are met; that is, we may transform the hi
individually. Finally, by considering the bias-corrected MLE the
conditions of Corollary 1 are met, and the transformation will be
optimal. As a consequence, and also to keep the algebra as brief as
possible, we will only consider the case where the mean function for
all of the regressions depends only upon λi =
exp{α + βwi}, for covariates
wi satisfying
[sum ]i wi = 0.
We will assume α is known and that we are interested in a
homogeneity hypothesis, that is, H0 : β = 0.
Assuming α is unknown and replacing it with an
-consistent
estimator would not affect the order of error of the approximation.
For each case, the density of the ith observation is
where φ(z) is the standard normal density.
The simplifications we have placed upon the regressions give, for
each case and under H0 : β = 0,
where kα is a constant depending upon the
value of α and the particular characteristics of each likelihood.
Indeed, after some algebra, we find
where
.
So, given a value α, the success of low-order Edgeworth
approximations for the density of the standardized MLE
,
even for these very simple cases, depends crucially upon the value of
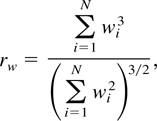
the sample skewness coefficient of the covariate w =
(w1,…,wN)′.
Because in all cases the conditions of Theorem 2 are met, the
transformation we seek satisfies
so that upon standardization,
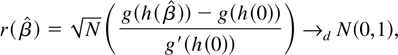
and solving (25) we find
To assess the numerical performance, for each model we fix α = 1
and N = 25 and consider two sets of (centered) covariates. Set
(i) was generated from an exponential random variable with mean 2.718
and set (ii) from a uniform [0,5], giving values of (24);
rw(i) = 12.538 and
rw(ii) = 5.693,
respectively. Based on likelihoods from (22) and setting
were simulated with 20,000 replications, using the internal numerical
optimization routine in Mathematica.
The quantiles for the empirical distribution of
,
for each model configuration, are given in Table
1, along with those for the standard normal, the limiting
distribution for either. Although the numerical accuracy of the
transformation is by no means perfect, there is an obvious improvement
over that of the bias-corrected MLE. This is particularly so for the
binary choice models and when the covariate has significant skewness.
Thus for these cases, the theoretical improvement implied by Corollary
1 manifests itself in the improved ability of the standard normal to
approximate the distribution of the transformed statistic (26).
Quantiles of the empirical distribution of the bias-corrected MLE
and the transformed statistic
The second set of experiments concerns the application of the
bootstrap in these nonlinear models, specifically the logit and
exponential regressions. Of interest will be the true cumulative
probabilities of bootstrap critical values for both the standardized MLE
and the transformed statistic
.
The procedure used is the k-step bootstrap described by Andrews
(2002).
Let YN =
(y1,…,yN) be
the data having likelihood f
(YN;β) and yielding MLE
.
A bootstrap sample YN* is generated from the
likelihood
and a k-step bootstrap estimator based on a Newton–Raphson
iterative routine is defined by
where
.
For the parametric bootstrap to be employed here it is sufficient to consider
k = 1,2 for the one- and two-step bootstrap to have the same order of
error in coverage probability as a bootstrap procedure based on full
estimation of the parameter (see Andrews,
2002).
Define the k-step standardized MLE and transformed statistic
by h(k) =
h(β(k)*) and
r(k) =
r(β(k)*) and let
be their empirical bootstrap distributions based on B
bootstrap iterations. Notice that for the transformed statistic at
least two steps are needed to ensure that
have coincident asymptotic skewness. We will also consider the two-step
bootstrap for h(2). Following Beran (1988) let
denote the empirical bootstrap distribution of the prepivoted
standardized MLE. Finally, denote the bootstrap critical values, of
nominal size ρ, by, respectively,
ch,N(ρ),
cr,N(ρ), and
c1,N(ρ) as the
[ρB] th element in the bootstrap empirical
distributions
Fh,N,Fr,N,
and F1,N. These critical values have error
in probabilities of order O(N−1),
O(N−3/2), and
O(N−3/2) (see Beran, 1988; and Corollary 2 in Section 3 of this
paper).
Details of these experiments are as follows. For both the logit and
exponential regression, data were generated with β = 0 and α =
1, for two sample sizes, N = 25 and N = 50; the set
of regressors (i) was used (in the case N = 50, the same set
was sampled twice). The full bias-corrected MLE was evaluated, say,
,
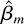
for m = 1,…,2,500 Monte Carlo replications. For each value of
a bootstrap sample
YNb1 was
generated and using (27) the k-step bootstrap estimates
calculated, and from that,
h(1)b1,
h(2)b1, and
r(2)b1, for
b1 = 1,…,400 bootstrap iterations. Similarly
the distribution of
h(2)b1 itself was
bootstrapped (prepivoted) giving values
Fh,Nb2
for b2 = 1,…,200 double bootstrap
replications. The bootstrap critical values, of nominal size ρ are
then found as the [ρB] th entry in the sorted
values for h(1)b1,
r(2)b1, and
Fh,Nb2,
giving ch,N(ρ),
cr,N(ρ), and
c1,N(ρ), respectively. The true
cumulative probability of these critical values is then calculated from
the empirical distributions of the
,
and the h(2)b1 for the
double bootstrap. The results are presented in Table
2.
Monte Carlo cumulative probabilities for bootstrap critical values
for the bias-corrected MLE
and the transformed statistic
The results confirm the relevance of Corollary 2. That is, the
one-step bootstrap applied to the transformed statistic does seem to
have improved finite sample performance compared with the one-step
bootstrap applied to the standardized estimator. However, the
asymptotic improvement offered by the transformation applies, in this
case, only for one-sided coverage probabilities. For symmetrical
confidence intervals the error orders are identical.
The performance of the double, or prepivoted, bootstrap is not
significantly better than that of the transformed statistic, whereas
the computation time for the latter is 200 times that of the one-step
bootstrap. The experiments were run on a 2 MHz PC. A single Monte Carlo
replication of 400 bootstrap iterations for a sample size of 25
required approximately 0.8 seconds, and a period of 160 seconds was
required for a double bootstrap with 200 iterations at the second
level. Consequently, with 2,500 Monte Carlo replications the single
bootstrap required just over an hour of computation time whereas the
double bootstrap required approximately 1 week. Times for the
experiments involving a sample size of 50 were approximately a third
longer.
6. CONCLUSIONS
This paper has generalized the results of Phillips (1979a) and Niki and Konishi (1986) on transformations in univariate Edgeworth
series to the multivariate case. To solve the system of differential
equations that the transformation must satisfy, (6), more structure on
the inferential problem was imposed, yielding an asymptotically local
solution. Although we lose some generality in the process, the
resultant theorem, Theorem 2, seems a powerful tool for higher order
inference in a multivariate setting. This is particularly the case if
the conditions required for Corollaries 1 and 2 hold. Specifically, we
can achieve accelerated asymptotic, that is,
O(N−1) normal, inference and thus
utilize the appropriate tabulated critical values and confidence
intervals. Moreover, in combination with the bootstrap, inference of
order O(N−3/2) is available with
a single bootstrap, offering a considerable computational saving over
the equivalent, in order of error, double bootstrap.
A full analysis of the properties of the transformation is obtained
in the special case of the exponential family. For general functions of
the sufficient statistics, the transformation is defined by a set of
second-order partial differential equations in the derivatives of the
log-likelihood. A similar result is obtained for transformations of the
class of statistics defined as a weighted average of the components of
the sufficient statistic. Perhaps more important than the analytic are
the numerical properties. For the class of simple nonlinear regression
models considered here, the transformation is relatively simple to
apply and has reasonable numerical properties.
Although the theoretical properties of such transformations are
precisely detailed in this paper, one potential weakness is the
practical difficulty of obtaining the transformation in cases more
complex than considered here. The transformed statistic is found by
solving the set of equations given in (8); how demanding this might be
will vary from case to case. However, a possible way forward might be
to utilize methods analogous to those of Andrews (2002): specifically, to find numerical solutions to
these equations that are equivalent to the analytic ones, up to some
appropriate order.
APPENDIX
We will require the cumulants of products of the elements of
X, the generalized cumulants, as detailed in McCullagh (1987, Ch. 3). For our purposes the first four will
suffice and, for reference, are
where [i] implies summation over similar objects,
for example,
κi1,i3 κi2,i4 [2]
=
κi1,i3 κi2,i4
+
κi1,i4 κi2,i3 .
Proof of Theorem 1. The transformed statistic is, upon
expansion,
and because E(XN − τ)
= Op(N−1/2),
then it is sufficient to consider only up to the quadratic term. We
write
where Z = X − τ,
gIv =
(∂vg(X)/∂X1i1…∂Xkik)|X=τ
and note that
have identical asymptotic skewness terms, which follows from before and
the expansion of cumulants in terms of generalized cumulants. Hence, for
notational convenience we drop the tildes. Following McCullagh (1987, Ch. 3),
where (G0r +
G1r +
G2r) is an operator acting on
X, with, for example,
G2rZ containing all
quadratic and bilinear terms in the elements of X. Denote this
operator by Dr, for a generic element of
g; then the cumulant generating function of g is
simply
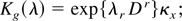
that is, exp{λr
Dr} is an operator acting upon the
cumulants of X. Expansion of this cumulant operator gives
The compound operators produce terms, for example, for the cubic,
and so on. Consequently, the cumulant generating function may be
written as
Now, for the skewness term, enclosed in the third set of brackets,
consider the objects in the third term, which contribute to the
asymptotic skewness of g, namely,
From (A.1) we have that
so, noting the cumulant expansions given in Assumption 1, particularly
denoting asymptotic equivalence by ∼, that is,
an ∼ bn
⇒ an
/bn = O(1), we have
Further, again because
κx,1i1 = 0,
which implies that
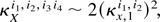
because E
[Xi1Xi2]
= E
[Xi2Xi1].
We note that (A.4) holds for all permutations over
i1,i2,i3,i4,
giving
Thus to reduce asymptotic skewness to zero, to our desired order, and
because
κXi1,i2,i3
∼
κx,1i1,i2,i3
we need to solve
Premultiplying twice by the inverse of the first derivative matrix
(which exists by Assumption 2(ii)) gives
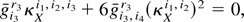
and noting the definition of
gi3,i4r3,
for r3 = 1,…,d, (A.5) proves the
result. █
Proof of Theorem 2. Suppose initially k = d.
Now X has asymptotic cumulants
κx,1i1,
κx,2i1,i2 ,
and so on, and in particular consider
which is a function of the m parameters and is by definition
is positive definite. Under the null H0 : θ =
θ0;
κXi1,i2
= Σ(θ0) with θ0 a fixed point in
Ωθ. Hence there exists a positive definite matrix
P0−1 =
P(θ0)−1 such that
We define
so z has cumulants
κz0i1,
Ik,
κz0i1,i2,i3 ,
and so on. For any
we say z is locally canonical for families
.
Moreover, for θ ∈ Ωθ′ and
zθ = P(θ)x we have
and denoting the cumulants of zθ
appropriately gives
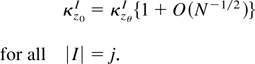
That is, the asymptotic cumulants of zθ and
zθ0 agree. Because, asymptotically,
the elements of z0 are independent we choose the
ith element of g to be a function of the ith
element of z0 alone. Thus we have the derivatives
of g(.) as
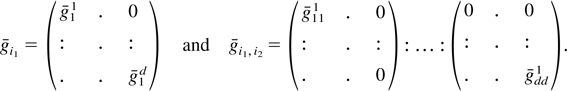
Substituting (A.7) into system (6) gives
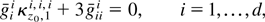
defined for the range of
κz0i1 in
,
Ωκ, say, implicitly defined by the set
Ωθ′, such that (A.6) holds. To prove the existence
of a solution we note first that each equation in system (A.8) is uncoupled
from every other, and second that each is simply a linear, homogeneous
second-order differential equation. Finally, a sufficient condition for a
solution is that
κz0,1i,i,i
is a continuous function of
κz0,1i1for
κz0,1i1
∈ Ωκ, and sufficient for this is that
P(θ) is continuous in Ωθ′.
Consider
Denoting derivatives with respect to θ by
Pθ and Σθ, we have
and Σθ exists in Ωθ′,
because b ≥ 3 in Assumption 1; then so does
Pθ. Hence P is continuous in a
neighborhood of θ0.
Returning to the k > d case, we make a
“pre-preliminary” transformation as
where
is the MLE for θ, c = Bx, and B is a
(k − d) × k matrix and is chosen,
using the implicit function theorem, such that
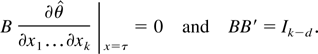
Now
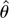
is locally sufficient in an O(N−1/2)
neighborhood of θ0 (see McCullagh,
1984) in that the density of X may be factored
and by (A.10)
and c are independent in this neighborhood. Hence, marginalizing
locally, noting from (A.10) that the Jacobian of the transformation (A.9)
does not depend on B, and then transforming from
,
where
retains the local properties required for the solution in the k =
d case, the analysis follows similarly. █
