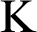1 Introduction
A logical decision problem is a pair
$(L,\Gamma)$
where L is the set of formulas of a certain logic and
$\Gamma $
is a subset of L. When looking at a logic from a semantic perspective we can consider two main decision problems. The satisfiability problem is the pair
$$ \begin{align*}(L,\{\gamma \in L: \gamma \text{ is a satisfiable formula}\})\end{align*} $$
and the validity problem is the pair
$$ \begin{align*}(L,\{\gamma \in L: \gamma \text{ is a valid formula}\}).\end{align*} $$
Logic decision problems were firstly stated by David Hilbert (Entscheidungsproblem; see [Reference Hilbert and Ackermann18, Reference Hilbert and Ackermann19]) for first-order logic in the following way. The Satisfiability Problem: Given a first-order formula
$\varphi $
, is
$\varphi $
satisfiable? The Validity Problem: Given a first-order formula
$\varphi $
, is
$\varphi $
valid? and the Provability Problem: Given a first-order formula
$\varphi $
, is
$\varphi $
provable (in a given proof system)?
The main interest in decision problems is related to their decidability. Intuitively speaking, a decision problem
$(L,\Gamma)$
is decidable if there is an algorithm (a recipe or a finite set of rules) that when applied to an argument
$\varphi \in L$
returns either
$1$
if
$\varphi \in \Gamma $
or
$0$
otherwise. When dealing with a decision problem in logic, we have two different options. Either we work with formulas all over or we convert our logical decision problem to the universe of the natural numbers (see, for instance, [Reference Griffor17, Reference Rogers26, Reference Shoenfield33]). The latter option was followed by Kurt Gödel while proving the Incompleteness Theorems, by giving what we now call Gödelization maps (see [Reference Epstein and Carnielli11, Reference Gödel13, Reference Sernadas and Sernadas28]). The essential requirement for a Gödelization map is to guarantee that the logical decision problem is decidable if and only if the corresponding problem in the natural numbers’ setting is decidable. When working with natural numbers, Turing machines and recursive functions are often adopted as the computation model (see [Reference Kleene20, Reference Soare34]). If we decide to work with other universes it seems interesting to use an abstract high level language (see [Reference Sernadas, Sernadas, Rasga and Ramos31]).
Proving or disproving decidability is not always a simple task. However, there are some techniques that can help besides the direct way of producing a program that computes the characteristic map of the set under consideration. The finite model property technique has been used in the context of first-order logic (see [Reference Börger, Grädel and Gurevich6, Reference Ebbinghaus and Flum10, Reference Libkin23]) and modal logic. In first-order logic the technique was used for showing that the satisfiability problems in
$\textrm {FO}(\exists ^*\forall ^*)$
(Bernays–Schönfinkel class),
$\textrm {FO}(\exists ^*\forall \exists ^*)$
(Ackermann class), and
$\textrm {FO}^2$
are decidable. In normal modal logic, filtrations have been used for showing that several normal modal logics have the finite model property (see [Reference Blackburn, de Rijke and Venema5]).
Another very important technique is reduction. Intuitively, a problem is reducible to another problem whenever a method (an algorithm) for solving the latter provides a method (an algorithm) for solving the former. The concept was introduced by Alan Turing (see [Reference Turing35]) in terms of oracles. Later on Stephen Kleene gave a notion of reduction using recursive functions (see [Reference Kleene21]) on the natural numbers.
Nowadays there is an abstract notion of many-to-one reducibility over the set of natural numbers (see [Reference Rogers26, Reference Soare34]). This notion can be adapted to logical decision problems, by saying that a reduction from
$(L,\Gamma)$
to
$(L',\Gamma ')$
is a computable map
$\tau: L \to L'$
such that, for each
$\varphi \in L$
,
$$ \begin{align*}\varphi \in \Gamma \quad \text{if and only if} \quad \tau(\varphi) \in \Gamma'.\end{align*} $$
However, we need a generalized version of this concept appropriate for meet-combination of logics (that provides an axiomatization of the product of matrix logics; see [Reference Rasga, Sernadas and Sernadas25, Reference Sernadas, Sernadas and Rasga30]). In the meet-combination of two logics a connective is a pair composed by a connective of each logic inheriting only the common logical properties of the component connectives. So, to transfer decidability results from the component logics to the meet-combination we need to extend the notion of reduction from one logical decision problem to a non-empty finite collection of logical decision problems.
The reductions described in the literature are for specific logics and no general mechanism is presented for reduction between logical decision problems. Moreover, in most of the cases the reduction is between the same kind of decision problems, that is, either between two satisfiability problems, or between two validity problems. One of the exceptions is related to the equivalence between the satisfiability problem and the validity problem for first-order logic, that is, the satisfiability problem for first-order logic is decidable if and only if the validity problem for first-order logic is decidable (see [Reference Hilbert and Ackermann18, Reference Hilbert and Ackermann19]).
The paper is organized as follows. In Section 2, we adopt the notion of satisfaction system (introduced in [Reference Barwise2]) as the appropriate framework for setting-up logical decision problems based on semantics. We define decision problem over a satisfaction system and provide examples of the satisfiability (respectively, the dual of the satisfiability) and of the validity (respectively, the dual of the validity) problems, proving that decidability is reflected by reduction. We end the section by establishing a sufficient condition for having a reduction from the validity problem in a satisfaction system to the satisfiability in another satisfaction system.
Section 3 concentrates on the important concept of reduction between a satisfaction system and a finite collection of satisfaction systems. Two main results are established: decidability of the satisfiability problem for the source satisfaction system whenever the satisfiability problem for each target satisfaction system is decidable and, under some mild conditions, decidability of the validity problem for the source satisfaction system whenever the validity problem for each target satisfaction system is decidable. Both results capitalize on the fact that a satisfaction system reduction induces a reduction between the corresponding satisfiability problems (similarly for validity problems). Three examples are provided. (1) Decidability of the satisfiability problem in
$\textrm {K}$
modal logic endowed with local Kripke semantics from the decidability of the satisfiability problem in
$\textrm {FO}^2$
first-order logic endowed with contextual satisfaction. (2) Decidability of the validity problem in
$\textrm {K}$
modal logic endowed with algebraic semantics from the decidability of the validity problem in
$\textrm {K}$
modal logic endowed with global Kripke semantics using Stone Representation Theorem and Jonssón–Tarski Theorem (see [Reference Blackburn, van Benthem, Blackburn, van Benthem and Wolter4, Reference Chagrov and Zakharyaschev9]). (3) Finally, decidability of the validity problem in intuitionistic logic endowed with algebraic semantics from the decidability of the validity problem in intuitionistic logic endowed with global Kripke semantics using Stone Representation Theorem (see [Reference Chagrov and Zakharyaschev9, Reference Rybakov27]).
Finally, in Section 4 we start by introducing the meet-combination of two (matrix) satisfaction systems. We show that there is a reduction from the satisfaction system for meet-combination to the collection composed by the component satisfaction systems and prove that the validity problem in meet-combination is decidable provided that the validity problem in each component logic is decidable as well. We end up the section by discussing the meet-combination of
$\textrm {K}$
modal logic and intuitionist logic both endowed with algebraic semantics.
2 Satisfaction system decision problems
The objective of this section is to introduce some important decision problems on logics presented by a satisfaction system.
Definition 2.1. A satisfaction system is a triple
$$ \begin{align*}S=(L,\mathcal{M},\Vdash),\end{align*} $$
where L is a non-empty set of formulas,
$\mathcal {M}$
is a class of semantic structures, and
$\Vdash \, \subseteq \mathcal {M} \times L$
is a binary relation called the satisfaction relation.
Example 2.2. The local Kripke satisfaction system
$$ \begin{align*}S^{\textrm{lk,K}}_{\Pi}=(L^{\textrm{ML}}_{\Pi},\mathcal{M}^{\textrm{lk,K}}_{\Pi},\Vdash^{\textrm{lk,K}}_{\Pi})\end{align*} $$
for
$\textrm {K}$
modal logic over a set
$\Pi $
of propositional symbols is such that
-
•
$L^{\textrm {ML}}_{\Pi }$
is the set of modal formulas inductively defined as follows:-
–
$\Pi \subseteq L^{\textrm {ML}}_\Pi $
; -
–
$\mathop {\neg } \varphi, {\Diamond } \varphi \in L^{\textrm {ML}}_\Pi $
provided that
$\varphi \in L^{\textrm {ML}}_\Pi $
; -
–
$\varphi _1 \mathbin {\supset } \varphi _2 \in L^{\textrm {ML}}_\Pi $
provided that
$\varphi _1,\varphi _2 \in L^{\textrm {ML}}_\Pi $
;
-
-
•
$\mathcal {M}^{\textrm {lk,K}}_{\Pi }$
is the class of all pointed Kripke structures, that is, pairs
$((W,R,V),w)$
where
$(W,R,V)$
is a Kripke structure, i.e.,-
– W is a non-empty set whose elements are called worlds;
-
–
$R \subseteq W^2$
is a relation called the accessibility relation; -
–
$V: \Pi \to \wp W$
is a map called valuation;
$w \in W$
;
-
-
•
$\Vdash ^{\textrm {lk,K}}_{\Pi } \subseteq \mathcal {M}^{\textrm {lk,K}}_{\Pi } \times L^{\textrm {lk,K}}_{\Pi }$
is the local satisfaction relation of a formula
$\varphi $
by
$((W,R,V),w)$
, written inductively defined as follows:
$$ \begin{align*}(W,R,V), w \Vdash^{\textrm{lk,K}}_{\Pi} \varphi\end{align*} $$
-
–
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } p$
whenever
$w \in V(p)$
for
$p \in \Pi $
; -
–
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } \mathop {\neg } \varphi $
whenever
$(W,R,V),w \not \Vdash ^{\textrm {lk,K}}_{\Pi } \varphi $
; -
–
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } \varphi _1 \mathbin {\supset } \varphi _2$
whenever either
$(W,R,V),w \not \Vdash ^{\textrm {lk,K}}_{\Pi } \varphi _1$
or
$(W,R,V),w \Vdash _{\Pi } \varphi _2$
; -
–
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } {\Diamond } \varphi $
whenever
$(W,R,V),w' \Vdash ^{\textrm {lk,K}}_{\Pi } \varphi $
for some
$w' \in W$
such that
$w \mathbin{R} w'$
.
-
We now present another modal satisfaction system using the previous example.
Example 2.3. The global satisfaction system
$$ \begin{align*}S^{\textrm{gk,K}}_{\Pi}=(L^{\textrm{ML}}_{\Pi},\mathcal{M}^{\textrm{gk,K}}_{\Pi},\Vdash^{\textrm{gk,K}}_{\Pi})\end{align*} $$
for
$\textrm {K}$
modal logic is such that
-
•
$\mathcal {M}^{\textrm {gk,K}}_{\Pi }$
is the class of all Kripke structures; -
•
$\Vdash ^{\textrm {gk,K}}_{\Pi } \subseteq \mathcal {M}^{\textrm {gk,K}}_{\Pi } \times L^{\textrm {ML}}_{\Pi }$
is the global satisfaction relation of a formula
$\varphi $
by
$(W,R,V)$
, written that holds when
$$ \begin{align*}(W,R,V) \Vdash^{\textrm{gk,K}}_{\Pi} \varphi\end{align*} $$
$(W,R,V), w \Vdash ^{\textrm {lk,K}}_{\Pi } \varphi $
for every
$w \in W$
.
Definition 2.4. A decision problem on a satisfaction system
$$ \begin{align*}S=(L,\mathcal{M},\Vdash)\end{align*} $$
is a pair
$(L,\Gamma)$
where
$\Gamma \subseteq L$
.
Informally, such a decision problem can be stated as
$$ \begin{align*}\text{given } \varphi \in L, \quad \text{is } \varphi \in \Gamma?\end{align*} $$
In order to discuss decision problems induced by the satisfaction system S we need some notions. A formula
$\varphi \in L$
is satisfiable if there is
$M \in \mathcal {M}$
such that
$M \Vdash \varphi $
. Moreover,
$\varphi $
is valid whenever
$M \Vdash \varphi $
for every
$M \in \mathcal {M}$
.
Definition 2.5. The satisfiability problem is the pair
$$ \begin{align*}\textrm{Sat}_S=(L,\{\varphi \in L: \varphi \text{ is satisfiable}\}).\end{align*} $$
The co-satisfiability problem is the pair
$$ \begin{align*}\textrm{co{-}Sat}_S=(L, \{\varphi \in L: \varphi \text{ is not satisfiable}\}).\end{align*} $$
The validity problem is the pair
$$ \begin{align*}\textrm{Val}_S=(L,\{\varphi \in L: \varphi \text{ is valid}\}).\end{align*} $$
The co-validity problem is the pair
$$ \begin{align*}\textrm{co{-}Val}_S=(L,\{\varphi \in L: \varphi \text{ is not valid}\}).\end{align*} $$
A decision problem
$(L,\Gamma)$
is decidable whenever the characteristic map
$$ \begin{align*}\chi_{(L,\Gamma)}: L \to \{0,1\}\end{align*} $$
defined as follows:
$$ \begin{align*}\chi_{(L,\Gamma)}(\varphi)= \begin{cases} 1 & \text{whenever } \varphi \in \Gamma,\\ 0 & \text{otherwise} \end{cases} \end{align*} $$
is computable (see [Reference Sernadas, Sernadas, Rasga and Ramos31]).
Proposition 2.6. Let
$(L,\Gamma)$
be a decision problem. Then
$$ \begin{align*}(L,\Gamma) \text{ is decidable } \quad \text{if and only if} \quad (L,L \setminus \Gamma) \text{ is decidable}.\end{align*} $$
Proof Observe that
$$ \begin{align*}\chi_{(L,L \setminus \Gamma)}(\varphi)=1-\chi_{(L,\Gamma)}(\varphi) \quad \text{and} \quad \chi_{(L,\Gamma)}(\varphi)=1-\chi_{(L,L \setminus \Gamma)}(\varphi).\end{align*} $$
So
$\chi _{(L,\Gamma)}$
is computable if and only if
$\chi _{(L,L \setminus \Gamma)}$
is computable.⊣
As a consequence,
$$ \begin{align*}\textrm{Sat}_S \text{ is decidable} \quad \text{if and only if} \quad \textrm{co{-}Sat}_S \text{ is decidable},\end{align*} $$
and
$$ \begin{align*}\textrm{Val}_S \text{ is decidable} \quad \text{if and only if} \quad \textrm{co{-}Val}_S \text{ is decidable}.\end{align*} $$
Definition 2.7. Let
$k \in {\mathbb {N}^+}$
,
$D_S=(L,\Gamma)$
be a decision problem on
$S=(L,\mathcal {M},\Vdash)$
, and
$D_{S^i}=(L^i,\Gamma ^i)$
a decision problem on
$S^i=(L^i,\mathcal {M}^i,\Vdash ^i)$
for each
$i=1,\dots,k$
. A collection of computable maps
$\tau ^i: L \to L^i$
for each
$i=1,\dots,k$
is a reduction from
$D_S$
to
$D_{S^1}, \dots,D_{S^k}$
, denoted by
$$ \begin{align*}(\tau^1,\dots,\tau^k): D_S \to D_{S^1}\times \dots \times D_{S^k},\end{align*} $$
whenever
$$ \begin{align*}\varphi \in \Gamma \quad \text{if and only if} \quad \tau^i(\varphi) \in \Gamma^i \quad \text{for each } i=1,\dots,k.\end{align*} $$
Proposition 2.8. Let
$(\tau ^1,\dots,\tau ^k): D_S \to D_{S^1}\times \dots \times D_{S^k}$
be a reduction. Then,
$D_S$
is decidable whenever
$D_{S^i}$
is decidable for each
$i=1,\dots,k$
.
Proof Assume that
$D_{S^i}$
is decidable for each
$i=1,\dots,k$
. Then,
$\chi _{D_{S^i}}$
is a computable map for each
$i=1,\dots,k$
. Observe that
$$ \begin{align*}\chi_{D_S}(\varphi)= \prod_{i=1}^k \; \chi_{D_{S^i}}\circ \tau_i(\varphi),\end{align*} $$
since
$(\tau ^1,\dots,\tau ^k)$
is a reduction. Hence,
$\chi _{D_S}$
is a computable map. Therefore,
$D_S$
is decidable.⊣
It is worthwhile to discuss the relationship between the satisfiability and the validity problems. For that we need to introduce the following notion.
Definition 2.9. A satisfaction system
$S'=(L',\mathcal {M}',\Vdash ')$
has a (standard) negation
$\mathop {\neg }$
if
$L'$
is closed for
$\mathop {\neg }$
, that is, if
$\varphi \in L'$
then
$\mathop {\neg } \varphi \in L'$
, and
$$ \begin{align*}M' \Vdash \varphi \quad \text{if and only if} \quad M' \not \Vdash \mathop{\neg} \varphi.\end{align*} $$
Observe that not all negations have the property above (see [Reference Carnielli and Coniglio7]).
Example 2.10. The local Kripke satisfaction system
$$ \begin{align*}S^{\textrm{lk,K}}_{\Pi}\end{align*} $$
defined in Example 2.2 has the negation
$\mathop {\neg }$
.
Proposition 2.11. Let
$S=(L,\mathcal {M},\Vdash)$
and
$S'=(L,\mathcal {M}',\Vdash ')$
be satisfaction systems such that
$S'$
has a negation
$\mathop {\neg }$
. Assume that there is a map
$f: \mathcal {M} \to \wp \mathcal {M}'$
such that
$f(\mathcal {M})=\mathcal {M}'$
and
$$ \begin{align*}M\Vdash \varphi \quad \text{if and only if} \quad M' \Vdash'\varphi \text{ for each } M' \in f(M).\end{align*} $$
Then, there is a reduction from
$\textrm {Val}_S$
to
$\textrm {co{-}Sat}_{S'}$
. Moreover,
$$ \begin{align*}\textrm{Sat}_{S'} \text{ is decidable} \quad \text{implies} \quad \textrm{Val}_S \text{ is decidable}.\end{align*} $$
Proof We start by showing that the map
$\tau: L \to L$
such that
$\psi \mapsto \mathop {\neg } \psi $
is a reduction from
$\textrm {Val}_S$
to
$\textrm {co{-}Sat}_{S'}$
.
-
(1) It is immediate to see that
$\tau $
is a computable map. -
(2) We must show that
$$ \begin{align*}\varphi \text{ is valid in } S \quad \text{if and only if} \quad \mathop{\neg} \varphi \text{ is not satisfiable in }S'.\end{align*} $$
$(\to)$
Assume that
$\varphi $
is valid in S. Thus,
$M \Vdash \varphi $
for every
$M \in \mathcal {M}$
. Therefore, by hypothesis,
$M' \Vdash ' \varphi $
for every
$M' \in f(M)$
and
$M \in \mathcal {M}$
. Hence,
$M' \not \Vdash ' \mathop {\neg } \varphi $
for every
$M' \in f(M)$
and
$M \in \mathcal {M}$
. Since
$f(\mathcal {M})=\mathcal {M}'$
then there is no
$M' \in \mathcal {M}'$
such that
$M' \Vdash ' \mathop {\neg } \varphi $
. Thus
$\mathop {\neg } \varphi $
is not satisfiable in
$S'$
.
$({{\leftarrow }})$
Assume that
$\mathop {\neg } \varphi $
is not satisfiable in
$S'$
. Then
$M' \not \Vdash ' \mathop {\neg } \varphi $
for every
$M' \in \mathcal {M}'$
. Hence,
$M' \Vdash ' \varphi $
for each
$M' \in \mathcal {M}'$
. Let
$M \in \mathcal {M}$
. Then
$M' \Vdash ' \varphi $
for every
$M' \in f(M)$
and so
$M \Vdash \varphi $
.
Assume that
$\textrm {Sat}_{S'}$
is decidable. Then,
$\textrm {co{-}Sat}_{S'}$
is decidable (see Proposition 2.6). Therefore,
$\textrm {Val}_{S}$
is decidable by Proposition 2.8.⊣
Proposition 2.12. The problem
$\textrm {Val}_{S^{\textrm {gk,K}}_{\Pi }}$
is decidable for every set
$\Pi $
of propositional symbols.
Proof We start by observing that
$S^{\textrm {gk,K}}_{\Pi }$
and
$S^{\textrm {lk,K}}_{\Pi }$
satisfy the requirements of Proposition 2.11 by taking
$f(W,R,V)=\{((W,R,V),w): w \in W\}$
. Again, by Proposition 2.11,
$$ \begin{align*}\textrm{Sat}_{S^{\textrm{lk,K}}_{\Pi}} \text{ is decidable} \quad \text{implies} \quad \textrm{Val}_{S^{\textrm{gk,K}}_{\Pi}} \text{ is decidable}.\end{align*} $$
The result follows since
$\textrm {Sat}_{S^{\textrm {lk,K}}_{\Pi }}$
is decidable as we will show in Proposition 3.11.⊣
3 Satisfaction system reductions
We now introduce the concept of reduction from one satisfaction system to a non-empty finite collection of satisfaction systems and discuss its impact on reductions between decision problems.
Definition 3.1. A reduction from satisfaction system
$(L,\mathcal {M},\Vdash)$
to satisfaction systems
$(L^1,\mathcal {M}^1,\Vdash ^1), \dots,(L^k,\mathcal {M}^k,\Vdash ^k)$
where
$k \in {\mathbb {N}^+}$
, is a tuple
$$ \begin{align*}(\tau^1,\dots,\tau^k,g^1,\dots,g^k,h),\end{align*} $$
where, for each
$i=1,\dots,k$
,
-
•
$\tau ^i: L \to L^i$
is a computable map; -
•
$g^i: \mathcal {M} \to \mathcal {M}^i$
is a map such that for every
$$ \begin{align*}\text{if } M \Vdash \varphi \text{ then } g^i(M) \Vdash^i \tau^i(\varphi)\end{align*} $$
$M \in \mathcal {M}$
;
and
$h: \mathcal {M}^1\times \dots \times \mathcal {M}^k \to \mathcal {M}$
is a map such that
$$ \begin{align*}\text{if} \quad M_1\Vdash^1 \tau^1(\varphi) \ \dots \ M_k\Vdash^k \tau^k(\varphi) \quad \text{then} \quad h(M_1,\dots,M_k) \Vdash \varphi\end{align*} $$
for every
$M_i \in \mathcal {M}^i$
with
$i=1,\dots,k$
.
In the sequel we denote such a reduction by
$$ \begin{align*}(\tau^1,\dots,\tau^k,g^1,\dots,g^k,h): (L,\mathcal{M},\Vdash) \to (L^1,\mathcal{M}^1,\Vdash^1) \times\dots \times (L^k,\mathcal{M}^k,\Vdash^k).\end{align*} $$
We compare the notion of reduction for
$k=1$
with the usual definition of satisfaction system morphism (see [Reference Barwise2, Reference Sernadas, Sernadas and Caleiro29]).
Definition 3.2. A satisfaction system morphism from
$S=(L,\mathcal {M},\Vdash)$
to
$S'=(L',\mathcal {M}',\Vdash ')$
is a pair
$({\overline {h}},{\underline {h}})$
where
${\overline {h}}:L \to L'$
and
${\underline {h}}: \mathcal {M}' \to \mathcal {M}$
are maps such that
$$ \begin{align*}M' \Vdash' {\overline{h}}(\varphi) \quad \text{if and only if} \quad {\underline{h}} (M') \Vdash \varphi.\end{align*} $$
Hence, without further assumptions, these two notions do not coincide. We now show that a satisfaction system reduction induces a reduction over the respective satisfiability problems.
Proposition 3.3. Let
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h): S \to S^1 \times \dots \times S^k$
be a satisfaction system reduction. Then,
$$ \begin{align*}(\tau^1,\dots,\tau^k)\end{align*} $$
is a reduction from
$\textrm {Sat}_S$
to
$\textrm {Sat}_{S_1},\dots,\textrm {Sat}_{S_k}$
.
Proof We must show that
$$ \begin{align*}\varphi \text{ is satisfiable in } S \quad \text{iff} \quad \tau^i(\varphi) \text{ is satisfiable in } S^i \text{ for each } i=1,\dots,k.\end{align*} $$
$(\to)$
Assume that
$\tau ^i(\varphi)$
is not satisfiable in
$S^i$
for some
$i=1,\dots,k$
. Then, there is no
$M_i \in \mathcal {M}^i$
such that
$M_i \Vdash ^i \tau ^i(\varphi)$
. Hence, there is no
$M \in \mathcal {M}$
such that
$g^i(M) \Vdash ^i \tau ^i(\varphi)$
. Therefore, there is no
$M \in \mathcal {M}$
such that
$M \Vdash \varphi $
. Thus,
$\varphi $
is not satisfiable in S.
$({{\leftarrow }})$
Assume that
$\tau ^i(\varphi)$
is satisfiable in
$S^i$
for each
$i=1,\dots,k$
. Then, there are
$M_1 \in \mathcal {M}^1, \dots, M_k \in \mathcal {M}^k$
such that
$M_i \Vdash ^i \tau ^i(\varphi)$
for each
$i=1,\dots,k$
. Hence,
$h(M_1,\dots,M_k) \Vdash \varphi $
. Therefore,
$\varphi $
is satisfiable in S.⊣
Proposition 3.4. Let
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h): S \to S^1 \times \dots \times S^k$
be a satisfaction system reduction. Then,
$\textrm {Sat}_{S}$
is decidable provided that
$\textrm {Sat}_{S^1},\dots,\textrm {Sat}_{S^k}$
are decidable.
Proof Assume
$\textrm {Sat}_{S^1},\dots,\textrm {Sat}_{S^k}$
are decidable. By Proposition 3.3,
$$ \begin{align*}(\tau^1,\dots,\tau^k):\textrm{Sat}_S \to \textrm{Sat}_{S_1}\times \dots \times \textrm{Sat}_{S_k}\end{align*} $$
is a reduction. Hence, by Proposition 2.8,
$\textrm {Sat}_{S}$
is decidable.⊣
Similarly, a satisfaction system reduction induces a reduction over the respective validity problems whenever the semantic translation maps are surjective up to satisfaction, as we define now.
Definition 3.5. Let
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h): S \to S^1 \times \dots \times S^k$
be a satisfaction system reduction. The maps
$g^1,\dots,g^k,h$
are surjective up to satisfaction whenever
-
• for every
$M \in \mathcal {M}$
,
$$ \begin{align*}h(g_1(M),\dots,g_k(M)) \Vdash \varphi \quad \text{if and only if} \quad M \Vdash \varphi;\end{align*} $$
-
• for every
$M_1 \in \mathcal {M}^1, \dots, M_k \in \mathcal {M}^k$
, for each
$$ \begin{align*}g_i(h(M_1,\dots,M_k)) \Vdash^i \tau^i(\varphi) \quad \text{if and only if} \quad M_i \Vdash^i \tau^i(\varphi)\end{align*} $$
$i=1,\dots,k$
.
Proposition 3.6. Let
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h): S \to S^1 \times \dots \times S^k$
be a satisfaction system reduction such that
$g^1,\dots,g^k,h$
are surjective up to satisfaction. Then,
$$ \begin{align*}(\tau^1,\dots,\tau^k)\end{align*} $$
is a reduction from
$\textrm {Val}_S$
to
$\textrm {Val}_{S_1},\dots,\textrm {Val}_{S_k}$
.
Proof We must show that
$$ \begin{align*}\varphi \text{ is valid in } S \quad \text{if and only if} \quad \tau^i(\varphi) \text{ is valid in } S^i \text{ for each } i=1,\dots,k.\end{align*} $$
$(\to)$
Let
$M_i \in \mathcal {M}^i$
for
$i=1,\dots,k$
. Then
$h(M_1,\dots,M_k) \in \mathcal {M}$
and so
$$ \begin{align*}h(M_1,\dots,M_k) \Vdash \varphi,\end{align*} $$
because
$\varphi $
is valid in S. Since
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h)$
is a reduction,
$$ \begin{align*}g^i(h(M_1,\dots,M_k)) \Vdash^i \tau^i(\varphi)\end{align*} $$
for every
$i=1,\dots,k$
. Therefore, by surjectivity up to satisfaction,
$$ \begin{align*}M_i \Vdash^i \tau^i(\varphi)\end{align*} $$
for every
$i=1,\dots,k$
.
$({{\leftarrow }})$
Let
$M \in \mathcal {M}$
. Then
$g^i(M) \in \mathcal {M}^i$
for each
$i=1,\dots,k$
. Hence
$$ \begin{align*}g^i(M) \Vdash^i \tau^i(\varphi),\end{align*} $$
because
$\tau ^i(\varphi)$
is valid for each
$i=1,\dots,k$
. Since
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h)$
is a reduction,
$$ \begin{align*}h(g^1(M),\dots,g^k(M)) \Vdash \varphi.\end{align*} $$
Moreover, by surjectivity up to satisfaction,
$M\Vdash \varphi $
.⊣
Proposition 3.7. Let
$(\tau ^1,\dots,\tau ^k,g^1,\dots,g^k,h): S \to S^1 \times \dots \times S^k$
be a satisfaction system reduction such that
$g^1,\dots,g^k,h$
are surjective up to satisfaction. Then,
$\textrm {Val}_{S}$
is decidable provided that
$\textrm {Val}_{S^1},\dots,\textrm {Val}_{S^k}$
are decidable.
Proof By Proposition 3.6,
$$ \begin{align*}(\tau^1,\dots,\tau^k):\textrm{Val}_S \to \textrm{Val}_{S_1}\times \dots \times \textrm{Val}_{S_k}\end{align*} $$
is a reduction. So, by Proposition 2.8,
$\textrm {Val}_{S}$
is decidable if
$\textrm {Val}_{S^1},\dots,\textrm {Val}_{S^k}$
are decidable.⊣
3.1 Satisfiability of
$S^{\mathrm {lk,K}}_{\Pi }$
from satisfiability of
$S^{\mathrm {FO}^2}_{\Sigma _{\mathrm {ML},\Pi }}$
We want to show, using the results in the previous section and [Reference Blackburn, van Benthem, Blackburn, van Benthem and Wolter4], that the satisfiability problem for
$\textrm {K}$
modal logic with local Kripke semantics is decidable by using the fact that the satisfiability problem for a fragment
$\textrm {FO}^2$
of
$\textrm {FOL}$
consisting of formulas using only a pair of variables is decidable (see [Reference Grädel, Kolaitis and Vardi16]).
Example 3.8
$\textrm {FO}^2$
-two variable first-order logic
Let
$\Sigma $
be a first-order logic signature with no function symbols and with a set
$P_n$
of predicate symbols of arity n for each
$n \in {\mathbb {N}^+}$
and
$X=\{x,y\}$
. A satisfaction system for
$\text {FO}^2$
$$ \begin{align*}S^{\text{FO}^2}_\Sigma=(L^{\text{FO}^2}_\Sigma,\mathcal{M}^{\text{FO}^2}_\Sigma,\Vdash^{\text{FO}^2}_\Sigma)\end{align*} $$
over signature
$\Sigma $
and X is such that
-
•
$L^{\text {FO}^2}_\Sigma $
is the set of formulas inductively defined as follows:-
–
$p(z_1,\dots,z_n) \in L^{\text {FO}^2}_\Sigma $
for every
$p \in P_n$
and
$z_1,\dots,z_n \in X$
; -
–
$\mathop {\neg } \varphi \in L^{\text {FO}^2}_\Sigma $
whenever
$\varphi \in L^{\text {FO}^2}_\Sigma $
; -
–
$\varphi _1 \mathbin {\supset } \varphi _2 \in L^{\text {FO}^2}_\Sigma $
whenever
$\varphi _1,\varphi _2 \in L^{\text {FO}^2}_\Sigma $
; -
–
$\exists z \, \varphi \in L^{\text {FO}^2}_\Sigma $
whenever
$z \in X$
and
$\varphi \in L^{\text {FO}^2}_\Sigma $
;
-
-
•
$\mathcal {M}^{\text {FO}^2}_\Sigma $
is the class of all pairs where I is a tuple
$$ \begin{align*}(I, \rho),\end{align*} $$
called an interpretation structure, such that
$$ \begin{align*}(D,\{\{p^I\}_{p \in P_n}\}_{n \in {\mathbb{N}^+}}),\end{align*} $$
-
– D is a non-empty set;
-
–
$p^I: D^n \to \{0,1\}$
is a map for each
$p \in P_n$
and
$n \in {\mathbb {N}^+}$
;
$\rho: X \to D$
is a map called an assignment;
-
-
•
$\Vdash ^{\text {FO}^2}_\Sigma \subseteq \mathcal {M}^{\text {FO}^2}_\Sigma \times L^{\text {FO}^2}_\Sigma $
is the satisfaction relation inductively defined as follows:-
–
$I,\rho \Vdash ^{\text {FO}^2}_\Sigma p(z_1,\dots,z_n)$
whenever
$p^I(\rho (z_1),\dots,\rho (z_n))=1$
; -
–
$I,\rho \Vdash ^{\text {FO}^2}_\Sigma \mathop {\neg } \varphi $
whenever
$I,\rho \not \Vdash ^{\text {FO}^2}_\Sigma \varphi $
; -
–
$I,\rho \Vdash ^{\text {FO}^2}_\Sigma \varphi _1 \mathbin {\supset } \varphi _2$
whenever either
$I,\rho \not \Vdash ^{\text {FO}^2}_\Sigma \varphi _1$
or
$I,\rho \Vdash ^{\text {FO}^2}_\Sigma \varphi _2$
;
$I,\rho \Vdash ^{\text {FO}^2}_\Sigma \exists z \, \varphi $
whenever
$I,\rho ' \Vdash ^{\text {FO}^2}_\Sigma \varphi $
for some
$\rho ' \equiv _{z} \rho $
, i.e., assignment
$\rho '$
such that
$\rho '(z')=\rho (z')$
for every
$z' \in X\setminus \{z\}$
.
-
Let
$\Sigma _{\textrm {ML},\Pi }$
be the
$\textrm {FO}^2$
signature induced by the
$\textrm {K}$
modal logic over
$\Pi $
with no function symbols, set of predicate symbols
$\{\bar p: p \in \Pi \}$
of arity
$1$
, and predicate symbol
$\bar R$
of arity two. In order to discuss the reduction from
$\textrm {K}$
modal logic to
$\textrm {FO}^2$
logic, we start by introducing an auxiliary map for each
$z \in X$
. Let
$$ \begin{align*}\tau_z: L^{\textrm{ML}}_\Pi \to L^{\textrm{FO}^2}_{\Sigma_{\textrm{ML},\Pi}}\end{align*} $$
be inductively defined as follows:
-
•
$\tau _z(p)=\bar {p}(z)$
; -
•
$\tau _z(\mathop {\neg } \varphi)=\mathop {\neg } \tau _z(\varphi)$
; -
•
$\tau _z(\varphi _1 \mathbin {\supset } \varphi _2)=\tau _z(\varphi _1) \mathbin {\supset } \tau _z(\varphi _2)$
; -
•
$\tau _z({\Diamond } \varphi)=\exists z' (\bar R(z,z') \mathbin {\wedge } \tau _{z'} (\varphi))$
, where
$z' \in X \setminus \{z\}$
.
Furthermore, for each
$z \in X$
, consider the map
$$ \begin{align*}g_z: \mathcal{M}^{\textrm{lk,K}}_{\Pi} \to \mathcal{M}^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}}\end{align*} $$
defined as follows:
$$ \begin{align*}g_z((W,R,V),w)=(I,\rho_z),\end{align*} $$
where
$I=(W,\{\bar p^{I}\}_{p \in \Pi },\bar R^{I})$
such that, for every
$w_1,w_2 \in W$
,
-
•
$\bar p^{I}(w_1)=1$
if and only if
$w_1 \in V(p)$
; -
•
$\bar R^{I}(w_1,w_2)=1$
if and only if
$w_1 \mathbin{R} w_2$
;
and
$\rho _z$
is an assignment such that
$\rho _z(z)=w$
.
We now show that local satisfaction carries over from
$\textrm {K}$
modal logic to
$\textrm {FO}^2$
logic.
Proposition 3.9. Let
$((W,R,V),w) \in \mathcal {M}^{\textrm {lk,K}}_{\Pi }$
and
$\varphi \in L^{\textrm {ML}}_\Pi $
. Then, for each
$z \in X$
,
$$ \begin{align*}(W,R,V),w \Vdash^{\textrm{lk,K}}_{\Pi} \varphi \quad \text{if and only if} \quad I,\rho_z \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \tau_z(\varphi),\end{align*} $$
where
$g_z((W,R,V),w)=(I,\rho _z)$
.
Proof We prove the result by induction on
$\varphi $
.
(Base) Let
$\varphi $
be
$p \in \Pi $
. Hence,
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } p$
if and only if
$w \in V(p)$
if and only if
$\bar p^{I}(w)=1$
if and only if
$ I,\rho _z \Vdash ^{\text {FO}^2}_{\Sigma _{\textrm {ML},\Pi }} \bar p(z)$
if and only if
$ I,\rho _z \Vdash ^{\text {FO}^2}_{\Sigma _{\textrm {ML},\Pi }} \tau _z(p)$
.
(Step) We only consider the case that
$\varphi $
is
${\Diamond } \psi $
. We start by showing that
$$ \begin{align*}(W,R,V),w \Vdash^{\textrm{lk,K}}_{\Pi} {\Diamond} \psi \quad \text{implies} \quad I,\rho_z \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \tau_z({\Diamond} \psi).\end{align*} $$
Assume that
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } {\Diamond } \psi $
. Then, there is
$w' \in W$
with
$w\mathbin{R}w'$
and
$(W,R,V),w' \Vdash ^{\textrm {lk,K}}_{\Pi } \psi $
. We must show that
$$ \begin{align*}I,\rho_z \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \exists z' (\bar R(z,z') \mathbin{\wedge} \tau_{z'}(\psi)),\end{align*} $$
where
$z' \in X\setminus \{z\}$
. Let
$\rho _{z'} \equiv _{z'} \rho _z$
be such that
$\rho _{z'}(z')=w'$
. Then,
$$ \begin{align*}I,\rho_{z'} \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \bar R(z,z'),\end{align*} $$
since
$\bar R^{I}(w,w')=1$
. Moreover,
$$ \begin{align*}I,\rho_{z'} \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \tau_{z'}(\psi)\end{align*} $$
by the induction hypothesis, since
$(W,R,V),w' \Vdash ^{\textrm {lk,K}}_{\Pi } \psi $
. We now prove that
$$ \begin{align*}I,\rho_z \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \tau_z({\Diamond} \psi) \quad \text{implies} \quad (W,R,V),w \Vdash^{\textrm{lk,K}}_{\Pi} {\Diamond} \psi.\end{align*} $$
Assume that
$I,\rho _z \Vdash ^{\text {FO}^2}_{\Sigma _{\textrm {ML},\Pi }} \tau _z({\Diamond } \psi)$
. Hence
$$ \begin{align*}I,\rho_z \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \exists z' (\bar R(z,z') \mathbin{\wedge} \tau_{z'}(\psi)).\end{align*} $$
Thus, there is
$\rho _{z'} \equiv _{z'} \rho _z$
such that
$$ \begin{align*}(\dagger) \quad I,\rho_{z'} \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \bar R(z,z')\end{align*} $$
and
$$ \begin{align*}(\ddagger) \quad I,\rho_{z'} \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \tau_{z'}(\psi).\end{align*} $$
From
$(\dagger)$
, we conclude that
$\rho _{z'}(z) \mathbin{R} \rho _{z'}(z')$
holds in
$(W,R,V)$
. So
$w \mathbin{R} \rho _{z'}(z')$
because
$\rho _{z'}(z)=\rho _z(z)=w$
. On the other hand, from
$(\ddagger)$
we can conclude, by the induction hypothesis, that
$(W,R,V),\rho _{z'}(z') \Vdash ^{\textrm {lk,K}}_{\Pi } \psi $
. Therefore,
$(W,R,V),w \Vdash ^{\textrm {lk,K}}_{\Pi } {\Diamond } \psi $
.⊣
Finally, for each
$z \in X$
, consider the map
$$ \begin{align*}h_z: \mathcal{M}^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \to \mathcal{M}^{\textrm{lk,K}}_{\Pi}\end{align*} $$
defined as follows:
$$ \begin{align*}h_z(I,\rho) = ((W,R,V),\rho(z)),\end{align*} $$
where
-
• W is the domain of I;
-
•
$R=\{(w_1,w_2) \in W^2: \bar R^{I}(w_1,w_2)=1\}$
; -
•
$V(p)=\{w \in W: \bar p^{I}(w)=1\}$
.
The following result shows that
$h_z$
preserves and reflects local satisfaction. We omit its proof since it follows the same steps as the proof of Proposition 3.9.
Proposition 3.10. Let
$(I,\rho) \in \mathcal {M}^{\text {FO}^2}_{\Sigma _{\textrm {ML},\Pi }}$
and
$\varphi \in L^{\textrm {ML}}_\Pi $
. Then, for each
$z \in X$
,
$$ \begin{align*}(W,R,V),\rho(z) \Vdash^{\textrm{lk,K}}_{\Pi} \varphi \quad \text{if and only if} \quad I,\rho \Vdash^{\text{FO}^2}_{\Sigma_{\textrm{ML},\Pi}} \tau_z(\varphi),\end{align*} $$
where
$h_z(I,\rho)=((W,R,V),\rho (z))$
.
Proposition 3.11. The satisfiability problem
$\textrm {Sat}_{S^{\textrm {lk,K}}_\Pi }$
for
$\textrm {K}$
modal logic is decidable for every set
$\Pi $
of propositional symbols.
Proof We start by observing that
$(\tau _x,g_x,h_x)$
is a reduction from
$S^{\textrm {lk,K}}_\Pi $
to
$S^{\text {FO}^2}_{\Sigma _{\textrm {ML},\Pi }}$
by Propositions 3.9 and 3.10 and since
$\tau _x$
is computable. The satisfiability problem
$\textrm {Sat}_{S^{\textrm {lk,K}}_\Pi }$
is decidable by Proposition 3.4 since the satisfiability problem
$\textrm {Sat}_{S^{\textrm {FO}^2}_{\Sigma _{\textrm {ML},\Pi }}}$
is decidable because
$\textrm {Sat}_{S^{\text {FO}^2}_\Sigma }$
is decidable for every signature
$\Sigma $
of
$\textrm {FO}^2$
(see [Reference Grädel, Kolaitis and Vardi16, Reference Libkin23, Reference Mortimer24]).⊣
3.2 Validity of
$S^{\mathrm {ga,K}}_{\Pi }$
from the validity of
$S^{\mathrm {gk,K}}_{\Pi }$
Herein, we prove that the validity problem of
$\textrm {K}$
modal logic endowed with an (global) algebraic semantics (see [Reference Goldblatt14, Reference Rybakov27]) is decidable taking into account the decidability of the validity problem of
$\textrm {K}$
modal logic endowed with a global Kripke semantics (see Proposition 2.12).
Example 3.12. The (global) algebraic satisfaction system
$$ \begin{align*}S^{\textrm{ga,K}}_{\Pi}=(L^{\textrm{ML}}_{\Pi},\mathcal{M}^{\textrm{ga,K}}_{\Pi},\Vdash^{\textrm{ga,K}}_{\Pi})\end{align*} $$
for
$\textrm {K}$
modal logic over a set
$\Pi $
of propositional symbols is such that
-
•
$L^{\textrm {ML}}_{\Pi }$
is as defined in Example 2.2; -
•
$\mathcal {M}^{\textrm {ga,K}}_{\Pi }$
is the class of all modal algebras with distinguished value, that is, pairs
$({\mathfrak {A}},D)$
such that-
–
${\mathfrak {A}}=(A,\sqcap,\sqcup,\sqsupset,{-},\top,{\underline {\Box }},V)$
where
$(A,\sqcap,\sqcup,\sqsupset,{-},\top)$
is a Boolean algebra,
${\underline {\Box }}: A \to A$
satisfies the following identities: and
$$ \begin{align*}{\underline{\Box}} (a_1 \sqcap a_2) =({\underline{\Box}} a_1 \sqcap {\underline{\Box}} a_2) \quad \text{and} \quad {\underline{\Box}} \top = \top,\end{align*} $$
$V: \Pi \to A$
is a map;
-
–
$D=\{\top \}$
;
-
-
•
$\Vdash ^{\textrm {ga,K}}_{\Pi } \subseteq \mathcal {M}^{\textrm {ga,K}}_{\Pi } \times L^{\textrm {ga,K}}_{\Pi }$
is the satisfaction relation such that whenever
$$ \begin{align*}({\mathfrak{A}},D) \Vdash^{\textrm{ga,K}}_{\Pi} \varphi\end{align*} $$
${{\lbrack \!\lbrack \varphi \rbrack \!\rbrack }}^{{\mathfrak {A}}}=\top $
where is inductively defined as follows:
$$ \begin{align*}{{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}}^{{\mathfrak{A}}} \in A\end{align*} $$
-
–
${{\lbrack \!\lbrack p \rbrack \!\rbrack }}^{{\mathfrak {A}}} = V(p)$
for
$p \in \Pi $
; -
–
${{\lbrack \!\lbrack \mathop {\neg } \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} = {-} {{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
; -
–
${{\lbrack \!\lbrack \psi _1 \mathbin {\supset } \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} = {{\lbrack \!\lbrack \psi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \sqsupset {{\lbrack \!\lbrack \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
; -
–
${{\lbrack \!\lbrack \Box \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} = {{\underline {\Box }}} {{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
.
-
We need to consider a restricted class of Kripke structures for
$\textrm {K}$
modal logic in order to provide a reduction from the algebraic semantics to the Kripke semantics.
Example 3.13. The descriptive global Kripke satisfaction system for
$\textrm {K}$
modal logic is the tuple
$$ \begin{align*}S^{\textrm{dgk,K}}_{\Pi}=(L^{\textrm{ML}}_{\Pi},\mathcal{M}^{\textrm{dgk,K}}_{\Pi},\Vdash^{\textrm{dgk,K}}_{\Pi})\end{align*} $$
over a set
$\Pi $
of propositional symbols obtained from
$S^{\textrm {gk,K}}_{\Pi }$
(see Example 2.3) by taking
$\mathcal {M}^{\textrm {dgk,K}}_{\Pi }$
as the subclass of
$\mathcal {M}^{\textrm {gk,K}}_{\Pi }$
composed by Kripke structures that are descriptive (that is, differentiated, tight, and compact; (see [Reference Chagrov and Zakharyaschev9, Reference Goldblatt14])) and
$\Vdash ^{\textrm {dgk,K}}_{\Pi }$
as the restriction of
$\Vdash ^{\textrm {gk,K}}_{\Pi }$
to
$\mathcal {M}^{\textrm {dgk,K}}_{\Pi }$
. Similarly for
$S^{\textrm {dlk,K}}_{\Pi }$
.
We now show that there is a map from modal algebras to descriptive Kripke structures that preserves and reflects satisfaction. Before we recall some notions.
Definition 3.14. A filter in a modal algebra
${\mathfrak {A}}$
is a set
$F \subseteq A$
such that:
-
•
$\top \in F$
; -
• if
$a,b \in F$
then
$a \sqcap b \in F$
; -
• if
$a \in F$
and
$a \leq b$
then
$b \in F$
where
$a \leq b$
whenever
$a \sqcap b=a$
.
A filter F is a ultrafilter whenever:
-
•
$\bot \notin F$
; -
• for every
$a \in A$
either
$a \in F$
or
$-a \in F$
.
Proposition 3.15. Let
$g: \mathcal {M}^{\mathrm {ga,K}}_{\Pi } \to \mathcal {M}^{\mathrm {dgk,K}}_{\Pi }$
be such that
$$ \begin{align*}g({\mathfrak{A}},\{\top\})=(W,R,{\underline{V}}),\end{align*} $$
where
-
• W is
$\{U \subseteq A: U \text { is an ultrafilter of } {\mathfrak {A}}\};$
-
•
$U \mathbin{R} U'$
whenever for every
$a \in A$
if
${\underline {\Box }} a \in U$
then
$a \in U';$
-
•
${\underline {V}}(p)=\{U \in W: V(p) \in U\}$
.
Then, for every
$U \in W$
,
$$ \begin{align*}{{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}}^{{\mathfrak{A}}} \in U \quad \text{if and only if} \quad (W,R,{\underline{V}}),U \Vdash_\Pi^{\mathrm{dlk,K}} \varphi.\end{align*} $$
Furthermore,
$$ \begin{align*}({\mathfrak{A}},\{\top\}) \Vdash_\Pi^{\mathrm{ga,K}} \varphi \quad \text{if and only if} \quad (W,R,{\underline{V}}) \Vdash_\Pi^{\mathrm{dgk,K}} \varphi.\end{align*} $$
Proof We start by observing that
$(W,R,{\underline {V}})$
is a descriptive global Kripke structure (see [Reference Goldblatt14, Theorem 1.10.5]). It is immediate to see that the second assertion about satisfaction of formulas follows from the first (taking into account Theorem 5.38 in [Reference Blackburn, de Rijke and Venema5]). The proof of the first statement follows by induction on
$\varphi $
and we only consider the step when
$\varphi $
is
$\Box \psi $
.
Before, we show that:
$$ \begin{align*}(\dagger) \quad {\underline{\Box}} a \in U \text{ provided that } a \in U' \text{ for every } U' \in W \text{ such that } U \mathbin{R} U'\end{align*} $$
for every
$U \in W$
and
$a \in A$
. Assume, by contradiction, that
$a \in U'$
for every
$U' \in W$
such that
$U \mathbin{R} U'$
and
${\underline {\Box }} a \notin U$
. Consider
$$ \begin{align*}F=\{b \in A: {\underline{\Box}} b \in U\}.\end{align*} $$
Observe that
$a \notin F$
. Moreover, F is a filter. Indeed,
-
(1)
$\top \in F$
. Since U is an ultrafilter
$\top \in U$
. Since
${\underline {\Box }} \top = \top $
then
${\underline {\Box }} \top \in U$
and so
$\top \in F$
. -
(2) Assume that
$b,b' \in F$
. Hence
${\underline {\Box }} b, {\underline {\Box }} b' \in U$
. Therefore,
${\underline {\Box }} b \sqcap {\underline {\Box }} b' \in U$
and so
${\underline {\Box }} (b \sqcap b') \in U$
because
${\underline {\Box }} (b \sqcap b')=({\underline {\Box }} b) \sqcap ({\underline {\Box }} b')$
. Thus,
$b \sqcap b' \in F$
. -
(3) Suppose that
$b \in F$
and
$b \leq b'$
. Thus,
$b \sqcap b'=b$
and so
${\underline {\Box }} (b \sqcap b') = {\underline {\Box }} b$
. Then,
$({\underline {\Box }} b) \sqcap ({\underline {\Box }} b') = {\underline {\Box }} b$
. Hence,
$({\underline {\Box }} b) \leq ({\underline {\Box }} b')$
. Therefore,
${\underline {\Box }} b' \in U$
since
${\underline {\Box }} b \in U$
and U is a filter. Hence,
$b' \in F$
.
Then, (see Proposition 5.38 of [Reference Blackburn, de Rijke and Venema5]) there is
$U'' \in W$
extending F such that
$a \notin U''$
. Moreover,
$U \mathbin{R} U''$
by definition of R. The existence of such
$U''$
contradicts the initial assumption.
We are ready to prove the step when
$\varphi $
is
$\Box \psi $
.
$(\to)$
Assume that
${{\lbrack \!\lbrack \Box \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
. Then,
${\underline {\Box }} {{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
. Let
$U' \in W$
be such that
$U \mathbin{R} U'$
. Thus, by definition of R,
${{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U'$
. Hence, by the induction hypothesis
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {dlk,K}} \psi $
. Therefore,
$(W,R,{\underline {V}}),U \Vdash _\Pi ^{\mathrm {dlk,K}} \varphi $
.
$({{\leftarrow }})$
Assume that
$(W,R,{\underline {V}}),U \Vdash _\Pi ^{\mathrm {dlk,K}} \Box \psi $
. Then,
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {dlk,K}} \psi $
for every
$U' \in W$
such that
$U\mathbin{R}U'$
. Thus, by the induction hypothesis,
${{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U'$
for every
$U' \in W$
such that
$U\mathbin{R}U'$
. Therefore, by
$(\dagger)$
, we can conclude that
${\underline {\Box }} \, {{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
.⊣
We now define a map from descriptive Kripke structures to modal algebras that preserves and reflects satisfaction.
Proposition 3.16. Let
$h: \mathcal {M}^{\mathrm {dgk,K}}_{\Pi } \to \mathcal {M}^{\mathrm {ga,K}}_{\Pi }$
be such that
$$ \begin{align*}h(W,R,V)=((\wp W, \cap,\cup, \sqsupset, {-},W,{\underline{\Box}}, V),\{W\}),\end{align*} $$
where
-
•
${-} Z=W \setminus Z;$
-
•
$Z_1 \sqsupset Z_2= {-}Z_1 \cup Z_2;$
-
•
${\underline {\Box }} \, Z=\{w \in W: w' \in Z \text { whenever } w \mathbin{R} w'\};$
for
$Z,Z_1,Z_2 \subseteq W$
. Then, for every
$w \in W$
,
$$ \begin{align*}(W,R,V),w \Vdash_\Pi^{\mathrm{dlk,K}} \varphi \quad \text{if and only if} \quad w \in {{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}}^{{\mathfrak{A}}}.\end{align*} $$
Furthermore,
$$ \begin{align*}(W,R,V) \Vdash_\Pi^{\mathrm{dgk,K}} \varphi \quad \text{iff} \quad ((\wp W, \cap,\cup, \sqsupset, {-},W,{\underline{\Box}}, V),\{W\}) \Vdash^{\mathrm{ga,K}}_{\Pi} \varphi.\end{align*} $$
Proof It is immediate to see that the second assertion follows from the first, so we only prove the first assertion by induction on
$\varphi $
. Consider the case of
$\Box $
.
(Step)
$\varphi $
is
$\Box \psi $
.
$(\to)$
Assume that
$(W,R,V),w \Vdash _\Pi ^{\mathrm {dlk,K}} \Box \psi $
. Then, for every
$w' \in W$
such that
$w \mathbin{R}w'$
,
$$ \begin{align*}(W,R,V),w' \Vdash_\Pi^{\mathrm{dlk,K}} \psi.\end{align*} $$
So by the induction hypothesis,
$$ \begin{align*}w' \in {{\lbrack\!\lbrack \psi \rbrack\!\rbrack}}^{{\mathfrak{A}}}\end{align*} $$
for every
$w' \in W$
such that
$w \mathbin{R}w'$
. Therefore,
$w \in {\underline {\Box }} {{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}}={{\lbrack \!\lbrack \varphi \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
.
$({{\leftarrow }})$
Assume that
$w \in {{\lbrack \!\lbrack \Box \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
. Then
$w' \in {{\lbrack \!\lbrack \psi \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
for every
$w' \in W$
such that
$w \mathbin{R}w'$
. Hence, by the induction hypothesis,
$(W,R,V),w' \Vdash _\Pi ^{\mathrm {dlk,K}} \psi $
for every
$w' \in W$
such that
$w \mathbin{R}w'$
. Thus,
$(W,R,V),w \Vdash _\Pi ^{\mathrm {dlk,K}} \varphi $
.⊣
In summary, we have the following reductions between decision problems:
$$ \begin{align*}\mathrm{Val}_{S^{\mathrm{gk,K}}_{\Pi}} \to_{\text{Prop~2.12}} \mathrm{Sat}_{S^{\mathrm{lk,K}}_{\Pi}} \quad \quad \mathrm{Sat}_{S^{\mathrm{lk,K}}_{\Pi}} \to_{\text{Prop~3.11}} \mathrm{Sat}_{S^{\mathrm{FO}^2}_{\Sigma_{\mathrm{ML},\Pi}}}\end{align*} $$
and
$$ \begin{align*}\mathrm{Val}_{S^{\mathrm{ga,K}}_{\Pi}} \to_{\text{Prop~3.17}} \mathrm{Val}_{S^{\mathrm{dgk,K}}_{\Pi}} \quad \quad \mathrm{Val}_{S^{\mathrm{dgk,K}}_{\Pi}} ={{}}_{\text{Cor}~1.10.6 \text{ of } [14]} \mathrm{Val}_{S^{\mathrm{gk,K}}_{\Pi}}.\end{align*} $$
We are ready to prove that the validity problem of
$\mathrm {K}$
modal logic with an algebraic semantics is decidable.
Proposition 3.17. The validity problem
$\mathrm {Val}_{S^{\mathrm {ga,K}}_{\Pi }}$
is decidable for every set
$\Pi $
of propositional symbols.
Proof Observe that
$$ \begin{align*}({\textsf{id}}_{L_{\mathrm{ML}}},g,h): S^{\mathrm{ga,K}}_{\Pi} \to S^{\mathrm{dgk,K}}_{\Pi},\end{align*} $$
where g and h are defined in Propositions 3.15 and 3.16, respectively, is a satisfaction system reduction since
${\textsf {id}}_{L_{\mathrm {ML}}}$
is computable. Observe that g and h are surjective up to satisfaction because for every modal algebra
${\mathfrak {A}}$
,
$$ \begin{align*}({\mathfrak{A}},\{\top\}) \Vdash^{\mathrm{ga,K}}_{\Pi}\varphi \quad \text{if and only if} \quad h(g({\mathfrak{A}},\{\top\})) \Vdash^{\mathrm{dgk,K}}_{\Pi} \varphi\end{align*} $$
(see [Reference Goldblatt14, p. 17]) and, for every descriptive Kripke structure
$(W,R,V)$
,
$$ \begin{align*}(W,R,V) \Vdash^{\mathrm{dgk,K}}_{\Pi} \varphi \quad \text{if and only if} \quad g(h(W,R,V) \Vdash^{\mathrm{ga,K}}_{\Pi} \varphi\end{align*} $$
(see [Reference Goldblatt14, Theorem 1.10.7]). Hence, by Proposition 3.7
$\mathrm {Val}_{S^{\mathrm {ga,K}}_{\Pi }}$
is decidable if
$\mathrm {Val}_{S^{\mathrm {dgk,K}}_{\Pi }}$
is decidable. Note also that
$$ \begin{align*}\varphi \text{ is valid in } S^{\mathrm{dgk,K}}_\Pi \quad \text{if and only if} \quad \varphi \text{ is valid in } S^{\mathrm{gk,K}}_\Pi\end{align*} $$
(see [Reference Goldblatt14, Corollary 1.10.6]). Thus,
$\mathrm {Val}_{S^{\mathrm {ga,K}}_{\Pi }}$
is decidable if
$\mathrm {Val}_{S^{\mathrm {gk,K}}_{\Pi }}$
is decidable. The thesis follows since
$\mathrm {Val}_{S^{\mathrm {gk,K}}_{\Pi }}$
is decidable, by Proposition 2.12.⊣
3.3 Validity in
$S^{\mathrm {ga,Int}}_{\Pi }$
from Hintikka systems
The objective of this subsection is to show that the validity problem for intuitionistic logic with an algebraic semantics is decidable. We start by showing that the dual of the validity problem for intuitionistic logic with a global Kripke semantics is decidable using Hintikka systems. After that, we show that there is a reduction from the satisfaction system for intuitionistic logic with a Heyting finite algebra semantics to the satisfaction system with finite Kripke structures.
Example 3.18 Intuitionistic logic
Let
$$ \begin{align*}S_\Pi^{\mathrm{gk,Int}}=(L^{\mathrm{Int}}_{\Pi},\mathcal{M}^{\mathrm{gk,Int}}_{\Pi},\Vdash^{\mathrm{gk,Int}}_{\Pi})\end{align*} $$
be a satisfaction system for intuitionistic logic where:
-
• the set of formulas
$L^{\mathrm {Int}}_{\Pi }$
is inductively defined as follows:-
–
$\Pi \cup \{{\mathsf {ff}}\} \subseteq L^{\mathrm {Int}}_{\Pi }$
; -
–
$\varphi _1 \Rightarrow \varphi _2,\varphi _1 \mathbin {\wedge } \varphi _2,\varphi _1 \mathbin {\vee } \varphi _2 \in L^{\mathrm {Int}}_{\Pi }$
provided that
$\varphi _1,\varphi _2 \in L^{\mathrm {Int}}_{\Pi }$
.
$\sim \varphi \in L^{\mathrm {Int}}_{\Pi }$
is defined as an abbreviation of
$\varphi \Rightarrow {\mathsf {ff}}$
provided that
$\varphi \in L^{\mathrm {Int}}_{\Pi }$
;
-
-
•
$\mathcal {M}^{\mathrm {gk,Int}}_{\Pi }$
is the class of all Kripke structures
$(W,R,V)$
such that-
– R is reflexive, transitive, and anti-symmetric;
-
– if
$w \in V(p)$
and
$w\mathbin{R}w'$
then
$w' \in V(p)$
;
-
-
•
$\Vdash ^{\mathrm {gk,Int}}_{\Pi }$
is such that whenever
$$ \begin{align*}(W,R,V) \Vdash^{\mathrm{gk,Int}}_{\Pi} \varphi\end{align*} $$
where
$$ \begin{align*}(W,R,V), w \Vdash^{\mathrm{lk,Int}}_{\Pi} \varphi \quad \text{for each } w \in W,\end{align*} $$
$\Vdash ^{\mathrm {lk,Int}}_{\Pi }$
is inductively defined as follows:-
–
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi } p$
whenever
$w \in V(p)$
; -
–
$(W,R,V),w \not \Vdash ^{\mathrm {lk,Int}}_{\Pi } {\mathsf {ff}}$
; -
–
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _1 \Rightarrow \varphi _2$
whenever if
$(W,R,V),w' \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _1$
then
$(W,R,V),w' \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _2$
for every
$w'$
such that
$w \mathbin{R}w'$
; -
–
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _1 \mathbin {\wedge } \varphi _2$
whenever
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _i$
for
$i=1,2$
; -
–
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi }\varphi _1 \mathbin {\vee } \varphi _2$
whenever either
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _1$
or
$(W,R,V),w \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi _2$
.
-
We want to investigate the validity problem in
$S_\Pi ^{\mathrm {gk,Int}}$
. For that we need to introduce the concepts of tableau and Hintikka system (see [Reference Chagrov and Zakharyaschev9]).
Definition 3.19. A tableau is a pair
$(\Gamma,\Delta)$
where
$\Gamma,\Delta \subseteq L^{\mathrm {Int}}_\Pi $
. A tableau
$(\Gamma,\Delta)$
is saturated if it fulfils the following closure conditions:
-
• if
$\gamma _1 \mathbin {\wedge } \gamma _2 \in \Gamma $
then
$\gamma _1 \in \Gamma $
and
$\gamma _2 \in \Gamma $
; -
• if
$\delta _1 \mathbin {\wedge } \delta _2 \in \Delta $
then either
$\delta _1 \in \Delta $
or
$\delta _2 \in \Delta $
; -
• if
$\gamma _1 \mathbin {\vee } \gamma _2 \in \Gamma $
then either
$\gamma _1 \in \Gamma $
or
$\gamma _2 \in \Gamma $
; -
• if
$\delta _1 \mathbin {\vee } \delta _2 \in \Delta $
then
$\delta _1 \in \Delta $
and
$\delta _2 \in \Delta $
; -
• if
$\delta \Rightarrow \gamma \in \Gamma $
then either
$\delta \in \Delta $
or
$\gamma \in \Gamma $
.
A saturated tableau
$(\Gamma,\Delta)$
is disjoint if
$\Gamma \cap \Delta = \emptyset $
and
${\mathsf {ff}} \notin \Gamma $
. A Hintikka system is a pair
$(\mathcal T,\preceq)$
where
$\mathcal T$
is a non-empty set of disjoint saturated tableaux and
$\preceq $
is a partial order on
$\mathcal T$
such that:
-
• if
$(\Gamma,\Delta),(\Gamma ',\Delta ') \in \mathcal T$
and
$(\Gamma,\Delta)\preceq (\Gamma ',\Delta ')$
then
$\Gamma \subseteq \Gamma '$
( hereditarity); -
• if
$(\Gamma,\Delta) \in \mathcal T$
and
$\gamma \Rightarrow \delta \in \Delta $
then there is
$(\Gamma ',\Delta ') \in \mathcal T$
such that
$(\Gamma,\Delta)\preceq (\Gamma ',\Delta ')$
,
$\gamma \in \Gamma '$
, and
$\delta \in \Delta '$
.
A pair
$(\mathcal T,\preceq)$
is a Hintikka system for
$(\Gamma,\Delta)$
if there is
$(\Gamma ',\Delta ') \in \mathcal T$
such that
$\Gamma \subseteq \Gamma '$
and
$\Delta \subseteq \Delta '$
. Moreover,
$(\mathcal T,\preceq)$
is a Hintikka system for
$\varphi $
whenever
$(\mathcal T,\preceq)$
is a Hintikka system for
$(\emptyset,\{\varphi \})$
.
For instance,
$(\emptyset,\{\varphi \})$
is a tableau provided that
$\varphi \in L^{\mathrm {Int}}_\Pi $
.
In the sequel, we denote by
$\text {sub}(\varphi)$
the set of subformulas of
$\varphi $
. For the next result we need to consider the following decision problem:
$$ \begin{align*}\mathrm{HS}_{S_\Pi^{\mathrm{gk,Int}}}=(L^{\mathrm{Int}}_\Pi,\{\varphi: \text{exists a Hintikka system } \mathcal T \text{ for } \varphi, |\mathcal T| \leq 2^{|\text{sub}(\varphi)|}\}).\end{align*} $$
Proposition 3.20. The decision problem
$\mathrm {co{-}Val}_{S_\Pi ^{\mathrm {gk,Int}}}$
is decidable, for every set
$\Pi $
of propositional symbols.
Proof We show that
${\textsf {id}}_{L^{\mathrm {Int}}_\Pi }$
is a reduction from
$\mathrm {co{-}Val}_{S_\Pi ^{\mathrm {gk,Int}}}$
to
$\mathrm {HS}_{S_\Pi ^{\mathrm {gk,Int}}}$
. It is immediate that
${\textsf {id}}_{L^{\mathrm {Int}}_\Pi }$
is computable. It remains to show that
$$ \begin{align*}\varphi \text{ is not valid in } S_\Pi^{\mathrm{gk,Int}}\quad \text{if and only if} \quad \begin{array}{l} \text{there is a Hintikka system } (\mathcal T,\preceq) \\ \text{for } \varphi \text{ and } |\mathcal T| \leq 2^{|\text{sub}(\varphi)|}. \end{array} \end{align*} $$
$(\to)$
Let
$(W,R,V) \in \mathcal {M}^{\mathrm {gk,Int}}_\Sigma $
and
$w \in W$
be such that
$(W,R,V),w \not \Vdash ^{\mathrm {lk,Int}}_{\Pi } \varphi $
. Consider the family
$$ \begin{align*}\mathcal T=\{(\Gamma_u,\Delta_u)\}_{u \in W}\end{align*} $$
of tableaux such that
$$ \begin{align*}\begin{cases} \Gamma_u=\{\psi \in \text{sub}(\varphi): (W,R,V),u \Vdash^{\mathrm{lk,Int}}_{\Pi} \psi\},\\ \Delta_u= \{\eta \in \text{sub}(\varphi): (W,R,V),u \not \Vdash^{\mathrm{lk,Int}}_{\Pi} \eta\}. \end{cases}\end{align*} $$
Define the relation
$\preceq $
over
$\mathcal T$
such that
$(\Gamma _u,\Delta _u) \preceq (\Gamma _{u'},\Delta _{u'})$
whenever
$\Gamma _u \subseteq \Gamma _{u'}$
. We now prove that
$(\mathcal T,\preceq)$
is a Hintikka system for
$\varphi $
with
$|\mathcal T| \leq 2^{|\text {sub}(\varphi)|}$
.
-
(1) Assume that
$(\Gamma _u,\Delta _u),(\Gamma _{u'},\Delta _{u'}) \in \mathcal T$
and
$(\Gamma _u,\Delta _u) \preceq (\Gamma _{u'},\Delta _{u'})$
. Then, by definition of
$\preceq $
,
$\Gamma _u \subseteq \Gamma _{u'}$
. -
(2) Suppose that
$(\Gamma _u,\Delta _u) \in \mathcal T$
and
$\gamma \Rightarrow \delta \in \Delta _u$
. So,
$(W,R,V),u \not \Vdash ^{\mathrm {lk,Int}}_{\Pi } \gamma \Rightarrow \delta $
. Therefore, there is
$u' \in W$
such that
$u\mathbin{R}u'$
,
$\gamma \in \Gamma _{u'}$
and
$\delta \in \Delta _{u'}$
. Moreover, by hereditarity (see [Reference Rybakov27]),
$\Gamma _u \subseteq \Gamma _{u'}$
and so
$(\Gamma _u,\Delta _u) \preceq (\Gamma _{u'},\Delta _{u'})$
. -
(3)
$(\mathcal T,\preceq)$
is a Hintikka system for
$\varphi $
since
$\emptyset \subseteq \Gamma _w$
and
$\varphi \in \Delta _w$
. -
(4) By construction, each
$\Gamma _u$
and
$\Delta _u$
are subsets of
$\text {sub}(\varphi)$
. Moreover,
$\Delta _u=\text {sub}(\varphi)\setminus \Gamma _u$
. Therefore,
$|\mathcal T| \leq 2^{|\text {sub}(\varphi)|}$
.
$({{\leftarrow }})~\text{Let }(\mathcal T,\preceq)$
be a Hintikka system for
$(\emptyset,\{\varphi \})$
with
$|\mathcal T| \leq 2^{|\text {sub}(\varphi)|}$
. Consider the Kripke structure
$(\mathcal T,{\preceq},V)$
where V is such that
$$ \begin{align*}V(p)=\{(\Gamma,\Delta): (\Gamma,\Delta) \in \mathcal T \text{ and } p \in \Gamma\}.\end{align*} $$
Observe that if
$(\Gamma,\Delta) \in V(p)$
and
$(\Gamma,\Delta) \preceq (\Gamma ',\Delta ')$
then, by the first property of Hintikka system,
$(\Gamma ',\Delta ') \in V(p)$
. We now show, for every
$(\Gamma,\Delta) \in \mathcal T$
, that
$$ \begin{align*}\begin{cases}\text{if } \eta \in \Gamma \text{ then }(\mathcal T,{\preceq},V),(\Gamma,\Delta) \Vdash^{\mathrm{lk,Int}}_\Pi \eta, \\[2mm]\text{if } \eta \in \Delta \text{ then } (\mathcal T,{\preceq},V),(\Gamma,\Delta) \not \Vdash^{\mathrm{lk,Int}}_\Pi \eta, \end{cases}\end{align*} $$
by induction on
$\eta $
. The base and the cases where
$\eta $
is either a conjunction or a disjunction are immediate. We concentrate on
$\eta $
being
$\eta _1 \Rightarrow \eta _2.$
-
(1) Assume, by contradiction,
$\eta _1 \Rightarrow \eta _2 \in \Gamma $
and
$(\mathcal T,{\preceq},V),(\Gamma,\Delta) \not \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _1 \Rightarrow \eta _2$
. Therefore, there exists
$(\Gamma ',\Delta ') \in \mathcal T$
such that
$(\Gamma,\Delta) \preceq (\Gamma ',\Delta ')$
,
$(\mathcal T,{\preceq},V),(\Gamma ',\Delta ') \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _1$
, and
$(\mathcal T,{\preceq},V),(\Gamma ',\Delta ') \not \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _2$
. Thus, by the first property of the Hintikka system,
$\eta _1 \Rightarrow \eta _2 \in \Gamma '$
. Then, either
$\eta _1 \in \Delta '$
or
$\eta _2 \in \Gamma '$
because
$(\Gamma ',\Delta ')$
is saturated. Hence, by the induction hypothesis, either
$(\mathcal T,{\preceq},V),(\Gamma ',\Delta ') \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _2$
or
$(\mathcal T,{\preceq}, V),(\Gamma ',\Delta ') \not \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _1$
which is a contradiction. -
(2) Assume that
$\eta _1 \Rightarrow \eta _2 \in \Delta $
. Then, by the second property of the Hintikka system, there is
$(\Gamma ',\Delta ') \in \mathcal T$
such that
$(\Gamma,\Delta) \preceq (\Gamma ',\Delta ')$
,
$\eta _1 \in \Gamma '$
, and
$\eta _2 \in \Delta '$
. Therefore, by the induction hypothesis,
$(\mathcal T,{\preceq}, V),(\Gamma ',\Delta ') \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _1$
and
$(\mathcal T,{\preceq},V),(\Gamma ',\Delta ') \not \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _2$
. So
$(\mathcal T,{\preceq}, V),(\Gamma,\Delta) \not \Vdash ^{\mathrm {lk,Int}}_\Pi \eta _1 \Rightarrow \eta _2$
.
Hence, we can conclude that
$\mathrm {co{-}Val}^{\mathrm {Int}}_\Pi $
is decidable, since
$\mathrm {HS}^{\mathrm {Int}}_\Pi $
is decidable for every set
$\Pi $
(see [Reference Chagrov and Zakharyaschev9, p. 39]) and there is a reduction from the former to the latter (see Proposition 2.8).⊣
The following result is a direct consequence of Propositions 2.6 and 3.20.
Proposition 3.21. The decision problem
$\mathrm {Val}_{S_\Pi ^{\mathrm {gk,Int}}}$
is decidable, for every set
$\Pi $
of propositional symbols.
We now describe an algebraic satisfaction system for intuitionistic logic.
Example 3.22. The (global) algebraic satisfaction system
$$ \begin{align*}S^{\mathrm{ga,Int}}_{\Pi}=(L^{\mathrm{Int}}_{\Pi},\, \mathcal{M}^{\mathrm{ga,Int}}_{\Pi},\Vdash^{\mathrm{ga,Int}}_{\Pi})\end{align*} $$
for intuitionistic logic over a set
$\Pi $
of propositional symbols is such that
-
•
$L^{\mathrm {Int}}_{\Pi }$
is as defined in Example 3.18; -
•
$\mathcal {M}^{\mathrm {ga,Int}}_{\Pi }$
is the class of all Heyting or pseudo-Boolean algebras with distinguished value, that is, pairs
$({\mathfrak {A}},D)$
such that-
–
${\mathfrak {A}}=(A,\,{\underline {\mathbin {\wedge }}},\,{\underline {\mathbin {\vee }}},\,{\underline {\Rightarrow }},\,\bot,V)$
where
$(A,\,{\underline {\mathbin {\wedge }}},\,{\underline {\mathbin {\vee }}},\,{\underline {\Rightarrow }},\bot)$
satisfies the following identities, where
$a_1 \leq a_2$
whenever
$a_1 {\underline {\mathbin {\wedge }}} a_2=a_1$
:-
*
$a_1 {\underline {\mathbin {\wedge }}} a_2=a_2 {\underline {\mathbin {\wedge }}} a_1$
and
$a_1 {\underline {\mathbin {\vee }}} a_2=a_2 {\underline {\mathbin {\vee }}} a_1$
; -
*
$(a_1 {\underline {\mathbin {\wedge }}} a_2) \mathbin {\wedge } a_3=a_1 {\underline {\mathbin {\wedge }}} (a_2 \mathbin {\wedge } a_3)$
and
$(a_1 {\underline {\mathbin {\vee }}} a_2) {\underline {\mathbin {\vee }}} a_3=a_1 {\underline {\mathbin {\vee }}} (a_2 {\underline {\mathbin {\vee }}} a_3)$
; -
*
$(a_1 {\underline {\mathbin {\wedge }}} a_2) {\underline {\mathbin {\vee }}} a_2=a_2$
and
$a_1 {\underline {\mathbin {\wedge }}} (a_1 {\underline {\mathbin {\vee }}} a_2)= a_1$
; -
*
$a_1 {\underline {\mathbin {\wedge }}} a_2 \leq a_3$
if and only if
$a_1 \leq a_2 {\underline {\Rightarrow }} a_3$
; -
*
$\bot \leq a$
;
and
$V: \Pi \to A$
is a map; -
-
–
$D=\{\top \}$
where
$\top $
is
$\bot {\underline {\Rightarrow }} \bot $
;
-
-
•
$\Vdash ^{\mathrm {ga,Int}}_{\Pi } \subseteq \mathcal {M}^{\mathrm {ga,Int}}_{\Pi } \times L^{\mathrm {Int}}_{\Pi }$
is the satisfaction relation such that whenever
$$ \begin{align*}({\mathfrak{A}},\{\top\}) \Vdash^{\mathrm{ga,Int}}_{\Pi} \varphi\end{align*} $$
${{\lbrack \!\lbrack \varphi \rbrack \!\rbrack }}^{{\mathfrak {A}}}=\top $
and is inductively defined as follows:
$$ \begin{align*}{{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}}^{{\mathfrak{A}}} \in A\end{align*} $$
-
–
${{\lbrack \!\lbrack p \rbrack \!\rbrack }}^{{\mathfrak {A}}} = V(p)$
for
$p \in \Pi $
; -
–
${{\lbrack \!\lbrack {\mathsf {ff}} \rbrack \!\rbrack }}^{{\mathfrak {A}}} = \bot $
; -
–
${{\lbrack \!\lbrack \psi _1 \mathbin {\wedge } \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} = {{\lbrack \!\lbrack \psi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\mathbin {\wedge }}} {{\lbrack \!\lbrack \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
; -
–
${{\lbrack \!\lbrack \psi _1 \mathbin {\vee } \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} = {{\lbrack \!\lbrack \psi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\mathbin {\vee }}} {{\lbrack \!\lbrack \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
; -
–
${{\lbrack \!\lbrack \psi _1 \Rightarrow \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} = {{\lbrack \!\lbrack \psi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\Rightarrow }} {{\lbrack \!\lbrack \psi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
.
-
We denote by
$$ \begin{align*}S_\Pi^{\mathrm{fga,Int}}\end{align*} $$
the satisfaction system obtained from
$S_\Pi ^{\mathrm {ga,Int}}$
by taking the elements of
$\mathcal {M}^{\mathrm {ga,Int}}_{\Pi }$
where the set A is finite. Similarly, we denote by
$$ \begin{align*}S_\Pi^{\mathrm{fgk,Int}}\end{align*} $$
the satisfaction system obtained from
$S_\Pi ^{\mathrm {gk,Int}}$
(see Example 3.18) by taking the elements of
$\mathcal {M}^{\mathrm {gk,Int}}_{\Pi }$
where the set W is finite.
Observe that from the point of view of validity it is equivalent to work with Heyting algebras or finite Heyting algebras (see [Reference Chagrov and Zakharyaschev9, Theorem 7.21]). We start by introducing two relevant concepts.
Definition 3.23. A filter U in a Heyting algebra
${\mathfrak {A}}$
is a subset of A such that:
-
•
$\top \in U$
; -
• if
$a, a {\underline {\Rightarrow }} b \in U$
then
$b \in U$
.
A filter U is prime whenever
$U \neq A$
and if
$a {\underline {\mathbin {\vee }}} b \in U$
then either
$a \in U$
or
$b \in U$
.
As a consequence we have that if
$a \in U$
and
$a \leq b$
then
$b \in U$
.
Proposition 3.24. Let
$g: \mathcal {M}^{\mathrm {fga,Int}}_{\Pi } \to \mathcal {M}^{\mathrm {fgk,Int}}_{\Pi }$
be such that
$$ \begin{align*}g({\mathfrak{A}},\{\top\})=(W,R,{\underline{V}}), \end{align*} $$
where
-
• W is the set of all prime filters in
${\mathfrak {A}};$
-
• R is such that
$U \mathbin{R} U'$
whenever
$U \subseteq U';$
-
•
${\underline {V}}(p)$
is
$\{U \in W: V(p) \in U\}$
.
Then, for every
$U \in W$
,
$$ \begin{align*}{{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}}^{{\mathfrak{A}}} \in U \quad \text{if and only if} \quad (W,R,{\underline{V}}),U \Vdash_\Pi^{\mathrm{fgk,Int}} \varphi.\end{align*} $$
Furthermore,
$$ \begin{align*}({\mathfrak{A}},\{\top\}) \Vdash^{\mathrm{fga,Int}}_{\Pi} \varphi \quad \text{if and only if} \quad (W,R,{\underline{V}}) \Vdash^{\mathrm{fgk,Int}}_{\Pi}\varphi. \end{align*} $$
Proof It is immediate to see that the second assertion follows from the first (taking into account Theorem 7.41 of [Reference Chagrov and Zakharyaschev9]). The proof of the first statement follows by induction on
$\varphi $
. We only prove the step where
$\varphi $
is
$\varphi _1 \Rightarrow \varphi _2$
.
$(\to)$
Assume that
${{\lbrack \!\lbrack \varphi _1 \Rightarrow \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
,
$U \mathbin{R} U'$
and
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _1$
. Hence, by the induction hypothesis,
${{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U'$
. Thus,
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U'$
because
$U'$
is a filter and
${{\lbrack \!\lbrack \varphi _1 \Rightarrow \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}={{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\Rightarrow }} {{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U'$
. So, by the induction hypothesis,
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _2$
. Hence,
$(W,R,{\underline {V}}),U \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _1 \Rightarrow \varphi _2$
.
$({{\leftarrow }})$
Assume that
$(W,R,{\underline {V}}),U \Vdash _\Pi ^{\mathrm {fgk,Int}} \varphi _1 \Rightarrow \varphi _2$
. Then, for every
$U' \in W$
such that
$U\mathbin{R}U'$
if
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {fgk,Int}} \varphi _1$
then
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {fgk,Int}} \varphi _2$
. Consider two cases:
-
(1) Assume that
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
. We show that
${{\lbrack \!\lbrack \varphi _1 \Rightarrow \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
. Observe that
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \leq {{\lbrack \!\lbrack \varphi _1 \Rightarrow \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
because
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\mathbin {\wedge }}} {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \leq {{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
. So, the thesis follows. -
(2) Assume that
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \notin U$
. Let
$$ \begin{align*}F=\{a \in A: \exists b \in U \, b {\underline{\mathbin{\wedge}}} {{\lbrack\!\lbrack \varphi_1 \rbrack\!\rbrack}}^{{\mathfrak{A}}} \leq a \}.\end{align*} $$
Observe that:
-
(a)
$U \subseteq F$
. It is enough to note that
$u {\underline {\mathbin {\wedge }}} {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \leq u$
for every
$u \in U$
. -
(b)
${{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in F$
since
$\top {\underline {\mathbin {\wedge }}} {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \leq {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
and
$\top \in U$
. -
(c) F is a filter. Indeed,
$\top \in F$
since
$\top {\underline {\mathbin {\wedge }}} {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \leq \top $
and
$\top \in U$
. For the other condition, assume that
$a_1, a_1 {\underline {\Rightarrow }} a_2 \in F$
. Then there are
$b_1, b \in U$
such that Hence,
$$ \begin{align*}b_1 {\underline{\mathbin{\wedge}}} {{\lbrack\!\lbrack \varphi_1 \rbrack\!\rbrack}}^{{\mathfrak{A}}} \leq a_1 \quad \text{and} \quad b {\underline{\mathbin{\wedge}}} {{\lbrack\!\lbrack \varphi_1 \rbrack\!\rbrack}}^{{\mathfrak{A}}} \leq a_1 {\underline{\Rightarrow}} a_2.\end{align*} $$
Thus,
$$ \begin{align*}b{\underline{\mathbin{\wedge}}} a_1 {\underline{\mathbin{\wedge}}} {{\lbrack\!\lbrack \varphi_1 \rbrack\!\rbrack}}^{{\mathfrak{A}}} \leq a_2.\end{align*} $$
Since
$$ \begin{align*}b{\underline{\mathbin{\wedge}}} b_1 {\underline{\mathbin{\wedge}}} {{\lbrack\!\lbrack \varphi_1 \rbrack\!\rbrack}}^{{\mathfrak{A}}} \leq a_2.\end{align*} $$
$b{\underline {\mathbin {\wedge }}} b_1 \in U$
then
$a_2 \in F$
.
-
(d) We prove that
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in F$
. Assume, by contradiction, that
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \notin F$
. Then (see [Reference Chagrov and Zakharyaschev9, Theorem Reference Carnielli and Coniglio7.41]) there is a prime filter
$U'$
such that
$F \subseteq U'$
and
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \notin U'$
. Thus,
$U \subseteq U'$
by (a) and so
$U\mathbin{R}U'$
. Therefore, by the induction hypothesis,
$(W,R,{\underline {V}}),U' \Vdash _\Pi ^{\mathrm {fgk,Int}} \varphi _1$
by (b) but
$(W,R,{\underline {V}}),U' \not \Vdash _\Pi ^{\mathrm {fgk,Int}} \varphi _2$
which is a contradiction because
$(W,R,{\underline {V}}),U \Vdash _\Pi ^{\mathrm {fgk,Int}} \varphi _1 \Rightarrow \varphi _2$
. Thus,
${{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in F$
and so there is
$b \in U$
such that Hence,
$$ \begin{align*}b {\underline{\mathbin{\wedge}}} {{\lbrack\!\lbrack \varphi_1 \rbrack\!\rbrack}}^{{\mathfrak{A}}} \leq {{\lbrack\!\lbrack \varphi_2 \rbrack\!\rbrack}}^{{\mathfrak{A}}}.\end{align*} $$
$b \leq {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\Rightarrow }} {{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
and, consequently,
${{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}} {\underline {\Rightarrow }} {{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}} \in U$
.⊣
We now define a map from finite Kripke structure for intuitionistic logics to finite pseudo-Boolean algebra that preserves and reflects satisfaction.
Proposition 3.25. Let
$h: \mathcal {M}^{\mathrm {fgk,Int}}_{\Pi } \to \mathcal {M}^{\mathrm {fga,Int}}_{\Pi }$
be such that
$$ \begin{align*}h(W,R,V)=((\mathrm{Up} W,\cap,\cup,\,{\underline{\Rightarrow}},\,\emptyset,\, {\underline{V}}), \{W\}), \end{align*} $$
where
-
•
$\mathrm {Up} W$
is the set of all subsets of W that are upwards closed with respect to
$R;$
-
•
$X {\underline {\Rightarrow }} Y$
is
$\{w \in W: \forall w' \in W \text { if } w \mathbin{R} w' \text { and } w' \in X \text { then } w'\in Y\};$
-
•
${\underline {V}}(p)=\{w \in W: w \in V(p)\}$
.
Then, for every
$w \in W$
,
$$ \begin{align*}(W,R,V),w \Vdash_\Pi^{\mathrm{fgk,Int}} \varphi \quad \text{if and only if} \quad w \in {{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}}^{{\mathfrak{A}}},\end{align*} $$
where
${\mathfrak {A}}=(\mathrm {Up} W,\cap,\cup,{\underline {\Rightarrow }},\emptyset, {\underline {V}})$
. Furthermore,
$$ \begin{align*}(W,R,V) \Vdash^{\mathrm{fgk,Int}}_{\Pi} \varphi \quad \text{if and only if} \quad ((\mathrm{Up} W,\cap,\cup,{\underline{\Rightarrow}},\emptyset, {\underline{V}}),\{W\}) \Vdash^{\mathrm{fga,Int}}_{\Pi} \varphi. \end{align*} $$
Proof It is immediate to see that the second assertion follows from the first, so we only prove the first assertion by induction on
$\varphi $
. Consider the case of
$\varphi _1 \Rightarrow \varphi _2$
.
$(\to)$
Assume that
$(W,R,V),w \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _1 \Rightarrow \varphi _2$
,
$w' \in W$
such that
$w\mathbin{R}w'$
and
$w' \in {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
. Then, by the induction hypothesis,
$(W,R,V),w' \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _1$
and so
$(W,R,V),w' \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _2$
. Thus, by the induction hypothesis,
$w' \in {{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
. Hence,
$w \in {{\lbrack \!\lbrack \varphi _1 \Rightarrow \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
.
$({{\leftarrow }})$
Assume
$w \in {{\lbrack \!\lbrack \varphi _1 \Rightarrow \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
,
$w' \in W$
,
$w\mathbin{R}w'$
, and
$(W,R,V),w' \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _1$
. Hence, by the induction hypothesis,
$w' \in {{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
and so
$w' \in {{\lbrack \!\lbrack \varphi _2 \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
. Once again by the induction hypothesis,
$(W,R,V),w' \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _2$
. Therefore,
$(W,R,V),w \Vdash _\Pi ^{\mathrm {fgk,Int}}\varphi _1 \Rightarrow \varphi _2$
.⊣
In summary, we have the following reductions between decision problems:
$$ \begin{align*}\mathrm{Val}_{S_\Pi^{\mathrm{gk,Int}}} \to_{\text{Prop}~3.21} \mathrm{co{-}Val}_{S_\Pi^{\mathrm{gk,Int}}} \to_{\text{Prop}~3.20} \mathrm{HS}_{S_\Pi^{\mathrm{gk,Int}}} \end{align*} $$
and
$$ \begin{align*}\mathrm{Val}_{S_\Pi^{\mathrm{fga,Int}}} \to_{\text{Prop}~3.26} \mathrm{Val}_{S_\Pi^{\mathrm{fgk,Int}}}\end{align*} $$
and
$$ \begin{align*}\mathrm{Val}_{S_\Pi^{\mathrm{ga,Int}}}=_{\text{Thm}~7.21 \text{ of}~[9]} \mathrm{Val}_{S_\Pi^{\mathrm{fga,Int}}}, \quad \mathrm{Val}_{S_\Pi^{\mathrm{gk,Int}}}=_{\text{Thm}~2.5.60 \text{ of}~[27]} \mathrm{Val}_{S_\Pi^{\mathrm{fgk,Int}}}.\end{align*} $$
We are ready to prove that the validity problem for the intuitionistic logic endowed with algebraic semantics is decidable.
Proposition 3.26. The validity problem
$\mathrm {Val}_{S^{\mathrm {ga,Int}}_{\Pi }}$
is decidable for every set
$\Pi $
of propositional symbols.
Proof Observe that
$$ \begin{align*}({\textsf{id}}_{L^{\mathrm{Int}}_{\Pi}},g,h),\end{align*} $$
where g and h are defined in Propositions 3.24 and 3.25, respectively, is a satisfaction system reduction. Moreover, g and h are surjective up to satisfaction because for every finite Heyting algebra
$({\mathfrak {A}},D)$
,
$$ \begin{align*}({\mathfrak{A}},D) \Vdash^{\mathrm{fga,Int}}_{\Pi}\varphi \quad \text{if and only if} \quad h(g({\mathfrak{A}},D)) \Vdash^{\mathrm{fga,Int}}_{\Pi} \varphi\end{align*} $$
(see [Reference Chagrov and Zakharyaschev9, Theorem 8.18]) and, for every finite Kripke structure
$(W,R,V)$
,
$$ \begin{align*}(W,R,V) \Vdash^{\mathrm{fgk,Int}}_{\Pi} \varphi \quad \text{if and only if} \quad g(h(W,R,V)) \Vdash^{\mathrm{fgk,Int}}_{\Pi} \varphi\end{align*} $$
(see [Reference Rybakov27, Theorem 2.5.60]). Therefore, by Proposition 3.7
$\mathrm {Val}_{S^{\mathrm {fga,Int}}_{\Pi }}$
is decidable if
$\mathrm {Val}_{S^{\mathrm {fgk,Int}}_{\Pi }}$
is decidable. On the other hand,
$\mathrm {Val}_{S^{\mathrm {ga,Int}}_{\Pi }}$
is decidable if and only if
$\mathrm {Val}_{S^{\mathrm {fga,Int}}_{\Pi }}$
is decidable (see [Reference Chagrov and Zakharyaschev9, Theorem 7.21]). Note also that
$$ \begin{align*}\varphi \text{ is valid in } S^{\mathrm{fgk,Int}}_\Pi \quad \text{if and only if} \quad \varphi \text{ is valid in } S^{\mathrm{gk,Int}}_\Pi\end{align*} $$
(see [Reference Bezhanishvili and de Jongh3]). The thesis follows because
$\mathrm {Val}_{S^{\mathrm {gk,Int}}_{\Pi }}$
is decidable, by Proposition 3.21.⊣
4 Reductions for meet-combination
Herein we discuss reductions between the satisfaction system resulting from meet-combination and their components. Meet-combination was introduced in [Reference Rasga, Sernadas and Sernadas25, Reference Sernadas, Sernadas and Rasga30] and it provides an axiomatization for the product of two matrix logics.
Let
$\Sigma $
be a signature, that is, a family
$\{\Sigma ^{(n)}\}$
where
$\Sigma ^{(n)}$
is a set for every
$n \in {\mathbb N}$
such that
${\mathsf {tt}},{\mathsf {ff}} \in \Sigma ^{(0)}$
. Each element of
$\Sigma ^{(n)}$
is a connective of arity n.
Definition 4.1. A matrix satisfaction system over
$\Sigma $
is a triple
$$ \begin{align*}(L_\Sigma,\mathcal{A}_\Sigma,\Vdash_\Sigma),\end{align*} $$
where
-
•
$L_\Sigma $
is inductively defined as follows:
$\Sigma ^{(0)} \subseteq L_\Sigma $
and if
$c \in \Sigma ^{(n)}$
and
$\varphi _1,\dots,\varphi _n \in L_\Sigma $
then
$c(\varphi _1,\dots,\varphi _n) \in L_\Sigma $
; -
•
$\mathcal {A}_\Sigma $
is a non-empty class of matrices over
$\Sigma $
, that is, pairs
$({\mathfrak {A}},D)$
where-
–
${\mathfrak {A}}$
is an algebra over
$\Sigma $
, that is, a pair
$(A,\{\{c^{\mathfrak {A}}\}_{c \in \Sigma ^{(n)}}\}_{n \in {\mathbb N}})$
where A is a non-empty set and
$c^{\mathfrak {A}}: A ^n \to A$
is a map for each
$c \in \Sigma ^{(n)}$
. Moreover, we denote by
${{\lbrack \!\lbrack \varphi \rbrack \!\rbrack }}^{{\mathfrak {A}}}$
the denotation of
$\varphi $
in
${\mathfrak {A}}$
; -
– D is a non-empty subset of A (the elements of D are called distinguished elements) such that
${\mathsf {tt}}^{\mathfrak {A}} \in D$
and
${\mathsf {ff}}^{\mathfrak {A}} \notin D$
;
-
-
•
$\Vdash _\Sigma \, \subseteq \mathcal {A}_\Sigma \times L_\Sigma $
is such that whenever
$$ \begin{align*}({\mathfrak{A}},D) \Vdash_\Sigma c(\varphi_1,\dots,\varphi_n)\end{align*} $$
$c^{{\mathfrak {A}}}({{\lbrack \!\lbrack \varphi _1 \rbrack \!\rbrack }}^{{\mathfrak {A}}},\dots,{{\lbrack \!\lbrack \varphi _n \rbrack \!\rbrack }}^{{\mathfrak {A}}}) \in D.$
Observe that a matrix satisfaction system is also a satisfaction system where each semantic structure in
$\mathcal {M}$
is a pair
$({\mathfrak {A}},D)$
.
Given signatures
$\Sigma _1$
and
$\Sigma _2$
, let
$$ \begin{align*}\Sigma_{\mathop{\lceil12\rceil}}\end{align*} $$
be the signature such that, for each
$n \in {\mathbb N}$
,
$\Sigma _{{\mathop {\lceil 12\rceil }}}^{(n)}$
is
$$ \begin{align*}\{\mathop{\lceil c_1c_2\rceil} \mid c_1 \in \Sigma_1^{(n)},c_2\in\Sigma_2^{(n)}\} \cup \{\mathop{\lceil c_1{\mathsf{tt}}_2\rceil} \mid c_1 \in \Sigma_1^{(n)}\} \cup \{\mathop{\lceil{\mathsf{tt}}_1 c_2\rceil} \mid c_2 \in \Sigma_2^{(n)}\},\end{align*} $$
where the constructor
$\mathop {\lceil c_1c_2\rceil }$
is the meet-combination of
$c_1$
and
$c_2$
. Observe that we look at signature
$\Sigma _{\mathop {\lceil 12\rceil }}$
as an enrichment of
$\Sigma _1$
via the embedding
$\eta _1:c_1 \mapsto \mathop {\lceil c_1{\mathsf {tt}}_2\rceil }$
for each
$c_1 \in \Sigma _1^{(n)}$
and similarly for
$\Sigma _2$
. For the sake of lightness of notation, in the context of
$\Sigma _{\mathop {\lceil 12\rceil }}$
, from now on, we may write
$c_1$
for
$\mathop {\lceil c_1{\mathsf {tt}}_2\rceil }$
when
$c_1\in \Sigma _1^{(n)}$
and
$c_2$
for
$\mathop {\lceil {\mathsf {tt}}_1c_2\rceil }$
when
$c_2\in \Sigma _2^{(n)}$
. In this vein, for
$k=1,2$
, we look at
$L_{\Sigma _k}$
as a subset of
$L_{\Sigma _{\mathop {\lceil 12\rceil }}}$
. Given a formula
$\varphi $
over
$\Sigma _{\mathop {\lceil 12\rceil }}$
and
$k\in \{1,2\}$
, we denote by
$\varphi |^{{}}_{k}$
the formula in
$L_{\Sigma _k}$
inductively defined as follows:
-
•
$\varphi |^{{}}_{k}$
is
${\mathsf {tt}}_k$
whenever
$\varphi $
is
$\mathop {\lceil c_1c_2\rceil }(\varphi _1,\dots,\varphi _n)$
and
$c_k$
is
${\mathsf {tt}}_k$
; -
•
$\varphi |^{{}}_{k}$
is
$c_k(\varphi _1|^{{}}_{k},\dots,\varphi _n|^{{}}_{k})$
whenever
$\varphi $
is
$\mathop {\lceil c_1c_2\rceil }(\varphi _1,\dots,\varphi _n)$
and
$c_k$
is not
${\mathsf {tt}}_k$
.
Definition 4.2. The meet-combination of matrix satisfaction systems
$S_{\Sigma _1}=(L_{\Sigma _1},\mathcal {A}_{\Sigma _1},\Vdash _{\Sigma _1})$
and
$S_{\Sigma _2}=(L_{\Sigma _2},\mathcal {A}_{\Sigma _2},\Vdash _{\Sigma _2})$
over signatures
$\Sigma _1$
and
$\Sigma _2$
, respectively, denoted by
$$ \begin{align*}\mathop{\lceil S_{\Sigma_1} \, S_{\Sigma_2}\rceil}\end{align*} $$
is the matrix satisfaction system
$$ \begin{align*}(L_{\Sigma_{\mathop{\lceil12\rceil}}},\mathcal{A}_{\Sigma_{\mathop{\lceil12\rceil}}},\Vdash_{\Sigma_{\mathop{\lceil12\rceil}}})\end{align*} $$
over the signature
$\Sigma _{\mathop {\lceil 12\rceil }}$
such that
$\mathcal {A}_{\Sigma _{\mathop {\lceil 12\rceil }}}$
is the class of product matrices
$$ \begin{align*}\{({\mathfrak{A}}_1,D_1) \times ({\mathfrak{A}}_2, D_2): ({\mathfrak{A}}_1,D_1) \in\mathcal{A}_{\Sigma_1} \; \text{and} \; ({\mathfrak{A}}_2,D_2)\in\mathcal{A}_{\Sigma_2}\}\end{align*} $$
over
$\Sigma _{\mathop {\lceil 12\rceil }}$
such that each
$({\mathfrak {A}}_1,D_1) \times ({\mathfrak {A}}_2,D_2) = ({\mathfrak {A}}_1 \times {\mathfrak {A}}_2,D_1 \times D_2)$
where
$$ \begin{align*}{\mathfrak{A}}_1 \times {\mathfrak{A}}_2 = (A_1 \times A_2,\{\{{\mathop{\lceil c_1c_2\rceil}}^{{\mathfrak{A}}_1 \times {\mathfrak{A}}_2}\}_{\mathop{\lceil c_1c_2\rceil}\in\Sigma_{{\mathop{\lceil12\rceil}}}^{(n)}}\}_{n\in{\mathbb N}})\end{align*} $$
with
$$ \begin{align*}\begin{array}{l}{\mathop{\lceil c_1c_2\rceil}}^{{\mathfrak{A}}_1 \times {\mathfrak{A}}_2}((a_1,b_1),\dots,(a_n,b_n)) =\\[3mm] \kern15mm\begin{cases} ({c_1}^{{\mathfrak{A}}_1}(a_1,\dots,a_n),{c_2}^{{\mathfrak{A}}_2}(b_1,\dots,b_n)) & \text{if }c_1 \in \Sigma_1^{(n)} \text{ and } c_2 \in \Sigma_2^{(n)}; \\[2mm] ({{\mathsf{tt}}_1}^{{\mathfrak{A}}_1},{c_2}^{{\mathfrak{A}}_2}(b_1,\dots,b_n)) & \text{if }c_1 \text{ is }{\mathsf{tt}}_1 \text{ and } c_2 \in \Sigma_2^{(n)};\\[2mm] ({c_1}^{{\mathfrak{A}}_1}(a_1,\dots,a_n),{{\mathsf{tt}}_2}^{{\mathfrak{A}}_2}) & \text{if }c_2 \text{ is }{\mathsf{tt}}_2 \text{ and } c_1 \in \Sigma_1^{(n)}. \end{cases} \end{array}\end{align*} $$
The following results were proved in [Reference Rasga, Sernadas and Sernadas25, Reference Sernadas, Sernadas and Rasga30].
Proposition 4.3. Let
$\varphi \in L_{\Sigma _1} \cup L_{\Sigma _2}$
,
$({\mathfrak {A}}_1,D_1) \in \mathcal {A}_{\Sigma _1}$
, and
$({\mathfrak {A}}_2,D_2) \in \mathcal {A}_{\Sigma _2}$
. Then
$$ \begin{align*}{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}^{{\mathfrak{A}}_1 \times {\mathfrak{A}}_2} = \begin{cases} ({\lbrack\!\lbrack \varphi \rbrack\!\rbrack}^{{\mathfrak{A}}_1},{\lbrack\!\lbrack {\mathsf{tt}}_2 \rbrack\!\rbrack}^{{\mathfrak{A}}_2}) & \text{ if } \varphi \text{ is in } L_{\Sigma_1}, \\[1mm] ({\lbrack\!\lbrack {\mathsf{tt}}_1 \rbrack\!\rbrack}^{{\mathfrak{A}}_1},{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}^{{\mathfrak{A}}_2}) & \text{ if } \varphi \text{ is in } L_{\Sigma_2}. \end{cases} \end{align*} $$
Proposition 4.4. Let
$\varphi \in L_{\Sigma _{\mathop {\lceil 12\rceil }}}$
,
$({\mathfrak {A}}_1,D_1) \in \mathcal {A}_{\Sigma _1}$
, and
$({\mathfrak {A}}_2,D_2) \in \mathcal {A}_{\Sigma _2}$
. Then
$$ \begin{align*}{\lbrack\!\lbrack \varphi \rbrack\!\rbrack}^{{\mathfrak{A}}_1 \times {\mathfrak{A}}_2} = \left(({\lbrack\!\lbrack \varphi|^{{}}_{1} \rbrack\!\rbrack}^{{\mathfrak{A}}_1 \times {\mathfrak{A}}_2})_1,({\lbrack\!\lbrack \varphi|^{{}}_{2} \rbrack\!\rbrack}^{{\mathfrak{A}}_1 \times {\mathfrak{A}}_2})_2 \right). \end{align*} $$
Proposition 4.5. Let
$\varphi \in L_{\Sigma _{\mathop {\lceil 12\rceil }}}$
,
$({\mathfrak {A}}_1,D_1) \in \mathcal {A}_{\Sigma _1}$
, and
$({\mathfrak {A}}_2,D_2) \in \mathcal {A}_{\Sigma _2}$
. Then
$$ \begin{align*}({\mathfrak{A}}_1,D_1) \times ({\mathfrak{A}}_2,D_2) \Vdash_{\Sigma_{\mathop{\lceil12\rceil}}} \varphi \quad \text{iff} \quad ({\mathfrak{A}}_1,D_1) \Vdash_{\Sigma_1} \varphi|^{{}}_{1} \text{ and } ({\mathfrak{A}}_2,D_2) \Vdash_{\Sigma_2} \varphi|^{{}}_{2}.\end{align*} $$
Proof Observe that
$({\mathfrak {A}}_1,D_1) \times ({\mathfrak {A}}_2,D_2) \Vdash _{\Sigma _{\mathop {\lceil 12\rceil }}} \varphi $
iff
${\lbrack \!\lbrack \varphi \rbrack \!\rbrack }^{{\mathfrak {A}}_1 \times {\mathfrak {A}}_2}$
is in
$D_1 \times D_2$
if and only if
$({\lbrack \!\lbrack \varphi |^{{}}_{1} \rbrack \!\rbrack }^{{\mathfrak {A}}_1 \times {\mathfrak {A}}_2})_1$
is in
$D_1$
,
$({\lbrack \!\lbrack \varphi |^{{}}_{2} \rbrack \!\rbrack }^{{\mathfrak {A}}_1 \times {\mathfrak {A}}_2})_2$
is in
$D_2$
, by Proposition 4.4, iff
${\lbrack \!\lbrack \varphi |^{{}}_{1} \rbrack \!\rbrack }^{{\mathfrak {A}}_1}$
is in
$D_1$
,
${\lbrack \!\lbrack \varphi |^{{}}_{2} \rbrack \!\rbrack }^{{\mathfrak {A}}_2}$
is in
$D_2$
, by Proposition 4.3, if and only if
$({\mathfrak {A}}_1,D_1) \Vdash _{\Sigma _1} \varphi |^{{}}_{1} \text { and } ({\mathfrak {A}}_2,D_2) \Vdash _{\Sigma _2} \varphi |^{{}}_{2}$
.⊣
We omit the proof of the following result since it is a straightforward consequence of Proposition 4.5.
Proposition 4.6. Let
$S_{\Sigma _1}\!=\!(L_{\Sigma _1},\mathcal {A}_{\Sigma _1},\Vdash _{\Sigma _1})$
and
$S_{\Sigma _2}\!=\!(L_{\Sigma _2},\mathcal {A}_{\Sigma _2},\Vdash _{\Sigma _2})$
be matrix satisfaction systems over signatures
$\Sigma _1$
and
$\Sigma _2$
, respectively. Then
$$ \begin{align*}(\tau^1,\tau^2,g^1,g^2,h),\end{align*} $$
where
-
•
$\tau ^k(\varphi)=\varphi |^{{}}_{k}$
for
$k=1,2;$
-
•
$g^k(({\mathfrak {A}}_1,D_1) \times ({\mathfrak {A}}_2,D_2)) = ({\mathfrak {A}}_k,D_k)$
for
$k=1,2;$
-
•
$h(({\mathfrak {A}}_1,D_1),({\mathfrak {A}}_2,D_2))=({\mathfrak {A}}_1,D_1) \times ({\mathfrak {A}}_2,D_2);$
is a satisfaction system reduction from
$\mathop {\lceil S_{\Sigma _1} \, S_{\Sigma _2}\rceil }$
to
$S_{\Sigma _1} \times S_{\Sigma _2}$
.
Proposition 4.7. Let
$S_{\Sigma _1}\!=\!(L_{\Sigma _1},\mathcal {A}_{\Sigma _1},\Vdash _{\Sigma _1})$
and
$S_{\Sigma _2}\!=\!(L_{\Sigma _2},\mathcal {A}_{\Sigma _2},\Vdash _{\Sigma _2})$
be matrix satisfaction systems over arbitrary signatures
$\Sigma _1$
and
$\Sigma _2$
, respectively. Then
$\mathrm {Val}_{\mathop {\lceil S_{\Sigma _1} \, S_{\Sigma _2}\rceil }}$
is decidable whenever
$\mathrm {Val}_{S_{\Sigma _1}}$
and
$\mathrm {Val}_{S_{\Sigma _2}}$
are decidable for every pair of signatures
$\Sigma _1$
and
$\Sigma _2$
.
Proof Assume that
$\mathrm {Val}_{S_{\Sigma _1}}$
and
$\mathrm {Val}_{S_{\Sigma _2}}$
are decidable. Since there is a satisfaction system reduction, by Proposition 4.6, from
$\mathop {\lceil S_{\Sigma _1} \, S_{\Sigma _2}\rceil }$
to
$S_{\Sigma _1} \times S_{\Sigma _2}$
where
$g^k$
for
$k=1,2$
and h are surjective up to satisfaction then
$\mathrm {Val}_{\mathop {\lceil S_{\Sigma _1} \, S_{\Sigma _2}\rceil }}$
is decidable by Proposition 3.7.⊣
We now consider the meet-combination
$$ \begin{align*}\mathop{\lceil S^{\mathrm{ga,K}}_{\Pi} \, S^{\mathrm{ga,Int}}_{\Pi}\rceil}\end{align*} $$
of the matrix satisfaction system for
$\mathrm {K}$
modal logic and the matrix satisfaction system for intuitionistic logic both endowed with algebraic semantics.
Proposition 4.8. The validity problem in the meet-combination
$$ \begin{align*}\mathop{\lceil S^{\mathrm{ga,K}}_{\Pi} \, S^{\mathrm{ga,Int}}_{\Pi}\rceil}\end{align*} $$
is decidable.
Proof We know from Propositions 3.17 and 3.26 that
$\mathrm {Val}_{S^{\mathrm {ga,K}}_{\Pi }}$
and
$\mathrm {Val}_{S^{\mathrm {ga,Int}}_{\Pi }}$
are decidable, respectively. Therefore, by Proposition 4.7,
$\mathrm {Val}_{\mathop {\lceil S^{\mathrm {ga,K}}_{\Pi } \, S^{\mathrm {ga,Int}}_{\Pi }\rceil }}$
is decidable.⊣
5 Concluding remarks
We presented satisfaction systems as the right general abstraction for analyzing in a semantic way logical decision problems. The essential notion of a reduction from a satisfaction system to a finite collection of satisfaction systems was here introduced. We showed that reductions between satisfaction systems induce reductions between the satisfiability and the validity problems leading to general results on decidability. We also consider the meet-combination of logics and proved that the validity problem in the meet-combination is decidable provided that the validity problem in the components is also decidable. An illustration was provided for the meet-combination of
$\mathrm {K}$
modal logic with algebraic semantics and intuitionistic logic with algebraic semantics.
We intend to extend the reduction technique proposed herein for obtaining results about entailment and deductive consequence problems (having hypotheses). The general setting should be defined over the notion of consequence system. In this case, preservation of semidecidability seems to play an important role. Moreover, it would also be interesting to use the fact that if some non-decidable problem can be reduced to another problem then the latter one is also not decidable.
We think that preservation of decidability for other forms of combination should also be considered. For instance, the preservation of decidability in fusion of modal logics (see [Reference Kracht and Wolter22]) was already addressed but not using reductions. The other case that comes to mind is to investigate reduction techniques in the fibring of logics (see [Reference Carnielli, Coniglio, Gabbay, Gouveia and Sernadas8, Reference Gabbay12, Reference Sernadas, Rasga and Carnielli32, Reference Zanardo, Sernadas and Sernadas36]).
Another challenging extension of this work is to adapt the reduction techniques to enumerable sets of logics, namely in the context of logics of formal inconsistency (see [Reference Carnielli and Coniglio7]) and many-valued logics (see [Reference Gottwald15]).
Moreover, we intend to obtain preservation results for complexity classes when in the presence of reductions. In particular we would like to relate the complexity class of logical decision problems for the meet-combination with the complexity classes of logical decision problems for the component logics.
Finally, following the recent work of [Reference Agudelo-Agudelo and Carnielli1], we intend to investigate logical decision problems and their reductions for logics presented by a polynomial ring calculus.
Acknowledgments
This work was supported by the Instituto de Telecomunicações, namely the Security and Quantum Information Group—Lx, by the Fundação para a Ciência e a Tecnologia (FCT) through national funds, by FEDER, COMPETE 2020, and by the Regional Operational Program of Lisbon, under UIDB/50008/2020, and also by the Department of Mathematics of Instituto Superior Técnico, Universidade de Lisboa. The third author acknowledges support from the National Council for Scientific and Technological Development (CNPq), Brazil, under research grant #307376/2018-4.
