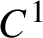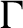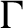We denote
![]() ${\mathbb T}={\mathbb R}/{\mathbb Z}$
the circle and
${\mathbb T}={\mathbb R}/{\mathbb Z}$
the circle and
![]() ${\mathbb A}={\mathbb T} \times {\mathbb R}$
the annulus. An important class of area-preserving maps of the annulus are the so-called twist maps or maps that deviate the vertical, because this class of maps describes the behavior of area preserving surface diffeomorphisms in the neighborhood of a generic elliptic periodic point (see [Reference ChencinerC85]).
${\mathbb A}={\mathbb T} \times {\mathbb R}$
the annulus. An important class of area-preserving maps of the annulus are the so-called twist maps or maps that deviate the vertical, because this class of maps describes the behavior of area preserving surface diffeomorphisms in the neighborhood of a generic elliptic periodic point (see [Reference ChencinerC85]).
More precisely, a
![]() $C^1$
diffeomorphism g of the annulus that is isotopic to identity is a positive twist map (respectively negative twist map) if for any given lift
$C^1$
diffeomorphism g of the annulus that is isotopic to identity is a positive twist map (respectively negative twist map) if for any given lift
![]() $\tilde {g} : {\mathbb R}^2 \to {\mathbb R}^2$
of g and for every
$\tilde {g} : {\mathbb R}^2 \to {\mathbb R}^2$
of g and for every
![]() $\theta \in {\mathbb R}$
, the maps
$\theta \in {\mathbb R}$
, the maps
![]() $r \mapsto \tilde {\pi } \circ \tilde {g}(\theta ,r)$
are increasing (respectively decreasing) diffeomorphisms. A twist map may be positive or negative. Here
$r \mapsto \tilde {\pi } \circ \tilde {g}(\theta ,r)$
are increasing (respectively decreasing) diffeomorphisms. A twist map may be positive or negative. Here
![]() $\tilde {\pi }$
denotes the lift of the first projection map.
$\tilde {\pi }$
denotes the lift of the first projection map.
An essential invariant curve by a diffeomorphism g of the annulus is a homotopically non-trivial simple loop that is invariant by g.
When f is a
![]() $C^1$
twist map, it is known from Birkhoff theory that any invariant essential curve by g is the graph of a Lipschitz map over
$C^1$
twist map, it is known from Birkhoff theory that any invariant essential curve by g is the graph of a Lipschitz map over
![]() ${\mathbb T}$
. Furthermore, it was proven by Arnaud in [Reference ArnaudA09] that the latter map must be
${\mathbb T}$
. Furthermore, it was proven by Arnaud in [Reference ArnaudA09] that the latter map must be
![]() $C^1$
on a
$C^1$
on a
![]() $G_\delta $
set of
$G_\delta $
set of
![]() ${\mathbb T}$
of full measure.
${\mathbb T}$
of full measure.
Numerical experiments show that the invariant curves of a smooth twist map are actually more regular than just what the Birkhoff theory predicts. Moreover, in the perturbative setting of quasi-integrable twist maps, the Kolmogorov–Arnold–Moser (KAM) theory provides a large measure set of smooth invariant curves. The question of the regularity of the invariant curves of twist maps is thus a natural question that is also related to the study of how the KAM curves disappear as the perturbation of integrable curves becomes large.
Another natural and related question is that of the regularity of the boundaries of Birkhoff instability zones. A Birkhoff instability zone of a twist map g is an open set of the annulus that is homeomorphic to the annulus, that does not contain any invariant essential curve, and that is maximal for these properties. By Birkhoff’s theory, the boundary of an instability zone is an invariant curve that is a Lipschitz graph. We refer to the nice introduction of [Reference ArnaudA11], where many features and questions are discussed about the boundaries of Birkhoff instability zones.
In [Reference Eliasson, Kuksin, Marmi, Yoccoz, Marmi and YoccozEKMY98], the following question was asked.
Question 1. (J. Mather [Reference Eliasson, Kuksin, Marmi, Yoccoz, Marmi and YoccozEKMY98, Problem 3.1.1])
Does there exist an example of a symplectic
![]() $C^r$
twist map with an essential invariant curve that is not
$C^r$
twist map with an essential invariant curve that is not
![]() $C^1$
and that contains no periodic point?
$C^1$
and that contains no periodic point?
In [Reference HermanH83, §III], Herman gave an example of a
![]() $C^2$
twist map of the annulus that has a
$C^2$
twist map of the annulus that has a
![]() $C^1$
invariant curve on which the dynamic is conjugated to that of a Denjoy counterexample. By Denjoy’s theorem on topological conjugacy of
$C^1$
invariant curve on which the dynamic is conjugated to that of a Denjoy counterexample. By Denjoy’s theorem on topological conjugacy of
![]() $C^2$
circle diffeomorphisms with irrational rotation number, such a curve cannot be
$C^2$
circle diffeomorphisms with irrational rotation number, such a curve cannot be
![]() $C^2$
.
$C^2$
.
In [Reference ArnaudA13], Arnaud gave an example of a
![]() $C^2$
twist map g of the annulus that has an invariant curve
$C^2$
twist map g of the annulus that has an invariant curve
![]() $\Gamma $
that is non-differentiable on which the dynamic is conjugated to that of a Denjoy counterexample. In addition, she showed that in any
$\Gamma $
that is non-differentiable on which the dynamic is conjugated to that of a Denjoy counterexample. In addition, she showed that in any
![]() $C^1$
neighborhood of g, there exist twist maps with Birkhoff instability zones having
$C^1$
neighborhood of g, there exist twist maps with Birkhoff instability zones having
![]() $\Gamma $
for a boundary and having the same dynamics as g on
$\Gamma $
for a boundary and having the same dynamics as g on
![]() $\Gamma $
.
$\Gamma $
.
In [Reference ArnaudA11], the following natural question was raised.
Question 2. (M.-C. Arnaud)
Does there exist a regular symplectic twist map of the annulus that has an essential invariant curve that is non-differentiable on which the restricted dynamics is minimal?
In this note, we give a positive answer to this question in low regularity.
Theorem 1. For every
![]() $\alpha \in {\mathbb R} \setminus {\mathbb Q}$
, there exists a symplectic
$\alpha \in {\mathbb R} \setminus {\mathbb Q}$
, there exists a symplectic
![]() $C^1$
twist map of the annulus that has a non differentiable essential invariant curve
$C^1$
twist map of the annulus that has a non differentiable essential invariant curve
![]() $\Gamma $
such that the restriction of g to
$\Gamma $
such that the restriction of g to
![]() $\Gamma $
is
$\Gamma $
is
![]() $C^0$
conjugated to the circle rotation of angle
$C^0$
conjugated to the circle rotation of angle
![]() $\alpha $
, and hence minimal.
$\alpha $
, and hence minimal.
Owing to [Reference ArnaudA11, Theorem 2], we can deduce the following.
Corollary 2. There exists a symplectic
![]() $C^1$
twist map g of the annulus that has a non-differentiable essential invariant curve
$C^1$
twist map g of the annulus that has a non-differentiable essential invariant curve
![]() $\Gamma $
such that the restriction of g to
$\Gamma $
such that the restriction of g to
![]() $\Gamma $
is minimal and such that
$\Gamma $
is minimal and such that
![]() $\Gamma $
is at the boundary of an instability zone of g.
$\Gamma $
is at the boundary of an instability zone of g.
The derivation of Corollary 2 from Theorem 1 follows from the general result of [Reference ArnaudA11, Theorem 2], which asserts that any essential invariant curve of a
![]() $C^1$
twist map g that has an irrational rotation number can be viewed as a boundary dynamics of Birkhoff instability zone of an arbitrarily nearby
$C^1$
twist map g that has an irrational rotation number can be viewed as a boundary dynamics of Birkhoff instability zone of an arbitrarily nearby
![]() $C^1\kern-1.5pt$
twist map. This result relies on a perturbation argument involving the Hayashi
$C^1\kern-1.5pt$
twist map. This result relies on a perturbation argument involving the Hayashi
![]() $C^1$
-closing lemma.
$C^1$
-closing lemma.
Owing to a construction by Herman in [Reference HermanH83, §II.2], Theorem 1 can be derived from the following result on circle homeomorphisms.
Theorem 3. For every
![]() $\alpha \in {\mathbb R} \setminus {\mathbb Q}$
, there exists a non-differentiable orientation preserving (minimal) homeomorphism of the circle f, topologically conjugate to the circle rotation of angle
$\alpha \in {\mathbb R} \setminus {\mathbb Q}$
, there exists a non-differentiable orientation preserving (minimal) homeomorphism of the circle f, topologically conjugate to the circle rotation of angle
![]() $\alpha $
, such that
$\alpha $
, such that
![]() $f+f^{-1}$
is of class
$f+f^{-1}$
is of class
![]() $C^1$
.
$C^1$
.
Proof of Theorem 1
To prove that Theorem 3 implies Theorem 1, we use Herman’s beautiful trick that associates to some circle homeomorphisms f a twist map of the annulus which preserves a circle that is determined by f and on which the restricted dynamics is given by f. For completeness, we state and prove Herman’s observation.
First of all, note that if
![]() $\tilde {f}$
is a lift of a circle homeomorphism f and if there exists a
$\tilde {f}$
is a lift of a circle homeomorphism f and if there exists a
![]() $C^1$
function
$C^1$
function
![]() $\phi :{\mathbb T} \to {\mathbb R}$
, which we also view as a function from
$\phi :{\mathbb T} \to {\mathbb R}$
, which we also view as a function from
![]() ${\mathbb R}$
to
${\mathbb R}$
to
![]() ${\mathbb R}$
of period
${\mathbb R}$
of period
![]() $1$
, satisfying
$1$
, satisfying
 $$ \begin{align} \mathrm{Id}_{{\mathbb R}}+ \frac{{\phi}(\cdot)}{2}= \frac{1}{2} (\tilde{f}(\cdot)+\tilde{f}^{-1}(\cdot)),\end{align} $$
$$ \begin{align} \mathrm{Id}_{{\mathbb R}}+ \frac{{\phi}(\cdot)}{2}= \frac{1}{2} (\tilde{f}(\cdot)+\tilde{f}^{-1}(\cdot)),\end{align} $$
then the map
is a
![]() $C^1$
Hamiltonian twist map of the annulus (this follows from the fact that
$C^1$
Hamiltonian twist map of the annulus (this follows from the fact that
![]() $\int _{{\mathbb T}}\phi (\theta )d\theta =0$
, as proved in [Reference HermanH83, §II.2.3]). Moreover, with
$\int _{{\mathbb T}}\phi (\theta )d\theta =0$
, as proved in [Reference HermanH83, §II.2.3]). Moreover, with
![]() $\psi :=\tilde {f}-id_{{\mathbb R}}$
, which we view as a function from
$\psi :=\tilde {f}-id_{{\mathbb R}}$
, which we view as a function from
![]() ${\mathbb T}$
to
${\mathbb T}$
to
![]() ${\mathbb R}$
, or from
${\mathbb R}$
, or from
![]() ${\mathbb R}$
to
${\mathbb R}$
to
![]() ${\mathbb R}$
of period
${\mathbb R}$
of period
![]() $1$
, the following holds.
$1$
, the following holds.
Claim. [Reference HermanH83, §II.2]
The graph
![]() $\Gamma $
of
$\Gamma $
of
![]() $\theta \mapsto \psi (\theta )$
is invariant by g and the dynamics of g restricted to
$\theta \mapsto \psi (\theta )$
is invariant by g and the dynamics of g restricted to
![]() $\Gamma $
is conjugated (via the first projection) to f.
$\Gamma $
is conjugated (via the first projection) to f.
Proof. From equation (1), we have that
so
and finally equation (2) implies
 $$ \begin{align*} g(\theta,\psi(\theta))&=(f(\theta),\psi(\theta)+ \phi(f(\theta)))\\&=(f(\theta),\psi(f(\theta))).\\[-37pt]\end{align*} $$
$$ \begin{align*} g(\theta,\psi(\theta))&=(f(\theta),\psi(\theta)+ \phi(f(\theta)))\\&=(f(\theta),\psi(f(\theta))).\\[-37pt]\end{align*} $$
The proof that Theorem 3 implies Theorem 1 is now straightforward from the claim.
To prove Theorem 3, we will work with a special class of circle diffeomorphisms that we call C-great.
Definition 1. Let
![]() $f:{\mathbb T} \to {\mathbb T}$
be a
$f:{\mathbb T} \to {\mathbb T}$
be a
![]() $C^1$
minimal diffeomorphism. For
$C^1$
minimal diffeomorphism. For
![]() $C>1$
, we say that x is C-good if
$C>1$
, we say that x is C-good if
 $\sum _{n \geq 0} |Df^n(x)|^{-2}<C$
, while
$\sum _{n \geq 0} |Df^n(x)|^{-2}<C$
, while
![]() $\sup _{n<0} |Df^n(x)|=\infty $
and
$\sup _{n<0} |Df^n(x)|=\infty $
and
 $\sum _{n<0} |Df^n(x)|^{-2}=\infty $
.
$\sum _{n<0} |Df^n(x)|^{-2}=\infty $
.
We say that f is C-great if the set of C-good points is uncountable and
![]() $\sup _{x\in {\mathbb T}} |Df(x)+Df^{-1}(x)|<C$
.
$\sup _{x\in {\mathbb T}} |Df(x)+Df^{-1}(x)|<C$
.
Moreover, we say that x is C-great if it is accumulated by an uncountable set of C-good points. We then say that the pair
![]() $(f,x)$
is C-great.
$(f,x)$
is C-great.
It is not hard to see that if f is C-great, then it has a C-great point x. Moreover, a C-great point is actually accumulated by an uncountable set of C-great points.
Let
![]() $0<u<v$
. For an injective map f defined from
$0<u<v$
. For an injective map f defined from
![]() $[x-v,x+v]$
to
$[x-v,x+v]$
to
![]() ${\mathbb R}$
, we define
${\mathbb R}$
, we define
 $$ \begin{align*}\Delta(f,x,u,v)=\frac{v}{u} \frac{f(x+u)-f(x)}{f(x+v)-f(x)}.\end{align*} $$
$$ \begin{align*}\Delta(f,x,u,v)=\frac{v}{u} \frac{f(x+u)-f(x)}{f(x+v)-f(x)}.\end{align*} $$
The following is a straightforward criterion of non-differentiability of f.
Lemma 4. If f is a differentiable circle diffeomorphism, then it must satisfy for every
![]() $x \in {\mathbb T}$
, the limit, as
$x \in {\mathbb T}$
, the limit, as
![]() $u,v$
go to
$u,v$
go to
![]() $0$
, of
$0$
, of
![]() $\Delta (f,x,u,v)$
exists and equals
$\Delta (f,x,u,v)$
exists and equals
![]() $1$
.
$1$
.
The proof of Theorem 3 is based on the following two lemmas.
Lemma 5. For every
![]() $\alpha \in {\mathbb R} \setminus {\mathbb Q}$
, there exist
$\alpha \in {\mathbb R} \setminus {\mathbb Q}$
, there exist
![]() $C>1$
and a circle diffeomorphism f topologically conjugate to the circle rotation of angle
$C>1$
and a circle diffeomorphism f topologically conjugate to the circle rotation of angle
![]() $\alpha $
that is C-great.
$\alpha $
that is C-great.
We will prove Lemma 5 at the end of the note.
We first show how, starting from a C-great diffeomorphism, we can prove Theorem 3. The proof is based on an inductive application of the following lemma.
Lemma 6. For every
![]() $C>1$
, there exists
$C>1$
, there exists
![]() $\epsilon _0>0$
with the following property. Let
$\epsilon _0>0$
with the following property. Let
![]() $(f,x)$
be C-great. Then for every
$(f,x)$
be C-great. Then for every
![]() $\epsilon>0$
, there exists a
$\epsilon>0$
, there exists a
![]() $C^1$
-diffeomorphism
$C^1$
-diffeomorphism
![]() $h:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
such that
$h:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
such that
![]() $g=h \circ f \circ h^{-1}$
satisfies:
$g=h \circ f \circ h^{-1}$
satisfies:
-
• h is
 $\epsilon $
-close to
$\epsilon $
-close to
 $\mathrm {Id}_{\mathbb T}$
in the
$\mathrm {Id}_{\mathbb T}$
in the
 $C^0$
topology;
$C^0$
topology; -
•
 $g+g^{-1}$
is
$g+g^{-1}$
is
 $\epsilon $
-close to
$\epsilon $
-close to
 $f+f^{-1}$
in the
$f+f^{-1}$
in the
 $C^1$
topology;
$C^1$
topology; -
• there exists
 $y\in {\mathbb T}$
such that
$y\in {\mathbb T}$
such that
 $|y-x|<{\epsilon }$
and
$|y-x|<{\epsilon }$
and
 $(g,y)$
is C-great, and there exists
$(g,y)$
is C-great, and there exists
 $u,v \in (0,{\epsilon })$
such that
$u,v \in (0,{\epsilon })$
such that
 $\Delta (g,y,u,v)>1+{\epsilon }_0$
.
$\Delta (g,y,u,v)>1+{\epsilon }_0$
.
Proof Proof that Lemmas 5 and 6 imply Theorem 3
Let
![]() $\alpha \in {\mathbb R} \setminus {\mathbb Q}$
. We want to construct a sequence of circle diffeomorphisms
$\alpha \in {\mathbb R} \setminus {\mathbb Q}$
. We want to construct a sequence of circle diffeomorphisms
![]() $(f_n)$
that converge to a circle homeomorphism
$(f_n)$
that converge to a circle homeomorphism
![]() $f_\infty $
that is topologically conjugated to
$f_\infty $
that is topologically conjugated to
![]() $R_\alpha $
and such that
$R_\alpha $
and such that
![]() $f_\infty $
is not a diffeomorphism while
$f_\infty $
is not a diffeomorphism while
![]() $f_\infty +f_\infty ^{-1}$
is
$f_\infty +f_\infty ^{-1}$
is
![]() $C^1$
. We will use the criterion of Lemma 4 to guarantee the non-differentiability of
$C^1$
. We will use the criterion of Lemma 4 to guarantee the non-differentiability of
![]() $f_\infty $
.
$f_\infty $
.
In light of Lemma 5, we can start with a
![]() $C^1$
circle diffeomorphism
$C^1$
circle diffeomorphism
![]() $f_0$
and
$f_0$
and
![]() $x_0$
such that
$x_0$
such that
![]() $(f_0,x_0)$
is C-great and
$(f_0,x_0)$
is C-great and
![]() $f_0$
is topologically conjugate to the circle rotation of angle
$f_0$
is topologically conjugate to the circle rotation of angle
![]() $\alpha $
. Using Lemma 6, we construct inductively, for
$\alpha $
. Using Lemma 6, we construct inductively, for
![]() $n\geq 1$
, sequences
$n\geq 1$
, sequences
![]() $(h_n)$
of circle diffeomorphisms,
$(h_n)$
of circle diffeomorphisms,
![]() $(x_n)$
of points in
$(x_n)$
of points in
![]() ${\mathbb T}$
, and
${\mathbb T}$
, and
![]() $(u_n)$
and
$(u_n)$
and
![]() $(v_n)$
of positive numbers, such that for
$(v_n)$
of positive numbers, such that for
 $$ \begin{align*}f_n:=h_n \circ f_{n-1} \circ h_n^{-1}, \quad F_n:=f_n+f_n^{-1}, \quad H_n:=h_n \circ \cdots \circ h_1,\end{align*} $$
$$ \begin{align*}f_n:=h_n \circ f_{n-1} \circ h_n^{-1}, \quad F_n:=f_n+f_n^{-1}, \quad H_n:=h_n \circ \cdots \circ h_1,\end{align*} $$
the following hold:
-
•
 $(f_n,x_n)$
is C-great;
$(f_n,x_n)$
is C-great; -
•
 $u_n+v_n\leq 2^{-n}$
;
$u_n+v_n\leq 2^{-n}$
; -
•
 $\|x_{n+1}-x_n\|\leq 2^{-n}$
;
$\|x_{n+1}-x_n\|\leq 2^{-n}$
; -
•
 $\Delta (f_n,x_n,u_n,v_n)>1+{\epsilon }_0$
;
$\Delta (f_n,x_n,u_n,v_n)>1+{\epsilon }_0$
; -
•
 $\|H_n-H_{n-1}\|_{C^0}\leq 2^{-n}$
;
$\|H_n-H_{n-1}\|_{C^0}\leq 2^{-n}$
; -
•
 $\|F_{n+1}-F_n\|_{C^1}\leq 2^{-n}$
.
$\|F_{n+1}-F_n\|_{C^1}\leq 2^{-n}$
.
We also ask that the convergence of
![]() $(H_n)$
and
$(H_n)$
and
![]() $(x_n)$
be sufficiently fast so that
$(x_n)$
be sufficiently fast so that
![]() $\Delta (f_m,x_m,u_n,v_n)>1+{\epsilon }_0$
for all
$\Delta (f_m,x_m,u_n,v_n)>1+{\epsilon }_0$
for all
![]() $m\geq n$
.
$m\geq n$
.
From the convergence of
![]() $H_n$
, we get that
$H_n$
, we get that
![]() $f_n$
converges to a circle homeomorphism
$f_n$
converges to a circle homeomorphism
![]() $f_\infty $
that is topologically conjugated to
$f_\infty $
that is topologically conjugated to
![]() $R_\alpha $
. In addition, the
$R_\alpha $
. In addition, the
![]() $C^1$
limit of
$C^1$
limit of
![]() $F_n$
must be
$F_n$
must be
![]() $f_\infty +f_\infty ^{-1}$
. Because
$f_\infty +f_\infty ^{-1}$
. Because
![]() $\Delta (f_m,x_m,u_n,v_n)>1+{\epsilon }_0$
for all
$\Delta (f_m,x_m,u_n,v_n)>1+{\epsilon }_0$
for all
![]() $m\geq n$
, we guarantee that the limit point
$m\geq n$
, we guarantee that the limit point
![]() $x_\infty $
of
$x_\infty $
of
![]() $(x_n)$
satisfies
$(x_n)$
satisfies
![]() $\Delta (f_\infty ,x_\infty ,u_n,v_n)>1+{\epsilon }_0$
for every n. Hence,
$\Delta (f_\infty ,x_\infty ,u_n,v_n)>1+{\epsilon }_0$
for every n. Hence,
![]() $f_\infty $
is not differentiable by Lemma 4.
$f_\infty $
is not differentiable by Lemma 4.
In conclusion,
![]() $f_\infty $
satisfies all the properties of Theorem 3.
$f_\infty $
satisfies all the properties of Theorem 3.
Proof of Lemma 6
To motivate what follows, note that if
![]() $g=h \circ f \circ h^{-1}$
with
$g=h \circ f \circ h^{-1}$
with
![]() $Dh(x)=1+e(x)$
, then, to have
$Dh(x)=1+e(x)$
, then, to have
![]() $g+g^{-1}=f+f^{-1}$
, one must have
$g+g^{-1}=f+f^{-1}$
, one must have
The latter implies that
 $$ \begin{align*}e(f(x)) Df(x)+\frac {e(f^{-1}(x))} {Df(f^{-1}(x))}=e(x) \bigg(Df(h(x))+\frac {1} {Df(f^{-1}(h(x))}\bigg)+\Delta,\end{align*} $$
$$ \begin{align*}e(f(x)) Df(x)+\frac {e(f^{-1}(x))} {Df(f^{-1}(x))}=e(x) \bigg(Df(h(x))+\frac {1} {Df(f^{-1}(h(x))}\bigg)+\Delta,\end{align*} $$
with
Assuming h is
![]() $C^0$
close to
$C^0$
close to
![]() $\mathrm {id}$
, we see that for
$\mathrm {id}$
, we see that for
![]() $g+g^{-1}$
to be
$g+g^{-1}$
to be
![]() $C^1$
-close to
$C^1$
-close to
![]() $f+f^{-1}$
, we should choose e such that
$f+f^{-1}$
, we should choose e such that
![]() $(e(f(x))-e(x)) Df(x) Df(f^{-1}(x))$
is close to
$(e(f(x))-e(x)) Df(x) Df(f^{-1}(x))$
is close to
![]() $e(x)-e(f^{-1}(x))$
.
$e(x)-e(f^{-1}(x))$
.
To construct the conjugacy h of Lemma 6, we start by defining a sequence
![]() $(e_j)_{j\in {\mathbb Z}}$
that will serve to define h along the orbit of a point that is C-good for f.
$(e_j)_{j\in {\mathbb Z}}$
that will serve to define h along the orbit of a point that is C-good for f.
Let x be a C-good point for f. Let
![]() $b_j=Df(f^j(x))$
,
$b_j=Df(f^j(x))$
,
![]() $j \in {\mathbb Z}$
. Define
$j \in {\mathbb Z}$
. Define
![]() $c_j$
,
$c_j$
,
![]() $j \in {\mathbb Z}$
by
$j \in {\mathbb Z}$
by
![]() $c_0=1$
and
$c_0=1$
and
![]() $c_j b_j b_{j-1}=c_{j-1}$
.
$c_j b_j b_{j-1}=c_{j-1}$
.
Sublemma 7. For any
![]() $\nu>0$
, we can define a sequence
$\nu>0$
, we can define a sequence
![]() $(e_j)_{j\in {\mathbb Z}}$
such that
$(e_j)_{j\in {\mathbb Z}}$
such that
![]() $e_j =0$
for
$e_j =0$
for
![]() $j \notin [-N',N]$
for some
$j \notin [-N',N]$
for some
![]() $N,N'\in {\mathbb {N}}^*$
as well as the following:
$N,N'\in {\mathbb {N}}^*$
as well as the following:
-
•
 $e_j \geq 0, \quad \text { for all } j \in {\mathbb Z}$
;
$e_j \geq 0, \quad \text { for all } j \in {\mathbb Z}$
; -
•
 $e_1-e_0=-1$
;
$e_1-e_0=-1$
; -
•
 $e_0\leq C^3$
;
$e_0\leq C^3$
; -
•
 $\eta _j:=|(e_{j+1}-e_j) b_j b_{j-1}+(e_{j-1}-e_j)|\leq \nu , \quad \text { for all } j \in {\mathbb Z}$
.
$\eta _j:=|(e_{j+1}-e_j) b_j b_{j-1}+(e_{j-1}-e_j)|\leq \nu , \quad \text { for all } j \in {\mathbb Z}$
.
Proof. We will need the following properties on the orbit of x that will be a consequence from the fact that x is C-good for f.
Claim. We have that
 $\sum _{j \geq 0} c_j\leq C^3$
and
$\sum _{j \geq 0} c_j\leq C^3$
and
 $\sum _{j \leq 0} c_j=\infty $
,
$\sum _{j \leq 0} c_j=\infty $
,
![]() $\liminf _{j \leq 0} c_j=0$
.
$\liminf _{j \leq 0} c_j=0$
.
Proof. We have that for
![]() $j\geq 0$
,
$j\geq 0$
,
 $c_j=({Df(x)Df(f^j(x))})/{(Df^{j+1}(x))^2}$
. Hence, it follows from Definition 1 that
$c_j=({Df(x)Df(f^j(x))})/{(Df^{j+1}(x))^2}$
. Hence, it follows from Definition 1 that
 $\sum _{j\geq 0} c_j \leq C^3$
.
$\sum _{j\geq 0} c_j \leq C^3$
.
For
![]() $j\leq -1$
, we have that
$j\leq -1$
, we have that
 $c_j=({Df(x)}/{Df(f^j(x))}) {1}/{(Df^{j}(x))^2}$
. Hence, it follows from Definition 1 that
$c_j=({Df(x)}/{Df(f^j(x))}) {1}/{(Df^{j}(x))^2}$
. Hence, it follows from Definition 1 that
 $\sum _{j< 0} c_j=\infty $
as well as
$\sum _{j< 0} c_j=\infty $
as well as
![]() $\liminf _{j \leq 0} c_j=0$
.
$\liminf _{j \leq 0} c_j=0$
.
Let us now define
![]() $e_j$
,
$e_j$
,
![]() $j \in {\mathbb Z}$
as follows. Fix N large such that
$j \in {\mathbb Z}$
as follows. Fix N large such that
![]() $c_{-N}$
is small. Note that by taking N sufficiently large, we will have that
$c_{-N}$
is small. Note that by taking N sufficiently large, we will have that
![]() $c_N$
is also small. We let
$c_N$
is also small. We let
![]() $e_j=0$
for
$e_j=0$
for
![]() $j>N$
. For
$j>N$
. For
![]() $|j| \leq N$
, we define
$|j| \leq N$
, we define
![]() $e_j$
so that
$e_j$
so that
![]() $e_{j+1}-e_j=-c_j$
. We now let
$e_{j+1}-e_j=-c_j$
. We now let
![]() $N'$
be much larger than N such that
$N'$
be much larger than N such that
![]() $c_{-N'+1}$
is small and such that
$c_{-N'+1}$
is small and such that
 $\alpha ={\sum _{-N' \leq j <-N} c_j}/{e_{-N}}$
is large. We set then
$\alpha ={\sum _{-N' \leq j <-N} c_j}/{e_{-N}}$
is large. We set then
![]() $e_{j+1}-e_j= {c_j}/{\alpha }$
for
$e_{j+1}-e_j= {c_j}/{\alpha }$
for
![]() $-N' \leq j \leq -N-1$
. We now define
$-N' \leq j \leq -N-1$
. We now define
![]() $e_j=0$
for
$e_j=0$
for
![]() $j<-N'$
. By construction,
$j<-N'$
. By construction,
![]() $e_1-e_0=-c_0=-1$
.
$e_1-e_0=-c_0=-1$
.
Note the following.
-
• For
 $j\in [-N,N]$
, we have that
$j\in [-N,N]$
, we have that
 $e_j=\sum _{k=j}^N c_k$
.
$e_j=\sum _{k=j}^N c_k$
. -
• For
 $j\in [-N',-N)$
, we have that
$j\in [-N',-N)$
, we have that
 $e_j=e_{-N}-({1}/{\alpha }) \sum _{k=j}^{-N-1}c_k$
.
$e_j=e_{-N}-({1}/{\alpha }) \sum _{k=j}^{-N-1}c_k$
.
From the definition of
![]() $\alpha $
, we deduce that
$\alpha $
, we deduce that
![]() $e_{-N'}=0$
and that
$e_{-N'}=0$
and that
![]() $e_j \geq 0$
for all
$e_j \geq 0$
for all
![]() $j\in {\mathbb Z}$
. Also,
$j\in {\mathbb Z}$
. Also,
 $-e_0=e_{N+1}-e_0=-\sum _{0 \leq j \leq N} c_j$
, so
$-e_0=e_{N+1}-e_0=-\sum _{0 \leq j \leq N} c_j$
, so
 $e_0=\sum _{0 \leq j \leq N} c_j\leq C^3$
.
$e_0=\sum _{0 \leq j \leq N} c_j\leq C^3$
.
Note that by construction, because
![]() $c_j b_j b_{j-1}=c_{j-1}$
, we have that
$c_j b_j b_{j-1}=c_{j-1}$
, we have that
for all
![]() $j \in {\mathbb Z}$
, except for
$j \in {\mathbb Z}$
, except for
![]() $j=-N'$
,
$j=-N'$
,
![]() $j=-N$
, and
$j=-N$
, and
![]() $j=N+1$
. We also have, because
$j=N+1$
. We also have, because
![]() $e_{-N'-1}=e_{-N'}=0$
, that
$e_{-N'-1}=e_{-N'}=0$
, that
![]() $\eta _{-N'}=c_{-N'}/\alpha $
is small as
$\eta _{-N'}=c_{-N'}/\alpha $
is small as
![]() $c_{-N'}$
is small and
$c_{-N'}$
is small and
![]() $\alpha $
is large. Next, we compute
$\alpha $
is large. Next, we compute
![]() $\eta _{-N}=-c_{-N-1}-({c_{-N-1}})/{\alpha }$
, which is also small because
$\eta _{-N}=-c_{-N-1}-({c_{-N-1}})/{\alpha }$
, which is also small because
![]() $c_{N}$
is small and
$c_{N}$
is small and
![]() $\alpha $
is large. Finally,
$\alpha $
is large. Finally,
![]() $\eta _{N+1}=c_N$
is also small by our choice of N.
$\eta _{N+1}=c_N$
is also small by our choice of N.
We want now to modify f by conjugation along a neighborhood of the orbit of x between the times
![]() $-N'$
and N to obtain the diffeomorphism g with the required properties of Lemma 6. We will look for the conjugacy under the form
$-N'$
and N to obtain the diffeomorphism g with the required properties of Lemma 6. We will look for the conjugacy under the form
![]() $Dh(x)=1+e(x)$
. The choice of the sequence
$Dh(x)=1+e(x)$
. The choice of the sequence
![]() $(e_j)$
in Sublemma 7, would essentially allow to get a good control on g and
$(e_j)$
in Sublemma 7, would essentially allow to get a good control on g and
![]() $g+g^{-1}$
along the orbit of the point x if the function e takes the values
$g+g^{-1}$
along the orbit of the point x if the function e takes the values
![]() $e_j$
along the orbit of x. We need however to define h in the neighborhood of the orbit of x without losing the required properties on g and
$e_j$
along the orbit of x. We need however to define h in the neighborhood of the orbit of x without losing the required properties on g and
![]() $g+g^{-1}$
and this will will require some additional technicalities that we now address.
$g+g^{-1}$
and this will will require some additional technicalities that we now address.
To guarantee a good control of
![]() $g+g^{-1}$
everywhere, we start by slightly modifying f to make it affine along the
$g+g^{-1}$
everywhere, we start by slightly modifying f to make it affine along the
![]() $-N'$
to N orbit of a small interval around x. For this, choose a small interval
$-N'$
to N orbit of a small interval around x. For this, choose a small interval
![]() $I_0$
centered around x, and let
$I_0$
centered around x, and let
![]() $I_j=f^j(I_0)$
,
$I_j=f^j(I_0)$
,
![]() $j \in {\mathbb Z}$
. We may assume that
$j \in {\mathbb Z}$
. We may assume that
![]() $I_j \cap I_{j'}=\emptyset $
if
$I_j \cap I_{j'}=\emptyset $
if
![]() $0<|j-j'| \leq 2 N'$
. Then for every
$0<|j-j'| \leq 2 N'$
. Then for every
![]() $\delta>0$
, we can define a diffeomorphism
$\delta>0$
, we can define a diffeomorphism
![]() $h':{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
, which is the identity outside
$h':{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
, which is the identity outside
![]() $\cup _{-N'+1 \leq j \leq N+1} I_j$
such that
$\cup _{-N'+1 \leq j \leq N+1} I_j$
such that
 $\sup _y |Dh'(y)-1|<\delta $
, and such that letting
$\sup _y |Dh'(y)-1|<\delta $
, and such that letting
![]() $f'=h' \circ f \circ h^{\prime \,-1}$
, we have
$f'=h' \circ f \circ h^{\prime \,-1}$
, we have
 $f'(y)=f^{j+1}(x)+b_j(y-f^j(x))$
whenever y is near
$f'(y)=f^{j+1}(x)+b_j(y-f^j(x))$
whenever y is near
![]() $f^j(x)$
and
$f^j(x)$
and
![]() $-N' \leq j \leq N$
.
$-N' \leq j \leq N$
.
Let us now select an interval
![]() $I^{\prime }_0 \subset I_0$
centered around x such that letting
$I^{\prime }_0 \subset I_0$
centered around x such that letting
 $I^{\prime }_j=f^{\prime \,j}(I^{\prime }_0)$
,
$I^{\prime }_j=f^{\prime \,j}(I^{\prime }_0)$
,
![]() $j \in {\mathbb Z}$
, we have that
$j \in {\mathbb Z}$
, we have that
 $f'|I^{\prime }_j$
is affine for
$f'|I^{\prime }_j$
is affine for
![]() $-N' \leq j \leq N$
.
$-N' \leq j \leq N$
.
Note that by choosing
![]() $\delta>0$
small, we get that
$\delta>0$
small, we get that
![]() $F'=f'+f^{\prime \,-1}$
is
$F'=f'+f^{\prime \,-1}$
is
![]() $C^1$
close to
$C^1$
close to
![]() $F=f+f^{-1}$
.
$F=f+f^{-1}$
.
We now define another diffeomorphism
![]() $h:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
which is the identity outside
$h:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
which is the identity outside
 $\cup _{-N'+1 \leq j \leq N} I^{\prime }_j$
as follows. To specify h, it is enough to define
$\cup _{-N'+1 \leq j \leq N} I^{\prime }_j$
as follows. To specify h, it is enough to define
![]() $Dh$
on
$Dh$
on
![]() $I^{\prime }_j$
for
$I^{\prime }_j$
for
![]() $-N'+1 \leq j \leq N$
. We let
$-N'+1 \leq j \leq N$
. We let
![]() $\phi :{\mathbb R} \to [-\delta ,1]$
be a smooth function supported on
$\phi :{\mathbb R} \to [-\delta ,1]$
be a smooth function supported on
![]() $(-1/2,1/2)$
, symmetric around
$(-1/2,1/2)$
, symmetric around
![]() $0$
, and such that
$0$
, and such that
![]() $\phi (0)=1$
and
$\phi (0)=1$
and
![]() $\int \phi (x) dx=0$
. We then let
$\int \phi (x) dx=0$
. We then let
![]() $Dh=1+e_j \phi \circ A_j$
, where
$Dh=1+e_j \phi \circ A_j$
, where
 $A_j:I^{\prime }_j \to [-1/2,1/2]$
is an affine homeomorphism. If
$A_j:I^{\prime }_j \to [-1/2,1/2]$
is an affine homeomorphism. If
![]() $\delta>0$
is chosen sufficiently small, h is indeed a diffeomorphism because all the
$\delta>0$
is chosen sufficiently small, h is indeed a diffeomorphism because all the
![]() $e_j$
are positive.
$e_j$
are positive.
Finally, let
Claim. The diffeomorphism g satisfies the requirements of Lemma 6.
Proof. Let us show that
![]() $G=g+g^{-1}$
is
$G=g+g^{-1}$
is
![]() $C^1$
close to
$C^1$
close to
![]() $F'=f'+f^{\prime \,-1}$
. Note that
$F'=f'+f^{\prime \,-1}$
. Note that
![]() $G=F'$
in the complement of
$G=F'$
in the complement of
 $\bigcup _{-N' \leq j \leq N} I^{\prime }_j$
, so it is enough to show that
$\bigcup _{-N' \leq j \leq N} I^{\prime }_j$
, so it is enough to show that
![]() $DG-DF'$
is small in each
$DG-DF'$
is small in each
![]() $I^{\prime }_j$
,
$I^{\prime }_j$
,
![]() $-N' \leq j \leq N$
. Indeed for
$-N' \leq j \leq N$
. Indeed for
 $y \in I^{\prime }_j$
, letting
$y \in I^{\prime }_j$
, letting
![]() $\kappa =\phi \circ A_j(y)$
, we have
$\kappa =\phi \circ A_j(y)$
, we have
 $$ \begin{align*}DG(h(y))-DF'(h(y))=\frac {\kappa} {(1+e_j \kappa) b_{j-1}} ((e_{j+1}-e_j) b_j b_{j-1}+e_{j-1}-e_j),\end{align*} $$
$$ \begin{align*}DG(h(y))-DF'(h(y))=\frac {\kappa} {(1+e_j \kappa) b_{j-1}} ((e_{j+1}-e_j) b_j b_{j-1}+e_{j-1}-e_j),\end{align*} $$
which is small because the term
![]() ${\kappa }/{(1+e_j \kappa ) b_{j-1}}$
is bounded. Indeed,
${\kappa }/{(1+e_j \kappa ) b_{j-1}}$
is bounded. Indeed,
![]() $-\delta \leq \kappa \leq 1$
, and
$-\delta \leq \kappa \leq 1$
, and
![]() $1+e_j \kappa \geq 1-e_j \delta \geq 1/2$
provided
$1+e_j \kappa \geq 1-e_j \delta \geq 1/2$
provided
![]() $\delta $
is chosen sufficiently small, and finally
$\delta $
is chosen sufficiently small, and finally
 $b_{j-1}>C^{-1}$
because
$b_{j-1}>C^{-1}$
because
![]() $\sup _{x\in {\mathbb T}} |Df(x)+Df^{-1}(x)|<C$
.
$\sup _{x\in {\mathbb T}} |Df(x)+Df^{-1}(x)|<C$
.
Moreover, we have
![]() $Dg(x)-Df(x)= ({(1+e_1) b_0})/({1+e_0})-b_0= {-b_0}/({1+e_0}) <-({1}/{C (1+C^3)})$
. Because
$Dg(x)-Df(x)= ({(1+e_1) b_0})/({1+e_0})-b_0= {-b_0}/({1+e_0}) <-({1}/{C (1+C^3)})$
. Because
![]() $(({g(x+u)-g(x)})/{u}) \sim Dg(x)$
for
$(({g(x+u)-g(x)})/{u}) \sim Dg(x)$
for
![]() $u \ll |I_0|$
, while
$u \ll |I_0|$
, while
![]() $(({g(x+v)-g(x)})/{v}) \sim Df(x)$
for
$(({g(x+v)-g(x)})/{v}) \sim Df(x)$
for
![]() $1\gg u \gg |I_0|$
, this allows to exhibit u and v such that
$1\gg u \gg |I_0|$
, this allows to exhibit u and v such that
![]() $\Delta (g,x,u,v) \geq 1+{\epsilon }_0$
with
$\Delta (g,x,u,v) \geq 1+{\epsilon }_0$
with
![]() ${\epsilon }_0= {1}/({2C^2 (1+C^3)})$
.
${\epsilon }_0= {1}/({2C^2 (1+C^3)})$
.
To conclude, we must show that there exists arbitrary close to x a point y such that
![]() $(g,y)$
is C-great. It suffices for this to show that in any interval J around x, there is an uncountable set of C-good points for g. By definition of x, we know that the latter is true for f. Note that if y is C-good for f, then
$(g,y)$
is C-great. It suffices for this to show that in any interval J around x, there is an uncountable set of C-good points for g. By definition of x, we know that the latter is true for f. Note that if y is C-good for f, then
![]() $y'=h(h'(y))$
is C-good for g if
$y'=h(h'(y))$
is C-good for g if
 $\sum _{n \geq 0} |Dg^n(y')|^{-2}<C$
.
$\sum _{n \geq 0} |Dg^n(y')|^{-2}<C$
.
Fix some
![]() $\Lambda>0$
much larger than
$\Lambda>0$
much larger than
![]() $\sup e_j$
. Notice that for small
$\sup e_j$
. Notice that for small
![]() $\lambda>0$
, we can choose
$\lambda>0$
, we can choose
![]() $m>0$
such that there is an uncountable set
$m>0$
such that there is an uncountable set
![]() $K' \subset J$
of y such that
$K' \subset J$
of y such that
 $$ \begin{align*}\sum_{n \geq 0} |Df^n(y)|^{-2}<C-\lambda, \quad \text{and} \quad \sum_{n \geq m} |Df^n(y)|^{-2}<\lambda/\Lambda.\end{align*} $$
$$ \begin{align*}\sum_{n \geq 0} |Df^n(y)|^{-2}<C-\lambda, \quad \text{and} \quad \sum_{n \geq m} |Df^n(y)|^{-2}<\lambda/\Lambda.\end{align*} $$
Now, notice that
![]() $h \circ h'=\mathrm {id}$
except in
$h \circ h'=\mathrm {id}$
except in
![]() $\cup _{-N'+1 \leq j \leq N+1} I_j$
, and the derivative of
$\cup _{-N'+1 \leq j \leq N+1} I_j$
, and the derivative of
![]() $h \circ h'$
is bounded by
$h \circ h'$
is bounded by
![]() $(1+\delta ) (1+\sup e_j)$
. In particular, if
$(1+\delta ) (1+\sup e_j)$
. In particular, if
![]() $y \in K'$
, then
$y \in K'$
, then
![]() $h(h'(y))$
will be C-good for g provided
$h(h'(y))$
will be C-good for g provided
![]() $g^n(y) \notin \cup _{-N'+1 \leq j \leq N+1} I_j$
for
$g^n(y) \notin \cup _{-N'+1 \leq j \leq N+1} I_j$
for
![]() $0 \leq n \leq m$
. If we choose the size of
$0 \leq n \leq m$
. If we choose the size of
![]() $I_0$
sufficiently small, we will have the latter property for uncountably many
$I_0$
sufficiently small, we will have the latter property for uncountably many
![]() $y \in K' \subset J$
.
$y \in K' \subset J$
.
The proof of Lemma 6 is thus accomplished.
To finish we still need to show the existence of C-great diffeomorphisms.
Proof of Lemma 5
Given an interval
![]() $I=[a,b]$
, let
$I=[a,b]$
, let
 $l(I)=a+\tfrac {3} {8}(b-a)$
and
$l(I)=a+\tfrac {3} {8}(b-a)$
and
 $r(I)=a+\tfrac {5} {8} (b-a)$
.
$r(I)=a+\tfrac {5} {8} (b-a)$
.
Our construction will depend on a sequence of integers
![]() $m_n \in {\mathbb {N}}$
,
$m_n \in {\mathbb {N}}$
,
![]() $n \geq 0$
, such that
$n \geq 0$
, such that
![]() $m_0$
is large and
$m_0$
is large and
![]() $m_{n+1}$
is much larger than
$m_{n+1}$
is much larger than
![]() $m_n$
.
$m_n$
.
Let
![]() $\Omega $
be the set of all finite sequences
$\Omega $
be the set of all finite sequences
![]() $\omega =(\omega _1,\ldots ,\omega _n)$
of l and r and length
$\omega =(\omega _1,\ldots ,\omega _n)$
of l and r and length
![]() $|\omega | \geq 0$
. For
$|\omega | \geq 0$
. For
![]() $\omega \in \Omega $
, we define intervals
$\omega \in \Omega $
, we define intervals
![]() $I_\omega $
inductively as follows. Let
$I_\omega $
inductively as follows. Let
![]() $n=|\omega |$
. If
$n=|\omega |$
. If
![]() $n=0$
, we let
$n=0$
, we let
![]() $I_\omega $
be the interval of length
$I_\omega $
be the interval of length
![]() $2^{-m_0}$
centered on
$2^{-m_0}$
centered on
![]() $0$
. If
$0$
. If
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $\omega '$
consist of
$\omega '$
consist of
![]() $\omega $
stripped of its last digit, and let
$\omega $
stripped of its last digit, and let
![]() $I_\omega $
be the interval of length
$I_\omega $
be the interval of length
![]() $2^{-m_n}$
centered on
$2^{-m_n}$
centered on
![]() $t(I_{\omega '})$
, where
$t(I_{\omega '})$
, where
![]() $t \in \{l,r\}$
is the last digit of
$t \in \{l,r\}$
is the last digit of
![]() $\omega $
.
$\omega $
.
Let
![]() $\phi :{\mathbb R} \to [0,1]$
be a smooth function symmetric around
$\phi :{\mathbb R} \to [0,1]$
be a smooth function symmetric around
![]() $0$
, supported on
$0$
, supported on
![]() $[-1/2,1/2]$
and such that
$[-1/2,1/2]$
and such that
![]() $\phi |[-1/4,1/4]=1$
.
$\phi |[-1/4,1/4]=1$
.
Let
![]() $A^\omega :I_\omega \to [-1/2,1/2]$
be an affine homeomorphism. Let us now define functions smooth functions
$A^\omega :I_\omega \to [-1/2,1/2]$
be an affine homeomorphism. Let us now define functions smooth functions
![]() $\phi ^\omega :{\mathbb R}/{\mathbb Z} \to {\mathbb R}$
supported inside the intervals
$\phi ^\omega :{\mathbb R}/{\mathbb Z} \to {\mathbb R}$
supported inside the intervals
![]() $I_\omega +k \alpha $
,
$I_\omega +k \alpha $
,
![]() $1 \leq k \leq 2 n-1$
, such that
$1 \leq k \leq 2 n-1$
, such that
Note that by selecting
![]() $m_n$
sufficiently large, we may assume the following property.
$m_n$
sufficiently large, we may assume the following property.
Low recurrence. For any
![]() $n\in {\mathbb {N}}$
, for all
$n\in {\mathbb {N}}$
, for all
![]() $|\omega |=|\omega '|=n$
for any
$|\omega |=|\omega '|=n$
for any
![]() $0 \leq |k| \leq 2^{2^n}$
,
$0 \leq |k| \leq 2^{2^n}$
,
![]() $I_\omega +k \alpha $
does not intersect
$I_\omega +k \alpha $
does not intersect
![]() $I_{\omega '}$
. In particular, the supports of
$I_{\omega '}$
. In particular, the supports of
![]() $\phi ^\omega $
and
$\phi ^\omega $
and
![]() $\phi ^{\omega '}$
do not intersect.
$\phi ^{\omega '}$
do not intersect.
We let
 $\phi _n=\sum _{|\omega |=n} \phi _\omega $
. Note that low recurrence implies that, for any
$\phi _n=\sum _{|\omega |=n} \phi _\omega $
. Note that low recurrence implies that, for any
![]() $x\in {\mathbb R} / {\mathbb Z}$
, the following hold:
$x\in {\mathbb R} / {\mathbb Z}$
, the following hold:
-
(L1)
 $|\phi _n(x+\alpha )-\phi _n(x)| \leq 1$
;
$|\phi _n(x+\alpha )-\phi _n(x)| \leq 1$
; -
(L2)
 $\phi _n(x-m \alpha )=0$
if
$\phi _n(x-m \alpha )=0$
if
 $m \geq 0$
and
$m \geq 0$
and
 $2n-1+m \leq 2^{2^n}$
;
$2n-1+m \leq 2^{2^n}$
; -
(L3)
 $\phi _n(x)\leq n$
.
$\phi _n(x)\leq n$
.
Finally, define a non-decreasing sequence of smooth function
![]() $\Phi _N:{\mathbb R}/{\mathbb Z} \to {\mathbb R}$
by
$\Phi _N:{\mathbb R}/{\mathbb Z} \to {\mathbb R}$
by
 $$ \begin{align*}\Phi_N=\sum_{0 \leq n \leq N} \frac {1} {(n+1)^{4/3}} \phi_n.\end{align*} $$
$$ \begin{align*}\Phi_N=\sum_{0 \leq n \leq N} \frac {1} {(n+1)^{4/3}} \phi_n.\end{align*} $$
Define the uncountable set
 $K:=\bigcap _n \bigcup _{|\omega |=n} I_\omega $
. Note that for
$K:=\bigcap _n \bigcup _{|\omega |=n} I_\omega $
. Note that for
![]() $x\in K$
, we have the following for
$x\in K$
, we have the following for
![]() $N\geq ~1$
:
$N\geq ~1$
:
-
(K1)
 $\Phi _N(x)=0$
;
$\Phi _N(x)=0$
; -
(K2)
 $\Phi _N(x+N \alpha ) \geq ({1}/ {10}) N^{2/3}$
;
$\Phi _N(x+N \alpha ) \geq ({1}/ {10}) N^{2/3}$
; -
(K3) for
 $m\in [0, 2^{2^n}-2n+1]$
,
$m\in [0, 2^{2^n}-2n+1]$
,
 $\Phi _N(x-m \alpha ) \leq {n (n+1)}/ {2}$
.
$\Phi _N(x-m \alpha ) \leq {n (n+1)}/ {2}$
.
To see the last item, just observe that if
![]() $\Phi _N(x-m \alpha ) \geq {n (n+1)}/ {2}$
, then
$\Phi _N(x-m \alpha ) \geq {n (n+1)}/ {2}$
, then
![]() $\phi _{n'}(x-m\alpha )>0$
for some
$\phi _{n'}(x-m\alpha )>0$
for some
![]() $n \leq n' \leq N$
[because
$n \leq n' \leq N$
[because
![]() $\phi _n \leq n$
by item (L3)], and by item (L2), we must have
$\phi _n \leq n$
by item (L3)], and by item (L2), we must have
![]() $m>2^{2^n}-2n+1$
.
$m>2^{2^n}-2n+1$
.
Next, observe that item (L1) implies that
![]() $\Phi _N(\cdot +\alpha )-\Phi _N(\cdot )$
converges in the
$\Phi _N(\cdot +\alpha )-\Phi _N(\cdot )$
converges in the
![]() $C^0$
topology to some continuous function
$C^0$
topology to some continuous function
![]() $\Theta : {\mathbb R} / {\mathbb Z} \to {\mathbb R}$
.
$\Theta : {\mathbb R} / {\mathbb Z} \to {\mathbb R}$
.
Introduce
 $\xi _N:=\int e^{\Phi _N(x)} dx$
and
$\xi _N:=\int e^{\Phi _N(x)} dx$
and
![]() $\Psi _N:=e^{\Phi _N}/\xi _N$
. Again, by letting the integers
$\Psi _N:=e^{\Phi _N}/\xi _N$
. Again, by letting the integers
![]() $m_n$
grow fast, we obtain that
$m_n$
grow fast, we obtain that
![]() $\xi _N$
is close to
$\xi _N$
is close to
![]() $1$
for all
$1$
for all
![]() $N \geq 1$
, and that if we consider the circle homeomorphism
$N \geq 1$
, and that if we consider the circle homeomorphism
![]() $h_n:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
given by
$h_n:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
given by
![]() $Dh_n=\Psi _n$
and
$Dh_n=\Psi _n$
and
![]() $h_n(0)=0$
, we get that
$h_n(0)=0$
, we get that
![]() $h_n$
converges in the
$h_n$
converges in the
![]() $C^0$
topology to some homeomorphism
$C^0$
topology to some homeomorphism
![]() $h:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
.
$h:{\mathbb R}/{\mathbb Z} \to {\mathbb R}/{\mathbb Z}$
.
Because
![]() $\Phi _N(x+\alpha )-\Phi _N(x)$
converges in
$\Phi _N(x+\alpha )-\Phi _N(x)$
converges in
![]() $C^0$
to a continuous function
$C^0$
to a continuous function
![]() $\Theta $
, we get that
$\Theta $
, we get that
![]() $f_n(x)=h_n(h_n^{-1}(x)+\alpha )$
is converging in the
$f_n(x)=h_n(h_n^{-1}(x)+\alpha )$
is converging in the
![]() $C^1$
topology to some f satisfying
$C^1$
topology to some f satisfying
![]() $f(x)=h(h^{-1}(x)+\alpha )$
and
$f(x)=h(h^{-1}(x)+\alpha )$
and
![]() $\ln Df=\Theta \circ h^{-1}$
. In particular, f is minimal.
$\ln Df=\Theta \circ h^{-1}$
. In particular, f is minimal.
Note that all
![]() $x \in h(K)$
are C-good for some absolute C, because
$x \in h(K)$
are C-good for some absolute C, because
 $Df^n(x)\geq e^{{n^{2/3}}/{10}}$
for
$Df^n(x)\geq e^{{n^{2/3}}/{10}}$
for
![]() $x\in h(K)$
by item (K2).
$x\in h(K)$
by item (K2).
However, item (K2) also implies that for each x, from time to time,
![]() $h^{-1}(x)-n \alpha $
, for
$h^{-1}(x)-n \alpha $
, for
![]() $n\geq 0$
, will visit regions where
$n\geq 0$
, will visit regions where
![]() $\sup _N \Phi _N$
is large, so for
$\sup _N \Phi _N$
is large, so for
![]() $x \in h(K)$
,
$x \in h(K)$
,
![]() $Df^{-n}(x)$
will be large, because
$Df^{-n}(x)$
will be large, because
![]() $\Phi _N(h^{-1}(x))=0$
by item (K1). Moreover, if
$\Phi _N(h^{-1}(x))=0$
by item (K1). Moreover, if
![]() $x \in h(K)$
, item (K3) implies that
$x \in h(K)$
, item (K3) implies that
![]() $\Phi _N(h^{-1}(x)-n \alpha )$
is at most of order
$\Phi _N(h^{-1}(x)-n \alpha )$
is at most of order
![]() $(\ln \ln n)^2$
, so
$(\ln \ln n)^2$
, so
 $\sum _{n \geq 1} |Df^{-n}(x)|^{-2}=\infty $
.
$\sum _{n \geq 1} |Df^{-n}(x)|^{-2}=\infty $
.
Acknowledgement
We are grateful to the referee for many useful comments on the first versions of this paper.