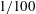1. Introduction
Linear stability analysis of the wake of a rotating cylinder in uniform flow (Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
), covering the parameter space
${\it\alpha}\leqslant 2.5$
,
$\mathit{Re}\leqslant 350$
, shows that several three-dimensional (3D) wake modes become unstable on either the steady or periodic two-dimensional (2D) base flows. Here,
${\it\alpha}={\it\omega}D/2U$
is the ratio of the surface speed of the cylinder (
${\it\omega}D/2$
) to the flow speed (
$U$
) and
$\mathit{Re}=UD/{\it\nu}$
is the Reynolds number, where
$D$
is the cylinder diameter,
${\it\nu}$
is the kinematic viscosity, and
${\it\omega}$
is the cylinder angular velocity. For the periodic base flow, where the analogue of the Bénard–von Kármán (BvK) vortex street is observed, five 3D modes are predicted to become unstable, depending on the control parameters. At low rotation rates (
${\it\alpha}\lesssim 1.25$
), the development of three-dimensionality is similar to that for a non-rotating cylinder; mode A becomes unstable first, followed by mode B at higher Reynolds numbers. At higher rotation rates of
$1.5\lesssim {\it\alpha}\lesssim 1.85$
, however, mode C, which does not occur for a non-rotating cylinder without external perturbations, is the first 3D mode to become unstable as the Reynolds number is increased.
An experimental study by Radi et al. (Reference Radi, Thompson, Rao, Hourigan and Sheridan2013), exploring the same parameter space as Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
) using hydrogen bubble visualisation, confirmed the existence of the 3D modes predicted by Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
); however, it was observed in the experiments that mode C first appeared at much lower rotation rates than numerically predicted (also see: movie 1 of Radi et al.
Reference Radi, Thompson, Rao, Hourigan and Sheridan2013). The original parameter map from Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
) showing the regions where each mode is unstable is reproduced in figure 1. Points marked with blue circles show where mode C was observed in these experiments using a hydrogen bubble wire for visualisation. At
$\mathit{Re}=275$
, for
$0.5\lesssim {\it\alpha}\lesssim 0.7$
, mode C was observed alongside mode B, and for
$1\lesssim {\it\alpha}\lesssim 1.7$
, mode C was the single dominant mode. Thus, mode C was found to be amplified for
${\it\alpha}>0.5$
, a significantly lower onset value than predicted via stability analysis (
${\it\alpha}\geqslant 1.5$
). Notably, a thin platinum wire was used to generate hydrogen bubbles for these experimental visualisations, and these bubbles were then illuminated by a laser sheet. This wire was placed approximately five diameters upstream of the rotating cylinder and one diameter above the centreline. Figure 2 shows a flow visualisation of the mode C instability at
${\it\alpha}=1,\mathit{Re}=275$
. The images, which are shown one shedding period apart, clearly confirm the subharmonic nature of the flow, as expected from the predicted nature of mode C. However, the stability analysis suggests this mode should not be unstable below
${\it\alpha}<1.5$
.
Figure 1. (
$\mathit{Re},{\it\alpha}$
) parameter space map adapted from Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
) showing the critical curves for flow transition from a steady or unsteady 2D base-flow state. Modes A and B correspond to the first two 3D transitions for a non-rotating cylinder. The points marked with blue circles show locations where mode C was observed in the experiments of Radi et al. (Reference Radi, Thompson, Rao, Hourigan and Sheridan2013), clearly extending well below the lower boundary of the mode C region.
Figure 2. Experimental flow visualisation of the saturated mode C wake at
${\it\alpha}=1$
,
$\mathit{Re}=275$
. The span shown is
$\simeq 8D$
. The two images are one period apart. The white guidelines show the mushroom vortical structures are displaced by half a spanwise wavelength from one period to the next. The upstream wire is not shown. Flow is from bottom to top, with the rear of the cylinder visible at the bottom of the images. (a)
$t=t_{0}$
; (b)
$t=t_{0}+T$
.
Thus, it is hypothesised that the wake of the fine platinum wire placed well upstream of the rotating cylinder can perturb the flow sufficiently to significantly alter the stability of at least some 3D wake modes.
The effect of small perturbations on the development of cylinder wakes was made clear by the work of Strykowski & Sreenivasan (Reference Strykowski and Sreenivasan1990), who showed that a correctly positioned small control cylinder (in their case, near to but above the cylinder) can be used to suppress shedding from a circular cylinder. Since then, there has been considerable work exploring the underlying physical and mathematical mechanisms in greater detail. More generally, the stabilisation of wake flows using passive control devices was probably first proposed by Hill (Reference Hill1992). A decade later, theoretical studies examined the sensitivity of eigenvalues (defining the growth rate and frequencies of unstable modes) to base-flow modifications (Bottaro, Corbett & Luchini Reference Bottaro, Corbett and Luchini2003) or turbulence transition (Gavarini, Bottaro & Nieuwstadt Reference Gavarini, Bottaro and Nieuwstadt2004). The role of perturbations to non-normal operators leading to large modifications to eigenvalues was examined by Chomaz (Reference Chomaz2005), highlighting the critical nature of the adjoint mode and noting that the impact was largest in the overlap region between adjoint and normal modes (e.g. Lauga & Bewley Reference Lauga and Bewley2004). For circular cylinders, an analysis of structural sensitivity, i.e. modifications to the perturbation mode or base flow (the case here) on the growth rate and frequency of the instability mode, was undertaken in a series of papers (Giannetti & Luchini Reference Giannetti and Luchini2007; Luchini, Giannetti & Pralits Reference Luchini, Giannetti and Pralits2008, Reference Luchini, Giannetti and Pralits2009; Giannetti, Camarri & Luchini Reference Giannetti, Camarri and Luchini2010), the latter examining structural stability of perturbation modes A and B. In addition, Marquet, Sipp & Jacquin (Reference Marquet, Sipp and Jacquin2008a ) developed sensitivity analyses for arbitrary base-flow modifications and Marquet et al. (Reference Marquet, Sipp, Jacquin and Chomaz2008b ) developed a multiple-scale sensitivity analysis to predict sensitivity to steady and unsteady force perturbations. The structural sensitivity of the 2D shedding modes of a rotating circular cylinder has also been examined recently by Pralits, Brandt & Giannetti (Reference Pralits, Brandt and Giannetti2010). As before, the shift in the growth rate or shedding frequency of the linear mode depends on the overlap of the adjoint and global linear instability modes for perturbations to the global mode, and the overlap of base-flow field with the adjoint perturbation mode for perturbations to the base flow. These authors also used DNS to simulate the enhancement or suppression of shedding using a small control cylinder placed very close to the rotating cylinder, showing that the direction and magnitude of the eigenvalue shift aligns with the predictions of the theory. However, despite these recent advances in adjoint methods in predicting the shift in growth rate and frequency due to base-flow perturbations for a steady to unsteady transition, the method is yet to be applied to unsteady 2D to 3D transition. Given this, the stability analysis presented in the paper is based on including the wire in the flow simulation explicitly, which still enables the surprisingly large effect for a wide range of fixed wire positions to be quantified.
Of relevance to the current findings, previous experimental investigations for a non-rotating cylinder (Zhang et al.
Reference Zhang, Fey, Noack, Konig and Eckelemann1995; Yildirim, Rindt & van Steenhoven Reference Yildirim, Rindt and van Steenhoven2013a
,Reference Yildirim, Rindt and van Steenhoven
b
) show that a subharmonic mode develops when a trip wire is placed downstream and above the cylinder for
$160\lesssim \mathit{Re}\lesssim 300$
. The spanwise wavelength of this wake mode is approximately
$2D$
(Sheard, Thompson & Hourigan Reference Sheard, Thompson and Hourigan2005; Blackburn & Sheard Reference Blackburn and Sheard2010). The combination of dominant wavelength and its subharmonic nature suggests that this wake mode may be related to mode C, which occurs naturally in a rotating cylinder wake, and further suggests that the early onset of this mode may be due to the perturbation introduced by the upstream wire. In a sense this is more broadly related to the observed sensitivity to small geometrical/flow perturbations causing large changes in flow fields and flow stability in many other fluid dynamical problems, such as vortex breakdown (Thompson & Hourigan Reference Thompson and Hourigan2003; Brons, Thompson & Hourigan Reference Brøns, Thompson and Hourigan2009), sensitivity to corner sharpness of bluff bodies (Leontini & Thompson Reference Leontini and Thompson2013) and streamwise bluff body misalignment (Blackburn & Sheard Reference Blackburn and Sheard2010).
To explore this hypothesis further, numerical modelling of the system was undertaken with the platinum wire modelled as a circular cylinder of diameter
$d$
, set to 1/100th of that of the rotating cylinder. This is the same diameter ratio as for the wire used in the experiments of Radi et al. (Reference Radi, Thompson, Rao, Hourigan and Sheridan2013). Two-dimensional base flows were generated for
$0\leqslant {\it\alpha}\leqslant 2$
for
$\mathit{Re}\leqslant 400$
for two scenarios: (a) with the wire upstream and above the cylinder, and (b) with the wire equidistant upstream but below the cylinder. Floquet/linear stability analysis was then performed for a few selected cases to observe the influence of the wire on the different wake modes. The results are compared with those for an isolated rotating cylinder (Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
).
2. Methodology
A schematic of the numerical set-up is shown in figure 3. A rotating cylinder of diameter
$D$
is centred at the origin, with a wire of diameter
$d$
placed upstream of the cylinder at streamwise position
$x\;({<}0)$
and cross-stream position
$y$
. In the discussions that follow, the wire is considered to be placed above the cylinder centreline for
$y>0$
and below the cylinder centreline for
$y<0$
.
Figure 3. Schematic of the numerical set-up. The wire, of diameter
$d$
, is placed upstream of the rotating cylinder (diameter
$D$
). The cylinder centreline is show by dashed lines (- -).
The inlet boundary was placed
$40D$
upstream of the rotating cylinder, and the lateral and outlet boundaries placed
$80D$
downstream of the cylinder. Similar large domain sizes have previously been used to limit blockage effects (Stewart et al.
Reference Stewart, Thompson, Leweke and Hourigan2010; Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
,Reference Rao, Thompson, Leweke and Hourigan
c
). Initial spatial resolution studies were carried out for the rotating cylinder at
${\it\alpha}=1.25,\mathit{Re}=300$
. However, to ensure that the mesh resolution was sufficient to capture the flow at higher rotation rates, a similar spatial resolution study was undertaken at
${\it\alpha}=2,\mathit{Re}=400$
for the wire positioned
$(-5D,D)$
relative to the cylinder centre. The number of internal node points of each quadrilateral element was varied between
$N^{2}=4^{2}$
and
$N^{2}=11^{2}$
. For all cases tested, at a resolution of
$N=7$
, the time-averaged force coefficients and Strouhal numbers were well within 0.5 % of their values at
$N=11$
. Note that the simulations presented in this paper follow closely those reported in Rao et al. (Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
), and more details on the methodology, domain and resolution studies can be found there and references therein. Further details of the particular spectral-element implementation can be found in Ryan, Thompson & Hourigan (Reference Ryan, Thompson and Hourigan2005) and Thompson et al. (Reference Thompson, Hourigan, Cheung and Leweke2006).
A secondary validation check was undertaken to confirm that the subharmonic mode observed in the studies of Zhang et al. (Reference Zhang, Fey, Noack, Konig and Eckelemann1995), Yildirim et al. (Reference Yildirim, Rindt and van Steenhoven2013b
) can indeed be observed when a wire of diameter
$d=D/100$
is placed downstream of a non-rotating cylinder for
$\mathit{Re}\leqslant 300$
. Shown in figure 4 are perturbation contours of spanwise vorticity at
$\mathit{Re}=200$
, where the maximum growth rate occurs at
${\it\lambda}/D\simeq 1.4$
. Clearly, this mode is subharmonic, with the perturbation contours alternating sign every successive period.
Figure 4. (a,b) Spanwise perturbation vorticity contours at
${\it\alpha}=0,\mathit{Re}=200,{\it\lambda}/D=1.4$
, showing the subharmonic mode C instability over one period of vortex shedding. The wire is located downstream of the non-rotating cylinder at the location
$(x,y)=(0.75,0.75)$
with respect to the centre of the cylinder at
$(x_{o},y_{o})=(0,0)$
. Positive/negative vorticity is shown by the red/blue colouring. These are overlaid with vorticity contours at
$\pm 0.2D/U$
, showing the relative positions of the wake vortices. (a)
$t=t_{0}$
; (b)
$t=t_{0}+T$
.
The following section deals with the results from the stability analysis for the wire placed upstream of the rotating cylinder.
3. Results
3.1. Comparison with the experimental findings
For the non-rotating cylinder, the presence of a wire of diameter
$D/100$
upstream does not trigger the mode C instability, and does not suppress mode A and mode B instabilities, at least at
$\mathit{Re}=275$
, well above the critical Reynolds numbers for the mode A and B transition. This is similar to the situation for the wire placed downstream (Zhang et al.
Reference Zhang, Fey, Noack, Konig and Eckelemann1995; Yildirim et al.
Reference Yildirim, Rindt and van Steenhoven2013b
).
On increasing the rotation rate at this Reynolds number, the first instance of the subharmonic mode is predicted experimentally at
${\it\alpha}=0.5$
. Figure 5(a) shows the numerically determined mode growth rate (
${\it\sigma}$
) of the dominant mode as a function of spanwise wavelength at
${\it\alpha}=0.5$
,
$\mathit{Re}=275$
for three situations: no wire, wire below the cylinder (at
$(x,y)=(-5D,-1D)$
), and the wire above the cylinder (at
$(-5D,1D)$
). The growth rates of modes A and B are only marginally affected by the presence or position of the wire for this combination of
$({\it\alpha},\mathit{Re})$
. Mode C, however, is strongly affected. The growth rate increases when the wire is present, and for the case where the wire is positioned above the cylinder centreline, the growth rate curve shows that mode C reaches approximately neutral stability at this rotation rate. Interpolation indicates the actual transition occurs at
${\it\alpha}_{crit}\simeq 0.53$
.
Figure 5. (a) Comparison of the computed growth rates of 3D perturbations when the wire is positioned upstream and above (▪)
$((x,y)=(-5D,1D))$
, and below (○)
$((-5D,-1D))$
, the rotating cylinder, together with the case without the wire (▵) at
${\it\alpha}=0.5,\mathit{Re}=275$
. The subharmonic mode C is observed to reach almost neutral stability only when the upstream wire is positioned above the cylinder centreline. (b) The predicted and experimentally measured spanwise wavelengths of mode C as a function of rotation rate at
$\mathit{Re}=275$
when the wire is positioned upstream at
$(-5D,1D)$
. The experimental values from Radi et al. (Reference Radi, Thompson, Rao, Hourigan and Sheridan2013) are shown by open circles (○) and predicted values by filled circles (●).
The premature onset of mode C when the wire is present above the axial centreline of the cylinder may be associated with some distortion of the upper vortex, which is not only influenced by the rotation of the cylinder, but also by the wake of the wire upstream. The wake asymmetry allows the formation of the subharmonic mode (Blackburn & Sheard Reference Blackburn and Sheard2010; Sheard Reference Sheard2011).
The numerical stability analysis indicates that mode C continues to be unstable up to a rotation rate of
${\it\alpha}\simeq 1.65$
. These findings are in excellent agreement with the experimental observations (Radi et al.
Reference Radi, Thompson, Rao, Hourigan and Sheridan2013).
Figure 5(b) shows the comparison between the experimentally observed spanwise wavelength of the mode C instability with rotation rate at
$\mathit{Re}=275$
and the numerically computed values of spanwise wavelength corresponding to the maximum growth rate from the stability analysis at
$\mathit{Re}=275$
. Again, the numerical predictions are in good agreement with the experimental findings, noting that the predicted wavelengths are generally within 10 % of the experimentally measured values over a wide range of rotation rates.
Figure 6 shows visualisations of the mode C instability for different rotation rates with the wire in position above the axial centreline of the cylinder. The most interesting aspect of these plots is that at the onset rotation rate for Mode C at
$\mathit{Re}=275$
(
${\it\alpha}\gtrsim 0.5$
), most of the wake of the wire does not impinge on the cylinder, but flows over the top. However, as indicated above, just above
${\it\alpha}=0.5$
, the effect of the wire is still strong enough to trigger mode C.
Figure 6. Spanwise perturbation vorticity contours at increasing rotation rates, showing the mode C instability with the upstream wire positioned above the cylinder centreline at
$(-5D,1D)$
for
$\mathit{Re}=275$
. Contour shading is as per figure 4. (a):
${\it\alpha}=0.50,{\it\lambda}_{z}/D=1.6$
; (b):
${\it\alpha}=0.75,{\it\lambda}_{z}/D=1.55$
; (c):
${\it\alpha}=1.25,{\it\lambda}_{z}/D=1.35$
.
3.2. Wire placed below the rotating cylinder centreline
Additional simulations were carried out to observe the influence of the wire when placed upstream but below the axial centreline of the cylinder at
$(x,y)=(-5D,1D)$
. Three rotation rates of
${\it\alpha}=0.5,0.75$
and 1 were considered for
$\mathit{Re}=275$
and stability analysis was carried out. These simulations showed that the flow remained stable to the subharmonic mode C. Also shown in figure 5(a) are growth rate data for modes A, B and C for the rotating cylinder at
${\it\alpha}=0.5,\mathit{Re}=275$
, for the wire placed below the axial centreline of the cylinder, in addition to the curves for when it is placed above. While the growth rate curves for mode A for each case (no wire, wire above, wire below) are effectively coincident, those for mode B show slight differences, although this mode remains unstable in all three cases.
3.3. Influence of wire location
Having previously investigated the influence of a wire at a fixed upstream position, it is useful to characterise the effect on mode C transition as its upstream location is varied. For the following, the rotation rate and Reynolds number are set to
${\it\alpha}=1$
and
$\mathit{Re}=275$
. Recall that mode C is not amplified for an isolated rotating cylinder at
$\mathit{Re}=275$
for
${\it\alpha}\lesssim 1.5$
. For the first set of simulations, the streamwise location is varied in the range
$-30\leqslant x/D\leqslant -2.5$
, for a fixed transverse position of
$y/D=1$
. The second set varied the transverse position
$-1\leqslant y/D\leqslant 2$
for a fixed upstream position of
$x/D=-5$
. Floquet stability analysis was performed on the 2D base flows corresponding to particular wire positions to determine the growth rate as a function of wavelength within the mode C range. Figure 7 shows the preferred-wavelength mode C growth rate, and the change to the base-flow Strouhal number with respect to the no-wire case. Figure 7(a) provides these variations as the wire is positioned further upstream. Note that the mode C growth rate without the wire is
${\it\sigma}\simeq -0.027$
. The maximum effect on both the growth rate and the Strouhal number occurs for
$x/D\simeq -7$
. However, the growth rate remains positive for the wire placed up to almost
$20D$
upstream of the cylinder. Figure 7(b) shows the Strouhal number/growth rate variations as a function of the transverse position of the wire. For
$0.55\lesssim y/D\lesssim 1.5$
, mode C has a positive growth rate, with the maximum effect at
$y/D\simeq 0.7$
. A significant shift in the base-flow Strouhal number also occurs for a similar range. Also of interest, placing the wire at
$y/D\lesssim 0.5$
stabilises mode C with respect to the case without the wire.
Figure 7. Variation of the change in Strouhal number relative to the no-wire case,
${\rm\Delta}\mathit{St}$
(○, dashed lines), and the growth rate
${\it\sigma}$
(▫, solid lines) of the mode C instability as the wire location is varied in (a) the streamwise direction (
$x/D$
) (
$y/D=1$
), and (b) the transverse direction (
$y/D$
) (
$x/D=-5$
) for
${\it\alpha}=1$
,
$\mathit{Re}=275$
.
3.4. Influence of wire diameter
Figure 8 shows the effect of the diameter of the perturbing wire on the mode C transition. This shows the predicted growth rate against spanwise wavelength as the wire diameter is varied between
$1/25$
th and
$1/200$
th of the cylinder diameter. Figure 8(a) and (b) correspond to
${\it\alpha}=0.5$
and 1.0, respectively. These plots illustrate that even a wire of diameter
$1/200$
th
$D$
has a substantial effect on the mode C growth rate, showing that such a wire triggers mode C growth at
${\it\alpha}=1$
, well below the critical value of
${\it\alpha}=1.5$
without the wire.
Figure 8. Variation of the growth rate of mode C as a function of spanwise wavelength for different wire diameters: (a)
${\it\alpha}=0.5$
; (b)
${\it\alpha}=1.0$
. The corresponding growth rate curves for the cases without the wire are also shown, confirming mode C remains stable. Wire position
$(x,y)=(-5D,1D)$
and
$\mathit{Re}=275$
.
3.5. Effect on the saturated flow: three-dimensional simulations
An interesting question is whether the presence of a small-diameter wire placed many cylinder diameters upstream can alter the sequence of transitions, which may result in a distinctly different fully developed flow state. Indeed, this certainly occurs. The stability analysis indicates that at
${\it\alpha}=1,\mathit{Re}=275$
, an upstream wire prematurely triggers mode C and suppresses mode A, while mode A is slightly unstable without the wire. Figure 9 shows the final saturated flow state at
$\mathit{Re}=280$
for
${\it\alpha}=1$
, with and without a wire of diameter
$D/25$
. Note that the slightly higher Reynolds number and larger diameter wire chosen here provide larger grow rates of each mode, allowing the expensive simulations to reach their saturated states more quickly. Figure 9(a) shows the saturated mode C 3D flow visualised by streamwise vorticity isosurfaces, with the upstream wire in place. The subharmonic state of this mode is clearly seen through the alternating colour of the aligned streamwise vortices from one shedding cycle to the next. This wake is quite different from the saturated mode A wake shown in figure 9(b) when there is no upstream wire. For mode C, five spanwise wavelengths of the mode are observed over the selected spanwise domain of
$z/D=8D$
, giving a wavelength of
$1.6D$
. For mode A, there are only two spanwise wavelengths, giving the typical mode A wavelength of
${\sim}4D$
. In this instance, a ‘pure’ mode A saturated state is observed, as the Reynolds number is close to the onset for this mode (
$\mathit{Re}_{c}\simeq 270$
, Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014). These simulations were run starting from white-noise perturbed 2D solutions, using 64 Fourier planes in the spanwise direction, sufficient to accurately capture the fully evolved flow at this Reynolds number.
Figure 9. (a) Mode C (with wire); top view of streamwise vorticity isosurfaces showing saturated mode C state at
${\it\alpha}=1,\mathit{Re}=280$
. Flow is from left to right and the cylinder spans
$8D$
. The wire, which in this case is modelled as a cylinder of diameter
$1/25$
th
$D$
, is seen far left in this image. (b) Mode A (without wire) shows the top view of the wake without the wire for the same
${\it\alpha}$
and
$\mathit{Re}$
. In this case, the flow saturates to the mode A state.
3.6. Influence of the wire at higher rotation rates
Although not the main focus of the current paper, it is interesting to assess the effect of the wire on other transitions. At a rotation rate of
${\it\alpha}=1.9$
, for the rotating cylinder with no wire, three shedding regimes are observed (Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
). These regimes cover the ranges (i)
$120\lesssim \mathit{Re}\lesssim 190$
, (ii)
$260\lesssim \mathit{Re}\lesssim 350$
and (iii)
$\mathit{Re}\gtrsim 350$
(Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
). In the range
$190\lesssim \mathit{Re}\lesssim 260$
, the flow is steady. Regimes (i) and (iii) correspond to low-frequency shedding analogous to Bénard–von Kármán shedding, while for regime (ii), the shedding frequency is higher. However, when the wire is placed upstream and above the cylinder at
$(x,y=-5,1)$
, the flow remains steady up to
$\mathit{Re}\simeq 280$
, beyond which the high-frequency branch of vortex shedding is observed. For
$\mathit{Re}\gtrsim 390$
, the shedding frequency drops down to the lower branch (regime (iii)). Figure 10 shows the effect on the Strouhal number and the Reynolds number ranges for flows without the upstream wire, and with the wire placed above or below the cylinder centreline.
Figure 10. Comparison of the shedding frequencies for the rotating cylinder at
${\it\alpha}=1.9$
, when the wire is positioned above (●) and below (○) the cylinder and the case without the wire (▫).
The 3D mode E instability grows on the steady base flow (Rao et al.
Reference Rao, Leontini, Thompson and Hourigan2013a
,Reference Rao, Leontini, Thompson and Hourigan
b
, Reference Rao, Radi, Leontini, Thompson, Sheridan and Hourigan2014) (see figure 1). Unlike for mode C, mode E is stabilised by the presence of the wire upstream and above the cylinder, and its onset delayed to higher Reynolds numbers. At
${\it\alpha}=1.9$
, the critical Reynolds number for the onset of mode E was found to be
$\mathit{Re}_{c}\simeq 204$
, as compared to
$\mathit{Re}_{c}\simeq 192$
for the no-wire case. A similar increase was observed at
${\it\alpha}=2$
, with
$\mathit{Re}_{c}\simeq 224$
, as compared to the isolated case (
$\mathit{Re}_{c}\simeq 207$
). This shift in stability is demonstrated in figure 11, which shows growth rate curves for the mode E instability at
${\it\alpha}=2$
and
$\mathit{Re}=220$
for the two cases. The presence of the wire shifts the transition Reynolds number by around 8 %.
Figure 11. Comparison of the growth rate curves for the mode E instability at
${\it\alpha}=2$
,
$\mathit{Re}=220$
with the wire above the cylinder centreline (-●-) and without the wire (-▫-). This 3D mode is stabilised by the wire, with the critical Reynolds number shifted from
$\mathit{Re}\simeq 207$
to
${\gtrsim}220$
at this rotation rate.
4. Conclusions
These simulations collectively indicate an early onset of the mode C transition, prematurely triggered by the presence of an upstream wire. This occurs for rotation rates noticeably lower than without the wire. Furthermore, linear stability analysis with the wire present accurately predicts the preferred spanwise wavelength for this mode, in line with experiments, and shows that modes A and B are more resilient to external disturbances than mode C. Three-dimensional DNS with the wire also confirms the onset and saturation of mode C at
${\it\alpha}=1,\mathit{Re}=280$
, rather than mode A, which is the case without the wire. When the streamwise location of the wire was varied, mode C was found to remain unstable for wire locations up to
$x/D\simeq -20$
, demonstrating the non-negligible influence of the wire even at extreme upstream distances. When the transverse position of the wire is varied at a fixed upstream distance, the maximum growth rate of mode C was found to occur for a wire position at
$y/D\simeq 0.75$
.
In terms of other transitions, at higher rotation rates, the presence of the wire also noticeably increases the transition Reynolds numbers for the onset of unsteady flow. Furthermore, the onset of the 3D steady mode E wake state is delayed to higher Reynolds numbers with the wire upstream of the cylinder. Collectively, perhaps these results serve as a reminder that surprising care is required even from apparently minimally intrusive flow visualisation and measurement systems in producing results that mimic those from an unperturbed system.
Acknowledgements
The support from Australian Research Council Discovery Grants DP130100822, DP150102879 and computing time from the National Computational Infrastructure (NCI), Victorian Life Sciences Computation Initiative (VLSCI) and Pawsey Supercomputing Centre are gratefully acknowledged. This research was also supported in part by the Monash e-Research Centre and eSolutions-Research Support Services through the use of the Monash Campus HPC Cluster. The authors would also like to acknowledge the storage space provided via VicNode/RDSI grant allocation 2014R8.2.
