1. Introduction
Multi-dimensional Feller processes have been useful for modelling the evolution of dynamical systems that are spatially inhomogeneous. These processes have been important models in finance and physics [Reference Böttcher3]. Of particular interest is the study of the dependence between the marginal processes. Some different notions of positive dependence include association (A), positive supermodular association (PSA), positive supermodular dependence (PSD), and positive orthant dependence (POD). If a process exemplifies a certain notion of positive dependence between the marginals, then one can better study the evolution of the process.
It is known that Lévy processes in ℝd can be characterized by their characteristic triplet (b, ∑, ν), where b ∊ Rd is the nonrandom linear drift, ∑ is the covariance matrix of the (continuous) Brownian motion, and ν is the Lévy measure which characterizes the jump behaviour of the process. Feller processes have behaviour that is ‘locally Lévy’, that is, for a Feller process ![]() [${(X_t^x)_{t \ge 0}}$ that starts at point x (
[${(X_t^x)_{t \ge 0}}$ that starts at point x (![]() [$X_0^x = x$ a.s.), there exists a Lévy process (Yt)t ≥0 such that, over a short time, the behaviour of
[$X_0^x = x$ a.s.), there exists a Lévy process (Yt)t ≥0 such that, over a short time, the behaviour of ![]() [${(X_t^x)_{t \ge 0}}$ can be approximated by the behaviour of (Yt + x)t ≥0 [Reference Böttcher, Schilling and Wang5, p. 46]. This idea is related to the notion that, if the domain 𝒟(𝒜) is ‘rich’, i.e. contains
[${(X_t^x)_{t \ge 0}}$ can be approximated by the behaviour of (Yt + x)t ≥0 [Reference Böttcher, Schilling and Wang5, p. 46]. This idea is related to the notion that, if the domain 𝒟(𝒜) is ‘rich’, i.e. contains ![]() [$C_c^\infty ({^d})$, the space of smooth functions with compact support, then the Feller process can be described by a characteristic triplet (b(x), ∑(x), ν(x, dy)), where the function b: ℝd → ℝd represents the nonrandom component, ∑ : ℝd → ℝd × d represents the continuous diffusion-like behaviour, and x ↦ ν(x, dy) is a measurable kernel representing the jump behaviour of the process. Unlike the Lévy process, the Feller process triplet has dependence on x, the state variable of the process, representing its spatial inhomogeneity. We will characterize the different notions of positive dependence via these triplets.
[$C_c^\infty ({^d})$, the space of smooth functions with compact support, then the Feller process can be described by a characteristic triplet (b(x), ∑(x), ν(x, dy)), where the function b: ℝd → ℝd represents the nonrandom component, ∑ : ℝd → ℝd × d represents the continuous diffusion-like behaviour, and x ↦ ν(x, dy) is a measurable kernel representing the jump behaviour of the process. Unlike the Lévy process, the Feller process triplet has dependence on x, the state variable of the process, representing its spatial inhomogeneity. We will characterize the different notions of positive dependence via these triplets.
Association, the strongest form of positive dependence that we will examine, has been well studied for infinitely divisible distributions. Infinitely divisible random vectors X also have a characteristic triplet (b, ∑, ν) by the famous Lévy–Khintchine formula, where b represents the nonrandom component, ∑ is covariance of the Gaussian component, and ν is the Lévy measure of the Poisson component. Pitt [Reference Pitt21] characterized association for Gaussian distributions (b, Q, 0) under the condition that the entries ∑ij of ∑ are nonnegative. Resnick [Reference Resnick22] proved that a sufficient condition for association of Poisson distributions (0, 0, ν) is that ν be concentrated on the positive and negative orthants ![]() [$_ + ^d$ and
[$_ + ^d$ and ![]() [$_ - ^d$, i.e.
[$_ - ^d$, i.e.
These results lead to the characterization of association between the marginal processes of a Lévy process, since, for a Lévy process Y = (Yt)t ≥0, Yt is infinitely divisible for each t ≥ 0, and the process can be described by its characteristic triplet (b, ∑, ν). Herbst and Pitt [Reference Herbst and Pitt13] extended Pitt’s result in [Reference Pitt21] to Brownian motion with covariance matrix ∑. For jump-Lévy processes Y ~ (0, 0, ν), Samorodnitsky [Reference Samorodnitsky25] showed that condition (1.1) is a sufficient and necessary condition for the association of each Yt. This result was also proved by Houdré et al. [Reference Houdré, Pérez-abreu and Surgailis14] using a covariance identity. Bäuerle et al. [Reference Bäuerle, Blatter and Müller2] extended Samorodnitsky’s results for jump-Lévy processes to association in time, and showed that condition (1.1) is also equivalent to PSD and POD. Liggett [Reference Liggett18] proved a necessary and sufficient condition for association of stochastically monotone Markov processes on compact state spaces based on the generator of the process. Szekli [Reference Szekli29, Chapter 3.7] and Rüschendorf [Reference Rüschendorf23, Corollary 3.1] extended this result to more general state spaces. Rüschendorf [Reference Rüschendorf23, Corollary 3.4] also extended the Liggett condition for PSA of the Markov process.
In this paper, we want to characterize various forms of positive dependence for stochastically monotone Feller process. Those forms of dependence include association, weak association (WA), PSA, PSD, POD, positive upper orthant dependence (PUOD), and positive lower orthant dependence (PLOD). The association of diffusion processes, i.e. (b(x), ∑(x), 0), has been characterized by Chen [Reference Chen and Wang7], so we will only focus on jump-Feller process (b(x), 0, ν(x, dy)). Association of jump-Feller processes, i.e. (b(x), 0, ν(x, dy)), was given by Wang [Reference Wang32, Theorem 1.4], but under certain continuity and integrability conditions on the characteristic triplet (see Remark 2.2). Here, we will relax those conditions, allowing us to consider a larger class of Feller processes. Additionally, we characterize WA, PSA, PSD, POD, PUOD, and PLOD for jump-Feller processes. Our techniques extend the ideas of Liggett, Szekli, and Rüschendorf to the extended generator of the process, an integro-differential operator. We use ideas of the probabilistic symbol p(x, ξ) of the process developed by Jacob and Schilling [Reference Böttcher, Schilling and Wang5, pp. 57–58]. Furthermore, for proving the necessary condition of association, WA, PSA, PSD, POD, PUOD, PLOD, we use the technique of small-time asymptotics of the Feller process [Reference Kühn and Schilling16], which will allow us to avoid the use of the (extended) generator and use solely the state-space dependent Lévy measure ν(x, dy). Finally, we provide examples of Feller processes satisfying the conditions of our main results.
In a concurrent paper of ours, entitled ‘Association and other forms of positive dependence for Feller evolution systems’ [Reference Tu31], we characterize dependence structures for Feller evolution processes (FEP), which are time-inhomogeneous Markov processes having strongly continuous Markov evolutions and Lévy-type behaviour. These FEPs are more general than the Feller processes (time-homogeneous) in this paper, but we need the results of this paper in order to characterize dependence structures of FEPs. We utilize Böttcher’s transformation of time-inhomogeneous FEPs into time-homogeneous Feller processes (see [Reference Böttcher4]) and, in a nontrivial way, use our results in this paper to prove characterizations of positive dependence for FEPs. This yields positive dependence characterizations for interesting time-inhomogeneous processes, such as additive processes. For a more comprehensive overview of time-inhomogeneous Markov processes, we recommend that the reader explore the paper by Rüschendorf et al. [Reference Rüschendorf, Schnurr and Wolf24], which also discusses comparison theorems of time-inhomogeneous Markov processes.
The present paper is organized in the following way. In Section 2, we give some background on the positive dependence structures, association, WA, PSA, PSD, POD, PUOD, and PLOD, along with definitions of various stochastic orderings. We also provide background on Lévy processes, Feller processes, and the different tools we use to analyse them. In Section 3, we state and prove our main results about the positive dependence structures of jump-Feller processes. Finally, in Section 4, we give a collection of interesting examples of multi-dimensional Feller processes to which we can apply these results.
2. Background
2.1. Dependence and stochastic orderings
Let X = (X 1,..., Xd) be a random vector in ℝd. We say X is positively correlated (PC) if Cov(Xi, Xj) ≥ 0 for all i, j ∊{1,..., d}. This is one of the weakest forms of positive dependence, and we are interested in stronger forms of positive dependence which will be of greater use in our study of stochastic processes. Association is the strongest form of positive dependence that we will study.
Definition 2.1. X = (X 1,..., Xd) is associated (A) if we have
for all f, g: ℝd → ℝ nondecreasing in each component, such that Cov( f (X), g(X)) exists.
We will also study other forms of positive dependence that are weaker than association but stronger than positive correlation. We list them below.
Definition 2.2. A random vector X = (X 1,..., Xd)is weakly associated (WA) if, for any pair of disjoint subsets I, J ⊆ {1,..., d}, with |I|= k, |J|= n,
where XI ≔ (Xi : i ∊ I), XJ ≔ (Xj : j ∊ J), for any f : ℝk → ℝ, g: ℝn → ℝ nondecreasing, such that Cov( f (XI), g(XJ)) exists.
Definition 2.3. X is positive supermodular associated (PSA) if Cov( f (X), g(X)) ≥ 0 for all f, g ∊ ℱism:= {h: ℝd → ℝ, nondecreasing, supermodular}. Here, f supermodular means, for all x, y ∊ ℝd, f (x ∧ y) + f (x ∨ y) ≥ f (x) + f (y), where x ∧ y is the component-wise minimum, and x ∨ y is the component-wise maximum.
Now let ![]() [$\hat X = ({\hat X_1}, \ldots ,{\hat X_d})$ be a random vector such that for all i,
[$\hat X = ({\hat X_1}, \ldots ,{\hat X_d})$ be a random vector such that for all i, ![]() [${\hat X_i}\mathop = \limits^d {X_i}$ and
[${\hat X_i}\mathop = \limits^d {X_i}$ and ![]() [${\hat X_i}$ are mutually independent.
[${\hat X_i}$ are mutually independent.
Definition 2.4. X is positive supermodular dependent (PSD) if, for all f : ℝd → ℝ supermodular, ![]() [$f(\hat X) \le f(X)$.
[$f(\hat X) \le f(X)$.

Figure 1: Implication map of various positive dependence structures.
Definition 2.5. X is positive upper orthant dependent (PUOD) if, for all t 1, ..., td ∈ ℝ,
Definition 2.6. X is positive lower orthant dependent (PLOD) if, for all t 1, ..., td ∈ ℝ,
Definition 2.7. X is positive orthant dependent (POD) if X is PUOD and PLOD.
One can state another equivalent definition to PUOD (PLOD). For i = 1, ..., d, let fi : ℝ → ℝ+ be nondecreasing (nonincreasing) functions. Then X = (X 1, ..., Xd) PUOD (PLOD) if and only if
 [$$({X_1} \le {t_1}, \ldots ,{X_d} \le {t_d}) \ge ({X_1} \le {t_1}) \cdots ({X_d} \le {t_d}).$$
[$$({X_1} \le {t_1}, \ldots ,{X_d} \le {t_d}) \ge ({X_1} \le {t_1}) \cdots ({X_d} \le {t_d}).$$
Note. Definition 2.1 first appeared in [Reference Esary, Proschan and Walkup11], and as Definition 2.2 in [Reference Burton, Dabrowski and Dehling6], Definition 2.3 in [Reference Rüschendorf23, p. 284], Definition 2.4 in [Reference Hu15], and Definitions 2.5–2.7 in [Reference Lehmann17]. Definitions 2.4–2.7 can also be stated in terms of stochastic orderings. For more on this, we refer the reader to Müller and Stoyan’s book [Reference Müller and Stoyan19, Chapter 3]. It is useful to see the relationship between these different forms of positive dependence. We state the relationships in the following proposition.
Proposition 2.1. The implications in Figure 1 hold.
Proof. Proofs for these implications can be found in Müller and Stoyan’s book [Reference Müller and Stoyan19, Chapter 3], and implications involving PSD can be found in [Reference Christofides and Vaggelatou8].
These notions of dependence can be extended from random vectors to stochastic processes. Let X = (Xt)t ≥ 0 be a stochastic process in ℝd.
(a) Process X is associated in space or spatially associated if, for every t ≥ 0, the random vector
 [${X_t} = (X_t^{(1)}, \ldots ,X_t^{(d)})$ is associated.
[${X_t} = (X_t^{(1)}, \ldots ,X_t^{(d)})$ is associated.(b) Process X is associated in time or temporally associated if, for all 0 ≤ t 1 < ⋅⋅⋅ < tn, the random vector
 [$({X_{{t_1}}}, \ldots ,{X_{{t_n}}})$ in ℝdn is associated.
[$({X_{{t_1}}}, \ldots ,{X_{{t_n}}})$ in ℝdn is associated.
(i) Clearly, (b) is stronger than (a) in the above definition.
(ii) We can define other forms of positive dependence in stochastic processes if we replace ‘associated’ in Definitions 2.8 (a) and (b) with ‘WA’, ‘PSA’, ‘PSD’, ‘POD’, ‘PUOD’, ‘PLOD’.
(iii) Definition (a) is equivalent to the statement that the ‘process preserves positive correlations’, as given in [Reference Liggett18, p. 80] and [Reference Chen and Wang7].
2.2. Feller processes, extended generators, small-time asymptotics
2.2.1 Feller process
Consider a time-homogeneous Markov process X = (Xt)t ≥ 0 on the space (Ω, 𝒢, (𝒢t)t ≥ 0, ℙx)x ∈ℝd. Here (𝒢t)t ≥ 0 is the filtration, and the index ‘x’ indicates the starting point of the process: ℙx(X 0 = x) = 1. We associate with a Markov process X a positivity-preserving, contraction semigroup of bounded operators (Tt)t ≥ 0 defined by
where f ∈ Bb(ℝd), the space of bounded measurable functions on ℝd. Let (C 0(ℝd), ⋅ ∞) be the Banach space of continuous functions that vanish at infinity, i.e. lim|x |→ ∞ f (x) = 0, where ⋅ ∞ is the sup-norm. Define ℱi:={f : ℝd → ℝ, nondecreasing in each component}. A Markov process is stochastically monotone if Ttf ∈ℱi for all f ∈ℱi. We define the generator 𝔸 of the process X to be
for all f ∈ 𝒟(𝒜), where D(A) is the domain of the generator defined to be
𝒟 (𝒜) = {u ∈ C 0(ℝd): limit on right-hand side of (2.1) exists uniformly}.
The Markov process is a Feller process if the semigroup (Tt)t ≥ 0 satisfies the following properties:
(i) Tt: C 0(ℝd) → C 0(ℝd),
(ii) limt → 0 Ttu − u ∞ = 0.
If, additionally, the domain of the generator contains smooth functions with compact support, i.e. ![]() [${\cal D}({\cal A}) \supset C_c^\infty ({^d})$, we call the process X a rich Feller process. It follows from Courrège’s theorem [Reference Courrège9] that −𝒜 becomes a pseudo-differential operator p(x, D) on the space of
[${\cal D}({\cal A}) \supset C_c^\infty ({^d})$, we call the process X a rich Feller process. It follows from Courrège’s theorem [Reference Courrège9] that −𝒜 becomes a pseudo-differential operator p(x, D) on the space of ![]() [$C_c^\infty ({^d}):{\cal A}{|_{C_c^\infty ({^d})}} = - p(x,D)$, where p(x, D) is defined to be
[$C_c^\infty ({^d}):{\cal A}{|_{C_c^\infty ({^d})}} = - p(x,D)$, where p(x, D) is defined to be
The function −p(x, ⋅) is a continuous negative definite function, in the sense of Schoenberg, for all x ∈ ℝd, which yields a Lévy–Khintchine representation for each x:
 [$$ - p(x,\xi ) = - {\rm{i}}b(x) \cdot \xi + {1 \over 2}\xi \cdot \Sigma (x)\xi - \int_{{^d}\backslash \{ 0\} } ({{\rm{e}}^{black{\rm{i}}\xi \cdot y}} - 1 - {\rm{i}}\xi \cdot y\chi (y))\nu (x,{\rm{d}}y),$$
[$$ - p(x,\xi ) = - {\rm{i}}b(x) \cdot \xi + {1 \over 2}\xi \cdot \Sigma (x)\xi - \int_{{^d}\backslash \{ 0\} } ({{\rm{e}}^{black{\rm{i}}\xi \cdot y}} - 1 - {\rm{i}}\xi \cdot y\chi (y))\nu (x,{\rm{d}}y),$$
where χ : ℝd → ℝ is a cut-off function. In this paper, unless otherwise mentioned, we will assume χ(y) = 1(0, 1) (|y|). For each x,(b(x), (x), ν(x, dy)) is the (Lévy) characteristic triplet, where b(x) ∈ ℝd, (x) ∈ ℝd × d a symmetric positive definite matrix, and ν(x, dy), the Lévy measure, is a σ-finite measure on ℝd \{0} satisfying ![]() [$\int_{{^d}\backslash \{ 0\} } (1 \wedge |y{|^2})\nu (x,{\rm{d}}y) /lt \infty $. We call the function p(x, ξ)the symbol of the process. We also write X ~ (b(x), (x), ν(x, dy)) to signify that X is a Feller process with that characteristic triplet.
[$\int_{{^d}\backslash \{ 0\} } (1 \wedge |y{|^2})\nu (x,{\rm{d}}y) /lt \infty $. We call the function p(x, ξ)the symbol of the process. We also write X ~ (b(x), (x), ν(x, dy)) to signify that X is a Feller process with that characteristic triplet.
When the symbol and the corresponding triplet are constant in x, i.e. p(x, ξ) = p(ξ) and triplet (b(x), (x), ν(x, dy)) = (b, ∑, ν), then process X is a Lévy process, i.e. a stochastically continuous Markov process with stationary and independent increments. The symbol p(ξ) is also the Lévy symbol of the process, with characteristic function ![]() [${\phi _{{X_t}}}(\xi ) = {{\rm{e}}^{tp(\xi )}}$. In the Lévy case, b is the nonrandom linear drift, ∑ is covariance of the Brownian motion, and ν is a measure representing the jumps of the process.
[${\phi _{{X_t}}}(\xi ) = {{\rm{e}}^{tp(\xi )}}$. In the Lévy case, b is the nonrandom linear drift, ∑ is covariance of the Brownian motion, and ν is a measure representing the jumps of the process.
Continuous negative definite functions p(x, ξ) which are associated with a Feller process have a form of local boundedness in the first argument. In other words, we say the symbol p(x, ξ) is locally bounded if, for all K ⊂ ℝd compact, there exists cK > 0 such that
We say the symbol is bounded if (2.4) holds for K = ℝd. The local boundedness (or boundedness) of the symbol corresponds to the local boundedness (boundedness) of the characteristics (b(x), ∑(x), ν(x, dy)) (see [Reference Schilling27, Lemma 2.1]).
2.2.2 Integro-differential operator
For any rich Feller process, the triplet (b(x), (x), ν(x, dy)) characterizes the behaviour of the process, with b(x) representing nonrandom continuous behaviour, ∑(x) representing the diffusion-like continuous behaviour, and ν(x, dy) representing the jump behaviour. To analyse the process, one of the crucial tools we will use is the extended generator. For the case of rich Feller processes, when we substitute (2.3) into the right-hand side of (2.2), by elementary Fourier analysis, we get an integro-differential operator I(p),
 [$$I(p) f(x) = b(x) \cdot \nabla f(x) + {1 \over 2}\nabla \cdot \Sigma (x)\nabla f(x) + \int_{y \ne 0} (\,f(x + y) - f(x) - y \cdot \nabla f(x)\chi (y))\nu (x,{\rm{d}}y),$$
[$$I(p) f(x) = b(x) \cdot \nabla f(x) + {1 \over 2}\nabla \cdot \Sigma (x)\nabla f(x) + \int_{y \ne 0} (\,f(x + y) - f(x) - y \cdot \nabla f(x)\chi (y))\nu (x,{\rm{d}}y),$$
where
 [$$\nabla \cdot \Sigma (x)\nabla f(x) = \sum\limits_{j,k = 1}^d {\Sigma _{jk}}(x){\partial _j}{\partial _k} f(x).$$
[$$\nabla \cdot \Sigma (x)\nabla f(x) = \sum\limits_{j,k = 1}^d {\Sigma _{jk}}(x){\partial _j}{\partial _k} f(x).$$
Clearly, the operator I(p) is defined on ![]() [$C_b^2({^d})$, the space of continuous twice-differentiable bounded functions. When the symbol p(x, ξ) is bounded, I(p) is an extension of −p(x, D),
[$C_b^2({^d})$, the space of continuous twice-differentiable bounded functions. When the symbol p(x, ξ) is bounded, I(p) is an extension of −p(x, D),
and an extension of generator 𝒜: I(p)|𝒟(𝒟) = 𝒜, as shown by Schilling [Reference Schilling27, Lemma 2.3]. Our interest in this integro-differential operator I(p) comes with wanting to use the idea of Liggett’s characterization of association via the generator.
Theorem 2.1. (Liggett [Reference Liggett18], p. 80.) Let X = (Xt)t ≥ 0 be a Feller process on state space E with generator (𝒜,𝒟(𝒜)) and semigroup (Tt )t ≥ 0. If X is stochastically monotone, then
if and only if Xt is associated for all t ≥ 0 with respect to ℙx for all x ∈ E.
Liggett proved this for E compact and 𝒜 bounded. This was extended by Szekli and Rüschendorf to more general Polish spaces E and 𝒜 unbounded ([Reference Szekli29, Chapter 3.7], [Reference Rüschendorf23, Corollary 3.1]). For the Feller processes we consider in the above setting, particularly those of the jump variety, the domain 𝒟(𝒜) is often defined to be a dense subspace of C 0 (ℝd), and thus𝒟(𝒜) ∩ℱi = {f ≡ 0}. Hence, in that case, inequality (2.6) would always hold. Thus, we would like to extend Theorem 2.1 to the extended generator I(p).
2.2.3 Small-time asymptotics
The (extended) generator gives us a connection between the notion of association and the Lévy characteristics (b, ∑(x), (x), ν(x, dy)) due to the representation of the integro-differential operator. Thus, to characterize association for Feller processes using the Lévy characteristics, an extension of Theorem 2.1 becomes quite useful. However, under weaker conditions on the symbol p(x, ξ), such as local boundedness, it is useful to avoid using the generator (as we will show in Section 3) and show a more direct connection between the Lévy characteristics and the notion of association. We will establish such a connection by looking at small-time asymptotics of a Feller process. Additionally, this notion will allow us to characterize weaker forms of positive dependence under the Lévy characteristics.
The classical results of small-time asymptotics have been primarily established for Lévy processes. For a given Lévy process L = (Lt)t ≥ 0, it is known that, for all f ∈ Cc(ℝd \ {0}),
 [$$\mathop {\lim }\limits_{t \searrow 0} {1 \over t}{^0}f({L_t}) = \int_{{^d}\backslash \{ 0\} } f(y)\nu ({\rm{d}}y)$$
[$$\mathop {\lim }\limits_{t \searrow 0} {1 \over t}{^0}f({L_t}) = \int_{{^d}\backslash \{ 0\} } f(y)\nu ({\rm{d}}y)$$
(see [Reference Kühn and Schilling16, p. 2] for a reference). Thus, by the Portmanteau Theorem,(2.7) implies
for all A ∈ ℬ(ℝd \{0}) with ![]() [$0 \notin \overline A $ and ν(∂A) = 0. This result naturally extends to a general starting point x: for every x ∈ ℝd,
[$0 \notin \overline A $ and ν(∂A) = 0. This result naturally extends to a general starting point x: for every x ∈ ℝd, ![]() [$\mathop {\lim }\nolimits_{t \searrow 0} {\textstyle{1 \over t}}{^x}({L_t} - x \in A) = \nu (A)$ by translation invariance of a Lévy process. Until recently, an analogous statement of the above for Feller processes was not known. However, Kühn and Schilling [Reference Kühn and Schilling16] proved such a statement for these processes.
[$\mathop {\lim }\nolimits_{t \searrow 0} {\textstyle{1 \over t}}{^x}({L_t} - x \in A) = \nu (A)$ by translation invariance of a Lévy process. Until recently, an analogous statement of the above for Feller processes was not known. However, Kühn and Schilling [Reference Kühn and Schilling16] proved such a statement for these processes.
Theorem 2.2. (Kühn, Schilling (2016) [Reference Kühn and Schilling16], Corollary 3.3.) Let X = (Xt) t ≥ 0 be a rich Feller process with symbol p (x, ξ) and characteristics (b(x), (x), ν (x, dy)). If f ∈ C 0(ℝd) and f |B(0, δ) = 0 for some δ > 0, then
 [$$\mathop {\lim }\limits_{t \searrow 0} {1 \over t}{^x}f({X_t} - x) = \int_{{^d}\backslash \{ 0\} } f(y)\nu (x,{\rm{d}}y).$$
[$$\mathop {\lim }\limits_{t \searrow 0} {1 \over t}{^x}f({X_t} - x) = \int_{{^d}\backslash \{ 0\} } f(y)\nu (x,{\rm{d}}y).$$
Additionally, by the Portmanteau Theorem,
for all A ∈ ℬ(ℝd \{0}) such that ![]() [$0 \notin \overline A $ and ν (x, ∂) = 0.
[$0 \notin \overline A $ and ν (x, ∂) = 0.
The small-time asymptotics given by Theorem 2.2 give us a direct connection between the Lévy measure and the Feller process, avoiding the representation of the generator. Also, note that the result holds for more general, locally bounded symbols.
Our interest focuses on jump-Feller processes, i.e. X ~ (b(x), 0, ν(x, dy)), since the association of diffusion processes X ~ (b(x), (x), 0) was completed by Mu-Fa Chen [Reference Chen and Wang7]. In the following section, we will prove a sufficient and necessary condition for the jump-Feller process to be associated, WA, PSA, PSD, POD, PUOD, and PLOD in space, where the condition is
Remark 2.2. We note that Jie Ming Wang [Reference Wang32, Theorem 1.4] proved that spatial association is equivalent to (2.8) under certain continuity and integrability conditions (unknown to the author at the time). These assumptions include the following:
bi, ij ∈ C(ℝd), for all i, j,
∫ hi(z)(ν(⋅, dz) − ν(⋅, d(−z))) ∈ C(ℝd), where h: ℝd → ℝd is defined by
 [$${h_i}(z) = {\rm{sgn}}({z_i})(1 \wedge |{z_i}|),$$
[$${h_i}(z) = {\rm{sgn}}({z_i})(1 \wedge |{z_i}|),$$
∫ A |h(z)|2ν(⋅, dz) ∈ C(ℝd) for all A ∈ ℬ(ℝd),
∫ g(z)ν(⋅, dz) ∈ C(ℝd) for any g ∈Cb(ℝd) that is 0 near the origin.
We relax these conditions, and furthermore our work includes characterizations of the other dependence structures mentioned in Definitions 2.1–2.7.

Figure 2: Equivalence of dependences under condition (2.8) for Feller processes.
3. Main results
Consider a rich Feller process X = (Xt)t ≥ 0 on the space ![]() [${(\Omega ,{\cal G},({{\cal G}_t}{)_{t \ge 0}},{^x})_{x \in {^d}}}$ with Lévy characteristics (b(x), 0, ν(x, dy)). If we assume that X is stochastically monotone, then condition (2.8) is a necessary and sufficient condition for the association, WA, PSA, PSD, POD, PUOD, and PLOD in the space of the process X. These equivalences can be illustrated in the implication map in Figure 2. The dashed arrows are the implications we will prove.
[${(\Omega ,{\cal G},({{\cal G}_t}{)_{t \ge 0}},{^x})_{x \in {^d}}}$ with Lévy characteristics (b(x), 0, ν(x, dy)). If we assume that X is stochastically monotone, then condition (2.8) is a necessary and sufficient condition for the association, WA, PSA, PSD, POD, PUOD, and PLOD in the space of the process X. These equivalences can be illustrated in the implication map in Figure 2. The dashed arrows are the implications we will prove.
To show these equivalences, we first give a proof that, under stochastic monotonicity, condition (2.8) is equivalent to association in space. We show this in Section 3.1. Then, in Section 3.2, we show that PUOD in space (and, similarly, PLOD) implies condition (2.8).
3.1. Association is equivalent to condition (2.8)
Theorem 3.1. Let X = (Xt)t ≥ 0 be a rich Feller process with stochastically monotone transition semigroup (Tt)t ≥ 0, a generator (𝒜,𝒟(𝒜)), bounded symbol p(x, ξ), and (b(x), 0, ν(x, dy)). Then Xt is associated for all t ≥ 0 if and only if (2.8), ![]() [$\nu (x,(_ + ^d \cup _ - ^d{)^c}) = 0$, is satisfied.
[$\nu (x,(_ + ^d \cup _ - ^d{)^c}) = 0$, is satisfied.
We prove this by first showing that association of X t is equivalent to a Liggett-type inequality for the extended generator, the statement of which is in the following theorem.
Theorem 3.2. Let X = (Xt)t ≥ 0 be a rich Feller processes with stochastically monotone transition semigroup (Tt)t ≥ 0, a generator (𝒜,𝒟(𝒜)), bounded symbol p(x, ξ), and an (extended) integro-differential operator I(p). Assume x → p(x, 0) is continuous. Then
if and only if, for all t ≥ 0,
Inequality (3.2) in Theorem 3.2 is another way to formulate that Xt is associated for all t ≥ 0. Since (3.2) means, for all x ∈ ℝd, 𝔼xf (Xt)g(Xt) ≥ 𝔼xf (Xt) 𝔼xg(Xt), then Xt is associated with respect to ℙx. Inequality (3.1) intuitively means that the process moves either up or down, which, in multidimensional Euclidean space, means that if the process is currently at point x, then it can only move to another point y if y ≥ x or y ≤ x component-wise.
Note that in Theorem 3.2 we are using the extended generator I(p). In previous statements of Liggett’s characterization, the generator 𝒜 is used, but we need to use I(p) for the reasons given in the comments after Theorem 2.1. Hence, it is necessary to show the Liggett-type inequality as a characterization of association for rich Feller processes. Such an extension has not been seen by the author of this paper. We first need the following lemmas to prove Theorem 2.1. We will often assume Setting 3.1 throughout this section.
Setting 3.1. Let X = (Xt)t ≥ 0 be a rich Feller process, semigroup (Tt)t ≥ 0, generator (𝔸,𝒟(𝒜)), symbol p(x, ξ), (extended) integro-differential operator I(p), and characteristics
where b, ∑, ν are the same as before, except that we have an additional characteristic a: ℝd → ℝ+ which represents the ‘killing rate’.
Remark 3.1. With the additional characteristic a(x), function −p(x, ξ) would look like a(x) + the right-hand side of equation (2.3). Also, I(p)f (x) would look like −a(x) f (x) + the right-hand side of equation (2.5). Unless stated otherwise, we will assume that a(x) ≡ 0. For more on the case when a(x) ≡ 0, see the paper by Schnurr [Reference Schnurr28], which discusses such processes satisfying a(x) ≡ 0 and their connection to the symbol.
Lemma 3.1. Assume Setting 3.1 and that p(x, ξ) is bounded. Then I(p) generates the semigroup (Tt)t ≥ 0 locally uniformly, i.e.
where the convergence is locally uniform.
For a detailed proof, see the appendix.
Lemma 3.2. Assume Setting 3.1 and the symbol p(x, ξ) is bounded. For all ![]() [$f \in C_b^2({^d})$,
[$f \in C_b^2({^d})$,
where the derivative is defined based on locally uniform convergence.
For a detailed proof, see the appendix. Finally, we can extend Liggett’s solution to a Cauchy problem [Reference Liggett18, Theorem 2.5, p. 19] to integro-differential operators that generate a semigroup locally uniformly.
Lemma 3.3. (Cauchy problem.) Let (𝒜,𝒟(𝒜)) be a (rich) Feller generator of a semigroup (Tt)t ≥ 0 with bounded Lévy characteristics and symbol p(x, ξ) Let I(p) be the extended generator on ![]() [$C_b^2({^d})$. Suppose F, G: [0, ∞) → Cb(ℝd) such that
[$C_b^2({^d})$. Suppose F, G: [0, ∞) → Cb(ℝd) such that
(a) F(t) ∈ 𝒟(I(p)) for all t ≥ 0,
(b) G(t) is continuous on [0, ∞) (locally uniformly),
(c) F(t) = I(p)F(t) + G(t) for all t ≥ 0.
Then ![]() [$F(t) = {T_t} f(0) + \int_0^t {T_{t - s}}G(s) {\rm{d}}s$.
[$F(t) = {T_t} f(0) + \int_0^t {T_{t - s}}G(s) {\rm{d}}s$.
For a detailed proof, see the appendix. We are now ready to prove the main theorems of this section.
Proof of Theorem 3.2. (⇐) Assume Tt fg ≥ Tt fTtg for all ![]() [$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. This implies
[$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. This implies
Hence, for all t > 0, 1 t
Therefore,
 [$$\matrix{{I(p) fg = \mathop {\lim }\limits_{t \searrow 0} {1 \over t}({T_t} fg - fg) \ge \mathop {\lim }\limits_{t \searrow 0} ({T_t} f\,{{{T_t}g - g} \over t} + g\,{{{T_t} f - f} \over t})} \hfill \cr { = (\mathop {\lim }\limits_{t \searrow 0} {T_t} f)\,(\mathop {\lim }\limits_{t \searrow 0} {{{T_t}g - g} \over t}) + g\,(\mathop {\lim }\limits_{t \searrow 0} {{{T_t} f - f} \over t})} \hfill \cr { = fI(p)g + gI(p) f,} \hfill \cr } $$
[$$\matrix{{I(p) fg = \mathop {\lim }\limits_{t \searrow 0} {1 \over t}({T_t} fg - fg) \ge \mathop {\lim }\limits_{t \searrow 0} ({T_t} f\,{{{T_t}g - g} \over t} + g\,{{{T_t} f - f} \over t})} \hfill \cr { = (\mathop {\lim }\limits_{t \searrow 0} {T_t} f)\,(\mathop {\lim }\limits_{t \searrow 0} {{{T_t}g - g} \over t}) + g\,(\mathop {\lim }\limits_{t \searrow 0} {{{T_t} f - f} \over t})} \hfill \cr { = fI(p)g + gI(p) f,} \hfill \cr } $$
where the convergence is locally uniform.
(⇒) Assume I(p) fg ≥ fI(p)g + gI(p) f for all f, ![]() [$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. By monotonicity, Tt f,
[$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. By monotonicity, Tt f, ![]() [${T_t} f,{T_t}g \in C_b^2({^d}) \cap {{\cal F}_i}$, which implies
[${T_t} f,{T_t}g \in C_b^2({^d}) \cap {{\cal F}_i}$, which implies
Define F(t) := Tt fg − Tt fTtg. Then, by Lemma 3.2, we have
 [$$\matrix{ {F'(t) = I(p){T_t} fg - ({T_t} f[I(p){T_t}g] + {T_t}g[I(p){T_t} f]) \ge I(p){T_t} fg - (I(p){T_t} f\,{T_t}g)} \hfill \cr { = I(p)({T_t} fg - {T_t} f\,{T_t}g)} \hfill \cr { = I(p)F(t),} \hfill \cr } $$
[$$\matrix{ {F'(t) = I(p){T_t} fg - ({T_t} f[I(p){T_t}g] + {T_t}g[I(p){T_t} f]) \ge I(p){T_t} fg - (I(p){T_t} f\,{T_t}g)} \hfill \cr { = I(p)({T_t} fg - {T_t} f\,{T_t}g)} \hfill \cr { = I(p)F(t),} \hfill \cr } $$
where the inequality comes from (3.3). Define G(t) := F (t) − I(p)F(t) ≥ 0. Then, by Lemma 3.3, the solution to the Cauchy problem F′ (t) = G(t) + I(p)F(t)is given by
 [$$F(t) = {T_t} f(0) + \int_0^t {T_{t - s}}G(s) {\rm{d}}s = \int_0^t {T_{t - s}}G(s) {\rm{d}}s$$
[$$F(t) = {T_t} f(0) + \int_0^t {T_{t - s}}G(s) {\rm{d}}s = \int_0^t {T_{t - s}}G(s) {\rm{d}}s$$
since F(0) = 0. Since G(s) ≥ 0 for all s, and Tt −s is a positivity-preserving linear operator, F(t) ≥ 0 for all t ≥ 0. Thus, Tt fg ≥ Tt f ⋅ Ttg for all f, ![]() [$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. This inequality also holds for all f, g ∈ Cb(ℝd) ∩ℱi, since we can approximate nondecreasing, continuous, bounded functions by nondecreasing smooth, bounded functions, and then use a dominated convergence argument.
[$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. This inequality also holds for all f, g ∈ Cb(ℝd) ∩ℱi, since we can approximate nondecreasing, continuous, bounded functions by nondecreasing smooth, bounded functions, and then use a dominated convergence argument.
Remark 3.2. For the necessary condition, we did not need stochastic monotonicity.
Proof of Theorem 3.1. ( ⇐)Fix x ∈ ℝd. Assume ![]() [$\nu (x,(_ + ^d \cup _ - ^d{)^c}) = 0$. Then, for all f,
[$\nu (x,(_ + ^d \cup _ - ^d{)^c}) = 0$. Then, for all f, ![]() [$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$,
[$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$,
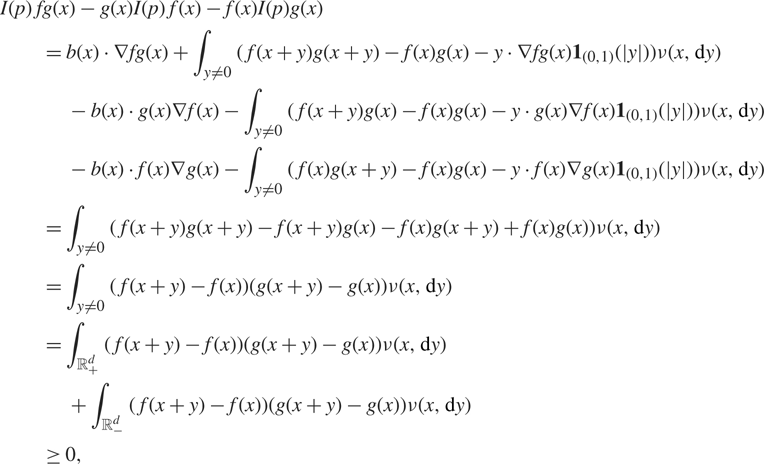 [$$\matrix{ {I(p) fg(x) - g(x)I(p) f(x) - f(x)I(p)g(x)} \hfill \cr {\quad \quad = b(x) \cdot \nabla fg(x) + \int_{y \ne 0} (\,f(x + y)g(x + y) - f(x)g(x) - y \cdot \nabla fg(x{{)1}_{(0,1)}}(|y|))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \quad - b(x) \cdot g(x)\nabla f(x) - \int_{y \ne 0} (\,f(x + y)g(x) - f(x)g(x) - y \cdot g(x)\nabla f(x{{)1}_{(0,1)}}(|y|))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \quad - b(x) \cdot f(x)\nabla g(x) - \int_{y \ne 0} (\,f(x)g(x + y) - f(x)g(x) - y \cdot f(x)\nabla g(x{{)1}_{(0,1)}}(|y|))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad = \int_{y \ne 0} (\,f(x + y)g(x + y) - f(x + y)g(x) - f(x)g(x + y) + f(x)g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad = \int_{y \ne 0} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad = \int_{_ + ^d} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \quad + \int_{_ - ^d} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \ge 0,} \hfill \cr } $$
[$$\matrix{ {I(p) fg(x) - g(x)I(p) f(x) - f(x)I(p)g(x)} \hfill \cr {\quad \quad = b(x) \cdot \nabla fg(x) + \int_{y \ne 0} (\,f(x + y)g(x + y) - f(x)g(x) - y \cdot \nabla fg(x{{)1}_{(0,1)}}(|y|))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \quad - b(x) \cdot g(x)\nabla f(x) - \int_{y \ne 0} (\,f(x + y)g(x) - f(x)g(x) - y \cdot g(x)\nabla f(x{{)1}_{(0,1)}}(|y|))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \quad - b(x) \cdot f(x)\nabla g(x) - \int_{y \ne 0} (\,f(x)g(x + y) - f(x)g(x) - y \cdot f(x)\nabla g(x{{)1}_{(0,1)}}(|y|))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad = \int_{y \ne 0} (\,f(x + y)g(x + y) - f(x + y)g(x) - f(x)g(x + y) + f(x)g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad = \int_{y \ne 0} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad = \int_{_ + ^d} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \quad + \int_{_ - ^d} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr {\quad \quad \ge 0,} \hfill \cr } $$
where the drift terms and the cut-off term in the integrand vanish because
Additionally, we get positivity at the end there because, for all ![]() [$y \in _ + ^d$, f (x + y) − f (x) ≥ 0, and g(x + y) − g(x) ≥ 0, so ( f (x + y) − f (x))(g(x + y) − g(x)) ≥ 0 on
[$y \in _ + ^d$, f (x + y) − f (x) ≥ 0, and g(x + y) − g(x) ≥ 0, so ( f (x + y) − f (x))(g(x + y) − g(x)) ≥ 0 on ![]() [$_ + ^d$. A similar result holds on
[$_ + ^d$. A similar result holds on ![]() [$_ - ^d$. By Theorem 3.1, this implies Tt fg(x) ≥ Tt f (x)Ttg(x), where
[$_ - ^d$. By Theorem 3.1, this implies Tt fg(x) ≥ Tt f (x)Ttg(x), where ![]() [$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. Now, to obtain association of Xt, this inequality needs to hold for all
[$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$. Now, to obtain association of Xt, this inequality needs to hold for all ![]() [$f,g \in {C_b}({^d}) \cap {{\cal F}_i}$. However, we can use an approximation of a function f ∈ Cb(ℝd) ∩ℱi by
[$f,g \in {C_b}({^d}) \cap {{\cal F}_i}$. However, we can use an approximation of a function f ∈ Cb(ℝd) ∩ℱi by ![]() [${f_n} \in C_b^\infty ({^d}) \cap {{\cal F}_i}$, which gives us the desired result.
[${f_n} \in C_b^\infty ({^d}) \cap {{\cal F}_i}$, which gives us the desired result.
(⇒) Assume that Xt is associated for all t ≥ 0. This means Tt fg(x) ≥ Ttf (x)Ttg(x) for all x ∈ ℝd, for all ![]() [$f,g \in {C_b}({^d}) \cap {{\cal F}_i}$. So this inequality of course holds for
[$f,g \in {C_b}({^d}) \cap {{\cal F}_i}$. So this inequality of course holds for ![]() [$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$ which yields I(p)fg ≥ gI(p) f + fI(p)g for such f, g by Theorem 3.1. This implies, by a similar calculation in the ( ⇐ ) direction, that
[$f,g \in C_b^2({^d}) \cap {{\cal F}_i}$ which yields I(p)fg ≥ gI(p) f + fI(p)g for such f, g by Theorem 3.1. This implies, by a similar calculation in the ( ⇐ ) direction, that
 [$$\int_{y \ne 0} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y) \ge 0.$$
[$$\int_{y \ne 0} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y) \ge 0.$$
For simplicity, assume d = 2, but note that we can easily generalize this result to higher dimensions using correction functions. Fix x = (x 1, x 2) ∈ ℝ2. Assume for contradiction that Resnick’s condition is not satisfied. Without loss of generality, let us say ν(x, (0, ∞) × (−∞, 0)) > 0. By continuity of measure, there exists a > 0 such that ν(x, (a, ∞) × (−∞, a)) > 0. Let ε ∈ (0, 1), and define ![]() [$f,g \in C_b^\infty ({^2}) \cap {{\cal F}_i}$ by
[$f,g \in C_b^\infty ({^2}) \cap {{\cal F}_i}$ by
 [$$f({y_1},{y_2}) = \left( {\matrix{ 0 & {{\rm{if}}{{\rm{y}}_{\rm{1}}} \le {{\rm{x}}_{\rm{1}}} + \varepsilon {\rm{a,}}} \cr 1 & {{\rm{if}}{{\rm{y}}_{\rm{1}}} \ge {{\rm{x}}_{\rm{1}}} + {\rm{a,}}} \cr {} & {} \cr } } \right.\quad \quad g({y_1},{y_2}) = \left( {\matrix{ 0 & {{\rm{if}}{{\rm{y}}_{\rm{2}}} \ge {{\rm{x}}_{\rm{2}}} - \varepsilon {\rm{a,}}} \cr { - 1} & {{\rm{if}}{{\rm{y}}_{\rm{2}}} \le {{\rm{x}}_{\rm{2}}} - {\rm{a}}{\rm{.}}} \cr {} & {} \cr } } \right.$$
[$$f({y_1},{y_2}) = \left( {\matrix{ 0 & {{\rm{if}}{{\rm{y}}_{\rm{1}}} \le {{\rm{x}}_{\rm{1}}} + \varepsilon {\rm{a,}}} \cr 1 & {{\rm{if}}{{\rm{y}}_{\rm{1}}} \ge {{\rm{x}}_{\rm{1}}} + {\rm{a,}}} \cr {} & {} \cr } } \right.\quad \quad g({y_1},{y_2}) = \left( {\matrix{ 0 & {{\rm{if}}{{\rm{y}}_{\rm{2}}} \ge {{\rm{x}}_{\rm{2}}} - \varepsilon {\rm{a,}}} \cr { - 1} & {{\rm{if}}{{\rm{y}}_{\rm{2}}} \le {{\rm{x}}_{\rm{2}}} - {\rm{a}}{\rm{.}}} \cr {} & {} \cr } } \right.$$
This implies f (x) = g(x) = 0. Hence,
 [$$\matrix{ {0 \le \int_{y \ne 0} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr { = \int_{y \ne 0} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr { = \int_{(a,\infty ) \times ( - \infty , - a)} f(x + y)g(x + y)\nu (x,{\rm{d}}y) + \int_{(a,\infty ) \times [ - a, - \varepsilon a]} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr {\quad + \int_{[\varepsilon a,a] \times ( - \infty , - a)} f(x + y)g(x + y)\nu (x,{\rm{d}}y) + \int_{[\varepsilon a,a] \times [ - a, - \varepsilon a]} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr { = - \nu (x,(a,\infty ) \times ( - \infty , - a)) - \int_{(a,\infty ) \times [ - a, - \varepsilon a]} g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr {\quad + \int_{[\varepsilon a,a] \times ( - \infty , - a)} f(x + y)\nu (x,{\rm{d}}y) + \int_{[\varepsilon a,a] \times [ - a, - \varepsilon a]} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr { \le - \nu (x,(a,\infty ) \times ( - \infty , - a)),} \hfill \cr } $$
[$$\matrix{ {0 \le \int_{y \ne 0} (\,f(x + y) - f(x))(g(x + y) - g(x))\nu (x,{\rm{d}}y)} \hfill \cr { = \int_{y \ne 0} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr { = \int_{(a,\infty ) \times ( - \infty , - a)} f(x + y)g(x + y)\nu (x,{\rm{d}}y) + \int_{(a,\infty ) \times [ - a, - \varepsilon a]} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr {\quad + \int_{[\varepsilon a,a] \times ( - \infty , - a)} f(x + y)g(x + y)\nu (x,{\rm{d}}y) + \int_{[\varepsilon a,a] \times [ - a, - \varepsilon a]} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr { = - \nu (x,(a,\infty ) \times ( - \infty , - a)) - \int_{(a,\infty ) \times [ - a, - \varepsilon a]} g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr {\quad + \int_{[\varepsilon a,a] \times ( - \infty , - a)} f(x + y)\nu (x,{\rm{d}}y) + \int_{[\varepsilon a,a] \times [ - a, - \varepsilon a]} f(x + y)g(x + y)\nu (x,{\rm{d}}y)} \hfill \cr { \le - \nu (x,(a,\infty ) \times ( - \infty , - a)),} \hfill \cr } $$
implying ν(x, (a, ∞) × (−∞, −a)) ≤ 0. Hence, ν(x, (a, ∞) × (−∞, −a)) = 0, a contradiction.
3.2. PUOD implies condition (2.8)
Lemma 3.4. If Y = (Y 1, ..., Yd) is PUOD, then ![]() [$({Y_{{k_1}}}, \ldots ,{Y_{{k_n}}})$ is PUOD for all multi-indices
[$({Y_{{k_1}}}, \ldots ,{Y_{{k_n}}})$ is PUOD for all multi-indices ![]() [$\{ {k_j}\} _{j = 1}^n \subset \{ 1, \ldots ,d\}$.
[$\{ {k_j}\} _{j = 1}^n \subset \{ 1, \ldots ,d\}$.
Proof. If Y PUOD, then we know ![]() [$(\prod\nolimits_{i = 1}^d {f_i}({Y_i})) \ge \prod\nolimits_{i = 1}^d {f_i}({Y_i})$, where fi : ℝ → ℝ+ non-decreasing. So for all
[$(\prod\nolimits_{i = 1}^d {f_i}({Y_i})) \ge \prod\nolimits_{i = 1}^d {f_i}({Y_i})$, where fi : ℝ → ℝ+ non-decreasing. So for all ![]() [$i \in \{ 1, \ldots ,d\} \backslash \{ {k_j}\} _{j = 1}^n$, set fi = 1ℝ. Then the above inequality becomes
[$i \in \{ 1, \ldots ,d\} \backslash \{ {k_j}\} _{j = 1}^n$, set fi = 1ℝ. Then the above inequality becomes
 [$$(\prod\limits_{j = 1}^n {f_j}({Y_{{k_j}}})) \ge \prod\limits_{j = 1}^n {f_j}({Y_{{k_j}}}).$$
[$$(\prod\limits_{j = 1}^n {f_j}({Y_{{k_j}}})) \ge \prod\limits_{j = 1}^n {f_j}({Y_{{k_j}}}).$$
Thus, ![]() [$({Y_{{k_1}}}, \ldots ,{Y_{{k_n}}})$ is PUOD.
[$({Y_{{k_1}}}, \ldots ,{Y_{{k_n}}})$ is PUOD.
Theorem 3.3. Let X = (Xt)t ≥ 0 be a rich Feller process with symbol p(x, ξ) and triplet
If X t is PUOD for each t ≥ 0, then condition (2.8) is satisfied, i.e.
Proof. Assume Xt is PUOD (with respect to ℙx) for each t ≥ 0. Fix x = (x 1, ..., xd) ∈ ℝd. Since Xt is PUOD, then Xt − x is PUOD for all t ≥ 0. Assume for contradiction that ν is not concentrated on ![]() [$_ + ^d \cup _ - ^d$. Without loss of generality, say ν(x, (0, ∞)d − 1 × (−∞, 0)) > 0. By continuity of measure, there exists a > 0 such that
[$_ + ^d \cup _ - ^d$. Without loss of generality, say ν(x, (0, ∞)d − 1 × (−∞, 0)) > 0. By continuity of measure, there exists a > 0 such that
and
Then, by Theorem 2.2,
Hence,
 [$$\matrix{ {0 /lt \nu (x,(a,\infty {)^{d - 1}} \times ( - \infty , - a))} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}({X_t} - x \in {{(a,\infty )}^{d - 1}} \times ( - \infty , - a))} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a, \ldots ,X_t^{(d - 1)} - {x_{d - 1}} > a,X_t^{(d)} - {x_d} /lt - a)} \hfill \cr { \le \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a, \ldots ,X_t^{(d - 1)} - {x_{d - 1}} > a,X_t^{(d)} - {x_d} \le - a)} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(\{ X_t^{(1)} - {x_1} > a\} \backslash [\{ X_t^{(1)} - {x_1} > a\} \cap {{\{ X_t^{(2)} - {x_2} > a, \ldots ,X_t^{(d)} - {x_d} \le - a\} }^c}])} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)} \hfill \cr {\quad \quad - {^x}(\{ X_t^{(1)} - {x_1} > a\} \cap {{\{ X_t^{(2)} - {x_2} > a, \ldots ,X_t^{(d)} - {x_d} \le - a\} }^c})]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)} \hfill \cr {\quad \quad - {^x}(\{ X_t^{(1)} - {x_1} > a\} \cap [\{ X_t^{(2)} - {x_2} \le a\} \cup \cdots \cup \{ X_t^{(d)} - {x_d} > - a\} ]])]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)} \hfill \cr {\quad \quad - {^x}(\{ X_t^{(1)} - {x_1} > a,X_t^{(2)} - {x_2} \le a\} \cup \cdots \cup \{ X_t^{(1)} - {x_1} > a,X_t^{(d)} - {x_d} > - a\} ])]} \hfill \cr { \le \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a) - {^x}(X_t^{(1)} - {x_1} > a,X_t^{(d)} - {x_d} > - a])]} \hfill \cr { \le \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a) - {^x}(X_t^{(1)} - {x_1} > a){^x}(X_t^{(d)} - {x_d} > - a])]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)(1 - {^x}(X_t^{(d)} - {x_d} > - a]))]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a){^x}(X_t^{(d)} - {x_d} \le - a])} \hfill \cr { = [\mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a)][\mathop {\lim }\limits_{t \to 0} {^x}(X_t^{(d)} - {x_d} \le - a])]} \hfill \cr { = \nu (x,(a,\infty ) \times {^{d - 1}}){^x}(X_0^{(d)} - {x_d} \le - a)} \hfill \cr { = 0.} \hfill \cr } $$
[$$\matrix{ {0 /lt \nu (x,(a,\infty {)^{d - 1}} \times ( - \infty , - a))} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}({X_t} - x \in {{(a,\infty )}^{d - 1}} \times ( - \infty , - a))} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a, \ldots ,X_t^{(d - 1)} - {x_{d - 1}} > a,X_t^{(d)} - {x_d} /lt - a)} \hfill \cr { \le \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a, \ldots ,X_t^{(d - 1)} - {x_{d - 1}} > a,X_t^{(d)} - {x_d} \le - a)} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(\{ X_t^{(1)} - {x_1} > a\} \backslash [\{ X_t^{(1)} - {x_1} > a\} \cap {{\{ X_t^{(2)} - {x_2} > a, \ldots ,X_t^{(d)} - {x_d} \le - a\} }^c}])} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)} \hfill \cr {\quad \quad - {^x}(\{ X_t^{(1)} - {x_1} > a\} \cap {{\{ X_t^{(2)} - {x_2} > a, \ldots ,X_t^{(d)} - {x_d} \le - a\} }^c})]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)} \hfill \cr {\quad \quad - {^x}(\{ X_t^{(1)} - {x_1} > a\} \cap [\{ X_t^{(2)} - {x_2} \le a\} \cup \cdots \cup \{ X_t^{(d)} - {x_d} > - a\} ]])]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)} \hfill \cr {\quad \quad - {^x}(\{ X_t^{(1)} - {x_1} > a,X_t^{(2)} - {x_2} \le a\} \cup \cdots \cup \{ X_t^{(1)} - {x_1} > a,X_t^{(d)} - {x_d} > - a\} ])]} \hfill \cr { \le \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a) - {^x}(X_t^{(1)} - {x_1} > a,X_t^{(d)} - {x_d} > - a])]} \hfill \cr { \le \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a) - {^x}(X_t^{(1)} - {x_1} > a){^x}(X_t^{(d)} - {x_d} > - a])]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}[{^x}(X_t^{(1)} - {x_1} > a)(1 - {^x}(X_t^{(d)} - {x_d} > - a]))]} \hfill \cr { = \mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a){^x}(X_t^{(d)} - {x_d} \le - a])} \hfill \cr { = [\mathop {\lim }\limits_{t \to 0} {1 \over t}{^x}(X_t^{(1)} - {x_1} > a)][\mathop {\lim }\limits_{t \to 0} {^x}(X_t^{(d)} - {x_d} \le - a])]} \hfill \cr { = \nu (x,(a,\infty ) \times {^{d - 1}}){^x}(X_0^{(d)} - {x_d} \le - a)} \hfill \cr { = 0.} \hfill \cr } $$
We obtain lines 4, 9 by set containment, line 5 by the fact that A ∩ B = A \ (A ∩ Bc), line 10 by Lemma 3.4, and line 14 by Theorem 2.2. This contradiction gives us the desired result.
(i) We could also have shown that PLOD implies condition (2.8)using techniques similar to those above.
(ii) Symbol p(x, ξ) in the above theorem need not be bounded, only locally bounded.
Corollary 3.1. For stochastically monotone jump-Feller processes, i.e. X ~ (b(x), 0, ν(x, dy)) with bounded symbols p(x, ξ), then condition (2.8), ![]() [$\nu (x,(_ + ^d \cup _ - ^d{)^c}) = 0$, is equivalent to X being associated, WA, PSA, PSD, POD, PUOD, and PLOD in space.
[$\nu (x,(_ + ^d \cup _ - ^d{)^c}) = 0$, is equivalent to X being associated, WA, PSA, PSD, POD, PUOD, and PLOD in space.
3.3. Association in time
Our results can also be used to study the temporal association of Feller processes. We first examine the case of Lévy processes, a subclass of Feller processes with constant characteristic triplet (b, Q, ν). For Lévy processes, spatial association is equivalent to temporal association.
Theorem 3.4. Let X = (Xt)t ≥ 0 be a stochastic process in ℝd with independent and stationary increments, i.e. Xt − Xs ⊥⊥ Xs − Xr, for all 0 ≤ r < s < t, and ![]() [${X_t} - {X_s}\matrix{ d \cr = \cr } {X_{t - s}}$ for all 0 ≤ s < t. Then X is associated in time if and only if X is associated in space.
[${X_t} - {X_s}\matrix{ d \cr = \cr } {X_{t - s}}$ for all 0 ≤ s < t. Then X is associated in time if and only if X is associated in space.
Proof. The forward direction is trivial by definition. We only need to prove the backward direction. Assume Xt is associated in ℝd for every t ≥ 0. Choose 0 ≤ t 1 < ⋅⋅⋅ < tn. Then
 [$$\matrix{ {({X_{{t_1}}}, \ldots ,{X_{{t_n}}}) = ({X_{{t_1}}},{X_{{t_1}}} + ({X_{{t_2}}} - {X_{{t_1}}}), \ldots ,{X_{{t_1}}} + ({X_{{t_2}}} - {X_{{t_1}}}) + \cdots + ({X_{{t_n}}} - {X_{{t_{n - 1}}}})).} \cr { = ({X_{{t_1}}}, \ldots ,{X_{{t_1}}}) + (0,{X_{{t_2}}} - {X_{{t_1}}}, \ldots ,{X_{{t_2}}} - {X_{{t_1}}}) + \cdots + (0, \ldots ,0,{X_{{t_n}}} - {X_{{t_{n - 1}}}})} \cr } $$
[$$\matrix{ {({X_{{t_1}}}, \ldots ,{X_{{t_n}}}) = ({X_{{t_1}}},{X_{{t_1}}} + ({X_{{t_2}}} - {X_{{t_1}}}), \ldots ,{X_{{t_1}}} + ({X_{{t_2}}} - {X_{{t_1}}}) + \cdots + ({X_{{t_n}}} - {X_{{t_{n - 1}}}})).} \cr { = ({X_{{t_1}}}, \ldots ,{X_{{t_1}}}) + (0,{X_{{t_2}}} - {X_{{t_1}}}, \ldots ,{X_{{t_2}}} - {X_{{t_1}}}) + \cdots + (0, \ldots ,0,{X_{{t_n}}} - {X_{{t_{n - 1}}}})} \cr } $$
Now observe that by stationary increments, ![]() [${X_{{t_{k + 1}}}} - {X_{{t_k}}}\mathop = \limits^d {X_{{t_{k + 1}} - {t_k}}}$ and
[${X_{{t_{k + 1}}}} - {X_{{t_k}}}\mathop = \limits^d {X_{{t_{k + 1}} - {t_k}}}$ and ![]() [${X_{{t_{k + 1}}}} - {X_{{t_k}}}$ is associated, which makes
[${X_{{t_{k + 1}}}} - {X_{{t_k}}}$ is associated, which makes ![]() [${X_{{t_{k + 1}}}} - {X_{{t_k}}}$ associated (association is preserved under equality in distribution), for all k ∈{1, ..., n − 1}. Further, if
[${X_{{t_{k + 1}}}} - {X_{{t_k}}}$ associated (association is preserved under equality in distribution), for all k ∈{1, ..., n − 1}. Further, if ![]() [$\hat X$ is associated in ℝd, then each block
[$\hat X$ is associated in ℝd, then each block ![]() [$(0, \ldots ,0,\hat X, \ldots ,\hat X)$ is associated in ℝdn, where there are k 0 vectors and (n − k)
[$(0, \ldots ,0,\hat X, \ldots ,\hat X)$ is associated in ℝdn, where there are k 0 vectors and (n − k) ![]() [$(0, \ldots ,0,{X_{{t_{k + 1}}}} - {X_{{t_k}}}, \ldots ,{X_{{t_{k + 1}}}} - {X_{{t_k}}})$ vectors. Therefore, each block
[$(0, \ldots ,0,{X_{{t_{k + 1}}}} - {X_{{t_k}}}, \ldots ,{X_{{t_{k + 1}}}} - {X_{{t_k}}})$ vectors. Therefore, each block ![]() [$({X_{{t_1}}}, \ldots ,{X_{{t_n}}})$ is associated, for each k ∈ {1, ..., n − 1}. By independent increments, each block is independent. Therefore, since the sum of independent random vectors, each of which is associated, is associated, then
[$({X_{{t_1}}}, \ldots ,{X_{{t_n}}})$ is associated, for each k ∈ {1, ..., n − 1}. By independent increments, each block is independent. Therefore, since the sum of independent random vectors, each of which is associated, is associated, then ![]() [$({X_{{t_1}}}, \ldots ,{X_{{t_n}}})$ is associated.
[$({X_{{t_1}}}, \ldots ,{X_{{t_n}}})$ is associated.
Corollary 3.2. Any Lévy process X that is associated in space is also associated in time. Additionally, if X has triplet (b, 0, ν), then X is associated in time if and only if ![]() [$\nu ((_ + ^d \cup _ - ^d{)^c}) = 0$.
[$\nu ((_ + ^d \cup _ - ^d{)^c}) = 0$.
Proof. Any Lévy process has independent and stationary increments, thus the result holds by Theorem 3.4.
We would also like to consider conditions for temporal association of general Feller processes. Early work on this has been done by Harris [Reference Harris12, Corollary 1.2] and Liggett [Reference Liggett18, p. 82] for Feller processes with a countable state space. This can be extended to more general state spaces, as given in the following theorem.
Theorem 3.5. Let X = (Xt)t ≥ 0 be a time-homogeneous, stochastically monotone Feller process on ℝd. If X is spatially associated, and X 0 ~ μ, where μ satisfies
then X is temporally associated.
The proof is similar to Liggett’s proof found in [Reference Liggett18, p. 82]. For details on the proof, we refer the reader to the author’s dissertation [Reference Tu30, p. 59]. Theorem 3.5 yields the following corollary about jump-Feller processes.
4. Examples
We give a collection of interesting Feller processes that satisfy stochastic monotonicity.
4.1. Lévy processes
Any Lévy process satisfies stochastic monotonicity. Let (Tt)t ≥ 0 be a semigroup of a Lévy process. Then, for f ∊ ℱi, we have
Thus monotonicity of function f and of the expectation 𝔼0 gives us Tt f ∊ ℱi.
Let X = (Xt)t ≥ 0 be a jump-Lévy process whose Lévy characteristics look like (b, 0, ν), where there is no state-space dependence. Then ![]() [$\nu ((_ + ^d \cup _ - ^d{)^c}) = 0$ is equivalent to Xt being associated, WA, PSA, PSD, POD, PUOD, and PLOD since all Lévy processes are stochastically monotone. This was proved in [Reference Bäuerle, Blatter and Müller2] for association, PSD, and POD, but not for the other dependence structures. Furthermore, the technique in [Reference Bäuerle, Blatter and Müller2] to prove condition (1.1)is equivalent to PSD and POD, and required Lévy copulas. Our method of short-time asymptotics avoids Lévy copulas altogether, and solely uses the Lévy measure. Additionally, condition (1.1) is equivalent to temporal association of X, by Corollary 3.3.
[$\nu ((_ + ^d \cup _ - ^d{)^c}) = 0$ is equivalent to Xt being associated, WA, PSA, PSD, POD, PUOD, and PLOD since all Lévy processes are stochastically monotone. This was proved in [Reference Bäuerle, Blatter and Müller2] for association, PSD, and POD, but not for the other dependence structures. Furthermore, the technique in [Reference Bäuerle, Blatter and Müller2] to prove condition (1.1)is equivalent to PSD and POD, and required Lévy copulas. Our method of short-time asymptotics avoids Lévy copulas altogether, and solely uses the Lévy measure. Additionally, condition (1.1) is equivalent to temporal association of X, by Corollary 3.3.
4.2. Ornstein–Uhlenbeck process
An Ornstein–Uhlenbeck (OU) process X = (Xt)t ≥ 0 in ℝd is the solution to the general Langevin equation
where λ > 0, L = (Lt)t ≥ 0 ∼ (bL, L, νL) is a Lévy process in ℝd, and x ∊ ℝd. Then the OU process looks like
 [$${X_t} = {{\rm{e}}^{ - \lambda t}}x + \int_0^t {{\rm{e}}^{ - \lambda (t - s)}}{\rm{d}}{L_t}$$
[$${X_t} = {{\rm{e}}^{ - \lambda t}}x + \int_0^t {{\rm{e}}^{ - \lambda (t - s)}}{\rm{d}}{L_t}$$
The semigroup (Tt)t ≥ 0 of this process is called the Mehler semigroup and is given by
Claim 4.1. The OU process is stochastically monotone.
Proof. Let f ∊ Bb(ℝd) be an increasing function. Assume x < y, and fix some t ≥ 0. Then e−λt x < e−λt y. This implies f (e−λt x + z) ≤ f (e−λt y + z) for all z ∊ Rd. Hence,
Thus, Tt f is an increasing function on ℝd.
Process X has a characteristic triplet, (bL − λx, ΣL, νL)[1]. Thus, the characterization of positive dependence (association, WA, PSA, PSD, POD, PUOD, PLOD) is equivalent to ![]() [${\nu _L}((_ + ^d \cup _ - ^d{)^c}) = 0$ when Σ = 0.
[${\nu _L}((_ + ^d \cup _ - ^d{)^c}) = 0$ when Σ = 0.
4.3. Feller’s pseudo-Poisson process
Here we construct a stochastically monotone pseudo-Poisson process. Let S = (S(n))n ∊ ℕ be a homogeneous Markov process taking values in ℝd. Let (q (n))n ∊ ℕ define the n-step transition probabilities,
for all B ∊ ℬ(ℝd). Let Q be the transition operator of S, defined by
for all f ∊ Bb(ℝd), x ∊ ℝd. Note that ![]() [${Q^n}f(x) = \int_{{^d}} f(y){q^{(n)}}(x,{\rm{d}}y)$. Let N = (Nt)t ≥ 0 be a Poisson process with rate λ that is independent of S. Define X = (Xt)t ≥ 0 by subordination:
[${Q^n}f(x) = \int_{{^d}} f(y){q^{(n)}}(x,{\rm{d}}y)$. Let N = (Nt)t ≥ 0 be a Poisson process with rate λ that is independent of S. Define X = (Xt)t ≥ 0 by subordination:
Process X, called Feller’s pseudo-Poisson process, is a Feller process.
The semigroup (Tt)t ≥ 0 and generator 𝒜 of X are given by
 [$$\matrix{ {{T_t} f(x) = {{\rm{e}}^{t[\lambda (Q - I)]}}f(x) = {{\rm{e}}^{ - \lambda t}}\sum\limits_{n = 0}^\infty {{{{(\lambda t)}^n}} \over {n!}}{Q^n}f(x),} \cr {{\cal A}f(x) = \lambda (Q - I) f(x) = \int_{{^d}} [f(y) - f(x)]\lambda q(x,{\rm{d}}y).} \cr } $$
[$$\matrix{ {{T_t} f(x) = {{\rm{e}}^{t[\lambda (Q - I)]}}f(x) = {{\rm{e}}^{ - \lambda t}}\sum\limits_{n = 0}^\infty {{{{(\lambda t)}^n}} \over {n!}}{Q^n}f(x),} \cr {{\cal A}f(x) = \lambda (Q - I) f(x) = \int_{{^d}} [f(y) - f(x)]\lambda q(x,{\rm{d}}y).} \cr } $$
Claim 4.2. If S is a stochastically monotone Markov process, then X is stochastically monotone.
Proof. We will show that if f ∊ ℱi then Tt f ∊ ℱi. Observe that, since S is stochastically monotone, we deduce that q(x, B) is a monotone function in x for any monotone set B ∊ ℬ(ℝd). Additionally, for ![]() [$f \in {B_b}({^d}) \cap {{\cal F}_i},Qf(x) = \int_{{^d}} f(y)q(x,{\rm{d}}y)$ is a monotone function. We show, by induction, that for all n
[$f \in {B_b}({^d}) \cap {{\cal F}_i},Qf(x) = \int_{{^d}} f(y)q(x,{\rm{d}}y)$ is a monotone function. We show, by induction, that for all n
is a nondecreasing function.
For the base case, n = 0, G 0(x) = e−λtf (x) is nondecreasing. For n = 1,
is nondecreasing.
Induction hypothesis. Assume that
is a nondecreasing function.
Inductive step. We have
 [$$\matrix{ {{G_{n + 1}}(x) = {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}{Q^{n + 1}}f(x)} \cr { = {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}\int_{{^d}} f(z)\,{q^{(n + 1)}}(x,{\rm{d}}z)} \cr } \matrix{ { = {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}\int_{{^d}} (\int_{{^d}} f(z)\,{q^{(n)}}(y,{\rm{d}}z))q(x,{\rm{d}}y)} \cr { = : {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}\int_{{^d}} H(y)q(x,{\rm{d}}y),} \cr } $$
[$$\matrix{ {{G_{n + 1}}(x) = {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}{Q^{n + 1}}f(x)} \cr { = {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}\int_{{^d}} f(z)\,{q^{(n + 1)}}(x,{\rm{d}}z)} \cr } \matrix{ { = {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}\int_{{^d}} (\int_{{^d}} f(z)\,{q^{(n)}}(y,{\rm{d}}z))q(x,{\rm{d}}y)} \cr { = : {{\rm{e}}^{ - \lambda t}}{{{{(\lambda t)}^{n + 1}}} \over {(n + 1)!}}\int_{{^d}} H(y)q(x,{\rm{d}}y),} \cr } $$
where ![]() [$H(y) = \int_{{^d}} f(z){q^{(n)}}(y,{\rm{d}}z)$ is a nondecreasing function in y by induction hypothesis, and we have used the Chapman–Kolmogorov equations. Thus, by the base case, the integral
[$H(y) = \int_{{^d}} f(z){q^{(n)}}(y,{\rm{d}}z)$ is a nondecreasing function in y by induction hypothesis, and we have used the Chapman–Kolmogorov equations. Thus, by the base case, the integral ![]() [$\int_{{^d}} H(y)q(x,{\rm{d}}y)$ is nondecreasing in x. Hence we deduce that Gn is a nondecreasing function for all n. Hence, Ttf is nondecreasing, giving us our desired result.
[$\int_{{^d}} H(y)q(x,{\rm{d}}y)$ is nondecreasing in x. Hence we deduce that Gn is a nondecreasing function for all n. Hence, Ttf is nondecreasing, giving us our desired result.
Now, to find the characteristic triplet (b(x), Σ(x), ν(x, dy)), we consider the generator:
 [$$\matrix{ {{\cal A}f(x) = \int_{{^d}} (\,f(z) - f(x))\lambda q(x,{\rm{d}}z)} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x))\lambda q(x,{\rm{d}}z + x)} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x))\lambda \hat q(x,{\rm{d}}z),\quad {\rm{where }}\hat q(x,B)q(x,B + x),} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x) - \nabla f(x) \cdot z\chi (z))\lambda \hat q(x,{\rm{d}}z) + \int_{{^d}} \nabla f(x) \cdot z\chi (z)\lambda \hat q(x,{\rm{d}}z)} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x) - \nabla f(x) \cdot z\chi (z))\lambda \hat q(x,{\rm{d}}z) + \nabla f(x) \cdot (\int_{{^d}} z\chi (z)\lambda \hat q(x,{\rm{d}}z)).} \hfill \cr } $$
[$$\matrix{ {{\cal A}f(x) = \int_{{^d}} (\,f(z) - f(x))\lambda q(x,{\rm{d}}z)} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x))\lambda q(x,{\rm{d}}z + x)} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x))\lambda \hat q(x,{\rm{d}}z),\quad {\rm{where }}\hat q(x,B)q(x,B + x),} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x) - \nabla f(x) \cdot z\chi (z))\lambda \hat q(x,{\rm{d}}z) + \int_{{^d}} \nabla f(x) \cdot z\chi (z)\lambda \hat q(x,{\rm{d}}z)} \hfill \cr { = \int_{{^d}} (\,f(x + z) - f(x) - \nabla f(x) \cdot z\chi (z))\lambda \hat q(x,{\rm{d}}z) + \nabla f(x) \cdot (\int_{{^d}} z\chi (z)\lambda \hat q(x,{\rm{d}}z)).} \hfill \cr } $$
Thus, the Lévy triplet will be (b(x), Σ(x), ν(x, dy)), where
4.4. Bochner’s subordination of a Feller process
Consider a continuous-time Feller process Y = (Y(t))t ≥ 0 with semigroup (Tt)t ≥ 0 and generator (𝒜, 𝒟(𝒜)). Let N = Nt be a subordinator independent of Y with Lévy characteristics (b, λ), i.e. it has Lévy symbol ![]() [$\eta (u) = {\rm{i}}bu + \int_0^\infty ({{\rm{e}}^{{\rm{i}}uy}} - 1)\lambda ({\rm{d}}y)$, where
[$\eta (u) = {\rm{i}}bu + \int_0^\infty ({{\rm{e}}^{{\rm{i}}uy}} - 1)\lambda ({\rm{d}}y)$, where ![]() [$ {{\rm{e}}^{{\rm{i}}u{N_t}}} = {{\rm{e}}^{t\eta (u)}}$. Additionally, we can attain a Laplace transform of the subordinator,
[$ {{\rm{e}}^{{\rm{i}}u{N_t}}} = {{\rm{e}}^{t\eta (u)}}$. Additionally, we can attain a Laplace transform of the subordinator, ![]() [${{\rm{e}}^{ - u{N_t}}} = {{\rm{e}}^{ - t\psi (u)}}$, where
[${{\rm{e}}^{ - u{N_t}}} = {{\rm{e}}^{ - t\psi (u)}}$, where
Function ψ is called the Laplace symbol or Bernstein function of the subordinator. The following is a theorem of Phillips.
Theorem 4.1. (Phillips [Reference Phillips20].) Let X = (Xt)t ≥ 0 be given by the prescription Xt = Y(Nt). Then X is a Feller process with semigroup ![]() [${(T_t^X)_{t \ge 0}}$ and generator (𝒜X, 𝒟(𝒜X)), given by
[${(T_t^X)_{t \ge 0}}$ and generator (𝒜X, 𝒟(𝒜X)), given by
Claim 4.3. If Y is a stochastically monotone Feller process with semigroup (Tt)t ≥ 0, i.e. Ttf ∊ ℱi for f ∊ ℱi, and N = (Nt)t ≥ 0 is a subordinator, then X = (Xt)t ≥ 0 given by Xt = Y(Nt)is a stochastically monotone Feller process.
Proof. We already know that X is Feller with semigroup ![]() [${(T_t^X)_{t \ge 0}}$. So choose f ∊ ℱi ∩ Cb(ℝd). Then Tsf ∊ Fi ∩ Cb(Rd) for all s ≥ 0. Choose x < y. Then Tsf (x) ≤ Tsf (y) for all s ≥ 0. Hence,
[${(T_t^X)_{t \ge 0}}$. So choose f ∊ ℱi ∩ Cb(ℝd). Then Tsf ∊ Fi ∩ Cb(Rd) for all s ≥ 0. Choose x < y. Then Tsf (x) ≤ Tsf (y) for all s ≥ 0. Hence,
Thus, ![]() [$T_t^Xf \in {{\cal F}_i}$.
[$T_t^Xf \in {{\cal F}_i}$.
Let Y have symbol p(x, ξ). Then X = Y(N) is a Feller process with symbol pX(x, ξ) that is given by
This ‘perturbation’ is ‘measured in a suitable scale of anisotropic function spaces’ [Reference Böttcher, Schilling and Wang5, p. 104]. Particularly interesting examples are when N is an α-stable subordinator, inverse Gaussian subordinator, and Gamma subordinator, and Y is a diffusion process Y ∼ (b(x), Q(x), 0).
Example 4.1. Let Y be a stochastically monotone diffusion process in ℝd. This means that Y has Lévy characteristics (b(x), Q(x), 0). Mu-Fa Chen and Feng-yu Wang [Reference Chen and Wang7] proved that such a process is stochastically monotone if and only if qij(x) only depends on xi and xj, and bi(x) ≤ bi(y) whenever x ≤ y with xi = yi. The generator of Y is given by
Let N be an α-stable subordinator with Lévy characteristics (0,λ), where
The generator 𝒜X of process X = Y(N) looks like
Appendix A. Proofs of some lemmas from Section 3
Throughout this appendix, we assume Setting 3.1.
Lemma A.1. (Schilling [Reference Schilling26], Theorem 4.3.) Assume p(x, ξ) is bounded. If x ↦ p(x, 0) is continuous, then (Tt)t ≥ 0 extends to a Cb-Feller semigroup, i.e. it satisfies
(a) Tt : Cb(ℝd) → Cb(ℝd),
(b)
 [$\mathop {\lim }\nolimits_{h \searrow 0} \parallel {T_{t + h}}u - {T_t}u{\parallel _{\infty ,K}} = 0$ for all K ⊂ ℝd compact, u ∊ Cb(ℝd), t ≥ 0, where ||u||∞,K ≔ supy∊K |u(y)|, i.e. locally uniformly continuous.
[$\mathop {\lim }\nolimits_{h \searrow 0} \parallel {T_{t + h}}u - {T_t}u{\parallel _{\infty ,K}} = 0$ for all K ⊂ ℝd compact, u ∊ Cb(ℝd), t ≥ 0, where ||u||∞,K ≔ supy∊K |u(y)|, i.e. locally uniformly continuous.
Proof. For a proof, see [Reference Schilling26, p. 247].
Proof of Lemma 3.1. The process
 [$$M_t^ff({X_t}) - f({X_0}) - \int_0^t I(p) f({X_{s - }}) {\rm{d}}s$$
[$$M_t^ff({X_t}) - f({X_0}) - \int_0^t I(p) f({X_{s - }}) {\rm{d}}s$$
is, for every ![]() [$f \in C_b^2({^d})$, a martingale with respect to ℙx, for all x (see [Reference Schilling27, Lemma 3.2, p. 579]). This implies
[$f \in C_b^2({^d})$, a martingale with respect to ℙx, for all x (see [Reference Schilling27, Lemma 3.2, p. 579]). This implies
 [$$\matrix{ {0 = {^x}f({X_t}) - {^x}f({X_0}) - {^x}\int_0^t I(p) f({X_{s - }}) {\rm{d}}s} \cr { = {T_t} f(x) - f(x) - \int_0^t {^x}I(p) f({X_{s - }}) {\rm{d}}s} \cr { = {T_t} f(x) - f(x) - \int_0^t {T_s}I(p) f(x){\rm{d}}s} \cr } $$
[$$\matrix{ {0 = {^x}f({X_t}) - {^x}f({X_0}) - {^x}\int_0^t I(p) f({X_{s - }}) {\rm{d}}s} \cr { = {T_t} f(x) - f(x) - \int_0^t {^x}I(p) f({X_{s - }}) {\rm{d}}s} \cr { = {T_t} f(x) - f(x) - \int_0^t {T_s}I(p) f(x){\rm{d}}s} \cr } $$
for every x ∊ ℝd, t ≥ 0. Note that we can switch integrals in line 2 because I(p)f ∊ Cb(ℝd)by Remark 4.5(ii) in [Reference Schilling26]. This implies
 [$${1 \over t}({T_t} f - f) = {1 \over t}\int_0^t {T_s}I(p) f {\rm{d}}s.$$
[$${1 \over t}({T_t} f - f) = {1 \over t}\int_0^t {T_s}I(p) f {\rm{d}}s.$$
We argue that when taking the limit as t ↘ 0, the right-hand side converges locally uniformly to I(p) f. Note that since I(p)f ∊ Cb(Rd), then (TsI(p) f )1K is continuous in s for every compact set K by the Cb-Feller property, i.e.
So, the function T (·)I(p) f 1K is the integrand of a Bochner-type integral that is continuous in s and integrable on any closed interval [a, b]. Therefore, by the Fundamental Theorem of Calculus for Bochner integrals [Reference Dynkin10, pp. 21–22],
 [$$\mathop {\lim }\limits_{t \searrow 0} {1 \over t}({T_t} f - f{)1_K} = \mathop {\lim }\limits_{t \searrow 0} {1 \over t}\int_0^t ({T_s}I(p) f{)1_K} {\rm{d}}s = (I(p) f{)1_K}$$
[$$\mathop {\lim }\limits_{t \searrow 0} {1 \over t}({T_t} f - f{)1_K} = \mathop {\lim }\limits_{t \searrow 0} {1 \over t}\int_0^t ({T_s}I(p) f{)1_K} {\rm{d}}s = (I(p) f{)1_K}$$
for all K ⊂ ℝd compact. Hence, ![]() [$I(p)f = \mathop {\lim }\nolimits_{t \searrow 0} {\textstyle{1 \over t}}({T_t} f - f)$, where convergence is locally uniform.
[$I(p)f = \mathop {\lim }\nolimits_{t \searrow 0} {\textstyle{1 \over t}}({T_t} f - f)$, where convergence is locally uniform.
Proof of Lemma 3.2. By Lemma A.1, our semigroup (Tt)t ≥ 0 satisfies the Cb-Feller property. Choose ![]() [$f \in C_b^2({^d})$. Observe that for all x ∊ ℝd,
[$f \in C_b^2({^d})$. Observe that for all x ∊ ℝd,
 [$$\matrix{ {{T_{t + h}}f(x) - {T_t}f(x) = {T_t}({T_h}f(x) - f(x))} \hfill \cr { = {T_t}\int_0^h {T_s}I(p) f(x){\rm{d}}s} \hfill \cr { = {^x}\int_0^h {T_s}I(p) f({X_t}) {\rm{d}}s} \hfill \cr { = \int_0^h {^x}{T_s}I(p) f({X_t}) {\rm{d}}s,\quad {\rm{byFubini's theorem}},} \hfill \cr { = \int_0^h {T_t}{T_s}I(p) f(x) {\rm{d}}s} \hfill \cr { = \int_0^h {T_s}{T_t}I(p) f(x){\rm{d}}s.} \hfill \cr } $$
[$$\matrix{ {{T_{t + h}}f(x) - {T_t}f(x) = {T_t}({T_h}f(x) - f(x))} \hfill \cr { = {T_t}\int_0^h {T_s}I(p) f(x){\rm{d}}s} \hfill \cr { = {^x}\int_0^h {T_s}I(p) f({X_t}) {\rm{d}}s} \hfill \cr { = \int_0^h {^x}{T_s}I(p) f({X_t}) {\rm{d}}s,\quad {\rm{byFubini's theorem}},} \hfill \cr { = \int_0^h {T_t}{T_s}I(p) f(x) {\rm{d}}s} \hfill \cr { = \int_0^h {T_s}{T_t}I(p) f(x){\rm{d}}s.} \hfill \cr } $$
Thus,
 [$$\mathop {\lim }\limits_{h \to 0} {1 \over h}({T_{t + h}}f - {T_t}f) = \mathop {\lim }\limits_{h \to 0} {1 \over h}\int_0^h {T_s}{T_t}I(p) f {\rm{d}}s = {T_t}I(p) f$$
[$$\mathop {\lim }\limits_{h \to 0} {1 \over h}({T_{t + h}}f - {T_t}f) = \mathop {\lim }\limits_{h \to 0} {1 \over h}\int_0^h {T_s}{T_t}I(p) f {\rm{d}}s = {T_t}I(p) f$$
because TtI(p) f ∊ Cb(ℝd) by the Cb-Feller property, thus making TsTtI(p) f 1K continuous in s for every compact K. Once again, by the Fundamental Theorem of Calculus for Bochner integrals (see [Reference Dynkin10, pp. 21–22]), we get the convergence shown above.
Finally, we want to show I(p)Tt f = TtI(p)f. We choose ![]() [${({\phi _n})_{n \in }} \subset C_c^\infty ({^d})$ such that 1B(0,n) ≤ ϕn ≤ 1 for all n. Hence,
[${({\phi _n})_{n \in }} \subset C_c^\infty ({^d})$ such that 1B(0,n) ≤ ϕn ≤ 1 for all n. Hence, ![]() [$f{\phi _n} \in C_c^2({^d}) \subset {\cal D}({\cal A})$, the domain of generator 𝒜, and we have I(p)Ttfϕn = TtI(p) f ϕn. By an approximation argument, we get our desired result.
[$f{\phi _n} \in C_c^2({^d}) \subset {\cal D}({\cal A})$, the domain of generator 𝒜, and we have I(p)Ttfϕn = TtI(p) f ϕn. By an approximation argument, we get our desired result.
Proof of Lemma 3.3. Observe that all limits (and corresponding derivatives) we take here are with respect to locally uniform convergence. Note that by the assumption that x ↦ p(x, 0) is continuous, our semigroup (Tt)t ≥ 0 satisfies the Cb-Feller property by Lemma A.1. Also, by Lemma 3.1, we have ![]() [$\mathop {\lim }\nolimits_{t \searrow 0} {\textstyle{1 \over t}}({T_t}u - u) = I(p)u$ for all
[$\mathop {\lim }\nolimits_{t \searrow 0} {\textstyle{1 \over t}}({T_t}u - u) = I(p)u$ for all ![]() [$u \in C_b^2({^d})$. Observe that we will define the derivative F ′ (s) by
[$u \in C_b^2({^d})$. Observe that we will define the derivative F ′ (s) by
where the limit is under locally uniform convergence. Also, our statement of (b) is different from that of Liggett.
 [$$\matrix{ {{\rm{Liggett's:}}\quad {\rm{if }}{{\rm{t}}_{\rm{n}}} \to {\rm{t, then}}\parallel {\rm{G(}}{{\rm{t}}_{\rm{n}}}{\rm{)}} - {\rm{G(t)}}{\parallel _\infty } \to {\rm{0 as n}} \to \infty {\rm{.}}} \cr {{\rm{Ours: if }}{{\rm{t}}_{\rm{n}}} \to {\rm{t, then}}\parallel {\rm{G(}}{{\rm{t}}_{\rm{n}}}{\rm{)}} - {\rm{G(t)}}{\parallel _{\infty {\rm{,K}}}} \to {\rm{0 as n}} \to \infty \;{\rm{for all K compact}}{\rm{.}}} \cr } $$
[$$\matrix{ {{\rm{Liggett's:}}\quad {\rm{if }}{{\rm{t}}_{\rm{n}}} \to {\rm{t, then}}\parallel {\rm{G(}}{{\rm{t}}_{\rm{n}}}{\rm{)}} - {\rm{G(t)}}{\parallel _\infty } \to {\rm{0 as n}} \to \infty {\rm{.}}} \cr {{\rm{Ours: if }}{{\rm{t}}_{\rm{n}}} \to {\rm{t, then}}\parallel {\rm{G(}}{{\rm{t}}_{\rm{n}}}{\rm{)}} - {\rm{G(t)}}{\parallel _{\infty {\rm{,K}}}} \to {\rm{0 as n}} \to \infty \;{\rm{for all K compact}}{\rm{.}}} \cr } $$
Although Liggett’s assumption would be sufficient, we do not need something that strong in our setting, and our G will satisfy locally uniform continuity. Choosing any compact set K ⊂ ℝd, we have
 [$$\matrix{ {{{{T_{t - s - h}}F(s + h) - {T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad = {{{T_{t - s - h}}F(s + h)} \over h} \cdot {1_K} - {{{T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad \quad + [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K} - [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K}} \hfill \cr {\quad \quad \quad + {{{T_{t - s - h}}F(s)} \over h} \cdot {1_K} - {{{T_{t - s - h}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad \quad + {{{T_{t - s}}F(s + h)} \over h} \cdot {1_K} - {{{T_{t - s}}F(s + h)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad \quad + {{{T_{t - s}}F(s)} \over h} \cdot {1_K} - {{{T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad = : (1) + (2) + (3) + (4) + (5) + (6) + (7) + (8) + (9) + (10)} \hfill \cr {\quad \quad = [(2) + (7)] + [(5) + (10)] + [(3)] + [(4) + (1) + (9) + (8) + (6)]} \hfill \cr {\quad \quad = {T_{t - s}}[{{F(s + h) - F(s)} \over h}] \cdot {1_K} + [{{{T_{t - s - h}} - {T_{t - s}}} \over h}]F(s) \cdot {1_K}} \hfill \cr {\quad \quad \quad + [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K} + [{T_{t - s - h}} - {T_{t - s}}][{{F(s + h) - F(s)} \over h} - F'(s)] \cdot {1_K}} \hfill \cr {\quad \quad = : (I) + (II) + (III) + (IV).} \hfill \cr } $$
[$$\matrix{ {{{{T_{t - s - h}}F(s + h) - {T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad = {{{T_{t - s - h}}F(s + h)} \over h} \cdot {1_K} - {{{T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad \quad + [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K} - [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K}} \hfill \cr {\quad \quad \quad + {{{T_{t - s - h}}F(s)} \over h} \cdot {1_K} - {{{T_{t - s - h}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad \quad + {{{T_{t - s}}F(s + h)} \over h} \cdot {1_K} - {{{T_{t - s}}F(s + h)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad \quad + {{{T_{t - s}}F(s)} \over h} \cdot {1_K} - {{{T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr {\quad \quad = : (1) + (2) + (3) + (4) + (5) + (6) + (7) + (8) + (9) + (10)} \hfill \cr {\quad \quad = [(2) + (7)] + [(5) + (10)] + [(3)] + [(4) + (1) + (9) + (8) + (6)]} \hfill \cr {\quad \quad = {T_{t - s}}[{{F(s + h) - F(s)} \over h}] \cdot {1_K} + [{{{T_{t - s - h}} - {T_{t - s}}} \over h}]F(s) \cdot {1_K}} \hfill \cr {\quad \quad \quad + [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K} + [{T_{t - s - h}} - {T_{t - s}}][{{F(s + h) - F(s)} \over h} - F'(s)] \cdot {1_K}} \hfill \cr {\quad \quad = : (I) + (II) + (III) + (IV).} \hfill \cr } $$
Now we consider the limits as h goes to 0 for each of these four terms.
(I)
because Tt −s is a bounded operator, which means it is a continuous operator. [$$\matrix{ {\mathop {\lim }\limits_{h \searrow 0} {T_{t - s}}[{{F(s + h) - F(s)} \over h}] \cdot {1_K} = {T_{t - s}}\mathop {\lim }\limits_{h \searrow 0} [{{F(s + h) - F(s)} \over h}] \cdot {1_K}} \cr { = {T_{t - s}}F'(s) \cdot {1_K}} \cr } $$
[$$\matrix{ {\mathop {\lim }\limits_{h \searrow 0} {T_{t - s}}[{{F(s + h) - F(s)} \over h}] \cdot {1_K} = {T_{t - s}}\mathop {\lim }\limits_{h \searrow 0} [{{F(s + h) - F(s)} \over h}] \cdot {1_K}} \cr { = {T_{t - s}}F'(s) \cdot {1_K}} \cr } $$
(II) Let u = t − s. Then s = t − u and ds =−du. For a function f ∊ Cb(ℝd),
Therefore, [$$\matrix{ {\mathop {\lim }\limits_{h \searrow 0} [{{{T_{t - s - h}} - {T_{t - s}}} \over h}] f \cdot {1_K} = {{\rm{d}} \over {{\rm{d}}s}}{T_{t - s}}f \cdot {1_K}} \cr { = - {{\rm{d}} \over {{\rm{d}}u}}{T_u}f \cdot {1_K}} \cr { = - I(p){T_u}f \cdot {1_K}} \cr { = - I(p){T_{t - s}}f \cdot {1_K}.} \cr } $$
[$$\matrix{ {\mathop {\lim }\limits_{h \searrow 0} [{{{T_{t - s - h}} - {T_{t - s}}} \over h}] f \cdot {1_K} = {{\rm{d}} \over {{\rm{d}}s}}{T_{t - s}}f \cdot {1_K}} \cr { = - {{\rm{d}} \over {{\rm{d}}u}}{T_u}f \cdot {1_K}} \cr { = - I(p){T_u}f \cdot {1_K}} \cr { = - I(p){T_{t - s}}f \cdot {1_K}.} \cr } $$
 [$$\mathop {\lim }\limits_{h \searrow 0} [{{{T_{t - s - h}} - {T_{t - s}}} \over h}]F(s) \cdot {1_K} = - I(p){T_{t - s}}F(s) \cdot {1_K} = - {T_{t - s}}I(p)F(s) \cdot {1_K}.$$
[$$\mathop {\lim }\limits_{h \searrow 0} [{{{T_{t - s - h}} - {T_{t - s}}} \over h}]F(s) \cdot {1_K} = - I(p){T_{t - s}}F(s) \cdot {1_K} = - {T_{t - s}}I(p)F(s) \cdot {1_K}.$$
(III) By the Cb-Feller property, since F ′ (s) ∊ Cb(ℝd),
 [$\mathop {\lim }\nolimits_{h \searrow 0} [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K} = 0$ uniformly.
[$\mathop {\lim }\nolimits_{h \searrow 0} [{T_{t - s - h}} - {T_{t - s}}]F'(s) \cdot {1_K} = 0$ uniformly.(IV) Observe that T t − s − h and Tt −s are both contractions. Hence,
as h → 0. Thus, we have, for 0 < s < t, [$$\matrix{ {\parallel |[{T_{t - s - h}} - {T_{t - s}}][{{F(s + h) - F(s)} \over h} - F'(s)]{\parallel _{\infty ,K}}} \cr {\quad \quad \le \parallel {T_{t - s - h}} - {T_{t - s}}\parallel \cdot \parallel [{{F(s + h) - F(s)} \over h} - F'(s)]{\parallel _{\infty ,K}}} \cr {\quad \quad \le 2\parallel [{{F(s + h) - F(s)} \over h} - F'(s)]{\parallel _{\infty ,K}} \to 0} \cr } $$
The right-hand side is a continuous function of s because G is a continuous function of s and the semigroup is uniformly continuous on K by the Cb-Feller property. We justify this as follows.
[$$\matrix{ {\parallel |[{T_{t - s - h}} - {T_{t - s}}][{{F(s + h) - F(s)} \over h} - F'(s)]{\parallel _{\infty ,K}}} \cr {\quad \quad \le \parallel {T_{t - s - h}} - {T_{t - s}}\parallel \cdot \parallel [{{F(s + h) - F(s)} \over h} - F'(s)]{\parallel _{\infty ,K}}} \cr {\quad \quad \le 2\parallel [{{F(s + h) - F(s)} \over h} - F'(s)]{\parallel _{\infty ,K}} \to 0} \cr } $$
The right-hand side is a continuous function of s because G is a continuous function of s and the semigroup is uniformly continuous on K by the Cb-Feller property. We justify this as follows. [$$\matrix{ {{{\rm{d}} \over {{\rm{d}}s}}{T_{t - s}}F(s) \cdot {1_K} = \mathop {\lim }\limits_{h \searrow 0} {{{T_{t - (s + h)}}F(s + h) - {T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr { = \mathop {\lim }\limits_{h \searrow 0} [(I) + (II) + (III) + (IV)]} \hfill \cr { = {T_{t - s}}F'(s) \cdot {1_K} - {T_{t - s}}I(p)F(s) \cdot {1_K}} \hfill \cr { = {T_{t - s}}[F'(s) - I(p)F(s)] \cdot {1_K}} \hfill \cr {\mathop = \limits^{{\rm{(c)}}} {T_{t - s}}G(s) \cdot {1_K}.} \hfill \cr } $$
[$$\matrix{ {{{\rm{d}} \over {{\rm{d}}s}}{T_{t - s}}F(s) \cdot {1_K} = \mathop {\lim }\limits_{h \searrow 0} {{{T_{t - (s + h)}}F(s + h) - {T_{t - s}}F(s)} \over h} \cdot {1_K}} \hfill \cr { = \mathop {\lim }\limits_{h \searrow 0} [(I) + (II) + (III) + (IV)]} \hfill \cr { = {T_{t - s}}F'(s) \cdot {1_K} - {T_{t - s}}I(p)F(s) \cdot {1_K}} \hfill \cr { = {T_{t - s}}[F'(s) - I(p)F(s)] \cdot {1_K}} \hfill \cr {\mathop = \limits^{{\rm{(c)}}} {T_{t - s}}G(s) \cdot {1_K}.} \hfill \cr } $$
Let ∊ > 0. Then there exists N such that ||G(sn) − G(s)||∞, K < ∊/2 for all n ≥ N. Also, there exists N ′ such that ![]() [$\parallel {T_{t - {s_n}}}G({s_N}) - {T_{t - s}}G({s_N}){\parallel _{\infty ,K}} = \parallel ({T_{t - {s_n}}} - {T_{t - s}})G({s_N}){\parallel _{\infty ,K}} /lt \varepsilon /2$ for all n ≤ N′, since the semigroup operator is uniformly continuous on compact sets. Let M = max (N, N ′ ). Then,
[$\parallel {T_{t - {s_n}}}G({s_N}) - {T_{t - s}}G({s_N}){\parallel _{\infty ,K}} = \parallel ({T_{t - {s_n}}} - {T_{t - s}})G({s_N}){\parallel _{\infty ,K}} /lt \varepsilon /2$ for all n ≤ N′, since the semigroup operator is uniformly continuous on compact sets. Let M = max (N, N ′ ). Then,
 [$$\matrix{ {\parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad = \parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G({s_M}) + {T_{t - s}}G({s_M}) - {T_{t - s}}G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad \le \parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G({s_M}){\parallel _{\infty ,K}} + \parallel {T_{t - s}}G({s_M}) - {T_{t - s}}G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad \le \parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G({s_M}){\parallel _{\infty ,K}} + \parallel G({s_M}) - G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad /lt {\varepsilon \over 2} + {\varepsilon \over 2}} \hfill \cr {\quad \quad = \varepsilon.} \hfill \cr } $$
[$$\matrix{ {\parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad = \parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G({s_M}) + {T_{t - s}}G({s_M}) - {T_{t - s}}G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad \le \parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G({s_M}){\parallel _{\infty ,K}} + \parallel {T_{t - s}}G({s_M}) - {T_{t - s}}G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad \le \parallel {T_{t - {s_M}}}G({s_M}) - {T_{t - s}}G({s_M}){\parallel _{\infty ,K}} + \parallel G({s_M}) - G(s){\parallel _{\infty ,K}}} \hfill \cr {\quad \quad /lt {\varepsilon \over 2} + {\varepsilon \over 2}} \hfill \cr {\quad \quad = \varepsilon.} \hfill \cr } $$
Therefore we can integrate these functions with respect to s from 0 to t. By the Fundamental Theorem of Calculus for Bochner integrals (see [Reference Dynkin10, pp. 21–22]), we obtain
 [$$\matrix{ {\int_0^t {T_{t - s}}G(s) {\rm{d}}s \cdot {1_K} = \int_0^t {{\rm{d}} \over {{\rm{d}}s}}{T_{t - s}}F(s){\rm{d}}s \cdot {1_K}} \cr { = ({T_{t - t}}F(t) - {T_t} f{{(0))1}_K}} \cr { = (F(t) - {T_t} f{{(0))1}_K}.} \cr } $$
[$$\matrix{ {\int_0^t {T_{t - s}}G(s) {\rm{d}}s \cdot {1_K} = \int_0^t {{\rm{d}} \over {{\rm{d}}s}}{T_{t - s}}F(s){\rm{d}}s \cdot {1_K}} \cr { = ({T_{t - t}}F(t) - {T_t} f{{(0))1}_K}} \cr { = (F(t) - {T_t} f{{(0))1}_K}.} \cr } $$
Since K was an arbitrary compact set, we have established our desired result: ![]() [$F(t) = {T_t} f(0) + \int_0^t {T_{t - s}}G(s){\rm{d}}s$.
[$F(t) = {T_t} f(0) + \int_0^t {T_{t - s}}G(s){\rm{d}}s$.
Acknowledgement
The author would like to thank Dr Jan Rosinski for his helpful advice and guidance regarding the ideas of this paper.









