Introduction
Development of highly intense laser beams has evoked interest in various wave-particle phenomena which are prevalent in laser plasma interactions viz., parametric instabilities (Mori, Reference Mori1994; Fuchs et al., Reference Fuchs, Labaune, Depierreux, Tikhonchuk and Baldis2000), filamentation (Chekalin and Kandidov, Reference Chekalin and Kandidov2013), higher harmonic generation (Gibbon, Reference Gibbon1997), super continuum generation (Corkum et al., Reference Corkum, Rolland and Srinivasan-Rao1986), etc. All these processes have remarkable significance in various applications such as laser-based accelerators (Tajima and Dawson, Reference Tajima and Dawson1979), coherent X-ray sources (Suckewer and Skinner, Reference Suckewer and Skinner1990; Eder et al., Reference Eder, Amendt, Dasilva, London, MacGowan, Matthews, Penetrante, Rosen, Wilksm, Donnelly, Falcone and Strobel1994), and most importantly inertial confinement fusion (ICF) (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Hora, Reference Hora2007). The main impetus for the development of laser plasma physics was provided by the invention of chirped pulse amplification (CPA) technique (Strickland and Mourou, Reference Strickland and Mourou1985) which dramatically increased the laser intensities up to 1022 W/cm2. Diffraction broadening of the laser beam is the harsh limitation in aforesaid applications. Laser propagation in plasma gives rise to the so-called self-action effects due to the dependence of the complex dielectric function on the incident electromagnetic wave intensity such that the plasma serves as a focusing lens for the incident wave. Relativistic self-focusing is a result of quiver motion of plasma electrons with a speed comparable to the speed of light when the intense laser field interacts with plasma. As the quiver motion of electrons is highly relativistic, the mass of electrons increases leading to the change in dielectric properties of plasma and hence refractive index. For simple Gaussian intensity distribution the beam energy is maximum at the center which reduces the plasma frequency by the Lorentz factor γ and correspondingly increases the refractive index which converges the minimum intensity wave fronts toward the center causing self-focusing of the laser beam.
Generation of optical harmonics of the fundamental beam is a vast area of research in plasma physics. The optically nonlinear medium plasma hold promise for converting the laser light into coherent harmonics with higher efficiency and for exploiting higher laser intensities because it imposes no restriction on the strength of incident laser field. Higher harmonic ultraviolet radiation emerging from laser-driven plasmas have applicability in powerful spectroscopy techniques and provide insight into the fundamental properties of plasma as well as plasma parameters such as electrical conductivity, opacity, local electron density, etc. Harmonic radiation enhances the laser penetration to the overdense regions of plasma thus have special relevance to the ICF process. Optical harmonics can be generated through many mechanisms, but excitation of plasma wave at pump frequency is the most common mechanism for higher harmonic generation, particularly second harmonic generation (SHG), in plasma. Plasma waves are the collective oscillations of electrons on a background of heavier, stationary ions and exhibit the intrinsic characteristics of plasma. Nonlinear interactions between the laser beam and the plasma electrons during laser propagation cause the generation of strongly nonlinear plasma waves suitable for particle acceleration in plasma accelerators and higher harmonic generation. This resonantly generated plasma wave further interacts with the pump beam to produce its second harmonics.
Franken et al. (Reference Franken, Hill, Peters and Weinreich1961) have reported the first experimentally generated second harmonics of high intensity laser beam of wavelength 6943 Å through crystalline quartz. Afterward, a lot of work has been carried out on the production and analysis of second harmonic radiation. Rax et al. (Reference Rax, Robiche and Kostyukov2000) analyzed the relativistic SHG with highly intense laser pulses in weakly magnetized plasma by considering the effect of pump depletion, phase matching, and relativistic tapering. Carrasco et al. (Reference Carrasco, Saleh, Teich and Fourkas2006) considered the SHG and third harmonic generation (THG) in a nonlinear optical crystal illuminated by a vector Gaussian beam. Dahiya et al. (Reference Dahiya, Sajal and Sharma2007) developed a 2D particle-in-cell simulation code for the generation of second and third harmonics of an ultrashort laser pulse in an underdense plasma having a density ripple. Faez et al. (Reference Faez, Johnson, Mazurenko and Lagendijk2009) experimentally measured the distribution of the second-harmonic intensity which is generated inside a highly scattering slab of porous gallium phosphide. Purohit et al. (Reference Purohit, Rawat and Gauniyal2016) have reported the effect of self-focused hollow Gaussian laser beam (carrying null intensity in the center) on the excitation of electron plasma wave (EPW) and SHG in collisionless plasma. Singh and Gupta (Reference Singh and Gupta2016) investigated the SHG by the relativistic self-focusing of cosh-Gaussian laser beam in underdense plasma using the method of moments. Recently, Sharma et al. (Reference Sharma, Thakur and Kant2018) observed the influence of density ripple on pulse slippage of THG in plasma.
The perusal of literature shows that, most of the theoretical investigations on SHG in plasma are carried out with the Gaussian intensity distribution of the laser beam. Gaussian modes are the lowest order solution to the free-space paraxial wave equation but real lasers elect to oscillate in higher order Gaussian modes (Siegman, Reference Siegman1986). The higher order solution to the wave equation can take the form either of Hermite–Gaussian functions in rectangular coordinates (Siegman, Reference Siegman1973), or of Laguerre–Gaussian functions in cylindrical coordinates (Courtial et al., Reference Courtial, Dholakia, Allen and Padgett1997). These higher order Gaussian modes are of considerable importance in practical lasers and in optical beam analyses and communication. Recently such class of laser beams such as Hermite–Gaussian, hollow Gaussian, Hermite–cosh-Gaussian is gaining interest among researchers. Patil et al. (Reference Patil, Takale, Navare and Dongare2010) investigated the focusing of Hermite–cosh-Gaussian beams in collisionless magneto plasma in paraxial approximation. Also, paraxial ray approximation has been widely used to study the nonlinear dynamics of laser plasma interactions which takes into account only the paraxial region of the laser beam. Moreover if the intensity distribution of the laser beam is not perfectly Gaussian and the intensity of off-axial part is relatively more than that of axial intensity, as in the case of Hermite–Gaussian profile, the off-axial part cannot be neglected and paraxial approximation leads to large errors in the analysis. Recently, propagation dynamics of Hermite–Gaussian beams (Takale et al., Reference Takale, Navare, Patil, Fulari and Dongare2009; Kant et al., Reference Kant, Wani and Kumar2012) in plasma have been studied using paraxial approximation which is suitable only for m = 0 mode (Gaussian) and not for higher order modes (m = 1, 2, …). This gives strong motivation to use moment theory approach, which is a global approach and takes into account the whole intensity profile of the laser beam. To the best of author's knowledge no earlier investigations on the production of SHG in relativistic plasma have been carried out with Hermite–Gaussian intensity profile of laser beam with method of moments.
This paper is structured as follows: In the section “Theoretical formulation”, the detailed theoretical formulation of dielectric function of plasma under the effect of relativistic electron mass variation and the nonlinear coupled differential equations for beam width parameters in the transverse x and y directions is given. In the section “Plasma wave excitation”, the excitation of EPW and the source term for SHG have been derived. The normalized second-harmonic yield has been obtained in the section “Second-harmonic yield”. The detailed discussion and conclusions drawn from the results of present investigation have been summarized in the sections “Results and discussion” and “Conclusions”, respectively.
Theoretical formulation
The optical wave-field E(x, y, z) of the circularly polarized laser beam having angular frequency ω0 and wave number k 0( = ω0(ϵ 0)1/2/c) propagating in homogeneous plasma along the z-axis is taken as
$$E(x,y,z) = {\rm \psi (}x,y,z{\rm )exp}\lpar {\dot{\iota} \lcub {{\rm \omega}_0t-k_0z} \rcub } \rpar ,$$where ψ(x, y, z) is the complex amplitude of the electric field vector of the Hermite–Gaussian laser beam which is a function of x, y, and z, the transverse co-ordinates in the rectangular co-ordinate system and is given by the following equation:
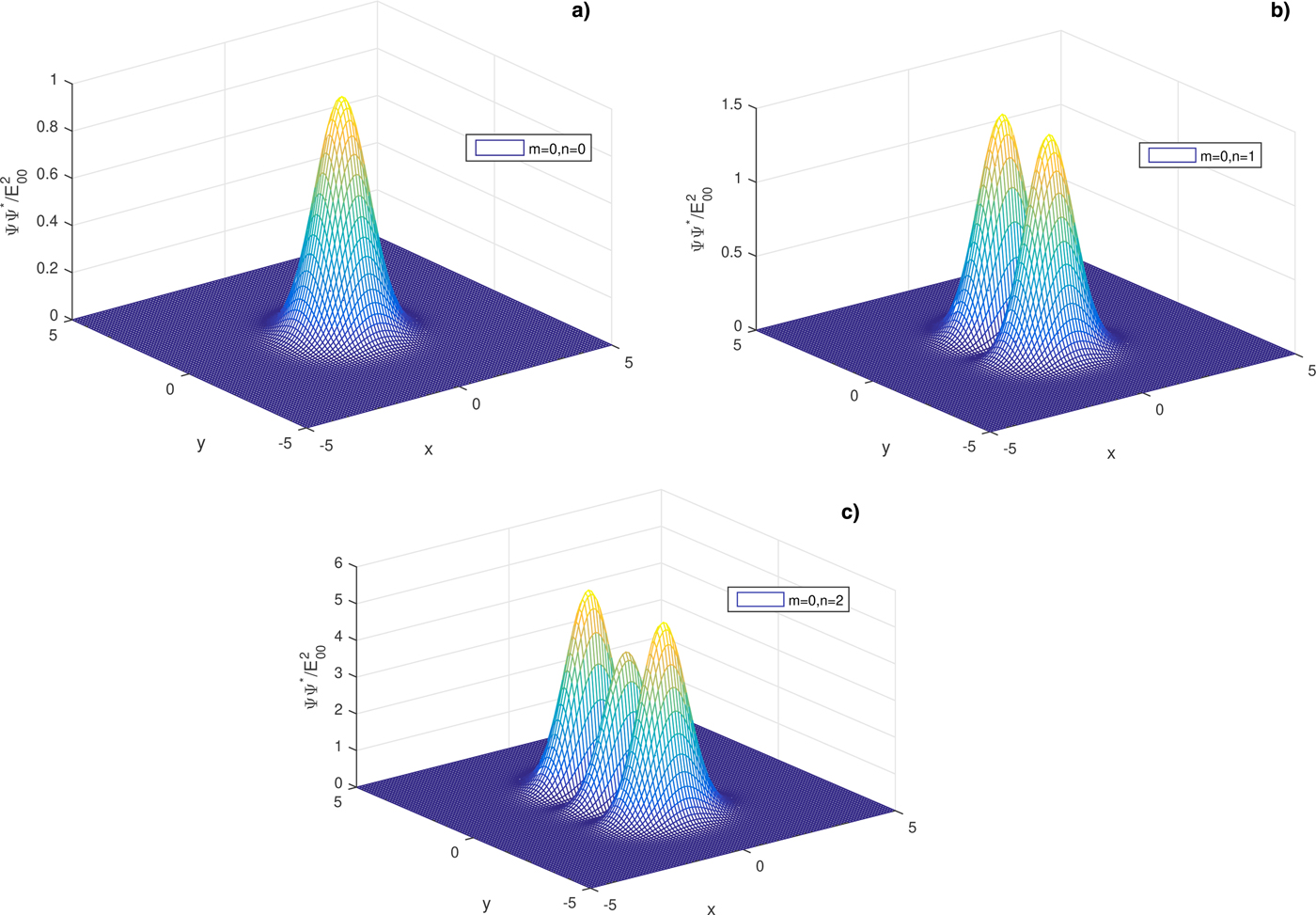
$$\eqalign{{\rm \psi} {\rm \psi} ^{\rm \star} & = \displaystyle{{E_{00}^2} \over {\,f_xf_y}}{\rm exp}\left( {-\left( {\displaystyle{{x^2} \over {a^2f_x^2}} + \displaystyle{{y^2} \over {b^2f_y^2}}} \right)} \right)\cr & \quad \times \left( {H_m\left( {\displaystyle{x \over {af_x}}} \right)} \right)^2\left( {H_n\left( {\displaystyle{y \over {bf_y}}} \right)} \right)^2},$$where E 00 represents the axial amplitude of the electric field of laser beam, af x and bf y are associated with the beam waists in the transverse x and y directions respectively, and H m and H n are the Hermite polynomials of TEM modes (m, n) corresponding to the x and y directions. The mode TEM00 of Hermite polynomial in the abovementioned profile represents the fundamental Gaussian beam. The normalized intensity profiles of first few modes are shown in Figure 1.
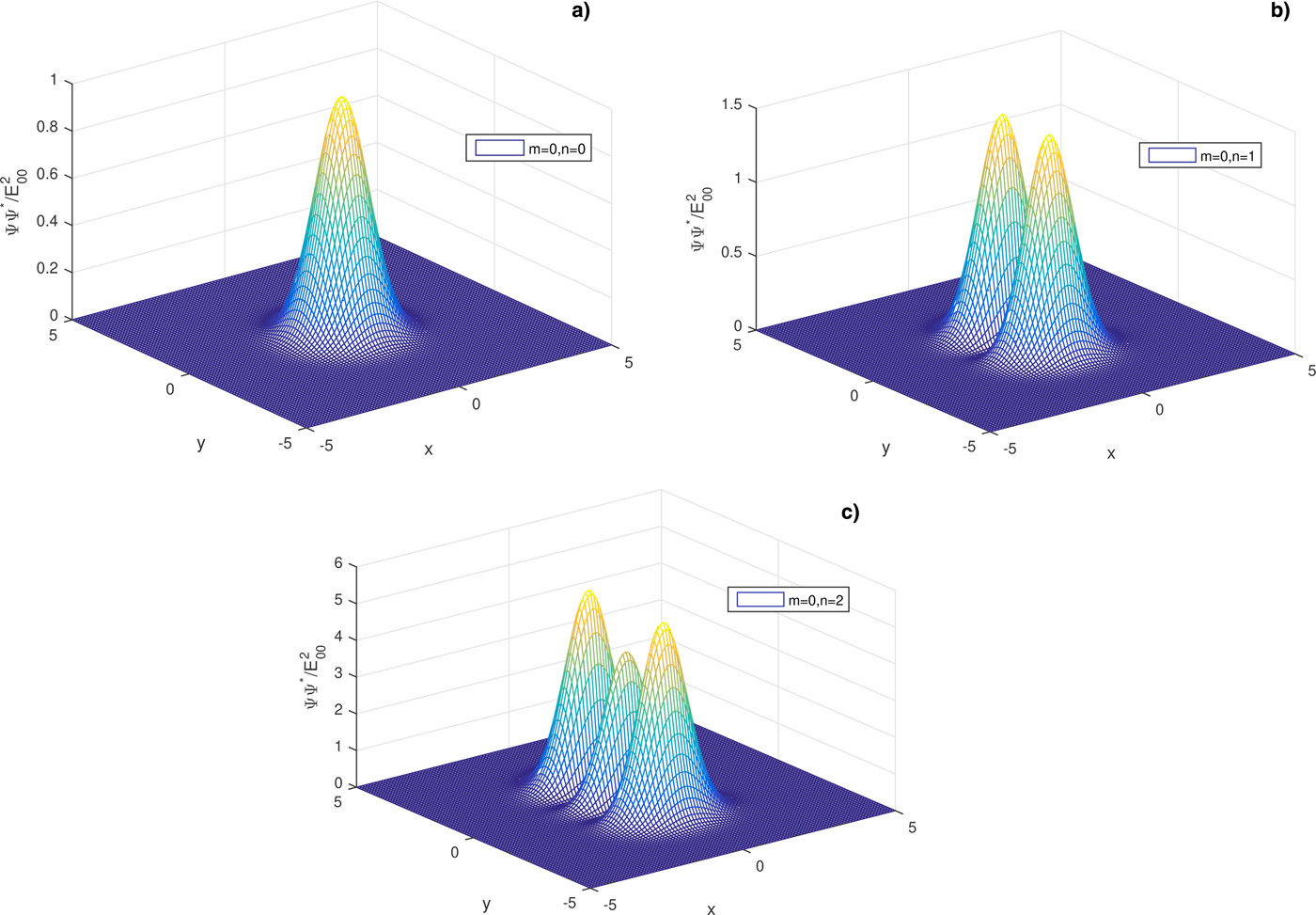
Fig. 1. Normalized intensity distribution of Hermite–Gaussian laser beam with transverse distances x and y for three different modes: (a) TEM00, (b) TEM01, and (c) TEM02.
Propagation of high intensity laser beam alters the properties of plasma as the plasma electrons resonantly respond to the incident beam and the motion becomes highly relativistic with velocity comparable to that of light. Hence refractive index as well as dielectric function of plasma 
$({\rm \epsilon} = 1-{\rm \omega} _{{\rm pe}}^2 /{\rm \omega} _0^2 ;{\rm \;\ \omega} _{{\rm pe}}^2 = 4{\rm \pi} e^2n_{\rm e}/m)$ changes as the mass of electrons m is replaced by the relativistic mass m 0γ. Therefore, the modified dielectric function for plasma can be written in the form of linear and nonlinear parts as:
$${\epsilon} = {\epsilon} _0 + {\rm \Phi (}EE^{\rm \star} {\rm )},$$where
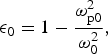$${\epsilon} _0 = 1-\displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} _0^2}}, $$
$${\rm \Phi (}EE^{\rm \star} {\rm )} = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} _0^2}} \left( {1-\displaystyle{1 \over {\rm \gamma}}} \right),$$
$${\rm \gamma} = (1 + {\rm \beta} EE^{\rm \star} )^{1/2}.$$ In Eq. (3) ϵ 0 represents the linear part and 
${\rm \Phi (}EE^{\rm \star} {\rm )}$ determines the nonlinear change in the dielectric function due to the presence of the laser beam.
Under the WKB approximation, the wave field vector of the laser beam satisfies the following wave equation:
$$\nabla ^2{\bf E} + \displaystyle{{{\rm \omega} _0^2} \over {c^2}}{\epsilon} {\bf E} = 0.$$Substituting Eq. (1) in Eq. (7) and using the assumption that the variations in the z direction are slower than those in the transverse directions, we get the following quasi-optic wave equation:
$$\dot{\iota} \displaystyle{{d{\rm \psi}} \over {dz}} = \displaystyle{1 \over {2k_0}}{\rm \;} \nabla _\bot ^2 {\rm \psi} + \displaystyle{{k_0} \over {2{\epsilon} _0}}{\rm \;\ \Phi} \lpar {EE^{\rm \star}} \rpar {\rm \psi}. $$Following Lam et al. (Reference Lam, Lippmann and Tappert1977), the definitions of zeroth and second-order spatial moments of the intensity distribution of the laser beam, the intensity and mean square radius of the laser beam are given by
$$I_0 = \int \int {\rm \;\ \psi} {\rm \psi} ^{\rm \star} {\rm \;} dx{\rm \;} dy,$$and
$$\langle{r_{{\rm rms}}^2} \rangle = \displaystyle{1 \over {I_0}} \int \int (x^2 + y^2){\rm \;\ \psi} {\rm \psi} ^{\rm \star} {\rm \;} dx{\rm \;} dy.$$Differentiating Eq. (10) twice with respect to z and using Eq. (8) we get
$$\displaystyle{{d^2} \over {dz^2}}\langle{r_{{\rm rms}}^2} \rangle = 4\displaystyle{{I_2} \over {I_0}} + 4\displaystyle{H \over {I_0}},$$where
$$I_2 = \int \int {\rm \;} ( \vert \nabla _\bot {\rm \psi} \vert ^2-F){\rm \;} dx{\rm \;} dy,$$
$$F\lpar {{\rm \psi} {\rm \psi}^{\rm \star}} \rpar = \displaystyle{1 \over {2{\epsilon} _0}}\int_0^{{\rm \psi} {\rm \psi} ^{\rm \star}} {{\rm \;\ \Phi} \lpar {{\rm \psi} {\rm \psi}^{\rm \star}} \rpar {\rm \;} d\lpar {{\rm \psi} {\rm \psi}^{\rm \star}} \rpar ,} $$and
$$H = \mathop \int \nolimits \int \nolimits^ {\rm \;} \left( {2F-\displaystyle{1 \over {2{\epsilon}_0}}{\rm \;\ \psi} {\rm \psi}^{\rm \star} {\rm \;\ \Phi} \lpar {{\rm \psi} {\rm \psi}^{\rm \star}} \rpar } \right){\rm \;} dx{\rm \;} dy.$$Substituting Eq. (2) in Eqs. (9) and (10) one can get,
$$I_0 = {\rm \pi} E_{00}^2 {\rm \;} ab{\rm \;} 2^{m + n}{\rm \;} m!{\rm \;} n!,$$and
$$\eqalign{& \matrix{ {\langle{r_{{\rm rms}}^2} \rangle = \langle{r_x^2} \rangle + \langle{r_y^2} \rangle}} \cr & \,\,\, \hskip2pt \qquad{= a^2f_x^2 \left( {m + \displaystyle{1 \over 2}} \right) + b^2f_y^2 \left( {n + \displaystyle{1 \over 2}} \right).} \cr} $$Differentiating Eq. (16) twice with respect to z and using Eqs. (2) and (8)–(15), we get the following coupled differential equations for the transverse beam width parameters f x and f y in the x and y directions respectively:
$$\eqalign{& \displaystyle{{d^2f_x} \over {d{\rm \xi} ^2}} + \displaystyle{1 \over {\,f_x}}\left( {\displaystyle{{df_x} \over {d{\rm \xi}}}} \right)^2 \cr& = \displaystyle{1 \over {\,f_x^3}} + \displaystyle{{\beta E_{00}^2} \over {{\rm \pi} f_x^2 f_y}}\left( {\displaystyle{{{\rm \omega}_{{\rm p}0}^2 a^2} \over {c^2}}} \right)\displaystyle{{I_1} \over {\lpar {m + 1/2} \rpar \; 2^{m + n + 1}\; m!\; n!}}},$$
$$\eqalign{& \displaystyle{{d^2f_y} \over {d{\rm \xi} ^2}} + \displaystyle{1 \over {\,f_y}}\left( {\displaystyle{{df_y} \over {d{\rm \xi}}}} \right)^2 \cr& = \displaystyle{{{(a/b)}^4} \over {\,f_y^3}} + (a/b)^2\displaystyle{{{\rm \beta} E_{00}^2} \over {{\rm \pi} f_xf_y^2}} \left( {\displaystyle{{{\rm \omega}_{{\rm p}0}^2 a^2} \over {c^2}}} \right)\displaystyle{{I_2} \over {\lpar {n + 1/2} \rpar \; 2^{m + n + 1}\; m!\; n!}}},$$where
$$\eqalign{I_1 = & \mathop \int \nolimits_{-\infty} ^\infty \mathop \int \nolimits_{-\infty} ^\infty ue^{-2(u^2 + v^2)}H_m^3 (u)H_n^4 (v)\lcub {uH_m(u)-H_{m + 1}(u)} \rcub {\rm \;} \cr & (J(u,v))^{{\rm -}3/2}{\rm \;} du{\rm \;} dv},$$
$$\eqalign{I_2 = & \mathop \int \nolimits_{-\infty} ^\infty \mathop \int \nolimits_{-\infty} ^\infty ve^{-2(u^2 + v^2)}H_m^4 (u)H_n^3 (v)\lcub {vH_n(v)-H_{n + 1}(v)} \rcub {\rm \;} \cr& (J(u,v))^{-3/2}{\rm \;} du{\rm \;} dv},$$
$$J(u,v) = \left( {1 + \displaystyle{{{\rm \beta} E_{00}^2} \over {\,f_xf_y}}H_m^2 (u)H_n^2 (v)e^{-(u^2 + v^2)}} \right),$$
$$u = \displaystyle{x \over {af_x}},$$
$$v = \displaystyle{y \over {bf_y}},$$and, ξ = z/k 0a 2 is the dimensionless distance of propagation. Equations (17) and (18) are subjected to the boundary conditions f x,y = 1 and df x,y/dξ = 0 at ξ = 0, and are the basic equations to study the dynamics of Hermite–Gaussian laser beam as it propagates in plasma under the effect of relativistic nonlinearity. These equations have been solved numerically by using the Runge–Kutta method for the current work.
Plasma wave excitation
To excite the EPW at pump frequency we consider the high frequency oscillations of electrons over the neutralizing background of ions in plasma. Relativistic mass variation of electrons modifies the plasma density and hence amplitude of EPW. The equation governing the excitation of EPW can be derived by using the following fluid equations viz., equation of continuity, equation of momentum, adiabatic equation of state, and Poisson's equation:
$$\displaystyle{{\partial n_{\rm e}} \over {\partial t}} + \nabla \cdot \lpar {n_{\rm e}{\bf v}} \rpar = 0,$$
$$m\left( {\displaystyle{{\partial {\bi v}} \over {\partial t}} + \lpar {{\bf v}\cdot \nabla} \rpar {\bf v}} \right) = -\displaystyle{{\nabla P} \over {n_{\rm e}}}-e{\bf E},$$
$$\displaystyle{P \over {n_{\rm e}^3}} = {\rm const}.,$$
$$\nabla \cdot {\bf E} = -4{\rm \pi} n_{\rm e}e,$$where n e represents the total electron density comprises of equilibrium plasma density (n 0) and perturbed density (n 1) associated with EPW, v is the fluid velocity, E is the total electric field vector of laser beam and field associated with plasma wave, and P is the fluid pressure. Using the linear perturbation theory for Eqs. (19)–(22) one can have the following equation governing for density perturbation:
$$-{\rm \omega} _0^2 n_1 + v_{{\rm th}}^2 \nabla ^2n_1 + \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {\rm \gamma}} = -\displaystyle{e \over m}n_0\nabla {\rm \psi}, $$
where 
$v_{{\rm th}}^2 = 2K_{\rm B}T_0/m_0$ is the thermal velocity of electrons. Taking 
$n_1\propto e^{\iota (k_0z-{\rm \omega} _0t)}$ and using Eq. (2) in the above equation, the source term for SHG is found to be
$$\eqalign{n_1 = &-\displaystyle{{en_0} \over m}\displaystyle{{E_{00}} \over {\sqrt {\,f_xf_y}}} e^{-1/2\lpar {x^2/a^2f_x^2 + y^2/b^2f_y^2} \rpar }\,\, \cr&\left( {H_m\left( {\displaystyle{x \over {af_x}}} \right)H_n\left( {\displaystyle{y \over {bf_y}}} \right)\left( {\displaystyle{x \over {a^2f_x^2}} + \displaystyle{y \over {b^2f_y^2}}} \right)} \right. \cr& \left. {-\displaystyle{1 \over {af_x}}H_{m + 1}\left( {\displaystyle{x \over {af_x}}} \right)H_n\left( {\displaystyle{y \over {bf_y}}} \right)-\displaystyle{1 \over {bf_y}}H_m\left( {\displaystyle{x \over {af_x}}} \right)H_{n + 1}\left( {\displaystyle{y \over {bf_y}}} \right)} \right) \cr&\times \displaystyle{1 \over {\lcub {{\rm \omega}_0^2 -k_0^2 v_{{\rm th}}^2 -{\rm \omega}_{{\rm p}0}^2 /{\rm \gamma}} \rcub }}.} $$Second-harmonic yield
Following Sodha et al. (Reference Sodha, Sharma, Tewari, Sharma and Kaushik1978), the electric field vector E2 of the second harmonic of incident laser beam satisfies the following wave equation:
$$\nabla ^2{\bf E}_2 + \displaystyle{{{\rm \omega} _2^2} \over {c^2}}{\epsilon} _2({\rm \omega} _2){\bf E}_2 = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {c^2}}\displaystyle{{n_1} \over {n_0}}{\rm \psi}, $$
where ω2 = 2ω0 is the frequency of generated second harmonic radiation and ϵ 2 is the corresponding effective dielectric constant. Above equation can be solved for E2 by taking 
${\bf E}_2\propto {\rm \psi} _2e^{\iota (k_2z-{\rm \omega} _2t)}$ as shown below:
$${\rm \psi} _2 = \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {c^2}}\displaystyle{{n_1} \over {n_0}}\displaystyle{{\rm \psi} \over {\lpar {k_2^2 -4k_0^2} \rpar }}.$$The normalized conversion efficiency of SHG in plasma can be defined as the ratio of power of generated second harmonic radiation to that of incident pump beam:
$${\rm \eta} = \displaystyle{{\mathop \int \nolimits_{-\infty} ^\infty \mathop \int \nolimits_{-\infty} ^\infty {\rm \psi} _2{\rm \psi} _2^{\rm \star} \; dx\; dy} \over {\mathop \int \nolimits_{-\infty} ^\infty \mathop \int \nolimits_{-\infty} ^\infty {\rm \psi} {\rm \psi} ^{\rm \star} \; dx\; dy}}.$$Using Eqs. (2), (24), and (26) in (27), we have the following second-harmonic yield or conversion efficiency (η) for incident Hermite–Gaussian laser beam:
$${\rm \eta} = \displaystyle{1 \over {9{\rm \pi}}} \displaystyle{{{\rm \beta} E_{00}^2} \over {\,f_xf_y}}\left( {\displaystyle{{{\rm \omega}_{{\rm p}0}^2 a^2} \over {c^2}}} \right)\displaystyle{{I_3} \over {m!\; n!\; 2^{m + n}}},$$where
$$\hskip5pc\eqalign{I_3 = &\mathop \int \nolimits_{-\infty} ^\infty \mathop \int \nolimits_{-\infty} ^\infty e^{-(u^2 + v^2)}H_m^2 (u)H_n^2 (v)\left\{ {H_m^2 (u)H_n^2 (v)\left( {\displaystyle{{u^2} \over {\,f_x^2}} + {\left( {\displaystyle{a \over b}} \right)}^2\displaystyle{{v^2} \over {\,f_y^2}}} \right) + \displaystyle{1 \over {\,f_x^2}} H_{m + 1}^2 (u)H_n^2 (v)} \right. \cr & + \left. {{\left( {\displaystyle{a \over b}} \right)}^2\displaystyle{1 \over {\,f_y^2}} H_m^2 (u)H_{n + 1}^2 (v)-2\displaystyle{u \over {\,f_x^2}} H_m(u)H_{m + 1}(u)H_n^2 (v)-2{\left( {\displaystyle{a \over b}} \right)}^2\displaystyle{v \over {\,f_y^2}} H_m^2 (u)H_n(v)H_{n + 1}(v)} \right\} \cr & \times \displaystyle{1 \over {{\lcub {{\rm \omega}_0^2 a^2/c^2-\lpar {{\rm \omega}_0^2 a^2/c^2-{\rm \omega}_{{\rm p}0}^2 a^2/c^2} \rpar v_{{\rm th}}^2 /c^2-{\rm \omega}_{{\rm p}0}^2 a^2/c^2\; {(J(u,v))}^{-1/2}} \rcub }^2}}{\rm \;} du{\rm \;} dv.} $$Results and discussion
The second-order differential Eqs. (17) and (18) and Eq. (28) have been solved numerically for the transverse beam width parameters f x and f y and second-harmonic yield respectively with distance of propagation ξ, to envision the effect of propagation dynamics of Hermite–Gaussian laser beam in relativistic plasma. Following set of laser parameters have been used to analyze the effect of different TEM modes of Hermite–Gaussian laser beam and plasma density on self-focusing as well as on the generation of second harmonics: ω0 = 1.78 × 1015 rad/s; a = 15 μ T 0 = 106 K.
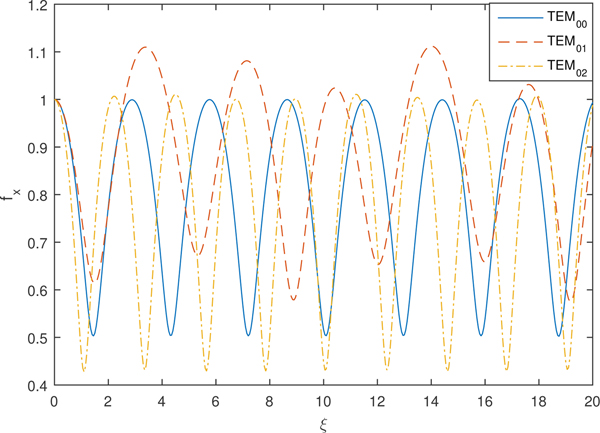
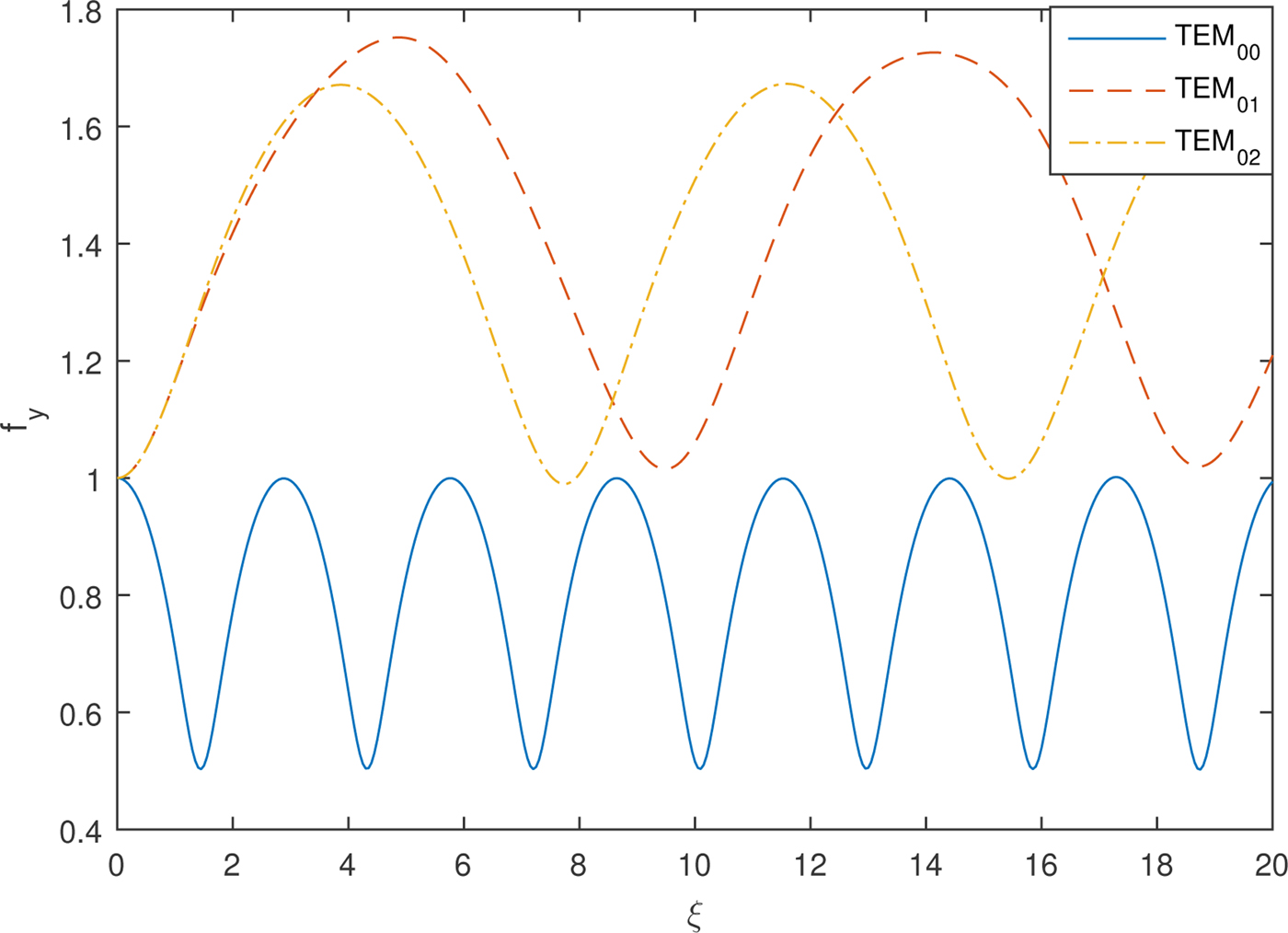
Figures 2 and 3 depict the oscillatory focusing and de-focusing of the transverse beam width parameters f x and f y with dimensionless distance of propagation ξ for different modes of Hermite–Gaussian beams, that is TEM00, TEM01, and TEM02 respectively. Synchronized focusing is observed for both f x and f y for lowest order Gaussian mode TEM00. For modes TEM01 and TEM02 f x and f y behave exactly opposite. From the intensity profile of TEM01 mode in Figure 1(b), it is clear that intensity has a central dip along the y-axis but Gaussian along the x-axis with no central dip. Therefore, laser beam undergoes oscillatory de-focusing along the transverse y direction and oscillatory focusing along the x-axis as focusing is observed mainly due to the contribution of axial intensity. Moreover, there is observed less focusing for TEM01 as compared to Gaussian mode for f x this is due to the large divergence of beam in the y direction as both these beam width parameters are coupled to each other. For TEM02 there is a greater extent of self-focusing along the x-axis among all three modes and f y also observes less de-focusing as compared with TEM01. This is due to the fact that intensity profile of TEM02 mode in Figure 1(c) is symmetrically distributed in three lobes along the y-axis with maximum intensity distributed to the off-axial parts. The central part (axial-part) enhances the focusing of the beam in the y direction which results in greater focusing in the x direction.
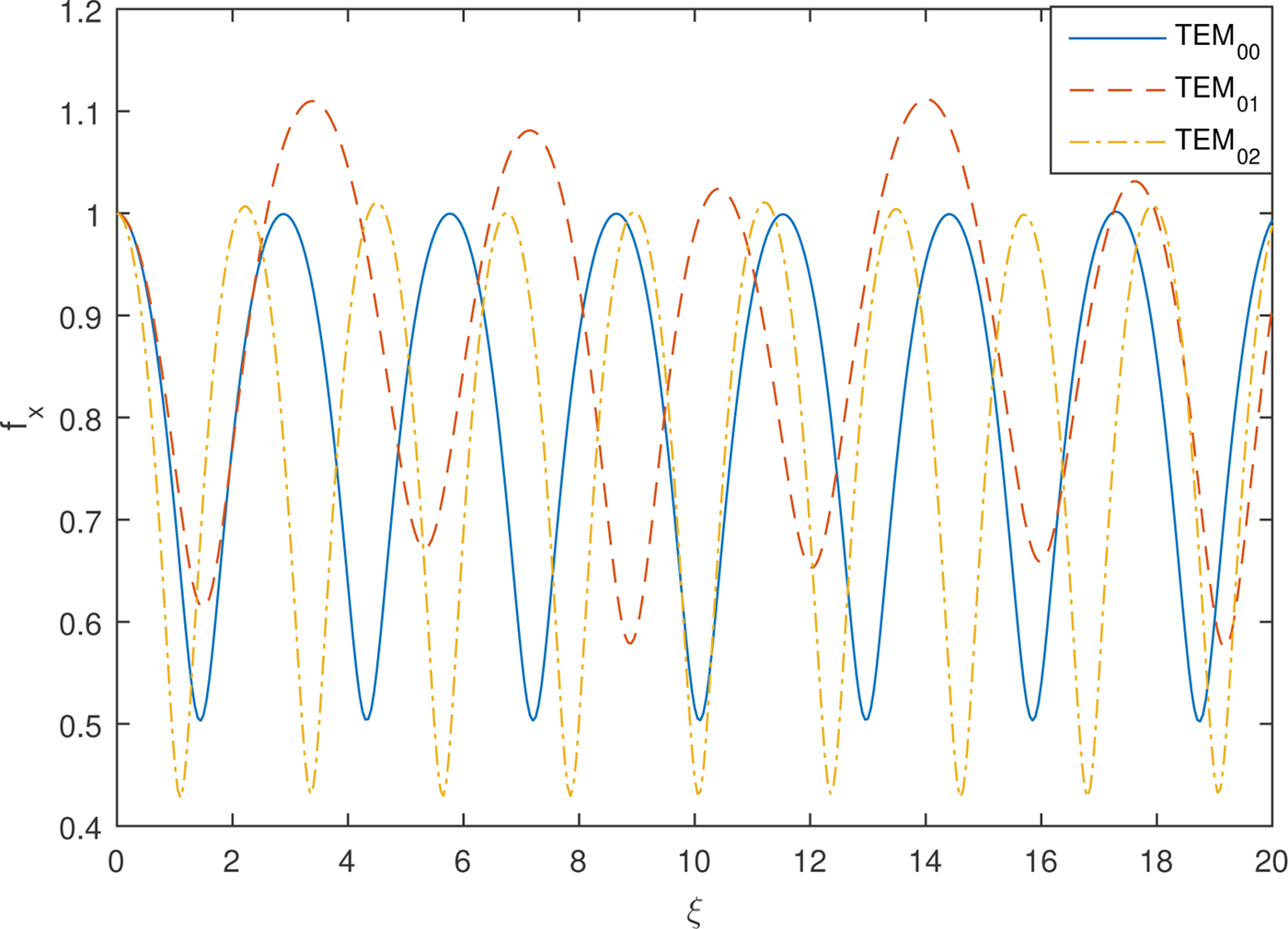
Fig. 2. Variation of transverse beam width parameter f x against the distance of propagation ξ for different TEMmn modes and fixed values of plasma density 
${\rm \omega} _{{\rm p}0}^2 a^2/c^2 = 12$, laser intensity 
${\rm \beta} E_{00}^2 = 2$ and a/b = 1.
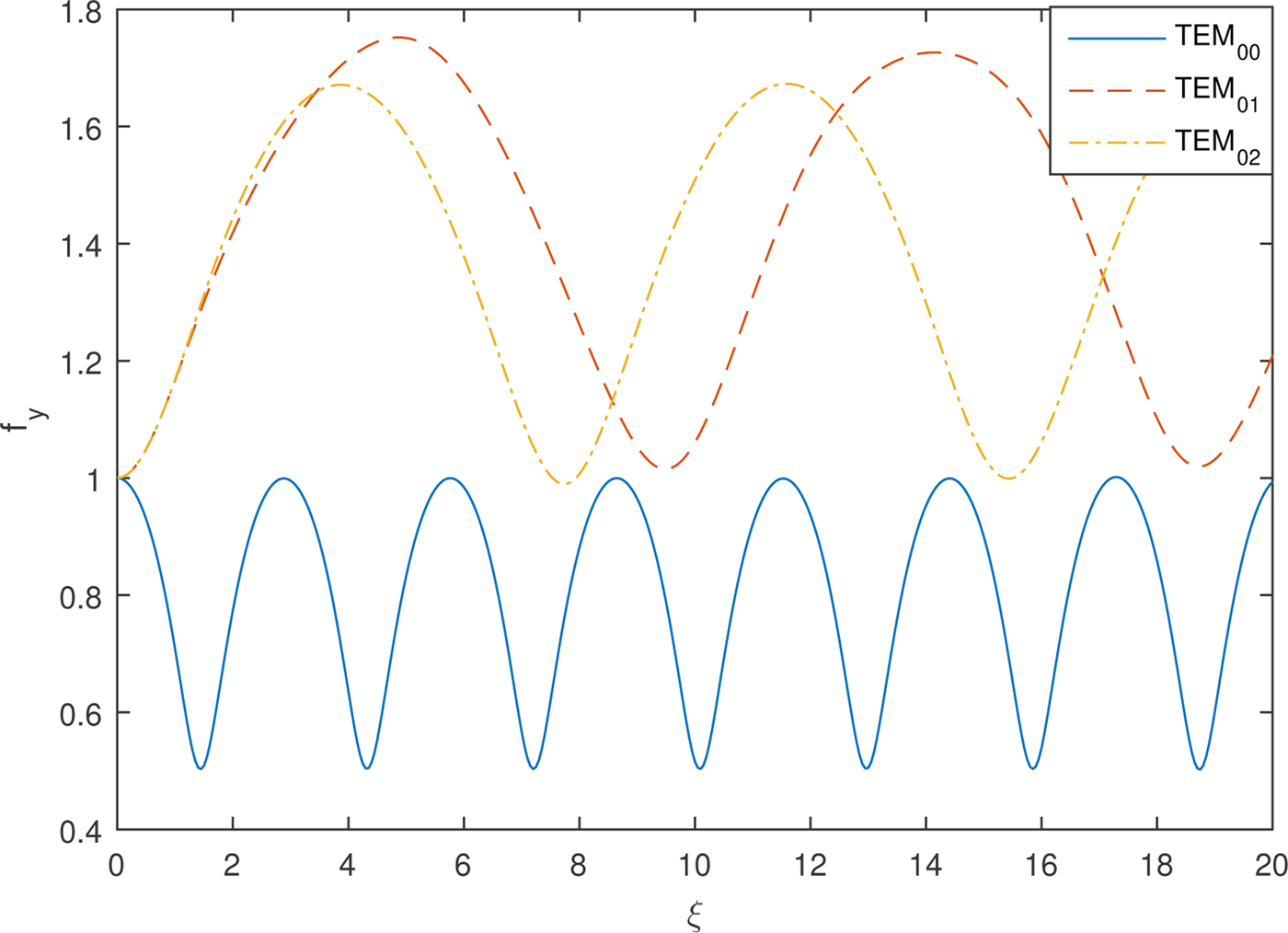
Fig. 3. Variation of transverse beam width parameter f y with the distance of propagation ξ for different TEMmn modes and fixed values of plasma density 
${\rm \omega} _{{\rm p}0}^2 a^2/c^2 = 12$, laser intensity 
${\rm \beta} E_{00}^2 = 2$ and a/b = 1.
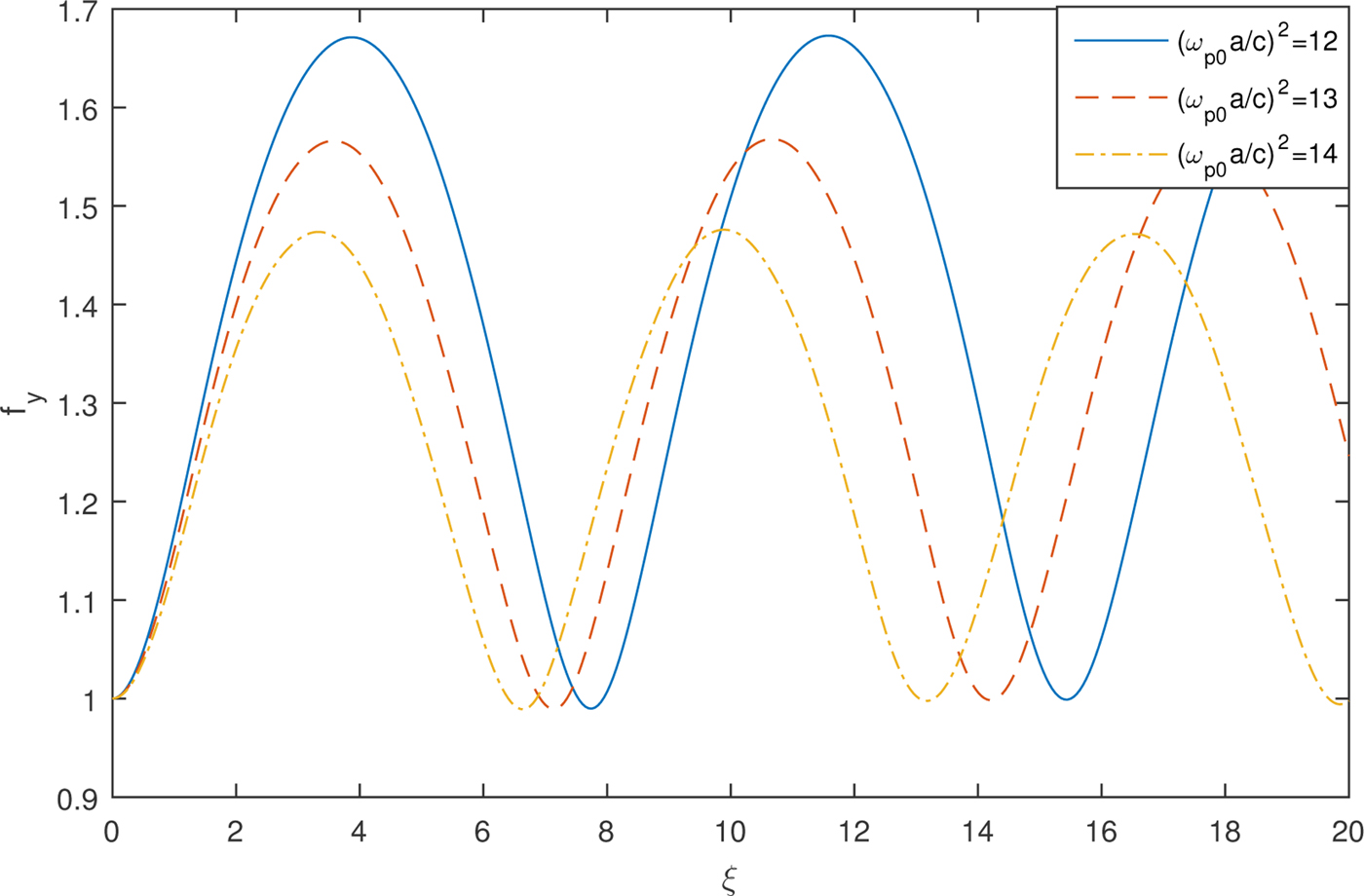
Figures 4 and 5 depict the effect of plasma density on the evolution of spot size of Hermite–Gaussian laser beam in the transverse x and y directions respectively for TEM02 mode. Strong focusing is observed for the beam width parameter f x with an increase in plasma density whereas, decrease in defocusing is observed in the case of f y.
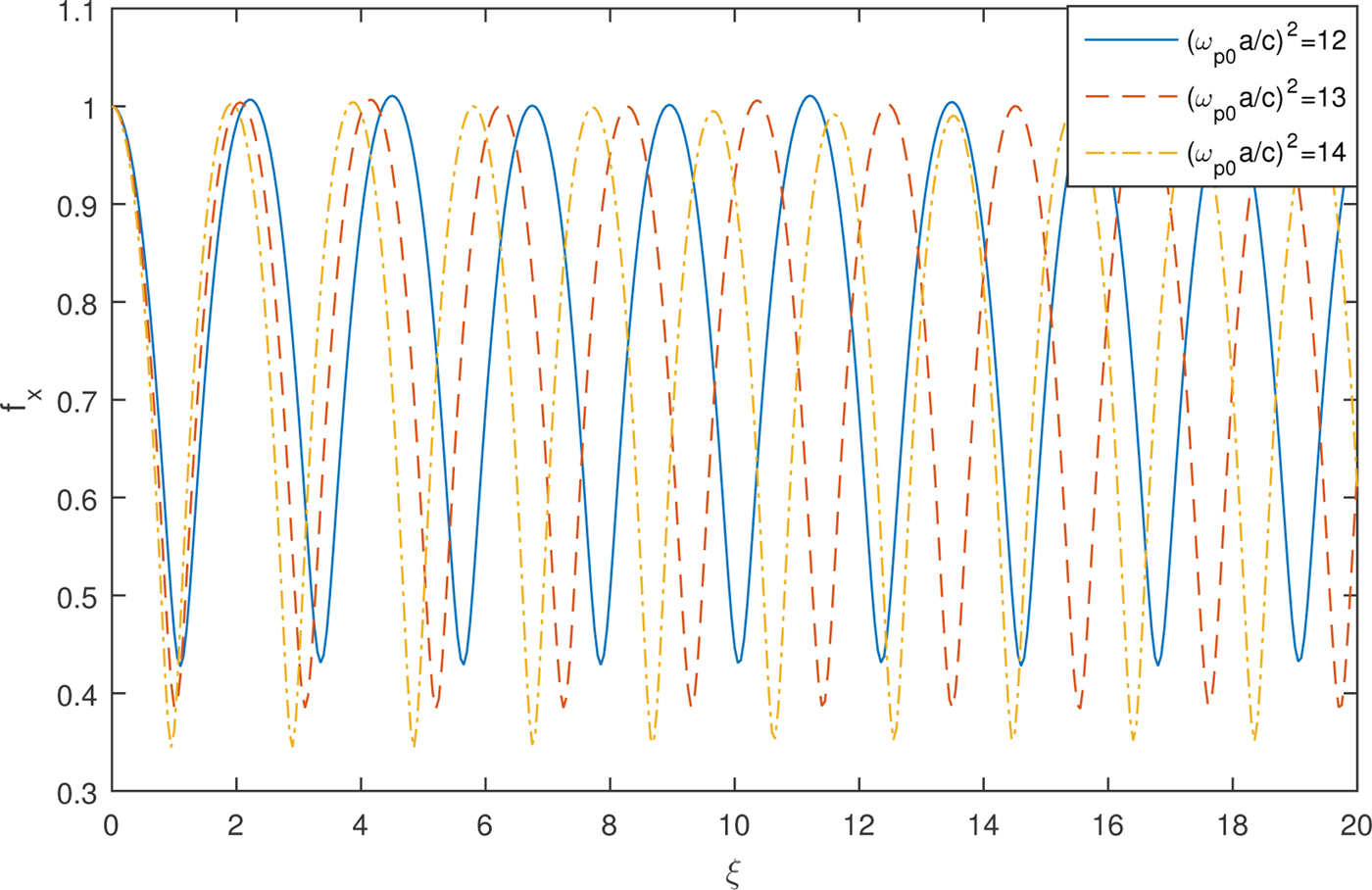
Fig. 4. Variation of transverse beam width parameter f x for TEM02 mode against the distance of propagation ξ with different values of plasma density and fixed values of laser intensity 
${\rm \beta} E_{00}^2 = 2$ and a/b = 1.
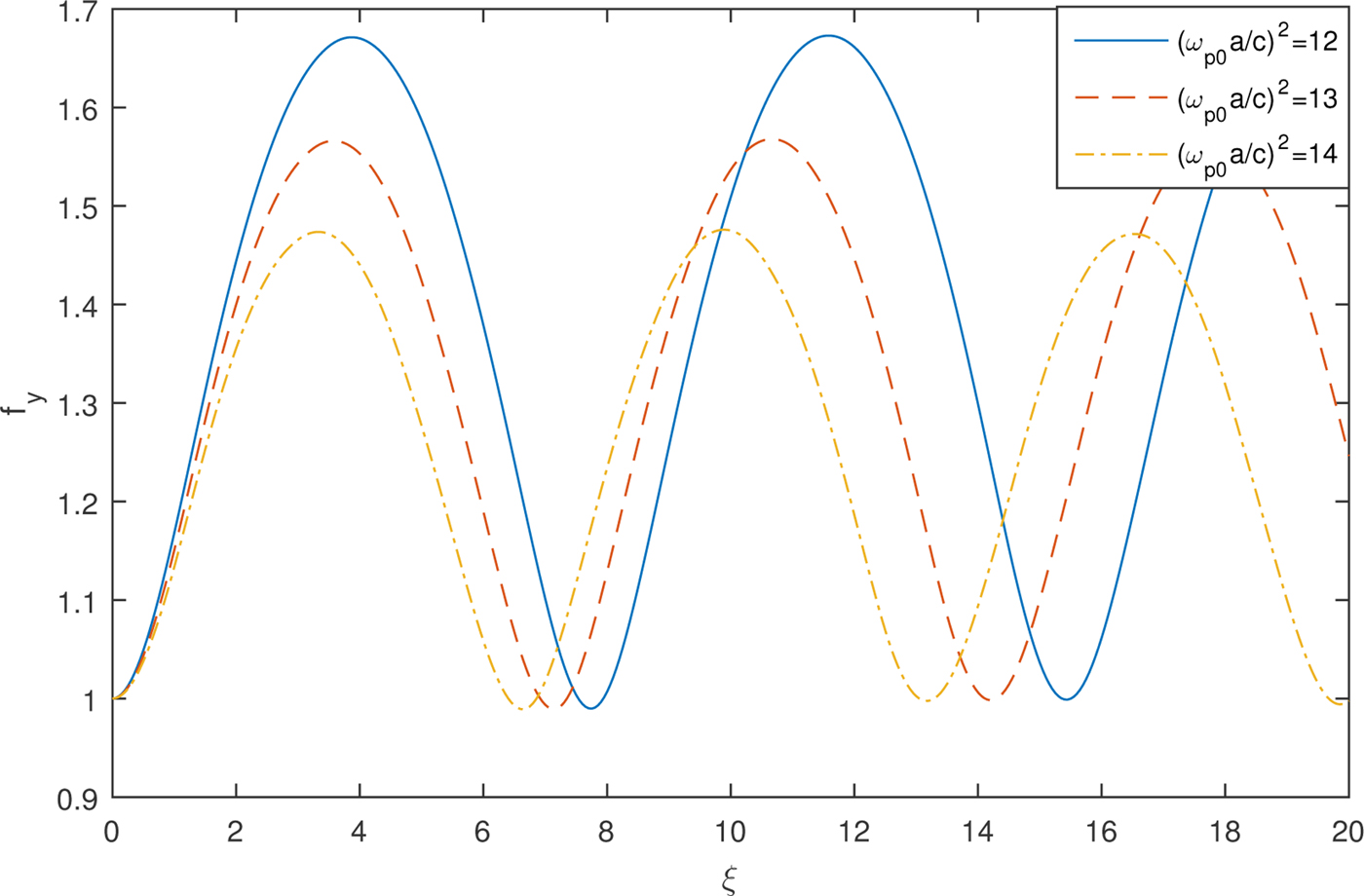
Fig. 5. Variation of transverse beam width parameter f y for TEM02 mode against the distance of propagation ξ with different values of plasma density and fixed values of laser intensity 
${\rm \beta} E_{00}^2 = 2$ and a/b = 1.
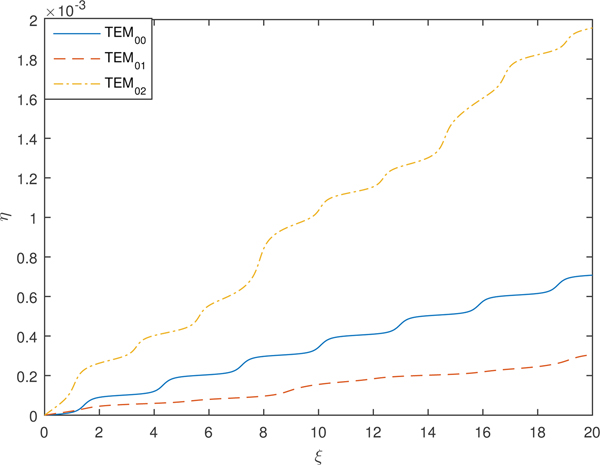
Figure 6 depicts the variation of second-harmonic yield, that is, η with a dimensionless distance of propagation ξ for different modes of Hermite–Gaussian laser beam and fixed values of normalized beam intensity and plasma density. It has been observed that second-harmonic yield shows a step-like variation corresponding to periodical positions of minimum beam waists during propagation and highest yield is obtained for mode TEM02. This is due to the fact that η is dependent on normalized distance of propagation ξ through transverse beam widths f x and f y. Therefore, if f x and f y are oscillatory, then η will also be oscillatory as well, giving rise to a step-like behavior in η. Another reason for this is that the focal spots of the laser beams are the regions of very high intensity. As a result of which the amplitude of the plasma wave and hence second-harmonic yield is maximum at the focal spots.
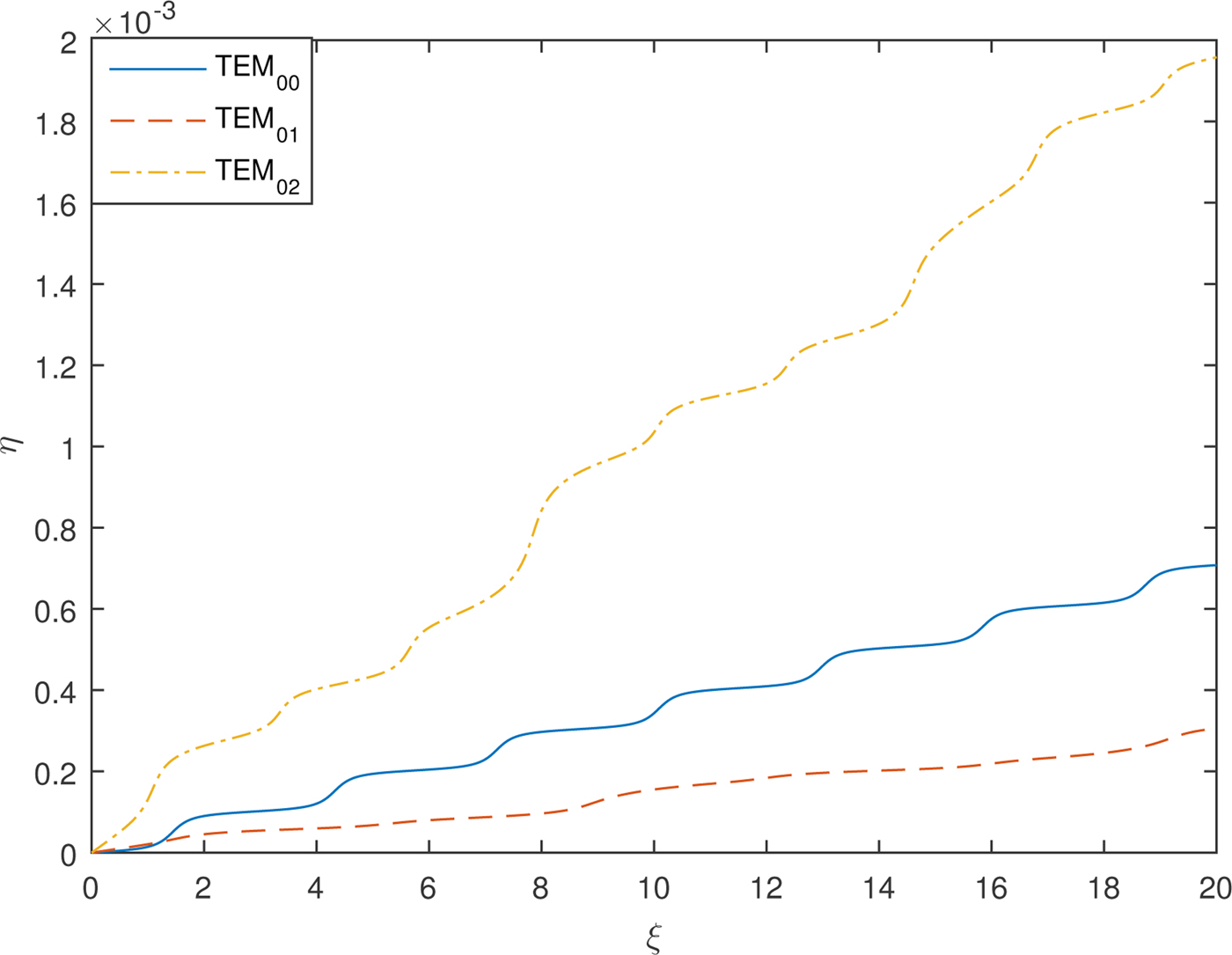
Fig. 6. Variation of η with the distance of propagation ξ for different TEMmn modes of Hermite–Gaussian beam and fixed values of plasma density 
${\rm \omega} _{{\rm p}0}^2 a^2/c^2 = 8$, laser intensity 
${\rm \beta} E_{00}^2 = 2$ and a/b = 1.
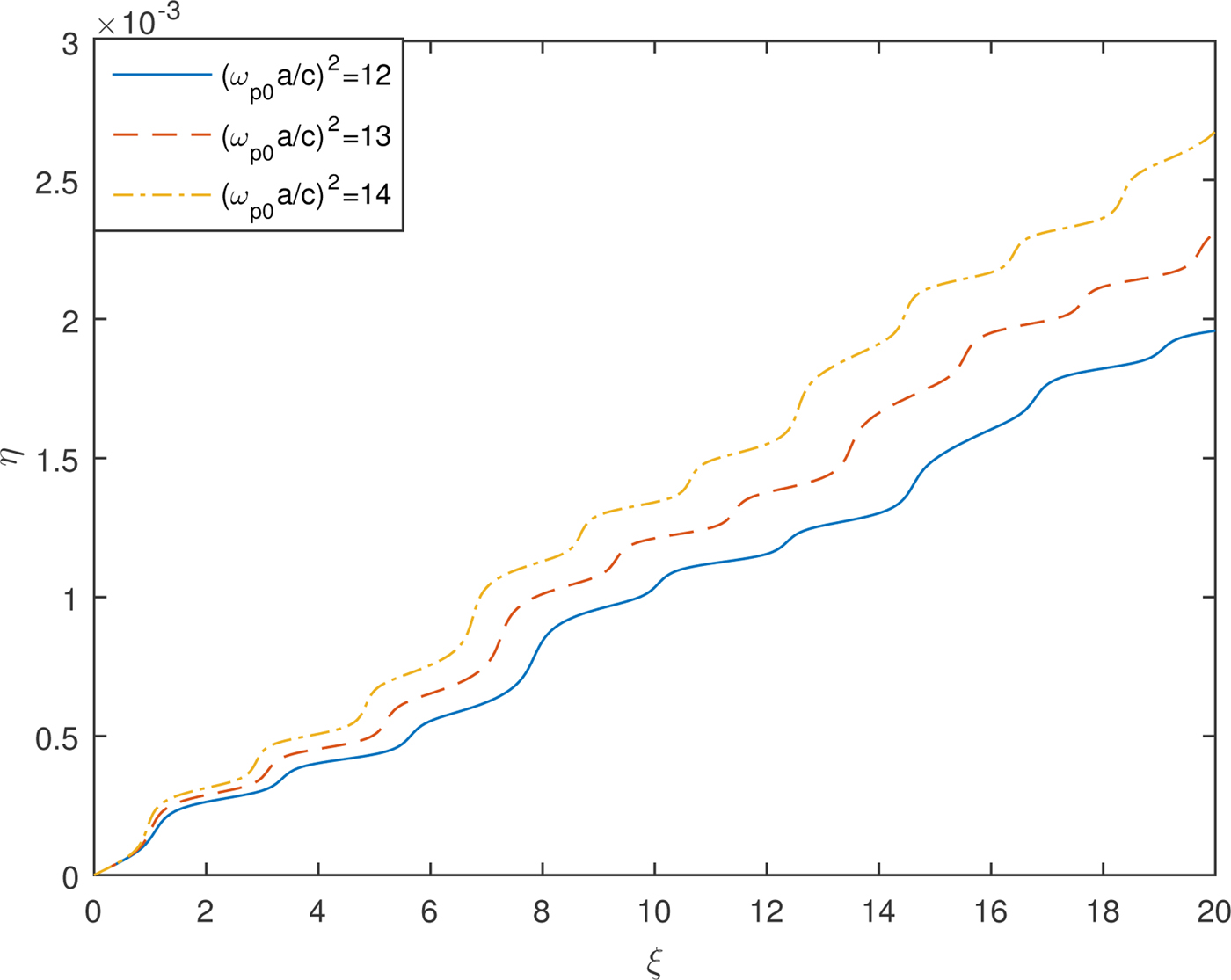
Figure 7 depicts the effect of increased plasma density on the second-harmonic yield of TEM02 mode of Hermite–Gaussian laser beam. It is observed that with increase in plasma density there is an increase in second-harmonic yield. This is because of the strong self-focusing of the beam width parameter f x and decrease in defocusing in case of f y of the laser beam with the increase in plasma density which results in steeper density gradients and amplified plasma wave at the focal regions and hence greater conversion efficiency, that is η.
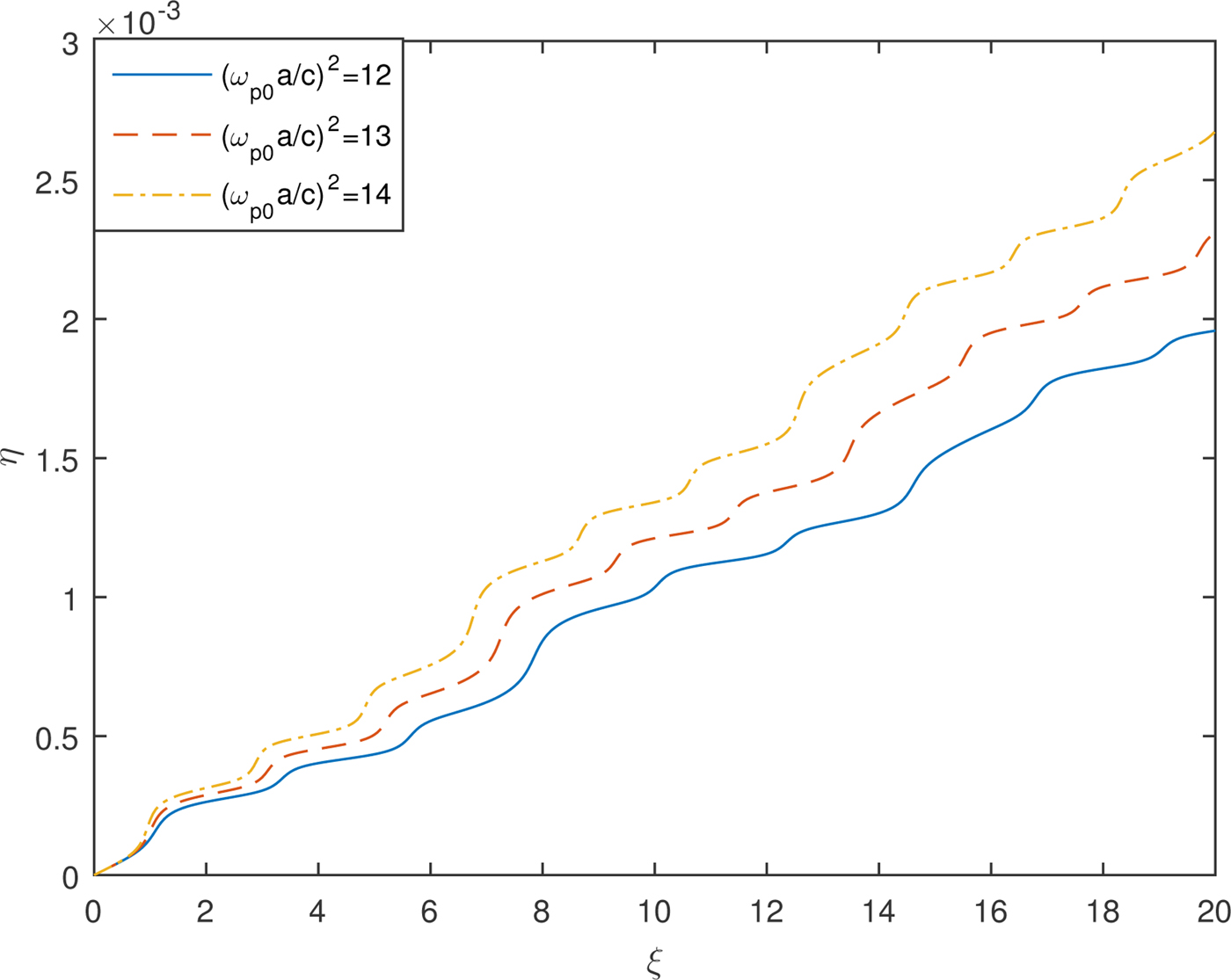
Fig. 7. Variation of η of TEM02 mode of Hermite–Gaussian beam against distance of propagation ξ for different values of plasma density and fixed values of laser intensity 
${\rm \beta} E_{00}^2 = 2$ and a/b = 1.
Conclusions
In this work, theoretical approach has been developed by using method of moments for the generation of second harmonics of Hermite–Gaussian laser beam in plasma and following important conclusions have been drawn from the present analysis.
• Self-focusing as well as second-harmonic yield is greater for TEM02 mode as compared to TEM00 and TEM01 which is one of the important investigations as far as the second-harmonic yield is concerned and would be helpful for the experimentalists working in the area of laser-induced fusion.
• Plasma density has a significant effect on second-harmonic yield as it increases with increase in plasma density.
Acknowledgements
The authors are thankful to the Ministry of Human Resources and Development (MHRD) of India for the financial support to carry out this research work.
