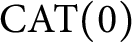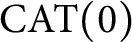1 Introduction
A classical result of [Reference Attouch2] establishes a set of equivalences between Mosco convergence, convergence of proximal mappings and of Moreau–Yosida approximates for a sequence of proper closed convex functions defined on a smooth reflexive Banach space. This result has a natural extension to any metric space equipped with a convex structure that allows for an appropriate notion of weak convergence. We consider these equivalences in the setting of a complete
$\operatorname {\mathrm {CAT}}(0)$
space. A
$\operatorname {\mathrm {CAT}}(0)$
space is a uniquely geodesic metric space that is endowed with a canonical convex structure and allows for a suitable notion of weak convergence. The main feature that distinguishes
$\operatorname {\mathrm {CAT}}(0)$
spaces from other geodesic metric spaces is the fact that every geodesic triangle in a
$\operatorname {\mathrm {CAT}}(0)$
space is at least as thin as its comparison triangle in the Euclidean plane. These spaces were formally introduced by Gromov [Reference Effland, Neumayer and Rumpf11] in recognition of the seminal work of Alexandrov [Reference Alexandrov1] and are often referred to as spaces of nonpositive curvature, e.g., [Reference Bërdëllima6, Reference Baćak8]. The main motivation for studying Mosco convergence in a
$\operatorname {\mathrm {CAT}}(0)$
space is the implications it has in the theory of the gradient flow initiated by Mayer [Reference Lim15] and Jost [Reference Jost13]. More recently, Mosco convergence is applied in numerical schemes for the so called metamorphosis models on Hadamard manifolds [Reference Burago, Burago and Ivanov10]. In relation to the theory of the gradient flow, Bačak [Reference Baćak3] proved that Mosco convergence implies pointwise convergence of Moreau approximates and of proximal mappings, and in turn convergence of proximal mappings yields pointwise convergence of the gradient flow semigroup. Later in [Reference Ballmann5], Bačak et al. showed that pointwise convergence of Moreau approximates yields Mosco convergence. However, it is not known whether pointwise convergence of the proximal mappings implies Mosco convergence. That convergence of proximal mappings alone is not enough was known to Bačak [Reference Baćak, Montag and Steidl4]. Indeed, consider a sequence of constant functions
$0,1,0,1,\ldots $
defined on
$\mathbb {R}$
. These are closed and convex functions but they do not converge in the sense of Mosco to any function f, however, their proximal mappings
$x\mapsto J_{\lambda }x$
equal the identity for all
$\lambda>0$
. It is the purpose of this note to establish a suitable condition under which convergenve of proximal mappings guarantees Mosco convergence for a sequence of proper closed convex functions.
2 Preliminaries
We follow standard terminology from metric geometry theory about
$\operatorname {\mathrm {CAT}}(0)$
spaces, e.g., [Reference Baćak8, Reference Tean, Ariza-Ruiz and López-Acedo9]. By
$(X,d)$
we denote a complete
$\operatorname {\mathrm {CAT}}(0)$
space, unless otherwise stated. Given
$x\in X$
let
$$\begin{align*}\Gamma_x(X):=\{\gamma:[0,1]\to X\;|\;\gamma(0)=x\}\end{align*}$$
denote the set of all geodesic segments emanating from x. A convex combination of two elements
$x,y\in X$
with parameter
$t\in [0,1]$
is an element
$x_t\in [x,y]$
satisfying
$d(x,x_t)=td(x,y)$
. We write
$x_t:= (1-t)x\oplus ty$
. Such a convex combination is uniquely determined. We often denote by
$[x,y]$
the unique geodesic segment connecting x with y. A set
$C\subseteq X$
is a convex set if for every
$x,y\in C$
and
$t\in [0,1]$
it holds that
$(1-t)x\oplus ty\in C$
. A set C is closed if its complement
$X\backslash C$
is open in the usual metric topology. In particular, geodesic segments are closed and convex. Let
$d(x,C):= \inf \{d(x,y)\;|\;y\in C\}$
and
$P_Cx:= \{z\in C\;|\; d(x,z)=d(x,C)\}$
. We use the following definition for weak convergence in a
$\operatorname {\mathrm {CAT}}(0)$
space which is due to [Reference Gromov12].
Definition 2.1 A sequence
$(x_n)$
weakly converges to x and we write
$x_n\overset {w}\to x$
if and only if
$\lim _{n\to +\infty }P_{\gamma }x_n=x$
for every
$\gamma \in \Gamma _x(X)$
.
This notion of convergence is well defined since projection onto a closed convex set always exists and is unique. On bounded sets, weak convergence coincides with the so-called
$\Delta $
-convergence introduced by Lim [Reference Jost14] and shares with it the desirable properties of Opial and Kadec–Klee. Moreover, every bounded sequence has a weakly convergent subsequence [Reference Bridson and Haefliger7, Chapter 3]. Moreover, weak limits are unique. Indeed if
$x_n\overset {w}\to x$
and
$x_n\overset {w}\to y$
then for
$\gamma := [x,y]$
and
$\tilde {\gamma }:= [y,x]$
we obtain
$x=\lim _{n\to +\infty }P_{\gamma }x_n=\lim _{n\to +\infty }P_{\tilde {\gamma }}x_n=y$
.
Definition 2.2 A sequence of functions
$f^n:X\to (-\infty ,+\infty ]$
is said to be Mosco convergent to
$f: X\to (-\infty ,+\infty ]$
and we write
$M-\lim _{n\to +\infty }f^n=f$
if for each
$x\in X$
:
-
(1)
$f(x)\leq \liminf _{n\to +\infty }f^n(x_n)$
whenever
$x_n\overset {w}\to x$
and -
(2) there exists some sequence
$(y_n)\subset X$
such that
$y_n\to x$
and
$f(x)\geq \limsup _{n\to +\infty } f^n(y_n)$
.
One of the difficulties in Attouch’s theorem is that it involves the dual space in its formulation. This is problematic in the setting of a
$\operatorname {\mathrm {CAT}}(0)$
space since a proper dual space corresponding to the weak convergence in Definition 2.1 is not yet fully understood. However the following concept becomes helpful and plays the role of a “subgradient.”Footnote
1
Definition 2.3 Let
$f:X\to (-\infty ,+\infty ]$
be some (extended) real-valued function and let
$x\in \operatorname {\mathrm {dom}} f:= \{x\in X\;|\; f(x)<+\infty \}$
. The absolute slope of f at x is defined as
$$ \begin{align} |\partial f|(x):=\limsup_{y\to x}\frac{\max\{f(x)-f(y),0\}}{d(x,y)}. \end{align} $$
If
$f(x)=+\infty $
we set
$|\partial f|(x):= +\infty $
.
To this end, we assume that our functions are real valued and satisfy:
-
(1) (proper) there exists no
$x\in X$
such that
$f(x)=-\infty $
and
$f\not \equiv +\infty $
. -
(2) (convex)
$f((1-t)x\oplus ty)\leq (1-t)f(x)+t(y)$
for all
$x,y\in X$
and
$t\in [0,1]$
. -
(3) (closed)
$f(x)\leq \liminf _{y\to x}f(y)$
for every
$x\in X$
.
Lemma 2.1 [Reference Baćak3, Lemma 5.1.2]
Let
$f:X\to (-\infty ,+\infty ]$
be a closed convex function. Then
$$ \begin{align} |\partial f|(x)=\sup_{y\in H\backslash\{x\}}\frac{\max\{f(x)-f(y),0\}}{d(x,y)}, \hspace{0.2cm}x\in\operatorname{\mathrm{dom}} f. \end{align} $$
Given
$x\in X$
and a geodesic segment
$\gamma $
containing x, we define the function
$\operatorname {\mathrm {\text {sign}}}(\,\cdot \,;\gamma ):\gamma \to \{-1,1\}$
as
$\operatorname {\mathrm {\text {sign}}}(y;\gamma )=1$
if
$y\in (x,\gamma (1)]$
and
$\operatorname {\mathrm {\text {sign}}}(y;\gamma )=-1$
if
$y\in [\gamma (0),x]$
. Another notion for the slope of a function f is that of the geodesic derivative.
Definition 2.4 Let
$f:X\to (-\infty ,+\infty ]$
. The geodesic lower derivative of f at
$x\in X$
along a geodesic
$\gamma $
containing x is defined asFootnote
2
$$ \begin{align} f^{\prime}_{-}(x;\gamma):=\liminf_{y\overset{\gamma}\to x}\frac{f(y)-f(x)}{\operatorname{\mathrm{\text{sign}}}(y;\gamma)\,d(y,x)}. \end{align} $$
Analogously, the geodesic upper derivative, denoted by
$f^{\prime }_{+}(x;\gamma )$
, is defined with
$\liminf $
replaced by
$\limsup $
. If both limits exist and coincide then we say that f is geodesically differentiable at x along
$\gamma $
and denote it by
$f'(x;\gamma )$
.
For a given closed convex function
$f:X\to (-\infty ,+\infty ]$
and parameter
$\lambda>0$
the Moreau approximate
$f_{\lambda }$
of f is defined as
$$ \begin{align} f_{\lambda}(x):=\inf_{y\in X}\Big\{f(y)+\frac{1}{2\lambda}d(y,x)^2\Big\},\;\text{for each}\; x\in X \end{align} $$
and the proximal mapping of f
$$ \begin{align} J_{\lambda}x:=\arg\min _{y\in X}\Big\{f(y)+\frac{1}{2\lambda}d(y,x)^2\Big\},\;\text{for each}\; x\in X. \end{align} $$
In general,
$J_{\lambda }x$
can be a multivalued operator if X is some arbitrary metric space, however, in a
$\operatorname {\mathrm {CAT}}(0)$
space
$J_{\lambda }x$
exists and is always unique (see [Reference Baćak3]). We use also the following two results for complete
$\operatorname {\mathrm {CAT}}(0)$
spaces.
Theorem 2.2 [Reference Baćak3, Theorem 5.2.4]
Let
$f^n:X\to (-\infty ,+\infty ]$
a sequence of closed convex functions. If
$M-\lim _{n\to +\infty }f^n(x)=f(x)$
, then it holds
$\lim _{n\to +\infty } f^n_{\lambda }(x)=f_{\lambda }(x)$
and
$\lim _{n\to +\infty } J^n_{\lambda }x=J_{\lambda }x$
for each
$x\in X$
.
Theorem 2.3 [Reference Ballmann5, Theorem 3.2]
Let
$f, f^n:X\to (-\infty ,+\infty ]$
be a sequence of closed convex functions. If
$\lim _{n\to +\infty } f^n_{\lambda }(x)=f_{\lambda }(x)$
then
$M-\lim _{n\to +\infty }f^n(x)=f(x)$
for all
$x\in X$
.
3 Main result
3.1 A normalization condition
Definition 3.1 A sequence of functions
$(f^n)_{n\in \mathbb {N}}, f$
satisfies the normalization condition if there exists some sequence
$(x_n)_{n\in \mathbb {N}}\subset X$
and
$x\in X$
such that
$x_n\to x, f^n(x_n)\to f(x)$
and
$|\partial f^n|(x_n)\to |\partial f|(x)$
as
$n\to +\infty $
.
Lemma 3.1 A sequence of closed convex functions
$(f^n)_{n\in \mathbb {N}},f:X\to (-\infty ,+\infty ]$
satisfies the normalization condition whenever
$M-\lim _{n\to +\infty }f^n=f$
.
Proof Let
$x_0\in X$
and
$M-\lim _{n\to +\infty }f^n=f$
. Then by Theorem 2.2, we have
$\lim _{n\to +\infty }J^n_{\lambda }x_0=J_{\lambda }x_0$
for any
$\lambda>0$
. Take
$x_n:= J^n_{\lambda }x_0$
and
$x:= J_{\lambda }x_0$
. By definition of
$J_{\lambda }$
we have
$$\begin{align*}f^n(x_n)+\frac{1}{2\lambda}d(x_0,x_n)^2\leq f^n(y)+\frac{1}{2\lambda}d(x_0,y)^2,\quad\forall y\in X.\end{align*}$$
Let
$(\xi _n)_{n\in \mathbb {N}}\subset X$
be a sequence strongly converging to x. From the last inequality, we obtain in particular that
$$\begin{align*}f^n(x_n)+\frac{1}{2\lambda}d(x_0,x_n)^2\leq f^n(\xi_n)+\frac{1}{2\lambda}d(x_0,\xi_n)^2,\quad\forall n\in \mathbb{N}\end{align*}$$
implying
$\limsup _{n\to +\infty }f^n(x_n)\leq \limsup _{n\to +\infty }f^n(\xi _n)_{n\in \mathbb {N}}$
. On the other hand, by definition of Mosco convergence there exists a sequence
$(\xi _n)_{n\in \mathbb {N}}$
such that
$\limsup _{n\to +\infty }f^n(\xi _n)\leq f(x)$
. Hence,
$\limsup _{n\to +\infty }f^n(x_n)\leq f(x)$
. Moreover,
$\lim _{n\to +\infty }x_n=x$
implies, in particular, that
$x_n\overset {w}\to x$
. Again by definition of Mosco convergence, we obtain
$f(x)\leq \liminf _{n\to +\infty }f^n(x_n)$
. Therefore,
$f(x)=\lim _{n\to +\infty }f^n(x_n)$
as desired. Next, we need to show the property about the slopes. Note that by Lemma 2.1, we have
$$\begin{align*}\frac{\max\{f^n(x_n)-f^n(y),0\}}{d(x_n,y)}\leq|\partial f^n|(x_n),\quad\forall y\in X\backslash\{x_n\},\forall n\in\mathbb{N}.\end{align*}$$
Again by Mosco convergence for each
$y\in X$
there is a sequence
$(\xi _n)_{n\in \mathbb {N}}$
strongly converging to y such that
$\limsup _{n\to +\infty }f^n(\xi _n)\leq f(y)$
. Applying the last inequality for
$\xi _n$
, we have
$$\begin{align*}\frac{\max\{f^n(x_n)-f^n(\xi_n),0\}}{d(x_n,y)}\leq|\partial f^n|(x_n),\quad\forall n\in\mathbb{N},\end{align*}$$
which in turn yields
$$\begin{align*}\frac{\max\{f(x)-\limsup_{n\to+\infty}f^n(\xi_n),0\}}{d(x,y)}\leq\liminf_{n\to+\infty}|\partial f^n|(x_n).\end{align*}$$
Using
$\limsup _{n\to +\infty }f^n(\xi _n)\leq f(y)$
, we get
$$\begin{align*}\frac{\max\{f(x)-f(y),0\}}{d(x,y)}\leq\liminf_{n\to+\infty}|\partial f^n|(x_n).\end{align*}$$
Because the last inequality holds for any
$y\in X\backslash \{x_n\}$
then
$|\partial f|(x)\leq \liminf _{n\to +\infty } |\partial f^n|(x_n)$
. Now by Definition 2.3, we obtain
$$\begin{align*}|\partial f^n|(x_n)\leq \frac{\max\{f^n(x_n)-f^n(y_n),0\}}{d(x_n,y_n)}+\varepsilon_n,\quad\forall n\in\mathbb{N}\end{align*}$$
for sufficiently small
$\varepsilon _n>0$
and
$y_n$
sufficiently close to
$x_n$
. Note that strong convergence of
$x_n$
to x implies that for any
$\delta>0$
, all but finitely many of the terms
$y_n\in \mathbb {B}(x,\delta )$
. In particular,
$(y_n)$
is a bounded sequence, hence it has a weakly convergent subsequence
$(y_{n_k})$
. But
$\operatorname {\mathrm {cl}}\mathbb {B}(x,\delta )$
is a closed convex set and since weak convergence coincides on bounded sets with the
$\Delta $
-convergence then by [Reference Baćak3, Lemma 3.2.1]
$y_{n_k}\overset {w}\to y\in \operatorname {\mathrm {cl}}\mathbb {B}(x,\delta )$
. One can choose
$(\varepsilon _n)$
such that
$\lim _{k\to +\infty }\varepsilon _{n_k}=0$
. Moreover,
$d(x,\cdot )$
is weakly lsc [Reference Baćak3, Corollary 3.2.4] implying
$$\begin{align*}\limsup_{k\to+\infty}|\partial f^{n_k}|(x_{n_k})\leq\frac{\max\{f(x)-\liminf_kf^{n_k}(y_{n_k}),0\}}{d(x,y)}.\end{align*}$$
By definition of Mosco convergence, it follows that
$\liminf _{k\to +\infty }f^{n_k}(y_{n_k})\geq f(y)$
. Hence,
$$\begin{align*}\limsup_{n\to+\infty}|\partial f^n|(x_n)\leq\limsup_{k\to+\infty}|\partial f^{n_k}|(x_{n_k})\leq\frac{\max\{f(x)-f(y),0\}}{d(x,y)}.\end{align*}$$
The last inequality implies
$\limsup _{n\to +\infty }|\partial f^n|(x_n)\leq |\partial f|(x)$
.▪
Definition 3.2 A family of functions
$f^n:X\to (-\infty ,+\infty ]$
is said to be equi locally Lipschitz if for any bounded set
$K\subseteq X$
, there is a constant
$C_K>0$
such that
$$ \begin{align} |f^n(x)-f^n(y)|\leq C_Kd(x,y),\quad\forall x,y\in K, \forall n\in\mathbb{N}. \end{align} $$
Lemma 3.2 Let
$f^n:X\to (-\infty ,+\infty ]$
be a sequence of closed convex functions such that
$\lim _{n\to +\infty }f^n_{\lambda }(x_0)=\alpha _0\in \mathbb {R}$
for some
$x_0\in X$
and some
$\lambda>0$
. Then
$(f^n_{\lambda })_{n\in \mathbb {N}}$
are equi locally Lipschitz functions.
Proof By virtue of [Reference Attouch2, Theorem 2.64 (ii)], it suffices to show that there is
$r>0$
and
$x_0\in X$
such that
$f^n(x)+r(d(x,x_0)^2+1)\geq 0$
for all
$x\in X$
and all
$n\in \mathbb {N}$
. Let
$x_0\in X$
be such that
$\lim _{n\to +\infty }f^n_{\lambda }(x_0)=\alpha _0\in \mathbb {R}$
. Notice that by definition of Moreau envelope, we have
$$\begin{align*}f^n(x)\geq f^n_{\lambda}(x_0)-\frac{1}{2\lambda}d(x_0,x)^2\geq \alpha_0-\delta-\frac{1}{2\lambda}d(x_0,x)^2\end{align*}$$
for some
$\delta>0$
and sufficiently large n. If one takes
$\delta =\alpha _0+1/2\lambda $
, then one gets
$$\begin{align*}f^n(x)\geq -\frac{1}{2\lambda}(d(x_0,x)^2+1),\quad\forall x\in X.\end{align*}$$
For any
$r\geq 1/2\lambda $
, we obtain
$f^n(x)+r(d(x_0,x)^2+1)\geq 0$
for all
$x\in X$
and all
$n\in \mathbb {N}$
.
3.2 Attouch’s theorem for complete
$\operatorname {\mathrm {CAT}}(0)$
spaces
Theorem 3.3 Let
$f^n,f:X\to (-\infty ,+\infty ]$
be proper closed convex functions such that
-
(1)
$\forall \lambda>0,\forall x\in X$
it holds
$\lim _{n\to +\infty }J^n_{\lambda }x=J_{\lambda }x$
. -
(2)
$(f^n)_{n\in \mathbb {N}}$
satisfies the normalization condition. -
(3)
$\lim _{n\to +\infty }(f^n_{\lambda })'(x;\gamma )=f^{\prime }_{\lambda }(x;\gamma )$
for all
$\gamma \in \Gamma _{x_0}(X)$
and
$x\in \gamma $
.
Then
$\lim _{n\to +\infty }f^n_{\lambda }(x)=f_{\lambda }(x)$
for any
$\lambda>0, x\in X$
.
Proof Let
$(f^n)_{n\in \mathbb {N}},f$
satisfy the normalization condition. Then there exists
$(x_n),x_0\subset X$
such that
$\lim _{n\to +\infty }x_n=x_0,\lim _{n\to +\infty }f^n(x_n)=f(x_0)$
and
$\lim _{n\to +\infty } |\partial f^n|(x_n)=|\partial f|(x_0)$
. Assume that
$\lambda>0$
. First, we claim that
$\lim _{n\to +\infty }f^n_{\lambda }(x_0)=f_{\lambda }(x_0)$
. Introduce the variables
$u_n:= J^n_{\lambda }x_n$
for each
$n\in \mathbb {N}$
and
$u_0:= J_{\lambda }x_0$
. Note that by assumption (3.3) for each fixed
$m\in \mathbb {N}$
, we have
$\lim _{n\to +\infty }J^n_{\lambda }x_m=J_{\lambda }x_m$
. Since the mapping
$x\mapsto J_{\lambda }x$
is nonexpansive and therefore continuous, then
$\lim _mJ_{\lambda }x_m=J_{\lambda }x_0$
. By triangle inequality
$d(J^n_{\lambda }x_n,J_{\lambda }x_0)\leq d(J^n_{\lambda }x_n,J^n_{\lambda }x_m)+d(J^n_{\lambda }x_m,J_{\lambda }x_0)$
and nonexpansiveness of
$J^n_{\lambda }$
, we have
$$\begin{align*}d(J^n_{\lambda}x_n,J_{\lambda}x_0)\leq d(x_n,x_m)+d(J^n_{\lambda}x_m,J_{\lambda}x_0).\end{align*}$$
Passing in the limit as
$m,n\to +\infty $
, we get
$\lim _{n\to +\infty }u_n=\lim _{n\to +\infty }J^n_{\lambda }x_n=J_{\lambda }x_0=u_0$
. On the other hand,
$$\begin{align*}|f^n(u_n)-f(u_0)|\leq |f^n(u_n)-f^n(x_n)|+|f^n(x_n)-f(x_0)|+|f(x_0)-f(u_0)|.\end{align*}$$
By normalization condition (3.3) and using
$\lim _{\lambda \downarrow 0}u_n=\lim _{\lambda \downarrow 0}J^n_{\lambda }x_n=x_n$
and
$\lim _{\lambda \downarrow 0}u_0=\lim _{\lambda \downarrow 0}J_{\lambda }x_0=x_0$
together with the lsc of
$f^n$
and f imply in the limit as
$\lambda \downarrow 0$
and
$n\to +\infty $
that
$\lim _{n\to +\infty }f^n(u_n)=f(u_0)$
. Again by definition of Moreau envelope as
$n\to +\infty $
$$\begin{align*}f^n_{\lambda}(x_n)=f^n(u_n)+\frac{1}{2\lambda}d(x_n,u_n)^2\to f(u_0)+\frac{1}{2\lambda}d(x_0,u_0)^2:= f_{\lambda}(x_0).\end{align*}$$
Note that
$$\begin{align*}f^n_{\lambda}(x_0)\leq f^n(x_n)+\frac{1}{2\lambda}d(x_0,x_n)^2\to f(x_0)\quad\text{as}\quad n\to+\infty.\end{align*}$$
On the other hand, we have
$$ \begin{align*} f^n_{\lambda}(x_0)\geq f^n(J^n_{\lambda}x_0)&\geq f^n(x_n)-|\partial f^n|(x_n)d(J^n_{\lambda}x_0,x_n)\\&\to f(x_0)-|\partial f|(x_0)d(J_{\lambda}x_0,x_0)>-\infty\quad\text{as}\quad n\to+\infty. \end{align*} $$
In particular we get
$-\infty <\liminf _{n\to +\infty }f^n_{\lambda }(x_0)\leq \limsup _{n\to +\infty }f^n_{\lambda }(x_0)<+\infty $
(we can assume wlog that
$x_0\in \operatorname {\mathrm {dom}} f$
). By Lemma 3.2, we get that
$(f^n_{\lambda })_{n\in \mathbb {N}}$
is equi locally Lipschitz in X. Then for any bounded domain
$K\subseteq X$
, there is
$C_K>0$
such that
$$\begin{align*}|f^n_{\lambda}(x)-f^n_{\lambda}(y)|\leq C_Kd(x,y),\quad\forall x,y\in K,\forall n\in\mathbb{N}.\end{align*}$$
From this and the estimate
$$ \begin{align*} |f^n_{\lambda}(x_0)-f_{\lambda}(x_0)|&\leq |f^n_{\lambda}(x_0)-f^n_{\lambda}(x_n)|+|f^n_{\lambda}(x_n)-f_{\lambda}(x_0)|\\&\leq C_Kd(x_n,x_0)+|f^n_{\lambda}(x_n)-f_{\lambda}(x_0)| \end{align*} $$
follows that
$\lim _{n\to +\infty }f^n_{\lambda }(x_0)=f_{\lambda }(x_0)$
. Now define
$g_{n,\lambda }(t):= f^n_{\lambda }(x_t)$
and
$g_{\lambda }(t):= f_{\lambda }(x_t)$
, where
$x_t:= (1-t)x_0\oplus tx$
and
$x\in X$
is arbitrary. Consider
$$\begin{align*}g^{\prime}_{n,\lambda}(t):=\lim_{s\to 0}\frac{g_{n,\lambda}(t+s)-g_{n,\lambda}(s)}{s},\;t\in(0,1).\end{align*}$$
Since
$f^n_{\lambda }$
is convex for each
$n\in \mathbb {N}$
then it is absolutely continuous on every geodesic segment. In particular,
$g^{\prime }_{n,\lambda }(t)$
exists almost everywhere on
$[0,1]$
, it is Lebesgue integrable on the interval
$[0,1]$
and satifies
$$ \begin{align} g_{n,\lambda}(1)=g_{n,\lambda}(0)+\int^1_0g^{\prime}_{n,\lambda}(t)\,dt. \end{align} $$
On the other hand,
$g^{\prime }_{n,\lambda }(t)=(f^n_{\lambda })'(x_t;\gamma )d(x_0,x)$
where
$\gamma \in \Gamma _{x_0}(X)$
connects
$x_0$
with x and
$x_t\in \gamma $
. Assumption (3.3) implies
$\lim _{n\to +\infty }g^{\prime }_{n,\lambda }(t)=g^{\prime }_{\lambda }(t)$
for all
$t\in [0,1]$
. Moreover equi locally Lipschitz property of
$(f^n_{\lambda })_{n\in \mathbb {N}}$
implies that
$\sup _n|g^{\prime }_{n,\lambda }(t)|\leq C_K d(x_0,x)$
for any bounded domain K around
$x_0$
and
$x\in K$
. Upon replacing
$g_{n,\lambda }(1)$
with
$f^n_{\lambda }(x)$
and
$g_{n,\lambda }(0)$
with
$f^n_{\lambda }(x_0)$
in (3.2), by Lebesgue dominated convergence theorem we obtain in the limit
$$\begin{align*}\lim_{n\to+\infty}f^n_{\lambda}(x)=f_{\lambda}(x_0)+\int^1_0\lim_{n\to+\infty}g^{\prime}_{n,\lambda}(t)\,dt=f_{\lambda}(x_0)+\int^1_0g^{\prime}_{\lambda}(t)\,dt=f_{\lambda}(x).\end{align*}$$
Example 3.4 Consider again the sequence of functions
$f^n:[0,1]\to \mathbb R$
given by
$$\begin{align*}f^n(x) =\left\{ \begin{array}{ll} 0 & n\;\text{odd}, \\ 1 & n\;\text{even}, \end{array} \right.\quad \forall x\in[0,1].\end{align*}$$
Let
$f(x)=1/2$
for all
$x\in [0,1]$
. Then
$(f^n)_{n\in \mathbb N},f$
is a family of proper closed convex functions satisfying
$\lim _{n\to +\infty }J_{\lambda }^nx=J_{\lambda }x$
for any
$\lambda>0$
and every
$x\in [0,1]$
. However, assumption (2) is not fulfilled since for any sequence
$(x_n)_{n\in \mathbb N}\subset X$
and for any
$x_0\in X$
such that
$\lim _{n\to +\infty }x_n=x_0$
we have
$\liminf _{n\to +\infty }f^n(x_n)=0<1/2=f(x_0)$
. Moreover, for any
$x\in [0,1]$
it holds that
$\liminf _{n\to +\infty }f^n(x)=0<1/2=f(x)$
consequently since
$f^n_{\lambda }(x)=f^n(x)$
and
$f_{\lambda }(x)=f(x)$
for all
$\lambda>0$
it follows that
$\lim _{n\to +\infty }f_{\lambda }^n(x)\neq f_{\lambda }(x)$
. Note that in this case,
$(f^n_{\lambda })'(x;\gamma )=(f^n)'(x;\gamma )=0$
and
$(f_{\lambda })'(x;\gamma )=f'(x;\gamma )=0$
i.e.,
$\lim _{n\to +\infty }(f^n_{\lambda })'(x;\gamma )=f'(x;\gamma )=0$
for all
$\gamma \in \Gamma _{x_0}(X)$
and
$x\in \gamma $
. This example shows that condition (2) cannot be removed.
Example 3.5 Let
$(\mathcal H,\|\cdot \|)$
be a separable Hilbert space equipped with the canonical norm
$\|\cdot \|$
. Let
$\{e_k\}_{k\in \mathbb N}$
be the usual orthonormal basis in
$\mathcal H$
. Denote by
$X=\displaystyle \bigcup _{k\in \mathbb N}X_k$
where
$$\begin{align*}X_k=\{x\in \mathcal H\,:\, x=t\,e_k,\;0\leq t\leq 1\}.\end{align*}$$
When X is equipped with the length metric, that we denote by
$d_{\ell }$
, then
$(X, d_{\ell })$
is a complete
$\operatorname {\mathrm {CAT}}(0)$
space. Let
$f^n:X\to \mathbb R$
be defined by the formula
$f^n(x)=d_{\ell }({\textbf {0}},x)/n$
for all
$x\in X$
and
$n\in \mathbb N$
. Here,
${\textbf {0}}$
is the usual origin in
$\mathcal H$
, i.e.,
$\{{\textbf {0}}\}=\displaystyle \bigcap _{k\in \mathbb N}X_k$
. Let
$f:X\to \mathbb R$
be the identical zero function i.e.,
$f(x)=0$
for all
$x\in X$
. Two elements
$x,y\in X$
are equivalent whenever
$x,y\in X_k$
for some
$k\in \mathbb N$
, and we write
$x\sim y$
. Note that
$$\begin{align*}d_{\ell}(x,y)=\left\{ \begin{array}{ll} \|x-y\| & x\sim y, \\ \|x\|+\|y\| & \text{else}. \end{array} \right.\end{align*}$$
In particular, we obtain
$f^n(x)=\|x\|/n$
for all
$x\in X$
and
$n\in \mathbb N$
. Then
$$\begin{align*}f^n(y)+\frac{1}{2\,\lambda}\,d_{\ell}^2(x,y)=\left\{ \begin{array}{ll} \displaystyle\frac{\|y\|}{n}+\frac{1}{2\lambda}\,\|x-y\|^2 & x\sim y, \\[1em] \displaystyle\frac{\|y\|}{n}+\frac{1}{2\lambda}\,(\|x\|+\|y\|)^2 & \text{else}. \end{array} \right.\end{align*}$$
By virtue of triangle inquality
$\|x-y\|\leq \|x\|+\|y\|$
, we obtain that
$$\begin{align*}\inf_{y\in X}\Big\{f^n(y)+\frac{1}{2\,\lambda}\,d_{\ell}^2(x,y)\Big\}=\inf_{y\sim x}\Big\{f^n(y)+\frac{1}{2\,\lambda}\,d_{\ell}^2(x,y)\Big\},\quad \forall x\in X.\end{align*}$$
Consequently
$$\begin{align*}f^n_{\lambda}(x)=\inf_{y\sim x}\Big\{f^n(y)+\frac{1}{2\,\lambda}\,\|x-y\|^2\Big\}.\end{align*}$$
Since
$x\sim y$
then there are
$s,t\in [0,1]$
such that
$x=te_k$
and
$y=se_k$
for some
$k\in \mathbb N$
. Hence, in terms of the variables
$s,t$
we can write
$$\begin{align*}g(t)=f^n_{\lambda}(te_k)=\inf_{s\in[0,1]}\Big\{\frac{s}{n}+\frac{1}{2\,\lambda}\,(s-t)^2\Big\}\end{align*}$$
minimum of which is achieved for
$s_n=t-\lambda /n$
. Hence,
$J_{\lambda }^nx=J^n_{\lambda }(t\,e_k)=(t-\lambda /n)\,e_k\to te_k=x$
as
$n\to +\infty $
. On the other hand,
$J_{\lambda }x=x$
since trivially
$f(x)=0$
for all
$x\in X$
. This means that
$\lim _{n\to +\infty }J^n_{\lambda }x=J_{\lambda }x$
for all
$x\in X$
and for all
$\lambda>0$
. Consequently condition (1) is satisfied. Now let
$x_n=e_n/n$
for
$n\in \mathbb N$
. Then
$\lim _{n\to +\infty }x_n={\textbf {0}}$
and
$\lim _{n\to +\infty }f^n(x_n)=\lim _{n\to +\infty }1/n^2=0=f({\textbf {0}})$
. Moreover, by virtue of Lemma 2.1, we have
$$ \begin{align*} |\partial f^n|(x_n)&=\sup_{y\in X\backslash\{x_n\}}\frac{\max\{\|x_n\|/n-\|y\|/n,0\}}{d_{\ell}(x_n,y)}\\&\leq \sup_{y\in X\backslash\{x_n\}}\frac{\max\{\|x_n\|/n-\|y\|/n,0\}}{\|x_n-y\|}\leq \frac{1}{n}\to 0,\quad\text{as}\;n\to+\infty. \end{align*} $$
Also
$|\partial f|({\textbf {0}})=0$
, hence
$\lim _{n\to +\infty } |\partial f^n|(x_n)=|\partial f|({\textbf {0}})$
. Therefore, condition (2) is also satisfied. Now let
$\gamma \in \Gamma _{{\textbf {0}}}(X)$
and
$x\in \gamma $
. From the above calculations, we obtain that
$$ \begin{align} f^n_{\lambda}(x)=f^n(J^n_{\lambda}x)+\frac{1}{2\lambda}\,\|x-J^n_{\lambda}x\|^2=\frac{|t-\lambda/n|}{n}+\frac{\lambda}{2\,n^2}:=g_{n,\lambda}(t). \end{align} $$
For sufficiently large n we get
$g^{\prime }_{n,\lambda }(t)=1/n^2\to 0$
as
$n\to +\infty $
. The relation
$g^{\prime }_{n,\lambda }(t)=(f^n_{\lambda })'(x;\gamma )\,d_{\ell }({\textbf {0}},\gamma (1))$
yields
$(f^n_{\lambda })'(x;\gamma )\to 0$
as
$n\to +\infty $
. On the other side,
$f_{\lambda }(x)=0$
for all
$x\in X$
implies
$(f_{\lambda })'(x;\gamma )=0$
for every
$\gamma \in \Gamma _{{\textbf {0}}}(X)$
and all
$x\in X$
. Consequently, we get
$\lim _{n\to +\infty }(f^n_{\lambda })'(x;\gamma )=(f_{\lambda })'(x;\gamma )$
. This confirms condition (3). By Theorem 3.3,
$\lim _{n\to +\infty }f^n_{\lambda }(x)=f_{\lambda }(x)$
for all
$x\in X$
and
$\lambda>0$
. Last conclusion can be easily verified directly from (3.3).
Theorem 3.6 Let
$(f^n), f:X\to (-\infty ,+\infty ]$
be proper closed and convex functions such that for some
$x_0\in X$
it holds that
$\lim _{n\to +\infty }(f^n_{\lambda })'(x;\gamma )=f^{\prime }_{\lambda }(x;\gamma )$
for all
$\gamma \in \Gamma _{x_0}(X)$
and
$x\in \gamma $
. Then the following statements are equivalent:
-
(1)
$M-\lim _{n\to +\infty }f^n=f$
. -
(2)
$\forall \lambda>0,\forall x\in X$
it holds
$\lim _{n\to +\infty }J^n_{\lambda }x=J_{\lambda }x$
and
$(f^n)_{n\in \mathbb {N}}$
satisfies the normalization condition with some
$(x_n)_{n\in \mathbb {N}}$
converging to
$x_0$
. -
(3)
$\lim _{n\to +\infty }f^n_{\lambda }(x)=f_{\lambda }(x)$
for any
$\lambda>0,\forall x\in X$
.
Acknowledgment
I am grateful to my advisor Prof. D. R. Luke for his helpful comments in improving the quality of this work. I would like to thank as well the anonymous referee for their qualitative suggestions. The author was supported by Deutscher Akademischer Austauschdienst (DAAD) and partially by Germany’s Excellence Strategy–The Berlin Mathematics Research Center MATH+ (EXC-2046/1, Projektnummer: 390685689).
