1 Introduction
Binomial edge ideals generalize in a natural way the determinantal ideals generated by the two-minors of a generic matrix of type
$2\times n.$
They were independently introduced a decade ago in the papers [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22] and [Reference Ohtani34]. Since then, they have been intensively studied and there exists a rich recent literature on this subject. Fundamental results on their Gröbner bases, primary decomposition, and their resolutions are presented in the monograph [Reference Herzog, Hibi and Ohsugi23].
Binomial edge ideals with quadratic Gröbner basis are of particular interest since their initial ideals are monomial edge ideals associated with bipartite graphs. Therefore, the theory of monomial edge ideals can be employed in deriving information about binomial edge ideals.
While many questions regarding binomial edge ideals have been already answered, much less is known about their powers. In [Reference Jayanthan, Kumar and Sarkar28], first steps in studying the regularity of powers of binomial edge ideals have been done. By using quadratic sequences, the authors obtain bounds for the regularity of powers of binomial edge ideals which are almost complete intersection. For the same class of ideals, in the paper [Reference Jayanthan, Kumar and Sarkar29], the Rees rings are considered. Another direction of research was pursued in [Reference Ene, Herzog, Stamate and Szemberg13]. Here, it is shown that binomial edge ideals with quadratic Gröbner basis have the nice property that their ordinary and symbolic powers coincide.
Let G be a simple graph (i.e., an undirected graph with no multiple edges and no loops) on the vertex set
$[n]=\{1,2,\ldots ,n\}$
and let
$S=K[x_1,x_2,\ldots ,x_n,y_1,y_2,\ldots ,y_n]$
be the polynomial ring in
$2n$
variables over the field
$K.$
For
$1\leq i<j\leq n,$
we set
$f_{ij}=x_iy_j-x_jy_i.$
The binomial edge ideal of the graph G is
$$ \begin{align*}J_G=(f_{ij}: i<j, \{i,j\} \text{ is an edge of }G).\end{align*} $$
We consider the polynomial ring S endowed with the lexicographic order induced by the natural order of the variables, namely
$x_1>x_2>\cdots >x_n>y_1>y_2\cdots >y_n.$
The Gröbner basis of
$J_G$
with respect to this order was computed in [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22]. The graphs G with the property that
$J_G$
has a quadratic Gröbner basis were characterized in the same paper and they were called closed. Later on, it turned out that closed graphs coincide with the proper interval graphs, see [Reference Crupi and Rinaldo10], which have a history of about 50 years in combinatorics. In Section 2, we survey various combinatorial characterizations of closed graphs which are very useful in working with their associated binomial edge ideals. Closed graphs with Cohen–Macaulay binomial edge ideals are classified in [Reference Ene, Herzog and Hibi14, Th. 3.1]. Roughly speaking, they are “chains” of cliques (i.e., complete graphs) with the property that every two consecutive cliques intersect in one vertex. For Cohen–Macaulay binomial edge ideals of closed graphs, we compute the depth function in Theorem 3.1 and Proposition 3.6. For this class of ideals, we show that
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{J_G^i}=\operatorname{\mathrm{depth}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)} \end{align*} $$
and this common value depends on the cardinality of the maximal cliques of
$G.$
The proof of Theorem 3.1 follows from several technical lemmas. The basic idea of the proof is the following. Starting with a closed graph G whose binomial edge ideal is Cohen–Macaulay, we consider a disconnected graph
$G'$
whose connected components are complete graphs of the same size as the maximal cliques of
$G.$
By using the techniques developed in [Reference Hà, Trung and Trung19] for computing the depth of powers of sums of ideals, we are able to calculate the depth of the powers of
$J_{G'}.$
Next, by using a regular sequence of linear forms, we can recover the powers of
$J_G$
from the powers of
$J_{G'}$
, and, finally we can compute the depth of the powers of
$J_G.$
Similar arguments are used to compute the depth for the powers of
$ \operatorname {\mathrm {in}}_<(J_G).$
In addition, Proposition 3.6 implies that the depth function of
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
is nonincreasing. We expect the same behavior for every closed graph, not only for those whose binomial edge ideal is Cohen–Macaulay; see Question 6.1. However, we are able to show that for every closed graph G, the limit depth for
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
coincide and we compute this value in Theorem 3.10. On the other hand, in Proposition 3.12, we show that the initial ideal
$ \operatorname {\mathrm {in}}_<(J_G)$
has a nonincreasing depth function. An important step in deriving Theorem 3.10 is Proposition 3.9 where we prove that the Rees rings
${\mathcal R}(J_G)$
and
${\mathcal R}( \operatorname {\mathrm {in}}_<(J_G))$
are Cohen–Macaulay. This reduces the proof of the equality
$$ \begin{align*} \lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S}{J_G^k}=\lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^k} \end{align*} $$
by showing that
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
have the same analytic spread. This is shown by using the Sagbi basis theory.
One of the problems that we have considered at the beginning of this project was to characterize the graphs G such that
$J_G ^k$
is Cohen–Macaulay for (some)
$k\geq 2.$
We still do not have a complete solution for this problem which is probably very difficult in the largest generality, but we can solve it if we restrict to closed or connected block graphs; see Proposition 3.7 and Proposition 5.2. In the last part of Section 3, we show that binomial edge ideals of closed graphs have the strong persistence property, as their initial ideals do.
In Section 4, we compute the regularity of the powers of
$J_G$
, when G is closed. In Theorem 4.1, we prove that if G is connected, then, for every
$k\geq 1,$
$$ \begin{align*} \operatorname{\mathrm{reg}}\frac{S}{J_G^k}=\operatorname{\mathrm{reg}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^k)}=\ell+2(k-1), \end{align*} $$
where
$\ell $
is the length of the longest induced path in
$G.$
The inequality
$ \operatorname {\mathrm {reg}} S/J_G^k\geq \ell +2(k-1)$
follows from a result in [Reference Jayanthan, Kumar and Sarkar28]. For the rest of the proof, we combine various known facts about the regularity of the powers of edge ideals of bipartite graphs. The statement is extended to disconnected closed graphs in Proposition 4.2.
In Section 5, we consider block graphs. These are chordal graphs with the property that every two maximal cliques intersect in at most one vertex. For the block graphs whose binomial edge ideal is Cohen–Macaulay, in Theorem 5.1, we show that the symbolic powers coincide with the ordinary ones if and only if the graph is closed. This theorem shows, in particular, that the equality between the symbolic and ordinary powers of binomial edge ideals does not hold for all chordal graphs. Finally, in Proposition 5.2, we show that for every connected block graph G which is not a path,
$J_G^k$
is not Cohen–Macaulay for
$k\geq 2.$
In the last section of the paper, we discuss a few open questions. The most intriguing is related to a conjecture which appeared in [Reference Ene, Herzog and Hibi14] and which is still open. This conjecture states that for every closed graph
$G,$
we have
$\beta _{ij}(J_G)=\beta _{ij}( \operatorname {\mathrm {in}}_<(J_G)).$
While doing some calculations with the computer, we observed an interesting phenomenon, namely that the graded Betti numbers are the same also for powers of
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G).$
Moreover, as we explain in Section 6, the equalities between the graded Betti numbers are true for complete and path graphs. Taking into account also our results on the regularity and depth of the powers of
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G),$
we were tempted to conjecture that for every closed graph G and every
$k\geq 1,$
we have
$\beta _{ij}(J_G^k)=\beta _{ij}(( \operatorname {\mathrm {in}}_<(J_G))^k).$
Another interesting question concerns block graphs. By computer calculation, we observed that the net graph N (Figure 2) which plays an important role in Theorem 5.1 has the property that
$J_N^{(2)}$
is Cohen–Macaulay, but
$J_N^2$
is not Cohen–Macaulay. It would be of interest to classify all the block graphs with the property that the second symbolic power of the associated binomial edge ideal is Cohen–Macaulay.
2 Preliminaries
Let G be a graphFootnote
1
on the vertex set
$V(G)=[n]$
and edge set
$E(G).$
Let
$S=K[x_1,\ldots ,x_n,y_1,\ldots ,y_n]$
be the polynomial ring in
$2n$
variables over the field
$K.$
The binomial edge ideal
$J_G$
associated with G is generated by the binomials
$f_{ij}=x_iy_j-x_jy_i\in S$
where
$\{i,j\}\in E(G).$
In other words,
$J_G$
is generated by the maximal minors of the generic
$2\times n$
-matrix
$X=\left ( \begin {array}{cccc} x_1 & x_2 & \cdots & x_n\\ y_1 & y_2 & \cdots & y_n \end {array}\right ) $
whose column indices correspond to the edges of G. Two simple examples of binomial edge ideals are the ideal
$I_2(X)$
generated by all the maximal minors of X which in our notation is denoted by
$J_{K_n}$
where
$K_n$
is the complete graph on the vertex set
$[n],$
and the ideal generated by the adjacent minors of X which coincides with
$J_{P_n},$
where
$P_n$
is the path graph with edges
$\{i,i+1\}, 1\leq i \leq n-1.$
We consider the polynomial ring S endowed with the lexicographic order induced by the natural order of the variables. Let
$ \operatorname {\mathrm {in}}_<(J_G)$
be the initial ideal of
$J_G$
with respect to this monomial order. By [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22, Cor. 2.2],
$J_G$
is a radical ideal. In the same paper, it was shown that the minimal prime ideals can be characterized in terms of the combinatorics of the graph
$G.$
In order to recall this characterization, we introduce the following notation. Let
$W\subset [n]$
be a (possibly empty) subset of
$[n]$
, and let
$G_1,\ldots ,G_{c(W)}$
be the connected components of
$G_{[n]\setminus W}$
where
$G_{[n]\setminus W}$
is the induced subgraph of G on the vertex set
$[n]\setminus W,$
and
$c(W)$
denotes the number of connected components of
$G_{[n]\setminus W}$
. For
$1\leq i\leq c(W),$
let
$\widetilde {G}_i$
be the complete graph on the vertex set
$V(G_i).$
Let
$$ \begin{align*}P_{W}(G)=(\{x_i,y_i\}_{i\in W}) +J_{\widetilde{G}_1}+\cdots +J_{\widetilde{G}_{c(W)}}.\end{align*} $$
Then
$P_{W}(G)$
is a prime ideal of height equal to
$n-c(W)+|W|$
for every
$W\subset [n],$
[Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22, Lem. 3.1].
By [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22, Th. 3.2],
$J_G=\bigcap _{W\subset [n]}P_{W}(G).$
In particular, the minimal primes of
$J_G$
are among the prime ideals
$P_{W}(G)$
with
$W\subset [n].$
Proposition 2.1. [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22, Cor. 3.9]
$P_{W}(G)$
is a minimal prime of
$J_G$
if and only if either
$W=\emptyset $
or W is nonempty and for each
$i\in W, c(W\setminus \{i\})<c(W)$
.
In graph theoretical terms,
$P_{W}(G)$
is a minimal prime ideal of
$J_G$
if and only if W is empty or W is nonempty and is a cut-point set of
$G,$
that is, i is a cut point of the induced subgraph
$G_{([n]\setminus W)\cup \{i\}}$
for every
$i\in W.$
Let
${\mathcal C}(G)$
be the set of all sets
$W\subset [n]$
such that
$P_{W}(G)\in \operatorname {\mathrm {Min}}(J_G),$
where
$ \operatorname {\mathrm {Min}}(J_G)$
is the set of minimal prime ideals of
$J_G.$
In particular, it follows that
$$ \begin{align} \dim S/J_G=\max\{n+c(W)-|W|: W \in {\mathcal C}(G)\}. \end{align} $$
For
$W=\emptyset , c=c(\emptyset )$
is the number of connected components
$G_1,\ldots ,G_c$
of
$G.$
In addition, one can easily see that
$P_{\emptyset }(G)=J_{\widetilde {G}_1}+\cdots +J_{\widetilde {G}_c}$
is a minimal prime of
$J_G.$
Therefore, if
$J_G$
is unmixed (which is the case, for instance, if
$J_G$
is Cohen–Macaulay), then all the minimal primes of
$J_G$
have dimension equal to
$n+c.$
In particular, if G is connected, then
$J_G$
is unmixed if and only if, for every minimal prime
$P_{W}(G)$
of
$G,$
we have
$n+c(W)-|W|=n+1,$
that is,
$c(W)-|W|=1.$
By [Reference Conca, De Negri and Gorla6, Th. 3.1] and [Reference Conca, De Negri and Gorla6, Cor. 2.12], we have
$$ \begin{align} \operatorname{\mathrm{in}}_<(J_G)=\bigcap_{W \in {\mathcal C}(G)} \operatorname{\mathrm{in}}_< P_{W}(G). \end{align} $$
In what follows, we are mainly interested in binomial edge ideals with quadratic Gröbner bases. We recall the following result from [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22, Th. 1.1].
Theorem 2.2 [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22]
Let G be a graph on the vertex set
$[n]$
with the edge set
$E(G)$
, and let
$<$
be the lexicographic order on S induced by
$x_1>\cdots > x_n> y_1>\cdots >y_n$
. Then the following conditions are equivalent:
-
(a) The generators
$f_{ij}$
of
$J_G$
form a quadratic Gröbner basis. -
(b) For all edges
$\{i,j\}$
and
$\{i,k\}$
with
$j>i<k$
or
$j<i>k$
one has
$\{j,k\}\in E(G)$
.
According to [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22], a graph G endowed with a labeling which satisfies condition (b) in the above theorem is called closed with respect to the given labeling. Therefore, the generators of
$J_G $
form a Gröbner basis with respect to the lexicographic order if and only if G is closed with respect to its given labeling. Moreover, a graph G is called closed if there exists a labeling of its vertices such that G is closed with respect to it. Later on, Crupi and Rinaldo proved in [Reference Crupi and Rinaldo10] that closed graphs coincide with the so-called proper interval graphs, a class of graphs with a rich history in combinatorics. However, in this paper, we will call them closed graphs. There are several characterizations of closed graphs. Before discussing them, let us recall some notions of graph theory. A graph is called chordal if it has no induced cycle of length greater than or equal to
$4.$
A graph is called claw-free if it has no induced subgraph isomorphic to the one displayed in Figure 1. A clique of a graph G is a complete subgraph of
$G.$
The cliques of G form a simplicial complex
$\Delta (G)$
which is called the clique complex of
$G.$
Figure 1 Claw graph
Figure 2 Net and tent
The equivalences of the following theorem collects several results proved in [Reference Baskoroputro, Ene and Ion3], [Reference Crupi and Rinaldo9], [Reference Crupi and Rinaldo10], [Reference Ene, Herzog and Hibi14], [Reference Herzog, Hibi, Hreinsdóttir, Kahle and Rauh22].
Theorem 2.3. Let G be a graph on the vertex set
$[n].$
The following statements are equivalent:
-
(i) G is a closed graph with respect to the given labeling, or equivalently, the generators of
$J_G$
form a Gröbner basis with respect to the lexicographic order induced by
$x_1>\cdots >x_n>y_1>\cdots >y_n;$
-
(ii) for all
$\{i,j\},\{k,\ell \}\in E(G)$
with
$i<j$
and
$k<\ell ,$
one has
$\{j,\ell \}\in E(G)$
if
$i=k, j\neq \ell $
, and
$\{i,k\}\in E(G)$
if
$j=\ell , i\neq k;$
-
(iii) The facets, say
$F_1,\ldots , F_r,$
of the clique complex
$\Delta (G)$
of G are intervals of the form
$F_i=[a_i,b_i]$
which can be ordered such that
$1=a_1<\cdots < a_r<b_r=n;$
-
(iv) for any
$1\leq i<j<k\leq n,$
if
$\{i,k\}\in E(G),$
then
$\{i,j\},\{j,k\}\in E(G); and$
-
(v) G is a chordal and claw-free graph which does not contain any subgraph isomorphic to the graphs displayed in Figure 2.
The connected closed graphs with Cohen–Macaulay binomial edge ideals were characterized in [Reference Ene, Herzog and Hibi14].
Theorem 2.4. [Reference Ene, Herzog and Hibi14, Th. 3.1]
Let G be a connected graph on
$[n]$
which is closed with respect to the given labeling. Then the following conditions are equivalent:
-
(a)
$J_G$
is unmixed; -
(b)
$J_G$
is Cohen–Macaulay; -
(c)
$ \operatorname {\mathrm {in}}_< (J_G)$
is Cohen–Macaulay; -
(d) G satisfies the following condition: if
$\{i,j+1\}, \{j,k+1\}\in E(G)$
with
$i<j<k$
, then
$\{i,k+1\}\in E(G)$
; and -
(e) there exist integers
$1=a_1<a_2<\cdots <a_r<a_{r+1}=n$
and a leaf order of the facets
$F_1,\ldots ,F_r$
of
$\Delta (G)$
such that
$F_i=[a_i,a_{i+1}]$
for all
$i=1,\ldots ,r$
.
Let us remark that if G is closed and has the connected components
$G_1,G_2,\ldots ,,G_c,$
then
$$ \begin{align*} \frac{S}{J_G}\cong \frac{S_1}{J_{G_1}}\otimes \frac{S_2}{J_{G_2}}\otimes \cdots \otimes \frac{S_c}{J_{G_c}}, \end{align*} $$
where
$S_i=K[\{x_j,y_j: j\in V(G_i)\}]$
for
$1\leq i\leq c.$
Thus,
$J_G$
is Cohen–Macaulay if and only if each
$S_i/J_{G_i}$
is Cohen–Macaulay.
Let G be a closed graph. Then the generators of
$J_G$
form a reduced Gröbner basis with respect to the lexicographic order. This implies that
$ \operatorname {\mathrm {in}}_<(J_G)=(x_iy_j: i<j, \{i,j\}\in E(G)).$
Thus,
$ \operatorname {\mathrm {in}}_<(J_G)$
is the monomial edge ideal of a bipartite graph, let us call it
$H,$
on the vertex set
$\{x_1,x_2,\ldots ,x_n\}\cup \{y_1,y_2,\ldots ,y_n\}$
whose edges are
$\{x_i,y_j\}$
where
$\{i,j\}\in E(G).$
Since H is bipartite, it follows that the edge ideal
$I(H)= \operatorname {\mathrm {in}}_<(J_G)$
has the property that its ordinary powers coincide with the symbolic ones [Reference Simis, Vasconcelos and Villarreal36, Th. 5.9]. Combining (2) with the proof of [Reference Ene, Herzog, Stamate and Szemberg13, Lem. 3.1], it follows that if G is closed, then
$$ \begin{align} \operatorname{\mathrm{in}}_<(J_G^i)=(\operatorname{\mathrm{in}}_<(J_G))^i, \text{ for every }i\geq 1. \end{align} $$
In other words, if G is closed, then the generators of
$J_G^i$
form a Gröbner basis of
$J_G^i$
for
$i\geq 1.$
Moreover, with the same assumption on the graph G, by [Reference Ene, Herzog, Stamate and Szemberg13, Cor. 3.4, Prop. 2.5], we have
$$ \begin{align} J_G^i=J_G^{(i)}\text{ for every }i\geq 1, \end{align} $$
where
$J_G^{(i)}$
denotes the ith symbolic power of
$J_G.$
In other words, for a closed graph
$G,$
the symbolic powers of the binomial edge ideal
$J_G$
coincide with the ordinary powers. We recall the notion of symbolic power. Let
$I\subset R$
be an ideal in a Noetherian ring
$R,$
and let
$ \operatorname {\mathrm {Min}}(I)$
be the set of the minimal prime ideals of
$I.$
For an integer
$k\geq 1,$
one defines the kth symbolic power of I as follows:
$$ \begin{align*} I^{(k)}=\bigcap_{{\frak p}\in\operatorname{\mathrm{Min}}(I)}(I^kR_{\frak p}\cap R). \end{align*} $$
By the definition of the symbolic power, we have
$I^k\subseteq I^{(k)}$
for
$k\geq 1. $
Symbolic powers do not, in general, coincide with the ordinary powers.
3 Depth of powers
The first main result of this section is the following.
Theorem 3.1. Let G be a connected closed graph on the vertex set
$[n]$
such that
$J_G$
is Cohen–Macaulay. Let
$F_1,F_2,\ldots ,F_r$
be the maximal cliques of G and
$d_i=\dim F_i=\# F_i-1$
for
$1\leq i\leq r.$
Assume that
$d_1\geq d_2\geq \cdots \geq d_r\geq 1.$
Footnote
2
Then the following equalities hold:
-
(a)
$ \operatorname {\mathrm {depth}}\frac {S}{J_G^i}= \operatorname {\mathrm {depth}}\frac {S}{ \operatorname {\mathrm {in}}_<(J_G^i)}=n-\sum _{j=1}^{i-1}d_j+i \text { for }1\leq i\leq r,$
-
(b)
$ \operatorname {\mathrm {depth}}\frac {S}{J_G^i}= \operatorname {\mathrm {depth}}\frac {S}{ \operatorname {\mathrm {in}}_<(J_G^i)}=r+2 \text { for } i\geq r+1.$
For the proof of this theorem, we need a few lemmas. The proof of the first preparatory lemma is a straightforward extension of the proof of [Reference Huneke26, Th. 4.4].
Lemma 3.2. Let G be a complete graph on the vertex set
$[n]$
and
$J_G$
its binomial edge ideal. Then
$y_{n-2}-x_{n-1},y_{n-1}-x_n,y_n$
is a maximal regular sequence on
$S/J_G^i$
for all
$i\geq 2.$
In particular,
$ \operatorname {\mathrm {depth}} S/J_G^i=3$
for
$i\geq 2.$
Proof Let
$R=S/(y_{n-2}-x_{n-1},y_{n-1}-x_n,y_n)=K[x_1,\ldots ,x_{n-2},y_1,\ldots ,y_{n-1}].$
The image of
$J_G$
in R is the ideal
$J'$
generated by all the
$2$
–minors of the matrix
$$ \begin{align*}X'=\left( \begin{array}{ccccc} x_1& \ldots & x_{n-2} & y_{n-2} & y_{n-1}\\ y_1 & \ldots & y_{n-2} & y_{n-1} & 0 \end{array}\right). \end{align*} $$
In order to prove our claim, it is enough to show that
${\frak m},$
that is, the maximal ideal of R is associated to
$(J')^i$
for
$i\geq 2.$
If we show that
$((J')^i:y_{n-1}^{2i-1})$
is
${\frak m}$
–primary, then
${\frak m}\in \operatorname {\mathrm {Ass}}(R/(J')^i)$
, which implies that
$ \operatorname {\mathrm {depth}}(R/(J')^i)=0$
and the claim follows.
Set
$y=y_{n-1}.$
Then
$y^{2i-1}\notin (J')^i$
since
$(J')^i$
is generated in degree
$2i.$
But
$y\cdot y^{2i-1}=(y^2)^i\in (J')^i$
since
$y^2\in J'.$
Therefore,
$y\in (J')^i:y^{2i-1}.$
For
$1\leq j\leq n-2,$
we have
$y_jy\in J'.$
Then
$y_j^{2i-1}y^{2i-1}\in (J')^{2i-1}\subseteq (J')^i,$
thus
$y_j^{2i-1}\in (J')^i:y^{2i-1}$
for
$1\leq j\leq n-2.$
Finally, since
$x_jy-y_jy_{n-2}\in J'$
for
$1\leq j\leq n-2,$
we get that for
$i\geq 2, y^{2i-2}(x_jy-y_jy_{n-2})\in (J')^{i-1}\cdot J'=(J')^i,$
since
$y^{2i-2}=(y^2)^{i-1}\in (J')^{i-1}.$
On the other hand,
$ y_jy_{n-2}y^{2i-2}=(y_jy)(y_{n-2}y)(y^2)^{i-2}\in (J')^i. $
It follows that
$x_jy^{2i-1}\in (J')^i,$
which implies that
$x_j\in (J')^i:y^{2i-1}$
for
$1\leq j\leq n-2.$
Lemma 3.3. Under the same assumption of Lemma 3.2, we have
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)} =3, \end{align*} $$
for all
$i\geq 2.$
Proof By (3), we have
$ \operatorname {\mathrm {in}}_<(J_G^i)=( \operatorname {\mathrm {in}}_<(J_G))^i$
for
$i\geq 1.$
Since
$y_1$
and
$x_n$
form a regular sequence on
$ \operatorname {\mathrm {in}}_<(J_G)$
and using Lemma 3.2, we get the following relations:
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{\overline{S}}{(\operatorname{\mathrm{in}}_<(J_G))^i}+2=\operatorname{\mathrm{depth}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^i}=\operatorname{\mathrm{depth}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)}\leq \operatorname{\mathrm{depth}}\frac{S}{J_G^i}=3, \end{align*} $$
where
$\overline {S}=K[\{x_i,y_j: 1\leq i\leq n-1, 2\leq j\leq n\}].$
By [Reference Trung37, Th. 4.4],
$ \operatorname {\mathrm {depth}}\overline {S}/( \operatorname {\mathrm {in}}_<(J_G))^i\geq 1$
for
$i\geq 1.$
Therefore, we get the desired equality.
In the following lemma, we use the following notation. If H is a graph on some vertex set
$V(H),$
then we denote by
$S(H)$
the polynomial ring over K in the variables
$x_k,y_k,$
where
$k\in V(H).$
Lemma 3.4. Let G be a closed graph on the vertex set
$[n]$
with maximal cliques
$[a_1,a_2],[a_2,a_3], \ldots ,[a_r,a_{r+1}]$
where
$1=a_1<a_2<\cdots <a_r<a_{r+1}=n.$
Let
$G'$
be the graph whose connected components are the mutually disjoint cliques
$$ \begin{align*}[a_1,a_2],[a_2+1,a_3+1],\ldots,[a_r+(r-1),a_{r+1}+(r-1)].\end{align*} $$
Then the following hold:
-
(a) The sequence of linear forms
is regular on
$$ \begin{align*} \underline{\ell}: \ell_1^y&=y_{a_2}-y_{a_2+1},\ell_1^x=x_{a_2}-x_{a_2+1}, \ell_2^y=y_{a_3+1}-y_{a_3+2},\ell_2^x=x_{a_3+1}-x_{a_3+2},\\&\ldots, \ell_{r-1}^y=y_{a_r+(r-2)}-y_{a_r+(r-1)},\ell_{r-1}^x=x_{a_r+(r-2)}-x_{a_r+(r-1)} \end{align*} $$
$S(G')/J_{G'}^j$
and for every
$$ \begin{align*} \frac{\frac{S(G')}{J_{G'}^j}}{(\underline{\ell})\frac{S(G')}{J_{G'}^j}}\cong \frac{S}{J_G^j}, \end{align*} $$
$j\geq 1.$
-
(b) The sequence of variables
$ \underline {\mu }: x_{a_2},y_{a_2+1},x_{a_3+1},\ldots ,y_{a_r+(r-1)} $
is regular on
$S(G')/ \operatorname {\mathrm {in}}_<(J_{G'}^j)$
and for every
$$ \begin{align*} \frac{\frac{S(G')}{\operatorname{\mathrm{in}}_<(J_{G'}^j)}}{(\underline{\mu})\frac{S(G')}{\operatorname{\mathrm{in}}_<(J_{G'}^j)}}\cong \frac{S}{\operatorname{\mathrm{in}}_<(J_G^j)}, \end{align*} $$
$j\geq 1.$
Proof (a) Let
$j\geq 1$
be an integer. We prove by induction on
$2\leq i\leq r$
that the sequence
$ \underline {\ell }_{i-1}:\ \ell _1^y,\ell _1^x,\ldots ,\ell _{i-1}^y,\ell _{i-1}^x$
is regular on
$S(G')/J_{G'}^j$
and
$$ \begin{align*} \frac{\frac{S(G')}{J_{G'}^j}}{(\underline{\ell}_{i-1})\frac{S(G')}{J_{G'}^j}}\cong \frac{S(\widetilde{G}_{i-1})}{J_{\widetilde{G}_{i-1}}^j}. \end{align*} $$
where, after relabeling the vertices,
$\widetilde {G}_{i-1}$
is a closed graph with maximal cliques
$$ \begin{align*}[a_1,a_2],[a_2,a_3],\ldots, [a_i,a_{i+1}], [a_{i+1}+1,a_{i+2}+1],\ldots,[a_r+(r-i),a_{r+1}+(r-i)].\end{align*} $$
Let us first check the claim for
$i=2.$
We have to show that
$\ell _1^y,\ell _1^x$
is regular on
$S(G')/J_{G'}^j.$
Note that
$J_{G'}$
is a prime ideal since it is the sum of r prime ideals in pairwise disjoint sets of variables corresponding to the r connected components of
$G'$
; see [Reference Herzog, Hibi and Ohsugi23, Lem. 7.14].
Let
$h\in S(G^{\prime })$
such that
$\ell _1^y h\in J_{G^{\prime }}^j.$
Since
$\ell _1^y\notin J_{G^{\prime }},$
because
$J_G^{\prime }$
is generated in degree
$2,$
it follows that
$h\in J_{G^{\prime }}^{(j)}=J_{G^{\prime }}^{j},$
thus
$\ell _1^y$
is regular on
$S(G^{\prime })/J_{G^{\prime }}^j.$
Now we show that
$\ell _1^x$
is regular on
$S(G^{\prime })/(J_{G^{\prime }}^j+(\ell _1^y)).$
We have
$$ \begin{align*} \frac{S(G')}{J_{G'}^j+(\ell_1^y)}\cong \frac{S(G')}{\overline{J}+(\ell_1^y)}, \end{align*} $$
where
$\overline {J} $
is the ideal in
$S(G')$
generated by the polynomials
$\overline {g}_1,\ldots , \overline {g}_m$
obtained from the generators
$g_1,\ldots , g_m$
of
$J_{G'}^j$
as follows. If
$g_k$
is a generator which contains the variable
$y_{a_2+1},$
we replace it by
$y_{a_2}$
and denote the new binomial by
$\overline {g}_k.$
If
$g_k$
contains the variable
$y_{a_2}$
, we replace it by
$y_{a_2+1},$
and denote the new binomial by
$\overline {g}_k.$
If a generator
$g_k$
of
$J_{G'}^j$
contains both variables
$y_{a_2}$
and
$y_{a_2+1}$
, then we exchange these variables and denote the new binomial by
$\overline {g}_k.$
Finally, if
$g_k$
is a generator of
$J_{G'}^j$
which does not contain any of the variables
$y_{a_2},y_{a_2+1}$
, we simply set
$\overline {g}_k=g_k.$
Then
$\overline {g}_1,\ldots , \overline {g}_m$
are the generators of the jth power of the binomial edge ideal associated with the graph
$G'$
and the matrix
$$ \begin{align*}X'=\left( \begin{array}{cccccccc} x_1 & \cdots & x_{a_2-1} & x_{a_2} & x_{a_2+1} & x_{a_2+2} &\cdots & x_{a_{r+1}+r-1}\\ y_1 & \cdots & y_{a_2-1} & y_{a_2+1} & y_{a_2} & y_{a_2+2} &\cdots & y_{a_{r+1}+r-1} \end{array}\right). \end{align*} $$
Since
$G'$
consists of r complete graphs, by (3) it follows that
$ \operatorname {\mathrm {in}}_<(\overline {J})$
is generated by the monomials
$ \operatorname {\mathrm {in}}_<(\overline {g}_1),\ldots , \operatorname {\mathrm {in}}_<(\overline {g}_m)$
where
$<$
is the lexicographic order on
$S(G').$
Note that
$ \operatorname {\mathrm {in}}_<(\overline {g}_k)$
differs from
$ \operatorname {\mathrm {in}}_<(g_k)$
if and only if
$y_{a_2}| \operatorname {\mathrm {in}}_<(g_k)$
and, in this case,
$ \operatorname {\mathrm {in}}_<(\overline {g}_k)$
is obtained from
$ \operatorname {\mathrm {in}}_<(g_k)$
by replacing the variable
$y_{a_2}$
with
$y_{a_2+1}.$
Then it follows that none of the generators of the initial ideal of
$\overline {J}+(\ell _1^y)$
is divisible by
$x_{a_2}$
since
$\{a_2,a_2+1\}$
is not an edge in
$G'.$
Therefore,
$x_{a_2}$
is regular on
$ \operatorname {\mathrm {in}}_<(\overline {J}+(\ell _1^y))$
and further,
$x_{a_2}-x_{a_2+1}$
is regular on
$S(G')/(J_{G'}^j+(\ell _1^y))$
. Moreover, we get
$$ \begin{align*} \frac{S(G')}{J_{G'}^j+(\ell_1^y,\ell_1^x)}\cong \frac{S(\widetilde{G}_1)}{J_{\widetilde{G}_1}^j}, \end{align*} $$
where
$\widetilde {G}_1$
is obtained from
$G'$
by identifying the vertices
$a_2$
and
$a_2+1$
and by relabeling the vertices k with
$k-1$
for
$k\geq a_2+2.$
Thus,
$\widetilde {G}_1$
has the maximal cliques
$$ \begin{align*}[a_1,a_2],[a_2,a_3], [a_3+1,a_4+1],\ldots, [a_r+(r-2),a_{r+1}+(r-2)].\end{align*} $$
In particular,
$\widetilde {G}_1$
is a closed graph which has
$r-1$
connected components.
Assume that the sequence
$ \underline {\ell }_{i-1}:\ \ell _1^y,\ell _1^x,\ldots ,\ell _{i-1}^y,\ell _{i-1}^x$
is a regular sequence on
$S(G')/J_{G'}^j$
and
$$ \begin{align*} \frac{\frac{S(G')}{J_{G'}^j}}{(\underline{\ell}_{i-1})\frac{S(G')}{J_{G'}^j}}\cong \frac{S(\widetilde{G}_{i-1})}{J_{\widetilde{G}_{i-1}}^j}, \end{align*} $$
where the graph
$\widetilde {G}_{i-1}$
has the first connected component consisting of the maximal cliques
$[a_1,a_2],[a_2,a_3],\ldots , [a_i,a_{i+1}]$
and the other connected components are pairwise disjoint cliques. We have to show that
$\ell _i^y,\ell _i^x$
is a regular sequence on
$S(\widetilde {G}_{i-1})/J_{\widetilde {G}_{i-1}}^j.$
In the closed graph
$\widetilde {G}_{i-1},$
the vertices
$a_{i+1}$
and
$a_{i+1}+1$
are free, thus
$\ell _i^y$
does not belong to any minimal prime ideal of
$\widetilde {G}_{i-1}$
by [Reference Rauf and Rinaldo35, Prop. 2.1] or [Reference Herzog, Hibi and Ohsugi23, Prop. 7.22]. This implies that
$\ell _i^y$
is regular on
$S(\widetilde {G}_{i-1})/J_{\widetilde {G}_{i-1}}^j$
since
$J_{\widetilde {G}_{i-1}}^j$
has no embedded component by (4). It remains to show that
$\ell _i^x$
is regular on
$S(\widetilde {G}_{i-1})/(J_{\widetilde {G}_{i-1}}^j+(\ell _i^y)).$
The argument is very similar to the induction basis. We observe that
$J_{\widetilde {G}_{i-1}}^j+(\ell _i^y)=\overline {J}+(\ell _i^y)$
where
$\overline {J}$
is obtained as follows. Let
$g_1,\ldots ,g_m$
be the generators of
$J_{\widetilde {G}_{i-1}}^j$
and denote by
$\overline {g}_1,\ldots ,\overline {g}_m$
the polynomials obtained in the following way. If
$g_k$
contains the variable
$y_{a_{i+1}},$
(respectively
$y_{a_{i+1}+1}$
) we replace it by
$y_{a_{i+1}+1}$
(respectively by
$y_{a_{i+1}}$
), and define
$\overline {g}_k$
to be this new binomial. If
$g_k$
contains both variables
$y_{a_{i+1}}$
and
$y_{a_{i+1}+1}$
, then we exchange these variables and denote the new binomial by
$\overline {g}_k.$
Finally, if
$g_k$
does not contain any of the variables
$y_{a_{i+1}}, y_{a_{i+1}+1}$
, we simply define
$\overline {g}_k=g_k.$
Then
$\overline {J}=(\overline {g}_1,\ldots ,\overline {g}_m)$
is the jth power of the binomial edge ideal corresponding to the closed graph
$\widetilde {G}_{i-1}$
and the matrix
$$ \begin{align*}X'=\left( \begin{array}{cccccccc} x_1 & \cdots & x_{a_{i+1}-1} & x_{a_{i+1}} & x_{a_{i+1}+1} & x_{a_{i+1}+2} &\cdots & x_{a_{r+1}+r-i}\\ y_1 & \cdots & y_{a_{i+1}-1} & y_{a_{i+1}+1} & y_{a_{i+1}} & y_{a_{i+1}+2} &\cdots & y_{a_{r+1}+r-i} \end{array}\right). \end{align*} $$
It follows that the initial ideal of
$\overline {J}$
is minimally generated by the monomial generators of
$ \operatorname {\mathrm {in}}_<(J_{\widetilde {G}_{i-1}}^j)$
in which we replaced the variable
$y_{a_{i+1}} $
with
$y_{a_{i+1}+1}.$
Hence
$\overline {g}_1,\ldots ,\overline {g}_m, \ell _i^y$
is a Gröbner basis of
$\overline {J}+(\ell _i^y).$
This implies that all the monomial minimal generators of
$ \operatorname {\mathrm {in}}_<(\overline {J}+(\ell _i^y))$
are not divisible by
$x_{a_{i+1}}.$
Therefore,
$x_{a_{i+1}}$
is regular on
$ \operatorname {\mathrm {in}}_<(\overline {J}+(\ell _1^y))$
and, consequently,
$\ell _i^x$
is regular on
$S/(\overline {J}+(\ell _i^y)).$
Moreover, we get the following isomorphism:
$$ \begin{align*} \frac{S(\widetilde{G}_{i-1})}{J_{\widetilde{G}_{i-1}}^j+(\ell_i^x,\ell_i^y)}\cong \frac{S(\widetilde{G}_{i})}{J_{\widetilde{G}_{i}}^j}, \end{align*} $$
where
$\widetilde {G}_i$
is a closed graph which is obtained from
$\widetilde {G}_{i-1}$
by identifying the vertex
$a_{i+1}+1$
with
$a_{i+1}$
and by relabeling the vertex k with
$k-1$
for
$k\geq a_{i+1}+2.$
Thus, the new graph
$\widetilde {G}_{i}$
has the maximal cliques
$$ \begin{align*} [a_1,a_2],\ldots,[a_i,a_{i+1}], [a_{i+1},a_{i+2}], [a_{i+2}+1, a_{i+3}+1],\ldots,[a_r+(r-i-1),a_{r+1}+(r-i-1)]. \end{align*} $$
(b) Since the variables from
$\underline {\mu }$
do not appear in the support of the minimal generators of
$ \operatorname {\mathrm {in}}_<(J_{G'}),$
it obviously follows that
$\underline {\mu }$
is a regular sequence on
$S(G')/( \operatorname {\mathrm {in}}_<(J_{G'}))^j=S(G')/ \operatorname {\mathrm {in}}_<(J_{G'}^j)$
and the desired conclusion follows.
Lemma 3.5. Let
$G'$
be the graph with the connected components
$H_1, H_2,\ldots ,H_r$
, where each
$H_i$
is a complete graph with
$d_i+1\geq 2$
vertices. Assume that
$d_1\geq d_2\geq \cdots \geq d_r\geq 1.$
Let
$J_{G'}$
be the binomial edge ideal of
$G'$
in the polynomial ring
$S'=K[\{x_i,y_i:i\in V(G')\}].$
Then:
-
(a)
$ \operatorname {\mathrm {depth}}\frac {S'}{J_{G'}^i}= \operatorname {\mathrm {depth}}\frac {S'}{ \operatorname {\mathrm {in}}_<(J_{G'}^i)}=d_i+d_{i+1}+\cdots +d_r+2r+i-1, \text { for } 1\leq i\leq r$
and -
(b)
$ \operatorname {\mathrm {depth}}\frac {S'}{J_{G'}^i}= \operatorname {\mathrm {depth}}\frac {S'}{ \operatorname {\mathrm {in}}_<(J_{G'}^i)}=3r, \text { for } i\geq r+1.$
Proof We proceed by induction on
$i.$
To simplify the notation, we set
$J_k=J_{H_k}$
for
$1\leq k\leq r.$
For
$i=1,$
we have
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S'}{J_{G'}}=\operatorname{\mathrm{depth}}\frac{S_1}{J_1}+\cdots +\operatorname{\mathrm{depth}}\frac{S_r}{J_r} \end{align*} $$
and
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S'}{\operatorname{\mathrm{in}}_<(J_{G'})}=\operatorname{\mathrm{depth}}\frac{S_1}{\operatorname{\mathrm{in}}_<(J_1)}+\cdots +\operatorname{\mathrm{depth}}\frac{S_r}{\operatorname{\mathrm{in}}_<(J_r)}, \end{align*} $$
where
$ S_k=K[\{x_j,y_j:j\in V(H_k)\}] $
for
$ 1\leq k\leq r.$
Since
$J_k$
and
$ \operatorname {\mathrm {in}}_<(J_k)$
are Cohen–Macaulay for all k and
$ \operatorname {\mathrm {depth}} S_k/ \operatorname {\mathrm {in}}_<(J_k)=d_k+2,$
we get
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S'}{J_{G'}}=\operatorname{\mathrm{depth}}\frac{S'}{\operatorname{\mathrm{in}}_<(J_{G'})}=(d_1+2)+(d_2+2)+\cdots+(d_r+2) =d_1+d_2+\cdots+d_r+2r. \end{align*} $$
The inductive step follows from the same argument for
$ \operatorname {\mathrm {depth}} S'/J_{G'}^i$
and for
$ \operatorname {\mathrm {depth}} S'/ \operatorname {\mathrm {in}}_<(J_{G'}^i).$
We will explain in detail the proof for
$ \operatorname {\mathrm {depth}} S'/J_{G'}^i$
and, in the final part we will point out the difference in the proof for
$ \operatorname {\mathrm {depth}} S'/ \operatorname {\mathrm {in}}_<(J_{G'}^i).$
Let us assume that
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S'}{J_{G'}^i}=d_i+d_{i+1}+\cdots +d_r+2r+i-1 \end{align*} $$
and
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S'}{\operatorname{\mathrm{in}}_<(J_{G'}^i)}=\operatorname{\mathrm{depth}}\frac{S'}{\operatorname{\mathrm{in}}_<(J_{G'})^i}=d_i+d_{i+1}+\cdots +d_r+2r+i-1 \end{align*} $$
for
$i\leq r-1.$
By [Reference Hà, Trung and Trung19, Th. 3.3], we have
$$ \begin{align} \operatorname{\mathrm{depth}}\frac{J_{G'}^i}{J_{G'}^{i+1}}=\min_{ j_1+j_2+\cdots+j_r=i}\left\{\operatorname{\mathrm{depth}}\frac{J_1^{j_1}}{J_1^{j_1+1}}+ \operatorname{\mathrm{depth}}\frac{J_2^{j_2}}{J_2^{j_2+1}}+\cdots+ \operatorname{\mathrm{depth}}\frac{J_r^{j_r}}{J_r^{j_r+1}}\right\}. \end{align} $$
We know that
$ \operatorname {\mathrm {depth}}\frac {S_i}{J_i}=d_i+2\geq 3$
since
$J_i$
is Cohen–Macaulay, and by Lemma 3.2 and the Depth Lemma,
$ \operatorname {\mathrm {depth}}\frac {J_i}{J_i^{2}}=3$
and
$ \operatorname {\mathrm {depth}}\frac {J_i^j}{J_i^{j+1}}\geq 3$
for
$j\geq 2$
.
If
$i\leq r-1,$
in the equality
$j_1+j_2+\cdots +j_r=i,$
at most i exponents among
$j_1,j_2,\ldots ,j_r$
are not
$0.$
Since
$d_1\geq d_2\geq \cdots \geq d_r,$
we get
$$ \begin{align*} \sum_{s=1}^r\operatorname{\mathrm{depth}}\frac{(J_i)^{j_s}}{(J_i)^{j_s+1}}\geq 3i+(d_{i+1}+2)+\cdots+ (d_r+2)=d_{i+1}+\cdots+d_r+2r+i. \end{align*} $$
Moreover, the minimal value
$d_{i+1}+\cdots +d_r+2r+i$
is achieved for
$j_1=\cdots =j_i=1$
and
$j_{i+1}=\cdots =j_r=0.$
Hence, equality (5) implies that
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{J_{G'}^i}{J_{G'}^{i+1}}=d_{i+1}+\cdots+d_r+2r+i. \end{align*} $$
We have the exact sequence of
$S'$
-modules:
$$ \begin{align*} 0\to \frac{J_{G'}^i}{J_{G'}^{i+1}}\to \frac{S'}{J_{G'}^{i+1}}\to \frac{S'}{J_{G'}^{i}}\to 0. \end{align*} $$
By the inductive hypothesis, since
$i\leq r-1,$
we have
$ \operatorname {\mathrm {depth}} \frac {S'}{J_{G'}^{i}}=d_i+d_{i+1}+\cdots + d_r+2r+{}(i-1).$
As
$d_{i+1}+\cdots +d_r+2r+i\leq d_i+d_{i+1}+\cdots + d_r+2r+(i-1),$
by the Depth Lemma applied to the above exact sequence, it follows that
$ \operatorname {\mathrm {depth}} \frac {S'}{J_{G'}^{i+1}}=d_{i+1}+\cdots +d_r+2r+i.$
Therefore, we proved part (a) of the statement. In particular, for
$i=r,$
we have
$ \operatorname {\mathrm {depth}} \frac {S'}{J_{G'}^{r}}=d_r+3r-1.$
To prove part (b), we apply again induction on
$i\geq r+1.$
We have the exact sequence of
$S'$
–modules:
$$ \begin{align*} 0\to \frac{J_{G'}^r}{J_{G'}^{r+1}}\to \frac{S'}{J_{G'}^{r+1}}\to \frac{S'}{J_{G'}^{r}}\to 0. \end{align*} $$
In equality (5), if we consider
$j_1+j_2+\cdots +j_r=r$
, we derive that
$$ \begin{align*} \sum_{s=1}^r\operatorname{\mathrm{depth}}\frac{(J_i)^{j_s}}{(J_i)^{j_s+1}}\geq 3r \end{align*} $$
and the minimal value
$3r$
is achieved for
$j_1=j_2=\cdots =j_r=1.$
Thus,
$ \operatorname {\mathrm {depth}} \frac {J_{G'}^r}{J_{G'}^{r+1}}=3r.$
Since
$3r\leq d_r+3r-1,$
the Depth Lemma applied to the above exact sequence yields
$ \operatorname {\mathrm {depth}} \frac {S'}{J_{G'}^{r+1}}=3r.$
For the inductive step, we consider the exact sequence
$$ \begin{align*} 0\to \frac{J_{G'}^i}{J_{G'}^{i+1}}\to \frac{S'}{J_{G'}^{i+1}}\to \frac{S'}{J_{G'}^{i}}\to 0 \end{align*} $$
for
$i\geq r+1.$
By hypothesis we have
$ \operatorname {\mathrm {depth}} \frac {S'}{J_{G'}^{i}}=3r,$
and we know from equality (5) that
$ \operatorname {\mathrm {depth}} \frac {J_{G'}^i}{J_{G'}^{i+1}}=3r.$
Then, by the Depth Lemma, we obtain
$ \operatorname {\mathrm {depth}} \frac {S'}{J_{G'}^{i+1}}=3r.$
As we have already mentioned, the inductive step for
$ \operatorname {\mathrm {depth}} S'/ \operatorname {\mathrm {in}}_<(J_{G'}^i)$
works in the same way. The only difference is that we need to apply Lemma 3.3 in order to derive that
$ \operatorname {\mathrm {depth}} \operatorname {\mathrm {in}}_<(J_i)/( \operatorname {\mathrm {in}}_<(J_i))^{2}=3$
and
$ \operatorname {\mathrm {depth}}( \operatorname {\mathrm {in}}_<(J_i))^j/( \operatorname {\mathrm {in}}_<(J_i))^{j+1}\geq 3$
for
$j\geq 2$
.
Proof Proof of Theorem 3.1
To begin with, we prove the formulas for the depth of
$S/J_G^i.$
Let
$[a_1,a_2],[a_2,a_3],\ldots ,[a_r,a_{r+1}]$
be the maximal cliques of
$G,$
where
$1=a_1<a_2<\cdots <a_r<a_{r+1}=n.$
Note that this is not necessarily the order with respect to the dimensions of the cliques. Let
$G'$
be the graph on
$[n+r-1]$
with the connected components
$[a_1,a_2],[a_2+1,a_3+1],\ldots ,[a_r+(r-1),a_{r+1}+(r-1)]$
and
$J_{G'}\subset S'=K[\{x_j,y_j:j\in V(G')\}]$
the associated binomial edge ideal. By Lemma 3.5, we have
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S'}{J_{G'}^i}=\operatorname{\mathrm{depth}}\frac{S'}{\operatorname{\mathrm{in}}_<(J_{G'}^i)}=\left\{ \begin{array}{ll} d_i+d_{i+1}+\cdots +d_r+2r+(i-1), & \text{ for } 1\leq i\leq r,\\ 3r, & \text{ for } i\geq r+1. \end{array}\right. \end{align*} $$
By Lemma 3.4, the sequence of
$2(r-1)$
linear forms
$$ \begin{align*} \underline{\ell}: \ell_1^y=y_{a_2}-y_{a_2+1},\ell_1^x=x_{a_2}-x_{a_2+1}, \ell_2^y=y_{a_3+1}-y_{a_3+2},\ell_2^x=x_{a_3+1}-x_{a_3+2}, \end{align*} $$
$$ \begin{align*}\ldots, \ell_{r-1}^y=y_{a_r+(r-2)}-y_{a_r+(r-1)},\ell_{r-1}^x=x_{a_r+(r-2)}-x_{a_r+(r-1)} \end{align*} $$
is regular on
$S'/J_{G'}^i$
and
$S'/(J_{G'}^i+(\underline {\ell }))\cong S/J_G^i$
for all
$i\geq 1.$
In addition, the sequence of
$2(r-1)$
elements
$$ \begin{align*} \underline{\mu}: x_{a_2},y_{a_2+1},x_{a_3+1},\ldots,y_{a_r+(r-1)} \end{align*} $$
is regular on
$S(G')/ \operatorname {\mathrm {in}}_<(J_{G'}^j)$
and
$$ \begin{align*} \frac{\frac{S(G')}{\operatorname{\mathrm{in}}_<(J_{G'}^j)}}{(\underline{\mu})\frac{S(G')}{\operatorname{\mathrm{in}}_<(J_{G'}^j)}}\cong \frac{S}{\operatorname{\mathrm{in}}_<(J_G^j)}. \end{align*} $$
for every
$j\geq 1.$
This implies that
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{J_{G}^i}=\operatorname{\mathrm{depth}} \frac{S}{\operatorname{\mathrm{in}}_<(J_G^j)}=\operatorname{\mathrm{depth}}\frac{S(G')}{J_{G'}^i}-2(r-1)=\end{align*} $$
$$ \begin{align*}=\left\{ \begin{array}{ll} \sum_{j=i}^r d_j+i+1=n-d_1-d_2\cdots-d_{i-1}+i, & \text{ for } 1\leq i\leq r,\\ r+2, & \text{ for } i\geq r+1, \end{array}\right. \end{align*} $$
where the second equality holds because
$n=\sum _{j=1}^r(d_j+1)-(r-1)=\sum _{j=1}^r d_j+1.$
With similar arguments as the ones we used for the connected case, we may derive the depth function for the powers of
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
in the case that G has several connected components, say
$G_1,\ldots ,G_c.$
The only difference is that we do not need to mod out by the entire sequences
$\underline {\ell }$
and
$\underline {\mu }$
of length
$2(r-1)$
but, instead, by sequences of length
$2(r-1)-2(c-1)=2(r-c).$
Consequently, we get the following.
Proposition 3.6. Let G be a closed graph on the vertex set
$[n]$
with the connected components
$G_1,G_2,\ldots ,G_c$
such that
$J_G$
is Cohen–Macaulay. Let
$F_1,F_2,\ldots ,F_r$
be the maximal cliques of G and
$d_i=\dim F_i=\# F_i-1$
for
$1\leq i\leq r.$
Assume that
$d_1\geq d_2\geq \cdots \geq d_r\geq 1.$
Then:
-
(a)
$ \operatorname {\mathrm {depth}}\frac {S}{J_G^i}= \operatorname {\mathrm {depth}}\frac {S}{ \operatorname {\mathrm {in}}_<(J_G^i)}=n-\sum _{j=1}^{i-1}d_j+i+c-1, \text { for }1\leq i\leq r and$
-
(b)
$ \operatorname {\mathrm {depth}}\frac {S}{J_G^i}= \operatorname {\mathrm {depth}}\frac {S}{ \operatorname {\mathrm {in}}_<(J_G^i)}=r+2c, \text { for } i\geq r+1.$
Proposition 3.7. Let G be a closed graph with the property that at least one of its connected components is not a path. Then
$J_G^i$
is not Cohen–Macaulay for
$i\geq 2.$
Proof If
$J_G$
is Cohen–Macaulay, then, by Proposition 3.6, it follows that
$$ \begin{align*}\operatorname{\mathrm{depth}}(S/J_G^i)<\operatorname{\mathrm{depth}}(S/J_G)=\dim(S/J_G)\end{align*} $$
for
$i\geq 2$
since G has cliques with at least three vertices. This implies that
$J_G^i$
is not Cohen–Macaulay.
If
$J_G$
is not Cohen–Macaulay, then, by Theorem 2.4,
$J_G$
is not unmixed. This implies that
$J_G^{(i)}$
is not unmixed, thus it is not Cohen–Macaulay. But we know that
$J_G^i=J_G^{(i)}$
for all
$i\geq 1,$
therefore,
$J_G^i$
is not Cohen–Macaulay for
$i\geq 1.$
Since all the powers of a complete intersection ideal in a polynomial ring are Cohen–Macaulay [Reference Achilles and Vogel1], [Reference Cowsik and Nori8], [Reference Waldi38], we get the following consequence of the above proposition.
Corollary 3.8. Let G be a closed graph. Then the following are equivalent:
-
(a) Each connected component of G is a path graph,
-
(b)
$J_G^i$
is Cohen–Macaulay for every
$i\geq 2,$
-
(c)
$J_G^i$
is Cohen–Macaulay for some
$i\geq 2, and$
-
(d)
$J_G^2$
is Cohen–Macaulay.
Proposition 3.9. Let G be a closed graph and let
$J_G$
be the associated binomial edge ideal. Then the Rees algebras
${\mathcal R}(J_G)$
and
${\mathcal R}( \operatorname {\mathrm {in}}_<(J_G))$
are Cohen–Macaulay and have the same dimension. In particular, the graded rings of
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
are Cohen–Macaulay.
Proof Since
$ \operatorname {\mathrm {in}}_<(J_G)$
is normally torsion free (by (3) and [Reference Ene, Herzog, Stamate and Szemberg13, Lem. 3.1]), it follows that
${\mathcal R}( \operatorname {\mathrm {in}}_<(J_G))$
is Cohen–Macaulay by [Reference Hochster25] and, by [Reference Conca, Herzog and Valla7, Th. 2.7], we have
${\mathcal R}( \operatorname {\mathrm {in}}_<(J_G))= \operatorname {\mathrm {in}}_{<'}({\mathcal R}(J_G)).$
Here,
$ \operatorname {\mathrm {in}}_{<'}({\mathcal R}(J_G))$
is the initial algebra of
${\mathcal R}(J_G)$
with respect to the monomial order
$<'$
on
$S[t]$
which extends the lexicographic order
$<$
on S as follows: given two monomials
$u,v\in S$
and two integers
$i,j\geq 0,$
we have
$ut^i<'vt^j$
if and only if
$i<j$
or
$i=j$
and
$u<v.$
Since
${\mathcal R}( \operatorname {\mathrm {in}}_<(J_G))$
is Cohen–Macaulay, it follows that
$ \operatorname {\mathrm {in}}_{<'}({\mathcal R}(J_G))$
is Cohen–Macaulay and this implies that
${\mathcal R}(J_G)$
shares the same property [Reference Conca, Herzog and Valla7, Cor. 2.3]. In addition, as
$ \operatorname {\mathrm {in}}_{<'}({\mathcal R}(J_G))$
and
${\mathcal R}(J_G)$
have the same Krull dimension [Reference Conca, Herzog and Valla7, Prop. 2.4], it follows that
${\mathcal R}(J_G)$
and
${\mathcal R}( \operatorname {\mathrm {in}}_<(J_G))$
have the same dimension.
The last part of the statement follows by [Reference Huneke27, Prop. 1.1].
Theorem 3.1 shows that the depth function of Cohen–Macaulay binomial edge ideals of closed graphs is nonincreasing. Moreover, it coincides with the depth function of their initial ideals. We expect that this behavior holds for every closed graph, but we could not prove it. Instead, in the next theorem we show that, for every closed graph
$G,$
the ideals
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
have the same limit depth and we compute its value. Moreover, in Proposition 3.12, we will show that
$ \operatorname {\mathrm {in}}_<(J_G)$
has a nonincreasing depth function.
Before stating the theorem, let us recall a few notions and results. A classical result of Brodmann [Reference Brodmann4] states that if I is a homogeneous ideal in a polynomial ring
$R=K[x_1,\ldots ,x_n]$
, then
$$ \begin{align} \lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{R}{I^k}\leq n-\ell(I), \end{align} $$
where
$\ell (I)=\dim {\mathcal R}(I)/{\frak m} {\mathcal R}(I)$
is the analytic spreadof
$I.$
Here
${\frak m}=(x_1,x_2,\ldots ,x_n)$
is the maximal graded ideal of R and
${\mathcal R}(I)$
is the Rees algebra of the ideal
$I.$
For an alternative proof of (6) we refer to [Reference Herzog and Hibi20, Th. 1.2]. In [Reference Eisenbud and Huneke11], it was shown that the equality holds in (6) if the ring
$ \operatorname {\mathrm {gr}}_I(R)$
is Cohen–Macaulay, which is the case if
${\mathcal R}(I)$
is Cohen–Macaulay [Reference Huneke27]. We should also recall that if I is generated by some polynomials, say
$f_1,\ldots , f_m,$
of the same degree, then the fiber ring
${\mathcal R}(I)/{\frak m} {\mathcal R}(I)$
is isomorphic to
$K[f_1,\ldots ,f_m]$
since we have the following isomorphism:
$$ \begin{align*} \frac{{\mathcal R}(I)}{{\frak m} {\mathcal R}(I)}\cong \frac{R}{{\frak m}}\oplus \frac{I}{{\frak m} I}\oplus\frac{I^2}{{\frak m} I^2}\oplus\cdots. \end{align*} $$
On the other hand, we need to recall some graph theoretical terminology. A vertex v of a graph G is called a free vertex if it belongs to exactly one maximal clique of
$G.$
A connected graph G is called decomposable if there exist
$G_1$
and
$G_2$
induced subgraphs of G such that
$G=G_1\cup G_2$
with
$V(G_1)\cap V(G_2)=\{v\}$
and v is a free vertex in
$G_1$
and
$G_2.$
A connected graph G is indecomposable if it is not decomposable. Clearly, every graph G (not necessarily connected) has a unique decomposition up to relabeling of the form
$G=G_1\cup G_2\cup \cdots \cup G_r$
where
$G_1,\ldots ,G_r$
are indecomposable graphs and for every
$1\leq i<j\leq r,$
we have either
$V(G_i)\cap V(G_j)=\emptyset $
or
$V(G_i)\cap V(G_j)=\{v\}$
where v is a free vertex in
$G_i$
and
$G_j.$
We call
$G_1,\ldots , G_r$
the indecomposable components of
$G.$
Theorem 3.10. Let G be a closed graph and
$J_G\subset S$
its binomial edge ideal. Let
$g_1,\ldots , g_m$
be the generators of
$J_G.$
Then the following hold:
-
(a) The set
$\{g_1,\ldots , g_m\}$
is a Sagbi basis of the K-algebra
$K[g_1,\ldots , g_m]$
with respect to the lexicographic order on
$S,$
that is,
$$ \begin{align*}\operatorname{\mathrm{in}}_<(K[g_1,\ldots, g_m])=K[\operatorname{\mathrm{in}}_<g_1,\ldots,\operatorname{\mathrm{in}}_<g_m].\end{align*} $$
-
(b) The ideals
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
have the same analytic spread. -
(c)
$\lim _{k\to \infty } \operatorname {\mathrm {depth}}\frac {S}{J_G^k}=\lim _{k\to \infty } \operatorname {\mathrm {depth}}\frac {S}{( \operatorname {\mathrm {in}}_<(J_G))^k}=r+2,$
where r is the number of indecomposable components of
$G.$
Proof Let
$A=K[g_1,\ldots , g_m]$
and
$B=K[ \operatorname {\mathrm {in}}_<g_1,\ldots , \operatorname {\mathrm {in}}_<g_m].$
(a). In order to show that
$\{g_1,\ldots , g_m\}$
is a Sagbi basis of
$A,$
we apply a criterion which plays a similar role to the Buchberger criterion in the Gröbner basis theory; see [Reference Ene and Herzog12, Th. 6.43]. Let
$ \varphi :K[t_1,\ldots ,t_m]\to A$
and
$\psi :K[t_1,\ldots ,t_m]\to B$
be the K-algebra homomorphisms defined by
$\varphi (t_i)=g_i$
and
$\psi (t_i)= \operatorname {\mathrm {in}}_<g_i$
for
$1\leq i\leq m.$
Let
$\mathbf {t}^{{\mathbf a}_1}-\mathbf {t}^{\mathbf {b}_1},\ldots ,\mathbf {t}^{{\mathbf a}_r}-\mathbf {t}^{\mathbf {b}_r}$
be a system of binomial generators for the toric ideal
$\ker \psi .$
Then
$\{g_1,\ldots , g_m\}$
is a Sagbi basis of A if and only if there exist some coefficients
$c_{{\mathbf a}}^{(j)}\in K$
such that
$$ \begin{align*} \mathbf{g}^{{\mathbf a}_j}-\mathbf{g}^{\mathbf{b}_j}=\sum_{{\mathbf a}}c_{{\mathbf a}}^{(j)} \mathbf{g}^{{\mathbf a}} \end{align*} $$
with
$ \operatorname {\mathrm {in}}_<(\mathbf {g}^{{\mathbf a}})< \operatorname {\mathrm {in}}_<(\mathbf {g}^{{\mathbf a}_j})$
for all
${\mathbf a},$
where by
$\mathbf {g}^{\mathbf a}$
we mean
$g_1^{a_1}\cdots g_m^{a_m}$
if
${\mathbf a}=(a_1,\ldots ,a_m).$
Thus, we first need to find a set of binomial generators for
$\ker \psi . $
The K-algebra B is the edge ring of the bipartite graph H on the vertex set
$V(H)=\{x_1,\ldots ,x_n\}\cup \{y_1,\ldots , y_n\}$
and edge set
$E(H)=\{\{x_i,y_j\}:i<j \text { and }\{i,j\}\in E(G)\}.$
By [Reference Ene and Zarojanu16, Lem. 3.3], we know that every induced cycle in H has length
$4.$
By [Reference Ohsugi and Hibi33], the toric ideal of B is generated by the binomials
$\beta _{\gamma _1},\ldots ,\beta _{\gamma _s}$
where
$\gamma _1,\ldots , \gamma _s$
are the four-cycles of H. If
$\gamma $
is a four-cycle in
$H,$
say
$\gamma =(x_i,y_j, x_k,y_\ell )$
with
$i<k<j<\ell ,$
and
$x_iy_j= \operatorname {\mathrm {in}}_<(g_{i_1}), x_iy_\ell = \operatorname {\mathrm {in}}_<(g_{i_2}), x_ky_j= \operatorname {\mathrm {in}}_<(g_{i_3}),x_ky_\ell = \operatorname {\mathrm {in}}_<(g_{i_4}),$
then
$\beta _\gamma =t_{i_1}t_{i_4}-t_{i_2}t_{i_3}$
. We have to lift the relations determined by the binomials
$\beta _\gamma $
to
$A.$
But this is very easy since
$$ \begin{align*} g_{i_1}g_{i_4}-g_{i_2}g_{i_3}=g_{i_5}g_{i_6}, \end{align*} $$
where
$g_{i_5}=x_iy_k-x_ky_i$
and
$g_{i_6}=x_jy_\ell -x_\ell y_j.$
Note that since
$i<k<j<\ell ,$
and
$\{i,\ell \}\in E(G),$
then
$\{i,k\}$
and
$\{j,\ell \}$
are edges in G as well, by Theorem 2.3 (iv). Moreover,
$$ \begin{align*}\operatorname{\mathrm{in}}_<(g_{i_5}g_{i_6})=x_ix_jy_ky_\ell<x_i x_ky_j y_\ell=\operatorname{\mathrm{in}}_<(g_{i_1}g_{i_4})\end{align*} $$
since
$k<j.$
(b) follows from (a) since
$\dim A=\dim \operatorname {\mathrm {in}}_<(A)$
by [Reference Conca, Herzog and Valla7, Prop. 2.4].
(c) By Proposition 3.9 and [Reference Eisenbud and Huneke11, Props. 3.1 and 3.3], we have
$$ \begin{align*} \lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S}{J_G^k}=\dim S-\ell(J_G) \text{ and } \lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^k}=\dim S-\ell(\operatorname{\mathrm{in}}_<(J_G)). \end{align*} $$
Therefore, we get the equality of the two limits by (b).
Since
$y_1$
and
$x_n$
are isolated vertices in the bipartite graph H whose edge ideal is equal to
$ \operatorname {\mathrm {in}}_<(J_G),$
we have
$$ \begin{align*} \lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^k}=\lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S'}{I(H)^k}+2, \end{align*} $$
where
$S'$
is the polynomial ring in the variables
$x_j, 1\leq j\leq n-1$
and
$y_j, 2\leq j\leq n.$
By [Reference Trung37, Th. 4.4] or [Reference Herzog and Hibi21, Cor. 10.3.18],
$$ \begin{align*} \lim_{k\to\infty}\operatorname{\mathrm{depth}}\frac{S'}{I(H)^k}=r, \end{align*} $$
where r is the number of connected components of
$H.$
But, taking into account the characterization of closed graphs given in Theorem 2.3 (iii), it is easily seen that this is exactly the number of indecomposable components of
$G.$
Remark 3.11. By using [Reference Almousa, Lin and Liske2, Th. 4.6 and Cor. 4.9], one may derive that the limit depth of the so-called closed determinantal facet ideals and their initial ideals is the same. This class of ideals was introduced in [Reference Ene, Herzog, Hibi and Mohammadi15].
Proposition 3.12. Let G be a closed graph and
$J_G$
its binomial edge ideal. Then
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^{k+1}}\leq \operatorname{\mathrm{depth}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^k} \end{align*} $$
for every
$k\geq 1.$
Proof The inequalities follow by [Reference Kimura, Terai and Yassemi31, Th. 5.2] since the bipartite graph H whose edge ideal is equal to
$ \operatorname {\mathrm {in}}_<(J_G)$
has at least one leaf, namely the vertex
$x_{n-1}.$
As we have seen in Section 2, for every closed graph
$G,$
we have
$J_G^i=J_G^{(i)}$
for
$i\geq 1.$
This equalities imply that
$ \operatorname {\mathrm {Ass}}(J_G^i)= \operatorname {\mathrm {Ass}}(J_G^{i+1})$
for
$i\geq 1,$
thus
$J_G$
has the persistence property, that is
$ \operatorname {\mathrm {Ass}}(J_G^i)\subseteq \operatorname {\mathrm {Ass}}(J_G^{i+1})$
for
$i\geq 1.$
But we can prove even more, namely, that
$J_G$
has the strong persistence property. Let us recall that an ideal I in a polynomial ring satisfies the strong persistence property if and only if
$I^{k+1}:I=I^k$
for all
$k;$
see [Reference Herzog and Asloob Qureshi24]. We will derive this property from a slightly more general statement.
Proposition 3.13. Let
$I\subset R=K[x_1,x_2,\ldots ,x_n]$
be a homogeneous ideal and assume that there exists a monomial order
$<$
on R such that the following conditions hold:
-
(a)
$ \operatorname {\mathrm {in}}_<(I)$
has the strong persistence property and -
(b)
$ \operatorname {\mathrm {in}}_<(I^j)=( \operatorname {\mathrm {in}}_<(I))^j$
for every
$j\geq 1.$
Then the ideal I has the strong persistence property. In particular, I has the persistence property.
Proof We have to prove that
$I^{j+1}:I=I^j$
for
$j\geq 1.$
Since
$I^j\subseteq I^{j+1}:I$
, it is enough to show that
$ \operatorname {\mathrm {in}}_<(I^j)= \operatorname {\mathrm {in}}_<(I^{j+1}:I).$
The inclusion
$ \operatorname {\mathrm {in}}_<(I^j)\subseteq \operatorname {\mathrm {in}}_<(I^{j+1}:I)$
is obvious. For the other inclusion, let us consider a monomial
$w\in \operatorname {\mathrm {in}}_<(I^{j+1}:I)$
. Then there exists a polynomial
$g\in I^{j+1}:I$
such that
$w= \operatorname {\mathrm {in}}_<(g).$
As
$g I\subseteq I^{j+1}$
, we get
$$ \begin{align*} w \operatorname{\mathrm{in}}_<(I)\subseteq \operatorname{\mathrm{in}}_<(I^{j+1})=(\operatorname{\mathrm{in}}_<(I))^{j+1}, \end{align*} $$
which yields
$$ \begin{align*} w\in (\operatorname{\mathrm{in}}_<(I))^{j+1}:\operatorname{\mathrm{in}}_<(I)=(\operatorname{\mathrm{in}}_<(I))^{j}=\operatorname{\mathrm{in}}_<(I^j). \end{align*} $$
Corollary 3.14. Let G be a closed graph. Then
$J_G$
has the strong persistence property.
Proof Let
$<$
be the lexicographic order on
$S.$
Then
$ \operatorname {\mathrm {in}}_<(J_G)=(x_iy_j:\{i,j\}\in E(G))$
is an edge ideal. Therefore, by [Reference Martinez-Bernal, Morey and Villarreal32, Lem. 2.12], it follows that
$ \operatorname {\mathrm {in}}_<(J_G)$
has the strong persistence property. Moreover, by (3), we also have
$ \operatorname {\mathrm {in}}_<(J_G^i)=( \operatorname {\mathrm {in}}_<(J_G))^i$
for every
$i\geq 1.$
The claim follows by Proposition 3.13.
4 Regularity
In this section, we compute the regularity of the powers of binomial edge ideals of closed graphs and of their initial ideals. First, we recall some notions and results from Graph Theory.
A graph G is called co-chordal if its complement graph
$G^c$
is chordal. The co-chordal cover number of G, denoted
$ \operatorname {\mathrm {co-chord}}(G),$
is the smallest number m for which there exist some co-chordal subgraphs
$G_1,\ldots ,G_m$
of G such that
$E(G)=\cup _{i=1}^mE(G_i).$
A graph G is weakly chordal if every induced cycle in G and in
$G^c$
has length at most
$4.$
For a graph
$G,$
we denote by
$ \operatorname {\mathrm {im}}(G)$
the number of edges in a largest induced matching of G. By an induced matching we mean an induced subgraph of G which consists of pairwise disjoint edges. In other words,
$ \operatorname {\mathrm {im}}(G)$
is the monomial grade of the edge ideal
$I(G),$
that is, the maximum length of a regular sequence of monomials in
$I(G)$
. In [Reference Busch, Dragan and Shritharan5, Prop. 3] it is proved that if G is weakly chordal, then
$ \operatorname {\mathrm {im}}(G)= \operatorname {\mathrm {co-chord}}(G).$
On the other hand, we will use [Reference Jayanthan, Narayanam and Selvaraja30, Th. 3.6] which states that if H is a bipartite graph and
$I(H)$
is its edge ideal, then, for
$i\geq 1,$
we have
$$ \begin{align} \operatorname{\mathrm{reg}}(I(H)^i)\leq \operatorname{\mathrm{co-chord}}(H)+2i-1. \end{align} $$
Theorem 4.1. Let G be a connected closed graph. Then, for every
$i\geq 1,$
we have
$$ \begin{align*} \operatorname{\mathrm{reg}}\frac{S}{J_G^i}=\operatorname{\mathrm{reg}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)}=\ell+2(i-1), \end{align*} $$
where
$\ell $
is the length of the longest induced path in
$G.$
Proof The inequality
$ \operatorname {\mathrm {reg}} S/J_G^i\geq \ell +2(i-1)$
follows by [Reference Jayanthan, Kumar and Sarkar28, Cor. 3.4]. Hence, we have
$$ \begin{align*}\operatorname{\mathrm{reg}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)}\geq \operatorname{\mathrm{reg}}\frac{S}{J_G^i}\geq \ell+2(i-1). \end{align*} $$
Thus, it is enough to prove that
$ \operatorname {\mathrm {reg}} S/ \operatorname {\mathrm {in}}_<(J_G^i)\leq \ell +2(i-1).$
Since G is closed, by (3), we have
$ \operatorname {\mathrm {in}}_<(J_G^i)=( \operatorname {\mathrm {in}}_<(J_G))^i.$
Therefore, we get
$$ \begin{align*} \operatorname{\mathrm{reg}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)}=\operatorname{\mathrm{reg}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^i}. \end{align*} $$
As we have already mentioned in Section 2, the monomial ideal
$ \operatorname {\mathrm {in}}_<(J_G)=(x_iy_j: \{i,j\}\in E(G))$
is the edge ideal
$I(H)$
of a bipartite graph on
$\{x_1,x_2,\ldots ,x_n\}\cup \{y_1,y_2,\ldots ,y_n\}.$
Then inequality (7) implies that
$$ \begin{align*} \operatorname{\mathrm{reg}}\frac{S}{(\operatorname{\mathrm{in}}_<(J_G))^i}\leq \operatorname{\mathrm{co-chord}}(H)+2(i-1). \end{align*} $$
In [Reference Ene and Zarojanu16, Lem. 3.3] it was proved that H is a weakly chordal graph. This implies that
$ \operatorname {\mathrm {co-chord}}(H)= \operatorname {\mathrm {im}}(H).$
On the other hand, by [Reference Ene and Zarojanu16, Prop. 3.5], it follows that
$ \operatorname {\mathrm {im}}(H)=\ell ,$
which completes the proof.
The arguments of the above proof can be extended to disconnected closed graphs.
Proposition 4.2. Let G be a closed graph with connected components
$G_1,\ldots ,G_c$
. Let
$\ell _i$
be the length of the longest induced path in the component
$G_i$
for
$1\leq i\leq c.$
Then, for all
$i\geq 1,$
we have
$$ \begin{align*} \operatorname{\mathrm{reg}}\frac{S}{J_G^i}=\operatorname{\mathrm{reg}}\frac{S}{\operatorname{\mathrm{in}}_<(J_G^i)}=\ell_1+\ell_2+\cdots+\ell_c+2(i-1). \end{align*} $$
Proof The inequality
$ \operatorname {\mathrm {reg}} S/J_G^i\geq \ell _1+\ell _2+\cdots +\ell _c+2(i-1)$
follows from [Reference Jayanthan, Kumar and Sarkar28, Prop. 3.3] and [Reference Jayanthan, Kumar and Sarkar28, Obser. 3.2] since the union of the longest induced paths in
$G_j, 1\leq j\leq c,$
form an induced subgraph in
$G,$
and the inequality
$ \operatorname {\mathrm {reg}} S/ \operatorname {\mathrm {in}}_<(J_G^i)\leq \ell _1+\ell _2+\cdots +\ell _c+2(i-1)$
holds since, obviously, in the bipartite graph H such that
$ \operatorname {\mathrm {in}}_<(J_G)=I(H)$
we have
$ \operatorname {\mathrm {im}}(H)=\ell _1+\ell _2+\cdots +\ell _c.$
5 Powers of binomial edge ideals of block graphs
In this section, we discuss powers of binomial edge ideals of block graphs. We recall that a graph G is called a block graph, if each block of G is a clique. A block of G is a connected subgraph of G that has no cutpoint and is maximal with respect to this property. A vertex v is a cutpoint of a graph H if the induced subgraph obtained by removing the vertex v has more connected components than
$H.$
The block graphs whose binomial edge ideal is Cohen–Macaulay are classified in [Reference Ene, Herzog and Hibi14, Th. 1.1]. It is shown that for a block graph
$G,$
the following conditions are equivalent:
-
(a)
$J_G$
is unmixed. -
(b)
$J_G$
is Cohen–Macaulay. -
(c) Each vertex of G is the intersection of at most two maximal cliques.
The following theorem shows that the equality between symbolic and ordinary powers does not hold, in general, for binomial edge ideals of block graphs.
Theorem 5.1. Let G be a block graph such that
$J_G$
is Cohen–Macaulay. Then, the following statements are equivalent:
-
(a) G is closed,
-
(b)
$J_G^i=J_G^{(i)}$
for all
$i\geq 2,$
-
(c)
$J_G^i=J_G^{(i)}$
for some
$i\geq 2,$
-
(d)
$J_G^2=J_G^{(2)},$
and -
(e) G is net-free, that is, it does not contain a net as an induced subgraph (see Figure 2).
Proof (a)
$\Rightarrow $
(b) follows by (4). The implications (b)
$\Rightarrow $
(c) and (b)
$\Rightarrow $
(d) are trivial.
Next, we prove (d)
$\Rightarrow $
(e). Let us assume that G contains as an induced subgraph the net N with the edge set
$E(N)=\{\{1,2\},\{3,4\},\{5,6\},\{2,3\},\{3,5\},\{2,5\}\}.$
Set
$g=x_3x_5x_6y_1y_2y_4-x_1x_5x_6y_2y_3y_4-x_3x_4x_5y_1y_2y_6+x_1x_2x_5y_3y_4y_6+x_1x_3x_4y_2y_5y_6-x_1x_2x_3y_4y_5y_6$
. We show that
$g\in J_G^{(2)}\setminus J_G^2.$
Since
$J_G=\bigcap _{ P_W(G)\in \operatorname {\mathrm {Ass}} (J_G)}P_W(G),$
we show that
$g\in (P_W(G))^2,$
for all W with the property that
$P_W(G)\in \operatorname {\mathrm {Ass}} (J_G)$
. Then it follows that
$g\in J_G^{(2)}$
, because, as it was observed in [Reference Ene, Herzog, Stamate and Szemberg13],
$P_W(G)^{(i)}=P_W(G)^i$
for all
$i\geq 1$
and all
$W\subset [n].$
We consider the following cases. Let
$W\subseteq [n].$
Case 1. If
$W \cap [6] \in \{\emptyset , \{1\}, \{4\}, \{6\}\},$
then
$g=x_5y_4(x_6y_2-x_2y_6)(x_3y_1-x_1y_3)+x_3y_6(x_4y_2-x_2y_4)(x_1y_5-x_5y_1) \in (P_W(G))^2$
.
Case 2.
$W \cap [6]= \{2\}.$
Then
$g=x_1x_2y_4y_6(x_5y_3-x_3y_5)+x_5x_6y_1y_2(x_3y_4-x_4y_3)+x_3x_4y_1y_2(x_6y_5-x_5y_6)+x_4x_6y_1y_2(x_5y_3-x_3y_5) +x_1x_5y_2y_3(x_4y_6-x_6y_4)+x_1x_4y_2y_6(x_3y_5-x_5y_3)\in (P_W(G))^2$
.
Case 3.
$W \cap [6]= \{3\}.$
Then
$g=x_1x_5y_3y_4(x_2y_6-x_6y_2)-x_3x_4y_1y_2(x_5y_6-x_6y_5)+x_1x_3y_4y_6(x_5y_2-x_2y_5)-x_3x_5y_2y_4(x_1y_6-x_6y_1) +x_3x_4y_2y_5(x_1y_6-x_6y_1)\in (P_W(G))^2$
.
Case 4.
$W \cap [6]= \{5\}.$
Then
$g=x_1x_3y_5y_6(x_4y_2-x_2y_4)+x_5x_6y_2y_4(x_3y_1-x_1y_3)+x_2x_5y_3y_6(x_1y_4-x_4y_1)+x_4x_5y_1y_6(x_2y_3-x_3y_2)\in (P_W(G))^2$
.
Next, we show that, if G contains N as an induced subgraph, then
$g \not \in J_G^{2}$
. Since N is an induced subgraph of G, by the proof of [Reference Jayanthan, Kumar and Sarkar28, Prop. 3.3], it follows that
$J_N^i=J_G^i\cap K[x_1,\ldots ,x_6,y_1,\ldots ,y_6]$
for all
$i\geq 1.$
Therefore, it suffices to show that
$g \not \in J_N^{2}$
.
Suppose
$g \in J_N^{2}$
. Then we have
$x_1x_2x_5y_3y_4y_6 \in J_N^{2}+(x_3, y_2)$
. Since
$\{x_1, y_4\}$
is a regular sequence on
$S/(J_N^{2}+(x_3, y_2))$
, we have
$x_2x_5y_3y_6 \in J_N^{2}+(x_3, y_2)$
. Since any monomial of degree
$4$
in
$ J_N^{2}+(x_3, y_2)$
which is not divided by neither
$x_3$
nor
$y_2$
is not divided by
$y_6$
, it follows
$x_2x_5y_3y_6 \not \in J_N^{2}+(x_3, y_2)$
, contradiction.
For (c)
$\Rightarrow $
(e), we show that
$g(x_2y_3-x_3y_2)^{i-2}\in J_G^{(i)} \setminus J_G^{i}.$
Taking into account the above arguments, it is obvious that
$g(x_2y_3-x_3y_2)^{i-2}\in (P_W(G))^i,$
for all W with the property that
$P_W(G)\in \operatorname {\mathrm {Ass}} (J_G)$
, thus
$g(x_2y_3-x_3y_2)^{i-2}\in J_G^{(i)}.$
We show that
$g(x_2y_3-x_3y_2)^{i-2} \not \in J_N^{i}$
. Suppose
$g(x_2y_3-x_3y_2)^{i-2} \in J_N^{i}$
. Then we have
$x_1x_2x_5y_3y_4y_6 (x_2y_3)^{i-2} \in J_N^{i}+(x_3, y_2)$
. Since
$\{x_1, y_4\}$
is a regular sequence on
$S/(J_N^{i}+(x_3, y_2))$
, we have
$x_2x_5y_3y_6(x_2y_3)^{i-2} \in J_N^{i}+(x_3, y_2)$
. Since any monomial of degree
$2i$
in
$ J_N^{i}+(x_3, y_2)$
which is not divided by neither
$x_3$
nor
$y_2$
is not divided by
$y_6$
, it follows that
$x_2x_5y_3y_6 (x_2y_3)^{i-2} \not \in J_N^{i}+(x_3, y_2)$
, contradiction.
Finally, we show that (e)
$\Rightarrow $
(a). Since G is a block graph, it follows that G is chordal and tent-free (see Figure 2). On the other hand, as
$J_G$
is Cohen–Macaulay and, in particular, unmixed, it follows that G is claw-free (see Figure 1). Therefore, the hypothesis implies that G is closed by Theorem 2.3 (v).
Proposition 5.2. Let G be a connected block graph which is not a path. Then
$J_G^i$
is not Cohen–Macaulay for every
$i\geq 2.$
Proof We analyze the following cases.
Case 1. Suppose that G is a net-free (see Figure 2) block graph which is not a path and
$J_G$
is Cohen–Macaulay. Then, by using Theorem 2.3 (v), it follows that G is a closed graph. Then, Proposition 3.7 implies that
$J_G^i$
is not Cohen–Macaulay for every
$i\geq 2.$
Case 2. Let G be a block graph which contains a net as an induced subgraph and such that
$J_G$
is Cohen–Macaulay. Then, by Theorem 5.1, we have
$J_G^i\subsetneq J_G^{(i)},$
for every
$i\geq 2$
and, in particular, it follows that
$J_G^i$
has embedded components. Consequently,
$J_G^i$
is not unmixed, and, therefore,
$J_G^i$
is not Cohen–Macaulay for
$i\geq 2.$
Case 3. Suppose that G is a block graph and
$J_G$
is not Cohen–Macaulay. Then
$J_G$
is not unmixed. It follows that
$J_G^{i}$
is not unmixed for all
$i,$
thus
$J_G^i$
is not Cohen–Macaulay as well.
6 Open problems
As we have seen in Section 3, the depth function of Cohen–Macaulay binomial edge ideals of closed graphs is non-increasing. The depth function of
$ \operatorname {\mathrm {in}}_<(J_G)$
is also nonincreasing for every closed graph
$G.$
Therefore it is natural to ask the following.
Question 6.1. Is it true that the depth function of
$J_G$
is nonincreasing for every closed graph
$G?$
Of course, taking into account Proposition 3.12, we can answer positively this question by showing that if G is closed, then
$ \operatorname {\mathrm {depth}} S/J_G^i= \operatorname {\mathrm {depth}} S/ \operatorname {\mathrm {in}}_<(J_G^i)$
for every
$i\geq 1.$
A partial positive answer to this question is the following. Let G be a closed graph with maximal cliques
$F_i=[a_i,b_i], 1\leq i\leq r,$
ordered as in Theorem 2.3 (iii). Assume that
$F_1=[1,2],$
in other words, the vertex
$1$
is a leaf of
$G.$
We claim that
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{J_G^{k+1}}\leq \operatorname{\mathrm{depth}}\frac{S}{J_G^k}, \end{align*} $$
for every
$k\geq 1.$
In order to prove this inequality, we first observe that
$J_G^{k+1}:f_{12}=J_G^k$
for all
$k.$
Indeed, since
$J_G^k\subseteq J_G^{k+1}:f_{12},$
it is enough to show that
$ \operatorname {\mathrm {in}}_<(J_G^{k+1}:f_{12})= \operatorname {\mathrm {in}}_<(J_G^k).$
Let us assume that
$ \operatorname {\mathrm {in}}_<(J_G^{k+1}:f_{12})\supsetneq \operatorname {\mathrm {in}}_<(J_G^k).$
Then there exists a monomial
$w\in \operatorname {\mathrm {in}}_<(J_G^{k+1}:f_{12})\setminus \operatorname {\mathrm {in}}_<(J_G^k).$
Let
$h\in J_G^{k+1}:f_{12}$
such that
$ \operatorname {\mathrm {in}}_<(h)=w.$
We can write
$h=w+h_1,$
where
$ \operatorname {\mathrm {in}}_<(h_1)<w.$
Then,
$f_{12}h=f_{12}(w+h_1)\in J_G^{k+1},$
which implies that
$$ \begin{align*}\operatorname{\mathrm{in}}_<(f_{12})w&=x_1y_2 w\in \operatorname{\mathrm{in}}_<(J_G^{k+1})=(\operatorname{\mathrm{in}}_<(J_G))^{k+1}=((x_1y_2)+\operatorname{\mathrm{in}}_<(J_{G-\{1\}}))^{k+1}\\&=(x_1y_2)(\operatorname{\mathrm{in}}_<(J_G))^k+(\operatorname{\mathrm{in}}_<(J_{G-\{1\}}))^{k+1}.\end{align*} $$
Since
$x_1$
and
$y_2$
do not divide any of the minimal monomial generators of
$ \operatorname {\mathrm {in}}_<(J_{G-\{1\}})$
and
$w\notin ( \operatorname {\mathrm {in}}_<(J_G))^k,$
thus
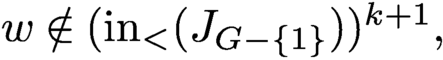$w\notin ( \operatorname {\mathrm {in}}_<(J_{G-\{1\}}))^{k+1},$
we get
$ \operatorname {\mathrm {in}}_<(f_{12})w\in (x_1y_2)( \operatorname {\mathrm {in}}_<(J_G))^k$
which yields
$w\in ( \operatorname {\mathrm {in}}_<(J_G))^k,$
a contradiction. Therefore, we have proved the equality
$J_G^{k+1}:f_{12}=J_G^k$
. We consider the exact sequence of S-modules
$$ \begin{align} 0\to \frac{S}{J_G^{k+1}:f_{12}}=\frac{S}{J_G^k}\to \frac{S}{J_G^{k+1}}\to \frac{S}{(J_G^{k+1},f_{12})}\to 0. \end{align} $$
Since
$J_G^{k+1}=(J_{G-\{1\}}+f_{12})^{k+1}=J_{G-\{1\}}^{k+1}+f_{12}J_G^k,$
it follows that
$(J_G^{k+1},f_{12})=(J_{G-\{1\}}^{k+1},f_{12}).$
But
$f_{12}$
is obviously regular on
$S/J_{G-\{1\}}^{k+1},$
thus
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{(J_G^{k+1},f_{12})}=\operatorname{\mathrm{depth}}\frac{S}{(J_{G-\{1\}}^{k+1},f_{12})}=\operatorname{\mathrm{depth}}\frac{S}{J_{G-\{1\}}^{k+1}}-1. \end{align*} $$
As
$G-\{1\}$
is an induced subgraph of
$G,$
by [Reference Jayanthan, Kumar and Sarkar28, Prop. 3.3] it follows that
$ \operatorname {\mathrm {depth}} S/J_{G-\{1\}}^{k+1}\geq \operatorname {\mathrm {depth}} S/J_G^{k+1}.$
Therefore, we obtain
$$ \begin{align*} \operatorname{\mathrm{depth}}\frac{S}{(J_G^{k+1},f_{12})}\geq \operatorname{\mathrm{depth}} \frac{S}{J_G^{k+1}}-1. \end{align*} $$
The Depth Lemma applied to sequence (8) gives the desired inequality.
The following conjecture, which is still open, was formulated in [Reference Ene, Herzog and Hibi14]: if G is a closed graph, then
$J_G$
and
$ \operatorname {\mathrm {in}}_<(J_G)$
have the same graded Betti numbers. On the other hand, from several computer experiments, we noticed that the same equality holds for small powers of
$J_G.$
Therefore, we suggest the following conjecture which extends the one in [Reference Ene, Herzog and Hibi14].
Conjecture 6.2. Let G be a closed graph. Then, for every
$i\geq 1, J_G^i$
and
$( \operatorname {\mathrm {in}}_<(J_G))^i= \operatorname {\mathrm {in}}_<(J_G^i)$
have the same graded Betti numbers.
Let us remark in support of our conjecture that in the previous sections we proved that
$ \operatorname {\mathrm {reg}} J_G^i= \operatorname {\mathrm {reg}}( \operatorname {\mathrm {in}}_<(J_G))^i$
for G closed and
$ \operatorname {\mathrm {depth}} J_G^i= \operatorname {\mathrm {depth}}( \operatorname {\mathrm {in}}_<(J_G))^i$
for G closed and with
$J_G$
Cohen–Macaulay. Of course, if the above conjecture is true, then it also answers Question 6.1.
In addition, we note that Conjecture 6.2 is true in two “extremal” cases, namely when G is a complete graph or a path.
Indeed, if
$G=K_n,$
then
$( \operatorname {\mathrm {in}}_<(J_G))^i$
has a linear resolution for every
$i\geq 1.$
Since
$( \operatorname {\mathrm {in}}_<(J_G))^i= \operatorname {\mathrm {in}}_<(J_G^i),$
it follows that
$J_G^i$
has a linear resolution for
$i\geq 1.$
As the Hilbert functions of
$J_G^i$
and
$ \operatorname {\mathrm {in}}_<(J_G^i)$
coincide, we derive that the conjecture is true when
$G=K_n$
. On the other hand, if
$G=P_n$
with the edges
$\{i,i+1\}, 1\leq i \leq n-1,$
then
$ \operatorname {\mathrm {in}}_<(J_G)$
and
$J_G$
are complete intersections generated in degree
$2$
and the conjecture is true by [Reference Guardo and Van Tuyl18, Cor. 1.3].
When G is a closed graph such that
$J_G$
is Cohen–Macaulay, we have
$\beta _{ij}(S/J_G)=\beta _{ij}(S/ \operatorname {\mathrm {in}}_<(J_G))$
for all
$i,j$
by [Reference Ene, Herzog and Hibi14, Prop. 3.2]. A possible strategy to prove Conjecture 6.2 in this case is the following. We begin with the following nice consequence of Lemma 3.4.
Corollary 6.3. With the same notation of Lemma 3.4, we have
$$ \begin{align*} \beta_{ij}^S\left(\frac{S}{J_G^k}\right)=\beta_{ij}^{S(G')}\left(\frac{S(G')}{J_{G'}^k}\right) \end{align*} $$
and
$$ \begin{align*} \beta_{ij}^S\left(\frac{S}{\operatorname{\mathrm{in}}_<(J_G^k)}\right)=\beta_{ij}^{S(G')}\left(\frac{S(G')}{\operatorname{\mathrm{in}}_<(J_{G'}^k)}\right), \end{align*} $$
for all
$i,j,$
and
$k\geq 1.$
This corollary implies that Conjecture 6.2 holds for the closed graphs with Cohen–Macaulay binomial edge ideal once we show that for every graph H whose connected components are complete graphs we have
$$ \begin{align*} \beta_{ij}^{S(H)}\left(\frac{S(H)}{J_H^k}\right)=\beta_{ij}^{S(H)}\left(\frac{S(H)}{\operatorname{\mathrm{in}}_<(J_H^k)}\right) \end{align*} $$
for all
$i,j,$
and
$k\geq 1.$
In Proposition 5.2, we proved that if G is a connected block graph, then
$J_G^i$
is Cohen–Macaulay for every
$i\geq 2$
if and only if G is a path. Then we may ask the following.
Question 6.4. Let G be a connected (chordal) graph. Is it true that
$J_G^i$
is Cohen–Macaulay for every
$i\geq 2$
if and only if G is a path?
The net graph N (see Figure 2) which plays an important role in Theorem 5.1 has the nice property that
$J_N^{(2)}$
is Cohen–Macaulay. On the other hand,
$J_N^2$
is not Cohen–Macaulay (see proof of Proposition 5.2, Case 2). This naturally yields the following.
Problem 6.5. Classify all the block graphs with the property that the second symbolic power of the associated binomial edge ideal is Cohen–Macaulay.
The last question is inspired by Theorem 5.1.
Question 6.6. Let G be a graph. Is it true that the following conditions are equivalent?
-
(a)
$J_G^i=J_G^{(i)}$
for all
$i\geq 2,$
-
(b)
$J_G^i=J_G^{(i)}$
for some
$i\geq 2,$
-
(c)
$J_G^2=J_G^{(2)}, and$
-
(d) G is net-free.
Computer experiments showed that for every graph G with at most eight vertices the equivalence (c)
$\Leftrightarrow $
(d) holds. Moreover, the implications (a)
$\Rightarrow $
(c)
$\Rightarrow $
(b)
$\Rightarrow $
(d) hold and they can be shown similarly to the proof of Theorem 5.1.
Acknowledgment
We thank Amin Fakhari and Arvind Kumar for their valuable comments on Section 6. We acknowledge the use of Macaulay2 [Reference Grayson and Stillman17] for our computations. We are grateful to the anonymous referee for valuable comments.
