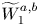1. Introduction
In the 2010s, various generalizations of classical optimal transport problems and Wasserstein distances have been introduced and investigated by numerous authors [Reference Alibert, Bouchitté and Champion2, Reference Backhoff-Veraguas, Beiglböck and Pammer4, Reference Caffarelli and McCann6, Reference Chizat, Peyré, Schmitzer and Vialard7, Reference Gozlan, Roberto, Samson and Tetali13, Reference Kondratyev, Monsaingeon and Vorotnikov17, Reference Liero, Mielke and Savaré18, Reference Piccoli and Rossi20, Reference Piccoli and Rossi21]. Recently, in 2021 we introduced unbalanced optimal entropy problems [Reference Chung and Trinh10] which cover both optimal entropy transport problems in [Reference Liero, Mielke and Savaré18] and weak optimal transport problems in [Reference Gozlan, Roberto, Samson and Tetali13]. In [Reference Chung and Trinh10], under certain conditions of entropy functionals we establish a Kantorovich duality for our unbalanced optimal transport problem. Before stating our first main result, let us review our unbalanced optimal entropy problems.
Given a metric space 
$X$, we denote by 
${{\mathcal {M}}}(X)$ and 
${{\mathcal {P}}}(X)$ the spaces of all Borel non-negative finite measures and probability measures on 
$X$, respectively. Let 
$X_1,X_2$ be Polish metric spaces and let 
$C:X_1\times {{\mathcal {P}}}(X_2)\to [0,\infty ]$ be a lower semi-continuous function satisfying that 
$C(x_1,\cdot )$ is convex for every 
$x_1\in X_1$. For every 
$\boldsymbol {\gamma }\in {{\mathcal {M}}}(X_1\times X_2)$, we denote 
$(\gamma _{x_1})_{x_1\in X_1}$ its disintegration with respect to its first marginal. Let 
$F_i:[0,\infty )\to [0,\infty ]$, 
$i=1,2$ be convex, lower semi-continuous entropy functions with their recession constants 
$(F_i)'_\infty :=\lim _{s\to \infty }{F_i(s)}/{s}$. Given 
$\mu _1\in {{\mathcal {M}}}(X_1), \mu _2\in {{\mathcal {M}}}(X_2)$ and 
$\boldsymbol {\gamma }\in {{\mathcal {M}}}(X_1\times X_2)$, we define
\begin{align*} {{\mathcal{F}}}_i(\gamma_i|\mu_i):&=\int_{X_i}F_i(f_i(x_i))\,\textrm{d}\mu_i(x_i)+(F_i)'_\infty \gamma_i^{{\perp}}(X),\\ {{\mathcal{E}}}(\boldsymbol{\gamma}|\mu_1,\mu_2):&=\sum_{i=1}^{2}{{\mathcal{F}}}_i(\gamma_i|\mu_i)+\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1), \end{align*}
where 
$\gamma _1,\gamma _2$ are the first and second marginals of 
$\boldsymbol {\gamma }$, and 
$\gamma _i=f_i\mu +\gamma _i^{\perp }$ is the Lebesgue decomposition of 
$\gamma _i$ with respect to 
$\mu _i$.
Our unbalanced optimal entropy-transport problem is defined as
\begin{align} {{\mathcal{E}}}(\mu_1,\mu_2):=\inf_{\boldsymbol{\gamma}\in {{\mathcal{M}}}(X_1\times X_2)} {{\mathcal{E}}}(\boldsymbol{\gamma}|\mu_1,\mu_2). \end{align}
Similarly to optimal entropy-transport problems in [Reference Liero, Mielke and Savaré18], to handle with problem (1.1) we often assume that 
$F_i$ is superlinear, i.e. 
$(F_i)'_\infty =+\infty$ for 
$i=1,2$. This assumption makes the problems easier as we can get rid of the part 
$(F_i)'_\infty \gamma _i^{\perp }(X_i)$ in the expression of 
${{\mathcal {F}}}_i$.
In the first part of the paper, we investigate problem (1.1) for a special case that 
$F_i$ is not superlinear, 
$i=1,2$. Given 
$a,b>0$, we consider the total variation entropy function 
$F_i(s):=a|s-1|$, 
$i=1,2$ and the cost function 
$b\cdot C$. In this case, problem (1.1) will become
\begin{align} {\textrm{E}}^{a,b}(\mu_1,\mu_2):=\inf_{\boldsymbol{\gamma}\in {{\mathcal{M}}}(X_1\times X_2)}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}|\mu_1,\mu_2), \end{align}
where 
${\textrm {E}}^{a,b}(\boldsymbol {\gamma }|\mu _1,\mu _2):=a\left \vert \mu _1-\gamma _1 \right \vert +a\left \vert \mu _2-\gamma _2 \right \vert +b\int _{X_1}C(x_1,\gamma _{x_1})d\gamma _1(x_1).$
As 
$F_i$ is not superlinear, to deal with problem (1.2) we need new techniques being different from [Reference Chung and Trinh10, Reference Liero, Mielke and Savaré18]. We define
\begin{align}
\Phi_I&:=\bigg\{(\varphi_1,\varphi_2)\in C_b(X_1)\times
C_b(X_2):\varphi_1(x_1),\varphi_2(x_2)\notag\\
&\geq{-}a\text{ for
every } x_i\in X_i,i=1,2\quad \text{and }\varphi_1(x_1)\notag\\
&+q(\varphi_2)\leq b\cdot C(x_1,q) \text{ for
every }x_1\in X_1, q\in{{\mathcal{P}}}(X_2)\bigg\}.
\end{align}
Next, we define the functional 
$J:\mathbb {R}\rightarrow (-\infty ,+\infty ]$ by
\begin{align} J(\phi)=\sup_{s>0}\frac{\phi-a\vert 1-s\vert}{s}= \begin{cases} +\infty & \text{ if }\phi>a,\\ \phi & \text{ if }-a\leq \phi\leq a,\\ - a & \text{ otherwise}. \end{cases}\end{align}Then we define
\begin{align}
\Phi_J&:=\bigg\{(\varphi_1,\varphi_2)\in C_b(X_1)\times
C_b(X_2):\varphi_1(x_1),\varphi_2(x_2)\notag\\
&\leq a\text{ for
every } x_i\in X_i,i=1,2\quad \text{and }J(\varphi_1(x_1))\notag\\
&+q(J(\varphi_2))\leq b\cdot C(x_1,q)
\text{ for every }x_1\in X_1,
q\in{{\mathcal{P}}}(X_2)\bigg\}.
\end{align}Our main result for the first part is a Kantorovich duality of problem (1.2).
Theorem 1.1 Let 
$X_1, X_2$ be locally compact, Polish metric spaces. Let 
$C:X_1\times {{\mathcal {P}}}(X_2)\to [0,\infty ]$ be a lower semi-continuous function such that 
$C(x_1,\cdot )$ is convex for every 
$x_1\in X_1$. Then for every 
$\mu _i\in {{\mathcal {M}}}(X_i),i=1,2$ we have
\begin{align*} {\textrm{E}}^{a,b}(\mu_1,\mu_2)&=\sup_{(\varphi_1,\varphi_2)\in \Phi_I}\sum_{i=1}^{2}\int_{X_i}I(\varphi_i(x_i))\,\textrm{d}\mu_i(x_i)\\ &=\sup_{(\varphi_1,\varphi_2)\in \Phi_J}\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}\mu_i(x_i), \end{align*}where
\begin{align}
I(\varphi):=\inf_{s\geq 0}\left(s\varphi+a\vert
1-s\vert\right)= \begin{cases} a & \text{
if } \varphi>a\\ \varphi & \text{ if } -a\leq \varphi\leq
a.\\ - \infty & \text{ otherwise }
\end{cases}
\end{align} We need the local compactness assumption on theorem 1.1 because in our proof we use Riesz representation theorem stating that 
${{\mathcal {M}}}_s(X)$, the space of all signed Borel measures with finite masses on 
$X$, is the dual space of 
$C_0(X)$, and it is only true for locally compact spaces. However, as the duality results for optimal entropy transport problems in [Reference Liero, Mielke and Savaré18] were proved for general Polish spaces by a different method, we expect that theorem 1.1 would still hold for these general spaces.
Now we present consequences of theorem 1.1. The first one is that we can get a version of [Reference Caffarelli and McCann6, corollary 2.6]. Let 
$X_1=X_2=X$ be a Polish space, 
$\mu _1,\mu _2\in {{\mathcal {M}}}(X)$, 
$a,b>0$ and 
$c_1: X\times X\to [0,+\infty ]$ be a lower semi-continuous function. We define 
$\hat {X}:=X\cup \{\hat {\infty }\}$ by attaching an isolated point 
$\hat {\infty }$ to 
$X$. We endow 
$\hat {X}$ with the topology induced from the topology of 
$X$ and the isolated point 
$\hat {\infty }$. We extend the cost function
\begin{align}
\hat{c}_1(x,y):= \left\lbrace\begin{array}{@{}cl@{}} b\cdot
c_1(x,y) & \text{ if } x\neq \hat{\infty} \mbox{ and } y
\neq \hat{\infty}, \\ a & \text{ if }x\in X,
y=\hat{\infty}\text{ or }x=\hat{\infty},y\in X,\\ 0 &
\text{ otherwise, } \end{array}\right.
\end{align}
and measures 
$\mu _1,\mu _2$ to 
$\hat {X}$ by adding a Dirac measure at infinity: 
$\hat {\mu }_1:=\mu _1+\vert \mu _2\vert \delta _{\hat {\infty }}$, 
$\hat {\mu }_2:=\mu _2+\vert \mu _1\vert \delta _{\hat {\infty }}$. Then the measures 
$\hat {\mu }_1$ and 
$\hat {\mu }_2$ have the same masses. We define
\begin{align*} \Gamma(\hat{\mu}_1,
\hat{\mu}_2)&:=\bigg\{\hat{\boldsymbol{\gamma}}\in
{{\mathcal{M}}}(\hat{X}\times
\hat{X}):\hat{\boldsymbol{\gamma}}(A\times
\hat{X})=\hat{\mu}_1(A),\hat{\boldsymbol{\gamma}}(\hat{X}\times
A )\\
&=\hat{\mu}_2(A) \mbox{ for Borel } A\subset
\hat{X}\bigg\}. \end{align*}Then we will get a version of [Reference Caffarelli and McCann6, corollary 2.6] as follows.
Corollary 1.2 Given a locally compact, Polish metric space 
$X$, 
$\mu _1,\mu _2\in {{\mathcal {M}}}(X)$, 
$a,b>0$, and a lower semi-continuous function 
$c_1: X\times X\to [0,+\infty ]$. Then
\[ \sup_{\substack{(\hat{\varphi}_1,\hat{\varphi}_2)\in L^{1}(\hat{\mu}_1)\times L^{1}(\hat{\mu}_2)\\\hat{\varphi}_1(x)+\hat{\varphi}_2(y)\leq \hat{c}_1(x,y)}}\sum_{i=1}^{2}\int_{\hat{X}}\hat{\varphi}_i(x)\,\textrm{d}\hat{\mu_i}(x)= \inf_{\hat{\boldsymbol{\gamma}}\in \Gamma(\hat{\mu}_1,\hat{\mu}_2)}\int_{\hat{X}\times \hat{X}}\hat{c}_1(x,y)\,\textrm{d}\hat{\boldsymbol{\gamma}}(x,y). \] Another consequence of theorem 1.1 is that we establish a Kantorovich duality for generalized Wasserstein distance 
$\widetilde {W}_p^{a,b}$, and a version of Kantorovich–Rubinstein theorem for generalized Wasserstein distance 
$\widetilde {W}_1^{a,b}$.
Let 
$(X,d)$ be a metric space. For a function 
$f:X\to {{\mathbb {R}}}$, we denote
\[ \|f\|_{Lip}:=\sup_{x,y\in X,x\neq y}\frac{|f(x)-f(y)|}{d(x,y)}. \]Corollary 1.3 Let 
$(X,d)$ be a locally compact and Polish metric space. Then for every 
$a,b>0, \mu ,\nu \in {{\mathcal {M}}}(X)$ and 
$p\geq 1$ we have
1.
$\widetilde {W}^{a,b}_p(\mu ,\nu )^{p}=\sup \limits _{(\varphi _1,\varphi _2)\in \Phi _W}\bigg \{ \int _X I(\varphi _1(x)) \textrm {d}\mu (x)+\int _X I(\varphi _2(x)) d\nu (x)\bigg \},$ where
\begin{align*} \Phi_W:= \{(\varphi_1,\varphi_2)\in C_b(X)\times C_b(X)\;\vert\; \varphi_1(x)+\varphi_2 (y)\leq (b\cdot d(x,y))^{p}\text{ and }\\ \varphi_1 (x), \varphi _2(y)\geq{-}a,\;\forall x,y\in X\}. \end{align*}2.
$\widetilde {W}_1^{a,b}(\mu ,\nu )=\sup \bigg \{\int _X fd(\mu -\nu ):f\in {{\mathbb {F}}}\bigg \},$ where
\[ {{\mathbb{F}}}:=\big\{f\in C_b(X), \|f\|_\infty\leq a, \|f\|_{Lip}\leq b\big\}. \]
Note that corollary 1.3 (1) is proved for the case 
$p=1$ in [Reference Chung and Trinh9], and corollary 1.3 (2) is a main result of [Reference Piccoli and Rossi21] proved by a different method there. In the second part of the paper, we apply corollary 1.3 to study barycenters of generalized Wasserstein distances. In 2002, Sturm investigated barycenters in non-positive curvature spaces as he showed the existence, uniqueness and contraction of barycenters in such spaces [Reference Sturm24]. Because Wassertein spaces are not in the framework of non-positive curvature spaces, to study the existence, uniqueness and properties of Wasserstein barycenters over 
${{\mathbb {R}}}^{n}$, Agueh and Carlier introduced dual problems of the primal barycenter problem and used convex analysis to handle them [Reference Agueh and Carlier1]. Recently, barycenters in Hellinger–Kantorovich spaces, siblings of Wasserstein spaces, have been investigated in [Reference Chung and Phung8, Reference Friesecke, Matthes and Schmitzer12].
On the other hand, in 2014, Piccoli and Rossi introduced generalized Wasserstein distances [Reference Piccoli and Rossi20] and established a duality Kantorovich–Rubinstein formula and a generalized Benamou–Breiner formula for them [Reference Piccoli and Rossi21]. Combining corollary 1.3 with the streamline of Agueh and Carlier's work [Reference Agueh and Carlier1], we study the existence and consistency of generalized Wasserstein barycenters.
More precisely, first we show the existence of generalized Wasserstein barycenters whenever starting measures have compact supports. Second, we introduce and investigate a dual problem of the barycenter problem. Although our barycenters are not unique, we still can establish their consistency as Boissard, Le Gouic and Loubes did in the Wasserstein case [Reference Boissard, Le Gouic and Loubes5].
Our paper is organized as follows. In § 2, we review basic notations and generalized Wasserstein distances 
$\widetilde {W}^{a,b}_p$. In § 3, we prove theorem 1.1, corollaries 1.2 and 1.3. In § 4, we study our primal barycenter problem and its dual problems. We also show the existence and consistency of generalized Wasserstein barycenters in this last section.
2. Preliminaries
Let 
$(X,d)$ be a metric space. We denote by 
$\mathcal {M}(X)$ and 
$\mathcal {P}(X)$ the sets of all non-negative Borel measures with finite mass and all probability Borel measures, respectively.
Given a Borel measure 
$\mu$, we denote its mass by 
$\vert \mu \vert :=\mu (X)$. In the general case, if 
$\mu =\mu ^{+}-\mu ^{-}$ is a signed Borel measure then 
$\vert \mu \vert :=\vert \mu ^{+}\vert +\vert \mu ^{-}\vert$. A set 
$M\subset \mathcal {M}(X)$ is bounded if 
$\sup _{\mu \in M}\vert \mu \vert <\infty$, and it is tight if for every 
$\varepsilon >0$, there exists a compact subset 
$K_\varepsilon$ of 
$X$ such that for all 
$\mu \in M$, we have 
$\mu (X\backslash K_\varepsilon )\leq \varepsilon$.
For every 
$\mu _1,\mu _2\in \mathcal {M}(X)$, we say that 
$\mu _1$ is absolutely continuous with respect to 
$\mu _2$ and write 
$\mu _1 \ll \mu _2$ if 
$\mu _2(A)=0$ yields 
$\mu _1(A)=0$ for every Borel subset 
$A$ of 
$X$. We call that 
$\mu _1$ and 
$\mu _2$ are mutually singular and write 
$\mu _1 \perp \mu _2$ if there exists a Borel subset 
$B$ of 
$X$ such that 
$\mu _1(B)=\mu _2(X\backslash B)=0$. We write 
$\mu _1\leq \mu _2$ if for all Borel subset 
$A$ of 
$X$ we have 
$\mu _1(A)\leq \mu _2(A)$.
For every 
$p\geq 1$, we denote by 
$\mathcal {M}_p(X)$ (reps. 
$\mathcal {P}_p (X)$) the space of all measures 
$\mu \in \mathcal {M}(X)$ (reps. 
$\mathcal {P}(X)$) with finite 
$p$-moment, i.e. there is some (and therefore any) 
$x_0\in X$ such that 
$\int _{X}d^{p}(x,x_0)d\mu (x)<\infty .$
For every measures 
$\mu _1,\mu _2\in \mathcal {M}(X)$, a Borel probability measure 
$\boldsymbol {\pi }$ on 
$X\times X$ is called a transference plan between 
$\mu _1$ and 
$\mu _2$ if
\[ \vert \mu_1\vert \boldsymbol{\pi} (A\times X)=\mu_1(A)\text{ and }\vert \mu_2\vert \boldsymbol{\pi} (X\times B)=\mu_2(B), \]
for every Borel subsets 
$A,B$ of 
$X$. We denote the set of all transference plan between 
$\mu _1$ and 
$\mu _2$ by 
$\Pi (\mu _1,\mu _2)$.
Given measures 
$\mu _1,\mu _2\in \mathcal {M}_p(X)$ with the same mass, i.e. 
$\vert \mu _1\vert =\vert \mu _2\vert$. The Wasserstein distance between 
$\mu _1$ and 
$\mu _2$ is defined by
\[ W_p(\mu_1,\mu_2):=\left(\vert \mu_1\vert\inf_{\pi\in \Pi (\mu_1,\mu_2)}\int_{X\times X}d^{p}(x,y)\,\textrm{d}\boldsymbol{\pi}(x,y)\right)^{1/p}. \]
For each 
$\mu _1,\mu _2\in \mathcal {M}(X)$ with 
$|\mu _1|=|\mu _2|$, we denote by 
${\textrm {Opt}}_p(\mu _1,\mu _2)$ the set of all 
$\boldsymbol {\pi }\in \Pi (\mu _1,\mu _2)$ such that 
$W^{p}_p(\mu _1,\mu _2)=\vert \mu _1\vert \int _{X\times X}d^{p}(x,y)d\boldsymbol {\pi }(x,y)$. If 
$(X,d)$ is a Polish metric space, i.e. 
$(X,d)$ is complete and separable then 
${\textrm {Opt}}_p(\mu _1,\mu _2)$ is non-empty [Reference Villani25, theorem 1.3].
Theorem 2.1 (Prokhorov's theorem) If 
$(X,d)$ is a Polish metric space then a subset 
$M\subset {{\mathcal {M}}}(X)$ is bounded and tight if and only if 
$M$ is relatively compact under the weak*-topology.
We now review the definitions of the generalized Wasserstein distances. They were introduced by Piccoli and Rossi in [Reference Piccoli and Rossi20, Reference Piccoli and Rossi21]. For convenience to establish Kantorovich duality formulas for the generalized Wasserstein distances, we adapt slightly the original ones.
Definition 2.2 Let 
$X$ be a Polish metric space and let 
$a,b>0,p\geq 1$. For every 
$\mu _1,\mu _2\in \mathcal {M}(X)$, the generalized Wasserstein distance 
$\widetilde {W}^{a,b}_p$ between 
$\mu _1$ and 
$\mu _2$ is defined by
\[ \widetilde{W}^{a,b}_p (\mu_1,\mu_2):=\left(\inf\left\{C\left(\widetilde{\mu_1}, \widetilde{\mu_2}\right)|\, \widetilde{\mu_1},\widetilde{\mu_2}\in \mathcal{M}_p(X),\vert \widetilde{\mu_1}\vert =\vert \widetilde{\mu_2}\vert \right\}\right)^{1/p}, \]
where 
$C(\widetilde {\mu _1}, \widetilde {\mu _2})= a\left \vert \mu _1-\widetilde {\mu _1}\right \vert +a\left \vert \mu _2-\widetilde {\mu _2}\right \vert +b^{p}\,W_p^{p}(\widetilde {\mu _1},\widetilde {\mu _2}).$
The following results can be adapted from the proofs of [Reference Piccoli and Rossi20, proposition 1 and theorem 3].
Proposition 2.3 [20, proposition 1] If 
$X$ is a Polish metric space then 
$(\mathcal {M}(X), \widetilde {W}^{a,b}_p)$ is a metric space. Moreover, there exist 
$\widetilde {\mu _1},\widetilde {\mu _2}\in \mathcal {M}_p(X)$ such that 
$\vert \widetilde {\mu _1}\vert = \vert \widetilde {\mu _2}\vert , \widetilde {\mu _1}\leq \mu _1, \widetilde {\mu _2}\leq \mu _2$, and 
$\widetilde {W}^{a,b}_p (\mu _1,\mu _2)^{p} = C(\widetilde {\mu _1}, \widetilde {\mu _2})$.
If measures 
$\widetilde {\mu _1}, \widetilde {\mu _2}\in \mathcal {M}_p(X)$ have the same mass such that 
$\widetilde {W}^{a,b}_p (\mu _1,\mu _2)^{p} = C(\widetilde {\mu _1}, \widetilde {\mu _2})$ then we say that 
$(\widetilde {\mu _1}, \widetilde {\mu _2})$ is an optimal for 
$\widetilde {W}^{a,b}_p (\mu _1,\mu _2)$.
Let 
$X_1,X_2$ be Polish metric spaces. For every 
$\boldsymbol {\gamma }\in {{\mathcal {M}}}(X_1\times X_2)$, we denote its disintegration with respect to its first marginal by 
$(\gamma _{x_1})_{x_1\in X_1}$. We also denote by 
$\gamma _1$ and 
$\gamma _2$ the first and second marginals of 
$\boldsymbol {\gamma }$, i.e.
\[ \gamma_1(B_1)=\boldsymbol{\gamma}(B_1\times X_2) \mbox{ and } \gamma_2(B_2)=\boldsymbol{\gamma}(X_1\times B_2) \mbox{ for Borel sets } B_i\subset X_i. \]3. Unbalanced optimal total variation transport problems
Let 
$C:X_1\times {{\mathcal {P}}}(X_2)\to [0,\infty ]$ be a lower semi-continuous function such that for every 
$x_1\in X_1$ we have
\[ C(x_1,tq_1+(1-t)q_2)\leq tC(x_1,q_1)+(1-t)C(x_1,q_2), \]
for every 
$t\in [0,1], q_1, q_2\in {{\mathcal {P}}}(X_2)$.
For every 
$a,b>0,\mu _i\in {{\mathcal {M}}} (X_i),i=1,2$ and every 
$\boldsymbol {\gamma }\in {{\mathcal {M}}}(X_1\times X_2)$, we recall
\[ {\textrm{E}}^{a,b}\left(\boldsymbol{\gamma}|\mu_1,\mu_2\right):=a\left\vert \mu_1-\gamma_1 \right\vert+a\left\vert \mu_2-\gamma_2 \right\vert+b\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1) \]
Then for every 
$\mu _i\in {{\mathcal {M}}}(X_i),i=1,2$ we have
\[ {\textrm{E}}^{a,b}(\mu_1,\mu_2):=\inf_{\boldsymbol{\gamma}\in{{\mathcal{M}}}(X_1\times X_2)}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}|\mu_1,\mu_2)=\inf_{\boldsymbol{\gamma}\in M}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}|\mu_1,\mu_2), \]
where 
$M:=\{\boldsymbol {\gamma }\in {{\mathcal {M}}}(X_1 \times X_2)|\int _XC(x_1,\gamma _{x_1})d\gamma _1(x_1)<\infty \}.$
Lemma 3.1 Let 
$X_1, X_2$ be Polish metric spaces and 
$a,b>0$. For every 
$\mu _1\in {{\mathcal {M}}}(X_1)$ and 
$\mu _2\in {{\mathcal {M}}}(X_2)$ we have
\[ {\textrm{E}}^{a,b}(\mu_1,\mu_2)=\inf_{\boldsymbol{\gamma}\in M}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}|\mu_1,\mu_2)=\inf_{\boldsymbol{\gamma}\in M^{{\leq}} (\mu_1,\mu_2)}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}|\mu_1,\mu_2), \]
where 
$M^{\leq } (\mu _1,\mu _2):=\{\boldsymbol {\gamma }\in M|\gamma _i\leq \mu _i,i=1,2\}.$
Proof. It is clear that we only need to prove that
\[ \inf_{\boldsymbol{\gamma}\in M}{\textrm{E}}^{a,b}\left(\boldsymbol{\gamma}|\mu_1,\mu_2\right)\geq \inf_{\boldsymbol{\gamma}\in M^{{\leq}} \left(\mu_1,\mu_2\right)}{\textrm{E}}^{a,b}\left(\boldsymbol{\gamma}|\mu_1,\mu_2\right). \]
For any 
$\boldsymbol {\alpha }\in M$, let 
$\alpha _1,\alpha _2$ be the first and second marginals of 
$\boldsymbol {\alpha }$. Suppose that 
$\alpha _1=f\mu _1+\mu _1^{\perp }$ is the Lebesgue decomposition of 
$\alpha _1$ with respect to 
$\mu _1$. We define 
$\overline {\alpha }_1:= \min \{f,1\}\mu _1.$ Then 
$\overline {\alpha }_1\leq \mu _1$ and 
$\overline {\alpha }_1\leq \alpha _1$. By the Radon–Nikodym theorem we get that there exists a measurable function 
$g:X_1\rightarrow [0,\infty )$ such that 
$\overline {\alpha }_1=g\alpha _1$ and 
$g\leq 1$ 
$\alpha _1$-a.e.
Next, for every Borel subsets 
$A_i$ of 
$X_i$, 
$i=1,2$, we define
\[ \overline{\boldsymbol{\alpha}}(A_1\times A_2):= \int_{A_1\times A_2}g(x_1)\,\textrm{d}\boldsymbol{\alpha} (x_1,x_2). \]
Then 
$\overline {\boldsymbol {\alpha }}(A_1\times X_2)=\int _{A_1}g(x_1)d\alpha _1(x_1)=\overline {\alpha }_1(A_1)$ for every Borel subset 
$A_1$ of 
$X_1$. For any Borel subset 
$A_2$ of 
$X_2$, we define 
$\overline {\alpha }_2(A_2):=\int _{X_1\times A_2}g(x_1)d\boldsymbol {\alpha } (x_1,x_2)$. Then 
$\overline {\alpha }_2(A_2)=\overline {\boldsymbol {\alpha }}(X_1\times A_2)$. This means that 
$\overline {\alpha }_1$ and 
$\overline {\alpha }_2$ are the first and second marginals of 
$\overline {\boldsymbol {\alpha }}$. Since 
$g\leq 1$ 
$\alpha _1$-a.e one has 
$\overline {\boldsymbol {\alpha }}\leq \boldsymbol {\alpha }$. Moreover, for every Borel function 
$h:X_1\times X_2\rightarrow [0,+\infty ]$ we have
\begin{align*} \int_{X_1\times X_2}h(x_1,x_2)\,\textrm{d}\overline{\boldsymbol{\alpha}}(x_1,x_2)&=\int_{X_1\times X_2}h(x_1,x_2)g(x_1)\,\textrm{d}\boldsymbol{\alpha}(x_1,x_2)\\ &=\int_{X_1}\left(\int_{X_2}h(x_1,x_2)g(x_1)\,\textrm{d}\alpha_{x_1}(x_2)\right)\textrm{d}\alpha_1(x_1)\\ &=\int_{X_1}\left(\int_{X_2}h(x_1,x_2)\,\textrm{d}\alpha_{x_1}(x_2)\right)\textrm{d}\overline{\alpha}_1(x_1). \end{align*}
Therefore, by the uniqueness of disintegration we get that 
$\overline {\alpha }_{x_1}=\alpha _{x_1}$ 
$\overline {\alpha }_1$-a.e. Then,
\begin{align*} \int_{X_1}C(x_1,\overline{\alpha}_{x_1})\,\textrm{d}\overline{\alpha}_1(x_1)\leq \int_{X_1}C(x_1,\alpha_{x_1})\,\textrm{d}\alpha_1(x_1). \end{align*}
Notice that as 
$\overline {\boldsymbol {\alpha }}\leq \boldsymbol {\alpha }$, we have 
$\overline {\alpha }_2\leq \alpha _2$.
On the other hand, putting 
$D:=\{x_1\in X_1: f(x_1)\leq 1\}$ then we get that
\begin{align*} \left\vert \mu_1-\alpha_1\right\vert & = \int_{X_1}\left\vert 1-f(x_1)\right\vert \textrm{d}\mu_1+\mu_1^{{\perp}} (X_1)\\ & = \int_{D}(1-f(x_1))\,\textrm{d}\mu_1+\int_{X_1\backslash D}(f(x_1)-1)\,\textrm{d}\mu_1+\mu_1^{{\perp}} (X_1)\\ & = \int_{D} \textrm{d}\mu_1-\int_{D}\textrm{d}\overline{\alpha}_1+\int_{X_1\backslash D}f(x_1)\,\textrm{d}\mu_1-\int_{X_1\backslash D}\textrm{d}\overline{\alpha}_1+\mu_1^{{\perp}} (X_1) \\ & = \int_{D} \textrm{d}\mu_1-\int_{D}\textrm{d}\overline{\alpha}_1+\int_{X_1\backslash D}\textrm{d}\alpha_1-\int_{X_1\backslash D}\textrm{d}\overline{\alpha}_1-\mu_1^{{\perp}}\left(X_1\backslash D\right)+\mu_1^{{\perp}} (X_1)\\ &=\int_{D} \textrm{d}\mu_1-\int_{D}\textrm{d}\overline{\alpha}_1+\int_{X_1\backslash D}\textrm{d}\alpha_1-\int_{X_1\backslash D}\textrm{d}\overline{\alpha}_1+\int_D \textrm{d}\alpha_1-\int_Df\textrm{d}\mu_1\\ & = \left\vert \mu_1-\overline{\alpha}_1\right\vert +\int_{X_1\backslash D}\textrm{d}\alpha_1-\int_{X_1\backslash D}\textrm{d}\overline{\alpha}_1 + \int_{D}\textrm{d}\alpha_1-\int_{D}\textrm{d}\overline{\alpha}_1\\ & = \left\vert \mu_1-\overline{\alpha}_1\right\vert+\left\vert \alpha_1-\overline{\alpha}_1\right\vert. \end{align*}
Observe that 
$\left \vert \alpha _1-\overline {\alpha }_1\right \vert =\left \vert \alpha _2-\overline {\alpha }_2\right \vert$, one gets
\begin{align*} \left\vert \mu_1-\overline{\alpha}_1\right\vert+\left\vert \mu_2-\overline{\alpha}_2\right\vert=\left\vert \mu_1-\alpha_1\right\vert-\left\vert \alpha_2-\overline{\alpha}_2\right\vert+\left\vert \mu_2-\overline{\alpha}_2\right\vert\leq \left\vert \mu_1-\alpha_1\right\vert+\left\vert \mu_2-\alpha_2\right\vert . \end{align*}
Hence, we obtain that 
${\textrm {E}}^{a,b}(\boldsymbol {\alpha }|\mu _1,\mu _2)\geq {\textrm {E}}^{a,b}(\overline {\boldsymbol {\alpha }}|\mu _1,\mu _2).$
Applying this process again for 
$\overline {\boldsymbol {\alpha }}$, we can find a plan 
$\widehat {\boldsymbol {\alpha }}\in M$ with its marginals are 
$\widehat {\alpha }_1$ and 
$\widehat {\alpha }_2$ such that 
$\widehat {\boldsymbol {\alpha }}\leq \overline {\boldsymbol {\alpha }}$ and
\[ {\textrm{E}}^{a,b}\left(\overline{\boldsymbol{\alpha}}|\mu_1,\mu_2\right)\geq {\textrm{E}}^{a,b}\left(\widehat{\boldsymbol{\alpha}}|\mu_1,\mu_2\right); \]
and 
$\widehat {\alpha }_2\leq \mu _2$, 
$\widehat {\alpha }_1\leq \overline {\alpha }_1\leq \mu _1$. Thus, 
$\widehat {\boldsymbol {\alpha }}\in M^{\leq } (\mu _1,\mu _2)$. Therefore, we get that
\[ {\textrm{E}}^{a,b}\left(\boldsymbol{\alpha}|\mu_1,\mu_2\right)\geq {\textrm{E}}\left(\overline{\boldsymbol{\alpha}}|\mu_1,\mu_2\right)\geq {\textrm{E}}^{a,b}\left(\widehat{\boldsymbol{\alpha}}|\mu_1,\mu_2\right)\geq \inf_{\boldsymbol{\gamma}\in M^{{\leq}} \left(\mu_1,\mu_2\right)}{\textrm{E}}^{a,b}\left(\boldsymbol{\gamma}|\mu_1,\mu_2\right). \]
This implies that 
$\inf _{\boldsymbol {\gamma }\in M}{\textrm {E}}^{a,b}(\boldsymbol {\gamma }|\mu _1,\mu _2)\geq \inf _{\boldsymbol {\gamma }\in M^{\leq } (\mu _1,\mu _2)}{\textrm {E}}^{a,b}(\boldsymbol {\gamma }|\mu _1,\mu _2)$.
For every 
$a,b>0$ and 
$(\mu _1,\mu _2)\in {{\mathcal {M}}}(X_1)\times {{\mathcal {M}}}(X_2)$ we denote by 
${\textrm {Opt}}^{a,b}(\mu _1,\mu _2)$ the set of all 
$\boldsymbol {\gamma }\in M^{\leq } (\mu _1,\mu _2)$ such that 
${\textrm {E}}^{a,b}(\mu _1,\mu _2)={\textrm {E}}^{a,b}(\boldsymbol {\gamma }|\mu _1,\mu _2)$.
Lemma 3.2 Let 
$X_1,X_2$ be Polish metric spaces. For every 
$a,b>0$ and 
$\mu _i\in {{\mathcal {M}}}(X_i),i=1,2$ the set 
${\textrm {Opt}}^{a,b}(\mu _1,\mu _2)$ is a non-empty subset of 
${{\mathcal {M}}}(X_1\times X_2)$.
Proof. From lemma 3.1, we choose a sequence of 
$\boldsymbol {\gamma }^{n}\in M^{\leq } (\mu _1,\mu _2)$ such that
\[ \lim_{n\to \infty}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}^{n}|\mu_1,\mu_2)= {\textrm{E}}^{a,b}(\mu_1,\mu_2). \]
Then 
$\gamma ^{n}_i\leq \mu _i$ for 
$i=1,2$ and every 
$n\in {{\mathbb {N}}}$. Since 
$\mu _i\in {{\mathcal {M}}}(X_i)$ for 
$i=1,2$, one has 
$\{\gamma _1^{n}\}_n$ and 
$\{\gamma _2^{n}\}_n$ are tight and bounded. By [Reference Ambrosio, Gigli and Savare3, Lemma 5.2.2] one gets that 
$\{\boldsymbol {\gamma }^{n}\}_{n\in {{\mathbb {N}}}}$ is also tight and bounded. Thus, by Prokhorov's theorem, passing to a subsequence we can assume that 
$\lim _{n\to \infty }\boldsymbol {\gamma }^{n}= \boldsymbol {\gamma }$ under the weak*-topology for some 
$\boldsymbol {\gamma }\in {{\mathcal {M}}}(X\times X)$.
Next, for any Borel subset 
$A_1$ of 
$X_1$ we have
\begin{align*} \gamma_1(A_1)&=\boldsymbol{\gamma}(A_1\times X_2)\\ &=\inf\{\boldsymbol{\gamma}(V): V\subset X_1\times X_2 \mbox{ open}, A_1\times X_2\subset V\}\\ &\leq \inf\{\boldsymbol{\gamma}(U\times X_2): U\subset X_1\mbox{ open}, A_1\subset U\}. \end{align*}
Applying [Reference Parthasarathy19, theorem 6.1 page 40] we obtain that 
$\boldsymbol {\gamma }(U\times X_2)\leq \liminf _{n\to \infty }\boldsymbol {\gamma }^{n} (U\times X_2)\leq \mu _1(U)$ for every open subset 
$U$ of 
$X_1$. This yields, 
$\gamma _1\leq \mu _1.$ Similarly, we also have 
$\gamma _2\leq \mu _2.$ Moreover, using [Reference Parthasarathy19, theorem 6.1 page 40] again we also have that 
$\limsup _{n\to \infty }\vert \boldsymbol {\gamma }^{n}\vert \leq \vert \boldsymbol {\gamma }\vert \leq \liminf _{n\to \infty } \vert \boldsymbol {\gamma }^{n}\vert .$ This implies that 
$\lim _{n\to \infty }\vert \boldsymbol {\gamma }^{n}\vert =\vert \boldsymbol {\gamma }\vert$. Hence, 
$\lim _{n\to \infty }\left \vert \mu _i-\gamma ^{n}_1\right \vert =\left \vert \mu _i-\gamma _i\right \vert ,$ for 
$i=1,2$.
Applying [Reference Chung and Trinh10, lemma 3.5] we obtain that
\[ \liminf_{n\to \infty}\int_{X_1}C(x_1,\gamma^{n}_{x_1})\,\textrm{d}\gamma^{n}_1(x_1)\geq \int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1). \]So, we get that
\[ a\left\vert \mu_1-\gamma_1\right\vert+a\left\vert \mu_2-\gamma_2\right\vert+b\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1)\leq {\textrm{E}}^{a,b}\left(\mu_1,\mu_2\right). \]
This implies that 
${\textrm {Opt}}^{a,b}(\mu _1,\mu _2)$ is non-empty.
We recall that the functionals 
$I,J$ are defined as in (1.6), (1.4) and 
$\Phi _I,\Phi _J$ are defined as in (1.3),(1.5), respectively. We also set
\[ \Phi_J^{0}:=\{\varphi=(\varphi_1,\varphi_2)\in C_0(X_1)\times C_0(X_2): \varphi\in \Phi_J\}. \]Lemma 3.3 For every 
$\mu _1\in {{\mathcal {M}}}(X_1)$ and 
$\mu _2\in {{\mathcal {M}}}(X_2)$ one has
\[ \sup_{(\varphi_1,\varphi_2)\in \Phi_J}\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}\mu_i(x_i)\leq\sup_{(\psi_1,\psi_2)\in \Phi_I}\sum_{i=1}^{2}\int_{X_i} I(\psi_i(x_i))\,\textrm{d}\mu_i(x_i). \]Proof. For every 
$(\varphi _1,\varphi _2)\in \Phi _J$ and 
$i\in \{1,2\}$ we define 
$\overline {\varphi }_i:=J(\varphi _i)$. Then for every 
$x_i\in X_i$ we have that 
$\overline {\varphi }_i(x_i)\in [-a,a]$ for 
$i=1,2$. Thus, from (1.6) one has 
$I(\overline {\varphi }_i)=\overline {\varphi }_i$. Moreover, by the definition of 
$\Phi _J$, we also get 
$\overline {\varphi }_1(x_1)+q(\overline {\varphi }_2)\leq b\cdot C(x_1,q)$ for every 
$x_1\in X_1,q\in {{\mathcal {P}}}(X_2)$. Since 
$J$ is continuous on 
$(-\infty ,a]$ we get that 
$(\overline {\varphi }_1,\overline {\varphi }_2)\in \Phi _I$. As 
$\overline {\varphi }_i=J(\varphi _i)\geq \varphi _i$ for 
$i=1,2$ we obtain that
\[ \sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}\mu_i(x_i)\leq\sum_{i=1}^{2}\int_{X_i} \overline{\varphi}_i(x_i) \textrm{d}\mu_i(x_i)= \sum_{i=1}^{2}\int_{X_i} I(\overline{\varphi}_i(x_i))\,\textrm{d}\mu_i(x_i). \]Hence, we get the result.
Lemma 3.4 Suppose that 
$X_1,X_2$ are Polish metric spaces. For every 
$a,b>0$ and 
$\mu _i\in \mathcal {M}(X_i), i=1,2$, we have
\begin{align*} {\textrm{E}}^{a,b}(\mu_1,\mu_2)\geq\sup\limits_{(\varphi_1,\varphi_2)\in\Phi_I} \sum_{i=1}^{2} \int_{X_i} I\left(\varphi_i(x_i)\right) \textrm{d}\mu_i(x_i). \end{align*}Proof. Let 
$\mu _i\in {{\mathcal {M}}}(X_i),i=1,2$. Thanks to lemma 3.2, let 
$\boldsymbol {\gamma }\in {\textrm {Opt}}^{a,b}(\mu _1,\mu _2)$. Then 
$\gamma _i\leq \mu _i$ for 
$i=1,2$. By Radon–Nikodym theorem, there exists a measurable function 
$f_i:X\rightarrow [0,\infty )$ such that 
$\gamma _i=f_i\mu _i$ and 
$f_i\leq 1$ 
$\mu _i$-a.e. Therefore, for every 
$(\varphi _1,\varphi _2)\in \Phi _I$ we get that
\begin{align*}
{\textrm{E}}^{a,b}\left(\mu_1,\mu_2\right) & =
\sum_{i=1}^{2}\int_{X_i}a\left(1-f_i(x_i)\right)\textrm{d}\mu_i(x_i)+b\int_{X_1}
C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1)\\ & \geq
\sum_{i=1}^{2}\int_{X_i}a\left(1-f_i(x_i)\right)\textrm{d}\mu_i(x_i)
+ \int_{X_1}
\left(\varphi_1(x_1)+\gamma_{x_1}(\varphi_2)\right)\textrm{d}\gamma_1(x_1)\\
&=
\sum_{i=1}^{2}\int_{X_i}a\left(1-f_i(x_i)\right)\textrm{d}\mu_i(x_i)
+
\int_{X_1}\varphi_1(x_1)\,\textrm{d}\gamma_1\\
&\quad +\int_{X_1}\int_{X_2}\varphi_2(x_2)\,\textrm{d}\gamma_{x_1}(x_2)\,\textrm{d}\gamma_1(x_1)\\
& =
\sum_{i=1}^{2}\int_{X_i}\left(a\left(1-f_i(x_i)\right)+f_i(x_i)\varphi_i(x_i)\right)\textrm{d}\mu_i(x_i).
\end{align*}
Furthermore, for all 
$x_i\in X_i$, since 
$f_i(x_i)\geq 0$, 
$f_i\leq 1$ 
$\mu _i$-a.e and (1.6) we get
\[ \int_{X_i}I(\varphi_i(x_i))\,\textrm{d}\mu_i(x_i)\leq\int_{X_i}( f_i(x_i)\varphi_i(x_i)+a(1-f_i(x_i))\,\textrm{d}\mu_i(x_i),\text{ for }i=1,2. \]Hence, we get the result.
For 
$i=1,2$, we denote by 
${{\mathcal {M}}}_s(X_i)$ the space of signed Borel measures with a finite mass on 
$X_i$. Then for every 
$a,b>0$ we define the functional 
${\textrm {ET}}^{a,b}:{{\mathcal {M}}}_s(X_1)\times {{\mathcal {M}}}_s(X_2)\to [0,+\infty ]$ by
\[
{\textrm{ET}}^{a,b}(\mu_1,\mu_2)=\begin{cases}
\inf_{\boldsymbol{\gamma}\in
M}{\textrm{E}}^{a,b}(\boldsymbol{\gamma}|\mu_1,\mu_2) &
\text{ if }(\mu_1,\mu_2)\in
{{\mathcal{M}}}(X_1)\times{{\mathcal{M}}}(X_2),\\ + \infty
& \text{ otherwise}. \end{cases} \]Lemma 3.5 Let 
$X_1,X_2$ be Polish metric spaces and 
$a,b>0$. Then
1.
${\textrm {ET}}^{a,b}$ is convex and satisfies that ${\textrm {ET}}^{a,b}(k\mu _1,k\mu _2)=k{\textrm {ET}}^{a,b}(\mu _1,\mu _2)$, for every $\mu _i\in {{\mathcal {M}}}_s(X_i),i=1,2$ and $k>0$.2. If moreover
$X_1$ and $X_2$ are locally compact then ${\textrm {ET}}^{a,b}$ is lower semi-continuous under the weak*-topology.
Proof. (1) Let 
$\mu _i\in {{\mathcal {M}}}_s(X_i),i=1,2$ and 
$k> 0$. If there exists 
$i\in \{1,2\}$ such that 
$\mu _i\not \in {{\mathcal {M}}}(X_i)$ then 
$k{\textrm {ET}}^{a,b}(\mu _1,\mu _2)=+\infty ={\textrm {ET}}^{a,b}(k\mu _1,k\mu _2).$ So we only need to consider 
$(\mu _1,\mu _2)\in {{\mathcal {M}}}(X_1)\times {{\mathcal {M}}}(X_2)$. Let 
$\boldsymbol {\gamma }\in {\textrm {Opt}}^{a,b}(k\mu _1,k\mu _2)$ then one has
\begin{align*}
{\textrm{ET}}^{a,b}(k\mu_1,k\mu_2)&=a\left\vert
k\mu_1-\gamma_1\right\vert+a\left\vert
k\mu_2-\gamma_2\right\vert+b\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1)\\
& =k\left(\vphantom{\int_{X_1}} a\left\vert
\mu_1-(\gamma_1/k)\right\vert+a\left\vert
\mu_2-(\gamma_2/k)\right\vert\right.\\
&\quad +\left. b\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}(\gamma_1(x_1)/k)\right)\\
&\geq k{\textrm{ET}}^{a,b}(\mu_1,\mu_2).
\end{align*}
Similarly, we also have 
$k{\textrm {ET}}^{a,b}(\mu _1,\mu _2)\geq {\textrm {ET}}^{a,b}(k\mu _1,k\mu _2)$ and thus 
${\textrm {ET}}^{a,b}(k\mu _1, k\mu _2)=k{\textrm {ET}}^{a,b}(\mu _1,\mu _2)$.
By this homogeneity property of 
${\textrm {ET}}^{a,b}$, to show that 
${\textrm {ET}}^{a,b}$ is convex, we only need to prove that
\[ {\textrm{ET}}^{a,b}(\mu_1,\mu_2)+{\textrm{ET}}^{a,b}(\nu_1,\nu_2)\geq {\textrm{ET}}^{a,b}(\mu_1+\nu_1,\mu_2+\nu_2), \]
for every 
$(\mu _1,\mu _2),(\nu _1,\nu _2)\,{\in}\, {{\mathcal {M}}}_s(X_1)\,{\times}\, {{\mathcal {M}}}_s(X_2)$. We will consider 
$(\mu _1,\mu _2),(\nu _1,\nu _2)\in {{\mathcal {M}}}(X_1)\times {{\mathcal {M}}}(X_2)$ (the other cases are trivial). Let 
$\boldsymbol {\gamma }\in {\textrm {Opt}}^{a,b}(\mu _1,\mu _2)\text { and } \overline {\boldsymbol {\gamma }}\in {\textrm {Opt}}^{a,b}(\nu _1,\nu _2)$. By the convexity of 
$C(x_1,\cdot )$ and observe that 
$((d\gamma _1/d(\gamma _1+\overline {\gamma }_1))\gamma _{x_1}+(d\overline {\gamma }_1/d(\gamma _1+\overline {\gamma }_1))\overline {\gamma }_{x_1})_{x_1\in X_1}$ is the disintegration of 
$\boldsymbol {\gamma }+\overline {\boldsymbol {\gamma }}$ with respect to 
$\gamma _1+\overline {\gamma }_1$, we have that
\[ \int_{X_1}C(x_1, (\gamma+\overline{\gamma})_{x_1})\,\textrm{d}(\gamma_1+\overline{\gamma}_1)\leq \int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1+\int_{X_1}C(x_1,\overline{\gamma}_{x_1})\,\textrm{d}\overline{\gamma}_1. \]This yields,
\begin{align*}
{\textrm{ET}}^{a,b}(\mu_1,\mu_2)+{\textrm{ET}}^{a,b}(\nu_1,\nu_2)&\geq
a\sum_{i=1}^{2}\vert(\mu_i+\nu_i)-(\gamma_i+\overline{\gamma}_i)\vert\\
&\quad +b\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1)\\
&\quad +b\int_{X_1}C(x_1,\overline{\gamma}_{x_1})\,\textrm{d}\overline{\gamma}_1(x_1)\\
&\geq {\textrm{ET}}^{a,b}(\mu_1+\nu_1,\mu_2+\nu_2).
\end{align*}(2) For
$i=1,2$, let $\{\mu _i^{n}\}\subset {{\mathcal {M}}}(X_i)$ such that $\mu _i^{n}\to \mu _i\in {{\mathcal {M}}}(X_i)$ as $n\to \infty$ under the weak*-topology. Then $\{\mu _i^{n}\}$ is relatively compact and by Prokhorov's theorem, $\{\mu _i^{n}\}$ is tight and bounded. For each $n\in {{\mathbb {N}}}$ let $\boldsymbol {\gamma }^{n}\in {\textrm {Opt}}^{a,b}(\mu _1^{n},\mu _2^{n})$ then $\gamma _i^{n}\leq \mu _i^{n}$ for $i=1,2$. This implies that $\{\gamma _i^{n}\}$ is also tight and bounded. Hence, by Prokhorov's theorem, passing to a subsequence we can assume that $\lim _{n\to \infty }\gamma _i^{n}=\gamma _i$ for $\gamma _i\in {{\mathcal {M}}}(X_i)$. Furthermore, for every $\mu ,\nu \in {{\mathcal {M}}}(X_i)$ by [Reference Rudin23, theorem 6.19] we have that
\[ \vert \mu-\nu\vert =\sup\bigg\{\int_{X_i}fd(\mu-\nu)|f\in C_0(X_i),\Vert f\Vert_\infty\leq 1\bigg\}. \]
From this formula, we get that 
$\liminf _{n\rightarrow \infty }\vert \mu _{i}^{n}-\gamma _{i}^{n}\vert \geq \vert \mu _i-\gamma _i\vert$ for 
$i=1,2$. By [Reference Chung and Trinh10, Lemma 3.5] we get that 
$\int _{X_1}C(x_1,\gamma _{x_1})d\gamma _1(x_1)$ is lower semi-continuous under the weak*-topology. Therefore,
\begin{align*}
\liminf_{n\rightarrow\infty}{\textrm{E}}^{a,b}(\mu_{1}^{n},\mu_{2}^{n})&\geq
a\vert \mu_1-\gamma_1\vert+a\vert
\mu_2-\gamma_2\vert+b\int_{X_1}C(x_1,\gamma_{x_1})\,\textrm{d}\gamma_1(x_1)\\
&\geq
{\textrm{E}}^{a,b}(\mu_1,\mu_2). \end{align*}
This means that 
${\textrm {E}}^{a,b}$ is lower semi-continuous. Therefore, 
${\textrm {ET}}^{a,b}$ is also lower semi-continuous since 
${{\mathcal {M}}}(X_1)\times {{\mathcal {M}}}(X_2)$ is closed.
Proof of theorem 1.1. Denote by 
$({\textrm {ET}}^{a,b})^{*}$ the Fenchel conjugate of 
${\textrm {ET}}^{a,b}$, i.e.
\begin{align*}
({\textrm{ET}}^{a,b})^{*}(\varphi_1,\varphi_2)&:=\sup_{(m_1,m_2)} \bigg\{\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}m_i(x_i)-{\textrm{E}}^{a,b}(m_1,m_2)\bigg\},
\end{align*}
where 
$(m_1,m_2)$ runs over 
${{\mathcal {M}}}_s(X_1) \times {{\mathcal {M}}}_s(X_2)$, for every 
$(\varphi _1,\varphi _2)\in C_0(X_1)\times C_0(X_2)$. Notice that the dual space of 
$C_0(X_i)$ is 
${{\mathcal {M}}}_s(X_i)$. By lemma 3.5 we get that
\[ ({\textrm{ET}}^{a,b})^{*}(\varphi_1,\varphi_2)=\left\lbrace\begin{array}{@{}ll} 0 & \text{ if }(\varphi_1,\varphi_2)\in \Phi_E,\\ + \infty & \text{ otherwise}, \end{array}\right. \]where
\begin{align*} \Phi_E:=\bigg\{(\varphi_1,\varphi_2)\in C_0(X_1)\times C_0(X_2)&: \sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}m_i(x_i)\leq {\textrm{ET}}^{a,b}(m_1,m_2)\\ & \mbox{ for every } (m_1,m_2)\in {{\mathcal{M}}}_s(X_1)\times{{\mathcal{M}}}_s(X_2)\bigg\}. \end{align*}
We now check that 
$\Phi _E=\Phi _J^{0}$. Let any 
$(\varphi _1,\varphi _2)\in \Phi _J^{0}$. Let 
$m_i\in {{\mathcal {M}}}_s(X_i)$, 
$i=1,2$. If 
${\textrm {ET}}^{a,b}(m_1,m_2)=+\infty$ then it is clear that 
$\sum _{i=1}^{2}\int _{X_i}\varphi _i(x_i)\textrm {d}m_i(x_i)\leq {\textrm {ET}}^{a,b}(m_1,m_2)$. Thus, we only consider 
$(m_1,m_2)\in {{\mathcal {M}}}(X_1)\times {{\mathcal {M}}}(X_2)$. By lemmas 3.3 and 3.4 we get that
\[ \sum_{i=1}^{2}\int_{X_i}\varphi_i\textrm{d}m_i\leq \sup_{(\phi_1,\phi_2)\in \Phi_I}\sum_{i=1}^{2}\int_{X_i}I(\phi_i)\,\textrm{d}m_i\leq {\textrm{E}}^{a,b}(m_1,m_2)={\textrm{ET}}^{a,b}(m_1,m_2). \]
Therefore, 
$(\varphi _1,\varphi _2)\in \Phi _E$ and thus 
$\Phi ^{0}_J\subset \Phi _E$.
Now, let any 
$(\varphi _1,\varphi _2)\in \Phi _E$. We will show that 
$(\varphi _1,\varphi _2)\in \Phi _J^{0}$. Denote by 
$\eta$ the null measure on 
$X_1\times X_2$. As 
$(\varphi _1,\varphi _2)\in \Phi _E$, for every 
$(m_1,m_2)\in {{\mathcal {M}}}(X_1)\times {{\mathcal {M}}}(X_2)$ one has
\[ \sum_{i=1}^{2}\int_{X_i} \varphi_i(x_i) \textrm{d}m_i(x_i)\leq {\textrm{E}}^{a,b}(m_1,m_2)\leq {\textrm{E}}^{a,b}(\eta|m_1,m_2)=a(\vert m_1\vert+\vert m_2\vert). \]
For every 
$z\in X_1$, setting 
$m_1:=\delta _{z}$ and 
$m_2$ is the null measure on 
$X_2$, we obtain that 
$\varphi _1(z)\leq a$. Similarly, we also have 
$\varphi _2\leq a$ on 
$X_2$.
On the other hand, for any 
$w\in X_1$ and 
$q\in {{\mathcal {P}}}(X_2)$ putting 
$m_1:=\delta _{w}, m_2:=q|_B$ and 
$\overline {\boldsymbol {\gamma }}:=\delta _{w}\otimes q$, where 
$B:=\{x_2\in X_2|\varphi _2(x_2)\geq -a\}$. Then
\begin{align*}
\varphi_1(w)+\int_B\varphi_2\textrm{d}q&=\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}m_i(x_i)\leq
{\textrm{E}}^{a,b}(\overline{\boldsymbol{\gamma}}|m_1,m_2)\\
&=a.q(X_2\backslash
B)+ b\cdot C(w,q). \end{align*}
From (1.4), if 
$\varphi _1(w)<-a$ then
\[ J(\varphi_1(w))+q(J(\varphi_2))\leq{-}a+a=0\leq b\cdot C(w,q), \]
and if 
$\varphi _1(w)\geq -a$ then
\begin{align*} J(\varphi_1(w))+q(J(\varphi_2))&= \varphi_1(w)+\int_BJ(\varphi_2)\,\textrm{d}q+\int_{X_2\backslash B}J(\varphi_2)\,\textrm{d}q\\ &= \varphi_1(w)+\int_B\varphi_2\textrm{d}q-a.q(X_2\backslash B)\\ &\leq b\cdot C(w,q). \end{align*}
Therefore, 
$(\varphi _1,\varphi _2)\in \Phi ^{0}_J$ and hence 
$\Phi _E\subset \Phi ^{0}_J$. Thus, 
$\Phi _E=\Phi ^{0}_J$.
Moreover, by lemma 3.5 one has 
${\textrm {ET}}^{a,b}$ is convex and lower semi-continuous. Hence, applying [Reference Ekeland and Témam11, proposition 3.1, page 14 and proposition 4.1, page 18] we get that 
$({\textrm {ET}}^{a,b})^{**}={\textrm {ET}}^{a,b}$. Therefore,
\begin{align*} {\textrm{ET}}^{a,b}(\mu_1,\mu_2)&=\sup_{(\varphi_1,\varphi_2)\in C_0(X_1)\times C_0(X_2)}\left\{\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}\mu_i(x_i)-({\textrm{ET}}^{a,b})^{*}(\varphi_1,\varphi_2)\right\}\\ &=\sup_{(\varphi_1,\varphi_2)\in \Phi^{0}_J}\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}\mu_i(x_i)\\ &\leq \sup_{(\varphi_1,\varphi_2)\in \Phi_J}\sum_{i=1}^{2}\int_{X_i}\varphi_i(x_i)\,\textrm{d}\mu_i(x_i). \end{align*}Proof of corollary 1.2. We define the cost function 
$C:X\times {{\mathcal {P}}}(X)\to [0,\infty ]$ by
\[ C(x,q):=\int_{X}c_1(x,y)dq(y), \]
for every 
$x\in X$ and 
$q\in {{\mathcal {P}}}(X)$. We will check that 
$C$ is lower semi-continuous on 
$X\times {{\mathcal {P}}}(X)$. Let 
$(x^{n},q^{n})\subset X\times {{\mathcal {P}}}(X)$ such that 
$(x^{n},q^{n})\to (x^{0},q^{0})$ as 
$n\to \infty$. Then as 
$c_1$ is lower semi-continuous on 
$X\times X$ and non-negative, by [Reference Chung and Trinh10, lemma 4.2] we get that
\[ \liminf_{n\to\infty} C(x^{n},q^{n})=\liminf_{n\to\infty}\int_Xc_1(x^{n},y)\,\textrm{d}q^{n}(y)\geq \int_Xc_1(x^{0},y)\,\textrm{d}q^{0}(y)=C(x^{0},q^{0}). \]
This means that 
$C$ is lower semi-continuous on 
$X\times {{\mathcal {P}}}(X)$. Next, a one-to-one correspondence between 
$\boldsymbol {\gamma }\in {{\mathcal {M}}}^{\leq } (\mu _1,\mu _2)$ and 
$\hat {\boldsymbol {\gamma }}\in \Gamma (\hat {\mu }_1,\hat {\mu }_2)$ is given by
\[ \hat{\boldsymbol{\gamma}}=\boldsymbol{\gamma}+\vert 1-f_1\vert\mu_1\otimes \delta_{\hat{\infty}}+\delta_{\hat{\infty}}\otimes\vert 1-f_2\vert\mu_2+\vert\boldsymbol{\gamma}\vert\delta_{(\hat{\infty},\hat{\infty})}, \]
where 
$f_i$ is the Radon–Nikodym derivative of 
$\gamma _i$ with respect to 
$\mu _i$. From this and theorem 1.1 we obtain that
\begin{align*} \inf_{\hat{\boldsymbol{\gamma}}\in \Gamma(\hat{\mu}_1,\hat{\mu}_2)}\int_{\hat{X}\times \hat{X}}\hat{c}_1(x,y)\,\textrm{d}\hat{\boldsymbol{\gamma}}(x,y)={\textrm{E}}^{a,b}(\mu_1,\mu_2)=\sup_{(\varphi_1,\varphi_2)\in \Phi_J}\sum_{i=1}^{2}\int_{X}\varphi_i(x)\,\textrm{d}\mu_i(x). \end{align*} Now, for any 
$(\varphi _1,\varphi _2)\in \Phi _J$ we define 
$\hat {\varphi _i}(x)=J(\varphi _i(x))$ if 
$x\in X$ and 
$\hat {\varphi }_i(x)=0$ if 
$x=\hat {\infty }$ for 
$i=1,2$. Then 
$\hat {\varphi }_i\in L^{1}(\hat {\mu }_i)$ for 
$i=1,2$. As 
$(\varphi _1,\varphi _2)\in \Phi _J$, for every 
$x,y\in X$ we have
\begin{align*} J(\varphi_1(x))+J(\varphi_2(y))=J(\varphi_1(x))+\delta_y(J(\varphi_2))\leq b\cdot C(x,\delta_y)=b\cdot c_1(x,y). \end{align*}
Hence 
$\hat {\varphi }_1(x)+\hat {\varphi }_2(y)\leq \hat {c}_1(x,y)\text { for every }x,y\in \hat {X}.$ Moreover, we also have
\[ \int_{\hat{X}}\hat{\varphi}_1\textrm{d}\hat{\mu}_1=\int_X\hat{\varphi}_1\textrm{d}\mu_1+\hat{\varphi}_1(\hat{\infty})|\mu_2|=\int_XJ(\varphi_1)\,\textrm{d}\mu_1 \geq\int_X\varphi_1\textrm{d}\mu_1. \]
Similarly, 
$\int _{\hat {X}}\hat {\varphi }_2d\hat {\mu }_2\geq \int _X\varphi _2d\mu _2$. Therefore,
\[ \sup_{(\varphi_1,\varphi_2)\in \Phi_J}\sum_{i=1}^{2}\int_{X}\varphi_i(x)\,\textrm{d}\mu_i(x)\leq \sup_{\substack{(\hat{\varphi}_1,\hat{\varphi}_2)\in L^{1}(\hat{\mu}_1)\times L^{1}(\hat{\mu}_2)\\\hat{\varphi}_1(x)+\hat{\varphi}_2(y)\leq \hat{c}_1(x,y)}}\sum_{i=1}^{2}\int_{\hat{X}}\hat{\varphi}_i(x)\,\textrm{d}\hat{\mu_i}(x). \]This implies that
\begin{align*} \inf_{\hat{\boldsymbol{\gamma}}\in \Gamma(\hat{\mu}_1,\hat{\mu}_2)}\int_{\hat{X}\times \hat{X}}\hat{c}_1(x,y)\,\textrm{d}\hat{\boldsymbol{\gamma}}(x,y)&\leq \sup_{\substack{(\hat{\varphi}_1,\hat{\varphi}_2)\in L^{1}(\hat{\mu}_1)\times L^{1}(\hat{\mu}_2)\\\hat{\varphi}_1(x)+\hat{\varphi}_2(y)\leq \hat{c}_1(x,y)}}\,\sum_{i=1}^{2}\int_{\hat{X}}\hat{\varphi}_i(x)\,\textrm{d}\hat{\mu_i}(x)\\ &\leq \inf_{\hat{\boldsymbol{\gamma}}\in \Gamma(\hat{\mu}_1,\hat{\mu}_2)}\int_{\hat{X}\times \hat{X}}\hat{c}_1(x,y)\,\textrm{d}\hat{\boldsymbol{\gamma}}(x,y). \end{align*}Hence, we get the result.
Proof of corollary 1.3. (1) Applying theorem 1.1 for 
$X_1=X_2=X$ and 
$C(x,q)=\int _Xc(x,y)dq(y)$, where 
$c(x,y)=(b\cdot d(x,y))^{p}$ for every 
$x,y\in X$ then we get the result.
(2) We use the techniques of the proof of [Reference Villani25, theorem 1.14] to prove (2). For every
$(\psi ,\varphi )\in \Phi _W$, we define $\varphi ^{d}(x):=\inf _{y\in X}[b\cdot d(x,y)-\varphi (y)]$ for every $x\in X$. Then $\varphi ^{d}$ is $b$-Lipschitz function and $\varphi ^{d}(x)\in [-a,a]$ for every $x\in X$. Therefore, $\varphi ^{d}\in {{\mathbb {F}}}$. Now we define $\varphi ^{dd}(y):=\inf _{x\in X}[b\cdot d(x,y)-\varphi ^{d}(x)]$ for every $y\in X$. Then $\varphi ^{dd}$ is $b$-Lipschitz and
\[ \varphi^{d}(x)+\varphi^{dd}(y)\leq b\cdot d(x,y), \mbox{ for every } x,y\in X. \]
As 
$-a\leq \varphi ^{d}(x)\leq a$ we also get that 
$-a\leq \varphi ^{dd}(y)\leq a$ for every 
$y\in X$. Therefore we have 
$\varphi ^{dd}\in {{\mathbb {F}}}$ and 
$(\varphi ^{d},\varphi ^{dd})\in \Phi _W$.
On the other hand, as 
$\psi (x)+\varphi (y)\leq b\cdot d(x,y)$ for every 
$x,y\in X$ we get that
\[ \psi(x)\leq \inf_{y\in X}[b\cdot d(x,y)-\varphi(y)]=\varphi^{d}(x) \mbox{ for every } x\in X. \]
Similarly, from the definitions of 
$\varphi ^{dd}$ we also have 
$\varphi ^{dd}(y)\geq \varphi (y)$ for every 
$y\in Y$. Hence
\begin{align*} \int_{X} I\left(\psi\right)\textrm{d}\mu+\int_{X} I\left(\varphi\right)\textrm{d}\nu \leq \int_{X} I\left(\varphi^{d}\right)\textrm{d}\mu+\int_{X} I\left(\varphi^{dd}\right)\textrm{d}\nu. \end{align*}Therefore,
\begin{align*}
&\sup_{(\psi,\varphi)\in \Phi_W}\bigg\{\int_{X}
I\left(\psi\right)\textrm{d}\mu+\int_{X}
I\left(\varphi\right)\textrm{d}\nu \bigg\}\\
&\quad \leq
\sup_{\varphi\in C_b(X)}\bigg\{\int_{X}
I\left(\varphi^{d}\right)\textrm{d}\mu+\int_{X}
I\left(\varphi^{dd}\right)\textrm{d}\nu \bigg\}.
\end{align*}
As 
$\varphi ^{d}$ is 
$b$-Lipschitz we get
\[ -\varphi^{d}(x)\leq \inf_{y\in X}[b\cdot d(x,y)-\varphi^{d}(y)]. \]
On the other hand, 
$\inf _{y\in X}[b\cdot d(x,y)-\varphi ^{d}(y)]\leq -\varphi ^{d}(x)$. Hence
\[ \varphi^{dd}(x)=\inf_{y\in X}[b\cdot d(x,y)-\varphi^{d}(y)]={-}\varphi^{d}(x). \]Thus
\begin{align*}
&\sup_{(\psi,\varphi)\in \Phi_W}\bigg\{\int_{X}
I(\psi)\,\textrm{d}\mu+\int_{X}
I(\varphi)\,\textrm{d}\nu \bigg\}\\
&\quad \leq
\sup_{\varphi\in C_b(X)}\bigg\{\int_{X}
I\left(\varphi^{d}\right)\textrm{d}\mu+\int_{X}
I\left(\varphi^{dd}\right)\textrm{d}\nu \bigg\} \\
&\quad =
\sup_{\varphi\in C_b(X)}\bigg\{\int_{X}
I\left(\varphi^{d}\right)\textrm{d}\mu+\int_{X}
I\left(-\varphi^{d}\right)\textrm{d}\nu \bigg\}\\
&\quad \leq \sup_{\varphi\in {{\mathbb{F}}}}\bigg\{\int_{X}
I\left(\varphi\right)\textrm{d}\mu+\int_{X}
I\left(-\varphi\right)\textrm{d}\nu \bigg\}\\
&\quad \leq
\sup_{(\psi,\varphi)\in \Phi_W}\bigg\{\int_{X}
I\left(\psi\right)\textrm{d}\mu+\int_{X}
I\left(\varphi\right)\textrm{d}\nu \bigg\}.
\end{align*}So we must have equality everywhere and get the result.
Remark 3.6 (1) Corollary 1.3 (2) has been proved in [Reference Piccoli and Rossi21, theorem 2] for the case 
$a=b=1$ and 
$X={{\mathbb {R}}}^{n}$ by a different method.
(2) [Reference Hanin14, Reference Hanin15] Let
$(X,d)$ be a Polish metric space. Let ${{\mathcal {M}}}^{0}(X)$ be the set of all $\mu \in {{\mathcal {M}}}_s(X)$ such that $\mu (X)=0$. For every $\mu \in {{\mathcal {M}}}^{0}(X)$, we denote by $\Psi _\mu$ the set of all non-negative measures $\boldsymbol {\gamma }\in {{\mathcal {M}}}(X\times X)$ such that $\boldsymbol {\gamma }(X\times A)-\boldsymbol {\gamma }(A\times X) =\mu (A)$ for every Borel $A\subset X$. Then we define for every $\mu \in {{\mathcal {M}}}^{0}(X)$,
\[ \|\mu\|^{0}_d:=\inf_{\boldsymbol{\gamma}\in \Psi_\mu}\bigg\{\int_{X\times X}d(x,y)d\boldsymbol{\gamma}(x,y)\bigg\}. \]
Now, on the vector space 
${{\mathcal {M}}}_s(X)$ we define an extension Kantorovich–Rubinstein norm as following
\[ \|\mu\|_d:=\inf_{\nu\in {{\mathcal{M}}}^{0}(X)}\bigg\{\|\nu\|^{0}_d+|\mu-\nu|(X)\bigg\}, \mbox{ for every } \mu\in {{\mathcal{M}}}_s(X). \]
Then from [Reference Hanin14, theorem 0] (when 
$X$ is compact) or [Reference Hanin15, theorem 1] (when 
$X$ is a general Polish metric space), applying Hahn–Banach theorem we get that
\[ \|\mu\|_d=\sup\bigg\{\int_X fd(\mu-\nu):f\in {{\mathbb{F}}}\bigg\}, \]
where 
${{\mathbb {F}}}:=\big \{f\in C_b(X), \|f\|_\infty \leq 1, \|f\|_{Lip}\leq 1\big \}$. We thank Benedetto Piccoli and Francesco Rossi for pointing [Reference Hanin14] out to us, and we have found [Reference Hanin15] after that.
Using corollary 1.3 (2) we get another proof of [Reference Piccoli, Rossi and Tournus22, lemma 5].
Corollary 3.7 Let 
$X$ be a locally compact, Polish metric space. For every 
$\mu ,\nu ,\eta \in {{\mathcal {M}}}(X)$ we have
\[ \widetilde{W}_1^{a,b}(\mu+\eta,\nu+\eta)=\widetilde{W}^{a,b}_1(\mu,\nu). \]4. Barycenter problem and an its dual problem
Let 
$(X,d)$ be a locally compact, Polish metric space. For every integer 
$k\geq 2$, we consider 
$k$ measures 
$\mu _1,\mu _2,\ldots ,\mu _k$ in 
$\mathcal {M}(X)$ such that 
$\text {supp}(\mu _i)$ is a compact subset of 
$X$ for every 
$i\in \{1,\ldots ,k\}$. Let 
$\lambda _1,\lambda _2,\ldots ,\lambda _k$ be positive real numbers such that 
$\sum _{i=1}^{k}\lambda _i=1$ and let 
$K={\bigcup} _{i=1}^{k} \text {supp}(\mu _i)$, we consider the following problem
\[ (B) \inf_{\text{supp}(\mu)\subset K} \sum_{i=1}^{k}\lambda_i \widetilde{W}^{a,b}_2\left(\mu_i,\mu\right)^{2}. \]Remark 4.1 Let 
$X={{\mathbb {R}}}^{d}$. For every 
$m>0, a,b\geq 0$ and 
$\mu _1,\mu _2\in {{\mathcal {M}}}(X)$ we define
\[ \widetilde{W}_{2,m}^{a,b}(\mu_1,\mu_2):=\inf_{\gamma_i\in {{\mathcal{M}}}_2(X), \gamma_i\leq \mu_i,\vert \boldsymbol{\gamma}\vert=m}a\sum_{i=1}^{2}\vert \mu_i-\gamma_i\vert+b\int_{X\times X} \vert x-y\vert^{2} \textrm{d}\boldsymbol{\gamma}(x,y). \]In [Reference Kitagawa and Pass16] Kitagawa and Pass introduced and investigated the following partial barycenter problem:
\[ \inf_{\mu\in{{\mathcal{M}}}(X),\vert \mu\vert=m}\sum_{i=1}^{k}\widetilde{W}_{2,m}^{0,1}(\mu_i,\mu)^{2}. \]The methods there are different from us as they study their partial barycenters via multi-marginal optimal transports while we use duality formulations for our barycenter problems in generalized Wasserstein spaces.
Theorem 4.2 Problem 
$(B)$ has solutions.
Proof. For every 
$\mu \in {{\mathcal {M}}}(X)$ such that 
$\text {supp}(\mu )\subset K$, let 
$J(\mu )=\sum _{i=1}^{k}\lambda _i \widetilde {W}^{a,b}_2(\mu _i,\mu )^{2}.$ Let 
$\left \{\mu ^{n}\right \}_{n\in \mathbb {N}}$ be a minimizing sequence of 
$(B)$. If there exists 
$n_0$ such that 
$\text {supp}(\mu ^{n_0})=X$ then 
$X=K$, and thus 
$X$ is compact. Hence, 
$\left \{\mu ^{n}\right \}_{n\in \mathbb {N}}$ is tight. Otherwise, for every 
$n\in \mathbb {N}$, let 
$x\not \in \text {supp}(\mu ^{n})$ then there exists an open neighborhood 
$U_x$ of 
$x$ such that 
$\mu ^{n}(U_x)=0$. Since 
$X$ is separable and 
$\left \{U_x\right \}_{x\in X\backslash \text {supp}(\mu ^{n})}$ is an open cover of 
$X\backslash \text {supp}(\mu ^{n})$, applying Lindelöf theorem there is a countable subcover 
$\left \{U_{x_i}\right \}_i$. Therefore, 
$\mu ^{n}(X\backslash \text {supp}(\mu ^{n}))=0$. Moreover, 
$\text {supp}(\mu ^{n})\subset K$ for every 
$n\in \mathbb {N}$. Thus, for every 
$n\in N$, 
$\mu ^{n}(X\backslash K)=0$. It implies that 
$\left \{\mu ^{n}\right \}_{n\in \mathbb {N}}$ is tight.
We now prove that 
$\left \{\mu ^{n}\right \}_{n\in \mathbb {N}}$ is bounded. For every 
$n\in \mathbb {N}$ and every 
$i\in \{1,2,\ldots ,k\}$, using corollary 1.3 (1) we get that
\begin{align*} \widetilde{W}^{a,b}_2\left(\mu^{n},\mu_i\right)^{2}=\sup\bigg\{\int_X\varphi_1(x) \textrm{d}\mu^{n}(x)+\int_X\varphi_2(x) \textrm{d}\mu_i(x)|\left(\varphi_1,\varphi_2\right)\in\Phi_W\bigg\}, \end{align*}
We set 
$\varphi _1(x)=a, \varphi _2(x)=-a$ for every 
$x\in X$ then
\[ \lambda_i.\widetilde{W}^{a,b}_2\left(\mu^{n},\mu_i\right)^{2}\geq \lambda_ia\mu^{n}(X)-\lambda_ia\mu_i(X) \]This yields,
\[ \left\vert \mu^{n}\right\vert\leq \dfrac{1}{a}J\left(\mu^{n}\right)+\sum_i^{k}\lambda_i\vert \mu_i\vert,\text{ for every }n\in\mathbb{N}. \]
As 
$\mu _i\in {{\mathcal {M}}}(X)$ for every 
$i\in \{1,2,\ldots ,k\}$ and 
$J(\mu ^{n})$ is bounded, we obtain that 
$\left \{\mu ^{n}\right \}_{n\in \mathbb {N}}$ is bounded. Therefore, applying Prokhorov's theorem, passing to a subsequence we can assume that 
$\mu ^{n}\rightarrow \mu$ as 
$n\rightarrow \infty$ in the weak*-topology for some 
$\mu \in {{\mathcal {M}}}(X)$.
We now show that 
$\text {supp}(\mu )\subset K$. As 
$X\backslash K$ is an open set, applying [Reference Parthasarathy19, theorem 6.1] we get that
\[ 0=\liminf_{n\rightarrow \infty}\mu^{n}(X\backslash K)\geq \mu(X\backslash K). \]
Therefore, 
$X\backslash K\subset X\backslash \text {supp}(\mu )$. Hence, 
$\text {supp}(\mu )\subset K$.
Next, we will check that 
$\widetilde {W}^{a,b}_2(\mu ^{n},\mu )\rightarrow 0$ as 
$n\rightarrow \infty$. If 
$\vert \mu \vert =0$ then we are done. If 
$\vert \mu \vert >0$ then there exists 
$N>0$ such that 
$\vert \mu ^{n}\vert >0$ for all 
$n\geq N$. For each 
$n\geq N$, we define 
$\nu ^{n}:=\vert \mu \vert \mu ^{n}/\vert \mu ^{n}\vert$ then 
$\vert \nu ^{n}\vert =\vert \mu \vert$. Therefore,
\begin{align*} \widetilde{W}^{a,b}_2(\mu^{n},\mu)^{2}\leq a\vert\mu^{n}-\nu^{n} \vert+b^{2}W_2^{2}(\nu^{n},\mu)=a\left\vert\vert\mu^{n}\vert-\vert \mu\vert\right\vert+b^{2}W_2^{2}(\nu^{n},\mu). \end{align*}
Moreover, since 
$\mu ^{n}\rightarrow \mu$ as 
$n\rightarrow \infty$ one has 
$\nu ^{n}\rightarrow \mu$ as 
$n\rightarrow \infty$. Observe that 
$\nu ^{n}$ and 
$\mu$ are concentrated in compact set 
$K$, applying [Reference Villani26, definition 6.8 and theorem 6.9] we obtain that 
$\lim _{n\rightarrow \infty }W_2(\nu ^{n},\mu )=0$. This yields,
\[ \limsup_{n\rightarrow \infty}\widetilde{W}^{a,b}_2(\mu^{n},\mu)^{2}\leq a\lim_{n\rightarrow\infty}\left\vert\vert\mu^{n}\vert-\vert \mu\vert\right\vert+\lim_{n\rightarrow\infty}b^{2}W_2^{2}(\mu^{n},\mu)=0. \]
Notice that 
$\liminf _{n\rightarrow \infty }\widetilde {W}^{a,b}_2(\mu ^{n},\mu )\geq 0$. Therefore, 
$\lim _{n\rightarrow \infty }\widetilde {W}^{a,b}_2(\mu ^{n},\mu )=0$. This implies that 
$\lim _{n\rightarrow \infty }J(\mu ^{n})=J(\mu )$. Hence, we get the result.
Definition 4.3 Let 
$X$ be a locally compact, Polish metric space. For every integer 
$k\geq 2$, let 
$\mu _1,\ldots ,\mu _k\in \mathcal {M}(X)$ such that 
$\text {supp}(\mu _i)$ is compact, for every 
$i\in \{1,\ldots ,k\}$. Let 
$\lambda _1,\ldots ,\lambda _k>0$ such that 
$\sum _{i=1}^{k}\lambda _i=1$. We say that 
$\mu \in {{\mathcal {M}}}(X)$ is a generalized Wasserstein barycenter of 
$(\mu _1,\ldots ,\mu _k)$ with weights 
$(\lambda _1,\ldots ,\lambda _k)$ if 
$\mu$ is a solution of 
$(B)$. We denote by 
$BC((\mu _i,\lambda _i)_{1\leq i\leq k})$ the set of all generalized Wasserstein barycenters of 
$(\mu _1,\ldots ,\mu _k)$ with weights 
$(\lambda _1,\ldots ,\lambda _k)$.
In general, barycenters in a generalized Wasserstein space are not unique.
Example 4.4 Let 
$X=\mathbb {R},a=b=1$ and 
$\lambda _1=\lambda _2=1/2$. For every 
$x\geq 0$ let 
$\mu _1=\delta _x$ and 
$\mu _2=3\delta _x$. Then we have 
$\left \{\mu \in {{\mathcal {M}}}(\mathbb {R})|\text {supp}(\mu )\subset \{x\}\right \}=\{q\delta _x|q\geq 0\}$. For every 
$q\geq 0$, let 
$(\widetilde {\mu }_1,\widetilde {\mu }_2)$ be an optimal for 
$\widetilde {W}^{1,1}_2(\delta _x,q\delta _x)$. Since 
$\vert \widetilde {\mu }_1\vert =\vert \widetilde {\mu }_2\vert , \widetilde {\mu }_1\leq \delta _x,\widetilde {\mu }_2\leq q\delta _x$, we must have 
$\widetilde {\mu }_1=\widetilde {\mu }_2=r\delta _x$ where 
$0\leq r\leq \min \{q,1\}$. Hence, we get that
\[ \widetilde{W}^{1,1}_2(\delta_x,q\delta_x)^{2}=\min\{q+1-2r|0\leq r\leq \min\{q,1\}\}. \]Similarly, we also get that
\[ \widetilde{W}^{1,1}_2(3\delta_x,q\delta_x)^{2}=\min\{q+3-2s|0\leq s\leq \min\{q,3\}\}. \]It is easy to check that
\begin{align*}
&\lambda_1.\min\{q+1-2r|0\leq r\leq
\min\{q,1\}\}\\
&\quad +\lambda_2.\min\{q+3-2s|0\leq s\leq
\min\{q,3\}\}=1, \end{align*}
and the minimum is attained when 
$q\in [1,3]$. Therefore, 
$BC((\mu _1,\lambda _1),(\mu _2,\lambda _2))=\{q\delta _x|q\in [1,3]\}.$
We now prove the consistency of barycenters in generalized Wasserstein spaces which has been shown in [Reference Boissard, Le Gouic and Loubes5, theorem 3.1] for the Wasserstein setting.
Theorem 4.5 Let 
$(X,d)$ be a locally compact, Polish metric space. For every integer 
$k\geq 2$, let 
$\left \{\mu ^{n}_i\right \}\subset {{\mathcal {M}}}(X)$ be sequences converging in the generalized Wasserstein distance to compactly supported measure 
$\mu _i\in {{\mathcal {M}}}(X)$ for every 
$i\in \{1,\ldots ,k\}$. Let 
$K={\bigcup} _{i=1}^{k}\text {supp}(\mu _i)$ and let sequences 
$\lambda ^{n}_1,\ldots ,\lambda ^{n}_k>0$ such that 
$\sum _{i=1}^{k}\lambda ^{n}_i=1$ for every 
$n\in \mathbb {N}$ and 
$\lambda _i^{n}$ converges to 
$\lambda _i>0$ for 
$i=1,\ldots ,k$. For each 
$n\in \mathbb {N}$, suppose that 
$\text {supp}(\mu _i^{n})\subset K$ for every 
$i\in \{1,\ldots ,k\}$. Then 
$BC((\mu _i^{n},\lambda _i^{n})_{1\leq i\leq k})$ is a non-empty set for every 
$n\in {{\mathbb {N}}}$. Moreover, for every 
$n\in {{\mathbb {N}}}$, let 
$\mu _B^{n}\in BC((\mu _i^{n},\lambda _i^{n})_{1\leq i\leq k})$ then the sequence 
$\left \{\mu ^{n}_B\right \}$ is precompact in 
$({{\mathcal {M}}}(X),\widetilde {W}^{a,b}_2)$ and any its limit point is a generalized Wasserstein barycenter of 
$(\mu _1,\ldots ,\mu _k)$ with weights 
$(\lambda _1,\ldots ,\lambda _k)$.
Proof. Since 
$\text {supp}(\mu _i^{n})\subset K$ and 
$K$ is compact, one has 
$\text {supp}(\mu _i^{n})$ is compact for every 
$n\in \mathbb {N}$ and every 
$i\in \{1,\ldots ,k\}$. Therefore, 
$BC((\mu _i^{n},\lambda _i^{n})_{1\leq i\leq k})$ is a non-empty set for every 
$n\in \mathbb {N}$, this follows from theorem 4.2.
We now prove the second part. Since 
$\mu _B^{n}\in BC((\mu _i^{n},\lambda _i^{n})_{1\leq i\leq k})$, we get that 
$\text {supp}(\mu _B^{n})\subset {\bigcup} _{i=1}^{k}\text {supp}(\mu _i^{n})\subset K$, for every 
$n\in {{\mathbb {N}}}$. Then 
$\mu _B^{n}(X\backslash K)=0$ for every 
$n\in {{\mathbb {N}}}$. Therefore, 
$\left \{\mu _B^{n}\right \}$ is tight. Let 
$\mu _B\in BC((\mu _i,\lambda _i)_{1\leq i\leq k})$. Since 
$\widetilde {W}^{a,b}_2(\mu _i^{n},\mu _i)\rightarrow 0$ as 
$n\rightarrow \infty$ for every 
$i\in \{1,\ldots ,k\}$ we get that
\[ \lim_{n\rightarrow\infty}\widetilde{W}^{a,b}_2\left(\mu_B,\mu_i^{n}\right)=\widetilde{W}^{a,b}_2\left(\mu_B,\mu_i\right)<\infty \]
Therefore, 
$\{\widetilde {W}^{a,b}_2(\mu _B,\mu _i^{n})\}_n$ is bounded for every 
$i\in \{1,\ldots ,k\}$. Moreover,
\begin{align} \sum_{i=1}^{k}\lambda_i^{n} \widetilde{W}^{a,b}_2\left(\mu_B^{n},\mu_i^{n}\right)^{2}\leq \sum_{i=1}^{k}\lambda_i^{n} \widetilde{W}^{a,b}_2\left(\mu_B,\mu_i^{n}\right)^{2},\text{ for every }n\in {{\mathbb{N}}}. \end{align}
This yields, 
$\widetilde {W}^{a,b}_2(\mu _B^{n},\mu _i^{n})$ is bounded for every 
$i\in \{1,\ldots ,k\}$. As 
$\mu ^{n}_i\rightarrow \mu _i$ as 
$n\rightarrow \infty$ in the weak*-topology, applying [Reference Parthasarathy19, theorem 6.1] we get that 
$\lim _{n\rightarrow \infty }\mu _i^{n}(X)=\mu _i(X)<\infty$. Thus, 
$\left \{\mu _i^{n}\right \}$ is bounded for every 
$i\in \{1,\ldots ,k\}$. Therefore, using corollary 1.3 (1) and by the same arguments as in the proof of theorem 4.2 we obtain that 
$\left \{\mu _B^{n}\right \}$ is bounded. Hence, applying Prokhorov's theorem, passing to a subsequence we can assume that 
$\mu _B^{n}\rightarrow \widehat {\mu }_B$ as 
$n\rightarrow \infty$ in the weak*-topology for some 
$\widehat {\mu }_B\in {{\mathcal {M}}}(X)$. Observe that, from 
$\mu ^{n}_B(X\backslash K)=0$ for every 
$n\in {{\mathbb {N}}}$ and 
$X\backslash K$ is an open set, we get that 
$\widehat {\mu }_B(X\backslash K)=0$ and thus 
$\text {supp}(\widehat {\mu }_B)\subset K$. By the same arguments in the proof of theorem 4.2 we also have 
$\widetilde {W}^{a,b}_2(\mu _B^{n},\widehat {\mu }_B)\rightarrow 0$ as 
$n\rightarrow \infty$. This implies that the sequence 
$\left \{\mu ^{n}_B\right \}$ is precompact in generalized Wasserstein topology and we also get that
\[ \lim_{n\rightarrow \infty}\widetilde{W}^{a,b}_2\left(\mu_B^{n},\mu_i^{n}\right)=\widetilde{W}^{a,b}_2\left(\widehat{\mu}_B,\mu_i\right),\text{ for every }i\in\{1,\ldots,k\}. \]Hence, since (4.1) we get that
\begin{align*} \sum_{i=1}^{k}\lambda_i \widetilde{W}^{a,b}_2\left(\widehat{\mu}_B,\mu_i\right)^{2}&=\lim_{n\rightarrow\infty}\sum_{i=1}^{k}\lambda_i^{n} \widetilde{W}^{a,b}_2\left(\mu_B^{n},\mu_i^{n}\right)^{2}\\ &\leq \lim_{n\rightarrow\infty}\sum_{i=1}^{k}\lambda_i^{n} \widetilde{W}^{a,b}_2\left(\mu_B,\mu_i^{n}\right)^{2}\\ &= \sum_{i=1}^{k}\lambda_i \widetilde{W}^{a,b}_2\left(\mu_B,\mu_i\right)^{2}. \end{align*}
Therefore, 
$\widehat {\mu }_B\in BC((\mu _i,\lambda _i)_{1\leq i\leq k})$.
Next, we will study the a dual problem of problem 
$(B)$. For every 
$\lambda >0$ and every function 
$f\in C_b(K)$ such that 
$f(x)\leq \lambda a$ for every 
$x\in K$ where 
$K={\bigcup} _{i=1}^{k}\text {supp}(\mu _i)$, we define 
$S_\lambda f(x):=\inf _{y\in K}\left \{\lambda b^{2} d^{2}(x,y)-f(y)\right \}$ and 
$\overline {S}_\lambda f(x):=\min \left \{S_\lambda f(x),\lambda a\right \}$. For every integer 
$k\geq 2$ and for each 
$i\in \{1,2,\ldots ,k\}$ we define function 
$H_i:C_b(K)\rightarrow \overline {\mathbb {R}}$ by
\[
H_i(f):=\begin{cases}
-\displaystyle\int_K
\overline{S}_{\lambda_i}f(x)d\mu_i(x) & \text{if } f\in
F_{\lambda_i}\\+\infty\quad \text{otherwise,
}\end{cases} \]
where 
$F_{\lambda _i}:=\left \{f\in C_b(K)| f(x)\leq \lambda _ia,\forall x\in K\right \}$. Then 
$H_i$ is convex on 
$F_{\lambda _i}$.
We denote by 
${{\mathcal {M}}}_s(K)$ (resp. 
${{\mathcal {M}}}_c(K))$ the space of signed (resp. non-negative) Radon measures 
$\mu$ with a finite mass on 
$X$ such that 
$\mu$ is concentrated on 
$K$, i.e. 
$\mu (X\backslash K)=0$. Then 
${{\mathcal {M}}}_s(K)$ is the dual space of 
$C_b(K)$, since 
$K$ is compact. For every 
$\mu \in {{\mathcal {M}}}_s(K)$, the Legendre–Fenchel transform of 
$H_i$ is
\begin{align*} H_i^{*}(\mu)&=\sup\left\{\int_K f(x)\,\textrm{d}\mu(x)-H_i(f)| f\in C_b(K)\right\}\\ &=\sup\left\{\int_K f(x)\,\textrm{d}\mu(x)-H_i(f)| f\in F_{\lambda_i}\right\}\\ &=\sup\left\{\int_K f(x)d\mu(x)+\int_K\overline{S}_{\lambda_i}f(x)\,\textrm{d}\mu_i(x)| f\in F_{\lambda_i}\right\}. \end{align*}We consider the following problem
\[ (B^{*})\;\sup\left\{ \sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x)|f_i\in F_{\lambda_i},\sum_{i=1}^{k}f_i=0\right\}. \]Lemma 4.6 Let 
$X$ be a locally compact, Polish metric space then 
$\inf (B)\geq \sup (B^{*})$.
Proof. For 
$i=1,2,\ldots ,k$ let any 
$f_i\in F_{\lambda _i}$ such that 
$\sum _{i=1}^{k}f_i=0$. Then 
$\overline {S}_{\lambda _i}f_i(x)+f_i(y)\leq \lambda _ib^{2}d^{2}(x,y)$ for every 
$x,y\in K$ and every 
$i\in \{1,2,\ldots ,k\}$. For every 
$\mu \in {{\mathcal {M}}}_c(K)$, let 
$\boldsymbol {\gamma }^{i}\in M^{\leq } (\mu ,\mu _i)$ be an optimal plan for 
$\widetilde {W}^{a,b}_2(\mu ,\mu _i)$. Since 
$\mu _i$ is concentrated on 
$K$ for every 
$i=1,\ldots ,k$, we get that
\[ \widetilde{W}^{a,b}_2\left(\mu,\mu_i\right)^{2}=a\left( \mu-\pi_\sharp^{1}\boldsymbol{\gamma}^{i}\right)(K)+a\left( \mu_i-\pi_\sharp^{2}\boldsymbol{\gamma}^{i}\right)(K)+b^{2}\int_{K\times K}d^{2}(x,y)\,\textrm{d}\boldsymbol{\gamma}^{i}(x,y). \]
As 
$\boldsymbol {\gamma }^{i}\in M^{\leq } (\mu ,\mu _i)$, by Radon–Nikodym theorem there exist measurable functions 
$\varphi _1,\varphi _2:K\rightarrow [0,+\infty )$ such that 
$\pi _\sharp ^{1}\boldsymbol {\gamma }^{i}=\varphi _1\mu$, 
$\pi _\sharp ^{2}\boldsymbol {\gamma }^{i}=\varphi _2\mu _i$ and 
$\varphi _1\leq 1 \;\mu$-a.e, 
$\varphi _2\leq 1 \;\mu _i$-a.e. Therefore, we get that
\begin{align*}
\widetilde{W}^{a,b}_2\left(\mu,\mu_i\right)^{2} &=
a\int_K\left(1-\varphi_1\right)\textrm{d}\mu+a\int_K\left(1-\varphi_2\right)\textrm{d}\mu_i+b^{2}\int_{K\times
K}d^{2}(x,y)\,\textrm{d}\boldsymbol{\gamma}^{i}(x,y)\\ &
\geq
a\int_K\left(1-\varphi_1\right)\textrm{d}\mu+a\int_K\left(1-\varphi_2\right)\textrm{d}\mu_i\\
&\quad +\dfrac{1}{\lambda_i}\int_{K\times
K}\left[f_i(x)+\overline{S}_{\lambda_i}f_i(y)\right]\textrm{d}\boldsymbol{\gamma}^{i}(x,y)\\
& =
\int_K\left[a\left(1-\varphi_1\right)+\dfrac{1}{\lambda_i}f_i.\varphi_1\right]\textrm{d}\mu+\int_K\left[a\left(1-\varphi_2\right)+\dfrac{1}{\lambda_i}\overline{S}_{\lambda_i}f_i.\varphi_2\right]\textrm{d}\mu_i.
\end{align*}
Moreover, 
$\varphi _1(x),\varphi _2(x)\geq 0$ for every 
$x\in X$ and 
$\varphi _1\leq 1 \;\mu$-a.e, 
$\varphi _2\leq 1 \;\mu _i$-a.e, 
$f_i(x)/\lambda _i\leq a$, 
$\overline {S}_{\lambda _i}f_i(x)/\lambda _i\leq a$ for every 
$x\in K$. Therefore, we obtain that
\begin{align*}
a\left(1-\varphi_1(x)\right)+\left(f_i(x)/\lambda_i\right).\varphi_i(x)&\geq
f_i(x)/\lambda_i,\;\mu-\text{a.e}, \\
a\left(1-\varphi_2(x)\right)+\left(\overline{S}_{\lambda_i}f_i(x)/\lambda_i\right).\varphi_2(x)&\geq
\overline{S}_{\lambda_i}f_i(x)/\lambda_i,\;\mu_i-\text{a.e}.
\end{align*}
Hence, for every 
$i\in \{1,2,\ldots ,k\}$, we get that
\begin{align} \lambda_i\widetilde{W}^{a,b}_2\left(\mu,\mu_i\right)^{2}\geq \int_K f_i(x)\,\textrm{d}\mu(x)+\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x). \end{align}Thus,
\begin{align*} \sum_{i=1}^{k}\lambda_i\widetilde{W}^{a,b}_2\left(\mu,\mu_i\right)^{2}&\geq \sum_{i=1}^{k}\int_K f_i(x)\,\textrm{d}\mu(x)+\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x)\\ &=\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x). \end{align*}This yields,
\[ \inf\left\{\sum_{i=1}^{k}\lambda_i\widetilde{W}^{a,b}_2\left(\mu,\mu_i\right)^{2}|\text{ supp}(\mu)\subset K\right\}\geq \sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x). \]Hence, we get the result.
Lemma 4.7 Let 
$X$ be a locally compact, Polish metric space. Then for every 
$i\in \{1,2,\ldots ,k\}$ we have 
$H_i^{*}(\mu )=\lambda _i\widetilde {W}^{a,b}_2(\mu ,\mu _i)^{2}$ if 
$\mu \in {{\mathcal {M}}}_c(K)$ and 
$+\infty$ otherwise.
Proof. If 
$\mu \in {{\mathcal {M}}}_s(K)\backslash {{\mathcal {M}}}_c(K)$ then there exists 
$g\in C_b(K),g\leq 0$ such that 
$\int _K g(x)d\mu (x)>0$. For every 
$t\in {{\mathbb {R}}},t\geq 0$ let 
$f=t.g$ then 
$f\in F_{\lambda _i}$ and 
$\overline {S}_{\lambda _i}(tf(x))\geq 0$ for every 
$x\in K$. Therefore, 
$H_i^{*}(\mu )\geq \sup _{t\geq 0}\int _K fd\mu =+\infty .$
We now consider 
$\mu \in {{\mathcal {M}}}_c(K)$. Since (4.2), it is clear that 
$\lambda _i\widetilde {W}^{a,b}_2(\mu ,\mu _i)^{2}\geq H_i^{*}(\mu )$. So we need to prove that 
$\lambda _i\widetilde {W}^{a,b}_2(\mu ,\mu _i)^{2}\leq H_i^{*}(\mu )$. We define
\begin{align*}
\Phi_K&:=\big\{(\varphi_1,\varphi_2)\in C_b(K)\times
C_b(K):\varphi_1(x)+\varphi_2(y)\leq b^{2}d^{2}(x,y),
\varphi_1(x),\varphi_2(y)\\
&\geq{-}a, \text{ for every }
x,y\in K\big\}. \end{align*}
Let any 
$(\varphi _1,\varphi _2)\in \Phi _K$ then 
$\lambda _i\varphi _1(x)+\lambda _i\varphi _2(y)\leq \lambda _ib^{2}d^{2}(x,y)$ for every 
$x,y\in K$ and every 
$i=1,\ldots ,k$. Therefore, 
$\lambda _i\varphi _2(y)\leq S_{\lambda _i}(\lambda _i\varphi _1(y))$ for every 
$y\in K$. Observe that 
$\varphi _2(y)\in [-a,a]$ for every 
$y\in K$, we get that 
$\lambda _i\varphi _2(y)\leq \overline {S}_{\lambda _i}(\lambda _i\varphi _1(y))$ for every 
$y\in K$. As 
$\lambda _i\varphi _1(x)\leq \lambda _ia$ for every 
$x\in K$, one has 
$\lambda _i\varphi _1\in F_{\lambda _i}$. Hence, we obtain that
\begin{align*}
&\int_K\lambda_i\varphi_1(x)\,\textrm{d}\mu(x)+\int_K\lambda_i\varphi_2(y)\,\textrm{d}\mu_i(y)\\
&\quad \leq
\int_K\lambda_i\varphi_1(x)\,\textrm{d}\mu(x)+\int_K\overline{S}_{\lambda_i}\left(\lambda_i\varphi_1(y)\right)\textrm{d}\mu_i(y)\\
&\quad \leq H_i^{*}(\mu). \end{align*}Applying corollary 1.3 (1) we get that
\[ \widetilde{W}^{a,b}_2\left(\mu,\mu_i\right)^{2}=\sup_{\left(\varphi_1,\varphi_2\right)\in \Phi_K}\left\{\int_K\varphi_1(x)\,\textrm{d}\mu(x)+\int_K\varphi_2(y)\,\textrm{d}\mu_i(y)\right\}\leq \dfrac{1}{\lambda_i}H_i^{*}(\mu). \]
Hence, 
$\lambda _i\widetilde {W}^{a,b}_2(\mu ,\mu _i)^{2}\leq H_i^{*}(\mu )$ for every 
$\mu \in {{\mathcal {M}}}_c(K)$ and every 
$i\in \{1,2,\ldots ,k\}$.
Let 
$F:=\left \{f\in C_b(K)|f(x)\leq a\text { for every }x\in K\right \}$. We define 
$H:C_b(K)\rightarrow \overline {\mathbb {R}}$ by 
$H(f)=\inf \left \{\sum _{i=1}^{k}H_i(f_i)|f_i\in F_{\lambda _i},\sum _{i=1}^{k}f_i=f\right \}$ if 
$f\in F$ and 
$+\infty$ otherwise.
Lemma 4.8 
$H$ is convex on 
$F$ and 
$H^{*}(\mu )=\sum _{i=1}^{k}H_i^{*}(\mu )$ for every 
$\mu \in M_s(K)$.
Proof. For every 
$g_1,g_2\in F$ and every 
$t\in [0,1]$ we will check that 
$H(tg_1+(1-t)g_2)\leq tH(g_1)+(1-t)H(g_2)$. Let any 
$\overline {f}_i,\widehat {f}_i\in F_{\lambda _i}$ such that 
$\sum _{i=1}^{k}\overline {f}_i=g_1$ and 
$\sum _{i=1}^{k}\widehat {f}_i=g_2$ then 
$t\overline {f}_i+(1-t)\widehat {f}_i\in F_{\lambda _i}$ and 
$\sum _{i=1}^{k}[t\overline {f}_i+(1-t)\widehat {f}_i]=tg_1+(1-t)g_2$. As 
$H_i$ is convex on 
$F_{\lambda _i}$ for every 
$i=1,\ldots ,k$, we get that
\begin{align*} t\sum_{i=1}^{k}H_i\left(\overline{f}_i\right)+(1-t)\sum_{i=1}^{k}H_i\left(\widehat{f}_i\right)&=\sum_{i=1}^{k}\left[tH_i\left(\overline{f}_i\right)+(1-t)H_i\left(\widehat{f}_i\right)\right]\\ &\geq \sum_{i=1}^{k}H_i\left(t\overline{f}_i+(1-t)\widehat{f}_i\right)\\ &\geq H\left(tg_1+(1-t)g_2\right). \end{align*}
Therefore, 
$H(tg_1+(1-t)g_2)\leq tH(g_1)+(1-t)H(g_2)$. Hence, 
$H$ is convex on 
$F$.
We now show that 
$H^{*}(\mu )=\sum _{i=1}^{k}H_i^{*}(\mu )$ for every 
$\mu \in M_s(K)$. For every 
$\mu \in {{\mathcal {M}}}_s(K)$, by definition of the Legendre–Fenchel one has
\begin{align*} H^{*}(\mu)&=\sup_{f\in C_b(K)}\left\{\int_Kf\textrm{d}\mu-H(f)\right\}\\ &=\sup_{f\in F}\left\{\int_Kf\textrm{d}\mu-H(f)\right\}\\ & = \sup_{f\in F}\left\{\int_Kf\textrm{d}\mu-\inf\left\{\sum_{i=1}^{k}H_i(f_i)|f_i\in F_{\lambda_i},\sum_{i=1}^{k}f_i=f\right\}\right\}\\ & = \sup_{f\in F}\left\{\int_Kf\textrm{d}\mu+\sup\left\{\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i\textrm{d}\mu_i|f_i\in F_{\lambda_i},\sum_{i=1}^{k}f_i=f\right\}\right\}. \end{align*}
For every 
$f_i\in F_{\lambda _i}$ let 
$f=\sum _{i=1}^{k}f_i$ then 
$f\in F$. Thus, for every 
$\mu \in {{\mathcal {M}}}_s(K)$ we get
\begin{align*}
&\sum_{i=1}^{k}\left(\int_Kf_i(x)\,\textrm{d}\mu(x)+\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x)\right)\\
&\quad =\int_Kf(x)\,\textrm{d}\mu(x)+\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x)\\
&\quad \leq H^{*}(\mu). \end{align*}This yields,
\begin{align*} \sum_{i=1}^{k}H_i^{*}(\mu)& = \sum_{i=1}^{k}\sup\left\{\int_Kf_i(x)\,\textrm{d}\mu(x)+\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x)|f_i\in F_{\lambda_i}\right\}\\ & = \sup\left\{\sum_{i=1}^{k}\left(\int_Kf_i(x)\,\textrm{d}\mu(x)+\int_K\overline{S}_{\lambda_i}f_i(x)\,\textrm{d}\mu_i(x)\right)|f_i\in F_{\lambda_i}\right\}\\ &\leq H^{*}(\mu). \end{align*}
Conversely, for every 
$f\in F$ let 
$G:=\left \{(f_1,\ldots ,f_k)|f_i\in F_{\lambda _i},\sum _{i=1}^{k}f_i=f\right \}$. Then,
\begin{align*}
&\int_Kf\textrm{d}\mu+\sup_{(f_1,\ldots,f_k)\in
G}\sum_{i=1}^{k}\int_k\overline{S}_{\lambda_i}f_i\textrm{d}\mu_i\\
&\quad
=\sup_{(f_1,\ldots,f_k)\in
G}\left\{\int_Kf\textrm{d}\mu+\sum_{i=1}^{k}\int_k\overline{S}_{\lambda_i}f_i\textrm{d}\mu_i\right\} \\
& \quad = \sup_{(f_1,\ldots,f_k)\in
G}\left\{\int_K\sum_{i=1}^{k}f_i\textrm{d}\mu+\sum_{i=1}^{k}\int_k\overline{S}_{\lambda_i}f_i\textrm{d}\mu_i\right\}\\
&\quad \leq \sum_{i=1}^{k}\sup_{f_i\in
F_{\lambda_i}}\left\{\int_Kf_i\textrm{d}\mu+\int_k\overline{S}_{\lambda_i}f_i\textrm{d}\mu_i\right\}\\
& \quad = \sum_{i=1}^{k}H_i^{*}(\mu). \end{align*}Hence, we get the result.
Inspired by [Reference Agueh and Carlier1, proposition 2.2] we get the following theorem.
Theorem 4.9 Let 
$(X,d)$ be a locally compact, Polish space then 
$\inf (B)=\sup (B^{*})$.
Proof. Combining lemmas 4.7 and 4.8 we obtain that
\[ \inf(B)=\inf_{\mu\in{{\mathcal{M}}}_c(K)}\sum_{i=1}^{k}H_i^{*}(\mu)={-}\left(\sum_{i=1}^{k}H_i^{*}\right)^{*}(0)={-}H^{**}(0). \]
Furthermore, we also have 
$\sup (B^{*})=-H(0)$. Thus, we only need to prove that 
$H^{**}(0)=H(0)$. For every 
$f\in F$, let 
$f_i\in F_{\lambda _i}$ such that 
$\sum _{i=1}^{k}f_i=f$. As 
$f_i(x)\leq \lambda _ia$ for every 
$x\in K$ and every 
$i=1,\ldots ,k$, one has
\[ S_{\lambda_i}f_i(x)=\inf_{y\in K}\left\{\lambda_ib^{2}d^{2}(x,y)-f_i(y)\right\}\geq{-}\lambda_ia \text{ for every }x\in K. \]
Therefore, 
$H_i(f_i)\leq \lambda _ia$. Moreover, since 
$\overline {S}_{\lambda _i}f(x)\leq \lambda _ia$ for every 
$x\in K$, we also have 
$H_i(f_i)\geq -\lambda _ia$. Hence 
$H$ is bounded on 
$F$. Thanks to lemma 4.8, one has 
$H$ is convex on 
$F$. We denote by 
$\mathring {F}$ the interior of 
$F$, then 
$\mathring {F}$ is also a convex set. Applying [Reference Ekeland and Témam11, lemma 2.1] we get that 
$H$ is continuous in 
$\mathring {F}$ endowed with the supremum norm 
$\|\cdot \|_\infty$. Observe that 
$0\in \mathring {F}$, using [Reference Ekeland and Témam11, propositions 3.1 and 4.1] we obtain that 
$H^{**}(0)=H(0)$. Hence, we get the result.
Lemma 4.10 Let 
$(X,d)$ be a Polish metric space. For every 
$\lambda >0$, let 
$f\in F_{\lambda }$ then 
$S_\lambda f$ and 
$(S_{\lambda }\circ S_{\lambda })f$ are 
$2\lambda b^{2}D$-Lipschitz functions on 
$K$, where 
$D=\text {diam}(K)$.
Proof. As 
$K$ is a compact subset of 
$X$ then 
$K$ is bounded and thus 
$D=\text {diam}(K)<\infty$. Let any 
$x_1,x_2\in K$. For every 
$\varepsilon >0$, there exists 
$y_0\in K$ such that 
$S_\lambda f (x_2)\geq \lambda b^{2}d^{2}(x_2,y_0)-f(y_0)-\varepsilon$. Moreover, it is clear that 
$S_\lambda f (x_1)\leq \lambda b^{2}d^{2}(x_1,y_0)-f(y_0)$. Hence, we get that
\begin{align*} S_\lambda f \left(x_1\right)-S_\lambda f \left(x_2\right)&\leq \lambda b^{2}\left[d^{2}\left(x_1,y_0\right)-d^{2}\left(x_2,y_0\right)\right]+\varepsilon\leq 2\lambda b^{2}D d\left(x_1,x_2\right)+\varepsilon. \end{align*}
Similarly, 
$S_\lambda f (x_2)-S_\lambda f (x_1)\leq 2\lambda b^{2}D d(x_1,x_2)+\varepsilon$. Therefore, 
$S_{\lambda }f$ is a 
$2\lambda b^{2} D$-Lipschitz function. By the same arguments above, we also get that 
$(S_{\lambda }\circ S_{\lambda })f$ is a 
$2\lambda b^{2} D$-Lipschitz function.
Theorem 4.11 Let 
$(X,d)$ be a Polish metric space then problem 
$(B^{*})$ has solutions.
Proof. Let 
$f^{n}=(f_1^{n},\ldots ,f_k^{n})$ be a maximizing sequence for 
$(B^{*})$. For each 
$i\in \{1,\ldots ,k-1\}$ we define 
$\widetilde {f}^{n}_i:=(S_{\lambda _i}\circ S_{\lambda _i})f^{n}_i$. Then 
$\widetilde {f}^{n}_i$ is bounded on 
$K$ for every 
$i=1,\ldots ,k-1$. Since 
$S_{\lambda _i}f_i(x)\geq -\lambda _ia$ for every 
$x\in K$ and every 
$i=1,\ldots ,k-1$, we get 
$\widetilde {f}^{n}_i(x)=\inf _{y\in K}\left \{\lambda _ib^{2}d^{2}(x,y)-S_{\lambda _i}f_i^{n}(y)\right \}\leq -S_{\lambda _i}f_i^{n}(x)\leq \lambda _ia$ for every 
$x\in K.$
Moreover, it is easy to see that 
$f_i^{n}\leq \widetilde {f}_i^{n}$ on 
$K$ and 
$S_{\lambda _i}\widetilde {f}^{n}_i=S_{\lambda _i}f^{n}_i$ for every 
$i=1,\ldots ,k-1$. Hence 
$\overline {S}_{\lambda _i}\widetilde {f}^{n}_i=\overline {S}_{\lambda _i}f^{n}_i$ for every 
$i=1,\ldots ,k-1$. For every 
$n\in {{\mathbb {N}}}$, we define 
$\widetilde {f}^{n}_k:=-\sum _{i=1}^{k-1}\widetilde {f}^{n}_i$. As 
$f_i^{n}\leq \widetilde {f}_i^{n}$ on 
$K$, one has 
$\widetilde {f}_k^{n}\leq -\sum _{i=1}^{k-1}f_i^{n}=f_k^{n}$. Thus, 
$\widetilde {f}_k^{n}(x)\leq \lambda _ka$ for every 
$x\in K$ and 
$S_{\lambda _k}\widetilde {f}_k^{n}\geq S_{\lambda _k}f^{n}_k$ for every 
$n\in {{\mathbb {N}}}$. Thus, 
$\overline {S}_{\lambda _k}\widetilde {f}_k^{n}\geq \overline {S}_{\lambda _k}f^{n}_k$ for every 
$n\in {{\mathbb {N}}}$. Therefore, we obtain that
\[ \limsup_{n\rightarrow \infty}\sum_{i=1}^{k}\int_K \overline{S}_{\lambda_i}\widetilde{f}_i^{n}(x)\,\textrm{d}\mu_i(x)\geq \lim_{n\rightarrow\infty}\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}f_i^{n}(x)\,\textrm{d}\mu_i(x)=\sup(B^{*}). \]
Using lemma 4.10 we get that 
$\widetilde {f}_i^{n}$ is a 
$2\lambda _i b^{2}D$-Lipschitz function on 
$K$ for every 
$i=1,\ldots ,k-1$ and every 
$n\in {{\mathbb {N}}}$. As 
$\widetilde {f}^{n}_k:=-\sum _{i=1}^{k-1}\widetilde {f}^{n}_i$ and 
$\sum _{i=1}^{k}\lambda _i=1$, we obtain that 
$\widetilde {f}_k^{n}$ is a 
$2(1-\lambda _k)b^{2}D$-Lipschitz function on 
$K$. Then applying Ascoli–Arzela theorem on compact set 
$K$ and using a standard diagonal argument there exists a subsequence of 
$\widetilde {f}^{n}=(\widetilde {f}_1^{n},\ldots ,\widetilde {f}_k^{n})$ which we still denote by 
$\left \{\widetilde {f}^{n}\right \}$ such that 
$\widetilde {f}^{n}$ converges uniformly to 
$\widetilde {f}=(\widetilde {f}_1,\ldots ,\widetilde {f}_k)$. Then 
$\widetilde {f}_i\in F_{\lambda _i}$ for every 
$i\in \{1,\ldots ,k\}$. As 
$\sum _{i=1}^{k}\widetilde {f}_i^{n}=0$ for every 
$n\in \mathbb {N}$, we get that 
$\sum _{i=1}^{k}\widetilde {f}_i=0$. This yields,
\begin{align*} \sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}\widetilde{f}_i(x)\,\textrm{d}\mu_i(x)&\leq \sup (B^{*})\leq\sum_{i=1}^{k} \limsup_{n\rightarrow \infty}\int_K \overline{S}_{\lambda_i}\widetilde{f}_i^{n}(x)\,\textrm{d}\mu_i(x). \end{align*}Applying Fatou lemma, we obtain that
\begin{align*}
&\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}\widetilde{f}_i(x)\,\textrm{d}\mu_i(x)\\
&\quad \leq\sum_{i=1}^{k} \int_K\limsup_{n\rightarrow \infty}
\overline{S}_{\lambda_i}\widetilde{f}_i^{n}(x)\,\textrm{d}\mu_i(x)\\
& \quad=\sum_{i=1}^{k} \int_K\limsup_{n\rightarrow
\infty}\left[\min\left\{ \inf_{y\in
K}\left\{\lambda_ib^{2}d^{2}(x,y)-\widetilde{f}_i^{n}(y)\right\},\lambda_ia\right\}\right]
\textrm{d}\mu_i(x)\\ &\quad\leq \sum_{i=1}^{k}
\int_K\min\left\{\inf_{y\in K}\left\{ \limsup_{n\rightarrow
\infty}\left(\lambda_ib^{2}d^{2}(x,y)-\widetilde{f}_i^{n}(y)\right)\right\},\lambda_ia\right\}
\textrm{d}\mu_i(x) \\ & \quad= \sum_{i=1}^{k}
\int_K\min\left\{\inf_{y\in
K}\left\{\lambda_ib^{2}d^{2}(x,y)-\widetilde{f}_i(y)\right\},\lambda_ia\right\}
\textrm{d}\mu_i(x)\\ & \quad=
\sum_{i=1}^{k}\int_K\overline{S}_{\lambda_i}\widetilde{f}_i(x)\,\textrm{d}\mu_i(x).
\end{align*}Therefore, we must have equality everywhere. Hence, we get the result.
Acknowledgements
Part of this paper was carried out when N.P. Chung visited University of Science, Vietnam National University at Hochiminh city on summer 2019. He is grateful to the math department there for its warm hospitality. The authors were partially supported by the National Research Foundation of Korea (NRF) grants funded by the Korea government nos. NRF-2016R1A5A1008055, NRF-2016R1D1A1B03931922, and NRF-2019R1C1C1007107. We thank the anonymous referee for useful comments, especially for improving the statement of theorem 4.5.
