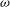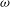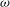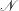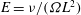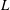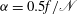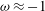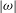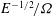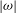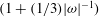1. Introduction
The dynamics of vortices (or lenses) of fluid floating inside another linearly stratified rotating fluid has attracted much attention due to its practical importance in geophysical and astrophysical phenomena, such as the persistent meddies in the Atlantic ocean (Armi et al. Reference Armi, Hebert, Oakey, Price, Richardson, Rossby and Ruddick1988), the propagation of volcanic clouds (Baines & Sparks Reference Baines and Sparks2005), and Jupiter’s anticyclonic red spots (Marcus Reference Marcus1993). This problem is also of interest in fluid dynamics due to its fundamental and intriguing character (e.g. Gill Reference Gill1981; Griffiths & Linden Reference Griffiths and Linden1981; Ungarish & Huppert Reference Ungarish and Huppert2004; Grant, Sundermeyer & Hebert Reference Grant, Sundermeyer and Hebert2011). A detailed outline of the previous investigation, and additional references, is given in the recent pair of papers by Aubert et al. (Reference Aubert, Le Bars, Le Gal and Marcus2012), Hassanzadeh, Marcus & Le Gal (Reference Hassanzadeh, Marcus and Le Gal2012), and we shall not repeat it here. Hereafter, these papers are referred to as ALM12 and HML12, respectively.
In the typical problem, the ambient fluid is ‘large’ (unbounded), rotating with constant
${\it\Omega}=f/2$
(about the vertical axis
$z$
) and of stable density stratification expressed by the buoyancy frequency
$\mathscr{N}$
. Essentially, the vortex is an ellipsoidal-like ‘small’ body of fluid, separated by a clear-cut interface, inside that ambient. The vortex floats at the neutral buoyancy level
$z=0$
, and rotates with
${\it\omega}$
(dimensionless, scaled with
${\it\Omega}$
) with respect to the rotating ambient frame. We shall consider only vortices with
${\it\omega}<0$
, called anticyclonic; the reason for this restriction will be explained later. We assume that the flow is axisymmetric about the
$z$
axis at
$r=0$
, and stable.
The salient property of the vortex is the ratio of maximal thickness to diameter,
${\it\alpha}$
. Theoretical and experimental studies (e.g. Gill Reference Gill1981; Griffiths & Linden Reference Griffiths and Linden1981; Hedstrom & Armi Reference Hedstrom and Armi1988; Grant et al.
Reference Grant, Sundermeyer and Hebert2011) have demonstrated that
${\it\alpha}\sim f/N$
, and decays with time over many rotations of the system. Recently, ALM12 and HML12 have developed and demonstrated a simple yet robust model that connects the shape of the vortex with the internal angular velocity
${\it\omega}$
. In particular, for the aspect ratio this model gives
$$\begin{eqnarray}{\it\alpha}\frac{\mathscr{N}}{f}=\frac{1}{2}[-{\it\omega}(2+{\it\omega})]^{1/2}.\end{eqnarray}$$
Here
${\it\omega}$
is taken as the space-averaged value inside the vortex, independent of
$r$
(radius from axis) and
$z$
. We note that ALM12 and HML12 use the Rossby number
$Ro={\it\omega}/2$
in their notation; we emphasize that (1.1) is for the case of constant
$\mathscr{N}$
in the ambient, while the vortex is anticyclonic and consists of homogeneous, well-mixed fluid (i.e. the internal stratification is zero).
The power of this model is the fact that this relationship holds for the entire long time of existence of the vortex (except for some initial adjustment time of about one revolution) and under the assumption that the flow is stable. In other words, we have a sharp universal connection between
${\it\alpha}(t)$
and
${\it\omega}(t)$
, where
$t$
is time. This provides a clear-cut insight into the reason for decay of the aspect ratio: the embedding fluid gradually reduces the angular speed difference
${\it\omega}$
. This is illustrated in figure 1.
Figure 1. The vortex shape according to the ALM12 and HML12 model at three times,
$t_{0}<t_{1}<t_{2}$
, assuming
${\it\omega}(t_{i})=-1,-0.2,-0.01$
.
$R(0)$
is the radius at
$t_{0}$
. The half-thickness
$h$
is scaled with
$R(0)\,f/\!\mathscr{N}$
.
This model has been convincingly demonstrated by laboratory experiments and three-dimensional Navier–Stokes simulations performed by ALM12 and HML12. However, it is evident that this is a descriptive rather than a predictive model. Accurate as it is, (1.1) is only one equation for two variables,
${\it\alpha}(t)$
and
${\it\omega}(t)$
. In general, we do not know the value of
${\it\omega}(t)$
needed for the calculation of
${\it\alpha}$
. If we determine
${\it\alpha}$
at some
$t_{k}$
we can calculate
${\it\omega}(t_{k})$
(or vice versa). Still, the available model is unable to predict the situation at a later given time (or estimate with confidence what it was at an earlier given time). We emphasize that the values of
${\it\omega}(t)$
used by ALM12 and HML12 for the verification of their model were obtained by laborious experiments or three-dimensional Navier–Stokes simulations. In the laboratory it is more difficult to measure
${\it\omega}$
than to determine the thickness-to-diameter aspect ratio
${\it\alpha}$
. However, large-scale geophysical and astrophysical vortices may be restricted to two-dimensional views, in which case it is possible to measure
${\it\omega}$
but not the depth (thickness) of the vortex.
Our objective is to close this gap in our knowledge: to extend the model of ALM12 and HML12 by incorporating a prediction for the variable
${\it\omega}(t)$
. To this end, we must model the physical effect of angular acceleration of the fluid, called ‘spin-up’.
In standard circumstances (a body of homogeneous fluid of low viscosity contained in a rigid axisymmetric container rotating with constant
${\it\Omega}$
) the flow-field during spin-up is amenable to quite accurate analytical solutions, and is well understood; see Greenspan (Reference Greenspan1968) or Ungarish (Reference Ungarish1993). The Ekman layer circulation (and torque) dominate the increase of angular momentum, and hence the internal
${\it\omega}$
decays like
$\exp (-t/{\it\tau})$
, where
${\it\tau}=E^{-1/2}/{\it\Omega}$
; here
$E={\it\nu}/({\it\Omega}H^{2})$
is the Ekman number,
$H$
is the half-height of the container, and
${\it\nu}$
the kinematic viscosity coefficient. The attempt to carry over this result to the present vortex problem fails. We illustrate this for the A1 case analysed in HML12. Letting
$H$
be the half-maximum-thickness of the vortex, we estimate
$E=1.3\times 10^{-4}$
, and hence
${\it\tau}{\it\Omega}/2{\rm\pi}=14$
revolutions. However, the simulations (figure 2a of that paper) demonstrate that the
$1/e\;{\it\omega}$
-decay time of the vortex (of fixed volume) is significantly longer, about 150 revolutions. The incompatibility is exacerbated for a vortex sustained by injection, because
$H$
changes with time and hence the value of
$E$
is evasive.
A closer examination reveals the reasons for incompatibility between the classical spin-up and that of the vortex. In the present case: the boundary of the spun-up fluid (i.e. the container) changes shape during the process; the spin-up torque is applied at an interface between two fluids (not by a solid surface); the spin-up of the vortex is accompanied by a spin-down of the embedding ambient fluid, and therefore the stratification in the latter is bound to suppress the Ekman layer circulation. Each of these features has been considered before (Walin Reference Walin1969; Flor, Ungarish & Bush Reference Flor, Ungarish and Bush2002; Ungarish & Mang Reference Ungarish and Mang2003) but their combination renders too formidable a problem for a detailed solution of the flow-field. We shall therefore attempt a bolder approximation: we will consider the angular acceleration of the entire body of the vortex without solving in detail the flow inside. We also restrict the analysis to a vortex of constant density,
${\it\rho}_{c}$
. We shall show that this simplification yields a manageable, and insightful, ODE for
${\it\omega}(t)$
. This, combined with (1.1), closes the predictive model: using given initial conditions, we can calculate, with insignificant computational effort, the global behaviour of the vortex (in particular the aspect ratio and relative rotation) as a function of time. Besides the quantitative values, the model also suggest qualitative insights into the mechanisms that influence and prolong the process. We shall see that the appropriate balances are strongly nonlinear and vary with time and the type of problem (fixed-volume or injection-sustained vortex). It is therefore not possible to capture well the spin-up process and vortex decay in terms of a constant time scale (like
${\it\tau}=E^{-1/2}/{\it\Omega}$
in the classical case).
The structure of the paper is as follows. In § 2 we briefly derive the vortex shape equation,
$h(r,t)$
, and
${\it\alpha}(t)$
. In particular, we point out the various underlying assumptions, and elucidate that, to leading order, the calculation of the shape can be decoupled from the angular momentum balance. We obtain closed algebraic formulas, but they contain the unknown
${\it\omega}(t)$
; these results are in agreement with the model of ALM12 and HML12. In § 3 we develop the angular momentum balance and the governing equation for the angular velocity
${\it\omega}(t)$
. This is a novel contribution. We first consider a vortex of fixed volume, then extend the analysis to a vortex sustained by injection. In both cases, we obtain one ODE for
${\it\omega}(t)$
which can be easily solved numerically. We show that the various terms provide useful insights into the spin-up and decay processes of the vortex, and thus clarify why this process extends for many more revolutions of the system than estimated by the classical spin-up time interval. Next, in § 5 we compare the predictions of the present model with previously published data from experiments and Navier–Stokes simulations. In § 6 we present some concluding remarks. Appendix A discusses the estimate of
${\it\omega}(0)$
.
2. The model for the shape
We use a cylindrical system
$r,{\it\theta},z$
which rotates with
${\it\Omega}\hat{\boldsymbol{z}}$
, while gravity
$g$
acts in the
$-z$
direction. The present work is restricted to vortices of constant density,
${\it\rho}_{c}$
, which are located at the level of neutral buoyancy,
$z=0$
, in a fluid of linear stratification,
${\it\rho}_{a}(z)={\it\rho}_{c}(1-{\it\sigma}z)$
, where
${\it\sigma}$
is a positive constant. This means that
$z=0$
is the plane of mirror-symmetry during the motion considered here, and that the buoyancy frequency
$\mathscr{N}>0$
is a constant (
$\mathscr{N}^{2}={\it\sigma}g$
). The flow is assumed axisymmetric and stable.
The volume of the vortex under consideration is
$4{\rm\pi}\mathscr{V}$
(i.e.
$\mathscr{V}$
is the volume of the upper half of the vortex, per radian). We shall first consider (unless stated otherwise) a fixed, given
$\mathscr{V}$
. At a later stage, we shall extend the analysis to
$\mathscr{V}(t)$
due to sustained influx (injection).
For simplicity, we hereafter use balances for the upper half and per radian, unless stated otherwise.
The shape (thickness)
$h(r,t)$
, for
$r\in [0,R(t)]$
, of the vortex has been considered in numerous previous papers.
$R(t)$
is the radius of the vortex. The recent papers of ALM12 and HML12 provide a review of the available results, and also present (and confirm) a more comprehensive formula.
We start with a short derivation of the shape. Evidently, the model which emerges in this work is an approximation for an ‘asymptotic’ range of parameters. For definiteness, we assume that
$f/\!\mathscr{N}$
is of the order of unity, and again, that the flow is axisymmetric and stable. Essential to our derivation are the following additional restrictions/assumptions. The domain of ambient is much larger than the vortex, and hence its basic rotation and stratification are negligibly affected by the motion of the vortex. The density differences between the vortex and the environment are small (Boussinesq case), and the kinematic viscosity of the ambient and the vortex fluids is the same
${\it\nu}$
(this can be relaxed). The buoyancy force is dominated by gravity,
$g\gg {\it\Omega}^{2}R$
. This implies that the pressure is hydrostatic in the
$z$
direction. The dynamic flow is dominated by rotation (Coriolis) effects; this can be expressed as
$E\ll 1$
, where the Ekman number of the vortex is
$$\begin{eqnarray}E=\frac{{\it\nu}}{{\it\Omega}L^{2}},\quad L=\mathscr{V}^{1/3}\left(\frac{f}{\mathscr{N}}\right)^{2/3}.\end{eqnarray}$$
The justification of this definition of
$E$
will emerge later. We also assume that the interface between the vortex and the ambient is sharp, and, again, the flow is axisymmetric and stable. These assumptions are relevant to systems in nature, and can be reproduced in the laboratory with moderate costs.
The motion starts at
$t=0$
, for definiteness, with some compatible initial conditions that will be discussed later.
The main point on which we focus attention in this section is that the derivation of the interface shape formula,
$z=h(r,t)$
for
$0\leqslant r\leqslant R(t)$
(or rather a good approximation), can be decoupled from the angular momentum equation of the flow-field.
The first governing equation is volume conservation
$$\begin{eqnarray}\int _{0}^{R}h(r,t)r\,\text{d}r=\mathscr{V},\end{eqnarray}$$
where
$\mathscr{V}$
is given.
The second equation is the height-averaged radial momentum balance
$$\begin{eqnarray}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}=-\frac{1}{2}\mathscr{N}^{2}\frac{\partial h^{2}}{\partial r}+{\it\Omega}^{2}r{\it\omega}(2+{\it\omega}).\end{eqnarray}$$
Here
$u$
is the radial velocity (dimensional) and
${\it\omega}$
is the angular velocity (dimensionless, scaled with
${\it\Omega}$
). This balance takes into account the hydrostatic pressure field of the vortex and ambient fluids, as well as pressure continuity at the interface; the result is that the pressure gradient
$-[\partial p/({\it\rho}_{c}\partial r)]$
is replaced by the first term on the right-hand side of (2.3). The underlying assumption in this equation is that the viscous shear is negligible in both the axial and radial momentum balances; this is fulfilled when
$E\ll 1$
. Various derivations of this equation are available in the literature (e.g. Ungarish Reference Ungarish2009 § 13.1 for
$S=1$
; ALM12 and HML12), and we shall not repeat it here.
Three major simplifications are introduced next: the inertial acceleration term on the left-hand side is negligible,
$z=h(r,t)$
is continuous, and
${\it\omega}$
is a function of
$t$
(but not of
$r$
). These assumptions are, typically, justifiable when
$E\ll 1$
, and after the formation (initial adjustment) of the vortex. The informal justification of the first two simplifications is what can be called ‘common knowledge’ in the branches of rotating fluids and gravity currents: Greenspan (Reference Greenspan1968) demonstrates that in axisymmetric bodies of rotating fluid with small
$E$
, significant radial motion,
$O({\it\Omega}{\it\omega}r)$
can be sustained only in thin viscous layers; and Ungarish (Reference Ungarish2009) shows that Coriolis effects stop the radial propagation of a typical intrusion after about a
$1/{\it\Omega}$
time interval from release, and that this is accompanied by a sharp (but continuous) decrease of
$h$
to
$0$
at the outer radius
$r=R$
of the vortex. The third simplification is supported by consistency with observations.
The power of these simplifications is that (2.3) (with zero left-hand side) can be integrated subject to the boundary condition
$h=0$
at the outer radius
$r=R$
. This yields the height of the vortex
$$\begin{eqnarray}h(r,t)=\frac{f}{2\mathscr{N}}{\it\phi}^{1/2}R(t)(1-{\it\xi}^{2})^{1/2},\end{eqnarray}$$
where
$R=R(t)$
is the radius of the vortex,
${\it\xi}$
is the reduced radial coordinate,
$$\begin{eqnarray}{\it\xi}=r/R\quad {\it\xi}\in [0,1],\end{eqnarray}$$
and
$$\begin{eqnarray}{\it\phi}={\it\phi}(t)=-{\it\omega}(t)\left[2+{\it\omega}(t)\right].\end{eqnarray}$$
The aspect ratio is
$$\begin{eqnarray}{\it\alpha}={\it\alpha}(t)=h(r=0,t)/R(t)=\frac{f}{2\mathscr{N}}{\it\phi}^{1/2}=\frac{f}{2\mathscr{N}}\left\{-{\it\omega}(t)\left[2+{\it\omega}(t)\right]\right\}^{1/2}.\end{eqnarray}$$
Substitution of (2.4) into (2.2) yields the radius
$$\begin{eqnarray}R=R(t)=\left(6\frac{\mathscr{N}}{f}\mathscr{V}\right)^{1/3}\frac{1}{{\it\phi}^{1/6}}.\end{eqnarray}$$
We note that (2.4)–(2.8) are exactly the model of ALM12 and HML12, for a vortex of constant density, upon the change of notation that these papers use the Rossby number
$Ro={\it\omega}/2$
. We prefer here the use of the variable
${\it\omega}$
because of the direct connection with the analysis of the spin-up process. Moreover, the definition of
$Ro$
varies in the literature, and this may be confusing. We reiterate that our
${\it\omega}$
is the dimensionless angular velocity (scaled with
${\it\Omega}$
) with respect to the rotating frame.
We emphasize that these equations are for a general, as yet unspecified,
${\it\omega}(t)$
. Physical considerations indicate that
$-1\leqslant {\it\omega}<0$
. The lower bound is counter-rotation with respect to the ambient fluid in the rotating frame, i.e. fixed in the absolute (laboratory) frame. The upper bound is co-rotation with the ambient fluid.
ALM12 and HML12 pointed out that in realistic circumstances
$|{\it\omega}|$
decreases with
$t$
. Typically, the initial value of
${\it\omega}$
is close to
$-1$
(see appendix A). We therefore define the ‘standard’ or ‘reference’ situation as
$$\begin{eqnarray}{\it\omega}=-1,\quad {\it\phi}=1,\quad R=\left(6\frac{\mathscr{N}}{f}\mathscr{V}\right)^{1/3},\quad {\it\alpha}=\frac{1}{2}\frac{f}{\mathscr{N}}.\end{eqnarray}$$
These values are the maximum of
${\it\alpha}(t)$
and minimum of
$R(t)$
. Also, we note in passing that the ‘standard’ case is quite robust. If we take
${\it\omega}=-0.7$
instead of
$-1$
,
${\it\phi}$
decreases by
$9\,\%$
; therefore,
${\it\alpha}$
and
$R$
change by only
$-4.6\,\%$
and
$1.6\,\%$
, respectively.
ALM12 and HML12 provide experimental and Navier–Stokes simulation evidence that (2.7) is a reliable and accurate relationship for the aspect ratio of vortices in a wide range of circumstances. The most convincing component of this evidence is the observation that (2.7) is valid over very long periods of time (hundreds of revolutions of the system): in each tested system, the measured
${\it\omega}$
decays significantly, and this is accompanied by the decrease of the measured aspect ratio
${\it\alpha}$
in agreement with the theoretical correlation.
However, (2.7) is a descriptive rather than a predictive model. Accurate as it is, this is still only one equation for two variables,
${\it\alpha}(t)$
and
${\it\omega}(t)$
. In general, we do not know the value of
${\it\omega}(t)$
needed for the calculation of
${\it\alpha}$
(except for the initial situation when
${\it\omega}\approx -1$
). We emphasize that the values of
${\it\omega}(t)$
used by ALM12 and HML12 in their verification of (2.7) were obtained by laborious experiments or three-dimensional Navier–Stokes simulations, not by an asymptotic model. Indeed, (2.7) is a quasi-static result. It does not provide any information concerning the dynamic mechanisms that affect the possible change of
${\it\omega}$
with time. With hindsight, this is not surprising, because the derivation of (2.7), as discussed above, uses only momentum balances in
$z$
and
$r$
directions, plus volume conservation. We did not use any conservation law for
${\it\omega}$
. We conclude that the upgrade from the descriptive to the predictive model requires an additional equation: the angular momentum balance.
3. Angular momentum considerations
The angular velocity
${\it\omega}$
of a contained volume of fluid can increase with time in a process that is usually referred to as ‘spin-up’. The typical driving force is the shear due to the fact that the domain under consideration is embedded in a rigid container (of height
$2H$
) which rotates with a larger angular velocity
${\it\omega}_{b}$
. Viscous boundary layers appear at the boundary, and sustain a torque that is proportional to
${\it\omega}_{b}-{\it\omega}(t)$
and continuously reduces the difference to zero. During the spin-up, particles (or rather shells) of fluid change their
${\it\omega}$
due to radial displacement and change of height (the potential-vorticity effect). (For connection with our problem, suppose that the gravity acts parallel with the axis of rotation and
${\it\omega}_{b}=0$
.)
When
$E$
is small, this process is well understood, and amenable to accurate modelling, for a homogeneous fluid in a solid container (Greenspan Reference Greenspan1968). The dominant viscous effect is concentrated in Ekman boundary layers of thickness
$({\it\nu}/{\it\Omega})^{1/2}$
(in dimensionless form,
$E^{1/2}$
;
$E={\it\nu}/({\it\Omega}H^{2})$
). These layers form quickly (in about one revolution of the system) and are subsequently quasi-steady; they induce a weak ‘secondary flow’ (or circulation) inside the container that causes, roughly, the decay of the initial
${\it\omega}$
on the time scale
$E^{-1/2}/{\it\Omega}$
. Some residual discrepancies decay on the diffusion time scale
$E^{-1}/{\it\Omega}$
. Even this simple scenario requires some care and adaptations in practical circumstances: the height of the container may vary with radius; if an open boundary is present the spin-up time increases; side-wall boundary layers also contribute. The accuracy of the spin-up solution also depends on the accuracy of the initial condition
${\it\omega}(0)$
; in practical circumstances, this may also contain uncertainties.
Significant modifications occur when the spun-up domain is embedded in another fluid (rather than in a solid container), and gravity buoyancy is significant. First, at the interface between the fluids there is a double Ekman layer effect: while the ambient shears and pumps the embedded fluid in one direction, this fluid shears and pumps the ambient into the opposite direction; therefore, the effective Ekman shear layer is thicker (by roughly 2). Second, the shape of the fluid domain under consideration varies during the process; moreover, there is coupling between the shape and
${\it\omega}$
. Third, when the embedding fluid is linearly stratified, the buoyancy hinders the motion (circulation) of the particles activated by the the Ekman layer pumping, and consequently this effect may be ‘suppressed’ even before a significant reduction of
$|{\it\omega}|$
is attained. These features were analysed in the papers of Walin (Reference Walin1969), Flor et al. (Reference Flor, Ungarish and Bush2002), Ungarish & Mang (Reference Ungarish and Mang2003) and the references therein.
The vortex under present investigation contains the spin-up components in their more complicated form. The formulation and solution of the flow-field that matches in detail all the effects involved is a formidable task; moreover, the expected outcome will be too complicated for useful insights and quick computation. We shall therefore not pursue this approach here. For progress, we shall attempt only an approximate global solution for the entire vortex, as follows.
Consider the angular momentum balance of the vortex
$$\begin{eqnarray}\frac{\text{d}{\it\Gamma}}{\text{d}t}=M,\end{eqnarray}$$
where
${\it\Gamma}$
is the angular momentum of the volume inside the interface, and
$M$
is the shear torque on the envelope. The system is sketched in figure 2. Again, we make the budget for only the upper-half of the vortex, per radian.
Figure 2. Schematic description of the spin-up flow. The interface of the vortex (upper half) is shown by the thick (black) curve. The domain between the thin lines is the ‘boundary layer’
${\it\delta}$
in which transition of
${\it\omega}$
occurs. The density is
${\it\rho}_{c}$
(constant) inside the vortex, and
${\it\rho}_{c}(1-{\it\sigma}z)$
in the ambient fluid.
$\mathscr{N}^{2}={\it\sigma}g$
.
More explicitly,
$$\begin{eqnarray}\displaystyle {\it\Gamma} & = & \displaystyle {\it\rho}_{c}\int _{0}^{R}{\it\Omega}(1+{\it\omega})r^{2}h(r,t)r\,\text{d}r={\it\rho}_{c}{\it\Omega}(1+{\it\omega}){\it\phi}^{1/2}\frac{f}{2\mathscr{N}}\nonumber\\ \displaystyle & & \displaystyle \times \,R^{5}\int _{0}^{1}(1-{\it\xi}^{2})^{1/2}{\it\xi}^{3}\,\text{d}{\it\xi}=\frac{2}{5}{\it\rho}_{c}{\it\Omega}\mathscr{V}(1+{\it\omega})R^{2},\end{eqnarray}$$
where we used the assumption
${\it\omega}={\it\omega}(t)$
and the results (2.4), (2.8). Then, after some algebra (see appendix C) and recalling that here
$\mathscr{V}$
is constant, we obtain
$$\begin{eqnarray}\frac{\text{d}{\it\Gamma}}{\text{d}t}=\frac{2}{5}{\it\rho}_{c}{\it\Omega}\mathscr{V}R^{2}(t)J(t)\frac{\text{d}{\it\omega}}{\text{d}t},\end{eqnarray}$$
where
$$\begin{eqnarray}J=J(t)=1-\frac{2}{3}\frac{(1+{\it\omega})^{2}}{{\it\omega}(2+{\it\omega})}.\end{eqnarray}$$
Since
${\it\omega}<0$
, this term is always positive; its influence on the spin-up may be significant, as discussed later. Equations (3.3)–(3.4) reveal the complexity of the spin-up: the rate of change of angular momentum is distributed among several components, and not a linear function of
$\text{d}{\it\omega}/\text{d}t$
.
For the torque we write
$$\begin{eqnarray}M=-{\it\rho}_{c}{\it\nu}\int _{0}^{R}\frac{{\it\Omega}{\it\omega}r}{{\it\delta}}r^{2}\,\text{d}r.\end{eqnarray}$$
The fraction in the integral stands for the shear, while
${\it\delta}$
is the thickness of the transition layer from the domain with
${\it\omega}<0$
(inside the vortex) to the unperturbed ambient fluid where
${\it\omega}=0$
. While
${\it\omega}$
is negative, the torque is positive, and this drives the spin-up process. Since
${\it\omega}={\it\omega}(t)$
we rewrite (3.5) as
$$\begin{eqnarray}M=-\frac{1}{4}{\it\rho}_{c}{\it\nu}{\it\Omega}{\it\omega}R^{4}\frac{1}{\bar{{\it\delta}}}.\end{eqnarray}$$
Here
$\bar{{\it\delta}}=\bar{{\it\delta}}(t)$
is the weighted-average thickness of the angular momentum transfer layer, defined by
$$\begin{eqnarray}\frac{1}{\bar{{\it\delta}}}=\frac{1}{\bar{{\it\delta}}(t)}=4\int _{0}^{1}\frac{{\it\xi}^{3}\text{d}{\it\xi}}{{\it\delta}({\it\xi},t)}\end{eqnarray}$$
where
${\it\xi}=r/R$
. This definition is convenient because, when
${\it\delta}$
is
$r$
-independent, it returns
$\bar{{\it\delta}}={\it\delta}$
.
To close the model we must specify the effective thickness of the shear layer,
$\bar{{\it\delta}}(t)$
. This is the most challenging component of our model. To our knowledge, no direct investigation of this effect has been performed, and we must rely on pieces of theoretical results gained for related spin-up problems (Walin Reference Walin1969; Flor et al.
Reference Flor, Ungarish and Bush2002; Ungarish & Mang Reference Ungarish and Mang2003). We consider the spin-up process over a long time period. Evidently, the first stage is dominated by the double Ekman layer of thickness
${\it\delta}_{1}=2({\it\nu}/{\it\Omega})^{1/2}$
.
However, the stratification of the ambient fluid tends to suppress the upper part of the Ekman layer. The result is that on the time scale
$t_{s}$
the thickness of the transition layer of ambient fluid near the centre increases to
${\it\delta}_{0s}$
, where
$$\begin{eqnarray}t_{s}{\it\Omega}=0.52\frac{f}{\mathscr{N}}\frac{R(0)}{{\it\delta}_{1}},\quad {\it\delta}_{0s}=0.26\frac{f}{\mathscr{N}}R(0).\end{eqnarray}$$
Subsequently, the layer at the centre thickens further by diffusion according to
$[{\it\nu}(t-t_{s})]^{1/2}$
. The thicker layer prevails over half of the radius (approximately), then decreases to
${\it\delta}_{1}$
at
$r=R$
. Based on analytical considerations and numerical solutions (Walin Reference Walin1969; Flor et al.
Reference Flor, Ungarish and Bush2002; Ungarish & Mang Reference Ungarish and Mang2003), we therefore suggest that the boundary layer of the vortex can be approximated by the functions
$$\begin{eqnarray}{\it\delta}(r,t)=\left\{\begin{array}{@{}ll@{}}{\it\delta}_{0}(t)\quad & (0\leqslant r\leqslant R(t)/2),\\ \text{linear decrease from }{\it\delta}_{0}(t)\text{ to }{\it\delta}_{1}\quad & (R(t)/2<r\leqslant R(t)),\end{array}\right.\end{eqnarray}$$
where
$$\begin{eqnarray}{\it\delta}_{0}(t)={\it\delta}_{1}+({\it\delta}_{0s}-{\it\delta}_{1})[1-\exp (-t/t_{s})],\end{eqnarray}$$
to which we add the diffusion contribution for
$t>t_{s}$
when relevant. To improve the accuracy, we use the instantaneous
$R(t)$
instead of
$R(0)$
for the calculation of
${\it\delta}_{0s}$
in the last equation.
With (3.9) the integral in (3.7) can be calculated analytically, and we thus obtain
$\bar{{\it\delta}}(t)$
. The details are presented in appendix B.
We admit that the calculation of the shear term is a bold approximation, and that we have neglected the curvature of the interface. We are presently unable to estimate the approximation errors. The justifications for the use of this approximation are as follows. (i) In the present state of the art, such a closure is necessary for progress, and it will be quite straightforward to replace it with a better one when available. (ii) The predictions of the resulting model seem to be qualitatively correct and quantitatively in reasonable agreement when compared to the available data acquired by laboratory experiments and Navier–Stokes simulations.
Finally, we substitute (3.3) and (3.6) into the angular momentum balance (3.1). It is convenient to use the dimensionless time variable
$({\it\Omega}t)$
. We thus obtain the spin-up equation
$$\begin{eqnarray}J\frac{\text{d}{\it\omega}}{\text{d}({\it\Omega}t)}=-\frac{5}{8}\frac{{\it\nu}}{{\it\Omega}}{\it\omega}\frac{R^{2}}{\mathscr{V}}\frac{1}{\displaystyle \bar{{\it\delta}}}.\end{eqnarray}$$
Here
$\mathscr{V}$
is constant.
$J(t)$
and
$R(t)$
are explicit functions of
${\it\omega}(t)$
via (2.6)–(2.8) and (3.4), while
$\bar{{\it\delta}}(t)$
is also explicitly calculated as specified above.
We now have a closed predictive model. The background system (input parameters
${\it\Omega}=f/2,\mathscr{N}\!/f$
and
${\it\nu}$
), the volume of the vortex
$\mathscr{V}$
(dimensional), and the initial
${\it\omega}(0)$
are given. The solution of (3.11), combined with (2.6)–(2.8), provides
${\it\omega},R$
, and, most importantly,
${\it\alpha}$
for the subsequent motion. Theoretically, the integration of (3.11) can be carried out ‘to infinity’, but there are indications that in real systems instabilities become dominant when
$|{\it\omega}|<0.01$
, and hence we think that
${\it\omega}=-0.01$
is a plausible end point for the prediction of our model.
3.1. Some qualitative insights
We can estimate the influence of the main flow-field parameters on the spin-up (vortex decay/spread-out) time,
$\mathscr{T}$
(scaled with
$1/{\it\Omega}$
). For definiteness, we focus on the case with
${\it\omega}(0)\approx -1$
and follow the process until
${\it\omega}\approx -0.01$
. We distinguish between two main stages: unhindered and hindered spin-up.
Unhindered spin-up
$J$
is close to
$1$
. This corresponds to
${\it\omega}<-0.3$
, roughly. Taking
$J=1$
, (3.11) provides the order of magnitude of the decay time as
$$\begin{eqnarray}\mathscr{T}\sim \left[\frac{{\it\nu}}{{\it\Omega}}\frac{1}{\bar{{\it\delta}}}\frac{R^{2}}{\mathscr{V}}\right]^{-1},\end{eqnarray}$$
and recall that
$R\sim (\mathscr{N}\!/f)^{1/3}\mathscr{V}^{1/3}$
. Here we neglect the influence of
${\it\phi}^{-1/6}$
on
$R$
. We must again distinguish between two sub-stages: when the Ekman layers are dominant,
$\bar{{\it\delta}}~\sim ({\it\nu}/{\it\Omega})^{1/2}$
, and when they are suppressed by the stratification,
$\bar{{\it\delta}}\sim (f/\!\mathscr{N})R$
.
For the case
$\bar{{\it\delta}}~\sim ({\it\nu}/{\it\Omega})^{1/2}$
,
$$\begin{eqnarray}\mathscr{T}_{1}\sim \frac{\mathscr{V}^{1/3}}{({\it\nu}/{\it\Omega})^{1/2}}\left(\frac{f}{\mathscr{N}}\right)^{2/3}.\end{eqnarray}$$
Note that this result can be rewritten as
$E^{-1/2}$
using the Ekman number defined by (2.1a,b
). Now we see the justification for this definition.
For the case
$\bar{{\it\delta}}\sim (f/\!\mathscr{N})R$
, after some algebra, (3.12) yields the typical time scale
$$\begin{eqnarray}\mathscr{T}_{2}\sim \frac{\mathscr{V}^{2/3}}{({\it\nu}/{\it\Omega})}\left(\frac{f}{\mathscr{N}}\right)^{4/3}=\mathscr{T}_{1}^{2}.\end{eqnarray}$$
The relation between
$\mathscr{T}_{1}$
and
$\mathscr{T}_{2}$
is interesting, and, with hindsight, not surprising: the first is proportional to
$E^{-1/2}$
, the second to
$E^{-1}$
. We conclude that, in general, the spin-up time increases when the volume increases and when the
$f/\!\mathscr{N}$
ratio increases. The relevant parameter is the Ekman number defined with the length
$\mathscr{V}^{1/3}(f/\!\mathscr{N})^{2/3}$
, which represents the height of the vortex.
On the face of it, this is not much progress, because the dependences are analogous to classical spin-up and diffusion processes. The novelty is twofold. (i) We have derived these estimates from a more rigorous model, that actually demonstrates that the estimates
$\mathscr{T}_{1},\mathscr{T}_{2}$
are only qualitative time intervals of overlapping processes in the first stage of motion. A sharper estimate of
$\mathscr{T}_{1},\mathscr{T}_{2}$
can be attempted with the aid of some prefactors. However, it is not useful to pursue this, because the behaviour of
${\it\omega}(t)$
is nonlinear and cannot be captured well by constant parameters. (ii) Most importantly, the system (when stable) spends most of the time in the second stage, considered next.
Hindered spin-up
In this stage, the changes of
${\it\omega}$
are affected by the dynamic influence of the variable denoted
$J$
, which can be regarded as the effective momentum of inertia. When
$|{\it\omega}|$
is small,
$J$
increases monotonically with the progress of the spin-up process
$(J\approx 1+(1/3)|{\it\omega}|^{-1})$
. In other words, it becomes ever more difficult for a given torque to spin up the vortex. This effect also contributes to the explanation as to why a stable vortex appears so robust for many revolutions of the system. Let us illustrate this: for
${\it\omega}=-0.05$
, the normalized aspect ratio is
${\it\alpha}\mathscr{N}/f=0.16$
and
$J=7.5$
. It will therefore take a considerably longer time than
$\mathscr{T}_{1}$
to achieve
${\it\omega}=-0.02$
, and when this happens,
${\it\alpha}\mathscr{N}\!/f=0.10$
.
This discussion points out the subtlety of the angular-speed determination:
${\it\omega}(t)$
depends on an initial condition which varies with the generating mechanism; then Ekman layer torque acts for some time to reduce
${\it\omega}$
, but this effect is suppressed to some extent by the stratification, which is then overcome by diffusion of angular momentum from the ambient core. On the other hand, while
${\it\omega}$
is reduced the vortex expands, its momentum of inertia increases, and this hinders the spin-up process. All of this works under the assumption that the flow is stable.
4. Slow sustained injection
Suppose that the vortex is produced and sustained by injection (influx) from a source about the axis at rate
$q$
, which is active for many rotations of the system. We assume that the injection is ‘slow’, so that our model can be used within some small extensions. This implies that a relatively small volume is added per
$1/{\it\Omega}$
, or
$q{\it\Omega}\ll \mathscr{V}_{0}=qt_{0}$
, where
$t_{0}$
is the time at which we start using the model. The result
$t_{0}\gg 1/{\it\Omega}$
is quite trivial, and, surprisingly, independent of
$q$
. (A more stringent criterion could involve the Ekman layer circulation speed, but the result is too cumbersome for useful insights.)
We therefore assume that a vortex which satisfies (2.4)–(2.8) exists for
$t\geqslant t_{0}=3/{\it\Omega}$
, with initial
${\it\omega}(0)$
. The volume is
$qt$
(per half-vortex per radian). We wish to predict the subsequent
${\it\omega}(t)$
and
${\it\alpha}(t)$
.
The extension of the model is as follows. First, we replace the constant
$\mathscr{V}$
with the time-dependent counterpart
$\mathscr{V}(t)=qt$
in (2.2), (2.8) and (3.2). The results (2.4)–(2.8) carry over.
The presence of
$\mathscr{V}(t)$
in (3.2) contributes a significant dynamic effect on the spin-up process via a modification of
$\text{d}{\it\Gamma}/\text{d}t$
for (3.1). After some algebra (see appendix C) and arrangement, the spin-up equation reads
$$\begin{eqnarray}J\frac{\text{d}{\it\omega}}{\text{d}({\it\Omega}t)}=-\frac{5}{8}{\it\omega}\frac{{\it\nu}}{{\it\Omega}}\frac{R^{2}}{\mathscr{V}(t)}\frac{1}{\bar{{\it\delta}}}-\frac{5}{3}(1+{\it\omega})\frac{1}{({\it\Omega}t)}.\end{eqnarray}$$
Here
$\bar{{\it\delta}}$
is calculated as before, using the appropriate
$R(t)$
.
The last term on the right-hand side of (4.1) is the dynamic contribution of the injection to the angular momentum variation. It reproduces the fact that the particles of injected fluid that propagate to larger radii are decelerated by Coriolis effects. This is actually a ‘spin-down’ contribution to the entire vortex, or a ‘sink’ that absorbs part of the external torque. This spin-down effect is strong when (i)
${\it\omega}$
is close to zero, and (ii)
${\it\Omega}t$
is not large. (We note in passing that this term essentially explains why ‘rapid injection’ creates
${\it\omega}(0)\approx -1$
: when the contribution of the first term is small,
${\it\omega}$
tends to
$-1$
in less than one
$1/{\it\Omega}$
.)
However, in a long spin-up process, the effect of the spin-down (last) term is not so dramatic. The first reason is the obvious trade-off between the terms on the right-hand side of (4.1). The spin-up (first and positive) term becomes dominant as the second (negative) term drives
${\it\omega}$
to
$-1$
. This keeps a balance during which
${\it\omega}$
is spun up. The second reason is the fairly rapid decay of the spin-down term like
$({\it\Omega}t)^{-1}$
. The
$R^{2}/\mathscr{V}(t)$
factor in the first term also decays with time, but more slowly,
${\sim}({\it\Omega}t)^{-1/3}$
. The hindering effect of
$J$
is like in the fixed-volume case.
In general, it is not straightforward to compare the time-dependent behaviour of the fixed-volume and slow-injection vortices. Both are expected to display
${\it\omega}\approx -1$
in the initial stage (with
${\it\alpha}\mathscr{N}\!/f\approx 0.5$
), and both will eventually be spun up to small
$|{\it\omega}|$
(accompanied by
${\it\alpha}\mathscr{N}\!/f\approx 0.5(2|{\it\omega}|)^{1/2}$
). The details, however, depend on the values of
$q$
(for the injection case) and
$\mathscr{V}$
(of the fixed vortex). We could not find a simple similarity rule between these systems.
Another immediate extension of the model is to the case of slow sustained injection over a finite period of time,
$t\geqslant t_{i}$
, after which a vortex of fixed volume exists. In this case we integrate (4.1) as follows: with both right-hand side terms up to
$t_{i}$
; then, for
$t>t_{i}$
, with the second term on the right-hand side turned off (set to zero). For
$t>t_{i}$
the fixed-volume vortex behaviour is recovered; however, the ‘initial conditions’ are, typically, different from the standard fixed-volume case. Technically, our model can now imitate the vortex of fixed
$\mathscr{V}$
created by rapid injection: take
$q=\mathscr{V}{\it\Omega}/n$
, and turn off the source at
$t_{i}=n/{\it\Omega}$
, where
$n=4$
or
$5$
. For definiteness, take
${\it\omega}(0)=-0.5$
; tests show that an adjustment towards
$-1$
occurs. We keep in mind, however, that the results in this initial stage lack physical accuracy. The underlying assumptions concerning the hydrostatic and radial-momentum balances cannot be justified during this
$t_{i}$
. These assumption gain validity around
$t_{i}$
, and it is therefore justified to consider the solution for the subsequent time.
Finally, we note that the assumption of constant-rate injection can be relaxed. For a prescribed general smoothly increasing
$\mathscr{V}(t)$
, the only change in the previous model will be to replace
$1/({\it\Omega}t)$
in (4.1) with
$[1/({\it\Omega}\mathscr{V}(t))](\text{d}\mathscr{V}/\text{d}t)$
.
Figure 3. Comparison with fixed-volume experiment of ALM12:
${\it\alpha}\mathscr{N}\!/f$
as a function of
$t/T$
(number of revolutions, where
$T=2{\rm\pi}/{\it\Omega}$
). The thick solid line shows the model prediction, the symbols joined by the thin line are experimental data,
$f=6.8~\text{s}^{-1},\mathscr{N}=1.6~\text{s}^{-1}$
. The model uses
$f/\!\mathscr{N}=4.25$
,
$E=5.1\times 10^{-5}$
,
${\it\omega}(0)=-0.95$
.
5. Comparisons
Given the bold approximations and simplifications of our model, confirmation by comparison with experimental and Navier–Stokes simulations is needed. Unfortunately, most of the pertinent available data are concerned with the short time interval of formation and adjustment (up to about 20 revolutions, say). In other cases, clear-cut comparisons are not possible because the reported data were obtained with initial conditions incompatible with the model, or use implicit scalings, or were contaminated by instabilities. For example, in the experiments of Grant et al. (Reference Grant, Sundermeyer and Hebert2011), the vortex (lens) was created by an oscillating grid (at the middle of the tank). The volume of the resulting vortex, and the value of the initial
${\it\omega}(0)$
, which are needed in our model, cannot be well estimated. All we can say is that the observations are consistent with our model if we use some plausible estimates of
$\mathscr{V}$
and
${\it\omega}(0)$
.
We have therefore restricted our comparison to four cases. In these comparisons the time is rescaled for the number of revolutions
$t/T$
, where
$T=2{\rm\pi}/{\it\Omega}$
. The experimental data concern water, and hence for the corresponding
$E$
we use
${\it\nu}=0.01~\text{cm}^{2}~\text{s}^{-1}$
.
5.1. Fixed volume
The experiment presented in ALM12 figure 2 allows a stringent comparison for a significant time,
$1453$
revolutions. The experiments were performed in a rotating container of
$50\times 50\times 70~\text{cm}^{3}$
using salt water. The vortex of total volume
$4{\rm\pi}\mathscr{V}=300~\text{cm}^{3}$
was created by rapid injection. We estimated the initial conditions
${\it\omega}(0)=-0.95$
. In this case
$f=6.8~\text{s}^{-1},\mathscr{N}=1.6~\text{s}^{-1}$
and hence
$f/N=4.25$
and
$E=5.1\times 10^{-5}$
. The typical radius of the vortex is
$4~\text{cm}$
.
Figure 4. Comparison with fixed-volume Navier–Stokes simulation of HML12:
${\it\alpha}\mathscr{N}\!/f$
as a function of
$t/T$
. The thick solid line shows the model, the symbols joined by the thin line are the simulation data. The model uses
$f/\!\mathscr{N}=5$
,
$E=7.7\times 10^{-5}$
,
${\it\omega}(0)=-0.40$
.
The comparison is shown in figure 3. The agreement between the prediction of the model and the experiment is good. Although
$E$
is very small, a significant decay of the aspect ratio occurs due to the spin-up mechanism elucidated above. However, this occurs over a very large number of revolutions of the system. Moreover, we see that the rate of decay (and spin-up) of the real vortex becomes milder with time, which confirms the theoretical prediction that the resistance to the external torques increases at large times.
Needless to say, there are various uncertainties in this comparison, such as experimental errors, and the value of the initial
${\it\omega}(0)$
. We shall not dwell on these issues because there is presently insufficient data and theoretical knowledge for a reliable evaluation of errors. We have run the model with other plausible
${\it\omega}(0)$
, and found relatively small variations about the result displayed in the figure. We have also run the influx version of the model, imposing the condition that the final volume is attained in
$t_{i}=4/{\it\Omega}$
. The differences from the fixed-volume results are insignificant.
Another useful comparison was performed with the Navier–Stokes simulation of HML12, case A1 (displayed in figure 2a of that paper). The input parameters are
$f/N=5,{\it\omega}(0)=-0.4,E=7.7\times 10^{-5}$
. (The simulation results are reported in dimensionless units, and hence the physical values of the volume of the vortex and of
${\it\nu}$
can be omitted in this comparison.) The results are shown in figure 4. Again, the agreement is good. We wish to emphasize that the Navier–Stokes points were obtained with a big programming effort that produced a three-dimensional pseudo-spectral code, followed by long/expensive computations for
$256^{3}$
modes in a triply periodic domain. The model requires a small programming effort, and insignificant run time. We do not claim that the model is a substitute for the simulations. The Navier–Stokes computations are of course much more accurate, produce detailed information about the flow-field inside and outside the vortex, and can take into account more complex initial conditions than the model (including internal stratification of the vortex). The model is just a useful approximation in the tool kit that can be employed for the analysis and understanding of the problem.
Compare figures 3 and 4. In the latter,
${\it\alpha}\mathscr{N}\!/f$
starts at a significantly smaller value. This is because the initial condition
${\it\omega}(0)=-0.4$
is imposed in the Navier–Stokes computation, while the rapid-injection laboratory vortex starts with
${\it\omega}(0)\approx -1$
, as explained above.
Figure 5. Comparison with experiment of Hedstrom & Armi (Reference Hedstrom and Armi1988):
${\it\alpha}\mathscr{N}/f$
as a function of
$t/T$
. Injection stops at
$t/T=40$
. The thick solid line shows the model prediction, the symbols (joined by the thin line) are the experiment; the triangles denote an unstable domain. The model uses
$f/\!\mathscr{N}=1.88$
;
$E$
decreases with time, from
$1.3\times 10^{-2}$
at
$t/T=3$
to
$2.3\times 10^{-4}$
at
$t/T\geqslant 40$
.
5.2. Sustained injection
Hedstrom & Armi (Reference Hedstrom and Armi1988) performed experiments with vortices of about
$1000{-}2000~\text{cm}^{3}$
created by slow injection in a container of diameter and height of
$120$
and
$60$
cm, respectively, using salt water. They report the decay of the angular velocity with time, but the presented data is in terms of a Rossby number based on the values of the angular velocity near the centre, which in general differs from our
${\it\omega}(t)$
. Therefore a reliable comparison between the
${\it\omega}(t)$
predictions of our model and the data of that paper is in general not feasible. However, figure 7 of that paper presents
${\it\alpha}N/f$
versus
$t/T$
for which a comparison can be attempted. In this case
$f=1.35~\text{s}^{-1},\mathscr{N}=0.72~\text{s}^{-1}$
. The value of the influx was not measured, but on account of the values reported in table 1 of that paper we estimated that
$q=5~\text{cm}^{3}~\text{s}^{-1}$
. The injection was sustained during
$0<t/T\leqslant 40$
, then stopped.
Figure 5 shows the predictions of the model and the measured points. There is fair agreement. The appearance and development of an instability was observed in the experiment, and the last three points are certainly affected by this perturbation. It is therefore not possible to conclude whether the discrepancies are due to simplification errors of the model or should be attributed to the unstable flow. We note the kink in the experimental curve at
$t/T=50$
. This indicates that the shut-down of the injection pump was accompanied by some strong perturbation of the shape. Up to this point the theoretical curve is higher than the measured points, afterwards below. This may be a result of the radial-inertia impulse of the sudden decay of the internal radial velocity. Since the experiment was not repeated, it is not possible to determine whether this is a general feature or just some incidental occurrence.
Figure 6. Comparison with experiment of ALM12:
${\it\alpha}\mathscr{N}\!/f$
as a function of
$t/T$
. Injection active all time. The thick solid line shows the model prediction, the symbols show the experimental data. The model uses
$f/\!\mathscr{N}=0.70$
;
$E$
decreases with time, from
$3.9\times 10^{-2}$
at
$t/T=3$
to
$4.1\times 10^{-3}$
at
$t/T=100$
.
In any case, we think that the model provides some useful quantitative and qualitative information for the flow-field under consideration. We emphasize that the prediction curve is obtained with insignificant computational efforts: the integration of one first-order ODE for
${\it\omega}(t)$
.
Consider next the case of ALM12 figure 3: in the experimental tank of
$50\times 50\times 70~\text{cm}^{3}$
mentioned above, they created a vortex sustained by constant injection
$q=0.17~\text{cm}^{3}~\text{s}^{-1}$
,
$f=1.6~\text{s}^{-1},\mathscr{N}=2.3~\text{s}^{-1}$
. The comparison is shown in figure 6. There is evidently a very significant discrepancy between the model and the experiments. We have no clear-cut explanation for this. The experiment shows some ‘strange’ behaviour: an extreme lack of reaction to the expected spin-up torque. This experimental result is in strong contrast not only to our model but also to the experiment of Hedstrom & Armi (Reference Hedstrom and Armi1988) (HeAr below) considered above. Let us compare the two experiments at
$t/T=100$
. Using the volume of the vortex at this time, we estimate
$E=4.1\times 10^{-3}$
and
$2.3\times 10^{-4}$
for ALM12 and HeAr, respectively. This
$20$
times larger
$E$
indicates that the spin-up in the influx experiment of ALM12 is expected to be significantly faster than in the experiment of HeAr. Figures 5 and 6 clearly show the opposite. At an earlier time (say
$t/T=50$
) the
$E$
ratio is even larger, yet the ALM12 experiment shows almost no spin-up at the first point
$t=77$
, which we think is very strange. Our speculation is that the viscous layer was somehow peeled away from the interface of the vortex by a local instability during the process. This conjecture is supported by the fact that in figure 3 of ALM12 we see that (i) the measured experimental interface is jagged, and (ii) the measured volume of the vortex is smaller than the theoretically injected fluid. (In all our estimates we took into account the fact that in the experiment of ALM12 there was sustained injection.) HeAr also have influx (and a stronger one) during
$t/T\leqslant 40$
, but this did not prevent the spin-up, and the agreement with the model was preserved, during this time interval. We leave this puzzling point open for future verification and interpretations.
6. Concluding remarks
We considered the time-dependent motion of an axisymmetric anticyclonic vortex in a large ambient stratified fluid rotating with constant
${\it\Omega}$
. We focused attention on the long-time behaviour (many revolutions of the system) that follow the initial adjustment (2–3 revolutions say). We developed a closed simple model for the prediction of the aspect ratio
${\it\alpha}$
(and actually the shape) and internal angular velocity
${\it\omega}$
as functions of time
$t$
. (In our model
${\it\omega}$
is scaled with
${\it\Omega}$
; the literature sometimes uses the Rossby number
$Ro={\it\omega}/2$
.) This model is an extension of the model of ALM12 and HML12, which derived the connection between
${\it\alpha}$
and
${\it\omega}$
. We added the balance of angular momentum, and analysed the spin-up process. The solution is obtained numerically by the integration of one ODE, with insignificant computational effort. The model can be applied to cases of both fixed-volume and injection-sustained vortices.
The model elucidates, qualitatively and quantitatively, the salient features of the vortex on the long-time scale. The continuous ‘decay’ of the aspect ratio of the vortex over many revolutions of the system can be attributed to the spin-up effect. Both the fixed-volume and injection-sustained vortices start with
${\it\omega}\approx -1$
, typically. The model provides useful insights into the spin-up mechanism, as follows. For the fixed-volume vortex, the shear torque decays with time because the thickness of the boundary layer,
$\bar{{\it\delta}}$
, increases. It starts as a double Ekman layer (between two fluids) but it quite quickly expands due to stratification effects, and later by viscous diffusion. This prolongs the spin-up somewhat beyond the classical
$E^{-1/2}/{\it\Omega}$
time interval. In this case
${\it\omega}$
decays continuously towards
$0$
, and
${\it\alpha}$
decreases (the vortex expands), but the notable changes of
${\it\alpha}$
occur, typically, over many revolutions of the system. Moreover, when
$|{\it\omega}|$
becomes small, the momentum of angular inertia of the vortex increases like
$(1+(1/3)|{\it\omega}|^{-1})$
; this further hinders the spin-up, and prolongs the process. For the sustained-injection vortex, the injected volume tends to spin down the vortex, and counteracts the effect of the shear torque. However, after some time interval (say 10 revolutions) the vortex is sufficiently large to render the spin-down effect of injection marginal. Then, the spin-up is roughly like in the fixed-volume case. In particular, the hindrance mechanism of the increasing momentum of angular inertia like
$(1+(1/3)|{\it\omega}|^{-1})$
is relevant when
$|{\it\omega}|$
is small.
We admit that our spin-up equation contains bold simplification. We ignored the variation of
${\it\omega}$
with
$r$
, and the effect of the curvature of the interface on the torque. We also discarded the fact that the spin-up of the vortex and its elongation are bound to modify the stratification of the ambient in the vicinity of the vortex. To assess the importance of these effects it is necessary to perform special experiments and Navier–Stokes computations which must be left for future work. Our model assumes a sharp interface between the vortex and the ambient; however, in realistic circumstances the turbulence and component diffusion may blur the boundary and invalidate the predictions.
Comparisons of the prediction of the model with experimental and Navier–Stokes simulation data were performed for four cases. In three cases the agreement is good. In one case, the model predicts a much faster spin-up than the observed one; we could not find a clear-cut explanation for this discrepancy.
We think that this model is a useful contribution to the investigation of the vortex in a rotating stratified ambient, and a valuable extension to the model of ALM12 and HML12. The present model is restricted to an anticyclonic vortex (
${\it\omega}<0$
) of constant density (i.e. the internal stratification
$\mathscr{N}_{c}=0$
). The study of ALM12 and HML12 also considered (i) cases with internal stratification,
$\mathscr{N}_{c}>0$
, and (ii) the cyclonic vortex with
${\it\omega}>0$
. We are presently unable to extend the spin-up considerations to these cases, because (i) there are indications that the spin-up circulation affects
$\mathscr{N}_{c}$
, but a mathematical approximation for this behaviour is still unavailable, to our knowledge, and (ii) HML12 shows that
${\it\omega}>0$
requires
$\mathscr{N}_{c}>0$
. Extension of the model to these important regimes must be left for future work.
Acknowledgements
Thanks to Professor P. Le Gal for valuable clarifications concerning the results of the papers ALM12 and HML12.
Appendix A. On
${\it\omega}(0)$
and consistency
The typical time scale of the model discussed here is the spin-up time interval, which is many revolutions of the system. The situation after the adjustment during the first few revolutions of the system can be considered as
$t=0$
.
The value of
${\it\omega}(0)$
can be estimated with the help of (3.1). Suppose that the fluid which will form the vortex has some initial angular momentum
${\it\Gamma}_{0}$
. After adjustment, the vortex attains the ellipsoidal shape with some
${\it\omega}(0),R(0)$
, and (3.2) is applicable. We argue that during the short-time adjustment the contribution of the torque is negligible, i.e. the total angular momentum is conserved,
$$\begin{eqnarray}{\textstyle \frac{2}{5}}{\it\rho}_{c}{\it\Omega}\mathscr{V}[1+{\it\omega}(0)]R^{2}(0)={\it\Gamma}_{0},\end{eqnarray}$$
which gives
$$\begin{eqnarray}{\it\omega}(0)=-1+\frac{5}{2}\frac{{\it\Gamma}_{0}}{{\it\rho}_{c}{\it\Omega}\mathscr{V}}\frac{1}{R^{2}(0)}.\end{eqnarray}$$
Let
${\it\Gamma}_{0}/({\it\rho}_{c}{\it\Omega}\mathscr{V})$
be represented by
${\it\gamma}(1+{\it\omega}_{i})r_{i}^{2}$
, where
${\it\gamma}$
is a constant,
$r_{i}$
and
${\it\omega}_{i}$
are the initial radius and angular velocity (in the rotating frame) of the volume of fluid under consideration. We obtain
$$\begin{eqnarray}{\it\omega}(0)=-1+\frac{5{\it\gamma}}{2}(1+{\it\omega}_{i})\left(\frac{r_{i}}{R(0)}\right)^{2}.\end{eqnarray}$$
Typically, the fluid that makes up the vortex is released with
${\it\omega}_{i}\leqslant 0$
, and
${\it\gamma}\approx 0.5$
(
${\it\gamma}=1/2$
and
$2/5$
for a cylinder and a sphere, respectively). Therefore, if the initial radius of release is significantly smaller than the radius of the vortex (say by factor 3), then
${\it\omega}(0)=-1$
is a good approximation. In this estimate, the standard value of
$R$
(see (2.9)) can be used for
$R(0)$
.
For example, if the initial volume is a cylinder of radius and height
$r_{i},h_{i}$
then (A 3) predicts
$$\begin{eqnarray}{\it\omega}(0)=-1+(1+{\it\omega}_{i})\frac{5}{4}C,\quad C=\left[\frac{r_{i}}{h_{i}}\frac{f}{3\mathscr{N}}\right]^{2/3}.\end{eqnarray}$$
A more rigorous calculation for the release of a cylinder co-rotating with the ambient (
${\it\omega}_{i}=0$
), taking into account the potential vorticity conservation, is presented in Ungarish (Reference Ungarish2009, § 13.1.1.1). This confirms the estimate (A 4a,b
) for small
$C$
.
We think that (A 4a,b
) can serve as a general approximation for a vortex of fixed volume, and that some estimate for
${\it\omega}_{i}$
and
$C$
can be obtained for cases of interest. If no specific information is available, it makes sense to assume that
$(1+{\it\omega}_{i})C\ll 1$
and hence
${\it\omega}(0)\approx -1$
. We also note that the determination of
${\it\omega}(0)$
from the initial aspect ratio becomes ill-conditioned when
${\it\omega}(0)$
is close to
$-1$
, because
$|\text{d}{\it\alpha}/\text{d}{\it\omega}|\sim (1+{\it\omega})$
(see (2.7)). Vortices created by rapid injection in the laboratory are made of fluid released with
${\it\omega}_{i}=0$
at a relatively small radius,
$r_{i}\ll R(0)$
, and hence also consistent with the
${\it\omega}(0)\approx -1$
suggestion.
An essential assumption in the derivation of our model was that the inertial acceleration terms,
$\text{D}u/\text{d}t$
, on the left-hand side of (2.3) are negligible. This is verified as follows. We argue that
$u\sim \text{d}R/\text{d}t=(\text{d}R/\text{d}{\it\omega})(\text{d}{\it\omega}/\text{d}t)\sim E^{1/2}{\it\Omega}R$
. We conclude that the contribution of
$\text{D}u/\text{D}t$
is
$O(E^{1/2})$
as compared to the right-hand side terms of (2.3). The fact that
$u$
is so small is also a vindication of the lack of viscous terms in (2.3), and an indirect validation of the hydrostatic pressure embedded in this equation. We conclude that, overall, the use of the quasi-steady results for the shape of the vortex is consistent with the spin-up time-dependent behaviour when
$E$
is small. When injection is present, the validity analysis excludes the domain close to the source (
$r<0.1R$
say), but we argue that this is insignificant because of the small volume in this domain.
Appendix B. Calculation of
$\bar{{\it\delta}}$
Consider a fixed time, and let
${\it\xi}=r/R\in [0,1]$
. Now
${\it\delta}({\it\xi})$
is equal to
${\it\delta}_{0}$
over the first half of the interval, then decreases linearly to a smaller
${\it\delta}_{1}$
at
${\it\xi}=1$
. The latter domain is expressed as
$$\begin{eqnarray}{\it\delta}({\it\xi})=a(1+b{\it\xi}),\quad a=2{\it\delta}_{0}-{\it\delta}_{1},\quad b=2\frac{{\it\delta}_{1}-{\it\delta}_{0}}{a}\quad {\it\xi}\in [0.5,1].\end{eqnarray}$$
According to our definition,
$$\begin{eqnarray}\frac{1}{\bar{{\it\delta}}}=4\left(\int _{0}^{0.5}\frac{{\it\xi}^{3}}{{\it\delta}_{0}}\text{d}{\it\xi}+\int _{0.5}^{1}\frac{{\it\xi}^{3}}{{\it\delta}({\it\xi})}\right)=\frac{0.5^{4}}{{\it\delta}_{0}}+\frac{4}{a}\left[I(1)-I(0.5)\right].\end{eqnarray}$$
We use
$$\begin{eqnarray}I(x)=\int \frac{x^{3}}{1+bx}\,\text{d}x=\left[y-\frac{1}{2}y^{2}+\frac{1}{3}y^{3}-\log (1+y)\right]\bigg/b^{4},\end{eqnarray}$$
where
$y=bx$
.
In our model
${\it\delta}_{0}$
varies with time, and hence this calculation is performed every time step. The physical situation implies
$a>0,b<0$
, and
$0<x\leqslant 1$
. Some care is needed when
$|b|$
is small, because the subtraction in (B 3) is prone to cancellation errors. An expansion for small
$y=bx$
yields
$$\begin{eqnarray}I(x)=\frac{x^{4}}{4}\left[1-\frac{4}{5}y+\frac{2}{3}y^{2}\right]\end{eqnarray}$$
with relative error
$O(y^{3})$
.
Appendix C. On the derivation of (3.3) and (4.1)
It is convenient to use the logarithmic form of (3.2),
$$\begin{eqnarray}\log {\it\Gamma}=\log \mathscr{V}+\log (1+{\it\omega})+2\log R+\log C_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \log R={\textstyle \frac{1}{3}}\log \mathscr{V}-{\textstyle \frac{1}{6}}\log {\it\phi}+\log C_{2}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \log {\it\phi}=\log (-{\it\omega})+\log (2+{\it\omega}), & & \displaystyle\end{eqnarray}$$
where
$C_{1},C_{2}$
are constants, and
${\it\omega},R,\mathscr{V}$
are functions of
$t$
.
We take the time derivative of these equations, and denote by an upper dot the time derivative of a variable. We obtain
$$\begin{eqnarray}\frac{\dot{{\it\Gamma}}}{{\it\Gamma}}=\frac{\dot{\mathscr{V}}}{\mathscr{V}}+\frac{\dot{{\it\omega}}}{1+{\it\omega}}+2\frac{{\dot{R}}}{R},\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\dot{R}}}{R}=\frac{1}{3}\frac{\dot{\mathscr{V}}}{\mathscr{V}}-\frac{1}{6}\frac{\dot{{\it\phi}}}{{\it\phi}};\quad \frac{\dot{{\it\phi}}}{{\it\phi}}=\frac{\dot{{\it\omega}}}{{\it\omega}}+\frac{\dot{{\it\omega}}}{2+{\it\omega}}.\end{eqnarray}$$
Combining these equations we get
$$\begin{eqnarray}\frac{\dot{{\it\Gamma}}}{{\it\Gamma}}=\dot{{\it\omega}}\frac{1}{1+{\it\omega}}\left[1-\frac{2}{3}\frac{(1+{\it\omega})^{2}}{{\it\omega}(2+{\it\omega})}\right]+\frac{5}{3}\frac{\dot{\mathscr{V}}}{\mathscr{V}}.\end{eqnarray}$$
The term in the brackets is denoted
$J$
.
$\dot{{\it\Gamma}}$
is the product of (C 6) with
${\it\Gamma}=(2/5){\it\rho}_{c}{\it\Omega}\mathscr{V}(1+{\it\omega})R^{2}$
. The last term of (C 6) vanished for the constant volume case, or when the injection influx is stopped; in this case, we obtain (3.3).
We can substitute the general
$\dot{{\it\Gamma}}$
result and (3.6) into (3.1), and write
$$\begin{eqnarray}\frac{2}{5}{\it\rho}_{c}{\it\Omega}R^{2}\mathscr{V}(1+{\it\omega})\frac{\dot{{\it\Gamma}}}{{\it\Gamma}}=-\frac{1}{4}{\it\rho}_{c}{\it\Omega}R^{4}{\it\nu}\frac{1}{\bar{{\it\delta}}}.\end{eqnarray}$$
For the constant injection case, (C 6) and (C 7) yield (4.1).
