1 Introduction
Modern statistical dynamical closure theory, initially applied to the iconic problem of homogeneous isotropic turbulence (McComb Reference McComb2014), has its origin in the pioneering works of Kraichnan (Reference Kraichnan1959a
) who derived the equations for his Eulerian direct interaction approximation (DIA) closure on the basis of formal renormalized perturbation theory. His approach had elements in common with the renormalized perturbation theory and functional approaches to quantum electrodynamics (QED) developed in the mid-twentieth century by Tomonaga, Schwinger and Feynman (Frederiksen (Reference Frederiksen2017) reviewed the related literature). Unlike QED, where the fine structure constant, measuring interaction strength is only
![]() ${\sim}1/137$
, turbulence at high Reynolds number is a problem of strong interaction. The DIA is a two-point non-Markovian closure for the renormalized two-time covariances or cumulants and response functions but the interaction coefficients, or vertices, are unrenormalized or bare. Herring (Reference Herring1965, Reference Herring1966) subsequently developed the self-consistent field theory (SCFT) closure and McComb (Reference McComb1974, Reference McComb1990, Reference McComb2014) developed the local energy transfer (LET) closure through independent approaches. These two-point non-Markovian closures were later shown to differ from the DIA only in how a fluctuation–dissipation theorem (FDT) (Kraichnan Reference Kraichnan1959b
; Deker & Haake Reference Deker and Haake1975) is invoked (Frederiksen, Davies & Bell Reference Frederiksen, Davies and Bell1994; Kiyani & McComb Reference Kiyani and McComb2004). The prior-time FDT (Carnevale & Frederiksen Reference Carnevale and Frederiksen1983a
, equation (3.5)) relates the two-time spectral covariance
${\sim}1/137$
, turbulence at high Reynolds number is a problem of strong interaction. The DIA is a two-point non-Markovian closure for the renormalized two-time covariances or cumulants and response functions but the interaction coefficients, or vertices, are unrenormalized or bare. Herring (Reference Herring1965, Reference Herring1966) subsequently developed the self-consistent field theory (SCFT) closure and McComb (Reference McComb1974, Reference McComb1990, Reference McComb2014) developed the local energy transfer (LET) closure through independent approaches. These two-point non-Markovian closures were later shown to differ from the DIA only in how a fluctuation–dissipation theorem (FDT) (Kraichnan Reference Kraichnan1959b
; Deker & Haake Reference Deker and Haake1975) is invoked (Frederiksen, Davies & Bell Reference Frederiksen, Davies and Bell1994; Kiyani & McComb Reference Kiyani and McComb2004). The prior-time FDT (Carnevale & Frederiksen Reference Carnevale and Frederiksen1983a
, equation (3.5)) relates the two-time spectral covariance
![]() $C_{\boldsymbol{k}}(t,t^{\prime })$
at wavenumber
$C_{\boldsymbol{k}}(t,t^{\prime })$
at wavenumber
![]() $\boldsymbol{k}$
to the response function
$\boldsymbol{k}$
to the response function
![]() $R_{\boldsymbol{k}}(t,t^{\prime })$
and the prior single-time covariance
$R_{\boldsymbol{k}}(t,t^{\prime })$
and the prior single-time covariance
![]() $C_{\boldsymbol{k}}(t^{\prime },t^{\prime })$
through
$C_{\boldsymbol{k}}(t^{\prime },t^{\prime })$
through
for
![]() $t\geqslant t^{\prime }$
as discussed in more detail in § 5. The SCFT has the same statistical dynamical equations for the single-time covariance and response function as the DIA but replaces the two-time covariance with the approximate expression in the FDT. The LET on the other hand has the same equations for the single-time and two-time covariances as the DIA but uses (1.1) to determine the response function.
$t\geqslant t^{\prime }$
as discussed in more detail in § 5. The SCFT has the same statistical dynamical equations for the single-time covariance and response function as the DIA but replaces the two-time covariance with the approximate expression in the FDT. The LET on the other hand has the same equations for the single-time and two-time covariances as the DIA but uses (1.1) to determine the response function.
Two space scale versions of the DIA closure have also been developed (Carnevale & Martin Reference Carnevale and Martin1982; Carnevale & Frederiksen Reference Carnevale and Frederiksen1983b
) including mean fields (Yoshizawa Reference Yoshizawa1984) as well as associated Markovian versions (Carnevale & Martin Reference Carnevale and Martin1982; Carnevale & Frederiksen Reference Carnevale and Frederiksen1983b
; Yoshizawa et al.
Reference Yoshizawa, Liou, Yokoi and Shih1997). In particular, Carnevale & Frederiksen (Reference Carnevale and Frederiksen1983b
) showed that the eddy-damped quasi-normal Markovian (EDQNM) reduces to the Boltzmann equation for the wave action density in the resonant interaction limit (Hasselmann Reference Hasselmann1966) of ‘wave turbulence’ (Newell & Rumpf (Reference Newell and Rumpf2011) reviewed the related literature). Moreover, it was shown that in the resonant interaction limit there is an additional quadratic invariant know as
![]() $y$
-momentum for Rossby waves and
$y$
-momentum for Rossby waves and
![]() $z$
-momentum for internal gravity waves (Carnevale & Frederiksen Reference Carnevale and Frederiksen1983b
). Throughout this paper we consider strong turbulence, and its interaction with Rossby waves in the inhomogeneous case, rather than weak ‘wave turbulence’.
$z$
-momentum for internal gravity waves (Carnevale & Frederiksen Reference Carnevale and Frederiksen1983b
). Throughout this paper we consider strong turbulence, and its interaction with Rossby waves in the inhomogeneous case, rather than weak ‘wave turbulence’.
The Eulerian DIA and the SCFT and LET closures result in energy spectra that generally agree well with the statistics of DNS in the energy-containing range of the larger scales. However, at high Reynolds numbers, the DIA power laws differ slightly from the classical
![]() $k^{-5/3}$
energy and
$k^{-5/3}$
energy and
![]() $k^{-3}$
enstrophy cascading inertial ranges. These discrepancies have been attributed to the fact that the DIA does not distinguish adequately between sweeping effects and intrinsic distortion effects, resulting in spurious non-local interactions between the large- and small-scale eddies (Kraichnan (Reference Kraichnan1964a
), Herring et al. (Reference Herring, Orszag, Kraichnan and Fox1974) and Frederiksen & Davies (Reference Frederiksen and Davies2000) reviewed the related literature). To overcome these power law deficiencies, quasi-Lagrangian versions of the direct interaction theories were developed by Kraichnan (Kraichnan Reference Kraichnan1965, Reference Kraichnan1977; Kraichnan & Herring Reference Kraichnan and Herring1978) and Kaneda (Kaneda Reference Kaneda1981; Gotoh, Kaneda & Bekki Reference Gotoh, Kaneda and Bekki1988). The non-Markovian quasi-Lagrangian theories, in common with the Eulerian DIA, contain no ad hoc parameters, but the results depend on whether the closure is formulated in terms of labelling time derivatives, like Kraichnan’s Lagrangian-history direct interaction (LHDI) or in terms of measuring time derivatives, like Kaneda’s Lagrangian renormalized approximation (LRA) and also on an ad hoc choice of the basic variables used (Kraichnan (Reference Kraichnan1977), Herring & Kraichnan (Reference Herring and Kraichnan1979), Kaneda (Reference Kaneda1981) and Frederiksen & Davies (Reference Frederiksen and Davies2004) reviewed the related literature). Interestingly, the Eulerian LET closure of McComb (Reference McComb1974, Reference McComb1990), is also consistent with the Kolmogorov (Reference Kolmogorov1941) classical
$k^{-3}$
enstrophy cascading inertial ranges. These discrepancies have been attributed to the fact that the DIA does not distinguish adequately between sweeping effects and intrinsic distortion effects, resulting in spurious non-local interactions between the large- and small-scale eddies (Kraichnan (Reference Kraichnan1964a
), Herring et al. (Reference Herring, Orszag, Kraichnan and Fox1974) and Frederiksen & Davies (Reference Frederiksen and Davies2000) reviewed the related literature). To overcome these power law deficiencies, quasi-Lagrangian versions of the direct interaction theories were developed by Kraichnan (Kraichnan Reference Kraichnan1965, Reference Kraichnan1977; Kraichnan & Herring Reference Kraichnan and Herring1978) and Kaneda (Kaneda Reference Kaneda1981; Gotoh, Kaneda & Bekki Reference Gotoh, Kaneda and Bekki1988). The non-Markovian quasi-Lagrangian theories, in common with the Eulerian DIA, contain no ad hoc parameters, but the results depend on whether the closure is formulated in terms of labelling time derivatives, like Kraichnan’s Lagrangian-history direct interaction (LHDI) or in terms of measuring time derivatives, like Kaneda’s Lagrangian renormalized approximation (LRA) and also on an ad hoc choice of the basic variables used (Kraichnan (Reference Kraichnan1977), Herring & Kraichnan (Reference Herring and Kraichnan1979), Kaneda (Reference Kaneda1981) and Frederiksen & Davies (Reference Frederiksen and Davies2004) reviewed the related literature). Interestingly, the Eulerian LET closure of McComb (Reference McComb1974, Reference McComb1990), is also consistent with the Kolmogorov (Reference Kolmogorov1941) classical
![]() $k^{-5/3}$
inertial range for high-Reynolds-number three-dimensional turbulence. In addition, in contrast to the quasi-Lagrangian closures, the LET, like the Eulerian DIA, is independent of the choice of basic variables such as velocity, vorticity and strain. At finite resolution and moderate Reynolds numbers the performance of the Eulerian DIA, SCFT and LET closures are quite similar, and in two dimensions all tend to underestimate the amplitudes of the small-scale energy spectra (Frederiksen & Davies Reference Frederiksen and Davies2000, Reference Frederiksen and Davies2004).
$k^{-5/3}$
inertial range for high-Reynolds-number three-dimensional turbulence. In addition, in contrast to the quasi-Lagrangian closures, the LET, like the Eulerian DIA, is independent of the choice of basic variables such as velocity, vorticity and strain. At finite resolution and moderate Reynolds numbers the performance of the Eulerian DIA, SCFT and LET closures are quite similar, and in two dimensions all tend to underestimate the amplitudes of the small-scale energy spectra (Frederiksen & Davies Reference Frederiksen and Davies2000, Reference Frederiksen and Davies2004).
The Eulerian and quasi-Lagrangian closures describe the evolution of the renormalized ‘propagators’, the response functions and two-point cumulants, but have deficiencies that arise from not accounting systematically for ‘vertex’ renormalization, the modification of the strength and form of the interaction coefficients. As noted by Martin, Siggia & Rose (Reference Martin, Siggia and Rose1973) ‘the whole problem of strong turbulence is contained in a proper treatment of vertex renormalization’. This is an unsolved problem for strongly interacting fields in general. However, Kraichnan (Reference Kraichnan1964c
) proposed removing some of the convection effects of the large scales on the small scales so that the modified Eulerian DIA becomes consistent with the Kolmogorov inertial range spectra. He zeroed the interaction coefficients, vertex functions, to localize the interactions between triads of wavenumbers dependent on a cut-off ratio
![]() $\unicode[STIX]{x1D6FC}$
(our appendix C has further details). Interestingly, we have found that the value of
$\unicode[STIX]{x1D6FC}$
(our appendix C has further details). Interestingly, we have found that the value of
![]() $\unicode[STIX]{x1D6FC}$
that gives close agreement at all scales of the energy spectra between ensembles of DNS and these regularized closures is essentially universal (Frederiksen & Davies Reference Frederiksen and Davies2004; O’Kane & Frederiksen Reference O’Kane and Frederiksen2004, hereafter OF04).
$\unicode[STIX]{x1D6FC}$
that gives close agreement at all scales of the energy spectra between ensembles of DNS and these regularized closures is essentially universal (Frederiksen & Davies Reference Frederiksen and Davies2004; O’Kane & Frederiksen Reference O’Kane and Frederiksen2004, hereafter OF04).
Non-Markovian closures with potentially long time-history integrals present a significant computational challenge, particularly at high resolution, and even more so if the general inhomogeneous problem is attempted. For a total integration time of
![]() $T$
, the computational effort of non-Markovian closures typically scales as
$T$
, the computational effort of non-Markovian closures typically scales as
![]() $\text{O}(T^{3})$
, whereas for Markovian closures the scaling is O(
$\text{O}(T^{3})$
, whereas for Markovian closures the scaling is O(
![]() $T$
). Orszag (Reference Orszag1970) developed a Markovian closure with the aim of overcoming the problems of possible negative energies (Ogura Reference Ogura1963) in closures based on the quasi-normal, or fourth-order cumulant discard, approximation (Millionshtchikov Reference Millionshtchikov1941). Orszag (Reference Orszag1970) recognized that an empirical damping of the third-order cumulant was needed, as well as Markovianization, to stabilize the quasi-normal closure. The consequent closure, denoted the EDQNM closure, describes the evolution of the single-time covariance associated with homogeneous isotropic turbulence. To reproduce the Kolmogorov inertial range at small scales, Orszag (Reference Orszag1970) augmented the molecular viscosity by an eddy viscosity that has a functional form consistent with the Kolmogorov power law and a strength determined by an empirical constant. Interestingly, the EDQNM closure for homogeneous isotropic turbulence satisfies an H-theorem that guarantees the monotonic increase of entropy for the inviscid system and approach to a canonical equilibrium solution for two- and three-dimensional systems (Carnevale, Frisch & Salmon Reference Carnevale, Frisch and Salmon1981). The EDQNM closure can also be derived by modifying the Eulerian DIA: first, the response function is replaced by a Markovian form with this eddy viscosity and second the two-time covariance is determined from the current-time FDT
$T$
). Orszag (Reference Orszag1970) developed a Markovian closure with the aim of overcoming the problems of possible negative energies (Ogura Reference Ogura1963) in closures based on the quasi-normal, or fourth-order cumulant discard, approximation (Millionshtchikov Reference Millionshtchikov1941). Orszag (Reference Orszag1970) recognized that an empirical damping of the third-order cumulant was needed, as well as Markovianization, to stabilize the quasi-normal closure. The consequent closure, denoted the EDQNM closure, describes the evolution of the single-time covariance associated with homogeneous isotropic turbulence. To reproduce the Kolmogorov inertial range at small scales, Orszag (Reference Orszag1970) augmented the molecular viscosity by an eddy viscosity that has a functional form consistent with the Kolmogorov power law and a strength determined by an empirical constant. Interestingly, the EDQNM closure for homogeneous isotropic turbulence satisfies an H-theorem that guarantees the monotonic increase of entropy for the inviscid system and approach to a canonical equilibrium solution for two- and three-dimensional systems (Carnevale, Frisch & Salmon Reference Carnevale, Frisch and Salmon1981). The EDQNM closure can also be derived by modifying the Eulerian DIA: first, the response function is replaced by a Markovian form with this eddy viscosity and second the two-time covariance is determined from the current-time FDT
for
![]() $t\geqslant t^{\prime }$
(see § 5). Another one-parameter Markovian closure, the test-field model (TFM), was developed by Kraichnan (Reference Kraichnan1971) to yield the Kolmogorov inertial range in three-dimensional turbulence and by Leith & Kraichnan (Reference Leith and Kraichnan1972) for two-dimensional turbulence.
$t\geqslant t^{\prime }$
(see § 5). Another one-parameter Markovian closure, the test-field model (TFM), was developed by Kraichnan (Reference Kraichnan1971) to yield the Kolmogorov inertial range in three-dimensional turbulence and by Leith & Kraichnan (Reference Leith and Kraichnan1972) for two-dimensional turbulence.
Leith (Reference Leith1971) pioneered the numerical implementation of the EDQNM closure for two-dimensional turbulence with application to atmospheric predictability and subgrid modelling. Subsequently the EDQNM has been widely applied to both isotropic and anisotropic problems in two- and three-dimensional turbulence and the interaction of waves and turbulence (Carnevale & Martin (Reference Carnevale and Martin1982), Carnevale & Frederiksen (Reference Carnevale and Frederiksen1983b ), Bowman, Krommes & Ottaviani (Reference Bowman, Krommes and Ottaviani1993), Frederiksen & Davies (Reference Frederiksen and Davies1997) and Cambon et al. (Reference Cambon, Mons, Gréa and Rubinstein2017) reviewed the related literature). Leith & Kraichnan (Reference Leith and Kraichnan1972) implemented and employed the TFM closure for studying error growth in two- and three-dimensional turbulent flows. Herring (Reference Herring1977) and Holloway (Reference Holloway1978) applied generalizations of the TFM for studying turbulent homogeneous flows over random topography with zero mean. The TFM has also been applied in many other studies of both isotropic and anisotropic turbulence (Bowman & Krommes (Reference Bowman and Krommes1997) reviewed the literature).
Markovian closures based on a third-order cumulant discard hypothesis and on eddy-damped quasi-normal forms have also been applied to problems in statistical dynamical prediction (Epstein Reference Epstein1969a ,Reference Epstein b ; Fleming Reference Fleming1971a ,Reference Fleming b ; Epstein & Pitcher Reference Epstein and Pitcher1972; Pitcher Reference Pitcher1977). O’Kane & Frederiksen (Reference O’Kane and Frederiksen2008a ) have also examined the effects of the third-order cumulant discard hypothesis within the QDIA formalism for ensemble prediction. In recent years the interaction of zonal flows with waves and eddies has also been studied with closures where the third-order cumulant is discarded, also called the quasi-linear approximation (e.g. Srinivasan & Young Reference Srinivasan and Young2012), or replaced by empirical stochastic noise and damping (e.g. Farrell & Ioannou Reference Farrell and Ioannou2007), or with closures where the empirical eddy-damped quasi-normal approximation is employed (Marston, Qi & Tobias (Reference Marston, Qi and Tobias2016) reviewed the related literature).
Bowman (Reference Bowman, Krommes and Ottaviani1993) showed that for anisotropic turbulence in the presence of linear wave phenomena, EDQNM-type closures may be potentially non-realizable. They demonstrated that this was a possibility if the EDQNM was derived as a modification of the DIA closure with Markovian response functions and the two-time covariances determined by the current-time FDT in (1.2) or the prior-time FDT in (1.1). However, they established a realizable Markovian closure (RMC) by using a response function with positive damping and specifying the two-time covariance through the correlation FDT
for
![]() $t\geqslant t^{\prime }$
(see § 5). That is, equation (1.3) states that the correlation function
$t\geqslant t^{\prime }$
(see § 5). That is, equation (1.3) states that the correlation function
![]() $C_{\boldsymbol{k}}(t,t^{\prime })[C_{\boldsymbol{k}}(t,t)]^{-1/2}[C_{\boldsymbol{k}}(t^{\prime },t^{\prime })]^{-1/2}$
is equal to the response function
$C_{\boldsymbol{k}}(t,t^{\prime })[C_{\boldsymbol{k}}(t,t)]^{-1/2}[C_{\boldsymbol{k}}(t^{\prime },t^{\prime })]^{-1/2}$
is equal to the response function
![]() $R_{\boldsymbol{k}}(t,t^{\prime })$
. They determined Markovian equations for the triad relaxation functions rather than specifying empirical analytical forms and also considered multi-field versions. Bowman & Krommes (Reference Bowman and Krommes1997) also developed a realizable test-field model (RTFM) closure for anisotropic turbulence and applied it and the RMC to study turbulence in the presence of plasma drift waves through the Hasegawa–Mima equation, whereas Hu, Krommes & Bowman (Reference Hu, Krommes and Bowman1997) performed similar studies for the two-field Hasegawa–Wakatani equations (Krommes (Reference Krommes2002) reviewed the related plasma physics literature).
$R_{\boldsymbol{k}}(t,t^{\prime })$
. They determined Markovian equations for the triad relaxation functions rather than specifying empirical analytical forms and also considered multi-field versions. Bowman & Krommes (Reference Bowman and Krommes1997) also developed a realizable test-field model (RTFM) closure for anisotropic turbulence and applied it and the RMC to study turbulence in the presence of plasma drift waves through the Hasegawa–Mima equation, whereas Hu, Krommes & Bowman (Reference Hu, Krommes and Bowman1997) performed similar studies for the two-field Hasegawa–Wakatani equations (Krommes (Reference Krommes2002) reviewed the related plasma physics literature).
The aim of this article is to formulate and apply three versions of the Markovian inhomogeneous closure (MIC) to the problem of general two-dimensional inhomogeneous turbulent flows interacting with Rossby waves and topography on a generalized
![]() $\unicode[STIX]{x1D6FD}$
-plane. In doing so, we extend the EDQNM and RMC closures for homogeneous turbulence to Markovian closures for the general problem of the interaction of inhomogeneous turbulent flows with waves and orography. Three versions of the MIC are obtained from the quasi-diagonal direct interaction approximation (QDIA) theory for inhomogeneous flows by modifying the response function to a Markovian form and replacing the two-time covariance by the three forms of the FDT in (1.1)–(1.3), respectively.
$\unicode[STIX]{x1D6FD}$
-plane. In doing so, we extend the EDQNM and RMC closures for homogeneous turbulence to Markovian closures for the general problem of the interaction of inhomogeneous turbulent flows with waves and orography. Three versions of the MIC are obtained from the quasi-diagonal direct interaction approximation (QDIA) theory for inhomogeneous flows by modifying the response function to a Markovian form and replacing the two-time covariance by the three forms of the FDT in (1.1)–(1.3), respectively.
The QDIA closure was developed for two-dimensional inhomogeneous turbulent flows over topography on an
![]() $f$
-plane by Frederiksen (Reference Frederiksen1999, hereafter F99) and generalized to include non-Gaussian and inhomogeneous initial conditions by O’Kane & Frederiksen (OF04) and to Rossby wave turbulence on a
$f$
-plane by Frederiksen (Reference Frederiksen1999, hereafter F99) and generalized to include non-Gaussian and inhomogeneous initial conditions by O’Kane & Frederiksen (OF04) and to Rossby wave turbulence on a
![]() $\unicode[STIX]{x1D6FD}$
-plane by Frederiksen & O’Kane (Reference Frederiksen and O’Kane2005, hereafter FO05). It was subsequently formulated for general classical field theories with first-order time derivatives (Frederiksen Reference Frederiksen2012a
,Reference Frederiksen
b
) and for classical and quantum field theories with first- or second-order time derivatives and non-Gaussian noise and non-Gaussian initial conditions (Frederiksen Reference Frederiksen2017). For inviscid flows the QDIA closure relaxes to a canonical equilibrium solution (Carnevale & Frederiksen Reference Carnevale and Frederiksen1987) as shown in F99.
$\unicode[STIX]{x1D6FD}$
-plane by Frederiksen & O’Kane (Reference Frederiksen and O’Kane2005, hereafter FO05). It was subsequently formulated for general classical field theories with first-order time derivatives (Frederiksen Reference Frederiksen2012a
,Reference Frederiksen
b
) and for classical and quantum field theories with first- or second-order time derivatives and non-Gaussian noise and non-Gaussian initial conditions (Frederiksen Reference Frederiksen2017). For inviscid flows the QDIA closure relaxes to a canonical equilibrium solution (Carnevale & Frederiksen Reference Carnevale and Frederiksen1987) as shown in F99.
The QDIA was numerically implemented for turbulent flows over topography on an
![]() $f$
-plane (OF04) and
$f$
-plane (OF04) and
![]() $\unicode[STIX]{x1D6FD}$
-plane (FO05). It was shown to be only a few times more computationally demanding than the homogeneous DIA (Frederiksen & Davies Reference Frederiksen and Davies2000, Reference Frederiksen and Davies2004) unlike Kraichnan’s (Reference Kraichnan1964b
, Reference Kraichnan1972) inhomogeneous DIA (IDIA), which has not been computed for turbulent fluids. At moderate Reynolds numbers the QDIA compares very favourably with large ensembles of DNS (FO05) whereas at high Reynolds numbers a regularized version (appendix C) of the QDIA yields the right small-scale power law behaviour (OF04) as for homogeneous turbulence (Frederiksen & Davies Reference Frederiksen and Davies2004). The computational efficiency of the QDIA has also been enhanced through a cumulant update restart procedure (Rose Reference Rose1985; Frederiksen et al.
Reference Frederiksen, Davies and Bell1994) that uses non-Gaussian terms in the initial conditions (OF04; FO05). This variant is termed the cumulant update QDIA (CUQDIA). The QDIA closure has been comprehensively tested against large ensembles of DNS for problems in predictability (FO05; O’Kane & Frederiksen Reference O’Kane and Frederiksen2008a
), data assimilation using Kalman and related filters (O’Kane & Frederiksen Reference O’Kane and Frederiksen2008b
, Reference O’Kane and Frederiksen2010) and subgrid-scale parameterizations (Frederiksen & O’Kane Reference Frederiksen and O’Kane2008; O’Kane & Frederiksen Reference O’Kane and Frederiksen2008c
). The QDIA theory has also been the framework for developing accurate subgrid-scale parameterizations for atmospheric and oceanic turbulent flows within quasi-geostrophic and primitive equation models and for three-dimensional boundary layer turbulence in channels as reviewed by Frederiksen et al. (Reference Frederiksen, Kitsios, O’Kane, Zidikheri, Franzke and O’Kane2017).
$\unicode[STIX]{x1D6FD}$
-plane (FO05). It was shown to be only a few times more computationally demanding than the homogeneous DIA (Frederiksen & Davies Reference Frederiksen and Davies2000, Reference Frederiksen and Davies2004) unlike Kraichnan’s (Reference Kraichnan1964b
, Reference Kraichnan1972) inhomogeneous DIA (IDIA), which has not been computed for turbulent fluids. At moderate Reynolds numbers the QDIA compares very favourably with large ensembles of DNS (FO05) whereas at high Reynolds numbers a regularized version (appendix C) of the QDIA yields the right small-scale power law behaviour (OF04) as for homogeneous turbulence (Frederiksen & Davies Reference Frederiksen and Davies2004). The computational efficiency of the QDIA has also been enhanced through a cumulant update restart procedure (Rose Reference Rose1985; Frederiksen et al.
Reference Frederiksen, Davies and Bell1994) that uses non-Gaussian terms in the initial conditions (OF04; FO05). This variant is termed the cumulant update QDIA (CUQDIA). The QDIA closure has been comprehensively tested against large ensembles of DNS for problems in predictability (FO05; O’Kane & Frederiksen Reference O’Kane and Frederiksen2008a
), data assimilation using Kalman and related filters (O’Kane & Frederiksen Reference O’Kane and Frederiksen2008b
, Reference O’Kane and Frederiksen2010) and subgrid-scale parameterizations (Frederiksen & O’Kane Reference Frederiksen and O’Kane2008; O’Kane & Frederiksen Reference O’Kane and Frederiksen2008c
). The QDIA theory has also been the framework for developing accurate subgrid-scale parameterizations for atmospheric and oceanic turbulent flows within quasi-geostrophic and primitive equation models and for three-dimensional boundary layer turbulence in channels as reviewed by Frederiksen et al. (Reference Frederiksen, Kitsios, O’Kane, Zidikheri, Franzke and O’Kane2017).
Renormalization methods (McComb Reference McComb2004), and in particular renormalized field theory (Frederiksen Reference Frederiksen2017), form the basis of much progress in many branches of statistical physics including scattering, equilibrium and time-dependent non-equilibrium systems in QED, strong interaction hadron particle physics, critical phenomena, Bose–Einstein condensation, magnetism, plasma physics and cosmology, in addition to fluid turbulence. These methods allow systematic derivation of realizable closures such as the DIA and QDIA for both classical and quantum fields (Frederiksen Reference Frederiksen2017).
The paper is structured as follows. In § 2, we summarize the equations for general two-dimensional flows over topography on a generalized
![]() $\unicode[STIX]{x1D6FD}$
-plane with doubly periodic boundary conditions. The flows consist of a large-scale component with a zonal velocity that satisfies the form-drag equation and a spectrum of smaller scales that satisfy the barotropic vorticity equation. The corresponding spectral equations are documented in § 3. The QDIA closure model is presented in § 4 and the derivation of three versions of the MIC is formulated in § 5 based on a Markovian form of the response function and using the three FDT relations in (1.1)–(1.3), respectively, for the two-time covariance. The performance of the three versions of the MIC, compared with the two variants of the non-Markovian QDIA (with and without cumulant update restarts) and an ensemble of 1800 DNS, is described in § 6. The significance of our findings and conclusions and suggested future studies are presented in § 7. Appendix A documents the interaction coefficients used in the spectral equations, appendix B lists relationships between off-diagonal and diagonal elements of the two-point and three-point cumulants and response functions needed for establishing the closures, and appendix C outlines the steps in developing regularized variants of the MIC.
$\unicode[STIX]{x1D6FD}$
-plane with doubly periodic boundary conditions. The flows consist of a large-scale component with a zonal velocity that satisfies the form-drag equation and a spectrum of smaller scales that satisfy the barotropic vorticity equation. The corresponding spectral equations are documented in § 3. The QDIA closure model is presented in § 4 and the derivation of three versions of the MIC is formulated in § 5 based on a Markovian form of the response function and using the three FDT relations in (1.1)–(1.3), respectively, for the two-time covariance. The performance of the three versions of the MIC, compared with the two variants of the non-Markovian QDIA (with and without cumulant update restarts) and an ensemble of 1800 DNS, is described in § 6. The significance of our findings and conclusions and suggested future studies are presented in § 7. Appendix A documents the interaction coefficients used in the spectral equations, appendix B lists relationships between off-diagonal and diagonal elements of the two-point and three-point cumulants and response functions needed for establishing the closures, and appendix C outlines the steps in developing regularized variants of the MIC.
2 Two-dimensional flow over topography on a generalized
 $\unicode[STIX]{x1D6FD}$
-plane
$\unicode[STIX]{x1D6FD}$
-plane
For this study of the development and performance of three versions of the MIC model we employ the same equations for two-dimensional flow over topography on a generalized
![]() $\unicode[STIX]{x1D6FD}$
-plane as introduced by FO05. Again the streamfunction is written in the form
$\unicode[STIX]{x1D6FD}$
-plane as introduced by FO05. Again the streamfunction is written in the form
![]() $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D713}-Uy$
where the ‘small scales’ are determined by
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D713}-Uy$
where the ‘small scales’ are determined by
![]() $\unicode[STIX]{x1D713}$
and the large-scale westerly flow by
$\unicode[STIX]{x1D713}$
and the large-scale westerly flow by
![]() $U$
.
$U$
.
2.1 Barotropic vorticity equation for the small scales
The ‘small scales’ evolve according to the barotropic vorticity equation in the presence of the large-scale flow and topography,
Here,
![]() $\unicode[STIX]{x1D701}$
is the vorticity,
$\unicode[STIX]{x1D701}$
is the vorticity,
![]() $h$
is the scaled topography,
$h$
is the scaled topography,
![]() $\hat{\unicode[STIX]{x1D708}}$
is the viscosity,
$\hat{\unicode[STIX]{x1D708}}$
is the viscosity,
![]() $f^{0}$
is a forcing function,
$f^{0}$
is a forcing function,
![]() $\unicode[STIX]{x1D6FD}$
is the beta effect and
$\unicode[STIX]{x1D6FD}$
is the beta effect and
![]() $k_{0}$
is a wavenumber that, on a sphere, would determine the strength of the vorticity of the solid-body rotation. This wavenumber can be made as small as desirable to recover the standard
$k_{0}$
is a wavenumber that, on a sphere, would determine the strength of the vorticity of the solid-body rotation. This wavenumber can be made as small as desirable to recover the standard
![]() $\unicode[STIX]{x1D6FD}$
-plane equations. However, the advantage of retaining a small
$\unicode[STIX]{x1D6FD}$
-plane equations. However, the advantage of retaining a small
![]() $k_{0}$
is that it allows us to combine the spectral equations for the small and large scales into a single elegant form. As shown in FO05, there is then a one-to-one correspondence between the spherical geometry and
$k_{0}$
is that it allows us to combine the spectral equations for the small and large scales into a single elegant form. As shown in FO05, there is then a one-to-one correspondence between the spherical geometry and
![]() $\unicode[STIX]{x1D6FD}$
-plane equations that extends to the statistical mechanics equilibrium solutions in the two geometries. The Jacobian is
$\unicode[STIX]{x1D6FD}$
-plane equations that extends to the statistical mechanics equilibrium solutions in the two geometries. The Jacobian is
and the vorticity is related to the streamfunction through
2.2 Large-scale flow equation
The large-scale flow
![]() $U$
evolves according to the form-drag equation
$U$
evolves according to the form-drag equation
The integrations of equations (2.1) and (2.2) are carried out for flows on the doubly periodic plane
![]() $0\leqslant x\leqslant 2\unicode[STIX]{x03C0},0\leqslant y\leqslant 2\unicode[STIX]{x03C0}$
. Here
$0\leqslant x\leqslant 2\unicode[STIX]{x03C0},0\leqslant y\leqslant 2\unicode[STIX]{x03C0}$
. Here
![]() $\boldsymbol{x}=(x,y)$
and the flow
$\boldsymbol{x}=(x,y)$
and the flow
![]() $U$
is forced by relaxing it towards
$U$
is forced by relaxing it towards
![]() $\bar{U}$
with relaxation coefficient
$\bar{U}$
with relaxation coefficient
![]() $\unicode[STIX]{x1D6FC}_{U}$
.
$\unicode[STIX]{x1D6FC}_{U}$
.
3 Spectral equations
Spectral equations corresponding to the system in § 2 are derived by expanding each of the ‘small-scale’ functions in a Fourier series. For example,
where
![]() $\boldsymbol{x}=(x,y),\boldsymbol{k}=(k_{x},k_{y}),k=(k_{x}^{2}+k_{y}^{2})^{1/2},\unicode[STIX]{x1D701}_{-\boldsymbol{k}}=\unicode[STIX]{x1D701}_{\boldsymbol{k}}^{\ast }$
and
$\boldsymbol{x}=(x,y),\boldsymbol{k}=(k_{x},k_{y}),k=(k_{x}^{2}+k_{y}^{2})^{1/2},\unicode[STIX]{x1D701}_{-\boldsymbol{k}}=\unicode[STIX]{x1D701}_{\boldsymbol{k}}^{\ast }$
and
![]() $\boldsymbol{R}$
is a circular domain in wavenumber space excluding the origin
$\boldsymbol{R}$
is a circular domain in wavenumber space excluding the origin
![]() $\mathbf{0}$
. As noted in FO05, it is possible to combine the spectral equations for the ‘small scales’ with the spectral representation of the form drag equation by defining
$\mathbf{0}$
. As noted in FO05, it is possible to combine the spectral equations for the ‘small scales’ with the spectral representation of the form drag equation by defining
as the zero wavenumber spectral component. In addition, the interaction coefficients
![]() $A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
and
$A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
and
![]() $K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
need to be generalized as summarized in appendix A. Thus, the spectral form of the vorticity equation may be written as in the same form as for flows on a non-rotating domain (F99; OF04),
$K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
need to be generalized as summarized in appendix A. Thus, the spectral form of the vorticity equation may be written as in the same form as for flows on a non-rotating domain (F99; OF04),
where
![]() $\boldsymbol{T}=\boldsymbol{R}\cup \mathbf{0}$
. From (A 1c
),
$\boldsymbol{T}=\boldsymbol{R}\cup \mathbf{0}$
. From (A 1c
),
![]() $\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})=1$
if
$\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})=1$
if
![]() $\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q}=0$
and otherwise is zero. In addition
$\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q}=0$
and otherwise is zero. In addition
and the Rossby wave frequency
The
![]() $\boldsymbol{k}=\mathbf{0}$
components of
$\boldsymbol{k}=\mathbf{0}$
components of
![]() $f_{\boldsymbol{k}}^{0}$
and
$f_{\boldsymbol{k}}^{0}$
and
![]() $\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})$
are defined by
$\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})$
are defined by
4 QDIA closure equations
We consider next an ensemble of flows satisfying (3.3) where the ensemble mean is denoted by
![]() $\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}\rangle$
and angle brackets denote expectation value. Then we can express the vorticity component for a given realization by
$\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}\rangle$
and angle brackets denote expectation value. Then we can express the vorticity component for a given realization by
where
![]() $\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{k}}$
denotes the deviation from the ensemble mean. The spectral equations (3.3) can then be expressed in terms of
$\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{k}}$
denotes the deviation from the ensemble mean. The spectral equations (3.3) can then be expressed in terms of
![]() $\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}\rangle$
and
$\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}\rangle$
and
![]() $\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{k}}$
as follows:
$\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{k}}$
as follows:
 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\langle \unicode[STIX]{x1D701}_{\boldsymbol{ k}}\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[\!K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\{\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle +C_{-\boldsymbol{p},-\boldsymbol{q}}(t,t)\}\nonumber\\ \displaystyle & & \displaystyle +\,A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle h_{-\boldsymbol{q}}\! ]+\,\bar{f}_{\boldsymbol{k}}^{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\langle \unicode[STIX]{x1D701}_{\boldsymbol{ k}}\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[\!K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\{\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle +C_{-\boldsymbol{p},-\boldsymbol{q}}(t,t)\}\nonumber\\ \displaystyle & & \displaystyle +\,A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle h_{-\boldsymbol{q}}\! ]+\,\bar{f}_{\boldsymbol{k}}^{0},\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{ k}} & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[\!K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\{\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{q}}+\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{q}}-C_{-\boldsymbol{p},-\boldsymbol{q}}(t,t)\!\}+A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}h_{-\boldsymbol{q}}\! ]+\tilde{f}_{\boldsymbol{k}}^{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{ k}} & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[\!K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\{\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{q}}+\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{q}}-C_{-\boldsymbol{p},-\boldsymbol{q}}(t,t)\!\}+A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}h_{-\boldsymbol{q}}\! ]+\tilde{f}_{\boldsymbol{k}}^{0}.\end{eqnarray}$$
Here, and in subsequent equations, the wave vectors lie in the larger
![]() $\boldsymbol{T}$
domain and
$\boldsymbol{T}$
domain and
with
and
are two-time covariance (and also two-point cumulant) matrix elements.
We briefly outline the derivation of the QDIA closure equations for barotropic flow over topography by employing the expressions for the off-diagonal elements of the two- and three-point cumulants and response functions, in terms of the diagonal elements for the QDIA closure equations, as described in appendix B. First, to close (4.2a
) we need the expression for the two-point cumulant
![]() $C_{-\boldsymbol{p},-\boldsymbol{q}}(t,t)$
in (B 1). This results in the expression
$C_{-\boldsymbol{p},-\boldsymbol{q}}(t,t)$
in (B 1). This results in the expression
where
and
with
Here,
![]() $\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)$
is the nonlinear damping,
$\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)$
is the nonlinear damping,
![]() $\unicode[STIX]{x1D712}_{\boldsymbol{k}}(t,s)$
is a measure of the strength of the interaction of the transient eddies with the topography and
$\unicode[STIX]{x1D712}_{\boldsymbol{k}}(t,s)$
is a measure of the strength of the interaction of the transient eddies with the topography and
![]() $f_{\boldsymbol{k}}^{h}(t)$
is the eddy–topographic force. The response function is defined for
$f_{\boldsymbol{k}}^{h}(t)$
is the eddy–topographic force. The response function is defined for
![]() $t\geqslant t^{\prime }$
through the functional derivative
$t\geqslant t^{\prime }$
through the functional derivative
In (4.5) we have also used the shortened notation
Substituting (4.4) into (4.2a ) yields
 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\langle \unicode[STIX]{x1D701}_{\boldsymbol{ k}}(t)\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}(t)\rangle h_{-\boldsymbol{q}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}(t)\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\int _{t_{o}}^{t}\text{d}s\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(s)\rangle +f_{\boldsymbol{k}}^{h}(t)+\bar{f}_{\boldsymbol{k}}^{0}(t).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\langle \unicode[STIX]{x1D701}_{\boldsymbol{ k}}(t)\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}(t)\rangle h_{-\boldsymbol{q}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}(t)\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \nonumber\\ \displaystyle & & \displaystyle -\,\int _{t_{o}}^{t}\text{d}s\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(s)\rangle +f_{\boldsymbol{k}}^{h}(t)+\bar{f}_{\boldsymbol{k}}^{0}(t).\end{eqnarray}$$
From (4.2b
), we can obtain an equation for the diagonal two-time cumulant, needed in (4.5), by multiplying by
![]() $\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{k}}(t^{\prime })$
. Then taking the expectation value we have
$\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{k}}(t^{\prime })$
. Then taking the expectation value we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)C_{\boldsymbol{ k}}(t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})C_{-\boldsymbol{p},-\boldsymbol{k}}(t,t^{\prime })h_{-\boldsymbol{q}}+\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,[\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}(t)\rangle C_{-\boldsymbol{q},-\boldsymbol{k}}(t,t^{\prime })+C_{-\boldsymbol{p},-\boldsymbol{k}}(t,t^{\prime })\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle +\langle \tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}(t)\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{q}}(t)\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{k}}(t^{\prime })\rangle ]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{t_{0}}^{t^{\prime }}\text{d}sF_{\boldsymbol{k}}^{0}(t,s)R_{-\boldsymbol{k}}(t^{\prime },s),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)C_{\boldsymbol{ k}}(t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})C_{-\boldsymbol{p},-\boldsymbol{k}}(t,t^{\prime })h_{-\boldsymbol{q}}+\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,[\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}(t)\rangle C_{-\boldsymbol{q},-\boldsymbol{k}}(t,t^{\prime })+C_{-\boldsymbol{p},-\boldsymbol{k}}(t,t^{\prime })\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle +\langle \tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{p}}(t)\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{q}}(t)\tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{k}}(t^{\prime })\rangle ]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{t_{0}}^{t^{\prime }}\text{d}sF_{\boldsymbol{k}}^{0}(t,s)R_{-\boldsymbol{k}}(t^{\prime },s),\end{eqnarray}$$
where
![]() $t>t^{\prime }$
and
$t>t^{\prime }$
and
![]() $C_{\boldsymbol{k}}(t,t^{\prime })=C_{-\boldsymbol{k}}(t^{\prime },t)$
for
$C_{\boldsymbol{k}}(t,t^{\prime })=C_{-\boldsymbol{k}}(t^{\prime },t)$
for
![]() $t^{\prime }>t$
and
$t^{\prime }>t$
and
Again, equation (B 1) can be used to express the off-diagonal elements of the two-time cumulant in terms of the diagonal elements. In the quasi-diagonal approximation, the treatment of the three-point cumulant in (4.8) is the same as in the standard DIA closure for homogeneous turbulence (Kraichnan Reference Kraichnan1959a ; Frederiksen et al. Reference Frederiksen, Davies and Bell1994; Frederiksen (Reference Frederiksen, Ball and Akhmediev2003) contains a simple derivation) and is given in (B 3). Thus,
 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)C_{\boldsymbol{ k}}(t,t^{\prime }) & = & \displaystyle \int _{t_{0}}^{t^{\prime }}\text{d}s(S_{\boldsymbol{k}}(t,s)+P_{\boldsymbol{k}}(t,s)+F_{\boldsymbol{k}}^{0}(t,s))R_{-\boldsymbol{k}}(t^{\prime },s)\nonumber\\ \displaystyle & & \displaystyle -\,\int _{t_{0}}^{t}\text{d}s(\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)+\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t^{\prime },s).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)C_{\boldsymbol{ k}}(t,t^{\prime }) & = & \displaystyle \int _{t_{0}}^{t^{\prime }}\text{d}s(S_{\boldsymbol{k}}(t,s)+P_{\boldsymbol{k}}(t,s)+F_{\boldsymbol{k}}^{0}(t,s))R_{-\boldsymbol{k}}(t^{\prime },s)\nonumber\\ \displaystyle & & \displaystyle -\,\int _{t_{0}}^{t}\text{d}s(\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)+\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t^{\prime },s).\end{eqnarray}$$
In (4.9),
 $$\begin{eqnarray}\displaystyle P_{\boldsymbol{k}}(t,s) & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})C_{-\boldsymbol{p}}(t,s)[2K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle +A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})h_{-\boldsymbol{q}}]\nonumber\\ \displaystyle & & \displaystyle \times \,[2K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle +A(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})h_{\boldsymbol{q}}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{\boldsymbol{k}}(t,s) & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})C_{-\boldsymbol{p}}(t,s)[2K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle +A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})h_{-\boldsymbol{q}}]\nonumber\\ \displaystyle & & \displaystyle \times \,[2K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle +A(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})h_{\boldsymbol{q}}],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s) & = & \displaystyle -\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})R_{-\boldsymbol{p}}(t,s)[2K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle +A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})h_{-\boldsymbol{q}}]\nonumber\\ \displaystyle & & \displaystyle \times \,[2K(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle +A(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})h_{\boldsymbol{q}}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s) & = & \displaystyle -\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})R_{-\boldsymbol{p}}(t,s)[2K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle +A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})h_{-\boldsymbol{q}}]\nonumber\\ \displaystyle & & \displaystyle \times \,[2K(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle +A(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})h_{\boldsymbol{q}}],\end{eqnarray}$$
The equation for the diagonal response function is derived in a similar way using (B 2) and (B 4). We find (F99; FO05)
for
![]() $t\geqslant t^{\prime }$
, where the delta function implies that
$t\geqslant t^{\prime }$
, where the delta function implies that
![]() $R_{\boldsymbol{k}}(t,t)=1$
. Finally, the single-time cumulant equation takes the form
$R_{\boldsymbol{k}}(t,t)=1$
. Finally, the single-time cumulant equation takes the form
 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+2Re\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)C_{\boldsymbol{ k}}(t,t) & = & \displaystyle 2Re\int _{t_{0}}^{t}\text{d}s(S_{\boldsymbol{ k}}(t,s)+P_{\boldsymbol{k}}(t,s)+F_{\boldsymbol{k}}^{0}(t,s))R_{-\boldsymbol{k}}(t,s)\nonumber\\ \displaystyle & & \displaystyle -\,2Re\int _{t_{0}}^{t}\text{d}s(\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)+\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t,s).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+2Re\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)C_{\boldsymbol{ k}}(t,t) & = & \displaystyle 2Re\int _{t_{0}}^{t}\text{d}s(S_{\boldsymbol{ k}}(t,s)+P_{\boldsymbol{k}}(t,s)+F_{\boldsymbol{k}}^{0}(t,s))R_{-\boldsymbol{k}}(t,s)\nonumber\\ \displaystyle & & \displaystyle -\,2Re\int _{t_{0}}^{t}\text{d}s(\unicode[STIX]{x1D702}_{\boldsymbol{k}}(t,s)+\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t,s).\end{eqnarray}$$
The CUQDIA closure, the cumulant update version of the QDIA, uses non-Gaussian and inhomogeneous cumulants, accumulated in the integrations, in the initial conditions of the periodic restarts, as described in the Appendix of FO05. For the sake of brevity these terms are not included here since they are not needed for the development of our three MIC models that follows next.
5 MIC equations
In this section, we formulate three slightly different versions of the MIC equations. We employ three commonly used versions of the FDT together with a Markovian version of the response function equation in the derivation. We begin by reformulating the single-time covariance equation (4.9), which we first write in the form
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}C_{\boldsymbol{k}}(t,t) & = & \displaystyle 2Re[{\mathcal{F}}_{\boldsymbol{k}}^{S}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PA}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PB}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PC}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PD}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{0}(t)]\nonumber\\ \displaystyle & & \displaystyle -\,2Re[{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x1D702}}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}A}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}B}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}C}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}D}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{0}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}C_{\boldsymbol{k}}(t,t) & = & \displaystyle 2Re[{\mathcal{F}}_{\boldsymbol{k}}^{S}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PA}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PB}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PC}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{PD}(t)+{\mathcal{F}}_{\boldsymbol{ k}}^{0}(t)]\nonumber\\ \displaystyle & & \displaystyle -\,2Re[{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x1D702}}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}A}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}B}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}C}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}D}(t)+{\mathcal{N}}_{\boldsymbol{k}}^{0}].\end{eqnarray}$$
Here, we have first split up the
![]() $P_{\boldsymbol{k}}(t,s)$
and
$P_{\boldsymbol{k}}(t,s)$
and
![]() $\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s)$
terms into their mean vorticity, topographic and cross terms. Simple algebra shows that the
$\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s)$
terms into their mean vorticity, topographic and cross terms. Simple algebra shows that the
![]() ${\mathcal{F}}_{\boldsymbol{k}}(t)$
and
${\mathcal{F}}_{\boldsymbol{k}}(t)$
and
![]() ${\mathcal{N}}_{\boldsymbol{k}}(t)$
functions have the following expressions:
${\mathcal{N}}_{\boldsymbol{k}}(t)$
functions have the following expressions:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}A}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t)=\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{k}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}A},}\equiv \unicode[STIX]{x1D6E5}^{PA}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}A}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t)=\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{k}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}A},}\equiv \unicode[STIX]{x1D6E5}^{PA}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}C}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t)=\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle h_{\boldsymbol{q}}\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{k}}(t,s) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}C}(t)=}\equiv \unicode[STIX]{x1D6E5}^{PC}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}C}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t)=\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle h_{\boldsymbol{q}}\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{k}}(t,s) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}C}(t)=}\equiv \unicode[STIX]{x1D6E5}^{PC}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}D}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t)=h_{-\boldsymbol{q}}\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{k}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}D}(t)=,}\equiv \unicode[STIX]{x1D6E5}^{PD}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}D}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t)=h_{-\boldsymbol{q}}\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{k}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{q}}(s)\rangle & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\unicode[STIX]{x1D6E5}^{\unicode[STIX]{x03C0}D}(t)=,}\equiv \unicode[STIX]{x1D6E5}^{PD}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
for
![]() $t\geqslant t^{\prime }$
and
$t\geqslant t^{\prime }$
and
![]() $C_{\boldsymbol{k}}(t,t^{\prime })=C_{-\boldsymbol{k}}(t^{\prime },t)$
for
$C_{\boldsymbol{k}}(t,t^{\prime })=C_{-\boldsymbol{k}}(t^{\prime },t)$
for
![]() $t^{\prime }>t$
. Here
$t^{\prime }>t$
. Here
![]() $X=0$
corresponds to the current-time FDT (see Frederiksen & Davies (Reference Frederiksen and Davies1997, equation (A.16)) and references therein) usually used in the EDQNM,
$X=0$
corresponds to the current-time FDT (see Frederiksen & Davies (Reference Frederiksen and Davies1997, equation (A.16)) and references therein) usually used in the EDQNM,
![]() $X=1/2$
is the correlation FDT in Bowman (Reference Bowman, Krommes and Ottaviani1993, equation (61)) and
$X=1/2$
is the correlation FDT in Bowman (Reference Bowman, Krommes and Ottaviani1993, equation (61)) and
![]() $X=1$
is the prior-time FDT (see Carnevale & Frederiksen (Reference Carnevale and Frederiksen1983a
, equation (3.5)) and references therein). Bowman (Reference Bowman, Krommes and Ottaviani1993) pointed out that in the presence of wave phenomena it is possible for the forms with
$X=1$
is the prior-time FDT (see Carnevale & Frederiksen (Reference Carnevale and Frederiksen1983a
, equation (3.5)) and references therein). Bowman (Reference Bowman, Krommes and Ottaviani1993) pointed out that in the presence of wave phenomena it is possible for the forms with
![]() $X=0$
and
$X=0$
and
![]() $X=1$
to lead to unphysical results whereas the form with
$X=1$
to lead to unphysical results whereas the form with
![]() $X=1/2$
(together with Markovian response functions with positive damping) will always be realizable. Their demonstration showing that
$X=1/2$
(together with Markovian response functions with positive damping) will always be realizable. Their demonstration showing that
![]() $C_{\boldsymbol{k}}(t,t)$
is real and non-negative when
$C_{\boldsymbol{k}}(t,t)$
is real and non-negative when
![]() $X=1/2$
, in their equation (65), applies equally in the QDIA inhomogeneous formalism. This follows by replacing their eddy–eddy nonlinear noise
$X=1/2$
, in their equation (65), applies equally in the QDIA inhomogeneous formalism. This follows by replacing their eddy–eddy nonlinear noise
![]() $\mathscr{F}_{\boldsymbol{k}}$
by our total nonlinear noise
$\mathscr{F}_{\boldsymbol{k}}$
by our total nonlinear noise
![]() $[S_{\boldsymbol{k}}+P_{\boldsymbol{k}}]$
. This is an important point in general, but whether unphysical results ensue will of course also depend on the parameter regime of the flow. For that reason we examine all three cases in this study.
$[S_{\boldsymbol{k}}+P_{\boldsymbol{k}}]$
. This is an important point in general, but whether unphysical results ensue will of course also depend on the parameter regime of the flow. For that reason we examine all three cases in this study.
With (5.4) substituted into equations (5.2) and (5.3) it is then possible to express the nonlinear noises and dampings in forms that involve triad relaxation functions
![]() $\unicode[STIX]{x1D6E9}^{X}$
,
$\unicode[STIX]{x1D6E9}^{X}$
,
![]() $\unicode[STIX]{x1D6F7}^{X}$
and
$\unicode[STIX]{x1D6F7}^{X}$
and
![]() $\unicode[STIX]{x1D6F9}^{X}$
. Thus,
$\unicode[STIX]{x1D6F9}^{X}$
. Thus,
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{S}(t)=2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2\sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)C_{-\boldsymbol{q}}^{X}(t,t)\unicode[STIX]{x1D6E9}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{S}(t)=2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2\sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)C_{-\boldsymbol{q}}^{X}(t,t)\unicode[STIX]{x1D6E9}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PA}(t)=4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2\sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PA}(t)=4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2\sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PB}(t)=\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2\sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)h_{-\boldsymbol{q}}h_{\boldsymbol{q}}\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PB}(t)=\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2\sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)h_{-\boldsymbol{q}}h_{\boldsymbol{q}}\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
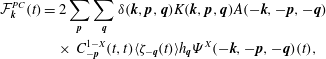 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PC}(t)=2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\sum \sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle h_{\boldsymbol{q}}\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PC}(t)=2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\sum \sum }\times \,\mathop{C}_{-\boldsymbol{p}}^{1-X}(t,t)\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle h_{\boldsymbol{q}}\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PD}(t)=2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2}\times \,C_{-\boldsymbol{p}}^{1-X}(t,t)h_{-\boldsymbol{q}}\unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{\boldsymbol{k}}^{PD}(t)=2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2}\times \,C_{-\boldsymbol{p}}^{1-X}(t,t)h_{-\boldsymbol{q}}\unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{k},-\boldsymbol{p},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x1D702}}(t)=-4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\sum }\times \,\mathop{C}_{-\boldsymbol{q}}^{1-X}(t,t)C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6E9}^{X}(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x1D702}}(t)=-4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{\sum }\times \,\mathop{C}_{-\boldsymbol{q}}^{1-X}(t,t)C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6E9}^{X}(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}A}(t)=-4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2-}\times \,C_{-\boldsymbol{k}}^{-X}(t,t)\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}A}(t)=-4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \hphantom{2-}\times \,C_{-\boldsymbol{k}}^{-X}(t,t)\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle \unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}B}(t)=-\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})h_{-\boldsymbol{q}}h_{\boldsymbol{q}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \times \,C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t),\hphantom{\sum \sum ,} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}B}(t)=-\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})h_{-\boldsymbol{q}}h_{\boldsymbol{q}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \times \,C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t),\hphantom{\sum \sum ,} & \displaystyle\end{eqnarray}$$
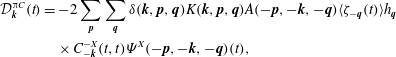 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}C}(t)=-2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle h_{\boldsymbol{q}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \times \,C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t),\hphantom{2\sum \sum \sum ,} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}C}(t)=-2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}(t)\rangle h_{\boldsymbol{q}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \times \,C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6F9}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t),\hphantom{2\sum \sum \sum ,} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}D}(t)=-2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})h_{-\boldsymbol{q}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \times \,C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t),\hphantom{2\sum \sum } & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{\unicode[STIX]{x03C0}D}(t)=-2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})h_{-\boldsymbol{q}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \times \,C_{-\boldsymbol{k}}^{-X}(t,t)\unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{p},-\boldsymbol{k},-\boldsymbol{q})(t),\hphantom{2\sum \sum } & \displaystyle\end{eqnarray}$$
Note that
![]() $C_{\boldsymbol{k}}(t,t)=C_{-\boldsymbol{k}}(t,t)$
since
$C_{\boldsymbol{k}}(t,t)=C_{-\boldsymbol{k}}(t,t)$
since
![]() $C_{\boldsymbol{k}}(t,t)$
is real. It convenient then to define
$C_{\boldsymbol{k}}(t,t)$
is real. It convenient then to define
From equations (4.12) and (5.1) we see that
Thus,
Now to complete the Markovianization, the response function equation (4.11) must also be replaced by
From equation (5.7k ) we see that (5.9) is equivalent to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}R_{\boldsymbol{k}}(t,t^{\prime })+\left[\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}+\int _{t_{0}}^{t}\text{d}s\{(\unicode[STIX]{x1D702}_{\boldsymbol{ k}}(t,s)+\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t,s)[C_{\boldsymbol{k}}(t,t)]^{-1}\}\right]R_{\boldsymbol{ k}}(t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle =\unicode[STIX]{x1D6FF}(t-t^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}R_{\boldsymbol{k}}(t,t^{\prime })+\left[\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}+\int _{t_{0}}^{t}\text{d}s\{(\unicode[STIX]{x1D702}_{\boldsymbol{ k}}(t,s)+\unicode[STIX]{x03C0}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t,s)[C_{\boldsymbol{k}}(t,t)]^{-1}\}\right]R_{\boldsymbol{ k}}(t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle =\unicode[STIX]{x1D6FF}(t-t^{\prime }).\end{eqnarray}$$
The advantage of the forms (5.8) and (5.9) is however that the integral terms can be replaced by manifestly Markovian equations for the triad relaxation times that also involve the damping terms
![]() ${\mathcal{D}}_{\boldsymbol{k}}(t)$
. This can be seen as follows. The integral expression for the relaxation time,
${\mathcal{D}}_{\boldsymbol{k}}(t)$
. This can be seen as follows. The integral expression for the relaxation time,
is equivalent to the differential equation
with
![]() $\unicode[STIX]{x1D6E9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(0)=0$
. In addition,
$\unicode[STIX]{x1D6E9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(0)=0$
. In addition,
is equivalent to
with
![]() $\unicode[STIX]{x1D6F7}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(0)=0$
. Finally,
$\unicode[STIX]{x1D6F7}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(0)=0$
. Finally,
is equivalent to
with
![]() $\unicode[STIX]{x1D6F9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(0)=0$
.
$\unicode[STIX]{x1D6F9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(0)=0$
.
To close the Markovian equations for the single-time diagonal cumulant and response function, with auxiliary equations for the triad relaxation times, we need to formulate a Markov version of the mean field equation. From (4.7) we have
 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\langle \unicode[STIX]{x1D701}_{\boldsymbol{ k}}\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[\!K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle h_{-\boldsymbol{q}}\! ]-{\mathcal{N}}_{\boldsymbol{k}}^{M}(t)+f_{\boldsymbol{k}}^{h}(t)+\bar{f}_{\boldsymbol{k}}^{0}(t).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}\right)\langle \unicode[STIX]{x1D701}_{\boldsymbol{ k}}\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[\!K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle \nonumber\\ \displaystyle & & \displaystyle +\,A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle h_{-\boldsymbol{q}}\! ]-{\mathcal{N}}_{\boldsymbol{k}}^{M}(t)+f_{\boldsymbol{k}}^{h}(t)+\bar{f}_{\boldsymbol{k}}^{0}(t).\end{eqnarray}$$
Here, the nonlinear damping and eddy–topographic force are given by
 $$\begin{eqnarray}\displaystyle {\mathcal{N}}_{\boldsymbol{k}}^{M}(t) & = & \displaystyle -4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{q}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(s)\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{N}}_{\boldsymbol{k}}^{M}(t) & = & \displaystyle -4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{q}}(t,s)\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(s)\rangle ,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle f_{\boldsymbol{k}}^{h}(t) & = & \displaystyle 2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,h_{\boldsymbol{k}}\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{q}}(t,s).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{\boldsymbol{k}}^{h}(t) & = & \displaystyle 2\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})A(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,h_{\boldsymbol{k}}\int _{t_{0}}^{t}\text{d}sR_{-\boldsymbol{p}}(t,s)C_{-\boldsymbol{q}}(t,s).\end{eqnarray}$$
and
Next, we again use the FDT (5.4) for
![]() $t\geqslant t^{\prime }$
. Then we have
$t\geqslant t^{\prime }$
. Then we have
where
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{M}(t) & = & \displaystyle -4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,C_{-\boldsymbol{q}}^{1-X}(t,t)\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(t)\rangle ^{-1}\unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})(t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\boldsymbol{k}}^{M}(t) & = & \displaystyle -4\mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})K(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})\nonumber\\ \displaystyle & & \displaystyle \times \,C_{-\boldsymbol{q}}^{1-X}(t,t)\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(t)\rangle ^{-1}\unicode[STIX]{x1D6F7}^{X}(-\boldsymbol{p},-\boldsymbol{q},-\boldsymbol{k})(t),\end{eqnarray}$$
and
Here, the expressions for
![]() $\unicode[STIX]{x1D6F7}^{X}$
and
$\unicode[STIX]{x1D6F7}^{X}$
and
![]() $\unicode[STIX]{x1D6F9}^{X}$
are the same as in (5.5). Similarly, we have the manifestly Markovian equations for the triad relaxation times associated with the mean field as in (5.11).
$\unicode[STIX]{x1D6F9}^{X}$
are the same as in (5.5). Similarly, we have the manifestly Markovian equations for the triad relaxation times associated with the mean field as in (5.11).
Now, equation (5.12) can be written in the form
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle +A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle h_{-\boldsymbol{q}}]\nonumber\\ \displaystyle & & \displaystyle -\,[{\mathcal{D}}_{\boldsymbol{k}}^{0}+{\mathcal{D}}_{\boldsymbol{k}}^{M}(t)]\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(t)\rangle +f_{\boldsymbol{k}}^{h}(t)+\bar{f}_{\boldsymbol{k}}^{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}\rangle & = & \displaystyle \mathop{\sum }_{\boldsymbol{p}}\mathop{\sum }_{\boldsymbol{q}}\unicode[STIX]{x1D6FF}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})[K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle \langle \unicode[STIX]{x1D701}_{-\boldsymbol{q}}\rangle +A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\langle \unicode[STIX]{x1D701}_{-\boldsymbol{p}}\rangle h_{-\boldsymbol{q}}]\nonumber\\ \displaystyle & & \displaystyle -\,[{\mathcal{D}}_{\boldsymbol{k}}^{0}+{\mathcal{D}}_{\boldsymbol{k}}^{M}(t)]\langle \unicode[STIX]{x1D701}_{\boldsymbol{k}}(t)\rangle +f_{\boldsymbol{k}}^{h}(t)+\bar{f}_{\boldsymbol{k}}^{0}.\end{eqnarray}$$
This then closes the equations for the three versions of the MIC with the unique triad relaxation times being
![]() $\unicode[STIX]{x1D6E9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(t),\unicode[STIX]{x1D6F7}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(t)$
and
$\unicode[STIX]{x1D6E9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(t),\unicode[STIX]{x1D6F7}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(t)$
and
![]() $\unicode[STIX]{x1D6F9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(t)$
. Of course, rather than performing the integrals over time, the partial differential equations for the triad relaxation times must be solved. The relative efficiency of the methods will depend on how long the integration needs to be done before a cumulant update restart can be performed (OF04; FO05) and the dimensionality of the problem. However, the MIC also offers the possibility of analytic forms of the triad relaxation times, such as is typically used in EDQNM calculations, and this of course would speed up the calculations enormously.
$\unicode[STIX]{x1D6F9}^{X}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})(t)$
. Of course, rather than performing the integrals over time, the partial differential equations for the triad relaxation times must be solved. The relative efficiency of the methods will depend on how long the integration needs to be done before a cumulant update restart can be performed (OF04; FO05) and the dimensionality of the problem. However, the MIC also offers the possibility of analytic forms of the triad relaxation times, such as is typically used in EDQNM calculations, and this of course would speed up the calculations enormously.
6 Performance of MIC models for turbulent flow and Rossby waves over topography
We test the performance of the three versions of the MIC model, described in § 5, against two variants of the non-Markovian QDIA and against a large ensemble of direct numerical simulations (DNS) for the case of inhomogeneous turbulent flows over an isolated topographic feature. The numerical simulation and closure calculation setup is similar to that described by FO05. We consider the turbulent interaction of an initial two-dimensional eastward mean flow
![]() $U$
impinging on isolated topography on a
$U$
impinging on isolated topography on a
![]() $\unicode[STIX]{x1D6FD}$
-plane. As noted by FO05, where many references are given, this is an iconic problem in mean flow–topographic interaction going back to the work of Kasahara (Reference Kasahara1966). This is a far from equilibrium problem that is a severe test of the closures with the Rossby wavetrains rapidly spun up in the presence of turbulence. The topography is a circular conical mountain centred at
$\unicode[STIX]{x1D6FD}$
-plane. As noted by FO05, where many references are given, this is an iconic problem in mean flow–topographic interaction going back to the work of Kasahara (Reference Kasahara1966). This is a far from equilibrium problem that is a severe test of the closures with the Rossby wavetrains rapidly spun up in the presence of turbulence. The topography is a circular conical mountain centred at
![]() $30~^{\circ }\text{N}$
,
$30~^{\circ }\text{N}$
,
![]() $180~^{\circ }\text{W}$
, with a height of 2.5 km and a diameter of
$180~^{\circ }\text{W}$
, with a height of 2.5 km and a diameter of
![]() $45^{\circ }$
latitude (figure 1 of FO05) and is also similar to that used in the linear and nonlinear study on the sphere by Frederiksen (Reference Frederiksen1982).
$45^{\circ }$
latitude (figure 1 of FO05) and is also similar to that used in the linear and nonlinear study on the sphere by Frederiksen (Reference Frederiksen1982).
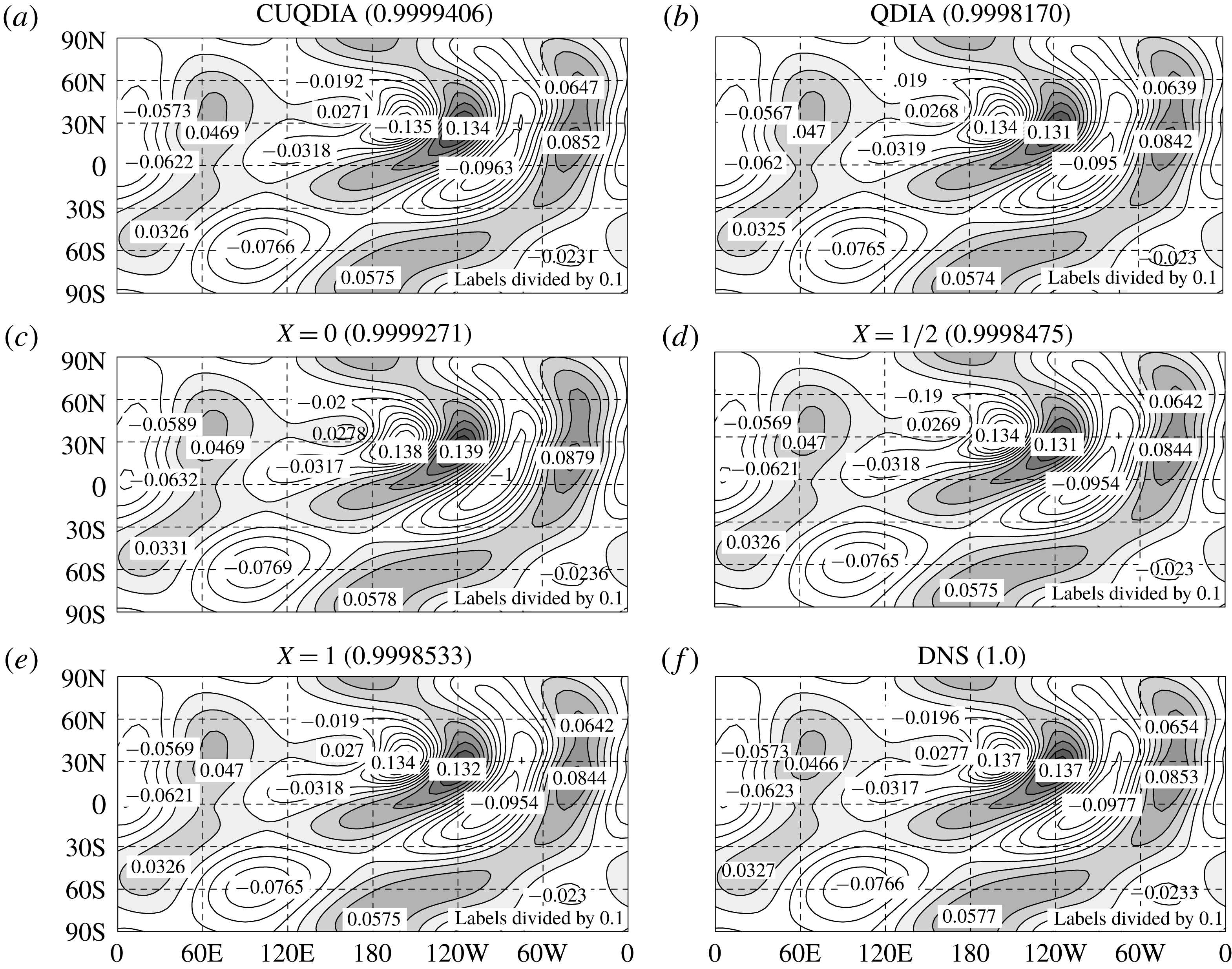
Figure 1. (a) The evolved day 10 CUQDIA, (b) QDIA, (c) MIC with
![]() $X=0$
, (d) MIC with
$X=0$
, (d) MIC with
![]() $X=1/2$
, (e) MIC with
$X=1/2$
, (e) MIC with
![]() $X=1$
and (f) ensemble of DNS Rossby wave streamfunction in non-dimensional units. Multiply values by
$X=1$
and (f) ensemble of DNS Rossby wave streamfunction in non-dimensional units. Multiply values by
![]() $(1/4)a_{e}^{2}\unicode[STIX]{x1D6FA}^{-1}=740~\text{km}^{2}~\text{s}^{-1}$
to convert into units of
$(1/4)a_{e}^{2}\unicode[STIX]{x1D6FA}^{-1}=740~\text{km}^{2}~\text{s}^{-1}$
to convert into units of
![]() $\text{km}^{2}~\text{s}^{-1}$
.
$\text{km}^{2}~\text{s}^{-1}$
.
The focus here is on a case similar to case 1 of FO05 where the initial mean flow
![]() $U$
is eastward at
$U$
is eastward at
![]() $7.5~\text{m}~\text{s}^{-1}$
and the
$7.5~\text{m}~\text{s}^{-1}$
and the
![]() $\unicode[STIX]{x1D6FD}$
-effect is
$\unicode[STIX]{x1D6FD}$
-effect is
![]() $1.15\times 10^{-11}~\text{m}^{-1}~\text{s}^{-1}$
. Throughout we use a length scale of one-half of the Earth’s radius,
$1.15\times 10^{-11}~\text{m}^{-1}~\text{s}^{-1}$
. Throughout we use a length scale of one-half of the Earth’s radius,
![]() $a_{e}/2$
, and a time scale of the inverse of the Earth’s rotation rate,
$a_{e}/2$
, and a time scale of the inverse of the Earth’s rotation rate,
![]() $\unicode[STIX]{x1D6FA}^{-1}$
, which means the non-dimensional values are
$\unicode[STIX]{x1D6FA}^{-1}$
, which means the non-dimensional values are
![]() $U=0.0325$
,
$U=0.0325$
,
![]() $\unicode[STIX]{x1D6FD}=1/2$
and
$\unicode[STIX]{x1D6FD}=1/2$
and
![]() $k_{0}^{2}=1/2$
, and the
$k_{0}^{2}=1/2$
, and the
![]() $\unicode[STIX]{x1D6FD}$
-effect is typical of that at
$\unicode[STIX]{x1D6FD}$
-effect is typical of that at
![]() $60^{\circ }$
latitude. The viscosity is
$60^{\circ }$
latitude. The viscosity is
![]() $2.5\times 10^{4}~\text{m}^{2}~\text{s}^{-1}$
or
$2.5\times 10^{4}~\text{m}^{2}~\text{s}^{-1}$
or
![]() $\hat{\unicode[STIX]{x1D708}}=3.378\times 10^{-5}$
in non-dimensional units and
$\hat{\unicode[STIX]{x1D708}}=3.378\times 10^{-5}$
in non-dimensional units and
![]() $f^{0}=0=\unicode[STIX]{x1D6FC}_{U}$
. Other details of the initial setup are specified in table 1. As well as the large-scale flow
$f^{0}=0=\unicode[STIX]{x1D6FC}_{U}$
. Other details of the initial setup are specified in table 1. As well as the large-scale flow
![]() $U$
the initial conditions include a small-amplitude mean flow, which is localized over the isolated topography, and an isotropic transient spectrum, both of which are specified in table 1. The calculations are started from this mean field, to which is added Gaussian isotropic perturbations with the spectrum given in table 1. The calculations use a circular C16 resolution, with
$U$
the initial conditions include a small-amplitude mean flow, which is localized over the isolated topography, and an isotropic transient spectrum, both of which are specified in table 1. The calculations are started from this mean field, to which is added Gaussian isotropic perturbations with the spectrum given in table 1. The calculations use a circular C16 resolution, with
![]() $k\leqslant 16$
, which is adequate for studying Rossby wave dispersion in a turbulent environment.
$k\leqslant 16$
, which is adequate for studying Rossby wave dispersion in a turbulent environment.
Table 1. Parameters and initial conditions used in the calculations and for figures.
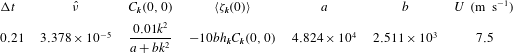
Some care is needed in setting up the 1800 initial conditions for the ensemble of DNS fields that the closure calculations are compared with, as noted by FO05. First a field is constructed as a Gaussian sample with zero mean and unit variance. Then from this field further initial members are obtained by moving its origin by a given increment in the
![]() $x$
-direction and then in the
$x$
-direction and then in the
![]() $y$
-direction. A total of
$y$
-direction. A total of
![]() $n$
realizations are obtained by successively moving the initial field by
$n$
realizations are obtained by successively moving the initial field by
![]() $2\unicode[STIX]{x03C0}/n$
in the
$2\unicode[STIX]{x03C0}/n$
in the
![]() $x$
-direction. By subsequently moving each of these
$x$
-direction. By subsequently moving each of these
![]() $n$
realizations by
$n$
realizations by
![]() $2\unicode[STIX]{x03C0}/n$
in the
$2\unicode[STIX]{x03C0}/n$
in the
![]() $y$
-direction we obtain a total of
$y$
-direction we obtain a total of
![]() $n^{2}$
realizations, and also taking the negative values of each gives
$n^{2}$
realizations, and also taking the negative values of each gives
![]() $2n^{2}$
realizations. The process can be repeated until the required number of realizations are arrived at and the fields then scaled as required and added to the mean vorticity in table 1. The method ensures that the DNS covariance matrix is nearly isotropic for sufficiently large
$2n^{2}$
realizations. The process can be repeated until the required number of realizations are arrived at and the fields then scaled as required and added to the mean vorticity in table 1. The method ensures that the DNS covariance matrix is nearly isotropic for sufficiently large
![]() $n$
.
$n$
.
The time evolutions with the DNS, with two variants of the non-Markovian QDIA and with the three versions of the MIC, are carried out with a time step of
![]() $1/30$
day (non-dimensional
$1/30$
day (non-dimensional
![]() $\unicode[STIX]{x0394}t=0.21$
) for a total of 10 days each. The time stepping employs a predictor–corrector method and the integrals are performed using the trapezoidal rule (Frederiksen et al.
Reference Frederiksen, Davies and Bell1994; OF04; FO05). The CUQDIA calculations use a restart every day as in FO05, but we also integrate the non-Markovian QDIA equations with the full 10-day integrals evaluated without restart. As noted, the CUQDIA uses the calculated off-diagonal elements of the two- and three-point cumulants in the new initial conditions of the periodic restart procedure. This makes the code more efficient at the expense of a judicious choice of the restart time. However, here we have also performed the much larger computational task with the full non-Markovian QDIA to make a very clean comparison with the Markovian closures.
$\unicode[STIX]{x0394}t=0.21$
) for a total of 10 days each. The time stepping employs a predictor–corrector method and the integrals are performed using the trapezoidal rule (Frederiksen et al.
Reference Frederiksen, Davies and Bell1994; OF04; FO05). The CUQDIA calculations use a restart every day as in FO05, but we also integrate the non-Markovian QDIA equations with the full 10-day integrals evaluated without restart. As noted, the CUQDIA uses the calculated off-diagonal elements of the two- and three-point cumulants in the new initial conditions of the periodic restart procedure. This makes the code more efficient at the expense of a judicious choice of the restart time. However, here we have also performed the much larger computational task with the full non-Markovian QDIA to make a very clean comparison with the Markovian closures.
Figure 1 shows the Rossby wavetrains in the zonally asymmetric component of the mean streamfunction on day 10 for the non-Markovian CUQDIA and QDIA closures, for the three variants of the MIC model and for the ensemble of DNS. The wave patterns show the typical Rossby wave dispersion found in both linearized models and in nonlinear simulations (see FO05 and references therein). The results in all six panels are extremely similar. The numbers in brackets above each figure panel are the pattern correlations between each of the closure results and those from the ensemble of DNS. The agreement between the DNS and the three MICs and the non-Markovian QDIA and CUQDIA closures is excellent, with pattern correlations greater than 0.9998 in all cases.
Next we examine the evolution of the statistics through the band-averaged kinetic energy spectra where the mean and transient components are defined as
Here, the average is taken over all
![]() $\boldsymbol{k}$
that lie within a band of unit width at a radius
$\boldsymbol{k}$
that lie within a band of unit width at a radius
![]() $k_{i}$
and the energy of the large-scale flow is plotted at zero wavenumber.
$k_{i}$
and the energy of the large-scale flow is plotted at zero wavenumber.
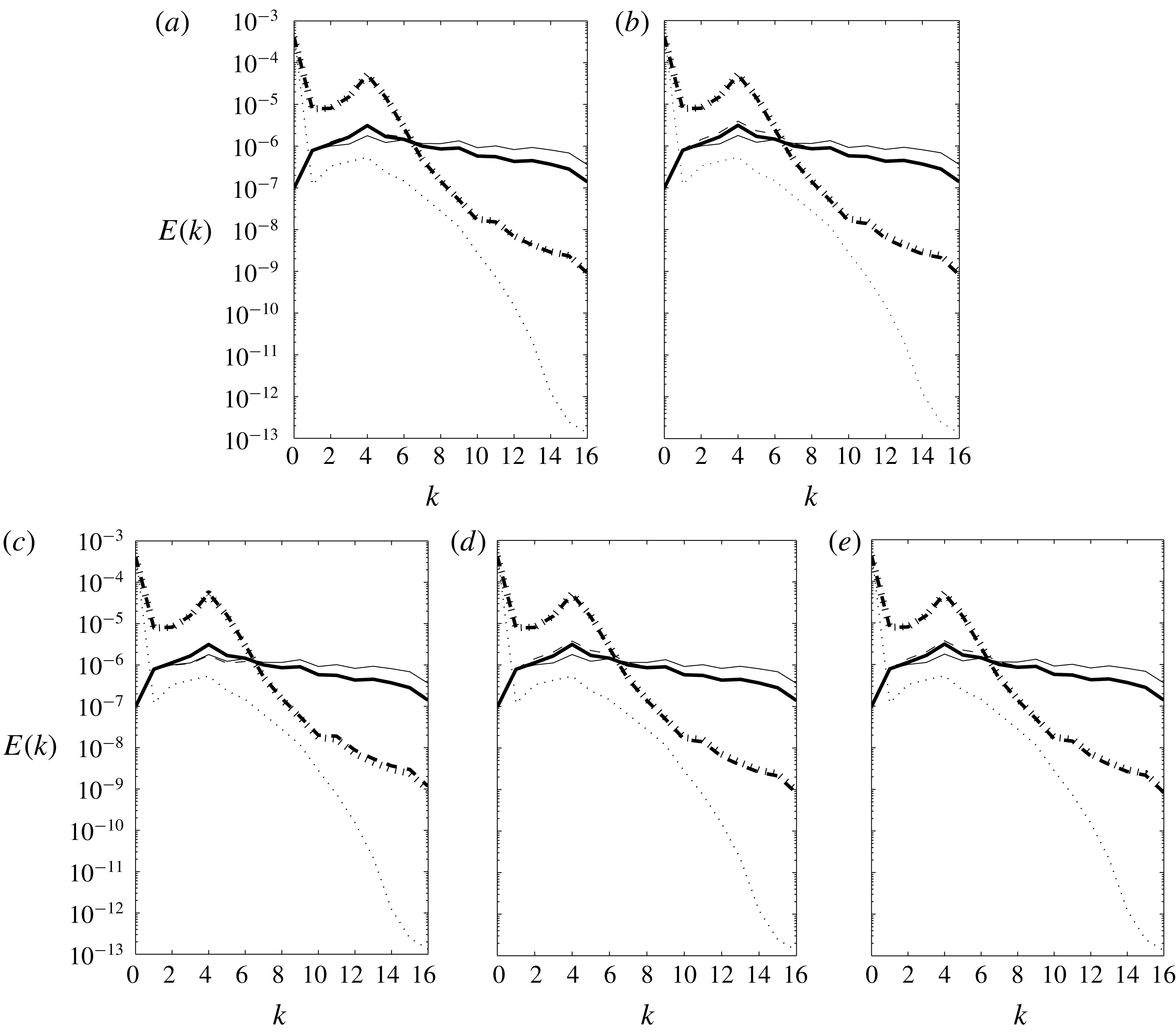
Figure 2. The evolved non-dimensional kinetic energy spectra for the five inhomogeneous closures (a) CUQDIA, (b) QDIA, (c) MIC with
![]() $X=0$
, (d) MIC with
$X=0$
, (d) MIC with
![]() $X=1/2$
, (e) MIC with
$X=1/2$
, (e) MIC with
![]() $X=1$
, and the ensemble of DNS in each panel. Shown are initial mean energy (dotted), initial transient energy (thin solid), evolved DNS transient energy (thick solid), evolved DNS mean energy (short wide dashed), evolved closure transient energy (thin dashed) and evolved closure mean energy (thick dashed). Multiply by
$X=1$
, and the ensemble of DNS in each panel. Shown are initial mean energy (dotted), initial transient energy (thin solid), evolved DNS transient energy (thick solid), evolved DNS mean energy (short wide dashed), evolved closure transient energy (thin dashed) and evolved closure mean energy (thick dashed). Multiply by
![]() $(1/4)a_{e}^{2}\unicode[STIX]{x1D6FA}^{-2}=5.4\times 10^{4}~\text{m}^{2}~\text{s}^{-2}$
to convert into units of
$(1/4)a_{e}^{2}\unicode[STIX]{x1D6FA}^{-2}=5.4\times 10^{4}~\text{m}^{2}~\text{s}^{-2}$
to convert into units of
![]() $\text{m}^{2}~\text{s}^{-2}$
.
$\text{m}^{2}~\text{s}^{-2}$
.
Figure 2 shows the initial and 10-day evolved mean and transient kinetic energy spectra for the non-Markovian CUQDIA and QDIA closures and each of the three variants of the MIC model, and spectra for the ensemble of DNS are also depicted in each panel for comparison. There are only slight differences in the six sets of results on day 10. The CUQDIA kinetic spectra, both mean and transient, are virtually identical to those of the ensemble of DNS, as are the QDIA spectra with just the slightest increase in the transients between wavenumbers 2 and 6. The realizable MIC that employs the correlation FDT (
![]() $X=1/2$
) and the MIC that uses the prior-time FDT (
$X=1/2$
) and the MIC that uses the prior-time FDT (
![]() $X=1$
) again perform exceptionally. For both, the evolved mean kinetic energy spectra are virtually indistinguishable from the ensemble of DNS, as are the transient spectra but with some slight increases between wavenumbers 2 and 6. This range of wavenumbers is of course where the changes in the mean kinetic energy are largest as the Rossby waves amplify, and it is also where there is some increase in the turbulent kinetic energy. The MIC that uses the current-time FDT (
$X=1$
) again perform exceptionally. For both, the evolved mean kinetic energy spectra are virtually indistinguishable from the ensemble of DNS, as are the transient spectra but with some slight increases between wavenumbers 2 and 6. This range of wavenumbers is of course where the changes in the mean kinetic energy are largest as the Rossby waves amplify, and it is also where there is some increase in the turbulent kinetic energy. The MIC that uses the current-time FDT (
![]() $X=0$
) again has evolved mean and transient kinetic energy spectra in close agreement with the ensemble of DNS but with somewhat weaker transients between wavenumbers 2 and 6 than the DNS and other closures. The method of Markovianization for this MIC (with
$X=0$
) again has evolved mean and transient kinetic energy spectra in close agreement with the ensemble of DNS but with somewhat weaker transients between wavenumbers 2 and 6 than the DNS and other closures. The method of Markovianization for this MIC (with
![]() $X=0$
) is of course closest to that employed for the EDQNM where the current-time FDT in (1.2) is also used. Interestingly, the large-amplitude Rossby waves between wavenumbers 2 and 6 will tend to reduce the kinetic energy transfer into those wavenumbers as is the case for the EDQNM (see Frederiksen, Dix & Kepert Reference Frederiksen, Dix and Kepert1996 and references therein). The magnitude of the 10-day evolved relative kinetic energy difference between the closures and DNS,
$X=0$
) is of course closest to that employed for the EDQNM where the current-time FDT in (1.2) is also used. Interestingly, the large-amplitude Rossby waves between wavenumbers 2 and 6 will tend to reduce the kinetic energy transfer into those wavenumbers as is the case for the EDQNM (see Frederiksen, Dix & Kepert Reference Frederiksen, Dix and Kepert1996 and references therein). The magnitude of the 10-day evolved relative kinetic energy difference between the closures and DNS,
![]() $|E(k)-E^{DNS}(k)|/E^{DNS}(k)$
, has a root mean square (r.m.s.) value, over
$|E(k)-E^{DNS}(k)|/E^{DNS}(k)$
, has a root mean square (r.m.s.) value, over
![]() $k$
, that varies little between the closures. The r.m.s. difference is less than 1.8 % for the QDIA, CUQDIA and MIC closure with
$k$
, that varies little between the closures. The r.m.s. difference is less than 1.8 % for the QDIA, CUQDIA and MIC closure with
![]() $X=1$
, for the MIC closure with
$X=1$
, for the MIC closure with
![]() $X=1/2$
it is 1.9 % whereas for
$X=1/2$
it is 1.9 % whereas for
![]() $X=0$
it is 2.1 %. For the QDIA, CUQDIA and MIC closures with
$X=0$
it is 2.1 %. For the QDIA, CUQDIA and MIC closures with
![]() $X=1/2$
and
$X=1/2$
and
![]() $X=1$
the maximum difference in
$X=1$
the maximum difference in
![]() $|E(k)-E^{DNS}(k)|/E^{DNS}(k)$
is
$|E(k)-E^{DNS}(k)|/E^{DNS}(k)$
is
![]() ${\sim}3\,\%$
between wavenumbers 7 and 9 whereas for the MIC with
${\sim}3\,\%$
between wavenumbers 7 and 9 whereas for the MIC with
![]() $X=0$
the peak magnitudes of
$X=0$
the peak magnitudes of
![]() ${\sim}4\,\%$
occur at wavenumbers 11 and 16.
${\sim}4\,\%$
occur at wavenumbers 11 and 16.
Altogether, the performance of the three versions of the MIC model, and of the non-Markovian CUQDIA and QDIA closures, is quite remarkable in this parameter regime of large-scale Rossby wave dispersion over topography in a turbulent environment. As noted, the performance of the MIC with
![]() $X=0$
is slightly poorer in terms of the kinetic energy spectra than the other closures. For higher resolution and higher Reynolds numbers we expect that the MICs, like the non-Markovian DIA (Frederiksen & Davies Reference Frederiksen and Davies2004) and QDIA (OF04), will need to incorporate a regularization, or empirical vertex renormalization, to yield the correct small-scale spectra. The regularized MICs are documented in appendix C.
$X=0$
is slightly poorer in terms of the kinetic energy spectra than the other closures. For higher resolution and higher Reynolds numbers we expect that the MICs, like the non-Markovian DIA (Frederiksen & Davies Reference Frederiksen and Davies2004) and QDIA (OF04), will need to incorporate a regularization, or empirical vertex renormalization, to yield the correct small-scale spectra. The regularized MICs are documented in appendix C.
The results here show the potential of the MICs to reproduce the mean and transient statistics of ensembles of DNS in a strongly inhomogeneous context. If broadly universal and analytic expressions for the triad relaxation times, or the underlying response functions, can be established in the presence of waves and inhomogeneities, then very efficient closures, like the EDQNM, can be developed to tackle the general problem of inhomogeneous turbulent flows.
7 Discussion and conclusions
We have formulated manifestly MIC models for turbulent flows and Rossby waves over topography on a generalized
![]() $\unicode[STIX]{x1D6FD}$
-plane. These have been derived as modifications of the non-Markovian QDIA closure (F99; OF04; FO05) in which the diagonal two-time covariance is replaced by one of three versions of the FDT and the diagonal response function equation is modified to a form that is Markovian. The three different MICs employ the current-time FDT (quasi-stationary), the prior-time FDT (non-stationary) and the correlation FDT, respectively. Bowman (Reference Bowman, Krommes and Ottaviani1993) pointed out that the correlation FDT for homogeneous turbulence, in the presence of waves, together with positive damping in Markovian response functions, resulted in an RMC that guaranteed real and non-negative cumulants
$\unicode[STIX]{x1D6FD}$
-plane. These have been derived as modifications of the non-Markovian QDIA closure (F99; OF04; FO05) in which the diagonal two-time covariance is replaced by one of three versions of the FDT and the diagonal response function equation is modified to a form that is Markovian. The three different MICs employ the current-time FDT (quasi-stationary), the prior-time FDT (non-stationary) and the correlation FDT, respectively. Bowman (Reference Bowman, Krommes and Ottaviani1993) pointed out that the correlation FDT for homogeneous turbulence, in the presence of waves, together with positive damping in Markovian response functions, resulted in an RMC that guaranteed real and non-negative cumulants
![]() $C_{\boldsymbol{k}}(t,t)$
. We have noted that the cumulants
$C_{\boldsymbol{k}}(t,t)$
. We have noted that the cumulants
![]() $C_{\boldsymbol{k}}(t,t)$
are again realizable in the more complex inhomogeneous MIC formalism with the correlation FDT, but, as in the homogeneous case, not necessarily with the current-time FDT or the prior-time FDT. Of course, whether unphysical results arise will depend on the parameter regimes of the flows, and in this article we have documented results for each of the three Markovian closures in the same regimes.
$C_{\boldsymbol{k}}(t,t)$
are again realizable in the more complex inhomogeneous MIC formalism with the correlation FDT, but, as in the homogeneous case, not necessarily with the current-time FDT or the prior-time FDT. Of course, whether unphysical results arise will depend on the parameter regimes of the flows, and in this article we have documented results for each of the three Markovian closures in the same regimes.
The MICs differ from the non-Markovian QDIA closure in that the response function has been modified to a form that is Markovian and the time history integrals have also been modified by the FDTs in such a way that their information can be characterized by three triad relaxation functions (for each variant) that satisfy auxiliary Markovian tendency equations. Thus, the MICs contain much the same information as the non-Markovian QDIA, but the time history integrals can be replaced by differential equations that become relatively more efficient for long integrations. In addition, there is the prospect of developing analytical forms of the triad relaxation functions, or underpinning response functions, as is the case for isotropic EDQNM closures, that would increase the computational efficiency enormously.
The performance of the three MICs has been compared with results from an 1800 member ensemble of DNS and with the non-Markovian QDIA and CUQDIA closures for turbulent flow over isolated topography on a generalized
![]() $\unicode[STIX]{x1D6FD}$
-plane. For each of these calculations, the initial flow consists of an eastward mean flow
$\unicode[STIX]{x1D6FD}$
-plane. For each of these calculations, the initial flow consists of an eastward mean flow
![]() $U$
, together with smaller-amplitude mean and transient ‘small scales’. The impact of the mean flow on the conical mountain topography results in the rapid generation of large-amplitude Rossby waves in a turbulent environment in 10-day integrations. The calculations are performed at a C16 resolution with wavenumbers
$U$
, together with smaller-amplitude mean and transient ‘small scales’. The impact of the mean flow on the conical mountain topography results in the rapid generation of large-amplitude Rossby waves in a turbulent environment in 10-day integrations. The calculations are performed at a C16 resolution with wavenumbers
![]() $k\leqslant 16$
, which is sufficient for this large-scale process. This is a far from equilibrium process (Frederiksen Reference Frederiksen1982; FO05), which severely tests the closures. The performance of each of the three MICs, and the non-Markovian QDIA integrated without a restart over the 10 days, is excellent, like the CUQDIA closure calculations with periodic 1-day restarts (FO05). In all cases, the pattern correlations of the day 10 mean Rossby wave streamfunction for the closures with the ensemble result for 1800 DNS are greater than 0.9998. Over the 10 days, there is significant evolution of the mean and transient energy spectra particularly between wavenumbers 2 and 6 where the Rossby waves amplify by orders of magnitude in the mean; in this range, there are some slight differences in the transient kinetic energy between the MIC calculations and the ensemble of 1800 DNS. The MIC with
$k\leqslant 16$
, which is sufficient for this large-scale process. This is a far from equilibrium process (Frederiksen Reference Frederiksen1982; FO05), which severely tests the closures. The performance of each of the three MICs, and the non-Markovian QDIA integrated without a restart over the 10 days, is excellent, like the CUQDIA closure calculations with periodic 1-day restarts (FO05). In all cases, the pattern correlations of the day 10 mean Rossby wave streamfunction for the closures with the ensemble result for 1800 DNS are greater than 0.9998. Over the 10 days, there is significant evolution of the mean and transient energy spectra particularly between wavenumbers 2 and 6 where the Rossby waves amplify by orders of magnitude in the mean; in this range, there are some slight differences in the transient kinetic energy between the MIC calculations and the ensemble of 1800 DNS. The MIC with
![]() $X=0$
is slightly poorer in terms of the kinetic energy spectra than the other closures.
$X=0$
is slightly poorer in terms of the kinetic energy spectra than the other closures.
We have also formulated a regularized version of the inhomogeneous closures, along the lines of the regularized DIA closure of Frederiksen & Davies (Reference Frederiksen and Davies2004) and the regularized QDIA closure of OF04, which are needed for high-resolution and high-Reynolds-number calculations. The regularized closures have a wavenumber cut-off parameter
![]() $\unicode[STIX]{x1D6FC}$
which localizes the interactions, and corresponds to an empirical vertex renormalization (C.1). It has been found that the value of
$\unicode[STIX]{x1D6FC}$
which localizes the interactions, and corresponds to an empirical vertex renormalization (C.1). It has been found that the value of
![]() $\unicode[STIX]{x1D6FC}$
that is consistent with inertial range behaviour in the DIA (Frederiksen & Davies Reference Frederiksen and Davies2004) and QDIA (OF04) is essentially universal.
$\unicode[STIX]{x1D6FC}$
that is consistent with inertial range behaviour in the DIA (Frederiksen & Davies Reference Frederiksen and Davies2004) and QDIA (OF04) is essentially universal.
In future studies we aim to experiment with different analytical expressions of the triad relaxation functions, or underpinning Markovian response functions, to see whether it is possible to establish Markovian closures for the inhomogeneous problem in the presence of waves that have similar computational efficiency to the EDQNM closure for isotropic turbulence. We also aim to examine the performance of regularized versions of the Markovian closures at high resolution and Reynolds numbers. We further seek to generalize the LET closure of McComb (Reference McComb1974, Reference McComb1990, Reference McComb2014) to inhomogeneous turbulent flows and compare the performance of non-Markovian and Markovian variants.
Acknowledgement
T.J.O. is supported by the CSIRO Decadal Forecasting project (https://research.csiro.au/dfp).
Appendix A. Interaction coefficients
As discussed in FO05, when the spectral equations for the small-scale and the large-scale flow are combined into a single equation as in (3.3), the required interaction coefficients are
and
Here, the zero wave vector representing the large-scale flow is included by defining
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $\hat{q}_{y}$
and
$\hat{q}_{y}$
and
![]() $\hat{p}_{y}$
as follows:
$\hat{p}_{y}$
as follows:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}-{\textstyle \frac{1}{2}}k_{0}\quad & \text{if }\boldsymbol{k}=\mathbf{0},\\ k_{0}\quad & \text{if }\boldsymbol{q}=\mathbf{0}\text{ or }\boldsymbol{p}=\mathbf{0},\\ 1\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}-{\textstyle \frac{1}{2}}k_{0}\quad & \text{if }\boldsymbol{k}=\mathbf{0},\\ k_{0}\quad & \text{if }\boldsymbol{q}=\mathbf{0}\text{ or }\boldsymbol{p}=\mathbf{0},\\ 1\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
and
Appendix B. QDIA two- and three-point cumulant and response function terms
Here we summarize expressions and relations for the two-point and three-point cumulants and response functions that are needed to close the QDIA equations. The first two relationships determine the QDIA off-diagonal elements of the two-point cumulant and response function through
 $$\begin{eqnarray}\displaystyle & & \displaystyle C_{\boldsymbol{k},-\boldsymbol{l}}(t,t^{\prime })=\int _{t_{0}}^{t}\text{d}s\,R_{\boldsymbol{k}}(t,s)C_{\boldsymbol{l}}(s,t^{\prime })[A(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})h_{(\boldsymbol{k}-\boldsymbol{l})}+2K(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\langle \unicode[STIX]{x1D701}_{(\boldsymbol{k}-\boldsymbol{l})}(s)\rangle ]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{t_{0}}^{t^{\prime }}\text{d}s\,R_{-\boldsymbol{l}}(t^{\prime },s)C_{\boldsymbol{k}}(t,s)[A(-\boldsymbol{l},\boldsymbol{k},\boldsymbol{l}-\boldsymbol{k})h_{(\boldsymbol{k}-\boldsymbol{l})}+2K(-\boldsymbol{l},\boldsymbol{k},\boldsymbol{l}-\boldsymbol{k})\langle \unicode[STIX]{x1D701}_{(\boldsymbol{k}-\boldsymbol{l})}(s)\rangle ]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C_{\boldsymbol{k},-\boldsymbol{l}}(t,t^{\prime })=\int _{t_{0}}^{t}\text{d}s\,R_{\boldsymbol{k}}(t,s)C_{\boldsymbol{l}}(s,t^{\prime })[A(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})h_{(\boldsymbol{k}-\boldsymbol{l})}+2K(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\langle \unicode[STIX]{x1D701}_{(\boldsymbol{k}-\boldsymbol{l})}(s)\rangle ]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{t_{0}}^{t^{\prime }}\text{d}s\,R_{-\boldsymbol{l}}(t^{\prime },s)C_{\boldsymbol{k}}(t,s)[A(-\boldsymbol{l},\boldsymbol{k},\boldsymbol{l}-\boldsymbol{k})h_{(\boldsymbol{k}-\boldsymbol{l})}+2K(-\boldsymbol{l},\boldsymbol{k},\boldsymbol{l}-\boldsymbol{k})\langle \unicode[STIX]{x1D701}_{(\boldsymbol{k}-\boldsymbol{l})}(s)\rangle ]\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle R_{\boldsymbol{k},\boldsymbol{l}}(t,t^{\prime }) & = & \displaystyle \int _{t^{\prime }}^{t}\text{d}s\,R_{\boldsymbol{k}}(t,s)R_{\boldsymbol{l}}(s,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,[A(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})h_{(\boldsymbol{k}-\boldsymbol{l})}+2K(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\langle \unicode[STIX]{x1D701}_{(\boldsymbol{k}-\boldsymbol{l})}(s)\rangle ].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{\boldsymbol{k},\boldsymbol{l}}(t,t^{\prime }) & = & \displaystyle \int _{t^{\prime }}^{t}\text{d}s\,R_{\boldsymbol{k}}(t,s)R_{\boldsymbol{l}}(s,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \times \,[A(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})h_{(\boldsymbol{k}-\boldsymbol{l})}+2K(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\langle \unicode[STIX]{x1D701}_{(\boldsymbol{k}-\boldsymbol{l})}(s)\rangle ].\end{eqnarray}$$
These relationships between the first-order renormalized off-diagonal elements of the two-point cumulant, or covariance, and response function and the diagonal components and mean field and topography were derived in F99. They apply for the case of homogeneous initial conditions. For inhomogeneous initial conditions an extra term appears in the two-point cumulant as given in equation (5.4) of FO05.
We shall also need expressions for the three-point cumulant and between the response function and perturbation field, which for the QDIA are
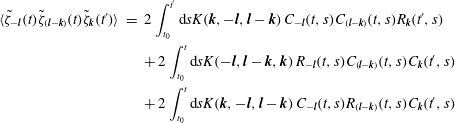 $$\begin{eqnarray}\displaystyle \langle \tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{l}}(t)\tilde{\unicode[STIX]{x1D701}}_{(\boldsymbol{l}-\boldsymbol{k})}(t)\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{k}}(t^{\prime })\rangle & = & \displaystyle 2\int _{t_{0}}^{t^{\prime }}\text{d}sK(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\,C_{-\boldsymbol{l}}(t,s)C_{(\boldsymbol{l}-\boldsymbol{k})}(t,s)R_{\boldsymbol{k}}(t^{\prime },s)\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{t_{0}}^{t}\text{d}sK(-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k},\boldsymbol{k})\,R_{-\boldsymbol{l}}(t,s)C_{(\boldsymbol{l}-\boldsymbol{k})}(t,s)C_{\boldsymbol{k}}(t^{\prime },s)\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{t_{0}}^{t}\text{d}sK(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\,C_{-\boldsymbol{l}}(t,s)R_{(\boldsymbol{l}-\boldsymbol{k})}(t,s)C_{\boldsymbol{k}}(t^{\prime },s)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \tilde{\unicode[STIX]{x1D701}}_{-\boldsymbol{l}}(t)\tilde{\unicode[STIX]{x1D701}}_{(\boldsymbol{l}-\boldsymbol{k})}(t)\tilde{\unicode[STIX]{x1D701}}_{\boldsymbol{k}}(t^{\prime })\rangle & = & \displaystyle 2\int _{t_{0}}^{t^{\prime }}\text{d}sK(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\,C_{-\boldsymbol{l}}(t,s)C_{(\boldsymbol{l}-\boldsymbol{k})}(t,s)R_{\boldsymbol{k}}(t^{\prime },s)\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{t_{0}}^{t}\text{d}sK(-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k},\boldsymbol{k})\,R_{-\boldsymbol{l}}(t,s)C_{(\boldsymbol{l}-\boldsymbol{k})}(t,s)C_{\boldsymbol{k}}(t^{\prime },s)\nonumber\\ \displaystyle & & \displaystyle +\,2\int _{t_{0}}^{t}\text{d}sK(\boldsymbol{k},-\boldsymbol{l},\boldsymbol{l}-\boldsymbol{k})\,C_{-\boldsymbol{l}}(t,s)R_{(\boldsymbol{l}-\boldsymbol{k})}(t,s)C_{\boldsymbol{k}}(t^{\prime },s)\end{eqnarray}$$
and
A simple derivation of these relationships that apply to the DIA, and to the QDIA, appears in Frederiksen (Reference Frederiksen, Ball and Akhmediev2003) for the case of Gaussian initial conditions. For non-Gaussian initial conditions the initial three-point function also appears as shown in (5.8) of FO05. A complete derivation of the two-point and three-point terms needed in the cumulant update QDIA closure is also presented by O’Kane & Frederiksen (Reference O’Kane and Frederiksen2010).
Appendix C. Regularization of MICs
Here, we summarize the regularization of the MICs that will be needed to simulate the small scales of high-Reynolds-number turbulence just as is needed for the non-Markovian DIA (Frederiksen & Davies Reference Frederiksen and Davies2004) and QDIA (OF04) closures. The regularization involves modifying the interaction coefficients, vertices, to localize the interactions. The reasons for this are discussed in some detail by Frederiksen & Davies (Reference Frederiksen and Davies2004 and references therein). Thus, the interaction coefficients are modified to
Here,
![]() $\breve{{\mathcal{D}}}_{\boldsymbol{k}}^{j}$
are defined through equations (5.6) and (5.7) with the replacements
$\breve{{\mathcal{D}}}_{\boldsymbol{k}}^{j}$
are defined through equations (5.6) and (5.7) with the replacements
![]() $A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{A}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
and
$A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{A}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
and
![]() $K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{K}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
. In the original notation the regularized Markov version of response function equation takes the form
$K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{K}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
. In the original notation the regularized Markov version of response function equation takes the form
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}R_{\boldsymbol{k}}(t,t^{\prime })+\left[\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}+\int _{t_{0}}^{t}\text{d}s\{(\breve{\unicode[STIX]{x1D702}}_{\boldsymbol{ k}}(t,s)+\breve{\unicode[STIX]{x03C0}}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t,s)[C_{\boldsymbol{k}}(t,t)]^{-1}\}\right]R_{\boldsymbol{ k}}(t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \phantom{\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}R_{\boldsymbol{k}}(t,t^{\prime })+}=\unicode[STIX]{x1D6FF}(t-t^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}R_{\boldsymbol{k}}(t,t^{\prime })+\left[\unicode[STIX]{x1D708}_{0}(\boldsymbol{k})k^{2}+\int _{t_{0}}^{t}\text{d}s\{(\breve{\unicode[STIX]{x1D702}}_{\boldsymbol{ k}}(t,s)+\breve{\unicode[STIX]{x03C0}}_{\boldsymbol{k}}(t,s))C_{-\boldsymbol{k}}(t,s)[C_{\boldsymbol{k}}(t,t)]^{-1}\}\right]R_{\boldsymbol{ k}}(t,t^{\prime })\nonumber\\ \displaystyle & & \displaystyle \phantom{\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}R_{\boldsymbol{k}}(t,t^{\prime })+}=\unicode[STIX]{x1D6FF}(t-t^{\prime })\end{eqnarray}$$
for
![]() $t\geqslant t^{\prime }$
. Here,
$t\geqslant t^{\prime }$
. Here,
![]() $\breve{\unicode[STIX]{x1D702}}_{\boldsymbol{k}}(t,s)$
is given by (4.5a
) and
$\breve{\unicode[STIX]{x1D702}}_{\boldsymbol{k}}(t,s)$
is given by (4.5a
) and
![]() $\breve{\unicode[STIX]{x03C0}}_{\boldsymbol{k}}(t,s)$
by (4.10c
) with the replacements
$\breve{\unicode[STIX]{x03C0}}_{\boldsymbol{k}}(t,s)$
by (4.10c
) with the replacements
![]() $A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{A}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
and
$A(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{A}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
and
![]() $K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{K}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
. In the equations for the triad relaxation times
$K(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})\rightarrow \breve{K}(\boldsymbol{k},\boldsymbol{p},\boldsymbol{q})$
. In the equations for the triad relaxation times
![]() $\breve{{\mathcal{D}}}_{\boldsymbol{k}}^{j}$
replace
$\breve{{\mathcal{D}}}_{\boldsymbol{k}}^{j}$
replace
![]() ${\mathcal{D}}_{\boldsymbol{k}}^{j}$
, but the single-time covariance equations (4.9) and (5.8) and the mean-field equations (4.7) and (5.12) remain unchanged.
${\mathcal{D}}_{\boldsymbol{k}}^{j}$
, but the single-time covariance equations (4.9) and (5.8) and the mean-field equations (4.7) and (5.12) remain unchanged.
The studies of Frederiksen & Davies (Reference Frederiksen and Davies2004) and OF04 suggest that the correct small-scale spectral behaviour is obtained with a value of
![]() $\unicode[STIX]{x1D6FC}$
, which is essentially universal or only weakly flow-dependent.
$\unicode[STIX]{x1D6FC}$
, which is essentially universal or only weakly flow-dependent.







