1 Introduction
The asset allocation, performance and risk of a defined-contribution (DC) pension plan during its accumulation and decumulation phases have received considerable interest in the literature since DC plans became viable alternatives to defined-benefit (DB) plans.Footnote 1 Two important characteristics of a DC plan are that affiliates (participants) bear the risk associated with fluctuations in asset values and that imposed administrative charges have direct and significant effects on the terminal wealth of the corresponding individual retirement accounts (IAs).Footnote 2 Substantial attention has been devoted to these charges, particularly in countries that have partially or completely transformed their public DB pension systems into individual capitalization systems.Footnote 3 Furthermore, high charges in IA systems are a primary target of criticism; these charges discourage participation, damage systems' reputations, reduce future pensions and increase future costs for the government in cases involving a guaranteed minimum pension (James et al., Reference James, Smalhout and Vittas2001 and Whitehouse, Reference Whitehouse2001).
The objective of this paper is to compare the outcome when fees are levied proportional to flow (or as a percentage of the affiliate's salary) with the outcome when fees are proportional to assets (the balance in the IA).Footnote 4 These two types of administrative charges are the most common fees in IA pension systems (Kritzer et al., Reference Kritzer, Kay and Sinha2011).Footnote 5 This study was partly motivated by the most recent reform of the Peruvian Private Pension System (PPS), which occurred in 2012 and required participants to choose one of the two aforementioned types of fees. With the objective of evaluating the likely impact of this reform and similar reforms on the welfare of participants in IA pension systems, we construct a model to compare both types of fees and analyze how these fees affect welfare when interacting with both risk aversion and the stability of contributions over an affiliate's working life. Such stability can be measured by density of contribution (DoC), which is defined as the ratio between the periods during which contributions are paid or credited and the total number of potential contribution periods.Footnote 6 , Footnote 7
As noted in the literature review, the optimal asset allocation of DC funds is primarily studied using an expected utility maximization criterion; however, when administrative charges are compared, it is customary to utilize procedures or techniques that are based either on an IA's expected terminal wealth or on the assumption of risk-neutral preferences. Therefore, we close this literature gap by introducing risk aversion into comparisons of fees on flow and balance. To perform these comparisons, we use the ratio between the expected utility of terminal wealth generated with a charge on balance and the corresponding expected utility for a charge on flow. Assuming that both charges yield the same expected terminal wealth and the expected DoC remains constant during the accumulation phase, we prove that the more risk-averse the affiliate is, the more the charge on balance improves with respect to the charge on flow. We also compare the fee schemes using the ratio between expected value and the standard deviation of terminal wealth and demonstrate that the charge on balance always generates a better ratio when the contribution stream is uninterrupted. However, if DoC is introduced into this final scenario, then the growth rate of the IA must be greater than the growth in contributions (salaries) to achieve the same theoretical result.
We apply the proposed methodology in comparisons of the fees charged to the PPS's participants. For a constant charge of 1% on balances (as a ratio of total fees to total assets of the system) and a charge on flow equal to 16.2% of every contribution (the PPS's average fee), a representative participant with an accumulation period of 45 years and a high degree of risk aversion could obtain an 8% greater certainty equivalent for terminal wealth when fees are levied on flow instead of balance. In a case involving a low degree of risk aversion, this difference is reduced to 4%. However, if the accumulation phase is only 15 years, the charge on balance generates a certainty equivalent 10% greater than the certainty equivalent for the charge on flow, and the effect of risk aversion becomes almost negligible. Moreover, for all examined degrees of risk aversion, assuming fixed charges as specified above, the charge on flow is preferable for participants younger than 28 years of age, whereas the charge on balance is preferable for affiliates older than 34 years of age. Finally, DoC does not constitute an important variable in these comparisons because certainty equivalent ratios remain approximately constant despite dramatic changes in DoC.
The remainder of the paper proceeds as follows. Section 2 introduces a methodology for mathematically representing charges on balance and flow and the interruption of contributions in a DC pension plan. Section 3 presents and analyzes the ratios used for comparisons of the aforementioned administrative charges. Section 4 discusses the application of the methodology to the Peruvian PPS, and Section 5 draws conclusions.
2 Methodology
Consider i ∈ ℕ and T ∈ ℕ+ such that 0 ≤ i ≤ T − 1, where i represents a particular month and T is the number of months before the affiliate's retirement, i.e., the length of her accumulation phase. We assume that the share value, V, of a representative pension fund managed by a Pension Fund Administrator (PFA) at time t ∈ ℝ+ (expressed in months) satisfies the following stochastic differential equation (SDE):
$$dV(t) = \mu V(t)dt + \sigma V(t)dB(t),\quad V(0) = {V_0},$$
where μ is the monthly growth rate of the share value, σ is the monthly volatility of its log-returns, V 0 is the initial share value, and B is a one-dimensional standard Brownian motion. The SDE in (1) is a common specification to model asset values, and it is heavily utilized in the stochastic control of DC pension funds, as mentioned in the introduction. Next, we describe in detail the charges on flow and balance using a structure similar to those considered in Shah (Reference Shah1997), Diamond (Reference Diamond and Shoven2000), Blake and Board (Reference Blake and Board2000), Whitehouse (2001), Devesa-Carpio et al. (Reference Devesa-Carpio, Rodríguez-Barrera and Vidal-Meliá2003) and Gómez-Hernández and Stewart (Reference Gómez-Hernández and Stewart2008).
2.1 Charge on balance
Let δ > 0 be the monthly charge on balanceFootnote
8
expressed in continuous time, and let
${{\rm {\cal W}}_T} = \{ {W_i}\;\vert \;{W_i} \gt 0,\;0 \le i \le T - 1\} $
be the affiliate's contribution stream. Then, at the beginning of month i the affiliate contributes an amount W
i
to her individual account.Footnote
9
If the share value, V, is normalized to the unit in month i, then contribution W
i
is equivalent to the same number of shares. For t ≥ i, and considering the SDE in (1), month i's contribution will evolve according to the following geometric Brownian motion (GBM):
$$W_s^i (t) = {W_i}{e^{(\mu - \delta - ({\sigma ^2}/2))(t - i) + \sigma (B(t) - B(i))}},\quad i \le t \le T.$$
It is in the affiliate's interest to determine the value of her IA at the end of the accumulation period. We denote the final wealth as W s (T), and it corresponds to the sum of the terminal values of all contributions made according to (2). Consequently,
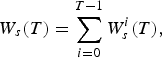$${W_s}(T) = \sum\limits_{i = 0}^{T - 1} W_s^i (T),$$
where all processes
$W_s^i $
are driven by the same source of uncertainty B in SDE (1).
2.2 Charge on flow
Let α > 0 be the charge on flow.Footnote
10
If the affiliate makes a contribution W
i
in month i, then the charge she will pay to the PFA (at the moment the contribution is made) will be equal to C
i
= W
i
(1 − e
−α
). Considering that C
i
is not discounted from W
i
(which is the most common case in DC pension funds), it could have been invested in the fund, so it is possible to express contribution W
i
as e
−α
W
i
to adjust for the opportunity cost of C
i
. Under this assumption, the adjusted contribution in month i,
$W_f^i $
, will evolve based on the following GBM:
$$W_f^i (t) = {W_i}{e^{ - \alpha}} {e^{(\mu - ({\sigma ^2}/2))(t - i) + \sigma (B(t) - B(i))}},\quad i \le t \le T.$$
The affiliate considers it important to compute her final wealth adjusted for the charge on flow. If we denote this amount as W f (T), we obtain
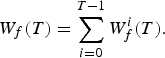$${W_f}(T) = \sum\limits_{i = 0}^{T - 1} W_f^i (T).$$
Recall that W f (T) represents not the affiliate's true wealth at the end of the accumulation phase but her final wealth adjusted for the opportunity cost generated by the charge on flow. The terminal wealth in her individual account will be equal to e α W f (T). Consequently, only when the opportunity cost is considered can variables W f (T) and W s (T) be compared.
2.3 Interruption in contributions
There is a possibility that for some month i, the affiliate will not be able to contribute an amount W
i
to her IA. To represent such interruptions, we introduce sequence
${{\rm {\cal P}}_T} = \{ {p_i}\;\vert \;{p_i} \in [0,1],0 \le i \le T - 1\} $
and a stochastic process Z = {Z
i
, 0 ≤ i ≤ T − 1}, independent of process B, such that Z is a sequence of independent Bernoulli(p
i
) random variables with at least one i* such that p
i* > 0. If Z
i
= 0, then there is no contribution in period i, which occurs with probability 1 − p
i
. Note that process Z is one of the simplest ways to introduce interruptions in
${{\rm {\cal W}}_T}$
. We also define
$${\widehat{W}_s}(T) = \sum\limits_{i = 0}^{T - 1} {Z_i}W_s^i (T),$$
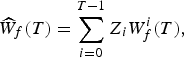$${\widehat{W}_f}(T) = \sum\limits_{i = 0}^{T - 1} {Z_i}W_f^i (T),$$
where
$W_s^i (T)$
and
$W_f^i (T)$
are given by (2) and (4), respectively. Both
${\widehat{W}_s}(T)$
and
${\widehat{W}_f}(T)$
represent the adjusted terminal wealth (under balance and flow charges) when interruptions are introduced by means of the stochastic process Z.
If we compute the expected values of
${\widehat{W}_s}(T)$
and
${\widehat{W}_f}(T)$
, we have
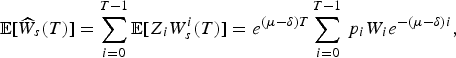$${\rm {\opf E}}[{\widehat{W}_s}(T)] = \sum\limits_{i = 0}^{T - 1} {\rm {\opf E}}[{Z_i}W_s^i (T)] = {e^{(\mu - \delta )T}}\sum\limits_{i = 0}^{T - 1} {\,p_i}{W_i}{e^{ - (\mu - \delta )i}},$$
$${\rm {\opf E}}[{\widehat{W}_f}(T)] = \sum\limits_{i = 0}^{T - 1} {\rm {\opf E}}[{Z_i}W_f^i (T)] = {e^{ - \alpha + \mu T}}\sum\limits_{i = 0}^{T - 1} {p_i}{W_i}{e^{ - \mu i}}.$$
To obtain (8) and (9), we used the independence of Z
i
with respect to
$W_s^i (T)$
and
$W_f^i (T)$
. Moreover, the variances of
${\widehat{W}_s}(T)$
and
${\widehat{W}_f}(T)$
can be determined using the following proposition.
Proposition 2.1
(Variance of adjusted terminal wealth).
Under interruption process Z, the variances of
${\widehat{W}_s}(T)$
and
${\widehat{W}_f}(T)$
in (6) and (7) are
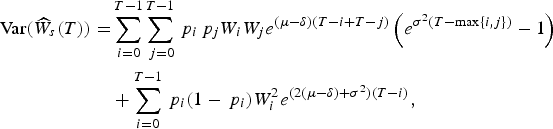$$\eqalign{{\rm Var}({\widehat{W}_s}(T)) = & \sum\limits_{i = 0}^{T - 1} \sum\limits_{\,j = 0}^{T - 1} {\,p_i}{\,p_j}{W_i}{W_j}{e^{(\mu - \delta )(T - i + T - j)}}\left( {{e^{{\sigma ^2}(T - {\rm max}\{ i,j\} )}} - 1} \right) \cr & + \sum\limits_{i = 0}^{T - 1} {\,p_i}(1 - {\,p_i})W_i^2 {e^{(2(\mu - \delta ) + {\sigma ^2})(T - i)}},} $$
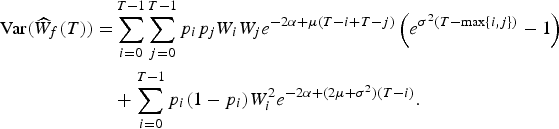$$\eqalign{{\rm Var}({\widehat{W}_f}(T)) = & \sum\limits_{i = 0}^{T - 1} \sum\limits_{j = 0}^{T - 1} {p_i}{p_j}{W_i}{W_j}{e^{ - 2\alpha + \mu (T - i + T - j)}}\left( {{e^{{\sigma ^2}(T - {\rm max}\{ i,j\} )}} - 1} \right) \cr & + \sum\limits_{i = 0}^{T - 1} {p_i}(1 - {p_i})W_i^2 {e^{ - 2\alpha + (2\mu + {\sigma ^2})(T - i)}}.} $$
Proof. See Appendix A.1 (online).
The variances in the absence of interruptions, Var(W s (T)) and Var(W f (T)), can be found considering p i = 1 for all i in (10) and (11). If we assume p i = p for all 0 ≤ i ≤ T − 1, then the affiliate has the same probability of contributing each month, and p can be interpreted as the affiliate's DoC.
2.4 Risk factors
So far, we have considered two main risk factors: the return on assets given by SDE (1) and the interruption in contributions given by the stochastic process Z defined in Section 2.3. We have not considered randomness in the level of contributions, even though they are often expressed as a percentage of wages and are indexed to inflation. Moreover, in a market with stochastic returns, it is well known that a correlation exists between inflation rates and returns.Footnote
11
Consequently, introducing randomness to returns but not to contributions could lead to false conclusions because both depend on inflation. We could work in nominal terms imposing a stochastic process to
${{\rm {\cal W}}_T}$
with some correlation with process V; however, we preferred to work with a deterministic sequence of contributions
${{\rm {\cal W}}_T}$
; to account for inflation, we are considering and calibrating both returns (given by process V) and contributions in real terms.
2.5 Terminology
Throughout this section, we have used terminology related to DC pension plans in Peru and other countries in Latin America with private pension systems – more specifically, the cases of Chile, Colombia and Mexico. However, there is a possibility that either the definitions or the methodology might be opaque to an audience familiar with DC institutions in other countries. In an effort to add clarity to the paper, we will try to relate our definitions to those for 401(k) plans in the USA.
The employer serves as the plan sponsor for the 401(k) and hires a firm, the plan vendor (it may be a mutual fund company, a brokerage firm or an insurance company), to administer the plan and its investments. In our methodology, the PFA acts as the plan vendor but with the difference that it is never selected by the employer but instead it is chosen by the employee. Therefore, the figure of the plan sponsor does not exist in our case. Once an employee voluntarily signs up for a 401(k), she becomes a participant (or what we call an ‘affiliate’), and then she decides how much to contribute to her individual account. In our framework, participation in the DC plan is mandatory and the rate of contribution is fixed as a percentage of the employee's monthly wage.Footnote 12 Typically, a 401(k) participant cannot withdraw her money before reaching 59.5 years of age, and early withdrawals are usually subject to a penalty. For example, in the Peruvian PPS, it is not possible to withdraw any part of the individual fund before reaching 65 years of age (the common retirement age); there are options for early retirement after the age of 50 but only in cases of prolonged unemployment.Footnote 13
Plan vendors in the USA usually offer a wide array of investment alternatives to participants; on the contrary, Latin American PFAs generally offer limited choices. As an example, Peruvian PFAs manage only three funds – high, medium (default option) and low risk – and the affiliate decides in which to invest her contributions. To cover the expenses of providing a 401(k) plan,Footnote 14 fees are paid by the plan itself, the employer, and/or the plan participants. These fees can be levied based on the number of participants, the amount of assets, or as a fixed dollar amount for the plan as a whole. In Latin American DC funds, the administrative charges introduced in Sections 2.1 and 2.2 cover the aforementioned expenses and are levied by the PFA but are paid only by the affiliate; i.e., the employer does not pay any fee or charge to the PFA. Finally, it is common that the PFA establishes a unique fee (either on balance or flow) for all its affiliates, so the fee structure is simpler than that of 401(k) plans.
3 Comparing charges on balance and flow
A particular affiliate wants to determine or assess the suitability of the administrative charges by contrasting
${\widehat{W}_s}(T)$
and
${\widehat{W}_f}(T)$
. The comparison could be performed using, among other forms, expected values, ratios of expected value to standard deviation, and expected utilities. We proceed to describe each of the three methods in detail.
3.1 Expected terminal wealth
If a comparison is performed using the expected value of adjusted terminal wealth, then we can define
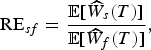$${\rm R}{{\rm E}_{sf}} = \displaystyle{{{\rm {\opf E}}[{{\widehat{W}}_s}(T)]} \over {{\rm {\opf E}}[{{\widehat{W}}_f}(T)]}},$$
where
${\rm {\opf E}}[{\widehat{W}_s}(T)]$
and
${\rm {\opf E}}[{\widehat{W}_f}(T)]$
are given by expressions (8) and (9), respectively. In this criterion, if RE
sf
> 1, the charge on balance will be preferred. If RE
sf
< 1, then the charge on flow will be preferred. This criterion will be adequate for a risk-neutral affiliate who only cares about adjusted terminal wealth. The next proposition studies the effect of the growth rate μ on RE
sf
.
Proposition 3.1
(Derivative of RE sf with respect to μ).
In process Z, we assume there exists i** ≠ i* such that p i ** ∈ (0, 1] and i* was defined in Section 2.3. If we consider RE sf in (12) as a function of the growth rate μ, then for every μ and T >1:
$$\displaystyle{{\partial {\rm R}{{\rm E}_{sf}}(\mu )} \over {\partial \mu}} \lt 0.$$
Proof. See Appendix A.2 (online).
Proposition 3.1 shows that higher growth rates benefit the charge on flow relative to the charge on balance, or more intuitively, if the mean return increases, then the fund tends to become more important. Thus, not surprisingly, fees on balance are less interesting to the affiliate. Note that result (13) is independent of the structure of sequences
${{\rm {\cal W}}_T}$
and
${{\rm {\cal P}}_T}$
. Moreover, if p
i
= p for all i with p ∈ (0, 1], RE
sf
will be independent of the interruption process Z and the DoC, p. Next, we introduce the equivalent charge on balance for a risk-neutral affiliate.
Definition 3.1
(Risk-neutral equivalent charge on balance).
Given a set of parameters
${\bf I} = \left\{ {T,\alpha, \mu, {\sigma ^2},{{\rm {\cal W}}_T},{{\rm {\cal P}}_T}} \right\}$
, we define the risk-neutral equivalent charge on balance,
$\delta _{\rm I}^{\ast} ({\bf I})$
, as the value of δ such that RE
sf
= 1 under scenario
${\bf I}$
.
For example, if we want to show the explicit dependence of
$\delta _{\rm I}^{\ast} ({\bf I})$
with respect to T, α, or both, we can use
$\delta _{\rm I}^{\ast} (T)$
,
$\delta _{\rm I}^{\ast} (\alpha )$
and
$\delta _{\rm I}^{\ast} (T,\alpha )$
, respectively. Additionally, we will use
$\delta _{\rm I}^{\ast} $
when we refer to this equivalent charge in a general situation. Note that
$\delta _{\rm I}^{\ast} (T = 1,\alpha ) = \alpha $
and
${\partial _\alpha} \delta _{\rm I}^{\ast} (T,\alpha ) \gt 0$
for any scenario
${\bf I}$
, and by Proposition 3.1 we have
${\partial _\mu} \delta _{\rm I}^{\ast} (T,\mu ) \lt 0$
for T >1. Finally, because sequences
${{\rm {\cal W}}_T}$
and
${{\rm {\cal P}}_T}$
are assumed to be unstructured, we are not able to infer, for example, that
$\delta _{\rm I}^{\ast} (T)$
is a decreasing function in T.
3.2 Ratio of expected value to the standard deviation of terminal wealth
It is also possible to determine the convenience of one of the two schemes using the ratio of expected terminal wealth (adjusted for charges) to its corresponding standard deviation. For the charges considered, the ratios are
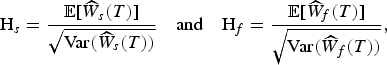$${{\rm H}_s} = \displaystyle{{{\rm {\opf E}}[{{\widehat{W}}_s}(T)]} \over {\sqrt {{\rm Var}({{\widehat{W}}_s}(T))}}} \quad {\rm and}\quad {{\rm H}_f} = \displaystyle{{{\rm {\opf E}}[{{\widehat{W}}_f}(T)]} \over {\sqrt {{\rm Var}({{\widehat{W}}_f}(T))}}}, $$
where
${\rm {\opf E}}[{\widehat{W}_s}(T)]$
and
${\rm {\opf E}}[{\widehat{W}_f}(T)]$
are given by (8) and (9), and
${\rm Var}({\widehat{W}_s}(T))$
and
${\rm Var}({\widehat{W}_f}(T))$
are given by (10) and (11), respectively. With this criterion, if a particular set of parameters satisfies H
s
> H
f
, then the charge based on assets will be preferred. The next proposition establishes the conditions for process Z such that H
s
> H
f
holds.
Proposition 3.2
(Derivative of H f with respect to μ under no interruptions).
In process Z, we assume p i = 1 for all i, and we consider H f in (14) as a function of the growth rate μ. Then, for any μ and T >1 we have
$$\displaystyle{{\partial {{\rm H}_f}(\mu )} \over {\partial \mu}} \lt 0.$$
Proof. See Appendix A.3 (online).
Expression (15) is equivalent to H s > H f for any common set of parameters and T > 1 because H f > 0, δ > 0, and α cancels in H f . Consequently, the charge on balance, in the absence of interruptions, always generates a better ratio H than that for the charge on flow. Proposition 3.2 also establishes that the standard deviation of the adjusted terminal wealth grows faster than its expected value as the fund's growth rate increases. If we assume p i = p ∈ (0,1] for all i and express the ratios in (14) as a function of the DoC, then we have H s (p) and H f (p), and their partial derivatives satisfy ∂ p H s (p) > 0 and ∂ p H f (p) > 0. Hence, increments in the probability of contributing improve the corresponding ratios. The next proposition gives conditions under which H s (p) > H f (p) holds when 0 < p < 1.
Proposition 3.3
(Effect of DoCs on H s and H f ).
If μ − δ + σ 2 > 0, T > 1, W i+1 ≤ W i and p i = p for all 0 ≤ i ≤ T − 1 with p ∈ (0,1], then H s (p) > H f (p) for all p.
Proof. See Appendix A.4 (online).
We can assume that
${{\rm {\cal W}}_T}$
satisfies the corresponding exponential growth model
$${W_i} = {W_0}{e^{\beta i}},\quad \beta \in {\rm {\opf R}},\quad {W_0} \gt 0\quad {\rm and}\quad 0 \le i \le T - 1.$$
Then, β is the monthly real growth rate of contributions, and the initial contribution is equal to W 0. Note that in this modelFootnote 15 we have W i > 0 for all i. The next corollary studies Proposition 3.3 when the contributions follow model (16).
Corollary 3.1
(Proposition under the exponential growth model of contributions).
If μ − δ + σ 2 > β, p ∈ (0,1], T > 1, W i as in (16) and p i = p for all 0 ≤ i ≤ T − 1, then H s (p) > H f (p) for all p.
Proof. See Appendix A.5 (online).
Corollary 3.1 states that if the fund's net growth rate, μ − δ, is greater than the growth in contributions, β, then the charge on balance will always be preferred (using the ratio of expected value to standard deviation criterion) even in the presence of interruptions.
3.3 Expected utility of terminal wealth
We assume the affiliate exhibits a Constant Relative Risk Aversion (CRRA) utility function given by
$$U(\widehat{W}) = \displaystyle{{{{\widehat{W}}^{1 - \gamma}}} \over {1 - \gamma}}, $$
where
$\widehat{W} \gt 0$
is a realization of adjusted terminal wealth, and γ > 0 measures the degree of relative risk aversion.Footnote
16
To determine the most appropriate charge scheme, the affiliate compares the expected utilities
${\rm {\opf E}}[U({\widehat{W}_s}(T))]$
and
${\rm {\opf E}}[U({\widehat{W}_f}(T))]$
, or their corresponding certainty equivalents,
${\rm CE}[{\widehat{W}_s}(T)]$
and
${\rm CE}[{\widehat{W}_f}(T)]$
, using the following expressions:
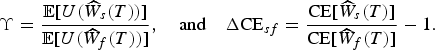$$\Upsilon = \displaystyle{{{\rm {\opf E}}[U({{\widehat{W}}_s}(T))]} \over {{\rm {\opf E}}[U({{\widehat{W}}_f}(T))]}},\quad {\rm and}\quad \Delta {\rm C}{{\rm E}_{sf}} = \displaystyle{{{\rm CE}[{{\widehat{W}}_s}(T)]} \over {{\rm CE}[{{\widehat{W}}_f}(T)]}} - 1.$$
Under the expected utility criterion, if ΔCE
sf
> 0, the charge on balance will be preferred. If ΔCE
sf
< 0, then the charge on flow will be preferred. However, if she uses
$\Upsilon $
for the comparison, then different cases need to be considered. For example, γ > 1 implies
$U(\widehat{W}) \lt 0$
, so the charge on balance will be preferred if
$\Upsilon \lt 1$
. On the contrary, γ < 1 implies
$U(\widehat{W}) \gt 0$
, and the charge on balance will be preferred if
$\Upsilon \gt 1$
. An interesting feature of utility (17) is that it preserves indifferences and preferences when multiplied by a positive constant factor. For example, if
${{\rm {\cal W}}_T}$
satisfies (16), then the ratios in (18) become independent of the initial contribution.
Closed-form expressions for expected utilities and certainty equivalents in (18) are not available, and although simulation is a good technique for obtaining the corresponding estimators, the error involved in such computations (due to the embedded stochastic processes and the complicated relationship of the variables) is likely to obscure the analysis or reduce its scope. An alternative approach consists of constructing a Taylor series expansion of (17) around the expected value of adjusted terminal wealth,
${\rm {\opf E}}[\widehat{W}]$
. Expressing
$U(\widehat{W})$
for some
$\widehat{W}$
, we obtain
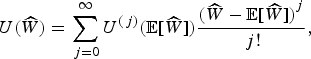$$U(\widehat{W}) = \sum\limits_{\,j = 0}^\infty {U^{(\,j)}}({\rm {\opf E}}[\widehat{W}])\displaystyle{{{{(\widehat{W} - {\rm {\opf E}}[\widehat{W}])}^j}} \over {\,j!}},$$
where
${U^{(j)}}({\rm {\opf E}}[\widehat{W}])$
is the jth derivative of the utility function at
${\rm {\opf E}}[\widehat{W}]$
. Loistl (Reference Loistl1976) showed that (19) converges for the CRRA utility when
$0 \lt \widehat{W} \lt 2{\rm {\opf E}}[\widehat{W}]$
. Because we have derived closed-form expressions for the first and second moments of
$\widehat{W}$
, we find it interesting to use the second-order approximation of (17), U
MV, given by
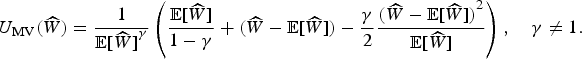$${U_{{\rm MV}}}(\widehat{W}) = \displaystyle{1 \over {{\rm {\opf E}}{{[\widehat{W}]}^\gamma}}} \left( {\displaystyle{{{\rm {\opf E}}[\widehat{W}]} \over {1 - \gamma}} + (\widehat{W} - {\rm {\opf E}}[\widehat{W}]) - \displaystyle{\gamma \over 2}\displaystyle{{{{(\widehat{W} - {\rm {\opf E}}[\widehat{W}])}^2}} \over {{\rm {\opf E}}[\widehat{W}]}}} \right),\quad \gamma \ne 1.$$
Equation (20) generates the following expectations of U MV for the charges on balance and flow:Footnote 17
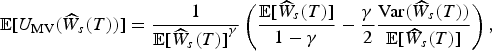$${\rm {\opf E}}[{U_{{\rm MV}}}({\widehat{W}_s}(T))] = \displaystyle{1 \over {{\rm {\opf E}}{{[{{\widehat{W}}_s}(T)]}^\gamma}}} \left( {\displaystyle{{{\rm {\opf E}}[{{\widehat{W}}_s}(T)]} \over {1 - \gamma}} - \displaystyle{\gamma \over 2}\displaystyle{{{\rm Var}({{\widehat{W}}_s}(T))} \over {{\rm {\opf E}}[{{\widehat{W}}_s}(T)]}}} \right),$$
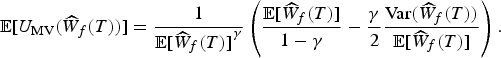$${\rm {\opf E}}[{U_{{\rm MV}}}({\widehat{W}_f}(T))] = \displaystyle{1 \over {{\rm {\opf E}}{{[{{\widehat{W}}_f}(T)]}^\gamma}}} \left( {\displaystyle{{{\rm {\opf E}}[{{\widehat{W}}_f}(T)]} \over {1 - \gamma}} - \displaystyle{\gamma \over 2}\displaystyle{{{\rm Var}({{\widehat{W}}_f}(T))} \over {{\rm {\opf E}}[{{\widehat{W}}_f}(T)]}}} \right).$$
Then, we define
${\Upsilon _{{\rm MV}}}$
to be the ratio of
${\rm {\opf E}}[{U_{{\rm MV}}}({\widehat{W}_s}(T))]$
to
${\rm {\opf E}}[{U_{{\rm MV}}}({\widehat{W}_f}(T))]$
, and we express it as a function of γ,
${{\rm {\cal P}}_T}$
and δ. Assuming p
i
= p ∈ (0,1] in process Z, we obtain
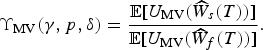$${\Upsilon _{{\rm MV}}}(\gamma, p,\delta ) = \displaystyle{{{\rm {\opf E}}[{U_{{\rm MV}}}({{\widehat{W}}_s}(T))]} \over {{\rm {\opf E}}[{U_{{\rm MV}}}({{\widehat{W}}_f}(T))]}}.$$
We expect (22) and (23) to be good approximations of the expected utility.Footnote
18
Hence,
${\Upsilon _{{\rm MV}}}$
would exhibit a behavior similar to that of
$\Upsilon $
. Additionally, we have not considered
$\Upsilon $
or
${\Upsilon _{{\rm MV}}}$
to be function of α because
${\partial _\alpha} \Upsilon = (1 - \gamma )\Upsilon $
and
${\partial _\alpha} {\Upsilon _{{\rm MV}}} = (1 - \gamma ){\Upsilon _{{\rm MV}}}$
for γ ≠ 1. Then, the charge on flow will always become less attractive with respect to the charge on balance as α increases.
To interpret
${\Upsilon _{{\rm MV}}}$
unambiguously, we will assume γ > 1 so
${U_{{\rm MV}}}({\widehat{W}_s}(T))$
and
${U_{{\rm MV}}}({\widehat{W}_f}(T))$
yield negative expectations. Therefore, the affiliate will prefer the charge on balance when
${\Upsilon _{{\rm MV}}} \lt 1$
, and she will prefer that on flow when
${\Upsilon _{{\rm MV}}} \gt 1$
. The next proposition analyzes the behavior of
${\Upsilon _{{\rm MV}}}$
with respect to the charge on balance and the degree of relative risk aversion.
Proposition 3.4
(Effect of the charge on balance and risk aversion on
${\Upsilon _{{\rm MV}}}$
).
Let γ > 1, T > 1, p
i
= p ∈ (0,1] in process Z, and let
$\delta _{\rm I}^{\ast} = \delta _{\rm I}^{\ast} ({\bf I})$
be the risk-neutral equivalent charge on balance of Definition 3.1, where
${\bf I} = \{ T,\alpha, \mu, {\sigma ^2},{{\rm {\cal W}}_T}\} $
. The following statements hold:
-
1. If both
${\sigma ^2} \le \displaystyle{1 \over T}\ln (2p)$
and
(25)hold, then
$${\rm {\opf E}}[{\widehat{W}_s}{(T)^2}] \ge \left( {1 + \displaystyle{2 \over {{\gamma ^2}}}} \right){\rm {\opf E}}{[{\widehat{W}_s}(T)]^2}$$
${\partial _\delta} {\Upsilon _{{\rm MV}}}(\gamma, p,\delta ) \gt 0$
.
-
2. If
$\mu - \delta _{\rm I}^{{\ast}} + {\sigma ^2} \gt 0$
and W
i+1 ≤ W
i
for all 0 ≤ i ≤ T − 1, then
${\Upsilon _{{\rm MV}}}(\gamma, p,\delta _{\rm I}^{\ast} ) \lt 1$
and
${\partial _\gamma} {\Upsilon _{{\rm MV}}}(\gamma, p,\delta _{\rm I}^{\ast} ) \lt 0$
. -
3. If
${{\rm {\cal W}}_T}$
is given by (16) and
$\mu - \delta _{\rm I}^{\ast} + {\sigma ^2} \gt \beta $
, then
${\Upsilon _{{\rm MV}}}(\gamma, p,\delta _{\rm I}^{\ast} ) \lt 1$
and
${\partial _\gamma} {\Upsilon _{{\rm MV}}}(\gamma, p,\delta _{\rm I}^{\ast} ) \lt 0$
.
Proof. See Appendix A.6 (online)Footnote 19
Statement (1) establishes conditions under which
${\Upsilon _{{\rm MV}}}$
is an increasing function of δ, i.e., the charge on flow improves with respect to the charge on balance as δ increases. Statements (2) and (3) give conditions under which the charge on balance is preferred or under which the latter improves with respect to the charge on flow as risk aversion increases. Because the aforementioned conditions are the same as those in Proposition 3.3, the intuition behind those results is that the risk (standard deviation) is greater for the charge on flow; and, therefore the more risk-averse the affiliate is, the more the charge on balance improves with respect to that on flow. Statement (2) is more general than (3) because it requires
$\mu + {\sigma ^2} \gt \delta _{\rm I}^{\ast} $
and a decreasing sequence of contributions. On the contrary, claim (3) requires a growth rate for contributions, β, not exceeding
$\mu - \delta _{\rm I}^{\ast} + {\sigma ^2}$
. Note that we have assumed
$\delta = \delta _{\rm I}^{\ast} $
, so arbitrary choices for δ cannot guarantee that (2) and (3) will hold. The effect of DoC, p, on
${\Upsilon _{{\rm MV}}}$
, i.e., the sign of
${\partial _p}{\Upsilon _{{\rm MV}}}(\gamma, p,\delta _{\rm I}^{\ast} ) \gt 0$
, cannot be determined even under assumptions such as those in Proposition 3.4; it will be studied empirically in Section 4.
4 Application to the Peruvian PPS
In this section, we present an application of the proposed methodology to the Peruvian PPS. This application is relevant because the PPS is going through an important reform exactly 20 years after its creation. Part of the reform consists of replacing the charge on flow with a charge on balance, and this situation has partially motivated the present research paper.Footnote 20
4.1 Parameters of the model
We are considering a retirement age of 65 years and a moderate scenario that corresponds to the medium-risk (default option) pension fund available for PPS's affiliates. Additionally, we fix the charge on flow to α = 0.1761. This value is related to the PPS's average charge as of December 2013, which was
$f = 1.615\% $
of the affiliate's salary under a constant contribution rate of 10%, i.e., α = −ln(1 − 10f).
We also need to determine parameters μ and σ for process V given by (1). For the moderate scenario, the monthly volatility is
${\sigma _M} = 2.511\% $
estimated from the daily real log-returns of the PPS's Type 2 (medium-risk) funds. For calibration purposes, we have considered the daily real returns of Integra'sFootnote
21
Type 2 fund from the period 01/02/2009 to 05/30/2013. Additionally, we have assumed an expected real return of 5.00% per year. Based on GBM's properties, we have
${r_M} = {\mu _M} - 0.5\sigma _M^2 $
, where r
M
is the expected monthly real return expressed in continuous time. After adequate transformations, we obtain
${\mu _M} = 0.44\% $
.
The monthly sequence of real contributions,
${{\rm {\cal W}}_T}$
, is assumed such that
$${W_{i + 1}} = (1 + {\tau}_i){W_i},\quad {W_0} \gt 0,\quad {\tau}_i \in {\open R} \,{\nltrie} \quad {\rm and}\quad i = 0,{\ldots}, T - 1,$$
where factors τ i are considered to be the sum of the growth along the salary curve plus a component related to productivity growth. Additionally, τ i depends on three characteristics: the affiliate's gender, education level and age. The calibration details are presented in Appendix B (online); however, it is important to mention that for young affiliates, the average growth factors fluctuate between 2.5% and 3.5% per year.
Although the independence assumptions are strong, the interruption process Z is flexible enough because the sequence of likelihoods p i can reflect different contribution profiles for affiliates. For the numerical experiments, we have considered its simplest specification: p i = p for all i. The goal behind this assumption is to show, in the most direct form, the effect of p on the comparison between both charge schemes. We consider three scenarios for the DoC: p = 1.00 (non-interrupted stream of contributions), p = 0.51 (the PPS average), and p = 0.18 (the average for affiliates less than 21 years of age).
4.2 Numerical results
4.2.1 Risk-neutral equivalent charge on balance:
$\delta _{\rm I}^{\ast} $
Figure 1 shows the plot of
$\delta _{\rm I}^{\ast} $
(see Definition 3.1) annualized and in percentage form for certain ages and contribution profiles and in a moderate scenario (an expected fund return of 5.00% per year). Detailed values can be found in Table C1 in online Appendix C. In the case of a 32-year-old risk-neutral female affiliate without a college education (F/NC profile), we have T = (65 − 32) × 12 = 396 months and the risk-neutral equivalent charge on balance is 0.93% per year. This implies that a charge on balance smaller than 0.93% makes such a scheme convenient for this particular risk-neutral affiliate when the charge on flow is α = 0.1761. We can observe that
$\delta _{\rm I}^{\ast} $
is strictly increasing in age; i.e., the charge on balance improves with age. This is intuitive because as the accumulation horizon (T) decreases, the fund becomes less important; thus, the fees on balance become more attractive. Note that
$\delta _{\rm I}^{\ast} \gt 0.65\% $
for all profiles and ages in online Table C1 (the value corresponds to a 20-year-old with F/NC profile), and this level would make the charge on balance preferable for all considered affiliates. Additionally, the differences between
$\delta _{\rm I}^{\ast} $
s for the same age are very small (<0.04% for affiliates younger than 40 years of age), implying that different growth rates in wages generate similar values of
$\delta _{\rm I}^{\ast} $
. Finally, recall that
$\delta _{\rm I}^{\ast} $
is independent of the DoC because p cancels in RE
sf
.
Figure 1. (Colour online) Risk-neutral equivalent charge on balance,
$\delta _{\rm I}^{\ast} $
, in percentage (%) and annualized for different ages in years (x-axis) and gender/education combinations in a moderate scenario (an expected fund return of 5.00% per year). We have assumed α = 0.1761 (which corresponds to a charge on flow of 1.615% of the salary with a constant contribution rate of 10%) and a retirement age of 65 years.
4.2.2 Percentage difference on certainty equivalent: ΔCE sf
In this section, we study (empirically) the percentage difference, ΔCE
sf
, given by (18). For utility (17), closed-form expressions for
${\rm CE}[{\widehat{W}_s}(T)]$
and
${\rm CE}[{\widehat{W}_f}(T)]$
are not available; thus, we will rely on a stochastic simulation to obtain an estimator of ΔCE
sf
. Figures 2 and 3 and online Tables C2 and C3 show estimated values of ΔCE
sf
for different values of DoC (p = 1.00, p = 0.51 and p = 0.18) and relative risk aversion, γ. Following Poterba et al. (Reference Poterba, Rauh, Venti, Wise and Wise2005), we select γ = 1 for a low degree of risk aversion, γ = 4 for a moderate degree of risk aversion, and γ = 8 for a high degree of risk aversion. In every scenario of Figure 2 and Table C2 (online), the charge on balance, δ, was fixed at its corresponding risk-neutral equivalent charge,
$\delta _{\rm I}^{\ast} $
. In Figure 3 and Table C3, the value of δ was fixed to 1.00% per year (current ratio of total fees to total assets of the system). The number of sample paths of adjusted wealth to estimate ΔCE
sf
(for every scenario) was determined using the sequential procedure of Kelton and Law (Reference Kelton and Law2000) with a relative error of 0.0001 and a confidence level of 99%. Additionally, we report only results for contribution profile F/NC (see Appendix B online) because the others generate very similar outputs.
Figure 2. (Colour online) Estimated values of
$\Delta {\rm C}{{\rm E}_{sf}} = {\rm CE}[{\widehat{W}_s}(T)]/{\rm CE}[{\widehat{W}_f}(T)] - 1$
in percentage (%) for different ages in years (x-axis), values of relative risk aversion (γ = 1, 4, 8) and density of contribution (p = 1.00, 0.51, 0.18) under a moderate scenario (an expected fund return of 5.00% per year) and F/NC contribution profile. We have also assumed
$\delta = \delta _{\rm I}^{\ast} $
, α = 0.1761 (which corresponds to a charge on flow of 1.615% of salary with a constant contribution rate of 10%) and a retirement age of 65 years.
Figure 3. (Colour online) Estimated values of
$\Delta {\rm C}{{\rm E}_{sf}} = {\rm CE}[{\widehat{W}_s}(T)]/{\rm CE}[{\widehat{W}_f}(T)] - 1$
in percentage (%) for different ages in years (x-axis), values of relative risk aversion (γ = 1, 4, 8) and density of contribution (p = 1.00, 0.51, 0.18) under a moderate scenario (an expected fund return of 5.00% per year) and F/NC contribution profile. We have also assumed
$\delta = 1.0\% $
per year, α = 0.1761 (which corresponds to a charge on flow of 1.615% of salary with a constant contribution rate of 10%) and a retirement age of 65 years.
From Figure 2 (
$\delta = \delta _{\rm I}^{\ast} $
), we observe that ΔCE
sf
> 0 for every scenario and that γ clearly has a stronger effect on ΔCE
sf
than p. Moreover, note that as risk aversion increases, ΔCE
sf
also increases. This fact is in line with the theoretical results of Proposition 3.4. For example, in the case of a 20-year-old F/NC affiliate, we have
$\Delta {\rm C}{{\rm E}_{sf}} \approx 0.5\% $
for γ = 1,
$\Delta {\rm C}{{\rm E}_{sf}} \approx 1.7\% $
for γ = 4 and
$\Delta {\rm C}{{\rm E}_{sf}} \approx 3.2\% $
for γ = 8. On the contrary, the effect of p on ΔCE
sf
for a fixed γ is not clear (in the sense that for older affiliates, small values of p benefit the charge on flow, whereas the opposite is true for younger ones), and it is almost negligible in magnitude. Figure 3 considers a fixed
$\delta = 1\% $
per year and, as opposed to Figure 2, we can observe that ΔCE
sf
> 0 does not hold for every scenario. For example, if γ = 4, then we have ΔCE
sf
> 0 only for affiliates older than 31 years of age, i.e., the charge on balance will be preferable for the aforementioned group of affiliates. The same threshold is approximately equal to 33 years for γ = 1 and 29 years for γ = 8. This observation and the fact that ΔCE
sf
is increasing in γ (for a fixed age and p) shows (again) that the charge on balance improves with respect to that on flow as risk aversion increases. Finally, we can verify the almost null effect that p has on ΔCE
sf
because for a common γ, the curves in the figure are almost overlapping (the largest difference is <0.1%).
4.2.3 The effect of age on ΔCE sf
In Figure 1, we can observe that
$\delta _{\rm I}^{\ast} $
is approximately 1% for age 35, i.e.,
$\delta _{\rm I}^{\ast} (35) \approx 1\% $
. For ages x < 35 we have
$\delta _{\rm I}^{\ast} (35) \lt 1\% $
and for ages x > 35 we have
$\delta _{\rm I}^{\ast} (35) \gt 1\% $
. This implies that a constant charge on balance of 1% is too high for risk-neutral affiliates younger than 35 and too low for affiliates older than 35. Consequently, with
$\delta = 1\% $
young affiliates will pay a charge on balance that is too high but old affiliates will pay a charge on balance that is too low. This explains why for young affiliates in Figure 3 ΔCE
sf
is negative (i.e., the charge on flow is better) and for old affiliates not only ΔCE
sf
is positive but it also takes high values, such as 10% for age 50. Also, we can notice from Figures 2 and 3 that the effect of relative risk aversion on ΔCE
sf
decreases as age increases. For example, in Figure 2 the difference in ΔCE
sf
for γ = 8 and γ = 1, i.e., ΔCE
sf
(γ = 8) − ΔCE
sf
(γ = 1), is approximately 2.6% for age 20 and the same difference is 1% for age 50. The same fact also appears in Figure 3 but the corresponding difference is 4% for age 20 and it is almost negligible for age 50. Finally, if age increases, then the effect of DoC on ΔCE
sf
is noticeable only when
$\delta = \delta _{\rm I}^{\ast} $
, risk aversion is high (γ = 8) and DoC is in its worst scenario (p = 0.18).
5 Conclusions
This paper studies how the affiliate's degree of risk aversion and DoC affects the comparison of proportional charges on flow and balance in DC pension systems with individual accounts. Assuming a GBM for the share value of a representative pension fund and using an independent process to model the interruption of contributions, we represent the terminal wealth in the affiliate's account assuming an arbitrary sequence of contributions and fixed values for the corresponding charges. Additionally, we proposed three ways to compare the aforementioned charges: the ratio of expected values of terminal wealth, the ratio of the expected value to the standard deviation of terminal wealth, and the ratio of expected utilities of terminal wealth. We derive theoretical results that explain the behavior of the charges with respect to the key parameters of the model and to the three methods of comparison. It is important to mention that under mild assumptions, the charge on balance improves its performance relative to that on flow as risk aversion increases. On the contrary, the effect of the DoC in the comparison is almost negligible when it is assumed to be constant during the accumulation phase. Finally, it is possible to include many refinements to the proposed methodology that can generate new research articles. For example, we can consider a variable charge on balance (which can be related to the total system's fund size) or work under the assumption of a complete market and provide expressions for an arbitrage-free relationship between the types of charges.
Acknowledgement
The author would like to thank the Editor and the anonymous reviewers for their helpful and constructive comments that greatly contributed to improving the final version of the paper.
Supplementary material
The supplementary material for this paper can be found at http://dx.doi.org/10.1017/S1474747216000068.
