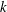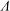1. Introduction
In natural swimming and flying, rapid manoeuvring is generally achieved via undulating or flapping fins, flukes or wings, often with a swept leading edge. In particular, the flapping wings of insects are known to exploit leading-edge vortices (LEVs) for lift enhancement, as discussed by Ellington et al. (Reference Ellington, van den Berg, Willmott and Thomas1996). These LEVs are the dominant contributor to circulation on stalled profiles at low Reynolds numbers, as demonstrated by Pitt Ford & Babinsky (Reference Pitt Ford and Babinsky2013), and have been observed on rotating and translating profiles over a broad range of Reynolds numbers (
$200\leqslant Re\leqslant 60\,000$
), such as by Lentink & Dickinson (Reference Lentink and Dickinson2009) and Garmann, Visbal & Orkwis (Reference Garmann, Visbal and Orkwis2013), Strouhal numbers (
$0.1\leqslant St\leqslant 0.6$
) and reduced frequencies (
$0.2\leqslant k\leqslant 1$
), by Rival & Tropea (Reference Rival and Tropea2010) and Baik et al. (Reference Baik, Bernal, Granlund and Ol2012), and aspect ratios (
$2.9\leqslant AR\leqslant 7.3$
), by Harbig, Sheridan & Thompson (Reference Harbig, Sheridan and Thompson2013). The above parameters vary the lift and drag production of an LEV, as observed by Garmann et al. (Reference Garmann, Visbal and Orkwis2013) with respect to Reynolds number, or alter the propulsive efficiency, as observed by Taylor, Nudds & Thomas (Reference Taylor, Nudds and Thomas2003) with respect to Strouhal number. However, the parameter of rotation is unique in that rotating cases often exhibit vortex stability, where both the convection speed of the LEV relative to the profile and the growth rate of the LEV are near zero, as observed by Ozen & Rockwell (Reference Ozen and Rockwell2012), Cheng et al. (Reference Cheng, Sane, Barbera, Troolin, Strand and Deng2013) and Wojcik & Buchholz (Reference Wojcik and Buchholz2014), to name a few.
A number of mechanisms for vortex stability have been proposed. Lentink & Dickinson (Reference Lentink and Dickinson2009) suggested that large rotational accelerations associated with low-aspect-ratio profiles stabilized LEVs. However, Harbig et al. (Reference Harbig, Sheridan and Thompson2013) identified stable LEVs on profiles in the range of aspect ratios
$2.9\leqslant AR\leqslant 7.3$
. Over a similar aspect ratio range of
$2\leqslant AR\leqslant 4$
, Jones, Ford & Babinsky (Reference Jones, Ford and Babinsky2012) did not observe LEV stability. It has been suggested by Ellington et al. (Reference Ellington, van den Berg, Willmott and Thomas1996) that spanwise flow transported vorticity to the tip vortex, and therefore was responsible for LEV stability. However, by translating profiles at sweep angles as high as
${\it\Lambda}=45^{\circ }$
. Beem, Rival & Triantafyllou (Reference Beem, Rival and Triantafyllou2012) showed that the spanwise flow in isolation was not responsible for vortex stability, which corroborated previous findings by Birch & Dickinson (Reference Birch and Dickinson2001) that spanwise flow was not responsible for LEV stability on rotating wings. However, nominally two-dimensional spanwise flow, such as that investigated by Beem et al. (Reference Beem, Rival and Triantafyllou2012), cannot result in three-dimensional effects such as the convection of spanwise-oriented vorticity, which depends also on a gradient of vorticity magnitude. Neglecting viscous diffusion, the transport of spanwise-oriented vorticity (
${\it\omega}_{z}$
) is governed by the spanwise component of the vorticity-transport equation:
$$\begin{eqnarray}\frac{\partial {\it\omega}_{z}}{\partial t}+u\frac{\partial {\it\omega}_{z}}{\partial x}+v\frac{\partial {\it\omega}_{z}}{\partial y}+w\frac{\partial {\it\omega}_{z}}{\partial z}={\it\omega}_{x}\frac{\partial w}{\partial x}+{\it\omega}_{y}\frac{\partial w}{\partial y}+{\it\omega}_{z}\frac{\partial w}{\partial z},\end{eqnarray}$$
where the terms from left to right represent the rate of change of vorticity due to unsteadiness, convection of vorticity in the streamwise (
$x$
), wall-normal (
$y$
) and spanwise (
$z$
) directions, vortex tilting in the streamwise and wall-normal directions, and vortex stretching, respectively. A hypothetical balance of vorticity is shown in figure 1, where spanwise-oriented vorticity entering the LEV from the leading-edge shear layer is balanced by a spanwise convection of vorticity.
Figure 1. A flat-plate profile undergoing a flapping motion has a spanwise variation in effective velocity and spanwise flow, resulting in vortex stretching (
${\it\omega}_{z}(\partial w/\partial z)$
) and vorticity convection (
$w(\partial {\it\omega}_{z}/\partial z)$
). The balance between the spanwise transport of vorticity and vorticity flux through the leading-edge shear layer is hypothesized here as the mechanism of LEV stability.
It has been shown by Rival et al. (Reference Rival, Kriegseis, Schaub, Widmann and Tropea2014) that LEV attachment is only topologically compatible with vortices smaller than one chord length
$c$
in scale. The vorticity generated in the leading-edge shear layer of a rotating profile must therefore be balanced by either the transport or annihilation of vorticity in order to limit vortex growth as a necessary condition for LEV stability. A recent study by Wojcik & Buchholz (Reference Wojcik and Buchholz2014) conducted a vorticity balance within the LEV on a rotating profile, utilizing direct measurements of the circulation transport through the leading-edge shear layer and via spanwise vorticity convection. It was concluded that spanwise vorticity convection was insufficient to balance vorticity production, and that the large residual in the vorticity balance must be accounted for by vorticity annihilation. Similarly, Cheng et al. (Reference Cheng, Sane, Barbera, Troolin, Strand and Deng2013) found that spanwise vorticity convection was negligible relative to convection in the streamwise and wall-normal directions. However, in natural swimming and flight, the full benefit of a stable LEV is realized when the LEV is maintained for at least one half-stroke of motion, rather than an indefinite period. Thus, it is sensible to measure the relative stability of an LEV in terms of its convection speed relative to the profile, as opposed to a binary stable or unstable condition. This relative LEV stability is an important characteristic of natural swimming and flight that has not been investigated in terms of vorticity transport. By comparing profiles of varying rotation rate and sweep angle, the current study investigates the role of both vortex stretching and vorticity convection on relative LEV stability.
2. The moderation of LEV growth with vorticity transport
Based on the limiting length-scale criterion of Rival et al. (Reference Rival, Kriegseis, Schaub, Widmann and Tropea2014), low vortex growth rates represent more stable LEVs. This can be accomplished by reducing the LEV feeding velocity, moderating LEV growth through vorticity convection, or contracting LEV size through vortex stretching. Figure 1 shows the hypothetical vorticity balance for a flapping profile. The rotational velocity
${\it\Omega}$
results in a spanwise variation in vorticity magnitude
$\partial {\it\omega}_{z}/\partial z$
, which couples with spanwise flow
$w$
from rotational accelerations to convect vorticity down the span of the profile. This convection of vorticity balances the flux of vorticity into the vortex from the leading-edge shear layer. Vortex stretching acts to modify the size of the vortex, but does not alter the balance of circulation on any two-dimensional slice. It is hypothesized that spanwise vorticity convection moderates LEV strength, while simultaneously vortex stretching can act to limit LEV growth.
2.1. The effect of reduced frequency on LEV saturation
In order to compare the growth rate of an LEV to the limiting length scale of one chord
$c$
, it is necessary to produce an estimate for the circulation entering that LEV. A model for the vorticity flux into a leading-edge vortex was proposed and validated by Wong, Kriegseis & Rival (Reference Wong, Kriegseis and Rival2013), shown in figure 2 for a profile experiencing an effective velocity
$u_{eff}$
and effective incidence
${\it\alpha}_{eff}$
. In the vorticity-flux model, the mass per unit span
$m^{\prime }$
entering the vortex was described as:
$$\begin{eqnarray}m^{\prime }={\it\rho}\int _{0}^{t_{0}}\int _{0}^{d}u({\it\xi},t)\text{d}{\it\xi}\text{d}t,\end{eqnarray}$$
where
${\it\xi}$
is the shear-layer coordinate as shown in figure 2,
${\it\rho}$
is the fluid density,
$d$
is the shear-layer thickness and
$u$
is the shear-layer velocity. Assuming that the shear-layer velocity scales with the effective velocity
$u_{eff}$
, this results in a mass flow into the vortex proportional to:
$$\begin{eqnarray}\frac{\partial m^{\prime }}{\partial t}\propto {\it\rho}\text{d}u_{eff}.\end{eqnarray}$$
Mass entering the vortex has an associated circulation
${\it\Gamma}$
, which can be determined via a path integral around the shear layer. The rate of circulation growth within the LEV is therefore approximately:
$$\begin{eqnarray}\frac{\partial {\it\Gamma}}{\partial t}=\frac{\partial {\it\Gamma}}{\partial m^{\prime }}\frac{\partial m^{\prime }}{\partial t}\propto \left(\frac{u_{eff}l}{{\it\rho}dl}\right)\left({\it\rho}\text{d}u_{eff}\right)=u_{eff}^{2}.\end{eqnarray}$$
Figure 2. The integration of vorticity within a shear-layer segment of length
$l$
and thickness
$d$
. For a fluid of density
${\it\rho}$
, this results in a rate of circulation growth
$(\partial {\it\Gamma}/\partial t)=(\partial {\it\Gamma}/\partial m^{\prime })(\partial m^{\prime }/\partial t)$
of approximately the square of effective velocity
$u_{eff}^{2}$
.
Didden (Reference Didden1979) derived a similar expression for the rate of circulation growth for a vortex ring generated by a piston–cylinder apparatus:
$$\begin{eqnarray}\frac{\partial {\it\Gamma}}{\partial t}=\frac{1}{2}U^{2},\end{eqnarray}$$
which scaled well with experimental data, where
$U$
was the piston velocity.
As vorticity-containing mass enters the LEV the vortex grows in size, and therefore it reaches its limiting length scale
$c$
with an area of the order of
$c^{2}$
. For a period of motion
$T$
, comparing the resulting maximum allowable LEV growth of
$c^{2}/T$
to the circulation developed in one period of motion
$u_{eff}^{2}T$
gives an analogous relationship with reduced frequency
$k={\rm\pi}fc/U_{\infty }$
:
$$\begin{eqnarray}\frac{c^{2}/T}{u_{eff}^{2}T}=\left(\frac{fc}{u_{eff}}\right)^{2}\approx \frac{1}{{\rm\pi}^{2}}\left(\frac{{\rm\pi}fc}{U_{\infty }}\right)^{2}=\frac{1}{{\rm\pi}^{2}}k^{2},\end{eqnarray}$$
where
$f=1/T$
is the frequency of motion and
$U_{\infty }$
is the free-stream velocity. Here, larger reduced frequencies represent a larger allowable vortex area for a given expected circulation, or in other words a more stable LEV. This is in agreement with the findings of Baik et al. (Reference Baik, Bernal, Granlund and Ol2012) that larger reduced frequencies result in more stable LEVs in two-dimensional plunging and pitching cases. It is therefore reasonable to expect that the same parameter is significant for LEV stability in flapping cases as well.
2.2. The effect of vorticity convection on LEV circulation
In addition to having a larger limiting length scale for a given circulation, as estimated by the reduced frequency
$k$
above, it is hypothesized that relative LEV stability can be improved by moderating circulation growth with vorticity convection. As done by Wojcik & Buchholz (Reference Wojcik and Buchholz2014), the rate of circulation change due to vorticity convection can be determined from the integral of the unsteady and spanwise convection terms of the vorticity-transport equation across the vortex-core area:
$$\begin{eqnarray}\int \frac{\partial {\it\omega}_{z}}{\partial t}\text{d}A=\int -w\frac{\partial {\it\omega}_{z}}{\partial z}\text{d}A.\end{eqnarray}$$
Using mean values across the vortex-core area, (2.6) reduces to:
$$\begin{eqnarray}\frac{\partial {\it\Gamma}}{\partial t}=\overline{-w\frac{\partial {\it\omega}_{z}}{\partial z}}A,\end{eqnarray}$$
where
$A$
is the cross-sectional area of the vortex core. The presence of the spanwise flow
$w$
indicates that circulation transport, and in turn relative LEV stability, can be improved by the presence of a sweep angle
${\it\Lambda}$
, as suggested by Wong et al. (Reference Wong, Kriegseis and Rival2013).
2.3. The effect of vortex stretching on LEV cross-sectional area
Vortex stretching acts to increase the centre-line vorticity of a vortex at a constant circulation, such that the vortex must contract in size to conserve momentum. In this way, vortex stretching can improve LEV stability by directly modifying the vortex size, avoiding the critical length scale
$c$
. Assuming mean values, vorticity and circulation are related through the vortex-core area:
$$\begin{eqnarray}{\it\omega}_{z}=\frac{{\it\Gamma}}{A},\end{eqnarray}$$
which can be differentiated with respect to time, while holding circulation constant:
$$\begin{eqnarray}\frac{\partial {\it\omega}_{z}}{\partial t}={\it\Gamma}\frac{\partial }{\partial t}\frac{1}{A}=-\frac{{\it\Gamma}}{A^{2}}\frac{\partial A}{\partial t}.\end{eqnarray}$$
This rate of change of vorticity can be substituted with the vortex stretching term of the vorticity-transport equation:
$$\begin{eqnarray}{\it\omega}_{z}\frac{\partial w}{\partial z}=-\frac{{\it\Gamma}}{A^{2}}\frac{\partial A}{\partial t},\end{eqnarray}$$
which can be rearranged for the rate of vortex growth as:
$$\begin{eqnarray}\frac{\partial A}{\partial t}=-{\it\omega}_{z}\frac{\partial w}{\partial z}\frac{A^{2}}{{\it\Gamma}}.\end{eqnarray}$$
Thus, three factors are expected to improve relative LEV stability: vortex stretching; vorticity convection modified through profile sweep
${\it\Lambda}$
; and increased reduced frequency
$k$
. The experimental procedures for investigating these effects are detailed in the following section.
3. Methods
All experiments were conducted in a horizontal free-surface water tunnel at the University of Calgary, while model kinematics were produced with a custom six-degree-of-freedom hexapod manipulator. A detailed description of these facilities can be found in Wong et al. (Reference Wong, Kriegseis and Rival2013). The water-tunnel test section has a diverging rectangular cross-section with a mean width of 385 mm. Water depth was maintained at 432 mm. The hexapod manipulator was mounted above the water-tunnel test section. The current study investigates root-flapping kinematics on aluminium flat-plate profiles. These flat-plate profiles were oriented vertically with zero geometric angle of attack relative to the free stream. In order to minimize free-end effects such as the inboard-directed spanwise flow or vortex compression observed by Hartloper, Kinzel & Rival (Reference Hartloper, Kinzel and Rival2013), the model pierced the free surface in each test case and maintained a tip gap with the water-tunnel floor of less than 3 mm. The axis of the root-flapping motion was in the streamwise direction and fixed at the water-tunnel floor, maintained as a virtual hinge by the hexapod. The reference rotation profile for all test cases is shown in figure 3, where the profile starts from rest and undergoes a sinusoidal ramp-up over a period of time
$t_{r}$
to the peak rotational speed
${\it\Omega}_{max}$
. The peak rotational speed
${\it\Omega}_{max}$
is then maintained for a set period of time
$t_{c}$
, and then finally the profile is returned to rest with a sinusoidal ramp-down over
$t_{r}$
.
Figure 3. The prescribed velocity of the flat-plate profiles follows three sections: a sinusoidal ramp-up from zero velocity to maximum velocity over a period
$t_{r}$
; a constant-velocity section over a period
$t_{c}$
; and a sinusoidal ramp-down over a period
$t_{r}$
. The duration of the constant-velocity section is varied in order to vary Strouhal number.
In order to compare the rotating cases investigated here to two-dimensional cases from the literature, it is possible to define a modified Strouhal number based on the displacement of the midspan of the flapping profile:
$$\begin{eqnarray}St^{\ast }=\frac{(R{\it\phi}_{max})f}{U_{\infty }},\end{eqnarray}$$
where
${\it\phi}_{max}$
is the maximum angular displacement of the profile,
$R$
is the physical profile span and
$f$
is the frequency of motion.
$R{\it\phi}_{max}$
is therefore the displacement of the half-span
$R/2$
over a range of
$\pm {\it\phi}_{max}$
. In order to determine the point at which
$St^{\ast }$
diverges from
$St$
, a large range of modified Strouhal numbers
$St^{\ast }$
and reduced frequencies
$k$
were investigated using phase-averaged planar particle image velocimetry (PIV). Subsequently, vorticity transport on swept and unswept profiles at the specific modified Strouhal number
$St^{\ast }$
that diverged from two-dimensional cases (
$St^{\ast }=0.54$
) were investigated using three-dimensional particle tracking velocimetry (3D-PTV). The details of the exact parameter space, as well as a detailed description of the PIV and 3D-PTV set-ups, are found below.
3.1. Parameter space
The range of modified Strouhal numbers
$St^{\ast }$
and reduced frequencies
$k$
that were investigated in this study are shown in figure 4. The parameter space of Baik et al. (Reference Baik, Bernal, Granlund and Ol2012) is superimposed, as it is used as a reference in § 4 in order to determine the effect of the modified Strouhal number
$St^{\ast }$
in comparison to the Strouhal number
$St$
. In order to vary the flapping frequency without changing the effective angle of attack
${\it\alpha}_{eff}$
, the velocity profile was modified from the reference profile shown in figure 3 by varying the duration of constant rotational speed
$t_{c}$
while maintaining the ramp-up and ramp-down duration
$t_{r}$
. By simultaneously varying the profile chord length and peak speed duration
$t_{c}$
, both reduced frequency and modified Strouhal number could be varied independently over the range
$St=0.33$
, 0.45 and 0.54 and
$k=0.45$
, 0.89 and 1.33. The varying chord length resulted in varying Reynolds numbers; however, the effect of Reynolds number on LEV convection speed is secondary within the range
$200\leqslant Re\leqslant 60\,000$
, as shown by Garmann et al. (Reference Garmann, Visbal and Orkwis2013). Nevertheless, the variation in Reynolds number was kept as small as possible by varying the water-tunnel temperature between
$20$
and
$40\,^{\circ }\text{C}$
, resulting in a range of
$1875\leqslant Re\leqslant 7500$
for all cases. Following the identification of the modified Strouhal numbers
$St^{\ast }$
and reduced frequencies
$k$
with large three-dimensional effects, a sweep angle
${\it\Lambda}$
was included as an additional parameter to vary spanwise vorticity convection. Two sweep angles were considered:
${\it\Lambda}=0^{\circ }$
and
$45^{\circ }$
.
Figure 4. The
$k{-}St^{\ast }$
parameter space for the current study. The
$k{-}St$
parameter space of the two-dimensional study by Baik et al. (Reference Baik, Bernal, Granlund and Ol2012) is superimposed for comparison. The first stage of this study is to determine when three-dimensional effects begin to dominate vortex growth.
Figure 5. Swept and unswept flat-plate profiles (A) manoeuvre through the cylindrical PTV control volume of length
$l=200~\text{mm}$
and diameter
$d=80~\text{mm}$
. The volume is illuminated with the aid of a mirror (B) reflecting light upstream from a high-intensity discharge light source collimated with 40 mm and 300 mm lenses (C). Also shown are the four pco.edge sCMOS cameras (D) and the hexapod manipulator (E). The mirror (B) was moved upstream relative to the real experimental set-up for the purposes of this photo. (a) Experimental set-up; (b) schematic of control volume.
3.2. PIV set-up
A 1 W continuous-wave laser (
${\it\lambda}=532~\text{nm}$
) was used to illuminate a spanwise-oriented plane at the half-span of each test case. The flow was seeded with silver-coated hollow glass spheres of
$100~{\rm\mu}\text{m}$
diameter, with a Stokes number of
$2.4\times 10^{-3}$
. Images of the flow were captured with a Photron SA4 high-speed camera at a frame rate of 250 Hz and a pixel resolution of
$1024\times 1024$
. The images were subsequently processed with LaVision DaVis 8.1.3. Profile motions were repeated and captured ten times per test case, and the results were then ensemble-averaged in order to produce the final vector fields. Vortex-core identification followed the
${\it\gamma}_{1}$
criterion detailed by Graftieaux, Michard & Grosjean (Reference Graftieaux, Michard and Grosjean2001):
$$\begin{eqnarray}{\it\gamma}_{1}(P)=\frac{1}{N}\mathop{\sum }_{S}\sin {\it\theta}_{M},\end{eqnarray}$$
where
${\it\theta}_{M}$
is the angle formed between the velocity
$u(M)$
at point
$M$
and the direction
$PM$
to the point
$M$
from the point of interest
$P$
, while
$N$
is the number of points
$M$
inside the region
$S$
.
3.3. 3D-PTV set-up
The features of the 3D-PTV set-up are illustrated in figure 5. A high-intensity discharge lamp was used as a light source to illuminate a streamwise-oriented cylindrical control volume centred at the midspan of each test profile, after being collimated with a 300 mm primary and 40 mm secondary lens. The measurement volume had a diameter of 80 mm and a length of approximately 200 mm. The light column entered the water tunnel vertically and was reflected into the streamwise direction with a mirror approximately 15 chords downstream of the test profiles. The effect of the mirror on the flow within the control volume was tested by measuring the flow in an otherwise empty channel and checking that the pathline curvature was in fact negligible, and that the flow velocity was undisturbed. The same seeding particles were used as in the PIV experiments, but at a substantially lower seeding density. Images of the flow were captured with four pco.edge sCMOS cameras at a frame rate of 165 Hz and a pixel resolution of
$2560\times 1280$
. The Lagrangian velocities and accelerations were determined by differentiation of the particle tracks. The mean interparticle distance was approximately 3 mm during the experiments. For each test case ten Lagrangian datasets were superimposed and interpolated onto an Eulerian grid with 4 mm grid spacing. Vortex-core identification followed a normalized helicity criterion detailed by Levy, Degani & Arnan (Reference Levy, Degani and Arnan1990):
$$\begin{eqnarray}H_{n}=\frac{\boldsymbol{u}\boldsymbol{\cdot }{\bf\omega}}{|\boldsymbol{u}|\,|{\bf\omega}|},\end{eqnarray}$$
where in the limiting case of
$H_{n}=\pm 1$
, the local vorticity and velocity vectors are parallel.
4. Results
In the following we will test the hypotheses proposed in § 2 with direct measurements of vorticity transport. However, the modified Strouhal numbers and reduced frequencies that produce strong spanwise vorticity transport will first be determined via planar PIV at the midspan position.
4.1. The effect of the modified Strouhal number and reduced frequency on vortex development
Vortices were tracked over the range of modified Strouhal numbers
$St^{\ast }=0.33$
, 0.45 and 0.54, and reduced frequencies
$k=0.45$
, 0.89 and 1.33 utilizing the
${\it\gamma}_{1}$
criterion, as shown in figure 6 for
$t/T=0.5$
. Vortex-core convection speed decreases with increasing reduced frequency, similar to two-dimensional plunging cases. The dependence on reduced frequency is seen much more clearly in figure 7, which shows the displacement of the
${\it\gamma}_{1}$
peak over the range of phases
$0.1\leqslant t/T\leqslant 0.5$
. Here it is shown that vortex-core displacement varies only with respect to reduced frequency, while the modified Strouhal number plays no role. The dependence on reduced frequency suggests that the ratio between the maximum allowable growth rate of the LEV and the feeding of circulation into the LEV (from the leading-edge shear layer) determines LEV stability, as suggested by (2.5).
Figure 6. Vortex-core locations were determined with the
$|{\it\gamma}_{1}|$
criterion and tracked through time, shown here for all modified Strouhal numbers
$St^{\ast }$
and reduced frequencies
$k$
tested, at the phase
$t/T=0.5$
. The modified Strouhal number does not effect vortex convection speed.
Figure 7. (a) Vortex locations are tracked, relative to
$t/T=0.1$
, showing a collapse of LEV displacement as a function of reduced frequency
$k$
. (b) Vortex circulation is affected by both modified Strouhal number
$St^{\ast }$
and reduced frequency
$k$
: larger
$k$
results in a lower circulation
${\it\Gamma}$
; sensitivity to
$St^{\ast }$
is low until
$St^{\ast }=0.54$
, at which point dramatic increases in circulation are observed.
Baik et al. (Reference Baik, Bernal, Granlund and Ol2012) observed that LEV circulation decreased with increasing reduced frequency for two-dimensional plunging cases, which is also observed for the flapping cases in the current study, again seen in figure 7. However, while two-dimensional plunging cases showed that circulation had only a low dependence on Strouhal number, the
$St^{\ast }=0.54$
cases exhibit a drastically increased circulation to that of the other modified Strouhal numbers. The large variation in circulation with respect to
$St^{\ast }$
suggests that the investigated flapping cases cannot be approximated as bulk two-dimensional at these increasingly faster motions. Therefore, as the
$St^{\ast }=0.54$
cases bear the least resemblance to two-dimensional plunging, these cases will be investigated with 3D-PTV below in order to determine how spanwise vorticity transport affects LEV stability.
4.2. The effect of vorticity transport on vortex development
Despite the divergence between
$St$
and
$St^{\ast }$
for
$St^{\ast }\geqslant 0.54$
, LEV stability is determined by the reduced frequency
$k$
alone, similar to two-dimensional plunging cases. Therefore, at first glance the influence of vorticity transport on LEV stability appears to be secondary. In order to reconcile this observation with the hypotheses in § 2, a profile sweep
${\it\Lambda}$
can be introduced in order to vary vorticity convection by varying the spanwise flow, thus acting as a vorticity sink. Figure 8 shows isosurfaces of vorticity magnitude and vorticity convection for two sweep angles
${\it\Lambda}=0^{\circ }$
and
$45^{\circ }$
and two reduced frequencies
$k=0.89$
and 1.33, as measured with 3D-PTV. Vorticity convection magnitude is found to increase both with increasing reduced frequency and increasing profile sweep, which can also be seen in figure 9. The spanwise flow, circulation, vorticity transport and vortex convection shown in figure 9 were measured at the midspan of each profile, and values for vorticity convection, vortex stretching and spanwise flow were determined from the average value within an isolevel of vorticity
${\it\omega}_{z}c/U_{\infty }=5$
. The vortices are tracked using the maximum normalized helicity criterion over the range
$0.2\leqslant t/T\leqslant 0.4$
, as a strong peak of normalized helicity was observed across this interval.
Figure 8. (a, c, e, g) Isosurfaces of vorticity magnitude (
${\it\omega}c/U_{\infty }=5$
, 10 and 20) for phase
$t/T=0.5$
. (b, d, f, h) Isosurfaces of vorticity convection (
$w(\partial {\it\omega}_{z}/\partial z)(c^{2}/U_{\infty }^{2})=20$
, 50 and 100). The four cases shown are: (a,b)
$k=0.89,{\it\Lambda}=0^{\circ }$
; (c,d)
$k=1.33,{\it\Lambda}=0^{\circ }$
; (e, f)
$k=0.89,{\it\Lambda}=45^{\circ }$
; and (g,h)
$k=1.33,{\it\Lambda}=45^{\circ }$
.
Figure 9. Spanwise flow, vortex circulation, vorticity transport and vortex location for four test cases: (a) spanwise flow; (b) circulation; (c) vorticity convection; (d) vortex stretching; (e) streamwise vortex convection; (f) wall-normal vortex convection. Streamwise vortex position shows a large dependence on both sweep angle and reduced frequency. This sensitivity to reduced frequency can be explained in terms of the limiting length scale of the profile chord for stable LEV growth.
The ability of profile sweep to modulate spanwise vorticity transport agrees with the findings of Wong et al. (Reference Wong, Kriegseis and Rival2013). Increased spanwise vorticity transport corresponds to a reduced LEV convection speed, and both higher sweep angles and higher reduced frequencies result in a slower streamwise vortex convection. However, the effect of vortex stretching and vorticity convection on streamwise vortex convection is not linear. For instance, the
${\it\Lambda}=45^{\circ },k=0.89$
case and the
${\it\Lambda}=0^{\circ },k=1.33$
case have nearly identical vortex convection paths despite having very different levels of vorticity convection and vortex stretching. In other words, relative LEV stability is increased by two mechanisms: (i) the addition of vorticity sinks, such as from profile sweep; or (ii) the reduction of vorticity feeding for a given limiting length scale
$c$
. This latter mechanism of increasing LEV stability is governed by the reduced frequency, as shown in § 2.
5. Discussion
In § 2 it was predicted that both larger reduced frequencies and larger sweep angles would result in more stable LEVs on flapping profiles. Even in the rotating cases investigated here, the reduced frequency was found to govern the ratio between the limiting growth rate of the LEV (
$c^{2}/T$
) and the feeding of circulation into the LEV from the leading-edge shear layer (
$u_{eff}^{2}T$
). Meanwhile, larger sweep angles result in larger spanwise vorticity transport, acting as a vorticity sink.
For rotating cases, the vorticity feeding rate is a function of the profile span. Therefore, while aspect ratio sensitivity was not investigated explicitly in this study, the reduced frequency is analogous to the aspect ratio
$AR$
for rotating profiles:
$$\begin{eqnarray}k\approx \frac{{\rm\pi}fc}{u_{eff}}\approx \frac{{\rm\pi}fc}{{\it\Omega}R}\approx \frac{{\rm\pi}f}{{\it\Omega}AR},\end{eqnarray}$$
where
$R$
is the profile span. Larger reduced frequencies
$k$
represent larger allowable LEV growth rates relative to shear-layer feeding, and thus more stable LEVs. In turn, the most stable LEVs also correspond to the smallest aspect ratios, similar to the findings of Lentink & Dickinson (Reference Lentink and Dickinson2009). This analogy between the aspect ratio
$AR$
and the reduced frequency
$k$
of course neglects effects such as vorticity convection and vortex stretching, which have been shown here to also improve relative LEV stability.
In addition to vorticity transport, Wojcik & Buchholz (Reference Wojcik and Buchholz2014) found that vorticity annihilation was a significant mechanism for regulating LEV growth and was generally much larger in magnitude than vorticity convection. However, as an extension to these findings, it has been shown here that relative LEV stability can be improved by moderating LEV growth through vorticity convection and vortex stretching.
Finally, with respect to the findings of Beem et al. (Reference Beem, Rival and Triantafyllou2012) that profile sweep does not affect LEV stability for plunging cases, it was found that profile sweep did, in fact, affect LEV stability for flapping cases in contrast with plunging cases. The addition of spanwise flow from profile sweep increased the vorticity transport that was already present for the rotating, unswept cases, in agreement with the findings of Wong et al. (Reference Wong, Kriegseis and Rival2013). Beem et al. (Reference Beem, Rival and Triantafyllou2012) had ignored rotating cases in their study on purely plunging profiles. The current result demonstrating the effect of profile sweep alludes to the evolutionary convergence of swept profiles found in nature, ranging from large marine animals down to small flapping birds, and provides us with a step forward towards designing more efficient autonomous vehicles and energy extraction devices.
6. Conclusions
In this study relative LEV stability on impulsively started flapping profiles was proposed and tested using phase-averaged planar PIV and volumetric 3D-PTV measurements. The circulation flux into an LEV from the leading-edge shear layer was moderated by the spanwise convection of vorticity. Moreover, vortex stretching was observed to limit LEV growth and further enhance relative LEV stability.
This study resulted in the following primary conclusions:
-
(i) The ratio between the limiting length scale of an LEV (the profile chord) and the shear-layer feeding rate can be approximated by the reduced frequency
$k$
, with larger reduced frequencies increasing LEV stability. In the specific case of rotating profiles, the shear-layer feeding rate is a function of the profile span. It is therefore speculated that the ratio between the limiting length scale of an LEV and the shear-layer feeding rate depends on the aspect ratio
$AR$
, with smaller aspect ratios increasing LEV stability in agreement with Lentink & Dickinson (Reference Lentink and Dickinson2009). -
(ii) In addition to the above ratio, LEV stability can be improved by draining vorticity through spanwise vorticity transport. Spanwise vorticity transport, and therefore LEV stability, can be increased by introducing profile sweep. This effect may explain the ubiquity of profile sweep in natural swimming and flying, throughout length scales ranging from the wings of small birds to the flukes of whales.
Acknowledgements
The authors gratefully acknowledge the support of the US Air Force Office of Scientific Research under grant number FA9550-13-1-0117, monitored by Dr D. Smith.
