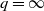1. Introduction and main results
One of the central aspects of high-dimensional probability theory is the study of random geometric quantities and the phenomena that occur as the dimension of the ambient space tends to infinity. The field is intimately connected to geometric functional analysis as well as convex and discrete geometry, and has attracted considerable attention in the last decade. This is in part because of numerous applications that can be found in the statistics and machine learning literature related to high-dimensional data, e.g. in the form of dimensionality reduction in information retrieval, clustering, principal component regression, community detection, or covariance estimation; see [Reference Vershynin28] as well as the references provided therein. A famous example of a high-dimensional limit theorem is the Maxwell–Poincaré–Borel lemma (see, e.g., [Reference Diaconis and Freedman8]) stating that, for fixed
$k\in\mathbb N$
, the distribution of the first k coordinates of a point chosen uniformly at random from the n-dimensional Euclidean ball or sphere of radius one converges weakly to a k-dimensional Gaussian distribution as the space dimension n tends to infinity.
Today, there is a vast literature on high-dimensional central limit theorems, which describe the Gaussian fluctuations for various random geometric quantities in different contexts, for instance the famous central limit theorem for convex bodies [Reference Klartag20], a central limit theorem for the volume of random projections of the cube [Reference Paouris, Pivovarov and Zinn24], or a central limit theorem for the q-norm (Euclidean norm) of (projections of) points chosen randomly from
$\ell_p^n$
-balls [Reference Alonso-Gutiérrez, Prochno and Thäle2, Reference Kabluchko, Prochno and Thäle15, Reference Kabluchko, Prochno and Thäle17], to mention just a few. Other limit theorems, such as moderate deviations principles and large deviations principles, have only been studied in high-dimensional probability related to the geometry of convex bodies since their introduction in [Reference Alonso-Gutiérrez, Prochno and Thäle1, Reference Gantert11, Reference Kabluchko, Prochno and Thäle15, Reference Kabluchko, Prochno and Thäle17]. In fact, those kinds of limit theorems are more sensitive to the randomness involved and display a non-universal behavior in their speed and/or rate function. The latter fact makes the subject particularly interesting as, contrary to a central limit theorem which implies the somewhat negative result that fluctuations do not provide much information because of universality, the moderate and large deviations limit theorems are distribution dependent and encode subtle geometric information about the underlying structure. In the past three years a number of interesting results in this direction have been obtained, and we refer the reader to [Reference Gantert, Kim, Ramanan and Letzter10, Reference Kabluchko, Prochno and Thäle16, Reference Kim and Ramanan18, Reference Kim and Ramanan19, Reference Liao and Ramanan21]. A link between the study of moderate and large deviations and the famous Kannan–Lovász–Simonovits conjecture has recently been discovered [Reference Alonso-Gutiérrez, Prochno and Thäle3].
In this work we study limit theorems for (suitably normalized)
$\ell_q$
-norms of points chosen uniformly at random in a centered and regular simplex. When
$1\leq q < \infty$
, we provide a Berry–Esseen-type rate of convergence to a standard Gaussian distribution. For the case where
$q=+\infty$
, we complement this result with a non-central limit theorem, establishing the weak convergence to a Gumbel distribution, and provide both moderate and large deviations principles. Moreover, as an application of our central limit theorem, we present a version of the Schechtman–Schmuckenschläger result [Reference Schechtman, Schmuckenschläger, Lindenstrauss, Milman and Springer25] and compute the volume of the intersection of an
$\ell_p$
-ball with a regular simplex. We note that the method of proof in the Berry–Esseen-type central limit theorem differs from the previously mentioned ones in the sense that here we use a connection to the asymptotic theory of sums of random spacings and do not rely on a Schechtman–Zinn-type probabilistic representation.
In order to be more precise, let
$n\in\mathbb N$
and consider the
$(n-1)$
-dimensional simplex
$\Delta_{n-1}\,{:\!=}\,\big\{x\in\mathbb R^n \,{:}\, x_i\geq 0,\, \sum_{i=1}^n x_i=1\big\} = \mathrm{conv}\{e_1,\dots,e_n \}$
, where
$\mathrm{conv}(A)$
denotes the convex hull of a set A and
$e_1,\ldots,e_n$
represent the unit vectors of the standard orthonormal basis of
$\mathbb R^n$
. Consider a sequence
$(E_i)_{i\in\mathbb N}$
of independent random variables with an exponential distribution of mean 1 and, for each
$n\in\mathbb N$
, let
$S_n\,{:\!=}\,\sum_{i=1}^n E_i$
denote the nth partial sum. We study the sequence of random vectors
\begin{equation*}Z_n\,{:\!=}\,\left(\frac{E_1}{S_n}-\frac{1}{n},\dots,\frac{E_n}{S_n}-\frac{1}{n}\right)\in \Delta_{n-1}-\frac{1}{n}(e_1+\cdots+e_n),\qquad n\in\mathbb N.\end{equation*}
In fact, uniformly distributed points in the standard centered simplex in
$\mathbb R^n$
,
$\Delta_{n-1}-\frac{1}{n}(e_1+\cdots+e_n)$
, have the same distribution as
$Z_n$
(see, e.g., [Reference Mathai22]). A different method to generate uniform random vectors in the simplex is by letting
$U_1,\ldots, U_{n-1}$
be independent and identically distributed random variables with a uniform distribution on [0,1] and considering
$G_{n,i}\,{:\!=}\,U_{(i)}-U_{(i-1)}$
,
$i=1,\ldots,n$
, where
$U_{(i)}$
is the ith order statistic of
$U_1,\ldots,U_{n-1}$
, with the convention that
$U_{(0)}\,{:\!=}\,0$
,
$U_{(n)}\,{:\!=}\,1$
. Then the vector
$G_n\,{:\!=}\,\big(G_{n,1},\ldots,G_{n,n}\big)$
is uniformly distributed in
$\Delta_{n-1}$
and
$Z_n\overset{\mathrm{d}}{=} G_n-\frac{1}{n}(e_1+\cdots+e_n)$
. A proof of this fact can be found, for instance, in [Reference David and Nagaraja5, Section 6.4].
The first main result of this paper is the following Berry–Esseen-type theorem for the
$\ell_q$
-norm
$\|\cdot\|_q$
(
$1\leq q<\infty$
) of uniform random points in
$\Delta_{n-1}-\frac 1n (e_1+\cdots+e_n)$
. Define
$\mu_q\,{:\!=}\,\mathbb{E}\left[ {\left|{E_1-1}\right|^q}\right]$
and
$\sigma_q^2\,{:\!=}\,q^{-2}\mu_q^{-2}\big(\mu_{2q}-\big(q^2+2q+2\big)\mu_q^2+2(q+1)\mu_q-1\big)$
. For example,
$\mu_1=2\mathrm{e}^{-1},\sigma_1=2\mathrm{e}-5$
, and
$\mu_2=\sigma_2=1$
.
Theorem 1.1 Let
$1\leq q<\infty$
. There exists some constant
$c_q>0$
depending only on q such that, for all
$n\in \mathbb{N}$
,
\begin{equation*} \sup_{x\in\mathbb R}\left| \mathbb{P}\Bigg[\sqrt{n}\Bigg(\frac{n^{1-1/q}\Vert Z_n\Vert_q\,\mu_q^{-1/q} -1}{\sigma_q}\Bigg)\leq x\Bigg]-\mathbb{P}[N\leq x]\right| \leq c_q\frac{\log n}{\sqrt{n}}, \end{equation*}
where
$N\sim\mathcal N(0,1)$
is a standard Gaussian random variable.
In the proof of this result we use a connection to the asymptotic theory of sums of random spacings. This allows us to use a Berry–Esseen result of Mirakhmedov [Reference Mirakhmedov23], who improved a theorem due to Does and Klaassen [Reference Does and Klaassen9].
As a direct corollary of Theorem 1.1, we obtain the following central limit theorem, which is the analogue for the regular simplex of the corresponding central limit theorems in [Reference Kabluchko, Prochno and Thäle15, Reference Kabluchko, Prochno and Thäle17] for
$\ell_p^n$
-balls. It will find an application in Section 4.
Corollary 1.1 For all
$1\leq q<\infty$
,
\begin{equation*} \sqrt{n}\Big(n^{1-1/q}\| Z_n \|_q\,\mu_q^{-1/q} -1\Big)\xrightarrow[n\to\infty]{\mathrm{d}} Z \sim {{\mathcal{N}}}(0,\sigma_q^2). \end{equation*}
When the parameter q satisfies
$q=\infty$
, we cannot expect convergence in distribution of
$\|Z_n\|_\infty$
to a Gaussian random variable. However, we establish a non-central limit theorem with a double exponential (also known as Gumbel) distribution in the limit. The result in this case reads as follows.
Theorem 1.2 We have
\begin{equation*} n\Vert Z_n\Vert_{\infty}-(\log n-1)\xrightarrow[n\to\infty]{\mathrm{d}} G, \end{equation*}
where G has a standard Gumbel distribution, i.e.
$\mathbb{P}[G\leq x]=\exp(\!-\mathrm{e}^{-x})$
for
$x\in\mathbb R$
.
The next result describes the upper and lower deviations on a moderate scale, which lies between the Gaussian fluctuations of a central limit theorem and the large deviations which occur on the scale of a law of large numbers. For a formal definition of a large deviations principle (LDP), see Section 2.2.
Theorem 1.3 Let
$(s_n)_{n\in\mathbb N}$
be a positive sequence with
$s_n\to \infty$
and
$s_n/\log n\to 0$
. Then, the sequence
$\Big(\frac{\log n}{s_n}\Big(\frac{n}{\log n}\|Z_n\|_{\infty}-1\Big)\Big)_{n\in\mathbb{N}}$
satisfies an LDP with speed
$s_n$
and rate function
\begin{equation*} \mathbb{I}(z) \,{:\!=}\, \begin{cases} z , & z\geq 0,\\ +\infty , & z<0. \end{cases} \end{equation*}
As a last result, we establish the following large deviations principle for the
$\ell_\infty$
-norm, which we compare in Section 4 to the LDP for random points in the n-dimensional crosspolytope, i.e. the
$\ell_1$
-ball in
$\mathbb R^n$
.
Theorem 1.4 The sequence
$\Big(\frac{n}{\log n}\Vert Z_n\Vert_{\infty}\Big)_{n\in\mathbb{N}} $
satisfies an LDP with speed
$ s_n=\log n $
and rate function
\begin{equation*}\mathbb{I}(z) \,{:\!=}\, \begin{cases} z-1 , & z\geq 1,\\ +\infty , & z<1. \end{cases} \end{equation*}
The rest of the paper is organized as follows. In Section 2 we collect some background material on large deviations and introduce the notation we use throughout the paper. Section 3 is then devoted to the proofs of Theorems 1.1, 1.2, 1.3, and 1.4. In Section 4 we compare the LDP for the simplex with the one for
$\ell_p^n$
-balls, in particular the one for the crosspolytope, and present an application of the central limit theorem to high-dimensional intersection volumes.
2. Preliminaries
2.1. General notation
Let
$n\in\mathbb{N}$
. Given
$1\leq q\leq \infty$
and a vector
$x=(x_1,\ldots,x_n)\in\mathbb{R}^n$
, we write
\begin{equation*}\left\|{x}\right\|_q=\begin{cases} \Bigl(\sum_{i=1}^n \left|{x_i}\right|^q\Bigr)^{1/q} , & q<\infty, \\ \\[-7pt] \max_{1\leq i\leq n} \left|{x_i}\right|, & q=\infty.\end{cases}\end{equation*}
We will assume that all random quantities are defined on a common probability space
$(\Omega,\Sigma,\mathbb{P})$
and we write
$\mathbb{P}\left[ \,{\cdot}\,\right]$
and
$\mathbb{E}\left[ {\,{\cdot}\,}\right]$
for the probability of an event and the expectation of an (integrable) random variable, respectively. For a sequence of independent and identically distributed (i.i.d.) random vectors
$(X_i)_{i\in\mathbb{N}}$
we denote by
$\bar{X}_n=\frac{1}{n}\sum_{i=1}^n X_i $
the empirical average. Throughout,
$E,E_1,E_2,\ldots$
will be independent exponential random variables having rate 1 and
$\bar{E}_n=\frac{1}{n}\sum_{i=1}^n E_i$
. Note that
$\mathbb{P}\left[ \bar{E}_n=0\right]=0$
and thus we can ignore this event in our analysis. By
$\mathcal{N}(\mu,\Sigma)$
we denote the (multivariate) Gaussian distribution with mean
$\mu$
and covariance matrix
$\Sigma$
. If a random variable N is distributed according to
$\mathcal{N}(\mu,\Sigma)$
, we write
$N\sim\mathcal{N}(\mu,\Sigma)$
. With
$\xrightarrow{\mathrm{d}}$
and
$\xrightarrow{\mathbb{P}}$
we indicate convergence in distribution and in probability, respectively. We say that a sequence of real-valued random variables
$(X_n)_{n\in\mathbb{N}}$
satisfies a central limit theorem (CLT) if there exists a sequence
$(a_n)_{n\in\mathbb{N}}$
of real numbers such that
$\sqrt{n}(a_nX_n-1)\xrightarrow{\mathrm{d}} N\sim \mathcal{N}(0,1)$
as
$n\to\infty$
. For further background material on asymptotic probability theory consult, for example, [Reference DasGupta4].
2.2. Large and moderate deviations
In the following, we recall facts from the theory of large deviations as developed, for example, in [Reference Dembo and Zeitouni6].
A sequence
$(X_n)_{n\in\mathbb{N}} $
of real-valued random variables is said to satisfy an LDP with speed
$ (s_n)_{n\in\mathbb{N}}\subset (0,\infty) $
and rate function
$ \mathbb{I} \,{:}\, \mathbb{R}\rightarrow [0,\infty] $
if
$\mathbb{I}$
is lower semi-continuous, has compact level sets
$\{z\in\mathbb{R} \,{:}\, \mathbb{I}(z)\leq \alpha\}$
,
$\alpha\in\mathbb{R}$
, and if, for all Borel sets
$ A\subset \mathbb{R} $
,
\begin{equation*}-\inf_{z\in A^{\circ}} \mathbb{I}(z)\leq \liminf_{n\to\infty} s_n^{-1}\log\,\mathbb{P}\left[ X_n\in A\right]\leq \limsup_{n\to\infty} s_n^{-1}\log\,\mathbb{P}\left[ X_n\in A\right]\leq -\inf_{z\in\bar{A}}\mathbb{I}(z).\end{equation*}
Here,
$A^\circ$
denotes the interior and
$\bar{A}$
the closure of A. For the empirical average of i.i.d. (real-valued) random variables an LDP holds according to Cramér’s theorem, which we state next.
Lemma 2.1 (Cramérs theorem [Reference Dembo and Zeitouni6, Theorem 2.2.3]) Let
$ X,X_1,X_2,\ldots $
be i.i.d. real-valued random variables. Assume that the origin is an interior point of the domain of the cumulant-generating function
$ \Lambda(u)=\log \mathbb{E}[\!\exp(uX)] $
. Then the sequence of partial sums
$ \bar{X}_n=\frac{1}{n} \sum_{i=1}^n X_i$
,
$n\in\mathbb{N}$
, satisfies an LDP on
$ \mathbb{R} $
with speed n and rate function
$ \Lambda^*$
, where
$\Lambda^*(z)=\sup_{u\in\mathbb{R}}(uz-\Lambda(u))$
for all
$z\in\mathbb{R}$
.
It is often useful to transfer an LDP for a sequence of random variables to another such sequence when they do not differ too much from each other. The following lemma provides a condition (called exponential equivalence) under which such an attempt is possible.
Lemma 2.2 (Exponential equivalence[Reference Dembo and Zeitouni6, Theorem 4.2.13]) Let
$ (X_n)_{n\in\mathbb{N}} $
and
$(Y_n)_{n\in\mathbb{N}} $
be two sequences of real-valued random variables, and assume that
$ (X_n)_{n\in\mathbb{N}} $
satisfies an LDP with speed
$ s_n $
and rate function
$ \mathbb{I} $
. If
$ (X_n)_{n\in\mathbb{N}} $
and
$ (Y_n)_{n\in\mathbb{N}} $
are exponentially equivalent at speed
$s_n$
, i.e. we have, for any
$ \delta>0 $
,
$\limsup_{n\to\infty} s_n^{-1}\log\, \mathbb{P}\left[ |X_n-Y_n|>\delta\right]=-\infty$
, then
$ (Y_n)_{n\in\mathbb{N}} $
satisfies an LDP with the same speed and rate function as
$ (X_n)_{n\in\mathbb{N}} $
.
We shall need the following result for moderate deviations of the empirical average of i.i.d. random variables.
Lemma 2.3 (Moderate deviations [Reference Dembo and Zeitouni6, Theorem 3.7.1]) Let
$ X,X_1,X_2,\ldots $
be i.i.d. real-valued random variables with
$\mathbb{E}\left[ {X}\right]=\mu$
and
$\mathrm{Var} X=\sigma^2>0$
. Assume that the origin is an interior point of the domain of the cumulant-generating function
$ \Lambda(u)=\log \mathbb{E}\exp(uX)$
. Fix a sequence
$(a_n)_{n\in\mathbb{N}}$
with
$a_n\to 0$
and
$na_n\to \infty$
. Then, the sequence
$\sqrt{na_n}\big(\bar{X}_n-\mu\big)$
satisfies an LDP on
$ \mathbb{R} $
with speed
$ a_n^{-1} $
and rate function
$\mathbb{I}(z)={z^2} / {2\sigma^2}$
.
3. The proofs
We now present the proofs of Theorems 1.1, 1.2, 1.3, and 1.4, and start with the Berry–Esseen-type central limit theorem followed by the non-central limit theorem together with the moderate and large deviations principles when
$q=\infty$
.
3.1. Proof of the Berry–Esseen CLT
The general philosophy of the proof is similar to that in [Reference Johnston and Prochno14]. However, as already explained, we shall use a connection to the asymptotic theory of sums of spacings. The following lemma is a version of [Reference Alonso-Gutiérrez, Prochno and Thäle2, Lemma 4.1] (see also [Reference Johnston and Prochno14, Lemma 2.8]).
Lemma 3.1 For any real-valued random variables X, Y and any
$\varepsilon>0$
,
\begin{equation*} \sup_{x\in\mathbb R}\big| \mathbb{P}[Y\leq x]-\mathbb{P}[N\leq x]\big| \leq \sup_{x\in\mathbb R}\vert \mathbb{P}[X\leq x]-\mathbb{P}[N\leq x]\vert +\mathbb{P}[\vert X-Y\vert>\varepsilon]+\frac{\varepsilon}{\sqrt{2\pi}\,}, \end{equation*}
where N is a standard Gaussian random variable.
Proof. Let
$x\in\mathbb R$
and
$\varepsilon>0$
. Then,
\begin{align*} \mathbb{P}[Y\leq x]-\mathbb{P}[N\leq x]&\leq \mathbb{P}[Y\leq x, \vert X-Y\vert\leq \varepsilon] + \mathbb{P}[\vert X-Y\vert>\varepsilon]-\mathbb{P}[N\leq x]\\[3pt] & \leq \mathbb{P}[X\leq x+\varepsilon]+ \mathbb{P}[\vert X-Y\vert>\varepsilon] -\mathbb{P}[N\leq x]\\[3pt] & =\mathbb{P}[X\leq x+\varepsilon]-\mathbb{P}[N\leq x+\varepsilon]+\mathbb{P}[\vert X-Y\vert>\varepsilon]\\[3pt] & \quad + \mathbb{P}[N\leq x+\varepsilon]-\mathbb{P}[N\leq x]. \end{align*}
Using that
$\mathbb{P}[N\leq x+\varepsilon]-\mathbb{P}[N\leq x]\leq \varepsilon/\sqrt{2\pi}$
for all
$x\in\mathbb R$
, taking absolute values, and forming the supremum completes the proof.
The next lemma shows that, similar to CLTs, Berry–Esseen-type bounds can also be transferred by “nice” functions.
Lemma 3.2 Let
$(X_n)_{n\in\mathbb N}$
be a sequence of real-valued random variables. Suppose that there exist constants
$\mu\in\mathbb{R}$
and
$\sigma>0$
such that the Berry–Esseen-type bound
\begin{equation*} \sup_{x\in\mathbb R}\bigg|\mathbb{P}\left[\sqrt{n}\left(\frac{X_n-\mu}{\sigma}\right)\leq x\right]-\mathbb{P}[N\leq x]\bigg|\leq a_n \end{equation*}
holds for some sequence
$(a_n)_{n\in\mathbb{N}}$
and all
$n\in\mathbb{N}$
, where N is a standard Gaussian random variable. If
$g \,{:}\, \mathbb R\to\mathbb R$
is twice continuously differentiable at
$\mu$
with
$g'(\mu)>0$
then, for some constant
$C>0$
and all
$n\in\mathbb{N}$
,
\begin{equation*} \sup_{x\in\mathbb R}\bigg|\mathbb{P}\left[\sqrt{n}\left(\frac{g(X_n)-g(\mu)}{g'(\mu)\sigma}\right)\leq x\right]-\mathbb{P}[N\leq x]\bigg|\leq C\max\left\{a_n,\frac{\log n}{\sqrt{n}}\right\}. \end{equation*}
Proof. Set
$\xi_n\,{:\!=}\,\sqrt{n}(X_n-\mu)/\sigma$
and
$\zeta_n\,{:\!=}\,\sqrt{n}(g(X_n)-g(\mu))/g'(\mu)\sigma$
. We use Lemma 3.1 to infer, for each
$n\in\mathbb{N}$
and every
$\varepsilon>0$
, that
\begin{equation} \sup_{x\in\mathbb R} \big\vert \mathbb{P}[\zeta_n\leq x]-\mathbb{P}[N\leq x] \big\vert \leq \sup_{x\in\mathbb R} \big\vert \mathbb{P}[\xi_n \leq x]-\mathbb{P}[N\leq x] \big\vert +\mathbb{P}[\vert \xi_n-\zeta_n\vert>\varepsilon]+\frac{\varepsilon}{\sqrt{2\pi}\,}. \end{equation}
Fix
$n\in\mathbb{N}$
. We will estimate
$\mathbb{P}[\vert \xi_n-\zeta_n\vert>\varepsilon]$
and choose
$\varepsilon$
suitably.
Making use of the Taylor expansion of g at
$\mu$
yields that there exists some
$\delta>0$
such that, for all
$x\in (\mu-\delta,\mu+\delta)$
,
$g(x)-g(\mu)=g'(\mu)(x-\mu)+\Phi(x-\mu)$
, where
$\Phi \,{:}\, \mathbb R\to\mathbb R$
is a function such that, for all
$x\in (\mu-\delta,\mu+\delta)$
,
$\vert \Phi(x)\vert \leq M_g\vert x-\mu\vert^2$
for
$M_g=\sup_{x\in (\mu-\delta,\mu+\delta)}\vert g''(x)\vert/2$
. Thus, if
$\vert X_n-\mu\vert<\delta$
,
$\left|{g(X_n)-g(\mu)-g'(\mu)(X_n-\mu)}\right|\leq M_g \left|{X_n-\mu}\right|^2$
. We get, after division by
$g'(\mu)\sigma$
and multiplication by
$\sqrt{n}$
,
\begin{equation*} \vert \xi_n-\zeta_n\vert\leq \frac{M_g}{g'(\mu)\sigma}\sqrt{n}\vert X_n-\mu\vert^2. \end{equation*}
Therefore, for every
$n\in\mathbb{N}$
,
\begin{equation} \mathbb{P}[\vert \xi_n-\zeta_n\vert> \varepsilon]\leq \mathbb{P}\left[\big|\sqrt{n} (X_n-\mu)\Big|>\sqrt{\frac{\varepsilon g'(\mu)\sigma\sqrt{n}}{M_g}}\right] + \mathbb{P}\Big[\big|\sqrt{n}(X_n-\mu)\big|>\delta\sqrt{n}\Big]. \end{equation}
If
$M_g=0$
, the first summand disappears and we can set
$\varepsilon=a_n$
. By the assumed Berry–Esseen bound and the symmetry of a Gaussian random variable, for each
$n\in\mathbb{N}$
and every
$x\in\mathbb{R}$
,
\begin{align*} \mathbb{P}\left[ \left|{\sqrt{n}(X_n-\mu)}\right|>\sigma x\right]&=\mathbb{P}\left[ \sqrt{n}(X_n-\mu)<-\sigma x\right]+\mathbb{P}\left[ \sqrt{n}(X_n-\mu)>\sigma x\right]\\ & \leq 2\bigl(\mathbb{P}\left[ N\geq x\right]+a_n\bigr). \end{align*}
Together with the bound
$\mathbb{P}\left[ N\geq x\right]\leq \mathrm{e}^{-x^2/2}$
, the second summand in (3.2) is
\begin{equation*} {{\mathbb{P}\left[ \left|{\sqrt{n}(X_n-\mu)}\right|>\delta\sqrt{n}\right]\leq 2\left(\!\exp\bigg\{{-}\frac{\delta^2}{2\sigma^2} n\bigg\}+a_n\right)\leq c\max\left\{a_n,\frac{\log n}{\sqrt{n}}\right\}}} \end{equation*}
for some
$c>0$
independent of
$n\in\mathbb{N}$
. If
$M_g>0$
, by setting
$\varepsilon=\sigma M_g g'(\mu)^{-1}n^{-1/2}\log n$
for each
$n\in\mathbb{N}$
, the first summand is
\begin{equation*} {{\mathbb{P}\left[ {\left|{\sqrt{n}(X_n-\mu)}\right|>\sigma\sqrt{\log n}}\right]\leq 2(n^{-1/2}+a_n)\leq c'\max\left\{a_n,\frac{\log n}{\sqrt{n}}\right\}}} \end{equation*}
for some constant
$c'>0$
independent of n. This choice of
$\varepsilon$
yields
\begin{equation*} \mathbb{P}[\vert \xi_n-\zeta_n\vert> \sigma M_g g'(\mu)^{-1}n^{-1/2}\log n]\leq (c+c')\max\left\{a_n,\frac{\log n}{\sqrt{n}}\right\}. \end{equation*}
Together with inequality (3.1) we have, for all
$n\in\mathbb{N}$
,
\begin{equation*} \sup_{x\in\mathbb R} \big\vert \mathbb{P}[\zeta_n\leq x]-\mathbb{P}[N\leq x] \big\vert \leq a_n +(c+c')\max\left\{a_n,\frac{\log n}{\sqrt{n}}\right\}+\frac{\sigma M_g}{\sqrt{2\pi} g'(\mu)}\frac{\log n}{\sqrt{n}}, \end{equation*}
whereupon choosing
$C>0$
suitably completes the proof.
Remark 3.1 There exist results in the literature which are similar to Lemma 3.2. For example, [Reference DasGupta4, Theorem 11.6] deals with the case of
$X_n$
being empirical averages and g a function with Hölder-continuous derivative. In this case we have
$a_n=n^{-1/2}$
and the guaranteed bound for the modified sequence is of order
${\log n} / {\sqrt{n}}$
. We do not know if this rate in Lemma 3.2 can be improved in general.
Recall the definition of the spacings in the introduction by
$G_{n,i}=U_{(i)}-U_{(i-1)}$
,
$i=1,\ldots,n$
, where
$U_{(i)}$
is the ith order statistic of
$U_1,\ldots,U_{n-1}$
, sampled independently and uniformly from the unit interval, with the convention that
$U_{(0)}=0$
,
$U_{(n)}=1$
. Also recall that E denotes an exponential random variable with rate 1.
We deduce the following theorem from [Reference Mirakhmedov23] which refined a Berry–Esseen theorem from [Reference Does and Klaassen9].
Theorem 3.1 Let
$G_{n,1},\ldots, G_{n,n}$
be as above. Suppose
$f \,{:}\, \mathbb R\to\mathbb R$
is measurable with
$\mathbb{E}\left[ {f(E)^3}\right]<\infty$
and
$\sigma^2\,{:\!=}\,\mathrm{Var} f(E)-\operatorname{Cov}(E,f(E))^2>0$
. Then there exists a constant
$C>0$
such that, for all
$n\in\mathbb{N}$
,
\begin{equation*} \sup_{x\in\mathbb R}\Bigg|\mathbb{P}\left[\sqrt{n}\left(\frac{\frac{1}{n}\sum_{i=1}^nf(nG_{n,i})-\mathbb{E}[f(E)]}{\sigma}\right)\leq x\right]-\mathbb{P}[N\leq x]\Bigg| \leq \frac{C}{\sqrt{n}\,}, \end{equation*}
where N is a standard Gaussian random variable.
The following result will be used for the proof of Theorem 1.1 and we skip its elementary proof. Again, E stands for a standard exponential random variable.
Lemma 3.3 Let
$1\leq q<\infty$
. Then
$\operatorname{Cov}(E,\left|{E-1}\right|^q)=(q+1)\mathbb{E}\left[ {\left|{E-1}\right|^q}\right]-1$
, where
$\mathbb{E}\left[ {\left|{E-1}\right|^q}\right]=\mathrm{e}^{-1}\left(\Gamma(q+1)+\int_{0}^1 x^q \mathrm{e}^x\text{d}x\right)$
.
Proof of Theorem 1.1. Using the connection to the spacings
$G_{n,1},\ldots,G_{n,n}$
we have
\begin{equation*} \|Z_n\|_q^q=\sum_{i=1}^n \biggl|Z_{n,i}-\frac{1}{n}\biggr|^q\overset{\mathrm{d}}{=}\sum_{i=1}^n \biggl|G_{n,i}-\frac{1}{n}\biggr|^q=n^{-q}\sum_{i=1}^n |nG_{n,i}-1|^q. \end{equation*}
Thus, writing
$n^{q-1}\|Z_n\|_q^q\overset{\mathrm{d}}{=}\frac{1}{n}\sum_{i=1}^n f(nG_{n,i})$
, we are in the situation of Theorem 3.1 with
$f(x)=|x-1|^q$
, which is not of the form
$x\mapsto ax+b$
for any
$a,b\in\mathbb{R}$
and all
$x\in\mathbb{R}$
. Because of this and the fact that the exponential distribution has finite moments of all orders, the assumptions of Theorem 3.1 are satisfied and there exists a constant
$c_q>0$
depending only on q such that, for all
$n\in\mathbb{N}$
,
\begin{equation*} \sup_{x\in\mathbb R}\Bigg|\mathbb{P}\left[\sqrt{n}\left(\frac{n^{q-1}\Vert Z_n\Vert_q^q -\mu_q}{{{d_q}}}\right)\leq x\right]-\mathbb{P}[N\leq x]\Bigg| \leq \frac{c_q}{\sqrt{n}\,}, \end{equation*}
with
\begin{equation*}{{d_q^2=\mathrm{Var} \vert E-1\vert^q -\operatorname{Cov}\big(E,|E-1|^q\big)^2=\mu_{2q}-\mu_q^2-\big((q+1)\mu_q-1\big)^2}}\end{equation*}
and
$\mu_q$
=
$\mathbb{E}\left[ {|E-1|^q}\right]$
according to Lemma 3.3. Note that
$d_q^2>0$
due to the Cauchy–Schwarz inequality and the fact that E and
$|E-1|^q$
are linearly independent. Applying Lemma 3.2 with
$g(x)=x^{1/q}$
and
$g'(\mu_q)=q^{-1}\mu_q^{1/q-1}$
, and rearranging terms, concludes the proof.
Remark 3.2 Using the so-called delta method, we can alternatively derive the central limit theorem stated as Corollary 1.1 from a CLT for sum-functions of spacings [Reference Holst13].
Remark 3.3 We briefly want to put
$\mu_q$
in a more accessible form and compare it to the centering constant in the central limit theorem [Reference Kabluchko, Prochno and Thäle15, Theorem 1.1], stating for
$1<q\leq \infty$
and random vectors
$Y_n$
, which are uniformly distributed in the
$\ell_1^n$
-ball, that
\begin{equation*} \sqrt{n}\left(n^{1-1/q}\left\|{Y_n}\right\|_q M_1(q)^{-1/q}-1\right)\xrightarrow[n\to\infty]{\mathrm{d}} {{Z\sim\mathcal{N}}}\bigl(0,C_1(q,q)\bigr), \end{equation*}
where
$M_1(q)\,{:\!=}\,\Gamma(q+1)$
and
\begin{equation*} C_1(q,q)=q^{-2}\left(\frac{\Gamma(2q+1)}{\Gamma(q+1)^2}-1\right)-1. \end{equation*}
As can be seen from Corollary 1.1, the same rate of
$n^{1-1/q}$
appears. With repeated partial integration we can derive, for
$q\in \mathbb{N}$
,
\begin{equation*} \mu_q=\mathbb{E}\left[ {\left|{ E-1}\right|^q}\right]= \begin{cases} \mathbb{E}\left[ {(E-1)^q}\right], & q \text{ even}, \\ \\[-7pt] 2\mathrm{e}^{-1}q!-\mathbb{E}\left[ {(E-1)^q}\right], & q \text{ odd}, \end{cases} \end{equation*}
where
$\mathbb{E}\left[ {(E-1)^q}\right]$
equals the subfactorial
$!q=q!\sum_{i=0}^q{(\!-1)^i} / {i!}$
, which is also the nearest integer to
$\mathrm{e}^{-1}q!$
. This is smaller than
$M_1(q)=q!$
by roughly a factor of e.
3.2. Proof of the non-central limit theorem
In the following, we give a proof of Theorem 1.2 and analyze the limiting distribution of
\begin{equation*} n\Vert Z_n\Vert_{\infty}=n\max_{1\leq i\leq n} |Z_{n,i}|=n\max_{1\leq i\leq n} \bigg\vert \frac{E_i}{S_n}-\frac{1}{n}\bigg\vert.\end{equation*}
Set
$M_n\,{:\!=}\,\max_{1\leq i\leq n} E_i$
and let us recall the well-known fact that
$M_n-\log n\,{=\!:}\, G_n\xrightarrow[n\to\infty]{\mathrm{d}} G$
, where G is standard Gumbel distributed. First, we prove that
$\left\|{Z_n}\right\|_{\infty}$
and
\begin{equation*}T_n\,{:\!=}\,\max_{1\leq i\leq n} \left( \frac{E_i}{S_n}-\frac{1}{n}\right)=\frac{M_n}{S_n}-\frac{1}{n}\end{equation*}
are exponentially equivalent in the following sense.
Lemma 3.4
$\lim_{n\to\infty}n^{-1}\log \,\mathbb{P}\bigl[\| Z_n\|_{\infty}\neq T_n\bigr]<0$
.
Proof. We first prove that everywhere except for
$\{S_n=0\}$
we have the implication
$\Vert Z_n\Vert_{\infty}\neq T_n\Longrightarrow {M_n} / {S_n}< {2} / {n}$
. Note that
$\Vert Z_n\Vert_{\infty}\geq T_n$
, and if
$\Vert Z_n\Vert_{\infty}\neq T_n$
there must be some index
$i_0\in\{1,\ldots,n\}$
such that
\begin{equation*}\bigg\vert\frac{E_{i_0}}{S_n}-\frac{1}{n}\bigg\vert>T_n=\frac{M_n}{S_n}-\frac{1}{n}.\end{equation*}
This can only occur if
${E_{i_0}} / {S_n}- {1} / {n}$
is negative (otherwise we would have equality), i.e.
\begin{equation*}\frac{1}{n}-\frac{E_{i_0}}{S_n}=\bigg\vert\frac{E_{i_0}}{S_n}-\frac{1}{n}\bigg\vert> \frac{M_n}{S_n}-\frac{1}{n}.\end{equation*}
Since
${E_{i_0}} / {S_n}\geq 0$
, this gives the desired implication. Therefore,
\begin{equation*} \mathbb{P}\bigl[\Vert Z_n\Vert_{\infty}\neq T_n\bigr]\leq \mathbb{P}\bigg[M_n<2{{\frac{S_n}{n}}}\bigg]\leq \mathbb P[M_n<4]+{{\mathbb P\bigg[\frac{S_n}{n}>2\bigg]}}. \end{equation*}
By means of the inequality
$1+x\leq \mathrm{e}^x$
, the first summand evaluates to
$\mathbb P[M_n<4]=(1-\mathrm{e}^{-4})^n\leq \mathrm{e}^{-\mathrm{e}^{-4}n}$
and, by Cramér’s theorem, Lemma 2.1,
$\lim_{n\to\infty}n^{-1}\log {{\mathbb{P}\left[{{S_n} / {n}>2}\right]}}<0$
. This completes the proof of the lemma.
We return to the proof of Theorem 1.2. The previous lemma implies that
$n\Vert Z_n\Vert_{\infty}- nT_n\xrightarrow{\mathbb{P}}0$
, and to establish Theorem 1.2 it suffices to prove that
$nT_n-(\log n-1)\xrightarrow{\mathrm{d}} G$
.
The connection to the spacings
$G_n=(G_{n,1},\ldots,G_{n,n})$
gives
$nT_n\overset{\mathrm{d}}{=}n\max_{1\leq i\leq n} G_{n,i}-1$
. A classical result [Reference Devroye7, Lemma 2.4] states that
$n\max_{1\leq i\leq n} G_{n,i}-\log n\xrightarrow[n\to\infty]{\mathrm{d}} G$
, which was originally derived by Lévy. Rewriting this for
$nT_n$
gives
$nT_n-\log n+1\xrightarrow[n\to\infty]{\mathrm{d}} G$
and completes the proof.
Remark 3.4 We can read off from Theorem 1.2 that the maximum norm of random points in the shifted simplex converges to zero at the rate
${\log n} / {n}$
with fluctuations of order
$(\log n)^{-1}$
. Uniformly distributed random vectors
$Y_n$
in the
$\ell_1^n$
-ball exhibit similar behavior, as can be read off from [Reference Kabluchko, Prochno and Thäle15, Theorem 1.1(c)]. Namely,
$n\|Y_n\|_{\infty}-\log n\xrightarrow[n\to\infty]{\mathrm{d}} G$
.
3.3. Proof of the moderate deviations principle
We derive the proof of Theorem 1.3 from [Reference Devroye7, Lemma 3.2], which we rephrase in our notation.
Lemma 3.5 Let
$(a_n)_{n\in\mathbb{N}}$
be a sequence of positive numbers satisfying
$a_n\to 0$
and
$a_n\log n\to\infty$
as
$n\to\infty$
. Then
\begin{equation*} \lim_{n\to\infty} n^{a_n}\mathbb{P}\left[ {\frac{n}{\log n}\frac{M_n}{S_n}-1>a_n}\right]=1 , \qquad \lim_{n\to\infty} \exp(n^{a_n})\mathbb{P}\left[ {\frac{n}{\log n}\frac{M_n}{S_n}-1<-a_n}\right]=1. \end{equation*}
In order to prove Theorem 1.3, we restate this result in the following form.
Lemma 3.6 Let
$(s_n)_{n\in\mathbb N}$
be a positive sequence with
$s_n\to \infty$
and
$s_n/\log n\to 0$
as
$n\to\infty$
. Then, for any
$x>0$
,
\begin{align*} \lim_{n\to\infty}\frac{1}{s_n}\log \mathbb P\left[\frac{\log n}{s_n}\biggl(\frac{n}{\log n}\|Z_n\|_{\infty}-1\biggr)>x\right] & = -x , \\[4pt] \lim_{n\to\infty}\frac{1}{s_n}\log \mathbb P\left[\frac{\log n}{s_n}\biggl(\frac{n}{\log n}\|Z_n\|_{\infty}-1\biggr)<-x\right] & = -\infty. \end{align*}
Proof. Using the continuity of the logarithm and inserting
$T_n=M_n/S_n-1/n$
, we can deduce from Lemma 3.5 that
\begin{align} \lim_{n\to\infty} a_n\log n+\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1>a_n-\frac{1}{\log n}}\right] & = 0 , \end{align}
\begin{align} \lim_{n\to\infty} n^{a_n}+\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1<-a_n-\frac{1}{\log n}}\right] & = 0 \end{align}
for any such sequence
$(a_n)_{n\in\mathbb{N}}$
.
In the following, let
$x>0$
be arbitrary. First, set
$a_n=(s_n/\log n)x+1/\log n=(s_nx+1)/\log n$
, where
$(s_n)_{n\in\mathbb{N}}$
is any sequence with
$s_n\to \infty$
and
$s_n/\log n\rightarrow 0$
. This choice of
$(a_n)_{n\in\mathbb{N}}$
meets the assumptions of Lemma 3.5. Then, inserting into (3.3) gives
\begin{equation*} \lim_{n\to\infty} s_nx+1+\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1>\frac{s_n}{\log n}x}\right]=0, \end{equation*}
which, by considering the limit of the sequence divided by
$s_n$
, implies that
\begin{equation*} x+\lim_{n\to\infty} \frac{1}{s_n}\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1>\frac{s_n}{\log n}x}\right]=0. \end{equation*}
For (3.4) we choose
$a_n=(s_n/\log n)x-1/\log n=(s_nx-1)/\log n$
for all
$n\in\mathbb{N}$
such that
$s_nx-1>0$
and set
$a_n=1$
for all other
$n\in\mathbb{N}$
. Since
$s_n\to\infty$
, we have
$s_nx-1>0$
for all
$n\geq n_0$
, where
$n_0\in\mathbb{N}$
may depend on x, and only need to set finitely many terms
$a_n=1$
. This choice of
$(a_n)_{n\in\mathbb{N}}$
satisfies the assumptions of Lemma 3.5. Therefore,
\begin{equation*} \lim_{n\to\infty} n^{(s_nx-1)/\log n}+\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1<-\frac{s_n}{\log n}x}\right]=0. \end{equation*}
Proceeding as before,
\begin{equation*} \lim_{n\to\infty} \frac{1}{s_n}n^{(s_nx-1)/\log n}+\frac{1}{s_n}\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1<-\frac{s_n}{\log n}x}\right]=0. \end{equation*}
Noting that
$n^{(s_nx-1)/\log n}/s_n=\exp(s_nx-1)/s_n\to\infty$
, we have
\begin{equation*} \lim_{n\to\infty} \frac{1}{s_n}\log\,\mathbb{P}\left[ {\frac{n}{\log n}T_n-1<-\frac{s_n}{\log n}x}\right]=-\infty. \end{equation*}
Since
$s_n/n\to 0$
as
$n\to\infty$
, we can apply Lemma 3.4 and rearrange terms to complete the proof of Lemma 3.6.
We now deduce Theorem 1.3 using a standard technique in large deviations theory.
Proof of Theorem 1.3. Let
$(s_n)_{n\in\mathbb{N}}$
be an arbitrary positive sequence with
$s_n\to\infty$
and
$s_n/\log n\to 0$
. Theorem 1.3 follows if we can show for arbitrary open
$U\subset\mathbb{R}$
and closed
$C\subset \mathbb{R}$
the bounds
\begin{equation} \begin{aligned} \liminf_{n\to\infty}s_n^{-1}\log\mathbb{P}\left[ {X_n\in U}\right] & \geq -\inf_{z\in U} \mathbb{I}(z) , \\ \\[-9pt] \limsup_{n\to\infty}s_n^{-1}\log\mathbb{P}\left[ {X_n\in C}\right] & \leq -\inf_{z\in C} \mathbb{I}(z), \end{aligned} \end{equation}
where we used the notation
$X_n\,{:\!=}\,\frac{\log n}{s_n}\left(\frac{n}{\log n}\|Z_n\|_{\infty}-1\right)$
. Recall that
\begin{equation*} \mathbb{I}(z) \,{:\!=}\, \begin{cases} z, & z\geq 0, \\ \\[-9pt] +\infty , & z<0. \end{cases} \end{equation*}
If
$A\subset\mathbb{R}$
, we use the notation
$A_-\,{:\!=}\,A\cap (\!-\infty,0]$
and
$A_+\,{:\!=}\,A\cap [0,\infty)$
as well as
$a_-\,{:\!=}\,\sup A_-$
and
$a_+=\inf A_+$
such that
$\inf_{z\in A}\mathbb{I}(z)=a_+$
.
We first prove the upper bound in (3.5) and choose a closed set
$C\subset\mathbb{R}$
. If C is empty, the upper bound is trivial as the probability of
$X_n$
being in an empty set is zero. On the other hand, if
$0\in C$
, the infimum is zero and the upper bound is satisfied due to
$\mathbb{P}\left[ {X_n\in C}\right]\leq 1$
. Therefore, assume without loss of generality that at least one of
$C_-$
and
$C_+$
is not empty and that
$0\not\in C$
. If both are non-empty, then
$c_-<0<c_+$
and
$C= C_-\cup C_+ \subset (\!-\infty,c_-]\cup [c_+,\infty)$
, and
$\mathbb{P}\left[ {X_n\in C}\right]\leq \mathbb{P}\left[ {X_n<c_-}\right]+\mathbb{P}\left[ {X_n>c_+}\right]$
for
$n\in\mathbb{N}$
. This also makes sense if
$C_-$
is empty, i.e.
$c_-=-\infty$
or if
$C_+$
is empty, i.e.
$c_+=\infty$
, if we interpret
$\mathbb{P}\left[ {X_n<-\infty}\right]=\mathbb{P}\left[ {X_n>\infty}\right]=0$
. Because of the monotonicity of the logarithm and [Reference Dembo and Zeitouni6, Lemma 1.2.15],
$\limsup_{n\to\infty}s_n^{-1}\log\, \mathbb{P}\left[ {X_n\in C}\right]\leq \max\{M_-,M_+\}$
with
$M_-\,{:\!=}\, \limsup_{n\to\infty}s_n^{-1}\log\, \mathbb{P}\left[ {X_n<c_-}\right] \text{ and } M_+\,{:\!=}\,\limsup_{n\to\infty}s_n^{-1}\log\, \mathbb{P}\left[ {X_n>c_+}\right].$
Now the upper bound follows from Lemma 3.6 since
$M_-=-\infty$
and
$\max\{M_-,M_+\}=M_+=-c_+=-\inf_{z\in C}\mathbb{I}(z)$
.
We now prove the lower bound and choose an open set
$U\subset\mathbb{R}$
. If
$U_+$
is empty, the infimum is
$\infty$
and the lower bound is trivially satisfied. Assume therefore, without loss of generality, that
$U_+$
is not empty. Take any
$z\in U_{+}$
. We will show that
\begin{equation} \liminf_{n\to\infty} s_n^{-1} \log\, \mathbb{P}\left[ {X_n\in U}\right] \ge - \mathbb{I}(z). \end{equation}
This will conclude the proof of the lower bound in (3.5), since then
\begin{equation*} \liminf_{n\to\infty} s_n^{-1} \log\, \mathbb{P}\left[ {X_n\in U}\right] \ge - \inf_{z\in U_+} \mathbb{I}(z) = - \inf_{z\in U} \mathbb{I}(z). \end{equation*}
The openness of U yields that, for all
$\varepsilon\ge 0$
small enough,
$(z+\varepsilon,z+2\varepsilon]\subset U$
. Therefore,
\begin{align} \liminf_{n\to\infty} s_n^{-1} \log \mathbb{P}\left[ {X_n\in U}\right] & \ge \liminf_{n\to\infty} s_n^{-1} \log\, \mathbb{P}\left[ {X_n\in (z+\varepsilon,z+2\varepsilon]}\right] \nonumber \\[3pt]
&= \liminf_{n\to\infty} s_n^{-1} \log\, \big(\mathbb{P}\left[ {X_n\ge z+\varepsilon}\right] - \mathbb{P}\left[ {X_n \ge z+2\varepsilon}\right]\big) \nonumber \\[3pt]
& \ge \liminf_{n\to\infty} s_n^{-1} \log\, \mathbb{P}\left[ {X_n\ge z+\varepsilon}\right] \nonumber\\[3pt]
& \quad + \liminf_{n\to\infty} s_n^{-1} \log\, \left(1- \frac{\mathbb{P}\left[ {X_n \ge z+2\varepsilon}\right]}{\mathbb{P}\left[ {X_n\ge z+\varepsilon}\right]}\right) \end{align}
by the superadditivity of
$\liminf$
. We use Lemma 3.6 to conclude the proof. The first summand in (3.7) satisfies
$\liminf_{n\to\infty} s_n^{-1} \log\, \mathbb{P}\left[ {X_n>z+\varepsilon}\right]=-z-\varepsilon= -\mathbb{I}(z)-\varepsilon$
. Let
$\delta>0$
be small. For the second summand in (3.7) we choose
$n_0\in\mathbb N$
large enough such that both
$\mathbb{P}\left[ {X_n> z+2\varepsilon}\right] \le \mathrm{e}^{(\!-(z+2\varepsilon)+\delta)s_n}$
and
$\mathbb{P}\left[ {X_n> z+\varepsilon}\right] \ge \mathrm{e}^{(\!-(z+\varepsilon)-\delta)s_n}$
for
$n\ge n_0$
. This shows that the fraction in the second summand satisfies, for every
$n\ge n_0$
,
\begin{equation*} 0\le \frac{\mathbb{P}\left[ {X_n > z+2\varepsilon}\right]}{\mathbb{P}\left[ {X_n>z+\varepsilon}\right]} \le \mathrm{e}^{(2\delta-\varepsilon)s_n}, \end{equation*}
which tends to zero for
$n\to\infty$
if
$\delta<\frac{1}{2}\varepsilon$
. Thus, the second summand in (3.7) is equal to zero and, after letting
$\varepsilon\to 0$
, the inequality (3.6) is established for any
$z\in U_+$
, which proves the lower bound in (3.5) and thus Theorem 1.3.
3.4. Proof of the LDP
For the proof of Theorem 1.4 we use a rather general result on large deviations for maxima and minima [Reference Giuliano and Macci12, Proposition 3.1]. Recall that a function
$H \,{:}\, \mathbb{R}\to\mathbb{R}$
is said to be regularly varying at
$\infty $
of index
$\alpha\in\mathbb{R}$
if, for all
$u>0$
,
$\lim_{t\to\infty}[{H(ut)} / {H(t)}] = u^{\alpha}$
.
Lemma 3.7 Let
$X,X_1,X_2,\ldots$
be i.i.d. real-valued random variables with
$\mathbb{P}\left[ {X\leq x}\right]<1$
for all
$x>0$
such that
$-\log\mathbb{P}\left[ {X>x}\right] $
is regularly varying at
$\infty$
of index
$\alpha>0$
as a function of
$x\in\mathbb{R}$
. Choose
$m_n\in\mathbb{R}$
such that
$\mathbb{P}\left[ {X>m_n}\right]=\frac{1}{n}$
and set
$M_n=\max_{1\leq i\leq n}X_i$
. Then
$ \Big(\frac{M_n}{m_n}\Big)_{n\geq 1} $
satisfies an LDP with speed
$ s_n=\log n $
and good rate function
\begin{equation*}\mathbb{I}(z) \,{:\!=}\, \begin{cases} z^{\alpha}-1 , & z\geq 1, \\ +\infty , & z<1. \end{cases} \end{equation*}
In order to prove Theorem 1.4 we make use of this result, Lemma 2.2, and the next lemma, which states the exponential equivalence of the sequences in question.
Lemma 3.8 Set
$M_n=\max_{1\leq i\leq n} E_i$
. The sequences
$\Big(\frac{n}{\log n}\Vert Z_n\Vert_{\infty}\Big)_{n\in\mathbb{N}} $
and
$ \Big(\frac{M_n}{\log n}\Big)_{n\in\mathbb{N}} $
are exponentially equivalent at speed
$ \log n $
.
Proof. This amounts to showing that, for every
$ \delta>0 $
,
\begin{equation*} \limsup_{n\to\infty} \frac{1}{\log n}\log\, \mathbb{P}\bigl[ {\bigl|n\|Z_n\|_{\infty}-M_n\bigr|>\delta\log n}\bigr]=-\infty. \end{equation*}
Fix
$ \delta>0 $
. Then, for every
$n\in\mathbb{N}$
,
\begin{equation*} \mathbb{P}\left[ {\bigl|n\|Z_n\|_{\infty}-M_n\bigr|>\delta\log n}\right]\leq \mathbb{P}\left[ {\bigl|nT_n-M_n\bigr|>\delta\log n}\right]+\mathbb{P}\bigl[ {\|Z_{n}\|_{\infty}\neq T_n}\bigr]. \end{equation*}
By Lemma 3.4 the second summand satisfies
$\frac{1}{\log n}\log\mathbb{P}\bigl[ {\Vert Z_{n}\Vert_{\infty}\neq T_n}\bigr]\to -\infty$
as
$n\to\infty$
. Recall the notation
$\bar{E}_n=\frac{S_n}{n}$
. For the first summand we compute
$nT_n-M_n=M_n\bar{E}_n^{-1}-1-M_n=-\big(M_n\big(\bar{E}_n-1\big)\bar{E}_n^{-1}+1\big)$
. Setting
$A_n\,{:\!=}\,M_n(\bar{E}_n-1)\bar{E}_n^{-1}$
, it follows that
$\mathbb{P}\left[ {\bigl|nT_n-M_n\bigr|>\delta\log n}\right]=\mathbb{P}\left[ {\left|{A_n+1}\right|>\delta\log n}\right]$
. Whenever n is large enough
$ \log n>2\delta^{-1} $
holds, and thus
$\mathbb{P}\bigl[ {\left|{A_n+1}\right|>\delta\log n}\bigr]\leq \mathbb{P}\bigl[ {\left|{A_n+1}\right|>2}\bigr]\leq \mathbb{P}\bigl[ {\left|{A_n}\right|>1}\bigr]$
. Introducing
$B_n\,{:\!=}\, n^{-1/4}M_n $
and
$ C_n\,{:\!=}\,n^{1/4}(\bar{E}_n-1)\bar{E}_n^{-1} $
, such that
$A_n=B_nC_n$
, gives
$\mathbb{P}\bigl[ {\bigl|nT_n-M_n\bigr|>\delta\log n}\bigr]\leq \mathbb{P}\bigl[ {\left|{B_n}\right|>1/2}\bigr]+\mathbb{P}\bigl[ {\left|{C_n}\right|>2}\bigr]$
. By the union bound, the first summand satisfies
\begin{equation*} \mathbb{P}\bigl[ {\left|{B_n}\right|>1/2}\bigr]=\mathbb{P}\left[ {M_n>n^{1/4}/2}\right]\leq n\mathbb{P}\left[ {E_1>n^{1/4}/2}\right]=n\mathrm{e}^{-n^{1/4}/2}, \end{equation*}
and thus
\begin{equation*} \frac{1}{\log n}\log \,\mathbb{P}\bigl[ {\left|{B_n}\right|>1/2}\bigr]\leq 1-\frac{n^{1/4}}{2\log n}\xrightarrow{n\to\infty} -\infty. \end{equation*}
The other summand can be estimated by means of
$\mathbb{P}\bigl[ {\left|{C_n}\right|>2}\bigr]\leq \mathbb{P}\left[ {\bar{E}_n<1/2}\right]+\mathbb{P}\left[ {n^{1/4}|\bar{E}_n-1|>1}\right]$
. Cramér’s theorem (Lemma 2.1) implies that
\begin{equation*} \frac{1}{\log n}\log\mathbb{P}\left[ {\bar{E}_n<1/2}\right]\xrightarrow{n\to\infty} -\infty. \end{equation*}
After splitting the second summand into
\begin{equation*} \mathbb{P}\left[ {n^{1/4}\big|\bar{E}_n-1\big|>1}\right]=\mathbb{P}\left[ {n^{1/4}\big(\bar{E}_n-1\big)>1}\right]+\mathbb{P}\left[ {n^{1/4}\big(\bar{E}_n-1\big)<-1}\right], \end{equation*}
we apply the moderate deviations principle (Lemma 2.3) with
$a_n=n^{-1/2}$
,
$n\in\mathbb{N}$
, giving
\begin{align*} \lim_{n\to\infty}n^{-1/2}\log\mathbb{P}\left[ {n^{1/4}\big(\bar{E}_n-1\big)>1}\right] & = -\frac{1}{2} , \\ \lim_{n\to\infty}n^{-1/2}\log\mathbb{P}\left[ {n^{1/4}\big(\bar{E}_n-1\big)<-1}\right] & = -\frac{1}{2}. \end{align*}
Consequently,
\begin{equation*} \frac{1}{\log n}\log \,\mathbb{P}\left[ {n^{1/4}|\bar{E}_n-1|>1}\right]\xrightarrow{n\to\infty} -\infty, \end{equation*}
and thus
\begin{equation*} \frac{1}{\log n}\log\,\mathbb{P}\bigl[ {\left|{C_n}\right|>2}\bigr]\xrightarrow{n\to\infty} -\infty, \end{equation*}
completing the proof.
Remark 3.5 The choice of the sequence
$n^{1/4}$
was arbitrary; any sequence growing faster than
$\log n$
and slower than
$\bigl(\frac{n}{\log n}\bigr)^{1/2}$
would have done the job.
Proof of Theorem 1.4. We apply Lemma 3.7 to the case of standard exponential random variables and verify the assumptions. We have
$\mathbb{P}\left[ {X\leq x}\right]=1-\mathrm{e}^{-x}<1$
for all
$x\in\mathbb{R}$
and
$-\log\mathbb{P}\left[ {X>x}\right]=x$
, which is regularly varying at
$\infty$
of index
$\alpha=1$
. We choose
$m_n=\log n$
and thus obtain an LDP of speed
$\log n$
and rate function as in Lemma 3.7 with
$\alpha=1$
. By Lemma 2.2 the just-proven Lemma 3.8 implies Theorem 1.4.
4. Comparison with and application to
$\ell_p^n$
-balls
4.1. An LDP for
$\ell_p^n$
-balls
In [Reference Kabluchko, Prochno and Thäle15] LDPs for the
$\ell_q$
-norm of uniformly distributed points in
$\ell_p^n$
-balls were proven for the cases
$1\leq p<\infty$
,
$1\leq q<\infty$
and
$p=\infty$
,
$1\leq q\leq\infty$
. In order to compare the LDP for the simplex with the one for the crosspolytope (i.e. the unit ball in
$\ell_1^n$
), we complete the picture presented in [Reference Kabluchko, Prochno and Thäle15] by deriving, without making the argument more complicated, a slightly more general LDP covering all possible values
$1\leq p<\infty$
and put
$q=\infty$
. Let
$1\leq p<\infty$
and
$\mathbb{B}_p^n\,{:\!=}\,\{x\in \mathbb{R}^n\,{:}\, \|x\|_p\leq 1\}$
be the
$\ell_p^n$
-unit ball. Further, let
$Z_n^{\prime}$
be uniformly distributed in
$\mathbb{B}_p^n$
for all
$n\in\mathbb N$
.
Theorem 4.1 Let
$1\leq p<\infty$
. The sequence
$\bigl(({n} / {p\log n})^{1/p}\|{{Z_n^{\prime}}}\|_{\infty}\bigr)_{n\in\mathbb{N}}$
satisfies an LDP with speed
$\log n$
and rate function
\begin{equation*} \mathbb{I}(z)\,{:\!=}\, \begin{cases} z^p-1 , & z\geq 1, \\ \infty , & z<1. \end{cases} \end{equation*}
In particular, taking
$p=1$
and comparing the result to Theorem 1.4 we see that the LDPs for the
$\ell_\infty$
-norm of uniformly distributed random points in a crosspolytope and a regular simplex are identical.
The proof of Theorem 4.1 is based on the Schechtman–Zinn probabilistic representation, saying that for any
$n\in\mathbb N$
the distributional identity
\begin{equation*} {{Z_n^{\prime}}}\overset{\mathrm{d}}{=} U^{1/n}\frac{Y_n^{\prime}}{\| Y_n^{\prime}\|_p} \end{equation*}
holds, where U is uniformly distributed on [0,1] and independent of
$Y_n^{\prime}\,{:\!=}\,(Y_1,\ldots,Y_n)$
which has i.i.d. p-generalized Gaussian distributed entries; see [Reference Schechtman and Zinn26]. We recall that if a random variable Y is distributed according to the p-generalized Gaussian distribution its Lebesgue density
$f_p$
is given by
$c_p \mathrm{e}^{-|y|^p/p}$
,
$x\in\mathbb R$
, with the normalization constant given by
$c_p\,{:\!=}\,(2p^{1/p}\Gamma(1+1/p))^{-1}$
.
Next, we define for each
$n\in\mathbb{N}$
the number
$m_n(p)>0$
by
$\mathbb{P}[|Y|> m_n(p)]=\frac{1}{n}$
, where Y is a p-generalized Gaussian random variable. From lemma 3.7 we can deduce the following result for
$M_n(p)\,{:\!=}\,\max_{1\leq i\leq n} |Y_i|$
.
Lemma 4.1 Let
$1\leq p<\infty$
. The sequence
$(M_n(p) m_n(p)^{-1})_{n\in\mathbb{N}}$
satisfies an LDP with speed
$\log n$
and rate function
$\mathbb{I}$
as in Theorem 4.1.
Proof. We check the assumptions of Lemma 3.7, and note that by the symmetry of the generalized Gaussian distribution,
$\mathbb{P}\bigl[ {|Y|>x}\bigr]=2\mathbb{P}\left[ {Y>x}\right]>0$
for every
$x>0$
. In order to check if
$-\log \mathbb{P}\left[ {|Y|>x}\right]$
is regularly varying at
$\infty$
, we compute, for every
$u>0$
,
\begin{equation*} \lim_{t\to\infty}\frac{\log \,\mathbb{P}\bigl[ {|Y|>ut}\bigr]}{\log\, \mathbb{P}\bigl[ {|Y|>t}\bigr]}=\lim_{t\to\infty}\frac{\log 2+\log\, \mathbb{P}\left[ {Y>ut}\right]}{\log 2+\log\, \mathbb{P}\left[ {Y>t}\right]}=\lim_{t\to\infty} \frac{(ut)^p}{t^p}=u^p. \end{equation*}
Here, we used that according to the inequality
\begin{equation} \frac{x}{{{x^p+p-1}}}\mathrm{e}^{-x^p/p}\leq \int_x^{\infty} \mathrm{e}^{-y^p/p} \, \text{d}y \leq \frac{1}{x^{p-1}}\mathrm{e}^{-x^p/p}, \end{equation}
which is valid for all
$1\leq p<\infty$
and
$x>0$
,
$\log \mathbb{P}\bigl[ {|Y|>x}\bigr]$
is asymptotically equivalent to
$-x^p/p$
as
$x\to\infty$
. Thus, the assumptions of Lemma 3.7 are satisfied with
$\alpha=\alpha_p\,{:\!=}\,p>0$
, and we can complete the proof.
Lemma 4.2 The two sequences
$\big(M_n(p) m_n(p)^{-1}\big)_{n\in\mathbb{N}}$
and
$\big(n^{1/p}\|{{Z_n^{\prime}}}\|_{\infty}m_n(p)^{-1}\big)_{n\in\mathbb{N}}$
are exponentially equivalent at speed
$\log n$
for
$1\leq p<\infty$
.
Proof. Note that
\begin{equation*} n^{1/p}\|{{Z_n^{\prime}}}\|_{\infty}m_n(p)^{-1}\overset{\mathrm{d}}{=}U^{1/n}\frac{M_n(p) m_n(p)^{-1}}{\left(\frac{1}{n}\sum_{i=1}^n|Y_i|^p\right)^{1/p}}, \end{equation*}
with the
$Y_i^{\prime}$
being independent and p-generalized Gaussians. Then, the exponential equivalence is proved using Cramér’s theorem as in the proof of [Reference Kabluchko, Prochno and Thäle15, Theorem 1.3]. It remains to note that, for
$0<\varepsilon\leq\delta$
, we have, by Lemma 4.1,
\begin{equation*} \limsup_{n\to\infty} \frac{1}{\log n}\log\, \mathbb{P}\left[M_n(p) m_n(p)^{-1}>\frac{\delta}{\varepsilon}\right]=-\left(\Bigl(\frac{\delta}{\varepsilon}\Bigr)^p-1\right), \end{equation*}
which tends to
$-\infty$
as
$\varepsilon\to 0$
.
After these preparations, we can now complete the proof of Theorem 4.1.
Proof of Theorem 4.1. By Lemma 4.1 the sequence
$\big(M_n(p)m_n(p)^{-1}\big)_{n\in\mathbb{N}}$
satisfies the required LDP, and so does
$\big(n^{1/p}\|{{Z_n^{\prime}}}\|_{\infty}m_n(p)^{-1}\big)_{n\in\mathbb{N}}$
by Lemma 4.2. Using (4.1), we can see that
$m_n(p)(p\log n)^{-1/p}$
tends to 1 as
$n\to\infty$
. Consequently, the sequences
$\big(n^{1/p}\|{{Z_n^{\prime}}}\|_{\infty}m_n(p)^{-1}\big)_{n\in\mathbb{N}}$
and
$\bigl(({n} / {p\log n})^{1/p}\|{{Z_n^{\prime}}}\|_{\infty}\bigr)_{n\in\mathbb{N}}$
satisfy the same LDP.
4.2. Intersection with
$\ell_p^n$
-balls
As an application of our central limit theorem, we sketch here a geometric application in the spirit of classical results of [Reference Schechtman and Zinn26, Reference Schmuckenschläger27] on the intersection of two different
$\ell_p^n$
-balls. In our case, we consider the intersection volume of an
$\ell_p$
-ball and a regular simplex. To be precise, we denote by
$\mathbb{D}_p^n\,{:\!=}\,\mathbb{B}_p^n/|\mathbb{B}_p^n|_n$
the normalized
$\ell_p^n$
-ball, where
$|\cdot|_n$
is a shorthand notation for the n-dimensional Lebesgue measure. Similarly, we define the normalized
$(n-1)$
-dimensional regular simplex
$\Sigma_{n-1}\,{:\!=}\,\tilde{\Delta}_{n-1}/|\tilde{\Delta}_{n-1}|_{n-1}$
, where
$\tilde{\Delta}_{n-1}\,{:\!=}\,\Delta_{n-1}-\frac{1}{n}(e_1+\cdots+e_n)$
is the centered
$(n-1)$
-dimensional regular simplex (note that
$|\tilde{\Delta}_{n-1}|_{n-1}=|{\Delta}_{n-1}|_{n-1}$
).
Theorem 4.2 Let
$s>0$
,
$1\leq p<\infty$
, and define
$A_p\,{:\!=}\,2\mathrm{e}^{-1}\mu_p^{1/p}\Gamma\Big(1+\frac{1}{p}\Big)(p\mathrm{e})^{1/p}$
. Then
\begin{align*} \lim_{n\to \infty}\big|\Sigma_{n-1}\cap s\mathbb{D}_p^n\big|_{n-1}= \begin{cases} 1 , & sA_p^{-1}>1 , \\ \\[-9pt] \dfrac{1}{2} , & sA_p^{-1}=1 , \\ \\[-9pt] 0 , & sA_p^{-1}<1. \end{cases} \end{align*}
Proof. We start by introducing some notation. For each
$n\in\mathbb N$
we put
\begin{equation*}A_{p,n}\,{:\!=}\,\mu_p^{1/p}\frac{n^{1/p}\big|\mathbb{B}_p^n\big|_n^{1/n}}{ n|\tilde{\Delta}_{n-1}|_{n-1}^{1/(n-1)}}\end{equation*}
and let
$s_n$
be such that
$s_n({A_{p,n} / A_p})=s$
. Using Stirling’s formula repeatedly, we can verify that
$A_{p,n}=A_p\big(1+O(n^{-1}\log n)\big)$
. Indeed,
\begin{align*} A_{p,n} &= 2\mu_p^{1/p}\Gamma\bigg(1+\frac{1}{ p}\bigg) \bigg\{\frac{n^{1/p}}{\big(\sqrt{2\pi n/p}(n/(\mathrm{e} p))^{n/p}\big(1+O\big(n^{-1}\big)\big)\big)^{1/n}}\bigg\} \\[2pt]
& \quad \times \bigg\{{n\bigg(\frac{\sqrt{n}}{\sqrt{2\pi(n-1)}((n-1)/\mathrm{e})^{n-1}\big(1+O\big(n^{-1}\big)\big)}\bigg)^{1/(n-1)}}\bigg\}^{-1} \\[2pt]
& = 2\mu_p^{1/p}\Gamma\bigg(1+\frac{1}{p}\bigg)\frac{(\mathrm{e} p)^{1/p}}{\mathrm{e}}\frac{\big(1+O\big(n^{-1}\big)\big)^{1/n}}{ (n/p)^{1/(2n)}\big(1+O\big(n^{-1}\big)\big)^{1/n}} =A_p\big(1+O\big(n^{-1}\log n\big)\big), \end{align*}
where we used that
$(n/p)^{1/(2n)}=1+O\big(n^{-1}\log n\big)$
in the last step.
Next, we rewrite
$\big|\Sigma_{n-1}\cap s\mathbb{D}_p^n\big|_{n-1}$
in probabilistic terms by using the definition of
$s_n$
:
\begin{align*} \big|\Sigma_{n-1} & \cap s\mathbb{D}_p^n\big|_{n-1}\\[3pt]
&= \bigg|\bigg\{z\in\Sigma_{n-1} \,{:}\, z\in s_n\frac{A_{p,n}}{ A_p}\mathbb{D}_p^n\bigg\}\bigg|_{n-1}\\[3pt]
&=\Bigg|\Bigg\{z\in\Sigma_{n-1} \,{:}\, z\in s_nn^{\frac{1}{ p}-1}\mu_p^{1/p}A_p^{-1}\frac{|\mathbb{B}_p^n|_n^{1/n}}{\big|\Sigma_{n-1}\big|_{n-1}^{1/(n-1)}}\mathbb{D}_p^n\Bigg\}\Bigg|_{n-1}\\[3pt]
&=\Big|\Big\{z\in\big|\tilde{\Delta}_{n-1}\big|_{n-1}^{-1/(n-1)}\tilde{\Delta}_{n-1}\,{:}\,z\in s_nn^{\frac{1}{ p}-1}\mu_p^{1/p}A_p^{-1}\big|\tilde{\Delta}_{n-1}\big|_{n-1}^{-1/(n-1)}\mathbb{B}_p^n\Big\}\Big|_{n-1}
\end{align*}
\begin{align*}
\\[-40pt]
&=\frac{\Big|\Big\{z\in\tilde{\Delta}_{n-1}\,{:}\,z\in s_nn^{\frac{1}{p}-1}\mu_p^{1/p}A_p^{-1}\mathbb{B}_p^n\Big\}\Big|_{n-1}}{\big|\tilde{\Delta}_{n-1}\big|_{n-1}}\\
&=\mathbb{P}\bigl(\|Z_n\|_p\leq s_n n^{\frac{1}{p}-1}\mu_p^{1/p}A_p^{-1}\bigr), \end{align*}
where
$Z_n$
is uniformly distributed in
$\tilde{\Delta}_{n-1}$
. Now, we observe that
\begin{align*} \mathbb{P}\Big(\|Z_n\|_p\leq s_n n^{\frac{1}{p}-1}\mu_p^{1/p}A_p^{-1}\Big)&=\mathbb{P}\Big(\sqrt{n}\big(n^{1-\frac{1}{p}}\|Z_n\|_p\mu_p^{-1/p}-1\big)\leq \sqrt{n}\big(s_n A_p^{-1}-1\big)\Big). \end{align*}
This allows us to apply the central limit theorem from Corollary 1.1. Indeed, if
$sA_p^{-1}>1$
or
$sA_p^{-1}<1$
, then
$\sqrt{n}\big(s_nA_p^{-1}-1\big)\to +\infty$
or
$-\infty$
respectively as
$n\to\infty$
. In the equality case
$sA_p^{-1}=1$
, since
$s_n=s\big(1+O(n^{-1}\log n)\big)$
for arbitrary
$\varepsilon>0$
, we have
$\sqrt{n}\big(s_nA_p^{-1}-1\big)=\sqrt{n}\big(sA_p^{-1}(1+O(n^{-1}\log n))-1\big)=O\big(n^{-1/2}\log n\big)\to 0$
as
$n\to \infty$
. The proof is thus complete.
It is interesting to know the value of s in the critical case, i.e.
$s=A_p$
, for different choices of p. For example, if
$p=1$
, which corresponds to the intersection of the simplex with the crosspolytope, we have that
$s=A_1=2\mu_1=4/\mathrm{e}\approx 1.4715$
. For
$p=2$
, which corresponds to the intersection of the simplex with the Euclidean ball, we obtain
$s=A_2=\sqrt{{2\pi} / {\mathrm{e}}}\approx 1.5203$
.
Remark 4.1 As in the case of
$\ell_p$
-balls (see [Reference Kabluchko, Prochno and Thäle15, Corollary 2.2]) one can show that for any
$r\in(0,1)$
there exists a sequence
$\big(s_n^{(r)}\big)_{n\in\mathbb N}$
for which
$\big|\Sigma_{n-1}\cap s_n^{(r)}\mathbb{D}_p^n\big|_{n-1}\to r$
as
$n\to\infty$
.
Acknowledgements
We gratefully acknowledge the suggestions of an anonymous referee which improved the exposition.
Funding information
ZK has been supported by the German Research Foundation under Germany’s Excellence Strategy EXC 2044 – 390685587, Mathematics Münster: Dynamics - Geometry - Structure. JP and MS are supported by the Austrian Science Fund (FWF) Project P32405 Asymptotic geometric analysis and applications and MS also received support from Project FF5513-N26, which is part of the Special Research Program Quasi-Monte Carlo Methods: Theory and Applications. Most of this work was done while AB was a visiting PhD student at the University of Graz and we thank the RTG 2131 High-dimensional phenomena in probability – Fluctuations and discontinuity for the financial support.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
