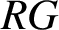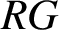1. Introduction
Let R be an associative ring with identity and let G be a group. A unit u in the group ring
$RG$
is said to be trivial if it is of the form
$rg$
for some unit
$r\in R$
and some
$g\in G$
. Any unit of
$RG$
not of this form is said to be a nontrivial unit.
A well-known conjecture on units of group rings, first formulated by Higman in his doctoral thesis [Reference Higman5] and made popular by Kaplansky [Reference Kaplansky6], states that if K is a field and G is a torsion-free group, then the group algebra
$KG$
has only trivial units. In an online talk on 22 February 2021, the mathematician Giles Gardam announced that this long-standing conjecture of more than 80 years is false. Gardam’s counterexample, where the field has order two and the group is virtually abelian, is available in a preprint [Reference Gardam2].
Conversely, questions have been asked on the conditions that the ring R and the group G would satisfy if the group ring
$RG$
has only trivial units. Among the results obtained on this question is the following result of Herman et al. [Reference Herman, Li and Parmenter4].
Proposition 1.1. ([Reference Herman, Li and Parmenter4], Proposition 8)
Let R be a commutative ring with identity of finite characteristic
$l>1$
and let G be a finite group such that
$RG$
has only trivial units. Then G is cyclic of order two or three.
A question that comes to mind then is whether Proposition 1.1 holds true even when R is not commutative. It turns out that the answer to this is in the affirmative when R has characteristic two and we present an elementary proof of this result here. We also consider commutative rings of odd prime characteristic and improve on Proposition 1.1 by showing that if G is a nontrivial locally finite group such that the units in
$RG$
are all trivial, then G is cyclic of order two.
It is worthwhile to mention here that in a continuation of the work in [Reference Herman, Li and Parmenter4], Herman and Li [Reference Herman and Li3] obtained necessary and sufficient conditions for the group ring
$RG$
to have only trivial units when R is the ring of integers of an algebraic number field and G is a nontrivial torsion group.
Throughout this paper,
$C_n$
is used to denote the cyclic group of order n and all rings considered are associative with identity.
2. Rings of characteristic two
We first give a constructive proof of the existence of nontrivial units.
Proposition 2.1. Let R be a ring of characteristic two and let G be a group. If G has an element of order n where
$n\ge 4$
, then
$RG$
has a nontrivial unit.
Proof. Suppose that
$x\in G$
has finite order n where
$n\ge 4$
. Consider the case
$n=2m$
where
$m\ge 2$
. Then it is easy to see that
$1+x+x^2+\dots +x^{2m-2}$
is a unit in
$RG$
because
$(1+x+x^2+\dots +x^{2m-2})^{-1}=1+x^2+x^3+\dots +x^{2m-1}$
.
Suppose now that
$n=2m+1$
where
$m\ge 2$
. Then
$1+x+x^2+\dots +x^{2m-2}$
is a unit in
$RG$
with
$$ \begin{align*} &(1+x+x^2+\dots +x^{2m-2})^{-1}\\ &\quad = \left\{ \begin{array}{ll} x+x^2+x^4+\dots +x^{2i}+\dots +x^{2m} &\mbox{ if } m\ge 2 \mbox{ is even,}\\ 1+x^3+x^5+\dots +x^{2i-1}+\dots +x^{2m-1} &\mbox{ if } m\ge 3 \mbox{ is odd}. \end{array} \right. \end{align*} $$
We have thus shown the existence of nontrivial units in
$RG$
.□
We now prove the main result in this section, which extends the characteristic-two case in Proposition 1.1 to rings that are not necessarily commutative.
Theorem 2.2. Let R be a ring of characteristic two and let G be a nontrivial torsion group. If the units in
$RG$
are all trivial, then G is cyclic of order two or three.
Proof. By Proposition 2.1, every nonidentity element of G has order two or three. Suppose that G is not cyclic. We consider the following cases.
Case 1: Every nonidentity element of G has order two. Then G is a
$2$
-group with a subgroup H isomorphic to the direct product
$C_2\times C_2$
. Let
$x,\,y$
be generators of
$C_2\times C_2$
. Then
$u=1+x+y\in RG$
and
$u^2=1$
. That is,
$RG$
has a nontrivial unit, which is a contradiction.
Case 2: Every nonidentity element of G has order three. Then G is a
$3$
-group with a subgroup H isomorphic to
$C_3\times C_3$
. Let
$x,\,y$
be generators of
$C_3\times C_3$
. Then
$v=1+x+x^2+y+xy\in RG$
is a unit with
$v^{-1}=1+x+x^2+y^2+x^2y^2$
. This tells us that
$RG$
has a nontrivial unit, which is a contradiction.
Case 3: G has at least one element of order two and at least one element of order three. Let P be a Sylow
$2$
-subgroup and Q a Sylow
$3$
-subgroup of G. Since every nonidentity element in P has order two, so P must be abelian. If
$|P|\ne 2$
, then P has a subgroup isomorphic to
$C_2\times C_2$
and, hence, by the same argument as in Case 1, there is a nontrivial unit in
$RG$
, which is a contradiction. It follows that
$|P|=2$
, that is,
$P\cong C_2$
. Now if Q is not cyclic, then since every nonidentity element in Q has order three, so Q has a subgroup isomorphic to
$C_3\times C_3$
and, by the same argument as in Case 2,
$RG$
would have a nontrivial unit, which again is a contradiction. Hence, we have
$Q\cong C_3$
. It follows that G has six elements and, since G is assumed to be not cyclic, P and Q cannot commute with one another. Therefore, G must be the symmetric group
$S_3$
, also known as the dihedral group of order six, given by the presentation
$\langle a, b\mid a^3=b^2=1, ba=a^2b\rangle $
. But then we have
$u=1+a+a^2+b+ab\in RG$
with
$u^2=1$
, that is, u is a nontrivial unit in
$RG$
, which gives us a contradiction.
In all the above cases, we have a contradiction. Therefore, G must be cyclic and has order two or three. □
Example 2.3. Let D be a division ring of characteristic two (such division rings do exist; see, for example, [Reference San Soucie8]). Then
$DG$
has a nontrivial unit for any nontrivial torsion group G except when
$G=C_2$
or
$C_3$
.
3. Rings of odd prime characteristic
By Proposition 1.1, we see that if
$\mathbb F$
is a field of prime characteristic and G is a finite group such that
$\mathbb FG$
has only trivial units, then G has order at most three. In fact, in the case where the field has odd prime characteristic, a sharper upper bound on the order of G is two (see [Reference Passman7]). For our purpose here, we prove the following version for fields of odd prime characteristic, which is somewhat analogous to Proposition 2.1.
Theorem 3.1. Let
$\mathbb F$
be a field of characteristic p where p is an odd prime and let G be a group with an element of finite order
$n\ge 3$
. Then
$\mathbb FG$
has a nontrivial unit.
Proof. Suppose that
$x\in G$
has finite order
$n\ge 3$
. Assume first that p does not divide n and let
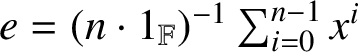$e=(n\cdot 1_{\mathbb F})^{-1}\sum _{i=0}^{n-1}x^i$
. Then e is an idempotent of
$\mathbb FG$
and
$u=1+(p-2)e$
is a unit of
$\mathbb FG$
with
$u^2=1$
. Note that
$$ \begin{align*} u = 1+(p-2)(n\cdot 1_{\mathbb F})^{-1} +(p-2)(n\cdot 1_{\mathbb F})^{-1} \sum_{i=1}^{n-1}\,x^i \ne kg \end{align*} $$
for any
$k\in \mathbb F\setminus \{0\}$
and
$g\in G$
. Thus, u is a nontrivial unit of
$\mathbb FG$
.
Now assume that p divides n. Then
$n=pm$
for some integer m and it follows that
$x^m$
has order p. Let
$\mathbb Z_p$
be the prime subfield of
$\mathbb F$
. Note that
$$ \begin{align*}(1+x^m+x^{2m}+\dots +x^{(p-1)m})(1-x^m)=1\end{align*} $$
in
$\mathbb Z_p\langle x^m\rangle $
. It follows that
$\mathbb Z_p\langle x^m\rangle $
(and hence
$\mathbb FG$
) contains a nontrivial unit. □
Now let R be a commutative ring. We first observe that if
$u\in R$
is a unit and
$x\in R$
is nilpotent, then
$u+x$
is a unit because
$$ \begin{align*}(1+u^{-1}x)(1-(u^{-1}x)+(u^{-1}x)^2-\dots +(-1)^{n-1}(u^{-1}x)^{n-1})=1,\end{align*} $$
where n is the smallest positive integer such that
$x^n=0$
. In the following, we obtain some conditions on R and the group G so that
$RG$
has a nontrivial unit.
Proposition 3.2. Let R be a commutative ring such that p is nilpotent in R for some odd prime p and let G be a nontrivial locally finite p-group. Then
$RG$
has a nontrivial unit.
Proof. By [Reference Connell1, Proposition 16(ii)], the augmentation ideal
$\Delta $
of
$RG$
is nil. Suppose that
$g_1,\, g_2\in G\setminus \{1\}$
are distinct elements in G. Then
$1-g_2\in \Delta $
is nilpotent and, hence,
$g_1+(1-g_2)$
is a nontrivial unit in
$RG$
. This completes the proof. □
Finally, we prove the following, which improves on Proposition 1.1 in the case where the ring R has odd prime characteristic.
Theorem 3.3. Let R be a commutative ring of odd prime characteristic p and let G be a nontrivial locally finite group. If the units in
$RG$
are all trivial, then G is cyclic of order two.
Proof. If the units in
$RG$
are all trivial, then it follows by Proposition 3.2 that G is not a p-group. Therefore, there exists
$x\in G$
such that x has order q for some prime q with
$q\ne p$
. If q is odd, then
$q\ge 3$
and, hence, it follows by Theorem 3.1 that
$(\mathbb Z/p\mathbb Z)\langle x\rangle $
(and, therefore,
$RG$
) has a nontrivial unit, which is a contradiction. Thus,
$q=2$
. We also note that none of the nonidentity elements in G has as its order a power of either p or
$2^k$
, where
$k\ge 2$
; otherwise, by Theorem 3.1 again,
$RG$
would contain a nontrivial unit, which is a contradiction. Thus, all the nonidentity elements in G have order two. If
$|G|\ne 2$
, then G has a subgroup H isomorphic to
$C_2\times C_2$
. Let
$x, y$
be generators of H. Then
$u=1+x+y-xy$
is a unit in
$(\mathbb Z/p\mathbb Z)H$
with
$u^{-1}=\lambda (1+x+y-xy)$
, where
$4\lambda \equiv 1\pmod {p}$
. Thus,
$RG$
has a nontrivial unit, which again is a contradiction. Therefore,
$|G|=2$
and G is cyclic, as asserted. □
Acknowledgement
The author would like to thank the referee for helpful suggestions which led to an improved paper.
