1. Introduction
Efficiency of natural resource use is strongly related to property rights regimes and market structures. For all privately owned resources, be they renewable or nonrenewable, resource use and efficiency depend on the market structure for the product derived from the natural resource. For the case of privately owned nonrenewable resource stocks this has been addressed in great detail in the literature (see, e.g., Dasgupta and Heal, Reference Dasgupta and Heal1979 and Groot et al., Reference Groot, Withagen and de Zeeuw2003 for a brief survey). Alternatively, and more scarcely, attention is paid to the case where there is a single nonrenewable resource that is common property of a given number of firms (see, e.g., Karp, Reference Karp1992). Usually, the focus is on welfare losses due to the common property regime. For renewable resources such as fisheries, open access is more common in the literature, based on real world evidence. In some respects, Datta and Mirman (Reference Datta and Mirman1999) have the same approach as Karp, but for renewable resources. They consider the case of two types of fish, harvested from spatially separated pools, where both are common property of a given number of countries. And they show that a noncooperative equilibrium is inefficient. In an international trade context the contributions by Chichilnisky (Reference Chichilnisky1994) and Brander and Taylor (Reference Brander and Taylor1998) should be mentioned. Chichilnisky shows that if two regions have different property rights regimes for a renewable resource, the free trade equilibrium is Pareto inefficient. Brander and Taylor (Reference Brander and Taylor1998) compare autarky and free trade and formally derive conditions under which a resource exporting country might lose under free trade. The two latter papers assume that in the case of trade, the world market for the resource is competitive.
So, it appears that in the trade papers private ownership of the renewable resource does not carry over to market power of the resource owner when the regions open up to trade. And, for the case where market power is assumed for the resource owners, these owners also share the resource stock. However, in the latter literature the case of autarky is not considered. This is the gap the present paper aims to bridge. So, we have two regions in which there is a homogeneous renewable resource, privately owned (by one owner) or commonly owned by a continuum of agents, so that open access is in place. In autarky the regional markets are separated. We then first consider market equilibrium in autarky. Next, we study the new market equilibrium when demand of both regions is aggregated on a single market. On this market perfect competition may prevail or the sole owner of the resource in one region may exploit some market power, or both private owners may play a Nash game. The objective is to characterize both autarky and common market equilibria in terms of (steady state) resource stocks and catch, under different assumptions with regard to natural growth functions and unit extraction cost functions. Among the findings we have that with two open access regimes the common market may lead to a higher steady state stock in one region and a lower one in the other region, depending on the cost structure. But it might also be the case that both stocks get exhausted. Another finding is that in the case of mixed ownership, one resource privately owned and the other with open access, the privately owned resource stock may increase under free trade. Clearly it is of interest to extend the analysis into a general equilibrium trade framework. This step will be made in future research. For that reason we also refrain from a welfare analysis for the time being.
An example where our analysis may be applicable are the alkaline lakes in Tanzania and Kenya. Due to the high concentration of alkaline, only certain kinds of tilapia can grow in these lakes and this fish is not found anywhere else. In addition no other fish grows here (Ramsar, 2001; Fishbase, 2005). Currently a regime of regulated open access prevails; fishermen can buy permits allowing them to catch whatever they want. In the future the two countries may opt for a different strategy of assigning property rights resulting in different market structures. Another example concerns lake trout in Trout Lake and Black Oak Lake in Northern America. Genetic tests showed that this fish is a unique species and only lives in these two lakes. The regulating government decides on the amount of fish that can be caught (Outdoor News Network, 2003). Both examples are real-life situations where there might be interaction between lakes. Furthermore, if one of these regions decides to introduce well-defined property rights this will lead to a new market structure and thus the interaction between the two regions changes. However, the field of application is broader. Markets for renewable resource commodities may be separated for a number of reasons, for example high transaction costs or transportation costs or for technological or regulatory reasons. This paper investigates the effects of these impediments disappearing.
In the next section we present the model. In the third section the equilibrium in autarky will be analyzed as a benchmark. The fourth section will analyze equilibria when the countries supply to a common market and section 5 will analyze the situation when the two countries cooperate. Section 6 concludes.
2. The model
To describe the different market structures and property rights regimes, a model with two separate lakes indexed by i (i = 1, 2) will be considered. Fish stock in lake i at instant of time t is denoted by Xi(t). The initial stocks are Xi 0 > 0. The natural growth function G i satisfies:
(A.1) G i (0) = Gi(Ki) = 0 for some Ki > 0. Gi is nonnegative and strictly concave on [0, Ki). Finally, Gi(X) = 0 for all X > Ki.
Here, Ki is the carrying capacity. By yi we denote total catch from lake i, which is required to be nonnegative. Hence the following holds
Fish from the two lakes is homogeneous. Local demand for fish is given by an identical inverse demand function P(yi) that is monotonically decreasing. The amount of fish caught depends on the current stock and the effort ei (see, for example, Clark, Reference Clark2005). The cost per unit of effort is wi. With constant returns to scale of effort, for a given stock, the cost of fishing is wiei = Ci(Xi)yi. With regard to Ci(Xi) the following assumption is made:
(A.2) Ci is decreasing and strictly convex. Moreover P(0) = C i (
i
) for some
i
> 0.
The latter condition implies that fishing is not profitable for all 0 ≤
X
i
≤ 
i
. The locus of points where P(y) = Ci(X) is increasing
for all (y, X)
> (0,
i
). The system P(yi) = Ci(Xi),
yi = Gi(Xi)
yields the steady states under open access. In general nothing can be said about the
number of solutions of the system. However, if the locus of points satisfying
P(y) =
Ci(X) is concave, the number of solutions is one, two or three, where the
case of two steady states is a border case (see figure 1). In the case of three steady states, one of
them will be on the downward-sloping part of the natural growth function G. Moreover, the steady state in the middle is
unstable. In the sequel we will assume:
Figure 1. Steady state in open access autarky
(A.3) The function y = fi(X) defined by P(y) = Ci(X) is concave.
In the sequel we will sometimes rely on simulations. The specific functional forms
used are: ![$G_i (X_i ) = rX_i [ {1 - \textstyle\frac{{X_i }}{{K_i }}} ]$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_inline1.gif?pub-status=live){kind=small}
. Here the constant r, assumed
positive, is the intrinsic growth rate and Ki is the carrying capacity of lake i.
With linear demand and market clearing we have P(y
i
) = 
− y
i
, where is the choke price.
, with a > b > 0, a
> and 0 <
c < 1. Since a > b we
have Ci(Ki) > 0. Since a > assumption
(A.2) is satisfied. The carrying capacity is included to allow, for example, for
higher search costs if the lake is larger. If 
then there is a unique point of intersection of the zero profit
curve and the steady state stock with G′ < 0.
For illustrative purposes we make numerical exercises as well. The parameter values
we are using are: r = 0.35,Footnote
1
K 2 = 3,750, = 200,Footnote
2
a = 250,Footnote
3
b = 157,Footnote
4
c = 0.5, α = 0.4 (from Perman et
al., Reference Perman, Ma, McGilvray and Common2003) and ρ = 0.05. The value of K 1 will vary between 1,250Footnote
5
and 20,000.
3. Autarky
The ownership regimes considered in autarky are open access and private ownership. In the latter regime we make a distinction between the case where the private owner can exercise market power and the case where he cannot. In the present section we omit the index i.
3.1. Open access
With open access anyone can start fishing without restrictions and fishermen will continue fishing as long as they make a profit. Hence, in the long run all rents dissipate (Gordon, Reference Gordon1954). Following the standard approach in fishery economics, entry and exit do not take place instantaneously. We introduce some delay in the response of the catch to changes in profitability
![\begin{equation}
\dot y(t) = \alpha [P(y(t)) - C(X(t))].
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU1.gif?pub-status=live){kind=small}
Here α denotes the speed of adjustment. As long as the price exceeds the unit cost of fishing, catch will increase. If fishing is not profitable, it gradually declines. We also have
In the case depicted in figure 1 there are two stable equilibria. The first one occurs if the initial stock is small. The other equilibrium occurs with a relatively high initial stock. From the existing literature we know that the approach path to the interior steady state is typically oscillating (see, e.g., Perman et al., Reference Perman, Ma, McGilvray and Common2003).
In the sequel we will occasionally consider the carrying capacity as a pivotal parameter to perform a sensitivity analysis. The carrying capacity can vary between lakes because of, for example, the size of the lakes or climatological circumstances.Footnote 6 For higher values of the carrying capacity the locus of points for which y = G(X) will lie entirely above the one with a lower carrying capacity. Let us start from the existence of two stable steady states (as in figure 1) and let us assume that the cost function does not depend on the carrying capacity. If we consider the case with a considerably higher carrying capacity, it could happen that only one steady state with a high steady state stock remains. In that newFootnote 7 steady state the harvest is larger than in the case of a low carrying capacity. If the alternative carrying capacity is only moderately larger, there will still be two steady states. Compared to the old steady states the new steady states are larger and they allow for higher steady state harvesting. The picture becomes slightly more complicated if the cost function depends on the carrying capacity as well. If the costs are increasing in the carrying capacity, for example due to increased search costs, then the locus of points for which P(y) = C(X) will move downwards. Hence, starting from two old steady states and keeping the growth function unchanged, the new steady state stocks are larger, with one having a lower steady state catch, and one having a higher steady state catch. When both the growth function and the cost function are affected, the result is no longer unambiguous. To analyze this further we make use of our specific functional forms. Note that in an open access steady state the zero profit condition reads
Total differentiation yields
The expression 2rX 2/K − rX is larger than 0 if and only if 
. Hence if K increases by 1
per cent and , the steady state increases by more than 1 per cent. Now
y increases since y = −
a + b(X/K)
c
. We thus experience an increase in y.Footnote
8
However, if 
and b is sufficiently
small, it might lead to a decrease of X and
of y.
For later reference we use the parameter values introduced above for a numerical exercise to confirm the effects of a change in the carrying capacity on the steady state amount of fish being caught and the size of the fish stock under open access in table 1. These parameter values imply a unique steady state at the decreasing part of the growth function.
Table 1. Steady states for a single open access lake
3.2. Private ownership
The private owner maximizes profits over time, discounted at the constant rate ρ > 0
subject to the natural growth equation. The current-value Hamiltonian is
![\begin{equation}
H(X,y,\lambda ) = P(y)y - C(X)y + \lambda [G(X) - y].
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU6.gif?pub-status=live){kind=small}
The necessary conditions for an interior solution read
![\begin{equation}
\frac{{\partial H}}{{\partial X}} = - \dot \lambda + \rho \lambda :\dot \lambda = C'(X)y - [G'(X) - \rho ]\lambda .
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqn4.gif?pub-status=live){kind=small}
Condition (3) requires that marginal revenue equals the marginal cost of harvesting (C′(X)) plus the marginal costs (λ) of having less fish left in the lake. Condition (4) is the arbitrage condition stating that the change in the future benefits is given by the stock effect (having more stock reduces the price of catching the fish C′(X)y) and the difference between the growth effect of having more fish in the lake and the discount rate ([G′(X) − ρ]λ). For the case of private ownership we consider first the case where the private owner is a price taker in order to have a benchmark for the market structures investigated in the sequel. Next we assume that the private owner acts as a monopolist.
If the private owner is a price taker, the first-order conditions for an interior solution boil down to
![\begin{equation}
\frac{{\partial H}}{{\partial X}} = - \dot \lambda + \rho \lambda :\dot \lambda = C'(X)y - [G'(X) - \rho ]\lambda .
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqn6.gif?pub-status=live){kind=small}
The steady state is defined by Ẋ =
0 and therefore 
= 0. The locus of
points for which Ẋ = 0 is the same
as under open access. It follows from (5) and (6) that along an interior path
There will only be supply if P(y) − C(X) > 0. Under
this condition and in view of the fact that C′ < 0, y
is increasing for G′(X) − ρ > 0. Consequently, in the steady state
we must have G′(X) − ρ < 0. In figure 2 an example is drawn of how an equilibrium
might look and how it can be reached. The example shows a case where the zero
profit manifold intersects with the growth function three times. We have also
drawn a ẏ = 0 curve. Note that it
cannot be the case that this curve intersects the growth function for values
lying above the zero profit manifold. For very low initial stocks there will be
no fishing for an initial interval of time. After some instant of time, where
the stock is reached, fishing
effort will increase until the steady state is reached. For high initial stock
values, the fishing effort will decrease monotonically until the steady state is
reached. This figure is an example only. The zero profit curve, the growth
function, and the ẏ = 0 isocline
may have different locations relative to each other, which would yield different
steady states as well as different approach paths. However, here we do not want
to go into a complete taxonomy of all possibilities. What can be said is that in
case of unique steady state stock it will be higher than in the case of open
access. This also holds when there are multiple steady states.
Figure 2. Steady state for a price-taking private owner in autarky
For the private owner acting as a monopolist we have a similar result as long as we make the usual innocuous assumption that the revenue function P(y)y is concave (so that P″(y)y + 2P′(y) < 0) and we have
The effects of changes in carrying capacity are given in table 2 in the case of price-taking behavior. For a monopolist the results are given in table 3.
Table 2. Steady states under price-taking private ownership
Table 3. Steady states for a monopolist
Comparing tables 2 and 3 with the results for open access confirms the analytical results as stock levels are higher for a price-taking private owner and even more so for a monopolistic private owner. Interestingly, for a price-taking private owner the profits are decreasing with an increase in carrying capacity, while for the monopolist the result is the other way around. The intuition for this seemingly surprising result is that the price-taking fisherman will supply ‘too’ much compared to the monopolist because the shadow price of the resource gets smaller with an increase in the carrying capacity, and the equilibrium therefore gets closer to the zero profit (open access) equilibrium, as can be seen from a comparison of tables 1 and 2.
4. Common market
If a common market for fish comes into existence, three regimes may unfold. One is
where the lakes in both regions have open access, one where one region has an open
access regime and the other lake is privately owned (the mixed regime), and,
finally, one with both lakes privately owned. In the sequel, autarky values and
values under the common market are distinguished by superscripts A and T
respectively. We have ![$P^T (y_1 + y_2 ) \equiv P({\textstyle{1 \over 2}}[y_1 + y_2 ])$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_inline6.gif?pub-status=live){kind=small}
. We are interested to see how the market interaction affects the
stocks and amounts of fish being caught. We also study the dynamic aspects of
introducing a common market. In particular, we will for some cases sketch the
approach paths to the new steady state, assuming that we start from an autarky
steady state, as is usual in the literature (see e.g. Brander and Taylor, Reference Brander and Taylor1998).
4.1. Open access
In the case of open access, a large variety of potential outcomes arises, even if the two lakes have equal growth functions and cost functions. Let us assume that this is the case. The dynamics are given by
![\begin{eqnarray*}
\dot{y}_1^T (t) & = & \alpha_1 \big[P \big(\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \big(y_1^T (t) + y_2^T (t)\big) - C \big(X_1^T (t)\big)\big] \\
\dot{y}_2^T (t) & = & \alpha_2 \big[P\big(\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} (y_1 (t) + y_2 (t)) - C\big(X_2^T (t)\big)\big],
\dot{X}_1^T (t) & = & G\big(X_1^T (t)\big) - y_1^T (t) \\
\dot{X}_2^T (t) & = & G\big(X_2^T (t)\big) - y_2^T (t) .
\end{eqnarray*}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU9.gif?pub-status=live)
The initial values are the autarky steady state values X
i
T
(0) = X
i
A
(∞), y
i
T
(0) = y
i
A
(∞). Now consider the picture below (figure 3), based on a numerical example.Footnote
9
Suppose lake 1 finds itself in the equilibrium with the low steady state
and the low catch, whereas lake 2 has a relatively high initial stock as well as
catch, where initial refers to the steady state in autarky. Then when the common
market comes into existence, there occurs a price drop for lake 1 fish and a
price hike for lake 2 fish. As a result, fishing in lake 1 will decrease,
whereas fishing in lake 2 will increase (seen from a purely mathematical
perspective, it can even be the case that fishing from lake 1 becomes negative,
which is obviously infeasible). In any case, if the speed of adjustment
α 1 is low, supply
from lake 1 will be at a low level for some time, say at 
1. The curve 
lies above the curve 
meaning that y 2
can increase from the initial steady state because profits are made. The
increase in y 2 induces a decrease
in X 2, which works against the
expansion of the fishery because of the high cost. However, it might be the case
that the zero profit locus is reached too late to prevent total exhaustion of
the second lake. The subsequent drop of the catch then boosts the price, which,
together with the increased stock in lake 1, enhances fishing in lake 1. The
outcome can be that eventually also the first lake gets exhausted. The situation
depicted here shows that the fact that the common market comes into existence
might have extreme consequences. But other possibilities arise as well.
Figure 3. Transition paths of X1 and X2 when a common market comes into existence
Let us assume that in autarky, with possibly differing growth and cost functions,
there exists a unique steady state for each lake, with both stocks corresponding
with the declining part of the growth function. Hence G′1(X 1
A
) < 0 and G′2(X 2
A
) < 0. For our functional forms this is the case if, for each
lake, − a + (1/2)
c
b <
1/4rK
i
. We consider several cases in detail. If G 1 ≡ G 2 and C 1 ≡ C 2, then nothing changes compared to autarky. Assume
next that G 1 ≡
G 2. Also assume that the cost
functions differ in the following sense: C 1(X) >
C 2(X) for all X > 0. The
locus of points for which P(y) = C 1(X) lies
strictly below the locus of points where P(y) = C 2(X), at least for points where y
> 0. For the common market we have in an interior steady state
C 1(XT 1)=C 2(XT 2). For every X 1 ≥ X 1
A
we can find X 2 <
XA 2 such that
C 1(X 1) = C 2(X 2).
For every such pair we can calculate the corresponding ys on the growth function. If we take X
A
1 as the starting point, then we have for the corresponding
ys that
1/2(y 1
A
+ y 2) >
y 1
A
, implying that the corresponding price would be smaller than P
A
(yA 1), which is
incompatible with the unchanged per unit extraction costs. Similarly, there will
exist an X such that the associated X 2 is X
A
2 with corresponding ys such
that 1/2(y 1
A
+ y 2) <
y 2
A
with a price higher than P
A
(yA 2). So,
following this procedure, we conclude that in the new equilibrium X
T
1 > XA 1 and X
T
2 < XA 2. Moreover, the catch in the low cost
lake goes up, the catch in the high cost lake decreases. This is also
intuitively clear from the dynamics behind the open access case. Initially, when
the new market opens, there is more supply from the low cost than from the high
cost lake. This implies that the price for the high cost lake decreases,
triggering less supply and therefore an increase in its stock. For the low cost
lake the situation is just the other way around. Finally, if we allow the growth
functions to differ as well as the cost functions, the same results will be
obtained, as long as these functions do not differ too much.
Turning now to our specific functional forms, it can be shown that K 1 > K 2 implies X
T
1 < XA 1, y
T
1 > yA 1 and P
T
> PA 1. The proof runs as follows. Clearly
C 1(X 1) = C 2(X 2)
if and only if 
. The autarky price in region 1 is
![\begin{equation}
P_1^A = \bar p - rX_1^A \left[ {1 - \frac{{X_1^A }}{{K_1 }}} \right] = a - b\left( {\frac{{X_1^A }}{{K_1 }}} \right)^c .
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU10.gif?pub-status=live){kind=small}
The price on the common market reads
![\begin{eqnarray*}
P^T &=& \bar p - \displaystyle\frac{1}{2}rX_1^T \left[ {1 - \frac{{X_1^T }}{{K_1 }}} \right] - \frac{1}{2}rX_1^T \frac{{K_2 }}{{K_1 }}\left[ {1 - \frac{{X_1^T }}{{K_1 }}} \right] \\
&=& \bar p - rX_1^T \left[ {1 - \frac{{X_1^T }}{{K_1 }}} \right]\left[ {\frac{{K_1 + K_2 }}{{2K_1 }}} \right] \\
&=& \bar p - r^ * X_1^T \left[ {1 - \frac{{X_1^T }}{{K_1 }}} \right] \\
&=& a - b\left( {\frac{{X_1^T }}{{K_1 }}} \right)^c
\end{eqnarray*}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU11.gif?pub-status=live)
with 
. Suppose K 1
> K 2. Then r* < r. It is then easily seen that X
T
1 < XA 1, y
T
1 > yA 1 and P
T
> PA 1.
Moreover, if for both lakes the equilibrium is on the declining part of the growth function, we have that an increase in K 1 implies an increase of X T 1/K 1. Therefore the equilibrium price is lower, and, moreover, also X T 2 is higher. These outcomes are confirmed by the numerical exercises with our specific functional forms (see table 4).
Table 4. Steady states for two open access lakes and a single market
In conclusion, there is no unambiguous answer to the question whether the common market leads to smaller or larger steady state resource stocks. The outcome depends on the growth functions as well as the cost functions. However, with similar functional forms and autarky equilibria it is to be expected that the new equilibrium price will be between the autarky market prices. With major differences in initial states (autarky) the dynamics can lead to new steady states where both lakes are completely depleted.
4.2. Mixed regime
In one region the lake is privately owned. The other region has a lake with open access. For the privately owned lake we consider two cases. One where the owner is a price taker, and one where the lake owner takes the supply from the other lake as given. The problem of the private owner of lake 1 reads
subject to (1). The current-value Hamiltonian is
![\begin{equation}
H_1 = P^T (y_1 + y_2 )y_1 - C_1 (X_1 )y_1 + \lambda_1 [ {G_1 (X_1 ) - y_1 } ].
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU13.gif?pub-status=live){kind=small}
The necessary conditions for an interior solution read
![\begin{equation}
\frac{\partial H_1}{\partial X_1} = {-} \dot{\lambda}_1 + \rho \lambda_1 : \dot{\lambda}_1 = C'_1 (X_1 )y_1 - [G'_1 (X_1 ) - \rho ]\lambda_1.
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU15.gif?pub-status=live){kind=small}
The steady states are characterized by
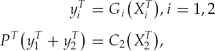
If the lake owner takes the common market price as given, i.e. (PT)′ = 0, the expression for the steady state is the same expression as under autarky. Assume identical growth functions as well as cost functions, some results can be derived analytically. So we assume that G 1 ≡ G 2 = G and C 1 ≡ C 2 = C. Moreover, as in the previous section where we discussed two open access lakes, we assume that the autarky equilibrium is unique and satisfies G′1(X 1 A ) < 0 and G′2(X 2 A ) < 0. We have C(X 2 T ) = C(X 1 T ) + λ1 T , implying X T 1 > XT 2. Hence, the steady state stock of the private owner is larger than the stock in the open access lake. Since by assumption the autarky steady state stocks are on the downward sloping part of the (identical) growth functions, we also have X A 1 > XA 2 and y A 1 < yA 2. Therefore, the open access lake will experience a price hike when the common market comes into existence, whereas for the privately owned lake the opposite occurs. As in the analysis of the previous section this implies that the new steady state for the open access lake is smaller than in autarky, whereas the reverse holds for the privately owned lake. Figure 4 depicts the transition paths from the autarky steady state to the steady state with the common market. Some additional results are the following. If G 1 ≡ G 2 and C 1(X) > C 2(X) for all X > 0, then X T 1 > XT 2 in equilibrium since C 2(X 2 T ) = C 1(X 1 T ) + λ1 T . If G 1(X) > G 2(X) for all X > 0 and C 1 ≡ C 2, then C 2(X 2 T ) = C 1(X 1 T ) + λ1 T still holds and thus X T 1 > XT 2.
Several interesting further comparisons can be made for more general cases than those discussed above. Table 5 contains information about the outcomes of the common market under price-taking behavior of the private owner.
Table 5. Steady states under a mixed regime with a price-taking private owner
First of all the outcomes confirm that with equal growth and cost functions (K 1 = K 2 = 3,750), the private owner has the higher steady state stock. However, even for the case of identical growth functions and costs functions, differing possibly only in a single parameter, namely the carrying capacity, no other unambiguous results are obtained.
We first compare autarky and common market outcomes. To this end consider tables 1 and 5. For a carrying capacity of the privately owned lake equal to K 1 = 3,750 the new steady state stock of the open access lake (3,345) is lower than in open access autarky (3,437), whereas for higher carrying capacities (K 1 = 20,000) we find the opposite result. This is due to the increased catch at higher carrying capacity levels of the privately owned lake resulting in a lower price. Comparison of tables 2 and 5 shows that for the price-taking private owner, the autarky steady state is lower for low carrying capacities and higher for high carrying capacities. The reason for the ambiguity lies in the fact that a higher carrying capacity on the one hand enhances natural growth but on the other hand increases the unit costs of fishing. We also see that the private owner loses from the common market coming into existence for low values of the carrying capacity, but gains for higher values.
Table 5 can also be used to see the effect of the carrying capacity on profitability, within the common market regime. The price-taking firm first experiences an increase in its profits with an increase in K 1. The initial increase is obtained because of the decrease of catch in the open access lake. The catch in the open access lake decreases as the increase in catch in lake 1 leads to a decrease in price and given the zero-profit condition the stock in lake 2 has to increase to reduce costs. This increase in stock leads to a lower catch, which in turn means a higher price, but this is a second-order effect. Thus, the reduced catch in lake 2 dampens the reduction in the price experienced by the private owner who still enjoys the benefit of selling more fish. However, as soon as more fish are being caught in the privately owned lake compared to the open access lake, profits decline with a further increase in the carrying capacity.
Next we assume the private owner is not a price taker, but sets the price, taking the supply by the open access lake fishermen as given. The equations of motion for the catch follow in a straightforward way from the necessary conditions and read
![\begin{eqnarray*}
\dot{y}_1 = \big[P^T (y_1 + y_2 ) - ^1{\!\!/\!}_2 \; y_2 - C_1 (X_1 )\big][G_1^{\prime} (X_1 ) - \rho ] \\
&&{-}\, ^1{\!\!/\!}_2 [\alpha [P^T (y_1 + y_2 ) - C_2 (X_2)] - C_1^{\prime}
(X_1 )G_1 (X_1),\\
\dot y_2 = \alpha [P^T (y_1 + y_2 ) - C_2 (X_2 )].
\end{eqnarray*}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU18.gif?pub-status=live)
We first consider the path towards equilibrium when the common market is established. As before we assume that the monopolistic private owner finds himself in the autarky steady state when the new market structure comes about.Footnote 10
When the common market comes into existence the open access lake will supply more fish due to an increased price. In view of the large supply of fish from the open access lake the private owner will reduce fishing, which results in a build up of its stock. Steady state values under alternative assumptions with regard to the carrying capacity of the former monopolist (lake 1) are given in table 6.
Table 6. Steady states under a mixed regime where the private owner plays Nash–Cournot
The private owner acting as a Nash player unambiguously loses under the common market coming into existence, at least in the steady state (compare with table 3). This comes as no surprise because of the fact that the open access lake fishermen definitely reduce the private owner's monopoly power initially held in autarky. This result is confirmed in a series of sensitivity analyses.Footnote 11 More interestingly, the profit is lower compared to the price-taking case. The underlying reasoning goes as follows. The private owner takes the supply of the open access lake as given and then sets its own supply to maximize profits. In performing the profit maximization process, the private owner only takes into account the supply from the open access lake. In other words, the private owner does not take into account that supply from the open access lake essentially determines everything, at least in the steady state. Indeed, steady state supply from the open access lake determines the steady state stock of the open access lake, and thereby the steady state costs and therefore the steady state price and, hence, the steady state supply from the private owner. Actually, with a given supply from the open access lake, the private owner has no degree of freedom, although the private owner is not aware of that fact. Consequently, market power actually leads to lower profits.
The private owner would do well to keep in mind the effect of his own actions on the actions of the agents managing the open access lake. This consideration calls for the Stackelberg equilibrium concept, where the private owner, if well-informed, can exploit its position better by acting as a Stackelberg leader. One option to the private owner is then to catch at an arbitrarily low rate initially, thereby setting a relatively high price. In an extreme case, this might lead to exhaustion of the other lake, after which the private lake owner can act as a monopolist. In a less extreme case, refraining initially from fully catching the Nash equilibrium amount of fish might also enhance a low stock level in the other lake. It is well-known that the open-loop Stackelberg equilibrium might lead to dynamic inconsistency (see, e.g., Gilbert, Reference Gilbert1978; Newbery, Reference Newbery1981; Groot et al., Reference Groot, Withagen and de Zeeuw1992, Reference Groot, Withagen and de Zeeuw2003, for similar problems occurring in the theory of nonrenewable natural resources). Hence, this would urge a closer examination of the feedback Stackelberg equilibrium. This is subject to further study. It is tempting to speculate on the results. However, it seems only safe to state that a small discount rate of the potential leader will stimulate him to act as a leader and let the follower extract in an early stage of the game.
4.3. Private owners
In this regime we have a private owner for each of the two lakes and the owners play a Nash game against each other, each one taking the quantities offered by the other as given. The optimization problem for the agent managing lake i can be stated as follows
subject to (1). The time path of yj (j ≠ i) is taken as given. The corresponding current-value Hamiltonian is
![\begin{equation}
H_i = P^T (y_1 + y_2 )y_i - C_i (X_i )y_i + \lambda _i \left[ {G_i (X_i ) - y_i } \right].\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU20.gif?pub-status=live){kind=small}
The necessary conditions for an interior solution read
![\begin{equation}
\frac{{\partial H_i }}{{\partial X_i }} = - \dot \lambda _i + \rho \lambda _i :\dot \lambda _i = C'_i (X_i )y_i - [G'_i (X_i ) - \rho ]\lambda _i .
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU22.gif?pub-status=live){kind=small}
The steady states are the solution of
A distinction could be made between many cases, depending on price-taking or monopolistic behaviour by each of the players before the common market comes into existence and on price-taking or Nash behaviour by each of the players afterwards. It goes beyond the scope of this paper to provide a full account of all possibilities. We will restrict ourselves to the two polar cases of both players being price takers throughout and both players being monopolists before and Nash players afterwards.
If the suppliers are price takers, in autarky as well as for the common market, and if they have identical growth and cost functions, the fact that the common market comes into existence does not change anything. The results of some numerical exercises are given in table 7.
Table 7. Steady states for two price-taking private owners
We see that with an increase in the carrying capacity of the first lake, both steady state stocks are increased. The supply from the second lake decreases, as well as the profit made. For the first lake the profits as a function of the carrying capacity are non-monotonic: they increase initially and decrease eventually. Compared to the case of autarky (see table 2) we observe a stock for lake 1 that is consistently lower, corresponding with more supply. For high carrying capacities this does not lead to lower profits. For example, when K 1 = 6,250 (and K 2 = 3,750), profits for the owner of lake 1 are higher than in autarky, due to the fact that supply by the competitor is reduced considerably. We have tested for the robustness of this result by performing a sensitivity analysis (see footnote 11) and found the same result throughout.
For the case of two monopolists becoming Nash players we can use the equations of motion to show the transition for the autarky steady state towards the steady state. The transition path is shown in figure 5. Both private owners reduce their steady state stock in a monotonic way.
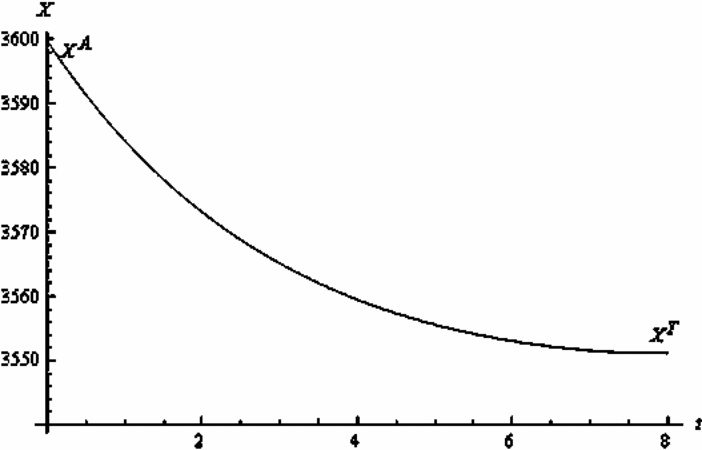
Figure 5. The transition path of two privately owned lakes from the autarky steady state towards the common market steady state (with K1 = K2 = 3,750)
Table 8 displays the outcomes of several calculations.
Table 8. Steady states for a Nash–Cournot game between two private owners
The conclusions drawn from the parametric change in the carrying capacity of lake 1 are similar to those drawn from the case of price taking (table 7). But in all cases the profits of both players are now considerably higher. Another result is that compared to the mixed regime (table 6) profits are higher for the owner of lake 1 when the other lake is properly managed. This is a result of reduced competition as the private owner supplies less fish to the market. Moreover, it also follows from a comparison of tables 6 and 8 that the private owner has a lower stock and a higher supply of fish when the other lake is also privately owned. More interesting perhaps is that for high carrying capacities the profits are higher than in the monopolistic case for a single lake (table 3). It can thus be profitable for the monopolist to give up its monopoly if it can thereby access a bigger market.
5. Cooperation
In this final scenario both lakes are privately owned and the owners cooperate by forming a monopoly. The optimization problem reads
![\begin{equation}
\max_{y_1, y_2} \int_0^\infty \{ P^T (y_1 + y_2 )[y_1 + y_2 ] - C_1 (X_1 )y_1 - C_2 (X_2 )y_2 \} e^{ - \rho t} dt
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU23.gif?pub-status=live){kind=small}
subject to (1) and (2). The corresponding current-value Hamiltonian is
![\begin{eqnarray*}
H & = & P^T (y_1 + y_2 )[y_1 + y_2 ] - C_1 (X_1 )y_1 - C_2 (X_2 )y_2 \\
&&{+}\, \lambda _1 (t) [ {G_1 (X_1 ) - y_1 } ] + \lambda _2 (t) [ {G_2 (X_2 ) - y_2 } ] .
\end{eqnarray*}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU24.gif?pub-status=live){kind=small}
The necessary conditions are
![\begin{eqnarray*}
\frac{\partial H}{\partial y_i} = 0:(P^T)' [y_1 + y_2 ] + P^T = C_i (X_i ) + \lambda _i (i = 1,2),\\
\frac{{\partial H}}{{\partial X_i }} = - \dot \lambda _i + \rho \lambda _i :\dot \lambda _i = C'_i (X_i )y_i - [G'_i (X_i ) - \rho ]\lambda _i {\rm }(i = 1,2).
\end{eqnarray*}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU25.gif?pub-status=live)
The new monopolistic firm takes into account that catching more fish in one lake will not only decrease the price of the fish from that lake but the price of fish from the other lake as well. The steady state is characterized by
![\begin{equation}
\rho = G'_i \big(X_i^T \big) - \frac{{C'_i \big(X_i^T \big)G_i \big(X_i^T \big)}}{{(P^T )'\big[y_1^T + y_2^T \big] + P^T - C_i \big(X_i^T \big)}}.
\end{equation}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920233610680-0331:S1355770X08004701:S1355770X08004701_eqnU27.gif?pub-status=live){kind=small}
A comparison with equation (7), for the steady state stocks in case of an uncoordinated Nash, reveals the intuitively appealing fact that for equal growth and cost functions the steady state stocks will be higher now. Compared to the case of an uncoordinated oligopoly, total supply is reduced. A further simulation exercise yields the outcomes given in table 9.
Table 9. Steady states for a monopolist with two lakes for different carrying capacities of the first lake
6. Conclusion
We have addressed several issues concerning trade and property rights regimes of lakes as well as market structures. We have characterized market equilibria in autarky as well as for a common market, mostly in terms of steady state stocks as well as steady state catch. We have also performed a sensitivity analysis employing specific functional forms, and in doing so mainly used the carrying capacity as a pivotal parameter.
The main conclusion that can be drawn is that the establishment of the common market can have quite large effects and that these effects are strikingly different according to the original type of competition and the new type of competition prevailing. When the new and the old markets are served by lakes with open access, the new situation might give rise to extinction of the fish stocks in both markets, depending on the speed of adjustment governing the adjustment of catch to profit opportunities. In less extreme circumstances it is to be expected that the new equilibrium price will be between the two autarky prices. If the common market is supplied by a lake with open access and another lake with a single owner, we obtain a similar result. But it could be that it is more profitable for the private owner to be a price taker than to act as a price setter while taking the supply from the open access lake as given. Finally, when two fishermen being monopolists previously are going to serve the common market we find that the steady state stocks decrease, compared to the autarky equilibria.
It was found that with higher carrying capacity in a lake the steady state stock of that lake always increases and that there is an ambiguous effect on the catch. We also see that with a decline in market power the stock decreases and supply increases (the monopolist had a higher stock compared to the private owner who had more compared to the amount of fish left in the lake in open access). This does not only hold in autarky: we found similar results for a common market. A private owner will keep a higher stock when there is an open access regime in the other lake compared to a private owner who has market power. We have also shown that market power does not necessarily result in a higher profit. Furthermore, opening up to a common market has ambiguous results on the profits of a private owner as the change in profits depends on whether the other lake is privately owned or governed by an open access regime. From the simulations of the equations of motion we have deduced the path from the autarky equilibrium towards the single market equilibrium in several cases.
For further research, a Stackelberg type equilibrium should be explored including the reaction of another private owner in the optimization process of the Stackelberg leader. Besides this we could think of investigating alternative cost structures. We could also think of the private owner buying better machineries when the carrying capacities increase, thereby changing the cost function.
or 
. This results in a value of b of 157 when the market price P(y) = 100.
. If there is a catch of 100, this would mean that K is at least 1,143. Furthermore, as Lake Nakuru is
a small lake, we use K = 1,250 as the minimum
value for the carrying capacity.
