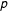1 Introduction
The consistency value fulfills an important role in Qualitative Comparative Analysis (QCA). Empirical QCA researchers use it as one, if not exclusive criterion to distinguish associations between a term and an outcome supporting the inference that a set relation is present from associations that fail to support it (Ragin Reference Ragin2006).Footnote
1
Braumoeller (Reference Braumoeller2015) recently pointed out that the consistency score is unsuitable for this purpose because we need to know the probability of obtaining such a value under the null hypothesis that there is, in fact, no set relation. Without determining the probability, we might commit a false positive by incorrectly inferring that a set relation is in place when it is not. Braumoeller shows for fuzzy-set QCA (fsQCA) that permutation tests allow one to derive the distribution of consistency values for calculating the
$p$
value and statistical significance for the observed consistency score.Footnote
2
Permutation tests and
$p$
-value calculation are valuable additions to the QCA toolbox for avoiding false positives. However, it is equally valuable to know the probability of rejecting the null hypothesis when it is false. This is a matter of the power of a truth table analysis that is inversely related to the probability of committing a false negative. So far, there has been no consideration of the role of power for truth table analyses in the QCA literature, although it is essential to avoiding producing and interpreting false QCA solutions.Footnote
3
In this paper, I introduce power analysis to further the development of truth table analyses and equip empirical researchers with a new tool that will contribute to the validity of their results. I first discuss what a null hypothesis and an alternative hypothesis are in QCA because they need to be specified for power estimation (Section 2). Throughout the paper, I discuss power analysis for set-relational analyses on sufficiency and note here that all arguments generalize to studies of necessity because they invoke consistency values for making similar decisions. Drawing on the distinction between a null and alternative hypothesis, I elaborate on the benefits of high power for a truth table analysis and the consequences of low-powered studies (Section 3). I argue that low power can have two consequences. First, it implies a high probability of falsely excluding truth table rows from the truth table minimization as being inconsistent that are in fact consistent. The solution derived from a wrong set of truth table rows cannot be identical to the true solution. However, the false and true solutions are not unrelated because the false solution is a subset of the true one. Second, even if this problem did not exist, low power might lead us to interpret minimal terms in the solution that are consistent as actually being inconsistent. The consequence is identical to the first problem because the solution we falsely take as the correct solution is a subset of the true solution we would obtain in a sufficiently powered study.
In Section 4, I present the setup for permutation tests that estimate power depending on different null and alternative hypotheses and numbers of cases. The results in Section 5 show that power estimates range from 1 to 0, with 48 simulations out of 75 displaying power of less than 0.5 and 15 have a power estimate of more than 0.8. The simulations show that power is positively correlated with the difference in the consistency values of the null and alternative hypothesis. The relationship between the number of cases and power is more involved because it is conditional on the difference between the consistency scores of the alternative and null hypothesis in ways described in detail in Section 5.2. In Section 6, I estimate power ex post for 63 published truth table analyses. Some are strongly powered, but about half of them display low power even under the most favorable null and alternative hypothesis.
The simulations and results speak in favor of calculating power prior to the truth table analysis and making adjustments to the sample size, if possible, to reach a desired level of power (Section 7). Section 8 extends the discussion to crisp-set and multivalue QCA and points out that power estimation for them differs from fsQCA in terms of the number of cases feeding into the procedure. In Section 9, I conclude by arguing that false-positive testing as introduced by Braumoeller and false-negative testing are complementary and should be used in tandem in empirical QCA research.
2 Alternative Hypotheses and Null Hypotheses in QCA
The terms “null hypothesis” and “alternative hypothesis” are neither used in empirical QCA research nor discussed in the methods literature.Footnote 4 This might not seem surprising because QCA is cast as a method that is different from quantitative research in which these terms are common (Ragin Reference Ragin2008, ch. 10, 11). However, the absence of these terms from the QCA literature does not necessarily mean that they are inherently inapplicable. On the contrary, the consistency value of a term is central to two stages of a QCA interested in a sufficient solution. The idea of an alternative and a null hypothesis about consistency scores come into play at these stages: first, when we assign outcome values to truth table rows to prepare the truth table for minimization and, second, when we interpret a QCA solution as the result of a simplified truth table.Footnote 5
One can argue that the very meaning of the consistency value implies an alternative hypothesis,
$H_{1}$
, which represents our expectation about the true consistency value of an empirical relation between sets. The consistency value captures the degree to which an empirical association between a term X and the outcome Y is in accord with the ideal, perfect relation of sufficiency as it is defined in propositional logic (Ragin Reference Ragin2006).Footnote
6
The ideal set relation is equivalent to an empirical set relation displaying a consistency value of 1 because classic propositional logic underlying QCA does not feature deviations from the ideal. Because a perfect set relation can be taken as the benchmark for interpreting any empirical consistency value, one can argue that
$H_{1}$
entails an expected consistency score of 1, which can be formalized as
$c_{H1}=1$
.
A consistency value of 1 for
$H_{1}$
is in line with logic and also reflects the understanding of QCA as a case-oriented,
$Y$
-centered method that seeks to fully explain the cases’ set membership values for the outcome (Ragin Reference Ragin1987, ch. 5). However, it is not mandatory to fix
$c_{H1}$
at 1 because it should reflect the researcher’s subjective, theoretical expectation about the consistency of a set relation. The most important aspect for specifying
$c_{H1}$
seems to be whether one believes that the empirical relation between
$X$
and
$Y$
is deterministic on an ontological level, that is, the observed consistency value would be unity with complete data measured without any error, and so forth.Footnote
7
Empirically, the observed consistency value might still be less than 1, but the belief in ontological determinism would allow one to set
$c_{H1}$
to 1. If it is thought the relation is probabilistic on an ontological dimension or one emphasizes epistemological probabilism, the set relation is assumed to fail the ideal from logic, even with perfect data, and so forth. This could be reflected in the specification of
$c_{H1}$
at a value of less than 1, the lower bound being the consistency value of the null hypothesis (see below).Footnote
8
In empirical research, one should not mechanically set
$c_{H1}$
to 1, but consider the consistency value one expects to govern a set relation.
Following its conventional use, the null hypothesis,
$H_{0}$
, should cover the largest possible consistency value
$c_{H0}$
representing an empirical association that is inconsistent with the statement that a set relation is given. In empirical research, this value is automatically fixed by determining the minimum consistency threshold that a term needs to surpass.Footnote
9
For sufficient relations, a value of 0.75 is customarily taken as the minimally acceptable consistency value with the option of fixing it at a higher level (Ragin Reference Ragin2006, 293).Footnote
10
Neither
$H_{1}$
nor
$H_{0}$
need to be the same during both stages of the analysis. For
$H_{0}$
, it is common practice to invoke different thresholds over the course of the truth table analysis (see Section 6). In deciding about the assignment of outcome values to truth table rows, empirical researchers frequently choose consistency thresholds higher than the minimally acceptable value of 0.75 (for example, Mello Reference Mello2012). A common strategy is to search for gaps or jumps in the consistency values of two adjacent rows that are ranked by their consistency values (for example, Freitag and Schlicht Reference Freitag and Schlicht2009, 63). For example, if one truth table row has a consistency of 0.87 and the next row only 0.8, we assign an outcome value of 1 to the former and of 0 to the latter, based on the belief that the conjunctions represented by the rows stand in a qualitatively different relationship to the outcome.Footnote
11
The assignment of outcome values based on gaps is common, but it has the potential to create an ambiguity that translates into uncertainty about the exact value of
$c_{H0}$
. In the hypothetical example, for the assignment of outcome values it does not matter whether the consistency threshold is fixed at 0.86 or 0.81. However, it makes a difference for power estimation because we need to fix
$c_{H0}$
at a specific value and because the level of power depends on the level of
$c_{H0}$
(see Section 5). For power analysis and, for the sake of transparency more generally, empirical researchers should not only identify gaps in consistency values, but also specify a consistency score when preparing the truth table for minimization.
For the second stage at which consistency plays a role, the interpretation of a QCA solution is usually not based on an explicit threshold distinguishing between sufficient and non-sufficient minimal terms. Implicitly, this means the threshold is fixed at 0.75 as the conventional minimum. As long as the consistency threshold for the assignment of outcome values is not 0.75, which it sometimes is (see Section 6), a single empirical study invokes two different null hypotheses at different stages of the analysis.
A rationale for choosing different values of
$c_{H0}$
and also of
$c_{H1}$
over the course of a truth table analysis is that they might relate to terms of varying complexity, where complexity is measured by the number of conjuncts in a configuration (see McCluskey Reference McCluskey1956). If the truth table rows that are taken as sufficient for the outcome are simplified in the truth table analysis, which usually is the case, the minimally sufficient terms in the solution are less complex than the sufficient truth table rows. Complexity is positively associated with the consistency value, that is, more complex terms tend to have consistency values equal to or higher than any other term that lacks at least one conjunct (Schneider and Wagemann Reference Schneider and Wagemann2012, 291–293). The formulation of different null and alternative hypotheses at both parts of the analysis would reflect that the terms to which the hypotheses apply are not identical and have different consistency scores for mechanical reasons. For the estimation of power, the specification of different levels of
$c_{H1}$
and
$c_{H0}$
is not a problem as long as the values of
$c_{H1}$
and
$c_{H0}$
at each stage of the analysis are transparent.
3 Consequences of High and Low Power
“Power” is the probability of rejecting
$H_{0}$
when it is false. Power equals 1-
$\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
being the probability of making the type-II error of not rejecting
$H_{0}$
when it is false, that is, of making a false negative. In a high-powered study, the observed consistency values allow us to separate terms that are sufficient from those that are not with a high rate of accuracy. Low power manifests itself differently at the two stages at which it matters, but the consequences for deriving and interpreting the QCA solution are similar.
First, when we assign outcome values to truth table rows, the probability of erroneously excluding rows from the minimization process increases as power decreases. This happens if the true, unknown consistency value of a truth table row is above
$c_{H0}$
, but the row’s observed score happens to fall below
$c_{H0}$
. If we commit a false negative and assign an outcome value of 0 when it should be 1, the QCA solution we derive cannot be identical to the true solution we would obtain if we were correctly assigning the outcome values. The reason is that assigning an outcome value of 0 excludes this row from the minimization process. The excluded row cannot contribute to singling out redundant conjuncts and the simplification of the truth table rows that do enter into the minimization procedure (Ragin Reference Ragin1987, ch. 6). Conjuncts that we could correctly identify as redundant if we had included the falsely excluded row appear to be non-redundant and remain falsely part of the QCA solution. Even if no minimization is possible, the derived solution would be different because a conjunction would be missing from it. A false negative stands in the way of deriving the true solution, but the wrong solution is not completely unrelated to the true one. The failure to minimize some configurations implies that the wrong solution is a more complex version of the true solution, making the wrong solution is a subset of the true one.Footnote
12
Second, low power comes into play in interpreting a QCA solution. Even if we do not commit a false negative when assigning outcome values, we may make one when interpreting the consistency values of the terms in a QCA solution. In a low-powered study, the observed consistency score of a term might fall below 0.75, the conventional minimum, with a high probability, although the true consistency value is above 0.75. We would have formally derived the true solution, but fail to recognize it as such, only giving a theoretical interpretation of the terms with a consistency value of 0.75 or higher. The consequences of too little power in the second stage are similar to those in the first stage because the exclusion of some terms from the theoretical discussion of the solution means focusing on a subset of the true model.
4 Permutation-based Power Analysis
4.1 Estimation procedure
I estimate power with permutation tests as a simple technique for deriving the distribution of the quantity of interest. One advantage of permutation tests is that we do not have to assume that the data at hand represent a random sample of a population (see Section 8 below, and Good (1994, ch. 1) and Carsey and Harden (Reference Carsey and Harden2013, Section 8.2)). For my purpose, the quantity of interest is the consistency value of a term that can be a condition, conjunction or disjunction of conditions or conjunctions.Footnote
13
In principle, one can easily estimate power before doing a fuzzy-set truth table analysis. We neither need to know the minimal terms of the QCA solution nor do we need to know the consistency value of any term or truth table row because the specification of
$c_{H1}$
and
$c_{H0}$
is independent of them. Regarding the number of cases as the third ingredient to power estimation (see Section 4.1), for fsQCA it suffices to know the total number of cases in the truth table analysis because all cases contribute to the consistency value of each truth table row and term in a solution. This differs for crisp-set QCA and multivalue QCA, the discussion of which I relegate to Section 8 because I first need to explain how power estimation is performed for fsQCA. The estimation procedure is summarized in Figure 1.
Figure 1. Summary of procedure for power estimation.
We first have to formulate
$H_{1}$
, stating that the consistency value is
$c_{H1}$
, and
$H_{0}$
that distinguishes consistent from inconsistent terms based on the consistency score
$c_{H0}$
. The starting point of power estimation is the assumption that
$H_{1}$
is correct. For any observational data, we do not know the data-generating process and whether it was generated in accord with
$H_{1}$
. Consequently, permutation tests for power estimation must be based on simulated data generated such that it is in accord with
$H_{1}$
and produces the consistency score
$c_{H1}$
.Footnote
14
If we set
$c_{H1}$
to 1, the consistency value for any simulated dataset must be 1. Let us denote a simulated dataset as
$s_{i}$
,
$i$
being a running index because we have to sample data multiple times for power estimation (see below). Each
$s_{i}$
consists of a term
$X$
and an outcome
$Y$
for which we observe set membership values for
$n$
cases.
A simulated dataset
$s_{i}$
is the starting point for the permutation test. We permute the dataset by keeping the cases’ membership in the term fixed and randomly assign them the outcome membership of another case in the data, that is, we resample outcome values without replacement (Braumoeller Reference Braumoeller2015, 479). Let us refer to the permuted data as
$r_{j}$
.
$r$
stands for randomized permutation and
$j$
is a running index for the number of permutations per simulated dataset
$s_{i}$
. I rely on randomized permutation tests because the number of cases quickly becomes too large for an exact permutation test that involves all possible permutations of the data (see Section 5 and Supplementary Appendix). A randomized permutation test permutes a simulated dataset
$s_{i}$
$j$
times,
$j$
being smaller than the total number of possible permutations. For each permuted dataset
$r_{j}$
, we calculate the consistency value
$c_{j}$
for the set relation of interest between
$X$
and
$Y$
. The process of permuting the same simulated dataset
$s_{i}$
and calculating consistency scores is iterated until
$j$
becomes sufficiently large to construct a distribution over all consistency values
$c_{1}$
to
$c_{j}$
. The distribution makes it possible to locate the consistency value
$c_{H0}$
in the distribution and derive the corresponding
$p$
value
$p_{H0}$
by performing a left-sided significance test.Footnote
15
We reject
$H_{0}$
if
$p_{H0}$
is smaller than the chosen level of
$\unicode[STIX]{x1D6FC}$
, which is what we expect because we know
$H_{0}$
is false, and fail to reject it otherwise.
There are no unambiguous guidelines for how many permutations
$j$
are needed per simulated dataset
$s_{i}$
to test
$H_{0}$
. I follow the guideline that
$j$
should be large enough to receive a precise estimate of
$p_{H0}$
(Braumoeller Reference Braumoeller2015, 479–480). The larger
$j$
becomes, the more precise the estimate and the more meaningful it becomes to test the consistency value
$c_{H0}$
for significance. The standard error of
$p_{H0}$
is the
$p$
value divided by
$\sqrt{j}$
and means we should be on the safe side when permuting each dataset
$s_{i}$
10000 times. In the simulations and power analysis for empirical studies, I take into account the uncertainty of
$p_{H0}$
by calculating its 95% confidence interval (two-sided) and testing whether the upper bound of the interval is smaller than
$\unicode[STIX]{x1D6FC}$
.
The process of simulating datasets according to
$H_{1}$
and permuting them
$j$
times is repeated until
$i$
becomes sufficiently large because we need to know the long-run probability of rejecting
$H_{0}$
when it is wrong. When
$i$
is large enough and we have tested
$c_{H0}$
for each dataset
$s_{i}$
for significance, the power estimate is the number of tests for which we could reject
$H_{0}$
relative to the total number of tests
$i$
. For example, a power estimate of 0.17 means that 17% of all tests of
$H_{0}$
turned out to be significant. There is no solid rule for how large
$i$
should be, but, initially, 1000 simulations seem appropriate for estimating power. Whether the chosen
$i$
is large enough for a reliable power estimate can be visually examined by plotting the running power estimate against
$i$
(see Figure 4 below). We can infer that
$i$
is sufficiently high to produce a reliable estimate if it settles into a specific range after a certain number of simulations. If the estimate is still moving up and down after
$i$
simulations,
$i$
should be increased until the estimate stabilizes and a reliable estimate can be derived.
In practice, the ex ante estimation of power is not possible for the truth table analysis if outcome values are assigned to rows based on a gap between the consistency values of adjacent rows (see Section 2).Footnote
16
The precise value of
$c_{H0}$
then depends on where the gap is and, if there is one, we only know this after creating the truth table and looking at the consistency values of its rows. Although we can calculate power following this procedure, it is preferable to calculate it beforehand because the decision about
$c_{H0}$
should not depend on where a gap happens to be. Instead, it should be considered a general decision to be made independent of the data.Footnote
17
4.2 The relation between power and its determinants
The relation between
$H_{1}$
and
$H_{0}$
and the power estimate should be the same as in quantitative research, while there is a difference as to the number of cases. Keeping
$c_{H1}$
and
$n$
fixed (but see below),
$c_{H0}$
should be negatively correlated with power. Holding
$c_{H0}$
and
$n$
constant,
$c_{H1}$
should be positively correlated with power. More generally, the larger the difference between
$c_{H1}$
and
$c_{H0}$
, the better we are able to distinguish between them empirically and the more often we are able to reject
$H_{0}$
if it is wrong.
In quantitative research, more cases mean higher power because the standard error of the estimate decreases and it becomes easier to empirically distinguish
$H_{0}$
from
$H_{1}$
. In QCA, more cases entail more information, which should contribute to a less widely dispersed distribution of permutation-based consistency values. In contrast to quantitative research, however, this does not necessarily imply that power increases with a growing number of cases. The smaller the number of cases, the more likely it gets that we simulate a dataset for which the permuted consistency values are always close to 1. This happens if all cases in the simulated dataset have membership values in the term that are close to 0. The membership values in the outcome is then likely to be larger than membership in the term and the consistency score is 1. If the membership value in
$X$
is small but not zero, we might assign membership values in
$Y$
that are smaller than in
$X$
and introduce a small degree of inconsistency. However, the small membership in
$X$
puts a cap on the degree to which this case can push the overall consistency value below 1 and it should not matter much (Ragin Reference Ragin2006, 295). For the permuted distribution of consistency values derived from such a dataset, this means it is narrow and located at the upper end of the range of possible values going from 0 to 1. Unless the chosen value of
$c_{H0}$
is very close to 1, we are able to reject the null hypothesis because
$c_{H0}$
falls into the left tail of the permuted distribution.
The more cases we use for simulating data, the less likely it is that they all receive small membership values in the term. Compared to a small-
$n$
setting, the location of the permuted distributed on the range of possible consistency values should be closer to the center of the scale. Because we perform a left-sided test of the consistency value of
$c_{H0}$
, it is therefore possible that we reject
$H_{0}$
if
$n$
is small and fail to reject it if
$n$
is large. This probability should decrease as the difference between
$c_{H1}$
and
$c_{H0}$
increases because an increasing difference makes it more likely that the consistency value of
$c_{H0}$
falls into the left tail of any permuted distribution.
In sum, it follows that the relation between
$n$
and power is conditional on the difference between
$c_{H1}$
and
$c_{H0}$
. For a sufficiently large difference, power should be increasing as the number of cases increases. What a “sufficiently large difference” is cannot be determined here in the abstract and will be reconsidered on the basis of the simulation results.
5 A Simulation Analysis
5.1 Setup and results
The simulations take a comprehensive perspective by evaluating the extent to which power depends on different formulations of
$H_{1}$
,
$H_{0}$
and levels of
$n$
.Footnote
18
This is necessary for evaluating the relationship between the three parameters and power and for offering broad guidance to empirical QCA researchers. I calculate power for consistency values of
$c_{H1}$
and
$c_{H0}$
in the range of 1 to 0.75 and in intervals of 0.05. If
$c_{H1}$
=1, I estimate power for values of
$c_{H0}$
equaling 0.95, 0.9, 0.85, 0.8 and 0.75 as the conventionally minimally acceptable value in a QCA on sufficiency; if
$c_{H1}$
is 0.95,
$c_{H0}$
is fixed at 0.9, 0.85, 0.8 and 0.75; and so on until the last pair of values is
$c_{H1}$
=0.8 and
$c_{H0}$
=0.75.Footnote
19
The numbers of cases is set to 10, 20, 30, 40 and 50.
Each value of
$n$
is combined with each possible combination of
$c_{H1}$
and
$c_{H0}$
, yielding 75 constellations in total. For each combination of
$c_{H1}$
,
$c_{H0}$
and
$n$
, I simulate 1000 datasets in accord with
$H_{1}$
. Each simulated dataset is permuted 10000 times to retrieve the distribution of consistency values for a dataset
$i$
. For each distribution, I calculate the upper bound of the 95% confidence interval of
$p_{H0}$
and test its significance for an
$\unicode[STIX]{x1D6FC}$
of 0.05. The power estimates derived from simulations with the parameter values for
$c_{H1}$
,
$c_{H0}$
and
$n$
are summarized in Figure 2.
Figure 2. Power estimates for five values of
$c_{H1}$
and
$c_{H0}$
.
The estimated levels of power convey that they can reach levels considered high in statistical research. The bar chart in Figure 3 summarizes the simulation results by collapsing the estimates into intervals of 0.1 and counting how many estimates fall within each interval. 15 out of 75 estimates are higher than 0.8, which is conventionally taken as high power (Ellis Reference Ellis2010, ch. 3). Of these 15 estimates, nine fall in the range of 0.9–1 and 6 in the range of 0.8–0.9. This indicates that power can be high in truth table analyses, but the broader view reveals that power is moderate or low for most combinations of the three parameters. Only a total of 27 estimates are above 0.5, meaning that for 48 constellations, the probability of correctly rejecting
$H_{0}$
is a coin flip or less. The category of 0–0.1 is the mode of the distribution of power estimates with a count of 26.
Figure 3. Summary of power estimates.
As a check as to whether 1000 simulations are sufficient to reliably estimate power, Figure 4 presents two plots illustrating how the power estimate develops over the course of the 1000 simulations. The left chart captures the largest possible difference between
$c_{H1}$
and
$c_{H0}$
for an
$n$
of 10. The right panel contains the power estimates for the smallest possible difference between both hypotheses and an
$n$
of 50. Both panels indicate that 1000 simulations clearly suffice for getting a reliable estimate. In both setups, the power estimate stabilizes at around 200 simulations and remains in a narrow range as the number of simulations increases.
The results in Figure 2 corroborate the arguments about the effect of choosing
$c_{H1}$
,
$c_{H0}$
and
$n$
on power. Each of the five panels shows that if we keep
$n$
fixed, power increases with an increasing difference between
$c_{H1}$
and
$c_{H0}$
. The relationship between
$n$
and power is more involved because the results show that the effect of
$n$
is conditional on
$c_{H1}$
and
$c_{H0}$
. For
$c_{H1}=1$
and
$c_{H1}=0.95$
, more cases only yield higher power if the difference between
$c_{H1}$
and
$c_{H0}$
is larger than 0.1. If
$c_{H1}=0.9$
and
$c_{H1}=0.85$
, power is estimated to be higher for a larger number of cases if the difference is more than 0.05. For those parameter constellations for which power gets larger as
$n$
increases, increasing
$n$
from 10 to 50 promises an increase power up to 0.25 to 0.35 points. On the other hand, if the difference between
$c_{H1}$
and
$c_{H0}$
is sufficiently small, power is estimated to be higher for a smaller number of cases with a maximum difference of about 0.15 points (
$c_{H1}=1$
,
$c_{H0}=0.9$
,
$n=10$
vs.
$n=50$
).
Figure 4. Development of power estimate over simulations.
An additional insight is that the power estimates are not similar for the same difference between
$c_{H1}$
and
$c_{H0}$
. For example, for
$n=50$
power is about 0.1 if
$c_{H1}=1$
and
$c_{H0}=0.9$
. In contrast, we get a power estimate of about 0.5 if we fix
$c_{H1}$
at 0.85 and
$c_{H0}$
at 0.75. The conditional relationship between
$n$
and the power estimate requires more scrutiny because it might seem counterintuitive and is different from quantitative research.
5.2 The relationship between n and power estimates
An empirical examination of the link between
$n$
and power estimates requires taking a look at the permuted distributions of consistency values that underlie an individual estimate. Figure 5 contains two panels, each with ten distributions of permutation-based consistency values.Footnote
20
The rugs at the bottom denote the 5%-quantile of a curve.
Figure 5. Consistency value distributions and 5%-quantiles for ten simulations.
The figure conveys three insights. First, the distributions tend to be less smooth with 10 cases than with 50 cases. This is to be expected because the number of possible permutations and consistency values is more restricted with 10 cases than with 50. Second, the distributions are narrower with 50 cases than with 10 cases because more cases imply more information about the distribution under the assumption
$H_{1}$
is correct. Third, with 50 cases, the dispersion of the consistency values of the 5th percentile of each curve are closer to each other than with 10 cases. The range of 5%-quantiles goes from 0.69 to 0.94 for 10 cases and from 0.8 to 0.89 for 50 cases.
Figure 5 highlights that the power estimates in Figure 2 have a very different basis in terms of the permuted distributions. To make the basis transparent and enhance interpretation of power estimates, I report the point estimate together with the underlying distribution of 5%-quantiles. I propose presenting the 5%-quantiles instead of the
$p$
values because the latter can be less insightful. Two permuted distributions can have a different shape and location on the possible range of consistency values, but yield two
$p$
values that are so small that it becomes little insightful to compare them.Footnote
21
This information should also be presented if we were running exact permutation tests because the variability of the quantiles is tied to the number of cases and not to the degree to which a randomized permutation test approaches the exact test (see Supplementary Appendix). Figure 6 contains sina plots for an
$n$
of 10 to 50 in steps of 10 cases, each for five values of
$c_{H1}$
. For orientation, each figure includes two dashed lines representing
$c_{H0}=0.95$
(upper line) and
$c_{H0}=0.8$
(lower line). In visual terms, the share of dots above the line relative to all dots is the estimated level of power.
Figure 6. Distribution of 5%-quantiles for five values of
$c_{H1}$
.
For each value of
$c_{H1}$
, the dispersion of 5%-quantiles decreases as
$n$
increases. The figure demonstrates why this has direct implications for the power estimate and why power can be larger for fewer cases. If
$c_{H1}=1$
and
$n=10$
, the wider distribution of quantiles implies that some are above 0.95, that is, they allow us to reject
$H_{0}$
. The larger
$n$
gets, the narrower the distribution becomes, the fewer quantiles are above the line and the lower the power estimate. In combination with this insight, the lower dashed line demonstrates that the power estimate is conditional on the difference between
$c_{H1}$
and
$c_{H0}$
because power then increases as
$n$
increases. The five panels further show that the location of a distribution on the
$y$
-axis depends on the value of
$c_{H1}$
. The lower the value of
$c_{H1}$
, the more the distribution moves south on the
$y$
-axis. Taken together, this means that the number of cases determines the width of the distribution and the value of
$c_{H1}$
its location on the range of consistency values.
The distribution’s location on the
$y$
-axis is central for understanding why power estimates can differ widely for the same difference between
$c_{H1}$
and
$c_{H0}$
. This can be illustrated with the panels for
$c_{H1}=1$
and
$c_{H1}=0.85$
and values of
$c_{H0}$
that are 0.1 points lower, which are the values that I also discussed in Section 5 in relation with Figure 2. Power is higher if we set
$c_{H1}$
to 0.85 instead of 1 because there is a bigger share of quantiles that is larger than the respective value of
$c_{H0}$
. In simple terms, it means that if we reduce
$c_{H1}$
and
$c_{H0}$
by the same amount, it can happen that the distribution of quantiles moves south on the
$y$
-axis, but less so than
$c_{H0}$
. As a consequence of this asymmetry, the difference between
$c_{H1}$
and
$c_{H0}$
remains constant and the power estimate increases.Footnote
22
For power estimation in empirical research, the bottom line is that the larger the variability of quantiles, the more careful we should be in interpreting the power estimate. If power is estimated to be higher for fewer cases, it is best to consider it an artifact of the low information contained in a small number of cases and, if possible, increase the number of cases to estimate power (see Section 7).
6 Ex post Power Analysis for Empirical QCA Studies
Simulations allow one to determine how power depends on the specification of
$H_{1}$
,
$H_{0}$
and the number of cases, but necessarily remain silent on the power of empirical QCA studies. To get a better idea of how large power is in empirical research, I distill the consistency thresholds for assigning outcome values to truth table rows and the number of cases from 63 truth table analyses published in 2014 and 2015.Footnote
23
No author explicitly devises an alternative hypothesis, which makes it necessary to simulate power for different assumed levels of
$c_{H1}$
. As for the simulations,
$c_{H1}$
is first set at 1 and gradually decreased in intervals of 0.05 as long as
$c_{H1}$
remains larger than the chosen consistency threshold in the truth table analysis.
The ex post estimation of power is confined to the consistency thresholds and does not additionally cover the consistency values of the solution terms. The value of
$c_{H0}$
would be set to 0.75 for all studies because they do not explicitly specify a higher one and the only difference would be the number of cases. Compared to the simulations, the analysis does not promise significant additional insights. This is different for the consistency thresholds because, together with the number of cases, they vary considerably across the empirical studies. Figure 7 summarizes the two parameters for the 63 truth table analyses.
Figure 7. Distribution of parameters for 63 truth table analyses.
The number of cases ranges from a minimum of 8 to a maximum of 123, with a median of 31. The consistency threshold variable has a minimum of 0.7 and a maximum of 1 and has a median number of 0.8. For the maximum value of
$c_{H0}=1$
, it automatically follows that power is 0. A threshold of 0.7, which is specified in two analyses, falls below the conventional minimum of 0.75. As this is only a convention, it is possible to set
$c_{H0}$
at this level and test the associated level of power for different values of
$c_{H1}$
.Footnote
24
Figure 8 summarizes the distribution of power estimates for each level of
$c_{H1}$
. The number of power estimates underlying the distribution decreases with a decreasing level of
$c_{H1}$
because studies that set the consistency threshold higher than the assumed level of
$c_{H1}$
have to be excluded from the estimation procedure. The numbers of estimates are given next to the value of
$c_{H1}$
on the
$x$
-axis and show that they range from 63 for
$c_{H1}=1$
to 14 for
$c_{H1}=0.8$
.
Figure 8. Ex post power estimates for 63 truth table analyses.
The results of the power analysis are mixed if we set
$c_{H1}$
to the most favorable value of 1. The median estimate is 0.81 and meets the value of 0.8 that conventionally denotes high power. For the maximum value of
$c_{H1}$
, this means half of the studies can be said to have sufficient power while the other half does not. The distribution of power estimates is left-skewed and the first quartile is 0.3, meaning the probability of correctly rejecting
$H_{0}$
is one out of three for 19 studies.
If we fix
$c_{H1}$
at 0.95, the third quartile is 0.89, which is high, and there are 17 analyses with a
$p$
value of at least 0.8. The median estimate drops to 0.50 and 30 of 59 studies have an equal probability of correctly or falsely rejecting
$H_{0}$
. The distribution of power estimates is wide and the first quartile is only 0.07, implying that 16 truth table analyses run a high risk of committing a false negative.
For all values of
$c_{H1}$
that are 0.9 or less, the distribution of power estimates becomes right-skewed and the median estimate decreases. It drops to 0.27 for
$c_{H1}=0.9$
and falls below 0.10 if
$c_{H1}$
equals 0.85 and 0.8.Footnote
25
For
$c_{H1}=0.9$
, the third quartile equals 0.68 and falls short of reaching a power level of 0.8. In absolute numbers, 11 studies out of 45 reach the conventional value indicating high power. If
$c_{H1}$
is 0.85, the number of analyses reaching a power estimate of at least 0.8 drops to four out of 36. The third quartile takes a value of 0.49, meaning that 27 studies correctly reject
$H_{0}$
with the probability of a coin flip.
In a broader view, the ex post estimates confirm the simulation results in Section 5 because power decreases with a decreasing value of
$c_{H1}$
. If we take a power of value of 0.8 as the benchmark for high power, the estimates show that empirical studies can reach that level. However, the results are mixed at best because even under the most favorable value of 1 for
$c_{H1}$
, almost half of the analyzed truth table analyses do not reach a value of 0.8.
7 Ex ante Calculation of Power and Required Number of Cases
For empirical researchers planning a truth table analysis, the benefit of considering power before the analysis is that they can estimate how many cases are needed to reach a desired level of power, given the preferred alternative and null hypothesis. In principle, this can only be done if one has the opportunity to collect more cases. If this is possible, estimating the required level of
$n$
needs the parameters
$c_{H1}$
,
$c_{H0}$
,
$\unicode[STIX]{x1D6FC}$
as input and the required level of power as the target parameter. Because it is simulation-based, calculating
$n$
has to take an iterative approach by starting with the best guess as to how many cases are needed and running the simulations. Based on a comparison of the estimated power and the target level,
$n$
has to be adjusted and the simulation run again until the desired degree of power is reached.Footnote
26
If one is not able to add cases, either because the entire population is already covered or because this is not feasible due to resource constraints or for other reasons (Ragin Reference Ragin2000, chaps. 2, 7), one should use the parameters
$c_{H1}$
,
$c_{H0}$
and
$n$
to estimate power and derive the probability of making the right decision.
For five different combinations of
$c_{H1}$
and
$c_{H0}$
and an
$\unicode[STIX]{x1D6FC}$
of 0.05, Table 1 exemplifies how many cases one needs to achieve a power level of 0.7, 0.8 and 0.9.Footnote
27
The case numbers do not exactly yield the desired level of power, but come sufficiently close.Footnote
28
Depending on the alternative and null hypothesis and the desired level of power, the required number of cases can be relatively small with 10 cases, but can also go up to 9000 cases if the difference between
$c_{H1}$
and
$c_{H0}$
is small and the required power level large.Footnote
29
For each parameter combination, one can further see that an increase in the target level of power by 0.1 points leads to a disproportionate increase in the required number of cases. Compared to an increase of power from 0.7 to 0.8, lifting the desired level from 0.8 to 0.9 entails an increase in
$n$
by a factor of 1.3 (
$c_{H1}=0.8$
,
$c_{H0}=0.75$
) to about 2 (
$c_{H1}=0.95$
,
$c_{H0}=0.8$
).
Table 1. Cases required for achieving different power levels.
Although it depends on the research question and data at hand, it seems safe to argue that thousands of cases are not available for a truth table analysis in most QCA studies. In particular, the number of cases is limited in macro research with countries or regions as the spatial unit of analysis, which traditionally has been and remains the main type of data subject to a truth table analysis (Marx, Rihoux and Ragin Reference Marx, Rihoux and Ragin2014). In such a situation, calculating the required number of cases is still valuable because it makes transparent how many cases we are lacking to achieve the desired level of power.
8 Power Estimation for Crisp-set QCA and Multivalue QCA
Crisp-set QCA (csQCA) and multivalue QCA (mvQCA) involve sets that only establish qualitative differences between cases (Schneider and Wagemann Reference Schneider and Wagemann2012, ch. 1). In principle, this feature of sets in csQCA and mvQCA allows us using the binomial distribution for calculating
$p$
values (Ragin Reference Ragin2000, chaps. 4, 5; Braumoeller Reference Braumoeller2015, 484–485). However, this implies the assumption that the cases at hand were randomly sampled from a population. This assumption is often not met because the cases were not selected randomly, or the cases constitute the population, or because the population cannot be easily demarcated (Ragin Reference Ragin2000, chaps. 2, 7; Athey and Imbens Reference Athey and Imbens2016, 7–8).
Permutation tests do not require the assumption of random sampling from a population and allow one to estimate
$p$
values without invoking the binomial distribution for csQCA and mvQCA. In randomization inference, the rationale for calculating
$p$
values is our uncertainty about the unobserved, potential outcomes of each case (Abadie et al.
Reference Abadie, Athey, Imbens and Wooldridge2014, 1). This source of uncertainty is different from the uncertainty that underlies the analytical calculation of
$p$
values because it follows from random sampling from a population. Formally seen, randomization analysis is not simply the resampling-based equivalent to the analytical calculation of
$p$
values, but has a different rationale for deriving the
$p$
value for a quantity of interest. Because the random-sampling assumption can be infeasible or problematic in csQCA and mvQCA, permutation-based power analysis can also be done for these two variants.Footnote
30
A crucial difference between fsQCA and the two other variants lies in the number of cases that enter into the power analysis and the implications for ex ante power estimation. For fsQCA,
$n$
equals the total number of cases because all cases feed into the consistency score of each truth table row and term of a solution. In csQCA and mvQCA,
$n$
equals the number of cases that are members of the row or term under scrutiny because only these cases affect the consistency value (see Schneider and Wagemann Reference Schneider and Wagemann2012, Section 5.2). This makes it impossible to calculate power ex ante as described in Section 7. We can only estimate power for the assignment of outcome values to truth table rows after we have determined how many members the truth table row in question has. Similarly, we can only estimate power for terms in a QCA solution after we have produced the solution and know how many cases are members of a term.
If one wants to estimate power ex ante in csQCA or mvQCA without running a truth table analysis, the only feasible route is to assume how many cases might fall in a truth table row. For the assignment of outcome values to truth table rows, the upper limit is the total number of members in the analysis and the lower limit is 1. It is possible that all cases fall in one truth table row, but it is more reasonable to assume a lower number than the total number of all cases. However, this cannot be more than an informed guess that might be far from the actual number of members in a row.
A similar protocol can be followed for terms in the QCA solution. The upper bound of members of a term equals the number of cases across all consistent truth table rows entering the minimization procedure. The lower bound is the minimum number of cases in a consistent truth table row. This shows that power analysis is possible with csQCA and mvQCA, but that ex ante power estimation differs from fsQCA because of uncertainty about the size of
$n$
feeding into power estimate.
9 Conclusion
QCA is often used for testing hypotheses and the consistency value plays a central role in this regard. Thus far, the consistency score is taken at face value and there is little reflection on whether the value is the product of a systematic or a non-systematic process. Building on recent work in false-positive testing (Braumoeller Reference Braumoeller2015), I introduce the idea of power analysis for the analysis of truth tables. I argue that it is meaningful to specify an alternative and a null hypothesis in QCA and use them for permutation-based power analysis. Power increases with an increasing difference between the consistency values of the null and alternative hypotheses. Except for specific constellations between the values of both hypotheses, power also increases with an increasing number of cases. The consequences of low power in QCA are important because it implies a high probability of designating a term as inconsistent with a set-relational claim that should be considered consistent. For the QCA solution as the result of a truth table analysis, this translates into a high probability of deriving a wrong model that is, however, a subset of the true model.
Ex post power analyses of published truth table analyses indicate that empirical research can reach high levels of power when assigning outcome values to truth table rows. Even in the most favorable setting, however, the picture is mixed because about half of 63 truth table analyses fail to reach 0.8 as the value conventionally denoting high power. Future empirical studies should estimate power ex ante and, whenever possible, select the appropriate number of cases achieving the desired level of power.
In combination with false-positive testing, power estimation and false-negative testing can add to the rigor of empirical QCA research. From a broader perspective, the discussion of power and false negatives on the one hand, and false positives (Braumoeller Reference Braumoeller2015) on the other points to a trade off when assigning outcome values to truth table rows. Avoiding a false positive is more likely if the consistency threshold is high because we hope for a consistency value of a term that is in the right tail of the permuted distribution of consistency scores (Braumoeller Reference Braumoeller2015, 479–482). At the same time, a high threshold makes it more likely to commit a false negative because of a small difference between the consistency values stipulated by the alternative hypothesis and null hypothesis. Although it is possible that a study suffers from neither a false positive nor a false negative, QCA researchers should determine the probabilities of both types of error and carefully weigh their consequences in the context of their research question and empirical analysis.
Funding
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement nr. 638425).
Acknowledgements
I am grateful to Bear Braumoeller for comments on an earlier version of the paper and the constructive comments of two reviewers. Holger Döring was of tremendous help in programming the simulations. Charlotte Brommer-Wierig, Lion Behrens, Nancy Deyo, Sven Hillen and Jonathan Klatt provided valuable research assistance. The reproduction material is available on Dataverse (Rohlfing Reference Rohlfing2017).
Supplementary Materials
For supplementary materials accompanying this paper, please visit https://doi.org/10.1017/pan.2017.30.
