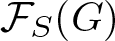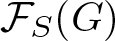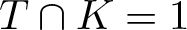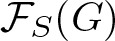1. Introduction
In recent years, the study of fusion category and fusion system theory has become a meaningful direction in finite group theory. Plenty of findings exist regarding nilpotent fusion systems, as well as several established conclusions concerning saturated fusion systems, as documented in [Reference Cantarero, Scherer and Viruel5, Reference Diaz, Glesser, Mazza and Park7, Reference Kessar and Linckelmann10] and [Reference Liao and Liu11]. Lluis Puig was the first to introduce the concept of a saturated fusion system, which has been continuously studied by a cohort of scholars. They obtained the following important results, which will provide a train of thought for the proof in this article. Given a finite group G and a p-subgroup 
$S \leqslant G,$ 
$\mathcal{F}_{S}(G)$ is used to represent the fusion category of G on 
$S:$ the objects of 
$\mathcal{F}_{S}(G)$ are all subgroups of S and morphisms in 
$\mathcal{F}_{S}(G)$ are the group homomorphisms between subgroups of S induced by conjugation in G. A fusion system over S is a category 
$\mathcal{F}$ whose objects are all subgroups of S and whose morphisms behave as though they are induced by conjugation inside a group including S as a p-subgroup. In [Reference Aschbacher, Kessar and Oliver2], it was shown that for a p-group P and 
$\mathcal{F},$ 
$\mathcal{F}$ is solvable when there is a series of strongly 
$\mathcal{F}$-closed subgroups 
$1=P_0 \leqslant P_1 \leqslant P_2 \leqslant \cdots \leqslant P_n=P$ and with 
$P_{i+1} / P_i$ abelian for 
$0 \leqslant i \leqslant n$. A saturated fusion system 
$\mathcal{F}$ over a p-group P is nilpotent (
$\mathcal{F}=\mathcal{F}_{P}(P)$) if and only if 
$Aut_{\mathcal{F}}(S)$ is a p-group for each subgroup S of P. In [Reference Kessar and Linckelmann10], Linckelmann and Kessar generalized the p-nilpotent theorem to fusion systems, demonstrating that 
$\mathcal{F}=\mathcal{F}_{P}(P)$ if and only if 
$N_{\mathcal{F}}(Z(J(P)))=\mathcal{F}_{P}(P)$. Shen and Zhang in [Reference Shen and Zhang14] investigated the p-supersolvable fusion systems. They gave the p-supersolvability of normal subsystems and they proved that the models of p-supersolvable fusion systems are p-supersolvable groups. Shen also provided a criterion for a saturated fusion system 
$\mathcal{F}$ to be nilpotent in [Reference Shen13]. The article draws on information from reference [Reference Aschbacher, Kessar and Oliver2] for a more complete description of fusion systems, and any unfamiliar terminology or symbols can be found in that book. Additionally, Gorenstein [Reference Gorenstein9] provides explanations of certain definitions that may be unfamiliar to readers and only finite groups will be considered.
Enlightened by current advances in the research of normality of subgroups, in [Reference Ru, Zhang and Shen12], Ru and Shen consider the influence of the normality of some subgroups of S on the supersolvability of 
$\mathcal{F}_{S}(G)$. Theorems 1.1 and 1.2 are cases in point. Following this line of thought, we contrive to combine the normality of subgroups and complement subgroups and we find a few conditions that make the supersolvability of 
$\mathcal{F}_{S}(G)$ hold.
Theorem 1.1. [Reference Ru, Zhang and Shen12]
Let G be a finite group and 
$S \leqslant G$ be a Sylow p-subgroup where p is a prime. If all subgroups of S of order p or 4 
$(p=2)$ are normal in G. Then 
$\mathcal{F}_{S}(G)$ is supersolvable.
Theorem 1.2. [Reference Ru, Zhang and Shen12]
Let G be a finite group and 
$S \leqslant G$ is a Sylow p-subgroup where p is an odd prime. Suppose there is a subgroup U < S with 
$1 \lt |U| \lt |S|$ and any subgroup of S with order 
$|U|$ is normal in G. Then 
$\mathcal{F}_{S}(G)$ is supersolvable.
In this article, our target is to explore how do normal subgroups or normal complement subgroups affect the supersolvability of 
$\mathcal{F}_{S}(G)$. Our main theorems are as follows. Firstly, we start with the subgroups of order p case.
Theorem A.
Suppose G is finite and 
$S \leqslant G$ is a Sylow p-subgroup where p is an odd prime. If all subgroups of S with order p are normal in G or have normal complement in G. Then 
$\mathcal{F}_{S}(G)$ is supersolvable.
Next we consider the maximal subgroup case.
Theorem B.
Let G be a finite group and 
$S \leqslant G$ be a Sylow p-subgroup where p is an odd prime. If all maximal subgroups of S are normal in G or have normal complement in G. Then 
$\mathcal{F}_{S}(G)$ is supersolvable.
Theorems A and B indicate that 
$\mathcal{F}_{S}(G)$ is supersolvable. Nevertheless, G may not be p-supersolvable. See the following example.
Example. Set 
$G=A_{5}$ and 
$S \in Syl_{5}(G)$. We have S is isomorphic to C 5. Then all maximal subgroups of S are normal in G or have normal complement in 
$G,$ but G is not 5-supersolvable.
In the end, we discuss a general case.
Theorem C.
Suppose G is a group and 
$S \in Syl_{p}(G)$ where p is an odd prime dividing 
$|G|$. Assume S has a subgroup U satisfying 
$1 \lt |U| \lt |S|$ and any subgroup of S with order 
$|U|$ or 
$p|U|$ is normal in G or has normal complement in G. Then 
$\mathcal{F}_{S}(G)$ is supersolvable.
2. Preliminaries
In this section, we provide a plethora of lemmas that we will need later. 
$Z_\mathcal{{U}}(G)$ represents the greatest normal subgroup of G whose G-chief factors are cyclic. As a special case of complement subgroups, the next lemma is clear.
Lemma 2.1. [Reference Bray and Weinstein4]
Suppose G is finite and 
$N \unicode{x2AA8} G$. Then 
$N / \Phi(N) \leqslant Z_\mathcal{{U}}(G / \Phi(N))$ if and only if 
$N \leqslant Z_\mathcal{{U}}(G)$.
Lemma 2.2. Suppose G is finite and 
$H \unicode{x2AA8} G$.
(1) If M has normal complement in G and 
$M \leqslant N \leqslant G,$ then M has normal complement in N.
(2) If M has normal complement in G and M contains 
$H,$ then 
$M/H$ has normal complement in 
$G/H$.
Based on [Reference Asaad1, Lemma 3.7], we obtain the following lemma.
Lemma 2.3. Let S be a normal p-subgroup of G. Suppose there exists a subgroup U of S with 
$1 \lt |U| \lt |S|$. If all subgroups of S of order 
$|U|$ and 
$p|U|$ have normal complement in 
$G,$ then 
$S \leqslant Z_\mathcal{{U}}(G)$.
Lemma 2.4. Let S be a normal p-subgroup of G where p is an odd prime. If all subgroups of S with order p are normal in G or have normal complement in 
$G,$ then 
$S \leqslant Z_\mathcal{{U}}(G)$.
Proof. We use the induction method on 
$|G|+|S|$ to solve this statement. If all minimal subgroups of S are normal in 
$G,$ then 
$\Omega_{1}(S) \unicode{x2AA8} G$ and all chief factors of G that lie below 
$\Omega_{1}(S)$ are cyclic with order p. This means 
$\Omega_{1}(S)\leqslant Z_\mathcal{{U}}(G)$. The lemma holds if 
$S=\Omega_{1}(S)$. So let 
$\Omega_{1}(S) \lt S$. Pick 
$a \in S$ such that 
$o(a)=p^{2}$ and g be any element in G. Then 
$\langle a^{p} \rangle \unicode{x2AA8} G$ and 
$(a^{g})^{p}=(a^{p})^{g}=a^{pi}=(a^{i})^{p}$ for some integer i. Thus we have 
$(a^{g}(a^{i})^{-1})^{p}=1,$ which indicate 
$a^{g}(a^{i})^{-1} \in \Omega_{1}(S)$. Then 
$a^{g}=a^{i}y$ where 
$y \in \Omega_{1}(S)$. Now all minimal subgroups of 
$S/\Omega_{1}(S)$ are normal in 
$G/\Omega_{1}(S)$ and so 
$S/\Omega_{1}(S) \leqslant Z_\mathcal{{U}}(G/\Omega_{1}(S))$ by induction on 
$|G|+|S|$. If follows from 
$\Omega_{1}(S)\leqslant Z_\mathcal{{U}}(G)$ that 
$S/\Omega_{1}(S) \leqslant Z_\mathcal{{U}}(G)/\Omega_{1}(S)$. Hence 
$S \leqslant Z_\mathcal{{U}}(G)$. Therefore, there exists a subgroup H of S with order p such that 
$H \not \unicode{x2AA8} G$ and H has normal complement in G. Then there is a normal subgroup L of G such that G = HL and 
$H \cap L=1$. Note that 
$S=G \cap S=HL \cap S=H(L \cap S)$ and 
$L \cap S \unicode{x2AA8} G$. So all minimal subgroups of 
$L \cap S$ are normal in G or have normal complement in 
$G,$ which means 
$L \cap S \leqslant Z_\mathcal{{U}}(G)$ by our induction. Furthermore, since 
$S/L \cap S \unicode{x2AA8} G/L \cap S$ and 
$|S/L \cap S|=p,$ we have 
$S/L \cap S \leqslant Z_\mathcal{{U}}(G/L \cap S)$. If follows from 
$Z_\mathcal{{U}}(G/L \cap S)=Z_\mathcal{{U}}(G)/(L \cap S)$ that 
$S \leqslant Z_\mathcal{{U}}(G)$.
Lemma 2.5. [Reference Aseeri and Kaspczyk3]
Suppose G is finite and 
$S \leqslant G$ is a Sylow p-subgroup. Assume for any proper subgroup K < G satisfying 
$S \cap K \in Syl_{p}(K)$ and 
$O_p(G) \lt S \cap K,$ 
$\mathcal{F}_{S\cap K}(K)$ is supersolvable. If 
$O_p(G) \leqslant Z_\mathcal{{U}}(G),$ 
$\mathcal{F}_{S}(G)$ is supersolvable.
Lemma 2.6. [Reference Doerk and Hawkes8]
Let 
$R,$ S and T be subgroups of 
$G,$ then the following statements are equivalent:
(1) 
$R \cap ST=(R \cap S)(R \cap T)$.
(2) 
$RS \cap RT=R(S \cap T)$.
Lemma 2.7. See [Reference Shen and Zhang14]
Let 
$\mathcal{F}$ be a p-supersolvable fusion system on a p-group. Suppose 
$\mathcal{F}_{1}$ is a normal subsystem of 
$\mathcal{F}$. Then 
$\mathcal{F}_{1}$ is p-supersolvable.
Now with these lemmas in the hand, we are able to offer the proof of our main theorems, showing the supersolvability of 
$\mathcal{F}_{S}(G)$.
3. Main results
3.1. Proof of Theorem A
Proof. If the theorem is false, we consider a counterexample 
$\mathcal{F}=\mathcal{F}_{S}(G)$ for which 
$|G|$ is smallest. If any subgroup of 
$O_p(G)$ with order p is normal in G or has normal complement in 
$G,$ by Lemma 2.4, 
$O_p(G) \leqslant Z_\mathcal{{U}}(G)$. Next choose L < G with 
$S \cap L \in Syl_{p}(L)$. Then the subgroups in 
$S \cap L$ with order p are normal G or have normal complement in G. Applying Lemma 2.2, these subgroups are normal in L or have normal complement in L. Then 
$\mathcal{F}_{S\cap L}(L)$ is supersolvable due to the minimality of 
$\mathcal{F}$. Now if L < G with 
$S \cap L \in Syl_{p}(L)$ and 
$O_p(G) \lt S \cap L,$ we have 
$\mathcal{F}_{S\cap L}(L)$ is supersolvable. Using Lemma 2.5, 
$\mathcal{F}_{S}(G)$ is supersolvable.
3.2. Proof of Theorem B
Proof. Assume the theorem is wrong and let 
$\mathcal{F}=\mathcal{F}_{S}(G)$ be a counterexample for which 
$|G|$ is smallest.
Step 1. 
$O_{p'}(G)=1$.
Set 
$Q=O_{p'}(G)$. If 
$Q \neq 1,$ then 
$SQ/Q \in Syl_{p}(G/Q)$. Set 
$M/Q$ as a maximal subgroup of 
$SQ/Q$. Then we have a maximal subgroup S 1 of S with 
$M=S_{1}Q$. If S 1 has a normal complement in 
$G,$ by Lemma 2.2, 
$M/Q=S_{1}Q/Q$ has a normal complement in 
$G/Q$. If 
$S_{1} \unicode{x2AA8} G,$ 
$S_{1}Q/Q \unicode{x2AA8} G/Q$. In both cases, the minimality of 
$\mathcal{F}$ shows that 
$\mathcal{F}_{SQ/Q}(G/Q)$ is supersolvable and hence 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction.
Step 2. Let N be a minimal normal subgroup, then 
$\mathcal{F}_{SN/N}(G/N)$ is supersolvable.
Choose 
$M/N$ as a maximal subgroup of 
$SN/N$. So we can find a maximal subgroup S 1 of S with 
$M=NS_{1}$ and 
$S \cap N=S_{1} \cap N \in Syl_{p}(N)$. If S 1 has normal complement in 
$G,$ there is a normal subgroup T of G satisfying 
$G=S_{1}T$ and 
$T \cap S_{1}=1$. Note that 
$G/N=(S_{1}N/N)(TN/N)$. Since 
$(|N:S_{1} \cap N|,|N:T \cap N|)=1,$ we have 
$(S_{1} \cap N)(T \cap N)=N=G \cap N=S_{1}T \cap N$. Therefore 
$TN \cap NS_{1}=(S_{1} \cap T)N$ by Lemma 2.6. So 
$(S_{1}N/N) \cap (TN/N)=(NS_{1} \cap NT)/N=(S_{1} \cap T)N/N=1$. Then 
$M/N$ has normal complement in 
$G/N$. If 
$S_{1} \unicode{x2AA8} G,$ then 
$M=NS_{1}$ is also normal in 
$G,$ which means 
$M/N \unicode{x2AA8} G/N$. Therefore, the assumption in the theorem is valid for 
$(G/N, S/N)$. The minimal choice of 
$\mathcal{F}$ shows 
$\mathcal{F}_{SN/N}(G/N)$ is supersolvable.
Step 3. The minimal normal subgroup N of G is unique.
If not, assume that there is a minimal normal subgroup N 1 with 
$N \neq N_{1}$. Then Step 2 tells us that 
$\mathcal{F}_{SN/N}(G/N)$ and 
$\mathcal{F}_{SN_{1}/N_{1}}(G/N_{1})$ are both supersolvable. Thus we conclude from the fact 
$N_1 \cap N_2 =1$ and [Reference Zhang and Shen15, Theorem 3.2] that 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction.
Step 4. 
$N \nleq \Phi(S)$.
If all of the maximal subgroups of S are normal in G, then all of them are normal in 
$\mathcal{F}_S (G)$. Therefore, we obtain from Theorem 1.2 that 
$\mathcal{F}_S (G)$ is supersolvable, which is impossible. Therefore, there exists some maximal subgroup S 1 of S which is not normal in G. This implies that S 1 has a normal complement K of G. Obviously K must contain N by the uniqueness of N, so that 
$S_1 \cap N = 1$. Hence 
$N \nleq \Phi(S),$ as required.
Step 5. 
$1 \lt N \cap S \lt S$.
If 
$N \cap S=S,$ then 
$S \leqslant N,$ contradicting to the minimality of N. Since p divides 
$|N|$ by Step 1, 
$N \cap S \neq 1$.
Step 6. 
$O_{p}(\mathcal{F})=1$.
If not, then 
$N \leqslant O_{p}(\mathcal{F})$. In view of Step 4, we choose a maximal subgroup S 0 of S with 
$S=NS_{0}$. If 
$S_{0} \unicode{x2AA8} G,$ then 
$N \cap S_{0} \unicode{x2AA8} G$. By the minimal choice of 
$N,$ 
$N \cap S_{0}=N$ or 
$N \cap S_{0}=1$. If 
$N \cap S_{0}=N,$ then 
$N \leqslant S_{0},$ a contradiction. Thus 
$N \cap S_{0}=1,$ which indicates that 
$|N|=p$. If follows from Step 2 that 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction. If S 0 has normal complement in G. Then there is a normal subgroup K of G such that 
$G=S_{0}K$ and 
$S_{0} \cap K=1$. By the uniqueness of 
$N,$ we have 
$N \leqslant K$ and 
$|K_{p}|=p,$ which indicates 
$|N|=p$. Then by Step 2, we have 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction.
Step 7. Final contradiction.
By Step 5, there exists a maximal subgroup S 1 of S such that 
$N \cap S \leqslant S_{1}$. By assumption, if 
$S_{1} \unicode{x2AA8} G,$ then 
$S_{1} \cap N \unicode{x2AA8} G$. By the choice of 
$N,$ 
$S_{1} \cap N =N$ or 
$S_{1} \cap N =1$. If 
$S_{1} \cap N =1,$ then 
$|N|=p$ and hence 
$\mathcal{F}_{S}(G)$ is supersolvable. If 
$S_{1} \cap N =N,$ 
$N \leqslant S_{1}$. So N is a normal p-subgroup of G and 
$N \leqslant O_{p}(\mathcal{F})=1$ by Step 6, a contradiction. If S 1 has normal complement in 
$G,$ then there is a normal subgroup L of G such that 
$G=S_{1}L$ and 
$S_{1} \cap L=1$. Notice that 
$N \cap L \unicode{x2AA8} G$ and hence 
$N \cap L=1$ or 
$N \cap L=N$. If 
$N \cap L=N,$ then 
$N \leqslant L$. So 
$N \cap S \leqslant L \cap S_{1}=1$. This indicates N is a p ʹ-group, contrary to Step 1. If 
$N \cap L=1,$ then 
$N \leqslant O_{p}(\mathcal{F})$. This is contrary to Step 6, asserting 
$O_{p}(\mathcal{F})=1$. The contradiction ends the proof.
3.3. Proof of Theorem C
Proof. Assume the result is false and set 
$\mathcal{F}=\mathcal{F}_{S}(G)$ be a minimal counterexample for which 
$|G|$ is the smallest.
Step 1. 
$O_{p'}(G)=1$.
If 
$O_{p'}(G) \neq 1,$ then 
$SO_{p'}(G)/O_{p'}(G) \in Syl_{p}(G/O_{p'}(G))$. So 
$SO_{p'}(G)/O_{p'}(G)$ and 
$G/O_{p'}(G)$ satisfy the assumption in the theorem. By the minimal choice of 
$\mathcal{F},$ 
$\mathcal{F}_{SO_{p'}(G)/O_{p'}(G)}(G/O_{p'}(G))$ is supersolvable. Therefore we conclude from [Reference Craven6, Theorem 5.20] that 
$\mathcal{F}_{SO_{p'}(G)/O_{p'}(G)}(G/O_{p'}(G))$ is isomorphic to 
$\mathcal{F}_S (G) / (O_{p'} (G) \cap S) = \mathcal{F}_S (G)$ by the fact that 
$ O_{p'} (G) \cap S=1$, which implies that 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction.
Step 2. 
$p \lt |U|$.
If 
$|U| \leqslant p,$ then all subgroups of S with order p are normal in G or have normal complement in G. So we have that 
$\mathcal{F}_{S}(G)$ is supersolvable in view of Theorem A, which is a contradiction. So 
$p \lt |U|$.
Step 3. 
$p|U| \lt |S|$.
By assumption in the theorem, 
$|S| \geq p|U|$. If 
$|S|=p|U|,$ then all maximal subgroups of S are normal in G or have normal complement in G. Then by Theorem B, 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction.
Step 4. Let 
$N \leqslant S$ be a minimal normal subgroup of G. Then N < S.
Since 
$O_{p'}(\mathcal{F})=1$ and 
$S \cap O^{p}(G) \in Syl_{p}(O^{p}(G)),$ we have 
$S \cap O^{p}(G) \neq 1$. If any subgroup of S with order 
$|U|$ is normal in 
$G,$ then 
$\mathcal{F}_{S}(G)$ is supersolvable by Theorem 1.2, a contradiction. So there exists a subgroup R of S with order 
$|U|$ satisfying 
$R \not \unicode{x2AA8} G$. Then R has normal complement in G. There is a normal subgroup K of G such that G = RK and 
$G/K$ is a p-group. By the properties of p-groups, there exists a maximal subgroup M of G such that 
$K \leqslant M \unicode{x2AA8} G$ and 
$|G/M|=p$. Since 
$|U| \lt |M|$ and 
$O^{p}(G) \leqslant M,$ 
$\mathcal{F}_{S \cap O^{p}(G)}(O^{p}(G))$ is supersolvable. We obtain 
$S \cap O^{p}(G) \unicode{x2AA8} G$ by 
$S \cap O^{p}(G)$ char 
$O^{p}(G) \unicode{x2AA8} G$.
If 
$N=S,$ then Step 3 shows 
$|S|=|N| \gt p|U|$. Choose T < N with order 
$|U|$. By assumption, if 
$T \unicode{x2AA8} G,$ then T = 1 by the minimality of 
$N,$ a contradiction. Thus T has normal complement in G. So there exists a normal subgroup K of G satisfying G = TK and 
$T \cap K=1$. Note that G = NK and 
$N \cap K$ is also normal in G. If 
$N \cap K =N,$ then 
$N \leqslant K$. This shows that 
$G=NK=K,$ a contradiction. If 
$N \cap K=1,$ then 
$T=N,$ a contradiction. So Step 4 holds.
Step 5. 
$|U| \gt |N|$ for an arbitrary minimal normal subgroup N of G contained in 
$S \cap O^{p}(G)$.
Suppose 
$p \lt |U| \lt |N|$. Since 
$N \lt S,$ then N and G meet the assumption in Lemma 2.3, so we have 
$N \leqslant Z_{\mathcal{U}}(G)$. Therefore 
$|N|=p \geq p|U|,$ which indicates that 
$|U|=1$. This contradicts Step 2.
Suppose 
$|U|=|N|$. So the assumption in Theorem A is valid for 
$(G/N, S/N)$ by Lemma 2.2. Then 
$\mathcal{F}_{S/N}(G/N)$ is supersolvable. Pick 
$R/N$ as a minimal normal subgroup of 
$S/N$ and then 
$|R/N|=p$. We denote 
$R=N\langle a \rangle,$ where 
$ a \not \in N$ and 
$a^{p} \in N$. If 
$N=\Phi(R),$ 
$R=\langle a \rangle$ is cyclic and so N is cyclic. This means 
$|N|=p$ and so 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction. Then 
$N \gt \Phi(R)$. Since 
$\Phi(R)$ char 
$R \unicode{x2AA8} S,$ 
$\Phi(R) \unicode{x2AA8} S$. We choose N 1 as a maximal subgroup of N such that 
$\Phi(R) \leqslant N$ and 
$N_{1} \unicode{x2AA8} S$. Write 
$H=N_{1}\langle a \rangle$. It follows from 
$a^{p} \in \Phi(R) \leqslant N_{1}$ that 
$|N|=|H|=|U|$. If 
$H \unicode{x2AA8} G,$ by the minimality of 
$N,$ 
$H=1,$ a contradiction. Therefore, H has normal complement in G. There is a normal subgroup T of G such that G = HT and 
$H \cap T=1$. Since 
$N \leqslant O^{p}(G) \leqslant T,$ 
$N_{1}=H \cap N \leqslant H \cap O^{p}(G) \leqslant H \cap T=1$. This means N is of order p and so 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction.
Step 6. Complete the proof.
Since 
$|U| \gt |N|,$ by Lemma 2.2, 
$S/N$ and 
$G/N$ satisfy the assumption in this theorem and so 
$\mathcal{F}_{S/N}(G/N)$ is supersolvable, by the minimal choice of 
$\mathcal{F}$. Note that 
$N \nleq \Phi(G)$. We choose a maximal subgroup V of G such that G = NV. In addition, 
$S=N(S \cap V)$ and 
$S \cap V \neq 1$. We pick S 1 as a maximal subgroup of S containing 
$S \cap V$. So 
$S=NS_{1}$ and 
$N \cap S_{1} \lt N$. If 
$N \cap S_{1}=1,$ then 
$|N|$ is a prime and hence 
$\mathcal{F}_{S}(G)$ is supersolvable, a contradiction. Then 
$N \cap S_{1} \neq 1$. We select a subgroup E of S 1 containing 
$N \cap S_{1}$ satisfying 
$|E|=|U|$ and 
$E \unicode{x2AA8} S$. Then 
$N \cap E=N \cap S_{1} \neq 1$. By assumption, if E is normal in 
$G,$ then 
$N \cap E \unicode{x2AA8} G$. Since 
$N \cap E=N \cap S_{1} \lt N,$ by the minimality of 
$N,$ 
$N \cap E=1,$ a contradiction. If E has normal complement in 
$G,$ then there is a normal subgroup F of G such that G = EF and 
$E \cap F=1$. Now 
$N \cap E \leqslant O^{p}(G) \cap E \leqslant F \cap E=1$ and thus 
$N \cap E=1$. This is a contradiction.
Data availability statement
The authors declare that data supporting the findings of this study are available within the article.
Acknowledgements
The authors are very grateful to the referee for providing detailed reports, correcting the grammatical errors and for improving the results presented in the paper considerably.
Competing interests
We declare that we have no competing interests.
