Introduction
In recent years, there has been a rapid increase in the study of whistler waves. Having been discovered more than a century ago (Preece, Reference Preece1894), these waves are still a subject of intense interest. Whistler (also known as helicon in solid-state plasma) is one of the most important electromagnetic waves in plasma, being circularly polarized guided along external magnetic field in the dense plasma. Whistler waves are observed in outer Earth's radiation belt, Earth's magnetopause (Stenberg et al., Reference Stenberg, Oscarsson, Andr, Vaivads, Backrud-Ivgren, Khotyaintsev, Rosenqvist, Sahraoui, Cornilleau-Wehrlin, Fazakerley, Ludin and Decreau2007), beam-plasma systems (Volokitin et al., Reference Volokitin, Krafft and Matthieussent1995; Starodubstev et al., Reference Starodubstev, Krafft, Thevenet and Kostrov1999) immersed in external magnetic field and in several laboratory experiments (Stenzel, Reference Stenzel1975, Reference Stenzel1976; Compernolle et al., Reference Compernolle, Bortnik, Pribyl, Gekelman, Nakamoto, Tao and Thorne2014, Reference Compernolle, An, Bortnik, Thorne, Pribyl and Gekelman2015). These waves are excited essentially in plasma by collective electron oscillations in the presence of an external or self-consistent large-scale magnetic field. The nonlinear dynamics of whistler wave in magnetized plasma has been investigated (Baker & Hall, Reference Baker and Hall1974; Sharma and Tripathi, Reference Sharma and Tripathi1993; Martino et al., Reference Martino, Falanga and Tzenov2005; Streltsov et al., Reference Streltsov, Lampe, Manheimer, Ganguli and Joyce2006; Karavaev et al., Reference Karavaev, Gumerov, Papadopoulos, Shao, Sharma, Gekelman, Gigliotti, Pribyl and Vincena2010; Gupta et al., Reference Gupta, Prakash, Sharma and Vijayshri2015).
The study of electromagnetic wave–plasma interaction is an active area of research in the context of harmonic generation. Over the last few years, the generation of harmonics of electromagnetic radiation in plasma has been a subject of extensive study (Krenz and kino, Reference Krenz and Kino1965; Tamaki, Reference Tamaki1999; Banerjee, Reference Banerjee2002; Mihailescu et al., Reference Mihailescu, Stancalie and Pais2014; Tang et al., Reference Tang, Kumar and Keitel2017) because of wide range of applications. Harmonics provide valuable diagnostics for plasma parameters such as local electron density, electrical conductivity, and can also be used to detect the presence of large electric and magnetic fields and plasma waves. Plasma is an attractive medium for harmonic generation which can convert the fundamental frequency of whistler into linear and nonlinear harmonics. Nonlinear even harmonic especially second harmonic generation (SHG) has its unique place as it converts the fundamental frequency of whistler into twice that is, ω2 = 2ω0. In the case of second harmonic, the main mechanism is the presence of density gradient produced by electron plasma wave excited by propagation of whistler pulse. Even harmonic generation in plasma has been studied both experimentally and theoretically by many authors (Malka et al., Reference Malka, Modena, Najmudin, Dangor, Clayton, Marsh, Joshi, Danson, Neely and Walsh1997; Agarwal et al., Reference Agarwal, Pandey and Sharma2001; Kant and Sharma, Reference Kant and Sharma2004; Kaur et al., Reference Kaur, Sharma and Salih2009; Aggarwal et al., Reference Aggarwal, Vij and Kant2015; Iwai et al., Reference Iwai, Nakamura, Bambina and Sakai2015).
In high-density plasma, where the de-Broglie wavelength of particles is of the order of or greater than the interparticle distance, the study of quantum effects becomes important. When the temperature of such plasma is less than the Fermi temperature degeneracy of particles comes into the picture. During the last decade, the focus is on investigating new aspects of quantum plasma due to its important applications in nanoscale and nanoelectronic devices (Abrahams et al., Reference Abrahams, Kravchenko and Sarachik2001; Magnus and Schoemaker, Reference Magnus and Schoemaker2002), in superdense astrophysical objects (Lai, Reference Lai2001; Opher et al., Reference Opher, Silva, Dauger, Decyk and Dawson2001; Chabrieret et al., Reference Chabrier, Douchin and Potekhin2002) (such as white dwarfs, neutron stars, magnetostars and supernova), quantum plasma echoes (Manfredi and Fexi, Reference Manfredi and Fexi1996), quantum X-ray free electron laser (Piovella et al., Reference Piovella, Cola, Volpe, Schiavi and Bonifacio2008), intense laser-solid density plasma experiments (Malkin et al., Reference Malkin, Fisch and Wurtele2007; Hartemann et al., Reference Hartemann, Siders and Barty2008). Most of the theoretical investigations on whistler waves have been focused on classical plasma, however, the nonlinear dynamics, collisional damping of the whistler mode (Watanabe et al., Reference Watanabe, Sugita and Nagao1967), dispersion of linear wave (Ren et al., Reference Ren, Wu and Chu2007), generation of Wakefield by whistler pulse (Mishra et al., Reference Mishra, Brodin, Maklund and Shukla2010b), circularly polarized modes (Mishra et al., Reference Mishra, Brodin, Maklund and Shukla2010a), whistler mode turbulence (Trukhanova, Reference Trukhanova2013) have been studied for quantum plasma. To the best of our knowledge, till now no attempt has been made to investigate excitation of SHG due to whistler propagation in strongly magnetized dense quantum plasma. Our objective in this paper is to present a theoretical study of the propagation of whistler pulse through quantum magnetoplasma embedded in an external magnetic field. When an external magnetic field is applied to quantum plasma, electron dynamics is modified and leads to nonlinear current modification. The density perturbation produced by magnetic field coupled with electron quiver motion leads to generation of harmonic radiation.
In the present paper, the interaction dynamics of whistler with plasma has been built in the mildly relativistic regime, using the recently developed quantum hydrodynamic (QHD) (Ren et al., Reference Ren, Wu and Chu2007; Mishra et al., Reference Mishra, Brodin, Marklund and Shukla2010c; Ghosh et al., Reference Ghosh, Chandra and Paul2012; Hass and Eliasson, Reference Hass and Eliasson2015) model which is generalization of classical fluid model for plasma with inclusion of quantum correction terms. It has been observed in the perturbative analysis that the relativistic effects become important in higher orders of perturbation only (Ghorbanalilu, Reference Ghorbanalilu2012). The momentum equation has been modified to incorporate the effects of spin magnetic moment (Mishra et al., Reference Mishra, Brodin, Maklund and Shukla2010a, Reference Mishra, Brodin, Maklund and Shuklab, Reference Mishra, Brodin, Marklund and Shuklac) and the relativistic variation of mass (Ghosh et al., Reference Ghosh, Chandra and Paul2012). The advantages of the QHD model over kinetic ones are its numerical efficiency, the direct use of macroscopic variables of interest such as momentum and energy and the easy way the boundary conditions are implemented. This allows considering the nonlinear phenomena relatively easier and so the QHD approach is preferred for describing such phenomena in quantum plasma (Shukla and Ali, Reference Shukla and Ali2006; Shukla and Eliasson, Reference Shukla and Eliasson2010; Vladimirov and Tyshetskiy, Reference Vladimirov and Tyshetskiy2011). The effects of Fermi statistical pressure, the quantum Bohm potential and electron spin have been incorporated. The systematic organization of this paper is as follows: The section ‘Whistler wave propagation’ is organized by using perturbation technique in mildly relativistic regime to setup the oscillatory electron velocities, perturbed density and nonlinear current density for the propagation of whistler in high-density plasma. In mildly relativistic regime, the relativistic effect comes into play in third and higher order velocity components and higher order. In the section ‘Second harmonic conversion efficiency’ the nonlinear wave equation is solved and conversion efficiency of second radiation generation is estimated. The section ‘Summary and discussion’ is devoted to summary and discussion.
Whistler wave propagation
Consider a whistler beam propagating parallel to an externally applied static magnetic field in the uniform quantum plasma. The magnetic field is assumed to be along the z-axis
$(B_0 = b\hat{e}_z)$. The electric and magnetic fields of the right circularly polarized whistler pulse are
$$\vec{{\it E}} = {\it E}(z,t)(\hat{x}-i\hat{y})e^{i(k_1z-{\rm \omega} _1t)} + c.c.,$$
$$\vec{{\it B}} = \displaystyle{{c({\vec{k}}_1 \times \vec{E})} \over {{\rm \omega} _1}},$$where E(z, t) is the slowly varying amplitude of fundamental whistler pulse inside plasma, c is speed of light in vacuum and k 1 is propagating wave vector at whistler wave frequency ω1. As the pulse propagates through magnetized plasma the current density at 2ω1 arises and acts as a source for second harmonic.
The QHD equations governing the motion of an electron in the presence of whistler field and static external magnetic fields are given by
$$\eqalign{\left( {\displaystyle{\partial \over {\partial t}} + \vec{v}.\nabla} \right)({\rm \gamma} \vec{v}\hskip2pt) = & -\displaystyle{e \over m}[ {\vec{{\rm E}} + (\vec{{\rm \nu}} \times \vec{{\rm B}})} ] \cr & -\displaystyle{{\nabla P} \over {mn}} + \displaystyle{{\hbar ^2} \over {2m^2{\rm \gamma} ^2}}\vec{\nabla} \left( {\displaystyle{1 \over {\sqrt n}} {\vec{\nabla}}^2\sqrt n} \right) \cr & -\displaystyle{{2{\rm \mu} _{\rm B}} \over {m{\rm \gamma} \hbar}} \overrightarrow S. (\vec{\nabla} \vec{{\rm B}}),} $$
$$\left( {\displaystyle{\partial \over {\partial t}} + \vec{v}.\nabla} \right)\vec{S} = \displaystyle{{2{\rm \mu} _{\rm B}} \over \hbar} (\vec{{\rm B}} \times \vec{S}\hskip2pt),$$and the continuity equation
$$\displaystyle{{\partial n} \over {\partial t}} + \nabla (n\vec{v}\hskip2pt) = 0,$$where, n is electron density, m is the electron rest mass, 
$\hbar $ is the Planck's constant, 
$\vec{v}$ is the velocity of electron, 
$\vec{S}$ is the spin magnetic moment with its absolute value 
$\vert {S_0} \vert = (\hbar /2)$, γ is the relativistic factor and 
${\rm \mu} _{\rm B} = ((e\hbar )/(2m))$ is the Bohr magneton. The second term on the left-hand side of Eq. (3) is the convective derivative of velocity field. On the other hand, the first term on the right-hand side of Eq. (3) is the Lorentz force, the second term denotes electron Fermi pressure 
$(P = mv_F^2 n^{{5 / 3}}/5n_0^{{2 / 3}} ),$ where 
$v_{\rm F} = {{\hbar {(3{\rm \pi} ^2n_0)}^{{1 / 3}}} / m}$ is the Fermi velocity, the third term is the Bohm force due to quantum correction in density fluctuations. The last term is the force due to the spin magnetic moment of plasma electrons. The classical equations may be recovered in the limit 
$\vec{J}$. The wave equation for source current 
$\hbar = 0 $ is
$$\left( {{\vec{\nabla}}^2-\displaystyle{1 \over {c^2}}\displaystyle{{\partial^2} \over {\partial t^2}}} \right)\vec{E} = \displaystyle{{4{\rm \pi}} \over {c^2}}\displaystyle{{\partial \vec{J}} \over {\partial t}}.$$Assuming that the ions form a neutralizing background in dense plasma, the perturbative expansion of the set of QHD equations [Eqs (3)–(5)] governing interaction dynamics for first order of electromagnetic whistler field gives
$$\eqalign{\displaystyle{{\partial {\vec{{\rm \nu}}} ^{\hskip1.5pt(1)}} \over {\partial t}} = & -\displaystyle{{e{\vec{{\rm E}}}^{\hskip1.5pt(1)}} \over m}-\displaystyle{{e({\vec{v}}^{\hskip1.5pt(1)} \times {\vec{B}}^{\hskip1.5pt(1)})} \over {mc}} \cr & -\displaystyle{{\vec{{\rm \nu}} _{\rm F}^2} \over {n_0}}\vec{\nabla} n^{(1)} + \displaystyle{{\hbar ^2} \over {4m^2}}\left( {\displaystyle{1 \over {n_0}}\vec{\nabla} ({\vec{\nabla}}^2n^{(1)})} \right) \cr & -\displaystyle{{2{\rm \mu} _{\rm B}S_0} \over {m\hbar}} (\vec{\nabla} {\vec{{\rm B}}}^{\hskip1.5pt(1)}),} $$
$$\displaystyle{{\partial {\vec{S}}^{\hskip2pt(1)}} \over {\partial t}} = \displaystyle{{2{\rm \mu} _{\rm B}} \over \hbar} (\vec{B}^{(1)} \times S^{(0)}),$$
$$\displaystyle{{\partial n^{(1)}} \over {\partial t}} + n_0.\nabla \vec{v}^{(1)} = 0.$$From Eq. (7) the first order perturbed equations for transverse quiver velocity components are obtained as
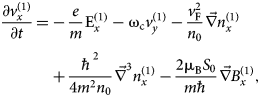$$\eqalign{\displaystyle{{\partial v_x^{\lpar 1 \rpar }} \over {\partial t}} = & -\displaystyle{e \over m}{\rm E}_x^{(1)} -{\rm \omega} _{\rm c}v_y^{\lpar 1 \rpar } -\displaystyle{{v_{\rm F}^2} \over {n_0}}\vec{\nabla} n_x^{\lpar 1 \rpar } \cr & + \displaystyle{{\hbar ^2} \over {4m^2n{}_0}}{\vec{\nabla}} ^3n_x^{\lpar 1 \rpar } -\displaystyle{{2{\rm \mu} _{\rm B}S_0} \over {m\hbar}} \vec{\nabla} {\it B}_x^{\lpar 1 \rpar },} $$
$$\eqalign{\displaystyle{{\partial {\rm \nu} _y^{(1)}} \over {\partial t}} = & -\displaystyle{e \over m}{\it E}_y^{\hskip1.5pt(1)} -{\rm \omega} _{\rm c}v_x^{\lpar 1 \rpar } \cr & -\displaystyle{{v_F^2} \over {n_0}}\vec{\nabla} n_y^{\lpar 1 \rpar } + \displaystyle{{\hbar ^2} \over {4m^2n{}_0}}{\vec{\nabla}} ^3n_y^{\lpar 1 \rpar } -\displaystyle{{2{\rm \mu} _{\rm B}S_0} \over {m\hbar}} \vec{\nabla} {\it B}_y^{\lpar 1 \rpar }.} $$In order to study the propagation of whistler pulse Eqs (10) and (11) are to be solved simultaneously. The plasma electrons interact with the whistler pulse to acquire the transverse quiver velocity,
$$\left( {\matrix{ {{\rm \nu}_x^{(1)}} \cr {v_y^{(1)}} \cr}} \right) = \left( {\matrix{ {v_{x1}} \cr {v_{y1}} \cr}} \right){\it E}(z,t)e^{i(k_1z-{\rm \omega} _1t)} + c.c.,$$where
$$\eqalign{v_{x1} & = \displaystyle{1 \over {\lpar {{\rm \omega}_{\rm c}^2 -{\rm \omega}_1^2} \rpar }} \cr & \left[ {\displaystyle{{ie({\rm \omega}_1-{\rm \omega}_{\rm c})} \over m} + \displaystyle{{k_1Q(i{\rm \omega}_{\rm c}n_{y1}-{\rm \omega}_1n_{x1})} \over {n_0}} + \displaystyle{{2i{\rm \mu}_{\rm B}k_1S_0({\rm \omega}_{\rm c}-{\rm \omega}_1)} \over {m\hbar}}} \right],} $$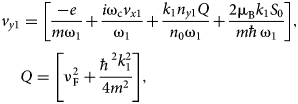
$$\eqalign{v_{y1} & = \left[ {\displaystyle{{-e} \over {m{\rm \omega}_1}} + \displaystyle{{i{\rm \omega}_{\rm c}v_{x1}} \over {{\rm \omega}_1}} + \displaystyle{{k_1n_{y1}Q} \over {n_0{\rm \omega}_1}} + \displaystyle{{2{\rm \mu}_{\rm B}k_1S_0} \over {m\hbar {\rm \omega}_1}}} \right],\, \cr & Q = \left[ {{\rm \nu}_{\rm F}^2 + \displaystyle{{\hbar^2k_1^2} \over {4m^2}}} \right],} $$and ωc = ((eb)/m) is the cyclotron frequency of plasma electrons.
The first order perturbed electron density is obtained by substituting the quiver velocities in the perturbed first order continuity equation,
$$\left( {\matrix{ {n_x^{(1)}} \cr {n_y^{(1)}} \cr}} \right) = \left( {\matrix{ {n_{x1}} \cr {n_{y1}} \cr}} \right){\rm E}(z,t)e^{i(k_1z-{\rm \omega} _1t)} + c.c.,$$where
$$\eqalign{n_{x1} = & \displaystyle{{n_0k} \over {{\rm \omega} _1\lcub {k_1^2 Q + \lpar {{\rm \omega}_{\rm c}^2 -{\rm \omega}_1^2} \rpar } \rcub }} \cr & \left[ {\displaystyle{{ie({\rm \omega}_1-{\rm \omega}_{\rm c})} \over m} + \displaystyle{{ik_1Q{\rm \omega}_{\rm c}n_{y1}} \over {n_0}} + \displaystyle{{2i{\rm \mu}_{\rm B}S_0k_1({\rm \omega}_{\rm c}-{\rm \omega}_1)} \over {m\hbar}}} \right],} $$and
$$ \hskip-2pt \eqalign{n_{y1} = & \displaystyle{{n_0k_1\lpar {{\rm \omega}_{\rm c}^2 -{\rm \omega}_1^2} \rpar } \over {\lcub {({\rm \omega}_1^2 -k_1^2 )({\rm \omega}_{\rm c}^2 -{\rm \omega}_1^2 ) + k_1^2 Q{\rm \omega}_{\rm c}^2} \rcub }} \cr & \!\left[ \!{\displaystyle{{-e} \over m} \!+ \!\displaystyle{{e{\rm \omega}_{\rm c}} \over {m({\rm \omega}_{\rm c} + {\rm \omega}_1)}}-\displaystyle{{ik_1Q{\rm \omega}_1{\rm \omega}_{\rm c}n_{x1}} \over {n_0({\rm \omega}_{\rm c}^2 -{\rm \omega}_1^2 )}}-\displaystyle{{2{\rm \omega}_{\rm c}{\rm \mu}_{\rm B}S_0k_1} \over {m\hbar ({\rm \omega}_{\rm c} + {\rm \omega}_1)}} \!+\! \displaystyle{{2{\rm \mu}_{\rm B}S_0k_1} \over {m\hbar}}} \right].} $$Spin is an important property of quantum degenerate plasma. It plays a crucial role in exposing the plasma to the external magnetic field, the effect of which can be ascertained in the perturbed spin magnetic moment for plasma electron through the spin angular momentum
$$\left( {\matrix{ {S_x^{(1)}} \cr {S_y^{(1)}} \cr {S_z^{(1)}} \cr}} \right) = \left( {\matrix{ {S_{x1}} \cr {S_{y1}} \cr {S_{z1}} \cr}} \right){\rm E}(z,t)e^{i(k_1z-{\rm \omega} _1t)} + c.c.,$$where
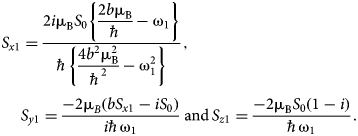$$\eqalign{S_{x1} & = \displaystyle{{2i{\rm \mu} _{\rm B}S_0\left\{ {\displaystyle{{2b{\rm \mu}_{\rm B}} \over \hbar} -{\rm \omega}_1} \right\}} \over {\hbar \left\{ {\displaystyle{{4b^2{\rm \mu}_{\rm B}^2} \over {\hbar^2}}-{\rm \omega}_1^2} \right\}}},\, \cr & S_{y1} = \displaystyle{{-2{\rm \mu} _B(bS_{x1}-iS_0)} \over {i\hbar {\rm \omega} _1}}\,{\rm and}\,S_{z1} = \displaystyle{{-2{\rm \mu} _{\rm B}S_0(1-i)} \over {\hbar {\rm \omega} _1}}.} $$ By following similar steps for nth harmonic, the quiver velocity, perturbed density and spin magnetic moment component can be obtained by substituting ω1 → nω 1, E(z, t) → En(z, t), (k 1z − ω1t) → (k nz − nω 1t), in Eqs (12–14). Hence, the linear part of induced current density for nth harmonic, 
$J^{(1)}(n{\rm \omega} _1) = J_{\rm c}^{(1)} (n{\rm \omega} _1) + J_{\rm s}^{(1)} (n{\rm \omega} _1)$ can be written as,
$$J^{(1)}(n{\rm \omega} _1) = [J_{\rm c}^{(1)} (n{\rm \omega} _1) + J_{\rm s}^{(1)} (n{\rm \omega} _1)]{\rm E}_n(z,t)e^{i(k_nz-n{\rm \omega} _1t)} + c.c.$$where, 
$\vec{J}_s = -((2{\rm \mu} _{\rm B})/\hbar )\nabla (n.S),$ is the current density due to spin magnetic moment and 
$\vec{J}_{\rm c} = -e(n.v)$ is the conventional current. Substitution of Eq. (15) in the wave Eq. (6) for nth harmonic yields the dispersion equation
$$c^2k_n^2 = n^2{\rm \omega} _1^2 + {\rm \omega} _p^2 \displaystyle{{imn{\rm \omega} _1\lcub {J_{\rm c}^{(1)} (n{\rm \omega}_{1}) + J_{\rm s}^{(1)} (n{\rm \omega}_1)} \rcub } \over {n_0e^2}}.$$Now, we proceed to obtain the second order perturbed velocity and particle density which are obtained using the same procedure as adopted for the first order fields,
$$\left( {\matrix{ {\nu _x^{(2)} } \cr {\nu _y^{(2)} } \cr {\nu _z^{(2)} } \cr } } \right) = \left( {\matrix{ {\nu _{x2}} \cr {\nu _{y2}} \cr {\nu _{z2}} \cr } } \right){\it E}^2(z,t)e^{2i(k_1z-\omega _1t)} + c.c.$$
$$\left( {\matrix{ {n_x^{(2)}} \cr {n_y^{(2)}} \cr {n_z^{(2)}} \cr}} \right) = \left( {\matrix{ {n_{x2}} \cr {n_{y2}} \cr {n_{z2}} \cr}} \right){\it E}^2(z,t)e^{2i(k_1z-{\rm \omega} _1t)} + c.c.$$where
$$\eqalign{v_{x2} & = \left[ {\displaystyle{{2i{\rm \mu}_Bk_1({\rm \omega}_{\rm c}S_{y1}-2{\rm \omega}_1S_{x1})} \over {m\hbar ({\rm \omega}_{\rm c}^2 -4{\rm \omega}_1^2 )}}} \right],\, \cr & v_{y2} = \left[ {\displaystyle{{i{\rm \omega}_{\rm c}v_{x2}} \over {2{\rm \omega}_1}} + \displaystyle{{{\rm \mu}_{\rm B}k_1S_{y1}} \over {m\hbar {\rm \omega}_1}}} \right],\,v_{z2} = \left[ {\displaystyle{{-ie(v_{x1}-iv_{y1})} \over {2m{\rm \omega}_1c}}} \right]} $$
$$\eqalign{n_{x2} & = \left[ {\displaystyle{{k_1n_0{\rm \nu}_{x2}} \over {{\rm \omega}_1}} + \displaystyle{{k_1n_{x1}v_{x1}} \over {{\rm \omega}_1}}} \right],\, \cr & n_{y2} = \left[ {\displaystyle{{k_1n_0v_{y2}} \over {{\rm \omega}_1}} + \displaystyle{{k_1n_{y1}v_{y1}} \over {{\rm \omega}_1}}} \right]\,{\rm and}\,n_{z2} = \left[ {\displaystyle{{k_1n_0v_{z2}} \over {{\rm \omega}_1}} + \displaystyle{{k_1n_{z1}v_{z1}} \over {{\rm \omega}_1}}} \right].} $$Thus, the second order velocity components of plasma electrons oscillate with frequency twice that of fundamental whistler frequency. This effect arises from the coupling of propagating magnetic field of whistler pulse with the external magnetic field. The second order spin magnetic moment is obtained as
$$\left( {\matrix{ {S_x^{(2)}} \cr {S_y^{(2)}} \cr {S_z^{(2)}} \cr}} \right) = \left( {\matrix{ {S_{x2}} \cr {S_{y2}} \cr {S_{z2}} \cr}} \right){\it E}^2(z,t)e^{2i(k_1z-{\rm \omega} _1t)} + c.c.$$where
$$\eqalign{&S_{x2} = \displaystyle{{[ {((2b{\rm \mu}_{\rm B})/\hbar )\lcub {((2i{\rm \mu}_{\rm B}/)\hbar ) + ik_1s_{y1}v_{y1}} \rcub}}} \cr&\qquad\,\, - 2i{\rm \omega}_1\lcub {((2{\rm \mu}_{\rm B}S_{z1})/\hbar )-ik_1v_{x1}S_{x1}} \rcub]} } \over {\lcub {((4{\rm \mu}_{\rm B}^2 b^2)/\hbar^2)-4{\rm \omega}_1^2} \rcub }},}$$
$$S_{y2} = \left[ {\displaystyle{{ib{\rm \mu}_{\rm B}S_{x2}} \over {\hbar {\rm \omega}_1}} + \displaystyle{{{\rm \mu}_{\rm B}S_{z1}} \over {\hbar {\rm \omega}_1}} + \displaystyle{{k_1S_{y1}v_{y1}} \over {2{\rm \omega}_1}}} \right]\,{\rm and}\,S_{z2} = \displaystyle{{i{\rm \mu} _{\rm B}(iS_{y1}-S_{x1})} \over {\hbar {\rm \omega} _1}}.$$The first order quiver velocity beats with the first order density to produce second harmonic nonlinear current density which leads to even second harmonic radiation generation at (2ω1, 2k 1) as,
$$\vec{J}_{NL}^{\hskip2pt(2)} = (J_{{\rm S}2} + J_{{\rm c}2}){\it E}^2(z,t)e^{2i(k_1z-{\rm \omega} _1t)} + c.c.$$where
$$\eqalign{J_{{\rm S}2} = & -\displaystyle{{4ik_0{\rm \mu} _{\rm B}} \over \hbar} \cr & [ {n_0S_{x2} + S_0n_{x2} + n_{x1}S_{x1} + n_0S_{y2} + S_0n_{y2}} \cr& + {n_{y1}S_{y1} + n_0S_{z2} + S_0n_{z2} + S_{z1}n_{z1}} ] } $$and
$$J_{{\rm c}2} = -e.[ {n_0v_{x2} + n_{x1}v{}_{x1} + n_0v_{y2} + n_{y1}v_{y1} + n_0v_{z2} + n_{z1}{\rm \nu}_{z1}} ] .$$ There also exists a self-consistent even second harmonic field 
$\vec{{\it E}}^{(2)} = {\it E}_2(z,t)e^{i(k_2z-2{\rm \omega} _1t)} + c.c$ due to which the linear current density is given by
$$\vec{J}_L^{\hskip2pt(2)} = \left( {\displaystyle{{ie^2n_0{\it E}_2(z,t)} \over {2m{\rm \omega}_1}}} \right)e^{i(k_2z-2{\rm \omega} _1t)} + c.c.$$Second harmonic conversion efficiency
The normalized amplitude for phase mismatched second harmonic is obtained by substituting linear and nonlinear current densities in the wave equation [Eq. (6)] governing the second harmonic field 
$\vec{E}^{(2)}$, which on simplification yields
$$\displaystyle{{E_2(z,t)} \over {E(z,t)}} = \displaystyle{{8{\rm \pi} ia_0mc(J_{{\rm s}2} + J_{{\rm c}2}){({\rm \omega} _1/{\rm \omega} _p)}^2} \over {\lcub {((2im{\rm \omega}_1[J_{\rm c}(2{\rm \omega}_1) + J_{\rm s}(2{\rm \omega}_1)])/(en_0)) + e} \rcub }}e^{i{\rm \Delta} kZ},$$where, Δk = (k 2 − 2k 1) represents the phase difference between the generated even second harmonic and the fundamental frequency. We get the second harmonic conversion efficiency as
$${\rm \eta} _2 = \displaystyle{{64{\rm \pi} ^2m^2c^2a_0^2 {(J_{{\rm s}2} + J_{{\rm c}2})}^2} \over {e^2{\lpar {(({\rm \omega}_p)/({\rm \omega}_1))} \rpar }^4{\lcub {((2im{\rm \omega}_1)/(n_0e^2))[ {J_{\rm c}(2{\rm \omega}_1) + J_{\rm s}(2{\rm \omega}_1)} ] + 1} \rcub }^2}},$$where
$$\eqalign{J_{\rm s}(2{\rm \omega} _1) & = -\displaystyle{{2ik_1{\rm \mu} _{\rm B}} \over \hbar} [n_0S_{x1} + S_0n_{_{x1}} \cr & \quad + n_0S_{y1} + S_0n_{_{y1}} + n_0S_{z1} + S_0n_{z1}](2{\rm \omega} _1)}$$
$$J_{\rm c}(2{\rm \omega} _1) = -en_0[v_{x1} + v_{y1} + v_{z1}](2{\rm \omega} _1)\,{\rm and}\,a_0 = \displaystyle{{eE_0} \over {mc{\rm \omega}}}. $$The conversion efficiency is proportional to the plasma electron density, strength of the magnetic field and the intensity of whistler pulse.
Figure 1, shows the variation of conversion efficiency 
$({\rm \eta} _2\% )$ with normalized plasma electron density for different values of magnetic field strength. The figure shows that for a constant magnetic field, harmonic radiation grows with increase in the plasma density until saturation. The saturation value of plasma density depends on the applied magnetic field and is more for the weaker magnetic field.
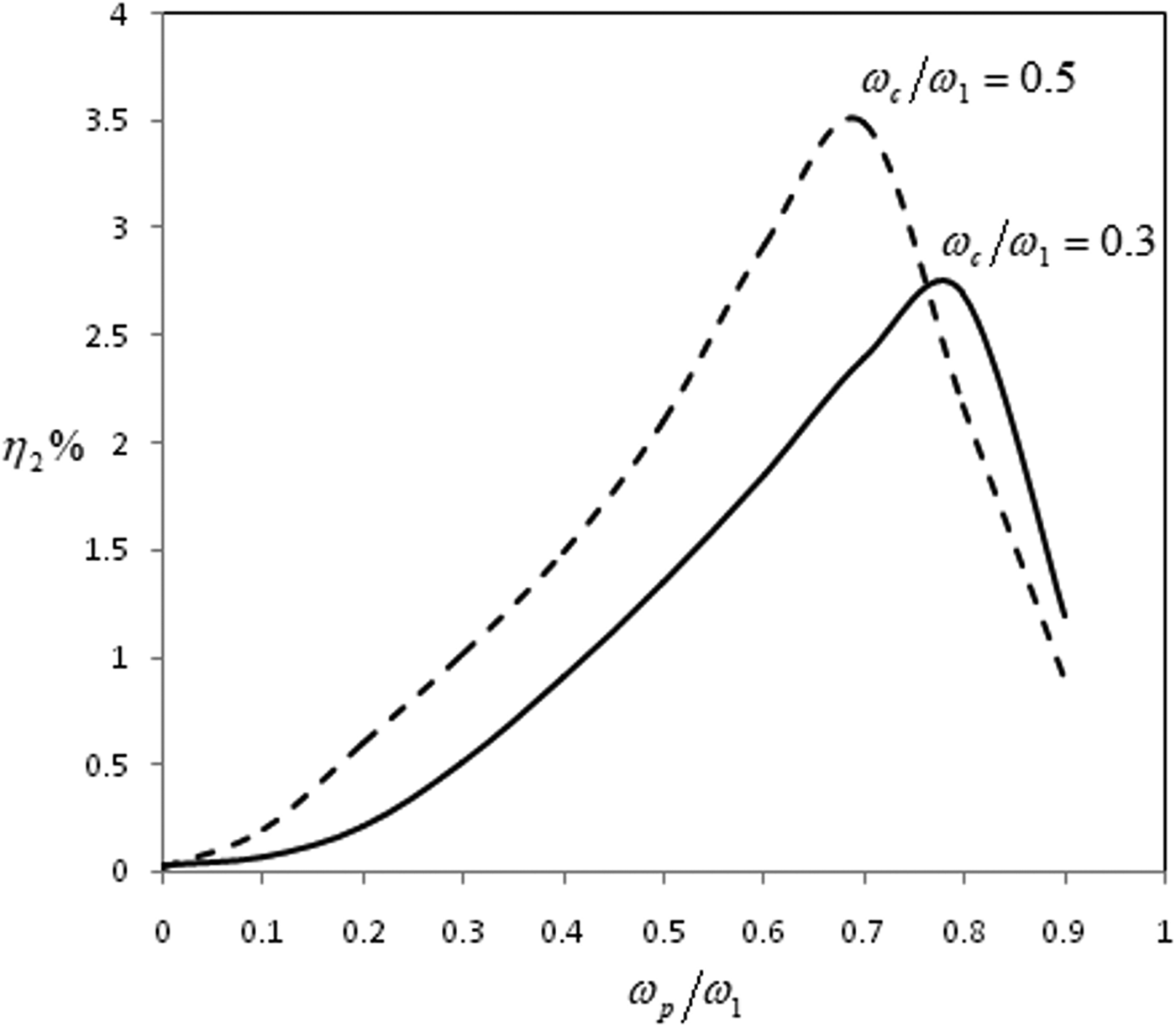
Fig. 1. Variation of conversion efficiency as a function of ωp/ω1 for a 0 = 0.271, n = 1030 m −3 and different value of ωc/ω1.
Figure 2, shows the variation of second harmonic conversion efficiency 
$({\rm \eta} _2\% )$ with the magnetic field strength at the varying value of normalized plasma density. The dark line is for ωp/ω1 = 0.3 and the dashed line is for ωp/ω1 = 0.5. It is observed that the efficiency increases with the magnetic field and approaches to saturation. The saturation strength increases for the lower density of plasma.
Fig. 2. Variation of conversion efficiency as a function of ωc/ω1 for a 0 = 0.271, n = 1030 m −3 and different value of ωp/ω1.
Figure 3, shows the variation of second harmonic conversion efficiency as a function of the intensity of the whistler pulse for different values of normalized plasma density. The dark line is for ωp/ω1 = 0.3, while the dashed line is for ωp/ω1 = 0.5. The efficiency increases for lower values of intensity, however conversion efficiency saturates at large value of the intensity of whistler pulse.
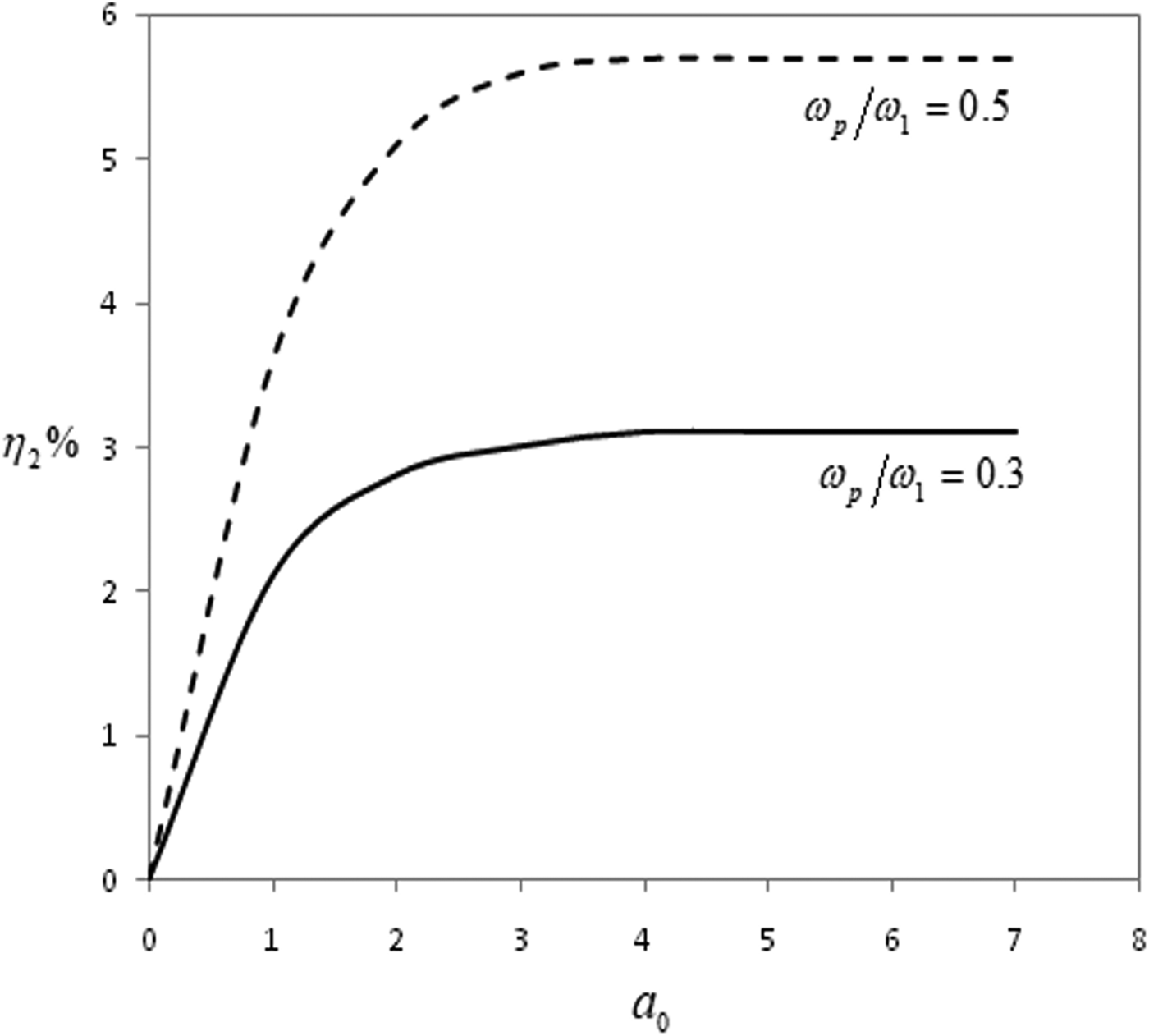
Fig. 3. Variation of conversion efficiency against normalized fundamental whistler intensity a 0 for various values of ωp/ω1.
Figure 4 shows the variation of harmonic conversion efficiency as a function of whistler pulse intensity for various values of magnetic field strength (ωc/ω1 = 0.4 for dark line and ωc/ω1 = 0.6 for dashed line). The figure depicts that the conversion efficiency of even second harmonic radiation generation increases with increase in whistler intensity and magnetic field. The increase in the conversion efficiency of second harmonic with the intensity of fundamental whistler pulse is due to the generation of strong nonlinear current. The efficiency tends to saturate for high value of a 0.
Fig. 4. Variation of conversion efficiency of second harmonic with normalized fundamental whistler intensity a 0 for various values of ωc/ω1.
In order to compare the conversion efficiency of second harmonic with the classical case, Figure 5 has been plotted for parameters ωc/ω1 = 0.3, a 0 = 0.271 and n = 1030m −3. The upper solid line shows the variation of conversion efficiency in presence of quantum effects and the dashed line is in the absence of quantum effects (in the limit 
$\hbar = 0$). It is evident from the figure that the conversion efficiency of second harmonic is more by about 11% due to the presence of quantum effects in magentoplasma because quantum diffraction effects play a crucial role by modifying the efficiency of second harmonic of whistler pulse.
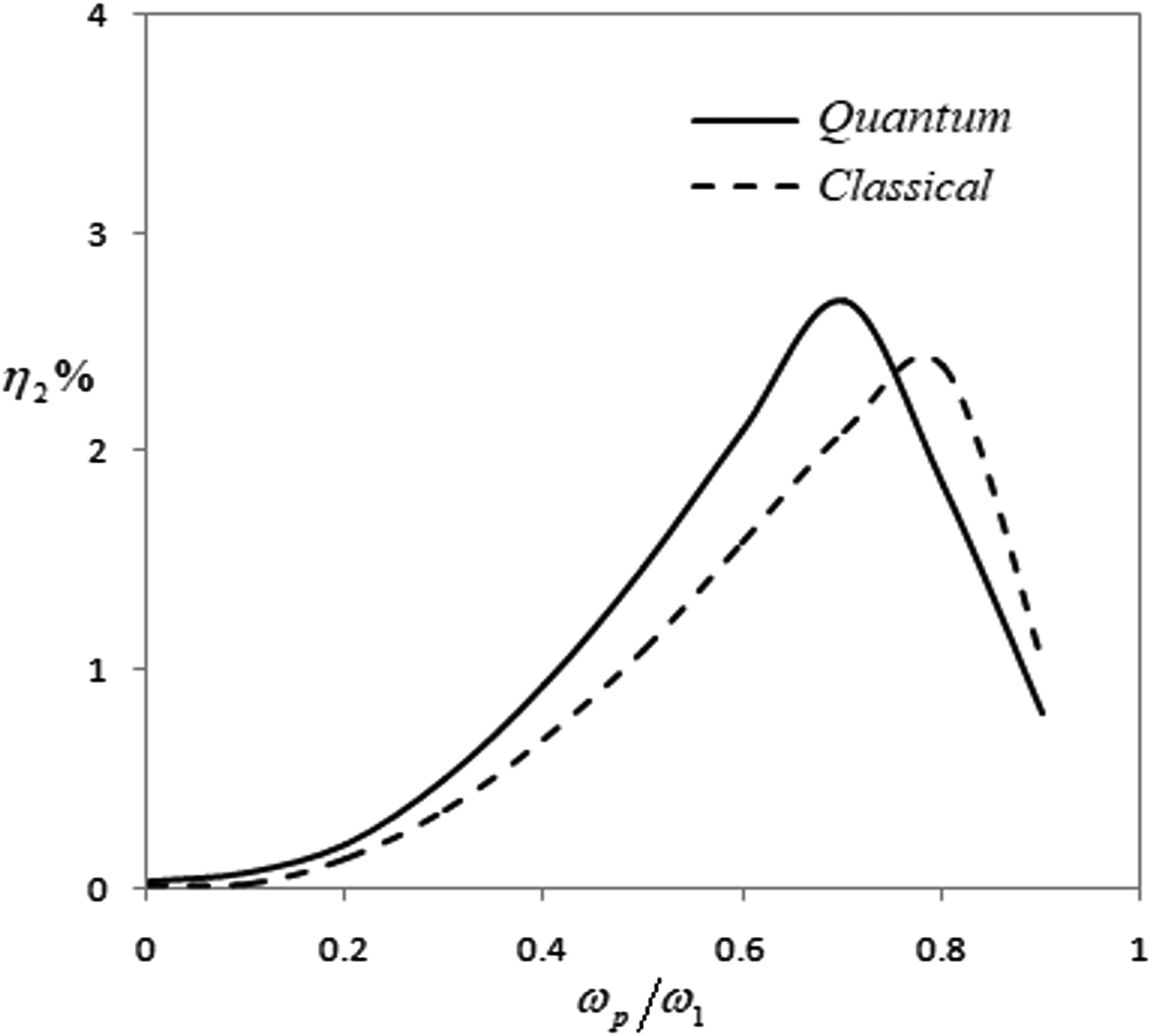
Fig. 5. Variation of conversion efficiency as a function of ωp/ω1, (i) solid line in the presence of quantum effects and (ii) dashed line in absence of quantum effects.
Summary and discussion
A study of SHG resulting from propagation of whistler wave in homogenous high-density magnetized quantum plasma is presented. The static magnetic field applied for magnetization is in the longitudinal direction. The interaction mechanism has been built using the recently developed QHD model. The effects of Fermi statistical pressure, the quantum Bohm potential, and the spin of electron have been taken into account. The quiver and second order velocities along with electron densities and the spin angular momenta have been obtained through the perturbative expansion of QHD equations. The nonlinear current density is the sum of conventional current and the current due to spin magnetic moment. The linear current results from the self-consistent field. The efficiency of SHG has been obtained for the phase mismatched case. It has been found that the SHG grows with the plasma density and the magnetic field up to the respective saturation values. The harmonic generation stops beyond saturation. The saturation of plasma density occurs earlier for increasing magnetic field. This is due to the polarization field effect in strongly magnetized dense plasma. The efficiency of SHG also increases with intensity of whistler pulse. The noteworthy observation is occurrence of enhanced SHG for high-density degenerate plasma at lower values of external magnetic field strength. The present study of second harmonic of whistler will be useful in acceleration of whistler pulse in astrophysical environments, fabrication of microelectronic devices, for high-quality plasma processing and to derive dc current in toroidal fusion devices.
Acknowledgements
The work has been carried out under DAE-BRNS sponsored research project no. 39/14/12/2016-BRNS, India.
