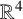1 Introduction
Recent decades have seen intense study of solitons for the mean curvature flow. The simplest example is the grim reaper
$y = \ln ( \cos x )$
which moves by downward translation under the mean curvature flow. There are geometric dualities between solitons for the mean curvature flow and minimal submanifolds [Reference Colding and Minicozzi4, Reference Smoczyk16, Reference White18].
A surface is a translator [Reference White18] for the mean curvature flow when its mean curvature vector field agrees with the normal component of a constant Killing vector field. Translators arise as Hamilton’s convex eternal solutions and Huisken–Sinestrari Type II singularities for the mean curvature flow, and provide a natural generalisation of minimal surfaces.
Altschuler and Wu [Reference Altschuler and Wu1] showed the existence of the convex, rotationally symmetric, entire graphical translator. Clutterbuck et al. [Reference Clutterbuck, Schnürer and Schulze3] constructed the winglike bigraphical translators, which are analogous to catenoids. Halldorsson [Reference Halldorsson5] proved the existence of helicoidal translators. Nguyen [Reference Nguyen14] used Scherk’s minimal towers to desingularise the intersection of a grim reaper product and a plane, and obtained a complete embedded translator. See also her generalisation [Reference Nguyen15].
Our main goal is to adapt the splitting of the generalised Gauss map of oriented surfaces in
${\mathbb {R}}^{4}$
to construct an explicit Weierstrass-type representation formula for translators in
${\mathbb {R}}^{4}$
.
2 Main results
We first introduce the complexification of the generalised Gauss map. Inside the complex projective space
${\mathbb {C}}{\mathbb {P}}^{3}$
, we take the variety
$$ \begin{align*} {\mathcal{Q}}_{2}=\{ [{\zeta}]=[{{\zeta}}_{1}: \cdots: {{\zeta}}_{4} ] \in {\mathbb{C}}{\mathbb{P}}^{3} : {\zeta}_{1}^{2} + \cdots + {\zeta}_{4}^{2} =0 \}, \end{align*} $$
which becomes a model for the Grassmannian manifold
${\mathcal {G}}_{2,2}$
of oriented planes in
${\mathbb {R}}^{4}$
. Hoffman and Osserman [Reference Hoffman and Osserman6, Reference Hoffman and Osserman7] defined the generalised Gauss map of a conformal immersion
${\mathbf {X}}:\Sigma \rightarrow {\mathbb {R}}^{4}$
,
$z \mapsto {\mathbf {X}}(z)$
, as follows:
$$ \begin{align*} \mathcal{G}(z)=\bigg[ \frac{\partial {\mathbf{X}}}{\partial {z}} \bigg]= [ 1+{g}_{1}{g}_{2}, i(1-{g}_{1}{g}_{2}), {g}_{1}-{g}_{2}, -i({g}_{1}+{g}_{2} ) ] \in {\mathcal{Q}}_{2} \subset {\mathbb{C}}{\mathbb{P}}^{3}. \end{align*} $$
We call the induced pair
$(g_{1}, g_{2})$
the complexified Gauss map of the immersion
${\mathbf {X}}$
.
Lemma 2.1 (Poincaré’s lemma)
Let
$\xi : \Omega \rightarrow \mathbb {C}$
be a function on a simply connected domain
$\Omega \subset \mathbb {C}$
. If
${\partial }\xi (z)/{\partial \overline {z}} \in \mathbb {R}$
for all
$z \in \Omega $
, then there exists a function
$x: \Omega \rightarrow \mathbb {R}$
such that
${\partial } x(z)/{\partial {z}}=\xi (z)$
.
Theorem 2.2 (Correspondence from null curves in
${\mathbb {C}}^{4}$
to translators in
${\mathbb {R}}^{4}$
)
Let
$({g}_{1}, g_{2})$
be a pair of nowhere-holomorphic
${\mathcal {C}}^{2}$
functions from a simply connected domain
$\Omega \subset \mathbb {C}$
to the open unit disc
$\mathbb {D}:=\{w \in \mathbb {C} \; \vert \; \vert w \vert < 1 \}$
satisfying the compatibility condition
$$ \begin{align} {\mathcal{F}}:=\frac{{({g}_{1})}_{\overline{z}}}{(1-g_{1}\overline{g_{2}})(1+{\vert g_{1}\vert}^{2})} =\frac{{({g}_{2})}_{\overline{z}}}{(1-\overline{g_{1}}g_{2})(1+{\vert g_{2}\vert}^{2})}, \quad z \in \Omega. \end{align} $$
Assume that one of the following two integrability conditions holds on
$\Omega $
:
$$ \begin{align} &0= {({g}_{1})}_{z \overline{z}} + \bigg(\frac{\overline{g_{2}}}{1-g_{1}\overline{g_{2}}} - \frac{\overline{g_{1}}}{1+{\vert g_{1}\vert}^{2}}\bigg) {({g}_{1})}_{z}{({g}_{1})}_{\overline{z}} +\frac{g_{1}+g_{2}}{(1-\overline{g_{1}}g_{2})(1+{\vert g_{1}\vert}^{2})} {\vert {({g}_{1})}_{\overline{z}} \vert}^{2}, \end{align} $$
$$ \begin{align} &0= {({g}_{2})}_{z \overline{z}} + \bigg(\frac{\overline{g_{1}}}{1-\overline{g_{1}}g_{2}} - \frac{\overline{g_{2}}}{1+{\vert g_{2}\vert}^{2}}\bigg) {({g}_{2})}_{z}{({g}_{2})}_{\overline{z}} +\frac{g_{1}+g_{2}}{(1-g_{1}\overline{g_{2}})(1+{\vert g_{2}\vert}^{2})} {\vert {({g}_{2})}_{\overline{z}} \vert}^{2}. \end{align} $$
-
(a) Both (2.2) and (2.3) hold. (In fact, we claim that (2.2) is equivalent to (2.3).)
-
(b) The complex curve
$\phi :=({\phi }_{1}, {\phi }_{2}, {\phi }_{3}, {\phi }_{4} ) : \Omega \rightarrow {\mathbb {C}}^{4}$
defined by satisfies the following three properties on the domain
$$ \begin{align*} \phi=f (1 + {g}_{1}{g}_{2}, i(1 - {g}_{1}{g}_{2}), {g}_{1} - {g}_{2}, -i({g}_{1} + {g}_{2}) ), \quad f:=-2i{\overline{\mathcal{F}}}, \end{align*} $$
$\Omega $
:
(b1) nullity:
$\phi \cdot \phi ={\phi }_{1}^{2}+{\phi }_{2}^{2}+{\phi }_{3}^{2}+{\phi }_{4}^{2}=0$
;(b2) nondegeneracy:
${\vert \phi \vert }^{2} ={\vert {\phi }_{1} \vert }^{2}+{\vert {\phi }_{2} \vert }^{2}+{\vert {\phi }_{3} \vert }^{2}+{\vert {\phi }_{4} \vert }^{2}>0$
;(b3) integrability:
${\partial {\phi } }/{\partial \overline {z}} = ({\partial {\phi }_{1}}/{\partial \overline {z}}, {\partial {\phi }_{2}}/{\partial \overline {z}}, {\partial {\phi }_{3}}/{\partial \overline {z}}, {\partial {\phi }_{4}}/{\partial \overline {z}} ) \in {\mathbb {R}}^{4}$
.
-
(c) Integrating the complex null immersion
$\phi : \Omega \rightarrow {\mathbb {C}}^{4}$
yields a translator
$\Sigma $
in
${\mathbb {R}}^{4}$
.(c1) There exists a conformal immersion
${\mathbf {X}}=( x_{1}, x_{2}, x_{3}, x_{4} ): \Omega \rightarrow {\mathbb {R}}^{4}$
satisfying
${\mathbf {X}}_{z} = \phi .$
(c2) The induced metric
$ds^{2}$
on the z-domain
$\Omega $
by the immersion
${\mathbf {X}}$
is
$$ \begin{align*} ds^{2}= \frac{ 16 \, {\vert {({g}_{1})}_{\overline{z}} \vert}^{2} }{ {\vert 1 - g_{1} \overline{{g}_{2}} \vert}^{2} } \cdot \frac{ 1+{\vert g_{2}\vert}^{2} }{ 1+{\vert g_{1}\vert}^{2} } {\vert dz \vert}^{2} = \frac{ 16 \, {\vert {({g}_{2})}_{\overline{z}} \vert}^{2} }{ {\vert 1 - \overline{{g}_{1}} g_{2} \vert}^{2} } \cdot \frac{ 1+{\vert g_{1}\vert}^{2} }{ 1+{\vert g_{2}\vert}^{2} } {\vert dz \vert}^{2}. \end{align*} $$
(c3) The pair
$({g}_{1}, g_{2})$
is the complexified Gauss map of the surface
$\Sigma = {\mathbf {X}}( \Omega )$
, that is, the generalised Gauss map of the conformal immersion
${\mathbf {X}}$
is
$$ \begin{align*} [{\mathbf{X}}_{z} ] = [ 1+{g}_{1}{g}_{2}, i(1-{g}_{1}{g}_{2}), {g}_{1}-{g}_{2}, -i({g}_{1}+{g}_{2}) ] \in {\mathcal{Q}}_{2} \subset {\mathbb{C}}{\mathbb{P}}^{3}. \end{align*} $$
(c4) The surface
$\Sigma $
becomes a translator with translating velocity given by
$-\mathbf {e}_{4}=(0,0,0,-1)$
.
Proof. Step A. For the proof of (a), we first set up the notation
$$ \begin{align*} &{\mathcal{L}}:= {({g}_{1})}_{z \overline{z}} + \bigg(\frac{\overline{g_{2}}}{1-g_{1}\overline{g_{2}}} - \frac{\overline{g_{1}}}{1+{\vert g_{1}\vert}^{2}}\bigg) {({g}_{1})}_{z}{({g}_{1})}_{\overline{z}}\, +\frac{g_{1}+g_{2}}{(1-\overline{g_{1}}g_{2})(1+{\vert g_{1}\vert}^{2})} {\vert {({g}_{1})}_{\overline{z}} \vert}^{2}, \\ &{\mathcal{R}}:={({g}_{2})}_{z \overline{z}} + \bigg(\frac{\overline{g_{1}}}{1-\overline{g_{1}}g_{2}} - \frac{\overline{g_{2}}}{1+{\vert g_{2}\vert}^{2}}\bigg) {({g}_{2})}_{z}{({g}_{2})}_{\overline{z}}\, +\frac{g_{1}+g_{2}}{(1-g_{1}\overline{g_{2}})(1+{\vert g_{2}\vert}^{2})} {\vert {({g}_{2}}_{\overline{z}} \vert}^{2}. \end{align*} $$
We first assume only (2.1). Taking the conjugation in (2.1) yields
$$ \begin{align*} \overline{\mathcal{F}}= \frac{ {(\overline{g_{2}})}_{z} } { (1 - g_{1}\overline{g_{2}}) (1+{\vert g_{2}\vert}^{2})} = \frac{ {(\overline{g_{1}})}_{z} } { (1 - \overline{g_{1}} g_{2}) )(1+{\vert g_{1}\vert}^{2}) }. \end{align*} $$
Taking this into account,
$$ \begin{align*} \frac{{\mathcal{F}}_{z}}{{\mathcal{F}}} &= \frac{{(g_{1})}_{z \overline{z}}}{{(g_{1})}_{\overline{z}}} + \bigg(\frac{\overline{g_{2}}}{1-g_{1}\overline{g_{2}}} - \frac{\overline{g_{1}}}{1+{\vert g_{1}\vert}^{2}}\bigg) {({g}_{1})}_{z} + \bigg( \frac{ 1+{\vert g_{2}\vert}^{2} }{1- \overline{g_{1}}g_{2}} - 1 \bigg) \cdot \frac{g_{1}}{ 1+{\vert g_{1}\vert}^{2} } {(\overline{g_{1}})}_{z} \\ &= \frac{{\mathcal{L}}}{{(g_{1})}_{\overline{z}}} - \overline{F} [ g_{1} ( 1-{\vert g_{2}\vert}^{2} ) + g_{2} ( 1-{\vert g_{1}\vert}^{2} ) ] \end{align*} $$
and
$$ \begin{align*} \frac{{\mathcal{F}}_{z}}{{\mathcal{F}}} &= \frac{{(g_{2})}_{z \overline{z}}}{{(g_{2})}_{\overline{z}}} + \bigg(\frac{\overline{g_{1}}}{1-g_{2}\overline{g_{2}}} - \frac{\overline{g_{2}}}{1+{\vert g_{2}\vert}^{2}}\bigg) {({g}_{2})}_{z} + \bigg( \frac{ 1+{\vert g_{1}\vert}^{2} }{1- g_{1} \overline{g_{2}}} - 1 \bigg) \cdot \frac{g_{2}}{ 1+{\vert g_{2}\vert}^{2} } {(\overline{g_{2}})}_{z} \\ &= \frac{{\mathcal{R}}}{{(g_{2})}_{\overline{z}}} - \overline{F} [ g_{1} ( 1-{\vert g_{2}\vert}^{2} ) + g_{2} ( 1-{\vert g_{1}\vert}^{2} ) ]. \end{align*} $$
From these two equalities,
$$ \begin{align*} \frac{{\mathcal{L}}}{{(g_{1})}_{\overline{z}}} = \frac{{\mathcal{R}}}{{(g_{2})}_{\overline{z}}}, \end{align*} $$
which gives the desired implications: (2.2)
$\Longleftrightarrow \mathcal {L}=0 \Longleftrightarrow \mathcal {R}=0 \Longleftrightarrow $
(2.3).
Step B. We deduce several equalities which will be used in the proof of (b) and (c). According to (a), from now on, we assume that both (2.2) and (2.3) hold. Since both
$\mathcal {L}$
and
$\mathcal {R}$
vanish, the previous equalities imply
$$ \begin{align*} {\mathcal{F}}_{z} = - {\vert \mathcal{F} \vert}^{2} [ g_{1} ( 1-\vert g_{2}\vert^{2} ) + g_{2} ( 1-{\vert g_{1}\vert}^{2} ) ]. \end{align*} $$
Conjugating this and using the definition
$f=-2i{\overline {\mathcal {F}}}$
, we arrive at the equality
$$ \begin{align} {f}_{\overline{z}} = \frac{i}{2} {\vert f \vert}^{2} [ \overline{g_{1}} ( 1-{\vert g_{2}\vert}^{2} ) + \overline{g_{2}} ( 1-{\vert g_{1}\vert}^{2} ) ]. \end{align} $$
The compatibility condition (2.1) can be written in terms of
$f=-2i{\overline {\mathcal {F}}}$
as
$$ \begin{align} \overline{f} =\frac{2i{({g}_{1})}_{\overline{z}}}{(1-g_{1}\overline{g_{2}})(1+{\vert g_{1}\vert}^{2})} =\frac{2i{({g}_{2})}_{\overline{z}}}{(1-\overline{g_{1}}g_{2})(1+{\vert g_{2}\vert}^{2})}. \end{align} $$
It immediately follows from (2.4) and (2.5) that
$$ \begin{align} {(fg_{1} )}_{\overline{z}} = {f}_{\overline{z}} g_{1} + {(g_{1} )}_{\overline{z}} f = - \frac{i}{2} {\vert f \vert}^{2} ( 1 - 2 g_{1} \overline{g_{2}} + {\vert g_{1}\vert}^{2} {\vert g_{2}\vert}^{2} ) \end{align} $$
and
$$ \begin{align} {(fg_{2} )}_{\overline{z}} ={f}_{\overline{z}} g_{2} + {(g_{2} )}_{\overline{z}} f = - \frac{i}{2} {\vert f \vert}^{2} ( 1 - 2 \overline{g_{1}} g_{2} + {\vert g_{1}\vert}^{2} {\vert g_{2}\vert}^{2} ). \end{align} $$
Another computation taking into account (2.5) and (2.6) shows that
$$ \begin{align} {(fg_{1}g_{2} )}_{\overline{z}} = {(fg_{1} )}_{\overline{z}} g_{2} + {(g_{2} )}_{\overline{z}} fg_{1} = - \frac{i}{2} {\vert f \vert}^{2} [ {g_{1}} ( 1-{\vert g_{2}\vert}^{2} ) + {g_{2}} ( 1-{\vert g_{1}\vert}^{2} ) ]. \end{align} $$
Step C. Our aim here is to establish the claims in (b) on the complex curve
$$ \begin{align*} \phi=({\phi}_{1}, {\phi}_{2}, {\phi}_{3}, {\phi}_{4} )=f (1 + {g}_{1}{g}_{2}, i(1 - {g}_{1}{g}_{2}), {g}_{1} - {g}_{2}, -i({g}_{1} + {g}_{2}) ). \end{align*} $$
First, the equality in (b1) is obvious. Next, by the assumptions on
$g_{1}$
and
$g_{2}$
, we see that
$f=-2i{\overline {\mathcal {F}}}$
never vanishes. Assertion (b2) follows from the equality
$$ \begin{align} {\vert {\phi}_{1} \vert}^{2}+{\vert {\phi}_{2} \vert}^{2}+{\vert {\phi}_{3} \vert}^{2}+{\vert {\phi}_{4} \vert}^{2} = 2 {\vert f \vert}^{2} ( 1 + {\vert g_{1}\vert}^{2} ) ( 1 + {\vert g_{2}\vert}^{2} ). \end{align} $$
We employ the equalities in step B to show assertion (b3). Combining (2.4), (2.6), (2.7) and (2.8) and the definition of
$\phi $
, we obtain
$$ \begin{align} \begin{cases} {({\phi}_{1})}_{\overline{z}} = {\vert f \vert}^{2} [ ( 1 - {\vert g_{2} \vert}^{2} ) \mathrm{Im }\,g_{1} + ( 1 - {\vert g_{1} \vert}^{2} ) \mathrm{Im }\,g_{2} ], \\ {({\phi}_{2})}_{\overline{z}} = -{\vert f \vert}^{2} [ ( 1 - {\vert g_{2} \vert}^{2} ) \mathrm{Re }\,g_{1} + ( 1 - {\vert g_{1} \vert}^{2} ) \mathrm{Re }\,g_{2} ], \\ {({\phi}_{3})}_{\overline{z}} = \, 2 {\vert f \vert}^{2} \; \mathrm{Im }\, ( \overline{g_{1}} g_{2} ), \\ {({\phi}_{4})}_{\overline{z}} = -{\vert f \vert}^{2} [ 1 - 2 \mathrm{Re }\, ( \overline{g_{1}} g_{2} ) + {\vert g_{1} \vert}^{2} {\vert g_{2} \vert}^{2} ]. \end{cases} \end{align} $$
These four equalities guarantee the integrability condition
$$ \begin{align*} \bigg( \frac{\partial {\phi}_{1}}{\partial \overline{z}}, \frac{\partial {\phi}_{2}}{\partial \overline{z}}, \frac{\partial {\phi}_{3}}{\partial \overline{z}}, \frac{\partial {\phi}_{4}}{\partial \overline{z}} \bigg) \in {\mathbb{R}}^{4}. \end{align*} $$
Step D. We prove claims (c1), (c2) and (c3). Thanks to (b3), we can integrate the curve
$\phi $
. Since
$\Omega $
is simply connected, applying Lemma 2.1 to the complex curve
$\phi $
shows the existence of a function
$ {\mathbf {X}}=( x_{1}, x_{2}, x_{3}, x_{4} ): \Omega \rightarrow {\mathbb {R}}^{4}$
satisfying
$$ \begin{align*} {\mathbf{X}}_{z} = \phi=f ( 1 + {g}_{1}{g}_{2}, i(1 - {g}_{1}{g}_{2}), {g}_{1} - {g}_{2}, -i({g}_{1} + {g}_{2}) ). \end{align*} $$
This and the nullity of
$\phi $
guarantee that the mapping
$ {\mathbf {X}}$
is conformal. From (2.9), the induced metric
$ds^{2}= {\Lambda }^{2} {\vert dz\vert }^{2}$
by the immersion
${\mathbf {X}}$
is
$$ \begin{align} ds^{2}= {\Lambda}^{2} {\vert dz\vert}^{2}= 4 {\vert f \vert}^{2} ( 1 + {\vert g_{1}\vert}^{2} ) ( 1 + {\vert g_{2}\vert}^{2} ) {\vert dz\vert}^{2}. \end{align} $$
Since f never vanishes, this completes the proof of (c1). Combining (2.5) and (2.11) gives the equality in (c2). The integrability
${\mathbf {X}}_{z} = \phi $
and the definition of
$\phi $
give
$$ \begin{align*} [ {\mathbf{X}}_{z} ] = [ 1+{g}_{1}{g}_{2}, i(1-{g}_{1}{g}_{2}), {g}_{1}-{g}_{2}, -i({g}_{1}+{g}_{2})], \end{align*} $$
which completes the proof of (c3).
Step E. Finally, we prove claim (c4). First, we find the normal component of the vector field
$-\mathbf {e}_{4}=(0,0,0,-1)$
in terms of
$g_{1}$
and
$g_{2}$
. We compute
$$ \begin{align*} {(-\mathbf{e}_{4})}^{\perp} &= -\mathbf{e}_{4} - \bigg[ \bigg( \frac{ {\mathbf{X}}_{u}}{\Lambda} \cdot (-\mathbf{e}_{4} ) \bigg) \frac{ {\mathbf{X}}_{u}}{\Lambda} + \bigg( \frac{ {\mathbf{X}}_{v}}{\Lambda} \cdot (-\mathbf{e}_{4} ) \bigg) \frac{ {\mathbf{X}}_{v}}{\Lambda} \bigg] \\ &= -\mathbf{e}_{4} + \frac{2}{{\Lambda}^{2}} [ ( {\mathbf{X}}_{\overline{z}} \cdot \mathbf{e}_{4} ) {\mathbf{X}}_{z} + ( {\mathbf{X}}_{z} \cdot \mathbf{e}_{4} ) {\mathbf{X}}_{\overline{z}} ] \\ &= \begin{bmatrix} 0 \\ 0\\ 0 \\ -1 \end{bmatrix} + \frac{4}{{\Lambda}^{2}} \begin{bmatrix} \mathrm{Re }\, ( {\phi}_{1} \overline{{\phi}_{4}} ) \\ \mathrm{Re }\, ( {\phi}_{2} \overline{{\phi}_{4}} ) \\ \mathrm{Re }\, ( {\phi}_{3} \overline{{\phi}_{4}} ) \\ {\vert {\phi}_{4} \vert}^{2} \end{bmatrix}. \end{align*} $$
Combining this with (2.10), and (2.11) yields
$$ \begin{align*} {(-\mathbf{e}_{4})}^{\perp}= \frac{1}{( 1 + {\vert g_{1}\vert}^{2} ) ( 1 + {\vert g_{2}\vert}^{2} )} \begin{bmatrix} [ ( 1 - {\vert g_{2} \vert}^{2} ) \mathrm{Im }\,g_{1} + ( 1 - {\vert g_{1} \vert}^{2} ) \mathrm{Im }\,g_{2} ] \\ - [ ( 1 - {\vert g_{2} \vert}^{2} ) \mathrm{Re }\,g_{1} + (1 - {\vert g_{1} \vert}^{2} ) \mathrm{Re }\,g_{2} ] \\ 2 \; \mathrm{Im }\, ( \overline{g_{1}} g_{2} ) \\ - [ 1 - 2 \mathrm{Re }\, ( \overline{g_{1}} g_{2} ) + {\vert g_{1} \vert}^{2} {\vert g_{2} \vert}^{2} ] \end{bmatrix}. \end{align*} $$
Second, we find the mean curvature vector
$$ \begin{align*} \mathcal{H}={\triangle}_{ds^{2}} {\mathbf{X}}= \frac{4}{ {\Lambda}^{2} } \frac{\partial }{\partial \overline{z}} \bigg( \frac{\partial }{\partial z} {\mathbf{X}} \bigg) = \frac{4}{ {\Lambda}^{2} } {\phi}_{\overline{z}} \end{align*} $$
on the surface
$\Sigma =\mathbf {X}( \Omega )$
. Using this, (2.10) and (2.11), we can write the mean curvature vector
$\mathcal {H}$
in terms of
$g_{1}$
and
$g_{2}$
:
$$ \begin{align*} \mathcal{H}= \frac{1}{( 1 + {\vert g_{1}\vert}^{2} ) ( 1 + {\vert g_{2}\vert}^{2} )} \begin{bmatrix} \;\, [ ( 1 - {\vert g_{2} \vert}^{2} ) \mathrm{Im }\,g_{1} + ( 1 - {\vert g_{1} \vert}^{2} ) \mathrm{Im }\,g_{2} ] \\ - [ ( 1 - {\vert g_{2} \vert}^{2} ) \mathrm{Re }\,g_{1} + ( 1 - {\vert g_{1} \vert}^{2} ) \mathrm{Re }\,g_{2} ] \\ 2 \; \mathrm{Im } \, ( \overline{g_{1}} g_{2} ) \\ - [ 1 - 2 \mathrm{Re }\, ( \overline{g_{1}} g_{2} ) + {\vert g_{1} \vert}^{2} {\vert g_{2} \vert}^{2} ] \end{bmatrix}. \end{align*} $$
We therefore conclude that
$\mathcal {H}={(-\mathbf {e}_{4})}^{\perp }$
.
Remark 2.3 (Ilmanen’s correspondence)
Theorem 2.2 generalises the classical Weierstrass construction from holomorphic null immersions in
${\mathbb {C}}^{3}$
to conformal minimal immersions in
${\mathbb {R}}^{3}$
. The key ingredient behind Theorem 2.2 is the Ilmanen correspondence between translators and minimal surfaces (see [Reference Ilmanen8, Reference White18]). We deform the flat metric of
${\mathbb {R}}^{4}$
conformally to introduce the four-dimensional Riemannian manifold
$$ \begin{align*} {\mathcal{I}}^{4}=( {\mathbb{R}}^{4}, e^{-x_{4}}(dx_{1}^{2}+ dx_{2}^{2}+dx_{3}^{2}+dx_{4}^{2}) ). \end{align*} $$
Any conformal immersion
${\mathbf {X}}: \Omega \rightarrow {\mathbb {R}}^{4}$
of a downward translator with the translating velocity
$-\mathbf {e}_{4}=(0,0,0,-1)$
in Euclidean space
${\mathbb {R}}^{4}$
can then be identified as a conformal minimal immersion
${\mathbf {X}}: \Omega \rightarrow {\mathcal {I}}^{4}$
.
Example 2.4 (The Hamiltonian stationary Lagrangian translator in
${\mathbb {C}}^{2}$
)
Interesting Lagrangian translators in the complex plane
${\mathbb {C}}^{2}$
are described in [Reference Castro and Lerma2, Reference Joyce, Lee and Tsui10, Reference Nakahara12]. In 2010, Castro and Lerma [Reference Castro and Lerma2, Corollary 2] classified all Hamiltonian stationary Lagrangian translators in
${\mathbb {C}}^{2}$
. Locally, they are unique up to dilations (except for the totally geodesic ones) [Reference Castro and Lerma2, Corollary 3]. The point of this example is to explicitly recover the Hoffman–Osserman Gauss map of the Castro–Lerma translator in
$\mathbb {R}^{4}={\mathbb {C}}^{2}$
.
We first notice that Theorem 2.2 still holds when we regard the prescribed Gauss map
$(g_{1}, g_{2})$
as a pair of functions from a simply connected domain
$\Omega $
to the complex plane (not just the unit disc). However, in this case, the induced mapping
${\mathbf {X}}: \Omega \rightarrow {\mathbb {R}}^{4}$
of the translator may admit the branch points where
$\overline {g_{1}}g_{2}=1$
(or equivalently,
${g_{1}\overline {g_{2}}=1}$
).
Imposing the additional condition
$\vert g_{1} \vert =1$
produces Lagrangian translators with the velocity
$-\mathbf {e}_{4}=( 0,0,0,-1 )$
. Then the integrability condition in (c1) for downward translators can be rewritten as
$$ \begin{align*} {\mathbf{X}}_{z} = ( {(x_{1})}_{z}, {(x_{2})}_{z}, {(x_{3})}_{z}, {(x_{4})}_{z} ) = - {\theta}_{z} \bigg(\frac{1+g_{1}g_{2}}{g_{1}-g_{2}}, i \frac{1-g_{1}g_{2}}{g_{1}-g_{2}}, 1, - i \frac{g_{1}+ g_{2}}{g_{1}-g_{2}} \bigg), \end{align*} $$
where
$\theta $
denotes the Lagrangian angle with
$ig_{1}=e^{i\theta }$
. The third term
${(x_{3})}_{z}=-{\theta }_{z}$
can be compared to [Reference Castro and Lerma2, Proposition 1], [Reference Joyce, Lee and Tsui10, Proposition 2.5] and [Reference Neves and Tian13, Proposition 2.1].
We consider a complexified Gauss map of the form,
$$ \begin{align*} ( g_{1}(z), g_{2}(z) ) = ( e^{iv}, \mathcal{G}(u) e^{iv} ),\quad z=u+iv \in \mathbb{R}+i\mathbb{R}, \end{align*} $$
for some
$\mathbb {R}$
-valued function
$\mathcal {G}$
, and aim to solve the system (2.1) and (2.2). First, the compatibility condition (2.1) induces the ordinary differential equation
$$ \begin{align*} \frac{1}{2} = \frac{1}{1+{\mathcal{G}}^{2}} \bigg( \mathcal{G} - \frac{d\mathcal{G}}{du} \bigg) \end{align*} $$
and a canonical solution is
$\mathcal {G}(u)={(u+1)}/{(u-1)}$
. It is straightforward to check that
$$ \begin{align*} ( g_{1}(z), g_{2}(z) ) = ( e^{iv}, \mathcal{G}(u) e^{iv} )= \bigg( e^{iv}, \frac{u+1}{u-1} e^{iv} \bigg) \end{align*} $$
satisfies the integrability condition (2.2). Then the induced Lagrangian translator
$\Sigma $
with the velocity
$-\mathbf {e}_{4}$
admits the conformal parameterisation
$$ \begin{align*} {\mathbf{X}}(u, v) = \big( u \sin v, - u \cos v, -v, - \tfrac{1}{2} u^{2} \big). \end{align*} $$
Since the induced metric on
$\Sigma $
is
$ds^{2} = ( 1+ u^{2} ) ( du^{2} + dv^{2} )$
, the Lagrangian angle function
$\theta (u,v) = \tfrac 12\pi + v$
with
$ig_{1}=e^{i\theta }$
is harmonic on
$\Sigma $
. This Hamiltonian stationary Lagrangian translator
$\Sigma $
with the velocity
$( 0,0,0,-1 )$
coincides with the Castro–Lerma translator [Reference Castro and Lerma2, Corollary 2] with the velocity
$(1,0,0,0 )$
by a suitable change of coordinates.
Theorem 2.5 (Correspondence from null curves in
${\mathbb {C}}^{3}$
to translators in
${\mathbb {R}}^{3}$
)
Given a nowhere-holomorphic
${\mathcal {C}}^{2}$
function
$G:\Omega \rightarrow \mathbb {D}$
from a simply connected domain
$\Omega \subset \mathbb {C}$
to the open unit disc
$\mathbb {D}:=\{w \in \mathbb {C} \; \vert \; \vert w \vert < 1 \}$
satisfying the translator equation
$$ \begin{align} {G}_{z \overline{z}} + 2 \frac{ \overline{G} \, {\vert G \vert}^{2}}{ 1 -{\vert G \vert}^{4} } G_{z} G_{\overline{z}} + 2 \frac{ G }{ 1 -{\vert G \vert}^{4}} {\vert G_{\overline{z}} \vert}^{2}=0, \quad z \in \Omega, \end{align} $$
we associate a complex curve
$\phi ={\phi }_{{}_{G}}=({\phi }_{1}, {\phi }_{2}, {\phi }_{3}) : \Omega \rightarrow {\mathbb {C}}^{3}$
by
$$ \begin{align*} \phi = \frac{2 {\overline{G}}_{z} }{ {\vert G \vert}^{4} -1 } ( 1-{G}^{2}, i ( 1 + G^{2} ), 2 G ). \end{align*} $$
-
(a) The complex curve
$\phi $
satisfies the following three properties on the domain
$\Omega $
:(a1) nullity:
$\phi \cdot \phi ={\phi }_{1}^{2} + {\phi }_{2}^{2} +{\phi }_{3}^{2}=0$
;(a2) nondegeneracy:
${\vert \phi \vert }^{2} ={\vert {\phi }_{1} \vert }^{2}+{\vert {\phi }_{2} \vert }^{2}+{\vert {\phi }_{3} \vert }^{2}>0$
;(a3) integrability:
${\partial {\phi } }/{\partial \overline {z}}= ( {\partial {\phi }_{1}}/{\partial \overline {z}},\ {\partial {\phi }_{2}}{\partial \overline {z}},\ {\partial {\phi }_{3}}/{\partial \overline {z}} ) \in {\mathbb {R}}^{3}$
.
-
(b) Integrating
${\mathbf {X}}_{z} = \phi $
on
$\Omega $
yields a downward translator
$\Sigma =\mathbf {X}( \Omega )$
with the velocity
$-\mathbf {e}_{3}=(0,0,-1)$
in
${\mathbb {R}}^{3}$
. The prescribed map G becomes the complexified Gauss map of the induced surface
$\Sigma =\mathbf {X}( \Omega )$
via the stereographic projection from the north pole. The induced metric
$ds^{2}$
by the immersion
${\mathbf {X}}$
is
$$ \begin{align*}ds^{2}= \frac{ 16 \, {\vert {G}_{\overline{z}} \vert}^{2} }{ {( {\vert G \vert}^{2} - 1 )}^{2} }{\vert dz \vert}^{2}.\end{align*} $$
Proof. We take
$(g_{1}, g_{2})=(iG, iG)$
in Theorem 2.2.
Remark 2.6. For the same Weierstrass representation formula for translators in
${\mathbb {R}}^{3}$
with the same Gauss map equation, see the recent preprint by Martínez and Martínez-Triviño [Reference Martínez and Martínez-Triviño11, Proposition 2.2 and Theorem 3.2].
Example 2.7 (Grim reaper product as an analogue of Scherk’s surface)
${}_{}$
-
(a) An application of our representation formula in Theorem 2.5 to the solution
of the translator equation (2.12) yields the conformal immersion
$$ \begin{align*} G(z)=G(u+iv)=\tanh u \in (-1,1), \quad u+iv \in {\mathbb{C}}, \end{align*} $$
$\mathbf {X}: {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}^{3}$
given by
$$ \begin{align*} \mathbf{X}(u,v)=(x_{1}, x_{2}, x_{3} ) = ( -2 {\tan}^{-1} ( \tanh u ), 2v, - \ln ( \cosh (2u) ) ), \end{align*} $$
-
(b) This represents the graphical translator with the translating velocity
$-\mathbf {e}_{3}$
: It can be viewed as an analogue of the classical Jenkins–Serrin minimal graph [Reference Jenkins and Serrin9, Reference Spruck17], discovered by Scherk in 1834,
$$ \begin{align*} x_{3} = \mathcal{F} ( x_{1}, x_{2} )= \ln ( \cos x_{1} ), \quad ( x_{1}, x_{2} ) \in \bigg(\! {-}\frac{\pi}{2} , \frac{\pi}{2} \bigg) \times {\mathbb{R}}. \end{align*} $$
$$ \begin{align*} x_{3} = \ln ( \cos x_{1} )-\ln ( \cos x_{2} ), \quad ( x_{1}, x_{2} ) \in \bigg(\! {-}\frac{\pi}{2} , \frac{\pi}{2} \bigg) \times \bigg(\! {-}\frac{\pi}{2} , \frac{\pi}{2} \bigg). \end{align*} $$
Example 2.8 (Deformations of the grim reaper product)
Let
$\theta \in \mathbb {R}$
be a constant.
-
(a) We begin with the solution
$G=G^{\theta }(z)$
of the translator equation (2.12): Theorem 2.5 induces the conformal immersion
$$ \begin{align*} G(z)=G(u+iv)=\frac{\cosh \theta \sinh (2u) + i \sinh \theta}{1+ \cosh \theta \cosh (2u)} , \quad u+iv \in {\mathbb{C}}. \end{align*} $$
${\mathbf {X}}^{\theta }=(x_{1}, x_{2}, x_{3} ): {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}^{3}$
given by The translator
$$ \begin{align*} \begin{cases} x_{1} (u,v) = -2 \cosh \theta \, {\tan}^{-1} ( \tanh u ), \\ x_{2} (u,v) = \sinh \theta \ln ( \cosh (2u) ) + 2v, \\ x_{3} (u,v) = - \ln ( \cosh (2u) ) + 2v \sinh \theta. \end{cases} \end{align*} $$
${\mathbf {G}}^{\theta }={\mathbf {X}}^{\theta }({\mathbb {R}}^{2})$
has the translating velocity
$(0,0,-1)$
.
-
(b) Using the patch
${\mathbf {X}}^{\theta }$
, we find that the Gauss map of the translator
${\mathbf {G}}^{\theta }$
lies on a half circle. Let us introduce a new linear coordinate and an orthonormal basis
$$ \begin{align*} x_{0}=\frac{1}{\cosh \theta} x_{2}+\frac{\sinh \theta}{\cosh \theta} x_{3} \end{align*} $$
The surface
$$ \begin{align*} {\mathcal{U}}_{1}=(1,0,0), \quad {\mathcal{U}}_{2}^{\theta} =\bigg(0,- \frac{\sinh \theta}{\cosh \theta},\frac{1}{\cosh \theta}\bigg), \quad {\mathcal{U}}_{3}^{\theta}=\bigg(0,\frac{1}{\cosh \theta},\frac{\sinh \theta}{\cosh \theta}\bigg). \end{align*} $$
${\mathbf {G}}^{\theta }$
admits a patch Here,
$$ \begin{align*} (x_{1}, x_{2}, x_{3} ) = {\widehat{\mathbf{X}}}^{\theta}(x_{1},x_{0}) = x_{1} \, {\mathcal{U}}_{1} + {\mathbf{T}}^{\theta}(x_{1}) \, {\mathcal{U}}_{2}^{\theta} + x_{0} \, {\mathcal{U}}_{3}^{\theta}. \end{align*} $$
${\mathbf {T}}^{\theta }(\cdot )=\cosh \theta \ln ( \cos ( {\cdot }/{\cosh \theta } ) )$
is a parabolic rescaling of the downward unit-speed grim reaper function. The surface
${\mathbf {G}}^{\theta }$
can be obtained by translating a parabolically rescaled grim reaper curve in the plane spanned by
${\mathcal {U}}_{1}$
and
${\mathcal {U}}_{2}^{\theta }$
.
-
(c) The one-parameter family
$\{{\mathbf {G}}^{\theta }\}_{\theta \in {\mathbb {R}}}$
of translators with the same translating velocity has a simple geometric description. Applying a suitable rotation in the ambient space
${\mathbb {R}}^{3}$
to the grim reaper product
${\mathbf {G}}^{0}$
with velocity
$-{\mathcal {U}}_{2}^{0}=(0,0,-1)$
, we obtain the congruent surface parameterised by
$$ \begin{align*} (x_{1}, x_{0}) \in \bigg(\! {-}\frac{\pi}{2}, \frac{\pi}{2} \bigg) \times \mathbb{R} \mapsto {\widehat{\mathbf{X}}}^{0}(x_{1},x_{0}) = x_{1} {\mathcal{U}}_{1} + {\mathbf{T}}^{0}(x_{1}) {\mathcal{U}}_{2}^{0} + x_{0} {\mathcal{U}}_{3}^{0}, \end{align*} $$
$$ \begin{align*} (x_{1}, x_{0}) \in \bigg(\! {-}\frac{\pi}{2}, \frac{\pi}{2} \bigg) \times \mathbb{R} \mapsto x_{1} {\mathcal{U}}_{1} + {\mathbf{T}}^{0}(x_{1}) {\mathcal{U}}_{2}^{\theta} + x_{0} {\mathcal{U}}_{3}^{\theta}, \end{align*} $$
which translates with the rotated velocity
$-{\mathcal {U}}_{2}^{\theta }$
under the mean curvature flow. However, we observe that this rotated surface can also be viewed as a translator with new velocity
${-}\cosh \theta \, {\mathcal {U}}_{2}^{0}=(0,0,{-}\cosh \theta )$
. The surface
${\mathbf {G}}^{\theta }$
parameterised by translates with velocity
$$ \begin{align*} (x_{1}, x_{0}) \in \bigg(\! {-}\frac{\pi}{2}\cosh \theta, \frac{\pi}{2}\cosh \theta \bigg) \times \mathbb{R} \mapsto {\widehat{\mathbf{X}}}^{\theta}(x_{1},x_{0}) = x_{1} {\mathcal{U}}_{1} + {\mathbf{T}}^{\theta}(x_{1}) {\mathcal{U}}_{2}^{\theta} + x_{0} {\mathcal{U}}_{3}^{\theta}, \end{align*} $$
$-{\mathcal {U}}_{2}^{0}=(0,0,-1)$
under the mean curvature flow.
