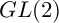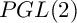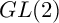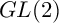1 Introduction
Let
![]() $p \geq 5$
be a prime, which is our assumption throughout the article. Let G be a compact noncommutative torsion-free p-adic analytic group. Let
$p \geq 5$
be a prime, which is our assumption throughout the article. Let G be a compact noncommutative torsion-free p-adic analytic group. Let
![]() $\Lambda (G)={\mathbb Z}_p[[G]]$
be the Iwasawa algebra of G. An ideal J of
$\Lambda (G)={\mathbb Z}_p[[G]]$
be the Iwasawa algebra of G. An ideal J of
![]() $\Lambda (G)$
is called left reflexive ideal if the natural map
$\Lambda (G)$
is called left reflexive ideal if the natural map
is an isomorphism as
![]() $\Lambda (G)$
-modules. We can also define a right reflexive ideal in a similar fashion. A two-sided ideal is called reflexive if it is both right and left reflexive. In [Reference ArdakovA], Ardakov showed that if
$\Lambda (G)$
-modules. We can also define a right reflexive ideal in a similar fashion. A two-sided ideal is called reflexive if it is both right and left reflexive. In [Reference ArdakovA], Ardakov showed that if
![]() $G \cong H \times C$
where H is a torsion-free pro-p group with split semisimple Lie algebra and
$G \cong H \times C$
where H is a torsion-free pro-p group with split semisimple Lie algebra and
![]() $C\cong {\mathbb Z}_p$
, the two-sided reflexive ideals of G are of the form
$C\cong {\mathbb Z}_p$
, the two-sided reflexive ideals of G are of the form
![]() $J=f\Lambda (G) $
, where f is a distinguished polynomial in
$J=f\Lambda (G) $
, where f is a distinguished polynomial in
![]() $\Lambda (C)$
(see [Reference ArdakovA, Cor. 4.8]).
$\Lambda (C)$
(see [Reference ArdakovA, Cor. 4.8]).
Reflexive ideals occur naturally in the study of Selmer groups of elliptic curves with good ordinary reduction at p over noncommutative p-adic Lie towers. More precisely, let E be an elliptic curve over a number field F such that E has good ordinary reduction at all the primes of F lying over an odd prime p. Let
![]() $F_{\infty }=F[E_{p^{\infty }}]$
be the noncommutative p-adic Lie extension with Galois group
$F_{\infty }=F[E_{p^{\infty }}]$
be the noncommutative p-adic Lie extension with Galois group
![]() $G={\mathrm {Gal}}(F_{\infty }/F)$
having center C. Since
$G={\mathrm {Gal}}(F_{\infty }/F)$
having center C. Since
![]() $p \geq 5$
, G is p-torsion-free compact p-adic Lie group (cf. Lemma 2.1). We also assume throughout our article that G is a pro-p group. Therefore,
$p \geq 5$
, G is p-torsion-free compact p-adic Lie group (cf. Lemma 2.1). We also assume throughout our article that G is a pro-p group. Therefore,
![]() $\Lambda (G)$
is an Auslander regular local ring [Reference VenjakobV, Th. 3.26]. Let
$\Lambda (G)$
is an Auslander regular local ring [Reference VenjakobV, Th. 3.26]. Let
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
be the Pontryagin dual of the Selmer group over
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
be the Pontryagin dual of the Selmer group over
![]() $F_{\infty }$
; it is easily seen to be a finitely generated module over the Iwasawa algebra
$F_{\infty }$
; it is easily seen to be a finitely generated module over the Iwasawa algebra
![]() $\Lambda (G)$
. In [Reference CoatesCFK+], the authors study Iwasawa theory over this noncommutative extension
$\Lambda (G)$
. In [Reference CoatesCFK+], the authors study Iwasawa theory over this noncommutative extension
![]() $F_{\infty }$
. If
$F_{\infty }$
. If
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is torsion (see Theorem 2.4), we have the following (weak) structure theorem:
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is torsion (see Theorem 2.4), we have the following (weak) structure theorem:
where
![]() $J_i$
are nonzero left reflexive ideals in
$J_i$
are nonzero left reflexive ideals in
![]() $\Lambda (G)$
and
$\Lambda (G)$
and
![]() $\sim $
is a pseudoisomorphism of left
$\sim $
is a pseudoisomorphism of left
![]() $\Lambda (G)$
-modules [Reference CremonaCSS, p. 74]. Note that Ardakov’s result mentioned above only applies to two-sided reflexive ideals. However, there can be ideals in the structure theorem which are left reflexive but not right reflexive. Note also that Ardakov’s result does not give us whether a particular two-sided reflexive ideal actually appears in the structure theorem for Selmer groups in (1.1). Therefore, in order to better understand the structure of the Selmer groups, it is crucial to classify all the reflexive (left) ideals that can occur in the decomposition in (1.1).
$\Lambda (G)$
-modules [Reference CremonaCSS, p. 74]. Note that Ardakov’s result mentioned above only applies to two-sided reflexive ideals. However, there can be ideals in the structure theorem which are left reflexive but not right reflexive. Note also that Ardakov’s result does not give us whether a particular two-sided reflexive ideal actually appears in the structure theorem for Selmer groups in (1.1). Therefore, in order to better understand the structure of the Selmer groups, it is crucial to classify all the reflexive (left) ideals that can occur in the decomposition in (1.1).
Our point of interest in this article is to understand when the augmentation ideal
![]() $I(C)$
can occur in the decomposition in (1.1). We show that this question is crucially related with the question of understanding whether the dual Selmer group for the
$I(C)$
can occur in the decomposition in (1.1). We show that this question is crucially related with the question of understanding whether the dual Selmer group for the
![]() $PGL(2)$
extension is torsion over the corresponding Iwasawa algebra. In the following, we discuss the main result in our article.
$PGL(2)$
extension is torsion over the corresponding Iwasawa algebra. In the following, we discuss the main result in our article.
Let
![]() $K_{\infty }$
be the fixed field of
$K_{\infty }$
be the fixed field of
![]() $F_{\infty }$
under the center C. Let
$F_{\infty }$
under the center C. Let
![]() ${\mathrm {Sel}}(E/K_{\infty })$
be the Selmer group over
${\mathrm {Sel}}(E/K_{\infty })$
be the Selmer group over
![]() $K_{\infty }$
; its dual is again a finitely generated module over the Iwasawa algebra
$K_{\infty }$
; its dual is again a finitely generated module over the Iwasawa algebra
![]() $\Lambda ({\mathrm {PG}})=\Lambda (G/C)$
. As
$\Lambda ({\mathrm {PG}})=\Lambda (G/C)$
. As
![]() $p\geq 5$
, one easily obtains that
$p\geq 5$
, one easily obtains that
![]() ${\mathrm {PG}}$
has no p-torsion (cf. Lemma 2.1). Since Iwasawa algebras of compact, p-torsion-free, p-adic Lie groups are Auslander regular [Reference VenjakobV, Th. 3.26],
${\mathrm {PG}}$
has no p-torsion (cf. Lemma 2.1). Since Iwasawa algebras of compact, p-torsion-free, p-adic Lie groups are Auslander regular [Reference VenjakobV, Th. 3.26],
![]() $\Lambda ({\mathrm {PG}})$
is also an Auslander regular local ring. By using our main theorem (see Theorem 1.1), we can classify when
$\Lambda ({\mathrm {PG}})$
is also an Auslander regular local ring. By using our main theorem (see Theorem 1.1), we can classify when
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is cotorsion as a
${\mathrm {Sel}}(E/K_{\infty })$
is cotorsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module in terms of the ideals
$\Lambda ({\mathrm {PG}})$
-module in terms of the ideals
![]() $J_i$
. We can prove that all the ideals
$J_i$
. We can prove that all the ideals
![]() $J_i$
cannot be the augmentation ideal
$J_i$
cannot be the augmentation ideal
![]() $I(C)$
(because the center cannot act trivially on
$I(C)$
(because the center cannot act trivially on
![]() ${\mathrm {Sel}}(E/F_{\infty })$
; see Proposition 3.8). Now, on the one hand, if any of these ideals is
${\mathrm {Sel}}(E/F_{\infty })$
; see Proposition 3.8). Now, on the one hand, if any of these ideals is
![]() $I(C)$
, then
$I(C)$
, then
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is not a cotorsion
${\mathrm {Sel}}(E/K_{\infty })$
is not a cotorsion
![]() $\Lambda ({\mathrm {PG}})$
-module. On the other hand, if none of the ideals are contained in
$\Lambda ({\mathrm {PG}})$
-module. On the other hand, if none of the ideals are contained in
![]() $I(C)$
, then
$I(C)$
, then
![]() ${{\mathrm {Sel}}(E/K_{\infty })}$
is a cotorsion
${{\mathrm {Sel}}(E/K_{\infty })}$
is a cotorsion
![]() $\Lambda ({\mathrm {PG}})$
-module (see Theorem 3.6 and Remark 3.7). This gives a complete classification of when
$\Lambda ({\mathrm {PG}})$
-module (see Theorem 3.6 and Remark 3.7). This gives a complete classification of when
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
can be a torsion
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
can be a torsion
![]() $\Lambda ({\mathrm {PG}})$
-module.
$\Lambda ({\mathrm {PG}})$
-module.
Under suitable hypotheses, Coates showed that the dual Selmer group over the
![]() $GL(2)$
extension is torsion over
$GL(2)$
extension is torsion over
![]() $\Lambda (G)$
(cf. [Reference Coates and HowsonCo1, Th. 4.5]). In particular, in [Reference Coates and HowsonCo1, Th. 4.5], it was shown that if the dual Selmer group of the elliptic curve over the cyclotomic extension is torsion and has
$\Lambda (G)$
(cf. [Reference Coates and HowsonCo1, Th. 4.5]). In particular, in [Reference Coates and HowsonCo1, Th. 4.5], it was shown that if the dual Selmer group of the elliptic curve over the cyclotomic extension is torsion and has
![]() $\mu $
-invariant zero, then the dual Selmer group of the elliptic curve over the
$\mu $
-invariant zero, then the dual Selmer group of the elliptic curve over the
![]() $GL(2)$
extension is
$GL(2)$
extension is
![]() $\Lambda (G)$
-torsion. As a consequence of our main result in this article, we can show that if the dual Selmer group of the elliptic curve over the
$\Lambda (G)$
-torsion. As a consequence of our main result in this article, we can show that if the dual Selmer group of the elliptic curve over the
![]() ${\mathrm {PGL}}(2)$
extension is torsion, this implies that the dual Selmer group over the
${\mathrm {PGL}}(2)$
extension is torsion, this implies that the dual Selmer group over the
![]() $GL(2)$
extension is also torsion. Hence, our result gives an alternative criterion under which the dual Selmer group of the elliptic curve over the
$GL(2)$
extension is also torsion. Hence, our result gives an alternative criterion under which the dual Selmer group of the elliptic curve over the
![]() $GL(2)$
extension is torsion.
$GL(2)$
extension is torsion.
Our main result can be summarized as follows (see Theorems 3.1 and 3.5).
Theorem 1.1. Let
![]() $p \geq 5$
, and let G be a pro-p compact p-adic Lie group.
$p \geq 5$
, and let G be a pro-p compact p-adic Lie group.
-
1. As
 $\Lambda ({\mathrm {PG}})$
-modules, the Selmer group
$\Lambda ({\mathrm {PG}})$
-modules, the Selmer group
 ${\mathrm {Sel}}(E/K_{\infty })$
is isomorphic to the Selmer group
${\mathrm {Sel}}(E/K_{\infty })$
is isomorphic to the Selmer group
 ${\mathrm {Sel}}(E/F_{\infty })$
invariant by the center C.
${\mathrm {Sel}}(E/F_{\infty })$
invariant by the center C. -
2. The dual Selmer group
 $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
 $\Lambda ({\mathrm {PG}})$
-module if and only if
$\Lambda ({\mathrm {PG}})$
-module if and only if
 $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
 $\Lambda (G)$
-module and
$\Lambda (G)$
-module and
 $H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})=0$
.
$H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})=0$
.
Furthermore, any of the following conditions are sufficient to conclude that
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
![]() $\Lambda ({\mathrm {PG}})$
-module.
$\Lambda ({\mathrm {PG}})$
-module.
-
• The Selmer group
 ${\mathrm {Sel}}(E/F)$
is finite and
${\mathrm {Sel}}(E/F)$
is finite and
 $H_2({\mathrm {PG}}, \widehat {{\mathrm {Sel}}(E/K_{\infty })})$
is finite.
$H_2({\mathrm {PG}}, \widehat {{\mathrm {Sel}}(E/K_{\infty })})$
is finite. -
• The Selmer group
 ${\mathrm {Sel}}(E/F)$
is finite,
${\mathrm {Sel}}(E/F)$
is finite,
 $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
 $\Lambda (G)$
-module, and
$\Lambda (G)$
-module, and
 $H_0({\mathrm {PG}}, H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})$
is finite.
$H_0({\mathrm {PG}}, H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})$
is finite.
Note that part (1) of the theorem above gives an isomorphism and not just a pseudo-isomorphism, whereas the natural map
has finite kernel and cokernel (see Theorem 4.2). We could prove part (2) only because of the interesting isomorphism in part (1). In the context of Iwasawa theory over a noncommutative p-adic Lie extension, one mainly considers admissible p-adic Lie extensions. We define a Galois extension
![]() $M_{\infty }$
of F to be an admissible p-adic Lie extension of F if (i)
$M_{\infty }$
of F to be an admissible p-adic Lie extension of F if (i)
![]() $ {\mathrm {Gal}}(M_{\infty }/F)$
is a p-adic Lie group, (ii)
$ {\mathrm {Gal}}(M_{\infty }/F)$
is a p-adic Lie group, (ii)
![]() $ M_{\infty } /F$
is unramified outside a finite set of primes of F, and (iii)
$ M_{\infty } /F$
is unramified outside a finite set of primes of F, and (iii)
![]() $ M_{\infty }$
contains the cyclotomic
$ M_{\infty }$
contains the cyclotomic
![]() ${\mathbb Z}_p$
-extension of F [Reference Coates and SujathaCS2, §2]. Results from cyclotomic Iwasawa theory are then used to obtain results in noncommutative Iwasawa theory. In this article, an attempt is made to rephrase the question of whether the two-sided reflexive ideal
${\mathbb Z}_p$
-extension of F [Reference Coates and SujathaCS2, §2]. Results from cyclotomic Iwasawa theory are then used to obtain results in noncommutative Iwasawa theory. In this article, an attempt is made to rephrase the question of whether the two-sided reflexive ideal
![]() $I(C)$
can occur in the structure theorem of
$I(C)$
can occur in the structure theorem of
![]() ${\mathrm {Sel}}(E/F_{\infty })$
in terms of whether
${\mathrm {Sel}}(E/F_{\infty })$
in terms of whether
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is cotorsion over
${\mathrm {Sel}}(E/K_{\infty })$
is cotorsion over
![]() $\Lambda ({\mathrm {PG}})$
. For this, we adopt a descent approach, since the
$\Lambda ({\mathrm {PG}})$
. For this, we adopt a descent approach, since the
![]() $PGL(2)$
extension does not contain the cyclotomic extension. For our descent argument, we use
$PGL(2)$
extension does not contain the cyclotomic extension. For our descent argument, we use
![]() $GL(2)$
Iwasawa theory to try and gain insights into
$GL(2)$
Iwasawa theory to try and gain insights into
![]() $PGL(2)$
Iwasawa theory. Moreover, we also ascend the Iwasawa theoretic tower from the
$PGL(2)$
Iwasawa theory. Moreover, we also ascend the Iwasawa theoretic tower from the
![]() $PGL(2)$
extension to the
$PGL(2)$
extension to the
![]() $GL(2)$
extension and derive conditions when the dual Selmer group over the
$GL(2)$
extension and derive conditions when the dual Selmer group over the
![]() $GL(2)$
extension is torsion.
$GL(2)$
extension is torsion.
Another reason to consider the
![]() $PGL(2)$
extension is the following. The Lie algebra of
$PGL(2)$
extension is the following. The Lie algebra of
![]() $PGL(2)$
is a simple (noncommutative) Lie algebra. Unlike
$PGL(2)$
is a simple (noncommutative) Lie algebra. Unlike
![]() $SL(2)$
, the
$SL(2)$
, the
![]() $PGL(2)$
extension occurs naturally as a p-adic Lie extension of the number field F in Iwasawa theory of elliptic curves. Over the
$PGL(2)$
extension occurs naturally as a p-adic Lie extension of the number field F in Iwasawa theory of elliptic curves. Over the
![]() $GL(2)$
extension,
$GL(2)$
extension,
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })} \otimes _{{\mathbb Z}_p} {\mathbb Q}_p$
is an infinite dimensional
$\widehat {{\mathrm {Sel}}(E/F_{\infty })} \otimes _{{\mathbb Z}_p} {\mathbb Q}_p$
is an infinite dimensional
![]() ${\mathbb Q}_p$
-representation [Reference Coates and HowsonCo1, Th. 1.5]. Therefore, it is interesting to explore if the corresponding result holds for
${\mathbb Q}_p$
-representation [Reference Coates and HowsonCo1, Th. 1.5]. Therefore, it is interesting to explore if the corresponding result holds for
![]() $PGL(2)$
extension. One can also enquire if the Lie algebra representation theory of
$PGL(2)$
extension. One can also enquire if the Lie algebra representation theory of
![]() $PGL(2)$
enables us to study the module structure of the dual Selmer group
$PGL(2)$
enables us to study the module structure of the dual Selmer group
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
, and thus giving us more insight into the arithmetic theory of elliptic curves.
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
, and thus giving us more insight into the arithmetic theory of elliptic curves.
This article consists of four sections including the introduction. In §2, we set up notation and collect the preliminary results that are needed. In §3, the defining exact sequences for the Selmer groups are used to compare the Selmer groups over the
![]() $GL(2)$
extension and the
$GL(2)$
extension and the
![]() $PGL(2)$
extension (see Theorem 3.1). Furthermore, using a descent approach from the Selmer group over the
$PGL(2)$
extension (see Theorem 3.1). Furthermore, using a descent approach from the Selmer group over the
![]() $GL(2)$
extension, we prove various equivalent conditions that are sufficient to ensure that the dual Selmer over the
$GL(2)$
extension, we prove various equivalent conditions that are sufficient to ensure that the dual Selmer over the
![]() $PGL(2)$
extension is a cotorsion module over the corresponding Iwasawa algebra (see Theorems 3.5 and 3.6). As applications, §4 deals with regular growth of ranks of Selmer groups as we descend from the
$PGL(2)$
extension is a cotorsion module over the corresponding Iwasawa algebra (see Theorems 3.5 and 3.6). As applications, §4 deals with regular growth of ranks of Selmer groups as we descend from the
![]() $GL(2)$
extension to the
$GL(2)$
extension to the
![]() $PGL(2)$
extension (see Proposition 4.1). Moreover, we study the relation between the Selmer group over the base field F and the Selmer group over the
$PGL(2)$
extension (see Proposition 4.1). Moreover, we study the relation between the Selmer group over the base field F and the Selmer group over the
![]() $PGL(2)$
extension (see Theorem 4.2).
$PGL(2)$
extension (see Theorem 4.2).
Under the assumption that the dual Selmer group over the
![]() $PGL(2)$
extension is torsion, its Euler characteristic and the nonexistence of its nontrivial pseudonull submodules have been shown in §4. These questions have been dealt in Howson’s dissertation [Reference HowsonHo1, Th. 5.34] and Zerbes’ dissertation [Reference ZerbesZ, Chaps. 8 and 9], but our proofs are different and much simpler.
$PGL(2)$
extension is torsion, its Euler characteristic and the nonexistence of its nontrivial pseudonull submodules have been shown in §4. These questions have been dealt in Howson’s dissertation [Reference HowsonHo1, Th. 5.34] and Zerbes’ dissertation [Reference ZerbesZ, Chaps. 8 and 9], but our proofs are different and much simpler.
It is clear that our methods in this article are extendable to a broader class of Galois representations. Our case of representations arising from elliptic curves should be seen as a first step.
2 Preliminaries
Lemma 2.1. For
![]() $p>n+1$
, there are no elements of p-power order in
$p>n+1$
, there are no elements of p-power order in
![]() $GL_n({\mathbb Z}_p) $
and
$GL_n({\mathbb Z}_p) $
and
![]() $PGL_n({\mathbb Z}_p)$
.
$PGL_n({\mathbb Z}_p)$
.
Proof. First, consider the case for
![]() $GL_n({\mathbb Z}_p) $
. Suppose
$GL_n({\mathbb Z}_p) $
. Suppose
![]() $X\in GL_n({\mathbb Z}_p)$
and
$X\in GL_n({\mathbb Z}_p)$
and
![]() $X^p=1$
. Since
$X^p=1$
. Since
![]() $X^p-1=(X-1)(X^{p-1}+\cdots +1)$
and
$X^p-1=(X-1)(X^{p-1}+\cdots +1)$
and
![]() $(X^{p-1}+\cdots +1)$
is irreducible over
$(X^{p-1}+\cdots +1)$
is irreducible over
![]() ${\mathbb Z}_p$
, we deduce that the minimal polynomial of X is of degree
${\mathbb Z}_p$
, we deduce that the minimal polynomial of X is of degree
![]() $p-1$
. We know that the characteristic polynomial of X is of degree n. Hence,
$p-1$
. We know that the characteristic polynomial of X is of degree n. Hence,
![]() $n \geq p-1$
, which is a contradiction.
$n \geq p-1$
, which is a contradiction.
Next, consider the case for
![]() $PGL_n({\mathbb Z}_p)$
. Suppose
$PGL_n({\mathbb Z}_p)$
. Suppose
![]() $X \in PGL_n({\mathbb Z}_p)$
and
$X \in PGL_n({\mathbb Z}_p)$
and
![]() $X^p=1$
. Let Z be a lift of X in
$X^p=1$
. Let Z be a lift of X in
![]() $GL(n,{\mathbb Z}_p)$
. Then
$GL(n,{\mathbb Z}_p)$
. Then
![]() $Z^p=cI_n$
for some
$Z^p=cI_n$
for some
![]() $c \in {\mathbb Z}_p$
(c is actually in
$c \in {\mathbb Z}_p$
(c is actually in
![]() ${\mathbb Z}_p^{\times }$
) and
${\mathbb Z}_p^{\times }$
) and
![]() $I_n$
is the identity matrix. Suppose c is not a pth power. Then the polynomial
$I_n$
is the identity matrix. Suppose c is not a pth power. Then the polynomial
![]() $T^p-c$
is irreducible. (This follows from a general fact that if F is a field, p is a prime, and
$T^p-c$
is irreducible. (This follows from a general fact that if F is a field, p is a prime, and
![]() $c\in F$
, then
$c\in F$
, then
![]() $x^p-c$
is irreducible in
$x^p-c$
is irreducible in
![]() $F[x]$
if and only if
$F[x]$
if and only if
![]() $x^p-c$
does not have any root in F.) Hence,
$x^p-c$
does not have any root in F.) Hence,
![]() $n\geq p$
, which is a contradiction.
$n\geq p$
, which is a contradiction.
Suppose
![]() $c=k^p$
where
$c=k^p$
where
![]() $k \in {\mathbb Z}_p^{\times }$
, then
$k \in {\mathbb Z}_p^{\times }$
, then
![]() $Z^p-cI_n=0$
is the same as
$Z^p-cI_n=0$
is the same as
![]() $(k^{-1}Z)^p-I_n=0$
. But then we can invoke the fact from
$(k^{-1}Z)^p-I_n=0$
. But then we can invoke the fact from
![]() $GL_n({\mathbb Z}_p)$
and deduce that
$GL_n({\mathbb Z}_p)$
and deduce that
![]() $k^{-1}Z=I_n$
which gives that
$k^{-1}Z=I_n$
which gives that
![]() $Z=kI_n$
and hence Z belongs to the center.
$Z=kI_n$
and hence Z belongs to the center.
Suppose
![]() $p \geq 5$
and G is a pro-p, compact open subgroup of
$p \geq 5$
and G is a pro-p, compact open subgroup of
![]() $GL_2({\mathbb Z}_p)$
with center C. Let
$GL_2({\mathbb Z}_p)$
with center C. Let
![]() ${\mathrm {PG}}$
be the quotient
${\mathrm {PG}}$
be the quotient
![]() $G/C$
. Then G and
$G/C$
. Then G and
![]() ${\mathrm {PG}}$
are p-torsion-free, and hence their Iwasawa algebras are Auslander regular local rings (cf. [Reference VenjakobV, Th. 3.26]) and so we have a dimension theory. Furthermore, the usual notion of rank of a module over these Iwasawa algebras (cf. [Reference VenjakobV, Def. 1.2]) coincides with the homological rank (see [Reference HowsonHo2]). The module is torsion if and only if its rank over the corresponding Iwasawa algebra is zero. Finally, note that the p-cohomological dimensions of G and
${\mathrm {PG}}$
are p-torsion-free, and hence their Iwasawa algebras are Auslander regular local rings (cf. [Reference VenjakobV, Th. 3.26]) and so we have a dimension theory. Furthermore, the usual notion of rank of a module over these Iwasawa algebras (cf. [Reference VenjakobV, Def. 1.2]) coincides with the homological rank (see [Reference HowsonHo2]). The module is torsion if and only if its rank over the corresponding Iwasawa algebra is zero. Finally, note that the p-cohomological dimensions of G and
![]() ${\mathrm {PG}}$
are
${\mathrm {PG}}$
are
![]() $4$
and
$4$
and
![]() $3$
, respectively.
$3$
, respectively.
Now, suppose G is not necessarily pro-p (still assuming
![]() $p>3$
). Let
$p>3$
). Let
![]() $G^{\prime }$
be a compact open pro-p subgroup of G. Both
$G^{\prime }$
be a compact open pro-p subgroup of G. Both
![]() $\Lambda (G)$
and
$\Lambda (G)$
and
![]() $\Lambda (G^{\prime })$
are Auslander regular integral domains. (This result does not need the pro-p assumption (see [Reference VenjakobV, Th. 3.36]).) Suppose M is a finitely generated
$\Lambda (G^{\prime })$
are Auslander regular integral domains. (This result does not need the pro-p assumption (see [Reference VenjakobV, Th. 3.36]).) Suppose M is a finitely generated
![]() $\Lambda (G)$
-module. Then M is
$\Lambda (G)$
-module. Then M is
![]() $\Lambda (G)$
-torsion if and only if
$\Lambda (G)$
-torsion if and only if
Given a finitely generated
![]() $\Lambda (G)$
-module M, there is an exact sequence
$\Lambda (G)$
-module M, there is an exact sequence
(see [Reference VenjakobV, Prop. 2.5]). This submodule
![]() ${\mathrm E}^1_{\Lambda (G)}DM$
is the
${\mathrm E}^1_{\Lambda (G)}DM$
is the
![]() $\Lambda (G)$
-torsion submodule of M (see [Reference VenjakobV, Def. 2.6]). Hence, the module M is said to be
$\Lambda (G)$
-torsion submodule of M (see [Reference VenjakobV, Def. 2.6]). Hence, the module M is said to be
![]() $\Lambda (G)$
-torsion if and only if
$\Lambda (G)$
-torsion if and only if
It is easy to see that if
![]() $G^{\prime }$
is an open pro-p subgroup, then there are natural isomorphisms
$G^{\prime }$
is an open pro-p subgroup, then there are natural isomorphisms
(see [Reference VenjakobV, Prop. 2.7(ii)] and the discussion after Definition 2.6 of [Reference VenjakobV]). Consequently, M is torsion as a
![]() $\Lambda (G)$
-module if and only if M is torsion as a
$\Lambda (G)$
-module if and only if M is torsion as a
![]() $\Lambda (G^{\prime })$
-module. Thus, in order to show that M is a torsion
$\Lambda (G^{\prime })$
-module. Thus, in order to show that M is a torsion
![]() $\Lambda (G)$
-module, it suffices to show that the homological rank of M as a
$\Lambda (G)$
-module, it suffices to show that the homological rank of M as a
![]() $\Lambda (G^{\prime })$
-module is zero. Since any compact p-adic analytic group contains an open characteristic subgroup which is uniform and extrapowerful pro-p group, one may study modules over
$\Lambda (G^{\prime })$
-module is zero. Since any compact p-adic analytic group contains an open characteristic subgroup which is uniform and extrapowerful pro-p group, one may study modules over
![]() $\Lambda (G^{\prime })$
by restriction of scalars (see [Reference VenjakobV, Rem. 3.23]).
$\Lambda (G^{\prime })$
by restriction of scalars (see [Reference VenjakobV, Rem. 3.23]).
Let E be an elliptic curve over a number field F without complex multiplication, and let
![]() $p\geq 5$
. Let us suppose that E has good ordinary reduction at the primes of F above p. Let S be a finite set of primes of F including those above
$p\geq 5$
. Let us suppose that E has good ordinary reduction at the primes of F above p. Let S be a finite set of primes of F including those above
![]() $\{p,\infty \} $
and the primes where E has bad reduction. Suppose
$\{p,\infty \} $
and the primes where E has bad reduction. Suppose
![]() $F_S$
is the maximal extension of F unramified outside S. Assume that
$F_S$
is the maximal extension of F unramified outside S. Assume that
![]() $H_{\infty }$
is an infinite Galois extension of F, contained in
$H_{\infty }$
is an infinite Galois extension of F, contained in
![]() $F_S$
, whose Galois group
$F_S$
, whose Galois group
![]() ${\mathrm {Gal}}(H_{\infty }/F)$
is a pro-p, compact, p-torsion-free, p-adic Lie group of positive dimension.
${\mathrm {Gal}}(H_{\infty }/F)$
is a pro-p, compact, p-torsion-free, p-adic Lie group of positive dimension.
For such a p-adic Lie extension
![]() $H_{\infty }$
of F, we can define the Selmer group of E over
$H_{\infty }$
of F, we can define the Selmer group of E over
![]() $H_{\infty }$
as a kernel of a natural global to local cohomological map defined by the following sequence:
$H_{\infty }$
as a kernel of a natural global to local cohomological map defined by the following sequence:
Here,
![]() $J_v(H_{\infty })$
’s are local cohomology groups defined as follows (cf. [Reference Coates and HowsonCo1, §3.1]). Let
$J_v(H_{\infty })$
’s are local cohomology groups defined as follows (cf. [Reference Coates and HowsonCo1, §3.1]). Let
![]() $H_{\infty }$
be the union of an increasing tower of finite extensions
$H_{\infty }$
be the union of an increasing tower of finite extensions
![]() $H_n$
of F. Let
$H_n$
of F. Let
![]() $v \in S$
, and for each n, denote by
$v \in S$
, and for each n, denote by
![]() $H_{n,\omega _n}$
the completion of
$H_{n,\omega _n}$
the completion of
![]() $H_n$
with respect to a prime
$H_n$
with respect to a prime
![]() $\omega _n$
of
$\omega _n$
of
![]() $H_n$
such that
$H_n$
such that
![]() $\omega _n$
divides v and such that
$\omega _n$
divides v and such that
![]() $\omega _n$
form a compatible sequence of primes
$\omega _n$
form a compatible sequence of primes
![]() $\omega _{n+1}\mid \omega _n$
. Then
$\omega _{n+1}\mid \omega _n$
. Then
where the limit is taken with respect to the restriction maps.
The Selmer group encodes several p-adic arithmetic information about the elliptic curve. It follows immediately from Kummer theory of E over
![]() $H_{\infty }$
that we have the following exact sequence:
$H_{\infty }$
that we have the following exact sequence:
where
is the Tate–Shafarevich group (cf. [Reference Coates and SujathaCS1, p. 15]).
It is easy to see that the dual Selmer group is a finitely generated module over the Iwasawa algebra
where W runs over all open normal subgroups of
![]() $\Omega ={\mathrm {Gal}}(H_{\infty }/F)$
. In the rest of the text,
$\Omega ={\mathrm {Gal}}(H_{\infty }/F)$
. In the rest of the text,
![]() $H_{\infty }$
is either the cyclotomic
$H_{\infty }$
is either the cyclotomic
![]() ${\mathbb Z}_p$
-extension of F, or a pro-p noncommutative
${\mathbb Z}_p$
-extension of F, or a pro-p noncommutative
![]() $GL(2)$
extension of F, or a pro-p noncommutative
$GL(2)$
extension of F, or a pro-p noncommutative
![]() $PGL(2)$
extension of F (see below). Since we are assuming
$PGL(2)$
extension of F (see below). Since we are assuming
![]() $p\geq 5$
, the corresponding Galois groups are p-torsion-free, pro-p, compact p-adic Lie groups. It is natural to study the structure of this Selmer group. In the classical case, when the group
$p\geq 5$
, the corresponding Galois groups are p-torsion-free, pro-p, compact p-adic Lie groups. It is natural to study the structure of this Selmer group. In the classical case, when the group
![]() $\Omega ={\mathrm {Gal}}(F_{\mathrm {cyc}}/F)\cong {\mathbb Z}_p$
is commutative, the Iwasawa algebra
$\Omega ={\mathrm {Gal}}(F_{\mathrm {cyc}}/F)\cong {\mathbb Z}_p$
is commutative, the Iwasawa algebra
![]() $\Lambda (\Omega )$
is a commutative local ring. One may then use the well-known structure theorem of finitely generated modules over
$\Lambda (\Omega )$
is a commutative local ring. One may then use the well-known structure theorem of finitely generated modules over
![]() $\Lambda ({\mathrm {Gal}}(F_{\mathrm {cyc}}/F))$
in this setting [Reference Backhausz and ZábrádiBo, Chap. VII, §4]. In the noncommutative cases, when
$\Lambda ({\mathrm {Gal}}(F_{\mathrm {cyc}}/F))$
in this setting [Reference Backhausz and ZábrádiBo, Chap. VII, §4]. In the noncommutative cases, when
![]() $\Omega $
is a compact pro-p, p-adic analytic group without p-torsion, the Iwasawa algebra
$\Omega $
is a compact pro-p, p-adic analytic group without p-torsion, the Iwasawa algebra
![]() $\Lambda (\Omega )$
is an Auslander regular local ring [Reference VenjakobV, Th. 3.26], and hence there is a dimension theory for modules in this setting. Suppose M is a finitely generated module over a noncommutative Iwasawa algebra
$\Lambda (\Omega )$
is an Auslander regular local ring [Reference VenjakobV, Th. 3.26], and hence there is a dimension theory for modules in this setting. Suppose M is a finitely generated module over a noncommutative Iwasawa algebra
![]() $\Lambda (\Omega )$
. Then M is a torsion
$\Lambda (\Omega )$
. Then M is a torsion
![]() $\Lambda (\Omega )$
-module if
$\Lambda (\Omega )$
-module if
![]() $\dim M \leq \dim \Lambda (\Omega ) - 1 $
. The module M is pseudonull if
$\dim M \leq \dim \Lambda (\Omega ) - 1 $
. The module M is pseudonull if
![]() $\dim M \leq \dim \Lambda (\Omega ) - 2$
(see [Reference VenjakobV, §3]). There is also a weak structure theorem [Reference CremonaCSS].
$\dim M \leq \dim \Lambda (\Omega ) - 2$
(see [Reference VenjakobV, §3]). There is also a weak structure theorem [Reference CremonaCSS].
Set
and write
By a well-known result of Serre [Reference SerreS], G is open in
![]() $GL_2({\mathbb Z}_p)$
for all primes and
$GL_2({\mathbb Z}_p)$
for all primes and
![]() $G=GL_2({\mathbb Z}_p)$
for all but a finite number of primes. Note that
$G=GL_2({\mathbb Z}_p)$
for all but a finite number of primes. Note that
![]() $F_{\infty }$
contains
$F_{\infty }$
contains
![]() $F_{\mathrm {cyc}}$
, the cyclotomic
$F_{\mathrm {cyc}}$
, the cyclotomic
![]() ${\mathbb Z}_p$
-extension over F with Galois group
${\mathbb Z}_p$
-extension over F with Galois group
![]() $\Gamma $
, a p-adic Lie group of dimension
$\Gamma $
, a p-adic Lie group of dimension
![]() $1$
.
$1$
.
A deep conjecture of [Reference MazurMa] asserts the following conjecture.
Conjecture 2.2.
![]() ${\mathrm {Sel}}(E/F_{\mathrm {cyc}})$
is a finitely generated cotorsion
${\mathrm {Sel}}(E/F_{\mathrm {cyc}})$
is a finitely generated cotorsion
![]() $\Lambda (\Gamma )$
-module.
$\Lambda (\Gamma )$
-module.
This conjecture is known to hold in some cases (e.g., when
![]() $F={\mathbb Q}$
), thanks to a celebrated result of Kato [Reference KatoK]. Coates and Howson in [Reference Coates, Fukaya, Kato, Sujatha and VenjakobCH1], [Reference Coates and GreenbergCH2], developed Iwasawa theory over the
$F={\mathbb Q}$
), thanks to a celebrated result of Kato [Reference KatoK]. Coates and Howson in [Reference Coates, Fukaya, Kato, Sujatha and VenjakobCH1], [Reference Coates and GreenbergCH2], developed Iwasawa theory over the
![]() $GL(2)$
extension
$GL(2)$
extension
![]() $F_{\infty }$
and provided conditions under which the Selmer group
$F_{\infty }$
and provided conditions under which the Selmer group
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion as a module over the noncommutative Iwasawa algebra
${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion as a module over the noncommutative Iwasawa algebra
![]() $\Lambda (G).$
In particular, they showed the following results (cf. Lemmas 4.7 and 4.8, Proposition 4.3, and Theorem 4.5 of [Reference Coates and HowsonCo1]).
$\Lambda (G).$
In particular, they showed the following results (cf. Lemmas 4.7 and 4.8, Proposition 4.3, and Theorem 4.5 of [Reference Coates and HowsonCo1]).
Theorem 2.3. If
![]() ${\mathrm {Sel}}(E/F)$
is finite, then
${\mathrm {Sel}}(E/F)$
is finite, then
![]() $H^i(G,{\mathrm {Sel}}(E/F_{\infty }))$
is finite for
$H^i(G,{\mathrm {Sel}}(E/F_{\infty }))$
is finite for
![]() $i=0,1$
. Additionally, if
$i=0,1$
. Additionally, if
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is
${\mathrm {Sel}}(E/F_{\infty })$
is
![]() $\Lambda (G)$
-cotorsion, then
$\Lambda (G)$
-cotorsion, then
![]() $H^i(G,{\mathrm {Sel}}(E/F_{\infty }))$
is
$H^i(G,{\mathrm {Sel}}(E/F_{\infty }))$
is
![]() $0$
for
$0$
for
![]() $i =2,3,4$
.
$i =2,3,4$
.
Theorem 2.4. If
![]() ${\mathrm {Sel}}(E/F_{{\mathrm {cyc}}})$
is a cotorsion
${\mathrm {Sel}}(E/F_{{\mathrm {cyc}}})$
is a cotorsion
![]() $\Lambda (\Gamma )$
-module and has
$\Lambda (\Gamma )$
-module and has
![]() $\mu $
-invariant
$\mu $
-invariant
![]() $0$
, then
$0$
, then
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is a cotorsion
${\mathrm {Sel}}(E/F_{\infty })$
is a cotorsion
![]() $\Lambda (G)$
-module.
$\Lambda (G)$
-module.
Coates and Howson have also calculated an explicit formula for the Euler characteristic
![]() $\chi (G,{\mathrm {Sel}}(E/F_{\infty })$
(cf. [Reference Coates and GreenbergCH2, Th. 1.1]) under the assumption that
$\chi (G,{\mathrm {Sel}}(E/F_{\infty })$
(cf. [Reference Coates and GreenbergCH2, Th. 1.1]) under the assumption that
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion as a
${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion as a
![]() $\Lambda (G)$
-module. Their point of view was to understand how Iwasawa theory over the cyclotomic extension
$\Lambda (G)$
-module. Their point of view was to understand how Iwasawa theory over the cyclotomic extension
![]() $F_{\mathrm {cyc}}$
influences the Iwasawa theory when one climbs up the tower to
$F_{\mathrm {cyc}}$
influences the Iwasawa theory when one climbs up the tower to
![]() $F_{\infty }$
.
$F_{\infty }$
.
Let N be a module endowed with the discrete topology and a continuous action of a profinite group G. Let H be a closed normal subgroup of G. Recall the Hochschild–Serre spectral sequence
We shall make repeated use of this sequence with
![]() $H=C$
, the center of G.
$H=C$
, the center of G.
3 Descent from
 $GL(2)$
Iwasawa theory to
$GL(2)$
Iwasawa theory to
 $PGL(2)$
Iwasawa theory
$PGL(2)$
Iwasawa theory
Let us make the following assumptions throughout the rest of this article. Assume that G is a pro-p group. Since
![]() $p \geq 5$
, we note that the compact p-adic pro-p Lie groups G, C, and
$p \geq 5$
, we note that the compact p-adic pro-p Lie groups G, C, and
![]() ${\mathrm {PG}}$
are all p-torsion-free and hence have p-cohomological dimensions
${\mathrm {PG}}$
are all p-torsion-free and hence have p-cohomological dimensions
![]() $4, 1$
, and
$4, 1$
, and
![]() $3$
, respectively. Hence, their Iwasawa algebras are all Auslander regular local rings by [Reference VenjakobV, Th. 3.26].
$3$
, respectively. Hence, their Iwasawa algebras are all Auslander regular local rings by [Reference VenjakobV, Th. 3.26].
From the Hochschild–Serre spectral sequence (see (2.2)) with
![]() $G={\mathrm {Gal}}(F_{\infty }/F)$
,
$G={\mathrm {Gal}}(F_{\infty }/F)$
,
![]() $H=C$
, and
$H=C$
, and
![]() $G/H={\mathrm {PG}}$
, it is easy to see that we obtain the commutative diagram (3.1) with exact rows.
$G/H={\mathrm {PG}}$
, it is easy to see that we obtain the commutative diagram (3.1) with exact rows.

The vertical maps are given by restriction maps. Our first objective is to prove the following theorem.
Theorem 3.1. The vertical maps
![]() $\alpha , \beta , \gamma $
in the fundamental diagram (3.1) are all isomorphisms. In particular,
$\alpha , \beta , \gamma $
in the fundamental diagram (3.1) are all isomorphisms. In particular,
as
![]() $\Lambda ({\mathrm {PG}})$
-modules.
$\Lambda ({\mathrm {PG}})$
-modules.
Proof. From the Hochschild–Serre spectral sequence, we have the following exact sequence:
Since the p-cohomological dimension of C is
![]() $1$
,
$1$
,
![]() $H^2(C,E_{p^{\infty }})=0$
, and hence the cokernel of the map
$H^2(C,E_{p^{\infty }})=0$
, and hence the cokernel of the map
![]() $\beta $
is zero. By applying Shapiro’s lemma (cf. the proof of [Reference Coates and HowsonCo1, Lem. 3.1]), we have the following exact sequence:
$\beta $
is zero. By applying Shapiro’s lemma (cf. the proof of [Reference Coates and HowsonCo1, Lem. 3.1]), we have the following exact sequence:
where w is a prime of
![]() $F_{\infty }$
above v and
$F_{\infty }$
above v and
![]() $\Theta _{w}^C$
is the decomposition group of C at w (see also [Reference Coates and GreenbergCH2, (19), (133), and (134)] for the corresponding exact sequence when
$\Theta _{w}^C$
is the decomposition group of C at w (see also [Reference Coates and GreenbergCH2, (19), (133), and (134)] for the corresponding exact sequence when
![]() $K_{\infty }$
is replaced by
$K_{\infty }$
is replaced by
![]() $F_{\mathrm {cyc}}$
). As
$F_{\mathrm {cyc}}$
). As
![]() $\Theta _{w}^C$
is a closed subgroup of C which is of dimension
$\Theta _{w}^C$
is a closed subgroup of C which is of dimension
![]() $1$
as a p-adic Lie group,
$1$
as a p-adic Lie group,
![]() $H^2(\Theta _{w}^C, E(F_{\infty , w}))(p)=0,$
which proves that the cokernel of
$H^2(\Theta _{w}^C, E(F_{\infty , w}))(p)=0,$
which proves that the cokernel of
![]() $\gamma _v$
is zero.
$\gamma _v$
is zero.
The following argument shows that
![]() $\ker (\beta )= H^1(C, E_{p^{\infty }})$
is zero. The congruence subgroups of
$\ker (\beta )= H^1(C, E_{p^{\infty }})$
is zero. The congruence subgroups of
![]() $GL_2({\mathbb Z}_p)$
form a base of neighborhood for its topology, and thus C must contain a scalar matrix
$GL_2({\mathbb Z}_p)$
form a base of neighborhood for its topology, and thus C must contain a scalar matrix
 $$\begin{align*}x= \left(\!\! {\begin{array}{cc} 1+p^n & 0 \\ 0 & 1+p^n \\ \end{array} } \!\!\right) \end{align*}$$
$$\begin{align*}x= \left(\!\! {\begin{array}{cc} 1+p^n & 0 \\ 0 & 1+p^n \\ \end{array} } \!\!\right) \end{align*}$$
for n sufficiently large. However, x lies in C, so
![]() $x-1$
annihilates
$x-1$
annihilates
![]() $H^1(C,E_{p^{\infty }})$
(see [Reference MilneMi, Chap. I, Lem. 6.21]). Therefore,
$H^1(C,E_{p^{\infty }})$
(see [Reference MilneMi, Chap. I, Lem. 6.21]). Therefore,
![]() $p^nH^1(C,E_{p^{\infty }})=0.$
Now, consider the short exact sequence
$p^nH^1(C,E_{p^{\infty }})=0.$
Now, consider the short exact sequence
As
![]() $p^nH^1(C,E_{p^{\infty }})=0$
, the long exact sequence corresponding to (3.3) gives rise to the following short exact sequence:
$p^nH^1(C,E_{p^{\infty }})=0$
, the long exact sequence corresponding to (3.3) gives rise to the following short exact sequence:
Now, C has p-cohomological dimension
![]() $1$
, and hence
$1$
, and hence
![]() $H^2(C,E_{p^n})=0$
. Therefore,
$H^2(C,E_{p^n})=0$
. Therefore,
![]() $H^1(C, E_{p^{\infty }})=0$
by (3.4). This shows that the map
$H^1(C, E_{p^{\infty }})=0$
by (3.4). This shows that the map
![]() $\beta $
is injective.
$\beta $
is injective.
Writing
![]() $\gamma =\oplus _{v \in S} \gamma _v$
, (3.2) gives
$\gamma =\oplus _{v \in S} \gamma _v$
, (3.2) gives
where w is a prime of
![]() $F_{\infty }$
above v and
$F_{\infty }$
above v and
![]() $\Theta _{w}^C$
is the decomposition group of C at w. In the following, it is shown that
$\Theta _{w}^C$
is the decomposition group of C at w. In the following, it is shown that
The decomposition subgroup
![]() $\Theta _w^C$
is a subgroup of C which is pro-p. Therefore,
$\Theta _w^C$
is a subgroup of C which is pro-p. Therefore,
![]() $\Theta _w^C$
is a subgroup of
$\Theta _w^C$
is a subgroup of
![]() $1+p{\mathbb Z}_p$
and hence a procyclic group. Choose
$1+p{\mathbb Z}_p$
and hence a procyclic group. Choose
![]() $\sigma $
to be a topological generator of
$\sigma $
to be a topological generator of
![]() $\Theta _w^C$
; for instance,
$\Theta _w^C$
; for instance,
![]() $\sigma =1+p^n$
for some n. By [Reference Neukirch, Schmidt and WingbergNS, Prop. 1.7.7],
$\sigma =1+p^n$
for some n. By [Reference Neukirch, Schmidt and WingbergNS, Prop. 1.7.7],
As
![]() $E_{p^{\infty }}$
is a p-divisible group,
$E_{p^{\infty }}$
is a p-divisible group,
![]() $E_{p^{\infty }}/p^nE_{p^{\infty }}=0$
, giving us
$E_{p^{\infty }}/p^nE_{p^{\infty }}=0$
, giving us
![]() $H^1(\Theta _w^C,E_{p^{\infty }})=0$
.
$H^1(\Theta _w^C,E_{p^{\infty }})=0$
.
If
![]() $v \nmid p$
, by Kummer theory [Reference GreenbergG, §2],
$v \nmid p$
, by Kummer theory [Reference GreenbergG, §2],
![]() $H^1(\Theta _{w}^C, E(F_{\infty , w}))(p)=H^1(\Theta _w^C,E_{p^{\infty }})$
, which vanishes by (3.6). This proves that
$H^1(\Theta _{w}^C, E(F_{\infty , w}))(p)=H^1(\Theta _w^C,E_{p^{\infty }})$
, which vanishes by (3.6). This proves that
![]() ${\mathrm {Ker}}(\gamma _v)=0$
when
${\mathrm {Ker}}(\gamma _v)=0$
when
![]() $v \nmid p$
.
$v \nmid p$
.
Now, suppose that
![]() $v \mid p$
. Let u be the prime of
$v \mid p$
. Let u be the prime of
![]() $K_{\infty }$
such that
$K_{\infty }$
such that
![]() $w\mid u$
and
$w\mid u$
and
![]() $u\mid v$
, and let
$u\mid v$
, and let
![]() $I_u$
be the inertia subgroup of
$I_u$
be the inertia subgroup of
![]() $K_{\infty }$
over F at the prime u. Since
$K_{\infty }$
over F at the prime u. Since
![]() $I_u$
is infinite,
$I_u$
is infinite,
![]() $K_{\infty , u}$
is deeply ramified (see [Reference Coates, Fieker and KohelCG]). It is also well known that
$K_{\infty , u}$
is deeply ramified (see [Reference Coates, Fieker and KohelCG]). It is also well known that
![]() $F_{\infty ,w}$
is deeply ramified.
$F_{\infty ,w}$
is deeply ramified.
Hence, [Reference Coates, Fieker and KohelCG, Prop. 4.8 and Th. 2.13] gives
where D can be identified with
![]() $\tilde {E}_{v,p^{\infty }}$
, the p-primary subgroup of the reduction of E modulo v. Note that E has good ordinary reduction at primes of F above p. By [Reference Coates, Fieker and KohelCG], the module D also satisfies the following exact sequence:
$\tilde {E}_{v,p^{\infty }}$
, the p-primary subgroup of the reduction of E modulo v. Note that E has good ordinary reduction at primes of F above p. By [Reference Coates, Fieker and KohelCG], the module D also satisfies the following exact sequence:
where
![]() $C^{\prime }$
is divisible and D is the maximal quotient of
$C^{\prime }$
is divisible and D is the maximal quotient of
![]() $E_{p^{\infty }}$
by a divisible subgroup such that
$E_{p^{\infty }}$
by a divisible subgroup such that
![]() $I_v$
acts on D via a finite quotient. Note that the following sequence is exact:
$I_v$
acts on D via a finite quotient. Note that the following sequence is exact:
Hence, using (3.7) and (3.8) into the above exact sequence, it is easy to see that
The exact sequence (3.9) gives that the following sequence
is exact. By (3.6), we know that
![]() $H^1(\Theta _w^C,E_{p^{\infty }}) =0$
, and since
$H^1(\Theta _w^C,E_{p^{\infty }}) =0$
, and since
![]() $\Theta _w^C$
is a subgroup of C which has p-cohomological dimension
$\Theta _w^C$
is a subgroup of C which has p-cohomological dimension
![]() $1$
, we have
$1$
, we have
![]() $H^2(\Theta _w^C,C)=0$
. Therefore, it is clear that
$H^2(\Theta _w^C,C)=0$
. Therefore, it is clear that
![]() $H^1(\Theta _w^C,D)=0, $
which shows that
$H^1(\Theta _w^C,D)=0, $
which shows that
![]() $\ker (\gamma _v)=0$
for
$\ker (\gamma _v)=0$
for
![]() $v \mid p$
.
$v \mid p$
.
Thus, the maps
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are isomorphisms. The theorem now follows from the snake lemma applied to the fundamental diagram (3.1).
$\gamma $
are isomorphisms. The theorem now follows from the snake lemma applied to the fundamental diagram (3.1).
Corollary 3.2. If
![]() $H^1(G, {\mathrm {Sel}}(E/F_{\infty }))$
is finite, then
$H^1(G, {\mathrm {Sel}}(E/F_{\infty }))$
is finite, then
![]() $H^1({\mathrm {PG}}, {\mathrm {Sel}}(E/K_{\infty }))$
is also finite.
$H^1({\mathrm {PG}}, {\mathrm {Sel}}(E/K_{\infty }))$
is also finite.
Proof. The assertion follows from the natural injection
and Theorem 3.1.
The reader is referred to Theorem 2.3 in §2 for cases where
![]() $H^1(G,{\mathrm {Sel}}(E/F_{\infty }))$
is known to be finite.
$H^1(G,{\mathrm {Sel}}(E/F_{\infty }))$
is known to be finite.
3.3 Conditions when the Selmer over
 ${\mathrm {PGL}}(2)$
extension is cotorsion
${\mathrm {PGL}}(2)$
extension is cotorsion
The following theorems give several conditions when
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module.
$\Lambda ({\mathrm {PG}})$
-module.
Theorem 3.4. Assume weak Leopoldt’s conjecture at
![]() $K_{\infty }$
, that is,
$K_{\infty }$
, that is,
![]() $H^2(F_S/K_{\infty }, E_{p^{\infty }})=0$
. Then the dual Selmer group
$H^2(F_S/K_{\infty }, E_{p^{\infty }})=0$
. Then the dual Selmer group
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is
![]() $\Lambda ({\mathrm {PG}})$
-torsion if and only if the map
$\Lambda ({\mathrm {PG}})$
-torsion if and only if the map
![]() $\lambda _{K_{\infty }}$
in (3.1) is surjective.
$\lambda _{K_{\infty }}$
in (3.1) is surjective.
Proof. The proof follows from [Reference Shekhar and SujathaSS, Th. 7.2].
Theorem 3.5. The dual Selmer group
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
![]() $\Lambda ({\mathrm {PG}})$
-module if any of the following conditions hold:
$\Lambda ({\mathrm {PG}})$
-module if any of the following conditions hold:
-
1. The Selmer group
 ${\mathrm {Sel}}(E/F)$
is finite and
${\mathrm {Sel}}(E/F)$
is finite and
 $H_2({\mathrm {PG}}, \widehat {{\mathrm {Sel}}(E/K_{\infty })})$
is finite.
$H_2({\mathrm {PG}}, \widehat {{\mathrm {Sel}}(E/K_{\infty })})$
is finite. -
2. The Selmer group
 ${\mathrm {Sel}}(E/F)$
is finite,
${\mathrm {Sel}}(E/F)$
is finite,
 $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
 $\Lambda (G)$
-module, and
$\Lambda (G)$
-module, and
 $H_0({\mathrm {PG}}, H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})$
is finite.
$H_0({\mathrm {PG}}, H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})$
is finite. -
3.
 $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a torsion
 $\Lambda (G)$
-module and
$\Lambda (G)$
-module and
 $H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})=0$
.
$H_1(C, \widehat {{\mathrm {Sel}}(E/F_{\infty })})=0$
.
Conversely, if
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
![]() $\Lambda ({\mathrm {PG}})$
-module, then
$\Lambda ({\mathrm {PG}})$
-module, then
![]() $(3)$
holds.
$(3)$
holds.
Proof. Let
![]() $M=\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
. We have
$M=\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
. We have
![]() $M_G \cong H_0({\mathrm {PG}},M_C)$
and
$M_G \cong H_0({\mathrm {PG}},M_C)$
and
![]() $M_C \cong \widehat {{\mathrm {Sel}}(E/K_{\infty })}$
. Now, since
$M_C \cong \widehat {{\mathrm {Sel}}(E/K_{\infty })}$
. Now, since
![]() ${\mathrm {Sel}}(E/F)$
is finite, by Theorem 2.3, it follows that
${\mathrm {Sel}}(E/F)$
is finite, by Theorem 2.3, it follows that
![]() $H_0({\mathrm {PG}}, M_C)$
is finite. By assumption,
$H_0({\mathrm {PG}}, M_C)$
is finite. By assumption,
![]() $H_2({\mathrm {PG}}, M_C)$
is also finite. Since
$H_2({\mathrm {PG}}, M_C)$
is also finite. Since
 $$ \begin{align*} {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M_C &=\sum_{k \geq 0}^{3}(-1)^k{\mathrm{rank}}_{{\mathbb Z}_p}H_k({\mathrm{PG}},M_C) \end{align*} $$
$$ \begin{align*} {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M_C &=\sum_{k \geq 0}^{3}(-1)^k{\mathrm{rank}}_{{\mathbb Z}_p}H_k({\mathrm{PG}},M_C) \end{align*} $$
(see [Reference HowsonHo2, Th. 1.1]), we obtain
![]() ${\mathrm {rank}}_{\Lambda ({\mathrm {PG}})}M_C=0$
and hence
${\mathrm {rank}}_{\Lambda ({\mathrm {PG}})}M_C=0$
and hence
![]() $M_C$
is
$M_C$
is
![]() $\Lambda ({\mathrm {PG}})$
-torsion. This shows that
$\Lambda ({\mathrm {PG}})$
-torsion. This shows that
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion as a
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module and hence proves that the condition (1) is sufficient.
$\Lambda ({\mathrm {PG}})$
-module and hence proves that the condition (1) is sufficient.
To show that the condition in (2) is also sufficient, note that if M is
![]() $\Lambda (G)$
-torsion and
$\Lambda (G)$
-torsion and
![]() ${\mathrm {Sel}}(E/F)$
is finite, then
${\mathrm {Sel}}(E/F)$
is finite, then
![]() $H_1(G,M)$
is finite and
$H_1(G,M)$
is finite and
![]() $H_2(G,M)=0$
(see Theorem 2.3). By Hochschild–Serre spectral sequence, we conclude that
$H_2(G,M)=0$
(see Theorem 2.3). By Hochschild–Serre spectral sequence, we conclude that
![]() $H_0({\mathrm {PG}}, H_1(C, M))$
is finite if and only if
$H_0({\mathrm {PG}}, H_1(C, M))$
is finite if and only if
![]() $H_2({\mathrm {PG}},M_C)$
is finite, and hence (2) follows from (1).
$H_2({\mathrm {PG}},M_C)$
is finite, and hence (2) follows from (1).
For (3), note that it follows from [Reference HowsonHo2, Th. 1.1] the Hochschild–Serre spectral sequence (use (2.2) with
![]() $H=C$
and
$H=C$
and
![]() $N=H_l(C,M)$
) that
$N=H_l(C,M)$
) that
 $$ \begin{align} {\mathrm{rank}}_{\Lambda(G)}M &=\sum_{k \geq 0}(-1)^k{\mathrm{rank}}_{{\mathbb Z}_p}H_k(G,M) \hspace{9pc} \end{align} $$
$$ \begin{align} {\mathrm{rank}}_{\Lambda(G)}M &=\sum_{k \geq 0}(-1)^k{\mathrm{rank}}_{{\mathbb Z}_p}H_k(G,M) \hspace{9pc} \end{align} $$
 $$ \begin{align} &=\sum_{k,l \geq 0}(-1)^{k+l}{\mathrm{rank}}_{{\mathbb Z}_p}H_k({\mathrm{PG}}, H_l(C,M)) \end{align} $$
$$ \begin{align} &=\sum_{k,l \geq 0}(-1)^{k+l}{\mathrm{rank}}_{{\mathbb Z}_p}H_k({\mathrm{PG}}, H_l(C,M)) \end{align} $$
 $$ \begin{align} &=\sum_{l\geq 0}(-1)^l{\mathrm{rank}}_{\Lambda({\mathrm{PG}})}H_l(C,M) \end{align} $$
$$ \begin{align} &=\sum_{l\geq 0}(-1)^l{\mathrm{rank}}_{\Lambda({\mathrm{PG}})}H_l(C,M) \end{align} $$
Suppose (3) holds. Since
![]() $H_1(C,M)$
is precisely the
$H_1(C,M)$
is precisely the
![]() $\Lambda (G)$
-submodule of M consisting of the elements in M annihilated by the augmentation ideal
$\Lambda (G)$
-submodule of M consisting of the elements in M annihilated by the augmentation ideal
![]() $I(C)=\langle c-1 \rangle $
, we have
$I(C)=\langle c-1 \rangle $
, we have
![]() $H_1(C,M)=0$
. Hence, the conclusion follows from (3.13) and Theorem 3.1.
$H_1(C,M)=0$
. Hence, the conclusion follows from (3.13) and Theorem 3.1.
Finally, suppose if
![]() $M_C \cong \widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
$M_C \cong \widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is a torsion
![]() $\Lambda ({\mathrm {PG}})$
-module. Then it follows from (3.13) that M is torsion as a
$\Lambda ({\mathrm {PG}})$
-module. Then it follows from (3.13) that M is torsion as a
![]() $\Lambda (G)$
-module and
$\Lambda (G)$
-module and
![]() $H_1(C,M)$
is torsion as a
$H_1(C,M)$
is torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module. Then
$\Lambda ({\mathrm {PG}})$
-module. Then
![]() $H_1(C,M)$
is pseudonull as a
$H_1(C,M)$
is pseudonull as a
![]() $\Lambda (G)$
-module. However, M has no nonzero pseudonull submodules (see [Reference Ochi and VenjakobOV, Th. 5.1]), and therefore
$\Lambda (G)$
-module. However, M has no nonzero pseudonull submodules (see [Reference Ochi and VenjakobOV, Th. 5.1]), and therefore
![]() $H_1(C,M)=0$
.
$H_1(C,M)=0$
.
The following theorem gives a restatement of condition (3) in Theorem 3.5 using the structure theorem of dual Selmer groups over noncommutative Iwasawa algebras [Reference CremonaCSS]. By [Reference CremonaCSS], there is an injection of
![]() $\Lambda (G)$
-modules
$\Lambda (G)$
-modules
with pseudonull cokernel. Here,
![]() $J_i$
’s are reflexive ideals in
$J_i$
’s are reflexive ideals in
![]() $\Lambda (G)$
which are pure of grade
$\Lambda (G)$
which are pure of grade
![]() $1$
, and
$1$
, and
![]() $M_0$
is the maximal pseudonull submodule of M. Recall that
$M_0$
is the maximal pseudonull submodule of M. Recall that
![]() $M=\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
; hence, M has no nontrivial pseudonull submodule and therefore
$M=\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
; hence, M has no nontrivial pseudonull submodule and therefore
![]() $M_0=0.$
This gives the exact sequence
$M_0=0.$
This gives the exact sequence
where N is a pseudonull
![]() $\Lambda (G)$
-module.
$\Lambda (G)$
-module.
Theorem 3.6. The Selmer group
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is a cotorsion
${\mathrm {Sel}}(E/K_{\infty })$
is a cotorsion
![]() $\Lambda ({\mathrm {PG}})$
-module if and only if
$\Lambda ({\mathrm {PG}})$
-module if and only if
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is a cotorsion
${\mathrm {Sel}}(E/F_{\infty })$
is a cotorsion
![]() $\Lambda (G)$
-module and
$\Lambda (G)$
-module and
![]() $H_1(C,\oplus _{i=1}^m\Lambda (G)/J_i)=0$
.
$H_1(C,\oplus _{i=1}^m\Lambda (G)/J_i)=0$
.
Proof. Since the center C has p-cohomological dimension
![]() $1$
, the sequence (3.14) gives the following exact sequence of
$1$
, the sequence (3.14) gives the following exact sequence of
![]() $\Lambda ({\mathrm {PG}})$
-modules:
$\Lambda ({\mathrm {PG}})$
-modules:
Let
![]() $\overline {J_i}$
be the image of
$\overline {J_i}$
be the image of
![]() $J_i$
under the natural projection
$J_i$
under the natural projection
![]() $\Lambda (G) \rightarrow \Lambda (G/C)=\Lambda (G)/I(C)$
. Since
$\Lambda (G) \rightarrow \Lambda (G/C)=\Lambda (G)/I(C)$
. Since
![]() $H_1(C,\Lambda (G)/J_i)=0$
for each
$H_1(C,\Lambda (G)/J_i)=0$
for each
![]() $i=[1,m]$
by assumption, then
$i=[1,m]$
by assumption, then
![]() $J_i \nsubseteq I(C)$
and hence
$J_i \nsubseteq I(C)$
and hence
![]() $\overline {J_i}$
is nonzero. Therefore, we have
$\overline {J_i}$
is nonzero. Therefore, we have
which implies that
![]() $(\Lambda (G)/J_i)_C $
is
$(\Lambda (G)/J_i)_C $
is
![]() $\Lambda ({\mathrm {PG}})$
-torsion. Now, as N is a pseudonull
$\Lambda ({\mathrm {PG}})$
-torsion. Now, as N is a pseudonull
![]() $\Lambda (G)$
-module,
$\Lambda (G)$
-module,
This implies that
![]() $N_C$
is a torsion
$N_C$
is a torsion
![]() $\Lambda ({\mathrm {PG}})$
-module, and the same holds for the module
$\Lambda ({\mathrm {PG}})$
-module, and the same holds for the module
![]() $M_C$
from (3.17) and (3.16).
$M_C$
from (3.17) and (3.16).
Conversely, suppose that
![]() $M_C \cong \widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
$M_C \cong \widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module. Then, by Theorem 3.5, M is torsion as a
$\Lambda ({\mathrm {PG}})$
-module. Then, by Theorem 3.5, M is torsion as a
![]() $\Lambda (G)$
-module and
$\Lambda (G)$
-module and
![]() $H_1(C, M)=0$
whence
$H_1(C, M)=0$
whence
![]() $H_1(C, \oplus _{i=1}^m \Lambda (G)/J_i)=0$
by (3.15).
$H_1(C, \oplus _{i=1}^m \Lambda (G)/J_i)=0$
by (3.15).
Remark 3.7. We note that the ideals
![]() $J_i$
cannot be
$J_i$
cannot be
![]() $I(C)$
for all
$I(C)$
for all
![]() $ i\geq 1$
because the center C cannot act trivially on the Selmer group at
$ i\geq 1$
because the center C cannot act trivially on the Selmer group at
![]() $F_{\infty }$
(see Proposition 3.8).
$F_{\infty }$
(see Proposition 3.8).
Suppose none of the ideals
![]() $J_i$
are contained in
$J_i$
are contained in
![]() $I(C)$
. Then
$I(C)$
. Then
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module. On the other hand, if
$\Lambda ({\mathrm {PG}})$
-module. On the other hand, if
![]() $J_i=I(C)$
for some i, then
$J_i=I(C)$
for some i, then
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
cannot be torsion as a
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
cannot be torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module (see Theorem 3.6).
$\Lambda ({\mathrm {PG}})$
-module (see Theorem 3.6).
Suppose
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion as a
${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion as a
![]() $\Lambda (G)$
-module, and
$\Lambda (G)$
-module, and
![]() ${\mathrm {Sel}}(E/F)$
and
${\mathrm {Sel}}(E/F)$
and
![]() $H_1(G,N)$
are finite. Then none of the ideals
$H_1(G,N)$
are finite. Then none of the ideals
![]() $J_i$
can be contained in
$J_i$
can be contained in
![]() $I(C)$
. This is because, from (3.14), we obtain the exact sequence
$I(C)$
. This is because, from (3.14), we obtain the exact sequence
whose first and last terms are finite. In this case,
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
is torsion as a
![]() $\Lambda ({\mathrm {PG}})$
-module.
$\Lambda ({\mathrm {PG}})$
-module.
In [Reference CremonaCSS, Prop. 8.10], for the elliptic curve
![]() $E=X_1(11): y^2+y=x^3-x^2$
of conductor
$E=X_1(11): y^2+y=x^3-x^2$
of conductor
![]() $11$
and prime
$11$
and prime
![]() $p=5$
, the authors show that the center C cannot act trivially on
$p=5$
, the authors show that the center C cannot act trivially on
![]() ${\mathrm {Sel}}(E/F_{\infty })$
. The following proposition generalizes this for any elliptic curve without complex multiplication and with good ordinary reduction for the primes above p.
${\mathrm {Sel}}(E/F_{\infty })$
. The following proposition generalizes this for any elliptic curve without complex multiplication and with good ordinary reduction for the primes above p.
Proposition 3.8. Suppose
![]() $G \cong C \times {\mathrm {PG}}$
, and
$G \cong C \times {\mathrm {PG}}$
, and
![]() ${\mathrm {Sel}}(E/F)$
is finite. Then the center C cannot act trivially on
${\mathrm {Sel}}(E/F)$
is finite. Then the center C cannot act trivially on
![]() ${\mathrm {Sel}}(E/F_{\infty })$
.
${\mathrm {Sel}}(E/F_{\infty })$
.
Proof. If C acts trivially on
![]() ${\mathrm {Sel}}(E/F_{\infty })$
, then
${\mathrm {Sel}}(E/F_{\infty })$
, then
Hoewever,
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is cofinitely generated over
${\mathrm {Sel}}(E/K_{\infty })$
is cofinitely generated over
![]() $\Lambda ({\mathrm {PG}})$
and so with the above identification,
$\Lambda ({\mathrm {PG}})$
and so with the above identification,
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion over
${\mathrm {Sel}}(E/F_{\infty })$
is cotorsion over
![]() $\Lambda (G)$
. As
$\Lambda (G)$
. As
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is
${\mathrm {Sel}}(E/F_{\infty })$
is
![]() $\Lambda (G)$
-cotorsion and
$\Lambda (G)$
-cotorsion and
![]() ${\mathrm {Sel}}(E/F)$
is finite, the cohomology groups
${\mathrm {Sel}}(E/F)$
is finite, the cohomology groups
![]() $H^i(G,{\mathrm {Sel}}(E/F_{\infty }))$
are finite for all i. The degeneration of the Hochschild–Serre spectral sequence (see [Reference Neukirch, Schmidt and WingbergNS, Prop. 2.4.5]) gives an injection
$H^i(G,{\mathrm {Sel}}(E/F_{\infty }))$
are finite for all i. The degeneration of the Hochschild–Serre spectral sequence (see [Reference Neukirch, Schmidt and WingbergNS, Prop. 2.4.5]) gives an injection
This implies that the cohomology groups
![]() $H^i({\mathrm {PG}},{\mathrm {Sel}}(E/K_{\infty }))$
are finite for all i. Hence,
$H^i({\mathrm {PG}},{\mathrm {Sel}}(E/K_{\infty }))$
are finite for all i. Hence,
 $$ \begin{align*}{\mathrm{rank}}_{\Lambda({\mathrm{PG}})}\widehat{{\mathrm{Sel}}(E/K_{\infty})}=\sum_{i \geq 0}(-1)^i{\mathrm{rank}}_{{\mathbb Z}_p}H_i({\mathrm{PG}}, \widehat{{\mathrm{Sel}}(E/K_{\infty})})=0,\end{align*} $$
$$ \begin{align*}{\mathrm{rank}}_{\Lambda({\mathrm{PG}})}\widehat{{\mathrm{Sel}}(E/K_{\infty})}=\sum_{i \geq 0}(-1)^i{\mathrm{rank}}_{{\mathbb Z}_p}H_i({\mathrm{PG}}, \widehat{{\mathrm{Sel}}(E/K_{\infty})})=0,\end{align*} $$
whereby
![]() ${\mathrm {Sel}}(E/K_{\infty }) $
is
${\mathrm {Sel}}(E/K_{\infty }) $
is
![]() $\Lambda ({\mathrm {PG}})$
-cotorsion. We deduce that
$\Lambda ({\mathrm {PG}})$
-cotorsion. We deduce that
This would imply that
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a pseudonull
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is a pseudonull
![]() $\Lambda (G)$
-module. However,
$\Lambda (G)$
-module. However,
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
has no nonzero pseudonull submodules. Hence,
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
has no nonzero pseudonull submodules. Hence,
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })}=0$
. On the other hand, it is known that
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}=0$
. On the other hand, it is known that
![]() $\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is infinite dimensional as a
$\widehat {{\mathrm {Sel}}(E/F_{\infty })}$
is infinite dimensional as a
![]() ${\mathbb Q}_p$
-vector space (see [Reference Coates and HowsonCo1, Th. 1.5]). This gives us a contradiction.
${\mathbb Q}_p$
-vector space (see [Reference Coates and HowsonCo1, Th. 1.5]). This gives us a contradiction.
Examples 3.9. Here are some examples of elliptic curves E such that
![]() $G={\mathrm {Gal}}(F_{\infty }/F)$
is a direct product of its center C and
$G={\mathrm {Gal}}(F_{\infty }/F)$
is a direct product of its center C and
![]() ${\mathrm {PG}}$
. We follow the nomenclature from Cremona tables [Reference Coates, Schneider and SujathaCr].
${\mathrm {PG}}$
. We follow the nomenclature from Cremona tables [Reference Coates, Schneider and SujathaCr].
-
1. Let E be the elliptic curve
 $X_1(11)$
, namely E is the curve
$X_1(11)$
, namely E is the curve
 $y^2+y=x^3-x^2$
and prime
$y^2+y=x^3-x^2$
and prime
 $p=5$
. This is a curve of conductor
$p=5$
. This is a curve of conductor
 $11$
defined over
$11$
defined over
 ${\mathbb Q}$
, but we consider it over
${\mathbb Q}$
, but we consider it over
 $F={\mathbb Q}(\mu _5)$
. Put
$F={\mathbb Q}(\mu _5)$
. Put
 $F_{\infty }=F(E_{5^{\infty }})$
. Then
$F_{\infty }=F(E_{5^{\infty }})$
. Then
 $G={\mathrm {Gal}}(F_{\infty }/F)$
has the form
$G={\mathrm {Gal}}(F_{\infty }/F)$
has the form
 $G=C \times PG$
[Reference CremonaCSS, Exam. 8.7, p. 104].
$G=C \times PG$
[Reference CremonaCSS, Exam. 8.7, p. 104]. -
2. Let E be the elliptic curve
 $X_0(11)$
, namely E is the curve
$X_0(11)$
, namely E is the curve
 $y^2+y=x^3-x^2-10x-20$
and
$y^2+y=x^3-x^2-10x-20$
and
 $p=5$
. This is a curve of conductor
$p=5$
. This is a curve of conductor
 $11$
defined over
$11$
defined over
 ${\mathbb Q}$
, but we consider it over
${\mathbb Q}$
, but we consider it over
 $F={\mathbb Q}(\mu _5)$
. Put
$F={\mathbb Q}(\mu _5)$
. Put
 $F_{\infty }=F(E_{5^{\infty }})$
. Then the Galois group
$F_{\infty }=F(E_{5^{\infty }})$
. Then the Galois group
 $G={\mathrm {Gal}}(F_{\infty }/F)$
is a subgroup of the first congruence kernel of
$G={\mathrm {Gal}}(F_{\infty }/F)$
is a subgroup of the first congruence kernel of
 $GL_2({\mathbb Z}_5)$
[Reference FisherF, (3), p. 586]. Hence, G is of the form
$GL_2({\mathbb Z}_5)$
[Reference FisherF, (3), p. 586]. Hence, G is of the form
 $C \times {\mathrm {PG}}$
.
$C \times {\mathrm {PG}}$
. -
3. For any general elliptic curve E over F without complex multiplication and with good ordinary reduction for the primes above p, we can always find an integer k large enough such that, over the base field
 $F[E_{p^k}]$
, the Galois group
$F[E_{p^k}]$
, the Galois group
 $G={\mathrm {Gal}}(F_{\infty }/F[E_{p^k}])$
lies inside the first congruence kernel of
$G={\mathrm {Gal}}(F_{\infty }/F[E_{p^k}])$
lies inside the first congruence kernel of
 $GL_2({\mathbb Z}_p)$
and hence can be written in the form
$GL_2({\mathbb Z}_p)$
and hence can be written in the form
 $C \times {\mathrm {PG}}$
. The center C can be identified with a subgroup of diagonal matrices of a certain form (see [Reference VenjakobV, Rem. 4.11]).
$C \times {\mathrm {PG}}$
. The center C can be identified with a subgroup of diagonal matrices of a certain form (see [Reference VenjakobV, Rem. 4.11]).
4 Applications
Suppose
![]() $G \cong {\mathrm {PG}} \times C$
. Let
$G \cong {\mathrm {PG}} \times C$
. Let
![]() $C_n=C^{p^n}$
and
$C_n=C^{p^n}$
and
![]() $G_n={\mathrm {PG}} \times C_n$
. Note that
$G_n={\mathrm {PG}} \times C_n$
. Note that
![]() $G_n \neq G^{p^n}$
. Let
$G_n \neq G^{p^n}$
. Let
![]() $M = \widehat {{\mathrm {Sel}}(E/F_{\infty })}$
.
$M = \widehat {{\mathrm {Sel}}(E/F_{\infty })}$
.
Proposition 4.1. Suppose that M is a torsion
![]() $\Lambda (G)$
-module. Then, for all large n,
$\Lambda (G)$
-module. Then, for all large n,
![]() ${\mathrm {rank}}_{\Lambda ({\mathrm {PG}})}M_{C_n}$
is a constant, independent of
${\mathrm {rank}}_{\Lambda ({\mathrm {PG}})}M_{C_n}$
is a constant, independent of
![]() $n.$
$n.$
Proof. As
![]() $G_n$
is of finite index in G, M is also a finitely generated module over
$G_n$
is of finite index in G, M is also a finitely generated module over
![]() $\Lambda (G_n)$
. As
$\Lambda (G_n)$
. As
![]() $C_n \cong {\mathbb Z}_p$
, we can identify
$C_n \cong {\mathbb Z}_p$
, we can identify
![]() $M^{C_n}$
with
$M^{C_n}$
with
![]() $ H_1(C_n,M)$
and then they both are finitely generated over
$ H_1(C_n,M)$
and then they both are finitely generated over
![]() $\Lambda ({\mathrm {PG}})$
. The Hochschild–Serre spectral sequence
$\Lambda ({\mathrm {PG}})$
. The Hochschild–Serre spectral sequence
![]() $H^r({\mathrm {PG}},H^s(C_n,M)) \implies H^{r+s}(G,M)$
and the argument as in (3.10)–(3.13) give
$H^r({\mathrm {PG}},H^s(C_n,M)) \implies H^{r+s}(G,M)$
and the argument as in (3.10)–(3.13) give
Identifying
![]() $M^{C_n}$
with
$M^{C_n}$
with
![]() $ H_1(C_n,M)$
, we deduce
$ H_1(C_n,M)$
, we deduce
 $$ \begin{align*} {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M_{C_n} &= {\mathrm{rank}}_{\Lambda(G_n)}M + {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M^{C_n}\\[3pt] &=p^n{\mathrm{rank}}_{\Lambda(G)}M + {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M^{C_n}\\[3pt] &={\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M^{C_n}. \end{align*} $$
$$ \begin{align*} {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M_{C_n} &= {\mathrm{rank}}_{\Lambda(G_n)}M + {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M^{C_n}\\[3pt] &=p^n{\mathrm{rank}}_{\Lambda(G)}M + {\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M^{C_n}\\[3pt] &={\mathrm{rank}}_{\Lambda({\mathrm{PG}})}M^{C_n}. \end{align*} $$
(The second equality follows since
![]() $G_n$
is of index
$G_n$
is of index
![]() $p^n$
in G, and the third equality follows as M is a torsion
$p^n$
in G, and the third equality follows as M is a torsion
![]() $\Lambda (G)$
-module by assumption.) Note that
$\Lambda (G)$
-module by assumption.) Note that
![]() $C_n$
is in the center, and hence abelian, and therefore
$C_n$
is in the center, and hence abelian, and therefore
![]() $M^{C_n}$
is a
$M^{C_n}$
is a
![]() $\Lambda (G)$
-submodule of M. However, M is a finitely generated module over
$\Lambda (G)$
-submodule of M. However, M is a finitely generated module over
![]() $\Lambda (G)$
, and hence M is a Noetherian module and satisfies the ascending chain condition on its submodules. Hence, the chain
$\Lambda (G)$
, and hence M is a Noetherian module and satisfies the ascending chain condition on its submodules. Hence, the chain
stabilizes and so
![]() ${\mathrm {rank}}_{\Lambda ({\mathrm {PG}})}M^{C_n}$
is a constant independent of n, for all sufficiently large n.
${\mathrm {rank}}_{\Lambda ({\mathrm {PG}})}M^{C_n}$
is a constant independent of n, for all sufficiently large n.
Consider the following fundamental diagram:

Let
![]() ${\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}})$
be the cokernel of the map
${\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}})$
be the cokernel of the map
![]() $\lambda _{K_{\infty }}^{\mathrm {PG}}$
in (4.1).
$\lambda _{K_{\infty }}^{\mathrm {PG}}$
in (4.1).
Theorem 4.2. The vertical maps
![]() $f,g,h$
in the fundamental diagram (4.1) have finite kernels and cokernels. Furthermore, if
$f,g,h$
in the fundamental diagram (4.1) have finite kernels and cokernels. Furthermore, if
![]() ${\mathrm {Sel}}(E/F)$
is finite, then
${\mathrm {Sel}}(E/F)$
is finite, then
![]() ${\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}})$
is finite.
${\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}})$
is finite.
Proof. Since
![]() $H^1(C, E_{p^{\infty }})=0$
, using Hochschild–Serre spectral sequence and noting that the cohomology groups
$H^1(C, E_{p^{\infty }})=0$
, using Hochschild–Serre spectral sequence and noting that the cohomology groups
are finite for
![]() $i\geq 1$
, it is easy to see that the kernel and the cokernel of g are finite.
$i\geq 1$
, it is easy to see that the kernel and the cokernel of g are finite.
Next, we decompose h into local components
![]() $h =\oplus _{v \in S}h_v$
and analyze the kernel of cokernel of the map
$h =\oplus _{v \in S}h_v$
and analyze the kernel of cokernel of the map
![]() $h_v$
.
$h_v$
.
Let w be a prime of
![]() $F_{\infty }$
above
$F_{\infty }$
above
![]() $v \in S$
, and let u be a prime of
$v \in S$
, and let u be a prime of
![]() $K_{\infty }$
below w. If one denotes
$K_{\infty }$
below w. If one denotes
![]() $\Theta _u$
(resp.,
$\Theta _u$
(resp.,
![]() $\Delta _w$
) the decomposition group of
$\Delta _w$
) the decomposition group of
![]() ${\mathrm {PG}}$
at u (resp., the decomposition group of G at w), then one has an isomorphism
${\mathrm {PG}}$
at u (resp., the decomposition group of G at w), then one has an isomorphism
![]() $\Theta _u=\Delta _w/C\cap \Delta _w$
.
$\Theta _u=\Delta _w/C\cap \Delta _w$
.
By Shapiro’s lemma,
![]() $H^i({\mathrm {PG}},J_v(K_{\infty })) \cong H^i(\Theta _u,H^1(K_{\infty ,u},E)(p)).$
$H^i({\mathrm {PG}},J_v(K_{\infty })) \cong H^i(\Theta _u,H^1(K_{\infty ,u},E)(p)).$
By Hochschild–Serre spectral sequence, the following sequence is exact:
 $$ \begin{align*} 0 \rightarrow H^1(\Theta_u,E(K_{\infty,u}))(p) &\rightarrow H^1(F_v,E)(p) \xrightarrow{h_v}H^1(K_{\infty,u},E)(p)^{\Theta_u}\\ &\rightarrow H^2(\Theta_u,E(K_{\infty,u}))(p). \end{align*} $$
$$ \begin{align*} 0 \rightarrow H^1(\Theta_u,E(K_{\infty,u}))(p) &\rightarrow H^1(F_v,E)(p) \xrightarrow{h_v}H^1(K_{\infty,u},E)(p)^{\Theta_u}\\ &\rightarrow H^2(\Theta_u,E(K_{\infty,u}))(p). \end{align*} $$
Therefore, to prove that
![]() $\ker (h_v)$
and
$\ker (h_v)$
and
![]() $\mathrm {cokernel}(h_v)$
are finite, it is sufficient to show that
$\mathrm {cokernel}(h_v)$
are finite, it is sufficient to show that
-
1.
 $H^1(\Theta _u,E(K_{\infty ,u}))(p)$
is finite, and
$H^1(\Theta _u,E(K_{\infty ,u}))(p)$
is finite, and -
2.
 $H^2(\Theta _u,E(K_{\infty ,u}))(p)$
is finite.
$H^2(\Theta _u,E(K_{\infty ,u}))(p)$
is finite.
Consider the following exact sequence:
With
![]() $\Theta _w^C=C \cap \Delta _w$
, the third term of the above exact sequence is
$\Theta _w^C=C \cap \Delta _w$
, the third term of the above exact sequence is
The last equality is due to (3.5), which is zero by Theorem 3.1.
Therefore, by the exact sequence (4.2), it suffices to show that
-
1.
 $H^1(\Delta _w,E(F_{\infty ,w}))(p)$
is finite, and
$H^1(\Delta _w,E(F_{\infty ,w}))(p)$
is finite, and -
2.
 $H^2(\Delta _w,E(F_{\infty ,w}))(p)$
is finite.
$H^2(\Delta _w,E(F_{\infty ,w}))(p)$
is finite.
However,
![]() $H^1(\Delta _w,E(F_{\infty ,w}))(p)$
and
$H^1(\Delta _w,E(F_{\infty ,w}))(p)$
and
![]() $H^2(\Delta _w,E(F_{\infty ,w}))(p)$
are the kernel and cokernel of the map
$H^2(\Delta _w,E(F_{\infty ,w}))(p)$
are the kernel and cokernel of the map
![]() $\delta _v$
, the local map of the following fundamental diagram which is known to be finite by the work of Coates and Howson (cf. proof of [Reference Coates and GreenbergCH2, Prop. 3.3] or Proposition
$\delta _v$
, the local map of the following fundamental diagram which is known to be finite by the work of Coates and Howson (cf. proof of [Reference Coates and GreenbergCH2, Prop. 3.3] or Proposition
![]() $5.21$
of [Reference HowsonHo1]):
$5.21$
of [Reference HowsonHo1]):

Therefore, the kernel and cokernel of h are finite. By the snake lemma, we deduce that the same is true for f.
If
![]() ${\mathrm {Sel}}(E/F)$
is finite,
${\mathrm {Sel}}(E/F)$
is finite,
![]() ${\mathrm {Coker}}(\lambda _F)$
is finite (cf. [Reference Coates and SujathaCS1, p. 35]). This implies that
${\mathrm {Coker}}(\lambda _F)$
is finite (cf. [Reference Coates and SujathaCS1, p. 35]). This implies that
![]() ${\mathrm {Coker}}(h \circ \lambda _F)$
is finite. However,
${\mathrm {Coker}}(h \circ \lambda _F)$
is finite. However,
![]() ${\mathrm {Coker}}(h \circ \lambda _F)={\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}} \circ g)$
, and hence
${\mathrm {Coker}}(h \circ \lambda _F)={\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}} \circ g)$
, and hence
![]() ${\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}})$
is finite.
${\mathrm {Coker}}(\lambda _{K_{\infty }}^{\mathrm {PG}})$
is finite.
Let
![]() $\mathcal {M}$
be the category of all finitely generated
$\mathcal {M}$
be the category of all finitely generated
![]() $\Lambda (G)$
-modules, let
$\Lambda (G)$
-modules, let
![]() $\mathcal {C}$
be the full subcategory of all pseudonull modules in
$\mathcal {C}$
be the full subcategory of all pseudonull modules in
![]() $\mathcal {M}$
, and let
$\mathcal {M}$
, and let
![]() $q:\mathcal {M} \rightarrow \mathcal {M}/\mathcal {C}$
denote the quotient functor. From [Reference ArdakovA, §1.3], recall that an object
$q:\mathcal {M} \rightarrow \mathcal {M}/\mathcal {C}$
denote the quotient functor. From [Reference ArdakovA, §1.3], recall that an object
![]() $q(M)$
in the quotient category
$q(M)$
in the quotient category
![]() $\mathcal {M}/\mathcal {C}$
is said to be completely faithful if
$\mathcal {M}/\mathcal {C}$
is said to be completely faithful if
![]() $\text {Ann}(N)=0$
for any
$\text {Ann}(N)=0$
for any
![]() $N \in \mathcal {M}$
such that
$N \in \mathcal {M}$
such that
![]() $q(N)$
is isomorphic to a nonzero subquotient of
$q(N)$
is isomorphic to a nonzero subquotient of
![]() $q(M)$
.
$q(M)$
.
Lemma 4.3. (see [Reference Coates and HowsonCo2, Lem. 9]Footnote
1
) Suppose
![]() $q(\widehat {{\mathrm {Sel}}(E/F_{\infty })})$
is completely faithful. Then
$q(\widehat {{\mathrm {Sel}}(E/F_{\infty })})$
is completely faithful. Then
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is
${\mathrm {Sel}}(E/K_{\infty })$
is
![]() $\Lambda ({\mathrm {PG}})$
-cotorsion.
$\Lambda ({\mathrm {PG}})$
-cotorsion.
Remark 4.4. In [Reference BourbakiBZ, §7], the authors consider an elliptic curve E over a number field and study the dual Selmer group of E over a
![]() ${\mathrm {PG}}$
-extension that arises from the trivializing extension of the Galois representation associated with another elliptic curve A. The example in [Reference BourbakiBZ, §7] combined with the method of the proof of [Reference Coates and HowsonCo2, Lem. 9] extend to give an example of the dual Selmer group of E which is cotorsion over the
${\mathrm {PG}}$
-extension that arises from the trivializing extension of the Galois representation associated with another elliptic curve A. The example in [Reference BourbakiBZ, §7] combined with the method of the proof of [Reference Coates and HowsonCo2, Lem. 9] extend to give an example of the dual Selmer group of E which is cotorsion over the
![]() ${\mathrm {PG}}$
-extension arising from the trivializing extension defined by the elliptic curve A. However, we are primarily interested in studying the cotorsion property of the dual Selmer group over the
${\mathrm {PG}}$
-extension arising from the trivializing extension defined by the elliptic curve A. However, we are primarily interested in studying the cotorsion property of the dual Selmer group over the
![]() ${\mathrm {PG}}$
-extension of the number field contained in the trivializing extension of the same elliptic curve. A detailed study is currently underway in a broader context.
${\mathrm {PG}}$
-extension of the number field contained in the trivializing extension of the same elliptic curve. A detailed study is currently underway in a broader context.
The Euler characteristic of the Selmer group of the
![]() $PGL(2)$
extension has been computed in Zerbes’ dissertation [Reference ZerbesZ, Chap. 8] and Howson’s dissertation [Reference HowsonHo1, Th. 5.34], but we include a simpler proof here.
$PGL(2)$
extension has been computed in Zerbes’ dissertation [Reference ZerbesZ, Chap. 8] and Howson’s dissertation [Reference HowsonHo1, Th. 5.34], but we include a simpler proof here.
Let
![]() $\chi ({\mathrm {PG}}, {\mathrm {Sel}}(E/K_{\infty }))$
be the Euler characteristic of Selmer group of the
$\chi ({\mathrm {PG}}, {\mathrm {Sel}}(E/K_{\infty }))$
be the Euler characteristic of Selmer group of the
![]() ${\mathrm {PGL}}(2)$
extension, and let
${\mathrm {PGL}}(2)$
extension, and let
 $$ \begin{align} \xi_p(E/F)=\rho_p(E/F) \times \prod_{v \in B}(1/L_v(E,1))^{(p)} \end{align} $$
$$ \begin{align} \xi_p(E/F)=\rho_p(E/F) \times \prod_{v \in B}(1/L_v(E,1))^{(p)} \end{align} $$
be defined as in [Reference Coates and SujathaCS1, §3.14].
Theorem 4.5. Suppose
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is
${\mathrm {Sel}}(E/K_{\infty })$
is
![]() $\Lambda ({\mathrm {PG}})$
-cotorsion and
$\Lambda ({\mathrm {PG}})$
-cotorsion and
![]() ${\mathrm {Sel}}(E/F)$
is finite. Then
${\mathrm {Sel}}(E/F)$
is finite. Then
![]() ${\mathrm {Sel}}(E/K_{\infty })$
has finite Euler characteristic given by
${\mathrm {Sel}}(E/K_{\infty })$
has finite Euler characteristic given by
where
![]() $\xi _p(E/F)$
is as in (4.5).
$\xi _p(E/F)$
is as in (4.5).
Proof. Since
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is
${\mathrm {Sel}}(E/K_{\infty })$
is
![]() $\Lambda ({\mathrm {PG}})$
-cotorsion, it implies that
$\Lambda ({\mathrm {PG}})$
-cotorsion, it implies that
![]() ${\mathrm {Sel}}(E/F_{\infty })$
is
${\mathrm {Sel}}(E/F_{\infty })$
is
![]() $\Lambda (G)$
-torsion and
$\Lambda (G)$
-torsion and
![]() $H^1(C,{\mathrm {Sel}}(E/F_{\infty }))=0$
(cf. Theorems 3.5 and 3.6). The Hochschild–Serre spectral sequence
$H^1(C,{\mathrm {Sel}}(E/F_{\infty }))=0$
(cf. Theorems 3.5 and 3.6). The Hochschild–Serre spectral sequence
gives
 $$ \begin{align*}\chi(G, {\mathrm{Sel}}(E/F_{\infty}))=\sum_{i\geq 0}(-1)^i\chi({\mathrm{PG}}, H^i(C,{\mathrm{Sel}}(E/F_{\infty})))=\chi({\mathrm{PG}}, {\mathrm{Sel}}(E/K_{\infty})).\end{align*} $$
$$ \begin{align*}\chi(G, {\mathrm{Sel}}(E/F_{\infty}))=\sum_{i\geq 0}(-1)^i\chi({\mathrm{PG}}, H^i(C,{\mathrm{Sel}}(E/F_{\infty})))=\chi({\mathrm{PG}}, {\mathrm{Sel}}(E/K_{\infty})).\end{align*} $$
Under the assumption that
![]() ${\mathrm {Sel}}(E/F)$
is finite,
${\mathrm {Sel}}(E/F)$
is finite,
![]() $\chi (G, {\mathrm {Sel}}(E/F_{\infty }))$
equals
$\chi (G, {\mathrm {Sel}}(E/F_{\infty }))$
equals
![]() $\xi _p(E/F)$
by [Reference Coates and SujathaCS1, Th. 3.16].
$\xi _p(E/F)$
by [Reference Coates and SujathaCS1, Th. 3.16].
The quantity
![]() $\xi _p(E/F)$
in (4.5) is related to the exact formula of the p-part of Birch and Swinnerton-Dyer conjecture, which in turn gives the value of the p-part of the leading coefficient of the complex L-value at
$\xi _p(E/F)$
in (4.5) is related to the exact formula of the p-part of Birch and Swinnerton-Dyer conjecture, which in turn gives the value of the p-part of the leading coefficient of the complex L-value at
![]() $1$
.
$1$
.
Suppose that
![]() $\widehat {{\mathrm {Sel}}(E/F_{\mathrm {cyc}})}$
is
$\widehat {{\mathrm {Sel}}(E/F_{\mathrm {cyc}})}$
is
![]() $\Lambda (\Gamma )$
-torsion (e.g.,
$\Lambda (\Gamma )$
-torsion (e.g.,
![]() $F={\mathbb Q}$
) and
$F={\mathbb Q}$
) and
![]() ${\mathrm {Sel}}(E/F)$
is finite. It is well known that
${\mathrm {Sel}}(E/F)$
is finite. It is well known that
![]() $\chi (\Gamma , {\mathrm {Sel}}(E/F_{\mathrm {cyc}}))=\rho _p(E/F) $
(cf. [Reference Coates and SujathaCS1, Th. 3.3]). From (4.5) and (4.6), we obtain
$\chi (\Gamma , {\mathrm {Sel}}(E/F_{\mathrm {cyc}}))=\rho _p(E/F) $
(cf. [Reference Coates and SujathaCS1, Th. 3.3]). From (4.5) and (4.6), we obtain
 $$ \begin{align*}\chi({\mathrm{PG}}, {\mathrm{Sel}}(E/K_{\infty}))=\chi(G,{\mathrm{Sel}}(E/F_{\infty}))=\chi(\Gamma, {\mathrm{Sel}}(E/F_{\mathrm{cyc}})) \times \prod_{v \in B}(1/L_v(E,1))^{(p)}.\end{align*} $$
$$ \begin{align*}\chi({\mathrm{PG}}, {\mathrm{Sel}}(E/K_{\infty}))=\chi(G,{\mathrm{Sel}}(E/F_{\infty}))=\chi(\Gamma, {\mathrm{Sel}}(E/F_{\mathrm{cyc}})) \times \prod_{v \in B}(1/L_v(E,1))^{(p)}.\end{align*} $$
Then the Iwasawa Main Conjecture predicts that the characteristic ideal of
![]() $\widehat {{\mathrm {Sel}}(E/F_{\mathrm {cyc}})}$
is generated by a p-adic L-function
$\widehat {{\mathrm {Sel}}(E/F_{\mathrm {cyc}})}$
is generated by a p-adic L-function
![]() $f_E(T)\in \Lambda (\Gamma )$
. Since
$f_E(T)\in \Lambda (\Gamma )$
. Since
![]() ${{\mathrm {Sel}}(E/F_{\mathrm {cyc}})}$
is
${{\mathrm {Sel}}(E/F_{\mathrm {cyc}})}$
is
![]() $\Lambda (\Gamma )$
-cotorsion, we deduce that the leading term of
$\Lambda (\Gamma )$
-cotorsion, we deduce that the leading term of
![]() $f_E(T)$
is nonzero and
$f_E(T)$
is nonzero and
Here,
![]() $a \sim b$
means that a and b both have the same p-adic valuation (cf. [Reference GreenbergG, Lem. 4.2]). This gives a conjectural connection of
$a \sim b$
means that a and b both have the same p-adic valuation (cf. [Reference GreenbergG, Lem. 4.2]). This gives a conjectural connection of
![]() $f_E(T)$
with the value of the Hasse–Weil complex L-function
$f_E(T)$
with the value of the Hasse–Weil complex L-function
![]() $L(E/F, s)$
at
$L(E/F, s)$
at
![]() $s=1$
. This is based on the Birch and Swinnerton-Dyer conjecture for E over F. The conjecture then asserts that
$s=1$
. This is based on the Birch and Swinnerton-Dyer conjecture for E over F. The conjecture then asserts that
![]() $L(E/F, 1) \neq 0$
, and for a suitably defined period
$L(E/F, 1) \neq 0$
, and for a suitably defined period
![]() $\Omega (E/F)$
, the value
$\Omega (E/F)$
, the value
![]() $L(E/F, 1)/\Omega (E/F)$
is rational. One would then expect
$L(E/F, 1)/\Omega (E/F)$
is rational. One would then expect
 $$ \begin{align*}f_E(0) \sim \Big(\prod_{v \mid p}(1-\beta_vN(v)^{-1})^2\Big)L(E/F, 1)/\Omega(E/F),\end{align*} $$
$$ \begin{align*}f_E(0) \sim \Big(\prod_{v \mid p}(1-\beta_vN(v)^{-1})^2\Big)L(E/F, 1)/\Omega(E/F),\end{align*} $$
where
![]() $(1-\beta _vN(v)^{-1})^2$
is a certain Euler factor as in [Reference GreenbergG, p. 91].
$(1-\beta _vN(v)^{-1})^2$
is a certain Euler factor as in [Reference GreenbergG, p. 91].
The nonexistence of nontrivial pseudonull submodules of
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
has been dealt with in Zerbes’ dissertation [Reference ZerbesZ, Chap. 9, §3]. The referee suggested that we include a proof of this assertion. This is done in the following theorem. Our proof is different to that of [Reference ZerbesZ, Chap. 9, §3]. The proof uses a standard result from Iwasawa theory and is originally due to Greenberg for commutative Iwasawa algebras.
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
has been dealt with in Zerbes’ dissertation [Reference ZerbesZ, Chap. 9, §3]. The referee suggested that we include a proof of this assertion. This is done in the following theorem. Our proof is different to that of [Reference ZerbesZ, Chap. 9, §3]. The proof uses a standard result from Iwasawa theory and is originally due to Greenberg for commutative Iwasawa algebras.
Theorem 4.6. Assume weak Leopoldt’s conjecture at
![]() $K_{\infty }$
, that is,
$K_{\infty }$
, that is,
![]() $H^2(F_S/K_{\infty }, E_{p^{\infty }})=0$
. Suppose
$H^2(F_S/K_{\infty }, E_{p^{\infty }})=0$
. Suppose
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is
${\mathrm {Sel}}(E/K_{\infty })$
is
![]() $\Lambda ({\mathrm {PG}})$
-cotorsion. Then
$\Lambda ({\mathrm {PG}})$
-cotorsion. Then
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
has no nontrivial pseudonull submodule.
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
has no nontrivial pseudonull submodule.
Proof. Let
![]() $S_p$
be the set of places of S above the prime p. As
$S_p$
be the set of places of S above the prime p. As
![]() ${\mathrm {Sel}}(E/K_{\infty })$
is
${\mathrm {Sel}}(E/K_{\infty })$
is
![]() $\Lambda ({\mathrm {PG}})$
-cotorsion, Theorem 3.4 gives the exact sequence
$\Lambda ({\mathrm {PG}})$
-cotorsion, Theorem 3.4 gives the exact sequence
By Theorem 3.1,
![]() $\widehat {J_v(K_{\infty })}=\widehat {J_v(F_{\infty })}_C $
for all
$\widehat {J_v(K_{\infty })}=\widehat {J_v(F_{\infty })}_C $
for all
![]() $v \in S$
.
$v \in S$
.
For
![]() $v \in S_p$
, the corresponding decomposition subgroup of the Galois group of the trivializing extension
$v \in S_p$
, the corresponding decomposition subgroup of the Galois group of the trivializing extension
![]() $F_{\infty }$
is of dimension
$F_{\infty }$
is of dimension
![]() $3$
(see [Reference Coates and GreenbergCH2, Lem. 5.1]). Hence,
$3$
(see [Reference Coates and GreenbergCH2, Lem. 5.1]). Hence,
![]() $\widehat {J_v(F_{\infty })}$
is free as a
$\widehat {J_v(F_{\infty })}$
is free as a
![]() $\Lambda (G)$
-module (see [Reference Ochi and VenjakobOV, Lem. 5.4(i)]), whence
$\Lambda (G)$
-module (see [Reference Ochi and VenjakobOV, Lem. 5.4(i)]), whence
![]() $\widehat {J_v(K_{\infty })}$
is free as a
$\widehat {J_v(K_{\infty })}$
is free as a
![]() $\Lambda ({\mathrm {PG}})$
-module.
$\Lambda ({\mathrm {PG}})$
-module.
For
![]() $v \in S\backslash S_p$
,
$v \in S\backslash S_p$
,
![]() $J_v(F_{\infty })=0$
(see [Reference Coates and GreenbergCH2, Lem. 5.4]), and hence
$J_v(F_{\infty })=0$
(see [Reference Coates and GreenbergCH2, Lem. 5.4]), and hence
![]() $J_v(K_{\infty })=0$
.
$J_v(K_{\infty })=0$
.
Since
![]() $H^2(F_S/K_{\infty }, E_{p^{\infty }})=0$
, [Reference Ochi and VenjakobOV, Th. 4.7] allows us to conclude that
$H^2(F_S/K_{\infty }, E_{p^{\infty }})=0$
, [Reference Ochi and VenjakobOV, Th. 4.7] allows us to conclude that
![]() $\widehat {H^1(F_S/K_{\infty }, E_{p^{\infty }})} $
has no nonzero pseudonull submodule.
$\widehat {H^1(F_S/K_{\infty }, E_{p^{\infty }})} $
has no nonzero pseudonull submodule.
Now, (4.7) gives an exact sequence where the first term is
![]() $\Lambda ({\mathrm {PG}})$
-free, and the middle term has no nonzero pseudonull submodule. An analogue of the argument by Greenberg referred to above (see [Reference Hachimori and OchiaiHO, Prop. 3.5]) allows us to conclude that
$\Lambda ({\mathrm {PG}})$
-free, and the middle term has no nonzero pseudonull submodule. An analogue of the argument by Greenberg referred to above (see [Reference Hachimori and OchiaiHO, Prop. 3.5]) allows us to conclude that
![]() $\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
has no nontrivial pseudonull submodule.
$\widehat {{\mathrm {Sel}}(E/K_{\infty })}$
has no nontrivial pseudonull submodule.
It seems to us that the full strength of the structure theorem has not been exploited. Specifically, the ideals in the summands are reflexive and pure of grade
![]() $1$
. It might be possible to use this effectively to study the homology groups
$1$
. It might be possible to use this effectively to study the homology groups
![]() $H_j({\mathrm {PG}}, \Lambda (G)/J_i).$
This would then yield finer results on the structure of the dual Selmer group. We hope to return to this line of investigation later.
$H_j({\mathrm {PG}}, \Lambda (G)/J_i).$
This would then yield finer results on the structure of the dual Selmer group. We hope to return to this line of investigation later.
Acknowledgments
The authors would like to thank Konstantin Ardakov, Srikanth B. Iyengar, Antonio Lei, and Dipendra Prasad for helpful discussions. Jishnu Ray would also like to thank the organizers of “Iwasawa 2019” conference (June 2019, Bordeaux) for invitation to speak. Theorem 3.1 in this article was announced in that conference. Jishnu Ray is very grateful to Sarah Zerbes for sending him a copy of her Ph.D. dissertation on Selmer groups over p-adic Lie extensions. Finally, the authors thank the referees for their careful reading of the article and suggestions, which helped improve the exposition.