Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-11T19:22:38.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Electron acceleration in a rectangular waveguide filled with unmagnetized inhomogeneous cold plasma

Published online by Cambridge University Press:  16 June 2008

H.K. Malik ,
S. Kumar  and
K.P. Singh
H.K. Malik*
Affiliation:
Plasma Waves and Particle Acceleration Laboratory, Department of Physics, Indian Institute of Technology Delhi, New Delhi, India
S. Kumar
Affiliation:
Department of Physics, Pohang University of Science and Technology, Pohang, Korea
K.P. Singh
Affiliation:
Simutech, Gainesville, Florida
*
Address correspondence and reprint requests to: Hitendra K. Malik, Plasma Waves and Particle Acceleration Laboratory, Department of Physics, Indian Institute of Technology Delhi, New Delhi – 110 016, India. E-mail: hkmalik@physics.iitd.ac.in
Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the study of propagation of electromagnetic wave in a rectangular waveguide filled with an inhomogeneous plasma in which electron density varies linearly in a transverse direction to the mode propagation. A transcendental equation in ω (microwave frequency) is obtained that governs the mode propagation. In addition, an attempt is made to examine the effect of density inhomogeneity on the energy gain acquired by the electron (electron bunch) when it is injected in the waveguide along the direction of the mode propagation. On the basis of angle of deflection of the electron motion we optimize the microwave parameters so that the electron does not strike with the waveguide walls. Conditions have been discussed for achieving larger energy gain. The plasma density inhomogeneity is found to play a crucial role on the cutoff frequency, fields and dispersion relation of the TE10 mode as well as on the acceleration gradient in the waveguide.

Keywords

Electron accelerationRectangular waveguideInhomogeneous plasmaMicrowave
Type
Research Article
Information
Laser and Particle Beams , Volume 26 , Issue 2 , June 2008 , pp. 197 - 205
Copyright
Copyright © Cambridge University Press 2008

INTRODUCTION

The subject particle acceleration has been fascinating due to its diverse applications in the field of nuclear physics, high energy physics, harmonic generation, nonlinear phenomena observed during laser plasma interaction, etc. In this direction, various experimental and theoretical investigations (Balakirev et al., Reference Balakirev, Karas, Karas and Levchenko2001; Reitsma & Jaroszynski, Reference Reitsma and Jaroszynski2004; Baiwen et al., Reference Baiwen, Ishiguro, Skoric, Takamaru and Sato2004; Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Koyama et al., Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006; Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006; Kumar et al., Reference Kumar, Malik and Nishida2006; Sakai et al., Reference Sakai, Miyazaki, Kawata, Hasumi and Kikuchi2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Gupta & Suk, Reference Gupta and Suk2007; Malik et al., Reference Malik, Kumar and Nishida2007; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007; Zhou et al., Reference Zhou, Yu and He2007) have been made along with the use of high peak power lasers that could be developed with the help of chirped pulse amplification (CPA) technique. The lasers have proved to be an effective tool to produce ultrahigh acceleration gradients using plasmas as the accelerating media as they can sustain large electric fields being in ionized state. Baiwen et al. (Reference Baiwen, Ishiguro, Skoric, Takamaru and Sato2004) have investigated the electron acceleration by an intense laser pulse in a low density plasma and observed a short high quality well collimated relativistic electron beam in the direction opposite to the laser propagation. Lifschitz et al. (Reference Lifschitz, Faure, Glinec, Malka and Mora2006) have proposed a design of a two stage compact GeV electron accelerator. Flippo et al. (Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007) have shown in a laser driven ion accelerator that the spectral shape of the accelerated particles can be controlled to yield a range of distribution, from Maxwellian to ones possessing a monoenergetic peak at high energy. Nickles et al. (Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007) have reviewed the ultrafast ion acceleration experiments in laser plasma and discussed the interaction of laser pulse with intensities above 1019 W/cm2 with water and heavy water droplets as well as with thin foils.

In addition, efforts have been made related to wakefield excitation by relativistic electron bunch (Balakirev et al., Reference Balakirev, Karas, Karas and Levchenko2001; Zhou et al., Reference Zhou, Yu and He2007), by different shapes of laser pulses (Kumar et al., Reference Kumar, Malik and Nishida2006; Malik et al., Reference Malik, Kumar and Nishida2007), and coupling of longitudinal and transverse motion of accelerated electrons in laser wakefield (Reitsma & Jaroszynski, Reference Reitsma and Jaroszynski2004). Also Koyama et al. (Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006) have experimentally generated monoenergetic electron beam by focusing 2 TW laser pulses of 50 fs on supersonic gas jet targets. Lotov (Reference Lotov2001) has analytically studied the laser wakefield acceleration in narrow plasma filled channels. With regard to the importance of polarization effects, Kado et al. (Reference Kado, Daido, Fukumi, Li, Orimo, Hayashi, Nishiuchi, Sagisaka, Ogura, Mori, Nakamura, Noda, Iwashita, Shirai, Tongu, Takeuchi, Yamazaki, Itoh, Souda, Nemoto, Oishi, Nayuki, Kiriyama, Kanazawa, Aoyama, Akahane, Inoue, Tsuji, Nakai, Yamamoto, Kotaki, Kondo, Bulanov, Esirkepov, Utsumi, Nagashima, Kimura and Yamakawa2006) have observed strongly collimated proton beam from Tantalum targets when irradiated with circularly polarized laser pulses. With the help of radially polarized ultra relativistic laser pulses, Karmakar and Pukhov (Reference Karmakar and Pukhov2007) have shown that collimated attosecond GeV electron bunches can be produced by ionization of high-Z material. They also compared the results with the case of Gaussian laser pulses and found that the radially polarized laser pulses are superior both in the maximum energy gain and in the quality of the produced electron beams. Xu et al. (Reference Xu, Kong, Chen, Wang, Wang, Lin and Ho2007) made a comparison between circularly polarized (CP) and linearly polarized (LP) fields with regard to the laser driven electron acceleration in vacuum and found that the CP field can give rise to greater acceleration efficiency. In such schemes of wakefield acceleration, a large amplitude plasma wave is generated which is used for the particle acceleration. However, when this wave achieves a sufficiently large amplitude it becomes susceptible to the oscillating two stream instability (OTSI), which is an important issue in nonlinear plasma physics and has been studied in different plasma models (Nicholson, Reference Nicholson1981; Kumar & Malik, Reference Kumar and Malik2006a; Malik, Reference Malik2007).

On the other hand, the researchers have studied the propagation of electromagnetic waves in circular waveguides (Alexov & Ivanov, Reference Alexov and Ivanov1993; Maraghechi et al., Reference Maraghechi, Willett and Mehdian1994; Watanabe et al., Reference Watanabe, Nishimura and Matsuo1995; Ivanov & Nikolaev, Reference Ivanov and Nikolaev1998; Ding et al., Reference Ding, Liu and Ma2001, Reference Ding, Chen and Wang2004) considering different models, viz. partially plasma filled waveguides, completely plasma filled waveguides, unmagnetized, magnetized plasma filled waveguide etc. in view of their applications to a variety of sources including backward wave oscillators (BWO), traveling wave tube (TWT) amplifiers, gyrotrons, etc. Microwaves have also been used for the purpose of particle acceleration (Palmer, Reference Palmer1972; Hirshfield et al., Reference Hirshfield, Lapointe, Ganguly, Yoder and Wang1996; Park & Hirshfield, Reference Park and Hirshfield1997; Zhang et al., Reference Zhang, Hirshfield, Marshall and Hafizi1997; Yoder et al., Reference Yoder, Marshall and Hirshfield2001; Jing et al., Reference Jing, Liu, Xiao, Gai and Schoessow2003; Malik, Reference Malik2003; Jawla et al., Reference Jawla, Kumar and Malik2005; Kumar & Malik, Reference Kumar and Malik2006b). On the basis of interaction of relativistic particles with free electromagnetic waves in the presence of a static helical magnet, Palmer (Reference Palmer1972) has shown that the particles can be accelerated when they move in the direction of propagation of the circularly polarized radiation. Hirshfield et al. (Reference Hirshfield, Lapointe, Ganguly, Yoder and Wang1996) have discussed cyclotron auto-resonance accelerator (CARA) using radiofrequency (rf) gyroresonant acceleration where the maximum energy achieved by the electron beam is up to 2.82 MeV. Zhang et al. (Reference Zhang, Hirshfield, Marshall and Hafizi1997) have attempted for a wakefield accelerator using a dielectric lined waveguide structure and showed that the acceleration gradient for electrons or positrons can be achieved in the range of 50–100 MV/m for a few nC driving bunches. Using a uniform circular waveguide with a helical wiggler and axial magnetic field, Yoder et al. (Reference Yoder, Marshall and Hirshfield2001) have measured the energy gain of about 360 keV for a 6 MeV electron bunch, and an accelerating gradient of 0.43 MV/m in a microwave inverse free electron laser accelerator. A theory was given by Park and Hirshfield (Reference Park and Hirshfield1997) for wakefield in a dielectric lined waveguide, and a peak acceleration gradient of 155 MeV/m was predicted for a 2 nC rectangular drive bunch. Jing et al. (Reference Jing, Liu, Xiao, Gai and Schoessow2003) have calculated dipole-mode wakefields in dielectric-loaded rectangular waveguide accelerating structure and predicted transverse wakefields of about 0.13 MeV/mnC (0.2 MeV/mnC) due to X-dipole modes (Y-dipole modes) in an X-band structure generated by an electron bunch. Jawla et al. (Reference Jawla, Kumar and Malik2005) have shown that the modified mode excited in a plasma filled waveguide under the effect of an external magnetic field can be quite useful for the electron acceleration using high intensity microwaves. Kumar and Malik (Reference Kumar and Malik2006b) have discussed the importance of obliquely applied magnetic field to an electron acceleration and obtained that the larger acceleration is possible when the condition ωp>ωc (ωp is the electron plasma frequency and ωc is the electron cyclotron frequency) is achieved in the plasma filled waveguide.

Since invariably we encounter with the inhomogeneous plasmas (Kovalenko & Kovalenko, Reference Kovalenko and Kovalenko1996; Cho, Reference Cho2004) and the waveguide can guide the electromagnetic radiations for longer distances, it would be of great interest to evaluate the effect of plasma density inhomogeneity on the electron motion and its acceleration in a rectangular waveguide when it is injected in the waveguide along the direction of mode propagation (schematic is shown in Fig. 1). In this paper we therefore discuss this problem by considering a weak gradient in the plasma density in the transverse direction to the mode propagation.

Fig. 1. Geometry of the plasma filled rectangular waveguide with a linear density variation along the x-axis and the mode propagation along the z-axis.

MODE FIELD: ANALYTICAL APPROACH

We focus on the transverse electric (TE) mode that is excited by a high intensity microwave in a lossless inhomogeneous unmagnetized plasma filled rectangular waveguide of dimensions a × b cm2. For calculating the fields of the mode, we proceed with the following Maxwell's equations for the time dependence as e −iωt

(1)
\eqalign{\matrix{&\vec \nabla \cdot \vec D = 0\comma \; \hfill& \vec \nabla \cdot \vec B = 0\comma \; \hfill \cr &\vec \nabla \times \vec E = i\omega \mu_0 \vec {H}\comma \; & \vec \nabla \times \vec H = - ne \vec v - i\omega \varepsilon_0 \vec E.}}

Here the velocity $\vec v$ is obtained from the electron equation of motion as $\vec v = \lpar e\vec E / m_e i\omega\rpar $. With the use of this expression in the above equations we get

(2)
\vec \nabla \times \vec H = - {ne^2 \vec E \over m_e i\omega} - i\omega \varepsilon_0 \vec E=- i\omega \varepsilon_0 \varepsilon \vec E\comma \; \eqno\lpar 2\rpar

where ɛ is the plasma dielectric function, given by ɛ (ω, x) = 1 − (ωp2 (x)/ω2) together with the plasma density n = n 0 (x), as we consider the density variation only in the x-direction. The curl of Eq. (2) together with the use of other Maxwell's equations and the standard identity $\vec \nabla \times \varepsilon \vec E = \varepsilon \vec \nabla \times \vec E + \vec \nabla \varepsilon \times \vec E$ yields

(3)
\nabla^2 \vec H + {\omega^2 \over c^2} \varepsilon \vec H + {1 \over \varepsilon} \vec \nabla \varepsilon \times \lpar \vec \nabla \times \vec H\rpar = 0.\eqno\lpar 3\rpar

The above equation for Hz can be written as

(4)
\nabla^2 H_z + {\omega^2 \over c^2} \varepsilon H_z - {1 \over \varepsilon} {d\varepsilon \over dx} {\partial H_z \over \partial x} = 0.\eqno\lpar 4\rpar

We consider weak inhomogeneity, i.e., n is treated as a slow varying function of x as long as its variation length scale is far longer than the wavelength of the wave, or in other words, (1/k gn) (dn/dx) <<1 together with kg as the guide propagation constant. In view of this, the last term of Eq. (4) can be dropped. Further we assume that the plasma density is a linear function of space, i.e., n = n cr (x/L), where n cr (≡ɛ0m e ω2/e 2) is the critical density, which we will call as reference plasma density n0. Therefore, Eq. 4 reads

(5)
\nabla^2 H_z + {\omega^2 \over c^2} \left(1 - {x \over L} \right)H_z = 0.\eqno\lpar 5\rpar

Using separation of variable method Eq. (5) can be solved by taking H z (x, y, z) = F(x)G(y)I(z). With this we obtain

(6)
{1 \over F} {\partial^2 F \over \partial x^2} + {1 \over G}{\partial^2 G \over \partial y^2} + {1 \over I} {\partial^2 I \over \partial z^2} = - k^2\comma \; \eqno\lpar 6\rpar

where k 2 = (ω2/c 2(1 − (x/L)). Taking −k 2 = k x2 + k y2 + k z2 we may write the following from the above equation

(7)
{1 \over F} {d^2 F \over dx^2} = k_x^2\comma \; \quad {1 \over G} {d^2 G \over dy^2} = k_y^2 \quad {1 \over I} {d^2 I \over dz^2} = k_z^2 = k_g^2.\eqno\lpar 7\rpar

With a change of variables to η = (ω2/c2L)1/3(x − L), the x-dependent part takes the following form

(8)
{d^2 F \over d\eta^2} - \eta F = 0.\eqno\lpar 8\rpar

This differential equation defines the well-documented Airy functions A i and B i together with the general solution as

(9)
F\lpar \eta\rpar = \alpha A_i \lpar \eta \rpar + \beta B_i \lpar \eta\rpar \comma \; \eqno\lpar 9\rpar

where α and β are constants that can be determined by matching to the boundary conditions. Since it is seen that B i(η) → ∞ as η → ∞, we choose β = 0. Then the constant α is obtained by matching the magnetic field with the field of the incident wave at the interface between the vacuum and the front of plasma filled waveguide at x = 0, i.e., at η =−(ωL/c)2/3. Further if we assume that (ωL/c)>>1 and use the asymptotic representation $A_i \lpar \eta\rpar = \lpar 1/\sqrt {\pi} \eta^{1/4}\rpar \cos \lpar \lpar 2/3\rpar \eta^{2/3} - \lpar \pi / 4\rpar \rpar $, we obtain $\alpha = 2\sqrt {\pi} \lpar \omega L / c\rpar ^{1/6} A_0$. Here A 0 is the value of magnetic field in the free space corresponding to the microwave intensity I 0. With this we write the expression for the F(x) component as

F \lpar x\rpar = 2A_0 \left({L \over x - L}\right)^{1/4} \cos \left[{2 \over 3} \left({\omega^2\over Lc^2}\right)^{2/9} \lpar x - L\rpar ^{2/3} - {\pi \over 4}\right].

With the use of solutions for the y- and z- dependence of H z one can write the complete solution as

(10)
\eqalign{H_z \lpar x\comma \; y\comma \; z\rpar =&\, 2A_0 \left({L \over x - L} \right)^{1/4} \cos \cr & \times \left[{2 \over 3}\left({\omega^2 \over Lc^2} \right)^{2/9} \lpar x - L\rpar ^{2/3} - {\pi \over 4} \right]\cos \left({n\pi y \over b} \right)e^{ik_g z}.}

Here $k_g = \sqrt {k^2 - k_c^2}$ together with −k c2 = k x2 + k y2. One can obtain the following expressions for H x, H y, E x, and E y in terms of H z from the Maxwell's equations for the space dependence as e ik gz

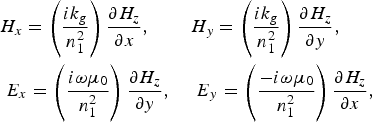
\eqalign{H_x &= \left({ik_g \over n_1^2} \right){\partial H_z \over \partial x}\comma \; \quad \quad \hskip -1.9pt H_y = \left({ik_g \over n_1^2}\right){\partial H_z \over \partial y}\comma \; \cr & \hskip -.8pcE_x = \left({i\omega \mu_0 \over n_1^2}\right) {\partial H_z \over \partial y}\comma \;\quad E_y= \left({ - i\omega \mu_0 \over n_1^2} \right){\partial H_z \over \partial x}\comma \;}

where n 12 = [k g2 − (ω2/c 2) (1 − (ωp2/ω2))].

The above relations are general expressions. The contribution of waveguide can be entered through the property of a pure conductor in view of which the tangential component of the electric field (e.g., E y) vanishes at the conducting waveguide walls, i.e., at x = 0 and a. This condition is equivalent to (∂H z/∂x)x=0,a = 0, which yields the following

(11a)
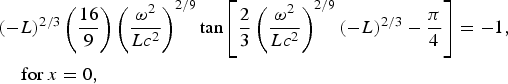
\eqalign{&\lpar - L\rpar ^{2/3} \left\lpar{16 \over 9} \right\rpar\left \lpar{\omega^2 \over Lc^2 }\right\rpar^{2/9} \tan \left\lsqb{2 \over 3} \left\lpar{\omega^2 \over Lc^2} \right\rpar^{2/9} \lpar - L\rpar ^{2/3} - {\pi \over 4} \right\rsqb =- 1\comma \cr &\quad \hbox{ for } x = 0\comma}
(11b)
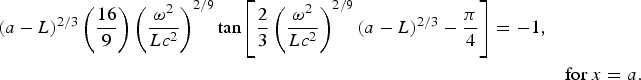
\eqalign{\lpar a - L\rpar ^{2 / 3} \left\lpar{16 \over 9}\right\rpar\left\lpar{\omega^2 \over Lc^2}\right\rpar^{2/9} \tan \left\lsqb{2 \over 3}\left\lpar{\omega^2 \over Lc^2} \right\rpar^{2 / 9} \lpar a - L\rpar ^{2/3} - {\pi \over 4} \right\rsqb = - 1\comma \cr & \quad\hbox{for } x = a.}

For typical values of microwave frequency ω and waveguide width a, we solve these two coupled equations and obtain the common values of L for which the field components would be applicable to the waveguide. Keeping this in mind and taking X a = (1/(x − L)) and a 1 = (2/3) (ω2/Lc 2)2/9 (x − L)2/3 − (π/4), we write the solution of H z in the simpler form as H z(x, y, z) = 2A 0 (LX a)1/4 cos a 1 cos (nπy/b)e ik gz.

Finally one can obtain the complete set of field components of the fundamental TE10 mode as given below

(12)
\eqalignno{H_x &= \left({ik_g \over n_1^2} \right)2A_0 \lpar LX_a \rpar ^{1/4} \left[- {X_a \over 4}\cos a_1 - {4 \over 9X_a^{1/3}} \left({\omega^2 \over Lc^2}\right)^{2/9} \sin a_1 \right]e^{ik_g z}\comma \; \cr E_y &= \left({i\omega \mu_0 \over n_1^2} \right)2A_0 \lpar LX_a\rpar ^{1/4} \left[{X_a \over 4}\cos a_1 + {4 \over 9X_a^{1/3}} \left({\omega^2\over Lc^2} \right)^{2/9} \sin a_1 \right]e^{ik_g z}\comma \; \cr H_z &= 2A_0 \lpar LX_a \rpar ^{1/4} \cos a_1 e^{ik_g z}.&\lpar 12\rpar}

Figures 2 to 4 show the variation of field components E y, H x, and H z, of the TE10 mode in a 4.0 cm × 2.5 cm waveguide for one guide wavelength when I 0 = 1 × 1010 W/cm2, f =11.6 GHz, and n 0 = 5 × 1016/m3. Here we mention that due to some problem in programming, we are unable to show the variation until the wall x = 0. However, the field component Ey vanishes at both the walls at x = 0 and a, which confirms the appropriateness of field components to the TE10 mode in the waveguide. Further, a comparison of Figure 3 with Figure 4 reveals that the component H x dominates over the component H z.

Fig. 2. (Color online) 3D variation of the resultant electric field E y in the waveguide for one guide wavelength when I 0 = 1×1010 W/cm2, f =11.6 GHz, and n 0 = 5 × 1016/m3 in a 4.0 cm × 2.5 cm rectangular waveguide.

Fig. 3. (Color online) 3D variation of the resultant magnetic field H x in the waveguide for one guide wavelength and the same parameters as in Figure 2.

Fig. 4. (Color online) 3D variation of the resultant magnetic field H z in the waveguide for one guide wavelength. Here, the parameters are the same as in Figure 2.

DISCUSSION ON MODE PROPAGATION

By putting the solution of H z in Eq. (5), we get the following dispersion relation for the TE10 mode

(13)
\eqalign{\omega^2 &= \omega_p^2 + c^2 \left[k_g^2 - {5 \over 16} X_a^2 - {10 \over 27} \left({2\omega^2 \over ac^2}\right)^{2 / 9} X_a^{4 / 3} \tan\right. \cr &\quad \left.\times \left\{{2 \over 3} \left({2\omega^2 \over ac^2} \right)^{2 / 9} \lpar x - L\rpar ^{2 / 3} - {\pi \over 4} \right\}+ {16 \over 81} \left({2\omega^2 \over ac^2} \right)^{4 / 9} X_a^{2 / 3}\right].}

Since we have already put the expression of the density (which is the function of x), we obtain this transcendental equation in ω that describes the propagation of the mode in the waveguide filled with an inhomogeneous plasma. In this context, the lower cut-off frequency is calculated by putting k g = 0 and ω = ωcutoff = 2πf L. With this one obtains the following equation

(14)
\eqalign{\omega_{cutoff}^2 &= \omega_p^2 + c^2 \left[- {5 \over 16} X_a^2 - {10 \over 27} \left({2\omega_{cutoff}^2 \over ac^2} \right)^{2 / 9} X_a^{4 / 3} \tan\right. \cr &\quad \times \left. \left\{{2 \over 3} \left({2\omega_{cutoff}^2 \over ac^2} \right)^{2 / 9} \lpar x - L\rpar ^{2 / 3} - {\pi \over 4} \right\}+ {16 \over 81} \left({2\omega_{cutoff}^2 \over ac^2} \right)^{4 / 9} X_a^{2 / 3} \right].}\eqno\lpar 14\rpar

The above equation can be solved for the typical values of x along the waveguide width, the reference plasma density n0, and waveguide width a in order to obtain the lower cut-off frequency for the propagation of the mode. However, the upper cut-off frequency can be obtained by replacing the width a by the height b of the waveguide in the above equation. Since the plasma has a density gradient along the waveguide width, the cut-off frequency will vary along the width. For example, the values of lower cut-off frequency f L when n 0 is taken as 5 × 1016/m3 in a 4.0 cm × 2.5 cm rectangular waveguide come out to be 7.96 GHz (at x = 2.4 cm), 7.97 GHz (at x = 2.8 cm), 7.99 GHz (at x = 3.2 cm), and 8.0 GHz (at x = 3.6 cm).

In order to discuss the dispersion characteristics of the mode, Figure 5 shows the behavior of ck g/ωp and ω/ωp with respect to x for different values of plasma density. Here the solid graphs k1, k2, and k3 correspond to ck g/ωp for three different plasma densities 5×1016/m3, 8×1016/m3, and 10×1016/m3, respectively. Similarly the dotted graphs ω1, ω2, and ω3 correspond to ω/ωp for the same respective values of plasma density. This is clear from the figure that as we move away from x = a/2 toward x = a, ω/ωp as well as ck g/ωp get reduced. For a fixed microwave frequency, the decrease of ck g/ωp means the propagation constant kg gets smaller or the mode velocity gets larger. Moreover, the wavelength of the microwave, i.e., guide wavelength λg (=2π/kg) becomes larger as we move toward x = a, i.e., toward the region of higher plasma density. On the other hand, for a fixed reference plasma density n 0, ω/ωp decreases as we move toward x = a; this is because of the increased plasma oscillation frequency ωp due to the density gradient.

Fig. 5. Behavior of ω/ωp and ckg/ωp of the TE10 mode along the waveguide width or the distance x in a 4.0 cm × 2.5 cm waveguide when I 0 = 1 × 1010W/cm2.

ELECTRON MOTION IN THE WAVEGUIDE

Now we study the motion of the electron (or electron bunch) in the field of the mode, when it is injected along the direction of mode propagation. Here we assume that the electron bunch does not affect the fields of the mode and employ the same approach as used by Malik (Reference Malik2003) and Jawla et al. (Reference Jawla, Kumar and Malik2005) for calculating the expression of the angle of deflection of the electron motion from the direction of mode propagation (z-axis). The y-component of electron momentum equation under the effect of field components E y, H x, and H z gives rise to the following expression for the angle θ

(15)
\eqalign{\tan \theta &= {eE_0 \over m_e v_z \omega k_g^2 \lpar T_2 + T_3\rpar ^2} \left[k_g \left\{\left({\omega + v_{z_0} k_g \over v_{z_0}} \right)\right.\right. \cr &\quad \left.\left. - \left({\omega + v_z k_g \over v_z } \right)\cos k_g z \right\}\lpar T_2 + T_3 \rpar ^2 + n_1^4 \lpar \cos k_g z - 1\rpar \cos^2 a_1 \right]\comma \; }\eqno\lpar 15\rpar

where T 2 = (1/8) X a cos a 1, T 3 = (4/9) (2ω2/ac 2)2/9 (X a)1/3 sin a 1, v z0 is the initial velocity of electron corresponding to its energy with which it is injected in the waveguide and E 0 is the field corresponding to the microwave intensity I 0. It is clear from this relation that the angle of deflection is directly proportional to E 0 and it also has a dependence on the waveguide width a, microwave frequency ω and reference plasma density n 0. Here it is also evident that the electron will execute sinusoidal oscillations in the waveguide. Therefore, the microwave parameters and the waveguide dimensions should be optimized such that the amplitude of oscillations always remains less than half of the waveguide height. We will take this point into consideration, when analyze the acceleration of the electron in the next section.

ELECTRON ACCELERATION: ENERGY GAIN

In order to analyze the electron acceleration in the waveguide, we employ the momentum equation $\lpar d \vec p / dt\rpar = - e \lpar \vec E + \mu_0 \vec v \times \vec H\rpar $ and energy equation $\lpar d\lpar m_e \gamma c^2\rpar / dt\rpar = - e\lpar \vec v.\vec E\rpar $ of the electron (or electron bunch) under the effect of the mode field components. Since TE10 mode is a fast wave (v p>c), a synchronous interaction of the moderate energy (few hundred keV) electrons with the mode is not possible. However, in the present paper, we are interested in accelerating such electrons and therefore analyze the simple interaction on the scale of velocity v g. We transform the coordinates to ς=v gt − z and obtain the following relations from the energy and momentum equations

(16)
{\lpar v_g - v_z \rpar d \lpar m_e \gamma v_y \rpar \over d\varsigma} = - e\lsqb \vec E_y + \mu_0 \lpar v_z H_x - v_x H_z \rpar \rsqb \comma \; \eqno\lpar 16\rpar
(17)
{\lpar v_g - v_z \rpar d \lpar m_e \gamma c^2\rpar \over d\varsigma } = - e \lpar v_x H_x + v_y H_y + v_z H_z \rpar .\eqno\lpar 17\rpar

Also, the following relation between v x and v z is realized

(18)
{d\lpar \gamma v_x \rpar \over d\varsigma} + \left({H_z \over H_x} \right){d\lpar \gamma v_z\rpar \over d\varsigma} = 0.\eqno\lpar 18\rpar

Then with the use of Eqs. (16) to (18) we obtain the following second order differential equation

(19)
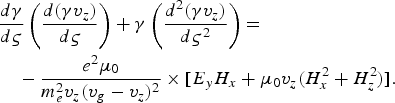
\eqalign{&{d\gamma \over d\varsigma} \left({d\lpar \gamma v_z \rpar \over d\varsigma} \right)+ \gamma \left({d^2 \lpar \gamma v_z \rpar \over d\varsigma^2}\right)= \cr &\quad- {e^2 \mu_0 \over m_e^2 v_z \lpar v_g - v_z \rpar ^2} \times\lsqb E_y H_x + \mu_0 v_z \lpar H_x^2 + H_z^2\rpar \rsqb .}

Now we substitute the values of field components E y, H x, and H z in the above equation and obtain the following solution by treating γ (or v z) as a slowly varying function

(20)
\eqalign{\left({d\gamma \over dz}\right)&= {eE_0 \over m_e \omega \lpar T_2 + T_3\rpar }\cr &\quad \times \left[\matrix{\matrix{k_g \lpar T_2 + T_3\rpar ^2 \left\{\left(\displaystyle{\gamma_0 \over \gamma} \right)^2 \left(\displaystyle{\omega + v_{z0} k_g \over v_{z0} \lpar v_g - v_z\rpar ^2} \right)\right.\cr \quad \left.- \left(\displaystyle{\omega + v_z k_g \over v_z \lpar v_g - v_z \rpar ^2} \right)\cos \lpar 2\, k_g z\rpar \right\}}\cr + n_1^4 \left\{\displaystyle{\cos \lpar 2\, k_gz\rpar \over \lpar v_g - v_z\rpar ^2 } - \left(\displaystyle{\gamma_0 \over \gamma} \right)^2 \left(\displaystyle{1 \over \lpar v_g - v_z\rpar ^2} \right)\right\}\cos^2 a_1} \right]^{1 / 2}\hskip-1pc .}\eqno\lpar 20\rpar

This relation gives the change in γ per unit length for the electron during its motion in the waveguide. Therefore, by multiplying it with the factor (m ec 2/e) we can obtain the energy gain or acceleration gradient in eV/m as

(21)
\eqalign{\left({\Delta U \over \Delta z}\right)_{ev/m} &= \left({c^2 E_0 \over \omega \lpar T_2 + T_3\rpar }\right)\cr &\quad \times \left[\matrix{k_g \lpar T_2 + T_3\rpar ^2 \left\{\matrix{\left(\displaystyle{\gamma_0 \over \gamma} \right)^2 \left(\displaystyle{\omega + v_{z0} k_g \over v_{z0} \lpar v_g - v_{z0}\rpar ^2}\right)\cr - \left(\displaystyle{\omega + v_z k_g \over v_z \lpar v_g - v_z\rpar ^2} \right)\cr \times \cos \lpar 2\, k_g z\rpar } \right\}\cr + n_1^4 \left\{\displaystyle{\cos \lpar 2\, k_gz\rpar \over \lpar v_g - v_z \rpar ^2} - \left(\displaystyle{\gamma_0 \over \gamma} \right)^2 \left(\displaystyle{1 \over \lpar v_g - v_z \rpar ^2 }\right)\right\}\cos^2 a_1} \right]^{1/2}\hskip -1pc.}\eqno\lpar 21\rpar

CONDITION FOR LARGER ENERGY GAIN

This is clear from Eq. (21) that the acceleration gradient is strongly affected by the plasma density inhomogeneity via a 1 and X a terms (in the expressions of T2 and T3) and it increases for the higher field E 0 or the microwave intensity I 0. We can obtain the point of injection and position where the electron will achieve larger energy gain (or the acceleration gradient). For this an approximate estimation of the point of injection can be obtained from the term cosa 1 for which a 1 should be zero. This reads

(22)
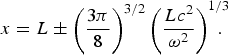
x = L \pm \left({3\pi \over 8}\right)^{3/2} \left({Lc^2 \over \omega^2}\right)^{1/3}\hskip -.7pc.\eqno\lpar 22\rpar

It means larger energy gain depends on the microwave frequency ω and the density inhomogeneity scale length L. On the other hand, the value of x cannot be exactly 0 or a. This point leads to the following condition for the minimum value of L

(23)
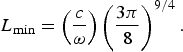
L_{\min} = \left({c \over \omega}\right)\left({3\pi \over 8}\right)^{9/4}.\eqno\lpar 23\rpar

Interestingly, the above equation infers that the waveguide filled with inhomogeneous plasma having lower scale of density gradient is more appropriate for getting effective acceleration if we use larger frequency microwave for exciting the fundamental TE10 mode, otherwise vice-versa is true. Now with Eq. (22) we obtain the following expression for larger acceleration gradient in eV/m

(24)
\left({\Delta U\over \Delta z}\right)_{\lpar ev/m\rpar _L } = \left({8c^2 E_0 \over \omega X_a}\right)\left[\matrix{\matrix{\left(\displaystyle{k_g \over 64 \lpar x - L\rpar ^2} \right)\left\{\left(\displaystyle{\gamma_0 \over \gamma} \right)^2 \left(\displaystyle{\omega + v_{z0} k_g \over v_{z0} \lpar v_g - v_z \rpar ^2}\right)\right.\cr \left.- \left(\displaystyle{\omega + v_z k_g \over v_z \lpar v_g - v_z \rpar ^2} \right)\cos \lpar 2\, k_g z\rpar \right\}} \cr + n_1^4 \left\{\displaystyle{\cos \lpar 2\, k_g z\rpar \over \lpar v_g - v_z \rpar ^2} - \left(\displaystyle{\gamma_0 \over \gamma}\right)^2 \left(\displaystyle{1 \over \lpar v_g - v_z\rpar ^2}\right)\right\}}\right]^{1 / 2}\hskip-1pc.\eqno\lpar 24\rpar

In addition to above Eqs. (22) and (23), we can see from the above equation that the maximum gradient is attained when the electron completes the distance z = λg/4 in the waveguide. In view of this for showing the results graphically we will restrict our calculations for energy gain and acceleration till z = λg/4.

RESULTS AND DISCUSSION

In view of the discussion made in the above sections, now we present the results by giving typical values to I 0, f, a, n 0, and initial electron energy E in. Figure 6 shows the variation of the energy gain and the acceleration gradient along the z-axis in a 4.0 cm × 2.5 cm rectangular waveguide when f = 11.66 GHz, I 0 = 1 × 1010 W/cm2 and E in = 500 keV. This is clear that the acceleration gradient as well as the energy gain achieved by the electron are increased during its motion in the waveguide.

Fig. 6. Variation of the energy gain (EG) and acceleration gradient (AGD) up to λg/4 in a 4.0 cm × 2.5 cm waveguide for two different values of n 0 as 5 × 1016/m3 (graphs AGD5 and EG5) and 8 × 1016/m3 (graphs AGD8 and EG58), when I 0 = 1 × 1010W/cm2, f = 11.66 GHz, E in = 500 keV and point of injection x = 3.2 cm.

Effect of Plasma Density and Waveguide Width

In Figure 7, the effect of plasma density n 0 on the total energy gain (TEG) and the maximum acceleration gradient (MGD) acquired by a 500 keV electron is shown for the parameters mentioned in the figure caption. Here, this can be seen that the effect of plasma density as well as the waveguide width is to enhance the energy gain and the acceleration gradient: the gain is increased from 0.62 MeV to 5.94 MeV whereas increase in the acceleration gradient is from 119 MeV/m to 248 MeV/m, when the plasma density is raised from 4.5 × 1016/m3 to 8.0 × 1016/m3 and the waveguide width remains fixed at a = 4.0 cm. However, for 4.2 cm width of the waveguide, the gradient is increased to 266 MeV/m and the gain to 8.20 MeV, which is quite a good amount of gain for a 500 keV electron. Also, we realize that these acceleration gradient and the energy gain are larger than those obtained by other investigators (Hirshfield et al., Reference Hirshfield, Lapointe, Ganguly, Yoder and Wang1996; Park & Hirshfield, Reference Park and Hirshfield1997; Yoder et al., Reference Yoder, Marshall and Hirshfield2001; Jing et al., Reference Jing, Liu, Xiao, Gai and Schoessow2003).

Fig. 7. Effect of the plasma density n 0 on the total energy gain (TEG) as well as on the maximum acceleration gradient (MGD) for two different widths of the waveguide when I 0 = 1 × 1010W/cm2, f = 11.66 GHz, and the electron is injected with energy of 500 keV in the waveguide at x = 3.4 cm. Graphs TEG4.0 (MGD4.0) and TEG4.2 (MGD4.2) are for the width a = 4.0 cm and 4.2 cm, respectively.

The increase in gain with plasma density can be explained on the basis of the interaction of the electron with the mode fields via the waveguide wavelength λg. Since the propagation constant k g decreases (hence λg increases) with the increasing plasma density (Fig. 5), an increase in the density finally enhances the interaction length for the effective electron acceleration.

Effect of Initial Electron Energy and Microwave Intensity

In Figure 8, we analyze the effect of electron's initial energy E in on the total energy gain and the acceleration gradient for the parameters mentioned in the caption. It is clear that electrons injected with larger energy achieve larger energy gain and also higher gradient is realized. The same effect is obtained for the increasing microwave intensity: the gain (gradient) is increased from 1.05 MeV (260 MeV/m) to 3.52 MeV (440 MeV/m) when the intensity is raised from 1 × 1010 W/cm2 to 1.5 × 1010 W/cm2 and the electrons are injected with 550 keV energy. This is due to the increased amplitude of the electric field of the mode, which provides the accelerating force to the electron. Due to the increased force on the electron the velocity of the electron gets larger and hence its interaction with the mode fields becomes stronger, which leads to the larger acceleration gradient and higher energy gain to the electrons.

Fig. 8. Effect of initial electron energy on the maximum acceleration gradient (MGD) and total energy gain (TEG) for different values of microwave intensity I 0 = 1 × 1010W/cm2 (graphs MGD1.0 and TEG1.0) and 1.5 × 1010W/cm2 (graphs MGD1.5 and TEG1.5) in a 4.0 cm ×2.5 cm rectangular waveguide when n 0 = 5 × 1016/m3, f = 11.66 GHz and point of injection x = 3.4 cm.

Effect of Microwave Frequency and Point of Electron Injection

The effect of point of injection of the electrons and the microwave frequency on the total energy gain is shown in Figure 9 for a 500 keV electron at I 0 = 1 × 1010 W/cm2 in a 4.0 cm × 2.5 cm rectangular waveguide. Here, it can be seen that the energy gain is enhanced from 3.92 MeV to 4.49 MeV when the microwave frequency is raised from 11.33 GHz to 11.66 GHz. It means the microwave frequency has a significant effect on the electron energy gain and the acceleration gradient. Since cut-off frequency of the microwave is decided by the plasma density in addition to the waveguide width, the plasma density plays a crucial role in selecting the microwave frequency for achieving larger electron acceleration. Moreover, the energy gain is larger when the electrons are injected at larger values of x, i.e., toward the side of higher plasma density region (Fig. 9). This reveals that a stronger density gradient would be more helpful to achieve larger energy gain.

Fig. 9. Effect of point of injection on the total energy gain for a 500 keV electron at 11.33 GHz and 11.66 GHz microwave frequencies, when I 0 = 1 × 1010 W/cm2 and n 0 = 8 × 1016/m3.

CONCLUDING REMARK

By considering a more realistic case of inhomogeneous plasma in a rectangular waveguide, the present analysis shows that larger acceleration gradient and energy gain can be achieved at the larger microwave frequency, higher intensity, longer waveguide width and higher plasma density. Since both the waveguide wavelength and the cut-off frequency level are enhanced for the increasing plasma density and the gain is increased for the higher microwave frequency, a waveguide filled with higher density plasma and/or a plasma having a stronger density gradient are more suitable for the effective particle acceleration.

ACKNOWLEDGEMENT

Department of Science and Technology (DST) and Indian Institute of Technology (IIT) Delhi, Government of India are thankfully acknowledged for the financial support.

References

REFERENCES

Alexov, E.G. & Ivanov, S.T. (1993). Nonreciprocal effects in a plasma waveguide. IEEE Trans. Plasma Sci. 21, 254–257.CrossRefGoogle Scholar
Baiwen, L.I., Ishiguro, S., Skoric, M.M., Takamaru, H. & Sato, T. (2004). Acceleration of high-quality, well-collimated return beam of relativistic electrons by intense laser pulse in a low-density plasma. Laser Part. Beams 22, 307–314.CrossRefGoogle Scholar
Balakirev, V.A., Karas, V.I., Karas, I.V. & Levchenko, V.D. (2001). Plasma wake-field excitation by relativistic electron bunches and charged particle acceleration in the presence of external magnetic field. Laser Part. Beams 19, 597–604.CrossRefGoogle Scholar
Cho, S. (2004). Dispersion characteristics and field structure of surface waves in a warm inhomogeneous plasma column. Phys. Plasmas 11, 4399–4406.CrossRefGoogle Scholar
Ding, Z., Liu, X. & Ma, T. (2001). Polarities of electromagnetic-wave modes in a magnetoplasma-filled cylindrical waveguide. Jpn. J. Appl. Phys 40, 837–838.CrossRefGoogle Scholar
Ding, Z.F., Chen, L.W. & Wang, Y.N. (2004). Splitting and mating properties of dispersion curves of wave modes in a cold magnetoplasma-filled cylindrical conducing waveguide. Phys. Plasmas 11, 1168–1172.CrossRefGoogle Scholar
Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRefGoogle Scholar
Gupta, D.N. & Suk, H. (2007). Electron acceleration to high energy by using two chirped lasers. Laser Part. Beams 25, 31–36.CrossRefGoogle Scholar
Hirshfield, J.L., Lapointe, M.A., Ganguly, A.K., Yoder, R.B. & Wang, C. (1996). Multimegawatt cyclotron autoresonance accelerator. Phys. Plasmas 3, 2163–2168.CrossRefGoogle Scholar
Ivanov, S.T. & Nikolaev, N.I. (1998). The spectrum of electromagnetic waves in a planar gyrotropic plasma waveguide. Jpn. J. Appl. Phys. 37, 5033–5088.CrossRefGoogle Scholar
Jawla, S.K., Kumar, S. & Malik, H.K. (2005). Evaluation of mode fields in a magnetized plasma waveguide and electron acceleration. Opt. Comm. 251, 346–360.CrossRefGoogle Scholar
Jing, C., Liu, W., Xiao, L., Gai, W. & Schoessow, P. (2003). Dipole-mode wakefields in dielectric-loaded rectangular waveguide accelerating structures. Phys. Rev. E. 6, 016502 (1–6).Google Scholar
Kado, M., Daido, H., Fukumi, A., Li, Z., Orimo, S., Hayashi, Y., Nishiuchi, M., Sagisaka, A., Ogura, K., Mori, M., Nakamura, S., Noda, A., Iwashita, Y., Shirai, T., Tongu, H., Takeuchi, T., Yamazaki, A., Itoh, H., Souda, H., Nemoto, K., Oishi, Y., Nayuki, T., Kiriyama, H., Kanazawa, S., Aoyama, M., Akahane, Y., Inoue, N., Tsuji, K., Nakai, Y., Yamamoto, Y., Kotaki, H., Kondo, S., Bulanov, S., Esirkepov, T., Utsumi, T., Nagashima, A., Kimura, T. & Yamakawa, K. (2006). Observation of strongly collimated proton beam from Tantalum targets irradiated with circular polarized laser pulses. Laser Part. Beams 24, 117–123.CrossRefGoogle Scholar
Karmakar, A. & Pukhov, A. (2007). Collimated attosecond GeV electron bunches from ionization of high-Z material by radially polarized ultra-relativistic laser pulses. Laser Part. Beams 25, 371–377.CrossRefGoogle Scholar
Kawata, S., Kong, Q., Miyazaki, S., Miyauchi, K., Sonobe, R., Sakai, K., Nakajima, K., Masuda, S., Ho, Y.K., Miyanaga, N., Limpouch, J. & Andreev, A.A. (2005). Electron bunch acceleration and trapping by ponderomotive force of an intense short-pulse laser. Laser Part. Beams 23, 61–67.CrossRefGoogle Scholar
Kovalenko, A.V. & Kovalenko, V.P. (1996). Langmuir oscillations in a cold inhomogeneous plasma. Phys. Rev. E 53, 4046–4050.CrossRefGoogle Scholar
Koyama, K., Adachi, M., Miura, E., Kato, S., Masuda, S., Watanabe, T., Ogata, A. & Tanimoto, M. (2006). Monoenergetic electron beam generation from a laser-plasma accelerator. Laser Part. Beams 24, 95–100.CrossRefGoogle Scholar
Kumar, S. & Malik, H.K. (2006a). Effect of negative ions on oscillating two stream instability of a laser driven plasma beat wave in a homogeneous plasma. Phys. Scripta 74, 304–309.CrossRefGoogle Scholar
Kumar, S. & Malik, H.K. (2006b). Electron acceleration in a plasma filled rectangular waveguide under obliquely applied magnetic field. J. Plasma Phys. 72, 983–987.CrossRefGoogle Scholar
Kumar, S., Malik, H.K. & Nishida, Y. (2006). Wake field excitation and electron acceleration by triangular and sawtooth laser pulses in a plasma: An analytical approach. Phys. Scripta 74, 525–530.CrossRefGoogle Scholar
Lifschitz, A.F., Faure, J., Glinec, Y., Malka, V. & Mora, P. (2006). Proposed scheme for compact GeV laser plasma accelerator. Laser Part. Beams 24, 255–259.CrossRefGoogle Scholar
Lotov, K.V. (2001). Laser wakefield acceleration in narrow plasma-filled channels: Laser Part. Beams 19, 219–222.CrossRefGoogle Scholar
Malik, H.K. (2003). Energy gain by an electron in the fundamental mode of a rectangular waveguide by microwave radiation. J. Plasma Phys. 69, 59–67.Google Scholar
Malik, H.K. (2007). Oscillating two stream instability of a plasma wave in a negative ion containing plasma with hot and cold positive ions. Laser Part. Beams 25, 397–406.CrossRefGoogle Scholar
Malik, H.K., Kumar, S. & Nishida, Y. (2007). Electron acceleration by laser produced wake field: Pulse shaper effect. Opt. Comm. 280, 417–423.CrossRefGoogle Scholar
Maraghechi, B., Willett, J.E. & Mehdian, H. (1994). High-frequency waves in a plasma waveguide. Phys. Plasmas 1, 3181–3188.CrossRefGoogle Scholar
Nicholson, D.R. (1981). Oscillating two-stream instability with pump of finite extent. Phys. Fluids 24, 908–910.CrossRefGoogle Scholar
Nickles, P.V., Ter-Avetisyan, S., Schnuerer, M., Sokollik, T., Sandner, W., Schreiber, J., Hilscher, D., Jahnke, U., Andreev, A. & Tikhonchuk, V. (2007). Review of ultrafast ion acceleration experiments in laser plasma at Max Born Institute. Laser Part. Beams 25, 347–363.CrossRefGoogle Scholar
Palmer, R.B. (1972). Interaction of relativistic particles and free electromagnetic waves in the presence of a static helical magnet. J. Appl. Phys. 43, 3014–3023.CrossRefGoogle Scholar
Park, S.Y. & Hirshfield, J.L. (1997). Theory of wakefields in a dielectric-lined waveguide. Phys. Rev. E 62, 1266–1283.CrossRefGoogle Scholar
Reitsma, A.J.W. & Jaroszynski, D.A. (2004). Coupling of longitudinal and transverse motion of accelerated electrons in laser wakefield acceleration. Laser Part. Beams 22, 407–413.CrossRefGoogle Scholar
Sakai, K., Miyazaki, S., Kawata, S., Hasumi, S. & Kikuchi, T. (2006). High-energy-density attosecond electron beam production by intense short-pulse laser with a plasma separator. Laser Part. Beams 24, 321–327.CrossRefGoogle Scholar
Watanabe, I., Nishimura, H. & Matsuo, S. (1995). Wave propagation in a cylindrical electron cyclotron resonance plasma chamber. Jpn. J. Appl. Phys. 34, 3675–3682.CrossRefGoogle Scholar
Xu, J.J., Kong, Q., Chen, Z., Wang, P.X., Wang, W., Lin, D. & Ho, Y.K. (2007). Polarization effect of fields on vacuum laser acceleration. Laser Part. Beams 25, 253–257.CrossRefGoogle Scholar
Yoder, R.B., Marshall, T.C. & Hirshfield, J.L. (2001). Energy-gain measurements from a microwave inverse free-electron-laser accelerator. Phys. Rev. Lett. 86, 1765–1768.CrossRefGoogle ScholarPubMed
Zhang, T.B., Hirshfield, J.L., Marshall, T.C. & Hafizi, B. (1997). Stimulated dielectric wake-field accelerator. Phys. Rev. E 56, 4647–4655.CrossRefGoogle Scholar
Zhou, C.T., Yu, M.Y. & He, X.T. (2007). Electron acceleration by high current-density relativistic electron bunch in plasmas. Laser Part. Beams 25, 313–319.CrossRefGoogle Scholar
Figure 0

Fig. 1. Geometry of the plasma filled rectangular waveguide with a linear density variation along the x-axis and the mode propagation along the z-axis.

Figure 1

Fig. 2. (Color online) 3D variation of the resultant electric field Ey in the waveguide for one guide wavelength when I0 = 1×1010 W/cm2, f =11.6 GHz, and n0 = 5 × 1016/m3 in a 4.0 cm × 2.5 cm rectangular waveguide.

Figure 2

Fig. 3. (Color online) 3D variation of the resultant magnetic field Hx in the waveguide for one guide wavelength and the same parameters as in Figure 2.

Figure 3

Fig. 4. (Color online) 3D variation of the resultant magnetic field Hz in the waveguide for one guide wavelength. Here, the parameters are the same as in Figure 2.

Figure 4

Fig. 5. Behavior of ω/ωp and ckg/ωp of the TE10 mode along the waveguide width or the distance x in a 4.0 cm × 2.5 cm waveguide when I0 = 1 × 1010W/cm2.

Figure 5

Fig. 6. Variation of the energy gain (EG) and acceleration gradient (AGD) up to λg/4 in a 4.0 cm × 2.5 cm waveguide for two different values of n0 as 5 × 1016/m3 (graphs AGD5 and EG5) and 8 × 1016/m3 (graphs AGD8 and EG58), when I0 = 1 × 1010W/cm2, f = 11.66 GHz, Ein = 500 keV and point of injection x = 3.2 cm.

Figure 6

Fig. 7. Effect of the plasma density n0 on the total energy gain (TEG) as well as on the maximum acceleration gradient (MGD) for two different widths of the waveguide when I0 = 1 × 1010W/cm2, f = 11.66 GHz, and the electron is injected with energy of 500 keV in the waveguide at x = 3.4 cm. Graphs TEG4.0 (MGD4.0) and TEG4.2 (MGD4.2) are for the width a = 4.0 cm and 4.2 cm, respectively.

Figure 7

Fig. 8. Effect of initial electron energy on the maximum acceleration gradient (MGD) and total energy gain (TEG) for different values of microwave intensity I0 = 1 × 1010W/cm2 (graphs MGD1.0 and TEG1.0) and 1.5 × 1010W/cm2 (graphs MGD1.5 and TEG1.5) in a 4.0 cm ×2.5 cm rectangular waveguide when n0 = 5 × 1016/m3, f = 11.66 GHz and point of injection x = 3.4 cm.

Figure 8

Fig. 9. Effect of point of injection on the total energy gain for a 500 keV electron at 11.33 GHz and 11.66 GHz microwave frequencies, when I0 = 1 × 1010 W/cm2 and n0 = 8 × 1016/m3.