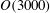1 Introduction
The momentum and energy transfer between wind and ocean surface waves is an essential component in air–sea interactions. It directly impacts the dynamics of the lower marine atmospheric boundary layer and the upper oceans. A solid understanding of the wind–wave interaction processes would bring benefits to society in applications, including marine weather forecasting, coping with natural and anthropologic hazards, energy harvest in offshore wind and wave farms, and marine ecosystem conservation, etc.
For deep water waves, it is wind forcing, nonlinear wave interactions, and wave breaking dissipation that dominate the dynamics of the wave field (Holthuijsen Reference Holthuijsen2007). Wave energy originates primarily from the wind blowing over the sea surface, an energy transfer process referred to as wind input. Jeffreys (Reference Jeffreys1925, Reference Jeffreys1926) first proposed a separation sheltering mechanism to interpret the wind input to waves. He attributed wave growth to flow separation on the leeward side of the waves. His prediction of wave growth rate was found to be too low compared with measurements (see e.g. Young Reference Young1999). Belcher & Hunt (Reference Belcher and Hunt1993) developed a non-separated sheltering theory, in which the thickening of the boundary layer on the leeward side of a wave causes a displacement of the mean flow and a pressure asymmetry in the outer region that contributes to the wave growth. The non-separated sheltering theory agrees much better with measurement data. Phillips (Reference Phillips1957) proposed a theory in which he attributed the main source of energy input to the resonance between the waves and the wind turbulence field, whereas the resulting linear growth rate is valid at the initial stage of wave generation. Miles (Reference Miles1957) used a quasi-linear theory to derive the Rayleigh equation for this problem and analysed the wave induced pressure perturbation using a predefined mean wind velocity profile. Miles’ theory showed the importance of a characteristic height where the wind speed matches the phase speed of the progressive wave. A major limitation of Miles’ theory is that the effect of turbulence was excluded from analysis. Real winds are much more complex. For example, their gustiness may have a significant impact on the wind–wave energy transfer (Nikolayeva & Tsimring Reference Nikolayeva and Tsimring1986). Through direct measurement of the airflow, a number of experimental studies conducted in the laboratory have revealed the impact of waves on the momentum and energy transfer between wind and waves. Typical wind–wave conditions include strong (hurricane) winds (Donelan Reference Donelan2004; Troitskaya et al. Reference Troitskaya, Sergeev, Kandaurov, Kazakov and Lupo2011b , Reference Troitskaya, Sergeev, Kandaurov, Baidakov, Vdovin and Kazakov2012; Sergeev et al. Reference Sergeev, Kandaurov, Troitskaya, Caulliez, Bopp and Jaehne2017), slow to moderate wind over wind-waves and mechanically generated swells (Veron, Saxena & Misra Reference Veron, Saxena and Misra2007; Buckley & Veron Reference Buckley and Veron2016, Reference Buckley and Veron2017), and steep (breaking) wave conditions (Reul, Branger & Giovanangeli Reference Reul, Branger and Giovanangeli1999, Reference Reul, Branger and Giovanangeli2008, Troitskaya et al. Reference Troitskaya, Sergeev, Ermakova and Balandina2011a ). While providing substantial insights to the canonical problem of monochromatic waves, many of these studies did not address complex wind–wave systems, especially when the wave field has a broad-band spectrum. One of the main objectives of the present study is to investigate the energy transfer process in complex wind–wave systems.
In the evolution of wave field, nonlinear resonant wave interactions, i.e., the energy transfer among different wave components, play an important role. Resonant interactions occur when certain conditions are satisfied in a group of wave components, which is a quadruplet for surface waves in the deep water. Hasselmann (Reference Hasselmann1962, Reference Hasselmann1963a ,Reference Hasselmann b ) derived a kinetic equation, known as the Hasselmann equation, for the calculation of resonant quadruplet wave interactions. The Hasselmann equation quantifies energy transfer due to four-wave interaction in the long term, where the non-resonant nonlinear terms vanish because of the asymptotic form of this kinetic equation. Recently, growing computer capacity has enabled phase-resolving simulations of broad-band waves, where the long-term characteristics of nonlinear wave fields have been studied (e.g. Gagnaire-Renou, Benoit & Badulin Reference Gagnaire-Renou, Benoit and Badulin2011; Annenkov & Shrira Reference Annenkov and Shrira2013), and the four-wave resonant interaction is found to be crucial in the process. In the present study of wind–wave interactions, we also perform phase-resolving simulations of broad-band waves, which is coupled with wind turbulence simulation, and the four-wave resonant interaction is directly captured in our simulations.
Extensive studies have been performed to develop a universal law on the evolution of wave fields in time and space. Sverdrup & Munk (Reference Sverdrup and Munk1947) proposed quantities necessary for the determination of such a law, including significant wave height, significant wave period, wind speed, fetch and duration. For decades, power law has been widely used to relate these quantities to wave growth, where the wind appears to control the wave evolution. In attempts to determine the constants in these power laws, studies have discovered an intrinsic feature of evolving wave fields, namely, self-similarity (see Hasselmann et al. Reference Hasselmann, Barnett, Bouws, Carlson, Cartwright, Enke, Ewing, Gienapp, Hasselmann and Kruseman1973). Badulin et al. (Reference Badulin, Pushkarev, Resio and Zakharov2005) conducted a series of numerical experiments, using parameterised models based on field measurements, to show that the wave spectra shapes are independent of the specific forms of wind input and dissipation. The result led to the weakly turbulent law for wave growth in support of the dominant role of nonlinear transfer (Badulin et al. Reference Badulin, Babanin, Zakharov and Resio2007). In a later study (Gagnaire-Renou et al. Reference Gagnaire-Renou, Benoit and Badulin2011), the self-similar parameter in the wave growth law (Badulin et al. Reference Badulin, Babanin, Zakharov and Resio2007) was quantified through numerical simulations for fetch-limited cases. Recently, Zakharov et al. (Reference Zakharov, Badulin, Hwang and Caulliez2015) developed a universal law that is entirely associated with intrinsic wave properties such as wave energy, peak wave frequency and peak wavenumber, while the wind speed is excluded from the formula. Their argument is also based on the dominant role of nonlinear interactions. Despite the above efforts in understanding wave field evolution, it is unclear whether the waves would evolve differently if the wind input were evaluated directly from first principles rather than by using parameterised models. Among the parameterised models, there is no consensus about which one is the best. In the operational wave model (The WAVEWATCH III® Development Group 2016) for instance, there are five different types of wind input source terms provided. In this regard, it would be desirable to examine the nonlinear interactions in the long-term evolution of a wave field using deterministic numerical tools where the wind turbulence is resolved.
The history of numerical study of wind–wave interaction that involves turbulence simulation is relatively short due to the complexity of the physical processes. The wave surface serves as an irregular bottom boundary of the wind field, which increases the complexity of solving the turbulence motions. Moreover, wave evolution involves nonlinear interactions that have a very large time scale, posing great challenges to the computational cost. In early studies, the focus was placed on wind turbulence, and only prescribed monochromatic waves were considered (Sullivan, Mcwilliams & Moeng Reference Sullivan, Mcwilliams and Moeng2000; Kihara et al. Reference Kihara, Hanazaki, Mizuya and Ueda2007; Yang & Shen Reference Yang and Shen2010). Simulations have also been applied to both air and water to study the initial stage of wave growth (Lin et al. Reference Lin, Moeng, Tsai, Sullivan and Belcher2008; Zonta, Soldati & Onorato Reference Zonta, Soldati and Onorato2015; Campbell, Hendrickson & Liu Reference Campbell, Hendrickson and Liu2016), wherein the time durations of wave evolution in these studies are limited. Some recent studies focused on the interaction between wind and breaking waves with simple wave configurations, including a two-dimensional (2-D) simulation of wind over a narrow-banded breaking wave train (Iafrati, De Vita & Verzicco Reference Iafrati, De Vita and Verzicco2019), and a three-dimensional simulation of wind over monochromatic breaking waves (Yang, Deng & Shen Reference Yang, Deng and Shen2018).
In the present study, we simulate the coupled wind–wave system based on a computational framework developed by Yang & Shen (Reference Yang and Shen2011a
,Reference Yang and Shen
b
) and Yang, Meneveau & Shen (Reference Yang, Meneveau and Shen2013). For wind turbulence, we perform large-eddy simulation (LES) on a curvilinear grid that dynamically fits the wave surface motions. For the wave field, we use a high-order spectral method (Dommermuth & Yue Reference Dommermuth and Yue1987) to capture its nonlinear evolution. The wind LES and wave simulations are dynamically coupled. The wave field evolves for a long duration up to
$O(3000)$
peak wave periods to have appreciable change in the wave spectrum. To our knowledge, this is the first wind and wave coupled simulation for such a long duration with the wave phases and turbulence eddies resolved. The analyses in this paper focus on the wave signature in the turbulence wind field, the energy transfer induced by the wind input and nonlinear interactions, and the statistical behaviours of an evolving wind–wave field. Our study aims to contribute to the fundamental understanding of the long-term wind-forced wave field evolution, and to pave the way for future wind–wave studies from the deterministic perspective. The remainder of this paper is organized as follows. In § 2, we briefly introduce the wind–wave coupled solver and problem setting. In § 3, we examine the numerical results including wind turbulence over waves, wind input to waves, wave statistics, and features of the nonlinear wave field in long-term evolution. Finally, conclusions are given in § 4.
2 Numerical method and problem setup
2.1 LES of wind over surface waves
The turbulent airflow is computed with LES (Yang et al.
Reference Yang, Meneveau and Shen2013), in which the air is treated as incompressible and is driven by a mean pressure gradient caused by the geostrophic wind forcing (Calaf, Meneveau & Meyers Reference Calaf, Meneveau and Meyers2010). The stratification is neglected. The molecular viscous effect is negligible due to the large Reynolds number in the problem of interest. Following the convention in the literature (e.g. Sullivan et al.
Reference Sullivan, Mcwilliams and Moeng2000, Reference Sullivan, Edson, Hristov and McWilliams2008), the streamwise, spanwise and vertical coordinates are denoted by
$(x,y,z)$
and equivalently
$(x_{1},x_{2},x_{3})$
. The governing equations for the airflow are (Pope Reference Pope2000)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\widetilde{u}_{i}}{\unicode[STIX]{x2202}x_{i}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\widetilde{u}_{i}}{\unicode[STIX]{x2202}t}+\widetilde{u}_{j}\frac{\unicode[STIX]{x2202}\widetilde{u}_{i}}{\unicode[STIX]{x2202}x_{j}}=-\frac{1}{\unicode[STIX]{x1D70C}_{a}}\frac{\unicode[STIX]{x2202}\widetilde{p}^{\ast }}{\unicode[STIX]{x2202}x_{i}}-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{ij}^{d}}{\unicode[STIX]{x2202}x_{j}}-\frac{1}{\unicode[STIX]{x1D70C}_{a}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x}\unicode[STIX]{x1D6FF}_{i1}, & \displaystyle\end{eqnarray}$$
where
$\widetilde{u}_{i}~(i=1,2,3)=(\widetilde{u},\widetilde{v},\widetilde{w})$
is the filtered velocity in which
$\widetilde{\ldots }$
denotes the filtered quantity at the grid scale,
$\widetilde{p}^{\ast }$
is the filtered modified pressure,
$\unicode[STIX]{x1D70F}_{ij}^{d}$
is the trace-free part of the subgrid-scale (SGS) stress tensor,
$\unicode[STIX]{x1D70C}_{a}$
is the density of air and
$\unicode[STIX]{x2202}p_{\infty }/\unicode[STIX]{x2202}x$
denotes the mean streamwise pressure gradient that drives the flow. The SGS stress tensor is calculated using the dynamic Smagorinsky model (see Germano et al.
Reference Germano, Piomelli, Moin and Cabot1991; Lilly Reference Lilly1992).
In the simulation, the filtered Navier–Stokes equations are transformed into the computational domain
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}=t,\quad \unicode[STIX]{x1D709}=x,\quad \unicode[STIX]{x1D713}=y,\quad \unicode[STIX]{x1D701}=\frac{z-\tilde{\unicode[STIX]{x1D702}}(x,y,t)}{h-\tilde{\unicode[STIX]{x1D702}}(x,y,t)}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D70F}$
are the space and time coordinates in the computational domain, and
$\bar{h}$
is the mean domain height with
$\overline{\cdots \,}$
denoting the averaging on the surface of a constant
$\unicode[STIX]{x1D701}$
. The coordinate transformation is illustrated in figure 1. As shown in figure 1(b), in the vertical direction,
$(u,v,p)$
are defined at the regular grid points, while
$w$
is defined on a staggered grid (Yang & Shen Reference Yang and Shen2011a
). The only exception is at the bottom and top boundary, where
$(u,v,w,p)$
are defined on the same grid points. The Jacobian matrix corresponding to the transformation (2.3) is
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D645}=\left[\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}z}\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}z}\\ \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}{\unicode[STIX]{x2202}z}\end{array}\right]=\left[\begin{array}{@{}ccc@{}}\displaystyle 1 & \displaystyle 0 & \displaystyle 0\\ \displaystyle 0 & \displaystyle 1 & \displaystyle 0\\ \displaystyle \frac{\unicode[STIX]{x1D701}-1}{h-\tilde{\unicode[STIX]{x1D702}}}\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x1D701}-1}{h-\tilde{\unicode[STIX]{x1D702}}}\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x2202}y} & \displaystyle \frac{1}{h-\tilde{\unicode[STIX]{x1D702}}}\end{array}\right]. & & \displaystyle\end{eqnarray}$$
Then the governing equations (2.1)–(2.2) become
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+\unicode[STIX]{x1D701}_{t}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+\tilde{u} \left(\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)+\tilde{v}\left(\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)+\tilde{w}\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{\unicode[STIX]{x1D70C}_{a}}\left(\frac{\unicode[STIX]{x2202}\tilde{p}^{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\tilde{p}^{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)-\frac{\unicode[STIX]{x1D70F}_{11}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{11}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\frac{\unicode[STIX]{x1D70F}_{12}^{d}}{\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{12}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{13}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\frac{1}{\unicode[STIX]{x1D70C}_{a}}\frac{\unicode[STIX]{x2202}p_{\infty }}{\unicode[STIX]{x2202}x},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+\unicode[STIX]{x1D701}_{t}\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+\tilde{u} \left(\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)+\tilde{v}\left(\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)+\tilde{w}\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\tilde{v}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{\unicode[STIX]{x1D70C}_{a}}\left(\frac{\unicode[STIX]{x2202}\tilde{p}^{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\tilde{p}^{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)-\frac{\unicode[STIX]{x1D70F}_{21}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{21}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\frac{\unicode[STIX]{x1D70F}_{22}^{d}}{\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{22}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{23}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+\unicode[STIX]{x1D701}_{t}\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+\tilde{u} \left(\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)+\tilde{v}\left(\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}+\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)+\tilde{w}\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\tilde{w}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{\unicode[STIX]{x1D70C}_{a}}\left(\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\tilde{p}^{\ast }}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)-\frac{\unicode[STIX]{x1D70F}_{31}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{31}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\frac{\unicode[STIX]{x1D70F}_{32}^{d}}{\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{32}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-\unicode[STIX]{x1D701}_{z}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}_{33}^{d}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}},\end{eqnarray}$$
where the time derivative in the physical space is associated with that in the transformed coordinates by
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}+\frac{\unicode[STIX]{x1D701}-1}{\bar{h}-\tilde{\unicode[STIX]{x1D702}}}\frac{\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D702}}}{\unicode[STIX]{x2202}t}, & & \displaystyle\end{eqnarray}$$
and the Laplacian operator in the transformed coordinates is
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}^{2}=\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}^{2}}+2\unicode[STIX]{x1D701}_{x}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+2\unicode[STIX]{x1D701}_{y}\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+(\unicode[STIX]{x1D701}_{x}^{2}+\unicode[STIX]{x1D701}_{y}^{2}+\unicode[STIX]{x1D701}_{z}^{2})\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}^{2}}+(\unicode[STIX]{x1D701}_{xx}+\unicode[STIX]{x1D701}_{yy})\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Figure 1. Sketch of the coordinates and grid in: (a) the physical domain and (b) the computational domain. For clarity, we only show part of the grid in each domain and the grid sizes are exaggerated. The grid points defining
$(u,v,p)$
and
$w$
are denoted by ● and *, respectively.
The upper boundary of the air flow is treated as shear free, while at the bottom boundary a wall model is used to estimate the shear stress at the wave surface (Yang, Meneveau & Shen Reference Yang, Meneveau and Shen2014a ,Reference Yang, Meneveau and Shen b )
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{i3}(x,y,t) & = & \displaystyle -\widehat{\widetilde{U}}_{r}(x,y,t)\left[\frac{\unicode[STIX]{x1D705}}{\ln (d_{2}/z_{0})}\right]^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,[\widehat{\widetilde{u}}_{r,i}(x,y,t)\cos \unicode[STIX]{x1D703}_{i}+\widehat{\widetilde{u}}_{r,3}(x,y,t)\sin \unicode[STIX]{x1D703}_{i}],\quad (i=1,2),\end{eqnarray}$$
where
$\widehat{\widetilde{\ldots }}$
denotes quantities filtered at the test-filter scale;
$\widehat{\widetilde{U}}_{r}(x,y,t)$
is the magnitude of the test-filtered air velocity in the horizontal directions relative to the ocean surface;
$\unicode[STIX]{x1D705}=0.41$
is the von Kármán constant;
$\widehat{\widetilde{u}}_{r,i}(x,y,t)=\widehat{\widetilde{u}}_{i}(x,y,d_{2},t)-\widehat{\widetilde{u}}_{s,i}(x,y,t)~(i=1,2,3)$
are the test-filtered velocity components on the first off-surface grid point relative to the sea-surface velocity
$\widehat{\widetilde{u}}_{s,i}(x,y,t)$
; and
$\unicode[STIX]{x1D703}_{i}$
are the local inclination angles of the surface. The wall model has been applied to the study of wind over waves of short to intermediate lengths (Sullivan et al.
Reference Sullivan, Edson, Hristov and McWilliams2008; Liu et al.
Reference Liu, Yang, Guo and Shen2010; Yang et al.
Reference Yang, Meneveau and Shen2013) as well as wind over swells (Nilsson et al.
Reference Nilsson, Rutgersson, Smedman and Sullivan2012; Yang et al.
Reference Yang, Meneveau and Shen2014a
,Reference Yang, Meneveau and Shen
b
). Note that for swell cases, there might be flow inversion very close to the wave surface (see Veron et al.
Reference Veron, Saxena and Misra2007; Buckley & Veron Reference Buckley and Veron2016, Reference Buckley and Veron2017) affecting the basic assumption of the wall model and thus its accuracy. The wall model also requires the wave surface to be well-defined with a small to intermediate steepness such that no violent wave breaking occurs. Otherwise, the resulting wave breaking may affect the wind–wave momentum transfer (e.g., Yang et al.
Reference Yang, Deng and Shen2018). In general, the logarithmic-law-based wall-layer model is valid when the turbulent eddies are in equilibrium within the grid (Piomelli & Balaras Reference Piomelli and Balaras2002). This assumption holds in this study because we focus on wind-generated waves instead of swells, and wave breaking is expected to be low at the present wind conditions.
Here we briefly outline the key steps in the numerical scheme. Derivatives are calculated in the horizontal directions using Fourier transform, while those in the vertical direction are calculated using second-order finite difference. The second-order Adam–Bashforth method is used for time advancement. The advection equations of the velocity field are first integrated in time excluding the pressure term. By imposing the divergence-free condition, the pressure field is computed from the Poisson equation. Due to the coordinate transformation, the operator (2.10) contains nonlinear terms and the Poisson equation is solved in an iteration process. The velocity field is then corrected in the second step with the integration of the pressure term. The initial condition of the wind turbulence is generated by adding random turbulence fluctuations to a logarithmic mean profile, and data for analysis is collected from the fully coupled wind–wave simulation. The details of the numerical schemes for simulating (2.1) and (2.2) with the use of (2.11) and the validations are given in Yang & Shen (Reference Yang and Shen2011a ,Reference Yang and Shen b ) and Yang et al. (Reference Yang, Meneveau and Shen2013).
2.2 High-order spectral method for wave simulation
The high-order spectral (HOS) method is used to simulate the evolution of wave fields denoted by the surface elevation at each position,
$\unicode[STIX]{x1D702}(x,y,t)$
. In the HOS method, the water motion is treated as a potential flow of an incompressible fluid where the effects of viscosity, turbulence and surface tension are negligibly small. The derivation by Zakharov (Reference Zakharov1968) shows that the nonlinear wave system is Hamiltonian and can be uniquely determined by the surface elevation
$\unicode[STIX]{x1D702}(x,y,t)$
and the surface velocity potential
$\unicode[STIX]{x1D6F7}^{S}(x,y,t)\equiv \unicode[STIX]{x1D6F7}(x,y,\unicode[STIX]{x1D702}(x,y,t),t)$
. The velocity potential
$\unicode[STIX]{x1D6F7}(x,y,z,t)$
in the domain can be evaluated through
$\unicode[STIX]{x1D702}(x,y,t)$
and
$\unicode[STIX]{x1D6F7}^{S}(x,y,t)$
up to an arbitrary perturbation order-
$M$
. The governing equations are (Dommermuth & Yue Reference Dommermuth and Yue1987)
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D702}_{t}+\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D6F7}^{S}-(1+\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle \quad \times \left[\mathop{\sum }_{m=1}^{M}\mathop{\sum }_{l=0}^{M-m}\frac{\unicode[STIX]{x1D702}^{l}}{l!}\mathop{\sum }_{n=1}^{N}\unicode[STIX]{x1D6F7}_{n}^{m}(t)\frac{\unicode[STIX]{x2202}^{l+1}}{\unicode[STIX]{x2202}z^{l+1}}\left.\unicode[STIX]{x1D6F9}_{n}(\boldsymbol{x},z)\right|_{z=0}\right]=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F7}_{t}^{S}+g\unicode[STIX]{x1D702}+\frac{1}{2}\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D6F7}^{S}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D6F7}^{S}-\frac{1}{2}(1+\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle \quad \times \left[\mathop{\sum }_{m=1}^{M}\mathop{\sum }_{l=0}^{M-m}\frac{\unicode[STIX]{x1D702}^{l}}{l!}\mathop{\sum }_{n=1}^{N}\unicode[STIX]{x1D6F7}_{n}^{m}(t)\frac{\unicode[STIX]{x2202}^{l+1}}{\unicode[STIX]{x2202}z^{l+1}}\left.\unicode[STIX]{x1D6F9}_{n}(\boldsymbol{x},z)\right|_{z=0}\right]^{2}=-\frac{p_{a}(\boldsymbol{x},t)}{\unicode[STIX]{x1D70C}_{w}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D735}_{\boldsymbol{x}}\equiv (\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x,\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$
is the gradient operator in horizontal directions,
$\unicode[STIX]{x1D70C}_{w}$
is the density of water,
$p_{a}(\boldsymbol{x},t)$
is the air pressure at the surface,
$\unicode[STIX]{x1D6F9}_{n}(\boldsymbol{x},z)=\exp (\text{i}\boldsymbol{k}_{\boldsymbol{n}}\boldsymbol{\cdot }\boldsymbol{x}+k_{n}z)$
is the basis function for deep water, and
$\unicode[STIX]{x1D6F7}_{n}^{m}(\boldsymbol{k}_{\boldsymbol{n}},t)$
is the corresponding Fourier coefficient of wavenumber
$\boldsymbol{k}_{\boldsymbol{n}}$
.
Physically, equations (2.12) and (2.13) are, respectively, the kinematic and dynamic boundary conditions at the wave surface. Given an initial field constructed from realistic waves, these equations can be integrated numerically. The linear terms, e.g.
$\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D6F7}^{S}$
, are first calculated in the spectral space and then transformed back to the physical space via the fast Fourier transform. The computation of the nonlinear terms, e.g.
$\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D702}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{x}}\unicode[STIX]{x1D6F7}^{S}$
, is completed in the physical space at each grid point. The fourth-order Runge–Kutta scheme is used for time integration, thus obtaining the evolution of the nonlinear wave field with the wave phases resolved. The details of the numerical schemes for simulating (2.12) and (2.13) and the validations are given in Dommermuth & Yue (Reference Dommermuth and Yue1987) and Xiao et al. (Reference Xiao, Liu, Wu and Yue2013).
The HOS method is a useful tool for simulating wave field evolution with the following advantages: (i) the wind input can be directly incorporated into the wave evolution through the pressure
$p_{a}(\boldsymbol{x},t)$
at the ocean surface; (ii) the maximum order-
$M$
can be easily adjusted based on the wave problem; (iii) it imposes much less restrictions upon the bandwidth of the wave spectrum compared with the nonlinear Schrödinger equation; and (iv) it has a relatively low computational cost for high numerical accuracy, which is a major advantage in large-scale simulations (Wu Reference Wu2004). However, the HOS method might fail when there are steep waves or wave breaking, due to the potential flow assumption and the perturbation expansion technique. Therefore, a numerical dissipation model is necessary to mimic the wave energy dissipation due to wave breaking. In the present study, following Xiao et al. (Reference Xiao, Liu, Wu and Yue2013), we apply an adaptive filter to the surface quantities
$\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D6F7}^{S}$
$$\begin{eqnarray}\displaystyle \left[\begin{array}{@{}c@{}}\hat{\unicode[STIX]{x1D702}}_{f}(\boldsymbol{k})\\ \hat{\unicode[STIX]{x1D6F7}}_{f}^{S}(\boldsymbol{k})\\ \end{array}\right]=\left[\begin{array}{@{}c@{}}\hat{\unicode[STIX]{x1D702}}(\boldsymbol{k})\\ \hat{\unicode[STIX]{x1D6F7}}^{S}(\boldsymbol{k})\\ \end{array}\right]G(k;C_{1},C_{2}), & & \displaystyle\end{eqnarray}$$
where
$G(k;C_{1},C_{2})=\exp [-(k/C_{1}k_{p})^{C_{2}}]$
is the filter function,
$C_{1}=8$
and
$C_{2}=30$
are constants that control the strength of the filter, and
$(\hat{\unicode[STIX]{x1D702}}_{f},\hat{\unicode[STIX]{x1D6F7}}_{f}^{S})$
are the filtered quantities in the wavenumber space. The corresponding filter in the frequency domain is
$G^{\prime }(f;C_{1},C_{2})=(4\unicode[STIX]{x03C0}^{2}f\sqrt{2f}/g)\exp [-(4\unicode[STIX]{x03C0}^{2}f/C_{1}gk_{p})^{C_{2}}]$
. As shown,
$G$
and
$G^{\prime }$
are low-pass filters that dissipate wave energy at short lengthscales and high frequencies. In cases such as steep waves in shallow water studied by Kirby & Kaihatu (Reference Kirby and Kaihatu1996) and Kaihatu et al. (Reference Kaihatu, Veeramony, Edwards and Kirby2007), the frequency distribution of the filter was found to have a controlling impact on the spectrum evolution. In the present deep water wave simulation using the filters given above and with the wave steepness set to be small, the impact of dissipation on spectrum evolution is insignificant compared with wind input and nonlinear wave interactions. Also note that while this model can ensure the stability of wave simulation using HOS, it should not be treated as a high-order tool for simulating steep waves. In those conditions, the separation of airflow occurs (Reul et al.
Reference Reul, Branger and Giovanangeli1999, Reference Reul, Branger and Giovanangeli2008; Buckley & Veron Reference Buckley and Veron2016, Reference Buckley and Veron2017), inducing a significant pressure gradient that affects the wind input. The filter would smooth out the wave surface before flow separation. Therefore, the filter is more appropriate to use for applications in wave fields of small to intermediate steepness, which is the case of this study.
2.3 Simulation set-up
A typical wave field in the open ocean has wavelengths ranging from a few centimetres to hundreds of meters. Apparently, the computational cost would become far beyond the current computer power to fully resolve such a broad range of fluid motions. It is crucial therefore to choose appropriate dimensions for the wind field and wave field. Since the focus of this study is the evolution of the coupled wind–wave system, we choose a Joint North Sea Wave Project (JONSWAP) (Hasselmann et al. Reference Hasselmann, Barnett, Bouws, Carlson, Cartwright, Enke, Ewing, Gienapp, Hasselmann and Kruseman1973) spectrum at an early stage of wave growth to initialise the wave simulation
$$\begin{eqnarray}\displaystyle E(f)=\frac{\unicode[STIX]{x1D6FC}_{p}g^{2}}{(2\unicode[STIX]{x03C0})^{4}f^{5}}\exp \left[-\frac{5}{4}\left(\frac{f}{f_{p}}\right)^{-4}\right]\unicode[STIX]{x1D6FE}_{J}^{\exp [-(f-f_{p})^{2}/2\unicode[STIX]{x1D70E}_{J}^{2}f_{p}^{2}]}, & & \displaystyle\end{eqnarray}$$
where
$E(f)$
is the frequency spectrum,
$\unicode[STIX]{x1D6FC}_{p}$
is the Phillips parameter (Phillips Reference Phillips1958),
$f_{p}$
is the peak wave frequency,
$\unicode[STIX]{x1D6FE}_{J}=3.3$
and
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}_{J}=\left\{\begin{array}{@{}ll@{}}0.07 & f\leqslant f_{p},\\ 0.09 & f>f_{p}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
It is generally assumed that the directional spectrum can be written as the product of the omnidirectional spectrum and a spreading function (Longuet-Higgins Reference Longuet-Higgins1963)
$$\begin{eqnarray}\displaystyle E(f,\unicode[STIX]{x1D703})=E(f)D(f,\unicode[STIX]{x1D703}). & & \displaystyle\end{eqnarray}$$
In this study, we adopt the widely used spreading function
$D(f,\unicode[STIX]{x1D703})=(2/\unicode[STIX]{x03C0})\cos ^{2}\unicode[STIX]{x1D703}$
to generate the initial wave field. The physical parameters of the wave field are summarised in table 1. In this paper, we use the subscript ‘0’ to indicate quantities of the initial condition unless otherwise specified. For the wave simulation using the HOS method, we set the perturbation order to
$M=3$
because resonant wave interactions (Hasselmann Reference Hasselmann1962) can be fully resolved (Tanaka Reference Tanaka2001). Besides, previous studies (Annenkov & Shrira Reference Annenkov and Shrira2013; Xiao et al.
Reference Xiao, Liu, Wu and Yue2013) have suggested that higher order wave statistics including skewness and kurtosis can be accurately captured when the wave nonlinearity is resolved up to the third order in long-term wave evolution. This is primarily because the dominant terms of skewness and kurtosis are determined by the wave energy up to the sixth order in terms of wave steepness parameter
$\unicode[STIX]{x1D716}$
(Janssen Reference Janssen2009). Note that while in principle we could start the simulations with other spectra or even white noise and let the physical wind-waves develop eventually, the computational cost would be too high for the present computing power. For convenience, phase-resolved wave field simulations, such as the ones using the HOS method, often start with an empirical wave spectrum that is already in the similarity form, such as the JONSWAP spectrum. The total energy of the initial spectrum is often deliberately controlled so that the wave steepness and magnitude are within the applicable range. In the present study, where mild waves are of interest, the Phillips parameter
$\unicode[STIX]{x1D6FC}_{p}$
that is associated with the total energy is set to a relatively small value (table 1), which is comparable to those in previous studies, e.g.,
$\unicode[STIX]{x1D6FC}_{p}=0.0131$
used in Tanaka (Reference Tanaka2001).
Table 1. Parameters of the initial JONSWAP wave field, where
$\unicode[STIX]{x1D6FC}_{p}$
is the Phillips parameter,
$f_{p0}$
is the peak wave frequency,
$\unicode[STIX]{x1D706}_{p0}$
is the peak wavelength,
$c_{p0}$
is the peak wave speed and
$T_{p0}$
is the peak wave period. The subscript ‘0’ denotes the initial condition.
Table 2. Parameters of the airflow above wave surface, where
$U_{10}$
is the wind speed at 10 m above the mean ocean surface,
$u_{\ast }$
is the air-side friction velocity,
$Re_{\ast }$
is the Reynolds number based on the wavelength and friction velocity, and
$T_{s}$
is the simulation time duration. The velocity ratios
$c_{p0}/U_{10}$
and
$c_{p0}/u_{\ast }$
are called the ‘wave age’. Here,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of air.
The computational domain size of the wind field is
$200~\text{m}\times 100~\text{m}\times 100~\text{m}$
with a grid number of
$256\times 128\times 256$
. The wave field has the same horizontal dimension of
$200~\text{m}\times 100~\text{m}$
with a grid number of
$512\times 256$
. These parameters are chosen with deliberation. The grid resolution is chosen such that the peak wave length contains enough grid points to resolve most of the energy-containing eddies in the air turbulence. According to Pope (Reference Pope2000), the grid resolution is sufficiently high once the bulk (
${\sim}$
80 %) turbulence energy is resolved everywhere except for the near-wall region. In the following spectral analysis of the wind turbulence, this requirement is examined in detail. In the wind simulation, we use an evenly spaced grid in all three directions, and the grid size is 0.78 m in horizontal directions and 0.39 m in the vertical direction. As a comparison, some previous studies on wind turbulence over waves have used coarser grids, such as
$4.8~\text{m}\times 4.8~\text{m}\times 1~\text{m}$
(Sullivan et al.
Reference Sullivan, Edson, Hristov and McWilliams2008) and
$24.5~\text{m}\times 24.5~\text{m}\times 7.8~\text{m}$
(Yang et al.
Reference Yang, Meneveau and Shen2014b
). Note that the grid in Sullivan et al. (Reference Sullivan, Edson, Hristov and McWilliams2008) is non-uniform in the vertical direction and the grid size varies from 1 m to 28 m. We would like to emphasise that for the wall-layer model to be valid, the size of the first grid near the wave surface cannot be too fine because the wall-layer model implicitly assumes a Reynolds-averaged inner layer (Piomelli & Balaras Reference Piomelli and Balaras2002). In the wall-modelled LES, the aerodynamic roughness
$z_{0}$
is required because the viscous sublayer is not resolved. Here, we choose a typical open-sea value of
$2\times 10^{-4}~\text{m}$
following Sullivan et al. (Reference Sullivan, Edson, Hristov and McWilliams2008) and Jiang et al. (Reference Jiang, Sullivan, Wang, Doyle and Vincent2016). Since the roughness is used as a property of the mean velocity profile, rather than the instantaneous turbulence field, the fixed value is acceptable when the change in the wind–wave condition is not significant. The parameters of the wind turbulence are summarised in table 2. We choose the four wind speeds to ensure that the wave ages fall into the representative region of wave growth in the real ocean condition while the wave breaking effect is not significant. The total number of the grid points in our wave simulation is eight times the grid number
$(256\times 64)$
in Chalikov, Babanin & Sanina (Reference Chalikov, Babanin and Sanina2014) and Chalikov (Reference Chalikov2016), slightly smaller than the maximum grid number
$(1025\times 257)$
in Engsig-Karup, Bingham & Lindberg (Reference Engsig-Karup, Bingham and Lindberg2009). The time duration of our simulation,
$O(3000T_{p0})$
, is nearly ten times that in Chalikov et al. (Reference Chalikov, Babanin and Sanina2014) and Chalikov (Reference Chalikov2016), and much longer than the maximum simulation time,
$O(50T_{p0})$
, in Engsig-Karup et al. (Reference Engsig-Karup, Bingham and Lindberg2009). Besides, these studies only involve the wave simulation, while the wind turbulence is not simulated. The present study has wind simulation in addition to the wave simulation, which substantially increases the computational cost. The wave parameters have also been justified by performing independent wave simulations at different grid numbers and perturbation orders (see appendix A).
Figure 2. Snapshot of the wind–wave field. Contours plotted in the
$x{-}z$
and
$y{-}z$
planes represent the streamwise wind velocity
$\tilde{u} _{1}$
normalised by the friction velocity
$u_{\ast }$
. Contours plotted in the
$x{-}y$
plane are the surface elevation
$\unicode[STIX]{x1D702}$
normalised by the mean vertical height of the wind field
$H$
.
We initialise the wind field with random fluctuations superposed to a mean logarithmic profile over a flat surface. At the same time, the wave field is initialised using the summation of various wave components in the directional JONSWAP spectrum as stated above, and it first evolves independent of the wind input. After a sufficiently long period of wind and wave simulations, separately, the wind turbulence becomes fully developed and the nonlinearity of the wave field has also been fully developed. The wind field and the wave field are then dynamically coupled gradually through a relaxation process, with the wind field providing air pressure to the waves and the wave field in return providing the surface elevation and velocity as the bottom boundary conditions to the wind field above. The data for analysis is collected after the relaxation is completed and the coupled wind–wave field has evolved
$O(100T_{p})$
to eliminate the relaxation effect. We then continue the fully coupled wind–wave simulations for
$O(3,000T_{p0})$
(table 2) to capture the long-term wave dynamics. For illustration purpose, we plot a snapshot of the streamwise velocity for the fully coupled wind–wave field in figure 2.
3 Results
In this section, we present the results of the numerical experiment. We first analyse the wave effect on wind turbulence by examining the mean profile, the turbulence energy spectrum, and the contribution to the shear stress in different quadrants. Next, we quantify the wind input to assess its role in the energy transfer process. Finally, we investigate key statistical properties of the wave field and study the long-term evolution of the wind-forced wave field.
3.1 Wind turbulence over waves
The marine atmospheric boundary layer is dynamically coupled with the oceans through the waves, which have spatial variations in both the wavy surface geometry and wave orbital velocity. As a result, the turbulent air flow over waves is more complex than that over a flat wall. In this section, we conduct analyses on the wind turbulence field with an emphasis on the wave effects.
3.1.1 Velocity profile and correlation with waves
Table 3. Wave age and features of the wind velocity profile. Here TE1-TE5 denote the wind–wave cases in a tank experiment (Buckley & Veron Reference Buckley and Veron2016, Reference Buckley and Veron2017).
The wind velocity profile over waves can be quantified by the von Kármán constant
$\unicode[STIX]{x1D705}$
and the aerodynamic surface roughness
$z_{0}$
in the logarithmic region. In table 3, we list our result and that of the recent tank experiments by Buckley & Veron (Reference Buckley and Veron2016, Reference Buckley and Veron2017), in which the wind velocity field near the wave surface is measured at a high resolution. For our simulation result, the mean velocity is calculated by taking the time-averaging of the streamwise velocity. The experimental result is estimated using the data extracted from the figures in Buckley & Veron (Reference Buckley and Veron2017). While a logarithmic region is found in each velocity profile in our simulation cases, and the experimental cases (Buckley & Veron Reference Buckley and Veron2016, Reference Buckley and Veron2017) and the ranges of parameters are consistent, the values of
$\unicode[STIX]{x1D705}$
and
$z_{0}$
vary with different wind–wave conditions, indicating the wave effect on wind turbulence. The wave effect can also be revealed by the correlation between the turbulence velocity and surface elevation as shown in figure 3. We also plot in the inset of figure 3 the correlation coefficient:
$\text{Corr}(u,\unicode[STIX]{x1D702})=\overline{u\unicode[STIX]{x1D702}}/(\overline{uu}\cdot \overline{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}})^{1/2}$
, which decreases monotonically with the height. The results shown here are calculated using data near the end of the simulation. The magnitude of
$\overline{u\unicode[STIX]{x1D702}}$
, a measure of the wave-coherent motion in the wind turbulence, decreases exponentially with height
${\sim}\exp (-k_{p}z)$
. The other trend line
${\sim}\exp (-k_{p0}z)$
, which uses the initial peak wavenumber
$k_{p0}$
, has appreciable deviation. This result indicates that the wind and wave fields are coupled.
Figure 3. Vertical distribution of the normalised correlation between the wind turbulence velocity and surface wave elevation. The inset is the vertical distribution of the correlation coefficient. Also plotted are two trend lines decreasing exponentially with height, denoted by black solid lines. Here,
$k_{p}$
and
$k_{p0}$
are the average peak wavenumber in the corresponding time duration and the peak wavenumber of the initial spectrum, respectively.
3.1.2 Spectral analysis
We examine the properties of the wind turbulence from the perspective of space–time correlations. Instead of calculating the correlation functions directly, we compute the full wavenumber–frequency spectrum of the streamwise velocity of the turbulence field because it provides a more intuitive approach to investigate turbulence motions of different scales (Pope Reference Pope2000). The spectrum is calculated at different vertical heights above the mean wave surface, using numerical data collected at a sampling time interval comparable to the time scale of the smallest resolved eddies in the present simulation. For demonstration purposes, we integrate the full spectrum
$F_{11}(\boldsymbol{k},\unicode[STIX]{x1D714};z)$
along the spanwise wavenumber
$k_{2}$
to obtain the projected spectrum
$F_{11}(k_{1},\unicode[STIX]{x1D714};z)$
on the
$k_{1}{-}\unicode[STIX]{x1D714}$
plane
$$\begin{eqnarray}\displaystyle F_{11}(k_{1},\unicode[STIX]{x1D714};z)=\int F_{11}(\boldsymbol{k},\unicode[STIX]{x1D714};z)\,\text{d}k_{2}. & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D714}$
is the angular frequency.
For comparison, we also calculate the wavenumber–frequency spectrum of turbulence over a flat wall using the model proposed by Wilczek & Narita (Reference Wilczek and Narita2012), which is written as
$$\begin{eqnarray}\displaystyle F_{11}(\boldsymbol{k},\unicode[STIX]{x1D714};z)=F_{11}(\boldsymbol{k};z)[2\unicode[STIX]{x03C0}\langle (\boldsymbol{V}\boldsymbol{\cdot }\boldsymbol{k})^{2}\rangle ]^{-1/2}\exp \left[-\frac{(\unicode[STIX]{x1D714}-\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{U})^{2}}{\langle (\boldsymbol{V}\boldsymbol{\cdot }\boldsymbol{k})^{2}\rangle }\right], & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{U}=\boldsymbol{U}(z)$
is the mean velocity at the corresponding height,
$\langle \cdot \rangle$
is the averaging operator on a horizontal plane, and
$\boldsymbol{V}$
is the velocity of large random eddies with a Gaussian distribution. The wavenumber spectrum
$F_{11}(\boldsymbol{k};z)$
is calculated using 2-D Fourier transform at each height, while the random eddy effect yields
$(\boldsymbol{V}\boldsymbol{\cdot }\boldsymbol{k})^{2}\approx \langle \tilde{u} ^{\prime }\tilde{u} ^{\prime }\rangle k_{1}^{2}+\langle \tilde{v}^{\prime }\tilde{v}^{\prime }\rangle k_{2}^{2}$
(Wilczek & Narita Reference Wilczek and Narita2012).
The numerical results of the wavenumber–frequency spectrum of wind turbulence over waves (3.1) and the model results of turbulence over a flat wall (3.2) are plotted in figure 4. Because the calculation of the spectrum requires data with high resolution in time, we continue the simulation for a period of
$33.4T_{p0}$
and output data at a sampling rate of approximately
$0.087T_{p0}$
. As shown, our simulation results capture the Doppler shift by the mean velocity and demonstrate the Doppler broadening due to turbulence eddies, consistent with the model for turbulence over a flat wall. The frozen turbulence hypothesis (Taylor Reference Taylor1938) only predicts the Doppler shift effect, and neglects the correlations induced by the turbulence eddies. He, Jin & Yang (Reference He, Jin and Yang2017) pointed out that the inclusion of the random eddy effect in Wilczek & Narita (Reference Wilczek and Narita2012)’s model can be seen as a theoretical validation of the elliptic model (He & Zhang Reference He and Zhang2006) of spatial–temporal correlation functions. It should be noted that in our results shown in figure 4(a,c,e,g,i), the energy at very small wavenumbers (
$k<0.067\sim 0.080k_{p,0}$
) is distributed over a relatively wide region along the frequency axis, which is not seen in the model results of (3.2). Such a discrepancy is caused by the limitation in the time duration of the numerical data and the computational domain size. For wavenumbers higher than this range, the limitation associated with the domain size does not affect the accuracy of energy spectra. The agreement between our numerical result and the random sweeping model can be seen as evidence that the small scale turbulence is adequately resolved.
The wave signature in the wind turbulence is distinct in our numerical results, as indicated by the dispersion relation of water waves in figure 4(c,e,g,i). This phenomenon can be qualitatively explained as follows. At the wave surface, where physically there is the no-slip boundary condition for the airflow, the velocity of air equals that of the water, namely the wave orbital velocity. The contours of the wavenumber–frequency spectrum of wind turbulence at the wave surface should then fall precisely along the wave dispersion relation, while the Doppler effect of the mean wind and the effect of large eddies do not exist at the surface. As the vertical height increases, the wave effect decreases, and the mean flow, along with the large eddies, becomes the dominant effect in the turbulence spectrum. Eventually, the wave effect vanishes above a certain height, and our result in figure 4(a) shows that this height is of
$O(1/k_{p})$
, consistent with the concept of wave boundary layer (Sullivan & McWilliams Reference Sullivan and McWilliams2010). For monochromatic waves, the wave effect can be evaluated by extracting the wave-coherent turbulence from the full turbulence via triple decomposition (Buckley & Veron Reference Buckley and Veron2016, Reference Buckley and Veron2017). By performing integration on
$F_{11}$
in different regions of figure 4(i), we estimate that approximately 90 % of the total energy is contained by turbulent motions of length scales greater than 9.2 m. Therefore, our grid size satisfies the requirement of resolving the bulk turbulent energy. Meanwhile, it is sufficiently high to capture the wave signature on turbulence as shown in figure 4. The presence of the wave signature shows that the dynamic coupling between the wind turbulence and wave field involves complex nonlinear processes, which cannot be captured by existing empirical parameterised models. The quantitative analysis of the wave effect on the wind wavenumber–frequency spectrum is beyond the scope of this study and will be investigated in the future.
Figure 4. Contours of the wavenumber–frequency spectrum for the streamwise velocity
$F_{11}$
, normalised by its maximum value
$F_{m}$
. From (a) to (j), the height
$z/\unicode[STIX]{x1D706}_{p0}=\{0.98,0.51,0.35,0.20,0.12\}$
. (a,c,e,g,i) Simulation results of wind turbulence over waves; (b,d,f,h,j): prediction of the random-sweeping model for turbulence over a flat wall. In (a,c,e,g,i), the Doppler shift
$\unicode[STIX]{x1D714}=k_{1}U(z)$
is denoted by – – –, and the dispersion relation for deep water wave
$\unicode[STIX]{x1D714}=\sqrt{gk_{1}}$
is denoted by — ⋅ —. Case WW6 is presented here.
3.1.3 Quadrant analysis
Figure 5. Joint probability distribution function (j.p.d.f.) of the normalised velocity fluctuations at the height of (a)
$z/\bar{h}=0.014$
(
$z/\unicode[STIX]{x1D706}_{p,0}=0.14$
) and (b)
$z/\bar{h}=0.1$
(
$z/\unicode[STIX]{x1D706}_{p,0}=1.0$
). The white dashed line denotes the constant hole size
$H=|u^{\prime }w^{\prime }|/|\widehat{u^{\prime }w^{\prime }}|=3$
. The result of case WW6 is shown.
In this section, we conduct quadrant analysis on the wind turbulence field and explore how waves affect the key turbulence events. First proposed by Wallace, Eckelmann & Brodkey (Reference Wallace, Eckelmann and Brodkey1972), the quadrant analysis divides the turbulent velocity fluctuations
$u^{\prime }$
and
$w^{\prime }$
into four parts, each denoting a certain category of turbulence events:
$Q1(u^{\prime }>0,w^{\prime }>0)$
, outward interaction;
$Q2(u^{\prime }<0,w^{\prime }>0)$
, ejection;
$Q3(u^{\prime }<0,w^{\prime }<0)$
, inward interaction;
$Q4(u^{\prime }>0,w^{\prime }<0)$
, sweep. As an example, we plot the joint probability distribution function of the normalised velocity fluctuations of case WW6 in figure 5. The difference between the quadrant distributions at two different heights is apparent: close to the wave surface (figure 5
a), the quadrant distribution is dominated by the
$Q4$
sweep events, whereas far from the wave surface (figure 5
b), both
$Q2$
and
$Q4$
become significant.
Figure 6. Magnitude of the stress fraction
$S_{i,H}~(i=1,2,3,4)$
as a function of the hole size
$H$
. The results in Raupach (Reference Raupach1981) for a turbulent flow over a smooth surface are denoted by ●,
$z/\bar{h}=0.06$
and ▴,
$z/\bar{h}=0.19$
.
To quantify the contributions to the shear stress from different events, we use the method proposed by Lu & Willmarth (Reference Lu and Willmarth1973). Given a positive constant
$H$
, we can calculate the conditional statistics
$S_{i,H}=\widehat{u^{\prime }w^{\prime }}_{i,H}/|\widehat{u^{\prime }w^{\prime }}|,(i=1,2,3,4)$
, for all velocity fluctuations satisfying
$|u^{\prime }w^{\prime }|/|\widehat{u^{\prime }w^{\prime }}|\geqslant H$
in four quadrants. Hereafter, the operator
$\widehat{\cdots }_{i,H}$
is the conditional version of the Reynolds averaging operator
$\widehat{\cdots }$
, and the Reynolds stress
$\widehat{u^{\prime }w^{\prime }}$
is calculated at different heights. Our definition of
$S_{i,H}$
is the same as the one proposed by Raupach (Reference Raupach1981), which differs slightly from the original one in Lu & Willmarth (Reference Lu and Willmarth1973) by a factor of the correlation coefficient. The stress fraction
$S_{i,H}$
measures the momentum flux contributed by events stronger than the threshold
$H$
in the
$i$
th quadrant. For each constant value of
$H$
, the curve
$H=|u^{\prime }w^{\prime }|/|\widehat{u^{\prime }w^{\prime }}|$
(see the red dashed lines in figure 5) divides each quadrant into two regions: the ‘hole’ with weak events and the outer region with strong events. The value of
$H$
is therefore a measure of the ‘hole’ size. When
$H=0$
, all the events are taken into consideration, and thus we have
$\sum _{i=1}^{4}S_{i,H=0}=1$
.
Figure 6 shows the result of the present study compared with the experimental result in a turbulent boundary layer over a smooth surface (Raupach Reference Raupach1981). For clarity, we present the results of case WW6 and WW9 considering that those of case WW7 and WW8 are not qualitatively different. Our results at
$z/\bar{h}=0.1$
(
$z/\unicode[STIX]{x1D706}_{p,0}=1.0$
) collapse to the smooth surface result (Raupach Reference Raupach1981) in all four quadrants. At such height, the wave effect becomes negligibly small and the turbulence barely ‘feels’ its impact. This is in sharp contrast to the near-surface region, where the contributions of various events deviate from the smooth surface result. The near-surface results in case WW6 and WW9 are nearly identical except for some deviations in the contribution of the inward interaction (
$Q3$
). The contribution from ejection (
$Q2$
) remains largely unchanged compared with the smooth surface result, whereas the contributions of outward interaction (
$Q1$
) and sweep (
$Q4$
) events to the shear stress are greatly enhanced. When
$H=0$
, for instance, the contributions of sweep and outward interaction events have increased from 60 % to 80 %, and 17 % to 27 %, respectively. Recognizing the challenges in distinguishing the broad-band-wave effect on wind turbulence, we further calculate the quadrant ratio
$Q_{r}=-(Q2+Q4)/(Q1+Q3)$
in the same way as in Sullivan et al. (Reference Sullivan, Edson, Hristov and McWilliams2008). Here,
$Q_{r}$
characterizes the ratio of downward momentum flux to upward flux. The value of
$Q_{r}$
is evaluated at
$z/\unicode[STIX]{x1D706}_{p,0}=0.18$
above the mean surface. For waves along the wind,
$Q_{r}$
obtained from experiments decreases with the wave age, which is expected because the momentum transfer from wind to waves in the downward direction is smaller for longer and faster waves. We find that the quadrant ratio in our simulations is close to the range obtained from experiments (Smedman et al.
Reference Smedman, Högström, Bergström and Rutgersson1999; Edson et al.
Reference Edson, Crawford, Crescenti, Farrar, Frew, Gerbi, Helmis, Hristov, Khelif and Jessup2007; Buckley & Veron Reference Buckley and Veron2016) for the similar wave age. Note that the instantaneous wave ages in all cases slowly increase with time as the coupled system evolves towards the wind–wave equilibrium state, which is associated with the frequency downshift phenomenon discussed in detail in § 3.3.2.
3.2 Wind input to waves
In this section, we investigate the wind input to quantify the net energy transfer from the wind to the waves. We consider the wave growth rate for a wave component defined as (see Donelan Reference Donelan, Sajjadi, Thomas and Hunt1999; Li, Xu & Taylor Reference Li, Xu and Taylor2000)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}=\frac{2}{\unicode[STIX]{x1D706}(ak)^{2}}\int _{0}^{\unicode[STIX]{x1D706}}\frac{p}{\unicode[STIX]{x1D70C}_{a}u_{\ast }^{2}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}x}\,\text{d}x, & & \displaystyle\end{eqnarray}$$
where
$p$
denotes the pressure at the wave surface, and
$ak$
is the wave steepness. Here, we have assumed that the wind input is primarily caused by the pressure (normal stress) as it can be shown that the work done by tangential stress is negligibly small (appendix D). For the broad-band wave field, we use the technique proposed by Liu et al. (Reference Liu, Yang, Guo and Shen2010) to evaluate
$\unicode[STIX]{x1D6FD}$
with the pressure and wave fields decomposed in the Fourier space. Suppose one component of the surface elevation is
$\unicode[STIX]{x1D702}(x,t)=a_{\unicode[STIX]{x1D702}}\cos (kx-\unicode[STIX]{x1D714}t+\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D702}})$
and the surface pressure is
$p(x,t)=a_{p}\cos (kx-\unicode[STIX]{x1D714}t+\unicode[STIX]{x1D703}_{p})$
, where
$a_{\unicode[STIX]{x1D702}}$
and
$a_{p}$
denote the amplitudes in the Fourier space, and
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D702}}$
and
$\unicode[STIX]{x1D703}_{p}$
the corresponding phases. The wave growth rate is then obtained as
$\unicode[STIX]{x1D6FD}=a_{p}\sin (\unicode[STIX]{x1D703}_{p}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D702}})/a_{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D70C}_{a}u_{\ast }^{2}$
. Note that the magnitude and the phase of the pressure play a decisive role, and their values can only be determined from the wind turbulence simulation.
The wind input can also be quantified by the temporal growth rate (Donelan & Pierson Reference Donelan and Pierson1987)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}=S_{\unicode[STIX]{x1D706}/2}\left(\frac{U_{\unicode[STIX]{x1D706}/2}}{c}-1\right)\left|\frac{U_{\unicode[STIX]{x1D706}/2}}{c}-1\right|, & & \displaystyle\end{eqnarray}$$
where
$S_{\unicode[STIX]{x1D706}/2}$
is the coefficient originated from the flow-separation-induced sheltering mechanism proposed by Jeffreys (Reference Jeffreys1925, Reference Jeffreys1926), and
$U_{\unicode[STIX]{x1D706}/2}$
is the mean wind velocity at the reference height
$z=\unicode[STIX]{x1D706}/2$
. Note that the theory of Jeffreys has been known to be inapplicable for wave growth unless the wave breaks (Banner & Melville Reference Banner and Melville1976). While there is no rigorous criterion for choosing the reference height,
$\unicode[STIX]{x1D706}/2$
(or
$\unicode[STIX]{x1D706}$
) has been found effective for reducing scattering (Donelan & Pierson Reference Donelan and Pierson1987; Donelan Reference Donelan, Sajjadi, Thomas and Hunt1999; Donelan et al.
Reference Donelan, Babanin, Young and Banner2006; Yang & Shen Reference Yang and Shen2010).
Figure 7. Wave growth rate
$\unicode[STIX]{x1D6FD}$
as a function of wave age
$c/u_{\ast }$
. Measurement data are plotted for comparison: ▪, Mastenbroek et al. (Reference Mastenbroek, Makin, Garat and Giovanangeli1996); ●, Grare et al. (Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013). Also plotted are numerical data for comparison: ▿, DNS, Sullivan et al. (Reference Sullivan, Mcwilliams and Moeng2000); ▹, RANS (Reynolds-averaged Navier–Stokes), Li et al. (Reference Li, Xu and Taylor2000); ◃, DNS, Kihara et al. (Reference Kihara, Hanazaki, Mizuya and Ueda2007); ♢, DNS, Yang & Shen (Reference Yang and Shen2010); ▫, LES, Liu et al. (Reference Liu, Yang, Guo and Shen2010). The horizontal solid lines are the upper (
$\unicode[STIX]{x1D6FD}=48$
) and lower limit (
$\unicode[STIX]{x1D6FD}=16$
) of the empirical formula by Plant (Reference Plant1982). The growth rate values predicted from Miles (Reference Miles1993) theory are denoted by – – –. Present simulation results are denoted by:
$\otimes$
, case WW6;
$\times$
, case WW7;
$\oplus$
, case WW8;
$+$
, case WW9.
Figure 8. Temporal growth rate
$\unicode[STIX]{x1D6FE}$
as a function of
$(U_{\unicode[STIX]{x1D706}/2}/c-1)|U_{\unicode[STIX]{x1D706}/2}/c-1|$
. Present simulation results are denoted by:
$\otimes$
, case WW6;
$\times$
, case WW7;
$\oplus$
, case WW8;
$+$
, case WW9. Also plotted are: ▾, measurement data, Donelan (Reference Donelan, Sajjadi, Thomas and Hunt1999); ▫, DNS of monochromatic waves, Yang & Shen (Reference Yang and Shen2010). The parameterisations are denoted by lines: ——,
$\unicode[STIX]{x1D6FE}=0.17(U_{\unicode[STIX]{x1D706}/2}/c-1)|U_{\unicode[STIX]{x1D706}/2}/c-1|$
, Donelan et al. (Reference Donelan, Babanin, Young and Banner2006); – – –,
$\unicode[STIX]{x1D6FE}=0.28(U_{\unicode[STIX]{x1D706}/2}/c-1)|U_{\unicode[STIX]{x1D706}/2}/c-1|$
, Donelan (Reference Donelan, Sajjadi, Thomas and Hunt1999).
We plot the wave growth rate
$\unicode[STIX]{x1D6FD}$
as a function of the wave age
$c/u_{\ast }$
for all four simulation cases in figure 7. The data points correspond to the wave modes in the range of
$k_{p}/2<k<2k_{p}$
, where wind turbulence and wave motions are best resolved. The values presented here as well as in figure 8 are the time-averaged result over
$100T_{p0}$
using the raw data at the end of the simulation in each case (see table 2). As shown, most data points fall into the range proposed by Plant (Reference Plant1982), which is based on experimental data assuming ‘the air–water interface to be well defined’. In other words, the energy dissipation caused by wave breaking was negligibly small for the compiled data (Plant Reference Plant1982), which has the same assumption as in the setup of our numerical experiments. For measurements completed in wave tanks (Mastenbroek et al.
Reference Mastenbroek, Makin, Garat and Giovanangeli1996; Grare et al.
Reference Grare, Peirson, Branger, Walker, Giovanangeli and Makin2013), due to the restriction on the tank size, the wavelengths are small and so are the wave ages. In our four simulation cases of WW6–WW9, as
$U_{10}$
increases from
$6~\text{m}~\text{s}^{-1}$
to
$9~\text{m}~\text{s}^{-1}$
, the data sets move to the left as the wave age decreases. In each case, the wave growth rates induced by wind input vary among different wave components, where fast (respectively, slow) waves have smaller (respectively, larger) growth rates. The dependence of
$\unicode[STIX]{x1D6FD}$
on
$c/u_{\ast }$
is similar to previous numerical results (Li et al.
Reference Li, Xu and Taylor2000; Sullivan et al.
Reference Sullivan, Mcwilliams and Moeng2000; Kihara et al.
Reference Kihara, Hanazaki, Mizuya and Ueda2007; Liu et al.
Reference Liu, Yang, Guo and Shen2010; Yang & Shen Reference Yang and Shen2010). For those results obtained with direct numerical simulations (DNS),
$\unicode[STIX]{x1D6FD}$
tends to be underestimated because of the low Reynolds numbers in DNS (Sullivan et al.
Reference Sullivan, Mcwilliams and Moeng2000; Yang & Shen Reference Yang and Shen2010). In the present LES results, the Reynolds number is realistically large.
Figure 8 shows the variation of the temporal growth rate
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FD}(u_{\ast }/c)^{2}$
with the inverse wave age function
$(U_{\unicode[STIX]{x1D706}/2}/c-1)|U_{\unicode[STIX]{x1D706}/2}/c-1|$
. The present result directly calculated from the surface pressure of the turbulent flow is compared with the parameterisations in terms of
$U_{\unicode[STIX]{x1D706}/2}$
. It should be noted that, due to the LES used in the present study, we are able to simulate wind–wave interaction at a much larger scale than the previous DNS study of Yang & Shen (Reference Yang and Shen2010). Consistent with the previous DNS results for monochromatic waves, the present LES results for broad-band wave fields support the parameterisations proposed by Donelan (Reference Donelan, Sajjadi, Thomas and Hunt1999) and Donelan et al. (Reference Donelan, Babanin, Young and Banner2006).
3.3 Wind-forced wave field
3.3.1 Wave statistics
Figure 9. Probability density function (p.d.f.) of the normalised surface elevation
$\unicode[STIX]{x1D702}/\bar{\unicode[STIX]{x1D702}^{2}}^{1/2}$
. The embedded figure is a zoom-in view of the peak region. The present result is denoted by ●. Also plotted are: the standard Gaussian distribution (——), the second-order approximation by Tayfun (Reference Tayfun1980) and Socquet-Juglard et al. (Reference Socquet-Juglard, Dysthe, Trulsen, Krogstad and Liu2005) (
$\cdots \cdots$
), and the Gram–Charlier series (– – –). The result is shown for case WW6.
We first present the statistical properties of the wind-waves, including the probability density function of the surface elevation and other key wave statistics such as skewness and kurtosis. The p.d.f. of the normalised surface elevation,
$\unicode[STIX]{x1D702}/\bar{\unicode[STIX]{x1D702}^{2}}^{1/2}$
, is shown in figure 9. Also shown is the standard Gaussian distribution, a second-order approximation (Tayfun Reference Tayfun1980; Socquet-Juglard et al.
Reference Socquet-Juglard, Dysthe, Trulsen, Krogstad and Liu2005), and the Gram–Charlier (GC) series, which utilizes the third- and fourth-order statistics to approximate the statistical distribution (see appendix B). The features of the wave statistics are similar for the cases WW6–WW9 in the present study, and we choose case WW6 as an example to present these features in this section. Under linear approximation, the p.d.f. of surface elevation is Gaussian, while our result exhibits a deviation from Gaussian in that the distribution function is tilted, consistent with field measurements (see e.g. Ochi & Wang Reference Ochi and Wang1984). This feature of p.d.f. corresponds to a positive skewness, and is caused by the shape of nonlinear waves with flatter troughs and sharper crests (Holthuijsen Reference Holthuijsen2007). Our numerical result agrees better with the second-order approximation and the GC series than with the Gaussian distribution, likely due to the higher-order nonlinearity (Agafontsev & Zakharov Reference Agafontsev and Zakharov2015). The greatest deviation from the Gaussian distribution occurs at large absolute values of surface elevations that indicate extreme waves associated with strong nonlinearity, similar to laboratory measurement (Onorato et al.
Reference Onorato, Cavaleri, Fouques, Gramstad, Janssen, Monbaliu, Osborne, Pakozdi, Serio and Stansberg2009). Note that in experiments, it is challenging to obtain a large data set of instantaneous surface elevations with the environment unchanged, and the p.d.f. is usually calculated from the temporal record of wave surface assuming that ensemble averages are identical to time averages. In this study, we compute the p.d.f. of surface elevation using the instantaneous data following Tanaka (Reference Tanaka2001) so that the number of independent observations of the surface elevation is much larger than what is required for an accurate estimate (Tayfun & Fedele Reference Tayfun and Fedele2007). In this regard, the p.d.f. obtained from our numerical result is useful as a measurement of the statistical behaviour of the irregular wave field.
Skewness and kurtosis are important statistics associated with the physical features of a nonlinear wave field. Specifically, the skewness indicates the deviation of the wave profile from a sinusoidal shape as mentioned above, while the wave kurtosis may suggest the occurrence of extreme waves (Onorato et al.
Reference Onorato, Cavaleri, Fouques, Gramstad, Janssen, Monbaliu, Osborne, Pakozdi, Serio and Stansberg2009; Xiao et al.
Reference Xiao, Liu, Wu and Yue2013). We calculate the skewness
$C_{3}$
and the kurtosis
$C_{4}$
from the instantaneous surface elevation as
$$\begin{eqnarray}\displaystyle & \displaystyle C_{3}=\frac{\overline{\unicode[STIX]{x1D702}^{3}}}{(\overline{\unicode[STIX]{x1D702}^{2}})^{3/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{4}=\frac{\overline{\unicode[STIX]{x1D702}^{4}}}{(\overline{\unicode[STIX]{x1D702}^{2}})^{2}}. & \displaystyle\end{eqnarray}$$
In nonlinear wave fields, bound waves occur in the form of harmonics, which result in a change in skewness and kurtosis. For narrow-band wave fields, the second-order nonlinear effect of bound waves has been investigated (Longuet-Higgins Reference Longuet-Higgins1963) and the statistics are found to be
$$\begin{eqnarray}\displaystyle & \displaystyle C_{3L} & \displaystyle =3k_{p}\overline{\unicode[STIX]{x1D702}^{2}}^{1/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{4L} & \displaystyle =3+24k_{p}^{2}\overline{\unicode[STIX]{x1D702}^{2}}.\end{eqnarray}$$
Additionally, the wave statistics may be influenced by resonant interactions (Janssen Reference Janssen2009; Annenkov & Shrira Reference Annenkov and Shrira2013). Taking into consideration this dynamic effect, Annenkov & Shrira (Reference Annenkov and Shrira2014) computed the skewness and kurtosis for a wide range of JONSWAP spectrum parameters and directional spreadings. Their result is written in the form of the following empirical formula,
$$\begin{eqnarray}\displaystyle & \displaystyle C_{3A}=(0.0897+0.02\unicode[STIX]{x1D6FE}_{J}^{-0.5})\unicode[STIX]{x1D700}_{c}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{4A}=12.6\unicode[STIX]{x1D6FE}_{J}^{-0.328}\unicode[STIX]{x1D700}_{c}^{2}+3, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D700}_{c}$
is a characteristic wave steepness.
Figure 10. Evolution of the skewness (●) and kurtosis (▴) of the wave field. The result is shown for case WW6.
The evolution of the skewness and kurtosis is plotted in figure 10. There is a clear difference between our result and the statistics of a standard Gaussian distribution, which has
$C_{3}=0$
and
$C_{4}=3$
(for more details see appendix B), largely due to the wave nonlinearity. This phenomenon is consistent with the result obtained by Tanaka (Reference Tanaka2001), who monitored both quantities in simulations of relatively short duration, such as
$25T_{P}$
and
$100T_{P}$
. The values of skewness and kurtosis are summarised in table 4, where
$C_{iL}$
and
$C_{iA}~(i=3,4)$
are computed using the corresponding parameters of our case set-up. The time-averages (denoted by subscript ‘
$+$
’) are an average measure of the non-Gaussianity of the irregular wave field, while the maximum values (denoted by subscript ‘
$m$
’) can serve as an indicator of extreme wave events (Xiao et al.
Reference Xiao, Liu, Wu and Yue2013). Again, we present here the result in case WW6 because the skewness and kurtosis of the wave fields share similar behaviours among the different cases WW6–WW9 and their dependence on the wind speed is less significant. The discrepancy among different results in table 4 is primarily due to the different wave properties, including the frequency bandwidth, directional spreading, wave nonlinearity, etc. The frequency bandwidth can affect the probability of extreme wave occurrence, causing an increase in the maximum values of the kurtosis (Xiao et al.
Reference Xiao, Liu, Wu and Yue2013). The directional spreading can also change the value of the high-order statistics (Onorato et al.
Reference Onorato, Cavaleri, Fouques, Gramstad, Janssen, Monbaliu, Osborne, Pakozdi, Serio and Stansberg2009; Toffoli et al.
Reference Toffoli, Benoit, Onorato and Bitner-Gregersen2009; Annenkov & Shrira Reference Annenkov and Shrira2014). The wave nonlinearity has the most prominent impact on the values of the skewness and kurtosis because it is the decisive factor for the deviation from Gaussianity.
Table 4. Skewness and kurtosis estimated from different approaches. Subscript
$+$
and
$m$
, respectively, denote the time-averages and the maxima of our results (case WW6). Other subscripts are:
$L$
, (3.7) and (3.8), theoretical prediction of Longuet-Higgins (Reference Longuet-Higgins1963);
$A$
, (3.9) and (3.10), empirical equations of Annenkov & Shrira (Reference Annenkov and Shrira2014);
$X$
, numerical result of Xiao et al. (Reference Xiao, Liu, Wu and Yue2013);
$T$
, numerical result of Tanaka (Reference Tanaka2001).
3.3.2 Wave evolution
One of the main goals of the present study is to investigate how wave fields would evolve from the deterministic perspective, where both the wind input and nonlinear wave interaction are resolved from first principles. In this section, we focus on the long-term evolution of the wave field, including the frequency downshift phenomenon and wave-based scaling law.
In statistical phase-averaging models, the wave evolution is described by the wave energy balance equation (Komen et al. Reference Komen, Cavaleri, Donelan, Hasselmann, Hasselmann and Janssen1994)
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}E}{\unicode[STIX]{x2202}t}+\boldsymbol{C}_{\boldsymbol{g}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\boldsymbol{x}}E=S_{tot}, & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{C}_{\boldsymbol{g}}$
is the group velocity, and
$S_{tot}=S_{nl}+S_{in}+S_{dis}$
is the sum of source terms representing different physical processes, including nonlinear wave interaction
$S_{nl}$
, wind input
$S_{in}$
, and dissipation
$S_{dis}$
. The wave energy balance equation can be written in the wavenumber
$(k_{x},k_{y})$
space or the directional frequency
$(f,\unicode[STIX]{x1D703})$
space (see appendix C). While both forms have been used in the literature, the directional form of wave spectrum is used almost exclusively in experiments and the output of the aforementioned operational wave models. Therefore, our numerical results in this section are calculated in the directional frequency space and then presented in the form of an omnidirectional spectrum.
Figure 11. Normalised rate of change of the omnidirectional energy density function (——) at different time instants. Also plotted is the normalised
$S_{nl}$
(– – –) calculated for the initial wave spectrum using the Webb–Resio–Tracy (WRT) method. Here,
${\dot{E}}_{m}$
is the maximum value of
$S_{nl}$
. The result is shown for case WW6.
For the dynamically coupled wind–wave field, separating the nonlinear interactions from wind input and dissipation in the data analysis is difficult (Plant Reference Plant1982). We plot the rate of change of the omnidirectional spectrum
$\unicode[STIX]{x0394}E/\unicode[STIX]{x0394}t$
in figure 11. Interestingly, the shapes of
$\unicode[STIX]{x0394}E/\unicode[STIX]{x0394}t$
at different time instants are similar, with a shift in frequency, to that of the
$S_{nl}$
calculated with the initial decoupled wind–wave field using the WRT method (Webb Reference Webb1978; Tracy & Resio Reference Tracy and Resio1982). The downshift of the peaks of
$\unicode[STIX]{x0394}E/\unicode[STIX]{x0394}t$
can be seen as an indication of the frequency downshift of the wave spectrum. Even in the absence of wind forcing, we would expect the frequency downshift to be present as a consequence of the four-wave interaction except that the overall wave energy growth rate can be different. Note that the frequency downshift may also occur in a narrow-banded wave field accompanied by wave breaking (Tulin & Waseda Reference Tulin and Waseda1999). Because of the turbulence generated in wave breaking, in those cases the wave turbulence framework that is based on weak nonlinearity is not valid any more.
We next examine the evolution of the wind-forced wave field through analysis of the wave spectrum. Acknowledging that the nonlinear interactions are dominant locally in the spectral space allows one to further simplify the spectral evolution equation as (Badulin et al. Reference Badulin, Pushkarev, Resio and Zakharov2005, Reference Badulin, Babanin, Zakharov and Resio2007)
$$\begin{eqnarray}\displaystyle \frac{\text{d}E}{\text{d}t}\approx S_{nl}. & & \displaystyle\end{eqnarray}$$
Meanwhile, because the nonlinear interaction process conserves the total energy, its corresponding term vanishes in the integral form of (3.11)
$$\begin{eqnarray}\displaystyle \int \frac{\text{d}E}{\text{d}t}\,\text{d}\boldsymbol{k}=\int (S_{in}+S_{dis})\,\text{d}\boldsymbol{k}. & & \displaystyle\end{eqnarray}$$
In figure 12, we provide the numerical evidence of self-similarity by showing the frequency downshift phenomenon is consistent with field measurements (e.g. Hasselmann et al. Reference Hasselmann, Barnett, Bouws, Carlson, Cartwright, Enke, Ewing, Gienapp, Hasselmann and Kruseman1973). The peak wave frequency sees a downshift due to the nonlinear interactions, whereas the total wave energy increases as a result of wind input. The frequency downshift is essentially the inverse cascade of wave energy because the wave field has not reached a stationary state, whereas for the classic stationary solution of the kinetic equation (Hasselmann Reference Hasselmann1962, Reference Hasselmann1963a ,Reference Hasselmann b ), the energy flux to low frequencies is zero (Kats & Kontorovich Reference Kats and Kontorovich1973, Reference Kats and Kontorovich1974; Zakharov & Zaslavskii Reference Zakharov and Zaslavskii1982). Figure 12 shows that over the duration of evolution in our simulations, and for the different wind speeds considered, the shape change in the wave spectrum is largely consistent for all the simulation cases.
Figure 12. Evolution of the normalised omnidirectional frequency spectrum
$E(f)/E_{0}$
, where
$E_{0}=E(f_{p0})$
is the peak wave energy density of the initial wave field. (a–d) correspond to cases WW6–WW9, respectively. Arrows indicate the direction of time increase. The evolution period is from
$t=1039T_{p0}$
(denoted by ——) to
$t=2424T_{p0}$
(denoted by — ⋅ ⋅ —) and the interval between each two consecutive curves is approximately
$277T_{p0}$
.
Figure 13. Universal constant
$\unicode[STIX]{x1D6FC}_{0}$
as a function of the normalised peak wave frequency
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D714}_{p}U_{10}/g$
. The present simulation results are denoted by:
$\otimes$
, case WW6;
$\times$
, case WW7;
$\oplus$
, case WW8;
$+$
, case WW9. Data compiled by Zakharov et al. (Reference Zakharov, Badulin, Hwang and Caulliez2015) are superposed for comparison, including the duration-limited data of: ▪, DeLeonibus & Simpson (Reference DeLeonibus and Simpson1972); ▾, Liu (Reference Liu1985); ◂, Hwang & Wang (Reference Hwang and Wang2004), and fetch-limited data of: ▫, Burling (Reference Burling1959); ♢, Donelan (Reference Donelan and Nihoul1979); ○, García-Nava et al. (Reference García-Nava, Ocampo-Torres, Osuna and Donelan2009); ▵, Romero & Melville (Reference Romero and Melville2010). The solid line corresponds to the theoretical value proposed by Zakharov et al. (Reference Zakharov, Badulin, Hwang and Caulliez2015).
According to Zakharov et al. (Reference Zakharov, Badulin, Hwang and Caulliez2015), the evolution of the wind-forced wave field can be summarised in a concise form
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}^{4}\unicode[STIX]{x1D708}=\unicode[STIX]{x1D6FC}_{0}^{3}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}=E^{1/2}\unicode[STIX]{x1D714}_{p}^{2}/g$
is a measure of the wave steepness,
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D714}_{p}t$
(respectively,
$\unicode[STIX]{x1D708}=2|\boldsymbol{k}_{p}|x$
) is the dimensionless duration (respectively, fetch) for duration-limited growth (respectively, fetch-limited growth), and
$\unicode[STIX]{x1D6FC}_{0}$
is a universal constant. Here, we use the simulation time to approximate the time duration of wave evolution. In the spirit of converting the time derivative to the space derivative (see Zakharov et al.
Reference Zakharov, Badulin, Hwang and Caulliez2015), the fetch can be estimated using
$$\begin{eqnarray}\displaystyle x=x_{0}+\int _{0}^{t}C_{charac}\,\text{d}t, & & \displaystyle\end{eqnarray}$$
where
$x_{0}$
is the fetch of the initial JONSWAP spectrum and
$C_{charac}=\int C_{g}E\,\text{d}\boldsymbol{k}/\int E\,\text{d}\boldsymbol{k}$
is a characteristic wave speed. Note that the choice of
$C_{charac}$
is not unique. For instance, one can also choose the peak wave group velocity
$C_{charac}=C_{g}$
. These two definitions are essentially the same when the bandwidth of the wave field is small because the weight function
$E/\int E\,\text{d}\boldsymbol{k}$
approximates a
$\unicode[STIX]{x1D6FF}$
function. For the broad-band wave field in our study, there is a 10 % difference between these two definitions. To determine the dependence of
$\unicode[STIX]{x1D6FC}_{0}$
on fetch and duration, we calculate
$\unicode[STIX]{x1D6FC}_{0}$
using the numerical data and plot in figure 13 its values as the wave field evolves. The data points are calculated from the instantaneous results of the raw data in the entire simulation period (see table 2). As shown, while the values are less than
$\unicode[STIX]{x1D6FC}_{0}\approx 0.7$
proposed by Zakharov et al. (Reference Zakharov, Badulin, Hwang and Caulliez2015), the simulation data show much less scattering than the experimental data, and remain almost constant. Our simulation result can be seen as a numerical support to the Zakharov law in the wind–wave region considered. We would like to point out that several factors may contribute to the difference in the value of
$\unicode[STIX]{x1D6FC}_{0}$
. The wave growth here is essentially duration-limited rather than fetch-limited. Besides, the choice of the reference fetch in (3.15) can affect
$\unicode[STIX]{x1D6FC}_{0}$
. Another possible explanation for the deviation is that the wave field is not fully self-similar. The same issue may occur when the universal law is validated against laboratory observations (e.g. Toba Reference Toba1972) where the wave ages are too small. As discussed by Zakharov et al. (Reference Zakharov, Badulin, Hwang and Caulliez2015), this error may be eliminated by using experimental data obtained from large water tanks at large fetch (e.g. Caulliez Reference Caulliez2013), where the self-similarity of waves has been established.
4 Summary and remarks
In this study, we have used a coupled wind LES and wave HOS computational approaches to study the energy transfer processes in an interacting wave system. The features of the numerical experiments include representative wave ages, broad-band wave field, and long-term wave evolution up to
$O(3,000T_{p0})$
. The LES and HOS capture a wide range of motions that constitute the most energetic part of wind turbulence and nonlinear waves.
Here, we briefly summarise our main findings. We have calculated the full wavenumber–frequency spectrum of the streamwise wind velocity, which is found to manifest a combined effect of mean flow, large energy-containing eddies, and wave effect that is identified for the first time. As expected, the wave effect on the wind turbulence spectrum is most prominent within a layer of a thickness that is comparable to the peak wavelength. Via quadrant analysis on the wind turbulence field, we have shown that the contributions of sweep and outward interaction events to the shear stress are greatly enhanced by the waves. We have also quantified the energy growth rate for each wave component in the broad-band wave field. The wind input is responsible for the wave energy increase while the energy dissipation related to the wave breaking model is small compared with the wind input (appendix D).
We have examined the statistical properties of the wind–wave field. The probability density function of the surface elevation and high-order wave statistics show a deviation from the Gaussian distribution due to the wave nonlinearity. We have calculated the total energy change in the wave spectrum. The result shows a positive–negative sign change across the peak frequency. The shape of the energy change is similar to that of the nonlinear interactions, suggesting that nonlinear interactions play a dominant role in the wave field evolution although they have no net contribution to the total wave energy growth. The presence of the nonlinear interactions in the wind-forced wave field results in the frequency downshift phenomenon throughout the numerical experiment, which is observed for the first time in numerical studies when the wind turbulence is resolved using LES. To quantitatively determine the role of the nonlinear interactions, we compute the value of
$\unicode[STIX]{x1D6FC}_{0}$
that arises from the scaling based on intrinsic wave properties. Our numerical result shows that while lower than the recommended value
$0.7$
,
$\unicode[STIX]{x1D6FC}_{0}$
remains largely constant in the evolution period and for the different simulation cases considered. In summary, the present numerical result supports the dominant role of nonlinear interactions in long-term wave evolution, and consequently the universal wave evolution law based on the scaling of wave properties.
Finally, we remark that the deterministic numerical simulation used in this study is a valuable research tool, but is also computationally demanding (for example, a typical case takes about two months to run on a parallel computer using 384 cores). This poses challenges to further increase the evolution period of the wave field with the existing computer power. In the future, with the increase of computer power, when the simulations can be carried out for much longer evolution periods, it would be helpful to provide further quantitative analysis on the wave evolution process when the wave properties, including the total wave energy, peak wavenumber and peak wave frequency, are plotted as functions of time or fetch. These functions are valuable to the further assessment of the wave turbulence theory (see Badulin et al. Reference Badulin, Pushkarev, Resio and Zakharov2005; Gagnaire-Renou et al. Reference Gagnaire-Renou, Benoit and Badulin2011) and may provide additional support for the significance of nonlinear interactions in the wind-forced wave evolution. The computation framework developed in this study will be useful for such studies. In addition, the energy dissipation of wave breaking is excluded in the analysis of the present study. In the design of our numerical experiments, we deliberately chose relatively weak wind speeds to reduce the impact of wave breaking that cannot be directly resolved by the HOS method due to the potential flow assumption. The complexity of wave breaking requires substantial work in modelling and validation, which is beyond the scope of this study. In future study, it will be beneficial to improve the heuristic wave breaking model in the present numerical tool to better capture the energy dissipation caused by different types of breakers (Melville Reference Melville1996; Duncan Reference Duncan2001, Perlin, Choi & Tian Reference Perlin, Choi and Tian2013).
Acknowledgements
The authors gratefully acknowledge the anonymous referees for their constructive and valuable comments. This work is supported by the Office of Naval Research, National Science Foundation and Minnesota Sea Grant.
Appendix A. Grid resolution and perturbation order in HOS simulation
Figure 14. Normalised omnidirectional frequency spectrum calculated with: (a) different grid numbers; and (b) different perturbation orders. In (a), the results are from cases BM, GN256, GN1024 and GN2048. In (b), results are from cases BM, PO2, PO4 and PO5. The spectra are calculated from the instantaneous wave field at
$t/T_{p0}=104$
.
Table 5. Numerical parameters of the test cases. Case BM has the same settings as the wave part in the coupled LES–HOS simulation. Cases GNx are designed to test the effect of grid number. Cases POx are designed to test the effect of maximum perturbation order.
We design a numerical experiment to assess the effect of grid number and order of nonlinearity in the wave simulation. For the sake of computational cost, the experiment involves only the wave simulation solving equations (2.12) and (2.13). The physical parameter setting of the initial wave field is the same as that in table 1. The numerical parameters are listed in table 5, where the case BM simply repeats the wave portion in the coupled wind–wave simulation. For all simulations, the time step is approximately
$8.7\times 10^{-3}T_{p0}$
and the simulation duration is
$104T_{p0}$
, comparable to the study of Tanaka (Reference Tanaka2001). The maximum grid number (case GN2048) is about
$2\times 10^{6}$
, the same as that in Korotkevich et al. (Reference Korotkevich, Pushkarev, Resio and Zakharov2008). When the grid number is reduced (case GN256), the high frequency part of wave spectrum is not accurately resolved (figure 14
a) because of low resolution. On the other hand, the results in the cases BM, GN1024 and GN2048 collapse for all frequencies, suggesting that the grid resolution
$(512,256)$
is sufficiently high to resolve wave dynamics. In figure 14(b), we observe a significant deviation in spectrum when the perturbation expansion order is two, showing that the nonlinear interactions are not captured. On the other hand, the result of case BM is consistent with those in cases PO4 and PO5. In conclusion, the result of this test shows that our choice of numerical parameters is appropriate in the coupled wind–wave simulation.
Appendix B. Gram–Charlier series
The Gram–Charlier series is an approximation to the Gaussian distribution (see Kolassa Reference Kolassa2006, chap. 3). It has the following form when truncated to the finite order
$$\begin{eqnarray}\displaystyle f(x) & = & \displaystyle \frac{1}{\sqrt{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{2}}}\exp \left[-\frac{(x-\unicode[STIX]{x1D705}_{1})^{2}}{2\unicode[STIX]{x1D705}_{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \times \left[1+\frac{\unicode[STIX]{x1D705}_{3}}{3!\unicode[STIX]{x1D705}_{2}^{3/2}}H_{3}\left(\frac{x-\unicode[STIX]{x1D705}_{1}}{\unicode[STIX]{x1D705}_{2}^{1/2}}\right)+\frac{\unicode[STIX]{x1D705}_{4}}{4!\unicode[STIX]{x1D705}_{2}^{2}}H_{4}\left(\frac{x-\unicode[STIX]{x1D705}_{1}}{\unicode[STIX]{x1D705}_{2}^{1/2}}\right)\right],\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}_{i}$
is the
$i$
th cumulant, and
$H_{3}(\cdot )$
and
$H_{4}(\cdot )$
are the third and fourth Hermite polynomials, respectively.
Equation (B 1) is valid under the condition that the distribution of the data is approximately Gaussian. Otherwise, the series do not converge and thus the approximation fails to hold rigorously. For the distribution of ocean surface elevation with a zero mean,
$\unicode[STIX]{x1D705}_{3}$
and
$\unicode[STIX]{x1D705}_{4}$
can be approximated using the skewness
$C_{3}$
and kurtosis
$C_{4}$
, respectively. For the standard Gaussian distribution,
$C_{3}=0$
and
$C_{4}=3$
.
Appendix C. Surface wave spectrum
Here we briefly review two types of spectrum commonly used in the analysis of surface wave energy: the wavenumber spectrum and the directional frequency spectrum. The reader is referred to Young (Reference Young1999) and Holthuijsen (Reference Holthuijsen2007) for more details. The wavenumber spectrum is defined as
$$\begin{eqnarray}\displaystyle E(k_{x},k_{y})=\lim _{\unicode[STIX]{x0394}k_{x}\rightarrow 0}\lim _{\unicode[STIX]{x0394}k_{x}\rightarrow 0}\frac{1}{\unicode[STIX]{x0394}k_{x}\unicode[STIX]{x0394}k_{y}}E\left\{\frac{1}{2}a^{2}\right\}, & & \displaystyle\end{eqnarray}$$
where
$a$
is the amplitude of the corresponding wave component and
$E\{\frac{1}{2}a^{2}\}$
denotes the variance in a spectral bin
$(\unicode[STIX]{x0394}k_{x},\unicode[STIX]{x0394}k_{y})$
. The directional spectrum is defined as
$$\begin{eqnarray}\displaystyle E(f,\unicode[STIX]{x1D703})=\lim _{\unicode[STIX]{x0394}f\rightarrow 0}\lim _{\unicode[STIX]{x0394}\unicode[STIX]{x1D703}\rightarrow 0}\frac{1}{\unicode[STIX]{x0394}f\unicode[STIX]{x0394}\unicode[STIX]{x1D703}}E\left\{\frac{1}{2}a^{2}\right\}. & & \displaystyle\end{eqnarray}$$
Equations (C 1) and (C 2) are related by
$$\begin{eqnarray}\displaystyle E(f,\unicode[STIX]{x1D703})=E(k_{x},k_{y})\frac{\unicode[STIX]{x2202}(f,\unicode[STIX]{x1D703})}{\unicode[STIX]{x2202}(k_{x},k_{y})}, & & \displaystyle\end{eqnarray}$$
where the Jacobian
$\unicode[STIX]{x2202}(f,\unicode[STIX]{x1D703})/\unicode[STIX]{x2202}(k_{x},k_{y})$
can be readily obtained from the dispersion relation.
Appendix D. Wind input by tangential stress and wave energy dissipation
The energy transfer from wind to wave can be caused by normal stress and tangential stress. Generally, the work done by the tangential stress is small compared with that done by normal stress (Young Reference Young1999). Under certain sea states, the air flow separation may occur and the effect of the tangential stress cannot be neglected (Tian, Perlin & Choi Reference Tian, Perlin and Choi2010). In figure 15, we compare the wind–wave conditions of each individual wave component in our simulation with experimental data (Kawai Reference Kawai1981; Donelan et al. Reference Donelan, Babanin, Young and Banner2006; Tian et al. Reference Tian, Perlin and Choi2010). While there is no rigorous criterion for determining the boundary of separation as indicated by the study of Tian et al. (Reference Tian, Perlin and Choi2010), our result shows that both the wave steepness and the wind speed relative to the waves are small, suggesting that the air flow separation is unlikely to occur for the wind field in the present study. Consequently, we expect the energy transfer related to the tangential stress to be negligibly small.
Figure 15. Wind–wave conditions related to air flow separation over water waves. Here,
$U_{\infty }$
denotes the free-stream wind speed. In Tian et al. (Reference Tian, Perlin and Choi2010), the conditions are divided into the following categories: no separations, denoted by ▫; separation undetermined, denoted by ▵; separations over non-breaking waves, denoted by ●; separations over breaking waves, denoted by ▴. Also included in their paper are results from Kawai (Reference Kawai1981), denoted by ○, and Donelan et al. (Reference Donelan, Babanin, Young and Banner2006), denoted by ◃. The trends of non-separation and separation are denoted by blue arrows. The present simulation results are denoted by
$\otimes$
, case WW6;
$\times$
, case WW7;
$\oplus$
, case WW8;
$+$
, case WW9.
Figure 16. Time history of the work done by stress at the wave surface. The work done by tangential stress
$P_{\unicode[STIX]{x1D708}}$
is denoted by the smaller symbols while that done by the pressure
$P_{p}$
is denoted by the larger ones. The present simulation results are denoted by:
$\otimes$
, case WW6;
$\times$
, case WW7;
$\oplus$
, case WW8;
$+$
, case WW9.
To quantitatively assess the significance of tangential stress, we define the work done by the tangential stress and the pressure per unit area per unit time as
$$\begin{eqnarray}\displaystyle & \displaystyle P_{\unicode[STIX]{x1D708}}=\frac{1}{A}\int _{A}\left(u_{\ast }^{2}-\frac{p_{a}}{\unicode[STIX]{x1D70C}_{a}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}x}\right)u_{s}\,\text{d}A, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P_{p}=\frac{1}{A}\int _{A}\frac{p_{a}}{\unicode[STIX]{x1D70C}_{a}}u_{n}\,\text{d}A, & \displaystyle\end{eqnarray}$$
where
$u_{s}$
is the streamwise velocity component at the wave surface,
$u_{n}$
is the velocity component normal to the wave surface, and
$A$
denotes the area of the entire wave field. Note that the tangential stress on the air side is not directly calculated from the velocity profile as in the DNS of Yang & Shen (Reference Yang and Shen2010). Instead, in the present study, it is estimated by subtracting the horizontal component of the pressure-induced stress from the total stress. As shown in figure 16, the work done by the tangential stress is one order of magnitude smaller than that done by pressure.
Figure 17. Time history of the ratio of the wave energy dissipation rate to the wind input induced by pressure. The present simulation results are denoted by:
$\otimes$
, case WW6;
$\times$
, case WW7;
$\oplus$
, case WW8;
$+$
, case WW9.
The wave energy dissipation modelled by the adaptive filter (2.14) can be estimated by
$$\begin{eqnarray}\displaystyle P_{ds}=\int \frac{\unicode[STIX]{x1D702}^{2}(\boldsymbol{k})}{\unicode[STIX]{x0394}t}[1-G^{2}(k;C_{1},C_{2})]\,\text{d}\boldsymbol{k}. & & \displaystyle\end{eqnarray}$$
The value of
$P_{ds}$
is therefore a measure of the wave energy dissipated via the filter per unit area per unit time. By comparing it with the work done by the pressure, we find that the magnitude of
$P_{ds}$
is generally one to three orders smaller than
$P_{p}$
(figure 17). Therefore, this energy dissipation is not a significant issue with regards to the wave evolution in the present study. Note that wave breaking in the real ocean is a very complex process, and the value calculated from (D 3) shall not be viewed as a high-accuracy measure of the energy dissipation induced by wave breaking.
