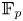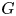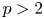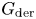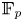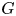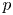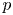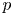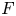1. Introduction
1.1 Motivation
Let ![]() $E$ be a local field of characteristic
$E$ be a local field of characteristic ![]() $p > 0$ with ring of integers
$p > 0$ with ring of integers ![]() $\mathcal {O}_E$ and residue field
$\mathcal {O}_E$ and residue field ![]() $\mathbb {F}_q$ where
$\mathbb {F}_q$ where ![]() $q$ is a power of
$q$ is a power of ![]() $p$. Let
$p$. Let ![]() $G$ be a split connected reductive group defined over
$G$ be a split connected reductive group defined over ![]() $E$, and fix a maximal torus and a Borel subgroup
$E$, and fix a maximal torus and a Borel subgroup ![]() $T \subset B \subset G$. Let
$T \subset B \subset G$. Let ![]() $X_*(T)$ be the group of cocharacters of
$X_*(T)$ be the group of cocharacters of ![]() $G$ and let
$G$ and let ![]() $X_*(T)^+$ be the monoid of dominant cocharacters. For a compact open subgroup
$X_*(T)^+$ be the monoid of dominant cocharacters. For a compact open subgroup ![]() $H \subset G(E)$ let
$H \subset G(E)$ let
The multiplication on ![]() $\mathcal {H}_H$ is by convolution of functions. The mod
$\mathcal {H}_H$ is by convolution of functions. The mod ![]() $p$ Hecke algebras
$p$ Hecke algebras ![]() $\mathcal {H}_H$ are important in the study of smooth admissible representations of
$\mathcal {H}_H$ are important in the study of smooth admissible representations of ![]() $G(E)$.
$G(E)$.
As ![]() $G$ is split we may let
$G$ is split we may let ![]() $K = G(\mathcal {O}_E)$. Then Herzig [Reference HerzigHer11b] (and Henniart and Vignéras [Reference Henniart and VignérasHV15] for more general coefficients) constructed a mod
$K = G(\mathcal {O}_E)$. Then Herzig [Reference HerzigHer11b] (and Henniart and Vignéras [Reference Henniart and VignérasHV15] for more general coefficients) constructed a mod ![]() $p$ Satake isomorphism
$p$ Satake isomorphism
We note that the mod ![]() $p$ Satake isomorphism is related to the usual Satake isomorphism by an integral Satake isomorphism constructed by Zhu in [Reference ZhuZhu20]. In [Reference CassCas19] we constructed a symmetric monoidal category of perverse
$p$ Satake isomorphism is related to the usual Satake isomorphism by an integral Satake isomorphism constructed by Zhu in [Reference ZhuZhu20]. In [Reference CassCas19] we constructed a symmetric monoidal category of perverse ![]() $\mathbb {F}_p$-sheaves on the affine Grassmannian of
$\mathbb {F}_p$-sheaves on the affine Grassmannian of ![]() $G$ which gives a geometrization of the inverse of
$G$ which gives a geometrization of the inverse of ![]() $\mathcal {S}$.
$\mathcal {S}$.
Now let ![]() $I \subset K$ be the Iwahori subgroup determined by
$I \subset K$ be the Iwahori subgroup determined by ![]() $B$ and let
$B$ and let ![]() $Z(\mathcal {H}_I)$ be the center of
$Z(\mathcal {H}_I)$ be the center of ![]() $\mathcal {H}_I$. If
$\mathcal {H}_I$. If ![]() ${\mathbb {1}}_K \in \mathcal {H}_I$ is the function which is
${\mathbb {1}}_K \in \mathcal {H}_I$ is the function which is ![]() $1$ on
$1$ on ![]() $K$ and
$K$ and ![]() $0$ elsewhere then by work of Vignéras [Reference VignérasVig05] and Ollivier [Reference OllivierOll14] there is an isomorphism of
$0$ elsewhere then by work of Vignéras [Reference VignérasVig05] and Ollivier [Reference OllivierOll14] there is an isomorphism of ![]() $\mathbb {F}_p$-algebras
$\mathbb {F}_p$-algebras
In this paper we will construct a functor on perverse ![]() $\mathbb {F}_p$-sheaves which geometrizes the inverse of
$\mathbb {F}_p$-sheaves which geometrizes the inverse of ![]() $\mathcal {C}$. This allows us to give geometric proofs of certain combinatorial identities in Iwahori mod
$\mathcal {C}$. This allows us to give geometric proofs of certain combinatorial identities in Iwahori mod ![]() $p$ Hecke algebras.
$p$ Hecke algebras.
This paper is the next step in a project aimed at providing a categorification of the representation theory of affine mod ![]() $p$ Hecke algebras. In future joint work with C. Pépin and T. Schmidt we plan to apply the results in this paper as well as [Reference Pépin and SchmidtPS20] to construct a mod
$p$ Hecke algebras. In future joint work with C. Pépin and T. Schmidt we plan to apply the results in this paper as well as [Reference Pépin and SchmidtPS20] to construct a mod ![]() $p$ version of Bezrukavnikov's equivalence in [Reference BezrukavnikovBez16], which we expect will have applications to a mod
$p$ version of Bezrukavnikov's equivalence in [Reference BezrukavnikovBez16], which we expect will have applications to a mod ![]() $p$ local Langlands correspondence. In particular, we hope to give a geometric construction of some instances of Grosse-Klönne's functor [Reference Grosse-KlönneGK16] from supersingular mod
$p$ local Langlands correspondence. In particular, we hope to give a geometric construction of some instances of Grosse-Klönne's functor [Reference Grosse-KlönneGK16] from supersingular mod ![]() $p$ Hecke modules to Galois representations. We refer the reader to the introduction in [Reference CassCas19] for more information on the relation between the objects studied in this paper and the
$p$ Hecke modules to Galois representations. We refer the reader to the introduction in [Reference CassCas19] for more information on the relation between the objects studied in this paper and the ![]() $p$-adic Langlands program.
$p$-adic Langlands program.
1.2 Main results
Let ![]() $G$ be a connected reductive group over an algebraically closed field
$G$ be a connected reductive group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p > 2$ such that
$p > 2$ such that ![]() $G_\text {der}$ is almost simple. Fix a maximal torus and a Borel subgroup
$G_\text {der}$ is almost simple. Fix a maximal torus and a Borel subgroup ![]() $T \subset B \subset G$. Let
$T \subset B \subset G$. Let ![]() $I \subset L^+G$ be the Iwahori group given by the fiber of
$I \subset L^+G$ be the Iwahori group given by the fiber of ![]() $B$ under the projection
$B$ under the projection ![]() $L^+G \rightarrow G$ (see § 2.1 for the definitions). Let
$L^+G \rightarrow G$ (see § 2.1 for the definitions). Let ![]() $\operatorname {Gr}$ be the affine Grassmannian of
$\operatorname {Gr}$ be the affine Grassmannian of ![]() $G$, let
$G$, let ![]() $\mathcal {F}\ell$ be the Iwahori affine flag variety, and let
$\mathcal {F}\ell$ be the Iwahori affine flag variety, and let ![]() $\pi \colon \mathcal {F}\ell \rightarrow \operatorname {Gr}$ be the projection.
$\pi \colon \mathcal {F}\ell \rightarrow \operatorname {Gr}$ be the projection.
In [Reference CassCas19, § 6] we defined the categories of equivariant perverse ![]() $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ and
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ and ![]() $P_I(\mathcal {F}\ell , \mathbb {F}_p)$ as well as a convolution product
$P_I(\mathcal {F}\ell , \mathbb {F}_p)$ as well as a convolution product ![]() $*$ on
$*$ on ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$. The convolution product on
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$. The convolution product on ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ preserves the full subcategory of semisimple objects
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ preserves the full subcategory of semisimple objects ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}} \subset P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$. In § 2.3 we define the convolution product
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}} \subset P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$. In § 2.3 we define the convolution product ![]() $\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet } \in D_c^b(\mathcal {F}\ell _\unicode{x00E9}{\text{t}}, \mathbb {F}_p)$ of two
$\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet } \in D_c^b(\mathcal {F}\ell _\unicode{x00E9}{\text{t}}, \mathbb {F}_p)$ of two ![]() $I$-equivariant perverse sheaves
$I$-equivariant perverse sheaves ![]() $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$, ![]() $\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell , \mathbb {F}_p)$.
$\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell , \mathbb {F}_p)$.
Let ![]() $W$ be the Weyl group of
$W$ be the Weyl group of ![]() $G$ and let
$G$ and let ![]() $\tilde {W}$ be the Iwahori–Weyl group of
$\tilde {W}$ be the Iwahori–Weyl group of ![]() $G(k (\!( t )\!))$. For
$G(k (\!( t )\!))$. For ![]() $\mu \in X_*(T)^+$ let
$\mu \in X_*(T)^+$ let ![]() $\operatorname {Gr}_{\leq \mu } \subset \operatorname {Gr}$ be the corresponding reduced
$\operatorname {Gr}_{\leq \mu } \subset \operatorname {Gr}$ be the corresponding reduced ![]() $L^+G$-orbit closure, and for
$L^+G$-orbit closure, and for ![]() $w \in \tilde {W}$ let
$w \in \tilde {W}$ let ![]() $\mathcal {F}\ell _w \subset \mathcal {F}\ell$ be the corresponding reduced
$\mathcal {F}\ell _w \subset \mathcal {F}\ell$ be the corresponding reduced ![]() $I$-orbit closure. Let
$I$-orbit closure. Let ![]() $\operatorname {IC}_\mu \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ be the shifted constant sheaf
$\operatorname {IC}_\mu \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ be the shifted constant sheaf ![]() $\mathbb {F}_p[\dim \operatorname {Gr}_{\leq \mu }]$ supported on
$\mathbb {F}_p[\dim \operatorname {Gr}_{\leq \mu }]$ supported on ![]() $\operatorname {Gr}_{\leq \mu }$ (see Theorem 2.10).
$\operatorname {Gr}_{\leq \mu }$ (see Theorem 2.10).
Given ![]() $\mu \in X_*(T)^+$, let
$\mu \in X_*(T)^+$, let ![]() $\text {Adm}(\mu ) \subset \tilde {W}$ be the
$\text {Adm}(\mu ) \subset \tilde {W}$ be the ![]() $\mu$-admissible set defined in (2.1). Set
$\mu$-admissible set defined in (2.1). Set
Let ![]() $\mathcal {Z}_{\mathcal {A}(\mu )} \in D_c^b(\mathcal {F}\ell _\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ be the shifted constant sheaf
$\mathcal {Z}_{\mathcal {A}(\mu )} \in D_c^b(\mathcal {F}\ell _\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ be the shifted constant sheaf ![]() $\mathbb {F}_p[\dim \mathcal {A}(\mu )]$ supported on
$\mathbb {F}_p[\dim \mathcal {A}(\mu )]$ supported on ![]() $\mathcal {A}(\mu )$.
$\mathcal {A}(\mu )$.
Our main theorem is as follows.
Theorem 1.1 There exists an exact functor ![]() $\mathcal {Z} \colon P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}} \rightarrow P_{I}(\mathcal {F}\ell , \mathbb {F}_p)$ that satisfies the following assertions.
$\mathcal {Z} \colon P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}} \rightarrow P_{I}(\mathcal {F}\ell , \mathbb {F}_p)$ that satisfies the following assertions.
(i) For all
 $\mu \in X_*(T)^+$ there is a canonical isomorphism
$\mu \in X_*(T)^+$ there is a canonical isomorphism
 \[ \mathcal{Z}(\operatorname{IC}_\mu) \cong \mathcal{Z}_{\mathcal{A}(\mu)}. \]
\[ \mathcal{Z}(\operatorname{IC}_\mu) \cong \mathcal{Z}_{\mathcal{A}(\mu)}. \](ii) For all
 $\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ there is a canonical isomorphism
$\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ there is a canonical isomorphism
 \[ R\pi_!(\mathcal{Z}(\mathcal{F}^\bullet)) \cong \mathcal{F}^\bullet. \]
\[ R\pi_!(\mathcal{Z}(\mathcal{F}^\bullet)) \cong \mathcal{F}^\bullet. \](iii) For all
 $\mathcal {F}_1^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ and
$\mathcal {F}_1^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ and  $\mathcal {F}_2^{\bullet } \in P_{I}(\mathcal {F}\ell , \mathbb {F}_p)$ the convolution product
is perverse and
$\mathcal {F}_2^{\bullet } \in P_{I}(\mathcal {F}\ell , \mathbb {F}_p)$ the convolution product
is perverse and \[ \mathcal{Z}(\mathcal{F}_1^\bullet) * \mathcal{F}_2^{{\bullet}} \]
\[ \mathcal{Z}(\mathcal{F}_1^\bullet) * \mathcal{F}_2^{{\bullet}} \] $I$-equivariant.
$I$-equivariant.(iv) For all
 $\mathcal {F}_1^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ and
$\mathcal {F}_1^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ and  $\mathcal {F}_2^{\bullet } \in P_{I}(\mathcal {F}\ell , \mathbb {F}_p)$ there is a canonical isomorphism
$\mathcal {F}_2^{\bullet } \in P_{I}(\mathcal {F}\ell , \mathbb {F}_p)$ there is a canonical isomorphism
 \[ \mathcal{Z}(\mathcal{F}_1^\bullet) * \mathcal{F}_2^{{\bullet}} \cong \mathcal{F}_2^{{\bullet}} * \mathcal{Z}(\mathcal{F}_1^\bullet). \]
\[ \mathcal{Z}(\mathcal{F}_1^\bullet) * \mathcal{F}_2^{{\bullet}} \cong \mathcal{F}_2^{{\bullet}} * \mathcal{Z}(\mathcal{F}_1^\bullet). \](v) For all
 $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$,  $\mathcal {F}_2^{\bullet } \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ there is a canonical isomorphism
$\mathcal {F}_2^{\bullet } \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ there is a canonical isomorphism
 \[ \mathcal{Z}(\mathcal{F}_1^\bullet * \mathcal{F}_2^{{\bullet}}) \cong \mathcal{Z}(\mathcal{F}_1^\bullet) * \mathcal{Z}(\mathcal{F}_2^{{\bullet}}). \]
\[ \mathcal{Z}(\mathcal{F}_1^\bullet * \mathcal{F}_2^{{\bullet}}) \cong \mathcal{Z}(\mathcal{F}_1^\bullet) * \mathcal{Z}(\mathcal{F}_2^{{\bullet}}). \]
Our method is analogous to the case of ![]() $\overline {\mathbb {Q}}_\ell$-coefficients considered in [Reference GaitsgoryGai01] and [Reference ZhuZhu14], but it involves some new ideas because we use a different notion of the nearby cycles functor which is well suited for our purposes (see Remark 2.9 for the usual definition). As in [Reference CassCas19], we exploit subtle properties of the singularities of affine Schubert varieties. In particular, we use Frobenius splitting techniques to verify that our ad-hoc construction of the nearby cycles functor satisfies the necessary properties. This requires us to prove some new results on the
$\overline {\mathbb {Q}}_\ell$-coefficients considered in [Reference GaitsgoryGai01] and [Reference ZhuZhu14], but it involves some new ideas because we use a different notion of the nearby cycles functor which is well suited for our purposes (see Remark 2.9 for the usual definition). As in [Reference CassCas19], we exploit subtle properties of the singularities of affine Schubert varieties. In particular, we use Frobenius splitting techniques to verify that our ad-hoc construction of the nearby cycles functor satisfies the necessary properties. This requires us to prove some new results on the ![]() $F$-singularities of affine Schubert varieties, which will be explained in § 1.4.
$F$-singularities of affine Schubert varieties, which will be explained in § 1.4.
The relevant facts from the theory of ![]() $F$-singularities are that if
$F$-singularities are that if ![]() $X$ is an integral
$X$ is an integral ![]() $F$-rational variety of dimension
$F$-rational variety of dimension ![]() $d$ then the shifted constant sheaf
$d$ then the shifted constant sheaf ![]() $\mathbb {F}_p[d] \in D_c^b(X_\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ is a simple perverse sheaf by [Reference CassCas19, 1.7], and that
$\mathbb {F}_p[d] \in D_c^b(X_\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ is a simple perverse sheaf by [Reference CassCas19, 1.7], and that ![]() $F$-rational singularities are pseudo-rational by a result of Smith [Reference SmithSmi97]. We will combine these facts with a result of Kovács [Reference KovácsKov17] to deduce that our nearby cycles functor commutes with pushforward along birational morphisms between certain
$F$-rational singularities are pseudo-rational by a result of Smith [Reference SmithSmi97]. We will combine these facts with a result of Kovács [Reference KovácsKov17] to deduce that our nearby cycles functor commutes with pushforward along birational morphisms between certain ![]() $F$-rational varieties.
$F$-rational varieties.
Remark 1.2 The functor ![]() $\mathcal {Z}$ in Theorem 1.1 can be defined on the category
$\mathcal {Z}$ in Theorem 1.1 can be defined on the category ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$, but then it is not clear that this functor is exact. This is why we restrict to the subcategory
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$, but then it is not clear that this functor is exact. This is why we restrict to the subcategory ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$.
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$.
1.3 Applications to mod  $p$ Hecke algebras
$p$ Hecke algebras
Let ![]() $G$ be a split connected reductive group defined over a local field
$G$ be a split connected reductive group defined over a local field ![]() $E$ of characteristic
$E$ of characteristic ![]() $p > 2$ and residue field
$p > 2$ and residue field ![]() $\mathbb {F}_q$. Fix a maximal torus and a Borel subgroup
$\mathbb {F}_q$. Fix a maximal torus and a Borel subgroup ![]() $T \subset B \subset G$. We assume that
$T \subset B \subset G$. We assume that ![]() $T$ and
$T$ and ![]() $B$ are defined over
$B$ are defined over ![]() $\mathbb {F}_q$ and that
$\mathbb {F}_q$ and that ![]() $G_{\text {der}}$ is absolutely almost simple. Let
$G_{\text {der}}$ is absolutely almost simple. Let ![]() $K = G(\mathcal {O}_E)$ and let
$K = G(\mathcal {O}_E)$ and let ![]() $t$ be a uniformizer of
$t$ be a uniformizer of ![]() $E$. Then
$E$. Then ![]() $\mathcal {H}_K$ has a natural basis
$\mathcal {H}_K$ has a natural basis ![]() $\{{\mathbb {1}}_\mu \}$ indexed by the dominant cocharacters
$\{{\mathbb {1}}_\mu \}$ indexed by the dominant cocharacters ![]() $X_*(T)^+$ where
$X_*(T)^+$ where ![]() ${\mathbb {1}}_\mu$ is the characteristic function of the double coset
${\mathbb {1}}_\mu$ is the characteristic function of the double coset ![]() $K \mu (t) K$. Similarly, if
$K \mu (t) K$. Similarly, if ![]() $I \subset K$ is the Iwahori subgroup determined by
$I \subset K$ is the Iwahori subgroup determined by ![]() $B$ then
$B$ then ![]() $\mathcal {H}_I$ has a basis
$\mathcal {H}_I$ has a basis ![]() $\{{\mathbb {1}}_w\}$ indexed by
$\{{\mathbb {1}}_w\}$ indexed by ![]() $\tilde {W}$. Let
$\tilde {W}$. Let ![]() ${\mathbb {1}}_K \in \mathcal {H}_I$ be the function which is
${\mathbb {1}}_K \in \mathcal {H}_I$ be the function which is ![]() $1$ on
$1$ on ![]() $K$ and
$K$ and ![]() $0$ elsewhere. In § 4 we will show that a version of Theorem 1.1 also holds when we view
$0$ elsewhere. In § 4 we will show that a version of Theorem 1.1 also holds when we view ![]() $\operatorname {Gr}$ and
$\operatorname {Gr}$ and ![]() $\mathcal {F}\ell$ as ind-schemes over the finite field
$\mathcal {F}\ell$ as ind-schemes over the finite field ![]() $\mathbb {F}_q$. Then by applying the function-sheaf correspondence we will derive the following explicit formula for
$\mathbb {F}_q$. Then by applying the function-sheaf correspondence we will derive the following explicit formula for ![]() $\mathcal {C}^{-1} \colon \mathcal {H}_K \rightarrow Z(\mathcal {H}_I)$.
$\mathcal {C}^{-1} \colon \mathcal {H}_K \rightarrow Z(\mathcal {H}_I)$.
Theorem 1.3 Let ![]() $\mathcal {C}$ be the isomorphism
$\mathcal {C}$ be the isomorphism ![]() $Z(\mathcal {H}_I) \rightarrow \mathcal {H}_K$ such that
$Z(\mathcal {H}_I) \rightarrow \mathcal {H}_K$ such that ![]() $\mathcal {C}(f) = f * {\mathbb {1}}_K$. Then
$\mathcal {C}(f) = f * {\mathbb {1}}_K$. Then
 \[ \mathcal{C}^{{-}1} \biggl( \sum_{\lambda \leq \mu} {\mathbb 1}_{\lambda} \biggr) = \sum_{w \in \text{Adm}(\mu)} {\mathbb 1}_{w}. \]
\[ \mathcal{C}^{{-}1} \biggl( \sum_{\lambda \leq \mu} {\mathbb 1}_{\lambda} \biggr) = \sum_{w \in \text{Adm}(\mu)} {\mathbb 1}_{w}. \] For ![]() $\mu \in X_*(T)^+$ let
$\mu \in X_*(T)^+$ let ![]() $t_\mu$ be the element
$t_\mu$ be the element ![]() $\mu$ regarded as an element of
$\mu$ regarded as an element of ![]() $\tilde {W}$, and let
$\tilde {W}$, and let ![]() $\Lambda _\mu \subset X_*(T)$ be the
$\Lambda _\mu \subset X_*(T)$ be the ![]() $W$-orbit of
$W$-orbit of ![]() $\mu$. In [Reference VignérasVig05], Vignéras constructed integral Bernstein elements
$\mu$. In [Reference VignérasVig05], Vignéras constructed integral Bernstein elements ![]() $B(\lambda ) \in \mathcal {H}_I$ for
$B(\lambda ) \in \mathcal {H}_I$ for ![]() $\lambda \in X_*(T)$ and showed that
$\lambda \in X_*(T)$ and showed that ![]() $\{\sum _{\lambda \in \Lambda _\mu } B(\lambda )\}_{\mu \in X_*(T)^+}$ is an
$\{\sum _{\lambda \in \Lambda _\mu } B(\lambda )\}_{\mu \in X_*(T)^+}$ is an ![]() $\mathbb {F}_p$-basis for
$\mathbb {F}_p$-basis for ![]() $Z(\mathcal {H}_I)$. Ollivier [Reference OllivierOll14] showed that these Bernstein elements give rise to an isomorphism of
$Z(\mathcal {H}_I)$. Ollivier [Reference OllivierOll14] showed that these Bernstein elements give rise to an isomorphism of ![]() $\mathbb {F}_p$-algebras
$\mathbb {F}_p$-algebras
Ollivier also showed that ![]() $\mathcal {B}$ is compatible with the mod
$\mathcal {B}$ is compatible with the mod ![]() $p$ Satake isomorphism in the sense that
$p$ Satake isomorphism in the sense that ![]() $\mathcal {B} = \mathcal {C}^{-1} \circ \mathcal {S}^{-1}$.
$\mathcal {B} = \mathcal {C}^{-1} \circ \mathcal {S}^{-1}$.
For our last application, we note that by [Reference OllivierOll14, 2.3] the coefficient of ![]() ${\mathbb {1}}_w$ appearing in
${\mathbb {1}}_w$ appearing in ![]() $\sum _{\lambda \in \Lambda _\mu } B(\lambda ) \in \mathcal {H}_I$ is
$\sum _{\lambda \in \Lambda _\mu } B(\lambda ) \in \mathcal {H}_I$ is ![]() $0$ if
$0$ if ![]() $w \notin \text {Adm}(\mu )$ and is
$w \notin \text {Adm}(\mu )$ and is ![]() $1$ if
$1$ if ![]() $w \in \text {Adm}(\mu )$ and
$w \in \text {Adm}(\mu )$ and ![]() $\ell (w) = \ell (t_\mu )$, where
$\ell (w) = \ell (t_\mu )$, where ![]() $\ell$ is the length function on
$\ell$ is the length function on ![]() $\tilde {W}$. Using Theorem 1.3, we can compute the rest of the coefficients (cf. [Reference OllivierOll15, 5.2]).
$\tilde {W}$. Using Theorem 1.3, we can compute the rest of the coefficients (cf. [Reference OllivierOll15, 5.2]).
Corollary 1.4 Let ![]() $\mu \in X_*(T)^+$. Then the integral Bernstein elements satisfy
$\mu \in X_*(T)^+$. Then the integral Bernstein elements satisfy
Remark 1.5 Let ![]() $\tilde {I} \subset I$ be the pro-
$\tilde {I} \subset I$ be the pro-![]() $p$ Sylow subgroup. The integral Bernstein elements are usually defined in the larger Hecke algebra
$p$ Sylow subgroup. The integral Bernstein elements are usually defined in the larger Hecke algebra ![]() $\mathcal {H}_{\tilde {I}}$. There is a central idempotent
$\mathcal {H}_{\tilde {I}}$. There is a central idempotent ![]() $\epsilon _1 \in \mathcal {H}_{\tilde {I}}$ such that
$\epsilon _1 \in \mathcal {H}_{\tilde {I}}$ such that ![]() $\mathcal {H}_I = \epsilon _1\mathcal {H}_{\tilde {I}}$ (see [Reference OllivierOll14, 2.14]). The Bernstein elements we are considering in this paper are the images of the Bernstein elements in [Reference OllivierOll14] after multiplication by
$\mathcal {H}_I = \epsilon _1\mathcal {H}_{\tilde {I}}$ (see [Reference OllivierOll14, 2.14]). The Bernstein elements we are considering in this paper are the images of the Bernstein elements in [Reference OllivierOll14] after multiplication by ![]() $\epsilon _1$. The integral Bernstein elements in [Reference OllivierOll14] also depend on a choice of a sign (
$\epsilon _1$. The integral Bernstein elements in [Reference OllivierOll14] also depend on a choice of a sign (![]() $\pm$) and a Weyl chamber, but the central integral Bernstein elements
$\pm$) and a Weyl chamber, but the central integral Bernstein elements ![]() $\sum _{\lambda \in \Lambda _\mu } B(\lambda )$ do not depend on these choices by [Reference OllivierOll14, 3.4].
$\sum _{\lambda \in \Lambda _\mu } B(\lambda )$ do not depend on these choices by [Reference OllivierOll14, 3.4].
1.4 F-singularities of local models
During the course of proving Theorem 1.1 we will also prove a result about the singularities of equal characteristic analogues of local models of Shimura varieties. Following the notation in § 1.3, let ![]() $\operatorname {Gr}$ be the affine Grassmannian of
$\operatorname {Gr}$ be the affine Grassmannian of ![]() $G$ viewed as an ind-scheme over
$G$ viewed as an ind-scheme over ![]() $\mathbb {F}_q$. Then for
$\mathbb {F}_q$. Then for ![]() $\mu \in X_*(T)^+$ there is an associated local model
$\mu \in X_*(T)^+$ there is an associated local model ![]() $M_{\mu } \rightarrow \operatorname {Spec}(\mathcal {O}_E)$ such that the generic fiber of
$M_{\mu } \rightarrow \operatorname {Spec}(\mathcal {O}_E)$ such that the generic fiber of ![]() $M_{\mu }$ is isomorphic to
$M_{\mu }$ is isomorphic to ![]() $\operatorname {Gr}_{\leq \mu } \times \operatorname {Spec}(E)$ and the reduced special fiber is isomorphic to
$\operatorname {Gr}_{\leq \mu } \times \operatorname {Spec}(E)$ and the reduced special fiber is isomorphic to ![]() $\mathcal {A}(\mu )$ (see Definition 2.3).
$\mathcal {A}(\mu )$ (see Definition 2.3).
Theorem 1.6 Suppose that ![]() $p > 2$ and that
$p > 2$ and that ![]() $G_{\text {der}}$ is absolutely almost simple and simply connected. Then for any
$G_{\text {der}}$ is absolutely almost simple and simply connected. Then for any ![]() $\mu \in X_*(T)^+$, every local ring in
$\mu \in X_*(T)^+$, every local ring in ![]() $M_{\mu }$ is strongly
$M_{\mu }$ is strongly ![]() $F$-regular,
$F$-regular, ![]() $F$-rational, and has pseudo-rational singularities.
$F$-rational, and has pseudo-rational singularities.
In the mixed characteristic case, local models are used to study the étale local structure of integral models of Shimura varieties with parahoric level structure. In the equal characteristic case they are related to moduli spaces of shtukas. We refer the reader to [Reference Haines and RicharzHR19] for more information on local models, where it is also shown that certain local models are Cohen–Macaulay by using Frobenius splittings of global affine Schubert varieties constructed in [Reference ZhuZhu14].
We prove Theorem 1.6 by combining the same Frobenius splittings in [Reference ZhuZhu14] with our previous results on the global ![]() $F$-regularity of affine Schubert varieties in [Reference CassCas19]. In fact, we prove that certain global affine Schubert varieties are strongly
$F$-regularity of affine Schubert varieties in [Reference CassCas19]. In fact, we prove that certain global affine Schubert varieties are strongly ![]() $F$-regular (Theorem 2.17) and then we deduce the local statement in Theorem 1.6. We also show that Schubert subvarieties in related Beilinson–Drinfeld and convolution Grassmannians are strongly
$F$-regular (Theorem 2.17) and then we deduce the local statement in Theorem 1.6. We also show that Schubert subvarieties in related Beilinson–Drinfeld and convolution Grassmannians are strongly ![]() $F$-regular in Theorem 3.6.
$F$-regular in Theorem 3.6.
2. Construction of the functor  $\mathcal {Z}$
$\mathcal {Z}$
2.1 Local affine Schubert varieties
Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p > 0$. For a smooth affine group scheme
$p > 0$. For a smooth affine group scheme ![]() $G$ over the power series ring
$G$ over the power series ring ![]() $k[\![t]\!]$ we define the loop group
$k[\![t]\!]$ we define the loop group ![]() $LG$ as the functor on
$LG$ as the functor on ![]() $k$-algebras
$k$-algebras
The positive loop group ![]() $L^+G$ is the functor
$L^+G$ is the functor
For each integer ![]() $n>0$ we also have the
$n>0$ we also have the ![]() $n$th jet group
$n$th jet group
We now specialize to the case where ![]() $G$ is a split connected reductive group defined over
$G$ is a split connected reductive group defined over ![]() $k$ (note that
$k$ (note that ![]() $G$ can also be viewed as a constant group scheme over
$G$ can also be viewed as a constant group scheme over ![]() $k[\![t]\!]$). Let
$k[\![t]\!]$). Let ![]() $T \subset B \subset G$ be a maximal torus and a Borel subgroup. Let
$T \subset B \subset G$ be a maximal torus and a Borel subgroup. Let ![]() $I \subset L^+G$ be the Iwahori group given by the fiber of
$I \subset L^+G$ be the Iwahori group given by the fiber of ![]() $B$ under the projection
$B$ under the projection ![]() $L^+G \rightarrow G$. The affine Grassmannian is the fpqc-quotient
$L^+G \rightarrow G$. The affine Grassmannian is the fpqc-quotient ![]() $\operatorname {Gr} : = LG/L^+G$ and the affine flag variety is the fpqc-quotient
$\operatorname {Gr} : = LG/L^+G$ and the affine flag variety is the fpqc-quotient ![]() $\mathcal {F}\ell : = LG/I.$ Both
$\mathcal {F}\ell : = LG/I.$ Both ![]() $\operatorname {Gr}$ and
$\operatorname {Gr}$ and ![]() $\mathcal {F}\ell$ are represented by ind-projective
$\mathcal {F}\ell$ are represented by ind-projective ![]() $k$-schemes.
$k$-schemes.
The left ![]() $L^+G$-orbits in
$L^+G$-orbits in ![]() $\operatorname {Gr}$ are indexed by the set of dominant cocharacters
$\operatorname {Gr}$ are indexed by the set of dominant cocharacters ![]() $X_*(T)^+$ and the left
$X_*(T)^+$ and the left ![]() $I$-orbits in
$I$-orbits in ![]() $\mathcal {F}\ell$ are indexed by the Iwahori–Weyl group
$\mathcal {F}\ell$ are indexed by the Iwahori–Weyl group ![]() $\tilde {W}$ of
$\tilde {W}$ of ![]() $G(k (\!( t )\!))$. Given
$G(k (\!( t )\!))$. Given ![]() $\mu \in X_*(T)^+$, let
$\mu \in X_*(T)^+$, let ![]() $\operatorname {Gr}_\mu = L^+G \cdot \mu (t)$ be the corresponding reduced orbit. The reduced closure of
$\operatorname {Gr}_\mu = L^+G \cdot \mu (t)$ be the corresponding reduced orbit. The reduced closure of ![]() $\operatorname {Gr}_\mu$ is denoted
$\operatorname {Gr}_\mu$ is denoted ![]() $\operatorname {Gr}_{\leq \mu }$, and it is the union of those
$\operatorname {Gr}_{\leq \mu }$, and it is the union of those ![]() $\operatorname {Gr}_\lambda$ for
$\operatorname {Gr}_\lambda$ for ![]() $\lambda \leq \mu$. For
$\lambda \leq \mu$. For ![]() $w \in \tilde {W}$ we define
$w \in \tilde {W}$ we define ![]() $C(w)$ to be the corresponding reduced
$C(w)$ to be the corresponding reduced ![]() $I$-orbit and we denote its reduced closure by
$I$-orbit and we denote its reduced closure by ![]() $\mathcal {F}\ell _{w}$. The scheme
$\mathcal {F}\ell _{w}$. The scheme ![]() $C(w)$ is isomorphic to
$C(w)$ is isomorphic to ![]() $\mathbb {A}_k^{\ell (w)}$. If
$\mathbb {A}_k^{\ell (w)}$. If ![]() $\lambda \in X_*(T)$ we denote by
$\lambda \in X_*(T)$ we denote by ![]() $t_\lambda$ the element
$t_\lambda$ the element ![]() $\lambda$ viewed as an element of
$\lambda$ viewed as an element of ![]() $\tilde {W}$. Note that
$\tilde {W}$. Note that ![]() $\mu - \lambda$ is a sum of positive coroots with non-negative integer coefficients if and only if
$\mu - \lambda$ is a sum of positive coroots with non-negative integer coefficients if and only if ![]() $t_\lambda \leq t_\mu$ in the Bruhat order on
$t_\lambda \leq t_\mu$ in the Bruhat order on ![]() $\tilde {W}$ by [Reference ZhuZhu14, 9.4], so there is no ambiguity in the choice of order on
$\tilde {W}$ by [Reference ZhuZhu14, 9.4], so there is no ambiguity in the choice of order on ![]() $X_*(T)^+$. See [Reference ZhuZhu17] or [Reference CassCas19, § 5.1] for more details on these affine Schubert varieties. Note that we used the notation
$X_*(T)^+$. See [Reference ZhuZhu17] or [Reference CassCas19, § 5.1] for more details on these affine Schubert varieties. Note that we used the notation ![]() $S_w$ in [Reference CassCas19, § 5.1] instead of
$S_w$ in [Reference CassCas19, § 5.1] instead of ![]() $\mathcal {F}\ell _{w}$.
$\mathcal {F}\ell _{w}$.
We now give the definition of the ![]() $\mu$-admissible set appearing in Theorem 1.1. Given
$\mu$-admissible set appearing in Theorem 1.1. Given ![]() $\mu \in X_*(T)$ let
$\mu \in X_*(T)$ let ![]() $\Lambda _\mu = W \cdot \mu \subset X_*(T)$ be the orbit of
$\Lambda _\mu = W \cdot \mu \subset X_*(T)$ be the orbit of ![]() $\mu$ in
$\mu$ in ![]() $X_*(T)$ under the action of the Weyl group
$X_*(T)$ under the action of the Weyl group ![]() $W$. The
$W$. The ![]() $\mu$-admissible set is
$\mu$-admissible set is
By [Reference FaltingsFal03] and [Reference Pappas and RapoportPR08], affine Schubert varieties are normal, Cohen–Macaulay, Frobenius split and have rational singularities if ![]() $p \nmid |\pi _1(G_{\text {der}})|$. Additionally, we have the following theorem.
$p \nmid |\pi _1(G_{\text {der}})|$. Additionally, we have the following theorem.
Theorem 2.1 [Reference CassCas19, 1.4]
If ![]() $p \nmid |\pi _1(G_{\text {der}})|$ the affine Schubert varieties
$p \nmid |\pi _1(G_{\text {der}})|$ the affine Schubert varieties ![]() $\operatorname {Gr}_{\leq \mu }$ and
$\operatorname {Gr}_{\leq \mu }$ and ![]() $\mathcal {F}\ell _{w}$ are globally
$\mathcal {F}\ell _{w}$ are globally ![]() $F$-regular, strongly
$F$-regular, strongly ![]() $F$-regular, and
$F$-regular, and ![]() $F$-rational.
$F$-rational.
We refer the reader to [Reference SmithSmi00] for the definition of global ![]() $F$-regularity and to [Reference Hochster and HunekeHH94] for the definitions of strong
$F$-regularity and to [Reference Hochster and HunekeHH94] for the definitions of strong ![]() $F$-regularity and
$F$-regularity and ![]() $F$-rationality. Global
$F$-rationality. Global ![]() $F$-regularity is a property of projective
$F$-regularity is a property of projective ![]() $k$-schemes. Strong
$k$-schemes. Strong ![]() $F$-regularity is defined for noetherian rings
$F$-regularity is defined for noetherian rings ![]() $R$ of characteristic
$R$ of characteristic ![]() $p > 0$ that are
$p > 0$ that are ![]() $F$-finite (meaning
$F$-finite (meaning ![]() $F_*R$ is a finite
$F_*R$ is a finite ![]() $R$-module). If
$R$-module). If ![]() $R$ is reduced then
$R$ is reduced then ![]() $R$ is
$R$ is ![]() $F$-finite if and only if
$F$-finite if and only if ![]() $R^{1/p}$ is a finite
$R^{1/p}$ is a finite ![]() $R$-module. A finitely generated
$R$-module. A finitely generated ![]() $k$-algebra is
$k$-algebra is ![]() $F$-finite since
$F$-finite since ![]() $k$ is perfect.
$k$ is perfect.
By [Reference Hochster and HunekeHH89, 3.1(a)], ![]() $R$ is strongly
$R$ is strongly ![]() $F$-regular if and only if
$F$-regular if and only if ![]() $R_P$ is strongly
$R_P$ is strongly ![]() $F$-regular for every prime ideal
$F$-regular for every prime ideal ![]() $P$, so it makes sense to say a locally noetherian scheme is strongly
$P$, so it makes sense to say a locally noetherian scheme is strongly ![]() $F$-regular if all of its local rings are strongly
$F$-regular if all of its local rings are strongly ![]() $F$-regular. The property of
$F$-regular. The property of ![]() $F$-rationality is defined for noetherian rings of characteristic
$F$-rationality is defined for noetherian rings of characteristic ![]() $p > 0$, and we say that a locally noetherian scheme is
$p > 0$, and we say that a locally noetherian scheme is ![]() $F$-rational if all of its local rings are
$F$-rational if all of its local rings are ![]() $F$-rational. If
$F$-rational. If ![]() $R$ is a homomorphic image of a Cohen–Macaulay ring, then
$R$ is a homomorphic image of a Cohen–Macaulay ring, then ![]() $R$ is
$R$ is ![]() $F$-rational if and only if all of its local rings are
$F$-rational if and only if all of its local rings are ![]() $F$-rational by [Reference Hochster and HunekeHH94, 4.2(e)]. We have the following chain of implications for projective
$F$-rational by [Reference Hochster and HunekeHH94, 4.2(e)]. We have the following chain of implications for projective ![]() $k$-schemes (or more generally projective schemes over an
$k$-schemes (or more generally projective schemes over an ![]() $F$-finite field):
$F$-finite field):
 \[ \begin{array}{lr} \text{Globally } \\ F \text{-regular} \\ \end{array} \overset{\text{[Smi00, 3.10]}}{\Longrightarrow} \begin{array}{lr} \text{Strongly } \\ F\text{-regular} \\ \end{array} \overset{\text{[HH89, 3.1]}}{\Longrightarrow} F\text{-rational} \overset{\begin{array}{lr} \text{ [Smi97, 3.1]} \\ \text{[HH94, 4.2]} \\ \end{array}}{\Longrightarrow} \begin{array}{lr} \text{Pseudo-rational}\\ \text{singularities, normal,}\\ \text{Cohen}-\text{Macaulay.}\\ \end{array} \]
\[ \begin{array}{lr} \text{Globally } \\ F \text{-regular} \\ \end{array} \overset{\text{[Smi00, 3.10]}}{\Longrightarrow} \begin{array}{lr} \text{Strongly } \\ F\text{-regular} \\ \end{array} \overset{\text{[HH89, 3.1]}}{\Longrightarrow} F\text{-rational} \overset{\begin{array}{lr} \text{ [Smi97, 3.1]} \\ \text{[HH94, 4.2]} \\ \end{array}}{\Longrightarrow} \begin{array}{lr} \text{Pseudo-rational}\\ \text{singularities, normal,}\\ \text{Cohen}-\text{Macaulay.}\\ \end{array} \]Remark 2.2 We will also use the notion of pseudo-rationality as defined in [Reference KovácsKov17]. Using [Reference SmithSmi97, 1.13] and the flat base change theorem, one can verify the following assertion. If ![]() $X$ is a
$X$ is a ![]() $k$-scheme of finite type such that every local ring of
$k$-scheme of finite type such that every local ring of ![]() $X$ is pseudo-rational as defined in [Reference SmithSmi97, 1.8], then
$X$ is pseudo-rational as defined in [Reference SmithSmi97, 1.8], then ![]() $X$ is also pseudo-rational as defined in [Reference KovácsKov17, 1.2].
$X$ is also pseudo-rational as defined in [Reference KovácsKov17, 1.2].
2.2 Global affine Schubert varieties
We continue using the notation introduced in § 2.1. Let ![]() $C = \mathbb {A}^1_k$. Throughout this paper we will denote by
$C = \mathbb {A}^1_k$. Throughout this paper we will denote by ![]() $0$ the origin viewed as a closed point in
$0$ the origin viewed as a closed point in ![]() $C$. Let
$C$. Let ![]() $\hat {\mathcal {O}}_{0}$ be the completed local ring of
$\hat {\mathcal {O}}_{0}$ be the completed local ring of ![]() $C$ at
$C$ at ![]() $0$ and let
$0$ and let ![]() $C^\circ = C - 0$. Let
$C^\circ = C - 0$. Let ![]() $\mathcal {G}$ be a Bruhat–Tits group scheme over
$\mathcal {G}$ be a Bruhat–Tits group scheme over ![]() $C$ equipped with isomorphisms
$C$ equipped with isomorphisms
See [Reference ZhuZhu14, § 3.2] for more information on the construction of ![]() $\mathcal {G}$.
$\mathcal {G}$.
For any smooth group scheme ![]() $H$ over
$H$ over ![]() $C$ (including
$C$ (including ![]() $\mathcal {G}$) we let
$\mathcal {G}$) we let ![]() $\mathcal {E}_0$ be
$\mathcal {E}_0$ be ![]() $H$ regarded as a trivial
$H$ regarded as a trivial ![]() $H$-torsor. For a
$H$-torsor. For a ![]() $k$-algebra
$k$-algebra ![]() $R$ let
$R$ let ![]() $C_R = C \times _{\operatorname {Spec}(k)} \operatorname {Spec}(R)$. If
$C_R = C \times _{\operatorname {Spec}(k)} \operatorname {Spec}(R)$. If ![]() $x \in C(R)$ let
$x \in C(R)$ let ![]() $\Gamma _x \subset C_R$ be the graph of
$\Gamma _x \subset C_R$ be the graph of ![]() $x$, that is, the closed subscheme
$x$, that is, the closed subscheme ![]() $\operatorname {Spec}(R) \xrightarrow {(x, \operatorname {id})} C \times _{\operatorname {Spec}(k)} \operatorname {Spec}(R)$. The global affine Grassmannian
$\operatorname {Spec}(R) \xrightarrow {(x, \operatorname {id})} C \times _{\operatorname {Spec}(k)} \operatorname {Spec}(R)$. The global affine Grassmannian ![]() $\operatorname {Gr}_{\mathcal {G}}$ is the functor on
$\operatorname {Gr}_{\mathcal {G}}$ is the functor on ![]() $k$-algebras defined by
$k$-algebras defined by
In the above definition we really mean the set of such objects up to the equivalence relation ![]() $(x, \mathcal {E}, \beta ) \sim (x, \mathcal {E}', \beta ')$ if there is an isomorphism
$(x, \mathcal {E}, \beta ) \sim (x, \mathcal {E}', \beta ')$ if there is an isomorphism ![]() $\mathcal {E} \cong \mathcal {E}'$ which respects the trivializations, but we will suppress this detail. The functor
$\mathcal {E} \cong \mathcal {E}'$ which respects the trivializations, but we will suppress this detail. The functor ![]() $\operatorname {Gr}_{\mathcal {G}}$ is represented by an ind-projective scheme over
$\operatorname {Gr}_{\mathcal {G}}$ is represented by an ind-projective scheme over ![]() $C$ by [Reference Pappas and ZhuPZ13, 5.5].
$C$ by [Reference Pappas and ZhuPZ13, 5.5].
Given ![]() $x \in C(R)$ let
$x \in C(R)$ let ![]() $\hat {\Gamma }_x$ be the formal completion of
$\hat {\Gamma }_x$ be the formal completion of ![]() $C_R$ along
$C_R$ along ![]() $\Gamma _x$ and let
$\Gamma _x$ and let ![]() $\hat {\Gamma }^\circ _x = \hat {\Gamma }_x - \Gamma _x$. The global analogue of
$\hat {\Gamma }^\circ _x = \hat {\Gamma }_x - \Gamma _x$. The global analogue of ![]() $LG$ is the functor
$LG$ is the functor
The global analogue of ![]() $L^+G$ is the functor
$L^+G$ is the functor
As in [Reference ZhuZhu14, 3.1], a lemma of Beauville and Laszlo [Reference Beauville and LaszloBL95] implies that there is a natural bijection
Then ![]() $\mathcal {L}^+\mathcal {G}$ acts on
$\mathcal {L}^+\mathcal {G}$ acts on ![]() $\operatorname {Gr}_{\mathcal {G}}$ by changing the trivialization
$\operatorname {Gr}_{\mathcal {G}}$ by changing the trivialization ![]() $\beta$, and there is an isomorphism
$\beta$, and there is an isomorphism
Our choice of isomorphisms in (2.2) induces isomorphisms
and
Via the isomorphisms (2.3) and (2.4), the action of ![]() $\mathcal {L}^+ \mathcal {G}$ on
$\mathcal {L}^+ \mathcal {G}$ on ![]() $\operatorname {Gr}_{\mathcal {G}}$ is compatible with the action of
$\operatorname {Gr}_{\mathcal {G}}$ is compatible with the action of ![]() $L^+G$ on
$L^+G$ on ![]() $\operatorname {Gr}$ and the action of
$\operatorname {Gr}$ and the action of ![]() $I$ on
$I$ on ![]() $\mathcal {F}\ell$.
$\mathcal {F}\ell$.
We define ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ to be the reduced closure of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ to be the reduced closure of ![]() $\operatorname {Gr}_{\leq \mu } \times C^{\circ }$ in
$\operatorname {Gr}_{\leq \mu } \times C^{\circ }$ in ![]() $\operatorname {Gr}_{\mathcal {G}}$. The scheme
$\operatorname {Gr}_{\mathcal {G}}$. The scheme ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is stable under the action of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is stable under the action of ![]() $\mathcal {L}^+ \mathcal {G}$, and our definition agrees with that in [Reference ZhuZhu14, 3.1] because
$\mathcal {L}^+ \mathcal {G}$, and our definition agrees with that in [Reference ZhuZhu14, 3.1] because ![]() $G$ is split. We can now define the local model
$G$ is split. We can now define the local model ![]() $M_{\mu }$.
$M_{\mu }$.
Definition 2.3 The local model ![]() $M_\mu$ is the fiber of
$M_\mu$ is the fiber of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ over the completed local ring at
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ over the completed local ring at ![]() $0 \in C$.
$0 \in C$.
Thus the generic fiber of ![]() $M_\mu$ is isomorphic to
$M_\mu$ is isomorphic to ![]() $\operatorname {Gr}_{\leq \mu } \times \operatorname {Spec}(k(\!( t )\!))$. The following theorem is due to Zhu in the case where
$\operatorname {Gr}_{\leq \mu } \times \operatorname {Spec}(k(\!( t )\!))$. The following theorem is due to Zhu in the case where ![]() $G_{\text {der}}$ is absolutely almost simple and simply connected and was extended by Haines and Richarz to the general case.
$G_{\text {der}}$ is absolutely almost simple and simply connected and was extended by Haines and Richarz to the general case.
Theorem 2.4 ([Reference ZhuZhu14, Theorem 3], [Reference Haines and RicharzHR20, 5.14], [Reference Haines and RicharzHR19, 2.1])
If ![]() $p \nmid |\pi _1(G_{\text {der}})|$ the fiber
$p \nmid |\pi _1(G_{\text {der}})|$ the fiber ![]() ${(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}}$ is reduced. Without any assumptions on
${(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}}$ is reduced. Without any assumptions on ![]() $p$, the reduced fiber satisfies
$p$, the reduced fiber satisfies
For each integer ![]() $n > 0$ let
$n > 0$ let ![]() $\Gamma _{x,n}$ be the
$\Gamma _{x,n}$ be the ![]() $n$th nilpotent thickening of
$n$th nilpotent thickening of ![]() $\Gamma _x$. The
$\Gamma _x$. The ![]() $n$th jet group of
$n$th jet group of ![]() $\mathcal {G}$ is
$\mathcal {G}$ is
This functor is represented by a smooth affine group scheme over ![]() $C$. For each
$C$. For each ![]() $\mu \in X_*(T)^+$ the action of
$\mu \in X_*(T)^+$ the action of ![]() $\mathcal {L}^+ \mathcal {G}$ on
$\mathcal {L}^+ \mathcal {G}$ on ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ factors through
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ factors through ![]() $\mathcal {L}^+_n \mathcal {G}$ for sufficiently large
$\mathcal {L}^+_n \mathcal {G}$ for sufficiently large ![]() $n$ depending on
$n$ depending on ![]() $\mu$. If
$\mu$. If ![]() $x \in C^\circ (k)$ then
$x \in C^\circ (k)$ then ![]() $(\mathcal {L}^+_n \mathcal {G})_x \cong L^n G$ and
$(\mathcal {L}^+_n \mathcal {G})_x \cong L^n G$ and ![]() $(\mathcal {L}^+_n \mathcal {G})_0 \cong L^n( {\mathcal {G}}\left|_{{\hat {\mathcal {O}}_{0}}}\right.)$.
$(\mathcal {L}^+_n \mathcal {G})_0 \cong L^n( {\mathcal {G}}\left|_{{\hat {\mathcal {O}}_{0}}}\right.)$.
Finally, let ![]() $\underline {G}$ be the constant group scheme
$\underline {G}$ be the constant group scheme ![]() $G \times C$. By replacing
$G \times C$. By replacing ![]() $\mathcal {G}$ with
$\mathcal {G}$ with ![]() $\underline {G}$ in the above definitions we get the ind-scheme
$\underline {G}$ in the above definitions we get the ind-scheme ![]() $\operatorname {Gr}_{\underline {G}}$, which is naturally isomorphic to
$\operatorname {Gr}_{\underline {G}}$, which is naturally isomorphic to ![]() $\operatorname {Gr} \times C$. There is a natural morphism
$\operatorname {Gr} \times C$. There is a natural morphism ![]() $\mathcal {G} \rightarrow \underline {G}$ which induces a morphism
$\mathcal {G} \rightarrow \underline {G}$ which induces a morphism ![]() $\pi _{\mathcal {G}} \colon \operatorname {Gr}_{\mathcal {G}} \rightarrow \operatorname {Gr}_{\underline {G}}$. By taking the fibers of
$\pi _{\mathcal {G}} \colon \operatorname {Gr}_{\mathcal {G}} \rightarrow \operatorname {Gr}_{\underline {G}}$. By taking the fibers of ![]() $\pi _{\mathcal {G}}$ over
$\pi _{\mathcal {G}}$ over ![]() $C^{\circ }$ and
$C^{\circ }$ and ![]() $0$ we get the following diagram with Cartesian squares.
$0$ we get the following diagram with Cartesian squares.

2.3 The definition of  $\mathcal {Z}$
$\mathcal {Z}$
For this section we assume that ![]() $k$ is an algebraically closed field of characteristic
$k$ is an algebraically closed field of characteristic ![]() $p > 0$. We refer the reader to [Reference CassCas19, § 2] for an introduction to the category
$p > 0$. We refer the reader to [Reference CassCas19, § 2] for an introduction to the category ![]() $P_c^b(X, \mathbb {F}_p)$ of perverse
$P_c^b(X, \mathbb {F}_p)$ of perverse ![]() $\mathbb {F}_p$-sheaves on a separated scheme
$\mathbb {F}_p$-sheaves on a separated scheme ![]() $X$ of finite type over
$X$ of finite type over ![]() $k$. This is an abelian subcategory of
$k$. This is an abelian subcategory of ![]() $D_c^b(X_\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ in which every object has finite length. As in the case of perverse
$D_c^b(X_\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ in which every object has finite length. As in the case of perverse ![]() $\overline {\mathbb {Q}}_\ell$-sheaves, there are operations such as the intermediate extension functor and pullback along smooth morphisms.
$\overline {\mathbb {Q}}_\ell$-sheaves, there are operations such as the intermediate extension functor and pullback along smooth morphisms.
Now suppose ![]() $X$ is a separated scheme of finite type over
$X$ is a separated scheme of finite type over ![]() $C$. Let
$C$. Let ![]() $j \colon U \rightarrow X$ be the inclusion of the fiber of
$j \colon U \rightarrow X$ be the inclusion of the fiber of ![]() $X$ over
$X$ over ![]() $C^\circ$ and let
$C^\circ$ and let ![]() $i \colon Z \rightarrow X$ be the inclusion of the fiber of
$i \colon Z \rightarrow X$ be the inclusion of the fiber of ![]() $X$ over
$X$ over ![]() $0$. For
$0$. For ![]() $\mathcal {F}^\bullet \in P_c^b(U, \mathbb {F}_p)$ we define the nearby cycles of
$\mathcal {F}^\bullet \in P_c^b(U, \mathbb {F}_p)$ we define the nearby cycles of ![]() $\mathcal {F}^\bullet$ by
$\mathcal {F}^\bullet$ by
This defines an additive functor
Proposition 2.5 Suppose ![]() $f \colon X' \rightarrow X$ is a smooth, separated morphism over
$f \colon X' \rightarrow X$ is a smooth, separated morphism over ![]() $C$ of relative dimension
$C$ of relative dimension ![]() $d$ and that
$d$ and that ![]() $X'$ has fibers
$X'$ has fibers ![]() $U'$ and
$U'$ and ![]() $Z'$ over
$Z'$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$, respectively. Then there is a natural isomorphism of functors
$0$, respectively. Then there is a natural isomorphism of functors
Proof. This follows from the fact that pullback along a smooth morphism commutes with taking intermediate extensions by [Reference CassCas19, 2.16].
Remark 2.6 If ![]() $f \colon X' \rightarrow X$ is a proper morphism then the functor
$f \colon X' \rightarrow X$ is a proper morphism then the functor ![]() $Rf_!$ does not preserve perversity in general. However, if
$Rf_!$ does not preserve perversity in general. However, if ![]() $\mathcal {F}^\bullet \in P_c^b(U', \mathbb {F}_p)$ and
$\mathcal {F}^\bullet \in P_c^b(U', \mathbb {F}_p)$ and ![]() $R({f}\left|_{U'}\right.)_!(\mathcal {F}^\bullet )$ happens to be perverse, then it makes sense to ask whether
$R({f}\left|_{U'}\right.)_!(\mathcal {F}^\bullet )$ happens to be perverse, then it makes sense to ask whether ![]() $R({f}\left|_{Z'}\right.)_!(\Psi _{X'} (\mathcal {F}^\bullet ))$ and
$R({f}\left|_{Z'}\right.)_!(\Psi _{X'} (\mathcal {F}^\bullet ))$ and ![]() $\Psi _{X}(R({f}\left|_{U'}\right.)_!(\mathcal {F}^\bullet ))$ are isomorphic. We will see examples (such as the proof of Theorem 1.1(ii)) where the presence of
$\Psi _{X}(R({f}\left|_{U'}\right.)_!(\mathcal {F}^\bullet ))$ are isomorphic. We will see examples (such as the proof of Theorem 1.1(ii)) where the presence of ![]() $F$-rational singularities allows us to prove there is such an isomorphism, but we are unsure about the general case. By [Reference Deligne and KatzSGA7II, Exp. XIII 2.1.7.1], the analogous fact is true for the usual definition of the nearby cycles functor (see Remark 2.9) due to the proper base change theorem.
$F$-rational singularities allows us to prove there is such an isomorphism, but we are unsure about the general case. By [Reference Deligne and KatzSGA7II, Exp. XIII 2.1.7.1], the analogous fact is true for the usual definition of the nearby cycles functor (see Remark 2.9) due to the proper base change theorem.
Remark 2.7 We note that by [Reference CassCas19, 2.7(ii)], ![]() $\Psi _X(\mathcal {F}^\bullet ) \in {}^pD^{\leq 0}({Z_\unicode{x00E9}\text {t}}, \mathbb {F}_p)$. By [Reference Beilinson, Bernstein and DeligneBBD82, 4.4.2], the same is true for
$\Psi _X(\mathcal {F}^\bullet ) \in {}^pD^{\leq 0}({Z_\unicode{x00E9}\text {t}}, \mathbb {F}_p)$. By [Reference Beilinson, Bernstein and DeligneBBD82, 4.4.2], the same is true for ![]() $\mathbb {F}_{\ell }$-sheaves with
$\mathbb {F}_{\ell }$-sheaves with ![]() $\ell \neq p$ using the usual definition of the nearby cycles functor. As the usual nearby cycles functor commutes with Verdier duality for
$\ell \neq p$ using the usual definition of the nearby cycles functor. As the usual nearby cycles functor commutes with Verdier duality for ![]() $\mathbb {F}_{\ell }$-sheaves by [Reference IllusieIll94, 4.2], it preserves perversity. There is no duality functor for
$\mathbb {F}_{\ell }$-sheaves by [Reference IllusieIll94, 4.2], it preserves perversity. There is no duality functor for ![]() $\mathbb {F}_p$-sheaves, and we do not know if
$\mathbb {F}_p$-sheaves, and we do not know if ![]() $\Psi _X(\mathcal {F}^\bullet )$ is always perverse, but it is perverse in all of the examples we have computed.
$\Psi _X(\mathcal {F}^\bullet )$ is always perverse, but it is perverse in all of the examples we have computed.
By the following lemma, we can naturally extend the definition of the nearby cycles functor to the ind-scheme ![]() $\operatorname {Gr}_{\mathcal {G}}$.
$\operatorname {Gr}_{\mathcal {G}}$.
Lemma 2.8 Suppose ![]() $h \colon X' \rightarrow X$ is a closed immersion of separated
$h \colon X' \rightarrow X$ is a closed immersion of separated ![]() $C$-schemes of finite type and that
$C$-schemes of finite type and that ![]() $X'$ has fibers
$X'$ has fibers ![]() $U'$ and
$U'$ and ![]() $Z'$ over
$Z'$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$, respectively. Then there is a natural isomorphism of functors
$0$, respectively. Then there is a natural isomorphism of functors
Proof. By taking the fibers of ![]() $h$ over
$h$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$ we get the following diagram with Cartesian squares.
$0$ we get the following diagram with Cartesian squares.

Because the intermediate extension functor agrees with the usual pushforward functor for closed immersions, by [Reference CassCas19, 2.6] we have
Now the lemma follows by applying ![]() $Ri^*$ and the proper base change theorem.
$Ri^*$ and the proper base change theorem.
Remark 2.9 Following [Reference Deligne and KatzSGA7II, Exp. XIII § 1.3], there is another nearby cycles functor ![]() $\Psi _X'$ defined as follows. Replace
$\Psi _X'$ defined as follows. Replace ![]() $C$ with the henselization of its local ring at
$C$ with the henselization of its local ring at ![]() $0$. Let
$0$. Let ![]() $\bar {\eta }$ be the spectrum of an algebraic closure of the function field of
$\bar {\eta }$ be the spectrum of an algebraic closure of the function field of ![]() $C$, and let
$C$, and let ![]() $\bar {C}$ be the normalization of
$\bar {C}$ be the normalization of ![]() $C$ in
$C$ in ![]() $\bar {\eta }$. Let
$\bar {\eta }$. Let ![]() $X_{\bar {C}} = X \times _C \bar {C}$ and
$X_{\bar {C}} = X \times _C \bar {C}$ and ![]() $X_{\bar {\eta }} = X \times _C \bar {\eta }$. Then there are natural morphisms
$X_{\bar {\eta }} = X \times _C \bar {\eta }$. Then there are natural morphisms ![]() $\bar {j} \colon X_{\bar {\eta }} \rightarrow X_{\bar {C}}$ and
$\bar {j} \colon X_{\bar {\eta }} \rightarrow X_{\bar {C}}$ and ![]() $\bar {i} \colon Z \rightarrow X_{\bar {C}}$. If
$\bar {i} \colon Z \rightarrow X_{\bar {C}}$. If ![]() ${\mathcal {F}^\bullet }\left|_{\bar {\eta }}\right.$ is the restriction of
${\mathcal {F}^\bullet }\left|_{\bar {\eta }}\right.$ is the restriction of ![]() $\mathcal {F}^\bullet \in D^b_c(U_\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ to
$\mathcal {F}^\bullet \in D^b_c(U_\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ to ![]() $X_{\bar {\eta }}$, one can define
$X_{\bar {\eta }}$, one can define
For ![]() $\mathbb {F}_{\ell }$-sheaves with
$\mathbb {F}_{\ell }$-sheaves with ![]() $\ell \neq p$, the functor
$\ell \neq p$, the functor ![]() $\Psi _X'$ preserves constructibility by [Reference DeligneSGA
$\Psi _X'$ preserves constructibility by [Reference DeligneSGA![]() , Exp. 7, Th. 3.2] and commutes with smooth base change as in Proposition 2.5 by [Reference Deligne and KatzSGA7II, Exp. XIII 2.1.7]. The proofs make essential use of the hypothesis
, Exp. 7, Th. 3.2] and commutes with smooth base change as in Proposition 2.5 by [Reference Deligne and KatzSGA7II, Exp. XIII 2.1.7]. The proofs make essential use of the hypothesis ![]() $\ell \neq p$, and part of our original motivation for defining
$\ell \neq p$, and part of our original motivation for defining ![]() $\Psi _X$ was to give short proofs of these two facts for
$\Psi _X$ was to give short proofs of these two facts for ![]() $\mathbb {F}_p$-sheaves. It would be interesting to compare the functors
$\mathbb {F}_p$-sheaves. It would be interesting to compare the functors ![]() $\Psi _X$ and
$\Psi _X$ and ![]() $\Psi _X'$ for
$\Psi _X'$ for ![]() $\mathbb {F}_p$-sheaves.
$\mathbb {F}_p$-sheaves.
In [Reference CassCas19, § 6] we defined the category ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ of
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ of ![]() $L^+G$-equivariant perverse
$L^+G$-equivariant perverse ![]() $\mathbb {F}_p$-sheaves on
$\mathbb {F}_p$-sheaves on ![]() $\operatorname {Gr}$. We also defined the category
$\operatorname {Gr}$. We also defined the category ![]() $P_I(\mathcal {F} \ell , \mathbb {F}_p)$ and proved the following theorem.
$P_I(\mathcal {F} \ell , \mathbb {F}_p)$ and proved the following theorem.
Theorem 2.10 [Reference CassCas19, 1.5]
The simple objects in ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ and
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ and ![]() $P_I(\mathcal {F} \ell , \mathbb {F}_p)$ are the shifted constant sheaves
$P_I(\mathcal {F} \ell , \mathbb {F}_p)$ are the shifted constant sheaves
for ![]() $\mu \in X_*(T)^+$,
$\mu \in X_*(T)^+$, ![]() $w \in \tilde {W}$.
$w \in \tilde {W}$.
Let ![]() $\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$. Since
$\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$. Since ![]() $C$ is smooth,
$C$ is smooth, ![]() $\mathcal {F}^\bullet \overset {L}{\boxtimes } \mathbb {F}_p[1] \in P_c^b(\operatorname {Gr} \times C, \mathbb {F}_p)$ by [Reference CassCas19, 2.15]. Via the isomorphism
$\mathcal {F}^\bullet \overset {L}{\boxtimes } \mathbb {F}_p[1] \in P_c^b(\operatorname {Gr} \times C, \mathbb {F}_p)$ by [Reference CassCas19, 2.15]. Via the isomorphism ![]() ${\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right. \cong \operatorname {Gr} \times C^\circ$ we view
${\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right. \cong \operatorname {Gr} \times C^\circ$ we view ![]() $\mathcal {F}^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.$ as a perverse sheaf on
$\mathcal {F}^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.$ as a perverse sheaf on ![]() $ {\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right.$. We set
$ {\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right.$. We set
In [Reference CassCas19, § 6] we defined the convolution product ![]() $\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet }$ of
$\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet }$ of ![]() $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$, ![]() $\mathcal {F}_2^{\bullet } \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$. We now define the convolution product of two perverse sheaves in
$\mathcal {F}_2^{\bullet } \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$. We now define the convolution product of two perverse sheaves in ![]() $P_I(\mathcal {F}\ell , \mathbb {F}_p)$. Since the situation is analogous to
$P_I(\mathcal {F}\ell , \mathbb {F}_p)$. Since the situation is analogous to ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ we will be brief. To begin, we have the following convolution diagram.
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ we will be brief. To begin, we have the following convolution diagram.
Here ![]() $p$ is the quotient map
$p$ is the quotient map ![]() $LG \rightarrow \mathcal {F}\ell$ on the first factor and the identity map on the second factor. The map
$LG \rightarrow \mathcal {F}\ell$ on the first factor and the identity map on the second factor. The map ![]() $q$ is the quotient by the diagonal action of
$q$ is the quotient by the diagonal action of ![]() $I$ given by
$I$ given by ![]() $g \cdot (g_1, g_2) = (g_1 g^{-1}, g g_2)$, and
$g \cdot (g_1, g_2) = (g_1 g^{-1}, g g_2)$, and ![]() $m$ is the multiplication map. We will also use the notation
$m$ is the multiplication map. We will also use the notation ![]() $\mathcal {F}\ell {\tilde{ \times }} \mathcal {F}\ell$ for
$\mathcal {F}\ell {\tilde{ \times }} \mathcal {F}\ell$ for ![]() $LG \times ^I \mathcal {F}\ell$.
$LG \times ^I \mathcal {F}\ell$.
Given ![]() $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$, ![]() $\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F} \ell , \mathbb {F}_p)$ we claim that there is a unique perverse sheaf
$\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F} \ell , \mathbb {F}_p)$ we claim that there is a unique perverse sheaf ![]() $\mathcal {F}_1^\bullet \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet } \in P_I(LG \times ^{I} \mathcal {F}\ell , \mathbb {F}_p)$ such that
$\mathcal {F}_1^\bullet \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet } \in P_I(LG \times ^{I} \mathcal {F}\ell , \mathbb {F}_p)$ such that ![]() $Rp^*(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet } ) \cong Rq^*(\mathcal {F}_1^\bullet \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet } ).$ The proof of this is analogous to the case of the affine Grassmannian in [Reference CassCas19, 6.2], so we omit it. We are also suppressing the fact that because
$Rp^*(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet } ) \cong Rq^*(\mathcal {F}_1^\bullet \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet } ).$ The proof of this is analogous to the case of the affine Grassmannian in [Reference CassCas19, 6.2], so we omit it. We are also suppressing the fact that because ![]() $LG \times \mathcal {F}\ell$ is not of ind-finite type, we must replace the
$LG \times \mathcal {F}\ell$ is not of ind-finite type, we must replace the ![]() $I$-torsors
$I$-torsors ![]() $p$ and
$p$ and ![]() $q$ by torsors for a finite type quotient of
$q$ by torsors for a finite type quotient of ![]() $I$ depending on the support of
$I$ depending on the support of ![]() $\mathcal {F}_1^\bullet$ and
$\mathcal {F}_1^\bullet$ and ![]() $\mathcal {F}_2^{\bullet }$.
$\mathcal {F}_2^{\bullet }$.
The convolution of ![]() $\mathcal {F}_1^\bullet$ and
$\mathcal {F}_1^\bullet$ and ![]() $\mathcal {F}_2^{\bullet }$ is
$\mathcal {F}_2^{\bullet }$ is
We may also write ![]() $Rm_*$ instead of
$Rm_*$ instead of ![]() $Rm_!$ because
$Rm_!$ because ![]() $\mathcal {F}_1^\bullet \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet }$ is supported on a proper scheme. As in the case of
$\mathcal {F}_1^\bullet \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet }$ is supported on a proper scheme. As in the case of ![]() $\bar {\mathbb {Q}} _\ell$-coefficients,
$\bar {\mathbb {Q}} _\ell$-coefficients, ![]() $\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet }$ is not perverse in general. However, if
$\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet }$ is not perverse in general. However, if ![]() $\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet }$ is perverse then it is also
$\mathcal {F}_1^\bullet * \mathcal {F}_2^{\bullet }$ is perverse then it is also ![]() $I$-equivariant by [Reference CassCas19, 3.2].
$I$-equivariant by [Reference CassCas19, 3.2].
Remark 2.11 Using the method in [Reference CassCas19, 3.13], we can define the category ![]() $P_{\mathcal {L}^+\mathcal {G}}(\operatorname {Gr}_{\mathcal {G}}, \mathbb {F}_p)$ of
$P_{\mathcal {L}^+\mathcal {G}}(\operatorname {Gr}_{\mathcal {G}}, \mathbb {F}_p)$ of ![]() $\mathcal {L}^+\mathcal {G}$-equivariant perverse
$\mathcal {L}^+\mathcal {G}$-equivariant perverse ![]() $\mathbb {F}_p$-sheaves on
$\mathbb {F}_p$-sheaves on ![]() $\operatorname {Gr}_{\mathcal {G}}$. By the same reasoning we can define other categories of equivariant perverse sheaves on ind-schemes we introduce later, such as
$\operatorname {Gr}_{\mathcal {G}}$. By the same reasoning we can define other categories of equivariant perverse sheaves on ind-schemes we introduce later, such as ![]() $P_{\mathcal {L}^+\mathcal {G}}(\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}}, \mathbb {F}_p)$ (see § 3.1). As
$P_{\mathcal {L}^+\mathcal {G}}(\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}}, \mathbb {F}_p)$ (see § 3.1). As ![]() $\mathcal {L}^+_n \mathcal {G} \rightarrow C$ has geometrically connected fibers for every
$\mathcal {L}^+_n \mathcal {G} \rightarrow C$ has geometrically connected fibers for every ![]() $n$ then
$n$ then ![]() $P_{\mathcal {L}^+\mathcal {G}}(\operatorname {Gr}_{\mathcal {G}}, \mathbb {F}_p)$ is a full subcategory of
$P_{\mathcal {L}^+\mathcal {G}}(\operatorname {Gr}_{\mathcal {G}}, \mathbb {F}_p)$ is a full subcategory of ![]() $P_c^b(\operatorname {Gr}_{\mathcal {G}}, \mathbb {F}_p)$.
$P_c^b(\operatorname {Gr}_{\mathcal {G}}, \mathbb {F}_p)$.
2.4 First properties of  $\mathcal {Z}$
$\mathcal {Z}$
In this section we prove parts (i) and (ii) of Theorem 1.1. The main ingredient will be the ![]() $F$-rationality of
$F$-rationality of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$. We assume that
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$. We assume that ![]() $k$ is a perfect field of characteristic
$k$ is a perfect field of characteristic ![]() $p> 2$ until Proposition 2.19, where we require
$p> 2$ until Proposition 2.19, where we require ![]() $k$ to be algebraically closed. Throughout this section we also assume that
$k$ to be algebraically closed. Throughout this section we also assume that ![]() $G_{\text {der}}$ is absolutely almost simple and simply connected. We will explain how to remove the simple connectedness hypothesis in Remark 3.9. To begin, we recall the following results.
$G_{\text {der}}$ is absolutely almost simple and simply connected. We will explain how to remove the simple connectedness hypothesis in Remark 3.9. To begin, we recall the following results.
Theorem 2.12 ([Reference Pappas and ZhuPZ13, 9.1], [Reference Haines and RicharzHR19, 2.1])
The schemes ![]() $\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ and
$\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ are integral, normal, and Cohen–Macaulay.
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ are integral, normal, and Cohen–Macaulay.
Corollary 2.13 The fiber ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ is Cohen–Macaulay, connected, and equidimensional of dimension equal to that of
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ is Cohen–Macaulay, connected, and equidimensional of dimension equal to that of ![]() $\operatorname {Gr}_{\leq \mu }$.
$\operatorname {Gr}_{\leq \mu }$.
Proof. Since ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is Cohen–Macaulay and integral,
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is Cohen–Macaulay and integral, ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ is also Cohen–Macaulay by [Sta21, OC6G]. Note that the morphism
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ is also Cohen–Macaulay by [Sta21, OC6G]. Note that the morphism ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow C$ is flat by [Reference HartshorneHar77, III 9.7]. Now because the generic fiber of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow C$ is flat by [Reference HartshorneHar77, III 9.7]. Now because the generic fiber of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow C$ is connected, then so is
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow C$ is connected, then so is ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ by [Reference Grothendieck and DieudonnéEGAIV3, 15.5.4]. Finally,
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ by [Reference Grothendieck and DieudonnéEGAIV3, 15.5.4]. Finally, ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ is equidimensional because it is Cohen–Macaulay and connected, and
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ is equidimensional because it is Cohen–Macaulay and connected, and ![]() $\dim \,(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0} = \dim \operatorname {Gr}_{\leq \mu }$ by [Reference HartshorneHar77, III 9.6].
$\dim \,(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0} = \dim \operatorname {Gr}_{\leq \mu }$ by [Reference HartshorneHar77, III 9.6].
Lemmas 2.14–2.16 below are well known to experts, but because we could not find detailed proofs in the literature we provide them here. These three lemmas are also valid if ![]() $p=2$.
$p=2$.
Lemma 2.14 Let ![]() $A$ and
$A$ and ![]() $B$ be domains that are strongly
$B$ be domains that are strongly ![]() $F$-regular
$F$-regular ![]() $k$-algebras of finite type. Then if
$k$-algebras of finite type. Then if ![]() $A \otimes _k B$ is a domain it is strongly
$A \otimes _k B$ is a domain it is strongly ![]() $F$-regular.
$F$-regular.
Proof. This is proven in [Reference HashimotoHas03, 5.2] when ![]() $A$ and
$A$ and ![]() $B$ are graded rings, but the same proof works in general. Let
$B$ are graded rings, but the same proof works in general. Let ![]() $R = A \otimes _k B$ and let
$R = A \otimes _k B$ and let ![]() $a \in A$ and
$a \in A$ and ![]() $b \in B$ be such that the localizations
$b \in B$ be such that the localizations ![]() $A_a$ and
$A_a$ and ![]() $B_b$ are smooth. Then
$B_b$ are smooth. Then ![]() $A_a \otimes _k B_b$ is smooth and hence strongly
$A_a \otimes _k B_b$ is smooth and hence strongly ![]() $F$-regular by [Reference Hochster and HunekeHH89, 3.1(c)], so by [Reference Hochster and HunekeHH89, 3.3(a)] it suffices to construct a splitting of
$F$-regular by [Reference Hochster and HunekeHH89, 3.1(c)], so by [Reference Hochster and HunekeHH89, 3.3(a)] it suffices to construct a splitting of ![]() $R [(a \otimes b)^{1/q}] \subset R^{1/q}$ for some
$R [(a \otimes b)^{1/q}] \subset R^{1/q}$ for some ![]() $q = p^e$. Because
$q = p^e$. Because ![]() $k$ is perfect, such a splitting can be constructed from splittings of
$k$ is perfect, such a splitting can be constructed from splittings of ![]() $A[a^{1/q}] \subset A^{1/q}$ and
$A[a^{1/q}] \subset A^{1/q}$ and ![]() $B[b^{1/q}] \subset B^{1/q}$, which exist for some common
$B[b^{1/q}] \subset B^{1/q}$, which exist for some common ![]() $q$ because
$q$ because ![]() $A_a$ and
$A_a$ and ![]() $B_b$ are strongly
$B_b$ are strongly ![]() $F$-regular.
$F$-regular.
Lemma 2.15 Let ![]() $R$ be a domain that is a strongly
$R$ be a domain that is a strongly ![]() $F$-regular
$F$-regular ![]() $k$-algebra of finite type and let
$k$-algebra of finite type and let ![]() $E$ be an
$E$ be an ![]() $F$-finite field containing
$F$-finite field containing ![]() $k$. Then if
$k$. Then if ![]() $R \otimes _k E$ is a domain it is strongly
$R \otimes _k E$ is a domain it is strongly ![]() $F$-regular.
$F$-regular.
Proof. Let ![]() $R_E = R \otimes _k E$ and let
$R_E = R \otimes _k E$ and let ![]() $c \in R$ be such that the localization
$c \in R$ be such that the localization ![]() $R_c$ is a smooth
$R_c$ is a smooth ![]() $k$-algebra. Since
$k$-algebra. Since ![]() $R_c \otimes _k E$ is a smooth
$R_c \otimes _k E$ is a smooth ![]() $E$-algebra, it is regular. Hence by [Reference Hochster and HunekeHH89, 3.1(c)],
$E$-algebra, it is regular. Hence by [Reference Hochster and HunekeHH89, 3.1(c)], ![]() $R_c \otimes _k E$ is strongly
$R_c \otimes _k E$ is strongly ![]() $F$-regular. Thus, to prove
$F$-regular. Thus, to prove ![]() $R_E$ is strongly
$R_E$ is strongly ![]() $F$-regular, by [Reference Hochster and HunekeHH89, 3.3(a)] it suffices to show that the inclusion
$F$-regular, by [Reference Hochster and HunekeHH89, 3.3(a)] it suffices to show that the inclusion ![]() $R_E[c^{1/q} \otimes 1] \subset R_E^{1/q}$ splits for some
$R_E[c^{1/q} \otimes 1] \subset R_E^{1/q}$ splits for some ![]() $q = p^e$. Because
$q = p^e$. Because ![]() $k$ is perfect, such a splitting can be constructed from splittings of
$k$ is perfect, such a splitting can be constructed from splittings of ![]() $R[c^{1/q}] \subset R^{1/q}$ and
$R[c^{1/q}] \subset R^{1/q}$ and ![]() $E \subset E^{1/q}$. A splitting of
$E \subset E^{1/q}$. A splitting of ![]() $R[c^{1/q}] \subset R^{1/q}$ exists for some
$R[c^{1/q}] \subset R^{1/q}$ exists for some ![]() $q$ because
$q$ because ![]() $R$ is strongly
$R$ is strongly ![]() $F$-regular, and a splitting of
$F$-regular, and a splitting of ![]() $E \subset E^{1/q}$ exists because
$E \subset E^{1/q}$ exists because ![]() $E$ is
$E$ is ![]() $F$-finite and it is a field.
$F$-finite and it is a field.
Lemma 2.16 Let ![]() $f \colon Y \rightarrow X$ be a smooth surjective morphism between reduced
$f \colon Y \rightarrow X$ be a smooth surjective morphism between reduced ![]() $k$-schemes of finite type. Then
$k$-schemes of finite type. Then ![]() $X$ is strongly
$X$ is strongly ![]() $F$-regular if and only if
$F$-regular if and only if ![]() $Y$ is strongly
$Y$ is strongly ![]() $F$-regular.
$F$-regular.
Proof. If ![]() $Y$ is strongly
$Y$ is strongly ![]() $F$-regular then
$F$-regular then ![]() $X$ is strongly
$X$ is strongly ![]() $F$-regular by [Reference Hochster and HunekeHH89, 3.1(b)]. Conversely, if
$F$-regular by [Reference Hochster and HunekeHH89, 3.1(b)]. Conversely, if ![]() $X$ is strongly
$X$ is strongly ![]() $F$-regular then
$F$-regular then ![]() $Y$ is strongly
$Y$ is strongly ![]() $F$-regular by [Reference AberbachAbe01, 3.6]. In order to apply [Reference AberbachAbe01, 3.6] we are using the fact that the local rings of a smooth scheme over a field are regular, and hence they are Gorenstein and
$F$-regular by [Reference AberbachAbe01, 3.6]. In order to apply [Reference AberbachAbe01, 3.6] we are using the fact that the local rings of a smooth scheme over a field are regular, and hence they are Gorenstein and ![]() $F$-rational by [Reference Hochster and HunekeHH94, 3.4].
$F$-rational by [Reference Hochster and HunekeHH94, 3.4].
We can now prove that the global Schubert varieties are strongly ![]() $F$-regular.
$F$-regular.
Theorem 2.17 The schemes ![]() $\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ and
$\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ are strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ are strongly ![]() $F$-regular,
$F$-regular, ![]() $F$-rational, and have pseudo-rational singularities.
$F$-rational, and have pseudo-rational singularities.
Proof. By the implications following Theorem 2.1 it suffices to prove these schemes are strongly ![]() $F$-regular. By [Reference CassCas19, 1.4],
$F$-regular. By [Reference CassCas19, 1.4], ![]() $\operatorname {Gr}_{\leq \mu }$ is globally
$\operatorname {Gr}_{\leq \mu }$ is globally ![]() $F$-regular and hence also strongly
$F$-regular and hence also strongly ![]() $F$-regular. As
$F$-regular. As ![]() $C$ is smooth, it is strongly
$C$ is smooth, it is strongly ![]() $F$-regular by [Reference Hochster and HunekeHH89, 3.1(c)]. Thus since
$F$-regular by [Reference Hochster and HunekeHH89, 3.1(c)]. Thus since ![]() $\overline {\operatorname {Gr}}_{\underline {G}, \mu } \cong \operatorname {Gr}_{\leq \mu } \times C$, it follows that
$\overline {\operatorname {Gr}}_{\underline {G}, \mu } \cong \operatorname {Gr}_{\leq \mu } \times C$, it follows that ![]() $\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ is strongly
$\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ is strongly ![]() $F$-regular by Theorem 2.12 and Lemma 2.14.
$F$-regular by Theorem 2.12 and Lemma 2.14.
Since ![]() ${\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right. \cong {\operatorname {Gr}_{\underline {G\!}}}\left|_{C^{\circ }}\right.$, we have that
${\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right. \cong {\operatorname {Gr}_{\underline {G\!}}}\left|_{C^{\circ }}\right.$, we have that ![]() $ {\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right.$ is strongly
$ {\operatorname {Gr}_{\mathcal {G\!}}}\left|_{C^{\circ }}\right.$ is strongly ![]() $F$-regular. Hence by [Reference Hochster and HunekeHH89, 3.3(a)], to prove
$F$-regular. Hence by [Reference Hochster and HunekeHH89, 3.3(a)], to prove ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is strongly ![]() $F$-regular it suffices to prove
$F$-regular it suffices to prove ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is Frobenius split along the effective Cartier divisor
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is Frobenius split along the effective Cartier divisor ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$. As
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$. As ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is Frobenius split compatibly with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is Frobenius split compatibly with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ by [Reference ZhuZhu14, 6.5], it is also Frobenius split along
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ by [Reference ZhuZhu14, 6.5], it is also Frobenius split along ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ (see, for example, [Reference CassCas19, 5.7]).
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ (see, for example, [Reference CassCas19, 5.7]).
Remark 2.18 We expect that by essentially the same proof, Theorem 2.17 is true more generally for any parahoric subgroup of a tamely ramified connected reductive group ![]() $G$ over
$G$ over ![]() $k(\!(t)\!)$ such that
$k(\!(t)\!)$ such that ![]() $p > 2$ and
$p > 2$ and ![]() $G_{\text {der}}$ is absolutely almost simple and simply connected. This is because the necessary inputs from [Reference Pappas and RapoportPR08] and [Reference ZhuZhu14] are proved under these more general assumptions.
$G_{\text {der}}$ is absolutely almost simple and simply connected. This is because the necessary inputs from [Reference Pappas and RapoportPR08] and [Reference ZhuZhu14] are proved under these more general assumptions.
Before proceeding, we prove Theorem 1.6. Recall that in the setup of Theorem 1.6, ![]() $E$ is a local field of characteristic
$E$ is a local field of characteristic ![]() $p > 2$ with ring of integers
$p > 2$ with ring of integers ![]() $\mathcal {O}_E$ and residue field
$\mathcal {O}_E$ and residue field ![]() $\mathbb {F}_q$. The group
$\mathbb {F}_q$. The group ![]() $G$ is a split connected reductive group defined over
$G$ is a split connected reductive group defined over ![]() $E$ such that
$E$ such that ![]() $G_{\text {der}}$ is absolutely almost simple and simply connected. We assume that
$G_{\text {der}}$ is absolutely almost simple and simply connected. We assume that ![]() $G$ is the base extension of a split Chevalley group over
$G$ is the base extension of a split Chevalley group over ![]() $\mathbb {Z}$ and that
$\mathbb {Z}$ and that ![]() $T$ and
$T$ and ![]() $B$ are defined over
$B$ are defined over ![]() $\mathbb {F}_q$. Let
$\mathbb {F}_q$. Let ![]() $\operatorname {Gr}$ be the affine Grassmannian of
$\operatorname {Gr}$ be the affine Grassmannian of ![]() $G$ viewed as a group scheme over
$G$ viewed as a group scheme over ![]() $\mathbb {F}_q$. After choosing an isomorphism
$\mathbb {F}_q$. After choosing an isomorphism ![]() $\mathbb {F}_q [\![ t ]\!] \cong \mathcal {O}_E$ we can view
$\mathbb {F}_q [\![ t ]\!] \cong \mathcal {O}_E$ we can view ![]() $M_{\mu }$ as a projective
$M_{\mu }$ as a projective ![]() $\mathcal {O}_E$-scheme.
$\mathcal {O}_E$-scheme.
Proof of Theorem 1.6. Let ![]() $x \in M_{\mu }$ and let
$x \in M_{\mu }$ and let ![]() $\mathcal {O}_x$ be the local ring at
$\mathcal {O}_x$ be the local ring at ![]() $x$. As
$x$. As ![]() $\mathcal {O}_E$ is an excellent ring and
$\mathcal {O}_E$ is an excellent ring and ![]() $M_{\mu }$ is a projective
$M_{\mu }$ is a projective ![]() $\mathcal {O}_E$-scheme,
$\mathcal {O}_E$-scheme, ![]() $\mathcal {O}_x$ is excellent. Hence by [Reference SmithSmi97, 3.1] pseudo-rationality will follow if we prove that
$\mathcal {O}_x$ is excellent. Hence by [Reference SmithSmi97, 3.1] pseudo-rationality will follow if we prove that ![]() $\mathcal {O}_x$ is
$\mathcal {O}_x$ is ![]() $F$-rational. The residue field of
$F$-rational. The residue field of ![]() $\mathcal {O}_x$ is
$\mathcal {O}_x$ is ![]() $F$-finite because it is finitely generated as a field over the perfect field
$F$-finite because it is finitely generated as a field over the perfect field ![]() $k$. Thus
$k$. Thus ![]() $\mathcal {O}_x$ is
$\mathcal {O}_x$ is ![]() $F$-finite by [Reference KunzKun76, 2.6]. By [Reference Hochster and HunekeHH89, 3.1(d)] it suffices to show
$F$-finite by [Reference KunzKun76, 2.6]. By [Reference Hochster and HunekeHH89, 3.1(d)] it suffices to show ![]() $\mathcal {O}_x$ is strongly
$\mathcal {O}_x$ is strongly ![]() $F$-regular.
$F$-regular.
First suppose ![]() $x \in M_{\mu }$ lies in the closed fiber of
$x \in M_{\mu }$ lies in the closed fiber of ![]() $M_\mu \rightarrow \operatorname {Spec}(\mathcal {O}_E)$. The completion
$M_\mu \rightarrow \operatorname {Spec}(\mathcal {O}_E)$. The completion ![]() $\hat {\mathcal {O}}_x$ is excellent and has an
$\hat {\mathcal {O}}_x$ is excellent and has an ![]() $F$-finite residue field, so it is
$F$-finite residue field, so it is ![]() $F$-finite by [Reference KunzKun76, 2.6]. To prove
$F$-finite by [Reference KunzKun76, 2.6]. To prove ![]() $\mathcal {O}_x$ is strongly
$\mathcal {O}_x$ is strongly ![]() $F$-regular it suffices to prove
$F$-regular it suffices to prove ![]() $\hat {\mathcal {O}}_x$ is strongly
$\hat {\mathcal {O}}_x$ is strongly ![]() $F$-regular by [Reference Hochster and HunekeHH89, 3.1(b)]. The ring
$F$-regular by [Reference Hochster and HunekeHH89, 3.1(b)]. The ring ![]() $\hat {\mathcal {O}}_x$ is isomorphic to the completion of a local ring in
$\hat {\mathcal {O}}_x$ is isomorphic to the completion of a local ring in ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$. Thus, it suffices to take
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$. Thus, it suffices to take ![]() $y \in \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ and show that the completion
$y \in \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ and show that the completion ![]() $\hat {\mathcal {O}}_y$ of the local ring
$\hat {\mathcal {O}}_y$ of the local ring ![]() $\mathcal {O}_y$ is strongly
$\mathcal {O}_y$ is strongly ![]() $F$-regular. Note that the map
$F$-regular. Note that the map ![]() $\mathcal {O}_y \rightarrow \hat {\mathcal {O}}_y$ is a flat map between
$\mathcal {O}_y \rightarrow \hat {\mathcal {O}}_y$ is a flat map between ![]() $F$-finite noetherian local rings. Since
$F$-finite noetherian local rings. Since ![]() $\mathcal {O}_y$ is reduced and excellent,
$\mathcal {O}_y$ is reduced and excellent, ![]() $\hat {\mathcal {O}}_y$ is also reduced. Moreover, the fibers of this map are regular by [Reference Grothendieck and DieudonnéEGAIV2, 7.8.3 (v)]. Thus, since
$\hat {\mathcal {O}}_y$ is also reduced. Moreover, the fibers of this map are regular by [Reference Grothendieck and DieudonnéEGAIV2, 7.8.3 (v)]. Thus, since ![]() $\mathcal {O}_y$ is strongly
$\mathcal {O}_y$ is strongly ![]() $F$-regular (Theorem 2.17),
$F$-regular (Theorem 2.17), ![]() $\hat {\mathcal {O}}_y$ is strongly
$\hat {\mathcal {O}}_y$ is strongly ![]() $F$-regular by [Reference AberbachAbe01, 3.6]. This shows that
$F$-regular by [Reference AberbachAbe01, 3.6]. This shows that ![]() $\mathcal {O}_x$ is strongly
$\mathcal {O}_x$ is strongly ![]() $F$-regular if
$F$-regular if ![]() $x$ lies in the closed fiber of
$x$ lies in the closed fiber of ![]() $M_\mu \rightarrow \operatorname {Spec}(\mathcal {O}_E)$.
$M_\mu \rightarrow \operatorname {Spec}(\mathcal {O}_E)$.
To complete the proof we need to show that the generic fiber ![]() $M_{\mu } \times _{\operatorname {Spec}(\mathcal {O}_E)} \operatorname {Spec}(E) = \operatorname {Gr}_{\mathbb {F}_q, \leq \mu } \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(E)$ is strongly
$M_{\mu } \times _{\operatorname {Spec}(\mathcal {O}_E)} \operatorname {Spec}(E) = \operatorname {Gr}_{\mathbb {F}_q, \leq \mu } \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(E)$ is strongly ![]() $F$-regular. The property of strong
$F$-regular. The property of strong ![]() $F$-regularity is Zariski local by definition, so it suffices to take an arbitrary open affine
$F$-regularity is Zariski local by definition, so it suffices to take an arbitrary open affine ![]() $\operatorname {Spec}(R) \subset \operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ and show that
$\operatorname {Spec}(R) \subset \operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ and show that ![]() $R \otimes _{\mathbb {F}_q} E$ is strongly
$R \otimes _{\mathbb {F}_q} E$ is strongly ![]() $F$-regular. Thus by Lemma 2.15 we are reduced to showing that
$F$-regular. Thus by Lemma 2.15 we are reduced to showing that ![]() $\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ is geometrically integral.
$\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ is geometrically integral.
We first show that the orbit ![]() $\operatorname {Gr}_{\mathbb {F}_q, \mu }$ is geometrically integral. Let
$\operatorname {Gr}_{\mathbb {F}_q, \mu }$ is geometrically integral. Let ![]() $F/\mathbb {F}_q$ be a field extension and let
$F/\mathbb {F}_q$ be a field extension and let ![]() $G_F = G \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(F)$. By definition
$G_F = G \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(F)$. By definition ![]() $\operatorname {Gr}_{F, \mu }$ is the scheme-theoretic image of the orbit map
$\operatorname {Gr}_{F, \mu }$ is the scheme-theoretic image of the orbit map ![]() $L^n(G_F) \rightarrow \operatorname {Gr}_{F}$,
$L^n(G_F) \rightarrow \operatorname {Gr}_{F}$, ![]() $g \mapsto g \cdot \mu (t)$ for
$g \mapsto g \cdot \mu (t)$ for ![]() $n \gg 0$. Since
$n \gg 0$. Since ![]() $L^nG$ is geometrically integral and taking scheme theoretic images commutes with flat base change it follows that
$L^nG$ is geometrically integral and taking scheme theoretic images commutes with flat base change it follows that ![]() $\operatorname {Gr}_{\mathbb {F}_q, \mu } \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(F) \cong \operatorname {Gr}_{F, \mu }$ is integral.
$\operatorname {Gr}_{\mathbb {F}_q, \mu } \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(F) \cong \operatorname {Gr}_{F, \mu }$ is integral.
Now assume ![]() $F$ is an algebraic closure of
$F$ is an algebraic closure of ![]() $\mathbb {F}_q$. Because the Cartan decompositions of
$\mathbb {F}_q$. Because the Cartan decompositions of ![]() $G(\mathbb {F}_q(\!(t)\!))$ and
$G(\mathbb {F}_q(\!(t)\!))$ and ![]() $G(F(\!(t)\!))$ are both indexed by
$G(F(\!(t)\!))$ are both indexed by ![]() $X_*(T)^+$, the reduced subscheme of
$X_*(T)^+$, the reduced subscheme of ![]() $\operatorname {Gr}_{\mathbb {F}_q, \leq \mu } \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(F)$ is isomorphic to
$\operatorname {Gr}_{\mathbb {F}_q, \leq \mu } \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(F)$ is isomorphic to ![]() $\operatorname {Gr}_{F, \leq \mu }$. Thus
$\operatorname {Gr}_{F, \leq \mu }$. Thus ![]() $\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ is geometrically irreducible by [Sta21, 038I]. Finally, since
$\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ is geometrically irreducible by [Sta21, 038I]. Finally, since ![]() $\mathbb {F}_q$ is perfect,
$\mathbb {F}_q$ is perfect, ![]() $\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ is geometrically reduced and hence also geometrically integral.
$\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$ is geometrically reduced and hence also geometrically integral.
We now begin proving parts (i) and (ii) of Theorem 1.1. For the rest of this section we assume that ![]() $k$ is an algebraically closed field of characteristic
$k$ is an algebraically closed field of characteristic ![]() $p > 2$ and that
$p > 2$ and that ![]() $G$ is a connected reductive group over
$G$ is a connected reductive group over ![]() $k$ such that
$k$ such that ![]() $G_{\text {der}}$ is almost simple and simply connected.
$G_{\text {der}}$ is almost simple and simply connected.
Proposition 2.19 The perverse sheaf ![]() $j_{\mathcal {G}, !*} (\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is isomorphic to the shifted constant sheaf
$j_{\mathcal {G}, !*} (\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is isomorphic to the shifted constant sheaf ![]() $\mathbb {F}_p[\dim \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }]$ supported on
$\mathbb {F}_p[\dim \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }]$ supported on ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$.
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$.
Proof. Since ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is integral and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is integral and ![]() $F$-rational,
$F$-rational, ![]() $\mathbb {F}_p[\dim \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }]$ is a simple perverse sheaf by [Reference CassCas19, 1.7]. Now the lemma follows by applying loc. cit. on
$\mathbb {F}_p[\dim \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }]$ is a simple perverse sheaf by [Reference CassCas19, 1.7]. Now the lemma follows by applying loc. cit. on ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}\left|_{C^\circ }\right.$ and using the fact that
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}\left|_{C^\circ }\right.$ and using the fact that ![]() $j_{\mathcal {G}, !*} (\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is simple by [Reference CassCas19, 2.9].
$j_{\mathcal {G}, !*} (\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is simple by [Reference CassCas19, 2.9].
Proposition 2.20 The functor ![]() $\mathcal {Z}$ is exact and preserves perversity, and
$\mathcal {Z}$ is exact and preserves perversity, and ![]() $\mathcal {Z}(\operatorname {IC}_\mu ) \cong \mathcal {Z}_{\mathcal {A}(\mu )}$.
$\mathcal {Z}(\operatorname {IC}_\mu ) \cong \mathcal {Z}_{\mathcal {A}(\mu )}$.
Proof. The isomorphism ![]() $\mathcal {Z}(\operatorname {IC}_\mu ) \cong \mathcal {Z}_{\mathcal {A}(\mu )}$ follows from Theorem 2.4 and Proposition 2.19, and the fact that
$\mathcal {Z}(\operatorname {IC}_\mu ) \cong \mathcal {Z}_{\mathcal {A}(\mu )}$ follows from Theorem 2.4 and Proposition 2.19, and the fact that ![]() $\dim \mathcal {A}(\mu ) = \dim \operatorname {Gr}_{\leq \mu }$. As
$\dim \mathcal {A}(\mu ) = \dim \operatorname {Gr}_{\leq \mu }$. As ![]() $\mathcal {A}(\mu )$ is Cohen–Macaulay and equidimensional (Corollary 2.13),
$\mathcal {A}(\mu )$ is Cohen–Macaulay and equidimensional (Corollary 2.13), ![]() $\mathcal {Z}_{\mathcal {A}(\mu )}$ is perverse by [Reference CassCas19, 1.6]. Since
$\mathcal {Z}_{\mathcal {A}(\mu )}$ is perverse by [Reference CassCas19, 1.6]. Since ![]() $P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ is semisimple,
$P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ is semisimple, ![]() $\mathcal {Z}$ is also exact and preserves perversity.
$\mathcal {Z}$ is also exact and preserves perversity.
Proposition 2.21 ![]() $\mathcal {Z}(\mathcal {F}^\bullet )$ is
$\mathcal {Z}(\mathcal {F}^\bullet )$ is ![]() $I$-equivariant.
$I$-equivariant.
Proof. Note that ![]() $\mathcal {F}^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.$ is equivariant for the action of
$\mathcal {F}^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.$ is equivariant for the action of ![]() $ {\mathcal {L}^+ \mathcal {G}}\left|_{C^\circ }\right. = L^+G \times C^\circ$ on
$ {\mathcal {L}^+ \mathcal {G}}\left|_{C^\circ }\right. = L^+G \times C^\circ$ on ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}\left|_{C^\circ }\right. = \operatorname {Gr}_{\leq \mu } \times C^\circ$. Using the fact that taking intermediate extensions commutes with smooth pullback ([Reference CassCas19, 2.16]), one can check that the perverse sheaf
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}\left|_{C^\circ }\right. = \operatorname {Gr}_{\leq \mu } \times C^\circ$. Using the fact that taking intermediate extensions commutes with smooth pullback ([Reference CassCas19, 2.16]), one can check that the perverse sheaf ![]() $j_{\mathcal {G}, !*}(\mathcal {F}^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) \in P_c^b(\overline {\operatorname {Gr}}_{\mathcal {G}, {\mu }}, \mathbb {F}_p)$ is
$j_{\mathcal {G}, !*}(\mathcal {F}^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) \in P_c^b(\overline {\operatorname {Gr}}_{\mathcal {G}, {\mu }}, \mathbb {F}_p)$ is ![]() $\mathcal {L}^+ \mathcal {G}$-equivariant. By taking the fiber over
$\mathcal {L}^+ \mathcal {G}$-equivariant. By taking the fiber over ![]() $0$ it follows that
$0$ it follows that ![]() $\mathcal {Z}(\mathcal {F}^\bullet )$ is
$\mathcal {Z}(\mathcal {F}^\bullet )$ is ![]() $I$-equivariant.
$I$-equivariant.
This completes the proof of the properties of ![]() $\mathcal {Z}$ asserted at the beginning of Theorem 1.1 and also part (i).
$\mathcal {Z}$ asserted at the beginning of Theorem 1.1 and also part (i).
Proof of Theorem 1.1(ii). We first show that ![]() $R\pi _! (\mathcal {Z}_{\mathcal {A}(\mu )}) \cong \operatorname {IC}_\mu$. Since
$R\pi _! (\mathcal {Z}_{\mathcal {A}(\mu )}) \cong \operatorname {IC}_\mu$. Since ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ and ![]() $\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ are normal, Cohen–Macaulay, and have pseudo-rational singularities, we have
$\overline {\operatorname {Gr}}_{\underline {G}, \mu }$ are normal, Cohen–Macaulay, and have pseudo-rational singularities, we have ![]() $R\pi _{\mathcal {G},*}(\mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}) \cong \mathcal {O}_{\overline {\operatorname {Gr}}_{\underline {G}, \mu }}$ by [Reference KovácsKov17, 1.8]. Because
$R\pi _{\mathcal {G},*}(\mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}) \cong \mathcal {O}_{\overline {\operatorname {Gr}}_{\underline {G}, \mu }}$ by [Reference KovácsKov17, 1.8]. Because ![]() $\pi _{\mathcal {G},*} = \pi _{\mathcal {G},!}$ as functors on
$\pi _{\mathcal {G},*} = \pi _{\mathcal {G},!}$ as functors on ![]() $\mathbb {F}_p$-sheaves, it follows by applying the Artin–Schreier sequence and Proposition 2.19 that
$\mathbb {F}_p$-sheaves, it follows by applying the Artin–Schreier sequence and Proposition 2.19 that
Now by semisimplicity, for general ![]() $\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\text {ss}}$ there exists an isomorphism
$\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\text {ss}}$ there exists an isomorphism
We can select a canonical isomorphism by requiring that it restricts to the identity map over ![]() $C^\circ$. By restricting this canonical isomorphism to
$C^\circ$. By restricting this canonical isomorphism to ![]() $0$ and applying the proper base change theorem we get a canonical isomorphism
$0$ and applying the proper base change theorem we get a canonical isomorphism
3. Proofs
3.1 Beilinson–Drinfeld and convolution Grassmannians
In this section we establish some ![]() $F$-regularity results that we will use to prove the remaining parts of Theorem 1.1. Let
$F$-regularity results that we will use to prove the remaining parts of Theorem 1.1. Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p > 2$ and let
$p > 2$ and let ![]() $G$ be a connected reductive group over
$G$ be a connected reductive group over ![]() $k$ such that
$k$ such that ![]() $G_{\text {der}}$ is almost simple. We also assume that
$G_{\text {der}}$ is almost simple. We also assume that ![]() $G_{\text {der}}$ is simply connected until Remark 3.9. In our proofs we will use the same geometric objects as in [Reference ZhuZhu14]. First, we have the Beilinson–Drinfeld Grassmannian for
$G_{\text {der}}$ is simply connected until Remark 3.9. In our proofs we will use the same geometric objects as in [Reference ZhuZhu14]. First, we have the Beilinson–Drinfeld Grassmannian for ![]() $\mathcal {G}$ over
$\mathcal {G}$ over ![]() $C$ defined by the functor
$C$ defined by the functor
This is an ind-proper scheme over ![]() $C$ by [Reference ZhuZhu14, 6.2.1]. By arguments similar to those in [Reference GaitsgoryGai01, Prop. 5],
$C$ by [Reference ZhuZhu14, 6.2.1]. By arguments similar to those in [Reference GaitsgoryGai01, Prop. 5],
Let ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ be the reduced closure of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ be the reduced closure of ![]() $\operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$ in
$\operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$ in ![]() $\operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$.
$\operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$.
The global convolution Grassmannian for ![]() $\mathcal {G}$ is the functor
$\mathcal {G}$ is the functor
 \[ \operatorname{Gr}_{\mathcal{G}}^{\mathrm{conv}}(R) = \left\{ (x, \mathcal{E}_1, \mathcal{E}_2, \beta_1, \beta_2) : \begin{array}{lr@{}} x \in C(R),\ \mathcal{E}_1, \mathcal{E}_2 \text{ are } \mathcal{G}\text{-torsors on } C_R,\\ \beta_1 \colon {\mathcal{E}_1}\left|_{C_R - \Gamma_x}\right. \cong { \mathcal{E}_0}\left|_{C_R - \Gamma_x}\right.,\ \beta_2 \colon {\mathcal{E}_2}\left|_{C_R^\circ}\right. \cong {\mathcal{E}_1}\left|_{C_R^\circ}\right. \\ \end{array}\!\!\!\right\}. \]
\[ \operatorname{Gr}_{\mathcal{G}}^{\mathrm{conv}}(R) = \left\{ (x, \mathcal{E}_1, \mathcal{E}_2, \beta_1, \beta_2) : \begin{array}{lr@{}} x \in C(R),\ \mathcal{E}_1, \mathcal{E}_2 \text{ are } \mathcal{G}\text{-torsors on } C_R,\\ \beta_1 \colon {\mathcal{E}_1}\left|_{C_R - \Gamma_x}\right. \cong { \mathcal{E}_0}\left|_{C_R - \Gamma_x}\right.,\ \beta_2 \colon {\mathcal{E}_2}\left|_{C_R^\circ}\right. \cong {\mathcal{E}_1}\left|_{C_R^\circ}\right. \\ \end{array}\!\!\!\right\}. \]
This is an ind-projective scheme over ![]() $C$ by [Reference ZhuZhu14, 6.2.3]. There is a map
$C$ by [Reference ZhuZhu14, 6.2.3]. There is a map ![]() $m_{\mathcal {G}} \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$ which sends
$m_{\mathcal {G}} \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$ which sends ![]() $(x, \mathcal {E}_1, \mathcal {E}_2, \beta _1, \beta _2)$ to
$(x, \mathcal {E}_1, \mathcal {E}_2, \beta _1, \beta _2)$ to ![]() $(x, \mathcal {E}_2, \beta _1 \circ \beta _2)$. The map
$(x, \mathcal {E}_2, \beta _1 \circ \beta _2)$. The map ![]() $m_{\mathcal {G}}$ is an isomorphism over
$m_{\mathcal {G}}$ is an isomorphism over ![]() $C^\circ$. By taking the fibers over
$C^\circ$. By taking the fibers over ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$ we get the following diagram with Cartesian squares.
$0$ we get the following diagram with Cartesian squares.

We define ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ to be the reduced closure of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ to be the reduced closure of ![]() $\operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$ in
$\operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$ in ![]() $\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}}$. In Theorem 3.6 we will show that
$\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}}$. In Theorem 3.6 we will show that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ are strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ are strongly ![]() $F$-regular. Before we can prove this, we need to show that
$F$-regular. Before we can prove this, we need to show that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is Frobenius split compatibly with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is Frobenius split compatibly with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$. Zhu proved such a splitting exists for
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$. Zhu proved such a splitting exists for ![]() $w \in X_*(T)^+$ sufficiently dominant [Reference ZhuZhu14, 6.5], and our argument will require only a minor modification of Zhu's argument.
$w \in X_*(T)^+$ sufficiently dominant [Reference ZhuZhu14, 6.5], and our argument will require only a minor modification of Zhu's argument.
In our proofs we will use the following facts and notation. Recall that for ![]() $\lambda \in X_*(T)^+$ we write
$\lambda \in X_*(T)^+$ we write ![]() $t_\lambda$ for the element
$t_\lambda$ for the element ![]() $\lambda$ viewed as an element of
$\lambda$ viewed as an element of ![]() $\tilde {W}$. If we write
$\tilde {W}$. If we write ![]() $\tilde {W} = X_*(T) \rtimes W$, then
$\tilde {W} = X_*(T) \rtimes W$, then
Additionally, for ![]() $\mu \in X_*(T)^+$ we have
$\mu \in X_*(T)^+$ we have
In this case, if ![]() $\ell$ is the length function on
$\ell$ is the length function on ![]() $\tilde {W}$ we have
$\tilde {W}$ we have
This can be proved using the formula for ![]() $\ell$ in [Reference GörtzGör10, § 1.1] (see also [Reference ZhuZhu14, § 9.1]).
$\ell$ in [Reference GörtzGör10, § 1.1] (see also [Reference ZhuZhu14, § 9.1]).
Proposition 3.1 Let ![]() $\mu$,
$\mu$, ![]() $\lambda \in X_*(T)^+$ and let
$\lambda \in X_*(T)^+$ and let ![]() $w = t_{\lambda }^{w_0} \in \tilde {W}$. Then
$w = t_{\lambda }^{w_0} \in \tilde {W}$. Then ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is normal, and the fiber
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is normal, and the fiber ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced and isomorphic to
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced and isomorphic to ![]() $\mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$.
$\mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$.
Proof. Let ![]() $\operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ be the functor
$\operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ be the functor
Then by [Reference GaitsgoryGai01, 3.1.1], ![]() $\operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ is ind-projective, and there are isomorphisms
$\operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ is ind-projective, and there are isomorphisms
The map ![]() $\mathcal {G} \rightarrow \underline {G}$ induces a map
$\mathcal {G} \rightarrow \underline {G}$ induces a map ![]() $\pi _{\mathrm {BD}} \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}} \rightarrow \operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$. Over closed points in
$\pi _{\mathrm {BD}} \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}} \rightarrow \operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$. Over closed points in ![]() $C^\circ$ this is the map
$C^\circ$ this is the map ![]() $\operatorname {id} \times \pi \colon \operatorname {Gr} \times \mathcal {F}\ell \rightarrow \operatorname {Gr} \times \operatorname {Gr}$, and over
$\operatorname {id} \times \pi \colon \operatorname {Gr} \times \mathcal {F}\ell \rightarrow \operatorname {Gr} \times \operatorname {Gr}$, and over ![]() $0$ this is
$0$ this is ![]() $\pi \colon \mathcal {F}\ell \rightarrow \operatorname {Gr}$. Let
$\pi \colon \mathcal {F}\ell \rightarrow \operatorname {Gr}$. Let ![]() $\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda } \subset \operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ be the reduced closure of
$\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda } \subset \operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ be the reduced closure of ![]() $\operatorname {Gr}_{\leq \mu } \times C^\circ \times \operatorname {Gr}_{\leq \lambda }$.
$\operatorname {Gr}_{\leq \mu } \times C^\circ \times \operatorname {Gr}_{\leq \lambda }$.
The fiber ![]() $(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda })_{0}$ is reduced and isomorphic to
$(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda })_{0}$ is reduced and isomorphic to ![]() $\operatorname {Gr}_{\leq \mu + \lambda }$ by [Reference ZhuZhu09, 1.2.4] (see also [Reference ZhuZhu17, 3.1.14]). As
$\operatorname {Gr}_{\leq \mu + \lambda }$ by [Reference ZhuZhu09, 1.2.4] (see also [Reference ZhuZhu17, 3.1.14]). As ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}} \subset \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda })$, we have that
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}} \subset \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda })$, we have that ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0, \, \text {red}} \subset \mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$. Furthermore,
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0, \, \text {red}} \subset \mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$. Furthermore, ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}} \rightarrow C$ is flat by [Reference HartshorneHar77, 9.7], and hence by [Reference HartshorneHar77, 9.6] the irreducible components of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}} \rightarrow C$ is flat by [Reference HartshorneHar77, 9.7], and hence by [Reference HartshorneHar77, 9.6] the irreducible components of ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0, \, \text {red}}$ all have dimension equal to
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0, \, \text {red}}$ all have dimension equal to ![]() $\dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _{t_\lambda ^{w_0}}$. Thus, since
$\dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _{t_\lambda ^{w_0}}$. Thus, since ![]() $\dim \mathcal {F} \ell _{t_{\mu +\lambda }^{w_0}} = \dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _{t_\lambda ^{w_0}}$, it follows that
$\dim \mathcal {F} \ell _{t_{\mu +\lambda }^{w_0}} = \dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _{t_\lambda ^{w_0}}$, it follows that ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0, \, \text {red}} = \mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$ and
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0, \, \text {red}} = \mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$ and ![]() $( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{\text {red}} = \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$.
$( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{\text {red}} = \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$.
As ![]() $\mathcal {F}\ell$ is a
$\mathcal {F}\ell$ is a ![]() $G/B$ fibration over
$G/B$ fibration over ![]() $\operatorname {Gr}$, we have that
$\operatorname {Gr}$, we have that ![]() $( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{0}$ is a
$( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{0}$ is a ![]() $G/B$ fibration over
$G/B$ fibration over ![]() $(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda })_{0}$. Since
$(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda })_{0}$. Since ![]() $(\overline {\operatorname {Gr}}_{\underline {G}, \mu , \lambda }^{\mathrm {BD}})_{0}$ is reduced, so is
$(\overline {\operatorname {Gr}}_{\underline {G}, \mu , \lambda }^{\mathrm {BD}})_{0}$ is reduced, so is ![]() $( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{0}$. As
$( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{0}$. As ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is a closed subscheme of
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is a closed subscheme of ![]() $( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{0}$, and these two schemes have the same reductions,
$( \pi _{\mathrm {BD}}^{-1}(\overline {\operatorname {Gr}}^{\mathrm {BD}}_{\underline {G}, \mu , \lambda }))_{0}$, and these two schemes have the same reductions, ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced. Finally, since
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced. Finally, since ![]() $\mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$ is normal and
$\mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}}$ is normal and ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{t_{\lambda }^{w_0}}$ is also normal,
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{t_{\lambda }^{w_0}}$ is also normal, ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is normal by Hironaka's lemma [Reference Grothendieck and DieudonnéEGAIV2, 5.12.8].
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is normal by Hironaka's lemma [Reference Grothendieck and DieudonnéEGAIV2, 5.12.8].
Remark 3.2 The functors ![]() $\operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$ and
$\operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$ and ![]() $\operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ can also be described as the restrictions to
$\operatorname {Gr}_{\underline {G}}^{\mathrm {BD}}$ can also be described as the restrictions to ![]() $C \times \{0\}$ of quotients of global loop groups over
$C \times \{0\}$ of quotients of global loop groups over ![]() $C^2$ which are similar to
$C^2$ which are similar to ![]() $\mathcal {L}\mathcal {G}$ and
$\mathcal {L}\mathcal {G}$ and ![]() $\mathcal {L}^+\mathcal {G}$ from § 2.2 (see also [Reference ZhuZhu17, § 3.1]). The referee has pointed out that it is possible to use this fact to show that
$\mathcal {L}^+\mathcal {G}$ from § 2.2 (see also [Reference ZhuZhu17, § 3.1]). The referee has pointed out that it is possible to use this fact to show that ![]() $\pi _{\mathrm {BD}}$ is a
$\pi _{\mathrm {BD}}$ is a ![]() $G/B$ fibration, and in particular it is smooth. Since normality and reducedness are local in the smooth topology, this leads to an alternative proof of Proposition 3.1.
$G/B$ fibration, and in particular it is smooth. Since normality and reducedness are local in the smooth topology, this leads to an alternative proof of Proposition 3.1.
The following proposition is well known, but because we could not find a complete proof in the literature we provide one here.
Proposition 3.3 Let ![]() $w$,
$w$, ![]() $w' \in \tilde {W}$ be such that
$w' \in \tilde {W}$ be such that ![]() $\ell (w) + \ell (w') = \ell (w \cdot w')$. Then the convolution morphism
$\ell (w) + \ell (w') = \ell (w \cdot w')$. Then the convolution morphism ![]() $m \colon LG \times ^I \mathcal {F}\ell \rightarrow \mathcal {F}{\ell }$ maps
$m \colon LG \times ^I \mathcal {F}\ell \rightarrow \mathcal {F}{\ell }$ maps ![]() $C(w) {\tilde{ \times }} C(w')$ isomorphically onto
$C(w) {\tilde{ \times }} C(w')$ isomorphically onto ![]() $C(w \cdot w')$.
$C(w \cdot w')$.
Proof. Let ![]() $W_{\text {aff}}$ be the affine Weyl group of
$W_{\text {aff}}$ be the affine Weyl group of ![]() $G$ and let
$G$ and let ![]() $\Omega \subset \tilde {W}$ be the subgroup of length
$\Omega \subset \tilde {W}$ be the subgroup of length ![]() $0$ elements. Then we have a decomposition
$0$ elements. Then we have a decomposition ![]() $\tilde {W} = W_{\text {aff}} \rtimes \Omega$. First suppose that
$\tilde {W} = W_{\text {aff}} \rtimes \Omega$. First suppose that ![]() $w$,
$w$, ![]() $w' \in W_{\text {aff}}$. Let
$w' \in W_{\text {aff}}$. Let ![]() $w = s_1 \cdots s_{\ell (w)}$ and
$w = s_1 \cdots s_{\ell (w)}$ and ![]() $w' = s_1' \cdots s_{\ell (w')}'$ be reduced expressions for
$w' = s_1' \cdots s_{\ell (w')}'$ be reduced expressions for ![]() $w$ and
$w$ and ![]() $w'$ as products of simple reflections. For each
$w'$ as products of simple reflections. For each ![]() $i$ let
$i$ let ![]() $\mathcal {P}_i$ be the parahoric group scheme corresponding to
$\mathcal {P}_i$ be the parahoric group scheme corresponding to ![]() $s_i$. Then
$s_i$. Then ![]() ${L^+(\mathcal {P}_i)/ I \cong \mathcal {F}\ell _{s_i}}$, and each
${L^+(\mathcal {P}_i)/ I \cong \mathcal {F}\ell _{s_i}}$, and each ![]() $\mathcal {F}\ell _{s_i}$ is abstractly isomorphic to
$\mathcal {F}\ell _{s_i}$ is abstractly isomorphic to ![]() $\mathbb {P}^1$. There is an affine Demazure resolution
$\mathbb {P}^1$. There is an affine Demazure resolution
By [Reference FaltingsFal03, § 3], since the product of the ![]() $s_i$ and the
$s_i$ and the ![]() $s_j'$ gives a reduced expression for
$s_j'$ gives a reduced expression for ![]() $w \cdot w'$, the morphism
$w \cdot w'$, the morphism ![]() $\pi _{w \cdot w'}$ induces an isomorphism
$\pi _{w \cdot w'}$ induces an isomorphism
As ![]() $\pi _{w \cdot w'} = m \circ (\pi _w {\tilde{ \times }} \pi _{w'})$, we see by also applying loc. cit. to the factors
$\pi _{w \cdot w'} = m \circ (\pi _w {\tilde{ \times }} \pi _{w'})$, we see by also applying loc. cit. to the factors ![]() ${\tilde{ \times }} \mathcal {F}\ell _{s_i}$ and
${\tilde{ \times }} \mathcal {F}\ell _{s_i}$ and ![]() ${\tilde{ \times }} \mathcal {F}\ell _{s'_j}$ that
${\tilde{ \times }} \mathcal {F}\ell _{s'_j}$ that ![]() $m$ maps
$m$ maps ![]() $C(w) {\tilde{ \times }} C(w')$ isomorphically onto
$C(w) {\tilde{ \times }} C(w')$ isomorphically onto ![]() $C(w \cdot w')$.
$C(w \cdot w')$.
For the general case, write ![]() $w = \tau w_{a}$ and
$w = \tau w_{a}$ and ![]() $w' = w'_{a}\tau '$ for
$w' = w'_{a}\tau '$ for ![]() $w_a$,
$w_a$, ![]() $w'_a \in W_{\text {aff}}$ and
$w'_a \in W_{\text {aff}}$ and ![]() $\tau$,
$\tau$, ![]() $\tau ' \in \Omega$. Then
$\tau ' \in \Omega$. Then ![]() $\ell (w) = \ell (w_a)$,
$\ell (w) = \ell (w_a)$, ![]() $\ell (w') = \ell (w_a')$ and
$\ell (w') = \ell (w_a')$ and ![]() $\ell (w \cdot w') = \ell (w_a \cdot w'_a)$. Because
$\ell (w \cdot w') = \ell (w_a \cdot w'_a)$. Because ![]() $\Omega$ normalizes
$\Omega$ normalizes ![]() $I$, we have that
$I$, we have that ![]() $\Omega$ acts on both
$\Omega$ acts on both ![]() $\mathcal {F}\ell$ and
$\mathcal {F}\ell$ and ![]() $LG \times ^I \mathcal {F}\ell$ by right multiplication. Furthermore, any lift
$LG \times ^I \mathcal {F}\ell$ by right multiplication. Furthermore, any lift ![]() $\dot {\tau }^{-1} \in LG(k)$ induces isomorphisms on both of these ind-schemes by left multiplication, and all of these isomorphisms send
$\dot {\tau }^{-1} \in LG(k)$ induces isomorphisms on both of these ind-schemes by left multiplication, and all of these isomorphisms send ![]() $I$-orbits to
$I$-orbits to ![]() $I$-orbits. In particular, there is a commutative diagram as follows.
$I$-orbits. In particular, there is a commutative diagram as follows.

We have shown the morphism on the right is an isomorphism, thus so is the morphism on the left.
Proposition 3.4 For any ![]() $\mu \in X_*(T)^+$ and
$\mu \in X_*(T)^+$ and ![]() $w \in \tilde {W}$ the scheme
$w \in \tilde {W}$ the scheme ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is Frobenius split compatibly with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is Frobenius split compatibly with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$.
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$.
Proof. If ![]() $w = t_\nu$ for
$w = t_\nu$ for ![]() $\nu \in X_*(T)^+$ sufficiently dominant then this is [Reference ZhuZhu14, 6.5]. If
$\nu \in X_*(T)^+$ sufficiently dominant then this is [Reference ZhuZhu14, 6.5]. If ![]() $\lambda < \nu$ is also dominant then this splitting is compatible with the closed subscheme
$\lambda < \nu$ is also dominant then this splitting is compatible with the closed subscheme ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}} \subset \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\nu }^{\mathrm {BD}}$ by [Reference ZhuZhu14, 6.8] and [Reference Brion and KumarBK05, 1.1.7 (ii)]. A splitting of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}} \subset \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\nu }^{\mathrm {BD}}$ by [Reference ZhuZhu14, 6.8] and [Reference Brion and KumarBK05, 1.1.7 (ii)]. A splitting of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\nu }^{\mathrm {BD}}$ compatible with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\nu }^{\mathrm {BD}}$ compatible with ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}}$ and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}}$ and ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\nu }^{\mathrm {BD}})_{0}$ induces a splitting of
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\nu }^{\mathrm {BD}})_{0}$ induces a splitting of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}}$ compatible with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}}$ compatible with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}})_{0}$. This proves the proposition when
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_\lambda }^{\mathrm {BD}})_{0}$. This proves the proposition when ![]() $w = t_\lambda$ for any dominant cocharacter
$w = t_\lambda$ for any dominant cocharacter ![]() $\lambda$.
$\lambda$.
For the general case, note that for every ![]() $w' \in \tilde {W}$ there exists
$w' \in \tilde {W}$ there exists ![]() $\lambda \in X_*(T)^+$ such that
$\lambda \in X_*(T)^+$ such that ![]() $w' \leq t_{\lambda }^{w_0}$, so it suffices to show
$w' \leq t_{\lambda }^{w_0}$, so it suffices to show ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_{\lambda }^{w_0}}^{\mathrm {BD}}$ is compatibly Frobenius split with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_{\lambda }^{w_0}}^{\mathrm {BD}}$ is compatibly Frobenius split with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_{\lambda }^{w_0}}^{\mathrm {BD}})_{0}$ and
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , t_{\lambda }^{w_0}}^{\mathrm {BD}})_{0}$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w'}^{\mathrm {BD}}$ for all
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w'}^{\mathrm {BD}}$ for all ![]() $\lambda \in X_*(T)^+$ and
$\lambda \in X_*(T)^+$ and ![]() $w' \leq t_{\lambda }^{w_0}$. Henceforth we fix
$w' \leq t_{\lambda }^{w_0}$. Henceforth we fix ![]() $\lambda \in X_*(T)^+$ and
$\lambda \in X_*(T)^+$ and ![]() $w = t_{\lambda }^{w_0} \in \tilde {W}$.
$w = t_{\lambda }^{w_0} \in \tilde {W}$.
We will proceed by a similar argument to that in [Reference ZhuZhu14, 6.7]. More precisely, we will construct an open subscheme ![]() $U \subset \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ such that the following assertions hold.
$U \subset \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ such that the following assertions hold.
(i) The scheme
 $U$ maps isomorphically onto its image under
$U$ maps isomorphically onto its image under  $m \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}} \rightarrow \overline {\operatorname {Gr}}^{\mathrm {BD}}_{\mathcal {G}, \mu , w}$.
$m \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}} \rightarrow \overline {\operatorname {Gr}}^{\mathrm {BD}}_{\mathcal {G}, \mu , w}$.(ii) The complement of
 $m(U)$ in
$m(U)$ in  $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ has codimension two.
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ has codimension two.(iii) The scheme
 $U$ is Frobenius split. Since
$U$ is Frobenius split. Since  $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is normal, by [Reference Brion and KumarBK05, 1.1.7] the spitting of
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is normal, by [Reference Brion and KumarBK05, 1.1.7] the spitting of  $m(U)$ extends to a splitting of
$m(U)$ extends to a splitting of  $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$. We will complete the proof of the proposition by showing
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$. We will complete the proof of the proposition by showing(iv) The resulting splitting of
 $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is compatible with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is compatible with  $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ and
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ and  $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w'}^{\mathrm {BD}}$ for all
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w'}^{\mathrm {BD}}$ for all  $w' < w$.
$w' < w$.
As in [Reference ZhuZhu14], we define ![]() $U_1 \subset \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ to be the open subscheme which is
$U_1 \subset \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ to be the open subscheme which is ![]() $\operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w}$ over
$\operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w}$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $C(t_\mu ) {\tilde{ \times }} \mathcal {F}\ell _{w}$ over
$C(t_\mu ) {\tilde{ \times }} \mathcal {F}\ell _{w}$ over ![]() $0$. We also define
$0$. We also define ![]() $U \subset U_1$ to be the open subscheme which is
$U \subset U_1$ to be the open subscheme which is ![]() $\operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w}$ over
$\operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w}$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $C(t_\mu ) {\tilde{ \times }} C(w)$ over
$C(t_\mu ) {\tilde{ \times }} C(w)$ over ![]() $0$. Since the lengths of
$0$. Since the lengths of ![]() $t_\mu$ and
$t_\mu$ and ![]() $w$ add,
$w$ add, ![]() $C(t_\mu ) {\tilde{ \times }} C(w)$ maps isomorphically onto
$C(t_\mu ) {\tilde{ \times }} C(w)$ maps isomorphically onto ![]() $C(t_{\mu +\lambda }^{w_0})$ by Proposition 3.3. Thus
$C(t_{\mu +\lambda }^{w_0})$ by Proposition 3.3. Thus ![]() $(U)_0$ maps isomorphically onto
$(U)_0$ maps isomorphically onto ![]() $m(U)_0$. Hence the morphism from
$m(U)_0$. Hence the morphism from ![]() $U$ to
$U$ to ![]() $m(U)$ is a bijective birational morphism between normal integral
$m(U)$ is a bijective birational morphism between normal integral ![]() $k$-schemes, so it is an isomorphism by Grothendieck's reformulation of Zariski's main theorem [Reference GrothendieckEGAIII1, 4.4.3].
$k$-schemes, so it is an isomorphism by Grothendieck's reformulation of Zariski's main theorem [Reference GrothendieckEGAIII1, 4.4.3].
As ![]() $\operatorname {Gr}_{\leq \mu } - \operatorname {Gr}_{\mu }$ has codimension two in
$\operatorname {Gr}_{\leq \mu } - \operatorname {Gr}_{\mu }$ has codimension two in ![]() $\operatorname {Gr}_{\leq \mu }$, the complement of
$\operatorname {Gr}_{\leq \mu }$, the complement of ![]() $ {m(U)}\left|_{C^\circ }\right. = \operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w}$ has codimension two in
$ {m(U)}\left|_{C^\circ }\right. = \operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w}$ has codimension two in ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. = \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$. By Proposition 3.1,
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. = \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$. By Proposition 3.1, ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0} - m(U)_{0} = \mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}} - C(t_{\mu +\lambda }^{w_0})$ has codimension one, so we conclude that
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0} - m(U)_{0} = \mathcal {F}\ell _{t_{\mu +\lambda }^{w_0}} - C(t_{\mu +\lambda }^{w_0})$ has codimension one, so we conclude that ![]() $U$ satisfies (ii). Finally, (iii) and (iv) follow from the fact that
$U$ satisfies (ii). Finally, (iii) and (iv) follow from the fact that ![]() $U_1$ is Frobenius split compatibly with
$U_1$ is Frobenius split compatibly with ![]() $(U_1)_{0}$ and
$(U_1)_{0}$ and ![]() $U_1 \cap (\operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w'})$ for all
$U_1 \cap (\operatorname {Gr}_{\mu } \times C^\circ \times \mathcal {F}\ell _{w'})$ for all ![]() $w' \leq w$ by [Reference ZhuZhu14, 6.8].
$w' \leq w$ by [Reference ZhuZhu14, 6.8].
Corollary 3.5 For any ![]() $\mu \in X_*(T)^+$ and
$\mu \in X_*(T)^+$ and ![]() $w \in \tilde {W}$ the scheme
$w \in \tilde {W}$ the scheme ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced, Cohen–Macaulay, Frobenius split, and equidimensional of dimension
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced, Cohen–Macaulay, Frobenius split, and equidimensional of dimension ![]() $\dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _w$.
$\dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _w$.
Proof. A Frobenius splitting of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ compatible with
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ compatible with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ induces a Frobenius splitting of
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ induces a Frobenius splitting of ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$. Thus
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$. Thus ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced by [Reference Brion and KumarBK05, 1.2.1]. Furthermore, as
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is reduced by [Reference Brion and KumarBK05, 1.2.1]. Furthermore, as ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$ is Cohen–Macaulay,
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$ is Cohen–Macaulay, ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is Cohen–Macaulay by [Reference Blickle and SchwedeBS13, 5.4] (see also [Reference Haines and RicharzHR19, 5.5]). Thus
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is Cohen–Macaulay by [Reference Blickle and SchwedeBS13, 5.4] (see also [Reference Haines and RicharzHR19, 5.5]). Thus ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is also Cohen–Macaulay by [Sta21, OC6G]. Finally, the morphism
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is also Cohen–Macaulay by [Sta21, OC6G]. Finally, the morphism ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}} \rightarrow C$ is flat by [Reference HartshorneHar77, III 9.7], so by [Reference HartshorneHar77, III 9.6] the fiber
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}} \rightarrow C$ is flat by [Reference HartshorneHar77, III 9.7], so by [Reference HartshorneHar77, III 9.6] the fiber ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is equidimensional of dimension
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is equidimensional of dimension ![]() $\dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _w$.
$\dim \operatorname {Gr}_{\leq \mu } + \dim \mathcal {F}\ell _w$.
Theorem 3.6 For any ![]() $\mu \in X_*(T)^+$ and
$\mu \in X_*(T)^+$ and ![]() $w \in \tilde {W}$ the schemes
$w \in \tilde {W}$ the schemes ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ are strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ are strongly ![]() $F$-regular,
$F$-regular, ![]() $F$-rational, and have pseudo-rational singularities.
$F$-rational, and have pseudo-rational singularities.
Proof. As in the proof of Theorem 2.17, it suffices to prove these schemes are strongly ![]() $F$-regular. Since
$F$-regular. Since ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$, it follows that
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right. \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _{w}$, it follows that ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right.$ is strongly
$ {\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}\left|_{C^\circ }\right.$ is strongly ![]() $F$-regular by Lemma 2.14 and Theorem 2.1. Now as in the proof of Theorem 2.17, it follows that
$F$-regular by Lemma 2.14 and Theorem 2.1. Now as in the proof of Theorem 2.17, it follows that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is strongly ![]() $F$-regular because it is Frobenius split compatibly with
$F$-regular because it is Frobenius split compatibly with ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$.
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$.
To prove ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ is strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ is strongly ![]() $F$-regular, we first note that
$F$-regular, we first note that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times \mathcal {F}\ell _{w}$ is strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times \mathcal {F}\ell _{w}$ is strongly ![]() $F$-regular by Lemma 2.14. By the isomorphism proceeding [Reference ZhuZhu14, 6.2.3],
$F$-regular by Lemma 2.14. By the isomorphism proceeding [Reference ZhuZhu14, 6.2.3], ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times \mathcal {F}\ell _{w}$ have a common smooth cover. Since the property of strong
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times \mathcal {F}\ell _{w}$ have a common smooth cover. Since the property of strong ![]() $F$-regularity is local in the smooth topology (Lemma 2.16),
$F$-regularity is local in the smooth topology (Lemma 2.16), ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ is strongly
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ is strongly ![]() $F$-regular.
$F$-regular.
3.2 Proofs of main results
We continue using the notation introduced in § 3.1. For ![]() $\mu \in X_*(T)^+$ and
$\mu \in X_*(T)^+$ and ![]() $w \in \tilde {W}$, let
$w \in \tilde {W}$, let ![]() $\mathcal {Z}_{\mu , w}$ be the shifted constant sheaf
$\mathcal {Z}_{\mu , w}$ be the shifted constant sheaf ![]() $\mathbb {F}_p[\dim (\operatorname {Gr}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}]$ supported on
$\mathbb {F}_p[\dim (\operatorname {Gr}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}]$ supported on ![]() $(\operatorname {Gr}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$. Parts (iii) and (iv) of Theorem 1.1 follow from the following proposition.
$(\operatorname {Gr}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$. Parts (iii) and (iv) of Theorem 1.1 follow from the following proposition.
Proposition 3.7 For ![]() $\mathcal {F}_1^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ and
$\mathcal {F}_1^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)^{\operatorname {ss}}$ and ![]() $\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell , \mathbb {F}_p)$ there are natural isomorphisms
$\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell , \mathbb {F}_p)$ there are natural isomorphisms
(i)
 $\Psi _{\operatorname {Gr}^{\mathrm {BD}}_{\mathcal {G}}}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \operatorname {IC}_w^{\mathcal {F}\ell }) \cong \mathcal {Z}_{\mu , w}$,
$\Psi _{\operatorname {Gr}^{\mathrm {BD}}_{\mathcal {G}}}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \operatorname {IC}_w^{\mathcal {F}\ell }) \cong \mathcal {Z}_{\mu , w}$,(ii)
 $\Psi _{\operatorname {Gr}^{\mathrm {BD}}_{\mathcal {G}}}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }) \cong \mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$,
$\Psi _{\operatorname {Gr}^{\mathrm {BD}}_{\mathcal {G}}}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }) \cong \mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$,(iii)
 $\Psi _{\operatorname {Gr}^{\mathrm {BD}}_{\mathcal {G}}}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }) \cong \mathcal {F}_2^{\bullet } * \mathcal {Z}(\mathcal {F}_1^{\bullet }).$
$\Psi _{\operatorname {Gr}^{\mathrm {BD}}_{\mathcal {G}}}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }) \cong \mathcal {F}_2^{\bullet } * \mathcal {Z}(\mathcal {F}_1^{\bullet }).$
Furthermore, each of these complexes is perverse and ![]() $I$-equivariant.
$I$-equivariant.
Proof. Since ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is integral and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is integral and ![]() $F$-rational,
$F$-rational, ![]() $j_{!*}^{\mathrm {BD}}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \operatorname {IC}_w^{\mathcal {F}\ell } )$ is the constant sheaf
$j_{!*}^{\mathrm {BD}}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \operatorname {IC}_w^{\mathcal {F}\ell } )$ is the constant sheaf ![]() $\mathbb {F}_p[\dim \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}]$ supported on
$\mathbb {F}_p[\dim \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}]$ supported on ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ by [Reference CassCas19, 1.7]. Hence the isomorphism in (i) follows. As
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ by [Reference CassCas19, 1.7]. Hence the isomorphism in (i) follows. As ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is Cohen–Macaulay and equidimensional,
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}})_{0}$ is Cohen–Macaulay and equidimensional, ![]() $\mathcal {Z}_{\mu , w}$ is perverse by [Reference CassCas19, 1.6].
$\mathcal {Z}_{\mu , w}$ is perverse by [Reference CassCas19, 1.6].
For (ii), suppose that ![]() $\mathcal {F}_1^\bullet$ is supported on
$\mathcal {F}_1^\bullet$ is supported on ![]() $\operatorname {Gr}_{\leq \mu }$ and
$\operatorname {Gr}_{\leq \mu }$ and ![]() $\mathcal {F}_2^{\bullet }$ is supported on
$\mathcal {F}_2^{\bullet }$ is supported on ![]() $\mathcal {F}\ell _{w}$. Let
$\mathcal {F}\ell _{w}$. Let ![]() $I_n := L^n( {\mathcal {G}}\left|_{{\hat {\mathcal {O}}_{0}}}\right.)$. As in [Reference ZhuZhu14, 6.2.3], for some
$I_n := L^n( {\mathcal {G}}\left|_{{\hat {\mathcal {O}}_{0}}}\right.)$. As in [Reference ZhuZhu14, 6.2.3], for some ![]() $n$ there is an
$n$ there is an ![]() $I_n$-torsor
$I_n$-torsor ![]() $\operatorname {Gr}_{\mathcal {G}, 0 ,n}$ over
$\operatorname {Gr}_{\mathcal {G}, 0 ,n}$ over ![]() $\operatorname {Gr}_{\mathcal {G}}$ such that
$\operatorname {Gr}_{\mathcal {G}}$ such that
Let ![]() $\varphi _n^{\mathrm {conv}} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times _{\operatorname {Gr}_{\mathcal {G}}} \operatorname {Gr}_{\mathcal {G}, 0 ,n} \times \mathcal {F}\ell _{w} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ be the resulting
$\varphi _n^{\mathrm {conv}} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times _{\operatorname {Gr}_{\mathcal {G}}} \operatorname {Gr}_{\mathcal {G}, 0 ,n} \times \mathcal {F}\ell _{w} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$ be the resulting ![]() $I_n$-torsor over
$I_n$-torsor over ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$.
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}$.
By similar reasoning to that in [Reference CassCas19, 6.2] we can form the perverse sheaf
The key point is that ![]() $j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) {\overset {L}{\boxtimes }} \, \mathcal {F}_2^{\bullet }$ is perverse when
$j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) {\overset {L}{\boxtimes }} \, \mathcal {F}_2^{\bullet }$ is perverse when ![]() $\mathcal {F}_1^\bullet$ and
$\mathcal {F}_1^\bullet$ and ![]() $\mathcal {F}_2^{\bullet }$ are simple because then
$\mathcal {F}_2^{\bullet }$ are simple because then ![]() $j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }$ is a constant sheaf supported on an equidimensional Cohen–Macaulay scheme. Thus
$j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }$ is a constant sheaf supported on an equidimensional Cohen–Macaulay scheme. Thus ![]() $j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) {\overset {L}{\boxtimes }} \, \mathcal {F}_2^{\bullet }$ is perverse for general
$j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) {\overset {L}{\boxtimes }} \, \mathcal {F}_2^{\bullet }$ is perverse for general ![]() $\mathcal {F}_1^\bullet$ and
$\mathcal {F}_1^\bullet$ and ![]() $\mathcal {F}_2^{\bullet }$ by induction on their lengths.
$\mathcal {F}_2^{\bullet }$ by induction on their lengths.
We claim there is an isomorphism
Let ![]() $\varphi _n \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times _{\operatorname {Gr}_{\mathcal {G}}} \operatorname {Gr}_{\mathcal {G}, 0 ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ be the pullback of
$\varphi _n \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \times _{\operatorname {Gr}_{\mathcal {G}}} \operatorname {Gr}_{\mathcal {G}, 0 ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ be the pullback of ![]() $\operatorname {Gr}_{\mathcal {G}, 0 ,n} \rightarrow \operatorname {Gr}_{\mathcal {G}}$ along
$\operatorname {Gr}_{\mathcal {G}, 0 ,n} \rightarrow \operatorname {Gr}_{\mathcal {G}}$ along ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow \operatorname {Gr}_{\mathcal {G}}$ and let
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow \operatorname {Gr}_{\mathcal {G}}$ and let ![]() $\varphi _{0, n} \colon (\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_{0, n} \rightarrow (\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ be the fiber of
$\varphi _{0, n} \colon (\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_{0, n} \rightarrow (\overline {\operatorname {Gr}}_{\mathcal {G}, \mu })_{0}$ be the fiber of ![]() $\varphi _n$ over
$\varphi _n$ over ![]() $0$. By taking the fiber of
$0$. By taking the fiber of ![]() $\varphi _n^{\mathrm {conv}}$ over
$\varphi _n^{\mathrm {conv}}$ over ![]() $0$ we get the following Cartesian diagram.
$0$ we get the following Cartesian diagram.

Then (3.2) follows from the following calculation:
 \begin{align*} R\varphi_{0,n}^{{\rm conv}, *} & \Bigl(Ri^{{\rm conv},*}[{-}1] \Bigl(j_{\mathcal{G}, !*} \Bigl(\mathcal{F}_1^\bullet \overset{L}{\boxtimes} {\mathbb{F}_p[1]}\left|_{C^\circ}\right. \Bigr) \overset{\sim}{\boxtimes} \mathcal{F}_2^{{\bullet}} \Bigr)\Bigr) \\ & \cong Ri_n^{{\rm conv},*}[{-}1] \Bigl(R\varphi_n^* \Bigl(j_{\mathcal{G}, !*} \Bigl(\mathcal{F}_1^\bullet \overset{L}{\boxtimes} {\mathbb{F}_p[1]}\left|_{C^\circ}\right. \Bigr)\Bigr) \overset{L}{\boxtimes} \mathcal{F}_2^{{\bullet}} \Bigr)\\ & \cong R\varphi_{0, n}^* \Bigl(Ri_{\mathcal{G}}^*[{-}1] \Bigl(j_{\mathcal{G}, !*} \Bigl(\mathcal{F}_1^\bullet \overset{L}{\boxtimes} {\mathbb{F}_p[1]}\left|_{C^\circ}\right.\Bigr)\Bigr)\Bigr) \overset{L}{\boxtimes} \mathcal{F}_2^{{\bullet}} \cong R\varphi_{0, n}^*(\mathcal{Z}(\mathcal{F}_1^\bullet)) \overset{L}{\boxtimes} \mathcal{F}_2^{{\bullet}}. \end{align*}
\begin{align*} R\varphi_{0,n}^{{\rm conv}, *} & \Bigl(Ri^{{\rm conv},*}[{-}1] \Bigl(j_{\mathcal{G}, !*} \Bigl(\mathcal{F}_1^\bullet \overset{L}{\boxtimes} {\mathbb{F}_p[1]}\left|_{C^\circ}\right. \Bigr) \overset{\sim}{\boxtimes} \mathcal{F}_2^{{\bullet}} \Bigr)\Bigr) \\ & \cong Ri_n^{{\rm conv},*}[{-}1] \Bigl(R\varphi_n^* \Bigl(j_{\mathcal{G}, !*} \Bigl(\mathcal{F}_1^\bullet \overset{L}{\boxtimes} {\mathbb{F}_p[1]}\left|_{C^\circ}\right. \Bigr)\Bigr) \overset{L}{\boxtimes} \mathcal{F}_2^{{\bullet}} \Bigr)\\ & \cong R\varphi_{0, n}^* \Bigl(Ri_{\mathcal{G}}^*[{-}1] \Bigl(j_{\mathcal{G}, !*} \Bigl(\mathcal{F}_1^\bullet \overset{L}{\boxtimes} {\mathbb{F}_p[1]}\left|_{C^\circ}\right.\Bigr)\Bigr)\Bigr) \overset{L}{\boxtimes} \mathcal{F}_2^{{\bullet}} \cong R\varphi_{0, n}^*(\mathcal{Z}(\mathcal{F}_1^\bullet)) \overset{L}{\boxtimes} \mathcal{F}_2^{{\bullet}}. \end{align*}To finish the proof of (ii) it suffices to construct a natural isomorphism
By the proper base change theorem, to establish an isomorphism as in (3.3) it suffices to construct an isomorphism
Since ![]() $m_{\mathcal {G}}$ is an isomorphism over
$m_{\mathcal {G}}$ is an isomorphism over ![]() $C^\circ$ then the left-hand side of (3.4) is naturally an extension of
$C^\circ$ then the left-hand side of (3.4) is naturally an extension of ![]() $\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }$, so we just have to show it is the intermediate extension. Indeed, once we know the left-hand side is isomorphic to the intermediate extension, then by [Reference CassCas19, 2.11] there is a unique isomorphism as in (3.4) which restricts to the identity map on
$\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }$, so we just have to show it is the intermediate extension. Indeed, once we know the left-hand side is isomorphic to the intermediate extension, then by [Reference CassCas19, 2.11] there is a unique isomorphism as in (3.4) which restricts to the identity map on ![]() $\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }$.
$\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \mathcal {F}_2^{\bullet }$.
Since the middle term in an exact triangle is an intermediate extension if the outer terms are intermediate extensions (see the proof of [Reference CassCas19, 7.8]), by induction on the lengths of ![]() $\mathcal {F}_1^\bullet$ and
$\mathcal {F}_1^\bullet$ and ![]() $\mathcal {F}_2^{\bullet }$ we reduce to the case
$\mathcal {F}_2^{\bullet }$ we reduce to the case ![]() $\mathcal {F}_1^\bullet = \operatorname {IC}_{\mu }$ and
$\mathcal {F}_1^\bullet = \operatorname {IC}_{\mu }$ and ![]() $\mathcal {F}_2^{\bullet } = \operatorname {IC}_w^{\mathcal {F}\ell }$. Because all of the schemes appearing are integral and
$\mathcal {F}_2^{\bullet } = \operatorname {IC}_w^{\mathcal {F}\ell }$. Because all of the schemes appearing are integral and ![]() $F$-rational, both
$F$-rational, both ![]() $j_{\mathcal {G}, !*}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) \overset {\sim }{\boxtimes } \operatorname {IC}_{w}^{\mathcal {F}\ell }$ and
$j_{\mathcal {G}, !*}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.) \overset {\sim }{\boxtimes } \operatorname {IC}_{w}^{\mathcal {F}\ell }$ and ![]() $j_{!*}^{\mathrm {BD}}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \operatorname {IC}_{w}^{\mathcal {F}\ell })$ are constant sheaves.
$j_{!*}^{\mathrm {BD}}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right. \overset {L}{\boxtimes } \operatorname {IC}_{w}^{\mathcal {F}\ell })$ are constant sheaves.
The map ![]() $m \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is a birational map between normal, Cohen–Macaulay
$m \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}$ is a birational map between normal, Cohen–Macaulay ![]() $k$-schemes having pseudo-rational singularities. Thus by [Reference KovácsKov17, 1.8],
$k$-schemes having pseudo-rational singularities. Thus by [Reference KovácsKov17, 1.8], ![]() $Rm_*(\mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}}) \cong \mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}$. By applying the Artin–Schreier sequence we complete the proof of (3.4) and (ii). Applying (i), this also shows that
$Rm_*(\mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {conv}}}) \cong \mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu , w}^{\mathrm {BD}}}$. By applying the Artin–Schreier sequence we complete the proof of (3.4) and (ii). Applying (i), this also shows that ![]() $\mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$ is perverse if
$\mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$ is perverse if ![]() $\mathcal {F}_1^\bullet = \operatorname {IC}_{\mu }$ and
$\mathcal {F}_1^\bullet = \operatorname {IC}_{\mu }$ and ![]() $\mathcal {F}_2^{\bullet } = \operatorname {IC}_w^{\mathcal {F}\ell }$. Convolution on the left by
$\mathcal {F}_2^{\bullet } = \operatorname {IC}_w^{\mathcal {F}\ell }$. Convolution on the left by ![]() $\mathcal {Z}(\mathcal {F}_1^\bullet )$ sends short exact sequences in
$\mathcal {Z}(\mathcal {F}_1^\bullet )$ sends short exact sequences in ![]() $P_I(\mathcal {F}\ell , \mathbb {F}_p)$ to exact triangles in
$P_I(\mathcal {F}\ell , \mathbb {F}_p)$ to exact triangles in ![]() $D_c^b(\mathcal {F}\ell _\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ by a proof analogous to the one in [Reference CassCas19, 6.7]. Thus, by induction on the lengths of
$D_c^b(\mathcal {F}\ell _\unicode{x00E9}{\text {t}}, \mathbb {F}_p)$ by a proof analogous to the one in [Reference CassCas19, 6.7]. Thus, by induction on the lengths of ![]() $\mathcal {F}_1^\bullet$ and
$\mathcal {F}_1^\bullet$ and ![]() $\mathcal {F}_2^{\bullet }$ we conclude that
$\mathcal {F}_2^{\bullet }$ we conclude that ![]() $\mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$ is perverse in general. For equivariance, we note that because
$\mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$ is perverse in general. For equivariance, we note that because ![]() $\mathcal {Z}(\mathcal {F}_1^\bullet )$ is
$\mathcal {Z}(\mathcal {F}_1^\bullet )$ is ![]() $I$-equivariant,
$I$-equivariant, ![]() $\mathcal {Z}(\mathcal {F}_1^\bullet ) \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet }$ is
$\mathcal {Z}(\mathcal {F}_1^\bullet ) \overset {\sim }{\boxtimes } \mathcal {F}_2^{\bullet }$ is ![]() $I$-equivariant for the action of
$I$-equivariant for the action of ![]() $I$ on the left factor of
$I$ on the left factor of ![]() $LG \times ^I \mathcal {F}\ell$. As the map
$LG \times ^I \mathcal {F}\ell$. As the map ![]() $m$ is
$m$ is ![]() $I$-equivariant,
$I$-equivariant, ![]() $\mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$
$\mathcal {Z}(\mathcal {F}_1^\bullet ) * \mathcal {F}_2^{\bullet }$ ![]() $I$-equivariant by [Reference CassCas19, 3.2].
$I$-equivariant by [Reference CassCas19, 3.2].
To prove (iii) we use the functor
 \[ \operatorname{Gr}_{\mathcal{G}}^{\mathrm{conv}'}(R) = \left\{ (x, \mathcal{E}_1, \mathcal{E}_2, \beta_1, \beta_2) : \begin{array}{lr@{}} x \in C(R),\ \mathcal{E}_1, \mathcal{E}_2 \text{ are } \mathcal{G}\text{-torsors on } C_R,\\ \beta_1 \colon {\mathcal{E}_1}\left|_{C_R^\circ}\right. \cong { \mathcal{E}_0}\left|_{C_R^\circ}\right.,\ \beta_2 \colon {\mathcal{E}_2}\left|_{C_R - \Gamma_x}\right. \cong {\mathcal{E}_1}\left|_{C_R - \Gamma_x}\right. \\ \end{array} \!\!\!\right\}. \]
\[ \operatorname{Gr}_{\mathcal{G}}^{\mathrm{conv}'}(R) = \left\{ (x, \mathcal{E}_1, \mathcal{E}_2, \beta_1, \beta_2) : \begin{array}{lr@{}} x \in C(R),\ \mathcal{E}_1, \mathcal{E}_2 \text{ are } \mathcal{G}\text{-torsors on } C_R,\\ \beta_1 \colon {\mathcal{E}_1}\left|_{C_R^\circ}\right. \cong { \mathcal{E}_0}\left|_{C_R^\circ}\right.,\ \beta_2 \colon {\mathcal{E}_2}\left|_{C_R - \Gamma_x}\right. \cong {\mathcal{E}_1}\left|_{C_R - \Gamma_x}\right. \\ \end{array} \!\!\!\right\}. \]
By [Reference ZhuZhu14, 7.2.6], ![]() $\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}'}$ is ind-proper over
$\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}'}$ is ind-proper over ![]() $C$. There is also a map
$C$. There is also a map ![]() $m_{\mathcal {G}}' \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}'} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$ which sends
$m_{\mathcal {G}}' \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}'} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$ which sends ![]() $(x, \mathcal {E}_1, \mathcal {E}_2, \beta _1, \beta _2)$ to
$(x, \mathcal {E}_1, \mathcal {E}_2, \beta _1, \beta _2)$ to ![]() $(x, \mathcal {E}_2, \beta _1 \circ \beta _2)$. The map
$(x, \mathcal {E}_2, \beta _1 \circ \beta _2)$. The map ![]() $m_{\mathcal {G}}'$ is an isomorphism over
$m_{\mathcal {G}}'$ is an isomorphism over ![]() $C^\circ$ and it restricts to the convolution map
$C^\circ$ and it restricts to the convolution map ![]() $m \colon LG \times ^I \mathcal {F}\ell \rightarrow \mathcal {F}\ell$ over
$m \colon LG \times ^I \mathcal {F}\ell \rightarrow \mathcal {F}\ell$ over ![]() $0$.
$0$.
Suppose ![]() $\mathcal {F}_1^\bullet$ is supported on
$\mathcal {F}_1^\bullet$ is supported on ![]() $\operatorname {Gr}_{\leq \mu }$ and
$\operatorname {Gr}_{\leq \mu }$ and ![]() $\mathcal {F}_2^{\bullet }$ is supported on
$\mathcal {F}_2^{\bullet }$ is supported on ![]() $\mathcal {F}\ell _{w}$. Let
$\mathcal {F}\ell _{w}$. Let ![]() $n$ be an integer large enough so that
$n$ be an integer large enough so that ![]() $\mathcal {L}^+ \mathcal {G}$ acts on
$\mathcal {L}^+ \mathcal {G}$ acts on ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ through the quotient
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ through the quotient ![]() $\mathcal {L}^+_n \mathcal {G}$. Then as in the proof of [Reference ZhuZhu14, 7.4 (ii)] there is an
$\mathcal {L}^+_n \mathcal {G}$. Then as in the proof of [Reference ZhuZhu14, 7.4 (ii)] there is an ![]() $\mathcal {L}^+_n \mathcal {G}$-torsor
$\mathcal {L}^+_n \mathcal {G}$-torsor ![]() $\mathcal {P}_n$ over
$\mathcal {P}_n$ over ![]() $\mathcal {F}\ell _{w} \times C$ such that
$\mathcal {F}\ell _{w} \times C$ such that ![]() $\mathcal {P}_n \times ^{\mathcal {L}^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \subset \overline {\operatorname {Gr}}_{\mathcal {G}}^{\mathrm {conv}'}$ is a closed subscheme with
$\mathcal {P}_n \times ^{\mathcal {L}^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \subset \overline {\operatorname {Gr}}_{\mathcal {G}}^{\mathrm {conv}'}$ is a closed subscheme with
The scheme ![]() $\mathcal {P}_n \times ^{L^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is strongly
$\mathcal {P}_n \times ^{L^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is strongly ![]() $F$-regular by Lemma 2.14 and because this property is local in the smooth topology by Lemma 2.16. Let
$F$-regular by Lemma 2.14 and because this property is local in the smooth topology by Lemma 2.16. Let ![]() $\varphi _n^{\mathrm {conv}'} \colon \mathcal {P}_n \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow \mathcal {P}_n \times ^{\mathcal {L}^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ be the resulting
$\varphi _n^{\mathrm {conv}'} \colon \mathcal {P}_n \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \mu } \rightarrow \mathcal {P}_n \times ^{\mathcal {L}^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ be the resulting ![]() $\mathcal {L}^+_n \mathcal {G}$-torsor.
$\mathcal {L}^+_n \mathcal {G}$-torsor.
Since ![]() $j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is
$j_{\mathcal {G}, !*}(\mathcal {F}_1^\bullet \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is ![]() $\mathcal {L}^+_n \mathcal {G}$-equivariant (see the proof of Proposition 2.21), by arguments analogous to those in the proof of (ii) we can form the perverse sheaf
$\mathcal {L}^+_n \mathcal {G}$-equivariant (see the proof of Proposition 2.21), by arguments analogous to those in the proof of (ii) we can form the perverse sheaf
which is supported on ![]() $\mathcal {P}_n \times ^{L^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$. Here we are applying the operation
$\mathcal {P}_n \times ^{L^+_n \mathcal {G}} \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$. Here we are applying the operation ![]() $\overset {\sim }{\boxtimes }$ with respect to the fiber product of
$\overset {\sim }{\boxtimes }$ with respect to the fiber product of ![]() $C$-schemes rather than
$C$-schemes rather than ![]() $k$-schemes. If
$k$-schemes. If ![]() $\mathcal {F}_1^\bullet = \operatorname {IC}_\mu$ and
$\mathcal {F}_1^\bullet = \operatorname {IC}_\mu$ and ![]() $\mathcal {F}_2^{\bullet } = \operatorname {IC}_{w}^{\mathcal {F}\ell }$ then
$\mathcal {F}_2^{\bullet } = \operatorname {IC}_{w}^{\mathcal {F}\ell }$ then ![]() $(\operatorname {IC}_{w}^{\mathcal {F}\ell } \overset {L}{\boxtimes } \, \mathbb {F}_p[1]) \overset {\sim }{\boxtimes } j_{\mathcal {G}, !*}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is a constant sheaf. Let
$(\operatorname {IC}_{w}^{\mathcal {F}\ell } \overset {L}{\boxtimes } \, \mathbb {F}_p[1]) \overset {\sim }{\boxtimes } j_{\mathcal {G}, !*}(\operatorname {IC}_\mu \overset {L}{\boxtimes } \, {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$ is a constant sheaf. Let ![]() $\mathcal {F}\ell _{w, n}$ be the
$\mathcal {F}\ell _{w, n}$ be the ![]() $I_n$-torsor
$I_n$-torsor ![]() $(\mathcal {P}_n)_{0}$ over
$(\mathcal {P}_n)_{0}$ over ![]() $\mathcal {F}\ell _{w}$. By taking the fiber over
$\mathcal {F}\ell _{w}$. By taking the fiber over ![]() $0$ we get the following Cartesian diagram.
$0$ we get the following Cartesian diagram.

Now we can finish the proof by following arguments analogous to those in the proof of (ii) to establish isomorphisms
and
In this last isomorphism we are applying the natural isomorphism ![]() $\mathcal {F}\ell _w \times C^\circ \times \operatorname {Gr}_{\leq \mu } \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _w$. We leave the details to the reader.
$\mathcal {F}\ell _w \times C^\circ \times \operatorname {Gr}_{\leq \mu } \cong \operatorname {Gr}_{\leq \mu } \times C^\circ \times \mathcal {F}\ell _w$. We leave the details to the reader.
Before we finish the proof of Theorem 1.1 we introduce the functor
There are isomorphisms
Moreover, by arguments similar to those proceeding [Reference ZhuZhu14, 6.2.3],
Thus ![]() $\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''}$ is ind-proper over
$\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''}$ is ind-proper over ![]() $C$. We define
$C$. We define ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ to be the reduced closure of the subscheme
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ to be the reduced closure of the subscheme ![]() $\operatorname {Gr}_{\leq \mu } {\tilde{ \times }} \operatorname {Gr}_{\leq \lambda } \times C^{\circ } \subset \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''}$.
$\operatorname {Gr}_{\leq \mu } {\tilde{ \times }} \operatorname {Gr}_{\leq \lambda } \times C^{\circ } \subset \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''}$.
Proposition 3.8 The scheme ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ is Cohen–Macaulay,
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ is Cohen–Macaulay, ![]() $(\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda })_0$ is reduced, and
$(\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda })_0$ is reduced, and
Proof. Note that ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ is a closed subscheme of
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ is a closed subscheme of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$, and these two schemes are isomorphic over
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$, and these two schemes are isomorphic over ![]() $C^\circ$. Thus the isomorphism in the proposition will follow if we show that
$C^\circ$. Thus the isomorphism in the proposition will follow if we show that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible.
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible.
To prove that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible, fix an integer
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible, fix an integer ![]() $n$ large enough so that
$n$ large enough so that ![]() $\mathcal {L}^+\mathcal {G}$ acts on
$\mathcal {L}^+\mathcal {G}$ acts on ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ through the quotient
$\overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ through the quotient ![]() $\mathcal {L}^+_n \mathcal {G}$. Let
$\mathcal {L}^+_n \mathcal {G}$. Let ![]() $\mathcal {L}\mathcal {G}_{\leq \mu }$ be the preimage of
$\mathcal {L}\mathcal {G}_{\leq \mu }$ be the preimage of ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ under the quotient map
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ under the quotient map ![]() $\mathcal {L} \mathcal {G} \rightarrow \mathcal {L} \mathcal {G} / \mathcal {L}^+ \mathcal {G} \cong \operatorname {Gr}_{\mathcal {G}}$, and let
$\mathcal {L} \mathcal {G} \rightarrow \mathcal {L} \mathcal {G} / \mathcal {L}^+ \mathcal {G} \cong \operatorname {Gr}_{\mathcal {G}}$, and let
Then there is a right ![]() $\mathcal {L}^+_n \mathcal {G}$-torsor
$\mathcal {L}^+_n \mathcal {G}$-torsor ![]() $\varphi _{\mathcal {G}, n} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ such that
$\varphi _{\mathcal {G}, n} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ such that
Thus it suffices to show that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ is irreducible.
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ is irreducible.
Because ![]() $\mathcal {L}^+_n \mathcal {G}$ has geometrically irreducible fibers, to prove that
$\mathcal {L}^+_n \mathcal {G}$ has geometrically irreducible fibers, to prove that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ is irreducible it suffices to prove that
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ is irreducible it suffices to prove that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible. Since
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible. Since ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu }$ and
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu }$ and ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ are flat over
$\overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ are flat over ![]() $C$, it follows that
$C$, it follows that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is flat over
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is flat over ![]() $C$. Thus since
$C$. Thus since ![]() $ {\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }}\left|_{C^\circ }\right. = \operatorname {Gr}_{\leq \mu } \times \operatorname {Gr}_{\leq \lambda } \times C^\circ$ is irreducible it follows that
$ {\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }}\left|_{C^\circ }\right. = \operatorname {Gr}_{\leq \mu } \times \operatorname {Gr}_{\leq \lambda } \times C^\circ$ is irreducible it follows that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible. Putting this all together, we have shown that
$\overline {\operatorname {Gr}}_{\mathcal {G},\mu } \times _C \overline {\operatorname {Gr}}_{\mathcal {G},\lambda }$ is irreducible. Putting this all together, we have shown that ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda } \cong (\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_{\text {red}}$.
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda } \cong (\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_{\text {red}}$.
By Corollary 2.13, the fibers ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0$ and
$(\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0$ and ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ are reduced and Cohen–Macaulay. Hence the product
$(\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ are reduced and Cohen–Macaulay. Hence the product ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0 \times (\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ is also reduced and Cohen–Macaulay. As these two properties are local in the smooth topology,
$(\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0 \times (\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ is also reduced and Cohen–Macaulay. As these two properties are local in the smooth topology, ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0 {\tilde{ \times }} (\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ is reduced and Cohen–Macaulay. Thus by the isomorphism
$(\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0 {\tilde{ \times }} (\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ is reduced and Cohen–Macaulay. Thus by the isomorphism ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda } \cong (\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_{\text {red}}$ it follows that
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda } \cong (\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_{\text {red}}$ it follows that ![]() $(\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda })_0 \cong (\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0 {\tilde{ \times }} (\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ is reduced and Cohen–Macaulay. As
$(\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda })_0 \cong (\overline {\operatorname {Gr}}_{\mathcal {G},\mu })_0 {\tilde{ \times }} (\overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_0$ is reduced and Cohen–Macaulay. As ![]() $ {\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }}\left|_{C^\circ }\right.$ is also Cohen–Macaulay then
$ {\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }}\left|_{C^\circ }\right.$ is also Cohen–Macaulay then ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ is Cohen–Macaulay.
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ is Cohen–Macaulay.
Proof of Theorem 1.1(v). There is a morphism ![]() $m_{\mathcal {G}}'' \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''} \rightarrow \operatorname {Gr}_{\mathcal {G}}$ which sends the element
$m_{\mathcal {G}}'' \colon \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''} \rightarrow \operatorname {Gr}_{\mathcal {G}}$ which sends the element ![]() $(x, \mathcal {E}_1, \mathcal {E}_2, \beta _1, \beta _2)$ to
$(x, \mathcal {E}_1, \mathcal {E}_2, \beta _1, \beta _2)$ to ![]() $(x, \mathcal {E}_2, \beta _1 \circ \beta _2)$. Over points in
$(x, \mathcal {E}_2, \beta _1 \circ \beta _2)$. Over points in ![]() $C^\circ (k)$ the morphism
$C^\circ (k)$ the morphism ![]() $m_{\mathcal {G}}''$ is the convolution morphism
$m_{\mathcal {G}}''$ is the convolution morphism ![]() $LG \times ^{L^+G} \operatorname {Gr} \rightarrow \operatorname {Gr}$ and over
$LG \times ^{L^+G} \operatorname {Gr} \rightarrow \operatorname {Gr}$ and over ![]() $0$ the morphism
$0$ the morphism ![]() $m_{\mathcal {G}}''$ is
$m_{\mathcal {G}}''$ is ![]() $m \colon LG \times ^I \mathcal {F}\ell \rightarrow \mathcal {F}\ell$. By taking the fibers of
$m \colon LG \times ^I \mathcal {F}\ell \rightarrow \mathcal {F}\ell$. By taking the fibers of ![]() $m_{\mathcal {G}}''$ over
$m_{\mathcal {G}}''$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$ we get the following diagram with Cartesian squares.
$0$ we get the following diagram with Cartesian squares.

Because the schemes ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda } = (\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_{\text {red}}$ for
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda } = (\overline {\operatorname {Gr}}_{\mathcal {G},\mu } {\tilde{ \times }} \overline {\operatorname {Gr}}_{\mathcal {G},\lambda })_{\text {red}}$ for ![]() $\mu$,
$\mu$, ![]() $\lambda \in X_*(T)^+$ are Cohen–Macaulay, by similar reasoning to that in [Reference CassCas19, 6.2] we can form the perverse sheaf
$\lambda \in X_*(T)^+$ are Cohen–Macaulay, by similar reasoning to that in [Reference CassCas19, 6.2] we can form the perverse sheaf
To complete the proof it suffices to construct natural isomorphisms
(i)
 $Ri^{{\rm conv}'',*}[-1](\mathcal {F}_{1,2}^\bullet ) \cong \mathcal {Z}(\mathcal {F}_1^\bullet ) \overset {\sim }{\boxtimes } \mathcal {Z}(\mathcal {F}_1^\bullet )$,
$Ri^{{\rm conv}'',*}[-1](\mathcal {F}_{1,2}^\bullet ) \cong \mathcal {Z}(\mathcal {F}_1^\bullet ) \overset {\sim }{\boxtimes } \mathcal {Z}(\mathcal {F}_1^\bullet )$,(ii)
 $Rm_*(Ri^{{\rm conv}'',*}[-1](\mathcal {F}_{1,2}^\bullet )) \cong \mathcal {Z}( \mathcal {F}_1^\bullet * \mathcal {F}^\bullet _2).$
$Rm_*(Ri^{{\rm conv}'',*}[-1](\mathcal {F}_{1,2}^\bullet )) \cong \mathcal {Z}( \mathcal {F}_1^\bullet * \mathcal {F}^\bullet _2).$
Suppose ![]() $\mathcal {F}_1^\bullet$ is supported on
$\mathcal {F}_1^\bullet$ is supported on ![]() $\operatorname {Gr}_{\leq \mu }$ and
$\operatorname {Gr}_{\leq \mu }$ and ![]() $\mathcal {F}_2^{\bullet }$ is supported on
$\mathcal {F}_2^{\bullet }$ is supported on ![]() $\operatorname {Gr}_{\leq \lambda }$. As in the proof of Proposition 3.8, fix an integer
$\operatorname {Gr}_{\leq \lambda }$. As in the proof of Proposition 3.8, fix an integer ![]() $n$ large enough so that
$n$ large enough so that ![]() $\mathcal {L}^+\mathcal {G}$ acts on
$\mathcal {L}^+\mathcal {G}$ acts on ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ through the quotient
$\overline {\operatorname {Gr}}_{\mathcal {G}, \lambda }$ through the quotient ![]() $\mathcal {L}^+_n \mathcal {G}$. Let
$\mathcal {L}^+_n \mathcal {G}$. Let ![]() $\varphi _{\mathcal {G}, n} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ be the right
$\varphi _{\mathcal {G}, n} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ be the right ![]() $\mathcal {L}^+_n \mathcal {G}$-torsor such that
$\mathcal {L}^+_n \mathcal {G}$-torsor such that
Let ![]() $\varphi _n^{\mathrm {conv}''} \colon (\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \lambda })_{\text {red}} \rightarrow \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ be the resulting
$\varphi _n^{\mathrm {conv}''} \colon (\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \times _C \overline {\operatorname {Gr}}_{\mathcal {G}, \lambda })_{\text {red}} \rightarrow \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$ be the resulting ![]() $\mathcal {L}^+_n \mathcal {G}$-torsor over
$\mathcal {L}^+_n \mathcal {G}$-torsor over ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$. Over points in
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu , \lambda }$. Over points in ![]() $C^\circ$ the map
$C^\circ$ the map ![]() $\varphi _{\mathcal {G},n} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ restricts to an
$\varphi _{\mathcal {G},n} \colon \overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ restricts to an ![]() $L^nG$-torsor
$L^nG$-torsor ![]() $p_n \colon \operatorname {Gr}_{\leq \mu , n} \rightarrow \operatorname {Gr}_{\leq \mu }$. By taking the fibers of
$p_n \colon \operatorname {Gr}_{\leq \mu , n} \rightarrow \operatorname {Gr}_{\leq \mu }$. By taking the fibers of ![]() $\varphi _n^{\mathrm {conv}''}$ over
$\varphi _n^{\mathrm {conv}''}$ over ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$ we get the following diagram with Cartesian squares.
$0$ we get the following diagram with Cartesian squares.

An isomorphism as in (i) can be constructed in a manner similar to (3.2) by pulling everything back to ![]() $(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n})_{0} \times (\overline {\operatorname {Gr}}_{\mathcal {G}, \lambda })_0$. We leave the details to the reader. By using the left-hand side of the above diagram one can also prove that
$(\overline {\operatorname {Gr}}_{\mathcal {G}, \mu ,n})_{0} \times (\overline {\operatorname {Gr}}_{\mathcal {G}, \lambda })_0$. We leave the details to the reader. By using the left-hand side of the above diagram one can also prove that
By the proper base change theorem, to prove (ii) it suffices to construct a natural isomorphism
(iii)
 $Rm_{\mathcal {G},*}''(\mathcal {F}_{1,2}^\bullet ) \cong j_{\mathcal {G},!*}((\mathcal {F}_1^\bullet * \mathcal {F}_2^\bullet ) \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$.
$Rm_{\mathcal {G},*}''(\mathcal {F}_{1,2}^\bullet ) \cong j_{\mathcal {G},!*}((\mathcal {F}_1^\bullet * \mathcal {F}_2^\bullet ) \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.)$.
By the description of ![]() $m_{\mathcal {G}}''$ over
$m_{\mathcal {G}}''$ over ![]() $C^\circ$ there is a natural isomorphism
$C^\circ$ there is a natural isomorphism
Thus the left-hand side of ![]() $({\rm iii})$ is naturally an extension of
$({\rm iii})$ is naturally an extension of ![]() $(\mathcal {F}_1^\bullet * \mathcal {F}_2^\bullet ) \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.$, so we just need to show it is isomorphic to the intermediate extension. By semisimplicity we reduce to the case
$(\mathcal {F}_1^\bullet * \mathcal {F}_2^\bullet ) \overset {L}{\boxtimes } {\mathbb {F}_p[1]}\left|_{C^\circ }\right.$, so we just need to show it is isomorphic to the intermediate extension. By semisimplicity we reduce to the case ![]() $\mathcal {F}_i^\bullet = \operatorname {IC}_{\mu _i}$ for
$\mathcal {F}_i^\bullet = \operatorname {IC}_{\mu _i}$ for ![]() $\mu _i \in X_*(T)^+$. Note that
$\mu _i \in X_*(T)^+$. Note that ![]() $m_{\mathcal {G}}''$ maps
$m_{\mathcal {G}}''$ maps ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}$ onto
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}$ onto ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$, where
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$, where ![]() $\mu = \mu _1+\mu _2$. Moreover,
$\mu = \mu _1+\mu _2$. Moreover, ![]() $\operatorname {IC}_{\mu _1} * \operatorname {IC}_{\mu _2} \cong \operatorname {IC}_\mu$ by [Reference CassCas19, 1.2]. Thus,
$\operatorname {IC}_{\mu _1} * \operatorname {IC}_{\mu _2} \cong \operatorname {IC}_\mu$ by [Reference CassCas19, 1.2]. Thus, ![]() $\mathcal {F}_{1,2}^\bullet$ and the right-hand side of
$\mathcal {F}_{1,2}^\bullet$ and the right-hand side of ![]() $({\rm iii})$ are shifted constant sheaves.
$({\rm iii})$ are shifted constant sheaves.
Because the convolution morphism ![]() $\operatorname {Gr}_{\leq \mu _1} {\tilde{ \times }} \operatorname {Gr}_{\leq \mu _2} \rightarrow \operatorname {Gr}_{\leq \mu }$ is birational, the morphism
$\operatorname {Gr}_{\leq \mu _1} {\tilde{ \times }} \operatorname {Gr}_{\leq \mu _2} \rightarrow \operatorname {Gr}_{\leq \mu }$ is birational, the morphism ![]() $m_{\mathcal {G}}'' \colon \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is also birational. We claim that
$m_{\mathcal {G}}'' \colon \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is also birational. We claim that ![]() $m_{\mathcal {G}}'' \colon \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is projective. To prove this, note that
$m_{\mathcal {G}}'' \colon \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is projective. To prove this, note that ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is projective over
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is projective over ![]() $C$ by [Reference Pappas and ZhuPZ13, 5.5]. As
$C$ by [Reference Pappas and ZhuPZ13, 5.5]. As ![]() $\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''} \cong \operatorname {Gr}_{\mathcal {G}} {\tilde{ \times }} \operatorname {Gr}_{\mathcal {G}} \cong \operatorname {Gr}_{\mathcal {G}} \times _C \operatorname {Gr}_{\mathcal {G}}$ (see, for example, [Reference ZhuZhu17, 1.2.14]),
$\operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}''} \cong \operatorname {Gr}_{\mathcal {G}} {\tilde{ \times }} \operatorname {Gr}_{\mathcal {G}} \cong \operatorname {Gr}_{\mathcal {G}} \times _C \operatorname {Gr}_{\mathcal {G}}$ (see, for example, [Reference ZhuZhu17, 1.2.14]), ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}$ is also projective over
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}$ is also projective over ![]() $C$. Thus
$C$. Thus ![]() $m_{\mathcal {G}}'' \colon \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is projective. Therefore, since
$m_{\mathcal {G}}'' \colon \overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2} \rightarrow \overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ is projective. Therefore, since ![]() $\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ has pseudo-rational singularities and
$\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }$ has pseudo-rational singularities and ![]() $\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}$ is Cohen–Macaulay we have
$\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}$ is Cohen–Macaulay we have ![]() $Rm_{\mathcal {G},*}''(\mathcal {O}_{\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}}) \cong \mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}$ by [Reference KovácsKov17, 1.4]. Now
$Rm_{\mathcal {G},*}''(\mathcal {O}_{\overline {\operatorname {Gr}}^{\mathrm {conv}''}_{\mathcal {G}, \mu _1, \mu _2}}) \cong \mathcal {O}_{\overline {\operatorname {Gr}}_{\mathcal {G}, \mu }}$ by [Reference KovácsKov17, 1.4]. Now ![]() $({\rm iii})$ follows by applying the Artin–Schreier sequence.
$({\rm iii})$ follows by applying the Artin–Schreier sequence.
Remark 3.9 We have proved Theorem 1.1 under the hypothesis that ![]() $G_{\text {der}}$ is simply connected and almost simple. We now explain how to remove the simple connectedness hypothesis using the same technique as in [Reference CassCas19, 7.12]. The same idea is also used in [Reference ZhuZhu14, 3.3].
$G_{\text {der}}$ is simply connected and almost simple. We now explain how to remove the simple connectedness hypothesis using the same technique as in [Reference CassCas19, 7.12]. The same idea is also used in [Reference ZhuZhu14, 3.3].
Let ![]() $G$ be a connected reductive group over
$G$ be a connected reductive group over ![]() $k$ such that
$k$ such that ![]() $G_{\text {der}}$ is almost simple. By [Reference Milne and ShihMS82, 3.1] there exists a central extension
$G_{\text {der}}$ is almost simple. By [Reference Milne and ShihMS82, 3.1] there exists a central extension
such that ![]() $G'_{\operatorname {der}}$ is simply connected and
$G'_{\operatorname {der}}$ is simply connected and ![]() $N$ is a connected torus. Since
$N$ is a connected torus. Since ![]() $G_{\text {der}}$ is almost simple, so is
$G_{\text {der}}$ is almost simple, so is ![]() $G'_{\text {der}}$. Let
$G'_{\text {der}}$. Let ![]() $T' \subset B' \subset G'$ be the maximal torus and Borel subgroup given by the preimages of
$T' \subset B' \subset G'$ be the maximal torus and Borel subgroup given by the preimages of ![]() $T$ and
$T$ and ![]() $B$, and let
$B$, and let ![]() $I' \subset L^+G'$ be the preimage of
$I' \subset L^+G'$ be the preimage of ![]() $B'$ under the projection
$B'$ under the projection ![]() $L^+G' \rightarrow G'$. Let
$L^+G' \rightarrow G'$. Let ![]() $\operatorname {Gr}_G$ and
$\operatorname {Gr}_G$ and ![]() $\operatorname {Gr}_{G'}$ be the affine Grassmannians for
$\operatorname {Gr}_{G'}$ be the affine Grassmannians for ![]() $G$ and
$G$ and ![]() $G'$, respectively. Similarly, let
$G'$, respectively. Similarly, let ![]() $\mathcal {F}\ell _{G}$ and
$\mathcal {F}\ell _{G}$ and ![]() $\mathcal {F}\ell _{G'}$ be the Iwahori affine flag varieties.
$\mathcal {F}\ell _{G'}$ be the Iwahori affine flag varieties.
Because ![]() $N$ is connected the map
$N$ is connected the map ![]() $X_*(T') \rightarrow X_*(T)$ is surjective. Hence the maps
$X_*(T') \rightarrow X_*(T)$ is surjective. Hence the maps ![]() $\operatorname {Gr}_{G'} \rightarrow \operatorname {Gr}_{G}$ and
$\operatorname {Gr}_{G'} \rightarrow \operatorname {Gr}_{G}$ and ![]() $\mathcal {F}\ell _{G'} \rightarrow \mathcal {F}\ell _{G}$ are surjective. Let
$\mathcal {F}\ell _{G'} \rightarrow \mathcal {F}\ell _{G}$ are surjective. Let ![]() $\varphi _1 \colon X_*(T')^+ \rightarrow X_*(T)^+$ be the induced surjection on dominant cocharacters and let
$\varphi _1 \colon X_*(T')^+ \rightarrow X_*(T)^+$ be the induced surjection on dominant cocharacters and let ![]() $\varphi _2 \colon \tilde {W}' \rightarrow \tilde {W}$ be the induced surjection on Iwahori–Weyl groups. Each connected component of
$\varphi _2 \colon \tilde {W}' \rightarrow \tilde {W}$ be the induced surjection on Iwahori–Weyl groups. Each connected component of ![]() $\operatorname {Gr}_{G'}$ maps onto its image in
$\operatorname {Gr}_{G'}$ maps onto its image in ![]() $\operatorname {Gr}_{G}$ via a universal homeomorphism by [Reference Hamacher and ViehmannHV18, 3.1]. The same is true of the map
$\operatorname {Gr}_{G}$ via a universal homeomorphism by [Reference Hamacher and ViehmannHV18, 3.1]. The same is true of the map ![]() $\mathcal {F}\ell _{G'} \rightarrow \mathcal {F}\ell _{G}$.
$\mathcal {F}\ell _{G'} \rightarrow \mathcal {F}\ell _{G}$.
There is also a Bruhat–Tits group scheme ![]() $\mathcal {G}'$ over
$\mathcal {G}'$ over ![]() $C$ satisfying the conditions (2.3) and equipped with a natural map
$C$ satisfying the conditions (2.3) and equipped with a natural map ![]() $\mathcal {G}' \rightarrow \mathcal {G}$. This induces a map
$\mathcal {G}' \rightarrow \mathcal {G}$. This induces a map ![]() $\operatorname {Gr}_{\mathcal {G}'} \rightarrow \operatorname {Gr}_{\mathcal {G}}$. By restricting this map to
$\operatorname {Gr}_{\mathcal {G}'} \rightarrow \operatorname {Gr}_{\mathcal {G}}$. By restricting this map to ![]() $C^\circ$ and
$C^\circ$ and ![]() $0$ one sees that
$0$ one sees that ![]() $\operatorname {Gr}_{\mathcal {G}'} \rightarrow \operatorname {Gr}_{\mathcal {G}}$ is surjective and maps each connected component of
$\operatorname {Gr}_{\mathcal {G}'} \rightarrow \operatorname {Gr}_{\mathcal {G}}$ is surjective and maps each connected component of ![]() $\operatorname {Gr}_{\mathcal {G}'}$ into its image via a universal homeomorphism. Similarly, there are maps
$\operatorname {Gr}_{\mathcal {G}'}$ into its image via a universal homeomorphism. Similarly, there are maps ![]() $\operatorname {Gr}_{\mathcal {G}'}^{\mathrm {BD}} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$,
$\operatorname {Gr}_{\mathcal {G}'}^{\mathrm {BD}} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {BD}}$, ![]() $\operatorname {Gr}_{\mathcal {G}'}^{\mathrm {conv}} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}}$, etc., which are surjective and restrict to universal homeomorphisms on connected components.
$\operatorname {Gr}_{\mathcal {G}'}^{\mathrm {conv}} \rightarrow \operatorname {Gr}_{\mathcal {G}}^{\mathrm {conv}}$, etc., which are surjective and restrict to universal homeomorphisms on connected components.
All of the diagrams of ![]() $C$-schemes we used in §§ 2 and 3 to prove Theorem 1.1 for
$C$-schemes we used in §§ 2 and 3 to prove Theorem 1.1 for ![]() $G'$ intertwine with the corresponding diagrams for
$G'$ intertwine with the corresponding diagrams for ![]() $G$. For example, we have the following commutative diagram.
$G$. For example, we have the following commutative diagram.

Thus, by the topological invariance of the étale site [Sta21, 04DY], our arguments in §§ 2 and 3 can be used to simultaneously prove Theorem 1.1 for both ![]() $G'$ and
$G'$ and ![]() $G$.
$G$.
4. Applications
4.1 The function–sheaf correspondence
Let ![]() $X_0$ be a separated scheme of finite type over
$X_0$ be a separated scheme of finite type over ![]() $\mathbb {F}_q$ and let
$\mathbb {F}_q$ and let ![]() $\mathcal {F}^\bullet _0 \in D_c^b(X_{0,\unicode{x00E9}\text {t}}, \mathbb {F}_p)$. Fix an embedding of
$\mathcal {F}^\bullet _0 \in D_c^b(X_{0,\unicode{x00E9}\text {t}}, \mathbb {F}_p)$. Fix an embedding of ![]() $\mathbb {F}_q$ into an algebraic closure
$\mathbb {F}_q$ into an algebraic closure ![]() $\overline {\mathbb {F}}_q$ and let
$\overline {\mathbb {F}}_q$ and let ![]() $F^* \in \operatorname {Gal}(\overline {\mathbb {F}}_q/\mathbb {F}_q)$ be the inverse of the map which sends
$F^* \in \operatorname {Gal}(\overline {\mathbb {F}}_q/\mathbb {F}_q)$ be the inverse of the map which sends ![]() $\alpha \mapsto \alpha ^q$. Let
$\alpha \mapsto \alpha ^q$. Let ![]() $X = X_0 \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(\overline {\mathbb {F}}_q)$ and let
$X = X_0 \times _{\operatorname {Spec}(\mathbb {F}_q)} \operatorname {Spec}(\overline {\mathbb {F}}_q)$ and let ![]() $\mathcal {F}^\bullet$ be the pullback of
$\mathcal {F}^\bullet$ be the pullback of ![]() $\mathcal {F}_0^\bullet$ to
$\mathcal {F}_0^\bullet$ to ![]() $X$. For
$X$. For ![]() $x \in X_0(\mathbb {F}_q)$ let
$x \in X_0(\mathbb {F}_q)$ let ![]() $\mathcal {F}^\bullet _x$ be the pullback of
$\mathcal {F}^\bullet _x$ be the pullback of ![]() $\mathcal {F}^\bullet$ along the composition
$\mathcal {F}^\bullet$ along the composition ![]() $\operatorname {Spec}(\overline {\mathbb {F}}_q) \rightarrow \operatorname {Spec}(\mathbb {F}_q) \xrightarrow {x} X_0$. Then each
$\operatorname {Spec}(\overline {\mathbb {F}}_q) \rightarrow \operatorname {Spec}(\mathbb {F}_q) \xrightarrow {x} X_0$. Then each ![]() $H^i(\mathcal {F}^\bullet _x)$ is a representation of
$H^i(\mathcal {F}^\bullet _x)$ is a representation of ![]() $\operatorname {Gal}(\overline {\mathbb {F}}_q/\mathbb {F}_q)$ and it makes sense to take the trace
$\operatorname {Gal}(\overline {\mathbb {F}}_q/\mathbb {F}_q)$ and it makes sense to take the trace ![]() $\operatorname {Tr}(F^*, H^i(\mathcal {F}^\bullet _x))$.
$\operatorname {Tr}(F^*, H^i(\mathcal {F}^\bullet _x))$.
We form a function ![]() $\operatorname {Tr}(\mathcal {F}^\bullet _0) \colon X_0(\mathbb {F}_q) \rightarrow \mathbb {F}_p$ by setting
$\operatorname {Tr}(\mathcal {F}^\bullet _0) \colon X_0(\mathbb {F}_q) \rightarrow \mathbb {F}_p$ by setting
See also [Reference DeligneSGA![]() , Ch. 2, § 1] for more information on the construction of the function
, Ch. 2, § 1] for more information on the construction of the function ![]() $\operatorname {Tr}(\mathcal {F}^\bullet _0)$. As in the case of
$\operatorname {Tr}(\mathcal {F}^\bullet _0)$. As in the case of ![]() $\overline {\mathbb {Q}}_{\ell }$-coefficients, we have the following theorem.
$\overline {\mathbb {Q}}_{\ell }$-coefficients, we have the following theorem.
Theorem 4.1 Let ![]() $X_0$ and
$X_0$ and ![]() $Y_0$ be separated schemes of finite type over
$Y_0$ be separated schemes of finite type over ![]() $\mathbb {F}_q$.
$\mathbb {F}_q$.
(i) Let
 $\mathcal {F}^\bullet _0 \in D_c^b(X_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$ and
$\mathcal {F}^\bullet _0 \in D_c^b(X_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$ and  $\mathcal {G}^\bullet _0 \in D_c^b(Y_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$. If
$\mathcal {G}^\bullet _0 \in D_c^b(Y_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$. If  $x \in (X_0 \times _{\operatorname {Spec}(\mathbb {F}_q)} Y_0)(\mathbb {F}_q)$ has images
$x \in (X_0 \times _{\operatorname {Spec}(\mathbb {F}_q)} Y_0)(\mathbb {F}_q)$ has images  $p_1(x) \in X_0(\mathbb {F}_q)$ and
$p_1(x) \in X_0(\mathbb {F}_q)$ and  $p_2(x) \in Y_0(\mathbb {F}_q)$ then
$p_2(x) \in Y_0(\mathbb {F}_q)$ then
 \[ \operatorname{Tr}\Bigl(\mathcal{F}^\bullet_0 \overset{L}{\boxtimes} \mathcal{G}^\bullet_0\Bigr)(x) = \operatorname{Tr}(\mathcal{F}^\bullet_0)(p_1(x)) \operatorname{Tr}(\mathcal{G}^\bullet_0)(p_2(x)). \]
\[ \operatorname{Tr}\Bigl(\mathcal{F}^\bullet_0 \overset{L}{\boxtimes} \mathcal{G}^\bullet_0\Bigr)(x) = \operatorname{Tr}(\mathcal{F}^\bullet_0)(p_1(x)) \operatorname{Tr}(\mathcal{G}^\bullet_0)(p_2(x)). \](ii) Let
 $f \colon Y_0 \rightarrow X_0$ be a morphism. If
$f \colon Y_0 \rightarrow X_0$ be a morphism. If  $\mathcal {F}^\bullet _0 \in D_c^b(X_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$ and
$\mathcal {F}^\bullet _0 \in D_c^b(X_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$ and  $y \in Y_0(\mathbb {F}_q)$ then
$y \in Y_0(\mathbb {F}_q)$ then
 \[ \operatorname{Tr}(Rf^* (\mathcal{F}^\bullet_0))(y) = \operatorname{Tr}(\mathcal{F}^\bullet_0)(f(y)). \]
\[ \operatorname{Tr}(Rf^* (\mathcal{F}^\bullet_0))(y) = \operatorname{Tr}(\mathcal{F}^\bullet_0)(f(y)). \](iii) If
 $\mathcal {F}^\bullet _0 \in D_c^b(X_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$ then
$\mathcal {F}^\bullet _0 \in D_c^b(X_{0, \unicode{x00E9} \text{t}}, \mathbb {F}_p)$ then
 \[ \displaystyle\sum_{x \in X_0(\mathbb{F}_q)} \operatorname{Tr}(\mathcal{F}^\bullet_0)(x) = \sum_i ({-}1)^i \operatorname{Tr}(F^*, R^i \Gamma_c (X,\mathcal{F}^\bullet)). \]
\[ \displaystyle\sum_{x \in X_0(\mathbb{F}_q)} \operatorname{Tr}(\mathcal{F}^\bullet_0)(x) = \sum_i ({-}1)^i \operatorname{Tr}(F^*, R^i \Gamma_c (X,\mathcal{F}^\bullet)). \]
Proof. Parts (i) and (ii) are immediate from the definitions, and part (iii) is [Reference DeligneSGA![]() , 4.1].
, 4.1].
4.2 Perverse  $\mathbb {F}_p$-sheaves over finite fields
$\mathbb {F}_p$-sheaves over finite fields
For the rest of § 4 we assume ![]() $G$ is a split connected reductive group defined over
$G$ is a split connected reductive group defined over ![]() $\mathbb {F}_q$ and that
$\mathbb {F}_q$ and that ![]() $G_{\operatorname {der}}$ is absolutely almost simple. Let
$G_{\operatorname {der}}$ is absolutely almost simple. Let ![]() $\operatorname {Gr}_{\mathbb {F}_q}$ and
$\operatorname {Gr}_{\mathbb {F}_q}$ and ![]() $\mathcal {F}\ell _{\mathbb {F}_q}$ denote the affine Grassmannian and affine flag variety viewed as ind-schemes over
$\mathcal {F}\ell _{\mathbb {F}_q}$ denote the affine Grassmannian and affine flag variety viewed as ind-schemes over ![]() $\mathbb {F}_q$. While we restricted to the case of an algebraically closed ground field in [Reference CassCas19], our constructions also work over an arbitrary perfect field of characteristic
$\mathbb {F}_q$. While we restricted to the case of an algebraically closed ground field in [Reference CassCas19], our constructions also work over an arbitrary perfect field of characteristic ![]() $p > 0$. In particular, we can construct the categories
$p > 0$. In particular, we can construct the categories ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ and
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ and ![]() $P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$. The main difference when working over
$P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$. The main difference when working over ![]() $\mathbb {F}_q$ is that there are more objects that are simple. In particular, [Reference CassCas19, 3.18] needs to be revised in this setting, as there are non-trivial simple étale local systems on
$\mathbb {F}_q$ is that there are more objects that are simple. In particular, [Reference CassCas19, 3.18] needs to be revised in this setting, as there are non-trivial simple étale local systems on ![]() $\operatorname {Spec}(\mathbb {F}_q)$.
$\operatorname {Spec}(\mathbb {F}_q)$.
As in the case of ![]() $\overline {\mathbb {Q}}_\ell$-coefficients in [Reference ZhuZhu17, 5.6], we will restrict ourselves to a certain subcategory of
$\overline {\mathbb {Q}}_\ell$-coefficients in [Reference ZhuZhu17, 5.6], we will restrict ourselves to a certain subcategory of ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ consisting of normalized perverse sheaves. More precisely, let
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ consisting of normalized perverse sheaves. More precisely, let ![]() $\mathcal {L}$ be the étale local system on
$\mathcal {L}$ be the étale local system on ![]() $\operatorname {Spec}(\mathbb {F}_q)$ corresponding to the representation
$\operatorname {Spec}(\mathbb {F}_q)$ corresponding to the representation ![]() $\operatorname {Gal}(\overline {\mathbb {F}}_q/ \mathbb {F}_q) \rightarrow \operatorname {GL}_1(\mathbb {F}_p)$ which sends
$\operatorname {Gal}(\overline {\mathbb {F}}_q/ \mathbb {F}_q) \rightarrow \operatorname {GL}_1(\mathbb {F}_p)$ which sends ![]() $F^*$ to
$F^*$ to ![]() $-1$. If
$-1$. If ![]() $X_0$ is a scheme over
$X_0$ is a scheme over ![]() $\mathbb {F}_q$ then we can also view
$\mathbb {F}_q$ then we can also view ![]() $\mathcal {L}$ as a local system on
$\mathcal {L}$ as a local system on ![]() $X_0$ by pulling back along
$X_0$ by pulling back along ![]() $X_0 \rightarrow \operatorname {Spec}(\mathbb {F}_q)$.
$X_0 \rightarrow \operatorname {Spec}(\mathbb {F}_q)$.
Let ![]() $\mu \in X_*(T)^+$ be such that
$\mu \in X_*(T)^+$ be such that ![]() $\dim \operatorname {Gr}_{\leq \mu }$ has parity
$\dim \operatorname {Gr}_{\leq \mu }$ has parity ![]() $p(\mu ) \in \{0, 1\}$. Because [Reference CassCas19, 1.7] also holds when
$p(\mu ) \in \{0, 1\}$. Because [Reference CassCas19, 1.7] also holds when ![]() $k$ is perfect (with the same proof),
$k$ is perfect (with the same proof), ![]() $\operatorname {IC}_\mu$ is isomorphic to the shifted constant sheaf
$\operatorname {IC}_\mu$ is isomorphic to the shifted constant sheaf ![]() $\mathbb {F}_p[\dim \operatorname {Gr}_{\leq \mu }]$ supported on
$\mathbb {F}_p[\dim \operatorname {Gr}_{\leq \mu }]$ supported on ![]() $\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$. We define the normalized
$\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$. We define the normalized ![]() $\operatorname {IC}$ complex
$\operatorname {IC}$ complex
Let ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}} \subset P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ be the Serre subcategory consisting of perverse sheaves whose simple subquotients are all of the form
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}} \subset P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ be the Serre subcategory consisting of perverse sheaves whose simple subquotients are all of the form ![]() $\operatorname {IC}_\mu ^{\mathrm {N}}$ for
$\operatorname {IC}_\mu ^{\mathrm {N}}$ for ![]() $\mu \in X_*(T)^+$.
$\mu \in X_*(T)^+$.
We claim the subcategory ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$ is monoidal. To prove this, we first note that the identity
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$ is monoidal. To prove this, we first note that the identity ![]() $\operatorname {IC}_{\mu _1} * \operatorname {IC}_{\mu _2} = \operatorname {IC}_{\mu _1+\mu _2}$ in [Reference CassCas19, 1.2] also holds over
$\operatorname {IC}_{\mu _1} * \operatorname {IC}_{\mu _2} = \operatorname {IC}_{\mu _1+\mu _2}$ in [Reference CassCas19, 1.2] also holds over ![]() $\mathbb {F}_q$. Indeed, this identity is derived from the result of Kovács [Reference KovácsKov17, 1.4] which is independent of the ground field. From this fact and the projection formula [Sta21, 0B54] it follows that
$\mathbb {F}_q$. Indeed, this identity is derived from the result of Kovács [Reference KovácsKov17, 1.4] which is independent of the ground field. From this fact and the projection formula [Sta21, 0B54] it follows that ![]() $\operatorname {IC}_{\mu _1}^{\mathrm {N}} * \operatorname {IC}_{\mu _2}^{\mathrm {N}} = \operatorname {IC}_{\mu _1+\mu _2}^{\mathrm {N}}$.
$\operatorname {IC}_{\mu _1}^{\mathrm {N}} * \operatorname {IC}_{\mu _2}^{\mathrm {N}} = \operatorname {IC}_{\mu _1+\mu _2}^{\mathrm {N}}$.
Using the same arguments as in [Reference CassCas19], one can show that ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$ is a symmetric monoidal category. For
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$ is a symmetric monoidal category. For ![]() $\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ let
$\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ let ![]() $\mathcal {F}_{\operatorname {Gr}}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ be its pullback to
$\mathcal {F}_{\operatorname {Gr}}^\bullet \in P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ be its pullback to ![]() $\operatorname {Gr}$. Then one can also show that
$\operatorname {Gr}$. Then one can also show that
is an exact, faithful, tensor functor.
For ![]() $\mu \in X_*(T)^+$ let
$\mu \in X_*(T)^+$ let
Let ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{N, \text {ss}} \subset P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$ be the tensor subcategory consisting of semisimple objects. If
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{N, \text {ss}} \subset P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$ be the tensor subcategory consisting of semisimple objects. If ![]() $p > 2$ the arguments in this paper also work over
$p > 2$ the arguments in this paper also work over ![]() $\mathbb {F}_q$ and give rise to a functor
$\mathbb {F}_q$ and give rise to a functor
which satisfies all parts of Theorem 1.1 and such that ![]() $\mathcal {Z}(\operatorname {IC}_\mu ^{\mathrm {N}}) \cong \mathcal {Z}_{\mathcal {A}(\mu )}^{\mathrm {N}}.$
$\mathcal {Z}(\operatorname {IC}_\mu ^{\mathrm {N}}) \cong \mathcal {Z}_{\mathcal {A}(\mu )}^{\mathrm {N}}.$
Remark 4.2 The functor ![]() $P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}} \rightarrow P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ induced by pullback is faithful and identifies the simple objects in these two categories, but it is not an equivalence of categories in general. The issue is that due to the failure of smooth base change, the group of extensions between two objects depends on the ground field (see the proof of [Reference CassCas19, 6.14]).
$P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}} \rightarrow P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)$ induced by pullback is faithful and identifies the simple objects in these two categories, but it is not an equivalence of categories in general. The issue is that due to the failure of smooth base change, the group of extensions between two objects depends on the ground field (see the proof of [Reference CassCas19, 6.14]).
4.3 Proofs of applications to Hecke algebras
In this section we prove Theorem 1.3 and Corollary 1.4. We fix an isomorphism ![]() $\mathbb {F}_q [\![ t ]\!] \cong \mathcal {O}_E$. Recall that if
$\mathbb {F}_q [\![ t ]\!] \cong \mathcal {O}_E$. Recall that if ![]() $H \subset G(E)$ is a compact open subgroup then the multiplication on
$H \subset G(E)$ is a compact open subgroup then the multiplication on ![]() $\mathcal {H}_H$ is defined by
$\mathcal {H}_H$ is defined by
We now verify that the function–sheaf correspondence respects the convolution of perverse sheaves and functions.
Lemma 4.3 If ![]() $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$, ![]() $\mathcal {F}_2^{\bullet } \in P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ then
$\mathcal {F}_2^{\bullet } \in P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)$ then
Similarly, if ![]() $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$, ![]() $\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$ then
$\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$ then
Proof. We will only consider the case ![]() $\mathcal {F}_1^\bullet$,
$\mathcal {F}_1^\bullet$, ![]() $\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$; the other case can be handled by similar methods. The proof is essentially the same as that of [Reference ZhuZhu17, 5.6.1] in the case of
$\mathcal {F}_2^{\bullet } \in P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$; the other case can be handled by similar methods. The proof is essentially the same as that of [Reference ZhuZhu17, 5.6.1] in the case of ![]() $\overline {\mathbb {Q}}_\ell$-coefficients, but because this lemma is important for our applications we will reproduce the details. Let
$\overline {\mathbb {Q}}_\ell$-coefficients, but because this lemma is important for our applications we will reproduce the details. Let ![]() $m \colon LG \times ^{I} \mathcal {F}\ell \rightarrow \mathcal {F}\ell$ be the multiplication map and let
$m \colon LG \times ^{I} \mathcal {F}\ell \rightarrow \mathcal {F}\ell$ be the multiplication map and let ![]() $x \in \mathcal {F}\ell _{\mathbb {F}_q}(\mathbb {F}_q) = G(E)/I$. There is a natural identification
$x \in \mathcal {F}\ell _{\mathbb {F}_q}(\mathbb {F}_q) = G(E)/I$. There is a natural identification ![]() $m^{-1}(x)(\mathbb {F}_q) = \{(xy, y^{-1}) : y \in G(E)/I\}$. By Theorem 4.1(iii) and the proper base change theorem,
$m^{-1}(x)(\mathbb {F}_q) = \{(xy, y^{-1}) : y \in G(E)/I\}$. By Theorem 4.1(iii) and the proper base change theorem,
Now viewing ![]() $xy$ and
$xy$ and ![]() $y^{-1}$ as elements of
$y^{-1}$ as elements of ![]() $G(E)/I$ and using Theorem 4.1(i) and (ii), we have
$G(E)/I$ and using Theorem 4.1(i) and (ii), we have
Lemma 4.4 Let ![]() $\mathcal {F}^\bullet \in P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$. Then
$\mathcal {F}^\bullet \in P_I(\mathcal {F}\ell _{\mathbb {F}_q}, \mathbb {F}_p)$. Then
Proof. If ![]() $x \in \operatorname {Gr}_{\mathbb {F}_q}(\mathbb {F}_q)$ then
$x \in \operatorname {Gr}_{\mathbb {F}_q}(\mathbb {F}_q)$ then ![]() $\pi ^{-1}(x)(\mathbb {F}_q) = \{xy : y \in K/I \}$. We claim that
$\pi ^{-1}(x)(\mathbb {F}_q) = \{xy : y \in K/I \}$. We claim that
The first equality follows from Theorem 4.1(iii) and the proper base change theorem. The other two equalities follow from the definitions.
Since ![]() $\operatorname {IC}_{\mu _1}^{\mathrm {N}} * \operatorname {IC}_{\mu _2}^{\mathrm {N}} = \operatorname {IC}_{\mu _1+\mu _2}^{\mathrm {N}}$ there is a natural isomorphism of
$\operatorname {IC}_{\mu _1}^{\mathrm {N}} * \operatorname {IC}_{\mu _2}^{\mathrm {N}} = \operatorname {IC}_{\mu _1+\mu _2}^{\mathrm {N}}$ there is a natural isomorphism of ![]() $\mathbb {F}_p$-algebras
$\mathbb {F}_p$-algebras
The next proposition shows that this isomorphism is compatible with the mod ![]() $p$ Satake isomorphism.
$p$ Satake isomorphism.
Proposition 4.5 The composition
is the inverse of the mod ![]() $p$ Satake isomorphism
$p$ Satake isomorphism ![]() $\mathcal {S}$.
$\mathcal {S}$.
Proof. When ![]() $G_{\text {der}}$ is simply connected, Herzig [Reference HerzigHer11a, 5.1] has computed
$G_{\text {der}}$ is simply connected, Herzig [Reference HerzigHer11a, 5.1] has computed
 \[ \mathcal{S}^{{-}1} \biggl( \sum_{\lambda \leq \mu} {\mathbb 1}_{\lambda} \biggr) = \mu \in \mathbb{F}_p[X_*(T)^+]. \]
\[ \mathcal{S}^{{-}1} \biggl( \sum_{\lambda \leq \mu} {\mathbb 1}_{\lambda} \biggr) = \mu \in \mathbb{F}_p[X_*(T)^+]. \]
While Herzig works with anti-dominant cocharacters, the formula above can be obtained from Herzig's formula by multiplying by the longest element of the Weyl group (see the proof of [Reference CassCas19, 1.3]). Herzig only uses the hypothesis that ![]() $G_{\text {der}}$ is simply connected to reduce to the case where the weight (a representation of
$G_{\text {der}}$ is simply connected to reduce to the case where the weight (a representation of ![]() $G(\mathbb {F}_q)$) is trivial. As the weight is trivial in our situation, the above formula is valid for any
$G(\mathbb {F}_q)$) is trivial. As the weight is trivial in our situation, the above formula is valid for any ![]() $G$. Since
$G$. Since ![]() $\operatorname {IC}_\mu$ is a constant sheaf supported on
$\operatorname {IC}_\mu$ is a constant sheaf supported on ![]() $\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$, the lemma now follows from our choice of normalized IC complexes
$\operatorname {Gr}_{\mathbb {F}_q, \leq \mu }$, the lemma now follows from our choice of normalized IC complexes ![]() $\operatorname {IC}_{\mu }^{\mathrm {N}}$.
$\operatorname {IC}_{\mu }^{\mathrm {N}}$.
Remark 4.6 In [Reference CassCas19] we worked over an algebraically closed field and described a natural map of ![]() $\mathbb {F}_p$-vector spaces
$\mathbb {F}_p$-vector spaces ![]() $K_0(P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)) \otimes \mathbb {F}_p \rightarrow \mathcal {H}_K$ which we proved is the inverse of the mod
$K_0(P_{L^+G}(\operatorname {Gr}, \mathbb {F}_p)) \otimes \mathbb {F}_p \rightarrow \mathcal {H}_K$ which we proved is the inverse of the mod ![]() $p$ Satake isomorphism, and hence also an isomorphism of
$p$ Satake isomorphism, and hence also an isomorphism of ![]() $\mathbb {F}_p$-algebras. It is possible to work over an algebraically closed field because, for
$\mathbb {F}_p$-algebras. It is possible to work over an algebraically closed field because, for ![]() $\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$,
$\mathcal {F}^\bullet \in P_{L^+G}(\operatorname {Gr}_{\mathbb {F}_q}, \mathbb {F}_p)^{\mathrm {N}}$, ![]() $\operatorname {Tr}(\mathcal {F}^\bullet )$ essentially counts the dimensions of the stalks of
$\operatorname {Tr}(\mathcal {F}^\bullet )$ essentially counts the dimensions of the stalks of ![]() $\mathcal {F}^\bullet$. However, one advantage of working over
$\mathcal {F}^\bullet$. However, one advantage of working over ![]() $\mathbb {F}_q$ is that Lemma 4.3 allows us to prove the existence of an isomorphism of
$\mathbb {F}_q$ is that Lemma 4.3 allows us to prove the existence of an isomorphism of ![]() $\mathbb {F}_p$-algebras
$\mathbb {F}_p$-algebras ![]() $\mathbb {F}_p[X_*(T)^+] \cong \mathcal {H}_K$ without using the existence of the mod
$\mathbb {F}_p[X_*(T)^+] \cong \mathcal {H}_K$ without using the existence of the mod ![]() $p$ Satake isomorphism.
$p$ Satake isomorphism.
Proof of Theorem 1.3 and Corollary 1.4. We observe that Theorem 1.3 follows immediately from Theorem 1.1 and Lemmas 4.3, 4.4. By [Reference OllivierOll14] the central integral Bernstein elements are uniquely determined by the identity ![]() $\mathcal {B} = \mathcal {C}^{-1} \circ \mathcal {S}^{-1}$, so Corollary 1.4 follows from Theorem 1.3 and Proposition 4.5.
$\mathcal {B} = \mathcal {C}^{-1} \circ \mathcal {S}^{-1}$, so Corollary 1.4 follows from Theorem 1.3 and Proposition 4.5.
Acknowledgements
It is a pleasure to thank M. Kisin, C. Pépin, and T. Schmidt for several discussions and comments on an earlier version of this paper. I thank the referee for their careful reading and helpful suggestions which improved the exposition and simplified some of the proofs. I also thank K. Koziol, R. Ollivier, M.-F. Vignéras, D. Yang, and X. Zhu for their interest and helpful conversations. Parts of this paper were written while the author visited the University of Paris 13 and the University of Rennes 1, and he would like to thank these institutions for their hospitality. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1144152.