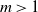1. Introduction
It is widely accepted that graphs/networks are an inherent feature of life today. The classical models
![]() $G_{n,m}$
and
$G_{n,m}$
and
![]() $G_{n,p}$
of Erdős and Rényi [Reference Erdős and Rényi17] and Gilbert [Reference Gilbert22], respectively, lacked some salient features of observed networks. In particular, they failed to have a degree distribution that decays polynomially. Barabási and Albert [Reference Barabási and Albert3] suggested the preferential attachment model (PAM) as a more realistic model of a ‘real-world’ network. There was a certain lack of rigor in [Reference Barabási and Albert3], and later Bollobás, Riordan, Spencer, and Tusnády [Reference Bollobás, Riordan, Spencer and Tusnády11] gave a rigorous definition.
$G_{n,p}$
of Erdős and Rényi [Reference Erdős and Rényi17] and Gilbert [Reference Gilbert22], respectively, lacked some salient features of observed networks. In particular, they failed to have a degree distribution that decays polynomially. Barabási and Albert [Reference Barabási and Albert3] suggested the preferential attachment model (PAM) as a more realistic model of a ‘real-world’ network. There was a certain lack of rigor in [Reference Barabási and Albert3], and later Bollobás, Riordan, Spencer, and Tusnády [Reference Bollobás, Riordan, Spencer and Tusnády11] gave a rigorous definition.
Many properties of this model have been studied. Bollobás and Riordan [Reference Bollobás and Riordan9] studied the diameter and proved that with high probability (w.h.p.) PAM with n vertices and
![]() $m>1$
attachments for every incoming vertex has diameter
$m>1$
attachments for every incoming vertex has diameter
![]() $\approx \log n/\log\log n$
. An earlier result by Pittel [Reference Pittel34] implied that for
$\approx \log n/\log\log n$
. An earlier result by Pittel [Reference Pittel34] implied that for
![]() $m=1$
w.h.p. the diameter of PAM is of exact order
$m=1$
w.h.p. the diameter of PAM is of exact order
![]() $\log n$
. Bollobás and Riordan [Reference Bollobás and Riordan7, Reference Bollobás and Riordan8] studied the effect on component size of deleting random edges from PAM and showed that it is quite robust w.h.p. The degree distribution was studied by Móri [Reference Móri30, Reference Móri31], Flaxman, Frieze, and Fenner [Reference Flaxman, Frieze and Fenner18], and Berger, Borgs, Chayes, and Saberi [Reference Berger, Borgs, Chayes and Saberi4]. Peköz, Röllin, and Ross [Reference Peköz, Röllin and Ross32] established convergence, with rate, of the joint distribution of the degrees of finitely many vertices. Acan and Hitczenko [Reference Acan and Hitczenko1] found an alternative proof, without rate, via a memory game. Pittel [Reference Pittel36] used the Bollobás–Riordan pairing model to approximate, with explicit error estimate, the degree sequence of the first
$\log n$
. Bollobás and Riordan [Reference Bollobás and Riordan7, Reference Bollobás and Riordan8] studied the effect on component size of deleting random edges from PAM and showed that it is quite robust w.h.p. The degree distribution was studied by Móri [Reference Móri30, Reference Móri31], Flaxman, Frieze, and Fenner [Reference Flaxman, Frieze and Fenner18], and Berger, Borgs, Chayes, and Saberi [Reference Berger, Borgs, Chayes and Saberi4]. Peköz, Röllin, and Ross [Reference Peköz, Röllin and Ross32] established convergence, with rate, of the joint distribution of the degrees of finitely many vertices. Acan and Hitczenko [Reference Acan and Hitczenko1] found an alternative proof, without rate, via a memory game. Pittel [Reference Pittel36] used the Bollobás–Riordan pairing model to approximate, with explicit error estimate, the degree sequence of the first
![]() $n^{m/(m+2)}$
vertices,
$n^{m/(m+2)}$
vertices,
![]() $m\ge 1$
, and proved that, for
$m\ge 1$
, and proved that, for
![]() $m>1$
, PAM is connected with probability
$m>1$
, PAM is connected with probability
![]() $\approx 1-{\textrm{O}}((\!\log n)^{-(m-1)/3})$
. Random walks on PAM have been considered in the work of Cooper and Frieze [Reference Cooper and Frieze14, Reference Cooper and Frieze15]. In [Reference Cooper and Frieze14] there are results on the proportion of vertices seen by a random walk on an evolving PAM and [Reference Cooper and Frieze15] determines the asymptotic cover time of a fully evolved PAM. Frieze and Pegden [Reference Frieze and Pegden20] used random walk in a ‘local algorithm’ to find vertex 1, improving results of Borgs et al. [Reference Borgs, Brautbar, Chayes, Khanna and Lucier12]. The mixing time of such a walk was analyzed by Mihail, Papadimitriou, and Saberi [Reference Mihail, Papadimitriou and Saberi28], who showed rapid mixing. Interpolating between Erdős–Rényi and preferential attachment, Pittel [Reference Pittel35] considered the birth of a giant component in a graph process
$\approx 1-{\textrm{O}}((\!\log n)^{-(m-1)/3})$
. Random walks on PAM have been considered in the work of Cooper and Frieze [Reference Cooper and Frieze14, Reference Cooper and Frieze15]. In [Reference Cooper and Frieze14] there are results on the proportion of vertices seen by a random walk on an evolving PAM and [Reference Cooper and Frieze15] determines the asymptotic cover time of a fully evolved PAM. Frieze and Pegden [Reference Frieze and Pegden20] used random walk in a ‘local algorithm’ to find vertex 1, improving results of Borgs et al. [Reference Borgs, Brautbar, Chayes, Khanna and Lucier12]. The mixing time of such a walk was analyzed by Mihail, Papadimitriou, and Saberi [Reference Mihail, Papadimitriou and Saberi28], who showed rapid mixing. Interpolating between Erdős–Rényi and preferential attachment, Pittel [Reference Pittel35] considered the birth of a giant component in a graph process
![]() $G_M$
on a fixed vertex set, when
$G_M$
on a fixed vertex set, when
![]() $G_{M+1}$
is obtained by inserting a new edge between vertices i and j with probability proportional to
$G_{M+1}$
is obtained by inserting a new edge between vertices i and j with probability proportional to
![]() $[\deg (i)+\delta]\cdot[\deg (j)+\delta]$
, with
$[\deg (i)+\delta]\cdot[\deg (j)+\delta]$
, with
![]() $\delta>0$
being fixed. Confirming a conjecture of Pittel [Reference Pittel35], Janson and Warnke [Reference Janson and Warnke25] recently determined the asymptotic size of the giant component in the supercritical phase in this graph model.
$\delta>0$
being fixed. Confirming a conjecture of Pittel [Reference Pittel35], Janson and Warnke [Reference Janson and Warnke25] recently determined the asymptotic size of the giant component in the supercritical phase in this graph model.
The paragraph above gives a small sample of results on PAM that can be related to its role as a model of a real-world network. It is safe to say that PAM has now been accepted into the pantheon of random graph models that can be studied from a purely combinatorial perspective. For example, Cooper, Klasing, and Zito [Reference Cooper, Klasing and Zito16] studied the size of the smallest dominating set and Frieze, Pérez-Giménez, Prałat, and Reiniger [Reference Frieze, Pérez-Giménez, Prałat and Reiniger21] studied the existence of perfect matchings and Hamilton cycles.
One source of our inspiration was the work of Móri [Reference Móri30, Reference Móri31]; see also Katona and Móri [Reference Katona and Móri27] and van der Hofstad [Reference van der Hofstad23]. They were able to construct a family of martingales in the form of factorial products, with arguments being the degrees of individual vertices. This allowed them to analyze the limiting behavior of vertex degrees in a
![]() $\delta$
-version of PAM. In this paper we construct a new factorial-type martingale with one argument being the total size of a ‘descendant’ subtree. This is a generalization of the martingale for
$\delta$
-version of PAM. In this paper we construct a new factorial-type martingale with one argument being the total size of a ‘descendant’ subtree. This is a generalization of the martingale for
![]() $\delta=0$
, found by Pittel [Reference Pittel36].
$\delta=0$
, found by Pittel [Reference Pittel36].
2. Our results
For each of the two models, PAM and UAM, we study the descendant tree of a given vertex v; it is a maximal subtree rooted at v and formed by increasing paths starting at v. The number of vertices in this subtree is a natural influence measure of vertex v. We also analyze the performance of two online greedy algorithms, for finding a large matching set and for a large independent set. Both algorithms are well known, and the classical random graphs are a gold mine for problems on the expected efficiency of these and similar algorithms, thanks to their homogeneity and independence. The PAM and UAM models are inherently more difficult, due to the rather limited scope of these properties. We carry out this analysis in the context of the PAM graph process described in [Reference Bollobás, Riordan, Spencer and Tusnády11] and its extension taken from [Reference van der Hofstad23, Chapter 8], and the UAM graph process; see [Reference Acan and Pittel2] and [Reference Frieze, Pérez-Giménez, Prałat and Reiniger21].
The PAM graph process,
![]() $\boldsymbol\delta$
-extension. Vertex 1 has m loops, so its degree is 2m initially. Recursively, vertex
$\boldsymbol\delta$
-extension. Vertex 1 has m loops, so its degree is 2m initially. Recursively, vertex
![]() $t+1$
has m edges, and it uses them one at a time either to connect to a vertex
$t+1$
has m edges, and it uses them one at a time either to connect to a vertex
![]() $x\in [t]$
or to loop back on itself.
$x\in [t]$
or to loop back on itself.
To describe the transition probabilities, let
![]() $d_{t,i-1}(x)$
denote the degree of vertex x just before the ith edge of vertex
$d_{t,i-1}(x)$
denote the degree of vertex x just before the ith edge of vertex
![]() $t+1$
arrives. Let w denote the random receiving end of the ith edge emanating from vertex
$t+1$
arrives. Let w denote the random receiving end of the ith edge emanating from vertex
![]() $t+1$
. Conditioned on
$t+1$
. Conditioned on
![]() $G_{m,\delta}(t)$
and the previous
$G_{m,\delta}(t)$
and the previous
![]() $i-1$
edges emanating from vertex
$i-1$
edges emanating from vertex
![]() $t+1$
, we have
$t+1$
, we have
 \begin{equation}\mathbb P(w=x) =\begin{cases} \dfrac{d_{t, i-1}(x) +\delta}{(2m + \delta)t + 2i-1 + i\delta/m} & \text{if $ x\in[t]$,}\\[15pt]\dfrac{d_{t,i-1}(t+1) +1+i\delta/m}{(2m + \delta)t + 2i-1 + i\delta/m} & \text{if $ x=t+1$.}\end{cases}\end{equation}
\begin{equation}\mathbb P(w=x) =\begin{cases} \dfrac{d_{t, i-1}(x) +\delta}{(2m + \delta)t + 2i-1 + i\delta/m} & \text{if $ x\in[t]$,}\\[15pt]\dfrac{d_{t,i-1}(t+1) +1+i\delta/m}{(2m + \delta)t + 2i-1 + i\delta/m} & \text{if $ x=t+1$.}\end{cases}\end{equation}
Thus one-step transition from
![]() $G_{m,\delta}(t)$
to
$G_{m,\delta}(t)$
to
![]() $G_{m,\delta}(t+1)$
is the m-long sequence of choices made by the m edges emanating from vertex
$G_{m,\delta}(t+1)$
is the m-long sequence of choices made by the m edges emanating from vertex
![]() $t+1$
, and given
$t+1$
, and given
![]() $G_{m,\delta}(t)$
, these choices form a Markov sequence.
$G_{m,\delta}(t)$
, these choices form a Markov sequence.
For
![]() $m=1$
, writing
$m=1$
, writing
![]() $d_t(x)$
for
$d_t(x)$
for
![]() $d_{t,0}(x)$
, the probabilities above can be written a little more simply in the form
$d_{t,0}(x)$
, the probabilities above can be written a little more simply in the form
 \begin{equation}\mathbb{P}({w=x})=\begin{cases} \dfrac{d_t(x)+\delta}{(2+\delta)t+(1+\delta)} & \text{if $ x \in [t]$,}\\[14pt] \dfrac{1+\delta}{(2+\delta)t+(1+\delta)} & \text{if $ x = t+1$.}\end{cases}\end{equation}
\begin{equation}\mathbb{P}({w=x})=\begin{cases} \dfrac{d_t(x)+\delta}{(2+\delta)t+(1+\delta)} & \text{if $ x \in [t]$,}\\[14pt] \dfrac{1+\delta}{(2+\delta)t+(1+\delta)} & \text{if $ x = t+1$.}\end{cases}\end{equation}
Bollobás and Riordan [Reference Bollobás and Riordan9] discovered the following coupling between
![]() $\{G_{m,0}(t)\}_t$
for
$\{G_{m,0}(t)\}_t$
for
![]() $m>1$
and
$m>1$
and
![]() $\{G_{1,0}(mt)\}_t$
. Start with the
$\{G_{1,0}(mt)\}_t$
. Start with the
![]() $\{G_{1,0}(t)\}$
random process and let the vertices be
$\{G_{1,0}(t)\}$
random process and let the vertices be
![]() $v_1,v_2,\dots$
. To obtain
$v_1,v_2,\dots$
. To obtain
![]() $\{G_{m,0}(t)\}$
from
$\{G_{m,0}(t)\}$
from
![]() $\{G_{1,0}(mt)\}$
:
$\{G_{1,0}(mt)\}$
:
-
(1) collapse the first m vertices
 $v_1,\dots,v_m$
into the first vertex
$v_1,\dots,v_m$
into the first vertex
 $w_1$
of
$w_1$
of
 $G_{m,0}(t)$
, the next m vertices
$G_{m,0}(t)$
, the next m vertices
 $v_{m+1},\dots,v_{2m}$
into the second vertex
$v_{m+1},\dots,v_{2m}$
into the second vertex
 $w_2$
of
$w_2$
of
 $G_{m,0}(t)$
, and so on;
$G_{m,0}(t)$
, and so on; -
(2) keep the full record of the multiple edges and loops formed by collapsing the blocks
 $\{v_{(i-1)m+1}, \dots, v_{im}\}$
for each i.
$\{v_{(i-1)m+1}, \dots, v_{im}\}$
for each i.
By doing this collapsing indefinitely we get the jointly defined Bollobás–Riordan graph processes
![]() $\{G_{m,0}(t)\}$
and
$\{G_{m,0}(t)\}$
and
![]() $\{G_{1,0}(mt)\}$
. The beauty of the
$\{G_{1,0}(mt)\}$
. The beauty of the
![]() $\delta$
-extended Bollobás–Riordan model is that, similarly, this collapsing operation applied to the process
$\delta$
-extended Bollobás–Riordan model is that, similarly, this collapsing operation applied to the process
![]() $\{G_{1,\delta/m}(mt)\}$
delivers the process
$\{G_{1,\delta/m}(mt)\}$
delivers the process
![]() $\{G_{m,\delta}(t)\}$
[Reference van der Hofstad23].
$\{G_{m,\delta}(t)\}$
[Reference van der Hofstad23].
(For the reader’s convenience we present the explanation in Appendix A.)
Remark 2.1. Note that the process is well-defined for
![]() $\delta\ge -m$
, since for such
$\delta\ge -m$
, since for such
![]() $\delta$
all the probabilities defined in (2.1) are non-negative and add up to 1. For
$\delta$
all the probabilities defined in (2.1) are non-negative and add up to 1. For
![]() $m=1$
and
$m=1$
and
![]() $\delta=-1$
, it is easy to see from (2.2) that there is no loop in the graph except the loop on the first vertex. Hence a vertex
$\delta=-1$
, it is easy to see from (2.2) that there is no loop in the graph except the loop on the first vertex. Hence a vertex
![]() $u>1$
starts with degree 1 and then its degree does not change, since as long as
$u>1$
starts with degree 1 and then its degree does not change, since as long as
![]() $d_t(u) + \delta = 0$
the vertex cannot attract any neighbors (again from (2.2)). As a result, in this case the graph is a star centered at vertex 1. It follows from the above coupling that
$d_t(u) + \delta = 0$
the vertex cannot attract any neighbors (again from (2.2)). As a result, in this case the graph is a star centered at vertex 1. It follows from the above coupling that
![]() $G_{m,-m}(t)$
is also a star centered at vertex 1, and the key problems we want to solve have trivial solutions in this extreme case.
$G_{m,-m}(t)$
is also a star centered at vertex 1, and the key problems we want to solve have trivial solutions in this extreme case.
The UAM graph process. Conceptually close to the preferential attachment model is the uniform attachment model (UAM). In this model, vertex
![]() $t+1$
selects uniformly at random (repetitions allowed) m vertices from the set [t] and attaches itself to these vertices. (See [Reference Acan and Pittel2] for connectivity and bootstrap percolation results.) This model can be thought of the limit of the PAM model as
$t+1$
selects uniformly at random (repetitions allowed) m vertices from the set [t] and attaches itself to these vertices. (See [Reference Acan and Pittel2] for connectivity and bootstrap percolation results.) This model can be thought of the limit of the PAM model as
![]() $\delta\to \infty$
except that loops are not allowed in this case.
$\delta\to \infty$
except that loops are not allowed in this case.
2.1. Number of descendants
Fix a positive integer r and let X(t) denote the number of descendants of r at time t. Here r is a descendant of r, and x is a descendant of r if and only if x chooses to attach itself to at least one descendant of r in step x. In other words, if we think of the graph as a directed graph with edges oriented towards the smaller vertices, vertex x is a descendant of r if and only if there is a directed decreasing path from x to r. In [Reference Pittel36] X(t) was proposed as an influence measure of vertex r at time t.
We prove two theorems.
Theorem 2.1. Suppose that r is fixed,
![]() $m=1$
and
$m=1$
and
![]() $\delta>-1$
, and set
$\delta>-1$
, and set
![]() $p_X(t)\,:\!=\, X(t)/t$
. Then almost surely (i.e. with probability
$p_X(t)\,:\!=\, X(t)/t$
. Then almost surely (i.e. with probability
![]() $\textrm{1}$
)
$\textrm{1}$
)
![]() $\lim p_X(t)$
exists, and its distribution is the mixture of two beta distributions, with parameters
$\lim p_X(t)$
exists, and its distribution is the mixture of two beta distributions, with parameters
weighted by
respectively. Consequently almost surely
![]() $\lim_{t\to\infty}p(t)>0$
.
$\lim_{t\to\infty}p(t)>0$
.
Remark 2.2. The two beta distributions in the theorem result from two possible scenarios for vertex r; if there is a loop on r we get the first beta distribution, otherwise we get the second one.
Note.
-
(i) The proof is based on a new family of martingales
where \[M_{\ell}(t)\,:\!=\, \dfrac{(X(t)+{{\gamma}/{(2+\delta)}})^{(\ell)}}{(t+\beta)^{(\ell)}},\]
\[M_{\ell}(t)\,:\!=\, \dfrac{(X(t)+{{\gamma}/{(2+\delta)}})^{(\ell)}}{(t+\beta)^{(\ell)}},\]
 $(z)^{(\ell)}$
stands for the rising factorial. This family definitely resembles the martingales used in [Reference Móri30, Reference Móri31] for the individual vertices’ degrees. For instance, if
$(z)^{(\ell)}$
stands for the rising factorial. This family definitely resembles the martingales used in [Reference Móri30, Reference Móri31] for the individual vertices’ degrees. For instance, if
 $D_j(t)$
is the degree of vertex j at time
$D_j(t)$
is the degree of vertex j at time
 $t\ge j$
, then for some deterministic
$t\ge j$
, then for some deterministic
 $\gamma_k(t)$
,
$\gamma_k(t)$
,
 $Z_{j,k}(t)\,:\!=\, \gamma_k(t)(D_j(t)+\delta)^{(k)}$
is a martingale [Reference van der Hofstad23]. However,
$Z_{j,k}(t)\,:\!=\, \gamma_k(t)(D_j(t)+\delta)^{(k)}$
is a martingale [Reference van der Hofstad23]. However,
 $M_{\ell}(t)$
depends on X(t), a global parameter of the PAM graph. Our initial proof was quite technical. We owe a debt of gratitude to an anonymous referee who was able to condense our argument to a few lines.
$M_{\ell}(t)$
depends on X(t), a global parameter of the PAM graph. Our initial proof was quite technical. We owe a debt of gratitude to an anonymous referee who was able to condense our argument to a few lines.
-
(ii) With high probability
 $G_{1,\delta}$
is a forest of
$G_{1,\delta}$
is a forest of
 $\Theta(\!\log t)$
trees rooted at vertices with loops. For the preferential attachment tree (no loops), Janson [Reference Janson24] recently proved that the scaled sizes of the principal subtrees, those rooted at the root’s children and ordered chronologically, converge almost surely (a.s.) to the GEM-distributed random variables. His techniques differ significantly from ours.
$\Theta(\!\log t)$
trees rooted at vertices with loops. For the preferential attachment tree (no loops), Janson [Reference Janson24] recently proved that the scaled sizes of the principal subtrees, those rooted at the root’s children and ordered chronologically, converge almost surely (a.s.) to the GEM-distributed random variables. His techniques differ significantly from ours.
For
![]() $m>1$
we use Theorem 2.1 to prove a somewhat surprising result that, for fixed r, almost surely all but a vanishingly small fraction of vertices are descendants of the vertex r (see [Reference Janson24]).
$m>1$
we use Theorem 2.1 to prove a somewhat surprising result that, for fixed r, almost surely all but a vanishingly small fraction of vertices are descendants of the vertex r (see [Reference Janson24]).
Theorem 2.2. Let r be fixed,
![]() $m>1$
and
$m>1$
and
![]() $\delta>-m$
, and let
$\delta>-m$
, and let
![]() $p_X(t)=X(t)/t$
,
$p_X(t)=X(t)/t$
,
![]() $p_Y(t)=Y(t)/(2mt)$
, where
$p_Y(t)=Y(t)/(2mt)$
, where
![]() $Y\big(t\big)$
is the total degree of the descendants of r at time t. Then almost surely
$Y\big(t\big)$
is the total degree of the descendants of r at time t. Then almost surely
![]() $\lim_{t\to\infty} p_X(t)=\lim_{t\to\infty} p_Y(t)=1$
.
$\lim_{t\to\infty} p_X(t)=\lim_{t\to\infty} p_Y(t)=1$
.
For the case of UAM we have the following result.
Theorem 2.3. Consider the UAM graph process
![]() $G_m(t)$
. Given a fixed
$G_m(t)$
. Given a fixed
![]() $r>1$
, let
$r>1$
, let
![]() $X\big(t\big)$
be the cardinality of the descendant tree rooted at vertex r, and let
$X\big(t\big)$
be the cardinality of the descendant tree rooted at vertex r, and let
![]() $p_X(t)\,:\!=\, X(t)/t$
.
$p_X(t)\,:\!=\, X(t)/t$
.
-
(i) For
 $m=1$
, almost surely
$m=1$
, almost surely
 $\lim p_X(t)$
exists, and it has the beta distribution with parameters 1 and r, which is the distribution of the minimum of r independent
$\lim p_X(t)$
exists, and it has the beta distribution with parameters 1 and r, which is the distribution of the minimum of r independent
 $[0, 1]$
-uniforms. Consequently a.s.
$[0, 1]$
-uniforms. Consequently a.s.
 $\liminf_{{t}\to\infty}p_X(t)>0$
.
$\liminf_{{t}\to\infty}p_X(t)>0$
. -
(ii) For
 $m>1$
, almost surely
$m>1$
, almost surely
 $\lim_{t\to\infty} p_X(t)=1$
.
$\lim_{t\to\infty} p_X(t)=1$
.
2.2. Greedy matching algorithm
We analyze a greedy matching algorithm; a.s. it delivers a surprisingly large matching set even for relatively small m. This algorithm generates the increasing sequence
![]() $\{ M(t)\}$
of partial matchings on the sets [t], with
$\{ M(t)\}$
of partial matchings on the sets [t], with
![]() $ M(1)=\emptyset$
. Suppose that X(t) is the set of unmatched vertices in [t] at time t. If
$ M(1)=\emptyset$
. Suppose that X(t) is the set of unmatched vertices in [t] at time t. If
![]() $t+1$
attaches itself to a vertex
$t+1$
attaches itself to a vertex
![]() $u\in X(t)$
, then
$u\in X(t)$
, then
![]() $M(t+1)=M(t)\cup\{\{u,t+1\}\}$
, otherwise
$M(t+1)=M(t)\cup\{\{u,t+1\}\}$
, otherwise
![]() $M(t+1)=M(t)$
. (If
$M(t+1)=M(t)$
. (If
![]() $t+1$
chooses multiple vertices from X(t), then we pick one of those as u arbitrarily.)
$t+1$
chooses multiple vertices from X(t), then we pick one of those as u arbitrarily.)
First consider the PAM graph. Let
and let
![]() $\rho=\rho_{m,\delta}$
be the unique solution of
$\rho=\rho_{m,\delta}$
be the unique solution of
![]() $h(z)=0$
in the interval [0, 1]. (We have
$h(z)=0$
in the interval [0, 1]. (We have
![]() $\rho_{m,\delta}\in (0,1)$
if
$\rho_{m,\delta}\in (0,1)$
if
![]() $\delta>-m$
.)
$\delta>-m$
.)
Theorem 2.4. Let
![]() $M\big(t\big)$
and
$M\big(t\big)$
and
![]() $X\big(t\big)$
, respectively, be the set of greedy matchings and the set of uncovered vertices at time t, and let
$X\big(t\big)$
, respectively, be the set of greedy matchings and the set of uncovered vertices at time t, and let
![]() $x(t)=X(t)/t$
. For any
$x(t)=X(t)/t$
. For any
![]() $\delta>-m$
and
$\delta>-m$
and
![]() $\alpha<1/3$
, almost surely
$\alpha<1/3$
, almost surely
In consequence, the greedy matching algorithm a.s. finds a sequence of nested matchings
![]() $\{M(t)\}$
, where the number of vertices in
$\{M(t)\}$
, where the number of vertices in
![]() $M\big(t\big)$
is asymptotically at least
$M\big(t\big)$
is asymptotically at least
![]() $(1-\rho_{m,\delta})t$
.
$(1-\rho_{m,\delta})t$
.
Remark 2.3. Observe that
![]() $\rho_{m,-m}=1$
, which makes it plausible that the maximum matching size is minuscule compared to t. In fact, by Remark 2.1,
$\rho_{m,-m}=1$
, which makes it plausible that the maximum matching size is minuscule compared to t. In fact, by Remark 2.1,
![]() $G_{m,-m}(t)$
is the star centered at vertex 1 and hence the maximum matching size is 1.
$G_{m,-m}(t)$
is the star centered at vertex 1 and hence the maximum matching size is 1.
Remark 2.4. Consider the case
![]() $\delta=0$
. Let
$\delta=0$
. Let
![]() $r_m\,:\!=\, 1-\rho_{m,0}$
; some values of
$r_m\,:\!=\, 1-\rho_{m,0}$
; some values of
![]() $r_m$
are
$r_m$
are
With a bit of calculus, we obtain
![]() $r_m=1- 2m^{-1}\log2 +{\textrm{O}}\big(m^{-2}\big)$
.
$r_m=1- 2m^{-1}\log2 +{\textrm{O}}\big(m^{-2}\big)$
.
Theorem 2.5. Let
![]() $M\big(t\big)$
denote the greedy matching set after t steps of the UAM process. Let
$M\big(t\big)$
denote the greedy matching set after t steps of the UAM process. Let
![]() $r_m$
denote the unique positive root of
$r_m$
denote the unique positive root of
![]() $2(1-z^m) -z=0$
, i.e.
$2(1-z^m) -z=0$
, i.e.
![]() $r_m=1-m^{-1}\log 2+{\textrm{O}}\big(m^{-2}\big)$
. Then, for any
$r_m=1-m^{-1}\log 2+{\textrm{O}}\big(m^{-2}\big)$
. Then, for any
![]() $\alpha<1/3$
, almost surely
$\alpha<1/3$
, almost surely
Some values of
![]() $r_m$
in this case are
$r_m$
in this case are
2.3. Greedy independent set algorithm
The algorithm generates an increasing sequence of independent sets
![]() $\{I(t)\}$
on vertex sets [t]. Namely,
$\{I(t)\}$
on vertex sets [t]. Namely,
![]() $I(1)=\{1\}$
, and
$I(1)=\{1\}$
, and
![]() $I(t+1)=I(t)\cup\{t+1\}$
if
$I(t+1)=I(t)\cup\{t+1\}$
if
![]() $t+1$
does not select any of the vertices in I(t); if it does, then
$t+1$
does not select any of the vertices in I(t); if it does, then
![]() $I(t+1)=I(t)$
. I(t) is also a dominating set for the PAM/UAM graph with vertex set [t]; indeed, if a vertex
$I(t+1)=I(t)$
. I(t) is also a dominating set for the PAM/UAM graph with vertex set [t]; indeed, if a vertex
![]() $\tau\in [t]\setminus I(t)$
did not have any neighbor in I(t), then vertex
$\tau\in [t]\setminus I(t)$
did not have any neighbor in I(t), then vertex
![]() $\tau$
would have been added to
$\tau$
would have been added to
![]() $I(\tau-1)$
at step
$I(\tau-1)$
at step
![]() $\tau$
. (Pittel [Reference Pittel33] analyzed the performance of this algorithm applied to the Erdős–Rényi random graph with a large but fixed vertex set.)
$\tau$
. (Pittel [Reference Pittel33] analyzed the performance of this algorithm applied to the Erdős–Rényi random graph with a large but fixed vertex set.)
For the PAM case we prove the following.
Theorem 2.6. Let
![]() $w_m$
denote the unique root of
$w_m$
denote the unique root of
![]() $(1-w)^m-w$
in
$(1-w)^m-w$
in
![]() $ (0,1)$
. For any
$ (0,1)$
. For any
almost surely
Remark 2.5. Thus the limiting scaled size of the greedy independent set does not depend on
![]() $\delta$
, but the convergence rate does.
$\delta$
, but the convergence rate does.
For the UAM case we prove an almost identical result.
Theorem 2.7. Let
![]() $w_m$
be the unique positive root of
$w_m$
be the unique positive root of
![]() $-w+(1-w)^m$
in
$-w+(1-w)^m$
in
![]() $ (0,1)$
. Then, for any
$ (0,1)$
. Then, for any
![]() $\alpha<1/3$
, almost surely
$\alpha<1/3$
, almost surely
Remark 2.6. Let
![]() $w_m$
be the unique positive root of
$w_m$
be the unique positive root of
![]() $(1-w)^m-w$
in (0, 1). As
$(1-w)^m-w$
in (0, 1). As
![]() $m\to\infty$
,
$m\to\infty$
,
So, for m large and both models, a.s. for all large enough t the greedy algorithm delivers an independent set containing a fraction
![]() $\sim{{\log m}/{m}}$
of all vertices in [t]. It was proved in [Reference Frieze, Pérez-Giménez, Prałat and Reiniger21] that for each large t with probability
$\sim{{\log m}/{m}}$
of all vertices in [t]. It was proved in [Reference Frieze, Pérez-Giménez, Prałat and Reiniger21] that for each large t with probability
![]() $1-{\textrm{o}}(1)$
, the fraction of vertices in the largest independent set in the PAM graph process and in the UAM graph process is at most
$1-{\textrm{o}}(1)$
, the fraction of vertices in the largest independent set in the PAM graph process and in the UAM graph process is at most
![]() $(4+{\textrm{o}}(1))\,{{\log m}/{m}}$
and
$(4+{\textrm{o}}(1))\,{{\log m}/{m}}$
and
![]() $(2+{\textrm{o}}(1))\,{{\log m}/{m}}$
, respectively. Since I(t) is dominating, our results prove a.s. existence for all large t of relatively small dominating sets, of cardinality
$(2+{\textrm{o}}(1))\,{{\log m}/{m}}$
, respectively. Since I(t) is dominating, our results prove a.s. existence for all large t of relatively small dominating sets, of cardinality
![]() $\le (1+\varepsilon_m) t\,{{\log m}/{m}}$
, (
$\le (1+\varepsilon_m) t\,{{\log m}/{m}}$
, (
![]() $\varepsilon_m\to 0$
).
$\varepsilon_m\to 0$
).
Remark 2.7. Let
![]() $\mathcal I(t)$
denote the cardinality of the largest independent set. We conjecture that for each of the processes there exists a corresponding constant c(m) such that a.s.
$\mathcal I(t)$
denote the cardinality of the largest independent set. We conjecture that for each of the processes there exists a corresponding constant c(m) such that a.s.
![]() $\lim_{t\to\infty}t^{-1}\mathcal I(t)=c(m)$
; of course,
$\lim_{t\to\infty}t^{-1}\mathcal I(t)=c(m)$
; of course,
![]() $c(m)\ge w_m$
.
$c(m)\ge w_m$
.
Notice that, for the UAM process, the existence of a deterministic function c(m,t), bounded away from 0 and 1 as
![]() $t\to\infty$
, such that the distribution of
$t\to\infty$
, such that the distribution of
![]() $\mathcal I(t)$
is sharply concentrated around tc(m,t), is not difficult to prove. Indeed,
$\mathcal I(t)$
is sharply concentrated around tc(m,t), is not difficult to prove. Indeed,
![]() $\mathcal I(t)$
is determined by
$\mathcal I(t)$
is determined by
![]() $t-1$
independent selections of m neighbors among the older vertices made by vertices
$t-1$
independent selections of m neighbors among the older vertices made by vertices
![]() $2,\dots, t$
. Obviously,
$2,\dots, t$
. Obviously,
![]() $\mathcal I(t)$
meets the following two conditions: (1) changing the outcome of any such selection can affect
$\mathcal I(t)$
meets the following two conditions: (1) changing the outcome of any such selection can affect
![]() $\mathcal I(t)$
by at most 1; (2) if
$\mathcal I(t)$
by at most 1; (2) if
![]() $\mathcal I(t)\ge s$
, then there are s vertices that form an independent set, which depends entirely on selections made by these vertices. Using Talagrand’s general inequality [Reference Talagrand37] (see also [Reference Molloy29]), we have, for
$\mathcal I(t)\ge s$
, then there are s vertices that form an independent set, which depends entirely on selections made by these vertices. Using Talagrand’s general inequality [Reference Talagrand37] (see also [Reference Molloy29]), we have, for
![]() $z\le \mathbb{E}[\mathcal I(t)]$
,
$z\le \mathbb{E}[\mathcal I(t)]$
,
That does it, since by Theorem 2.7
![]() $\mathbb{E}[\mathcal I(t)]\ge \mathbb{E}[I(t)]\ge 0.9 w_mt$
when t is large enough and, with exponentially high probability, we have
$\mathbb{E}[\mathcal I(t)]\ge \mathbb{E}[I(t)]\ge 0.9 w_mt$
when t is large enough and, with exponentially high probability, we have
![]() $\mathcal I(t)\le (\sigma+{\textrm{o}}(1))t$
, where
$\mathcal I(t)\le (\sigma+{\textrm{o}}(1))t$
, where
![]() $\sigma=\sigma(m)\in (0,1)$
is the root of
$\sigma=\sigma(m)\in (0,1)$
is the root of
![]() $\sigma\log\sigma+(1-\sigma)\log(1-\sigma)+\sigma^2m/2$
; see Lemma 9 of [Reference Frieze, Pérez-Giménez, Prałat and Reiniger21].
$\sigma\log\sigma+(1-\sigma)\log(1-\sigma)+\sigma^2m/2$
; see Lemma 9 of [Reference Frieze, Pérez-Giménez, Prałat and Reiniger21].
3. Descendant trees
Instead of referring the reader back to Section 2, we start this, and other proof sections, by formulating each claim in full.
3.1. Proof of Theorem 2.1
In this subsection we prove Theorem 2.1 restated below.
Theorem 2.1. Suppose that
![]() $m=1$
and
$m=1$
and
![]() $\delta>-1$
, and set
$\delta>-1$
, and set
![]() $p_X(t)\,:\!=\, X(t)/t$
. Then almost surely (i.e. with probability
$p_X(t)\,:\!=\, X(t)/t$
. Then almost surely (i.e. with probability
![]() $\textrm{1}$
)
$\textrm{1}$
)
![]() $\lim p_X(t)$
exists, and its distribution is the mixture of two beta distributions, with parameters
$\lim p_X(t)$
exists, and its distribution is the mixture of two beta distributions, with parameters
weighted by
respectively. Consequently a.s.
![]() $\lim_{t\to\infty}p_X(t)>0$
.
$\lim_{t\to\infty}p_X(t)>0$
.
Proof. For
![]() $t\ge r>1$
, let
$t\ge r>1$
, let
![]() $X(t)=X_{m,\delta}(t)=X_{m,\delta}(t,r)$
and
$X(t)=X_{m,\delta}(t)=X_{m,\delta}(t,r)$
and
![]() $Y(t)=Y_{m,\delta}(t)=Y_{m,\delta}(t,r)$
denote the size and total degree of the vertices in the descendant set rooted at r; so
$Y(t)=Y_{m,\delta}(t)=Y_{m,\delta}(t,r)$
denote the size and total degree of the vertices in the descendant set rooted at r; so
![]() $X(r)=1$
and
$X(r)=1$
and
![]() $Y(r)\in [m,2m]$
, where m (resp. 2m) is attained when vertex r forms no loops (resp. forms m loops) at itself. Introduce
$Y(r)\in [m,2m]$
, where m (resp. 2m) is attained when vertex r forms no loops (resp. forms m loops) at itself. Introduce
![]() $p_Y(t)={{Y(t)}/{(2mt)}}$
. This notation will be used in the proof of Theorem 2.2 as well, but of course
$p_Y(t)={{Y(t)}/{(2mt)}}$
. This notation will be used in the proof of Theorem 2.2 as well, but of course
![]() $m=1$
in Theorem 2.1.
$m=1$
in Theorem 2.1.
Here
 \[Y(t)=\begin{cases}2X(t) &\text{if}\ {r}\ \text{looped on itself,}\\[4pt]2X(t)-1 &\text{if}\ {r}\ \text{selected a vertex in}\ [r-1].\end{cases}\]
\[Y(t)=\begin{cases}2X(t) &\text{if}\ {r}\ \text{looped on itself,}\\[4pt]2X(t)-1 &\text{if}\ {r}\ \text{selected a vertex in}\ [r-1].\end{cases}\]
![]() $\big($
In particular,
$\big($
In particular,
![]() $p_Y(t) =p_X(t)+{\textrm{O}}\big(t^{-1}\big)$
.
$p_Y(t) =p_X(t)+{\textrm{O}}\big(t^{-1}\big)$
.
![]() $\big)$
So, by (2.2),
$\big)$
So, by (2.2),
 \begin{align*} \mathbb P(X(t+1)&=X(t)+1\mid \circ)\\ &=\dfrac{Y(t)+\delta X(t)}{(2+\delta)t +(1+\delta)}\\[5pt] &= \begin{cases}\dfrac{(2+\delta)X(t)}{(2+\delta)t+(1+\delta)} &\text{if}\ {r}\ \text{looped on itself,}\\[12pt] \dfrac{(2+\delta)X(t)-1}{(2+\delta)t+(1+\delta)} &\text{if}\ {r}\ \text{selected a vertex in}\ [r-1],\end{cases}\end{align*}
\begin{align*} \mathbb P(X(t+1)&=X(t)+1\mid \circ)\\ &=\dfrac{Y(t)+\delta X(t)}{(2+\delta)t +(1+\delta)}\\[5pt] &= \begin{cases}\dfrac{(2+\delta)X(t)}{(2+\delta)t+(1+\delta)} &\text{if}\ {r}\ \text{looped on itself,}\\[12pt] \dfrac{(2+\delta)X(t)-1}{(2+\delta)t+(1+\delta)} &\text{if}\ {r}\ \text{selected a vertex in}\ [r-1],\end{cases}\end{align*}
where ‘
![]() $\circ$
’ indicates conditioning on prehistory (particularly X(t) and Y(t)). Thus we are led to consider the process X(t) such that
$\circ$
’ indicates conditioning on prehistory (particularly X(t) and Y(t)). Thus we are led to consider the process X(t) such that
 \begin{align*}\mathbb P(X(t+1)=X(t)+1 \mid \circ) &= \dfrac{(2+\delta)X(t)+\gamma}{(2+\delta)t+(1+\delta)},\\\mathbb P(X(t+1)=X(t) \mid \circ) &= 1 - \mathbb P(X(t+1)=X(t)+1 \mid \circ) ,\end{align*}
\begin{align*}\mathbb P(X(t+1)=X(t)+1 \mid \circ) &= \dfrac{(2+\delta)X(t)+\gamma}{(2+\delta)t+(1+\delta)},\\\mathbb P(X(t+1)=X(t) \mid \circ) &= 1 - \mathbb P(X(t+1)=X(t)+1 \mid \circ) ,\end{align*}
![]() $\gamma=0$
if r looped on itself,
$\gamma=0$
if r looped on itself,
![]() $\gamma=-1$
if r selected a vertex in
$\gamma=-1$
if r selected a vertex in
![]() $[r-1]$
. So
$[r-1]$
. So
![]() $\gamma$
is determined by
$\gamma$
is determined by
![]() $G_{1,\delta}(t)$
. Letting
$G_{1,\delta}(t)$
. Letting
![]() $\beta={{(1+\delta)}/{(2+\delta)}}$
, the above equation can be written as
$\beta={{(1+\delta)}/{(2+\delta)}}$
, the above equation can be written as
 \begin{equation}\begin{aligned}\mathbb P(X(t+1)=X(t)+1 \mid \circ) &= \dfrac{X(t) + \gamma/(2+\delta)}{t+\beta},\\\mathbb P(X(t+1)=X(t) \mid \circ) &= 1 - \dfrac{X(t) + \gamma/(2+\delta)}{t+\beta}.\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\mathbb P(X(t+1)=X(t)+1 \mid \circ) &= \dfrac{X(t) + \gamma/(2+\delta)}{t+\beta},\\\mathbb P(X(t+1)=X(t) \mid \circ) &= 1 - \dfrac{X(t) + \gamma/(2+\delta)}{t+\beta}.\end{aligned}\end{equation}
For
![]() $\delta=0$
the following claim was proved in [Reference Pittel36]. We let
$\delta=0$
the following claim was proved in [Reference Pittel36]. We let
![]() $z^{(\ell)}$
denote the rising factorial
$z^{(\ell)}$
denote the rising factorial
![]() $\prod_{j=0}^{\ell-1}(z+j)$
.
$\prod_{j=0}^{\ell-1}(z+j)$
.
Lemma 3.1. Let
![]() $\beta={{(1+\delta)}/{(2+\delta)}}$
and
$\beta={{(1+\delta)}/{(2+\delta)}}$
and
![]() $Z(t) = X(t) + {{\gamma}/{(2+\delta)}}$
. Then, conditioned on the attachment record during the time interval
$Z(t) = X(t) + {{\gamma}/{(2+\delta)}}$
. Then, conditioned on the attachment record during the time interval
![]() $\big[r, t\big]$
, i.e. starting with the attachment decision by vertex r, we have
$\big[r, t\big]$
, i.e. starting with the attachment decision by vertex r, we have
Consequently
is a martingale.
We thank an anonymous referee for the following proof, which is much shorter than our original proof.
Proof. We have
 \begin{align*}\mathbb{E}[(Z(t+1)^{(\ell)} \mid \circ ]&= (Z(t)+1)^{(\ell)} \dfrac{Z(t)}{t+\beta} + Z(t)^{(\ell)} \biggl( 1- \dfrac{Z(t)}{t+\beta}\biggr)\\&= (Z(t)+\ell)\, Z(t)^{(\ell)} \dfrac{1}{t+\beta} + Z(t)^{(\ell)} - Z(t)^{(\ell)} \dfrac{Z(t)}{t+\beta}\\&= Z(t)^{(\ell)} \biggl(\dfrac{\ell+t+\beta}{t+\beta}\biggr).\end{align*}
\begin{align*}\mathbb{E}[(Z(t+1)^{(\ell)} \mid \circ ]&= (Z(t)+1)^{(\ell)} \dfrac{Z(t)}{t+\beta} + Z(t)^{(\ell)} \biggl( 1- \dfrac{Z(t)}{t+\beta}\biggr)\\&= (Z(t)+\ell)\, Z(t)^{(\ell)} \dfrac{1}{t+\beta} + Z(t)^{(\ell)} - Z(t)^{(\ell)} \dfrac{Z(t)}{t+\beta}\\&= Z(t)^{(\ell)} \biggl(\dfrac{\ell+t+\beta}{t+\beta}\biggr).\end{align*}
The second part follows from this immediately.
To identify the
![]() $\lim_{t\to\infty} p(t)$
, recall that the classical beta probability distribution has density
$\lim_{t\to\infty} p(t)$
, recall that the classical beta probability distribution has density
parametrized by two parameters
![]() $a>0$
,
$a>0$
,
![]() $b>0$
, and moments
$b>0$
, and moments
 \begin{equation*} \int_0^1 x^{\ell} f(x;a, b)\,{\textrm{d}} x=\prod_{j=0}^{\ell-1}\dfrac{a+j}{a+b+j}.\end{equation*}
\begin{equation*} \int_0^1 x^{\ell} f(x;a, b)\,{\textrm{d}} x=\prod_{j=0}^{\ell-1}\dfrac{a+j}{a+b+j}.\end{equation*}
We can now complete the proof of Theorem 2.1. By Lemma 3.1, we have, for all
![]() $t\ge r$
,
$t\ge r$
,
![]() $\mathbb E [M_{\ell}(t)\mid \gamma]=M_{\ell}(r)$
, or explicitly
$\mathbb E [M_{\ell}(t)\mid \gamma]=M_{\ell}(r)$
, or explicitly
Since
![]() $|\gamma/(2+\delta)|\le 1$
and
$|\gamma/(2+\delta)|\le 1$
and
![]() $X(t)\le t$
, we obtain
$X(t)\le t$
, we obtain
Therefore, for every
![]() $\ell\ge 1$
, by the martingale convergence theorem, conditioned on
$\ell\ge 1$
, by the martingale convergence theorem, conditioned on
![]() $\gamma$
, a.s. there exists
$\gamma$
, a.s. there exists
Since
![]() $X(t)\le t$
, it follows from (3.2) that a.s. there exists
$X(t)\le t$
, it follows from (3.2) that a.s. there exists
![]() $\lim_{t\to\infty}X(t)/t=\lim_{t\to\infty}p_X(t)$
, and
$\lim_{t\to\infty}X(t)/t=\lim_{t\to\infty}p_X(t)$
, and
 \begin{equation*} \lim_{t\to\infty}\mathbb{E}[p_X(t)^{\ell}]=\mathbb{E}[\mathcal M_{\gamma,\ell}]=\dfrac{(1+{{\gamma}/{(2+\delta)}})^{(\ell)}}{(r+\beta)^{(\ell)}}=\prod_{j=0}^{\ell-1}\dfrac{1+{{\gamma}/{(2+\delta)}}+j}{r+\beta+j}.\end{equation*}
\begin{equation*} \lim_{t\to\infty}\mathbb{E}[p_X(t)^{\ell}]=\mathbb{E}[\mathcal M_{\gamma,\ell}]=\dfrac{(1+{{\gamma}/{(2+\delta)}})^{(\ell)}}{(r+\beta)^{(\ell)}}=\prod_{j=0}^{\ell-1}\dfrac{1+{{\gamma}/{(2+\delta)}}+j}{r+\beta+j}.\end{equation*}
The sequence of the right-hand side products is the sequence of moments of a unique distribution, which is the beta distribution with parameters
![]() $1+{{\gamma}/{(2+\delta)}}$
and
$1+{{\gamma}/{(2+\delta)}}$
and
![]() $r+\beta-1-{{\gamma}/{(2+\delta)}}$
. By the definition of
$r+\beta-1-{{\gamma}/{(2+\delta)}}$
. By the definition of
![]() $\gamma$
and (2.2), we have
$\gamma$
and (2.2), we have
We conclude that
![]() $\lim_{t\to\infty}p_X(t)$
has the distribution which is the mixture of the two beta distributions, with parameters
$\lim_{t\to\infty}p_X(t)$
has the distribution which is the mixture of the two beta distributions, with parameters
weighted by
respectively. This completes the proof of Theorem 2.1.
3.2. Proof of Theorem 2.2
In this subsection we prove Theorem 2.2 restated below.
Theorem 2.2. Let
![]() $m>1$
and
$m>1$
and
![]() $\delta>-m$
, and let
$\delta>-m$
, and let
![]() $p_X(t)=X(t)/t$
,
$p_X(t)=X(t)/t$
,
![]() $p_Y(t)=Y(t)/(2mt)$
, where
$p_Y(t)=Y(t)/(2mt)$
, where
![]() $Y\big(t\big)$
is the total degree of the descendants of r at time t. Then almost surely
$Y\big(t\big)$
is the total degree of the descendants of r at time t. Then almost surely
![]() $\lim_{t\to\infty} p_X(t)=\lim_{t\to\infty} p_Y(t)=1$
.
$\lim_{t\to\infty} p_X(t)=\lim_{t\to\infty} p_Y(t)=1$
.
For the proof of this theorem, we need tractable formulas/bounds for the conditional distribution of
![]() $Y(t+1)-Y(t)$
. The existence of loops in a preferential attachment graph is a minor nuisance for stating exact conditional probabilities. Hence we will start with the scenario that we do not get a loop on vertex
$Y(t+1)-Y(t)$
. The existence of loops in a preferential attachment graph is a minor nuisance for stating exact conditional probabilities. Hence we will start with the scenario that we do not get a loop on vertex
![]() $t+1$
, in which case we can write the exact equations easily and we will then argue that the effect of loops is negligible. Let
$t+1$
, in which case we can write the exact equations easily and we will then argue that the effect of loops is negligible. Let
![]() $\mathcal E_m(t)$
be the event that vertex
$\mathcal E_m(t)$
be the event that vertex
![]() $t+1$
has no loop. Conditioned on
$t+1$
has no loop. Conditioned on
![]() $G_{m,\delta}(t)$
and
$G_{m,\delta}(t)$
and
![]() $\mathcal E_m(t)$
, by the transition probabilities given in (2.1), vertex
$\mathcal E_m(t)$
, by the transition probabilities given in (2.1), vertex
![]() $t+1$
chooses a vertex
$t+1$
chooses a vertex
![]() $x\in [t]$
with probability
$x\in [t]$
with probability
In the following lemma we use ‘
![]() $ \mid \circ)$
’ to denote conditioning on
$ \mid \circ)$
’ to denote conditioning on
![]() $G_{m,\delta}(t)$
and
$G_{m,\delta}(t)$
and
![]() $\mathcal E_m(t)$
.
$\mathcal E_m(t)$
.
Lemma 3.2. For
![]() $a\in [m]$
,
$a\in [m]$
,
and
Proof. Let V(t) denote the descendants of r at time t. Vertex
![]() $t+1$
selects, in m steps, a sequence
$t+1$
selects, in m steps, a sequence
![]() $\{v_1,\dots, v_m\}$
of m vertices from [t], with t choices for every selection. Introduce
$\{v_1,\dots, v_m\}$
of m vertices from [t], with t choices for every selection. Introduce
![]() $\textbf{I}=(\mathbb{I}_1,\dots,\mathbb{I}_m)$
, where
$\textbf{I}=(\mathbb{I}_1,\dots,\mathbb{I}_m)$
, where
![]() $\mathbb{I}_i$
is the indicator of the event
$\mathbb{I}_i$
is the indicator of the event
![]() $\{v_i \in V(t)\}$
. The total vertex degree of [t] (resp. V(t)) right before step i is
$\{v_i \in V(t)\}$
. The total vertex degree of [t] (resp. V(t)) right before step i is
![]() $2mt + i-1$
(resp.
$2mt + i-1$
(resp.
![]() $Y(t)+\mu_i$
,
$Y(t)+\mu_i$
,
![]() $\mu_i\,:\!=\, |\{j<i\colon \mathbb{I}_j=1\}|$
). Conditioned on
$\mu_i\,:\!=\, |\{j<i\colon \mathbb{I}_j=1\}|$
). Conditioned on
![]() $G_{m,\delta}(t)$
,
$G_{m,\delta}(t)$
,
![]() $\mathcal E_m(t)$
, and the outcomes of the previous
$\mathcal E_m(t)$
, and the outcomes of the previous
![]() $i-1$
steps, we have
$i-1$
steps, we have
 \begin{align*}\mathbb P(\mathbb{I}_i=1)&=\dfrac{Y(t)+\delta X(t)+\mu_i}{2mt+\delta t+i-1},\\[4pt] \mathbb P(\mathbb{I}_i=0)&=\dfrac{2mt-Y(t)+\delta(t-X(t))+i-1-\mu_i}{2mt+\delta t+ i -1}.\end{align*}
\begin{align*}\mathbb P(\mathbb{I}_i=1)&=\dfrac{Y(t)+\delta X(t)+\mu_i}{2mt+\delta t+i-1},\\[4pt] \mathbb P(\mathbb{I}_i=0)&=\dfrac{2mt-Y(t)+\delta(t-X(t))+i-1-\mu_i}{2mt+\delta t+ i -1}.\end{align*}
Therefore a sequence
![]() $(j_1,\dots,j_m)$
will be the outcome of the loopless m-step selection with probability
$(j_1,\dots,j_m)$
will be the outcome of the loopless m-step selection with probability
 \begin{align*}& \mathbb P(\textbf{I} =(j_1,\dots,j_m)) \\&\quad=\prod_{i\in [m]} ((2m+\delta)t +i-1)^{-1}\\&\quad \quad \times\prod_{i\colon j_i=1}(Y(t)+\delta X(t)+\mu_i)\times \prod_{i\colon j_i=0}(2mt-Y(t)+\delta(t-X(t))+i-1-\mu_i).\end{align*}
\begin{align*}& \mathbb P(\textbf{I} =(j_1,\dots,j_m)) \\&\quad=\prod_{i\in [m]} ((2m+\delta)t +i-1)^{-1}\\&\quad \quad \times\prod_{i\colon j_i=1}(Y(t)+\delta X(t)+\mu_i)\times \prod_{i\colon j_i=0}(2mt-Y(t)+\delta(t-X(t))+i-1-\mu_i).\end{align*}
For
![]() $j_1+\cdots+j_m = a \in [m]$
, the second product above equals
$j_1+\cdots+j_m = a \in [m]$
, the second product above equals
![]() $(Y(t)+\delta X(t))^{(a)}$
and the third product equals
$(Y(t)+\delta X(t))^{(a)}$
and the third product equals
![]() $(2mt-Y(t)+\delta(t-X(t))^{(m-a)}$
so that
$(2mt-Y(t)+\delta(t-X(t))^{(m-a)}$
so that
Since the total number of admissible sequences
![]() $(j_1,\dots,j_m)$
with
$(j_1,\dots,j_m)$
with
![]() $j_1+\cdots+j_m = a$
is
$j_1+\cdots+j_m = a$
is
![]() $\binom{m}{a}$
, we obtain the first formula in Lemma 3.2. The second formula is the case of
$\binom{m}{a}$
, we obtain the first formula in Lemma 3.2. The second formula is the case of
![]() $\mathbb P(\textbf{I} = (0,\dots,0))$
.
$\mathbb P(\textbf{I} = (0,\dots,0))$
.
Proof of Theorem 2.2. Lemma 3.2 gives the conditional probabilities for
![]() $Y(t+1)-Y(t)$
in the event that there is no loop on vertex
$Y(t+1)-Y(t)$
in the event that there is no loop on vertex
![]() $t+1$
. Now let us evaluate the probability that there is no loop on vertex
$t+1$
. Now let us evaluate the probability that there is no loop on vertex
![]() $t+1$
. For
$t+1$
. For
![]() $0\le i \le m$
, let
$0\le i \le m$
, let
![]() $\mathcal E_{i}(t)$
denote the event that no loop has been formed on vertex
$\mathcal E_{i}(t)$
denote the event that no loop has been formed on vertex
![]() $t+1$
in the first i steps when vertex
$t+1$
in the first i steps when vertex
![]() $t+1$
is choosing its neighbors. On the event
$t+1$
is choosing its neighbors. On the event
![]() $\mathcal E_{i-1}(t)$
, as the ith edge incident to
$\mathcal E_{i-1}(t)$
, as the ith edge incident to
![]() $t+1$
is about to attach its second end to a vertex in
$t+1$
is about to attach its second end to a vertex in
![]() $[t]\cup\{t+1\}$
, the total degree of vertices in [t] is
$[t]\cup\{t+1\}$
, the total degree of vertices in [t] is
![]() $2mt+i-1$
(
$2mt+i-1$
(
![]() $1\le i\le m$
). So, by the transition probabilities given in (2.1),
$1\le i\le m$
). So, by the transition probabilities given in (2.1),
Hence
It is clear from the proof of Lemma 3.2 that, given X(t) and Y(t),
is a probability distribution of a random variable D, a ‘rising-factorial’ counterpart of the binomial distribution
![]() $\mathcal D=\text{Bin}(m,p=Y(t)/2mt)$
. (We have not seen this distribution in the literature.) Define the falling factorial
$\mathcal D=\text{Bin}(m,p=Y(t)/2mt)$
. (We have not seen this distribution in the literature.) Define the falling factorial
![]() $(x)_{\ell}=x(x-1)\cdots (x-\ell+1)$
. It is well known that
$(x)_{\ell}=x(x-1)\cdots (x-\ell+1)$
. It is well known that
![]() $\mathbb E[(\mathcal D)_{\mu}]=(m)_{\mu} p^{\mu}$
,
$\mathbb E[(\mathcal D)_{\mu}]=(m)_{\mu} p^{\mu}$
,
![]() $(\mu\le m)$
. For D we have
$(\mu\le m)$
. For D we have
 \begin{align} \mathbb E[(D)_{\mu}]&=\sum_a(a)_{\mu} \mathbb P_m(a) \notag \\[3pt] &=\dfrac{(m)_{\mu}\,(Y(t)+\delta X(t))^{(\mu)}}{((2m+\delta)t)^{(\mu)}}\cdot \sum_{a\ge \mu}\binom{m-\mu}{a-\mu} \notag \\[3pt] &\quad \times \dfrac{(Y(t)+\delta X(t)+\mu)^{(a-\mu)}((2m+\delta)t+\mu-(Y(t)+\delta X(t)+\mu))^{((m-\mu)-(a-\mu))}}{(2mt+\mu)^{(m-\mu)}} \notag \\[3pt] &=\dfrac{(m)_{\mu}\,(Y(t)+\delta X(t))^{(\mu)}}{((2m+\delta)t)^{(\mu)}},\end{align}
\begin{align} \mathbb E[(D)_{\mu}]&=\sum_a(a)_{\mu} \mathbb P_m(a) \notag \\[3pt] &=\dfrac{(m)_{\mu}\,(Y(t)+\delta X(t))^{(\mu)}}{((2m+\delta)t)^{(\mu)}}\cdot \sum_{a\ge \mu}\binom{m-\mu}{a-\mu} \notag \\[3pt] &\quad \times \dfrac{(Y(t)+\delta X(t)+\mu)^{(a-\mu)}((2m+\delta)t+\mu-(Y(t)+\delta X(t)+\mu))^{((m-\mu)-(a-\mu))}}{(2mt+\mu)^{(m-\mu)}} \notag \\[3pt] &=\dfrac{(m)_{\mu}\,(Y(t)+\delta X(t))^{(\mu)}}{((2m+\delta)t)^{(\mu)}},\end{align}
since the sum over
![]() $a\ge \mu$
is
$a\ge \mu$
is
![]() $\sum_{\nu\ge 0}\mathbb P_{m-\mu}(\nu)=1$
.
$\sum_{\nu\ge 0}\mathbb P_{m-\mu}(\nu)=1$
.
By Lemma 3.2, (3.3), and (3.4),
 \begin{align}\mathbb E[Y(t+1)-Y(t)\mid\circ] &= \sum_{a=1}^m (a+m) \mathbb P_m(a) + {\textrm{O}}\big(t^{-1}\big) \notag \\[4pt]&= \biggl( \sum_{a=1}^m a \mathbb P_m(a) + \sum_{a=1}^m m \mathbb P_m(a) \biggr) + {\textrm{O}}\big(t^{-1}\big) \notag \\[4pt]&= \dfrac{m(Y(t)+\delta X(t))}{(2m+\delta)t}+ m\biggl(1-\dfrac{((2m+\delta)t-Y(t)-\delta X(t))^{(m)}}{((2m+\delta)t)^{(m)}}\biggr) +{\textrm{O}}\big(t^{-1}\big)\end{align}
\begin{align}\mathbb E[Y(t+1)-Y(t)\mid\circ] &= \sum_{a=1}^m (a+m) \mathbb P_m(a) + {\textrm{O}}\big(t^{-1}\big) \notag \\[4pt]&= \biggl( \sum_{a=1}^m a \mathbb P_m(a) + \sum_{a=1}^m m \mathbb P_m(a) \biggr) + {\textrm{O}}\big(t^{-1}\big) \notag \\[4pt]&= \dfrac{m(Y(t)+\delta X(t))}{(2m+\delta)t}+ m\biggl(1-\dfrac{((2m+\delta)t-Y(t)-\delta X(t))^{(m)}}{((2m+\delta)t)^{(m)}}\biggr) +{\textrm{O}}\big(t^{-1}\big)\end{align}
and
where ‘
![]() $\circ$
’ indicates conditioning on
$\circ$
’ indicates conditioning on
![]() $G_{m,\delta}(t)$
. (Note that
$G_{m,\delta}(t)$
. (Note that
![]() $X(t+1)=X(t)$
if and only if
$X(t+1)=X(t)$
if and only if
![]() $Y(t+1)=Y(t)$
.)
$Y(t+1)=Y(t)$
.)
To continue the proof of Theorem 2.2, we note first that
![]() $mX(t)\le Y(t)\le 2mX(t)$
. These inequalities follow from the fact that every time a vertex joins the descendant set, the total degree of the descendant set increases by an amount
$mX(t)\le Y(t)\le 2mX(t)$
. These inequalities follow from the fact that every time a vertex joins the descendant set, the total degree of the descendant set increases by an amount
![]() $m+a$
for some
$m+a$
for some
![]() $a\in [m]$
. Let
$a\in [m]$
. Let
where
![]() $p_Y(t)=Y(t)/(2mt)$
and
$p_Y(t)=Y(t)/(2mt)$
and
![]() $p_X(t)=X(t)/t$
as defined before. By the definition of p(t) and the above inequalities, we have
$p_X(t)=X(t)/t$
as defined before. By the definition of p(t) and the above inequalities, we have
in particular,
![]() $p(t)\in [0,1]$
since
$p(t)\in [0,1]$
since
![]() $\delta\ge -m$
. We will also need
$\delta\ge -m$
. We will also need
So, using (3.5), we compute
 \begin{equation} \begin{aligned}\mathbb E[p_Y(t+1) \mid \circ]&=\mathbb E\biggl[\dfrac{Y(t+1)}{2mt}\cdot \dfrac{t}{t+1}\Bigm| \circ\biggr] \\[3pt]&=\dfrac{t}{t+1} \biggl(p_Y(t)+\dfrac{1}{2t}\bigl[1+p(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big)\biggr) \\[3pt]&=p_Y(t)+q_Y(t), \\[3pt]q_Y(t)&\,:\!=\, \dfrac{1}{2(t+1)}\bigl[1+p(t)-2p_Y(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big).\end{aligned}\end{equation}
\begin{equation} \begin{aligned}\mathbb E[p_Y(t+1) \mid \circ]&=\mathbb E\biggl[\dfrac{Y(t+1)}{2mt}\cdot \dfrac{t}{t+1}\Bigm| \circ\biggr] \\[3pt]&=\dfrac{t}{t+1} \biggl(p_Y(t)+\dfrac{1}{2t}\bigl[1+p(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big)\biggr) \\[3pt]&=p_Y(t)+q_Y(t), \\[3pt]q_Y(t)&\,:\!=\, \dfrac{1}{2(t+1)}\bigl[1+p(t)-2p_Y(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big).\end{aligned}\end{equation}
Likewise
 \begin{equation}\begin{aligned}\mathbb E[p_X(t+1)\mid\circ]&=p_X(t)+q_X(t),\\[3pt]q_X(t)&=\dfrac{1}{t+1}\bigl[1-p_X(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big).\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\mathbb E[p_X(t+1)\mid\circ]&=p_X(t)+q_X(t),\\[3pt]q_X(t)&=\dfrac{1}{t+1}\bigl[1-p_X(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big).\end{aligned}\end{equation}
Multiplying (3.6) by
![]() ${{2m}/{(2m+\delta)}}$
and (3.7) by
${{2m}/{(2m+\delta)}}$
and (3.7) by
![]() ${{\delta}/{(2m+\delta)}}$
, and adding them, we obtain
${{\delta}/{(2m+\delta)}}$
, and adding them, we obtain
 \begin{equation}\begin{aligned}\mathbb E[p(t+1) \mid \circ]&=p(t) +q(t),\\[3pt]q(t)& \,:\!=\, \dfrac{m+\delta}{(2m+\delta)(t+1)}\bigl[1-p(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big).\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\mathbb E[p(t+1) \mid \circ]&=p(t) +q(t),\\[3pt]q(t)& \,:\!=\, \dfrac{m+\delta}{(2m+\delta)(t+1)}\bigl[1-p(t)-(1-p(t))^m\bigr]+{\textrm{O}}\big(t^{-2}\big).\end{aligned}\end{equation}
From the first line in (3.8) it follows that
implying that
Since
![]() $1-z-(1-z)^m\ge 0$
on [0, 1], the second line in (3.8) implies that
$1-z-(1-z)^m\ge 0$
on [0, 1], the second line in (3.8) implies that
![]() $|q(t)|\le q(t)+{\textrm{O}}\big(t^{-2}\big)$
. Since
$|q(t)|\le q(t)+{\textrm{O}}\big(t^{-2}\big)$
. Since
![]() $\sum_t t^{-2}<\infty$
, we see that
$\sum_t t^{-2}<\infty$
, we see that
![]() $\sum_t\mathbb E[|q(t)|]<\infty$
.
$\sum_t\mathbb E[|q(t)|]<\infty$
.
So a.s. there exists
![]() $Q\,:\!=\, \lim_{\tau\to\infty}\sum_{1\le t\le \tau} q(t)$
, with
$Q\,:\!=\, \lim_{\tau\to\infty}\sum_{1\le t\le \tau} q(t)$
, with
![]() $\mathbb E[|Q|]\le \sum_t\mathbb E[|q(t)|]<\infty$
, that is, a.s.
$\mathbb E[|Q|]\le \sum_t\mathbb E[|q(t)|]<\infty$
, that is, a.s.
![]() $|Q|<\infty$
. Introducing
$|Q|<\infty$
. Introducing
![]() $Q(t+1)=\sum_{\tau\le t}q(\tau) $
, we see from (3.8) that
$Q(t+1)=\sum_{\tau\le t}q(\tau) $
, we see from (3.8) that
![]() $\{p(t+1)-Q(t+1)\}_{t\ge 1}$
is a martingale with
$\{p(t+1)-Q(t+1)\}_{t\ge 1}$
is a martingale with
![]() $\sup_t |p(t+1)-Q(t+1)|\le 1 + \sum_{\tau\ge 1} |q(\tau)|$
. By the martingale convergence theorem we obtain that there exists an integrable
$\sup_t |p(t+1)-Q(t+1)|\le 1 + \sum_{\tau\ge 1} |q(\tau)|$
. By the martingale convergence theorem we obtain that there exists an integrable
![]() $\lim_{t\to\infty}(p(t)-Q(t))$
, implying that a.s. there exists a random
$\lim_{t\to\infty}(p(t)-Q(t))$
, implying that a.s. there exists a random
![]() $p(\infty)=\lim_{t\to\infty}p(t)$
. Equation (3.8) also implies that
$p(\infty)=\lim_{t\to\infty}p(t)$
. Equation (3.8) also implies that
Since
![]() $m+\delta>0$
and
$m+\delta>0$
and
and the series
![]() $\sum_{t\ge 1} t^{-1}$
diverges, we obtain that
$\sum_{t\ge 1} t^{-1}$
diverges, we obtain that
![]() $\mathbb P(p(\infty)\in \{0,1\})=1$
.
$\mathbb P(p(\infty)\in \{0,1\})=1$
.
Recall that
If we show that a.s.
![]() $\liminf_{t\to\infty}p_X(t)>0$
, it will follow that a.s.
$\liminf_{t\to\infty}p_X(t)>0$
, it will follow that a.s.
![]() $p(\infty)>0$
, whence a.s.
$p(\infty)>0$
, whence a.s.
![]() $p(\infty)=1$
, implying (by
$p(\infty)=1$
, implying (by
![]() $p(t)\le p_X(t)$
) that a.s.
$p(t)\le p_X(t)$
) that a.s.
![]() $p_X(\infty)$
exists, and is 1, and consequently (by the formula for p(t)) a.s.
$p_X(\infty)$
exists, and is 1, and consequently (by the formula for p(t)) a.s.
![]() $p_Y(\infty)$
exists, and is 1.
$p_Y(\infty)$
exists, and is 1.
So let us prove that a.s.
![]() $\liminf_{t\to\infty}p_X(t)>0$
. Recall that we did prove the latter for
$\liminf_{t\to\infty}p_X(t)>0$
. Recall that we did prove the latter for
![]() $m=1$
. To transfer this earlier result to
$m=1$
. To transfer this earlier result to
![]() $m>1$
we need to establish some kind of monotonicity with respect to m. The coupling described in Section 2 comes to the rescue!
$m>1$
we need to establish some kind of monotonicity with respect to m. The coupling described in Section 2 comes to the rescue!
Lemma 3.3. For the coupled processes
![]() $\{G_{m,\delta}(t)\}$
and
$\{G_{m,\delta}(t)\}$
and
![]() $\{G_{1,\delta/m}(mt)\}$
, we have
$\{G_{1,\delta/m}(mt)\}$
, we have
![]() $X_{m,\delta}(t,r) \ge m^{-1} X_{1,\delta/m}(mt,mr)$
.
$X_{m,\delta}(t,r) \ge m^{-1} X_{1,\delta/m}(mt,mr)$
.
Proof. Let us simply write
![]() $G_1$
and
$G_1$
and
![]() $G_m$
for the two graphs
$G_m$
for the two graphs
![]() $G_{1,\delta/m}(mt)$
and
$G_{1,\delta/m}(mt)$
and
![]() $G_{m,\delta}(t)$
, respectively. Similarly, write
$G_{m,\delta}(t)$
, respectively. Similarly, write
![]() $T_1$
and
$T_1$
and
![]() $T_m$
, respectively, for the descendant tree in
$T_m$
, respectively, for the descendant tree in
![]() $G_{1,\delta/m}(mt)$
rooted at mr and the descendant tree in
$G_{1,\delta/m}(mt)$
rooted at mr and the descendant tree in
![]() $G_{m,\delta}(t)$
rooted at r. If
$G_{m,\delta}(t)$
rooted at r. If
![]() $v_a\in T_1$
, i.e.
$v_a\in T_1$
, i.e.
![]() $v_a$
is a descendant of mr, then for
$v_a$
is a descendant of mr, then for
![]() $b=\lceil a/m \rceil $
we have
$b=\lceil a/m \rceil $
we have
![]() $w_b=\{v_{m(b-1)+i}\}_{i\in [m]}\ni v_a$
, implying that
$w_b=\{v_{m(b-1)+i}\}_{i\in [m]}\ni v_a$
, implying that
![]() $w_b$
is a descendant of r in
$w_b$
is a descendant of r in
![]() $G_m$
, i.e.
$G_m$
, i.e.
![]() $w_b\in T_m$
. (The converse is generally false: if
$w_b\in T_m$
. (The converse is generally false: if
![]() $w_b$
is a descendant of r, it does not mean that every
$w_b$
is a descendant of r, it does not mean that every
![]() $v_{m(b-1)+i}$
, (
$v_{m(b-1)+i}$
, (
![]() $i\in [m]$
), is a descendant of mr.) Therefore
$i\in [m]$
), is a descendant of mr.) Therefore
Thus, to complete the proof of the theorem, i.e. for
![]() $\delta>-m$
, we (a) use Theorem 2.1, to assert that for the process
$\delta>-m$
, we (a) use Theorem 2.1, to assert that for the process
![]() $\{G_{1,\delta/m}(t)\}$
, a.s.
$\{G_{1,\delta/m}(t)\}$
, a.s.
![]() $\lim_{t\to\infty} p_X (t)>0$
, (b) use Lemma 3.3, to assert that a.s.
$\lim_{t\to\infty} p_X (t)>0$
, (b) use Lemma 3.3, to assert that a.s.
![]() $\liminf_{t\to\infty} p_X (t)>0$
for
$\liminf_{t\to\infty} p_X (t)>0$
for
![]() $\{G_{m,\delta}(t)\}$
as well. The proof of Theorem 2.2 is complete.
$\{G_{m,\delta}(t)\}$
as well. The proof of Theorem 2.2 is complete.
3.3. Proof of Theorem 2.3
Theorem 2.3. Consider the UAM graph process
![]() $G_m(t)$
. Given
$G_m(t)$
. Given
![]() $r>1$
, let
$r>1$
, let
![]() $X\big(t\big)$
be the cardinality of the descendant tree rooted at vertex r, and let
$X\big(t\big)$
be the cardinality of the descendant tree rooted at vertex r, and let
![]() $p_X(t)\,:\!=\, X(t)/t$
.
$p_X(t)\,:\!=\, X(t)/t$
.
-
(i) For
 $m=1$
, almost surely
$m=1$
, almost surely
 $\lim p_X(t)$
exists and it has the same distribution as the minimum of
$\lim p_X(t)$
exists and it has the same distribution as the minimum of
 $(r-1)$
independent
$(r-1)$
independent
 $[0, 1]$
-uniforms. Consequently a.s.
$[0, 1]$
-uniforms. Consequently a.s.
 $\liminf_{t\to\infty}p_X(t)>0$
.
$\liminf_{t\to\infty}p_X(t)>0$
. -
(ii) For
 $m>1$
, almost surely
$m>1$
, almost surely
 $\lim_{t\to\infty} p_X(t)=1$
.
$\lim_{t\to\infty} p_X(t)=1$
.
Proof. By the definition of the UAM process, we have
Case (i). Consider
![]() $m=1$
. For
$m=1$
. For
![]() $r=1$
, we have
$r=1$
, we have
![]() $p(t)\equiv 1$
. Consider
$p(t)\equiv 1$
. Consider
![]() $r\ge 2$
. Equation (3.9) is the case
$r\ge 2$
. Equation (3.9) is the case
![]() $\delta=-1$
,
$\delta=-1$
,
![]() $\gamma=0$
of (3.1). By Lemma 3.1, we claim that
$\gamma=0$
of (3.1). By Lemma 3.1, we claim that
is a martingale. So arguing as in the proof of Theorem 2.1, we obtain that almost surely (a.s.)
![]() $\lim p_X(t)=p_X(\infty)$
exists, and the limiting distribution of
$\lim p_X(t)=p_X(\infty)$
exists, and the limiting distribution of
![]() $p_X(\infty)$
is a beta distribution with parameters
$p_X(\infty)$
is a beta distribution with parameters
![]() $a=1$
and
$a=1$
and
![]() $b=r$
. That is, the limiting density is
$b=r$
. That is, the limiting density is
![]() $r(1-x)^{r-1}$
,
$r(1-x)^{r-1}$
,
![]() $x\in [0,1]$
. Therefore a.s.
$x\in [0,1]$
. Therefore a.s.
![]() $\lim p_X(t)>0$
.
$\lim p_X(t)>0$
.
Case (ii). Consider
![]() $m>1$
. Clearly
$m>1$
. Clearly
![]() $G_1(t)\subset G_m(t)$
. Therefore a.s.
$G_1(t)\subset G_m(t)$
. Therefore a.s.
![]() $\liminf p_X(t)>0$
as well. Furthermore, it follows from (3.9) that
$\liminf p_X(t)>0$
as well. Furthermore, it follows from (3.9) that
(as before, ‘
![]() $ \mid \circ)$
’ means conditioning on
$ \mid \circ)$
’ means conditioning on
![]() $G_m(t)$
), which is a special case of (3.8), with
$G_m(t)$
), which is a special case of (3.8), with
![]() ${\textrm{O}}\big(t^{-2}\big)$
dropped. So we obtain that
${\textrm{O}}\big(t^{-2}\big)$
dropped. So we obtain that
![]() $\mathbb{P}(p(\infty)\in \{0,1\})=1$
, which in combination with
$\mathbb{P}(p(\infty)\in \{0,1\})=1$
, which in combination with
![]() $\mathbb{P}(p_X(\infty)>0)=1$
implies that
$\mathbb{P}(p_X(\infty)>0)=1$
implies that
![]() $\mathbb{P}(p_X(\infty)=1)=1$
.
$\mathbb{P}(p_X(\infty)=1)=1$
.
4. A technical lemma
In this section we will prove Lemma 4.1. We need the following Chernoff bound for its proof (see e.g. [Reference Janson, Łuczak and Ruciński26, Theorem 2.8]).
Theorem 4.1. If
![]() $X_1,\dots,X_n$
are independent Bernoulli random variables,
$X_1,\dots,X_n$
are independent Bernoulli random variables,
![]() $X=\sum_{i=1}^n X_i$
, and
$X=\sum_{i=1}^n X_i$
, and
![]() $\lambda = \mathbb{E}[X]$
, then
$\lambda = \mathbb{E}[X]$
, then
Lemma 4.1. Let
![]() $\{X(t)\}_{t\ge 0}$
be a sequence of random variables such that
$\{X(t)\}_{t\ge 0}$
be a sequence of random variables such that
![]() $X(0)=0$
and
$X(0)=0$
and
![]() $X(t+1)-X(t) \in \{0,1\}$
. Let
$X(t+1)-X(t) \in \{0,1\}$
. Let
![]() $x(t)=X(t)/t$
and, using ‘
$x(t)=X(t)/t$
and, using ‘
![]() $ \mid \circ)$
’ to denote conditioning on
$ \mid \circ)$
’ to denote conditioning on
![]() $\{x(s)\colon s\le t\}$
, let us assume
$\{x(s)\colon s\le t\}$
, let us assume
where h is a continuous, strictly decreasing function with
![]() $h(0)>0$
and
$h(0)>0$
and
![]() $h(1)<0$
, so that
$h(1)<0$
, so that
![]() $h\big(x\big)$
has a unique root
$h\big(x\big)$
has a unique root
![]() $\rho \in(0,1)$
. Assume also that
$\rho \in(0,1)$
. Assume also that
![]() $h'(x) < -1$
in
$h'(x) < -1$
in
![]() $(0,1)$
. Then, for any
$(0,1)$
. Then, for any
![]() $\gamma<1/3$
, almost surely
$\gamma<1/3$
, almost surely
Lemma 4.2. (Extensions of Lemma 4.1.)Lemma 4.1 can be extended in a couple of ways as follows.
-
(a) If the hypothesis
 $X(t+1)-X(t) \in \{0,1\}$
in Lemma 4.1 is replaced with
$X(t+1)-X(t) \in \{0,1\}$
in Lemma 4.1 is replaced with
 $X(t+1)-X(t) \in \{-1,1\}$
, then the conclusion of Lemma 4.1 still holds. This follows from minor modifications in the proof of Lemma 4.1.
$X(t+1)-X(t) \in \{-1,1\}$
, then the conclusion of Lemma 4.1 still holds. This follows from minor modifications in the proof of Lemma 4.1. -
(b) If the inequality sign in (4.1)is replaced with an equality sign, i.e. under the condition
we have the following conclusion: for any \[ {\mathbb{E}[{x(t+1) - x(t) \mid \circ}]} = \dfrac{h(x(t))}{t} +{\textrm{O}}\big(t^{-2}\big), \]
\[ {\mathbb{E}[{x(t+1) - x(t) \mid \circ}]} = \dfrac{h(x(t))}{t} +{\textrm{O}}\big(t^{-2}\big), \]
 $\gamma<1/3$
, almost surely
$\gamma<1/3$
, almost surely  \[\lim_{t\to\infty} t^{\gamma} (x(t)-\rho)=0.\]
\[\lim_{t\to\infty} t^{\gamma} (x(t)-\rho)=0.\]
Proof of Lemma 4.2(b). First of all, by Lemma 4.1, we have
![]() $\lim_{t\to\infty} t^{\gamma}\max\{0,x(t)-\rho\}=0$
almost surely. Second, let
$\lim_{t\to\infty} t^{\gamma}\max\{0,x(t)-\rho\}=0$
almost surely. Second, let
![]() $g(z) = -h(1-z)$
, so that
$g(z) = -h(1-z)$
, so that
![]() $g(0) >0$
and
$g(0) >0$
and
![]() $g(1)<0$
, and in (0, 1), we have
$g(1)<0$
, and in (0, 1), we have
![]() $g'(z) = h'(1-z)<-1$
. Letting
$g'(z) = h'(1-z)<-1$
. Letting
![]() $y(t) = 1-x(t)$
,
$y(t) = 1-x(t)$
,
 \begin{align*}{\mathbb{E}[{y(t+1) -y (t) \mid \circ}]} &= {\mathbb{E}[{(1-x(t+1)) -(1- x(t)) \mid \circ}]} \\&= -\dfrac{h(x(t))}{t} +{\textrm{O}}\big(t^{-2}\big)\\&= \dfrac{g(y(t))}{t} +{\textrm{O}}\big(t^{-2}\big).\end{align*}
\begin{align*}{\mathbb{E}[{y(t+1) -y (t) \mid \circ}]} &= {\mathbb{E}[{(1-x(t+1)) -(1- x(t)) \mid \circ}]} \\&= -\dfrac{h(x(t))}{t} +{\textrm{O}}\big(t^{-2}\big)\\&= \dfrac{g(y(t))}{t} +{\textrm{O}}\big(t^{-2}\big).\end{align*}
Applying Lemma 4.1 with
![]() $X_1(t) = t-X(t)$
, and then switching back to X(t), we see that
$X_1(t) = t-X(t)$
, and then switching back to X(t), we see that
![]() $\lim_{t\to\infty} t^{\gamma}\max\{0, \rho-x(t)\}=0$
almost surely, as well.
$\lim_{t\to\infty} t^{\gamma}\max\{0, \rho-x(t)\}=0$
almost surely, as well.
Proof of Lemma 4.1. Let
![]() $\varepsilon=\varepsilon_t\,:\!=\, t^{-1/3}\log t$
. We will show
$\varepsilon=\varepsilon_t\,:\!=\, t^{-1/3}\log t$
. We will show
Once we show (4.2), the Borel–Cantelli lemma gives
which proves what we want. Let us prove (4.2).
For
![]() $T\in [0,t)$
, let
$T\in [0,t)$
, let
![]() $\mathcal E_T$
be the event that {
$\mathcal E_T$
be the event that {
![]() $x(t)> \rho+\varepsilon$
and T is the last time such that
$x(t)> \rho+\varepsilon$
and T is the last time such that
![]() $X(\tau) \le (\rho+\varepsilon/2)\tau$
}, that is,
$X(\tau) \le (\rho+\varepsilon/2)\tau$
}, that is,
Since
![]() $X(t+1)-X(t) \in \{0,1\}$
, we have
$X(t+1)-X(t) \in \{0,1\}$
, we have
Using
![]() $X(t) = tx(t)$
above, we get
$X(t) = tx(t)$
above, we get
implying
We conclude that
Now let us fix a
![]() $T\in [0,s]$
and bound
$T\in [0,s]$
and bound
![]() $\mathbb P(\mathcal E_T)$
. The main idea of the proof is that, as long as
$\mathbb P(\mathcal E_T)$
. The main idea of the proof is that, as long as
![]() $x(\tau)>\rho$
, by (4.1), the process
$x(\tau)>\rho$
, by (4.1), the process
![]() $\{x(\tau)\}$
has a negative drift.
$\{x(\tau)\}$
has a negative drift.
Let
![]() $\xi_\tau$
denote the indicator of the event
$\xi_\tau$
denote the indicator of the event
![]() $\{x(\tau-1)>\rho+\varepsilon/2 \text{ and } X(\tau)=X(\tau-1)+1\}$
and let
$\{x(\tau-1)>\rho+\varepsilon/2 \text{ and } X(\tau)=X(\tau-1)+1\}$
and let
![]() $\mathcal Z_T\,:\!=\, \xi_{T+2}+\cdots+\xi_t$
. On the event
$\mathcal Z_T\,:\!=\, \xi_{T+2}+\cdots+\xi_t$
. On the event
![]() $\mathcal E_T$
, the sum
$\mathcal E_T$
, the sum
![]() $\mathcal Z_T$
counts the total number of upward unit jumps (
$\mathcal Z_T$
counts the total number of upward unit jumps (
![]() $X(\tau)-X(\tau-1)=1$
,
$X(\tau)-X(\tau-1)=1$
,
![]() $\tau\in [T+2,t]$
) and therefore
$\tau\in [T+2,t]$
) and therefore
Since
![]() $X(T+1) \le X(T)+1\le T(\rho+\varepsilon/2)+1$
, we must have
$X(T+1) \le X(T)+1\le T(\rho+\varepsilon/2)+1$
, we must have
Writing
![]() $p(x(\tau))\,:\!=\, \mathbb{P}({X(\tau+1) = X(\tau)+1 \mid \circ})$
,
$p(x(\tau))\,:\!=\, \mathbb{P}({X(\tau+1) = X(\tau)+1 \mid \circ})$
,
 \begin{align*}{\mathbb{E}[{x(\tau+1) \mid \circ}]} &= p(x(\tau)) \dfrac{X(\tau)+1}{\tau+1} + (1-p(x(\tau))) \dfrac{X(\tau)}{\tau+1} \\&= \dfrac{p(x(\tau))}{\tau+1} + \dfrac{\tau x(\tau)}{\tau+1} \\& = x(\tau) + \dfrac{p(x(\tau)) - x(\tau)}{\tau+1},\end{align*}
\begin{align*}{\mathbb{E}[{x(\tau+1) \mid \circ}]} &= p(x(\tau)) \dfrac{X(\tau)+1}{\tau+1} + (1-p(x(\tau))) \dfrac{X(\tau)}{\tau+1} \\&= \dfrac{p(x(\tau))}{\tau+1} + \dfrac{\tau x(\tau)}{\tau+1} \\& = x(\tau) + \dfrac{p(x(\tau)) - x(\tau)}{\tau+1},\end{align*}
so that
![]() $p(x(\tau)) = h(x(\tau)) + x(\tau) + {\textrm{O}}\left(\tau^{-1}\right)$
.
$p(x(\tau)) = h(x(\tau)) + x(\tau) + {\textrm{O}}\left(\tau^{-1}\right)$
.
Recall that for
![]() $\tau \ge T+1$
we have
$\tau \ge T+1$
we have
![]() $x(\tau) > \rho +\varepsilon/2$
. Since
$x(\tau) > \rho +\varepsilon/2$
. Since
![]() $h'(x)<-1$
in (0, 1), the sum
$h'(x)<-1$
in (0, 1), the sum
![]() $h(x) + x$
is decreasing in (0, 1). Hence, conditioning on the full record (up to and including time
$h(x) + x$
is decreasing in (0, 1). Hence, conditioning on the full record (up to and including time
![]() $\tau$
),
$\tau$
),
 \begin{align*}\mathbb P(\xi_{\tau+1}=1 \mid \circ) &=\mathbb P(X(\tau+1)=X(\tau)+1\mid \circ)\\&= h(x(\tau)) + x(\tau) +{\textrm{O}}\left(\tau^{-1}\right) \\&< h(\rho +\varepsilon/2) + \rho + \varepsilon/2 + {\textrm{O}}\left(\tau^{-1}\right)\\&= h(\rho) + (\varepsilon/2)\cdot h'(y) +\rho +\varepsilon/2 + {\textrm{O}}\left(\tau^{-1}\right) \quad \text{for some }y\in (\rho,\rho+\varepsilon/2)\\& < \rho + {\textrm{O}}\left(\tau^{-1}\right).\end{align*}
\begin{align*}\mathbb P(\xi_{\tau+1}=1 \mid \circ) &=\mathbb P(X(\tau+1)=X(\tau)+1\mid \circ)\\&= h(x(\tau)) + x(\tau) +{\textrm{O}}\left(\tau^{-1}\right) \\&< h(\rho +\varepsilon/2) + \rho + \varepsilon/2 + {\textrm{O}}\left(\tau^{-1}\right)\\&= h(\rho) + (\varepsilon/2)\cdot h'(y) +\rho +\varepsilon/2 + {\textrm{O}}\left(\tau^{-1}\right) \quad \text{for some }y\in (\rho,\rho+\varepsilon/2)\\& < \rho + {\textrm{O}}\left(\tau^{-1}\right).\end{align*}
Hence the sequence
![]() $\{\xi_\tau\}$
is stochastically dominated by the sequence of independent Bernoulli random variables
$\{\xi_\tau\}$
is stochastically dominated by the sequence of independent Bernoulli random variables
![]() $B_\tau$
with parameters
$B_\tau$
with parameters
![]() $\min\big(\rho+{\textrm{O}}\left(\tau^{-1}\right),1\big)$
. Consequently
$\min\big(\rho+{\textrm{O}}\left(\tau^{-1}\right),1\big)$
. Consequently
![]() $Z_T$
is stochastically dominated by
$Z_T$
is stochastically dominated by
![]() $1+\sum_{j=T+2}^t B_j$
, and
$1+\sum_{j=T+2}^t B_j$
, and
 \[\lambda\,:\!=\, \sum_{j=T+2}^t \mathbb E[B_j]=\rho(t-T) +{\textrm{O}}(\!\log t).\]
\[\lambda\,:\!=\, \sum_{j=T+2}^t \mathbb E[B_j]=\rho(t-T) +{\textrm{O}}(\!\log t).\]
For the choice of
![]() $\varepsilon$
we have, (4.3) gives
$\varepsilon$
we have, (4.3) gives
Thus, by the Chernoff bound in Theorem 4.1 and using (4.3),
 \begin{align*}\mathbb{P}({\mathcal{E}_T})&\le \mathbb P(Z_T>(t-T)(\rho+\varepsilon)) \\&\le \mathbb P(1+B_{T+2}+\cdots+B_t>(t-T)(\rho+\varepsilon)) \\&\le \mathbb P(1+B_{T+2}+\cdots+B_t> (1+\varepsilon/2)\lambda) \\&\le \exp({-}\Theta(\varepsilon^2(t-T))) \le {\textrm{e}}^{-\Theta\left(\log^3 t\right)}.\end{align*}
\begin{align*}\mathbb{P}({\mathcal{E}_T})&\le \mathbb P(Z_T>(t-T)(\rho+\varepsilon)) \\&\le \mathbb P(1+B_{T+2}+\cdots+B_t>(t-T)(\rho+\varepsilon)) \\&\le \mathbb P(1+B_{T+2}+\cdots+B_t> (1+\varepsilon/2)\lambda) \\&\le \exp({-}\Theta(\varepsilon^2(t-T))) \le {\textrm{e}}^{-\Theta\left(\log^3 t\right)}.\end{align*}
Using the union bound on T, we complete the proof of (4.2) and of the lemma.
Note. In the next sections we turn to the two greedy algorithms for the PAM and UAM Markov graph processes. We will continue using the symbol ‘
![]() $ \mid \circ)$
’ to denote conditioning on a current graph G(t).
$ \mid \circ)$
’ to denote conditioning on a current graph G(t).
5. Greedy matching algorithm
Recall that the greedy matching algorithm (for either of two graph models) generates the increasing sequence
![]() $\{ M(t)\}$
of partial matchings on the sets [t], with
$\{ M(t)\}$
of partial matchings on the sets [t], with
![]() $ M(1)=\emptyset$
. GivenM(t), let
$ M(1)=\emptyset$
. GivenM(t), let
 \begin{align*}X(t)&\,:\!=\, \text{number of unmatched vertices at time }t,\\Y(t)&\,:\!=\, \text{total degree of unmatched vertices at time }t,\\U(t)&\,:\!=\, \text{number of unmatched vertices selected by $t+1$ from $[t]\setminus M(t)$},\\x(t)&\,:\!=\, X(t)/t,\\y(t)&\,:\!=\, Y(t)/(2mt).\end{align*}
\begin{align*}X(t)&\,:\!=\, \text{number of unmatched vertices at time }t,\\Y(t)&\,:\!=\, \text{total degree of unmatched vertices at time }t,\\U(t)&\,:\!=\, \text{number of unmatched vertices selected by $t+1$ from $[t]\setminus M(t)$},\\x(t)&\,:\!=\, X(t)/t,\\y(t)&\,:\!=\, Y(t)/(2mt).\end{align*}
5.1. The PAM case
Theorem 2.4. Let
![]() $X\big(t\big)$
be the number of unmatched vertices at time t in the greedy matching algorithm. For
$X\big(t\big)$
be the number of unmatched vertices at time t in the greedy matching algorithm. For
![]() $\delta>-m$
, let
$\delta>-m$
, let
![]() $\rho_{m,\delta}$
be the unique root in
$\rho_{m,\delta}$
be the unique root in
![]() $ (0,1)$
of
$ (0,1)$
of
Then, for any
![]() $\alpha<1/3$
, almost surely
$\alpha<1/3$
, almost surely
In consequence, the greedy matching algorithm a.s. finds a sequence of nested matchings
![]() $\{M(t)\}$
, where the number of vertices in
$\{M(t)\}$
, where the number of vertices in
![]() $M\big(t\big)$
is asymptotically at least
$M\big(t\big)$
is asymptotically at least
![]() $(1-\rho_{m,\delta})t$
.
$(1-\rho_{m,\delta})t$
.
Proof. Notice first that for
![]() $\delta>-m$
the function h(z) is decreasing on (0, 1) and
$\delta>-m$
the function h(z) is decreasing on (0, 1) and
![]() $h(z)=0$
does have a unique solution in the same interval.
$h(z)=0$
does have a unique solution in the same interval.
We will prove our claim first for a slightly different model that does not allow any loops other than at the first vertex. In this model, vertex 1 has m loops, and the ith edge of vertex
![]() $t+1$
attaches to
$t+1$
attaches to
![]() $u\in [t]$
with probability
$u\in [t]$
with probability
Loops not allowed except at vertex 1. In this case, since each degree is at least m, we have
![]() $Y(t)\ge mX(t)$
and hence
$Y(t)\ge mX(t)$
and hence
![]() $y(t)\ge x(t)/2$
. Also, since
$y(t)\ge x(t)/2$
. Also, since
 \[X(t+1)=\begin{cases}X(t)+1 & \text{if $ U(t)=0$,}\\X(t)-1 & \text{if $ U(t)>0$,}\end{cases}\]
\[X(t+1)=\begin{cases}X(t)+1 & \text{if $ U(t)=0$,}\\X(t)-1 & \text{if $ U(t)>0$,}\end{cases}\]
we have
Since
![]() $\mathbb P(\text{vertex}\ t + 1\ \textrm{has some loop})= {\textrm{O}}\big(t^{-1}\big)$
, using
$\mathbb P(\text{vertex}\ t + 1\ \textrm{has some loop})= {\textrm{O}}\big(t^{-1}\big)$
, using
![]() $Y(t)\ge mX(t)$
in the last step below, by Lemma 3.2 we get
$Y(t)\ge mX(t)$
in the last step below, by Lemma 3.2 we get
 \begin{align}\mathbb P(U(t)=0 \mid \circ)&= \mathbb P(U(t)=0 \text{ and vertex $t+1$ has no loop} \mid \circ) +{\textrm{O}}\big(t^{-1}\big) \notag\\&= (1-{\textrm{O}}\big(t^{-1}\big))\dfrac{(2mt-Y(t)+\delta t-\delta X(t))^{(m)}}{(2mt+\delta t)^{(m)}}+{\textrm{O}}\big(t^{-1}\big) \notag\\&=\dfrac{(2mt+\delta t-Y(t)-\delta X(t))^{m}}{(2mt+\delta t)^{m}}+{\textrm{O}}\big(t^{-1}\big) \notag\\&=\biggl( 1-\dfrac{2m}{2m+\delta}\,y(t)-\dfrac{\delta}{2m+\delta}\,x(t)\biggr)^m+{\textrm{O}}\big(t^{-1}\big) \notag \\&\le \biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+ {\textrm{O}}\big(t^{-1}\big).\end{align}
\begin{align}\mathbb P(U(t)=0 \mid \circ)&= \mathbb P(U(t)=0 \text{ and vertex $t+1$ has no loop} \mid \circ) +{\textrm{O}}\big(t^{-1}\big) \notag\\&= (1-{\textrm{O}}\big(t^{-1}\big))\dfrac{(2mt-Y(t)+\delta t-\delta X(t))^{(m)}}{(2mt+\delta t)^{(m)}}+{\textrm{O}}\big(t^{-1}\big) \notag\\&=\dfrac{(2mt+\delta t-Y(t)-\delta X(t))^{m}}{(2mt+\delta t)^{m}}+{\textrm{O}}\big(t^{-1}\big) \notag\\&=\biggl( 1-\dfrac{2m}{2m+\delta}\,y(t)-\dfrac{\delta}{2m+\delta}\,x(t)\biggr)^m+{\textrm{O}}\big(t^{-1}\big) \notag \\&\le \biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+ {\textrm{O}}\big(t^{-1}\big).\end{align}
 \begin{align}\mathbb E[x(t+1) \mid \circ] &\le x(t)+ \dfrac1t\biggl[2\biggl( 1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m-x(t)-1\biggr] +{\textrm{O}}\big(t^{-2}\big) \notag \\[3pt]&=x(t)+\dfrac{1}{t}h(x(t))+{\textrm{O}}\big(t^{-2}\big),\end{align}
\begin{align}\mathbb E[x(t+1) \mid \circ] &\le x(t)+ \dfrac1t\biggl[2\biggl( 1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m-x(t)-1\biggr] +{\textrm{O}}\big(t^{-2}\big) \notag \\[3pt]&=x(t)+\dfrac{1}{t}h(x(t))+{\textrm{O}}\big(t^{-2}\big),\end{align}
where h(z) is as defined in (5.1). Note that
![]() $X(0) = 0$
and h(z) satisfies the conditions given in Lemmas 4.1 and 4.2, namely
$X(0) = 0$
and h(z) satisfies the conditions given in Lemmas 4.1 and 4.2, namely
![]() $h(0)>0$
,
$h(0)>0$
,
![]() $h(1)<0$
, and
$h(1)<0$
, and
![]() $h'(z) <- 1$
for
$h'(z) <- 1$
for
![]() $z\in (0,1)$
. The conclusion of the theorem follows from the first part of Lemma 4.2 in this case.
$z\in (0,1)$
. The conclusion of the theorem follows from the first part of Lemma 4.2 in this case.
Loops allowed everywhere. The above analysis is carried over to this more complicated case via an argument similar to that for the descendant trees in Section 2.1.Here is a proof sketch. First, the counterpart of (5.3) is
 \begin{align*}&\mathbb P(\{U(t)=0\}\cap \{\text{no loops at }t+1\} \mid \circ)\\&\quad =\Pi_m(t)\prod_{j=0}^{m-1}\biggl(\dfrac{2mt-Y(t)+\delta t-\delta X(t)+j}{2mt+2j+1+\delta t+(j+1)\,\delta/m}\biggr)\\&\quad \le \Pi_m(t)\biggl[\biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+ {\textrm{O}}\big(t^{-1}\big)\biggr]\\&\quad =\big(1-{\textrm{O}}\big(t^{-1}\big)\big)\biggl[\biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+ {\textrm{O}}\big(t^{-1}\big)\biggr]\\&\quad = \biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+{\textrm{O}}\big(t^{-1}\big);\end{align*}
\begin{align*}&\mathbb P(\{U(t)=0\}\cap \{\text{no loops at }t+1\} \mid \circ)\\&\quad =\Pi_m(t)\prod_{j=0}^{m-1}\biggl(\dfrac{2mt-Y(t)+\delta t-\delta X(t)+j}{2mt+2j+1+\delta t+(j+1)\,\delta/m}\biggr)\\&\quad \le \Pi_m(t)\biggl[\biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+ {\textrm{O}}\big(t^{-1}\big)\biggr]\\&\quad =\big(1-{\textrm{O}}\big(t^{-1}\big)\big)\biggl[\biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+ {\textrm{O}}\big(t^{-1}\big)\biggr]\\&\quad = \biggl(1-\dfrac{m+\delta}{2m+\delta}\,x(t)\biggr)^m+{\textrm{O}}\big(t^{-1}\big);\end{align*}
see (3.3) for
![]() $\Pi_m(t)$
. Therefore we again obtain (5.4). The rest of the proof remains the same.
$\Pi_m(t)$
. Therefore we again obtain (5.4). The rest of the proof remains the same.
Remark 5.1. Let
![]() $r=r_{m,\delta}\,:\!=\, 1-\rho_{m,\delta}$
, where
$r=r_{m,\delta}\,:\!=\, 1-\rho_{m,\delta}$
, where
![]() $\rho_{m,\delta}$
is the unique root in (0, 1) of
$\rho_{m,\delta}$
is the unique root in (0, 1) of
Then r is the unique root in (0, 1) of
Thus, by Theorem 2.4, we have
almost surely, where
![]() $1-x(t)$
is the fraction of the vertices in M(t). See (2.3) for various r values when
$1-x(t)$
is the fraction of the vertices in M(t). See (2.3) for various r values when
![]() $\delta=0$
.
$\delta=0$
.
Remark 5.2. When
![]() $\delta \to \infty$
, the function
$\delta \to \infty$
, the function
![]() $f_{m,\delta}(z)$
as defined above converges to
$f_{m,\delta}(z)$
as defined above converges to
![]() $2-z-2z^m$
in (0, 1). So it is plausible that for the case of uniform attachment model, the number of vertices in M(t) is asymptotically rt, where r is the unique root of
$2-z-2z^m$
in (0, 1). So it is plausible that for the case of uniform attachment model, the number of vertices in M(t) is asymptotically rt, where r is the unique root of
![]() $2-z-2z^m$
. This is in fact the case, as shown in the next theorem.
$2-z-2z^m$
. This is in fact the case, as shown in the next theorem.
5.2. The UAM case
Theorem 2.5. Let
![]() $M\big(t\big)$
denote the greedy matching set after t steps of the UAM process. Let
$M\big(t\big)$
denote the greedy matching set after t steps of the UAM process. Let
![]() $r_m$
denote the unique positive root of
$r_m$
denote the unique positive root of
![]() $2(1-z^m) -z=0$
, i.e.
$2(1-z^m) -z=0$
, i.e.
![]() $r_m=1-m^{-1}\log 2+{\textrm{O}}\!\left(m^{-2}\right)$
. Then, for any
$r_m=1-m^{-1}\log 2+{\textrm{O}}\!\left(m^{-2}\right)$
. Then, for any
![]() $\alpha<1/3$
, almost surely
$\alpha<1/3$
, almost surely
Proof. Let
![]() $X(t) = t-2|M(t)|$
as before. In particular, we have
$X(t) = t-2|M(t)|$
as before. In particular, we have
![]() $X(0)=0$
and
$X(0)=0$
and
![]() $X(1)=1$
. At each step
$X(1)=1$
. At each step
![]() $t\ge 2$
we check the edges incident to vertex t. If some of the edges end at vertices that do not belong to M(t), then we choose the largest (youngest) of those vertices, say w, and set
$t\ge 2$
we check the edges incident to vertex t. If some of the edges end at vertices that do not belong to M(t), then we choose the largest (youngest) of those vertices, say w, and set
![]() $M(t)\,:\!=\, M(t-1)\cup \{(t,w)\}$
and
$M(t)\,:\!=\, M(t-1)\cup \{(t,w)\}$
and
![]() $X(t)=X(t-1)-1$
. Otherwise
$X(t)=X(t-1)-1$
. Otherwise
![]() $M(t)=M(t-1)$
and
$M(t)=M(t-1)$
and
![]() $X(t)=X(t-1)+1$
. Let
$X(t)=X(t-1)+1$
. Let
![]() $x(t)=X(t)/t$
be the fraction of unmatched vertices after step t. Then X(t) is a Markov chain with
$x(t)=X(t)/t$
be the fraction of unmatched vertices after step t. Then X(t) is a Markov chain with
since for
![]() $X(t+1)-X(t) =1$
to happen, each of the m choices made by vertex
$X(t+1)-X(t) =1$
to happen, each of the m choices made by vertex
![]() $t+1$
must lie outside of M(t), the probability of each such choice is
$t+1$
must lie outside of M(t), the probability of each such choice is
![]() $1-x(t)$
, and the choices are independent of each other. With the remaining probability vertex
$1-x(t)$
, and the choices are independent of each other. With the remaining probability vertex
![]() $t+1$
chooses at least one of m vertices from X(t), in which case X(t) decreases by 1. Consequently
$t+1$
chooses at least one of m vertices from X(t), in which case X(t) decreases by 1. Consequently
Dividing both sides by
![]() $t+1$
, we obtain
$t+1$
, we obtain
where
![]() $h(z) = 2(1-z)^m-z-1$
. The function h meets the conditions of the second part of Lemma 4.2. Hence
$h(z) = 2(1-z)^m-z-1$
. The function h meets the conditions of the second part of Lemma 4.2. Hence
![]() $\lim_{t\to\infty} t^{\gamma}|x(t)-\rho_m| = 0$
a.s. On the other hand, if
$\lim_{t\to\infty} t^{\gamma}|x(t)-\rho_m| = 0$
a.s. On the other hand, if
![]() $\rho_m$
is the unique root of h in (0, 1), then
$\rho_m$
is the unique root of h in (0, 1), then
![]() $r_m\,:\!=\, 1-\rho_m$
is the unique root of
$r_m\,:\!=\, 1-\rho_m$
is the unique root of
![]() $2(1-z^m)-z$
in (0, 1). Since
$2(1-z^m)-z$
in (0, 1). Since
![]() $x(t)-\rho_m = (1 -2 |M(t)|/t) - (1-\rho_m) = \rho_m -2 |M(t)|/t$
, we also have a.s.
$x(t)-\rho_m = (1 -2 |M(t)|/t) - (1-\rho_m) = \rho_m -2 |M(t)|/t$
, we also have a.s.
This completes the proof.
6. Analysis of greedy independent set algorithm
The algorithm, for both the PAM and UAM cases, generates the increasing sequence of independent sets
![]() $\{I(t)\}$
on the sets [t], with
$\{I(t)\}$
on the sets [t], with
![]() $I(1)\,:\!=\, \{1\}$
. If vertex
$I(1)\,:\!=\, \{1\}$
. If vertex
![]() $t+1$
does not select a single vertex from t, we set
$t+1$
does not select a single vertex from t, we set
![]() $I(t+1)=I(t)\cup \{t+1\}$
; otherwise
$I(t+1)=I(t)\cup \{t+1\}$
; otherwise
![]() $I(t+1)\,:\!=\, I(t)$
. Given I(t), let
$I(t+1)\,:\!=\, I(t)$
. Given I(t), let
 \begin{align*}X(t)&\,:\!=\, \text{number of vertices} \le t\ \text{outside of the current independent set } I(t),\\Y(t)&\,:\!=\, \text{total degree of these outsiders} ,\\Z(t)&\,:\!=\, \text{number of insiders selected by outsiders by time}\ {t},\\U(t)&\,:\!=\, \text{number of insiders selected by vertex}\ t+1,\\x(t) &\,:\!=\, \dfrac{X(t)}{t},\quad y(t)\,:\!=\, \dfrac{Y(t)}{2mt},\quad z(t)=\dfrac{Z(t)}{mt}, \quad i(t)=\dfrac{|I(t)|}{t}.\end{align*}
\begin{align*}X(t)&\,:\!=\, \text{number of vertices} \le t\ \text{outside of the current independent set } I(t),\\Y(t)&\,:\!=\, \text{total degree of these outsiders} ,\\Z(t)&\,:\!=\, \text{number of insiders selected by outsiders by time}\ {t},\\U(t)&\,:\!=\, \text{number of insiders selected by vertex}\ t+1,\\x(t) &\,:\!=\, \dfrac{X(t)}{t},\quad y(t)\,:\!=\, \dfrac{Y(t)}{2mt},\quad z(t)=\dfrac{Z(t)}{mt}, \quad i(t)=\dfrac{|I(t)|}{t}.\end{align*}
Since each insider selects only among outsiders, the total degree of insiders is
![]() $m|I(t)| +Z(t)$
and
$m|I(t)| +Z(t)$
and
6.1. The PAM case
Theorem 2.6. Let
![]() $w_m$
denote the unique root of
$w_m$
denote the unique root of
![]() $-w+(1-w)^m$
in
$-w+(1-w)^m$
in
![]() $ (0, 1)$
. For any
$ (0, 1)$
. For any
almost surely
Proof. By the definition of the algorithm, we have
 \[|I(t+1)|=\begin{cases}|I(t)|+1 &\text{with probability $\mathbb{P}(U(t)=0 \mid \circ)$,}\\|I(t)| &\text{with probability $\mathbb{P}(U(t)>0 \mid \circ)$.}\end{cases}\]
\[|I(t+1)|=\begin{cases}|I(t)|+1 &\text{with probability $\mathbb{P}(U(t)=0 \mid \circ)$,}\\|I(t)| &\text{with probability $\mathbb{P}(U(t)>0 \mid \circ)$.}\end{cases}\]
Now
![]() $U(t)=0$
means that vertex
$U(t)=0$
means that vertex
![]() $t+1$
selects all m vertices from the outsiders set, so that
$t+1$
selects all m vertices from the outsiders set, so that
 \begin{align*}\mathbb{P}(U(t)=0 \mid \circ)&=\dfrac{(Y(t)+\delta X(t))^{(m)}}{((2m+\delta)t)^{(m)}}+{\textrm{O}}\big(t^{-1}\big)\\&=\biggl(\dfrac{2my(t)+\delta x(t)}{2m+\delta}\biggr)^m +{\textrm{O}}\big(t^{-1}\big)\\&=\biggl(1-\dfrac{m+\delta}{2m+\delta}\, i(t)-\dfrac{m}{2m+\delta}\,z(t)\biggr)^m +{\textrm{O}}\big(t^{-1}\big).\end{align*}
\begin{align*}\mathbb{P}(U(t)=0 \mid \circ)&=\dfrac{(Y(t)+\delta X(t))^{(m)}}{((2m+\delta)t)^{(m)}}+{\textrm{O}}\big(t^{-1}\big)\\&=\biggl(\dfrac{2my(t)+\delta x(t)}{2m+\delta}\biggr)^m +{\textrm{O}}\big(t^{-1}\big)\\&=\biggl(1-\dfrac{m+\delta}{2m+\delta}\, i(t)-\dfrac{m}{2m+\delta}\,z(t)\biggr)^m +{\textrm{O}}\big(t^{-1}\big).\end{align*}
The leading term in the first equality is the exact (conditional) probability of
![]() $\{U(t)=0\}$
when no loops at vertices other than the first vertex are allowed, and the extra
$\{U(t)=0\}$
when no loops at vertices other than the first vertex are allowed, and the extra
![]() ${\textrm{O}}\big(t^{-1}\big)$
is for our more general case when the loops are admissible. So, using
${\textrm{O}}\big(t^{-1}\big)$
is for our more general case when the loops are admissible. So, using
![]() $i(t)=|I(t)|/t$
, we have
$i(t)=|I(t)|/t$
, we have
Now
![]() $Z(t+1)=Z(t)+U(t)$
, so that
$Z(t+1)=Z(t)+U(t)$
, so that
 \begin{align*}\mathbb{E}[Z(t+1) \mid \circ]&= Z(t) +\mathbb{E}[U(t) \mid \circ]\\&=Z(t)+m\dfrac{I(t)(m+\delta)+Z(t)}{(2m+\delta)t}+{\textrm{O}}\big(t^{-1}\big),\end{align*}
\begin{align*}\mathbb{E}[Z(t+1) \mid \circ]&= Z(t) +\mathbb{E}[U(t) \mid \circ]\\&=Z(t)+m\dfrac{I(t)(m+\delta)+Z(t)}{(2m+\delta)t}+{\textrm{O}}\big(t^{-1}\big),\end{align*}
and using
![]() $z(t)=Z(t)/mt$
, we have
$z(t)=Z(t)/mt$
, we have
Introduce
Multiplying (6.1) and (6.2) by
![]() ${{(m+\delta)}/{(2m+\delta)}}$
and
${{(m+\delta)}/{(2m+\delta)}}$
and
![]() ${{m}/{(2m+\delta)}}$
and adding the products, we obtain
${{m}/{(2m+\delta)}}$
and adding the products, we obtain
 \begin{equation}\begin{aligned}\mathbb{E}[w(t+1) \mid \circ]&=w(t)+\dfrac{f(w(t))}{t+1}+{\textrm{O}}\big(t^{-2}\big),\\f(w)&\,:\!=\, \dfrac{m+\delta}{2m+\delta}\bigl[-w+(1-w)^m\bigr].\end{aligned}\end{equation}
\begin{equation}\begin{aligned}\mathbb{E}[w(t+1) \mid \circ]&=w(t)+\dfrac{f(w(t))}{t+1}+{\textrm{O}}\big(t^{-2}\big),\\f(w)&\,:\!=\, \dfrac{m+\delta}{2m+\delta}\bigl[-w+(1-w)^m\bigr].\end{aligned}\end{equation}
The function f is qualitatively similar to the function h in the proof of Theorem 2.4. Indeed, f(w) is strictly decreasing, with
![]() $f(0)=1$
and
$f(0)=1$
and
![]() $f(1)=-1$
. Therefore f(w) has a unique root
$f(1)=-1$
. Therefore f(w) has a unique root
![]() $w_m\in (0,1)$
; it is not difficult to see that
$w_m\in (0,1)$
; it is not difficult to see that
Let us prove that for any
and
![]() $A\ge A(\alpha)$
we have
$A\ge A(\alpha)$
we have
First
 \begin{align}|i(t+1)-i(t)|&=\bigg|\dfrac{|I(t+1)|}{t+1}-\dfrac{|I(t)|}{t}\bigg| \notag \\&\le \dfrac{1}{t+1}(|I(t+1)|-|I(t)|) +\dfrac{|I(t+1)|}{t+1}\notag \\&\le \dfrac{2}{t+1},\end{align}
\begin{align}|i(t+1)-i(t)|&=\bigg|\dfrac{|I(t+1)|}{t+1}-\dfrac{|I(t)|}{t}\bigg| \notag \\&\le \dfrac{1}{t+1}(|I(t+1)|-|I(t)|) +\dfrac{|I(t+1)|}{t+1}\notag \\&\le \dfrac{2}{t+1},\end{align}
and similarly
Therefore
![]() $|w(t+1)-w(t)|\le 2/(t+1)$
, and consequently
$|w(t+1)-w(t)|\le 2/(t+1)$
, and consequently
So, conditioning on prehistory, we have
 \begin{align*}\mathbb{E}\bigl[(w(t+1)-w_m)^2 \mid \circ\bigr]&\le (w(t)-w_m)^2+2(w(t)-w_m) \mathbb{E}[w(t+1)-w(t) \mid \circ] +{\textrm{O}}\big(t^{-2}\big)\\&=(w(t)-w_m)^2 +\dfrac{2(w(t)-w_m)}{t+1} f(w(t))+{\textrm{O}}\big(t^{-2}\big).\end{align*}
\begin{align*}\mathbb{E}\bigl[(w(t+1)-w_m)^2 \mid \circ\bigr]&\le (w(t)-w_m)^2+2(w(t)-w_m) \mathbb{E}[w(t+1)-w(t) \mid \circ] +{\textrm{O}}\big(t^{-2}\big)\\&=(w(t)-w_m)^2 +\dfrac{2(w(t)-w_m)}{t+1} f(w(t))+{\textrm{O}}\big(t^{-2}\big).\end{align*}
By (6.3),
Therefore, with
the last inequality gives
leading to a recursive inequality
The bound (6.4) follows from (6.6) by a straightforward induction on t. Next we use (6.4) to prove that, for
![]() $A_1$
large enough,
$A_1$
large enough,
Using (6.5), we have
Consequently
 \begin{align*}\mathbb{E}\bigl[(i(t+1)-w_m)^2 \mid \circ\bigr]&\le (i(t)-w_m)^2+2(i(t)-w_m) \mathbb{E}[i(t+1)-i(t) \mid \circ] +{\textrm{O}}\big(t^{-2}\big)\\&=(i(t)-w_m)^2 +\dfrac{2(i(t)-w_m)}{t+1} [-i(t)+(1-w(t))^m]+{\textrm{O}}\big(t^{-2}\big).\end{align*}
\begin{align*}\mathbb{E}\bigl[(i(t+1)-w_m)^2 \mid \circ\bigr]&\le (i(t)-w_m)^2+2(i(t)-w_m) \mathbb{E}[i(t+1)-i(t) \mid \circ] +{\textrm{O}}\big(t^{-2}\big)\\&=(i(t)-w_m)^2 +\dfrac{2(i(t)-w_m)}{t+1} [-i(t)+(1-w(t))^m]+{\textrm{O}}\big(t^{-2}\big).\end{align*}
Taking expectations of both sides, and using Cauchy’s inequality and (6.4), we obtain
 \begin{align*}\mathbb{E}\bigl[(i(t+1)-w_m)^2\bigr]&\le \biggl(1-\dfrac{2}{t+1}\biggr)\mathbb{E}\bigl[(i(t)-w_m)^2\bigr]\\&\quad\, +\dfrac{2}{t+1}\mathbb{E}^{1/2}\bigl[(i(t)-w_m)^2\bigr]\,\mathbb{E}^{1/2}\bigl[(w_m-(1-w(t))^m)^2\bigr]+{\textrm{O}}\big(t^{-2}\big)\\&\le \biggl(1-\dfrac{2}{t+1}\biggr)\mathbb{E}\bigl[(i(t)-w_m)^2\bigr] +\dfrac{2mA^{1/2}}{t^{1+\alpha/2}}\mathbb{E}^{1/2}\bigl[(i(t)-w_m)^2\bigr]+{\textrm{O}}\big(t^{-2}\big),\end{align*}
\begin{align*}\mathbb{E}\bigl[(i(t+1)-w_m)^2\bigr]&\le \biggl(1-\dfrac{2}{t+1}\biggr)\mathbb{E}\bigl[(i(t)-w_m)^2\bigr]\\&\quad\, +\dfrac{2}{t+1}\mathbb{E}^{1/2}\bigl[(i(t)-w_m)^2\bigr]\,\mathbb{E}^{1/2}\bigl[(w_m-(1-w(t))^m)^2\bigr]+{\textrm{O}}\big(t^{-2}\big)\\&\le \biggl(1-\dfrac{2}{t+1}\biggr)\mathbb{E}\bigl[(i(t)-w_m)^2\bigr] +\dfrac{2mA^{1/2}}{t^{1+\alpha/2}}\mathbb{E}^{1/2}\bigl[(i(t)-w_m)^2\bigr]+{\textrm{O}}\big(t^{-2}\big),\end{align*}
since
![]() $w_m=(1-w_m)^m$
, and
$w_m=(1-w_m)^m$
, and
So it suffices to show the existence of
![]() $A_1$
such that
$A_1$
such that
holds for
![]() $t>t_0$
, where
$t>t_0$
, where
![]() $t_0$
depends only on A and
$t_0$
depends only on A and
![]() $\alpha$
. For large t, the above inequality becomes
$\alpha$
. For large t, the above inequality becomes
and
does the job. So (6.7) is proved. Therefore, by Markov’s inequality,
This inequality already means that
![]() $i(t)\to w_m$
in probability. Let us show the considerably stronger statement that
$i(t)\to w_m$
in probability. Let us show the considerably stronger statement that
![]() $i(t)\to w_m$
with probability 1, at least as fast as
$i(t)\to w_m$
with probability 1, at least as fast as
![]() $t^{-\chi}$
, for any given
$t^{-\chi}$
, for any given
![]() $\chi<1/3$
. Pick
$\chi<1/3$
. Pick
![]() $\beta>1$
and introduce a sequence
$\beta>1$
and introduce a sequence
![]() $\{t_{\nu}\}$
,
$\{t_{\nu}\}$
,
![]() $t_{\nu}=\lfloor \nu^{\beta}\rfloor$
. By (6.8), we have
$t_{\nu}=\lfloor \nu^{\beta}\rfloor$
. By (6.8), we have
provided that
![]() $\beta>(\alpha-2\chi)^{-1}$
, which we assume from now. For such choice of
$\beta>(\alpha-2\chi)^{-1}$
, which we assume from now. For such choice of
![]() $\beta$
, by the Borel–Cantelli lemma with probability 1 for all but finitely many
$\beta$
, by the Borel–Cantelli lemma with probability 1 for all but finitely many
![]() $\nu$
, we have
$\nu$
, we have
![]() $|i(t_{\nu})-\rho|\le t_{\nu}^{-\chi}$
. Let
$|i(t_{\nu})-\rho|\le t_{\nu}^{-\chi}$
. Let
![]() $t\in [t_{\nu}, t_{\nu+1}]$
. By (6.5), we have
$t\in [t_{\nu}, t_{\nu+1}]$
. By (6.5), we have
uniformly for all
![]() $\nu$
. So if
$\nu$
. So if
![]() $|i(t_{\nu})-\rho|\le t_{\nu}^{-\chi}$
, then (using
$|i(t_{\nu})-\rho|\le t_{\nu}^{-\chi}$
, then (using
![]() $t_{\nu}=\Theta\big(\nu^{\beta}\big)$
) we have, for
$t_{\nu}=\Theta\big(\nu^{\beta}\big)$
) we have, for
![]() $t\in [t_{\nu},t_{\nu+1}]$
,
$t\in [t_{\nu},t_{\nu+1}]$
,
 \begin{align*}|i(t)-w_m|&\le t_{\nu}^{-\chi}+{\textrm{O}}\biggl(\dfrac{t_{\nu+1}-t_{\nu}}{t_{\nu}}\biggr)\\&={\textrm{O}}\left(\nu^{-\beta\chi}+\nu^{-1}\right)\\&={\textrm{O}}\left(\nu^{-\min(\beta\chi,1)}\right)\\&={\textrm{O}}\left(t^{-\min(\chi,\beta^{-1})}\right).\end{align*}
\begin{align*}|i(t)-w_m|&\le t_{\nu}^{-\chi}+{\textrm{O}}\biggl(\dfrac{t_{\nu+1}-t_{\nu}}{t_{\nu}}\biggr)\\&={\textrm{O}}\left(\nu^{-\beta\chi}+\nu^{-1}\right)\\&={\textrm{O}}\left(\nu^{-\min(\beta\chi,1)}\right)\\&={\textrm{O}}\left(t^{-\min(\chi,\beta^{-1})}\right).\end{align*}
Since
![]() $|i(t_{\nu})-w_m|\le t_{\nu}^{-\chi}$
holds almost surely (a.s.) for all but finitely many
$|i(t_{\nu})-w_m|\le t_{\nu}^{-\chi}$
holds almost surely (a.s.) for all but finitely many
![]() $\nu$
, we see then that a.s. so does the bound
$\nu$
, we see then that a.s. so does the bound
![]() $|i(t)-w_m|={\textrm{O}}(t^{-\min(\chi,\beta^{-1})})$
for all but finitely many t. Now, by taking
$|i(t)-w_m|={\textrm{O}}(t^{-\min(\chi,\beta^{-1})})$
for all but finitely many t. Now, by taking
![]() $\beta$
sufficiently close to
$\beta$
sufficiently close to
![]() $(\alpha-2\chi)^{-1}$
from above, we can make
$(\alpha-2\chi)^{-1}$
from above, we can make
![]() $\min(\chi,\beta^{-1})$
arbitrarily close to
$\min(\chi,\beta^{-1})$
arbitrarily close to
![]() $\min(\chi, \alpha-2\chi)$
from below. It remains to notice that
$\min(\chi, \alpha-2\chi)$
from below. It remains to notice that
![]() $\min(\chi, \alpha-2\chi)$
attains its maximum
$\min(\chi, \alpha-2\chi)$
attains its maximum
![]() $\alpha/3$
at
$\alpha/3$
at
![]() $\chi=\alpha/3$
. The proof of Theorem 2.6 is complete.
$\chi=\alpha/3$
. The proof of Theorem 2.6 is complete.
6.2. The UAM case
Theorem 2.7. Let
![]() $w_m$
be the unique root of
$w_m$
be the unique root of
![]() $-w+(1-w)^m$
in
$-w+(1-w)^m$
in
![]() $ (0, 1)$
. Then, for any
$ (0, 1)$
. Then, for any
![]() $\alpha<1/3$
, almost surely
$\alpha<1/3$
, almost surely
The following remark is already stated as Remark 2.3.
Remark 6.1. Thus, the convergence rate aside, almost surely the greedy independent algorithm delivers a sequence of independent sets of asymptotically the same size as for the PAM case.
Proof. Let
![]() $i(t)=|I(t)|/t$
. From the definition of the UAM process and the greedy independent set algorithm, we obtain
$i(t)=|I(t)|/t$
. From the definition of the UAM process and the greedy independent set algorithm, we obtain
 \[|I(t+1)|=\begin{cases}|I(t)|+1 &\text{with conditional probability $ (1-i(t))^m$,}\\|I(t)| &\text{with conditional probability $ 1-(1-i(t))^m$.}\end{cases}\]
\[|I(t+1)|=\begin{cases}|I(t)|+1 &\text{with conditional probability $ (1-i(t))^m$,}\\|I(t)| &\text{with conditional probability $ 1-(1-i(t))^m$.}\end{cases}\]
Therefore
or equivalently
The function
![]() $-x+(1-x)^m$
differs by a constant positive factor from the function f in (6.3). The function f meets the conditions of Lemma 4.1, and
$-x+(1-x)^m$
differs by a constant positive factor from the function f in (6.3). The function f meets the conditions of Lemma 4.1, and
![]() $r_m$
is a unique root of f. Therefore, for any
$r_m$
is a unique root of f. Therefore, for any
![]() $\alpha<1/3$
, a.s.
$\alpha<1/3$
, a.s.
![]() $\lim_{t\to\infty} t^{\alpha}|i(t)-r_m|=0$
.
$\lim_{t\to\infty} t^{\alpha}|i(t)-r_m|=0$
.
Appendix A. Coupling
 $\{{\boldsymbol{G}}_{{\boldsymbol{m,}}\textbf{0}}{(\boldsymbol{t})}\}_{{\boldsymbol{t}}}$
and
$\{{\boldsymbol{G}}_{{\boldsymbol{m,}}\textbf{0}}{(\boldsymbol{t})}\}_{{\boldsymbol{t}}}$
and
 $\{{\boldsymbol{G}}_{1,0}({\boldsymbol{mt}})\}_{{\boldsymbol{t}}}$
$\{{\boldsymbol{G}}_{1,0}({\boldsymbol{mt}})\}_{{\boldsymbol{t}}}$
In order to show that the coupling described in Section 2 really works, we can compute the probability that the ith edge of vertex
![]() $w_{t+1}$
connects to vertex
$w_{t+1}$
connects to vertex
![]() $w_x$
in the coupling and compare it with the probability in (2.1). Let
$w_x$
in the coupling and compare it with the probability in (2.1). Let
![]() $\{G^{\prime}_{m,\delta}(t)\}$
denote the process obtained by collapsing the vertices of
$\{G^{\prime}_{m,\delta}(t)\}$
denote the process obtained by collapsing the vertices of
![]() $\{G_{1,\delta/m}(mt)\}$
. Note that the
$\{G_{1,\delta/m}(mt)\}$
. Note that the
![]() $(mt+i)$
th edge of the
$(mt+i)$
th edge of the
![]() $\{G_{1,\delta/m}(mt)\}$
process becomes the ith edge of
$\{G_{1,\delta/m}(mt)\}$
process becomes the ith edge of
![]() $w_{t+1}$
after collapsing. Hence the ith edge of vertex
$w_{t+1}$
after collapsing. Hence the ith edge of vertex
![]() $w_{t+1}$
connects to
$w_{t+1}$
connects to
![]() $w_x$
(
$w_x$
(
![]() $x\le t$
) if and only if the
$x\le t$
) if and only if the
![]() $(mt+i)$
th edge of the
$(mt+i)$
th edge of the
![]() $\{G_{1,\delta/m}(mt)\}$
process connects
$\{G_{1,\delta/m}(mt)\}$
process connects
![]() $v_{mt+i}$
with one of the vertices
$v_{mt+i}$
with one of the vertices
![]() $v_{m(x-1)+1},\dots,v_{mx}$
. Let
$v_{m(x-1)+1},\dots,v_{mx}$
. Let
![]() $d_{mt+i-1}(v_y)$
denote the degree of
$d_{mt+i-1}(v_y)$
denote the degree of
![]() $v_y$
(
$v_y$
(
![]() $y\le mt+i$
) just before the
$y\le mt+i$
) just before the
![]() $(mt+i)$
th edge of the
$(mt+i)$
th edge of the
![]() $\{G_{1,\delta/m}\}$
process is drawn. Also, let
$\{G_{1,\delta/m}\}$
process is drawn. Also, let
![]() $D_{t,i-1}(w_x)$
denote the degree of
$D_{t,i-1}(w_x)$
denote the degree of
![]() $w_x$
at the exact same time. Hence, by definition,
$w_x$
at the exact same time. Hence, by definition,
 \[D_{t,i-1}(w_x)=\begin{cases}\displaystyle \sum_{y=mx-m+1}^{mx} \ d_{mt+i-1}(v_y) & x\le t,\\[17pt]\displaystyle \sum_{y=mt+1}^{mt+i}\ d_{mt+i-1}(v_y) & x=t+1.\end{cases}\]
\[D_{t,i-1}(w_x)=\begin{cases}\displaystyle \sum_{y=mx-m+1}^{mx} \ d_{mt+i-1}(v_y) & x\le t,\\[17pt]\displaystyle \sum_{y=mt+1}^{mt+i}\ d_{mt+i-1}(v_y) & x=t+1.\end{cases}\]
By (2.2), for
![]() $x\le t$
, the probability that
$x\le t$
, the probability that
![]() $v_{mt+i}$
connects to one of the vertices
$v_{mt+i}$
connects to one of the vertices
![]() $v_{m(x-1)+1},\dots,v_{mx}$
(equivalently, the probability that the ith edge of
$v_{m(x-1)+1},\dots,v_{mx}$
(equivalently, the probability that the ith edge of
![]() $w_{t+1}$
connects to
$w_{t+1}$
connects to
![]() $w_x$
) is
$w_x$
) is
 \begin{align*}\dfrac {\sum_{y=mx-m+1}^{mx} \ (d_{mt+i-1}(v_y)+\delta/m)} {(2+\delta/m)(mt+i-1)+1+\delta/m} &= \dfrac{\delta+ \sum_{y=mx-m+1}^{mx}\ d_{mt+i-1}(v_y)}{\delta(t+i/m)+2mt+2i-1}\\[5pt]&=\dfrac{\delta+ D_{t,i-1}(w_x)}{\delta(t+i/m)+2mt+2i-1}.\end{align*}
\begin{align*}\dfrac {\sum_{y=mx-m+1}^{mx} \ (d_{mt+i-1}(v_y)+\delta/m)} {(2+\delta/m)(mt+i-1)+1+\delta/m} &= \dfrac{\delta+ \sum_{y=mx-m+1}^{mx}\ d_{mt+i-1}(v_y)}{\delta(t+i/m)+2mt+2i-1}\\[5pt]&=\dfrac{\delta+ D_{t,i-1}(w_x)}{\delta(t+i/m)+2mt+2i-1}.\end{align*}
Similarly, the probability that
![]() $v_{mt+i}$
selects one of
$v_{mt+i}$
selects one of
![]() $v_{mt+1},\dots,v_{mt+i}$
(equivalently, the probability that the ith edge of
$v_{mt+1},\dots,v_{mt+i}$
(equivalently, the probability that the ith edge of
![]() $w_{t+1}$
is a loop) is
$w_{t+1}$
is a loop) is
Note that the two probabilities above are the same as those in (2.1) if we replace
![]() $D_{t,i-1}(w_x)$
with
$D_{t,i-1}(w_x)$
with
![]() $d_{t,i-1}(x)$
. Moreover, the two processes,
$d_{t,i-1}(x)$
. Moreover, the two processes,
![]() $\{G^{\prime}_{m,\delta}(t)\}$
and
$\{G^{\prime}_{m,\delta}(t)\}$
and
![]() $\{G_{m,\delta}(t)\}$
as defined by (2.1), both start with m loops on the first vertex, which implies
$\{G_{m,\delta}(t)\}$
as defined by (2.1), both start with m loops on the first vertex, which implies
![]() $d_{1,0}(\cdot)=D_{1,0}(\cdot)$
. This gives us that
$d_{1,0}(\cdot)=D_{1,0}(\cdot)$
. This gives us that
![]() $\{G_{m,\delta}(t)\}$
and
$\{G_{m,\delta}(t)\}$
and
![]() $\{G^{\prime}_{m,\delta}(t)\}$
are equivalent processes, that is, at every stage they produce the same random graph.
$\{G^{\prime}_{m,\delta}(t)\}$
are equivalent processes, that is, at every stage they produce the same random graph.
Acknowledgements
We thank the referees for numerous critical comments that genuinely helped us to improve the presentation of our results. We are sincerely grateful to the Editors for an efficient refereeing/editorial process. We dedicate this work to the memory of Irina Pittel, the wife of the third coauthor.
Funding information
During the time of this research, the first coauthor was supported by NSF Fellowship (award no. 1502650). Research of the second author is supported in part by NSF Grant DMS 1661063.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.