Published online by Cambridge University Press: 01 October 2004
We consider shot-noise and max-shot-noise processes driven by spatial stationary Cox (doubly stochastic Poisson) processes. We derive their upper and lower bounds in terms of the increasing convex order, which is known as the order relation to compare the variability of random variables. Furthermore, under some regularity assumption of the random intensity fields of Cox processes, we show the monotonicity result which implies that more variable shot patterns lead to more variable shot noises. These are direct applications of the results obtained for so-called Ross-type conjectures in queuing theory.
Let
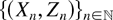
denote a marked point process on
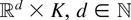
, defined on a probability space
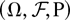
, where
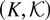
is some measurable mark space and
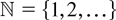
. We consider shot-noise process
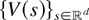
defined by
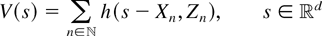
and max-shot-noise process
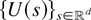
defined by
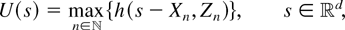
where

is called a response function and is measurable and finite almost everywhere (see, e.g., [7]). The mark process
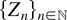
is a family of independent and identically distributed (i.i.d.) random elements and also independent of the point process
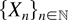
. The stability condition for |V(s)| < ∞, P-a.s., for each

, is investigated in Westcott [16, Thm.1] (see also [4,6]), and we assume that such a condition is fulfilled as far as (1) is concerned.
The random fields like (1) and (2) are often used as basic models in optics, meteorology, astronomy, and other fields (see, e.g., [2,15] and references therein). For example, if K is the set of compact subsets of

, the indicator of event {s ∈ z}, then (2) gives the indicator function if the position s is in a germ-grain model Un∈N {Xn + y : y ∈ Zn}. However, it should be noted that their characteristics are explicitly evaluated only in exceptional cases such as when

is Poisson (see, e.g., [15]). In this article, we consider the case where
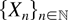
is a stationary Cox (doubly stochastic Poisson) process and h is nonnegative on

and semicontinuous in the first variable, and we investigate bounds and monotonicity of (1) and (2) in terms of some stochastic order. The stochastic order considered here is called increasing convex (icx) order and is known as the order relation to compare the variability of random variables (see, e.g., 10]). Our result shows that the upper bound is realized when
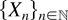
is a mixed Poisson process with the same marginal distribution of random intensity and that, under some positive dependence assumption of the random intensity field, the lower bound is realized when

is a homogeneous Poisson process with the same mean intensity. Furthermore, the monotonicity result states that under some regularity assumption of the random intensity field, more variable shot patterns lead to more variable noises. These are direct applications of the results obtained for so-called Ross-type conjectures in queuing theory (see, e.g., [1,3,8,11,12,13]) and provide an example that queuing theory applies into other fields.
This article is organized as follows. As a preliminary, in the next section, we give the definitions and some properties of the stochastic orders used. In Section 3, we derive the upper and lower bounds of (1) and (2) in terms of increasing convex order. The bounds of their Palm versions are also presented in a similar way. In Section 4, we consider the shot-noise processes (1) and (2) where the Cox point process has the random intensity fields

, defined by
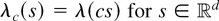
. We show that under some regularity assumption of

, (1) and (2) and their Palm versions are decreasing in c in terms of the increasing convex order. It is also noted that the bounds in Section 3 are given as two extremal cases of the monotonicity result.
In this section, we give the definitions and useful properties of some stochastic orders used in the article. A good reference for this section is a recent monograph by Müller and Stoyan [10]. First, we give the definitions of some classes of functions related to the stochastic orders. Throughout this article, we use “increasing” and “decreasing” in the nonstrict sense.
Definition 1:
(i) A function
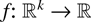
is said to be supermodular if for all
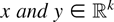
,
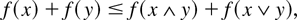
where x ∧ y and x ∨ y denote componentwise minimum and maximum, respectively.
(ii) A function
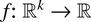
is said to be directionally convex (dcx) if for all
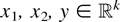
with x1 ≤ x2 and y ≥ 0,
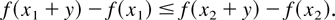
Note that a function is dcx if and only if it is supermodular and componentwise convex and note also that usual convexity neither implies nor is implied by directional convexity (see, e.g., [13]). Useful properties of increasing and dcx (idcx) functions, which often appear in stochastic models, are as follows (see [7,11]):
Lemma 1:
Let
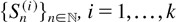
, denote k independent sequences of i.i.d. nonnegative random variables. If
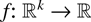
is idcx, then
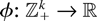
, defined by
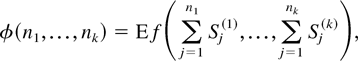
is idcx, where
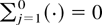
conventionally, and
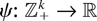
, defined by
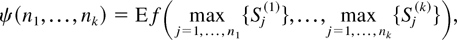
is also idcx, where we take maxj∈[empty ](·) = 0 since each Sj(i) is nonnegative.
(ii) Let Ni ; i = 1,…,k, denote k mutually independent Poisson random variables, where the mean of Ni is λi, i = 1,…,k. If
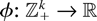
is idcx, then
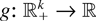
, defined by
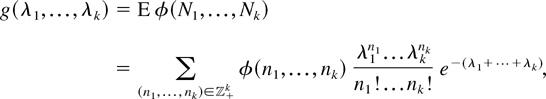
is also idcx.
Proof: The proof of the first part of (i) and that of (ii) are found in [11, Lemmas4 and 3] and [8, Lemmas2.17 and 2.18]. The second part of (i) seems new but is proved similar to the first part by replacing the sums with the maxima since x1 + ··· + xn and max{x1,…,xn} are both increasing and convex in xi, i = 1,…,n. █
Note that in Lemma 1(i),
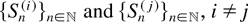
, are mutually independent, but they are not necessarily identical.
The following are the important stochastic orders used throughout this article:
Definition 2:
(i) For two
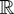
-valued random variables X and Y, we say that X is smaller than Y in the increasing convex (icx) order and write X ≤icx Y if E f (X) ≤ E f (Y) for all increasing and convex functions
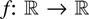
such that the expectations exist.
(ii) For two
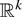
-valued random vectors X and Y, we say that X is smaller than Y in the supermodular order and write X ≤sm Y if
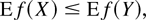
for all supermodular functions
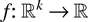
such that the expectations exist.
(iii) For two
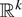
-valued random vectors X and Y, we say that X is smaller than Y in the increasing directionally convex (idcx) order and write X ≤idcx Y if (3) holds for all idcx functions
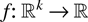
such that the expectations exist.
(iv) For two
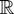
-valued random fields
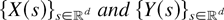
, we say that
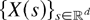
is smaller than

in the supermodular [idcx resp.] order and write
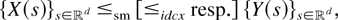
if for any

and all
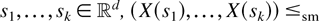
[≤idcx resp.] (Y(s1),…,Y(sk)).
Because each idcx function is supermodular, we have that X ≤sm Y implies X ≤idcx Y. Both supermodular and idcx orders are known as the order relations to compare the strength of positive dependence in random vectors (see, e.g., [10, Chap.3]). One of the most famous results, called Lorentz's inequality, is as follows (see, e.g., [10, Thm.3.9.8]):
Lemma 2 (Lorentz's Inequality): Let X1,…,Xk be
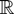
-valued random variables and let Fi denote the marginal distribution of Xi, i = 1,…,k. Then, for a random variable U uniformly distributed on [0,1),

where

.
In Lemma 2, the right-hand side is known as the random vector, which has the strongest positive dependence among ones with marginal distributions (F1,…,Fk). The next lemma, which is given by [8, Lemma3.3] (see also [9, Lemma3]) for stochastic processes on the real line, is often used in the following sections.
Lemma 3: Suppose that two
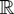
-valued random fields

are a.s. Riemann integrable. If
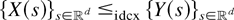
, then
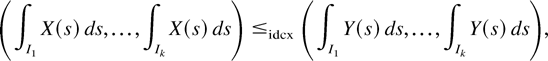
for any

and any disjoint and bounded

.
Before concluding this section we give the definition of a notion describing the positive dependence of random vectors and random fields (see [10, Def. 3.10.9] and [8, Def. 3.7]):
Definition 3:
(i) An
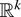
-valued random vector (X1,…,Xk) is said to be conditionally increasing if E[f (Xi)|Xj = xj,j ∈ J] is increasing in xj, j ∈ J, for all increasing function f, any i ∈ {1,…,k}, and any subset J ⊂ {1,…,k}.
(ii) An
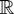
-valued random field
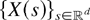
is said to be conditionally increasing if for any

and all
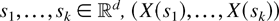
is conditionally increasing.
Combining Theorems 3.6 and 3.8 in [8], we have the following:
Lemma 4: Let X = (X1,…,Xk) be conditionally increasing and let Y = (Y1,…,Yk) be mutually independent random variables with Yi ≤icx Xi for all i = 1,…,k. Then, Y ≤idcx X.
In this section, we derive the upper and lower bounds of (1) and (2) and also those of their Palm versions, in terms of the increasing convex order. For notational convenience, we take s = 0 in (1) and (2) due to the stationarity, suppress the symbol 0, and change the sign of
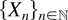
; that is, we consider
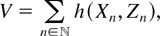
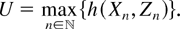
We consider {Xn}n∈N a stationary Cox process and let
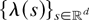
denote the stationary random intensity field of {Xn}n∈N. The corresponding random measure Λ is given by Λ(ds) = λ(s) ds. Then, lettting N denote the random counting measure which counts the points

, we have that, for any bounded
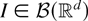
,
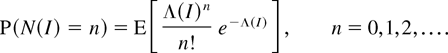
We assume that
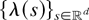
has positive and finite mean λ = E λ(0) and that
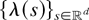
is a.s. Riemann integrable.
Two special cases of
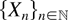
are the homogeneous Poisson process with constant intensity λ and the mixed Poisson process with random, but constant on

, intensity
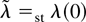
, where “=st” denotes equivalence in distribution. We compare (4) and (5) with the ones that have these special cases of Cox point processes and the identical mark process
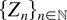
.
Theorem 1: Let Vmix and Umix denote respectively (4) and (5) where the point process
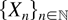
is the mixed Poisson process with random intensity

. Then,
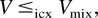

Furthermore, let Vhom and Uhom denote respectively (4) and (5) where the
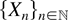
is the homogeneous Poisson process with intensity λ. If
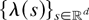
is conditionally increasing, then
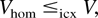
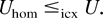
Proof: First, we show (6) and (8). For a positive integer k, let Ik = {Ik,j; j = 1,…,(k2k+1)d} denote a partition of [−k,k]d such that each Ik,j is a cube of side length 1/2k with ∪j Ik,j = [−k,k]d and Ik,j ∩ Ik,i = [empty ], j ≠ i. The first step is to show that for any increasing and convex f, there exists a family of idcx functions
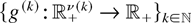
such that

where ν(k) = (k2k+1)d. Now, for any subset
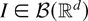
, we define
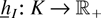
by
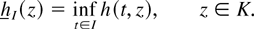
Note that hI is measurable on
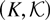
for any fixed
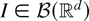
. Thus, defining

by
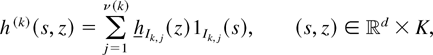
we have h(k)(s,z) ↑ h(s,z) as k → ∞ a.e. on
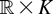
. Therefore, the random sequence
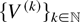
, given by
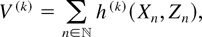
satisfies V(k) ↑ V a.s. as k → ∞. Since f is continuously increasing, by the monotone convergence theorem we have E f (V) = limk→∞ E f (V(k)). Now, for
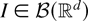
, let
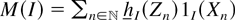
. Then, V(k) is expressed by
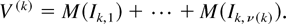
Clearly, g(x1,…,xk) = f (x1 + ··· + xk) is idcx for any increasing and convex f. Therefore, since
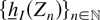
is a sequence of i.i.d. variables for fixed
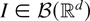
, by applying the first part of Lemma 1(i) (conditioning on N(Ik,1),…,N(Ik,ν(k))) and then by Lemma 1(ii) (conditioning on Λ(Ik,1),…,Λ(Ik,ν(k))), we have the form of (10).
Let
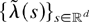
be such that
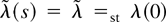
for all
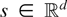
. Then, by Lemma 2 (Lorentz's inequality), we have
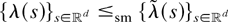
, and therefore by Lemma 3,
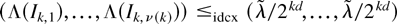
, where we use that the Lebesgue measure of Ik,j is given as |Ik,j| = 1/2kd for j = 1,…,ν(k). Hence, from (10),
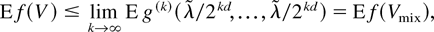
which completes the proof of (6). On the other hand, let
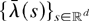
be such that λ(s) = λ = E λ(0) for all

. Since λ ≤icx λ(0) clearly by Jensen's inequality, we have by Lemma 4 that
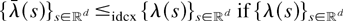
is conditionally increasing. Hence, similar to the above,
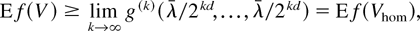
which completes the proof of (8).
Next, we show (7) and (9). Using h(k) in (11), we define the sequence

by
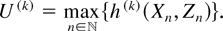
Then, U(k) ↑ U a.s. as k → ∞ and, therefore, E f (U) = limk→∞ E f (U(k)) by the monotone convergence theorem. Since hI is nonnegative and 1Ik,j(s) takes value one at most one j ∈ {1,…,ν(k)} for a given
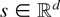
, we can rewrite (11) as h(k)(s,z) = maxj=1,…,ν(k){hIk,j(z)1Ik,j(s)}. Thus, defining
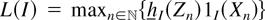
for
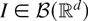
, we have
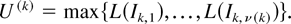
Finally, since g(x1,…,xk) = f (max{x1,…,xk}) is idcx for any increasing and convex f, we can show (7) and (9) similar to the above argument but using the second part of Lemma 1(i) instead of the first part. █
In the remainder of this section, we consider the Palm versions of (4) and (5), which are interpreted as those according to the conditional distribution given a point at the origin. Recall that the Palm version of a stationary Cox process driven by stationary random measure Λ is given by the Cox process driven by the random measure Λ° plus a point added at the origin, where Λ° is also the Palm version of Λ (see, e.g., [5, Thm.2 in Sect. 2.4]). Since the Palm probability PΛ0 with respect to the stationary random measure Λ satisfies
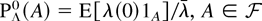
, we can define the Palm version
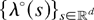
of the stationary process

by the finite-dimensional distributions:
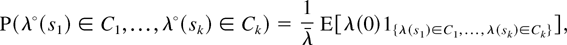
for any
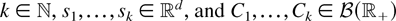
. The Palm version Λ° of the random measure Λ is then given by Λ°(ds) = λ°(s) ds. Therefore, the Palm versions of V in (4) and U in (5) are respectively given by
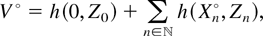
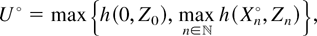
where
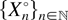
denotes the Cox process with driving random measure Λ°, and Z0 denotes a random element on
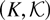
with the same distribution as Zn, n = 1,2,…, whereas Z0 is independent of
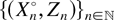
. Note that these Palm versions are not stationary in probability measure P but are so in the respective Palm probability measures.
We compare the Palm versions (13) and (14) with their special cases. Note that the Palm version of a homogeneous Poisson process is the same homogeneous Poisson process plus a point added at the origin. Also, the Palm version of the mixed Poisson process with random intensity
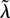
is the mixed Poisson process with random intensity

plus a point at the origin, where

. To obtain the Palm version of Theorem 1, we use the following lemma, the case of d = 1, which is implicitly used in [9].
Lemma 5: If two
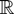
-valued random fields

are a.s. Riemann integrable and
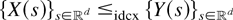
, then for any idcx
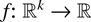
,
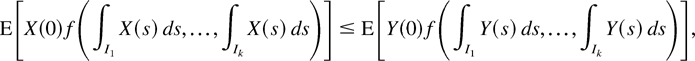
for any disjoint and bounded
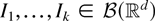
, provided that the expectations exist.
Proof: The proof is similar to that of Lemma 3 because we can easily check that if
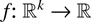
is idcx, then
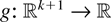
defined by g(x0,x1,…,xk) = x0 f (x1,…,xk) is also idcx (see [8, Lemma3.3] and [9, Lemma3]). █
Corollary 1: Let Vmix° and Umix° denote respectively (13) and (14) where
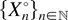
is the mixed Poisson process with random intensity

. Then,

Furthermore, let Vhom° and Uhom° denote respectively (13) and (14) where
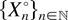
is the homogeneous Poisson process with intensity λ. If
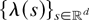
is conditionally increasing, then
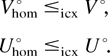
Proof: In a method similar to the proof of Theorem 1 and using (12), we have
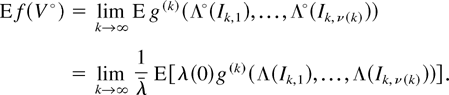
Hence, the result follows using Lemma 5 instead of Lemma 3. █
In this section, we introduce a regularity property for stationary and isotropic (i.e., motion-invariant; see, e.g., [15]) random fields, which serves as the assumption for the monotonicity results (see [9] for the version of stationary stochastic processes on the line).
Definition 4: A stationary and isotropic random field
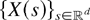
is said to be ≤sm-regular [≤idcx-regular resp.] if for any
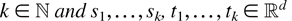
such that ∥si − sj∥ ≤ ∥ti − tj∥ for all i,j = 1,…,k,
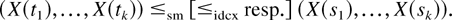
Note that if a random field
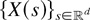
is ≤sm-regular, it is also ≤idcx-regular. The above-described regularity properties define the strength of positive dependence in random fields. The relation between the regularity property here and the conditionally increasing property in Section 2 needs further research. The regularity property in this section seems to require more than the conditionally increasing since the influence of the distance on the dependence is not concerned in the latter. However, in the case where d = 1, the one-dimensional case, and
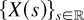
is Markovian, the conditionally increasing property reduces to doubly stochastic monotonicity, defined in [9] (see also [1]), and it is shown in [9] that stationary and doubly stochastic monotone Markov processes are ≤sm-regular.
Example 1: Consider a stationary and isotropic Gaussian field
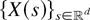
. Due to stationarity and isotropy, the covariance function is just a function of the distance and not of the direction; that is, Cov[X(si),X(sj)] = C(∥si − sj∥) for
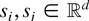
. Therefore, by Theorem 3.13.5 of [10], we have that

is ≤sm-regular if and only if the covariance function C is decreasing.
Lemma 6: Let a stationary and isotropic random field
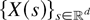
be ≤sm-regular [≤idcx-regular resp.]. Then, the random field

defined by
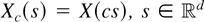
, is ≤sm-decreasing [≤idcx-decreasing resp.] in c > 0.
In Lemma 6,

fluctuates more actively as c increases while the mean value remains the same because of the stationarity. As an example of the ≤idcx-regular random intensity field of Cox process, we can choose
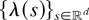
defined by
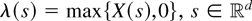
, for a stationary and isotropic Gaussian field
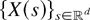
with decreasing covariance function since f (g1(·),…,gk(·)) is idcx for idcx

and increasing and convex
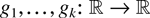
.
Theorem 2: Given a stationary and isotropic random field
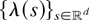
with mean λ, we define

, by λc(s) = λ(cs) for all

. Let Vc, Uc, Vc°, and Uc° denote respectively shot noise (4), max shot noise (5), and their Palm versions (13) and (14) where the point process

is the Cox process driven by the random intensity field

. If

is ≤idcx-regular, then Vc, Uc, Vc°, and Uc° are all ≤icx-decreasing in c (>0).
Proof: The proof is immediate from the proof of Theorem 1, applying Lemmas 3 and 6. For the Palm versions, we use (15) and Lemma 5 instead of Lemma 3. █
The bounds obtained in the previous section are considered the extremal cases of Theorem 2 in the sense that the limit as c → 0 reduces to the case of the mixed Poisson process and the limit as c → ∞ reduces to the case of the homogeneous Poisson process; that is, for any bounded subset

,
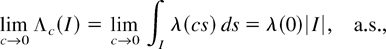
and if
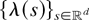
is ergodic,

where

.
The author wishes to thank Tomasz Rolski for stimulating the author's interest in the Ross-type problems.