1. Introduction
The boundary-layer separation from a body surface leads to a significant alteration of the flow field and of the forces experienced by the body. Therefore, it is not surprising that the separation phenomenon has been a focus of attention in fluid dynamics for many years. The first theoretical model of a separated flow was suggested by Kirchhoff (Reference Kirchhoff1869) who studied the flow past a flat plate perpendicular to the free-stream velocity with the separation taking place at the plate edges. Later, the Kirchhoff model was applied to other body shapes. In particular, Levi-Civita (Reference Levi-Civita1907) used it to study the separated flow past a circular cylinder. An important conclusion of this work was that the Euler equations admit a family of solutions with the position of the separation point on the cylinder surface playing the role of a free parameter. However, Kirchhoff's theory failed to reveal the physical processes leading to the separation, and provided no clues on how to choose the separation point.
Now we know that to find the location of the separation point, one needs to take into consideration the boundary layer that forms on the cylinder surface. According to Prandtl (Reference Prandtl1904), this is due to a specific behaviour of the flow in the boundary layer that separation takes place. Prandtl described the separation process as follows. Since the flow in the boundary layer has to satisfy the no-slip condition on the body surface, the fluid velocity decreases from the value dictated by the inviscid theory at the outer edge of the boundary layer to zero on the body surface. The slow moving fluid near the body surface is very sensitive to the pressure variations. On the front part of the body the pressure normally decreases in the downstream direction which makes the pressure gradient negative. It is referred to as the favourable pressure gradient because it acts to accelerate the flow keeping the boundary layer attached to the body surface. However, further downstream the pressure starts to rise, and the boundary layer finds itself under the action of a positive (adverse) pressure gradient. In these conditions the boundary layer tends to separate from the body surface. The reason for separation may be explained as follows. Since the velocity in the boundary layer decreases towards the wall, the kinetic energy of fluid particles inside the boundary layer appears to be less than that at the outer edge of the boundary layer. In fact, the closer a fluid particle is to the wall, the smaller its kinetic energy appears to be. This means that while the pressure rise in the outer flow may be quite significant, the fluid particles inside the boundary layer may not be able to get over it. Even a rather small increase of the pressure may cause the fluid particles near the wall to stop and then turn back to form a reverse flow region characteristic of separated flows. According to Prandtl, the separation point is identified as a point on the body surface where the skin friction ![]() $\tau _w = \mu ({\partial u}/{\partial y})|_{y = 0}$ becomes zero. Here we denote the longitudinal velocity by
$\tau _w = \mu ({\partial u}/{\partial y})|_{y = 0}$ becomes zero. Here we denote the longitudinal velocity by ![]() $u$, the distance from the body surface by
$u$, the distance from the body surface by ![]() $y$ and
$y$ and ![]() $\mu$ is the viscosity coefficient. Indeed, with
$\mu$ is the viscosity coefficient. Indeed, with ![]() $\tau _w$ being positive upstream of the separation point, the longitudinal velocity
$\tau _w$ being positive upstream of the separation point, the longitudinal velocity ![]() $u$ stays positive which means that the fluid particles in the boundary layer move downstream along the wall and the flow appears to be attached to the body surface. However, once the skin friction turns negative, a layer of reversed flow (
$u$ stays positive which means that the fluid particles in the boundary layer move downstream along the wall and the flow appears to be attached to the body surface. However, once the skin friction turns negative, a layer of reversed flow (![]() $u < 0$) forms near the wall, giving rise to a region of recirculation.
$u < 0$) forms near the wall, giving rise to a region of recirculation.
The above arguments relied on the kinematics of the flow, and seemed to be self-evident, but it was soon discovered that the flow reversal does not necessarily imply that the boundary layer breaks away from the body surface. The first example of such a situation was presented by Blasius (Reference Blasius1908) who considered a circular cylinder that is initially kept motionless in a stagnant fluid. At time ![]() $t = 0$, the cylinder is brought to motion with a constant velocity, which leads to a formation of the boundary layer on the cylinder surface. The solution of the boundary-layer equations showed that when the non-dimensional time reaches
$t = 0$, the cylinder is brought to motion with a constant velocity, which leads to a formation of the boundary layer on the cylinder surface. The solution of the boundary-layer equations showed that when the non-dimensional time reaches ![]() $t = 0.644$, the skin friction turned zero at the rear stagnation point, and then two symmetric recirculation regions formed inside the boundary layer, expanding upstream from the rear stagnation point. The appearance of the recirculation regions does not signify the boundary-layer separation. Indeed, experimental observations (see, for example, Nakayama Reference Nakayama1988) clearly show that the eruption of eddies from the boundary layer starts at
$t = 0.644$, the skin friction turned zero at the rear stagnation point, and then two symmetric recirculation regions formed inside the boundary layer, expanding upstream from the rear stagnation point. The appearance of the recirculation regions does not signify the boundary-layer separation. Indeed, experimental observations (see, for example, Nakayama Reference Nakayama1988) clearly show that the eruption of eddies from the boundary layer starts at ![]() $t \approx 3.0$. Before that the boundary layer remains thin, and does not influence the external inviscid part of the flow. The eddy eruption was found to start when a singularity forms in the solution of the boundary-layer equations. This behaviour is not restricted to an impulsively started cylinder, but is observed in various other flows. Inparticular, Walker(Reference Walker1978) studied the finite-time singularity in the boundary layer exposed to a rectilinear vortex. Soon after a detailed description of the finite-time singularity was given by van Dommelen & Shen (Reference van Dommelen and Shen1980). These results were re-examined with the help of numerical and analytical methods by various authors, including van Dommelen & Shen (Reference van Dommelen and Shen1982), Cowley (Reference Cowley1983), Elliott, Smith & Cowley (Reference Elliott, Smith and Cowley1983), Ingham (Reference Ingham1984), Peridier, Smith & Walker (Reference Peridier, Smith and Walker1991), Christov & Tsankov (Reference Christov and Tsankov1993), Cassel, Smith & Walker (Reference Cassel, Smith and Walker1996). They confirmed that in the case of a circular cylinder the flow reversal in the boundary layer is observed starting at
$t \approx 3.0$. Before that the boundary layer remains thin, and does not influence the external inviscid part of the flow. The eddy eruption was found to start when a singularity forms in the solution of the boundary-layer equations. This behaviour is not restricted to an impulsively started cylinder, but is observed in various other flows. Inparticular, Walker(Reference Walker1978) studied the finite-time singularity in the boundary layer exposed to a rectilinear vortex. Soon after a detailed description of the finite-time singularity was given by van Dommelen & Shen (Reference van Dommelen and Shen1980). These results were re-examined with the help of numerical and analytical methods by various authors, including van Dommelen & Shen (Reference van Dommelen and Shen1982), Cowley (Reference Cowley1983), Elliott, Smith & Cowley (Reference Elliott, Smith and Cowley1983), Ingham (Reference Ingham1984), Peridier, Smith & Walker (Reference Peridier, Smith and Walker1991), Christov & Tsankov (Reference Christov and Tsankov1993), Cassel, Smith & Walker (Reference Cassel, Smith and Walker1996). They confirmed that in the case of a circular cylinder the flow reversal in the boundary layer is observed starting at ![]() $t = 0.644$, but the solution remains smooth, which means that the eddies are still confined to a thin
$t = 0.644$, but the solution remains smooth, which means that the eddies are still confined to a thin ![]() $O (Re^{-1/2})$ region near the cylinder surface. This continues until
$O (Re^{-1/2})$ region near the cylinder surface. This continues until ![]() $t = 3.0$ when the solution develops a singularity at a position
$t = 3.0$ when the solution develops a singularity at a position ![]() $\theta = 111^{\circ }$ from the front stagnation point, signifying the start of the eddy eruption process.
$\theta = 111^{\circ }$ from the front stagnation point, signifying the start of the eddy eruption process.
For steady flows, a link between the separation and singular behaviour of the solution of the boundary-layer equations was first discovered by Howarth (Reference Howarth1938) and Hartree (Reference Hartree1939). They considered a flow where the velocity ![]() $U_e (x)$ at the outer edge of the boundary layer was a linearly decreasing function of the coordinate
$U_e (x)$ at the outer edge of the boundary layer was a linearly decreasing function of the coordinate ![]() $x$ measured along the body contour. Under these conditions the boundary layer is exposed to the adverse pressure gradient that causes the skin friction to decrease with
$x$ measured along the body contour. Under these conditions the boundary layer is exposed to the adverse pressure gradient that causes the skin friction to decrease with ![]() $x$. Howarth and Hartree found that the solution of the boundary-layer equations becomes singular at the point
$x$. Howarth and Hartree found that the solution of the boundary-layer equations becomes singular at the point ![]() $x = x_s$ where the skin friction is zero. The form of the singularity was later uncovered by Landau & Lifshitz (Reference Landau and Lifshitz1944). Making use of heuristic arguments they arrived at a conclusion that the skin friction decreases on approach to the separation point as
$x = x_s$ where the skin friction is zero. The form of the singularity was later uncovered by Landau & Lifshitz (Reference Landau and Lifshitz1944). Making use of heuristic arguments they arrived at a conclusion that the skin friction decreases on approach to the separation point as ![]() $\tau _w \sim \sqrt {x_s - x}$. They also found that the velocity component normal to the body surface experiences unbounded growth being proportional to
$\tau _w \sim \sqrt {x_s - x}$. They also found that the velocity component normal to the body surface experiences unbounded growth being proportional to ![]() $1/\sqrt {x_s - x}$. The latter appeared to explain the eruption of eddies from the boundary layer. Later Goldstein (Reference Goldstein1948) confirmed this result on a more rigorous basis, and (which is even more important) proved that the singularity at the separation precludes the solution to be continued beyond the point of zero skin friction.
$1/\sqrt {x_s - x}$. The latter appeared to explain the eruption of eddies from the boundary layer. Later Goldstein (Reference Goldstein1948) confirmed this result on a more rigorous basis, and (which is even more important) proved that the singularity at the separation precludes the solution to be continued beyond the point of zero skin friction.
Thus, it became clear that the boundary-layer theory in its classical form, as formulated by Prandtl (Reference Prandtl1904), could not be used in a vicinity of the separation point. A key element of the separation process that was not fully appreciated in Prandtl's description, was an interaction between the boundary layer and external inviscid flow, now referred to as the viscous–inviscid interaction. Asymptotic theory of the viscous–inviscid interaction, also known as the triple-deck theory, was formulated simultaneously by Neiland (Reference Neiland1969b) and Stewartson & Williams (Reference Stewartson and Williams1969) in their study of the ‘self-induced separation’ in a supersonic flow and by Stewartson (Reference Stewartson1969) and Messiter (Reference Messiter1970) for incompressible fluid flow near the trailing edge of a flat plate. The solution of the classical problem of the boundary-layer separation from a smooth body surface (like a circular cylinder) in a steady incompressible flow was presented by Sychev (Reference Sychev1972). Later, many researchers were involved in the development of the theory, and it became clear that the viscous–inviscid interaction plays a key role in a wide variety of fluid-dynamic phenomena. An exposition of applications of the theory to different forms of the boundary-layer separation may be found, for example, in Sychev et al. (Reference Sychev, Ruban, Sychev and Korolev1998), Neiland et al. (Reference Neiland, Bogolepov, Dudin and Lipatov2007) and Ruban (Reference Ruban2018).
Returning to the unsteady separation, it should be noted that an additional independent variable, time, makes the boundary-layer separation a rather complicated phenomenon that may assume various forms. Until now, the theoreticians have concentrated on two of these. The first one may be called the ‘incipient separation’, which emerges at a finite time at a particular point on the body surface in an otherwise attached boundary layer. The classical example of such a situation is an impulsive motion of a circular cylinder discussed above. This form of separation is observed in many other physical situations, most notably, at the leading edge of pitching up aerofoil (see, for example, Degani, Li & Walker Reference Degani, Li and Walker1996) where the erupting vortex leads to the phenomenon of dynamic stall.
In the second category are flows with ‘developed separation’. A typical example is the flow past a circular cylinder with the Kármán vortex street in its wake. In this flow each individual vortex forms near the cylinder surface through accumulation of vorticity in the boundary layer. Once the circulation around the vortex reaches a critical value, it is shed downstream, and another one starts to form in its place. During this cycle, the separation point moves up and down the cylinder surface.
Even before calculating the boundary-layer equations for this flow, one can predict that the solution will develop a singularity at the separation point. Indeed, if the solution remained regular, then the separation eddies could stay within the boundary layer, which is not what happens in reality. Once the fact of a singular behaviour of the boundary layer is accepted, an analogy between the unsteady separation over a fixed wall and a steady separation on a moving wall can be established (this analogy was mentioned for the first time by Sears (Reference Sears1956) and Moore (Reference Moore1958)). Indeed, on approach to the separation point, ![]() $\partial u / \partial x$ is expected to become infinitely large, making the convective acceleration of the fluid
$\partial u / \partial x$ is expected to become infinitely large, making the convective acceleration of the fluid ![]() $u \partial u / \partial x$ much larger than the local acceleration
$u \partial u / \partial x$ much larger than the local acceleration ![]() $\partial u / \partial t$, provided that the latter is calculated in the coordinate frame moving with the separation point. Of course, the fact that the flow near the separation point is governed by the steady equations does not yet mean that the theory of steady separation becomes applicable. Indeed, in the frame moving with the separation point, the body surface no longer remains motionless. Figure1 shows what happens when the separation point moves upstream along the cylinder surface and, correspondingly, for an ‘observer’ in the moving frame, the cylinder surface moves downstream. Due to the action of viscous forces, the fluid particles adjacent to the wall will be involved in the downstream motion, which precludes the recirculation region to start from a point on the body surface, as it happens in the case of steady flow separation. Instead, the separation now takes place from a point that lies in the middle of the boundary layer, as was first suggested by Rott (Reference Rott1956), Sears (Reference Sears1956) and Moore (Reference Moore1958). To explain how it happens, let us consider a sequence of cross-sections of the boundary layer corresponding to progressively larger values of the longitudinal coordinate
$\partial u / \partial t$, provided that the latter is calculated in the coordinate frame moving with the separation point. Of course, the fact that the flow near the separation point is governed by the steady equations does not yet mean that the theory of steady separation becomes applicable. Indeed, in the frame moving with the separation point, the body surface no longer remains motionless. Figure1 shows what happens when the separation point moves upstream along the cylinder surface and, correspondingly, for an ‘observer’ in the moving frame, the cylinder surface moves downstream. Due to the action of viscous forces, the fluid particles adjacent to the wall will be involved in the downstream motion, which precludes the recirculation region to start from a point on the body surface, as it happens in the case of steady flow separation. Instead, the separation now takes place from a point that lies in the middle of the boundary layer, as was first suggested by Rott (Reference Rott1956), Sears (Reference Sears1956) and Moore (Reference Moore1958). To explain how it happens, let us consider a sequence of cross-sections of the boundary layer corresponding to progressively larger values of the longitudinal coordinate ![]() $x$. In each cross-section the fluid velocity
$x$. In each cross-section the fluid velocity ![]() $u$ is a function of the normal coordinate
$u$ is a function of the normal coordinate ![]() $y$. If the boundary layer is exposed to an adverse pressure gradient then the fluid will experience a deceleration. As a result the velocity profile will have a minimum that lies some distance
$y$. If the boundary layer is exposed to an adverse pressure gradient then the fluid will experience a deceleration. As a result the velocity profile will have a minimum that lies some distance ![]() $y_{min}(x)$ from the wall. If the pressure gradient is strong enough then the minimal velocity will continue to decrease with
$y_{min}(x)$ from the wall. If the pressure gradient is strong enough then the minimal velocity will continue to decrease with ![]() $x$, leading to the separation point
$x$, leading to the separation point ![]() $( x_s , y_{min } (x_s) )$, where
$( x_s , y_{min } (x_s) )$, where ![]() $u$ is zero. At this point the so-called Moore–Rott–Sears condition
$u$ is zero. At this point the so-called Moore–Rott–Sears condition ![]() $u = {\partial u}/{\partial y} = 0$ holds.
$u = {\partial u}/{\partial y} = 0$ holds.

Figure 1. Boundary-layer separation on a downstream moving wall.
A significant breakthrough in this field was made in late 70s and 80s when the ideas of triple-deck theory were applied to the analysis of steady boundary-layer separation on a downstream moving wall. Firstly, Sychev (Reference Sychev1980) confirmed that the solution of the classical boundary-layer equations does develop a singularity at the Moore–Rott–Searspoint. Assuming that the pressure gradient remains regular on approach to this point, Sychev found that the minimum velocity decreases as ![]() $u_{min} \sim \sqrt {x_s - x}$. He also proved that the singularity precludes the solution to be continued downstream of the separation, which implies that the boundary-layer theory (in its classical formulation) is insufficient for describing the separation process.
$u_{min} \sim \sqrt {x_s - x}$. He also proved that the singularity precludes the solution to be continued downstream of the separation, which implies that the boundary-layer theory (in its classical formulation) is insufficient for describing the separation process.
A new theory was developed by Sychev (Reference Sychev1979, Reference Sychev1984, Reference Sychev1987) with help from van Dommelen & Shen (Reference van Dommelen and Shen1983) based on the asymptotic analysis of the Navier–Stokes equations at large values of the Reynolds number. It was shown that, similar to the case of a motionless wall (see Sychev Reference Sychev1972), a key element of the separation process is the mutual interaction of the boundary layer and the external inviscid part of the flow. However, unlike in the conventional triple-deck theory (Sychev Reference Sychev1972) the boundary layer on the downstream moving wall finds itself under the action of an extreme adverse pressure gradient even before the interaction region. As a consequence, the flow in the boundary layer experiences a sharp deceleration, leading to formation of a relatively thick region of retarded fluid near the point of minimal velocity. It modifies completely the process of the interaction between the boundary layer and external flow, making it predominantly inviscid. For these and other details of the theory, the reader is referred to Chapter 5 of the monograph by Sychev et al. (Reference Sychev, Ruban, Sychev and Korolev1998).
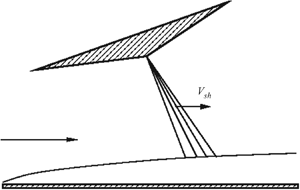
An analogue of this theory for supersonic flows was presented by Ruban et al. (Reference Ruban, Araki, Yapalparvi and Gajjar2011). They considered the boundary layer exposed to a shock wave that moves upstream. Initially it was assumed that the pressure jump across the shock ![]() ${\rm \Delta} \hat {p}$ is an order
${\rm \Delta} \hat {p}$ is an order ![]() $\hat {\rho }_{\infty } \hat {V}_{\infty }^{2} Re^{-1/4}$ quantity and the shock speed is
$\hat {\rho }_{\infty } \hat {V}_{\infty }^{2} Re^{-1/4}$ quantity and the shock speed is ![]() $\hat {V}_{sh} \sim \hat {V}_{\infty } Re^{-1/8}$, where
$\hat {V}_{sh} \sim \hat {V}_{\infty } Re^{-1/8}$, where ![]() $\hat {\rho }_{\infty }$ and
$\hat {\rho }_{\infty }$ and ![]() $\hat {V}_{\infty }$ are the free-stream density and velocity, respectively, and
$\hat {V}_{\infty }$ are the free-stream density and velocity, respectively, and ![]() $Re$ is the Reynolds number assumed large. Under these conditions the viscous–inviscid interaction is described by the equations of the classical triple-deck theory. These were first studied numerically. Then an analytic solution of the viscous–inviscid interaction problem was constructed under the assumption of a relatively large wall speed:
$Re$ is the Reynolds number assumed large. Under these conditions the viscous–inviscid interaction is described by the equations of the classical triple-deck theory. These were first studied numerically. Then an analytic solution of the viscous–inviscid interaction problem was constructed under the assumption of a relatively large wall speed: ![]() $\hat {V}_{sh} / \hat {V}_{\infty } \gg Re^{-1/8}$. It was found that, while there are mathematical differences, the physical processes leading to the separation are in essence the same as in the corresponding subsonic flow.
$\hat {V}_{sh} / \hat {V}_{\infty } \gg Re^{-1/8}$. It was found that, while there are mathematical differences, the physical processes leading to the separation are in essence the same as in the corresponding subsonic flow.
This study and the works listed above are restricted to the case of a downstream moving wall. The problem of boundary-layer separation on an upstream moving wall proved to be more difficult. The reason for this lies, at least partially, in an unclear topology of the flow. Both for the motionless wall and for the wall moving downstream, the separation may be identified by the onset of the flow reversal in the boundary layer. Contrary to that, for the upstream moving wall, a link between the flow reversal and boundary-layer separation does not appear to exist. This is illustrated in figure 2, where the classical Blasius boundary layer is considered. Figure 2(a) displays the velocity profile across the boundary layer in a conventional coordinate system attached to the body surface. Of course, this is the only coordinate system in which the flow is steady. For unsteady flows, such a ‘privileged’ coordinate system does not exist, and the velocity profile proves to be dependent on a particular coordinate system used. In figure 2(b) we consider the same flow in the coordinate frame that moves downstream along the plate surface. In this frame a ‘reverse flow’ region is observed near the plate surface. Of course, this does not mean that now the boundary layer develops a separation. Keeping this in mind, our aim in this paper will be to identify situations when a singularity develops in the boundary layer. Indeed, if the flow is free of singularities then no separation can be expected.

Figure 2. Blasius boundary layer in stationary and moving coordinates. (a) Velocity profile in a stationary coordinate frame. (b) Velocity profile in a downstream moving coordinate frame.
In the present study, we use the same formulation as in Ruban et al. (Reference Ruban, Araki, Yapalparvi and Gajjar2011), namely, we consider the boundary layer in the supersonic flow exposed to a shock or expansion fan. The triple-deck theory for such flows is easily generalized for the case of an upstream moving flow. Zhuk (Reference Zhuk1982) was the first to present a numerical solution of the triple-deck equations for the upstream moving wall. More recently the calculations were repeated by Yapalparvi & van Dommelen (Reference Yapalparvi and van Dommelen2012). The results of these works suggest that increasing wall speed suppresses the separation. In the present paper we show that the behaviour of the flow changes drastically when instead of the impinging shock the boundary layer is exposed to an expansion fan. With a large enough wall speed, the singularity develops in the boundary layer of the type first described by Neiland (Reference Neiland1969a) in his analysis of supersonic flow separation from a convex corner.
2. Problem formulation
In this paper we consider, as an example, the boundary layer on the surface of a flat plate that is aligned with the oncoming supersonic flow. Our interest is in the incipience of the separation caused by an impinging shock or expansion wave. The latter can be produced by an expansion ramp situated above the plate as shown in figure 3. We assume that the ramp and, hence, the shock/expansion fan are moving downstream with respect to the plate with velocity ![]() $\hat {V}_{sh}$. If one assumes that
$\hat {V}_{sh}$. If one assumes that ![]() $\hat {V}_{sh}/ \hat {V}_{\infty } \sim Re^{-1/8}$, where
$\hat {V}_{sh}/ \hat {V}_{\infty } \sim Re^{-1/8}$, where ![]() $\hat {V}_{\infty }$ is the free-stream velocity and
$\hat {V}_{\infty }$ is the free-stream velocity and ![]() $Re$ is the Reynolds number, then the triple-deck theory is applicable. In § 4 we will present the results of the numerical solution of the triple-deck equations. To make an analytic progress in the flow analysis we shall assume that
$Re$ is the Reynolds number, then the triple-deck theory is applicable. In § 4 we will present the results of the numerical solution of the triple-deck equations. To make an analytic progress in the flow analysis we shall assume that
The condition ![]() $\hat {V}_{sh}/ \hat {V}_{\infty } \ll 1$ ensures that the pressure stays unchanged across the boundary layer in the leading-order approximation.
$\hat {V}_{sh}/ \hat {V}_{\infty } \ll 1$ ensures that the pressure stays unchanged across the boundary layer in the leading-order approximation.

Figure 3. The flow layout.
In this study we are interested in nonlinear perturbations in the boundary layer. We therefore assume that the pressure jump across the shock/expansion fan is proportional to ![]() $( \hat {V}_{sh}/ \hat {V}_{\infty } ) ^{2}$ which, according to (2.1), is small. This means that while the perturbations in the boundary layer are nonlinear, the perturbations outside the boundary layer are weak and can be described in framework of the Ackeret theory. In this theory both the shock wave and expansion fan degenerate into a characteristic, such as the fan shown in figure3 becomes, in fact, infinitely narrow fan.
$( \hat {V}_{sh}/ \hat {V}_{\infty } ) ^{2}$ which, according to (2.1), is small. This means that while the perturbations in the boundary layer are nonlinear, the perturbations outside the boundary layer are weak and can be described in framework of the Ackeret theory. In this theory both the shock wave and expansion fan degenerate into a characteristic, such as the fan shown in figure3 becomes, in fact, infinitely narrow fan.
To study the flow we introduce a Cartesian coordinate frame ![]() $(\hat {x} , \hat {y})$ that moves along the plate with the shock/expansion fan;
$(\hat {x} , \hat {y})$ that moves along the plate with the shock/expansion fan; ![]() $\hat {x}$ is measured along the plate surface and
$\hat {x}$ is measured along the plate surface and ![]() $\hat {y}$ in the perpendicular direction. The velocity components in these coordinates are denoted by
$\hat {y}$ in the perpendicular direction. The velocity components in these coordinates are denoted by ![]() $(\hat {u} , \hat {v})$ and the streamfunction by
$(\hat {u} , \hat {v})$ and the streamfunction by ![]() $\hat {\psi }$. As usual, we denote the gas density by
$\hat {\psi }$. As usual, we denote the gas density by ![]() $\hat {\rho }$, pressure by
$\hat {\rho }$, pressure by ![]() $\hat {p}$, enthalpy by
$\hat {p}$, enthalpy by ![]() $\hat {h}$ and dynamic viscosity coefficient by
$\hat {h}$ and dynamic viscosity coefficient by ![]() $\hat {\mu }$. Here
$\hat {\mu }$. Here ![]() $\, \hat{} \,$ is used for dimensional variables. The non-dimensional variables are introduced as
$\, \hat{} \,$ is used for dimensional variables. The non-dimensional variables are introduced as
 \[ \begin{array}{lll} \hat{u} = \hat{V}_{\infty } u , & \hat{v} = \hat{V}_{\infty } v, & \hat{\psi } = \hat{\rho }_{\infty } \hat{V}_{\infty } \hat{L} \psi ,\\ \hat{\rho } = \hat{\rho }_{\infty } \rho , & \hat{h} = \hat{V}_{\infty }^{2} h, & \hat{p} = \hat{p}_{\infty } + \hat{\rho }_{\infty } \hat{V}_{\infty }^{2} p ,\\ \hat{\mu } = \hat{\mu }_{\infty } \mu , & \hat{x} = \hat{L} x , & \hat{y} = \hat{L} y , \end{array} \]
\[ \begin{array}{lll} \hat{u} = \hat{V}_{\infty } u , & \hat{v} = \hat{V}_{\infty } v, & \hat{\psi } = \hat{\rho }_{\infty } \hat{V}_{\infty } \hat{L} \psi ,\\ \hat{\rho } = \hat{\rho }_{\infty } \rho , & \hat{h} = \hat{V}_{\infty }^{2} h, & \hat{p} = \hat{p}_{\infty } + \hat{\rho }_{\infty } \hat{V}_{\infty }^{2} p ,\\ \hat{\mu } = \hat{\mu }_{\infty } \mu , & \hat{x} = \hat{L} x , & \hat{y} = \hat{L} y , \end{array} \]
where ![]() $\hat {\rho }_{\infty }$,
$\hat {\rho }_{\infty }$, ![]() $\hat {p}_{\infty }$ and
$\hat {p}_{\infty }$ and ![]() $\hat {\mu }_{\infty }$ are the values of density, pressure and viscosity coefficient in the oncoming flow;
$\hat {\mu }_{\infty }$ are the values of density, pressure and viscosity coefficient in the oncoming flow; ![]() $\hat {L}$ denotes the distance between the leading edge of the plate and current position of the point of interaction of the boundary layer with the shock/expansion fan. We calculate the Reynolds number as
$\hat {L}$ denotes the distance between the leading edge of the plate and current position of the point of interaction of the boundary layer with the shock/expansion fan. We calculate the Reynolds number as
and assume that the free-stream Mach number
 \[ M_{\infty } = \frac{\hat{V}_{\infty }}{\sqrt{\gamma \hat{p}_{\infty } / \hat{\rho }_{\infty }}} \]
\[ M_{\infty } = \frac{\hat{V}_{\infty }}{\sqrt{\gamma \hat{p}_{\infty } / \hat{\rho }_{\infty }}} \]
has a finite value larger than one; ![]() $\gamma$ denotes the specific heat ratio of the gas considered.
$\gamma$ denotes the specific heat ratio of the gas considered.
The mathematical analysis of the flow may be conducted by applying the limit ![]() $Re \to \infty$ to the Navier–Stokes equations. Alternately one can start with the triple-deck theory. We shall choose the latter approach. Remember that the interaction of the shock wave or expansion fan with the boundary layer leads to a formation of the three-tiered viscous–inviscid interaction region; see figure 4. The nonlinear processes, characteristic of the flow separation are confined to the near-wall layer (region 1).
$Re \to \infty$ to the Navier–Stokes equations. Alternately one can start with the triple-deck theory. We shall choose the latter approach. Remember that the interaction of the shock wave or expansion fan with the boundary layer leads to a formation of the three-tiered viscous–inviscid interaction region; see figure 4. The nonlinear processes, characteristic of the flow separation are confined to the near-wall layer (region 1).

Figure 4. Three-tiered structure of the interaction region.
The asymptotic solution of the Navier–Stokes equations in this layer is sought in the form (for details the reader is referred to § 2 in the textbook by Ruban Reference Ruban2018):
 \begin{equation} \left. \begin{array}{cc@{}} \displaystyle x = 1 + Re^{-3/8} \dfrac{\mu _w^{-1/4} \rho _w^{-1/2}} {\lambda ^{5/4} \beta ^{3/4}} \,X , & \displaystyle y = Re^{-5/8} \dfrac{\mu _w^{1/4} \rho _w^{-1/2}} {\lambda ^{3/4} \beta ^{1/4}}\, Y ,\\ \displaystyle u = Re^{-1/8} \dfrac{\mu _w^{1/4} \rho _w^{-1/2}}{\lambda ^{-1/4} \beta ^{1/4}} \, U + \cdots , & \displaystyle v = Re^{-3/8} \dfrac{\mu _w^{3/4} \rho _w^{-1/2}} {\lambda ^{-3/4} \beta ^{-1/4}} \, V + \cdots , \\ \displaystyle p = Re^{-1/4} \dfrac{\mu _w^{1/2}}{\lambda ^{-1/2} \beta ^{1/2}} \,P + \cdots , & \displaystyle \psi = Re^{-3/4} \dfrac{\mu _w^{1/2}}{\lambda ^{1/2} \beta ^{1/2}} \, \Psi + \cdots , \\ \rho = \rho _w + \cdots , & \mu = \mu _w + \cdots . \end{array}\right\} \end{equation}
\begin{equation} \left. \begin{array}{cc@{}} \displaystyle x = 1 + Re^{-3/8} \dfrac{\mu _w^{-1/4} \rho _w^{-1/2}} {\lambda ^{5/4} \beta ^{3/4}} \,X , & \displaystyle y = Re^{-5/8} \dfrac{\mu _w^{1/4} \rho _w^{-1/2}} {\lambda ^{3/4} \beta ^{1/4}}\, Y ,\\ \displaystyle u = Re^{-1/8} \dfrac{\mu _w^{1/4} \rho _w^{-1/2}}{\lambda ^{-1/4} \beta ^{1/4}} \, U + \cdots , & \displaystyle v = Re^{-3/8} \dfrac{\mu _w^{3/4} \rho _w^{-1/2}} {\lambda ^{-3/4} \beta ^{-1/4}} \, V + \cdots , \\ \displaystyle p = Re^{-1/4} \dfrac{\mu _w^{1/2}}{\lambda ^{-1/2} \beta ^{1/2}} \,P + \cdots , & \displaystyle \psi = Re^{-3/4} \dfrac{\mu _w^{1/2}}{\lambda ^{1/2} \beta ^{1/2}} \, \Psi + \cdots , \\ \rho = \rho _w + \cdots , & \mu = \mu _w + \cdots . \end{array}\right\} \end{equation}
Here, in addition to conventional scaling with respect to the small parameter ![]() $Re^{-1/8}$, we use affine transformations with
$Re^{-1/8}$, we use affine transformations with ![]() $\rho _w$ and
$\rho _w$ and ![]() $\mu _w$ being the dimensionless density and dynamic viscosity on the body surface immediately before the interaction region, and
$\mu _w$ being the dimensionless density and dynamic viscosity on the body surface immediately before the interaction region, and ![]() $\lambda$ denoting the dimensionless skin friction produced by a conventional boundary layer before the triple-deck region. It is given by the compressible version of the Blasius solution (see § 1.10 in Ruban Reference Ruban2018). The dependence of the solution in the triple-deck region on the free-stream Mach number,
$\lambda$ denoting the dimensionless skin friction produced by a conventional boundary layer before the triple-deck region. It is given by the compressible version of the Blasius solution (see § 1.10 in Ruban Reference Ruban2018). The dependence of the solution in the triple-deck region on the free-stream Mach number, ![]() $M_{\infty }$, is expressed through parameter
$M_{\infty }$, is expressed through parameter ![]() $\beta = \sqrt {M_{\infty }^{2} - 1}$. These transformations allow us to exclude
$\beta = \sqrt {M_{\infty }^{2} - 1}$. These transformations allow us to exclude ![]() $\rho _w$,
$\rho _w$, ![]() $\mu _w$,
$\mu _w$, ![]() $\lambda$ and
$\lambda$ and ![]() $\beta$ from the equations for the interaction region.
$\beta$ from the equations for the interaction region.
The flow in region 1 is described by the boundary-layer equations
with the pressure ![]() $P$ being a function of
$P$ being a function of ![]() $X$ only.
$X$ only.
The no-slip conditions on the plate surface are written as
Notice that in the coordinate frame moving with the expansion fan (see figure 3), the plate surface moves upstream. We denote its speed, scaled with ![]() $Re^{-1/8}$, as
$Re^{-1/8}$, as ![]() $U_w$. Equations (2.3a) and (2.3b) also require the far-field attenuation conditions
$U_w$. Equations (2.3a) and (2.3b) also require the far-field attenuation conditions
which follows from matching with the solution in the unperturbed boundary layer upstream and downstream of the interaction region. The matching condition with the solution in the main part of the boundary layer (region 2 in figure 4) is expressed as
Here ![]() $A (X)$ denotes the so called displacement function. It is used in the interaction law
$A (X)$ denotes the so called displacement function. It is used in the interaction law
which is deduced from the flow analysis in region 3 (see figure 4). The first term on the right-hand side of (2.3f) stands for the impinging shock/expansion fan, with ![]() $\mathcal {H}$ being the Heaviside function:
$\mathcal {H}$ being the Heaviside function:
 \[ \mathcal{H} (X) = \begin{cases} 0 & \text{if} \ X < 0, \\ 1 & \text{if} \ X \ge 0. \end{cases} \]
\[ \mathcal{H} (X) = \begin{cases} 0 & \text{if} \ X < 0, \\ 1 & \text{if} \ X \ge 0. \end{cases} \]
The strength of the shock/expansion fan is defined by factor ![]() $P_s$. It is positive for the shock and negative for the expansion wave. The second term in (2.3f) represents the displacement effect of the boundary layer.
$P_s$. It is positive for the shock and negative for the expansion wave. The second term in (2.3f) represents the displacement effect of the boundary layer.
The above formulation is applicable for a perfect gas flow, and remains valid both for an adiabatic wall and for the case when the wall temperature is kept constant at least locally in the triple-deck region. It involves two parameters that may be thought of as the similarity parameters of the flow: the shock strength ![]() $P_s$ and the wall speed
$P_s$ and the wall speed ![]() $U_w$. These are related to the pressure jump
$U_w$. These are related to the pressure jump ![]() ${\rm \Delta} \hat {p}_{sh}$ across the shock and the shock speed
${\rm \Delta} \hat {p}_{sh}$ across the shock and the shock speed ![]() $\hat {V}_{sh}$ as follows:
$\hat {V}_{sh}$ as follows:
 \[ P_s = \frac{{\rm \Delta} \hat{p}_{sh} Re^{1/4}}{\hat{\rho }_{\infty } \hat{V}_{\infty }^{2}} \frac{\mu _w^{-1/2}}{\lambda ^{1/2} \beta ^{-1/2}} , \quad U_w = \frac{\hat{V}_{sh} Re^{1/8}}{\hat{V}_{\infty }} \frac{\mu _w^{-1/4} \rho _w^{1/2}} {\lambda ^{1/4} \beta ^{-1/4}} . \]
\[ P_s = \frac{{\rm \Delta} \hat{p}_{sh} Re^{1/4}}{\hat{\rho }_{\infty } \hat{V}_{\infty }^{2}} \frac{\mu _w^{-1/2}}{\lambda ^{1/2} \beta ^{-1/2}} , \quad U_w = \frac{\hat{V}_{sh} Re^{1/8}}{\hat{V}_{\infty }} \frac{\mu _w^{-1/4} \rho _w^{1/2}} {\lambda ^{1/4} \beta ^{-1/4}} . \]In what follows we shall use the ‘Cartesian formulation’ (2.3) of the interaction problem for numerical analysis of the flow. For theoretical analysis, it is more convenient to express the problem in von Mises variables (see, for example, Ruban Reference Ruban2018) where the momentum (2.3a) and continuity (2.3b) equations assume the forms
These should be solved with the interaction law (2.3f), now written as
subject to the no-slip conditions (2.3c)
the far-field attenuation conditions (2.3d)
 \begin{equation} U|_{X = \pm \infty } = \begin{cases} - \sqrt{2 \Psi + U_w^{2}} & \text{if} \ \Psi \in \left[ 0 , - \frac{1}{2} U_w^{2} \right] ,\\ \sqrt{2 \Psi + U_w^{2}} & \text{if} \ \Psi > - \frac{1}{2} U_w^{2}, \end{cases} \end{equation}
\begin{equation} U|_{X = \pm \infty } = \begin{cases} - \sqrt{2 \Psi + U_w^{2}} & \text{if} \ \Psi \in \left[ 0 , - \frac{1}{2} U_w^{2} \right] ,\\ \sqrt{2 \Psi + U_w^{2}} & \text{if} \ \Psi > - \frac{1}{2} U_w^{2}, \end{cases} \end{equation}and the condition (2.3e) at the outer edge of the viscous sublayer (region 1 in figure 4):
The formulation of the interaction problem (2.3) is similar to the one in Ruban etal. (Reference Ruban, Araki, Yapalparvi and Gajjar2011). The main difference is that Ruban et al. (Reference Ruban, Araki, Yapalparvi and Gajjar2011) considered the case of a downstream moving wall. It was shown that for the flow to separate, the boundary layer on a downstream moving wall had to be exposed to a shock wave. The mathematical description of the separation process is somewhat different from that presented by Sychev (Reference Sychev1979, Reference Sychev1983, Reference Sychev1984, Reference Sychev1987) for the incompressible flow. However, the physical processes leading to the separation are rather similar. In the present paper we consider the case of an upstream moving flow. We shall see that in this case the shock wave does not cause separation. Surprisingly enough, the boundary layer has to be exposed to an expansion fan for the separation to take place.
To start the theoretical analysis of the flow, we note that when formulating the equations of the triple-deck theory, it is assumed that the wall speed is an order ![]() $O (Re^{-1/8})$ quantity. Therefore, to satisfy condition (2.1) we have to assume that
$O (Re^{-1/8})$ quantity. Therefore, to satisfy condition (2.1) we have to assume that
In this limit the near-wall region 1 splits into two regions: the nonlinear inviscid region![]() $1a$ and a thinner viscous region
$1a$ and a thinner viscous region ![]() $1b$ adjacent to the plate surface; see figure 5. We start our analysis with region
$1b$ adjacent to the plate surface; see figure 5. We start our analysis with region ![]() $1a$.
$1a$.

Figure 5. Splitting of region 1.
3. Flow analysis in region  $1a$
$1a$
The form of the asymptotic solution of the interaction problem (2.4) in region 1![]() $a$ may be determined using the principle of least degeneration. We start with the initial condition (2.4e). In order to avoid degeneration in (2.4e) we have to assume that
$a$ may be determined using the principle of least degeneration. We start with the initial condition (2.4e). In order to avoid degeneration in (2.4e) we have to assume that
Since the separation is a nonlinear process, we have to ensure that the two terms on the left-hand side of the momentum equation (2.4a) remain in balance with one another. Thisis only possible if
An estimate for the lateral velocity component ![]() $V$ is obtained, as usual, from the continuity equation (2.4b). The two sides of this equation remain in balance with each other provided that
$V$ is obtained, as usual, from the continuity equation (2.4b). The two sides of this equation remain in balance with each other provided that
Here ![]() ${\rm \Delta} X$ is the longitudinal scale of the interaction region. It may be found using the interaction law (2.4c). Balancing the pressure on the left-hand side of (2.4c) with the second term on the right-hand side, it is easily found that
${\rm \Delta} X$ is the longitudinal scale of the interaction region. It may be found using the interaction law (2.4c). Balancing the pressure on the left-hand side of (2.4c) with the second term on the right-hand side, it is easily found that
Substituting (3.2) back into (3.1), we find that
This suggests that the asymptotic solution of (2.4) in region 1![]() $a$ may be sought in the form
$a$ may be sought in the form
with the arguments ![]() $X_{\ast }$,
$X_{\ast }$, ![]() $\Psi _{\ast }$ of functions
$\Psi _{\ast }$ of functions ![]() $U_{\ast }$,
$U_{\ast }$, ![]() $V_{\ast }$ and
$V_{\ast }$ and ![]() $P_{\ast }$ defined by
$P_{\ast }$ defined by
Substitution of (3.3a--c), (3.4a,b) into (2.4) shows that, in the leading-order approximation, the flow in region ![]() $1a$ is governed by the equations
$1a$ is governed by the equations
that should be solved with the boundary conditions
 \begin{gather} U_{\ast } = \begin{cases} - \sqrt{2 \Psi _{\ast } + 1} & \text{if} \ \Psi _{\ast } \in \left[ 0 , - \frac{1}{2} \right] ,\\ \sqrt{2 \Psi _{\ast } + 1} & \text{if} \ \Psi _{\ast } > - \frac{1}{2} \end{cases} \quad \text{at} \ X_{\ast } = \infty ,\end{gather}
\begin{gather} U_{\ast } = \begin{cases} - \sqrt{2 \Psi _{\ast } + 1} & \text{if} \ \Psi _{\ast } \in \left[ 0 , - \frac{1}{2} \right] ,\\ \sqrt{2 \Psi _{\ast } + 1} & \text{if} \ \Psi _{\ast } > - \frac{1}{2} \end{cases} \quad \text{at} \ X_{\ast } = \infty ,\end{gather}Here it has been assumed that the strength of the shock/expansion fan is given by
with ![]() $\bar {P}_s$ being an order one parameter. Notice that the viscous term disappears from the momentum equation (3.5a), signifying that the flow in region 1
$\bar {P}_s$ being an order one parameter. Notice that the viscous term disappears from the momentum equation (3.5a), signifying that the flow in region 1![]() $a$ may be treated as inviscid. For this reason, we can only impose the impermeability condition (3.5d) on the body surface, leaving the task of satisfying the no-slip condition to the flow analysis in region 1
$a$ may be treated as inviscid. For this reason, we can only impose the impermeability condition (3.5d) on the body surface, leaving the task of satisfying the no-slip condition to the flow analysis in region 1![]() $b$. It should be also noticed that for an inviscid flow the far-field attenuation condition (2.3d), (2.4e) cannot be satisfied both upstream and downstream of the interaction region. When solving the inviscid interaction problem (3.5), we assume the velocity profile to be undisturbed downstream of the interaction region as stated in (3.5e). This is to ensure the existence of the solution in region
$b$. It should be also noticed that for an inviscid flow the far-field attenuation condition (2.3d), (2.4e) cannot be satisfied both upstream and downstream of the interaction region. When solving the inviscid interaction problem (3.5), we assume the velocity profile to be undisturbed downstream of the interaction region as stated in (3.5e). This is to ensure the existence of the solution in region ![]() $1b$; for a detailed discussion of this issue, the reader is referred to Kirsten (Reference Kirsten2018).
$1b$; for a detailed discussion of this issue, the reader is referred to Kirsten (Reference Kirsten2018).
The boundary-value problem (3.5) is solved as follows. Integrating the momentum equation (3.5a) with respect to ![]() $X_{\ast }$ we have
$X_{\ast }$ we have
To find the Bernoulli function ![]() $H_{\ast } (\Psi _{\ast })$, we set
$H_{\ast } (\Psi _{\ast })$, we set ![]() $X_{\ast } = \infty$ in (3.7) and use conditions (3.5e) and (3.5g):
$X_{\ast } = \infty$ in (3.7) and use conditions (3.5e) and (3.5g):
Now we can substitute (3.8) back into (3.7) and solve the resulting equation for ![]() $U_{\ast }$:
$U_{\ast }$:
 \begin{equation} U_{\ast } = \begin{cases} - \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \frac{1}{2} + \bar{P}_s \right) } & \text{if} \ \Psi _{\ast } \in \left[ 0 , P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) \right] ,\\ \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \frac{1}{2} + \bar{P}_s \right) } & \text{if} \ \Psi _{\ast } > P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) . \end{cases} \end{equation}
\begin{equation} U_{\ast } = \begin{cases} - \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \frac{1}{2} + \bar{P}_s \right) } & \text{if} \ \Psi _{\ast } \in \left[ 0 , P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) \right] ,\\ \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \frac{1}{2} + \bar{P}_s \right) } & \text{if} \ \Psi _{\ast } > P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) . \end{cases} \end{equation} In order to find the pressure ![]() $P_{\ast } (X_{\ast })$ we turn our attention to the continuity equation (3.5b). Integration of (3.5b) with respect to
$P_{\ast } (X_{\ast })$ we turn our attention to the continuity equation (3.5b). Integration of (3.5b) with respect to ![]() $\Psi _{\ast }$ with initial condition (3.5d) allows us to write
$\Psi _{\ast }$ with initial condition (3.5d) allows us to write
 \begin{equation} \frac{V_{\ast }}{U_{\ast }} = \frac{\partial }{\partial X_{\ast }} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} . \end{equation}
\begin{equation} \frac{V_{\ast }}{U_{\ast }} = \frac{\partial }{\partial X_{\ast }} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} . \end{equation}
We first consider the region near the plate surface where ![]() $U_{\ast }$ is negative and is given by the first equation in (3.9). We have
$U_{\ast }$ is negative and is given by the first equation in (3.9). We have
 \begin{equation} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} - \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \tfrac{1}{2} + \bar{P}_s \right) } . \end{equation}
\begin{equation} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} - \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \tfrac{1}{2} + \bar{P}_s \right) } . \end{equation}
At the position of flow reversal, where ![]() $U_{\ast } = 0$, the second term on the right-hand side of (3.11) vanishes, leading to
$U_{\ast } = 0$, the second term on the right-hand side of (3.11) vanishes, leading to
 \[ \int\limits_0^{P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) } \frac{\textrm{d} \Psi _{\ast }^{\prime }} {U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} . \]
\[ \int\limits_0^{P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) } \frac{\textrm{d} \Psi _{\ast }^{\prime }} {U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} . \]Above this point, we have to use the second equation in (3.9). We have
 \begin{align} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} &= \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} + \int\limits_{P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) }^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{\sqrt{2 \Psi _{\ast }^{\prime } - 2 P_{\ast } + 2 \left( \frac{1}{2} + \bar{P}_s \right) }} \nonumber\\ &= \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} + \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \tfrac{1}{2} + \bar{P}_s \right) } . \end{align}
\begin{align} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} &= \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} + \int\limits_{P_{\ast } - \left( \frac{1}{2} + \bar{P}_s \right) }^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{\sqrt{2 \Psi _{\ast }^{\prime } - 2 P_{\ast } + 2 \left( \frac{1}{2} + \bar{P}_s \right) }} \nonumber\\ &= \sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }} + \sqrt{2 \Psi _{\ast } - 2 P_{\ast } + 2 \left( \tfrac{1}{2} + \bar{P}_s \right) } . \end{align}
It remains to substitute (3.12) into (3.10) and then into the interaction law (3.5c), and we will have the following equation for ![]() $P_{\ast } (X_{\ast })$:
$P_{\ast } (X_{\ast })$:
 \begin{equation} P_{\ast } = \bar{P}_s \mathcal{H} (X_{\ast }) - \frac{1}{\sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }}} \frac{\textrm{d} P_{\ast }}{\textrm{d} X_{\ast }} . \end{equation}
\begin{equation} P_{\ast } = \bar{P}_s \mathcal{H} (X_{\ast }) - \frac{1}{\sqrt{2 \left( \tfrac{1}{2} + \bar{P}_s \right) - 2 P_{\ast }}} \frac{\textrm{d} P_{\ast }}{\textrm{d} X_{\ast }} . \end{equation}The solution to (3.13) is written as
 \begin{equation} P_{\ast } = \begin{cases} 0 & \text{if} \ X_{\ast } < 0 ,\\ \dfrac{1}{2} + \bar{P}_s - \dfrac{1}{2} \left( \dfrac{1 - C \,\textrm{e}^{-X_{\ast }}} {1 + C \,\textrm{e}^{-X_{\ast }}} \right) ^{2} & \text{if} \ X_{\ast } > 0 . \end{cases} \end{equation}
\begin{equation} P_{\ast } = \begin{cases} 0 & \text{if} \ X_{\ast } < 0 ,\\ \dfrac{1}{2} + \bar{P}_s - \dfrac{1}{2} \left( \dfrac{1 - C \,\textrm{e}^{-X_{\ast }}} {1 + C \,\textrm{e}^{-X_{\ast }}} \right) ^{2} & \text{if} \ X_{\ast } > 0 . \end{cases} \end{equation}
It satisfies conditions (3.5g), (3.5h) and is continuous at ![]() $X_{\ast } = 0$ provided that constant
$X_{\ast } = 0$ provided that constant ![]() $C$ is chosen to be
$C$ is chosen to be
 \begin{equation} C = \frac{1 - \sqrt{1 + 2 \bar{P}_s}}{1 + \sqrt{1 + 2 \bar{P}_s}} . \end{equation}
\begin{equation} C = \frac{1 - \sqrt{1 + 2 \bar{P}_s}}{1 + \sqrt{1 + 2 \bar{P}_s}} . \end{equation}3.1. Impinging shock or expansion fan
In the flow with impinging shock, ![]() $\bar {P}_s > 0$, and it follows from (3.14), (3.15) that the pressure displays a monotonic growth as
$\bar {P}_s > 0$, and it follows from (3.14), (3.15) that the pressure displays a monotonic growth as ![]() $X_{\ast }$ increases from
$X_{\ast }$ increases from ![]() $0$ to
$0$ to ![]() $\infty$. Consequently, the fluid in the viscous layer (region
$\infty$. Consequently, the fluid in the viscous layer (region ![]() $1b$ in figure 5), that moves in the direction opposite to the
$1b$ in figure 5), that moves in the direction opposite to the ![]() $X_{\ast }$-axis, finds itself under the action of a favourable pressure gradient. No boundary-layer separation can be expected under these conditions. Contrary to that, in the case of an expansion fan, the pressure is decaying in the positive
$X_{\ast }$-axis, finds itself under the action of a favourable pressure gradient. No boundary-layer separation can be expected under these conditions. Contrary to that, in the case of an expansion fan, the pressure is decaying in the positive ![]() $X_{\ast }$-direction, which means that the flow in region
$X_{\ast }$-direction, which means that the flow in region ![]() $1b$ appears to be under an adverse pressure gradient. Similar to the downstream moving wall (see Ruban et al. Reference Ruban, Araki, Yapalparvi and Gajjar2011) we expect a singularity to form in region
$1b$ appears to be under an adverse pressure gradient. Similar to the downstream moving wall (see Ruban et al. Reference Ruban, Araki, Yapalparvi and Gajjar2011) we expect a singularity to form in region ![]() $1b$ when the velocity
$1b$ when the velocity ![]() $U_e$ at the outer edge of this region turns zero.
$U_e$ at the outer edge of this region turns zero.
To find ![]() $U_e (X_{\ast })$, one needs to set
$U_e (X_{\ast })$, one needs to set ![]() $\Psi _{\ast } = 0$ in the first equation in (3.9), and use (3.14) for
$\Psi _{\ast } = 0$ in the first equation in (3.9), and use (3.14) for ![]() $P_{\ast }$. This gives
$P_{\ast }$. This gives
It is easily seen that ![]() $U_e$ first turns zero at
$U_e$ first turns zero at ![]() $X_{\ast } = 0$ when the strength
$X_{\ast } = 0$ when the strength ![]() $\bar {P}_s$ of the expansion fan assumes the value
$\bar {P}_s$ of the expansion fan assumes the value
In this case, (3.16) turns into
 \begin{equation} U_e = \begin{cases} 0 & \text{if} \ X_{\ast } < 0 ,\\ - \dfrac{1 - \textrm{e}^{-X_{\ast }}}{1 + \textrm{e}^{-X_{\ast }}} & \text{if} \ X_{\ast } > 0 , \end{cases} \end{equation}
\begin{equation} U_e = \begin{cases} 0 & \text{if} \ X_{\ast } < 0 ,\\ - \dfrac{1 - \textrm{e}^{-X_{\ast }}}{1 + \textrm{e}^{-X_{\ast }}} & \text{if} \ X_{\ast } > 0 , \end{cases} \end{equation}
and the pressure ![]() $P_{\ast }$ can be found from
$P_{\ast }$ can be found from
that is deduced by setting ![]() $\Psi _{\ast } = 0$ in (3.8) and combining it with (3.7).
$\Psi _{\ast } = 0$ in (3.8) and combining it with (3.7).
4. Numerical solution of the triple-deck problem
Here we return to the original triple-deck problem (2.3), and discuss the behaviour of the flow based on the numerical solution of (2.3) for ![]() $U_w = O (1)$. The calculations were conducted with the help of the numerical technique developed by Kravtsova, Zametaev & Ruban (Reference Kravtsova, Zametaev and Ruban2005). The interested reader is referred to this original paper for details of the method. Here we shall give a brief description of the method. To perform the calculations, we introduce a discrete mesh
$U_w = O (1)$. The calculations were conducted with the help of the numerical technique developed by Kravtsova, Zametaev & Ruban (Reference Kravtsova, Zametaev and Ruban2005). The interested reader is referred to this original paper for details of the method. Here we shall give a brief description of the method. To perform the calculations, we introduce a discrete mesh ![]() $\{ x_i \}$, where
$\{ x_i \}$, where ![]() $i = 1, \ldots , N$, and denote the vector composed of the values of the displacement function
$i = 1, \ldots , N$, and denote the vector composed of the values of the displacement function ![]() $A$ at the mesh point by
$A$ at the mesh point by ![]() $\boldsymbol {A}$. We also consider the vector
$\boldsymbol {A}$. We also consider the vector ![]() $\textrm {d}\boldsymbol {P}/\textrm {d}x$ whose elements are the values of the pressure gradient at the mesh points. Then finite-difference representation of the inviscid equation (2.3f) can be expressed in the form
$\textrm {d}\boldsymbol {P}/\textrm {d}x$ whose elements are the values of the pressure gradient at the mesh points. Then finite-difference representation of the inviscid equation (2.3f) can be expressed in the form
Also, for a given displacement function ![]() $\boldsymbol {A}$, (2.3a), (2.3b) allow us to calculate the velocity field and the pressure gradient in the viscous sublayer
$\boldsymbol {A}$, (2.3a), (2.3b) allow us to calculate the velocity field and the pressure gradient in the viscous sublayer
where the term ![]() $\boldsymbol {R}$ corresponds to the boundary-layer solution with
$\boldsymbol {R}$ corresponds to the boundary-layer solution with ![]() $\boldsymbol {A} =0$. The requirement that the pressure gradient should be the same in the viscous sublayer and at the ‘bottom’ of the upper deck leads to the following set of equations:
$\boldsymbol {A} =0$. The requirement that the pressure gradient should be the same in the viscous sublayer and at the ‘bottom’ of the upper deck leads to the following set of equations:
These are solved by means of Newtonian iterations. As usual the Newtonian iterations prove to be rather sensitive to the initial guess. Keeping this in mind, we started with a small value of ![]() $U_w$ and, after convergence was achieved, the obtained distribution of the fluid dynamic functions was used to initiate the calculations for the next value of
$U_w$ and, after convergence was achieved, the obtained distribution of the fluid dynamic functions was used to initiate the calculations for the next value of ![]() $U_w$. For each
$U_w$. For each ![]() $U_w$, the strength of the expansion fan was chosen according to (3.17) which, being combined with (3.6), gives
$U_w$, the strength of the expansion fan was chosen according to (3.17) which, being combined with (3.6), gives
Figure 6 displays the streamlines in the boundary layer on the wall moving upstream with velocities ![]() $U_w = 2.0$ and
$U_w = 2.0$ and ![]() $U_w = 3.0$. The pressure distribution in the interaction region is shown in figure 7. We see that two eddies are forming in the flow: one lies downstream of the impinging expansion fan and the other upstream of the fan. We shall call them the primary eddy and the secondary eddy, respectively. The primary eddy grows with
$U_w = 3.0$. The pressure distribution in the interaction region is shown in figure 7. We see that two eddies are forming in the flow: one lies downstream of the impinging expansion fan and the other upstream of the fan. We shall call them the primary eddy and the secondary eddy, respectively. The primary eddy grows with ![]() $U_w$, while the secondary eddy becomes relatively smaller. The formation of the primary eddy is explained as follows. If we consider a fluid particle situated near the wall downstream of the impinging expansion fan then initially this particle moves in the negative
$U_w$, while the secondary eddy becomes relatively smaller. The formation of the primary eddy is explained as follows. If we consider a fluid particle situated near the wall downstream of the impinging expansion fan then initially this particle moves in the negative ![]() $X$-direction. It encounters a growing pressure and, therefore, experiences a deceleration. If the fluid particle is sufficiently close to the wall then its kinetic energy is large enough to overcome the growing pressure, and it continues to move along the wall in the original direction. However, one can see from (2.3d) that there are always fluid particles with a smaller initial velocity. These are stopped by the growing pressure, and are forced to turn back. The smaller the initial velocity, the earlier this happens.
$X$-direction. It encounters a growing pressure and, therefore, experiences a deceleration. If the fluid particle is sufficiently close to the wall then its kinetic energy is large enough to overcome the growing pressure, and it continues to move along the wall in the original direction. However, one can see from (2.3d) that there are always fluid particles with a smaller initial velocity. These are stopped by the growing pressure, and are forced to turn back. The smaller the initial velocity, the earlier this happens.

Figure 6. The streamline pattern in the boundary layer exposed to an impinging expansion fan. (![]() $a$)
$a$) ![]() $U_w = 2.0$. The streamlines shown in black correspond to the following values of the streamfunction: 0.001; 1; 3; 6; 10; 15; 20. For the coloured lines, these are:
$U_w = 2.0$. The streamlines shown in black correspond to the following values of the streamfunction: 0.001; 1; 3; 6; 10; 15; 20. For the coloured lines, these are: ![]() $-0.4$;
$-0.4$; ![]() $-0.8$;
$-0.8$; ![]() $-1.2$;
$-1.2$; ![]() $-1.6$. (
$-1.6$. (![]() $b$)
$b$) ![]() $U_w = 3.0$. The streamlines shown in black correspond to the following values of the streamfunction: 0.001; 1; 3; 6; 10; 15; 20. For the coloured lines, these are:
$U_w = 3.0$. The streamlines shown in black correspond to the following values of the streamfunction: 0.001; 1; 3; 6; 10; 15; 20. For the coloured lines, these are: ![]() $-0.4$;
$-0.4$; ![]() $-0.8$;
$-0.8$; ![]() $-1.2$;
$-1.2$; ![]() $-1.6$;
$-1.6$; ![]() $-2$;
$-2$; ![]() $-2.4$.
$-2.4$.
The situation with the secondary eddy is more complicated. We observe in figure 6 that the fluid particles away from the wall continue travelling in the positive ![]() $X$-direction. However, those that are closer to the wall, decelerate before the impinging expansion fan and turn back despite being exposed to a favourable pressure. This can only be explained by action of viscous forces. Our computations indeed show that the viscous forces prove to be strong in the secondary eddy before it ‘collides’ with the primary vortex. Of course, the theory presented in the previous section shows that the fluid motion should become effectively inviscid as
$X$-direction. However, those that are closer to the wall, decelerate before the impinging expansion fan and turn back despite being exposed to a favourable pressure. This can only be explained by action of viscous forces. Our computations indeed show that the viscous forces prove to be strong in the secondary eddy before it ‘collides’ with the primary vortex. Of course, the theory presented in the previous section shows that the fluid motion should become effectively inviscid as ![]() $U_w \to \infty$. We expect that in this limit the secondary vortex will disappear, as shown in figure 10.
$U_w \to \infty$. We expect that in this limit the secondary vortex will disappear, as shown in figure 10.
5. Viscous region 1b
Here we continue the theoretical analysis of the flow we started in § 3. Now we turn our attention to a thin viscous near-wall layer shown as region ![]() $1b$ in figure 5. In this region the asymptotic solution of the interaction problem (2.4) is sought in the form
$1b$ in figure 5. In this region the asymptotic solution of the interaction problem (2.4) is sought in the form
Here, it is taken into account that region 1![]() $b$ has the same longitudinal extent as region 1
$b$ has the same longitudinal extent as region 1![]() $a$. The scaling for
$a$. The scaling for ![]() $U$ is dictated by the necessity to perform the matching with the solution in region 1
$U$ is dictated by the necessity to perform the matching with the solution in region 1![]() $a$. We also need to satisfy the no-slip condition on the body surface. The latter is only possible if the convective terms in the momentum equation (2.4a) remain in balance with the viscous term, that is,
$a$. We also need to satisfy the no-slip condition on the body surface. The latter is only possible if the convective terms in the momentum equation (2.4a) remain in balance with the viscous term, that is,
The above equation expresses in the von Mises variable standard Prandtl's requirement that is used to determine the thickness of the boundary layer. Since ![]() $X \sim U_w^{-1}$ and
$X \sim U_w^{-1}$ and ![]() $U \sim U_w$, it follows from (5.2) that
$U \sim U_w$, it follows from (5.2) that ![]() $\Psi = O (1)$. Using further the continuity equation (2.4b), one can deduce that
$\Psi = O (1)$. Using further the continuity equation (2.4b), one can deduce that ![]() $V \sim U_w$. Finally, the pressure
$V \sim U_w$. Finally, the pressure ![]() $P$ does not change across region 1
$P$ does not change across region 1![]() $b$ and stays the same as in region 1
$b$ and stays the same as in region 1![]() $a$:
$a$:
To find the velocity components ![]() $\widetilde {U}$ and
$\widetilde {U}$ and ![]() $\widetilde {V}$, one needs to solve the equations of classical boundary-layer theory:
$\widetilde {V}$, one needs to solve the equations of classical boundary-layer theory:
 \begin{gather} \widetilde{U} \frac{\partial \widetilde{U}}{\partial X_{\ast }} - U_e \frac{\textrm{d} U_e}{\textrm{d} X_{\ast }} = \widetilde{U} \frac{\partial }{\partial \Psi} \left( \widetilde{U} \frac{\partial \widetilde{U}}{\partial \Psi} \right) , \end{gather}
\begin{gather} \widetilde{U} \frac{\partial \widetilde{U}}{\partial X_{\ast }} - U_e \frac{\textrm{d} U_e}{\textrm{d} X_{\ast }} = \widetilde{U} \frac{\partial }{\partial \Psi} \left( \widetilde{U} \frac{\partial \widetilde{U}}{\partial \Psi} \right) , \end{gather} \begin{gather}\frac{\partial }{\partial \Psi } \left( \frac{\widetilde{V}}{\widetilde{U}} \right) = \frac{\partial }{\partial X_{\ast }} \left( \frac{1}{\widetilde{U}} \right) . \end{gather}
\begin{gather}\frac{\partial }{\partial \Psi } \left( \frac{\widetilde{V}}{\widetilde{U}} \right) = \frac{\partial }{\partial X_{\ast }} \left( \frac{1}{\widetilde{U}} \right) . \end{gather}
In (5.4a) we used the Bernoulli equation (3.19) to express the pressure gradient in terms of the velocity ![]() $U_e (X_{\ast })$ at the outer edge of region
$U_e (X_{\ast })$ at the outer edge of region ![]() $1b$; the latter is given by (3.18). The boundary conditions for (5.4) are
$1b$; the latter is given by (3.18). The boundary conditions for (5.4) are
The limit ![]() $\Psi \to -\infty$ in (5.4e) corresponds to the outer edge of region
$\Psi \to -\infty$ in (5.4e) corresponds to the outer edge of region ![]() $1b$.
$1b$.
In what follows our task will be to determine the behaviour of the solution of (5.4) near the outer edge of region 1![]() $b$ on approaching
$b$ on approaching ![]() $X_{\ast } = 0$, where
$X_{\ast } = 0$, where ![]() $U_e$ vanishes. To perform this task we start with the asymptotic analysis of (5.4) in the limit
$U_e$ vanishes. To perform this task we start with the asymptotic analysis of (5.4) in the limit ![]() $X_{\ast } \to \infty$. In this case, (3.18) may be expanded as
$X_{\ast } \to \infty$. In this case, (3.18) may be expanded as
Corresponding to this, the longitudinal velocity ![]() $\widetilde {U}$ inside region 1
$\widetilde {U}$ inside region 1![]() $b$ is sought in the form
$b$ is sought in the form
first suggested by Krapivskii & Neiland (Reference Krapivskii and Neiland1982). Substitution of (5.6) together with (5.5) into (5.4a), (5.4c) and (5.4e) results in the following boundary-value problem for function ![]() $f (\Psi )$:
$f (\Psi )$:
Its solution is easily found to be
Substitution of (5.7) back into (5.6) yields
Let us now consider the limit
At this stage it is convenient to introduce a modified Bernoulli function
which allows us to write (5.4a) as
Substitution of (5.8) together with (5.5) into (5.9) shows that
This suggests that for all finite values of ![]() $X_{\ast }$ the solution of (5.10) should be sought near the outer edge of region 1
$X_{\ast }$ the solution of (5.10) should be sought near the outer edge of region 1![]() $b$ in the form
$b$ in the form
where function ![]() $h (X_{\ast })$ is such that
$h (X_{\ast })$ is such that
We substitute (5.11) into (5.10) and take into account that at large negative values of ![]() $\Psi$ the coefficient
$\Psi$ the coefficient ![]() $\widetilde {U}$ on the right-hand side of (5.10) is given by (3.18). This leads to the following equation for function
$\widetilde {U}$ on the right-hand side of (5.10) is given by (3.18). This leads to the following equation for function ![]() $h (X_{\ast })$:
$h (X_{\ast })$:
The solution of this equation, satisfying the initial condition (5.12), is written as
Now we can substitute (5.13a,b) back into (5.11) and use for ![]() $\widetilde {H}$ its definition (5.9). Solving the resulting equation for
$\widetilde {H}$ its definition (5.9). Solving the resulting equation for ![]() $\widetilde {U}$, we find that near the outer edge of region 1
$\widetilde {U}$, we find that near the outer edge of region 1![]() $b$
$b$
 \begin{equation} \widetilde{U} = - \sqrt{U_e^{2} + \frac{4 \,\textrm{e}^{\Psi }}{\textrm{e}^{X_{\ast }} + 2 + \textrm{e}^{-X_{\ast }}}} + \cdots \quad \text{as} \ \Psi \to - \infty ,\quad X_{\ast } \in [0 , \infty ) . \end{equation}
\begin{equation} \widetilde{U} = - \sqrt{U_e^{2} + \frac{4 \,\textrm{e}^{\Psi }}{\textrm{e}^{X_{\ast }} + 2 + \textrm{e}^{-X_{\ast }}}} + \cdots \quad \text{as} \ \Psi \to - \infty ,\quad X_{\ast } \in [0 , \infty ) . \end{equation}
In particular, if ![]() $X_{\ast } \to 0^{+}$ then it follows from (3.18) that
$X_{\ast } \to 0^{+}$ then it follows from (3.18) that
and (5.14) reduces to
The asymptotic formula (5.16) has been obtained using a double limit procedure. We first assumed that ![]() $\Psi$ tends to minus infinity, with
$\Psi$ tends to minus infinity, with ![]() $X_{\ast }$ remaining an order one quantity; this led to (5.14). Then it was assumed that
$X_{\ast }$ remaining an order one quantity; this led to (5.14). Then it was assumed that ![]() $X_{\ast }$ tends to zero. Therefore, strictly speaking, (5.16) remains valid provided that the first term in the square root is much larger than the second one, and a new region (let us call it region 1
$X_{\ast }$ tends to zero. Therefore, strictly speaking, (5.16) remains valid provided that the first term in the square root is much larger than the second one, and a new region (let us call it region 1![]() $b^{\prime }$) should be introduced where
$b^{\prime }$) should be introduced where ![]() $\textrm {e}^{\Psi } / X_{\ast }^{2}$ becomes an order one quantity; see figure 8.
$\textrm {e}^{\Psi } / X_{\ast }^{2}$ becomes an order one quantity; see figure 8.

Figure 8. Formation of region ![]() $1a^{\prime }$.
$1a^{\prime }$.
5.1. Region  $1b^{\prime }$
$1b^{\prime }$
In region 1![]() $b^{\prime }$ a characteristic independent variable
$b^{\prime }$ a characteristic independent variable ![]() $\eta$ should satisfy the condition
$\eta$ should satisfy the condition
where ![]() $\phi$ is an arbitrary function of
$\phi$ is an arbitrary function of ![]() $\eta$. It is convenient to choose
$\eta$. It is convenient to choose ![]() $\phi (\eta ) = \textrm {e}^{\eta }$ (see Elliott etal. Reference Elliott, Smith and Cowley1983). Then we will have
$\phi (\eta ) = \textrm {e}^{\eta }$ (see Elliott etal. Reference Elliott, Smith and Cowley1983). Then we will have
Using (5.18) in (5.16), we find that on approaching region 1![]() $b^{\prime }$
$b^{\prime }$
This suggests that the solution in region 1![]() $b^{\prime }$ should be sought in the form
$b^{\prime }$ should be sought in the form
where function ![]() $F (\eta )$ is such that
$F (\eta )$ is such that
To find the function ![]() $F (\eta )$, we need to substitute (5.19), (5.18) and (5.15) into the momentum equation (5.4a). The three terms in this equation are calculated as
$F (\eta )$, we need to substitute (5.19), (5.18) and (5.15) into the momentum equation (5.4a). The three terms in this equation are calculated as
 \begin{gather*} \widetilde{U} \frac{\partial \widetilde{U}}{\partial X_{\ast }} = - X_{\ast } F \left( 2 F^{\prime } - F \right) , \quad U_e \frac{\textrm{d} U_e} {\textrm{d} X_{\ast }} = \frac{1}{4} X_{\ast } ,\\ \widetilde{U} \frac{\partial }{\partial \Psi} \left( \widetilde{U} \frac{\partial \widetilde{U}}{\partial \Psi} \right) = - X_{\ast }^{3} F \left( F F^{\prime } \right) ^{\prime } . \end{gather*}
\begin{gather*} \widetilde{U} \frac{\partial \widetilde{U}}{\partial X_{\ast }} = - X_{\ast } F \left( 2 F^{\prime } - F \right) , \quad U_e \frac{\textrm{d} U_e} {\textrm{d} X_{\ast }} = \frac{1}{4} X_{\ast } ,\\ \widetilde{U} \frac{\partial }{\partial \Psi} \left( \widetilde{U} \frac{\partial \widetilde{U}}{\partial \Psi} \right) = - X_{\ast }^{3} F \left( F F^{\prime } \right) ^{\prime } . \end{gather*}
We see that as ![]() $X_{\ast } \to 0^{+}$, the viscous term can be disregarded, which means that the flow in region 1
$X_{\ast } \to 0^{+}$, the viscous term can be disregarded, which means that the flow in region 1![]() $b^{\prime }$ appears to be effectively inviscid. The equation for
$b^{\prime }$ appears to be effectively inviscid. The equation for ![]() $F (\eta )$ assumes the form
$F (\eta )$ assumes the form
Its solution, satisfying the boundary condition (5.20), is easily found to be
Hence, the longitudinal velocity (5.19) in region 1![]() $b^{\prime }$ is written as
$b^{\prime }$ is written as
To have the solution in the entire region 1![]() $b$ (see figure 8), we shall, finally, consider the limit
$b$ (see figure 8), we shall, finally, consider the limit
Since the velocity ![]() $U_e (X_{\ast })$ at the outer edge of region 1
$U_e (X_{\ast })$ at the outer edge of region 1![]() $b$ is regular for all
$b$ is regular for all ![]() $X_{\ast } > 0$, the asymptotic solution of (5.4a) with respect to the limit (5.20a,b) can be sought in the form of the Taylor expansion
$X_{\ast } > 0$, the asymptotic solution of (5.4a) with respect to the limit (5.20a,b) can be sought in the form of the Taylor expansion
Substitution of (5.23) and (5.15) into (5.4a) yields
Here ![]() $\widetilde {U}_0 (\Psi )$ remains undetermined. We only know from matching of (5.23) with (5.21) that
$\widetilde {U}_0 (\Psi )$ remains undetermined. We only know from matching of (5.23) with (5.21) that
Now we can substitute (5.25) into (5.24). We find that
5.2. Displacement effect of region  $1b$
$1b$
The displacement effect of a boundary layer is characterised by the angle the streamlines make with the body surface. Integrating the continuity equation (5.4b) with initial condition (5.4c), we have
 \begin{equation} \frac{\widetilde{V}}{\widetilde{U}} = - \int\limits_0^{\Psi } \frac{1} {\widetilde{U}^{2}} \frac{\partial \widetilde{U}}{\partial X_{\ast }}\, \textrm{d} \psi . \end{equation}
\begin{equation} \frac{\widetilde{V}}{\widetilde{U}} = - \int\limits_0^{\Psi } \frac{1} {\widetilde{U}^{2}} \frac{\partial \widetilde{U}}{\partial X_{\ast }}\, \textrm{d} \psi . \end{equation}
Corresponding to two limits, (5.17) and (5.22a,b), that had to be considered in region 1![]() $b$, we shall subdivide the integration interval in (5.27) into two parts:
$b$, we shall subdivide the integration interval in (5.27) into two parts:
Here
with ![]() $\varDelta$ being a positive parameter satisfying the conditions
$\varDelta$ being a positive parameter satisfying the conditions ![]() $1 \ll \varDelta \ll - 2 \ln X_{\ast }$. The second interval in (5.28) corresponds to region
$1 \ll \varDelta \ll - 2 \ln X_{\ast }$. The second interval in (5.28) corresponds to region ![]() $1b^{\prime }$. In terms of variable
$1b^{\prime }$. In terms of variable ![]() $\eta$ it is written as
$\eta$ it is written as
Notice that the interval of variation of ![]() $\eta$ in (5.29) is ‘inverted’ to signify that the left-hand side boundary of (5.29) corresponds to the lower edge of region
$\eta$ in (5.29) is ‘inverted’ to signify that the left-hand side boundary of (5.29) corresponds to the lower edge of region ![]() $1b^{\prime }$, while the right-hand side boundary represents its upper edge.
$1b^{\prime }$, while the right-hand side boundary represents its upper edge.
When dealing with the first interval in (5.28), we need to use for ![]() $\widetilde {U}$ the asymptotic representation (5.23). Hence, we have
$\widetilde {U}$ the asymptotic representation (5.23). Hence, we have
 \begin{equation} - \int\limits_0^{\Psi _{\varDelta }} \frac{1}{\widetilde{U}^{2}} \frac{\partial \widetilde{U}} {\partial X_{\ast }}\, \textrm{d} \psi = - \int\limits_0^{\Psi _{\varDelta }} \frac{\widetilde{U}_1 (\psi )} {\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} \, \textrm{d} \psi + \cdots \quad \text{as} \ X_{\ast } \to 0^{+} . \end{equation}
\begin{equation} - \int\limits_0^{\Psi _{\varDelta }} \frac{1}{\widetilde{U}^{2}} \frac{\partial \widetilde{U}} {\partial X_{\ast }}\, \textrm{d} \psi = - \int\limits_0^{\Psi _{\varDelta }} \frac{\widetilde{U}_1 (\psi )} {\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} \, \textrm{d} \psi + \cdots \quad \text{as} \ X_{\ast } \to 0^{+} . \end{equation}It follows from (5.25) and (5.26) that
 \[ \frac{\widetilde{U}_1 (\psi )}{\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} \to \frac{1}{2} \quad \text{as} \ \psi \to -\infty . \]
\[ \frac{\widetilde{U}_1 (\psi )}{\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} \to \frac{1}{2} \quad \text{as} \ \psi \to -\infty . \]Keeping this in mind, we rearrange the integral on the right-hand side of (5.30) as
 \begin{align} - \int\limits_0^{\Psi _{\varDelta }} \frac{\widetilde{U}_1 (\psi )} {\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} \, \textrm{d} \psi & = - \int\limits_0^{2 \ln X^{\ast } + \varDelta } \left\{ \frac{\widetilde{U}_1 (\psi )}{\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} - \frac{1}{2} \right\} \textrm{d} \psi - \ln X^{\ast } - \frac{1}{2} \varDelta \nonumber\\ & = - \ln X^{\ast } - \frac{1}{2} \varDelta + D + \cdots \quad \text{as} \ X^{\ast } \to 0^{-} , \end{align}
\begin{align} - \int\limits_0^{\Psi _{\varDelta }} \frac{\widetilde{U}_1 (\psi )} {\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} \, \textrm{d} \psi & = - \int\limits_0^{2 \ln X^{\ast } + \varDelta } \left\{ \frac{\widetilde{U}_1 (\psi )}{\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} - \frac{1}{2} \right\} \textrm{d} \psi - \ln X^{\ast } - \frac{1}{2} \varDelta \nonumber\\ & = - \ln X^{\ast } - \frac{1}{2} \varDelta + D + \cdots \quad \text{as} \ X^{\ast } \to 0^{-} , \end{align}
with constant ![]() $D$ given by
$D$ given by
 \[ D = - \int\limits_0^{-\infty } \left\{ \frac{\widetilde{U}_1 (\psi )} {\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} - \frac{1}{2} \right\} \textrm{d} \psi . \]
\[ D = - \int\limits_0^{-\infty } \left\{ \frac{\widetilde{U}_1 (\psi )} {\left[ \widetilde{U}_0 (\psi ) \right] ^{2}} - \frac{1}{2} \right\} \textrm{d} \psi . \] Now we turn to the second interval in (5.28), where ![]() $\widetilde {U}$ is represented by (5.19). We see that
$\widetilde {U}$ is represented by (5.19). We see that
 \begin{align} - \int\limits_{\Psi _{\varDelta }}^{\Psi } \frac{1}{\widetilde{U}^{2}} \frac{\partial \widetilde{U}}{\partial X_{\ast }} \, \textrm{d} \psi &= \frac{1}{X_{\ast }^{2}} \int\limits_{\varDelta }^{\Psi - 2 \ln X_{\ast }} \left( \frac{1}{F} - 2 \frac{F^{\prime }}{F^{2}} \right) \textrm{d} \eta \nonumber\\ &= \frac{2}{X_{\ast }^{2}} \left[ \ln \frac{\sqrt{\frac{1}{4} + \textrm{e}^{\eta }} - \frac{1}{2}} {\sqrt{\frac{1}{4} + \textrm{e}^{\eta }} + \frac{1}{2}} + \frac{1}{\sqrt{\frac{1}{4} + \textrm{e}^{\eta }}}\right]_{\varDelta }^{\Psi - 2 \ln X_{\ast }} \nonumber\\ &= \frac{2}{X_{\ast }^{2}} \left[ \Psi - 2 \ln X_{\ast } + 2 \right] + \cdots . \end{align}
\begin{align} - \int\limits_{\Psi _{\varDelta }}^{\Psi } \frac{1}{\widetilde{U}^{2}} \frac{\partial \widetilde{U}}{\partial X_{\ast }} \, \textrm{d} \psi &= \frac{1}{X_{\ast }^{2}} \int\limits_{\varDelta }^{\Psi - 2 \ln X_{\ast }} \left( \frac{1}{F} - 2 \frac{F^{\prime }}{F^{2}} \right) \textrm{d} \eta \nonumber\\ &= \frac{2}{X_{\ast }^{2}} \left[ \ln \frac{\sqrt{\frac{1}{4} + \textrm{e}^{\eta }} - \frac{1}{2}} {\sqrt{\frac{1}{4} + \textrm{e}^{\eta }} + \frac{1}{2}} + \frac{1}{\sqrt{\frac{1}{4} + \textrm{e}^{\eta }}}\right]_{\varDelta }^{\Psi - 2 \ln X_{\ast }} \nonumber\\ &= \frac{2}{X_{\ast }^{2}} \left[ \Psi - 2 \ln X_{\ast } + 2 \right] + \cdots . \end{align} Comparing (5.32) with (5.31), it is easily seen that the displacement effect of region![]() $1b$ is predominantly due to region
$1b$ is predominantly due to region ![]() $1b^{\prime }$. Substituting (5.32) into (5.27) and rescaling the velocity components according to (5.1), we can conclude that at the outer edge of region
$1b^{\prime }$. Substituting (5.32) into (5.27) and rescaling the velocity components according to (5.1), we can conclude that at the outer edge of region![]() $1b^{\prime }$
$1b^{\prime }$
5.3. Displacement effect of region  $1a$
$1a$
Let us now calculate the streamline slope ![]() $V/U$ in region
$V/U$ in region ![]() $1a$. For this purpose, we can use (3.10). At the ‘bottom’ of region 1
$1a$. For this purpose, we can use (3.10). At the ‘bottom’ of region 1![]() $a$, where
$a$, where ![]() $\Psi _{\ast }$ is small, the integral on the right-hand side of (3.10) is given by (3.11). Setting
$\Psi _{\ast }$ is small, the integral on the right-hand side of (3.10) is given by (3.11). Setting ![]() $\bar {P}_s = - \frac {1}{2}$ in (3.11), we have
$\bar {P}_s = - \frac {1}{2}$ in (3.11), we have
 \begin{equation} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} =\sqrt{- 2 P_{\ast }} - \sqrt{2 \Psi _{\ast } - 2 P_{\ast }} . \end{equation}
\begin{equation} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} =\sqrt{- 2 P_{\ast }} - \sqrt{2 \Psi _{\ast } - 2 P_{\ast }} . \end{equation}
We are interested in small values of ![]() $X_{\ast }$ where
$X_{\ast }$ where ![]() $P_{\ast }$ may be obtained by substituting (5.15) into (3.19). We see that
$P_{\ast }$ may be obtained by substituting (5.15) into (3.19). We see that
which allows us to express (5.34) in the form
 \[ \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \frac{1}{2} X_{\ast } - \frac{1}{2} X_{\ast } \sqrt{1 + 8 \frac{\Psi _{\ast }}{X_{\ast }^{2}}} . \]
\[ \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \frac{1}{2} X_{\ast } - \frac{1}{2} X_{\ast } \sqrt{1 + 8 \frac{\Psi _{\ast }}{X_{\ast }^{2}}} . \]
For small values of ![]() $\Psi _{\ast } / X_{\ast }^{2}$,
$\Psi _{\ast } / X_{\ast }^{2}$,
 \[ \sqrt{1 + 8 \frac{\Psi _{\ast }}{X_{\ast }^{2}}} = 1 + 4 \frac{\Psi _{\ast }}{X_{\ast }^{2}} , \]
\[ \sqrt{1 + 8 \frac{\Psi _{\ast }}{X_{\ast }^{2}}} = 1 + 4 \frac{\Psi _{\ast }}{X_{\ast }^{2}} , \]and, therefore,
 \[ \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = - 2 \frac{\Psi _{\ast }}{X_{\ast }} . \]
\[ \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = - 2 \frac{\Psi _{\ast }}{X_{\ast }} . \]
It remains to rescale ![]() $V_{\ast }$,
$V_{\ast }$, ![]() $U_{\ast }$ and
$U_{\ast }$ and ![]() $\Psi _{\ast }$ with the help of (3.3a--c), and we can conclude that at the ‘bottom’ of region 1
$\Psi _{\ast }$ with the help of (3.3a--c), and we can conclude that at the ‘bottom’ of region 1![]() $a$
$a$
It is easily seen that (5.36) coincides with the first term in (5.33). Hence, the second term in (5.33) should be solely attributed to the displacement effect of region 1![]() $b$:
$b$:
To evaluate the displacement effect of region 1![]() $a$, we have to use instead of (3.11) equation (3.12). Setting
$a$, we have to use instead of (3.11) equation (3.12). Setting ![]() $\bar {P}_s = - \frac {1}{2}$ in (3.12) and using (5.35) for
$\bar {P}_s = - \frac {1}{2}$ in (3.12) and using (5.35) for ![]() $P_{\ast }$, we have
$P_{\ast }$, we have
 \begin{equation} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \frac{1}{2} X_{\ast } + \sqrt{2 \Psi _{\ast } + \frac{1}{4} X_{\ast }^{2}} . \end{equation}
\begin{equation} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }}{U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \frac{1}{2} X_{\ast } + \sqrt{2 \Psi _{\ast } + \frac{1}{4} X_{\ast }^{2}} . \end{equation}
Differentiation of (5.38) with respect to ![]() $X_{\ast }$ yields
$X_{\ast }$ yields
 \begin{equation} \frac{\partial }{\partial X_{\ast }} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }} {U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \frac{1}{2} + \frac{1}{2} \frac{1} {\sqrt{1 + 2 \xi }} , \end{equation}
\begin{equation} \frac{\partial }{\partial X_{\ast }} \int\limits_0^{\Psi _{\ast }} \frac{\textrm{d} \Psi _{\ast }^{\prime }} {U_{\ast } (X_{\ast } , \Psi _{\ast }^{\prime })} = \frac{1}{2} + \frac{1}{2} \frac{1} {\sqrt{1 + 2 \xi }} , \end{equation}where
It follows from (5.39) and (3.10) that at the outer edge of region 1![]() $a$
$a$
It also follows from (5.39) that the main contribution to the displacement effect of region1![]() $a$ is produced by region
$a$ is produced by region![]() $1a^{\prime }$ (see figure 8), where
$1a^{\prime }$ (see figure 8), where
With the help of (3.3a--c) we can express (5.40) in the form
Comparing (5.42) with (5.37), and keeping in mind that ![]() $U_w \gg 1$, one can conclude that as long as
$U_w \gg 1$, one can conclude that as long as ![]() $X_{\ast }$ is not too small, the displacement effect of region 1
$X_{\ast }$ is not too small, the displacement effect of region 1![]() $a$ is dominant. However, for any
$a$ is dominant. However, for any ![]() $U_w$, no matter how large, there always exists a vicinity of
$U_w$, no matter how large, there always exists a vicinity of ![]() $X_{\ast } = 0$, where the displacement effect of region 1
$X_{\ast } = 0$, where the displacement effect of region 1![]() $b$ can no longer be ignored. Our next task will be to examine the flow behaviour in this new region.
$b$ can no longer be ignored. Our next task will be to examine the flow behaviour in this new region.
6. Flow near singularity. Inviscid region  $\boldsymbol {C}$
$\boldsymbol {C}$
In the region in question (we shall call it region ![]() $C$; see figure 8) we introduce a new longitudinal coordinate,
$C$; see figure 8) we introduce a new longitudinal coordinate, ![]() $\breve {X}$, such that
$\breve {X}$, such that
where the scaling parameter ![]() $\sigma$ is defined by
$\sigma$ is defined by
This ensures that the streamline angle (5.37) produced by region 1![]() $b$ is the same order quantity as the streamline angle (5.42) produced by region 1
$b$ is the same order quantity as the streamline angle (5.42) produced by region 1![]() $a$.
$a$.
Region ![]() $C$ is composed of the stream filaments that pass through regions 1
$C$ is composed of the stream filaments that pass through regions 1![]() $a^{\prime }$ and 1
$a^{\prime }$ and 1![]() $b^{\prime }$; see figure 9. The longitudinal velocity
$b^{\prime }$; see figure 9. The longitudinal velocity ![]() $U_{\ast }$ in region 1
$U_{\ast }$ in region 1![]() $a^{\prime }$ is given by (3.9). Setting
$a^{\prime }$ is given by (3.9). Setting ![]() $\bar {P}_s= - \frac {1}{2}$ and taking into account that for small
$\bar {P}_s= - \frac {1}{2}$ and taking into account that for small ![]() $X_{\ast }$ the pressure is given by (5.35), we can express (3.9) in the form
$X_{\ast }$ the pressure is given by (5.35), we can express (3.9) in the form
 \begin{equation} U_{\ast } = \begin{cases} - \frac{1}{2} X_{\ast } \sqrt{1 + 2 \xi } & \text{if} \ \xi \in \left[ 0 , - \frac{1}{2} \right] ,\\ \frac{1}{2} X_{\ast } \sqrt{1 + 2 \xi } & \text{if} \ \xi > - \frac{1}{2} , \end{cases} \end{equation}
\begin{equation} U_{\ast } = \begin{cases} - \frac{1}{2} X_{\ast } \sqrt{1 + 2 \xi } & \text{if} \ \xi \in \left[ 0 , - \frac{1}{2} \right] ,\\ \frac{1}{2} X_{\ast } \sqrt{1 + 2 \xi } & \text{if} \ \xi > - \frac{1}{2} , \end{cases} \end{equation}
where ![]() $\xi$ is given by (5.41).
$\xi$ is given by (5.41).

Figure 9. Formation of region ![]() $C$.
$C$.
If we now express (5.35) and (6.3) in terms of the new coordinate (6.1), and return to the original variables ![]() $P$,
$P$, ![]() $U$ and
$U$ and ![]() $\Psi$ with the help of (3.3a--c) and (3.4a,b), then we will see that in region 1
$\Psi$ with the help of (3.3a--c) and (3.4a,b), then we will see that in region 1![]() $a^{\prime }$
$a^{\prime }$
 \begin{gather*} P = U_w^{2} \sigma ^{2} \left( - \tfrac{1}{8} \breve{X}^{2} \right) + \cdots , \\ U = \begin{cases} U_w \sigma \left( - \frac{1}{2} \breve{X} \sqrt{1 + 2 \xi } \right) +\cdots & \text{if} \ \xi \in \left[ 0 , - \frac{1}{2} \right] ,\\ U_w \sigma \left( \frac{1}{2} \breve{X} \sqrt{1 + 2 \xi } \right) + \cdots & \text{if} \ \xi > - \frac{1}{2} , \end{cases} \end{gather*}
\begin{gather*} P = U_w^{2} \sigma ^{2} \left( - \tfrac{1}{8} \breve{X}^{2} \right) + \cdots , \\ U = \begin{cases} U_w \sigma \left( - \frac{1}{2} \breve{X} \sqrt{1 + 2 \xi } \right) +\cdots & \text{if} \ \xi \in \left[ 0 , - \frac{1}{2} \right] ,\\ U_w \sigma \left( \frac{1}{2} \breve{X} \sqrt{1 + 2 \xi } \right) + \cdots & \text{if} \ \xi > - \frac{1}{2} , \end{cases} \end{gather*}where
This suggests that the solution in region ![]() $C$ has to be sought in the form
$C$ has to be sought in the form
 \begin{equation} \left.\begin{array}{cc@{}}
U = U_w \sigma \breve{U} + \cdots, & P = U_w^{2} \sigma
^{2} \breve{P} + \cdots ,\\ X = \dfrac{\sigma }{U_w}
\breve{X} , & \Psi = U_w^{2} \sigma ^{2} \breve{\Psi } ,
\end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{cc@{}}
U = U_w \sigma \breve{U} + \cdots, & P = U_w^{2} \sigma
^{2} \breve{P} + \cdots ,\\ X = \dfrac{\sigma }{U_w}
\breve{X} , & \Psi = U_w^{2} \sigma ^{2} \breve{\Psi } ,
\end{array}\right\} \end{equation}
with functions ![]() $\breve {U} (\breve {X} , \breve {\Psi })$ and
$\breve {U} (\breve {X} , \breve {\Psi })$ and ![]() $\breve {P} (\breve {X} , \breve {\Psi })$ satisfying the following matching condition with the solution in region 1
$\breve {P} (\breve {X} , \breve {\Psi })$ satisfying the following matching condition with the solution in region 1![]() $a^{\prime }$:
$a^{\prime }$:
 \begin{equation} \left.\begin{array}{c@{}}
\breve{P} = - \tfrac{1}{8} \breve{X}^{2} + \cdots ,\\
\breve{U} = \left\{\begin{array}{@{}cl@{}} - \frac{1}{2} \breve{X} \sqrt{1
+ 2 \xi } +\cdots & \text{if} \ \xi \in \left[ 0 , -
\frac{1}{2} \right] ,\\ \frac{1}{2} \breve{X} \sqrt{1 + 2
\xi } + \cdots & \text{if} \ \xi > - \frac{1}{2} ,
\end{array}\right. \end{array} \right\} \quad \text{as} \
\breve{X} \to \infty.
\end{equation}
\begin{equation} \left.\begin{array}{c@{}}
\breve{P} = - \tfrac{1}{8} \breve{X}^{2} + \cdots ,\\
\breve{U} = \left\{\begin{array}{@{}cl@{}} - \frac{1}{2} \breve{X} \sqrt{1
+ 2 \xi } +\cdots & \text{if} \ \xi \in \left[ 0 , -
\frac{1}{2} \right] ,\\ \frac{1}{2} \breve{X} \sqrt{1 + 2
\xi } + \cdots & \text{if} \ \xi > - \frac{1}{2} ,
\end{array}\right. \end{array} \right\} \quad \text{as} \
\breve{X} \to \infty.
\end{equation}
Here ![]() $\xi$ is expressed in terms of variables of region
$\xi$ is expressed in terms of variables of region ![]() $C$ by means of the equation
$C$ by means of the equation
To formulate the corresponding matching conditions with the solution in region 1![]() $b^{\prime }$, we need to return to (5.21). Combining it with the first equation in (5.1) and applying the rescaling (6.1), renders the solution in region 1
$b^{\prime }$, we need to return to (5.21). Combining it with the first equation in (5.1) and applying the rescaling (6.1), renders the solution in region 1![]() $b^{\prime }$ in the form
$b^{\prime }$ in the form
which means that the sought matching condition for the velocity ![]() $\breve {U}$ in region
$\breve {U}$ in region ![]() $C$ is written as
$C$ is written as
The similarity variable ![]() $\eta$ is defined by (5.18). We now need to express it in terms of the variables (6.4) of region
$\eta$ is defined by (5.18). We now need to express it in terms of the variables (6.4) of region ![]() $C$. Substituting (6.1) and the fourth equation in (6.4) into (5.18), we have
$C$. Substituting (6.1) and the fourth equation in (6.4) into (5.18), we have
Finally, it follows from (6.2) that ![]() $2 |\ln \sigma | = U_w^{2} \sigma ^{2}$ and, therefore, we can write
$2 |\ln \sigma | = U_w^{2} \sigma ^{2}$ and, therefore, we can write
where ![]() $\chi = 2 |\ln \sigma |$.
$\chi = 2 |\ln \sigma |$.
Before performing mathematical analysis of the flow in region ![]() $C$ we need to supplement (6.4) with the corresponding asymptotic representation of the lateral velocity
$C$ we need to supplement (6.4) with the corresponding asymptotic representation of the lateral velocity ![]() $V$. For this purpose,
$V$. For this purpose,
is used. Evaluating the left-hand side in (6.9) with the help of (6.4) it is easily seen that in region ![]() $C$ the lateral velocity should be sought in the form
$C$ the lateral velocity should be sought in the form
Now we can substitute (6.4) into the momentum equation (2.4a). We see that in the limit ![]() $U_w \to \infty$ this equation reduces to
$U_w \to \infty$ this equation reduces to
which shows that the flow in region ![]() $C$ can be treated as inviscid. This allows us to use the Bernoulli equation
$C$ can be treated as inviscid. This allows us to use the Bernoulli equation
The Bernoulli function ![]() $\breve {H} (\breve {\Psi })$ can be found by means of matching with solutions in regions
$\breve {H} (\breve {\Psi })$ can be found by means of matching with solutions in regions![]() $1a^{\prime }$ and
$1a^{\prime }$ and ![]() $1b^{\prime }$. We start with region
$1b^{\prime }$. We start with region ![]() $1a^{\prime }$, where we have to use (6.5) and (6.6). We see that
$1a^{\prime }$, where we have to use (6.5) and (6.6). We see that
When matching with region ![]() $1b^{\prime }$, (6.7) and (6.8) have to be used, leading to
$1b^{\prime }$, (6.7) and (6.8) have to be used, leading to
Notice that the matching between (6.12) and (6.13) is performed by setting ![]() $\breve {\Psi } \to 0$ in (6.12) and
$\breve {\Psi } \to 0$ in (6.12) and ![]() $\breve {\Psi } \to -\infty$ in (6.13). The composite Bernoulli function that is applicable to all streamlines in region
$\breve {\Psi } \to -\infty$ in (6.13). The composite Bernoulli function that is applicable to all streamlines in region ![]() $C$ is obtained by adding (6.12) to (6.13):
$C$ is obtained by adding (6.12) to (6.13):
Substituting (6.14) into (6.11) and solving the resulting equation for ![]() $\skew3\breve {U}$, we find that
$\skew3\breve {U}$, we find that
To decide where the velocity ![]() $\skew3\breve {U}$ is positive and where it is negative, we need to consider the topology of the streamlines in region
$\skew3\breve {U}$ is positive and where it is negative, we need to consider the topology of the streamlines in region ![]() $C$. We shall use for this purpose the streamline sketch in figure 10. We know that in region
$C$. We shall use for this purpose the streamline sketch in figure 10. We know that in region ![]() $1b^{\prime }$ and in the lower part of region
$1b^{\prime }$ and in the lower part of region ![]() $1b^{\prime }$ on the right-hand side of the sketch, the fluid particles move against the flow outside the boundary layer. As they do so, they encounter a growing pressure and experience a deceleration. In fact, given
$1b^{\prime }$ on the right-hand side of the sketch, the fluid particles move against the flow outside the boundary layer. As they do so, they encounter a growing pressure and experience a deceleration. In fact, given ![]() $\breve {\Psi }$ on the streamline considered, one can find the pressure
$\breve {\Psi }$ on the streamline considered, one can find the pressure ![]() $\breve {P}$ that makes the fluid stop and turn back. This means that any cross-section
$\breve {P}$ that makes the fluid stop and turn back. This means that any cross-section ![]() $A A^{\prime }$ in region
$A A^{\prime }$ in region ![]() $C$ has a ‘reverse’ point
$C$ has a ‘reverse’ point ![]() $R$, where
$R$, where
The value ![]() $\breve {\Psi }_R$ of the streamfunction on the streamline passing through point
$\breve {\Psi }_R$ of the streamfunction on the streamline passing through point ![]() $R$ is obtained by setting
$R$ is obtained by setting ![]() $\skew3\breve {U} = 0$ in (6.15). This leads to the equation
$\skew3\breve {U} = 0$ in (6.15). This leads to the equation
relating ![]() $\breve {\Psi }_R$ to the pressure
$\breve {\Psi }_R$ to the pressure ![]() $\breve {P}$ at cross-section
$\breve {P}$ at cross-section ![]() $A A^{\prime }$.
$A A^{\prime }$.

Figure 10. Streamline pattern in region ![]() $C$.
$C$.
To find the pressure distribution ![]() $\breve {P} (\breve {X})$ in region
$\breve {P} (\breve {X})$ in region ![]() $C$, we shall use the fact that this region is rather short and, therefore, the flow is subject to the conditions of the ‘condensed flow regime’ (see Bogolepov & Neiland Reference Bogolepov and Neiland1971). In this regime the streamline slope angle at the outer edge of region
$C$, we shall use the fact that this region is rather short and, therefore, the flow is subject to the conditions of the ‘condensed flow regime’ (see Bogolepov & Neiland Reference Bogolepov and Neiland1971). In this regime the streamline slope angle at the outer edge of region ![]() $C$ remains constant:
$C$ remains constant:
The value of the constant on the right-hand side of (6.17) may be obtained through matching with the solution (5.42) in region ![]() $1a$:
$1a$:
Applying the scalings (6.4) and (6.10) to the velocity components ![]() $U$ and
$U$ and ![]() $V$ on the left-hand side of (6.18), we can conclude that in region
$V$ on the left-hand side of (6.18), we can conclude that in region ![]() $C$ the following equation holds:
$C$ the following equation holds:
 \begin{equation} \left.\frac{\breve{V}}{\breve{U}}\right|_{\breve{Y} = \infty } = \frac{1}{2} . \end{equation}
\begin{equation} \left.\frac{\breve{V}}{\breve{U}}\right|_{\breve{Y} = \infty } = \frac{1}{2} . \end{equation} The left-hand side of (6.19) may be calculated using the continuity equation (2.4b). It is written in terms of variables (6.4), (6.10) of region ![]() $C$ as
$C$ as
 \begin{equation} \frac{\partial }{\partial \breve{\Psi }} \left( \frac{\breve{V}}{\breve{U}} \right) = \frac{\partial }{\partial \breve{X}} \left( \frac{1}{\breve{U}} \right) . \end{equation}
\begin{equation} \frac{\partial }{\partial \breve{\Psi }} \left( \frac{\breve{V}}{\breve{U}} \right) = \frac{\partial }{\partial \breve{X}} \left( \frac{1}{\breve{U}} \right) . \end{equation}
When integrating (6.20) across region ![]() $C$, one needs to distinguish three intervals on
$C$, one needs to distinguish three intervals on ![]() $A A^{\prime }$; see figure 10. The first one,
$A A^{\prime }$; see figure 10. The first one, ![]() $A R$, lies below the reversal point
$A R$, lies below the reversal point ![]() $R$. The fluid crosses this interval from right to left, and the velocity
$R$. The fluid crosses this interval from right to left, and the velocity ![]() $\skew3\breve {U}$ is given by (6.15) with the minus sign. Above point
$\skew3\breve {U}$ is given by (6.15) with the minus sign. Above point ![]() $R$ the velocity
$R$ the velocity ![]() $\skew3\breve {U}$ becomes positive, and we have to use (6.15) with the plus sign. Equation (6.15) remains valid until point
$\skew3\breve {U}$ becomes positive, and we have to use (6.15) with the plus sign. Equation (6.15) remains valid until point ![]() $M$ is reached. This point lies on the last streamline that originates in region
$M$ is reached. This point lies on the last streamline that originates in region ![]() $1b^{\prime }$ and turned back by the rising pressure. The value
$1b^{\prime }$ and turned back by the rising pressure. The value ![]() $\breve {\Psi }_M$ of the streamfunction at point
$\breve {\Psi }_M$ of the streamfunction at point ![]() $M$ is defined by the equation
$M$ is defined by the equation
Here ![]() $\breve {P}_M$ is the maximum value of pressure
$\breve {P}_M$ is the maximum value of pressure ![]() $\breve {P}$ in region
$\breve {P}$ in region ![]() $C$. The latter is defined by the strength of the impinging expansion fan:
$C$. The latter is defined by the strength of the impinging expansion fan:
The streamlines crossing ![]() $A A^{\prime }$ above point
$A A^{\prime }$ above point ![]() $M$ originate in the unperturbed flow region before the expansion fan (see figure 10), where
$M$ originate in the unperturbed flow region before the expansion fan (see figure 10), where ![]() $\breve {H}$ also should be a linear function of
$\breve {H}$ also should be a linear function of ![]() $\breve {\Psi }$, as it is in region 1
$\breve {\Psi }$, as it is in region 1![]() $a^{\prime }$. However, due to obvious misalignment of the streamline before and after the impinging expansion fan (see figure 6), we shall modify (6.12) as follows:
$a^{\prime }$. However, due to obvious misalignment of the streamline before and after the impinging expansion fan (see figure 6), we shall modify (6.12) as follows:
To find the shift parameter ![]() $\breve {\Psi }_0$, we consider the stagnation point
$\breve {\Psi }_0$, we consider the stagnation point ![]() $S$ in figure 10. At this point,
$S$ in figure 10. At this point, ![]() $\skew3\breve {U} = 0$ and
$\skew3\breve {U} = 0$ and ![]() $\breve {P} = \breve {P}_M$ and, therefore, the left-hand side of (6.23) is calculated as
$\breve {P} = \breve {P}_M$ and, therefore, the left-hand side of (6.23) is calculated as
while the right-hand side equals
This leads to the following equation:
Eliminating ![]() $\breve {P}_M$ from (6.24) with the help of (6.21), we find that
$\breve {P}_M$ from (6.24) with the help of (6.21), we find that
It remains to substitute (6.25) back into (6.23) and then into (6.11). Solving the resulting equation for ![]() $\skew3\breve {U}$, we see that above point
$\skew3\breve {U}$, we see that above point ![]() $M$,
$M$,
Consequently, for any ![]() $\breve {\Psi } > \breve {\Psi }_M$, we can express the result of the integration of (6.20) in the form
$\breve {\Psi } > \breve {\Psi }_M$, we can express the result of the integration of (6.20) in the form
 \begin{align*} \frac{\breve{V}}{\breve{U}} &= \frac{\partial }{\partial \breve{X}} \left[ - \int\limits_{+\infty }^{\breve{\Psi }_R}\frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} \right.\\ &\left.\quad + \int\limits_{\breve{\Psi }_R}^{\breve{\Psi }_M} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} + \int\limits_{\breve{\Psi }_M}^{\breve{\Psi }} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi }_M + 1)} - 2 \breve{P}}} \right] , \end{align*}
\begin{align*} \frac{\breve{V}}{\breve{U}} &= \frac{\partial }{\partial \breve{X}} \left[ - \int\limits_{+\infty }^{\breve{\Psi }_R}\frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} \right.\\ &\left.\quad + \int\limits_{\breve{\Psi }_R}^{\breve{\Psi }_M} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} + \int\limits_{\breve{\Psi }_M}^{\breve{\Psi }} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi }_M + 1)} - 2 \breve{P}}} \right] , \end{align*}or, equivalently,
 \begin{align} \frac{\breve{V}}{\breve{U}} &= \frac{\partial }{\partial \breve{X}} \left[ \int\limits_{\breve{\Psi }_M}^{+\infty } \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} \right. \nonumber\\ &\quad \left.+ 2 \int\limits_{\breve{\Psi }_R}^{\breve{\Psi }_M} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} + \int\limits_{\breve{\Psi }_M}^{\breve{\Psi }} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi }_M + 1)} - 2 \breve{P}}} \right] . \end{align}
\begin{align} \frac{\breve{V}}{\breve{U}} &= \frac{\partial }{\partial \breve{X}} \left[ \int\limits_{\breve{\Psi }_M}^{+\infty } \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} \right. \nonumber\\ &\quad \left.+ 2 \int\limits_{\breve{\Psi }_R}^{\breve{\Psi }_M} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} + \int\limits_{\breve{\Psi }_M}^{\breve{\Psi }} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi }_M + 1)} - 2 \breve{P}}} \right] . \end{align}
It remains to substitute (6.26) into (6.19), and we will have the following integro-differential equation for ![]() $\breve {P}$:
$\breve {P}$:
 \begin{align} \frac{1}{2} &= \frac{\textrm{d}}{\textrm{d} \breve{X}} \left[ 2 \int\limits_{\breve{\Psi }_R}^{\breve{\Psi }_M} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} \right]\nonumber\\ &\quad + \frac{\textrm{d} \breve{P}}{\textrm{d} \breve{X}} \left[ \int\limits_{\breve{\Psi }_M}^{+\infty } \frac{\textrm{d} \breve{\Psi }}{\left[ 2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P} \right] ^{3/2}} + \frac{1}{\sqrt{2 \breve{\Psi }_M + \textrm{e}^{\chi (\breve{\Psi }_M + 1)} - 2 \breve{P}}} \right] . \end{align}
\begin{align} \frac{1}{2} &= \frac{\textrm{d}}{\textrm{d} \breve{X}} \left[ 2 \int\limits_{\breve{\Psi }_R}^{\breve{\Psi }_M} \frac{\textrm{d} \breve{\Psi }} {\sqrt{2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} \right]\nonumber\\ &\quad + \frac{\textrm{d} \breve{P}}{\textrm{d} \breve{X}} \left[ \int\limits_{\breve{\Psi }_M}^{+\infty } \frac{\textrm{d} \breve{\Psi }}{\left[ 2 \breve{\Psi } + \textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P} \right] ^{3/2}} + \frac{1}{\sqrt{2 \breve{\Psi }_M + \textrm{e}^{\chi (\breve{\Psi }_M + 1)} - 2 \breve{P}}} \right] . \end{align}It should be solved together with (6.16) subject to the boundary condition
given by (6.5).
The results of the numerical solution of (6.27) are displayed in figure 11. We found that when performing the calculations, a really fine partition in ![]() $\breve {\Psi }$ is needed to make the results mesh independent. This is due to the fact that the first integral on the right-hand side of (6.27a) is singular at the lower limit of integration
$\breve {\Psi }$ is needed to make the results mesh independent. This is due to the fact that the first integral on the right-hand side of (6.27a) is singular at the lower limit of integration ![]() $\breve {\Psi } = \breve {\Psi }_R$. Its vicinity
$\breve {\Psi } = \breve {\Psi }_R$. Its vicinity ![]() $\breve {\Psi } \in [\breve {\Psi }_R , \breve {\Psi }_R + \delta ]$ requires a special treatment. We approximated
$\breve {\Psi } \in [\breve {\Psi }_R , \breve {\Psi }_R + \delta ]$ requires a special treatment. We approximated ![]() $2 \breve {\Psi } + \textrm {e}^{\chi (\breve {\Psi } + 1)} - 2 \breve {P}$ by a linear function
$2 \breve {\Psi } + \textrm {e}^{\chi (\breve {\Psi } + 1)} - 2 \breve {P}$ by a linear function
and calculated the resulting integral analytically.

Figure 11. Pressure variation in region ![]() $C$ for
$C$ for ![]() $\Psi _M = -0.4$ and
$\Psi _M = -0.4$ and ![]() $\chi = 3.0$,
$\chi = 3.0$, ![]() $4.0$ and
$4.0$ and ![]() $5.0$.
$5.0$.
Typical behaviour of the solution is shown in figure 11 where the results of the calculations performed for ![]() $\Psi _M = -0.4$ and three values of
$\Psi _M = -0.4$ and three values of ![]() $\chi = 3.0$,
$\chi = 3.0$, ![]() $4.0$ and
$4.0$ and ![]() $5.0$ are displayed. We found that for large enough
$5.0$ are displayed. We found that for large enough ![]() $\breve {X}$, the asymptote (6.27b) is followed very closely. Then the graphs corresponding to different values of
$\breve {X}$, the asymptote (6.27b) is followed very closely. Then the graphs corresponding to different values of ![]() $\chi$ start to deviate from one another. The larger parameter
$\chi$ start to deviate from one another. The larger parameter ![]() $\chi$, the lower
$\chi$, the lower ![]() $\breve {P}$ appears to be. Still, for all
$\breve {P}$ appears to be. Still, for all ![]() $\chi$, the pressure increases monotonically with decreasing
$\chi$, the pressure increases monotonically with decreasing ![]() $\breve {X}$. Interestingly enough, the solution terminates at a finite position
$\breve {X}$. Interestingly enough, the solution terminates at a finite position ![]() $\breve {X}_0$ where
$\breve {X}_0$ where ![]() $\breve {P}$ becomes infinite.
$\breve {P}$ becomes infinite.
6.1. Analysis of the singularity
The behaviour of the solution near singular point ![]() $\breve {X}_0$ may be studied analytically based on the following observations. When
$\breve {X}_0$ may be studied analytically based on the following observations. When ![]() $\breve {P}_M$ becomes large, the displacement effect of the boundary layer is predominantly due to the region that lies inside the loop formed by the streamline with
$\breve {P}_M$ becomes large, the displacement effect of the boundary layer is predominantly due to the region that lies inside the loop formed by the streamline with ![]() $\breve {\Psi } = \breve {\Psi }_M$; see figure 10. This allows us to disregard the two terms on the second line in (6.27a). We also note that the streamlines originating from region 1
$\breve {\Psi } = \breve {\Psi }_M$; see figure 10. This allows us to disregard the two terms on the second line in (6.27a). We also note that the streamlines originating from region 1![]() $a$ cannot penetrate the region with large
$a$ cannot penetrate the region with large ![]() $\breve {P}$. This means that the contribution (6.12) of region 1
$\breve {P}$. This means that the contribution (6.12) of region 1![]() $a^{\prime }$ into the composite Bernoulli function (6.14) can be disregarded. This reduces (6.27a) to
$a^{\prime }$ into the composite Bernoulli function (6.14) can be disregarded. This reduces (6.27a) to
 \begin{equation} \frac{1}{4} = \frac{\textrm{d}}{\textrm{d} \breve{X}} \int\limits_{\breve{\Psi }_R}^{\infty } \frac{\textrm{d} \breve{\Psi }} {\sqrt{\textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} . \end{equation}
\begin{equation} \frac{1}{4} = \frac{\textrm{d}}{\textrm{d} \breve{X}} \int\limits_{\breve{\Psi }_R}^{\infty } \frac{\textrm{d} \breve{\Psi }} {\sqrt{\textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} . \end{equation}
Here ![]() $\breve {\Psi }_R$ is related to the pressure
$\breve {\Psi }_R$ is related to the pressure ![]() $\breve {P}$ via the equation
$\breve {P}$ via the equation
that is obtained by disregarding ![]() $2 \breve {\Psi }_R$ in (6.16).
$2 \breve {\Psi }_R$ in (6.16).
The integral on the right-hand side of (6.28) is easily calculated:
 \begin{equation} \int\limits_{\breve{\Psi }_R}^{\infty } \frac{\textrm{d} \breve{\Psi }} {\sqrt{\textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} = \frac{{\rm \pi} } {\chi \sqrt{2 \breve{P}}} . \end{equation}
\begin{equation} \int\limits_{\breve{\Psi }_R}^{\infty } \frac{\textrm{d} \breve{\Psi }} {\sqrt{\textrm{e}^{\chi (\breve{\Psi } + 1)} - 2 \breve{P}}} = \frac{{\rm \pi} } {\chi \sqrt{2 \breve{P}}} . \end{equation}
It remains to substitute (6.29) into (6.28) and integrate the resulting equation with respect to ![]() $\breve {X}$. We find that
$\breve {X}$. We find that
with ![]() $\breve {X}_0$ denoting the position of the singularity. We found that (6.30) agrees very well with the numerical results of figure 11.
$\breve {X}_0$ denoting the position of the singularity. We found that (6.30) agrees very well with the numerical results of figure 11.
It should be noted that if the expansion fan strength parameter ![]() $\breve {P}_M$ as defined by (6.22) is finite, then the pressure
$\breve {P}_M$ as defined by (6.22) is finite, then the pressure ![]() $\breve {P}$ will only rise to
$\breve {P}$ will only rise to ![]() $\breve {P}_M$, and the above description gives a complete representation of the flow. However, the above theory is also applicable to the case of a self-induced pressure rise in region
$\breve {P}_M$, and the above description gives a complete representation of the flow. However, the above theory is also applicable to the case of a self-induced pressure rise in region ![]() $C$ which leads to a singularity. In this case a new region should be introduced near the singular point. In this region the variation of the pressure across the boundary layer becomes important. The situation is analogous to that discussed in Neiland & Sychev (Reference Neiland and Sychev1966) and Neiland (Reference Neiland1969a). We intend to study this analogy in detail and present the results in a subsequent publication.
$C$ which leads to a singularity. In this case a new region should be introduced near the singular point. In this region the variation of the pressure across the boundary layer becomes important. The situation is analogous to that discussed in Neiland & Sychev (Reference Neiland and Sychev1966) and Neiland (Reference Neiland1969a). We intend to study this analogy in detail and present the results in a subsequent publication.
7. Concluding remarks
Our objective in this paper is to understand if and when the boundary layer can separate from a rigid body surface that moves in the direction opposite to the main flow external to the boundary layer. Here we choose the external flow to be supersonic. The reason for this is twofold. First, in a supersonic flow the region of interest is relatively small which makes it easier to formulate the governing equations and boundary conditions. Second, we wanted to study both the flow with an adverse pressure gradient and the flow with a favourable pressure gradient. As we have seen the adverse and favourable pressure gradient can be easily achieved in supersonic flows by imposing either a shock wave or an expansion fan impinging on the boundary layer.
The interaction of the shock wave with the boundary layer is a classical problem of the triple-deck theory. Strictly speaking this theory is valid when the non-dimensional wall velocity ![]() $U_w = \hat {V}_{sh} / \hat {V}_{\infty }$ is an order
$U_w = \hat {V}_{sh} / \hat {V}_{\infty }$ is an order ![]() $O (Re^{-1/8})$ quantity. In § 4 we presented the results of the numerical solution of the triple-deck equations for the boundary layer on an upstream moving wall. The case of an impinging shock, when the boundary layer is exposed to the adverse pressure gradient, was analysed earlier by Zhuk (Reference Zhuk1982) and Yapalparvi & van Dommelen (Reference Yapalparvi and van Dommelen2012). Their calculations (and our theoretical arguments) suggest that the increasing wall speed suppresses the separation. Keeping this in mind, the main attention in the present work is payed to the boundary layer exposed to an expansion fan. We found that two eddies form in the boundary layer: one lies downstream of the impinging expansion fan and the other upstream of the fan. The former grows as the wall speed
$O (Re^{-1/8})$ quantity. In § 4 we presented the results of the numerical solution of the triple-deck equations for the boundary layer on an upstream moving wall. The case of an impinging shock, when the boundary layer is exposed to the adverse pressure gradient, was analysed earlier by Zhuk (Reference Zhuk1982) and Yapalparvi & van Dommelen (Reference Yapalparvi and van Dommelen2012). Their calculations (and our theoretical arguments) suggest that the increasing wall speed suppresses the separation. Keeping this in mind, the main attention in the present work is payed to the boundary layer exposed to an expansion fan. We found that two eddies form in the boundary layer: one lies downstream of the impinging expansion fan and the other upstream of the fan. The former grows as the wall speed ![]() $|U_w|$ increases, while the latter becomes relatively small. The observed flow behaviour resembles that in the so-called ‘pseudo-shock’ (see Ruban & Vonatsos Reference Ruban and Vonatsos2008), which establishes a link to the ‘collisional separation’ as described by Stewartson, Cebeci & Chang (Reference Stewartson, Cebeci and Chang1980) and Kluwick & Wohlfahrt (Reference Kluwick and Wohlfahrt1986).
$|U_w|$ increases, while the latter becomes relatively small. The observed flow behaviour resembles that in the so-called ‘pseudo-shock’ (see Ruban & Vonatsos Reference Ruban and Vonatsos2008), which establishes a link to the ‘collisional separation’ as described by Stewartson, Cebeci & Chang (Reference Stewartson, Cebeci and Chang1980) and Kluwick & Wohlfahrt (Reference Kluwick and Wohlfahrt1986).
These conclusions are confirmed by theoretical analysis of the flow that has been performed under the assumption that the wall speed is larger than that in the triple-deck theory, namely, ![]() $1 \gg V_{sh}/ V_{\infty } \gg Re^{-1/8}$. In this case the viscous lower tier of the triple-deck structure splits into the inviscid and viscous layers. The pressure distribution along the interaction region can be found by analysing the interaction of the inviscid layer with the external supersonic flow. Still, to satisfy the no-slip condition on the body surface, one has to study the flow behaviour in the near-wall viscous layer. We found that the solution for the viscous layer remains smooth in the case of an impinging shock, but develops a singularity when the boundary layer interacts with the expansion fan. A detailed analysis of the flow behaviour near the singularity shows that a new shorter region should be introduced in the vicinity of the separation point. In this vicinity the flow is governed by the integro-differential equation (6.27a). We found numerically and by means of theoretical analysis of (6.27a) that solution encounters yet another singularity (6.30). The physical processes that lead to its formation are essentially the same as those leading to a singularity in the expansion solution of the classical triple-deck theory; see Neiland (Reference Neiland1969a) and Neiland & Sychev (Reference Neiland and Sychev1966).
$1 \gg V_{sh}/ V_{\infty } \gg Re^{-1/8}$. In this case the viscous lower tier of the triple-deck structure splits into the inviscid and viscous layers. The pressure distribution along the interaction region can be found by analysing the interaction of the inviscid layer with the external supersonic flow. Still, to satisfy the no-slip condition on the body surface, one has to study the flow behaviour in the near-wall viscous layer. We found that the solution for the viscous layer remains smooth in the case of an impinging shock, but develops a singularity when the boundary layer interacts with the expansion fan. A detailed analysis of the flow behaviour near the singularity shows that a new shorter region should be introduced in the vicinity of the separation point. In this vicinity the flow is governed by the integro-differential equation (6.27a). We found numerically and by means of theoretical analysis of (6.27a) that solution encounters yet another singularity (6.30). The physical processes that lead to its formation are essentially the same as those leading to a singularity in the expansion solution of the classical triple-deck theory; see Neiland (Reference Neiland1969a) and Neiland & Sychev (Reference Neiland and Sychev1966).
Acknowledgements
We thank Professor V. V. Sychev for helpful comments on the paper.
Declaration of interests
The authors report no conflict of interest.