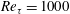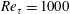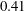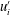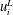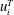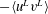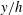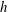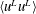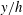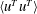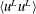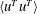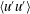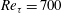1 Introduction
The interaction between wind-shear-driven currents and surface water waves generates Langmuir circulations (LCs), manifested by the long windrows (or streaks) extending along the wind direction at the water surface (Leibovich Reference Leibovich1983; Smith Reference Smith2001; Thorpe Reference Thorpe2004; Sullivan & McWilliams Reference Sullivan and McWilliams2010; D’Asaro Reference D’Asaro2014). LCs are named after Irving Langmuir for his pioneering contribution to the investigation of windrows based on a series of flow visualization experiments (Langmuir Reference Langmuir1938). He attributed the windrows to the convergent motion between pairs of counter-rotating streamwise vortices in the water. Following the work of Langmuir, many field observations and laboratory experiments were conducted to study the characteristics of LCs in the upper-ocean mixed layer (see, e.g. the reviews by Pollard Reference Pollard1977; Leibovich Reference Leibovich1983; Thorpe Reference Thorpe2004). The previous studies of LCs in deep water investigated the length scales of windrows, the vertical penetration depth of LCs and the intensities of the upwelling and downwelling motions induced by LCs (Langmuir Reference Langmuir1938; Scott et al. Reference Scott, Myer, Stewart and Walther1969; Assaf, Gerard & Gordon Reference Assaf, Gerard and Gordon1971; Smith, Pinkel & Weller Reference Smith, Pinkel and Weller1987; Weller & Price Reference Weller and Price1988; Nepf Reference Nepf1992; Thorpe Reference Thorpe1992; Farmer & Li Reference Farmer and Li1995). It was reported that the strong downwelling and upwelling motions of LCs enhance the vertical mixing and attenuate the mean shear in the mixed layer (Weller & Price Reference Weller and Price1988; Nepf Reference Nepf1992; Thorpe Reference Thorpe1992; Farmer & Li Reference Farmer and Li1995). In neutrally stratified shallow water, LCs can engulf the entire water column (Faller & Caponi Reference Faller and Caponi1978; Gargett et al. Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Gargett & Wells Reference Gargett and Wells2007; Kukulka, Plueddemann & Sullivan Reference Kukulka, Plueddemann and Sullivan2012; Savidge & Gargett Reference Savidge and Gargett2017). These large-scale full-depth LCs greatly enhance the vertical mixing of scalar quantities and momentum throughout the water column (Gargett et al. Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Dethleff & Kemepema Reference Dethleff and Kemepema2007; Gargett & Wells Reference Gargett and Wells2007; Dierssen et al. Reference Dierssen, Zimmerman, Drake and Burdige2009; Kukulka et al. Reference Kukulka, Plueddemann and Sullivan2012; Akan et al. Reference Akan, Tejada-Martínez, Grosch and Martinat2013), and have a significant impact on the bottom boundary layer (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007; Tejada-Martínez et al. Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012).
Craik & Leibovich (Reference Craik and Leibovich1976) and Leibovich (Reference Leibovich1977) derived the Craik–Leibovich (C–L) equations to explain the mechanism underlying LCs. The C–L equations describe the wave-phase-averaged effect of surface waves on the shear turbulence through a vortex force term in the momentum equations, which depends on the Stokes drift velocity of surface waves and the vorticity of flow field. The derivation of the C–L equations was also given in Andrews & McIntyre (Reference Andrews and McIntyre1978), Leibovich (Reference Leibovich1980) and Holm (Reference Holm1996). Through the stability analysis of the C–L equations, it was found that the vertical vorticity generated by the disturbance of the shear-driven current is tilted into the streamwise direction by the shear of the Stokes drift of surface waves to generate streamwise vortices (Craik Reference Craik1977).
The development of the C–L equations makes it possible to perform numerical simulations to study Langmuir turbulence without resolving the wave surface. Skyllingstad & Denbo (Reference Skyllingstad and Denbo1995) and McWilliams, Sullivan & Moeng (Reference McWilliams, Sullivan and Moeng1997) performed large-eddy simulations (LES) for Langmuir turbulence in the mixed layer based on the C–L equations. McWilliams et al. (Reference McWilliams, Sullivan and Moeng1997) pointed out that the turbulent Langmuir number,
![]() $La_{t}=\sqrt{u_{\unicode[STIX]{x1D70F}}/u_{s}^{\ast }}$
, is a key dimensionless parameter in Langmuir turbulence that quantifies the relative importance of the wind shear to the C–L vortex force related to the Stokes drift of surface waves. Here,
$La_{t}=\sqrt{u_{\unicode[STIX]{x1D70F}}/u_{s}^{\ast }}$
, is a key dimensionless parameter in Langmuir turbulence that quantifies the relative importance of the wind shear to the C–L vortex force related to the Stokes drift of surface waves. Here,
![]() $u_{\unicode[STIX]{x1D70F}}$
is the surface friction velocity, and
$u_{\unicode[STIX]{x1D70F}}$
is the surface friction velocity, and
![]() $u_{s}^{\ast }$
is the characteristic value of Stokes drift velocity, defined as the surface Stokes drift in deep-water Langmuir turbulence. As the value of
$u_{s}^{\ast }$
is the characteristic value of Stokes drift velocity, defined as the surface Stokes drift in deep-water Langmuir turbulence. As the value of
![]() $La_{t}$
decreases, the LCs are enhanced, characterized by the increase of the variance of vertical velocity fluctuations (Li, Garrett & Skyllingstad Reference Li, Garrett and Skyllingstad2005; Harcourt & D’Asaro Reference Harcourt and D’Asaro2008). The LCs are also influenced by the parameter
$La_{t}$
decreases, the LCs are enhanced, characterized by the increase of the variance of vertical velocity fluctuations (Li, Garrett & Skyllingstad Reference Li, Garrett and Skyllingstad2005; Harcourt & D’Asaro Reference Harcourt and D’Asaro2008). The LCs are also influenced by the parameter
![]() $kh$
, where
$kh$
, where
![]() $k$
is the wavenumber of the dominant wave and
$k$
is the wavenumber of the dominant wave and
![]() $h$
is the depth of mixed layer. It was found that the location of the maximum vertical velocity in deep-water Langmuir turbulence moves towards the water surface as
$h$
is the depth of mixed layer. It was found that the location of the maximum vertical velocity in deep-water Langmuir turbulence moves towards the water surface as
![]() $kh$
increases (Li et al.
Reference Li, Garrett and Skyllingstad2005; Harcourt & D’Asaro Reference Harcourt and D’Asaro2008). LES based on the C–L equations were also performed to study the deep-water Langmuir turbulence under complex sea conditions, including modelling for wave breaking (Noh, Min & Raasch Reference Noh, Min and Raasch2004; Sullivan, McWilliams & Melville Reference Sullivan, McWilliams and Melville2007), swells coexisting with wind seas (McWilliams et al.
Reference McWilliams, Huckle, Liang and Sullivan2014) and hurricanes (Sullivan et al.
Reference Sullivan, Romero, McWilliams and Melville2012).
$kh$
increases (Li et al.
Reference Li, Garrett and Skyllingstad2005; Harcourt & D’Asaro Reference Harcourt and D’Asaro2008). LES based on the C–L equations were also performed to study the deep-water Langmuir turbulence under complex sea conditions, including modelling for wave breaking (Noh, Min & Raasch Reference Noh, Min and Raasch2004; Sullivan, McWilliams & Melville Reference Sullivan, McWilliams and Melville2007), swells coexisting with wind seas (McWilliams et al.
Reference McWilliams, Huckle, Liang and Sullivan2014) and hurricanes (Sullivan et al.
Reference Sullivan, Romero, McWilliams and Melville2012).
While the C–L equations were solved numerically to study deep-water Langmuir turbulence as reviewed above, for shallow waters, LES based on the C–L equations were also conducted to study the influence of full-depth LCs on the turbulence in the bottom, core and surface regions of the neutrally stratified shallow-water column (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007; Kukulka et al.
Reference Kukulka, Plueddemann and Sullivan2012; Tejada-Martínez et al.
Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012; Akan et al.
Reference Akan, Tejada-Martínez, Grosch and Martinat2013; Tejada-Martínez et al.
Reference Tejada-Martínez, Akan, Sinha, Grosch and Martinat2013; Martinat, Grosch & Gatski Reference Martinat, Grosch and Gatski2014; Sinha et al.
Reference Sinha, Tejada-Martínez, Akan and Grosch2015). It was reported that in shallow-water Langmuir turbulence, the mean shear in the core region reduces and even becomes negative, and the logarithmic layer disappears due to the disruption effect of the LCs (Tejada-Martínez et al.
Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012, Reference Tejada-Martínez, Akan, Sinha, Grosch and Martinat2013; Sinha et al.
Reference Sinha, Tejada-Martínez, Akan and Grosch2015). In comparison with the pure shear-driven turbulence without LCs, the LCs significantly enhance the spanwise velocity fluctuations near the water bottom and the vertical velocity fluctuations in the core region of the water column (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007; Kukulka et al.
Reference Kukulka, Plueddemann and Sullivan2012; Akan et al.
Reference Akan, Tejada-Martínez, Grosch and Martinat2013; Martinat et al.
Reference Martinat, Grosch and Gatski2014; Sinha et al.
Reference Sinha, Tejada-Martínez, Akan and Grosch2015). The results obtained from the LES show good agreement with the observations of full-depth LCs in an unstratified shallow-water column (15 m) on the shelf approximately
![]() $6$
–
$6$
–
![]() $7$
km off the New Jersey coast (Gargett et al.
Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Gargett & Wells Reference Gargett and Wells2007). The effects of Coriolis force (Grosch & Gargett Reference Grosch and Gargett2016), surface heat flux (Gargett et al.
Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Gargett & Wells Reference Gargett and Wells2007; Gargett & Grosch Reference Gargett and Grosch2014; Gargett, Savidge & Wells Reference Gargett, Savidge and Wells2014; Walker, Tejada-Martínez & Grosch Reference Walker, Tejada-Martínez and Grosch2016) and tidal current (Kukulka et al.
Reference Kukulka, Plueddemann, Trowbridge and Sullivan2011; Martinat et al.
Reference Martinat, Xu, Grosch and Tejada-Martínez2011) on shallow-water Langmuir turbulence are also studied through LES and field measurements.
$7$
km off the New Jersey coast (Gargett et al.
Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Gargett & Wells Reference Gargett and Wells2007). The effects of Coriolis force (Grosch & Gargett Reference Grosch and Gargett2016), surface heat flux (Gargett et al.
Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Gargett & Wells Reference Gargett and Wells2007; Gargett & Grosch Reference Gargett and Grosch2014; Gargett, Savidge & Wells Reference Gargett, Savidge and Wells2014; Walker, Tejada-Martínez & Grosch Reference Walker, Tejada-Martínez and Grosch2016) and tidal current (Kukulka et al.
Reference Kukulka, Plueddemann, Trowbridge and Sullivan2011; Martinat et al.
Reference Martinat, Xu, Grosch and Tejada-Martínez2011) on shallow-water Langmuir turbulence are also studied through LES and field measurements.
To study the mechanism of the effect of full-depth LCs on turbulence statistics in the bottom boundary layer, wall-resolved LES (i.e. without wall-layer modelling) has been used in the literature to resolve the near-bottom region. Only full-depth LCs can deeply penetrate into the bottom boundary. This is the focus of the present study. Hereafter, full-depth LCs are called LCs for short. In previous studies, wall-resolved LES of shallow-water Langmuir turbulence was carried out at relatively low Reynolds numbers, e.g.
![]() $Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}=395$
and
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}=395$
and
![]() $590$
(Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007; Tejada-Martínez et al.
Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012). Here,
$590$
(Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007; Tejada-Martínez et al.
Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012). Here,
![]() $h$
is the half-water depth, and
$h$
is the half-water depth, and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity. The disruption of the logarithmic layer implies that the traditional wall-layer modelling based on the logarithmic law of the mean velocity (Cabot & Moin Reference Cabot and Moin2000; Piomelli & Balaras Reference Piomelli and Balaras2002) is inappropriate. The above conclusion is, however, based on relatively low Reynolds numbers, and needs to be further examined at higher Reynolds numbers. Furthermore, the increase of Reynolds number differentiates the inner and outer length scales. It was found that in canonical wall turbulence at high Reynolds numbers (
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. The disruption of the logarithmic layer implies that the traditional wall-layer modelling based on the logarithmic law of the mean velocity (Cabot & Moin Reference Cabot and Moin2000; Piomelli & Balaras Reference Piomelli and Balaras2002) is inappropriate. The above conclusion is, however, based on relatively low Reynolds numbers, and needs to be further examined at higher Reynolds numbers. Furthermore, the increase of Reynolds number differentiates the inner and outer length scales. It was found that in canonical wall turbulence at high Reynolds numbers (
![]() $Re_{\unicode[STIX]{x1D70F}}=O(10^{3}{-}10^{5})$
), the length scale separation leads to the emergence of large-scale motions scaled by the outer length scale, which make the shape of Reynolds normal stress profiles different from that at low Reynolds numbers (
$Re_{\unicode[STIX]{x1D70F}}=O(10^{3}{-}10^{5})$
), the length scale separation leads to the emergence of large-scale motions scaled by the outer length scale, which make the shape of Reynolds normal stress profiles different from that at low Reynolds numbers (
![]() $Re_{\unicode[STIX]{x1D70F}}=O(10^{2})$
) (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010; Jiménez Reference Jiménez2012). From the above review of previous studies of Langmuir turbulence and canonical wall turbulence, it is understood that wall-resolved LES at higher Reynolds numbers are needed to further study the effects of LCs on the bottom boundary layer. The recent growth in computer power allows us to perform wall-resolved LES at higher Reynolds numbers with a larger computational domain size. In the present study, we perform wall-resolved LES of shallow-water Langmuir turbulence at
$Re_{\unicode[STIX]{x1D70F}}=O(10^{2})$
) (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010; Jiménez Reference Jiménez2012). From the above review of previous studies of Langmuir turbulence and canonical wall turbulence, it is understood that wall-resolved LES at higher Reynolds numbers are needed to further study the effects of LCs on the bottom boundary layer. The recent growth in computer power allows us to perform wall-resolved LES at higher Reynolds numbers with a larger computational domain size. In the present study, we perform wall-resolved LES of shallow-water Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
,
$Re_{\unicode[STIX]{x1D70F}}=395$
,
![]() $700$
and
$700$
and
![]() $1000$
to study the Reynolds number effect. The effects of dimensionless parameters
$1000$
to study the Reynolds number effect. The effects of dimensionless parameters
![]() $kh$
and
$kh$
and
![]() $La_{t}$
are also investigated.
$La_{t}$
are also investigated.
The remainder of this paper is organized as follows. In § 2, the governing equations and numerical method are introduced. In § 3, the reappearance of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
is reported, and the effects of
$Re_{\unicode[STIX]{x1D70F}}=1000$
is reported, and the effects of
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the width of the logarithmic layer are studied. In § 4, the Reynolds stresses are analysed. The reappearance of the logarithmic layer at
$La_{t}$
on the width of the logarithmic layer are studied. In § 4, the Reynolds stresses are analysed. The reappearance of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
is explained by analysing the Reynolds shear stress. The bimodal shape in the profile of the variance of streamwise velocity fluctuations at
$Re_{\unicode[STIX]{x1D70F}}=1000$
is explained by analysing the Reynolds shear stress. The bimodal shape in the profile of the variance of streamwise velocity fluctuations at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
is reported and analysed based on the decomposition of the velocity fluctuations into a LC-coherent part and a residual turbulence part. In § 5, the budget of turbulence kinematic energy (TKE) is analysed to further study the effects of LCs on the turbulence statistics, followed by the summary in § 6.
$Re_{\unicode[STIX]{x1D70F}}=1000$
is reported and analysed based on the decomposition of the velocity fluctuations into a LC-coherent part and a residual turbulence part. In § 5, the budget of turbulence kinematic energy (TKE) is analysed to further study the effects of LCs on the turbulence statistics, followed by the summary in § 6.
2 Simulation set-up and numerical method
2.1 Governing equations

Figure 1. Sketch of the computational model for shear-driven shallow-water turbulence with LCs.
Figure 1 shows the computational domain and coordinates used in the present simulations. As shown,
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
represent the streamwise, vertical and spanwise directions, respectively. The water depth is
$z$
represent the streamwise, vertical and spanwise directions, respectively. The water depth is
![]() $H$
. Wall-resolved LES based on the C–L equations is performed to study the neutrally stratified shallow-water Langmuir turbulence. Following McWilliams et al. (Reference McWilliams, Sullivan and Moeng1997), a low-pass spatial filter is applied to obtain the wave-phase-averaged motions. The C–L equations read
$H$
. Wall-resolved LES based on the C–L equations is performed to study the neutrally stratified shallow-water Langmuir turbulence. Following McWilliams et al. (Reference McWilliams, Sullivan and Moeng1997), a low-pass spatial filter is applied to obtain the wave-phase-averaged motions. The C–L equations read
Here,
![]() $\overline{\boldsymbol{u}}=(\overline{u},\overline{v},\overline{w})$
is the resolved velocity with
$\overline{\boldsymbol{u}}=(\overline{u},\overline{v},\overline{w})$
is the resolved velocity with
![]() $\overline{u}$
,
$\overline{u}$
,
![]() $\overline{v}$
and
$\overline{v}$
and
![]() $\overline{w}$
denoting the velocity in the
$\overline{w}$
denoting the velocity in the
![]() $x$
-,
$x$
-,
![]() $y$
- and
$y$
- and
![]() $z$
-directions, respectively. The overline represents the implicit grid-level filter. The effective pressure
$z$
-directions, respectively. The overline represents the implicit grid-level filter. The effective pressure
![]() $\overline{\unicode[STIX]{x1D6F1}}=\overline{p}/\unicode[STIX]{x1D70C}+\overline{\unicode[STIX]{x1D6E4}}$
includes the resolved pressure
$\overline{\unicode[STIX]{x1D6F1}}=\overline{p}/\unicode[STIX]{x1D70C}+\overline{\unicode[STIX]{x1D6E4}}$
includes the resolved pressure
![]() $\overline{p}/\unicode[STIX]{x1D70C}$
and the additional term (McWilliams et al.
Reference McWilliams, Sullivan and Moeng1997)
$\overline{p}/\unicode[STIX]{x1D70C}$
and the additional term (McWilliams et al.
Reference McWilliams, Sullivan and Moeng1997)
In (2.2) and (2.3),
![]() $\boldsymbol{u}_{s}$
is the Stokes drift velocity induced by water waves. According to Longuet-Higgins (Reference Longuet-Higgins1953) and Phillips (Reference Phillips1967),
$\boldsymbol{u}_{s}$
is the Stokes drift velocity induced by water waves. According to Longuet-Higgins (Reference Longuet-Higgins1953) and Phillips (Reference Phillips1967),
![]() $\boldsymbol{u}_{s}$
induced by shallow-water potential waves is given as
$\boldsymbol{u}_{s}$
induced by shallow-water potential waves is given as
Here,
![]() $u_{s}^{\ast }=\unicode[STIX]{x1D70E}ka^{2}$
is the characteristic value of
$u_{s}^{\ast }=\unicode[STIX]{x1D70E}ka^{2}$
is the characteristic value of
![]() $u_{s}$
(Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007), with
$u_{s}$
(Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007), with
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $k$
and
$k$
and
![]() $a$
being the frequency, wavenumber and wave amplitude, respectively. In (2.2),
$a$
being the frequency, wavenumber and wave amplitude, respectively. In (2.2),
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity, and the subgrid-scale (SGS) stress tensor
$\unicode[STIX]{x1D708}$
is the kinematic viscosity, and the subgrid-scale (SGS) stress tensor
![]() $\unicode[STIX]{x1D749}^{sgs}$
is included due to the use of the low-pass spatial filter. The last term on the right-hand side of (2.2) is the C–L vortex force, with
$\unicode[STIX]{x1D749}^{sgs}$
is included due to the use of the low-pass spatial filter. The last term on the right-hand side of (2.2) is the C–L vortex force, with
![]() $\overline{\unicode[STIX]{x1D74E}}=\unicode[STIX]{x1D735}\times \overline{\boldsymbol{u}}$
being the vorticity. The value of
$\overline{\unicode[STIX]{x1D74E}}=\unicode[STIX]{x1D735}\times \overline{\boldsymbol{u}}$
being the vorticity. The value of
![]() $La_{t}^{2}$
characterizes the relative magnitude of the wind-shear forcing with respect to wave forcing. According to the definitions of the C–L vortex force (2.2) and Stokes drift (2.4), the increase of either
$La_{t}^{2}$
characterizes the relative magnitude of the wind-shear forcing with respect to wave forcing. According to the definitions of the C–L vortex force (2.2) and Stokes drift (2.4), the increase of either
![]() $La_{t}$
or
$La_{t}$
or
![]() $kh$
leads to the magnitude decrease of the C–L vortex force. Particularly, as the value of
$kh$
leads to the magnitude decrease of the C–L vortex force. Particularly, as the value of
![]() $La_{t}$
approaches infinity, the flow reduces to a shear-driven turbulence without LCs.
$La_{t}$
approaches infinity, the flow reduces to a shear-driven turbulence without LCs.
In the C–L equations derived by Craik & Leibovich (Reference Craik and Leibovich1976) and Leibovich (Reference Leibovich1977), the Stokes drift
![]() $u_{s}$
is obtained using the leading-order solution of potential waves with respect to the wave steepness
$u_{s}$
is obtained using the leading-order solution of potential waves with respect to the wave steepness
![]() $\unicode[STIX]{x1D716}$
. Near the wave surface and water bottom, the magnitude of Stokes drift in the context of viscous flow is different from that obtained from the potential theory due to the viscous boundary condition. For example, at the water bottom, the Stokes drift
$\unicode[STIX]{x1D716}$
. Near the wave surface and water bottom, the magnitude of Stokes drift in the context of viscous flow is different from that obtained from the potential theory due to the viscous boundary condition. For example, at the water bottom, the Stokes drift
![]() $u_{s}$
is zero due to the no-slip boundary condition, but the value given by (2.4) is non-zero. Nevertheless, the magnitude of the latter is very small. Among all the cases studied in this paper, the maximal value of
$u_{s}$
is zero due to the no-slip boundary condition, but the value given by (2.4) is non-zero. Nevertheless, the magnitude of the latter is very small. Among all the cases studied in this paper, the maximal value of
![]() $u_{s}$
is
$u_{s}$
is
![]() $2.26u_{\unicode[STIX]{x1D70F}}$
. Near the water surface, the viscous effect can also influence the Stokes drift. However, the influence of the viscous effect on the Stokes drift is confined in a thin layer. Longuet-Higgins (Reference Longuet-Higgins1953) showed that the leading-order approximation of shallow-water waves satisfies the potential solution in most of the water column, and only deviates from the potential solution in a thin viscous layer with a thickness comparable to that of the Stokes layer. The thickness of the Stokes layer
$2.26u_{\unicode[STIX]{x1D70F}}$
. Near the water surface, the viscous effect can also influence the Stokes drift. However, the influence of the viscous effect on the Stokes drift is confined in a thin layer. Longuet-Higgins (Reference Longuet-Higgins1953) showed that the leading-order approximation of shallow-water waves satisfies the potential solution in most of the water column, and only deviates from the potential solution in a thin viscous layer with a thickness comparable to that of the Stokes layer. The thickness of the Stokes layer
![]() $\unicode[STIX]{x1D6FF}_{s}$
is
$\unicode[STIX]{x1D6FF}_{s}$
is
![]() $\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D70E}}$
, which is small for water waves. For example, in the case of finite-depth waves, if
$\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D70E}}$
, which is small for water waves. For example, in the case of finite-depth waves, if
![]() $\unicode[STIX]{x1D70E}=2\unicode[STIX]{x03C0}~\text{rad}~\text{s}^{-1}$
, the thickness of its Stokes layer is only
$\unicode[STIX]{x1D70E}=2\unicode[STIX]{x03C0}~\text{rad}~\text{s}^{-1}$
, the thickness of its Stokes layer is only
![]() $0.56$
mm (Longuet-Higgins Reference Longuet-Higgins1953). The thickness of the Stokes layer can also be estimated from other studies of turbulent boundary layer subjected to an oscillatory pressure gradient. Based on the results of Ramaprian & Tu (Reference Ramaprian and Tu1983), Scotti & Piomelli (Reference Scotti and Piomelli2001) and Manna, Vacca & Verzicco (Reference Manna, Vacca and Verzicco2012), we can estimate that
$0.56$
mm (Longuet-Higgins Reference Longuet-Higgins1953). The thickness of the Stokes layer can also be estimated from other studies of turbulent boundary layer subjected to an oscillatory pressure gradient. Based on the results of Ramaprian & Tu (Reference Ramaprian and Tu1983), Scotti & Piomelli (Reference Scotti and Piomelli2001) and Manna, Vacca & Verzicco (Reference Manna, Vacca and Verzicco2012), we can estimate that
![]() $\unicode[STIX]{x1D6FF}_{s}$
is smaller than five wall units under the wave condition that Langmuir circulations are observed in the field by Gargett & Wells (Reference Gargett and Wells2007). This above discussions indicate that the viscous effects are confined in the viscous sublayer. According to the original theory of Craik & Leibovich (Reference Craik and Leibovich1976), the viscous effects may lead to a correction to the C–L equation. However, the correction is only subtle and is in a thin layer near the wave surface and water bottom. In Langmuir turbulence, due to the wind shear, the viscous effects near the wave surface and water bottom are much less important than the wind-induced shear. As a result of the above factors, it is believed that the viscous effects at the boundaries only have higher-order influence on the dynamics of the Langmuir turbulence. It was shown in previous LES studies of shallow-water Langmuir turbulence that the LES results based on the C–L equations with
$\unicode[STIX]{x1D6FF}_{s}$
is smaller than five wall units under the wave condition that Langmuir circulations are observed in the field by Gargett & Wells (Reference Gargett and Wells2007). This above discussions indicate that the viscous effects are confined in the viscous sublayer. According to the original theory of Craik & Leibovich (Reference Craik and Leibovich1976), the viscous effects may lead to a correction to the C–L equation. However, the correction is only subtle and is in a thin layer near the wave surface and water bottom. In Langmuir turbulence, due to the wind shear, the viscous effects near the wave surface and water bottom are much less important than the wind-induced shear. As a result of the above factors, it is believed that the viscous effects at the boundaries only have higher-order influence on the dynamics of the Langmuir turbulence. It was shown in previous LES studies of shallow-water Langmuir turbulence that the LES results based on the C–L equations with
![]() $u_{s}$
given by (2.4) (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007) agree well with the field measurement data (Gargett & Wells Reference Gargett and Wells2007). At last, we remark that when more computer power becomes available, one might conduct wave-phase-resolved simulations with full viscous boundary conditions to quantify the viscous effects at the boundaries, which requires a simulation framework different from the present one based on the C–L equations and is beyond the scope of this work.
$u_{s}$
given by (2.4) (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007) agree well with the field measurement data (Gargett & Wells Reference Gargett and Wells2007). At last, we remark that when more computer power becomes available, one might conduct wave-phase-resolved simulations with full viscous boundary conditions to quantify the viscous effects at the boundaries, which requires a simulation framework different from the present one based on the C–L equations and is beyond the scope of this work.
The surface boundary for the wave-phase-averaged motions described in the C–L equations is a rigid lid, which is obtained by keeping the leading-order term in the expansion of the boundary condition with respect to the wave steepness (Craik & Leibovich Reference Craik and Leibovich1976; Leibovich Reference Leibovich1977). According to Kemp & Simons (Reference Kemp and Simons1982) and McWilliams, Restrepo & Lane (Reference McWilliams, Restrepo and Lane2004), the difference in wave amplitude induced by wave–current interactions is a higher-order effect with respect to the wave steepness, which is omitted in the C–L theory. Therefore, it is believed that the C–L equation with a rigid-lid boundary condition at wave surface can still be used under the influence of wave–current interaction. In fact, the rigid-lid surface boundary condition has been widely used in LES of Langmuir turbulence (Skyllingstad & Denbo Reference Skyllingstad and Denbo1995; McWilliams et al.
Reference McWilliams, Sullivan and Moeng1997; Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007). The flow is driven by a constant wind-shear stress
![]() $\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D70C}u_{\unicode[STIX]{x1D70F}}^{2}$
at the water surface
$\unicode[STIX]{x1D70F}_{w}=\unicode[STIX]{x1D70C}u_{\unicode[STIX]{x1D70F}}^{2}$
at the water surface
![]() $y=2h$
, with
$y=2h$
, with
![]() $\unicode[STIX]{x1D70C}$
being the density of water. The no-slip boundary condition is applied at the bottom
$\unicode[STIX]{x1D70C}$
being the density of water. The no-slip boundary condition is applied at the bottom
![]() $y=0$
. Periodic boundary conditions are imposed in the
$y=0$
. Periodic boundary conditions are imposed in the
![]() $x$
- and
$x$
- and
![]() $z$
-directions.
$z$
-directions.
Table 1. Key parameters of simulation cases.

2.2 Computational parameters
Table 1 summarizes the key parameters of the present simulations. In the table,
![]() $L_{x}$
and
$L_{x}$
and
![]() $L_{z}$
denote the computation domain size in the
$L_{z}$
denote the computation domain size in the
![]() $x$
- and
$x$
- and
![]() $z$
-directions, respectively;
$z$
-directions, respectively;
![]() $N_{x}$
,
$N_{x}$
,
![]() $N_{y}$
and
$N_{y}$
and
![]() $N_{z}$
are the number of the grid points in the
$N_{z}$
are the number of the grid points in the
![]() $x$
-,
$x$
-,
![]() $y$
- and
$y$
- and
![]() $z$
-directions, respectively, with
$z$
-directions, respectively, with
![]() $\unicode[STIX]{x0394}x^{+}$
,
$\unicode[STIX]{x0394}x^{+}$
,
![]() $\unicode[STIX]{x0394}y_{min}^{+}$
and
$\unicode[STIX]{x0394}y_{min}^{+}$
and
![]() $\unicode[STIX]{x0394}z^{+}$
being the grid resolution in the corresponding directions. The superscript ‘
$\unicode[STIX]{x0394}z^{+}$
being the grid resolution in the corresponding directions. The superscript ‘
![]() $+$
’ denotes flow quantities normalized using the viscous length scale
$+$
’ denotes flow quantities normalized using the viscous length scale
![]() $\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
and surface friction velocity
$\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
and surface friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}$
. Note that due to the use of a conservative finite difference scheme for the discretization in the
$u_{\unicode[STIX]{x1D70F}}$
. Note that due to the use of a conservative finite difference scheme for the discretization in the
![]() $y$
-direction (Kim & Moin Reference Kim and Moin1985), the shear stress
$y$
-direction (Kim & Moin Reference Kim and Moin1985), the shear stress
![]() $\unicode[STIX]{x1D70F}_{w}$
prescribed at the top is balanced by the time-averaged shear stress at the bottom when the flow is fully developed to a statistically stationary state. Correspondingly, the value of
$\unicode[STIX]{x1D70F}_{w}$
prescribed at the top is balanced by the time-averaged shear stress at the bottom when the flow is fully developed to a statistically stationary state. Correspondingly, the value of
![]() $u_{\unicode[STIX]{x1D70F}}$
at the water bottom obtained from the simulation is also identical to that at the water surface. As a result, the values of
$u_{\unicode[STIX]{x1D70F}}$
at the water bottom obtained from the simulation is also identical to that at the water surface. As a result, the values of
![]() $\unicode[STIX]{x0394}x^{+}$
,
$\unicode[STIX]{x0394}x^{+}$
,
![]() $\unicode[STIX]{x0394}y_{min}^{+}$
and
$\unicode[STIX]{x0394}y_{min}^{+}$
and
![]() $\unicode[STIX]{x0394}z^{+}$
are all constants in different cases with the same
$\unicode[STIX]{x0394}z^{+}$
are all constants in different cases with the same
![]() $Re_{\unicode[STIX]{x1D70F}}$
. The details of the numerical scheme are given in § 2.3.
$Re_{\unicode[STIX]{x1D70F}}$
. The details of the numerical scheme are given in § 2.3.
Simulation cases 1–3 are conducted to study the effect of the Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}$
. The value of
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}h/\unicode[STIX]{x1D708}$
. The value of
![]() $Re_{\unicode[STIX]{x1D70F}}$
is
$Re_{\unicode[STIX]{x1D70F}}$
is
![]() $1000$
,
$1000$
,
![]() $700$
and
$700$
and
![]() $395$
in cases 1, 2 and 3, respectively. The dimensionless parameters
$395$
in cases 1, 2 and 3, respectively. The dimensionless parameters
![]() $La_{t}=0.7$
and
$La_{t}=0.7$
and
![]() $kh=0.5$
are chosen to match the typical field condition in the observation of Gargett & Wells (Reference Gargett and Wells2007). Cases 3S and 3L are performed to examine the influence of the computational domain size on the simulation results. The values of
$kh=0.5$
are chosen to match the typical field condition in the observation of Gargett & Wells (Reference Gargett and Wells2007). Cases 3S and 3L are performed to examine the influence of the computational domain size on the simulation results. The values of
![]() $Re_{\unicode[STIX]{x1D70F}}$
,
$Re_{\unicode[STIX]{x1D70F}}$
,
![]() $La_{t}$
and
$La_{t}$
and
![]() $kh$
in cases 3S and 3L are the same as those in case 3. The computational domain sizes of cases 3S and 3L are respectively one-half and four times that of case 3 in both the
$kh$
in cases 3S and 3L are the same as those in case 3. The computational domain sizes of cases 3S and 3L are respectively one-half and four times that of case 3 in both the
![]() $x$
- and
$x$
- and
![]() $z$
-directions. It is shown in § 2.4 that the computation domain size of case
$z$
-directions. It is shown in § 2.4 that the computation domain size of case
![]() $3$
,
$3$
,
![]() $L_{x}\times L_{z}=8\unicode[STIX]{x03C0}h\times 16\unicode[STIX]{x03C0}h/3$
, is sufficiently large to obtain accurate simulation results. As a result, the computational domain size of the other cases is set to that of case 3. Cases 1 and 4–6 are performed to investigate the effect of
$L_{x}\times L_{z}=8\unicode[STIX]{x03C0}h\times 16\unicode[STIX]{x03C0}h/3$
, is sufficiently large to obtain accurate simulation results. As a result, the computational domain size of the other cases is set to that of case 3. Cases 1 and 4–6 are performed to investigate the effect of
![]() $kh$
. In these cases, the value of
$kh$
. In these cases, the value of
![]() $kh$
varies from
$kh$
varies from
![]() $0.5$
to
$0.5$
to
![]() $2.0$
with the corresponding wavelength-to-depth ratio
$2.0$
with the corresponding wavelength-to-depth ratio
![]() $\unicode[STIX]{x1D706}/H$
varying from
$\unicode[STIX]{x1D706}/H$
varying from
![]() $2\unicode[STIX]{x03C0}$
to
$2\unicode[STIX]{x03C0}$
to
![]() $\unicode[STIX]{x03C0}/2$
, while
$\unicode[STIX]{x03C0}/2$
, while
![]() $Re_{\unicode[STIX]{x1D70F}}$
and
$Re_{\unicode[STIX]{x1D70F}}$
and
![]() $La_{t}$
are fixed at
$La_{t}$
are fixed at
![]() $1000$
and
$1000$
and
![]() $0.7$
, respectively. The effect of
$0.7$
, respectively. The effect of
![]() $La_{t}$
is studied through cases 1, 7 and 8. The value of
$La_{t}$
is studied through cases 1, 7 and 8. The value of
![]() $La_{t}$
is
$La_{t}$
is
![]() $0.4$
,
$0.4$
,
![]() $0.7$
and
$0.7$
and
![]() $0.9$
in cases 7, 1 and 8, respectively. Case 9 is the pure shear-driven turbulence case, which is used as a reference case to reveal the influence of LCs on turbulence statistics.
$0.9$
in cases 7, 1 and 8, respectively. Case 9 is the pure shear-driven turbulence case, which is used as a reference case to reveal the influence of LCs on turbulence statistics.
The grid is evenly distributed in the
![]() $x$
- and
$x$
- and
![]() $z$
-directions. In the
$z$
-directions. In the
![]() $y$
-direction, the grid lines are located at
$y$
-direction, the grid lines are located at
![]() $y_{j}/h=b^{-1}\tanh [(-1+2j/N_{y})\tanh ^{-1}(b)]+1$
for
$y_{j}/h=b^{-1}\tanh [(-1+2j/N_{y})\tanh ^{-1}(b)]+1$
for
![]() $j=0,1,\ldots ,N_{y}$
with
$j=0,1,\ldots ,N_{y}$
with
![]() $b=0.973$
, such that the grid is clustered near the water surface and water bottom. As shown in table 1, the minimum vertical grid resolution
$b=0.973$
, such that the grid is clustered near the water surface and water bottom. As shown in table 1, the minimum vertical grid resolution
![]() $\unicode[STIX]{x0394}y_{min}^{+}$
near the top and bottom is smaller than
$\unicode[STIX]{x0394}y_{min}^{+}$
near the top and bottom is smaller than
![]() $1.0$
, satisfying the grid resolution of wall-resolved LES. The grid resolution in the
$1.0$
, satisfying the grid resolution of wall-resolved LES. The grid resolution in the
![]() $x$
- and
$x$
- and
![]() $z$
-directions also satisfies the standard of wall-resolved LES, i.e.
$z$
-directions also satisfies the standard of wall-resolved LES, i.e.
![]() $\unicode[STIX]{x0394}x^{+}\simeq 50$
and
$\unicode[STIX]{x0394}x^{+}\simeq 50$
and
![]() $\unicode[STIX]{x0394}z^{+}\simeq 30$
(Chapman Reference Chapman1979; Choi & Moin Reference Choi and Moin2012). We have re-run case 1 by doubling the number of grid points in the
$\unicode[STIX]{x0394}z^{+}\simeq 30$
(Chapman Reference Chapman1979; Choi & Moin Reference Choi and Moin2012). We have re-run case 1 by doubling the number of grid points in the
![]() $x$
- and
$x$
- and
![]() $z$
-directions to examine the effect of grid resolution on the simulation results. It is found that the mean velocity and Reynolds stresses change by less than
$z$
-directions to examine the effect of grid resolution on the simulation results. It is found that the mean velocity and Reynolds stresses change by less than
![]() $2\,\%$
and
$2\,\%$
and
![]() $4\,\%$
, respectively.
$4\,\%$
, respectively.
2.3 Numerical method
In our simulations, the fractional-step projection method (Kim & Moin Reference Kim and Moin1985) is employed to solve (2.1) and (2.2). The second-order explicit Adams–Bashforth scheme and second-order implicit Crank–Nicolson scheme are used for the time integrations of the convective and viscous terms in the C–L equations, respectively. In the
![]() $x$
- and
$x$
- and
![]() $z$
-directions, the Fourier–Galerkin method is utilized for the spatial discretization. The
$z$
-directions, the Fourier–Galerkin method is utilized for the spatial discretization. The
![]() $3/2$
rule is employed to remove the aliasing error. In the vertical direction, the second-order finite-difference method is used to discretize the flow field. The vertical velocity component
$3/2$
rule is employed to remove the aliasing error. In the vertical direction, the second-order finite-difference method is used to discretize the flow field. The vertical velocity component
![]() $\overline{v}$
is defined at grid points, while horizontal velocity components
$\overline{v}$
is defined at grid points, while horizontal velocity components
![]() $\overline{u}$
,
$\overline{u}$
,
![]() $\overline{w}$
, and pressure
$\overline{w}$
, and pressure
![]() $\overline{\unicode[STIX]{x1D6F1}}$
are defined at the centres of grid lines.
$\overline{\unicode[STIX]{x1D6F1}}$
are defined at the centres of grid lines.
The SGS stress
![]() $\unicode[STIX]{x1D70F}_{ij}^{sgs}$
is calculated using the dynamic Smagorinsky model (Germano et al.
Reference Germano, Piomelli, Moin and Cabot1991; Lilly Reference Lilly1992). Hereinafter, the subscript
$\unicode[STIX]{x1D70F}_{ij}^{sgs}$
is calculated using the dynamic Smagorinsky model (Germano et al.
Reference Germano, Piomelli, Moin and Cabot1991; Lilly Reference Lilly1992). Hereinafter, the subscript
![]() $i$
(or
$i$
(or
![]() $j$
)
$j$
)
![]() $=$
1, 2 and 3 represents the component in the streamwise, vertical and spanwise directions, respectively. The SGS stress
$=$
1, 2 and 3 represents the component in the streamwise, vertical and spanwise directions, respectively. The SGS stress
![]() $\unicode[STIX]{x1D70F}_{ij}^{sgs}$
is calculated as
$\unicode[STIX]{x1D70F}_{ij}^{sgs}$
is calculated as
where the dilatational part of the SGS stress
![]() $\unicode[STIX]{x1D70F}_{kk}^{sgs}\unicode[STIX]{x1D6FF}_{ij}/3$
is absorbed into the modified pressure
$\unicode[STIX]{x1D70F}_{kk}^{sgs}\unicode[STIX]{x1D6FF}_{ij}/3$
is absorbed into the modified pressure
![]() $\bar{\unicode[STIX]{x1D6F1}}$
,
$\bar{\unicode[STIX]{x1D6F1}}$
,
![]() $C_{s}$
is the model coefficient,
$C_{s}$
is the model coefficient,
![]() $\overline{\unicode[STIX]{x1D6E5}}=(\unicode[STIX]{x0394}x\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)^{1/3}$
is the width of the grid-level filter,
$\overline{\unicode[STIX]{x1D6E5}}=(\unicode[STIX]{x0394}x\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)^{1/3}$
is the width of the grid-level filter,
![]() $\overline{\unicode[STIX]{x1D61A}}_{ij}=(\unicode[STIX]{x2202}\overline{u}_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}\overline{u}_{j}/\unicode[STIX]{x2202}x_{i})/2$
is the resolved strain-rate tensor and
$\overline{\unicode[STIX]{x1D61A}}_{ij}=(\unicode[STIX]{x2202}\overline{u}_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}\overline{u}_{j}/\unicode[STIX]{x2202}x_{i})/2$
is the resolved strain-rate tensor and
![]() $|\overline{S}|=(2\overline{\unicode[STIX]{x1D61A}}_{ij}\overline{\unicode[STIX]{x1D61A}}_{ij})^{1/2}$
is the norm of
$|\overline{S}|=(2\overline{\unicode[STIX]{x1D61A}}_{ij}\overline{\unicode[STIX]{x1D61A}}_{ij})^{1/2}$
is the norm of
![]() $\bar{\unicode[STIX]{x1D61A}}_{ij}$
. The model coefficient
$\bar{\unicode[STIX]{x1D61A}}_{ij}$
. The model coefficient
![]() $C_{s}$
is determined using a dynamic procedure as
$C_{s}$
is determined using a dynamic procedure as
where
and
Here,
![]() $\langle \rangle _{xz}$
denotes the averaging in the
$\langle \rangle _{xz}$
denotes the averaging in the
![]() $x$
- and
$x$
- and
![]() $z$
-directions, the tilde stands for a test-grid-level filter, and
$z$
-directions, the tilde stands for a test-grid-level filter, and
![]() $\widetilde{\unicode[STIX]{x1D6E5}}$
is the size of the test-grid-level filter.
$\widetilde{\unicode[STIX]{x1D6E5}}$
is the size of the test-grid-level filter.

Figure 2. Profiles of (a) the mean streamwise velocity
![]() $\langle u\rangle ^{+}$
and (b) Reynolds normal stresses in case 3S and comparison with the result of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007).
$\langle u\rangle ^{+}$
and (b) Reynolds normal stresses in case 3S and comparison with the result of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007).
To validate the code, we compare the results in case 3S with those in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). The computational domain size,
![]() $La_{t}$
, and
$La_{t}$
, and
![]() $Re_{\unicode[STIX]{x1D70F}}$
in case 3S are the same as those in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007), while the value of
$Re_{\unicode[STIX]{x1D70F}}$
in case 3S are the same as those in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007), while the value of
![]() $kh$
in case 3S (0.5) is close to that (0.52) in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). Figure 2 compares the profiles of the mean streamwise velocity
$kh$
in case 3S (0.5) is close to that (0.52) in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). Figure 2 compares the profiles of the mean streamwise velocity
![]() $\langle u\rangle ^{+}$
and Reynolds normal stresses
$\langle u\rangle ^{+}$
and Reynolds normal stresses
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
and
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
and
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
in case 3S with those in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) to validate the numerical algorithms. Here, the angular brackets
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
in case 3S with those in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) to validate the numerical algorithms. Here, the angular brackets
![]() $\langle ~\rangle$
represent the temporal and spatial averaging over a time duration of
$\langle ~\rangle$
represent the temporal and spatial averaging over a time duration of
![]() $t=120h/u_{\unicode[STIX]{x1D70F}}$
in
$t=120h/u_{\unicode[STIX]{x1D70F}}$
in
![]() $x$
–
$x$
–
![]() $z$
planes. The prime denotes fluctuations. For the convenience of presenting the results, the overline is omitted hereinafter. Figures 2(a) and 2(b) show that the results of case 3S are close to those of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). In the equilibrium shallow-water Langmuir turbulence, the viscous shear stress
$z$
planes. The prime denotes fluctuations. For the convenience of presenting the results, the overline is omitted hereinafter. Figures 2(a) and 2(b) show that the results of case 3S are close to those of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). In the equilibrium shallow-water Langmuir turbulence, the viscous shear stress
![]() $\text{d}\langle u\rangle ^{+}/\text{d}y^{+}$
, resolved Reynolds shear stress
$\text{d}\langle u\rangle ^{+}/\text{d}y^{+}$
, resolved Reynolds shear stress
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
and the SGS shear stress
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
and the SGS shear stress
![]() $\langle \unicode[STIX]{x1D70F}_{12}^{sgs}\rangle ^{+}$
satisfy (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007)
$\langle \unicode[STIX]{x1D70F}_{12}^{sgs}\rangle ^{+}$
satisfy (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007)
Figure 3 shows different terms in (2.9) in Langmuir turbulence (case 3S) and shear-driven turbulence (case 1). As shown, the viscous stress is important near the water bottom, while the resolved Reynolds shear stress is dominant away from the bottom of the water. The SGS shear stress is significantly smaller than the resolved Reynolds shear stress. The value of the total shear stress obtained from our LES is
![]() $1.0$
throughout the water column, indicating that the simulation reaches a statistically equilibrium state and the time duration used for performing time averaging is sufficiently long.
$1.0$
throughout the water column, indicating that the simulation reaches a statistically equilibrium state and the time duration used for performing time averaging is sufficiently long.
2.4 Effect of computational domain size
Figure 4 compares the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
,
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
,
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
and
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
and
![]() $\langle u^{\prime }v^{\prime }\rangle ^{+}$
among cases 3S, 3 and 3L to examine the effect of computational domain size on the Reynolds stresses. As shown, the profiles of
$\langle u^{\prime }v^{\prime }\rangle ^{+}$
among cases 3S, 3 and 3L to examine the effect of computational domain size on the Reynolds stresses. As shown, the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
,
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
,
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
and
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
and
![]() $\langle u^{\prime }v^{\prime }\rangle ^{+}$
in case 3 collapse with those in case 3L, indicating that the computational domain size of case 3 is adequate to obtain domain-size-independent results of Reynolds stresses. The domain size of case 3S, on the other hand, is inadequate as evident by the difference in the profiles of
$\langle u^{\prime }v^{\prime }\rangle ^{+}$
in case 3 collapse with those in case 3L, indicating that the computational domain size of case 3 is adequate to obtain domain-size-independent results of Reynolds stresses. The domain size of case 3S, on the other hand, is inadequate as evident by the difference in the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
and
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
and
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
of case 3S from those of cases 3 and 3L (figure 4
a–c).
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
of case 3S from those of cases 3 and 3L (figure 4
a–c).

Figure 3. Profiles of shear stresses in (a) case 3S and (b) case
![]() $1$
.
$1$
.

Figure 4. Profiles of (a)
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
, (b)
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
, (b)
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
, (c)
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
, (c)
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
and (d)
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
and (d)
![]() $\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases 3S, 3 and 3L with different domain sizes.
$\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases 3S, 3 and 3L with different domain sizes.

Figure 5. Contours of
![]() $\langle u^{L}\rangle _{t}^{+}$
and vectors consisting of
$\langle u^{L}\rangle _{t}^{+}$
and vectors consisting of
![]() $(\langle w^{L}\rangle _{t}^{+},\langle v^{L}\rangle _{t}^{+})$
in (a) case
$(\langle w^{L}\rangle _{t}^{+},\langle v^{L}\rangle _{t}^{+})$
in (a) case
![]() $3$
and (b) case
$3$
and (b) case
![]() $3$
L with different domain sizes.
$3$
L with different domain sizes.
We have also examined the effect of computational domain size on the scales and intensities of LCs. The LC quantities are extracted using a triple decomposition, viz.
Because the LCs are elongated along the wind direction (Gargett et al.
Reference Gargett, Wells, Tejada-Martínez and Grosch2004; Gargett & Wells Reference Gargett and Wells2007), the LC-coherent velocity
![]() $\boldsymbol{u}^{L}$
is defined as the streamwise averaging of
$\boldsymbol{u}^{L}$
is defined as the streamwise averaging of
![]() $\boldsymbol{u}^{\prime }$
. The residual turbulence fluctuations are denoted as
$\boldsymbol{u}^{\prime }$
. The residual turbulence fluctuations are denoted as
![]() $\boldsymbol{u}^{T}$
. The summation of
$\boldsymbol{u}^{T}$
. The summation of
![]() $\boldsymbol{u}^{L}$
and
$\boldsymbol{u}^{L}$
and
![]() $\boldsymbol{u}^{T}$
gives the total fluctuation
$\boldsymbol{u}^{T}$
gives the total fluctuation
![]() $\boldsymbol{u}^{\prime }$
. The same triple decomposition method was used by Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007), Kukulka et al. (Reference Kukulka, Plueddemann and Sullivan2012) and Tejada-Martínez et al. (Reference Tejada-Martínez, Akan, Sinha, Grosch and Martinat2013) in shallow-water Langmuir turbulence.
$\boldsymbol{u}^{\prime }$
. The same triple decomposition method was used by Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007), Kukulka et al. (Reference Kukulka, Plueddemann and Sullivan2012) and Tejada-Martínez et al. (Reference Tejada-Martínez, Akan, Sinha, Grosch and Martinat2013) in shallow-water Langmuir turbulence.
Figure 5 compares the LCs obtained from cases
![]() $3$
and
$3$
and
![]() $3$
L. The LCs are visualized using the vectors consisting of
$3$
L. The LCs are visualized using the vectors consisting of
![]() $(\langle w^{L}\rangle _{t}^{+},\langle v^{L}\rangle _{t}^{+})$
and the contours of
$(\langle w^{L}\rangle _{t}^{+},\langle v^{L}\rangle _{t}^{+})$
and the contours of
![]() $\langle u^{L}\rangle _{t}^{+}$
in an
$\langle u^{L}\rangle _{t}^{+}$
in an
![]() $z$
–
$z$
–
![]() $y$
plane, where
$y$
plane, where
![]() $\langle ~\rangle _{t}$
represents the time averaging over
$\langle ~\rangle _{t}$
represents the time averaging over
![]() $120h/u_{\unicode[STIX]{x1D70F}}$
. As highlighted by the red dashed boxes in figure 5(a,b), the positive
$120h/u_{\unicode[STIX]{x1D70F}}$
. As highlighted by the red dashed boxes in figure 5(a,b), the positive
![]() $u^{L}$
forms a mushroom-shaped region (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007), and each mushroom is accompanied by a pair of counter-rotating streamwise vortices, consistent with the observation of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). As pointed out by Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015), the magnitude of the time- and streamwise-averaged velocity is larger in the downwelling limbs than in the upwelling limbs, because
$u^{L}$
forms a mushroom-shaped region (Tejada-Martínez & Grosch Reference Tejada-Martínez and Grosch2007), and each mushroom is accompanied by a pair of counter-rotating streamwise vortices, consistent with the observation of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). As pointed out by Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015), the magnitude of the time- and streamwise-averaged velocity is larger in the downwelling limbs than in the upwelling limbs, because
![]() $u^{L}$
is positive and negative in the downwelling and upwelling limbs, respectively (figure 5). Furthermore, in the region away from the bottom, the decrease in the amplitude of
$u^{L}$
is positive and negative in the downwelling and upwelling limbs, respectively (figure 5). Furthermore, in the region away from the bottom, the decrease in the amplitude of
![]() $u^{L}$
with
$u^{L}$
with
![]() $y/h$
(figure 5) results in a negative and positive vertical gradient of
$y/h$
(figure 5) results in a negative and positive vertical gradient of
![]() $u^{L}$
in the downwelling and upwelling limbs, such that the velocity gradient in the upwelling limbs is relatively small in comparison with that in the downwelling limbs. Two and eight pairs of counter-rotating vortices are observed in cases
$u^{L}$
in the downwelling and upwelling limbs, such that the velocity gradient in the upwelling limbs is relatively small in comparison with that in the downwelling limbs. Two and eight pairs of counter-rotating vortices are observed in cases
![]() $3$
and
$3$
and
![]() $3$
L, respectively. The spanwise length scale of LCs obtained from the present LES is
$3$
L, respectively. The spanwise length scale of LCs obtained from the present LES is
![]() $8\unicode[STIX]{x03C0}h/3$
, agreeing with that in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). The spanwise domain size in the present study follows Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007), who set the spanwise domain size to
$8\unicode[STIX]{x03C0}h/3$
, agreeing with that in Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007). The spanwise domain size in the present study follows Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007), who set the spanwise domain size to
![]() $8\unicode[STIX]{x03C0}h/3$
, which approximates the spanwise length scale of LCs in the field measurements by Gargett et al. (Reference Gargett, Wells, Tejada-Martínez and Grosch2004) and Gargett & Wells (Reference Gargett and Wells2007). According to Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012), no Langmuir circulation is observed if the spanwise domain size is set to
$8\unicode[STIX]{x03C0}h/3$
, which approximates the spanwise length scale of LCs in the field measurements by Gargett et al. (Reference Gargett, Wells, Tejada-Martínez and Grosch2004) and Gargett & Wells (Reference Gargett and Wells2007). According to Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012), no Langmuir circulation is observed if the spanwise domain size is set to
![]() $12\unicode[STIX]{x03C0}h/3$
.
$12\unicode[STIX]{x03C0}h/3$
.

Figure 6. Profiles of (a)
![]() $\langle u^{L}u^{L}\rangle ^{+}$
, (b)
$\langle u^{L}u^{L}\rangle ^{+}$
, (b)
![]() $\langle v^{L}v^{L}\rangle ^{+}$
, (c)
$\langle v^{L}v^{L}\rangle ^{+}$
, (c)
![]() $\langle w^{L}w^{L}\rangle ^{+}$
and (d)
$\langle w^{L}w^{L}\rangle ^{+}$
and (d)
![]() $\langle u^{L}v^{L}\rangle ^{+}$
in cases
$\langle u^{L}v^{L}\rangle ^{+}$
in cases
![]() $3$
and
$3$
and
![]() $3$
L with different domain sizes.
$3$
L with different domain sizes.
The Reynolds stress can be further decomposed into the LC-coherent part and residual turbulence part as
The cross-term
![]() $\langle u_{i}^{L}u_{j}^{T}\rangle$
is zero (Akan et al.
Reference Akan, Tejada-Martínez, Grosch and Martinat2013; Martinat et al.
Reference Martinat, Grosch and Gatski2014), because
$\langle u_{i}^{L}u_{j}^{T}\rangle$
is zero (Akan et al.
Reference Akan, Tejada-Martínez, Grosch and Martinat2013; Martinat et al.
Reference Martinat, Grosch and Gatski2014), because
![]() $u_{i}^{L}$
are streamwise averaged and the streamwise-averaged value of
$u_{i}^{L}$
are streamwise averaged and the streamwise-averaged value of
![]() $u_{j}^{T}$
is zero. To further examine the domain-size effect on the intensity of LCs, we compare the profiles of LC-induced Reynolds stresses
$u_{j}^{T}$
is zero. To further examine the domain-size effect on the intensity of LCs, we compare the profiles of LC-induced Reynolds stresses
![]() $\langle u^{L}u^{L}\rangle ^{+}$
,
$\langle u^{L}u^{L}\rangle ^{+}$
,
![]() $\langle v^{L}v^{L}\rangle ^{+}$
,
$\langle v^{L}v^{L}\rangle ^{+}$
,
![]() $\langle w^{L}w^{L}\rangle ^{+}$
and
$\langle w^{L}w^{L}\rangle ^{+}$
and
![]() $\langle u^{L}v^{L}\rangle ^{+}$
between cases
$\langle u^{L}v^{L}\rangle ^{+}$
between cases
![]() $3$
and
$3$
and
![]() $3$
L in figure 6. As shown, the profiles in case
$3$
L in figure 6. As shown, the profiles in case
![]() $3$
agree with those in case
$3$
agree with those in case
![]() $3$
L. The results shown in figures 4–6 indicate that the computational domain size of
$3$
L. The results shown in figures 4–6 indicate that the computational domain size of
![]() $L_{x}\times L_{z}=8\unicode[STIX]{x03C0}h\times 16\unicode[STIX]{x03C0}h/3$
is sufficiently large for capturing LCs.
$L_{x}\times L_{z}=8\unicode[STIX]{x03C0}h\times 16\unicode[STIX]{x03C0}h/3$
is sufficiently large for capturing LCs.
3 Mean velocity
It was reported in Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) that the logarithmic layer over the bottom boundary is disrupted in the shallow-water Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
and
$Re_{\unicode[STIX]{x1D70F}}=395$
and
![]() $590$
with
$590$
with
![]() $La_{t}=0.7$
and
$La_{t}=0.7$
and
![]() $kh=0.5$
. In this paper, we start our analysis from the examination of the logarithmic law of the mean velocity at higher Reynolds numbers. In the logarithmic layer, the mean velocity satisfies (Millikan Reference Millikan1938; Rotta Reference Rotta1962; Townsend Reference Townsend1976)
$kh=0.5$
. In this paper, we start our analysis from the examination of the logarithmic law of the mean velocity at higher Reynolds numbers. In the logarithmic layer, the mean velocity satisfies (Millikan Reference Millikan1938; Rotta Reference Rotta1962; Townsend Reference Townsend1976)
where
![]() $\unicode[STIX]{x1D705}$
is the von Kármán constant, and
$\unicode[STIX]{x1D705}$
is the von Kármán constant, and
![]() $B$
is the intercept. The logarithmic law can be quantitatively identified by the diagnostic function
$B$
is the intercept. The logarithmic law can be quantitatively identified by the diagnostic function
The value of
![]() $F$
is a constant
$F$
is a constant
![]() $1/\unicode[STIX]{x1D705}$
if the logarithmic law (3.1) holds. However, at a finite Reynolds number, the value of
$1/\unicode[STIX]{x1D705}$
if the logarithmic law (3.1) holds. However, at a finite Reynolds number, the value of
![]() $F$
is not strictly identical to
$F$
is not strictly identical to
![]() $1/\unicode[STIX]{x1D705}$
, but increases slightly with
$1/\unicode[STIX]{x1D705}$
, but increases slightly with
![]() $y^{+}$
in a quasi-plateau region (Moser, Kim & Mansour Reference Moser, Kim and Mansour1999; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). This is because the logarithmic law is only the first-order truncation of the asymptotic expansion of the mean velocity with respect to
$y^{+}$
in a quasi-plateau region (Moser, Kim & Mansour Reference Moser, Kim and Mansour1999; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). This is because the logarithmic law is only the first-order truncation of the asymptotic expansion of the mean velocity with respect to
![]() $1/Re_{\unicode[STIX]{x1D70F}}$
(Afzal & Yajnik Reference Afzal and Yajnik1973; Zagarola, Perry & Smits Reference Zagarola, Perry and Smits1997; Jiménez & Moser Reference Jiménez and Moser2007; Mizuno & Jiménez Reference Mizuno and Jiménez2011).
$1/Re_{\unicode[STIX]{x1D70F}}$
(Afzal & Yajnik Reference Afzal and Yajnik1973; Zagarola, Perry & Smits Reference Zagarola, Perry and Smits1997; Jiménez & Moser Reference Jiménez and Moser2007; Mizuno & Jiménez Reference Mizuno and Jiménez2011).

Figure 7. Effect of Reynolds number on (a)
![]() $\langle u\rangle ^{+}$
and (b)
$\langle u\rangle ^{+}$
and (b)
![]() $F$
in the bottom half of the shallow-water Langmuir turbulence in cases
$F$
in the bottom half of the shallow-water Langmuir turbulence in cases
![]() $1$
–
$1$
–
![]() $3$
with
$3$
with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively. The logarithmic law in (a) is
$395$
, respectively. The logarithmic law in (a) is
![]() $\langle u\rangle ^{+}=\log (y^{+})/0.36+3.2$
. The open circles represent the results of case 9 (the shear-driven turbulence at
$\langle u\rangle ^{+}=\log (y^{+})/0.36+3.2$
. The open circles represent the results of case 9 (the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
).
$Re_{\unicode[STIX]{x1D70F}}=1000$
).
Figure 7 compares the profiles of
![]() $\langle u\rangle ^{+}$
and
$\langle u\rangle ^{+}$
and
![]() $F$
among cases 1, 2 and 3, with
$F$
among cases 1, 2 and 3, with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively. The results of case
$395$
, respectively. The results of case
![]() $9$
for the shear-driven turbulence at
$9$
for the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
are superimposed as a reference. As shown in figure 7(a), the profile of
$Re_{\unicode[STIX]{x1D70F}}=1000$
are superimposed as a reference. As shown in figure 7(a), the profile of
![]() $\langle u\rangle ^{+}$
at
$\langle u\rangle ^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
deviates from the logarithmic law, consistent with the results of Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012). However, the profile of
$Re_{\unicode[STIX]{x1D70F}}=395$
deviates from the logarithmic law, consistent with the results of Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012). However, the profile of
![]() $\langle u\rangle ^{+}$
approaches the logarithmic law progressively as the Reynolds number increases. This observation from figure 7(a) is further confirmed by the diagnostic function
$\langle u\rangle ^{+}$
approaches the logarithmic law progressively as the Reynolds number increases. This observation from figure 7(a) is further confirmed by the diagnostic function
![]() $F$
. Figure 7(b) shows that although the profile of
$F$
. Figure 7(b) shows that although the profile of
![]() $F$
in Langmuir turbulence deviates from that in shear-driven turbulence above
$F$
in Langmuir turbulence deviates from that in shear-driven turbulence above
![]() $y^{+}=100$
, the profile of
$y^{+}=100$
, the profile of
![]() $F$
below
$F$
below
![]() $y^{+}=100$
approaches that of shear-driven turbulence progressively as the Reynolds number increases. Particularly, at
$y^{+}=100$
approaches that of shear-driven turbulence progressively as the Reynolds number increases. Particularly, at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, the profiles of
$Re_{\unicode[STIX]{x1D70F}}=1000$
, the profiles of
![]() $F$
in the Langmuir turbulence and shear-driven turbulence are close to each other below
$F$
in the Langmuir turbulence and shear-driven turbulence are close to each other below
![]() $y^{+}=100$
, indicating a weak influence of LCs on the mean velocity in the near-bottom region. A plateau region can be observed in the profile of
$y^{+}=100$
, indicating a weak influence of LCs on the mean velocity in the near-bottom region. A plateau region can be observed in the profile of
![]() $F$
in the Langmuir turbulence at
$F$
in the Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, an indicator of the presence of logarithmic layer. The value of
$Re_{\unicode[STIX]{x1D70F}}=1000$
, an indicator of the presence of logarithmic layer. The value of
![]() $F$
in the plateau region is approximately
$F$
in the plateau region is approximately
![]() $2.77$
, and correspondingly, the value of the von Kármán constant is
$2.77$
, and correspondingly, the value of the von Kármán constant is
![]() $\unicode[STIX]{x1D705}=0.36$
. Note that
$\unicode[STIX]{x1D705}=0.36$
. Note that
![]() $\unicode[STIX]{x1D705}$
is not necessarily the conventional value of
$\unicode[STIX]{x1D705}$
is not necessarily the conventional value of
![]() $0.41$
. It also deviates from
$0.41$
. It also deviates from
![]() $0.41$
in canonical wall-bounded turbulence at finite Reynolds number (Nagib & Chauhan Reference Nagib and Chauhan2008; Klewicki, Fife & Wei Reference Klewicki, Fife and Wei2009; Mizuno & Jiménez Reference Mizuno and Jiménez2011; Jiménez Reference Jiménez2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smiths2013; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Lee & Moser Reference Lee and Moser2015). The conventional value
$0.41$
in canonical wall-bounded turbulence at finite Reynolds number (Nagib & Chauhan Reference Nagib and Chauhan2008; Klewicki, Fife & Wei Reference Klewicki, Fife and Wei2009; Mizuno & Jiménez Reference Mizuno and Jiménez2011; Jiménez Reference Jiménez2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smiths2013; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Lee & Moser Reference Lee and Moser2015). The conventional value
![]() $\unicode[STIX]{x1D705}=0.41$
is the asymptotic value as the Reynolds number approaches infinity (Jiménez & Moser Reference Jiménez and Moser2007; Mizuno & Jiménez Reference Mizuno and Jiménez2011). The presence of the logarithmic layer at
$\unicode[STIX]{x1D705}=0.41$
is the asymptotic value as the Reynolds number approaches infinity (Jiménez & Moser Reference Jiménez and Moser2007; Mizuno & Jiménez Reference Mizuno and Jiménez2011). The presence of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
indicates that the wall-layer model based on the logarithmic law is still appropriate in the shallow-water Langmuir turbulence at high Reynolds number. Because the logarithmic layer in Langmuir turbulence is thinner than that in shear-driven turbulence (figure 7
b), care must be taken to ensure that the first grid is located in the logarithmic layer when the wall-layer model is used. The reappearance of the logarithmic layer at
$Re_{\unicode[STIX]{x1D70F}}=1000$
indicates that the wall-layer model based on the logarithmic law is still appropriate in the shallow-water Langmuir turbulence at high Reynolds number. Because the logarithmic layer in Langmuir turbulence is thinner than that in shear-driven turbulence (figure 7
b), care must be taken to ensure that the first grid is located in the logarithmic layer when the wall-layer model is used. The reappearance of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
is further explained in § 4.2, based on the analysis of Reynolds shear stress, an indicator of the transport of mean momentum in the vertical direction.
$Re_{\unicode[STIX]{x1D70F}}=1000$
is further explained in § 4.2, based on the analysis of Reynolds shear stress, an indicator of the transport of mean momentum in the vertical direction.

Figure 8. Effect of
![]() $kh$
on (a)
$kh$
on (a)
![]() $\langle u\rangle ^{+}$
and (b) its diagnostic function
$\langle u\rangle ^{+}$
and (b) its diagnostic function
![]() $F$
in the bottom half of the shallow-water Langmuir turbulence in cases
$F$
in the bottom half of the shallow-water Langmuir turbulence in cases
![]() $1$
and
$1$
and
![]() $4$
–
$4$
–
![]() $6$
with
$6$
with
![]() $kh=0.5$
,
$kh=0.5$
,
![]() $1$
,
$1$
,
![]() $1.5$
and
$1.5$
and
![]() $2$
, respectively. The open circles represent the results in case 9 (the shear-driven turbulence at
$2$
, respectively. The open circles represent the results in case 9 (the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
).
$Re_{\unicode[STIX]{x1D70F}}=1000$
).

Figure 9. Effect of
![]() $La_{t}$
on (a)
$La_{t}$
on (a)
![]() $\langle u\rangle ^{+}$
and (b) its diagnostic function
$\langle u\rangle ^{+}$
and (b) its diagnostic function
![]() $F$
in the bottom half of the flow in cases
$F$
in the bottom half of the flow in cases
![]() $1$
,
$1$
,
![]() $7$
and
$7$
and
![]() $8$
with
$8$
with
![]() $La_{t}=0.7$
,
$La_{t}=0.7$
,
![]() $0.4$
and
$0.4$
and
![]() $0.9$
, respectively. The open circles represent the results in case 9 (the shear-driven turbulence at
$0.9$
, respectively. The open circles represent the results in case 9 (the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
).
$Re_{\unicode[STIX]{x1D70F}}=1000$
).
Figures 8 and 9 show respectively the effects of the dimensionless parameters
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the profiles of
$La_{t}$
on the profiles of
![]() $\langle u\rangle ^{+}$
and
$\langle u\rangle ^{+}$
and
![]() $F$
. The results in cases 1 and 4–6 with various values of
$F$
. The results in cases 1 and 4–6 with various values of
![]() $kh$
are shown in figure 8, while those of cases 1, 7 and 8 with various values of
$kh$
are shown in figure 8, while those of cases 1, 7 and 8 with various values of
![]() $La_{t}$
are shown in figure 9 (see table 1 for the parameters). The results of case 9 for shear-driven turbulence are superimposed in figures 8 and 9 for comparison. As pointed out above, at
$La_{t}$
are shown in figure 9 (see table 1 for the parameters). The results of case 9 for shear-driven turbulence are superimposed in figures 8 and 9 for comparison. As pointed out above, at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, the LCs do not significantly influence the mean velocity in the near-bottom region (figure 7). As a result, below
$Re_{\unicode[STIX]{x1D70F}}=1000$
, the LCs do not significantly influence the mean velocity in the near-bottom region (figure 7). As a result, below
![]() $y^{+}=80$
, both the profiles of
$y^{+}=80$
, both the profiles of
![]() $\langle u\rangle ^{+}$
and those of
$\langle u\rangle ^{+}$
and those of
![]() $F$
in cases 1 and 4–8 for Langmuir turbulence with various values of
$F$
in cases 1 and 4–8 for Langmuir turbulence with various values of
![]() $kh$
and
$kh$
and
![]() $La_{t}$
are coincident with those in case 9 for shear-driven turbulence. As the value of either
$La_{t}$
are coincident with those in case 9 for shear-driven turbulence. As the value of either
![]() $kh$
or
$kh$
or
![]() $La_{t}$
increases, the magnitude of the vortex force decreases ((2.2) and (2.4)), resulting in a weaker influence of the vortex force on the mean velocity. Therefore, the profile of
$La_{t}$
increases, the magnitude of the vortex force decreases ((2.2) and (2.4)), resulting in a weaker influence of the vortex force on the mean velocity. Therefore, the profile of
![]() $F$
above
$F$
above
![]() $y^{+}=80$
in Langmuir turbulence approaches that in shear-driven turbulence as the values of
$y^{+}=80$
in Langmuir turbulence approaches that in shear-driven turbulence as the values of
![]() $kh$
and
$kh$
and
![]() $La_{t}$
increase, leading to the thickness increase of the logarithmic layer (figures 8
b and 9
b). The effect of
$La_{t}$
increase, leading to the thickness increase of the logarithmic layer (figures 8
b and 9
b). The effect of
![]() $kh$
on the mean velocity at
$kh$
on the mean velocity at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
obtained from our LES is consistent with the trend observed by Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
$Re_{\unicode[STIX]{x1D70F}}=1000$
obtained from our LES is consistent with the trend observed by Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. According to the analysis above,
$Re_{\unicode[STIX]{x1D70F}}=395$
. According to the analysis above,
![]() $Re_{\unicode[STIX]{x1D70F}}$
,
$Re_{\unicode[STIX]{x1D70F}}$
,
![]() $kh$
and
$kh$
and
![]() $La_{t}$
all influence the thickness of the logarithmic layer in shallow-water Langmuir turbulence. In the future, if more measurement and simulation data are available, it will be interesting to derive an explicit expression of the thickness of the logarithmic layer as a function of these three parameters, which is however, infeasible at this stage due to the limitation in the present computer power and beyond the scope of this study.
$La_{t}$
all influence the thickness of the logarithmic layer in shallow-water Langmuir turbulence. In the future, if more measurement and simulation data are available, it will be interesting to derive an explicit expression of the thickness of the logarithmic layer as a function of these three parameters, which is however, infeasible at this stage due to the limitation in the present computer power and beyond the scope of this study.
Table 2. The von Kármán constant
![]() $\unicode[STIX]{x1D705}$
obtained at
$\unicode[STIX]{x1D705}$
obtained at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
.
$Re_{\unicode[STIX]{x1D70F}}=1000$
.

The von Kármán constant
![]() $\unicode[STIX]{x1D705}$
is an important parameter in the wall-layer modelling of wall turbulence (Cabot & Moin Reference Cabot and Moin2000; Piomelli & Balaras Reference Piomelli and Balaras2002). Table 2 lists the values of
$\unicode[STIX]{x1D705}$
is an important parameter in the wall-layer modelling of wall turbulence (Cabot & Moin Reference Cabot and Moin2000; Piomelli & Balaras Reference Piomelli and Balaras2002). Table 2 lists the values of
![]() $\unicode[STIX]{x1D705}$
in different cases, calculated by fitting the mean velocity in the plateau region of
$\unicode[STIX]{x1D705}$
in different cases, calculated by fitting the mean velocity in the plateau region of
![]() $F$
. Note that because the logarithmic layer is absent in cases 2, 3 and 7, table 2 only gives the value of
$F$
. Note that because the logarithmic layer is absent in cases 2, 3 and 7, table 2 only gives the value of
![]() $\unicode[STIX]{x1D705}$
in cases
$\unicode[STIX]{x1D705}$
in cases
![]() $1$
,
$1$
,
![]() $4$
–
$4$
–
![]() $6$
,
$6$
,
![]() $8$
and
$8$
and
![]() $9$
. In the shear-driven turbulence (case 9), the value of
$9$
. In the shear-driven turbulence (case 9), the value of
![]() $\unicode[STIX]{x1D705}$
is
$\unicode[STIX]{x1D705}$
is
![]() $0.386$
, close to that in canonical wall-bounded turbulence (Nagib & Chauhan Reference Nagib and Chauhan2008; Jiménez Reference Jiménez2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smiths2013; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Lee & Moser Reference Lee and Moser2015). As shown in table 2, the value of
$0.386$
, close to that in canonical wall-bounded turbulence (Nagib & Chauhan Reference Nagib and Chauhan2008; Jiménez Reference Jiménez2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smiths2013; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Lee & Moser Reference Lee and Moser2015). As shown in table 2, the value of
![]() $\unicode[STIX]{x1D705}$
varies in a narrow range with
$\unicode[STIX]{x1D705}$
varies in a narrow range with
![]() $0.362\pm 0.003$
, for the Langmuir turbulence considered in the present work, which is slightly smaller than that in the shear-driven turbulence. It was reported in the literature that the value of
$0.362\pm 0.003$
, for the Langmuir turbulence considered in the present work, which is slightly smaller than that in the shear-driven turbulence. It was reported in the literature that the value of
![]() $\unicode[STIX]{x1D705}$
is influenced by the boundary geometry (Nagib & Chauhan Reference Nagib and Chauhan2008; Marusic et al.
Reference Marusic, Monty, Hultmark and Smiths2013), body forces such as the buoyancy force (Scagliarini et al.
Reference Scagliarini, Einarsson, Gylfason and Toschi2015) and the streamwise mean pressure gradient (Luchini Reference Luchini2017). In the Langmuir turbulence, the small discrepancy in the value of
$\unicode[STIX]{x1D705}$
is influenced by the boundary geometry (Nagib & Chauhan Reference Nagib and Chauhan2008; Marusic et al.
Reference Marusic, Monty, Hultmark and Smiths2013), body forces such as the buoyancy force (Scagliarini et al.
Reference Scagliarini, Einarsson, Gylfason and Toschi2015) and the streamwise mean pressure gradient (Luchini Reference Luchini2017). In the Langmuir turbulence, the small discrepancy in the value of
![]() $\unicode[STIX]{x1D705}$
between the shallow-water Langmuir turbulence and shear-driven turbulence is correlated with the C–L vortex force, which acts as a body force in the C–L equations.
$\unicode[STIX]{x1D705}$
between the shallow-water Langmuir turbulence and shear-driven turbulence is correlated with the C–L vortex force, which acts as a body force in the C–L equations.
4 Structure and statistics of velocity fluctuations
4.1 Instantaneous velocity fluctuations

Figure 10. Instantaneous velocity fluctuations of (a1) (b1)
![]() $u^{\prime }$
, (a2) (b2)
$u^{\prime }$
, (a2) (b2)
![]() $v^{\prime }$
and (a3) (c3)
$v^{\prime }$
and (a3) (c3)
![]() $w^{\prime }$
in a
$w^{\prime }$
in a
![]() $x$
–
$x$
–
![]() $z$
plane at
$z$
plane at
![]() $y/h=0.12$
. (a1), (a2) and (a3) are results for case
$y/h=0.12$
. (a1), (a2) and (a3) are results for case
![]() $1$
(Langmuir turbulence), while (b1), (b2) and (b3) are for case
$1$
(Langmuir turbulence), while (b1), (b2) and (b3) are for case
![]() $9$
(shear-driven turbulence).
$9$
(shear-driven turbulence).
Figure 10 compares the instantaneous velocity fluctuations in an
![]() $x$
–
$x$
–
![]() $z$
plane at
$z$
plane at
![]() $y/h=0.12$
in the Langmuir turbulence (case
$y/h=0.12$
in the Langmuir turbulence (case
![]() $1$
) with those in the shear-driven turbulence (case
$1$
) with those in the shear-driven turbulence (case
![]() $9$
). The contours of
$9$
). The contours of
![]() $u^{\prime }$
in the shear-driven turbulence show large-scale streaks with spanwise length scale
$u^{\prime }$
in the shear-driven turbulence show large-scale streaks with spanwise length scale
![]() $5.6h$
, accompanied by smaller-scale streaks (figure 10
b1). The contours of
$5.6h$
, accompanied by smaller-scale streaks (figure 10
b1). The contours of
![]() $u^{\prime }$
in the Langmuir turbulence are more coherent and mainly dominated by large-scale streaks with spanwise length scale
$u^{\prime }$
in the Langmuir turbulence are more coherent and mainly dominated by large-scale streaks with spanwise length scale
![]() $8\unicode[STIX]{x03C0}h/3$
agreeing with those of LCs (figure 10
a1), indicating the important contribution of LCs to the streamwise velocity fluctuations. This observation is similar to that of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) at the centre of the water column at
$8\unicode[STIX]{x03C0}h/3$
agreeing with those of LCs (figure 10
a1), indicating the important contribution of LCs to the streamwise velocity fluctuations. This observation is similar to that of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) at the centre of the water column at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. Similarly, the comparison between figures 10(a3) and 10(b3) indicates that the spanwise velocity fluctuation
$Re_{\unicode[STIX]{x1D70F}}=395$
. Similarly, the comparison between figures 10(a3) and 10(b3) indicates that the spanwise velocity fluctuation
![]() $w^{\prime }$
is more coherent in the Langmuir turbulence than in the shear-driven turbulence. For the vertical velocity fluctuations, two negative streamwise-elongated streaks with spanwise separation of
$w^{\prime }$
is more coherent in the Langmuir turbulence than in the shear-driven turbulence. For the vertical velocity fluctuations, two negative streamwise-elongated streaks with spanwise separation of
![]() $8\unicode[STIX]{x03C0}h/3$
appear in the Langmuir turbulence (figure 10
a2), which are the footprints of the strong downwelling motions of LCs near the bottom. In contrast, the large-scale motion in the shear-driven turbulence is not sufficiently strong to leave footprints in
$8\unicode[STIX]{x03C0}h/3$
appear in the Langmuir turbulence (figure 10
a2), which are the footprints of the strong downwelling motions of LCs near the bottom. In contrast, the large-scale motion in the shear-driven turbulence is not sufficiently strong to leave footprints in
![]() $v^{\prime }$
near the water bottom.
$v^{\prime }$
near the water bottom.
4.2 Reynolds shear stress
According to (2.9), the mean velocity
![]() $\langle u\rangle$
and Reynolds shear stress
$\langle u\rangle$
and Reynolds shear stress
![]() $-\langle u^{\prime }v^{\prime }\rangle$
in the shallow-water Langmuir turbulence are related by the following balance equation of the mean streamwise shear stress
$-\langle u^{\prime }v^{\prime }\rangle$
in the shallow-water Langmuir turbulence are related by the following balance equation of the mean streamwise shear stress
Here, the mean SGS shear stress
![]() $\langle \unicode[STIX]{x1D70F}_{12}^{sgs}\rangle$
in (2.9) is neglected, because its magnitude is negligibly small in comparison with
$\langle \unicode[STIX]{x1D70F}_{12}^{sgs}\rangle$
in (2.9) is neglected, because its magnitude is negligibly small in comparison with
![]() $-\langle u^{\prime }v^{\prime }\rangle$
(figure 3). In this section, the reappearance of the logarithmic layer at
$-\langle u^{\prime }v^{\prime }\rangle$
(figure 3). In this section, the reappearance of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
and the effects of
$Re_{\unicode[STIX]{x1D70F}}=1000$
and the effects of
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the thickness of the logarithmic layer are further studied through the analysis of the Reynolds shear stress.
$La_{t}$
on the thickness of the logarithmic layer are further studied through the analysis of the Reynolds shear stress.
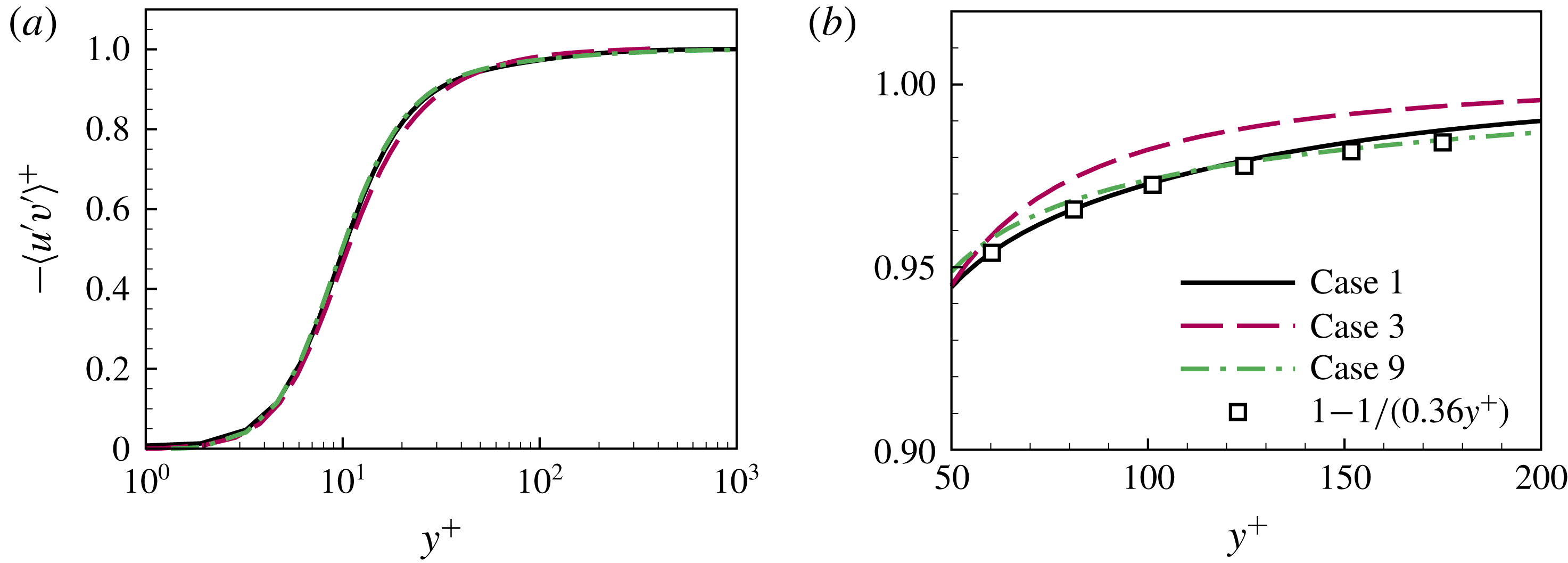
Figure 11. Profiles of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases
![]() $1$
,
$1$
,
![]() $3$
and
$3$
and
![]() $9$
and comparison with
$9$
and comparison with
![]() $1-1/(\unicode[STIX]{x1D705}y^{+})$
. LCs are present in cases
$1-1/(\unicode[STIX]{x1D705}y^{+})$
. LCs are present in cases
![]() $1$
and
$1$
and
![]() $3$
with
$3$
with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
and
$Re_{\unicode[STIX]{x1D70F}}=1000$
and
![]() $395$
, respectively, while LCs are absent in case
$395$
, respectively, while LCs are absent in case
![]() $9$
with
$9$
with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
.
$Re_{\unicode[STIX]{x1D70F}}=1000$
.
Figure 11(a) compares the profiles of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases 1 and 3 for Langmuir turbulence at
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases 1 and 3 for Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
and 395, respectively, with the result of case 9 for shear-driven turbulence superimposed. Figure 11(b) provides a zoom-in view of their distributions in the logarithmic layer. In all of these three cases, the value of
$Re_{\unicode[STIX]{x1D70F}}=1000$
and 395, respectively, with the result of case 9 for shear-driven turbulence superimposed. Figure 11(b) provides a zoom-in view of their distributions in the logarithmic layer. In all of these three cases, the value of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
increases monotonically as
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
increases monotonically as
![]() $y^{+}$
increases in the near-bottom region below
$y^{+}$
increases in the near-bottom region below
![]() $y^{+}=100$
, and approaches
$y^{+}=100$
, and approaches
![]() $1.0$
in the outer layer above
$1.0$
in the outer layer above
![]() $y^{+}=100$
. Substituting equation (4.1) into the definition of
$y^{+}=100$
. Substituting equation (4.1) into the definition of
![]() $F$
(3.2) gives the relationship between
$F$
(3.2) gives the relationship between
![]() $F$
and
$F$
and
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
as
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
as
According to this equation, although the difference in the profile of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
seems to be small between cases 1 and 3, it is amplified by the multiplication with
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
seems to be small between cases 1 and 3, it is amplified by the multiplication with
![]() $y^{+}$
to result in a more significant difference in the profile of
$y^{+}$
to result in a more significant difference in the profile of
![]() $F$
.
$F$
.
To further study the effect of the Reynolds shear stress on the logarithmic layer, we depict in figure 11(b) the profile of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases 1, 3 and 9 in the logarithmic layer of the shear-driven turbulence between
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
in cases 1, 3 and 9 in the logarithmic layer of the shear-driven turbulence between
![]() $y^{+}=50$
and 200. According to (4.1), the identity
$y^{+}=50$
and 200. According to (4.1), the identity
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}=1-1/(ky^{+})$
holds in the logarithmic layer. Figure 11(b) shows that in case 3 for Langmuir turbulence at
$-\langle u^{\prime }v^{\prime }\rangle ^{+}=1-1/(ky^{+})$
holds in the logarithmic layer. Figure 11(b) shows that in case 3 for Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
, the value of
$Re_{\unicode[STIX]{x1D70F}}=395$
, the value of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is larger than
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is larger than
![]() $1-1/(ky^{+})$
, indicating that the mean velocity deviates from the logarithmic law. In contrast, in case 1 for Langmuir turbulence at
$1-1/(ky^{+})$
, indicating that the mean velocity deviates from the logarithmic law. In contrast, in case 1 for Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, the profile of
$Re_{\unicode[STIX]{x1D70F}}=1000$
, the profile of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is close to that of
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is close to that of
![]() $1-1/(ky^{+})$
, meaning that the logarithmic layer reappears.
$1-1/(ky^{+})$
, meaning that the logarithmic layer reappears.

Figure 12. Profiles of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
and
$-\langle u^{T}v^{T}\rangle ^{+}$
and
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
in cases 1–3 with
$-\langle u^{L}v^{L}\rangle ^{+}$
in cases 1–3 with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively. (a) Profiles of
$395$
, respectively. (a) Profiles of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
in near-bottom coordinate
$-\langle u^{T}v^{T}\rangle ^{+}$
in near-bottom coordinate
![]() $y^{+}$
, and (b), (c) profiles of
$y^{+}$
, and (b), (c) profiles of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
in near-bottom coordinate
$-\langle u^{L}v^{L}\rangle ^{+}$
in near-bottom coordinate
![]() $y^{+}$
and water-column coordinate
$y^{+}$
and water-column coordinate
![]() $y/h$
, respectively.
$y/h$
, respectively.
The effect of LCs on the Reynolds shear stress can be further assessed through the decomposition of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
into the LC-coherent part
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
into the LC-coherent part
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
and the residual part
$-\langle u^{L}v^{L}\rangle ^{+}$
and the residual part
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
(2.11). Figures 12(a) and 12(b) compare respectively the profiles of
$-\langle u^{T}v^{T}\rangle ^{+}$
(2.11). Figures 12(a) and 12(b) compare respectively the profiles of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
and
$-\langle u^{T}v^{T}\rangle ^{+}$
and
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
in cases 1–3 in the near-bottom coordinate
$-\langle u^{L}v^{L}\rangle ^{+}$
in cases 1–3 in the near-bottom coordinate
![]() $y^{+}$
, while figure 12(c) compares the profile of
$y^{+}$
, while figure 12(c) compares the profile of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
in these cases in the water-column coordinate
$-\langle u^{L}v^{L}\rangle ^{+}$
in these cases in the water-column coordinate
![]() $y/h$
to further study the effect of the Reynolds number on the Reynolds shear stress. From the comparison between figures 12(a) and 12(b), it can be observed that the residual part
$y/h$
to further study the effect of the Reynolds number on the Reynolds shear stress. From the comparison between figures 12(a) and 12(b), it can be observed that the residual part
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
is dominant below
$-\langle u^{T}v^{T}\rangle ^{+}$
is dominant below
![]() $y^{+}=100$
, while the LC-coherent part
$y^{+}=100$
, while the LC-coherent part
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
is more important above
$-\langle u^{L}v^{L}\rangle ^{+}$
is more important above
![]() $y^{+}=100$
, consistent with the observations of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015). Figure 12(a) shows that, as the Reynolds number increases, the peak location of
$y^{+}=100$
, consistent with the observations of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015). Figure 12(a) shows that, as the Reynolds number increases, the peak location of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
remains almost unchanged in the near-bottom coordinate. Different from
$-\langle u^{T}v^{T}\rangle ^{+}$
remains almost unchanged in the near-bottom coordinate. Different from
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
, the peaks of
$-\langle u^{T}v^{T}\rangle ^{+}$
, the peaks of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
are collocated in the water-column coordinate at
$-\langle u^{L}v^{L}\rangle ^{+}$
are collocated in the water-column coordinate at
![]() $y/h=0.5$
(figure 12
c). Note that the near-bottom and water-column coordinates are related by the Reynolds number as
$y/h=0.5$
(figure 12
c). Note that the near-bottom and water-column coordinates are related by the Reynolds number as
![]() $y^{+}=Re_{\unicode[STIX]{x1D70F}}y/h$
. As a result, the peaks of
$y^{+}=Re_{\unicode[STIX]{x1D70F}}y/h$
. As a result, the peaks of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
collocated at the same value of
$-\langle u^{L}v^{L}\rangle ^{+}$
collocated at the same value of
![]() $y/h$
correspond to an increasing value of
$y/h$
correspond to an increasing value of
![]() $y^{+}$
as the Reynolds number increases (figure 12
b). This indicates a weaker influence of LCs on the momentum transfer near the water bottom at higher Reynolds number, characterized by the smaller magnitude of
$y^{+}$
as the Reynolds number increases (figure 12
b). This indicates a weaker influence of LCs on the momentum transfer near the water bottom at higher Reynolds number, characterized by the smaller magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
below
$-\langle u^{L}v^{L}\rangle ^{+}$
below
![]() $y^{+}=200$
(figure 12
b). This effect of Reynolds number leads to the reappearance of the logarithmic layer in the near-bottom region at
$y^{+}=200$
(figure 12
b). This effect of Reynolds number leads to the reappearance of the logarithmic layer in the near-bottom region at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
(figure 7).
$Re_{\unicode[STIX]{x1D70F}}=1000$
(figure 7).
Figure 13 shows the effects of
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the LC-coherent Reynolds shear stress
$La_{t}$
on the LC-coherent Reynolds shear stress
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
. As depicted in figure 13(a), as the value of
$-\langle u^{L}v^{L}\rangle ^{+}$
. As depicted in figure 13(a), as the value of
![]() $kh$
increases, the peak of
$kh$
increases, the peak of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
shifts to larger
$-\langle u^{L}v^{L}\rangle ^{+}$
shifts to larger
![]() $y^{+}$
, and the magnitude of
$y^{+}$
, and the magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
decreases below
$-\langle u^{L}v^{L}\rangle ^{+}$
decreases below
![]() $y^{+}=200$
. This indicates a weaker effect of LCs on the momentum transfer in the near-bottom region at larger value of
$y^{+}=200$
. This indicates a weaker effect of LCs on the momentum transfer in the near-bottom region at larger value of
![]() $kh$
. As a result, the logarithmic layer expands as the value of
$kh$
. As a result, the logarithmic layer expands as the value of
![]() $kh$
increases (figure 8).
$kh$
increases (figure 8).

Figure 13. Profiles of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
in (a) cases 1 and 4–6 with
$-\langle u^{L}v^{L}\rangle ^{+}$
in (a) cases 1 and 4–6 with
![]() $kh=0.5$
,
$kh=0.5$
,
![]() $1$
,
$1$
,
![]() $1.5$
and
$1.5$
and
![]() $2$
, respectively, and (b) cases 1, 7 and 8 with
$2$
, respectively, and (b) cases 1, 7 and 8 with
![]() $La_{t}=0.7$
,
$La_{t}=0.7$
,
![]() $0.4$
and
$0.4$
and
![]() $0.9$
, respectively.
$0.9$
, respectively.
The magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
is non-monotonic with the increase of
$-\langle u^{L}v^{L}\rangle ^{+}$
is non-monotonic with the increase of
![]() $La_{t}$
. As shown in figure 13(b), the magnitude of
$La_{t}$
. As shown in figure 13(b), the magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
at
$-\langle u^{L}v^{L}\rangle ^{+}$
at
![]() $La_{t}=0.7$
is larger than those at
$La_{t}=0.7$
is larger than those at
![]() $La_{t}=0.4$
and 0.9 between
$La_{t}=0.4$
and 0.9 between
![]() $y^{+}=20$
and
$y^{+}=20$
and
![]() $1000$
. The larger magnitude of
$1000$
. The larger magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
at
$-\langle u^{L}v^{L}\rangle ^{+}$
at
![]() $La_{t}=0.7$
than at
$La_{t}=0.7$
than at
![]() $La_{t}=0.9$
can be attributed to the stronger intensity of LCs due to the larger magnitude of vortex force at smaller value of
$La_{t}=0.9$
can be attributed to the stronger intensity of LCs due to the larger magnitude of vortex force at smaller value of
![]() $La_{t}$
(2.2). The magnitude of
$La_{t}$
(2.2). The magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
is smaller at
$-\langle u^{L}v^{L}\rangle ^{+}$
is smaller at
![]() $La_{t}=0.4$
than at
$La_{t}=0.4$
than at
![]() $La_{t}=0.7$
, indicating a less important contribution of LCs to the momentum transfer at
$La_{t}=0.7$
, indicating a less important contribution of LCs to the momentum transfer at
![]() $La_{t}=0.4$
, which is consistent with the observation of Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
$La_{t}=0.4$
, which is consistent with the observation of Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. As explained by Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015), the intensities of the upwelling motion induced by LCs become stronger at a smaller value of
$Re_{\unicode[STIX]{x1D70F}}=395$
. As explained by Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015), the intensities of the upwelling motion induced by LCs become stronger at a smaller value of
![]() $La_{t}$
due to the larger magnitude of C–L vortex forcing. The strong upwelling motion at
$La_{t}$
due to the larger magnitude of C–L vortex forcing. The strong upwelling motion at
![]() $La_{t}=0.4$
shifts LCs towards the water surface. As a result, the magnitude of the LC-coherent Reynolds stress is smaller at
$La_{t}=0.4$
shifts LCs towards the water surface. As a result, the magnitude of the LC-coherent Reynolds stress is smaller at
![]() $La_{t}=0.4$
than at
$La_{t}=0.4$
than at
![]() $La_{t}=0.7$
in the lower half of the water column. The residual turbulence motions become important in the momentum transfer at
$La_{t}=0.7$
in the lower half of the water column. The residual turbulence motions become important in the momentum transfer at
![]() $La_{t}=0.4$
, which is indicated by
$La_{t}=0.4$
, which is indicated by
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
. To further study the effects of
$-\langle u^{T}v^{T}\rangle ^{+}$
. To further study the effects of
![]() $La_{t}$
on the residual turbulence motions, we compare
$La_{t}$
on the residual turbulence motions, we compare
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
among cases 1, 7 and 8 in figure 14(a), and the pre-multiplied spanwise co-spectrum
$-\langle u^{T}v^{T}\rangle ^{+}$
among cases 1, 7 and 8 in figure 14(a), and the pre-multiplied spanwise co-spectrum
![]() $\unicode[STIX]{x1D719}_{uv}^{T}(y,k_{z})=k_{z}E_{uv}^{T}(y,k_{z})$
at a near-bottom plane
$\unicode[STIX]{x1D719}_{uv}^{T}(y,k_{z})=k_{z}E_{uv}^{T}(y,k_{z})$
at a near-bottom plane
![]() $y^{+}=120$
and a water-column central plane
$y^{+}=120$
and a water-column central plane
![]() $y/h=1.0$
in figures 14(b) and 14(c), respectively. Here,
$y/h=1.0$
in figures 14(b) and 14(c), respectively. Here,
![]() $k_{z}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{z}$
is the spanwise wavenumber corresponding to the spanwise length scale
$k_{z}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{z}$
is the spanwise wavenumber corresponding to the spanwise length scale
![]() $\unicode[STIX]{x1D706}_{z}$
, and
$\unicode[STIX]{x1D706}_{z}$
, and
![]() $E_{uv}^{T}(y,k_{z})$
is the spanwise co-spectrum between
$E_{uv}^{T}(y,k_{z})$
is the spanwise co-spectrum between
![]() $u^{T}$
and
$u^{T}$
and
![]() $v^{T}$
, which satisfies the normalization property
$v^{T}$
, which satisfies the normalization property

Figure 14. Residual part of Reynolds shear stress
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
and pre-multiplied co-spectrum
$-\langle u^{T}v^{T}\rangle ^{+}$
and pre-multiplied co-spectrum
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
in cases 1, 7 and 8 with
$-\unicode[STIX]{x1D719}_{uv}^{T}$
in cases 1, 7 and 8 with
![]() $La_{t}=0.7$
,
$La_{t}=0.7$
,
![]() $0.4$
and
$0.4$
and
![]() $0.9$
, respectively. (a) Profiles of
$0.9$
, respectively. (a) Profiles of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
, (b) pre-multiplied co-spectra
$-\langle u^{T}v^{T}\rangle ^{+}$
, (b) pre-multiplied co-spectra
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
at
$-\unicode[STIX]{x1D719}_{uv}^{T}$
at
![]() $y^{+}=120$
and (c) pre-multiplied co-spectra
$y^{+}=120$
and (c) pre-multiplied co-spectra
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
at
$-\unicode[STIX]{x1D719}_{uv}^{T}$
at
![]() $y/h=1$
.
$y/h=1$
.
As shown in figure 14(a), the magnitude of the residual turbulence part of Reynolds shear stress
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
is larger at
$-\langle u^{T}v^{T}\rangle ^{+}$
is larger at
![]() $La_{t}=0.4$
than at
$La_{t}=0.4$
than at
![]() $La_{t}=0.7$
above
$La_{t}=0.7$
above
![]() $y^{+}=20$
and
$y^{+}=20$
and
![]() $La_{t}=0.9$
above
$La_{t}=0.9$
above
![]() $y^{+}=100$
, which results from the intensification of residual turbulence motions. The effect of turbulence motions on
$y^{+}=100$
, which results from the intensification of residual turbulence motions. The effect of turbulence motions on
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
can be observed from the pre-multiplied spanwise co-spectrum
$-\langle u^{T}v^{T}\rangle ^{+}$
can be observed from the pre-multiplied spanwise co-spectrum
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
shown in figure 14(b,c). At the near-bottom plane
$-\unicode[STIX]{x1D719}_{uv}^{T}$
shown in figure 14(b,c). At the near-bottom plane
![]() $y^{+}=120$
(figure 14
b), the magnitude of
$y^{+}=120$
(figure 14
b), the magnitude of
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
at
$-\unicode[STIX]{x1D719}_{uv}^{T}$
at
![]() $La_{t}=0.4$
is larger than that at
$La_{t}=0.4$
is larger than that at
![]() $La_{t}=0.7$
for
$La_{t}=0.7$
for
![]() $\unicode[STIX]{x1D706}_{z}^{+}>200$
, indicating that the larger magnitude of
$\unicode[STIX]{x1D706}_{z}^{+}>200$
, indicating that the larger magnitude of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
at
$-\langle u^{T}v^{T}\rangle ^{+}$
at
![]() $La_{t}=0.4$
results from the enhancement of the large-scale turbulence motions (
$La_{t}=0.4$
results from the enhancement of the large-scale turbulence motions (
![]() $\unicode[STIX]{x1D706}_{z}^{+}>200$
). Akan et al. (Reference Akan, Tejada-Martínez, Grosch and Martinat2013) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) pointed out that the strong shear of Stokes drift at
$\unicode[STIX]{x1D706}_{z}^{+}>200$
). Akan et al. (Reference Akan, Tejada-Martínez, Grosch and Martinat2013) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) pointed out that the strong shear of Stokes drift at
![]() $La_{t}=0.4$
significantly enhances the large-scale turbulent motion in the vertical direction in the upper half of the water column. It is evident from figure 14(c) that the large-scale turbulent motions also lead to the magnitude increase of
$La_{t}=0.4$
significantly enhances the large-scale turbulent motion in the vertical direction in the upper half of the water column. It is evident from figure 14(c) that the large-scale turbulent motions also lead to the magnitude increase of
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
at spanwise scales larger than
$-\unicode[STIX]{x1D719}_{uv}^{T}$
at spanwise scales larger than
![]() $\unicode[STIX]{x1D706}_{z}^{+}=200$
at the centre of the water column
$\unicode[STIX]{x1D706}_{z}^{+}=200$
at the centre of the water column
![]() $y/h=1$
. By comparing figure 14(b) with figure 14(c), it is observed that as the value of
$y/h=1$
. By comparing figure 14(b) with figure 14(c), it is observed that as the value of
![]() $La_{t}$
decreases from
$La_{t}$
decreases from
![]() $0.7$
to
$0.7$
to
![]() $0.4$
, the magnitude of
$0.4$
, the magnitude of
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
increases at the same spanwise scales (
$-\unicode[STIX]{x1D719}_{uv}^{T}$
increases at the same spanwise scales (
![]() $\unicode[STIX]{x1D706}_{z}^{+}>200$
). This indicates that the large-scale turbulent motions are sufficiently strong to reach the near-bottom region. As a result, the magnitude of
$\unicode[STIX]{x1D706}_{z}^{+}>200$
). This indicates that the large-scale turbulent motions are sufficiently strong to reach the near-bottom region. As a result, the magnitude of
![]() $-\langle u^{T}v^{T}\rangle$
also becomes stronger at
$-\langle u^{T}v^{T}\rangle$
also becomes stronger at
![]() $La_{t}=0.4$
than at
$La_{t}=0.4$
than at
![]() $La_{t}=0.7$
near the water bottom. This effect of large-scale turbulence motion on the near-bottom momentum flux is absent at larger value of
$La_{t}=0.7$
near the water bottom. This effect of large-scale turbulence motion on the near-bottom momentum flux is absent at larger value of
![]() $La_{t}$
, because of the smaller Stokes shear. As shown in figure 14(b), the magnitude of
$La_{t}$
, because of the smaller Stokes shear. As shown in figure 14(b), the magnitude of
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
is larger at
$-\unicode[STIX]{x1D719}_{uv}^{T}$
is larger at
![]() $La_{t}=0.9$
than at
$La_{t}=0.9$
than at
![]() $La_{t}=0.7$
at all spanwise scales
$La_{t}=0.7$
at all spanwise scales
![]() $\unicode[STIX]{x1D706}_{z}^{+}$
. In contrast, as shown in figure 14(c), at
$\unicode[STIX]{x1D706}_{z}^{+}$
. In contrast, as shown in figure 14(c), at
![]() $y/h=1$
, the magnitudes of
$y/h=1$
, the magnitudes of
![]() $-\unicode[STIX]{x1D719}_{uv}^{T}$
at
$-\unicode[STIX]{x1D719}_{uv}^{T}$
at
![]() $La_{t}=0.9$
and 0.7 are comparable at most spanwise scales except for
$La_{t}=0.9$
and 0.7 are comparable at most spanwise scales except for
![]() $\unicode[STIX]{x1D706}_{z}^{+}\geqslant 7000$
. This indicates that the suppression of
$\unicode[STIX]{x1D706}_{z}^{+}\geqslant 7000$
. This indicates that the suppression of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
near the water bottom in response to the decrease of
$-\langle u^{T}v^{T}\rangle ^{+}$
near the water bottom in response to the decrease of
![]() $La_{t}$
from 0.9 to 0.7 cannot be attributed to large-scale turbulence motions at
$La_{t}$
from 0.9 to 0.7 cannot be attributed to large-scale turbulence motions at
![]() $y/h=1$
. Martinat et al. (Reference Martinat, Grosch and Gatski2014) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) pointed out that LCs tend to suppress the momentum flux induced by turbulent motions. Because the impact of LCs on the momentum flux near the bottom is weaker at
$y/h=1$
. Martinat et al. (Reference Martinat, Grosch and Gatski2014) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) pointed out that LCs tend to suppress the momentum flux induced by turbulent motions. Because the impact of LCs on the momentum flux near the bottom is weaker at
![]() $La_{t}=0.9$
than at
$La_{t}=0.9$
than at
![]() $La_{t}=0.7$
(figure 13
b), the magnitude of
$La_{t}=0.7$
(figure 13
b), the magnitude of
![]() $-\langle u^{T}v^{T}\rangle ^{+}$
becomes larger as
$-\langle u^{T}v^{T}\rangle ^{+}$
becomes larger as
![]() $La_{t}$
increases from
$La_{t}$
increases from
![]() $0.7$
to
$0.7$
to
![]() $0.9$
.
$0.9$
.
4.3 Reynolds normal stresses

Figure 15. Profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
in the coordinate of (a)
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
in the coordinate of (a)
![]() $y^{+}$
and (b)
$y^{+}$
and (b)
![]() $y/h$
in cases 1–3 with
$y/h$
in cases 1–3 with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively. In (a), the line with open circles represents the result in case
$395$
, respectively. In (a), the line with open circles represents the result in case
![]() $9$
(the shear-driven turbulence at
$9$
(the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
) as a reference.
$Re_{\unicode[STIX]{x1D70F}}=1000$
) as a reference.
We start our analyses of Reynolds normal stresses with the effect of the Reynolds number. Figure 15 compares the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
among cases 1–3 with different Reynolds numbers. The result of case 9 for shear-driven turbulence is superimposed for comparison. As shown in figure 15(a), at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
among cases 1–3 with different Reynolds numbers. The result of case 9 for shear-driven turbulence is superimposed for comparison. As shown in figure 15(a), at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
, there is a single peak in the profile of
$Re_{\unicode[STIX]{x1D70F}}=395$
, there is a single peak in the profile of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
. This peak is located at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
. This peak is located at
![]() $y^{+}=32$
, different from the peak location of
$y^{+}=32$
, different from the peak location of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
at
![]() $y^{+}=11$
in the shear-driven turbulence. As the Reynolds number increases to 700 and 1000, the profile of
$y^{+}=11$
in the shear-driven turbulence. As the Reynolds number increases to 700 and 1000, the profile of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
shows a bimodal shape. As shown in figure 15(a), the inner peak at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
shows a bimodal shape. As shown in figure 15(a), the inner peak at
![]() $y^{+}=12$
is close to that in the shear-driven turbulence. Although an outer peak of
$y^{+}=12$
is close to that in the shear-driven turbulence. Although an outer peak of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
also occurs in canonical wall-bounded turbulence for
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
also occurs in canonical wall-bounded turbulence for
![]() $Re_{\unicode[STIX]{x1D70F}}>15\,000$
(Alfredsson, Segalini & Örlü Reference Alfredsson, Segalini and Örlü2011), the one in Langmuir turbulence is different in three aspects. First, the outer peak of
$Re_{\unicode[STIX]{x1D70F}}>15\,000$
(Alfredsson, Segalini & Örlü Reference Alfredsson, Segalini and Örlü2011), the one in Langmuir turbulence is different in three aspects. First, the outer peak of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
in the Langmuir turbulence occurs at a much smaller Reynolds number of 700. Second, in the shallow-water Langmuir turbulence, the outer peak location is scaled by
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
in the Langmuir turbulence occurs at a much smaller Reynolds number of 700. Second, in the shallow-water Langmuir turbulence, the outer peak location is scaled by
![]() $h$
for various Reynolds numbers. As shown in figure 15(b), at
$h$
for various Reynolds numbers. As shown in figure 15(b), at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
and
$Re_{\unicode[STIX]{x1D70F}}=700$
and
![]() $1000$
, the outer peak of
$1000$
, the outer peak of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
is collocated at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
is collocated at
![]() $y/h=0.11$
. However, the outer peak in the canonical wall-bounded turbulence for
$y/h=0.11$
. However, the outer peak in the canonical wall-bounded turbulence for
![]() $Re_{\unicode[STIX]{x1D70F}}>15\,000$
is located at
$Re_{\unicode[STIX]{x1D70F}}>15\,000$
is located at
![]() $y^{+}\sim Re_{\unicode[STIX]{x1D70F}}^{1/2}$
(Alfredsson et al.
Reference Alfredsson, Segalini and Örlü2011). Third, as shown in figure 15(b), in the water-column coordinate
$y^{+}\sim Re_{\unicode[STIX]{x1D70F}}^{1/2}$
(Alfredsson et al.
Reference Alfredsson, Segalini and Örlü2011). Third, as shown in figure 15(b), in the water-column coordinate
![]() $y/h$
, the profiles of
$y/h$
, the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
in the outer layer of the Langmuir turbulence at various Reynolds numbers are close to each other. In contrast, in the canonical wall-bounded turbulence, the profiles of
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
in the outer layer of the Langmuir turbulence at various Reynolds numbers are close to each other. In contrast, in the canonical wall-bounded turbulence, the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
at various Reynolds numbers deviate from each other in the outer coordinate
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
at various Reynolds numbers deviate from each other in the outer coordinate
![]() $y/h$
(Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). It is evident from the above three points that the occurrence of LCs significantly alters the profile of
$y/h$
(Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). It is evident from the above three points that the occurrence of LCs significantly alters the profile of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
.
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
.

Figure 16. Profiles of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
in the coordinate of (a)
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
in the coordinate of (a)
![]() $y^{+}$
and (b)
$y^{+}$
and (b)
![]() $y/h$
in cases 1–3 with
$y/h$
in cases 1–3 with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively. In (a), the line with open circles represents the result in case
$395$
, respectively. In (a), the line with open circles represents the result in case
![]() $9$
(the shear-driven turbulence at
$9$
(the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
) as a reference.
$Re_{\unicode[STIX]{x1D70F}}=1000$
) as a reference.
Figure 16 shows the Reynolds number effect on the profiles of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
. As shown in figure 16(a), the value of
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
. As shown in figure 16(a), the value of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
increases monotonically with
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
increases monotonically with
![]() $y^{+}$
at
$y^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. In contrast, at
$Re_{\unicode[STIX]{x1D70F}}=395$
. In contrast, at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
and
$Re_{\unicode[STIX]{x1D70F}}=700$
and
![]() $1000$
, a local peak located at
$1000$
, a local peak located at
![]() $y^{+}=50$
occurs in the profile of
$y^{+}=50$
occurs in the profile of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
. As the distance from the bottom further increases, the profiles of
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
. As the distance from the bottom further increases, the profiles of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
at
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
and
$Re_{\unicode[STIX]{x1D70F}}=700$
and
![]() $1000$
first reach their local minimal values at
$1000$
first reach their local minimal values at
![]() $y/h\approx 0.17$
, and then increases again with
$y/h\approx 0.17$
, and then increases again with
![]() $y/h$
(figure 16
b). The shape of the
$y/h$
(figure 16
b). The shape of the
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
profile in shallow-water Langmuir turbulence is drastically different from that in the shear-driven turbulence and canonical wall-bounded turbulence (Kim, Moin & Moser Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). For example, the value of
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
profile in shallow-water Langmuir turbulence is drastically different from that in the shear-driven turbulence and canonical wall-bounded turbulence (Kim, Moin & Moser Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). For example, the value of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
in the turbulent Couette flow (Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014) and the shear-driven turbulence is close to a constant in the outer layer, while in the pressure-driven turbulent channel flow the magnitude of
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
in the turbulent Couette flow (Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014) and the shear-driven turbulence is close to a constant in the outer layer, while in the pressure-driven turbulent channel flow the magnitude of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
decreases with
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
decreases with
![]() $y^{+}$
in the outer layer (Kim et al.
Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Lee & Moser Reference Lee and Moser2015).
$y^{+}$
in the outer layer (Kim et al.
Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Lee & Moser Reference Lee and Moser2015).

Figure 17. Profiles of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
in the coordinate of (a)
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
in the coordinate of (a)
![]() $y^{+}$
and (b)
$y^{+}$
and (b)
![]() $y/h$
in cases 1–3 with
$y/h$
in cases 1–3 with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively. In (a), the line with open circles represents the result in case
$395$
, respectively. In (a), the line with open circles represents the result in case
![]() $9$
(the shear-driven turbulence at
$9$
(the shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
) as a reference.
$Re_{\unicode[STIX]{x1D70F}}=1000$
) as a reference.
Figure 17 compares the profiles of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
in shallow-water Langmuir turbulence at various Reynolds numbers. Figure 17(a) shows that in the wall coordinate
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
in shallow-water Langmuir turbulence at various Reynolds numbers. Figure 17(a) shows that in the wall coordinate
![]() $y^{+}$
, the magnitude of
$y^{+}$
, the magnitude of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
increases as the Reynolds number increases. In Langmuir turbulence at
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
increases as the Reynolds number increases. In Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
, 700 and 1000, the peak value of
$Re_{\unicode[STIX]{x1D70F}}=395$
, 700 and 1000, the peak value of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
is respectively
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
is respectively
![]() $5.7$
,
$5.7$
,
![]() $6.6$
and
$6.6$
and
![]() $7.2$
, significantly larger than those in the shear-driven turbulence (figure 17
a) and canonical wall-bounded turbulence at
$7.2$
, significantly larger than those in the shear-driven turbulence (figure 17
a) and canonical wall-bounded turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}\leqslant 1000$
(approximately 2.0–3.0, see e.g. Kim et al.
Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014). The peak location of
$Re_{\unicode[STIX]{x1D70F}}\leqslant 1000$
(approximately 2.0–3.0, see e.g. Kim et al.
Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014). The peak location of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
in Langmuir turbulence is also different from that in shear-driven turbulence and canonical wall-bounded turbulence. In Langmuir turbulence, the peak location of
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
in Langmuir turbulence is also different from that in shear-driven turbulence and canonical wall-bounded turbulence. In Langmuir turbulence, the peak location of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
is scaled by
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
is scaled by
![]() $h$
. As shown in figure 17(b), the peaks of
$h$
. As shown in figure 17(b), the peaks of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
at various Reynolds numbers collocate at
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
at various Reynolds numbers collocate at
![]() $y/h=0.15$
. In canonical wall-bounded turbulence, the peak of
$y/h=0.15$
. In canonical wall-bounded turbulence, the peak of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
is located at
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
is located at
![]() $y^{+}=30{-}40$
(Kim et al.
Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014), closer to the wall than in Langmuir turbulence. Similarly, in the shear-driven turbulence the peak is located at
$y^{+}=30{-}40$
(Kim et al.
Reference Kim, Moin and Moser1987; Hoyas & Jiménez Reference Hoyas and Jiménez2006; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014), closer to the wall than in Langmuir turbulence. Similarly, in the shear-driven turbulence the peak is located at
![]() $y^{+}=30$
(figure 17
a). From the comparison of the peak magnitude and location of
$y^{+}=30$
(figure 17
a). From the comparison of the peak magnitude and location of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
,
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
and
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
and
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
between the shallow-water Langmuir turbulence and canonical wall turbulence without LCs, it is evident that LCs make a substantial contribution to the Reynolds normal stresses in Langmuir turbulence.
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
between the shallow-water Langmuir turbulence and canonical wall turbulence without LCs, it is evident that LCs make a substantial contribution to the Reynolds normal stresses in Langmuir turbulence.

Figure 18. Profiles of (a)
![]() $\langle u^{L}u^{L}\rangle ^{+}$
in the coordinate of
$\langle u^{L}u^{L}\rangle ^{+}$
in the coordinate of
![]() $y/h$
, (b)
$y/h$
, (b)
![]() $\langle u^{L}u^{L}\rangle ^{+}$
and (c)
$\langle u^{L}u^{L}\rangle ^{+}$
and (c)
![]() $\langle u^{T}u^{T}\rangle ^{+}$
in the coordinate of
$\langle u^{T}u^{T}\rangle ^{+}$
in the coordinate of
![]() $y^{+}$
in cases
$y^{+}$
in cases
![]() $1$
–
$1$
–
![]() $3$
with
$3$
with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively.
$395$
, respectively.
Similar to the analyses of Reynolds shear stress in § 4.2, we employ the decomposition of the Reynolds stress (2.11) to study the effect of LCs on the Reynolds normal stresses in Langmuir turbulence at various Reynolds numbers. Figure 18 shows the profiles of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
and
$\langle u^{L}u^{L}\rangle ^{+}$
and
![]() $\langle u^{T}u^{T}\rangle ^{+}$
, while figures 19 and 20 show respectively those of
$\langle u^{T}u^{T}\rangle ^{+}$
, while figures 19 and 20 show respectively those of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
and
$\langle v^{L}v^{L}\rangle ^{+}$
and
![]() $\langle v^{T}v^{T}\rangle ^{+}$
and those of
$\langle v^{T}v^{T}\rangle ^{+}$
and those of
![]() $\langle w^{L}w^{L}\rangle ^{+}$
and
$\langle w^{L}w^{L}\rangle ^{+}$
and
![]() $\langle w^{T}w^{T}\rangle ^{+}$
at various Reynolds numbers. In each of these three figures, the left column compares the profiles of LC-coherent part in the water-column coordinate, while the middle and right columns compare respectively the profiles of LC-coherent and residual parts in the near-bottom coordinate.
$\langle w^{T}w^{T}\rangle ^{+}$
at various Reynolds numbers. In each of these three figures, the left column compares the profiles of LC-coherent part in the water-column coordinate, while the middle and right columns compare respectively the profiles of LC-coherent and residual parts in the near-bottom coordinate.
From the comparison among figures 15–20, it can be observed that in the outer layer, all of the three LC-coherent Reynolds normal stresses make important contributions to the total Reynolds normal stresses, which is consistent with the observations of Tejada-Martínez & Grosch (Reference Tejada-Martínez and Grosch2007) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. Figure 18(a) shows that the location of the
$Re_{\unicode[STIX]{x1D70F}}=395$
. Figure 18(a) shows that the location of the
![]() $\langle u^{L}u^{L}\rangle ^{+}$
peak is scaled by
$\langle u^{L}u^{L}\rangle ^{+}$
peak is scaled by
![]() $h$
. The peaks of
$h$
. The peaks of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
at various Reynolds numbers collocate at
$\langle u^{L}u^{L}\rangle ^{+}$
at various Reynolds numbers collocate at
![]() $y/h=0.11$
, which is consistent with the outer peak of
$y/h=0.11$
, which is consistent with the outer peak of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
and
$Re_{\unicode[STIX]{x1D70F}}=700$
and
![]() $1000$
(figure 15
b). From the comparison between figures 18(b) and 18(c), it can be observed that the magnitude of
$1000$
(figure 15
b). From the comparison between figures 18(b) and 18(c), it can be observed that the magnitude of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
is much larger than that of
$\langle u^{L}u^{L}\rangle ^{+}$
is much larger than that of
![]() $\langle u^{T}u^{T}\rangle ^{+}$
above
$\langle u^{T}u^{T}\rangle ^{+}$
above
![]() $y^{+}=100$
, indicating that the outer peaks of
$y^{+}=100$
, indicating that the outer peaks of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
at
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
and 1000 are induced by the LCs. Figure 19(b) shows that the value of
$Re_{\unicode[STIX]{x1D70F}}=700$
and 1000 are induced by the LCs. Figure 19(b) shows that the value of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
increases with
$\langle v^{L}v^{L}\rangle ^{+}$
increases with
![]() $y^{+}$
in the outer layer. In contrast, as depicted in figure 19(c), the profile of
$y^{+}$
in the outer layer. In contrast, as depicted in figure 19(c), the profile of
![]() $\langle v^{T}v^{T}\rangle ^{+}$
is relatively flat above
$\langle v^{T}v^{T}\rangle ^{+}$
is relatively flat above
![]() $y^{+}=100$
. This indicates that the increase of
$y^{+}=100$
. This indicates that the increase of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
with
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
with
![]() $y^{+}$
above
$y^{+}$
above
![]() $y^{+}=100$
(figure 16
b) is caused by the LCs. Similar to
$y^{+}=100$
(figure 16
b) is caused by the LCs. Similar to
![]() $\langle u^{L}u^{L}\rangle ^{+}$
, the peak location of
$\langle u^{L}u^{L}\rangle ^{+}$
, the peak location of
![]() $\langle w^{L}w^{L}\rangle ^{+}$
is scaled by
$\langle w^{L}w^{L}\rangle ^{+}$
is scaled by
![]() $h$
at various Reynolds numbers. As shown in figure 20(a), the peaks of
$h$
at various Reynolds numbers. As shown in figure 20(a), the peaks of
![]() $\langle w^{L}w^{L}\rangle ^{+}$
at various Reynolds numbers collocate at
$\langle w^{L}w^{L}\rangle ^{+}$
at various Reynolds numbers collocate at
![]() $y/h=0.16$
, which are close to those of
$y/h=0.16$
, which are close to those of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
at
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
at
![]() $y/h=0.15$
(figure 17
b). In contrast, as shown in figure 20(c), the magnitude of the
$y/h=0.15$
(figure 17
b). In contrast, as shown in figure 20(c), the magnitude of the
![]() $\langle w^{T}w^{T}\rangle ^{+}$
profile changes little with
$\langle w^{T}w^{T}\rangle ^{+}$
profile changes little with
![]() $y^{+}$
. Therefore, the peak of
$y^{+}$
. Therefore, the peak of
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
in the shallow-water Langmuir turbulence results from the contribution of LCs.
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
in the shallow-water Langmuir turbulence results from the contribution of LCs.

Figure 19. Profiles of (a)
![]() $\langle v^{L}v^{L}\rangle ^{+}$
in the coordinate of
$\langle v^{L}v^{L}\rangle ^{+}$
in the coordinate of
![]() $y/h$
, (b)
$y/h$
, (b)
![]() $\langle v^{L}v^{L}\rangle ^{+}$
and (c)
$\langle v^{L}v^{L}\rangle ^{+}$
and (c)
![]() $\langle v^{T}v^{T}\rangle ^{+}$
in the coordinate of
$\langle v^{T}v^{T}\rangle ^{+}$
in the coordinate of
![]() $y^{+}$
in cases
$y^{+}$
in cases
![]() $1$
–
$1$
–
![]() $3$
with
$3$
with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively.
$395$
, respectively.

Figure 20. Profiles of (a)
![]() $\langle w^{L}w^{L}\rangle ^{+}$
in the coordinate of
$\langle w^{L}w^{L}\rangle ^{+}$
in the coordinate of
![]() $y/h$
, (b)
$y/h$
, (b)
![]() $\langle w^{L}w^{L}\rangle ^{+}$
and (c)
$\langle w^{L}w^{L}\rangle ^{+}$
and (c)
![]() $\langle w^{T}w^{T}\rangle ^{+}$
in the coordinate of
$\langle w^{T}w^{T}\rangle ^{+}$
in the coordinate of
![]() $y^{+}$
in cases
$y^{+}$
in cases
![]() $1$
–
$1$
–
![]() $3$
with
$3$
with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively.
$395$
, respectively.
In the near-bottom region below
![]() $y^{+}=100$
, it can be observed from the comparisons between figures 18(b) and 18(c), and between figures 20(b) and 20(c) that the magnitudes of
$y^{+}=100$
, it can be observed from the comparisons between figures 18(b) and 18(c), and between figures 20(b) and 20(c) that the magnitudes of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
and
$\langle u^{L}u^{L}\rangle ^{+}$
and
![]() $\langle w^{L}w^{L}\rangle ^{+}$
are comparable to those of
$\langle w^{L}w^{L}\rangle ^{+}$
are comparable to those of
![]() $\langle u^{T}u^{T}\rangle ^{+}$
and
$\langle u^{T}u^{T}\rangle ^{+}$
and
![]() $\langle w^{T}w^{T}\rangle ^{+}$
, respectively. This indicates that both the LC-coherent and residual parts are important to the total Reynolds normal stresses
$\langle w^{T}w^{T}\rangle ^{+}$
, respectively. This indicates that both the LC-coherent and residual parts are important to the total Reynolds normal stresses
![]() $\langle u^{\prime }u^{\prime }\rangle$
and
$\langle u^{\prime }u^{\prime }\rangle$
and
![]() $\langle w^{\prime }w^{\prime }\rangle$
near the bottom. As shown in figure 18(c), the peaks of
$\langle w^{\prime }w^{\prime }\rangle$
near the bottom. As shown in figure 18(c), the peaks of
![]() $\langle u^{T}u^{T}\rangle ^{+}$
at various Reynolds numbers collocate at
$\langle u^{T}u^{T}\rangle ^{+}$
at various Reynolds numbers collocate at
![]() $y^{+}=12$
. At
$y^{+}=12$
. At
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
, because the peak of
$Re_{\unicode[STIX]{x1D70F}}=395$
, because the peak of
![]() $\langle u^{T}u^{T}\rangle ^{+}$
is close to that of
$\langle u^{T}u^{T}\rangle ^{+}$
is close to that of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
, neither of them alone is shown in the profile of the total Reynolds normal stress
$\langle u^{L}u^{L}\rangle ^{+}$
, neither of them alone is shown in the profile of the total Reynolds normal stress
![]() $\langle u^{\prime }u^{\prime }\rangle$
(figure 15
a). As the Reynolds number increases, the peak of
$\langle u^{\prime }u^{\prime }\rangle$
(figure 15
a). As the Reynolds number increases, the peak of
![]() $\langle u^{T}u^{T}\rangle ^{+}$
is located at the same
$\langle u^{T}u^{T}\rangle ^{+}$
is located at the same
![]() $y^{+}$
, but that of
$y^{+}$
, but that of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
moves to larger
$\langle u^{L}u^{L}\rangle ^{+}$
moves to larger
![]() $y^{+}$
. As a result, the peaks of both
$y^{+}$
. As a result, the peaks of both
![]() $\langle u^{T}u^{T}\rangle ^{+}$
and
$\langle u^{T}u^{T}\rangle ^{+}$
and
![]() $\langle u^{L}u^{L}\rangle$
are shown in the profile of
$\langle u^{L}u^{L}\rangle$
are shown in the profile of
![]() $\langle u^{\prime }u^{\prime }\rangle$
, forming a bimodal shape (figure 15
a). The peak of
$\langle u^{\prime }u^{\prime }\rangle$
, forming a bimodal shape (figure 15
a). The peak of
![]() $\langle w^{T}w^{T}\rangle ^{+}$
for various Reynolds numbers collocates at
$\langle w^{T}w^{T}\rangle ^{+}$
for various Reynolds numbers collocates at
![]() $y^{+}=30$
, where its magnitude is smaller than that of
$y^{+}=30$
, where its magnitude is smaller than that of
![]() $\langle w^{L}w^{L}\rangle ^{+}$
. As a result, the peak of
$\langle w^{L}w^{L}\rangle ^{+}$
. As a result, the peak of
![]() $\langle w^{T}w^{T}\rangle ^{+}$
is not shown in the profile of
$\langle w^{T}w^{T}\rangle ^{+}$
is not shown in the profile of
![]() $\langle w^{\prime }w^{\prime }\rangle$
(figure 17
a). From the comparison between figure 17(a) and figure 20(b), it can be deduced that the single peak of
$\langle w^{\prime }w^{\prime }\rangle$
(figure 17
a). From the comparison between figure 17(a) and figure 20(b), it can be deduced that the single peak of
![]() $\langle w^{\prime }w^{\prime }\rangle$
is induced by the LC-coherent part
$\langle w^{\prime }w^{\prime }\rangle$
is induced by the LC-coherent part
![]() $\langle w^{L}w^{L}\rangle ^{+}$
. The peak locations of
$\langle w^{L}w^{L}\rangle ^{+}$
. The peak locations of
![]() $\langle w^{\prime }w^{\prime }\rangle$
and
$\langle w^{\prime }w^{\prime }\rangle$
and
![]() $\langle w^{L}w^{L}\rangle ^{+}$
are close to each other. As the Reynolds number increases, they both shift away from the bottom, with their magnitude increasing.
$\langle w^{L}w^{L}\rangle ^{+}$
are close to each other. As the Reynolds number increases, they both shift away from the bottom, with their magnitude increasing.
Different from
![]() $\langle u^{L}u^{L}\rangle ^{+}$
and
$\langle u^{L}u^{L}\rangle ^{+}$
and
![]() $\langle w^{L}w^{L}\rangle ^{+}$
, the magnitude of
$\langle w^{L}w^{L}\rangle ^{+}$
, the magnitude of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
is much smaller than that of
$\langle v^{L}v^{L}\rangle ^{+}$
is much smaller than that of
![]() $\langle v^{T}v^{T}\rangle ^{+}$
near the water bottom (figure 19
b,c). In wall-bounded turbulent flows, the vertical mixing is responsible for the generation of Reynolds shear stresses (Blackwelder & Eckelmann Reference Blackwelder and Eckelmann1979; Robinson Reference Robinson1991; Jeong et al.
Reference Jeong, Hussain, Schoppa and Kim1997; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Panton Reference Panton2001). As a result, the magnitude of
$\langle v^{T}v^{T}\rangle ^{+}$
near the water bottom (figure 19
b,c). In wall-bounded turbulent flows, the vertical mixing is responsible for the generation of Reynolds shear stresses (Blackwelder & Eckelmann Reference Blackwelder and Eckelmann1979; Robinson Reference Robinson1991; Jeong et al.
Reference Jeong, Hussain, Schoppa and Kim1997; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Panton Reference Panton2001). As a result, the magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
is also small in the near-bottom region (figure 12
b). As the Reynolds number increases, the profile of
$-\langle u^{L}v^{L}\rangle ^{+}$
is also small in the near-bottom region (figure 12
b). As the Reynolds number increases, the profile of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
shifts to larger
$\langle v^{L}v^{L}\rangle ^{+}$
shifts to larger
![]() $y^{+}$
, leading to the thickness increase of the near-bottom region with a small magnitude of
$y^{+}$
, leading to the thickness increase of the near-bottom region with a small magnitude of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
. In response, the near-bottom region with a small magnitude of
$\langle v^{L}v^{L}\rangle ^{+}$
. In response, the near-bottom region with a small magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
also becomes thicker at higher Reynolds number, which in turn leads to the reappearance of the logarithmic layer at
$-\langle u^{L}v^{L}\rangle ^{+}$
also becomes thicker at higher Reynolds number, which in turn leads to the reappearance of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
.
$Re_{\unicode[STIX]{x1D70F}}=1000$
.

Figure 21. Profiles of (a1)
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
, (a2)
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
, (a2)
![]() $\langle u^{L}u^{L}\rangle ^{+}$
, (a3)
$\langle u^{L}u^{L}\rangle ^{+}$
, (a3)
![]() $\langle u^{T}u^{T}\rangle ^{+}$
, (b1)
$\langle u^{T}u^{T}\rangle ^{+}$
, (b1)
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
, (b2)
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
, (b2)
![]() $\langle v^{L}v^{L}\rangle ^{+}$
, (b3)
$\langle v^{L}v^{L}\rangle ^{+}$
, (b3)
![]() $\langle v^{T}v^{T}\rangle ^{+}$
, (c1)
$\langle v^{T}v^{T}\rangle ^{+}$
, (c1)
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
, (c2)
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
, (c2)
![]() $\langle w^{L}w^{L}\rangle ^{+}$
and (c3)
$\langle w^{L}w^{L}\rangle ^{+}$
and (c3)
![]() $\langle w^{T}w^{T}\rangle ^{+}$
in cases
$\langle w^{T}w^{T}\rangle ^{+}$
in cases
![]() $1$
and
$1$
and
![]() $4-6$
with
$4-6$
with
![]() $kh=0.5$
,
$kh=0.5$
,
![]() $1$
,
$1$
,
![]() $1.5$
and
$1.5$
and
![]() $2$
, respectively.
$2$
, respectively.
Figure 21 shows the effects of
![]() $kh$
on the Reynolds normal stresses, together with their LC-coherent parts and the residual turbulence parts. As the value of
$kh$
on the Reynolds normal stresses, together with their LC-coherent parts and the residual turbulence parts. As the value of
![]() $kh$
increases, the profile of Stokes drift velocity in (2.4) shifts towards the water surface, and the magnitude of vortex force term in the C–L equations (2.2) is suppressed in the bottom half of the water column, which weakens the intensity of LCs. In response, the profiles of the LC-coherent Reynolds normal stresses shift towards the water surface (figure 21
a2,b2,c2), with the magnitude of the
$kh$
increases, the profile of Stokes drift velocity in (2.4) shifts towards the water surface, and the magnitude of vortex force term in the C–L equations (2.2) is suppressed in the bottom half of the water column, which weakens the intensity of LCs. In response, the profiles of the LC-coherent Reynolds normal stresses shift towards the water surface (figure 21
a2,b2,c2), with the magnitude of the
![]() $\langle u^{L}u^{L}\rangle ^{+}$
peak decreasing slightly (figure 21
a2) and those of
$\langle u^{L}u^{L}\rangle ^{+}$
peak decreasing slightly (figure 21
a2) and those of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
and
$\langle v^{L}v^{L}\rangle ^{+}$
and
![]() $\langle w^{L}w^{L}\rangle ^{+}$
decreasing throughout the bottom half of the water column (figure 21
b2,c2). The present observation of the effects of
$\langle w^{L}w^{L}\rangle ^{+}$
decreasing throughout the bottom half of the water column (figure 21
b2,c2). The present observation of the effects of
![]() $kh$
on the intensity of LCs is consistent with that of Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
$kh$
on the intensity of LCs is consistent with that of Tejada-Martínez et al. (Reference Tejada-Martínez, Grosch, Sinha, Akan and Martinat2012) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. The smaller magnitude of
$Re_{\unicode[STIX]{x1D70F}}=395$
. The smaller magnitude of
![]() $\langle v^{L}v^{L}\rangle ^{+}$
indicates weaker vertical turbulence mixing coherent to the motion of LCs, such that the magnitude of
$\langle v^{L}v^{L}\rangle ^{+}$
indicates weaker vertical turbulence mixing coherent to the motion of LCs, such that the magnitude of
![]() $-\langle u^{L}v^{L}\rangle ^{+}$
decreases as the value of
$-\langle u^{L}v^{L}\rangle ^{+}$
decreases as the value of
![]() $kh$
increases (figure 13
a), resulting in the wider logarithmic layer at larger value of
$kh$
increases (figure 13
a), resulting in the wider logarithmic layer at larger value of
![]() $kh$
(figure 8).
$kh$
(figure 8).
In the outer layer, because the turbulence is dominated by the LCs, the effects of
![]() $kh$
on the Reynolds normal stresses are dominated by those on their LC-coherent parts. This is evident by comparing figures 21(a1), 21(b1), 21(c1) with figures 21(a2), 21(b2) and 21(c2), respectively. From the comparison, it can be observed that above
$kh$
on the Reynolds normal stresses are dominated by those on their LC-coherent parts. This is evident by comparing figures 21(a1), 21(b1), 21(c1) with figures 21(a2), 21(b2) and 21(c2), respectively. From the comparison, it can be observed that above
![]() $y^{+}=200$
, the effects of
$y^{+}=200$
, the effects of
![]() $kh$
on the total Reynolds normal stresses are consistent with those on their LC-coherent part.
$kh$
on the total Reynolds normal stresses are consistent with those on their LC-coherent part.
In the near-bottom region with
![]() $y^{+}<20$
, the profiles of
$y^{+}<20$
, the profiles of
![]() $\langle u^{T}u^{T}\rangle$
,
$\langle u^{T}u^{T}\rangle$
,
![]() $\langle v^{T}v^{T}\rangle$
and
$\langle v^{T}v^{T}\rangle$
and
![]() $\langle w^{T}w^{T}\rangle$
are barely influenced by
$\langle w^{T}w^{T}\rangle$
are barely influenced by
![]() $kh$
(figure 21
a3,b3,c3), indicating that the interaction between LCs and residual turbulence is week and the residual turbulence is not significantly influenced by the reduction in LC intensity. However, because the LC-coherent motion makes a considerable contribution to
$kh$
(figure 21
a3,b3,c3), indicating that the interaction between LCs and residual turbulence is week and the residual turbulence is not significantly influenced by the reduction in LC intensity. However, because the LC-coherent motion makes a considerable contribution to
![]() $\langle u^{\prime }u^{\prime }\rangle$
and
$\langle u^{\prime }u^{\prime }\rangle$
and
![]() $\langle w^{\prime }w^{\prime }\rangle$
in the inner layer (figure 21
a2,c2), the magnitudes of
$\langle w^{\prime }w^{\prime }\rangle$
in the inner layer (figure 21
a2,c2), the magnitudes of
![]() $\langle u^{\prime }u^{\prime }\rangle$
and
$\langle u^{\prime }u^{\prime }\rangle$
and
![]() $\langle w^{\prime }w^{\prime }\rangle$
decrease in the inner layer as the value of
$\langle w^{\prime }w^{\prime }\rangle$
decrease in the inner layer as the value of
![]() $kh$
increases. As shown in figures 21(a1) and 21(c1), the LC-coherent motion influences the profiles of
$kh$
increases. As shown in figures 21(a1) and 21(c1), the LC-coherent motion influences the profiles of
![]() $\langle u^{\prime }u^{\prime }\rangle$
and
$\langle u^{\prime }u^{\prime }\rangle$
and
![]() $\langle w^{\prime }w^{\prime }\rangle$
down to
$\langle w^{\prime }w^{\prime }\rangle$
down to
![]() $y^{+}=10$
and
$y^{+}=10$
and
![]() $y^{+}=4$
, respectively. Different from
$y^{+}=4$
, respectively. Different from
![]() $\langle u^{L}u^{L}\rangle$
and
$\langle u^{L}u^{L}\rangle$
and
![]() $\langle w^{L}w^{L}\rangle$
, the magnitude of
$\langle w^{L}w^{L}\rangle$
, the magnitude of
![]() $\langle v^{L}v^{L}\rangle$
is negligibly small in the inner layer below
$\langle v^{L}v^{L}\rangle$
is negligibly small in the inner layer below
![]() $y^{+}=100$
(figure 21
b2), such that the effect of
$y^{+}=100$
(figure 21
b2), such that the effect of
![]() $kh$
on
$kh$
on
![]() $\langle v^{\prime }v^{\prime }\rangle$
is consistent with that on
$\langle v^{\prime }v^{\prime }\rangle$
is consistent with that on
![]() $\langle v^{T}v^{T}\rangle$
. As shown in figure 21(b1,b3), between
$\langle v^{T}v^{T}\rangle$
. As shown in figure 21(b1,b3), between
![]() $y^{+}=40$
and
$y^{+}=40$
and
![]() $100$
, the magnitudes of
$100$
, the magnitudes of
![]() $\langle v^{\prime }v^{\prime }\rangle$
and
$\langle v^{\prime }v^{\prime }\rangle$
and
![]() $\langle v^{T}v^{T}\rangle$
both increase slightly as the value of
$\langle v^{T}v^{T}\rangle$
both increase slightly as the value of
![]() $kh$
increases.
$kh$
increases.

Figure 22. Profiles of (a1)
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
, (a2)
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
, (a2)
![]() $\langle u^{L}u^{L}\rangle ^{+}$
, (a3)
$\langle u^{L}u^{L}\rangle ^{+}$
, (a3)
![]() $\langle u^{T}u^{T}\rangle ^{+}$
, (b1)
$\langle u^{T}u^{T}\rangle ^{+}$
, (b1)
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
, (b2)
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
, (b2)
![]() $\langle v^{L}v^{L}\rangle ^{+}$
, (b3)
$\langle v^{L}v^{L}\rangle ^{+}$
, (b3)
![]() $\langle v^{T}v^{T}\rangle ^{+}$
, (c1)
$\langle v^{T}v^{T}\rangle ^{+}$
, (c1)
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
, (c2)
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
, (c2)
![]() $\langle w^{L}w^{L}\rangle ^{+}$
and (c3)
$\langle w^{L}w^{L}\rangle ^{+}$
and (c3)
![]() $\langle w^{T}w^{T}\rangle ^{+}$
in cases 1, 7 and 8 with
$\langle w^{T}w^{T}\rangle ^{+}$
in cases 1, 7 and 8 with
![]() $La_{t}=0.7$
,
$La_{t}=0.7$
,
![]() $0.4$
and
$0.4$
and
![]() $0.9$
, respectively.
$0.9$
, respectively.
Figure 22 shows the effect of
![]() $La_{t}$
on the profiles of the Reynolds normal stresses, their LC-coherent parts, and residual parts. Similar to the LC-coherent Reynolds shear stress discussed in § 4.2, the magnitudes of the LC-coherent Reynolds normal stresses are not monotonic with the increase of
$La_{t}$
on the profiles of the Reynolds normal stresses, their LC-coherent parts, and residual parts. Similar to the LC-coherent Reynolds shear stress discussed in § 4.2, the magnitudes of the LC-coherent Reynolds normal stresses are not monotonic with the increase of
![]() $La_{t}$
. As shown in figure 22(a2,b2,c2), the magnitudes of
$La_{t}$
. As shown in figure 22(a2,b2,c2), the magnitudes of
![]() $\langle u^{L}u^{L}\rangle ^{+}$
,
$\langle u^{L}u^{L}\rangle ^{+}$
,
![]() $\langle v^{L}v^{L}\rangle ^{+}$
and
$\langle v^{L}v^{L}\rangle ^{+}$
and
![]() $\langle w^{L}w^{L}\rangle ^{+}$
are all larger at
$\langle w^{L}w^{L}\rangle ^{+}$
are all larger at
![]() $La_{t}=0.7$
than at 0.4 and 0.9, indicating that the intensity of the LCs reverses at
$La_{t}=0.7$
than at 0.4 and 0.9, indicating that the intensity of the LCs reverses at
![]() $La_{t}=0.7$
. Further because the residual parts of the Reynolds normal stresses
$La_{t}=0.7$
. Further because the residual parts of the Reynolds normal stresses
![]() $\langle u^{T}u^{T}\rangle ^{+}$
and
$\langle u^{T}u^{T}\rangle ^{+}$
and
![]() $\langle w^{T}w^{T}\rangle ^{+}$
are not significantly influenced by the value of
$\langle w^{T}w^{T}\rangle ^{+}$
are not significantly influenced by the value of
![]() $La_{t}$
(figure 22
a3,c3), the magnitudes of
$La_{t}$
(figure 22
a3,c3), the magnitudes of
![]() $\langle u^{\prime }u^{\prime }\rangle ^{+}$
and
$\langle u^{\prime }u^{\prime }\rangle ^{+}$
and
![]() $\langle w^{\prime }w^{\prime }\rangle ^{+}$
also reverse at
$\langle w^{\prime }w^{\prime }\rangle ^{+}$
also reverse at
![]() $La_{t}=0.7$
(figure 22
a1,c1). In contrast, the magnitude of
$La_{t}=0.7$
(figure 22
a1,c1). In contrast, the magnitude of
![]() $\langle v^{\prime }v^{\prime }\rangle ^{+}$
is monotonic to the value increase of
$\langle v^{\prime }v^{\prime }\rangle ^{+}$
is monotonic to the value increase of
![]() $La_{t}$
(figure 22
b1), due to the magnitude increase of
$La_{t}$
(figure 22
b1), due to the magnitude increase of
![]() $\langle v^{T}v^{T}\rangle ^{+}$
as the value of
$\langle v^{T}v^{T}\rangle ^{+}$
as the value of
![]() $La_{t}$
decreases from 0.7 to 0.4, which is also observed by Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
$La_{t}$
decreases from 0.7 to 0.4, which is also observed by Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015) at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
.
$Re_{\unicode[STIX]{x1D70F}}=395$
.
5 Budget of turbulence kinematic energy
To further assess the effects of LCs on the energy transport, we study the budget of TKE. The transport equation of TKE reads
Here,
![]() $k=\langle u_{i}^{\prime }u_{i}^{\prime }\rangle /2$
is the TKE. The budget terms on the right-hand side are the production term
$k=\langle u_{i}^{\prime }u_{i}^{\prime }\rangle /2$
is the TKE. The budget terms on the right-hand side are the production term
![]() $P_{k}$
, turbulent diffusion term
$P_{k}$
, turbulent diffusion term
![]() $T_{k}$
, pressure diffusion term
$T_{k}$
, pressure diffusion term
![]() $\unicode[STIX]{x1D6F1}_{k}$
, viscous and SGS diffusion term
$\unicode[STIX]{x1D6F1}_{k}$
, viscous and SGS diffusion term
![]() $V_{k}$
, Stokes production term
$V_{k}$
, Stokes production term
![]() $S_{k}$
and viscous and SGS dissipation term
$S_{k}$
and viscous and SGS dissipation term
![]() $\unicode[STIX]{x1D700}_{k}$
, defined respectively as
$\unicode[STIX]{x1D700}_{k}$
, defined respectively as
The above equations can also be found in McWilliams et al. (Reference McWilliams, Sullivan and Moeng1997), Harcourt (Reference Harcourt2013) and Sinha et al. (Reference Sinha, Tejada-Martínez, Akan and Grosch2015).
The profiles of the budget terms of TKE pre-multiplied by
![]() $y$
are shown in figure 23 using the scaling of
$y$
are shown in figure 23 using the scaling of
![]() $u_{\unicode[STIX]{x1D70F}}^{3}$
, with a maximum balance error smaller than
$u_{\unicode[STIX]{x1D70F}}^{3}$
, with a maximum balance error smaller than
![]() $1\,\%$
of the dominant source terms. The pre-multiplication by
$1\,\%$
of the dominant source terms. The pre-multiplication by
![]() $y$
makes the balance relationship among the budget terms in the outer layer clear (Hoyas & Jiménez Reference Hoyas and Jiménez2008; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014). From the comparison between figures 23(a) and 23(b), it is evident that below
$y$
makes the balance relationship among the budget terms in the outer layer clear (Hoyas & Jiménez Reference Hoyas and Jiménez2008; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014). From the comparison between figures 23(a) and 23(b), it is evident that below
![]() $y^{+}=100$
, the balance relationship of budget terms in the shallow-water Langmuir turbulence is similar to that in the shear-driven turbulence. Above
$y^{+}=100$
, the balance relationship of budget terms in the shallow-water Langmuir turbulence is similar to that in the shear-driven turbulence. Above
![]() $y^{+}=10$
, the energy gained from the production term
$y^{+}=10$
, the energy gained from the production term
![]() $P_{k}$
is largely balanced by the viscous and SGS dissipation term
$P_{k}$
is largely balanced by the viscous and SGS dissipation term
![]() $\unicode[STIX]{x1D700}_{k}$
. The turbulent diffusion term
$\unicode[STIX]{x1D700}_{k}$
. The turbulent diffusion term
![]() $T_{k}$
transports the energy above
$T_{k}$
transports the energy above
![]() $y^{+}=10$
downward. The viscous diffusion term
$y^{+}=10$
downward. The viscous diffusion term
![]() $V_{k}$
transports the energy in the buffer layer downward into the viscous sublayer to balance the dissipation term
$V_{k}$
transports the energy in the buffer layer downward into the viscous sublayer to balance the dissipation term
![]() $\unicode[STIX]{x1D700}_{k}$
. The energy transport below
$\unicode[STIX]{x1D700}_{k}$
. The energy transport below
![]() $y^{+}=100$
shown in figure 23 is also similar to that in the canonical wall turbulence (Hoyas & Jiménez Reference Hoyas and Jiménez2008; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014), indicating that the effect of LCs on the TKE budget is weak in the near-bottom region.
$y^{+}=100$
shown in figure 23 is also similar to that in the canonical wall turbulence (Hoyas & Jiménez Reference Hoyas and Jiménez2008; Avsarkisov et al.
Reference Avsarkisov, Hoyas, Oberlack and Garcia-Galache2014), indicating that the effect of LCs on the TKE budget is weak in the near-bottom region.

Figure 23. Pre-multiplied budget terms of TKE in (a) Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $La_{t}=0.7$
and
$La_{t}=0.7$
and
![]() $kh=0.5$
(case 1) and (b) shear-driven turbulence at
$kh=0.5$
(case 1) and (b) shear-driven turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
(case 9).
$Re_{\unicode[STIX]{x1D70F}}=1000$
(case 9).
In the outer layer, the occurrence of LCs significantly alters the transport of TKE. In the Langmuir turbulence (figure 23
a), there is a plateau region in the profile of
![]() $y^{+}P_{k}^{+}$
between
$y^{+}P_{k}^{+}$
between
![]() $y^{+}=15$
and 100. In the shear-driven turbulence (figure 23
b), the plateau of
$y^{+}=15$
and 100. In the shear-driven turbulence (figure 23
b), the plateau of
![]() $y^{+}P_{k}^{+}$
extends to
$y^{+}P_{k}^{+}$
extends to
![]() $y^{+}=300$
. According to its definition (5.2), the value of
$y^{+}=300$
. According to its definition (5.2), the value of
![]() $P_{k}^{+}$
is determined by the Reynolds shear stress
$P_{k}^{+}$
is determined by the Reynolds shear stress
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
and the mean velocity gradient
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
and the mean velocity gradient
![]() $\text{d}u^{+}/\text{d}y^{+}$
. In the outer layer above
$\text{d}u^{+}/\text{d}y^{+}$
. In the outer layer above
![]() $y^{+}=100$
, the value of
$y^{+}=100$
, the value of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is approximately unity in both Langmuir turbulence and shear-driven turbulence (figure 11
d). As a result, the value of the pre-multiplied production term is approximately
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is approximately unity in both Langmuir turbulence and shear-driven turbulence (figure 11
d). As a result, the value of the pre-multiplied production term is approximately
![]() $y^{+}P_{k}^{+}\approx y^{+}\text{d}\langle u\rangle ^{+}/\text{d}y^{+}=F$
(see (3.2) for the definition of
$y^{+}P_{k}^{+}\approx y^{+}\text{d}\langle u\rangle ^{+}/\text{d}y^{+}=F$
(see (3.2) for the definition of
![]() $F$
). In the Langmuir turbulence, due to the occurrence of LCs, the mean shear is reduced above the logarithmic layer, resulting in the value decrease of
$F$
). In the Langmuir turbulence, due to the occurrence of LCs, the mean shear is reduced above the logarithmic layer, resulting in the value decrease of
![]() $F$
and
$F$
and
![]() $y^{+}P_{k}^{+}$
above
$y^{+}P_{k}^{+}$
above
![]() $y^{+}=100$
. Above
$y^{+}=100$
. Above
![]() $y^{+}=400$
, the major source of TKE changes from the production term
$y^{+}=400$
, the major source of TKE changes from the production term
![]() $P_{k}$
to the turbulence diffusion term
$P_{k}$
to the turbulence diffusion term
![]() $T_{k}$
and Stokes production term
$T_{k}$
and Stokes production term
![]() $S_{k}$
in the Langmuir turbulence (figure 23
a). It has been known that in the deep-water Langmuir turbulence,
$S_{k}$
in the Langmuir turbulence (figure 23
a). It has been known that in the deep-water Langmuir turbulence,
![]() $S_{k}$
is an important source term in the transport equation of TKE, resulting in a large magnitude of vertical velocity fluctuations (Skyllingstad & Denbo Reference Skyllingstad and Denbo1995; McWilliams et al.
Reference McWilliams, Sullivan and Moeng1997; Li et al.
Reference Li, Garrett and Skyllingstad2005; Kukulka et al.
Reference Kukulka, Plueddemann, Trowbridge and Sullivan2010). In the following content, we first study the
$S_{k}$
is an important source term in the transport equation of TKE, resulting in a large magnitude of vertical velocity fluctuations (Skyllingstad & Denbo Reference Skyllingstad and Denbo1995; McWilliams et al.
Reference McWilliams, Sullivan and Moeng1997; Li et al.
Reference Li, Garrett and Skyllingstad2005; Kukulka et al.
Reference Kukulka, Plueddemann, Trowbridge and Sullivan2010). In the following content, we first study the
![]() $S_{k}$
term to show the effect of Stokes drift of surface waves on the TKE budget in the shallow-water Langmuir turbulence.
$S_{k}$
term to show the effect of Stokes drift of surface waves on the TKE budget in the shallow-water Langmuir turbulence.

Figure 24. Profiles of the Stokes production term
![]() $S_{k}$
scaled by
$S_{k}$
scaled by
![]() $u_{\unicode[STIX]{x1D70F}}^{3}/h$
in the TKE budget in cases 1–3 with
$u_{\unicode[STIX]{x1D70F}}^{3}/h$
in the TKE budget in cases 1–3 with
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
,
$Re_{\unicode[STIX]{x1D70F}}=1000$
,
![]() $700$
and
$700$
and
![]() $395$
, respectively, in (a) water-column coordinate
$395$
, respectively, in (a) water-column coordinate
![]() $y/h$
and (b) near-bottom coordinate
$y/h$
and (b) near-bottom coordinate
![]() $y^{+}$
. The lines without symbols in (a) are
$y^{+}$
. The lines without symbols in (a) are
![]() $S_{k}^{L}$
.
$S_{k}^{L}$
.
Figure 24 compares the profiles of
![]() $S_{k}/(u_{\unicode[STIX]{x1D70F}}^{3}/h)$
in cases 1–3 with various Reynolds numbers. According to Harcourt (Reference Harcourt2013) and Suzuki & Fox-Kemper (Reference Suzuki and Fox-Kemper2016), it can be derived that the Stokes production terms in the transport equations of
$S_{k}/(u_{\unicode[STIX]{x1D70F}}^{3}/h)$
in cases 1–3 with various Reynolds numbers. According to Harcourt (Reference Harcourt2013) and Suzuki & Fox-Kemper (Reference Suzuki and Fox-Kemper2016), it can be derived that the Stokes production terms in the transport equations of
![]() $\langle u^{\prime }u^{\prime }\rangle$
,
$\langle u^{\prime }u^{\prime }\rangle$
,
![]() $\langle v^{\prime }v^{\prime }\rangle$
and
$\langle v^{\prime }v^{\prime }\rangle$
and
![]() $\langle w^{\prime }w^{\prime }\rangle$
are respectively
$\langle w^{\prime }w^{\prime }\rangle$
are respectively
Equation (5.8) indicates that the
![]() $S_{k}$
term is directly responsible for the enhancement of
$S_{k}$
term is directly responsible for the enhancement of
![]() $\langle v^{\prime }v^{\prime }\rangle$
in the outer layer of the Langmuir turbulence (figure 16). This deduction can be further confirmed by the comparison between the profiles of
$\langle v^{\prime }v^{\prime }\rangle$
in the outer layer of the Langmuir turbulence (figure 16). This deduction can be further confirmed by the comparison between the profiles of
![]() $\langle v^{\prime }v^{\prime }\rangle$
and
$\langle v^{\prime }v^{\prime }\rangle$
and
![]() $S_{k}$
. As shown in figures 16(a) and 24(a), above
$S_{k}$
. As shown in figures 16(a) and 24(a), above
![]() $y/h=0.2$
, both
$y/h=0.2$
, both
![]() $\langle v^{\prime }v^{\prime }\rangle$
and
$\langle v^{\prime }v^{\prime }\rangle$
and
![]() $S_{k}$
have large magnitudes, and their values increase fast as
$S_{k}$
have large magnitudes, and their values increase fast as
![]() $y/h$
increases.
$y/h$
increases.
According to its definition (5.6), the
![]() $S_{k}$
term is determined by
$S_{k}$
term is determined by
![]() $-\langle u^{\prime }v^{\prime }\rangle$
and
$-\langle u^{\prime }v^{\prime }\rangle$
and
![]() $\text{d}u_{s}/\text{d}y$
. The value of
$\text{d}u_{s}/\text{d}y$
. The value of
![]() $-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is approximately unity in the outer layer (figure 11
a), while
$-\langle u^{\prime }v^{\prime }\rangle ^{+}$
is approximately unity in the outer layer (figure 11
a), while
![]() $u_{s}/u_{\unicode[STIX]{x1D70F}}$
is independent of the Reynolds number by its definition (2.4). As a result, the value of
$u_{s}/u_{\unicode[STIX]{x1D70F}}$
is independent of the Reynolds number by its definition (2.4). As a result, the value of
![]() $S_{k}/(u_{\unicode[STIX]{x1D70F}}^{3}/h)$
is expected to be insensitive to the Reynolds number, which is confirmed by figure 24(a). However, the effect of the Stokes production term on the LC-coherent fluctuations is slightly dependent on the Reynolds number. This can be explained using the decomposition
$S_{k}/(u_{\unicode[STIX]{x1D70F}}^{3}/h)$
is expected to be insensitive to the Reynolds number, which is confirmed by figure 24(a). However, the effect of the Stokes production term on the LC-coherent fluctuations is slightly dependent on the Reynolds number. This can be explained using the decomposition
![]() $S_{k}=S_{k}^{L}+S_{k}^{T}$
, where
$S_{k}=S_{k}^{L}+S_{k}^{T}$
, where
![]() $S_{k}^{L}=-\langle u^{L}v^{L}\rangle \text{d}u_{s}/\text{d}y$
and
$S_{k}^{L}=-\langle u^{L}v^{L}\rangle \text{d}u_{s}/\text{d}y$
and
![]() $S_{k}^{T}=-\langle u^{T}v^{T}\rangle \text{d}u_{s}/\text{d}y$
are the Stokes productions of
$S_{k}^{T}=-\langle u^{T}v^{T}\rangle \text{d}u_{s}/\text{d}y$
are the Stokes productions of
![]() $\langle v^{L}v^{L}\rangle$
and
$\langle v^{L}v^{L}\rangle$
and
![]() $\langle v^{T}v^{T}\rangle$
, respectively. The profiles of
$\langle v^{T}v^{T}\rangle$
, respectively. The profiles of
![]() $S_{k}^{L}$
at various Reynolds numbers are also shown in figure 24(a). From the figure, it can be seen that the magnitude of
$S_{k}^{L}$
at various Reynolds numbers are also shown in figure 24(a). From the figure, it can be seen that the magnitude of
![]() $S_{k}^{L}$
increases slightly as the Reynolds number increases. Correspondingly, the magnitude of
$S_{k}^{L}$
increases slightly as the Reynolds number increases. Correspondingly, the magnitude of
![]() $\langle v^{L}v^{L}\rangle$
also increases with the Reynolds number in the water-column coordinate (figure 19
a). On the other hand, as shown in figure 24(b), the profiles of
$\langle v^{L}v^{L}\rangle$
also increases with the Reynolds number in the water-column coordinate (figure 19
a). On the other hand, as shown in figure 24(b), the profiles of
![]() $S_{k}$
shift to larger
$S_{k}$
shift to larger
![]() $y^{+}$
as
$y^{+}$
as
![]() $Re_{\unicode[STIX]{x1D70F}}$
increases. In response, when observed in the near-bottom coordinate
$Re_{\unicode[STIX]{x1D70F}}$
increases. In response, when observed in the near-bottom coordinate
![]() $y^{+}$
, the effect of Stokes production on
$y^{+}$
, the effect of Stokes production on
![]() $\langle v^{\prime }v^{\prime }\rangle$
is weakened near the bottom. Therefore, as the Reynolds number increases, the profiles of
$\langle v^{\prime }v^{\prime }\rangle$
is weakened near the bottom. Therefore, as the Reynolds number increases, the profiles of
![]() $\langle v^{\prime }v^{\prime }\rangle$
below
$\langle v^{\prime }v^{\prime }\rangle$
below
![]() $y^{+}=50$
in the Langmuir turbulence approach that in the shear-driven turbulence (figure 16
a).
$y^{+}=50$
in the Langmuir turbulence approach that in the shear-driven turbulence (figure 16
a).

Figure 25. Profiles of the Stokes production term
![]() $S_{k}$
scaled by
$S_{k}$
scaled by
![]() $u_{\unicode[STIX]{x1D70F}}^{3}/h$
(a) in cases
$u_{\unicode[STIX]{x1D70F}}^{3}/h$
(a) in cases
![]() $1$
and
$1$
and
![]() $4$
–
$4$
–
![]() $6$
with
$6$
with
![]() $kh=0.5$
,
$kh=0.5$
,
![]() $1$
,
$1$
,
![]() $1.5$
and
$1.5$
and
![]() $2$
, respectively and (b) cases
$2$
, respectively and (b) cases
![]() $1$
,
$1$
,
![]() $7$
and
$7$
and
![]() $8$
with
$8$
with
![]() $La_{t}=0.7$
,
$La_{t}=0.7$
,
![]() $0.4$
and
$0.4$
and
![]() $0.9$
, respectively.
$0.9$
, respectively.
Different from the Reynolds number effect,
![]() $kh$
and
$kh$
and
![]() $La_{t}$
affect the magnitude of
$La_{t}$
affect the magnitude of
![]() $S_{k}$
. Figure 25 shows the effects of
$S_{k}$
. Figure 25 shows the effects of
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the profile of
$La_{t}$
on the profile of
![]() $S_{k}$
. It can be observed from the figure that as the value of either
$S_{k}$
. It can be observed from the figure that as the value of either
![]() $kh$
or
$kh$
or
![]() $La_{t}$
increases, the magnitude of
$La_{t}$
increases, the magnitude of
![]() $S_{k}$
decreases. This is expected from the definitions of the
$S_{k}$
decreases. This is expected from the definitions of the
![]() $S_{k}$
term (5.6) and Stokes drift velocity (2.4). As a result of the reduction of
$S_{k}$
term (5.6) and Stokes drift velocity (2.4). As a result of the reduction of
![]() $S_{k}$
, the magnitude of
$S_{k}$
, the magnitude of
![]() $\langle v^{\prime }v^{\prime }\rangle$
also decreases in the outer layer (figures 21
b1 and 22
b1), which leads to the suppression of vertical mixing.
$\langle v^{\prime }v^{\prime }\rangle$
also decreases in the outer layer (figures 21
b1 and 22
b1), which leads to the suppression of vertical mixing.
It is shown in figure 23 that the turbulence diffusion term
![]() $T_{k}$
is the most important source in the transport equation of TKE above
$T_{k}$
is the most important source in the transport equation of TKE above
![]() $y^{+}=400$
in the Langmuir turbulence, and its magnitude is larger than that in the shear-driven turbulence. Here, we further study the effect of LCs on the
$y^{+}=400$
in the Langmuir turbulence, and its magnitude is larger than that in the shear-driven turbulence. Here, we further study the effect of LCs on the
![]() $T_{k}$
term. The
$T_{k}$
term. The
![]() $T_{k}$
term can be decomposed as
$T_{k}$
term can be decomposed as
Here, the
![]() $T_{k}^{T+}$
term is the turbulent diffusion only related to the residual velocity fluctuations, defined as
$T_{k}^{T+}$
term is the turbulent diffusion only related to the residual velocity fluctuations, defined as
The
![]() $T_{k}^{L\ast }$
term is defined as
$T_{k}^{L\ast }$
term is defined as
 $$\begin{eqnarray}T_{k}^{L\ast }=\underbrace{-\frac{1}{2}\frac{\text{d}\langle u_{i}^{L}u_{i}^{L}v^{L}+u_{i}^{T}u_{i}^{T}v^{L}\rangle }{\text{d}y}}_{T_{k}^{L1}}\underbrace{-\frac{\text{d}\langle u_{i}^{L}u_{i}^{T}v^{T}\rangle }{\text{d}y}}_{T_{k}^{L2}},\end{eqnarray}$$
$$\begin{eqnarray}T_{k}^{L\ast }=\underbrace{-\frac{1}{2}\frac{\text{d}\langle u_{i}^{L}u_{i}^{L}v^{L}+u_{i}^{T}u_{i}^{T}v^{L}\rangle }{\text{d}y}}_{T_{k}^{L1}}\underbrace{-\frac{\text{d}\langle u_{i}^{L}u_{i}^{T}v^{T}\rangle }{\text{d}y}}_{T_{k}^{L2}},\end{eqnarray}$$
which includes the LC-coherent velocity fluctuations and represents the effect of the LCs. A similar triple decomposition was used by Martinat et al. (Reference Martinat, Grosch and Gatski2014) to analyse the budget balance of
![]() $\langle u_{i}^{L}u_{i}^{L}\rangle /2$
and
$\langle u_{i}^{L}u_{i}^{L}\rangle /2$
and
![]() $\langle u_{i}^{T}u_{i}^{T}\rangle /2$
at
$\langle u_{i}^{T}u_{i}^{T}\rangle /2$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. Figure 26 compares the profiles of
$Re_{\unicode[STIX]{x1D70F}}=395$
. Figure 26 compares the profiles of
![]() $y^{+}T_{k}^{T+}$
,
$y^{+}T_{k}^{T+}$
,
![]() $y^{+}T_{k}^{L\ast +}$
and
$y^{+}T_{k}^{L\ast +}$
and
![]() $y^{+}T_{k}$
in Langmuir turbulence (case 1). As shown, above
$y^{+}T_{k}$
in Langmuir turbulence (case 1). As shown, above
![]() $y^{+}=200$
, the magnitude of
$y^{+}=200$
, the magnitude of
![]() $y^{+}T_{k}^{L\ast +}$
is significantly larger than that of
$y^{+}T_{k}^{L\ast +}$
is significantly larger than that of
![]() $y^{+}T_{k}^{T+}$
, and the profiles of
$y^{+}T_{k}^{T+}$
, and the profiles of
![]() $y^{+}T_{k}^{L\ast +}$
and
$y^{+}T_{k}^{L\ast +}$
and
![]() $y^{+}T_{k}^{+}$
almost collapse. This indicates that the large magnitude of the turbulent diffusion term in the outer layer is contributed by the LCs.
$y^{+}T_{k}^{+}$
almost collapse. This indicates that the large magnitude of the turbulent diffusion term in the outer layer is contributed by the LCs.

Figure 26. Profiles of pre-multiplied turbulent diffusion terms
![]() $y^{+}T_{k}^{+}$
,
$y^{+}T_{k}^{+}$
,
![]() $y^{+}T_{k}^{T+}$
and
$y^{+}T_{k}^{T+}$
and
![]() $y^{+}T_{k}^{L\ast +}$
in Langmuir turbulence (case 1).
$y^{+}T_{k}^{L\ast +}$
in Langmuir turbulence (case 1).

Figure 27. Profiles of pre-multiplied turbulent diffusion term
![]() $y^{+}T_{k}^{L\ast +}$
,
$y^{+}T_{k}^{L\ast +}$
,
![]() $y^{+}T_{k}^{L1+}$
and
$y^{+}T_{k}^{L1+}$
and
![]() $y^{+}T_{k}^{L2+}$
in Langmuir turbulence (case 1).
$y^{+}T_{k}^{L2+}$
in Langmuir turbulence (case 1).
According to (5.11),
![]() $T_{k}^{L\ast +}$
can be further decomposed into
$T_{k}^{L\ast +}$
can be further decomposed into
![]() $T_{k}^{L1+}$
and
$T_{k}^{L1+}$
and
![]() $T_{k}^{L2+}$
. The
$T_{k}^{L2+}$
. The
![]() $T_{k}^{L1+}$
term is the turbulence diffusion term induced by
$T_{k}^{L1+}$
term is the turbulence diffusion term induced by
![]() $v^{L}$
, and
$v^{L}$
, and
![]() $T_{k}^{L2+}$
is the interaction between the residual turbulence and LCs. Figure 27 compares the profiles of
$T_{k}^{L2+}$
is the interaction between the residual turbulence and LCs. Figure 27 compares the profiles of
![]() $y^{+}T_{k}^{L\ast +}$
,
$y^{+}T_{k}^{L\ast +}$
,
![]() $y^{+}T_{k}^{L1+}$
and
$y^{+}T_{k}^{L1+}$
and
![]() $y^{+}T_{k}^{L2+}$
in Langmuir turbulence (case 1). As shown, above
$y^{+}T_{k}^{L2+}$
in Langmuir turbulence (case 1). As shown, above
![]() $y^{+}=200$
, the magnitude of
$y^{+}=200$
, the magnitude of
![]() $y^{+}T_{k}^{L1+}$
is much larger than that of
$y^{+}T_{k}^{L1+}$
is much larger than that of
![]() $y^{+}T_{k}^{L2+}$
, indicating that the large magnitude of
$y^{+}T_{k}^{L2+}$
, indicating that the large magnitude of
![]() $T_{k}^{L\ast +}$
and
$T_{k}^{L\ast +}$
and
![]() $T_{k}^{+}$
in the outer layer is induced by the vertical mixing of the LCs. Therefore, the vertical velocity fluctuations of LCs generated by
$T_{k}^{+}$
in the outer layer is induced by the vertical mixing of the LCs. Therefore, the vertical velocity fluctuations of LCs generated by
![]() $S_{k}$
in the outer layer lead to the strong turbulent diffusion, which significantly alters the energy transport in the outer layer.
$S_{k}$
in the outer layer lead to the strong turbulent diffusion, which significantly alters the energy transport in the outer layer.
6 Summary
In this study, wall-resolved large-eddy simulations based on the C–L equations have been performed to investigate the influence of LCs on the turbulence in the bottom boundary layer of shallow water. The effect of Reynolds number
![]() $Re_{\unicode[STIX]{x1D70F}}$
on the mean velocity and Reynolds stresses is investigated by varying
$Re_{\unicode[STIX]{x1D70F}}$
on the mean velocity and Reynolds stresses is investigated by varying
![]() $Re_{\unicode[STIX]{x1D70F}}$
from
$Re_{\unicode[STIX]{x1D70F}}$
from
![]() $395$
up to
$395$
up to
![]() $1000$
. The wall-resolved LES of the shallow-water Langmuir turbulence at
$1000$
. The wall-resolved LES of the shallow-water Langmuir turbulence at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
is carried out for the first time. The effects of the dimensionless wavenumber of surface waves
$Re_{\unicode[STIX]{x1D70F}}=1000$
is carried out for the first time. The effects of the dimensionless wavenumber of surface waves
![]() $kh$
and turbulent Langmuir number
$kh$
and turbulent Langmuir number
![]() $La_{t}$
, two parameters dominating the intensity of LCs, are also studied. To analyse the result, the total velocity fluctuation
$La_{t}$
, two parameters dominating the intensity of LCs, are also studied. To analyse the result, the total velocity fluctuation
![]() $u_{i}^{\prime }$
is decomposed into the LC-coherent velocity fluctuation
$u_{i}^{\prime }$
is decomposed into the LC-coherent velocity fluctuation
![]() $u_{i}^{L}$
and residual turbulent velocity fluctuation
$u_{i}^{L}$
and residual turbulent velocity fluctuation
![]() $u_{i}^{T}$
, and their contributions to the Reynolds stresses are analysed. The transport equations of TKE are studied to further reveal the effect of LCs on the energy transport. The major findings of this paper are summarized as follows.
$u_{i}^{T}$
, and their contributions to the Reynolds stresses are analysed. The transport equations of TKE are studied to further reveal the effect of LCs on the energy transport. The major findings of this paper are summarized as follows.
In the analysis of the mean streamwise velocity, we focus on the effects of
![]() $Re$
,
$Re$
,
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the thickness of the logarithmic layer, identified as the plateau region in the profile of the diagnostic function
$La_{t}$
on the thickness of the logarithmic layer, identified as the plateau region in the profile of the diagnostic function
![]() $F$
. The present simulations show that the logarithmic layer is absent at low Reynolds numbers
$F$
. The present simulations show that the logarithmic layer is absent at low Reynolds numbers
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
and 700, but reappears at
$Re_{\unicode[STIX]{x1D70F}}=395$
and 700, but reappears at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
. As the value of either
$Re_{\unicode[STIX]{x1D70F}}=1000$
. As the value of either
![]() $kh$
or
$kh$
or
![]() $La_{t}$
increases, the magnitude of the C–L vortex force in the momentum equation decreases, leading to the thickness increase of the logarithmic layer. In the plateau region of
$La_{t}$
increases, the magnitude of the C–L vortex force in the momentum equation decreases, leading to the thickness increase of the logarithmic layer. In the plateau region of
![]() $F$
, the value of
$F$
, the value of
![]() $F$
is identical to the von Kármán constant. It is observed that the von Kármán constant in the bottom boundary of the Langmuir turbulence under investigation varies in a narrow range with
$F$
is identical to the von Kármán constant. It is observed that the von Kármán constant in the bottom boundary of the Langmuir turbulence under investigation varies in a narrow range with
![]() $0.362\pm 0.003$
, which is below the classic value 0.41.
$0.362\pm 0.003$
, which is below the classic value 0.41.
In the outer layer, the LC-coherent part makes important contributions to the total Reynolds stresses. In the water-column coordinate
![]() $y/h$
, the peak locations of
$y/h$
, the peak locations of
![]() $\langle -u^{L}v^{L}\rangle$
,
$\langle -u^{L}v^{L}\rangle$
,
![]() $\langle u^{L}u^{L}\rangle$
and
$\langle u^{L}u^{L}\rangle$
and
![]() $\langle w^{L}w^{L}\rangle$
remain the same at various
$\langle w^{L}w^{L}\rangle$
remain the same at various
![]() $Re_{\unicode[STIX]{x1D70F}}$
with given values of
$Re_{\unicode[STIX]{x1D70F}}$
with given values of
![]() $La_{t}$
and
$La_{t}$
and
![]() $kh$
, indicating that the locations of LCs are scaled by
$kh$
, indicating that the locations of LCs are scaled by
![]() $h$
. On the other hand, when observed in the near-bottom coordinate
$h$
. On the other hand, when observed in the near-bottom coordinate
![]() $y^{+}$
, the profile of
$y^{+}$
, the profile of
![]() $\langle -u^{L}v^{L}\rangle$
shifts to larger
$\langle -u^{L}v^{L}\rangle$
shifts to larger
![]() $y^{+}$
at higher Reynolds number, indicating a weaker influence of LCs on the momentum transfer near the bottom, which results in the reappearance of the logarithmic layer at
$y^{+}$
at higher Reynolds number, indicating a weaker influence of LCs on the momentum transfer near the bottom, which results in the reappearance of the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
. Furthermore, as the Reynolds number increases, the peak location of
$Re_{\unicode[STIX]{x1D70F}}=1000$
. Furthermore, as the Reynolds number increases, the peak location of
![]() $\langle u^{T}u^{T}\rangle$
remains unchanged, while that of
$\langle u^{T}u^{T}\rangle$
remains unchanged, while that of
![]() $\langle u^{L}u^{L}\rangle$
shifts to larger
$\langle u^{L}u^{L}\rangle$
shifts to larger
![]() $y^{+}$
. As a result, the peaks of both
$y^{+}$
. As a result, the peaks of both
![]() $\langle u^{T}u^{T}\rangle$
and
$\langle u^{T}u^{T}\rangle$
and
![]() $\langle u^{L}u^{L}\rangle$
are shown in the profile of
$\langle u^{L}u^{L}\rangle$
are shown in the profile of
![]() $\langle u^{\prime }u^{\prime }\rangle$
at
$\langle u^{\prime }u^{\prime }\rangle$
at
![]() $Re_{\unicode[STIX]{x1D70F}}=700$
and
$Re_{\unicode[STIX]{x1D70F}}=700$
and
![]() $1000$
, resulting in a bimodal shape. The profile of
$1000$
, resulting in a bimodal shape. The profile of
![]() $\langle w^{\prime }w^{\prime }\rangle$
only has a single peak, with its location close to the peak of
$\langle w^{\prime }w^{\prime }\rangle$
only has a single peak, with its location close to the peak of
![]() $\langle w^{L}w^{L}\rangle$
. Owing to the contribution of LCs, the magnitude of
$\langle w^{L}w^{L}\rangle$
. Owing to the contribution of LCs, the magnitude of
![]() $\langle v^{\prime }v^{\prime }\rangle$
increases fast with
$\langle v^{\prime }v^{\prime }\rangle$
increases fast with
![]() $y/h$
in the outer layer above
$y/h$
in the outer layer above
![]() $y/h=0.17$
at all of the Reynolds numbers under investigation.
$y/h=0.17$
at all of the Reynolds numbers under investigation.
As the value of
![]() $kh$
increases, the intensity of LCs is reduced, characterized by the magnitude decrease of
$kh$
increases, the intensity of LCs is reduced, characterized by the magnitude decrease of
![]() $\langle -u^{L}v^{L}\rangle$
,
$\langle -u^{L}v^{L}\rangle$
,
![]() $\langle u^{L}u^{L}\rangle$
,
$\langle u^{L}u^{L}\rangle$
,
![]() $\langle v^{L}v^{L}\rangle$
and
$\langle v^{L}v^{L}\rangle$
and
![]() $\langle w^{L}w^{L}\rangle$
in the outer layer, which leads to the magnitude decrease of their corresponding total Reynolds stresses. Furthermore, at larger value of
$\langle w^{L}w^{L}\rangle$
in the outer layer, which leads to the magnitude decrease of their corresponding total Reynolds stresses. Furthermore, at larger value of
![]() $kh$
, the peak locations of
$kh$
, the peak locations of
![]() $-\langle u^{L}v^{L}\rangle$
,
$-\langle u^{L}v^{L}\rangle$
,
![]() $\langle u^{L}u^{L}\rangle$
and
$\langle u^{L}u^{L}\rangle$
and
![]() $\langle w^{L}w^{L}\rangle$
are farther away from the bottom, indicating a weaker influence of LCs on the momentum and energy transfer in the bottom inner layer. As a result, the thickness of the logarithmic layer increases as the value of
$\langle w^{L}w^{L}\rangle$
are farther away from the bottom, indicating a weaker influence of LCs on the momentum and energy transfer in the bottom inner layer. As a result, the thickness of the logarithmic layer increases as the value of
![]() $kh$
increases.
$kh$
increases.
The intensity of LCs is not monotonic in response to the increase of
![]() $La_{t}$
. The magnitudes of
$La_{t}$
. The magnitudes of
![]() $-\langle u^{L}v^{L}\rangle$
,
$-\langle u^{L}v^{L}\rangle$
,
![]() $\langle u^{L}u^{L}\rangle$
,
$\langle u^{L}u^{L}\rangle$
,
![]() $\langle v^{L}v^{L}\rangle$
and
$\langle v^{L}v^{L}\rangle$
and
![]() $\langle w^{L}w^{L}\rangle$
all reverse at
$\langle w^{L}w^{L}\rangle$
all reverse at
![]() $La_{t}=0.7$
. As the value of
$La_{t}=0.7$
. As the value of
![]() $La_{t}$
decreases from 0.9 to 0.7, the logarithmic layer becomes thinner because of the stronger effect of LCs on the momentum transfer. As
$La_{t}$
decreases from 0.9 to 0.7, the logarithmic layer becomes thinner because of the stronger effect of LCs on the momentum transfer. As
![]() $La_{t}$
further decreases from
$La_{t}$
further decreases from
![]() $0.7$
to
$0.7$
to
![]() $0.4$
, although the LCs become weaker, the logarithmic layer is thinner at
$0.4$
, although the LCs become weaker, the logarithmic layer is thinner at
![]() $La_{t}=0.4$
due to the enhancement of outer-layer large-scale turbulence motions that penetrate to the near-bottom region. This effect alters the momentum transfer in the near-bottom region, and tends to disrupt the logarithmic law.
$La_{t}=0.4$
due to the enhancement of outer-layer large-scale turbulence motions that penetrate to the near-bottom region. This effect alters the momentum transfer in the near-bottom region, and tends to disrupt the logarithmic law.
The effects of
![]() $Re_{\unicode[STIX]{x1D70F}}$
,
$Re_{\unicode[STIX]{x1D70F}}$
,
![]() $kh$
and
$kh$
and
![]() $La_{t}$
on the intensity of LCs are further explained through the analyses of the Stokes production term
$La_{t}$
on the intensity of LCs are further explained through the analyses of the Stokes production term
![]() $S_{k}$
in the transport equation of TKE. The Stokes production term induces large magnitude of vertical velocity fluctuations in the outer layer mainly contributed by LCs. The contribution of the Stoke production term to LCs,
$S_{k}$
in the transport equation of TKE. The Stokes production term induces large magnitude of vertical velocity fluctuations in the outer layer mainly contributed by LCs. The contribution of the Stoke production term to LCs,
![]() $S_{k}^{L}$
, is slightly dependent on
$S_{k}^{L}$
, is slightly dependent on
![]() $Re_{\unicode[STIX]{x1D70F}}$
, so that
$Re_{\unicode[STIX]{x1D70F}}$
, so that
![]() $\langle v^{L}v^{L}\rangle$
varies with
$\langle v^{L}v^{L}\rangle$
varies with
![]() $Re_{\unicode[STIX]{x1D70F}}$
. As the value of either
$Re_{\unicode[STIX]{x1D70F}}$
. As the value of either
![]() $kh$
or
$kh$
or
![]() $La_{t}$
increases, the magnitude of
$La_{t}$
increases, the magnitude of
![]() $S_{k}$
decreases, leading to the smaller magnitude of
$S_{k}$
decreases, leading to the smaller magnitude of
![]() $\langle v^{\prime }v^{\prime }\rangle$
in the outer layer. Due to the occurrence of LCs, the turbulence diffusion term
$\langle v^{\prime }v^{\prime }\rangle$
in the outer layer. Due to the occurrence of LCs, the turbulence diffusion term
![]() $T_{k}$
is significantly amplified in the outer layer of the Langmuir turbulence, which becomes the most important source of TKE instead of the production term
$T_{k}$
is significantly amplified in the outer layer of the Langmuir turbulence, which becomes the most important source of TKE instead of the production term
![]() $P_{k}$
as in the shear-driven turbulence.
$P_{k}$
as in the shear-driven turbulence.
Finally, we remark that the present results show the capability of numerical simulations in the investigation of flow details of the bottom boundary layer in shallow-water Langmuir turbulence. Before we can reach a much higher Reynolds number of practical interest with wall-modelled LES, it is important to examine the logarithmic law using wall-resolved LES. Our LES results show that the disruption effect of LCs on the logarithmic law becomes less significant as the Reynolds number increases and the logarithmic layer reappears at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, indicating that the wall-layer modelling based on the logarithmic law can still be used at high Reynolds number. Recently, Golshan et al. (Reference Golshan, Tejada-Martínez, Juha and Bazilevs2017) conducted wall-modelled LES with the conventional wall-layer model based on the logarithmic law, and captured the disruption of the logarithmic layer in the profile of the mean velocity at
$Re_{\unicode[STIX]{x1D70F}}=1000$
, indicating that the wall-layer modelling based on the logarithmic law can still be used at high Reynolds number. Recently, Golshan et al. (Reference Golshan, Tejada-Martínez, Juha and Bazilevs2017) conducted wall-modelled LES with the conventional wall-layer model based on the logarithmic law, and captured the disruption of the logarithmic layer in the profile of the mean velocity at
![]() $Re_{\unicode[STIX]{x1D70F}}=395$
. In the future, it will be of interest to examine if the wall-layer model based on the logarithmic law can capture the reappearance of the logarithmic layer and the thinning effect of LCs on the logarithmic layer at
$Re_{\unicode[STIX]{x1D70F}}=395$
. In the future, it will be of interest to examine if the wall-layer model based on the logarithmic law can capture the reappearance of the logarithmic layer and the thinning effect of LCs on the logarithmic layer at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
and higher. However, care must be taken to ensure that the first grid is located in the logarithmic layer, given that the logarithmic layer is thinner in the Langmuir turbulence than in shear-driven turbulence.
$Re_{\unicode[STIX]{x1D70F}}=1000$
and higher. However, care must be taken to ensure that the first grid is located in the logarithmic layer, given that the logarithmic layer is thinner in the Langmuir turbulence than in shear-driven turbulence.
Acknowledgements
This work is partially supported by the Office of Naval Research, National Science Foundation and Minnesota Sea Grant.