2. NONLINEAR LASER EIGEN MODE

Consider a singly ionized cold collionless plasma of uniform electron density n ₀⁰. A two-dimensional intense short pulse laser propagates through it along $\hat{z}$ with fast phase variation as,

(1)$${\bf E}=\hat{y} A_T\lpar x\rpar e^{-i\lpar {\rm \omega} t-k_z z\rpar }.$$

The duration of the pulse is larger than the electron plasma period but much shorter than the ion plasma period, so that the ions remain immobile. We look for a suitable profile of A _T (x) that would propagate without convergence or divergence and allow A _T to acquire relativistically large values. The laser imparts oscillatory velocity to electrons, $\vec v=$$e{\bf E}/mi{\rm \omega} {\rm \gamma}$, where ${\rm \gamma}=\sqrt{1+a^2/2}\comma \; a=e \vert A_T \vert /m{\rm \omega} c\comma \; -e$ and m are the electronic charge and rest mass, and c is the speed of light in vacuum. The laser exerts a ponderomotive force on electrons,

(2)$${\bf F}_{\bf p}=e \nabla {\rm \phi}_p\comma \;$$

where ${\rm \phi}_p=-({mc^2 / e}) \lpar \sqrt {1+a^2/2}-1 \rpar.$ For an eigen mode, field amplitude does not change with z, hence the ponderomotive force has only x− component. It pushes the electrons outward (to higher values of |x|) producing a space charge field E_s = −∇ϕ_s. The radial movement of electrons takes place as long as $\vec F_p \gt e \vec E_s$. On the time scale of a plasma period ω⁻¹_p, a quasi-steady state is reached when F_p = e E_s, or ϕ_s = −ϕ_p. From the Poisson's equation,

(3)$$\nabla^2 {\rm \phi}_s=4{\rm \pi} e\lpar n_e-n_0^0\rpar \comma \;$$

one may write, using ϕ_s = −ϕ_p, the modified electron density

(4)$$n_e=n^0_0 - {1\over 4{\rm \pi} e} \nabla^2 {\rm \phi}_p\comma \;$$

where n ⁰₀ is the ion density (equal to unperturbed electron density). Since, n _e cannot be negative, Eq. (4) is valid only as long as

(5)$$n^0_0 \gt {1\over 4{\rm \pi} e}\nabla^2 {\rm \phi}_p.$$

Thus, the electron density in the channel can be written as,

(6)$$n_e = \left\{\matrix{0 & \hbox{for} x \lt r_{0p} \cr n_0^0 - {1 \over 4{\rm \pi} e}\nabla ^2 {\rm \phi} _p & {\rm for} x \gt r_{0p}}\right. \comma \;$$

where r _0p is the value of x at which

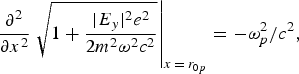(7)$${\partial^2 \over \partial x^2} \left. \sqrt{1+{\vert E_y \vert^2e^2 \over 2m^2{\rm \omega}^2c^2}}\right\vert_{x\,=\,r_{0p}} = -{\rm \omega}^2_p/c^2\comma \;$$

where ${\rm \omega}_p=\sqrt{4{\rm \pi} n^0_0 e^2/m}=k_{\,p}c.$ One may note that the electron density increases from zero at |x| = r _0p to higher values as |x| increases.

For x < r _0p (for a symmetric mode), the laser field E _y may be written as,

(8)$$E_y=A_0 cos\lpar {\rm \alpha} x\rpar e^{-i\lpar {\rm \omega} t-k_{z}z\rpar }\comma \;$$

where A ₀ is the amplitude of the laser at x = 0 and ${\rm \alpha}=\sqrt{({{\rm \omega}^2 / c^2})-k^2_z}.$ For x > r _0p, E _y is governed by the wave equation

(9)$${\partial^2 \over \partial x^2}E_y+ \left[{{\rm \omega}^2\over c^2}\left(1-{{\rm \omega}^2_p \over {\rm \omega}^2}{n_e\over {\rm \gamma} n^0_0}\right)-k^2_z \right]E_y=0.$$

The term ${\rm \omega}^2_p({ne/ {\rm \gamma} n^0_0})$ in the wave equation arises due to the contribution of current density, $\vec J = -n_e e \vec v$ driven by the laser pulse and $\vec v\lpar \!= \hat{y} e E_y/mi{\rm \omega} {\rm \gamma}\rpar $ is the oscillatory velocity imparted by the laser.

Using E _y from Eq. (1) in Eq. (9), writing A _T = A e ^iϕ with A and ϕ real, and separating out the real and imaginary parts of Eq. (9), we obtain

$$\displaystyle{d \over dx} \left(A^2 \displaystyle{d {\rm \phi} \over dx} \right)= 0 \Rightarrow A^2 \displaystyle{d {\rm \phi} \over dx} = constant = C_1\comma \;$$

(10)$$\displaystyle{d^2 A \over dx^2} - \displaystyle{C_1^2 \over A^3} + \left[\displaystyle{{\rm \omega}^2 \over c^2} \left(1 - \displaystyle{{\rm \omega}_p^2 \over {\rm \omega}^2} \displaystyle{n_e \over {\rm \gamma} n_0^0}\right)- k_z^2\right]A = 0.$$

One may multiply Eq. (10) by e/mωc and write it for normalized amplitude a = eA/mωc as,

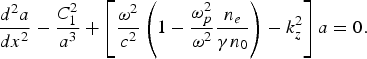(11)$$\displaystyle{d^2 a \over dx^2} - \displaystyle{C_1^2 \over a^3} + \left[\displaystyle{{\rm \omega}^2 \over c^2} \left(1 - \displaystyle{{\rm \omega}_p^2 \over {\rm \omega}^2} \displaystyle{n_e \over {\rm \gamma} n_0}\right)- k_z^2\right]a = 0.$$

Using the value of n _e/n ₀⁰ from Eq. (4),

(12)$$\displaystyle{n_e \over n_0^0} = 1 + \displaystyle{c^2 \over 2{\rm \omega}_p^2} \left(\displaystyle{a \over \sqrt{1 + a^2/2}} \displaystyle{d^2 a \over dx^2} + \displaystyle{1 \over \lpar 1 + a^2/2\rpar ^{3/2}}\left(\displaystyle{da \over dx}\right)^2\right)\comma \;$$

Eq. (11) can be written as

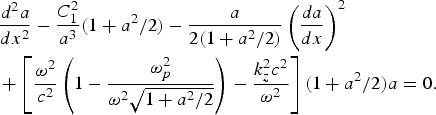(13)$$\eqalign{& \displaystyle{d^2 a \over dx^2} - {C_1^2 \over a^3} \lpar 1 + a^2/2\rpar - \displaystyle{a \over 2\lpar 1 + a^2/2\rpar } \left(\displaystyle{da \over dx}\right)^2 \cr & + \left[\displaystyle{{\rm \omega}^2 \over c^2}\left(1 - \displaystyle{{\rm \omega}_p^2 \over {\rm \omega}^2 \sqrt{1 + a^2/2}}\right)- \displaystyle{k_z^2 c^2 \over {\rm \omega}^2}\right]\lpar 1 + a^2/2\rpar a = 0.}$$

As x → ∞, the nonlinear terms vanish and a → 0. The equation will remain well behaved only when C₁ = 0. At x = r _0p, n _e/n ₀⁰ = 0, Eq. (12) gives

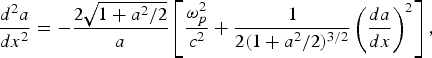(14)$$\displaystyle{d^2 a \over dx^2} = - \displaystyle{2 \sqrt{1 + a^2/2} \over a} \left[\displaystyle{{\rm \omega}_p^2 \over c^2} + \displaystyle{1 \over 2\lpar 1 + a^2/2\rpar ^{3/2}} \left(\displaystyle{da \over dx}\right)^2\right]\comma \;$$

while from Eq. (11), on putting n_e/n₀⁰ = 0, and C ₁ = 0, we get

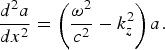(15)$$\displaystyle{d^2 a \over dx^2} = \left(\displaystyle{{\rm \omega}^2 \over c^2} - k_z^2\right)a.$$

Comparing Eq. (14) and (15), we obtain,

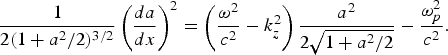(16)$$\displaystyle{1 \over 2\lpar 1 + a^2/2\rpar ^{3/2}} \left(\displaystyle{da \over dx}\right)^2 = \left(\displaystyle{{\rm \omega}^2 \over c^2} - k_z^2 \right)\displaystyle{a^2 \over 2 \sqrt{1 + a^2/2}} - \displaystyle{{\rm \omega}_p^2 \over c^2}.$$

We want a and da/dx to be continuous at x = r _0p, hence

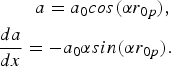(17)$$\eqalign{& \quad \quad a = a_0 cos\lpar {\rm \alpha} {r_{0p}}\rpar \comma \; \cr & \displaystyle{da \over dx} = - a_0 {\rm \alpha} sin\lpar {\rm \alpha} {r_{0p}}\rpar .}$$

Using these in Eq. (16) we get an equation governing r _0p,

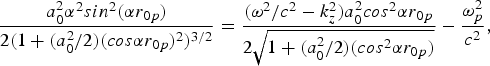(18)$$\displaystyle{a_0^2 {\rm \alpha}^2 sin^2 \lpar {\rm \alpha} {r_{0p}}\rpar \over 2\lpar 1 + \lpar a_0^2/2\rpar \lpar cos {\rm \alpha} {r_{0p}}\rpar ^2\rpar ^{3/2}} = \displaystyle{\lpar {\rm \omega}^2/c^2 - k_z^2\rpar a_0^2 cos^2 {\rm \alpha} {r_{0p}} \over 2 \sqrt{1 + \lpar a_0^2/2\rpar \lpar cos^2 {\rm \alpha} {r_{0p}}\rpar }} - \displaystyle{{\rm \omega}_p^2 \over c^2}\comma \;$$

One must choose k _z < ω/c, ω_p to be small and a ₀ such that the right hand side is +ve. Eq. (18) can be written as,

(19)$$\displaystyle{{\rm \alpha}^2 c^2 \over {\rm \omega}^2} = \displaystyle{2 {\rm \omega}_p ^2 \over {\rm \omega}^2} \displaystyle{\sqrt{1 + \lpar a_0^2/2\rpar cos^2 \lpar {\rm \alpha} {r_{0p}}\rpar } \over a_0^2 cos^2 \lpar {\rm \alpha} {r_{0p}}\rpar } + \displaystyle{\lpar {\rm \alpha}^2 c^2 / {\rm \omega}^2\rpar tan^2 \lpar {\rm \alpha} {r_{0p}}\rpar \over 1 + \lpar a_0^2/2\rpar \lpar cos^2 \lpar {\rm \alpha} {r_{0p}}\rpar }.$$

To obtain r _0p and α explicitly for a given ω_p/ω, we proceed as follows. At some large value of x we chose a small value of a. Now pick a value of ck _z/ω and take da/dx = −α′a, where ${\rm \alpha}^\prime=\lpar k^2_z+({{\rm \omega}^2_p / c^2})- ({{\rm \omega}^2 / c^2})\rpar ^{1/2}.$ Solve Eq. (13) backward to smaller x, up to a point where n _e = 0, i.e., Eq. (16) is satisfied. Call this point x = r _0p. At this point, the continuity conditions (17) demand, (1/a)(da/dx) = −αtan(αr _0p). If this condition is not met, we try a different value of ck _z/ω and repeat the same procedure until this condition is satisfied. Once we get a suitable ck _z/ω and have r _0p, α, Eq. (19) gives the value of a ₀.

We have plotted the hole half width of the electron (equivalent to hole radius) r _0pω_p/c with a ₀ in Figure 1 and ck _z/ω with a ₀ in Figure 2. The hole radius increases rapidly with a ₀ in the range of a ₀ → 1–4 with a strong dependence on ω_p/ω and tends to saturate for larger values of a ₀. With increase in ω_p/ω, the electron density on the shoulders of the channel increases resulting in considerable reduction in channel radius. From Figure 1 one may note that beyond a certain value of a ₀(= a _min) the electrons are completely removed from the axis forming an electron hole. The value a _min increases with increase in ω/ω_p and electron evacuation does not occur for a _min < 1. With increase in laser amplitude, as the hole size increases, there is corresponding reduction in the phase velocity of the eigen mode (see Fig. 2). This is because the effective refractive index increases with increase in laser amplitude a ₀. The dispersion relation is plotted in Figure 3 for a ₀ = 2(dot), 3(solid). One may note that the eigen frequency shows a monotonous increase with wave vector of the mode with a strong dependence on a ₀. For ω/ω_p = 1.2, k _zc/ω_p = 0.525 and a ₀ = 2, the phase velocity of the eigen mode turns out to be ω/k _zc = 2.25 and the value of ω/k _zc decreases with a ₀ as mentioned earlier. Figure 4 shows the mode structure, |a/a ₀|² versus normalized distance k _px, for a ₀ = 3, ω/ω_p = 1.2, k _zc/ω_p = 0.9 and k _pr _0p = 1. The eigen mode field varies cosinudally inside the channel (shown by solid line) and starts decaying from channel boundary (shown by dashed line) at k _px = k _pr _0p = 1. The mode intensity |a/a ₀|² falls off to half of its axial value at k _pr _0p = 1. The intensity decreases more rapidly inside the electron hole and near the channel boundary. Outside the channel, it decreases slowly. The value of |a|² reduces to 1/10 of its axial value at k _px = 1.5.

Fig. 1. Variation of normalized channel radius r _0pω_p/c with laser amplitude a ₀ for ω_p/ω = 0.86 (dot) and 0.83 (solid).

Fig. 2. Variation of k _zc/ω (inverse of phase velocity of eigen mode) with a ₀ for ω/ω_p= 1.2.

Fig. 3. Variation of ω/ω_p with k _zc/ω_p for a ₀ = 2 (dot) and 3 (dash).

Fig. 4. Variation of |a/a ₀|² with k _px for a ₀ = 2, ω/ω_p = 1.2, k _zc/ω_p = 0.9, and k _pr _0p = 1.

The power contained in the eigen mode per unit y width is,

(20)$$P = \displaystyle{m^2 c^4 {\rm \omega}^2 {\rm \epsilon}_0 \over 2e^2} \int_0^{\infty} \vert a\vert ^2 dx.$$

where |a|² is the laser eigen mode intensity obtained by solving Eq. (13) as mentioned earlier. Multiplying both sides of Eq. (20) by c/ω_p, one obtains the normalized power,

(21)$$\displaystyle{Pc/{\rm \omega}_p \over P_0} \,=\,\, \int_0^{\infty} \vert a\vert ^2 dx = \int_0^{r_{0p}} \vert a\vert ^2 dx + \int_{r_{0p}}^{\infty} \vert a\vert ^2 dx.$$

where $P_0=({{\rm \omega}^2/ {\rm \omega}^2_p})({m^2 c^5 \epsilon_0\! / 2e^2})=3.47{\left({\rm \omega} / {\rm \omega}_p\right)}^2\times10^9 W$ and x → xω_p/c. Figure 5 shows the variation of normalized power $(Pc/{\rm \omega}_p)/ P_0$ with a ₀. The normalized power $(Pc/{\rm \omega}_p)/ P_0$ varies almost linearly with a ₀. For a ₀ = 1.5, ω_p/ω = 0.83, the power turns out to be $Pc/{\rm \omega}_p=$$1.6{\left({\rm \omega} / {\rm \omega}_p\right)}^2 \times 10^{10}W.$ Hence for a ₀ = 1.5, the power obtained is slightly less than the critical power $\lpar P_c=1.78{\left({\rm \omega} / {\rm \omega}_p\right)}^2 \times 10^{10}W)$ needed for the formation of electron hole. Thus for the electrons to be completely removed from the axis, a ₀ must be kept higher for the same value of ω_p/ω such that the condition P/P _cr ≥ 1 is achieved. Increasing the value of a ₀ from 2 to 5 the normalized power $(Pc/{\rm \omega}_p )/ P_0$ increases by a factor of 2. How ever with increase in ω_p/ω, $(Pc/{\rm \omega}_p)/ P_0$ decreases, so as r _0p. For a ₀ = 5, ω_p/ω = 0.83 and r _0p = 1.38c/ω_p, the normalized power $(Pc/{\rm \omega}_p )/ P_0$ turns out to be 9.0058, which is very close to the value obtained by Sun et al. Reference Sun, Edward, Lee and Guzdar1987. Hence, the power contained in the eigen mode for a ₀ = 5 is $Pc/{\rm \omega}_p=$$3.948{\left({\rm \omega}/{\rm \omega}_p\right)}^2 \times 10^{10}W$, exceeding the critical power P _cr by a factor of 2.

Fig. 5. Variation of the normalized power $(Pc/{\rm \omega} p)/ P_0$ with a ₀ for ω/ω_p = 1.2 and k _zc/ω_p = 0.9.

3. THIRD HARMONIC GENERATION

The laser eigen mode (E _y) propagating through the plasma channel with density profile given by Eq. (6) exerts a second harmonic ponderomotive force on electrons,

(22)$${\bf F}_{2{\rm \omega}} = -\lpar 1/2\rpar e\!\mathop {{\rm v}} \limits^{\rightarrow} \times {\bf B} = - {\hat z} \displaystyle{e^2 k_z E_y^2 \over 2 mi{\rm \omega}^2 {\rm \gamma}}.$$

Using this in the equations of motion and continuity one obtains the oscillatory velocity $\vec{v}_{2{\rm \omega}}$ and density n _2ω.

(23)$$\vec{v}_{2{\rm \omega}} = - \displaystyle{{\bf F}_{2 {\rm \omega}} \over mi2{\rm \omega} {\rm \gamma}} = - {\hat z} \displaystyle{e^2 k_z E_y^2 \over 4 m^2 {\rm \omega}^3 {\rm \gamma}^2}\comma \;$$

(24)$$n_{2{\rm \omega}} =\displaystyle{n_e k_z {\rm v}_z \over {\rm \omega}} = - \displaystyle{n_e e^2 k_z^2 E_y^2 \over 4 m^2 {\rm \omega}^4 {\rm \gamma}^2}.$$

The density perturbation n _2ω couples with oscillatory velocity $\vec{v}$ to produce nonlinear current density at the third harmonic frequency (3ω),

(25)$${\bf J}^{NL} = - \lpar 1/2\rpar n_{2{\rm \omega}} e\!\mathop{{\rm v}}\limits^{\rightarrow} = - {\hat y} \displaystyle{{\rm \omega}_p^2\lpar n_e/n_0^0\rpar k_z^2 c^2 \over 8i {\rm \omega}^{4} {\rm \gamma}^2} a^2 {\rm \omega} {\rm \epsilon}_0 E_y\comma \;$$

where a = e|E _y|/mωc. The nonlinear third harmonic current density produces third harmonic electric field E_3ω. This field produces self consistent current density J ^L_3ω,

(26)$${\bf J}_{3{\rm \omega}}^L = i \displaystyle{n_0^0 e^2 {\bf E}_{3{\rm \omega}} \over 3 m{\rm \omega} {\rm \gamma}}.$$

The wave equation governing E_3ω can be deduced from Maxwell's equations,

(27)$$\nabla \times {\bf E}_{3{\rm \omega}} = 3i{\rm \omega}{\bf B}_{3{\rm \omega}}\comma \;$$

(28)$$\nabla \times {\bf B}_{3{\rm \omega}} = - 3i{\rm \omega} {\rm \mu}_0\lpar {\bf J}^{NL} + {\bf J}_{3{\rm \omega}}^{L}\rpar - i \displaystyle{3{\rm \omega} \over c^2} {\bf E}_{3{\rm \omega}}.$$

Since J ^NL is parallel to $\hat{y}$ (cf. Eq. (25)), E_3ω is also parallel to $\hat{y}$. Defining a _3ω = e E _3ωy/mωc and taking fast t,z variation as e _z^{−i(3ωt−k _3zz)}, we obtain from Eqs. (25)–(28),

(29)$$\eqalign{& \displaystyle{d^2 a_{3{\rm \omega}}\over dx^2} + 2ik_{3z} \displaystyle{\partial a_{3{\rm \omega}} \over \partial z} + \left(\displaystyle{9 {\rm \omega}^2 \over c^2} - \displaystyle{{\rm \omega}_p^2 \lpar n_e/n_0^0\rpar \over c^2 {\rm \gamma}} - k_{3z}^2\right) \times \cr & \quad a_{3{\rm \omega}} = \displaystyle{3 \over 8} a^3\lpar k_z c/{\rm \omega}\rpar ^2 \displaystyle{{\rm \omega}_p^2 \lpar n_e/n_0^0\rpar \over {\rm \gamma}^2 c^2}.}$$

One may note that the nonlinear third harmonic source current density is finite only in the outer region |x| > r _0p. It excites a number of eigen modes in the channel at the third harmonic. We consider the excitation of the fundamental mode of the third harmonic that has the mode structure similar to that of the pump laser,

(30)$$a_{3{\rm \omega}} = eE_{3{\rm \omega} y}/m{\rm \omega} c = A_{3{\rm \omega}}\lpar z\rpar F\lpar x\rpar e^{-i\lpar 3{\rm \omega} t-k_{3z}z\rpar }\comma \;$$

(31)$$F \lpar x \rpar = \left\{\matrix{a_0 cos \lpar {\rm \alpha} x \rpar & \hbox{for} \, 0 \lt \vert x \vert \lt {r_{0p}} \cr a \lpar x \rpar & \hbox{for} \, \vert x \vert \gt {r_{0p}}}. \right.$$

where 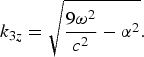$k_{3z}=\sqrt{{9{\rm \omega}^2 \over c^2}-{\rm \alpha}^2}.$

Substituting Eq. (30) in (29), multiplying the resulting equation by F(x) ^*dx and integrating from −∞ to ∞, we obtain,

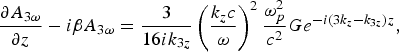(32)$$\displaystyle{\partial A_{3{\rm \omega}}\over \partial z} - i {\rm \beta} A_{3{\rm \omega}} = \displaystyle{3 \over 16ik_{3z}} \left(\displaystyle{k_z c \over {\rm \omega}}\right)^2 \displaystyle{{\rm \omega}_p^2 \over c^2}Ge^{-i\lpar 3k_z - k_{3z}\rpar z}\comma \;$$

where 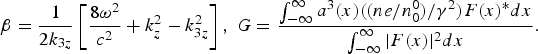${\rm \beta}={1 \over 2k_{3z}}\left[{8 {\rm \omega}^2 \over c^2}+{k^{2}_{z}}-{k^{2}_{3z}}\right]\comma \; G={\int^{\infty}_{- \infty} a^3\lpar x\rpar \lpar \lpar ne/n^0_0\rpar /{\rm \gamma}^2\rpar F\lpar x\rpar ^{\ast} {dx} \over \int^{\infty}_{-\infty}\vert F\lpar x\rpar \vert^{2} dx}.$

Effectively the integral in the numerator of G is the sum of two integrals one with limits −∞ to −r _0p and then from r _0p to ∞ as there are no electrons (n _e = 0) in the inner region. One may solve Eq. (32) on taking ∂/∂z = −iδ, δ = (3k _z − k _3z). Hence,

(33)$$\eqalign{& A_{3{\rm \omega}}\lpar z\rpar \cr & = \displaystyle{3\lpar k_z c/{\rm \omega}\rpar ^2 Ge^{-i\lpar {\rm \beta}+3k_z - {k_{3z}}\rpar z} \over 16[ 8\lpar {\rm \omega}/{\rm \omega}_p\rpar ^2 + \lpar k_z c/{\rm \omega}_p\rpar ^2 - 3\lpar {k_{3z}}c/{\rm \omega}_p\rpar ^2 + \lpar 6k_{3z} c/{\rm \omega}_p\rpar \lpar k_z c/{\rm \omega}_p\rpar ] }\comma \; }$$

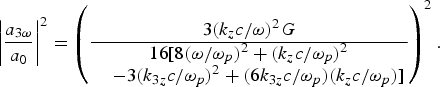(34)$$ \left \vert \displaystyle{a_{3{\rm \omega}} \over a_0}\right\vert^2 = \left(\displaystyle{3\lpar k_z c/{\rm \omega}\rpar ^2 G \over \matrix{16 [ 8 \lpar {\rm \omega}/{\rm \omega}_p \rpar ^2 + \lpar k_z c/{\rm \omega}_p \rpar ^2 \cr \quad- 3 \lpar {k_{3z}}c/{\rm \omega}_p\rpar ^2 + \lpar 6k_{3z} c/ {\rm \omega}_p \rpar \lpar k_z c/{\rm \omega}_p\rpar ] }}\right)^2.$$

In the fundamental mode, the amplitude of the third harmonic is maximum at the channel axis. The efficiency of the third harmonic shows a strong relationship with laser amplitude a ₀ and frequency ω. Figure 6 shows the variation of axial amplitude of the third harmonic with normalized laser frequency ω/ω_p for a ₀ = 3. With increase in normalized laser frequency ω/ω_p the fundamental and third harmonic wave vectors k _zc/ω_p, k _3zc/ω_p(≈ 3ω/ω_p) and inverse of the phase velocity k _zc/ω increases. Hence the denominator in Eq. (34) decreases steadily, whereas the numerator monotonously increases with ω/ω_p. The third harmonic efficiency |a _{3 ω}/a ₀|² at constant a ₀ shows a gradual increase in the range of ω/ω → 1.1–1.3 and increases bit faster beyond ω/ω_p = 1.3. Beyond ω/ω_p = 1.3 the denominator in Eq. (34) attains a fairly constant value.

Fig. 6. Variation of the square of normalized third harmonic amplitude | a _3ω/a ₀|² with ω/ω_p for a ₀ = 3.

From Figure 7 one may note that the efficiency gradually increases with the laser amplitude a ₀ for ω/ω_p = 1.2. However with the increase in a ₀, the cavitation radius r _0p increases and increasing r _0p adversely effects the growth of third harmonic efficiency |a _3ω/a ₀|². But the laser intensity amplitude a ²₀ is predominant both inside and outside the channel. Hence with increase in the laser amplitude a ₀ the lowering of third harmonic efficiency due to increasing r _0p can be compensated. However beyond a ₀ = 3, the channel radius r _0p tends to saturate and the third harmonic efficiency grows with a ₀.

Fig. 7. Variation of the square of normalized third harmonic amplitude | a _3ω/a ₀|² with a ₀ for ω/ω_p = 1.2 and k _zc/ω_p = 0.9.

To validate the efficacy of our analytical calculation we compare our results with the experimental results obtained by Kuo et al. (Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007). Kuo et al. (Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007) have experimentally demonstrated the enhancement of relativistic third-harmonic generation in both uniform and rippled density plasma waveguide using linearly polarized laser beam of amplitude a ₀ = 1. For the axially uniform channel case, they have obtained an efficiency of 1.1 × 10⁻⁸ at plasma density n ⁰₀ = 4.8 × 10¹⁸ cm ⁻³. For a comparison, we may calculate the conversion efficiency from Eq. (31) for the parameters: ω_p/ω0.05 (corresponding to n ₀⁰ = 4.8 × 10¹⁸ cm ⁻³ at 1μm laser wavelength) and a ₀ = 1.5. The conversion efficiency |a _3ω/a ₀|² of third harmonic for the aforementioned parameters turns out to be 1.95 × 10⁻⁸, which are within a factor of 2 from Kuo et al. (Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007). However the efficiency of the third harmonic can be improved by increasing the laser frequency or by increasing the laser amplitude a ₀ as shown in Figures 6 and 7.