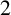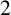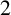1 Introduction
In this paper, all graphs are assumed to be finite and simple, and all groups are assumed to be finite.
A graph is a pair
![]() ${{\Gamma}}=(V,E)$
of a nonempty set V and a set E of
${{\Gamma}}=(V,E)$
of a nonempty set V and a set E of
![]() $2$
-subsets of V. The elements in V and E are called the vertices and edges of
$2$
-subsets of V. The elements in V and E are called the vertices and edges of
![]() ${{\Gamma}}$
, respectively. For
${{\Gamma}}$
, respectively. For
![]() $v\in V$
, the set
$v\in V$
, the set
![]() ${{\Gamma}}(v)=\{u\in V\mid \{u,v\}\in E\}$
is called the neighborhood of v in
${{\Gamma}}(v)=\{u\in V\mid \{u,v\}\in E\}$
is called the neighborhood of v in
![]() ${{\Gamma}}$
, while
${{\Gamma}}$
, while
![]() $|{{\Gamma}}(v)|$
is called the valency of v. We say that the graph
$|{{\Gamma}}(v)|$
is called the valency of v. We say that the graph
![]() ${{\Gamma}}$
has valency d or
${{\Gamma}}$
has valency d or
![]() ${{\Gamma}}$
is d-regular if its vertices have equal valency d. For an integer
${{\Gamma}}$
is d-regular if its vertices have equal valency d. For an integer
![]() $s\ge 1$
, an s-arc in
$s\ge 1$
, an s-arc in
![]() ${{\Gamma}}$
is an
${{\Gamma}}$
is an
![]() $(s{+}1)$
-tuple
$(s{+}1)$
-tuple
![]() $(v_0,v_1,\ldots , v_s)$
of vertices such that
$(v_0,v_1,\ldots , v_s)$
of vertices such that
![]() $\{v_{i-1},v_{i}\}\in E$
for
$\{v_{i-1},v_{i}\}\in E$
for
![]() $1\le i\le s$
and
$1\le i\le s$
and
![]() $v_{i-1}\ne v_{i+1}$
for
$v_{i-1}\ne v_{i+1}$
for
![]() $1\le i\le s-1$
. A
$1\le i\le s-1$
. A
![]() $1$
-arc is also called an arc.
$1$
-arc is also called an arc.
Let
![]() ${{\Gamma}}=(V,E)$
be a graph. A permutation g on V is called an automorphism of
${{\Gamma}}=(V,E)$
be a graph. A permutation g on V is called an automorphism of
![]() ${{\Gamma}}$
if
${{\Gamma}}$
if
![]() $\{u^g,v^g\}\in E$
for all
$\{u^g,v^g\}\in E$
for all
![]() $\{u,v\}\in E$
. All automorphisms of
$\{u,v\}\in E$
. All automorphisms of
![]() ${{\Gamma}}$
form a subgroup of the symmetric group
${{\Gamma}}$
form a subgroup of the symmetric group
![]() ${\mathrm{Sym}}(V)$
, denoted by
${\mathrm{Sym}}(V)$
, denoted by
![]() ${\sf Aut}{{\Gamma}}$
, that is called the automorphism group of
${\sf Aut}{{\Gamma}}$
, that is called the automorphism group of
![]() ${{\Gamma}}$
. The group
${{\Gamma}}$
. The group
![]() ${\sf Aut}{{\Gamma}}$
has a natural action on E, namely,
${\sf Aut}{{\Gamma}}$
has a natural action on E, namely,
![]() $\{u,v\}^g=\{u^g,v^g\}$
for
$\{u,v\}^g=\{u^g,v^g\}$
for
![]() $\{u,v\}\in E$
and
$\{u,v\}\in E$
and
![]() $g\in {\sf Aut}{{\Gamma}}$
. If this action is transitive, that is, for each pair of edges there exists some
$g\in {\sf Aut}{{\Gamma}}$
. If this action is transitive, that is, for each pair of edges there exists some
![]() $g\in {\sf Aut}{{\Gamma}}$
mapping one edge to the other one, then
$g\in {\sf Aut}{{\Gamma}}$
mapping one edge to the other one, then
![]() ${{\Gamma}}$
is called edge-transitive. Similarly, we may define the vertex-transitivity, arc-transitivity and s-arc-transitivity of
${{\Gamma}}$
is called edge-transitive. Similarly, we may define the vertex-transitivity, arc-transitivity and s-arc-transitivity of
![]() ${{\Gamma}}$
. The graph
${{\Gamma}}$
. The graph
![]() ${{\Gamma}}$
is called edge-primitive if
${{\Gamma}}$
is called edge-primitive if
![]() ${\sf Aut}{{\Gamma}}$
acts primitively on E, that is,
${\sf Aut}{{\Gamma}}$
acts primitively on E, that is,
![]() ${{\Gamma}}$
is edge-transitive and the stabilizer
${{\Gamma}}$
is edge-transitive and the stabilizer
![]() $({\sf Aut}{{\Gamma}})_{\{u,v\}}$
of some (and hence every) edge
$({\sf Aut}{{\Gamma}})_{\{u,v\}}$
of some (and hence every) edge
![]() $\{u,v\}$
in
$\{u,v\}$
in
![]() ${\sf Aut}{{\Gamma}}$
is a maximal subgroup.
${\sf Aut}{{\Gamma}}$
is a maximal subgroup.
The class of edge-primitive graphs includes many famous graphs such as the Heawood graph, Tutte’s
![]() $8$
-cage, the Biggs–Smith graph, the Hoffman–Singleton graph, the Higman–Sims graph and the rank-
$8$
-cage, the Biggs–Smith graph, the Hoffman–Singleton graph, the Higman–Sims graph and the rank-
![]() $3$
graphs associated with the sporadic simple groups
$3$
graphs associated with the sporadic simple groups
![]() ${\mathrm{M}}_{22}$
,
${\mathrm{M}}_{22}$
,
![]() ${\mathrm{J}}_2$
,
${\mathrm{J}}_2$
,
![]() ${\mathrm{McL}}$
,
${\mathrm{McL}}$
,
![]() ${\mathrm{Ru}}$
,
${\mathrm{Ru}}$
,
![]() ${\mathrm{Suz}}$
and
${\mathrm{Suz}}$
and
![]() ${\mathrm{Fi}}_{23}$
and so on. In 1973, Weiss [Reference Weiss34] determined all edge-primitive graphs of valency three. Up to isomorphism, all edge-primitive cubic graphs consist of the complete bipartite graph
${\mathrm{Fi}}_{23}$
and so on. In 1973, Weiss [Reference Weiss34] determined all edge-primitive graphs of valency three. Up to isomorphism, all edge-primitive cubic graphs consist of the complete bipartite graph
![]() ${\sf K}_{3,3}$
and the first three graphs mentioned above. After that, edge-primitive graphs had received little attention until Giudici and Li [Reference Giudici and Li9] systematically investigated the existence and the general structure of such graphs in 2010. Giudici and Li’s work has stimulated a lot of progress in the study of edge-primitive graphs; see [Reference Giudici and King8, Reference Guo, Feng and Li10, Reference Guo, Feng and Li11, Reference Li and Zhang17, Reference Lu21, Reference Pan, Wu and Yin24], for example. Also, their work reveals that those graphs associated with almost simple groups play an important role in the study of edge-primitive graphs. This is one of the main motivations of [Reference Lu21] and the present paper.
${\sf K}_{3,3}$
and the first three graphs mentioned above. After that, edge-primitive graphs had received little attention until Giudici and Li [Reference Giudici and Li9] systematically investigated the existence and the general structure of such graphs in 2010. Giudici and Li’s work has stimulated a lot of progress in the study of edge-primitive graphs; see [Reference Giudici and King8, Reference Guo, Feng and Li10, Reference Guo, Feng and Li11, Reference Li and Zhang17, Reference Lu21, Reference Pan, Wu and Yin24], for example. Also, their work reveals that those graphs associated with almost simple groups play an important role in the study of edge-primitive graphs. This is one of the main motivations of [Reference Lu21] and the present paper.
Let
![]() ${{\Gamma}}=(V,E)$
be an edge-primitive graph of valency no less than three. Then, as observed in [Reference Giudici and Li9],
${{\Gamma}}=(V,E)$
be an edge-primitive graph of valency no less than three. Then, as observed in [Reference Giudici and Li9],
![]() ${{\Gamma}}$
is also arc-transitive. If
${{\Gamma}}$
is also arc-transitive. If
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $2$
-arc-transitive, then Praeger’s reduction theorems [Reference Praeger25, Reference Praeger26] will be effective tools for us to investigate the group-theoretic and graph-theoretic properties of
$2$
-arc-transitive, then Praeger’s reduction theorems [Reference Praeger25, Reference Praeger26] will be effective tools for us to investigate the group-theoretic and graph-theoretic properties of
![]() ${{\Gamma}}$
. However,
${{\Gamma}}$
. However,
![]() ${{\Gamma}}$
is not necessarily
${{\Gamma}}$
is not necessarily
![]() $2$
-arc-transitive; for example, by the Atlas [Reference Conway, Norton, Parker and Wilson3], the sporadic Rudvalis group
$2$
-arc-transitive; for example, by the Atlas [Reference Conway, Norton, Parker and Wilson3], the sporadic Rudvalis group
![]() ${\mathrm{Ru}}$
is the automorphism group of a rank-three graph that is edge-primitive and of valency
${\mathrm{Ru}}$
is the automorphism group of a rank-three graph that is edge-primitive and of valency
![]() $2304$
but not
$2304$
but not
![]() $2$
-arc-transitive. Using the O’Nan–Scott theorem for (quasi)primitive groups [Reference Praeger25], Giudici and Li [Reference Giudici and Li9] gave a reduction theorem on the automorphism group of
$2$
-arc-transitive. Using the O’Nan–Scott theorem for (quasi)primitive groups [Reference Praeger25], Giudici and Li [Reference Giudici and Li9] gave a reduction theorem on the automorphism group of
![]() ${{\Gamma}}$
. They proved that, as a primitive group on E, only four of the eight O’Nan–Scott types for primitive groups may occur for
${{\Gamma}}$
. They proved that, as a primitive group on E, only four of the eight O’Nan–Scott types for primitive groups may occur for
![]() ${\sf Aut}{{\Gamma}}$
, namely SD, CD, PA and AS. They also considered the possible O’Nan–Scott types for
${\sf Aut}{{\Gamma}}$
, namely SD, CD, PA and AS. They also considered the possible O’Nan–Scott types for
![]() ${\sf Aut}{{\Gamma}}$
acting on V, and presented constructions or examples to verify the existence of corresponding graphs. Then what will happen if we assume further that
${\sf Aut}{{\Gamma}}$
acting on V, and presented constructions or examples to verify the existence of corresponding graphs. Then what will happen if we assume further that
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $2$
-arc-transitive? The third author of this paper showed that either
$2$
-arc-transitive? The third author of this paper showed that either
![]() ${\sf Aut}{{\Gamma}}$
is almost simple or
${\sf Aut}{{\Gamma}}$
is almost simple or
![]() ${{\Gamma}}$
is a complete bipartite graph if
${{\Gamma}}$
is a complete bipartite graph if
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $2$
-arc-transitive; see [Reference Lu21]. This stimulated our interest in classifying those edge-primitive graphs that are
$2$
-arc-transitive; see [Reference Lu21]. This stimulated our interest in classifying those edge-primitive graphs that are
![]() $2$
-arc-transitive.
$2$
-arc-transitive.
In this paper, we present a classification result stated as follows.
Theorem 1.1. Let
![]() ${{\Gamma}}=(V,E)$
be a graph of valency
${{\Gamma}}=(V,E)$
be a graph of valency
![]() $d\ge 6$
and let
$d\ge 6$
and let
![]() $G\le {\sf Aut}{{\Gamma}}$
be such that G acts primitively on the edge set and transitively on the
$G\le {\sf Aut}{{\Gamma}}$
be such that G acts primitively on the edge set and transitively on the
![]() $2$
-arc set of
$2$
-arc set of
![]() ${{\Gamma}}$
. Assume further that G is almost simple and, for
${{\Gamma}}$
. Assume further that G is almost simple and, for
![]() $\{u,v\}\in E$
, the edge-stabilizer
$\{u,v\}\in E$
, the edge-stabilizer
![]() $G_{\{u,v\}}$
is soluble. Then either
$G_{\{u,v\}}$
is soluble. Then either
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(G,4)$
-arc-transitive or G,
$(G,4)$
-arc-transitive or G,
![]() $G_{\{u,v\}}$
,
$G_{\{u,v\}}$
,
![]() $G_v$
and d are listed as in Table 1.
$G_v$
and d are listed as in Table 1.
Table 1 Graphs.

Remark 1.2. If
![]() ${{\Gamma}}$
is edge-primitive and either
${{\Gamma}}$
is edge-primitive and either
![]() $4$
-arc-transitive or of valency less than six, then the edge-stabilizers must be soluble. The reader may find a complete list of such graphs in [Reference Guo, Feng and Li10, Reference Guo, Feng and Li11, Reference Li and Zhang17, Reference Weiss34]. For each triple
$4$
-arc-transitive or of valency less than six, then the edge-stabilizers must be soluble. The reader may find a complete list of such graphs in [Reference Guo, Feng and Li10, Reference Guo, Feng and Li11, Reference Li and Zhang17, Reference Weiss34]. For each triple
![]() $(G, G_v, G_{\{u,v\}})$
listed in Table 1, the coset graph
$(G, G_v, G_{\{u,v\}})$
listed in Table 1, the coset graph
![]() ${\sf Cos}(G, G_v, G_{\{u,v\}})$
, see Section 2 for the definition, is both
${\sf Cos}(G, G_v, G_{\{u,v\}})$
, see Section 2 for the definition, is both
![]() $(G,2)$
-arc-transitive and G-edge-primitive.
$(G,2)$
-arc-transitive and G-edge-primitive.
2 Preliminaries
Let G be a finite group and
![]() $H,K\le G$
with
$H,K\le G$
with
![]() $|K:(H\cap K)|=2$
and
$|K:(H\cap K)|=2$
and
![]() $\cap _{g\in G}H^g=1$
, and let
$\cap _{g\in G}H^g=1$
, and let
![]() $[G:H]=\{Hx\mid x\in G\}$
. We define a graph
$[G:H]=\{Hx\mid x\in G\}$
. We define a graph
![]() ${\sf Cos}(G,H,K)$
on
${\sf Cos}(G,H,K)$
on
![]() $[G:H]$
such that
$[G:H]$
such that
![]() $\{Hx,Hy\}$
is an edge if and only if
$\{Hx,Hy\}$
is an edge if and only if
![]() $yx^{-1}\in HKH\setminus H$
. The group G can be viewed as a subgroup of
$yx^{-1}\in HKH\setminus H$
. The group G can be viewed as a subgroup of
![]() ${\sf Aut}{\sf Cos}(G,H,K)$
, where G acts on
${\sf Aut}{\sf Cos}(G,H,K)$
, where G acts on
![]() $[G:H]$
by right multiplication. Then
$[G:H]$
by right multiplication. Then
![]() ${\sf Cos}(G,H,K)$
is G-arc-transitive and, for
${\sf Cos}(G,H,K)$
is G-arc-transitive and, for
![]() $x\in K\setminus H$
, the edge
$x\in K\setminus H$
, the edge
![]() $\{H,Hx\}$
has stabilizer K in G. Thus,
$\{H,Hx\}$
has stabilizer K in G. Thus,
![]() ${\sf Cos}(G,H,K)$
is G-edge-primitive if and only if K is maximal in G.
${\sf Cos}(G,H,K)$
is G-edge-primitive if and only if K is maximal in G.
Assume that
![]() ${{\Gamma}}=(V,E)$
is a G-edge-primitive graph of valency
${{\Gamma}}=(V,E)$
is a G-edge-primitive graph of valency
![]() $d\ge 3$
. Then
$d\ge 3$
. Then
![]() ${{\Gamma}}$
is G-arc-transitive by [Reference Giudici and Li9, Lemma 3.4]. Take an edge
${{\Gamma}}$
is G-arc-transitive by [Reference Giudici and Li9, Lemma 3.4]. Take an edge
![]() $\{u,v\}\in E$
and let
$\{u,v\}\in E$
and let
![]() $H=G_v$
and
$H=G_v$
and
![]() $K=G_{\{u,v\}}$
. Then K is maximal in G, and
$K=G_{\{u,v\}}$
. Then K is maximal in G, and
![]() $H\cap K=G_{uv}$
that has index two in K. Noting that
$H\cap K=G_{uv}$
that has index two in K. Noting that
![]() $\cap _{g\in G}H^g$
fixes V pointwise,
$\cap _{g\in G}H^g$
fixes V pointwise,
![]() $\cap _{g\in G}H^g=1$
. Further,
$\cap _{g\in G}H^g=1$
. Further,
![]() $\,v^g\mapsto G_vg \,\text { for all } g\in G$
gives an isomorphism from
$\,v^g\mapsto G_vg \,\text { for all } g\in G$
gives an isomorphism from
![]() ${{\Gamma}}$
to
${{\Gamma}}$
to
![]() ${\sf Cos}(G,H,K)$
. Then, by [Reference Fang and Praeger5, Theorem 2.1], the following lemma holds.
${\sf Cos}(G,H,K)$
. Then, by [Reference Fang and Praeger5, Theorem 2.1], the following lemma holds.
Lemma 2.1. Let
![]() ${{\Gamma}}=(V,E)$
be a connected graph of valency
${{\Gamma}}=(V,E)$
be a connected graph of valency
![]() $d\ge 3$
and
$d\ge 3$
and
![]() $G\le {\sf Aut}{{\Gamma}}$
. Then
$G\le {\sf Aut}{{\Gamma}}$
. Then
![]() ${{\Gamma}}$
is both
${{\Gamma}}$
is both
![]() $(G,2)$
-arc-transitive and G-edge-primitive if and only if
$(G,2)$
-arc-transitive and G-edge-primitive if and only if
![]() ${{\Gamma}}\cong {\sf Cos}(G,H,K)$
for some subgroups H and K of G satisfying:
${{\Gamma}}\cong {\sf Cos}(G,H,K)$
for some subgroups H and K of G satisfying:
-
(1)
 $|K:(H\cap K)|=2$
,
$|K:(H\cap K)|=2$
,
 $\cap _{g\in G}H^g=1$
and K is maximal in G;
$\cap _{g\in G}H^g=1$
and K is maximal in G; -
(2) H acts
 $2$
-transitively on
$2$
-transitively on
 $[H:(H\cap K)]$
by right multiplication.
$[H:(H\cap K)]$
by right multiplication.
Let
![]() ${{\Gamma}}=(V,E)$
be a connected graph of valency at least 3,
${{\Gamma}}=(V,E)$
be a connected graph of valency at least 3,
![]() $\{u,v\}\in E$
and
$\{u,v\}\in E$
and
![]() $G\le {\sf Aut}{{\Gamma}}$
. Assume that
$G\le {\sf Aut}{{\Gamma}}$
. Assume that
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(G,s)$
-arc-transitive for some
$(G,s)$
-arc-transitive for some
![]() $s\ge 1$
, that is, G acts transitively on the s-arc set of
$s\ge 1$
, that is, G acts transitively on the s-arc set of
![]() ${{\Gamma}}$
. Then
${{\Gamma}}$
. Then
![]() $G_v$
acts transitively on the neighborhood
$G_v$
acts transitively on the neighborhood
![]() ${{\Gamma}}(v)$
of v in
${{\Gamma}}(v)$
of v in
![]() ${{\Gamma}}$
. Let
${{\Gamma}}$
. Let
![]() ${\mathrm{G}}_v^{{{\Gamma}}(v)}$
be the transitive permutation group induced by
${\mathrm{G}}_v^{{{\Gamma}}(v)}$
be the transitive permutation group induced by
![]() $G_v$
on
$G_v$
on
![]() ${{\Gamma}}(v)$
, and let
${{\Gamma}}(v)$
, and let
![]() $G_v^{[1]}$
be the kernel of
$G_v^{[1]}$
be the kernel of
![]() $G_v$
acting on
$G_v$
acting on
![]() ${{\Gamma}}(v)$
. Then
${{\Gamma}}(v)$
. Then
![]() $G_v^{{{\Gamma}}(v)}\cong G_v/G_v^{[1]}$
. Considering the action of
$G_v^{{{\Gamma}}(v)}\cong G_v/G_v^{[1]}$
. Considering the action of
![]() $G_{uv}$
on
$G_{uv}$
on
![]() ${{\Gamma}}(v)$
,
${{\Gamma}}(v)$
,
Similarly,
![]() $(G_u^{{{\Gamma}}(u)})_v=G_{uv}^{{{\Gamma}}(u)}\cong G_{uv}/G_u^{[1]}$
. Since G is transitive on the arcs of
$(G_u^{{{\Gamma}}(u)})_v=G_{uv}^{{{\Gamma}}(u)}\cong G_{uv}/G_u^{[1]}$
. Since G is transitive on the arcs of
![]() ${{\Gamma}}$
, there is some element in G interchanging u and v. This implies that
${{\Gamma}}$
, there is some element in G interchanging u and v. This implies that
Set
![]() $G_{uv}^{[1]}=G_u^{[1]}\cap G_v^{[1]}$
. Then
$G_{uv}^{[1]}=G_u^{[1]}\cap G_v^{[1]}$
. Then
![]() $G_{uv}^{[1]}$
is the kernel of
$G_{uv}^{[1]}$
is the kernel of
![]() $G_{uv}$
acting on
$G_{uv}$
acting on
![]() ${{\Gamma}}(u)\cup {{\Gamma}}(v)$
and, noting that
${{\Gamma}}(u)\cup {{\Gamma}}(v)$
and, noting that
![]() $G_{uv}/(G_{u}^{[1]}\cap G_{v}^{[1]})\lesssim (G_{uv}/G_{u}^{[1]})\times (G_{uv}/G_{v}^{[1]})$
,
$G_{uv}/(G_{u}^{[1]}\cap G_{v}^{[1]})\lesssim (G_{uv}/G_{u}^{[1]})\times (G_{uv}/G_{v}^{[1]})$
,
Since
![]() $G_v^{[1]}\unlhd G_{uv}$
, we know that
$G_v^{[1]}\unlhd G_{uv}$
, we know that
![]() $G_v^{[1]}$
induces a normal subgroup
$G_v^{[1]}$
induces a normal subgroup
![]() $(G_v^{[1]})^{{{\Gamma}}(u)}$
of
$(G_v^{[1]})^{{{\Gamma}}(u)}$
of
![]() $(G_{u}^{{{\Gamma}}(u)})_v$
. In particular,
$(G_{u}^{{{\Gamma}}(u)})_v$
. In particular,
Writing
![]() $G_v^{[1]}$
,
$G_v^{[1]}$
,
![]() $G_{uv}$
and
$G_{uv}$
and
![]() $G_v$
in group extensions, the next lemma follows.
$G_v$
in group extensions, the next lemma follows.
Lemma 2.2.
-
(1)
 $G_v^{[1]}=G_{uv}^{[1]}.(G_v^{[1]})^{{{\Gamma}}(u)}$
,
$G_v^{[1]}=G_{uv}^{[1]}.(G_v^{[1]})^{{{\Gamma}}(u)}$
,
 $(G_v^{[1]})^{{{\Gamma}}(u)}\unlhd (G_{u}^{{{\Gamma}}(u)})_v$
.
$(G_v^{[1]})^{{{\Gamma}}(u)}\unlhd (G_{u}^{{{\Gamma}}(u)})_v$
. -
(2)
 $G_{uv}=(G_{uv}^{[1]}.(G_v^{[1]})^{{{\Gamma}}(u)}).(G_v^{{{\Gamma}}(v)})_u$
,
$G_{uv}=(G_{uv}^{[1]}.(G_v^{[1]})^{{{\Gamma}}(u)}).(G_v^{{{\Gamma}}(v)})_u$
,
 $G_v=(G_{uv}^{[1]}.(G_v^{[1]})^{{{\Gamma}}(u)}).G_v^{{{\Gamma}}(v)}$
.
$G_v=(G_{uv}^{[1]}.(G_v^{[1]})^{{{\Gamma}}(u)}).G_v^{{{\Gamma}}(v)}$
. -
(3) If
 $G_{uv}^{[1]}=1$
, then
$G_{uv}^{[1]}=1$
, then
 $G_{uv}\lesssim (G_v^{{{\Gamma}}(v)})_u\times (G_{u}^{{{\Gamma}}(u)})_v$
.
$G_{uv}\lesssim (G_v^{{{\Gamma}}(v)})_u\times (G_{u}^{{{\Gamma}}(u)})_v$
.
By [Reference Weiss32],
![]() $s\le 7$
and, if
$s\le 7$
and, if
![]() $s\ge 2$
, then
$s\ge 2$
, then
![]() $G_{uv}^{[1]}$
is a p-group for some prime p; refer to [Reference Gardiner7]. Thus, Lemma 2.2 yields a fact as follows.
$G_{uv}^{[1]}$
is a p-group for some prime p; refer to [Reference Gardiner7]. Thus, Lemma 2.2 yields a fact as follows.
Corollary 2.3. Let
![]() ${{\Gamma}}=(V,E)$
be a connected
${{\Gamma}}=(V,E)$
be a connected
![]() $(G,2)$
-arc-transitive graph and
$(G,2)$
-arc-transitive graph and
![]() $\{u,v\}\in E$
. Then
$\{u,v\}\in E$
. Then
![]() $G_{\{u,v\}}$
is soluble if and only if
$G_{\{u,v\}}$
is soluble if and only if
![]() $(G_v^{{{\Gamma}}(v)})_u$
is soluble, and
$(G_v^{{{\Gamma}}(v)})_u$
is soluble, and
![]() $G_v$
is soluble if and only if
$G_v$
is soluble if and only if
![]() $G_v^{{{\Gamma}}(v)}$
is soluble.
$G_v^{{{\Gamma}}(v)}$
is soluble.
Choose s maximal, that is,
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(G,s)$
-arc-transitive but not
$(G,s)$
-arc-transitive but not
![]() $(G,s{+}1)$
-arc-transitive. In this case,
$(G,s{+}1)$
-arc-transitive. In this case,
![]() ${{\Gamma}}$
is said to be
${{\Gamma}}$
is said to be
![]() $(G,s)$
-transitive. If further
$(G,s)$
-transitive. If further
![]() $G_{uv}^{[1]}\ne 1$
, then one can read out the vertex-stabilizer
$G_{uv}^{[1]}\ne 1$
, then one can read out the vertex-stabilizer
![]() $G_v$
from [Reference Weiss31, Reference Weiss33] for
$G_v$
from [Reference Weiss31, Reference Weiss33] for
![]() $s\ge 4$
and from [Reference Trofimov, Ivanov, Liebeck and Saxl29] for
$s\ge 4$
and from [Reference Trofimov, Ivanov, Liebeck and Saxl29] for
![]() $2\le s\le 3$
. In particular, we have the following result from [Reference Trofimov, Ivanov, Liebeck and Saxl29, Reference Weiss33].
$2\le s\le 3$
. In particular, we have the following result from [Reference Trofimov, Ivanov, Liebeck and Saxl29, Reference Weiss33].
Theorem 2.4. Let
![]() ${{\Gamma}}=(V,E)$
be a connected
${{\Gamma}}=(V,E)$
be a connected
![]() $(G,s)$
-transitive graph of valency at least 3 and
$(G,s)$
-transitive graph of valency at least 3 and
![]() $\{u,v\}\in E$
. Assume that
$\{u,v\}\in E$
. Assume that
![]() $s\ge 2$
.
$s\ge 2$
.
-
(1) If
 $G_{uv}^{[1]}=1$
, then
$G_{uv}^{[1]}=1$
, then
 $s=2$
or
$s=2$
or
 $3$
.
$3$
. -
(2) If
 $G_{uv}^{[1]}\ne 1$
, then
$G_{uv}^{[1]}\ne 1$
, then
 $G_{uv}^{[1]}$
is a p-group for some prime p,
$G_{uv}^{[1]}$
is a p-group for some prime p,
 ${\mathrm{PSL}}_n(q)\unlhd G_v^{{{\Gamma}}(v)}$
,
${\mathrm{PSL}}_n(q)\unlhd G_v^{{{\Gamma}}(v)}$
,
 $ |{{\Gamma}}(v)|={({q^n-1})/({q-1})}$
and
$ |{{\Gamma}}(v)|={({q^n-1})/({q-1})}$
and
 $6\ne s\le 7$
, where
$6\ne s\le 7$
, where
 $n\ge 2$
and
$n\ge 2$
and
 $q=p^f$
for some integer
$q=p^f$
for some integer
 $f\ge 1$
; moreover, either:
$f\ge 1$
; moreover, either:-
(i)
 $n=2$
and
$n=2$
and
 $s\ge 4$
; or
$s\ge 4$
; or -
(ii)
 $n\ge 3$
,
$n\ge 3$
,
 $s\le 3$
and
$s\le 3$
and
 ${\mathrm{{\textbf {O}}}}_p(G_v)$
is given as in Table 2, where
${\mathrm{{\textbf {O}}}}_p(G_v)$
is given as in Table 2, where
 $\textbf {O}_p(G_v)$
is the maximal normal p-subgroup of
$\textbf {O}_p(G_v)$
is the maximal normal p-subgroup of
 $G_v$
.
$G_v$
.Table 2 Vertex-stabilizers.

-
Lemma 2.5. Let
![]() ${{\Gamma}}=(V,E)$
be a connected
${{\Gamma}}=(V,E)$
be a connected
![]() $(G,2)$
-arc-transitive graph and
$(G,2)$
-arc-transitive graph and
![]() $\{u,v\}\in E$
. If r is a prime divisor of
$\{u,v\}\in E$
. If r is a prime divisor of
![]() $|{{\Gamma}}(v)|$
, then
$|{{\Gamma}}(v)|$
, then
![]() $\textbf {O}_r(G_{v}^{[1]})=1$
,
$\textbf {O}_r(G_{v}^{[1]})=1$
,
![]() $\textbf {O}_r(G_{uv})=1$
and either
$\textbf {O}_r(G_{uv})=1$
and either
![]() $\textbf {O}_r(G_v)=1$
, or
$\textbf {O}_r(G_v)=1$
, or
![]() $\textbf {O}_r(G_v)\cong \mathbb Z_r^e\cong {\mathrm{soc}}(G_v^{{{\Gamma}}(v)})$
and
$\textbf {O}_r(G_v)\cong \mathbb Z_r^e\cong {\mathrm{soc}}(G_v^{{{\Gamma}}(v)})$
and
![]() $|{{\Gamma}}(v)|=r^e$
for some integer
$|{{\Gamma}}(v)|=r^e$
for some integer
![]() $e\ge 1$
.
$e\ge 1$
.
Proof. Since
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(G,2)$
-arc-transitive,
$(G,2)$
-arc-transitive,
![]() $G_v^{{{\Gamma}}(v)}$
is a
$G_v^{{{\Gamma}}(v)}$
is a
![]() $2$
-transitive group and thus
$2$
-transitive group and thus
![]() $G_{uv}$
is transitive on
$G_{uv}$
is transitive on
![]() ${{\Gamma}}(v)\setminus \{u\}$
. Since
${{\Gamma}}(v)\setminus \{u\}$
. Since
![]() $\textbf {O}_r(G_{uv}) \unlhd G_{uv}$
, all
$\textbf {O}_r(G_{uv}) \unlhd G_{uv}$
, all
![]() $\textbf {O}_r(G_{uv})$
-orbits on
$\textbf {O}_r(G_{uv})$
-orbits on
![]() ${{\Gamma}}(v)\setminus \{u\}$
have the same size. Noting that
${{\Gamma}}(v)\setminus \{u\}$
have the same size. Noting that
![]() $|{{\Gamma}}(v)\setminus \{u\}|$
is coprime to r, it follows that
$|{{\Gamma}}(v)\setminus \{u\}|$
is coprime to r, it follows that
![]() $\textbf {O}_r(G_{uv})\le G_v^{[1]}$
. Since
$\textbf {O}_r(G_{uv})\le G_v^{[1]}$
. Since
![]() $G_v^{[1]} \unlhd G_{uv}$
, we have
$G_v^{[1]} \unlhd G_{uv}$
, we have
![]() $\textbf {O}_r(G_v^{[1]})\le \textbf {O}_r(G_{uv})$
and so
$\textbf {O}_r(G_v^{[1]})\le \textbf {O}_r(G_{uv})$
and so
![]() $\textbf {O}_r(G_v^{[1]})=\textbf {O}_r(G_{uv})$
. Similarly, considering the action of
$\textbf {O}_r(G_v^{[1]})=\textbf {O}_r(G_{uv})$
. Similarly, considering the action of
![]() $G_{uv}$
on
$G_{uv}$
on
![]() ${{\Gamma}}(u)\setminus \{v\}$
, we get
${{\Gamma}}(u)\setminus \{v\}$
, we get
![]() $\textbf {O}_r(G_u^{[1]})=\textbf {O}_r(G_{uv})$
. Then
$\textbf {O}_r(G_u^{[1]})=\textbf {O}_r(G_{uv})$
. Then
![]() $\textbf {O}_r(G_u^{[1]})=\textbf {O}_r(G_{uv})=\textbf {O}_r(G_v^{[1]})\le G_{uv}^{[1]}$
. By Theorem 2.4, either
$\textbf {O}_r(G_u^{[1]})=\textbf {O}_r(G_{uv})=\textbf {O}_r(G_v^{[1]})\le G_{uv}^{[1]}$
. By Theorem 2.4, either
![]() $G_{uv}^{[1]}=1$
, or
$G_{uv}^{[1]}=1$
, or
![]() $G_{uv}^{[1]}$
is a nontrivial p-group for a prime divisor p of
$G_{uv}^{[1]}$
is a nontrivial p-group for a prime divisor p of
![]() $|{{\Gamma}}(v)|-1$
. It follows that
$|{{\Gamma}}(v)|-1$
. It follows that
![]() $\textbf {O}_r(G_u^{[1]})=\textbf {O}_r(G_{uv})=\textbf {O}_r(G_v^{[1]})=1$
.
$\textbf {O}_r(G_u^{[1]})=\textbf {O}_r(G_{uv})=\textbf {O}_r(G_v^{[1]})=1$
.
Note that
![]() $\textbf {O}_r(G_v)G_v^{[1]}/G_v^{[1]}\cong \textbf {O}_r(G_v)/(\textbf {O}_r(G_v)\cap G_v^{[1]})$
. Clearly,
$\textbf {O}_r(G_v)G_v^{[1]}/G_v^{[1]}\cong \textbf {O}_r(G_v)/(\textbf {O}_r(G_v)\cap G_v^{[1]})$
. Clearly,
![]() $\textbf {O}_r(G_v)\cap G_v^{[1]}\le \textbf {O}_r(G_v^{[1]})$
and we have
$\textbf {O}_r(G_v)\cap G_v^{[1]}\le \textbf {O}_r(G_v^{[1]})$
and we have
![]() $\textbf {O}_r(G_v)\cap G_v^{[1]}=1$
. It follows that
$\textbf {O}_r(G_v)\cap G_v^{[1]}=1$
. It follows that
![]() $\textbf {O}_r(G_v)\cong \textbf {O}_r(G_v)G_v^{[1]}/G_v^{[1]}\unlhd G_v/G_v^{[1]}\cong {\mathrm{G}}_v^{{{\Gamma}}(v)}$
. Thus,
$\textbf {O}_r(G_v)\cong \textbf {O}_r(G_v)G_v^{[1]}/G_v^{[1]}\unlhd G_v/G_v^{[1]}\cong {\mathrm{G}}_v^{{{\Gamma}}(v)}$
. Thus,
![]() $\textbf {O}_r(G_v)$
is isomorphic to a normal r-subgroup of
$\textbf {O}_r(G_v)$
is isomorphic to a normal r-subgroup of
![]() ${\mathrm{G}}_v^{{{\Gamma}}(v)}$
. This implies that either
${\mathrm{G}}_v^{{{\Gamma}}(v)}$
. This implies that either
![]() $\textbf {O}_r(G_v)=1$
, or
$\textbf {O}_r(G_v)=1$
, or
![]() ${\mathrm{G}}_v^{{{\Gamma}}(v)}$
is an affine
${\mathrm{G}}_v^{{{\Gamma}}(v)}$
is an affine
![]() $2$
-transitive group of degree
$2$
-transitive group of degree
![]() $r^e$
for some e. Thus, the lemma follows.
$r^e$
for some e. Thus, the lemma follows.
Let
![]() $a\ge 2$
and
$a\ge 2$
and
![]() $f\ge 1$
be integers. A prime divisor r of
$f\ge 1$
be integers. A prime divisor r of
![]() $a^f-1$
is primitive if r is not a divisor of
$a^f-1$
is primitive if r is not a divisor of
![]() $a^{e}-1$
for all
$a^{e}-1$
for all
![]() $1\le e< f$
. By Zsigmondy’s theorem [Reference Zsigmondy37], if
$1\le e< f$
. By Zsigmondy’s theorem [Reference Zsigmondy37], if
![]() $f>1$
and
$f>1$
and
![]() $a^f-1$
has no primitive prime divisor, then
$a^f-1$
has no primitive prime divisor, then
![]() $a^f=2^6$
, or
$a^f=2^6$
, or
![]() $f=2$
and
$f=2$
and
![]() $a=2^t-1$
for some prime t. Assume that
$a=2^t-1$
for some prime t. Assume that
![]() $a^f-1$
has a primitive prime divisor r. Then a has order f modulo r. Thus, f is a divisor of
$a^f-1$
has a primitive prime divisor r. Then a has order f modulo r. Thus, f is a divisor of
![]() $r-1$
and, if r is a divisor of
$r-1$
and, if r is a divisor of
![]() $a^{f'}-1$
for some
$a^{f'}-1$
for some
![]() $f'\ge 1$
, then f is a divisor of
$f'\ge 1$
, then f is a divisor of
![]() $f'$
. Thus, we have the following lemma.
$f'$
. Thus, we have the following lemma.
Lemma 2.6. Let
![]() $a\ge 2$
,
$a\ge 2$
,
![]() $f\ge 1$
and
$f\ge 1$
and
![]() $f'\ge 1$
be integers. If
$f'\ge 1$
be integers. If
![]() $a^f-1$
has a primitive prime divisor r, then f is a divisor of
$a^f-1$
has a primitive prime divisor r, then f is a divisor of
![]() $r-1$
, and r is a divisor of
$r-1$
, and r is a divisor of
![]() $a^{f'}-1$
if and only if f is a divisor of
$a^{f'}-1$
if and only if f is a divisor of
![]() $f'$
. If
$f'$
. If
![]() $f\ge 3$
, then
$f\ge 3$
, then
![]() $a^f-1$
has a prime divisor no less than 5.
$a^f-1$
has a prime divisor no less than 5.
We end this section with a fact on finite primitive groups.
Lemma 2.7. Assume that G is a finite primitive group with a point-stabilizer H. If H has a normal Sylow subgroup
![]() $P\ne 1$
, then P is also a Sylow subgroup of G.
$P\ne 1$
, then P is also a Sylow subgroup of G.
Proof. Assume that
![]() $P\ne 1$
is a normal Sylow subgroup of H. Clearly, P is not normal in G. Take a Sylow subgroup Q of G with
$P\ne 1$
is a normal Sylow subgroup of H. Clearly, P is not normal in G. Take a Sylow subgroup Q of G with
![]() $P\le Q$
. Then
$P\le Q$
. Then
![]() $H\le \langle \textbf {N}_Q(P),H\rangle \le \textbf {N}_G(P)\ne G$
. Since H is maximal in G, we have
$H\le \langle \textbf {N}_Q(P),H\rangle \le \textbf {N}_G(P)\ne G$
. Since H is maximal in G, we have
![]() $H=\langle \textbf {N}_Q(P),H\rangle $
and so
$H=\langle \textbf {N}_Q(P),H\rangle $
and so
![]() $\textbf {N}_Q(P)\le H$
. It follows that
$\textbf {N}_Q(P)\le H$
. It follows that
![]() $\textbf {N}_Q(P)=P$
and hence
$\textbf {N}_Q(P)=P$
and hence
![]() $P=Q$
. Then the lemma follows.
$P=Q$
. Then the lemma follows.
3 Some restrictions on stabilizers
In Sections 4 and 5, we prove Theorem 1.1 using the result given in [Reference Li and Zhang17] that classifies finite primitive groups with soluble point-stabilizers. Let
![]() ${{\Gamma}}=(V,E)$
be a graph of valency
${{\Gamma}}=(V,E)$
be a graph of valency
![]() $d\ge 6$
,
$d\ge 6$
,
![]() $\{u,v\}\in E$
and
$\{u,v\}\in E$
and
![]() $G\le {\sf Aut}{{\Gamma}}$
. Assume that G is almost simple,
$G\le {\sf Aut}{{\Gamma}}$
. Assume that G is almost simple,
![]() $G_{\{u,v\}}$
is soluble and
$G_{\{u,v\}}$
is soluble and
![]() ${{\Gamma}}$
is G-edge-primitive and
${{\Gamma}}$
is G-edge-primitive and
![]() $(G,2)$
-arc-transitive. Clearly, each nontrivial normal subgroup of G acts transitively on the edge set E. Choose a minimal X among the normal subgroups of G that act primitively on E. By the choice of X, we have
$(G,2)$
-arc-transitive. Clearly, each nontrivial normal subgroup of G acts transitively on the edge set E. Choose a minimal X among the normal subgroups of G that act primitively on E. By the choice of X, we have
![]() ${\mathrm{soc}}(X)={\mathrm{soc}}(G)$
,
${\mathrm{soc}}(X)={\mathrm{soc}}(G)$
,
![]() $X_{\{u,v\}}=X\cap G_{\{u,v\}}$
,
$X_{\{u,v\}}=X\cap G_{\{u,v\}}$
,
![]() $G=XG_{\{u,v\}}$
and
$G=XG_{\{u,v\}}$
and
![]() $G/X=XG_{\{u,v\}}/X\cong G_{\{u,v\}}/X_{\{u,v\}}$
. Then, considering the restrictions on both
$G/X=XG_{\{u,v\}}/X\cong G_{\{u,v\}}/X_{\{u,v\}}$
. Then, considering the restrictions on both
![]() $X_{\{u,v\}}$
and
$X_{\{u,v\}}$
and
![]() $X_v$
caused by the
$X_v$
caused by the
![]() $2$
-arc-transitivity of
$2$
-arc-transitivity of
![]() ${{\Gamma}}$
, we may work out the pair
${{\Gamma}}$
, we may work out the pair
![]() $(X,X_{\{u,v\}})$
from [Reference Li and Zhang17, Theorem 1.1] and then determine the group G and the graph
$(X,X_{\{u,v\}})$
from [Reference Li and Zhang17, Theorem 1.1] and then determine the group G and the graph
![]() ${{\Gamma}}$
. Thus, we make the following assumptions.
${{\Gamma}}$
. Thus, we make the following assumptions.
Hypothesis 3.1. Let
![]() ${{\Gamma}}=(V,E)$
be a G-edge-primitive graph of valency
${{\Gamma}}=(V,E)$
be a G-edge-primitive graph of valency
![]() $d\ge 6$
and
$d\ge 6$
and
![]() $\{u,v\}\in E$
, where G is an almost simple group with socle T. Assume that:
$\{u,v\}\in E$
, where G is an almost simple group with socle T. Assume that:
-
(1)
 ${{\Gamma}}$
is
${{\Gamma}}$
is
 $(G,2)$
-arc-transitive and the edge-stabilizer
$(G,2)$
-arc-transitive and the edge-stabilizer
 $G_{\{u,v\}}$
is soluble;
$G_{\{u,v\}}$
is soluble; -
(2) G has a normal subgroup X such that
 ${\mathrm{soc}}(X)=T$
,
${\mathrm{soc}}(X)=T$
,
 $X_{\{u,v\}}$
is maximal in X and
$X_{\{u,v\}}$
is maximal in X and
 $(X,X_{\{u,v\}})$
is one of the pairs
$(X,X_{\{u,v\}})$
is one of the pairs
 $(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20].
$(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20].
For the group X in Hypothesis 3.1, we have
![]() $1\ne X_v^{{{\Gamma}}(v)}\unlhd G_v^{{{\Gamma}}(v)}$
. Note that
$1\ne X_v^{{{\Gamma}}(v)}\unlhd G_v^{{{\Gamma}}(v)}$
. Note that
![]() $G_v^{{{\Gamma}}(v)}$
is
$G_v^{{{\Gamma}}(v)}$
is
![]() $2$
-transitive (on
$2$
-transitive (on
![]() ${{\Gamma}}(v)$
). Then
${{\Gamma}}(v)$
). Then
![]() $G_v^{{{\Gamma}}(v)}$
is affine or almost simple; see [Reference Dixon and Mortimer4, Theorem 4.1B], for example. It follows that
$G_v^{{{\Gamma}}(v)}$
is affine or almost simple; see [Reference Dixon and Mortimer4, Theorem 4.1B], for example. It follows that
![]() ${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})={\mathrm{soc}}(X_v^{{{\Gamma}}(v)})$
.
${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})={\mathrm{soc}}(X_v^{{{\Gamma}}(v)})$
.
3.1
Assume that
![]() $G_v$
is insoluble. Then
$G_v$
is insoluble. Then
![]() $G_v^{{{\Gamma}}(v)}$
is an almost simple
$G_v^{{{\Gamma}}(v)}$
is an almost simple
![]() $2$
-transitive group (on
$2$
-transitive group (on
![]() ${{\Gamma}}(v)$
). Recall that
${{\Gamma}}(v)$
). Recall that
![]() ${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})={\mathrm{soc}}(X_v^{{{\Gamma}}(v)})$
. Checking the point-stabilizers of almost simple
${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})={\mathrm{soc}}(X_v^{{{\Gamma}}(v)})$
. Checking the point-stabilizers of almost simple
![]() $2$
-transitive groups (see [Reference Li, Seress and Song16, Table 2.1], for example), since
$2$
-transitive groups (see [Reference Li, Seress and Song16, Table 2.1], for example), since
![]() $(G_v^{{{\Gamma}}(v)})_u$
is soluble, we conclude that either
$(G_v^{{{\Gamma}}(v)})_u$
is soluble, we conclude that either
![]() $X_v^{{{\Gamma}}(v)}$
is
$X_v^{{{\Gamma}}(v)}$
is
![]() $2$
-transitive, or
$2$
-transitive, or
![]() $G_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8){.}3$
and
$G_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8){.}3$
and
![]() $d=28$
. (For a complete list of finite
$d=28$
. (For a complete list of finite
![]() $2$
-transitive groups, the reader may refer to [Reference Cameron2, Tables 7.3 and 7.4].)
$2$
-transitive groups, the reader may refer to [Reference Cameron2, Tables 7.3 and 7.4].)
Lemma 3.2. Suppose that Hypothesis 3.1 holds. If
![]() $d=28$
, then
$d=28$
, then
![]() $G_v^{{{\Gamma}}(v)}$
is not isomorphic to
$G_v^{{{\Gamma}}(v)}$
is not isomorphic to
![]() ${\mathrm{PSL}}_2(8){.}3$
.
${\mathrm{PSL}}_2(8){.}3$
.
Proof. Suppose that
![]() $G_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8){.}3$
and
$G_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8){.}3$
and
![]() $d=28$
. Note that
$d=28$
. Note that
![]() $X_{uv}^{[1]}\le G_{uv}^{[1]}=1$
; see Theorem 2.4. Thus,
$X_{uv}^{[1]}\le G_{uv}^{[1]}=1$
; see Theorem 2.4. Thus,
![]() $X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
by Lemma 2.2.
$X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
by Lemma 2.2.
Assume that
![]() $X_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8)$
. Then
$X_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8)$
. Then
![]() $(X_v^{{{\Gamma}}(v)})_u\cong {\mathrm{D}}_{18}$
, and
$(X_v^{{{\Gamma}}(v)})_u\cong {\mathrm{D}}_{18}$
, and
![]() $X_{uv}\cong {\mathrm{D}}_{18}$
,
$X_{uv}\cong {\mathrm{D}}_{18}$
,
![]() $(\mathbb Z_3{\times }\mathbb Z_9){:}\mathbb Z_2$
,
$(\mathbb Z_3{\times }\mathbb Z_9){:}\mathbb Z_2$
,
![]() $(\mathbb Z_9{\times }\mathbb Z_9){:}\mathbb Z_2$
or
$(\mathbb Z_9{\times }\mathbb Z_9){:}\mathbb Z_2$
or
![]() ${\mathrm{D}}_{18}{\times } {\mathrm{D}}_{18}$
. In particular, the unique Sylow
${\mathrm{D}}_{18}{\times } {\mathrm{D}}_{18}$
. In particular, the unique Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $X_{\{u,v\}}=X_{uv}.2$
is isomorphic to
$X_{\{u,v\}}=X_{uv}.2$
is isomorphic to
![]() $\mathbb Z_m{\times } \mathbb Z_9$
, where
$\mathbb Z_m{\times } \mathbb Z_9$
, where
![]() $m=1$
,
$m=1$
,
![]() $3$
or
$3$
or
![]() $9$
. Checking the primitive groups listed in [Reference Li and Zhang17, Tables 14–20], we know that only the pairs
$9$
. Checking the primitive groups listed in [Reference Li and Zhang17, Tables 14–20], we know that only the pairs
![]() $({\mathrm{PSL}}_2(q),{\mathrm{D}}_{{2(q{\pm } 1)}/{(2,q-1)}})$
possibly meet our requirements on
$({\mathrm{PSL}}_2(q),{\mathrm{D}}_{{2(q{\pm } 1)}/{(2,q-1)}})$
possibly meet our requirements on
![]() $X_{\{u,v\}}$
, yielding
$X_{\{u,v\}}$
, yielding
![]() $X_{\{u,v\}}\cong {\mathrm{D}}_{{2(q{\pm } 1)}/{(2,q-1)}}$
. Then
$X_{\{u,v\}}\cong {\mathrm{D}}_{{2(q{\pm } 1)}/{(2,q-1)}}$
. Then
![]() ${\mathrm{D}}_{36}\cong X_{\{u,v\}}\cong {\mathrm{D}}_{{2(q{\pm } 1)}/{(2,q-1)}}$
. Calculation shows that
${\mathrm{D}}_{36}\cong X_{\{u,v\}}\cong {\mathrm{D}}_{{2(q{\pm } 1)}/{(2,q-1)}}$
. Calculation shows that
![]() $q=37$
; however,
$q=37$
; however,
![]() ${\mathrm{PSL}}_2(37)$
has no subgroup that has a quotient
${\mathrm{PSL}}_2(37)$
has no subgroup that has a quotient
![]() ${\mathrm{PSL}}_2(8)$
, which is a contradiction.
${\mathrm{PSL}}_2(8)$
, which is a contradiction.
Now let
![]() $X_v^{{{\Gamma}}(v)}=G_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8){.}3$
. Then
$X_v^{{{\Gamma}}(v)}=G_v^{{{\Gamma}}(v)}\cong {\mathrm{PSL}}_2(8){.}3$
. Then
![]() $(X_v^{{{\Gamma}}(v)})_u\cong (X_u^{{{\Gamma}}(u)})_v\cong \mathbb Z_9{:}\mathbb Z_6$
and
$(X_v^{{{\Gamma}}(v)})_u\cong (X_u^{{{\Gamma}}(u)})_v\cong \mathbb Z_9{:}\mathbb Z_6$
and
![]() $X_{uv}\lesssim \mathbb Z_9{:}\mathbb Z_6{\times } \mathbb Z_9{:}\mathbb Z_6$
. In particular, a Sylow
$X_{uv}\lesssim \mathbb Z_9{:}\mathbb Z_6{\times } \mathbb Z_9{:}\mathbb Z_6$
. In particular, a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $X_{\{u,v\}}=X_{uv}.2$
is not a cyclic group of order 8 and the unique Sylow
$X_{\{u,v\}}=X_{uv}.2$
is not a cyclic group of order 8 and the unique Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $X_{\{u,v\}}$
is nonabelian and contains elements of order 9. Since
$X_{\{u,v\}}$
is nonabelian and contains elements of order 9. Since
![]() $X_{\{u,v\}}=X_{uv}.2=X_v^{[1]}.(X_v^{{{\Gamma}}(v)})_u.2$
and
$X_{\{u,v\}}=X_{uv}.2=X_v^{[1]}.(X_v^{{{\Gamma}}(v)})_u.2$
and
![]() $X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v$
, we have
$X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v$
, we have
![]() $|X_{\{u,v\}}|=2^2\cdot 3^3$
,
$|X_{\{u,v\}}|=2^2\cdot 3^3$
,
![]() $2^2\cdot 3^4$
,
$2^2\cdot 3^4$
,
![]() $2^2\cdot 3^5$
,
$2^2\cdot 3^5$
,
![]() $2^2\cdot 3^6$
,
$2^2\cdot 3^6$
,
![]() $2^3\cdot 3^5$
or
$2^3\cdot 3^5$
or
![]() $2^3\cdot 3^6$
. Checking Tables 14–20 given in [Reference Li and Zhang17], we conclude that
$2^3\cdot 3^6$
. Checking Tables 14–20 given in [Reference Li and Zhang17], we conclude that
![]() $X={\mathrm{G}}_2(3).2$
and
$X={\mathrm{G}}_2(3).2$
and
![]() $X_{\{u,v\}}\cong [3^6]{:}{\mathrm{D}}_8$
. In this case,
$X_{\{u,v\}}\cong [3^6]{:}{\mathrm{D}}_8$
. In this case,
![]() $X_v^{[1]}\cong \mathbb Z_9{:}\mathbb Z_6$
and
$X_v^{[1]}\cong \mathbb Z_9{:}\mathbb Z_6$
and
![]() $X_v\cong \mathbb Z_9{:}\mathbb Z_6.{\mathrm{PSL}}_2(8){.}3$
; however, X has no such subgroup by the Atlas [Reference Conway, Norton, Parker and Wilson3], which is a contradiction. This completes the proof.
$X_v\cong \mathbb Z_9{:}\mathbb Z_6.{\mathrm{PSL}}_2(8){.}3$
; however, X has no such subgroup by the Atlas [Reference Conway, Norton, Parker and Wilson3], which is a contradiction. This completes the proof.
By Lemma 3.2, combining with Theorem 2.4, the next lemma follows from checking the point-stabilizers of finite almost simple
![]() $2$
-transitive groups; refer to [Reference Li, Seress and Song16, Table 2.1].
$2$
-transitive groups; refer to [Reference Li, Seress and Song16, Table 2.1].
Lemma 3.3. Suppose that Hypothesis 3.1 holds and
![]() $G_v^{{{\Gamma}}(v)}$
is almost simple. Then one of the following holds:
$G_v^{{{\Gamma}}(v)}$
is almost simple. Then one of the following holds:
-
(1)
 $G_v^{{{\Gamma}}(v)}=X_v^{{{\Gamma}}(v)}={\mathrm{PSL}}_3(2)$
or
$G_v^{{{\Gamma}}(v)}=X_v^{{{\Gamma}}(v)}={\mathrm{PSL}}_3(2)$
or
 ${\mathrm{PSL}}_3(3)$
, and
${\mathrm{PSL}}_3(3)$
, and
 $d=7$
or
$d=7$
or
 $13$
, respectively;
$13$
, respectively; -
(2)
 ${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{PSL}}_2(q)$
with
${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{PSL}}_2(q)$
with
 $q>4$
, and
$q>4$
, and
 $d=q{+}1$
;
$d=q{+}1$
; -
(3)
 $G_{uv}^{[1]}=1$
,
$G_{uv}^{[1]}=1$
,
 ${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{PSU}}_3(q)$
with
${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{PSU}}_3(q)$
with
 $q>2$
, and
$q>2$
, and
 $d=q^3{+}1$
;
$d=q^3{+}1$
; -
(4)
 $G_{uv}^{[1]}=1$
,
$G_{uv}^{[1]}=1$
,
 ${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{Sz}}(q)$
with
${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{Sz}}(q)$
with
 $q=2^{2n{+}1}>2$
, and
$q=2^{2n{+}1}>2$
, and
 $d=q^2{+}1$
;
$d=q^2{+}1$
; -
(5)
 $G_{uv}^{[1]}=1$
,
$G_{uv}^{[1]}=1$
,
 ${\mathrm{soc}}(X_v^{{{\Gamma}}(v)}) ={\mathrm{Ree}}(q)$
with
${\mathrm{soc}}(X_v^{{{\Gamma}}(v)}) ={\mathrm{Ree}}(q)$
with
 $q=3^{2n{+}1}>3$
, and
$q=3^{2n{+}1}>3$
, and
 $d=q^3{+}1$
.
$d=q^3{+}1$
.
In particular,
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(X,2)$
-arc-transitive.
$(X,2)$
-arc-transitive.
Recall that the Fitting subgroup
![]() ${\mathrm{Fit}}(H)$
of a finite group H is the direct product of
${\mathrm{Fit}}(H)$
of a finite group H is the direct product of
![]() $\textbf {O}_r(H)$
, where r runs over the set of prime divisors of
$\textbf {O}_r(H)$
, where r runs over the set of prime divisors of
![]() $|H|$
.
$|H|$
.
Lemma 3.4. Suppose that Hypothesis 3.1 holds and (2) or (5) of Lemma 3.3 occurs. Let
![]() $q=p^f$
for some prime p. Assume that
$q=p^f$
for some prime p. Assume that
![]() $X_{uv}^{[1]}=1$
. Then
$X_{uv}^{[1]}=1$
. Then
![]() ${\mathrm{Fit}}(X_{uv})=\textbf {O}_p(X_{uv})$
and either
${\mathrm{Fit}}(X_{uv})=\textbf {O}_p(X_{uv})$
and either
![]() ${\mathrm{Fit}}(X_{uv})={\mathrm{Fit}}(X_{\{u,v\}})$
or
${\mathrm{Fit}}(X_{uv})={\mathrm{Fit}}(X_{\{u,v\}})$
or
![]() ${\mathrm{Fit}}(X_{\{u,v\}})={\mathrm{Fit}}(X_{uv}).2$
; in particular, we have
${\mathrm{Fit}}(X_{\{u,v\}})={\mathrm{Fit}}(X_{uv}).2$
; in particular, we have
![]() $|{\mathrm{Fit}}(X_{\{u,v\}}):\textbf {O}_p(X_{\{u,v\}})|\le 2$
.
$|{\mathrm{Fit}}(X_{\{u,v\}}):\textbf {O}_p(X_{\{u,v\}})|\le 2$
.
Proof. Let r be a prime divisor of
![]() $|X_{uv}|$
. Then
$|X_{uv}|$
. Then
![]() $\textbf {O}_r(X_{uv})$
is normal in
$\textbf {O}_r(X_{uv})$
is normal in
![]() $X_{uv}$
. Since
$X_{uv}$
. Since
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(X,2)$
-arc-transitive,
$(X,2)$
-arc-transitive,
![]() $X_{uv}$
acts transitively on
$X_{uv}$
acts transitively on
![]() ${{\Gamma}}(v)\setminus \{u\}$
. Thus, all
${{\Gamma}}(v)\setminus \{u\}$
. Thus, all
![]() $\textbf {O}_r(X_{uv})$
-orbits (on
$\textbf {O}_r(X_{uv})$
-orbits (on
![]() ${{\Gamma}}(v)\setminus \{u\}$
) have equal size that is a power of r and a divisor of
${{\Gamma}}(v)\setminus \{u\}$
) have equal size that is a power of r and a divisor of
![]() $|{{\Gamma}}(v)\setminus \{u\}|$
. Note that
$|{{\Gamma}}(v)\setminus \{u\}|$
. Note that
![]() $|{{\Gamma}}(v)\setminus \{u\}|=d-1$
, which is a power of p. It follows that either
$|{{\Gamma}}(v)\setminus \{u\}|=d-1$
, which is a power of p. It follows that either
![]() $r=p$
or
$r=p$
or
![]() $\textbf {O}_r(X_{uv})=1$
. Then
$\textbf {O}_r(X_{uv})=1$
. Then
![]() ${\mathrm{Fit}}(X_{uv})=\textbf {O}_p(X_{uv})$
.
${\mathrm{Fit}}(X_{uv})=\textbf {O}_p(X_{uv})$
.
Note that
![]() $X_{uv}$
is normal in
$X_{uv}$
is normal in
![]() $X_{\{u,v\}}$
as
$X_{\{u,v\}}$
as
![]() $|X_{\{u,v\}}:X_{uv}|=2$
. Since
$|X_{\{u,v\}}:X_{uv}|=2$
. Since
![]() $\textbf {O}_p(X_{uv})$
is a characteristic subgroup of
$\textbf {O}_p(X_{uv})$
is a characteristic subgroup of
![]() $X_{uv}$
, it follows that
$X_{uv}$
, it follows that
![]() $\textbf {O}_p(X_{uv})$
is normal in
$\textbf {O}_p(X_{uv})$
is normal in
![]() $X_{\{u,v\}}$
and so
$X_{\{u,v\}}$
and so
![]() $\textbf {O}_p(X_{uv})\le \textbf {O}_p(X_{\{u,v\}})\le {\mathrm{Fit}}(X_{\{u,v\}})$
. For each odd prime divisor r of
$\textbf {O}_p(X_{uv})\le \textbf {O}_p(X_{\{u,v\}})\le {\mathrm{Fit}}(X_{\{u,v\}})$
. For each odd prime divisor r of
![]() $|X_{\{u,v\}}|$
, since
$|X_{\{u,v\}}|$
, since
![]() $|X_{\{u,v\}}:X_{uv}|=2$
, we have
$|X_{\{u,v\}}:X_{uv}|=2$
, we have
![]() $\textbf {O}_r(X_{\{u,v\}})\le X_{uv}$
and so
$\textbf {O}_r(X_{\{u,v\}})\le X_{uv}$
and so
![]() $\textbf {O}_r(X_{\{u,v\}})=\textbf {O}_r(X_{uv})$
. It follows that
$\textbf {O}_r(X_{\{u,v\}})=\textbf {O}_r(X_{uv})$
. It follows that
In particular,
![]() $\textbf {O}_p(X_{uv})=\textbf {O}_p(X_{\{u,v\}})$
if
$\textbf {O}_p(X_{uv})=\textbf {O}_p(X_{\{u,v\}})$
if
![]() $p\ne 2$
.
$p\ne 2$
.
It is easily shown that
![]() $X_{uv}\cap \textbf {O}_2(X_{\{u,v\}})=\textbf {O}_2(X_{uv})$
. If
$X_{uv}\cap \textbf {O}_2(X_{\{u,v\}})=\textbf {O}_2(X_{uv})$
. If
![]() $X_{uv}\ge \textbf {O}_2(X_{\{u,v\}})$
, then
$X_{uv}\ge \textbf {O}_2(X_{\{u,v\}})$
, then
![]() $p=2$
,
$p=2$
,
![]() ${\mathrm{Fit}}(X_{\{u,v\}})=\textbf {O}_2(X_{\{u,v\}})={\mathrm{Fit}}(X_{uv})$
and the lemma is true. Assume that
${\mathrm{Fit}}(X_{\{u,v\}})=\textbf {O}_2(X_{\{u,v\}})={\mathrm{Fit}}(X_{uv})$
and the lemma is true. Assume that
![]() $\textbf {O}_2(X_{\{u,v\}})\not \le X_{uv}$
. Since
$\textbf {O}_2(X_{\{u,v\}})\not \le X_{uv}$
. Since
![]() $|X_{\{u,v\}}:X_{uv}|=2$
, we have
$|X_{\{u,v\}}:X_{uv}|=2$
, we have
![]() $X_{\{u,v\}}=X_{uv}\textbf {O}_2(X_{\{u,v\}})$
. Then
$X_{\{u,v\}}=X_{uv}\textbf {O}_2(X_{\{u,v\}})$
. Then
 $$ \begin{align*} 2|X_{uv}|=|X_{\{u,v\}}|&=|X_{uv}||\textbf{O}_2(X_{\{u,v\}}):(X_{uv}\cap \textbf{O}_2(X_{\{u,v\}}))|\\ &=|X_{uv}||\textbf{O}_2(X_{\{u,v\}}):\textbf{O}_2(X_{uv})|, \end{align*} $$
$$ \begin{align*} 2|X_{uv}|=|X_{\{u,v\}}|&=|X_{uv}||\textbf{O}_2(X_{\{u,v\}}):(X_{uv}\cap \textbf{O}_2(X_{\{u,v\}}))|\\ &=|X_{uv}||\textbf{O}_2(X_{\{u,v\}}):\textbf{O}_2(X_{uv})|, \end{align*} $$
yielding
![]() $|\textbf {O}_2(X_{\{u,v\}}):\textbf {O}_2(X_{uv})|=2$
. If
$|\textbf {O}_2(X_{\{u,v\}}):\textbf {O}_2(X_{uv})|=2$
. If
![]() $p=2$
, then
$p=2$
, then
![]() ${\mathrm{Fit}}(X_{\{u,v\}})=\textbf {O}_2(X_{\{u,v\}})$
and
${\mathrm{Fit}}(X_{\{u,v\}})=\textbf {O}_2(X_{\{u,v\}})$
and
![]() ${\mathrm{Fit}}(X_{uv})=\textbf {O}_2(X_{uv})$
. If
${\mathrm{Fit}}(X_{uv})=\textbf {O}_2(X_{uv})$
. If
![]() $p\ne 2$
, then
$p\ne 2$
, then
![]() $\textbf {O}_2(X_{uv})=1$
,
$\textbf {O}_2(X_{uv})=1$
,
![]() $|\textbf {O}_2(X_{\{u,v\}})|=2$
and so
$|\textbf {O}_2(X_{\{u,v\}})|=2$
and so
![]() ${\mathrm{Fit}}(X_{\{u,v\}})=\textbf {O}_p(X_{uv})\times \mathbb Z_2$
. This completes the proof.
${\mathrm{Fit}}(X_{\{u,v\}})=\textbf {O}_p(X_{uv})\times \mathbb Z_2$
. This completes the proof.
3.2
Assume that Hypothesis 3.1 holds and
![]() $G_v$
is soluble. Then
$G_v$
is soluble. Then
![]() $G_v^{{{\Gamma}}(v)}$
is an affine
$G_v^{{{\Gamma}}(v)}$
is an affine
![]() $2$
-transitive group. Let
$2$
-transitive group. Let
![]() ${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})=\mathbb Z_p^f$
. Then
${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})=\mathbb Z_p^f$
. Then
![]() $d=p^f$
. Recalling that
$d=p^f$
. Recalling that
![]() $d\ge 6$
, we have
$d\ge 6$
, we have
![]() $G_{uv}^{[1]}=1$
by Theorem 2.4 and so
$G_{uv}^{[1]}=1$
by Theorem 2.4 and so
![]() $G_{uv}\lesssim (G_v^{{{\Gamma}}(v)})_u\,{\times }\, (G_u^{{{\Gamma}}(u)})_v$
. If
$G_{uv}\lesssim (G_v^{{{\Gamma}}(v)})_u\,{\times }\, (G_u^{{{\Gamma}}(u)})_v$
. If
![]() $G_{uv}$
is abelian, then
$G_{uv}$
is abelian, then
![]() ${{\Gamma}}$
is known from [Reference Lu21]. Thus, we assume further that
${{\Gamma}}$
is known from [Reference Lu21]. Thus, we assume further that
![]() $G_{uv}$
is not abelian. Then
$G_{uv}$
is not abelian. Then
![]() $(G_v^{{{\Gamma}}(v)})_u$
is nonabelian and so
$(G_v^{{{\Gamma}}(v)})_u$
is nonabelian and so
![]() $(G_v^{{{\Gamma}}(v)})_u\not \le {\mathrm{GL}}_1(p^f)$
; in particular,
$(G_v^{{{\Gamma}}(v)})_u\not \le {\mathrm{GL}}_1(p^f)$
; in particular,
![]() $f>1$
. Since
$f>1$
. Since
![]() $(G_v^{{{\Gamma}}(v)})_u$
is soluble, by [Reference Cameron2, Table 7.3], we have the following lemma.
$(G_v^{{{\Gamma}}(v)})_u$
is soluble, by [Reference Cameron2, Table 7.3], we have the following lemma.
Lemma 3.5. Suppose that Hypothesis 3.1 holds,
![]() $G_v$
is soluble and
$G_v$
is soluble and
![]() $G_{uv}$
is not abelian. Let
$G_{uv}$
is not abelian. Let
![]() ${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})=\mathbb Z_p^f$
, where p is a prime. Then
${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})=\mathbb Z_p^f$
, where p is a prime. Then
![]() $f>1$
and one of the following holds:
$f>1$
and one of the following holds:
-
(1)
 $f=2$
and either
$f=2$
and either
 ${\mathrm{SL}}_2(3)\unlhd (G_v^{{{\Gamma}}(v)})_u\le {\mathrm{GL}}_2(p)$
and
${\mathrm{SL}}_2(3)\unlhd (G_v^{{{\Gamma}}(v)})_u\le {\mathrm{GL}}_2(p)$
and
 $p\in \{3,5,7,11,23\}$
, or
$p\in \{3,5,7,11,23\}$
, or
 $p=3$
and
$p=3$
and
 $(G_v^{{{\Gamma}}(v)})_u={\mathrm{Q}}_8$
;
$(G_v^{{{\Gamma}}(v)})_u={\mathrm{Q}}_8$
; -
(2)
 $2_{+}^{1{+}4}{:}\mathbb Z_5\le (G_v^{{{\Gamma}}(v)})_u\le 2_{+}^{1{+}4}.(\mathbb Z_5{:}\mathbb Z_4)< 2_{+}^{1{+}4}.{\mathrm{S}}_5$
and
$2_{+}^{1{+}4}{:}\mathbb Z_5\le (G_v^{{{\Gamma}}(v)})_u\le 2_{+}^{1{+}4}.(\mathbb Z_5{:}\mathbb Z_4)< 2_{+}^{1{+}4}.{\mathrm{S}}_5$
and
 $p^f=3^4$
;
$p^f=3^4$
; -
(3)
 $(G_v^{{{\Gamma}}(v)})_u\not \le {\mathrm{GL}}_1(p^f)$
,
$(G_v^{{{\Gamma}}(v)})_u\not \le {\mathrm{GL}}_1(p^f)$
,
 $(G_v^{{{\Gamma}}(v)})_u\le {\Gamma \textrm{L}}_1(p^f)$
and
$(G_v^{{{\Gamma}}(v)})_u\le {\Gamma \textrm{L}}_1(p^f)$
and
 $|(G_v^{{{\Gamma}}(v)})_u|$
is divisible by
$|(G_v^{{{\Gamma}}(v)})_u|$
is divisible by
 $p^f-1$
.
$p^f-1$
.
Consider the case (3) in Lemma 3.5. Write
Let
![]() $\langle \tau \rangle \cap (G_v^{{{\Gamma}}(v)})_u=\langle \tau ^m\rangle $
, where
$\langle \tau \rangle \cap (G_v^{{{\Gamma}}(v)})_u=\langle \tau ^m\rangle $
, where
![]() $m\mid (p^f-1)$
. Then
$m\mid (p^f-1)$
. Then
Set
![]() $(G_v^{{{\Gamma}}(v)})_u/\langle \tau ^m\rangle \cong \langle \sigma ^e\rangle $
for some divisor e of f. Then
$(G_v^{{{\Gamma}}(v)})_u/\langle \tau ^m\rangle \cong \langle \sigma ^e\rangle $
for some divisor e of f. Then
Choose
![]() $\tau ^l\sigma ^k\in (G_v^{{{\Gamma}}(v)})_u$
with
$\tau ^l\sigma ^k\in (G_v^{{{\Gamma}}(v)})_u$
with
![]() $(G_v^{{{\Gamma}}(v)})_u=\langle \tau ^m\rangle \langle \tau ^l\sigma ^k\rangle $
. Then
$(G_v^{{{\Gamma}}(v)})_u=\langle \tau ^m\rangle \langle \tau ^l\sigma ^k\rangle $
. Then
![]() $(\tau ^l\sigma ^k)^{{f}/{e}}\in \langle \tau ^m\rangle $
but
$(\tau ^l\sigma ^k)^{{f}/{e}}\in \langle \tau ^m\rangle $
but
![]() $(\tau ^l\sigma ^k)^j\not \in \langle \tau ^m\rangle $
for
$(\tau ^l\sigma ^k)^j\not \in \langle \tau ^m\rangle $
for
![]() $1\le j< {f}/{e}$
. It follows that
$1\le j< {f}/{e}$
. It follows that
![]() $\sigma ^k$
has order
$\sigma ^k$
has order
![]() ${f}/{e}$
. Then
${f}/{e}$
. Then
![]() $\sigma ^k=\sigma ^{ie}$
for some i with
$\sigma ^k=\sigma ^{ie}$
for some i with
![]() $(i, {f}/{e})=1$
and then
$(i, {f}/{e})=1$
and then
![]() $(\sigma ^k)^{i'}=\sigma ^e$
for some
$(\sigma ^k)^{i'}=\sigma ^e$
for some
![]() $i'$
. Thus, replacing
$i'$
. Thus, replacing
![]() $\tau ^l\sigma ^k$
by a power of it if necessary, we may let
$\tau ^l\sigma ^k$
by a power of it if necessary, we may let
![]() $k=e$
. Then
$k=e$
. Then
Further,
![]() $(G_v^{{{\Gamma }}(v)})_u=\langle \tau ^m\rangle \langle (\tau ^m)^i\tau ^l\sigma ^e\rangle $
for an arbitrary integer i; thus, we may assume further that
$(G_v^{{{\Gamma }}(v)})_u=\langle \tau ^m\rangle \langle (\tau ^m)^i\tau ^l\sigma ^e\rangle $
for an arbitrary integer i; thus, we may assume further that
![]() $0\le l<m$
. By [Reference Foulser6, Proposition 15.3], letting
$0\le l<m$
. By [Reference Foulser6, Proposition 15.3], letting
![]() ${{\pi }}(n)$
be the set of prime divisors of a positive integer n:
${{\pi }}(n)$
be the set of prime divisors of a positive integer n:
-
(
 $\divideontimes $
)
$\divideontimes $
)
 ${{\pi }}(m)\subseteq {{\pi }}(p^e-1)$
,
${{\pi }}(m)\subseteq {{\pi }}(p^e-1)$
,
 $me\mid f$
and
$me\mid f$
and
 $(m,l)=1$
; in particular,
$(m,l)=1$
; in particular,
 $m=1$
if
$m=1$
if
 $l=0$
.
$l=0$
.
Suppose that
![]() $X_{uv}$
is nonabelian. (The case where
$X_{uv}$
is nonabelian. (The case where
![]() $X_{uv}$
is abelian is left to Section 5.) Since
$X_{uv}$
is abelian is left to Section 5.) Since
![]() $X_{uv}^{[1]}\le {\mathrm{G}}_{uv}^{[1]}=1$
,
$X_{uv}^{[1]}\le {\mathrm{G}}_{uv}^{[1]}=1$
,
This yields that
![]() $(X_v^{{{\Gamma}}(v)})_u$
is nonabelian. Then a limitation on
$(X_v^{{{\Gamma}}(v)})_u$
is nonabelian. Then a limitation on
![]() $\pi (|X_{uv}|)$
is given as follows.
$\pi (|X_{uv}|)$
is given as follows.
Lemma 3.6. Assume that Lemma 3.5(3) holds and
![]() $X_{uv}$
is nonabelian. Then
$X_{uv}$
is nonabelian. Then
![]() $(X_v^{{{\Gamma}}(v)})_u\cong \mathbb Z_{m'}.\mathbb Z_{{f}/{e'} }$
, where
$(X_v^{{{\Gamma}}(v)})_u\cong \mathbb Z_{m'}.\mathbb Z_{{f}/{e'} }$
, where
![]() $m'$
and
$m'$
and
![]() $e'$
satisfy:
$e'$
satisfy:
-
(1)
 $\mathbb Z_{m'}\cong (X_v^{{{\Gamma}}(v)})_u\cap \langle \tau ^m\rangle $
,
$\mathbb Z_{m'}\cong (X_v^{{{\Gamma}}(v)})_u\cap \langle \tau ^m\rangle $
,
 $mm'\mid p^f-1$
,
$mm'\mid p^f-1$
,
 $e\mid e'\mid f$
; and
$e\mid e'\mid f$
; and -
(2)
 $m'>1$
,
$m'>1$
,
 $e'<f$
,
$e'<f$
,
 ${{\pi }}(p^f-1)\setminus {{\pi }}(p^{e'}-1)\subseteq {{\pi }}(m')\subseteq \pi (|X_{uv}|)$
.
${{\pi }}(p^f-1)\setminus {{\pi }}(p^{e'}-1)\subseteq {{\pi }}(m')\subseteq \pi (|X_{uv}|)$
.
Proof. Recall that
![]() $(X_v^{{{\Gamma}}(v)})_u\unlhd (G_v^{{{\Gamma}}(v)})_u=\langle \tau ^m\rangle \langle \tau ^l\sigma ^e\rangle \cong \mathbb Z_{({p^f-1})/{m}}.\mathbb Z_{{f}/{e}}$
. Then
$(X_v^{{{\Gamma}}(v)})_u\unlhd (G_v^{{{\Gamma}}(v)})_u=\langle \tau ^m\rangle \langle \tau ^l\sigma ^e\rangle \cong \mathbb Z_{({p^f-1})/{m}}.\mathbb Z_{{f}/{e}}$
. Then
yielding
![]() $(X_v^{{{\Gamma}}(v)})_u\cong \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}$
with
$(X_v^{{{\Gamma}}(v)})_u\cong \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}$
with
![]() $m'$
and
$m'$
and
![]() $e'$
satisfying (1). Since
$e'$
satisfying (1). Since
![]() $X_{uv}$
is nonabelian,
$X_{uv}$
is nonabelian,
![]() $(X_v^{{{\Gamma}}(v)})_u$
is nonabelian and so
$(X_v^{{{\Gamma}}(v)})_u$
is nonabelian and so
![]() $m'>1$
and
$m'>1$
and
![]() $e'<f$
.
$e'<f$
.
By the above
![]() $(\divideontimes )$
, each prime
$(\divideontimes )$
, each prime
![]() $r\in {{\pi }}(p^f-1)\setminus {{\pi }}(p^{e'}-1)$
is a divisor of
$r\in {{\pi }}(p^f-1)\setminus {{\pi }}(p^{e'}-1)$
is a divisor of
![]() $|\langle \tau ^m\rangle |=({p^f-1})/{m}$
. Let R be the unique subgroup of order r of
$|\langle \tau ^m\rangle |=({p^f-1})/{m}$
. Let R be the unique subgroup of order r of
![]() $\langle \tau ^m\rangle $
. Then, since R is normal in
$\langle \tau ^m\rangle $
. Then, since R is normal in
![]() $(G_v^{{{\Gamma}}(v)})_u$
, either
$(G_v^{{{\Gamma}}(v)})_u$
, either
![]() $R\le (X_v^{{{\Gamma}}(v)})_u$
or
$R\le (X_v^{{{\Gamma}}(v)})_u$
or
![]() $R (X_v^{{{\Gamma}}(v)})_u=R{\times }(X_v^{{{\Gamma}}(v)})_u$
. Suppose that the latter case occurs. Since
$R (X_v^{{{\Gamma}}(v)})_u=R{\times }(X_v^{{{\Gamma}}(v)})_u$
. Suppose that the latter case occurs. Since
![]() $e'<f$
, we may let
$e'<f$
, we may let
![]() $\tau ^n\sigma ^{e'}\in (X_v^{{{\Gamma}}(v)})_u\setminus \langle \tau ^m\rangle $
. Then
$\tau ^n\sigma ^{e'}\in (X_v^{{{\Gamma}}(v)})_u\setminus \langle \tau ^m\rangle $
. Then
![]() $\sigma ^{e'}$
centralizes R. Thus,
$\sigma ^{e'}$
centralizes R. Thus,
![]() $x^{p^{e'}}=x$
for
$x^{p^{e'}}=x$
for
![]() $x\in R$
, yielding
$x\in R$
, yielding
![]() $r\mid (p^{e'}-1)$
, which is a contradiction. Then
$r\mid (p^{e'}-1)$
, which is a contradiction. Then
![]() $R\le (X_v^{{{\Gamma}}(v)})_u\cap \langle \tau ^m\rangle \cong \mathbb Z_{m'}$
. Noting that
$R\le (X_v^{{{\Gamma}}(v)})_u\cap \langle \tau ^m\rangle \cong \mathbb Z_{m'}$
. Noting that
![]() $m'$
is a divisor of
$m'$
is a divisor of
![]() $|X_{uv}|$
, the result follows.
$|X_{uv}|$
, the result follows.
4 Graphs with insoluble vertex-stabilizers
In this and the next sections, we prove Theorem 1.1. Thus, we let G, T, X and
![]() ${{\Gamma}}=(V,E)$
be as in Hypothesis 3.1. Our task is to determine which pair
${{\Gamma}}=(V,E)$
be as in Hypothesis 3.1. Our task is to determine which pair
![]() $(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20] is a possible candidate for
$(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20] is a possible candidate for
![]() $(X,X_{\{u,v\}})$
, and determine whether or not the resulting triple
$(X,X_{\{u,v\}})$
, and determine whether or not the resulting triple
![]() $(G,G_v,G_{\{u,v\}})$
meets the conditions (1) and (2) in Lemma 2.1.
$(G,G_v,G_{\{u,v\}})$
meets the conditions (1) and (2) in Lemma 2.1.
In this section, we deal with the case where
![]() $G_v$
is insoluble; that is,
$G_v$
is insoluble; that is,
![]() $X_v$
is described as in Lemma 3.3. First, by the following lemma, (4) and (5) of Lemma 3.3 are excluded.
$X_v$
is described as in Lemma 3.3. First, by the following lemma, (4) and (5) of Lemma 3.3 are excluded.
Lemma 4.1. (4) and (5) of Lemma 3.3 do not occur.
Proof. Suppose that Lemma 3.3(4) or (5) holds. By Theorem 2.4,
![]() $X_{uv}^{[1]}=1$
. Then
$X_{uv}^{[1]}=1$
. Then
![]() $X_v=X_v^{[1]}.X_v^{{{\Gamma}}(v)}$
,
$X_v=X_v^{[1]}.X_v^{{{\Gamma}}(v)}$
,
![]() $X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u$
and
$X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u$
and
![]() $X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
. Set
$X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
. Set
![]() $q=p^f$
with p a prime. Then the pair
$q=p^f$
with p a prime. Then the pair
![]() $(X_v^{{{\Gamma}}(v)}, (X_v^{{{\Gamma}}(v)})_u)$
is given as follows:
$(X_v^{{{\Gamma}}(v)}, (X_v^{{{\Gamma}}(v)})_u)$
is given as follows:
 $$ \begin{align*} \begin{array}{lll} X_v^{{{\Gamma}}(v)} & (X_v^{{{\Gamma}}(v)})_u & \\ {\mathrm{Sz}}(q).e & p^{f{+}f}{:}(q-1).e& e\mbox{ a divisor of } f,\,p=2,\, \mbox{odd } f>1 \\ {\mathrm{Ree}}(q).e & p^{f{+}2f}{:}(q-1).e &e\mbox{ a divisor of } f,\,p=3,\, \mbox{odd } f>1. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll} X_v^{{{\Gamma}}(v)} & (X_v^{{{\Gamma}}(v)})_u & \\ {\mathrm{Sz}}(q).e & p^{f{+}f}{:}(q-1).e& e\mbox{ a divisor of } f,\,p=2,\, \mbox{odd } f>1 \\ {\mathrm{Ree}}(q).e & p^{f{+}2f}{:}(q-1).e &e\mbox{ a divisor of } f,\,p=3,\, \mbox{odd } f>1. \end{array} \end{align*} $$
In particular,
![]() $\textbf {O}_p(X_{\{u,v\}})$
is not abelian.
$\textbf {O}_p(X_{\{u,v\}})$
is not abelian.
We next show that none of the pairs
![]() $(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] gives a desired pair
$(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] gives a desired pair
![]() $(X,X_{\{u,v\}})$
. Since
$(X,X_{\{u,v\}})$
. Since
![]() $\textbf {O}_p(X_{\{u,v\}})$
is nonabelian, those pairs
$\textbf {O}_p(X_{\{u,v\}})$
is nonabelian, those pairs
![]() $(G_0,H_0)$
with
$(G_0,H_0)$
with
![]() $\textbf {O}_p(H_0)$
abelian are not in our consideration. In particular,
$\textbf {O}_p(H_0)$
abelian are not in our consideration. In particular,
![]() ${\mathrm{soc}}(X)$
is not isomorphic to an alternating group. Also, noting that
${\mathrm{soc}}(X)$
is not isomorphic to an alternating group. Also, noting that
![]() $X_{\{u,v\}}$
has a subgroup of index 2, those
$X_{\{u,v\}}$
has a subgroup of index 2, those
![]() $H_0$
having no subgroup of index 2 are excluded.
$H_0$
having no subgroup of index 2 are excluded.
Case 1. Suppose that
![]() ${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{Ree}}(q)$
. Then
${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{Ree}}(q)$
. Then
![]() $p=3$
,
$p=3$
,
![]() $\textbf {O}_3(X_{\{u,v\}})$
is nonabelian and of order
$\textbf {O}_3(X_{\{u,v\}})$
is nonabelian and of order
![]() $3^{3f}$
,
$3^{3f}$
,
![]() $3^{4f}$
,
$3^{4f}$
,
![]() $3^{5f}$
or
$3^{5f}$
or
![]() $3^{6f}$
and
$3^{6f}$
and
![]() $|X_{\{u,v\}}|$
is a divisor of
$|X_{\{u,v\}}|$
is a divisor of
![]() $2\cdot 3^{6f}\cdot (q-1)^2f^2$
and divisible by
$2\cdot 3^{6f}\cdot (q-1)^2f^2$
and divisible by
![]() $2(q-1)$
. Checking the orders of those
$2(q-1)$
. Checking the orders of those
![]() $H_0$
given in [Reference Li and Zhang17, Table 15], we conclude that
$H_0$
given in [Reference Li and Zhang17, Table 15], we conclude that
![]() ${\mathrm{soc}}(X)$
is not a sporadic simple group.
${\mathrm{soc}}(X)$
is not a sporadic simple group.
Suppose that
![]() ${\mathrm{soc}}(X)$
is a simple exceptional group of Lie type. Checking [Reference Li and Zhang17, Table 20], we conclude that
${\mathrm{soc}}(X)$
is a simple exceptional group of Lie type. Checking [Reference Li and Zhang17, Table 20], we conclude that
![]() $(X,X_{\{u,v\}})$
is one of the pairs
$(X,X_{\{u,v\}})$
is one of the pairs
![]() $({\mathrm{Ree}}(3^t),[3^{3t}]{:}\mathbb Z_{3^t-1})$
and
$({\mathrm{Ree}}(3^t),[3^{3t}]{:}\mathbb Z_{3^t-1})$
and
![]() $({\mathrm{G}}_2(3^t).\mathbb Z_{2^{l+1}}, [3^{6t}]{:}\mathbb Z_{3^t-1}^2. \mathbb Z_{2^{l+1}})$
, where
$({\mathrm{G}}_2(3^t).\mathbb Z_{2^{l+1}}, [3^{6t}]{:}\mathbb Z_{3^t-1}^2. \mathbb Z_{2^{l+1}})$
, where
![]() $2^l$
is the
$2^l$
is the
![]() $2$
-part of t. Recall that
$2$
-part of t. Recall that
![]() $|X_{\{u,v\}}|$
is a divisor of
$|X_{\{u,v\}}|$
is a divisor of
![]() $2\cdot 3^{6f}\cdot (q-1)^2f^2$
and divisible by
$2\cdot 3^{6f}\cdot (q-1)^2f^2$
and divisible by
![]() $2(q-1)$
. It follows that
$2(q-1)$
. It follows that
![]() $f=t$
,
$f=t$
,
![]() $X={\mathrm{G}}_2(q).\mathbb Z_{2^{l+1}}$
and
$X={\mathrm{G}}_2(q).\mathbb Z_{2^{l+1}}$
and
![]() $X_{\{u,v\}}\cong [q^6]{:}\mathbb Z_{q-1}^2.\mathbb Z_{2^{l+1}}$
. This implies that
$X_{\{u,v\}}\cong [q^6]{:}\mathbb Z_{q-1}^2.\mathbb Z_{2^{l+1}}$
. This implies that
![]() $X_v^{[1]}\ne 1$
; in fact,
$X_v^{[1]}\ne 1$
; in fact,
![]() $|\textbf {O}_3(X_v^{[1]})|=q^3$
. Thus,
$|\textbf {O}_3(X_v^{[1]})|=q^3$
. Thus,
![]() $\textbf {O}_3(X_v)\ne 1$
and
$\textbf {O}_3(X_v)\ne 1$
and
![]() $X_v$
has a quotient
$X_v$
has a quotient
![]() ${\mathrm{Ree}}(q).e$
. Checking the maximal subgroups of
${\mathrm{Ree}}(q).e$
. Checking the maximal subgroups of
![]() ${\mathrm{G}}_2(q).\mathbb Z_{2^{l+1}}$
(refer to [Reference Kleidman15, Theorems A and B]) we conclude that
${\mathrm{G}}_2(q).\mathbb Z_{2^{l+1}}$
(refer to [Reference Kleidman15, Theorems A and B]) we conclude that
![]() ${\mathrm{G}}_2(q).\mathbb Z_{2^{l+1}}$
has no maximal subgroup containing such
${\mathrm{G}}_2(q).\mathbb Z_{2^{l+1}}$
has no maximal subgroup containing such
![]() $X_v$
as a subgroup, which is a contradiction.
$X_v$
as a subgroup, which is a contradiction.
Suppose that
![]() ${\mathrm{soc}}(X)$
is a simple classical group over a finite field of order
${\mathrm{soc}}(X)$
is a simple classical group over a finite field of order
![]() $r^t$
, where r is a prime. Since
$r^t$
, where r is a prime. Since
![]() $f>1$
is odd,
$f>1$
is odd,
![]() $3^f-1$
has an odd prime divisor and so
$3^f-1$
has an odd prime divisor and so
![]() $X_{\{u,v\}}$
is not a
$X_{\{u,v\}}$
is not a
![]() $\{2,3\}$
-group as
$\{2,3\}$
-group as
![]() $|X_{\{u,v\}}|$
is divisible by
$|X_{\{u,v\}}|$
is divisible by
![]() $3^f-1$
. Recall that
$3^f-1$
. Recall that
![]() $\textbf {O}_3(X_{\{u,v\}})$
is nonabelian and of order
$\textbf {O}_3(X_{\{u,v\}})$
is nonabelian and of order
![]() $3^{3f}$
,
$3^{3f}$
,
![]() $3^{4f}$
,
$3^{4f}$
,
![]() $3^{5f}$
or
$3^{5f}$
or
![]() $3^{6f}$
. Checking the groups
$3^{6f}$
. Checking the groups
![]() $H_0$
given in [Reference Li and Zhang17, Tables 16–19], we conclude that
$H_0$
given in [Reference Li and Zhang17, Tables 16–19], we conclude that
![]() ${\mathrm{soc}}(X)={\mathrm{PSL}}_n(r^t)$
or
${\mathrm{soc}}(X)={\mathrm{PSL}}_n(r^t)$
or
![]() ${\mathrm{PSU}}_n(r^t)$
, where
${\mathrm{PSU}}_n(r^t)$
, where
![]() $n\in \{3,4\}$
. Take a maximal subgroup M of X such that
$n\in \{3,4\}$
. Take a maximal subgroup M of X such that
![]() $X_v\le M$
. Then M has a simple section (that is, a quotient of some subgroup)
$X_v\le M$
. Then M has a simple section (that is, a quotient of some subgroup)
![]() ${\mathrm{Ree}}(q)$
. Recall that
${\mathrm{Ree}}(q)$
. Recall that
![]() $q>3$
. Checking Tables 8.3–8.6 and 8.8–8.11 given in [Reference Bray, Holt and Roney-Dougal1], we conclude that none of
$q>3$
. Checking Tables 8.3–8.6 and 8.8–8.11 given in [Reference Bray, Holt and Roney-Dougal1], we conclude that none of
![]() ${\mathrm{PSL}}_3(r^t)$
,
${\mathrm{PSL}}_3(r^t)$
,
![]() ${\mathrm{PSL}}_4(r^t)$
,
${\mathrm{PSL}}_4(r^t)$
,
![]() ${\mathrm{PSU}}_3(r^t)$
and
${\mathrm{PSU}}_3(r^t)$
and
![]() ${\mathrm{PSU}}_4(r^t)$
has such maximal subgroups, which is a contradiction.
${\mathrm{PSU}}_4(r^t)$
has such maximal subgroups, which is a contradiction.
Case 2. Suppose that
![]() ${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{Sz}}(q)$
. Then
${\mathrm{soc}}(X_v^{{{\Gamma}}(v)})={\mathrm{Sz}}(q)$
. Then
![]() $q=2^f$
,
$q=2^f$
,
![]() $|\textbf {O}_2(X_{\{u,v\}})|=2^{2f}a$
,
$|\textbf {O}_2(X_{\{u,v\}})|=2^{2f}a$
,
![]() $2^{3f}a$
or
$2^{3f}a$
or
![]() $2^{4f}a$
, where
$2^{4f}a$
, where
![]() $f>1$
is odd and
$f>1$
is odd and
![]() $a=1$
or
$a=1$
or
![]() $2$
. Noting that
$2$
. Noting that
![]() $|X_{\{u,v\}}|$
is divisible by
$|X_{\{u,v\}}|$
is divisible by
![]() $2(2^f-1)$
, by Lemma 2.6, we conclude that
$2(2^f-1)$
, by Lemma 2.6, we conclude that
![]() $X_{\{u,v\}}$
is not a
$X_{\{u,v\}}$
is not a
![]() $\{2,3\}$
-group. Since
$\{2,3\}$
-group. Since
![]() $X_{\{u,v\}}$
is nonabelian, it follows from [Reference Li and Zhang17, Tables 15–20] that either
$X_{\{u,v\}}$
is nonabelian, it follows from [Reference Li and Zhang17, Tables 15–20] that either
![]() $(X,X_{\{u,v\}})$
is one of
$(X,X_{\{u,v\}})$
is one of
![]() $({}^2{\mathrm{F}}_4(2)', [2^9]{:}5{:}4)$
,
$({}^2{\mathrm{F}}_4(2)', [2^9]{:}5{:}4)$
,
![]() $({\mathrm{Sz}}(2^t),[2^{2t}]{:}\mathbb Z_{2^t-1})$
and
$({\mathrm{Sz}}(2^t),[2^{2t}]{:}\mathbb Z_{2^t-1})$
and
![]() $({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, [2^{4t}]{:}\mathbb Z_{2^t-1}^2.\mathbb Z_{2^{l+1}})$
, or
$({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, [2^{4t}]{:}\mathbb Z_{2^t-1}^2.\mathbb Z_{2^{l+1}})$
, or
![]() ${\mathrm{soc}}(X)$
is one of
${\mathrm{soc}}(X)$
is one of
![]() ${\mathrm{PSL}}_n(r^t)$
and
${\mathrm{PSL}}_n(r^t)$
and
![]() ${\mathrm{PSU}}_n(r^t)$
, where
${\mathrm{PSU}}_n(r^t)$
, where
![]() $n\in \{3,4\}$
,
$n\in \{3,4\}$
,
![]() $2^l$
is the
$2^l$
is the
![]() $2$
-part of t and r is odd if
$2$
-part of t and r is odd if
![]() $n=4$
. The first pair leads to
$n=4$
. The first pair leads to
![]() $q=2^3$
and so
$q=2^3$
and so
![]() $|X_{\{u,v\}}|$
is divisible by
$|X_{\{u,v\}}|$
is divisible by
![]() $7$
, which is a contradiction. Checking the maximal subgroups of
$7$
, which is a contradiction. Checking the maximal subgroups of
![]() ${\mathrm{soc}}(X)$
(refer to [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6 and 8.8–8.14]), the groups
${\mathrm{soc}}(X)$
(refer to [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6 and 8.8–8.14]), the groups
![]() ${\mathrm{PSL}}_3(r^t)$
,
${\mathrm{PSL}}_3(r^t)$
,
![]() ${\mathrm{PSU}}_3(r^t)$
,
${\mathrm{PSU}}_3(r^t)$
,
![]() ${\mathrm{PSL}}_4(r^t)$
and
${\mathrm{PSL}}_4(r^t)$
and
![]() ${\mathrm{PSU}}_4(r^t)$
are excluded as they have no maximal subgroup with a simple section
${\mathrm{PSU}}_4(r^t)$
are excluded as they have no maximal subgroup with a simple section
![]() ${\mathrm{Sz}}(q)$
. Thus,
${\mathrm{Sz}}(q)$
. Thus,
![]() $(X,X_{\{u,v\}})=({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, [2^{4t}]{:}\mathbb Z_{2^t-1}^2.\mathbb Z_{2^{l+1}})$
or
$(X,X_{\{u,v\}})=({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, [2^{4t}]{:}\mathbb Z_{2^t-1}^2.\mathbb Z_{2^{l+1}})$
or
![]() $({\mathrm{Sz}}(2^t),[2^{2t}]{:}\mathbb Z_{2^t-1})$
. Note that
$({\mathrm{Sz}}(2^t),[2^{2t}]{:}\mathbb Z_{2^t-1})$
. Note that
![]() $|X_{\{u,v\}}|$
is a divisor of
$|X_{\{u,v\}}|$
is a divisor of
![]() $2\cdot 2^{4f}\cdot (q-1)^2f^2$
and is divisible by
$2\cdot 2^{4f}\cdot (q-1)^2f^2$
and is divisible by
![]() $2^{2f+1}(2^f-1)$
. It follows that
$2^{2f+1}(2^f-1)$
. It follows that
![]() $X={\mathrm{PSp}}_4(q).\mathbb Z_{2^{l+1}}$
and
$X={\mathrm{PSp}}_4(q).\mathbb Z_{2^{l+1}}$
and
![]() $X_v^{[1]}\cong [q^2]{:}\mathbb Z_{q-1}$
. However, by [Reference Bray, Holt and Roney-Dougal1, Table 8.14],
$X_v^{[1]}\cong [q^2]{:}\mathbb Z_{q-1}$
. However, by [Reference Bray, Holt and Roney-Dougal1, Table 8.14],
![]() ${\mathrm{PSp}}_4(q).\mathbb Z_{2^{l+1}}$
has no maximal subgroup containing
${\mathrm{PSp}}_4(q).\mathbb Z_{2^{l+1}}$
has no maximal subgroup containing
![]() $[q^2]{:}\mathbb Z_{q-1}.{\mathrm{Sz}}(q)$
, which is a contradiction. This completes the proof.
$[q^2]{:}\mathbb Z_{q-1}.{\mathrm{Sz}}(q)$
, which is a contradiction. This completes the proof.
Lemma 4.2. Assume that (1) of Lemma 3.3 occurs. Then G, X,
![]() $X_{\{u,v\}}$
and
$X_{\{u,v\}}$
and
![]() $X_v$
are as listed as in Table 3.
$X_v$
are as listed as in Table 3.
Table 3 Graphs for (1) of Lemma 3.3.

Proof. Assume first that
![]() $X_{uv}^{[1]}=1$
. Then
$X_{uv}^{[1]}=1$
. Then
![]() $X_v=X_v^{[1]}.X_v^{{{\Gamma}}(v)}$
,
$X_v=X_v^{[1]}.X_v^{{{\Gamma}}(v)}$
,
![]() $X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u$
and
$X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u$
and
![]() $X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
.
$X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
.
Suppose that
![]() $X_v^{{{\Gamma}}(v)}={\mathrm{PSL}}_3(2)$
. Then
$X_v^{{{\Gamma}}(v)}={\mathrm{PSL}}_3(2)$
. Then
![]() $(X_v^{{{\Gamma}}(v)})_u\cong {\mathrm{S}}_4$
and thus
$(X_v^{{{\Gamma}}(v)})_u\cong {\mathrm{S}}_4$
and thus
![]() $X_v^{[1]}$
and
$X_v^{[1]}$
and
![]() $X_{\{u,v\}}$
are given as follows:
$X_{\{u,v\}}$
are given as follows:
 $$ \begin{align*} \begin{array}{lllll} X_v^{[1]}& 1 & 2^2 &{\mathrm{A}}_4&{\mathrm{S}}_4\\ X_{\{u,v\}}& 2^2{:}{\mathrm{S}}_3.2& 2^4.{\mathrm{S}}_3.2&2^4{:}3^2.[4]& 2^4{:}{\mathrm{S}}_3^2.2. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lllll} X_v^{[1]}& 1 & 2^2 &{\mathrm{A}}_4&{\mathrm{S}}_4\\ X_{\{u,v\}}& 2^2{:}{\mathrm{S}}_3.2& 2^4.{\mathrm{S}}_3.2&2^4{:}3^2.[4]& 2^4{:}{\mathrm{S}}_3^2.2. \end{array} \end{align*} $$
In particular,
![]() $2^2\le |\textbf {O}_2(X_{\{u,v\}})|\le 2^5$
. Check all possible pairs
$2^2\le |\textbf {O}_2(X_{\{u,v\}})|\le 2^5$
. Check all possible pairs
![]() $(X,X_{\{u,v\}})$
in [Reference Li and Zhang17, Tables 14–20]. Noting that
$(X,X_{\{u,v\}})$
in [Reference Li and Zhang17, Tables 14–20]. Noting that
![]() ${\mathrm{A}}_8\cong {\mathrm{PSL}}_4(2)$
and
${\mathrm{A}}_8\cong {\mathrm{PSL}}_4(2)$
and
![]() ${\mathrm{PSU}}_4(2)\cong {\mathrm{PSp}}_4(3)$
, we conclude that
${\mathrm{PSU}}_4(2)\cong {\mathrm{PSp}}_4(3)$
, we conclude that
![]() $X\cong {\mathrm{A}}_8$
,
$X\cong {\mathrm{A}}_8$
,
![]() $X_{\{u,v\}}\cong 2^4{:}{\mathrm{S}}_3^2$
and
$X_{\{u,v\}}\cong 2^4{:}{\mathrm{S}}_3^2$
and
![]() $X_v^{[1]}\cong {\mathrm{A}}_4$
; or
$X_v^{[1]}\cong {\mathrm{A}}_4$
; or
![]() $X= {\mathrm{M}}_{12}$
with
$X= {\mathrm{M}}_{12}$
with
![]() $X_{\{u,v\}}\cong 2_{+}^{1{+}4}{:}{\mathrm{S}}_3$
; or
$X_{\{u,v\}}\cong 2_{+}^{1{+}4}{:}{\mathrm{S}}_3$
; or
![]() $X\cong {\mathrm{PSU}}_4(2)$
where
$X\cong {\mathrm{PSU}}_4(2)$
where
![]() $X_{\{u,v\}}\cong 2{\mathrm{A}}_4^2.2$
. The group
$X_{\{u,v\}}\cong 2{\mathrm{A}}_4^2.2$
. The group
![]() ${\mathrm{A}}_8$
is excluded as it has no subgroup of the form of
${\mathrm{A}}_8$
is excluded as it has no subgroup of the form of
![]() $X_v^{[1]}.{\mathrm{PSL}}_3(2)$
. The groups
$X_v^{[1]}.{\mathrm{PSL}}_3(2)$
. The groups
![]() ${\mathrm{M}}_{12}$
and
${\mathrm{M}}_{12}$
and
![]() ${\mathrm{PSU}}_4(2)$
are excluded as their orders are not divisible by
${\mathrm{PSU}}_4(2)$
are excluded as their orders are not divisible by
![]() $d=7$
.
$d=7$
.
Suppose that
![]() $X_v^{{{\Gamma}}(v)}={\mathrm{PSL}}_3(3)$
. Then
$X_v^{{{\Gamma}}(v)}={\mathrm{PSL}}_3(3)$
. Then
![]() $(X_v^{{{\Gamma}}(v)})_u\cong 3^2{:}2{\mathrm{S}}_4$
. Thus,
$(X_v^{{{\Gamma}}(v)})_u\cong 3^2{:}2{\mathrm{S}}_4$
. Thus,
![]() $X_v^{[1]}$
and
$X_v^{[1]}$
and
![]() $X_{\{u,v\}}$
are given as follows:
$X_{\{u,v\}}$
are given as follows:
 $$ \begin{align*} \begin{array}{cllllll} X_v^{[1]}& 1 & 3^2 &3^2{:}2&3^2{\mathrm{Q}}_8& 3^2{:}2{\mathrm{A}}_4& 3^2{:}2{\mathrm{S}}_4\\ X_{\{u,v\}}& 3^2{:}2{\mathrm{S}}_4{.}2& 3^4{:}2{\mathrm{S}}_4{.}2& 3^4{:}([4].{\mathrm{S}}_4){.}2&3^4{:}{\mathrm{Q}}_8^2{.}{\mathrm{S}}_3{.}2& 3^4{:}(2{\mathrm{A}}_4)^2{.}[4] &3^4{:}(2{\mathrm{S}}_4)^2{.}2. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cllllll} X_v^{[1]}& 1 & 3^2 &3^2{:}2&3^2{\mathrm{Q}}_8& 3^2{:}2{\mathrm{A}}_4& 3^2{:}2{\mathrm{S}}_4\\ X_{\{u,v\}}& 3^2{:}2{\mathrm{S}}_4{.}2& 3^4{:}2{\mathrm{S}}_4{.}2& 3^4{:}([4].{\mathrm{S}}_4){.}2&3^4{:}{\mathrm{Q}}_8^2{.}{\mathrm{S}}_3{.}2& 3^4{:}(2{\mathrm{A}}_4)^2{.}[4] &3^4{:}(2{\mathrm{S}}_4)^2{.}2. \end{array} \end{align*} $$
Note that
![]() $\textbf {O}_3(X_{\{u,v\}})\cong 3^2$
or
$\textbf {O}_3(X_{\{u,v\}})\cong 3^2$
or
![]() $3^4$
. Checking the possible pairs
$3^4$
. Checking the possible pairs
![]() $(X,X_{\{u,v\}})$
, we have
$(X,X_{\{u,v\}})$
, we have
![]() $X_{\{u,v\}}\cong 3^4{:}2^3{.}{\mathrm{S}}_4$
and
$X_{\{u,v\}}\cong 3^4{:}2^3{.}{\mathrm{S}}_4$
and
![]() $X= {\mathrm{A}}_{12}$
or
$X= {\mathrm{A}}_{12}$
or
![]() ${\mathrm {P\Omega }}^{+}_8(2)$
; in this case,
${\mathrm {P\Omega }}^{+}_8(2)$
; in this case,
![]() $d=13$
is not a divisor of
$d=13$
is not a divisor of
![]() $|X|$
, which is a contradiction.
$|X|$
, which is a contradiction.
Now let
![]() $X_{uv}^{[1]}$
be a nontrivial p-group. Then, by Theorem 2.4,
$X_{uv}^{[1]}$
be a nontrivial p-group. Then, by Theorem 2.4,
![]() $X_v$
and
$X_v$
and
![]() $X_{\{u,v\}}$
are given as shown in Table 4.
$X_{\{u,v\}}$
are given as shown in Table 4.
Table 4 Edge-stabilizers with
![]() $d=7$
or 13.
$d=7$
or 13.

Suppose that
![]() $p=2$
. Then
$p=2$
. Then
![]() $|X_{\{u,v\}}|$
is divisible by
$|X_{\{u,v\}}|$
is divisible by
![]() $9$
if and only if
$9$
if and only if
![]() $|\textbf {O}_2(X_{\{u,v\}})|\ge 8$
, and
$|\textbf {O}_2(X_{\{u,v\}})|\ge 8$
, and
![]() $\textbf {O}_2(X_{\{u,v\}})$
contains no elements of order 8 unless
$\textbf {O}_2(X_{\{u,v\}})$
contains no elements of order 8 unless
![]() $|\textbf {O}_2(X_{\{u,v\}})|\ge 2^{22}$
. Check the pairs
$|\textbf {O}_2(X_{\{u,v\}})|\ge 2^{22}$
. Check the pairs
![]() $(G_0,H_0)$
given in [Reference Li and Zhang17, Tables 14–20] by estimating
$(G_0,H_0)$
given in [Reference Li and Zhang17, Tables 14–20] by estimating
![]() $|H_0|$
and
$|H_0|$
and
![]() $|\textbf {O}_2(H_0)|$
. We conclude that one of the following holds:
$|\textbf {O}_2(H_0)|$
. We conclude that one of the following holds:
-
(i)
 $X={\mathrm{PSL}}_4(2).2\cong {\mathrm{S}}_8$
and
$X={\mathrm{PSL}}_4(2).2\cong {\mathrm{S}}_8$
and
 $X_{\{u,v\}}= 2^4{:}{\mathrm{S}}_4$
;
$X_{\{u,v\}}= 2^4{:}{\mathrm{S}}_4$
; -
(ii)
 $X= {\mathrm{PSL}}_5(2).2$
and
$X= {\mathrm{PSL}}_5(2).2$
and
 $X_{\{u,v\}}= [2^8]{.}{\mathrm{S}}_3^2.2$
;
$X_{\{u,v\}}= [2^8]{.}{\mathrm{S}}_3^2.2$
; -
(iii)
 $X= {\mathrm{F}}_4(2).2$
and
$X= {\mathrm{F}}_4(2).2$
and
 $X_{\{u,v\}}= [2^{22}]{.}{\mathrm{S}}_3^2.2$
;
$X_{\{u,v\}}= [2^{22}]{.}{\mathrm{S}}_3^2.2$
; -
(iv)
 ${\mathrm{soc}}(X)={\mathrm{PSL}}_3(4)$
and
${\mathrm{soc}}(X)={\mathrm{PSL}}_3(4)$
and
 $|\textbf {O}_2(X_{\{u,v\}})|=2^6$
;
$|\textbf {O}_2(X_{\{u,v\}})|=2^6$
; -
(v)
 $X= {\mathrm{PSU}}_4(3).2_3$
and
$X= {\mathrm{PSU}}_4(3).2_3$
and
 $|\textbf {O}_2(X_{\{u,v\}})|=2^7$
;
$|\textbf {O}_2(X_{\{u,v\}})|=2^7$
; -
(vi)
 $X= {\mathrm{He}}.2$
and
$X= {\mathrm{He}}.2$
and
 $X_{\{u,v\}}= [2^8]{:}{\mathrm{S}}_3^2.2$
.
$X_{\{u,v\}}= [2^8]{:}{\mathrm{S}}_3^2.2$
.
Case (iv) yields that
![]() $X_v\cong 2^3{:}{\mathrm{SL}}_3(2)$
or
$X_v\cong 2^3{:}{\mathrm{SL}}_3(2)$
or
![]() $2^4{:}{\mathrm{SL}}_3(2)$
; however, X has no such subgroup by the Atlas [Reference Conway, Norton, Parker and Wilson3]. Similarly, cases (v) and (vi) are excluded. For (i),
$2^4{:}{\mathrm{SL}}_3(2)$
; however, X has no such subgroup by the Atlas [Reference Conway, Norton, Parker and Wilson3]. Similarly, cases (v) and (vi) are excluded. For (i),
![]() $G=X$
and
$G=X$
and
![]() ${{\Gamma}}$
is (isomorphic to) the point–plane incidence graph of the projective geometry
${{\Gamma}}$
is (isomorphic to) the point–plane incidence graph of the projective geometry
![]() ${\mathrm{PG}}(3,2)$
. For (ii),
${\mathrm{PG}}(3,2)$
. For (ii),
![]() $G=X$
and
$G=X$
and
![]() ${{\Gamma}}$
is (isomorphic to) the line–plane incidence graph of the projective geometry
${{\Gamma}}$
is (isomorphic to) the line–plane incidence graph of the projective geometry
![]() ${\mathrm{PG}}(4,2)$
. If (iii) holds, then
${\mathrm{PG}}(4,2)$
. If (iii) holds, then
![]() $G=X$
and
$G=X$
and
![]() ${{\Gamma}}$
is the line–plane incidence graph of the metasymplectic space associated with
${{\Gamma}}$
is the line–plane incidence graph of the metasymplectic space associated with
![]() ${\mathrm{F}}_4(2)$
; see [Reference Weiss30].
${\mathrm{F}}_4(2)$
; see [Reference Weiss30].
Now let
![]() $p=3$
. Then
$p=3$
. Then
![]() $|\textbf {O}_3(X_{\{u,v\}})|=3^5$
or
$|\textbf {O}_3(X_{\{u,v\}})|=3^5$
or
![]() $3^8$
, and
$3^8$
, and
![]() $X_{\{u,v\}}$
has no normal Sylow subgroup. Checking all possible pairs
$X_{\{u,v\}}$
has no normal Sylow subgroup. Checking all possible pairs
![]() $(X,X_{\{u,v\}})$
in [Reference Li and Zhang17, Tables 14–20], we know that
$(X,X_{\{u,v\}})$
in [Reference Li and Zhang17, Tables 14–20], we know that
![]() $(X,X_{\{u,v\}})$
is one of the following pairs:
$(X,X_{\{u,v\}})$
is one of the following pairs:
 $$ \begin{align*}\begin{array}{l} ({\mathrm{F}}_4(8).2, 9^4.(2_{+}^{1{+}4}{:}{\mathrm{S}}_3^2).2),\\ ({\mathrm{PSL}}_5(3).2, [3^8]{:}(2{\mathrm{S}}_4)^2.2),\, ({\mathrm{PSL}}_4(3).2, 3_{+}^{1{+}4}{:}(2{\times} 2{\mathrm{S}}_4)). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\mathrm{F}}_4(8).2, 9^4.(2_{+}^{1{+}4}{:}{\mathrm{S}}_3^2).2),\\ ({\mathrm{PSL}}_5(3).2, [3^8]{:}(2{\mathrm{S}}_4)^2.2),\, ({\mathrm{PSL}}_4(3).2, 3_{+}^{1{+}4}{:}(2{\times} 2{\mathrm{S}}_4)). \end{array} \end{align*} $$
Note that
![]() $\textbf {O}_3(X_v)\le \textbf {O}_3(X_{\{u,v\}})$
. Then, for the first pair,
$\textbf {O}_3(X_v)\le \textbf {O}_3(X_{\{u,v\}})$
. Then, for the first pair,
![]() $\textbf {O}_3(X_{\{u,v\}})\cong \mathbb Z_9^4$
has no subgroup isomorphic to
$\textbf {O}_3(X_{\{u,v\}})\cong \mathbb Z_9^4$
has no subgroup isomorphic to
![]() $\mathbb Z_3^6$
, which is impossible. For the second pair,
$\mathbb Z_3^6$
, which is impossible. For the second pair,
![]() $G=X$
and
$G=X$
and
![]() ${{\Gamma}}$
is (isomorphic to) the line–plane incidence graph of the projective geometry
${{\Gamma}}$
is (isomorphic to) the line–plane incidence graph of the projective geometry
![]() ${\mathrm{PG}}(4,3)$
. The last pair implies that
${\mathrm{PG}}(4,3)$
. The last pair implies that
![]() $X\cong {\mathrm{PGL}}_4(3)$
,
$X\cong {\mathrm{PGL}}_4(3)$
,
![]() $G=X$
or
$G=X$
or
![]() $X.2$
, and
$X.2$
, and
![]() ${{\Gamma}}$
is (isomorphic to) the line–plane incidence graph of the projective geometry
${{\Gamma}}$
is (isomorphic to) the line–plane incidence graph of the projective geometry
![]() ${\mathrm{PG}}(3,3)$
. This completes the proof.
${\mathrm{PG}}(3,3)$
. This completes the proof.
Lemma 4.3. Assume that Lemma 3.3(2) holds. Then
![]() $d=q+1$
and either
$d=q+1$
and either
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(X,4)$
-arc-transitive or G, X,
$(X,4)$
-arc-transitive or G, X,
![]() $X_{\{u,v\}}$
and
$X_{\{u,v\}}$
and
![]() $X_v$
are as listed in Table 5.
$X_v$
are as listed in Table 5.
Table 5 Graphs for (2) of Lemma 3.3.

Proof. Let
![]() $X_v^{{{\Gamma}}(v)}= {\mathrm{PSL}}_2(q).[o]$
and
$X_v^{{{\Gamma}}(v)}= {\mathrm{PSL}}_2(q).[o]$
and
![]() $q=p^f> 4$
, where p is a prime and o is a divisor of
$q=p^f> 4$
, where p is a prime and o is a divisor of
![]() $(2,p-1)f$
. Note that
$(2,p-1)f$
. Note that
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(X,2)$
-arc-transitive; see Lemma 3.3. By Theorem 2.4, if
$(X,2)$
-arc-transitive; see Lemma 3.3. By Theorem 2.4, if
![]() $X_{uv}^{[1]}\ne 1$
, then
$X_{uv}^{[1]}\ne 1$
, then
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(X,4)$
-arc-transitive. Thus, we assume next that
$(X,4)$
-arc-transitive. Thus, we assume next that
![]() $X_{uv}^{[1]}=1$
and then Lemma 3.4 works.
$X_{uv}^{[1]}=1$
and then Lemma 3.4 works.
Note that
![]() $X_v=X_v^{[1]}.X_v^{{{\Gamma}}(v)}$
,
$X_v=X_v^{[1]}.X_v^{{{\Gamma}}(v)}$
,
 $$\begin{align*}X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u= p^f{:}({q-1})/{(2,q-1)}{.}[o]\end{align*}$$
$$\begin{align*}X_v^{[1]}\cong (X_v^{[1]})^{{{\Gamma}}(u)}\unlhd (X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u= p^f{:}({q-1})/{(2,q-1)}{.}[o]\end{align*}$$
and
![]() $X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
. We have
$X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
. We have
![]() $\textbf {O}_p(X_{\{u,v\}})=\mathbb Z_p^{if}.a$
, where
$\textbf {O}_p(X_{\{u,v\}})=\mathbb Z_p^{if}.a$
, where
![]() $i\in \{1,2\}$
and a is a divisor of
$i\in \{1,2\}$
and a is a divisor of
![]() $(2,p)$
. It is easily shown that
$(2,p)$
. It is easily shown that
![]() $i=2$
if and only if
$i=2$
if and only if
![]() $\textbf {O}_p(X_v^{[1]})=\mathbb Z_p^f$
. Combining with Lemma 3.4, we need only consider those pairs
$\textbf {O}_p(X_v^{[1]})=\mathbb Z_p^f$
. Combining with Lemma 3.4, we need only consider those pairs
![]() $(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] that satisfy:
$(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] that satisfy:
-
(a)
 $\textbf {O}_p(H_0)=\mathbb Z_p^{if}.a$
, where
$\textbf {O}_p(H_0)=\mathbb Z_p^{if}.a$
, where
 $i\in \{1,2\}$
$i\in \{1,2\}$
 $a\mid (2,p)$
;
$a\mid (2,p)$
;
 $|{\mathrm{Fit}}(H_0):\textbf {O}_p(H_0)|\le 2$
;
$|{\mathrm{Fit}}(H_0):\textbf {O}_p(H_0)|\le 2$
;
 $G_0$
has a subgroup, say
$G_0$
has a subgroup, say
 $M_0$
, such that
$M_0$
, such that
 $|M_0:(M_0\cap H_0)|=q+1$
,
$|M_0:(M_0\cap H_0)|=q+1$
,
 $|H_0:(M_0\cap H_0)|=2$
and
$|H_0:(M_0\cap H_0)|=2$
and
 $M_0$
has a simple section
$M_0$
has a simple section
 ${\mathrm{PSL}}_2(q)$
;
${\mathrm{PSL}}_2(q)$
; -
(b)
 $|H_0{:}\textbf {O}_p(H_0)|$
is a divisor of
$|H_0{:}\textbf {O}_p(H_0)|$
is a divisor of
 $2(q-1)^2f^2$
and divisible by
$2(q-1)^2f^2$
and divisible by
 $q-1$
; if
$q-1$
; if
 $i=1$
, then
$i=1$
, then
 $|H_0{:}\textbf {O}_p(H_0)|$
is a divisor of
$|H_0{:}\textbf {O}_p(H_0)|$
is a divisor of
 $2(q-1)f$
.
$2(q-1)f$
.
Case 1. Assume that
![]() ${\mathrm{soc}}(X)$
is an alternating group. Using [Reference Li and Zhang17, Table 14], we have
${\mathrm{soc}}(X)$
is an alternating group. Using [Reference Li and Zhang17, Table 14], we have
![]() $G=X={\mathrm{S}}_p$
and
$G=X={\mathrm{S}}_p$
and
![]() $X_{\{u,v\}}\cong \mathbb Z_p{:}\mathbb Z_{p-1}$
, where
$X_{\{u,v\}}\cong \mathbb Z_p{:}\mathbb Z_{p-1}$
, where
![]() $p\in \{7,11,17,23\}$
. Then
$p\in \{7,11,17,23\}$
. Then
![]() $X_v={\mathrm{PSL}}_2(p)$
and
$X_v={\mathrm{PSL}}_2(p)$
and
![]() $d=p{+}1$
. In particular,
$d=p{+}1$
. In particular,
![]() ${{\Gamma}}$
is a bipartite graph with two parts being the orbits of
${{\Gamma}}$
is a bipartite graph with two parts being the orbits of
![]() ${\mathrm{A}}_p$
on the vertex set V. For
${\mathrm{A}}_p$
on the vertex set V. For
![]() $p=17$
or
$p=17$
or
![]() $23$
, the group
$23$
, the group
![]() ${\mathrm{PSL}}_2(p)$
has no transitive permutation representation of degree p and thus it cannot occur as a subgroup of
${\mathrm{PSL}}_2(p)$
has no transitive permutation representation of degree p and thus it cannot occur as a subgroup of
![]() ${\mathrm{S}}_p$
. Therefore,
${\mathrm{S}}_p$
. Therefore,
![]() $p=7$
or
$p=7$
or
![]() $11$
, and G, X and
$11$
, and G, X and
![]() $X_{\{u,v\}}$
are as listed in Table 5. In fact,
$X_{\{u,v\}}$
are as listed in Table 5. In fact,
![]() $X_{uv}$
and
$X_{uv}$
and
![]() $X_{\{u,v\}}$
are the normalizers of some Sylow p-subgroup in
$X_{\{u,v\}}$
are the normalizers of some Sylow p-subgroup in
![]() ${\mathrm{PSL}}_2(p)$
and
${\mathrm{PSL}}_2(p)$
and
![]() ${\mathrm{S}}_p$
, respectively. (Note that
${\mathrm{S}}_p$
, respectively. (Note that
![]() ${\mathrm{A}}_7$
can be embedded in
${\mathrm{A}}_7$
can be embedded in
![]() ${\mathrm{PSL}}_4(2)$
acting on the projective points or the hyperplanes of the projective geometry
${\mathrm{PSL}}_4(2)$
acting on the projective points or the hyperplanes of the projective geometry
![]() ${\mathrm{PG}}(3,2)$
; see [Reference Liebeck, Praeger and Saxl18, Table III], for example. Then, for
${\mathrm{PG}}(3,2)$
; see [Reference Liebeck, Praeger and Saxl18, Table III], for example. Then, for
![]() $p=7$
, it is easily shown that the resulting graph is the point–plane nonincidence graph of
$p=7$
, it is easily shown that the resulting graph is the point–plane nonincidence graph of
![]() ${\mathrm{PG}}(3,2)$
.)
${\mathrm{PG}}(3,2)$
.)
Case 2. Assume that
![]() ${\mathrm{soc}}(X)$
is a simple sporadic group. By [Reference Li and Zhang17, Table 15], with the restrictions (a) and (b), the only pairs
${\mathrm{soc}}(X)$
is a simple sporadic group. By [Reference Li and Zhang17, Table 15], with the restrictions (a) and (b), the only pairs
![]() $(G_0,H_0)$
are listed as follows:
$(G_0,H_0)$
are listed as follows:
 $$ \begin{align*}\begin{array}{l} ({\rm M}_{11}, 3^2{:}{\rm Q}_8.2),\, ({\rm J}_1,\mathbb Z_{11}{:}\mathbb Z_{10}),\, ({\rm J}_1,\mathbb Z_{7}{:}\mathbb Z_{6}),\, ({\rm J}_3.2,\mathbb Z_{19}{:}\mathbb Z_{18}),\, ({\rm J}_4,\mathbb Z_{29}{:}\mathbb Z_{28}),\\ ({\rm O'N}.2,\mathbb Z_{31}{:}\mathbb Z_{30}),\, ({\rm B},\mathbb Z_{19}{:}\mathbb Z_{18}{\times} \mathbb Z_2),\, ({\rm B},\mathbb Z_{23}{:}\mathbb Z_{11}{\times} \mathbb Z_2),\\ ({\rm M},\mathbb Z_{41}{:}\mathbb Z_{40}), ({\rm M},\mathbb Z_{47}{:}\mathbb Z_{23}{\times} \mathbb Z_2).\end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\rm M}_{11}, 3^2{:}{\rm Q}_8.2),\, ({\rm J}_1,\mathbb Z_{11}{:}\mathbb Z_{10}),\, ({\rm J}_1,\mathbb Z_{7}{:}\mathbb Z_{6}),\, ({\rm J}_3.2,\mathbb Z_{19}{:}\mathbb Z_{18}),\, ({\rm J}_4,\mathbb Z_{29}{:}\mathbb Z_{28}),\\ ({\rm O'N}.2,\mathbb Z_{31}{:}\mathbb Z_{30}),\, ({\rm B},\mathbb Z_{19}{:}\mathbb Z_{18}{\times} \mathbb Z_2),\, ({\rm B},\mathbb Z_{23}{:}\mathbb Z_{11}{\times} \mathbb Z_2),\\ ({\rm M},\mathbb Z_{41}{:}\mathbb Z_{40}), ({\rm M},\mathbb Z_{47}{:}\mathbb Z_{23}{\times} \mathbb Z_2).\end{array}\end{align*} $$
In particular,
![]() $\textbf {O}_p(H_0)$
is a Sylow p-subgroup of
$\textbf {O}_p(H_0)$
is a Sylow p-subgroup of
![]() $G_0$
. This yields that
$G_0$
. This yields that
![]() $X_v^{[1]}=1$
and so
$X_v^{[1]}=1$
and so
![]() ${\mathrm{soc}}(X_v)={\mathrm{PSL}}_2(p^f)$
.
${\mathrm{soc}}(X_v)={\mathrm{PSL}}_2(p^f)$
.
If
![]() $(X,X_{\{u,v\}})$
is one of
$(X,X_{\{u,v\}})$
is one of
![]() $({\mathrm{J}}_1,\mathbb Z_{7}{:}\mathbb Z_{6})$
,
$({\mathrm{J}}_1,\mathbb Z_{7}{:}\mathbb Z_{6})$
,
![]() $({\mathrm{J}}_4,\mathbb Z_{29}{:}\mathbb Z_{28})$
and
$({\mathrm{J}}_4,\mathbb Z_{29}{:}\mathbb Z_{28})$
and
![]() $({\mathrm{M}},\mathbb Z_{47}{:}\mathbb Z_{23}{\times } \mathbb Z_2)$
, then
$({\mathrm{M}},\mathbb Z_{47}{:}\mathbb Z_{23}{\times } \mathbb Z_2)$
, then
![]() $X_v= {\mathrm{PSL}}_2(p)$
for
$X_v= {\mathrm{PSL}}_2(p)$
for
![]() $p=7$
,
$p=7$
,
![]() $29$
and
$29$
and
![]() $47$
, respectively; however, by the Atlas [Reference Conway, Norton, Parker and Wilson3] and [Reference Wilson36, Tables 5.6 and 5.11], X has no subgroup
$47$
, respectively; however, by the Atlas [Reference Conway, Norton, Parker and Wilson3] and [Reference Wilson36, Tables 5.6 and 5.11], X has no subgroup
![]() ${\mathrm{PSL}}_2(p)$
, which is a contradiction. Thus, G, X and
${\mathrm{PSL}}_2(p)$
, which is a contradiction. Thus, G, X and
![]() $X_{\{u,v\}}$
are as listed in Table 5. (Note that the Monster
$X_{\{u,v\}}$
are as listed in Table 5. (Note that the Monster
![]() ${\mathrm{M}}$
has a maximal subgroup
${\mathrm{M}}$
has a maximal subgroup
![]() ${\mathrm{PSL}}_2(41)$
by [Reference Norton and Wilson23].)
${\mathrm{PSL}}_2(41)$
by [Reference Norton and Wilson23].)
Case 3. Assume that
![]() ${\mathrm{soc}}(X)$
is a simple group of Lie type over a finite field of order
${\mathrm{soc}}(X)$
is a simple group of Lie type over a finite field of order
![]() $r^t$
, where r is a prime. We first show that
$r^t$
, where r is a prime. We first show that
![]() $r\ne p$
.
$r\ne p$
.
Suppose that
![]() $r=p$
. Then, by (a), either
$r=p$
. Then, by (a), either
![]() $\textbf {O}_p(H_0)$
is abelian or
$\textbf {O}_p(H_0)$
is abelian or
![]() $r=p=2$
. For
$r=p=2$
. For
![]() $r=p> 2$
, noting that
$r=p> 2$
, noting that
![]() $|H_0|$
has a divisor
$|H_0|$
has a divisor
![]() $q-1$
, there does not exist
$q-1$
, there does not exist
![]() $H_0$
in [Reference Li and Zhang17, Tables 16–20] such that
$H_0$
in [Reference Li and Zhang17, Tables 16–20] such that
![]() $\textbf {O}_p(H_0)$
is abelian. Thus, we have
$\textbf {O}_p(H_0)$
is abelian. Thus, we have
![]() $r=p=2$
. Recalling that
$r=p=2$
. Recalling that
![]() $p^f>4$
and
$p^f>4$
and
![]() $|H_0/\textbf {O}_p(H_0)|$
is divisible by
$|H_0/\textbf {O}_p(H_0)|$
is divisible by
![]() $2^f-1$
, it follows from Lemma 2.6 that
$2^f-1$
, it follows from Lemma 2.6 that
![]() $H_0/\textbf {O}_p(H_0)$
is not a
$H_0/\textbf {O}_p(H_0)$
is not a
![]() $\{2,3\}$
-group. Checking those
$\{2,3\}$
-group. Checking those
![]() $H_0$
given in [Reference Li and Zhang17, Tables 16–20], we conclude that
$H_0$
given in [Reference Li and Zhang17, Tables 16–20], we conclude that
![]() $(G_0,H_0)$
is one of the following pairs:
$(G_0,H_0)$
is one of the following pairs:
 $$ \begin{align*}\begin{array}{l} ({\mathrm{PSL}}_2(2^t), \mathbb Z_2^t{:}\mathbb Z_{2^t-1}),\,({\mathrm{PSL}}_3(2^t), [2^{3t}]{:}[{(2^t-1)^2}/{(3,2^t-1)}].2),\\ ({\mathrm{PSU}}_3(2^t), [2^{3t}]{:}\mathbb Z_{({2^{2t}-1})/{(3,2^t+1)}}),\\ ({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, [2^{4t}]{:}\mathbb Z_{2^{t}-1}^2.\mathbb Z_{2^{l+1}}), \mbox{ where }2^l \mbox{ is the }2\mbox{-part of }t,\\ ({\mathrm{Sz}}(2^t), [2^{2t}]{:}\mathbb Z_{2^{t}-1}), ({}^3{\mathrm{D}}_4(2), [2^{11}]{:}(\mathbb Z_7\times{\mathrm{S}}_3)),\, ({}^2{\mathrm{F}}_4(2)', [2^9]{:}5{:}4). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\mathrm{PSL}}_2(2^t), \mathbb Z_2^t{:}\mathbb Z_{2^t-1}),\,({\mathrm{PSL}}_3(2^t), [2^{3t}]{:}[{(2^t-1)^2}/{(3,2^t-1)}].2),\\ ({\mathrm{PSU}}_3(2^t), [2^{3t}]{:}\mathbb Z_{({2^{2t}-1})/{(3,2^t+1)}}),\\ ({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, [2^{4t}]{:}\mathbb Z_{2^{t}-1}^2.\mathbb Z_{2^{l+1}}), \mbox{ where }2^l \mbox{ is the }2\mbox{-part of }t,\\ ({\mathrm{Sz}}(2^t), [2^{2t}]{:}\mathbb Z_{2^{t}-1}), ({}^3{\mathrm{D}}_4(2), [2^{11}]{:}(\mathbb Z_7\times{\mathrm{S}}_3)),\, ({}^2{\mathrm{F}}_4(2)', [2^9]{:}5{:}4). \end{array}\end{align*} $$
First, the pair
![]() $({\mathrm{Sz}}(2^t), [2^{2t}]{:}\mathbb Z_{2^{t}-1})$
is excluded as
$({\mathrm{Sz}}(2^t), [2^{2t}]{:}\mathbb Z_{2^{t}-1})$
is excluded as
![]() ${\mathrm{Sz}}(2^t)$
has no subgroup with a section
${\mathrm{Sz}}(2^t)$
has no subgroup with a section
![]() ${\mathrm{PSL}}_2(2^f)$
. For the last two pairs, we have
${\mathrm{PSL}}_2(2^f)$
. For the last two pairs, we have
![]() $f=5$
and
$f=5$
and
![]() $4$
, respectively, which yields that
$4$
, respectively, which yields that
![]() $2^f-1$
is not a divisor of
$2^f-1$
is not a divisor of
![]() $|H_0|$
, which is a contradiction. For the three pairs after the first one, we have
$|H_0|$
, which is a contradiction. For the three pairs after the first one, we have
![]() $t<f$
and thus
$t<f$
and thus
![]() $G_0$
has no maximal subgroup with a section
$G_0$
has no maximal subgroup with a section
![]() ${\mathrm{PSL}}_2(2^f)$
, which is a contradiction. Suppose finally that
${\mathrm{PSL}}_2(2^f)$
, which is a contradiction. Suppose finally that
![]() $(X,X_{\{u,v\}})=({\mathrm{PSL}}_2(2^t), \mathbb Z_2^t{:}\mathbb Z_{2^t-1})$
. Then
$(X,X_{\{u,v\}})=({\mathrm{PSL}}_2(2^t), \mathbb Z_2^t{:}\mathbb Z_{2^t-1})$
. Then
![]() $3\le f<t\le 2f+1$
. Noting that
$3\le f<t\le 2f+1$
. Noting that
![]() $2^f-1$
is a divisor of
$2^f-1$
is a divisor of
![]() $2^t-1$
, it follows that f is a divisor of t and so
$2^t-1$
, it follows that f is a divisor of t and so
![]() $t=2f$
. Then
$t=2f$
. Then
![]() $\textbf {O}_2(X_{\{u,v\}})=2^{2f}$
, yielding
$\textbf {O}_2(X_{\{u,v\}})=2^{2f}$
, yielding
![]() $|\textbf {O}_2(X_v^{[1]})|=2^f$
. Thus,
$|\textbf {O}_2(X_v^{[1]})|=2^f$
. Thus,
![]() $\textbf {O}_2(X_v)\ne 1$
and
$\textbf {O}_2(X_v)\ne 1$
and
![]() $X_v$
has a section
$X_v$
has a section
![]() ${\mathrm{PSL}}_2(2^f)$
. Check the subgroups of
${\mathrm{PSL}}_2(2^f)$
. Check the subgroups of
![]() ${\mathrm{PSL}}_2(2^{2f})$
; refer to [Reference Huppert12, Hauptsatz II.8.27]. We conclude that
${\mathrm{PSL}}_2(2^{2f})$
; refer to [Reference Huppert12, Hauptsatz II.8.27]. We conclude that
![]() ${\mathrm{PSL}}_2(2^{2f})$
has no subgroup isomorphic to
${\mathrm{PSL}}_2(2^{2f})$
has no subgroup isomorphic to
![]() $X_v$
, which is a contradiction.
$X_v$
, which is a contradiction.
We assume that
![]() $r\ne p$
from now on.
$r\ne p$
from now on.
Subcase 3.1. We first deal with those pairs
![]() $(G_0,H_0)$
such that
$(G_0,H_0)$
such that
![]() $H_0$
is included in some infinite families in [Reference Li and Zhang17, Tables 16–20]. Note that
$H_0$
is included in some infinite families in [Reference Li and Zhang17, Tables 16–20]. Note that
![]() $r\ne p$
and we consider only those
$r\ne p$
and we consider only those
![]() $H_0$
having subgroups of index 2. It follows that either
$H_0$
having subgroups of index 2. It follows that either
![]() $H_0/{\mathrm{Fit}}(H_0)$
is a
$H_0/{\mathrm{Fit}}(H_0)$
is a
![]() $\{2,3\}$
-group, or
$\{2,3\}$
-group, or
![]() $G_0={\mathrm{E}}_8(q')$
and
$G_0={\mathrm{E}}_8(q')$
and
![]() $|H_0|=30(q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'{+}1)$
, where
$|H_0|=30(q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'{+}1)$
, where
![]() $q'=r^t$
. Suppose the latter case occurs. It is easily shown that
$q'=r^t$
. Suppose the latter case occurs. It is easily shown that
![]() $q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'{+}1$
is divisible by some primitive prime divisor s of
$q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'{+}1$
is divisible by some primitive prime divisor s of
![]() $q^{\prime 15}-1$
or of
$q^{\prime 15}-1$
or of
![]() $q^{\prime 30}-1$
. Noting that
$q^{\prime 30}-1$
. Noting that
![]() $s\ge 17$
, we know that
$s\ge 17$
, we know that
![]() $H_0$
has a normal cyclic Sylow s-subgroup. It follows from (a) that
$H_0$
has a normal cyclic Sylow s-subgroup. It follows from (a) that
![]() $17\le p=s=q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'{+}1$
. In particular,
$17\le p=s=q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'{+}1$
. In particular,
![]() $\textbf {O}_p(H_0)=\mathbb Z_p$
and
$\textbf {O}_p(H_0)=\mathbb Z_p$
and
![]() $f=1$
. By (b),
$f=1$
. By (b),
![]() $|H_0|$
is divisible by
$|H_0|$
is divisible by
![]() $p-1$
and then
$p-1$
and then
![]() $30$
is divisible by
$30$
is divisible by
![]() $p-1$
. This implies that
$p-1$
. This implies that
![]() $30=p-1=q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'$
, which is impossible. Therefore,
$30=p-1=q^{\prime 8}{\pm } q^{\prime 7}{\mp } q^{\prime 5}-q^{\prime 4}{\mp } q^{\prime 3}{\pm } q'$
, which is impossible. Therefore,
![]() $H_0/{\mathrm{Fit}}(H_0)$
is a
$H_0/{\mathrm{Fit}}(H_0)$
is a
![]() $\{2,3\}$
-group.
$\{2,3\}$
-group.
By (a),
![]() ${\mathrm{Fit}}(H_0)$
a
${\mathrm{Fit}}(H_0)$
a
![]() $\{2,p\}$
-group. Then
$\{2,p\}$
-group. Then
![]() $|H_0|$
has no prime divisor other than
$|H_0|$
has no prime divisor other than
![]() $2$
,
$2$
,
![]() $3$
and p. Since
$3$
and p. Since
![]() $p^f-1$
is a divisor of
$p^f-1$
is a divisor of
![]() $|H_0|$
, by Lemma 2.6, we have
$|H_0|$
, by Lemma 2.6, we have
![]() $f<3$
. Recall that
$f<3$
. Recall that
![]() $(X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u= p^f{:}({q-1})/{(2,q-1)}{.}[o]$
and
$(X_u^{{{\Gamma}}(u)})_v\cong (X_v^{{{\Gamma}}(v)})_u= p^f{:}({q-1})/{(2,q-1)}{.}[o]$
and
![]() $X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
, where o is a divisor of
$X_{uv}\lesssim (X_v^{{{\Gamma}}(v)})_u{\times } (X_u^{{{\Gamma}}(u)})_v$
, where o is a divisor of
![]() $(2,q-1)f$
. Then
$(2,q-1)f$
. Then
![]() $X_{uv}/\textbf {O}_p(X_{uv})$
has an abelian Hall
$X_{uv}/\textbf {O}_p(X_{uv})$
has an abelian Hall
![]() $2'$
-subgroup. Note that
$2'$
-subgroup. Note that
![]() $X_{uv}\textbf {O}_p(X_{\{u,v\}})/\textbf {O}_p(X_{\{u,v\}})\cong X_{uv}/(\textbf {O}_p(X_{\{u,v\}}\cap X_{uv})=X_{uv}/\textbf {O}_p(X_{uv})$
and also
$X_{uv}\textbf {O}_p(X_{\{u,v\}})/\textbf {O}_p(X_{\{u,v\}})\cong X_{uv}/(\textbf {O}_p(X_{\{u,v\}}\cap X_{uv})=X_{uv}/\textbf {O}_p(X_{uv})$
and also
![]() $|X_{\{u,v\}}:X_{uv}\textbf {O}_p(X_{\{u,v\}})|\le 2$
. It follows that
$|X_{\{u,v\}}:X_{uv}\textbf {O}_p(X_{\{u,v\}})|\le 2$
. It follows that
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has an abelian Hall
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has an abelian Hall
![]() $2'$
-subgroup. Thus, as a possible candidate for
$2'$
-subgroup. Thus, as a possible candidate for
![]() $X_{\{u,v\}}$
, the quotient of
$X_{\{u,v\}}$
, the quotient of
![]() $H_0$
over
$H_0$
over
![]() $\textbf {O}_p(H_0)$
has abelian Hall
$\textbf {O}_p(H_0)$
has abelian Hall
![]() $2'$
-subgroups. In particular,
$2'$
-subgroups. In particular,
![]() $H_0/\textbf {O}_p(H_0)$
has no section
$H_0/\textbf {O}_p(H_0)$
has no section
![]() $A_4$
.
$A_4$
.
Considering the restrictions on
![]() $H_0$
, r and f, we conclude that
$H_0$
, r and f, we conclude that
![]() $(G_0,H_0)$
can only be one of the following pairs:
$(G_0,H_0)$
can only be one of the following pairs:
 $$ \begin{align*}\def\arraystretch{1.18}\begin{array}{l} ({\mathrm{PSL}}_2(r^t), \mathbb Z_{({r^t\pm 1})/{(2,r^t-1)}}{:}\mathbb Z_2), \,({\mathrm{PSL}}_3(r^t), [{(r^t-1)^2}/{(3,r^t-1)}].{\mathrm{S}}_3),\\ ({\mathrm{PSU}}_3(r^t), [{(r^t+1)^2}/{(3,r^t+1)}].{\mathrm{S}}_3);\\ ({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{2^t\pm 1}^2.[2^{l+4}]), \,({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{2^{2t}+1}.[2^{l+3}]), \,t\ge 3;\\ ({\mathrm{Sz}}(2^t), \mathbb Z_{2^t-1}{:}\mathbb Z_2), \,({\mathrm{Sz}}(2^t), \mathbb Z_{2^t\pm \sqrt{2^{t+1}}+1}{:}\mathbb Z_4), \,t\ge 3; \\ ({\mathrm{Ree}}(3^t), \mathbb Z_{3^t\pm \sqrt{3^{t+1}}+1}{.}\mathbb Z_6), \,({\mathrm{Ree}}(3^t), \mathbb Z_{3^t+1}{.}\mathbb Z_6), \,t\ge 3;\\ ({\mathrm{G}}_2(3^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{3^t\pm 1}^2{.}[3\cdot2^{l+3}]), \,({\mathrm{G}}_2(3^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{3^{2t}\pm3^t+1}{.}[3\cdot2^{l+2}]), \,t\ge 2;\\ ({}^3{\mathrm{D}}_4(r^t), \mathbb Z_{r^{4t}-r^{2t}+1}{:}\mathbb Z_4), \,({}^2{\mathrm{F}}_4(2^t), \mathbb Z_{2^{2t}\pm \sqrt{2^{3t+1}}+2^{t}\pm \sqrt{2^{t+1}}+1}{.}\mathbb Z_{12}), \,t\ge 3; \\ ({\mathrm{F}}_4(2^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{2^{4t}-2^{2t}+1}{.}[3\cdot2^{l+3}]), \,t\ge 2, \end{array}\end{align*} $$
$$ \begin{align*}\def\arraystretch{1.18}\begin{array}{l} ({\mathrm{PSL}}_2(r^t), \mathbb Z_{({r^t\pm 1})/{(2,r^t-1)}}{:}\mathbb Z_2), \,({\mathrm{PSL}}_3(r^t), [{(r^t-1)^2}/{(3,r^t-1)}].{\mathrm{S}}_3),\\ ({\mathrm{PSU}}_3(r^t), [{(r^t+1)^2}/{(3,r^t+1)}].{\mathrm{S}}_3);\\ ({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{2^t\pm 1}^2.[2^{l+4}]), \,({\mathrm{PSp}}_4(2^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{2^{2t}+1}.[2^{l+3}]), \,t\ge 3;\\ ({\mathrm{Sz}}(2^t), \mathbb Z_{2^t-1}{:}\mathbb Z_2), \,({\mathrm{Sz}}(2^t), \mathbb Z_{2^t\pm \sqrt{2^{t+1}}+1}{:}\mathbb Z_4), \,t\ge 3; \\ ({\mathrm{Ree}}(3^t), \mathbb Z_{3^t\pm \sqrt{3^{t+1}}+1}{.}\mathbb Z_6), \,({\mathrm{Ree}}(3^t), \mathbb Z_{3^t+1}{.}\mathbb Z_6), \,t\ge 3;\\ ({\mathrm{G}}_2(3^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{3^t\pm 1}^2{.}[3\cdot2^{l+3}]), \,({\mathrm{G}}_2(3^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{3^{2t}\pm3^t+1}{.}[3\cdot2^{l+2}]), \,t\ge 2;\\ ({}^3{\mathrm{D}}_4(r^t), \mathbb Z_{r^{4t}-r^{2t}+1}{:}\mathbb Z_4), \,({}^2{\mathrm{F}}_4(2^t), \mathbb Z_{2^{2t}\pm \sqrt{2^{3t+1}}+2^{t}\pm \sqrt{2^{t+1}}+1}{.}\mathbb Z_{12}), \,t\ge 3; \\ ({\mathrm{F}}_4(2^t).\mathbb Z_{2^{l+1}}, \mathbb Z_{2^{4t}-2^{2t}+1}{.}[3\cdot2^{l+3}]), \,t\ge 2, \end{array}\end{align*} $$
where the power
![]() $2^l$
appearing means the
$2^l$
appearing means the
![]() $2$
-part of t. Recall that
$2$
-part of t. Recall that
![]() $|{\mathrm{Fit}}(H_0):\textbf {O}_p(H_0)|\le 2$
and
$|{\mathrm{Fit}}(H_0):\textbf {O}_p(H_0)|\le 2$
and
![]() $|H_0:\textbf {O}_p(H_0)|$
is divisible by
$|H_0:\textbf {O}_p(H_0)|$
is divisible by
![]() $p^f-1$
. This allows us determine the values of
$p^f-1$
. This allows us determine the values of
![]() $p^f$
and
$p^f$
and
![]() $r^t$
. As an example, we only deal with the second pair. Suppose that
$r^t$
. As an example, we only deal with the second pair. Suppose that
![]() $(G_0,H_0)=({\mathrm{PSL}}_3(r^t), [{(r^t-1)^2}/{(3,r^t-1)}].{\mathrm{S}}_3)$
. Considering the structures of
$(G_0,H_0)=({\mathrm{PSL}}_3(r^t), [{(r^t-1)^2}/{(3,r^t-1)}].{\mathrm{S}}_3)$
. Considering the structures of
![]() ${\mathrm{Fit}}(H_0)$
and
${\mathrm{Fit}}(H_0)$
and
![]() $\textbf {O}_p(H_0)$
, either
$\textbf {O}_p(H_0)$
, either
![]() $(3,r^t-1)=1$
,
$(3,r^t-1)=1$
,
![]() $p=r^t-1$
and
$p=r^t-1$
and
![]() $f\in \{1,2\}$
, or
$f\in \{1,2\}$
, or
![]() $f=1$
and
$f=1$
and
![]() $p=r^t-1=3$
. The latter implies that
$p=r^t-1=3$
. The latter implies that
![]() ${\mathrm{PSL}}_2(q)$
is soluble, which is not the case. Assume that the former case holds. Then
${\mathrm{PSL}}_2(q)$
is soluble, which is not the case. Assume that the former case holds. Then
![]() $|{\mathrm{S}}_3|$
is divisible by
$|{\mathrm{S}}_3|$
is divisible by
![]() $r^t-1-1$
or
$r^t-1-1$
or
![]() $(r^t-1)^2-1$
. Then the only possibility is that
$(r^t-1)^2-1$
. Then the only possibility is that
![]() $(p^f,r^t)=(7,8)$
. The other pairs can be determined in a similar way; the details are omitted here. Eventually, we conclude that
$(p^f,r^t)=(7,8)$
. The other pairs can be determined in a similar way; the details are omitted here. Eventually, we conclude that
![]() $(G_0,H_0, p,f)$
is one of
$(G_0,H_0, p,f)$
is one of
![]() $({\mathrm{PSL}}_2(19), {\mathrm{D}}_{20}, 5,1)$
,
$({\mathrm{PSL}}_2(19), {\mathrm{D}}_{20}, 5,1)$
,
![]() $({\mathrm{PSL}}_3(8), 7^2{:}{\mathrm{S}}_3,7,1)$
and
$({\mathrm{PSL}}_3(8), 7^2{:}{\mathrm{S}}_3,7,1)$
and
![]() $({\mathrm{Sz}}(8),\mathbb Z_5{:}\mathbb Z_4,5,1)$
. By the Atlas [Reference Conway, Norton, Parker and Wilson3], neither
$({\mathrm{Sz}}(8),\mathbb Z_5{:}\mathbb Z_4,5,1)$
. By the Atlas [Reference Conway, Norton, Parker and Wilson3], neither
![]() ${\mathrm{PSL}}_3(8)$
nor
${\mathrm{PSL}}_3(8)$
nor
![]() ${\mathrm{Sz}}(8)$
has subgroup with a section
${\mathrm{Sz}}(8)$
has subgroup with a section
![]() ${\mathrm{PSL}}_2(p)$
. Thus, in this case, G, X and
${\mathrm{PSL}}_2(p)$
. Thus, in this case, G, X and
![]() $X_{\{u,v\}}$
are as given in Table 5.
$X_{\{u,v\}}$
are as given in Table 5.
Subcase 3.2. For the pairs
![]() $(G_0,H_0)$
not appearing in Subcase 3.1, we check the finite number of
$(G_0,H_0)$
not appearing in Subcase 3.1, we check the finite number of
![]() $H_0$
one by one. We observe that either
$H_0$
one by one. We observe that either
![]() $p=2$
or
$p=2$
or
![]() $H_0/\textbf {O}_p(H_0)$
is a
$H_0/\textbf {O}_p(H_0)$
is a
![]() $\{2,3\}$
-group. Recall that
$\{2,3\}$
-group. Recall that
![]() $r\ne p$
.
$r\ne p$
.
Suppose that
![]() $p=2$
. Recalling that
$p=2$
. Recalling that
![]() $q=2^f>4$
, we have
$q=2^f>4$
, we have
![]() $f\ge 3$
. In particular, since
$f\ge 3$
. In particular, since
![]() $|H_0|$
is divisible by
$|H_0|$
is divisible by
![]() $2^f-1$
,
$2^f-1$
,
![]() $H_0$
is not a
$H_0$
is not a
![]() $\{2,3\}$
-group by Lemma 2.6. Then the only possibility is that
$\{2,3\}$
-group by Lemma 2.6. Then the only possibility is that
![]() $G_0={}^2{\mathrm{F}}_4(2)'$
and
$G_0={}^2{\mathrm{F}}_4(2)'$
and
![]() $H_0=[2^9]{:}5{:}4$
. Thus,
$H_0=[2^9]{:}5{:}4$
. Thus,
![]() $|\textbf {O}_2(H_0)|=2^9$
; it follows from (a) that
$|\textbf {O}_2(H_0)|=2^9$
; it follows from (a) that
![]() $f=4$
or
$f=4$
or
![]() $9$
and then
$9$
and then
![]() $G_0$
has a section
$G_0$
has a section
![]() ${\mathrm{PSL}}_2(2^4)$
or
${\mathrm{PSL}}_2(2^4)$
or
![]() ${\mathrm{PSL}}_2(2^9)$
, which is impossible by checking the (maximal) subgroups of
${\mathrm{PSL}}_2(2^9)$
, which is impossible by checking the (maximal) subgroups of
![]() ${}^2{\mathrm{F}}_4(2)'$
. Thus,
${}^2{\mathrm{F}}_4(2)'$
. Thus,
![]() $p>2$
and
$p>2$
and
![]() $H_0/\textbf {O}_p(H_0)$
is a
$H_0/\textbf {O}_p(H_0)$
is a
![]() $\{2,3\}$
-group; in particular, by (a),
$\{2,3\}$
-group; in particular, by (a),
![]() $\textbf {O}_p(H_0)=\mathbb Z_p^{if}$
for some
$\textbf {O}_p(H_0)=\mathbb Z_p^{if}$
for some
![]() $i\in \{1,2\}$
.
$i\in \{1,2\}$
.
Suppose that
![]() $H_0$
has a section
$H_0$
has a section
![]() ${\mathrm{A}}_4$
. Then
${\mathrm{A}}_4$
. Then
![]() $H_0$
has no normal Sylow
$H_0$
has no normal Sylow
![]() $3$
-subgroup. Further,
$3$
-subgroup. Further,
![]() $H_0$
has no quotient
$H_0$
has no quotient
![]() ${\mathrm{A}}_4$
as
${\mathrm{A}}_4$
as
![]() $H_0$
has a subgroup of index two. If
$H_0$
has a subgroup of index two. If
![]() $(3,(q-1)f)=1$
, then, by (b), we conclude that
$(3,(q-1)f)=1$
, then, by (b), we conclude that
![]() $p=3$
and
$p=3$
and
![]() $\textbf {O}_p(H_0)$
is the unique Sylow
$\textbf {O}_p(H_0)$
is the unique Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $H_0$
, which is a contradiction. Thus,
$H_0$
, which is a contradiction. Thus,
![]() $3$
is a divisor of
$3$
is a divisor of
![]() $(q-1)f$
. Check those
$(q-1)f$
. Check those
![]() $H_0$
in [Reference Li and Zhang17, Tables 16–20] which have a section
$H_0$
in [Reference Li and Zhang17, Tables 16–20] which have a section
![]() ${\mathrm{A}}_4$
and do not appear in Subcase 3.1. Recalling that
${\mathrm{A}}_4$
and do not appear in Subcase 3.1. Recalling that
![]() $r\ne p>2$
and
$r\ne p>2$
and
![]() $\textbf {O}_p(H_0)=\mathbb Z_p^{if}$
, it follows that either
$\textbf {O}_p(H_0)=\mathbb Z_p^{if}$
, it follows that either
![]() $\textbf {O}_p(H_0)=\mathbb Z_3^2$
or
$\textbf {O}_p(H_0)=\mathbb Z_3^2$
or
![]() $(G_0,H_0)=({\mathrm{F}}_4(2).4, \mathbb Z_7^2{:}(3\times {\mathrm{SL}}_2(3)).4)$
. Since
$(G_0,H_0)=({\mathrm{F}}_4(2).4, \mathbb Z_7^2{:}(3\times {\mathrm{SL}}_2(3)).4)$
. Since
![]() $3$
is a divisor of
$3$
is a divisor of
![]() $(q-1)f$
, we get
$(q-1)f$
, we get
![]() $G_0={\mathrm{F}}_4(2).4$
and
$G_0={\mathrm{F}}_4(2).4$
and
![]() $q=p^f=7$
or
$q=p^f=7$
or
![]() $7^2$
. By (b), for
$7^2$
. By (b), for
![]() $q=7$
or
$q=7$
or
![]() $7^2$
, the order of
$7^2$
, the order of
![]() $H_0$
should be a divisor of
$H_0$
should be a divisor of
![]() $72$
or
$72$
or
![]() $192$
, respectively, which is impossible.
$192$
, respectively, which is impossible.
The above argument allows us to ignore many cases without further inspection. Inspecting carefully the remaining pairs, the possible candidates for
![]() $(X,X_{\{u,v\}})$
are as follows:
$(X,X_{\{u,v\}})$
are as follows:
 $$ \begin{align*}\begin{array}{l} ({\mathrm{PGL}}_2(9), {\mathrm{D}}_{20}), \,({\mathrm{M}}_{10}, \mathbb Z_5{:}\mathbb Z_4), \,({\mathrm{PGL}}_2(11), {\mathrm{D}}_{20});\\ ({\mathrm{PSL}}_3(r), 3^2{:}{\mathrm{Q}}_8), \quad\mbox{where }r\equiv 4,7 \ \mod 9;\\ ({\mathrm{PSp}}_4(4).4, \mathbb Z_{17}{:}\mathbb Z_{16}), \,({\mathrm{PSp}}_4(4).4, 5^2{:}[2^5]);\\ ({\mathrm{PSU}}_3(r), 3^2{:}{\mathrm{Q}}_8), \quad\mbox{where }5<r\equiv 2,5 \ \mod 9;\\ ({\mathrm{PSU}}_3(2^t), 3^2{:}{\mathrm{Q}}_8), \quad\mbox{where }t \mbox{ is a prime no less than }5;\\ ({}^2{\mathrm{F}}_4(2), \mathbb Z_{13}{:}\mathbb Z_{12}). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\mathrm{PGL}}_2(9), {\mathrm{D}}_{20}), \,({\mathrm{M}}_{10}, \mathbb Z_5{:}\mathbb Z_4), \,({\mathrm{PGL}}_2(11), {\mathrm{D}}_{20});\\ ({\mathrm{PSL}}_3(r), 3^2{:}{\mathrm{Q}}_8), \quad\mbox{where }r\equiv 4,7 \ \mod 9;\\ ({\mathrm{PSp}}_4(4).4, \mathbb Z_{17}{:}\mathbb Z_{16}), \,({\mathrm{PSp}}_4(4).4, 5^2{:}[2^5]);\\ ({\mathrm{PSU}}_3(r), 3^2{:}{\mathrm{Q}}_8), \quad\mbox{where }5<r\equiv 2,5 \ \mod 9;\\ ({\mathrm{PSU}}_3(2^t), 3^2{:}{\mathrm{Q}}_8), \quad\mbox{where }t \mbox{ is a prime no less than }5;\\ ({}^2{\mathrm{F}}_4(2), \mathbb Z_{13}{:}\mathbb Z_{12}). \end{array} \end{align*} $$
For the first three pairs, G, X and
![]() $X_{\{u,v\}}$
are easily determined and as given in Table 5. The pair
$X_{\{u,v\}}$
are easily determined and as given in Table 5. The pair
![]() $({\mathrm{PSp}}_4(4).4, \mathbb Z_{17}{:}\mathbb Z_{16})$
is excluded as
$({\mathrm{PSp}}_4(4).4, \mathbb Z_{17}{:}\mathbb Z_{16})$
is excluded as
![]() ${\mathrm{PSp}}_4(4).4$
has no subgroup
${\mathrm{PSp}}_4(4).4$
has no subgroup
![]() ${\mathrm{PSL}}_2(17)$
and the pair
${\mathrm{PSL}}_2(17)$
and the pair
![]() $({}^2{\mathrm{F}}_4(2), \mathbb Z_{13}{:}\mathbb Z_{12})$
is excluded as
$({}^2{\mathrm{F}}_4(2), \mathbb Z_{13}{:}\mathbb Z_{12})$
is excluded as
![]() ${}^2{\mathrm{F}}_4(2)$
has no subgroup
${}^2{\mathrm{F}}_4(2)$
has no subgroup
![]() ${\mathrm{PSL}}_2(13)$
. Suppose that
${\mathrm{PSL}}_2(13)$
. Suppose that
![]() $X\cong {\mathrm{PSU}}_3(2^t)$
and
$X\cong {\mathrm{PSU}}_3(2^t)$
and
![]() $X_{\{u,v\}}\cong 3^2{:}{\mathrm{Q}}_8$
. Then we have
$X_{\{u,v\}}\cong 3^2{:}{\mathrm{Q}}_8$
. Then we have
![]() $X_v\cong {\mathrm{PSL}}_2(9)$
; however, by [Reference Bray, Holt and Roney-Dougal1, Tables 8.3 and 8.4],
$X_v\cong {\mathrm{PSL}}_2(9)$
; however, by [Reference Bray, Holt and Roney-Dougal1, Tables 8.3 and 8.4],
![]() ${\mathrm{PSU}}_3(2^t)$
has no subgroup
${\mathrm{PSU}}_3(2^t)$
has no subgroup
![]() ${\mathrm{PSL}}_2(9)$
, which is a contradiction. Suppose that
${\mathrm{PSL}}_2(9)$
, which is a contradiction. Suppose that
![]() $(X,X_{\{u,v\}})=({\mathrm{PSp}}_4(4).4, 5^2{:}[2^5])$
. Then
$(X,X_{\{u,v\}})=({\mathrm{PSp}}_4(4).4, 5^2{:}[2^5])$
. Then
![]() $X_v$
contains a Sylow
$X_v$
contains a Sylow
![]() $5$
-subgroup P of X and has a section
$5$
-subgroup P of X and has a section
![]() ${\mathrm{PSL}}_2(5)$
or
${\mathrm{PSL}}_2(5)$
or
![]() ${\mathrm{PSL}}_2(25)$
. By the information for
${\mathrm{PSL}}_2(25)$
. By the information for
![]() ${\mathrm{PSp}}_4(4).4$
given in the Atlas [Reference Conway, Norton, Parker and Wilson3], we conclude that
${\mathrm{PSp}}_4(4).4$
given in the Atlas [Reference Conway, Norton, Parker and Wilson3], we conclude that
![]() $X_v\le M\cong ({\mathrm{A}}_5\times {\mathrm{A}}_5){:}2^2<{\mathrm{PSp}}_4(4).2<{\mathrm{PSp}}_4(4).4$
. Note that
$X_v\le M\cong ({\mathrm{A}}_5\times {\mathrm{A}}_5){:}2^2<{\mathrm{PSp}}_4(4).2<{\mathrm{PSp}}_4(4).4$
. Note that
![]() $X_{uv}=5^2{:}[2^4]$
, which should be the normalizer of P in
$X_{uv}=5^2{:}[2^4]$
, which should be the normalizer of P in
![]() $X_v$
. Using GAP [28], computation shows that
$X_v$
. Using GAP [28], computation shows that
![]() $|\textbf {N}_L(P)|\le 200$
for any maximal subgroup L of M with
$|\textbf {N}_L(P)|\le 200$
for any maximal subgroup L of M with
![]() $P\le L$
. It follows that
$P\le L$
. It follows that
![]() $X_v=M\cong ({\mathrm{A}}_5\times {\mathrm{A}}_5){:}2^2$
, yielding
$X_v=M\cong ({\mathrm{A}}_5\times {\mathrm{A}}_5){:}2^2$
, yielding
![]() $d=|X_v:X_{uv}|=36\ne q+1$
, which is a contradiction.
$d=|X_v:X_{uv}|=36\ne q+1$
, which is a contradiction.
Let
![]() $(X,X_{\{u,v\}})=({\mathrm{PSL}}_3(r), 3^2{:}{\mathrm{Q}}_8)$
. Then
$(X,X_{\{u,v\}})=({\mathrm{PSL}}_3(r), 3^2{:}{\mathrm{Q}}_8)$
. Then
![]() $X_{uv}\cong 3^2{:}4$
. It is easily shown that
$X_{uv}\cong 3^2{:}4$
. It is easily shown that
![]() $p=3$
and
$p=3$
and
![]() $X_v\cong {\mathrm{PSL}}_2(9)$
. Since
$X_v\cong {\mathrm{PSL}}_2(9)$
. Since
![]() $r\equiv 4,7 \ \mod 9$
, we know that
$r\equiv 4,7 \ \mod 9$
, we know that
![]() ${\mathrm{PSL}}_3(r)$
has a Sylow
${\mathrm{PSL}}_3(r)$
has a Sylow
![]() $3$
-subgroup
$3$
-subgroup
![]() $\mathbb Z_3^2$
. By [Reference Bray, Holt and Roney-Dougal1, Tables 8.3 and 8.4],
$\mathbb Z_3^2$
. By [Reference Bray, Holt and Roney-Dougal1, Tables 8.3 and 8.4],
![]() ${\mathrm{PSL}}_3(r)$
has a subgroup
${\mathrm{PSL}}_3(r)$
has a subgroup
![]() ${\mathrm{PSL}}_2(9)$
if and only if
${\mathrm{PSL}}_2(9)$
if and only if
![]() $r\equiv 1,4 \ \mod 15$
. Thus, in this case, we have
$r\equiv 1,4 \ \mod 15$
. Thus, in this case, we have
![]() $r\equiv 11,14,29,41 \ \mod 45$
. For a subgroup
$r\equiv 11,14,29,41 \ \mod 45$
. For a subgroup
![]() ${\mathrm{PSL}}_2(9)$
of
${\mathrm{PSL}}_2(9)$
of
![]() ${\mathrm{PSL}}_3(r)$
, taking a Sylow
${\mathrm{PSL}}_3(r)$
, taking a Sylow
![]() $3$
-subgroup Q of
$3$
-subgroup Q of
![]() ${\mathrm{PSL}}_2(9)$
, the normalizers of Q in
${\mathrm{PSL}}_2(9)$
, the normalizers of Q in
![]() ${\mathrm{PSL}}_2(9)$
and
${\mathrm{PSL}}_2(9)$
and
![]() ${\mathrm{PSL}}_3(r)$
are (isomorphic to)
${\mathrm{PSL}}_3(r)$
are (isomorphic to)
![]() $3^2{:}4$
and
$3^2{:}4$
and
![]() $3^2{:}{\mathrm{Q}}_8$
, respectively. Then these two normalizers of Q can serve as the roles of
$3^2{:}{\mathrm{Q}}_8$
, respectively. Then these two normalizers of Q can serve as the roles of
![]() $X_{uv}$
and
$X_{uv}$
and
![]() $X_{\{u,v\}}$
, respectively. Thus, X and
$X_{\{u,v\}}$
, respectively. Thus, X and
![]() $X_{\{u,v\}}$
are as given in Table 5. Noting that
$X_{\{u,v\}}$
are as given in Table 5. Noting that
![]() $G=XG_{\{u,v\}}$
, we have
$G=XG_{\{u,v\}}$
, we have
![]() $G_{\{u,v\}}/X_{\{u,v\}}\cong G/X\lesssim {\sf Out}({\mathrm{PSL}}_3(r))\cong {\mathrm{S}}_3$
and so
$G_{\{u,v\}}/X_{\{u,v\}}\cong G/X\lesssim {\sf Out}({\mathrm{PSL}}_3(r))\cong {\mathrm{S}}_3$
and so
![]() $G=X.[m]$
and
$G=X.[m]$
and
![]() $G_{\{u,v\}}=X_{\{u,v\}}.[m]$
, where m is a divisor of
$G_{\{u,v\}}=X_{\{u,v\}}.[m]$
, where m is a divisor of
![]() $6$
. Thus,
$6$
. Thus,
![]() $|G_{uv}{:}X_{uv}|=m$
; since
$|G_{uv}{:}X_{uv}|=m$
; since
![]() $|G_v{:}G_{uv}|=10=|X_v{:}X_{uv}|$
, we have
$|G_v{:}G_{uv}|=10=|X_v{:}X_{uv}|$
, we have
![]() $|G_v{:}X_v|=m$
. By [Reference Bray, Holt and Roney-Dougal1, Table 8.4],
$|G_v{:}X_v|=m$
. By [Reference Bray, Holt and Roney-Dougal1, Table 8.4],
![]() $\textbf {N}_{{\sf Aut}({\mathrm{PSL}}_3(r))}(X_v)=X_v.2$
. Since
$\textbf {N}_{{\sf Aut}({\mathrm{PSL}}_3(r))}(X_v)=X_v.2$
. Since
![]() $X_v\unlhd G_v$
, it follows that
$X_v\unlhd G_v$
, it follows that
![]() $m\le 2$
. Thus,
$m\le 2$
. Thus,
![]() $G=X$
or
$G=X$
or
![]() $X.2$
and, if
$X.2$
and, if
![]() $G=X.2$
, then
$G=X.2$
, then
![]() $G_v=X_v.2\cong {\mathrm{PGL}}_2(9)$
and
$G_v=X_v.2\cong {\mathrm{PGL}}_2(9)$
and
![]() $G_{\{u,v\}}\cong 3^2{:}{\mathrm{Q}}_8.2$
. The pair
$G_{\{u,v\}}\cong 3^2{:}{\mathrm{Q}}_8.2$
. The pair
![]() $({\mathrm{PSU}}_3(r), 3^2{:}{\mathrm{Q}}_8)$
is similarly dealt with; the details are omitted. This completes the proof.
$({\mathrm{PSU}}_3(r), 3^2{:}{\mathrm{Q}}_8)$
is similarly dealt with; the details are omitted. This completes the proof.
Lemma 4.4. If (3) of Lemma 3.3 holds, then G, X,
![]() $X_{\{u,v\}}$
and
$X_{\{u,v\}}$
and
![]() $X_v$
are as listed in Table 6.
$X_v$
are as listed in Table 6.
Table 6 Graphs for (3) of Lemma 3.3.

Proof. Let
![]() $X_v^{{{\Gamma}}(v)}= {\mathrm{PSU}}_3(q).[o]$
and
$X_v^{{{\Gamma}}(v)}= {\mathrm{PSU}}_3(q).[o]$
and
![]() $q=p^f>2$
, where p is a prime and
$q=p^f>2$
, where p is a prime and
![]() $o\mid 2(3,q{+}1)f$
. Then
$o\mid 2(3,q{+}1)f$
. Then
![]() $(X_v^{{{\Gamma}}(v)})_u=p^{f{+}2f}{:}(({q^2-1})/{(3,q{+}1)}).[o]$
and
$(X_v^{{{\Gamma}}(v)})_u=p^{f{+}2f}{:}(({q^2-1})/{(3,q{+}1)}).[o]$
and
![]() $X_{uv}^{[1]}=1$
, by Theorem 2.4. Thus,
$X_{uv}^{[1]}=1$
, by Theorem 2.4. Thus,
![]() $|\textbf {O}_p(X_{\{u,v\}})|=p^{3f}.a$
,
$|\textbf {O}_p(X_{\{u,v\}})|=p^{3f}.a$
,
![]() $p^{4f}.a$
,
$p^{4f}.a$
,
![]() $p^{5f}.a$
or
$p^{5f}.a$
or
![]() $p^{6f}.a$
, where a is a divisor of
$p^{6f}.a$
, where a is a divisor of
![]() $(2,p)$
. Moreover,
$(2,p)$
. Moreover,
![]() $\textbf {O}_p(X_{\{u,v\}})$
is nonabelian and
$\textbf {O}_p(X_{\{u,v\}})$
is nonabelian and
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has a subgroup
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has a subgroup
![]() $\mathbb Z_{({q^2-1})/{(3,q{+}1)}}$
. We next determine which pair
$\mathbb Z_{({q^2-1})/{(3,q{+}1)}}$
. We next determine which pair
![]() $(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] is a possible candidate for
$(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] is a possible candidate for
![]() $(X,X_{\{u,v\}})$
. Note that we may ignore those
$(X,X_{\{u,v\}})$
. Note that we may ignore those
![]() $H_0$
that either have no subgroup of index two or have an abelian maximal normal p-subgroup. In particular,
$H_0$
that either have no subgroup of index two or have an abelian maximal normal p-subgroup. In particular,
![]() ${\mathrm{soc}}(X)$
is not an alternating group.
${\mathrm{soc}}(X)$
is not an alternating group.
Case 1. Let
![]() $(G_0,H_0)$
be a pair with
$(G_0,H_0)$
be a pair with
![]() $H_0$
included in some infinite families given in [Reference Li and Zhang17, Tables 16–20]. Since
$H_0$
included in some infinite families given in [Reference Li and Zhang17, Tables 16–20]. Since
![]() $\textbf {O}_p(X_{\{u,v\}})$
is nonabelian, we conclude that
$\textbf {O}_p(X_{\{u,v\}})$
is nonabelian, we conclude that
![]() $(X,\textbf {O}_p(X_{\{u,v\}}))$
is one of the following pairs:
$(X,\textbf {O}_p(X_{\{u,v\}}))$
is one of the following pairs:
 $$ \begin{align*}\begin{array}{l} ({\mathrm{PSL}}_3(p^t).2, [p^{3t}]), \,({\mathrm{PGL}}_3(p^t).2, [p^{3t}]) \mbox{ (with } p=2),\\ ({\mathrm{PSU}}_3(p^t), [p^{3t}]), \,({\mathrm{PSp}}_4(p^t).\mathbb Z_{2^{l+1}}, [p^{4t}]) \mbox{ (with }p=2), \\ ({\mathrm{Sz}}(p^t), [p^{2t}]), \,({\mathrm{Ree}}(p^t), [p^{3t}])\mbox{ and }({\mathrm{G}}_2(p^t).\mathbb Z_{2^{l+1}}, [p^{6t}]), \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\mathrm{PSL}}_3(p^t).2, [p^{3t}]), \,({\mathrm{PGL}}_3(p^t).2, [p^{3t}]) \mbox{ (with } p=2),\\ ({\mathrm{PSU}}_3(p^t), [p^{3t}]), \,({\mathrm{PSp}}_4(p^t).\mathbb Z_{2^{l+1}}, [p^{4t}]) \mbox{ (with }p=2), \\ ({\mathrm{Sz}}(p^t), [p^{2t}]), \,({\mathrm{Ree}}(p^t), [p^{3t}])\mbox{ and }({\mathrm{G}}_2(p^t).\mathbb Z_{2^{l+1}}, [p^{6t}]), \end{array}\end{align*} $$
where
![]() $2^{l}$
is the
$2^{l}$
is the
![]() $2$
-part of t. Check the maximal subgroups of
$2$
-part of t. Check the maximal subgroups of
![]() ${\mathrm{PSp}}_4(p^t).\mathbb Z_{2^{l+1}}$
,
${\mathrm{PSp}}_4(p^t).\mathbb Z_{2^{l+1}}$
,
![]() ${\mathrm{Sz}}(p^t)$
and
${\mathrm{Sz}}(p^t)$
and
![]() ${\mathrm{Ree}}(p^t)$
; refer to [Reference Bray, Holt and Roney-Dougal1, Table 8.14], [Reference Suzuki27, Theorem 9] and [Reference Kleidman15, Theorem C], respectively. We conclude that none of
${\mathrm{Ree}}(p^t)$
; refer to [Reference Bray, Holt and Roney-Dougal1, Table 8.14], [Reference Suzuki27, Theorem 9] and [Reference Kleidman15, Theorem C], respectively. We conclude that none of
![]() ${\mathrm{PSp}}_4(t^f).\mathbb Z_{2^{l+1}}$
,
${\mathrm{PSp}}_4(t^f).\mathbb Z_{2^{l+1}}$
,
![]() ${\mathrm{Sz}}(p^t)$
and
${\mathrm{Sz}}(p^t)$
and
![]() ${\mathrm{Ree}}(p^t)$
has maximal subgroups with a simple section
${\mathrm{Ree}}(p^t)$
has maximal subgroups with a simple section
![]() ${\mathrm{PSU}}_3(q)$
and they are excluded. For the first three and the last pairs,
${\mathrm{PSU}}_3(q)$
and they are excluded. For the first three and the last pairs,
![]() $|X/\textbf {O}_p(X_{\{u,v\}})|$
is a divisor of
$|X/\textbf {O}_p(X_{\{u,v\}})|$
is a divisor of
![]() $2(p^t-1)^2$
and
$2(p^t-1)^2$
and
![]() $\textbf {O}_p(X_{\{u,v\}})=[p^{3t}]$
or
$\textbf {O}_p(X_{\{u,v\}})=[p^{3t}]$
or
![]() $[p^{6t}]$
. Clearly,
$[p^{6t}]$
. Clearly,
![]() $t\le 2f$
.
$t\le 2f$
.
Suppose that
![]() $t=2f$
. Then
$t=2f$
. Then
![]() ${\mathrm{soc}}(X)={\mathrm{PSL}}_3(q^2)$
or
${\mathrm{soc}}(X)={\mathrm{PSL}}_3(q^2)$
or
![]() ${\mathrm{PSU}}_3(q^2)$
, and
${\mathrm{PSU}}_3(q^2)$
, and
![]() $\textbf {O}_p(X_{\{u,v\}})=[q^6]$
. It follows that
$\textbf {O}_p(X_{\{u,v\}})=[q^6]$
. It follows that
![]() $\textbf {O}_p(X_v^{[1]})=[q^3]$
. Thus,
$\textbf {O}_p(X_v^{[1]})=[q^3]$
. Thus,
![]() $\textbf {O}_p(X_v)\ne 1$
and
$\textbf {O}_p(X_v)\ne 1$
and
![]() $X_v$
has an almost simple quotient
$X_v$
has an almost simple quotient
![]() ${\mathrm{PSU}}_3(q).[o]$
. Checking Tables 8.3 and 8.5 given in [Reference Bray, Holt and Roney-Dougal1], we conclude that X has no maximal subgroup containing
${\mathrm{PSU}}_3(q).[o]$
. Checking Tables 8.3 and 8.5 given in [Reference Bray, Holt and Roney-Dougal1], we conclude that X has no maximal subgroup containing
![]() $X_v$
, which is a contradiction. If
$X_v$
, which is a contradiction. If
![]() $t=f$
, then we have
$t=f$
, then we have
![]() $(X,\textbf {O}_p(X_{\{u,v\}}))=({\mathrm{G}}_2(p^t).\mathbb Z_{2^{l+1}}, [q^6])$
and we get a similar contradiction by checking the maximal subgroups of
$(X,\textbf {O}_p(X_{\{u,v\}}))=({\mathrm{G}}_2(p^t).\mathbb Z_{2^{l+1}}, [q^6])$
and we get a similar contradiction by checking the maximal subgroups of
![]() ${\mathrm{G}}_2(p^t).\mathbb Z_{2^{l+1}}$
.
${\mathrm{G}}_2(p^t).\mathbb Z_{2^{l+1}}$
.
Suppose that
![]() $f\ne t<2f$
. Then
$f\ne t<2f$
. Then
![]() $f>1$
. Recalling that
$f>1$
. Recalling that
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has a subgroup
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has a subgroup
![]() $\mathbb Z_{({q^2-1})/{(3,q{+}1)}}$
, we know that
$\mathbb Z_{({q^2-1})/{(3,q{+}1)}}$
, we know that
![]() $p^{2f}-1$
is a divisor of
$p^{2f}-1$
is a divisor of
![]() $2(3,q+1)(p^t-1)^2$
. If
$2(3,q+1)(p^t-1)^2$
. If
![]() $p^{2f}-1$
has a primitive prime divisor, say s, then
$p^{2f}-1$
has a primitive prime divisor, say s, then
![]() $s\ge 2f+1\ge 5$
, and s is not a divisor of
$s\ge 2f+1\ge 5$
, and s is not a divisor of
![]() $2(3,q+1)(p^t-1)^2$
, which is a contradiction. It follows from Zsigmondy’s theorem that
$2(3,q+1)(p^t-1)^2$
, which is a contradiction. It follows from Zsigmondy’s theorem that
![]() $2f=6$
and
$2f=6$
and
![]() $p=2$
and so
$p=2$
and so
![]() $t=1$
or
$t=1$
or
![]() $2$
. Then
$2$
. Then
![]() $7$
is a divisor of
$7$
is a divisor of
![]() $p^{2f}-1$
but not a divisor of
$p^{2f}-1$
but not a divisor of
![]() $2(3,q+1) (p^t-1)^2$
, which is a contradiction.
$2(3,q+1) (p^t-1)^2$
, which is a contradiction.
Case 2. Let
![]() $(G_0,H_0)$
be one of the pairs in [Reference Li and Zhang17, Tables 15–20] that is not considered in Case 1. Assume that
$(G_0,H_0)$
be one of the pairs in [Reference Li and Zhang17, Tables 15–20] that is not considered in Case 1. Assume that
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
is a
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
is a
![]() $\{2,3\}$
-group. Then
$\{2,3\}$
-group. Then
![]() $p^{2f}-1$
has no prime divisor other than
$p^{2f}-1$
has no prime divisor other than
![]() $2$
and
$2$
and
![]() $3$
. It follows that
$3$
. It follows that
![]() $f=1$
and so
$f=1$
and so
![]() $p=q>2$
. Calculation shows that
$p=q>2$
. Calculation shows that
![]() $p\in \{3,5,7\}$
. For
$p\in \{3,5,7\}$
. For
![]() $q=p=3$
, it is easily shown that
$q=p=3$
, it is easily shown that
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
is a
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
is a
![]() $2$
-group. These observations yield that either
$2$
-group. These observations yield that either
![]() $q=p=3$
and
$q=p=3$
and
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
is a
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
is a
![]() $2$
-group, or
$2$
-group, or
![]() $X_{\{u,v\}}$
is not a
$X_{\{u,v\}}$
is not a
![]() $\{2,3\}$
-group.
$\{2,3\}$
-group.
Recall that
![]() $X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has a subgroup
$X_{\{u,v\}}/\textbf {O}_p(X_{\{u,v\}})$
has a subgroup
![]() $\mathbb Z_{({q^2-1})/{(3,q{+}1)}}$
and
$\mathbb Z_{({q^2-1})/{(3,q{+}1)}}$
and
![]() $\textbf {O}_p(X_{\{u,v\}})$
has order
$\textbf {O}_p(X_{\{u,v\}})$
has order
![]() $p^{if}.a$
, where
$p^{if}.a$
, where
![]() $3\le i\le 6$
. It follows that
$3\le i\le 6$
. It follows that
![]() $(X,X_{\{u,v\}})$
is one of the following pairs:
$(X,X_{\{u,v\}})$
is one of the following pairs:
Then
![]() $q=p\in \{5,11\}$
and
$q=p\in \{5,11\}$
and
![]() $X_v^{[1]}=1$
. In particular,
$X_v^{[1]}=1$
. In particular,
![]() ${\mathrm{soc}}(X_v)={\mathrm{PSU}}_3(p)$
, and
${\mathrm{soc}}(X_v)={\mathrm{PSU}}_3(p)$
, and
![]() $X_{\{u,v\}}$
is the normalizer
$X_{\{u,v\}}$
is the normalizer
![]() $\textbf {N}_X(P)$
of some Sylow p-subgroup P of X. Thus,
$\textbf {N}_X(P)$
of some Sylow p-subgroup P of X. Thus,
![]() $X_{uv}=X_v\cap X_{\{u,v\}}\le \textbf {N}_{X_v}(P)$
. For the pairs
$X_{uv}=X_v\cap X_{\{u,v\}}\le \textbf {N}_{X_v}(P)$
. For the pairs
![]() $({\mathrm{HS}}.2, [5^3]{:}[2^5])$
and
$({\mathrm{HS}}.2, [5^3]{:}[2^5])$
and
![]() $({\mathrm{Ru}}, [5^3]{:}[2^5])$
, by the Atlas [Reference Conway, Norton, Parker and Wilson3],
$({\mathrm{Ru}}, [5^3]{:}[2^5])$
, by the Atlas [Reference Conway, Norton, Parker and Wilson3],
![]() $X_{\{u,v\}}$
is a normalizer of some Sylow
$X_{\{u,v\}}$
is a normalizer of some Sylow
![]() $5$
-subgroup that intersects a maximal subgroup
$5$
-subgroup that intersects a maximal subgroup
![]() ${\mathrm{PSU}}_3(5){:}2$
of
${\mathrm{PSU}}_3(5){:}2$
of
![]() ${\mathrm{soc}}(X)$
at
${\mathrm{soc}}(X)$
at
![]() $[5^3]{:}8{:}2$
; thus G, X and
$[5^3]{:}8{:}2$
; thus G, X and
![]() $X_{\{u,v\}}$
are as listed in Table 6. The other pairs are excluded as follows.
$X_{\{u,v\}}$
are as listed in Table 6. The other pairs are excluded as follows.
First, the group
![]() ${\mathrm{Th}}$
is excluded as it has no maximal subgroup with a simple section
${\mathrm{Th}}$
is excluded as it has no maximal subgroup with a simple section
![]() ${\mathrm{PSU}}_3(5)$
; refer to [Reference Wilson36, Table 5.8]. For the pair
${\mathrm{PSU}}_3(5)$
; refer to [Reference Wilson36, Table 5.8]. For the pair
![]() $({\mathrm{McL}}, [5^3]{:}3{:}8)$
, by the Atlas [Reference Conway, Norton, Parker and Wilson3], we have
$({\mathrm{McL}}, [5^3]{:}3{:}8)$
, by the Atlas [Reference Conway, Norton, Parker and Wilson3], we have
![]() $X_v={\mathrm{PSU}}_3(5)$
and so
$X_v={\mathrm{PSU}}_3(5)$
and so
![]() $X_{uv}\le \textbf {N}_{{\mathrm{PSU}}_3(5)}(P)=[5^3]{:}8$
, which contradicts that
$X_{uv}\le \textbf {N}_{{\mathrm{PSU}}_3(5)}(P)=[5^3]{:}8$
, which contradicts that
![]() $|X_{\{u,v\}}:X_{uv}|=2$
. For the pair
$|X_{\{u,v\}}:X_{uv}|=2$
. For the pair
![]() $({\mathrm{J}}_4, [11^3]{:}(5\times 2{\mathrm{S}}_4))$
, by [Reference Wilson36, Table 5.8],
$({\mathrm{J}}_4, [11^3]{:}(5\times 2{\mathrm{S}}_4))$
, by [Reference Wilson36, Table 5.8],
![]() $X_v={\mathrm{PSU}}_3(11).2$
, yielding
$X_v={\mathrm{PSU}}_3(11).2$
, yielding
![]() $X_{uv}\le \textbf {N}_{X_v}(P)=[11^3]{:}(5\times 8{:}2)$
and we get a similar contradiction. For the pair
$X_{uv}\le \textbf {N}_{X_v}(P)=[11^3]{:}(5\times 8{:}2)$
and we get a similar contradiction. For the pair
![]() $(X,X_{\{u,v\}})=({\mathrm{Co}}_2, [5^3]{:}4{\mathrm{S}}_4)$
, by the Atlas [Reference Conway, Norton, Parker and Wilson3],
$(X,X_{\{u,v\}})=({\mathrm{Co}}_2, [5^3]{:}4{\mathrm{S}}_4)$
, by the Atlas [Reference Conway, Norton, Parker and Wilson3],
![]() $X_v<{\mathrm{HS}}.2<{\mathrm{Co}}_2$
. Checking the maximal subgroups of
$X_v<{\mathrm{HS}}.2<{\mathrm{Co}}_2$
. Checking the maximal subgroups of
![]() ${\mathrm{HS}}.2$
, we have
${\mathrm{HS}}.2$
, we have
![]() $X_v={\mathrm{PSU}}_3(5)$
or
$X_v={\mathrm{PSU}}_3(5)$
or
![]() $X_v={\mathrm{PSU}}_3(5){:}2$
. It follows that
$X_v={\mathrm{PSU}}_3(5){:}2$
. It follows that
![]() $X_{uv}\le \textbf {N}_{X_v}(P)=[5^3]{:}8$
or
$X_{uv}\le \textbf {N}_{X_v}(P)=[5^3]{:}8$
or
![]() $[5^3]{:}[2^5]$
and then
$[5^3]{:}[2^5]$
and then
![]() $|X_{\{u,v\}}:X_{uv}|\ne 2$
, which is a contradiction. This completes the proof.
$|X_{\{u,v\}}:X_{uv}|\ne 2$
, which is a contradiction. This completes the proof.
5 Graphs with soluble vertex-stabilizers
Let G, T, X and
![]() ${{\Gamma}}=(V,E)$
be as in Hypothesis 3.1. The following lemma says that if
${{\Gamma}}=(V,E)$
be as in Hypothesis 3.1. The following lemma says that if
![]() ${{\Gamma}}$
is a complete bipartite graph, then
${{\Gamma}}$
is a complete bipartite graph, then
![]() ${{\Gamma}}\cong {\sf K}_{6,6}$
and
${{\Gamma}}\cong {\sf K}_{6,6}$
and
![]() $G_v^{{{\Gamma}}(v)}$
is insoluble.
$G_v^{{{\Gamma}}(v)}$
is insoluble.
Lemma 5.1. Assume that
![]() ${{\Gamma}}\cong {\sf K}_{d,d}$
. Then
${{\Gamma}}\cong {\sf K}_{d,d}$
. Then
![]() $T\cong {\mathrm{A}}_6$
,
$T\cong {\mathrm{A}}_6$
,
![]() $d=6$
,
$d=6$
,
![]() $T_v={\mathrm{PSL}}_2(5)$
and
$T_v={\mathrm{PSL}}_2(5)$
and
![]() $T_{uv}\cong {\mathrm{D}}_{10}$
. In particular,
$T_{uv}\cong {\mathrm{D}}_{10}$
. In particular,
![]() $X_{uv}$
is nonabelian.
$X_{uv}$
is nonabelian.
Proof. Let
![]() $G^{+}$
be the subgroup of G fixing the bipartition of
$G^{+}$
be the subgroup of G fixing the bipartition of
![]() ${{\Gamma}}$
. Then
${{\Gamma}}$
. Then
![]() $G_v\le G^{+}$
and
$G_v\le G^{+}$
and
![]() $G_v$
is
$G_v$
is
![]() $2$
-transitive on the partite set that does not contain v. Thus,
$2$
-transitive on the partite set that does not contain v. Thus,
![]() $G^{+}$
acts
$G^{+}$
acts
![]() $2$
-transitively on each partite set and these two actions are not equivalent. Check the almost simple
$2$
-transitively on each partite set and these two actions are not equivalent. Check the almost simple
![]() $2$
-transitive groups; refer to [Reference Cameron2, Table 7.4]. We conclude that
$2$
-transitive groups; refer to [Reference Cameron2, Table 7.4]. We conclude that
![]() $T\cong {\mathrm{A}}_6$
or
$T\cong {\mathrm{A}}_6$
or
![]() ${\mathrm{M}}_{12}$
,
${\mathrm{M}}_{12}$
,
![]() $T_v\cong {\mathrm{A}}_5$
or
$T_v\cong {\mathrm{A}}_5$
or
![]() ${\mathrm{M}}_{11}$
and
${\mathrm{M}}_{11}$
and
![]() $T_{uv}\cong {\mathrm{D}}_{10}$
or
$T_{uv}\cong {\mathrm{D}}_{10}$
or
![]() ${\mathrm{PSL}}_2(11)$
, respectively. Since
${\mathrm{PSL}}_2(11)$
, respectively. Since
![]() $T_{uv}$
is soluble, the lemma follows.
$T_{uv}$
is soluble, the lemma follows.
Assume that
![]() $G_v$
is soluble and let
$G_v$
is soluble and let
![]() ${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})=\mathbb Z_p^f$
, where p is a prime. By Lemma 5.1, since
${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})=\mathbb Z_p^f$
, where p is a prime. By Lemma 5.1, since
![]() $G_v$
is soluble,
$G_v$
is soluble,
![]() ${{\Gamma}}$
is not a complete bipartite graph. Then we have the following result by [Reference Lu21, Theorem 3.3].
${{\Gamma}}$
is not a complete bipartite graph. Then we have the following result by [Reference Lu21, Theorem 3.3].
Lemma 5.2. Assume that
![]() $X_{uv}$
is abelian. Then one of the following holds:
$X_{uv}$
is abelian. Then one of the following holds:
-
(1)
 $T\cong {\mathrm{PSL}}_2(p^f)$
,
$T\cong {\mathrm{PSL}}_2(p^f)$
,
 $T_{\{u,v\}}\cong {\mathrm{D}}_{{2(p^{f}-1)}/{(2,p-1)}}$
,
$T_{\{u,v\}}\cong {\mathrm{D}}_{{2(p^{f}-1)}/{(2,p-1)}}$
,
 $T_v\cong \mathbb Z_p^{f}{:}\mathbb Z_{({p^{f}-1})/{(2,p-1)}}$
and
$T_v\cong \mathbb Z_p^{f}{:}\mathbb Z_{({p^{f}-1})/{(2,p-1)}}$
and
 ${{\Gamma}}\cong {\sf K}_{p^f{+}1}$
;
${{\Gamma}}\cong {\sf K}_{p^f{+}1}$
; -
(2)
 $T={\mathrm{Sz}}(2^f)$
,
$T={\mathrm{Sz}}(2^f)$
,
 $T_{\{u,v\}}\cong {\mathrm{D}}_{2(2^{f}-1)}$
,
$T_{\{u,v\}}\cong {\mathrm{D}}_{2(2^{f}-1)}$
,
 $T_v\cong \mathbb Z_2^{f}{:}\mathbb Z_{2^{f}-1}$
and
$T_v\cong \mathbb Z_2^{f}{:}\mathbb Z_{2^{f}-1}$
and
 ${{\Gamma}}$
is
${{\Gamma}}$
is
 $(T,2)$
-arc-transitive, where
$(T,2)$
-arc-transitive, where
 $f\ge 3$
is odd.
$f\ge 3$
is odd.
Remark 5.3. In Lemma 5.2,
![]() $T_{\{u,v\}}$
is soluble and maximal in T and thus
$T_{\{u,v\}}$
is soluble and maximal in T and thus
![]() $X=T$
by the choice of X. For part (1), since
$X=T$
by the choice of X. For part (1), since
![]() ${{\Gamma}}$
is
${{\Gamma}}$
is
![]() $(G,2)$
-arc-transitive, G is a
$(G,2)$
-arc-transitive, G is a
![]() $3$
-transitive group of degree
$3$
-transitive group of degree
![]() $p^f+1$
and thus
$p^f+1$
and thus
![]() $X\ne G$
if p is odd. The graphs satisfying part (2) are determined by [Reference Fang and Praeger5, Construction 5.4 and Proposition 5.5]; in particular, for any given odd
$X\ne G$
if p is odd. The graphs satisfying part (2) are determined by [Reference Fang and Praeger5, Construction 5.4 and Proposition 5.5]; in particular, for any given odd
![]() $f\ge 3$
, there is a unique
$f\ge 3$
, there is a unique
![]() $({\mathrm{Sz}}(2^f),2)$
-arc-transitive graph of valency
$({\mathrm{Sz}}(2^f),2)$
-arc-transitive graph of valency
![]() $2^f$
that has automorphism group
$2^f$
that has automorphism group
![]() ${\sf Aut}({\mathrm{Sz}}(2^f))$
.
${\sf Aut}({\mathrm{Sz}}(2^f))$
.
Lemma 5.4. Assume that (1) or (2) of Lemma 3.5 holds and
![]() $X_{uv}$
is nonabelian. Then one of the following holds:
$X_{uv}$
is nonabelian. Then one of the following holds:
-
(1)
 $G=X$
or
$G=X$
or
 $X.2$
,
$X.2$
,
 $X={\mathrm{M}}_{10}$
,
$X={\mathrm{M}}_{10}$
,
 $X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
,
$X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
,
 $X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
$X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
 ${{\Gamma}}\cong {\sf K}_{10}$
;
${{\Gamma}}\cong {\sf K}_{10}$
; -
(2)
 $G=X={\mathrm{PSL}}_3(3).2$
,
$G=X={\mathrm{PSL}}_3(3).2$
,
 $X_{\{u,v\}}\cong {\mathrm{GL}}_2(3){:}2$
,
$X_{\{u,v\}}\cong {\mathrm{GL}}_2(3){:}2$
,
 $X_v\cong 3^2{:}{\mathrm{GL}}_2(3)$
and
$X_v\cong 3^2{:}{\mathrm{GL}}_2(3)$
and
 ${{\Gamma}}$
is the point–line nonincidence graph of
${{\Gamma}}$
is the point–line nonincidence graph of
 ${\mathrm{PG}}(2,3)$
.
${\mathrm{PG}}(2,3)$
.
Proof.
Case 1. Assume that Lemma 3.5(1) holds. Suppose first that
![]() $(X_v^{{{\Gamma}}(v)})_u={\mathrm{Q}}_8$
. Then
$(X_v^{{{\Gamma}}(v)})_u={\mathrm{Q}}_8$
. Then
![]() $X_{uv}\lesssim {\mathrm{Q}}_8{\times }{\mathrm{Q}}_8$
. This implies that
$X_{uv}\lesssim {\mathrm{Q}}_8{\times }{\mathrm{Q}}_8$
. This implies that
![]() $|X_{\{u,v\}}|$
is a divisor of
$|X_{\{u,v\}}|$
is a divisor of
![]() $2^7$
and divisible by
$2^7$
and divisible by
![]() $2^4$
. Checking Tables 14–20 in [Reference Li and Zhang17], we have
$2^4$
. Checking Tables 14–20 in [Reference Li and Zhang17], we have
![]() $X\cong {\mathrm{PSL}}_2(9).2={\mathrm{M}}_{10}$
and
$X\cong {\mathrm{PSL}}_2(9).2={\mathrm{M}}_{10}$
and
![]() $X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
. In this case,
$X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
. In this case,
![]() $X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
$X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
![]() $d=9$
. Since
$d=9$
. Since
![]() ${{\Gamma}}$
has valency nine and order
${{\Gamma}}$
has valency nine and order
![]() $|X:X_v|=10$
, we have
$|X:X_v|=10$
, we have
![]() ${{\Gamma}}\cong {\sf K}_{10}$
, desired as in part (1).
${{\Gamma}}\cong {\sf K}_{10}$
, desired as in part (1).
Suppose that
![]() $(X_v^{{{\Gamma}}(v)})_u\ne {\mathrm{Q}}_8$
. If
$(X_v^{{{\Gamma}}(v)})_u\ne {\mathrm{Q}}_8$
. If
![]() $p=3$
and
$p=3$
and
![]() $(G_v^{{{\Gamma}}(v)})_u={\mathrm{Q}}_8$
, then
$(G_v^{{{\Gamma}}(v)})_u={\mathrm{Q}}_8$
, then
![]() $(X_v^{{{\Gamma}}(v)})_u$
is abelian; it follows that
$(X_v^{{{\Gamma}}(v)})_u$
is abelian; it follows that
![]() $X_{uv}$
is abelian, which is a contradiction. Thus, we have
$X_{uv}$
is abelian, which is a contradiction. Thus, we have
![]() ${\mathrm{SL}}_2(3)\unlhd (G_v^{{{\Gamma}}(v)})_u\le {\mathrm{GL}}_2(p)$
and
${\mathrm{SL}}_2(3)\unlhd (G_v^{{{\Gamma}}(v)})_u\le {\mathrm{GL}}_2(p)$
and
![]() $p\in \{3,5,7,11,23\}$
. Then
$p\in \{3,5,7,11,23\}$
. Then
![]() $(G_v^{{{\Gamma}}(v)})_u\le \textbf {N}_{{\mathrm{GL}}_2(p)}({\mathrm{SL}}_2(3))=\mathbb Z_{p-1}\circ {\mathrm{GL}}_2(3)$
. Since
$(G_v^{{{\Gamma}}(v)})_u\le \textbf {N}_{{\mathrm{GL}}_2(p)}({\mathrm{SL}}_2(3))=\mathbb Z_{p-1}\circ {\mathrm{GL}}_2(3)$
. Since
![]() $(X_v^{{{\Gamma}}(v)})_u$
is nonabelian and normal in
$(X_v^{{{\Gamma}}(v)})_u$
is nonabelian and normal in
![]() $(G_v^{{{\Gamma}}(v)})_u$
, we have
$(G_v^{{{\Gamma}}(v)})_u$
, we have
![]() ${\mathrm{Q}}_8\unlhd (X_v^{{{\Gamma}}(v)})_u$
and hence
${\mathrm{Q}}_8\unlhd (X_v^{{{\Gamma}}(v)})_u$
and hence
![]() ${\mathrm{SL}}_2(3)\unlhd (X_v^{{{\Gamma}}(v)})_u$
. Moreover,
${\mathrm{SL}}_2(3)\unlhd (X_v^{{{\Gamma}}(v)})_u$
. Moreover,
![]() $|X_{\{u,v\}}|$
is a divisor of
$|X_{\{u,v\}}|$
is a divisor of
![]() $2^7\cdot 3^2\cdot (p-1)^2$
and divisible by
$2^7\cdot 3^2\cdot (p-1)^2$
and divisible by
![]() $2^4$
. Let M be an arbitrary normal abelian subgroup of
$2^4$
. Let M be an arbitrary normal abelian subgroup of
![]() $X_{\{u,v\}}$
. Then
$X_{\{u,v\}}$
. Then
![]() $M\cap X_{uv}$
has index at most 2 in M, and
$M\cap X_{uv}$
has index at most 2 in M, and
![]() $(M\cap X_{uv})X_v^{[1]}/X_v^{[1]}$
is isomorphic to a normal subgroup of
$(M\cap X_{uv})X_v^{[1]}/X_v^{[1]}$
is isomorphic to a normal subgroup of
![]() $(X_v^{{{\Gamma}}(v)})_u$
. Thus,
$(X_v^{{{\Gamma}}(v)})_u$
. Thus,
![]() $(M\cap X_{uv})X_v^{[1]}/X_v^{[1]}\lesssim \mathbb Z_{p-1}$
. Since
$(M\cap X_{uv})X_v^{[1]}/X_v^{[1]}\lesssim \mathbb Z_{p-1}$
. Since
![]() $M\cap X_v^{[1]}\unlhd X_v^{[1]}$
and
$M\cap X_v^{[1]}\unlhd X_v^{[1]}$
and
![]() $X_v^{[1]}$
is isomorphic to a normal subgroup of
$X_v^{[1]}$
is isomorphic to a normal subgroup of
![]() $(X_v^{{{\Gamma}}(v)})_u$
, we have
$(X_v^{{{\Gamma}}(v)})_u$
, we have
![]() $M\cap X_v^{[1]}\lesssim \mathbb Z_{p-1}$
. Noting that
$M\cap X_v^{[1]}\lesssim \mathbb Z_{p-1}$
. Noting that
![]() $(M\cap X_{uv})X_v^{[1]}/X_v^{[1]}\cong M\cap X_{uv}/(M\cap X_v^{[1]})$
, it follows that
$(M\cap X_{uv})X_v^{[1]}/X_v^{[1]}\cong M\cap X_{uv}/(M\cap X_v^{[1]})$
, it follows that
![]() $|M\cap X_{uv}|$
is a divisor of
$|M\cap X_{uv}|$
is a divisor of
![]() $(p-1)^2$
. Thus,
$(p-1)^2$
. Thus,
![]() $|M|$
is a divisor of
$|M|$
is a divisor of
![]() $2(p-1)^2$
.
$2(p-1)^2$
.
The above observations allow us to consider only the pairs
![]() $(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] that satisfy the following conditions:
$(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20] that satisfy the following conditions:
-
(c1)
 $|H_0|$
is a divisor of
$|H_0|$
is a divisor of
 $2^7\cdot 3^2\cdot (p-1)^2$
and divisible by
$2^7\cdot 3^2\cdot (p-1)^2$
and divisible by
 $2^4$
;
$2^4$
;
 $H_0$
has a factor (a quotient of some subnormal subgroup)
$H_0$
has a factor (a quotient of some subnormal subgroup)
 ${\mathrm{Q}}_8$
; and
${\mathrm{Q}}_8$
; and
 $H_0$
has no element of order
$H_0$
has no element of order
 $3^2$
,
$3^2$
,
 $5^2$
or
$5^2$
or
 $11^2$
;
$11^2$
; -
(c2) if M is a normal abelian subgroup of
 $H_0$
, then
$H_0$
, then
 $|M|$
is a divisor of
$|M|$
is a divisor of
 $2(p-1)^2$
; if
$2(p-1)^2$
; if
 $p\in \{7,11,23\}$
, the order of
$p\in \{7,11,23\}$
, the order of
 $\textbf {O}_{({p-1})/{2}}(H_0)$
is a divisor of
$\textbf {O}_{({p-1})/{2}}(H_0)$
is a divisor of
 ${(p-1)^2}/{4}$
.
${(p-1)^2}/{4}$
.
Checking those
![]() $H_0$
that satisfy conditions (c1) and (c2), we conclude that the possible pairs
$H_0$
that satisfy conditions (c1) and (c2), we conclude that the possible pairs
![]() $(X,X_{\{u,v\}})$
are listed as follows:
$(X,X_{\{u,v\}})$
are listed as follows:
 $$ \begin{align*}\begin{array}{l} ({\rm M}_{11},3^2{:}{\rm Q}_8.2),\, ({\rm M}_{11},2{\rm S}_4),\, ({\rm M}_{12}, [2^5].{\rm S}_3),\, ({\rm M}_{12},3^2{:}2{\rm S}_4),\\ ({\rm J}_{2},[2^6]{:}(3{\times}{\rm S}_3)),\, ({\rm J}_{3},[2^6]{:}(3{\times}{\rm S}_3)),\, ({\rm Co}_3,[2^9].3^2.{\rm S}_3)),\\ ({\rm He}.2,[2^8]{:}3^2.{\rm D}_8)),\, ({\rm McL}.2, [2^6]{:}{\rm S}_3^2),\\ ({\rm PSL}_3(3), 3^2{:}2{\rm S}_4),\, ({\rm PSL}_3(3).2, 2{\rm S}_4{:}2),\, ({\rm PSL}_3(4).2, 2^{2{+}4}.3.2),\\ ({\rm PGL}_3(4){.}2, [2^6]{.}3{.}{\rm S}_3),\, ({\rm PSL}_4(3){.}2, 2{.}{\rm S}_4^2{.}2),\, ({\rm PSL}_5(2){.}2, [2^8]{.}{\rm S}_3^2{.}2),\\ ({\rm PSp}_4(4){.}4, [2^8]{:}3{.}12),\, ({\rm PSp}_4(4).4, 5^2{:}[2^5]),\, ({\rm PSp}_6(2), [2^7]{:}{\rm S}_3^2),\\ ({\rm PSp}_6(3), [2^8]{:}3^3.S_3),\, ({\rm PSU}_3(3), 4.{\rm S}_4),\, ({\rm PSU}_4(2), 2.{\rm A}_4^2.2),\\ ({\rm PSU}_4(3), 2.{\rm A}_4^2.4),\, ({\rm PSU}_4(3).2, [2^5].{\rm S}_4),\, ({\rm P\Omega}^{+}_8(3){.}{\rm A}_4, 10^2{:}4{\rm A}_4),\\ ({\rm G}_2(2)', 4.{\rm S}_4),\, ({\rm G}_2(3), {\rm SL}_2(3)\circ{\rm SL}_2(3){:}2),\, ({}^2{\rm F}_4(2)', 5^2{:}4{\rm A}_4).\end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\rm M}_{11},3^2{:}{\rm Q}_8.2),\, ({\rm M}_{11},2{\rm S}_4),\, ({\rm M}_{12}, [2^5].{\rm S}_3),\, ({\rm M}_{12},3^2{:}2{\rm S}_4),\\ ({\rm J}_{2},[2^6]{:}(3{\times}{\rm S}_3)),\, ({\rm J}_{3},[2^6]{:}(3{\times}{\rm S}_3)),\, ({\rm Co}_3,[2^9].3^2.{\rm S}_3)),\\ ({\rm He}.2,[2^8]{:}3^2.{\rm D}_8)),\, ({\rm McL}.2, [2^6]{:}{\rm S}_3^2),\\ ({\rm PSL}_3(3), 3^2{:}2{\rm S}_4),\, ({\rm PSL}_3(3).2, 2{\rm S}_4{:}2),\, ({\rm PSL}_3(4).2, 2^{2{+}4}.3.2),\\ ({\rm PGL}_3(4){.}2, [2^6]{.}3{.}{\rm S}_3),\, ({\rm PSL}_4(3){.}2, 2{.}{\rm S}_4^2{.}2),\, ({\rm PSL}_5(2){.}2, [2^8]{.}{\rm S}_3^2{.}2),\\ ({\rm PSp}_4(4){.}4, [2^8]{:}3{.}12),\, ({\rm PSp}_4(4).4, 5^2{:}[2^5]),\, ({\rm PSp}_6(2), [2^7]{:}{\rm S}_3^2),\\ ({\rm PSp}_6(3), [2^8]{:}3^3.S_3),\, ({\rm PSU}_3(3), 4.{\rm S}_4),\, ({\rm PSU}_4(2), 2.{\rm A}_4^2.2),\\ ({\rm PSU}_4(3), 2.{\rm A}_4^2.4),\, ({\rm PSU}_4(3).2, [2^5].{\rm S}_4),\, ({\rm P\Omega}^{+}_8(3){.}{\rm A}_4, 10^2{:}4{\rm A}_4),\\ ({\rm G}_2(2)', 4.{\rm S}_4),\, ({\rm G}_2(3), {\rm SL}_2(3)\circ{\rm SL}_2(3){:}2),\, ({}^2{\rm F}_4(2)', 5^2{:}4{\rm A}_4).\end{array}\end{align*} $$
Note that these groups X are included in the Atlas [Reference Conway, Norton, Parker and Wilson3]. Inspecting the subgroups of X, only the pair
![]() $({\mathrm{PSL}}_3(3).2, 2{\mathrm{S}}_4{:}2)$
gives a desired
$({\mathrm{PSL}}_3(3).2, 2{\mathrm{S}}_4{:}2)$
gives a desired
![]() $X_v\cong 3^2{:}{\mathrm{GL}}_2(3)$
and then the desired graph
$X_v\cong 3^2{:}{\mathrm{GL}}_2(3)$
and then the desired graph
![]() ${{\Gamma}}$
has valency
${{\Gamma}}$
has valency
![]() $d=9$
. In this case, the socle
$d=9$
. In this case, the socle
![]() ${\mathrm{PSL}}_3(3)$
of X has two orbits on the vertex set of
${\mathrm{PSL}}_3(3)$
of X has two orbits on the vertex set of
![]() ${{\Gamma}}$
; each of them has size
${{\Gamma}}$
; each of them has size
![]() $13$
and can be viewed as the point set or the line set of the projective plane
$13$
and can be viewed as the point set or the line set of the projective plane
![]() ${\mathrm{PG}}(2,3)$
. This forces that
${\mathrm{PG}}(2,3)$
. This forces that
![]() ${{\Gamma}}$
is (isomorphic to) one of the following graphs:
${{\Gamma}}$
is (isomorphic to) one of the following graphs:
![]() ${\sf K}_{13,13}-13{\sf K}_2$
, the point–line incidence graph and the point–line nonincidence graph of
${\sf K}_{13,13}-13{\sf K}_2$
, the point–line incidence graph and the point–line nonincidence graph of
![]() ${\mathrm{PG}}(2,3)$
. Since
${\mathrm{PG}}(2,3)$
. Since
![]() ${{\Gamma}}$
has valency 9, the graph
${{\Gamma}}$
has valency 9, the graph
![]() ${{\Gamma}}$
is the point–line nonincidence graph of
${{\Gamma}}$
is the point–line nonincidence graph of
![]() ${\mathrm{PG}}(2,3)$
. Then part (2) of this lemma follows.
${\mathrm{PG}}(2,3)$
. Then part (2) of this lemma follows.
Case 2. Let
![]() $2_{+}^{1{+}4}{:}\mathbb Z_5\le (G_v^{{{\Gamma}}(v)})_u\le 2_{+}^{1{+}4}.(\mathbb Z_5{:}\mathbb Z_4)$
. Then
$2_{+}^{1{+}4}{:}\mathbb Z_5\le (G_v^{{{\Gamma}}(v)})_u\le 2_{+}^{1{+}4}.(\mathbb Z_5{:}\mathbb Z_4)$
. Then
![]() $2_{+}^{1{+}4}\unlhd (X_v^{{{\Gamma}}(v)})_u$
and so
$2_{+}^{1{+}4}\unlhd (X_v^{{{\Gamma}}(v)})_u$
and so
![]() $|X_{\{u,v\}}|$
is a divisor of
$|X_{\{u,v\}}|$
is a divisor of
![]() $2^{15}\cdot 5^2$
and divisible by
$2^{15}\cdot 5^2$
and divisible by
![]() $2^6$
. Further, if M is a normal abelian subgroup of
$2^6$
. Further, if M is a normal abelian subgroup of
![]() $X_{\{u,v\}}$
, then a similar argument as in Case 1 yields that
$X_{\{u,v\}}$
, then a similar argument as in Case 1 yields that
![]() $|M|$
is a divisor of
$|M|$
is a divisor of
![]() $2^5$
. It is easily shown that
$2^5$
. It is easily shown that
![]() $\textbf {O}_2(X_{uv})\ne 1 $
and hence
$\textbf {O}_2(X_{uv})\ne 1 $
and hence
![]() $\textbf {O}_2(X_{\{u,v\}})\ne 1$
. Checking the pairs
$\textbf {O}_2(X_{\{u,v\}})\ne 1$
. Checking the pairs
![]() $(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20], either
$(G_0,H_0)$
in [Reference Li and Zhang17, Tables 14–20], either
![]() $\textbf {O}_2(H_0)=1$
or
$\textbf {O}_2(H_0)=1$
or
![]() $|H_0|$
has an odd prime divisor other than
$|H_0|$
has an odd prime divisor other than
![]() $5$
. Thus, in this case, no desired pair
$5$
. Thus, in this case, no desired pair
![]() $(X,X_{\{u,v\}})$
exists. This completes the proof.
$(X,X_{\{u,v\}})$
exists. This completes the proof.
We assume next that Lemma 3.5(3) occurs. Thus,
![]() $(G_v^{{{\Gamma}}(v)})_u\not \le {\mathrm{GL}}_1(p^f)$
and
$(G_v^{{{\Gamma}}(v)})_u\not \le {\mathrm{GL}}_1(p^f)$
and
![]() $(G_v^{{{\Gamma}}(v)})_u\le {\Gamma \textrm{L}}_1(p^f)$
. Then
$(G_v^{{{\Gamma}}(v)})_u\le {\Gamma \textrm{L}}_1(p^f)$
. Then
![]() $f>1$
and
$f>1$
and
![]() $(G_v^{{{\Gamma}}(v)})_u\lesssim \mathbb Z_{p^f-1}{:}\mathbb Z_f$
. Recalling that
$(G_v^{{{\Gamma}}(v)})_u\lesssim \mathbb Z_{p^f-1}{:}\mathbb Z_f$
. Recalling that
![]() $X_{uv}\lesssim (X_u^{{{\Gamma}}(u)})_v{\times } (X_v^{{{\Gamma}}(v)})_u\le (G_u^{{{\Gamma}}(u)})_v{\times } (G_v^{{{\Gamma}}(v)})_u$
, we have the following simple fact.
$X_{uv}\lesssim (X_u^{{{\Gamma}}(u)})_v{\times } (X_v^{{{\Gamma}}(v)})_u\le (G_u^{{{\Gamma}}(u)})_v{\times } (G_v^{{{\Gamma}}(v)})_u$
, we have the following simple fact.
Lemma 5.5. If (3) of Lemma 3.5 occurs, then
![]() $X_{\{u,v\}}$
has no section
$X_{\{u,v\}}$
has no section
![]() $\mathbb Z_t^3$
,
$\mathbb Z_t^3$
,
![]() $\mathbb Z_r^5$
or
$\mathbb Z_r^5$
or
![]() $\mathbb Z_2^6$
, where t is a primitive prime divisor of
$\mathbb Z_2^6$
, where t is a primitive prime divisor of
![]() $p^f-1$
and r is an arbitrary odd prime.
$p^f-1$
and r is an arbitrary odd prime.
Lemma 5.6. Assume that
![]() $X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Then
$X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Then
![]() $p^f\ne 2^6$
.
$p^f\ne 2^6$
.
Proof. Suppose that
![]() $p^f=2^6$
. Then X has order divisible by
$p^f=2^6$
. Then X has order divisible by
![]() $2^6$
,
$2^6$
,
![]() $X_{uv}\lesssim \mathbb Z_{63}{:}\mathbb Z_6\times \mathbb Z_{63}{:}\mathbb Z_6$
and thus
$X_{uv}\lesssim \mathbb Z_{63}{:}\mathbb Z_6\times \mathbb Z_{63}{:}\mathbb Z_6$
and thus
![]() $X_{\{u,v\}}$
has a normal Hall
$X_{\{u,v\}}$
has a normal Hall
![]() $2'$
-subgroup and
$2'$
-subgroup and
![]() $|X_{\{u,v\}}|$
is indivisible by
$|X_{\{u,v\}}|$
is indivisible by
![]() $2^4$
. Checking Tables 14–20 given in [Reference Li and Zhang17],
$2^4$
. Checking Tables 14–20 given in [Reference Li and Zhang17],
![]() $(X,X_{\{u,v\}})$
is one of the following pairs:
$(X,X_{\{u,v\}})$
is one of the following pairs:
The pair
![]() $({\mathrm{PSL}}_2(2^6),{\mathrm{D}}_{126})$
yields that
$({\mathrm{PSL}}_2(2^6),{\mathrm{D}}_{126})$
yields that
![]() $X_v\cong 2^6{:}\mathbb Z_{63}$
and thus
$X_v\cong 2^6{:}\mathbb Z_{63}$
and thus
![]() $X_{uv}$
is abelian; this is not the case. The other pairs are easily excluded as none of them gives a desired
$X_{uv}$
is abelian; this is not the case. The other pairs are easily excluded as none of them gives a desired
![]() $X_v$
. This completes the proof.
$X_v$
. This completes the proof.
Lemma 5.7. Assume that
![]() $X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Suppose that
$X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Suppose that
![]() $X_{uv}$
has a normal abelian Hall
$X_{uv}$
has a normal abelian Hall
![]() $2'$
-subgroup. Then
$2'$
-subgroup. Then
![]() $G=X$
or
$G=X$
or
![]() $X.2$
,
$X.2$
,
![]() $X={\mathrm{M}}_{10}$
,
$X={\mathrm{M}}_{10}$
,
![]() $X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
,
$X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
,
![]() $X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
$X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
![]() ${{\Gamma}}\cong {\sf K}_{10}$
.
${{\Gamma}}\cong {\sf K}_{10}$
.
Proof. Note that
![]() $X_{\{u,v\}}=X_{uv}.2$
. The unique Hall
$X_{\{u,v\}}=X_{uv}.2$
. The unique Hall
![]() $2'$
-subgroup of
$2'$
-subgroup of
![]() $X_{uv}$
is also the Hall
$X_{uv}$
is also the Hall
![]() $2'$
-subgroup of
$2'$
-subgroup of
![]() $X_{\{u,v\}}$
. Checking Tables 14–20 given in [Reference Li and Zhang17], we know that
$X_{\{u,v\}}$
. Checking Tables 14–20 given in [Reference Li and Zhang17], we know that
![]() $(X,X_{\{u,v\}})$
is one of the following pairs:
$(X,X_{\{u,v\}})$
is one of the following pairs:
-
(i)
 $({\mathrm{PGL}}_2(7),{\mathrm{D}}_{16})$
,
$({\mathrm{PGL}}_2(7),{\mathrm{D}}_{16})$
,
 $({\mathrm{PSL}}_3(2).2,{\mathrm{D}}_{16})$
,
$({\mathrm{PSL}}_3(2).2,{\mathrm{D}}_{16})$
,
 $({\mathrm{PGL}}_2(9),{\mathrm{D}}_{16})$
,
$({\mathrm{PGL}}_2(9),{\mathrm{D}}_{16})$
,
 $({\mathrm{M}}_{10},\mathbb Z_8{:}\mathbb Z_2)$
,
$({\mathrm{M}}_{10},\mathbb Z_8{:}\mathbb Z_2)$
,
 $({\mathrm{A}}_5,{\mathrm{D}}_{10})$
,
$({\mathrm{A}}_5,{\mathrm{D}}_{10})$
,
 $({\mathrm{A}}_6, 3^2{:}\mathbb Z_4)$
,
$({\mathrm{A}}_6, 3^2{:}\mathbb Z_4)$
,
 $({\mathrm{M}}_{11}, 3^2{:}{\mathrm{Q}}_8.2)$
,
$({\mathrm{M}}_{11}, 3^2{:}{\mathrm{Q}}_8.2)$
,
 $({\mathrm{J}}_1,{\mathrm{D}}_6{\times } {\mathrm{D}}_{10})$
,
$({\mathrm{J}}_1,{\mathrm{D}}_6{\times } {\mathrm{D}}_{10})$
,
 $({\mathrm{PGL}}_2(7), {\mathrm{D}}_{12})$
,
$({\mathrm{PGL}}_2(7), {\mathrm{D}}_{12})$
,
 $({\mathrm{PGL}}_2(9),{\mathrm{D}}_{20})$
,
$({\mathrm{PGL}}_2(9),{\mathrm{D}}_{20})$
,
 $({\mathrm{M}}_{10},\mathbb Z_5{:}\mathbb Z_4)$
,
$({\mathrm{M}}_{10},\mathbb Z_5{:}\mathbb Z_4)$
,
 $({\mathrm{PGL}}_2(11), {\mathrm{D}}_{20})$
,
$({\mathrm{PGL}}_2(11), {\mathrm{D}}_{20})$
,
 $({\mathrm{PSL}}_2(t^a), {\mathrm{D}}_{{2(t^a{\pm } 1)}/{(2,t-1)}})$
,
$({\mathrm{PSL}}_2(t^a), {\mathrm{D}}_{{2(t^a{\pm } 1)}/{(2,t-1)}})$
,
 $({\mathrm{PSp}}_4(4).4,\mathbb Z_{17}{:}\mathbb Z_{16})$
;
$({\mathrm{PSp}}_4(4).4,\mathbb Z_{17}{:}\mathbb Z_{16})$
; -
(ii)
 $({\mathrm{PSL}}_2(t^a), \mathbb Z_t^a{:}\mathbb Z_{({t^a-1})/{2}})$
, t is a prime,
$({\mathrm{PSL}}_2(t^a), \mathbb Z_t^a{:}\mathbb Z_{({t^a-1})/{2}})$
, t is a prime,
 $a\le 4$
and
$a\le 4$
and
 $t^a-1$
is a power of
$t^a-1$
is a power of
 $2$
;
$2$
;
 $({\mathrm{PSL}}_3(t),\mathbb Z_3^2{:}{\mathrm{Q}}_8)$
, t is a prime with
$({\mathrm{PSL}}_3(t),\mathbb Z_3^2{:}{\mathrm{Q}}_8)$
, t is a prime with
 $t\equiv 4,7 \ \mod 9$
;
$t\equiv 4,7 \ \mod 9$
;
 $({\mathrm{PSU}}_3(t),\mathbb Z_3^2{:}{\mathrm{Q}}_8)$
, t is a prime with
$({\mathrm{PSU}}_3(t),\mathbb Z_3^2{:}{\mathrm{Q}}_8)$
, t is a prime with
 $t\equiv 2,5 \ \mod 9$
;
$t\equiv 2,5 \ \mod 9$
;
 $({\mathrm{PSU}}_3(2^a),\mathbb Z_3^2{:}{\mathrm{Q}}_8)$
with a prime
$({\mathrm{PSU}}_3(2^a),\mathbb Z_3^2{:}{\mathrm{Q}}_8)$
with a prime
 $a>3$
;
$a>3$
;
 $({\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}, {\mathrm{D}}_{2(q{\pm } 1)}^2{:}2.\mathbb Z_{2^{b{+}1}})$
,
$({\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}, {\mathrm{D}}_{2(q{\pm } 1)}^2{:}2.\mathbb Z_{2^{b{+}1}})$
,
 $({\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}, \mathbb Z_{2^{2a}{+}1}.4.\mathbb Z_{2^{b{+}1}})$
,
$({\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}, \mathbb Z_{2^{2a}{+}1}.4.\mathbb Z_{2^{b{+}1}})$
,
 $2^b$
is the
$2^b$
is the
 $2$
-part of a;
$2$
-part of a;
 $({\mathrm{Sz}}(2^{2a{+}1}), {\mathrm{D}}_{2(2^{2a{+}1}-1)})$
,
$({\mathrm{Sz}}(2^{2a{+}1}), {\mathrm{D}}_{2(2^{2a{+}1}-1)})$
,
 $({\mathrm{Sz}}(2^{2a{+}1}), \mathbb Z_{2^{2a{+}1}{\pm } 2^{a{+}1}{+}1}{:}\mathbb Z_4)$
;
$({\mathrm{Sz}}(2^{2a{+}1}), \mathbb Z_{2^{2a{+}1}{\pm } 2^{a{+}1}{+}1}{:}\mathbb Z_4)$
;
 $({}^3{\mathrm{D}}_4(t^a), \mathbb Z_{t^{4a}-t^{2a}{+}1}{:}\mathbb Z_4)$
, t is a prime.
$({}^3{\mathrm{D}}_4(t^a), \mathbb Z_{t^{4a}-t^{2a}{+}1}{:}\mathbb Z_4)$
, t is a prime.
The pair
![]() $({\mathrm{M}}_{10},\mathbb Z_8{:}\mathbb Z_2)$
yields that
$({\mathrm{M}}_{10},\mathbb Z_8{:}\mathbb Z_2)$
yields that
![]() $X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
$X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
![]() $d=9$
. The third pair in (i) implies that
$d=9$
. The third pair in (i) implies that
![]() $X_v\cong \mathbb Z_3^2{:}\mathbb Z_8$
; however, then
$X_v\cong \mathbb Z_3^2{:}\mathbb Z_8$
; however, then
![]() $X_{uv}$
is abelian, which is not the case. For
$X_{uv}$
is abelian, which is not the case. For
![]() $({\mathrm{PSL}}_2(t^a), {\mathrm{D}}_{{2(t^a{\pm } 1)}/{(2,t^a-1)}})$
, checking the subgroups of
$({\mathrm{PSL}}_2(t^a), {\mathrm{D}}_{{2(t^a{\pm } 1)}/{(2,t^a-1)}})$
, checking the subgroups of
![]() ${\mathrm{PSL}}_2(t^a)$
, we have
${\mathrm{PSL}}_2(t^a)$
, we have
![]() $t^a=p^f$
and
$t^a=p^f$
and
![]() $X_v\cong \mathbb Z_p^f{:}\mathbb Z_{({p^f-1})/{(2,p-1)}}$
and then
$X_v\cong \mathbb Z_p^f{:}\mathbb Z_{({p^f-1})/{(2,p-1)}}$
and then
![]() $X_{uv}$
is abelian, which a contradiction. The other pairs in (i) are also excluded as
$X_{uv}$
is abelian, which a contradiction. The other pairs in (i) are also excluded as
![]() $|X|$
is indivisible by
$|X|$
is indivisible by
![]() $p^f$
. (Note that
$p^f$
. (Note that
![]() $f>1$
.)
$f>1$
.)
Now we deal with the pairs in (ii). Note that, for an odd prime r, the edge-stabilizer
![]() $X_{\{u,v\}}$
has a unique Sylow r-subgroup
$X_{\{u,v\}}$
has a unique Sylow r-subgroup
![]() $\textbf {O}_r(X_{\{u,v\}})$
. Then
$\textbf {O}_r(X_{\{u,v\}})$
. Then
![]() $\textbf {O}_r(X_{\{u,v\}})$
is a Sylow subgroup of X by Lemma 2.7. This implies that the unique Hall
$\textbf {O}_r(X_{\{u,v\}})$
is a Sylow subgroup of X by Lemma 2.7. This implies that the unique Hall
![]() $2'$
-subgroup of
$2'$
-subgroup of
![]() $X_{\{u,v\}}$
, say K, is a Hall subgroup of X. Since
$X_{\{u,v\}}$
, say K, is a Hall subgroup of X. Since
![]() $X_{\{u,v\}}=X_{uv}.2$
, we have
$X_{\{u,v\}}=X_{uv}.2$
, we have
![]() $K\le X_{uv}$
. Note that
$K\le X_{uv}$
. Note that
![]() $|X_v{:}X_{uv}|=d=p^f$
and
$|X_v{:}X_{uv}|=d=p^f$
and
![]() $X_v$
is contained in a maximal subgroup of X. We now check the maximal subgroups of X that contain K; refer to [Reference Huppert12, Hauptsatz II.8.27], [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6, 8.14 and 8.15] and [Reference Kleidman13, Reference Kleidman14, Reference Suzuki27]. Then one of the following occurs:
$X_v$
is contained in a maximal subgroup of X. We now check the maximal subgroups of X that contain K; refer to [Reference Huppert12, Hauptsatz II.8.27], [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6, 8.14 and 8.15] and [Reference Kleidman13, Reference Kleidman14, Reference Suzuki27]. Then one of the following occurs:
-
(iii)
 $X={\mathrm{Sz}}(2^{2a{+}1})$
and
$X={\mathrm{Sz}}(2^{2a{+}1})$
and
 $X_v\cong \mathbb Z_2^{2a{+}1}{:}\mathbb Z_{2^{2a{+}1}-1}$
;
$X_v\cong \mathbb Z_2^{2a{+}1}{:}\mathbb Z_{2^{2a{+}1}-1}$
; -
(iv)
 $X={\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}$
and
$X={\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}$
and
 $X_v\lesssim {\mathrm{Sp}}_2(2^{2a}){:}2.\mathbb Z_{2^b}$
;
$X_v\lesssim {\mathrm{Sp}}_2(2^{2a}){:}2.\mathbb Z_{2^b}$
; -
(v)
 $X={\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}$
and
$X={\mathrm{PSp}}_4(2^{a}).\mathbb Z_{2^{b{+}1}}$
and
 $X_v\lesssim {\mathrm{Sp}}_2(2^{a})\wr {\mathrm{S}}_2.\mathbb Z_{2^b}$
.
$X_v\lesssim {\mathrm{Sp}}_2(2^{a})\wr {\mathrm{S}}_2.\mathbb Z_{2^b}$
.
Item (iii) yields that
![]() $X_{uv}$
is abelian, which is not the case. Item (iv) gives
$X_{uv}$
is abelian, which is not the case. Item (iv) gives
![]() $X_{uv}=X_v$
, which is a contradiction. Suppose that (v) occurs; we have
$X_{uv}=X_v$
, which is a contradiction. Suppose that (v) occurs; we have
![]() $X_v\cong (\mathbb Z_2^{a}{:}\mathbb Z_{2^{a}-1})^2{:}2.\mathbb Z_{2^b}$
. Then
$X_v\cong (\mathbb Z_2^{a}{:}\mathbb Z_{2^{a}-1})^2{:}2.\mathbb Z_{2^b}$
. Then
![]() $1\ne \textbf {O}_2(X_v)\le \textbf {O}_2(G_v)$
and hence
$1\ne \textbf {O}_2(X_v)\le \textbf {O}_2(G_v)$
and hence
![]() $d=|\textbf {O}_2(G_v)|$
, by Lemma 2.5. Since
$d=|\textbf {O}_2(G_v)|$
, by Lemma 2.5. Since
![]() $X_v$
is transitive on
$X_v$
is transitive on
![]() ${{\Gamma}}(v)$
, it follows that
${{\Gamma}}(v)$
, it follows that
![]() $p^f=d=2^{2a}$
. Thus,
$p^f=d=2^{2a}$
. Thus,
![]() $|X_{uv}|=(2^{a}-1)^22^{b{+}1}$
and so
$|X_{uv}|=(2^{a}-1)^22^{b{+}1}$
and so
![]() $|X_{\{u,v\}}{:}X_{uv}|=8>2$
, which is a contradiction.
$|X_{\{u,v\}}{:}X_{uv}|=8>2$
, which is a contradiction.
Corollary 5.8. Assume that
![]() $X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. If
$X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. If
![]() $f=2$
, then
$f=2$
, then
![]() $G=X$
or
$G=X$
or
![]() $X.2$
,
$X.2$
,
![]() $X={\mathrm{M}}_{10}$
,
$X={\mathrm{M}}_{10}$
,
![]() $X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
,
$X_{\{u,v\}}\cong \mathbb Z_8{:}\mathbb Z_2$
,
![]() $X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
$X_v\cong 3^2{:}{\mathrm{Q}}_8$
and
![]() ${{\Gamma}}\cong {\sf K}_{10}$
.
${{\Gamma}}\cong {\sf K}_{10}$
.
Proof. Let
![]() $f=2$
. Then
$f=2$
. Then
![]() $(X_v^{{{\Gamma}}(v)})_u\lesssim \mathbb Z_{p^2-1}.\mathbb Z_{2}$
. Note that
$(X_v^{{{\Gamma}}(v)})_u\lesssim \mathbb Z_{p^2-1}.\mathbb Z_{2}$
. Note that
![]() $X_{\{u,v\}}=X_{uv}.2$
and
$X_{\{u,v\}}=X_{uv}.2$
and
![]() $X_{uv}\lesssim \mathbb Z_{p^2-1}.\mathbb Z_{2}{\times } \mathbb Z_{p^2-1}.\mathbb Z_{2}$
. Then Lemma 5.7 is applicable and the result follows.
$X_{uv}\lesssim \mathbb Z_{p^2-1}.\mathbb Z_{2}{\times } \mathbb Z_{p^2-1}.\mathbb Z_{2}$
. Then Lemma 5.7 is applicable and the result follows.
Let
![]() ${{\pi }}_0(p^f-1)$
be the set of primitive primes of
${{\pi }}_0(p^f-1)$
be the set of primitive primes of
![]() $p^f-1$
. By Zsigmondy’s theorem, if
$p^f-1$
. By Zsigmondy’s theorem, if
![]() ${{\pi }}_0(p^f-1)=\emptyset $
and
${{\pi }}_0(p^f-1)=\emptyset $
and
![]() $f>1$
, then
$f>1$
, then
![]() $p^f=2^6$
, or
$p^f=2^6$
, or
![]() $f=2$
and
$f=2$
and
![]() $p=2^t-1$
, where t is a prime. Thus, in view of Lemma 5.6 and Corollary 5.8, we assume next that
$p=2^t-1$
, where t is a prime. Thus, in view of Lemma 5.6 and Corollary 5.8, we assume next that
![]() ${{\pi }}_0(p^f-1)\ne \emptyset $
.
${{\pi }}_0(p^f-1)\ne \emptyset $
.
Lemma 5.9. Assume that
![]() $\pi {:}={{\pi }}_0(p^f-1)\ne \emptyset $
,
$\pi {:}={{\pi }}_0(p^f-1)\ne \emptyset $
,
![]() $X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Then
$X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Then
![]() $f\ge 3$
and:
$f\ge 3$
and:
-
(1)
 $\pi \ne \pi (|X_{\{u,v\}}|)\setminus \{2\}$
,
$\pi \ne \pi (|X_{\{u,v\}}|)\setminus \{2\}$
,
 $\min (\pi )\ge \max \{5,f{+}1\}$
;
$\min (\pi )\ge \max \{5,f{+}1\}$
; -
(2)
 $p\not \equiv {\pm } 1 \ \mod r$
and
$p\not \equiv {\pm } 1 \ \mod r$
and
 $\textbf {O}_r(X_{\{u,v\}})\ne 1$
for each
$\textbf {O}_r(X_{\{u,v\}})\ne 1$
for each
 $r\in \pi $
;
$r\in \pi $
; -
(3)
 $X_{\{u,v\}}$
has a unique (nontrivial) Hall
$X_{\{u,v\}}$
has a unique (nontrivial) Hall
 $\pi $
-subgroup that is either cyclic or a direct product of two cyclic subgroups.
$\pi $
-subgroup that is either cyclic or a direct product of two cyclic subgroups.
Proof. By the assumptions in this lemma and Lemma 3.6, we have that
![]() $(X_v^{{{\Gamma}}(v)})_u\cong \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}$
and
$(X_v^{{{\Gamma}}(v)})_u\cong \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}$
and
![]() $\emptyset \ne \pi ={{\pi }}_0(p^f-1)\subseteq {{\pi }}(m')$
. For
$\emptyset \ne \pi ={{\pi }}_0(p^f-1)\subseteq {{\pi }}(m')$
. For
![]() $r\in {{\pi }}$
, since
$r\in {{\pi }}$
, since
![]() $p^{r-1}\equiv 1 \ \mod r$
, we have
$p^{r-1}\equiv 1 \ \mod r$
, we have
![]() $f\le r-1$
and so
$f\le r-1$
and so
![]() $r\ge f{+}1$
. In particular,
$r\ge f{+}1$
. In particular,
![]() $r\ge 5$
and
$r\ge 5$
and
![]() $p\not \equiv {\pm } 1 \ \mod r$
. Recall that
$p\not \equiv {\pm } 1 \ \mod r$
. Recall that
![]() $X_{\{u,v\}}=X_{uv}.2$
and
$X_{\{u,v\}}=X_{uv}.2$
and
![]() $X_{uv}\lesssim \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}{\times } \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}$
. It follows that
$X_{uv}\lesssim \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}{\times } \mathbb Z_{m'}.\mathbb Z_{{f}/{e'}}$
. It follows that
![]() $\textbf {O}_r(X_{\{u,v\}})\ne 1$
and
$\textbf {O}_r(X_{\{u,v\}})\ne 1$
and
![]() $\textbf {O}_r(X_{\{u,v\}})$
is the unique Sylow r-subgroup of
$\textbf {O}_r(X_{\{u,v\}})$
is the unique Sylow r-subgroup of
![]() $X_{\{u,v\}}$
. Clearly,
$X_{\{u,v\}}$
. Clearly,
![]() $\textbf {O}_r(X_{\{u,v\}})$
is either cyclic or a direct product of two cyclic subgroups. Then
$\textbf {O}_r(X_{\{u,v\}})$
is either cyclic or a direct product of two cyclic subgroups. Then
![]() $X_{\{u,v\}}$
has a unique Hall
$X_{\{u,v\}}$
has a unique Hall
![]() $\pi $
-subgroup F that is either cyclic or a direct product of two cyclic subgroups. Clearly,
$\pi $
-subgroup F that is either cyclic or a direct product of two cyclic subgroups. Clearly,
![]() $F\ne 1$
and, by Lemma 5.7,
$F\ne 1$
and, by Lemma 5.7,
![]() $X_{\{u,v\}}$
has no normal abelian Hall
$X_{\{u,v\}}$
has no normal abelian Hall
![]() $2'$
-subgroup. Then
$2'$
-subgroup. Then
![]() $\pi \ne \pi (|X_{\{u,v\}}|)\setminus \{2\}$
and the lemma follows.
$\pi \ne \pi (|X_{\{u,v\}}|)\setminus \{2\}$
and the lemma follows.
Recall that
![]() $X_{\{u,v\}}$
has no section
$X_{\{u,v\}}$
has no section
![]() $\mathbb Z_2^6$
or
$\mathbb Z_2^6$
or
![]() $\mathbb Z_3^5$
; see Lemma 5.5. Combining with Lemma 5.9, we next check the pairs
$\mathbb Z_3^5$
; see Lemma 5.5. Combining with Lemma 5.9, we next check the pairs
![]() $(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20].
$(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20].
Lemma 5.10. Assume that
![]() ${{\pi }}_0(p^f-1)\ne \emptyset $
,
${{\pi }}_0(p^f-1)\ne \emptyset $
,
![]() $X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Then
$X_{uv}$
is nonabelian and (3) of Lemma 3.5 occurs. Then
![]() $T={\mathrm{soc}}(X)$
is not a simple group of Lie type.
$T={\mathrm{soc}}(X)$
is not a simple group of Lie type.
Proof. Suppose that T is a simple group of Lie type over a finite field of order
![]() $q'=t^a$
, where t is a prime. Since
$q'=t^a$
, where t is a prime. Since
![]() $T\unlhd G$
, we know that T is transitive on the edge set of
$T\unlhd G$
, we know that T is transitive on the edge set of
![]() ${{\Gamma}}$
. Then
${{\Gamma}}$
. Then
![]() $T_v^{{{\Gamma}}(v)}\ne 1$
. Noting that
$T_v^{{{\Gamma}}(v)}\ne 1$
. Noting that
![]() $T_v^{{{\Gamma}}(v)}\unlhd G_v^{{{\Gamma}}(v)}$
, we have
$T_v^{{{\Gamma}}(v)}\unlhd G_v^{{{\Gamma}}(v)}$
, we have
![]() ${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})\le T_v^{{{\Gamma}}(v)}$
. In particular,
${\mathrm{soc}}(G_v^{{{\Gamma}}(v)})\le T_v^{{{\Gamma}}(v)}$
. In particular,
![]() $T_v$
is transitive on
$T_v$
is transitive on
![]() ${{\Gamma}}(v)$
and so
${{\Gamma}}(v)$
and so
![]() $|T_v|=p^f|T_{uv}|$
. In view of this, noting that
$|T_v|=p^f|T_{uv}|$
. In view of this, noting that
![]() $T_v=T\cap X_v=T\cap G_v$
and
$T_v=T\cap X_v=T\cap G_v$
and
![]() $T_{\{u,v\}}=T\cap X_{\{u,v\}}=T\cap G_{\{u,v\}}$
, we sometimes work on the triple
$T_{\{u,v\}}=T\cap X_{\{u,v\}}=T\cap G_{\{u,v\}}$
, we sometimes work on the triple
![]() $(T,T_v,T_{\{u,v\}})$
instead of
$(T,T_v,T_{\{u,v\}})$
instead of
![]() $(X,X_v,X_{\{u,v\}})$
.
$(X,X_v,X_{\{u,v\}})$
.
By Lemmas 5.7 and 5.9,
![]() $X_{\{u,v\}}$
is not a
$X_{\{u,v\}}$
is not a
![]() $\{2,3\}$
-group and has no normal abelian Hall
$\{2,3\}$
-group and has no normal abelian Hall
![]() $2'$
-subgroup. Assume that
$2'$
-subgroup. Assume that
![]() $t\in \pi _0(p^f-1)$
. By Lemmas 5.5 and 5.9,
$t\in \pi _0(p^f-1)$
. By Lemmas 5.5 and 5.9,
![]() $t\ge 5$
,
$t\ge 5$
,
![]() $X_{\{u,v\}}$
has no section
$X_{\{u,v\}}$
has no section
![]() $\mathbb Z_t^3$
and
$\mathbb Z_t^3$
and
![]() $\textbf {O}_t(X_{\{u,v\}})\ne 1$
is abelian. Checking the pairs
$\textbf {O}_t(X_{\{u,v\}})\ne 1$
is abelian. Checking the pairs
![]() $(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 16–20], we have
$(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 16–20], we have
![]() $X={\mathrm{PSL}}_2(t^2)$
and
$X={\mathrm{PSL}}_2(t^2)$
and
![]() $X_{\{u,v\}}\cong \mathbb Z_t^2{:}\mathbb Z_{({t^2-1})/{2}}$
. For this case, checking the subgroups of
$X_{\{u,v\}}\cong \mathbb Z_t^2{:}\mathbb Z_{({t^2-1})/{2}}$
. For this case, checking the subgroups of
![]() ${\mathrm{PSL}}_2(t^2)$
, no desired
${\mathrm{PSL}}_2(t^2)$
, no desired
![]() $X_v$
arises, which is a contradiction. Therefore,
$X_v$
arises, which is a contradiction. Therefore,
![]() $t\not \in \pi _0 (p^f-1)$
.
$t\not \in \pi _0 (p^f-1)$
.
By Lemma 5.9,
![]() $\textbf {O}_r(X_{\{u,v\}})\ne 1$
for each
$\textbf {O}_r(X_{\{u,v\}})\ne 1$
for each
![]() $r\in \pi _0(p^f-1)$
. Recall that
$r\in \pi _0(p^f-1)$
. Recall that
![]() $X_{\{u,v\}}$
is not a
$X_{\{u,v\}}$
is not a
![]() $\{2,3\}$
-group and has a subgroup of index two. Checking the pairs
$\{2,3\}$
-group and has a subgroup of index two. Checking the pairs
![]() $(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 16–20], we conclude that
$(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 16–20], we conclude that
![]() $\textbf {O}_t(X_{\{u,v\}})=1$
. Further, we observe that a desired
$\textbf {O}_t(X_{\{u,v\}})=1$
. Further, we observe that a desired
![]() $X_{\{u,v\}}$
if it exists has the form of
$X_{\{u,v\}}$
if it exists has the form of
![]() $N.K$
, where N is an abelian subgroup of T and either K is a
$N.K$
, where N is an abelian subgroup of T and either K is a
![]() $\{2,3\}$
-group or
$\{2,3\}$
-group or
![]() $(X,K)=({\mathrm{E}}_8(q'),\mathbb Z_{30})$
. For the case where
$(X,K)=({\mathrm{E}}_8(q'),\mathbb Z_{30})$
. For the case where
![]() $K\not \cong \mathbb Z_{30}$
, by Lemma 3.6,
$K\not \cong \mathbb Z_{30}$
, by Lemma 3.6,
![]() $\pi _0(p^f-1)\subseteq \pi (|N|)$
and thus, by Lemma 5.5, N has no subgroup
$\pi _0(p^f-1)\subseteq \pi (|N|)$
and thus, by Lemma 5.5, N has no subgroup
![]() $\mathbb Z_r^3$
for
$\mathbb Z_r^3$
for
![]() $r\in \pi _0(p^f-1)$
. With these restrictions, only one of the following Cases 1–4 occurs.
$r\in \pi _0(p^f-1)$
. With these restrictions, only one of the following Cases 1–4 occurs.
Case 1. Either
![]() $X={\mathrm{PSL}}_3(q')$
and
$X={\mathrm{PSL}}_3(q')$
and
![]() $X_{\{u,v\}}\cong ({1}/{(3,q'-1)})\mathbb Z_{q'-1}^2.{\mathrm{S}}_3$
with
$X_{\{u,v\}}\cong ({1}/{(3,q'-1)})\mathbb Z_{q'-1}^2.{\mathrm{S}}_3$
with
![]() $q'\ne 2, \,4$
, or
$q'\ne 2, \,4$
, or
![]() $X={\mathrm{PSU}}_3(q')$
and
$X={\mathrm{PSU}}_3(q')$
and
![]() $X_{\{u,v\}}\cong ({1}/{(3,q'{+}1)})\mathbb Z_{q'{+}1}^2.{\mathrm{S}}_3$
. Then
$X_{\{u,v\}}\cong ({1}/{(3,q'{+}1)})\mathbb Z_{q'{+}1}^2.{\mathrm{S}}_3$
. Then
![]() $|X_v|=({3}/{(3,q'{\mp }1)})p^f(q'{\mp } 1)^2$
. Checking Tables 8.3–8.6 given in [Reference Bray, Holt and Roney-Dougal1], we have
$|X_v|=({3}/{(3,q'{\mp }1)})p^f(q'{\mp } 1)^2$
. Checking Tables 8.3–8.6 given in [Reference Bray, Holt and Roney-Dougal1], we have
![]() $X={\mathrm{PSL}}_3(q')$
and
$X={\mathrm{PSL}}_3(q')$
and
![]() $X_v\lesssim [q^{\prime 3}]{:} ({1}/ {(3,q'-1)})\mathbb Z_{q'-1}^2$
. It follows that
$X_v\lesssim [q^{\prime 3}]{:} ({1}/ {(3,q'-1)})\mathbb Z_{q'-1}^2$
. It follows that
![]() $p=t=3$
and
$p=t=3$
and
![]() $|\textbf {O}_3(X_v)|=3^{f{+}1}=3d$
, which contradicts Lemma 2.5.
$|\textbf {O}_3(X_v)|=3^{f{+}1}=3d$
, which contradicts Lemma 2.5.
Case 2.
![]() $T={\mathrm{soc}}(X)={\mathrm {P\Omega }}_8^{+}(q')$
and
$T={\mathrm{soc}}(X)={\mathrm {P\Omega }}_8^{+}(q')$
and
![]() $T_{\{u,v\}}\cong {\mathrm{D}}_{{2(q^{\prime 2}{+}1)}/{(2,q'-1)}}^2.[2^2]$
. In this case, noting that
$T_{\{u,v\}}\cong {\mathrm{D}}_{{2(q^{\prime 2}{+}1)}/{(2,q'-1)}}^2.[2^2]$
. In this case, noting that
![]() $|T_{\{u,v\}}{:}T_{uv}|\le 2$
, we have
$|T_{\{u,v\}}{:}T_{uv}|\le 2$
, we have
![]() $|T_v|=2^4p^f({(q^{\prime 2}{+}1)^2}/{(2,q'-1)^2})$
or
$|T_v|=2^4p^f({(q^{\prime 2}{+}1)^2}/{(2,q'-1)^2})$
or
![]() $2^3p^f({(q^{\prime 2}{+}1)^2}/ {(2,q'-1)^2})$
. Let M be a maximal subgroup of T with
$2^3p^f({(q^{\prime 2}{+}1)^2}/ {(2,q'-1)^2})$
. Let M be a maximal subgroup of T with
![]() $T_v\le M$
. By [Reference Kleidman13], since
$T_v\le M$
. By [Reference Kleidman13], since
![]() $|M|$
is divisible by
$|M|$
is divisible by
![]() $(q^{\prime 2}{+}1)^2$
, we have
$(q^{\prime 2}{+}1)^2$
, we have
![]() $M\cong {\mathrm{PSL}}_2(q^{\prime 2})^2.2^2$
. It is easily shown that
$M\cong {\mathrm{PSL}}_2(q^{\prime 2})^2.2^2$
. It is easily shown that
![]() ${\mathrm{PSL}}_2(q^{\prime 2})^2.2^2$
does not have subgroups of order
${\mathrm{PSL}}_2(q^{\prime 2})^2.2^2$
does not have subgroups of order
![]() $2^4p^f({(q^{\prime 2}{+}1)^2}/{(2,q'-1)^2})$
or
$2^4p^f({(q^{\prime 2}{+}1)^2}/{(2,q'-1)^2})$
or
![]() $2^3p^f({(q^{\prime 2}{+}1)^2}/{(2,q'-1)^2})$
, which is a contradiction.
$2^3p^f({(q^{\prime 2}{+}1)^2}/{(2,q'-1)^2})$
, which is a contradiction.
Case 3.
![]() $(X,X_{\{u,v\}})$
is one of
$(X,X_{\{u,v\}})$
is one of
![]() $({}^2{\mathrm{F}}_4(2)',5^2{:}4{\mathrm{A}}_4)$
and
$({}^2{\mathrm{F}}_4(2)',5^2{:}4{\mathrm{A}}_4)$
and
![]() $({}^2{\mathrm{F}}_4(2),13{:}12)$
. For the first pair, we have
$({}^2{\mathrm{F}}_4(2),13{:}12)$
. For the first pair, we have
![]() $\pi _0(p^f-1)=\{5\}$
and, since
$\pi _0(p^f-1)=\{5\}$
and, since
![]() $p^f$
is a divisor of
$p^f$
is a divisor of
![]() $|{}^2{\mathrm{F}}_4(2)'|$
, we conclude that
$|{}^2{\mathrm{F}}_4(2)'|$
, we conclude that
![]() $p^f=2^4$
or
$p^f=2^4$
or
![]() $3^4$
. The second pair implies that
$3^4$
. The second pair implies that
![]() $\pi _0(p^f-1)=\{13\}$
and then
$\pi _0(p^f-1)=\{13\}$
and then
![]() $p^f=2^{12}$
or
$p^f=2^{12}$
or
![]() $3^3$
. By the Atlas [Reference Conway, Norton, Parker and Wilson3], X has no maximal subgroup containing
$3^3$
. By the Atlas [Reference Conway, Norton, Parker and Wilson3], X has no maximal subgroup containing
![]() $X_{uv}$
as a subgroup of index divisible by
$X_{uv}$
as a subgroup of index divisible by
![]() $p^f$
, which is a contradiction.
$p^f$
, which is a contradiction.
Case 4.
![]() $T_{\{u,v\}}$
has a normal abelian subgroup N listed in Table 7. Let M be a maximal subgroup of T with
$T_{\{u,v\}}$
has a normal abelian subgroup N listed in Table 7. Let M be a maximal subgroup of T with
![]() $T_v\le M$
. Then
$T_v\le M$
. Then
![]() $|M|$
is divisible by
$|M|$
is divisible by
![]() $p^f|N|$
. Check the maximal subgroups of T of order divisible by
$p^f|N|$
. Check the maximal subgroups of T of order divisible by
![]() $|N|$
; refer to [Reference Kleidman15, Reference Liebeck, Seitz, Ivanov, Liebeck and Saxl20, Reference Malle22]. Then we may deduce a contradiction. First, by [Reference Kleidman15, Theorem C], we conclude that
$|N|$
; refer to [Reference Kleidman15, Reference Liebeck, Seitz, Ivanov, Liebeck and Saxl20, Reference Malle22]. Then we may deduce a contradiction. First, by [Reference Kleidman15, Theorem C], we conclude that
![]() ${\mathrm{Ree}}(3^a)$
has no maximal subgroup of order divisible by
${\mathrm{Ree}}(3^a)$
has no maximal subgroup of order divisible by
![]() $p^f|N|$
. Similarly, by [Reference Malle22], the group
$p^f|N|$
. Similarly, by [Reference Malle22], the group
![]() ${}^2{\mathrm{F}}_4(2^a)$
is excluded. We next deal with the remaining cases.
${}^2{\mathrm{F}}_4(2^a)$
is excluded. We next deal with the remaining cases.
Table 7 Edge-stabilizers in exceptional groups.

Suppose that
![]() $T={\mathrm{G}}_2(3^a)$
. For
$T={\mathrm{G}}_2(3^a)$
. For
![]() $|N|=3^{2a}{\pm } 3^a{+}1$
, since
$|N|=3^{2a}{\pm } 3^a{+}1$
, since
![]() $|M|$
is divisible by
$|M|$
is divisible by
![]() $3^{2a}{\pm } 3^a{+}1$
, we have
$3^{2a}{\pm } 3^a{+}1$
, we have
![]() $M\cong {\mathrm{SL}}_3(3^a){:}2$
or
$M\cong {\mathrm{SL}}_3(3^a){:}2$
or
![]() ${\mathrm{SU}}_3(3^a){:}2$
by [Reference Kleidman15, Theorems A and B]. By [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6], we conclude that
${\mathrm{SU}}_3(3^a){:}2$
by [Reference Kleidman15, Theorems A and B]. By [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6], we conclude that
![]() $T_v\lesssim \mathbb Z_{3^{2a}{\pm } 3^a{+}1}{:}[6]$
, which is impossible. Similarly, for
$T_v\lesssim \mathbb Z_{3^{2a}{\pm } 3^a{+}1}{:}[6]$
, which is impossible. Similarly, for
![]() $|N|=(3^a{\pm } 1)^2$
, we have that
$|N|=(3^a{\pm } 1)^2$
, we have that
![]() $T_v\lesssim ({\mathrm{SL}}_2(3^a)\circ {\mathrm{SL}}_2(3^a)).2$
,
$T_v\lesssim ({\mathrm{SL}}_2(3^a)\circ {\mathrm{SL}}_2(3^a)).2$
,
![]() ${\mathrm{SL}}_3(3^a){:}2$
or
${\mathrm{SL}}_3(3^a){:}2$
or
![]() ${\mathrm{SU}}_3(3^a){:}2$
. Since
${\mathrm{SU}}_3(3^a){:}2$
. Since
![]() $|T_v|$
is divisible by
$|T_v|$
is divisible by
![]() $\tfrac {1}{2}|T_{\{u,v\}}|p^f=6p^f(3^a{\pm } 1)^2$
, checking the maximal subgroups of
$\tfrac {1}{2}|T_{\{u,v\}}|p^f=6p^f(3^a{\pm } 1)^2$
, checking the maximal subgroups of
![]() ${\mathrm{SL}}_2(3^a)$
,
${\mathrm{SL}}_2(3^a)$
,
![]() ${\mathrm{SL}}_3(3^a)$
and
${\mathrm{SL}}_3(3^a)$
and
![]() ${\mathrm{SU}}_3(3^a)$
, we have
${\mathrm{SU}}_3(3^a)$
, we have
![]() $p=3$
and
$p=3$
and
![]() $T_v\lesssim [3^{ba}]{:}\mathbb Z_{3^a-1}^2.2$
for
$T_v\lesssim [3^{ba}]{:}\mathbb Z_{3^a-1}^2.2$
for
![]() $b=2$
or
$b=2$
or
![]() $3$
. Since
$3$
. Since
![]() $T_{uv}$
has order divisible by
$T_{uv}$
has order divisible by
![]() $3$
, it follows that
$3$
, it follows that
![]() $\textbf {O}_3(T_{uv})\ne 1$
, which contradicts Lemma 2.5.
$\textbf {O}_3(T_{uv})\ne 1$
, which contradicts Lemma 2.5.
Suppose that
![]() $T={\mathrm{F}}_4(2^a)$
. By [Reference Liebeck, Saxl and Seitz19, Reference Liebeck, Seitz, Ivanov, Liebeck and Saxl20], noting that
$T={\mathrm{F}}_4(2^a)$
. By [Reference Liebeck, Saxl and Seitz19, Reference Liebeck, Seitz, Ivanov, Liebeck and Saxl20], noting that
![]() $|M|$
is divisible by
$|M|$
is divisible by
![]() $p^f|N|$
, we conclude that
$p^f|N|$
, we conclude that
![]() $M\cong {\mathrm{Sp}}_8(2^a)$
or
$M\cong {\mathrm{Sp}}_8(2^a)$
or
![]() ${\mathrm {P\Omega }}_8^+(2^a).{\mathrm{S}}_3$
with
${\mathrm {P\Omega }}_8^+(2^a).{\mathrm{S}}_3$
with
![]() $|N|=(2^{2a}{+}1)^2$
, or
$|N|=(2^{2a}{+}1)^2$
, or
![]() $M\cong c.{\mathrm{PSL}}_3(2^a)^2.c.2$
or
$M\cong c.{\mathrm{PSL}}_3(2^a)^2.c.2$
or
![]() $c.{\mathrm{PSU}}_3(2^a)^2.c.2$
with
$c.{\mathrm{PSU}}_3(2^a)^2.c.2$
with
![]() $|N|=(2^{2a}{\pm } 2^a{+}1)^2$
, where
$|N|=(2^{2a}{\pm } 2^a{+}1)^2$
, where
![]() $c=(3,2^a\pm 1)$
. Then a contradiction follows from checking the maximal subgroups of
$c=(3,2^a\pm 1)$
. Then a contradiction follows from checking the maximal subgroups of
![]() ${\mathrm{Sp}}_8(2^a)$
,
${\mathrm{Sp}}_8(2^a)$
,
![]() ${\mathrm {P\Omega }}_8^+(2^a)$
,
${\mathrm {P\Omega }}_8^+(2^a)$
,
![]() ${\mathrm{PSL}}_3(2^a)$
and
${\mathrm{PSL}}_3(2^a)$
and
![]() ${\mathrm{PSU}}_3(2^a)$
; refer to [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6 and 8.48–8.50].
${\mathrm{PSU}}_3(2^a)$
; refer to [Reference Bray, Holt and Roney-Dougal1, Tables 8.3–8.6 and 8.48–8.50].
Finally, suppose that
![]() $T={\mathrm{E}}_8(q')$
. Then
$T={\mathrm{E}}_8(q')$
. Then
![]() $|N|=(q^{\prime 4}-q^{\prime 2} {+}1)^2$
and
$|N|=(q^{\prime 4}-q^{\prime 2} {+}1)^2$
and
![]() $M\cong {\mathrm{PSU}}_3(q^{\prime 2})^2.8$
. For this case, checking the maximal subgroups
$M\cong {\mathrm{PSU}}_3(q^{\prime 2})^2.8$
. For this case, checking the maximal subgroups
![]() ${\mathrm{PSU}}_3(q^{\prime 2})$
, we get a contradiction. This completes the proof.
${\mathrm{PSU}}_3(q^{\prime 2})$
, we get a contradiction. This completes the proof.
Lemma 5.11. Assume that
![]() ${{\pi }}_0(p^f-1)\ne \emptyset $
,
${{\pi }}_0(p^f-1)\ne \emptyset $
,
![]() $X_{uv}$
is not abelian and (3) of Lemma 3.5 occurs. Then
$X_{uv}$
is not abelian and (3) of Lemma 3.5 occurs. Then
![]() $G=X={\mathrm{J}}_1$
,
$G=X={\mathrm{J}}_1$
,
![]() $X_{\{u,v\}}\cong \mathbb Z_7{:}\mathbb Z_6$
,
$X_{\{u,v\}}\cong \mathbb Z_7{:}\mathbb Z_6$
,
![]() $X_v\cong \mathbb Z_2^3{:}\mathbb Z_7{:}\mathbb Z_3$
and
$X_v\cong \mathbb Z_2^3{:}\mathbb Z_7{:}\mathbb Z_3$
and
![]() $d=8$
.
$d=8$
.
Proof. By Lemma 5.10,
![]() $T={\mathrm{soc}}(X)$
is either an alternating group or a sporadic simple group. Note that
$T={\mathrm{soc}}(X)$
is either an alternating group or a sporadic simple group. Note that
![]() $X_{\{u,v\}}$
is not a
$X_{\{u,v\}}$
is not a
![]() $\{2,3\}$
-group and has no normal abelian Hall
$\{2,3\}$
-group and has no normal abelian Hall
![]() $2'$
-subgroup.
$2'$
-subgroup.
Assume that T is an alternating group. Then, by [Reference Li and Zhang17, Table 14], either
![]() $X={\mathrm{A}}_r$
and
$X={\mathrm{A}}_r$
and
![]() $X_{\{u,v\}}\cong \mathbb Z_r{:}\mathbb Z_{({r-1})/{2}}$
for
$X_{\{u,v\}}\cong \mathbb Z_r{:}\mathbb Z_{({r-1})/{2}}$
for
![]() $r\not \in \{7,11,17,23\}$
, or
$r\not \in \{7,11,17,23\}$
, or
![]() $X={\mathrm{S}}_r$
and
$X={\mathrm{S}}_r$
and
![]() $X_{\{u,v\}}\cong \mathbb Z_r{:}\mathbb Z_{r-1}$
for
$X_{\{u,v\}}\cong \mathbb Z_r{:}\mathbb Z_{r-1}$
for
![]() $r\in \{7,11,17,23\}$
. For these two cases,
$r\in \{7,11,17,23\}$
. For these two cases,
![]() $X_v$
is a transitive subgroup of
$X_v$
is a transitive subgroup of
![]() ${\mathrm{S}}_r$
in the natural action of
${\mathrm{S}}_r$
in the natural action of
![]() ${\mathrm{S}}_r$
. Then either
${\mathrm{S}}_r$
. Then either
![]() $X_v$
is almost simple or
$X_v$
is almost simple or
![]() $X_v\lesssim \mathbb Z_r{:}\mathbb Z_{r-1}$
(refer to [Reference Dixon and Mortimer4, page 99, Corollary 3.5B]), which is a contradiction.
$X_v\lesssim \mathbb Z_r{:}\mathbb Z_{r-1}$
(refer to [Reference Dixon and Mortimer4, page 99, Corollary 3.5B]), which is a contradiction.
Assume that T is a sporadic simple group and let
![]() $r\in \pi _0(p^f-1)$
. Then
$r\in \pi _0(p^f-1)$
. Then
![]() $(X,X_{\{u,v\}}, r)$
is one of the following triples:
$(X,X_{\{u,v\}}, r)$
is one of the following triples:
 $$ \begin{align*}\begin{array}{l} ({\mathrm{J}}_1, \mathbb Z_7{:}\mathbb Z_6,7), \,({\mathrm{J}}_1, \mathbb Z_{11}{:}\mathbb Z_{10},11), \,({\mathrm{J}}_1, \mathbb Z_{19}{:}\mathbb Z_{6},19), \,({\mathrm{J}}_2, \mathbb Z_{5}^2{:}{\mathrm{D}}_{12},5), \\ ({\mathrm{J}}_3.2, \mathbb Z_{19}{:}\mathbb Z_{18},19), \,({\mathrm{J}}_4, \mathbb Z_{29}{:}\mathbb Z_{28},29), \,({\mathrm{J}}_4, \mathbb Z_{37}{:}\mathbb Z_{12},37), \,({\mathrm{J}}_4, \mathbb Z_{43}{:}\mathbb Z_{14},43), \\ ({\mathrm{O'N}}.2, \mathbb Z_{31}{:}\mathbb Z_{30},31), \,({\mathrm{He}}, \mathbb Z_5^2{:}4{\mathrm{A}}_4, 5), \,({\mathrm{Co}}_1, \mathbb Z_{7}^2{:}(3{\times} 2{\mathrm{A}}_4),7),\\ ({\mathrm{Ly}}, \mathbb Z_{37}{:}\mathbb Z_{18},37), \,({\mathrm{Ly}}, \mathbb Z_{67}{:}\mathbb Z_{22},67), \,({\mathrm{Fi}}_{24}', \mathbb Z_{29}{:}\mathbb Z_{14},29), \\ ({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times} {\mathrm{S}}_4,13), \,({\mathrm{B}}, \mathbb Z_{19}{:}\mathbb Z_{18}{\times}\mathbb Z_2,19), \,({\mathrm{B}}, \mathbb Z_{23}{:}\mathbb Z_{11}{\times} 2,23), \\ ({\mathrm{M}}, \mathbb Z_{23}{:}\mathbb Z_{11}{\times} {\mathrm{S}}_4,23), \,({\mathrm{M}}, (\mathbb Z_{29}{:}\mathbb Z_{14}{\times} 3).2,29), \,({\mathrm{M}}, \mathbb Z_{31}{:}\mathbb Z_{15}{\times} {\mathrm{S}}_3,31), \\ ({\mathrm{M}}, \mathbb Z_{41}{:}\mathbb Z_{40},41), \,({\mathrm{M}}, \mathbb Z_{47}{:}\mathbb Z_{23}{\times} 2,47). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\mathrm{J}}_1, \mathbb Z_7{:}\mathbb Z_6,7), \,({\mathrm{J}}_1, \mathbb Z_{11}{:}\mathbb Z_{10},11), \,({\mathrm{J}}_1, \mathbb Z_{19}{:}\mathbb Z_{6},19), \,({\mathrm{J}}_2, \mathbb Z_{5}^2{:}{\mathrm{D}}_{12},5), \\ ({\mathrm{J}}_3.2, \mathbb Z_{19}{:}\mathbb Z_{18},19), \,({\mathrm{J}}_4, \mathbb Z_{29}{:}\mathbb Z_{28},29), \,({\mathrm{J}}_4, \mathbb Z_{37}{:}\mathbb Z_{12},37), \,({\mathrm{J}}_4, \mathbb Z_{43}{:}\mathbb Z_{14},43), \\ ({\mathrm{O'N}}.2, \mathbb Z_{31}{:}\mathbb Z_{30},31), \,({\mathrm{He}}, \mathbb Z_5^2{:}4{\mathrm{A}}_4, 5), \,({\mathrm{Co}}_1, \mathbb Z_{7}^2{:}(3{\times} 2{\mathrm{A}}_4),7),\\ ({\mathrm{Ly}}, \mathbb Z_{37}{:}\mathbb Z_{18},37), \,({\mathrm{Ly}}, \mathbb Z_{67}{:}\mathbb Z_{22},67), \,({\mathrm{Fi}}_{24}', \mathbb Z_{29}{:}\mathbb Z_{14},29), \\ ({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times} {\mathrm{S}}_4,13), \,({\mathrm{B}}, \mathbb Z_{19}{:}\mathbb Z_{18}{\times}\mathbb Z_2,19), \,({\mathrm{B}}, \mathbb Z_{23}{:}\mathbb Z_{11}{\times} 2,23), \\ ({\mathrm{M}}, \mathbb Z_{23}{:}\mathbb Z_{11}{\times} {\mathrm{S}}_4,23), \,({\mathrm{M}}, (\mathbb Z_{29}{:}\mathbb Z_{14}{\times} 3).2,29), \,({\mathrm{M}}, \mathbb Z_{31}{:}\mathbb Z_{15}{\times} {\mathrm{S}}_3,31), \\ ({\mathrm{M}}, \mathbb Z_{41}{:}\mathbb Z_{40},41), \,({\mathrm{M}}, \mathbb Z_{47}{:}\mathbb Z_{23}{\times} 2,47). \end{array} \end{align*} $$
Recall that
![]() $p^f$
is a divisor of
$p^f$
is a divisor of
![]() $|X|$
and r is a primitive prime divisor of
$|X|$
and r is a primitive prime divisor of
![]() $p^f-1$
. Searching all possible pairs
$p^f-1$
. Searching all possible pairs
![]() $(p^f,r)$
, we get Table 8.
$(p^f,r)$
, we get Table 8.
Table 8 Primitive prime divisors.

Recalling that
![]() $G_{\{u,v\}}=X_{\{u,v\}}.(G/X)$
, we have
$G_{\{u,v\}}=X_{\{u,v\}}.(G/X)$
, we have
![]() $2|G_{uv}|=|G_{\{u,v\}}|=|X_{\{u,v\}}||G{:}X|=2|X_{uv}||G{:}X|$
and so
$2|G_{uv}|=|G_{\{u,v\}}|=|X_{\{u,v\}}||G{:}X|=2|X_{uv}||G{:}X|$
and so
![]() $|G_{uv}|=|X_{uv}||G{:}X|$
. Since
$|G_{uv}|=|X_{uv}||G{:}X|$
. Since
![]() $G_v$
is
$G_v$
is
![]() $2$
-transitive on
$2$
-transitive on
![]() ${{\Gamma}}(v)$
, we know that
${{\Gamma}}(v)$
, we know that
![]() $(p^f-1)$
is a divisor of
$(p^f-1)$
is a divisor of
![]() $|G_{uv}|=|X_{uv}||G{:}X|$
. It follows that
$|G_{uv}|=|X_{uv}||G{:}X|$
. It follows that
![]() $(X,X_{\{u,v\}}, r, p^f)$
is one of the following quadruples:
$(X,X_{\{u,v\}}, r, p^f)$
is one of the following quadruples:
 $$ \begin{align*}\begin{array}{l} ({\mathrm{J}}_1, \mathbb Z_7{:}\mathbb Z_6,7, 2^3), \,({\mathrm{J}}_2, \mathbb Z_{5}^2{:}{\mathrm{D}}_{12},5, 2^4), \,({\mathrm{Co}}_1, \mathbb Z_{7}^2{:}(3{\times} 2{\mathrm{A}}_4),7, 2^3),\\ ({\mathrm{O'N}}.2, \mathbb Z_{31}{:}\mathbb Z_{30},31, 2^5), \,({\mathrm{He}}, \mathbb Z_5^2{:}4{\mathrm{A}}_4, 5,2^4), \,({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times} {\mathrm{S}}_4,13, 3^3), \\ ({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times} {\mathrm{S}}_4,13, 5^4), \,({\mathrm{M}}, \mathbb Z_{31}{:}\mathbb Z_{15}{\times} {\mathrm{S}}_3,31, 2^5). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} ({\mathrm{J}}_1, \mathbb Z_7{:}\mathbb Z_6,7, 2^3), \,({\mathrm{J}}_2, \mathbb Z_{5}^2{:}{\mathrm{D}}_{12},5, 2^4), \,({\mathrm{Co}}_1, \mathbb Z_{7}^2{:}(3{\times} 2{\mathrm{A}}_4),7, 2^3),\\ ({\mathrm{O'N}}.2, \mathbb Z_{31}{:}\mathbb Z_{30},31, 2^5), \,({\mathrm{He}}, \mathbb Z_5^2{:}4{\mathrm{A}}_4, 5,2^4), \,({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times} {\mathrm{S}}_4,13, 3^3), \\ ({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times} {\mathrm{S}}_4,13, 5^4), \,({\mathrm{M}}, \mathbb Z_{31}{:}\mathbb Z_{15}{\times} {\mathrm{S}}_3,31, 2^5). \end{array}\end{align*} $$
For
![]() $({\mathrm{Co}}_1, \mathbb Z_{7}^2{:}(3{\times } 2{\mathrm{A}}_4),7, 2^3)$
, we have
$({\mathrm{Co}}_1, \mathbb Z_{7}^2{:}(3{\times } 2{\mathrm{A}}_4),7, 2^3)$
, we have
![]() $X_{uv}\lesssim {\Gamma \textrm{L}}_1(2^3){\times } {\Gamma \textrm{L}}_1(2^3)$
, yielding that
$X_{uv}\lesssim {\Gamma \textrm{L}}_1(2^3){\times } {\Gamma \textrm{L}}_1(2^3)$
, yielding that
![]() $|X_{uv}|$
is odd, which is a contradiction. Similarly, for
$|X_{uv}|$
is odd, which is a contradiction. Similarly, for
![]() $({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times } {\mathrm{S}}_4,13, 3^3)$
, the order of
$({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times } {\mathrm{S}}_4,13, 3^3)$
, the order of
![]() $X_{uv}$
is indivisible by
$X_{uv}$
is indivisible by
![]() $2^4$
, which is a contradiction; for
$2^4$
, which is a contradiction; for
![]() $({\mathrm{M}}, \mathbb Z_{31}{:}\mathbb Z_{15}{\times } {\mathrm{S}}_3,31, 2^5)$
, the order of
$({\mathrm{M}}, \mathbb Z_{31}{:}\mathbb Z_{15}{\times } {\mathrm{S}}_3,31, 2^5)$
, the order of
![]() $X_{uv}$
is indivisible by
$X_{uv}$
is indivisible by
![]() $3$
, which is a contradiction. For
$3$
, which is a contradiction. For
![]() $({\mathrm{He}}, \mathbb Z_5^2{:}4{\mathrm{A}}_4, 5,2^4)$
, the order of
$({\mathrm{He}}, \mathbb Z_5^2{:}4{\mathrm{A}}_4, 5,2^4)$
, the order of
![]() $X_{uv}$
is divisible by
$X_{uv}$
is divisible by
![]() $2^3\cdot 3\cdot 5^2$
and, since
$2^3\cdot 3\cdot 5^2$
and, since
![]() $p^f=2^4$
, the order of
$p^f=2^4$
, the order of
![]() $X_u$
is divisible by
$X_u$
is divisible by
![]() $2^7\cdot 3\cdot 5^2$
; however,
$2^7\cdot 3\cdot 5^2$
; however,
![]() ${\mathrm{He}}$
has no soluble subgroup of order divisible by
${\mathrm{He}}$
has no soluble subgroup of order divisible by
![]() $2^7\cdot 3\cdot 5^2$
, which is a contradiction. Similarly,
$2^7\cdot 3\cdot 5^2$
, which is a contradiction. Similarly,
![]() $({\mathrm{O'N}}.2, \mathbb Z_{31}{:}\mathbb Z_{30},31, 2^5)$
is excluded as
$({\mathrm{O'N}}.2, \mathbb Z_{31}{:}\mathbb Z_{30},31, 2^5)$
is excluded as
![]() ${\mathrm{O'N}}.2$
has no soluble subgroup with order divisible by
${\mathrm{O'N}}.2$
has no soluble subgroup with order divisible by
![]() $2^5\cdot 31$
. (Note that
$2^5\cdot 31$
. (Note that
![]() $G_v$
is soluble.) By the Atlas [Reference Conway, Norton, Parker and Wilson3],
$G_v$
is soluble.) By the Atlas [Reference Conway, Norton, Parker and Wilson3],
![]() ${\mathrm{J}}_2$
has no subgroup with order divisible by
${\mathrm{J}}_2$
has no subgroup with order divisible by
![]() $2^4\cdot 5^2$
and then
$2^4\cdot 5^2$
and then
![]() $({\mathrm{J}}_2, \mathbb Z_{5}^2{:}{\mathrm{D}}_{12},5, 2^4)$
is excluded. By the Atlas [Reference Conway, Norton, Parker and Wilson3] and [Reference Wilson35, Theorem 2.1],
$({\mathrm{J}}_2, \mathbb Z_{5}^2{:}{\mathrm{D}}_{12},5, 2^4)$
is excluded. By the Atlas [Reference Conway, Norton, Parker and Wilson3] and [Reference Wilson35, Theorem 2.1],
![]() ${\mathrm{B}}$
has no subgroup with order divisible by
${\mathrm{B}}$
has no subgroup with order divisible by
![]() $3^2\cdot 5^4\cdot 13$
and so
$3^2\cdot 5^4\cdot 13$
and so
![]() $({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times } {\mathrm{S}}_4,13, 5^4)$
is excluded. Then only
$({\mathrm{B}}, \mathbb Z_{13}{:}\mathbb Z_{12}{\times } {\mathrm{S}}_4,13, 5^4)$
is excluded. Then only
![]() $({\mathrm{J}}_1, \mathbb Z_7{:}\mathbb Z_6,7, 2^3)$
is left, which gives
$({\mathrm{J}}_1, \mathbb Z_7{:}\mathbb Z_6,7, 2^3)$
is left, which gives
![]() $X_v\cong \mathbb Z_2^3{:}\mathbb Z_7{:}\mathbb Z_3$
,
$X_v\cong \mathbb Z_2^3{:}\mathbb Z_7{:}\mathbb Z_3$
,
![]() $d=p^f=8$
and
$d=p^f=8$
and
![]() $G=X$
. This completes the proof.
$G=X$
. This completes the proof.
Finally, we summarize the argument for proving Theorem 1.1 as follows.
Proof of Theorem 1.1 .
Clearly, each
![]() $(G,G_v, G_{\{u,v\}})$
in Table 1 gives a G-edge- primitive graph
$(G,G_v, G_{\{u,v\}})$
in Table 1 gives a G-edge- primitive graph
![]() ${\sf Cos}(G,G_v, G_{\{u,v\}})$
. It is not difficult to check the
${\sf Cos}(G,G_v, G_{\{u,v\}})$
. It is not difficult to check the
![]() $2$
-arc-transitivity of G acting on
$2$
-arc-transitivity of G acting on
![]() ${\sf Cos}(G,G_v, G_{\{u,v\}})$
; we omit the details.
${\sf Cos}(G,G_v, G_{\{u,v\}})$
; we omit the details.
Now let G and
![]() ${{\Gamma}}=(V,E)$
satisfy the assumptions in Theorem 1.1. Let
${{\Gamma}}=(V,E)$
satisfy the assumptions in Theorem 1.1. Let
![]() $T={\mathrm{soc}}(G)$
and
$T={\mathrm{soc}}(G)$
and
![]() $\{u,v\}\in E$
. Choose a minimal X among the normal subgroups of G that act primitively on E. Then
$\{u,v\}\in E$
. Choose a minimal X among the normal subgroups of G that act primitively on E. Then
![]() ${\mathrm{soc}}(X)=T$
. Since
${\mathrm{soc}}(X)=T$
. Since
![]() $G_{\{u,v\}}$
is soluble,
$G_{\{u,v\}}$
is soluble,
![]() $X_{\{u,v\}}$
is soluble. Then
$X_{\{u,v\}}$
is soluble. Then
![]() $(X,X_{\{u,v\}})$
is one of the pairs
$(X,X_{\{u,v\}})$
is one of the pairs
![]() $(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20]. Thus,
$(G_0,H_0)$
listed in [Reference Li and Zhang17, Tables 14–20]. Thus,
![]() ${{\Gamma}}$
, G,
${{\Gamma}}$
, G,
![]() $G_{\{u,v\}}$
, X and
$G_{\{u,v\}}$
, X and
![]() $X_{\{u,v\}}$
satisfy Hypothesis 3.1 and then Lemmas 3.3 and 3.5 work here. If
$X_{\{u,v\}}$
satisfy Hypothesis 3.1 and then Lemmas 3.3 and 3.5 work here. If
![]() $G_v^{{{\Gamma}}(v)}$
is an almost simple
$G_v^{{{\Gamma}}(v)}$
is an almost simple
![]() $2$
-transitive group, then, by Lemma 3.3 and Lemmas 4.1–4.4, the triple
$2$
-transitive group, then, by Lemma 3.3 and Lemmas 4.1–4.4, the triple
![]() $(G,G_v, G_{\{u,v\}})$
is as listed in Table 1. Assume next that
$(G,G_v, G_{\{u,v\}})$
is as listed in Table 1. Assume next that
![]() $G_v^{{{\Gamma}}(v)}$
is a soluble
$G_v^{{{\Gamma}}(v)}$
is a soluble
![]() $2$
-transitive group of degree
$2$
-transitive group of degree
![]() $d=p^f$
, where p is a prime.
$d=p^f$
, where p is a prime.
If
![]() $X_{uv}$
is abelian, then the triple
$X_{uv}$
is abelian, then the triple
![]() $(G,G_v, G_{\{u,v\}})$
is as desired in Table 1, by Lemma 5.2. Thus, assume further that
$(G,G_v, G_{\{u,v\}})$
is as desired in Table 1, by Lemma 5.2. Thus, assume further that
![]() $X_{uv}$
is nonabelian. Then
$X_{uv}$
is nonabelian. Then
![]() $G_{uv}$
is nonabelian. By Lemma 3.5, either
$G_{uv}$
is nonabelian. By Lemma 3.5, either
![]() $G_v^{{{\Gamma}}(v)}\not \le {\mathrm{GL}}_1(p^f)$
and
$G_v^{{{\Gamma}}(v)}\not \le {\mathrm{GL}}_1(p^f)$
and
![]() $G_v^{{{\Gamma}}(v)}\le {\Gamma \textrm{L}}_1(p^f)$
, or
$G_v^{{{\Gamma}}(v)}\le {\Gamma \textrm{L}}_1(p^f)$
, or
![]() $G_v^{{{\Gamma}}(v)}$
has a normal subgroup
$G_v^{{{\Gamma}}(v)}$
has a normal subgroup
![]() ${\mathrm{SL}}_2(3)$
or
${\mathrm{SL}}_2(3)$
or
![]() $2_+^{1+4}$
. For the latter case, the triple
$2_+^{1+4}$
. For the latter case, the triple
![]() $(G,G_v, G_{\{u,v\}})$
is known by Lemma 5.4. Let
$(G,G_v, G_{\{u,v\}})$
is known by Lemma 5.4. Let
![]() $G_v^{{{\Gamma}}(v)}\le {\Gamma \textrm{L}}_1(p^f)$
and consider the primitive prime divisors of
$G_v^{{{\Gamma}}(v)}\le {\Gamma \textrm{L}}_1(p^f)$
and consider the primitive prime divisors of
![]() $p^f-1$
. If
$p^f-1$
. If
![]() $p^f-1$
has no primitive prime divisor, then, by Lemma 5.6 and Corollary 5.8,
$p^f-1$
has no primitive prime divisor, then, by Lemma 5.6 and Corollary 5.8,
![]() $(G,G_v, G_{\{u,v\}})$
is as listed in Table 1. If
$(G,G_v, G_{\{u,v\}})$
is as listed in Table 1. If
![]() $p^f-1$
has primitive prime divisors, then
$p^f-1$
has primitive prime divisors, then
![]() $(G,G_v, G_{\{u,v\}})$
is known by Lemma 5.11. This completes the proof.
$(G,G_v, G_{\{u,v\}})$
is known by Lemma 5.11. This completes the proof.